判别分析作业3
多元统计分析课件第六章-判别分析例题与操作过程可修改文字

.
(一) 操作步骤 1. 在SPSS窗口中选择Analyze→Classify→Discriminate,调 出判别分析主界面,将左边的变量列表中的“group”变量选 入分组变量中,将—变量选入自变量中,并选择Enter independents together单选按钮,即使用所有自变量进行判 别分析。
1
5
50.06 23.03 2.83 23.74 112.52 63.3
1
6
33.24 6.24 1.18 22.9 160.01 65.4
2
7
32.22 4.22 1.06 20.7 124.7 68.7
2
8
41.15 10.08 2.32 32.84 172.06 65.85
2
9
53.04 25.74 4.06 34.87 152.03 63.5
由此表可知,两个Fisher判别函数分别为:
y1 74.99 1.861X1 1.656X 2 0.877 X3 0.798X 4 0.098X 5 1.579X 6 y2 29.482 0.867X1 1.155X 2 0.356X 3 0.089X 4 0.054X 5 0.69 X 6
判别分析例题
例1:设有两个正态总体 G1 和 G2 ,已知:
(1)
ห้องสมุดไป่ตู้
10 15
(2)
20 25
18 12 1=12 32
20 7
2
=
7
5
试用距离判别法判断:样品:
X
20 20
,应归属于哪一类
判别分析例题 解:比较X到两个总体的马氏距离的大小
所以X属于正态总体 G1
例2:
第4章判别分析习题

D 2 ( X , G1 ) ( X 1 )' 1 ( X 1 ) 5. 8 ((6,0) (5,1)) 2.1 5.8 (1,1) 2.1 2.1 7.6
1
2. 1 7. 6
1ห้องสมุดไป่ตู้
(6,0) (5,1)
1 1 0.4436602
D2 ( X , G2 ) ( X 2 )'1 ( X 2 ) 1.673809
由于 D(X,G2)>D(X,G1),所以X属于G1。
本章结束
4.6 试析距离判别法、贝叶斯判别法和费希尔判别法的异同 答:相同点:它们全是用来判别 p 维空间中的某个点到 底是来自哪个总体的一种算法。 区别是算法的不同,贝叶斯判别法是在距离判别法的基 础上,又考虑的判错问题。而费希尔判别法是以一种线 性组合的形式出现。 4.7 设有两个二元总体 G1 和 G2,从中分别抽取样本计算得到
5 X 1 ,
(1)
X
( 2)
3 2 ,
5.8 2.1 ˆ p 2.1 7.6
假设 1 2 ,试用距离判别法建立判别函数和规则。 样品 X (6,0)' 应属于哪个总体。
解:由式4.3及4.4式有
第四章 判别分析习题
思考与习题
4.1 简述欧氏距离与马氏距离的区别与联系 答:欧氏距离是马氏距离的特例。
2 1 D ( X , Y ) ( X Y )' (X Y ) , 在马氏距离的测定中,
当其中的协差阵等于单位距阵
I 时,马氏距离
就是欧氏距离。 4.2 试叙述判别分析的实质 答:判别分析就是希望利用已测得的变量数据,找出一 种判别函数,使得这一函数具有某种最优性质,能 把属于不同类别的样本点尽可能的区别开来。
判别分析作业
判别分析与聚类分析不同。
判别分析是在已知研究对象分成若干类型(或组别)并已取得各种类型的一批已知样品的观测数据,在此基础上根据某些准则建立判别式,然后对未知类型的样品进行判别分类。
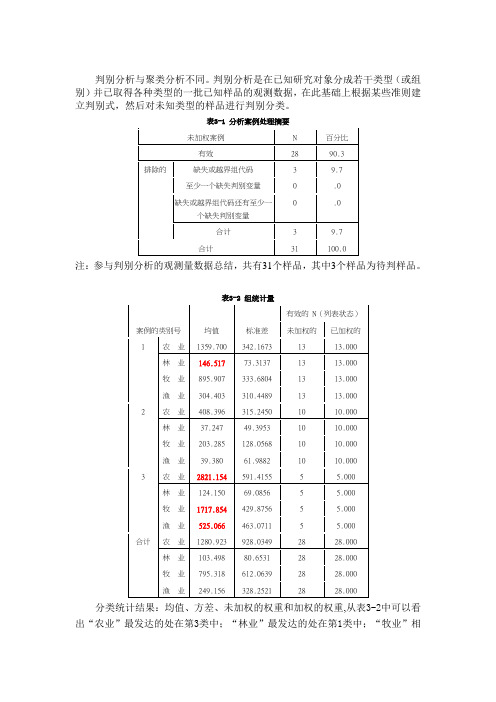
表3-1 分析案例处理摘要未加权案例N 百分比有效28 90.3排除的缺失或越界组代码 3 9.7至少一个缺失判别变量0 .0缺失或越界组代码还有至少一个缺失判别变量0 .0合计 3 9.7合计31 100.0注:参与判别分析的观测量数据总结,共有31个样品,其中3个样品为待判样品。
表3-2 组统计量案例的类别号均值标准差有效的 N(列表状态)未加权的已加权的1 农业1359.700 342.1673 13 13.000林业146.517 73.3137 13 13.000牧业895.907 333.6804 13 13.000渔业304.403 310.4489 13 13.0002 农业408.396 315.2450 10 10.000林业37.247 49.3953 10 10.000牧业203.285 128.0568 10 10.000渔业39.380 61.9882 10 10.0003 农业2821.154 591.4155 5 5.000林业124.150 69.0856 5 5.000牧业1717.854 429.8756 5 5.000渔业525.066 463.0711 5 5.000合计农业1280.923 928.0349 28 28.000林业103.498 80.6531 28 28.000牧业795.318 612.0639 28 28.000渔业249.156 328.2521 28 28.000 分类统计结果:均值、方差、未加权的权重和加权的权重,从表3-2中可以看出“农业”最发达的处在第3类中;“林业”最发达的处在第1类中;“牧业”相对比较发达的处在第3类中;“渔业”比较发达的处在第3类中.表3-3 汇聚的组内矩阵a农业林业牧业渔业协方差农业147937.808 32.329 53946.036 38237.523林业32.329 4221.968 763.564 5011.382牧业53946.036 763.564 88914.814 -1202.757渔业38237.523 5011.382 -1202.757 81954.578相关性农业 1.000 .001 .470 .347林业.001 1.000 .039 .269牧业.470 .039 1.000 -.014渔业.347 .269 -.014 1.000a. 协方差矩阵的自由度为 25。
判别分析练习题
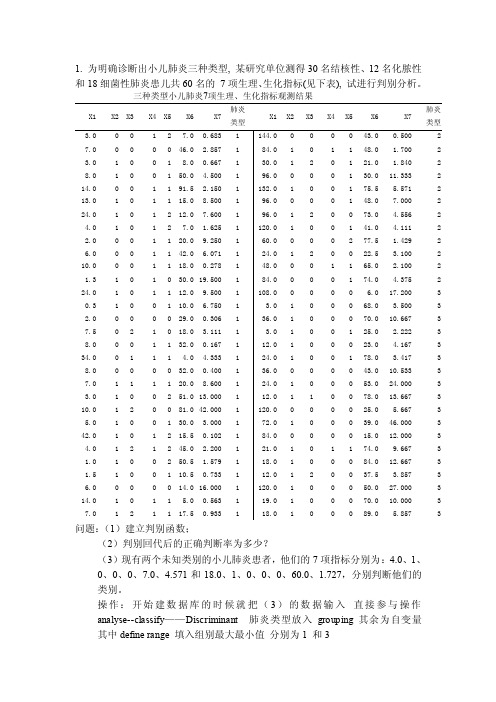
1. 为明确诊断出小儿肺炎三种类型, 某研究单位测得30名结核性、12名化脓性和18细菌性肺炎患儿共60名的7项生理、生化指标(见下表), 试进行判别分析。
三种类型小儿肺炎7项生理、生化指标观测结果X1 X2 X3 X4 X5 X6 X7 肺炎类型X1 X2 X3 X4 X5 X6 X7肺炎类型问题:(1)建立判别函数;(2)判别回代后的正确判断率为多少?(3)现有两个未知类别的小儿肺炎患者,他们的7项指标分别为:4.0、1、0、0、0、7.0、4.571和18.0、1、0、0、0、60.0、1.727,分别判断他们的类别。
操作:开始建数据库的时候就把(3)的数据输入直接参与操作analyse--classify——Discriminant 肺炎类型放入grouping 其余为自变量其中define range 填入组别最大最小值分别为1 和3Statistics 里面,fisher’s为bayes判别选择fisher’s Classify——display——summary table显示结果Save —(全选)—predicted group membership新数据的预测分类Probabilities of group membership 回代正确率Discriminant scores 判别得分结果中:classification function coefficients下标为fisher’s linear分为几类就有几个判别函数:y=0.033x1+1.617x2+…..Classification rescult’s 下标的88.3%为正确率2. 下表是10名健康人(group=1)和6名心肌梗塞患者(group=2)的三个心电图指标(X1,X2,X3)。
试进行判别分析。
group X1 X2 X31 436.70 49.59 2.321 290.67 30.02 2.461 352.53 36.23 2.361 340.91 38.28 2.441 332.83 41.92 2.281 319.97 31.42 2.491 361.31 37.99 2.021 366.5 39.87 2.421 292.56 26.07 2.161 276.84 16.60 2.912 510.47 67.64 1.732 510.41 62.71 1.582 470.30 54.40 1.682 364.12 46.26 2.092 416.07 45.37 1.902 515.70 84.59 1.75问题:(1)建立判别函数;(2)判别回代后的正确判断率为多少?(3)现有一人,他的3项指标为:420.50、32.42、1.98,判断他是健康人还是心肌梗塞患者?操作与上相同,要注意的是:F判别对数据分布无要求,适用于两组判别分析;B要求数据为多元正态分布,适用于多组判别分析。
判别分析练习题

判别分析练习题判别分析练习题在统计学中,判别分析是一种用于分类和预测的方法。
它通过对不同类别的样本进行分析,构建一个分类模型,以便将未知样本分配到正确的类别中。
判别分析在各个领域都有广泛的应用,如医学诊断、金融风险评估等。
下面我将给大家提供一些判别分析的练习题,希望能够帮助大家更好地理解和应用这一方法。
1. 假设有两个类别的样本,每个样本都有两个变量。
已知两个类别的样本均值和协方差矩阵如下:类别1:均值为(1, 2),协方差矩阵为[[2, 1], [1, 2]]类别2:均值为(3, 4),协方差矩阵为[[3, 1], [1, 3]]现有一个未知样本(2, 3),请利用判别分析方法判断该样本属于哪个类别。
解答:首先,我们需要计算两个类别的判别函数值。
对于类别1,判别函数为:g1(x) = -0.5 * (x - μ1) * Σ1^-1 * (x - μ1)T - 0.5 * ln(|Σ1|) + ln(P1)其中,x为未知样本,μ1为类别1的均值,Σ1为类别1的协方差矩阵,P1为类别1的先验概率。
类似地,对于类别2,判别函数为:g2(x) = -0.5 * (x - μ2) * Σ2^-1 * (x - μ2)T - 0.5 * ln(|Σ2|) + ln(P2)其中,μ2为类别2的均值,Σ2为类别2的协方差矩阵,P2为类别2的先验概率。
根据给定的均值和协方差矩阵,我们可以计算出:μ1 = (1, 2), Σ1 = [[2, 1], [1, 2]]μ2 = (3, 4), Σ2 = [[3, 1], [1, 3]]假设两个类别的先验概率相等,即P1 = P2 = 0.5。
将未知样本(2, 3)代入判别函数中,可以计算出:g1(2, 3) = -4.5g2(2, 3) = -5.5由于g2(2, 3)的值较小,所以未知样本更有可能属于类别2。
2. 现有一个三类别的样本,每个样本有三个变量。
已知三个类别的样本均值和协方差矩阵如下:类别1:均值为(1, 2, 3),协方差矩阵为[[2, 1, 1], [1, 2, 1], [1, 1, 2]]类别2:均值为(4, 5, 6),协方差矩阵为[[3, 1, 2], [1, 3, 2], [2, 2, 3]]类别3:均值为(7, 8, 9),协方差矩阵为[[4, 1, 2], [1, 4, 2], [2, 2, 4]]现有一个未知样本(3, 4, 5),请利用判别分析方法判断该样本属于哪个类别。
SPSS操作方法:判别分析例题

SPSS操作方法:判别分析例题为研究1991年中国城镇居民月平均收入状况,按标准化欧氏平方距离、离差平方和聚类方法将30个省、市、自治区.分为三种类型。
试建立判别函数,判定广东、西藏分别属于哪个收入类型。
判别指标及原始数据见表9-4。
1991年30个省、市、自治区城镇居民月平均收人数据表单位:元/人 x1:人均生活费收入 x6:人均各种奖金、超额工资(国有+集体) x2:人均国有经济单位职工工资 x7:人均各种津贴(国有+集体)x3:人均来源于国有经济单位标准工资x8:人均从工作单位得到的其他收入x4:人均集体所有制工资收入 x9:个体劳动者收入5贝叶斯判别的SPSS操作方法:1. 建立数据文件2.单击Analyze→ Classify→ Discriminant,打开Discriminant Analysis 判别分析对话框如图1所示:图1 Discriminant Analysis判别分析对话框3.从对话框左侧的变量列表中选中进行判别分析的有关变量x1~x9进入Independents 框,作为判别分析的基础数据变量。
从对话框左侧的变量列表中选分组变量Group进入Grouping Variable 框,并点击Define Range...钮,在打开的Discriminant Analysis: Define Range对话框中,定义判别原始数据的类别数,由于原始数据分为3类,则在Minimum(最小值)处输入1,在Maximum(最大值)处输入3(见图2)。
选择后点击Continue按钮返回Discriminant Analysis主对话框。
图2 Define Range对话框4、选择分析方法Enter independent together 所有变量全部参与判别分析(系统默认)。
本例选择此项。
Use stepwise method 采用逐步判别法自动筛选变量。
单击该项时Method 按钮激活,打开Stepwise Method对话框如图3所示,从中可进一步选择判别分析方法。
判别分析法(数学建模相关习题)

1 1 2 , a 1 1 2 2
W x a ' x
举例
2、μ1 ≠ μ2,∑1 ≠ ∑2
d 2 x,1 x 1 1 x 1
'
d 2 x, 2 x 2 1 x 2
化简
d 2 x, 1 d 2 x, 2 2 x
x 1 , 若d 2 x, 1 d 2 x, 2 x 2 , 若d 2 x, 1 d 2 x, 2
1 2
2
1 ' 1 2 2x a 2a x '
0.0784 0.0647 0.0197 0.0217 总体样本离差矩阵 s1 0.0647 0.1350 s2 0.0217 0.0389
平均协方差阵的估计ˆ V
0.0075 0.0066 1 s1 s2 0.0066 0.0134 n1 n2 2
1
2
例题:对28名一级和25名健将级标枪运动员测试了6个 影响标枪成绩的训练指标; 30米跑(x1)、 投小铅球( x2 )、 挺举重量( x3 )、
抛实心球( x4 )、前抛铅球( x5 )、 五级跳( x6 )。
编号 组别 x1
Hale Waihona Puke x24.30 4.10 : 4.20 4.00
4.30
x3
82.3 87.48 : 89.20 103.00
平均 y=0.9625x+0.6065 用它来判定发现不好 2、心型平分线 取Af和Apf的中心(1.41,1.80), (1.22,1.93),垂直平分线方程是 y=1.52576x-0.1485
多元统计作业-判别分析
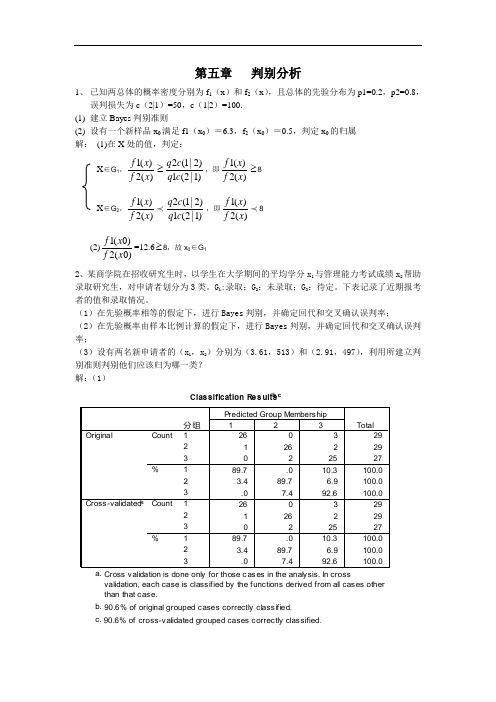
第五章 判别分析1、 已知两总体的概率密度分别为f 1(x )和f 2(x ),且总体的先验分布为p1=0.2,p2=0.8,误判损失为c (2|1)=50,c (1|2)=100. (1) 建立Bayes 判别准则(2) 设有一个新样品x 0满足f1(x 0)=6.3,f 2(x 0)=0.5,判定x 0的归属 解: (1)在X 处的值,判定:X ∈G 1,1()2()f x f x ≥2(1|2)1(2|1)q c q c ,即1()2()f x f x ≥8X ∈G 2,1()2()f x f x 2(1|2)1(2|1)q c q c ,即1()2()f x f x 8(2)1(0)2(0)f x f x =12.6≥8,故x 0∈G 12、某商学院在招收研究生时,以学生在大学期间的平均学分x 1与管理能力考试成绩x 2帮助录取研究生,对申请者划分为3类。
G 1:录取;G 2:未录取;G 3:待定。
下表记录了近期报考者的值和录取情况。
(1)在先验概率相等的假定下,进行Bayes 判别,并确定回代和交叉确认误判率;(2)在先验概率由样本比例计算的假定下,进行Bayes 判别,并确定回代和交叉确认误判率;(3)设有两名新申请者的(x 1,x 2)分别为(3.61,513)和(2.91,497),利用所建立判别准则判别他们应该归为哪一类? 解:(1)回代误判率:8/85=0.0941,交叉确认误判率同样为8/85=0.0941,第2号、3号、24号、30号、31号、58号、74号、75号被误判。
(2)号、30号、31号、58号、74号、75号被误判。
(3)建立Fisher线性判别准则W1=-151.902+60.431X1+0.172X2W2=-89.815+45.255X1+0.138X2W3=-110.818+53.024X1+0.137X2把(3.61,513)代入以上三式,W1=154.48991,W2=144.34955,W3=150.87964把(2.91,497)代入以上三式,W1=109.43621,W2=110.46305,W3=111.57084故第一个申请者判为W1(W1最大),第二个申请者判为W3(W3最大)。
第三章判别分析范文

第三章判别分析范文判别分析,也称为判别函数分析,是一种统计分析方法,旨在通过建立判别函数来确定样本的类别归属。
判别分析被广泛应用于各个领域,包括医学、经济学、社会科学等。
本章将介绍判别分析的基本原理、应用以及一些相关的方法和技巧。
3.1判别分析的基本原理判别分析的基本原理是通过在高维空间中找到一个判别函数,将样本划分为不同的组别。
这个判别函数的设计目标是使得同一组别内的样本尽可能相似,而不同组别之间的样本尽可能不同。
判别函数可以是线性或非线性的,具体的形式取决于具体的问题。
对于线性判别分析而言,判别函数可以表示为:D(x)=w'x+w0其中,x是样本的特征向量,w是权重向量,w0是一个常数。
为了找到最佳的权重向量 w,我们需要定义一个目标函数,常用的目标函数包括 Fisher 判别准则和最小误分类准则。
3.2判别分析的应用场景判别分析可以应用于多个场景,以下是一些常见的应用场景:1.医学诊断判别分析在医学领域中被广泛用于疾病的诊断和预测。
通过对患者的生理指标进行测量,可以建立一个判别函数,将患者分为患病组和健康组。
例如,在癌症诊断中,医生可以通过对患者的肿瘤大小、形状和血液指标等进行测量,来建立一个判别函数,判断患者是否患有癌症。
2.金融风险评估判别分析在金融领域中被广泛应用于风险评估。
通过对客户的个人信息、信用评级等进行分析,可以建立一个判别函数,将客户分为高风险组和低风险组。
这可以帮助银行机构评估客户的信用风险,并做出相应的贷款决策。
3.社会科学研究判别分析在社会科学研究中也有着广泛的应用。
例如,在心理学研究中,可以通过对被试者的个人特征、心理问卷得分等进行分析,来建立一个判别函数,将被试者分为不同的心理类型。
这有助于研究人员理解人类行为和心理特征之间的关系。
3.3判别分析的相关方法和技巧在进行判别分析时,有一些方法和技巧可以提高分析的准确性和可解释性。
1.特征选择在建立判别函数时,选择合适的特征是非常重要的。
判别分析作业

判别分析作业对教科书第P133页习题6做判别分析答:上述两个表对总体数据进行了一个基本的分析,由表我们得知根据分组,不同的数据在分组之后显著性差异有所不同.在分组后55岁组死亡概率、80岁组死亡概率,有明显的差异。
答:上表我们得知,由于0.299〉0.05,所以接受原假设,即个总体之间的协方差矩阵无显著差异,即相等。
答:上表说明:得出来的一个判别式,对原方差的解释为百分之百。
答:此表为Wilks' Lambda检验,目的是检验所得判别方程的显著性,从结果看判别方程是显著的。
上面两个表为标准化判别函数的系数(判别权重)与因子载荷,通过左面两个表,我们可以清楚地揭示出各个自变量对判别函数的贡献多少。
由此我们得出此判别函数主要是根据80岁组死亡概率,来判定其属于哪组的。
答:由上述两张表,我们可以清楚地看到未标准化判别系数及各组的重心,因此我们可以计算其临界点为-1.373,0.803,从而我们可以判断位置数据应属的组。
判别方程:Y1=0.076*X6-8.77答:此为先验概率,我们假设其相等Classification Function Coefficients答:上表为三个fisher判别函数Y1=0.582X6-30.209Y2=0.878X6-67.417Y3=0.546X6-26.761答:上表为经过保存后,数据窗口所保存的简历它们的意思依次为原序号,原组数,预测组数,根据Bayes判别函数所得的得分,在第一组的可能性,在第二组的可能性,在第三组的可能性。
由此我们看到,在原组数中有4个值为缺失值,此为待被判别组,由此我们得出结论。
根据判别函数我们推测原未知组1号,推断为属于第二组,原未知组2号,推断为属于第三组,原未知组3号,推断为属于第二组,原未知组4号,推断为属于第一组,判别结束。
判别分析作业

判别分析1、说明各判别方法的原理。
答: (1)距离判别法:样品和哪个总体的距离最近,就判断它属于哪个总体。
而距离使用的是马氏距离,即设总体G为m元总体,均值向量为,协方差阵为则样品与总体的马氏距离定义为当m=1时,(2)贝叶斯判别法:就是给出空间的一个划分,使得当通过划分来判别归类时,所带来的平均损失达到最小。
(3)Fisher判别:基本思想是投影。
将k组m元数据投影到某一个方向,使得投影后组与组之间尽可能分开。
以上判别方法的使用,均建立在各类别方差具有显著性差异的基础上。
2、下面是85个学生的GPA和GMAT数据表,经聚类分析,分为三类:接收、不接收、边缘。
(1)已知的分类情况是否可以进行判别分析?T ests of Equality of Group Means.194170.020282.000.53735.350282.000GPAx1GMATx2Wilk s 'LambdaF df1df2Sig.由上表可知,各组均值具有显著性差异,可以进行判别分析.(2)计算各类的样本均值及Si 。
计算B 及A ,求出A-1B 特征根。
Group Statistics3.4023.212413131.000561.225867.957693131.0002.4825.183442828.000447.071462.379922828.0002.9927.172322626.000446.230847.401532626.0002.9740.429058585.000488.447181.522358585.000GPAx1GMATx2GPAx1GMATx2GPAx1GMATx2GPAx1GMATx2组别123TotalMean Std. DeviationUnweighted WeightedValid N (listwise)由上表可知,各类的样本均值分别为:(3.4023,561.2258)、(2.4825,447.0714)、(2.9927,446.2308).Cov ariance Matrices.045.000.0004618.247.034-1.192-1.1923891.254.030-5.404-5.4042246.905GPAx1GMATx2GPAx1GMATx2GPAx1GMATx2组别123GPAx1GMATx2,,Cov ariance Matricesa.18416.04616.0466645.893GPAx1GMATx2组别TotalGPAx1GMATx2The total covariance matrix has 84 degrees of freedom.a.Eigenv alues5.560a 96.796.7.921.191a 3.3100.0.400Function 12Eigenvalue % of VarianceCumulative %Canonical CorrelationFirst 2 canonical discriminant functions were used in the analysis.a.(3)给出三类的领域图,并给出各类的中心值。
多元统计分析应用 第四章课后习题

第四章判别分析习题4.8(1)根据数据建立贝叶斯判别函数,并根据此判别函数对原样本进行回判。
(2)现有一新品牌的饮料在该超市试销,其销售价格为3.0,顾客对其口味评分为8,信任度评分平均为5,试预测该饮料的销售情况。
将数据导入SPSS,分析得到以下结果:1.典型判别函数的特征函数的特征值表表1-1 特征值表表1-1所示是典型判别函数的特征值表,只有两个判别函数,所以特征值只有2个。
函数1的特征值为17.791,函数2的特征值为0.720,判别函数的特征值越大,说明函数越具有区别判断力。
函数1方差的累积贡献率高达96.1%,且典型相关系数为0.973,而函数2方差的贡献率仅为3.9%,典型相关系数为0.647。
由此,说明函数1的区别判断力比函数2的强,函数1更具有区别判断力。
2.Wilks检验结果表1-2 Wilks 的Lambda上表中判别函数1和判别函数2的Wilks’Lambda值为0.031,判别函数2的Wilks’Lambda值为0.581。
“1到2”表示两个判别函数的平均数在三个类间的差异情况,P值=0.002<0.05表示差异达到显著水平“2”表示在排除了第一个判别函数后,第二个判别函数在三个组别间的差异情况,P值=0.197>0.05表示判别函数2未达到显著水平。
3.建立贝叶斯判别函数表1-3 贝叶斯判别法函数系数上表为贝叶斯判别函数的系数矩阵,用数学表达式表示各类的贝叶斯判别函数为:第一组:F1=-81.843-11.689X1+12.97X2+16.761X3第二组:F2=-94.536-10.707X1+13.361X2+17.086X3第三组:F3=-17.499-2.194X1+4.960X2+6.447X3将新品牌饮料样品的自变量值分别代入上述三个贝叶斯判别函数,得到三个函数值为:F1=65.271,F2=65.661,F3=47.884比较三个值,可以看出F2=65.661最大,据此得出新品牌饮料样品应该属于第二组,即该饮料的销售情况为平销。
数理统计作业1-三中判别分析

作业一一、人文发展指数是联合国开发计划署于1990年5月发表的第一份《人类发展报告》中公布的。
该报告建议,目前对人文发展的衡量应当以人生的三大要素为重点,衡量人生三大要素的指示分别采用出生时的预期寿命、成人识字率和实际人均GDP,将以上三个指示指标的数值合成为一个复合指数,即为人文发展指数。
资料来源UNDP《人类发展报告》1995年。
今从1995年世界各国人文发展指数的排序中,选取高发展水平、中等发展水平的国家各五个作为两组样品,另选四个国家作为待判样品作判别分析。
使用距离判别方法进行判别,并进行研究三者之间的关系。
一、距离判别法解:变量个数p=3,两类总体各有5个样品,即n1=n2=5 ,有4个待判样品,假定两总体协差阵相等。
由spss可计算出:协方差和平均值知道了均值和协方差可利用matlab 计算线性判别函数W (x )的判别系数a 和判别常数。
程序如下:v=[15.380,21.713,-555.875;21.713,66.613,-1446.098;-555.875,-1446.098,262546.500]; >> m1=[75.88;94.12;5343.4];m2=[70.44;91.74;3430.2];>> m=(m1+m2)/2;>> arfa=inv(v)*(m1-m2)arfa =0.65070.01330.0087>> c=arfa'*mc =87.1774则:()1774.870087.00133.06507.0321-++=x x x x W则将待判样品带入判别方程中得:-24.5071-15.584710.29514.1921故可知:中国和罗马尼亚属于第二类,而希腊和哥伦比亚属于第一类。
二、Fisher判别方法1、操作步骤:1)录入数据,选择菜单项Analyze→Classify→Discriminate,打开Discriminate Analysis对话框,如图2-1。
实验报告-判别分析(多元统计) (2)精选全文完整版

可编辑修改精选全文完整版实验报告5判别分析(设计性实验)(Discriminant analysis)实验原理:判别分析是判别样品所属类型的一种统计方法。
判别分析是在已知研究对象分成若干类型(或组别)并已取得各种类型的一批已知样品的观测数目,在此基础上根据某些准则建立判别式,然后对未知类型的样品进行判别分类。
本实验要求学生应用距离判别准则(即,对任给的一次观测,若它与第i类的重心距离最近,就认为它来自第i类),对两总体和多总体情形下分别进行判别分析。
实验中需注意协方差矩阵相等时,选取线性判别函数;协方差矩阵不相等时,应选取二次判别函数。
实验题目一:为了检测潜在的血友病A携带者,下表中给出了两组数据:(t11a8)其中x1=log10(AHF activity),x2=log10(AHF antigen)。
下表给出了五个新的观测,试对这些观测判别归类;(t11b8)实验要求:(1)分别检验两组数据是否大致满足二元正态性;(2)分别计算两组数据的协方差矩阵,是否可以认为两者近似相等?(3)对训练样本和新观测合并作散点图,不同的类用不同颜色标识;(4)用lda函数做判别分析,即在协方差矩阵相等的情形下作判别分析;(5)用qda函数做判别分析,即在协方差矩阵不相等的情形下作判别分析;(6)比较方法(4)和方法(5)的误判率。
实验题目二:某商学研究生院的招生官员利用指标――大学期间平均成绩GPA和研究生管理能力考试GMAT的成绩,将申请者分为三类:接受,不接受,待定。
下表中给出了三类申请者的GPA与GMAT成绩:(t11a6)GPA (x1)GMAT(x2)接受GPA(x1)GMAT(x2)不接受GPA(x1)GMAT(x2)待定2.96 596 1 2.54 446 2 2.86 494 33.14 473 1 2.43 425 2 2.85 496 3 3.22 482 1 2.2 474 2 3.14 419 3 3.29 527 1 2.36 531 2 3.28 371 3 3.69 505 1 2.57 542 2 2.89 447 3 3.46 693 1 2.35 406 2 3.15 313 3 3.03 626 1 2.51 412 2 3.5 402 3 3.19 663 1 2.51 458 2 2.89 485 3 3.63 447 1 2.36 399 2 2.8 444 33.59 588 1 2.36 482 2 3.13 416 33.3 563 1 2.66 420 2 3.01 471 33.4 553 1 2.68 414 2 2.79 490 33.5 572 1 2.48 533 2 2.89 431 33.78 591 1 2.46 509 2 2.91 446 33.44 692 1 2.63 504 2 2.75 546 33.48 528 1 2.44 336 2 2.73 467 33.47 552 1 2.13 408 2 3.12 463 33.35 520 1 2.41 469 2 3.08 440 33.39 543 1 2.55 538 2 3.03 419 33.28 523 1 2.31 505 2 3 509 33.21 530 1 2.41 489 2 3.03 438 33.58 564 1 2.19 411 2 3.05 399 33.33 565 1 2.35 321 2 2.85 483 33.4 431 1 2.6 394 2 3.01 453 33.38 605 1 2.55 528 2 3.03 414 33.26 664 1 2.72 399 2 3.04 446 33.6 609 1 2.85 381 23.37 559 1 2.9 384 23.8 521 13.76 646 13.24 467 1实验要求:(1)对上表中的数据作散点图,不同的类用不同的颜色标识;(2)用lda函数做判别分析,即在协方差矩阵相等的情形下作判别分析;(3)用qda函数做判别分析,即在协方差矩阵不相等的情形下作判别分析;(4)比较方法(2)和方法(3)的误判率;(5)现有一新申请者的GPA为3.21,GMAT成绩为497。
判别分析上机练习题

判别分析上机练习题一、基础题1. 给定一组数据,如何判断其适合进行判别分析?2. 简述费希尔判别法的基本思想。
3. 什么是马氏距离?它在判别分析中的作用是什么?4. 请列举至少三种常用的判别分析方法。
5. 在进行判别分析时,为什么要对数据进行标准化处理?二、选择题1. 判别分析的主要目的是:A. 分类B. 聚类C. 回归D. 相关性分析A. 费希尔判别法B. 贝叶斯判别法C. 线性回归D. 逐步判别法A. S_wB. S_bC. S_tD. S_o4. 贝叶斯判别法的分类原则是:A. 使总体概率最大B. 使后验概率最大C. 使先验概率最大D. 使损失函数最小三、计算题1. 已知某组数据的协方差矩阵如下,请计算马氏距离:S = | 2 1 || 1 3 |μ_1 = (1, 2, 3)μ_2 = (2, 3, 4)3. 设有两个总体G1和G2,它们的先验概率分别为P(G1) = 0.6,P(G2) = 0.4。
现有一观测向量X,其属于G1和G2的概率密度函数分别为f1(x)和f2(x)。
试计算X属于G1的后验概率。
G1: (1, 2), (2, 3), (3, 4)G2: (4, 5), (5, 6), (6, 7)四、应用题客户编号 | 年收入(万元) | 消费金额(万元)1 | 10 | 22 | 15 | 33 | 20 | 54 | 25 | 65 | 30 | 86 | 35 | 107 | 40 | 128 | 45 | 15类别1:(1, 2), (2, 3), (3, 4)类别2:(4, 5), (5, 6), (6, 7)新观测样本:(3, 5)五、案例分析题病人编号 | 肺活量(升) | 心率(次/分钟) | 疾病类型 | | |1 | 3.5 | 75 | A2 | 4.0 | 80 | A3 | 3.8 | 78 | A4 | 4.2 | 85 | B5 | 4.5 | 90 | B6 | 4.3 | 88 | B新病人 | 4.1 | 82 | ?用户编号 | 购买频率(次/月) | 平均消费金额(元) | 用户类别| | |1 | 3 | 500 | 高价值2 | 2 | 300 | 低价值3 |4 | 700 | 高价值4 | 1 | 200 | 低价值5 | 5 | 900 | 高价值新用户 | 4 | 600 | ?六、编程题1. 编写Python代码,实现费希尔线性判别函数。
高级统计学-判别分析作业

全国各地区消费水平的实例判别分析摘要:针对我国各省(直辖)市的2009年度消费水平数据,选取9个经济指标进行系统聚类分析,得到我国3类不同的地区消费水平类型;利用实例进行判别分析, 结合实际情况分析结果。
聚类结果为制订有针对性的地区消费市场战略提供依据。
关键词:SPSS;判别分析;消费水平。
1.引言由于传统的经济发展起点不同,加上地域、资源、技术和政策等条件的差异,各个地区的经济发展水平高低不齐,导致各地区的工资水平和消费水平的不同。
因此,对各地区消费水平进行分类、比较和研究,总结出有助于市场调节和商业发展的对策,有针对性地制订地区经济发展战略,对促进国民经济协调发展有重要意义。
聚类分析和判别分析是是进行以上分析的两个重要的方法。
1.1判别分析定义:判别分析是一种进行统计判别和分组的技术手段。
根据一定量案例的一个分组变量和相应的其他多元变量的已知信息,确定分组与其他多元变量之间的数量关系,建立判别函数,然后便可以利用这一数量关系对其他未知分组类型所属的案例进行判别分组。
判别分析的基本思想:对已知分类的数据建立由数值指标构成的分类规则即判别函数,然后把这样的规则应用到未知分类的样本去分类。
本文针对我国各省(直辖)市的2009年度消费消费价格分类指数数据,考虑到数据的可得性和来源的权威性,选取9个消费指标进行系统聚类分析并假定上年相应价格指数为100,得到我国3类不同的地区消费水平类型;并利用实例进行判别分析,以确认聚类效果。
聚类结果将为制订有针对性的地区经济发展战略提供依据。
下述数据来源于《中国统计摘要-2010》,利用社会经济统计软件SPSS19.0建立数据库并对数据进行分析处理。
表-1:国内31个省、直辖市、自治区的9项消费指标数据其中,北京、河北、山东、贵州、重庆五省、直辖市、自治区将作为实例样本数据利用判别分析进行分组归类,以检验聚类分析中的聚类结果。
2.判别分析2.1判别分析步骤将国内21省、直辖市、自治区的9项消费价格指标数据输入SPSS,做判别分析,具体步骤为:(1)在数据编辑窗口的主菜单中选择“分析(A)”→“分类(F)”→“判别(D)”(如图-1所示)。
判别分析实例讲解

例:人文与发展指数是联合国开发计划署于1990年5月发表的第一份《人类发展报告》中公布的。
该报告建议,目前对人文发展的衡量指标应当以人生的三大要素为重点。
衡量人生的三大要素的指标分别为:实际人均GDP指数、出生时的预期寿命指数、受教育程度指数(由成人识字率指数和综合总人学率指数按2/3、1/3的权重加权而得),将一生三个指数合成为一个指数就是人文发展指数。
今从2007年世界各国人文发展指数(2005年)的排序中,选取高发展水平、中等发展水平和低发展水平国家各6个作为三组样品,另选四个国家作为待判样品,资料如下表所示。
试用判别分析过程对以下数据资料进行判别分析,并据此对待data develop;input type gdp life rate zhrate@@;cards;1 41890 77.9 99.5 93.31 29461 79.1 99.2 881 23381 78.9 96 991 29663 79.4 92.5 87.31 28529 80.3 98.4 90.61 22029 77.9 99 962 6000 77.7 99.8 87.62 9060 71.9 97.3 76.82 8402 71.7 88.6 87.52 8677 69.6 92.6 71.22 5137 71 92.6 81.12 8407 71.4 87.4 68.73 1550 62.6 48.6 58.13 1128 46.5 69.1 56.23 2299 49.8 67.9 62.33 2370 64.6 49.9 403 3071 73.7 90.3 63.93 3843 69.7 90.4 68.2. 31267 82.3 99 85.9. 3452 63.7 61 63.8. 6757 72.5 90.9 69.1. 11110 50.8 82.4 77;proc discrim simple wcov distance list;/*simple:要求技术各类样品的简单描述统计量;选项WCOV要求计算类内协方差阵;选项DISTANCE要求计算马氏距离;选项LIST要求输出重复替换归类结果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
判别分析法
一、筛选变量
1、通过单因素方差分析剔除不显著变量:在SPSS软件中建立变量和已知数据表,通过Analyze-Classify-Discriminant进入判别分析对话框,由题意知分组变量group即为因变量,其范围定义为:最小值1,最大值2。
自变量为X1、X
2、X
3、X4,通过勾选Statistics选项中的单因素方差分析得到表3-1如下
3-1
由表中可看出收益性指标(X2)和生产效率指标(X4)的显著性水平均大于0.05,接受原假设,即这两个判别变量在各组间差异不显著,所以剔除X2、X4。
2、对判别变量选择逐步进入,得到表3-2至3-4
(3-2)
(3-3)
(3-4)
表3-2至3-3表示逐步判别法中每一步进入的变量;表3-4表示最终删除的变量,通过上表可以明显地看出最终删除的变量是收益性指标(X2)和生产效率指标(X4)。
二、判别分析
1.Box’s 检验:通过第一步将不显著变量剔除后,在SPSS软件中勾选Box’s M判断协方差阵是否相等,得到表3-5和3-6
(3-5)
(3-6)
表3-5反映的是协方差矩阵的秩和行列式的对数值,由行列式的值可以看出,协方差阵不是病态矩阵。
由表3-6可以看出总体协方差矩阵检验的P值0.01<0.05,拒绝原假设,即总体协方差阵不相等。
所以将Winthin-groups换为Separate-groups看两种协方差阵是否存在显著差异,结果表明两种方法没有差异,因此任选一种继续进行判别。
2、Fisher判别
通过在软件中选择非标准化判别得到表3-7至3-12
(3-7)
(3-8)
(3-9)
(3-10)
(3-11)
(3-12)
表3-11是非标准化的判别函数,由此可以写出判别函数的表达式:
y=-1.823+2.321*X1+0.777*X3
表3-7和3-8分析的是典型判别函数,其中表3-7反映了判别函数的特征值、解释方差的比例和典型相关系数,从表中可清楚的看出只有一个判别函数,而且它解释了100%的方差。
表3-8是对判别函数的显著性检验,由表中的P值可以看出显著的小于0.05,即该判别函数的检验是显著的。
表3-9是标准化的判别函数,标准化变量的系数是判别权重,表3-10是结构矩阵,即判别载荷。
从这两个表中可以看出判别变量对判别函数的影响大小,绝对值越大的影响越大,因此从表中系数可以看出短期支付能力(X3)对判别函数的影响要大于总负债率(X1)对判别函数的影响。
(3-13)
表3-13是分类矩阵表,这里交叉验证是“留一个在外”的。
即,每个观测都是通过除了这个观测以外的其他观测所推导出的判别函数来分类的。
由该表交错验证法得到的数据可以看出,在17个破产企业中有14个被判对,判对率为
82.4%;21个正常运行企业中有17个被判对,判对率为81%。
所以在38个企业中,共有31个企业的分类是正确的,故原始数据的判对率为31/38=94.7%。
由表3-13中的原始数据(original)中还可以看出8个待判企业中有4个第1类的,4个第2类的。
将待判的八个企业的X1和X3的值分别带入判别方程
计算得到y1、y2、 y3…… y8然后分别计算与表3-12的两种类型的重心的距
离,哪个距离小就判给哪一类,通过对save中的选项的勾选可以在SPSS数据表中输出待判企业的分类结果为前4个待判企业被判为第1类,后4个待判企业被判为第2类。
