判别分析作业
北航数理统计大作业2-聚类与判别分析

应用数理统计作业二学号:姓名:电话:二〇一四年十二月对NBA球队的聚类分析和判别分析摘要:NBA联盟作为篮球的最高殿堂深受广大球迷的喜爱,联盟的30支球队大家也耳熟能详,本文选取NBA联盟30支球队2013-2014常规赛赛季场均数据。
利用spss软件通过聚类分析对27个地区进行实力类型分类,并利用判断分析对其余3支球队对分类结果进行验证。
可以看出各球队实力类型与赛季实际结果相吻合。
关键词:聚类分析,判别分析,NBA目录1. 引言 (4)2、相关统计基础理论 (5)2.1、聚类分析 (5)2.2,判别分析 (6)3.聚类分析 (7)3.1数据文件 (7)3.2聚类分析过程 (9)3.3 聚类结果分析 (11)4、判别分析 (12)4.1 判别分析过程 (12)4.2判别检验 (17)5、结论 (20)参考文献 (21)致谢 (22)1. 引言1896年,美国第一个篮球组织"全国篮球联盟(简称NBL)"成立,但当时篮球规则还不完善,组织机构也不健全,经过几个赛季后,该组织就名存实亡了。
1946年4月6日,由美国波士顿花园老板沃尔特.阿.布朗发起成立了“美国篮球协会”(简称BAA)。
1949年在布朗的努力下,美国两大篮球组织BAA和NBL合并为“全国篮球协会”(简称NBA)。
NBA季前赛是 NBA各支队伍的热身赛,因为在每个赛季结束后,每支球队在阵容上都有相当大的变化,为了让各队磨合阵容,熟悉各自球队的打法,确定各队新赛季的比赛阵容、同时也能增进队员、教练员之间的沟通,所以在每个赛季开始之前,NBA就举办若干场季前赛,使他们能以比较好的状态投入到漫长的常规赛的比赛当中。
为了扩大NBA在全球的影响,季前赛有约三分之一的球队在美国以外的国家举办。
从总体上看,NBA的赛程安排分为常规赛、季后赛和总决赛。
常规赛采用主客场制,季后赛和总决赛采用七场四胜制的淘汰制。
[31]NBA常规赛从每年的11月的第一个星期二开罗,到次年的4月20日左右结束。
08聚类分析与判别分析的例题

聚类分析与判别分析的例题1、某超市经销十种品牌的饮料,其中有四种畅销,三种滞销,三种平销。
下表是这十种品牌饮料的销售价格(元)和顾客对各种饮料的口味评分、信任度评分的平均数。
(1)根据数据建立贝叶斯判别函数,并根据此判别函数对原样本进行回判。
(2)现有一新品牌的饮料再该超市试销,其销售价格为3.0,顾客对其口味的评分平均分为8,信任评分为5,试预测该饮料的销售情况。
2、银行的贷款部门需要判别每个客户的信用好坏(是否未履行还贷责任),以决定是否给予贷款。
可以根据贷款申请人的年龄、受教育程度、现从事工作的年龄、未变更住址的年数、收入,负债收入比例、信用卡债务、其他债务等来判断其信用情况。
下表是某银行的客户资料中抽取的部分数据,(1)根据样本资料分别用距离判别法、贝叶斯判别法和费系尔判别法建立判别函数和判别规则。
(2)某客户的如上情况资料为(53,1,9,18,50,11,20,2.02,3.58),对其进行信用好坏的判别。
目前信用好坏客户序号已履行还贷责任1 23 1 7 2 31 6.6 0.34 1.712 34 1 173 59 8.0 1.81 2.913 42 2 7 23 41 4.6 0.94 0.944 39 1 195 48 13.1 1.93 4.365 35 1 9 1 34 5.0 0.40 1.30未履行还贷责任6 37 1 1 3 24 15.1 1.80 1.827 29 1 13 1 42 7.4 1.46 1.658 32 2 11 6 75 23.3 7.76 9.729 28 2 2 3 23 6.4 0.19 1.2910 26 1 4 3 27 10.5 2.47 0.363、从胃癌患者、萎缩性胃炎患者和非胃炎患者中分别抽取五个病人进行思想生化指标的化验:血清铜蛋白、蓝色反应、尿吲哚乙酸和中性硫化物,数据见下表。
试用距离判别法建立判别函数,并根据此判别函数对原样本进行回判。
判别分析作业
判别分析与聚类分析不同。
判别分析是在已知研究对象分成若干类型(或组别)并已取得各种类型的一批已知样品的观测数据,在此基础上根据某些准则建立判别式,然后对未知类型的样品进行判别分类。
表3-1 分析案例处理摘要未加权案例N 百分比有效28 90.3排除的缺失或越界组代码 3 9.7至少一个缺失判别变量0 .0缺失或越界组代码还有至少一个缺失判别变量0 .0合计 3 9.7合计31 100.0注:参与判别分析的观测量数据总结,共有31个样品,其中3个样品为待判样品。
表3-2 组统计量案例的类别号均值标准差有效的 N(列表状态)未加权的已加权的1 农业1359.700 342.1673 13 13.000林业146.517 73.3137 13 13.000牧业895.907 333.6804 13 13.000渔业304.403 310.4489 13 13.0002 农业408.396 315.2450 10 10.000林业37.247 49.3953 10 10.000牧业203.285 128.0568 10 10.000渔业39.380 61.9882 10 10.0003 农业2821.154 591.4155 5 5.000林业124.150 69.0856 5 5.000牧业1717.854 429.8756 5 5.000渔业525.066 463.0711 5 5.000合计农业1280.923 928.0349 28 28.000林业103.498 80.6531 28 28.000牧业795.318 612.0639 28 28.000渔业249.156 328.2521 28 28.000 分类统计结果:均值、方差、未加权的权重和加权的权重,从表3-2中可以看出“农业”最发达的处在第3类中;“林业”最发达的处在第1类中;“牧业”相对比较发达的处在第3类中;“渔业”比较发达的处在第3类中.表3-3 汇聚的组内矩阵a农业林业牧业渔业协方差农业147937.808 32.329 53946.036 38237.523林业32.329 4221.968 763.564 5011.382牧业53946.036 763.564 88914.814 -1202.757渔业38237.523 5011.382 -1202.757 81954.578相关性农业 1.000 .001 .470 .347林业.001 1.000 .039 .269牧业.470 .039 1.000 -.014渔业.347 .269 -.014 1.000a. 协方差矩阵的自由度为 25。
数理统计大作业聚类分析和判别分析

数理统计大作业(2)全国各省、市及自治区产业类型聚类分析和判别分析院(系)名称航空科学与工程学院专业名称飞行器设计与工程学生姓名熊蕾学号ZY15054022015年12月全国各省、市及自治区产业类型聚类分析和判别分析ZY1505402 熊蕾摘要本文从中国统计年鉴(2014)中获得了2013年按三次产业分地区生产总值的数据,按各省的第一产业、第二产业和第三产业产值所占地区生产总值的比值不同,对全国23个省、4个直辖市和5个少数民族自治区进行聚类分析和判别分析。
关键词经济类型聚类分析判别分析一、引言产业是指具有某种同类属性的经济活动的集合或系统,是经济社会的物质生产部门。
世界各国把各种产业划分为三大类:第一产业、第二产业和第三产业。
第一产业是指提供生产资料的产业,包括种植业、林业、畜牧业、水产养殖业等直接以自然物为对象的生产部门。
第二产业是指加工产业,利用基本的生产资料进行加工并出售,包括采矿业、制造业、电力、燃气和水的生产和供应业和建筑业。
第三产业又称服务业,它是指第一、第二产业以外的其他行业。
第三产业行业广泛。
包括交通运输业、通讯业、商业、餐饮业、金融保险业、行政、家庭服务等非物质生产部门。
我国区域经济发展不平衡,各地区的产业类型和产业结构不尽相同,因此可以以各省的第一产业、第二产业和第三产业产值所占地区生产总值的比值对全国的23个省、4个直辖市和5个少数民族自治区进行分类。
二、聚类分析2.1数据输入从中国统计年鉴中得到了2013年按三次产业分地区生产总值的数据,如下表所示,产值单位均为亿元,由于各省经济发展程度不同,地区生产总值有较大的差别,因此要算出各地区三大产业所占的比值来进行聚类和判别分析。
表 1 原始数据2.2聚类分析从表1中选出湖南、安徽和西藏三个地区的数据以待判别,对其余地区的数据进行聚类分析。
表 2 聚类分析数据将表2数据导入SPSS,进行系统聚类分析,得到以下结果:表 3 聚类表阶群集组合系数首次出现阶群集下一阶群集 1 群集 2 群集 1 群集 21 7 13 .052 0 0 92 6 12 .109 0 0 133 14 20 .174 0 0 54 3 21 .244 0 0 95 14 27 .336 3 0 166 5 24 .465 0 0 127 8 23 .602 0 0 198 11 17 .742 0 0 109 3 7 .952 4 1 1510 10 11 1.163 0 8 1711 18 28 1.381 0 0 1812 5 26 1.641 6 0 2013 4 6 1.977 0 2 1614 16 25 2.315 0 0 1815 3 15 2.673 9 0 2016 4 14 3.149 13 5 2317 2 10 3.678 0 10 2318 16 18 4.238 14 11 2119 8 22 4.814 7 0 2120 3 5 5.523 15 12 2521 8 16 6.429 19 18 2422 1 9 7.640 0 0 2623 2 4 9.318 17 16 2524 8 19 11.431 21 0 2625 2 3 14.946 23 20 2726 1 8 20.495 22 24 2727 1 2 26.551 26 25 0表4 群集成员案例8 群集7 群集 6 群集 5 群集 4 群集 3 群集1:北京 1 1 1 1 1 1 2:天津 2 2 2 2 2 2 3:河北 3 3 3 3 3 2 4:山西 4 4 4 2 2 2 5:内蒙古 3 3 3 3 3 2 6:辽宁 4 4 4 2 2 2 7:吉林 3 3 3 3 3 2 8:黑龙江 5 5 5 4 4 3 9:上海 6 6 1 1 1 1 10:江苏 2 2 2 2 2 2 11:浙江 2 2 2 2 2 2 12:福建 4 4 4 2 2 2 13:江西 3 3 3 3 3 2 14:山东 4 4 4 2 2 2 15:河南 3 3 3 3 3 2 16:湖北7 5 5 4 4 3 17:广东 2 2 2 2 2 2 18:广西7 5 5 4 4 3 19:海南8 7 6 5 4 3 20:重庆 4 4 4 2 2 2 21:四川 3 3 3 3 3 2 22:贵州 5 5 5 4 4 3 23:云南 5 5 5 4 4 3 24:陕西 3 3 3 3 3 2 25:甘肃7 5 5 4 4 3 26:青海 3 3 3 3 3 2 27:宁夏 4 4 4 2 2 2 28:新疆7 5 5 4 4 3图1聚类分析树状图从树状图中,我们定下聚类分析最终得到四个组别:1为北京和上海,可以看出这两个直辖市的总产值中,第三产业也就是服务业占有绝对优势,因此可将第一组作为第三产业为主的地区;2为天津、山西、江苏、广东等10个省份,这些省份的第二产业占有较多的比重,而第一产业仅占极少的比重,说明第2组以第二、三产业为主;第三组包括河北、河南、吉林、江西等省份,这些省份虽然也是第二产业占有的比重最大,但它们的第一产业的比重与第1、2组相比更多;第四组的各个地区是传统的鱼米之乡,可以看到它们的第一产业的比重大于其他各组。
判别分析 实验报告

判别分析实验报告判别分析实验报告一、引言判别分析是一种常用的统计分析方法,广泛应用于数据挖掘、模式识别、生物信息学等领域。
本实验旨在通过对一个真实数据集的分析,探讨判别分析在实际问题中的应用效果。
二、数据集介绍本实验使用的数据集是一份关于肿瘤患者的临床数据,包括患者的年龄、性别、肿瘤大小、转移情况等多个变量。
我们的目标是根据这些变量,建立一个判别模型,能够准确地预测患者是否患有恶性肿瘤。
三、数据预处理在进行判别分析之前,我们首先对数据进行预处理。
这包括数据清洗、缺失值处理、异常值检测等步骤。
通过对数据的观察和分析,我们发现有部分数据存在缺失值,需要进行处理。
我们选择使用均值替代缺失值的方法进行处理,并对替代后的数据进行了异常值检测。
四、判别模型建立在本实验中,我们选择了线性判别分析(LDA)作为判别模型的建立方法。
LDA 是一种经典的判别分析方法,通过将数据投影到低维空间中,使得不同类别的样本在投影后的空间中能够更好地区分开来。
我们使用Python中的scikit-learn 库来实现LDA算法。
五、模型评估为了评估建立的判别模型的性能,我们将数据集划分为训练集和测试集。
使用训练集对模型进行训练,并使用测试集进行模型的评估。
我们选择了准确率、精确率、召回率和F1值等指标来评估模型的性能。
经过多次实验和交叉验证,我们得到了一个较为稳定的模型,并对其性能进行了详细的分析和解释。
六、结果与讨论经过模型评估,我们得到了一个在测试集上准确率为85%的判别模型。
该模型在预测恶性肿瘤时具有较高的精确率和召回率,说明了其在实际应用中的可行性和有效性。
但同时我们也发现,该模型在预测良性肿瘤时存在一定的误判率,可能需要进一步优化和改进。
七、结论本实验通过对一个真实数据集的判别分析,验证了判别分析方法在预测恶性肿瘤的应用效果。
通过建立判别模型,并对其性能进行评估,我们得到了一个在测试集上具有较高准确率的模型。
然而,我们也发现了该模型在预测良性肿瘤时存在一定的误判率,需要进一步的改进和优化。
多元作业判别分析

《多元统计分析》实验报告实验名称: 判别分析及正态检验专业:统计学班级:120802姓名:指导教师:2014 年6 月26 日给出血友病基因携带者数据1,共分2组,第一组为非携带者(1π),第二组为必然携带者(2π),分组变量为g ,变量x1表示()10log AHF 活性,变量x2表示()10log AHF 抗原,利用上述数据: (1)对两个组检查二元正态性假定;一通过菜单系统实现 二运行结果第一组的正态性检验一运行程序proc princomp data=sasuser.zu1 out=prin prefix=z standard;var x1 x2;run;proc univariate data=work.prin normal plot;var z1 z2;run;二运行结果三结论分析第二组的正态性检验一运行程序proc princomp data=sasuser.zu2 out=prin1 prefix=z standard; var x1 x2;run;proc univariate data=work.prin1 normal plot;var z1 z2;run;二运行结果三结论分析(2)假定两组先验概率相等,求样本线性判别函数,并估计误判概率;一运行程序proc discrim data=sasuser.liangzu listerr crosslisterr;class g;var x1-x2;run;二运行结果三结论分析(3)将血友病基因携带者数据2中的10个新事例用(2)得到的判别函数进行分类;一运行程序proc discrim data=sasuser.liangzu testdata=sasuser.daipan listerr crosslisterr testlist;class g;var x1-x2;run;二运行结果三结论分析(3)假定必然携带者(组2)的先验概率为0.25。
北航数理统计第二次数理统计大作业 判别分析

数理统计大作业(二)全国各省发展程度的聚类分析及判别分析指导教师院系名称材料科学与工程院学号学生姓名2015 年 12 月21 日目录全国各省发展程度的聚类分析及判别分析 (1)摘要: (1)引言 (1)1实验方案 (2)1.1数据统计 (2)1.2聚类分析 (3)1.3判别分析 (4)2结果分析与讨论 (5)2.1聚类分析结果 (5)2.2聚类分析结果分析: (8)2.3判别分析结果 (9)2.4 Fisher判别结果分析: (11)参考文献: (16)全国各省发展程度的聚类分析及判别分析摘要:利用SPSS软件对全国31个省、直辖市、自治区(浙江、安徽、甘肃除外)的主要经济指标进行多种聚类分析,分析选择最佳聚类类数,并对浙江、湖南、甘肃进行类型判别分析。
通过这两个方法对全国各省进行发展分类。
本文选取了7项社会发展指标作为决定发展程度的影响因素,其中经济因素为主要因素,同时评估城镇化率和人口素质因素。
各项数据均来自2014年国家统计年鉴。
分析结果表明:北京市和上海市和天津市为同一类;江苏省和山东省和广东省为同一类型;河北、湖北、河南、湖南、四川、辽宁为同一类;其余的为另一类。
关键词:聚类分析、判别分析、发展引言聚类分析是根据研究对象的特征对研究对象进行分类的多元统计分析技术的总称。
它直接比较各事物之间的性质,将性质相近的归为一类,将性质差别较大的归入不同的类。
系统聚类分析又称集群分析,是聚类分析中应用最广的一种方法,它根据样本的多指标(变量)、多个观察数据,定量地确定样品、指标之间存在的相似性或亲疏关系,并据此连结这些样品或指标,归成大小类群,构成分类树状图或冰柱图。
判别分析是根据多种因素(指标)对事物的影响来实现对事物的分类,从而对事物进行判别分类的统计方法。
判别分析适用于已经掌握了历史上分类的每一个类别的若干样品,希望根据这些历史的经验(样品),总结出分类的规律性(判别函数)来指导未来的分类。
判别分析练习题

判别分析练习题判别分析练习题在统计学中,判别分析是一种用于分类和预测的方法。
它通过对不同类别的样本进行分析,构建一个分类模型,以便将未知样本分配到正确的类别中。
判别分析在各个领域都有广泛的应用,如医学诊断、金融风险评估等。
下面我将给大家提供一些判别分析的练习题,希望能够帮助大家更好地理解和应用这一方法。
1. 假设有两个类别的样本,每个样本都有两个变量。
已知两个类别的样本均值和协方差矩阵如下:类别1:均值为(1, 2),协方差矩阵为[[2, 1], [1, 2]]类别2:均值为(3, 4),协方差矩阵为[[3, 1], [1, 3]]现有一个未知样本(2, 3),请利用判别分析方法判断该样本属于哪个类别。
解答:首先,我们需要计算两个类别的判别函数值。
对于类别1,判别函数为:g1(x) = -0.5 * (x - μ1) * Σ1^-1 * (x - μ1)T - 0.5 * ln(|Σ1|) + ln(P1)其中,x为未知样本,μ1为类别1的均值,Σ1为类别1的协方差矩阵,P1为类别1的先验概率。
类似地,对于类别2,判别函数为:g2(x) = -0.5 * (x - μ2) * Σ2^-1 * (x - μ2)T - 0.5 * ln(|Σ2|) + ln(P2)其中,μ2为类别2的均值,Σ2为类别2的协方差矩阵,P2为类别2的先验概率。
根据给定的均值和协方差矩阵,我们可以计算出:μ1 = (1, 2), Σ1 = [[2, 1], [1, 2]]μ2 = (3, 4), Σ2 = [[3, 1], [1, 3]]假设两个类别的先验概率相等,即P1 = P2 = 0.5。
将未知样本(2, 3)代入判别函数中,可以计算出:g1(2, 3) = -4.5g2(2, 3) = -5.5由于g2(2, 3)的值较小,所以未知样本更有可能属于类别2。
2. 现有一个三类别的样本,每个样本有三个变量。
已知三个类别的样本均值和协方差矩阵如下:类别1:均值为(1, 2, 3),协方差矩阵为[[2, 1, 1], [1, 2, 1], [1, 1, 2]]类别2:均值为(4, 5, 6),协方差矩阵为[[3, 1, 2], [1, 3, 2], [2, 2, 3]]类别3:均值为(7, 8, 9),协方差矩阵为[[4, 1, 2], [1, 4, 2], [2, 2, 4]]现有一个未知样本(3, 4, 5),请利用判别分析方法判断该样本属于哪个类别。
聚类与判别分析作业

利用SPSS对全国各省进行经济类型聚类和判别分析摘要:本文利用SPSS统计软件对中国大陆(除港、澳、台之外)的31个省、市、自治区2000年到2009年的经济总量进行聚类分析,将这31个省、市、自治区分为了三大类,即经济发达地区、中等水平区、经济落后区。
并以这31个省级行政区10年的经济数据为样本,进行判别分析,建立了Fisher判别模型。
从判回代统计表可以看出该判别模型有着很高的正确率。
关键词:SPSS 聚类分析判别分析Fisher判别法一、引言利用各省以往经济数据对各省进行经济类型的划分,有助于了解各省的经济发展的状况,特别是能有助于了解全国各区域经济发展状况。
这对于相关部门制定相应的经济政策有一定的参考意义。
本文利用SPSS统计软件对全国31个省级行政区近10年的经济总量进行了聚类分析,把这31个地区划分为三个大类,即经济发达地区、中等水平区、经济落后区,然后对分好的类进行了判别分析,建立了判别函数。
从结果可以看出,其判别效果较好。
二、聚类分析和判别分析简介1、聚类分析法俗话说:“物以类聚,人以群分”。
对研究对象进行适当的分类,进而发现其规律性,是人们认识世界的一种基本方法。
研究怎样对事物进行合理分类(归类)的统计方法称为聚类分析。
依据分类对象的不同可以把聚类分析再分成Q型聚类和R型聚类,Q聚类是对样品进行聚类,R聚类是指对变量进行聚类。
聚类分析的基本原理是把某种性质相似的对象归于同一类,而不同的类之间则存在较大的差异。
为此,首先需要能刻画各个变量之间或者各个样本点之间的相似性,Q聚类一般使用“距离”度量样本点之间的相似性,R聚类则使用“相似系数”作为变量相似性的度量。
定义样本之间的距离可以采用欧氏距离、明考夫斯基距离、马氏距离、兰氏距离等测度;定义各变量之间的相似系数则多采用样本相关系数、夹角余弦等测度。
系统聚类法(Hierarchical Clustering Method )是最常用的一种聚类方法。
判别分析实验报告

判别分析实验报告一、引言判别分析是一种常用的统计分析方法,用于解决分类问题。
它通过分析已知类别的训练样本,构建一个分类模型,再用该模型对新样本进行分类预测。
本实验旨在通过判别分析方法,对一组实验数据进行分类分析,并评估分类模型的准确性和可靠性。
二、实验设计本次实验采用了以下步骤进行判别分析:1.数据收集:收集一组有标签的实验数据,包括特征变量和类别标签。
2.数据预处理:对收集到的数据进行清洗和预处理,包括缺失值处理、异常值处理等。
3.特征选择:根据实际需求和特征变量的相关性,选择合适的特征作为判别分析的输入变量。
4.训练模型:使用训练数据集训练判别分析模型,建立分类模型。
5.模型评估:使用测试数据集对分类模型进行评估,包括分类准确度、召回率、精确率等指标。
6.模型优化:根据评估结果,对分类模型进行优化,如调整模型参数、增加特征变量等。
三、实验结果经过以上步骤,我们得到了一个判别分析模型,并进行了评估。
以下是实验结果的总结:1.数据集描述:我们使用了一个包含1000个样本的数据集,每个样本有5个特征变量和一个类别标签。
2.数据预处理:我们对数据集进行了缺失值处理和异常值处理,确保数据的完整性和准确性。
3.特征选择:根据特征变量与类别标签的相关性,我们选择了3个最相关的特征作为判别分析的输入变量。
4.模型训练:根据训练数据集,我们使用了判别分析算法来训练模型。
模型的训练过程中,我们使用了交叉验证方法来评估模型的性能。
5.模型评估:使用测试数据集,我们对模型进行了评估。
评估结果显示,该模型的分类准确度达到了90%,召回率为85%,精确率为92%。
6.模型优化:根据评估结果,我们对模型进行了优化。
我们尝试了不同的特征组合和参数调整,最终将模型的准确度提高到了92%。
四、讨论与总结通过本次实验,我们得到了一个准确度较高的判别分析模型,并对其进行了评估和优化。
然而,在实际应用中,我们还需注意以下几点:1.数据质量:数据质量对判别分析模型的准确性有重要影响。
判别分析法(数学建模相关习题)

1 1 2 , a 1 1 2 2
W x a ' x
举例
2、μ1 ≠ μ2,∑1 ≠ ∑2
d 2 x,1 x 1 1 x 1
'
d 2 x, 2 x 2 1 x 2
化简
d 2 x, 1 d 2 x, 2 2 x
x 1 , 若d 2 x, 1 d 2 x, 2 x 2 , 若d 2 x, 1 d 2 x, 2
1 2
2
1 ' 1 2 2x a 2a x '
0.0784 0.0647 0.0197 0.0217 总体样本离差矩阵 s1 0.0647 0.1350 s2 0.0217 0.0389
平均协方差阵的估计ˆ V
0.0075 0.0066 1 s1 s2 0.0066 0.0134 n1 n2 2
1
2
例题:对28名一级和25名健将级标枪运动员测试了6个 影响标枪成绩的训练指标; 30米跑(x1)、 投小铅球( x2 )、 挺举重量( x3 )、
抛实心球( x4 )、前抛铅球( x5 )、 五级跳( x6 )。
编号 组别 x1
Hale Waihona Puke x24.30 4.10 : 4.20 4.00
4.30
x3
82.3 87.48 : 89.20 103.00
平均 y=0.9625x+0.6065 用它来判定发现不好 2、心型平分线 取Af和Apf的中心(1.41,1.80), (1.22,1.93),垂直平分线方程是 y=1.52576x-0.1485
多元统计作业-判别分析
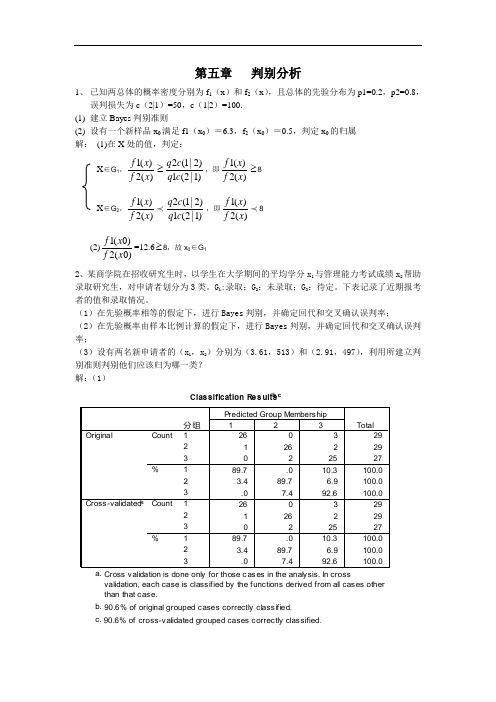
第五章 判别分析1、 已知两总体的概率密度分别为f 1(x )和f 2(x ),且总体的先验分布为p1=0.2,p2=0.8,误判损失为c (2|1)=50,c (1|2)=100. (1) 建立Bayes 判别准则(2) 设有一个新样品x 0满足f1(x 0)=6.3,f 2(x 0)=0.5,判定x 0的归属 解: (1)在X 处的值,判定:X ∈G 1,1()2()f x f x ≥2(1|2)1(2|1)q c q c ,即1()2()f x f x ≥8X ∈G 2,1()2()f x f x 2(1|2)1(2|1)q c q c ,即1()2()f x f x 8(2)1(0)2(0)f x f x =12.6≥8,故x 0∈G 12、某商学院在招收研究生时,以学生在大学期间的平均学分x 1与管理能力考试成绩x 2帮助录取研究生,对申请者划分为3类。
G 1:录取;G 2:未录取;G 3:待定。
下表记录了近期报考者的值和录取情况。
(1)在先验概率相等的假定下,进行Bayes 判别,并确定回代和交叉确认误判率;(2)在先验概率由样本比例计算的假定下,进行Bayes 判别,并确定回代和交叉确认误判率;(3)设有两名新申请者的(x 1,x 2)分别为(3.61,513)和(2.91,497),利用所建立判别准则判别他们应该归为哪一类? 解:(1)回代误判率:8/85=0.0941,交叉确认误判率同样为8/85=0.0941,第2号、3号、24号、30号、31号、58号、74号、75号被误判。
(2)号、30号、31号、58号、74号、75号被误判。
(3)建立Fisher线性判别准则W1=-151.902+60.431X1+0.172X2W2=-89.815+45.255X1+0.138X2W3=-110.818+53.024X1+0.137X2把(3.61,513)代入以上三式,W1=154.48991,W2=144.34955,W3=150.87964把(2.91,497)代入以上三式,W1=109.43621,W2=110.46305,W3=111.57084故第一个申请者判为W1(W1最大),第二个申请者判为W3(W3最大)。
判别分析

实验六判别分析(综合性实验 4学时)1、目的要求:熟练掌握判别分析的基本步骤,对给出的样本建立判别函数,进行判别分析。
2、实验内容:使用指定的数据按实验教材完成相关的操作。
3、主要仪器设备:计算机。
练习:1、为研究舒张期血压和血浆胆固醇对冠心病的作用,某医师测定了50—59岁冠心病人15例和正常人16例的舒张压和胆固醇指标,结果如下表所示。
试做判别分析,建立判别函数以便在临床中用于筛选在临床中用于筛选冠心病人。
操作步骤:Step1:读取数据文件。
其中,变量名“舒张压”、“胆固醇”代表两项指标值。
病人资料和正常人资料合并一同输入,定义变量名为“组别”的变量用于区分冠心病人资料和正常人资料,即冠心病人资料的“组别”值均为1,正常人资料的“组别”值均为2.Step2:选择“Analysis” →“Classify” →“Discriminant”命令,在“Discriminant Analysis”对话框中,选择“组别”变量进入“Grouping Variable”文本框;单击“Define Range”按钮,在“Minimum”文本框中输入1,在“Maximum”文本框中输入2,单击“Continue”按钮,返回主对话框。
Step3:选择变量“舒张压”和“胆固醇”移动到“Independents”列表框中,本例选择“Enterindependents together”判别方式作为判别分析的方法。
Step4:单击“Statistics”按钮,在“Descriptive”选项中选择“Mean”;在“Function Coefficients”选择“Unstandardized”。
单击“Continue”按钮,返回主对话框。
Step5:单击“Classify”按钮,在“Plot”选项组中选择“Combined-groups”选项,在“Display”选项组中选择“Casewise result”和“Summmary table”选项;单击“Continue”按钮,返回主对话框。
spss数据分析作业-中国区域经济类型的聚类和判别分析

应用数理统计(论文)中国区域经济类型的聚类和判别分析指导老师:**院系名称:材料科学与工程学号:SY********名:***2014年12月20日摘要区域经济发展的指标体系,包括人口总数、第一产业总产值、第二产业总产值、第三产业总产值、财政收入、社会消费品零售总额、货物进出口总额、平均工资、人均可支配收入和居民消费水平等。
本文主要通过系统类聚的方法,将全国31 个省市(自治区)的2013年经济发展状况进行归类分析,得出全国区域经济发展水平的一些基本情况,并进行了相应的判别分析,为我国经济在快速发展的前提下,做好协调发展提供一些启示。
关键字:区域经济聚类分析判别分析中国区域经济类型的聚类和判别分析目录1引言 (4)2数据收集 (5)3聚类分析 (8)3.1聚类分析概述 (8)3.2聚类分析过程及结果输出 (8)3.3讨论 (12)4判别分析 (14)4.1判别分析概述 (14)4.2判别分析过程及结果输出 (14)4.3讨论 (17)5结论 (18)参考文献 (19)应用数理统计(论文)1引言在制定国民经济和社会发展规划时,通常需要按照行政区域进行经济类型的划分,这有助于对不同地区经济发展存在的差异进行宏观调控,从而因地制宜出台相应的经济政策,促进各地区经济的协调发展,为国民经济持续协调健康发展奠定了坚实基础。
明确当前我国发达地区和落后地区的区间格局, 对于进一步的研究和分析我国各区域间经济发展的状况,并探求切实可行的区域协调发展政策以实现我国经济的可持续发展有着极为重要的现实意义。
在多元统计分析中,常常使用聚类分析和判别分析来解决样本的分类问题。
在事先并不知道应将样品或指标分为几类的情况下,可以使用聚类分析根据样本或指标的相似程度,将样本或指标归组分类;而在事先已经建立了样品分类,需要将新样本归入到已知分类的样本组中时,就可以使用判别分析。
本文试图通过聚类分析的方法,分析2013 年中国31 个省市(区域)经济发展发展状况和差异情况,从中寻找一些有用的信息,提出对我国经济如何在快速发展的基础上,做到协调发展的一些思考。
判别分析作业

判别分析1、说明各判别方法的原理。
答: (1)距离判别法:样品和哪个总体的距离最近,就判断它属于哪个总体。
而距离使用的是马氏距离,即设总体G为m元总体,均值向量为,协方差阵为则样品与总体的马氏距离定义为当m=1时,(2)贝叶斯判别法:就是给出空间的一个划分,使得当通过划分来判别归类时,所带来的平均损失达到最小。
(3)Fisher判别:基本思想是投影。
将k组m元数据投影到某一个方向,使得投影后组与组之间尽可能分开。
以上判别方法的使用,均建立在各类别方差具有显著性差异的基础上。
2、下面是85个学生的GPA和GMAT数据表,经聚类分析,分为三类:接收、不接收、边缘。
(1)已知的分类情况是否可以进行判别分析?T ests of Equality of Group Means.194170.020282.000.53735.350282.000GPAx1GMATx2Wilk s 'LambdaF df1df2Sig.由上表可知,各组均值具有显著性差异,可以进行判别分析.(2)计算各类的样本均值及Si 。
计算B 及A ,求出A-1B 特征根。
Group Statistics3.4023.212413131.000561.225867.957693131.0002.4825.183442828.000447.071462.379922828.0002.9927.172322626.000446.230847.401532626.0002.9740.429058585.000488.447181.522358585.000GPAx1GMATx2GPAx1GMATx2GPAx1GMATx2GPAx1GMATx2组别123TotalMean Std. DeviationUnweighted WeightedValid N (listwise)由上表可知,各类的样本均值分别为:(3.4023,561.2258)、(2.4825,447.0714)、(2.9927,446.2308).Cov ariance Matrices.045.000.0004618.247.034-1.192-1.1923891.254.030-5.404-5.4042246.905GPAx1GMATx2GPAx1GMATx2GPAx1GMATx2组别123GPAx1GMATx2,,Cov ariance Matricesa.18416.04616.0466645.893GPAx1GMATx2组别TotalGPAx1GMATx2The total covariance matrix has 84 degrees of freedom.a.Eigenv alues5.560a 96.796.7.921.191a 3.3100.0.400Function 12Eigenvalue % of VarianceCumulative %Canonical CorrelationFirst 2 canonical discriminant functions were used in the analysis.a.(3)给出三类的领域图,并给出各类的中心值。
数理统计作业1-三中判别分析

作业一一、人文发展指数是联合国开发计划署于1990年5月发表的第一份《人类发展报告》中公布的。
该报告建议,目前对人文发展的衡量应当以人生的三大要素为重点,衡量人生三大要素的指示分别采用出生时的预期寿命、成人识字率和实际人均GDP,将以上三个指示指标的数值合成为一个复合指数,即为人文发展指数。
资料来源UNDP《人类发展报告》1995年。
今从1995年世界各国人文发展指数的排序中,选取高发展水平、中等发展水平的国家各五个作为两组样品,另选四个国家作为待判样品作判别分析。
使用距离判别方法进行判别,并进行研究三者之间的关系。
一、距离判别法解:变量个数p=3,两类总体各有5个样品,即n1=n2=5 ,有4个待判样品,假定两总体协差阵相等。
由spss可计算出:协方差和平均值知道了均值和协方差可利用matlab 计算线性判别函数W (x )的判别系数a 和判别常数。
程序如下:v=[15.380,21.713,-555.875;21.713,66.613,-1446.098;-555.875,-1446.098,262546.500]; >> m1=[75.88;94.12;5343.4];m2=[70.44;91.74;3430.2];>> m=(m1+m2)/2;>> arfa=inv(v)*(m1-m2)arfa =0.65070.01330.0087>> c=arfa'*mc =87.1774则:()1774.870087.00133.06507.0321-++=x x x x W则将待判样品带入判别方程中得:-24.5071-15.584710.29514.1921故可知:中国和罗马尼亚属于第二类,而希腊和哥伦比亚属于第一类。
二、Fisher判别方法1、操作步骤:1)录入数据,选择菜单项Analyze→Classify→Discriminate,打开Discriminate Analysis对话框,如图2-1。
判别分析练习题1

1 292.56 26.07 2.16
1 276.84 16.60 2.91
2 510.47 67.64 1.73
2 510.41 62.71 1.58
2 470.30 54.40 1.68
2 364.12 46.26 2.09
2 416.07 45.37 1.90
2 515.70 84.59 1.75
3现有一人他的3项指标为420.50、32.42、1.98判断他是健康人
还是心肌梗塞患者2 心肌梗塞
10.0 1 2 0 0 81.0 42.000 1 120.0 0 0 0 0 25.0 5.667 3
5.0 1 0 0 1 30.0 3.000 1 72.0 1 0 0 0 39.0 46.000 3
42.0 1 0 1 2 15.5 0.102 1 84.0 0 0 0 0 15.0 12.000 3
X1 X2 X3
1 436.70 49.59 2.32
1 290.67 30.02 2.46
1 352.53 36.23 2.36
1 340.91 38.28 2.44
1 332.83 41.92 2.28
1 319.97 31.42 2.49
1 361.31 37.99 2.02
7.5 0 2 1 0 18.0 3.111 1 3.0 1 0 0 1 25.0 2.222 3
8.0 0 0 1 1 32.0 0.167 1 12.0 1 0 0 0 23.0 4.167 3
34.0 0 1 1 1 4.0 4.333 1 24.0 1 0 0 1 78.0 3.417 3
判别分析上机练习题

判别分析上机练习题一、基础题1. 给定一组数据,如何判断其适合进行判别分析?2. 简述费希尔判别法的基本思想。
3. 什么是马氏距离?它在判别分析中的作用是什么?4. 请列举至少三种常用的判别分析方法。
5. 在进行判别分析时,为什么要对数据进行标准化处理?二、选择题1. 判别分析的主要目的是:A. 分类B. 聚类C. 回归D. 相关性分析A. 费希尔判别法B. 贝叶斯判别法C. 线性回归D. 逐步判别法A. S_wB. S_bC. S_tD. S_o4. 贝叶斯判别法的分类原则是:A. 使总体概率最大B. 使后验概率最大C. 使先验概率最大D. 使损失函数最小三、计算题1. 已知某组数据的协方差矩阵如下,请计算马氏距离:S = | 2 1 || 1 3 |μ_1 = (1, 2, 3)μ_2 = (2, 3, 4)3. 设有两个总体G1和G2,它们的先验概率分别为P(G1) = 0.6,P(G2) = 0.4。
现有一观测向量X,其属于G1和G2的概率密度函数分别为f1(x)和f2(x)。
试计算X属于G1的后验概率。
G1: (1, 2), (2, 3), (3, 4)G2: (4, 5), (5, 6), (6, 7)四、应用题客户编号 | 年收入(万元) | 消费金额(万元)1 | 10 | 22 | 15 | 33 | 20 | 54 | 25 | 65 | 30 | 86 | 35 | 107 | 40 | 128 | 45 | 15类别1:(1, 2), (2, 3), (3, 4)类别2:(4, 5), (5, 6), (6, 7)新观测样本:(3, 5)五、案例分析题病人编号 | 肺活量(升) | 心率(次/分钟) | 疾病类型 | | |1 | 3.5 | 75 | A2 | 4.0 | 80 | A3 | 3.8 | 78 | A4 | 4.2 | 85 | B5 | 4.5 | 90 | B6 | 4.3 | 88 | B新病人 | 4.1 | 82 | ?用户编号 | 购买频率(次/月) | 平均消费金额(元) | 用户类别| | |1 | 3 | 500 | 高价值2 | 2 | 300 | 低价值3 |4 | 700 | 高价值4 | 1 | 200 | 低价值5 | 5 | 900 | 高价值新用户 | 4 | 600 | ?六、编程题1. 编写Python代码,实现费希尔线性判别函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
分类统计结果:均值、方差、未加权的权重和加权的权重,从表3-2中可以看出“农业”最发达的处在第3类中;“林业”最发达的处在第1类中;“牧业”相对比较发达的处在第3类中;“渔业”比较发达的处在第3类中.
※ 各类协方差矩阵和总协方差矩阵。
※ 第3类中农业之间的协方差数值最大为349772.315,牧业之间的协方差数值达到最大为184793.008,渔业之间的协方差数值达到最大为214434.833,第1类中林业之间的协方差数值达到最大为5374.905。
典型判别式函数摘要
表3-5 特征值
函数 特征值 方差的 % 累积 % 正则相关性 1 6.408a
94.7 94.7 .930 2
.358a
5.3
100.0
.514
a. 分析中使用了前 2 个典型判别式函数。
数越具有区别判断力。
最后一列表示是典则相关系数,是组间平方和与总平方和之比的平方根,表示判别函数分数与组别间的关联程度。
表3-6 Wilks 的 Lambda
函数检验 Wilks 的 Lambda 卡方 df Sig. 1 到 2 .099 54.258 8 .000 2
.736
7.199
3
.066
Wilk 的
表3-7 标准化的典型判别式函系数
函数
1 2 农 业 .747 -.403 林 业 .234 .923 牧 业 .383 .189 渔 业
-.063
.036
标准化后的典型判别式函数 ※ 112340.7470.2340.3830.063y x x x x =++-
※ 212340.4030.9230.1890.036y x x x x =-+++
表3-8 结构矩阵
函数
1 2 农 业 .906*
-.300 牧 业
.744*
.035
判别变量和标准化典型判别式函数之间的汇聚组间相关性按函数内相关的绝对大小排序的变量。
*. 每个变量和任意判别式函数间最大的绝对相关性。
※ 112340.9060.7440.2540.233y x x x x =+++
※ 212340.3000.0350.1420.940y x x x x =-+++
非标准化的典型判别式函数
※ 11230.0020.0040.001 3.827y x x x =++-
※ 21230.0010.0140.0010.664y x x x =-++-
Fisher 的线性判别式函数
※ 112340.0080.0360.0050.0211.034y x x x x =++-- ※ 21240.0030.0110.002 1.921y x x x =+--
※ 312340.0170.0310.0090.00333.332y x x x x =++--
根据判别函数,就可以对原各组样品以及待判样品进行回判和判别。
.
区域图
典则判别
函数 2
-8.0 -6.0 -4.0 -2.0 .0 2.0 4.0 6.0 8.0 +---------+---------+---------+---------+---------+---------+---------+---------+ 8.0 + 21 13 +
| 21 13 | | 21 13 |
| 21 13 | | 21 13 | 6.0 + + + 21 + + + + 13 + +
| 21 13 | | 21 13 | | 21 13 | | 21 13 | | 21 13 | 4.0 + + + 21+ + + 13 + +
| 21 13 | | 21 13 | | 21 13 | | 21 13 | | 21 13 | 2.0 + + + +21 + + 13 + + +
| 21 13 | | 21 13 | | 21 13 | | 21 * 13 | | 21 13 |
.0 + + + + 21 + + 13 + + + | * 21 13 | | 21 13 * | | 21 13 | | 21 13 | | 21 13 |
-2.0 + + + + 21+ 13+ + + + | 21 13 | | 21 13 | | 21 13 | | 21 13 | | 21 13 |
-4.0 + + + + +21 13 + + + + | 2113 | | 2113 | | 23 | | 23 | | 23 |
-6.0 + + + + + 23 + + + + | 23 | | 23 | | 23 | | 23 | | 23 |
+---------+---------+---------+---------+---------+---------+---------+---------+
-8.0 -6.0 -4.0 -2.0 .0 2.0 4.0 6.0 8.0
典则判别函数 1
区域图中使用的符号
符号组标签
---- -- --------------
1 1
2 2
3 3
* 表示一个组质心
单独组图表
如果您需要使用本文档,请点击下载按钮下载!
分析:回代率为百分之百,这与统计资料的结果相符,而待判的3个样品的判别结果表明:河南,湖北属于第3类,宁夏属于第2类。
(注:可编辑下载,若有不当之处,请指正,谢谢!)
授课:XXX。
