实数知识点、典型例题及练习题单元复习(供参考)
实数知识点及典型例题

实数知识点及典型例题一、实数知识点。
(一)实数的分类。
1. 有理数。
- 整数:正整数、0、负整数统称为整数。
例如:5,0,-3。
- 分数:正分数、负分数统称为分数。
分数都可以表示为有限小数或无限循环小数。
例如:(1)/(2)=0.5,(1)/(3)=0.333·s。
- 有理数:整数和分数统称为有理数。
2. 无理数。
- 无理数是无限不循环小数。
例如:√(2),π,0.1010010001·s(每两个1之间依次多一个0)。
3. 实数。
- 有理数和无理数统称为实数。
(二)实数的相关概念。
1. 数轴。
- 规定了原点、正方向和单位长度的直线叫做数轴。
- 实数与数轴上的点是一一对应的关系。
2. 相反数。
- 只有符号不同的两个数叫做互为相反数。
a的相反数是-a,0的相反数是0。
例如:3与-3互为相反数。
- 若a、b互为相反数,则a + b=0。
3. 绝对值。
- 数轴上表示数a的点与原点的距离叫做数a的绝对值,记作| a|。
- 当a≥slant0时,| a|=a;当a < 0时,| a|=-a。
例如:| 5| = 5,| -3|=3。
4. 倒数。
- 乘积为1的两个数互为倒数。
a(a≠0)的倒数是(1)/(a)。
例如:2的倒数是(1)/(2)。
(三)实数的运算。
1. 运算法则。
- 加法法则:同号两数相加,取相同的符号,并把绝对值相加;异号两数相加,绝对值相等时和为0,绝对值不等时,取绝对值较大的数的符号,并用较大的绝对值减去较小的绝对值;一个数同0相加,仍得这个数。
- 减法法则:减去一个数等于加上这个数的相反数。
- 乘法法则:两数相乘,同号得正,异号得负,并把绝对值相乘;任何数同0相乘都得0。
- 除法法则:除以一个数等于乘以这个数的倒数(除数不为0)。
2. 运算律。
- 加法交换律:a + b=b + a。
- 加法结合律:(a + b)+c=a+(b + c)。
- 乘法交换律:ab = ba。
(完整版)实数知识点及例题

实数习题集【知识要点】1.实数分类:2.相反数:互为相反数b a ,0=+b a 4.倒数:互为倒数没有倒数.b a ,0;1=ab 5.平方根,立方根:±.==x ,a x a x 记作的平方根叫做数则数若,2a 若a x ,a x a x 33,==记作的立方根叫做数则数6.数轴的概念与画法.实数与数轴上的点一一对应;利用数形结合的思想及数轴比较实数大小的方法.【课前热身】1、36的平方根是 ;的算术平方根是 ;162、8的立方根是 ;= ;327-3、的相反数是 ;绝对值等于的数是37-34、的倒数的平方是 ,2的立方根的倒数的立方是。
5、的绝对值是 ,的绝对值是 。
211-6、9的平方根的绝对值的相反数是 。
7的相反数是 ,的相反数的绝对值是。
+-8的相反数之和的倒数的平方为 。
--+【典型例题】例1、把下列各数分别填入相应的集合里:2,3.0,10,1010010001.0,125,722,0,1223π---∙- 有理数集合:{ };无理数集合:{ };负实数集合:{ };例2、比较数的大小(1)(2)2332与6756--与例3.化简:实数有理数无理数整数(包括正整数,零,负整数)分数(包括正分数,负整数)正无理数负无理数)0(>a 3.绝对值:=a a0a -)0(=a )0(<a(1)233221-+-+-(2+例4.已知是实数,且有,求的值.b a ,0)2(132=+++-b a b a ,例5 若|2x+1|与互为相反数,则-xy 的平方根的值是多少?x y 481+总结:若几个非负数的和为零,则每个非负数都为零,这个性质在代数式求值中经常被使用.例6.已知为有理数,且,求的平方根b a ,3)323(2b a +=-b a +例7. 已知实数x 、y 、z 在数轴上的对应点如图试化简:。
x zx y y z x z x z ---++++-【课堂练习】1.无限小数包括无限循环小数和 ,其中 是有理数, 是无理数.2.如果,则是一个 数,的整数部分是 .102=x x x 3.的平方根是 ,立方根是 .644.的相反数是 ,绝对值是 .51-5.若 .==x x 则66.当时,有意义;_______x 32-x 7.当时,有意义;_______x x -118.若一个正数的平方根是和,则,这个正数是 ;12-a 2+-a ____=a 9.当时,化简;10≤≤x __________12=-+x x 10.的位置如图所示,则下列各式中有意义的是( ).b a , A 、B 、C 、D 、b a +b a -ab ab -11.全体小数所在的集合是( ).A 、分数集合B 、有理数集合C 、无理数集合D 、实数集合12.等式成立的条件是( ).1112-=+⋅-x x x A 、B 、C 、D 、1≥x 1-≥x 11≤≤-x 11≥-≤或x 13.若,则等于( ).64611)23(3=-+x x A 、B 、C、D 、214141-49-14.计算:(1) (221--4-(3(4) 24+-+-++81214150232-+-ab15.若,求的值.054=-++-y x x xy16.设a 、b 是有理数,且满足,求的值(21a +=-b a17.若,求的值。
(完整版)实数知识点总结及习题练习,推荐文档

a a a a 2x x 1- x1、平方根实数知识点总结平方根、算数平方根和立方根 (3—10 分)如果一个数的平方等于 a ,那么这个数就叫做 a 的平方根(或二次方跟)。
一个数有两个平方根,他们互为相反数;零的平方根是零;负数没有平方根。
正数 a 的平方根记做“ ± ”。
2、算术平方根正数 a 的正的平方根叫做 a 的算术平方根,记作“ ”。
正数和零的算术平方根都只有一个,零的算术平方根是零。
a ( a ≥ 0)≥ 0= a =3、立方根- a ( a <0);注意 的双重非负性:a ≥ 0如果一个数的立方等于 a ,那么这个数就叫做 a 的立方根(或 a 的三次方根)。
一个正数有一个正的立方根;一个负数有一个负的立方根;零的立方根是零。
注意: 3 - a = -3 a ,这说明三次根号内的负号可以移到根号外面。
实数(平方根)单元习题练习思维启动如图是一块由两个正方形并排放在一起而成的硬纸板,请你用两刀把它裁成四块,然后拼成一个正方形,拼后的正方形边长为多少?综合探究探究一 由平方根和算术平方根的意义确定字母的取值范围 1.中被开方数为,根号下的被开方数必须是 才有意义,因此可列出不等式,x 的取值范围是.2. + 有意义,需要列出不等式组为. x 的取值范围a 2⎩是 .x3.x 的取值范围是 x +1答案:1. 2x ,非负数, 2x ≥ 0 , x ≥ 0 .⎧1- x ≥ 0,2. ⎨x ≥ 0. 3. x > -1 .0 ≤ x ≤ 1. 探究二 根据非负数性质求未知数的值已知 x 、 y 3(y - 2)2= 0 .1 3(y - 2)2+ 3(y - 2)2= 0 ,你能得到什么结论?.2.由 1,你能求出 x - y 的值吗?.答案:1.∵3(y - 2)2= 0 .≥ 0 , 3(y - 2)2≥ 0 , 3(y - 2)2= 0 = 0 ,2.由 1 得, x -1 = 0 , x = 1 ; y - 2 = 0 , y = 2 .∴ x - y = 1- 2 = -1. 探究三 平方根与简单的一元二次方程 1.由 x 2 -196 = 0 可得 , 2.据 1 得, x 是 196 的,所以 x =.3.由 1,2 的启示,请你试着求等式16 (x + 2)2- 81 = 0 中的 x 值..答案:1. x 2 = 196 . 2.平方根, x = ±14 .2 2 81 9 1 173.由16 (x + 2)-81 = 0 ,得(x + 2)=,∴ x + 2 =±16 4,∴x =或-.4 4探究四由平方根的意义确定字母的值3a - 22 和2a - 3 都是m 的平方根,求a 和m 的值.1.当3a - 22 与2a - 3 相等时,求a 和m 的值..2.当3a - 22 与2a - 3 互为相反数时,求a 和m 的值..3.讨论总结:m 的值为.答案:1.3a - 22 = 2a - 3 ,得a = 19 ,3a - 22 = 3⨯19 - 22 = 35 ,2a - 3 = 35 ,m = 352 = 1225 .2.3a - 22 + 2a - 3 = 0 ,得a = 5 ,3a - 22 = 3⨯ 5 - 22 =-7 ,2a-3=2⨯5-3=7,m=(-7)2= 72= 49 .3.m 的值为 1225 或49.探究五利用被开方数非负性求未知数的值已知x 、y 都是有理数,且y =+ 3 ,求y x+1 的平方根.1.表示x - 3 的,则x 的范围是.2.表示x - 3 的,则x 的范围是. 3.由1,2,得x =,y =. 4.讨论总结:y x+1 的平方根是多少?.答案:1.算术平方根,x ≥ 3 .2.算术平方根,x ≤3.3.x = 3 ,y = 3 .4.∵ y x+1 = 34 = 81,∴ y x+1 的平方根为±9 .探究六算术平方根与绝对值相综合题已知2009 -a +=aa - 2010 a - 2010 a - 20092 +15 a - 20092 +15 a - 2010 a - 2010 1. 由式子可以得出 a 的取值范围是什么?.2. 由 1,你能将等式 2009 - a + = a 中的绝对值去掉吗?.3. 由 2,你能求出 a - 20092 的值吗?.4. 讨论总结:求的值..答案:1.∵ a - 2010 ≥ 0 ,∴ a ≥ 2010 .2.原式变形为 a - 2009 + = a = 2009 .3. a - 2010 = 20092 , a - 20092 = 2010 .4. a - 20092 +15 = 2010 +15 = 2025 ,∴ = 45 . 探究七 平方根的实际应用一个开口的长方体盒子,是从一块正方形的马口铁的每个角剪掉一个 36cm 2的正方形后,再把它的边折起来做成的,如图,量得这个盒子的容积是 150cm 2,求原正方形的边长是多少?1. 由题意可知剪掉正方形的边长为cm .2. 设原正方形的边长为 x cm ,请你用x 表示盒子的容积..3. 由 1,2 的分析,请你列出方程,并解答,求原正方形的边长..答案:1.6.2. 6 (x - 6)2.3. 6 (x - 6)2= 150 , (x - 6)2= 25 , x - 6 = ±5 .∴ x = 11 或 x = 1 (舍去).即原25 121 25 121x 2 4 - y 29 - a 29 - a x - 4 a + b a +1 5正方形的边长为 11cm .随堂反馈251.的平方根的数学表达式是( )121A . = ±B .11= - 5 C . 11=5D . ± = ± 511112.9 的算术平方根是( )A . -3B .3C . ±3D .813. 当 x = -5 时,的值是()A .5B . -5C . ±5D .254. 正方形 M 的面积是正方形 N 的面积的 64 倍,那么正方形 M 的边长是正方形 N 的边长的( )A .4 倍B .8 倍C .16 倍D .2 倍5.一个数的算术平方根是它的本身,则这个数是. 6.= - ,则 xy 的算术平方根为.7. 代数式-5的最大值为.8. 已知 a , b+ b - 3a -1 = 0 ,求b 2 - 5a 的平方根.9. 如果 a的最大值及此时 a 的值.10. 已知2a -1 的平方根为±3 , 3a + b -1的平方根为±4 ,求 a + 2b 的平方根.参考答案25 121 25 121a +1 a +1 29 - a 7 79 352(-4)229 - a 9 9 (- 2)2⎩ ⎩1.D 2.B 3.A 4.B 5.0,1 6.4 7. -58.∵ ≥ 0 , b - 3a -1 ≥ 0 ,+ b - 3a -1 = 0 ,∴ 29 - a ≤ 29 , ≤ 5 .因此 的最大值为 5,此时 a 的值为 4.⎧2a -1 = 9,∴ = 0 , a = -1 ;b - 3a -1 = 0 , b - 3a -1 = 0 ,10.由题意,得⎨3a + b -1 = ⎧a = 5,⎨b = 2. 解得16. ∴ b = -2 .∴ b 2 - 5a = 9 , b 2 - 5a 的平方根为±3 . 9.∵ a 为正数,∴ a + 2b = 9 , a + 2b 的平方根为± 3.平方根跟踪练习(一)一、选择题1. 下列各式中无意义的是()A. - B . C. 12. 的算术平方根是()D . -41 111 A.B .C .16823. 下列运算正确的是()D . ±2A . -3 = 3B . -3 = -3C . = ±D . = -3二、填空题4. 若一个正方形的面积为 13,则正方形的边长为.5. 小明房间的面积为 10.8 米 2,房间地面恰好由 120 块相同的正方形地砖铺成,每块地砖的边长是.6. 计算:⑴=;⑵ =;⑶ =;⑷- =;⑸ ( 3)2 = .7. 若下列各式有意义,在后面的横线上写出 x 的取值范围:a +1 - 7(- 7)2x2 4 25 4 25 0.9 b -3 24 25 4 25 179⑴ ⑵8.若 a - 2 + = 0 ,则a 2 -b = .9. 一个正方形的面积扩大为原来的 4 倍,它的边长变为原来的倍,面积扩大为原来的 9 倍,它的边长变为原来的倍,面积扩大为原来的 n 倍,它的边长变为原来的倍.10.的算数平方根是它本身.三、解答题11. 求下列各数的算术平方根:⑴169⑵0.0256⑶124 25⑷ (- 2)212. 要种一块面积为 615.44 m 2 的圆形草地以美化家庭,它的半径应是多少米?(π 取3.14)平方根跟踪练习(二)一、选择题1. 下列说法中不正确的是()A. - 是 2 的平方根B. 是 2 的平方根C.2 的平方根是 12.的平方根是() D.2 的算术平方根是 41 111A.B.C.16 8 2423. “ 的平方根是± ”,用数学式子可以表示为()D. ±225A.= ± 55B. ±= ± 2C. = 25 5D. - = - 2 54. 下列各式中,正确的个数是()= ±42① = 0.3 ; ② ③ - 3 3 ;的平方根是-3; 5 - x222(- 5)216 (-9)21- a a -1 0.0004(- 0.1)20.81 0.04225713④ 的算术平方根是-5; ⑤ ± 是1 的平方根.6 36A.1 个B.2 个C.3 个D.4 个5.若 a 是(- 4)2的平方根,b 的一个平方根是 2,则代数式 a +b 的值为()A.8B.0C.8 或 0D.4 或-4 二、填空题6. 如果某数的一个平方根是-6,那么这个数为.7. 如果正数m 的平方根为 x + 1和x - 3 ,则m 的值是. 8.的算术平方根是, 的平方根是.9. 若b =+ + 4 ,则ab 的平方根是.三、解答题10. 求下列各式的值:⑴ ⑵ - ⑶ ±⑷ - ⑸ - ⑹一、选择题 1.C . 2.C .3.A . 二、填空题4.5.0.96.3;5;2;-4;3跟踪练习一答案7.x≥0;x≤58.19.2;3;10.0 和 1 三、解答题711.13;0.16; ;2512.14跟踪练习二答案12 1 4412 - 40213n一、选择题1.C2.D3.B4.A5.C二、填空题6.367.48.23 或-39.2 或-2三、解答题7 10.⑴15⑵-0.02⑶2⑷-0.1⑸0.7⑹9“”“”At the end, Xiao Bian gives you a passage. Minand once said, "people who learn to learn are very happy people.". In every wonderful life, learning is an eternal theme. As a professional clerical and teaching position, I understand the importance of continuous learning, "life is diligent, nothing can be gained", only continuous learning can achieve better self. Only by constantly learning and mastering the latest relevant knowledge, can employees from all walks of life keep up with the pace of enterprise development and innovate to meet the needs of the market. This document is also edited by my studio professionals, there may be errors in the document, if there are errors, please correct, thank you!。
初二(下)实数的知识点与练习题

第十三章 实数知识要点一: 1.实数的性质(1)实数范围内仍然适用在有理数范围内定义的一些概念(如倒数,相反数);(2)两实数的大小关系:正数大于0,0大于负数;两个正实数,绝对值大的实数大;两个负实数,绝对值大的实数反而小;(3)在实数范围内,加、减、乘、除(除数不为零)、乘方五种运算是畅通无阻的,但是开方运算要注意,正实数和零总能进行开方运算,而负实数只能开奇次方,不能开偶次方;(4)有理数范围内的运算律和运算顺序在实数范围内仍然相同. 2.实数与数轴的关系每一个实数都可以用数轴上的一个点表示;反之,数轴上每一个点都表示一个实数,即数轴上的点与实数是一一对应关系.3.实数的分类(1)按实数的定义分类:⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧⎭⎬⎫⎩⎨⎧⎪⎪⎪⎩⎪⎪⎪⎨⎧⎭⎬⎫⎩⎨⎧⎪⎩⎪⎨⎧无限不循环小数负无理数正无理数无理数数有限小数或无限循环小负分数正分数分数负整数零正整数整数有理数实数 (2)按实数的正负分类:⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧⎩⎨⎧负无理数负分数负整数负有理数负实数负数)零(既不是正数也不是正无理数正分数正整数正有理数正实数实数4.实数的大小比较两实数的大小关系如下:正实数都大于0,负实数都小于0,正数大于一切负数;两个正实数,绝对值大的实数较大;两个负实数,绝对值大的实数反而小.实数和数轴上的点一一对应,在数轴上表示的两个实数,右边的数总大于左边的数.【典型例题】2-1C B A 例1若a 为实数,下列代数式中,一定是负数的是( ) A. -a 2 B. -( a +1)2 C.-2a D.-(a -+1)分析:本题主要考查负数和非负数的概念,同时涉及考查字母表示数这个知识点.由于a 为实数, a 2、( a +1)2、2a 均为非负数,∴-a 2≤0,-( a +1)2≤0,-2a ≤0.而0既不是正数也不是负数,是介于正数与负数之间的中性数.因此,A 、B 、C 不一定是负数.又依据绝对值的概念及性质知-(a -+1)﹤0.故选D例2 实数a 在数轴上的位置如图所示, 化简:2)2(1-+-a a =分析:这里考查了数形结合的数学思想,要去掉绝对值符号,必须清楚绝对值符号内的数是正还是负.由数轴可知:1﹤a ﹤2,于是,22)2(,112a a a a a -=-=--=-所以, 2)2(1-+-a a =a -1+2-a =1.例3 如图所示,数轴上A 、B 两点分别表示实数1,5,点B 关于点A 的对称点为C ,则点C 所表示的实数为( ) A. 5-2 B. 2-5 C.5-3 D.3-5分析:这道题也考查了数形结合的数学思想,同时又考查了对称的性质.B 、C 两点关于点A 对称,因而B 、C 两点到点A 的距离是相同的,点B 到点A 的距离是5-1,所以点C 到点A 的距离也是5-1,设点C 到点O 的距离为a ,所以a +1=5-1,即a =5-2.又因为点C 所表示的实数为负数,所以点C 所表示的实数为2-5.例4 已知a 、b 是有理数,且满足(a -2)2+3-b =0,则a b 的值为分析:因为(a -2)2+3-b =0,所以a -2=0,b -3=0。
实数知识点总结及习题练习

实数知识点总结平方根、算数平方根和立方根(3— 10 分)1、平方根假如一个数的平方等于a,那么这个数就叫做 a 的平方根(或二次方跟)。
一个数有两个平方根,他们互为相反数;零的平方根是零;负数没有平方根。
正数 a 的平方根记做“ a ”。
2、算术平方根正数 a 的正的平方根叫做 a 的算术平方根,记作“ a ”。
正数和零的算术平方根都只有一个,零的算术平方根是零。
a ( a0)a0a2a;注意 a 的两重非负性:- a(a <0)a03、立方根假如一个数的立方等于a,那么这个数就叫做 a 的立方根(或 a 的三次方根)。
一个正数有一个正的立方根;一个负数有一个负的立方根;零的立方根是零。
注意:3a 3 a,这说明三次根号内的负号能够移到根号外面。
实数(平方根)单元习题练习思想启动如图是一块由两个正方形并排放在一同而成的硬纸板,请你用两刀把它裁成四块,而后拼成一个正方形,拼后的正方形边长为多少?综合研究研究一由平方根和算术平方根的意义确立字母的取值范围1.2x中被开方数为___________ ,根号下的被开方数一定是_____________ 才存心义,所以可列出不等式______________,x的取值范围是______________.2.要使 1 x x 存心义,需要列出不等式组为________________ .x 的取值范围是______________ .3.若x 存心义,则 x 的取值范围是 ______________ .x1答案: 1. 2x ,非负数, 2x 0 , x 0 .1 x 0,1.2.0 xx 0.3. x 1 .研究二依据非负数性质求未知数的值已知 x 、 y 为实数,且x 1 3 y220 .1.因为x 1 , 3 y 2 22都是非负数,联合已知x 1 3 y 2 0 ,你能获得什么结论?_________________________________________________________________________ .2.由 1,你能求出 x y 的值吗?_________________________________________________________________________ .答案: 1 .∵x1 0 , 320 , x 1 3 y 22x 1 0 ,y 20 ,∴20 .3 y 2.由 1 得,x 1 0 ,x 1; y 2 0 , y 2 .∴ x y 1 2 1.2研究三 平方根与简单的一元二次方程1.由 x 2196 0 可得 _______________ ,2.据 1 得, x 是 196 的 _______________,所以 x______________ .281 0 中的 x 值.3.由 1, 2 的启迪,请你试着求等式 16 x 2_________________________________________________________________________________________________________________________________________________________ .答案: 1. x 2 196 .2.平方根, x 14 .3.由 16 x 22281 9 1 17 81 0 ,得 x2,∴ x 2,∴ x或.16444研究四 由平方根的意义确立字母的值3a 22 和 2a 3都是m的平方根,求a和m的值.1.当3a 22与 2a 3 相等时,求a和m的值.______________________________________________________________________ .2.当3a22 与 2a 3 互为相反数时,求 a 和 m 的值._____________________________________________________________________ .3.议论总结:m 的值为____________.答案: 1 .3a22 2a 3 ,得 a 19 , 3a 22 3 19 22 35 , 2a 335 ,m 3521225 .2.3a 22 2a 3 0,得a 5 ,3a 22 3 5 227, 2a 32537,249 .m7723.m的值为 1225 或 49.研究五利用被开方数非负性求未知数的值已知 x 、y都是有理数,且 yx3 3 x 3 ,求 y x 1的平方根.1.x 3 表示x 3 的_________________,则x的范围是______________.2.3x 表示x 3 的_________________,则x的范围是______________..由,,得 x______________,y_______________.3124.议论总结:y x 1的平方根是多少?_________________________________________________________________ .答案: 1.算术平方根,x 3 .2.算术平方根,x 3..x 3, y3.34.∵y x 13481,∴ y x 1的平方根为9.研究六算术平方根与绝对值相综合题已知 2009a a2010 a ,求 a 20092 15 的值.1.由式子a2010能够得出 a 的取值范围是什么?________________________________________________________________________ .2.由 1,你能将等式2009 a a 2010 a 中的绝对值去掉吗?_______________________________________________________________________ .3.由 2,你能求出a20092的值吗?_______________________________________________________________________ .4.议论总结:求 a 2009215 的值._______________________________________________________________________ .答案: 1.∵a2010 0,∴a 2010 .2.原式变形为a 2009a2010 a ,即 a 20102009 .3.a201020092, a200922010 .4.a2009215 2010152025 ,∴a2009215 45.研究七平方根的实质应用一个张口的长方体盒子,是从一块正方形的马口铁的每个角剪掉一个36cm2的正方形后,再把它的边折起来做成的,如图,量得这个盒子的容积是150cm2,求原正方形的边长是多少?1.由题意可知剪掉正方形的边长为______________cm.2.设原正方形的边长为x cm,请你用 x表示盒子的容积.________________________________ .3.由 1, 2 的剖析,请你列出方程,并解答,求原正方形的边长._________________________________________________________________________ .答案: 1. 6.22.6 x6.225.∴ x 11或 x 1 (舍去).即原正3.6 x 6150 , x 625 , x 6方形的边长为11cm.随堂反应1.25的平方根的数学表达式是( )121A .25 5 25 5 25 512111B .11C .11121121 2. 9 的算术平方根是( )A . 3B . 3C . 33.当 x 5 时, x 2 的值是()A . 5B . 5C . 525 5 D .12111D . 81D . 254.正方形 M 的面积是正方形 N 的面积的 64 倍,那么正方形 M 的边长是正方形 N 的边长的()A .4 倍B .8 倍C .16 倍D .2 倍5.一个数的算术平方根是它的自己,则这个数是 ______________.6.若x 44 y ,则 xy 的算术平方根为 ______________ .7.代数式5a b 的最大值为 ______________ .8.已知 a , b 知足a 1b 3a 1 0 ,求 b 2 5a 的平方根.9.假如 a 为正数, 29 a 为整数,求 29 a 的最大值及此时 a 的值.10.已知 2a 1 的平方根为 3 , 3a b 1的平方根为 4 ,求 a 2b 的平方根.参照答案1.D 2 .B 3 .A 4 .B 5 .0,1 6 .4 7 . 58 . ∵ a10 ,b 3a 10 ,a 1b 3a 10 ,为4.∴ a 1 0,a 1 ;b 3a 10 ,10.由题意,得2a19,3a b解得1 16.b 3a 10 ,a 5,∴ b 2 .∴b25a 9 , b25a 的 b 2.平方根为3.∴ a 2b 9, a2b 的平方根为3.9.∵a为正数,∴ 29a29,29 a 5 .所以29 a 的最大值为5,此时a的值平方根追踪练习(一)一、选择题1.以下各式中无心义的是()A.7B.7 C.7D.722.1的算术平方根是()4A.1B.1C.1D.1 168223.以下运算正确的选项是()A. 3 3B.33C.93D.93二、填空题4.若一个正方形的面积为 13,则正方形的边长为 ___________.5.小明房间的面积为 10.8 米2,房间地面恰巧由120 块同样的正方形地砖铺成,每块地砖的边长是 _________.6.计算:⑴9 =_________;⑵52___________; ⑶22________;23)2.⑷- 4 =_______;⑸(_______7.若以下各式存心义,在后边的横线上写出 x 的取值范围:⑴x________⑵5x_______8.若a 2 b 3 0 ,则a2b_________.9.一个正方形的面积扩大为本来的 4 倍,它的边长变成本来的倍, 面积扩大为本来的 9 倍,它的边长变成本来的倍,面积扩大为本来的 n 倍,它的边长变成本来的_______倍 .10._______ 的算数平方根是它自己 . 三、解答题11.求以下各数的算术平方根 :⑴ 169⑵ 0.0256⑶124⑷ 2 22512. 要种一块面积为 615.44 m 2 的圆形草地以美化家庭, 它的半径应是多少米?(π取 3.14 )平方根追踪练习(二)一、选择题1.以下说法中不正确的选项是()A.2是 2的平方根B.2是 2的平方根C.2 的平方根是 2D.2 的算术平方根是22. 1的平方根是()4A.1B.1C.1D.1 168223.“ 4 的平方根是2”,用数学式子能够表示为()2554 2 4 2 4 2 D.4 2A.5B.5C.52552525254.以下各式中,正确的个数是()①0.9 0.3 ; ② 174 ③32 的平方根是- 3;93 ;④52的算术平方根是- 5; ⑤ 7 是113的平方根 .6 36A.1 个B.2 个C.3 个D.4 个 5. 若 a 是4 2 的平方根, b 的一个平方根是2,则代数式 a + b 的值为()A.8B.0C.8或 0D.4或- 4二、填空题6. 假如某数的一个平方根是 -6 ,那么这个数为 ________.7. 假如正数 m 的平方根为 x1和 x 3 ,则 m 的值是.8. 162的平方根是 .的算术平方根是, 9 9.若 b1 aa 14 ,则 a b 的平方根是 .三、解答题10.求以下各式的值 :⑴ 225⑷0.1 2一、选择题 1. C .2. C .3. A .二、填空题4. 135. 0.96. 3; 5; 2;- 4; 3⑵0.0004⑶1214⑸⑹412 402追踪练习一答案7. x ≥ 0; x ≤ 58. 19. 2; 3; n 10.0 和 1 三、解答题11. 13; 0.16 ; 7; 2512. 14追踪练习二答案一、选择题1. C 2. D 3. B 4. A5.C二、填空题6. 36 7. 48.23 或 -3 9.2 或-2三、解答题10.⑴ 15⑵-0.02 ⑶7 2⑷-0.1 ⑸0.7 ⑹9。
(完整版)实数知识点和练习
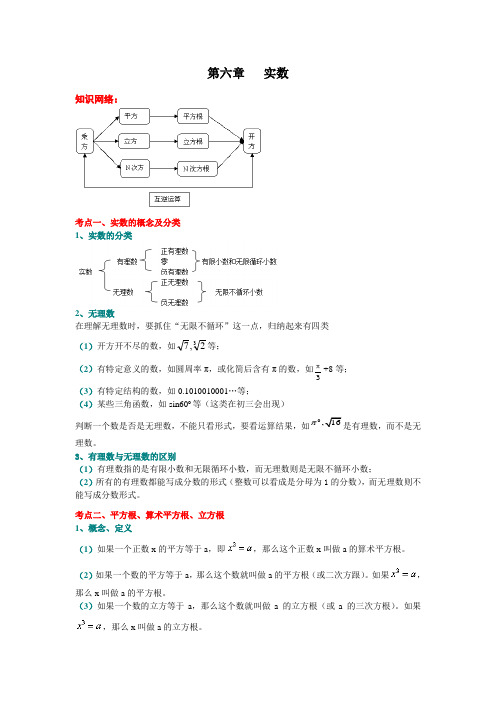
第六章实数知识网络:考点一、实数的概念及分类1、实数的分类2、无理数在理解无理数时,要抓住“无限不循环”这一点,归纳起来有四类,7等;(1)开方开不尽的数,如32π+8等;(2)有特定意义的数,如圆周率π,或化简后含有π的数,如3(3)有特定结构的数,如0.1010010001…等;(4)某些三角函数,如sin60o等(这类在初三会出现)是有理数,而不是无判断一个数是否是无理数,不能只看形式,要看运算结果,如0,16理数。
3、有理数与无理数的区别(1)有理数指的是有限小数和无限循环小数,而无理数则是无限不循环小数;(2)所有的有理数都能写成分数的形式(整数可以看成是分母为1的分数),而无理数则不能写成分数形式。
考点二、平方根、算术平方根、立方根1、概念、定义(1)如果一个正数x的平方等于a,即,那么这个正数x叫做a的算术平方根。
(2)如果一个数的平方等于a,那么这个数就叫做a的平方根(或二次方跟)。
如果,那么x叫做a的平方根。
(3)如果一个数的立方等于a,那么这个数就叫做a 的立方根(或a 的三次方根)。
如果,那么x叫做a的立方根。
2、运算名称(1)求一个正数a 的平方根的运算,叫做开平方。
平方与开平方互为逆运算。
(2)求一个数的立方根的运算,叫做开立方。
开立方和立方互为逆运算。
3、运算符号(1)正数a 的算术平方根,记作“a ”。
(2)a(a ≥0)的平方根的符号表达为。
(3)一个数a 的立方根,用表示,其中a 是被开方数,3是根指数。
4、运算公式4、开方规律小结(1)若a ≥0,则a 的平方根是a ±,a 的算术平方根a ;正数的平方根有两个,它们互为相反数,其中正的那个叫它的算术平方根;0的平方根和算术平方根都是0;负数没有平方根。
实数都有立方根,一个数的立方根有且只有一个,并且它的符号与被开方数的符号相同。
正数的立方根是正数,负数的立方根是负数,0的立方根是0。
(2)若a<0,则a 没有平方根和算术平方根;若a 为任意实数,则a 的立方根是。
《第6章实数》知识清单含例题+期末专题复习试卷(含答案).doc

2018年七年级数学下册实数知识清单+经典例题+专题复习试卷1、 定义:如果一个正数X 的平方等于a,即工=。
那么,这正数x 叫做a 的算术平方根。
记作氐 读作“根号屮。
a 叫做被开 算术平方根*方数,规定0的算术平方根还是0o2、 性质:双重非员性(a h 0,需X 0 )。
负数没有算术平方根。
'3、J 产=\a\ (a是任意数力(7^)2 =a (B 是非员数)。
1、定义:如果一个数X 的平方等于4即乂2 =4。
那么,这个X叫做a 的平方根。
记作土需,读作“正、员根号屮。
a 叫做被幵 方数。
规定0的算术平方根还是0o2、 性质:(1)正数有两个平方根,它们互为相反数。
(2) 0的平方根是0。
员数没有平方根。
3、 未知数次数是两次的方程,结果一般都有两个值。
72^1.414, 73^1.732,少恐2.236, J7俎26461、走义:如果一个数x 的立方等于匕 即x 3 =a o 那么,这个x 叫做a 的立方根。
记作砺,读作“三次根号护。
a 叫做被开方数。
2、性质:(1)正数的立方根是正数,员数的立方根是员数,0的立方根是0。
(2)1卜a 取任意数(3) (佝=° J分数(有理数和分数是相同的概念)rI 无限循环小数'1、开方开不尽的方根无理数无限不循环小数彳2、圆周率兀以及含有兀、3、具有特定结构的数(0.010010001……)有理数』r 正整数员整数(可以看成分母是1的分数)正实数o员实数有限小数平方根立方根【经典例题1】1、下列说法错误的是()4、若 a 2=4, b 2=9,且 ab<0,B. ±55、 设边长为3的正方形的对角线长为a.下列关于a 的四种说法: ®a 是无理数; ②a 可以用数轴上的一个点來表示;③3<a<4; ④a 是18的算术平方根.其中,所有正确说法的序号是 ( )A.①④B.②③C.①②④D.①③④ 6、 已知实数x 、y 满足心- l+|y+3|=0,则x+y 的值为( ) A. -2B. 2C.4D. -4【经典例题3】7、 一个自然数的算术平方根为a,则和这个自然数相邻的下一个自然数是( )A. a+1B. a 2+lC.寸/+1Va+1f x 二 2f inx+ny=88、 已知■是二元一次方程组{、的解,则加・n 的算术平方根为( )\ y=l[nx - iny^lA. ±2B. V2C. 2D. 49、 有一个数值转换器,原理如下:A. 5是25的算术平方根 C. (-4)2的平方根是一4 2、下列各式中,正确的是()B. 1是1的一个平方根 D. 0的平方根与算术平方根都是0B.-佇二 _ 3C.寸(±3严二 ±3D.佇二 ±33、716的平方根是(A. ±2【经典例题2】B. 2C. — 2D. 16C. 5A. 2B. 8当输入的x=64时,输出的y 等于()【经典例题4】10、平方等于16的数是________ ;立方等于本身的数是_______________________ •11、一个数的立方根是4,这个数的平方根是______________ ,12、若一2x ra_n y2与3x7^是同类项,则m-3n的立方根是_____________ .【经典例题5】13、求x 的值:25(X+1)2=16;14、求y 的值:(2y-3) 2 - 64=0;15、计算:^4-23-|-2|X(-7+5) 16、计算:舗一血+ 乂-3)' -磁-2【经典例题6】17、已知实数a, b在数轴上的位置如图所示,化简:寸(fl) 4-1)并|a・b|. -------- ------- 1---------------- 1 ----- >・ 1^0 b 118、阅读理解7 >^<75 <79* 即2<V5<3» A1<V5-1<2-・••厉_1的整数部分为1,小数部分为厉_2・解决问题:己知a是JI7-3的整数部分,D是的小数部分,求(-a)"+(b + 4)2的平方根.参考答案1、c;2、B3、A4、B5、C6、A7、B8、C9、D10、±4, 0, ±111、&-812、213、x = -0. 2, x=-l. 8;14、y=5. 5 或y= - 2. 5;15、10 ;16、-2;17、解:由数轴上点的位置关系,得-l<a<0<b<l.原式二a+1+2 - 2b - b+a=2a - 3b+3.18、由题意,得幺=1,i = T17-4 所以(一幺尸 + 0+4)2 = (-1尸 + (何_4+4)2 = 16 即+ @ + 4)2的平方根为±牛2018年 七年级数学下册 实数 期末复习试卷一、选择题:1、下列语句中正确的是(C. 9的算术平方根是±3D. 9的算术平方根是3设边长为3的正方形的对角线长为a.下列关于a 的I 川种说法: ①a 是无理数; ②a 可以用数轴上的一个点來表示; @3<a<4;④a 是18的算术平方根.其中,所有正确说法的序号是() A.①④B.②③C.①②④ D.①③④7、负的算术平方根是( )A. ±6B. 6C. ±A /6D. V68、下列各数中,3. 14159,-饭,0.3131131113- (2016春•潮州期末)下列各式表示正确的是9、己知实数x 、y 满足Jx=l+1 y+31二0,则x+y 的值为()10、若正数a 的算术平方根比它本身大,则( )A.・9的平方根是・3B. 9的平方根是3 2、下列结论正确的是(A- -{(-6)2二-6 B.(~{5)2二9 C. 7(~16) 2=± 16 D.-(2,16 ^25A- 4、 下列关于祈的说法中,错误的是( 灵是8的算术平方根 B. 2<品<3 下列各组数中互为相反数的一组是()C. 78= ±2^2D.灵是无理数A. ■⑵与寻PB.・4与・{(-4)2C.D. P 与法5^如果际〒二2. 872, ^3700 =28.72,则勺0・023厂(A. 0. 2872B. 28. 72C. 2. 872D. 0.02872 6、 B. ±725=5A. - 2B. 2C. 4( )lk •估计— 1在()A. 0〜1之间•B. 1〜2之间C. 2〜3之间D. 3〜4之间12、实数纸b在数轴上对应点的位置如图,则|a-b| -肯的结果是()•••Aa b0A. 2a - bB. b - 2aC. bD. - b二、填空题:13、(-9)2的算术平方根是_.14、如图,在数轴上点A和点B之间的整数是_________ .15^ 己知(x - 1) 2二3,则x= _ .16、如杲丽二1.732, A/30 =5.477,那么0. 0003的平方根是________ .17、若3、b互为相反数,c、d互为负倒数,则石匸尹+畅= _______________ •18、已知a, b为两个连续的整数,且a<V8<b,则a+b二____________ .三、解答题:19、求x 的值:9(3x - 2尸二64. 20、求x 的值:(5- 3x?=—4921、计算:7132-12222、计算:(亦尸+旷爾一加2一炉.23、已知x・1的平方根为±2, 3x+y・1的平方根为±4,求3x+5y的算术平方根.24、已知2a-l的平方根是±3, 3a+b_9的立方根是2, c是妬的整数部分,求a + 2D+f的值•25、阅读下面的文字,解答问题:大家知道迈是无理数,而无理数是无限不循环小数,因此迈的小数部分我们不可能全部写出来,于是小明用屁-1来表示典的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为近的整数部分是1,将这个数减去其整数部分,差就是小数部分.又例如:・・・2'<7<3,即2<听<3,・••听的整数部分为2,小数部分为听・2.请解答:(1)Vio的整数部分是__________ ,小数部分是 _________ .(2)如果衍的小数部分为a, 荷的整数部分为b,求a+br/^的值;(3)己知:x是3+^5的整数部分,y是其小数部分,请直接写出X- y的值的相反数.26、若实数a, b, c 在数轴上所对应点分别为A, B, C, a 为2的算术平方根,b 二3, C 点是A 点关 于B点的对称点,(1) 求数轴上AB 两点之间的距离; (2) 求c 点对应的数;27、已知字母a 、b 满足亦二+的_21 1 1 1~ab @ + 1)@ + 1)@+2)@ + 2)… @ + 2011)@ + 2001)第X 页共1()页(3) 3的整数部分为x, c 的小数部分为y,求2x^+2》的值(结果保留带根号的形式)的值.1、 D2、 A3、 C4、 C5、 A6、 C7、 D8、 C9、 A 10、 11、 12、 C 13、 9.14、 答案为:2. 15、 答案为:土近+1. 16、 ±0.01732. 17、 -118、 答案为:5.149 19、 开平方得:3 (3x-2)二±8 解得:Xi=—, x 2= - -T .9920、§或兰7 2116 T -10; 23、5 24、a=5, b 二2, c 二7, a + 2&+u 二 16・(2) V4<5<9,・・・2<任<3,即沪旋 ・2, V36<37<49, A6<V37<7,即 b 二6,贝lj a+b ・ 丽二4;(3) 根据题意得:x=5, y=3+{^ - 5二- 2,・;x - y=7 - 其相反数是A /5 - 7.26、(1) 3; (2) 6;72 ⑶尸2—屈.21、参考答案21、22、25、 解: (1) V10的整数部分是3,小数部分是V10- 3;故答案为:3; V10- 3;•解;、「7/o,丑-1~ o且-f 二o'弋鳥解得伫°b十@H"賊斗3化X昭十• • •十莎丽莎和 -丄丄亠」一-2 +A3十3*卩十・・・十二卜亍+土一土+》* +・・•十二 /_ Zo/27。
八上实数全章节题型分类知识点+例题+练习分类全面

三.开平方开平方的概念:求一个非负数的平方根的运算,叫做开平方.开平方与平方是互逆运算,可以通过平方运算来求一个数的平方根或算术平方根,以及检验一个数是不是另一个数的平方根或算术平方根.开平方运算的性质:1.当被开方数扩大(或缩小)二倍,它的算术平方根相应地扩大(或缩小)n倍(「:).2.平方根和算术平方根与被开方数之间的关系:(1)若二丁,则,'=-;;好叫.吟。
)(2)不管.;为何值,总有一八,;注意二者之间的区别及联系.题模一平方根例 1.1.1、士3 是 9 的()A、平方根B、相反数C、绝对值D、算术平方根例1.1.2、仪的平方根是()A、2B、±2C、22D、土 <2例1.1.3、若2a-1和a-5是一个正数m的两个平方根,则a=, m=.练习:1.的平方根为()C、二三D、二述2.若二二二,:=、户,则()A 、8 C 、8 或-2 3.4耳的平方根为()C 、二二例1.2.5、若也工T 有意义,则x 的取值范围是练习:1 . J8T 的算术平方根是B 、二三 D 、2 或-B 、2D 、二尤4.已知一个正数的平方根是3x-2和5x+6, 题模二算术平方根例1.2.1、4的算术平方根是( )A 、2 C 、±2例1.2.2、29的算术平方根是 例1.2.3、下列说法正确的是( )A 、4的算术平方根是2 C 、V 同的平方根是2例1.2.4、一个自然数的算术平方根为a , A 、a+1则这个数是. B 、-2 D 、五B 、0和1的相反数都是它本身D -—、-是分数则和这个自然数相邻的下一个自然数是( )B 、a 2+1 D 、知识点二:立方根知识精讲一•立方根立方根的定义及表示方法:如果一个数的立方等于「那么这个数叫做•;的立方根;若;:=•、则;就叫做・;的立方根,一个数•、的立方根可用符号表“石”,其中“3”叫做根指数,不能省略.立方根的特点:1.任意一个数都有立方根;2.正数立方根是正值;3.负数的立方根是负值;4.0的立方根是0二.开立方开立方的概念:求一个数的立方根的运算.开立方与立方是互逆运算,可以通过立方运算来求一个数的立方根,以及检验一个数是不是另一个数的立方根.开立方运算的性质:1.当被开方数(大于0)扩大(或缩小)::倍,它的立方根相应地扩大(或缩小):倍.易错点:1.平方根“F”其实省略了根指数“二”,即:H也可以表示为F,而立方根“盗” 的根指数“3”不能省略.2.立方根等于本身的数有“二[”和“0” .3.两个数互为相反数,则它们的立方根也互为相反数.题模一立方根例2.1.1、27的立方根是.q -例2.1.2、7的立方根是.64例2.1.3、一五的立方根是. 例2.1.4、9的立方根是. 例2.1.5、下列说法正确的是( )A 、16的算术平方根是-4B 、25的平方根是5C 、1的立方根是二1D 、-27的立方根是-3练习:1 .如果一个实数的平方根与它的立方根相等,则这个数是() A 、0 B 、正整数 C 、0 和 1D 、12 .下列说法正确的是()题模二开立方例2.2.1、求符合下列各条件中的x 的值. x* -1 = 0 -x 1 -1 = 0(1) -(2)-例2.2.2、已知343的立方根是7,那么343000的立方根是A 、如果一个数的立方根是这个数的本身,那么 这个数一定是零 B 、 一个数的立方根不是正数就是负数 C 、负数没有立方根D 、一个数的立方根与这个数同号,零的立方根 是零例2.2.3、已知与互为相反数,求.例2.2.4、已知“:是4的算术平方根,丁三是8的立方根,求;「「的平方根练习:1.下列各式中,正确的是()A、二忑=二二C、石一D、-# = 32.正确的个数是()①]”二一"②止〜与③0=二;④==-二A、B、C、D、3.若,则k的取值范围为(A、士B、C、< =-D、二为任意数4.求符合下列各条件中的x的值.(2)「3 —(1) J一一二5.如果,求―的值知识点三:实数知识精讲一.无理数无理数的概念:无理数是无限不循环小数;常见的无理数有:无限不循环小数(例如.), 开方开不尽的数.二.实数的概念及分类:实数的概念:有理数和无理数统称为实数.实数的性质:£1.有理数都可以写成有限小数或循环小数的形式,都可以表示成分数-二的形式;2.任何两个有理数的和、差、积、商还是有理数;3.两个无理数的和、差、积、商不一定是无理数.实数的分类■:正整数-整数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六章《实数》知识点总结及典型例题练习题
一、平方根
1.平方根的含义
如果一个数的平方等于a,那么这个数就叫做a的平方根。
即x2 a,x叫做a的平方根。
2.平方根的性质与表示
⑴表示:正数a的平方根用,a表示,..a叫做正平方根,也称为算术平方根,
、• a叫做a的负平方根。
⑵一个正数有两个平方根:■, a (根指数2省略)
0有一个平方根,为0,记作.0 0,负数没有平方根
⑶平方与开平方互为逆运算
开平方:求一个数a的平方根的运算。
Ja2e
a
刁==
a0\Q a
( a 0)
a a0
⑷Ja的双重非负性:a0 且Ja 0(应用较广)
例:Jx 4 v4x y 得知x 4, y0 \
⑸如果正数的小数点向右或者向左移动两位,它的正的平方根的小数点就相应
地向右或向左移动一位。
区分:4的平方根为_________ 打的平方根为___________ 44______ 4开平方
后,得_______
3.计算ja的方法非完全平方类47=47
精确到某位小数
*若a b 0,则. b
二、立方根和开立方
1.立方根的定义
如果一个数的立方等于a,呢么这个数叫做a的立方根,记作3 a
2.立方根的性质
任何实数都有唯一确定的立方根。
正数的立方根是一个正数。
负数的立方根
是一个负数。
0
的立方根是0 . \
3. 开立方与立方
开立方:求一个数的立方根的运算。
Va a 3 a3a 目—a 3 a (a取任何数)
这说明三次根号内的负号可以移到根号外面。
* 0的平方根和立方根都是0本身。
三、推广:n次方根
1 .如果一个数的n次方(n是大于1的整数)等于a,这个数就叫做a的n次方根。
当n为奇数时,这个数叫做a的奇次方根。
当n为偶数时,这个数叫做a的偶次方根。
2.正数的偶次方根有两个。
n a 0的偶次方根为0。
n 0 0 负数没有偶次方根。
正数的奇次方根为正。
0的奇次方根为0。
负数的奇次方根为负。
___ 1 2
例1 .已知实数a、b、c 满足,2|a-1|+ J2b+(c —) =0,,求a+b+c 的值.
2
6. -5的相反数是,绝对值是,倒数是
例2.若y .x 1 .. 1 x 1,求x, y 的值。
例3.若3 2a 1和31 3b互为相反数,求-的值。
b
跟踪练习:
1. y -.2 X x 2 x25,求y x的平方根和算术平方根。
3.若 ' x 1 I y 2 I 0,求x+y 的值。
实战演练:一、填空
2
1 •如果X 16,那么X ------------------ ;9.
0.0144
32;0
10.比较大小:
2
12 .若9x4,则x=
14.如果x 4 (y 6)
,若
(x
0,那么
3.14 n,
1)3 64
,则x=
15 .若a、
b
互为相反数,c、
d
互为倒数,则
5)2的平方根是_________
选择题
1.与数轴上的点---- 对应的是(
21
.
A.实数
B. 正数
C. 有理数
D. 整数
2 . 144的平方根是_______ , 64的立方根是_________ ;
5•要切一面积为16平方米的正方形钢板,它的边长是 ___________________ 米; 2
.
A.
C
.
3.
A.
F列说法正确的是().
(-5 )是52的算术平方根
2是-4的算术平方根
16的平方根是
.64的立方根是如果•. x 1有意义,则x可以取的最小整数为().
4 •若X 1 y 2 z 0 则x+2y+z= (
A. 6
5 一组数1,3.14, , .27 ,
3 2 尿 2 J2 V 343 13丄这几个数中,无理数,,,246
的个数是( )A. 2 B. 3 C. 4 D. 5
7•—个自然数的算术平方根是x,把么下一个与他它相邻的自然数的算术平方根是)A. x2 B. X 1 C. X 1 D. . X2 1
8.若一个数的平方根是则这个数的立方根是(
A. 2
B.
C. 2
D. 4
四、实数
1. 实数:有理数和无理数统称为实数
实数的分类:
①按属性分类:
打I fEKft
②按符号分类
分敛IE分散
Tift
+埠萨•.卜.7点
I負无鳏负工农.V无戰
2. 实数和数轴上的点的对应关系:
实数和数轴上的点 --- 对应,即每一个实数都可以用数轴上的一个点表示.
数轴上的每一个点都可以表示一个实数.
在数轴上表示无理数通常有两种情况:
思考:
(1)- a2一定是负数吗?一a 一定是正数吗?
(2)大家都知道.广是一个无理数,那么—1在哪两个整数之间?
(3)-. 15 的整数部分为a,小数部分为b,贝U a= _______________ , b= ____________
(4)判断下面的语句对不对?并说明判断的理由。
①无限小数都是无理数;
②无理数都是无限小数;
③带根号的数都是无理数;
④有理数都是实数,实数不都是有理数;
⑤实数都是无理数,无理数都是实数;
⑥实数的绝对值都是非负实数;
⑦有理数都可以表示成分数的形式。
3.实数大小比较的方法
一、平方法:比较—和•、3的大小
2 /
二、移动因式法:比较2 3和3 2的大小
■ 2的画法:画边长为1的正方形的对角线V5 1
三、求差法:比较------- 和1的大小
2
练习:
、比较下列各组数的大小:
②.15和34
5 1.当x= 时,3 5x 2有意义;
2.若x416,则x=;若3n81,则n=
.7 和—2.45练习: 平方根
1.36 的平方根是
2.平方数是它本身的数是
3.当x= 时,
4.下列各式中,正确的是(
(A) ( 2)2 2(B)(
10.若1 v x v 3,
练习:立方根
16的算术平方根是3)2
化简■■ x 3 2
);平方数是它的相反数的数是
(1有意义;
4.若n为正整数,则
A.-1
B. 1
5.求x的值:(2x
3
6. (1)
9 (C) 39 3 (D) (2) 31 0.973
3.若vx 2,贝y x=若364
2n -11等于(
C.
1)3 8
3-------
7 .
—1
8
D.2n+1
⑵ 4.49
1
、土一
2
316
⑶
3 8
;(10)22 12
(3) 3-343 . 0.25?3( 6)。
