电磁场与电磁波课后习题解答(第五章)
电磁场与电磁波基础教程--符果行版(第2版)习题解答

《电磁场与电磁波基础教程》(第2版)(符果行编著)习题解答第1章1.1 解:(1)==A B=C(2))))23452A x y zB y zC x z ==+-=-+=-,,;A a a a a a a a a a a A(3)()()+2431223x y z x y z =+-+-+=--=+;A B a a a a a a A B (4)()()23411x y z y z ⋅=+-⋅-+=-;A B a a a a a (5)()()234104x y z y z x y z ⨯=+-⨯-+=---;A B a a a a a a a a (6)()()()1045242x y z x z ⨯⋅=-++⋅-=-;A B C a a a a a(7)()()()x 104522405x y z x z y z ⨯⨯=-++⨯-=-+A B C a a a a a a a a 。
1.2解:cos 68.56θθ⋅===︒;A B A BA 在B 上的投影cos 1.37B A θ===A ;B 在A 上的投影cos 3.21A B θ===B 。
1.3 解:()()()()()()()4264280⋅=-++-=正交A B 。
1.4 解:1110x x y y z z x y y z z y ⋅=⋅=⋅=⋅=⋅=⋅=,,;;a a a a a a a a a a a a 0x x y y z z ⨯=⨯=⨯=;a a a a a a x y z y z x z x y ⨯=⨯=⨯=;,a a a a a a a a a 。
1.5 解:(1)111000z z z z ρρϕϕρϕϕρ⋅=⋅=⋅=⋅=⋅=⋅=,,;,,a a a a a a a a a a a a ;000z z z z z ρρϕϕρϕϕρρϕ⨯=⨯=⨯=⨯=⨯=⨯=,,;,,a a a a a a a a a a a a a a a 。
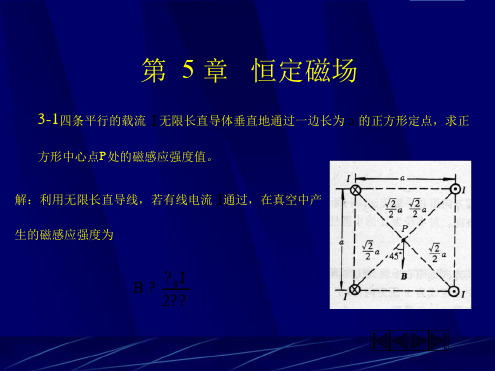
电磁场与电磁波第5版王家礼答案

电磁场与电磁波第5版王家礼答案电磁场与电磁波第5版王家礼答案第一章电磁场和电磁波的基本概念1.1 什么是电磁场?电磁场是描述电荷运动影响的物理场。
它可以被看作是一种对空间的划分,并且在各个空间区域内具有不同的物理状态。
1.2 电磁场的基本方程式是哪些?电磁场的基本方程式包括:麦克斯韦方程组、库仑定律、法拉第电磁感应定律、安培环路定律等。
1.3 什么是电磁波?电磁波是由振动的电荷和振动的磁场所产生的波动现象。
它具有电场和磁场的相互作用,且在真空和各种介质中都能传播。
第二章静电场和静磁场2.1 什么是静电场?静电场是指当电荷分布不随时间变化、不产生磁场时,所产生的电场。
2.2 静电场的基本定律有哪些?静电场的基本定律包括库仑定律、电场线、电势能和电势。
2.3 什么是静磁场?静磁场是指当电荷分布不随时间变化,但产生了磁场时,所产生的磁场。
2.4 静磁场的基本定律有哪些?静磁场的基本定律包括安培环路定律、比奥萨伐尔定律和洛伦兹力定律。
第三章时变电磁场和电磁波的基本概念3.1 什么是时变电磁场?时变电磁场是指电荷分布随时间变化,且产生了磁场时,所产生的电磁场。
3.2 时变电磁场的基本方程式是哪些?时变电磁场的基本方程式是麦克斯韦方程组,包括麦克斯韦-安培定律、麦克斯韦-法拉第定律、法拉第感应定律和电场定律等。
3.3 什么是电磁波?电磁波是由振动的电荷和振动的磁场所产生的波动现象,它具有电场和磁场的相互作用,可以在真空和各种介质中传播。
3.4 电磁波的基本特征有哪些?电磁波的基本特征包括电场和磁场垂直于传播方向、具有可见光、红外线、紫外线、X射线和γ射线等不同频率和能量等。
第四章电磁波在真空和介质中的传播4.1 电磁波如何在真空中传播?电磁波在真空中传播速度等于光速,即299792458m/s。
4.2 介质是如何影响电磁波传播的?介质对电磁波的传播速度、方向和振动方向都有影响,介质内的电磁波速度取决于介质的介电常数和磁导率。
电磁场与电磁波课后习题答案(杨儒贵编着)(第二版)

第五章 恒定磁场重点和难点该章重点及处理方法与静电场类似。
但是磁感应强度的定义需要详细介绍,尤其要强调磁场与运动电荷之间没有能量交换,电流元受到的磁场力垂直于电流的流动方向。
说明磁导率与介电常数不同,磁导率可以小于1,而且大多数媒质的磁导率接近1。
讲解恒定磁场时,应与静电场进行对比。
例如,静电场是无散场,而恒定磁场是无旋场。
在任何边界上电场强度的切向分量是连续的,而磁感应强度的法向分量是连续的。
重要公式磁感应强度定义:根据运动电荷受力: B v F ⨯=q 根据电流元受力: B l F ⨯=d I 根据电流环受力: B m T ⨯=真空中恒定磁场方程: 积分形式: I ⎰=⋅ll B 0d μ⎰=⋅SS B 0d微分形式:J B 0 μ=⨯∇0=⋅∇B已知电流分布求解电场强度:1,A B ⨯∇=V V ''-'=⎰'d )(4)( 0 r r r J r A πμ2,V V ''-'-⨯'=⎰'d )()( 4)(3 0 r r r r r J r B πμ 毕奥─萨伐定律。
3,I ⎰=⋅ll B 0d μ安培环路定律。
面电流产生的矢量磁位及磁感应强度分别为S ''-'=⎰'d )(4)(0r r r J r A S S πμS ''-'-⨯'=⎰'d )()(4)( 30 r r r r r J r B S S πμ 线电流产生的矢量磁位及磁感应强度分别为⎰''-'=l r r l r A d 4)(0I πμ ⎰''-'-⨯'=l r r r r l r B 30 )(d 4)(I πμ矢量磁位满足的微分方程:J A 0 2μ-=∇无源区中标量磁位满足的微分方程: 0 2=∇m ϕ 媒质中恒定磁场方程: 积分形式: I l =⋅⎰l H d⎰=⋅SS B 0d微分形式:J H =⨯∇ 0=⋅∇B磁性能均匀线性各向同性的媒质:场方程积分形式:⎰=⋅lI d μl B⎰=⋅BS H 0d场方程微分形式: J B μ=⨯∇ 0=⋅∇H矢量磁位微分方程:J A 2μ-=∇ 矢量磁位微分方程的解:V V ''-'=⎰'d )(4)(r r r J r A πμ 恒定磁场边界条件:1,t t H H 21=。
电磁场与电磁波5答案

式中, 是长为l的圆柱形电容器的电容。
流过电容器的传导电流为
可见
6.6由麦克斯韦方程组出发,导出点电荷的电场强度公式和泊松方程。
解点电荷q产生的电场满足麦克斯韦方程
和
由 得
据散度定理,上式即为
利用球对称性,得
故得点电荷的电场表示式
由于 ,可取 ,则得
即得泊松方程
5.7试将麦克斯方程的微分形式写成八个标量方程:(1)在直角坐标中;(2)在圆柱坐标中;(3)在球坐标中。
解如题6.12图所示,设第2区为理想导体( )。在分界面上取闭合路径 。对该闭合路径应用麦克斯韦第一方程可得
(1)
因为 为有限值,故上式中
而(1)式中的另一项
为闭合路径所包围的传导电流。取N为闭合路径所围面积的单位矢量(其指向与闭合路径的绕行方向成右手螺旋关系),则有
因
故式(1)可表示为
(2)
应用矢量运算公式 ,式(2)变为
第5章时变电磁场
5.1有一导体滑片在两根平行的轨道上滑动,整个装置位于正弦时变磁场 之中,如题6.1图所示。滑片的位置由 确定,轨道终端接有电阻 ,试求电流i.
解穿过导体回路abcda的磁通为
故感应电流为
5.2一根半径为a的长圆柱形介质棒放入均匀磁场 中与z轴平行。设棒以角速度 绕轴作等速旋转,求介质内的极化强度、体积内和表面上单位长度的极化电荷。
解(1)在直角坐标中
(2)在圆柱坐标中
(3)在球坐标系中
5.8已知在空气中 ,求 和 。
提示:将E代入直角坐标中的波方程,可求得 。
解电场E应满足波动方程
将已知的 代入方程,得
式中
故得
则
由
得
将上式对时间t积分,得
电磁场与电磁波(第三版)课后答案第5章

第五章习题解答5.1真空中直线长电流I 的磁场中有一等边三角形回路,如题 5.1图所示,求三角形回路内的磁通。
解根据安培环路定理,得到长直导线的电流I 产生的磁场2IrB e穿过三角形回路面积的磁通为d SB S32322[d ]d d 2db db zd dI I z z xxxx由题 5.1图可知,()tan63x d zx d ,故得到32d 3db dIx dxx3[ln(1)]223Ib d b d5.2通过电流密度为J 的均匀电流的长圆柱导体中有一平行的圆柱形空腔,如题 5.2图所示。
计算各部分的磁感应强度B ,并证明腔内的磁场是均匀的。
解将空腔中视为同时存在J 和J 的两种电流密度,这样可将原来的电流分布分解为两个均匀的电流分布:一个电流密度为J 、均匀分布在半径为b 的圆柱内,另一个电流密度为J 、均匀分布在半径为a 的圆柱内。
由安培环路定律,分别求出两个均匀分布电流的磁场,然后进行叠加即可得到圆柱内外的磁场。
由安培环路定律d CI B l,可得到电流密度为J 、均匀分布在半径为b 的圆柱内的电流产生的磁场为2222b b bbbbr bbr br J r B J r 电流密度为J 、均匀分布在半径为a 的圆柱内的电流产生的磁场为2222a a aaaar aar ar J r B J r 这里a r 和br 分别是点a o 和b o 到场点P 的位置矢量。
将aB 和bB 叠加,可得到空间各区域的磁场为圆柱外:22222babab a r rBJr r ()br b 圆柱内的空腔外:2022ba aar BJr r (,)b ar b r a 空腔内:22b aBJr r J d()ar a 式中d 是点和b o 到点a o 的位置矢量。
由此可见,空腔内的磁场是均匀的。
5.3下面的矢量函数中哪些可能是磁场?如果是,求其源变量J 。
dbIzx题 5.1 图Sbr ar Jboao ab题5.2图d(1) 0,r ar H e B H(圆柱坐标)(2) 0(),x y ay ax H e e BH(3) 0,x y axay H e e BH(4) 0,ar He BH (球坐标系)解根据恒定磁场的基本性质,满足0B 的矢量函数才可能是磁场的场矢量,否则,不是磁场的场矢量。
电磁场与电磁波(第4版)第5章部分习题参考解答-电磁场与电磁波第五章

5.1 在自由空间中,已知电场3(,)10sin() V/m y E z t e t z ωβ=−G G,试求磁场强度。
(,)H z t G解:以余弦为基准,重新写出已知的电场表示式3π(,)10cos( V/m 2y E z t e t z ωβ=−−G G这是一个沿方向传播的均匀平面波的电场,其初相角为z +90−D 。
与之相伴的磁场为300311π(,)(,)10cos(210πcos() 2.65sin() A/m120π2z z y x x H z t e E z t e e t z e t z e t z ωβηηωβωβ=×=×−−=−−−=−−G G G G G G G5.2 理想介质(参数为0μμ=、r 0εεε=、0σ=)中有一均匀平面波沿x 方向传播,已知其电场瞬时值表达式为9(,)377cos(105) V/m y E x t e t x =−G G试求:(1) 该理想介质的相对介电常数;(2) 与(,)E x t G相伴的磁场;(3) 该平面波的平均功率密度。
(,)H x t G 解:(1) 理想介质中的均匀平面波的电场E G应满足波动方程2220EE tμε∂∇−=∂G G据此即可求出欲使给定的E G满足方程所需的媒质参数。
方程中222929425cos(105)y y y y y E E e E e e t x x∂∇=∇==−−∂G G G G 221892237710cos(105)y y y E E e e t t x∂∂==−×−∂∂G G G x = 故得91899425cos(105)[37710cos(105)]0t x t x με−−+×−即18189425251037710με−==×× 故181882r 0025102510(310) 2.25εμε−−×==×××=其实,观察题目给定的电场表达式,可知它表征一个沿x +方向传播的均匀平面波,其相速为98p 10210 m/s 5v k ω===× 而8p 310v ====×故2r 3() 2.252ε==(2) 与电场相伴的磁场E G H G 可由0j E ωμ∇×=−H G G求得。
电磁场与电磁波课后答案

第一章 矢量场1.1 z y x C z y x B z y xA ˆˆˆ3;ˆ2ˆˆ;ˆˆ3ˆ2+-=-+=-+=ρρρ 求:(a) A ; (b) ∃b ; (c) ρρA B ⋅ ; (d) ρρB C ⨯ ; (e) ()ρρρA B C ⨯⨯ (f)()ρρρA B C ⨯⋅ 解:(a) 14132222222=++=++=z y x A A A A ; (b) )ˆ2ˆˆ(61ˆz y x BB b -+==ρρ( c) 7=⋅B A ρρ; (d) z y xC B ˆ4ˆ7ˆ---=⨯ρρ (e)z y x C B A ˆ4ˆ2ˆ2)(-+=⨯⨯ρρρ (f)19)(-=⋅⨯C B A ρρρ 1.2 ρA z =++2∃∃∃ρπϕ; ρB z =-+-∃∃∃ρϕ32 求:(a) A ; (b) ∃b ; (c) ρρA B ⋅ ; (d) ρρB A ⨯ ; (e) B A ρρ+解:(a) 25π+=A ;(b) )ˆ2ˆ3ˆ(141ˆz b -+-=ϕρ;(c) 43-=⋅πB A ρρ (d) z A B ˆ)6(ˆ3ˆ)23(+--+=⨯πϕρπρρ (e) z B A ˆˆ)3(ˆ-++=+ϕπρρρ 1.3 ρA r=+-22∃∃∃πθπϕ; ρB r =-∃∃πθ 求:(a) A ; (b) ∃b ; (c) ρρA B ⋅ ; (d) ρρB A ⨯ ; (e) ρρA B +解:(a) 254π+=A ; (b) )ˆˆ(11ˆ2θππ-+=r b ; (c) 22π-=⋅B A ρρ ; (d) ϕπθππˆ3ˆ2ˆ22++=⨯rA B ρρ ; (e) ϕπˆ2ˆ3-=+r B A ρρ 1.4 ρA x y z =+-∃∃∃2; ρB x y z =+-α∃∃∃3 当ρρA B ⊥时,求α。
解:当ρρA B ⊥时,ρρA B ⋅=0, 由此得 5-=α1.5 将直角坐标系中的矢量场ρρF x y z xF x y z y 12(,,)∃,(,,)∃==分别用圆柱和圆球坐标系中的坐标分量表示。
工程电磁场与电磁波 丁君版 答案第五章习题答案

习题五5-1 一圆柱形铝管,外半径为32 mm ,管壁厚6 mm ,求单位长度的电阻。
解:铝管的内半径为26mm ,设流过铝管的电流为I ,则: 662222211034810)2632()(⨯=⨯-=-=-πππI IR R IJ6/10348I E J σπσ==⨯13349.5103486103486-=⨯=⨯⨯=⋅=σπσπσII I d E R (Ω)5-2 一长为l m 的导体,电阻率为σ,导体各处的横截面相似,一端的面积为A m 2,另一端面的面积为kA m 2,求两端面间的电阻。
5-2.解:(此题应为导体各处的横截面相似且呈线性关系)。
z设流入导体的电流为I ,则设任一截面面积为()z S ,由⎩⎨⎧==kA l S A S )()0(得: ⎪⎩⎪⎨⎧-==A l k a A b 1则:AAz lk z S +-=1)(σE z S IJ ==)(σ⋅=∴)(z S I Ek Ak Il A z A lk dz I dz E U ln )1()1(11⋅-=+⋅-⋅=⋅=⎰⎰σσAk k l IU R ⋅-⋅==∴σ)1(ln5-3解:σb lU本题所求电感为跨接在内外导体间的r ar E E ˆ)(=r arl I J ˆ2π=E Jσ= r alr IE ˆ2σπ=ab lI dr lr I l d E U babaln22πσσπ==⋅=⎰⎰ab UI G ln 2πσ==球冠面积⎰⎰-==πθθπϕθθ20220)cos 1(2sin r d d r Sr a r E E ˆ)(= r r a r Ia S I J ˆ)c o s 1(2ˆ2θπ-== σS J E = ⎰⎰-=⋅-=21)cos 1(22r r dr r Il d E U σθπ2112)cos 1(2r r r r IU R θπσ--==5-5.解:设电容器板内的D 为0D ,则:d 1=1.0mm d 2=2.0mmd 3=2.5mm1r ε2r ε3r ε方法一:(1) n n D D 10=⎰⋅=⋅=Sn n S D dS D Q 11101111r n n d D d E U εε⋅=⋅=F d S UQ C r 93911011096.71013103613.0---⨯=⨯⨯⨯⨯=⋅==∴πεε(2)同理 F C 921031.5-⨯=(3)同理 F C 931037.6-⨯= F C C C C 93211012.21111-⨯=++=∴方法二:由介质边界条件nn n n D D D D 0321===⎰⎰⎰⎰++=⋅-=12132321d d d d d n n n dzE dz E dz E l d E Udz D dz D d d d r nd r n⎰⎰++=1212102001εεεεdz D d d d d rn⎰+++3122303εε)(3213210rrrond d d D εεεε++=SD ds D Q n 01=⋅=⎰ UQ C =5-6 解:设内导体单位长度带电量为Q ,E 、D只有r 方向分量,电荷将均匀分布在导体表面上,⎰⎰=⋅+⋅QS d D S d D 2211Q r E r E =+-12110)2(θεθπε 在介质与空气的分界面上t t E E 21=且没有ϕ方向分量,即 21E E E == rQE 1)2(110⋅+-=∴εθθπε)l n ()2(110abQdr E U ba⋅+-=⋅=∴⎰εθθπε[])l n (/)2(110abU QC εθθπε+-==∴5-7l设电轴的位置偏离轴心c mm a 85.68= mm h 53.8= M 点N 点的电位相等 120ln 2R R l περφ=ca c a h l M +-+=2ln20περφ ca c a h l N ---=2ln20περφ由此可得出ca c a h ca c a h ---=+-+22 所以c 满足0222=+-a hc c可求出0003.0=c 1)由于a h >>,求解导体电位时a 可以忽略。
《电磁场与电磁波》课后习题解答(第五章)

《电磁场与电磁波》课后习题解答(第五章)————————————————————————————————作者:————————————————————————————————日期:习题及参考答案5.1 一个点电荷 Q 与无穷大导体平面相距为d ,如果把它移动到无穷远处,需要作多少功?解:用镜像法计算。
导体面上的感应电荷的影响用镜像电荷来代替,镜像电荷的大小为-Q ,位于和原电荷对称的位置。
当电荷Q 离导体板的距离为x 时,电荷Q 受到的静电力为2)2(042x Q F επ-=静电力为引力,要将其移动到无穷远处,必须加一个和静电力相反的外力2)2(042x Q f επ=在移动过程中,外力f 所作的功为d Q d dx dx Q dx f 016220162επεπ=⎰∞⎰∞= 当用外力将电荷Q 移动到无穷远处时,同时也要将镜像电荷移动到无穷远处,所以,在整个过程中,外力作的总功为dq8/2επ。
也可以用静电能计算。
在移动以前,系统的静电能等于两个点电荷之间的相互作用能:d Q d Q Q d Q Q q q W 082)2(04)(21)2(042122211121επεπεπϕϕ-=-+-=+=移动点电荷Q 到无穷远处以后,系统的静电能为零。
因此,在这个过程中,外力作功等于系统静电能的增量,即外力作功为dq8/2επ。
5.2 一个点电荷放在直角导体内部(如图5-1),求出所有镜像电荷的位置和大小。
解:需要加三个镜像电荷代替 导体面上的感应电荷。
在(-a ,d )处,镜像电荷为-q ,在(错误!链接无效。
)处, 镜像电荷为q ,在(a ,-d )处,镜像电荷为-q 。
图5-1 5.3 证明:一个点电荷q 和一个带有电 荷Q 、半径为R 的导体球之间的作用力为]2)22(2[04R D DRq D D qR Q q F --+=επ其中D 是q 到球心的距离(D >R )。
证明:使用镜像法分析。
1 电磁场与电磁波课后习题答案第五章

5.3设y=0为两种磁介质的分界面,y<0为媒质1,其磁导率为1μ,y>0为媒质2,其磁导率为2μ,分界面上有电流密度s x J 2a A/m =分布的面电流,已知媒质1中磁场强度为123/x y z H a a a A m =++ 求媒质2中磁场强度2H 解:mA a a a H a n J H H n z y x y S /52)(2121212++=-==-⨯μμ其中则由到媒质设电磁波由媒质5.6已知在空气中,电场强度矢量为90.1sin(10)cos(610)/y E a x t z V m ππβ=⨯-求磁场强度H 和相位常数β 解:3939,0.2310sin(10)cos(61054.41)0.1310cos(10)sin(61054.14)20/x z E jwB B HH a x t z a x t z rad mμππππηωμεωνπ--∇⨯=-==-⨯⨯--⨯⨯-==÷=由得相位常数:5.7自由空间中,已知电场强度矢量为4cos()3cos()x y E a t z a t z ωβωβ=-+-求(1)磁场强度的复数表达式(2)坡印廷矢量的瞬时表达式(3)平均坡印廷矢量 解: (1)m/4)e a 3a (120113e a e 4a zj -y x z-j y z -j x )(V B H B j E E z βββπμω-==-=⨯∇+=得由 (2)z)-t (cos 245a H E S z)-t 4)cos(a 3a (1201z)-t 3cos(a z)-t cos(4a 2z y x ),(y x )t ,(βωπβωπβωβω=⨯=-=+=所以t z z H E w/m 2(3)()[]ππ485)43()34(120121HE Re 21S av zy x y x a a a a a =-⨯+=⨯=*5.9 将下列复数形式的场矢量变换成瞬时表达式,或作用反的变换 (1)43j z j z x y Ea e a je ββ--=+()()2(,)4Re[]3Re[]4cos()3cos()24cos()3sin()j t z j t z z t x y x y x y E a ea ea t z a t z a t z a t z πωβωβπωβωβωβωβ-+-=+=-+-+=---(2)4sin()sin()cos()cos()x z Ea x t z a x t z a aππωβωβ=-+-(,)()()2()2()4sin()cos()cos()cos()24sin()Re[]cos()Re[]4sin()cos()4sin()cos()z t x z j t z j t z x z j z j zz x z j z j zx z E a x t z a x t z a a a x e a x e a aE a x ea x e aaa j x e a x e a aπωβωβπββββπππωβωβππππππ--------=--+-=+=+=-+(3)cos()2sin()x y E a t z a t z ωβωβ=-+-(,)()()2()cos()2cos()2Re[]2Re[]2z t x y j t z j t z x y j z j zz x y E a t z a t z a ea eE a e a je πωβωβββπωβωβ-----=-+--=+=-(4)sin 3cos(cos )jkz y x Ea j k e θθ-=(sin )2()(sin )2(,)3cos(cos )3cos(cos )Re[]3cos(cos )cos(sin )23cos(cos )sin(sin )j kz z y x j t kz z t y x y x y x E a k eE a k ea k t kz a k t kz πθπωθθθπθωθθωθ---+===-+=--(5)2sin()y Ea t z ωβϕ=-+(,)()()()2cos()22Re[]2z t y j t z y j z z y E a t z a j e E a je ωβφβφπωβφ-+-+=-+-=-=-5.12 对于线性,均匀和各向同性导电媒质,设媒质的介电常数为,磁导率为电导率为,试证明无源区域中时谐电磁场所满足的波动方程为2222E jw E k E H jw H k Hμσμσ∇=-∇=-式中22k w με=解:H k H j H HH j H H Hj H H H E HH H E j E H Ej E D j J H2222220)j ()()(j )()(-=∇-=∇∴=⋅∇-⋅+=∇-⋅∇∇-=⨯∇⨯∇⨯∇+∇=⋅∇∇+⨯∇=⨯∇⨯∇+=+=⨯∇ωμσμεωωμσωμωεσωμωεσωεσω即代入上式将E k E j E 22:-=∇ωμσ同理5.15设电场强度和磁场强度分别为cos()cos()o e o m E E t H H t ωφωφ=+=+求其平均坡印廷矢量。
电磁场与电池波第五章 习题答案

+ a y 3e -j β z
由∇ × E = − jωμ0 H 得
H= ∇× E −1 = (a x 3 − a y 4)e -jβ z V / m − jωμ0 120π
(2) E ( z , t ) = ax 4 cos(ωt − β z ) + a y 3cos(ωt − β z )
2 2 2 2
H + ∇ × ∇ × H
∇ × E = − j ωμ H 代入上式 H = ( σ + j ωε ) ⋅ ( − j ωμ ) H H − ω H − k
2 2
H = j ωμσ H = j ωμσ
με H
H
同理 : ∇ 2 E = j ωμσ E − k 2 E
5.15 设电场强度和磁场强度分别为 解:
解:
∇ 2 E = jwμσ E − k 2 E ∇ 2 H = jwμσ H − k 2 H
式中
∇ × H = J + j ω D = σ E + j ωε E ∇ × ∇ × H = ∇ × ( σ E + j ωε E ) 将 ∇ (∇ ⋅ H ) = ∇ ∇ (∇ ⋅ H ) − ∇ ∵ ∇ ⋅H = 0 ∴ ∇ 即 ∇
β B sin(ωt-βz) μ0 ε0 m
∂B , 满足电磁场基本方程 ∂t
所以 ∇ × E = − a z ωBm cos(ωt-βz)= −
5.12 对于线性,均匀和各向同性导电媒质,设媒质的介电常数为 ε ,磁导率为 μ ,电导率为
σ ,试证明无源区域中时谐电磁场所满足的波动方程为
k 2 = w2 με
π
2
)
E ( x , y , z , t ) = a y 3 co s( k x co s θ ) R e[ e
电磁场与电磁波(金立军)第五章答案

半
圆
受
到
的
力
为
题 5-9 图
F2 Idl B I ade Be z
BIa e d
0
BIa (cos e y sin e x )d
0
2 BIae x
2 1.25 120 1a x 50ex
e z 0 I 5 z x 2 ( y 1) 2 ( z 5) 2 ln 2 2 2 4 5 z x ( y 1) ( z 5)
则 A(3, 4,0) = ez 4.5 10 Wb / m
-6
y 1 y 1 B = A = ex (5 z x 2 ( y 1) 2 ( z 5) 2 ) x 2 ( y 1) 2 ( z 5) 2 (5 z x 2 ( y 1) 2 ( z 5) 2 ) x 2 ( y 1) 2 ( z 5) 2 y 1 y 1 e x (5 z x 2 ( y 1) 2 ( z 5) 2 ) x 2 ( y 1) 2 ( z 5) 2 (5 z x 2 ( y 1) 2 ( z 5) 2 ) x 2 ( y 1) 2 ( z 5) 2 x x e y (5 z x 2 ( y 1) 2 ( z 5) 2 ) x 2 ( y 1) 2 ( z 5) 2 (5 z x 2 ( y 1) 2 ( z 5) 2 ) x 2 ( y 1) 2 ( z 5) 2 x x e y (5 z x 2 ( y 1) 2 ( z 5) 2 ) x 2 ( y 1) 2 ( z 5) 2 (5 z x 2 ( y 1) 2 ( z 5) 2 ) x 2 ( y 1) 2 ( z 5) 2
电磁场与电磁波课后习题答案全-杨儒贵

第一章矢量分析第一章 题 解1-1已知三个矢量分别为z y e e e A x 32-+=;z y e e e B x 23++=;z e e C x -=2。
试求①|| |,| |,|C B A ;②单位矢量c b a e e e , ,;③B A ⋅;④B A ⨯;⑤C B A ⨯⨯)(及B C A ⨯⨯)(;⑥B C A ⋅⨯)(及C B A ⋅⨯)(。
解 ① ()14321222222=-++=++=z y x A A A A14213222222=++=++=z y x B B B B()5102222222=-++=++=z y x C C C C② ()z y e e e A A A e x a 3214114-+===()z y e e e B B B e x b 2314114++===()z e e C C C e x c -===2515 ③ 1623-=-+=++=⋅z z y y x x B A B A B A B A④ z y zy z y xz y xz y B B B A A A e e e e e e e e e B A x x x5117213321--=-==⨯ ⑤ ()z y z y e e e e e e C B A x x22311125117+-=---=⨯⨯因z y zy zyxz y xC C C A A A e e e e e e e e e C A x x x x x45212321---=--==⨯则()z y z y e e e e e e B C A x x 1386213452+--=---=⨯⨯⑥ ()()()152131532=⨯+⨯-+⨯-=⋅⨯B C A()()()1915027=-⨯-++⨯=⋅⨯C B A 。
1-2 已知0=z 平面内的位置矢量A 与X 轴的夹角为α,位置矢量B 与X 轴的夹角为β,试证βαβαβαsin sin cos cos )cos(+=-证明 由于两矢量位于0=z 平面内,因此均为二维矢量,它们可以分别表示为ααsin cos A A y e e A x += ββsin cos B B y e e B x +=已知()βα-=⋅c o s B A B A ,求得()BA B A B A βαβαβαsin sin cos cos cos +=-即 βαβαβαsin sin cos cos )cos(+=-1-3 已知空间三角形的顶点坐标为)2 ,1,0(1-P ,)3 ,1 ,4(2-P 及)5 ,2 ,6(3P 。
电磁场课后习题第五章
?
?K
2
uuv ey
?
?K uuv
2 ey
? uuv
uuv
? 0.998 0 ? 80ey ??100.9 10?6 e y T
uuuv H2 ?
uuv B2
?
?
uuv 80e y
A/ m
uuuv M2
?
uuv B2
?
?
uuuv H2
?
uuv ? 0.16e y
A/ m
⑵在区域①,③内与上面的结论一致,在区域②内
2??
??? BH? 0 r ? 4 ? 10?7 ? 500? 144.96 ? 9.1? 10?2
B ,H 方向均沿安培环路的切线方向。
3-9 已知在 Z ? 0 的区域中,? r1 ? 4 ,在 Z ? 0 的区域中 ? r 2 ? 1 ,设在
Z ? 0 处B 是均的,其方向为 ? ? 60o,? ? 45o ,量值为 1Wb / m2 ,试求
?
l?z 2
1
? ??
z
?
l ?2 ?2
2 ??
? ?
?
?? ?
uuv ez
?
?
??
⑵当远离圆柱时,即 z ? l ,? ? a 时,可将此圆柱视为一个磁偶极子,磁
2
? 偶极矩 uuv
uuv
uuv
me? ImS z ? M0l a 2 ez
uvu
它在空间中产生的磁场可用磁矩 m 表示为
? ? uv ? ? ? ? ? B ?
式中 dz?是小圆环的宽度,每个小圆环电流在轴线上某点均产生磁感应强度。利
用圆环电流在其中心轴线一点的磁感应强度的表达式,可以写出 dI m 在轴线上产
电磁场与电磁波课后习题及答案五章习题解答

五章习题解答真空中直线长电流I 的磁场中有一等边三角形回路,如题图所示,求三角形回路内的磁通。
解 根据安培环路定理,得到长直导线的电流I 产生的磁场02I rφμπ=B e 穿过三角形回路面积的磁通为d S ψ==⎰B S 32320002[d ]d d 2d b d b z ddII zz x x x xμμππ=⎰ 由题图可知,()tan63z x d π=-=,故得到320d 3d b d x d x x ψπ-==⎰03[23I b b μπ 通过电流密度为J 的均匀电流的长圆柱导体中有一平行的圆柱形空腔,如题图所示。
计算各部分的磁感应强度B ,并证明腔内的磁场是均匀的。
解 将空腔中视为同时存在J 和J -的两种电流密度,这样可将原来的电流分布分解为两个均匀的电流分布:一个电流密度为J 、均匀分布在半径为b 的圆柱内,另一个电流密度为J -、均匀分布在半径为a 的圆柱内。
由安培环路定律,分别求出两个均匀分布电流的磁场,然后进行叠加即可得到圆柱内外的磁场。
dbIz题 图d S由安培环路定律d CI μ⋅=⎰B l ,可得到电流密度为J 、均匀分布在半径为b 的圆柱内的电流产生的磁场为 020222b b b b b b r b b r b r J r B J r μμ⎧⨯<⎪⎪=⎨⨯⎪>⎪⎩ 电流密度为J -、均匀分布在半径为a 的圆柱内的电流产生的磁场为 020222a a a a a a r a a r a r J r B J r μμ⎧-⨯<⎪⎪=⎨⨯⎪->⎪⎩这里a r 和b r 分别是点a o 和b o 到场点P 的位置矢量。
将a B 和b B 叠加,可得到空间各区域的磁场为圆柱外:22222b a ba b a r r B J r r μ⎛⎫=⨯- ⎪⎝⎭ ()b r b > 圆柱内的空腔外:2022b a a a r B J r r μ⎛⎫=⨯- ⎪⎝⎭ (,)b a r b r a <> 空腔内: ()0022b a B J r r J d μμ=⨯-=⨯ ()a r a < 式中d 是点和b o 到点a o 的位置矢量。
电磁场与电磁波金立军第五章答案

5-9
题
5-9
图示一个在
xy
平面上的弯曲线,通过
20A
电流。在这区域内的磁场为
B
1.25ezT
。求导
线所受的力。
解 两端直线受到力为 F1 F3 Idl B BIlex
1.25 20 4 100
半圆受到的力为
题 5-9 图
F2 Idl B I ade Bez
l z 2
dm
l z 2
(b2
m2 )3/ 2
ez
0b2 NI 2l
l z
arctan( 2 b
)
b sec2 d
b sec l
z
3
3
arctan( 2 )
b
ez
0 NI 2l
l z
2
( l z)2 b2
2
l z
2
(l 2
2.5107
上下两边产生的磁感应强度
B2
B4
2 10 4
左边产生的磁感应强度
B3
u0I 4
0
0.05da (0.05)a 0.053
6.28104
总的磁感应强度
B总
1.031035
题 5-2 图
5-3 在氢原子中,电子绕半径为 5.3×10-11m 的圆轨道运动,速度为 2200m/s,求圆轨道圆心处的磁场。
解 建立圆柱坐标系,另圆柱轴线为 z 轴。那么根据真空中的安培环路定律可知,
(1)在圆柱内线积分包围的部分电流为 I1
大学电磁场与电磁波第五章5.9正弦时变电磁场中的平均能量与功率

二次式的时间平均值
在时谐电磁场中,常常要关心二次式在一个时间周期 T 中的
平均值,即
∫ ∫ 平均电场能量密度 = weav
1 T
T
= 0 we dt
1 T
T
1
E
⋅
D
dt
02
∫ ∫ 平均磁场能量密度 = wmav
1 T
T
= 0 wm dt
1 T
T
1
H
⋅
B
dt
02
∫ ∫ 平均能流密度矢量
= Sav
其中E0、H0 和
解:(1w) = we +
k 为常数。求:(1)
wm =
1
(
E
⋅
D
+
B
⋅
2
w和
H) =
wav ;(2)
1 2
(ε
0
E
2
S
+
和 Sav。
µ0H 2 )
1 2
ε
0
E02
cos2
(ωt
−
kz
)
+
µ0
H
2 0
cos
2
(ωt
−
kz)
由于 E xˆ= ˆEˆ0ˆe− jkz , D* xε= 0E0e jkz , H y= H0e− jkz , B* yµ0H0e jkz
为
例1 E(z) =
已知无源的自由空间中,电磁场的电场强度复矢
yE0e−
jkz,其中k
和
E0
为常数。求:(1)磁场强度复矢量H
量 ;
(2)瞬时坡印廷矢量 S
;(3)平均坡印廷矢量
电磁场与电磁波(第四版)课后答案 第五章习题

5 Rˆ
5
EmI zˆj 5
可见
EmR EmI 5
zˆ Rˆ zˆ 1 xˆ 2yˆ 1 yˆ 2xˆ nˆ
5
5
Rˆ zˆ 1 xˆ 2yˆ zˆ 0
5
因为
EmR、E相mI 位相差
90 ,所以电场为一个左旋圆极化波。
与之相伴的磁场为
H r 1 nˆ E r 1 2xˆ yˆ xˆ 2 yˆ j 5zˆ e j2xy
S z,t E z,t H z,t ez153.6 cos2 6 108t 2 z W / m2
5.19自由空间中均匀平面波电场表达式为
E r,t xˆ 2yˆ zˆEzm 10cost 3x y zV / m
式中 Ezm 为待定量。试由表达式确定波的传播方向、角频率、
第五章 习题
5.6在自由空间传播的均匀平面波的电场强度的复矢量为
E
z
ex104 e
j 20 z
ey104 e
j
20
பைடு நூலகம்
z 2
V /m
试求(1)平面波的传播方向和频率 (2)波的极化方式 (3)磁场强度H (4)流过沿传播方向单位面积的平均功率
解:(1)传播方向为z方向 由题意知
k 20 00
试有此表达式确定波的传播方向、波长、极化状态,并求出磁场
H r
解:波的传播方向由波矢量的方向确定,由:
k r kxx ky y kzz 2x by cz
得
kx 2
ky b kz c
为确定b和c,利用
k Em 0
有 2xˆ byˆ czˆ • xˆ 2yˆ j 5zˆ 2 2b j 5c 0
波长 相速
2 2 m 1m 2
电磁场与电磁波课后习题答案全-杨儒贵

第一章矢量分析第一章 题 解1-1已知三个矢量分别为z y e e e A x 32-+=;z y e e e B x 23++=;z e e C x -=2。
试求①|| |,| |,|C B A ;②单位矢量c b a e e e , ,;③B A ⋅;④B A ⨯;⑤C B A ⨯⨯)(及B C A ⨯⨯)(;⑥B C A ⋅⨯)(及C B A ⋅⨯)(。
解 ① ()14321222222=-++=++=z y x A A A A14213222222=++=++=z y x B B B B()5102222222=-++=++=z y x C C C C② ()z y e e e A A A e x a 3214114-+===()z y e e e B B B e x b 2314114++===()z e e C C C e x c -===2515 ③ 1623-=-+=++=⋅z z y y x x B A B A B A B A④ z y zy z y xz y xz y B B B A A A e e e e e e e e e B A x x x5117213321--=-==⨯ ⑤ ()z y z y e e e e e e C B A x x22311125117+-=---=⨯⨯因z y zy zyxz y xC C C A A A e e e e e e e e e C A x x x x x45212321---=--==⨯则()z y z y e e e e e e B C A x x 1386213452+--=---=⨯⨯⑥ ()()()152131532=⨯+⨯-+⨯-=⋅⨯B C A()()()1915027=-⨯-++⨯=⋅⨯C B A 。
1-2 已知0=z 平面内的位置矢量A 与X 轴的夹角为α,位置矢量B 与X 轴的夹角为β,试证βαβαβαsin sin cos cos )cos(+=-证明 由于两矢量位于0=z 平面内,因此均为二维矢量,它们可以分别表示为ααsin cos A A y e e A x += ββsin cos B B y e e B x +=已知()βα-=⋅c o s B A B A ,求得()BA B A B A βαβαβαsin sin cos cos cos +=-即 βαβαβαsin sin cos cos )cos(+=-1-3 已知空间三角形的顶点坐标为)2 ,1,0(1-P ,)3 ,1 ,4(2-P 及)5 ,2 ,6(3P 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题及参考答案5.1 一个点电荷 Q 与无穷大导体平面相距为d ,如果把它移动到无穷远处,需要作多少功?解:用镜像法计算。
导体面上的感应电荷的影响用镜像电荷来代替,镜像电荷的大小为-Q ,位于和原电荷对称的位置。
当电荷Q 离导体板的距离为x 时,电荷Q 受到的静电力为 2)2(042x Q F επ-=静电力为引力,要将其移动到无穷远处,必须加一个和静电力相反的外力2)2(042x Q f επ=在移动过程中,外力f 所作的功为d Q d dx dx Q dx f 016220162επεπ=⎰∞⎰∞= 当用外力将电荷Q 移动到无穷远处时,同时也要将镜像电荷移动到无穷远处,所以,在整个过程中,外力作的总功为dq8/2επ。
也可以用静电能计算。
在移动以前,系统的静电能等于两个点电荷之间的相互作用能:d Q d Q Q d Q Q q q W 082)2(04)(21)2(042122211121επεπεπϕϕ-=-+-=+= 移动点电荷Q 到无穷远处以后,系统的静电能为零。
因此,在这个过程中,外力作功等于系统静电能的增量,即外力作功为dq8/2επ。
5.2 一个点电荷放在直角导体部(如图5-1),求出所有镜像电荷的位置和大小。
解:需要加三个镜像电荷代替 导体面上的感应电荷。
在(-a ,d ) 处,镜像电荷为-q ,在(错误!无效。
镜像电荷为q ,在(a ,-d )处,镜像电荷为-q 。
5.3 证明:一个点电荷q 和一个带有电 荷Q 、半径为R 的导体球之间的作用力为 ]2)22(2[04R D DRq D D qR Q q F--+=επ 其中D 是q 到球心的距离(D >R )。
证明:使用镜像法分析。
由于导体球不接地,本身又带电Q ,必须在导体球加上两个镜像电荷来等效导体球对球外的影响。
在距离球心b=R 2/D 处,镜像电荷为q '= -Rq/D ;在球心处,镜像电荷为D Rq Q q Q q /2+='-=。
点电荷q 受导体球的作用力就等于球两个镜像电荷对q 的作用力,即]2)2(2[04]2)(22[04DR D D q R D D q R Q q b D q D qq F --++=-'+=επεπ]2)22(2[04R D DRqD D q R Q q--+=επ 5.4 两个点电荷+Q 和-Q 位于一个半径为a 的接地导体球的直径的延长线上,分别距离球心D 和-D 。
(1)证明:镜像电荷构成一电偶极子,位于球心,偶极矩为2a 3Q/D 2。
(2)令Q 和D 分别趋于无穷,同时保持Q/D 2不变,计算球外的电场。
解:(1)使用导体球面的镜像法叠加原理分析。
在球应该加上两个镜像电荷:一个是Q 在球面上的镜像电荷,q 1 = -aQ/D ,距离球心b=a 2/D ;第二个是-Q 在球面上的镜像电荷,q 2 = aQ/D ,距离球心b 1=-a 2/D 。
当距离较大时,镜像电荷间的距离很小,等效为一个电偶极子,电偶极矩为232)1(1DQa b b q p --= (2)球外任意点的电场等于四个点电荷产生的电场的叠加。
设+Q 和-Q 位于坐标z 轴上,当Q 和D 分别趋于无穷,同时保持Q/D 2不变时,由+Q 和-Q 在空间产生的电场相当于均匀平板电容器的电场,是一个均匀场。
均匀场的大小为204/2D Q επ,方向在-e z 。
由镜像电荷产生的电场可以由电偶极子的公式计算:)θθθεπsin cos 2(34e r e r P E +=)θθθεπsin cos 2(230432e r e Dr Qa +-=5.5 接地无限大导体平板上有一个半径为a 的半球形突起,在点(0,0,d )处有一个点电荷q (如图5-5),求导体上方的电位。
解:计算导体上方的电位时,要保持 导体平板部分和半球部分的电位都为 零。
先找平面导体的镜像电荷q 1 = -q , 位于(0,0,-d )处。
再找球面镜像 电荷q 2 = -aq/d ,位于(0,0,b )处, b= a 2/d 。
当叠加这两个镜像电荷和原电荷共同产生的电位时,在导体平面上和 图5-5 球面上都不为零,应当在球再加上一个镜像电荷q 3 =aq/d ,位于(0,0,-b )处。
这时,三个镜像电荷和原电荷共同产生的电位在导体平面和球面上都为零。
而且三个镜像电荷在要计算的区域以外。
导体上方的电位为四个点电荷的叠加,即)(332211041rq r qr q R q+++=επϕ其中21]2)(22[d z y x R -++=21]2)(22[1d z y x r +++= 21]2)(22[2b z y x r -++= 21]2)(22[3b z y x r +++= 5.6 求截面为矩形的无限长区域(0<x<a ,0<y<b )的电位,其 四壁的电位为0,0,==)()(b x x ϕϕ0,0=)(y ϕ⎪⎩⎪⎨⎧<<-≤<=by b by U b y b yUy a 2),1(020,0,)(ϕ解:由边界条件0,0,==)()(b x x ϕϕ知,方程的基本解在y 方向应该为周期函数,且仅仅取正弦函数,即 )(sin b n nkynk nY π==在x 方向,考虑到是有限区域,选取双曲正弦和双曲余弦函数,使用边界条件0,0=)(y ϕ,得出仅仅选取双曲正弦函数,即 x b n shnX π=将基本解进行线性组合,得bxn n b x n sh n C ππϕ∑∞==1sin待定常数由x=a 处的边界条件确定,即bxn n b xn sh nC y a ππϕ∑∞==1sin),( 使用正弦函数的正交归一性质,有dy by n b y a b a n sh n C bπϕπ⎰=0sin ),(22]cos sin 2)[(0sin 020b b y n y n b b y n n b b U dy b y n b y U b πππππ-=⎰]2cos 222sin 2)[(0ππππn n b n n b b U-=2]cos sin 2)[(02cos 0sin )21(0b b b y n y n b b y n n b b U b b b y n n bU dy b yn b yb b U πππππππ---=⎰- πππππππn b n b b U n n b b Un n n bU cos 02sin 2)(0)2cos cos 0++--=(2cos20ππn bn b b U-化简以后得dy b y n b y a b an sh n C bπϕπ⎰=0sin ),(2=2sin2202ππn n b U 求出系数,代入电位表达式,得b x n shb y n ba n n n Un πππππϕsin sin2sin22041∑∞== 5.7一个截面如图5-7所示的长槽,向y 方向无限延伸,两则的电位是零,槽y →∞,φ→0,底部的电位为 00,U x =)(ϕ求槽的电位。
解:由于在x=0和x=a 两个边界的 电位为零,故在x 方向选取周期解,且仅仅取正弦函数,即)(sin a n nk xnk n Xπ== 图5-7在y 方向,区域包含无穷远处,故选取指数函数,在y →∞时,电位趋于零,所以选取由基本解的叠加构成电位的表示式为yy n k e nY -= 由基本解的叠加构成电位的表示式为ay n ea x n n n ππϕ-∑∞==sin 1C待定系数由y=0的边界条件确定。
在电位表示式中,令y=0,得a xn n nU πsin 1C 0∑∞==)cos 1(00sin 02πππn n aUdx a xn a U a n C-=⎰= 当n 为奇数时,πn UnC 04=,当n 为偶数时,00=C 。
最后,电位的解为ay n e ax n n U n πππϕ-∑∞==sin45,3,15.7 若上题的底部的电位为00,U x =)(ϕaxπ3sin重新求槽的电位。
解:同上题,在x 方向选取正弦函数,即)(sin an nk x nk nX π==,在y方向选取yn k e nY -=。
由基本解的叠加构成电位的表示式为ay n ea x n n n ππϕ-∑∞==sin 1C将y=0的电位代入,得0U a xπ3sin a xn n nπsin1C ∑∞== 应用正弦级数展开的唯一性,可以得到n=3时,03C C =,其余系数00=C ,所以ay e axππϕ33sin 0U -=5.9 一个矩形导体槽由两部分构成,如图5-9所示,两个导体板的电位分别是U 0和零,求槽的电位。
解:将原问题的电位看成是两个电 位的叠加。
一个电位与平行板电容 器的电位相同(上板电位为U 0,下 板电位为零),另一个电位为U ,即U y a+=Uϕ 图5-9其中,U 满足拉普拉斯方程,其边界条件为 y=0 , U=0 y=a , U=0 x=0时,⎪⎪⎩⎪⎪⎨⎧<<-<<-=-=20,02,000,0U a y ay U ay a a y U U ay U y )(ϕx →∞时,电位U 应该趋于零。
U 的形式解为ayφ=U 0a x n e a yn n nU ππ-∑∞==sin 1C待定系数用x=0的条件确定。
=)(y ,0U ay n n n U πsin1C ∑∞==dy ay n a y U n C aπ⎰=0sin ),0(22]cos sin 2)[(0sin 020a a y n y n a a y n n a a Udy a y n a y U aπππππ--=-⎰ ]2cos 222sin 2)([0ππππn n a n n a a U+-=2]cos sin 2)[(02cos 0sin )21(0a a a y n y n a a y n n a a U a a a y n n aU dy a yn a ya a U πππππππ---=⎰- πππππππn a n a a Un n a a Un n n aU cos 02sin 2)(0)2cos cos 0++--=(2cos20ππn an a a U-化简以后,得到dy a y n a y U n C aπ⎰=0sin ),0(2=2cos 0ππn n a U只有偶数项的系数不为零。
将系数求出,代入电位的表达式,得a xn ea y n n n Un y a Uππππϕ-∑∞=+=sin 2cos 02,4,20K5.10 将一个半径为a 的无限长导体管平分成两半,两部分之间互相绝缘,上半(0<Ф<π)接电压U 0,下半(π<Ф<2π)电位为零,如图5-10,求管的电位。
