2018年全国各省市中考数学几何压轴题

合集下载

2018年全国各地中考数学压轴题汇编：几何综合（湖南专版）（原卷）

2018年全国各地中考数学压轴题汇编：几何综合（湖南专版）（原卷）2018年全国各地中考数学压轴题汇编（湖南专版）几何综合1．（2018?长沙）如图，在△ABC中，AD是边BC上的中线，∠BAD=∠CAD，CE∥AD，CE交BA的延长线于点E，BC=8，AD=3．（1）求CE的长；（2）求证：△ABC为等腰三角形．（3）求△ABC的外接圆圆心P与内切圆圆心Q之间的距离．2．（2018?株洲）如图，在Rt△ABM和Rt△ADN的斜边分别为正方形的边AB和AD，其中AM=AN．（1）求证：Rt△ABM≌Rt△AND；（2）线段MN与线段AD相交于T，若AT=，求tan∠ABM的值．3．（2018?长沙）我们不妨约定：对角线互相垂直的凸四边形叫做“十字形”．（1）①在“平行四边形，矩形，菱形，正方形”中，一定是“十字形”的有；②在凸四边形ABCD中，AB=AD且CB≠CD，则该四边形“十字形”．（填“是”或“不是”）（2）如图1，A，B，C，D是半径为1的⊙O上按逆时针方向排列的四个动点，AC与BD 交于点E，∠ADB﹣∠CDB=∠ABD﹣∠CBD，当6≤AC2+BD2≤7时，求OE的取值范围；（3）如图2，在平面直角坐标系xOy中，抛物线y=ax2+bx+c（a，b，c为常数，a＞0，c ＜0）与x轴交于A，C两点（点A在点C的左侧），B是抛物线与y 轴的交点，点D的坐标为（0，﹣ac），记“十字形”ABCD的面积为S，记△AOB，△COD，△AOD，△BOC 的面积分别为S1，S2，S3，S4．求同时满足下列三个条件的抛物线的解析式；①=；②=；③“十字形”ABCD的周长为12．4．（2018?湘潭）如图，在正方形ABCD中，AF=BE，AE与DF 相交于点O．（1）求证：△DAF≌△ABE；（2）求∠AOD的度数．5．（2018?株洲）如图，已知AB为⊙O的直径，AB=8，点C和点D是⊙O上关于直线AB对称的两个点，连接OC、AC，且∠BOC ＜90°，直线BC和直线AD相交于点E，过点C作直线CG与线段AB的延长线相交于点F，与直线AD相交于点G，且∠GAF=∠GCE．（1）求证：直线CG为⊙O的切线；（2）若点H为线段OB上一点，连接CH，满足CB=CH，①△CBH∽△OBC；②求OH+HC的最大值．6．（2018?衡阳）如图，⊙O是△ABC的外接圆，AB为直径，∠BAC的平分线交⊙O于点D，过点D作DE⊥AC分别交AC、AB的延长线于点E、F．（1）求证：EF是⊙O的切线；（2）若AC=4，CE=2，求的长度．（结果保留π）7．（2018?湘潭）如图，AB是以O为圆心的半圆的直径，半径CO⊥AO，点M是上的动点，且不与点A、C、B重合，直线AM交直线OC于点D，连结OM与CM．（1）若半圆的半径为10．①当∠AOM=60°时，求DM的长；②当AM=12时，求DM的长．（2）探究：在点M运动的过程中，∠DMC的大小是否为定值？若是，求出该定值；若不是，请说明理由．8．（2018?衡阳）如图，在Rt△ABC中，∠C=90°，AC=BC=4cm，动点P从点C出发以1cm/s 的速度沿CA匀速运动，同时动点Q从点A出发以cm/s的速度沿AB匀速运动，当点P到达点A时，点P、Q同时停止运动，设运动时间为t（s）．（1）当t为何值时，点B在线段PQ的垂直平分线上？（2）是否存在某一时刻t，使△APQ是以PQ为腰的等腰三角形？若存在，求出t的值；若不存在，请说明理由；（3）以PC为边，往CB方向作正方形CPMN，设四边形QNCP 的面积为S，求S关于t 的函数关系式．9．（2018?邵阳）如图1所示，在四边形ABCD中，点O，E，F，G分别是AB，BC，CD，AD的中点，连接OE，EF，FG，GO，GE．（1）证明：四边形OEFG是平行四边形；（2）将△OGE绕点O顺时针旋转得到△OMN，如图2所示，连接GM，EN．①若OE=，OG=1，求的值；②试在四边形ABCD中添加一个条件，使GM，EN的长在旋转过程中始终相等．（不要求证明）10．（2018?常德）如图，已知⊙O是等边三角形ABC的外接圆，点D在圆上，在CD的延长线上有一点F，使DF=DA，AE∥BC交CF 于E．（1）求证：EA是⊙O的切线；（2）求证：BD=CF．11．（2018?岳阳）已知在Rt△ABC中，∠BAC=90°，CD为∠ACB的平分线，将∠ACB沿CD所在的直线对折，使点B落在点B′处，连结AB'，BB'，延长CD交BB'于点E，设∠ABC=2α（0°＜α＜45°）．（1）如图1，若AB=AC，求证：CD=2BE；（2）如图2，若AB≠AC，试求CD与BE的数量关系（用含α的式子表示）；（3）如图3，将（2）中的线段BC绕点C逆时针旋转角（α+45°），得到线段FC，连结EF交BC于点O，设△COE的面积为S1，△COF的面积为S2，求（用含α的式子表示）．12．（2018?张家界）如图，点P是⊙O的直径AB延长线上一点，且AB=4，点M为上一个动点（不与A，B重合），射线PM与⊙O交于点N（不与M重合）．（1）当M在什么位置时，△MAB的面积最大，并求出这个最大值；（2）求证：△PAN∽△PMB．13．（2018?常德）已知正方形ABCD中AC与BD交于O点，点M在线段BD上，作直线AM交直线DC于E，过D作DH⊥AE于H，设直线DH交AC于N．。

2018年广西各省市中考数学几何压轴题真题汇总

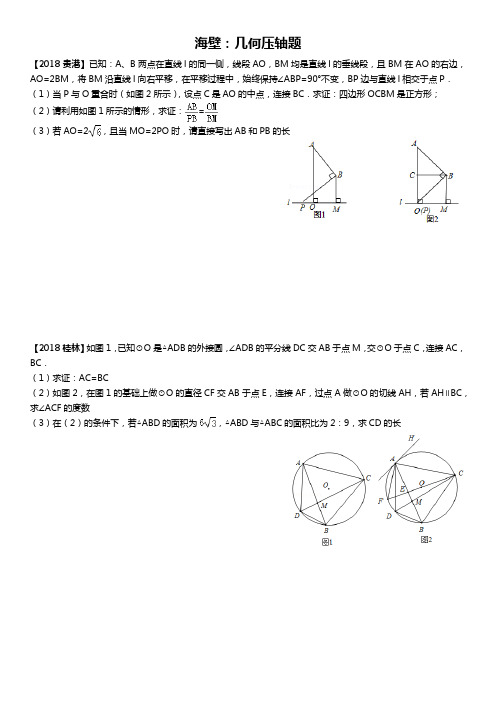
海壁：几何压轴题【2018贵港】已知：A、B两点在直线l的同一侧，线段AO，BM均是直线l的垂线段，且BM在AO的右边，AO=2BM，将BM沿直线l向右平移，在平移过程中，始终保持∠ABP=90°不变，BP边与直线l相交于点P．（1）当P与O重合时（如图2所示），设点C是AO的中点，连接BC．求证：四边形OCBM是正方形；（2）请利用如图1所示的情形，求证：=（3）若AO=2，且当MO=2PO时，请直接写出AB和PB的长【2018桂林】如图1，已知⊙O是△ADB的外接圆，∠ADB的平分线DC交AB于点M，交⊙O于点C，连接AC，BC．（1）求证：AC=BC（2）如图2，在图1的基础上做⊙O的直径CF交AB于点E，连接AF，过点A做⊙O的切线AH，若AH∥BC，求∠ACF的度数（3）在（2）的条件下，若△ABD的面积为，△ABD与△ABC的面积比为2：9，求CD的长【2018贺州】如图，AB 是⊙O 的弦，过AB 的中点E 作EC ⊥OA ，垂足为C ，过点B 作直线BD 交CE 的延长线于点D ，使得DB=DE ．（1）求证：BD 是⊙O 的切线（2）若AB=12，DB=5，求△AOB 的面积【2018南宁】如图，△ABC 内接于⊙O ，∠CBG =∠A ，CD 为直径，OC 与AB 相交于点E ，过点E 作EF ⊥BC ，垂足为F ，延长CD 交GB 的延长线于点P ，连接BD（1）求证：PG 与⊙O 相切（2）若85=AC EF ，求OCBE 的值（3）在（2）的条件下，若⊙O 的半径为8，PD= OD ，求OE 的长【2018玉林】在▱ABCD中，DC＞AD，四个角的平分线AE，DE，BF，CF的交点分别是E，F，过点E，F分别作DC与AB间的垂线MM'与NN'，在DC与AB上的垂足分别是M，N与M′，N′，连接EF．（1）求证：四边形EFNM是矩形（2）已知：AE=4，DE=3，DC=9，求EF的长【2018梧州】如图，AB 是⊙M 的直径，BC 是⊙M 的切线，切点为B，C 是B C 上（除B点外）的任意一点，连接C M 交⊙M 于点G，过点C作D C⊥BC 交B G 的延长线于点D，连接A G 并延长交B C 于点E．（1）求证：△ABE∽△BCD（2）若M B=BE=1，求C D 的长度。

2018年全国各地中考数学压轴题汇编：几何综合(西北专版)(解析卷)

2018年全国各地中考数学压轴题汇编（西北专版）几何综合参考答案与试题解析一．选择题（共10小题）1．（2018•陕西）如图，在△ABC中，AC=8，∠ABC=60°，∠C=45°，AD⊥BC，垂足为D，∠ABC的平分线交AD于点E，则AE的长为（）A．B．2C．D．3解：∵AD⊥BC，∴∠ADC=∠ADB=90°．在Rt△ADC中，AC=8，∠C=45°，∴AD=CD，∴AD=AC=4．在Rt△ADB中，AD=4，∠ABD=60°，∴BD=AD=．∵BE平分∠ABC，∴∠EBD=30°．在Rt△EBD中，BD=，∠EBD=30°，∴DE=BD=，∴AE=AD﹣DE=．故选：C．2．（2018•兰州）如图，矩形ABCD中，AB=3，BC=4，EF∥DF且BE与DF之间的距离为3，则AE的长是（）A．B．C．D．解：如图所示：过点D作DG⊥BE，垂足为G，则GD=3．∵∠A=∠G，∠AEB=∠GED，AB=GD=3，∴△AEB≌△GED．∴AE=EG．设AE=EG=x，则ED=4﹣x，在Rt△DEG中，ED2=GE2+GD2，x2+32=（4﹣x）2，解得：x=．故选：C．3．（2018•陕西）如图，在菱形ABCD中．点E、F、G、H分别是边AB、BC、CD和DA 的中点，连接EF、FG、GH和HE．若EH=2EF，则下列结论正确的是（）A．AB=EF B．AB=2EF C．AB=EF D．AB=EF解：连接AC、BD交于O，∵四边形ABCD是菱形，∴AC⊥BD，OA=OC，OB=OD，∵点E、F、G、H分别是边AB、BC、CD和DA的中点，∴EF=AC，EF∥AC，EH=BD，EH∥BD，∴四边形EFGH是矩形，∵EH=2EF，∴OB=2OA，∴AB==OA，∴AB=EF，故选：D．4．（2018•兰州）如图，将▱ABCD沿对角线BD折叠，使点A落在点E处，交BC于点F，若∠ABD=48°，∠CFD=40°，则∠E为（）A．102°B．112°C．122°D．92°解：∵AD∥BC，∴∠ADB=∠DBC，由折叠可得∠ADB=∠BDF，∴∠DBC=∠BDF，又∵∠DFC=40°，∴∠DBC=∠BDF=∠ADB=20°，又∵∠ABD=48°，∴△ABD中，∠A=180°﹣20°﹣48°=112°，∴∠E=∠A=112°，故选：B．5．（2018•陕西）如图，△ABC是⊙O的内接三角形，AB=AC，∠BCA=65°，作CD∥AB，并与⊙O相交于点D，连接BD，则∠DBC的大小为（）A．15°B．35°C．25°D．45°解：∵AB=AC、∠BCA=65°，∴∠CBA=∠BCA=65°，∠A=50°，∵CD∥AB，∴∠ACD=∠A=50°，又∵∠ABD=∠ACD=50°，∴∠DBC=∠CBA﹣∠ABD=15°，故选：A．6．（2018•白银）如图，点E是正方形ABCD的边DC上一点，把△ADE绕点A顺时针旋转90°到△ABF的位置，若四边形AECF的面积为25，DE=2，则AE的长为（）A．5 B．C．7 D．解：∵把△ADE顺时针旋转△ABF的位置，∴四边形AECF的面积等于正方形ABCD的面积等于25，∴AD=DC=5，∵DE=2，∴Rt△ADE中，AE==．故选：D．7．（2018•青海）小桐把一副直角三角尺按如图所示的方式摆放在一起，其中∠E=90°，∠C=90°，∠A=45°，∠D=30°，则∠1+∠2等于（）A．150°B．180°C．210°D．270°解：如图：∵∠1=∠D+∠DOA，∠2=∠E+∠EPB，∵∠DOA=∠COP，∠EPB=∠CPO，∴∠1+∠2=∠D+∠E+∠COP+∠CPO=∠D+∠E+180°﹣∠C=30°+90°+180°﹣90°=210°，故选：C．8．（2018•新疆）如图，矩形纸片ABCD中，AB=6cm，BC=8cm．现将其沿AE对折，使得点B落在边AD上的点B1处，折痕与边BC交于点E，则CE的长为（）A．6cm B．4cm C．3cm D．2cm解：∵沿AE对折点B落在边AD上的点B1处，∴∠B=∠AB1E=90°，AB=AB1，又∵∠BAD=90°，∴四边形ABEB1是正方形，∴BE=AB=6cm，∴CE=BC﹣BE=8﹣6=2cm．故选：D．9．（2018•白银）如图，⊙A过点O（0，0），C（，0），D（0，1），点B是x轴下方⊙A上的一点，连接BO，BD，则∠OBD的度数是（）A．15°B．30°C．45°D．60°解：连接DC，∵C（，0），D（0，1），∴∠DOC=90°，OD=1，OC=，∴∠DCO=30°，∴∠OBD=30°，故选：B．10．（2018•新疆）如图，点P是边长为1的菱形ABCD对角线AC上的一个动点，点M，N分别是AB，BC边上的中点，则MP+PN的最小值是（）A．B．1 C．D．2解：如图，作点M关于AC的对称点M′，连接M′N交AC于P，此时MP+NP有最小值，最小值为M′N 的长．∵菱形ABCD关于AC对称，M是AB边上的中点，∴M′是AD的中点，又∵N是BC边上的中点，∴AM′∥BN，AM′=BN，∴四边形ABNM′是平行四边形，∴M′N=AB=1，∴MP+NP=M′N=1，即MP+NP的最小值为1，故选：B．二．填空题（共7小题）11．（2018•陕西）如图，在正五边形ABCDE中，AC与BE相交于点F，则∠AFE的度数为72°．解：∵五边形ABCDE是正五边形，∴∠EAB=∠ABC==108°，∵BA=BC，∴∠BAC=∠BCA=36°，同理∠ABE=36°，∴∠AFE=∠ABF+∠BAF=36°+36°=72°，故答案为：72°．12．（2018•兰州）如图，M、N是正方形ABCD的边CD上的两个动点，满足AM=BN，连接AC交BN于点E，连接DE交AM于点F，连接CF，若正方形的边长为6，则线段CF的最小值是3﹣3．解：如图，在正方形ABCD中，AD=BC=CD，∠ADC=∠BCD，∠DCE=∠BCE，在Rt△ADM和Rt△BCN中，，∴Rt△ADM≌Rt△BCN（HL），∴∠DAM=∠CBN，在△DCE和△BCE中，，∴△DCE≌△BCE（SAS），∴∠CDE=∠CBE∴∠DCM=∠CDE，∵∠ADF+∠CDE=∠ADC=90°，∴∠DAM+∠ADF=90°，∴∠AFD=180°﹣90°=90°，取AD的中点O，连接OF、OC，则OF=DO=AD=3，在Rt△ODC中，OC==3根据三角形的三边关系，OF+CF＞OC，∴当O、F、C三点共线时，CF的长度最小，最小值=OC﹣OF=3﹣3．故答案为：3﹣3．13．（2018•青海）如图，四边形ABCD与四边形EFGH位似，其位似中心为点O，且=，则=．解：∵四边形ABCD与四边形EFGH位似，其位似中心为点O，且=，∴=，则==．故答案为：．14．（2018•陕西）如图，点O是▱ABCD的对称中心，AD＞AB，E、F是AB边上的点，且EF=AB；G、H是BC边上的点，且GH=BC，若S1，S2分别表示△EOF和△GOH的面积，则S1与S2之间的等量关系是=．解：∵==，==，∴S1=S△AOB，S2=S△BOC．∵点O是▱ABCD的对称中心，=S△BOC=S▱ABCD，∴S△AOB∴==．即S1与S2之间的等量关系是=．故答案为=．15．（2018•白银）如图，分别以等边三角形的每个顶点为圆心、以边长为半径，在另两个顶点间作一段圆弧，三段圆弧围成的曲边三角形称为勒洛三角形．若等边三角形的边长为a，则勒洛三角形的周长为πa．解：如图．∵△ABC是等边三角形，∴∠A=∠B=∠C=60°，AB=BC=CA=a，∴的长=的长=的长==，∴勒洛三角形的周长为×3=πa．故答案为πa．16．（2018•青海）如图，用一个半径为20cm，面积为150πcm2的扇形铁皮，制作一个无底的圆锥（不计接头损耗），则圆锥的底面半径r为7.5cm．解：解：设铁皮扇形的半径和弧长分别为R、l，圆锥形容器底面半径为r，则由题意得R=20，由Rl=150π得l=15π；由2πr=15π得r=7.5cm．故答案是：7.5cm．17．（2018•新疆）如图，△ABC是⊙O的内接正三角形，⊙O的半径为2，则图中阴影部分的面积是．解：∵△ABC是等边三角形，∴∠C=60°，根据圆周角定理可得∠AOB=2∠C=120°，∴阴影部分的面积是=π，故答案为：三．解答题（共15小题）18．（2018•陕西）如图，已知：在正方形ABCD中，M是BC边上一定点，连接AM．请用尺规作图法，在AM上作一点P，使△DPA∽△ABM．（不写作法，保留作图痕迹）解：如图所示，点P即为所求：∵DP⊥AM，∴∠APD=∠ABM=90°，∵∠BAM+∠PAD=90°，∠PAD+∠ADP=90°，∴∠BAM=∠ADP，∴△DPA∽△ABM．19．（2018•宁夏）已知：AB为⊙O的直径，延长AB到点P，过点P作圆O的切线，切点为C，连接AC，且AC=CP．（1）求∠P的度数；（2）若点D是弧AB的中点，连接CD交AB于点E，且DE•DC=20，求⊙O的面积．（π取3.14）解：（1）连接OC，∵PC为⊙O的切线，∴∠OCP=90°，即∠2+∠P=90°，∵OA=OC，∴∠CAO=∠1，∵AC=CP，∴∠P=∠CAO，又∵∠2是△AOC的一个外角，∴∠2=2∠CAO=2∠P，∴2∠P+∠P=90°，∴∠P=30°；（2）连接AD，∵D为的中点，∴∠ACD=∠DAE，∴△ACD∽△EAD，∴=，即AD2=DC•DE，∵DC•DE=20，∴AD=2，∵=，∴AD=BD，∵AB是⊙O的直径，∴Rt△ADB为等腰直角三角形，∴AB=2，∴OA=AB=，=π•OA2=10π=31.4．∴S⊙O20．（2018•陕西）如图，在Rt△ABC中，∠ACB=90°，以斜边AB上的中线CD为直径作⊙O，分别与AC、BC交于点M、N．（1）过点N作⊙O的切线NE与AB相交于点E，求证：NE⊥AB；（2）连接MD，求证：MD=NB．证明：（1）连接ON，如图，∵CD为斜边AB上的中线，∴CD=AD=DB，∴∠1=∠B，∵OC=ON，∴∠1=∠2，∴∠2=∠B，∴ON∥DB，∵NE为切线，∴ON⊥NE，∴NE⊥AB；（2）连接DN，如图，∵CD为直径，∴∠CMD=∠CND=90°，而∠MCB=90°，∴四边形CMDN为矩形，∴DM=CN，∵DN⊥BC，∠1=∠B，∴CN=BN，∴MD=NB．21．（2018•宁夏）已知点E为正方形ABCD的边AD上一点，连接BE，过点C作CN⊥BE，垂足为M，交AB于点N．（1）求证：△ABE≌△BCN；（2）若N为AB的中点，求tan∠ABE．（1）证明：∵四边形ABCD为正方形∴AB=BC，∠A=∠CBN=90°，∠1+∠2=90°∵CM⊥BE，∴∠2+∠3=90°∴∠1=∠3在△ABE和△BCN中∴△ABE≌△BCN（ASA）；（2）∵N为AB中点，∴BN=AB又∵△ABE≌△BCN，∴AE=BN=AB在Rt△ABE中，tan∠ABE═．22．（2018•兰州）如图，在△ABC中，过点C作CD∥AB，E是AC的中点，连接DE并延长，交AB于点F，交CB的延长线于点G，连接AD，CF．（1）求证：四边形AFCD是平行四边形．（2）若GB=3，BC=6，BF=，求AB的长．解：（1）∵E是AC的中点，∴AE=CE，∵AB∥CD，∴∠AFE=∠CDE，在△AEF和△CED中，∵，∴△AEF≌△CED（AAS），∴AF=CD，又AB∥CD，即AF∥CD，∴四边形AFCD是平行四边形；（2）∵AB∥CD，∴△GBF∽△GCD，∴=，即=，解得：CD=，∵四边形AFCD是平行四边形，∴AF=CD=，∴AB=AF+BF=+=6．23．（2018•白银）已知矩形ABCD中，E是AD边上的一个动点，点F，G，H分别是BC，BE，CE的中点．（1）求证：△BGF≌△FHC；（2）设AD=a，当四边形EGFH是正方形时，求矩形ABCD的面积．解：（1）∵点F，G，H分别是BC，BE，CE的中点，∴FH∥BE，FH=BE，FH=BG，∴∠CFH=∠CBG，∵BF=CF，∴△BGF≌△FHC，（2）当四边形EGFH是正方形时，可得：EF⊥GH且EF=GH，∵在△BEC中，点，H分别是BE，CE的中点，∴GH=，且GH∥BC，∴EF⊥BC，∵AD∥BC，AB⊥BC，∴AB=EF=GH=a，∴矩形ABCD的面积=．24．（2018•陕西）问题提出（1）如图①，在△ABC中，∠A=120°，AB=AC=5，则△ABC的外接圆半径R的值为5．问题探究（2）如图②，⊙O的半径为13，弦AB=24，M是AB的中点，P是⊙O上一动点，求PM 的最大值．问题解决（3）如图③所示，AB、AC、是某新区的三条规划路，其中AB=6km，AC=3km，∠BAC=60°，所对的圆心角为60°，新区管委会想在路边建物资总站点P，在AB，AC路边分别建物资分站点E、F，也就是，分别在、线段AB和AC上选取点P、E、F．由于总站工作人员每天都要将物资在各物资站点间按P→E→F→P的路径进行运输，因此，要在各物资站点之间规划道路PE、EF和FP．为了快捷、环保和节约成本．要使得线段PE、EF、FP 之和最短，试求PE+EF+FP的最小值．（各物资站点与所在道路之间的距离、路宽均忽略不计）解：（1）设O是△ABC的外接圆的圆心，∴OA=OB=OC，∵∠A=120°，AB=AC=5，∴△ABO是等边三角形，∴AB=OA=OB=5，（2）当PM⊥AB时，此时PM最大，连接OA，由垂径定理可知：AM=AB=12，∵OA=13，∴由勾股定理可知：OM=5，∴PM=OM+OP=18，（3）设连接AP，OP分别以AB、AC所在直线为对称轴，作出P关于AB的对称点为M，P关于AC的对称点为N，连接MN，交AB于点E，交AC于点F，连接PE、PF，∴AM=AP=AN，∵∠MAB=∠PAB，∠NAC=∠PAC，∴∠BAC=∠PAB+∠PAC=∠MAB+∠NAC=60°，∴∠MAN=120°∴M、P、N在以A为圆心，AP为半径的圆上，设AP=r，易求得：MN=r，∵PE=ME，PF=FN，∴PE+EF+PF=ME+EF+FN=MN=r，∴当AP最小时，PE+EF+PF可取得最小值，∵AP+OP≥OA，∴AP≥OA﹣OP，即点P在OA上时，AP可取得最小值，设AB的中点为Q，∴AQ=AC=3，∵∠BAC=60°，∴AQ=QC=AC=BQ=3，∴∠ABC=∠QCB=30°，∴∠ACB=90°，∴由勾股定理可知：BC=3，∵∠BOC=60°，OB=OC=3，∴△OBC是等边三角形，∴∠OBC=60°，∴∠ABO=90°∴由勾股定理可知：OA=3，∵OP=OB=3，∴AP=r=OA﹣OP=3﹣3，∴PE+EF+PF=MN=r=3﹣9∴PE+EF+PF的最小值为（3﹣9）km．25．（2018•兰州）如图，AB为⊙O的直径，C为⊙O上一点，D为BA延长线上一点，∠ACD=∠B．（1）求证：DC为⊙O的切线；（2）线段DF分别交AC，BC于点E，F且∠CEF=45°，⊙O的半径为5，sinB=，求CF 的长．（1）证明：连接OC，∵AB为⊙O的直径，∴∠ACB=∠BCO+∠OCA=90°，∵OB=OC，∴∠B=∠BCO，∵∠ACD=∠B，∴∠ACD=∠BCO，∴∠ACD+∠OCA=90°，即∠OCD=90°，∴DC为⊙O的切线；（2）解：Rt△ACB中，AB=10，sinB=，∴AC=6，BC=8，∵∠ACD=∠B，∠ADC=∠CDB，∴△CAD∽△BCD，∴，设AD=3x，CD=4x，Rt△OCD中，OC2+CD2=OD2，52+（4x）2=（5+3x）2，x=0（舍）或，∵∠CEF=45°，∠ACB=90°，∴CE=CF，设CF=a，∵∠CEF=∠ACD+∠CDE，∠CFE=∠B+∠BDF，∴∠CDE=∠BDF，∵∠ACD=∠B，∴△CED∽△BFD，∴，∴，a=，∴CF=．26．（2018•青海）如图，在平行四边形ABCD中，E为AB边上的中点，连接DE并延长，交CB的延长线于点F．（1）求证：AD=BF；（2）若平行四边形ABCD的面积为32，试求四边形EBCD的面积．解：（1）∵E是AB边上的中点，∴AE=BE．∵AD∥BC，∴∠ADE=∠F．在△ADE和△BFE中，∠ADE=∠F，∠DEA=∠FEB，AE=BE，∴△ADE≌△BFE．∴AD=BF．（2）过点D作DM⊥AB与M，则DM同时也是平行四边形ABCD的高．=•AB•DM=AB•DM=×32=8，∴S△AED=32﹣8=24．∴S四边形EBCD27．（2018•白银）如图，点O是△ABC的边AB上一点，⊙O与边AC相切于点E，与边BC，AB分别相交于点D，F，且DE=EF．（1）求证：∠C=90°；（2）当BC=3，sinA=时，求AF的长．解：（1）连接OE，BE，∵DE=EF，∴∴∠OBE=∠DBE∵OE=OB，∴∠OEB=∠OBE∴∠OEB=∠DBE，∴OE∥BC∵⊙O与边AC相切于点E，∴OE⊥AC∴BC⊥AC∴∠C=90°（2）在△ABC，∠C=90°，BC=3，sinA=∴AB=5，设⊙O的半径为r，则AO=5﹣r，在Rt△AOE中，sinA===∴r=∴AF=5﹣2×=28．（2018•青海）如图△ABC内接于⊙O，∠B=60°，CD是⊙O的直径，点P是CD延长线上一点，且AP=AC．（2）若PD=，求⊙O的直径．解：（1）证明：连接OA，∵∠B=60°，∴∠AOC=2∠B=120°，又∵OA=OC，∴∠OAC=∠OCA=30°，又∵AP=AC，∴∠P=∠ACP=30°，∴∠OAP=∠AOC﹣∠P=90°，∴OA⊥PA，∴PA是⊙O的切线．（2）在Rt△OAP中，∵∠P=30°，∴PO=2OA=OD+PD，又∵OA=OD，∴PD=OA，∵PD=，∴2OA=2PD=2．∴⊙O的直径为2．29．（2018•新疆）如图，▱ABCD的对角线AC，BD相交于点O．E，F是AC上的两点，并且AE=CF，连接DE，BF．（2）若BD=EF，连接EB，DF，判断四边形EBFD的形状，并说明理由．（1）证明：∵四边形ABCD是平行四边形，∴OA=OC，OB=OD，∵AE=CF，∴OE=OF，在△DEO和△BOF中，∴△DOE≌△BOF．（2）解：结论：四边形EBFD是矩形．理由：∵OD=OB，OE=OF，∴四边形EBFD是平行四边形，∵BD=EF，∴四边形EBFD是矩形．30．（2018•青海）请认真阅读下面的数学小探究系列，完成所提出的问题：（1）探究1：如图1，在等腰直角三角形ABC中，∠ACB=90°，BC=a，将边AB绕点B顺时针旋转90°得到线段BD，连接CD．求证：△BCD的面积为a2．（提示：过点D作BC 边上的高DE，可证△ABC≌△BDE）（2）探究2：如图2，在一般的Rt△ABC中，∠ACB=90°，BC=a，将边AB绕点B顺时针旋转90°得到线段BD，连接CD．请用含a的式子表示△BCD的面积，并说明理由．（3）探究3：如图3，在等腰三角形ABC中，AB=AC，BC=a，将边AB绕点B顺时针旋转90°得到线段BD，连接CD．试探究用含a的式子表示△BCD的面积，要有探究过程．解：（1）如图1，过点D作DE⊥CB交CB的延长线于E，∴∠BED=∠ACB=90°，由旋转知，AB=AD，∠ABD=90°，∴∠ABC+∠DBE=90°，∵∠A+∠ABC=90°，∴∠A=∠DBE，在△ABC和△BDE中，，∴△ABC≌△BDE（AAS）∴BC=DE=a．=BC•DE∵S△BCD=；∴S△BCD（2）△BCD的面积为．理由：如图2，过点D作BC的垂线，与BC的延长线交于点E．∴∠BED=∠ACB=90°，∵线段AB绕点B顺时针旋转90°得到线段BE，∴AB=BD，∠ABD=90°．∴∠ABC+∠DBE=90°．∵∠A+∠ABC=90°．∴∠A=∠DBE．在△ABC和△BDE中，，∴△ABC≌△BDE（AAS）∴BC=DE=a．=BC•DE∵S△BCD=；∴S△BCD（3）如图3，过点A作AF⊥BC与F，过点D作DE⊥BC的延长线于点E，∴∠AFB=∠E=90°，BF=BC=a．∴∠FAB+∠ABF=90°．∵∠ABD=90°，∴∠ABF+∠DBE=90°，∴∠FAB=∠EBD．∵线段BD是由线段AB旋转得到的，∴AB=BD．在△AFB和△BED中，，∴△AFB≌△BED（AAS），∴BF=DE=a．∵S△BCD=BC•DE=•a•a=a2．∴△BCD的面积为．31．（2018•宁夏）空间任意选定一点O，以点O为端点，作三条互相垂直的射线ox、oy、oz．这三条互相垂直的射线分别称作x轴、y轴、z轴，统称为坐标轴，它们的方向分别为ox（水平向前）、oy（水平向右）、oz（竖直向上）方向，这样的坐标系称为空间直角坐标系．将相邻三个面的面积记为S1、S2、S3，且S1＜S2＜S3的小长方体称为单位长方体，现将若干个单位长方体在空间直角坐标系内进行码放，要求码放时将单位长方体S1所在的面与x轴垂直，S2所在的面与y轴垂直，S3所在的面与z轴垂直，如图1所示．若将x轴方向表示的量称为几何体码放的排数，y轴方向表示的量称为几何体码放的列数，z轴方向表示的量称为几何体码放的层数；如图2是由若干个单位长方体在空间直角坐标内码放的一个几何体，其中这个几何体共码放了1排2列6层，用有序数组记作（1，2，6），如图3的几何体码放了2排3列4层，用有序数组记作（2，3，4）．这样我们就可用每一个有序数组（x，y，z）表示一种几何体的码放方式．（1）如图4是由若干个单位长方体码放的一个几何体的三视图，则这种码放方式的有序数组为（2，3，2），组成这个几何体的单位长方体的个数为12个；（2）对有序数组性质的理解，下列说法正确的是①②⑤；（只填序号）①每一个有序数组（x，y，z）表示一种几何体的码放方式．②有序数组中x、y、z的乘积就表示几何体中单位长方体的个数．③有序数组不同，所表示几何体的单位长方体个数不同．④不同的有序数组所表示的几何体的体积不同．⑤有序数组中x、y、z每两个乘积的2倍可分别确定几何体表面上S1、S2、S3的个数．（3）为了进一步探究有序数组（x，y，z）的几何体的表面积公式S（x，y，z），某同学针对若干个单位长方体进行码放，制作了下列表格：根据以上规律，请写出有序数组（x，y，z）的几何体表面积计算公式S（x，y，z）；（用x、y、z、S1、S2、S3表示）（4）当S1=2，S2=3，S3=4时，对由12个单位长方体码放的几何体进行打包，为了节约外包装材料，对12个单位长方体码放的几何体表面积最小的规律进行探究，根据探究的结果请写出使几何体表面积最小的有序数组，并用几何体表面积公式求出这个最小面积．（缝隙不计）解：（1）这种码放方式的有序数组为（2，3，2），组成这个几何体的单位长方体的个数为2×3×2=12个，故答案为（2，3，2），12；（2）正确的有①②⑤．故答案为①②⑤；（3）S（x，y，z）=2yzS1+2xzS2+2xyS3=2（yzS1+xzS2+xyS3）．（4）当S1=2，S2=3，S3=4时S（x，y，z）=2（yzS1+xzS2+xyS3）=2（2yz+3xz+4xy）欲使S（x，y，z）的值最小，不难看出x、y、z应满足x≤y≤z（x、y、z为正整数）．在由12个单位长方体码放的几何体中，满足条件的有序数组为（1，1，12），（1，2，6），（1，3，4），（2，2，3）．而S（1，1，12）=128，S（1，2，6）=100，S（1，3，4）=96，S（2，2，3）=92所以，由12个单位长方体码放的几何体表面积最小的有序数组为：（2，2，3），最小面积为S（2，2，3）=92．。

2018全国各地中考数学压轴题精选(含详细答案)

9．（厦门）如图，在直角梯形 OABD 中，DB∥OA，∠OAB=90°，点 O 为坐标原点，点 A 在 x 轴的正半轴上，对角线 OB，AD 相交于点 M．OA=2，AB=2 （1）求 OB 和 OM 的值；（2）求直线 OD 所对应的函数关系式；，BM：MO=1上（P 不与点 O，B 重合），经过点 A 和点 P 的直线交梯形 OABD 的边于点 E（E 异于点 A），设 OP=t，梯形 OABD 被夹在∠OAE 内的部分的面积为 S，求 S 关于 t 的函数关系式．
6
①求 b 与 k 的函数关系式； ②求折痕 EF 的长（用含 k 的代数式表示），并写出 k 的取值范围．
17．（厦门）已知点 P（m，n）（m＞0）在直线 y=x+b（0＜b＜3）上，点 A、B 在 x 轴上（点 A 在点 B 的左边），线段 AB 的长度为 b，设△PAB 的面积为 S，且 S= b2+ b．（1）若 b= ，求 S 的值；（2）若 S=4，求 n 的值；（3）若直线 y=x+b（0＜b＜3）与 y 轴交于点 C，△PAB 是等腰三角形，当 CA∥PB 时，求 b 的值．（乌鲁木齐）如图 1，在平面直角坐标系中，点 A 的坐标为（0，，点 B 坐标为， 18． O 为坐标原点， 6） BC∥y 轴且与 x 轴交于点 C，直线 OB 与直线 AC 相交于点 P．（1）求点 P 的坐标；（2）若以点 O 为圆心，OP 的长为半径作⊙O（如图 2），求证：直线 AC 与⊙O 相切于点 P；（3）过点 B 作 BD∥x 轴与 y 轴相交于点 D，以点 O 为圆心，r 为半径作⊙O，使点 D 在⊙O 内，点 C 在⊙O 外；以点 B 为圆心，R 为半径作⊙B，若⊙O 与⊙B 相切，试分别求出 r，R 的取值范围．

2018年全国各地中考数学压轴题汇编：几何综合(华北东北专版)(解析卷)

2018年全国各地中考数学压轴题汇编（华北东北专版）几何综合参考答案与试题解析1．（2018•北京）如图，在四边形ABCD中，AB∥DC，AB=AD，对角线AC，BD交于点O，AC平分∠BAD，过点C作CE⊥AB交AB的延长线于点E，连接OE．（1）求证：四边形ABCD是菱形；（2）若AB=，BD=2，求OE的长．解：（1）∵AB∥CD，∴∠OAB=∠DCA，∵AC为∠DAB的平分线，∴∠OAB=∠DAC，∴∠DCA=∠DAC，∴CD=AD=AB，∵AB∥CD，∴四边形ABCD是平行四边形，∵AD=AB，∴▱ABCD是菱形；（2）∵四边形ABCD是菱形，∴OA=OC，BD⊥AC，∵CE⊥AB，∴OE=OA=OC，∵BD=2，∴OB=BD=1，在Rt△AOB中，AB=，OB=1，∴OA==2，∴OE=OA=2．2．（2018•河北）如图，点A在数轴上对应的数为26，以原点O为圆心，OA为半径作优弧，使点B在O右下方，且tan∠AOB=，在优弧上任取一点P，且能过P作直线l∥OB交数轴于点Q，设Q在数轴上对应的数为x，连接OP．（1）若优弧上一段的长为13π，求∠AOP的度数及x的值；（2）求x的最小值，并指出此时直线l与所在圆的位置关系；（3）若线段PQ的长为12.5，直接写出这时x的值．解：（1）如图1中，由=13π，解得n=90°，∴∠POQ=90°，∵PQ∥OB，∴∠PQO=∠BOQ，∴tan∠PQO=tan∠QOB==，∴OQ=，∴x=．（2）如图当直线PQ与⊙O相切时时，x的值最小．在Rt△OPQ中，OQ=OP÷=32.5，此时x的值为﹣32.5．（3）分三种情况：①如图2中，作OH⊥PQ于H，设OH=4k，QH=3k．在Rt△OPH中，∵OP2=OH2+PH2，∴262=（4k）2+（12.5﹣3k）2，整理得：k2﹣3k﹣20.79=0，解得k=6.3或﹣3.3（舍弃），∴OQ=5k=31.5．此时x的值为31.5．②如图3中，作OH⊥PQ交PQ的延长线于H．设OH=4k，QH=3k．在Rt△在Rt△OPH中，∵OP2=OH2+PH2，∴262=（4k）2+（12.5+3k）2，整理得：k2+3k﹣20.79=0，解得k=﹣6.3（舍弃）或3.3，∴OQ=5k=16.5，此时x的值为﹣16.5．③如图4中，作OH⊥PQ于H，设OH=4k，AH=3k．在Rt△OPH中，∵OP2=OH2+PH2，∴262=（4k）2+（12.5﹣3k）2，整理得：k2﹣3k﹣20.79=0，解得k=6.3或﹣3.3（舍弃），∴OQ=5k=31.5不合题意舍弃．此时x的值为﹣31.5．综上所述，满足条件的x的值为﹣16.5或31.5或﹣31.5．3．（2018•北京）如图，AB是⊙O的直径，过⊙O外一点P作⊙O的两条切线PC，PD，切点分别为C，D，连接OP，CD．（1）求证：OP⊥CD；（2）连接AD，BC，若∠DAB=50°，∠CBA=70°，OA=2，求OP的长．解：（1）连接OC，OD，∴OC=OD，∵PD，PC是⊙O的切线，∵∠ODP=∠OCP=90°，在Rt△ODP和Rt△OCP中，，∴Rt△ODP≌Rt△OCP，∴∠DOP=∠COP，∵OD=OC，∴OP⊥CD；（2）如图，连接OD，OC，∴OA=OD=OC=OB=2，∴∠ADO=∠DAO=50°，∠BCO=∠CBO=70°，∴∠AOD=80°，∠BOC=40°，∴∠COD=60°，∵OD=OC，∴△COD是等边三角形，由（1）知，∠DOP=∠COP=30°，在Rt△ODP中，OP==．4．（2018•天津）在平面直角坐标系中，四边形AOBC是矩形，点O（0，0），点A（5，0），点B（0，3）．以点A为中心，顺时针旋转矩形AOBC，得到矩形ADEF，点O，B，C的对应点分别为D，E，F．（Ⅰ）如图①，当点D落在BC边上时，求点D的坐标；（Ⅱ）如图②，当点D落在线段BE上时，AD与BC交于点H．①求证△ADB≌△AOB；②求点H的坐标．（Ⅲ）记K为矩形AOBC对角线的交点，S为△KDE的面积，求S的取值范围（直接写出结果即可）．解：（Ⅰ）如图①中，∵A（5，0），B（0，3），∴OA=5，OB=3，∵四边形AOBC是矩形，∴AC=OB=3，OA=BC=5，∠OBC=∠C=90°，∵矩形ADEF是由矩形AOBC旋转得到，∴AD=AO=5，在Rt△ADC中，CD==4，∴BD=BC﹣CD=1，∴D（1，3）．（Ⅱ）①如图②中，由四边形ADEF是矩形，得到∠ADE=90°，∵点D在线段BE上，∴∠ADB=90°，由（Ⅰ）可知，AD=AO，又AB=AB，∠AOB=90°，∴Rt△ADB≌Rt△AOB（HL）．②如图②中，由△ADB≌△AOB，得到∠BAD=∠BAO，又在矩形AOBC中，OA∥BC，∴∠CBA=∠OAB，∴∠BAD=∠CBA，∴BH=AH，设AH=BH=m，则HC=BC﹣BH=5﹣m，在Rt△AHC中，∵AH2=HC2+AC2，∴m2=32+（5﹣m）2，∴m=，∴BH=，∴H（，3）．（Ⅲ）如图③中，当点D在线段BK上时，△DEK的面积最小，最小值=•DE•DK=×3×（5﹣）=，当点D在BA的延长线上时，△D′E′K的面积最大，最大面积=×D′E′×KD′=×3×（5+）=．综上所述，≤S≤．5．（2018•北京）如图，在正方形ABCD中，E是边AB上的一动点（不与点A、B重合），连接DE，点A关于直线DE的对称点为F，连接EF并延长交BC于点G，连接DG，过点E作EH⊥DE交DG的延长线于点H，连接BH．（1）求证：GF=GC；（2）用等式表示线段BH与AE的数量关系，并证明．证明：（1）如图1，连接DF，∵四边形ABCD是正方形，∴DA=DC，∠A=∠C=90°，∵点A关于直线DE的对称点为F，∴△ADE≌△FDE，∴DA=DF=DC，∠DFE=∠A=90°，∴∠DFG=90°，在Rt△DFG和Rt△DCG中，∵，∴Rt△DFG≌Rt△DCG（HL），∴GF=GC；（2）BH=AE，理由是：证法一：如图2，在线段AD上截取AM，使AM=AE，∵AD=AB，∴DM=BE，由（1）知：∠1=∠2，∠3=∠4，∵∠ADC=90°，∴∠1+∠2+∠3+∠4=90°，∴2∠2+2∠3=90°，∴∠2+∠3=45°，即∠EDG=45°，∵EH⊥DE，∴∠DEH=90°，△DEH是等腰直角三角形，∴∠AED+∠BEH=∠AED+∠1=90°，DE=EH，∴∠1=∠BEH，在△DME和△EBH中，∵，∴△DME≌△EBH，∴EM=BH，Rt△AEM中，∠A=90°，AM=AE，∴EM=AE，∴BH=AE；证法二：如图3，过点H作HN⊥AB于N，∴∠ENH=90°，由方法一可知：DE=EH，∠1=∠NEH，在△DAE和△ENH中，∵，∴△DAE≌△ENH，∴AE=HN，AD=EN，∵AD=AB，∴AB=EN=AE+BE=BE+BN，∴AE=BN=HN，∴△BNH是等腰直角三角形，∴BH=HN=AE．6．（2018•天津）已知AB是⊙O的直径，弦CD与AB相交，∠BAC=38°，（I）如图①，若D为的中点，求∠ABC和∠ABD的大小；（Ⅱ）如图②，过点D作⊙O的切线，与AB的延长线交于点P，若DP∥AC，求∠OCD 的大小．解：（Ⅰ）∵AB是⊙O的直径，弦CD与AB相交，∠BAC=38°，∴∠ACB=90°，∴∠ABC=∠ACB﹣∠BAC=90°﹣38°=52°，∵D为的中点，∠AOB=180°，∴∠AOD=90°，∴∠ABD=45°；（Ⅱ）连接OD，∵DP切⊙O于点D，∴OD⊥DP，即∠ODP=90°，由DP∥AC，又∠BAC=38°，∴∠P=∠BAC=38°，∵∠AOD是△ODP的一个外角，∴∠AOD=∠P+∠ODP=128°，∴∠ACD=64°，∵OC=OA，∠BAC=38°，∴∠OCA=∠BAC=38°，∴∠OCD=∠ACD﹣∠OCA=64°﹣38°=26°．7．（2018•山西）请阅读下列材料，并完成相应的任务：在数学中，利用图形在变化过程中的不变性质，常常可以找到解决问题的办消去．著名美籍匈牙利数学家波利亚在他所著的《数学的发现》一书中有这样一个例子：请问如何在一个三角形ABC的AC和BC两边上分别取一点X和Y，使得AX=BY=XY．（如图）解决这个问题的操作步骤如下：第一步，在CA上作出一点D，使得CD=CB，连接BD．第二步，在CB上取一点Y'，作Y'Z'∥CA，交BD于点Z'，并在AB上取一点A'，使Z'A'=Y'Z'．第三步，过点A作AZ∥A'Z'，交BD于点Z．第四步，过点Z作ZY∥AC，交BC于点Y，再过点Y作YX∥ZA，交AC于点X．则有AX=BY=XY．下面是该结论的部分证明：证明：∵AZ∥A'Z'，∴∠BA'Z'=∠BAZ，又∵∠A'BZ'=∠ABZ．∴△BA'Z'～△BAZ．∴．同理可得．∴．∵Z'A'=Y'Z'，∴ZA=YZ．任务：（1）请根据上面的操作步骤及部分证明过程，判断四边形AXYZ的形状，并加以证明；（2）请再仔细阅读上面的操作步骤，在（1）的基础上完成AX=BY=XY的证明过程；而确定了点Z，Y的位置，这里运用了下面一种图形的变化是D（或位似）．A．平移B．旋转C．轴对称D．位似解：（1）四边形AXYZ是菱形．证明：∵ZY∥AC，YX∥ZA，∴四边形AXYZ是平行四边形．∵ZA=YZ，∴平行四边形AXYZ是菱形．（2）证明：∵CD=CB，∴∠1=∠3．∵ZY∥AC，∴∠1=∠2．∴∠2=∠3．∴YB=YZ．∵四边形AXYZ是菱形，∴AX=XY=YZ．∴AX=BY=XY．（3）通过作平行线把四边形BA'Z'Y'放大得到四边形BAZY，从而确定了点Z，Y的位置，此时四边形BA'Z'Y'∽四边形BAZY，所以该变换形式是位似变换．故答案是：D（或位似）．8．（2018•北京）对于平面直角坐标系xOy中的图形M，N，给出如下定义：P为图形M 上任意一点，Q为图形N上任意一点，如果P，Q两点间的距离有最小值，那么称这个最小值为图形M，N间的“闭距离“，记作d（M，N）．已知点A（﹣2，6），B（﹣2，﹣2），C（6，﹣2）．（1）求d（点O，△ABC）；（2）记函数y=kx（﹣1≤x≤1，k≠0）的图象为图形G．若d（G，△ABC）=1，直接写（3）⊙T的圆心为T（t，0），半径为1．若d（⊙T，△ABC）=1，直接写出t的取值范围．解：（1）如图所示，点O到△ABC的距离的最小值为2，∴d（点O，△ABC）=2；（2）y=kx（k≠0）经过原点，在﹣1≤x≤1范围内，函数图象为线段，当y=kx（﹣1≤x≤1，k≠0）经过（1，﹣1）时，k=﹣1，此时d（G，△ABC）=1；当y=kx（﹣1≤x≤1，k≠0）经过（﹣1，﹣1）时，k=1，此时d（G，△ABC）=1；∴﹣1≤k≤1，∵k≠0，∴﹣1≤k≤1且k≠0；（3）⊙T与△ABC的位置关系分三种情况：①当⊙T在△ABC的左侧时，由d（⊙T，△ABC）=1知此时t=﹣4；②当⊙T在△ABC内部时，当点T与原点重合时，d（⊙T，△ABC）=1，知此时t=0；当点T位于T3位置时，由d（⊙T，△ABC）=1知T3M=2，∵AB=BC=8、∠ABC=90°，∴∠C=∠T3DM=45°，则T3D===2，∴t=4﹣2，故此时0≤t≤4﹣2；∵∠T4DC=∠C=45°，∴T4D===2，∴t=4+2；综上，t=﹣4或0≤t≤4﹣2或t=4+2．9．（2018•包头）如图，在Rt△ACB中，∠ACB=90°，以点A为圆心，AC长为半径的圆交AB于点D，BA的延长线交⊙A于点E，连接CE，CD，F是⊙A上一点，点F与点C位于BE两侧，且∠FAB=∠ABC，连接BF．（1）求证：∠BCD=∠BEC；（2）若BC=2，BD=1，求CE的长及sin∠ABF的值．解：（1）∵∠ACB=90°，∴∠BCD+∠ACD=90°，∵DE是⊙A的直径，∴∠DCE=90°，∴∠BEC+∠CDE=90°，∵AD=AC，∴∠CDE=∠ACD，∴∠BCD=∠BEC，（2）∵∠BCD=∠BEC，∠EBC=∠EBC，∴△BDC∽△BCE，∴，∵BC=2，BD=1，∴BE=4，EC=2CD，∴DE=BE﹣BD=3，在Rt△DCE中，DE2=CD2+CE2=9，过点F作FM⊥AB于M，∵∠FAB=∠ABC，∠FMA=∠ACB=90°，∴△AFM∽△BAC，∴，∵DE=3，∴AD=AF=AC=，AB=，∴FM=，过点F作FN⊥BC于N，∴∠FNC=90°，∵∠FAB=∠ABC，∴FA∥BC，∴∠FAC=∠ACB=90°，∴四边形FNCA是矩形，∴FN=AC=，NC=AF=，∴BN=，在Rt△FBN中，BF=，在Rt△FBM中，sin∠ABF=．10．（2018•山西）综合与实践问题情境：在数学活动课上，老师出示了这样一个问题：如图1，在矩形ABCD中，AD=2AB，E是AB延长线上一点，且BE=AB，连接DE，交BC于点M，以DE为一边在DE的左下方作正方形DEFG，连接AM．试判断线段AM与DE的位置关系．探究展示：勤奋小组发现，AM垂直平分DE，并展示了如下的证明方法：证明：∵BE=AB，∴AE=2AB．∵四边形ABCD是矩形，∴AD∥BC．∴．（依据1）∵BE=AB，∴．∴EM=DM．即AM是△ADE的DE边上的中线，又∵AD=AE，∴AM⊥DE．（依据2）∴AM垂直平分DE．反思交流：（1）①上述证明过程中的“依据1”“依据2”分别是指什么？②试判断图1中的点A是否在线段GF的垂直平分线上，请直接回答，不必证明；（2）创新小组受到勤奋小组的启发，继续进行探究，如图2，连接CE，以CE为一边在CE的左下方作正方形CEFG，发现点G在线段BC的垂直平分线上，请你给出证明；探索发现：（3）如图3，连接CE，以CE为一边在CE的右上方作正方形CEFG，可以发现点C，点B 都在线段AE的垂直平分线上，除此之外，请观察矩形ABCD和正方形CEFG的顶点与边，你还能发现哪个顶点在哪条边的垂直平分线上，请写出一个你发现的结论，并加以证明．解：（1）①依据1：两条直线被一组平行线所截，所得的对应线段成比例（或平行线分线段成比例）．依据2：等腰三角形顶角的平分线，底边上的中线及底边上的高互相重合（或等腰三角形的“三线合一”）．②答：点A在线段GF的垂直平分线上．理由：由问题情景知，AM⊥DE，∵四边形DEFG是正方形，∴DE∥FG，（2）证明：过点G作GH⊥BC于点H，∵四边形ABCD是矩形，点E在AB的延长线上，∴∠CBE=∠ABC=∠GHC=90°，∴∠BCE+∠BEC=90°．∵四边形CEFG为正方形，∴CG=CE，∠GCE=90°，∴∠BCE+∠BCG=90°．∴∠2BEC=∠BCG．∴△GHC≌△CBE．∴HC=BE，∵四边形ABCD是矩形，∴AD=BC．∵AD=2AB，BE=AB，∴BC=2BE=2HC，∴HC=BH．∴GH垂直平分BC．∴点G在BC的垂直平分线上．（3）答：点F在BC边的垂直平分线上（或点F在AD边的垂直平分线上）．证法一：过点F作FM⊥BC于点M，过点E作EN⊥FM于点N．∴∠BMN=∠ENM=∠ENF=90°．∵四边形ABCD是矩形，点E在AB的延长线上，∴∠CBE=∠ABC=90°，∴四边形BENM为矩形．∴BM=EN，∠BEN=90°．∴∠1+∠2=90°．∵四边形CEFG为正方形，∴EF=EC，∠CEF=90°．∴∠2+∠3=90°．∴∠1=∠3．∵∠CBE=∠ENF=90°，∴NE=BE．∴BM=BE．∵四边形ABCD是矩形，∴AD=BC．∵AD=2AB，AB=BE．∴BC=2BM．∴BM=MC．∴FM垂直平分BC．∴点F在BC边的垂直平分线上．11．（2018•呼和浩特）如图，已知BC⊥AC，圆心O在AC上，点M与点C分别是AC 与⊙O的交点，点D是MB与⊙O的交点，点P是AD延长线与BC的交点，且=．（1）求证：PD是⊙O的切线；（2）若AD=12，AM=MC，求的值．（1）证明：连接OD、OP、CD．∵=，∠A=∠A，∴△ADM∽△APO，∴∠ADM=∠APO，∴MD∥PO，∴∠1=∠4，∠2=∠3，∵OD=OM，∴∠3=∠4，∴∠1=∠2，∵OP=OP，OD=OC，∴∠ODP=∠OCP，∵BC⊥AC，∴∠OCP=90°，∴OD⊥AP，∴PD是⊙O的切线．（2）连接CD．由（1）可知：PC=PD，∵AM=MC，∴AM=2MO=2R，在Rt△AOD中，OD2+AD2=OA2，∴R2+122=9R2，∴R=3，∴OD=3，MC=6，∵==，∴DP=6，∵O是MC的中点，∴==，∴点P是BC的中点，∴BP=CP=DP=6，∵MC是⊙O的直径，∴∠BDC=∠CDM=90°，在Rt△BCM中，∵BC=2DP=12，MC=6，∴BM=6，∵△BCM∽△CDM，∴=，即=，∴MD=2，∴==．12．（2018•包头）如图，在矩形ABCD中，AB=3，BC=5，E是AD上的一个动点．（1）如图1，连接BD，O是对角线BD的中点，连接OE．当OE=DE时，求AE的长；（2）如图2，连接BE，EC，过点E作EF⊥EC交AB于点F，连接CF，与BE交于点G．当BE平分∠ABC时，求BG的长；（3）如图3，连接EC，点H在CD上，将矩形ABCD沿直线EH折叠，折叠后点D落在EC上的点D'处，过点D′作D′N⊥AD于点N，与EH交于点M，且AE=1．①求的值；②连接BE，△D'MH与△CBE是否相似？请说明理由．解：（1）如图1，连接OA，在矩形ABCD中，CD=AB=3，AD=BC=5，∠BAD=90°在Rt△ABD中，根据勾股定理得，BD=，∵O是BD中点，∴OD=OB=OA=，∴∠OAD=∠ODA，∵OE=DE，∴∠EOD=∠ODE=∠OAD，∴△ODE∽△ADO，∴，∴DO2=DE•DA，∴设AE=x，∴DE=5﹣x，∴（）2=5（5﹣x），∴x=，即：AE=；（2）如图2，在矩形ABCD中，∵BE平分∠ABC，∴∠ABE=∠EBC=45°，∵AD∥BC，∴∠AEB=∠EBC，∴∠ABE=∠AEB，∴AE=AB=3，∴AE=CD=3，∵EF⊥EC，∴∠FEC=90°，∴∠AEF+∠CED=90°，∵∠A=90°，∴∠AEF+∠AFE=90°，∴∠CED=∠AFE，∵∠D=∠A=90°，∴△AEF≌△DCE，∴AF=DE=2，∴BF=AB﹣AF=1，过点G作GK⊥BC于K，∴∠EBC=∠BGK=45°，∴BK=GK，∠ABC=∠GKC=90°，∵∠KCG=∠BCF，∴△CKG∽△CBF，∴，设BK=GK=y，∴CK=5﹣y，∴y=，∴BK=GK=，在Rt△GKB中，BG=；（3）①在矩形ABCD中，∠D=90°，∵AE=1，AD=5，∴DE=4，∵DC=3，∴EC=5，由折叠知，ED'=ED=4，D'H=DH，∠ED'H=∠D=90°，∴D'C=1，设D'H=DH=z，∴HC=3﹣z，根据勾股定理得，（3﹣z）2=1+z2，∴z=，∴DH=，CH=，∵D'N⊥AD，∴∠AND'=∠D=90°，∴D'N∥DC，∴△EMN∽△EHD，∴，∵D'N∥DC，∴∠ED'M=∠ECH，∵∠MED'=∠HEC，∴△ED'M∽△ECH，∴，∴，∴，∴；②相似，理由：由折叠知，∠EHD'=∠EHD，∠ED'H=∠D=90°，∴∠MD'H+∠ED'N=90°，∵∠END'=90°，∴∠ED'N+∠NED'=90°，∴∠MD'H=∠NED'，∵D'N∥DC，∴∠EHD=∠D'MH，∴∠EHD'=∠D'MH，∴D'M=D'H，∵AD∥BC，∴∠NED'=∠ECB，∴∠MD'H=∠ECB，∵CE=CB=5，∴，∴△D'MH∽△CBE．13．（2018•赤峰）如图，在Rt△ABC中，∠C=90°，AD平分∠BAC，交BC于点D，点O 在AB上，⊙O经过A、D两点，交AC于点E，交AB于点F．（1）求证：BC是⊙O的切线；（2）若⊙O的半径是2cm，E是的中点，求阴影部分的面积（结果保留π和根号）解：（1）连接OD ．、∵OA=OD ，∴∠OAD=∠ODA ，∵∠OAD=∠DAC ，∴∠ODA=∠DAC ，∴OD ∥AC ，∴∠ODB=∠C=90°，∴OD ⊥BC ，∴BC 是⊙O 的切线．（2）连接OE ，OE 交AD 于K ． ∵=，∴OE ⊥AD ，∵∠OAK=∠EAK ，AK=AK ，∠AKO=∠AKE=90°，∴△AKO ≌△AKE ，∴AO=AE=OE ，∴△AOE 是等边三角形，∴∠AOE=60°，∴S 阴=S 扇形OAE ﹣S △AOE =﹣×22=﹣．14．（2018•黑龙江）如图，在Rt △BCD 中，∠CBD=90°，BC=BD ，点A 在CB 的延长线上，且BA=BC ，点E 在直线BD 上移动，过点E 作射线EF ⊥EA ，交CD 所在直线于点F ．（1）当点E 在线段BD 上移动时，如图（1）所示，求证：BC ﹣DE=DF ．（2）当点E 在直线BD 上移动时，如图（2）、图（3）所示，线段BC 、DE 与DF 又有怎样的数量关系？请直接写出你的猜想，不需证明．（1）证明：如图1中，在BA上截取BH，使得BH=BE．∵BC=AB=BD，BE=BH，∴AH=ED，∵∠AEF=∠ABE=90°，∴∠AEB+∠FED=90°，∠AEB+∠BAE=90°，∴∠FED=∠HAE，∵∠BHE=∠CDB=45°，∴∠AHE=∠EDF=135°，∴△AHE≌△EDF，∴HE=DF，∴BC﹣DE=BD﹣DE=BE=EH=DF．∴BC﹣DE=DF．（2）解：如图2中，在BC上截取BH=BE，同法可证：DF=EH．可得：DE﹣BC=DF．如图3中，在BA上截取BH，使得BH=BE．同法可证：DF=HE，可得BC+DE=DF．15．（2018•通辽）如图，⊙O是△ABC的外接圆，点O在BC边上，∠BAC的平分线交⊙O于点D，连接BD、CD，过点D作BC的平行线与AC的延长线相交于点P．（1）求证：PD是⊙O的切线；（2）求证：△ABD∽△DCP；（3）当AB=5cm，AC=12cm时，求线段PC的长．解：（1）如图，连接OD，∵BC是⊙O的直径，∴∠BAC=90°，∵AD平分∠BAC，∴∠BAC=2∠BAD，∵∠BOD=2∠BAD，∴∠BOD=∠BAC=90°，∵DP∥BC，∴∠ODP=∠BOD=90°，∴PD⊥OD，∵OD是⊙O半径，∴PD是⊙O的切线；（2）∵PD∥BC，∴∠ACB=∠P，∵∠ACB=∠ADB，∴∠ADB=∠P，∵∠ABD+∠ACD=180°，∠ACD+∠DCP=180°，∴∠DCP=∠ABD，∴△ABD∽△DCP，（3）∵BC是⊙O的直径，∴∠BDC=∠BAC=90°，在Rt△ABC中，BC==13cm，∵AD平分∠BAC，∴∠BAD=∠CAD，∴∠BOD=∠COD，∴BD=CD，在Rt△BCD中，BD2+CD2=BC2，∴BC=CD=BC=，∵△ABD∽△DCP，∴，∴，∴CP=16.9cm．16．（2018•赤峰）将一副三角尺按图1摆放，等腰直角三角尺的直角边DF恰好垂直平分AB，与AC相交于点G，BC=2cm．（1）求GC的长；（2）如图2，将△DEF绕点D顺时针旋转，使直角边DF经过点C，另一直角边DE与AC 相交于点H，分别过H、C作AB的垂线，垂足分别为M、N，通过观察，猜想MD与ND 的数量关系，并验证你的猜想．（3）在（2）的条件下，将△DEF沿DB方向平移得到△D′E′F′，当D′E′恰好经过（1）中的点G时，请直接写出DD′的长度．解：（1）如图1中，在Rt△ABC中，∵BC=2，∠B=60°，∴AC=BC•tan60°=6，AB=2BC=4，在Rt△ADG中，AG==4，∴CG=AC=AG=6﹣4=2．（2）如图2中，结论：DM+DN=2或DM=DN．理由：∵HM⊥AB，CN⊥AB，∴∠AMH=∠DMH=∠CNB=∠CND=90°，∵∠A+∠B=90°，∠B+∠BCN=90°，∴∠A=∠BCN．∴△AHM∽△CBN，∴=①，同法可证：△DHM∽△CDN，∴=②由①②可得AM•BN=DN•DM，∴=，∴=，∴=，∵AD=BD，∴AM=DN，∴DM+DN=AM+DM=AD=2．或∵△ABC为直角三角形，D为斜边AB的中点，∴CD=BD=AD．又∠B=60°，∴△BDC为等边三角形，∴∠CDB=60°．又∠EDF=90°，∴∠MDA=30°．∵∠A=90°﹣∠B=30°，∴AH=HD，又HM⊥AD，∴MD=．在等边三角形BCD中，CN⊥BD，∴ND=NB．又AD=BD，∴MD=ND．（3）如图3中，作GK∥DE交AB由K．在△AGK中，AG=GK=4，∠A=∠GKD=30°，作GH⊥AB于H．则AH=AG•cos30°=2，可得AK=2AH=4，此时K与B重合．∴DD′=DB=2．17．（2018•哈尔滨）已知：⊙O是正方形ABCD的外接圆，点E在上，连接BE、DE，点F在上连接BF、DF，BF与DE、DA分别交于点G、点H，且DA平分∠EDF．（1）如图1，求证：∠CBE=∠DHG；（2）如图2，在线段AH上取一点N（点N不与点A、点H重合），连接BN交DE于点L，过点H作HK∥BN交DE于点K，过点E作EP⊥BN，垂足为点P，当BP=HF时，求证：BE=HK；（3）如图3，在（2）的条件下，当3HF=2DF时，延长EP交⊙O于点R，连接BR，若△BER的面积与△DHK的面积的差为，求线段BR的长．（1）证明：如图1，∵四边形ABCD是正方形，∴∠A=∠ABC=90°，∵∠F=∠A=90°，∴∠F=∠ABC，∵DA平分∠EDF，∴∠ADE=∠ADF，∵∠ABE=∠ADE，∴∠ABE=∠ADF，∵∠CBE=∠ABC+∠ABE，∠DHG=∠F+∠ADF，∴∠CBE=∠DHG；（2）如图2，过H作HM⊥KD，垂足为点M，∵∠F=90°，∴HF⊥FD，∵DA平分∠EDF，∴HM=FH，∵FH=BP，∴HN=BP，∵KH∥BN，∴∠DKH=∠DLN，∴∠ELP=∠DLN，∴∠DKH=∠ELP，∵∠BED=∠A=90°，∴∠BEP+∠LEP=90°，∵EP⊥BN，∴∠BPE=∠EPL=90°，∴∠LEP+∠ELP=90°，∴∠BEP=∠ELP=∠DKH，∵HM⊥KD，∴∠KMH=∠BPE=90°，∴△BEP≌△HKM，∴BE=HK；（3）解：如图3，连接BD，∵3HF=2DF，BP=FH，∴设HF=2a，DF=3a，∴BP=FH=2a，由（2）得：HM=BP，∠HMD=90°，∵∠F=∠A=90°，∴tan∠HDM=tan∠FDH，∴==，∴DM=3a，∵四边形ABCD为正方形，∴AB=AD，∴∠ABD=∠ADB=45°，∵∠ABF=∠ADF=∠ADE，∠DBF=45°﹣∠ABF，∠BDE=45°﹣∠ADE，∴∠DBF=∠BDE，∵∠BED=∠F，BD=BD，∴△BED≌△DFB，∴BE=FD=3a，过H作HS⊥BD，垂足为S，∵tan∠ABH=tan∠ADE==，∴设AB=3m，AH=2m，∴BD=AB=6m，DH=AD﹣AH=m，∵sin∠ADB==，∴HS=m，∴DS==m，∴BS=BD﹣DS=5m，∴tan∠BDE=tan∠DBF==，∵∠BDE=∠BRE，∴tanBRE==，∵BP=FH=2a，∴RP=10a，在ER上截取ET=DK，连接BT，由（2）得：∠BEP=∠HKD，∴△BET≌△HKD，∴∠BTE=∠KDH，∴tan∠BTE=tan∠KDH，∴=，即PT=3a，∴TR=RP﹣PT=7a，∵S△BER﹣S△DHK=，∴BP•ER﹣HM•DK=，∴BP•（ER﹣DK）=BP•（ER﹣ET）=，∴×2a×7a=，解得：a=（负值舍去），∴BP=1，PR=5，则BR==．18．（2018•黑龙江）如图，在平面直角坐标系中，菱形ABCD的边AB在x轴上，点B 坐标（﹣3，0），点C在y轴正半轴上，且sin∠CBO=，点P从原点O出发，以每秒一个单位长度的速度沿x轴正方向移动，移动时间为t（0≤t≤5）秒，过点P作平行于y 轴的直线l，直线l扫过四边形OCDA的面积为S．（1）求点D坐标．（2）求S关于t的函数关系式．（3）在直线l移动过程中，l上是否存在一点Q，使以B、C、Q为顶点的三角形是等腰直角三角形？若存在，直接写出Q点的坐标；若不存在，请说明理由．解：（1）在Rt△BOC中，OB=3，sin∠CBO==，设CO=4k，BC=5k，∵BC2=CO2+OB2，∴25k2=16k2+9，∴k=1或﹣1（舍弃），BC=5，OC=4，∵四边形ABCD是菱形，∴CD=BC=5，∴D（5，4）．（2）①如图1中，当0≤t≤2时，直线l扫过的图象是四边形CCQP，S=4t．②如图2中，当2＜t≤5时，直线l扫过的图形是五边形OCQTA．S=S梯形OCDA﹣S△DQT=×（2+5）×4﹣×（5﹣t）×（5﹣t）=﹣t2+t﹣．（3）如图3中，①当QB=QC，∠BQC=90°，Q（，）．②当BC=CQ′，∠BCQ′=90°时，Q′（4，1）；③当BC=BQ″，∠CBQ″=90°时，Q″（1，﹣3）；综上所述，满足条件的点Q坐标为（，）或（4，1）或（1，﹣3）．19．（2018•哈尔滨）已知：在四边形ABCD中，对角线AC、BD相交于点E，且AC⊥BD，作BF⊥CD，垂足为点F，BF与AC交于点G，∠BGE=∠ADE．（1）如图1，求证：AD=CD；（2）如图2，BH是△ABE的中线，若AE=2DE，DE=EG，在不添加任何辅助线的情况下，请直接写出图2中四个三角形，使写出的每个三角形的面积都等于△ADE面积的2倍．解：（1）∵∠BGE=∠ADE，∠BGE=∠CGF，∴∠ADE=∠CGF，∵AC⊥BD、BF⊥CD，∴∠ADE+∠DAE=∠CGF+∠GCF，∴∠DAE=∠GCF，∴AD=CD；（2）设DE=a，则AE=2DE=2a，EG=DE=a，=AE•DE=•2a•a=a2，∴S△ADE∵BH是△ABE的中线，∴AH=HE=a，∵AD=CD、AC⊥BD，∴CE=AE=2a，=AC•DE=•（2a+2a）•a=2a2=2S△ADE；则S△ADC在△ADE和△BGE中，∵，∴△ADE≌△BGE（ASA），∴BE=AE=2a，=AE•BE=•（2a）•2a=2a2，∴S△ABES△BCE=CE•BE=•（2a）•2a=2a2，S△BHG=HG•BE=•（a+a）•2a=2a2，综上，面积等于△ADE面积的2倍的三角形有△ACD、△ABE、△BCE、△BHG．20．（2018•齐齐哈尔）如图，以△ABC的边AB为直径画⊙O，交AC于点D，半径OE ∥BD，连接BE，DE，BD，设BE交AC于点F，若∠DEB=∠DBC．（1）求证：BC是⊙O的切线；（2）若BF=BC=2，求图中阴影部分的面积．证明：（1）∵AB是⊙O的直径，∴∠ADB=90°，∴∠A+∠ABD=90°，∵∠A=∠DEB，∠DEB=∠DBC，∴∠A=∠DBC，∵∠DBC+∠ABD=90°，∴BC是⊙O的切线；（2）连接OD，∵BF=BC=2，且∠ADB=90°，∴∠CBD=∠FBD，∵OE∥BD，∴∠FBD=∠OEB，∵OE=OB，∴∠OEB=∠OBE，∴∠CBD=∠OEB=∠OBE=∠ADB=90°=30°，∴∠C=60°，∴AB=BC=2，∴⊙O的半径为，∴阴影部分的面积=扇形DOB的面积﹣三角形DOB的面积=．．（2018•吉林）如图①，在△ABC中，AB=AC，过AB上一点D作DE∥AC交BC于点E，以E为顶点，ED为一边，作∠DEF=∠A，另一边EF交AC于点F．（1）求证：四边形ADEF为平行四边形；（2）当点D为AB中点时，▱ADEF的形状为菱形；（3）延长图①中的DE到点G，使EG=DE，连接AE，AG，FG，得到图②，若AD=AG，判断四边形AEGF的形状，并说明理由．（1）证明：∵DE∥AC，∴∠BDE=∠A，∵∠DEF=∠A，∴∠DEF=∠BDE，∴AD∥EF，又∵DE∥AC，∴四边形ADEF为平行四边形；（2）解：▱ADEF的形状为菱形，理由如下：∵点D为AB中点，∴AD=AB，∵DE∥AC，点D为AB中点，∴DE=AC，∵AB=AC，∴AD=DE，∴平行四边形ADEF为菱形，故答案为：菱形；（3）四边形AEGF是矩形，理由如下：由（1）得，四边形ADEF为平行四边形，∴AF∥DE，AF=DE，∵EG=DE，∴AF∥DE，AF=GE，∴四边形AEGF是平行四边形，∵AD=AG，EG=DE，∴AE⊥EG，∴四边形AEGF是矩形．22．（2018•大庆）如图，AB是⊙O的直径，点E为线段OB上一点（不与O，B重合），作EC⊥OB，交⊙O于点C，作直径CD，过点C的切线交DB的延长线于点P，作AF⊥PC 于点F，连接CB．（1）求证：AC平分∠FAB；（2）求证：BC2=CE•CP；（3）当AB=4且=时，求劣弧的长度．（1）证明：∵AB是直径，∴∠ACB=90°，∴∠BCP+∠ACF=90°，∠ACE+∠BCE=90°，∵∠BCP=∠BCE，∴∠ACF=∠ACE，即AC平分∠FAB．（2）证明：∵OC=OB，∴∠OCB=∠OBC，∵PF是⊙O的切线，CE⊥AB，∴∠OCP=∠CEB=90°，∴∠PCB+∠OCB=90°，∠BCE+∠OBC=90°，∴∠BCE=∠BCP，∵CD是直径，∴∠CBD=∠CBP=90°，∴△CBE∽△CPB，∴=，∴BC2=CE•CP；（3）解：作BM⊥PF于M．则CE=CM=CF，设CE=CM=CF=3a，PC=4a，PM=a，∵∠MCB+∠P=90°，∠P+∠PBM=90°，∴∠MCB=∠PBM，∵CD是直径，BM⊥PC，∴∠CMB=∠BMP=90°，∴△BMC∽△PMB，∴=，∴BM2=CM•PM=3a2，∴BM=a，∴tan∠BCM==，∴∠BCM=30°，∴∠OCB=∠OBC=∠BOC=60°，∠BOD=120°∴的长==π．23．（2018•齐齐哈尔）综合与实践折纸是一项有趣的活动，同学们小时候都玩过折纸，可能折过小动物、小花、飞机、小船等，折纸活动也伴随着我们初中数学的学习．在折纸过程中，我们可以通过研究图形的性质和运动、确定图形位置等，进一步发展空间观念，在经历借助图形思考问题的过程中，我们会初步建立几何直观，折纸往往从矩形纸片开始，今天，就让我们带着数学的眼光来玩一玩折纸，看看折叠矩形的对角线之后能得到哪些数学结论．实践操作如图1，将矩形纸片ABCD沿对角线AC翻折，使点B′落在矩形ABCD所在平面内，B'C和AD相交于点E，连接B′D．解决问题（1）在图1中，①B′D和AC的位置关系为平行；②将△AEC剪下后展开，得到的图形是菱形；（2）若图1中的矩形变为平行四边形时（AB≠BC），如图2所示，结论①和结论②是否成立，若成立，请挑选其中的一个结论加以证明，若不成立，请说明理由；（3）小红沿对角线折叠一张矩形纸片，发现所得图形是轴对称图形，沿对称轴再次折叠后，得到的仍是轴对称图形，则小红折叠的矩形纸片的长宽之比为1：1或：1；拓展应用（4）在图2中，若∠B=30°，AB=4，当△AB′D恰好为直角三角形时，BC的长度为4或6或8或12．解：（1）①BD′∥AC．②将△AEC剪下后展开，得到的图形是菱形；故答案为BD′∥AC，菱形；（2）①选择②证明如下：∵四边形ABCD是平行四边形，∴AD∥BC，∴∠DAC=∠ACB，∵将△ABC沿AC翻折至△AB′C，∴∠A CB′=∠ACB，∴∠DAC=∠ACB′，∴AE=CE，∴△AEC是等腰三角形；∴将△AEC剪下后展开，得到的图形四边相等，∴将△AEC剪下后展开，得到的图形四边是菱形．②选择①证明如下，∵四边形ABCD是平行四边形，∴AD=BC，∵将△ABC沿AC翻折至△AB′C，∵B′C=BC，∴B′C=AD，∴B′E=DE，∴∠CB′D=∠ADB′，∵∠AEC=∠B′ED，∠ACB′=∠CAD∴∠ADB′=∠DAC，∴B′D∥AC．（3）①当矩形的长宽相等时，满足条件，此时矩形纸片的长宽之比为1：1；∵∠AB′D+∠ADB′=90°，∴y﹣30°+y=90°，②当矩形的长宽之比为：1时，满足条件，此时可以证明四边形ACDB′是等腰梯形，是轴对称图形；综上所述，满足条件的矩形纸片的长宽之比为1：1或：1；（4）∵AD=BC，BC=B′C，∴AD=B′C，∵AC∥B′D，∴四边形ACB′D是等腰梯形，∵∠B=30°，∴∠AB′C=∠CDA=30°，∵△AB′D是直角三角形，当∠B′AD=90°，AB＞BC时，如图3中，设∠ADB′=∠CB′D=y，∴∠AB′D=y﹣30°，解得y=60°，∴∠AB′D=y﹣30°=30°，∵AB′=AB=4，∴AD=×4=4，∴BC=4，当∠ADB′=90°，AB＞BC时，如图4，∵AD=BC，BC=B′C，∴AD=B′C，∵AC∥B′D，∴四边形ACB′D是等腰梯形，∵∠ADB′=90°，∴四边形ACB′D是矩形，∴∠ACB′=90°，∴∠ACB=90°，∵∠B=30°，AB=4，∴BC=AB=×4=6；当∠B′AD=90°，AB＜BC时，如图5，∵AD=BC，BC=B′C，∴AD=B′C，∵AC∥B′D，∠B′AD=90°，∵∠B=30°，AB′=4，∴∠AB′C=30°，∴AE=4，BE′=2AE=8，∴AE=EC=4，∴CB′=12，当∠AB′D=90°时，如图6，∵AD=BC，BC=B′C，∴AD=B′C，∵AC∥B′D，∴四边形ACDB′是等腰梯形，∵∠AB′D=90°，∴四边形ACDB′是矩形，∴∠BAC=90°，∵∠B=30°，AB=4，∴BC=AB÷=8；∴已知当BC的长为4或6或8或12时，△AB′D是直角三角形．故答案为：平行，菱形，1：1或：1，4或6或8或12；24．（2018•吉林）如图，在矩形ABCD中，AB=2cm，∠ADB=30°．P，Q两点分别从A，B同时出发，点P沿折线AB﹣BC运动，在AB上的速度是2cm/s，在BC上的速度是2cm/s；点Q在BD上以2cm/s的速度向终点D运动，过点P作PN⊥AD，垂足为点N．连接PQ，以PQ，PN为邻边作▱PQMN．设运动的时间为x（s），▱PQMN与矩形ABCD重叠部分的图形面积为y（cm2）（1）当PQ⊥AB时，x=s；（2）求y关于x的函数解析式，并写出x的取值范围；（3）直线AM将矩形ABCD的面积分成1：3两部分时，直接写出x的值．解：（1）当PQ⊥AB时，BQ=2PB，∴2x=2（2﹣2x），∴x=s．故答案为s．（2）①如图1中，当0＜x≤时，重叠部分是四边形PQMN．y=2x×x=2x2．②如图②中，当＜x≤1时，重叠部分是四边形PQEN．y=（2﹣x+2tx×x=x2+x③如图3中，当1＜x＜2时，重叠部分是四边形PNEQ．y=（2﹣x+2）×[x﹣2（x﹣1）]=x2﹣3x+4；综上所述，y=．（3）①如图4中，当直线AM经过BC中点E时，满足条件．则有：tan∠EAB=tan∠QPB，∴=，解得x=．②如图5中，当直线AM经过CD的中点E时，满足条件．此时tan∠DEA=tan∠QPB，∴=，解得x=，综上所述，当x=或时，直线AM将矩形ABCD的面积分成1：3两部分．25．（2018•长春）在正方形ABCD中，E是边CD上一点（点E不与点C、D重合），连结BE．【感知】如图①，过点A作AF⊥BE交BC于点F．易证△ABF≌△BCE．（不需要证明）【探究】如图②，取BE的中点M，过点M作FG⊥BE交BC于点F，交AD于点G．（1）求证：BE=FG．（2）连结CM，若CM=1，则FG的长为2．【应用】如图③，取BE的中点M，连结CM．过点C作CG⊥BE交AD于点G，连结EG、MG．若CM=3，则四边形GMCE的面积为9．解：感知：∵四边形ABCD是正方形，∴AB=BC，∠BCE=∠ABC=90°，∴∠ABE+∠CBE=90°，∵AF⊥BE，∴∠ABE+∠BAF=90°，∴∠BAF=∠CBE，在△ABF和△BCE中，，∴△ABF≌△BCE（ASA）；探究：（1）如图②，过点G作GP⊥BC于P，∵四边形ABCD是正方形，∴AB=BC，∠A=∠ABC=90°，∴四边形ABPG是矩形，∴PG=AB，∴PG=BC，同感知的方法得，∠PGF=∠CBE，在△PGF和△CBE中，，∴△PGF≌△CBE（ASA），∴BE=FG，（2）由（1）知，FG=BE，连接CM，∵∠BCE=90°，点M是BE的中点，∴BE=2CM=2，∴FG=2，故答案为：2．应用：同探究（2）得，BE=2ME=2CM=6，∴ME=3，同探究（1）得，CG=BE=6，∵BE⊥CG，=CG×ME=×6×3=9，∴S四边形CEGM故答案为9．26．（2018•沈阳）如图，BE是O的直径，点A和点D是⊙O上的两点，过点A作⊙O 的切线交BE延长线于点C．（1）若∠ADE=25°，求∠C的度数；（2）若AB=AC，CE=2，求⊙O半径的长．解：（1）连接OA，∵AC是⊙O的切线，OA是⊙O的半径，∴OA⊥AC，∴∠OAC=90°，∵，∠ADE=25°，∴∠AOE=2∠ADE=50°，∴∠C=90°﹣∠AOE=90°﹣50°=40°；（2）∵AB=AC，∴∠B=∠C，∵，∴∠AOC=2∠B，∴∠AOC=2∠C，∵∠OAC=90°，∴∠AOC+∠C=90°，∴3∠C=90°，∴∠C=30°，∴OA=OC，设⊙O的半径为r，∵CE=2，∴r=，解得：r=2，∴⊙O的半径为2．27．（2018•长春）如图，在Rt△ABC中，∠C=90°，∠A=30°，AB=4，动点P从点A出发，沿AB以每秒2个单位长度的速度向终点B运动．过点P作PD⊥AC于点D（点P不与点A、B重合），作∠DPQ=60°，边PQ交射线DC于点Q．设点P的运动时间为t秒．（1）用含t的代数式表示线段DC的长；（2）当点Q与点C重合时，求t的值；（3）设△PDQ与△ABC重叠部分图形的面积为S，求S与t之间的函数关系式；（4）当线段PQ的垂直平分线经过△ABC一边中点时，直接写出t的值．解：（1）在Rt△ABC中，∠A=30°，AB=4，∴AC=2，∵PD⊥AC，∴∠ADP=∠CDP=90°，在Rt△ADP中，AP=2t，∴DP=t，AD=APcosA=2t×=t，∴CD=AC﹣AD=2﹣t（0＜t＜2）；（2）在Rt△PDQ中，∵∠DPC=60°，∴∠PQD=30°=∠A，∴PA=PQ，∵PD⊥AC，∴AD=DQ，∵点Q和点C重合，∴AD +DQ=AC ，∴2×t=2，∴t=1；（3）当0＜t ≤1时，S=S △PDQ =DQ ×DP=×t ×t=t 2；当1＜t ＜2时，如图2，CQ=AQ ﹣AC=2AD ﹣AC=2t ﹣2=2（t ﹣1），在Rt △CEQ 中，∠CQE=30°，∴CE=CQ•tan ∠CQE=2（t ﹣1）×=2（t ﹣1）， ∴S=S △PDQ ﹣S △ECQ =×t ×t ﹣×2（t ﹣1）×2（t ﹣1）=﹣t 2+4t ﹣2， ∴S=；（4）当PQ 的垂直平分线过AB 的中点F 时，如图3，∴∠PGF=90°，PG=PQ=AP=t ，AF=AB=2， ∵∠A=∠AQP=30°，∴∠FPG=60°，∴∠PFG=30°，∴PF=2PG=2t ，∴AP +PF=2t +2t=2，∴t=；。

2018年全国各省市中考数学几何压轴题

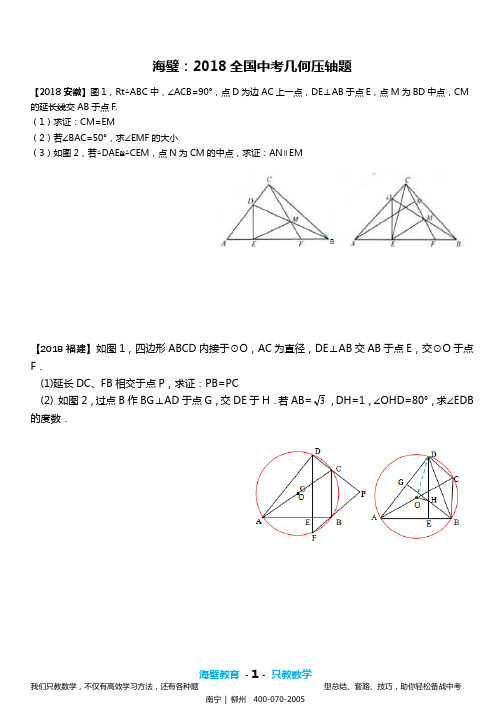
海璧：2018全国中考几何压轴题【2018安徽】图1，Rt△ABC中，∠ACB=90°，点D为边AC上一点，DE⊥AB于点E，点M为BD中点，CM 的延长线交AB于点F.（1）求证：CM=EM（2）若∠BAC=50°，求∠EMF的大小（3）如图2，若△DAE≌△CEM，点N为CM的中点，求证：AN∥EM【2018福建】如图1，四边形ABCD内接于⊙O，AC为直径，DE⊥AB交AB于点E，交⊙O于点F．(1)延长DC、FB相交于点P，求证：PB=PC(2) 如图2，过点B作BG⊥AD于点G，交DE于H．若AB=3，DH=1，∠OHD=80°，求∠EDB 的度数．【2018兰州】如图AB为⊙O的直径，C为⊙O上一点，D为BA延长线上一点，∠ACD=∠B. （1）求证：DC为⊙O的切线（2）线段DF分别交AC、BC于点E、F且∠CEF=45°，⊙O的半径为5，sinB=35,求CF的长.【2018定西】点O是△ABC的边AB上一点，⊙O与边AC相切于点E，与边BC，AB分别相交于点D，F，且DE=EF．（1）求证：∠C=90°（2）当BC=3，sinA=时，求AF的长．【2018广州】在四边形ABCD中，∠B=60°，∠D=30°，AB=BC．（2）连接BD，探究AD，BD，CD三者之间的数量关系，并说明理由；（3）若AB=1，点E在四边形ABCD内部运动，且满足AE2=BE2+CE2，求点E运动路径的长度．【2018深圳】如图9，⊙O是ABC=,2BC=，cos ABC∆的外接圆，AB AC∠=。

点D为AC上的动点，连接AD并延长，交BC的延长线于点E.（1）试求AB的长（2）试判断AD AE的值是否为定值？若为定值，请求出这个定值，若不为定值，请说明理由（3）如图10，连接BD，过点A作AH⊥BD于点H，连接CD，求证：BH CD DH=+【2018贵阳】如图，在矩形ABCD中，AB═2，AD=，P是BC边上的一点，且BP=2CP．（2）如图②，在（1）的条体下，判断EB是否平分∠AEC，并说明理由（3）如图③，在（2）的条件下，连接EP并廷长交AB的廷长线于点F，连接AP，不添加辅助线，△PFB能否由都经过P点的两次变换与△PAE组成一个等腰三角形？如果能，说明理由，并写出两种方法（指出对称轴、旋转中心、旋转方向和平移距离）【2018安顺】在△ABC中，AB=AC，O为BC的中点，AC与半圆O相切于点D．（1）求证：AB是半圆O所在圆的切线（2）若cos∠ABC=，AB=12，求半圆O所在圆的半径【2018铜仁】在三角形ABC中，AB=6，AC=BC=5，以BC为直径作⊙O交AB于点D，交AC于点G，直线DF是⊙O的切线，D为切点，交CB的延长线于点E．（1）求证：DF⊥AC（2）求tan∠E的值【2018遵义】AB是半圆O的直径，C是AB延长线上的点，AC的垂直平分线交半圆于点D，交AC于点E，连接DA，DC．已知半圆O的半径为3，BC=2．（1）求AD的长（2）点P是线段AC上一动点，连接DP，作∠DPF=∠DAC，PF交线段CD于点F．当△DPF为等腰三角形时，求AP的长【2018海南】已知，如图1，在▱ABCD 中，点E 是AB 中点，连接DE 并延长，交CB 的延长线于点F ．（1）求证：△ADE ≌△BFE（2）如图2，点G 是边BC 上任意一点（点G 不与点B 、C 重合），连接AG 交DF 于点H ，连接HC ，过点A 作AK ∥HC ，交DF 于点K①求证：HC=2AK②当点G 是边BC 中点时，恰有HD=n •HK （n 为正整数），求n 的值【2018河北】如图15，点A 在数轴上对应的数为26，以原点O 为圆心，OA 为半径作优弧AB ，使点B 在O 右下方，且34tan =∠AOB ，在优弧AB 上任取一点P ，且能过P 作直线l ∥OB 交数轴于点Q ，设Q 在数轴上对应的数为x ，连接OP(1)若优弧AB 上一段AP⌒ 的长为π13，求∠AOP 的度数及x 的值 (2)求x 的最小值，并指出此时直线l 与AB 所在圆的位置关系(3)若线段PQ 的长为12.5，直接写出这时x 的值【2018大庆】AB 是⊙O 的直径，点E 为线段OB 上一点（不与O ，B 重合），作EC ⊥OB ，交⊙O 于点C ，作直径CD ，过点C 的切线交DB 的延长线于点P ，作AF ⊥PC 于点F ，连接CB ．（1）求证：AC 平分∠FAB（2）求证：BC 2=CE •CP（3）当AB=43且CP CF =43时，求劣弧的长度【2018哈尔滨】已知：⊙O 是正方形ABCD 的外接圆，点E 在上，连接BE 、DE ，点F 在上连接BF 、DF ，BF 与DE 、DA 分别交于点G 、点H ，且DA 平分∠EDF ．（1）如图1，求证：∠CBE=∠DHG（2）如图2，在线段AH 上取一点N （点N 不与点A 、点H 重合），连接BN 交DE 于点L ，过点H 作HK ∥BN 交DE 于点K ，过点E 作EP ⊥BN ，垂足为点P ，当BP=HF 时，求证：BE=HK（3）如图3，在（2）的条件下，当3HF=2DF 时，延长EP 交⊙O 于点R ，连接BR ，若△BER 的面积与△DHK 的面积的差为47，求线段BR 的长【2018黄石】在△ABC中，E、F分别为线段AB、AC上的点（不与A、B、C重合）．（1）如图1，若EF∥BC，求证：（2）如图2，若EF不与BC平行，（1）中的结论是否仍然成立？请说明理由（3）如图3，若EF上一点G恰为△ABC的重心，，求的值【2018荆门】AB为⊙O的直径，C为⊙O上一点，经过点C的切线交AB的延长线于点E，AD⊥EC交EC的延长线于点D，AD交⊙O于F，FM⊥AB于H，分别交⊙O、AC于M、N，连接MB，BC．（1）求证：AC平分∠DAE（2）若cosM=，BE=1，①求⊙O的半径；②求FN的长【2018武汉】在△ABC 中，∠ABC ＝90°、(1) 如图1，分别过A 、C 两点作经过点B 的直线的垂线，垂足分别为M 、N ，求证：△ABM ∽△BCN(2) 如图2，P 是边BC 上一点，∠BAP ＝∠C ，tan ∠PAC ＝552，求tanC 的值 (3) 如图3，D 是边CA 延长线上一点，AE ＝AB ，∠DEB ＝90°，sin ∠BAC ＝53，52 AC AD ，直接写出tan ∠CEB 的值【2018天门】问题：如图①，在Rt △ABC 中，AB=AC ，D 为BC 边上一点（不与点B ，C 重合），将线段AD 绕点A 逆时针旋转90°得到AE ，连接EC ，则线段BC ，DC ，EC 之间满足的等量关系式为；探索：如图②，在Rt △ABC 与Rt △ADE 中，AB=AC ，AD=AE ，将△ADE 绕点A 旋转，使点D 落在BC 边上，试探索线段AD ，BD ，CD 之间满足的等量关系，并证明你的结论应用：如图③，在四边形ABCD 中，∠ABC=∠ACB=∠ADC=45°．若BD=9，CD=3，求AD 的长【2018孝感】如图，△ABC 中，AB=AC ，以AB 为直径的⊙O 交BC 于点D ，交AC 于点E ，过点D 作DF ⊥AC 于点F ，交AB 的延长线于点G ．（1）求证：DF 是⊙O 的切线（2）已知BD=2 ，CF=2，求AE 和BG 的长【2018十堰】已知正方形ABCD 与正方形CEFG ，M 是AF 的中点，连接DM ，EM .（1）如图1，点E 在CD 上，点G 在BC 的延长线上，请判断DM ，EM 的数量关系与位置关系，并直接写出结论；（2）如图2，点E 在DC 的延长线上，点G 在BC 上，（1）中结论是否仍然成立？请证明你的结论；（3）将图1中的正方形CEFG 绕点C 旋转，使D ，E ，F 三点在一条直线上，若13AB =，5CE =，请画出图形，并直接写出MF 的长.【2018宜昌】在矩形ABCD中，AB=12，P是边AB上一点，把ΔPBC沿直线PC折叠，顶点B的对应点是点G，过点B作BE⊥CG，垂足为E且在AD上，BE交PC于点F.（1）如图1，若点E是AD的中心，求证：ΔAEB≌ΔDEC（2）如图2，①求证：BP=BF②当AD=25，且AE＜DE时，求cos∠PCB的值③当BP=9时，求BE·EF的值【2018长沙】在∆ABC 中，AD 是边B C 上的中线，∠BAD =∠CAD ，CE//AD ，CE 交B A 的延长线于点E，BC =8，AD =3.（1）求CE的长（2）求证：∆ABC为等腰三角形（3）求∆ABC的外接圆圆心P与内切圆圆心Q之间的距离【2018常德】已知正方形ABCD中AC与BD交于O点，点M在线段BD上，作直线AM交直线DC于E，过D 作DH⊥AE于H，设直线DH交AC于N．（1）如图1，当M在线段BO上时，求证：MO=NO；（2）如图2，当M在线段OD上，连接NE，当EN∥BD时，求证：BM=AB；（3）在图3，当M在线段OD上，连接NE，当NE⊥EC时，求证：AN2=NC•AC．【2018郴州】在矩形ABCD中，AD＞AB，点P是CD边上的任意一点（不含C，D两端点），过点P作PF∥BC，交对角线BD于点F．（1）如图1，将△PDF沿对角线BD翻折得到△QDF，QF交AD于点E求证：△DEF是等腰三角形（2）如图2，将△PDF绕点D逆时针方向旋转得到△P'DF'，连接P'C，F'B．设旋转角为α（0°＜α＜180°）①若0°＜α＜∠BDC，即DF'在∠BDC的内部时，求证：△DP'C∽△DF'B②如图3，若点P是CD的中点，△DF'B能否为直角三角形？如果能，试求出此时tan∠DBF'的值，如果不能，请说明理由【2018衡阳】在Rt△ABC中，∠C=90°，AC=BC=4cm，动点P从点C出发以1cm/s的速度沿CA匀速运动，同时动点Q从点A出发以cm/s的速度沿AB匀速运动，当点P到达点A时，点P、Q同时停止运动，设运动时间为t（s）．（1）当t为何值时，点B在线段PQ的垂直平分线上？（2）是否存在某一时刻t，使△APQ是以PQ为腰的等腰三角形？若存在，求出t的值；若不存在，请说明理由；（3）以PC为边，往CB方向作正方形CPMN，设四边形QNCP的面积为S，求S关于t的函数关系式．【2018娄底】C、D是以AB为直径的⊙O上的点，=，弦CD交AB于点E．（1）当PB是⊙O的切线时，求证：∠PBD=∠DAB（2）求证：BC2﹣CE2=CE•DE（3）已知OA=4，E是半径OA的中点，求线段DE的长【2018湘潭】AB是以O为圆心的半圆的直径，半径CO⊥AO，点M是上的动点，且不与点A、C、B重合，直线AM交直线OC于点D，连结OM与CM．（1）若半圆的半径为10①当∠AOM=60°时，求DM的长②当AM=12时，求DM的长（2）探究：在点M运动的过程中，∠DMC的大小是否为定值？若是，求出该定值；若不是，请说明理由【2018永州】如图1，在△ABC中，矩形EFGH的一边EF在AB上，顶点G、H分别在BC、AC上，CD是边AB 上的高，CD交GH于点I．若CI=4，HI=3，AD=．矩形DFGI恰好为正方形．（1）求正方形DFGI的边长（2）如图2，延长AB至P．使得AC=CP，将矩形EFGH沿BP的方向向右平移，当点G刚好落在CP上时，试判断移动后的矩形与△CBP重叠部分的形状是三角形还是四边形，为什么？（3）如图3，连接DG，将正方形DFGI绕点D顺时针旋转一定的角度得到正方形DF′G′I′，正方形DF′G′I′分别与线段DG、DB相交于点M，N，求△MNG′的周长【2018岳阳】已知在Rt △ABC 中，∠BAC=90°，CD 为∠ACB 的平分线，将∠ACB 沿CD 所在的直线对折，使点B 落在点B ′处，连结AB'，BB'，延长CD 交BB'于点E ，设∠ABC=2α（0°＜α＜45°）．（1）如图1，若AB=AC ，求证：CD=2BE（2）如图2，若AB ≠AC ，试求CD 与BE 的数量关系（用含α的式子表示）（3）如图3，将（2）中的线段BC 绕点C 逆时针旋转角（α+45°），得到线段FC ，连结EF 交BC 于点O ，设△COE 的面积为S 1，△COF 的面积为S 2，求（用含α的式子表示）【2018株洲】已知AB 为⊙O 的直径，AB=8，点C 和点D 是⊙O 上关于直线AB 对称的两个点，连接OC 、AC ，且∠BOC ＜90°，直线BC 和直线AD 相交于点E ，过点C 作直线CG 与线段AB 的延长线相交于点F ，与直线AD 相交于点G ，且∠GAF ＝∠GCE（1）求证：直线CG 为⊙O 的切线（2）若点H 为线段OB 上一点，连接CH ，满足CB ＝CH①△CBH ∽△OBC②求OH ＋HC 的最大值A【2018益阳】如图1，矩形ABCD中，E是AD的中点，以点E直角顶点的直角三角形EFG的两边EF，EG分别过点B，C，∠F＝30°.（1）求证：BE＝CE（2）将△EFG绕点E按顺时针方向旋转，当旋转到EF与AD重合时停止转动。

2018全国各地中考数学压轴题精品

2018全国各省市中考数学压轴题25、（2018•北京）如图，在平面直角坐标系xOy中，我把由两条射线AE，BF和以AB为直径的半圆所组成的图形叫作图形C（注：不含AB线段）．已知A（﹣1，0），B（1，0），AE∥BF，且半圆与y轴的交点D在射线AE的反向延长线上．（1）求两条射线AE，BF所在直线的距离；（2）当一次函数y=x+b的图象与图形C恰好只有一个公共点时，写出b的取值范围；当一次函数y=x+b的图象与图形C恰好只有两个公共点时，写出b的取值范围；（3）已知▱AMPQ（四个顶点A，M，P，Q按顺时针方向排列）的各顶点都在图形C上，且不都在两条射线上，求点M的横坐标x的取值范围．26、（2018•河北）如图，在平面直角坐标系中，点P从原点O出发，沿x轴向右以毎秒1个单位长的速度运动t秒（t＞0），抛物线y=x2+bx+c经过点O和点P，已知矩形ABCD的三个顶点为 A （1，0），B （1，﹣5），D （4，0）．（1）求c，b （用含t的代数式表示）：（2）当4＜t＜5时，设抛物线分别与线段AB，CD交于点M，N．①在点P的运动过程中，你认为∠AMP的大小是否会变化？若变化，说明理由；若不变，求出∠AMP的值；②求△MPN的面积S与t的函数关系式，并求t为何值时，错误!未找到引用源。

；（3）在矩形ABCD的内部（不含边界），把横、纵坐标都是整数的点称为“好点”．若抛物线将这些“好点”分成数量相等的两部分，请直接写出t的取值范围．28．（2018•江苏南京）问题情境:已知矩形的面积为a（a为常数，a＞0），当该矩形的长为多少时，它的周长最小？最小值是多少？数学模型:设该矩形的长为x，周长为y，则y与x的函数关系式为2()(0)ay x xx=+＞．探索研究:⑴我们可以借鉴以前研究函数的经验，先探索函数1(0)y x xx=+＞的图象性质．①填写下表，画出函数的图象：x (1)413121 2 3 4 ……y …………②观察图象，写出该函数两条不同类型的性质；③在求二次函数y=ax2＋bx＋c（a≠0）的最大（小）值时，除了通过观察图象，还可以通过配方得到．请你通过配方求函数1y xx=+(x＞0)的最小值．解决问题:⑵用上述方法解决“问题情境”中的问题，直接写出答案．28．（2018•江苏杨州）在ABC△中，90BAC AB AC M∠=<°，，是BC边的中点，MN BC⊥交AC于点N．动点P从点B出发沿射线BA以每秒3厘米的速度运动．同时，动点Q从点N出发沿射线NC运动，且始终保持MQ MP⊥．设运动时间为t秒（0t>）．（1）PBM△与QNM△相似吗？以图１为例说明理由；（2）若6043ABC AB∠==°，厘米．①求动点Q的运动速度；②设APQ△的面积为S（平方厘米），求S与t的函数关系式；（3）探求22BP PQ CQ2、、三者之间的数量关系，以图１为例说明理由．1xyO 134522 3 54－1－1ABPNQCMAB CNM图1 图2（备用图）ADCBP 1 P 2 P 3 P 4Q 1 Q 2 Q 3 Q 4图328、（2018•江苏连云港）如图，在Rt △ABC 中，∠C=90°，AC=8，BC=6，点P 在AB 上，AP=2，点E 、F 同时从点P 出发，分别沿PA 、PB 以每秒1个单位长度的速度向点A 、B 匀速运动，点E 到达点A 后立刻以原速度沿AB 向点B 运动，点F 运动到点B 时停止，点E 也随之停止．在点E 、F 运动过程中，以EF 为边作正方形EFGH ，使它与△ABC 在线段AB 的同侧．设E 、F 运动的时间为t/秒（t ＞0），正方形EFGH 与△ABC 重叠部分面积为S ．（1）当时t=1时，正方形EFGH 的边长是 1 ．当t=3时，正方形EFGH 的边长是 4 ．（2）当0＜t≤2时，求S 与t 的函数关系式；（3）直接答出：在整个运动过程中，当t 为何值时，S 最大？最大面积是多少？28．（2018•江苏淮安）某课题研究小组就图形面积问题进行专题研究，他们发现如下结论：（1）有一条边对应相等的两个三角形面积之比等于这条边上的对应高之比；（2）有一个角对应相等的两个三角形面积之比等于夹这个角的两边乘积之比；…现请你继续对下面问题进行探究，探究过程可直接应用上述结论．（S 表示面积）问题1：如图1，现有一块三角形纸板ABC ，P 1，P 2三等分边AB ，R 1，R 2三等分边AC ．经探究知2121R R P P S 四边形＝13 S △ABC ，请证明．问题2：若有另一块三角形纸板，可将其与问题1中的拼合成四边形ABCD ，如图2，Q 1，Q 2三等分边DC ．请探究2211P Q Q P S 四边形与S 四边形ABCD 之间的数量关系．问题3：如图3，P 1，P 2，P 3，P 4五等分边AB ，Q 1，Q 2，Q 3，Q 4五等分边DC ．若 S 四边形ABCD ＝1，求3322P Q Q P S 四边形．问题4：如图4，P 1，P 2，P 3四等分边AB ，Q 1，Q 2，Q 3四等分边DC ，P 1Q 1，P 2Q 2，P 3Q 3将四边形ABCD 分成四个部分，面积分别为S 1，S 2，S 3，S 4．请直接写出含有S 1，S 2，S 3，S 4的一个等式． 28．（2018•江苏南通）如图，已知直线l 经过点A (1，0)，与双曲线y ＝mx(x ＞0)交于点B (2，1)．过点P (p ，p －1)(p ＞1)作x 轴的平行线分别交双曲线y ＝m x (x ＞0)和y ＝－mx(x ＜0)于点M 、N ．(1)求m 的值和直线l 的解析式；(2)若点P 在直线y ＝2上，求证：△PMB ∽△PNA ；(3)是否存在实数p ，使得S △AMN ＝4S △AMP ？若存在，请求出所有满足条件的p 的值；若不存在，请说明理由．29．（2018•江苏苏州）已知二次函数()()2680y a x x a =-+>的图象与x 轴分别交于点A 、B ，与y 轴交于点C ．点D 是抛物线的顶点．(1)如图①，连接AC ，将△OAC 沿直线AC 翻折，若点O 的对应点O'恰好落在该抛物线的对称轴上，求实数a 的值；(2)如图②，在正方形EFGH 中，点E 、F 的坐标分别是（4，4）、（4，3），边HG 位于边EF 的右侧．小林同学经过探索后发现了一个正确的命题：“若点P 是边EH 或边HG 上的任意一点，则四条线段PA 、PB 、PC 、PD 不能与任何一个平行四边形的四条边对应相等（即这四条线段不能构成平行四边形）．”若点P 是边EF 或边FG 上的任意一点，刚才的结论是否也成立？请你积极探索，并写出探索过程；(3)如图②，当点P 在抛物线对称轴上时，设点P 的纵坐标t 是大于3的常数，试问：是否存在一个正数a ，使得四条线段PA 、PB 、PC 、PD 与一个平行四边形的四条边对应相等（即这四条线段能构成平行四边形）？请说明理由．A BC图1P 1 P 2R 2R 1ABC图2P 1 P 2R 2R 1D Q 1Q 2ADP 1 P 2 P 3BQ 1Q 2 Q 3C图4S 1 S 2 S 3S 4 OABl xy28．（2018•江苏泰州）在平面直角坐标系xOy中，边长为a（a为大于0的常数）的正方形ABCD的对角线AC、BD相交于点P，顶点A在x轴正半轴上运动，顶点B在y轴正半轴上运动（x轴的正半轴、y轴的正半轴都不包含原点O），顶点C、D都在第一象限。

2018年全国各地中考数学压轴题汇编：几何综合(贵州专版)(解析卷)

2018年全国各地中考数学压轴题汇编（贵州专版）几何综合参考答案与试题解析一．选择题（共6小题）1．（2018•贵阳）如图，在菱形ABCD中，E是AC的中点，EF∥CB，交AB于点F，如果EF=3，那么菱形ABCD的周长为（）A．24 B．18 C．12 D．9解：∵E是AC中点，∵EF∥BC，交AB于点F，∴EF是△ABC的中位线，∴EF=BC，∴BC=6，∴菱形ABCD的周长是4×6=24．故选：A．2．（2018•遵义）如图，点P是矩形ABCD的对角线AC上一点，过点P作EF∥BC，分别交AB，CD于E、F，连接PB、PD．若AE=2，PF=8．则图中阴影部分的面积为（）A．10 B．12 C．16 D．18解：作PM⊥AD于M，交BC于N．则有四边形AEPM，四边形DFPM，四边形CFPN，四边形BEPN都是矩形，∴S△ADC =S△ABC，S△AMP=S△AEP，S△PBE=S△PBN，S△PFD=S△PDM，S△PFC=S△PCN，∴S△DFP=S△PBE=×2×8=8，∴S阴=8+8=16，故选：C．3．（2018•贵阳）如图，A、B、C是小正方形的顶点，且每个小正方形的边长为1，则tan∠BAC的值为（）A．B．1 C．D．解：连接BC，由网格可得AB=BC=，AC=，即AB2+BC2=AC2，∴△ABC为等腰直角三角形，∴∠BAC=45°，则tan∠BAC=1，故选：B．4．（2018•遵义）如图，四边形ABCD中，AD∥BC，∠ABC=90°，AB=5，BC=10，连接AC、BD，以BD为直径的圆交AC于点E．若DE=3，则AD的长为（）A．5 B．4 C．3D．2解：如图，在Rt△ABC中，AB=5，BC=10，∴AC=5过点D作DF⊥AC于F，∴∠AFD=∠CBA，∵AD∥BC，∴∠DAF=∠ACB，∴△ADF∽△CAB，∴，∴，设DF=x，则AD=x，在Rt△ABD中，BD==，∵∠DEF=∠DBA，∠DFE=∠DAB=90°，∴△DEF∽△DBA，∴，∴，∴x=2，∴AD=x=2，故选：D．5．（2018•安顺）已知⊙O的直径CD=10cm，AB是⊙O的弦，AB⊥CD，垂足为M，且AB=8cm，则AC的长为（）A．2cm B．4cm C．2cm或4cm D．2cm或4cm 解：连接AC，AO，∵⊙O的直径CD=10cm，AB⊥CD，AB=8cm，∴AM=AB=×8=4cm，OD=OC=5cm，当C点位置如图1所示时，∵OA=5cm，AM=4cm，CD⊥AB，∴OM===3cm，∴CM=OC+OM=5+3=8cm，∴AC===4cm；当C点位置如图2所示时，同理可得OM=3cm，∵OC=5cm，∴MC=5﹣3=2cm，在Rt△AMC中，AC===2cm．故选：C．6．（2018•铜仁市）在同一平面内，设a、b、c是三条互相平行的直线，已知a与b的距离为4cm，b与c的距离为1cm，则a与c的距离为（）A．1cm B．3cm C．5cm或3cm D．1cm或3cm解：当直线c在a、b之间时，∵a、b、c是三条平行直线，而a与b的距离为4cm，b与c的距离为1cm，∴a与c的距离=4﹣1=3（cm）；当直线c不在a、b之间时，∵a、b、c是三条平行直线，而a与b的距离为4cm，b与c的距离为1cm，∴a与c的距离=4+1=5（cm），综上所述，a与c的距离为3cm或3cm．故选：C．二．填空题（共8小题）7．（2018•贵阳）如图，点M、N分别是正五边形ABCDE的两边AB、BC上的点．且AM=BN，点O是正五边形的中心，则∠MON的度数是72度．解：连接OA、OB、OC，∠AOB==72°，∵∠AOB=∠BOC，OA=OB，OB=OC，∴∠OAB=∠OBC，在△AOM和△BON中，∴△AOM≌△BON，∴∠BON=∠AOM，∴∠MON=∠AOB=72°，故答案为：72．8．（2018•遵义）如图，△ABC中．点D在BC边上，BD=AD=AC，E为CD的中点．若∠CAE=16°，则∠B为37度．解：∵AD=AC，点E是CD中点，∴AE⊥CD，∴∠AEC=90°，∴∠C=90°﹣∠CAE=74°，∵AD=AC，∴∠ADC=∠C=74°，∵AD=BD，∴2∠B=∠ADC=74°，∴∠B=37°，故答案为37°．9．（2018•贵阳）如图，在△ABC中，BC=6，BC边上的高为4，在△ABC的内部作一个矩形EFGH，使EF在BC边上，另外两个顶点分别在AB、AC边上，则对角线EG长的最小值为．解：如图，作AQ⊥BC于点Q，交DG于点P，∵四边形DEFG是矩形，∴AQ⊥DG，GF=PQ，设GF=PQ=x，则AP=4﹣x，由DG∥BC知△ADG∽△ABC，∴=，即=，则EF=DG=（4﹣x），∴EG====，∴当x=时，EG取得最小值，最小值为，故答案为：．10．（2018•遵义）如图，在菱形ABCD中，∠ABC=120°，将菱形折叠，使点A恰好落在对角线BD上的点G处（不与B、D重合），折痕为EF，若DG=2，BG=6，则BE的长为2.8．解：作EH⊥BD于H，由折叠的性质可知，EG=EA，由题意得，BD=DG+BG=8，∵四边形ABCD是菱形，∴AD=AB，∠ABD=∠CBD=∠ABC=60°，∴△ABD为等边三角形，∴AB=BD=8，设BE=x，则EG=AE=8﹣x，在Rt△EHB中，BH=x，EH=x，在Rt△EHG中，EG2=EH2+GH2，即（8﹣x）2=（x）2+（6﹣x）2，解得，x=2.8，即BE=2.8，故答案为：2.8．11．（2018•安顺）如图，C 为半圆内一点，O 为圆心，直径AB 长为2cm ，∠BOC=60°，∠BCO=90°，将△BOC 绕圆心O 逆时针旋转至△B′OC′，点C′在OA 上，则边BC 扫过区域（图中阴影部分）的面积为 π cm 2．（结果保留π）解：∵∠BOC=60°，△B′OC′是△BOC 绕圆心O 逆时针旋转得到的，∴∠B′OC′=60°，△BCO=△B′C′O ，∴∠B′OC=60°，∠C′B′O=30°， ∴∠B′OB=120°，∵AB=2cm ，∴OB=1cm ，OC′=， ∴B′C′=，∴S 扇形B′OB ==π，S 扇形C′OC ==， ∵∴阴影部分面积=S 扇形B′OB +S △B′C′O ﹣S △BCO ﹣S 扇形C′OC =S 扇形B′OB ﹣S 扇形C′OC =π﹣=π；故答案为：π．12．（2018•黔西南州）已知一个菱形的边长为2，较长的对角线长为2，则这个菱形的面积是 2 ．解：依照题意画出图形，如图所示．在Rt△AOB中，AB=2，OB=，∴OA==1，∴AC=2OA=2，=AC•BD=×2×2=2．∴S菱形ABCD故答案为：2．13．（2018•铜仁市）在直角三角形ABC中，∠ACB=90°，D、E是边AB上两点，且CE 所在直线垂直平分线段AD，CD平分∠BCE，BC=2，则AB=4．解：∵CE所在直线垂直平分线段AD，∴CE平分∠ACD，∴∠ACE=∠DCE．∵CD平分∠BCE，∴∠DCE=∠DCB．∵∠ACB=90°，∴∠ACE=∠ACB=30°，∴∠A=60°，∴AB===4．故答案为：4．14．（2018•黔西南州）如图，已知在△ABC中，BC边上的高AD与AC边上的高BE交于点F，且∠BAC=45°，BD=6，CD=4，则△ABC的面积为60．解：∵AD⊥BC，BE⊥AC，∴∠AEF=∠BEC=∠BDF=90°，∵∠BAC=45°，∴AE=EB，∵∠EAF+∠C=90°，∠CBE+∠C=90°，∴∠EAF=∠CBE，∴△AEF≌△BEC，∴AF=BC=10，设DF=x．∵△ADC∽△BDF，∴=，∴=，整理得x2+10x﹣24=0，解得x=2或﹣12（舍弃），∴AD=AF+DF=12，=•BC•AD=×10×12=60．∴S△ABC故答案为60．三．解答题（共9小题）15．（2018•贵阳）如图，在平行四边形ABCD中，AE是BC边上的高，点F是DE的中点，AB与AG关于AE对称，AE与AF关于AG对称．（1）求证：△AEF是等边三角形；（2）若AB=2，求△AFD的面积．解：（1）∵AB与AG关于AE对称，∴AE⊥BC，∵四边形ABCD是平行四边形，∴AD∥BC，∴AE⊥AD，即∠DAE=90°，∵点F是DE的中点，即AF是Rt△ADE的中线，∴AF=EF=DF，∵AE与AF关于AG对称，∴AE=AF，则AE=AF=EF，∴△AEF是等边三角形；（2）记AG、EF交点为H，∵△AEF是等边三角形，且AE与AF关于AG对称，∴∠EAG=30°，AG⊥EF，∵AB与AG关于AE对称，∴∠BAE=∠GAE=30°，∠AEB=90°，∵AB=2，∴BE=1、DF=AF=AE=，则EH=AE=、AH=，=××=．∴S△ADF16．（2018•遵义）如图，正方形ABCD的对角线交于点O，点E、F分别在AB、BC上（AE ＜BE），且∠EOF=90°，OE、DA的延长线交于点M，OF、AB的延长线交于点N，连接MN．（1）求证：OM=ON．（2）若正方形ABCD的边长为4，E为OM的中点，求MN的长．解：（1）∵四边形ABCD是正方形，∴OA=OB，∠DAO=45°，∠OBA=45°，∴∠OAM=∠OBN=135°，∵∠EOF=90°，∠AOB=90°，∴∠AOM=∠BON，∴△OAM≌△OBN（ASA），∴OM=ON；（2）如图，过点O作OH⊥AD于点H，∵正方形的边长为4，∴OH=HA=2，∵E为OM的中点，∴HM=4，则OM==2，∴MN=OM=2．17．（2018•贵阳）如图，AB为⊙O的直径，且AB=4，点C在半圆上，OC⊥AB，垂足为点O，P为半圆上任意一点，过P点作PE⊥OC于点E，设△OPE的内心为M，连接OM、PM．（1）求∠OMP的度数；（2）当点P在半圆上从点B运动到点A时，求内心M所经过的路径长．解：（1）∵△OPE的内心为M，∴∠MOP=∠MOC，∠MPO=∠MPE，∴∠PMO=180°﹣∠MPO﹣∠MOP=180°﹣（∠EOP+∠OPE），∵PE⊥OC，即∠PEO=90°，∴∠PMO=180°﹣（∠EOP+∠OPE）=180°﹣（180°﹣90°）=135°，（2）如图，∵OP=OC，OM=OM，而∠MOP=∠MOC，∴△OPM≌△OCM，∴∠CMO=∠PMO=135°，所以点M在以OC为弦，并且所对的圆周角为135°的两段劣弧上（和）；点M在扇形BOC内时，过C、M、O三点作⊙O′，连O′C，O′O，在优弧CO取点D，连DA，DO，∵∠CMO=135°，∴∠CDO=180°﹣135°=45°，∴∠CO′O=90°，而OA=2cm，∴O′O=OC=×2=，∴弧OMC的长==π（cm），同理：点M在扇形AOC内时，同①的方法得，弧ONC的长为πcm，所以内心M所经过的路径长为2×π=πcm．18．（2018•遵义）如图，AB是半圆O的直径，C是AB延长线上的点，AC的垂直平分线交半圆于点D，交AC于点E，连接DA，DC．已知半圆O的半径为3，BC=2．（1）求AD的长．（2）点P是线段AC上一动点，连接DP，作∠DPF=∠DAC，PF交线段CD于点F．当△DPF为等腰三角形时，求AP的长．解：（1）如图1，连接OD，∵OA=OD=3，BC=2，∴AC=8，∵DE是AC的垂直平分线，∴AE=AC=4，∴OE=AE﹣OA=1，在Rt△ODE中，DE==2；在Rt△ADE中，AD==2；（2）当DP=DF时，如图2，点P与A重合，F与C重合，则AP=0；当DP=PF时，如图4，∴∠CDP=∠PFD，∵DE是AC的垂直平分线，∠DPF=∠DAC，∴∠DPF=∠C，∵∠PDF=∠CDP，∴△PDF∽△CDP，∴∠DFP=∠DPC，∴∠CDP=∠CPD，∴CP=CD，∴AP=AC﹣CP=AC﹣CD=AC﹣AD=8﹣2；当PF=DF时，如图3，∴∠FDP=∠FPD，∵∠DPF=∠DAC=∠C，∴△DAC∽△PDC，∴，∴，∴AP=5，即：当△DPF是等腰三角形时，AP的长为0或5或8﹣2．19．（2018•安顺）如图，在△ABC中，AD是BC边上的中线，E是AD的中点，过点A 作BC的平行线交BE的延长线于点F，连接CF．（1）求证：AF=DC；（2）若AC⊥AB，试判断四边形ADCF的形状，并证明你的结论．（1）证明：连接DF，∵E为AD的中点，∴AE=DE，∵AF∥BC，∴∠AFE=∠DBE，在△AFE和△DBE中，，∴△AFE≌△DBE（AAS），∴EF=BE，∵AE=DE，∴四边形AFDB是平行四边形，∴BD=AF，∵AD为中线，∴DC=BD，∴AF=DC；（2）四边形ADCF的形状是菱形，理由如下：∵AF=DC，AF∥BC，∴四边形ADCF是平行四边形，∵∴∵AD为中线∴AD=BC=DC，∴平行四边形ADCF是菱形；20．（2018•铜仁市）如图，在三角形ABC中，AB=6，AC=BC=5，以BC为直径作⊙O交AB于点D，交AC于点G，直线DF是⊙O的切线，D为切点，交CB的延长线于点E．（1）求证：DF⊥AC；（2）求tan∠E的值．（1）证明：如图，连接OC，∵BC是⊙O的直径，∴∠BDC=90°，∴CD⊥AB，∵AC=BC，∴AD=BD，∵OB=OC，∴OD是△ABC的中位线∴OD∥AC，∵DF为⊙O的切线，∴OD⊥DF，∴DF⊥AC；（2）解：如图，连接BG，∵BC是⊙O的直径，∴∠BGC=90°，∵∠EFC=90°=∠BGC，∴EF∥BG，∴∠CBG=∠E，Rt△BDC中，∵BD=3，BC=5，∴CD=4，S△ABC=，6×4=5BG，BG=，由勾股定理得：CG==，∴tan∠CBG=tan∠E===．21．（2018•安顺）如图，在△ABC中，AB=AC，O为BC的中点，AC与半圆O相切于点D．（1）求证：AB是半圆O所在圆的切线；（2）若cos∠ABC=，AB=12，求半圆O所在圆的半径．解：（1）如图，作OE⊥AB于E，连接OD，OA，∵AB=AC，点O是BC的中点，∴∠CAO=∠BAO，∵AC与半圆O相切于D，∴OD⊥AC，∵OE⊥AB，∴OD=OE，∵AB径半圆O的半径的外端点，∴AB是半圆O所在圆的切线；（2）∵AB=AC，O是BC的中点，∴AO⊥BC，在Rt△AOB中，OB=AB•cos∠ABC=12×=8，根据勾股定理得，OA==4，=AB•OE=OB•OA，由三角形的面积得，S△AOB∴OE==，即：半圆O所在圆的半径为．22．（2018•贵阳）如图，在矩形ABCD中，AB═2，AD=，P是BC边上的一点，且BP=2CP．（1）用尺规在图①中作出CD边上的中点E，连接AE、BE（保留作图痕迹，不写作法）；（2）如图②，在（1）的条件下，判断EB是否平分∠AEC，并说明理由；（3）如图③，在（2）的条件下，连接EP并廷长交AB的廷长线于点F，连接AP，不添加辅助线，△PFB能否由都经过P点的两次变换与△PAE组成一个等腰三角形？如果能，说明理由，并写出两种方法（指出对称轴、旋转中心、旋转方向和平移距离）解：（1）依题意作出图形如图①所示，（2）EB是平分∠AEC，理由：∵四边形ABCD是矩形，∴∠C=∠D=90°，CD=AB=2，BC=AD=，∵点E是CD的中点，∴DE=CE=CD=1，在△ADE和△BCE中，，∴△ADE≌△BCE，∴∠AED=∠BEC，在Rt△ADE中，AD=，DE=1，∴tan∠AED==，∴∠AED=60°，∴∠BCE=∠AED=60°，∴∠AEB=180°﹣∠AED﹣∠BEC=60°=∠BEC，∴BE平分∠AEC；（3）∵BP=2CP，BC=，∴CP=，BP=，在Rt△CEP中，tan∠CEP==，∴∠CEP=30°，∴∠BEP=30°，∴∠AEP=90°，∵CD∥AB，∴∠F=∠CEP=30°，在Rt△ABP中，tan∠BAP==，∴∠PAB=30°，∴∠EAP=30°=∠F=∠PAB，∵CB⊥AF，∴AP=FP，∴△AEP≌△FBP，∴△PFB能由都经过P点的两次变换与△PAE组成一个等腰三角形，变换的方法为：将△BPF绕点B顺时针旋转120°和△EPA重合，①沿PF折叠，②沿AE 折叠．23．（2018•黔西南州）如图1，已知矩形AOCB，AB=6cm，BC=16cm，动点P从点A出发，以3cm/s的速度向点O运动，直到点O为止；动点Q同时从点C出发，以2cm/s 的速度向点B运动，与点P同时结束运动．（1）点P到达终点O的运动时间是s，此时点Q的运动距离是cm；（2）当运动时间为2s时，P、Q两点的距离为6cm；（3）请你计算出发多久时，点P和点Q之间的距离是10cm；（4）如图2，以点O为坐标原点，OC所在直线为x轴，OA所在直线为y轴，1cm长为单位长度建立平面直角坐标系，连结AC，与PQ相交于点D，若双曲线y=过点D，问k 的值是否会变化？若会变化，说明理由；若不会变化，请求出k的值．解：（1）∵四边形AOCB是矩形，∴OA=BC=16，∵动点P从点A出发，以3cm/s的速度向点O运动，∴,此时，点Q的运动距离是cm（2）如图1，由运动知，AP=3×2=6cm，CQ=2×2=4cm，过点P作PE⊥BC于E，过点Q作QF⊥OA于F，∴四边形APEB是矩形，∴PE=AB=6，BE=6，∴EQ=BC﹣BE﹣CQ=16﹣6﹣4=6，根据勾股定理得，PQ=6，故答案为6；（3）设运动时间为t秒时，由运动知，AP=3t，CQ=2t，同（2）的方法得，PE=6，EQ=16﹣3t﹣2t=16﹣5t，∵点P和点Q之间的距离是10cm，∴62+（16﹣5t）2=100，∴t=或t=；（4）k的值是不会变化，理由：∵四边形AOCB是矩形，∴OC=AB=6，OA=16，∴C（6，0），A（0，16），∴直线AC的解析式为y=﹣x+16①，设运动时间为t，∴AP=3t，CQ=2t，∴OP=16﹣3t，∴P（0，16﹣3t），Q（6，2t），∴PQ解析式为y=x+16﹣3t②，联立①②得，﹣x+16=x+16﹣3t，∴x+x=3t，∴5tx﹣16x+16x=3t，∴x=，∴y=，∴D（，）∴k=×=是定值．。

2018年全国各地中考数学压轴题精品

2018年全国各地中考数学压轴题专集1．（北京市）在□ABCD 中，过点C 作CE ⊥CD 交AD 于点E ，将线段EC 绕点E 逆时针旋转90°得到线段EF （如图1）．（1）在图1中画图探究：①当P 1为射线CD 上任意一点（P 1不与C 点重合）时，连结EP 1，将线段EP 1绕点E 逆时针旋转90°得到线段EG 1，判断直线FG 1与直线CD 的位置关系并加以证明； ②当P 2为线段DC 的延长线上任意一点时，连结EP 2，将线段EP 2绕点E 逆时针旋转90°得到线段EG 2，判断直线G 1G 2与直线CD 的位置关系，画出图形并直接写出你的结论．（2）若AD ＝6，tan B ＝34，AE ＝1，在①的条件下，设CP 1＝x ，S △P 1FG 1＝y ，求y 与x 之间的函数关系式，并写出自变量x 的取值范围．2．（北京市）如图，在平面直角坐标系xO y 中，△ABC 三个顶点的坐标分别为A (－6，0)，B (6，0)， C (0，34)，延长AC 到点D ，使CD ＝21AC ，过D 点作DE ∥AB 交BC 的延长线于点E ．（1）求D 点的坐标；（2）作C 点关于直线DE 的对称点F ，分别连结DF 、EF ，若过B 点的直线y kx b =+将四边形CDFE 分成周长相等的两个四边形，确定此直线的解析式；（3）设G 为y 轴上一点，点P 从直线y ＝kx ＋b 与y 轴的交点出发，先沿y 轴到达G 点，再沿GA 到达A 点，若P 点在y 轴上运动的速度是它在直线GA 上运动速度的2倍，试确定G 点的位置，使P 点按照上述要求到达A 点所用的时间最短．（要求：简述确定G 点位置的方法，但不要求证明） 3．（天津市）已知一个直角三角形纸片OAB ，其中∠AOB ＝90°，OA ＝2，OB ＝4．如图，将该纸片放置在平面直角坐标系中，折叠该纸片，折痕与边OB 交于点C ，与边AB 交于点D ．（Ⅰ）若折叠后使点B 与点A 重合，求点C 的坐标；（Ⅱ）若折叠后点B 落在边OA 上的点为B ′，设OB ′＝x ，OC ＝y ，试写出y 关于x 的函数解析式，并确定y 的取值范围；（Ⅲ）若折叠后点B 落在边OA 上的点为B ′′，且使B ′′D ∥OB ，求此时点C 的坐标．4．（天津市）已知函数y 1＝x ，y 2＝x2＋bx ＋c ，α，β为方程y 1－y 2＝0的两个根，点M (1，T )在函数y 2的图象上．（Ⅰ）若α＝31，β＝21，求函数y 2的解析式；（Ⅱ）在（Ⅰ）的条件下，若函数y 1与y 2的图象的两个交点为A ，B ，当△ABM 的面积为3121时，求t 的值；（Ⅲ）若0＜α＜β＜1，当0＜t ＜1时，试确定T ，α，β三者之间的大小关系，并说明理由．5．（上海市）在直角坐标平面内，O 为原点，点A 的坐标为（1，0），点C 的坐标为（0，4），直线CM ∥x 轴（如图所示）．点B 与点A 关于原点对称，直线y ＝x ＋b （b 为常数）经过点B ，且与直线CM 相交于点D ，联结OD ．（1）求b 的值和点D 的坐标；（2）设点P 在x 轴的正半轴上，若△POD 是等腰三角形，求点P的坐标；（3）在（2）的条件下，如果以PD 为半径的圆P 与圆O 外切，求圆O 的半径．6．（上海市）已知∠ABC ＝90°，AB ＝2，BC ＝3，AD ∥BC ，P 为线段BD 上的动点，点Q 在射线AB 上，且满足PC PQ ＝ABAD（如图1所示）．（1）当AD ＝2，且点Q 与点B 重合时（如图2所示），求线段PC 的长；（2）在图1中，联结AP ．当AD ＝23，且点Q 在线段AB 上时，设点B 、Q 之间的距离为x ，PBC APQ S S △△＝y ，其中APQ S △表示△APQ 的面积，PBC S △表示△PBC 的面积，求y 关于x 的函数解析式，并写出函数定义域；（3）当AD＜AB ，且点Q 在线段AB 的延长线上时（如图3所示），求∠QPC 的大小．图1 图2（备用）D APCB(Q ) 图2图3CADPBQ图117．（重庆市）已知：如图，在平面直角坐标系xO y 中，矩形OABC 的边OA 在y 轴的正半轴上，OC 在x 轴的正半轴上，OA ＝2，OC ＝3．过原点O 作∠AOC 的平分线交AB 于点D ，连接DC ，过点D 作DE ⊥DC ，交OA 于点E ．（1）求过点E 、D 、C 的抛物线的解析式；（2）将∠EDC 绕点D 按顺时针方向旋转后，角的一边与y 轴的正半轴交于点F ，另一边与线段OC 交于点G ．如果DF 与（1）中的抛物线交于另一点M ，点M 的横坐标为56，那么EF ＝2GO 是否成立？若成立，请给予证明；若不成立，请说明理由；（3）对于（2）中的点G ，在位于第一象限内的该抛物线上是否存在点Q ，使得直线GQ 与AB 的交点P 与点C 、G 构成的△PCG 是等腰三角形？若存在，请求出点Q 的坐标；若不存在，请说明理由．8．（重庆市江津区）如图，抛物线y ＝－x2＋bx ＋c 与x 轴交于A (1，0)，B (－3，0)两点．（1）求该抛物线的解析式；（2）设（1）中的抛物线交y 轴于C 点，在该抛物线的对称轴上是否存在点Q ，使得△QAC 的周长最小？若存在，求出点Q 的坐标；若不存在，请说明理由；（3）在（1）中的抛物线上的第二象限内是否存在一点P ，使△PBC的面积最大？，若存在，求出点P 的坐标及△PBC 的面积最大值；若不存在，请说明理由．9．（重庆市綦江县）如图，已知抛物线y ＝a (x －1)2＋33(a ≠0)经过点A (－2，0)，抛物线的顶点为D ，过O 作射线OM ∥AD ．过顶点D 平行于x 轴的直线交射线OM 于点C ，B 在x 轴正半轴上，连结BC ．（1）求该抛物线的解析式；（2）若动点P 从点O 出发，以每秒1个长度单位的速度沿射线OM 运动，设点P 运动的时间为t （s ）．问：当t 为何值时，四边形DAOP 分别为平行四边形？直角梯形？等腰梯形？（3）若OC ＝OB ，动点P 和动点Q 分别从点O 和点B 同时出发，分别以每秒1个长度单位和2个长度单位的速度沿OC 和BO 运动，当其中一个点停止运动时另一个点也随之停止运动．设它们的运动的时间为t （s ），连接PQ ，当t 为何值时，四边形BCPQ 的面积最小？并求出最小值及此时PQ 的长． 10．（江苏省）如图，已知二次函数y ＝x2－2x －1的图象的顶点为A ，二次函数y ＝ax2＋bx 的图象与x 轴交于原点O 及另一点C ，它的顶点B 在函数y ＝x2－2x －1的图象的对称轴上．（1）求点A 与点C 的坐标；（2）当四边形AOBC 为菱形时，求函数y ＝ax2＋bx 的关系式．11．（江苏省）如图，已知射线DE 与x 轴和y 轴分别交于点D （3，0）和点E （0，4），动点C 从点M （5，0）出发，以1个单位长度/秒的速度沿x 轴向左作匀速运动，与此同时，动点P 从点D 出发，也以1个单位长度/秒的速度沿射线DE 的方向作匀速运动．设运动时间为t 秒．（1）请用含t 的代数式分别表示出点C 与点P 的坐标；（2）以点C 为圆心、21t 个单位长度为半径的⊙C 与x 轴交于A 、B 两点（点A 在点B 的左侧），连接P A 、PB ． ① 当⊙C 与射线DE 有公共点时，求t 的取值范围； ② 当△P AB 为等腰三角形时，求t 的值．12．（浙江省杭州市）已知平行于x 轴的直线y ＝a (a ≠0)与函数y ＝x 和函数y ＝x1的图象分别交于点A 和点B ，又有定点P (2，0)．（1）若a ＞0，且tan ∠POB ＝91，求线段AB 的长；（2）在过A ，B 两点且顶点在直线y ＝x 上的抛物线中，已知线段AB＝38，且在它的对称轴左边时，y 随着x 的增大而增大，试求出满足条件的抛物线的解析式；（3）已知经过A ，B ，P 三点的抛物线，平移后能得到y ＝59x2的图象，求点P 到直线AB 的距离．13．（浙江省台州市）如图，已知直线y ＝－21x ＋1交坐标轴于A 、B 两点，以线段AB 为边向上作正方形ABCD ，过点A ，D ，C 的抛物线与直线另一个交点为E ．（1）请直接写出点C ，D 的坐标；（2）求抛物线的解析式；（3）若正方形以每秒5个单位长度的速度沿射线AB 下滑，直至顶点D 落在x 轴上时停止．设正方形落在x 轴下方部分的面积为S ，求S 关于滑行时间t 的函数关系式，并写出相应自变量t 的取值范围；（4）在（3）的条件下，抛物线与正方形一起平移，直至顶点D 落在x 轴上时停止，求抛物线上C 、E 两点间的抛物线弧所扫过的面积．14．（浙江省温州市）如图，在平面直角坐标系中，点A （3，0），B （33，2），C （0，2）．动点D 以每秒1个单位的速度从点O 出发沿OC 向终点C 运动，同时动点E 以每秒2个单位的速度从点A 出发沿AB 向终点B 运动．过点E 作EF ⊥AB ，交BC 于点F ，连结DA 、DF ．设运动时间为t 秒．（1）求∠ABC 的度数；（2）当t 为何值时，AB ∥DF ；（3）设四边形AEFD 的面积为S ． ①求S 关于t 的函数关系式； ②若一抛物线y ＝－x2＋mx 经过动点E ，当S ＜23时，求m 的取值范围（写出答案即可）．15．（浙江省湖州市）已知：抛物线y ＝x2－2x ＋a （a＜0）与y 轴相交于点A ，顶点为M ．直线y ＝21x －a 分别与x 轴，y 轴相交于B ，C 两点，并且与直线AM 相交于点N ．（1）填空：试用含a 的代数式分别表示点M 与N 的坐标，则M （，），N （，）；（2）如图，将△NAC 沿y 轴翻折，若点N 的对应点N′恰好落在抛物线上，AN′与x 轴交于点D ，连结CD ，求a 的值和四边形ADCN 的面积；（3）在抛物线y ＝x2－2x ＋a （a＜0）上是否存在一点P ，使得以P ，A ，C ，N 为顶点的四边形是平行四边形？若存在，求出P 点的坐标；若不存在，试说明理由．16．（浙江省衢州市、舟山市）如图，已知点A （－4，8）和点B （2，n ）在抛物线y ＝ax2上．（1）求a 的值及点B 关于x 轴对称点P 的坐标，并在x 轴上找一点Q ，使得AQ ＋QB 最短，求出点Q 的坐标；（2）平移抛物线y ＝ax2，记平移后点A 的对应点为A ′，点B 的对应点为B ′，点C （－2，0）和点D （－4，0）是x 轴上的两个定点．① 当抛物线向左平移到某个位置时，A ′C ＋CB′最短，求此时抛物线的函数解析式；② 当抛物线向左或向右平移时，是否存在某个位置，使四边形A ′B ′CD 的周长最短？若存在，求出此时抛物线的函数解析式；若不存在，请说明理由．17．（浙江省宁波市）如图1，在平面直角坐标系中，O 为坐标原点，点A 的坐标为（－8，0），直线BC 经过点B （－8，6），C （0，6），将四边形OABC 绕点O 按顺时针方向旋转α度得到四边形OA ′B ′C ′，此时直线OA′、直线B′C′分别与直线BC 相交于P 、Q ．（1）四边形OABC 的形状是_______________，当α＝90°时，BQBP的值是____________；（2）①如图2，当四边形OA ′B ′C ′的顶点B ′落在y 轴正半轴上时，求BQBP的值； ②如图3，当四边形OA ′B ′C ′的顶点B ′落在直线BC 上时，求ΔOPB ′的面积．（3）在四边形OABC 旋转过程中，当0＜α≤180°时，是否存在这样的点P 和点Q ，使BP ＝21BQ ？若存在，请直接写出点P 的坐标；若不存在，请说明理由．18．（浙江省金华市）如图，在平面直角坐标系中，点A （0，6），点B 是x 轴上的一个动点，连结AB ，取AB的中点M ，将线段MB绕着点B 按顺时针方向旋转90°，得到线段BC ．过点B 作x 轴的垂线交直线AC 于点D ．设点B 坐标是（t ，0）．（1）当t＝4时，求直线AB 的解析式；（2）当t ＞0时，用含t的代数式表示点C 的坐标及△ABC 的面积；（3）是否存在点B ，使△ABD 为等腰三角形？若存在，请求出所有符合条件的点B的坐标；若不存在，请说明理由．121+-=x备用图图1 图2 ) 图3 备用图19．（浙江省绍兴市）定义一种变换：平移抛物线F 1得到抛物线F 2，使F 2经过F 1的顶点A ．设F 2的对称轴分别交F 1，F 2于点D ，B ，点C 是点A 关于直线BD 的对称点．（1）如图1，若F 1：y ＝x2，经过变换后，得到F 2：y ＝x2＋bx ，点C 的坐标为（2，0），则①b 的值等于__________； ②四边形ABCD 为（）；A ．平行四边形B ．矩形C ．菱形D ．正方形（2）如图2，若F 1：y ＝ax2＋c ，经过变换后，点B 的坐标为（2，c －1），求△ABD 的面积；（3）如图3，若F 1：y ＝31x2－32x ＋37，经过变换后，AC ＝32，点P 是直线AC 上的动点，求点P 到点D的距离和到直线AD 的距离之和的最小值．20．（浙江省嘉兴市）如图，已知A 、B 是线段MN 上的两点，MN ＝4，MA ＝1，MB ＞1．以A 为中心顺时针旋转点M ，以B 为中心逆时针旋转点N ，使M 、N 两点重合成一点C ，构成△ABC ，设AB ＝x ．（1）求x 的取值范围；（2）若△ABC 为直角三角形，求x 的值；（3）探究：△ABC 的最大面积？21．（浙江省义乌市）已知点A 、B 分别是x 轴、y 轴上的动点，点C 、D 是某个函数图像上的点，当四边形ABCD（A 、B 、C 、D 各点依次排列）为正方形时，称这个正方形为此函数图像的伴侣正方形．例如：如图，正方形ABCD 是一次函数y ＝x ＋1图像的其中一个伴侣正方形．（1）若某函数是一次函数y ＝x ＋1，求它的图像的所有伴侣正方形的边长；（2）若某函数是反比例函数y ＝xk（k ＞0），它的图像的伴侣正方形为ABCD ，点D （2，m ）（m ＜2）在反比例函数图像上，求m 的值及反比例函数的解析式；（3）若某函数是二次函数y ＝ax2＋c （a ≠0），它的图像的伴侣正方形为ABCD ，C 、D 中的一个点坐标为（3，4）．写出伴侣正方形在抛物线上的另一个顶点坐标__________，写出符合题意的其中一条抛物线解析式________________，并判断你写出的抛物线的伴侣正方形的个数是奇数还是偶数？__________．（本小题只需直接写出答案）22．（浙江省丽水市）如图，已知在等腰△ABC 中，∠A ＝∠B ＝30°，过点C 作CD ⊥AC 交AB 于点D ．（1）尺规作图：过A ，D ，C 三点作⊙O （只要求作出图形，保留痕迹，不要求写作法）；（2）求证：BC 是过A ，D ，C 三点的圆的切线；（3）若过A ，D ，C 三点的圆的半径为3，则线段BC 上是否存在一点P ，使得以P ，D ，B 为顶点的三角形与△BCO 相似，若存在，求出DP 的长；若不存在，请说明理由．23．（浙江省丽水市）已知直角坐标系中菱形ABCD 的位置如图，C ，D 两点的坐标分别为（4，0），（0，3）．现有两动点P ，Q 分别从A ，C 同时出发，点P 沿线段AD 向终点D 运动，点Q 沿折线CBA 向终点A 运动，设运动时间为t 秒．（1）填空：菱形ABCD 的边长是________、面积是________、高BE 的长是________；（2）探究下列问题：①若点P 的速度为每秒1个单位，点Q 的速度为每秒2个单位，当点Q 在线段BA 上时，求△APQ 的面积S 关于t 的函数关系式，以及S 的最大值；②若点P 的速度为每秒1个单位，点Q 的速度变为每秒k 个单位，在运动过程中，任何时刻都有相应的k 值，使得△APQ 沿它的一边翻折，翻折前后两个三角形组成的四边形为菱形．请探究当t ＝4秒时的情形，并求出k 的值．24．（浙江省慈溪中学保送生招生考试）已知：抛物线y ＝ax2＋bx ＋c 经过点（－1，1），且对于任意的实数x ，有4x －4≤ax2＋bx ＋c ≤2x2－4x ＋4恒成立．（1）求4a ＋2b ＋c 的值．（2）求y ＝ax2＋bx ＋c 的解析式．（3）设点M （x ，y ）是抛物线上任一点，点B （0，2），求线段MB 的长度的最小值．25．（浙江省奉化市保送生考试）如图，射线OA ⊥射线OB ，半径r ＝2cm 的动圆M 与OB 相切于点Q （圆M 与OA •没有公共点），P 是OA 上的动点，且PM ＝3cm ，设OP ＝x cm ，OQ ＝y cm ．2 （图1）（图2）（图3）图（1）（1）求x、y所满足的关系式，并写出x的取值范围．（2）当△MOP为等腰三角形时，求相应的x的值．（3）是否存在大于2的实数x，使△MQO∽△OMP？若存在，求相应x的值，若不存在，请说明理由．26．（河南省）如图，在平面直角坐标系中，已知矩形ABCD的三个顶点B（4，0）、C（8，0）、D（8，8）．抛物线y＝ax2＋bx过A、C两点．（1）直接写出点A（2）动点P从点A发，沿线段CD向终点D时间为t秒．过点P作PE①过点E作EF⊥AD于点FEG最长？②连接EQ，在点P、Q△CEQ27．（安徽省）所示．中画出该函数图象；指出金额在什么范围内，以同样的资金可以批发到较多数量的该种水果．（3）经调查，某经销商销售该种水果的日最高销量与零售价之间的函数关系如图（2）所示．该经销商拟每日售出60kg以上该种水果，且当日零售价不变，请你帮助该经销商设计进货和销售的方案，使得当日获得的利润最大．28．（安徽省芜湖市）如图，在平面直角坐标系中放置一直角三角板，其顶点为A（－1，0），B（0，3），O（0，0），将此三角板绕原点O顺时针旋转90°，得到△A′B′O．（1）如图，一抛物线经过点A、B、B′，求该抛物线解析式；（2）设点P是在第一象限内抛物线上一动点，求使四边形PBAB′的面积达到最大时点P的坐标及面积的最大值．29．（安徽省蚌埠二中高一自主招生考试）已知关于x的方程(m2－1)x2－3(3m－1)x＋18＝0有两个正整数根（m是整数），△ABC的三边a、b、c满足c＝32，m2＋a2m－8a＝0，m2＋b2m－8b＝0．求：（1）m的值；（2）△ABC的面积．30．（吉林省）如图所示，菱形ABCD的边长为6厘米，∠B＝60°．从初始时刻开始，点P、Q同时从A点出发，点P以1厘米/秒的速度沿A→C→B的方向运动，点Q以2厘米/秒的速度沿A→B→C→D的方向运动，当点Q运动到D点时，P、Q两点同时停止运动．设P、Q运动的时间为x秒时，△APQ与△ABC重叠部分．．．．的面积为y平方厘米（这里规定：点和线段是面积为0的三角形），解答下列问题：（1）点P、Q从出发到相遇所用时间是__________秒；（2）点P、Q从开始运动到停止的过程中，当△APQ是等边三角形时x的值是__________秒；（3）求y与x之间的函数关系式．31．（吉林省长春市）如图，直线y＝－43x＋6分别与x轴、y轴交于A、B两点；直线y＝45x与AB交于点C，与过点A且平行于y轴的直线交于点D．点E从点A出发，以每秒1个单位的速度沿x轴向左运动．过点E作x轴的垂线，分别交直线AB、OD于P、Q两点，以PQ为边向右作正方形PQMN，设正方形PQMN与△ACD重叠部分（阴影部分）的面积为S（平方单位），点E的运动时间为t（秒）．（1）求点C的坐标；（2）当0＜t＜5时，求S与t之间的函数关系式；（3）求（2）中S的最大值；（4）当t＞0时，直接写出点（4，29）在正方形PQMN内部时t的取值范围．32．（山西省）如图，已知直线l1：y＝32x＋38与直线l2：y＝－2x＋16相交于点C，l1、l2分别交x轴于A、B两点．矩形DEFG的顶点D、E分别在直线l1、l2上，顶点F、G都在x轴上，且点G与点B重合．（1）求△ABC的面积；（2）求矩形DEFG的边DE与EF的长；（3）若矩形DEFG从原地出发，沿x轴的反方向以每秒1个单位长度的速度平移，设移动时间为t（0≤t≤12）秒，矩形DEFG与△ABC重叠部分的面积为S，求S关于t的函数关系式，并写出相应的t的取值范围；（4）S是否存在最大值？若存在，请直接写出最大值及相应的t值，若不存在，请说明理由．QEDCBA MF图（1）33．（山西省太原市）问题解决如图（1），将正方形纸片ABCD 折叠，使点B 落在CD 边上一点E （不与点C ，D 重合），压平后得到折痕MN ．当CD CE ＝21时，求BNAM 的值．类比归纳在图（1）中，若CD CE ＝31，则BN AM 的值等于___________；若CD CE ＝41，则BN AM 的值等于___________；若CDCE ＝n 1（n 为整数），则BN AM 的值等于___________．（用含n 的式子表示）联系拓广如图（2），将矩形纸片ABCD 折叠，使点B 落在CD 边上一点E （不与点C ，D 重合），压平后得到折痕MN ，设BC AB ＝m 1（m ＞1），CD CE＝n1，则BN AM 的值等于_______________．（用含m ，n 的式子表示）34．（江西省、江西省南昌市）如图，抛物线y ＝－x2＋2x ＋3与x 轴相交于A 、B 两点（点A 在点B 的左侧），与y 轴相交于点C ，顶点为D．（1）直接写出A 、B 、C 三点的坐标和抛物线的对称轴；（2）连结BC ，与抛物线的对称轴交于点E ，点P 为线段BC 上的一个动点，过点P 作PF∥DE 交抛物线于点F ，设点P 的横坐标为m ．①用含m 的代数式表示线段PF 的长，并求出当m 为何值时，四边形PEDF 为平行四边形？②设△BCF 的面积为S ，求S 与m 的函数关系式．35．（江西省、江西省南昌市）如图1，在等腰梯形ABCD 中，AD ∥BC ，E 是AB 的中点，过点E 作EF ∥BC 交CD 于点F ．AB ＝4，BC ＝6，∠B ＝60°．（1）求点E 到BC 的距离；（2）点P 为线段EF 上的一个动点，过P 作PM ⊥EF 交BC 于点M ，过M 作MN ∥AB 交折线ADC 于点N ，连结PN ，设EP ＝x ．①当点N 在线段AD 上时（如图2），△PMN 的形状是否发生改变？若不变，求出△PMN 的周长；若改变，请说明理由；②当点N 在线段DC 上时（如图3），是否存在点P ，使△PMN 为等腰三角形？若存在，请求出所有满足要求的x 的值；若不存在，请说明理由．36．（青海省）矩形OABC 在平面直角坐标系中位置如图所示，A 、C 两点的坐标分别为A （6，0），C （0，－3），直线y ＝－43x 与BC 边相交于D 点．（1）求点D 的坐标；（2）若抛物线y ＝ax2－49x 经过点A ，试确定此抛物线的表达式；（3）设（2）中的抛物线的对称轴与直线OD 交于点M ，点P为对称轴上一动点，以P 、O 、M 为顶点的三角形与△OCD 相似，求符合条件的点P 的坐标．37．（青海省西宁市）已知OABC 是一张矩形纸片，AB ＝6．（1）如图1，在AB 上取一点M ，使得△CBM 与△CB ′′M 关于CM 所在直线对称，点B ′′恰好在边OA 上，且△OB ′C 的面积为24cm 2，求BC 的长；（2）如图2．以O 为原点，OA 、OC 所在直线分别为x 轴、y 轴建立平面直角坐标系．求对称轴CM 所在直线的函数关系式；（3）作B ′G ∥AB 交CM 于点G ，若抛物线y ＝61x2＋m 过点G ，求这条抛物线所对应的函数关系式．38．（新疆维吾尔自治区、新疆生产建设兵团）某公交公司的公共汽车和出租车每天从乌鲁木齐市出发往返于乌鲁木齐市和石河子市两地，出租车比公共汽车多往返一趟，如图表示出租车距乌鲁木齐市的路程y （单位：千米）与所用时间x （单位：小时）的函数图象。

2018年全国各地中考数学压轴题汇编：几何综合(浙江专版)(原卷)

2018年全国各地中考数学压轴题汇编（浙江专版）几何综合1．数学课上，张老师举了下面的例题：例1等腰三角形ABC中，∠A=110°，求∠B的度数．（答案：35°）例2等腰三角形ABC中，∠A=40°，求∠B的度数，（答案：40°或70°或100°）张老师启发同学们进行变式，小敏编了如下一题：变式等腰三角形ABC中，∠A=80°，求∠B的度数．（1）请你解答以上的变式题．（2）解（1）后，小敏发现，∠A的度数不同，得到∠B的度数的个数也可能不同，如果在等腰三角形ABC中，设∠A=x°，当∠B有三个不同的度数时，请你探索x的取值范围．2．如图，在Rt△ABC中，点O在斜边AB上，以O为圆心，OB为半径作圆，分别与BC，AB相交于点D，E，连结AD．已知∠CAD=∠B．（1）求证：AD是⊙O的切线．（2）若BC=8，tanB=，求⊙O的半径．3．如图，在6×6的网格中，每个小正方形的边长为1，点A在格点（小正方形的顶点）上．试在各网格中画出顶点在格点上，面积为6，且符合相应条件的图形．4．如图，在四边形ABCD中，E是AB的中点，AD∥EC，∠AED=∠B．（1）求证：△AED≌△EBC．（2）当AB=6时，求CD的长．5．如图，已知AB是⊙O的直径，C，D是⊙O上的点，OC∥BD，交AD于点E，连结BC．（1）求证：AE=ED；（2）若AB=10，∠CBD=36°，求的长．6．如图，在△ABC中，∠ACB=90°，以点B为圆心，BC长为半径画弧，交线段AB于点D；以点A为圆心，AD长为半径画弧，交线段AC于点E，连结CD．（1）若∠A=28°，求∠ACD的度数．（2）设BC=a，AC=b．①线段AD的长是方程x2+2ax﹣b2=0的一个根吗？说明理由．②若AD=EC，求的值．7．在5×3的方格纸中，△ABC的三个顶点都在格点上．（1）在图1中画出线段BD，使BD∥AC，其中D是格点；（2）在图2中画出线段BE，使BE⊥AC，其中E是格点．8．如图，在▱ABCD中，AC是对角线，BE⊥AC，DF⊥AC，垂足分别为点E，F，求证：AE=CF．9．已知：在△ABC中，AB=AC，D为AC的中点，DE⊥AB，DF⊥BC，垂足分别为点E，F，且DE=DF．求证：△ABC是等边三角形．10．如图，D是△ABC的BC边上一点，连接AD，作△ABD的外接圆，将△ADC 沿直线AD折叠，点C的对应点E落在BD上．（1）求证：AE=AB．（2）若∠CAB=90°，cos∠ADB=，BE=2，求BC的长．11．在Rt△ABC中，∠ACB=90°，AC=12．点D在直线CB上，以CA，CD为边作矩形ACDE，直线AB与直线CE，DE的交点分别为F，G．（1）如图，点D在线段CB上，四边形ACDE是正方形．①若点G为DE中点，求FG的长．②若DG=GF，求BC的长．（2）已知BC=9，是否存在点D，使得△DFG是等腰三角形？若存在，求该三角形的腰长；若不存在，试说明理由．12．如图，△ABC是⊙O的内接三角形，点D在上，点E在弦AB上（E不与A重合），且四边形BDCE为菱形．（1）求证：AC=CE；（2）求证：BC2﹣AC2=AB•AC；（3）已知⊙O的半径为3．①若=，求BC的长；②当为何值时，AB•AC的值最大？13．小敏思考解决如下问题：原题：如图1，点P，Q分别在菱形ABCD的边BC，CD上，∠PAQ=∠B，求证：AP=AQ．（1）小敏进行探索，若将点P，Q的位置特殊化；把∠PAQ绕点A旋转得到∠EAF，使AE⊥BC，点E，F分别在边BC，CD上，如图2．此时她证明了AE=AF，请你证明．（2）受以上（1）的启发，在原题中，添加辅助线：如图3，作AE⊥BC，AF⊥CD，垂足分别为E，F．请你继续完成原题的证明．（3）如果在原题中添加条件：AB=4，∠B=60°，如图1，请你编制一个计算题（不标注新的字母），并直接给出答案（根据编出的问题层次，给不同的得分）．14．如图，已知P为锐角∠MAN内部一点，过点P作PB⊥AM于点B，PC⊥AN 于点C，以PB为直径作⊙O，交直线CP于点D，连接AP，BD，AP交⊙O于点E．（1）求证：∠BPD=∠BAC．（2）连接EB，ED，当tan∠MAN=2，AB=2时，在点P的整个运动过程中．①若∠BDE=45°，求PD的长．②若△BED为等腰三角形，求所有满足条件的BD的长．（3）连接OC，EC，OC交AP于点F，当tan∠MAN=1，OC∥BE时，记△OFP 的面积为S1，△CFE的面积为S2，请写出的值．15．如图，在Rt△ABC中，AC=BC，∠ACB=90°，点D，E分别在AC，BC上，且CD=CE．（1）如图1，求证：∠CAE=∠CBD；（2）如图2，F是BD的中点，求证：AE⊥CF；（3）如图3，F，G分别是BD，AE的中点，若AC=2，CE=1，求△CGF的面积．16．如图1，直线l：y=﹣x+b与x轴交于点A（4，0），与y轴交于点B，点C 是线段OA上一动点（0＜AC＜）．以点A为圆心，AC长为半径作⊙A交x 轴于另一点D，交线段AB于点E，连结OE并延长交⊙A于点F．（1）求直线l的函数表达式和tan∠BAO的值；（2）如图2，连结CE，当CE=EF时，①求证：△OCE∽△OEA；②求点E的坐标；（3）当点C在线段OA上运动时，求OE•EF的最大值．。

2018年全国各地中考数学压轴题汇编：几何综合(江苏专版)(解析卷)

2018年全国各地中考数学压轴题汇编（江苏专版）几何综合参考答案与试题解析一．解答题（共18小题）1．（2018•无锡）如图，四边形ABCD内接于⊙O，AB=17，CD=10，∠A=90°，cosB=，求AD的长．解：∵四边形ABCD内接于⊙O，∠A=90°，∴∠C=180°﹣∠A=90°，∠ABC+∠ADC=180°．作AE⊥BC于E，DF⊥AE于F，则CDFE是矩形，EF=CD=10．在Rt△AEB中，∵∠AEB=90°，AB=17，cos∠ABC=，∴BE=AB•cos∠ABE=，∴AE==，∴AF=AE﹣EF=﹣10=．∵∠ABC+∠ADC=180°，∠CDF=90°，∴∠ABC+∠ADF=90°，∵cos∠ABC=，∴sin∠ADF=cos∠ABC=．在Rt△ADF中，∵∠AFD=90°，sin∠ADF=，∴AD===6．2．（2018•南京）如图，在四边形ABCD中，BC=CD，∠C=2∠BAD．O是四边形ABCD 内一点，且OA=OB=OD．求证：（1）∠BOD=∠C；（2）四边形OBCD是菱形．证明：（1）延长OA到E，∵OA=OB，∴∠ABO=∠BAO，又∠BOE=∠ABO+∠BAO，∴∠BOE=2∠BAO，同理∠DOE=2∠DAO，∴∠BOE+∠DOE=2∠BAO+2∠DAO=2（∠BAO+∠DAO）即∠BOD=2∠BAD，又∠C=2∠BAD，∴∠BOD=∠C；（2）连接OC，∵OB=OD，CB=CD，OC=OC，∴△OBC≌△ODC，∴∠BOC=∠DOC，∠BCO=∠DCO，∵∠BOD=∠BOC+∠DOC，∠BCD=∠BCO+∠DCO，∴∠BOC=∠BOD，∠BCO=∠BCD，又∠BOD=∠BCD，∴∠BOC=∠BCO，∴BO=BC，又OB=OD，BC=CD，∴OB=BC=CD=DO，∴四边形OBCD是菱形．3．（2018•淮安）如图，AB是⊙O的直径，AC是⊙O的切线，切点为A，BC交⊙O于点D，点E是AC的中点．（1）试判断直线DE与⊙O的位置关系，并说明理由；（2）若⊙O的半径为2，∠B=50°，AC=4.8，求图中阴影部分的面积．解：（1）直线DE与⊙O相切．理由如下：连接OE、OD，如图，∵AC是⊙O的切线，∴AB⊥AC，∴∠OAC=90°，∵点E是AC的中点，O点为AB的中点，∴OE∥BC，∴∠1=∠B，∠2=∠3，∵OB=OD，∴∠B=∠3，∴∠1=∠2，，∴△AOE≌△DOE，∴∠ODE=∠OAE=90°，∴OA⊥AE，∴DE为⊙O的切线；（2）∵点E是AC的中点，∴AE=AC=2.4，∵∠AOD=2∠B=2×50°=100°，∴图中阴影部分的面积=2•×2×2.4﹣=4.8﹣π．4．（2018•连云港）如图，矩形ABCD中，E是AD的中点，延长CE，BA交于点F，连接AC，DF．（1）求证：四边形ACDF是平行四边形；（2）当CF平分∠BCD时，写出BC与CD的数量关系，并说明理由．解：（1）∵四边形ABCD是矩形，∴AB∥CD，∴∠FAE=∠CDE，∵E是AD的中点，∴AE=DE，又∵∠FEA=∠CED，∴CD=FA，又∵CD∥AF，∴四边形ACDF是平行四边形；（2）BC=2CD．证明：∵CF平分∠BCD，∴∠DCE=45°，∵∠CDE=90°，∴△CDE是等腰直角三角形，∴CD=DE，∵E是AD的中点，∴AD=2CD，∵AD=BC，∴BC=2CD．5．（2018•南京）如图，在正方形ABCD中，E是AB上一点，连接DE．过点A作AF ⊥DE，垂足为F，⊙O经过点C、D、F，与AD相交于点G．（1）求证：△AFG∽△DFC；（2）若正方形ABCD的边长为4，AE=1，求⊙O的半径．（1）证明：在正方形ABCD中，∠ADC=90°，∴∠CDF+∠ADF=90°，∵AF⊥DE，∴∠AFD=90°，∴∠DAF+∠ADF=90°，∴∠DAF=∠CDF，∵四边形GFCD是⊙O的内接四边形，∴∠FCD+∠DGF=180°，∵∠FGA+∠DGF=180°，∴∠FGA=∠FCD，∴△AFG∽△DFC．（2）解：如图，连接CG．∵∠EAD=∠AFD=90°，∠EDA=∠ADF，∴△EDA∽△ADF，∴=，即=，∵△AFG∽△DFC，∴=，∴=，在正方形ABCD中，DA=DC，∴AG=EA=1，DG=DA﹣AG=4﹣1=3，∴CG==5，∵∠CDG=90°，∴CG是⊙O的直径，∴⊙O的半径为．6．（2018•无锡）如图，矩形ABCD中，AB=m，BC=n，将此矩形绕点B顺时针方向旋转θ（0°＜θ＜90°）得到矩形A1BC1D1，点A1在边CD上．（1）若m=2，n=1，求在旋转过程中，点D到点D1所经过路径的长度；（2）将矩形A1BC1D1继续绕点B顺时针方向旋转得到矩形A2BC2D2，点D2在BC的延长线上，设边A2B与CD交于点E，若=﹣1，求的值．解：（1）作A1H⊥AB于H，连接BD，BD1，则四边形ADA1H是矩形．∴AD=HA1=n=1，在Rt△A1HB中，∵BA1=BA=m=2，∴BA1=2HA1，∴∠ABA1=30°，∴旋转角为30°，∵BD==，∴D到点D1所经过路径的长度==π．（2）∵△BCE∽△BA2D2，∴==，∴CE=∵=﹣1∴=，∴AC=•，∴BH=AC==•，∴m2﹣n2=6•，∴m4﹣m2n2=6n4，1﹣=6•，∴=（负根已经舍弃）．7．（2018•泰州）如图，AB为⊙O的直径，C为⊙O上一点，∠ABC的平分线交⊙O于点D，DE⊥BC于点E．（1）试判断DE与⊙O的位置关系，并说明理由；（2）过点D作DF⊥AB于点F，若BE=3，DF=3，求图中阴影部分的面积．解：（1）DE与⊙O相切，理由：连接DO，∵DO=BO，∴∠ODB=∠OBD，∵∠ABC的平分线交⊙O于点D，∴∠EBD=∠DBO，∴∠EBD=∠BDO，∴DO∥BE，∵DE⊥BC，∴∠DEB=∠EDO=90°，∴DE与⊙O相切；（2）∵∠ABC的平分线交⊙O于点D，DE⊥BE，DF⊥AB，∴DE=DF=3，∴BD==6，∵sin∠DBF==，∴∠DBA=30°，∴∠DOF=60°，∴sin60°===，∴DO=2，则FO=，故图中阴影部分的面积为：﹣××3=2π﹣．8．（2018•扬州）如图，在平行四边形ABCD中，DB=DA，点F是AB的中点，连接DF并延长，交CB的延长线于点E，连接AE．（1）求证：四边形AEBD是菱形；（2）若DC=，tan∠DCB=3，求菱形AEBD的面积．（1）证明：∵四边形ABCD是平行四边形，∴AD∥CE，∴∠DAF=∠EBF，∵∠AFD=∠EFB，AF=FB，∴△AFD≌△BFE，∴AD=EB，∵AD∥EB，∴四边形AEBD是平行四边形，∴四边形AEBD是菱形．（2）解：∵四边形ABCD是平行四边形，∴CD=AB=，AB∥CD，∴∠ABE=∠DCB，∴tan∠ABE=tan∠DCB=3，∵四边形AEBD是菱形，∴AB⊥DE，AF=FB，EF=DF，∴tan∠ABE==3，∵BF=，∴EF=，∴DE=3，=•AB•DE=•3=15．∴S菱形AEBD9．（2018•宿迁）如图，AB、AC分别是⊙O的直径和弦，OD⊥AC于点D．过点A作⊙O的切线与OD的延长线交于点P，PC、AB的延长线交于点F．（1）求证：PC是⊙O的切线；（2）若∠ABC=60°，AB=10，求线段CF的长．解：（1）连接OC，∵OD⊥AC，OD经过圆心O，∴AD=CD，∴PA=PC，在△OAP和△OCP中，∵，∴△OAP≌△OCP（SSS），∴∠OCP=∠OAP∵PA是半⊙O的切线，∴∠OAP=90°．∴∠OCP=90°，即OC⊥PC∴PC是⊙O的切线．（2）∵OB=OC，∠OBC=60°，∴△OBC是等边三角形，∴∠COB=60°，∵AB=10，∴OC=5，由（1）知∠OCF=90°，∴CF=OCtan∠COB=5．10．（2018•淮安）如果三角形的两个内角α与β满足2α+β=90°，那么我们称这样的三角形为“准互余三角形”．（1）若△ABC是“准互余三角形”，∠C＞90°，∠A=60°，则∠B=15°；（2）如图①，在Rt△ABC中，∠ACB=90°，AC=4，BC=5．若AD是∠BAC的平分线，不难证明△ABD是“准互余三角形”．试问在边BC上是否存在点E（异于点D），使得△ABE也是“准互余三角形”？若存在，请求出BE的长；若不存在，请说明理由．（3）如图②，在四边形ABCD中，AB=7，CD=12，BD⊥CD，∠ABD=2∠BCD，且△ABC是“准互余三角形”，求对角线AC的长．解：（1）∵△ABC是“准互余三角形”，∠C＞90°，∠A=60°，∴2∠B+∠A=60°，解得，∠B=15°，故答案为：15°；（2）如图①中，在Rt△ABC中，∵∠B+∠BAC=90°，∠BAC=2∠BAD，∴∠B+2∠BAD=90°，∴△ABD是“准互余三角形”，∵△ABE也是“准互余三角形”，∴只有2∠A+∠BAE=90°，∵∠A+∠BAE+∠EAC=90°，∴∠CAE=∠B，∵∠C=∠C=90°，∴△CAE∽△CBA，可得CA2=CE•CB，∴CE=，∴BE=5﹣=．（3）如图②中，将△BCD沿BC翻折得到△BCF．∴CF=CD=12，∠BCF=∠BCD，∠CBF=∠CBD，∵∠ABD=2∠BCD，∠BCD+∠CBD=90°，∴∠ABD+∠DBC+∠CBF=180°，∴A、B、F共线，∴∠A+∠ACF=90°∴2∠ACB+∠CAB≠90°，∴只有2∠BAC+∠ACB=90°，∴∠FCB=∠FAC，∵∠F=∠F，∴△FCB∽△FAC，∴CF2=FB•FA，设FB=x，则有：x（x+7）=122，∴x=9或﹣16（舍弃），∴AF=7+9=16，在Rt△ACF中，AC===20．11．（2018•盐城）如图，在以线段AB为直径的⊙O上取一点C，连接AC、BC．将△ABC沿AB翻折后得到△ABD．（1）试说明点D在⊙O上；（2）在线段AD的延长线上取一点E，使AB2=AC•AE．求证：BE为⊙O的切线；（3）在（2）的条件下，分别延长线段AE、CB相交于点F，若BC=2，AC=4，求线段EF的长．解：（1）∵AB为⊙O的直径，∴∠C=90°，∵将△ABC沿AB翻折后得到△ABD，∴△ABC≌△ABD，∴∠ADB=∠C=90°，∴点D在以AB为直径的⊙O上；（2）∵△ABC≌△ABD，∴AC=AD，∵AB2=AC•AE，∴AB2=AD•AE，即=，∵∠BAD=∠EAB，∴△ABD∽△AEB，∴∠ABE=∠ADB=90°，∵AB为⊙O的直径，∴BE是⊙O的切线；（3）∵AD=AC=4、BD=BC=2，∠ADB=90°，∴AB===2，∵=，∴=，解得：DE=1，∴BE==，∵四边形ACBD内接于⊙O，∴∠FBD=∠FAC，即∠FBE+∠DBE=∠BAE+∠BAC，又∵∠DBE+∠ABD=∠BAE+∠ABD=90°，∴∠DBE=∠BAE，∴∠FBE=∠BAC，又∠BAC=∠BAD，∴∠FBE=∠BAD，∴△FBE∽△FAB，∴=，即==，∴FB=2FE，在Rt△ACF中，∵AF2=AC2+CF2，∴（5+EF）2=42+（2+2EF）2，整理，得：3EF2﹣2EF﹣5=0，解得：EF=﹣1（舍）或EF=，∴EF=．12．（2018•扬州）如图，在△ABC中，AB=AC，AO⊥BC于点O，OE⊥AB于点E，以点O为圆心，OE为半径作半圆，交AO于点F．（1）求证：AC是⊙O的切线；（2）若点F是A的中点，OE=3，求图中阴影部分的面积；（3）在（2）的条件下，点P是BC边上的动点，当PE+PF取最小值时，直接写出BP 的长．（1）证明：作OH⊥AC于H，如图，∵AB=AC，AO⊥BC于点O，∴AO平分∠BAC，∵OE⊥AB，OH⊥AC，∴OH=OE，∴AC是⊙O的切线；（2）解：∵点F是AO的中点，∴AO=2OF=3，而OE=3，∴∠OAE=30°，∠AOE=60°，∴AE=OE=3，∴图中阴影部分的面积=S△AOE ﹣S扇形EOF=×3×3﹣=；（3）解：作F点关于BC的对称点F′，连接EF′交BC于P，如图，∵PF=PF′，∴PE+PF=PE+PF′=EF′，此时EP+FP最小，∵OF′=OF=OE，∴∠F′=∠OEF′，而∠AOE=∠F′+∠OEF′=60°，∴∠F′=30°，∴∠F′=∠EAF′，∴EF′=EA=3，即PE+PF最小值为3，在Rt△OPF′中，OP=OF′=，在Rt△ABO中，OB=OA=×6=2，∴BP=2﹣=，即当PE+PF取最小值时，BP的长为．13．（2018•南京）结果如此巧合!下面是小颖对一道题目的解答．题目：如图，Rt△ABC的内切圆与斜边AB相切于点D，AD=3，BD=4，求△ABC的面积．解：设△ABC的内切圆分别与AC、BC相切于点E、F，CE的长为x．根据切线长定理，得AE=AD=3，BF=BD=4，CF=CE=x．根据勾股定理，得（x+3）2+（x+4）2=（3+4）2．整理，得x2+7x=12．=AC•BC所以S△ABC=（x+3）（x+4）=（x2+7x+12）=×（12+12）=12．小颖发现12恰好就是3×4，即△ABC的面积等于AD与BD的积．这仅仅是巧合吗？请你帮她完成下面的探索．已知：△ABC的内切圆与AB相切于点D，AD=m，BD=n．可以一般化吗？（1）若∠C=90°，求证：△ABC的面积等于mn．倒过来思考呢？（2）若AC•BC=2mn，求证∠C=90°．改变一下条件……（3）若∠C=60°，用m、n表示△ABC的面积．解：设△ABC的内切圆分别与AC、BC相切于点E、F，CE的长为x，根据切线长定理，得：AE=AD=m、BF=BD=n、CF=CE=x，（1）如图1，在Rt△ABC中，根据勾股定理，得：（x+m）2+（x+n）2=（m+n）2，整理，得：x2+（m+n）x=mn，=AC•BC所以S△ABC=（x+m）（x+n）= [x2+（m+n）x+mn]=（mn+mn）=mn，（2）由AC•BC=2mn，得：（x+m）（x+n）=2mn，整理，得：x2+（m+n）x=mn，∴AC2+BC2=（x+m）2+（x+n）2=2[x2+（m+n）x]+m2+n2=2mn+m2+n2=（m+n）2=AB2，根据勾股定理逆定理可得∠C=90°；（3）如图2，过点A作AG⊥BC于点G，在Rt△ACG中，AG=AC•sin60°=（x+m），CG=AC•cos60°=（x+m），∴BG=BC﹣CG=（x+n）﹣（x+m），在Rt△ABG中，根据勾股定理可得：[（x+m）]2+[（x+n）﹣（x+m）]2=（m+n）2，整理，得：x2+（m+n）x=3mn，=BC•AG∴S△ABC=×（x+n）•（x+m）= [x2+（m+n）x+mn]=×（3mn+mn）=mn．14．（2018•盐城）【发现】如图①，已知等边△ABC，将直角三角板的60°角顶点D任意放在BC边上（点D不与点B、C重合），使两边分别交线段AB、AC于点E、F．（1）若AB=6，AE=4，BD=2，则CF=4；（2）求证：△EBD∽△DCF．【思考】若将图①中的三角板的顶点D在BC边上移动，保持三角板与边AB、AC的两个交点E、F都存在，连接EF，如图②所示，问：点D是否存在某一位置，使ED平分∠BEF且FD平分∠CFE？若存在，求出的值；若不存在，请说明理由．【探索】如图③，在等腰△ABC中，AB=AC，点O为BC边的中点，将三角形透明纸板的一个顶点放在点O处（其中∠MON=∠B），使两条边分别交边AB、AC于点E、F （点E、F均不与△ABC的顶点重合），连接EF．设∠B=α，则△AEF与△ABC的周长之比为1﹣cosα（用含α的表达式表示）．（1）解：∵△ABC是等边三角形，∴AB=BC=AC=6，∠B=∠C=60°．∵AE=4，∴BE=2，则BE=BD，∴△BDE是等边三角形，∴∠BED=60°，又∵∠EDF=60°，∴∠CDF=180°﹣∠EDF﹣∠B=60°，则∠CDF=∠C=60°，∴△CDF是等边三角形，∴CF=CD=BC=BD=6﹣2=4．故答案是：4；（2）证明：如图①，∵∠EDF=60°，∠B=60°，∴∠CDF+BDE=120°，∠BED+∠BDE=120°，∴∠BED=∠CDF．又∠B=∠C=60°，∴△EBD∽△DCF；【思考】存在，如图②，过D作DM⊥BE，DG⊥EF，DN⊥CF，垂足分别是M、G、N，∵ED平分∠BEF且FD平分∠CFE．∴DM=DG=DN．又∠B=∠C=60°，∠BMD=∠CND=90°，∴△BDM≌△CDN，∴BD=CD，即点D是BC的中点，∴=；【探索】如图③，连接AO，作OG⊥BE，OD⊥EF，OH⊥CF，垂足分别是G、D、H．则∠BGO=∠CHO=90°，∵AB=AC，O是BC的中点，∴∠B=∠C，OB=OC，∴△OBG≌△OCH，∴OG=OH，GB=CH，∠BOG=∠COH=90°﹣α，则∠GOH=180°﹣（∠BOG+∠COH）=2α，∴∠EOF=∠B=α则∠GOH=2∠EOF=2α．由（2）题可猜想应用EF=ED+DF=GE+FH（可通过半角旋转证明），AE+EF+AF=AE+EG+FH+AF=AG+AH=2AG，则C△AEF设AB=m，则OB=mcosα，GB=mcos2α．====1﹣cosα．故答案是：1﹣cosα．15．（2018•扬州）问题呈现如图1，在边长为1的正方形网格中，连接格点D，N和E，C，DN和EC相交于点P，求tan∠CPN的值．方法归纳求一个锐角的三角函数值，我们往往需要找出（或构造出）一个直角三角形．观察发现问题中∠CPN不在直角三角形中，我们常常利用网格画平行线等方法解决此类问题，比如连接格点M，N，可得MN∥EC，则∠DNM=∠CPN，连接DM，那么∠CPN就变换到Rt△DMN中．问题解决（1）直接写出图1中tan∠CPN的值为2；（2）如图2，在边长为1的正方形网格中，AN与CM相交于点P，求cos∠CPN的值；思维拓展（3）如图3，AB⊥BC，AB=4BC，点M在AB上，且AM=BC，延长CB到N，使BN=2BC，连接AN交CM的延长线于点P，用上述方法构造网格求∠CPN的度数．解：（1）如图1中，∵EC∥MN，∴∠CPN=∠DNM，∴tan∠CPN=tan∠DNM，∵∠DMN=90°，∴tan∠CPN=tan∠DNM===2，故答案为2．（2）如图2中，取格点D，连接CD，DM．∵CD∥AN，∴∠CPN=∠DCM，∵△DCM是等腰直角三角形，∴∠DCM=∠D=45°，∴cos∠CPN=cos∠DCM=．（3）如图3中，如图取格点M，连接AN、MN．∵PC∥MN，∴∠CPN=∠ANM，∵AM=MN，∠AMN=90°，∴∠ANM=∠MAN=45°，∴∠CPN=45°．16．（2018•泰州）对给定的一张矩形纸片ABCD进行如下操作：先沿CE折叠，使点B 落在CD边上（如图①），再沿CH折叠，这时发现点E恰好与点D重合（如图②）（1）根据以上操作和发现，求的值；（2）将该矩形纸片展开．①如图③，折叠该矩形纸片，使点C与点H重合，折痕与AB相交于点P，再将该矩形纸片展开．求证：∠HPC=90°；②不借助工具，利用图④探索一种新的折叠方法，找出与图③中位置相同的P点，要求只有一条折痕，且点P在折痕上，请简要说明折叠方法．（不需说明理由）解：（1）由图①，可得∠BCE=∠BCD=45°，又∵∠B=90°，∴△BCE是等腰直角三角形，∴=cos45°=，即CE=BC，由图②，可得CE=CD，而AD=BC，∴CD=AD，∴=；（2）①设AD=BC=a，则AB=CD=a，BE=a，∴AE=（﹣1）a，如图③，连接EH，则∠CEH=∠CDH=90°，∵∠BEC=45°，∠A=90°，∴∠AEH=45°=∠AHE，∴AH=AE=（﹣1）a，设AP=x，则BP=a﹣x，由翻折可得，PH=PC，即PH2=PC2，∴AH2+AP2=BP2+BC2，即[（﹣1）a]2+x2=（a﹣x）2+a2，解得x=a，即AP=BC，又∵PH=CP，∠A=∠B=90°，∴Rt△APH≌Rt△BCP（HL），∴∠APH=∠BCP，又∵Rt△BCP中，∠BCP+∠BPC=90°，∴∠APH+∠BPC=90°，∴∠CPH=90°；②折法：如图，由AP=BC=AD，可得△ADP是等腰直角三角形，PD平分∠ADC，故沿着过D的直线翻折，使点A落在CD边上，此时折痕与AB的交点即为P；折法：如图，由∠BCE=∠PCH=45°，可得∠BCP=∠ECH，由∠DCE=∠PCH=45°，可得∠PCE=∠DCH，又∵∠DCH=∠ECH，∴∠BCP=∠PCE，即CP平分∠BCE，故沿着过点C的直线折叠，使点B落在CE上，此时，折痕与AB的交点即为P．17．（2018•宿迁）如图，在边长为1的正方形ABCD中，动点E、F分别在边AB、CD 上，将正方形ABCD沿直线EF折叠，使点B的对应点M始终落在边AD上（点M不与点A、D重合），点C落在点N处，MN与CD交于点P，设BE=x．（1）当AM=时，求x的值；（2）随着点M在边AD上位置的变化，△PDM的周长是否发生变化？如变化，请说明理由；如不变，请求出该定值；（3）设四边形BEFC的面积为S，求S与x之间的函数表达式，并求出S的最小值．解：（1）如图，在Rt△AEM中，AE=1﹣x，EM=BE=x，AM=，∵AE2+AM2=EM2，∴（1﹣x）2+（）2=x2，∴x=．（2）△PDM的周长不变，为2．理由：设AM=y，则BE=EM=x，MD=1﹣y，在Rt△AEM中，由勾股定理得AE2+AM2=EM2，（1﹣x）2+y2=x2，解得1+y2=2x，∴1﹣y2=2（1﹣x）∵∠EMP=90°，∠A=∠D，∴Rt△AEM∽Rt△DMP，∴=，即=，解得DM+MP+DP==2．∴△DMP的周长为2．（3）作FH⊥AB于H．则四边形BCFH是矩形．连接BM交FN于O，交FH于K．在Rt△AEM中，AM==，∵B、M关于EF对称，∴BM⊥EF，∴∠KOF=∠KHB，∵∠OKF=∠BKH，∴∠KFO=∠KBH，∵AB=BC=FH，∠A=∠FHE=90°，∴△ABM≌△HFE，∴EH=AM=，∴CF=BH=x﹣，∴S=（BE+CF）•BC=（x+x﹣）= [（）2﹣+1]=（﹣）2+．当=时，S有最小值=．18．（2018•连云港）在数学兴趣小组活动中，小亮进行数学探究活动．△ABC是边长为2的等边三角形，E是AC上一点，小亮以BE为边向BE的右侧作等边三角形BEF，连接CF．（1）如图1，当点E在线段AC上时，EF、BC相交于点D，小亮发现有两个三角形全等，请你找出来，并证明．（2）当点E在线段上运动时，点F也随着运动，若四边形ABFC的面积为，求AE 的长．（3）如图2，当点E在AC的延长线上运动时，CF、BE相交于点D，请你探求△ECD的面积S 1与△DBF 的面积S 2之间的数量关系．并说明理由．（4）如图2，当△ECD 的面积S 1=时，求AE 的长．解：（1）结论：△ABE ≌△CBF ．理由：如图1中，∴∵△ABC ，△BEF 都是等边三角形， ∴BA=BC ，BE=BF ，∠ABC=∠EBF ， ∴∠ABE=∠CBF ，∴△ABE ≌△CBF ．（2）如图1中，∵△ABE ≌△CBF ， ∴S △ABE =S △BCF ，∴S 四边形BECF =S △BEC +s △BCF =S △BCE +S △ABE =S △ABC =， ∵S 四边形ABCF =， ∴S △ABE =， ∴•AE•AB•siin60°=， ∴AE=．（3）结论：S 2﹣S 1=．理由：如图2中，∵△ABC ，△BEF 都是等边三角形， ∴BA=BC ，BE=BF ，∠ABC=∠EBF ， ∴∠ABE=∠CBF ，∴△ABE ≌△CBF ，∴S △ABE =S △BCF ，∵S △BCF ﹣S △BCE =S 2﹣S 1，∴S 2﹣S 1=S △ABE ﹣S △BCE =S △ABC =．（4）由（3）可知：S △BDF ﹣S △ECD =，∵S △ECD =， ∴S △BDF =，∵△ABE ≌△CBF ，∴AE=CF ，∠BAE=∠BCF=60°， ∴∠ABC=∠DCB ，∴CF ∥AB ，则△BDF 的BF 边上的高为，可得DF=，设CE=x ，则2+x=CD +DF=CD +，∴CD=x ﹣，∵CD ∥AB ， ∴=，即=，化简得：3x 2﹣x ﹣2=0，解得x=1或﹣（舍弃），∴CE=1，AE=3．。

2018年全国各地中考数学压轴题汇编：几何综合(湖北专版)(解析版)

2018年全国各地中考数学压轴题汇编（湖北专版）几何综合参考答案与试题解析1．（2018•武汉）如图，PA是⊙O的切线，A是切点，AC是直径，AB是弦，连接PB、PC，PC交AB于点E，且PA=PB．（1）求证：PB是⊙O的切线；（2）若∠APC=3∠BPC，求的值．（1）证明：连接OP、OB．∵PA是⊙O的切线，∴PA⊥OA，∴∠PAO=90°，∵PA=PB，PO=PO，OA=OB，∴△PAO≌△PBO．∴∠PAO=∠PBO=90°，∴PB⊥OB，∴PB是⊙O的切线．（2）设OP交AB于K．∵AB是直径，∴∠ABC=90°，∴AB⊥BC，∵PA、PB都是切线，∴PA=PB，∠APO=∠BPO，∵OA=OB，∴OP垂直平分线段AB，∴OK∥BC，∵AO=OC，∴AK=BK，∴BC=2OK，设OK=a，则BC=2a，∵∠APC=3∠BPC，∠APO=∠OPB，∴∠OPC=∠BPC=∠PCB，∴BC=PB=PA=2a，∵△PAK∽△POA，∴PA2=PK•PO，设PK=x，则有：x2+ax﹣4a2=0，解得x=a（负根已经舍弃），∴PK=a，∵PK∥BC，∴==．2．（2018•天门）问题：如图①，在Rt△ABC中，AB=AC，D为BC边上一点（不与点B，C重合），将线段AD绕点A逆时针旋转90°得到AE，连接EC，则线段BC，DC，EC之间满足的等量关系式为BC=DC+EC；探索：如图②，在Rt△ABC与Rt△ADE中，AB=AC，AD=AE，将△ADE绕点A旋转，使点D落在BC边上，试探索线段AD，BD，CD之间满足的等量关系，并证明你的结论；应用：如图③，在四边形ABCD中，∠ABC=∠ACB=∠ADC=45°．若BD=9，CD=3，求AD 的长．解：（1）BC=DC+EC，理由如下：∵∠BAC=∠DAE=90°，∴∠BAC﹣∠DAC=∠DAE﹣∠DAC，即∠BAD=∠CAE，在△BAD和△CAE中，，∴△BAD≌△CAE，∴BD=CE，∴BC=BD+CD=EC+CD，故答案为：BC=DC+EC；（2）BD2+CD2=2AD2，理由如下：连接CE，由（1）得，△BAD≌△CAE，∴BD=CE，∠ACE=∠B，∴∠DCE=90°，∴CE2+CD2=ED2，在Rt△ADE中，AD2+AE2=ED2，又AD=AE，∴BD2+CD2=2AD2；（3）作AE⊥AD，使AE=AD，连接CE，DE，∵∠BAC+∠CAD=∠DAE+∠CAD，即∠BAD=∠CAD′，在△BAD与△CAE中，，∴△BAD≌△CAE（SAS），∴BD=CE=9，∵∠ADC=45°，∠EDA=45°，∴∠EDC=90°，∴DE==6，∵∠DAE=90°，∴AD=AE=DE=6．3．（2018•黄石）如图，已知A、B、C、D、E是⊙O上五点，⊙O的直径BE=2，∠BCD=120°，A为的中点，延长BA到点P，使BA=AP，连接PE．（1）求线段BD的长；（2）求证：直线PE是⊙O的切线．（1）解：连接DB，如图，∵∠BCD+∠DEB=180°，∴∠DEB=180°﹣120°=60°，∵BE为直径，∴∠BDE=90°，在Rt△BDE中，DE=BE=×2=，BD=DE=×=3；（2）证明：连接EA，如图，∵BE为直径，∴∠BAE=90°，∵A为的中点，∴∠ABE=45°，∵BA=AP，而EA⊥BA，∴△BEP为等腰直角三角形，∴∠PEB=90°，∴PE⊥BE，∴直线PE是⊙O的切线．4．（2018•武汉）在△ABC中，∠ABC=90°．（1）如图1，分别过A、C两点作经过点B的直线的垂线，垂足分别为M、N，求证：△ABM∽△BCN；（2）如图2，P是边BC上一点，∠BAP=∠C，tan∠PAC=，求tanC的值；（3）如图3，D是边CA延长线上一点，AE=AB，∠DEB=90°，sin∠BAC=，，直接写出tan∠CEB的值．解：（1）∵AM⊥MN，CN⊥MN，∴∠AMB=∠BNC=90°，∴∠BAM+∠ABM=90°，∵∠ABC=90°，∴∠ABM+∠CBN=90°，∴∠BAM=∠CBN，∵∠AMB=∠NBC，∴△ABM∽△BCN；（2）如图2，过点P作PF⊥AP交AC于F，在Rt△AFP中，tan∠PAC===，同（1）的方法得，△ABP∽△PQF，∴=，设AB=a，PQ=2a，BP=b，FQ=2b（a＞0，b＞0），∵∠BAP=∠C，∠B=∠CQF=90°，∴△ABP∽△CQF，∴，∴CQ==2a，∵BC=BP+PQ+CQ=b+2a+2a=4a+b∵∠BAP=∠C，∠B=∠B=90°，∴△ABP∽△CBA，∴=，∴BC===，∴4a+b=，a=b，∴BC=4×b+b=5b，AB=a=5b，在Rt△ABC中，tanC==；（3）在Rt△ABC中，sin∠BAC==，过点A作AG⊥BE于G，过点C作CH⊥BE交EB的延长线于H，∵∠DEB=90°，∴CH∥AG∥DE，∴=同（1）的方法得，△ABG∽△BCH∴，设BG=4m，CH=3m，AG=4n，BH=3n，∵AB=AE，AG⊥BE，∴EG=BG=4m，∴GH=BG+BH=4m+3n，∴，∴n=2m，∴EH=EG+GH=4m+4m+3n=8m+3n=8m+6m=14m，在Rt△CEH中，tan∠BEC==．5．（2018•随州）如图，AB是⊙O的直径，点C为⊙O上一点，CN为⊙O的切线，OM ⊥AB于点O，分别交AC、CN于D、M两点．（1）求证：MD=MC；（2）若⊙O的半径为5，AC=4，求MC的长．解：（1）连接OC，∵CN为⊙O的切线，∴OC⊥CM，∠OCA+∠ACM=90°，∵OM⊥AB，∴∠OAC+∠ODA=90°，∵OA=OC，∴∠OAC=∠OCA，∴∠ACM=∠ODA=∠CDM，∴MD=MC；（2）由题意可知AB=5×2=10，AC=4，∵AB是⊙O的直径，∴∠ACB=90°，∴BC=，∵∠AOD=∠ACB，∠A=∠A，∴△AOD∽△ACB，∴，即，可得：OD=2.5，设MC=MD=x，在Rt△OCM中，由勾股定理得：（x+2.5）2=x2+52，解得：x=，即MC=．6．（2018•天门）如图，在⊙O中，AB为直径，AC为弦．过BC延长线上一点G，作GD ⊥AO于点D，交AC于点E，交⊙O于点F，M是GE的中点，连接CF，CM．（1）判断CM与⊙O的位置关系，并说明理由；（2）若∠ECF=2∠A，CM=6，CF=4，求MF的长．解：（1）CM与⊙O相切．理由如下：连接OC，如图，∵GD⊥AO于点D，∴∠G+∠GBD=90°，∵AB为直径，∴∠ACB=90°，∵M点为GE的中点，∴MC=MG=ME，∴∠G=∠1，∵OB=OC，∴∠B=∠2，∴∠1+∠2=90°，∴∠OCM=90°，∴OC⊥CM，∴CM为⊙O的切线；（2）∵∠1+∠3+∠4=90°，∠5+∠3+∠4=90°，∴∠1=∠5，而∠1=∠G，∠5=∠A，∴∠G=∠A，∵∠4=2∠A，∴∠4=2∠G，而∠EMC=∠G+∠1=2∠G，∴∠EMC=∠4，而∠FEC=∠CEM，∴△EFC∽△ECM，∴==，即==，∴CE=4，EF=，∴MF=ME﹣EF=6﹣=．7．（2018•黄石）在△ABC中，E、F分别为线段AB、AC上的点（不与A、B、C重合）．（1）如图1，若EF∥BC，求证：（2）如图2，若EF不与BC平行，（1）中的结论是否仍然成立？请说明理由；（3）如图3，若EF上一点G恰为△ABC的重心，，求的值．解：（1）∵EF∥BC，∴△AEF∽△ABC，∴=，∴=（）2=•=；（2）若EF不与BC平行，（1）中的结论仍然成立，分别过点F、C作AB的垂线，垂足分别为N、H，∵FN⊥AB、CH⊥AB，∴FN∥CH，∴△AFN∽△ACH，∴=，∴==；（3）连接AG并延长交BC于点M，连接BG并延长交AC于点N，连接MN，则MN分别是BC、AC的中点，∴MN∥AB，且MN=AB，=S△ACM，∴==，且S△ABM∴=，设=a，由（2）知：==×=，==a，则==+=+a，而==a，∴+a=a，解得：a=，∴=×=．8．（2018•襄阳）如图，AB是⊙O的直径，AM和BN是⊙O的两条切线，E为⊙O上一点，过点E作直线DC分别交AM，BN于点D，C，且CB=CE．（1）求证：DA=DE；（2）若AB=6，CD=4，求图中阴影部分的面积．解：（1）证明：连接OE、OC．∵OB=OE，∴∠OBE=∠OEB．∵BC=EC，∴∠CBE=∠CEB，∴∠OBC=∠OEC．∵BC为⊙O的切线，∴∠OEC=∠OBC=90°；∵OE为半径，∴CD为⊙O的切线，∵AD切⊙O于点A，∴DA=DE；（2）如图，过点D作DF⊥BC于点F，则四边形ABFD是矩形，∴AD=BF，DF=AB=6，∴DC=BC+AD=4．∵FC==2，∴BC﹣AD=2，∴BC=3．在直角△OBC中，tan∠BOE==，∴∠BOC=60°．在△OEC与△OBC中，，∴△OEC≌△OBC（SSS），∴∠BOE=2∠BOC=120°．∴S阴影部分=S四边形BCEO﹣S扇形OBE=2×BC•OB﹣=9﹣3π．9．（2018•咸宁）如图，以△ABC的边AC为直径的⊙O恰为△ABC的外接圆，∠ABC的平分线交⊙O于点D，过点D作DE∥AC交BC的延长线于点E．（1）求证：DE是⊙O的切线；（2）若AB=25，BC=，求DE的长．（1）证明：连接OD，∵AC是⊙O的直径，∴∠ABC=90°，∵BD平分∠ABC，∴∠ABD=45°，∴∠AOD=90°，∵DE∥AC，∴∠ODE=∠AOD=90°，∴DE是⊙O的切线；（2）解：在Rt△ABC中，AB=2，BC=，∴AC==5，∴OD=，过点C作CG⊥DE，垂足为G，则四边形ODGC为正方形，∴DG=CG=OD=，∵DE∥AC，∴∠CEG=∠ACB，∴tan∠CEG=tan∠ACB，∴=，即=，解得：GE=，∴DE=DG+GE=．10．（2018•宜昌）在矩形ABCD中，AB=12，P是边AB上一点，把△PBC沿直线PC折叠，顶点B的对应点是点G，过点B作BE⊥CG，垂足为E且在AD上，BE交PC于点F．（1）如图1，若点E是AD的中点，求证：△AEB≌△DEC；（2）如图2，①求证：BP=BF；②当AD=25，且AE＜DE时，求cos∠PCB的值；③当BP=9时，求BE•EF的值．解：（1）在矩形ABCD中，∠A=∠D=90°，AB=DC，∵E是AD中点，∴AE=DE，在△ABE和△DCE中，，∴△ABE≌△DCE（SAS）；（2）①在矩形ABCD，∠ABC=90°，∵△BPC沿PC折叠得到△GPC，∴∠PGC=∠PBC=90°，∠BPC=∠GPC，∵BE⊥CG，∴BE∥PG，∴∠GPF=∠PFB，∴∠BPF=∠BFP，∴BP=BF；②当AD=25时，∵∠BEC=90°，∴∠AEB+∠CED=90°，∵∠AEB+∠ABE=90°，∴∠CED=∠ABE，∵∠A=∠D=90°，∴△ABE∽△DEC，∴，设AE=x，∴DE=25﹣x，∴，∴x=9或x=16，∵AE＜DE，∴AE=9，DE=16，∴CE=20，BE=15，由折叠得，BP=PG，∴BP=BF=PG，∵BE∥PG，∴△ECF∽△GCP，∴，设BP=BF=PG=y，∴，∴y=，∴BP=，在Rt△PBC中，PC=，cos∠PCB==；③如图，连接FG，∵∠GEF=∠BAE=90°，∵BF∥PG，BF=PG，∴▱BPGF是菱形，∴BP∥GF，∴∠GFE=∠ABE，∴△GEF∽△EAB，∴，∴BE•EF=AB•GF=12×9=108．11．（2018•荆门）如图，AB为⊙O的直径，C为⊙O上一点，经过点C的切线交AB的延长线于点E，AD⊥EC交EC的延长线于点D，AD交⊙O于F，FM⊥AB于H，分别交⊙O、AC于M、N，连接MB，BC．（1）求证：AC平分∠DAE；（2）若cosM=，BE=1，①求⊙O的半径；②求FN的长．（1）证明：连接OC，如图，∵直线DE与⊙O相切于点C，∴OC⊥DE，又∵AD⊥DE，∴OC∥AD．∴∠1=∠3∵OA=OC，∴∠2=∠3，∴∠1=∠2，∴AC平方∠DAE；（2）解：①∵AB为直径，∴∠AFB=90°，而DE⊥AD，∴BF∥DE，∴OC⊥BF，∴=，∴∠COE=∠FAB，而∠FAB=∠M，∴∠COE=∠M，设⊙O的半径为r，在Rt△OCE中，cos∠COE==，即=，解得r=4，即⊙O的半径为4；②连接BF，如图，在Rt△AFB中，cos∠FAB=，∴AF=8×=在Rt△OCE中，OE=5，OC=4，∴CE=3，∵AB⊥FM，∴，∴∠5=∠4，∵FB∥DE，∴∠5=∠E=∠4，∵=，∴∠1=∠2，∴△AFN∽△AEC，∴=，即=，∴FN=．12．（2018•黄冈）如图，AD是⊙O的直径，AB为⊙O的弦，OP⊥AD，OP与AB的延长线交于点P，过B点的切线交OP于点C．（1）求证：∠CBP=∠ADB．（2）若OA=2，AB=1，求线段BP的长．（1）证明：连接OB，如图，∵AD是⊙O的直径，∴∠ABD=90°，∴∠A+∠ADB=90°，∵BC为切线，∴OB⊥BC，∴∠OBC=90°，∴∠OBA+∠CBP=90°，而OA=OB，∴∠A=∠OBA，∴∠CBP=∠ADB；（2）解：∵OP⊥AD，∴∠POA=90°，∴∠P+∠A=90°，∴∠P=∠D，∴△AOP∽△ABD，∴=，即=，∴BP=7．13．（2018•襄阳）如图（1），已知点G在正方形ABCD的对角线AC上，GE⊥BC，垂足为点E，GF⊥CD，垂足为点F．（1）证明与推断：①求证：四边形CEGF是正方形；②推断：的值为：（2）探究与证明：将正方形CEGF绕点C顺时针方向旋转α角（0°＜α＜45°），如图（2）所示，试探究线段AG与BE之间的数量关系，并说明理由：（3）拓展与运用：正方形CEGF在旋转过程中，当B，E，F三点在一条直线上时，如图（3）所示，延长CG 交AD于点H．若AG=6，GH=2，则BC=3．解：（1）①∵四边形ABCD是正方形，∴∠BCD=90°，∠BCA=45°，∵GE⊥BC、GF⊥CD，∴∠CEG=∠CFG=∠ECF=90°，∴四边形CEGF是矩形，∠CGE=∠ECG=45°，∴EG=EC，∴四边形CEGF是正方形；②由①知四边形CEGF是正方形，∴∠CEG=∠B=90°，∠ECG=45°，∴=，GE∥AB，∴==，故答案为：；（2）连接CG，由旋转性质知∠BCE=∠ACG=α，在Rt△CEG和Rt△CBA中，=cos45°=、=cos45°=，∴==，∴△ACG∽△BCE，∴==，∴线段AG与BE之间的数量关系为AG=BE；（3）∵∠CEF=45°，点B、E、F三点共线，∴∠BEC=135°，∵△ACG∽△BCE，∴∠AGC=∠BEC=135°，∴∠AGH=∠CAH=45°，∵∠CHA=∠AHG，∴△AHG∽△CHA，∴==，设BC=CD=AD=a，则AC=a，则由=得=，∴AH=a，则DH=AD﹣AH=a，CH==a，∴=得=，解得：a=3，即BC=3，故答案为：3．14．（2018•宜昌）如图，在△ABC中，AB=AC，以AB为直径的圆交AC于点D，交BC 于点E，延长AE至点F，使EF=AE，连接FB，FC．（1）求证：四边形ABFC是菱形；（2）若AD=7，BE=2，求半圆和菱形ABFC的面积．（1）证明：∵AB是直径，∴∠AEB=90°，∴AE⊥BC，∵AB=AC，∴BE=CE，∵AE=EF，∴四边形ABFC是平行四边形，∵AC=AB，∴四边形ABFC是菱形．（2）设CD=x．连接BD．∵AB是直径，∴∠ADB=∠BDC=90°，∴AB2﹣AD2=CB2﹣CD2，∴（7+x）2﹣72=42﹣x2，解得x=1或﹣8（舍弃）∴AC=8，BD==，=8．∴S菱形ABFC•π•42=8π．∴S半圆=15．（2018•黄冈）如图，在直角坐标系xOy中，菱形OABC的边OA在x轴正半轴上，点B，C在第一象限，∠C=120°，边长OA=8．点M从原点O出发沿x轴正半轴以每秒1个单位长的速度作匀速运动，点N从A出发沿边AB﹣BC﹣CO以每秒2个单位长的速度作匀速运动，过点M作直线MP垂直于x轴并交折线OCB于P，交对角线OB于Q，点M和点N同时出发，分别沿各自路线运动，点N运动到原点O时，M和N两点同时停止运动．（1）当t=2时，求线段PQ的长；（2）求t为何值时，点P与N重合；（3）设△APN的面积为S，求S与t的函数关系式及t的取值范围．解：（1）当t=2时，OM=2，在Rt△OPM中，∠POM=60°，∴PM=OM•tan60°=2，在Rt△OMQ中，∠QOM=30°，∴QM=OM•tan30°=，∴PQ=CN﹣QM=2﹣=．（2）由题意：8+（t﹣4）+2t=24，解得t=．（3）①当0＜x ＜4时，S=•2t•4=4t ． ②当4≤x ＜时，S=×[8﹣（t ﹣4）﹣（2t ﹣8）]×4=40﹣6t ． ③当≤x ＜8时．S=×[（t ﹣4）+（2t ﹣8）﹣8]×4=6t ﹣40．④当8≤x ≤12时，S=S菱形ABCO ﹣S △AON ﹣S △ABP =32﹣•（24﹣2t ）•4﹣•[8﹣（t ﹣4）]•4=6t ﹣40．16．（2018•孝感）如图，△ABC 中，AB=AC ，以AB 为直径的⊙O 交BC 于点D ，交AC 于点E ，过点D 作DF ⊥AC 于点F ，交AB 的延长线于点G ．（1）求证：DF 是⊙O 的切线；（2）已知BD=2，CF=2，求AE 和BG 的长．解：（1）连接OD ，AD ，∵AB 为⊙O 的直径，∴∠ADB=90°，即AD ⊥BC ，∵AB=AC ，∴BD=CD ，又∵OA=OB ，∴OD ∥AC ，∵DG ⊥AC ，∴OD ⊥FG ，∴直线FG 与⊙O 相切；（2）连接BE ．∵BD=2， ∴， ∵CF=2，∴DF==4，∴BE=2DF=8，∵cos∠C=cos∠ABC，∴=，∴=，∴AB=10，∴AE==6，∵BE⊥AC，DF⊥AC，∴BE∥GF，∴△AEB∽△AFG，∴=，∴=，∴BG=．17．（2018•恩施州）如图，AB为⊙O直径，P点为半径OA上异于O点和A点的一个点，过P点作与直径AB垂直的弦CD，连接AD，作BE⊥AB，OE∥AD交BE于E点，连接AE、DE、AE交CD于F点．（1）求证：DE为⊙O切线；（2）若⊙O的半径为3，sin∠ADP=，求AD；（3）请猜想PF与FD的数量关系，并加以证明．证明：（1）如图1，连接OD、BD，BD交OE于M，∵AB是⊙O的直径，∴∠ADB=90°，AD⊥BD，∵OE∥AD，∴OE⊥BD，∴BM=DM，∵OB=OD，∴∠BOM=∠DOM，∵OE=OE，∴△BOE≌△DOE（SAS），∴∠ODE=∠OBE=90°，∴DE为⊙O切线；（2）设AP=a，∵sin∠ADP==，∴AD=3a，∴PD===2a，∵OP=3﹣a，∴OD2=OP2+PD2，∴32=（3﹣a）2+（2a）2，9=9﹣6a+a2+8a2，a1=，a2=0（舍），当a=时，AD=3a=2，∴AD=2；（3）PF=FD，理由是：∵∠APD=∠ABE=90°，∠PAD=∠BAE，∴△APF∽△ABE，∴，∴PF=，∵OE∥AD，∴∠BOE=∠PAD，∵∠OBE=∠APD=90°，∴△ADP∽△OEB，∴，∴PD=，∵AB=2OB，∴PD=2PF，∴PF=FD．18．（2018•咸宁）定义：我们知道，四边形的一条对角线把这个四边形分成了两个三角形，如果这两个三角形相似（不全等），我们就把这条对角线叫做这个四边形的“相似对角线”．理解：（1）如图1，已知Rt△ABC在正方形网格中，请你只用无刻度的直尺在网格中找到一点D，使四边形ABCD是以AC为“相似对角线”的四边形（保留画图痕迹，找出3个即可）；（2）如图2，在四边形ABCD中，∠ABC=80°，∠ADC=140°，对角线BD平分∠ABC．求证：BD是四边形ABCD的“相似对角线”；（3）如图3，已知FH是四边形EFCH的“相似对角线”，∠EFH=∠HFG=30°，连接EG，若△EFG的面积为2，求FH的长．解：（1）由图1知，AB=，BC=2，∠ABC=90°，AC=5，∵四边形ABCD是以AC为“相似对角线”的四边形，①当∠ACD=90°时，△ACD∽△ABC或△ACD∽△CBA，∴=或=2，∴CD=10或CD=2.5同理：当∠CAD=90°时，AD=2.5或AD=10，（2）证明：∵∠ABC=80°，BD平分∠ABC，∴∠ABD=∠DBC=40°，∴∠A+∠ADB=140°∵∠ADC=140°，∴∠BDC+∠ADB=140°，∴∠A=∠BDC，∴△ABD∽△BDC，∴BD是四边形ABCD的“相似对角线”；（3）如图3，∵FH是四边形EFGH的“相似对角线”，∴△EFG与△HFG相似，∵∠EFH=∠HFG，∴△FEH∽△FHG，∴，∴FH2=FE•FG，过点E作EQ⊥FG于Q，∴EQ=FE•sin60°=FE，∵FG×EQ=2，∴FG×FE=2，∴FG•FE=8，∴FH2=FE•FG=8，∴FH=2．。

2018年全国各地中考数学压轴题汇编：几何综合(山东专版)(解析卷)

2018年全国各地中考数学压轴题汇编（山东专版）几何综合参考答案与试题解析1．（2018•威海）如图，将矩形ABCD（纸片）折叠，使点B与AD边上的点K重合，EG 为折痕；点C与AD边上的点K重合，FH为折痕．已知∠1=67.5°，∠2=75°，EF=+1，求BC的长．解：由题意，得：∠3=180°﹣2∠1=45°，∠4=180°﹣2∠2=30°，BE=KE、KF=FC，如图，过点K作KM⊥BC于点M，设KM=x，则EM=x、MF=x，∴x+x=+1，解得：x=1，∴EK=、KF=2，∴BC=BE+EF+FC=EK+EF+KF=3++，∴BC的长为3++．2．（2018•枣庄）如图，在4×4的方格纸中，△ABC的三个顶点都在格点上．（1）在图1中，画出一个与△ABC成中心对称的格点三角形；（2）在图2中，画出一个与△ABC成轴对称且与△ABC有公共边的格点三角形；（3）在图3中，画出△ABC绕着点C按顺时针方向旋转90°后的三角形．解：（1）如图所示，△DCE为所求作（2）如图所示，△ACD为所求作（3）如图所示△ECD为所求作3．（2018•枣庄）如图，在Rt△ACB中，∠C=90°，AC=3cm，BC=4cm，以BC为直径作⊙O交AB于点D．（1）求线段AD的长度；（2）点E是线段AC上的一点，试问：当点E在什么位置时，直线ED与⊙O相切？请说明理由．解：（1）在Rt△ACB中，∵AC=3cm，BC=4cm，∠ACB=90°，∴AB=5cm；连接CD，∵BC为直径，∴∠ADC=∠BDC=90°；∵∠A=∠A，∠ADC=∠ACB，∴Rt△ADC∽Rt△ACB；∴，∴；（2）当点E是AC的中点时，ED与⊙O相切；证明：连接OD，∵DE是Rt△ADC的中线；∴ED=EC，∴∠EDC=∠ECD；∵OC=OD，∴∠ODC=∠OCD；∴∠EDO=∠EDC+∠ODC=∠ECD+∠OCD=∠ACB=90°；∴ED⊥OD，∴ED与⊙O相切．4．（2018•潍坊）如图，点M是正方形ABCD边CD上一点，连接AM，作DE⊥AM于点E，BF⊥AM于点F，连接BE．（1）求证：AE=BF；（2）已知AF=2，四边形ABED的面积为24，求∠EBF的正弦值．（1）证明：∵四边形ABCD为正方形，∴BA=AD，∠BAD=90°，∵DE⊥AM于点E，BF⊥AM于点F，∴∠AFB=90°，∠DEA=90°，∵∠ABF+∠BAF=90°，∠EAD+∠BAF=90°，∴∠ABF=∠EAD，在△ABF和△DEA中，∴△ABF≌△DEA（AAS），∴BF=AE；（2）解：设AE=x，则BF=x，DE=AF=2，∵四边形ABED的面积为24，∴•x•x+•x•2=24，解得x1=6，x2=﹣8（舍去），∴EF=x﹣2=4，在Rt△BEF中，BE==2，∴sin∠EBF===．5．（2018•淄博）如图，以AB为直径的⊙O外接于△ABC，过A点的切线AP与BC的延长线交于点P，∠APB的平分线分别交AB，AC于点D，E，其中AE，BD（AE＜BD）的长是一元二次方程x2﹣5x+6=0的两个实数根．（1）求证：PA•BD=PB•AE；（2）在线段BC上是否存在一点M，使得四边形ADME是菱形？若存在，请给予证明，并求其面积；若不存在，说明理由．解：（1）∵DP平分∠APB，∴∠APE=∠BPD，∵AP与⊙O相切，∴∠BAP=∠BAC+∠EAP=90°，∵AB是⊙O的直径，∴∠ACB=∠BAC+∠B=90°，∴∠EAP=∠B，∴△PAE∽△PBD，∴，∴PA•BD=PB•AE；（2）过点D作DF⊥PB于点F，作DG⊥AC于点G，∵DP平分∠APB，AD⊥AP，DF⊥PB，∴AD=DF，∵∠EAP=∠B，∴∠APC=∠BAC，易证：DF∥AC，∴∠BDF=∠BAC，由于AE，BD（AE＜BD）的长是x2﹣5x+6=0，解得：AE=2，BD=3，∴由（1）可知：，∴cos∠APC==，∴cos∠BDF=cos∠APC=，∴，∴DF=2，∴DF=AE，∴四边形ADFE是平行四边形，∵AD=AE，∴四边形ADFE是菱形，此时点F即为M点，∵cos∠BAC=cos∠APC=，∴sin∠BAC=，∴，∴DG=，∴在线段BC上是否存在一点M，使得四边形ADME是菱形其面积为：DG•AE=2×=6．（2018•烟台）【问题解决】一节数学课上，老师提出了这样一个问题：如图1，点P是正方形ABCD内一点，PA=1，PB=2，PC=3．你能求出∠APB的度数吗？小明通过观察、分析、思考，形成了如下思路：思路一：将△BPC绕点B逆时针旋转90°，得到△BP′A，连接PP′，求出∠APB的度数；思路二：将△APB绕点B顺时针旋转90°，得到△CP'B，连接PP′，求出∠APB的度数．请参考小明的思路，任选一种写出完整的解答过程．【类比探究】如图2，若点P是正方形ABCD外一点，PA=3，PB=1，PC=，求∠APB的度数．解：（1）思路一、如图1，将△BPC绕点B逆时针旋转90°，得到△BP′A，连接PP′，∴△ABP'≌△CBP，∴∠PBP'=90°，BP'=BP=2，AP'=CP=3，在Rt△PBP'中，BP=BP'=2，∴∠BPP'=45°，根据勾股定理得，PP'=BP=2，∵AP=1，∴AP2+PP'2=1+8=9，∵AP'2=32=9，∴AP2+PP'2=AP'2，∴△APP'是直角三角形，且∠APP'=90°，∴∠APB=∠APP'+∠BPP'=90°+45°=135°；思路二、同思路一的方法；（2）如图2，将△BPC绕点B逆时针旋转90°，得到△BP′A，连接PP′，∴△ABP'≌△CBP，∴∠PBP'=90°，BP'=BP=1，AP'=CP=，在Rt△PBP'中，BP=BP'=1，∴∠BPP'=45°，根据勾股定理得，PP'=BP=，∵AP=3，∴AP2+PP'2=9+2=11，∵AP'2=（）2=11，∴AP2+PP'2=AP'2，∴△APP'是直角三角形，且∠APP'=90°，∴∠APB=∠APP'﹣∠BPP'=90°﹣45°=45°．7．（2018•东营）如图，CD是⊙O的切线，点C在直径AB的延长线上．（1）求证：∠CAD=∠BDC；（2）若BD=AD，AC=3，求CD的长．（1）证明：连接OD，如图所示．∵OB=OD，∴∠OBD=∠ODB．∵CD是⊙O的切线，OD是⊙O的半径，∴∠ODB+∠BDC=90°．∵AB是⊙O的直径，∴∠ADB=90°，∴∠OBD+∠CAD=90°，∴∠CAD=∠BDC．（2）解：∵∠C=∠C，∠CAD=∠CDB，∴△CDB∽△CAD，∴=．∵BD=AD，∴=，∴=，又∵AC=3，∴CD=2．8．（2018•济宁）在一次数学活动课中，某数学小组探究求环形花坛（如图所示）面积的方法，现有以下工具；①卷尺；②直棒EF；③T型尺（CD所在的直线垂直平分线段AB）．（1）在图1中，请你画出用T形尺找大圆圆心的示意图（保留画图痕迹，不写画法）；（2）如图2，小华说：“我只用一根直棒和一个卷尺就可以求出环形花坛的面积，具体做法如下：将直棒放置到与小圆相切，用卷尺量出此时直棒与大圆两交点M，N之间的距离，就可求出环形花坛的面积”如果测得MN=10m，请你求出这个环形花坛的面积．解：（1）如图点O即为所求；（2）设切点为C，连接OM，OC．∵MN是切线，∴OC⊥MN，∴CM=CN=5，∴OM2﹣OC2=CM2=25，=π•OM2﹣π•OC2=25π．∴S圆环9．（2018•潍坊）如图，BD为△ABC外接圆⊙O的直径，且∠BAE=∠C．（1）求证：AE与⊙O相切于点A；（2）若AE∥BC，BC=2，AC=2，求AD的长．证明：（1）连接OA，交BC于F，则OA=OB，∴∠D=∠DAO，∵∠D=∠C，∴∠C=∠DAO，∵∠BAE=∠C，∴∠BAE=∠DAO，（2分）∵BD是⊙O的直径，∴∠BAD=90°，即∠DAO+∠BAO=90°，（3分）∴∠BAE+∠BAO=90°，即∠OAE=90°，∴AE⊥OA，∴AE与⊙O相切于点A；（4分）（2）∵AE∥BC，AE⊥OA，∴OA⊥BC，（5分）∴，FB=BC，∴AB=AC，∵BC=2，AC=2，∴BF=，AB=2，在Rt△ABF中，AF==1，在Rt△OFB中，OB2=BF2+（OB﹣AF）2，∴OB=4，（7分）∴BD=8，∴在Rt△ABD中，AD====2．（8分）10．（2018•东营）（1）某学校“智慧方园”数学社团遇到这样一个题目：如图1，在△ABC中，点O在线段BC上，∠BAO=30°，∠OAC=75°，AO=，BO：CO=1：3，求AB的长．经过社团成员讨论发现，过点B作BD∥AC，交AO的延长线于点D，通过构造△ABD就可以解决问题（如图2）．请回答：∠ADB=75°，AB=4．（2）请参考以上解决思路，解决问题：如图3，在四边形ABCD中，对角线AC与BD相交于点O，AC⊥AD，AO=，∠ABC=∠ACB=75°，BO：OD=1：3，求DC的长．解：（1）∵BD∥AC，∴∠ADB=∠OAC=75°．∵∠BOD=∠COA，∴△BOD∽△COA，∴==．又∵AO=，∴OD=AO=，∴AD=AO+OD=4．∵∠BAD=30°，∠ADB=75°，∴∠ABD=180°﹣∠BAD﹣∠ADB=75°=∠ADB，∴AB=AD=4．故答案为：75；4．（2）过点B作BE∥AD交AC于点E，如图所示．∵AC⊥AD，BE∥AD，∴∠DAC=∠BEA=90°．∵∠AOD=∠EOB，∴△AOD∽△EOB，∴==．∵BO：OD=1：3，∴==．∵AO=3，∴EO=，∴AE=4．∵∠ABC=∠ACB=75°，∴∠BAC=30°，AB=AC，∴AB=2BE．在Rt△AEB中，BE2+AE2=AB2，即（4）2+BE2=（2BE）2，解得：BE=4，∴AB=AC=8，AD=12．在Rt△CAD中，AC2+AD2=CD2，即82+122=CD2，解得：CD=4．11．（2018•枣庄）如图，将矩形ABCD沿AF折叠，使点D落在BC边的点E处，过点E 作EG∥CD交AF于点G，连接DG．（1）求证：四边形EFDG是菱形；（2）探究线段EG、GF、AF之间的数量关系，并说明理由；（3）若AG=6，EG=2，求BE的长．解：（1）证明：∵GE∥DF，∴∠EGF=∠DFG．∵由翻折的性质可知：GD=GE，DF=EF，∠DGF=∠EGF，∴∠DGF=∠DFG．∴GD=DF．∴DG=GE=DF=EF．∴四边形EFDG为菱形．（2）EG2=GF•AF．理由：如图1所示：连接DE，交AF于点O．∵四边形EFDG为菱形，∴GF⊥DE，OG=OF=GF．∵∠DOF=∠ADF=90°，∠OFD=∠DFA，∴△DOF∽△ADF．∴，即DF2=FO•AF．∵FO=GF，DF=EG，∴EG2=GF•AF．（3）如图2所示：过点G作GH⊥DC，垂足为H．∵EG2=GF•AF，AG=6，EG=2，∴20=FG（FG+6），整理得：FG2+6FG﹣40=0．解得：FG=4，FG=﹣10（舍去）．∵DF=GE=2，AF=10，∴AD==4．∵GH⊥DC，AD⊥DC，∴GH∥AD．∴△FGH∽△FAD．∴，即=．∴GH=．∴BE=AD﹣GH=4﹣=．12．（2018•烟台）如图，已知D，E分别为△ABC的边AB，BC上两点，点A，C，E在⊙D上，点B，D在⊙E上．F为上一点，连接FE并延长交AC的延长线于点N，交AB 于点M．（1）若∠EBD为α，请将∠CAD用含α的代数式表示；（2）若EM=MB，请说明当∠CAD为多少度时，直线EF为⊙D的切线；（3）在（2）的条件下，若AD=，求的值．解：（1）连接CD、DE，⊙E中，∵ED=EB，∴∠EDB=∠EBD=α，∴∠CED=∠EDB+∠EBD=2α，⊙D中，∵DC=DE=AD，∴∠CAD=∠ACD，∠DCE=∠DEC=2α，△ACB中，∠CAD+∠ACD+∠DCE+∠EBD=180°，∴∠CAD==；（2）设∠MBE=x，∵EM=MB，∴∠EMB=∠MBE=x，当EF为⊙D的切线时，∠DEF=90°，∴∠CED+∠MEB=90°，∴∠CED=∠DCE=90°﹣x，△ACB中，同理得，∠CAD+∠ACD+∠DCE+∠EBD=180°，∴2∠CAD=180°﹣90∴=90∴，∴∠CAD=45°；（3）由（2）得：∠CAD=45°；由（1）得：∠CAD=；∴∠MBE=30°，∴∠CED=2∠MBE=60°，∵CD=DE，∴△CDE是等边三角形，∴CD=CE=DE=EF=AD=，Rt△DEM中，∠EDM=30°，DE=，∴EM=1，MF=EF﹣EM=﹣1，△ACB中，∠NCB=45°+30°=75°，△CNE中，∠CEN=∠BEF=30°，∴∠CNE=75°，∴∠CNE=∠NCB=75°，∴EN=CE=，∴===2+．13．（2018•泰安）如图，△ABC中，D是AB上一点，DE⊥AC于点E，F是AD的中点，FG⊥BC于点G，与DE交于点H，若FG=AF，AG平分∠CAB，连接GE，CD．（1）求证：△ECG≌△GHD；（2）小亮同学经过探究发现：AD=AC+EC．请你帮助小亮同学证明这一结论．（3）若∠B=30°，判定四边形AEGF是否为菱形，并说明理由．解：（1）∵AF=FG，∴∠FAG=∠FGA，∵AG平分∠CAB，∴∠CAG=∠FGA，∴∠CAG=∠FGA，∴AC∥FG，∵DE⊥AC，∴FG⊥DE，∵FG⊥BC，∴DE∥BC，∴AC⊥BC，∴∠C=∠DHG=90°，∠CGE=∠GED，∵F是AD的中点，FG∥AE，∴H是ED的中点，∴FG是线段ED的垂直平分线，∴GE=GD，∠GDE=∠GED，∴∠CGE=∠GDE，∴△ECG≌△GHD；（2）证明：过点G作GP⊥AB于P，∴GC=GP，而AG=AG，∴△CAG≌△PAG，∴AC=AP，由（1）可得EG=DG，∴Rt△ECG≌Rt△GPD，∴EC=PD，∴AD=AP+PD=AC+EC；（3）四边形AEGF是菱形，证明：∵∠B=30°，∴∠ADE=30°，∴AE=AD，∴AE=AF=FG，由（1）得AE∥FG，∴四边形AECF是平行四边形，∴四边形AEGF是菱形．14．（2018•淄博）（1）操作发现：如图①，小明画了一个等腰三角形ABC，其中AB=AC，在△ABC的外侧分别以AB，AC为腰作了两个等腰直角三角形ABD，ACE，分别取BD，CE，BC的中点M，N，G，连接GM，GN．小明发现了：线段GM与GN的数量关系是MG=NG；位置关系是MG⊥NG．（2）类比思考：如图②，小明在此基础上进行了深入思考．把等腰三角形ABC换为一般的锐角三角形，其中AB＞AC，其它条件不变，小明发现的上述结论还成立吗？请说明理由．（3）深入研究：如图③，小明在（2）的基础上，又作了进一步的探究．向△ABC的内侧分别作等腰直角三角形ABD，ACE，其它条件不变，试判断△GMN的形状，并给与证明．解：（1）连接BE，CD相交于H，∵△ABD和△ACE都是等腰直角三角形，∴AB=AD，AC=AE，∠BAD=∠CAE=90°∴∠CAD=∠BAE，∴△ACD≌△AEB（SAS），∴CD=BE，∠ADC=∠ABE，∴∠BDC+∠DBH=∠BDC+∠ABD+∠ABE=∠BDC+∠ABD+∠ADC=∠ADB+∠ABD=90°，∴∠BHD=90°，∴CD⊥BE，∵点M，G分别是BD，BC的中点，∴MG CD，同理：NG BE，∴MG=NG，MG⊥NG，故答案为：MG=NG，MG⊥NG；（2）连接CD，BE相交于点H，同（1）的方法得，MG=NG，MG⊥NG；（3）连接EB，DC，延长线相交于H，同（1）的方法得，MG=NG，同（1）的方法得，△ABE≌△ADC，∴∠AEB=∠ACD，∴∠CEH+∠ECH=∠AEH﹣∠AEC+180°﹣∠ACD﹣∠ACE=∠ACD﹣45°+180°﹣∠ACD﹣45°=90°，∴∠DHE=90°，同（1）的方法得，MG⊥NG．15．（2018•泰安）如图，在菱形ABCD中，AC与BD交于点O，E是BD上一点，EF∥AB，∠EAB=∠EBA，过点B作DA的垂线，交DA的延长线于点G．（1）∠DEF和∠AEF是否相等？若相等，请证明；若不相等，请说明理由；（2）找出图中与△AGB相似的三角形，并证明；（3）BF的延长线交CD的延长线于点H，交AC于点M．求证：BM2=MF•MH．解：（1）∠DEF=∠AEF，理由：∵EF∥AB，∴∠DEF=∠EBA，∠AEF=∠EAB，∵∠EAB=∠EBA，∴∠DEF=∠AEF；（2）△EOA∽△AGB，理由：∵四边形ABCD是菱形，∴AB=AD，AC⊥BD，∴∠GAB=∠ABE+∠ADB=2∠ABE，∵∠AEO=∠ABE+∠BAE=2∠ABE，∵∠GAB=∠AEO，∠GAB=∠AOE=90°，∴△EOA∽△AGB；（3）如图，连接DM，∵四边形ABCD是菱形，由对称性可知，BM=DM，∠ADM=∠ABM，∵AB∥CH，∴∠ABM=∠H，∴∠ADM=∠H，∵∠DMH=∠FMD，∴△MFD∽△MDH，∴，∴DM2=MF•MH，∴BM2=MF•MH．16．（2018•潍坊）如图1，在▱ABCD中，DH⊥AB于点H，CD的垂直平分线交CD于点E，交AB于点F，AB=6，DH=4，BF：FA=1：5．（1）如图2，作FG⊥AD于点G，交DH于点M，将△DGM沿DC方向平移，得到△CG′M′，连接M′B．①求四边形BHMM′的面积；②直线EF上有一动点N，求△DNM周长的最小值．（2）如图3，延长CB交EF于点Q，过点Q作QK∥AB，过CD边上的动点P作PK∥EF，并与QK交于点K，将△PKQ沿直线PQ翻折，使点K的对应点K′恰好落在直线AB上，求线段CP的长．解：（1）①在▱ABCD中，AB=6，直线EF垂直平分CD，∴DE=FH=3，又BF：FA=1：5，∴AH=2，∵Rt△AHD∽Rt△MHF，∴，即，∴HM=1.5，根据平移的性质，MM'=CD=6，连接BM，如图1，四边形BHMM′的面积=；②连接CM交直线EF于点N，连接DN，如图2，∵直线EF垂直平分CD，∴CN=DN，∵MH=1.5，∴DM=2.5，在Rt△CDM中，MC2=DC2+DM2，∴MC2=62+（2.5）2，即MC=6.5，∵MN+DN=MN+CN=MC，∴△DNM周长的最小值为9．（2）∵BF∥CE，∴，∴QF=2，∴PK=PK'=6，过点K'作E'F'∥EF，分别交CD于点E'，交QK于点F'，如图3，当点P在线段CE上时，在Rt△PK'E'中，PE'2=PK'2﹣E'K'2，∴，∵Rt△PE'K'∽Rt△K'F'Q，∴，即，解得：，∴PE=PE'﹣EE'=，∴，同理可得，当点P在线段DE上时，，如图4，综上所述，CP的长为或．17．（2018•青岛）已知：如图，四边形ABCD，AB∥DC，CB⊥AB，AB=16cm，BC=6cm，CD=8cm，动点P从点D开始沿DA边匀速运动，动点Q从点A开始沿AB边匀速运动，它们的运动速度均为2cm/s．点P和点Q同时出发，以QA、QP为边作平行四边形AQPE，设运动的时间为t（s），0＜t＜5．根据题意解答下列问题：（1）用含t的代数式表示AP；（2）设四边形CPQB的面积为S（cm2），求S与t的函数关系式；（3）当QP⊥BD时，求t的值；（4）在运动过程中，是否存在某一时刻t，使点E在∠ABD的平分线上？若存在，求出t的值；若不存在，请说明理由．解：（1）如图作DH⊥AB于H，则四边形DHBC是矩形，∴CD=BH=8，DH=BC=6，∴AH=AB﹣BH=8，AD==10，BD==10，由题意AP=AD﹣DP=10﹣2t．（2）作PN⊥AB于N．连接PB．在Rt△APN中，PA=10﹣2t，∴PN=PA•sin∠DAH=（10﹣2t），AN=PA•cos∠DAH=（10﹣2t），∴BN=16﹣AN=16﹣（10﹣2t），S=S△PQB+S△BCP=•（16﹣2t）•（10﹣2t）+×6×[16﹣（10﹣2t）]=t2﹣t+72（3）当PQ⊥BD时，∠PQN+∠DBA=90°，∵∠QPN+∠PQN=90°，∴∠QPN=∠DBA，∴tan∠QPN==，∴=，解得t=，经检验：t=是分式方程的解，∴当t=s时，PQ⊥BD．（4）存在．理由：连接BE交DH于K，作KM⊥BD于M．当BE平分∠ABD时，△KBH≌△KBM，∴KH=KM，BH=BM=8，设KH=KM=x，在Rt△DKM中，（6﹣x）2=22+x2，解得x=，作EF⊥AB于F，则△AEF≌△QPN，∴EF=PN=（10﹣2t），AF=QN=（10﹣2t）﹣2t，∴BF=16﹣[（10﹣2t）﹣2t]，∵KH∥EF，∴=，∴=，解得：t=，经检验：t=是分式方程的解，∴当t=s时，点E在∠ABD的平分线．18．（2018•威海）如图①，在四边形BCDE中，BC⊥CD，DE⊥CD，AB⊥AE，垂足分别为C，D，A，BC≠AC，点M，N，F分别为AB，AE，BE的中点，连接MN，MF，NF．（1）如图②，当BC=4，DE=5，tan∠FMN=1时，求的值；（2）若tan∠FMN=，BC=4，则可求出图中哪些线段的长？写出解答过程；（3）连接CM，DN，CF，DF．试证明△FMC与△DNF全等；（4）在（3）的条件下，图中还有哪些其它的全等三角形？请直接写出．解：（1）∵点M，N，F分别为AB，AE，BE的中点，∴MF，NF都是△ABE的中位线，∴MF=AE=AN，NF=AB=AM，∴四边形ANFM是平行四边形，又∵AB⊥AE，∴四边形ANFM是矩形，又∵tan∠FMN=1，∴FN=FM，∴矩形ANFM是正方形，AB=AE，又∵∠1+∠2=90°，∠2+∠3=90°，∴∠1=∠3，∵∠C=∠D=90°，∴△ABC≌△EAD（AAS），∴BC=AD=4，CA=DE=5，∴=；（2）可求线段AD的长．由（1）可得，四边形MANF为矩形，MF=AE，NF=AB，∵tan∠FMN=，即=，∴=，∵∠1=∠3，∠C=∠D=90°，（3）∵BC⊥CD，DE⊥CD，∴△ABC和△ADE都是直角三角形，∵M，N分别是AB，AE的中点，∴BM=CM，NA=ND，∴∠4=2∠1，∠5=2∠3，∵∠1=∠3，∴∠4=∠5，∵∠FMC=90°+∠4，∠FND=90°+∠5，∴∠FMC=∠FND，∵FM=DN，CM=NF，∴△FMC≌△DNF（SAS）；（4）在（3）的条件下，BM=AM=FN，MF=AN=NE，∠FMB=∠MFN=∠MAN=∠ENF=90°，∴图中有：△BMF≌△NFM≌△MAN≌△FNE．。

中考数学试题-2018年全国中考数学压轴题精选精析(5份) 最新

2018年全国中考数学压轴题精选精析（二）14（18江苏常州）（本题答案暂缺）28.如图,抛物线24y x x =+与x 轴分别相交于点B 、O ,它的顶点为A ,连接AB,把AB 所的直线沿y 轴向上平移,使它经过原点O,得到直线l ,设P 是直线l 上一动点.(1) 求点A 的坐标; (2) 以点A 、B 、O 、P 为顶点的四边形中,有菱形、等腰梯形、直角梯形,请分别直接写出这些特殊四边形的顶点P 的坐标;(3) 设以点A 、B 、O 、P 为顶点的四边形的面积为S,点P 的横坐标为x,当46S +≤≤+,求x 的取值范围.13（18江苏淮安）（本题答案暂缺）28．(本小题14分)如图所示，在平面直角坐标系中．二次函数y=a(x-2)2-1图象的顶点为P ，与x 轴交点为 A 、B ，与y 轴交点为C ．连结BP 并延长交y 轴于点D. (1)写出点P 的坐标；(2)连结AP ，如果△APB 为等腰直角三角形，求a 的值及点C 、D 的坐标； (3)在(2)的条件下，连结BC 、AC 、AD ，点E(0，b)在线段CD(端点C 、D 除外)上,将△BCD 绕点E 逆时针方向旋转90°，得到一个新三角形．设该三角形与△ACD 重叠部分的面积为S ，根据不同情况，分别用含b 的代数式表示S ．选择其中一种情况给出解答过程，其它情况直接写出结果；判断当b 为何值时,重叠部分的面积最大?写出最大值．14（18江苏连云港）24．（本小题满分14分）如图，现有两块全等的直角三角形纸板Ⅰ，Ⅱ，它们两直角边的长分别为1和2．将它们分别放置于平面直角坐标系中的AOB △，COD △处，直角边OB OD ，在x 轴上．一直尺从上方紧靠两纸板放置，让纸板Ⅰ沿直尺边缘平行移动．当纸板Ⅰ移动至PEF △处时，设PE PF ，与OC 分别交于点M N ，，与x 轴分别交于点G H ，．(第28题）（第24题图）（1）求直线AC 所对应的函数关系式；（2）当点P 是线段AC （端点除外）上的动点时，试探究：①点M 到x 轴的距离h 与线段BH 的长是否总相等？请说明理由；②两块纸板重叠部分（图中的阴影部分）的面积S 是否存在最大值？若存在，求出这个最大值及S 取最大值时点P 的坐标；若不存在，请说明理由．（18江苏连云港24题解析）24．解：（1）由直角三角形纸板的两直角边的长为1和2，知A C ，两点的坐标分别为(12)(21)，，，．设直线AC 所对应的函数关系式为y kx b =+． ················ 2分有221k b k b +=⎧⎨+=⎩，．解得13k b =-⎧⎨=⎩，．所以，直线AC 所对应的函数关系式为3y x =-+． ·············· 4分（2）①点M 到x 轴距离h 与线段BH 的长总相等．因为点C 的坐标为(21)，，所以，直线OC 所对应的函数关系式为12y x =．又因为点P 在直线AC 上，所以可设点P 的坐标为(3)a a -，．过点M 作x 轴的垂线，设垂足为点K ，则有MK h =．因为点M 在直线OC 上，所以有(2)M h h ，． ······ 6分因为纸板为平行移动，故有EF OB ∥，即EF GH ∥．又EF PF ⊥，所以PH GH ⊥．法一：故Rt Rt Rt MKG PHG PFE △∽△∽△，从而有12GK GH EF MK PH PF ===．得1122GK MK h ==，11(3)22GH PH a ==-．（第24题答图）所以13222OG OK GK h h h =-=-=．又有13(3)(1)22OG OH GH a a a =-=--=-． ··············· 8分所以33(1)22h a =-，得1h a =-，而1BH OH OB a =-=-，从而总有h BH =． ···························· 10分法二：故Rt Rt PHG PFE △∽△，可得12GH EF PH PF =-．故11(3)22GH PH a ==-．所以13(3)(1)22OG OH GH a a a =-=--=-．故G 点坐标为3(1)02a ⎛⎫-⎪⎝⎭，．设直线PG 所对应的函数关系式为y cx d =+，则有330(1)2a ca d c a d -=+⎧⎪⎨=-+⎪⎩，．解得233c d a =⎧⎨=-⎩ 所以，直线PG 所对的函数关系式为2(33)y x a =+-． ············ 8分将点M 的坐标代入，可得4(33)h h a =+-．解得1h a =-．而1BH OH OB a --=-，从而总有h BH =． ················ 10分 ②由①知，点M 的坐标为(221)a a --，，点N 的坐标为12a a ⎛⎫ ⎪⎝⎭，．ONH ONG S S S =-△△1111133(1)222222a NH OH OG h a a a -=⨯-⨯=⨯⨯-⨯⨯- 22133133224228a a a ⎛⎫=-+-=--+ ⎪⎝⎭． ···················12分当32a =时，S 有最大值，最大值为38． S 取最大值时点P 的坐标为3322⎛⎫⎪⎝⎭，． ···················· 14分15（18江苏连云港）25．（本小题满分12分）我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆．例如线段AB 的最小覆盖圆就是以线段AB 为直径的圆．（1）请分别作出图1中两个三角形的最小覆盖圆（要求用尺规作图，保留作图痕迹，不写AA作法）；（2）探究三角形的最小覆盖圆有何规律？请写出你所得到的结论（不要求证明）；（3）某地有四个村庄E F G H ，，，（其位置如图2所示），现拟建一个电视信号中转站，为了使这四个村庄的居民都能接收到电视信号，且使中转站所需发射功率最小（距离越小，所需功率越小），此中转站应建在何处？请说明理由．（18江苏连云港25题解析）25．解：（1）如图所示： ············· 4分（注：正确画出1个图得2分，无作图痕迹或痕迹不正确不得分）（2）若三角形为锐角三角形，则其最小覆盖圆为其外接圆； ··········· 6分若三角形为直角或钝角三角形，则其最小覆盖圆是以三角形最长边（直角或钝角所对的边）为直径的圆． ······························· 8分（3）此中转站应建在EFH △的外接圆圆心处（线段EF 的垂直平分线与线段EH 的垂直平分线的交点处）． ················ 10分理由如下：由47.835.182.9HEF HEG GEF ∠=∠+∠=+=，50.0EHF ∠=，47.1EFH ∠=，G49.8F53.8 44.0 47.1 35.1 47.8 50.0 （第25题图2） 80 100 （第25题答图1）32.4 49.8 F53.8 44.047.135.147.8 50.0故EFH △是锐角三角形，所以其最小覆盖圆为EFH △的外接圆，设此外接圆为O ，直线EG 与O 交于点E M ，，则50.053.8EMF EHF EGF ∠=∠=<=∠．故点G 在O 内，从而O 也是四边形EFGH 的最小覆盖圆．所以中转站建在EFH △的外接圆圆心处，能够符合题中要求．························ 12分16（18江苏南京）28．（10分）一列快车从甲地驶往乙地，一列慢车从乙地驶往甲地，两车同时出发，设慢车行驶的时间为(h)x ，两车之间的距离．．．．．．．为(km)y ，图中的折线表示y 与x 之间的函数关系．根据图象进行以下探究：信息读取（1）甲、乙两地之间的距离为 km ；（2）请解释图中点B 的实际意义；图象理解（3）求慢车和快车的速度；（4）求线段BC 所表示的y 与x 之间的函数关系式，并写出自变量x 的取值范围；问题解决（5）若第二列快车也从甲地出发驶往乙地，速度与第一列快车相同．在第一列快车与慢车相遇30分钟后，第二列快车与慢车相遇．求第二列快车比第一列快车晚出发多少小时？（18江苏南京28题解析）28．（本题10分）解：（1）900； ······························· 1分（2）图中点B 的实际意义是：当慢车行驶4h 时，慢车和快车相遇． ······· 2分（3）由图象可知，慢车12h 行驶的路程为900km ，所以慢车的速度为90075(km /h)12=； ···················· 3分当慢车行驶4h 时，慢车和快车相遇，两车行驶的路程之和为900km ，所以慢车和快车行驶的速度之和为900225(km /h)4=，所以快车的速度为150km/h ． ········· 4分（4）根据题意，快车行驶900km 到达乙地，所以快车行驶9006(h)150=到达乙地，此时两车之间的距离为675450(km)⨯=，所以点C 的坐标为(6450)，．设线段BC 所表示的y 与x 之间的函数关系式为y kx b =+，把(40)，，(6450)，代入得 044506.k b k b =+⎧⎨=+⎩，（第28题）y解得225900.k b =⎧⎨=-⎩，所以，线段BC 所表示的y 与x 之间的函数关系式为225900y x =-． ······ 6分自变量x 的取值范围是46x ≤≤． ····················· 7分（5）慢车与第一列快车相遇30分钟后与第二列快车相遇，此时，慢车的行驶时间是4.5h ．把 4.5x =代入225900y x =-，得112.5y =．此时，慢车与第一列快车之间的距离等于两列快车之间的距离是112.5km ，所以两列快车出发的间隔时间是112.51500.75(h)÷=，即第二列快车比第一列快车晚出发0.75h ． · 10分 17（18江苏南通）（第28题14分） 28．已知双曲线k y x =与直线14y x =相交于A 、B 两点．第一象限上的点M （m ，n ）（在A 点左侧）是双曲线ky x=上的动点．过点B 作BD ∥y 轴交x 轴于点D ．过N （0，－n ）作NC ∥x 轴交双曲线ky x=于点E ，交BD 于点C ．（1）若点D 坐标是（－8，0），求A 、B 两点坐标及k 的值．（2）若B 是CD 的中点，四边形OBCE 的面积为4，求直线CM 的解析式．（3）设直线AM 、BM 分别与y 轴相交于P 、Q 两点，且MA =pMP ，MB =qMQ ，求p －q 的值．（18江苏南通28题解析）28．解：（1）∵D （－8，0），∴B 点的横坐标为－8，代入14y x =中，得y =－2．∴B 点坐标为（－8，－2）．而A 、B 两点关于原点对称，∴A （8，2）．从而8k =⨯．……………………………………………………………………3分（2）∵N （0，－n ），B 是CD 的中点，A 、B 、M 、E 四点均在双曲线上，∴mn k =，B （－2m ，－2n ），C （－2m ，－n ），E （－m ，－n ）． ……………4分（第28题）S 矩形DCNO 22mn k ==，S △DBO =1122mn k =，S △OEN =1122mn k =， ………………7分∴S 四边形OBCE = S 矩形DCNO －S △DBO － S △OEN =k ．∴4k =． …………………………8分由直线14y x =及双曲线4y x=，得A （4，1），B （－4，－1）， ∴C （－4，－2），M （2，2）．………………………………………………………9分设直线CM 的解析式是y ax b =+，由C 、M 两点在这条直线上，得 42,2 2.a b a b -+=-⎧⎨+=⎩ 解得23a b ==． ∴直线CM 的解析式是2233y x =+．………………………………………………11分（3）如图，分别作AA 1⊥x 轴，MM 1⊥x 轴，垂足分别为A 1、M 1．设A 点的横坐标为a ，则B 点的横坐标为－a ．于是111A M MA a mp MP M O m-===．同理Bm q Qm=13分∴2a m m ap q m m-+-=-=-．……………………14分18（18江苏宿迁）27．（本题满分12分）如图，⊙O 的半径为1，正方形ABCD 顶点B 坐标为)0,5(，顶点D 在⊙O 上运动． (1)当点D 运动到与点A 、O 在同一条直线上时,试证明直线CD 与⊙O 相切；(2)当直线CD 与⊙O 相切时，求CD 所在直线对应的函数关系式；(3)设点D 的横坐标为x ，正方形ABCD 的面积为S ，求S 与x 之间的函数关系式，并求出S 的最大值与最小值．（18江苏宿迁27题解析）27．解：(1) ∵四边形ABCD 为正方形 ∴CD AD ⊥ ∵A 、O 、D 在同一条直线上 ∴︒=∠90ODC ∴直线CD 与⊙O 相切； (2)直线CD 与⊙O 相切分两种情况:①如图1, 设1D 点在第二象限时,过1D 作x E D ⊥11轴于点1E ,设此时的正方形的边长为a ,则2225)1(=+-a a ,解得4=a 或3-=a (舍去)．由BOA Rt ∆∽11OE D Rt ∆ 得OBOD BA E D OA OE 1111== ∴54,53111==E D OE ∴)54,53(1-D ，故直线OD 的函数关系式为x y 34-=；②如图2, 设2D 点在第四象限时,过2D 作x E D ⊥22轴于点2E ,设此时的正方形的边长为b ,则2225)1(=++b b ,解得3=b 或4-=b (舍去)．由BOA Rt ∆∽22OE D Rt ∆得OBOD BA E D OA OE 2222==第27题图1第27题图2∴53,54222==E D OE ∴)53,54(2-D ，故直线OD 的函数关系式为x y 43-=. (3)设),(0y x D ,则201x y -±=,由)0,5(B 得x x x DB 1026)1()5(22-=-+-=∴x x BD S 513)1026(21212-=-==∵11≤≤-x∴851318513=-==+=最小值最大值，S S .19（18江苏泰州）29．已知二次函数)0(21≠++=a c bx ax y 的图象经过三点（1，0），（-3，0），（0，23-）。

2018年山西数学中考试题“几何压轴题”分析

2018年山西数学中考试题“几何压轴题”分析2018年山西数学中考试题分析（5）sdfd作为一名初中数学教师，有必要对中考题进行认真分析，希望可以给今后的教学一些指导，同时也希望给有心的人一点启示。

现在正是假期，可以作点实事。

几何压轴题22．综合与实践问题情境：在数学活动课上，老师出示了这样一个问题：如图1，在矩形ABCD中，AD=2AB，E是AB延长线上一点，且BE=AB，连接DE，交BC于点M，以DE为一边在DE的左下方作正方形DEFG，连接AM．试判断线段AM与DE的位置关系．探究展示：勤奋小组发现，AM垂直平分DE，并展示了如下的证明方法：证明：∵BE=AB，∴AE=2AB．∵AD=2AB，∴AD=AE．∵四边形ABCD是矩形，∴AD∥BC．即AM是△ADE的DE边上的中线，又∵AD=AE，∴AM⊥DE．（依据2）∴AM垂直平分DE．反思交流：（1）①上述证明过程中的“依据1”“依据2”分别是指什么？②试判断图1中的点A是否在线段GF的垂直平分线上，请直接回答，不必证明；（2）创新小组受到勤奋小组的启发，继续进行探究，如图2，连接CE，以CE为一边在CE的左下方作正方形CEFG，发现点G在线段BC的垂直平分线上，请你给出证明；探索发现：（3）如图3，连接CE，以CE为一边在CE的右上方作正方形CEFG，可以发现点C，点B都在线段AE的垂直平分线上，除此之外，请观察矩形ABCD和正方形CEFG的顶点与边，你还能发现哪个顶点在哪条边的垂直平分线上，请写出一个你发现的结论，并加以证明．【解答】解：（1）①依据1：两条直线被一组平行线所截，所得的对应线段成比例（或平行线分线段成比例）．依据2：等腰三角形顶角的平分线，底边上的中线及底边上的高互相重合（或等腰三角形的“三线合一”）．②答：点A在线段GF的垂直平分线上．理由：∵DG∥AM∥EF，DE∥FG，且AM垂直平分DE，∴AM也垂直平分GF,即点A在线段GF的垂直平分线上．（2）证明：如图2，过点G作GH⊥BC于点H，∵四边形ABCD是矩形，点E在AB的延长线上，∴∠CBE=∠ABC=∠GHC=90°，∴∠BCE+∠BEC=90°．∵四边形CEFG为正方形，∴CG=CE，∠GCE=90°，∴∠BCE+∠BCG=90°．∴∠2BEC=∠BCG．∴△GHC≌△CBE．∴HC=BE，∵四边形ABCD是矩形，∴AD=BC．∵AD=2AB，BE=AB，∴BC=2BE=2HC，∴HC=BH．∴GH垂直平分BC．∴点G在BC的垂直平分线上．（3）答：点F在BC边的垂直平分线上（或点F在AD边的垂直平分线上）．证明：如图3，过点F作FM⊥BC于点M，过点E作EN⊥FM于点N．∴∠BMN=∠ENM=∠ENF=90°．∵四边形ABCD是矩形，点E在AB的延长线上，∴∠CBE=∠ABC=90°，∴四边形BENM为矩形．∴BM=EN，∠BEN=90°．∴∠1+∠2=90°．∵四边形CEFG为正方形，∴EF=EC，∠CEF=90°．∴∠2+∠3=90°．∴∠1=∠3．∵∠CBE=∠ENF=90°，∴△ENF≌△EBC．∴NE=BE．∴BM=BE．∵四边形ABCD是矩形，∴AD=BC．∵AD=2AB，AB=BE．∴BC=2BM．∴BM=MC．∴FM垂直平分BC．∴点F在BC边的垂直平分线上．【点评】此题是几何综合题，以特殊矩形与正方形为背景，围绕判断点在线段的垂直平分线上展开探究，主要考查了正方形、矩形的性质，全等三角形的判定和性质，线段垂直平分线的判定和性质，构造全等三角形是解决问题的关键．sdfd【总评】2018年山西数学中考试题中的几何压轴题并没有以平移、旋转、轴对称构图,而是以变换顶点、变换相对位置进行构图；在第（1）小题中还对证明过程中的依据进行了考查，特别是“依据1”考查了“平行线分线段成比例定理”还很容易填错，再次提醒我们虽然证明过程中的依据不要求写，但你必须清楚地知道依据是什么；勾股弦图不仅给我们提供了证明勾股定理的方法，还提供了以正方形的边为斜边的全等三角形的构造方法；第（3）小题中“点A在线段CE的垂直平分线上”是错解，这儿就需要我们严谨的求学态度，而决不能是看见像。

2018年全国各地中考数学压轴题汇编：几何综合(中南西南)(解析卷)

2018年全国各地中考数学压轴题汇编（中南西南）几何综合参考答案与试题解析一．选择题（共3小题）1．（2018•重庆）如图，已知AB是⊙O的直径，点P在BA的延长线上，PD与⊙O相切于点D，过点B作PD的垂线交PD的延长线于点C，若⊙O的半径为4，BC=6，则PA的长为（）A．4 B．2C．3 D．2.5解：连接DO，∵PD与⊙O相切于点D，∴∠PDO=90°，∵∠C=90°，∴DO∥BC，∴△PDO∽△PCB，∴===，设PA=x，则=，解得：x=4，故PA=4．故选：A．2．（2018•海南）如图1，分别沿长方形纸片ABCD和正方形纸片EFGH的对角线AC，EG剪开，拼成如图2所示的▱KLMN，若中间空白部分四边形OPQR恰好是正方形，且▱KLMN 的面积为50，则正方形EFGH的面积为（）A．24 B．25 C．26 D．27解：如图，设PM=PL=NR=KR=a，正方形ORQP的边长为b．由题意：a2+b2+（a+b）（a﹣b）=50，∴a2=25，∴正方形EFGH的面积=a2=25，故选：B．3．（2018•曲靖）如图，在正方形ABCD中，连接AC，以点A为圆心，适当长为半径画弧，交AB、AC于点M，N，分别以M，N为圆心，大于MN长的一半为半径画弧，两弧交于点H，连结AH并延长交BC于点E，再分别以A、E为圆心，以大于AE长的一半为半径画弧，两弧交于点P，Q，作直线PQ，分别交CD，AC，AB于点F，G，L，交CB的延长线于点K，连接GE，下列结论：①∠LKB=22.5°，②GE∥AB，③tan∠CGF=，④S△CGE：S△CAB=1：4．其中正确的是（）A．①②③B．②③④C．①③④D．①②④解：①∵四边形ABCD是正方形，∴∠BAC=∠BAD=45°，由作图可知：AE平分∠BAC，∴∠BAE=∠CAE=22.5°，∵PQ是AE的中垂线，∴AE⊥PQ，∴∠AOL=90°，∵∠AOL=∠LBK=90°，∠ALO=∠KLB，∴∠LKB=∠BAE=22.5°；故①正确；②∵OG是AE的中垂线，∴AG=EG，∴∠AEG=∠EAG=22.5°=∠BAE，∴EG∥AB，故②正确；③∵∠LAO=∠GAO，∠AOL=∠AOG=90°，∴∠ALO=∠AGO，∵∠CGF=∠AGO，∠BLK=∠ALO，∴∠CGF=∠BLK，在Rt△BKL中，tan∠CGF=tan∠BLK=，故③正确；④连接EL，∵AL=AG=EG，EG∥AB，∴四边形ALEG是菱形，∴AL=EL=EG＞BL，∴，∵EG∥AB，∴△CEG∽△CBA，∴=，故④不正确；本题正确的是：①②③，故选：A．二．填空题（共9小题）4．（2018•广东）如图，矩形ABCD中，BC=4，CD=2，以AD为直径的半圆O与BC相切于点E，连接BD，则阴影部分的面积为π．（结果保留π）解：连接OE，如图，∵以AD为直径的半圆O与BC相切于点E，∴OD=2，OE⊥BC，易得四边形OECD为正方形，∴由弧DE、线段EC、CD所围成的面积=S正方形OECD ﹣S扇形EOD=22﹣=4﹣π，∴阴影部分的面积=×2×4﹣（4﹣π）=π．故答案为π．5．（2018•深圳）如图，四边形ACDF是正方形，∠CEA和∠ABF都是直角且点E，A，B 三点共线，AB=4，则阴影部分的面积是8．解：∵四边形ACDF是正方形，∴AC=AF，∠CAF=90°，∴∠EAC+∠FAB=90°，∵∠ABF=90°，∴∠AFB+∠FAB=90°，∴∠EAC=∠AFB，在△CAE和△AFB中，，∴△CAE≌△AFB，∴EC=AB=4，∴阴影部分的面积=×AB×CE=8，故答案为：8．6．（2018•广州）如图，CE是▱ABCD的边AB的垂直平分线，垂足为点O，CE与DA的延长线交于点E．连接AC，BE，DO，DO与AC交于点F，则下列结论：①四边形ACBE是菱形；②∠ACD=∠BAE；③AF：BE=2：3；④S四边形AFOE ：S△COD=2：3．其中正确的结论有①②④．（填写所有正确结论的序号）解：∵四边形ABCD是平行四边形，∴AB∥CD，AB=CD，∵EC垂直平分AB，∴OA=OB=AB=DC，CD⊥CE，∵OA∥DC，∴===，∴AE=AD，OE=OC，∵OA=OB，OE=OC，∴四边形ACBE是平行四边形，∵AB⊥EC，∴四边形ACBE是菱形，故①正确，∵∠DCE=90°，DA=AE，∴AC=AD=AE，∴∠ACD=∠ADC=∠BAE，故②正确，∵OA∥CD，∴==，∴==，故③错误，设△AOF的面积为a，则△OFC的面积为2a，△CDF的面积为4a，△AOC的面积=△AOE 的面积=3a，∴四边形AFOE的面积为4a，△ODC的面积为6a∴S四边形AFOE ：S△COD=2：3．故④正确，故答案为①②④．7．（2018•河南）如图，在△ABC中，∠ACB=90°，AC=BC=2，将△ABC绕AC的中点D 逆时针旋转90°得到△A'B′C'，其中点B的运动路径为，则图中阴影部分的面积为π﹣．解：△ABC绕AC的中点D逆时针旋转90°得到△A'B′C'，此时点A′在斜边AB上，CA′⊥AB，DB′==，A′B′==2，1×2÷2﹣（2﹣）×÷2=π﹣．∴S阴=﹣故答案为π﹣．8．（2018•深圳）在Rt△ABC中，∠C=90°，AD平分∠CAB，BE平分∠ABC，AD、BE相交于点F，且AF=4，EF=，则AC=．解：如图，∵AD，BE是分别是∠BAC和∠ABC的平分线，∴∠1=∠2，∠3=∠4，∵∠ACB=90°，∴2（∠2+∠4）=90°，∴∠2+∠4=45°，∴∠EFG=∠2+∠4=45°，过点E作EG⊥AD于G，在Rt△EFG中，EF=，∴FG=EG=1，∵AF=4，∴AG=AF﹣FG=3，根据勾股定理得，AE==，连接CF，∵AD平分∠CAB，BE平分∠ABC，∴CF是∠ACB的平分线，∴∠ACF=45°=∠AFE，∵∠CAF=∠FAE，∴△AEF∽△AFC，∴，∴AC===，故答案为．9．（2018•河南）如图，∠MAN=90°，点C在边AM上，AC=4，点B为边AN上一动点，连接BC，△A′BC与△ABC关于BC所在直线对称，点D，E分别为AC，BC的中点，连接DE并延长交A′B所在直线于点F，连接A′E．当△A′EF为直角三角形时，AB的长为4或4．解：当△A′EF为直角三角形时，存在两种情况：①当∠A'EF=90°时，如图1，∵△A′BC与△ABC关于BC所在直线对称，∴A'C=AC=4，∠ACB=∠A'CB，∵点D，E分别为AC，BC的中点，∴D、E是△ABC的中位线，∴DE∥AB，∴∠CDE=∠MAN=90°，∴∠CDE=∠A'EF，∴AC∥A'E，∴∠ACB=∠A'EC，∴∠A'CB=∠A'EC，∴A'C=A'E=4，Rt△A'CB中，∵E是斜边BC的中点，∴BC=2A'E=8，由勾股定理得：AB2=BC2﹣AC2，∴AB==4；②当∠A'FE=90°时，如图2，∵∠ADF=∠A=∠DFB=90°，∴∠ABF=90°，∵△A′BC与△ABC关于BC所在直线对称，∴∠ABC=∠CBA'=45°，∴△ABC是等腰直角三角形，∴AB=AC=4；综上所述，AB的长为4或4；故答案为：4或4；10．（2018•重庆）如图，把三角形纸片折叠，使点B、点C都与点A重合，折痕分别为DE、FG，得到∠AGE=30°，若AE=EG=2厘米，则△ABC的边BC的长为6+4厘米．解：∵把三角形纸片折叠，使点B、点C都与点A重合，折痕分别为DE，FG，∴BE=AE，AG=GC，∵∠AGE=30°，AE=EG=2厘米，∴AG=6，∴BE=AE=2，GC=AG=6，∴BC=BE+EG+GC=6+4，故答案为：6+4，11．（2018•昆明）如图，正六边形ABCDEF的边长为1，以点A为圆心，AB的长为半径，作扇形ABF，则图中阴影部分的面积为﹣（结果保留根号和π）．解：正六边形的中心为点O，连接OD、OE，作OH⊥DE于H，∠DOE==60°，∴OD=OE=DE=1，∴OH=，∴正六边形ABCDEF的面积=×1××6=，∠A==120°，∴扇形ABF的面积==，∴图中阴影部分的面积=﹣，故答案为：﹣．12．（2018•曲靖）如图：在△ABC中，AB=13，BC=12，点D，E分别是AB，BC的中点，连接DE，CD，如果DE=2.5，那么△ACD的周长是18．解：∵D，E分别是AB，BC的中点，∴AC=2DE=5，AC∥DE，AC2+BC2=52+122=169，AB2=132=169，∴AC2+BC2=AB2，∴∠ACB=90°，∵AC∥DE，∴∠DEB=90°，又∵E是BC的中点，∴直线DE是线段BC的垂直平分线，∴DC=BD，∴△ACD的周长=AC+AD+CD=AC+AD+BD=AC+AB=18，故答案为：18．三．解答题（共16小题）13．（2018•广东）如图，四边形ABCD中，AB=AD=CD，以AB为直径的⊙O经过点C，连接AC、OD交于点E．（1）证明：OD∥BC；（2）若tan∠ABC=2，证明：DA与⊙O相切；（3）在（2）条件下，连接BD交⊙O于点F，连接EF，若BC=1，求EF的长．解：（1）连接OC，在△OAD和△OCD中，∵，∴△OAD≌△OCD（SSS），∴∠ADO=∠CDO，又AD=CD，∴DE⊥AC，∵AB为⊙O的直径，∴∠ACB=90°，∴∠ACB=90°，即BC⊥AC，∴OD∥BC；（2）∵tan∠ABC==2，∴设BC=a、则AC=2a，∴AD=AB==，∵OE∥BC，且AO=BO，∴OE=BC=a，AE=CE=AC=a，在△AED中，DE==2a，在△AOD中，AO2+AD2=（）2+（a）2=a2，OD2=（OE+DE）2=（a+2a）2=a2，∴AO2+AD2=OD2，∴∠OAD=90°，则DA与⊙O相切；（3）连接AF，∵AB是⊙O的直径，∴∠AFD=∠BAD=90°，∵∠ADF=∠BDA，∴△AFD∽△BAD，∴=，即DF•BD=AD2①，又∵∠AED=∠OAD=90°，∠ADE=∠ODA，∴△AED∽△OAD，∴=，即OD•DE=AD2②，由①②可得DF•BD=OD•DE，即=，又∵∠EDF=∠BDO，∴△EDF∽△BDO，∵BC=1，∴AB=AD=、OD=、ED=2、BD=、OB=，∴=，即=，解得：EF=．14．（2018•广州）如图，在四边形ABCD中，∠B=∠C=90°，AB＞CD，AD=AB+CD．（1）利用尺规作∠ADC的平分线DE，交BC于点E，连接AE（保留作图痕迹，不写作法）；（2）在（1）的条件下，①证明：AE⊥DE；②若CD=2，AB=4，点M，N分别是AE，AB上的动点，求BM+MN的最小值．解：（1）如图，∠ADC的平分线DE如图所示．（2）①延长DE交AB的延长线于F．∵CD∥AF，∴∠CDE=∠F，∵∠CDE=∠ADE，∴∠ADF=∠F，∴AD=AF，∵AD=AB+CD=AB+BF，∴CD=BF，∵∠DEC=∠BEF，∴△DEC≌△FEB，∴DE=EF，∵AD=AF，∴AE⊥DE．②作点B关于AE的对称点K，连接EK，作KH⊥AB于H，DG⊥AB于G．连接MK．∵AD=AF，DE=EF，∴AE平分∠DAF，则△AEK≌△AEB，∴AK=AB=4，在Rt△ADG中，DG==4，∵KH∥DG，∴=，∴=，∴KH=，∵MB=MK，∴MB+MN=KM+MN，∴当K、M、N共线，且与KH重合时，KM+MN的值最小，最小值为KH的长，∴BM+MN的最小值为．15．（2018•广东）已知Rt△OAB，∠OAB=90°，∠ABO=30°，斜边OB=4，将Rt△OAB绕点O顺时针旋转60°，如图1，连接BC．（1）填空：∠OBC=60°；（2）如图1，连接AC，作OP⊥AC，垂足为P，求OP的长度；（3）如图2，点M，N同时从点O出发，在△OCB边上运动，M沿O→C→B路径匀速运动，N沿O→B→C路径匀速运动，当两点相遇时运动停止，已知点M的运动速度为1.5单位/秒，点N的运动速度为1单位/秒，设运动时间为x秒，△OMN的面积为y，求当x为何值时y取得最大值？最大值为多少？解：（1）由旋转性质可知：OB=OC，∠BOC=60°，∴△OBC是等边三角形，∴∠OBC=60°．故答案为60．（2）如图1中，∵OB=4，∠ABO=30°，∴OA=OB=2，AB=OA=2，=•OA•AB=×2×2=2，∴S△AOC∵△BOC是等边三角形，∴∠OBC=60°，∠ABC=∠ABO+∠OBC=90°，∴AC==2，∴OP===．（3）①当0＜x≤时，M在OC上运动，N在OB上运动，此时过点N作NE⊥OC且交OC于点E．则NE=ON•sin60°=x，=•OM•NE=×1.5x×x，∴S△OMN∴y=x2．∴x=时，y有最大值，最大值=．②当＜x≤4时，M在BC上运动，N在OB上运动．作MH⊥OB于H．则BM=8﹣1.5x，MH=BM•sin60°=（8﹣1.5x），∴y=×ON×MH=﹣x2+2x．当x=时，y取最大值，y＜，③当4＜x≤4.8时，M、N都在BC上运动，作OG⊥BC于G．MN=12﹣2.5x，OG=AB=2，∴y=•MN•OG=12﹣x，当x=4时，y有最大值，最大值=2，综上所述，y有最大值，最大值为．16．（2018•深圳）已知菱形的一个角与三角形的一个角重合，然后它的对角顶点在这个重合角的对边上，这个菱形称为这个三角形的亲密菱形，如图，在△CFE中，CF=6，CE=12，∠FCE=45°，以点C为圆心，以任意长为半径作AD，再分别以点A和点D为圆心，大于AD 长为半径作弧，交EF于点B，AB∥CD．（1）求证：四边形ACDB为△FEC的亲密菱形；（2）求四边形ACDB的面积．（1）证明：∵由已知得：AC=CD，AB=DB，由已知尺规作图痕迹得：BC是∠FCE的角平分线，∴∠ACB=∠DCB，又∵AB∥CD，∴∠ABC=∠DCB，∴∠ACB=∠ABC，∴AC=AB，又∵AC=CD，AB=DB，∴AC=CD=DB=BA∴四边形ACDB是菱形，∵∠ACD与△FCE中的∠FCE重合，它的对角∠ABD顶点在EF上，∴四边形ACDB为△FEC的亲密菱形；（2）解：设菱形ACDB的边长为x，∵四边形ACDB是菱形，∴AB∥CE，∴∠FAB=∠FCE，∠FBA=∠E，∴△FAB∽△FCE∴，即，解得：x=4，过A点作AH⊥CD于H点，∵在Rt△ACH中，∠ACH=45°，∴，∴四边形ACDB的面积为：．17．（2018•广州）如图，在四边形ABCD中，∠B=60°，∠D=30°，AB=BC．（1）求∠A+∠C的度数；（2）连接BD，探究AD，BD，CD三者之间的数量关系，并说明理由；（3）若AB=1，点E在四边形ABCD内部运动，且满足AE2=BE2+CE2，求点E运动路径的长度．解：（1）如图1中，在四边形ABCD中，∵∠A+∠B+∠C+∠D=360°，∠B=60°，∠C=30°，∴∠A+∠C=360°﹣60°﹣30°=270°．（2）如图2中，结论：DB2=DA2+DC2．理由：连接BD．以BD为边向下作等边三角形△BDQ．∵∠ABC=∠DBQ=60°，∴∠ABD=∠CBQ，∵AB=BC，DB=BQ，∴△ABD≌△CBQ，∴AD=CQ，∠A=∠BCQ，∵∠A+∠BCD=∠BCQ+∠BCD=270°，∴∠DCQ=90°，∴DQ2=DC2+CQ2，∵CQ=DA，DQ=DB，∴DB2=DA2+DC2．（3）如图3中，连接AC，将△ACE绕点A顺时针旋转60°得到△ABR，连接RE．则△AER是等边三角形，∵EA2=EB2+EC2，EA=RE，EC=RB，∴RE2=RB2+EB2，∴∠EBR=90°，∴∠RAE+∠RBE=150°，∴∠ARB+∠AEB=∠AEC+∠AEB=0°，∴∠BEC=150°，∴点E的运动轨迹在O为圆心的圆上，在⊙O上取一点K，连接KB，KC，OB，OC，∵∠K+∠BEC=180°，∴∠K=30°，∠BOC=60°，∵OB=OC，∴△OBC是等边三角形，∴点E的运动路径==．18．（2018•河南）如图，AB是⊙O的直径，DO⊥AB于点O，连接DA交⊙O于点C，过点C作⊙O的切线交DO于点E，连接BC交DO于点F．（1）求证：CE=EF；（2）连接AF并延长，交⊙O于点G．填空：①当∠D的度数为30°时，四边形ECFG为菱形；②当∠D的度数为22.5°时，四边形ECOG为正方形．（1）证明：连接OC，如图，∵CE为切线，∴OC⊥CE，∴∠OCE=90°，即∠1+∠4=90°，∵DO⊥AB，∴∠3+∠B=90°，而∠2=∠3，∴∠2+∠B=90°，而OB=OC，∴∠4=∠B，∴∠1=∠2，∴CE=FE；（2）解：①当∠D=30°时，∠DAO=60°，而AB为直径，∴∠ACB=90°，∴∠B=30°，∴∠3=∠2=60°，而CE=FE，∴△CEF为等边三角形，∴CE=CF=EF，同理可得∠GFE=60°，利用对称得FG=FC，∵FG=EF，∴△FEG为等边三角形，∴EG=FG，∴EF=FG=GE=CE，∴四边形ECFG为菱形；②当∠D=22.5°时，∠DAO=67.5°，而OA=OC，∴∠OCA=∠OAC=67.5°，∴∠AOC=180°﹣67.5°﹣67.5°=45°，∴∠AOC=45°，∴∠COE=45°，利用对称得∠EOG=45°，∴∠COG=90°，易得△OEC≌△OEG，∴∠OEG=∠OCE=90°，∴四边形ECOG为矩形，而OC=OG，∴四边形ECOG为正方形．故答案为30°，22.5°．19．（2018•深圳）如图在⊙O中，BC=2，AB=AC，点D为AE上的动点，且cosB=．（1）求AB的长度；（2）求AD•AE的值；（3）过A点作AH⊥BD，求证：BH=CD+DH．解：（1）作AM⊥BC，∵AB=AC，AM⊥BC，BC=2BM，∴CM=BC=1，∵cosB==，在Rt△AMB中，BM=1，∴AB==；（2）连接DC，∵AB=AC，∴∠ACB=∠ABC，∵四边形ABCD内接于圆O，∴∠ADC+∠ABC=180°，∵∠ACE+∠ACB=180°，∴∠ADC=∠ACE，∵∠CAE公共角，∴△EAC∽△CAD，∴=，∴AD•AE=AC2=10；（3）在BD上取一点N，使得BN=CD，在△ABN和△ACD中，∴△ABN≌△ACD（SAS），∴AN=AD，∵AN=AD，AH⊥BD，∴NH=HD，∵BN=CD，NH=HD，∴BN+NH=CD+HD=BH．20．（2018•海南）已知，如图1，在▱ABCD中，点E是AB中点，连接DE并延长，交CB的延长线于点F．（1）求证：△ADE≌△BFE；（2）如图2，点G是边BC上任意一点（点G不与点B、C重合），连接AG交DF于点H，连接HC，过点A作AK∥HC，交DF于点K．①求证：HC=2AK；②当点G是边BC中点时，恰有HD=n•HK（n为正整数），求n的值．（1）证明：∵四边形ABCD是平行四边形，∴AD∥BC，∴∠ADE=∠BFE，∠A=∠FBE，在△ADE和△BFE中，，∴△ADE≌△BFE；（2）如图2，作BN∥HC交EF于N，∵△ADE≌△BFE，∴BF=AD=BC，∴BN=HC，由（1）的方法可知，△AEK≌△BEN，∴AK=BN，∴HC=2AK；（3）如图3，作GM∥DF交HC于M，∵点G是边BC中点，∴CG=CF，∵GM∥DF，∴△CMG∽△CHF，∴==，∵AD∥FC，∴△AHD∽△GHF，∴===，∴=，∵AK∥HC，GM∥DF，∴△AHK∽△HGM，∴==，∴=，即HD=4HK，∴n=4．．（2018•云南）如图，已知AB是⊙O的直径，C是⊙O上的点，点D在AB的延长线上，∠BCD=∠BAC．（1）求证：CD是⊙O的切线；（2）若∠D=30°，BD=2，求图中阴影部分的面积．解：（1）连接OC，∵OA=OC，∴∠BAC=∠OCA，∵∠BCD=∠BAC，∴∠BCD=∠OCA，∵AB是直径，∴∠ACB=90°，∴∠OCA+OCB=∠BCD+∠OCB=90°∴∠OCD=90°∵OC是半径，∴CD是⊙O的切线（2）设⊙O的半径为r，∴AB=2r，∵∠D=30°，∠OCD=90°，∴OD=2r，∠COB=60°∴r+2=2r，∴r=2，∠AOC=120°∴BC=2，∴由勾股定理可知：AC=2=×2×1=易求S△AOCS扇形OAC==∴阴影部分面积为﹣22．（2018•重庆）如图，在平行四边形ABCD中，点O是对角线AC的中点，点E是BC 上一点，且AB=AE，连接EO并延长交AD于点F．过点B作AE的垂线，垂足为H，交AC于点G．（1）若AH=3，HE=1，求△ABE的面积；（2）若∠ACB=45°，求证：DF=CG．解：（1）∵AH=3，HE=1，∴AB=AE=4，又∵Rt△ABH中，BH==，=AE×BH=×4×=；∴S△ABE（2）如图，过A作AM⊥BC于M，交BG于K，过G作GN⊥BC于N，则∠AMB=∠AME=∠BNG=90°，∵∠ACB=45°，∴∠MAC=∠NGC=45°，∵AB=AE，∴BM=EM=BE，∠BAM=∠EAM，又∵AE⊥BG，∴∠AHK=90°=∠BMK，而∠AKH=∠BKM，∴∠MAE=∠NBG，设∠BAM=∠MAE=∠NBG=α，则∠BAG=∠45°+α，∠BGA=∠GCN+∠GBC=45°+α，∴AB=BG，∴AE=BG，在△AME和△BNG中，，∴△AME≌△BNG（AAS），∴ME=NG，在等腰Rt△CNG中，NG=NC，∴GC=NG=ME=BE，∴BE=GC，∵O是AC的中点，∴OA=OC，∵四边形ABCD是平行四边形，∴AD∥BC，AD=BC，∴∠OAF=∠OCE，∠AFO=∠CEO，∴△AFO≌△CEO（AAS），∴AF=CE，∴AD﹣AF=BC﹣EC，即DF=BE，∴DF=BE=CG．23．（2018•昆明）如图，AB是⊙O的直径，ED切⊙O于点C，AD交⊙O于点F，AC平分∠BAD，连接BF．（1）求证：AD⊥ED；（2）若CD=4，AF=2，求⊙O的半径．（1）证明：连接OC，如图，∵AC平分∠BAD，∴∠1=∠2，∵OA=OC，∴∠1=∠3，∴∠2=∠3，∴OC∥AD，∵ED切⊙O于点C，∴OC⊥DE，∴AD⊥ED；（2）解：OC交BF于H，如图，∵AB为直径，∴∠AFB=90°，易得四边形CDFH为矩形，∴FH=CD=4，∠CHF=90°，∴OH⊥BF，∴BH=FH=4，∴BF=8，在Rt△ABF中，AB===2，∴⊙O的半径为．24．（2018•云南）如图，在平行四边形ABCD中，点E是CD的中点，点F是BC边上的点，AF=AD+FC，平行四边形ABCD的面积为S，由A、E、F三点确定的圆的周长为l．（1）若△ABE的面积为30，直接写出S的值；（2）求证：AE平分∠DAF；（3）若AE=BE，AB=4，AD=5，求l的值．解：（1）如图，作EG⊥AB于点G，=×AB×EG=30，则AB•EG=60，则S△ABE∴平行四边形ABCD的面积为60；（2）延长AE交BC延长线于点H，∵四边形ABCD是平行四边形，∴AD∥BC，∴∠ADE=∠HCE，∠DAE=∠CHE，∵E为CD的中点，∴CE=ED，∴△ADE≌△HCE，∴AD=HC、AE=HE，∴AD+FC=HC+FC，由AF=AD+FC和FH=HC+FC得AF=FH，∴∠FAE=∠CHE，又∵∠DAE=∠CHE，∴∠DAE=∠FAE，∴AE平分∠DAF；（3）连接EF，∵AE=BE、AE=HE，∴AE=BE=HE，∴∠BAE=∠ABE，∠HBE=∠BHE，∵∠DAE=∠CHE，∴∠BAE+∠DAE=∠ABE+∠HBE，即∠DAB=∠CBA，由四边形ABCD是平行四边形得∠DAB+∠CBA=180°，∴∠CBA=90°，∴AF2=AB2+BF2=16+（5﹣FC）2=（FC+CH）2=（FC+5）2，解得：FC=，∴AF=FC+CH=，∵AE=HE、AF=FH，∴FE⊥AH，∴AF是△AEF的外接圆直径，∴△AEF的外接圆的周长l=π．25．（2018•曲靖）如图：在平行四边形ABCD的边AB，CD上截取AF，CE，使得AF=CE，连接EF，点M，N是线段EF上两点，且EM=FN，连接AN，CM．（1）求证：△AFN≌△CEM；（2）若∠CMF=107°，∠CEM=72°，求∠NAF的度数．（1）证明：∵四边形ABCD是平行四边形，∴CD∥AB，∴∠AFN=∠CEM，∵FN=EM，AF=CE，∴△AFN≌△CEM（SAS）．（2）解：∵△AFN≌△CEM，∴∠NAF=∠ECM，∵∠CMF=∠CEM+∠ECM，∴107°=72°+∠ECM，∴∠ECM=35°，∴∠NAF=35°．26．（2018•昆明）如图1，在矩形ABCD中，P为CD边上一点（DP＜CP），∠APB=90°．将△ADP沿AP翻折得到△AD′P，PD′的延长线交边AB于点M，过点B作BN∥MP交DC于点N．（1）求证：AD2=DP•PC；（2）请判断四边形PMBN的形状，并说明理由；（3）如图2，连接AC，分别交PM，PB于点E，F．若=，求的值．解：（1）过点P作PG⊥AB于点G，∴易知四边形DPGA，四边形PCBG是矩形，∴AD=PG，DP=AG，GB=PC∵∠APB=90°，∴∠APG+∠GPB=∠GPB+∠PBG=90°，∴∠APG=∠PBG，∴△APG∽△PBG，∴，∴PG2=AG•GB，即AD2=DP•PC；（2）∵DP∥AB，∴∠DPA=∠PAM，由题意可知：∠DPA=∠APM，∴∠PAM=∠APM，∵∠APB﹣∠PAM=∠APB﹣∠APM，即∠ABP=∠MPB∴AM=PM，PM=MB，∴PM=MB，又易证四边形PMBN是平行四边形，∴四边形PMBN是菱形；（3）由于=，可设DP=1，AD=2，由（1）可知：AG=DP=1，PG=AD=2，∵PG2=AG•GB，∴4=1•GB，∴GB=PC=4，AB=AG+GB=5，∵CP∥AB，∴△PCF∽△BAF，∴==，∴，又易证：△PCE∽△MAE，AM=AB=∴===∴，∴EF=AF﹣AE=AC﹣=AC，∴==27．（2018•曲靖）如图，AB为⊙O的直径，点C为⊙O上一点，将弧BC沿直线BC翻折，使弧BC的中点D恰好与圆心O重合，连接OC，CD，BD，过点C的切线与线段BA 的延长线交于点P，连接AD，在PB的另一侧作∠MPB=∠ADC．（1）判断PM与⊙O的位置关系，并说明理由；（2）若PC=，求四边形OCDB的面积．解：（1）PM与⊙O相切．理由如下：连接DO并延长交PM于E，如图，∵弧BC沿直线BC翻折，使弧BC的中点D恰好与圆心O重合，∴OC=DC，BO=BD，∴OC=DC=BO=BD，∴四边形OBDC为菱形，∴OD⊥BC，∴△OCD和△OBD都是等边三角形，∴∠COD=∠BOD=60°，∴∠COP=∠EOP=60°，∵∠MPB=∠ADC，而∠ADC=∠ABC，∴∠ABC=∠MPB，∴PM∥BC，∴OE⊥PM，∴OE=OP，∵PC为⊙O的切线，∴OC⊥PC，∴OC=OP，∴OE=OC，而OE⊥PC，∴PM是⊙O的切线；（2）在Rt△OPC中，OC=PC=×=1，=2××12=．∴四边形OCDB的面积=2S△OCD28．（2018•河南）（1）问题发现如图1，在△OAB和△OCD中，OA=OB，OC=OD，∠AOB=∠COD=40°，连接AC，BD交于点M．填空：①的值为1；②∠AMB的度数为40°．（2）类比探究如图2，在△OAB和△OCD中，∠AOB=∠COD=90°，∠OAB=∠OCD=30°，连接AC交BD 的延长线于点M．请判断的值及∠AMB的度数，并说明理由；（3）拓展延伸在（2）的条件下，将△OCD绕点O在平面内旋转，AC，BD所在直线交于点M，若OD=1，OB=，请直接写出当点C与点M重合时AC的长．解：（1）问题发现①如图1，∵∠AOB=∠COD=40°，∴∠COA=∠DOB，∵OC=OD，OA=OB，∴△COA≌△DOB（SAS），∴AC=BD，∴=1，②∵△COA≌△DOB，∴∠CAO=∠DBO，∵∠AOB=40°，∴∠OAB+∠ABO=140°，在△AMB中，∠AMB=180°﹣（∠CAO+∠OAB+∠ABD）=180°﹣（∠DBO+∠OAB+∠ABD）=180°﹣140°=40°，故答案为：①1；②40°；（2）类比探究如图2，=，∠AMB=90°，理由是：Rt△COD中，∠DCO=30°，∠DOC=90°，∴，同理得：，∴，∵∠AOB=∠COD=90°，∴∠AOC=∠BOD，∴△AOC∽△BOD，∴=，∠CAO=∠DBO，在△AMB中，∠AMB=180°﹣（∠MAB+∠ABM）=180°﹣（∠OAB+∠ABM+∠DBO）=90°；（3）拓展延伸①点C与点M重合时，如图3，同理得：△AOC∽△BOD，∴∠AMB=90°，，设BD=x，则AC=x，Rt△COD中，∠OCD=30°，OD=1，∴CD=2，BC=x﹣2，Rt△AOB中，∠OAB=30°，OB=，∴AB=2OB=2，在Rt△AMB中，由勾股定理得：AC2+BC2=AB2，，x2﹣x﹣6=0，（x﹣3）（x+2）=0，x1=3，x2=﹣2，∴AC=3；②点C与点M重合时，如图4，同理得：∠AMB=90°，，设BD=x，则AC=x，在Rt△AMB中，由勾股定理得：AC2+BC2=AB2，+（x+2）2=x2+x﹣6=0，（x+3）（x﹣2）=0，x1=﹣3，x2=2，∴AC=2；综上所述，AC的长为3或2．。

2018年全国各省市中考数学几何压轴题

2018年全国各地中考数学压轴题汇编：几何综合（湖南专版）（原卷）

2018年广西各省市中考数学几何压轴题真题汇总

2018年全国各地中考数学压轴题汇编：几何综合(西北专版)(解析卷)

2018全国各地中考数学压轴题精选(含详细答案)

2018年全国各地中考数学压轴题汇编：几何综合(华北东北专版)(解析卷)

2018年全国各省市中考数学几何压轴题

2018全国各地中考数学压轴题 精品

2018年全国各地中考数学压轴题汇编：几何综合(贵州专版)(解析卷)

2018年全国各地中考数学压轴题 精品

2018年全国各地中考数学压轴题汇编：几何综合(浙江专版)(原卷)

2018年全国各地中考数学压轴题汇编：几何综合(江苏专版)(解析卷)

2018年全国各地中考数学压轴题汇编：几何综合(湖北专版)(解析版)

2018年全国各地中考数学压轴题汇编：几何综合(山东专版)(解析卷)

中考数学试题-2018年全国中考数学压轴题精选精析(5份) 最新

2018年山西数学中考试题“几何压轴题”分析

2018年全国各地中考数学压轴题汇编：几何综合(中南西南)(解析卷)

最新-2018年全国各地中考数学压轴题专集 7平行四边形、矩形、菱形、正方形、梯形 精品

2018全国各地中考数学压轴题精品

2018年全国各地中考数学压轴题精品

最新-2018年全国各地中考数学压轴题专集 7平行四边形、矩形、菱形、正方形、梯形精品