高思导引 四年级第三讲 还 原问题与年龄问题教师版
四年级下册数学专题培优 优秀PPT(第九讲)还原问题与年龄问题一 全国通用

四年级下册数学专题培优 优秀PPT(第九讲)还原问题与年龄问 题一 全国通用
退一步,海阔天空。
例(6)今年父亲的年龄是48岁,哥哥的年龄是弟弟的2倍, 当弟弟长到哥哥现在的年龄时,父亲的年龄恰好等于兄弟 俩年龄之和。请问:今年哥哥多少岁?
例(4)兄弟两个年龄之和是32岁. 当哥哥是弟弟现在这么大 时,哥哥的年龄是当时弟弟年龄的3倍;求哥哥现在的年 龄。
四年级下册数学专题培优 优秀PPT(第九讲)还原问题与年龄问 题一 全国通用
四年级下册数学专题培优 优秀PPT(第九讲)还原问题与年龄问 题一 全国通用
退一步,海阔天空。
例(5)学生问老师多少岁,老师说:“当我像你这么大时, 你刚3岁;当你像我这么大时,我已经39岁了” 。求老师 和学生现在的年龄。
退一步,海阔天空。
例(3)今年,费叔叔的年龄比小悦、冬冬、阿奇三人年龄 的总和还多6岁, 多少年后,费叔叔的年龄将比他们三人年 龄的总和少6岁?
四年级下册数学专题培优 优秀PPT(第九讲)还原问题与年龄问 题一 全国通用
四年级下册数学专题培优 优秀PPT(第九讲)还原问题与年龄问 题一 全国通用
退一步,海阔天空。
四年级下册数学专题培优 优秀PPT(第九讲)还原问题与年龄问 题一 全国通用
四年级下册数学专题培优 优秀PPT(第九讲)还原问题与年龄问 题一 全国通用
人们都说数学与生活息息相关,此话不假。 中国有句话叫:“退一步,海阔天空。”这便是倒
推 法在生活中的反映。有了倒推法,生活中不少的难 题都会迎刃而解。
(一斗等于八两)
四年级下册数学专题培优 优秀PPT(第九讲)还原问题与年龄问 题一 全国通用
四年级高斯数学导引第三讲超越篇

四年级高斯数学导引第三讲超越篇(原创实用版)目录1.导引简介2.高斯数学导引的内容3.四年级高斯数学导引第三讲的主要内容4.超越篇的含义和作用5.超越篇的主要知识点6.总结正文一、导引简介《四年级高斯数学导引》是一本针对小学四年级学生的数学辅导教材,以德国数学家高斯的教学理念为基础,结合我国的教育实际,为学生提供系统、全面的数学知识。
本书的内容涵盖了四年级数学课程的全部知识点,旨在帮助学生更好地理解和掌握数学知识,提高学生的数学素养和解题能力。
二、高斯数学导引的内容《四年级高斯数学导引》共分为十讲,内容包括:算术、代数、几何、测量、组合、概率、逻辑、方法、策略、竞赛等。
每讲都按照知识点的难易程度和学生的接受能力进行编排,既有基本概念的讲解,也有综合运用的训练,让学生在掌握知识的同时,也能学会解题的方法和技巧。
三、四年级高斯数学导引第三讲的主要内容第三讲为超越篇,主要介绍了一些基本的超越数及其性质。
超越数是指不能表示为两个整数的比值的实数,例如圆周率π和自然对数的底数 e等。
本讲的主要内容包括:超越数的概念、性质、分类和一些著名的超越数等。
四、超越篇的含义和作用超越篇的含义是指那些不能用有理数表示的实数,它们在数学中有着广泛的应用。
学习超越数,有助于学生更好地理解实数的概念,丰富学生的数学知识,提高学生的数学素养。
同时,超越数的学习也为以后学习更高级的数学知识打下基础。
五、超越篇的主要知识点1.超越数的概念:不能表示为两个整数的比值的实数。
2.超越数的性质:无理数、无限不循环小数、不能表示为整系数方程的根等。
3.超越数的分类:代数无理数、无理代数数、超越代数数等。
4.著名的超越数:圆周率π、自然对数的底数 e、黄金分割比例φ等。
六、总结《四年级高斯数学导引》第三讲超越篇为学生介绍了一些基本的超越数及其性质,让学生了解到超越数的概念、性质、分类和一些著名的超越数等知识。
高思课本对应导引目录

三年级上(二升三暑假&三年级秋季)第1讲乘除法巧算三年级导引第1讲第2讲枚举法中的字典排列三年级导引第3讲第3讲移多补少与等量代换三年级导引第8讲第4讲寻找隐藏周期三年级导引第7讲第5讲植树问题三年级导引第19讲第6讲复杂间隔问题三年级导引第19讲第7讲和倍与和差三年级导引第5讲第8讲归一问题三年级导引第2讲第9讲假设法解鸡兔同笼三年级导引第8讲第10讲分组法解鸡兔同笼三年级导引第8讲第11讲乘法分配律三年级导引第13讲第12讲差倍三年级导引第5讲第13讲多个对象和差倍三年级导引第5讲第14讲树形图三年级导引第14讲第15讲多重周期问题三年级导引第7讲第16讲复杂周期问题三年级导引第7讲第17讲数字趣题三年级导引第23讲第18讲假设法进阶三年级导引第17讲第19讲分组法进阶三年级导引第17讲第20讲等差数列初步三年级导引第9讲第21讲等差数列求和三年级导引第9讲第22讲等差数列应用三年级导引第9讲第23讲基本盈亏问题三年级导引第11讲三年级下(三年级寒假&三年级春季)第1讲和差倍中的隐藏条件三年级导引第15讲第2讲复杂和差倍三年级导引第15讲第3讲假设分组综合提高三年级导引第17讲第4讲数字计数三年级导引第14讲第5讲巧填算符进阶三年级导引第20讲第6讲算符与数字三年级导引第20讲第7讲数阵图初步四年级导引第2讲第8讲盈亏条件的转化三年级导引第21讲第9讲复杂盈亏问题三年级导引第21讲第10讲四则混合运算三年级导引第13讲第11讲简单乘法竖式三年级导引第16讲第12讲简单除法竖式三年级导引第16讲第13讲简单抽屉原理四年级导引第6讲第14讲还原问题四年级导引第9讲第15讲长度计算三年级导引第22讲第16讲角度计算三年级导引第22讲第17讲找位置四年级导引第10讲第18讲阵列问题三年级导引第19讲第19讲几何图形剪拼四年级导引第4讲第20讲思维游戏四年级导引第23讲第1讲整数计算综合四年级导引第01讲第2讲和差倍中的分组比较四年级导引第08讲第3讲基本直线形面积公式四年级导引第07讲第4讲字母竖式四年级导引第03讲第5讲加法原理与乘法原理四年级导引第11讲第6讲相遇问题四年级导引第05讲第7讲追及问题四年级导引第05讲第8讲数列规律计算四年级导引第10讲第9讲统筹规划四年级导引第12讲第10讲游戏策略四年级导引第12讲第11讲整数数列计算四年级导引第01讲第12讲乘法原理进阶四年级导引第11讲第13讲变倍问题四年级导引第08讲第14讲年龄问题四年级导引第09讲第15讲逻辑推理一四年级导引第24讲第16讲多位数巧算四年级导引第13讲第17讲复杂竖式四年级导引第15讲第18讲火车行程初步四年级导引第18讲第19讲火车行程进阶四年级导引第18讲第20讲底高的选取与组合四年级导引第07讲第21讲等积变形四年级导引第07讲第22讲数表规律计算四年级导引第10讲第23讲最值问题一四年级导引第23讲第1讲从洛书到幻方四年级导引第20讲第2讲小数巧算四年级导引第13讲第3讲多人多次相遇与追及四年级导引第18讲第4讲格点图形面积计算四年级导引第17讲第5讲割补法巧算面积四年级导引第17讲第6讲横式问题四年级导引第16讲第7讲平均数问题四年级导引第14讲第8讲复杂数阵图四年级导引第20讲第9讲排列组合公式四年级导引第21讲第10讲排列组合应用四年级导引第21讲第11讲分段计算的行程问题四年级导引第19讲第12讲直线形面积计算综合提高五年级导引第14讲第13讲多次往返相遇与追及四年级导引第19讲第14讲有特殊要求的挑选四年级导引第22讲第15讲捆绑法与插空法四年级导引第22讲第16讲奇偶性分析五年级导引第23讲第17讲牛吃草问题五年级导引第18讲第18讲整数裂项五年级导引第13讲第19讲容斥原理五年级导引第04讲第20讲复杂抽屉原理五年级导引第24讲第1讲整除问题初步五年级导引第2讲第2讲整除问题进阶五年级导引第2讲第3讲质数与合数五年级导引第3讲第4讲环形路线五年级导引第5讲第5讲分数基本计算五年级导引第1讲第6讲直线形计算中的倍数关系五年级导引第14讲第7讲解方程与方程组六年级导引第4讲第8讲分数计算与比较大小五年级导引第1讲第9讲流水行船问题五年级导引第5讲第10讲约数与倍数五年级导引第7讲第11讲分数与循环小数五年级导引第8讲第12讲几何计数五年级导引第6讲第13讲逻辑推理二无对应讲次第14讲公约数与公倍数初步五年级导引第7讲第15讲公约数与公倍数进阶五年级导引第7讲第16讲分数应用题五年级导引第11讲第17讲比例应用题五年级导引第12讲第18讲直线形计算中的比例关系五年级导引第19讲第19讲分数裂项六年级导引第1讲第20讲数字谜综合一五年级导引第10讲第21讲余数的性质与计算五年级导引第16讲第22讲物不知数与同余五年级导引第16讲第23讲工程问题五年级导引第17讲第24讲列方程解应用题六年级导引第4讲第25讲燕尾模型六年级导引第10讲第26讲比较与估算五年级导引第9讲第1讲圆与扇形初步五年级导引第15讲第2讲圆与扇形进阶五年级导引第15讲第3讲行程问题综合一无对应讲次第4讲计算综合一五年级导引第13讲第5讲计数综合一无对应讲次第6讲钟表问题五年级导引第18讲第7讲位值原理五年级导引第21讲第8讲水管问题五年级导引第17讲第9讲立体几何六年级导引第9讲第10讲比例计算与列表分析六年级导引第3讲第11讲正反比例的概念与应用六年级导引第3讲第12讲行程问题中的比例关系六年级导引第14讲第13讲沙漏与金字塔五年级导引第19讲六年级导引第10讲第14讲数论相关的计数五年级导引第22讲第15讲数字谜中的计数五年级导引第22讲第16讲不确定性问题五年级导引第12讲第17讲浓度问题六年级导引第5讲第18讲经济问题六年级导引第5讲第19讲变速行程问题一五年级导引第20讲第20讲行程问题中的分段与比较五年级导引第20讲第1讲比赛中的推理六年级导引第6讲第2讲计算综合二六年级导引第2讲第3讲递推计数六年级导引第12讲第4讲对应计数六年级导引第13讲第5讲进位制六年级导引第19讲第6讲取整问题六年级导引第19讲第7讲不定方程六年级导引第8讲第8讲复杂直线形计算六年级导引第10讲第9讲几何综合六年级导引第11讲第10讲复杂应用题串讲六年级导引第17讲第11讲间隔发车问题六年级导引第14讲第12讲复杂行程问题六年级导引第14讲第13讲概率初步六年级导引第23讲第14讲工程问题综合无对应讲次第15讲整除问题综合无对应讲次第16讲约数与倍数综合无对应讲次第17讲整数型计算综合无对应讲次第18讲最值问题二六年级导引第7讲第19讲计数综合二无对应讲次第20讲计数综合三无对应讲次第21讲数字谜综合二六年级导引第16讲第22讲分数、百分数应用题综合无对应讲次第23讲行程问题综合二无对应讲次第24讲构造论证二六年级导引第22讲第25讲直线形计算综合无对应讲次第26讲应用题综合六年级导引第18讲第1讲浓度与经济问题综合无对应讲次第2讲余数问题综合无对应讲次第3讲分数计算综合无对应讲次第4讲曲线形计算综合无对应讲次第5讲抽屉原理综合六年级导引第24讲第6讲变速行程问题二无对应讲次第7讲计算综合练习第8讲几何综合练习第9讲应用题综合练习第10讲数字谜综合练习第11讲数论综合练习第12讲计数综合练习第13讲组合综合练习第14讲小升初综合模拟测试一第15讲小升初综合模拟测试二第16讲小升初综合模拟测试三第17讲小升初综合模拟测试四第18讲小升初综合模拟测试五第19讲小升初综合模拟测试六第20讲小升初综合模拟测试七第21讲小升初综合模拟测试八第22讲小升初综合模拟测试九。
高思导引--四年级第三讲-还原问题与年龄问题教师版汇编

第3讲还原问题与年龄问题内容概述学会用逆推法求解还原问题,处理多个对象时可采用列表的形式,在年龄问题中,通常采用和差倍问题的分析方法,有时需注意任意两人的年龄差保持不变。
典型问题兴趣篇1. 某数加上6,再乘以6,再减去6,再除以6,其结果等于6,则这个数是多少?答案:这个数是详解:+6 x6 -6 +662. 有一个人非常喜欢喝酒,他每经过一个酒店都要买酒喝. 这个人出门带了一个酒葫芦,看到一个酒店就把酒葫芦中的酒加一倍,然后喝下8两酒,这天他一共遇到3家酒店,在最后一家酒店喝完酒后,葫芦里的酒刚好喝完. 问:原来酒葫芦里有多少两酒?答案:7两酒。
详解:每经过一个酒店,葫芦里酒的数量就先乘2,再减8,利用倒推法,我们反过来应该先加8,再除以2.那么到酒店C之前葫芦里应该有(0+8)÷2=4两酒,他在到酒店B的时候应该有(4+8)÷2=6两酒,所以他原来的酒葫芦应该有(6+8)÷2=7两酒。
0+8=8,8÷2=4,4+8=12,12÷2=6,6+8=14,14÷2=73. 某人发现了一条魔道,下面有一个存钱的小箱子,当他从魔道走过去的时候,箱子里的一些钱会飞到人的身上使人身上的钱增加一倍,这人很高兴;当他从魔道走回来时,身上的钱会飞到箱子里,使箱子里的钱增加一倍;这人一连走了3个来回后,箱子里的钱和人身上的钱都是64枚一元的硬币,那么原来这人身上有多少元?箱子里有多少元?答案:原来这个人身上有43元,箱子里有85元。
详解:4. 三棵树上共有48只鸟. 后来,第一棵树上有一半的鸟飞到了第二棵树上;之后,第二棵树上又有与第三棵树同样数目的鸟飞到了第三棵树上;最后,第三棵树上又有10只鸟飞到了第一棵树上,此时三棵树上的鸟一样多. 问:一开始三棵树上各有几只鸟?答案:第一棵树上有12,第二棵23,第三棵13详解:5. 1997年张伯伯45岁,小方9岁,在哪一年张伯伯的年龄是小方年龄的4倍?答案:小方12岁那年。
学而思讲义四年级第三讲(游戏与对策)(2024版)

第三讲 游戏与对策一、基本前提游戏双方足够聪明,目的都是获胜。
二、方法:倒推三、游戏类型(一)拿火柴棍/抢数如:桌子上放着10根火柴,二人轮流每次取走1—2根,规定谁取走最后一根火柴谁获胜。
你知道必胜的方法吗?分析:如果从开始分析,“局面”太大,有太多种取法要讨论。
所以我们尝试从结果倒推。
如上图,要必胜,也就是要让自己拿到10号火柴,那就应给对方留下8,9,10三根火柴供他取,这样对方不管取一根还是两根,自己都能拿到最后的10号火柴。
照这样分析,自己应该拿到7号火柴(这样就是给对方留下了8,9,10号三根)就必胜。
同理分析,要想取7号,就应该取4号,要想取4号,就应该取1号。
那么,本题的制胜点就是1,4,7,10号火柴,对于足够聪明的人来说,拿到第一个制胜点1号火柴,一定能拿到其余的制胜点。
所以本题要必胜,就要抢先取1根,然后对方取a 根,自己就取3-a 根,这样保证自己能取到每一个制胜点,最终取到10号火柴。
总结一下,同学们应该能看出,这里面有周期现象(只是周期是从后往前排布的),周期是几呢?是可取的最大限度2再加1等于3,制胜点是哪些呢?是每个周期的最后一根。
掌握此规律,就不难总结出这类题的解题方法了:解题方法:(1)找周期:周期等于可拿最大限度+1(2)总数÷周期1 桌子上放着60根火柴,聪明昊、神奇涛二人轮流每次取走1—3根,规定谁取走最后一根火柴谁获胜。
你知道必胜的方法吗?解析: 周期为 3+1=4(根)60÷4=15(组) (整除,应该抢后)制胜点:4,8,12 (60)做法:1、让对方先取2、对方取a 根,自己就取4-a 根2 有一种抢数游戏,是两个人从自然数1开始轮流报数,规定每次至少报几个数与至多报几个数(都是自然数),最后谁报到规定的“某个数字”为胜。
如“抢50”,规定每次必须报1或2个1 2 3 4 5 6 7 8 9 10有余数:抢先拿余数整除(余数为0):抢后自然数,从1开始,谁抢报到50为胜。
高思导引 四年级第三讲 还原问题与年龄问题教师版汇编

学习-----好资料第3讲还原问题与年龄问题内容概述学会用逆推法求解还原问题,处理多个对象时可采用列表的形式,在年龄问题中,通常采用和差倍问题的分析方法,有时需注意任意两人的年龄差保持不变。
典型问题兴趣篇1. 某数加上6,再乘以6,再减去6,再除以6,其结果等于6,则这个数是多少?答案:这个数是详解:+6 x6 -6 +636761422. 有一个人非常喜欢喝酒,他每经过一个酒店都要买酒喝. 这个人出门带了一个酒葫芦,看到一个酒店就把酒葫芦中的酒加一倍,然后喝下8两酒,这天他一共遇到3家酒店,在最后一家酒店喝完酒后,葫芦里的酒刚好喝完. 问:原来酒葫芦里有多少两酒?答案:7两酒。
详解:每经过一个酒店,葫芦里酒的数量就先乘2,再减8,利用倒推法,我们反过来应该先加8,再除以2.那么到酒店C之前葫芦里应该有(0+8)÷2=4两酒,他在到酒店B的时候应该有(4+8)÷2=6两酒,所以他原来的酒葫芦应该有(6+8)÷2=7两酒。
2=714÷2=6,6+8=14,,,8÷2=4,4+8=1212÷0+8=83. 某人发现了一条魔道,下面有一个存钱的小箱子,当他从魔道走过去的时候,箱子里的一些钱会飞到人的身上使人身上的钱增加一倍,这人很高兴;当他从魔道走回来时,身上的钱会飞到箱子里,使箱子里的钱增加一倍;这人一连走了3个来回后,箱子里的钱和人身上的钱都是64枚一元的硬币,那么原来这人身上有多少元?箱子里有多少元?答案:原来这个人身上有43元,箱子里有85元。
详解:箱子里的钱身上的钱85 43 开始时86 42 第一次走过去后44 84 第一次走回来后88 40 第二次走过去后48 80 第二次走回来后96 32 第三次走过去后64 64 第三次走回来后后来,第一棵树上有一半的鸟飞到了第二棵树上;之后,第二棵树只鸟. 4. 三棵树上共有48只鸟飞到了第上又有与第三棵树同样数目的鸟飞到了第三棵树上;最后,第三棵树上又有10 问:一开始三棵树上各有几只鸟?一棵树上,此时三棵树上的鸟一样多.13 ,第三棵12,第二棵23答案:第一棵树上有详解:第三棵第一棵第二颗131223开始时61329第一棵飞到第二棵后616 26 第二棵飞到第三棵后16 16 16 第三棵飞到第一棵后更多精品文档.好资料学习-----倍?45岁,小方9岁,在哪一年张伯伯的年龄是小方年龄的45. 1997年张伯伯岁那年。
四年级下册数学课件-专题培优:PPT(第十讲)还原问题与年龄问题二 全国通用 (共10页)

四年级下册数学课件-专题培优:PPT( 第十讲 )还原 问题与 年龄问 题二 全国通用 (共10页)
退一步,海阔天空。
例(5)有老师和甲、乙、丙三个学生,现在老师年龄恰为 三个学生年龄之和;9年后,老师年龄为甲、乙两学生年 龄之和;又过了3年,老师年龄为甲、丙学生年龄之和; 再过3年,老师年龄为乙、丙两学生年龄之和,求现在各 人的年龄。
四年级下册数学课件-专题培优:PPT( 第十讲 )还原 问题与 年龄问 题二 全国通用 (共10页)
四年级下册数学课件-专题培优:PPT( 第十讲 )还原 问题与 年龄问 题二 全国通用 (共10页)
退一步,海阔天空。
例(4)去年哥哥的年龄是明年兄弟二人年龄和的一半,前 年哥哥的年龄是弟弟的2倍. 求哥哥和弟弟现在的年龄。
•
2.同学们,相信你们大多数同学都有 旅游的 经历, 请大家 交流一 下,到 过哪些 名山大 川,有 什么感 受?大 自然中 的山水 ,不仅 能给我 们带来 美感也 给我们 带来灵 感,今 天让我 们从诸 子大家 对山水 的体悟 中,学 习为人 为事的 道理。
•
3.说起胡同,我们并不陌生,有的甚 至熟视 无睹了 ,不论 是农村 还是城 镇,往 来于胡 同之中 的经验 是有的 。但对 于胡同 中蕴含 的文化 内涵却 不大注 意。
退一步,海阔天空。
例(2)今年,父亲年龄是儿子年龄的5倍;15年后,父亲年 龄是儿子年龄的2倍. 问:现在父子的年龄各是多少?
四年级下册数学课件-专题培优:PPT( 第十讲 )还原 问题与 年龄问 题二 全国通用 (共10页)
退一步,海阔天空。
例(3)甲、乙、丙三人的钱数各不相同,甲最多,他拿出 一些钱给乙和丙,使乙和丙的钱数都比原来增加了2倍, 结果乙的钱最多;接着乙拿出一些钱给甲和丙,使甲和丙 的钱数各增加了2倍,结果丙的钱最多;最后丙又拿出一 些钱给甲和乙,使他们的钱数和增加2倍,结果三人的钱 数一样多,如果他们三人共有81元,那么三人原来分别有 多少钱?
四年级高思奥数之还原问题与年龄问题含答案

第3讲还原问题与年龄问题内容概述学会用逆推法求解还原问题,处理多个对象时可采用列表的形式,在年龄问题中,通常采用和差倍问题的分析方法,有时需注意任意两人的年龄差保持不变。
典型问题兴趣篇1. 某数加上6,再乘以6,再减去6,再除以6,其结果等于6,则这个数是多少?2. 有一个人非常喜欢喝酒,他每经过一个酒店都要买酒喝. 这个人出门带了一个酒葫芦,看到一个酒店就把酒葫芦中的酒加一倍,然后喝下8两酒,这天他一共遇到3家酒店,在最后一家酒店喝完酒后,葫芦里的酒刚好喝完. 问:原来酒葫芦里有多少两酒?3. 某人发现了一条魔道,下面有一个存钱的小箱子,当他从魔道走过去的时候,箱子里的一些钱会飞到人的身上使人身上的钱增加一倍,这人很高兴;当他从魔道走回来时,身上的钱会飞到箱子里,使箱子里的钱增加一倍;这人一连走了3个来回后,箱子里的钱和人身上的钱都是64枚一元的硬币,那么原来这人身上有多少元?箱子里有多少元?4. 三棵树上共有48只鸟. 后来,第一棵树上有一半的鸟飞到了第二棵树上;之后,第二棵树上又有与第三棵树同样数目的鸟飞到了第三棵树上;最后,第三棵树上又有10只鸟飞到了第一棵树上,此时三棵树上的鸟一样多. 问:一开始三棵树上各有几只鸟?5. 1997年张伯伯45岁,小方9岁,在哪一年张伯伯的年龄是小方年龄的4倍?6. 今年,小明的年龄等于他父母的年龄差;4年后,小明的年龄等于他父母年龄差的3倍. 今年小明多少岁?7. 今年,父亲年龄是儿子年龄的5倍;15年后,父亲年龄是儿子年龄的2倍. 问:现在父子的年龄各是多少?8. 兄弟两个年龄之和是32岁. 当哥哥是弟弟现在这么大时,哥哥的年龄是当时弟弟年龄的3倍.求哥哥现在的年龄.9. 学生问老师多少岁,老师说:“当我像你这么大时,你刚3岁;当你像我这么大时,我已经39岁了.”求老师和学生现在的年龄.10. 今年,费叔叔的年龄比小悦、冬冬、阿奇三人年龄的总和还多6岁, 多少年后,费叔叔的年龄将比他们三人年龄的总和少6岁?拓展篇1. 有一个数,把它加上37,再乘以18,减去323,得到的结果用23去除,商是16,余数是11.这个数原来是多少?2. 果园里有一棵桃树. 有一天,三只猴子吃了两个桃子并摘下了剩下桃子的一半,最后第三只猴子吃了三个桃子并摘下了剩下桃子的一半. 这时树上刚好还有四个桃子,原来树上一共有几个桃子?3. 地上有26地砖,兄弟二人争着去挑. 弟弟抢在前面,刚挑起一些砖,哥哥赶到了,挑了剩下的砖. 哥哥看弟弟挑得太多,就从弟弟那儿抢过一半. 弟弟不肯,又从哥哥那儿抢走一半. 哥哥不服,弟弟只好再给哥哥5块,这时哥哥比弟弟多挑2块,请问:最初弟弟准备挑多少块砖?4. 甲、乙各有糖若干块,每操作一次是由糖多的人给糖少的人一些糖,使得糖少的人的糖数增加一倍,经过三次这样的操作后,甲有5块糖,乙有12块糖,两个人原来的糖数分别是多少?5. 甲、乙、丙三人的钱数各不相同,甲最多,他拿出一些钱给乙和丙,使乙和丙的钱数都比原来增加了2倍,结果乙的钱最多;接着乙拿出一些钱给甲和丙,使甲和丙的钱数各增加了2倍,结果丙的钱最多;最后丙又拿出一些钱给甲和乙,使他们的钱数和增加2倍,结果三人的钱数一样多,如果他们三人共有81元,那么三人原来分别有多少钱?6. 今年张明15岁,他父亲45岁,请问:多少年后,父亲年龄是张明年龄的2倍?多少年前,父亲年龄是张明年龄的4倍?7. 12年前,父亲的年龄是女儿年龄的11倍;今年,父亲的年龄是女儿年龄的3倍. 请问:多少年后父亲年龄是女儿年龄的2倍?8. 去年哥哥的年龄是明年兄弟二人年龄和的一半,前年哥哥的年龄是弟弟的2倍. 求哥哥和弟弟现在的年龄。
第八讲 还原问题1 教师版-四年级数学思维拓展

第8讲还原问题1序,从最后一步出发,一步一步倒着往前推算,问题就很容易解决。
这种思考问题的方法叫做还原法,用还原法来解决的问题称为还原问题。
例1有一位老人说:“把我的年龄加上14以后除以3,再减去26,最后用25乘,恰巧是100岁。
”这位老人今年多少岁?解 (100÷25+26)×3-14=30×3-14=76(岁)答:这位老人今年76岁。
【思路点拨】这道题目可以倒过来想,从最后一步“最后用25乘,恰巧是100岁”,一步一步往前推算。
这就是还原问题,我们可以用倒推法解决。
100岁是乘25后得到的,没有用25乘之前应是100÷25=4(岁);“减去26后”是4岁没有减去26之前是4+26=30(岁)。
下面该怎样算了,“除以3”是30岁,没有除以3之前应是30×3=90(岁);把老人的年龄加上14后是90岁,所以,这位老人今年的岁数应是90-14=76(岁)。
例2在做一道加法算式题时,小芳把个位上的5看成了9,把十位上的8看成了3,结果所得的和是123。
正确的答案是多少?解方法一:9-5=480-30=50123+50-4=169方法二:123-39+85=84+85=169答:正确的答案是169。
【思路点拨】把个位上的5看做9,相当于把正确的和多算了9-5=4,把十位上的8看做3,相当于把正确的和少算了80-30=50。
这样就可以把这道题理解为:一个数加上4,减去50,得123,求这个数是几。
采用倒推法,也就是123加上50,减去4。
我认为要求正确的和,就要知道两个正确的加数。
看错的加数是39,因此得到错误的和是123,根据逆运算可得到另一个没看错的加数是123-39=84,题中已知一个正确的加数是85,所以,正确的和是85+84=169。
例3甲、乙、丙三个组共有图书90本,如果乙组向甲组借3本后,又送给丙组5本,那么三个组拥有图书的本数刚好相等。
高斯小学奥数含答案二年级下第03讲年龄问题初步

第三讲年龄问题初步前续知识点:二年级第一讲;XX模块第X讲后续知识点:X年级第X讲;XX模块第X讲把里面的人物换成相应红字标明的人物.“年龄问题”是我们以后会学到的“和差倍问题”的基础.本讲我们将初步接触年龄问题.年龄问题当然是讲年龄了.今年呆呆7岁,瓜瓜8岁.10年后,呆呆17岁,瓜瓜18岁.他们的年龄都变了10岁,那什么没有变呢?例题1弟弟今年8岁,姐姐13岁,10年后,姐姐比弟弟大几岁?【提示】对于两个人来说,每过一年,两个人的年龄都会增长一岁,那么他们的年龄差变了吗?练习1皮皮今年7岁,爸爸比他大30岁,3年前,皮皮比爸爸小几岁?“年龄问题”的特点之一是“年龄差”不变.想一想,对不对?我们可以利用“年龄差” 不变这个特点解决很多问题.例题2小林今年10岁,他比爸爸小25岁.5年前,爸爸是多少岁?【提示】根据年龄差不变,可先计算出5年前小林的年龄,再计算出爸爸5年前的年龄;或根据小林今年的年龄计算出爸爸今年的年龄,再计算爸爸5年前的年龄.练习2佳佳今年12岁,她比张阿姨小20岁.5年后,张阿姨是多少岁?不是所有的问题都会用到“年龄差”不变,我们要灵活应用!例题3(1)灵灵今年6岁,4年后,灵灵的年龄和晶晶今年的岁数相同.晶晶今年几岁?(2)姐姐今年是12岁,姐姐3年前的年龄与妹妹2年后的年龄相等,问妹妹今年多少岁?【提示】先找出两人之间的年龄差!练习3朵朵今年是6岁,朵朵5年后的年龄与阳阳4年前的年龄相等,问阳阳今年多少岁?“年龄问题”第二个特点是“年龄和”.一个人每过一年长一岁,过两年长两岁.两个人每过一年,“年龄和”大2,过两年大4.三个人呢,四个人呢?有没有发现什么规律?例题4(1)妹妹今年9岁,4年后妹妹和姐姐的年龄和是30岁,姐姐今年多少岁?(2)小杰今年4岁,爸爸今年32岁.当两人年龄的和是50岁时,小杰和爸爸各是几岁?【提示】两人年龄和,随着时间的推移,同增同减相等的量.练习4妈妈今年30岁,女儿今年2岁,多少年以后母女俩的年龄之和是60岁?例题5奶奶今年56岁,妈妈今年32岁,壮壮今年6岁,再过多少年,他们三个人的年龄和是100岁?【提示】他们三个人今年的年龄和是多少岁?例题6爷爷今年70岁,他有三个孙子,大孙子20岁,二孙子15岁,三孙子才5岁.再过多少年后,三个孙子年龄的和同爷爷那时的年龄相等?【提示】每过一年,三个孙子年龄的和增加几岁?爷爷增加几岁?课堂内外年龄的那些事古人对高寿人常给以美称,如花甲、古稀等等.但如果年龄未到整数,比如七十七岁,八十八岁,九十九岁,怎么称呼呢?有人把七十七岁称为‘喜寿’,八十八岁称为‘米寿’,九十九岁称为‘白寿’.原来这是三个字谜.喜字,草写,是由七十七三个字组成;米字是由八十八三个字组成;白字是百字缺一,正好九十九!三十而立,四十而不惑,五十知天命,六十花甲,七十古稀.未满周岁的儿童一一襁褓;2 —3岁一一孩提;童年一一总角,垂髫;8岁(男)一一龆年;10岁以下一一黄口;10岁(女)——髻年;12岁(女)一一金钗之年;13—14岁(女)一一豆蔻年华;13—15岁一一舞勺之年;15岁(女)——及笄之年;15岁(男)一一志学之年,束发;16岁(女)一一碧玉年华;15—20岁——舞象之年;20岁(男)一一弱冠;20岁(女)一一桃李年华;24岁(女)一一花禧(信)年华;出嫁一一标梅之年;30岁(女)一一半老徐娘;30岁(男)一一而立之年;40岁(男)一一不惑之年;50岁一一知命之年、半百;60岁一一花甲,平头之年、耳顺之年,杖乡之年;70岁一一古稀、杖国之年;77岁——喜寿;80岁一一杖朝之年;88岁——米寿;80—90岁一一耄耋之年;90岁一一鲐(台,骀)背之年;99岁一一白寿;100岁一一期后队人瑞;108岁——茶寿.作业1.妞妞今年10岁,妈妈今年36岁,7年后,妈妈比妞妞大几岁?2.平平今年9岁,他比叔叔小21岁.6年前,叔叔是多少岁?3.小贝今年25岁,5年前,小贝和弟弟的年龄和是30岁,弟弟今年几岁?4.果果今年8岁,弟弟今年6岁,几年以后,他们的年龄之和是28岁?5.大雄今年7岁,爸爸今年38岁,妈妈今年35岁.再过几年,他们三个人的年龄和是89岁?第三讲年龄问题初步1.例题1答案:5详解:方法一:今年姐姐比弟弟大13-8 = 5 (岁),根据年龄差不变,所以10年后,姐姐比弟弟还是大5岁;方法二:10年后,姐姐13 +10 = 23 (岁),弟弟8 +10 = 18 (岁),姐姐比弟弟大23-18 = 5 (岁).2.例题2答案:30详解:方法一:根据题意可以知道今年爸爸是10 + 25 = 35 (岁),那么5年前,爸爸是35-5 = 30 (岁).方法二:根据题意知道5年前小林是10-5 = 5 (岁),再由年龄差不变,所以5年前爸爸是5 + 25 = 30 (岁).3.例题3答案:(1)10;(2)7详解:(1)方法一:根据题意可以知道4年后灵灵是6 + 4 = 10 (岁),并且4年后,灵灵的年龄和晶晶今年的岁数相同,那么晶晶今年就是10岁.方法二:因为4年后,灵灵的年龄和晶晶今年的岁数相同,所以灵灵和晶晶的年龄差是4岁,并且是晶晶比灵灵大4岁,所以晶晶今年是6 + 4 = 10 (岁).(2)方法一:根据题意可以知道姐姐3年前是12-3 = 9 (岁)并且姐姐3年前的年龄与妹妹2年后的年龄相等,那么妹妹今年就是9-2 = 7 (岁).方法二:因为姐姐3年前的年龄与妹妹2年后的年龄相等,所以姐姐和妹妹的年龄差是3 + 2 = 5 (岁),并且是姐姐比妹妹大5岁,所以妹妹今年是12-5 = 7 (岁).4.例题4答案:(1)13;(2)39详解:(1)方法一:根据题意可以知道4年后妹妹是9 + 4 = 13 (岁)那么4年后姐姐的年龄是30-13 = 17 (岁)姐姐今年就是17-4 = 13 (岁).方法二:因为4年后妹妹和姐姐的年龄和是30岁,所以今年妹妹和姐姐的年龄和是30-4x2 = 22 (岁),那么姐姐今年是22-9 = 13 (岁).(2)小杰和爸爸今年年龄和是4 + 32 = 36 (岁),当两人年龄的和是50岁时,是过了(50-36)+ 2 = 7 (年),那么7年后,小杰是4 + 7 = 11 (岁),爸爸是32 + 7 = 39 (岁).5.例题5答案:2详解:今年三人的年龄和是56 + 32 + 6 = 94 (岁),那么再过(100 -94)+ 3 = 2 (年),三人的年龄和是100岁.6.例题6答案:15详解:今年三个孙子的年龄和是20+15 + 5 = 40 (岁),那么今年爷爷比三个孙子的年龄大70-40 = 30 (岁),因为爷孙四人年龄同时增加,所以再过30 + (3-1)= 15 (年)后,三个孙子年龄的和同爷爷那时的年龄相等.7.练习1答案:30简答:根据年龄差不变,今年爸爸比他大30岁,3年前,皮皮比爸爸还是小30岁.8.练习2答案:37 简答:方法一:根据题意可以知道今年张阿姨是12 + 20 = 32 (岁),那么5年后,张阿姨是32+5 = 37 (岁).方法二:根据题意知道5年后小林是12+5 = 17(岁),再由年龄差不变,所以5年后张阿姨是17 + 20 = 37 (岁).9.练习3答案:15简答:方法一:根据题意可以知道5年后朵朵是6 + 5 = 11 (岁),并且与阳阳4年前的年龄相等,那么阳阳今年就是11+4 = 15 (岁).方法二:因为朵朵5年后的年龄与阳阳4年前的年龄相等,所以朵朵和阳阳的年龄差是4 + 5 = 9(岁),并且是阳阳比朵朵大9岁,所以阳阳今年是6 + 9 = 15 (岁).10.练习4答案:14简答:母女俩今年年龄和是30 + 2 = 32 (岁),当两人年龄的和是60岁时,是过了(60-32)+ 2 = 14 (年).11.作业1答案:26简答:根据年龄差不变,今年妈妈比妞妞大36-10 = 26 (岁),7年后,妈妈比妞妞还是大26岁.12.作业2答案:24简答:方法一:根据题意可以知道今年叔叔是9 + 21 = 30 (岁),那么6年前,叔叔是30-6 = 24 (岁).方法二:根据题意知道6年前平平是9-6 = 3 (岁),再由年龄差不变,所以6年前叔叔是3 + 21 = 24 (岁).13.作业3答案:15简答:方法一:根据题意可以知道5年前小贝是25-5 = 20 (岁),那么弟弟今年就是20-5 = 15 (岁).方法二: 因为小贝5年前的年龄和弟弟5年后的年龄相等,所以小贝和弟弟的年龄差是5 + 5 = 10 (岁),并且是小贝比弟弟大10岁,所以弟弟今年是25-10 = 15 (岁).14.作业4答案:7简答:今年果果和弟弟的年龄和是8 + 6 = 14 (岁),28-14 = 14 (岁),因为两人年龄同增同减,所以是在14 + 2 =7 (年)后,他们的年龄和是28岁.15.作业5答案:3简答:首先知道大雄、爸爸和妈妈三人今年的年龄和是7 + 38 + 35 = 80 (岁),当三人年龄和是89岁,三人年龄和共增加了89-80=9 (岁);然后根据年龄同增同减,应是再过9 + 3 = 3 (年),三人年龄和才是89岁.6.。
高思学校竞赛数学导引 四年级

&!!"!!))#,,.,,#,&+,&#,-.,-#,*+%+’#$.$#"+"#!!
’!5678!)))&9:+;)$ 3<=’>+?3&&+@,)% 3<=’>+?3$ &+@,!$ A% &B-./&
(!CD! !;<=+&,!
! # % ' !#% " $ & "$& ! # % ' !#%' " $ & "$& # % ' !#%'
" $
"!#!)")%),)!);¨©ªc’*+,c’«+)¬|+®)¯wc’®°! !
±<=t&®°²³£´Z)µ,-./&
! "
! #
$
%
&
’
(
#!!"!!.$+*.!)+!(."!+"&.%+’,()!
$!EFGHBIJ!"".#"/""+###"".##!!"! !))"+,,".,&".,-"+,*"+,(".,’".,$"+%+’"+$"."".!"!
! $
四年级导引解析-《华数思维训练导引》四年级上学期 还原与年龄

四年级导引解析->《华数思维训练导引》四年级上学期还原与年龄华数思维训练导引----还原与年龄四年级上学期第03讲应用题第08讲1. 某数加上6,乘以6,减去6,除以6,其结果等于6,则这个数是多少?解答:(6×6+6)÷6-6=1,这个数是1.2. 两个两位数相加,其中一个加数是73,另一个加数不知道,只知道另一个加数的十位数字增加5,个位数字增加1,那么求得的和的后两位数字是72,问另一个加数原来是多少?解答:和的后两位数字是72,说明另一个加数是99。
十位数字增加5,个位数字增加1,那么原来的加数是99-51=48。
3. 有砖26块,兄弟二人争着去挑。
弟弟抢在前面,刚摆好砖,哥哥赶到了。
哥哥看弟弟挑的太多,就抢过一半。
弟弟不肯,又从哥哥那儿抢走一半。
哥哥不服,弟弟只好给哥哥5块,这时哥哥比弟弟多挑2块。
问最初弟弟准备挑多少块?解答:先看最后兄弟俩各挑几块:哥哥比弟弟多挑2块,这是一个和差问题,哥哥挑的块数=(26+2)÷2=14块,弟弟=26-14=12块;然后再还原:哥哥还给弟弟5块:哥哥=14-5=9块,弟弟=12+5=17块;弟弟把抢走的一半还给哥哥:哥哥=9+9=18块,弟弟=17-9=8块;哥哥把抢走的一半还给弟弟:弟弟原来是8+8=16块。
4. 甲、乙、丙三人钱数各不相同,甲最多,他拿出一些钱给乙和丙,使乙和丙的钱数都比原来增加了两倍,结果乙的钱最多;接着乙拿出一些钱给甲和丙,使甲和丙的钱数都比原来增加了两倍,结果丙的钱最多;最后丙拿出一些钱给甲和乙,使甲和乙的钱数都比原来增加了两倍,结果三人钱数一样多了。
如果他们三人共有81元,那么三人原来的钱分别是多少元?解答:三人最后一样多,那么每人都是81÷3=27元;还原:甲和乙把钱还给丙:每人增加2倍,就是原来的3倍,那么甲和乙都是27/3=9元,丙是27+2*2*9=63元;甲和丙把钱还给乙:甲=9/3=3元,丙=63/3=21元,乙=9+2*3+2*21=57元;乙和丙把钱还给甲:乙=57/3=19元,丙=21/3=7元,甲=3+2*19+2*7==55元。
高思导引 四年级第三讲 还原问题与年龄问题教师版
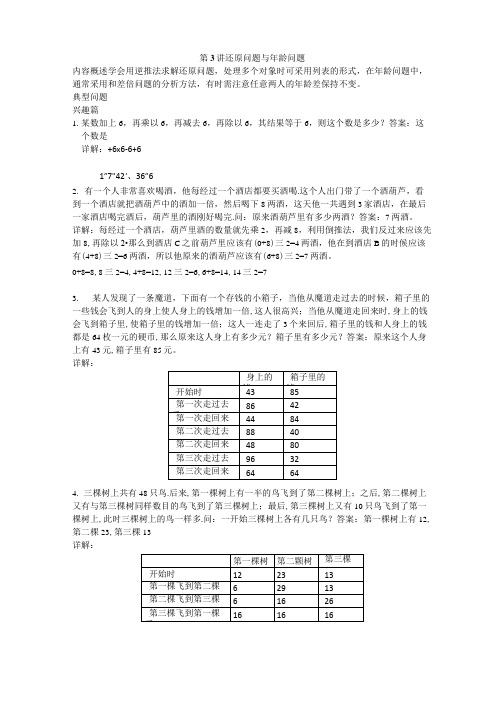
第3讲还原问题与年龄问题内容概述学会用逆推法求解还原问题,处理多个对象时可采用列表的形式,在年龄问题中,通常采用和差倍问题的分析方法,有时需注意任意两人的年龄差保持不变。
典型问题兴趣篇1.某数加上6,再乘以6,再减去6,再除以6,其结果等于6,则这个数是多少?答案:这个数是详解:+6x6-6+61”7"42'、36”62.有一个人非常喜欢喝酒,他每经过一个酒店都要买酒喝.这个人出门带了一个酒葫芦,看到一个酒店就把酒葫芦中的酒加一倍,然后喝下8两酒,这天他一共遇到3家酒店,在最后一家酒店喝完酒后,葫芦里的酒刚好喝完.问:原来酒葫芦里有多少两酒?答案:7两酒。
详解:每经过一个酒店,葫芦里酒的数量就先乘2,再减8,利用倒推法,我们反过来应该先加8,再除以2•那么到酒店C之前葫芦里应该有(0+8)三2=4两酒,他在到酒店B的时候应该有(4+8)三2=6两酒,所以他原来的酒葫芦应该有(6+8)三2=7两酒。
0+8=8,8三2=4,4+8=12,12三2=6,6+8=14,14三2=73.某人发现了一条魔道,下面有一个存钱的小箱子,当他从魔道走过去的时候,箱子里的一些钱会飞到人的身上使人身上的钱增加一倍,这人很高兴;当他从魔道走回来时,身上的钱会飞到箱子里,使箱子里的钱增加一倍;这人一连走了3个来回后,箱子里的钱和人身上的钱都是64枚一元的硬币,那么原来这人身上有多少元?箱子里有多少元?答案:原来这个人身上有43元,箱子里有85元。
详解:4.三棵树上共有48只鸟.后来,第一棵树上有一半的鸟飞到了第二棵树上;之后,第二棵树上又有与第三棵树同样数目的鸟飞到了第三棵树上;最后,第三棵树上又有10只鸟飞到了第一棵树上,此时三棵树上的鸟一样多.问:一开始三棵树上各有几只鸟?答案:第一棵树上有12,第二棵23,第三棵13详解:5.1997年张伯伯45岁,小方9岁,在哪一年张伯伯的年龄是小方年龄的4倍?答案:小方12岁那年。
高思数学_4年级上-第13讲-年龄问题(彩色)

在与年龄有关的应用题中,年龄一般只与年份有关,比如某人在2010年是30岁,那么他在2011年一定是31岁,不用具体考虑他今年是否已经过完生日.在这类应用题中,给出的条件一般是几个人的具体年龄,或者他们年龄之间的和差倍关系.所以年龄问题其实是一类特殊的和差倍问题.对于两个人来说,每过一年,两个人的年龄都会增长一岁,但是他们的年龄差保持不变!分析 张明和父亲的年龄差是不变的,怎么把年龄差与年龄的倍数关系联系起来呢?今年张明15岁,他父亲45岁,请问:多少年后,父亲年龄是张明的2倍?多少年前,父亲年龄是张明的4倍?例题1练习1.父亲今年32岁,儿子今年4岁,当父亲的年龄是儿子的3倍时,父子的年龄和是多少岁?分析 父女年龄的倍数关系发生变化,是一个典型的变倍问题.选取哪个量作为合适的单位“1”呢?练习2. 6年前母亲的年龄是女儿的10倍,18年后,母亲的年龄是女儿的两倍.那么现在母亲的年龄是多少岁?对于比较复杂的问题,只考虑年龄差往往是不够的,这时画好线段图就显得尤为重要.我们一般把每个人的年龄用不同的线段表示,那么经过若干年后,每条线段就增加同样长的一段;而若干年前,每条线段就减少同样长的一段. 分析 我们可以根据兄弟年龄的倍数关系画出线段图,再用不同的线标出弟弟长到哥哥现在的年龄时各人的年龄.想一想,父亲的年龄该怎么画呢?练习3.哥哥和弟弟现在的年龄和为60岁,当哥哥为弟弟现在的年龄时,弟弟的年龄为哥是女儿的3倍.请问:例题2弟弟长到哥哥现在的年龄时,父亲的年龄恰好等于兄弟俩年龄之和.请问:今年哥哥多少岁?哥的一半,请问哥哥现在多少岁? 分析 本题中过去、现在、将来的时间都出现了,你能在一个图里把这些时间都表示出来吗?练习4.甲对乙说:“当我的岁数是你现在的岁数时,你才4岁.”乙对甲说:“当我的岁数是你现在的岁数时,你将61岁.”请问:甲、乙二人现在各多少岁?前面所说的年龄差不变,指的是两个人的年龄差不变,不一定适用于多个人的年龄差.比如每过一年,父亲、母亲、儿子的年龄各增加了一岁,但父母年龄和增加了两岁,父母年龄和与儿子年龄的差就肯定要改变了.分析 这是关于父母年龄和与兄弟年龄和的变倍问题,我们是不是应该把父母二人分成一组,兄弟二人分成另一组来计算呢?练习5.今年某教授与两名学生的年龄之和为100岁,12年后教授年龄是这两位学生年龄之和.那么这位教授今年的年龄是多少?岁;父母的年龄和是兄弟二人年龄和的多少岁?本一、“两人年龄差不变”是年龄问题中最重要的性质,但年龄差不变不一定适用于多人的年龄差.二、年龄问题可以转化为其他类型的和差倍问题,可以画出线段图辅助思考.作业1. 2010年张伯伯45岁,小聪9岁,那么在哪一年张伯伯的年龄是小聪的3倍?2. 2008年,母亲的年龄是女儿的5倍;2010年,母亲的年龄是女儿的4倍.求哪一年母亲的年龄是女儿的3倍?3.李家有三兄弟,当老二像老三那么大时,老二的年龄是老三的3倍,老大的年龄是老二、老三的年龄之和.已知现在三兄弟年龄之和为28岁,请问:现在老大、老二、老三的年龄分别是多少?4.哥哥对弟弟说:“当我到爸爸现在的年龄时,爸爸就70岁了.”弟弟又对哥哥说:“当我到妈妈现在的年龄时,妈妈也70岁了.”已知爸爸比妈妈大2岁,那么哥哥比弟弟大多少岁?5. 5年前父母的年龄和是兄弟二人年龄和的10倍,明年父母的年龄和是兄弟二人年龄和的4倍,那么从今年起多少年后父母的年龄和是兄弟二人年龄和的2倍?龄之和是。
小学奥林匹克数学 竞赛数学 四年级导引 2-6 还原问题与年龄问题

一、 还原问题 (1)还原问题:已知过程和最终结果,求初始状态.(2)基本方法:倒推法.即从结果出发,进行逆向操作,直至求得初始状态.(3)若为单对象,可考虑写出流程图;若涉及多对象,可考虑列表.(4)部分复杂题在倒推时有多种可能,若不能排除某些情况,需逐一计算(即分类讨论).二、 年龄问题(1)两人年龄差不变是最常用的突破口.(2)若两组人的人数相同,则各组年龄和之差也不变.(不能倒退至出现某人未出生时)(3)很多时候需要画线段图或设份数来分析问题.【例1】 口渴的三个和尚分别捧着一个水罐.最初,老和尚的水最多,并且有一个和尚没水喝.于是,老和尚把自己的水全部平均分给了大、小两个和尚;接着,大和尚又把自己的水全部平均分给了老、小两个和尚;然后,小和尚又把自己的水全部平均分给了另外两个和尚.就这样,三人轮流谦让了一阵.结果太阳落山时,老和尚的水罐里有10升水,小和尚的水罐则装着20升水.请问:最初大和尚的水罐有多少升水?第14讲 还原问题与年龄问题知识点超越篇题目【例2】甲和乙各有若干块糖,甲的糖数比乙少.每次操作由糖多的人给糖少的人一些糖,使其糖数增加1倍;经过2005次这样的操作以后,甲有10块糖,乙有8块糖.请问:两个人原来分别有多少块糖?【例3】哥哥对弟弟说:“你长到我这么大的时候,我恰好获得博士学位;我在你这么大的时候,你刚刚上幼儿园.”已知哥哥和弟弟现在的年龄和为32岁,哥哥获得博士学位的年龄是弟弟上幼儿园年龄的7倍,求哥哥获得博士学位的年龄是多少岁.【例4】小明跟爷爷聊天.爷爷对小明说:“当我的岁数是你爸现在的岁数时,你才5岁呢.”小明对爷爷说:“我的岁数是您现在的岁数时,我爸都89岁了.”请问:小明的爸爸今年多少岁?【例5】1996年时,父母的年龄之和是78岁,兄弟二人的年龄之和是17岁;4年后,父亲年龄是弟弟年龄的4倍,母亲年龄是哥哥年龄的3倍.试问:当父亲年龄是哥哥年龄的3倍时是公元多少年?【例6】全家4口人,父亲比母亲大3岁,姐姐比弟弟大2岁.4年前全家人的年龄之和是58岁,而现在是73岁.问:现在各人的年龄分别是多少岁?【例7】老师在黑板上写了三个不同的整数,小明每次先擦掉第一个数,然后在最后写上另两个数的平均数,如此做了7次,这时黑板上三个数的和为159.如果开始时老师在黑板上写的三个数之和为2008,且所有写过的数都是整数.请问:开始时老师在黑板上写的第一个数是多少?【例8】甲、乙、丙三人现在年龄的和是113岁.当乙的岁数是丙的岁数的一半时,甲是17岁.请问:乙现在多少岁?补充题目【习题1】n名海盗分金币.第1名海盗先拿1枚金币,再将剩下金币平分为100份,拿走其中1份;然后,第2名海盗先拿2枚,再将剩下金币平分为100份,拿走其中1份;第3名海盗先拿3枚,再将剩下金币平分为100份,拿走其中1份;……第n名海盗拿n枚,结果金币全被分完.已知每位海盗拿的金币都一样多,那么金币共多少枚?【习题2】把任意一个2位数进行一次操作,就是把这个2位数的各个数位上的数字相乘得到一新的2位数,若乘积为1位数,则把这个数再写一遍,由此得到一个新的2位数.那么,经过4次操作所得到的数为88的有多少个?【习题3】甲乙丙丁四个人今年的年龄之和是72岁.几年前(至少一年)甲是22岁时,乙是16岁.又知道,当甲是19的时候,丙的年龄是丁的3倍(此时丁至少1岁).如果甲乙丙丁四个人的年龄互不相同,那么今年甲可能是几岁?【习题4】材料阅读题:对于数列1、2、4、8、16…有求和公式12311222221n n ++++++=− .定义一种对单个数进行的运算β:对任意一个数n ,()()52n n β=+÷.而多个β可嵌套在一起,例如,()()()()()()995277526ββββ=+÷==+÷=.已知()()()()()10013k ββββββ= (((( (((( 个,请写出k 的一个简洁表达式. (k 很大,无需求出具体值,但不要表示成一个长串算式)。
高斯小学奥数四年级上册含答案第14讲_年龄问题

第十四讲年龄问题在与年龄有关的应用题中,年龄一般只与年份有关,比如某人在 2012年是----------------- n,在多少岁吗?30岁,那么他在2013年一定是31岁,不用具体考虑他今年是否已经过完生日.这类应用题中,给出的条件一般是两个人或者多个人的具体年龄或者他们年龄之间的和差倍关系•所以年龄问题其实就是一类特殊的和差倍问题.与其他和差倍问题相同,年龄问题也可以通过画线段图来分析,但和其他和差倍相比,年龄问题中时常包含着一些隐藏条件,需要大家格外关注.我们先来看一下只与两个人的年龄有关的几类问题.今年小高12岁,他父亲42岁,请问:多少年后,父亲年龄是小高的2倍?多少年前,父亲年龄是小高的4倍?「分析」小高和父亲的年龄差是不变的,怎么把年龄差与年龄的倍数关系联系起来呢?练习1今年小高10岁,他父亲30岁,请问:多少年前,父亲年龄是小高的5倍?多少年前,父亲年龄是小高的6倍?对于两个人来说,每过一年,两个人的年龄都会增长一岁,但是他们的年龄差不变•抓住这一不变量,很多问题就可以迎刃而解了.例题2今年爸爸的年龄是儿子的4倍,4年以后,爸爸年龄就只有儿子的 3 倍,请问今年爸爸、儿子各几岁?「分析」父子年龄的倍数关系发生了变化,是一个典型的变倍问题,其中的不变量是什么呢?把不变量设为几份呢?今年,母亲年龄是儿子年龄的3倍;10年后,母亲年龄是儿子年龄的2倍•请问:今年母亲的年龄是多少岁?年龄问题中,我们有时需要比较两个人在不同时间的年龄•对这类问题,我们仍然像解决基本和差倍问题一样,画出线段图来.小高问师傅多少岁,师傅说:“当我像你这么大时,你刚3岁;当你像我这么大时,我已经39岁了.”请问:师傅和小高现在分别多少岁?「分析」本题中过去、现在、将来的时间都出现了,你能在一个图里把这些时间都表示出来吗?叔叔对亮亮说:“当你像我这么大的时候,我已经60岁了;当我像你这么大的时候,你才24岁•”请问:亮亮和叔叔今年各多少岁?例题4兄弟现在两个年龄之和是32岁,当哥哥像弟弟现在这么大时,哥哥的年龄是当时弟弟年龄的3倍.请问:哥哥现在多少岁了?「分析」这个题目中只有现在和过去,应该先画哪个时间点呢?和差倍问题, 有倍数我们就要优先画出倍数关系.练习4小姐妹两个现在年龄之和是35岁.当姐姐是妹妹现在这么大时,姐姐当时的年龄是当时妹妹年龄的2倍.请问:姐姐现在的年龄是多少?1年前,父母的年龄和是兄弟二人年龄和的7倍;4年后,父母的年龄和是兄弟二人年龄和的4倍.已知爸爸和妈妈同岁,妈妈今年多少岁?「分析」这是关于父母年龄和与兄弟年龄和的变倍问题,我们是不是应该把父母二人分成一组,兄弟二人分成另一组来计算呢?例题6 哥哥对弟弟说:“你长到我这么大的时候,我恰好获得博士学位;我在你这么大的时候,你刚刚上幼儿园.”已知哥哥和弟弟现在的年龄和为32岁,哥哥获得博士学位时的年龄是弟弟上幼儿园时年龄的7倍,请问:哥哥获得博士学位时的年龄是多少岁?「分析」和差倍问题,有倍数时要优先画倍数.你可以根据兄弟年龄的倍数关系以及“两个人年龄差不变”画出线段图吗?年龄“外号”知多少总角:指童年•语出《诗经》,如《诗卫风氓》“总角之宴”.垂髫(chu iti co):指童年. 古时童子未冠,头发下垂,因而以“垂髫"代指童年.束发:指青少年. 一般指15岁左右,这时应该学会各种技艺.及笄(j i) j指女子15岁. 语出《礼记内则》“女子十有五年而笄待年:指女子成年待嫁,又称“待字弱冠:指男子20岁. 语出《礼记曲礼上》“二十曰弱,冠”.古代男子20岁行冠礼,表示已经成年.而立:指30岁. 语出《论语为政》“三十而立” •以后称三十岁为“而立”之年.不惑:指40岁. 语出《论语为政》“四十而不惑” •以后用“不惑”作40岁的代称.艾:指50岁•语出《礼记曲礼上》“五十曰艾” •老年头发苍白如艾.花甲:指60岁•以天干地支名号错综参互而得名.古稀:指70岁•语出杜甫《曲江》诗:“酒债寻常行处有,人生七十古来稀•” 皓首:指老年,又称“白首”.黄发:指长寿老人•语出《诗经》,如《诗鲁颂•宫》“黄发台背” •老人头发由白转黄.鲐背:指长寿老人.语出《诗经》,如《诗大雅行苇》“黄台背”,“台”与“鲐”通用.耄:古称大约七十至九十岁的年纪.老夫耄矣,无能为也. 一一《左传隐公四年》耋: 年八十曰耊•字亦作耋. 一一《易 离》•马注:“七十曰耋•”期颐:指百岁•语出《礼记 曲礼上》“百年曰期,颐” •谓百岁老人应由后代赡养.孑«I-養十有A厨志于孝r *=十:r二^做 凹十两平孤.%--'「岂JI十帀知A4-作业1.2010年张伯伯45岁,小聪9岁,那么在哪一年张伯伯的年龄是小聪的 3倍?2.今年,父亲年龄是儿子年龄的 4倍;24年后,父亲年龄是儿子年龄的 2倍•今年父亲多少岁?3.李家有三兄弟,老大、老二、老三•当老二像老三那么大时,老二的年龄是老三的 3倍,老大的年龄是老二、老三的年龄之和.已知现在三兄弟年龄之和为 28岁,现在老大多少岁?4.哥哥对弟弟说:“当我到爸爸现在的年龄时, 爸爸就70岁了. ”弟弟又对哥哥说:“当我 到妈妈现在的年龄时, 妈妈也70岁了. ”已知爸爸比妈妈大 2岁,那么哥哥比弟弟大多 少岁?5.5年前父母的年龄和是兄弟二人年龄和的 10倍,明年父母的年龄和是兄弟二人年龄和的4倍,那么从今年起多少年后父母的年龄和是兄弟二人年龄和的2倍?第十四讲年龄问题1. 例题1答案:18年后;2年前详解:小高和父亲年龄差30岁,根据年龄差不变的性质,当父亲年龄是小高2倍时,设小高年龄为“ 1”,父亲年龄为“ 2”,差值为“1”,即30岁,则当小高30岁,父亲60岁时,父亲年龄 是小高的2倍,这是在18年后;同理,当父亲年龄是小高 4倍时,设小高年龄为“ 1”,父亲年 龄为“ 4”,差值为“ 3”,即30岁,则“ 1”为10岁,小高为10岁,那是在2年前.详解:设年龄差为“6”,则儿子今年年龄为“2 ”, 爸爸今年年龄为“8 ”,4年后,儿子年龄为“ 3 ”, 爸爸年龄为“ 9”,则“ 1”为4年,那么儿子今 年8岁,爸爸今年32岁.1”,则4年后的父母年龄和为 “8”,兄弟年龄和为“ 2”,则10岁为“ 1 ”,所以爸爸妈妈今年年龄和为 72,所以妈妈今年36岁.6. 例题6 答案:28岁详解:如右图所示,根据 7倍可得年龄差是弟弟上幼儿园时年龄的2倍,设弟弟上幼儿园时年2.例题2答案:儿子8岁;爸爸32岁3. 例题3答案:小高15岁;师傅27岁详解:画“过去、现在、将来”图,如右图所示.设 年龄差为“ 1”,发现“ 3”恰好是3岁到39岁, 即36岁,则“ 1”为12岁,所以现在小高和师 傅分别是15岁和27岁.4. 例题4 答案:20岁详解:画出“过去、现在”图,如右图所示•设哥哥像弟 1” ------ “ 3”__ I 45.弟现在这么大时,弟弟年龄为“ 1”,哥哥年龄为“ 3”,年龄差为“ 2”,则现在弟弟年龄“ 3”,哥哥年龄为“ 5”,年 龄和为“ 8”,即是32岁,则“ 1 ”为4岁,所以哥哥现例题5 答案:36岁详解:将父母年龄和看成一组,将兄弟二人年龄和看成一组,根据 之差统一为“ 6”.则1年前父母年龄和为“ 7”,兄弟年龄和为“ 倍和4倍,把两组年龄和 将龄为“1”,则哥哥获博士学位年龄为 “ 7 ”, 弟 1 则现在弟弟年龄为“ 3”哥哥年龄为“ 5 ” 两个人的年龄和为“ 8”,32岁,则“ 1”为 4岁;那么哥哥获得博士学位的年龄为 28岁.练习1答案:5年前;6年前详解:小高和父亲年龄差20岁,根据年龄 差不变的性质,当父亲年龄是小高5倍时, 设小高年龄为“ 1 ”,父亲年龄为“ 5”,差 值为“ 4”,即20岁,则当小高5岁,父亲 25岁时,父亲年龄是小高的 5倍,这是在龄为“ 1”,父亲年龄为“ 6”,差值为“ 5”,即20岁,则“ 1”为4岁,小高为4岁,那是在6 年前.8. 练习2 答案:30岁详解:设年龄差为“ 2”则儿子今年年龄为“ 1”母亲今年年龄为“ 3”,10年后,儿子年龄为 “2”母亲年龄为“ 4”,则“ 1”为10年,那么儿子今年10岁,母亲今年30岁.9. 练习3答案:亮亮36岁;叔叔48岁简答:方法同例3,画出线段图,设年龄差为“ 1 ”,发现“ 3”恰好是24岁到60岁,即36岁, 贝U“1 ”为12岁,所以现在亮亮和叔叔分别是 36岁和48岁.10. 练习4答案:21岁简答:方法同例4,画出线段图,设姐姐像妹妹现在这么大时,妹妹年龄为“ 1 ”,姐姐年龄为“2”年龄差为“1”,则现在妹妹年龄“ 2”,姐姐年龄为“ 3 ”,年龄和为“ 5”,即35岁,则“ 1 ”为7 岁,所以姐姐现在21岁.11. 作业1答案:2019年简答:两人年龄差为45 9 36岁.张伯伯年龄是小聪的 3倍时,小聪的年龄为36 3 1 18岁, 这是在18 9 9年后,为2019年.12. 作业2答案:48岁简答:设年龄差是“ 3”.今年父亲的年龄是“ 4”,今年儿子的年龄是“ 1 ”,24年后儿子的年龄7.5年前;同理,当父亲年龄是小高 6倍时,设小高年是“ 3”,父亲年龄是“ 6”. “1”份是12年,今年父亲的年龄是12 4 48岁. 13. 作业3答案:12岁简答:当老二像老三那么大时,假设老三的年龄为“1”,则老二的年龄为“ 3”,老大的年龄为“ 4”,如下图所示•老三、老二的年龄差为“ 2”,则现在老三年龄为“ 3”,老二年龄为“ 5”, 老大年龄为“ 6”,“1 ”为28 3 5 62岁.因此现在老大12岁,老二10岁,老三6岁.现在现在卜28岁现在14. 作业4答案:4岁简答:先根据父母年龄差 2岁画出线段图,如下所示•从图中看出,由于爸爸比妈妈大2岁,所以弟弟与妈妈年龄差比哥哥与爸爸年龄差大 2岁,比哥哥与妈妈年龄差大 2 2 4岁,所以哥 哥和弟弟年龄差为4岁.为“3”,相差的“ 2”相当于5 1 2 12年,即“1”相当于6年.5年前兄弟年龄和为6岁,父母年龄和为6 1060岁,今年兄弟年龄和为 6 5 2 16岁,父母年龄和为60 5 270岁,父母年龄和与兄弟年龄和之差为 70 16 54岁.当父母年龄和是兄弟年龄和的2倍时,兄弟年龄和为542 154岁,是在 54 162 19年后.老二1”,明年兄弟年龄和。
四年级第五讲和还原问题与年龄问题 提高班教师版

讲义是乐谱,学生是听众,老师是指挥家,每节课都是一篇乐章,老师您辛苦了!——学而思小学奥数讲义组第五讲还原问题与年龄问题教学目标1.掌握倒推法解决还原问题;2.能够独立解决较复杂的年龄问题;想有119只蜜蜂在三棵枣树上采蜜.一会儿有10只蜜蜂从第一棵枣树上飞到第二棵枣树上;过了一会儿,又有20只蜜蜂从第二棵枣树上飞走了.这时三棵枣树上的蜜蜂正好一样多,第二棵枣树上原来有多少只蜜蜂?挑战吗?分析:第二棵(119-20)÷3=33(只),33+20-10=43(只)。
还原问题像上面“想挑战吗”这种问题,依照题意叙述由后往前推算,最终解决问题的方法,叫做还原法(或称倒推法).这种问题叫做还原问题.解答还原问题的一般方法是:1.从最后的结果出发,采用与原题中相反的逆运算方法,原题加的用减,减的用加,乘的用除,除的用乘.2.根据原题的叙述顺序,从上面列出数量关系式,再用逆运算方法得出原数.【例1】马小虎做一道整数减法题时,把减数个位上的1看成7,把减数十位上的7看成1,结果得出差是111.问正确答案应是几?分析:马小虎错把减数个位上1看成7,使差减少7-1=6,把十位上的7看成1,使差增加70—10=60.因此归结为某数减6,加60得111,求某数是几的问题.111-(70—10)+(7—1)=57。
[拓展]两个两位数相加,其中一个加数是73,另一个加数不知道,只知道另一个加数的十位数字增加5,个位数字增加1,那么求得的和的后两位数字是72,问另一个加数原来是多少?分析:和的后两位数字是72,说明另一加数变成99,所以原加数是99-51=48.学而思教育08年寒假四年级提高班第五讲教师版Page31【例2】村姑卖鸡蛋,第一次卖出一篮的一半又二个;第二次卖出余下的一半又二个;第三次卖出再剩下的一半又二个,这时篮里只剩下二个蛋,问这篮鸡蛋有多少个?分析:从上面线段图可以看出:最后剩下2个再加上第三次卖出的再余下的一半以外的2个,就是再余下的一半,由此可求出再余下的是(2+2)×2=8(个);8个再加上第二次卖出余下的一半以外的2个就是余下的一半,因此可求出余下的是:(8+2)×2=20(个);20个再加上第一次卖出一篮的一半以外的2个就是全篮的一半,因此可求出全篮鸡蛋的个数是:(20+2)×2=44(个)。
0923年龄与还原问题

第三讲年龄与还原问题知识点(一):两人年龄问题1.3年前,父亲的年龄是女儿年龄的11倍;9年后,父亲的年龄是女儿年龄的3倍.那么今年父亲________岁,女儿________岁.2.已知儿子现在的年龄为5岁.当儿子长到爸爸现在的年龄时,父子俩人的年龄和为85岁,那么爸爸现在________岁.3.学生问老师多少岁,老师说:“当我像你这么大时,你刚3岁;当你像我这么大时,我已经39岁。
”那么老师现在的年龄是_____岁,学生现在的年龄是_____岁.知识点(二):多人年龄问题4.甲、乙、丙、丁四人现在的年龄和是64岁.已知当甲21岁时,乙17岁;当甲18岁时,丙的年龄是丁的3倍;当甲15岁时,乙比丙小1岁.那么丁现在是________岁.5.今年父亲的年龄是48岁,哥哥的年龄是弟弟年龄的2倍.当弟弟长到哥哥现在年龄时,父亲的年龄恰等于兄弟俩年龄之和,那么今年哥哥________岁.知识点(三):还原问题6.甲乙两个油桶各装了15千克油.售货员卖了14千克.后来,售货员从剩下较多油的甲桶倒一部分给乙桶使乙桶油增加一倍;然后从乙桶倒一部分给甲桶,使甲桶油也增加一倍,这时甲桶油恰好是乙桶油的3倍.问:售货员从两个桶里各卖了多少千克油?7.三筐苹果共48个,先从第一个筐中拿出一半放入第二个筐,再从第二个筐里拿出与第三个筐数目相同的苹果放入第三个筐,最后再从第三个筐里拿出与这时第一个筐数目相等的苹果放入第一个筐.结________个.8.甲、乙、丙三人的钱数各不相同,甲最多,他拿出一些钱分给乙、丙,使两人各自的钱数增加2倍,结果乙的钱变成最多,于是他拿出一些钱分给甲、丙,使两人各自的钱数变成原来的2倍,结果丙的钱变成最多,于是他把自己钱的一半平分给甲、乙,这时每人手中都有48元钱,那么甲原有________元、乙原有________元、丙原有________元.第三讲年龄与还原问题课堂练习1.2006年,爷爷72岁,孙子12岁,_____年爷爷为孙子的5倍,_____年爷爷为孙子的13倍;2.一个数加上6,再乘以6,再减去6,再除以6得到6,原来的数字是______.3.有一个财迷总想使自己的钱成倍增长,一天他在一座桥上碰见一个老人,老人对他说:“你只要走过这座桥再回来,你身上的钱就会增加一倍,但作为报酬,你每走一个来回要给我32个铜板.”财迷想想挺合算,就同意了.他走过桥去又走回来,身上的钱果然增加了一倍,他很高兴地给了老人32个铜板.这样走完第五个来回,身上的最后32个铜板都给了老人,一个铜板也没剩下.那么财迷身上原有________个铜板.4.哥哥对弟弟说:“你和我一样大的时候,我将24岁;我在你这么大的时候,你刚刚9岁。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
今年小明年龄;
4年后小明年龄: 4岁
小明张了4岁,那么他变大的4岁就是“2”份,所以“1”份就是4÷2=2岁,也 就是小明今年2岁。 7. 今年,父亲年龄是儿子年龄的5倍;15年后,父亲年龄是儿子年龄的2 倍. 问:现在父子的年龄各是多少? 答案:儿子5岁。父亲25岁。 详解:根据分析,父亲和儿子的年龄差是今年儿子年龄的4倍,也是15年 后儿子年龄的1倍。所以我们把年龄差看成“4”份,那么今年儿子的年龄 是“1”份,15年后儿子的年龄就是“4”份。 15年后儿子的年龄是比今年的年龄多了“3”份,正好是15岁。因此“1”份就 是15÷3=5岁。于是 今年儿子5岁,父亲今年是5×5=25岁
超越篇 1、口渴的三个和尚分别捧着一个水罐。最初,老和尚的水最多,并且 有一个和尚没水喝。于是,老和尚把自己的水全部平均分给了大、小两 个和尚;接着,大和尚又把自己的水全部平均分给了老、小两个和尚; 然后,小和尚又把自己的水全部平均分给了另外两个和尚。就这样,三 人轮流谦让了一阵。结果太阳落山时,老和尚的水罐里有10升水,小和 尚的水罐则装着20升水。请问:最初大和尚的水罐里有多少升水? 答案:10升 详解:设最初为3,则最后总数不变,得出: (10+20)÷3=10(升)
8. 兄弟两个年龄之和是32岁. 当哥哥是弟弟现在这么大时,哥哥的年龄 是当时弟弟年龄的3倍.求哥哥现在的年龄. 答案:20 详解:32÷(3+3+2)=4(岁)32-(4×3)=20(岁)
9. 学生问老师多少岁,老师说:“当我像你这么大时,你刚3岁;当你像 我这么大时,我已经39岁了.” 求老师和学生现在的年龄. 答案:学生15岁,老师27岁。 详解:39岁与3岁的差别正好是年龄差的3倍,所以师生的年龄差为 (39-3)÷3=12岁。 那么学生现在3+12=15岁 老师现在15+12=27岁。
次数
甲乙
开始
7 10
第一次给 14 3 糖后
第二次给 11 6 糖后
第三次给 5 12 糖后
5. 甲、乙、丙三人的钱数各不相同,甲最多,他拿出一些钱给乙和丙, 使乙和丙的钱数都比原来增加了2倍,结果乙的钱最多;接着乙拿出一 些钱给甲和丙,使甲和丙的钱数各增加了2倍,结果丙的钱最多;最后 丙又拿出一些钱给甲和乙,使他们的钱数和增加2倍,结果三人的钱数 一样多,如果他们三人共有81元,那么三人原来分别有多少钱? 答案:甲原来有55元,乙原来有19元,丙原来有7元。 详解:
第3讲 还原问题与年龄问题 内容概述 学会用逆推法求解还原问题,处理多个对象时可采用列表的形式,在年 龄问题中,通常采用和差倍问题的分析方法,有时需注意任意两人的年 龄差保持不变。 典型问题 兴趣篇 1. 某数加上6,再乘以6, 再减去6,再除以6, 其结果等于6,则这个数 是多少?
答案:这个数是
详解:+6 x6 -6 +6 1742366
3. 地上有26地砖,兄弟二人争着去挑. 弟弟抢在前面,刚挑起一些砖, 哥哥赶到了,挑了剩下的砖. 哥哥看弟弟挑得太多,就从弟弟那儿抢过 一半. 弟弟不肯,又从哥哥那儿抢走一半. 哥哥不服,弟弟只好再给哥哥 5块,这时哥哥比弟弟多挑2块,请问:最初弟弟准备挑多少块砖? 答案:最初弟弟挑了16块砖。 详解:
9. 今年父亲的年龄是48岁,哥哥的年龄是弟弟的2倍, 当弟弟长到哥哥现 在的年龄时,父亲的年龄恰好等于兄弟俩年龄之和,请问:今年哥哥多 少岁? 答案:24岁。 详解:当弟弟长到哥哥现在的年龄是,弟弟年龄为2份,哥哥的年龄为 2+1=3份,父亲的年龄是兄弟的年龄和2+3=5份,由此得到今年父亲的 年龄是5-1=4份,为48岁,所以今年弟弟的年龄是48÷4=12岁,哥哥今 年的年龄是12÷2=24岁。
哥哥挑的砖 弟弟挑的砖
开始
10
16
弟弟减半后
18
8
哥哥减半后
9
17
弟弟给哥哥5块后 14
12
4. 甲、乙各有糖若干块,每操作一次是由糖多的人给糖少的人一些糖, 使得糖少的人的糖数增加一倍,经过三次这样的操作后,甲有5块糖, 乙有12块糖,两个人原来的糖数分别是多少? 答案:甲原来有7块糖,乙原来有10块糖。 详解:
后,第三棵树上又有10只鸟飞到了第一棵树上,此时三棵树上的鸟一样
多. 问:一开始三棵树上各有几只鸟?
答案:第一棵树上有12,第二棵23,第三棵13
详解:
第一棵
第一棵飞到第二棵后 6
29
13
第二棵飞到第三棵后 6
16
26
5. 1997年张
第三棵飞到第一棵后 16
3. 某人发现了一条魔道,下面有一个存钱的小箱子,当他从魔道走过去 的时候,箱子里的一些钱会飞到人的身上使人身上的钱增加一倍,这人 很高兴;当他从魔道走回来时,身上的钱会飞到箱子里,使箱子里的钱 增加一倍;这人一连走了3个来回后,箱子里的钱和人身上的钱都是64 枚一元的硬币,那么原来这人身上有多少元?箱子里有多少元? 答案:原来这个人身上有43元,箱子里有85元。 详解:
2. 有一个人非常喜欢喝酒,他每经过一个酒店都要买酒喝. 这个人出门 带了一个酒葫芦,看到一个酒店就把酒葫芦中的酒加一倍,然后喝下8 两酒,这天他一共遇到3家酒店,在最后一家酒店喝完酒后,葫芦里的 酒刚好喝完. 问:原来酒葫芦里有多少两酒? 答案:7两酒。 详解:每经过一个酒店,葫芦里酒的数量就先乘2,再减8,利用倒推 法,我们反过来应该先加8,再除以2.那么到酒店C之前葫芦里应该有 (0+8)÷2=4两酒,他在到酒店B的时候应该有(4+8)÷2=6两酒,所 以他原来的酒葫芦应该有(6+8)÷2=7两酒。 0+8=8,8÷2=4,4+8=12,12÷2=6,6+8=14,14÷2=7
16
16
伯伯45岁,
小方9岁,在
哪一年张伯伯的年龄是小方年龄的4倍?
答案:小方12岁那年。
详解;我们把小方的年龄看成“1”份,那么张伯伯的年龄就是“4”份,那
么他们的年龄差就是“3”份,因此“1”份是36÷3=12岁。于是小方的年龄
应该是12岁,张伯伯的年龄是小方的4倍。
6. 今年,小明的年龄等于他父母的年龄差;4年后,小明的年龄等于他父 母年龄差的3倍. 今年小明多少岁? 答案:2岁。 详解: 父母的年龄差是不变的,所以我们把父母的年龄差看成“1”份,那么小明 现在的年龄是“1”份,而4年后小明的年龄变成了“3”份。画出线段图。
比,相当于30-15=15年后。
8. 去年哥哥的年龄是明年兄弟二人年龄和的一半,前年哥哥的年龄是弟弟 的2倍. 求哥哥和弟弟现在的年龄。 答案:弟弟的年龄是6岁,哥哥是10岁。 详解:前年弟弟的年龄是1份、哥哥的年龄是2份,去年哥哥的年龄是2 份+1岁,明年弟弟的年龄是1份+3岁,哥哥的年龄是2份+3岁。所以(2份 +1岁)×2=(1份+3岁)+( 2份+3岁) 1份是4岁。弟弟的年龄是4+2=6岁,哥哥的年龄是2×4+2=10岁。
10. 学生问老师多少岁,老师说:“当我像你这么大时,你刚5岁;当你 像我这么大时,我已经50岁了。“求老师和学生现在的年龄。 答案:学生20岁,老师35岁 详解:
5岁
50岁 ☆
☆ :师生现在的年龄 ◇ :将来学生像老师这么大时 △:过去老师像学生这么大时 从上面可以看出,50-5=45岁正好是3个年龄差,所以师生的年龄差为 45÷3=15岁
所以现在学生为5+15=20岁,老师魏15+20=35岁。
11. 有老师和甲、乙、丙三个学生,现在老师年龄恰为三个学生年龄之 和;9年后,老师年龄为甲、乙两学生年龄之和;又过了3年,老师年龄 为甲、丙学生年龄之和;再过3年,老师年龄为乙、丙两学生年龄之 和,求现在各人的年龄。 答案:甲15岁,乙12岁,丙9岁,老师36岁。 详解:老师是1人增加年龄,而学生是3人增加年龄,9年后增加的正好 是丙的年龄。同理(9+3}年后增加的是乙的年龄,(9+3+3)年后增加 的是甲的年龄。15+12+9=36(岁)
身上的钱 箱子里的钱
开始时
43
85
第一次走过去后 86
42
第一次走回来后 44
84
第二次走过去后 88
40
第二次走回来后 48
80
第三次走过去后 96
32
4. 三棵树上共有48只鸟. 后
第三次走回来后 64
64
来,第一棵树上有一半的
鸟飞到了第二棵树上;之
后,第二棵树上又有与第三棵树同样数目的鸟飞到了第三棵树上;最
次数
甲乙丙
开始
55 19 7
甲将钱分给乙和丙后 3 57 21
乙将钱分给甲和丙后 9 9 63
丙将钱分给甲和乙后 27 27 27
6. 今年张明15岁,他父亲45岁,请问:多少年后,父亲年龄是张明年龄 的2倍?多少年前,父亲年龄是张明年龄的4倍? 答案:15年后,5年前。 详解:张明和他父亲的年龄差不变,始终是45-15=30岁。当“父亲年龄 是张明年龄的2倍”时,假设张明年龄是1份,那么父亲的年龄是2份,两 人的年龄差也是“1”份,由于年龄差是30岁,那么此时张明的年龄就是 30×1=30岁,是现在的30-15=15年后 当“父亲年龄是张明年龄的4倍”时,假设张明年龄是1份,那么父亲的年 龄是4份,年龄差就是“3”份,这时“1”份对应30÷3=10岁,张明的年龄 就是10岁,是现在的15-10=5年前。 7. 12年前,父亲的年龄是女儿年龄的11倍;今年,父亲的年龄是女儿年 龄的3倍. 请问:多少年后父亲年龄是女儿年龄的2倍? 答案:15年后 详解:父亲和女儿的年龄差是今年女儿年龄的2倍,也是12年前女儿年 龄的10倍,所以把父亲和女儿的年龄差设为10份,那么今年女儿的年龄 就是5份,而12年前女儿的年龄是1份,12年前女儿的年龄是比今年的年 龄多了4份,因此能算出1份是12÷4=3岁,于是今年女儿是5行=15岁, 而父亲今年是15×3=45岁,父女年龄差45-15=30岁。当父亲年龄是女儿 年龄的2倍时,那时的女儿年龄就等于年龄差30岁,与女儿今年15岁相
