高思导引 四年级第十二讲 复杂竖式教师版
高思学校竞赛数学导引(四年级)

$应用题第#*讲% !!!!!!!!!! &)
第!%讲!!复杂竖式
$数字谜问题第(讲%!!!!!!!!! &$
第!&讲!!横式问题
$数字谜问题第%讲%!!!!!!!!! $(
第!’讲!!格点与割补
$几何问题第’讲% !!!!!!!!! #"#
第!(讲!!行程问题二
$应用题第#)讲%!!!!!!!!!! #"&
)!012"’#(3!" ##/""+!##"#.!#!4!"! "!#&#!)$!!!!!!!!!!!!""#!)#&!
!*!012"’ (3!" #/"##.""+##!4!"! "!#( &$!!!""#& ($!!!"$#"* (# ’$!!!"’#* "( ’#!
$%#
!!!"!"!#-"#"-#&&%",#!!#!"#$!!""#$!#!"!.&&#!"(%"!)))%!"!#!
目 录
!目!录
第 ! 讲!!整数计算综合
$计算问题第(讲% !!!!!!!!!! #
第 " 讲!!数阵图初步
$数字谜问题第)讲% !!!!!!!!! %
第 # 讲!!竖式问题
$数字谜问题第’讲%!!!!!!!!! #’
第 $ 讲!!几何图形剪拼
$几何问题第*讲%!!!!!!!!!! !!
高思导引-四年级-竖式问题教师版汇编

学习-----好资料第5讲竖式问题内容概述以字母或汉字表示数字的竖式问题,学会选择适当的突破口,并逐步解决问题;能够将文字叙述的题目转化为数字谜形式,便于直观地解决问题。
典型问题兴趣篇1.如图5-1所示,每个英文字母代表一个数字,不同的字母代表不同的数字,其中“G”代表“5”,“A”代表“9”,“D”代表“0”,“H”代表“6”.问:“I”代表的数字是多少?分析:也一定有A+E=HC=4,A+D=D,所以,它们的和一定有进位,所以,、2、F分别是1没有用,所以1、2、3、8B,现在还剩进位,所以E=7I=3.的加法竖式中,不同的汉字代表不同的数字,相同的汉字代)在图5-22. (1 表相同的数字,那么每个汉字各代表什么数字?的减法竖式中,不同的汉字代表不同的数字,相同的汉字代表相在图5-3(2)同的数字,那么每个汉字各代表什么数字?分析:,卒=1(1)观察可得:车,马=卒,所以兵=5=0,兵+兵马,所炮=,+1=5,所以马=4炮+=2以炮5240+5210=10450=2=马,所以:兵,=12)观察可得:炮,兵—兵=马,一定有借位,所以马=9,炮—兵(292=929—1221的竖式中,相同的汉字代表相同的3. 在图5-4+如果23+解数字,不同的汉字代表不同的数字,”所代表的三,那么“字++谜=30 数数字谜位数是多少?更多精品文档.学习-----好资料不同的汉字代表不同的数字,每个汉字代表一个数字,图5-5所示的竖式中,4. ”代表的四位数是多少?那么“北京奥运分析:奥++京,北+奥=0,所以可得要进位,所以;京=8 观察可得:北=1,北+京=9 ,运位,所以:奥=0+运=8,所以要进2=1809 北京奥运ABCDE所示的乘法竖式成立,那么5. 已知图5-6是多少?相同的符号代5-7的竖式中,6. (1) 在图表相同的数字,不同的符号代表不同的数字,那么☆、△、○分别代表什么数字?的竖式中,相同的符号代表5-8(2) 在图不同的符号代表不同的数字,相同的数字,那么☆、△、○分别代表什么数字?分析:三种可能,因为是三位数5、9,×△=△,所以△=1、)(1△,○=1,☆乘一位数等于四位数,所以1排除,经分析:△=5=2=2 ,○,当△=5时,☆=4、)△=15、6三种可能,排除12 (=3○=5时,△当=6☆,更多精品文档.学习-----好资料7. 如图5-9,相同的字母表示相同的数字,不同的字母表示不同的数字,那么十个方框中数字之和是多少?分析:B×B=B,所以B=1、5、6,三种可能,经分析1排除,A×B=B,所以B=5,A为奇数,三位数乘B得三位数,所以第一个方格中添1,一百多乘一位数得四位数,所以A只能是7、9,当A=7时,C=7,矛盾不成立;当A=9时,C=7,成立;所以:195×95=18525 1+9+1+7+5+1+8+5+2+5=448. 在图5-10和图5-11中的方格内填入适当的数字,使下列除法竖式成立.分析:,所以除数9=783(1)除数×=6003 ,所以被除数×6=522=87,8787=69÷6003=2465 5=145,所以被除数8=232,所以除数=29,29×(2)除数×29=85÷2465所示的除法竖式中填入合适的数字,使得竖式成立,那么其中的商5-129.在图是多少?分析:三= 除数×7=两位数,除数×另一个一位数,所以除数只能是位数,且三位数的十位上是2 ,9=12614,14×7=98,14×=79所以除数更多精品文档.好资料学习-----后所得乘积恰好是将原来的四位数各位数字顺序910. 有一个四位数,它乘以.颠倒而得的新四位数,求原来的四位数拓展篇不同的汉字代表不同的数字,相同的汉字代表相同的数字,和5-14中,1. 在图5-13. 求出它们使竖式成立的值分析:,四个语、语=5 (1)观察得:巧=1,所以三个英相加得数,进2相加得20,所,向前进2的个位是8,所以英得6 以学=4 以学+学得数个位也是8,所1465+林=7,奥++=6,奥林+匹进2,所以林2 ()观察的奥+林有进1,所以奥6789=83,所以匹,克=9 匹+克进,在这个算式中,相2. 如图5-15不同的同的字母代表相同的数字,、A字母代表不同的数字,那么数字分别是多少?B、C分析:有借位,没有借位,C—BCA=A,—B=B,所以C—AC观察—A=4A=A,所以B=9,所以有借位且,C=8,已知C—B—B=B8、4、9不同的字母表示不同的数在图5-16的竖式中,相同的字母表示相同的数字,3. 字,并且A<B<C<D. 问:竖式中的和是多少?分析:D=5 C=4,,,观察得A=2B=3 2233+3344+4455=10032更多精品文档.学习-----好资料4. 在图5-17的竖式中,相同的汉字表示相同的数字,不同的汉字表示不同的数字,那么“”所代表的七位数是多少?携手上海世博会分析:,个=9,手=0,上观察得,黄金三角:携=1,所=7位数的和肯定要进位,要使进1为,则博,=6位,办海=4,假设百位向前进2以会只能是2,,位,办=5,成立,1094382 ;假设百位向前进3=8当世=3时,在;,成立,1094872=8时,在=3当世小悦写了一个四位数,冬冬把这个四位数的个位抹掉,变成了一个三位数,5. 阿奇又把这个三位数的个位抹掉,变成了一个两位数,最后把这三个数加起来,小悦原来写的四位数是多少?结果刚好是7826.分析:利用位值原理ABCD+ABC+AB=78261000A+100B+10C+D+100A+10B+C+10A+B=1110A+111B+11C+D=7826D=1 56-55=1 则当则B=0 C=5时-时当A=778267770=56 7051即一个各位数字互不相同的三位数,用它的三个数字组成一个最大的三位数,6. 再用这三个数字组成一个最小的三位数,组成的这两个三位数之差正好是原来. 求原来的三位数的三位数.更多精品文档.学习-----好资料移到左边首位数字前面,所构成44,将这个7. (1) 一个自然数的个位数字是 4倍,那么原数最小是多少?的新数恰好是原数的一个五位数,将它的各位数字顺序颠倒就可以得到一个新的五位数,而且(2)/4倍,那么原来的五位数是多少这个新的五位数恰好是原数的)(1219782)(中的一个数字,不同的字母2,……908. 如图5-18,每一个英文字母代表,1 、RF分别代表什么数字?、、、代表不同的数字,则字母AQT更多精品文档.学习-----好资料分析:不QAQ×T=1符合题意,当Q=6时为5或6 当Q=5时A=2 .........QTAQ等于T=1 则........AQ×T=AQF=3R=7,Q=5,T=1,A=2,所以“美”三个汉字分别代表三个各不相同的“峡”、中的竖式里,“江”、9. 图5-19. 数字,请把这个竖式写出来分析:=6 ,所以美0,1,5,6中的一个,通过实验排除0,1,5先确定美是□□江,则=×江4或8之一,又因为江峡美或美通过确定江是2 排除,所以江=24或8=8=□□□峡,则峡由于江峡美×峡所示的除法5-2010. 请把如图竖式中空缺的数字补上,其中的商是多少?分析:1 7 则除数个位是7,商的十位数字是=6.........6□□×□□除数的十位数3=×□□□61 则商的个位数字是,7.........6□8 字是更多精品文档.学习-----好资料11. 请把图5-21中的除法竖式补充完整。
高斯小学奥数四年级下册含答案第12讲_直线形面积计算综合提高

第十二讲直线形面积计算综合提高我们已经学过了基本直线形面积计算公式及其反求、等积变形、格点图形面积、割补法巧算面积等几何知识,本讲就是在之前学习的基础上,加强对基本公式、一些常见模型的掌握以及对画辅助线解决几何问题的过程深刻理解,并在此基础上学习勾股定理.1. 面积计算公式2. 常见模型在计算一些不规则图形的面积时,往往需要利用一些技巧把不规则图形变成规则图形来求解.常用的技巧有割补和平移,在割补和平移的同时往往需要连辅助线,画辅助线巧妙的解决问题是几何学习中的重点、也是一大难点.我们在之前学过的“等积变形”一讲中已经学习过了这一模块中的基本知识点,如下图所示:上面两个图形中,阴影部分面积都是其所在平行四边形面积的一半.一些特殊的平行四边形(如长方形、正方形)中存在这样的基本模型.AD三角形面积=底×高÷2阴影部分面积是长方形面积的一半 阴影部分面积是长方形(平行四边形)面积的一半正方形面积=对角线的平方÷2阴影部分面积是大正方形面积的一半2S ah =÷三角形 2S a =22S b =÷ 正方形 a 等腰直角三角形22=÷S a24=÷S b例题1如图,正方形ABCD 面积为20,E 是BC 上任意一点,DF 与AE 垂直.已知AE 长5,求DF 长度.「分析」已知正方形面积,我们可以计算出哪一块图形的面积呢?练习1如图,长方形ABCD 的长BC 为15,AE =6,DF =10.那么AB 长多少?例题2如图,在长方形ABCD 中,三角形ADE 的面积为20平方厘米,三角形BEF 的面积为12平方厘米.求三角形CDF 的面积. 「分析」你能找出图中哪些图形面积是长方形的一半吗?哪些与题目所给的20、12以及△CDF 有关系呢? 练习2如图,E 、F 分别是平行四边形ABCD 两条边上的点.已知△AFM 面积为12,△BNF 面积为8,△CEN 面积为11.那么△DEM 的面积是多少?128 11ABCDEF MN勾股定理如右图所示的直角三角形ABC 中,∠A =90°,直角边AC 与直角边AB长度的平方和等于斜边BC 长度的平方.即:反之,若三角形三边符合上述等式,则此三角形为直角三角形,BC 为斜边. 勾股图与弦图勾股图法:如上左图,小正方形内接于大正方形中,所截得的4个全等直角三角形的边长均已标出.大正方形的面积为()2a b +,小正方形的面积等于大正方形的面积减去4个全等直角三角形的面积.因此有:()22224222aba b a ab b ab c +-=++-=,所以222c a b =+. 弦图法:如上右图,将大正方形分成4个全等的直角三角形和1个小正方形,各边长均已在图中标出.小正方形的面积加上4个全等的直角三角形的面积就等于大正方形的面积.因此有:()22224222aba b a ab b ab c -+=-++=,所以222c a b =+.aabCB例题3(1)如右上图所示,直角三角形ABC 中,∠ABC =90°,已知AB =5cm ,BC =12cm ,求AC 的长度.(2)如右下图所示,直角三角形ABC 中,∠ABC =90°,已知BC =40cm ,AC =50cm ,求AB 的长度.「分析」直接应用勾股定理公式进行计算吧!注意:是2次方而不是乘2哦!练习3如图所示,其中AC 的长为12,BC 的长为16,BD 的长是15,那么AD 的长是多少?例题4如图,请根据所给出的条件,计算出大梯形的面积.(单位:厘米)「分析」要求梯形面积,就必须知道梯形的高,好好思考一下,能根据直角三角形的两条直角边计算出梯形的高吗?梯形的高与直角三角形有什么关系呢? 练习4如图,请根据给出的数据,求出直角三角形的斜边上的高的长度.A B512D3 4接下来我们看两道比较复杂的题目,要解决它们,我们需要灵活应用前面所学的模型与方法,有时甚至需要我们自己画辅助线构造如上模型. 例题5如图,四边形ABCD 和AEFG 分别是长方形和正方形.已知正方形的边长是10,△DFG 的面积是18.求长方形ABCD 的面积.「分析」你能从这个复杂的图中找出基本的“一半”关系吗? 例题6如图,四边形ABCD 各边的边长均已标在图中,其中∠A = 90°,求四边形ABCD 的面积.「分析」有90°直角,能否应用勾股定理呢?这个图中有直角三角形吗? 课堂内外勾股定理勾股定理,是几何学中一颗光彩夺目的明珠,被称为“几何学的基石”,而且在高等数学和其他学科中也有着极为广泛的应用.正因为这样,世界上几个文明古国都已发现并且进行了广泛深入的研究,因此有许多名称.中国是发现和研究勾股定理最古老的国家之一.中国古代数学家称直角三角形为勾股形,较短的直角边称为勾,另一直角边称为股,斜边称为弦,所以勾股定理也称为勾股弦定理.在公元前1000多年,据记载,商高(约公元前1120年)答周公曰:“故折矩,以为句广三,股修四,径隅五.既方之,外半其一矩,环而共盘,得成三四五.两矩共长二十有五,是谓积矩.”因此,勾股定理在中国又称“商高定理”.在公元前7至6世纪一中国学者陈子,24 C曾经给出过任意直角三角形的三边关系即“以日下为勾,日高为股,勾、股各乘并开方除之得邪至日.”在法国和比利时,勾股定理又叫“驴桥定理”.还有的国家称勾股定理为“平方定理”.在陈子后一二百年,希腊的著名数学家毕达哥拉斯发现了这个定理,因此世界上许多国家都称勾股定理为“毕达哥拉斯”定理.为了庆祝这一定理的发现,毕达哥拉斯学派杀了一百头牛酬谢供奉神灵,因此这个定理又有人叫做“百牛定理”.作业1.如图,ABCD是长方形,EF与宽平行,GH与长平行,AB的长是8厘米,BC的长是6厘米,那么图中阴影部分的面积是多少平方厘米.?2.如图,已知平行四边形面积为60平方厘米,那么长方形面积是多少平方厘米?3.已知甲、乙从同一位置出发,甲往西走了5米,乙往南走了12米,这时甲、乙相距多少米?4. 如下图,在△ABC 中,∠ACB =90°,AC =12,BC =5,AM =AC ,BN =BC ,则MN 的长多少?5. 如图,已知大梯形的下底为35,根据图中给出的条件,请求出大梯形的面积.CBNMA第十二讲 直线形面积计算综合提高1. 例题1答案:3.2详解:正方形边长为4,面积为16;三角形ADE 面积是正方形的一半,为8.三角形面积等于2AE DF ⨯÷,所以DF 长为825 3.2⨯÷=.2. 例题2答案:32平方厘米详解:ADE BEF DEF ++面积和是长方形的一半;CDF DEF +面积和是长方形的一半;比较可得,CDF 面积恰好等于ADE 与BEF 面积和,为201232+=平方厘米. 3. 例题3答案:13厘米;30厘米详解:(1)222512AC +=,AC =13;(2)2224050AB +=,AB =30. 4. 例题4答案:60平方厘米详解:画如图虚线,原图中的直角三角形直角边分别是6、8,所以斜边是10,即梯形上底为10;梯形的高即为直角三角形的高,如图虚线,高为6810 4.8⨯÷=厘米;梯形面积为()1015 4.8260+⨯÷=平方厘米.5. 例题5答案:64详解:如图,连接DE .首先,三角形ADE 与DFG 的面积和为正方形AEFG 的一半,等于50;其中DFG 面积为18,所以ADE 面积为32;而三角形ADE 面积为长方形ABCD 的一半,所以长方形面积为64.E6. 例题6答案:96详解:如图,连接BD .ABD 中,BD 为10.BCD 中,三边分别为10、24、26,有222102426+=,所以BCD 为直角三角形.三角形BCD 面积为10242120⨯÷=,三角形ABD 面积为68224⨯÷=,所以ABCD 面积为1202496-=. 7. 练习1答案:4详解:三角形AED 面积为610230⨯÷=,则长方形面积为60,长为15,所以宽AB 为60154÷=.8. 练习2答案:9详解:AMF BNF MENF ++面积和是长方形的一半;DME CNE MENF ++面积和是长方形的一半;比较可得,AMF BNF +面积恰好等于DME CNE +,所以DME 面积为128119+-=平方厘米.9. 练习3答案:25 简答:2221216AB +=,AB =20;2222015AD +=,AD =25.10. 练习4答案:2.4简答:直角三角形直角边分别是3、4,所以斜边是5,高为345 2.4⨯÷=厘米.11. 作业1答案:24 简答:四个阴影三角形面积分别等于各自所在的长方形面积的一半,所以阴影部分总面积即为大长方形ABCD 的一半,为68224⨯÷=平方厘米.12. 作业2答案:60简答:长方形和平行四边形面积都等于直角三角形的两倍,所以他们面积相等.24 C13.作业3答案:13简答:甲往西走了5米,乙往南走了12米,两个人的方向垂直,所以此时两人的距离即为两条直角边长分别为5和12的直角三角形的斜边长度,等于13.14.作业4答案:4简答:AC=12,BC=5,所以斜边AB=13;AM=AC=12,所以BM=1;而BN=BC=5,所以514=-=-=.MN BN BM15.作业5答案:360简答:直角三角形两条直角边分别是15、20,根据勾股定理可得斜边(即梯形上底)为25,因此斜边上的高(即梯形的高)为20152512⨯÷=.而梯形面积为()+⨯÷=.2535122360。
高思数学_4年级下第十二讲分段计算的行程问题

行程问题主要有三组共9个基本公式,它们分别是:(1),,;(2),,;(3),,.对于运动过程较为复杂的行程问题,不仅要会灵活运用公式,通过已知的条件求出未知的路程、速度或时间,还要学会分段、比较、从整体考虑等各种辅助手段.分析 要是能求出甲、乙两人的速度就好办了,你能求出他们的速度吗?练习1.甲车每小时行 40千米,乙车每小时行 60千米.甲车从 A 地、乙车从B 地同时出发相向而行,两车相遇后9小时,甲车到达B 地.请问A 、B 两地相距多少千米?分段比较,主要在速度相同、时间相同或路程相同的前提下进行,因而按时间流程来画线段图是非常重要的!有时候,我们还给相同时间点标上相同的记号,使线段图更加一目了然.分析 本题中甲、乙两人的行程过程较为复杂,不画出线段图实在很难想清楚.画出线段图,并注意在图中标出甲出发的时刻、乙出发的时刻、甲到达A 地的时刻、乙到达A 地的时刻.大家自己把已知条件在图中标出来,看看有什么发现. 5分钟后与乙相遇,这时乙距离甲出发A 地,此时甲距离起点ķ˖ ѻ ԅ ĸ˖ ѻ ԅĹ˖ ӾӒA ԙԅĺ˖ ӾӒA ԙԅ练习2.甲、乙分别从 A 、B 两地出发相向而行,甲比乙早出发10分钟,甲每分钟走 60米,乙每分钟走90米.两人相遇后,甲再走12分钟到B 地.请问A 、B 两地相距多少米?在路程、速度与时间这行程三要素中,有时我们只知道其中的一个量,这时我们就可以通过设份数来解决.此外,我们还经常需要用到以下这三个基本倍数关系:当运动的速度相同时,时间的倍数关系等于路程的倍数关系;当运动的时间相同时,速度的倍数关系等于路程的倍数关系;当运动的路程相同时,时间的倍数关系等于速度的反倍数关系:时间长的速度慢,时间短的速度快.因此我们要仔细分析在同一段时间或者同一段路程中,不同运动对象的运动过程. 分析 大家试着自己画出线段图,并把关键时刻标注在线段图中,看看能不能算出自行车队12分钟经过的路程?能不能找到相同时间内,自行车队与摩托车经过的路程之间有什么关系?练习3.肖马虎步行去上学,从家出发5分钟后爸爸发现他没带文具盒,于是骑摩托车去追,在距离家600米的地方追上了他.肖马虎拿着文具盒继续向学校走去,爸爸返回家后发现他作业也没带,于是带上作业又骑摩托车去追,刚好在学校门口追上了他.已知家到学校门口的距离为1000米,请问肖马虎每分钟走多少米?距出发点发点后通信员又马上掉头去追自行车队,再次追上时恰好离出发点自行车队每分钟行多少千米?摩托车每分钟行多少千米?分析 大家先画出线段图,想想兔子睡觉的过程该怎么画.有时候逆向思维会带来意想不到的效果.我们可以不去考虑兔子睡觉的过程,而考虑兔子没睡觉时兔子和乌龟各跑了多远.练习4.乌龟与蜗牛进行100米赛跑,乌龟的速度是蜗牛的10倍.当它们从起点一起出发后,蜗牛不停地爬,乌龟爬到某一地点开始睡觉.乌龟醒来时发现蜗牛已经领先它20米,于是奋起直追.当蜗牛到达终点时,乌龟仍落后10米.请问:乌龟睡觉期间,蜗牛爬了多少米? 龟兔赛跑 第一次比赛:兔子中途睡觉,结果乌龟赢了.第二次比赛:兔子不服气,要再赛一次,乌龟也答应了.枪声一响,兔子拼命往前跑.只差一步到终点时,兔子想回头看乌龟到哪了,它刚转过身,就听到乌龟在它后面笑着说:“老弟,我在这呐,你又输了.”因为,枪声一响,乌龟就一口咬住了兔子的尾巴.第三次比赛:兔子更不服气,还要再赛一次,乌龟同样答应了.枪声一响,兔子拼命往前跑,当它冲过终点时,发现乌龟已在终点等它了,原来乌龟这次叫了计程车.第四次比赛:兔子找到乌龟要再比一次,乌龟说:“好呀,地点我来定.”兔子快到终点时傻眼了,原来终点设在河心的小岛上,它实在没办法上去.第五次比赛:兔子找乌龟雪耻,乌龟说:“线路我选.”兔子说:“可以,但全要选山路.”乌龟说:“没问题,三天后比,全程跑完七座山.”比赛那天,兔子每跑到半山腰,都听见乌龟在山顶上喊:“兔子加油,我就在你前面.”兔子拼尽全力满怀希望跑到第七座山的山腰,还是那个声音“兔子加油,我就在你前面.”原来乌龟找了7个同伴来帮忙了.倍.当它们从起点一起出发后,乌龟不停地跑,兔子跑到某一地点开始睡觉.兔子醒来时发现乌龟已经领先它终点时,兔子仍落后分析 我们既不知道两车速度的关系,也不知道有关的路程,只知道时间.所以应该搞清楚在每个时间阶段内,甲、乙各自的路程与速度之间的关系.我们知道,当路程一定时,速度的倍数关系与时间的倍数关系恰好相反.你能求出两车速度的倍数关系吗?练习5.甲、乙两车分别从A 、B 两地同时出发,相向而行,18小时后在C 地相遇.相遇后,两车并不停顿,继续前进.甲车在相遇后继续行驶12小时到达B 地.请问甲车到达B 地后乙车还要再开几小时才能到达A 地?时后在行驶经过每天早上7:30司机开车原速返回王经理家.一天早上,王经理想要锻炼一下,因此中途下车走到公司,结果理步行速度的多少倍?如果第二天,王经理仍然中途下车,但是下车地点比前一天距离公司要近一些,题本一、行程问题中的三个基本倍数关系: 1.当运动的速度相同时,时间的倍数关系等于路程的倍数关系;2.当运动的时间相同时,速度的倍数关系等于路程的倍数关系;3.当运动的路程相同时,时间的倍数关系等于速度的反倍数关系.二、按时间流程画线段图的方法.画线段图在求解行程问题中是至关重要的,画好线段图,能使题目条件一目了然,对解题颇有益处.三、分段与比较的想法.主要依据行程问题的三个基本倍数关系,来得到不同行程过程之间的关系.当按时间流程画出线段图后:1.同一个人的不同过程之间,速度相同,可以得到路程与时间之间的关系;2.两个时刻之间所经过的时间相同,可以得到不同对象之间路程与速度的关系;3.长度相同的线段,路程相同,可以得到速度与时间之间的关系.作业1.甲、乙同时从A、B两地出发相向而行.甲每小时走5千米,两人相遇后,乙再走50千米到A地,甲再走8小时到B地.请问乙每小时走多少千米?2.甲、乙两人从同一个地点出发同向而行,甲比乙先出发.甲走了2400米到达A地时,乙落后甲600米.又过了5分钟乙到达A地,此时乙还落后甲500米.请问乙比甲晚出发多少分钟?3.下午3点,小强放学了,从学校开始向家走.同时小强家的宠物狗大壮从家出发,迎接小强.小强与大壮在距离小强家2000米的地方相遇,相遇后大壮立即调头向家跑,跑到家之后再返回迎接小强,在距离小强家500米的地方再次与小强相遇.请问小强家到学校的距离为多少米?4.小高和小娅比赛骑自行车,赛程是2000米.小高骑自行车的速度是小娅的2倍,小娅从出发点很顺利行驶到达终点.而小高的车在中途爆胎了,小高停下来花了些时间换上备用轮胎.换完后,小娅已经骑到他前面200米处.于是小高奋起直追,终于在距离终点200米处追上了小娅,最终赢得了比赛的胜利.那么小高换轮胎期间,小娅骑了多远?如果小高换轮胎花了5分钟,那么小高每分钟骑多少米?5.快羊羊和慢羊羊分别从绵羊村的村东头和村西头同时出发,相向而行,30分钟后它们在途中某地相遇.相遇后两只羊并不停留,继续按原来方向前行,快羊羊又走了10分钟到达村西头.这时,快羊羊马上返回追慢羊羊,请问它追上慢羊羊还需要多少分钟?。
小学数学四年级第12课时 求未知加数

第八单元10以内的加法和减法第12课时求未知加数教学内容:课本第68-69页。
教学目标:1、让学生认识求未知加数的算式,探索并掌握求未知加数的方法,初步体会加减法之间的联系。
2、让学生积累把一个数凑成10的经验,为将来学习进位加作准备。
3、发展学生的数学理解能力和发散思维能力,继续培养独立思考、与人交流的学习习惯。
教学重点:掌握求未知加数的不同方法。
教学难点:正确求出未知加数。
课前准备:教学挂图、学具教学过程:一、情境导入1、口算:口算卡片练习。
2、今天数学课,智慧爷爷来到了我们的课堂,他带来了一个盒子。
二、探究交流1、教学例题。
(1)媒体出示装了苹果的盒子图。
问:图中盒子里如果装满苹果,可以装几个?已经装了几个?还差几个?(2)进行说明:同学们,盒子里可以装10个苹果,我们已经装了8个,还有几个没有装的。
(教师边说边板书:8+()=10)(3)如果不是我们已经算出来了,我们就不知道还有几个没有装,所以我们把没有装的,也就是不知道的这个数用括号括起来,表示不知道的意思。
(4)这个算式就读做:8加几等于10。
(5)通过图我们知道了还有2个没有装,也就是8加2等于10。
(教师在黑板上填写。
)如果没有图,你该怎么想8加几等于10呢?小组讨论。
(6)学生说的只要有道理就可以了,教师可以引导学生回答。
讨论后形成如下板书:因为10可以分成8和2,所以8+(2)=10。
8和2合成10,所以8+(2)=10。
10-8=2,所以8+(2)=10。
(7)思考:6+()=10,小朋友可以怎么想?发表意见,只要说的有道理。
2、延伸。
(1)把数字卡片贴在黑板上,再在黑板上写上 4+()=103+()=7 ()+5=10 7+()=10三、反馈完善1、完成第2题。
(1)看书上题目,明确要求:先画满10个图形,再填空。
(2)学生独立在书上画图形填空。
指名说出每一行画了几个图形,()里填了什么数。
2.完成第3题。
(1)谈话:信鸽在天上飞呀飞,迷失了方向,智慧爷爷要让小朋友帮个忙,用自己的办法帮信鸽把信送到邮局。
四年级数学思维训练导引(奥数)第12讲 复杂竖式
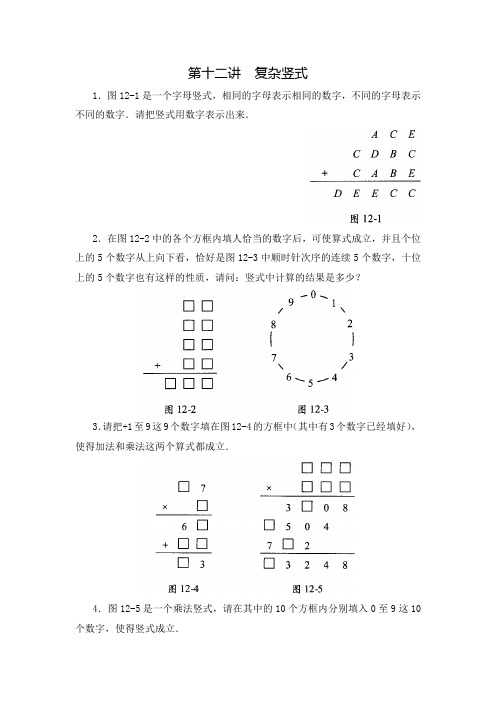
第十二讲复杂竖式1.图12-1是一个字母竖式,相同的字母表示相同的数字,不同的字母表示不同的数字.请把竖式用数字表示出来.2.在图12-2中的各个方框内填人恰当的数字后,可使算式成立,并且个位上的5个数字从上向下看,恰好是图12-3中顺时针次序的连续5个数字,十位上的5个数字也有这样的性质,请问:竖式中计算的结果是多少?3.请把+1至9这9个数字填在图12-4的方框中(其中有3个数字已经填好),使得加法和乘法这两个算式都成立.4.图12-5是一个乘法竖式,请在其中的10个方框内分别填入0至9这10个数字,使得竖式成立.5.如图12-6,在乘法竖式的每个方框中填入一个数字,使其成为正确的竖式,那么所得的乘积应该是多少?6.如图12-7,在乘法竖式的每个方框中填入一个数字,使其成为正确的竖式,那么所得的乘积应该是多少?7.在图12-8的方框内填人恰当的数字,可以得到一个正确的乘法竖式.已知这样的填法有两种,这两种填法所得到的两个不同的乘积相差多少?8.在图12-9的方框内填上适当的数字,使得竖式成立,请写出所有的答案.9.请把图12-10中的除法竖式补充完整.10.请把图12-11中的除法竖式补充完整,这个算式的被除数、除数以及商的总和是多少?1.在图12-12的字母竖式中,相同的字母代表相同的数字,不同的字母代表不同的数字.已知个位向十位的进位为2,且E是奇数,则A、曰、C、D分别代表什么数字?2.在图12-13中,相同的字母代表相同的数字,不同的字母代表不同的数字,请给出两种使竖式成立的填法,3.在图12-14所示的乘法竖式中,每个方框和字母都代表一个数字,相同的字母代表相同的数字,不同的字母代表不同的数字.请问:A、B、C、D各代表什么数字?4.在图12-15所示的乘法竖式中,每个方框和汉字都代表一个数字,相同的汉字代表相同的数字,不同的汉字代表不同的数字.请问:这个乘法算式最后的乘积是多少?5.图12-16是一个乘法竖式,其中的每个方框和汉字都代表一个数字,相同的汉字代表相同的数字,不同的汉字代表不同的数字.试问:当算式成立时,“巴西法国争夺冠军”所代表的八位数是多少?6.如图12-17,请把这个乘法竖式补充完整.7.如图12-18,请把这个乘法竖式补充完整.8.请把图12-19中的除法竖式补充完整,其中被除数是多少?(注意本题有小数点)9.在如图12-20所示的除法竖式中,在各个方框里填入适当的数字后可使竖式成立,那么在这15个方框中填入的数字最多能有多少个是偶数?10.在图12-21的除法竖式中,相同的字母代表相同的数字,不同的字母代表不同的数字,请问:被除数DEFGF是多少?11.请把图12-22中的除法竖式补充完整.12.请在图12-23中的每个方框内填入恰当的数字,使得除法竖式成立.1.在图12-24的加法竖式中,相同的字母代表相同的数字,不同的字母代表不同的数字,这个算式的结果是多少?2.在图12-25的加法竖式中,相同的字母代表相同的数字,不同的字母代表不同的数字.请问:丽鬲万所代表的五位数最多是多少?3.在图12-26的乘法竖式中,口、扫、c、d、P分别代表不同的数字,且口十易+c=P.请问adde:所代表的四位数是多少?4.请把图12-27中的除法竖式补充完整.5.在图12-28的竖式中,“奇”代表奇数,“偶”代表偶数,请把竖式补充完整.6.在图12-29的方框内填人适当的数字,使下面的小数除法竖式成立.7.电子数字0至9如图12-30所示,图12-31是由电子数字组成的乘法算式,但有些已经模糊不清.请将图12-31中的的电子数字恢复,并将它写成横式:8.请将图12-32中的除法竖式补充完整.。
高斯小学奥数四年级上册含答案第12讲_乘法原理进阶

第十二讲乘法原理进阶在之前我们学习了 “加法原理与乘法原理” 一讲,即分类相加与分步相乘的 思想. 如果完成一件事分为几个步骤,在每一个步骤中又有不同的方法,那么把每 步的方法数相乘就得到所有的方法数一一这就是乘法原理.要想把过程分成几个步骤从而应用乘法原理,必须保证各步骤之间满足下面 两个要求:1. 每步都只是整件事情的一个部分,必须全部完成才算做完这件事;2. 步骤之间要有先后顺序,先确定好一步,再做下一步, 直到最后.那么是不是只要分步骤完成整件事情就可以直接用乘法原理呢?沽你来当服装 设讣人师.给小高 挑迭帽子、上衣" 棘了、柱了.如采 这四件衣物械不 可.但只能甸种选 -件'有多少种不 同的搭配?如下图,把A、B、C三部分用三种不同的颜色染色,要求相邻两部分不能同色,那么一共有多少种不同的染法呢?其实,整个染色过程是需要分为三步的,即分别给其中一块染色:当染色顺序为A-B-C时,那么A有3种染法,B不能和A 一样,有2种染法,同样C 有2种,那么一共就有“ 3 2 2 ”种染法;(C-B-A同理)当染色顺序为B-A-C时,那么B有3种染法,A不能和B 一样,有2种染法,同样C 有2种,那么一共就有“ 3 2 2 ”种染法;(B-C-A同理)当染色顺序为A-C-B时,那么A有3种染法,第二步C没有限制,也有3种染法,但是最后的B就出问题了,我们没法确定它有2种还是1种染法一一如果C和A同色,则B 有2种染法;如果C和A不同色,则B只有1种染法一—此时,根据分步相乘的思想计算整个过程的染色方法“ 3 3 ? ”就不再适用了. (C-A- B 同理)因此,并不是只要分步完成整件事情就一定可以应用乘法原理,要想应用乘法原理,还必须满足第三个要求:3.做完一步时,这一步的结果很可能会影响后面步骤的结果,但一定不能影响后面步骤的方法数.如果这一步的不同结果会导致后面某一步的方法数发—变化,就不能直接用乘法原理计算—--- 简称“前不影响后原则”染色问题,是应用乘法原理最常见的一类题型,其实,从上面对A、B、C三部分的染色分析我们应该可以发现,染色的时候,要尽量避免“隔”着染,一定不要“跳”着染,而且,第一步要尽量去染“接触最多”的那一部分,这样,才能够使得后面的染色过程尽量避开“前影响后”.例题1如图,把A、B、C、D、E这五部分用4种不同的颜色染色,且相邻的部分不能使用同一种颜色.请问:这幅图共有多少种不同的染色方法?「分析」分五步染色,先染哪一块呢?能否按照A、B、C、D、E的顺序染呢?练习1如图,把A、B、C、D这四部分用4种不同的颜色染色,且相邻的部分不能使用同一种颜色.请问: 这幅图共有多少种不同的染色方法?例题2某市实行垃圾分类处理.每个地方放置五个垃圾桶,从左向右依次标明:电池、塑料、废纸、易拉罐、其它.现在准备把五个垃圾桶染成红、绿、蓝这3种颜色之一.(1)要求相邻两个垃圾桶颜色不同,一共有多少种染色方法?(2)要求相邻两个垃圾桶颜色不同且回收易拉罐的垃圾桶不能染成红色,一共有多少种染色方法?「分析」如果我们先染废纸垃圾桶:当它染红色时,回收易拉罐的垃圾桶可以染绿、蓝两种颜色;而当它染绿色(蓝色)时,回收废纸的垃圾桶只能染蓝色(绿色).因此先染废纸垃圾桶时,会影响易拉罐垃圾桶的染色方法数,就不能直接用乘法原理计算了.那么我们应该先给哪个垃圾桶染色呢?练习2麦兜很挑食,只吃带有鱼丸或粗面的搭配.一天它和3位同学来餐厅吃东西, 一开口就要鱼丸粗面,结果老板说没有.这个时候,由于时间太晚,餐厅快打烊了,只能做牛肚河粉,鱼丸油面,猪肉米线和牛肉拉面各一份,请问它们四只猪各点一份,有几种点法?在例题2中,有一个垃圾桶是有特殊要求的一一易拉罐垃圾桶不能染成红色,我们通过尝试可知:如果一开始先染其他的垃圾桶,那么前面垃圾桶的染色方法就会影响到易拉罐垃圾桶的染色方法数,即不能满足“前不影响后”原则,而如果首先染易拉罐垃圾桶,则不会出现该问题,所以一般而言,如果题目中有些对象是有特殊要求的,那么我们分步分析计算的时候,首先要考虑这些特殊的对象.卡莉娅、墨莫、小高和大头4名同学竞选班委.有班长、学习委员、生活委员三个职位,每个人只能担任一个职位,并且每个职位只能由一个人担任.(1)有多少种可能的选举结果?(2)如果班长必须由卡莉娅来担任,有多少种可能的选举结果?(3)如果生活委员只能在墨莫和大头之中选,有多少种可能的选举结果?(4)如果学习委员不能由小高担任,有多少种可能的选举结果?「分析」可以按照职位一一确定,第(2)问中,班长只能由卡莉娅来担任,那么先确定哪一个职位的人选呢?其他小问呢?甲、乙、丙、丁、戊5个人竞选班委.有班长、副班长、纪律委员、卫生委员四个职位,每个人只能担任一个职位,并且每个职位只能由一个人担任:请问:(1) 一共有多少种可能的选举结果?( 2)如果副班长只能在甲、丁和戊中选,有多少种可能的选举结果? ( 3)如果卫生委员不能由乙、丙担任,有多少种可能的选举结果?甲、乙、丙、丁四个人要住进A、B、C、D四间房间,每个房间住一个人.其中甲不住A房间,丙只住D房间.请问:这四个人住进四个房间有多少种住法?「分析」本题中甲和丙有特殊要求,我们应该先考虑甲还是丙呢?练习4甲、乙、丙、丁四个人要住进A、B、C、D四间房间,每个房间住一个人.其中甲只住A或B房间,丙只住A、B或C房间.请问:这四个人住进四个房间有多少种住法?例题5甲、乙、丙、丁、戊五人要驾驶A、B、C、D、E这五辆不同型号的汽车,请计算在下列情况下,分别共有多少种不同的安排方案:(1)只有甲能开汽车A,乙不会开汽车B;(2)会开A的只有甲和乙,会开E的只有甲、乙、丙.「分析」第(1)问中,甲和丙两人有特殊要求,我们应该先考虑哪一个人呢?第(2)问中,A和E两车有特殊要求,我们应该先考虑哪辆车呢?接下来我们分析一下“放相同棋子”的问题.如右图,将2枚相同的棋子放入2X2的方格内,每个格子只能放1枚,且要求每行每列最多只能放1枚,那么一共会有几种方法呢?其实,要把两枚相同的棋子放进格子内,只需要选出两个格子即可,然后每个格子里放一枚棋子.一共有两行,所以必定会是每行一枚,所以我们完全可以分行选格子,第行有两种选法,第一行选好后,第二行就只有一种选法了,所以一共有2X1=2 种.例题6右图是一个阶梯形方格表,在方格中放入五枚相同的棋子,使得每行、每列中都只有一枚棋子,这样的放法共有多少种?「分析」容易看出,每行只能有1枚棋子,每列也只能由一枚棋子, 我们可以把放五枚棋子的过程分成五步:一行一行或一列一列的放.课堂内外四色定理读书的格斯里向他的老师一一著名数学家摩根提出了这个问题,摩根没有能找到解决这个问题的途径.“四色问题”提出以后,最初并没有引起广泛的重视,许多数学家低估了它的难度.就连素以谦虚著称的德国数论专家闵可夫斯基在大学上拓扑课时也说:四色问题之所以一直没有获得解决,那仅仅是由于没有一流的数学家来解决它.说罢,他拿起粉笔,竟要当堂给学生推导出来,结果没有成功.下一节课他又去试,还是没有成功.过了几个星期,仍无进展.有一天,他刚跨进教室,适逢天上雷声大作,震耳欲聋.他马上对学生说:“上天在责备我自大,我也无法解决四色问题.”这样,四色问题就成了世界最著名的问题之一. 100多年中, “四色问题”使数学家们深为困扰.没有人能证明它,也没有人推翻它.电子计算机问世以后,由于演算速度迅速提高,加之人机对话的出现,大大加快了四色猜想的证明进程.就在1976年6月,哈肯与阿佩尔在美国伊利诺斯大学的两台不同的电子计算机上,用了1200个小时,作了100亿次判断,终于完成了四色定理的证明,轰动了世界.作业1.五个座位排成一排,小高、墨莫、萱萱、阿呆、阿瓜每人选一个座位坐下,其中每个座位只能坐一个人,且萱萱不坐在中间的位置•这五个人有多少种坐法?2.如图,把A、B、C这三部分用4种不同的颜色染色,且相邻的部分不能使用同一种颜色•请问,这幅图共有多少种不同的染色方法?3.把A、B、C、D、E这五部分用4种不同的颜色染色,且相邻的部分不能使用同一种颜色.这幅图共有多少种不同的染色方法?AL D亠4.甲、乙、丙、丁四个人排成一队,甲不当排头,乙不当排头也不当排尾,共有多少种不同的排法?5.在2 4的方格中放入两枚相同的棋子,要求两枚棋子既不在同一行也不在同一列,共有多少种放法?第十二讲乘法原理进阶1. 例题1答案:96详解:分步,分别给E、B、C、A、D染色,分别有4、3、2、2、2种染法,所以一共有4 3 2 2 2 96 种染色方法.2. 例题2答案:48; 32详解:(1)从左往右依次染色,分别有3、2、2、2、2种染法,共有3 2 2 2 2 48种染色方法;(2)分步,先染易拉罐垃圾桶,再分别给废纸、塑料、电池、其他这四个垃圾桶染色,五个垃圾桶分别有2、2、2、2、2种染法,所以一共有 2 2 2 2 2 32种染色方法.3. 例题3答案:24; 6; 12; 18详解:(1 )分别确定班长、学委、生活委员的人选,分别有4、3、2种选法,所以共有4 3 2 24种;(2)分别确定班长、学委、生活委员的人选,分别有1、3、2种选法,所以共有1 3 2 6种;(3)分别确定生活委员、学委、班长的人选,分别有2、3、2种选法,所以共有2 3 2 12种;(4)分别确定学委、班长、生活委员的人选,分别有3、3、2种选法,所以共有3 3 2 18种.4. 例题4答案:4详解:分步,分别安排丙、甲、乙、丁,分别有1、2、2、1种选法,所以一共有12 2 14 种选法.5. 例题5答案:18;24详解:(1 )先考虑甲,后考虑乙,再考虑其他三个人,分别有1、3、3、2、1种可能,共有1 3 32 1 18 种;(2)先考虑A,后考虑E,再考虑其他三辆车,分别有2、2、3、2、1种可能,所以共有2 23 2 1 24 种.6. 例题6答案:16详解:一共要选5个格子放棋子,一行一行选,每行1个,而且不能在同一列,从上往下,5行分别有2、2、2、2、1种选法,所以一共有2 2 2 2 1 16种选法.7. 练习1答案:48详解:分步,分别给B、C、A、D染色,分别有4、3、2、2种染法,所以一共有4 3 2 2 48种染色方法.8. 练习2答案:6详解:先让麦兜点,只有鱼丸油面1种可选,然后让其他3位同学依次点,分别有3、2、1种选法,共分四步,乘法原理,所以共有13 2 1 6中不同的选法.9. 练习3答案:120; 72; 72简答:(1) 5 4 3 2 120 种;(2)先确定副班长,再依次确定其他,共有 3 4 3 2 72种;(3)先确定卫生委员,再依次确定其他,共有 3 4 3 2 72种.10. 练习4答案:8简答:分步,分别安排甲、丙、乙、丁,分别有2、2、2、1种选法,所以一共有2 2 2 1 8种选法.11. 作业1答案:96.简答:可以按照萱萱、小高、墨莫、阿呆、阿瓜的顺序安排座位,有 4 4 3 2 1 96种•安排座位的顺序不唯一.12. 作业2答案:24简答:可以按照A、B、C的顺序染色,4 3 2 24种.染色顺序不唯一.13. 作业3答案:96简答:可以按照A、B、C、D、E的顺序染色,有4 3 2 2 2 96种.染色顺序不唯一.14. 作业4答案:8简答:按照乙、甲、丙、丁的顺序安排,有 2 2 2 1 8种排法.15. 作业5答案:12简答:一行一行选位置,第一行有4个格子可选,即4种选法;第二行还有3个格子可选,即有 3 种选法. 因此有 4 3 12 种不同的放法.。
四年级-第12讲-正推与逆推

1.学会使用正推或逆推的方法解决数学问题.(此环节设计时间在10—15分钟)案例1:小胖见到了一位白发苍苍的老爷爷,他问老爷爷有多大年纪?老爷爷说:“把我的年龄加上10除以4,减去15后用10乘,结果正好是100岁。
请问这位老爷爷有多大年岁?(用正推加以验证)案例2:猜数游戏(我能猜出你心中想的数)每个同学想一个数,写在卡片上。
按照我给你的游戏规则运算一下。
你只要告诉我运算结果,我就能猜出你们纸上所写的数。
规则:想一个数;把这个数减去1;再乘以2;最后加上4;告诉老师结果。
(此环节设计时间在40—50分钟)例题1:如图,根据算盒求输出的数。
(要求画树状算图,列算式计算)输入输出参考答案:树状算图如右上图方法一:分步列式方法二:综合算式12+16=28(12+16)÷728÷7=4=28÷4=7试一试:根据流程图画出树状算图,并列出综合式计算。
树状算图:综合算式:参考答案:树状算图略,综合算式为:(980-75)÷5+789=970例题2:如图,根据算盒求输入的数。
输入参考答案:树状算图如右上图方法一:分步列式 方法二:综合算式4×7=28 4×7-1628-16=12 =28-16=12试一试:根据流程图画出树状算图,并列出综合式计算。
树状算图: 综合算式:参考答案:树状算图略,综合算式为:(32+99)×3+83=476例题3:一个数减去85,再除以5,最后加上218,结果是246,这个数是几?教学说明:建议让学生画出以下图形参考答案:(246-218)×5+85=28×5+85=140+85=225试一试:一个数加上87,再乘5,最后减去74,结果是451,这个数是几?参考答案:(451+74)÷5-87=18 (?) ( ) ÷5 ( ) +218 246 -85输出课外拓展:小胖、小巧、小亚和小丁丁四人共有图书180本,小胖给小巧6本,小巧给小亚12本,小亚给小丁丁12本,小丁丁给小胖4本,这时四人的图书本数相等。
高思导引-四年级-竖式问题教师版汇编

学习-----好资料第5讲竖式问题内容概述以字母或汉字表示数字的竖式问题,学会选择适当的突破口,并逐步解决问题;能够将文字叙述的题目转化为数字谜形式,便于直观地解决问题。
典型问题兴趣篇1.如图5-1所示,每个英文字母代表一个数字,不同的字母代表不同的数字,其中“G”代表“5”,“A”代表“9”,“D”代表“0”,“H”代表“6”.问:“I”代表的数字是多少?分析:也一定有A+E=HC=4,A+D=D,所以,它们的和一定有进位,所以,、2、F分别是1没有用,所以1、2、3、8B,现在还剩进位,所以E=7I=3.的加法竖式中,不同的汉字代表不同的数字,相同的汉字代)在图5-22. (1 表相同的数字,那么每个汉字各代表什么数字?的减法竖式中,不同的汉字代表不同的数字,相同的汉字代表相在图5-3(2)同的数字,那么每个汉字各代表什么数字?分析:,卒=1(1)观察可得:车,马=卒,所以兵=5=0,兵+兵马,所炮=,+1=5,所以马=4炮+=2以炮5240+5210=10450=2=马,所以:兵,=12)观察可得:炮,兵—兵=马,一定有借位,所以马=9,炮—兵(292=929—1221的竖式中,相同的汉字代表相同的3. 在图5-4+如果23+解数字,不同的汉字代表不同的数字,”所代表的三,那么“字++谜=30 数数字谜位数是多少?更多精品文档.学习-----好资料不同的汉字代表不同的数字,每个汉字代表一个数字,图5-5所示的竖式中,4. ”代表的四位数是多少?那么“北京奥运分析:奥++京,北+奥=0,所以可得要进位,所以;京=8 观察可得:北=1,北+京=9 ,运位,所以:奥=0+运=8,所以要进2=1809 北京奥运ABCDE所示的乘法竖式成立,那么5. 已知图5-6是多少?相同的符号代5-7的竖式中,6. (1) 在图表相同的数字,不同的符号代表不同的数字,那么☆、△、○分别代表什么数字?的竖式中,相同的符号代表5-8(2) 在图不同的符号代表不同的数字,相同的数字,那么☆、△、○分别代表什么数字?分析:三种可能,因为是三位数5、9,×△=△,所以△=1、)(1△,○=1,☆乘一位数等于四位数,所以1排除,经分析:△=5=2=2 ,○,当△=5时,☆=4、)△=15、6三种可能,排除12 (=3○=5时,△当=6☆,更多精品文档.学习-----好资料7. 如图5-9,相同的字母表示相同的数字,不同的字母表示不同的数字,那么十个方框中数字之和是多少?分析:B×B=B,所以B=1、5、6,三种可能,经分析1排除,A×B=B,所以B=5,A为奇数,三位数乘B得三位数,所以第一个方格中添1,一百多乘一位数得四位数,所以A只能是7、9,当A=7时,C=7,矛盾不成立;当A=9时,C=7,成立;所以:195×95=18525 1+9+1+7+5+1+8+5+2+5=448. 在图5-10和图5-11中的方格内填入适当的数字,使下列除法竖式成立.分析:,所以除数9=783(1)除数×=6003 ,所以被除数×6=522=87,8787=69÷6003=2465 5=145,所以被除数8=232,所以除数=29,29×(2)除数×29=85÷2465所示的除法竖式中填入合适的数字,使得竖式成立,那么其中的商5-129.在图是多少?分析:三= 除数×7=两位数,除数×另一个一位数,所以除数只能是位数,且三位数的十位上是2 ,9=12614,14×7=98,14×=79所以除数更多精品文档.好资料学习-----后所得乘积恰好是将原来的四位数各位数字顺序910. 有一个四位数,它乘以.颠倒而得的新四位数,求原来的四位数拓展篇不同的汉字代表不同的数字,相同的汉字代表相同的数字,和5-14中,1. 在图5-13. 求出它们使竖式成立的值分析:,四个语、语=5 (1)观察得:巧=1,所以三个英相加得数,进2相加得20,所,向前进2的个位是8,所以英得6 以学=4 以学+学得数个位也是8,所1465+林=7,奥++=6,奥林+匹进2,所以林2 ()观察的奥+林有进1,所以奥6789=83,所以匹,克=9 匹+克进,在这个算式中,相2. 如图5-15不同的同的字母代表相同的数字,、A字母代表不同的数字,那么数字分别是多少?B、C分析:有借位,没有借位,C—BCA=A,—B=B,所以C—AC观察—A=4A=A,所以B=9,所以有借位且,C=8,已知C—B—B=B8、4、9不同的字母表示不同的数在图5-16的竖式中,相同的字母表示相同的数字,3. 字,并且A<B<C<D. 问:竖式中的和是多少?分析:D=5 C=4,,,观察得A=2B=3 2233+3344+4455=10032更多精品文档.学习-----好资料4. 在图5-17的竖式中,相同的汉字表示相同的数字,不同的汉字表示不同的数字,那么“”所代表的七位数是多少?携手上海世博会分析:,个=9,手=0,上观察得,黄金三角:携=1,所=7位数的和肯定要进位,要使进1为,则博,=6位,办海=4,假设百位向前进2以会只能是2,,位,办=5,成立,1094382 ;假设百位向前进3=8当世=3时,在;,成立,1094872=8时,在=3当世小悦写了一个四位数,冬冬把这个四位数的个位抹掉,变成了一个三位数,5. 阿奇又把这个三位数的个位抹掉,变成了一个两位数,最后把这三个数加起来,小悦原来写的四位数是多少?结果刚好是7826.分析:利用位值原理ABCD+ABC+AB=78261000A+100B+10C+D+100A+10B+C+10A+B=1110A+111B+11C+D=7826D=1 56-55=1 则当则B=0 C=5时-时当A=778267770=56 7051即一个各位数字互不相同的三位数,用它的三个数字组成一个最大的三位数,6. 再用这三个数字组成一个最小的三位数,组成的这两个三位数之差正好是原来. 求原来的三位数的三位数.更多精品文档.学习-----好资料移到左边首位数字前面,所构成44,将这个7. (1) 一个自然数的个位数字是 4倍,那么原数最小是多少?的新数恰好是原数的一个五位数,将它的各位数字顺序颠倒就可以得到一个新的五位数,而且(2)/4倍,那么原来的五位数是多少这个新的五位数恰好是原数的)(1219782)(中的一个数字,不同的字母2,……908. 如图5-18,每一个英文字母代表,1 、RF分别代表什么数字?、、、代表不同的数字,则字母AQT更多精品文档.学习-----好资料分析:不QAQ×T=1符合题意,当Q=6时为5或6 当Q=5时A=2 .........QTAQ等于T=1 则........AQ×T=AQF=3R=7,Q=5,T=1,A=2,所以“美”三个汉字分别代表三个各不相同的“峡”、中的竖式里,“江”、9. 图5-19. 数字,请把这个竖式写出来分析:=6 ,所以美0,1,5,6中的一个,通过实验排除0,1,5先确定美是□□江,则=×江4或8之一,又因为江峡美或美通过确定江是2 排除,所以江=24或8=8=□□□峡,则峡由于江峡美×峡所示的除法5-2010. 请把如图竖式中空缺的数字补上,其中的商是多少?分析:1 7 则除数个位是7,商的十位数字是=6.........6□□×□□除数的十位数3=×□□□61 则商的个位数字是,7.........6□8 字是更多精品文档.学习-----好资料11. 请把图5-21中的除法竖式补充完整。
高斯小学奥数四年级上册含答案第12讲_乘法原理进阶

第十二讲乘法原理进阶在之前我们学习了“加法原理与乘法原理”一讲,即分类相加与分步相乘的思想.如果完成一件事分为几个步骤,在每一个步骤中又有不同的方法,那么把每步的方法数相乘就得到所有的方法数——这就是乘法原理.要想把过程分成几个步骤从而应用乘法原理,必须保证各步骤之间满足下面两个要求:1.2.那么是不是只要分步骤完成整件事情就可以直接用乘法原理呢?如下图,把A、B、C三部分用三种不同的颜色染色,要求相邻两部分不能同色,那么一共有多少种不同的染法呢?A B C其实,整个染色过程是需要分为三步的,即分别给其中一块染色:当染色顺序为A→B→C时,那么A有3种染法,B不能和A一样,有2种染法,同样C有2种,那么一共就有“322⨯⨯”种染法;(C→B→A同理)当染色顺序为B→A→C时,那么B有3种染法,A不能和B一样,有2种染法,同样C有2种,那么一共就有“322⨯⨯”种染法;(B→C→A同理)当染色顺序为A→C→B时,那么A有3种染法,第二步C没有限制,也有3种染法,但是最后的B就出问题了,我们没法确定它有2种还是1种染法——如果C和A同色,则B有2种染法;如果C和A不同色,则B只有1种染法——此时,根据分步相乘的思想计算整个过程的染色方法“33?⨯⨯”就不再适用了.(C→A→B同理)因此,并不是只要分步完成整件事情就一定可以应用乘法原理,要想应用乘法原理,还必须满足第三个要求:3.——简称“前不影响后.....原则”染色问题,是应用乘法原理最常见的一类题型,其实,从上面对A、B、C 三部分的染色分析我们应该可以发现,染色的时候,要尽量避免“隔”着染,一定不要“跳”着染,而且,第一步要尽量去染“接触最多”的那一部分,这样,才能够使得后面的染色过程尽量避开“前影响后”.例题1如图,把A 、B 、C 、D 、E 这五部分用4种不同的颜色染色,且相邻的部分不能使用同一种颜色.请问:这幅图共有多少种不同的染色方法?「分析」分五步染色,先染哪一块呢?能否按照A 、B 、C 、D 、E 的顺序染呢? 练习1如图,把A 、B 、C 、D 这四部分用4种不同的颜色染色,且相邻的部分不能使用同一种颜色.请问:这幅图共有多少种不同的染色方法?例题2某市实行垃圾分类处理.每个地方放置五个垃圾桶,从左向右依次标明:电池、塑料、废纸、易拉罐、其它.现在准备把五个垃圾桶染成红、绿、蓝这3种颜色之一.(1)要求相邻两个垃圾桶颜色不同,一共有多少种染色方法? (2)要求相邻两个垃圾桶颜色不同且回收易拉罐的垃圾桶不能染成红色,一共有多少种染色方法?「分析」如果我们先染废纸垃圾桶:当它染红色时,回收易拉罐的垃圾桶可以染绿、蓝两种颜色;而当它染绿色(蓝色)时,回收废纸的垃圾桶只能染蓝色(绿色).因此先染废纸垃圾桶时,会影响易拉罐垃圾桶的染色方法数,就不能直接用乘法原理计算了.那么我们应该先给哪个垃圾桶染色呢?练习2麦兜很挑食,只吃带有鱼丸或粗面的搭配.一天它和3位同学来餐厅吃东西,一开口就要鱼丸粗面,结果老板说没有.这个时候,由于时间太晚,餐厅快打烊了,只能做牛肚河粉,鱼丸油面,猪肉米线和牛肉拉面各一份,请问它们四只猪各点一份,有几种点法?在例题2中,有一个垃圾桶是有特殊要求的——易拉罐垃圾桶不能染成红色,我们通过尝试可知:如果一开始先染其他的垃圾桶,那么前面垃圾桶的染色方法就会影响到易拉罐垃圾桶的染色方法数,即不能满足“前不影响后”原则,而如果首先染易拉罐垃圾桶,则不会出现该问题,所以一般而言,如果题目中有些对象是有特殊要求的,那么我们分步..分析计算的时候,首先要考虑这些特殊的对象.例题3卡莉娅、墨莫、小高和大头4名同学竞选班委.有班长、学习委员、生活委员三个职位,每个人只能担任一个职位,并且每个职位只能由一个人担任.(1)有多少种可能的选举结果?(2)如果班长必须由卡莉娅来担任,有多少种可能的选举结果?(3)如果生活委员只能在墨莫和大头之中选,有多少种可能的选举结果?(4)如果学习委员不能由小高担任,有多少种可能的选举结果?「分析」可以按照职位一一确定,第(2)问中,班长只能由卡莉娅来担任,那么先确定哪一个职位的人选呢?其他小问呢?练习3甲、乙、丙、丁、戊5个人竞选班委.有班长、副班长、纪律委员、卫生委员四个职位,每个人只能担任一个职位,并且每个职位只能由一个人担任:请问:(1)一共有多少种可能的选举结果?(2)如果副班长只能在甲、丁和戊中选,有多少种可能的选举结果?(3)如果卫生委员不能由乙、丙担任,有多少种可能的选举结果?例题4甲、乙、丙、丁四个人要住进A、B、C、D四间房间,每个房间住一个人.其中甲不住A房间,丙只住D房间.请问:这四个人住进四个房间有多少种住法?「分析」本题中甲和丙有特殊要求,我们应该先考虑甲还是丙呢?练习4甲、乙、丙、丁四个人要住进A 、B 、C 、D 四间房间,每个房间住一个人.其中甲只住A 或B 房间,丙只住A 、B 或C 房间.请问:这四个人住进四个房间有多少种住法?例题5甲、乙、丙、丁、戊五人要驾驶A 、B 、C 、D 、E 这五辆不同型号的汽车,请计算在下列情况下,分别共有多少种不同的安排方案: (1)只有甲能开汽车A ,乙不会开汽车B ;(2)会开A 的只有甲和乙,会开E 的只有甲、乙、丙.「分析」第(1)问中,甲和丙两人有特殊要求,我们应该先考虑哪一个人呢?第(2)问中,A 和E 两车有特殊要求,我们应该先考虑哪辆车呢?接下来我们分析一下“放相同棋子”的问题.如右图,将2枚相同的棋子放入2×2的方格内,每个格子只能放1枚,且要求每行每列最多只能放1枚,那么一共会有几种方法呢?其实,要把两枚相同的棋子放进格子内,只需要选出两个格子即可,然后每个格子里放一枚棋子.一共有两行,所以必定会是每行一枚,所以我们完全可以分行选格子,第一行有两种选法,第一行选好后,第二行就只有一种选法了,所以一共有2×1=2种.例题6右图是一个阶梯形方格表,在方格中放入五枚相同的棋子,使得每行、每列中都只有一枚棋子,这样的放法共有多少种?「分析」容易看出,每行只能有1枚棋子,每列也只能由一枚棋子,我们可以把放五枚棋子的过程分成五步:一行一行或一列一列的放.课堂内外四色定理四色定理与费马大定理、哥德巴赫猜想并称为近代数学三大难题.四色定理的内容是:对于任何一张地图,只用四种颜色,就可以把有相邻边界的国家染上不同的颜色.四色问题的提出来自英国.1852年,在大学读书的格斯里向他的老师——著名数学家摩根提出了这个问题,摩根没有能找到解决这个问题的途径.“四色问题”提出以后,最初并没有引起广泛的重视,许多数学家低估了它的难度.就连素以谦虚著称的德国数论专家闵可夫斯基在大学上拓扑课时也说:四色问题之所以一直没有获得解决,那仅仅是由于没有一流的数学家来解决它.说罢,他拿起粉笔,竟要当堂给学生推导出来,结果没有成功.下一节课他又去试,还是没有成功.过了几个星期,仍无进展.有一天,他刚跨进教室,适逢天上雷声大作,震耳欲聋.他马上对学生说:“上天在责备我自大,我也无法解决四色问题.”这样,四色问题就成了世界最著名的问题之一.l00多年中,“四色问题”使数学家们深为困扰.没有人能证明它,也没有人推翻它.电子计算机问世以后,由于演算速度迅速提高,加之人机对话的出现,大大加快了四色猜想的证明进程.就在1976年6月,哈肯与阿佩尔在美国伊利诺斯大学的两台不同的电子计算机上,用了1200个小时,作了100亿次判断,终于完成了四色定理的证明,轰动了世界.作业1. 五个座位排成一排,小高、墨莫、萱萱、阿呆、阿瓜每人选一个座位坐下,其中每个座位只能坐一个人,且萱萱不坐在中间的位置.这五个人有多少种坐法?2. 如图,把A 、B 、C 这三部分用4种不同的颜色染色,且相邻的部分不能使用同一种颜色.请问,这幅图共有多少种不同的染色方法?3. 把A 、B 、C 、D 、E 这五部分用4种不同的颜色染色,且相邻的部分不能使用同一种颜色.这幅图共有多少种不同的染色方法?4. 甲、乙、丙、丁四个人排成一队,甲不当排头,乙不当排头也不当排尾,共有多少种不同的排法?5. 在的方格中放入两枚相同的棋子,要求两枚棋子既不在同一行也不在同一列,共有多少种放法?24 ABCD E第十二讲乘法原理进阶1.例题1答案:96详解:分步,分别给E、B、C、A、D染色,分别有4、3、2、2、2种染法,所以一共有4322296⨯⨯⨯⨯=种染色方法.2.例题2答案:48;32方法;(2)分步,先染易拉罐垃圾桶,再分别给废纸、塑料、电池、其他这四个垃圾桶染色,五个垃圾桶分别有2、2、2、2、2种染法,所以一共有2222232⨯⨯⨯⨯=种染色方法.3.例题3答案:24;6;12;18种;(2)分别确定班长、学委、生活委员的人选,分别有1、3、2种选法,所以共有1326⨯⨯=种;(3)分别确定生活委员、学委、班长的人选,分别有2、3、2种选法,所以共有23212⨯⨯=种;(4)分别确定学委、班长、生活委员的人选,分别有3、3、2种选法,所以共有33218⨯⨯=种.4.例题4答案:4种选法.5.例题5答案:18;24详解:(1)先考虑甲,后考虑乙,再考虑其他三个人,分别有1、3、3、2、1种可能,共有⨯⨯⨯⨯=种;1332118(2)先考虑A,后考虑E,再考虑其他三辆车,分别有2、2、3、2、1种可能,所以共有⨯⨯⨯⨯=种.22321246.例题6答案:16详解:一共要选5个格子放棋子,一行一行选,每行1个,而且不能在同一列,从上往下,5行分别有2、2、2、2、1种选法,所以一共有2222116⨯⨯⨯⨯=种选法.7.练习1答案:48详解:分步,分别给B、C、A、D染色,分别有4、3、2、2种染法,所以一共有⨯⨯⨯=种染色方法.4322488.练习2答案:6详解:先让麦兜点,只有鱼丸油面1种可选,然后让其他3位同学依次点,分别有3、2、1种选法,共分四步,乘法原理,所以共有13216⨯⨯⨯=中不同的选法.9.练习3答案:120;72;72⨯⨯⨯=5432120(2)先确定副班长,再依次确定其他,共有343272⨯⨯⨯=种;(3)先确定卫生委员,再依次确定其他,共有343272⨯⨯⨯=种.10.练习4答案:8种选法.11.作业1答案:96.简答:可以按照萱萱、小高、墨莫、阿呆、阿瓜的顺序安排座位,有4432196⨯⨯⨯⨯=种.安排座位的顺序不唯一.12.作业2答案:24简答:可以按照A、B、C的顺序染色,43224⨯⨯=种.染色顺序不唯一.13.作业3答案:96简答:可以按照A、B、C、D、E的顺序染色,有4322296⨯⨯⨯⨯=种.染色顺序不唯一.14.作业4答案:8简答:按照乙、甲、丙、丁的顺序安排,有22218⨯⨯⨯=种排法.15.作业5答案:12简答:一行一行选位置,第一行有4个格子可选,即4种选法;第二行还有3个格子可选,即有3种选法.因此有4312⨯=种不同的放法.。
苏教版-小学数学四年级第12课时 求未知加数

第八单元10以内的加法和减法第12课时求未知加数教学内容:课本第68-69页。
教学目标:1、让学生认识求未知加数的算式,探索并掌握求未知加数的方法,初步体会加减法之间的联系。
2、让学生积累把一个数凑成10的经验,为将来学习进位加作准备。
3、发展学生的数学理解能力和发散思维能力,继续培养独立思考、与人交流的学习习惯。
教学重点:掌握求未知加数的不同方法。
教学难点:正确求出未知加数。
课前准备:教学挂图、学具教学过程:一、情境导入1、口算:口算卡片练习。
2、今天数学课,智慧爷爷来到了我们的课堂,他带来了一个盒子。
二、探究交流1、教学例题。
(1)媒体出示装了苹果的盒子图。
问:图中盒子里如果装满苹果,可以装几个?已经装了几个?还差几个?(2)进行说明:同学们,盒子里可以装10个苹果,我们已经装了8个,还有几个没有装的。
(教师边说边板书:8+()=10)(3)如果不是我们已经算出来了,我们就不知道还有几个没有装,所以我们把没有装的,也就是不知道的这个数用括号括起来,表示不知道的意思。
(4)这个算式就读做:8加几等于10。
丹青骈丽工方好,水墨清华写亦奇;欲画荷花比西子,浓妆淡抹各相宜。
画荷,当然以宋人的“夺造化而移精神”为正宗大道。
但宋人画荷留存至今的作品却并不多。
有几件小品如《出水芙蓉》《太液风荷》等,或朵花片叶,或锦机密云,无不活色生香,精美绝伦,可惜皆佚名。
名家的作品,如赵佶《池塘秋晚图》长卷中的片断,钱选《百花图》长卷中的片断以及《白莲图》短卷,皆水墨勾染,淡宕清空,又别是一番韵致。
至明代中后期,以白阳、青藤为代表,演为波澜壮阔的水墨大写意,给人以振聋发聩之感。
不过,画荷真正蔚成中国画科中的一门大宗,是在清代之后,至近世三百数十年间,名家辈出,名作纷陈,迈绝前代。
尤以八大山人、齐白石、吴湖帆、张大千、潘天寿、刘海粟、唐云、谢稚柳、程十髮九家的风格、成就为最著,也都是我长年心慕手追的典范。
育儿知识大全网/ 。
西南师范版-小学数学四年级第12课时 求未知加数

第八单元10以内的加法和减法第12课时求未知加数教学内容:课本第68-69页。
教学目标:1、让学生认识求未知加数的算式,探索并掌握求未知加数的方法,初步体会加减法之间的联系。
2、让学生积累把一个数凑成10的经验,为将来学习进位加作准备。
3、发展学生的数学理解能力和发散思维能力,继续培养独立思考、与人交流的学习习惯。
教学重点:掌握求未知加数的不同方法。
教学难点:正确求出未知加数。
课前准备:教学挂图、学具教学过程:一、情境导入1、口算:口算卡片练习。
2、今天数学课,智慧爷爷来到了我们的课堂,他带来了一个盒子。
二、探究交流1、教学例题。
期刊发表详细问题了解下!(1)媒体出示装了苹果的盒子图。
问:图中盒子里如果装满苹果,可以装几个?已经装了几个?还差几个?(2)进行说明:同学们,盒子里可以装10个苹果,我们已经装了8个,还有几个没有装的。
(教师边说边板书:8+()=10)(3)如果不是我们已经算出来了,我们就不知道还有几个没有装,所以我们把没有装的,也就是不知道的这个数用括号括起来,表示不知道的意思。
(4)这个算式就读做:8加几等于10。
(5)通过图我们知道了还有2个没有装,也就是8加2等于10。
(教师在黑板上填写。
)如果没有图,你该怎么想8加几等于10呢?小组讨论。
(6)学生说的只要有道理就可以了,教师可以引导学生回答。
讨论后形成如下板书:因为10可以分成8和2,所以8+(2)=10。
8和2合成10,所以8+(2)=10。
10-8=2,所以8+(2)=10。
(7)思考:6+()=10,小朋友可以怎么想?发表意见,只要说的有道理。
2、延伸。
(1)把数字卡片贴在黑板上,再在黑板上写上 4+()=103+()=7 ()+5=10 7+()=10三、反馈完善1、完成第2题。
(1)看书上题目,明确要求:先画满10个图形,再填空。
(2)学生独立在书上画图形填空。
指名说出每一行画了几个图形,()里填了什么数。
2.完成第3题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第12讲复杂竖式
内容概述
需要较强推理能力的竖式问题.学会运用奇偶分析、整体分析、分粪讨论等技巧性较高的方法.
典型问题
兴趣篇
1.图12-1是一个字母竖式,相同的字母表示相同的数字,不同的字母表示不同的数字.请把竖式用数字表示出来.
2.在图12-2中的各个方框内填人恰当的数字后,可使算式成立,并且个位上的5个数字从上向下看,恰好是图12-3中顺时针次序的连续5个数字,十位上的5个数字也有这样的性质.请问:竖式中计算的结果是多少?
3. 请把1至9这9个数字填在图12-4的方框中(其中有3个数字已经填好),使得加法和乘法这两个算式都成立.
4. 图12-5是一个乘法竖式,请在其中的10个方框内分别填入0至9这10个数字,使得竖式成立.
5.如图12-6,在乘法竖式的每个方框中填入一个数字,使其成为正确的竖式,那么所得的乘积应该是多少?
6. 如图12-7,在乘法竖式的每个方框中填入一个数字,使其成为正确的竖式,那么所得的
乘积应该是多少?
7. 在图12-8的方框内填入恰当的数字,可以得到一个正确的乘法竖式. 已知这样的填法有两种,这两种填法所得到的两个不同的乘积相差多少?
8. 在图12-9的方框内填上适当的数字,使得竖式成立,请写出所有的答案.
9. 请把图12-10中的除法竖式补充完整.
10. 请把图12-11中的除法竖式补充完整. 这个算式的被除数、除数以及商的总和是多少?
拓展篇
1. 在图12-12中的字母竖式中,相同的字母代表相同的数字,不同的字母代表不同的数字. 已知个位向十位的进位为2,且E是奇数,则A、B、C、D分别代表什么数字?
2. 在图12-13中,相同的字母代表相同的数字,不同的字母代表不同的数字. 请给出两种使竖式成立的填法.
3. 在图12-14所示的乘法竖式中,每个方框和字母都代表一个数字,相同的字母代表相同的数字,不同的字母代表不同的数字,请问:A、B、C、D各代表什么数字?
4. 在图12-15所示的乘法竖式中,每个方框和汉字都代表一个数字,相同的汉字代表相同的数字,不同的汉字代表不同的数字. 请问:这个乘法算式最后的乘积是多少?
5. 图12-16是一个乘法竖式,其中的每个方框和汉字都代表一个数字,相同的汉字代表相同的数字,不同的汉字代表不同的数字. 试问:当算式成立时,“ ”所代表的八位数是多少?
6. 如图12-17,请把这个乘法竖式补充完整.
7. 如图12-18,请把这个乘法竖式补充完整.
8. 请把图12-19中的除法竖式补充完整,其中被除数是多少?(注意本题有小数点)
9. 在如图12-20
所示的除法竖式中,在各个方框里填入适当的数字后可使竖式成立,那么巴西法国争夺冠军
在这15个方框中填入的数字最多能有多少个是偶数?
10. 在图12-21的除法竖式中,相同的字母代表相同的数字,不同的字母代表不同的数
字. 请问:被除数DEFGF是多少?
11. 请把图12-22中的除法竖式补充完整.
12. 请在图12-23中的每个方框内填入恰当的数字,使得除法竖式成立.
超越篇
1.在图12-24的加法竖式中,相同的字母代表相同的数字,不同的字母代表不同的数字,这个算式的结果是多少?
2.在图12-25的加法竖式中,相同的字母代表相同的数字,不同的字母代表不同的数字. 请
问:money所代表的五位数最多是多少?
3. 在图12-26的乘法竖式中,a、b、c、d、e分别代表不同的数字,且a+b+c=e. 请问adde:所代表的四位数是多少?
4. 请把图12-27中的除法竖式补充完整.
5. 在图12-28的竖式中,“奇”代表奇数,“偶”代表偶数,请把竖式补充完整.
6. 在图12-29的方框内填入适当的数字,使下面的小数除法竖式成立.
7. 电子数字0至9如图12-30所示,图12-31是由电子数字组成的乘法算式,但有一些已经模湖不清. 请将图12-31中的电子数字恢复,并将它写成横式:
8. 请将图12-32中的除法竖式补充完整.。
