高思竞赛数学导引 五年级第十三讲 数字谜综合学生版
五年级奥数.数字谜综合

数字谜综合涉及分数与小数的各种类型的数字谜问题,包括竖式的补填、算式的构造、小数的舍人与变化等.较为复杂的数字问题,以及其他略有综合性的数字谜问题.1.有一个四位整数,在它的某位数字前面加上一个小数点,再与这个四位数相加,得数是2000.81.求这个四位数是多少?【分析与解】设四位整数4的某位数字前加上一个小数点得到一个新的数B,A与B 的和为2000.81,而小数只能由B得到,且0.81为B的小数部分,所以小数点加在A的百位与十位之间,即缩小了100倍.有A+0.01A=2000.81,所以A=1981.2.老师在黑板上写了13个自然数,让小明计算平均数(保留两位小数),小明计算出的答数是12.43.老师说最后一位数字错了,其他的数字都对.正确答案应该是什么?【分析与解】老师说最后一位数字错了,那么前3位数字是正确的,所以正确的平均数在12.40~12.5(不能取12.5)之间,那么这13个数的和在161.2~162.5(不能取162.5),因为这13个数都是自然数,所以它们的和也应该是自然数.那么这13个数的和只能是162,它们的平均数应该是162÷13≈12.46.所以正确的平均数应该是12.46.3.两个带小数相乘,乘积四舍五人以后是22.5.这两个数都只有一位小数,且个位数字都是4.这两个数的乘积四舍五入前是多少?【分析与解】因为这两个带小数均只有一位小数,那么给它们均乘以10,则这两个数均是整数.开始它们的乘积在22.45~22.55(不能取22.55)之间,所以在这两个数在均乘以10以后再相乘而得到的乘积应该在2245~2255(不能取2255)之间.一一验证,2245=5×449,2246=2×1123,2247=3×7×107,2248=2×2×2×281,2249=13×173,2250=2×3×3×5×5×5,2251为质数,2252=2×2×563,2253=3×751,2254=2×7×7×23.其中只有2254可以表达为(2×23)×(7×7)=46×49,两个十位数字均为4的数的乘积.所以,四舍五人前的乘积应为2254÷10÷10=22.54.即两个数的乘积四舍五人前是22.54.4.[4.2×5-(1÷2.5+9.1÷0.7)]÷O.04=100改动上面算式中一个数的小数点的位置,使其成为一个正确的等式,那么被改动的数变为多少?【分析与解】我们先把题中左边算式计算一遍,在计算过程中发现问题.[4.2×5-(1÷2.5+9.1÷0.7)]÷0.04=[21-(0.4+13) ]÷0.04=[21-13.4]÷0.04=7.6÷0.04=190注意到在“[21-(0.4+13)]÷O.04”这一步中如果(0.4+13)是(4+13),那么最终的结果为100.所以只需将1÷2.5改为1÷0.25,即将2.5改为O.25即可.5.在算式2÷3÷4÷5÷6中添上若干个括号,使算式的结果是整数,并且尽可能小.试写出添加完括号后的算式.【分析与解】注意到将除号前加一个括号,可以使括号内的除号在脱括号之后变为乘号.又注意到2、3、4、5、6只有5含有质因数5,就是说其他的质因数可能经过变换运算法则除去,而质因数只能保留,且只能作为乘数,也就是说题中算式变化后是最终的结果最小为5.有2÷3÷4÷5÷6=EFCD,现在要得到5,扩大了5÷1180=900,所以必须将原来作为除数的30变为乘数30,有5×6=30,所以将5、6由除数变为乘数.有2÷3÷(4÷5÷6)=5,此式即为所求.6.用1,4,5,6四个数,并适当选择加号、减号、乘号、除号以及括号,组成一个结果等于24的正确算式.【分析与解】有24=2×2×2×3,常规的方法,无法使1,4,5,6通过运算得到24,但是注意到可利用分数:有4÷16=24,6÷14=24等.于是有下面两个算式满足:4÷(1-5÷6)=24,6÷(5÷4-1)=24.评注:此类题是常说的“24点”游戏:从一副扑克牌中除去大王、小王,A表示1,J 表示11,Q表示12,K表示13,其他的牌表示的数等于牌面数字.从剩下的52张牌中任意抽取4张,通过选择运算使它们最终的计算结果为24.7.1+1+1≈0.658上式是经过四舍五入得到的等式,其中每个△代表一个一位数.那么这3个△所代表的3个数分别是多少?【分析与解】设△代表的三个数从小到大为a、b、c.当a取最小值2时,1+1+1最小为12+18+19≈0.736,所以a最小取3.当a=3,b最小取 4时, 1+1+1最小为13+14+19≈0.694,所以b最小取5.当a=3,b=5时,1+1+1最小为13+15+19≈0.644,有可能.验证当,a=3,b=5,c=8时有13+15+18≈0.658.满足.所以这三个数分别为3、5、8.评注:此题从极端情况开始一一枚举而得.8.用0,1,2,…,9这10个数字组成5个两位数,每个数字只用一次,要求它们的和是一个奇数,并且尽可能的大.那么这5个两位数的和是多少?【分析与解】要求5个数的和是奇数,所以这5个数中有奇数个奇数,如果用9、8、7、6、5作十位数字,那么个位数字为0、1、2、3、4,这样组成的5个数中有2个数是奇数.所以调整,将9、8、7、6、4作为十位数字,0、1、2、3、5作为个位数字,那么组成的5个两位数的和是(9+8+7+6+4)×10+(0+1+2+3+5)=351.因为已经使十位数字尽可能的大,所以所得的和为最大值.即在满足题意下,得到的5个两位数的和为351.9.将I,2,3,4,5,6,7,8这8个数分成3组,分别计算各组数的和.已知这3个和互不相等,且最大的和是最小的和的2倍,那么最小的和是多少?【分析与解】设分成的3组数的和从大到小依次为a、b、c,a=2c,并且有a+b+c=b+3c=1+2+3+…+8=36.3c为3的倍数,36为3的倍数.所以b为3的倍数.解得b3c11a2c22=⎧⎪=⎨⎪==⎩,b6c10a2c20=⎧⎪=⎨⎪==⎩,b9c9a2c18=⎧⎪=⎨⎪==⎩,b12c8a2c16=⎧⎪=⎨⎪==⎩,b15c7a2c14=⎧⎪=⎨⎪==⎩,不难看出随着b的增大,a在减小,所以其他情况不用再讨论.满足条件的解只有b=12,c=8,a=16.1,2,3,4,5,6,7,8可以分成{1,2,3,4,6}、{5,7}、{8}这三组.所以满足题意的最小一组数的和为8.10.用1,2,3,4,5,6,7,8,9这9个数字组成3个三位数(每个数字只用一次),使其中最大的三位数被3除余2,并且尽可能的小;次大的三位数被3除余1;最小的三位数能被3整除.那么,最大的三位数是多少?【分析与解】被3除余2、1、0的数,其数字和除以3也分别余2、1、0.为了使最大的三位数尽可能的小,所以其百位最小取3,因为如果取1或2,那么剩下两个三位中的某一个其百位数字大于3,显然不满足.当最大三位数的百位取3时,1,2,3,4,5,6,7,8,9组成的三个三位数只能是3口口、2口口、l口口,而3口口的十位最小取4,百位与十位的数字和为7,则个位只能取7.所以满足条件的最大三位数是347.11.红、黄、蓝和白色卡片各一张,每张上写有一个数字.小明将这4张卡片如图7-l 放置,使它们构成一个四位数,并计算这个四位数与它的数字之和的10倍的差.结果小明发现,无论白色卡片上是什么数字,计算结果都是1998.问红、黄、蓝3张卡片上各是什么数字?红黄白蓝图7—1【分析与解】设这个四位数为abcd,其中a、b、c、d依次代表红、黄、白、蓝.有abcd=1000a+lOOb+10c+d,而abcd的数字和为a+b+c+d,所求的差为:(1000a+100b+10c+d)-10(a+b+c+d)=1998,即990a+90b-9d=1998.因为a、b、d均为小于10的自然数,所以a=2,b=l,d=8.即红、黄、蓝3张卡片上的数字分别为2、1、8.评注:对于用字母表示的数,注意到其在10进制中与其各个位数数字的关系.如:abcde 中的a在万位表示10000a,b在千位表示1000b,….12.一个四位数的数码都是由非零的偶数码组成,它又恰是某两个偶数码组成的数的平方.问这个四位数是多少?【分析与解】设这个四位数为A=abcd,其为B=ef的平方,因为f只能取0、2、4、6、8,所以B平方后的个位为0、4、6.即d为4或6.而B中的十位数字e只能取4、6、8这三个数,不然平方后得到的不是4位数.验证有68×68=4624满足.13.一个整数乘以13后,乘积的最后三位数是123.这样的整数中最小的是多少?【分析与解】设A=cba,B=123,有cba×13=123.方法一:123一定是13的倍数,而13的倍数满足其后三位与前面隔开,差是13的倍数.123÷13=9……6,那么6123一定是13的倍数,且为满足条件的最小自然数.那么题中所求的最小整数为6123÷13=471.方法二:有A的个位a只能是1,不然其与13的乘积的个位不是3.显然有A的个位1与13相乘过程中进有1,则A的十位b乘以13得到的数的个位为2-1=1,显然只有当b=7时才能满足.此时A的十位7与13相乘过程中进有9,则A的百位c乘以13得到的数的个位为(1+10)-9=2,显然只有c=4.于是417而乘以13后得到的积其最后三位数是123.而这样的数中最小的是471.14.将1,2,3,4,5,6,7,8,9分别填入图7-2中的9个圆圈内,使其中一条边上的4个数之和与另一条边的4个数之和的比值最大.那么这个比值是多少?【分析与解】为了使比值尽可能的大,那么一边应尽可能的小,另一边尽可能的大.有两种情况:第一种情况,两边上各自4个数字和的比值为47894321++++++=2810=2.8,第二种情况,两边上各自4个数字和的比值为6+7+8+96+1+2+3=3012=2.5.显然有第一种情况的比值最大,为2.8.15.在图7-3所示的除法算式中,只知道一个数字“3”,且商是一个循环小数.问被除数是多少?【分析与解】为了方便说明,标出字母.O.A3B =A3B999=A3B÷999=EF÷CD,被除数与除数均为两位数.所以A3B999可以约分后为EFCD,999为除数CD的倍数,999=3×3×3×37,999的约数中只有27、37为两位数,所以除数CD只能是27或37.第四行对应为CD×3,且为三位数,所以CD=37.那么第四行为37×3=111.则第五行首位为0减1,借位后为9.所以第五行为90,对应为CD×B+EF=37×B+EF(EF<CD).当B=1时,37×B+EF小于37×(1+1)=54,不满足;当B=2时,37×B+EF=37×2+EF=90,解得被除数EF=16.数字谜涉及质数与合数等概念,以及需要利用数的整除特征、分解质因数等数论手段解的数字谜问题.1.试将1,2,3,4,5,6,7分别填入下面的方框中,每个数字只用一次: 口口口(这是一个三位数).口口口(这是一个三位数),口(这是一个一位数),使得这三个数中任意两个都互质.已知其中一个三位数已填好,它是714,求其他两个数.【分析与解】714=2×3×7×17.由此可以看出,要使最下面方框中的数与714互质,在剩下未填的数字2,3,5,6中只能选5,也就是说,第三个数只能是5.现在来讨论第二个数的三个方框中应该怎样填2,3,6这3个数字.因为任意两个偶数都有公约数2,而714是偶数,所以第二个的三位数不能是偶数,因此个位数字只能是3.这样一来,第二个三位数只能是263或623.但是623能被7整除,所以623与714不互质.最后来看263这个数.通过检验可知:714的质因数2,3,7和17都不是263的因数,所以714与263这两个数互质.显然,263与5也互质.因此,其他两个数为263和5.2.如图19-1,4个小三角形的顶点处有6个圆圈.如果在这些圆圈中分别填上6个质数,它们的和是20,而且每个小三角形3个顶点上的数之和相等.问这6个质数的积是多少?【分析与解】设每个小三角形三个顶点上的数的和都是S.4个小三角形的和S相加时,中间三角形每个顶点上的数被算了3次,所以 4S=2S+20,即S=10.这样,每个小三角形顶点上出现的三个质数只能是2,3,5,从而六个质数是2,2,3,3,5,5,它们的积是:2×2×3×3×5×5=9003.在图19-2.所示算式的每个方框内填人一个数字,要求所填的数字都是质数,并使竖式成立.【分析与解】记两个乘数为7a b 和cd 其中a 、b 、c 、d 的值只能取自2、3、5或7.由已知条件,b 与c 相乘的个位数字仍为质数,这只可能是b 与c 中有一个是5另一个是3、5或7,如果b 不是5,那么c 必然是5,但73×5=365、77×5=385的十位数字都不是质数.因此b 是5,c 是3、5、7中的一个,同样道理,d 也是3、5、7中的一个.再由已知条件,75a 的乘积的各位数字全是质数,所以乘积肯定大于2000,满足积大于2000且a 、c 取质数,只有以下六种情况:775×3=2325,575×5=2875,775×5=3875,375×7=2625,575×7=4025,775×7=5425.其中只有第一组的结果各位数字是质数,因此a=7,c=3,同理,d 也是3.最终算式即为775×33=255754.把一个两位数的个位数字与其十位数字交换后得到一个新数,它与原来的数加起来恰好是某个自然数的平方.那么这个和数是多少?【分析与解】 设原来的两位数为xy ,则交换十位数字与个位数字后的两位数为,两个数的和为yx ,两个数和为 xy +yx =1010x y x y +++()11x y =+是ll 的倍数,因为它是完全平方数,所以也是11 ×11=121的倍数.但是这个和小于100+100=200 <121×2,所以这个和数只能是121.5. 迎杯×春杯=好好好在上面的乘法算式中,不同的汉字表示不同的数字,相同的汉字表示相同的数字.那么“迎+春+杯+好”之和等于多少?【分析与解】 好好好=好×111=好×3×37.那么37必定是“迎杯”或“春杯”的约数,不妨设为“迎杯”的约数,那么“迎杯”为37或74. 当“迎杯”为37时,“春杯”为“好”×3,且“杯”为7,此时“春杯”为27,“好”为9,“迎+春+杯+好”之和为3+2+7+9=21;当“迎杯”为74时,“春杯”为“好”×3÷2,且“杯”为4,此时“春杯”为24,“好”为16,显然不满足.所以“迎+春+杯+好”之和为3+2+7+9=21.6.数数×科学=学数学在上面的算式中,每一汉字代表一个数字,不同的汉字代表不同的数字.那么“数学”所代表的两位数是多少?【分析与解】“学数学”是“数数”的倍数,因而是“数”与1l的倍数.学数学=学×101+数×10是“数”的倍数,而101是质数,所以“学”一定是“数”的倍数.又“学数学”是11的倍数,因而:“学+学-数”为11的倍数.因为“学”是“数”的倍数,从上式推出“数”是11的约数,所以“数”=1,“学”=(11+1)÷2=6.“数学”所代表的两位数是16.7.将1,2,3,4,5,6,7,8,9这9个数字分别填人下式的各个方框中,可使此等式成立:口口×口口=口口×口口口=3634.填好后得到三个两位数和一个三位数,这三个两位数中最大的一个是多少?【分析与解】3634=2×23×79,表达为两个两位数的乘积只能是(2×23)×79,即46×79;表达为一个两位数与一个三位数的乘积,只能是23×(2×79)=23×158.满足题意,所以这三个两位数中最大的一个是79.8.六年级的学生总人数是三位数,其中男生占35,男生人数也是三位数,而组成以上两个三位数的6个数字,恰好是l,2,3,4,5,6.那么六年级共有学生多少人?【分析与解】设六年级总人数为xyz,其中男生有abc人.有xyz×35=abc,即5abc=3xyz,其中xyz为5的倍数,所以z为5.而abc为3的倍数,所以其数字和a+b+c应为3的倍数,则在剩下的5个数中,a、b、c(不计顺序)只能为1,2,6或l,2,3或4,2,6或4,2,3.而c不能是偶数(不然z应为0),所以只能是l,2,6或1,2,3或4,2,3可能满足;又因为xyz最大为645,对应abc为387,即c不超过3.于是abc有可能为261,123,321,213,231,243这6种可能,验证只有当abc=261时,对应xyz为261÷3×5=435.所以六年级共有学毕435人.9.图19-3是三位数与一位数相乘的算式,在每个方格填入一个数字,使算式成立.那么共有多少种不同的填法?【分析与解】设1992=abc×d(a,b,c,d可以相同),有1992=2×2×2×3×83,其中d可以取2,3,4,6,8这5种,对应的算式填法有5种.10.在图19-4残缺的算式中,只写出3个数字l,其余的数字都不是1.那么这个算式的乘积是多少?【分析与解】如下图所示,为了方便说明,将某些数用字母标出.第4行口口1对应为AB×C,其个位为1,那么B×C的个位数字也是1,而B、C又均不能为1,所以只有3×7,9×9对应为1,那么B为9、7或3.第3行10口对应为AB×D,可能为100、102、103、104、105、106、107、108、109.103、107、109均为质数,没有两位数的约数,不满足;100、105没有个位数字为3、7、9的约数,不满足;102=17×6、104=13×8、106=53×2、108=27×4,但102、104对应的AB中4均为1,不满足.所以AB为53或27.当AB为27时,第4行为27×C,且个位数字为1,所以只能为27×3=8l,但不是三位数,不满足.当AB为53时,第4行为53×C,且个位数字为1,所以只能为53×7=371,因此被乘数必须为53,乘数为72,积为3816.11.图19-5是一个残缺的乘法竖式,在每个方框中填入一个不是2的数字,可使其成为正确的算式.那么所得的乘积是多少?【分析与解】方法一:由已知条件,最后结果的首位数字不能是2,因此只能是3.这说明千位上作加法时有进位.百位数上相加时最多向千位进2,所以要使千位数有进位,其中的未知数字至少是10-2-2=6,即三个三位数加数中的第二个至少是600.因为它是第一个乘数与一个一位数字的乘积,因此该乘数肯定大于60.第二个乘数的百位数字与第一个乘数的乘积在220~229之间,所以它只能是3(否则4×60>229).而220~229之间个位数字不是2且是3的倍数的只有225=3×75和228=3×76.如果第一乘数是75,又第二个乘数的百位数字是3,那么它们的乘积小于75×400=30000,它的首位数字也就不可能是3,不满足.乘数是76,另一个乘数就要大于30000÷76>394,那么只有395、396、397、398、399这五种可能,它们与76的乘积依次为30020、30096、30172、30248、30324.由于各个数字都不能是2,所以只有76×396=30096满足题目的要求.算式中所得的乘积为30096.方法二:为了方便说明,将某些位置标上字母,如下图所示,因为干位最多进1,而最终的乘积万位又不能是2,所以只能是3:而第5行对应为22口=AB×C,其中C不可能为1,又不能为2,那么最小为3.当C为3时,22口=AB×3,那么A只能为7,B只能为4,5或6,(1)当B为4时,74×3=222,第5行个位为2,不满足题意;(2)当B为5时,AB×CDE对应为75×3DE,小于30000,不满足;(3)当B为6时,AB×CDE对应为76×3DE,D只能为9,此时第4行对应为AB×D即76×9=684.因为30000÷76>394,所以39E只有395、396、397、398、399这五种可能,它们与76的乘积依次为30020、30096、30172、30248、30324.由于各个数字都不能是2,所以只有76×396=30096满足题目的要求.验证C取其他值时没有满足题意的解.所以算式中所得的乘积为30096.【分析与解】易知除号下第二行的首位为9.除号下第一行开头两位为1、0,商的十位为0.第二行9口对应为CD×A,(1)9口不可能为90,不然第一行前三位10口与第二行90的差不可能为一位数,不满足第三行特征;(2)9口对应为91时,第三行的首位对应为10口-91,最小为9,所以只能为9,那么有91=CD×A,928=CD×B,不可能;(3)9口对应为92时,第三行的首位对应为10口-92,最小为8,所以可能为8、9,①如果为9,那么对应有92=CD×A,928=CD×B,不可能;②如果为8,那么对应有92=CD×A,828=CD×B,不难得知A=l,B=9,CD=92时满足,那么被除数为92×109=10028.验证没有其他的情况满足,所以这个除法算式的商数为109.13.若用相同汉字表示相同数字,不同汉字表示不同数字,则在等式学习好勤动脑×5=勤动脑学习好×8中,“学习好勤动脑”所表示的六位数最小是多少?【分析与解】设“学习好”为x,“勤动脑”为Y,则“学习好勤动脑”为1000X+Y,“勤动脑学习好”为1000y+x,有(1000x+Y)×5=(1000y+x)×8,化简有4992x=7995y,4992=128×3×13,7995=3×41×5×13,即128x=205y,有205,128xy=⎧⎨=⎩410,256xy=⎧⎨=⎩615,384xy=⎧⎨=⎩820512xy=⎧⎨=⎩所以,“学习好勤动脑”所表示的六位数可能为205128,410256,615384,820512,但是不能有重复数字,所以只有410256,615384满足,其中最小的是41025614.互为反序的两个自然数的积是92565,求这两个互为反序的自然数.(例如102和201,35和53,11和11,…,称为互为反序的数,但120和2l 不是互为反序的数.)【分析与解】 首先可以确定这两个自然数均为三位数,不然得到的乘积不可能为五位数. 设ABC ×CBA =92565,那么C 、A 中必定有一个为5,一个为奇数.不妨设C 为5.5AB ×5BA =92565,那么A 只能为1,1551B B =92565.又注意到92565=3×3×5×11×1l×17.验证只有15B 为165时满足,所以这两个自然数为165、561.15.开放的中国盼奥运×口=盼盼盼盼盼盼盼盼盼上面的横式中不同的汉字代表不同的数字,口代表某个一位数.那么,“盼”字所代表的数字是多少?【分析与解】 我们从“口”中所应填入的一位自然数开始分析,设A=“开放的中国盼奥运”,B=“盼盼盼盼盼盼盼盼盼”.于是B=A×口.显然口内不会是1.由于口是B 的约数,因此口不会是“盼”所代表的数字,要不然A 就等于111111111,这说明口内不会是5,而111111111不是7的倍数,说明口内也不会是7.如果口内填3,则“盼”只能是1或2,当“盼”是1时,B÷3=37037037,不符合要求;当“盼”时2时,B ÷3=74074074,也不符合要求;说明口内不能填入3.口内也不会是偶数数字2、4、6和8.因为口内是偶数数字时,“盼”也是偶数数字,口内显然不会是2,如果口内是4,根据被4整除的特征,“盼”只能是8,这时A 就成了一个九位数,说明口内不能是4;类似的,可以说明口内不能是6和8.综上所需,口的数字只能是9,这时利用91111...1个=12345679×9,可以得到9个盼盼盼盼...盼=12345679×9×盼.于是“盼”代表的数字必须同时满足下面两个条件:经验证知◇=盼=7,即86419753×9=777777777.。
高思学校竞赛数学导引(四年级)

$应用题第#*讲% !!!!!!!!!! &)
第!%讲!!复杂竖式
$数字谜问题第(讲%!!!!!!!!! &$
第!&讲!!横式问题
$数字谜问题第%讲%!!!!!!!!! $(
第!’讲!!格点与割补
$几何问题第’讲% !!!!!!!!! #"#
第!(讲!!行程问题二
$应用题第#)讲%!!!!!!!!!! #"&
)!012"’#(3!" ##/""+!##"#.!#!4!"! "!#&#!)$!!!!!!!!!!!!""#!)#&!
!*!012"’ (3!" #/"##.""+##!4!"! "!#( &$!!!""#& ($!!!"$#"* (# ’$!!!"’#* "( ’#!
$%#
!!!"!"!#-"#"-#&&%",#!!#!"#$!!""#$!#!"!.&&#!"(%"!)))%!"!#!
目 录
!目!录
第 ! 讲!!整数计算综合
$计算问题第(讲% !!!!!!!!!! #
第 " 讲!!数阵图初步
$数字谜问题第)讲% !!!!!!!!! %
第 # 讲!!竖式问题
$数字谜问题第’讲%!!!!!!!!! #’
第 $ 讲!!几何图形剪拼
$几何问题第*讲%!!!!!!!!!! !!
小学五年级奥数基础教程目30讲全

小学奥数根底教程(五年级) 第1讲数字迷〔一〕第2讲数字谜(二)第3讲定义新运算(一)第4讲定义新运算(二)第5讲数的整除性(一)第6讲数的整除性(二)第7讲奇偶性〔一〕第8讲奇偶性〔二〕第9讲奇偶性〔三〕第10讲质数与合数第11讲分解质因数第12讲最大公约数与最小公倍数〔一〕第13讲最大公约数与最小公倍数〔二〕第14讲余数问题第15讲孙子问题与逐步约束法第16讲巧算24第17讲位置原那么第18讲最大最小第19讲图形的分割与拼接第20讲多边形的面积第21讲用等量代换求面积第22 用割补法求面积第23讲列方程解应用题第24讲行程问题〔一〕第25讲行程问题〔二〕第26讲行程问题〔三〕第27讲逻辑问题〔一〕第28讲逻辑问题〔二〕第29讲抽屉原理(一)第30讲抽屉原理(二)第1讲数字谜〔一〕数字谜的内容在三年级与四年级都讲过,同学们已经掌握了不少方法。
例如用猜测、拼凑、排除、枚举等方法解题。
数字谜涉与的知识多,思考性强,所以很能锻炼我们的思维。
这两讲除了复习稳固学过的知识外,还要讲述数字谜的代数解法与小数的除法竖式问题。
例1 把+,-,×,÷四个运算符号,分别填入下面等式的○内,使等式成立〔每个运算符号只准使用一次〕:〔5○13○7〕○〔17○9〕=12。
分析与解:因为运算结果是整数,在四那么运算中只有除法运算可能出现分数,所以应首先确定“÷〞的位置。
当“÷〞在第一个○内时,因为除数是13,要想得到整数,只有第二个括号内是13的倍数,此时只有下面一种填法,不合题意。
〔5÷13-7〕×〔17+9〕。
当“÷〞在第二或第四个○内时,运算结果不可能是整数。
当“÷〞在第三个○内时,可得下面的填法:〔5+13×7〕÷〔17-9〕=12。
例2 将1~9这九个数字分别填入下式中的□中,使等式成立:□□□×□□=□□×□□=5568。
高思竞赛数学导引-五年级和差倍分问题学生版汇编

学习-----好资料第6讲和差倍分问题内容概述在和差倍问题中引入“分数倍”的概念,并理解其含义。
解题中应合理选取单位“1”,题目中隐藏的不变量或公共量往往是关键。
典型问题兴趣篇5,其余都是手榴弹。
由于遇上敌军伏枚弹药送到前线,其中炮弹占了1、运输连要将450923,而手榴弹只剩下击,炮弹损失了,送到是还剩多少枚弹药?582、学校举行新年自助餐会,一共准备了1000瓶饮料,其中一部分是可乐,剩下的全是果汁。
1,但可乐的数量却没有改变。
如果此时饮料还剩果汁已经减少了872瓶,那一个小时后,5么可乐的数量是多少瓶?11,黄球占总球数的,绿、口袋里装着红、黄、绿三种颜色的球。
其中红球占总球数的334个。
口袋里一共有几个球?球比黄球多505,现在已完成计划的、游戏公司计划生产一批限量版的游戏机。
4如果再生产340台,总121,原计划生产多少台?产量就超过计划的8更多精品文档.学习-----好资料11,第二天完成了剩下部分的,前5、一个工人加工一批机器零件,第一天完成了任务的53 56个。
请问:这批零件共有几个?两天一共完成了1,第二车间的人数、红星机械厂有三个车间,第一车间的人数是第二、三车间人数和的621,第三车间有105是第一、三车间人数和的人。
求该厂工人的总数。
311,丙桶中的水比甲桶中的少。
7、甲桶中的水笔乙桶中的多请问:乙、丙两桶哪桶水多?55如果把三桶水倒入一个大缸里,甲桶中的水占其中的几分之几?35,竹林占圆形的6-1是某市的园林规划图,其中草地占正方形的,正方形和圆形、图847的公共部分是水池。
已知竹林的面积比草地的面积少450平方米。
问:水池的面积是多少平方米?3阿奇的科普书数量是小悦的。
后来小悦送给阿奇11、阿奇和小悦都有很多科普书,9本书84后,阿奇的科普书数量就变成了小悦的。
原来阿奇比小悦少多少本书?7更多精品文档.学习-----好资料2,后来又来了12、课间同学们都在操场上活动,其中女生占总人数的10个女生,使得女93,操场上现在有多少名同学?生人数达到男生人数的7拓展篇1、等候公共汽车的人整齐地排列成一列,阿奇也在其中。
五年级奥数讲义(学生版)30讲全

-1-五年级奥数第1讲数字迷〔一〕第16讲巧算24第2讲数字谜(二)第17讲位置原那么第3讲定义新运算(一)第18讲最大最小第4讲定义新运算(二)第19讲图形的分割与拼接第5讲数的整除性(一)第20讲多边形的面积第6讲数的整除性(二)第21讲用等量代换求面积第7讲奇偶性〔一〕第22用割补法求面积第8讲奇偶性〔二〕第23讲列方程解应用题第9讲奇偶性〔三〕第24讲行程问题〔一〕第10讲质数与合数第25讲行程问题〔二〕第11讲分解质因数第26讲行程问题〔三〕第12讲最大公约数与最小公倍数〔一〕第27讲逻辑问题〔一〕第13讲最大公约数与最小公倍数〔二〕第28讲逻辑问题〔二〕第14讲余数问题第29讲抽屉原理(一)第15讲孙子问题与逐步约束法第30讲抽屉原理(二)-2-第1讲数字谜〔一〕例1把+,-,×,÷四个运算符号,分别填入下面等式的○内,使等式成立〔每个运算符号只准使用一次〕:〔5○13○7〕○〔17○9〕=12。
例2将1~9这九个数字分别填入下式中的□中,使等式成立:□□□×□□=□□×□□=5568。
例3在443后面添上一个三位数,使得到的六位数能被573整除。
例4六位数33□□44是89的倍数,求这个六位数。
例5在左下方的加法竖式中,不同的字母代表不同的数字,相同的字母代表相同的数字,请你用适当的数字代替字母,使加法竖式成立。
FORTYTENTENSIXTY例6在左下方的减法算式中,每个字母代表一个数字,不同的字母代表不同的数字。
请你填上适当的数字,使竖式成立。
练习11.在一个四位数的末尾添零后,把所得的数减去原有的四位数,差是621819,求原来的四位数。
在以下竖式中,不同的字母代表不同的数字,相同的字母代表相同的数字。
请你用适当的数字代替字母,使竖式成立:〔1〕AB (2)ABAB+BCA - ACAABC BAAC在下面的算式中填上括号,使得计算结果最大:1÷2÷3÷4÷5÷6÷7÷8÷9。
高思杯数学五年级试题及答案

钥”打开(例如“高思育教”、“高思高思”、“高高思思”等,汉字可以重复使用),一共有
( )种不同的“密钥”.
A、24
B、64
C、128
D、256
知识点:计数问题
难易度:★★(两颗星)
答案:D.
高思学校 2012 年春季
高思杯五年级试卷解析
年级
5. 2012 年的 1 月份和 2 月份,墨莫每隔.2 天来高思上一次课(如果周三墨莫上课,那么下次上课 是在周六),萱萱每隔.3 天来高思上一次课,第一次两人上课都是在 1 月 1 日,那么这两个月中 有( )天两人都来高思上课.
五、填空题 II(每小题 8 分,共 32 分) 17.___165___ 18. __62.8___ 19. ___5_____ 20. ___25____
六.填空题 III(每小题 9 分,共 18 分) 21.____135/38___________ 22.______444.888__________
9. 下面是一个数列:1、4、9、16、25、……,这个数列前十项的和是______.
10. 如图所示,四个半径是 1 厘米的圆放在一起,四个圆的圆心刚好在一个边长 是 2 厘米的正方形的四个顶点上,图中阴影部分的面积是_______平方厘 米.(π 取 3.14)
11. 2011 年 12 月 22 日,北京数学学校集训队成立仪式在北京大学图书馆南配殿隆重举行,北京数学 学校集训队是北京数学会唯一指定的官方集训队.如果把这天的日期的年份从正中间拆开,加上月 份和日子,可以得到 4 个数:20、11、12、22,它们的和是 65.那么在 2012 年,共有_______个 日期,拆成的 4 个数的和为 65(这 4 个数不一定都是两位数,例如 2012 年 6 月 5 日,可以分成 20、 12、6、5).
期末测试秋季高斯数学五年级竞赛体系(3课时)试卷

尖子A 班测试 高思学校五年级快乐思维尖子班 秋季5 年级【学生注意】本次测验分为两试,第一试满分120分,第二试附加题满分30分,考试时间80分钟.第十五讲 期末测验第一试一、填空题I (本题共有10小题,每题6分,共60分)1. 20122013除以8和9的余数分别是_________、_________.2. 胡小涂帮妈妈洗碗,打烂了其中的,还剩10个碗是好的.他打烂了_______个碗.3. 小高家养了很多鸡和兔子,其中鸡和兔子的数量比是3:4.已知兔子有20只,那么鸡有______只.4. ,那么x =_________.5. 某次秋游人数总数为85人,其中男生和女生之比为3:2,女生与老师之比为3:1.这次秋游有_________位老师.6. 小温和小林合作一项工程,需要10天完成.如果小温单独完成这项工程,需要30天完成.如果小林单独完成这项工程,需要________天完成.7. 一个两位数除以5余3,除以9余3,这个两位数最小是_______.8. 两个数的最小公倍数是90,最大公约数是3,其中一个数是9,那么另一个数是________. 9. 如图,不规则四边形ABCD 中,三角形BOC 的面积为6,三角形AOB 的面积为4,三角形AOD 的面积为2,那么图中阴影部分面积是__________.10. 算式中,相同字母代表相同数字,不同字母代表不同数字,那么三位数___________.二、 填空题II (本题共有5小题,每题8分,共40分)11. 计算:________. 12. 如图,D 点是靠近B 点的三等分点,AE :EC =2:3,且四边形EODC 与△AOB 的面积相差12.那么△ABC 的面积是_______. 13. = ×大朱小朱 珠珠珠中,不同的汉字表示不同的数字,相同的汉字表示相同的数字,那么大小朱珠表示的四位数最大..为_______.14. 一个带余除法算式中,被除数是129,余数是24,除数可能是_________.11123341920+++=××× ABC =AA AA BCB ×= ()12123x +−=27姓名:_______________ABCEO尖子A 班测试 高思学校五年级快乐思维尖子班 秋季5年级15. 加工一批零件,单独1人做,甲要10天完成,乙要15天完成,丙要12天完成.如果先由甲、乙两人合做5天后,剩下的由丙1人做,还要_______天完成.三、解答题(本题共有2小题,每题10分,共20分,请给出必要步骤,否则不得分)16. 大朱去早市买水果,苹果和梨一共买了20斤,其中苹果5元一斤,梨4元一斤,共花92元.请问苹果、梨各买了多少斤?(请列方程求解)17. 甲乙共同完成一件工作需要10小时,他们共同工作3小时后甲离开了,乙再干了21小时完成了这件工作,那么甲单独干完这件工作需要多少小时?第二试(本试共有3小题,每题10分.共30分.本试不用解答过程.)1. 算式87654321×−的结果除以9的余数是__________.2. 一个三位数除以3余2,除以5余4,除以11余6.这个三位数最大是________.3. 如图,AB =30,AD =16,AE :ED =3:1,BF :BE =1:3,G 、H 分别是CF 和DG 的中点,阴影部分面积为_______.。
高思竞赛数学导引-五年级第十二讲-余数学生版

第12讲余数内容概述掌握余数的概念与基本性质,掌握除以某些特殊数的余数的计算方法.学会利用余数的可加性、可减性和可乘性计算余数;学会运用同期性处理各类余数计算问题;学会求解“物不知数’问题.典型问题兴趣篇1.72除以一个数,余数是7.商可能是多少?2. 100和84除以同一个数,得到的余数相同,但余数不为0.这个除数可能是多少?3. 20080808除以9的余数是多少?除以8和25的余数分别是多少?除以11的余数是多少?4.4个运动员进行乒乓球比赛,他们的号码分别为101、126、173、193.规定每两人之间比赛的盘数是他们号码的和除以3所得的余数.请问:比赛盘数最多的运动员打了多少盘?5.某工厂有128名工人生产零件,他们每个月工作23天,在工作期间每人每天可以生产300个零件.月底将这些零件按17个一包的规格打包,发现最后一包不够17个.请问:最后一包有多少个零件?6.(1) 220除以7的余数是多少?(2)1414除以11的余数是多少?(3) 28121除以13的余数是多少?7.810888888个⨯⨯⨯++⨯+除以5的余数是多少?8.一个三位数除以21余17,除以20也余17.这个数最小是多少?9.有一个数,除以3的余数是2,除以4的余数是1.请问:这个数除以12余数是几?10.100多名小朋友站成一列,从第一人开始依次按1,2,3,…,11的顺序循环报数,最后一名同学报的数是9;如果按1,2,3,…,13的顺序循环报数,那么最后一名同学报的数是11.请问:一共有多少名小朋友?拓展篇1.1111除以一个两位数,余数是66. 求这个两位数.2.(1) 42121421421421个除以4和125的余数分别是多少?(2) 80821808808808个除以9和11的余数分别是多少?3.一年有365天,轮船制造厂每天都可以生产零件1234个,年终将这些零件按19个一包的规格打包,最后一包不够19个.请问:最后一包有多少个零件?4.自然数12222267-⨯⨯⨯⨯个的个位数字是多少?5.算式20072007200720072006321++++ 计算结果的个位数是多少?6.一个自然数除以49余23,除以48也余23.这个自然数被14除的余数是多少?7.一个自然数除以19余9,除以23余7.这个自然数最小是多少?8.刘叔叔养了400多只兔子,如果每3只兔子关在一个笼子里,那么最后一个笼子里有2只;如果每5只兔子关在一个笼子里,那么最后一个笼子里有4只;如果每7只兔子关在一个笼子里,那么最后一个笼子里有5只.请问:刘叔叔一共养了多少只兔子?9. 123123123123123个除以99的余数是多少?10.把63个苹果,90个橘子,130个梨平均分给一些同学,最后一共剩下25个水果没有分出去.请问:剩下个数最多的水果剩下多少个?11.有一个大于l的整数,用它除300、262、205得到相同的余数,求这个数.12.用61和90分别除以某一个数,除完后发现两次除法都除不尽,而且前一次所得的余数是后一次的2倍,如果这个数大于1,那么这个数是多少?超越篇1.从l 依次写到99,可以组成一个多位数12345…979899.这个多位数除以11的余数是多少?2.算式72008777777个⨯⨯⨯++⨯+计算结果的末两位数字是多少?3.算式20077531⨯⨯⨯⨯⨯ 计算结果的末两位数字是多少?4.有5000多根牙签,按以下6种规格分成小包:如果10根一包,最后还剩9根;如果9根一包,最后还剩8根;如果依次以8、7、6、5根为一包,最后分别剩7、6、5、4根.原来一共有牙签多少根?5.有三个连续的自然数,它们从小到大依次是5、7、9的倍数,这三个连续自然数最小是多少?6.请找出所有的三位数,使它除以7、11、13的余数之和尽可能大.7.已知.0000940909421717!21CD AB 那么四位数ABCD 是多少?8.有一些自然数n ,满足:2n - n 是3的倍数,3n - n是5的倍数,5n - n 是2的倍数,请问:这样的,n 中最小的是多少?。
高思竞赛数学导引-五年级第十讲-几何计数学生版
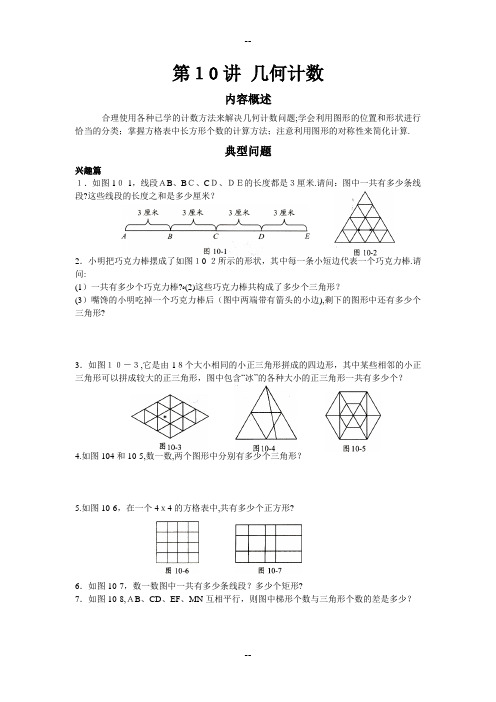
第10讲几何计数内容概述合理使用各种已学的计数方法来解决几何计数问题;学会利用图形的位置和形状进行恰当的分类;掌握方格表中长方形个数的计算方法;注意利用图形的对称性来简化计算.典型问题兴趣篇1.如图10-1,线段AB、BC、CD、DE的长度都是3厘米.请问:图中一共有多少条线段?这些线段的长度之和是多少厘米?2.小明把巧克力棒摆成了如图10-2所示的形状,其中每一条小短边代表一个巧克力棒.请问:(1)一共有多少个巧克力棒?ﻩ(2)这些巧克力棒共构成了多少个三角形?(3)嘴馋的小明吃掉一个巧克力棒后(图中两端带有箭头的小边),剩下的图形中还有多少个三角形?3.如图10-3,它是由18个大小相同的小正三角形拼成的四边形,其中某些相邻的小正三角形可以拼成较大的正三角形,图中包含“冰”的各种大小的正三角形一共有多少个?4.如图104和10-5,数一数,两个图形中分别有多少个三角形?5.如图10-6,在一个4x4的方格表中,共有多少个正方形?6.如图10-7,数一数图中一共有多少条线段?多少个矩形?7.如图10-8,AB、CD、EF、MN互相平行,则图中梯形个数与三角形个数的差是多少?8.如图10-9,125个黑色与白色小立方体相间排列拼成了一个大立方体,其中露在表面上的黑色小立方体有多少个?9.如图10-10,木板上钉着12枚钉子,排成三行四列的长方阵.用橡皮筋一共可以套出多少个不同的三角形?10.如图10-11,在2x3的长方形中,每个小正方形的面积都是1.请问:以A、B、C、D、E、,、G为顶点且面积为1的三角形共有多少个?拓展篇1.如图10-12,数一数,图中有多少个三角形?2.如图10-13,数一数下面的三个图形中分别有多少个三角形.3.如图10-14,数一数,图中有多少个三角形?4.如图10-15,数一数.,图中共有多少个长方形?(正方形是一种特殊的长方形)5.如图10-16,四条边长度都相等的四边形称为菱形,用16个同样大小的菱形组成如图的一个大菱形.数一数,图中共有多少个菱形?6.如图10-17,这是一个长为9,宽为4的网格,每一个小格都是一个正方形.请问:(1)从中可以数出多少个长方形?(2)从中可以数出包含黑点的长方形有多少个?7.如图10-18,数一数,图中共有多少个长方形?8.如图10-19,数一数,图中共有多少个平行四边形?9.如图10-20,18个大小相同的小正三角形拼成了一个平行四边形,数一数,图中共有多少个梯形?10.如图10-21,方格纸上放了20枚棋子,以这些棋子为顶点,可以连出多少个正方形?11.一个平面封闭图形,只要组成它的边中有一条边不是直线段,就将这个图形称为曲边形,例如圆、半圆、扇形等都是曲边形.在图10-22中,共有多少个不同的曲边形?12.如图10-23,一个2×3的网格中,每个小正方形的面积都是1.以这些格点为顶点,可以连成多少个面积为l的三角形?超越篇1.图10-24是一个等边三角形的点阵.以这些点为顶点,可以画出多少个等腰三角形(包括等边三角形)?2.如图10-25,数一数,图中共有多少个三角形?3.如图10-26,这是一个4x8的矩形网格,每一个小格都是一个正方形.请问:(1)包含有两个“★”的矩形共有多少个?(2)至少包含一个“★”的矩形有多少个?4.如图10-27,在图中的3×3正方形格子中,格线的交点称为格点.例如:A,B,C这3个点都是格点,那么,以格点为顶点,且完全覆盖了阴影部分小方格的三角形共有多少个?5.如图10-28,用12个点将圆周12等分,以这些点为顶点的梯形共有多少个?6.一个平面封闭图形,只要组成它的边中有一条边不是直线段,就将这个图形称为曲边形,例如圆、半圆、扇形等都是曲边形,在图10-29中,共有多少个不同的曲边形?7.如图10-30,木板上钉着16枚钉子,排成四行四列的方阵.用橡皮筋一共可以套出多少个不同的等腰三角形?8.如图10-31,在3×3的方格表内,每个小正方形的面积均为1.请问:(1)以格点为顶点共可以连出多少个面积为4的三角形?(2)以格点为顶点共可以连出多少个面积为3的三角形?(3)以格点为顶点共可以连出多少个面积为1.5的三角形?。
2010-2015年高思杯数学五年级试题及答案

18. 墨莫、萱萱和卡莉娅在比较他们获得的高思积分卡,墨莫比萱萱多 26 分,墨莫的积分比卡莉娅和
萱萱加起来的多
1 6
,卡莉娅的积分比萱萱的少
2 5
,那么墨莫有________分.
A
B
19. 如图,正方形 ABCD 和正方形 CEFG 放在一起,∠BCE 是直角,已
知 AB 9 , IG 12 ,那么三角形 CFI 的面积是________.
8. 一个两位数除以 5 余 1,除以 8 余 4.这个两位数最小是_______. 知识点:余数问题 难易度:☆(半颗星) 答案: 36.
9. 下面是一个数列:1、4、9、16、25、„„,这个数列前十项的和是______. 知识点:计算问题 难易度:★(一颗星) 答案: 385.
10. 如图所示,四个半径是 1 厘米的圆放在一起,四个圆的圆心刚好在一个边长 是 2 厘米的正方形的四个顶点上,图中阴影部分的面积是_______平方厘 米.(π 取 3.14) 知识点:几何——圆面积计算 难易度:☆(半颗星) 答案: 9.42.
14. a、b、c、d、e、f 分别代表 0~5 中的 6 个不同数字, abca d ebf ,则 abca ________.
15. 在 1 到 100 这 100 个正整数中,不能被 2、3、5、7 中任何一个数整除的数有________个.
三、填空题 II
16.
计算:
22 1 1 3
42 1 35
62 1 57
20122 1 2011 2013
=
________.
17. 一天晚上,亨亨同学熬夜写作业,写到凌晨 2 点多时,实在不行了,倒在床上就开始呼呼大睡.睡 觉前他看了一下闹钟,发现了一件有趣的事情——时钟上的时针和分针正好重合在了一起.早晨 8 点多时,亨亨被闹钟闹醒.他看了一下闹钟,又发现了一件有意思的事——此时时钟上的时针和分 针正好张开成一条直线.亨亨睡了_________小时.
2010-2015年高思杯数学五年级试题及答案

打开(例如“高思育教”、“高思高思”、“高高思思”等,汉字可以重复使用),一共有()种不
同的“密钥”.
A、24
B、64
C、128
D、256
5. 2012 年的 1 月份和 2 月份,墨莫每隔.2 天来高思上一次课(如果周三墨莫上课,那么下次上课是 在周六),萱萱每隔.3 天来高思上一次课,第一次两人上课都是在 1 月 1 日,那么这两个月中有() 天两人都来高思上课.
三、计算题(每小题 6 分,共 24 分) 9.___5/12____ 10. _12300__ 11. _2012/2013_ 12. __32/15__
四、填空题 I(每小题 7 分,共 28 分) 13.___88___ 14. __10_____ 15. __21.6___ 16. ___1_____
18. 墨莫、萱萱和卡莉娅在比较他们获得的高思积分卡,墨莫比萱萱多 26 分,墨莫的积分比卡莉娅和
萱萱加起来的多
1 6
,卡莉娅的积分比萱萱的少
2 5
,那么墨莫有________分.
A
B
19. 如图,正方形 ABCD 和正方形 CEFG 放在一起,∠BCE 是直角,已
知 AB 9 , IG 12 ,那么三角形 CFI 的面积是________.
钥”打开(例如“高思育教”、“高思高思”、“高高思思”等,汉字可以重复使用),一共有
( )种不同的“密钥”.
A、24
B、64
C、128
D、256
知识点:计数问题
难易度:★★(两颗星)
答案:D.
高思学校 2012 年春季
高思杯五年级试卷解析
年级
5. 2012 年的 1 月份和 2 月份,墨莫每隔.2 天来高思上一次课(如果周三墨莫上课,那么下次上课 是在周六),萱萱每隔.3 天来高思上一次课,第一次两人上课都是在 1 月 1 日,那么这两个月中 有( )天两人都来高思上课.
北京市小学生第五届高思杯

高思学校 2014年北京市小学生第五届高思杯•360°学习体检综合解答及评析五年级·思维部分1、2、3、4、本题评析:本题可以通过凑整进行巧算.5、 答案:6、 答案:2本题评析:分数四则混合运算是计算的基本功,需要同学们多多练习.29高思学校 2014年7、 答案:40详解:8、9、10本题评析:本题考查的是等比数列求和,对于公比是2的等比数列可以采用大数乘以2再减去小数的方法计算.765=111820++-11910++-()288120.452288125528812540=⨯+⨯=⨯+⨯=+⨯=原式高思学校 2014年本大题评析:本大题主要是考查同学们基本的运算能力,重点是考查同学们五年级才接触的分数加减乘除运算,以及分数巧算、分数裂项等内容,希望同学们在平时勤加练习.计算能力提高了,解题速度和正确率也就会大幅提高.二、选择题11、 答案:C1.从312应13“1”份,男生为“7”份,女生比男生少“1”份,少的“1”份占男生的,因此女生比男生少. 本题评析:对于分数应用题,分清楚单位“1”是谁非常重要,在本题中“女生比男生少几分之几?”是以男生为单位“1”,因此要看少的“1”份占男生的几分之几.1717 521=高思学校 2014年三、填空题I14、 答案:24知识点:数论,最大公约数和最小公倍数详解:120个苹果和72个桔子恰好分完,说明同学的数量既是120的约数,又是72的约数,即为120和72的公约数,最大为24.15161718种不同的方法;选2名女生有种不同的方法,共计35种不同的方法.本题评析:本题也可以从反面考虑问题,用总数减去不满足条件的方法数.即种不同的方法.779735C C -=252721C C ⨯= 62714C =高思学校 2014年19、 答案:20知识点:应用题,工程问题详解:由题目知,甲工效为,甲做了3天,做了总工程的,乙又接着独做了4天,两人完成整个工程的,说明乙4天完成总工程的,乙的效率为,单独完成需要20天. 20211星或22详解:本题要注意题目中两个分数所对应的单位“1”是不一样的,不能直接对它们进行相加减.可以采用倒推法.15题占剩下题目的,因此完成全部题目的后,还剩下道,全部题目有道.本题评析:本题也可以通过统一单位“1”的方法来解决,剩下题目的占全部题目的,因此15道题占全部题目的,一共有105道. 4211777--= 4221737⎛⎫-⨯= ⎪⎝⎭2344511057⎛⎫÷-= ⎪⎝⎭ 115453÷= 47 21133-= 120 1312105-=12310110高思学校 2014年23、 答案:15知识点:应用题,工程问题详解:甲、乙的合作效率为,看到合作的效率我们要找合作的天数,可以将条件“甲单独做了3天,乙接着独做了4天”转化为“甲、乙合作3天,乙又单独做了1天”,甲、乙合作3天完成全部的,乙1天完成,由此可求出甲的效率为,甲单独完成整2425.26,27详解:本题可以用重叠法来求图中阴影部分的面积.通过观察不难发现,图中阴影部分的面积等于边上三个圆的面积减去中间一个圆的面积,即等于两个圆的面积,为.本大题评析:本大题难度要高于前面的题目,考查内容涉及到应用题,数论,数字谜,几何等,主要是2星或3星难度的题目,做这部分题目时要胆大心细.2210628π⨯= 56= 319= 111103015-= 13131030-=310 110高思学校 2014年五、改错题28、 答案:(1)第一行,;(2)第一行,.知识点:计算,解方程详解:(1)第一次出现错误是在第一行,移项过程中要注意改变符号,第一行改正后为.(2)第一次出现错误是在第一行,去括号的时候,如果括号前面有数,括号里每一项都要乘以这个数,第一行改正后为.本大题评析:方程对于高年级的同学来说是非常有力的解决问题的工具,在应用题,几何问题,行程问题等许多问题中都有着广泛的应用.但同学们在解方程过程中常常会犯这样或那样的错误,例如在解分数方程过程中,去分母,去括号,移项都很容易出错.希望同学们在平时做题的过程中就要注意总结.六、文字材料题29、 答案:10知识点:几何详解:直角三角形的两条直角边长度分别为6和8,则斜边的平方为,斜边长为10.30、 答案:1334知识点:几何详解:两条直角边长度分别为7和24,则斜边的平方为,斜边长为25.直角三角形面积为,三个正方形的面积为,整个图形的面积为.31、 答案:500知识点:几何详解:通过第30题的例子我们可以发现,如果三个正方形的边长恰好为一组勾股数,则它们的面积和为最大正方形面积的2倍.在图中的“勾股树”中,我们可以反复应用这个结论,最终可以发现,图中所有正方形面积之和恰好为最大正方形面积的5倍,即500.8412501334+=222724251250++=724284⨯÷= 2227244957662525+=+== 2226810010+==13467x x -+=-101152x x +=+13467x x -+=-101152x x +=+高思学校 2014年本大题评析:对于文字材料题,一定要认真读题,读懂题,并且要注意不同问题之间的联系.七、解答题32、 答案:星期五知识点:数论,余数问题详解:利用7的整除特性,可以很容易求出2014除以7的余数为5,因此再过2014天是星期五.33、 答案:星期四知识点:数论,余数问题详解:利用特性求余法和替换求余法,可知除以7的余数等于除以7的余数,余数为4,因此再过天是星期四.34、 答案:星期二知识点:数论,余数问题详解:仍然利用特性求余法和替换求余法,可知除以7的余数等于除以7的余数,然后我们利用周期求余法,除以7余5,除以7余4,除以7余6,除以7余2,除以7余3,除以7余1,因此是6个一周期,2014除以6余4,即周期中的第4个,余数为2,因此再过天是星期二.本大题评析:对于解答题,由于要求书写过程,因此难度并不是很大,尤其是前两个小问,历年的高思杯都是比较容易的,同学们只要认真解答都会得一些分.二试八、填空题III35、 答案:3420142014 65 55 45 35 25 1520145555⨯⨯⨯个20142014201420142014⨯⨯⨯个20142014⨯55⨯20142014⨯高思学校 2014年知识点:数字谜详解:首先分析的首位,可以确定代表的数只能为1,再看,可以确定或应为7的倍数,则或.若,则,,分36 (3)解得:,由于各班人数均少于40人,因此不满足条件. (4)解得:,由于A 班人数最多,因此不满足条件. 综合上述,A 班有38人.37333638a b c d =⎧⎪=⎪⎨=⎪⎪=⎩364432a b c d a b c b d c +++=⨯⎧⎪-=⎪⎨-=⎪⎪-=⎩ 3335c d ⎨=⎪⎪=⎩32b c d c ⎨-=⎪⎪-=⎩ 2 思2=数41思14=高好14=高思14=高好高思高好 7=数好高好高思高⨯=数好高思数学好高思学校 2014年37、 答案:6930知识点:几何详解:如右图1所示,连接AC ,BE :AE =3:2,设三角形BCE 的面积为“3”份,则三角形ACE 的面积为“2”份,三角形BCE 、四边形AECF 和三角形CDF 面积相等,因此均为“3”38而考虑到,百位所填的0、1、8除以3的余数恰好分别为0、1、2.当万位、千位、十位和个位确定后,百位所填的0、1、8有且只有一个数满足条件,因此全部满足条件的种数有种.本题评析:本题也可以进行分类求解,但利用对应的这一想法,能够很好地化简问题.60320÷=ABD EF“3”“2”“1” “3”C解析 高思学校2014年 5年级39、 答案:180知识点:应用题,行程问题 详解:如图,相同时间用相同线来表示,设甲、乙、丙第一次相遇于D 点,比较甲与丙,当甲从A 走到D 时,丙从C 走到D .当甲从D 走回A 时,丙从D 走到E ,甲的速度变为原来的4倍,走相同的路程,因此时间变为原来的,丙的速度始终不变,因此所走的路程为原来的,CFDA 12:5,“1”份为1414学校工作总结本学期,我校工作在全体师生的大力支持下,按照学校工作计划及行事历工作安排,紧紧围绕提高教育教学质量的工作思路,不断强化学校内部管理,着力推进教师队伍建设,进一步提高学校办学水平,提升学校办学品位,取得了显著的成绩。
2016年第七届高思杯五年级数学答案
1 6
29
16 4 11
学习新知识能力检测部分
五、 文字材料题(本大题共 4 小题,第 34 题 2 分,第 35 题 3 分,第 36 题 6 分,第 37 题
7 分,共 18 分) 题号 答案 34 60,50 35 20~40 分钟
36. 【答案】650,10
【解析】设 y=a-b× t,将 t 40, y 250 和 t 45, y 200 带入得到
250 a 40b 200 a 45b a 650 解得 b 10
所以 y 650 10t 40 t 60
37. 【答案】能,12~44 分钟(介于 12~44 分钟,且差大于等于 30 分钟的其它答案也正
确,例如:12~42 分钟等). 【解析】注意力上升阶段,12 分钟的时候注意力开始达到 210 点,注意力下降阶 段,44 分钟的时候注意力刚好为 210 点,这之间共有 32 分钟,所以老师能在学生 注意力达到所需状态下讲完这道题目,时间段为 12~44 分钟之间.
拓展知识能力检测部分
三、 计算题 II(本大题共 4 小题,每题 4 分,共 16 分)
题号 答案 16 1 17
4 1 3
18
64 16 17
19 2015
四、 填空题 II(本大题共 14 小题,每题 4 分,共 56 分)
题号 答案 题号 答案 题号 答案 20 320166 25 77 30 7 21 7 26 44 31 448 22 502 27 6 32 400 23 42 28 157 33 1507.2 24
2016 年第七届高思杯(五年级)·数学部分 答案
常规知识能力检测部分
一、 计算题 I(本大题共 5 小题,每题 4 分,共 20 分)
高思杯数学五年级试题及答案

18. 墨莫、萱萱和卡莉娅在比较他们获得的高思积分卡,墨莫比萱萱多 26 分,墨莫的积分比卡莉娅和
萱萱加起来的多
1 6
,卡莉娅的积分比萱萱的少
2 5
,那么墨莫有________分.
A
B
19. 如图,正方形 ABCD 和正方形 CEFG 放在一起,∠BCE 是直角,已
知 AB 9 , IG 12 ,那么三角形 CFI 的面积是________.
高思学校 2012 年春季
年级
高思杯五年级试卷解析
11. 2011 年 12 月 22 日,北京数学学校集训队成立仪式在北京大学图书馆南配殿隆重举行,北京数 学学校集训队是北京数学会唯一指定的官方集训队.如果把这天的日期的年份从正中间拆开, 加上月份和日子,可以得到 4 个数:20、11、12、22,它们的和是 65.那么在 2012 年,共有 _______个日期,拆成的 4 个数的和为 65(这 4 个数不一定都是两位数,例如 2012 年 6 月 5 日, 可以分成 20、12、6、5). 知识点:计数问题 难易度:★★(两颗星) 答案: 10.
题的解答填在答.题.纸.上,只填在原题上不得分!
一、选择题
1. 同时满足以下条件的数是( ).
①所有因数的和为 31;②是 5 的倍数;③有奇数个因数.
A、30
B、27
C、25
D、20
知识点:数论知识
难易度:☆(半颗星)
答案:C.
2. 一个三角形中,其中两个角的度数的平均值是 45,这个三角形是( A、锐角 B、直角 C、钝角 D、无法确定
8. 一个两位数除以 5 余 1,除以 8 余 4.这个两位数最小是_______. 知识点:余数问题 难易度:☆(半颗星) 答案: 36.
高思杯数学五年级试题及答案

六.填空题 III(每小题 9 分,共 18 分) 21.____135/38___________ 22.______444.888__________
12. 甲从 A 地出发去一个地方办事,速度是 1 米/分.11 分钟以后,乙发现甲在出发地落了东西,于是 以甲 2 倍的速度去追甲;又过了 2 分钟,甲也发现自己落了东西,便以原速返回去取,最后甲乙相 遇.那么从乙出发到甲乙相遇一共用了________分钟.
13. 三个不同的两位数的和是完全平方数,这三个数的和最大是_______.
打开(例如“高思育教”、“高思高思”、“高高思思”等,汉字可以重复使用),一共有()种不
同的“密钥”.
A、24
B、64
C、128
D、256
5. 2012 年的 1 月份和 2 月份,墨莫每隔.2 天来高思上一次课(如果周三墨莫上课,那么下次上课是 在周六),萱萱每隔.3 天来高思上一次课,第一次两人上课都是在 1 月 1 日,那么这两个月中有() 天两人都来高思上课.
知识点:几何问题 难易度:☆(半颗星) 答案:B.
)三角形.
3. 周长相等的长方形和平行四边形相比,长方形的面积( )平行四边形的面积. A、大于 B、等于 C、小于 D、无法确定
知识点:组合数学 难易度:★(一颗星) 答案:D. 提示:排除法.
4. 高思教育的积分卡宝盒要由“高”、“思”、“教”、“育”四个汉字随意组合成的四位“密
A、10
B、9
C、6
D、5
6. 2012 个 2012 相乘的末位数字是().
2010-2015年高思杯数学五年级试题及答案

第二届高思杯五年级综合素质测评思维部分答案(总分:150 分时间:90 分钟)判断、选择、填空阅卷人复查人得分总分一、判断题(每小题3 分,共12 分)1.___√____2.___√____3.___√____4.___×____二、选择题(每小题5 分,共20 分)5.____A____6.___C____7.___C_____8.___D_____三、计算题(每小题6 分,共24 分)9.___5/12____ 10._12300__ 11._2012/2013_ 12.__32/15__四、填空题I(每小题7 分,共28 分)13.___88___ 14.__10_____ 15.__21.6___ 16.___1_____五、填空题II(每小题8 分,共32 分)17.___165___ 18.__62.8___ 19.___5_____ 20.___25____六.填空题III(每小题9 分,共18 分)21.____135/38___________ 22.______444.888__________注意:解答题过程写在答题纸背面!解答题部分 5年级七、解答题(请写出解题过程,每个小题分.别.写答.四 道小题的分值分别为:3 分,4 分,4 分,5 分) 第 23阅 卷 人 复 查 人得 分 23.解: 题第三届高思杯五年级综合素质测评思维部分(总分:150 分时间:90 分钟)【学生注意】本试卷共24 小题,请务必将1至22 题的答案和23、24 题的解答填在答.题.纸.上,只填在原题上不得分!一、选择题1. 同时满足以下条件的数是().①所有因数的和为31;②是5 的倍数;③有奇数个因数.A、30B、27C、25D、202. 一个三角形中,其中两个角的度数的平均值是45,这个三角形是()三角形.A、锐角B、直角C、钝角D、无法确定3. 周长相等的长方形和平行四边形相比,长方形的面积()平行四边形的面积.A、大于B、等于C、小于D、无法确定4. 高思教育的积分卡宝盒要由“高”、“思”、“教”、“育”四个汉字随意组合成的四位“密钥”打开(例如“高思育教”、“高思高思”、“高高思思”等,汉字可以重复使用),一共有()种不同的“密钥”.A、24B、64C、128D、2565. 2012 年的1 月份和2 月份,墨莫每隔.2 天来高思上一次课(如果周三墨莫上课,那么下次上课是在周六),萱萱每隔.3 天来高思上一次课,第一次两人上课都是在1 月 1 日,那么这两个月中有()天两人都来高思上课.A、10B、9C、6D、56. 2012 个2012 相乘的末位数字是().A、2B、4C、6D、8二、填空题I7. 一项工程,小高单独完成需要12 天,墨莫单独完成需要24 天.如果两人合作,需要_____天才能1完成这项工程的.48. 一个两位数除以5 余1,除以8 余4.这个两位数最小是_______.9. 下面是一个数列:1、4、9、16、25、……,这个数列前十项的和是______.10. 如图所示,四个半径是1 厘米的圆放在一起,四个圆的圆心刚好在一个边长是 2 厘米的正方形的四个顶点上,图中阴影部分的面积是_______平方厘米.(π取3.14)11. 2011 年12 月22 日,北京数学学校集训队成立仪式在北京大学图书馆南配殿隆重举行,北京数学学校集训队是北京数学会唯一指定的官方集训队.如果把这天的日期的年份从正中间拆开,加上月份和日子,可以得到4 个数:20、11、12、22,它们的和是65.那么在2012 年,共有_______个日期,拆成的4 个数的和为65(这4 个数不一定都是两位数,例如2012 年6 月5 日,可以分成20、12、6、5).12. 甲从A地出发去一个地方办事,速度是1 米/分.11 分钟以后,乙发现甲在出发地落了东西,于是以甲2 倍的速度去追甲;又过了2 分钟,甲也发现自己落了东西,便以原速返回去取,最后甲乙相遇.那么从乙出发到甲乙相遇一共用了________分钟.13. 三个不同的两位数的和是完全平方数,这三个数的和最大是_______.14. a、b、c、d、e、f分别代表0~5 中的6 个不同数字,abca d ebf,则abca________.15. 在1 到100 这100 个正整数中,不能被2、3、5、7 中任何一个数整除的数有________个.三、填空题II2 1 4 1 6 1 2012 12 2 2 216. 计算:= ________.1 3 3 5 57 2011201317. 一天晚上,亨亨同学熬夜写作业,写到凌晨2 点多时,实在不行了,倒在床上就开始呼呼大睡.睡觉前他看了一下闹钟,发现了一件有趣的事情——时钟上的时针和分针正好重合在了一起.早晨8点多时,亨亨被闹钟闹醒.他看了一下闹钟,又发现了一件有意思的事——此时时钟上的时针和分针正好张开成一条直线.亨亨睡了_________小时.18. 墨莫、萱萱和卡莉娅在比较他们获得的高思积分卡,墨莫比萱萱多26 分,墨莫的积分比卡莉娅和1 2萱萱加起来的多,卡莉娅的积分比萱萱的少,那么墨莫有________分.6 5A B19. 如图,正方形ABCD 和正方形CEF G 放在一起,∠BCE 是直角,已C 知AB 9,IG 12 ,那么三角形CFI 的面积是________. EDHIG F四、填空题III高思思集集训训队20. 一个五位数由5 个不同的非零数字组成.已知、、高思集训队高思集训队高思集思集训集训队这3 个数除以3 的余数互不相同.那么高思集训队所代表的五位数最大是__________.21. 阿呆、阿瓜两人同时从A 地出发前往B 地,与此同时萱萱从B 地出发前往A 地.阿呆与萱萱的速度比是5:3,他们在途中的C 点相遇.相遇后萱萱马上调头返回,速度不变,一段时间后被阿瓜追上.此时萱萱再一次调头,速度仍然不变.当萱萱再次到达C 点时,阿呆恰好到达B 地,而阿瓜距B 地6 千米.那么A、B 两地之间的距离是_______________千米.22. 将4、5、6、…、43、44、45 排成一行,满足:从左到右第k 个位置的数能被k 整除,那么一共有________种不同的排法.五、解答题23. 张勇老师沿江乘船顺流而下前往A港口,途中不慎将一袋宝石(宝石会沉入水中)和一个空酒葫芦(葫芦会随水漂流)掉入江中,到达A港时,他将草帽丢入江中(草帽也会随水漂流),并下船去集市上买了一块表和一套潜水服,返回船上时正好中午12 点.他立刻乘船继续沿江向下航行,并于13 点追上之前掉入江中的酒葫芦.14 点时又追上自己的草帽,于是立刻返航,回到A港时是17 点.那么:(1)船的静水速度和水速的比是多少?(2)之前他在A港停泊了多少小时?(3)他再向上游航行多少小时就到达宝石丢失点?24. 正整数1、2、3、……按螺旋形排列成右图中的数表.在这个数表中:21 22 23 24 25 26(1)与25 相邻的右上角的数是多少?(2)以100 为中心的9 个数可以组成一个33 的数表,这9 个数的和是多少?20 7 8 9 10 ⋮19 6 1 2 11 ⋮18 5 4 3 12(3)2012 所在的横行中,最小的数是多少?17 16 15 14 13 (4)2012 所在的竖列中,最小的数是多少?年级高思杯五年级试卷解析第三届高思杯五年级综合素质测评思维部分(总分:150 分时间:90 分钟)【学生注意】本试卷共24小题,请务必将1至22题的答案和23、24 题的解答填在答.题.纸.上,只填在原题上不得分!一、选择题1. 同时满足以下条件的数是().①所有因数的和为 31;②是 5 的倍数;③有奇数个因数.A、30B、27C、25D、20知识点:数论知识难易度:☆(半颗星)答案:C.2. 一个三角形中,其中两个角的度数的平均值是 45,这个三角形是()三角形.A、锐角B、直角C、钝角D、无法确定知识点:几何问题难易度:☆(半颗星)答案:B.3. 周长相等的长方形和平行四边形相比,长方形的面积()平行四边形的面积.A、大于B、等于C、小于D、无法确定知识点:组合数学难易度:★(一颗星)答案:D.提示:排除法.4. 高思教育的积分卡宝盒要由“高”、“思”、“教”、“育”四个汉字随意组合成的四位“密钥”打开(例如“高思育教”、“高思高思”、“高高思思”等,汉字可以重复使用),一共有()种不同的“密钥”.A、24B、64C、128D、256知识点:计数问题难易度:★★(两颗星)答案:D.高思杯五年级试卷解析年级5. 2012 年的 1 月份和 2 月份,墨莫每隔.2 天来高思上一次课(如果周三墨莫上课,那么下次上课是在周六),萱萱每隔.3 天来高思上一次课,第一次两人上课都是在 1 月 1 日,那么这两个月中有()天两人都来高思上课.A、10B、9C、6D、5知识点:找规律计算难易度:★(一颗星)答案:D.6. 2012 个 2012 相乘的末位数字是().A、2B、4C、6D、8知识点:周期问题难易度:★(一颗星)答案:C.二、填空题I7. 一项工程,小高单独完成需要 12 天,墨莫单独完成需要 24 天.如果两人合作,需要_____天才1能完成这项工程的.4知识点:工程问题难易度:☆(半颗星)答案:2 天.8. 一个两位数除以 5 余 1,除以 8 余 4.这个两位数最小是_______.知识点:余数问题难易度:☆(半颗星)答案:36.9. 下面是一个数列:1、4、9、16、25、……,这个数列前十项的和是______.知识点:计算问题难易度:★(一颗星)答案:385.10. 如图所示,四个半径是 1 厘米的圆放在一起,四个圆的圆心刚好在一个边长是 2 厘米的正方形的四个顶点上,图中阴影部分的面积是_______平方厘米.(π取 3.14)知识点:几何——圆面积计算难易度:☆(半颗星)答案:9.42.年级高思杯五年级试卷解析11. 2011 年 12 月 22 日,北京数学学校集训队成立仪式在北京大学图书馆南配殿隆重举行,北京数学学校集训队是北京数学会唯一指定的官方集训队.如果把这天的日期的年份从正中间拆开,加上月份和日子,可以得到 4 个数:20、11、12、22,它们的和是 65.那么在 2012 年,共有_______个日期,拆成的 4 个数的和为 6 5(这 4 个数不一定都是两位数,例如 2012 年 6 月 5 日,可以分成 20、12、6、5).知识点:计数问题难易度:★★(两颗星)答案:10.12. 甲从A 地出发去一个地方办事,速度是 1 米/分.11 分钟以后,乙发现甲在出发地落了东西,于是以甲 2 倍的速度去追甲;又过了 2 分钟,甲也发现自己落了东西,便以原速返回去取,最后甲乙相遇.那么从乙出发到甲乙相遇一共用了________分钟.知识点:行程问题难易度:★(一颗星)答案:5.13. 三个不同的两位数的和是完全平方数,这三个数的和最大是_______.知识点:最值问题难易度:★★(两颗星)答案:289.14. a、b、c、d、e、f 分别代表 0~5 中的 6 个不同数字,abca d ebf ,则abca ________.知识点:数字谜问题难易度:★★☆(两颗半星)答案:2012.15. 在 1 到 100 这 100 个正整数中,不能被 2、3、5、7 中任何一个数整除的数有________个.知识点:数论问题难易度:★★☆(两颗半星)答案:22.三、填空题II2 1 4 1 6 1 2012 12 2 2 216. 计算:= ________.1 3 3 5 5 7 2011 2013知识点:计算——分数裂项难易度:★★(两颗星)高思杯五年级试卷解析年级2012答案:.20131006解答:我们可以先计算出几项的结果,然后寻找一下规律,不难发现,每一项的分子都比分母多 2,可以以此为突破口对题目进行求解…….原式=2 1 4 1 6 1 2012 12 2 221 3 3 5 5 7 2011 20132 2 2 2=1 1 1 (1)1 3 3 5 57 2011 20131 1 1 1 1 1 1 1=1006+……1 3 3 5 5 7 2011 2013=100620122013.17.一天晚上,亨亨同学熬夜写作业,写到凌晨2点多时,实在不行了,倒在床上就开始呼呼大睡.睡觉前他看了一下闹钟,发现了一件有趣的事情——时钟上的时针和分针正好重合在了一起.早晨8点多时,亨亨被闹钟闹醒.他看了一下闹钟,又发现了一件有意思的事——此时时钟上的时针和分针正好张开成一条直线.亨亨睡了_________小时.知识点:时钟问题难易度:★★(两颗星)答案:6小时.解答:首先算出亨亨开始睡觉的时间:1 1201010 11012 111110,即:2点分1011然后算出亨亨醒来的时间:1 1201010 11012 11 1110,即:8点分,1011所以,亨亨睡了6个小时.18.墨莫、萱萱和卡莉娅在比较他们获得的高思积分卡,墨莫比萱萱多26分,墨莫的积分比卡莉娅1 2和萱萱加起来的多,卡莉娅的积分比萱萱的少,那么墨莫有________分.6 5知识点:比列解应用题难易度:★★☆(两颗半星)答案:56分.解答:墨莫的积分与卡莉娅加萱萱的总和的比是7:6,卡莉娅与萱萱的积分比是3:5;年级高思杯五年级试卷解析所以设:墨莫的积分是56份,则卡莉娅的积分为18份,萱萱的积分是30份,那么墨莫比萱萱多 26份的积分,刚好对应实际的26分,说明1份等于1分,所以,墨莫有积分56分.19. 如图,正方形 ABCD 和正方形 CEFG 放在一起,∠BCE 是AB直角,已知 , 12 ,那么三角形 CFI 的面积是AB 9IG________. 知识点:几何问题D HCE难易度:★★★(三颗星)I答案: 54.解答:连接 DG (如图中虚线所示),可知四边形 CDGF 是 梯形,根据蝴蝶模型可知三角形 DGI 和阴影部分是面积相等GF的两个三角形,三角形 DGI 是以 IG 为底 DC 为高的钝角三 912 2 54 角形,面积是:.四、填空题 III20. 一 个 五 位 数 高思集训队 由 5 个 不 同 的 非 零 数 字 组 成 . 已 知 高思集训队 、高思思集 集训 训队高思集 思集训 集训队、这 3 个数除以 3 的余数互不相同.那么高思集训队 所代表的五位数最大是__________.知识点:数论问题难易度:★★★(三颗星) 答案: 98746.高思思集 集训 训队高思集思集训 集训队解答:比较“高思集训队 ”、“”、“”三组数字和分别是:高+思+集+训+队、高+2 思+2 集+2 训+队、高+2 思+3 集+2 训+队,要想使三 个数除以 3 的余数互不相同,也就是这三组数数字之和除以 3 的余数互不相同;第二组比第一 组多了“思+集+训”,根据余数的性质,可以得出“思+集+训”的数字和一定不是 3 倍数,而 第三组比第二组多了一个“集”,同理“集”也一定不是 3 倍数,比较一、三组可知“思+2 集+ 训”的和也一定不是 3 的倍数,而“思+集+训”和“集”都不是 3 的倍数说明“思+训”一定 是 3 的倍数.我们知道由 5 个不同的非零自然数组成的五位数最大是 98765,但是简单验证可知 98765 不 合题意,在保证五位数尽可能大的情况下,我们优先保证不动的一定是万位、其次是千位、再次是百位等.由上可得万位 9 不动,千位的 8 必须与十位上的数数字之和是 3 的倍数,推出十位是 4,百位的七符合题意(不是 3 的倍数),此时个位最大为 6,带回题目验证符合题意,所以五位数最大是 98746.高思杯五年级试卷解析年级21.阿呆、阿瓜两人同时从A 地出发前往B 地,与此同时萱萱从B 地出发前往A 地.阿呆与萱萱的速度比是5:3,他们在途中的C 点相遇.相遇后萱萱马上调头返回,速度不变,一段时间后被阿瓜追上.此时萱萱再一次调头,速度仍然不变.当萱萱再次到达C 点时,阿呆恰好到达B 地,而阿瓜距B 地 6 千米.那么A、B 两地之间的距离是_______________千米.知识点:比例解行程问题难易度:★★★☆(三颗半星)答案:65.解答:根据“阿呆与萱萱的速度比是 5:3”可得:他们在C 点相遇时所走路程也是 5:3,不妨把全程设为 8 份,如图所示:A CB 阿呆萱萱由“相遇后萱萱马上调头返回,速度不变,一段时间后被阿瓜追上.此时萱萱再一次调头,速度仍然不变.”假设萱萱从C 点返回在D 点被阿瓜追上,画出路线图:A C BD阿呆萱萱阿瓜不难发现萱萱从C 点返回到D 点和从D 点返回到C 点所走路程是相同的即两个CD 的长度,那么对应时间一定相等,而萱萱走两个CD 时间阿呆刚好从C 点走到B 点,所以萱萱走一个CD的时间阿呆刚好走到CB 的中点,我们可以由此求出CD 的长度:因为萱萱与阿呆的速度比是3:5,所以阿呆从C 点走到CB 的中点,走了 1.5 份的路程,此时萱萱走了 0.9 份,即CD 的长度是 0.9 份.又由于萱萱到达D 点时刚好被阿瓜追上即,阿瓜走了 5.9 的路程是,阿呆走了 6.5 份的路程,如下如所示:AB 阿呆阿瓜由此可推出阿呆与阿瓜的速度比是65:59,那么最后当阿呆到达B 点时,阿瓜距B 点还有6千米可以看做阿呆走了 65 份,阿瓜走了 59 份,推出全程 65 千米.22.将 4、5、6、…、43、44、45 排成一行,满足:从左到右第k 个位置的数能被k 整除,那么一共有________种不同的排法.知识点:计数问题难易度:★★★★(四颗星)答案:9 种.解答:这个题目要把 42 个数排成一行,每个数要能被它的位置号整除,所以我们先列一个表格:年级高思杯五年级试卷解析所填数字位置号 1 号 2 号 3 号 4 号…40 号41 号42 号很明显,43 只能写在 1 号,而对其它数字较小的位置,可填的数范围比较广,比如 3 号位置,在 4~45 中有 14 个数可以写,不好确定;相反,数字较大的位置,可填的数比较容易确定,比如 42 号,只能填 42,所以我们倒着推算,先看 23~42 这 20 个位置:可填数字23 24 25 26 …40 41 42位置号23 号24 号25 号26 号…40 号41 号42 号明显:42 号填 42,41 号填 41,40 号填 40,…,23 号填 23.下面看 16~22 这 7 个位置:可填数字16、32 17、34 18、36 19、38 20、40 21、42 22、44位置号16 号17 号18 号19 号20 号21 号22 号上面的红色数字表示这个数已经被用过.从 16 号开始我们只有 22 号没有填数字,在 16 以后的数字,有 22、44、45 没有用.现在我们看一下 10~15 这 6 个位置(红色的数字表示已经在前面用过)可填数字10、20、30、40 11、22、33、44 12、24、36 13、26、39 14、28、42 15、45位置号10 号11 号12 号13 号14 号15 号下面看一下 6~9 这 4 个位置,目前,只有 45、44、22、15、11 这几个数字没有填.可填数字 6 7 8 9、45位置号 6 号7 号8 号9 号明显,6~8 号位置也确定了.到目前,还未确定的位置是 2、3、4、5、9、15、22,未确定的数是 4、5、9、15、22、44、45.可填数字4、22、44 9、15、45 4、44 5、15、45 9、45 15、45 22、44 22、44 位置号 2 号 3 号 4 号 5 号9 号15 号22 号22 号接下来,我们把这个表拆成两个小表格进行计算,第一个是 2、4、22 这 3 个位置、第二个是 3、5、9、15 这 4 个位置:(1)2、4、22 号位置:可填数字4、22、44 4、44 22、44位置号 2 号 4 号22 号所填数字22 4 44 4 44 22 44 4 22高思杯五年级试卷解析年级(2)3、5、9、45 号位置:可填数字9、15、45 5、15、45 9、45 15、45位置号 3 号 5 号9 号15 号45 5 9 15所填数字9 5 45 1525 5 9 453 3 9所以共种可能.五、解答题23. 张勇老师沿江乘船顺流而下前往A 港口,途中不慎将一袋宝石(宝石会沉入水中)和一个空酒葫芦(葫芦会随水漂流)掉入江中,到达A 港时,他将草帽丢入江中(草帽也会随水漂流),并下船去集市上买了一块表和一套潜水服,返回船上时正好中午 12 点.他立刻乘船继续沿江向下航行,并于13 点追上之前掉入江中的酒葫芦.14 点时又追上自己的草帽,于是立刻返航,回到A 港时是 17 点.那么:(1)船的静水速度和水速的比是多少?(2)之前他在A 港停泊了多少小时?(3)他再向上游航行多少小时就到达宝石丢失点?知识点:行程中的流水行船问题难易度:★★★★☆(四颗半星)答案:5:1;10 小时;1.5 小时.【解答】(1)从张勇老师12 点开始继续航行,14 点追上草帽返航,可知这段时间他航行了2 个小时,接下来返航从 14 点到 17 点回到A 港,可知他走了 3 小时,两段路程相同,时间比是2:5,所以顺水速度:逆水速度=3:2,不妨设顺水速度为“3”份,则逆水速度“2”份,由公式:静水速度=顺水速度+逆水速度 2 水流速度= 顺水速度-逆水速度 2,,可得水速为“0.5”份,船的静水速度是“2.5”份,所以静水速度和水速的比是 5:1.(2)不妨设船的顺水速度是 6 份/时,水流速度是 1 份/时,那么船从A 港出发 2 个小时后追上草帽,相当于知道了速度差(5 份/时),追及时间(2 小时),那么路程差是 10 份,以草帽 1 份/时的速度,若想走 10 份的路程需 10 小时,所以张勇老师在A 港停泊了 10 小时.(3)(方法同上)设船的顺水速度是 6 份/时,水流速度是 1 份/时,那么船从A 港出发 1 个小时后追上空葫芦,相当于知道了速度差是 5 份/时,追及时间是 1 小时,那么路程差是 5 份,以空葫芦 1 份/时的速度可知若想产生 5 份的路程需 5 小时,又由于张勇老师在A 港停泊了 10 小时,年级高思杯五年级试卷解析可知张勇老师到达 A 港时酒葫芦还有 5 小时才能到达 A 港,也就是此时张勇老师与酒葫芦有 5 份的路程差,由这个条件可以求出张勇老师是在到达 A 港前 1 小时丢的宝石和葫芦,即宝石在 距 A 港 6 份路程的上游处,因为逆水速度是 4 份/时,所以张勇再向上游行 1.5 小时就能到达宝 石丢失点.24. 正整数 1、2、3、……按螺旋形排列成右图中的数表.在21 22 23 24 25 26这个数表中:2078910⋮(1)与 25 相邻的右上角的数是多少?(2)以 100 为中心的 9 个数可以组成一个 3×3 的数表,19 6 1 2 11 ⋮ 1854312这 9 个数的和是多少?17 16 15 14 13(3)2012 所在的横行中,最小的数是多少? (4)2012 所在的竖列中,最小的数是多少? 知识点:复杂数列、数表问题 难易度:★★★★★(五颗星) 答案: 49;960;1981;290.⋮ 21 22 23 24 25 26 【解答】首先,通过观察可以发现,数表中,有两条对角线 ⋮2078910 27上的数都是平方数,其中奇数的平方在右上,偶数的平方在⋮1961211 28左下. ⋮ 18 5 4 3 12 29(1)很明显,25 右上角的数是 7 249 ;(2)100 是偶数的平方,所以在左下方,画出以 100 为中心⋮17 16 15 14 13 30⋯ 36 35 34 33 32 31的 3×3 表格,先把 100 的右上方和左下方的数写出来,分别 是 64 和 144.(图 1)6465 64从原图中可以看出,每个偶数的平方 a 2的左侧是 a 21,右侧是 a 21,填好后见图 2.100101 10099此时只有一个位置没有填,从题目中的图中可以看出,它是 102,144144 143 142 于是这个表格中所有数之和是 960.图 1图 2 (3)把 1 所在的列看作第 1 列,1 左侧和右侧相邻的列都看作第 2 列,……第23第1第10第23 列列列列把 1 所在的行看作第 1 行,1 上侧和下侧的行都看第 23 行1981 ...2003 ...2012 (2025)做第 2 行,……,得到图 3.因为 1~2025 组成了一个 45×45 的数表且 1 在最中间,于是 2025 在第…………………23 行、第 23 列.第 10 行…………361 ……………………… 于是第23 行第 1 列的数是 2025 22 2003,左侧第 1 行…… 1 …………图 3高思杯五年级试卷解析年级的 23 行 23 列的数是2003 22 1981,所以 2012 在第 23 行.如果一个数的行数或者列数中有一个大于 23,那么它肯定会大于 2025,所以 2012 所在行的最小数是 1981.(4)因为2012 2003 9 ,所以 2012 在第 10 列从题目中的图可以看出 9 在第 2 行第 2 列,25 在第 3 行第 3 列,……,所以第 10 行第 10 列的数是210 1 361.2观察 9 和 25 所在列可以发现:第 2 列的最小数是12 1,第 3 列最小数是32 110 ,……所以第 10 列的最小数在 361 的下方,是172 1 290 .结束语:相信大家一定能通过这次高思杯考试对自己最近的学习情况进行一次系统的检测,对照完答案后,我们首要做的一件事情是反思,反思自己考试成功的地方,反思自己考试失误的地方,同时吃透这套试题中的题目及相关的知识点,把所发现的进步和不足记录下来,为接下来的学习和考试提供指导.祝大家百尺竿头更进一步!高思教育2012年4月2013 高思杯·“7龙珠”学习文化节五年级·思维部分【学生注意】请把答案写在答题纸上,只填在原题上不得分.考试时间90 分钟,总分150 分一、判断题(请在答题纸上写上“√”或“×”,本大题共5 小题,每题2 分,共10 分)四、填空题I(请在答题纸上写出正确的答案,本大题共7 小题,每题4 分,共28 分)1. 若两数的乘积为1,那么这两个数互为倒数.()19.1~100 这100 个自然数中质数有25 个,合数有__________个.2. 互质的两个数,一定都是质数.()20.已知小圆的半径是大圆半径的一半,那么大圆的面积是小圆面积的______倍.21.100 以内的自然数中,除以9 余 2 的有________个.3. 任何一个圆都有无数条对称轴.()4. 等腰三角形一定是锐角三角形.()2x=3y: 3: 2x y=5. 如果,那么.()22.苏小琳和陈小琪在一条周长为400 米的环形跑道上散步.两人同时同地出发,相背而行.第一次相遇时距离出发地100 米.如果她们继续保持原来的速度匀速前进,第三次相遇的地点将距离出发地_______米.(与出发地的距离取不大于200 米的那一个)二、选择题(请在答题纸上写出正确的选项,本大题共3 小题,每题3 分,共9 分)6. 单独盖一栋房子,小勇需要15 天,大勇需要10 天.如果两人合作,盖好这栋房子需要( )天.A.5 B.6 C.25 23.王萍在外地工作,收入很高,她很孝敬自己的妈妈,每月都到邮局汇相等数额的钱给妈妈,汇费是1汇款的,她一年光是汇费就花了144 元,每月寄___________元钱给妈妈.4024.李栗栗有一个电子邮箱,密码是12349 ×94321 的乘积结果.但是她只记得密码是1164 70029,第五位数字不记得了.请你告诉她,密码的第五位数字是_______.7. 周长相同的下列平面图形中,面积最大的是()A.等边三角形B.正方形C.圆25.使用数字4、5、6、7 以及加、减、乘、除、括号组成一个算式,使得算式结果是24,算式为___________.五、操作题(请在答题纸上写出正确的答案,本大题共1 小题,每题10 分,共10 分)8. 现有五种动物:狮子、老虎、河马、蝙蝠和鸵鸟.要从中选出三种动物参加运动会,但是要求至少有一种是鸟类.一共有()种不同的选法.26.“7 龙珠”学习文化节中的“名师PK”活动正进行的如火如荼.五年级共有五个队,分别是金星队、木星队、水星队、火星队和土星队.在活动还在进行时,贺老师查了一下各队的人数,发现以下事A.C =10 B.C ×C +C ×C =9 C.32 1 1 2 C2 =65 3 2 3 2 4实:(1)火星队的男生有50 人;(2)土星队的男生比水星队的男生多83 人;(3)金星队和木星队的男生一共有167 人;(4)金星队的女生占所有参加活动人数的十分之一;三、计算题(请在答题纸上写出正确的答案,本大题共10 小题,每题2.5 分,共25 分)9. 356 += 452 __________.10.35×35 =__________.(5)木星队的男生和女生一样多;11.123456×999999 =__________.(6)火星队和水星队一共有170 人;(7)水星队、火星队和土星队的女生人数之比为20:10:29;4 112.8×+8×2 =__________.5 51 1 1÷÷=13. __________.3 4 54 5 1 1÷−+=14. __________.9 6 6 32x−3 =3(x−2)x=15. ,那么_____.(8)参加活动的一共有680 人,且男生与女生之比为9:8.请将下表填完整,并回答后面的问题.金星队木星队水星队火星队土星队总男2 +4 +8+16 ++512 =16. ________.女1 +2 +3 ++15 =17. __________.2 2 2 21 1 1 118. + __________.1 3 3 5 5 7 23 25×+×+×+×=18. + __________.总已知金星队平均每人得到3 个龙珠环,木星队平均每人得到2 个龙珠环,水星队平均每人得到4 个龙珠环,土星队平均每人得到3 个龙珠环.那么这四个队平均每人得到_______个龙珠环.-1- -2-2013 高思杯·“7 龙珠”学习文化节五年级·思维部分六、 文字材料题(请在答题纸上写出正确的答案,本大题共 1 小题,每题 6 分,共 6 分)34.刘钟、王明和朱迪三人都从A 出发在AB 两地间做匀速往返运动,C 是靠近B 的三等分点.刘钟先27. 2013 年春季,北京一直被雾霾笼罩.汽车燃烧汽油排放出的尾气是造成这种情况的罪魁祸首之一.为出发,当刘钟走到C 时,王明出发;当王明走到C 时,朱迪出发.已知朱迪在第一次到达B 点时第了减少环境污染,我国有些城市采用天然气作为汽车的燃料.天然气的主要成分是甲烷(读音同“完”), 一次遇到刘钟,在第一次返回C 点时第一次追上王明.当刘钟和朱迪第三次相遇时(迎面相遇和追 一个甲烷分子由一个碳(符号为C )原子和四个氢(符号为H )原子组成,化学式是CH 4. 上都算相遇),王明距离C 点360 千米,那么AB 两地间的距离是__________千米.(1)除了甲烷之外,天然气中还有少量的乙烷、丙烷和丁烷,化学式分别是C 2H 6、C 3H 8 和C 4H 10.由 此可以推断,含有五个碳原子的戊烷的化学式是__________.八、 解答题(请在答题纸上给出具体过程并作答,本大题共 2 小题,其中第 35 题 8 分,第 36 题 12 分,共(2)乙烷中碳原子的排布方式为C —C ,丙烷中碳原子的排布方式为C —C —C ,丁烷中碳原子的排20 分)C —C —C C —C —C 布方式有两种:C —C —C —C 和 (C —C —C —C 和 算一种).那么戊烷中碳原子的 C C 35.(本题答案已经给出,请根据解答在横线上写出适当的算式.)须师傅要装修高思大厦,他独立完成需要12 天.现在须师傅工作了4 天之后,徐师傅来帮忙.两人 排布方式有_________种(旋转或翻转相同算同一种).又工作了6 天才装修完.如果徐师傅自己装修的话,需要多少天才能完成? 七、 填空题 II (请在答题纸上写出正确的答案,本大题共 7 小题,每题 6 分,共 42 分)28.如图,已知△ABC 的面积是2013,D 是AC 上一点,F 是BC 延长线上一点,A1解:设装修高思大厦的工作量为单位1,那么须师傅的效率是 .由题意可知须师傅一共工作了12 10 天,徐师傅一共工作了6 天.且BC = 3CF .又知道四边形DCFE 是平行四边形,那么阴影部分的面积是 第一步,求出须师傅10 天的工作量,____________________________._______. D E第二步,求出徐师傅的工作量,____________________________.29.如图,正六边形的边长为2.以它的各顶点为圆心,边长的一半为半径画弧, 得到图中实线围成的图形.该图形的周长为_________.(π 取 3.14)B C第28 题F第三步,求出徐师傅的工作效率,____________________________.第四步,求出徐师傅单独工作需要的天数,____________________________.答:徐师傅自己装修需要36天. 30.一个水池上装有一个进水管和一个排水管,而且进水管进水的效率是排水管排水效率的1.5 倍.同时打开两个水管,6 个小时可以把水池注满.现36.五年级一班的同学们准备开一个联欢晚会.晚会共有7 个节目,1 个小品,2 个相声,3 个歌曲以及早上8:00 时将两管同时打开,中间某时刻将排水管关闭,中午12:00 时1 个魔术.但是对于节目的安排顺序,同学们意见不一.就已经将水池注满.那么关闭排水管的时刻是________.(1) 贺一淳说,歌曲比较多,最好不要连着演.如果我们采用贺一淳的意见,其它节目任意排的话,共有多少种安排节目的方法?31.4 个自然数的和是44,它们两两之间的差分别是1、3、4、5、6、9,那(2) 路二亨说,这次相声节目,我们请的是郭德纲和于谦,我特爱听他俩的相声,所以希望两个相么最大的那个数最大可能是__________.第29 题声连着演.如果我们采用路二亨的意见,其它节目任意排的话,共有多少种安排节目的方法?32.高思学校要颁发七龙珠活动的神秘大奖,小哼也是获奖者之一.获奖者在台上站成一排,分别编号(3) 温三金说,这次魔术节目,我们请的是刘谦,这个节目最好作为压轴节目,可以放在最后一个为1、2、3、….小哼发现获奖者不超过20 个,而且更有意思的是,小哼左边所有获奖者编号的乘或倒数第二个.如果我们采用温三金的意见,其它节目任意排的话,共有多少种安排节目的方 积与小哼右边所有获奖者编号的乘积正好相等.那么小哼的编号是_________.法?33.如图,A 、B 两齿轮互相咬合,且A 齿轮有12 齿,B 齿轮有16 齿(图。
2016年第七届高思杯五年级数学详细解答

7. 【答案】150
【解析】根据一半模型,阴影部分面积等于长方形 ABCD 的面积的一 半.20× 15÷ 2=150.
8. 【答案】150
【解析】a=[2,15,25]=150
9. 【答案】24
【解析】60× 2 =24 张. 5
10. 【答案】18
【解析】设工作总量为 1 份,石老师和张老师的工作效率分别是 合作时工作效率为:
2016 年第七届高思杯(五年级)·数学部分 详细解答
常规知识能力检测部分
一、 计算题 I(本大题共 5 小题,每题 4 分,共 20 分) 1. 【答案】20.16
【解析】 20.09 0.07 20.16
2. 【答案】
1 6 1 1 2 3 5 1 【解析】 15 10 30 30 30 6 4 25 2 5 2 2 4 【解析】 5 2 5 5 25
【解析】 设 a 6x , 其中 x 和 y 互质, 那么 a, b 6 xy 72 , 所以 xy 12 , b 6y , 由于 a 和 b 不成倍数关系,所以 x 和 y 也不成倍数关系,再根据互质的要求, x 和
y 应该分别是 3 和 4,那么 a 和 b 分别是 18 和 24, a b 18 24 42 .
D A 甲 C B 乙
33. 【答案】1507.2
【解析】旋转之后形成的立体图形上半部分是一个圆锥,下半部分是一个圆柱, 梯形的下底长度为 90 2 6 10 20 厘米,所以圆锥的高度是 20 10 10 厘米, 1 整个立体图形的体积是 62 10 62 10 480 1507.2 立方厘米. 3
1 1 1 1 ,所以需要 1 18 分钟. 30 45 18 18 1 1 和 ,两人 30 45
高思竞赛数学导引-五年级第十三讲-数字谜综合学生版

第13讲 数字谜综合一内容概述涉及小数、分数、循环小数酌数字谜问题;须要利用数论学问解决的数字谜问题.典型问题爱好篇1.有一个四位数,在它的某位数字后加上一个小数点,得到一个小数,再把这个小数和原来的四位数相加,得数是4003.64求这个四位数.2.试将1、2、3、4、5、6、7分别填人下面的方框中,每个数字只用一次:口口口(这是一个三位数),口口口(这是一个三位数),口(这是一个一位数),使得这三个数中随意两个都互质.已知其中一个三位数已填好,它是714,求另外两个数.3.用1至9这9个数字各一次组成若干个数,这些数中最多有多少个合数?4.如图13-!,4个小三角形的顶点处有6个圆圈,在这些圆圈中分别填上6个质数(可以重复),使得它们的和是20,而且每个小三角形3个顶点上的数之和相等,请问:这6个质数的乘积是多少?5.在一个带有余数的除法算式中,商比除数大2,在被除数、除数、商和余数中,最大数与最小数之差是1023.请问:此算式中的4个数之和最大可能是多少?6.在乘法算式“好好好春杯迎杯=⨯”中,不同的汉字表示不同的数字,相同的汉字表示相同的数字.请问:“迎+春+杯+好”等于多少?7.将1至9这9个数填入下面算式中的9个方框内(每个数字只能用一次),使等式成立.口口口×口口=口口×口口=55688.循环小数B A.0化成最简分数后,分子与分母之和为40,那么A 和B 分别是多少?9.在算式“7=+金杯竞赛华罗庚数学”中,华、罗、庚、金、杯、数、学、竞、赛九个字,分别代表数字1、2、3、4、5、6、7、8、9.已知“竞 = 8,赛 = 6”,请把这个算式写出来.10.已知“GOOD BAD BAD =+”是一个正确的加法算式,其中相同的字母代表相同的数字,不同的字母代表不同的数字,已知GOOD 不是8的倍数.请问:ABGD 代表的四位数是什么?拓展篇1.[4.2×5 - (1+2.5 + 9.1 + 0.7)] + 0.04=100.2.用0至9这10个数字恰好组成一位数、两位数、三位数、四位数各一个(每个数字只能用一次),且这四个数两两互质.其中的四位数是2940,另外三个数可能是多少?3.学数学科学数数=⨯.在上面的算式中,每一个汉字代表一个数字,不同的汉字代表不同的数字.请问:“数学”所代表的两位数是多少?4.在等式“口△×△口×口O×◇△=口△口△口△”中,口、△、O 、◇分别代表不同的数字.四位数◇O 口△是多少?5.将1、2、3、4、5、6、7、8、9这9个数字分别填人下式的各个方框中,使等式成立:口口×口口=口口×口口口=3634.6.已知a 是一个自然数,A 、B 是1至9中的数字,最简分数差B A a 33.0222=.请问:a 是多少?7.把质数373按数位拆开(不变更各数之间的依次),只能得到3、7、37、73这四个数,它们仍旧都是质数,请找出全部具有这种性质的质数.8.在下面各题中,请你用给出的四个数,适当进行加、减、乘、除运算,每个数恰好用一次,使得计算结果等于24. (1)1,4,5,6; (2)1,5,5,5; (3)3,3,7,7; (4)3,3,8,8.9.把1至6填人下面的方框中,每个数字恰好运用一次,使得等式成立,请写出所有的答案. 口.口×口.口=口.口10.如图13-2所示,三角形纸片盖住的都是质数数字,正方形纸片盖住的都是合数数字,要使得两个加数的差尽可能小,较大的加数是多少?11.在下面两个算式中,相同的汉字表示相同的数字,不同的汉字表示不同的数字.花相似人不同代表的六位数是多少? 花相似岁岁年年=⨯ 不同人年年年年÷=÷12.在图13-3所示的算式中,每个字母代表一个数字,不同的字母代表不同的数字.假如CHINA 代表的五位数能被24整除,那么这个五位数是多少?超越篇1.两个学生计算同一个乘法算式,两个乘数都是两位数,他们各抄错了一个数字,但计算结果都是1360.事实上正确结果的个位不是0,那么正确结果应当是多少?2.用0至9这10个数字组成一些质数(每个数字恰好用一次),这些质数的和最小是多少?3.已知b 13a.0A 是纯循环小数,将它写成最简分数后,使得分母最小.那么这个分数是多少?4.数学家维纳在博士毕业典礼上说:“我现在年龄的三次方是一个四位数,现在年龄的四次方是一个六位数,并且这两个数刚好包含数字0至9各一次,所以全部数字都得朝拜我,我将在数学领域干出一番大事业.”请问:他是几岁毕业的?5.一个四位数的每一位数字都是非零的偶数,它又恰好是某个偶数数字组成的数的平方,请问:这个四位数是多少?6.在图134所示算式的每个方框内填人一个数字,要求所填的数字都是质数,并使竖式成立. 答案:775×33=255757.a 、b 、c 是三个互不相同的自然数,且满意cba ×7bc =bca ×abc ,求三位数abc8.已知算式234235286 = cab ×bca ×abc ,其中a > b > c .后来发觉右边的乘积的数字依次出现错。
高思竞赛数学导引五年级第二十三讲计数综合二学生版

高思竞赛数学导引五年级第二十三讲计数综合二学生版第23讲计数综合二(学生版)内容概述涉及整数知识,具有教字或数阵图形式的计数问题.解题中需要灵活应用已学的各种计数方法,并注意结合题目的具体形式.典型问题兴趣篇1.同时能被6、7、8、9整除的四位数有多少个?2.从1,2,3,…,9这9个数中选出2个数,请问:(1)要使两数之和是3的倍数,一共有多少种不同的选法?(2)要使两数之积是3的倍数,一共有多少种不同的选法?3.在所有由1、3、5、7、9中的3个不同数字组成的三位数中,有多少个是3的倍数?4.用0至5这6个数字可以组成多少个能被5整除且各位数字互不相同的五位数?5.个位比十位大的两位数共有多少个?个位比十位大,十位比百位大的三位数共有多少个?6. 如果称能被8整除或者含有数字8的自然数为“吉利数”,那么在l至200这200个自然数中有多少个“吉利数”?7.一个正整数,如果从左到右看和从右到左看都是一样的,那么称这个数称为“回文数”,例如:1331,7,202,66都是回文数,而220则不是“回文数”,请问:从一位到六位的“回文数”一共有多少个?其中第1997个“回文数”是什么?8有一些四位数的4个数字分别是2个不同的奇数和2个不同的偶数,而且不含有数字0,这样的四位数有几个?9.把2005、2006、2007、2008、2009这5个数分别填人图23-1的东、南、西、北、中5个方格内,使横、竖3个数的和相等,一共有多少种不同的填法?10.从1至7中选出6个数字填入图23.2的的表中,使得相邻的两个方框内,下面的数字比上面大,右边的数字比左边大.请先给出一种填法,然后考虑一共有多少种填法?拓展篇1.分子小于6,分母小于20的最简真分数共有多少个?2.从l、2、3、4、5、6、7这7个数中选出3个数,请问:(1)要使这3个数的乘积能被3整除,一共有多少种不同的选法?(2)要使这3个数的和能被3整除,一共有多少种不同的选法?3,小明的衣服口袋中有10张卡片,分别写着1,2,3, (10)现从中拿出两张卡片,使得卡片上两个数的乘积能被6整除,这样的选法共有多少种?(注:9不能颠倒当作6来使用,6也不能颠倒当作9来使用)4.六位数123475能被11整除,如果将这个六位数的6个数字重新排列,还能排出多少个能被1 1整除的六位数?5.三个2,两个1和一个0可以组成多少个不同的六位数?求所有符合条件的六位数的和.6. 有一种“上升数”,这些数的数字从左往右依次增大,将所有的四位“上升数”按从小到大的顺序排成一行:1234,1235,1236,(6789)请问:此列数中的第100个数是多少?7. 有一些三位数的相邻两位数字为2和3,例如132、235等等,这样的三位数一共有多少个?8.在图23—3的方框内填入3、4、5、6中的一个数字,使得竖式成立.请问:所填的九个数字之和是多少?一共有多少种填法?9. 在1000,1001,…,2000这1001个自然数中,可以找到多少对相邻的自然数,满足它们相加时不进位?10.将1至7分别填入图234中的7个方框中,使得每行每列中既有奇数又有偶数,一共有多少种不同的填法?11.在图23。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第13讲 数字谜综合一
内容概述
涉及小数、分数、循环小数酌数字谜问题;需要利用数论知识解决的数字谜问题.
典型问题
兴趣篇
1.有一个四位数,在它的某位数字后加上一个小数点,得到一个小数,再把这个小数和原来的四位数相加,得数是4003.64求这个四位数.
2.试将1、2、3、4、5、6、7分别填人下面的方框中,每个数字只用一次:口口口(这是一个三位数),口口口(这是一个三位数),口(这是一个一位数),使得这三个数中任意两个都互质.已知其中一个三位数已填好,它是714,求另外两个数.
3.用1至9这9个数字各一次组成若干个数,这些数中最多有多少个合数?
4.如图13-!,4个小三角形的顶点处有6个圆圈,在这些圆圈中分别填上6个质数(可以重复),使得它们的和是20,而且每个小三角形3个顶点上的数之和相等,请问:这6个质数的乘积是多少?
5.在一个带有余数的除法算式中,商比除数大2,在被除数、除数、商和余数中,最大数与最小数之差是1023.请问:此算式中的4个数之和最大可能是多少?
6.在乘法算式“好好好春杯迎杯=⨯”中,不同的汉字表示不同的数字,相同的汉字表示相同的数字.请问:“迎+春+杯+好”等于多少?
7.将1至9这9个数填入下面算式中的9个方框内(每个数字只能用一次),使等式成立. 口口口×口口=口口×口口=5568
8.循环小数B A
.0化成最简分数后,分子与分母之和为40,那么A 和B 分别是多少?
9.在算式“7=+金杯
竞赛华罗庚数学”中,华、罗、庚、金、杯、数、学、竞、赛九个字,分别代表数字1、2、3、4、5、6、7、8、9.已知“竞 = 8,赛 = 6”,请把这个算式写出来.
10.已知“GOOD BAD BAD =+”是一个正确的加法算式,其中相同的字母代表相同的数字,不同的字母代表不同的数字,已知GOOD 不是8的倍数.请问:ABGD 代表的四位数是什么?
拓展篇
1.[4.2×5 - (1+2.5 + 9.1 + 0.7)] + 0.04=100.
2.用0至9这10个数字恰好组成一位数、两位数、三位数、四位数各一个(每个数字只能用一次),且这四个数两两互质.其中的四位数是2940,另外三个数可能是多少?
3.学数学科学数数=⨯.在上面的算式中,每一个汉字代表一个数字,不同的汉字代表不同的数字.请问:“数学”所代表的两位数是多少?
4.在等式“口△×△口×口O×◇△=口△口△口△”中,口、△、O 、◇分别代表不同的数字.四位数◇O 口△是多少?
5.将1、2、3、4、5、6、7、8、9这9个数字分别填人下式的各个方框中,使等式成立:口口×口口=口口×口口口=3634.
6.已知a 是一个自然数,A 、B 是1至9中的数字,最简分数差B A a 33.0222
=.请问:a 是多少?
7.把质数373按数位拆开(不改变各数之间的顺序),只能得到3、7、37、73这四个数,它们仍然都是质数,请找出所有具有这种性质的质数.
8.在下面各题中,请你用给出的四个数,适当进行加、减、乘、除运算,每个数恰好用一次,使得计算结果等于24. (1)1,4,5,6; (2)1,5,5,5; (3)3,3,7,7; (4)3,3,8,8.
9.把1至6填人下面的方框中,每个数字恰好使用一次,使得等式成立,请写出所
有的答案. 口.口×口.口=口.口
10.如图13-2所示,三角形纸片盖住的都是质数数字,正方形纸片盖住的都是合数数字,要使得两
个加数的差尽可能小,较大的加数是多少?
11.在下面两个算式中,相同的汉字表示相同的数字,不同的汉字表示不同的数字.花相似人不同代表的六位数是多少? 花相似岁岁年年=⨯ 不同人年年年年÷=÷
12.在图13-3所示的算式中,每个字母代表一个数字,不同的字母代表不同的数字.如果CHINA
代表的五位数能被24整除,那么这个五位数是多少?
超越篇
1.两个学生计算同一个乘法算式,两个乘数都是两位数,他们各抄错了一个数字,但计算结果都是1360.实际上正确结果的个位不是0,那么正确结果应该是多少?
2.用0至9这10个数字组成一些质数(每个数字恰好用一次),这些质数的和最小是多少?
3.已知b 13a
.0A 是纯循环小数,将它写成最简分数后,使得分母最小.那么这个分数是多少?
4.数学家维纳在博士毕业典礼上说:“我现在年龄的三次方是一个四位数,现在年龄的四次方是一个六位数,并且这两个数刚好包含数字0至9各一次,所以所有数字都得朝拜我,我将在数学领域干出一番大事业.”请问:他是几岁毕业的?
5.一个四位数的每一位数字都是非零的偶数,它又恰好是某个偶数数字组成的数的平方,请问:这个四位数是多少?
6.在图134所示算式的每个方框内填人一个数字,要求所填的数字都是质数,并使竖式成立.
答案:775×33=25575
7.a 、b 、c 是三个互不相同的自然数,且满足cba ×7bc =bca ×abc ,求三位数abc
8.已知算式234235286
= cab ×bca ×abc ,其中a > b > c .后来发现右边的乘积的数字顺序出现错。
