动力学第十三章
第十三章 机械振动与机械波1 第1讲 机械振动-2024-2025学年高考物理一轮复习课件

对点练1.(多选)如图甲所示,悬挂在 竖直方向上的弹簧振子,在C、D两点 之间做简谐运动,O点为平衡位置。振 子到达D点时开始计时,以竖直向上为 正方向,一个周期内的振动图像如图乙所示,下列说法正确的是
√A.振子在O点受到的弹簧弹力等于小球的重力
B.振子在C点和D点的回复力相同
√C.t=0.3 s时,振子的速度方向为竖直向上
√√BC..小弹球簧的振质子量的为频率F1为-2gF432t0
D.若弹簧振子的振幅为A,则从计时开始到13t0时,小球的路程为36A
由题图乙可知,t=0时刻小球所受弹力最 大,方向竖直向上,所以小球处于最低点, 故A错误;根据对称性,小球在最高点和 最低点的加速度大小相等、方向相反,根 据 F解1-得牛mf顿=g第=43t二m0 ,a定;故律解C,得正小m确球=;在F由1最-2于g高F132点,t0=,故9有BT正F+2确+34;Tm,由g=所题m以图a小;乙球小可的球知路在34T程最=为低t0s,点=T,9=·4有A1f , +3A=39A,故D错误。故选BC。
位移大小相等
对称性 (2)物体由P到O所用的时间等于由O到P′所用的时间,即tPO=tOP′
(3)物体往复过程中通过同一段路程(如OP段)所用的时间相等,即tOP
=tPO
(4)相隔
T 2
或
(2n+1)T 2
(n为正整数)的两个时刻,物体位置关于平
衡位置对称,位移、速度、加速度大小相等、方向相反
考向1 简谐运动的基本物理量 例1 如图所示,在光滑水平面上有一质量为m的小物块与左端固定的轻 质弹簧相连,构成一个水平弹簧振子,弹簧处于原长时小物块位于O点。 现使小物块在M、N两点间沿光滑水平面做简谐运动,在此过程中 A.小物块运动到M点时回复力与位移方向相同
第十三章 达朗贝尔原理

HOHAI UNIVERSITY ENGINEERING MECHANICS
O
η
θ
mg
dFI A y
η
3. 建立平衡方程:
ω
M
Oxi
l mg sin cosdFI 0 2 0
l
3g arccos 2 2 l
§2 刚体动力学中的达朗贝尔原理
刚体为一个质点系,其上每一个质点加上惯性 力后,成为一个分布力系,此力系应与刚体所受外 力构成平衡力系。
ma a
FW
FI
一、质点的达朗贝尔原理
则有 F FN FI 0
记 FI ma
ma FR F FN F FN ma 0
M
称为质点的惯性力, 与加速度方向相反
a FN
F
FR
F FN FI 0
ω
C i FI FIi FIin
故定轴转动刚体惯性力系简化为:
作用在转轴上,且与质心加速 度方向相反的惯性力FI=maC
在对称平面内,转向与角加速度方 向相反的惯性力偶MIO=JOα
ω α
MIO
O
FI C
aC
主矢和主矩作用在转动轴与对称平面相交的O点处
在对称面内向质心C简化
HOHAI UNIVERSITY ENGINEERING MECHANICS
FI mi ai maC
主矩
mi ri ri i )
FIit
FIin
若转轴过质心,则惯性力系 简化的结果仅为一力偶,其矩与 角加速度方向相反,MIC=JCα
FI
MIO
第十三章动量矩定理
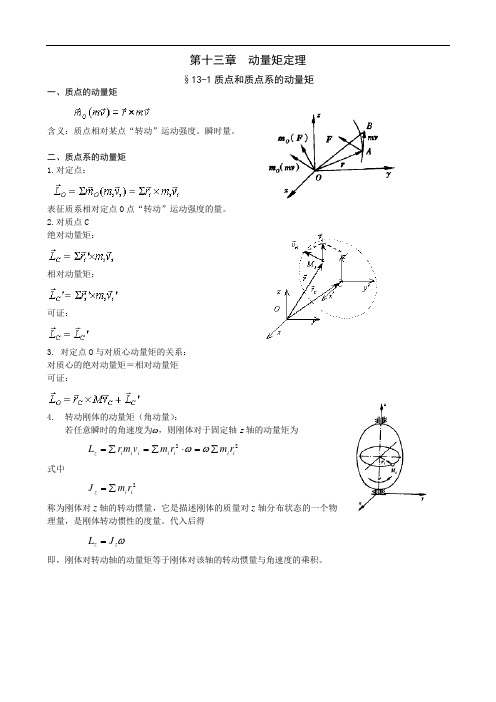
第十三章 动量矩定理§13-1质点和质点系的动量矩一、质点的动量矩含义:质点相对某点“转动”运动强度。
瞬时量。
二、质点系的动量矩 1.对定点:表征质系相对定点O 点“转动”运动强度的量。
2.对质点C绝对动量矩:相对动量矩:可证:3. 对定点O 与对质心动量矩的关系: 对质心的绝对动量矩=相对动量矩 可证:4. 转动刚体的动量矩(角动量):若任意瞬时的角速度为ω,则刚体对于固定轴z 轴的动量矩为22i i i i i i i z r m r m v m r L ∑=⋅∑=∑=ωω式中2i i z r m J ∑=称为刚体对z 轴的转动惯量,它是描述刚体的质量对z 轴分布状态的一个物理量,是刚体转动惯性的度量。
代入后得 ωz z J L =即,刚体对转动轴的动量矩等于刚体对该轴的转动惯量与角速度的乘积。
§13-2 动量矩定理一. 质点动量矩定理如图所示质点M 的动量对于O 点的矩,定义为质点对于O 点的动量矩,即v r v M m m O ⨯=)(质点对于O 点的动量矩为矢量,它垂直于矢径r 与动量mv 所形成的平面,指向按右手法则确定,其大小为 mvd OMD m O ==∆2)(v M 将上式对时间求一次导数,有 )()()(F M F r v r v r v M O O m dtd m dt d m dt d =⨯=⨯+⨯= 得)()(F M v M O O m dtd= 上式为质点的动量矩定理,即:质点对固定点O 的动量矩对时间的一阶导数等于作用于质点上的力对同一点的力矩。
二.质系动量矩定理设质系内有n 个质点,对于任意质点M i 有n i m dtde i i i O i i O 1)()()()()(=+=F M F M v M O式中)()(,e i i i F F 分别为作用于质点上的内力和外力。
求n 个方程的矢量和有∑∑∑===+=ni e i O ni n i i i O i i O m dt d 1)(11)()()()(F M F M v M式中∑==ni i i O1)(0)(F M,∑∑===⨯=ni ni e O i e i O 11)()()(M F r F M (e)i 为作用于系统上的外力系对于O 点的主矩。
《理论力学》--第十三章 达朗贝尔原理(动静法)

例13-7 已知:如图所示,轮盘(连同轴)的质量 m 20kg, 转轴AB与轮盘的质量对称面垂直,但轮盘的质心 C不在转轴上,偏心距 e 0.1mm. 当轮盘以均转速 转动. n 12000 r min 求:轴承A,B的约束力
解:
0.1 12000π 1 2 an e m s 158 m s 2 1000 30
2
FI man 3160 N 1 FNA FNB mg FI 2
1 20 9.8 3160N 1680N 2
(e) Fi 为作用于第i个质点上质点系外部物体的作用力. (i) Fi 为作用于第i个质点上质点系内部的力. (e) (i) Fi Fi Fi 0 i 1,2,, n
例13-2 已知:如图所示,定滑轮的半径为r ,质量为m 均匀分布在轮缘 上,绕水平轴O转动.垮过滑轮的无重绳的两端挂有质量 为m1 和m2 的重物(m1>m2),绳与轮间不打滑,轴承摩擦 忽略不计。 求:重物的加速度.
例13-1 已知: 求:
m 0.1kg , l 0.3m , 60
v, FT .
解:
v2 FI man m l sin mg FT FI 0
Fb Fn
0, FT cos mg 0 0, FT sin FI 0
Fs f s FN f s m1 m2 g
Fs 3m1 fs FN 2m1 m2
D
§ 13-4
绕定轴转动刚体的轴承动约束力
F
x
0 FA x FB x FR x FI x 0
F
y
0 FA y FB y FR y FI y 0
理论力学-第13章 动力学普遍方程和第二类拉格朗日方程

*第13章 动力学普遍方程和第二类拉格朗日方程
第二类拉格朗日方程
返回
第二类拉格朗日方程
在动力学普遍方程中,由于系统存在约束,一般情形下,各 质点的虚位移并不完全独立,应用时须建立各虚位移与广义坐标 之间的关系。
第二类拉格朗日方程
N
(Qk Qk*) δ qk 0
k 1
其中Qk为对应于广义所标qk的广义力(generalized forces); Qk*为广义惯性力(generalized inertia forces)
Qk
n i 1
Fi
ri qk
Qk*
n i 1
miai
ri qk
由于在完整约束下,δq1, δq2,…, δqN 相互独立,
Qk*
n i 1
miri
ri qk
d dt
n
(
i 1
miri
ri qk
)
n i 1
miri
d dt
( ri qk
)
d dt
n i1
mi
ri
ri qk
n i1
mi
ri
ri qk
d dt
qk
n
(
i 1
1 2
miri2 )
qk
n
(
i 1
1 2
miri2 )
d dt
(
T qk
理论力学
第3篇 工程动力学基础
第3篇 工程动力学基础
*第13章 动力学普遍方程 和第二类拉格朗日方程
*第13章 动力学普遍方程和第二类拉格朗日方程
第十三章 振动分析的矩阵迭代法

(13-27)
M1
不包含第一振型的试探形状为
0 0 20 v v 1Y 2 1
(13-28)
§13.4 高阶振型分析 在试探向量中消除第一振型分量的方便方法是 应用淘汰矩阵S1
2 v 0 v 0 2 1 11T mv 0 S1v 0 2 2 M1
ˆ ˆ v=n 2Dvn
v1 =Dv1
1 0
(13-5)
(13-5a)
§13.2 基本振型分析—Stodola法
高等结构动力学
1
2 1
1 =v1 v
1 1
(13-6*)
考虑任一点k的位移
1
12
1 vk0 =vk1 1
(13-7*)
2 1
0 v
k1 1 vk1
该方程最后一个等号成立,第一振型的系数远大于其它的系数.1 3
2s
(13-23)
最终结果可视为
v1
s
1Y1(0) 1 (0) max(1Y1 )
(13-24)
§13.3 收敛性的证明
高等结构动力学
(13-32)
D2 =DS1
(13-33)
此时可用下式计算频率
2 2 (1)
(1) T (v 2 ) mv(0) 2 (1) (1) v 2 mv 2
(13-34)
v 2 D 2 v(0) 2
§13.4 高阶振型分析 第三和更高振型的分析
高等结构动力学
净化了的第三振型的形状为
(0) 3 v (0) Y (0) Y (0) v 3 1 1 2 2
N
k
i
第三篇动力学

转动惯量是描述刚体的质量分布的另一个 特征量。
刚体的转动惯量是刚体转动时惯性的度量,
它等于刚体内各质点的质量与其到转轴的垂
直距离平方的乘积之和。
n
I z
mi ri 2
i 1
由此可见,转动惯量的大小不仅与质量大小有关,
而且与质量的分布情况有关。
若刚体的质量是连续分布的,刚体的转动惯量公式
Iz
这个速度称之为物体在液体中自由下沉的极限速度
讨论:由此可以看出在阻尼系数基本相同的 情况下(即物体的大小、形状基本相同时), 物体的质量越大,它趋近于极限速度所需的 时间越长。工程中的选矿、选种工作,就是 应用了这个道理。
注意到运动的起始条件为
t 0 x0 H , v0 0
v g 1 ebt b
I O杆
I C杆
M1
1 2 2
IO杆
l 12
M
1l
2
M1
l2 4
1 3
M1l
2
I O盘
I C盘
M
2
l
d 2
2
IO盘
1 2
M
2
d 2
2
M
2
l
d 2
2
Βιβλιοθήκη M2 3 8
d
2
l2
ld
IO
IO杆
IO盘
1 3
已知物体的运动规律,求作用在此物 体上的力;
已知作用于物体上的力,求此物体产 生什么样的运动。
《理论力学》第十三章 达朗贝尔原理.ppt

O
aCn C
A
Fix FOx-ma2lCn 2 mg sin 0
aCτ α
4.由动能定理计算2,T1-T2=∑Wi
1 2
J O 2
0
mg
l 2
sin
外力只有重力
例4: OB质量不计,AB长l、质量m。试求绳OA剪
HOHAI UNIVERSITY ENGINEERING MECHANICS
Fix FOx 0 (3)
4.补充方程
aC l / 2
FOx
0;
FOy
1 4
mg ;
3g
2l
HOHAI UNIVERSITY ENGINEERING MECHANICS
例3: 约束均质杆A端的绳索突然被剪断,试求杆转
到任一位置时的角加速度 、角速度及O处约束力
惯性系中:
0 FR ma FR FI
达朗贝尔原理将动力学加速度问题形 式上转换成静力学中的平衡问题,也 叫动静法
一、质点的达朗贝尔原理
ma FR F FN
FI
F
记
F N
ma
FI ma
0
称为质点的惯性力, 与加速度方向相反
则有 F FN FI 0
MIO MO (FIi ) MO FIi
MO miii miii
mi i2 JO
ω
MIO
FaOICFCρIii
i FIin
故定轴转动刚体惯性力系简化为:
作用在转轴上,且与质心加速 度方向相反的惯性力FI=maC 在对称平面内,转向与角加速度方 向相反的惯性力偶MIO=JOα
理论力学第十三章 动量定理和动量矩定理

冲量是矢量,它与力F的方向一致。在国际单位制中,冲量的单位是N·s, 它与动量的单位相同
§13-1 动量定理
动量定理
I. 质点的动量定理
(1) 动量定理的微分形式
质点动量的微分等于作用于该质点上的各力元冲量的矢量和。
(2)动量定理的积分形式
质点动量在任一时间间隔内的变化,等于作用于该质点上各力在同一时间 间隔内的冲量的矢量和。
若作用于质点系的外力的矢量和恒等于零.则该质点系的动 量保持不变。 若作用于质点系的外力在轴x上投影的代数和等于零,即∑F(xe)=0,可得
若作用于质点系的外力在某轴上的投影代数和恒等于零,则 该质点系的动量在该轴上的投影保持不变。
§13-1 动量定理
例13-1 质量为75kg的跳伞运动员,从飞机中跳出
解鼓轮作平面运动其受力如图所示建立鼓轮平面运动微分方程为123因鼓轮沿平直轨道作无滑动的滚动故有如下关系将上述关系和代入式34将式4与式1联立求解得轮心0的加速度为由此得到使鼓轮作无滑动滚动时的摩擦力为135动力学普遍定理的综合应用一般方法11首先判断是否是某种运动守恒问题如动量守恒质心运动守恒动量矩守恒或相对于质心的动量矩守恒等
(1)判定给定问题是否可用动量定理或质心运动定理求解。求约束反力、速 度和加速度时可用动量定理或质心运动定理;求质心速度、质心位置或质点 系内部质点速度的改变时多用动量守恒定律或质心运动守恒定律。
(2)根据题意选择研究对象。研究对象可以是单个质点、质点系内部部分质 点或整个质点系。
(3)受力分析。受力图中只画外力,不画内力。分析作用在研究对象上的外力 主矢或外力在某轴上投影的代数和是否为零,若为零可选择动量守恒或质心 运动守恒定律求解。
第十三章 动量定理
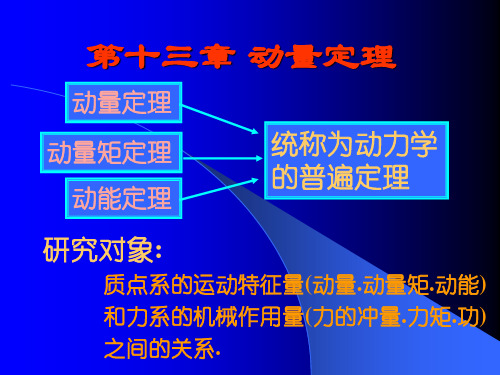
⑵方向与V一致Kx=m来自Vx⑶单位. kg·m/s ; N·s Ky=m·Vy
⑷动量是状态量
Kz=m·Vz
13.22 质点系的动量
1定义: 质点系各质点动量的矢量和称为 质点系的动量.
K= ∑Ki = ∑miVi
⑴总动量不一定总大于分动量
⑵总动量为零时,质点动量不一 定为零.
K=∑(mi·dri / dt)
注意两点: ⑴重力场中,质心和重心重合;
⑵.质心比重心更具广泛的意义. (重心只在重力场中有意义)
13.2 质点和质点系的动量 力的冲量
13.21 质点的动量(物体机械运动量的量度)
1.定义: 质点的质量与其瞬 时运动速度的乘积
K = m ·V
2.注意: ⑴动量是矢量
3.动量在直角坐标系 中的分量式
冲量是力在 一段时间间隔内的累计作用效果, 等于力矢量对时间的定积分.当力是常力时, 力的冲量等于力矢量与作用时间的乘积.
3.合力的冲量: 合力的冲量=分力冲量的矢量和
S(R) = ∑ S(Fi)
4.单位: N·S
13.3 动量定律
13.31 质点动量定律
1.质点动量定律微分形式: m dv F
其中: Gi = mi g G= M g 所以: XC=∑miXi / M 这就是质心坐标公式
YC=∑miYi / M ZC=∑miZi / M
由该公式确定的几何 点称为物体的质心
XC=∑miXi / M YC=∑miYi / M ZC=∑miZi / M
该公式表明:
质心的坐标等于质点系 各质点坐标对质量的加 权平均
第十三章 动量定理
动量定理
动量矩定理 动能定理
统称为动力学 的普遍定理
第13章质点系动能定理

1k 2
(12
22
)
初变形 1 未变形2
转动刚体上作用力的功
WM
2
mz (F )d
mz(F) C
W mz (F )(2 1)
1
力偶的功 WM M(2 1)
摩檫力的功 •两物有相对滑动, 摩擦力 作负功
vO O
P Fs
纯滚动时, 作用在速度瞬心P点 的摩擦力F 所作元功为
1
T ( 2i
mi )vC2
i
1 2
mi
vi2r
Te
Tr
质点系的动能(绝对运动动能),等于系统跟 随质心平移的动能(牵连运动动能)与相对于质 心平移系运动的动能(相对运动动能)之和。
结论与讨论
正确计算刚体 平面运动时的动能
x
vA xA
OA
x
B
均质杆AB长度为l、质量为m , A端与小圆滚轮铰接,小圆滚轮
dt
dt
力(偶)矩的功率: P W M d M
质点系动能定理 dt
dt
质点: m dv F m dv v F v
d( 1 mv 2 ) 2
P
dt
质点系:d(
1
2 dt
mv
2
)
dt
P
dT dt
dt
P — 功率方程
dT Pdt dT W -微分形式
W
O
Ax
为求物块A下降至 任意位置(x)时的加速 度,可以采用哪一个
动力学定理?
W x
结论与讨论
关于动能定理 与
第十三章 动量定理
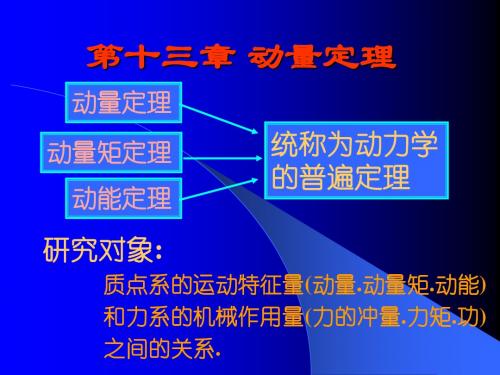
t1 t2
同样,应用动量定理时,常取它们在直角坐标 轴上的投影式. dt 即质点系动量在某轴上 ex X F dK X 的投影对时间的导数等 dt 于作用于质点系的全部 eY F Y Y dK 外力在同一轴上的投影 dt 之代数和。 eZ
1.恒力的冲量:
S = F ·( t2 - t1 )
⑵取决于力的作用时间.
力对物体的作用效果: ⑴取决于力的大小;
2.变力的冲量: 元冲量: 力F与它所作用的微小 dS=F· dt 时间间隔dt的乘积 变力的 冲量: 等于每一时间间隔的 S=∫F· dt 元冲量的矢量和
冲量是力在 一段时间间隔内的累计作用效果, 等于力矢量对时间的定积分.当力是常力时, 力的冲量等于力矢量与作用时间的乘积. 3.合力的冲量: 合力的冲量=分力冲量的矢量和
第十三章 动量定理
动量定理
动量矩定理 动能定理
统称为动力学 的普遍定理
研究对象:
质点系的运动特征量(动量.动量矩.动能) 和力系的机械作用量(力的冲量.力矩.功) 之间的关系.
13.1质点系的质量中心(质心)
1.质量中心的坐标:
由重心坐标公式:
XC=∑GiXi / G
其中: 所以:
YC=∑GiYi / G
由上式作图(b)。并取MXY坐标如图,将上式 向XY轴方向投影: Sx=k2x- k1X=- mv· co s(180°- 135°)-mV o =- O.14(40×cos45°十50)=- 11(N· S) Sy=k2y- kly=mV· sin(180°- 135°) =0.14×40Sin45°=3.96(N· S) S=√sx2十sY2=√(-11)2十3.962=11.69(N· S)
第十三章 热、质同时传递的过程

2、传质速率 N A = kg ( ps − p) PS为液相温度对应的平衡分压 N A = kH (HS − H ) 以湿度差为推动力
气体湿度 H 的定义: 单位质量干气体带有的水汽量 kg水汽 kg干气
空气湿度
H=
湿空气中水汽质量 湿空气中干空气质量
=
m水汽 m干气
=
M 水n水 M 气n气
=
18 • 29
=
0.0303kg 水气
/ kg干气
四、热质同时传递过程的计算
1、湿空气热焓 I
单位 kJ / kg干气
定义:1 kg干气焓 + H kg水汽焓
焓基准:干气0℃ 水汽0℃
所以: I = CPg t + HC PV t + Hro
干气比热 + 水汽比热 + 水汽化热
= (CPg + CPV H )t + r0 H = CPH 固定不变,液相状态变化(湿球温度计 )
液相极限温度—— 湿球温度 tw
t
过程分析: 起初 t = θ水
由于 p水汽 < pS ,过程逆转(传热)
tw
水汽化从其自身吸热使水温θ ↓
气体
此时,t气 > θ水,空气传递显热给水,
空气 传 热 水
水 传 质 空气 ps > p
如果这一热量不足以补偿水的汽化所需 热量,水温θ继续下降,降至tw时,在ttw温差下,空气传给水的显热与水汽化 所需热量相等,达到平衡状态,水温θ
第十三章 热、质同时传递的过程
一、热质同时传递过程的特征与过程方向判断 二、热质同时传递过程的速率 三、热质同时传递过程的极限 四、热质同时传递过程的计算
一、热质同时传递过程的特征与方向判断
第十三章动量矩定理

M (e) O2
mO2 (F (e) )
, LO2
1 2
P2 g
r22
w2
P3 g
vr2
d dt
(1 2
P2 g
r22
w2
P3 g
vr2 )
T 'r2
P3
r2
(2)
③运动学补充方程:
r1e1 r2e2 (3)
v r2w2, a r2e2 (4)
化简(2)
得:P2
2P3 2g
⒊ 质点的动量矩守恒情况
若 mO(F ) 0 mz (F ) 0则 mO (mv ) 常矢量 mz (mv) 常量
[例2] 单摆 已知m,l,t =0时= 0,从静止
开始释放。 求单摆的运动规律。
解:研究小球,将小球视为质点。受力如图示。
mO (F )mO (T )mO (mg)mglsin
a
T
'P3
化简(1) 得:
P1 a M1 T
2g
r1
a 2(M1 / r1 P3) g P1 P2 2P3
§12-2 动量矩
质点 动量定理: 质点系 动量的改变—外力(外力系主矢)
质心运动定理:质心的运动—外力(外力系主矢)
若当质心为固定轴上一点时,vC=0,则其动量恒等于零, 质心无运动,可是质点系确受外力的作用。动量矩定理建立了 质点和质点系相对于某固定点(固定轴)的动量矩的改变与外 力对同一点(轴)之矩两者之间的关系。 一.质点的动量矩
l
代入初始条件 (t 0, 0,0 0)
则运动方程
0 cos
第十三章阅读材料---衍射运动学理论和动力学理论

6.6衍衬运动学理论的局限性运动学理论假设:1) 试样的反射面不严格处于精确的布拉格位置,及S ≠0。
2) 衍射束与透射束相比强度很小,它们的相互作用可以忽略不计。
3) 试样较薄,吸收效应可以忽略不计。
在此基础上,求得在完整晶体下表面处的衍射强度:22222)()(sin s st A I g gg ππξπ≈= 当s=0时,上式变为:222)(gg g t A I ξπ≈=∞→∞→g I t 不合理当t 很大时,I g 可超过入射电子强度,这是不可能的,原因是运动学理论有问题。
根据能量守恒原理:22)(gt ξπ≤1(入射强度已归一),即3~gg t ξπξ≤。
当V=100kV 时,一般材料的消光距离g ξ为150-500Å,故若要把运动学理论用在s=0的情况,晶体厚度t 必须<100 Å。
而事实上,在电镜中所用的薄晶体厚度在几百Å甚至更厚一些(通常10g ξ厚)。
由运动学理论导出的等厚条纹间距为1/s ,当s →0时,条纹间距→无穷大,而实际上条纹间距是一个有限值。
另外,电子衍射强度I g 往往可与透射强度相比,以致常发生二次衍射效应及透射束与衍射束之间的相互作用。
还有由于吸收出现的反常衬度效应等衍衬象的细节等。
这些都是运动学理论无法处理的,必须发展动力学理论。
6.7电子衍衬动力学理论动力学理论的数学推导较繁琐,物理图像也较抽象,这儿只介绍一些基本概念。
为了处理简单,仅考虑双束近似的情况,也就是说晶103体内只有一个强衍射束和一个透射束,在它们之间不断交换能量,保持动态平衡,根据动力学理论,在晶体内透射束和衍射束的强度是交替变化的,而不是象在运动学情况下,透射束不断减弱,衍射束一直在加强。
设透射束振幅为φ0,衍射束振幅为φg ,则φ0、φg 随深度的变化可表示为: )2exp()2exp(00000isz ii dz d isz ii dz d g g g g gπφξπφξπφπφξπφξπφ-+=+= (6-8)0ξ是→g =0时的消光距离。
13-理论力学-第三部分动力学第十三章达朗贝尔原理

由于小车具有惯性,力图保持原来的运动状态,对于施力物体
(人手)产生的反抗力(反作用力),称为小车的惯性力。 F' F ma
动力学/达朗伯原理
二、质点的达朗贝尔原理
非自由质点M,质量m,受主动
FI
力 为
F
a
,约束反力 FN ,获得的加速度
。 由牛顿第二定律:
FN
F
FN
ma
F FN ma 0
▼任意点
Mi 切向加速度
a i
法向加速度
ain
▼
Mi 虚加上的惯性力
FIi
mi
ai
,
FIin
miain
α
所有的点组成一个平面内的惯性力系
α
ain aiτ
FIiτ
FIin
动力学/达朗伯原理
▼
Mi 虚加上的惯性力
FIi
mi
ai
,
FIin
miain
▼O为转轴 z与质量对称平面的交点,向O点简化:
理论力学
第三部分 动 力 学
第十三章
达 朗 贝尔原 理
2021年7月22日
动力学/达朗伯原理
第十三章
达朗贝尔原理
达朗贝尔原理是十八世纪为解决机器动力学问题 提出的,实质就是在动力学方程中引入惯性力,将动 力学问题从形式上转化为静力学中的力的平衡问题, 应用静力学的平衡理论求解。
本章介绍动力学的这一重要原理——达朗伯尔原 理 (也称动静法)。
FA
mg 4
cos0
FAτ
(与图示反向)
FAn
FIR
动力学/达朗伯原理
●用动量矩定理+质心运动定理再求解此题:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
动力学第十三章达朗伯原理达朗伯原理是一种解决非自由质点和质点系动力学问题的普遍方法。
这种方法是用静力学中研究平衡问题的方法来研究动力学问题,因此又称为动静法。
本章介绍达朗伯原理和定轴转动刚体的轴承动反力,以及静平衡和动平衡的概念。
第一节达朗伯原理一、质点惯性力的概念当质点受到其他物体作用而使运动状态发生变化时,由于质点本身的惯性,对施力物体产生反作用力,这种反作用力称为质点的惯性力。
惯性力的大小等于质点的质量与其加速度的乘积,方向与加速度的方向相反,但作用于施力物体上。
若用F I表示惯性力,则。
例如,工人沿光滑的水平直线轨道推动质量为m的小车,作用力为F,小车在力的方向上产生加速度a,有。
根据作用反作用定律,此时工人手上必受到小车的反作用力F I,此力是由于小车具有惯性,力图保持其原来的运动状态,对手进行反抗而产生的,即小车的惯性力,有。
二、质点的达朗伯原理设质量为m的质点M,受主动力F和约束反力F N的作用,沿曲线运动,产生加速度a,如图13-1所示。
根据牛顿第二定律,有此时质点由于运动状态发生改变,它的惯性力为将以上两式相加,得(13-1)上式表明:任一瞬时,作用于质点上的主动力、约束反力和虚加在质点上的惯性力在形式上组成平衡力系。
这就是质点的达朗伯原理。
图13-1必须指出:由于质点的惯性力并不作用于质点本身,而是假想地虚加在质点上的,质点实际上也并不平衡。
式(13-1)反映了力与运动的关系,实质上仍然是动力学问题,但它提供了将动力学问题转化为静力学平衡问题的研究方法。
这种方法对求解质点的动力学问题并未带来明显的方便,但在研究方法上显然是个新的突破,而且,它对求解非自由质点系的动力学问题是十分有益的。
三、质点系的达朗伯原理设有n个质点组成的非自由质点系,取其中任意一质量为m i的质点M i,在该质点上作用有主动力F i,约束反力F Ni,其加速度为a i。
根据质点的达朗伯原理,如在质点M i上假想地加上惯性力,则F i、F Ni和F Ii构成一平衡力系,有对质点系的每个质点都作这样的处理,则作用于整个质点系的主动力系、约束力系和惯性力系组成一空间力系,此时力系的主矢和力系向任一点O简化的主矩都等于零,即(13-2)上式表明:任一瞬时,作用于质点系上的主动力系、约束力系和虚加在质点系上惯性力系在形式上构成一平衡力系。
这就是质点系的达朗伯原理。
如果将力系按外力系和内力系划分,用和分别表示质点系外力系主矢和内力系主矢;和分别表示质点系外力系和内力系对任一点O的主矩,由于质点系内力系的主矢和主矩均等于零,故式(13-2)可以改写为(13-3)上式表明:任一瞬时,作用于质点系上的外力系和虚加在质点系上的惯性力系在形式上构成一平衡力系。
第二节刚体惯性力系的简化应用达朗伯原理解决质点系的动力学问题时,从理论上讲,在每个质点上虚加上惯性力是可行的。
但质点系中质点很多时计算非常困难,对于由无穷多质点组成的刚体更是不可能。
因此,对于刚体动力学问题,一般先用力系简化理论将刚体上的惯性力系加以简化,然后将惯性力系的简化结果直接虚加在刚体上。
下面仅就刚体作平动、定轴转动和平面运动三种情况,来研究惯性力系的简化。
一、刚体作平动刚体平动时,刚体上各点的加速度都相同,惯性力系构成一个同向空间平行力系。
如图13-4所示,将此惯性力系向刚体的质心C简化,得惯性力系的主矢为即(13-4)图13-4惯性力系对质心C的主矩为式中r i为质点Mi相对于质心C的矢径,由质心矢径表达式(3-25)知式中r c为质心的矢径,由于质心C为简化中心,r c=0 ,于是有上述结果表明:刚体作平动时,惯性力系简化的结果为一个通过质心的合力F IR,其大小等于刚体的质量与质心加速度的乘积,方向与质心加速度的方向相反。
二、刚体作定轴转动仅讨论工程中常见的比较简单的情况。
设刚体具有质量对称平面,且转轴垂直于质量对称平面。
先将惯性力系简化为在质量对称平面内的平面力系,再将它向平面与转轴的交点O简化,如图13-5所示。
图13-5先研究惯性力系的主矢。
设刚体内任一质点M i的质量为m i,加速度为a i,刚体的总质量为m,质心的加速度为a C,则惯性力系的主矢为由质心公式对时间求两阶导数,可得故有(13-5)再研究惯性力系对坐标原点O的主矩。
由于刚体转动时任一质点M i的惯性力F Ii可以分解为切向惯性力F Iiτ和法向惯性力F Ii n,如图13-5所示。
故惯性力系对O点的主矩为即(13-6)式中Jz为刚体对通过点O的转轴z的转动惯量,α为刚体转动的角加速度,负号表示主矩与a转向相反。
上述结果表明:刚体绕垂直于质量对称平面的转轴转动时,惯性力系向转轴与对称面的交点O简化的结果为一个主矢和主矩。
主矢的大小等于刚体的质量与质心加速度的乘积,方向与质心加速度的方向相反;主矩的大小等于刚体对转轴的转动惯量与角加速度的乘积,转向与角加速度的转向相反。
下面讨论几种特殊情况:1.刚体转轴不通过质心,作匀速转动如图13-6a所示,由于角加速度α=0,故,因而惯性力系简化为一通过O 点的法向惯性力,大小等于,方向与质心法向加速度方向相反,其作用线通过质心C。
2.刚体绕质心轴转动,角加速度α≠0如图13-6b所示,由于质心加速度a C=0,此时,惯性力系仅简化为一个力偶,其力偶矩。
图13-63. 刚体绕质心轴匀速转动如图13-6c所示,由于a C=0,α=0,惯性力系向O点简化的主矢和主矩都等于零。
三、刚体作平面运动仅讨论刚体具有质量对称平面,且刚体平行于对称平面作平面运动的情况。
此时,刚体惯性力系可简化为在对称平面内的平面力系。
刚体的平面运动可分解为随质心的平动和绕质心的转动,将惯性力系向质心C简化,如图13-7所示,可得惯性主矢和主矩分别为(13-7)图13-7上式表明:具有质量对称平面且平行于此平面作平面运动的刚体,惯性力系向质心C简化的结果为一个主矢和一个主矩。
主矢过质心C,大小等于刚体质量与质心加速度的乘积,方向与质心加速度的方向相反;主矩的大小等于刚体对质心轴的转动惯量与角加速度的乘积,转向与角加速度的转向相反。
第三节达朗伯原理的应用应用达朗伯原理求解刚体动力学问题时,首先应根据题意选取研究对象,分析其所受的外力,画出受力图;然后再根据刚体的运动方式在受力图上虚加惯性力及惯性力偶;最后根据达朗伯原理列平衡方程求解未知量。
下面通过举例来说明达朗伯原理的应用。
第四节定轴转动刚体的轴承动反力在高速转动的机械中,由于转子质量的不均匀性以及制造或安装时的误差,转子对于转轴常常产生偏心或偏角,转动时就会引起轴的振动和轴承动反力。
这种动反力的极值有时会达到静反力的十倍以上。
因此,如何消除轴承动反力的问题就成为高速转动机械的重要问题。
下面将着重研究轴承动反力的计算和如何消除轴承动反力。
一、一般情况下转动刚体惯性力系的简化现在研究一般情况下定轴转动刚体的惯性力系的简化问题。
如图13-11所示,设刚体绕定轴z转动,在某瞬时的角速度为ω,角加速度为α。
在质点M i上虚加惯性力图13-11则惯性力系向O点简化的主矢为(13-8)惯性力系向O点简化的主矩可用在x、y、z三坐标轴上的投影M IOx、M IOy、M IOz来表示。
根据合力矩定理,有质点惯性力可以分解为切向惯性力和法向惯性力,它们的方向如图所示,大小分别为则由图13-11可知于是得(13-9)式中和取决于刚体质量对于坐标轴分布的情况,并具有转动惯量的量纲,分别称为刚体对通过O点的轴x、z和轴y、z的惯性积,也称为离心转动惯量。
惯性积可正、可负,也可为零。
同理可得惯性力系对于y轴的矩为(13-10)因为各质点的法向惯性力通过轴线,有,于是有(13-11)式中负号表示力矩转向与角加速度转向相反。
二、一般情况下轴承的动反力设刚体绕AB轴转动,如图13-12所示,某瞬时的角速度为ω,角加速度为α。
作用于刚体的主动力系和虚加于刚体的惯性力系向转轴上任一点O简化,分别得力和,力偶矩矢M O和M IO。
轴承A、B的约束反力如图所示。
图13-12为求轴承反力,取O点为直角坐标系的原点,z轴为转轴。
根据达朗伯原理,可列出下列六个平衡方程由前五个方程解得轴承反力(13-12)由式(13-12)可知,由于惯性力系分布在垂直于转轴的各平面内,止推轴承沿z轴的反力F Bz 与惯性力无关;与z轴垂直的轴承反力F Ax、F Ay、F Bx、F By由两部分组成:(1)由主动力引起的静反力;(2)由惯性力引起的动反力。
要使动反力等于零,必须有即轴承动反力等于零的条件是:惯性力系的主矢等于零,惯性力系对于x轴和y轴之矩等于零。
由式(13-8)、式(13-9)和式(13-10)知由此可见,要使惯性力系主矢等于零,必须有a c=0,即转轴必须通过质心;要使惯性力系对于x轴和y轴之矩等于零,必须有,即刚体对于转轴的惯性积等于零。
如果刚体对于通过O点的z轴的惯性积J xz和J yz等于零,则此z轴称为该点的惯性主轴,通过质心的惯性主轴称为中心惯性主轴。
因此,避免出现轴承动反力的条件是:刚体的转轴应为刚体的中心惯性主轴。
三、定轴转动刚体的静平衡和动平衡的概念设刚体的转轴通过质心,且刚体除受到重力作用外,没有受到其它主动力的作用,则刚体在任何位置均能保持静止不动,这种现象称为静平衡。
当刚体绕定轴转动时,不出现轴承动反力的现象称为动平衡。
在工程中,为了消除轴承动反力,对转速较高的物体如汽轮机转子、电动机转子等,要求转轴是中心惯性主轴,所以一般将它们设计成具有对称轴或有对称面,并且转轴是对称轴或通过质心并垂直于对称面。
然而在实际上,由于在制造或安装中难免出现误差,以及材料的不均匀性等,转子的质心和转轴的方位仍然会产生一定的偏离,需要在一定的试验设备上进行静平衡或动平衡试验加以校正。
第十三章思考题·13-1 设质点在空中运动时,只受到重力作用,问在下列三种情况下,质点惯性力的大小和方向:(1)质点作自由落体运动;(2)质点被垂直上抛;(3)质点沿抛物线运动。
·13-2 一列火车在启动过程中,哪一节车厢的挂钩受力最大,为什么?·13-3 均质薄圆盘半径为R,质量为m,以角速度ω和角加速度α绕O轴转动,圆盘的偏心矩OC=e,如图13-14所示。
试证明按平面运动情况对圆盘惯性力系进行简化的结果与按定轴转动情况对圆盘的惯性力系进行简化的结果是一致的。
图13-14·13-4 滑轮对O轴的转动惯量为J O,绳两端物重W1=W2,如图13-15所示,问在下述两种情况下滑轮两端绳的拉力是否相等?(1)物块B作匀速运动;(2)在物块B上加力使物块作匀加速运动。
图13-15第十三章习题·13-1 如图13-16所示,一飞机以匀加速度a沿与水平线成仰角β的方向作直线运动。
