电力系统稳态分析大作业——基于高斯赛德尔法潮流计算
电力系统中潮流计算算法研究

电力系统中潮流计算算法研究随着电力系统的不断发展,潮流计算算法成为了电力系统运行中不可或缺的一环。
潮流计算算法主要是用来分析电力系统中电流、电压以及功率等各种参数的变化。
它是电力系统稳态分析中最基本、最重要的一项计算,对于保证电网的安全可靠运行起到了举足轻重的作用。
一、潮流计算算法的基本原理潮流计算算法的基本原理是基于电力系统中的潮流方程,通过求解潮流计算方程来得到电力系统中各支路及各节点的电流、电压和功率等参数。
其主要求解过程包括节点电压的估计、节点功率的平衡以及潮流方程的求解等方面。
潮流计算算法可以通过数学方法实现,也可以利用计算机程序来求解。
二、潮流计算中常用的算法1. 高斯-赛德尔迭代法高斯-赛德尔迭代法是潮流计算中最早也是最经典的算法之一。
该算法是根据潮流计算方程的特点而设计出来的,主要通过迭代的方式求解方程组,并逐步逼近方程的最终解。
该算法虽然存在收敛速度较慢、收敛极限不明确等缺点,但是其稳定性较好,可以准确地计算出电力系统中的各项参数。
2. 牛顿-拉夫逊方法牛顿-拉夫逊方法是一种基于二次对数频率计算的方法,其主要特点是通过求解雅克比矩阵而不是求解逆矩阵来建立方程组。
该算法收敛速度较快、计算精度高,被广泛应用于大规模电力系统的潮流计算中。
3. 变权系数法变权系数法是一种改进的潮流计算算法,其主要特点是通过加大潮流方程中电压较小的节点的权数,从而使迭代效率更高,收敛速度更快。
该方法适用于电力系统中节点数较多、计算强度较大的情况。
三、潮流计算在电力系统中的应用潮流计算通常被广泛应用于电力系统的运行和规划中,主要包括以下几个方面:1. 性能评估潮流计算可以用来评估电力系统的性能,包括电压稳定性、电网负荷能力、电网安全裕度等方面。
通过对潮流计算结果的分析,电力系统工作者可以预测电力系统可能出现的问题,并采取相应的措施来保证电网的安全稳定运行。
2. 计划管理潮流计算可以用来指导电力系统的规划和管理工作。
高斯赛德尔法潮流计算
高斯——赛德尔法潮流计算潮流计算高斯——赛德尔迭代法(Gauss 一Seidel method)是求解电力系统潮流的方法。
潮流计算高斯——赛德尔迭代 法又分导纳矩阵迭代法和阻抗矩阵迭代法两种。
前者 是以节点导纳矩阵为基础建立的赛德尔迭代格式;后者是以节点阻扰矩阵为基础建立的赛德尔迭代格式。
高斯——赛德尔迭代法这是数学上求解线性或非 线性方程组的一种常用的迭代方法。
本实验通过对电力网数学模型形成的计算机程序的编制与调试,获得形成电力网数学模型:高斯---赛德尔法的计算机程序,使数学模型能够由计算机自行形成,即根据已知的电力网的接线图及各支路参数由计算程序运行形成该电力网的节点导纳矩阵和各节点电压、功率。
通过实验教学加深学生对高斯---赛德尔法概念的理解,学会运用数学知识建立电力系统的数学模型,掌握数学模型的形成过程及其特点,熟悉各种常用应用软件,熟悉硬件设备的使用方法,加强编制调试计算机程序的能力,提高工程计算的能力,学习如何将理论知识和实际工程问题结合起来。
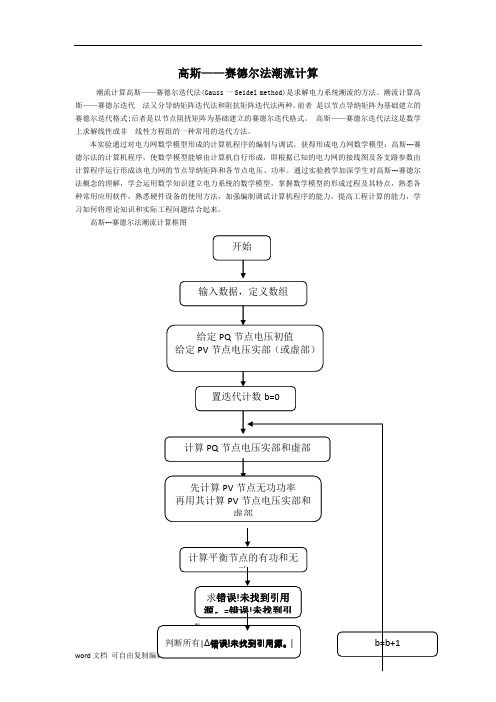
高斯---赛德尔法潮流计算框图N开始输入数据,定义数组给定PQ 节点电压初值给定PV 节点电压实部(或虚部)置迭代计数b=0计算PQ 节点电压实部和虚部先计算PV 节点无功功率 再用其计算PV 节点电压实部和虚部计算平衡节点的有功和无功判断所有|Δ错误!未找到引用源。
b=b+1求错误!未找到引用源。
=错误!未找到引Y[1]系统节点的分类根据给定的控制变量和状态变量的不同分类如下① P 、Q 节点(负荷节点),给定Pi 、Qi 求Vi 、Si ,所求数量最多;② 负荷节点,变电站节点(联络节点、浮游节点),给定P Gi 、Q Gi 的发电机节点,给定Q Gi 的无功电源节点;③ PV 节点(调节节点、电压控制节点),给定P i 、Q i 求Q n 、S n ,所求数量少,可以无有功储备的发电机节点和可调节的无功电源节点;④ 平衡节点(松弛节点、参考节点(基准相角)、S 节点、VS 节点、缓冲节点),给定V i ,δi =0,求P n 、Q n (V s 、δs 、P s 、Q s )。
电力系统中的潮流计算与分析

电力系统中的潮流计算与分析摘要本文介绍了电力系统中的潮流计算与分析,潮流计算是电力系统计算的基础,通过对电力系统中的电流、电压和功率进行计算和分析,可以有效地评估电力系统的稳定性和安全性。
在本文中,我们讨论了潮流计算的原理和方法,并介绍了一种基于改进的高斯-赛德尔迭代算法的潮流计算方法。
同时,我们还介绍了一种基于Python语言的潮流计算程序的设计和实现,该程序可以对电力系统进行潮流计算和分析,并生成相关的报告和图表。
最后,我们利用该程序对IEEE 14节点测试系统进行了潮流计算和分析,并分析了系统的稳定性和安全性。
关键词:电力系统;潮流计算;高斯-赛德尔迭代算法;Python语言AbstractThis paper introduces the load flow calculation and analysis in power system. Load flow calculation is the basis of power system calculation. By calculating and analyzing the current, voltage and power in the power system, the stability and safety of the power system can be effectively evaluated. In this paper, we discuss the principles and methods of load flow calculation, and introduce an improved Gauss-Seidel iterative algorithm based load flow calculation method. At the same time, we also introduce the design and implementation of a load flow calculation program based on the Python language. The program can perform load flow calculation and analysis on the power system, and generate relevant reports and charts. Finally, we use the program to perform load flow calculation and analysis on the IEEE 14-bus test system, and analyze the stability and safety of the system.Keywords: power system; load flow calculation; Gauss-Seidel iterative algorithm; Python language一、引言电力系统是现代工业和生活的基础设施之一,它承担着输送和分配电能的重要任务。
电力系统稳态分析--潮流计算

电力系统稳态分析--潮流计算(总36页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--电力系统稳态分析摘要电力系统潮流计算是研究电力系统稳态运行情况的一种重要的分析计算,它根据给定的运行条件及系统接线情况确定整个电力系统各部分的运行状态:各母线的电压,各元件中流过的功率,系统的功率损耗。
所以,电力系统潮流计算是进行电力系统故障计算,继电保护整定,安全分析的必要工具。
本文介绍了基于MATLAB软件的牛顿-拉夫逊法和P-Q分解法潮流计算的程序,该程序用于计算中小型电力网络的潮流。
在本文中,采用的是一个5节点的算例进行分析,并对仿真结果进行比较,算例的结果验证了程序的正确性和迭代法的有效性。
关键词:电力系统潮流计算;MATLAB;牛顿-拉夫逊法;P-Q分解法;目次1 绪论 ..................................................................................................... 错误!未定义书签。
背景及意义......................................................................................... 错误!未定义书签。
相关理论 ............................................................................................ 错误!未定义书签。
本文的主要工作 ................................................................................ 错误!未定义书签。
2 潮流计算的基本理论 ......................................................................... 错误!未定义书签。
高斯赛德尔法潮流计算

3
& =S & −S &′ ∆S 12 12 12
其它支路相同求法。
迭代结束
& ( k +1) − U & (k ) ≤ ε U 2 2
( k + 1) (k ) & & U3 − U3 ≤ ε
ห้องสมุดไป่ตู้
求各支路输入功率、输出功率、功率损失。
1
& S 12
y12
&′ S 12
2
y13
y23
∗ ∗ & & & & & & S12 = U1 I 12 = U1 y12 (U1 − U 2 ) ∗ ∗ & & & & & & ′ S12 = U 2 I 12 = U 2 y12 (U1 − U 2 )
节点电压 发电机注入功率 & MW Mvar U 1.05+j0.0 ? ? 1.03 20 ? 0 0 ?
i
负荷 MW Mvar 0 0 50 20 60 25
分析:
由已知条件可知:节点1为平衡节点,节点2 为PV节点,节点3为PQ节点。
解:(1)形成节点导纳矩阵
y23 = 1/ Z 23 = 1.667 − j5.0
& = 1.05∠0o ,U & = 1.03∠0o ,U & = 1.0∠0o 设U 1 2 3
(0) & (0) ∑ Y 2 j U j ) =Im(U Q2 2 j =1 3 ∗ ∗ (0)
=Im[1.03∠0o × (−1.25 − j 3.73) × 1.05∠0o + 1.03∠0o × (2.9167 + j8.75) × 1.03∠0o + 1.03∠0o × (−1.6667 − j 5.0) × 1.0∠0o ] = 0.07766
电力系统稳态实验报告

电力系统稳态潮流计算上机实验报告一、问题如下图所示的电力系统网络,分别用牛顿拉夫逊法、PQ解耦法、高斯赛德尔法、保留非线性法计算该电力系统的潮流。
发电机的参数如下,*表示任意值负荷参数如下,如上图所示的电力系统,可以看出,节点1、2、3是PQ节点,节点4是PV节点,而将节点5作为平衡节点。
根据问题所需,采用牛顿拉夫逊法、PQ解耦法、高斯赛德尔法、保留非线性法,通过对每次修正量的收敛判据的判断,得出整个电力系统的潮流,并分析这四种方法的收敛速度等等。
算法分析1.牛顿拉夫逊法节点5为平衡节点,不参加整个的迭代过程,节点1、2、3为PQ节点,节点4为PV 节点,计算修正方程中各量,进而得到修正量,判断修正量是否收敛,如果不收敛,迭代继续,如果收敛,算出PQ节点的电压幅值以及电压相角,得出PV节点的无功量以及电压相角,得出平衡节点的输出功率。
潮流方程的直角坐标形式,()()∑∑∈∈++-=ij j ij j ij i ij j ij j ij i i e B f G f f B e G e P()()∑∑∈∈+--=ij j ij j ij i ij j ij j ij i i e B f G e f B e G f Q直角坐标形式的修正方程式,11112n n n m n m -----∆⎡⎤⎡⎤∆⎡⎤⎢⎥⎢⎥∆=-⎢⎥⎢⎥⎢⎥∆⎣⎦⎢⎥⎢⎥∆⎣⎦⎣⎦PHN e Q M L f UR S修正方程式中的各量值的计算,()()][∑∑∈∈++--=∆ij j ij j ij i ij j ij j ij i is i e B f G f f B e G e p P()()][∑∑∈∈+---=∆ij j ij j ij i ij j ij j ij i is i e B f G e f B e G f Q Q)(2222i i is i f e U U +-=∆Jacobi 矩阵的元素计算,()()()ij i ij i i ijij j ij j ii i ii i jj iB e G f j i Q M G f B e B e G f j i e ∈-⎧≠∂∆⎪==⎨++-=∂⎪⎩∑()()()ij i ij i i ijij j ij j ii i ii i jj iG e B f j i Q L G e B f G e B f j i f ∈+⎧≠∂∆⎪==⎨--++=∂⎪⎩∑)()(202i j i j e e U R ijij i =≠⎩⎨⎧-=∂∆∂=)()(202i j i j f f U S ijij i =≠⎩⎨⎧-=∂∆∂=牛顿拉夫逊法潮流计算的流程图如下,2.PQ 解耦法如同牛顿拉夫逊法,快速解耦法的前提是,输电线路的阻抗要比电阻大得多,并且输电线路两端的电压相角相差不大,此时可利用PQ 快速解耦法,来计算整个电力系统网络的潮流。
电力系统中的潮流计算方法及精度评估研究

电力系统中的潮流计算方法及精度评估研究概述电力系统潮流计算是电力系统运行和规划的关键技术之一。
它用于计算电力系统中各节点的电压和功率流向,以评估系统的稳定性、安全性和经济性。
本文将介绍电力系统中常用的潮流计算方法,并探讨潮流计算结果的精度评估方法。
一、潮流计算方法1. 高斯-赛德尔迭代法高斯-赛德尔迭代法是最早应用于电力系统潮流计算的方法之一。
该方法通过迭代计算每个节点的电压值,直到满足潮流平衡方程。
然而,由于其收敛速度较慢,只适用于较小规模的电力系统。
2. 牛顿-拉夫逊迭代法牛顿-拉夫逊迭代法是目前应用较广的潮流计算方法。
该方法通过建立潮流计算的牛顿方程组,并迭代求解节点电压值。
相比高斯-赛德尔迭代法,牛顿-拉夫逊迭代法具有更快的收敛速度和更好的稳定性。
3. 直流潮流计算法直流潮流计算法是一种快速计算潮流的方法,主要用于大规模电力系统的运行和规划。
该方法基于直流潮流模型,忽略了交流系统中的谐波和动态特性,降低了计算的复杂性。
然而,由于其模型简化,直流潮流计算法在评估系统安全性和稳定性方面的准确性较低。
二、潮流计算结果的精度评估1. 误差分析法误差分析法是一种常用的潮流计算结果的精度评估方法。
它通过比较潮流计算结果与实际测量值之间的差异来评估计算结果的准确性。
误差分析法通常涉及计算误差、输入误差和观测误差等方面的考虑。
2. 灵敏度分析法灵敏度分析法是一种用于评估潮流计算结果的精度和稳定性的方法。
通过计算各个输入参数对潮流计算结果的影响程度,可以评估计算结果对输入参数变化的敏感度,并识别不确定性因素。
3. 置信区间分析法置信区间分析法是一种用于评估潮流计算结果的不确定性的方法。
它通过构建置信区间,表示潮流计算结果的可信程度。
置信区间分析法可以在统计学框架下对潮流计算结果进行准确的可信度评估。
三、研究展望1. 基于深度学习的潮流计算方法近年来,深度学习在电力系统领域取得了显著的应用成果。
基于深度学习的潮流计算方法能够利用大量的数据和高级模型进行潮流计算,提高计算效率和准确性。
电力系统潮流计算222(实际讲稿)

f ( x ( 0 ) ) + f ′( x ( 0 ) )∆x ( 0 ) = 0
原理:
∆x
(0)
f (x ) =− ′( x ( 0) ) f
( 0)
修正 x (1) = x ( 0 ) + ∆x ( 0) ∆x
直至
(1)
f ( x (1) ) =− f ′( x (1) )
x
( k+3)
x(k+2) x(k+1) x(k )
PQ节点 节点
N11 H12 L11 J1p N21 H22 L21 J22
N12
H1p
N1p
H1n
L1p J1p L1p J1n N22 H2 p N2 p H2n L22 J2 p L2 p J2n
PV节点 节点
L L L L L L N p1 H p2 N p2 H pp N pp H pn S p1 Rp2 S p2 Rpp S pp Rpn Nn1 Hn2 Nn2 Hnp Sn1 Rn2 Sn2 Rnp Nnp Hnn Snp Rnn
N1n ∆f1 L1n ∆e1 N2n ∆f2 L2n ∆e2 L L N pn ∆f p S pn ∆ep Nnn ∆fn Snn ∆en
( k +1) 3
LL
& Ui
(k+1)
1 Pi −jQ (k+1) (k) (k) i & & & & = ∗ −Yi1U1 −L−Yii−1Ui−1 −Yii+1Ui+1 L−YinUn Yii U (k) i 1 Pn−jQ (k+1) (k+1) n & & = ∗ −Yn1U1 −Yn2U2 −L nn−1Un−1 Y & Ynn U (k) n
电力系统稳态分析大作业——基于高斯赛德尔法潮流计算

电力系统稳态分析姓名: 学号:学院(系):自动化学院专业: 电气工程题目: 基于Matlab的高斯和高斯—赛德尔法的潮流计算指导老师:2014年12月摘要电力系统潮流计算是电力系统稳态运行分析中最基本和最重要的计算之一,是电力系统其他分析计算的基础,也是电力网规划、运行研究分析的一种方法,在电力系统中具有举足轻重的作用。
经典算法有高斯法,高斯-赛德尔迭代法及牛顿法等,近年来学者们开始应用非线性规划法及智能算法等优化方法求解潮流问题,提高了收敛的可靠性。
高斯-赛德尔迭代法开始于上世纪50年代,是一种直接迭代求解方程的算法,既可以解线性方程组,可以解非线性方程组。
高斯法求解节点电压的特点是: 在计算节点 i第k+1次的迭代电压时,前后所用的电压都是第k次迭代的结果,整个一轮潮流迭代完成后,把所有计算出的电压新值用于下一轮电压新值的计算过程中。
该计算方法简单,占用计算机内存小,能直接利用迭代求解节点电压方程,对电压初值的选取要求不是很严格。
但它的收敛性能较差,系统规模增大时,迭代次数急剧上升。
本文首先对高斯—赛德尔算法进行了综述,然后推导了该算法的计算过程,通过MATLAB软件计算了该算法的实例。
关键字:潮流计算高斯法高斯-赛德尔法迭代AbstractPower flow calculation is the one of the most basic and the most important calculation in the steady state analysis of power system .It is the foundation of other analytical calculation of power system, a method of analysis and planning, operation of power network.So it plays a decisive role in the power system. The classical algorithm is the Gauss method, Gauss - Seidel iterative method and Newton's method, in recent years.Scholars began to applicate nonlinear programming method and intelligent algorithm optimization method for solving power flow problem, enhances the reliability of convergence.Gauss - Seidel iterative method began in the 50's of last century, is a direct iteration equation algorithm, which can solve the linear equation and nonlinear equations. Characteristics of Gauss's method to calculate the node voltage is: in the iterative calculation of node i’s K + 1-times voltage, the voltage is used the results of K-times iterative.After completing the whole round of power flow iteration, all voltage value is used to calculate the next round of new voltage value of . The method is simple and captures small memory.It also can directly use the iterative solution of the node voltage equation .the selection of initial values are not very strict. But it has poor convergence performance. The system scale increases,when the number of iterations rise.This paper gives an overview of the Gauss Seidel algorithm at the first.Then it show the calculation process of this algorithm through the MATLAB software.Keywords: Gauss Gauss - Seidel iterative method the method of power flow calculation目录1 高斯迭代法和高斯—赛德尔迭代法概述 (5)2 节点导纳矩阵 (6)2.1不定导纳矩阵 (6)2.2导纳矩阵 (6)3 高斯迭代法 (7)4 高斯-赛德尔迭代法 (8)4.1高斯-赛德尔法的原理 (8)4.2 关于高斯法和高斯-赛德尔法的讨论 (8)5实例验证 (9)5.1 案例描述 (9)5.2 模型的建立 (10)5.3 案例程序流程图 (11)5.4 案例程序 (13)5.5 程序运行步骤和结果 (17)6结果分析 (20)7总结 (21)7参考文献 (22)一高斯迭代法和高斯—赛德尔迭代法概述电力系统潮流计算是研究电力系统稳态运行情况的一种基本电气计算。
电力系统分析潮流计算最终完整版

电力系统分析潮流计算最终完整版电力系统潮流计算是电力系统运行的基础,它对电力系统的稳定运行和安全运行具有重要意义。
本文将介绍电力系统潮流计算的主要内容和步骤,并阐述其在电力系统运行中的应用。
电力系统潮流计算是指对电力系统中各节点的电压和功率进行计算和分析的过程。
它主要用于确定电力系统中各个节点的电压和相应的功率,以评估电力系统的稳定性和安全性。
潮流计算的结果可以用于电力系统的规划、调度和运行等各个环节。
潮流计算的主要步骤主要包括:建立电力系统潮流模型、制定潮流计算方程、选择潮流计算方法和求解潮流计算方程。
建立电力系统潮流模型是潮流计算的第一步,它主要包括确定电力系统的拓扑结构、电气参数和发电机和负荷模型等。
通过建立电力系统的拓扑结构和电气参数,可以确定电力系统中各个节点之间的连接关系和传输条件。
发电机和负荷模型则用于描述电力系统中的发电机和负荷之间的相互作用。
制定潮流计算方程是潮流计算的第二步,它主要是根据电力系统的拓扑结构和电气参数,建立潮流计算的数学模型。
潮流计算方程主要包括功率方程、节点电压方程和变压器方程等。
功率方程用于描述发电机和负荷之间的功率平衡关系,节点电压方程用于描述电力系统中各个节点的电压平衡关系,变压器方程用于描述变压器的运行状况。
选择潮流计算方法是潮流计算的第三步,它主要是选择合适的方法来求解潮流计算方程。
常见的方法包括直接迭代法、高斯-赛德尔迭代法、牛顿-拉夫逊迭代法和快速迭代法等。
不同的方法在精度和收敛速度上有所差异,根据实际情况选择合适的方法。
求解潮流计算方程是潮流计算的最后一步,它主要是通过迭代计算,求解潮流计算方程得到电力系统各个节点的电压和功率值。
在求解过程中,需要根据实际情况设置迭代的初始值和收敛条件,以保证计算结果的准确性和稳定性。
电力系统潮流计算在电力系统运行中具有广泛的应用。
它可以用于电力系统规划,通过计算电力系统中各个节点的电压和功率,评估电力系统的输电能力和供电质量,为电力系统的扩容和优化提供指导。
煤矿电力系统高斯赛德尔法潮流计算与实现

煤矿电力系统高斯赛德尔法潮流计算与实现[摘要]分析了电力系统分析中的一种最基本的计算:潮流计算。
以导纳矩阵为基础的高斯-塞德尔潮流计算方法简单,占用计算机内存小,但它的收敛性能较差,当系统规模增大时,迭代次数急剧上升。
通过matlab编程计算算例,证明了该方法更加适用于为其它潮流计算方法计算合适的初值。
[关键词]电力系统;潮流计算;高斯-赛德尔中图分类号:tm744 文献标识码:a 文章编号:1009-914x(2013)22-0014-02一、电力系统潮流计算概述1.1 潮流计算简介电力系统潮流计算是研究电力系统稳态运行情况的一种基本电气计算。
它的任务是根据给定的运行条件和网路结构确定整个系统的运行状态,如电力系统中电压,有功功率和无功功率的分布等。
电力系统潮流计算的结果是电力系统稳定计算和故障分析的基础。
潮流计算也分为离线计算和在线计算。
前者主要用于系统规划设计和安排系统运行方式,后者用于正在运行系统的经常监视以及实时控制。
对潮流计算的要求可以归纳为下面几点:(1)算法的可靠性或收敛性(2)计算速度和内存占用量(3)计算的方便性和灵活性电力系统潮流计算问题在数学上是一组多元非线性方程式求解问题,其解法离不开迭代。
因此对潮流计算方法,首先要求它可靠地收敛,并给出正确答案。
随着电力系统规模的不断扩大,潮流问题的方程式阶数越来越高,目前已达到几千阶甚至上万阶,对这样规模的方程式并不是采用任何数学方法都能保证给出正确答案的。
这种情况促使电力系统的研究人员不断寻求新的更可靠的计算方法。
1.2 潮流计算的意义与作用电流系统潮流计算的主要作用可以通过下述体现:(1)在电网规划阶段,通过潮流计算,合理规划电源容量及接入点,合理规划网架,选择无功补偿方案,满足规划水平的大、小方式下潮流交换控制、调峰、调相、调压的要求。
(2)在编制年运行方式时,在预计负荷增长及新设备投运基础上,选择典型方式进行潮流计算,发现电网中薄弱环节,供调度员日常调度控制参考,并对规划、基建部门提出改进网架结构,加快基建进度的建议。
电力系统三种潮流计算方法的比较

电力系统三种潮流计算方法的比较 一、高斯-赛德尔迭代法:以导纳矩阵为基础,并应用高斯--塞德尔迭代的算法是在电力系统中最早得到应用的潮流计算方法,目前高斯一塞德尔法已很少使用。
将所求方程改写为 不能直接得出方程的根,给一个猜测值 得 又可取x1为猜测值,进一步得:反复猜测则方程的根优点:1. 原理简单,程序设计十分容易。
2. 导纳矩阵是一个对称且高度稀疏的矩阵,因此占用内存非常节省。
3. 就每次迭代所需的计算量而言,是各种潮流算法中最小的,并且和网络所包含的节点数成正比关系。
缺点:1. 收敛速度很慢。
2. 对病态条件系统,计算往往会发生收敛困难:如节点间相位角差很大的重负荷系统、包含有负电抗支路(如某些三绕组变压器或线路串联电容等)的系统、具有较长的辐射形线路的系统、长线路与短线路接在同一节点上,而且长短线路的长度比值又很大的系统。
3. 平衡节点所在位置的不同选择,也会影响到收敛性能。
二、牛顿-拉夫逊法:求解 设 ,则按牛顿二项式展开:当△x 不大,则取线性化(仅取一次项)则可得修正量对 得: 作变量修正:,求解修正方程 ()0f x =()0f x =10()x x ϕ=迭代 0x 21()x x ϕ=1()k k x x ϕ+=()x x ϕ=()0f x =k k x x lim *∞→=0x x x =+∆0()0f x x +∆=23000011()()()()()()02!3!f x f x x f x x f x x ''''''+∆+∆+∆+=00()()0f x f x x '+∆=()100()()x f x f x -'∆=-10x x x =+∆00()()f x x f x '∆=-1k k k x x x +=+∆牛顿法是数学中求解非线性方程式的典型方法,有较好的收敛性。
自从20世纪60年代中期采用了最佳顺序消去法以后,牛顿法在收敛性、内存要求、计算速度方面都超过了其他方法,成为直到目前仍被广泛采用的方法。
电力系统的潮流计算

电力系统的潮流计算电力系统的潮流计算是电力系统分析中的基础工作,主要用于计算电力系统中各节点的电压和功率流动情况。
通过潮流计算可以得到电力系统的电压、功率、功率因数等关键参数,为电力系统的运行和规划提供有效的参考依据。
本文将介绍电力系统潮流计算的基本原理、计算方法和应用。
一、电力系统潮流计算的基本原理电力系统潮流计算基于电力系统的能量守恒原理和基尔霍夫电流定律,通过建立电力系统的节点电压和功率平衡方程组来描述系统中各节点间的电压和功率流动关系。
潮流计算的基本原理可简述为以下三个步骤:1.建立节点电压方程:根据基尔霍夫电流定律,将电力系统中各节点的电流状况表达为节点电压和导纳矩阵之间的乘积关系。
2.建立功率平衡方程:根据能量守恒原理,将电力系统中各支路的功率流动表达为节点电压和导纳矩阵之间的乘积关系。
3.解算节点电压:通过求解节点电压方程组,得到系统中各节点的电压值。
二、电力系统潮流计算的常用方法电力系统潮流计算常用的方法有高斯-赛德尔迭代法、牛顿-拉夫逊迭代法和快速潮流法等。
其中,高斯-赛德尔迭代法是一种基于节点电压的迭代算法,通过在每一次迭代中更新节点电压值来逐步逼近系统潮流平衡状态。
牛顿-拉夫逊迭代法是一种基于节点电压和节点功率的迭代算法,通过在每一次迭代中同时更新节点电压和节点功率值来逼近系统潮流平衡状态。
快速潮流法则是一种通过行列式运算直接求解节点电压的方法,对于大规模复杂的电力系统具有较高的计算效率和精度。
三、电力系统潮流计算的应用电力系统潮流计算在电力系统的规划和运行中有广泛应用。
具体应用包括:1.电力系统规划:通过潮流计算可以预测系统中各节点的电压和功率流动情况,为电力系统的设计和扩建提供参考依据。
2.电力系统稳定性分析:潮流计算可以帮助分析系统中节点电压偏差、功率瓶颈等问题,为系统的稳态和暂态稳定性分析提供基础数据。
3.运行状态分析:潮流计算可以实时监测系统中各节点的电压和功率流动情况,为电力系统的运行调度提供参考。
第四章复杂电力系统潮流计算-高斯-赛德尔法潮流计算概要

I
Y
U
节 点 电 压 列 向 量
导纳矩阵
Y11 Y21 Y Yi 1 Yn1
Y
Y12 Y22 Y1i Y2 i Yii Yni
n
Yi 2 Yn 2
n
Y1n Y2 n Yin Ynn
非对角元素 Yij : 节点 i 和 j 之间支路 导纳的负值
I ij I ij
j
I ik
I ij yij (U i U j )
i
Ii
k
I il
Ii
j 0, j i
n
n
I ij
j 0, j i n
n
yij (U i U j ) yijU j
l
j 0, j i
yijU i
j 0, j i
n个节点,n= 0表示地节点且U0=0
导纳矩阵Y为
10 j 40 20 j 89.96 10 j 50 Y 10 j 50 30 j120 20 j 70 10 j 40 20 j 70 30 j109.96
导纳矩阵的修改
电力系统运行方式常会发生某种变化,通常只 是对局部区域或个别元件作一些变化,例如投入或 切除一条线路或一台变压器。这只影响了该支路两 端节点的自导纳和它们的互导纳,因此不必重新形 成新的导纳矩阵,只需在原有的导纳矩阵上做适当 修改即可。
Yij yij
节点 i 的自导纳 则
节点 i 和 i 之间的互自导纳
I i YijU j
j 1
n
Yi 1U 1 Yi 2U 2
YiiU i
电力系统稳态分析大作业——基于高斯赛德尔法潮流计算

电力系统稳态分析大作业——基于高斯赛德尔法潮流计算电力系统稳态分析姓名: 学号:学院(系):自动化学院专业: 电气工程题目: 基于Matlab的高斯和高斯—赛德尔法的潮流计算指导老师:2014年12月摘要电力系统潮流计算是电力系统稳态运行分析中最基本和最重要的计算之一,是电力系统其他分析计算的基础,也是电力网规划、运行研究分析的一种方法,在电力系统中具有举足轻重的作用。
经典算法有高斯法,高斯-赛德尔迭代法及牛顿法等,近年来学者们开始应用非线性规划法及智能算法等优化方法求解潮流问题,提高了收敛的可靠性。
高斯-赛德尔迭代法开始于上世纪50年代,是一种直接迭代求解方程的算法,既可以解线性方程组,可以解非线性方程组。
高斯法求解节点电压的特点是: 在计算节点 i第k+1次的迭代电压时,前后所用的电压都是第k次迭代的结果,整个一轮潮流迭代完成后,把所有计算出的电压新值用于下一轮电压新值的计算过程中。
该计算方法简单,占用计算机内存小,能直接利用迭代求解节点电压方程,对电压初值的选取要求不是很严格。
但它的收敛性能较差,系统规模增大时,迭代次数急剧上升。
本文首先对高斯—赛德尔算法进行了综述,然后推导了该算法的计算过程,通过MATLAB软件计算了该算法的实例。
关键字:潮流计算高斯法高斯-赛德尔法迭代AbstractPower flow calculation is the one of the most basic and the most important calculation in the steady state analysis of power system .It is the foundation of other analytical calculation of power system, a method of analysis and planning, operation of power network.So it plays a decisive role in the power system. The classical algorithm is the Gauss method, Gauss - Seidel iterative method and Newton's method, in recent years.Scholars began to applicate nonlinear programming method and intelligent algorithm optimization method for solving power flow problem, enhances the reliability of convergence.Gauss - Seidel iterative method began in the 50's of last century, is a direct iteration equation algorithm, which can solve the linear equation and nonlinear equations. Characteristics of Gauss's method to calculate the node voltage is: in the iterative calculation of node i’s K + 1-times voltage, the voltage is used the results of K-times iterative.After completing the whole round of power flow iteration, all voltage value is used to calculate the next round of new voltage value of . The method is simple and captures small memory.It also can directly use the iterative solution of the node voltage equation .the selection of initial values are not very strict. But it has poor convergence performance. The system scale increases,when the number of iterations rise.This paper gives an overview of the Gauss Seidel algorithm at the first.Then it show the calculation process of this algorithm through the MATLAB software.Keywords: Gauss Gauss - Seidel iterative method the method of power flow calculation一高斯迭代法和高斯—赛德尔迭代法概述电力系统潮流计算是研究电力系统稳态运行情况的一种基本电气计算。
电力系统稳态 高斯—赛德尔

clear;format short;N=input(' 请输入节点个数:N= ');A=input(' 请输入广义节点支路关联矩阵:A=\n');AYb=input(' 请输入各支路导纳: \n');n=2*N;YY=zeros(n);for i=1:(n*n)m=floor(i/n);if(i==(n*m+m+1))YY(i)=Yb(m+1);endYY(n*n)=Yb(n);endB=A*YY;disp(' 导纳矩阵为: ');Yn=B*(A.') %形成导纳矩阵DD=diag(Yn);D=zeros(N);for i=1:N*Nm=floor(i/N);if(i==(m*N+m+1))D(i)=DD(m+1);endD(N*N)=DD(N); %严格对角矩阵DendL=tril(Y) -D; %严格下三角矩阵LU=triu(Y) -D; %严格上三角矩阵ULL=zeros(N-1);%考虑第N 个节点为平衡节点,对L,D,U 进行处理DD=zeros(N-1);UU=zeros(N-1);LL=L(1:(N-1),1:(N-1));DD=D(1:(N-1),1:(N-1));UU=U(1:(N-1),1:(N-1)) ;%取矩阵n-1*n-1S=input(' 请输入节点1 到节点n-1 的注入功率S=\n' );V0=input(' 请给定节点电压初值V0=\n');Vs=input(' 请输入平衡节点N 的电压Vs=\n');ee=input(' 请输入收敛判断值:e=\n');Vk=zeros(N-1,1);Vk1=zeros(N-1,1);Vk=V0;D1=inv(DD);Ys=Y(N,1:N-1);Ys0=(Ys*Vs).';k=1;V1(1,1:2)=(V0);%记录每次迭代过程中各节点电压值V2(1,1)=0;jj=1;I=zeros(1,2);eee=zeros(1,2);while(jj==1) %循环计算k=k+1;Vk1=Vk;I1=conj(S(1))/conj(Vk(1));Lk1=LL(1,1)*Vk(1)+LL(1,2)*Vk(2);Uk1=UU(1,1)*Vk(1)+UU(1,2)*Vk(2);Vk(1)=D1(1,1)*(I1-Ys0(1)-Lk1-Uk1);I2=conj(S(2))/conj(Vk(2));Lk2=LL(2,1)*Vk(1)+LL(2,2)*Vk(2);Uk2=UU(2,1)*Vk(1)+UU(2,2)*Vk(2);Vk(2)=D1(2,2)*(I2-Ys0(2)-Lk2-Uk2);eee(1)=Vk(1)-Vk1(1);eee(2)=Vk(2)-Vk1(2);eee=max(eee.');eeee=sqrt((real(eee))^2+(imag(eee))^2);V1(k,1:2)=(Vk);V2(k,1)=eeee;V=[V1,V2];if eeee<ee %判断误差值是否满足条件jj=0; %若满足条件,设置标志位,停止迭代endendfprintf(' 迭代次数%d\n',(k-1)); %输出结果disp(' 整个迭代过程如下:');disp(' V1(k) V2(k) max(V(k+1) -V(k))'); disp(V);[-1 -1/1.05 0 1 0 0;1 0 -1 0 1 0;0 1 1 0 0 1][0.2494-4.9875i,0.9901-9.9010i,0.49505-4.9505i,0.01i,0.03i,0.02i] [-2-1i,0.5+0.415i][1 1]I=。
(完整word版)电力系统三种潮流计算方法的比较

反复猜测
x2 ( x1 ) xk 1 ( xk )
迭代
则方程的根 x* lim xk k
优点: 1. 原理简单,程序设计十分容易。 2. 导纳矩阵是一个对称且高度稀疏的矩阵,因此占用内存非常节省。 3. 就每次迭代所需的计算量而言,是各种潮流算法中最小的,并且和网络所包
含的节点数成正比关系。 缺点: 1. 收敛速度很慢。 2. 对病态条件系统,计算往往会发生收敛困难:如节点间相位角差很大的重负
0
牛顿法是数学中求解非线性方程式的典型方法,有较好的收敛性。自从 20 世纪 60 年代中期采用了最佳顺序消去法以后,牛顿法在收敛性、内存要求、计算速 度方面都超过了其他方法,成为直到目前仍被广泛采用的方法。 优点: 1. 收敛速度快,若选择到一个较好的初值,算法将具有平方收敛特性,一般迭
代 4—5 次便可以收敛到一个非常精确的解。而且其迭代次数与所计算网络 的规模基本无关。 2. 具有良好的收敛可靠性,对于前面提到的对以节点导纳矩阵为基础的高斯一 塞德尔法呈病态的系统,牛顿法均能可靠地收敛。 3. 牛顿法所需的内存量及每次迭代所需时间均较前述的高斯一塞德尔法为多, 并与程序设计技巧有密切关系。 缺点: 牛顿法的可靠收敛取决于有一个良好的启动初值。如果初值选择不当,算法有可 能根本不收敛或收敛到一个无法运行的解点上。 解决方法: 对于正常运行的系统,各节点电压一般均在额定值附近,偏移不会太大,并且各 节点间的相位角差也不大,所以对各节点可以采用统一的电压初值(也称为“平 直电压”),“平直电压”法假定:
代替原来的(n+m-1)阶变化的、不对称的系数矩阵 M,以此提高计算速度,降
低对计算机贮存容量的要求。P-Q 分解法在计算速度方面有显著的提高,迅速得
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
电力系统稳态分析姓名: 学号:学院(系):自动化学院专业: 电气工程题目: 基于Matlab的高斯和高斯—赛德尔法的潮流计算指导老师:2014年12月摘要电力系统潮流计算是电力系统稳态运行分析中最基本和最重要的计算之一,是电力系统其他分析计算的基础,也是电力网规划、运行研究分析的一种方法,在电力系统中具有举足轻重的作用。
经典算法有高斯法,高斯-赛德尔迭代法及牛顿法等,近年来学者们开始应用非线性规划法及智能算法等优化方法求解潮流问题,提高了收敛的可靠性。
高斯-赛德尔迭代法开始于上世纪50年代,是一种直接迭代求解方程的算法,既可以解线性方程组,可以解非线性方程组。
高斯法求解节点电压的特点是: 在计算节点 i第k+1次的迭代电压时,前后所用的电压都是第k次迭代的结果,整个一轮潮流迭代完成后,把所有计算出的电压新值用于下一轮电压新值的计算过程中。
该计算方法简单,占用计算机内存小,能直接利用迭代求解节点电压方程,对电压初值的选取要求不是很严格。
但它的收敛性能较差,系统规模增大时,迭代次数急剧上升。
本文首先对高斯—赛德尔算法进行了综述,然后推导了该算法的计算过程,通过MATLAB软件计算了该算法的实例。
关键字:潮流计算高斯法高斯-赛德尔法迭代AbstractPower flow calculation is the one of the most basic and the most important calculation in the steady state analysis of power system .It is the foundation of other analytical calculation of power system, a method of analysis and planning, operation of power network.So it plays a decisive role in the power system. The classical algorithm is the Gauss method, Gauss - Seidel iterative method and Newton's method, in recent years.Scholars began to applicate nonlinear programming method and intelligent algorithm optimization method for solving power flow problem, enhances the reliability of convergence.Gauss - Seidel iterative method began in the 50's of last century, is a direct iteration equation algorithm, which can solve the linear equation and nonlinear equations. Characteristics of Gauss's method to calculate the node voltage is: in the iterative calculation of node i’s K + 1-times voltage, the voltage is used the results of K-times iterative.After completing the whole round of power flow iteration, all voltage value is used to calculate the next round of new voltage value of . The method is simple and captures small memory.It also can directly use the iterative solution of the node voltage equation .the selection of initial values are not very strict. But it has poor convergence performance. The system scale increases,when the number of iterations rise.This paper gives an overview of the Gauss Seidel algorithm at the first.Then it show the calculation process of this algorithm through the MATLAB software.Keywords: Gauss Gauss - Seidel iterative method the method of power flow calculation目录1 高斯迭代法和高斯—赛德尔迭代法概述 (5)2 节点导纳矩阵 (6)2.1不定导纳矩阵 (6)2.2导纳矩阵 (6)3 高斯迭代法 (7)4 高斯-赛德尔迭代法 (8)4.1高斯-赛德尔法的原理 (8)4.2 关于高斯法和高斯-赛德尔法的讨论 (8)5实例验证 (9)5.1 案例描述 (9)5.2 模型的建立 (10)5.3 案例程序流程图 (11)5.4 案例程序 (13)5.5 程序运行步骤和结果 (17)6结果分析 (20)7总结 (21)7参考文献 (22)一高斯迭代法和高斯—赛德尔迭代法概述电力系统潮流计算是研究电力系统稳态运行情况的一种基本电气计算。
它的任务是根据给定的运行条件和网路结构确定整个系统的运行状态,如各母线上的电压(幅值及相角)、网络中的功率分布以及功率损耗等。
电力系统潮流计算的结果是电力系统稳定计算和故障分析的基础。
给定电力系统的网络结构,参数和决定系统运行状况的边界条件,电力系统的稳态运行状态便随之确定。
潮流计算就是要通过数值仿真的方法把电力系统的详细运行状态呈现给运行和工作人员,以便研究系统在给定条件下的稳定运行特点。
潮流计算是电力系统分析中最基本、最重要的计算,是电力系统运行、规划以及安全性、可靠性分析和优化的基础,也是各种电磁暂态和机电暂态分析的基础和出发点。
20世纪50年代中期,随着电子计算机的发展,人们开始在计算机上用数学模拟的方法进行潮流计算。
最初在计算机上实现的潮流计算方法是以导纳矩阵为基础的高斯迭代法( Gauss 法)。
这种方法内存需求小,但收敛性差。
后来在高斯迭代法上进行改进,这就是高斯——赛德尔迭代法(Gauss一Seidel method),潮流计算高斯—赛德尔迭代法,分为导纳矩阵迭代法和阻抗矩阵迭代法两种。
前者是以节点导纳矩阵为基础建立的赛德尔迭代格式,后者是以节点阻扰矩阵为基础建立的赛德尔迭代格式。
高斯——赛德尔迭代法这是数学上求解线性或非线性方程组的一种常用的迭代方法。
牛顿-拉夫逊方法是解非线性代数方程组的一种基本方法,在潮流计算中也得到了应用。
20世纪60年代中后期,系数矩阵技术和编号优化技术的提出使牛顿-拉夫逊的解题规模和计算效率进一步提高,至今仍是潮流计算中的广泛采用的优秀算法。
20世纪70年代中期,Stott在大量计算实践的基础上提出了潮流计算的快速分解法,是潮流计算的速度大大提高,可以应用于在线,但是直至20世纪80年代末期才对快速分解法潮流的收敛性给出了比较满意的解释。
由于潮流计算在电力系统中的特殊地位和作用,对其计算方法有如下较高的要求:1.要有可靠的收敛性,对不同的系统及不同的运行条件都能收敛;2.占用内存小、计算速度快;3. 调整和修改容易,使用灵活方便。
本文使用的高斯法和高斯-赛德尔迭代法,开始于上世纪50年代,是一种直接迭代求解方程的算法,既可以解线性方程组,可以解非线性方程组。
高斯法求解节点电压的特点是: 在计算节点 i 第k+1次的迭代电压时,前后所用的电压都是第k 次迭代的结果,整个一轮潮流迭代完成后,把所有计算出的电压新值用于下一轮电压新值的计算过程中。
高斯-赛德尔法是刚刚计算出的x 值在下次迭代中被立即使用。
两种方法都计算方法简单,占用计算机内存小,能直接利用迭代求解节点电压方程,对电压初值的选取要求不是很严格,但收敛性能较差 ,系统规模增大时,迭代次数急剧上升。
二 节点导纳矩阵1 不定导纳矩阵令连通的电力网络的节点数为N ,大地作为节点未包括在内。
网络中有b 条支路,包括接地支路。
如果把地节点增广进来,电网的(N+1)×b 阶节点支路的关联矩阵A0,b 阶支路导纳矩阵是yb ,定义(N+1)×(N+1)阶节点导纳矩阵Y0为T b A y A Y 000= (2-1) 并有网络方程.0.0I V Y = (2-2)2 导纳矩阵选地节点为电压参考点,将它排在第N+1位,令参考点点位为零,则可将节点不定导纳矩阵表示的网络方程(2-1)写成分块的形式[Y y 0y oT y 00][V 0]=[I I 0] (2-3) 展开后有YV =I (2-4)和y 0T V =I 0 (2-5)式(2-5)中Y 为N ×N 阶矩阵,V 和I 分别为N 维节点电压和电流列矢量,I0为流入地节点的电流。
三 高斯迭代法高斯迭代法是最早在计算机上实现的潮流计算方法。
这种方法编程简单,在某些应用领域,如配电网计算潮流计算中还有应用。
另外,也用于为牛顿-拉夫逊法提供初值。
考察基于节点导纳矩阵的高斯迭代法。
在网络方程(2-4)中,将平衡点 s 排在最后,并将导纳矩阵写成分块的形式,取出前 n 个方程有Y n V n +Y s V s =I n (3-1)平衡节点 s 的电压V s 给定,n 个节点的注入电流矢量I n 已知,则有Y n V n =I n −Y s V s (3-2)实际电力系统给定量是 n 个节点的注入功率。
注入电流和注入功率之间的关系是I i =S i ̃V i ̃ i =1,2,3….n (3-3)其中V i ̃和S i ̃为V i 和S i的共轭复数。
写成矢量的形式 I n =[S i ̃V i ̃] (3-4) 再把Y n 写成对角线矩阵D 和严格上三角矩阵U 以及严格下三角矩阵L 的和,可以得到Y n =L +D +U其中L =[ 0Y 21⋮⋱Y n,1…Y n,n−10] , D =[ Y 11Y 22Y 33Y 44] , U =[0Y 12…Y 1n ⋱⋮Y n−1,n] 代入式(2-2),经过整理可得到V n=D −1{I n −Y s V s −LV n −UV n } (3-5)考虑到电流和功率的关系式,(3-5)可以写成为V i(k+1)=1Y ii {S ĩV ĩ(k)−Y is V s−∑Y iji−1j=1V j(k)−∑Y ijnj=i+1V j(k)} i=1,2,…n(3-6)给定,i=1,2,…n,代入上式中可得电压新值,逐次迭代直到前后两次迭代求得的电压值的差小于某一收敛精度为止。
