数字谜之竖式谜(一)讲课讲稿
竖式谜问题二三年级讲课精品教案

竖式谜问题二三年级讲课精品教案一、教学内容本节课选自小学数学教材三年级下册第九单元《笔算多位数加减法》中的竖式谜问题。
详细内容包括:理解竖式谜的概念,掌握竖式谜的解题步骤,运用加减法运算定律解决竖式谜问题。
二、教学目标1. 知识与技能:学生能理解竖式谜的概念,掌握竖式谜的解题方法,灵活运用加减法运算定律。
2. 过程与方法:通过实践情景引入,培养学生观察、分析、解决问题的能力。
3. 情感态度价值观:激发学生学习数学的兴趣,提高学生合作交流的意识。
三、教学难点与重点教学难点:竖式谜的解题步骤及运用加减法运算定律。
教学重点:理解竖式谜的概念,掌握竖式谜的解题方法。
四、教具与学具准备教具:PPT、黑板、粉笔、教鞭。
学具:练习本、铅笔、直尺。
五、教学过程1. 导入(5分钟)实践情景引入:通过展示一个关于购物找零的情景,让学生思考如何计算,引出竖式谜问题。
2. 新课讲解(15分钟)(1)讲解竖式谜的概念,让学生明白什么是竖式谜。
(2)通过例题讲解,展示竖式谜的解题步骤,引导学生掌握解题方法。
3. 随堂练习(15分钟)(1)让学生独立完成一道竖式谜题目,教师巡回指导。
4. 合作交流(10分钟)将学生分成小组,讨论并解决一道较难的竖式谜题目,培养学生的合作交流能力。
教师引导学生回顾本节课所学内容,巩固竖式谜的解题方法。
六、板书设计1. 竖式谜问题2. 内容:(1)竖式谜的概念(2)竖式谜的解题步骤(3)例题及解题过程(4)随堂练习题目七、作业设计1. 作业题目:(1)完成课后练习第1、2题。
(2)思考:如何运用加减法运算定律解决竖式谜问题?2. 答案:(1)课后练习第1题答案:7;课后练习第2题答案:14。
(2)运用加减法运算定律,通过逐位相加或相减,找出缺失的数字。
八、课后反思及拓展延伸1. 课后反思:教师在本节课结束后,及时反思教学效果,针对学生的掌握情况,调整教学方法。
2. 拓展延伸:鼓励学生课后寻找生活中的竖式谜问题,将所学知识运用到实际中,提高解决问题的能力。
横(竖)式数字谜(一)

横(竖)式数字谜(一)在一个数学式子(横式或竖式)中擦去部分数字,或用字母、文字来代替部分数字的不完整的算式或竖式,叫做数字谜题目。
解数字谜题就是求出这些被擦去的数或用字母、文字代替的数的数值。
例如,求算式324+□=528中□所代表的数。
根据“加数=和-另一个加数”知,□=582-324=258。
又如,求右竖式中字母A,B所代表的数字。
显然个位数相减时必须借位,所以,由12-B=5知,B=12-5=7;由A-1=3知,A=3+1=4。
解数字谜问题既能增强数字运用能力,又能加深对运算的理解,还是培养和提高分析问题能力的有效方法。
这一讲介绍简单的算式(横式)数字谜的解法。
解横式数字谜,首先要熟知下面的运算规则:(1)一个加数+另一个加数=和;(2)被减数-减数=差;(3)被乘数×乘数=积;(4)被除数÷除数=商。
由它们推演还可以得到以下运算规则:由(1),得和 - 一个加数=另一个加数;其次,要熟悉数字运算和拆分。
例如,8可用加法拆分为8=0+8=1+7=2+6=3+5=4+4;24可用乘法拆分为24=1×24=2×12=3×8=4×6(两个数之积)=1×2×12=2×2×6=…(三个数之积)=1×2×2×6=2×2×2×3=…(四个数之积)例1下列算式中,□,○,△,☆,*各代表什么数?(1)□+5=13-6;(2)28-○=15+7;(3)3×△=54;(4)☆÷3=87;(5)56÷*=7。
解:(1)由加法运算规则知,□=13-6-5=2;(2)由减法运算规则知,○=28-(15+7)=6;(3)由乘法运算规则知,△=54÷3=18;(4)由除法运算规则知,☆=87×3=261;(5)由除法运算规则知,*=56÷7=8。
小学三年级奥数讲解.竖式数字谜教案资料

竖式数字谜第1部分:加、减法竖式数字谜这一部分主要讲加、减法竖式的数字谜问题。
解加、减法数字谜问题的基本功,在于掌握好上一讲中介绍的运算规则(1)(2)及其推演的变形规则,另外还要掌握数的加、减的“拆分”。
关键是通过综合观察、分析,找出解题的“突破口”。
题目不同,分析的方法不同,其“突破口”也就不同。
这需要通过不断的“学”和“练”,逐步积累知识和经验,总结提高解题能力。
例1:在下列各竖式的□中填上适当的数字,使竖式成立解:加数都是两位数,从第一个加数个位是5与和的个位数是9,可以推断第二个加数的个位数必定是4。
即5+?=9。
从和的百位数与十位数是18,可断定,两个加数的十位数都是9,这样,谜便揭开了.例2:在下列各竖式的□中填上适当的数字,使竖式成立解:三个加数,只知道其中两个加数的个位分别是7、5,而和的个位却是8,肯定是进位造成的。
从7+5+?=□8,可判断另一个加数的个位必为6,十位上5+□+7=□7,可断定:□加上个位进上来的1是5,去掉进上来的1应是4。
百位上2+□=6,可知:□=4,去掉进上来的1,□=3。
例3:在下列各竖式的□中填上适当的数字,使竖式成立解:这个减法算式,只告知了减数是1,被减数、减数都不知道!全式应有八个数字,其中七个都是未知数,初看是比较难解的。
但是认真分析一下减法算式各部分的数位,便可以找到突破口。
被减数有四位,减去1后,差却成了三位数,只有相减时连续退位,才会如此。
那么,什么数减去1需要向高位借数呢?只有“0”!而最高位退1后成了0,表明被减数的最高位就是“1”。
这样,就可以断定被减数是1000。
知道了被减数和减数,差就迎刃而解了!例4:在下列各竖式的□中填上适当的数字,使竖式成立解:个位上,被减数是7,差是6,可知减数是1。
十位上,减数是8,差是9,可知被减数必小于8,借位后才使差比减数大的。
那么,?-8=9,可知被减数十位上是7。
再看百位,因为被减数是四位数。
小学数学《竖式谜 (1)》教学设计

竖式谜教学目标:1.在探索加减法算式中的“竖式谜”问题过程中,学习用推理的方法解决问题,初步获得一些简单推理的经验。
2、分析每个已知数字和要求数字之间的关系,再根据加减运算法则,正确运算。
3、.经历简单推理的过程,培养学生思维的条理性和严密性,提高逻辑思维能力和分析解决问题的能力,发展学生的代数思想。
4、在解决问题的过程中,激发学生学习数学的兴趣和欲望,体验成功的乐趣,产生学好数学的自信心。
教学重、难点:学习用推理的方法解决问题,初步获得一些简单推理的经验。
一、创设情境,梳理加减法各部分之间关系。
1、(出示ppt情境图)同学们,认识他吗?(大雄)大雄的学习成绩一向不好,每次都被他的妈妈批评,我们一起来帮帮他吧。
2、(出示大雄的小测0分)看,今天他三道题都不会做,心情很沮丧。
我们看看能不能帮个忙。
(出示第一道题)45+()=87 ,这个空里该填多少?赶紧在草稿本上算一算,你是怎么算出来的?(87—45=42 也就是说想要知道这其中一个加数是多少,你要怎么做?和—一个加数=另一个加数)3、(出示第二道题)96—()=28那这道呢?又该怎么算?看看你用什么方法?(96—28=68,也就是说你是把被减数—差=减数)4、(出示第三道题)()—35=46,最后一道题,请你再帮忙算一算?(46+35=81,也就是差+减数=被减数)经过大家的共同努力,大雄终于弄明白了。
二、探究解开竖式谜的秘密。
1、大雄要用上这些方法,完成今天的家庭作业。
我们和他一起研究一下吧。
(1)5 □ 5 □+ □6-□69 8 2 2你知道叶子底下藏着什么数吗?说说你是怎么想到?(A 先看个位2+6=8还可以怎么想8—6=2,用上什么知识?再看十位5+4=9 ,也可以想9—3=6 B先看十位再看个位)(2)想个位8—6=2 或者2+6=8 十位5—3=2或者5—2=3(3)小结,同学们刚才在解开竖式谜的时候用上了什么方法?有什么好的经验吗?2、 3 □ 5 □+ □6-□89 4 2 6(1)带着你总结出来的方法,再帮大雄解决这两道题。
二年级奥数.计算.竖式谜(1)

在这一节课中,教材内容中主要是通过不同的符号,汉字或字母来组成各种不同的竖式数字谜,让学生根据竖式的结构来计算(求出)这些未知的数字.弄清楚加减法各部分之间的数量关系是我们学习数字谜的基础.解答数字谜的关键是找准突破口.通过这节课的学习,要使学生掌握解答竖式数字谜的一般技巧.先要观察数字的特点,然后找出“关键位置”认真分析,一般可以引导学生从各个不同的数位进行考虑.解答完题目以后,教师还要培养学生验算的好习惯.我们经常会看到一些残缺不全的算式,要求我们在方格内填上合适的数字,使算式成立.我们也经常看到在一个算式里面有很多的汉字或字母,要我们猜猜它们代表几,像这样的问题都是数字谜问题.在填数字时,要认真分析数字的特点,充分运用加、减法之间的关系,巧妙地安排每一个数,很快就能求出方格里应填的数字.今天这节课我们就一起来解答数字谜问题.解这种题应按三个步骤分析思考:(1)审题审题就是找出算式中数字之间的关系和特征,挖掘题目中的隐含条件,它是确定各空格内应该填什么数字的主要依据.(2)选择解题突破口在审题的基础上,认真思考找出算式中容易填出或关键性的空格,做为解题的突破口.这一步是填空格的关键.(3)确定各空格填什么数字从突破口开始,依据竖式的已知条件,逐个填出各空格中的数字.【例1】在“庆元旦”晚会上,主持人小丽出了这样两道题目:请大家想一想,被纸片盖住的是什么数字?【例2】在下面算式的空格内,各填上一个合适的数字,使算式成立.知识框架竖式谜例题精讲【例3】用0、1、2、3、4、5、6、7、8、9这十个数字组成下面的加法算式,每个数字只许用一次,现已写出3个数字,请把这个算式补齐.【例4】在下面算式的空格内,各填入一个合适的数字,使算式成立.【例5】把数字1~5分别填写在下面算式中的口里.【例6】下面的算式里四个小纸片各盖住一个数字,问被盖住的四个数字的和是多少?【例7】在下面算式的空格内,各填入一个合适的数字,使算式成立.【例8】算下面竖式中的汉字各代表多少?我=( ) 爱=( ) 数=( ) 学=( )【例9】求当它们各代表什么数字时,能够使算式成立?【例10】请你猜一猜,每个算式中的汉字各表示几【例11】相同的英文字母代表相同的数字,你知道下面A、B、C代表几?【随练1】请你算一算,下面竖式中每个字各代表几?+ 兵炮马卒兵炮车卒车卒马兵卒【随练2】下面各数字表示几?【随练3】在下面的加法算式中,第—个加数的各位数字之和恰好是和的各位数字之和的2倍.则第一个加数是多少?【随练4】下面的算式里,每个方框代表一个数字,问:这6个方框中数字的总和是多少?课堂检测【作业1】在下列竖式的空格内,各填入一个合适的数字,使竖式成立. 【作业2】填一填.【作业3】下面方框可以填什么数?【作业4】下面的方框各应该填几?【作业5】下面的符号和汉字各代表几?【作业6】下面竖式中的字母和符号各代表多少?家庭作业【作业7】在下列竖式的空格内,各填入一个合适的数字,使竖式成立.【作业8】下面的符号各表示几?【作业9】请你猜一猜,每个算式中的汉字各表示几?【作业10】下边的加法算式中,□内这四个数字之和是多少?。
小学三年级奥数讲解.竖式数字谜讲课稿

竖式数字谜第1部分:加、减法竖式数字谜这一部分主要讲加、减法竖式的数字谜问题。
解加、减法数字谜问题的基本功,在于掌握好上一讲中介绍的运算规则(1)(2)及其推演的变形规则,另外还要掌握数的加、减的“拆分”。
关键是通过综合观察、分析,找出解题的“突破口”。
题目不同,分析的方法不同,其“突破口”也就不同。
这需要通过不断的“学”和“练”,逐步积累知识和经验,总结提高解题能力。
例1:在下列各竖式的□中填上适当的数字,使竖式成立解:加数都是两位数,从第一个加数个位是5与和的个位数是9,可以推断第二个加数的个位数必定是4。
即5+?=9。
从和的百位数与十位数是18,可断定,两个加数的十位数都是9,这样,谜便揭开了.例2:在下列各竖式的□中填上适当的数字,使竖式成立解:三个加数,只知道其中两个加数的个位分别是7、5,而和的个位却是8,肯定是进位造成的。
从7+5+?=□8,可判断另一个加数的个位必为6,十位上5+□+7=□7,可断定:□加上个位进上来的1是5,去掉进上来的1应是4。
百位上2+□=6,可知:□=4,去掉进上来的1,□=3。
例3:在下列各竖式的□中填上适当的数字,使竖式成立解:这个减法算式,只告知了减数是1,被减数、减数都不知道!全式应有八个数字,其中七个都是未知数,初看是比较难解的。
但是认真分析一下减法算式各部分的数位,便可以找到突破口。
被减数有四位,减去1后,差却成了三位数,只有相减时连续退位,才会如此。
那么,什么数减去1需要向高位借数呢?只有“0”!而最高位退1后成了0,表明被减数的最高位就是“1”。
这样,就可以断定被减数是1000。
知道了被减数和减数,差就迎刃而解了!例4:在下列各竖式的□中填上适当的数字,使竖式成立解:个位上,被减数是7,差是6,可知减数是1。
十位上,减数是8,差是9,可知被减数必小于8,借位后才使差比减数大的。
那么,?-8=9,可知被减数十位上是7。
再看百位,因为被减数是四位数。
第五讲竖式数字谜(一)

在下列□中填上合适的数,使 竖式成立
□ 7 □ + 4 □ 7 □ 2 4 0
在下列□中填上合适的数,使 竖式成立
□ 7 □ 4 - 1 □ 7 6 2 0 1 □
在下列□中填上合适的数,使 竖式成立
□ 7 □ 4 - 1 □ 7 6 2 0 1 □
在下列□中填上合适的数,使 竖式成立
7
□ 8 + □ 2 □
□ □ 1 9
在下列□中填上合适的数,使 竖式成立
□ 0
9
9 □
0 9
- 8 □ □ 9
在下列□中填上合适的数,使 竖式成立
5 □ □ 6 - □ 7 5 □
□ 6
2
7
在下列□中填上合适的数,使 竖式成立
6
3
□ □ 7 8
- □ □
□
0
2
在下列□中填上合适的数,使 竖式成立
3 □ 2 □ 8 □ + □ 3 8 □ 1
在下列算式中,每个字母代表 不同的数,找出每个字母各代 表什么数字,使竖式成立
3 - B
B
A A
C
B 6
A
在下列算式中,每个字母代表 不同的数,找出每个字母各代 表什么数字,使竖式成立
A +
2
B D
0
C E
3
C -
D E B C A B C D
A C A C
在下列算式中不同的汉字代表不同的数 字,相同的汉字代表相同的数字,每个 字母各代表什么数字时竖式成立
学 数 学
爱 数 学 + 喜 爱 数 学
2 0 0 0
在下列算式中不同的汉字代表不同的数 字,相同的汉字代表相同的数字,每个 字母各代表什么数字时竖式成立
小学三年级奥数讲解.竖式数字谜之欧阳语创编

竖式数字谜第1部分:加、减法竖式数字谜这一部分主要讲加、减法竖式的数字谜问题。
解加、减法数字谜问题的基本功,在于掌握好上一讲中介绍的运算规则(1)(2)及其推演的变形规则,另外还要掌握数的加、减的“拆分”。
关键是通过综合观察、分析,找出解题的“突破口”。
题目不同,分析的方法不同,其“突破口”也就不同。
这需要通过不断的“学”和“练”,逐步积累知识和经验,总结提高解题能力。
例1:在下列各竖式的□中填上适当的数字,使竖式成立解:加数都是两位数,从第一个加数个位是5与和的个位数是9,可以推断第二个加数的个位数必定是4。
即5+?=9。
从和的百位数与十位数是18,可断定,两个加数的十位数都是9,这样,谜便揭开了.例2:在下列各竖式的□中填上适当的数字,使竖式成立解:三个加数,只知道其中两个加数的个位分别是7、5,而和的个位却是8,肯定是进位造成的。
从7+5+?=□8,可判断另一个加数的个位必为6,十位上5+□+7=□7,可断定:□加上个位进上来的1是5,去掉进上来的1应是4。
百位上2+□=6,可知:□=4,去掉进上来的1,□=3。
例3:在下列各竖式的□中填上适当的数字,使竖式成立解:这个减法算式,只告知了减数是1,被减数、减数都不知道!全式应有八个数字,其中七个都是未知数,初看是比较难解的。
但是认真分析一下减法算式各部分的数位,便可以找到突破口。
被减数有四位,减去1后,差却成了三位数,只有相减时连续退位,才会如此。
那么,什么数减去1需要向高位借数呢?只有“0”!而最高位退1后成了0,表明被减数的最高位就是“1”。
这样,就可以断定被减数是1000。
知道了被减数和减数,差就迎刃而解了!例4:在下列各竖式的□中填上适当的数字,使竖式成立解:个位上,被减数是7,差是6,可知减数是1。
十位上,减数是8,差是9,可知被减数必小于8,借位后才使差比减数大的。
那么,?-8=9,可知被减数十位上是7。
再看百位,因为被减数是四位数。
三年级奥数基础教程竖式数字谜小学

三年级奥数基础教程竖式数字(shùzì)谜小学这一讲主要讲加、减法竖式的数字(shùzì)谜问题。
解加、减法数字谜问题的基本功,在于掌握好上一讲中介绍的运算(yùn suàn)规则(1)(2)及其推演(tuīyǎn)的变形规则,另外(lìnɡ wài)还要掌握数的加、减的“拆分”。
关键是通过综合观察、分析,找出解题的“突破口”。
题目不同,分析的方法不同,其“突破口”也就不同。
这需要通过不断的“学”和“练”,逐步积累知识和经验,总结提高解题能力。
例1 在右边的竖式中,A,B,C,D各代表什么数字?解:显然,C=5,D=1(因两个数字之和只能进一位)。
由于A+4+1即A+5的个位数为3,且必进一位(因为4>3),所以A+5=13,从而A=13-5=8。
同理,由7+B+1=12,即B+8=12,得到B=12-8=4。
故所求的A=8,B=4,C=5,D=1。
例2 求下面各竖式中两个加数的各个数位上的数字之和:分析与解:(1)由于和的个位数字是9,两个加数的个位数字之和不大于9+9=18,所以两个加数的个位上的两个方框里的数字之和只能是9。
(这是“突破口”)再由两个加数的个位数之和未进位,因而两个加数的十位数字之和就是14。
故这两个加数的四个数字之和是9+14=23。
(2)由于和的最高两位数是19,而任何两个一位数相加的和都不超过18,因此,两个加数的个位数相加后必进一位。
(这是“突破口”,与(1)不同) 这样,两个加数的个位数字相加之和是15,十位数字相加之和是18。
所求的两个加数的四个数字之和是15+18=33。
注意:(1)(2)两题虽然题型相同,但两题的“突破口”不同。
(1)是从和的个位着手分析,(2)是从和的最高两位着手分析。
例3 在下面的竖式中,A,B,C,D,E各代表什么数?分析与解:解减法竖式数字谜,与解加法竖式数字谜的分析方法一样,所不同的是“减法”。
5-1-2-2 乘除法数字谜(一).教师版

5-1-2-2.乘除法数字谜(一)
教学目标
数字谜是杯赛中非常重要的一块,特别是迎春杯,数字谜是必考的,一般学生在做数字谜的时候都采用尝试的方式,但是这样会在考试中浪费很多时间.本模块主要讲乘除竖式数字谜的解题方法,学会通过找突
1.数字谜定义:一般是指那些含有未知数字或未知运算符号的算式.
模块一、乘法数字谜
是一个残缺的乘法竖式,其中
【难度】2星【题型】填空
所以b≥6,从而d≥6.由22□÷c≥60和c>2知c=3,
de=
76
30 000,所以.再由乘积不小于30000
下面残缺的算式中,只写出了3个数字1,其余的数字都不是
【难度】2星 【题型】填空
了说明的方便,这个算式中的关键数字用英文字母表示.很明显e= 0三数之一,两位数应是(100+f )的因数.101,103,102=17×6,则C 只能取3,,ab 317=⨯,,53ab =
【题型】填空
⨯=
.510)2161080
【答案】。
三年级数奥第4讲-竖式数字谜(一)

三年级数奥第四讲 竖式数字谜姓名竖式数字谜就是填出竖式运算中的空格,本讲先讨论加减法的竖式。
例1右图的算式里,四个小纸片各盖住了一个数字, 问:被盖住的四个数字总和是多少?例2在下面竖式的□内各填一个合适的数字,使竖式成立。
例3 在下列空格中,各填一个数字,使算式成立。
例4 下面每个汉字各代表一个数字,不同的汉字表示不同的数字,相同的汉字表示相同的数字。
问:这些汉字各代表什么数字? 海 宁 海 宁 市+ 爱 海 宁 市 爱=( );海=( ); 1 9 9 9 宁=( );市=( );例5 右面算式,不同的汉字表示不同的数字,相同的 汉字表示相同的数字,问:每个汉字各代表什么数字?真=( ) 奇=( ) 妙=( ) 啊=( )例6 在右面算式中,汉字“第、十、一、届、华、杯、赛”代表1、2、3、4、5、6、7、8、9中的7个数字,不同的汉字代表不同的数字,“第、十、一、届、华、杯、赛”所代表的7个数字的和等于多少?(第十一届华罗庚金杯赛初赛试题)练 习 四1、在下列空格中,各填一个数字,使算式成立。
+ 4910 5+ 39 1 09妙 啊 妙+真 奇 妙 真 奇 妙 啊6 + 8218 35 7 + 43282、下面每题的6个方框中的数字被盖住了,求这6个数字的和。
3、在下列空格中,各填一个数字,使算式成立。
4、下面每个汉字各代表一个数字,不同的汉字表示不同的数字,相同的汉字表示相同的数字。
问:这些汉字各代表什么数字?5、下面各式中,不同的字母代表不同的数字,相同的字母表示相同的数字。
问,它们各代表什么数字?6、不同的汉字表示不同的数字,相同的汉字表示相同的数字,问:它们各代表什么数字? 助助 人助 人 为+助 人 为 乐1 9 9 3+ 99 11+ 99 13-490 -9 1 2 7家 家 + 学 大 上 上 学 爱 学 学 大 爱 大 登 登 + 峰攀 高 高 峰 高 峰 登 攀 我 攀 B A -C D CCD B CD A A C D C B C + EFCD BP - H G F CDPPE A + B C AA B A A + B A。
实用文库汇编之小学三年级奥数讲解.竖式数字谜

作者:方升座作品编号: 58001984419960354创作日期:2020年12月20日实用文库汇编之竖式数字谜第1部分:加、减法竖式数字谜这一部分主要讲加、减法竖式的数字谜问题。
解加、减法数字谜问题的基本功,在于掌握好上一讲中介绍的运算规则(1)(2)及其推演的变形规则,另外还要掌握数的加、减的“拆分”。
关键是通过综合观察、分析,找出解题的“突破口”。
题目不同,分析的方法不同,其“突破口”也就不同。
这需要通过不断的“学”和“练”,逐步积累知识和经验,总结提高解题能力。
例1:在下列各竖式的□中填上适当的数字,使竖式成立解:加数都是两位数,从第一个加数个位是5与和的个位数是9,可以推断第二个加数的个位数必定是4。
即5+?=9。
从和的百位数与十位数是18,可断定,两个加数的十位数都是9,这样,谜便揭开了.例2:在下列各竖式的□中填上适当的数字,使竖式成立解:三个加数,只知道其中两个加数的个位分别是7、5,而和的个位却是8,肯定是进位造成的。
从7+5+?=□8,可判断另一个加数的个位必为6,十位上5+□+7=□7,可断定:□加上个位进上来的1是5,去掉进上来的1应是4。
百位上2+□=6,可知:□=4,去掉进上来的1,□=3。
例3:在下列各竖式的□中填上适当的数字,使竖式成立解:这个减法算式,只告知了减数是1,被减数、减数都不知道!全式应有八个数字,其中七个都是未知数,初看是比较难解的。
但是认真分析一下减法算式各部分的数位,便可以找到突破口。
被减数有四位,减去1后,差却成了三位数,只有相减时连续退位,才会如此。
那么,什么数减去1需要向高位借数呢?只有“0”!而最高位退1后成了0,表明被减数的最高位就是“1”。
这样,就可以断定被减数是1000。
知道了被减数和减数,差就迎刃而解了!例4:在下列各竖式的□中填上适当的数字,使竖式成立解:个位上,被减数是7,差是6,可知减数是1。
十位上,减数是8,差是9,可知被减数必小于8,借位后才使差比减数大的。
《?竖式数字迷》教案

《竖式数字迷》教案
《竖式数字迷》教案
知识点:
一、竖式数字谜的类型
(1)空格类
去掉的数字用空格表示,空格中只能填0至9中的某个数字。
(2)符号类
去掉的数字用字母、汉字或图形表示,代表的数字只能取0至9中的某个数字。
一般相同的符号代表相同的数字,不同的符号代表不同的数字。
空格类数字谜与符号类数字谜的解题步骤类似,需要仔细审题找到突破口,用数字表示出竖式后要再验算一遍。
二、竖式问题的常见突破口
(1)加、减法竖式
可以利用首、末位分析,进、退位规律,重复数分析以及特殊结构“黄金三角”等方法解加、减法竖式问题。
(2)乘法竖式
可以利用尾数分析、首位分析、位数分析等方法解乘法竖式问题。
在进行尾数分析时,要注意先减去后一位进位的数再计算。
多位数的乘法竖式有时候要从加法部分进行突破。
(3)除法竖式
从除法竖式中分解出乘法和减法,然后用乘法竖式和减法竖式的分析方法解决。
在有余数的除法竖式中,一定要注意余数要比除数小。
课上习题:手写P65。
数字谜之竖式谜(一)word版本

数字谜之竖式谜(一)A12标准奥数教程数字谜之竖式谜【知识点与基本方法】跟横式数字谜一样也是一种猜数的游戏。
解竖式谜旧的根据有关的运算法则、数的性质(和差积商的位数、数的整除性、奇偶性、尾数规律等)来进行正确地推理、判断解答竖式数字谜是应注意的问题:(1)空格中只能填写0、1、2、3、4、5、6、7、8、9,而且最高位不能为0;(2)进位要留意,不能漏掉(3)答案有时候不唯一(4)两数字相加,最大进位为1,三个数字相加最大进位为2,(5)两个数字相乘,最大进位为8(6)相同的字母(汉字或符号)代表相同的数字,不同的字母(汉字或符号)代表不同的数字加(7)一个问题,读取整数型,并计算所有各位上数字的总和,直到该和降至一位数。
例如:数字是1256sum=1+2+5+6=14;sum=1+4=5;【例题精讲】求100~999一共900个三位数的各位数字之和也就是2700个数的和只需计算处各个数字出现的次数便可0出现的次数这样算0在个位上出现次数100~990共90次0在十位上出现次数a00~a09,a为1~9,共10*9=90次即数字0共出现了180次而数字1~9出现的次数相同为(2700-180)/9=280次所以所求数等于280*(1+2+……+9)=280*45=12600【例题精讲】例1.下面的算式中,只有5个数字已写出,请补充其他的数字6□7+ □ 2 □□□ 1 5分析:在5个方格中,要个填写一个数字,是运算式成立,先填哪一个?那就要我们找问题的突破口了从百位来看,和的千位数字只能是1.从市委相加来看,进位到百位,也只能进1,因此□2 □的百位是九,和的百位是0.通过上面的分析就找到了问题的突破口了,15-7-6=2 11-2-1=8就得到算式的结果6□7+ □ 2 □□□ 1 5例3.图中,有四个小纸片各盖住了一个数字,问:被盖住的四个数字综合是多少?□□+ □□1 4 9分析:先看个位,因为两个数字相加,最大为9+9=18,所以两个数的和不能是19.从而两个被盖住的个位数字之和等于9.由于个位数字相加不向十位进位,所以两个被盖住的十位数字的和14.因此被盖主的四个数字的总和是14+9=23例4.在下面的方框中填上何时得数字□7 6×□□18 □□□□□□3 1 □□ 0分析:由于积的各位舒适0,乘数的个位数是5,由此我们可以得到被乘得数与5相乘的1880,被乘数的百位数字是3,最后因为被乘数是376,积是31□□0,所以乘数的十位数字是8解: 3 7 6× 8 51 8 8 03 0 0 83 1 8 6 0例5.下面每个汉字个代表一个数字,不同的汉字表示不同的数字,相同的汉字表示相同的数字,问:这些汉字个代表什么数字?北京北京市+ 爱北京市1 9 9 9分析:首先,我们立即得到“爱”表示=1,所以百位数字相加不进位,“北”小于5.又因为三个数字相加小于100+100+100=300所以“北”+“北”大于6,从而“北”=4,知道“爱”和“北”个代表什么数字问题就很好解决了解:爱=1,北”=4 “京”=7 “市”=6例6.在图6-1算式的每个空格中,各填入一个合适的数字,使竖式成立。
尖子名师-数字谜之乘除法竖式(1)
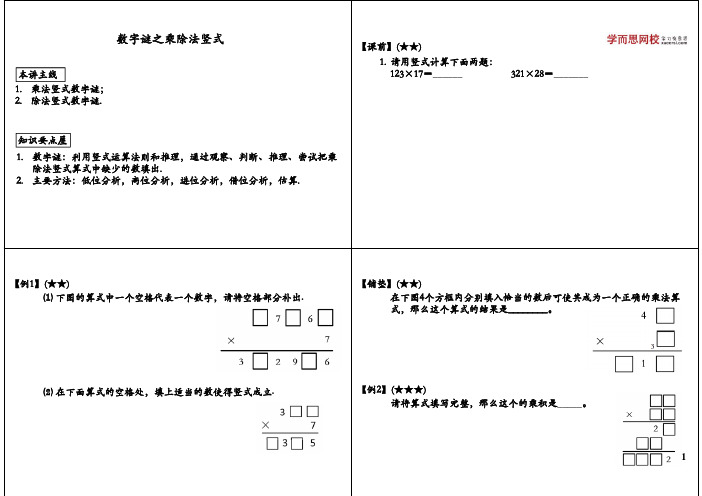
⑴下图的算式中一个空格代表一个数字,请将空格部分补出.
⑵在下面算式的空格处,填上适当的数使得竖式成立.
在下图4个方框内分别填入恰当的数后可使其成为一个正确的乘法算
式,那么这个算式的结果是________。
【】★★★
请将算式填写完整,那么这个的乘积是_____。
【例2】(★★★)
下面这个算式中,是一个四位数,且P 、Q 、R 及S 分别为不同的PQRS 数码. 则四位数是____。
PQRS 请将算式填写完整。
【例3】(★★★★)
【例5】(★★★★)在下图所示除法竖式的每个方框中,填入适当的数字,使算式成立。
【例5】(★★★★) 那么算式中的被除数是多少?
在下面空格填入适当的数。
【超常大挑战】(★★★★)。
加减法竖式谜pptx

利用竖式谜作为教学案例,引导学生发现数学在现实生活中的应用价值 ,培养他们的数学应用意识。
拓展延伸:其他类型竖式谜简
05
介
乘法竖式谜
乘法竖式谜的构造
通过特定的数字排列组合,使得 乘法竖式的结果呈现出有趣的图
案或文字。
未来加减法竖式谜的发展趋势
未来加减法竖式谜可能会更加注重与其他学科的融合和交叉,如物理、化学等。同时,随着科技的发展和应用, 可能会出现更多形式的加减法竖式谜,如数字化、虚拟化等。这些新的形式将为学生提供更加丰富多彩的学习体 验和挑战。
谢谢聆听
加减法竖式谜pptx
目录
• 竖式谜基本概念与规则 • 加减法竖式谜解题技巧 • 实例分析:加减法竖式谜求解过程 • 竖式谜在数学教育中的应用价值
目录
• 拓展延伸:其他类型竖式谜简介 • 总结回顾与展望未来发展趋势
01 竖式谜基本概念与规则
竖式谜定义及特点
01
竖式谜是一种数学游戏,玩家需要通过逻辑推理和运算 技巧来解开谜题。
结合多种方法
综合运用观察法、尝试法 和排除法,提高解题效率 和准确性。
实例分析:加减法竖式谜求解
03
过程
简单实例讲解与演示
选择简单加减法竖式 谜题目,如“123 + 456 = 579”
通过PPT动画效果, 演示每一步的求解过 程,帮助学生理解
逐步解析竖式谜的求 解过程,包括数字对 应关系和逻辑推理
底。
除法竖式谜的实例
如一个除法竖式,商为循环小数 ,且循环节与除数相同。
混合运算竖式谜
1 2
混合运算竖式谜的构造
三年级数学奥数讲义-数字谜之乘除法竖式通用版

2
【本讲总结】 一、几种方法
1.首位分析 2.末位分析 3.位数分析 4.奇偶性分析 5.进位分析 6.退位分析 二、一般步骤: 1.寻找突破口 2.结合枚举法 3.检验 对于数字谜问题的解法有很多,其实并不难,需要同学ห้องสมุดไป่ตู้多多练习, 有 良好的数感哦!
3
数字谜之乘除法竖式
数字谜,一般是指那些含有未知数字或未知运算符号的算式。这种不 完整的算式,就像“谜”一样,要解开这样的谜,就得根据有关的运算法则、 数的性质(和差积商的位数,数的整除性、奇偶性、尾数规律等)来进行正确的 推理、判断。
关键:寻找突破口 几点注意: ⑴数字谜中的文字、字母或其它符号,只取0~9中的某个数字; ⑵认真分析算式中所包含的数量关系,找出尽可能多的隐蔽条件; ⑶必要时,枚举和筛选相结合的方法(试验法),逐步淘汰不符合题意的数字; ⑷数字谜解出之后,最好验算一遍。
竖式数字谜

全方位教学辅导教案学科:奥数任课教师:教务:授课时间:2014年月日星期学生性别年级小2 总课时:小时第次课教学内容竖式数字谜重点难点加减乘除运算规则教学目标熟练掌握加减乘除运算规则,并会解应用题针对性授课第2讲竖式数字谜第1部分:加、减法竖式数字谜这一部分主要讲加、减法竖式的数字谜问题。
解加、减法数字谜问题的基本功,在于掌握好上一讲中介绍的运算规则(1)(2)及其推演的变形规则,另外还要掌握数的加、减的“拆分”。
关键是通过综合观察、分析,找出解题的“突破口”。
题目不同,分析的方法不同,其“突破口”也就不同。
这需要通过不断的“学”和“练”,逐步积累知识和经验,总结提高解题能力。
例1:在以下各竖式的□中填上适当的数字,使竖式成立解:加数都是两位数,从第一个加数个位是5与和的个位数是9,可以推断第二个加数的个位数必定是4。
即5+?=9。
从和的百位数与十位数是18,可断定,两个加数的十位数都是9,这样,谜便揭开了.例2:在以下各竖式的□中填上适当的数字,使竖式成立解:三个加数,只知道其中两个加数的个位分别是7、5,而和的个位却是8,肯定是进位造成的。
从7+5+?=□8,可判断另一个加数的个位必为6,十位上5+□+7=□7,可断定:□加上个位进上来的1是5,去掉进上来的1应是4。
百位上2+□=6,可知:□=4,去掉进上来的1,□=3。
例3:在以下各竖式的□中填上适当的数字,使竖式成立解:这个减法算式,只告知了减数是1,被减数、减数都不知道!全式应有八个数字,其中七个都是未知数,初看是比较难解的。
但是认真分析一下减法算式各部分的数位,便可以找到突破口。
被减数有四位,减去1后,差却成了三位数,只有相减时连续退位,才会如此。
那么,什么数减去1需要向高位借数呢?只有“0”!而最高位退1后成了0,说明被减数的最高位就是“1”。
这样,就可以断定被减数是1000。
知道了被减数和减数,差就迎刃而解了!例4:在以下各竖式的□中填上适当的数字,使竖式成立解:个位上,被减数是7,差是6,可知减数是1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数字谜之竖式谜(一)A12标准奥数教程数字谜之竖式谜【知识点与基本方法】跟横式数字谜一样也是一种猜数的游戏。
解竖式谜旧的根据有关的运算法则、数的性质(和差积商的位数、数的整除性、奇偶性、尾数规律等)来进行正确地推理、判断解答竖式数字谜是应注意的问题:(1)空格中只能填写0、1、2、3、4、5、6、7、8、9,而且最高位不能为0;(2)进位要留意,不能漏掉(3)答案有时候不唯一(4)两数字相加,最大进位为1,三个数字相加最大进位为2,(5)两个数字相乘,最大进位为8(6)相同的字母(汉字或符号)代表相同的数字,不同的字母(汉字或符号)代表不同的数字加(7)一个问题,读取整数型,并计算所有各位上数字的总和,直到该和降至一位数。
例如:数字是1256sum=1+2+5+6=14;sum=1+4=5;【例题精讲】求100~999一共900个三位数的各位数字之和也就是2700个数的和只需计算处各个数字出现的次数便可0出现的次数这样算0在个位上出现次数100~990共90次0在十位上出现次数a00~a09,a为1~9,共10*9=90次即数字0共出现了180次而数字1~9出现的次数相同为(2700-180)/9=280次所以所求数等于280*(1+2+……+9)=280*45=12600【例题精讲】例1.下面的算式中,只有5个数字已写出,请补充其他的数字6□7+ □ 2 □□□ 1 5分析:在5个方格中,要个填写一个数字,是运算式成立,先填哪一个?那就要我们找问题的突破口了从百位来看,和的千位数字只能是1.从市委相加来看,进位到百位,也只能进1,因此□2 □的百位是九,和的百位是0.通过上面的分析就找到了问题的突破口了,15-7-6=2 11-2-1=8就得到算式的结果6□7+ □ 2 □□□ 1 5例3.图中,有四个小纸片各盖住了一个数字,问:被盖住的四个数字综合是多少?□□+ □□1 4 9分析:先看个位,因为两个数字相加,最大为9+9=18,所以两个数的和不能是19.从而两个被盖住的个位数字之和等于9.由于个位数字相加不向十位进位,所以两个被盖住的十位数字的和14.因此被盖主的四个数字的总和是14+9=23例4.在下面的方框中填上何时得数字□7 6×□□18 □□□□□□3 1 □□ 0分析:由于积的各位舒适0,乘数的个位数是5,由此我们可以得到被乘得数与5相乘的1880,被乘数的百位数字是3,最后因为被乘数是376,积是31□□0,所以乘数的十位数字是8解: 3 7 6× 8 51 8 8 03 0 0 83 1 8 6 0例5.下面每个汉字个代表一个数字,不同的汉字表示不同的数字,相同的汉字表示相同的数字,问:这些汉字个代表什么数字?北京北京市+ 爱北京市1 9 9 9分析:首先,我们立即得到“爱”表示=1,所以百位数字相加不进位,“北”小于5.又因为三个数字相加小于100+100+100=300所以“北”+“北”大于6,从而“北”=4,知道“爱”和“北”个代表什么数字问题就很好解决了解:爱=1,北”=4 “京”=7 “市”=6例6.在图6-1算式的每个空格中,各填入一个合适的数字,使竖式成立。
分析:首先根据十位上8+5得到4可知,个位有一个进位,所以,个位的空格中必定是9;再根据百位上两个数相加,再加一个进位后得到9,并有进位可知,百位两个空格中都是9;结果中的千位只能是1,于是得到:例7.如图6-2,用0,1,2,3,4,5,6,7,8,9这10个数字各一次,可组成一个正确的加法竖式。
现已写出3个数字,那么这个算式的结果是多少?分析:首先,结果中的千位为1;第二,百位上第一个数至少是7,最多是9;如为7,那么,结果中的百位为0,并十位要有进位;由此第一个数的十位可以填6,第二个数的个位填9;如为9,显然不行。
所以,结果只能是:【课后练习题】6.在如图6-3所示的算式中,3个加数的各位数字均是某两个相邻数字中的一个,那么这个算式的计算结果可能是多少?7.在图6-6所示的算式中,每个方框代表一个数字。
问:这6个方框中的数字的总和是多少?8.将1到9这9个数码分别填入图6-8的9个空格中,要求先填1,再在与1相邻(即左、右或上、下)的格中填2,再在与2相邻的空格中填3,依次类推,……,最后填9,使得加法算式成立。
二加法与减法中数字和的变化在数字和的问题上,有许多有趣的、富于思考的问题。
首先,计算两个数相加,数字和会怎样变化,我们分开不进位加和进位加这两种情况进行讨论。
先看546+453与546+435两题,这两题每题两个加数的各位上的数字的和是5+4+6+4+5+3=5+4+6+4+3+5=27,而546+453=999,加的过程没有进位,所得的和999各位上的数字的和9+9+9=27;546+435=981,两个加数的数字和是27,加的过程个位上满10向十位进1,有一次进位,所得的和981各位上的数字和9+8+1=18,比没有进位时,和的数字和少9;再计算546+534,两个加数各位上的数字的和也是27,546+534=1080,加的过程中,个位和百位分别都满10,各向前一位进1,有两次进位,所得的和1080各位上的数字的和1+0+8+0=9,比没有进位时少了18,即少了2个9。
由此我们可以得到这样的规律:计算加法,没有进位时,加得的和的数字和等于加数的数字和;有进位时,每进位一次,加得的和的数字和就减少1个9。
同样,我们也可以归纳出减法中数字和的变化规律:计算减法,没有退位时,减得的差的数字和等于被减数的数字和减去减数的数字和的差;有退位时,每退位一次,减得的差的数字和就增加1个9。
下面,我们用上面的规律来解答几个问题。
例1:有A、B两个整数,A的各位数字的和是35,B的各位数字的和是29,如果A和B相加时有三次进位,那么把A+B 所得的和的各位数字相加,和是多少?解:如果相加时没有进位,A+B所得的和的各位数字相加的和,等于A和B两个加数数字和相加的和。
35+29=64,相加时,每进位一次,得数的数字和减少1个9,现有三次进位,得数的数字和减少3个9,所以A+B所得的和的各位数字相加,和是64-27=37。
答:A+B的和的数字和是37。
例2:整数A减整数B有两次退位,减得的差的数字和是13,已知A的各位数字的和是8,B的各位数字和是多少?解:A的各位数字的和是8,A减B的差的数字和却是13,这有可能吗?如果连同退位使差的数字和增加这一因素考虑在内,这个结果是很正常的。
A减B有两次退位,使减得的差比不退位时增加2×9=18,也可以看作是13由被减数A的数字和8增加了18减去B的数字和得到的。
所以B的各位数字的和是8+18-13=13。
答:B的各位数字的和是13。
例3:整数A的各位数字的和是24,整数B的各位数字的和是22,而A+B的和的各位数字的和是10,在加的过程中有多少次进位?解:如果A+B在计算中没有进位,所得的和的各位数字的和是24+22=46,现在A+B的和的各位数字的和是10,比不进位时减少了46-10=36,36里面包含9的个数是36÷9=4,所以加的过程中有4次进位。
答:在加的过程中有4次进位。
例4:甲数和乙数的数字和都能被7整除,甲数加乙数,得数的数字和是3,甲数减乙数,差最小是几?解:甲数和乙数的数字和都能被7整除,相加时如果没有进位,所得的和的数字和也能被7整除,现已知甲数加乙数得数的数字和是3,不能被7整除,因此,甲数加乙数必定有若干次进位,3至少加上2个9,得到3+2×9=21,能被7整除,而21=7+14,即甲数和乙数的数字和一个是7,一个是14,并且甲数加乙数有两位进位。
当甲数是61,乙数是59时,甲数减乙数的差为61-59=2,这是最小的差。
答:差最小是2。
例5:1~1000这1000个自然数所有数字的和是多少?解:1~1000这1000个自然数所有数字的和比1~1000这1000个数的和小得多,这是因为把1~1000这1000个数相加时,有多次进位,每进位1次,比不进位时数字和都减少9,把加得的和按数字和计算的进位次数减去9的个数,才得到所有数字的和,但这样计算太繁了。
为了简便地计算这1000个数所有数字的和,可以把这1000个数按以下的方法分组,使每一组相加时都不进位,然后算出每组和的数字和,再求出各组数字和的总和,就是1000个数所有数字的和。
1 2 3 4 (499)1000 999 998 997 996 995 (500)1000 999 999 999 999 999 … 999 ——各组数的和1 27 27 27 27 27 …999 ——各个和的数字和这样算得1000个数所有数字的和是1+27×500=13501。
答:所有数字的和是13501。
*例6:两个四位数相加,第一个四位数的每个数字都不小于5,第二个四位数仅仅是第一个四位数的数字调换了位置。
某同学做出的答案是16246。
试问该同学的答数正确吗?如果正确,写出这两个四位数,如果不正确,请说明理由。
解:在对这一题思考时,如果试图按题中的条件找出四位数拼出加法算式,要找出很多的四位数,进行许多的尝试,而且不能进行严密的推理,因此这不是可取的方法。
比较好的做法是,先按规律说明是否可能按题目的条件做出这个答数,有可能时,才拼算式,如果不可能,这个答数就是错的。
由于第一个四位数的每个数字都不小于5,不管把这四个数字怎样调换组成第二个四位数,第二个四位数的每个数字也都不小于5,两个数相加,四个数位上都要进位,共有四次进位,而两个四位数数字的和是第一个四位数数字和的2倍,是偶数,四次进位使和的数字和比原来八个数字的和减少4个9,所得的和的数字和仍然是偶数,而该同学的答数16246的数字的和1+6+2+4+6=19,是个奇数,所以这个答数是错的。
应用练习二1.有A、B两个整数,A的各位上的数字的和是31,B的各位上的数字的和是19,A和B相加,得数的各位上的数字的和是32,相加时有几次进位?2.A的各位上的数字的和是4,A减去一个两位数,差的各位上的数字的和是24,减数最大是几?3.甲数和乙数的数字和都是17的倍数,甲数减乙数,差的数字和是10,甲数最小是几?4.甲数和乙数的和是753,两个数的数字和都是11的倍数,两个数中较大的一个最大是几?5.1~10000这10000个自然数所有数字的和是多少?6.一个三位数,它的各位上的数字的和能被8整除,这个三位数加1得到的数各位上的数字的和也能被8整除,在所有满足条件的三位数中,最大的一个是几?*7.的差是一个自然数的平方,这个自然数的各位数字的和是几?*8.的积的各位数字的和是几?课后练习二1.甲数各位数字之和是28,乙数各位数字之和是18,甲、乙两数相加时有三次进位,那么甲、乙两数之和的各位数字之和是多少?2.甲数各位数字之和是9,乙数各位数字之和是10,如果甲数减乙数有两次要从前一位退1再减。
