高三周末学情检测
江苏省盐城市联盟校2023-2024学年高三上学期第一次学情调研检测英语参考答案及评分标准

2023-2024学年第一学期联盟校第一次学情调研检测高三年级英语参考答案及评分标准第一部分听力(共两节,每小题2.5分,满分30分)1-5CCACB6-10BCBAC11-15ABCAA16-20CBAAB第二部分阅读理解(共两节,每小题2.5分,满分50分)21-25BACDA26-30DBBDB31-35CDACD36-40GBCFE第三部分语言运用(共两节,满分30分)第一节完形填空(共15小题;每小题1分,满分15分)41-45ACDCB46-50DABDC51-55BADCB第二节语篇填空(共10小题:每小题1.5分,满分15分)56.which57.At58.voiced59.accounting60.deeply61.is based62.country’s63.a64.themselves65.to push第四部分写作(共两节,满分40分)第一节应用文写作(满分15分)Read Classics,Learn EnglishDear fellow schoolmates,Aimed at appreciating the charm of English classics and promoting English learning,the school English Club will host the“Read Classics,Learn English”activity.This activity will last roughly2weeks,scheduled from April1st to14th.Various activities have been designed, ranging from attending a lecture on reading tips to recommending the favourite English classics, followed by exchanging reading experiences as well as reading skills.Anyone who shows interest in reading English classics is welcome.Looking forward to your participation.English Club 第二节读后续写(满分25分)Paragraph1:My father shouted at us to run back to the hotel.He grabbed my hand and pulled me with him.As we reached the hotel gate,we heard a roaring sound behind us.Quickly,my father pushed us towards the stairs.Fear gripped us and we reached the first floor when we heard the roar of rushing water and glass breaking.My father yelled at us to keep climbing.We stopped on the fourth floor and looked down at the water below us.It had stopped rising.After some minutes,it began to drop.Paragraph2:We waited a long time before going downstairs.Hardly had the rushing water dropped when we saw the unrecognizable hotel gate.There was dirt and broken furniture everywhere. Some people who were caught in the water were either unconscious or burst into tears with pain. What we saw weakened our heart and we decided to help the victims after a narrow escape.Never had I had such a thrilling yet dangerous vacation before.The special trip to Penang was deeply impressed in my mind.附英语听力录音稿和部分答案解析:英语听力录音稿第一节Text1M:Excuse me,I’ve been all over the building looking for the Chemistry office but I could only find the Chinese and Geography office.Is this the right place?W:Yes,this is the Chemistry office.Text2M:Good afternoon,City Police Station.Can I help you?W:Oh,hello,I’d like to report a man not wearing a mask here.M:Just a minute and I’ll put you through.Text3W:Hi there,Martin.How are you going with your report?M:I’ve finished it actually.After some consideration,I decided to look at the Chinese traditional Double Ninth Festival.W:Lucky you.I’m still trying to find an interesting topic.Text4W:You are from Indonesia,Luki.How do you find Suzhou?M:Well,I like it here.I think the city is very beautiful.W:What about your accommodation?Is that OK?M:Yes,OK.At first I stayed with a family for three months.They were very kind to me but they had two naughty boys and I found it difficult to study.Text5W:Darling,what do you think of this street?M:Good.It’s quiet and calm.And the neighbors don’t party on the weekends.W:Yes,everything is okay except the Blacks’dog often barks.第一节到此结束。
常州市联盟学校 2024—2025 学年度第一学期学情调研高三年级数学试卷答案

常州市联盟学校2024—2025学年度第一学期学情调研高三年级数学试卷答案2024.10一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.A 2.C 3.B 4.D 5.B 6.D 7.C 8.C二、多选题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.ACD 10.BC 11.BCD三、填空题:本题共4小题,每小题5分,共20分.12.613.⎥⎦⎤⎢⎣⎡3,2314.2四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.15.(13分)(1)0m n m n ⊥∴⋅=…………1分()()22222cos 2sin 1cos 2sin 1cos 21cos 2CC C C C C -=+-=+--22cos cos 10C C =+-=解得:cos 1C =-或1cos 2C =,()0,C π∈ ,3C π∴=;…………6分(2)因为2π3C =.由正弦定理,2sin sin sin a b c A B C ===,…………8分所以sin 2bB =,sin 2a A =.又因为sin sin 2A B +=,所以22a b +=,得a b +=由余弦定理有:2222cos c a b ab C =+-,所以1ab =.所以11sin 122ABC S ab C ==⨯⨯ .…………13分16.(15分)(1)当a =0时,f (x )=2)1(+x x(x ≠-1),则f (0)=0,因为3')1(1)(+-=x xx f ,所以f ′(0)=1.所以曲线y =f (x )在(0,0)处的切线方程为y =x .…………5分(2)函数的定义域为(-∞,-1)∪(-1,+∞).3')1())12(()(++--=x a x x f ,令f ′(x )=0,解得x =2a +1.…………7分①当2a +1=-1,即a =-1时,0)1(1)1(1)(23'<+-=+--=x x x x f 所以函数f (x )的单调递减区间为(-∞,-1)和(-1,+∞),无单调递增区间;………9分②当2a +1<-1,即a <-1时,令f ′(x )<0,则x ∈(-∞,2a +1)∪(-1,+∞),令f ′(x )>0,则x ∈(a +1,-1),函数f (x )的单调递减区间为(-∞,2a +1)和(-1,+∞),单调递增区间为(2a +1,-1);…12分③当2a +1>-1,即a >-1时,令f ′(x )<0,则x ∈(-∞,-1)∪(2a +1,+∞),令f ′(x )>0,则x ∈(-1,2a +1),函数f (x )的单调递减区间为(-∞,-1)和(2a +1,+∞),单调递增区间为(-1,2a +1).…14分综上所述:当a =-2时,函数f (x )的单调递减区间为(-∞,-1)和(-1,+∞),无单调递增区间;当a <-2时,函数f (x )的单调递减区间为(-∞,a +1)和(-1,+∞),单调递增区间为(a +1,-1);当a >-2时,函数f (x )的单调递减区间为(-∞,-1)和(a +1,+∞),单调递增区间为(-1,a +1).…………15分17.(15分)(1)证明:如图取CE 的中点G ,连接FG 、BG .F 为CD 的中点,//GF DE ∴且12GF DE =,由AB ⊥平面ACD ,DE ⊥平面ACD ,//AB DE ∴,//GF AB ∴.又12AB DE =,GF AB ∴=,∴四边形GFAB 为平行四边形,则//AF BG ,AF ⊄ 平面BCE ,BG ⊂平面BCE ,//AF ∴平面BCE .…………5分(2)证明:ACD 为等边三角形,F 为CD 的中点,AF CD ∴⊥.DE ⊥ 平面ACD ,AF ⊂平面ACD ,DE AF ∴⊥,//BG AF ,所以DE BG ⊥,BG CD ⊥,又CD DE E = ,CD 、DE ⊂平面CDE ,BG ∴⊥平面CDE ,BG ⊂ 平面BCE ,∴平面BCE ⊥平面CDE .…………10分(3)如图:在平面CDE 内,过F 作FH CE ⊥于点H ,连接BH ,平面BCE ⊥平面CDE ,平面BCE 平面CDE CE =,FH ⊂平面CDE ,FH ⊥ 平面BCE .FBH ∴∠为BF 和平面BCE 所成的角,因为4AD DE ==,2AB =,则sin 45FH CF =︒4BF ==,在Rt FHB 中,sin 4FH FBH BF∠==,∴直线BF 和平面BCE .…………15分(向量法略)18.(17分)(1)在ABC V 中,由余弦定理,2222cos b a c ac ABC =+-∠,因为2221)sin 2S b a c ac ABC =--=∠,所以sin ABC ABC =∠∠,即tan B =(0,180)B ∈︒︒,所以120ABC ∠=︒.…………4分26AB BC BAC ACB π==∴∠=∠=,设CBD θ∠=,则2π03θ<<,在BCE 中,由正弦定理得sin sin CE BE ACB θ=∠,在ABE 中,由正弦定理得2πsin sin 3BEAE BACθ=∠⎛⎫- ⎪⎝⎭,26AB BC BAC ACB π==∴∠=∠=,2πsin sin 3CEAE θθ∴=⎛⎫- ⎪⎝⎭,因为23AE AC = ,则2AE CE =,所以,2πsin 32sin AE CE θθ⎛⎫- ⎪⎝⎭==,333cos sin tan 223θθθ=∴因为2π03θ<<,所以,π6θ=,即6CBD π∠=…………10分(2)解:2AD CD =,且π3ADC ∠=,BAC α∠=,由余弦定理可得22222cos 3AC AD CD AD CD ADC CD =+-⋅∠=,2222AC AC CD AD ACD π∴∴+=∴∠=在ABC △中,2AB BC ==,BAC ACB α∴∠=∠=由正弦定理得sin(2)sin AC AB παα=-,2sin(2)4cos sin AC πααα-∴==4cos AC α∴=,CD α=在BCD △中,2BC =,π2BCD α∠=+,由余弦定理可得2222π16432cos()4cos 22cos sin 233BD BC CD BC CD αααα=+-⋅+=++⋅⋅⋅,()2816π2041cos 2sin 2sin 23363BD ααα⎛⎫=++=++ ⎪⎝⎭,易知π02α<<,则ππ5π2666α<+<,故当ππ262α+=时,即当π6α=时,BD取最大值,且最大值为 (17)分19.(17分)(1)若()()f x f x -=当0x <时,则0x ->,3411x x x ∴-=∴=-,无实数解,舍去;当0x >时,则0x -<,3411x x x ∴=∴=--,无实数解,舍去;则()f x 不是“弱偶函数”,…………2分若()()f x f x -=-当0x <时,则0x ->,3411x x x ∴-=-∴=,解得1x =-(正舍),当0x >时,则0x -<,若31x x -=-,解得1x =(负舍),则存在实数01x =±,满足()()00f x f x -=-,所以()f x 是“弱奇函数”.…………5分(2)()()23234,14,1x x m x g x x ⎧-⋅-≥-⎪=⎨-<-⎪⎩,定义域为R .①当在区间[]1,1-上存在0x ,满足()()00g x g x -=-时,则()()00022323432340x x x x m m ---⋅-+-⋅-=,即()()0000233233100x x x x m --+-⋅+-=.令0033x x t -=+,则2t ≥=,当且仅当00x =时取等号.又[]01,1x ∈-,所以1110333t -≤+=,即102,3t ⎡⎤∈⎢⎥⎣⎦,所以()()00002233233102100x x x x m t mt --+-⋅+-=--=,所以210531,2226t t m t t -⎡⎤==-∈-⎢⎥⎣⎦②当在区间(),1∞--上存在0x ,满足()()00g x g x -=-时,则()0232344x x m ---⋅-=,即0014323x x m =-⋅⋅有解.因为0014323x x y =-⋅⋅在区间(),1∞--上单调递减,所以16m >.③当在区间()1,+∞上存在0x ,满足()()00g x g x -=-时,则()243234x x m ⎡⎤-=--⋅-⎢⎥⎣⎦,即003423x x m =-有解.因为03423x x y =-在区间()1,+∞上单调递增,所以16m >.综上所述,实数m 的取值范围为32m m ⎧⎫≥-⎨⎬⎩⎭.…………11分(3)由题意知,31,2b ⎡⎤∀∈⎢⎥⎣⎦,()()h x h x -=-在[]1,1x ∈-上都有解,即31,2b ⎡⎤∀∈⎢⎥⎣⎦,()()22ln 1ln 1x a x x b x a x x b -+++--=-++--+在[]1,1x ∈-上都有解,即31,2b ⎡⎤∀∈⎢⎥⎣⎦,()222ln 122a x x b ⎡⎤+-+=⎣⎦在[]1,1x ∈-上都有解,令[]20,1x s =∈,令()()2ln 12s a s s ϕ⎡⎤=+-+⎣⎦,由题意知()s ϕ在[]0,1s ∈上的值域包含[]2,3,因为()()2121s a sϕ-=++-',又因为[]()0,1,1,s a ∞∈∈+,所以()213a s +->,所以()0s ϕ'>,所以()s ϕ在[]0,1s ∈上单调递增,所以()()1021311e 111a e a a a a ϕϕ≤-⎧⎧≤⎪⎪≥⇒≥⇒<≤-⎨⎨⎪⎪>>⎩⎩综上:1e 1a <≤-.…………17分。
江苏省南京市2024-2025学年高三9月学情调研考试 数学 含答案

南京市2025届高三年级学情调研数 学 2024.09.19 注意事项:1.本试卷考试时间为120分钟,试卷满分150分.2.本试卷中所有试题必须作答在答题卡上规定的位置,否则不给分.3.答题前,务必将自己的姓名、准考证号用0.5毫米黑色墨水签字笔填写在试卷及答题卡上.一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的,请把答案填涂在答题卡相应位置上.1.已知集合A ={x |x -3>0},B ={x |x 2-5x +4>0},则A ∩B =A .(-∞,1)B .(-∞,3)C .(3,+∞)D .(4,+∞)2.已知a x =4,log a 3=y ,则a x +y =A .5B .6C .7D .123.已知|a |=3,|b |=1.若(a +2b )⊥a ,则cos<a ,b >=A .-32B .-33C .33D .324.已知数列{a n }为等差数列,前n 项和为S n .若S 3=6,S 6=3,则S 9=A .-18B .-9C .9D .185.若a 是第二象限角,4sin2α=tan α,则tan α= A .-7 B .-77 C .77D .7 6.甲、乙、丙、丁共4名同学参加某知识竞赛,已决出了第1名到第4名(没有并列名次).甲、乙、丙三人向老师询问成绩,老师对甲和乙说:“你俩名次相邻”,对丙说:“很遗憾,你没有得到第1名”.从这个回答分析,4人的名次排列情况种数为A .4B .6C .8D .127.若正四棱锥的高为8,且所有顶点都在半径为5的球面上,则该正四棱锥的侧面积为A .24B .32C .96D .1288.已知抛物线C :y 2=8x 的焦点为F ,准线为l ,点P 在C 上,点Q 在l 上.若PF =2QF ,PF ⊥QF ,则△PFQ 的面积为A .254B .25C .552D .55二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.已知复数z ,下列命题正确的是A .若z +1∈R ,则z ∈RB .若z +i ∈R ,则z 的虚部为-1C .若|z |=1,则z =±1D .若z 2∈R ,则z ∈R10.对于随机事件A ,B ,若P (A )=25,P (B )=35,P (B |A )=14,则 A .P (AB )=320 B .P (A |B )=16 C .P (A +B )=910 D .P (―AB )=1211.设函数f (x )=1|sin x |+8|cos x |,则 A .f (x )的定义域为{x |x ≠k π2,k ∈Z } B .f (x )的图象关于x =π4对称 C .f (x )的最小值为5 5 D .方程f (x )=12在(0,2π)上所有根的和为8π三、填空题:本题共3小题,每小题5分,共15分.请把答案填写在答题卡相应位置上.12.(2x +1x)4展开式中的常数项是 ▲ . 13.与圆柱底面成45°角的平面截圆柱得到如图所示的几何体.截面上的点到圆柱底面距离的最大值为4,最小值为2,则该几何体的体积为 ▲ .(第13题图)14.已知椭圆C 的左、右焦点分别为F 1,F 2,上顶点为B ,直线BF 2与C 相交于另一点A .当cos ∠F 1AB 最小时,C 的离心率为 ▲ .四、解答题;本大题共5小题,共77分.请在答题卡指定区域内作答,解答时应写出必要的文字说明,证明过程或演算步骤.15.(本小题满分13分)小王早晨7:30从家出发上班,有A ,B 两个出行方选择,他统计了最近100天分别选择A ,B 两个出行方案到达单位的时间,制成如下表格:(1)判断并说明理由:是否有95%的把握认为在8点前到单位与方案选择有关;(2)小王准备下周一选择A方案上班,下周二至下周五选择B方案上班,记小王下周一至下周五这五天中,8点前到单位的天数为随机变量X.若用频率估计概率,求P(X=3).附:χ2=n(ad-bc)2(a+b)(c+d)(a+c)(b+d),其中n=a+b+c+d,16.(本小题满分15分)如图,在四面体ABCD中,△ACD是边长为3的正三角形,△ABC是以AB为斜边的等腰直角三角形,E,F分别为线段AB,BC的中点,→AM=2→MD,→CN=2→ND.(1)求证:EF∥平面MNB;(2)若平面ACD⊥平面ABC,求直线BD与平面MNB所成角的正弦值.(第16题图)已知数列{a n },{b n },a n =(-1)n +2n ,b n =a n +1-λa n (λ>0),且{b n }为等比数列.(1)求λ的值;(2)记数列{b n ⋅n 2}的前n 项和为T n .若T i ⋅T i +2=15T i +1(i ∈N *),求i 的值.18.(本小题满分17分)已知 F 1,F 2是双曲线线C :x 2a 2-y 2b 2=1(a >0,b >0)的左、右焦点,F 1F 2=26,点T (26,10)在C 上.(1)求C 的方程;(2)设直线l 过点D (1,0),且与C 交于A ,B 两点.①若→DA =3→DB ,求△F 1F 2A 的面积;②以线段AB 为直径的圆交x 轴于P ,Q 两点,若|PQ |=2,求直线l 的方程.已知函数f(x)=e x-a+ax2-3ax+1,a∈R.(1)当a=1时,求曲线y=f(x)在x=1处切线的方程;(2)当a>1时,试判断f(x)在[1,+∞)上零点的个数,并说明理由;(3)当x≥0时,f(x)≥0恒成立,求a的取值范围.。
江苏省淮安市五校联盟2023-2024学年高三上学期10月学情调查测试数学试题(解析版)

2024届高三五校联盟10月学情调查测试数学试题试卷满分:150分 考试时长:120分钟一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合{}{}2780,31,A x x x B x x k k =--<==-∈N ∣∣,则A B = ( )A. {}2,5B. {}1,2,5- C. {}2,5,8 D. {}1,2,5,8-【答案】A 【解析】【分析】根据一元二次不等式化简集合A ,即可由交集运算求解.【详解】由{}2780A xx x =--<∣可得{}18,A x x =-<<∣又{}{}31,1,2,5,8,B x x k k ==-∈=-N ∣,所以A B = {}2,5,故选:A2. 已知复数z 满足()2i 2i z +=-,则z =( )A.54i 3+ B.C.34i 5+ D.34i 5-【答案】D 【解析】【分析】根据复数除法的运算法则进行求解即可.【详解】由()()()()22i 2i44i 1342i 2i i 2i 2i 2i 555z z ----+=-⇒====-++-,故选:D3. 已知m ∈R ,命题2:,420p x x x m ∀∈-+≥R ,命题:3q m ≥,则p 是q 的( )A. 充分不必要条件 B. 必要不充分条件C. 充要条件 D. 既不充分也不必要条件【答案】B 【解析】【分析】根据一元二次不等式恒成立,利用判别式即可求解2m ≥,利用集合间的关系即可求解.【详解】2:,420p x x x m ∀∈-+≥R 为真命题,则1680m ∆=-≤,故2m ≥,由于{}3m m ≥ {}2m m ≥,所以p 是q 的必要不充分条件,故选:B4. 数学家杨辉在其专著《详解九章算术法》和《算法通变本末》中,提出了一些新的高阶等差数列.其中二阶等差数列是一个常见的高阶等差数列,如数列2,4,7,11,16从第二项起,每一项与前一项的差组成的新数列2,3,4,5是等差数列,则称数列2,4,7,11,16为二阶等差数列.现有二阶等差数列{}n a ,其前六项分别为1,3,6,10,15,21,则11n a n ++的最小值为( )A.12B. 34C. 1D.32【答案】C 【解析】【分析】先得出递推公式,叠加法求通项公式,再用基本不等式求最小值即可.【详解】数列{}n a 前六项分别为1,3,6,10,15,21,依题知21324312,3,4,,n n a a a a a a a a n --=-=-=-= ,叠加可得:()()()1122322n n n a a n n -+-=+++=≥ ,得()222n n na n +=≥,当1n =时,211112a +==,满足22n n na +=,所以22n n na +=,所以1111111212122n a n n n n n ++=+=+-≥-+++,当且仅当1121n n +=+时,即1n =时,等号成立,又n ∈*N ,所以等号取不了,所以最小值在1n =取得,当1n =时,111n a n +=+,所以最小值为1.故选:C5. 已知α为锐角,πcos 3α⎛⎫+= ⎪⎝⎭,则πcos 23α⎛⎫-= ⎪⎝⎭( )A. 35-B.35C. 45-D.45【答案】D 【解析】【分析】根据二倍角公式以及诱导公式即可求解.【详解】由于πcos 3α⎛⎫+= ⎪⎝⎭,所以22ππ4cos 22cos 1335αα⎛⎫⎛⎫+=+-=- ⎪ ⎪⎝⎭⎝⎭,πcos 23α⎛⎫-= ⎪⎝⎭2π2π4cos 2πcos 2335αα⎛⎫⎛⎫+-=-+= ⎪ ⎪⎝⎭⎝⎭,故选:D6. 已知函数()()ln 1f x x =-,则使不等式()()12f x f x +<成立的x 的取值范围是( )A. ()(),11,-∞-⋃+∞ B. ()2,1--C. ()(),21,-∞-+∞ D. ()()1,1,3-∞-⋃+∞【答案】C 【解析】【分析】根据函数的奇偶性以及单调性即可列不等式求解.【详解】由于()()ln 1f x x =-的定义域为()(),11,-∞-⋃+∞,关于原点对称,且()()()()ln 1ln 1,f x x x f x -=--=-=故()f x 为偶函数,而当()1,ln(1)x f x x >=-为单调递增函数,故当1x <-,()f x 单调递减,由()()12f x f x +<可得112x x <+<,平方得()22114x x <+<,解得<2x -或1x >,故x 的取值范围是()(),21,-∞-+∞ ,故选:C7. 已知等差数列{}n a 和等差数列{}n b 的前n 项和分别为n S 和n T ,且5633n n S n T n +=+,则使得n na b 为整数的正整数n 的个数为( )A. 6 B. 7C. 8D. 9【答案】B 【解析】【分析】根据等差数列前n 项和公式以及等差数列的性质可得()2121n n S n a -=-,进而可求解.【详解】由于()()()()12121212212122n n n na a n a n S n a --+--===-所以()21215216352924521311n n n n n S a b n T n n n ---++===-+=+++,要使nna b 为整数,则1n +为24的因数,由于12n +≥,故1n +可以为2,3,4,6,8,12,24,故满足条件的正整数n 的个数为7个,故选:B 8. 已知6644log log log log 49,96xxyyx y =-=+,则xy的值为( )A.B.C.1+D.1-【答案】B 【解析】【分析】根据对数和指数的互化关系可得,m n 均满足方程233122kk ⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭,进而根据一元二次方程210t t +-=的解,即可结合32xy ⎛⎫= ⎪⎝⎭的单调性求解.【详解】令64log ,log x m y n ==,则6,4m n x y ==,由6644log log log log 49,96xx y y x y =-=+可得649,496m m m n n n =-=+,进而可得2331,22mm⎛⎫⎛⎫=- ⎪ ⎪⎝⎭⎝⎭故233122mm⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭,同理可得233122nn ⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭,令210t t t +-=⇒=t =,故330,022m n⎛⎫⎛⎫>> ⎪ ⎪⎝⎭⎝⎭,均为方程210t t +-=的实数根,故32m⎛⎫= ⎪⎝⎭,32n⎛⎫= ⎪⎝⎭由于函数32xy ⎛⎫= ⎪⎝⎭为单调递增函数,所以m n =,6342mm n x y ⎛⎫===⎪⎝⎭,故选:B二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9. 已知{}n a 为等比数列,n S 是其前n 项和.若375416,a a a a =与52a 的等差中项为20,则( )A. 11a = B. 公比2q =-C. 12n n a -= D. 21n n S =-【答案】ACD 【解析】【分析】根据等比数列基本量的计算即可求解公比和首项,进而由求和公式以及通项公式即可求解.【详解】由37516a a a =得52551616a a a ⇒==,又4a 与52a 的等差中项为20,则4454082a a a +=⇒=,所以公比为542a q a ==,故31411a q a a =⇒=,故1122,2112nn n n n a S --===--,故ACD 正确,B 错误,故选:ACD10. 已知正数,a b 满足21a b +=,则( )A. ab 的最大值为14B.12a b+的最小值为9C. 224a b +的最小值为14D. 24a b +的最小值为【答案】BD【解析】【分析】运用基本不等式逐一判断即可.【详解】A :因为,a b 是正数,所以1128a b ab =+≥⇒≤,当且仅当2a b =时取等号,即当11,24a b ==时,ab 有最大值为18,因此本选项不正确;B :因为,a b 是正数,21a b +=,所以()12222559b a a b a b a b ⎛⎫++=++≥+= ⎪⎝⎭,当且仅当22b a a b =时取等号,即当13a b ==取等号,故本选项正确;C :因为,a b 是正数,21a b +=,所以2221422a b a b +≤⇒+≥,当且仅当2a b =时取等号,即当11,24a b ==时, 224a b +有最小值12,因此本选项不正确;D :因为,a b 是正数,21a b +=,所以24a b +≥=,当且仅当2a b =时取等号,即当11,24a b ==时,24a b +的最小值为因此本选项正确,故选:BD11. 已知函数()323f x x x =-,则( )A. ()f x 的图象关于原点中心对称B. ()f x 在区间[]2,1-上的最小值为C. 过点()2,10有且仅有1条直线与曲线()y f x =相切D. 若过点()1,P t 存在3条直线与曲线()y f x =相切,则实数t 的取值范围是()3,1--【答案】AD 【解析】【分析】根据奇函数的定义即可判断A ,求导得函数的单调性,即可求解函数的最值,进而判断B ,求解切点处的切线方程,将经过的点代入,利用方程的根即可判断DC.【详解】()323f x x x =-的定义域为R ,且()()()()332323f x x x x x f x -=---=-+=-,所以()f x 为奇函数,故图象关于原点对称,故A 正确,()2636f x x x x ⎛'=-= ⎝,令()0f x ¢>得x >或x <,故()f x 在,,⎛⎫-∞+∞ ⎪ ⎪⎝⎭单调递增,在⎛ ⎝单调递减,故()f x 在区间2,⎡-⎢⎣单调递增,在⎛ ⎝单调递减,在⎫⎪⎪⎭单调递增,又()210f f =-=-,最小值为10-,故B 错误,设切点为()00,x y ,则切点处切线方程为()()2300006323y x x x xx =--+-,若切线经过()2,10,则将()2,10代入可得()()2320000340210x x x x -+=⇒--=,所以01x =或02x =,故经过()2,10会有两条切线,C 错误,若切线经过()1,P t ,则将()1,P t 代入()()2300006323y x x x xx =--+-得3200463x x t -+-=,令()()322463,()12121g x x x g x x x x x '=-+-=-+=--,则当01,()0,x g x '<<>因此()g x 在()0,1单调递增,在(),0∞-和()1,+∞单调递减,作出()g x 的图象如下:()()()()1103g x g g x g ==-==-极大值极小值,,要使过点()1,P t 存在3条直线与曲线()y f x =相切,则直线过点y t =与()g x 的图象有三个不同的交点,故3<1m -<-,D 正确,故选:AD12. 已知函数()()sin (0)f x x ωϕω=+>,则( )A. 12,x x 是方程()1f x =的两个不等实根,且12x x -最小值为π,则2ω=B. 若()π,6f x ϕ=在[]0,2π上有且仅有4个零点,则2329,1212ω⎡⎫∈⎪⎢⎣⎭C. 若()π,6f x ϕ=在ππ,64⎡⎤-⎢⎥⎣⎦上单调递增,则()f x 在()0,2π上的零点最多有3个D. 若()1,f x ω=的图象与直线(01)y m m =<<连续的三个公共点从左到右依次为,,M N P ,若3PN MN =,则m =【答案】ABD 【解析】【分析】根据正弦函数性质和周期公式可判断A ;函数()f x 由小到大的第4个零点在区间[]0,2π内,第5个零点大于2π求解可判断B ;根据单调性和第3个零点在区间()0,2π内分别求出ω范围即可判断C ;数形结合可得π2MN =,然后可得π2π,4M x k k ϕ+=+∈Z ,即可求出m ,可判断D .【详解】A 选项:由题可知πT =,所以2π2π2πT ω===,A 正确;B 选项:若π6ϕ=,令()πsin 06f x x ω⎛⎫=+= ⎪⎝⎭得ππ6x k ω+=,即ππ,6k x k ωω=-+∈Z ,所以,函数()f x 由小到大的第4个零点为π4π6ωω-+,第5个零点为π5π6ωω-+,由题知,π4π2π6π5π2π6ωωωω⎧-+≤⎪⎪⎨⎪-+>⎪⎩,解得23291212ω≤<,B 正确;C 选项:由πππ262x ω-≤+≤得2ππ33x ωω-≤≤,因为()f x 在ππ,64⎡⎤-⎢⎥⎣⎦上单调递增,所以2ππ36ππ34ωω⎧-≤-⎪⎪⎨⎪≥⎪⎩,解得403ω<≤,若()f x 在()0,2π上有3个零点,则π3π2π6ωω-+<,解得1712ω>,因174123>,所以C 错误;D 选项:由图可知,2πMP =,又3PN MN =,所以π2MN =,即π2N M x x -=,因为π2π,22MN x x k k ϕ++=+∈Z ,所以π2π,4M x k k ϕ+=+∈Z ,所以()πsin sin 2π4M m x k ϕ⎛⎫=+=+=⎪⎝⎭D 正确.故选:ABD .三、填空题:本题共4小题,每小题5分,共20分.13. 数列{}n a 满足1111,2n na a a +=-=,则2024a =__________.【答案】12##0.5【解析】【分析】根据递推式得到数列的周期,应用周期性求对应项.【详解】由题设312411,2, (2)2,,a a a a =-===,所以{}n a 是周期为3的数列,则202436742212a a a ⨯+===.故答案为:1214. 已知函数()22ln f x x x =-,若()f x 在区间()2,1m m +上单调递增,则实数m 的取值范围是__________.为【答案】1[,1)4【解析】【分析】由导数求解函数的单调递增区间,即可列不等式求解.【详解】由()22ln f x x x =-得()21414x f x x x x-'=-=,由于函数()f x 的定义域为()0,∞+,故令()0f x '≥,解得12x ≥,故()f x 的单调递增区间为1,2⎡⎫+∞⎪⎢⎣⎭,若()f x 在区间()2,1m m +上单调递增,则12212m m m ⎧≥⎪⎨⎪+>⎩,解得114m ≤<,故答案:1[,1)415. 在ABC 中,角,,A B C 的对边分别为,,,a b c D 为BC 边中点,若222,24AD b c =+=,则ABC 面积S 的最大值为__________.【答案】【解析】【分析】根据向量模长公式即可2cos 8bc A =-,结合基本不等式即可求解12bc ≤,进而根据三角函数的单调性,结合面积公式即可求解.【详解】由于D 为BC 边中点,所以()12AD AB AC =+,平方2222242162cos AD AB AC AB AC c b bc A =++⋅⇒=++,因此2cos 8bc A =-,由于22242b c bc +=≥,所以12bc ≤,当且仅当b c ==时等号成立,故41cos 3A bc -=≤-,由于cos y x =在()0,π单调递减,故当1cos 3A =-时,A 最小,且为钝角,114sin sin 2tan 22cos ABC S bc A A A A-===- ,由于tan y x =在π,π2⎛⎫⎪⎝⎭单调递增,故当tan A 取最小值时,此时面积最大,故当1cos 3A =-时,此时A最小,进而tan A 最小,故面积最大,为由1cos 3A =-可得sin tan A A ==-,故面积的最大值为,故答案为:16. 已知函数()212ln 8f x a x a x ⎛⎫=-- ⎪⎝⎭,若()0f x ≥恒成立,则满足条件的所有整数a 的取值集合为__________.(参考数据:ln20.6931,ln5 1.6094≈≈)【答案】{1,2,3,4}【解析】【分析】对函数求导,讨论0a ≤、0a >研究单调性,转化为极小值0f ≥恒成立,构造中间函数2()1ln 8a a a ϕ=+-研究使()0a ϕ≥对应a 的区间,即得答案.【详解】由题意()222(1)2ax f x ax x x-'=-=且,()0x ∈+∞,当0a ≤时()0f x '<,即()f x 在,()0x ∈+∞上递减,又()1(108af a =-≤,所以,定义域内存在()0f x <,不符合题意;当0a >时,0x <<时()0f x '<,()f x 递减;x >()0f x ¢>,()f x 递增;所以()21ln 8a f x f a ≥=+-,要使()0f x ≥恒成立,只需21ln 08a a +-≥,令2()1ln 8a a a ϕ=+-且0a >,则214()44a a a a aϕ-'=-=,所以,02a <<时()0a ϕ'>,()a ϕ递增;2a >时()0a ϕ'<,()a ϕ递减;由211717(0(1),(4)2ln 210(5)ln 5e8e 88ϕϕϕϕ=-<<==->>=-,所以()a ϕ在1(,1),(4,5)e各有一个零点,且a 取两个零点之间的值(含零点)时()0a ϕ≥,故整数{1,2,3,4}a ∈时()0f x ≥恒成立.故答案为:{1,2,3,4}【点睛】关键点点睛:利用导数研究()f x 单调性,特殊值判断0a ≤是否能使()0f x ≥恒成立,对于0a >求()f x 的极小值,构造中间函数研究极小值恒大于等于0的情况.四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17. 已知函数()sin (0)f x x x t ωωω=++>,且()f x 的最大值为3,最小正周期为π.(1)求()f x 的解析式;(2)求()f x 在ππ,36-⎡⎤⎢⎥⎣⎦上的值域,并指出()f x 取得最大值时自变量x 的值.【答案】(1)π()2sin(213f x x =++ (2)值域为[1,()f x 取最大值时自变量x 值为π12【解析】【分析】(1)由辅助角公式化简()f x ,即可由周期公式求解2ω=,根据最值可得1t =,(2)由[]x ∈π6得ππ2π2[,]333x +∈-,即可结合三角函数的性质求解.【小问1详解】1()sin 2(sin cos 2sin(23f x x x t x x t x t ωωωωωπ=++=⋅++=++,所以()f x 的最小正周期2ππT ω==,则2ω=;且()f x 的最大值23t +=,则1t =.所以π()2sin(213f x x =++.【小问2详解】因为[]x ∈-ππ,36,所以ππ2π2[,]333x +∈-,则πsin(2)[3x +∈,则2sin(2)1[13x π++∈,所以()f x 的值域为[1.当()f x 取得最大值时,ππ2=32x +,所以自变量x 的值为π12.18. 已知n S 是等差数列{}n a 的前n 项和,且7943,3a S a =-=.(1)求数列{}n a 通项公式与前n 项和n S ;(2)若n n b a =,求数列{}n b 的前n 项和n T .的的【答案】(1)211210n n a n S n n =-=-,(2)2210,51050,6n n n n T n n n ⎧-≤=⎨-+≥⎩【解析】【分析】(1)根据等差数列基本量的计算可得公差和首项,进而根据公式即可求解,(2)根据当5n ≤时,0n a >,n n n b a a ==;当6n ≥时,0n a <,n n n b a a ==-,即可分类求解,结合等差数列求和公式即可.【小问1详解】设等差数列{}n a 的公差为d ,则111639363(3)a d a d a d +=-⎧⎨+=+⎩,解得192a d =⎧⎨=-⎩.所以数列{}n a 的通项公式为9(1)(2)112n a n n =+-⋅-=-,数列{}n a 的前n 项和29112102n nS n n n +-=⋅=-.【小问2详解】由1120n a n =->得112n <,所以当5n ≤时,0n a >,n n n b a a ==;由1120n a n =-<得112n >,所以当6n ≥时,0n a <,n n n b a a ==-.所以,当5n ≤时,210n n T S n n ==-;当6n ≥时,1212567()n n n T b b b a a a a a a =++⋅⋅⋅+=++⋅⋅⋅+-++⋅⋅⋅+1251252()()2n na a a a a a S S =++⋅⋅⋅+-++⋅⋅⋅+=-2222(1055)(10)1050n n n n =⨯---=-+.所以,2210,51050,6n n n n T n n n ⎧-≤=⎨-+≥⎩.19. 已知函数()()221ln ,f x x a x a x a =-++∈R .(1)若()f x 在1x =处取得极值,求()f x 的极值;(2)若()f x 在[]1,e 上的最小值为2a -,求a 的取值范围.【答案】(1)极大值为5ln 24--,极小值为2- (2)(,1]-∞【解析】【分析】(1)根据极值点可得()10f '=,进而可得1a =,利用导数即可求解函数的单调区间,进而可求解极值,(2)根据导数确定函数单调性,结合分类讨论即可求解.【小问1详解】2()(21)ln f x x a x a x =-++,()2(21)af x x a x'=-++,0x >.因为()f x 在1x =处取得极值,所以(1)2(21)0f a a '=-++=,则1a =.所以2()3ln =-+f x x x x ,21231(21)(1)()23-+--'=-+==x x x x f x x x x x,令()0f x '=得12x =或1,列表得所以()f x 的极大值为11315(ln ln 224224f =-+=--,极小值为(1)13ln12f =-+=-.【小问2详解】22(21)(21)()()2(21)a x a x a x x a f x x a x x x-++--=-++=='.①当1a ≤时,()[1,e],0x f x '∈>,所以()f x 在[1,e]上单调递增,()f x 的最小值为(1)2f a =-,满足题意;②当1e a <<时,令()0f x ¢>,则x a >或102x <<,所以()f x [1,]a 上单调递减,在[,e]a 上单调递增,此时,()f x 的最小值为()(1)2f a f a <=-,不满足题意;③当e a ≥时,()f x 在[1,e]上单调递减,()f x 的最小值为(e)(1)2f f a <=-,不满足题意.综上可知,实数a 的取值范围时(,1]-∞.20. 已知数列{}n a 的前n 项和为n S ,且1342n n S n a -=-.在(1)求数列{}n a 的通项公式;(2)若1n n b a =,求证:数列{}n b 的前n 项和32n T <.【答案】(1)131n n a -=+(2)证明见解析【解析】【分析】(1)根据,n n S a 的关系可得132n n a a -=-,进而可得{1}n a -为等比数列,即可求解,(2)利用放缩法,结合等比数列求和公式即可求证.【小问1详解】因为1342n n S n a -=-,所以322n n S a n =+-①当1n =时,1113122a S a ==+-,所以12a =;当2n ≥时,113(1)22n n S a n --=+--②①-②得133122n n n a a a -=-+,即132n n a a -=-,则113(1)n n a a --=-,所以数列{1}n a -构成以111a -=为首项,3为公比的等比数列,则113n n a --=,所以131n n a -=+.【小问2详解】因为131n n a -=+,所以11131n n n b a -==+,所以1221111111313131n n n T b b b -=++⋅⋅⋅+=+++⋅⋅⋅+++++2111()111133133(11333223213nn n --<+++⋅⋅⋅+==-⋅<-.21. ABC 中,角,,A B C 的对边为()223,,,sin sin sin sin sin 222B A a b c a b c A B b A ⎛⎫+++= ⎪⎝⎭.(1)求角C 的大小;(2)若3,c ABC =内切圆的半径r =ABC 的面积.【答案】(1)π3C =(2)【解析】【分析】(1)利用正弦定理的角边化及降幂公式,结合余弦定理的推论及三角函数的特殊值对应的特殊角即可求解;(2)根据(1)的结论及三角形的面积公式即可求解.【小问1详解】由正弦定理得223()(sinsin 222B A a b c a b ab +++=,因为221cos 1cos 1sinsin (cos cos )222222B A B A a b a b a b a B b A --++=⋅+⋅=-+2222221(22222a b a c b b c a a b ca b ac bc ++-+-+-=-⋅+⋅=,所以3()22a b c a b c ab +-++⋅=,则22()3a b c ab +-=,即222a b c ab +-=,由余弦定理得2221cos 22a b c C ab +-==,又0πC <<,所以π3C =.【小问2详解】由(1)知22()3a b c ab +-=,因为3c =,所以2()93a b ab +-=(*).又ABC 的面积11sin ()22S ab C a b c r ==++⋅,即11sin (3)232ab a b π⋅=++,则2(3)ab a b =++,代入(*)式得2()96(3)a b a b +-=++,即(3)(3)6(3)a b a b a b +++-=++,所以36a b +-=,则9a b +=,所以ABC 的面积11()1222S a b c r =++⋅=⨯=.22. 已知函数()()cos 1,x f x g x ax x x==-.(1)若函数()f x 在点π,02A ⎛⎫⎪⎝⎭处的切线与函数()g x 的图象有公共点,求实数a 的取值范围;(2)若函数()f x 和函数()g x 的图象没有公共点,求实数a 的取值范围.【答案】(1)214a -π≥(2)1(,0)[,)2-∞⋃+∞【解析】【分析】(1)求导,即可根据点斜式求解切线方程,联立方程转化为一元二次方程,利用判别式即可求解,(2)将问题转化为2()cos 10h x x ax =+-=没有实数根,求导,利用导数确定函数的单调性,分类讨论,进而结合零点存在性定理即可求解.【小问1详解】因为cos ()x f x x=,所以2sin cos ()x x xf x x --'=,则()f x 在点π,02A ⎛⎫⎪⎝⎭处的切线斜率为2()2f π'=-π,所以切线方程为2()2y x π=--π,即21πy x =-+.由21π1y x y axx ⎧=-+⎪⎪⎨⎪=-⎪⎩得211x ax x -+=-π,即22(10a x x -+-=π.因为函数定义域为{|0}x x ≠,所以方程22()10a x x -+-=π有非零实数根,当2πa =时,1x =,符合题意,当2πa ≠时,则214()0a ∆=+-π≥,即214a -π≥,且2πa ≠,所以实数a 的取值范围是21π4a ≥-.【小问2详解】因为函数()f x 和函数()g x 的图象没有公共点,所以()()f x g x =,即cos 1x ax x x=-无实根,所以当0x ≠时,2()cos 10h x x ax =+-=无实根,因为()()h x h x -=,即()h x 是偶函数,所以2()cos 10h x x ax =+-=在(0,)+∞上无实根.()2sin h x ax x '=-,记()()2sin m x h x ax x '==-则()2cos m x a x '=-,,()0x ∈+∞.①当0a <时,20ax <,又1cos 1x -≤≤,则cos 10x -≤,所以2()cos 10h x x ax =+-<,满足()0h x =在(0,)+∞上无实根.②当0a =时,()cos 10h x x =-=在(0,)+∞上有实根,不合题意,舍去.③当12a ≥时,()2cos 0m x a x '=-≥,所以()2sin h x ax x '=-在(0,)+∞单调递增,则()(0)0h x h ''>=,所以2()cos 10h x x ax =+-=在(0,)+∞上单调递增,所以()(0)0h x h >=,满足()0h x =在(0,)+∞上无实根.④当102a <<时,因为()2cos m x a x '=-在π(0,)2单调递增,且(0)210m a '=-<,(202m a π'=>,则存在唯一的0π(0,)2x ∈,使00()2cos 0m x a x '=-=,列表得所以当0(0,)x x ∈时,()(0)0h x h ''<=,则()h x 在0(0,)x 单调递减,则()(0)0h x h <=,又因为2(2)40h a π=π>,且()h x 在(0,)+∞上连续,所以2()cos 10h x x ax =+-=在(0,2π)上有实根,不合题意.综上可知,实数a 的取值范围是1(,0)[,)2-∞⋃+∞.【点睛】方法点睛:1. 导函数中常用的两种常用的转化方法:一是利用导数研究含参函数的单调性,常化为不等式恒成立问题.注意分类讨论与数形结合思想的应用;二是函数的零点、不等式证明常转化为函数的单调性、极(最)值问题处理.2.利用导数解决含参函数的单调性问题时,一般将其转化为不等式恒成立问题,解题过程中要注意分类讨论和数形结合思想的应用.3.证明不等式,构造一个适当的函数,利用它的单调性进行解题,是一种常用技巧.许多问题,如果运用这种思想去解决,往往能获得简洁明快的思路,有着非凡的功效.。
南京市2025届高三年级零模学情调研(解析卷)

一、选择题(共11题,每题4分)1.【答案】B【解析】结合v-t 图像的知识可知:运动学图像只能描述直线运动,图中质点速度大小呈周期性变化,所以不是匀速直线运动,A 错误;速度的方向未发生变化,所以做单向直线运动,位移一直在增大,B 正确D 错误;斜率正负表示加速度的方向,发生变化,C 错误,综上所述,正确答案为B 2024-2025学年南京高三零模解析卷。
2.【答案】A【解析】油膜法测分子直径实验中,将油酸稀释配置成一定浓度的油酸酒精溶液,为清晰显示轮廓,先在浅盘中均匀撒上一层痱子粉,然后滴入1滴油酸酒精溶液,最后形成单分子油膜,若将油酸分子简化成球形模型,认为它们紧密排列,则该油膜的厚度即为油酸分子的直径,A 正确B 错误;根据溶液的浓度可以求出1滴溶液中纯油酸的体积V,等轮廓稳定后利用数格数的方法,不足半格的舍去,大于半格的当做一格,记下格数,则轮廓的面积等于格数乘以每格的面积,记作S,根据公式d =VS 从而计算出油酸分子的直径,如果描绘轮廓时油酸还未散开就会导致S 偏小从而导致测得的分子直径偏大,CD 错误,综上所述,正确答案为A。
3.【答案】A【解析】根据天体环绕规律可知:高轨低速大周期,A 正确;卫星运行过程中,加速度大小不变方向始终在变化,B 错误;圆轨道上近地卫星的环绕速度最大为第一宇宙速度,其他圆轨道均小于第一宇宙速度,C 错误;根据万有引力公式,地球外部同一物体所受万有引力与距离之间满足平方反比,D 错误;综上所述,正确答案为A。
【答案】D【解析】根据振动图像与波形图的相关知识:=0.5m/s,A错误;a图中�=2m,b图T=4s,波速v=λT由b图可知t=0时刻质点P振动方向沿y轴正方向,在a图中结合同侧法可知,波沿x轴负方向传播,B错误;振幅A=4cm,0-4s内,质点P运动的路程为s=4A=16cm,C错误;b图斜率表示速度,正负表示方向,t=2s时质点P沿y轴负方向运动,D正确;综上所述,正确答案为D。
2024-2025学年第一学期高三化学第一次学情检测答案

(第1页 共计8页) 2024-2025学年第一学期高三第一次学情检测化学答案单项选择题(本题包括13小题,每题3分,共39分。
每小题只有一个....选项符合题意) 1.B 2.A 3.D 4.B 5.D 6.C 7.C 8.A 9.B 10.A11. C 12.D 13. B非选择题(包括4小题,共61分)14.(12分)(每空2分)(1)MgCO 3+H 2SO 4===MgSO 4+H 2O +CO 2↑ 使MgCO 3完全转化为MgSO 4(2)Fe(OH)3 Mn 2++ClO -+H 2O===MnO 2↓+2H ++Cl -(3)温度过低,反应速率慢;温度过高,碳酸铵分解(或轻质碳酸镁分解)2MgSO 4+2(NH 4)2CO 3+3H 2O===MgCO 3·Mg(OH)2·2H 2O ↓+2(NH 4)2SO 4+CO 2↑ 15.(19分)(最后一空5分)(1)点燃 Fe 3+水解生成的Fe(OH)3胶体具有吸附性,能吸附水中的悬浮杂质 (2)d(3)Cl 2+2OH -===Cl -+ClO -+H 2O(4)2FeCl 3+3NaClO +10NaOH===2Na 2FeO 4+9NaCl +5H 2O 3∶2(5)碱性溶液中,上述反应向逆反应方向进行,可减少洗涤时K 2FeO 4的损失(6)63.1%16.(16分)(每空2分)(1)高温下KOH 能与玻璃中的SiO 2发生反应(2)3MnO 2+6KOH +KClO 3=====高温3K 2MnO 4+KCl +3H 2O(3)①3MnO 2-4+2CO 2===2MnO -4+MnO 2↓+2CO 2-3②二氧化碳过量会生成溶解度比K 2CO 3小得多的KHCO 3,可能与KMnO 4同时析出 ③滤纸上有紫红色④加热浓缩 趁热过滤(4)MnO 217.(14分)(每空2分)(1) 7N A 或7×6.02×1023平面正三角形 SO 3(或BF 3) (2)1∶1 Cu 失去一个电子时,核外电子排布从[Ar]3d 104s 1变为[Ar]3d 10能量较低的稳定结构较容易;Zn 失去一个电子时,核外电子排布从[Ar]3d 104s 2变为[Ar]3d 104s 1较难(3)sp 2、sp 3 bcd。
江苏省南京市2025届高三六校联合体学情调研测试语文试题[含答案]
![江苏省南京市2025届高三六校联合体学情调研测试语文试题[含答案]](https://img.taocdn.com/s3/m/9d2b60b2846a561252d380eb6294dd88d0d23d39.png)
江苏省南京市2025届高三六校联合体学情调研测试语文试题一、现代文阅读(35分)(一)现代文阅读I(本题共5小题,19分)阅读下面的文字,完成1~5题。
材料一:逻辑不仅是一门独特的科学,还是一门奇异的艺术。
科学在知的方面使理性臻于完善,艺术在行的方面使理性臻于完善。
从这一意义上讲,逻辑的目的就是艺术的目的。
然而,除非逻辑既是一门艺术,同时又是一门科学,否则这一目的是不能达到的。
人类理智的本性就是要成为理性,对于人来说,理智生活是一种发展着的东西,理性并非意味着不会犯错。
人类理性的活动是推演性的,而推演活动又是一种生产性的或构造性的,理性并不保证它在生产或构造或构成中不会出错,相反,它可能会做出错误的定义或划分,推理会出现疵,思想会产生混乱。
自在的理性需要一种逻辑的力量来克服它的这种先天的不确定性,从而使理性的德行臻于完善。
逻辑不仅仅是科学,是艺术,还是一种精神,一种理性精神。
正是这种精神激发、促进、鼓舞和驱使人们将人类的思维得以运用到最完善的程度,并尽其所能地去探求和确立已经确立的知识的最深刻和最完美的内涵。
公理化的逻辑体系表达出人类对臻至完美的理论所应当具有的形态的认识和向往。
其中逻辑公理的选择体现出人们对理论本身的最深思熟虑的判断和洞察力。
逻辑规则和定义体现出人们为追求无可置疑结论而对推论施加的严苛条件。
推理链条的环环相扣反映出人们对思维编织的精细严密的要求。
从公理出发,一些简单的定理立刻就能得到证明,这些定理进而成为那些更深奥的定理的基石。
这样,一座精美的大厦就严密地建立起来了。
可以想象,如果一个理论将其中所有的论证一一抽出,那么这一理论就会因只剩下一堆描述性语句而坍塌,理论的结构性力量和活力由此丧失殆尽。
而一个确定了逻辑有效性的理论则意味着它获得了一种逻辑的品行。
它因逻辑而变得简洁、精美、严格、强大,内部和谐、外部精巧、经久耐用。
逻辑能力是存在于人的大脑中的一种能力,这种能力是在人的成长过程中逐步形成的。
地理丨江苏省盐城五校联盟2025届高三10月第一次学情调研检测考试地理试卷及答案
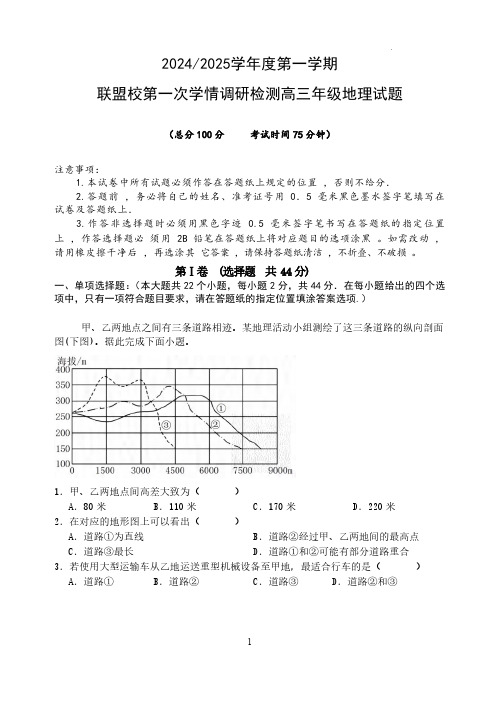
2024/2025学年度第一学期联盟校第一次学情调研检测高三年级地理试题(总分100分考试时间75分钟)注意事项:1.本试卷中所有试题必须作答在答题纸上规定的位置,否则不给分.2.答题前,务必将自己的姓名、准考证号用0.5毫米黑色墨水签字笔填写在试卷及答题纸上.3.作答非选择题时必须用黑色字迹0.5毫米签字笔书写在答题纸的指定位置上,作答选择题必须用2B铅笔在答题纸上将对应题目的选项涂黑。
如需改动,请用橡皮擦干净后,再选涂其它答案,请保持答题纸清洁,不折叠、不破损。
第Ⅰ卷(选择题共44分)一、单项选择题:(本大题共22个小题,每小题2分,共44分.在每小题给出的四个选项中,只有一项符合题目要求,请在答题纸的指定位置填涂答案选项.)甲、乙两地点之间有三条道路相迹。
某地理活动小组测绘了这三条道路的纵向剖面图(下图)。
据此完成下面小题。
1.甲、乙两地点间高差大致为()A.80米B.110米C.170米D.220米2.在对应的地形图上可以看出()A.道路①为直线B.道路②经过甲、乙两地间的最高点C.道路③最长D.道路①和②可能有部分道路重合3.若使用大型运输车从乙地运送重型机械设备至甲地,最适合行车的是()A.道路①B.道路②C.道路③D.道路②和③2024年9月7日是二十四节气中的白露。
下表示意二十四节气排列顺序。
完成下面小题。
立春雨水惊蛰春分清明谷雨立夏小满芒种夏至小暑大暑立秋处暑白露秋分寒露霜降立冬小雪大雪冬玉小木大寒4.白露节气前后各一个月,地球公转速度的变化是()A.越来越快B.越来越慢C.先快后慢D.先慢后快5.与白露节气昼长大致相同的节气是()A.芒种B.惊蛰C.清明D.寒露太阳时是以太阳日为标准来计算的时间,可分为真太阳时(各地日晷时间)与平太阳时(由各地经度计量的地方时)。
由于地球公转速度等因素的影响,真太阳时可能比平太阳时推迟或提前。
图为“真太阳时与平太阳时的时差曲线图”。
完成下面小题。
高三检测学情反馈报告-历史1

生
问
题
反
馈
1.学生知识结构还不够系统完整,知识体系的形成有待进一步提高,某些知识点掌握不透彻,知识的整合及迁移能力有待进一步提升。
2.选择题部分正确率要进一步提高,主观题要强化训练,提升学生的理解、提炼和归纳能力,部分同学的卷面书写质量有待提高。
3.由于历史学科主观题排在文综试卷的最后,导致部分同学最后两道主观题做不完,从试卷分析看,不少同学第41题来不及做或因作答仓促,导致得分低,所以平时要加强主观题训练,答题时要兼顾答题质量与答题效率。尤其强调同学们要重视这学期每次周日的文综考试训练。
地理
试
卷
分
析
学
生
问
题
反
馈
安庆一中2017届高三下学期周六、周日、月考
检测学情分析报告
时间:2017年月日
检测类型:
语
文
试
卷
分
析
学
生
问
题
反
馈
文
数
试
卷
分
析
学
生
问
题
反
馈
理
数
试
卷
分
析
学
生
问
题
反
馈
英语
试
卷
分
析
学
生
问
题
反
馈
物理
试
卷
分
析
学
生
问
题
反
馈
化学
试
卷
分
析
学
生
问
题
反
馈
生
物
试
卷
分
析
学
2024届南京高三上学期9月学情调研数学试题及答案

南京市2024届高三年级学情调研数 学 2023.09(第13题~第16题)、解答题(第17题~第22题)四部分.本试卷满分为150分,考试时间为120分钟.2.答卷前,考生务必将自己的学校、姓名、考生号填涂在答题卡上指定的位置.3.作答选择题时,选出每小题的答案后,用2B 注意事项:1.本试卷包括单项选择题(第1题~第8题)、多项选择题(第9题~第12题)、填空题铅笔在答题卡上将对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案.答案不能答在试卷上.4.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内,在其他位置作答一律无效.一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的,请把答案填涂在答题卡相应位置上. 1.已知集合A ={x |x 2-4x +3≤0},B ={x |2<x <4},则A ∩B =A .{x |3≤x <4}B .{x |1≤x ≤3}C .{x |2<x ≤3}D .{x |1≤x <4}2.若z =3-i1+i,则z 的虚部为 A .2B .-2C .2iD .-2i3.(x -2x)4的展开式中常数项为A .-24B .-4C .4D .244.在△ABC 中,点D 为边AB 的中点.记CA →=m ,CD →=n ,则CB →=A .2m +nB .m 2C .2m -nD .-m +2n 5.设O 为坐标原点,A 为圆C :x 2+y 2-4x +2=0上一个动点,则∠AOC 的最大值为A .π12B .π6C . π4D .π36.在正方体ABCD -A 1B 1C 1D 1中,过点B 的平面α与直线A 1C 垂直,则α截该正方体所得截面的形状为 A .三角形B .四边形C .五边形D .六边形7.新风机的工作原理是,从室外吸入空气,净化后输入室内,同时将等体积的室内空气排向室外.假设某房间的体积为v 0,初始时刻室内空气中含有颗粒物的质量为m .已知某款新风机工作时,单位时间内从室外吸入的空气体积为v (v >1),室内空气中颗粒物的浓度与时刻t 的函数关系为ρ(t )=(1-λ)m v 0+λm v 0e -vt ,其中常数λ为过滤效率.若该款新风机的过滤效率为45,且t =1时室内空气中颗粒物的浓度是t =2时的32倍,则v 的值约为(参考数据:ln2≈0.6931,ln3≈1.0986) A .1.3862B .1.7917C .2.1972D .3.58348.若函数f (x )=sin(ωcos x )-1(ω>0)在区间(0,2π)恰有2个零点,则ω的取值范围是A .(0,π2)B .(π2,3π2)C .(π2,5π2)D .(π2,+∞)二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分. 9.若a <0<b ,且a +b >0,则A .ab>-1B .|a |<|b |C .1a +1bD .(a -1)(b -1)<110.有一组样本数据x 1,x 2,x 3,x 4,x 5,已知∑5i =1x i =10,∑5i =1x i 2=30,则该组数据的A .平均数为2B .中位数为2C .方差为2D .标准差为211.在△ABC 中,∠ACB =90º,AC =BC =22,D 是AB 的中点.将△ACD 沿CD 翻折,得到三棱锥A'-BCD ,则 A .CD ⊥A'BB .当A'D ⊥BD 时,三棱锥A'-BCD 的体积为83C .当A'B =23时,二面角A'-CD -B 的大小为2π3D .当∠A'DB =2π3时,三棱锥A'-BCD 的外接球的表面积为20π12.函数f (x )及其导函数f '(x )的定义域均为R ,且f (x )-f (-x )=2x ,f '(1+x )+f '(1-x )=0,则A .y =f (x )+x 为偶函数B .f (x )的图象关于直线x =1对称C .f '(0)=1D .f '(x +2)=f '(x )+2三、填空题:本题共4小题,每小题5分,共20分.13.已知角α的顶点为坐标原点,始边与x 轴的非负半轴重合,终边经过点 P (3,4),则sin(π+α)=▲________. 14.某批麦种中,一等麦种占90%,二等麦种占10%,一、二等麦种种植后所结麦穗含有50粒以上麦粒的概率分别为0.6,0.2,则这批麦种种植后所结麦穗含有50粒以上麦粒的概率为▲________.15.记S n 为数列{a n }的前n 项和,已知a n = 2n (n +2),n 为奇数,a n -1, n 为偶数,则S 8=▲________. 16.已知双曲线C :x 2a 2-y 2b2=1(a >0,b >0)的左、右焦点分别为F 1,F 2,P 是C 右支上一点,线段PF 1与C 的左支交于点M .若∠F 1PF 2=π3,且|PM |=|PF 2|,则C 的离心率为▲________. 四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤. 17.(10分)已知公比大于1的等比数列{a n }满足:a 1+a 4=18,a 2a 3=32. (1)求{a n }的通项公式;(2)记数列{b n }的前n 项和为S n ,若S n =2b n -a n ,n ∈N *,证明:b n a n 是等差数列.(2)若a =3,sin B sin C =14,求△ABC 的面积.19.(12分)某地区对某次考试成绩进行分析,随机抽取100名学生的A ,B 两门学科成绩作为样本.将他们的A 学科成绩整理得到如下频率分布直方图,且规定成绩达到70分为良好.已知他们中B 学科良好的有50人,两门学科均良好的有40人.(1)根据所给数据,完成下面的2×2列联表,并根据列联表,判断是否有95%的把握认为这次考试学生的A 学科良好与B 学科良好有关;(23人中A ,B 学科均良好的人数为随机变量X ,求X 的分布列与数学期望.附:K2=n (ad -bc )2(a +b )(c +d )(a +c )(b +d ),其中n =a +b +c +d .P (K 2≥k 0)0.150.100.050.025 0.010 0.0050.001k 02.072 2.7063.841 5.024 6.635 7.879 10.828O0.005 (第19题图)点G 是线段BF 的中点. (1)证明:EG ∥平面DAF ;(2)求直线EF 与平面DAF 所成角的正弦值.21.(12分)已知O 为坐标原点,F (1,0)是椭圆C :x 2a 2+y 2b 2=1(a >b >0)的右焦点,过F 且不与坐标轴垂直的直线l 交椭圆C 于A ,B 两点.当A 为短轴顶点时,△OAF 的周长为3+3. (1)求C 的方程;(2)若线段AB 的垂直平分线分别交x 轴、y 轴于点P ,Q ,M 为线段AB 的中点,求|PM |·|PQ |的取值范围.22.(12分)已知函数f (x )=a e x -x -a ,其中a >0. (1)若a =1,证明:f (x )≥0;(2)设函数g (x )=xf (x ),若x =0为g (x)的极大值点,求a 的取值范围.EO FG (第20题图)数学参考答案2023.09一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的,请把答案填涂在答题卡相应位置上.1.C 2.B 3.D 4.D 5.C 6.A 7.B 8.B二、选择题:本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求,请把答案填涂在答题卡相应位置上.全部选对得5分,部分选对得2分,不选或有错选的得0分. 9.ABD 10.AC 11.ACD 12.BC三、填空题:本大题共4小题,每小题5分,共20分.请把答案填写在答题卡相应位置上. 13.-4514.0.56 15.169 16.7四、解答题:本大题共6小题,共70分.请在答题卡指定区域内作答,解答时应写出必要的文字说明,证明过程或演算步骤. 17.(10分) 解:(1)方法1:因为{a n }是等比数列,所以a 2a 3=a 1a 4=32,又a 1+a 4=18,所以 a 1=2,a 4=16或 a 1=16,a 4=2. ···················································· 2分又q >1,所以a 1=2,a 4=16,所以q 3=8,q =2. ················································ 4分 因此a n =a 1q n -1=2n .分方法2:由基本量得出 a 1=2,q =2或a 1=16,q =12. ························································ 2分又q >1,所以a 1=2,q =2.··········································································· 4分 因此a n =a 1q n -1=2n . ··············································································· 5分 (2)由(1)得S n =2b n -2n ,所以S n +1=2b n +1-2n +1,两式作差可得b n +1-2b n =2n ,n ∈N *. ·························································· 7分 所以b n +12n +1-b n 2n =12,即b n +1a n +1-b n a n =12(n ∈N *). ··················································· 9分 所以数列 b n a n 是公差为12的等差数列. ························································· 10分因为A ∈(0,π),所以A =2π3.···································································· 6分(2)解法1:由正弦定理a sin A =b sin B =c sin C ,所以b sin B =c sin C =332=23,因此b =23sin B ,c =23sin C . ································································· 9分 所以bc =(23)2×sin B sin C =3.································································ 10分 所以,△ABC 的面积为S =12bc sin A =12×3×23=334. ································· 12分解法2:因为sin B sin C =14,B =π-A -C =π3-C ,所以sin(π3-C )sin C =14.化简得cos(2C -π3)=1,因为C ∈(0,π3),所以2C -π3∈(-π3,π3),故C =π6. ········ 9分因此B =π3-C =π6,进而可解得b =c =3. ················································· 10分所以△ABC 的面积为S =12×3×3×sin 2π3=334. ····································· 12分19.(12分)解:(1)由直方图可得A 学科良好的人数为100×(0.040+0.025+0.005)×10=70,所以2×2列联表如下:B 学科良好 B 学科不够良好 合计A 学科良好 40 30 70 A 学科不够良好10 20 30 合计5050100············································································································ 2分 假设H 0:A 学科良好与B 学科良好无关, ····················································· 3分 K2=n (ad -bc )2(a +b )(c +d )(a +c )(b +d )=100×(30×10-40×20)270×30×50×50=10021≈4.8>3.841, ········ 5分所以有95%把握认为A B 学科良好有关. ······································ 6分(2)AB 学科均良好的概率P =40100=25,X 的可能取值为0,1,2,3,且X ~B (3,25).所以P (X =0)=C 03·(25)0·(35)3=27125,P (X =1)=C 13·(25)1·(35)2=54125, P (X =2)=C 23·(25)2·(35)1=36125,P (X =3)=C 33·(25)3·(35)0=8125. ······························· 10分 所以X 的分布列为因为X ~B (3,25),所以E (X )=3×25=65. ······················································· 12分20.(12分)(1)证法一:连接OE ,OG .在圆柱OE 中,四边形ABCD 是圆柱OE 的轴截面,所以OE ∥DA .又OE ⊄平面DAF ,DA ⊂平面DAF ,所以OE ∥平面DAF . ············· 2分 在△ABF 中,点O ,G 分别是AB 和BF 的中点,所以OG ∥AF . 又OG ⊄平面DAF ,AF ⊂平面DAF ,所以OG ∥平面DAF .又OE ∩OG =O ,OE ,OG ⊂平面OEG ,所以平面OEG ∥平面DAF . 4分 又EG ⊂平面OEG ,所以EG ∥平面DAF .··································· 6分 证法二:取AF 的中点M ,连接MD ,MG .因为点M ,G 分别是F A 和FB 的中点,所以MG _∥AO . ················ 2分 在圆柱OE 的轴截面四边形ABCD 中,AO _∥DE . 所以MG _∥DE ,因此四边形DEGM 是平行四边形. ······················ 4分 因此EG ∥DM .又EG ⊄平面DAF ,DM ⊂平面DAF ,所以EG ∥平面DAF . ············ 6分 证法三:以O 为坐标原点,AB 的中垂线为x 轴,OB 为y 轴,OE 为z 轴,建立如图所示的空间直角坐标系.则B (0,3,0),E (0,0,3). 因为AB 为底面圆O 的直径,点F 在圆O 上,所以BF ⊥AF . 又OA =OB =BF =3,所以∠BOF =60º,因此F (32,32,0).因为点G 是线段BF 的中点,所以G (34,3340),因此GE →=(-34,-334,3). ·················································· 2分因为AD ⊥平面ABF ,BF ⊂平面ABF ,所以BF ⊥AD .又BF ⊥AF ,AF ∩AD =A ,AF ,AD ⊂平面DAF ,所以BF ⊥平面DAF , 因此→FB =(-32,32,0)是平面DAF 的一个法向量. ···················· 4分因为BF →·EG →=-32×34+32×0×3=0,又EG ⊄平面DAF ,所以EG ∥平面DAF . ··································· 6分 (2)解:法一:以O 为坐标原点,AB 的中垂线为x 轴,OB 为y 轴,OE 为z 轴,建立如图所示的空间直角坐标系.则B (0,3,0),E (0,0,3). ···· 7分 因为AB 为底面圆O 的直径,点F 在圆O 上,所以BF ⊥AF . 又OA =OB =BF =3,所以∠BOF =60º,因此F (32,32,0).因此F (32,32,0),→EF =(32,32,-3). ··································· 8分因为AD ⊥平面ABF ,BF ⊂平面ABF ,所以BF ⊥AD .又BF ⊥AF ,AF ∩AD =A ,AF ,AD ⊂平面DAF ,所以BF ⊥平面DAF . 因此→FB =(-32,32,0)是平面DAF 的一个法向量. ··················· 10分设EF 与平面DAF 所成角为θ,则sin θ=|cos <→EF ,→FB >|=|→EF ·→FB ||→EF |·|→FB |=3223×3=14,DEOFGMDECBOF GyxDECBOFGyx所以EF 与平面DAF 所成角的正弦值为14. ································ 12分法二:由(1)得EG ∥平面DAF ,所以点E 到平面DAF 的距离等于点G 到平面DAF 的距离. 因为AD ⊥平面ABF ,BF ⊂平面ABF ,所以BF ⊥AD . 因为AB 为底面圆O 的直径,点F 在圆O 上,所以BF ⊥AF . 又AF ∩AD =A ,AF ,AD ⊂平面DAF ,所以BF ⊥平面DAF .所以点E 到平面DAF 的距离d =GF =12BF =32. ························· 9分连结OE ,OF ,易得OF =3,所以EF =OF 2+OE 2=23. ······· 10分 设EF 与平面DAF 所成角为θ,则sin θ=dEF =3223=14, 所以EF 与平面DAF 所成角的正弦值为14. ······························· 12分法三:过F 作AD 的平行线交上底面于点H ,连结DH ,平面ADF 即为平面AFH D . 过E 作EK ⊥DH ,K 为垂足,又因为AD ⊥EK ,AD ∩DH =D ,则EK ⊥平面AFHD ,则∠EFK 为EF 与平面ADF 所成的角. 8分得EK =32,EF =OF 2+OE 2=23. ····································· 10分设EF 与平面DAF 所成角为θ,则sin θ=EKEF =3223=14,所以EF 与平面DAF 所成角的正弦值为14. ······························· 12分21.(12分)解:(1)设椭圆C 的焦距为2c ,由题得c =1.当A 为短轴顶点时,△OAF 的周长a +b +1=3+3. ·················· 1分 又a 2=b 2+1,所以a 2=(2+3-a )2+1,解得a =2,b =3. ········ 3分 所以,椭圆C 的标准方程为x 24+y 23=1. ······································ 4分(2)法一:易得F (1,0),设直线AB :y =k (x -1).联立 y =k (x -1),x 24+y 23=1,消去y 并整理得(4k 2+3)x 2-8k 2x +4k 2-12=0, 设A (x 1,y 1),B (x 2,y 2),则x 1+x 2=8k 24k 2+3,y 1+y 2=k (x 1+x 2)-2k =-6k 4k 2+3,则M (4k 24k 2+3,-3k 4k 2+3). ············································································· 6分于是线段AB 的垂直平分线的方程为y =-1k(x -4k 24k 2+3)-3k 4k 2+3.BM yP xO AFQ ADECB OFGADE CB OFGKH令y =0,得x P =k 24k 2+3. ··········································································· 8分处理法1:因为k ≠0,所以x P =k 24k 2+3=14-34(4k 2+3)∈(0,14). ······························ 9分 因为∠POQ =∠PMF =90º,所以Q ,O ,M ,F 四点共圆,由相交弦定理可得|PM |·|PQ |=|PO |·|PF |=x P (1-x P )=x P -x P 2. ···················· 11分 因为x P ∈(0,14),且函数y =x P -x P 2在(0,14)上递增,所以|PM |·|PQ |=x P -x P 2∈(0,316). ·························································· 12分处理法2:易得△OPQ ∽△MPF ,所以PO PM =PQPF ,所以PM ·PQ =PO ·PF .处理法3:|PM |·|PQ |=1+1k2|x M -x P |·1+1k2|x P | =(1+1k 2)|4k 24k 2+3-k 24k 2+3|·|k 24k 2+3|=3k 2(k 2+1)(4k 2+3)2. ················· 10分令t =4k2+3>3,则|PM |·|PQ |=3k 2(k 2+1)(4k 2+3)2=3(t 2-2t -3)16t2=316[-3(1t )2-21t +1], 因为t >3,所以1t ∈(0,13),因此-3(1t )2-21t +1∈(0,1),因此|PM |·|PQ |=316[-3(1t )2-21t +1]∈(0,316). ·········································· 12分法二:易得F (1,0),设直线AB :x =my +1.联立 x =my +1,x 24+y 23=1,消去x 并整理得(3m 2+4)y 2+6my -9=0, 设A (x 1,y 1),B (x 2,y 2),则y +y 2=-6m 3m 2+4,x 1+x 2=m (y 1+y 2)+2=83m 2+4,则M (43m 2+4,-3m 3m 2+4). ··········································································· 6分于是线段AB 的垂直平分线的方程为y =-m (x -43m 2+4)-3m3m 2+4.令y =0,得x P =13m 2+4. ·········································································· 8分处理法1:因为m ≠0,所以x P =13m 2+4∈(0,14). ··············································· 9分因为∠POQ =∠PMF =90º,所以Q ,O ,M ,F 四点共圆,由相交弦定理可得|PM |·|PQ |=|PO |·|PF |=x P (1-x P )=x P -x P 2. ···················· 11分 因为x P ∈(0,14),且函数y =x P -x P 2在(0,14)上递增,所以|PM |·|PQ |=x P -x P 2∈(0,316). ·························································· 12分处理法2:易得△OPQ ∽△MPF ,所以PO PM =PQPF ,所以PM ·PQ =PO ·PF .处理法3:|PM |·|PQ |=1+m 2|x M -x P |·1+m 2|x P |=(1+m 2)|43m 2+4-13m 2+4|·|13m 2+4|=3(m 2+1)(3m 2+4)2. ·············· 10分令t =3m 2+4>4,则|PM |·|PQ |=3(m 2+1)(3m 2+4)2=t -1t2=-1t 2+1t ∈(0,316). ············ 12分 处理法4:|PM |·|PQ |=3(m 2+1)(3m 2+4)2. 令t =3(m 2+1)>3,则|PM |·|PQ |=3(m 2+1)(3m 2+4)2=t (t +1)2=1t +1t+2∈(0,316). ······· 12分 22.(12分)(1)证明:若a =1,则f (x )=e x -x -1,f '(x )=e x -1, ············································· 1分令f '(x )=0,得x =0.在(-∞,0)上,f '(x )<0,f (x )单调递减;在(0,+∞)上,f '(x )>0,f (x )单调递增; ······················································ 3分 故f (x )≥f (0)=0. ····················································································· 4分 (2)解:g (x )=ax e x -x 2-ax ,g'(x )=a (x +1)e x -2x -a =a [(x +1)e x -1]-2x .当x >0时,易得(x +1)e x -1>0,所以由(1)可得,若a ≥1,则g'(x )=a [(x +1)e x -1]-2x ≥(x +1)e x -2x -1>(x +1)2-2x -1=x 2>0, 所以g (x )在(0,+∞)上单调递增,这与x =0为函数g (x )的极大值点相矛盾. ····················································· 7分 若0<a <1,g''(x )=a (x +2)e x -2,因为g'''(x )=a (x +3)e x >0对x >-3恒成立, 所以g''(x )在(-3,+∞)上单调递增. ·························································· 8分 又g''(0)=2a -2<0,g''(2a -2)>a (2a -2+2)-2=0,因为0<a <1,所以2a -2>0,因此存在唯一x 0∈(0,2a -2)g''(x 0)=0.··············································· 9分 所以,在(-3,x 0)上,g''(x )<0,g'(x )单调递减. ··········································· 10分 又g'(0)=0,所以在(-3,0)上,g'(x )>0,故g (x )单调递增;在(0,x 0)上,g'(x )<0,故g (x )单调递减. ···················································· 11分 所以x =0为函数f (x )的极大值点,满足题意.综上,a 的取值范围为(0,1). ·································································· 12分。
天津市滨海新区塘沽紫云中学2024-2025学年高三上学期第二次学情检测数学试题

红灯的概率都是
1 3
,那么该生在上学路上到第
3
个路口首次遇到红灯的概率为
.
13.已知正方体 ABCD - A1B1C1D1 的棱长为 1,除面 ABCD 外,该正方体其余各面的中心分
别为点 E,F,G,H,M(如图),则四棱锥 M - EFGH 的体积为
.
14.已知正数 x,y 满足 x + 2 y = 4 ,则 x + 8y 的最小值为
A.{0}
B. {0,1, 3, 5}
C.{0,1, 2, 4}
D.{0, 2,3, 4}
2.在V ABC 中,“ cos A < cos B ”是“ tan A > tan B ”的( )
A.充分不必要条件 C.既不充分也不必要条件
B.必要不充分条件 D.充要条件
3.函数
f
(x)
=
x
cos
x
-
1 x
.
xy
15.如图梯形
ABCD
,
AB//CD
且
AB
=
5
,
AD
=
2DC
=
4
,
E
在线段
BC
上,
uuur AC
×
uuur BD
=
0
,
则
uuur AE
×
uuur DE
的最小值为
.
16.已知 a
>
0
,函数
f
(x)
=
ì x2 + 2ax + a, x £ 0, íî-x2 + 2ax - 2a, x > 0.
若关于
AB
政治丨江苏省盐城五校联盟2025届高三10月第一次学情调研检测考试政治试卷及答案

2024/2025学年度第一学期联盟校第一次学情调研检测高三年级政治试题(总分100分考试时间75分钟)注意事项:1.本试卷中所有试题必须作答在答题纸上规定的位置,否则不给分.2.答题前,务必将自己的姓名、准考证号用0.5毫米黑色墨水签字笔填写在试卷及答题纸上.3.作答非选择题时必须用黑色字迹0.5毫米签字笔书写在答题纸的指定位置上,作答选择题必须用2B 铅笔在答题纸上将对应题目的选项涂黑。
如需改动,请用橡皮擦干净后,再选涂其它答案,请保持答题纸清洁,不折叠、不破损。
第Ⅰ卷(选择题共48分)一、单项选择题:(本大题共16个小题,每小题3分,共48分.在每小题给出的四个选项中,只有一项符合题目要求,请在答题纸的指定位置填涂答案选项.)1.下列对“两个必然”和“两个决不会”关系认识正确的是()①两者都依据社会基本矛盾运动规律阐释社会形态的更替问题②两者都论证了社会主义终将代替资本主义,但过程是漫长的③前者揭示社会形态更替的必然性,后者揭示其实现的条件性④前者反映资本主义社会的运行方式,后者反映社会形态更替的实现方式A.①③B.①④C.②③D.②④2.《共产党宣言》指出,过去的一切运动都是少数人的或者为少数人谋利益的运动,无产阶级的运动是绝大多数人的、为绝大多数人谋利益的独立的运动。
这一鲜明的政治立场()A.全面阐述了马克思主义政党的崇高理想B.深刻揭露了资本主义生产方式的内在矛盾C.毫不掩饰地揭示了马克思主义政党的阶级性D.科学论证了无产阶级是先进生产力的代表者3.中国共产党人信仰马克思主义,是因为马克思主义能够让中国先进分子“用无产阶级的宇宙观作为观察国家命运的工具”,去“重新考虑中国问题”;中国共产党人坚持马克思主义,就是为了用马克思主义之“箭”射中国革命之“的”,“有的放矢”;中国共产党人发展马克思主义,就是为了用发展着的马克思主义指导中国发展着的实践。
由此可见()“两个必然”:1848年,马克思、恩格斯在《共产党宣言》中指出:“资产阶级的灭亡和无产阶级的胜利是同样不可避免的。
六校联合体2024-2025学年高三上学期学情调研测试物理试卷

2024-2025学年第一学期六校联合体学情调研测试高三物理一、单项选择题:共11题,每题4分,共44分。
每题只有一个选项符合题意,错选、多选、未选均不得分。
1.喷泉a、b形成如图所示的形状,其中OA OB,不计空气阻力,则喷泉a、b的()A.最高点的速度相同B.加速度相同C.在空中的时间相同D.初速度相同2.2024年3月20日,我国探月工程四期鹊桥二号中继星成功发射升空。
当抵达距离月球表面某高度时,鹊桥二号开始进行近月制动,并顺利进入捕获轨道运行,如图所示,轨道的半长轴约为51900km。
后经多次轨道调整,进入冻结轨道运行,轨道的半长轴约为9900km,周期约为24h。
则鹊桥二号在捕获轨道运行时()A.周期小于24hB.近月点的速度小于远月点的速度C.近月点的速度大于在冻结轨道运行时近月点的速度D.近月点的加速度大于在冻结轨道运行时近月点的加速度3.2024年是中国航天大年,神舟十八号、嫦娥六号等已陆续飞天,部分航天器装载了具有抗干扰性强的核电池。
已知9038Sr衰变为9039Y的半衰期约为29年;23894Pu衰变为23492U的半衰期约为87年。
现用相同数目的90 38Sr和23894Pu各做一块核电池,下列说法正确的是()A.9038Sr 衰变为9039Y 时产生α粒子B.23894Pu 衰变过程中满足动量守恒,机械能守恒C.29年后,衰变的9038Sr 数目大于23894Pu 的数目D.87年后,剩余的9038Sr 数目大于23894Pu 的数目4.如图所示,固定的光滑斜面上有一木板,其下端与斜面上A 点距离为L 。
木板由静止释放,若木板长度为L ,上端到达A 点时的速度为1v ;若木板长度为2L ,上端到达A 点时的速度为2v 。
则21:v v 为()A.2:1 B.3:1C.31):21)(( D.3:25.如图,弹簧测力计下端挂有一质量为0.20kg 的光滑均匀球体,球体静止于带有固定挡板的斜面上,斜面倾角为30°,挡板与斜面夹角为60°,若弹簧测力计位于竖直方向,读数为1.0N ,g 取210m/s g ,则球体对斜面的压力大小为()A.3N 3B.1.0NC.2.0ND.3N6.污水中的污泥絮体经处理后带负电,可利用电泳技术对其进行沉淀去污,基本原理如图所示。
江苏省南京市2024-2025学年高三上学期学情调研化学试卷(含答案)

南京市2025届高三年级学情调研化学2024.09本试卷分选择题和非选择题两部分,共100分。
考试用时75分钟。
注意事项:答题前,考生务必将自己的学校、姓名写在答题卡上。
考试结束后,交回答题卡。
可能用到的相对原子质量:H1 C12 N14 O16 Na23 S32 Cl35.5 Pb207一、单项选择题:共13题,每题3分,共39分。
每题只有一个选项最符合题意。
1.氮是自然界各种生物体生命活动不可缺少的重要元素。
下列过程属于氮的固定的是( )A.将转化成硝酸盐B.将NO 转化成硝酸C.将转化成铵盐D.将转化成氮气2.反应可用于生产磨砂玻璃。
下列说法正确的是( )A.为分子晶体B.HF 分子间可形成氢键C.中Si 元素的化合价为-4D.的电子式为3.水合肼()具有强还原性,其制备原理为。
下列关于实验室制备水合肼的装置不能达到实验目的的是()A.装置甲用于制取氨气B.装置乙作为制备过程的安全瓶C.装置丙用于制取水合肼D.装置丁用于吸收尾气中的氨气4.磷酸二氢钙和硫酸钾均可用作化肥。
下列说法正确的是( )A.半径:B.碱性:C.热稳定性:D.第一电离能:阅读下列材料,完成5~7题:催化反应广泛存在,如植物光合作用、合成氨、和重整制和CO 、工业尾气中的无害化处理、的催化氧化[和生成放出98.3kJ 的热量]等。
催化剂有选择性,2N 3NH 2NO 242SiO 4HF SiF 2H O +=↑+2SiO 4SiF 2H O 242N H H O ⋅3242NaClO 2NH N H H O NaCl +=⋅+()242Ca H PO ⎡⎤⎣⎦()24K SO ()()2Ca K r r ++>2Ca(OH)KOH>22H S H O >11(P)(S )I I >4CH 2H O 2H 3NH 2SO ()2SO g ()2O g ()31molSO g如酸性条件下锑电催化还原,生成HCOOH 的选择性大于CO 。
南京市2024-2025学年高三9月学情调研考试 语文 含答案

南京市2025届高三年级学情调研语文2024.09注意事项:1.本试卷考试时间为150分钟,试卷满分150分,考试形式闭卷;2.本试卷中所有试题必须作答在答题卡上规定的位置,否则不给分;3.答题前,务必将自己的学校、班级、姓名、准考证号用0.5毫米黑色墨水签字笔填写在试卷及答题卡上。
一、现代文阅读(35分)(一)现代文阅读I (本题共5小题,19分)阅读下面的文字,完成1~5题。
两千多年来,孔丘一直被世人尊称为孔子,这已是妇孺皆知的常识。
但是,孔丘为什么会被尊称为孔子呢?学者大概有两种见解。
第一种以大名鼎鼎的《论语正义》为代表,认为“子”本指男子,而孔丘是男性,所以就被尊称为孔子。
“子”的本意指婴儿,婴儿有男有女,“子”未必一定就指男子,所以“男子称子说”不可能成立。
第二种是近现代大多数学者的意见。
孔丘因道德崇高,学问伟大,所以其弟子后学都尊称他为孔子,久而久之,成为了后人的思维习惯和语言习惯。
这种意见恐怕也难成立:其一,春秋时代道德崇高,学问伟大者,远不止孔丘一人,例如孔子入室弟子颜回,虽然道德学问都非常了不起,却不能尊称为“颜子”。
根据传世文献,战国时代才尊称颜回为“颜子”,而这是违反春秋礼制的,说明战国时代周礼已荡然无存。
其二,春秋时代华夏大国的一些普通的公卿,例如鲁国的公卿“三桓”,也被尊称为“某子”,但他们并没有什么崇高的道德、伟大的学问。
所以,孔丘被尊称为孔子,“男子说”和“道德学问说”,都难自圆其说。
“子”在西周时代是对部分诸侯的贬称。
据春秋传世文献,大体上,华夏大国诸侯称“公”也称“侯”;诸侯称霸者则称“伯”;华夏小国诸侯和蛮夷戎狄诸侯,则笼统称“子”或称“男”,其中“男”爵的地位似乎更低。
蛮夷戎狄诸侯,则无论大小一律称“子”。
春秋初期出现了新情况,以文明之国、强大之国自居的华夏大国,将自己的公卿视作华夏小国之君和蛮夷戎狄之君,有提高华夏大国诸侯政治地位的意思。
尊称华夏大国公卿为“子”的最早例子是《左传·隐公四年》中卫国君子尊称该国公卿石磺为“石子”,因为石醋选择国家大义。
江苏省南京市2023-2024学年高三上学期学情调研物理试卷及参考答案

南京市2024届高三年级学情调研物理2023.09 本试卷分选择题和非选择题两部分,共100分.考试用时75分钟.注意事项:答题前,考生务必将自己的学校、班级写在答题卡上.选择题答案按要求填涂在答题卡上;非选择题的答案写在答题卡上对应题目的答案空格内,答案不写在试卷上.考试结束后,交回答题卡。
一、单项选择题:共10题,每题4分;共40分.每题只有--个选项最符合题意.1.2023年4月12日,我国“人造太阳”之称的全超导托卡马克聚变试验装置(EAST)创造了新的运行世界纪录.此装置中,21H与31H发生核反应,生成新核42He和X.已知21H、31H、42He的质量分别为m1、m2、m3,真空中的光速为c,下列说法正确的是A.X为电子B.该反应属于轻核聚变C.该反应属于β衰变D.一次核反应释放的能量为(m1+m2-m3)c22.2023年春晚舞蹈《锦绣》,改编自舞剧《五星出东方》.图(a)是一个优美且难度大的动作.人后仰平衡时,可简化为图(b) ,头部受到重力G、肌肉拉力F2和颈椎支持力F1.头部受力示意图可能正确的是3.如图所示,圆形金属线圈放置于粗糙的水平面.上,磁场方向垂直线圈平面向里,磁感应强度按B= kt(k>0)规律变化,线圈始终保持静止,下列说法正确的是A.线圈中产生逆时针方向的感应电流B.线圈有扩张的趋势C.线圈有向右运动的趋势D.线圈中的张力保持不变4.如图所示,将一-等腰直角玻璃棱镜截去棱角,使AD边平行于底面,可制成“道威棱镜”一束复色光从AB边上的E点射入,最终从DC边射出,甲、乙两束光相比,下列说法正确的是A.乙光子能量比较小B.在棱镜内传播的速度,乙光较小C.玻璃砖对乙光的折射率比对甲光的折射率小D.照射同一狭缝,乙光通过狭继后的衍射现象更明显5.在“用油膜法估测分子的大小”的实验中,把1滴油酸酒精溶液滴入盛水的浅盘里,待水面稳定后,画出如图所示的油膜形状.已知该溶液依度为η,n 滴溶液的体积为V,油膜面积为S,则A.油酸分子直径为V SB.实验中,应先滴溶液后撒爽身粉C. nD.计算油膜面积时,将不足一格都当作一格计入面积,将导致所测分子直径偏大6.如图所示,S 点为振源,其频率为50Hz,所产生的横波向右传播,波速为40m/s,PQ 是传播路径中的两点,已知SP=4.6m,SQ=5.0m,当S 通过平衡位置向上运动时A.P 、Q 都在波谷B.P 在波峰,Q 在波谷C.P 在波谷,Q 在波峰D. P 通过平衡位置向上运动,Q 通过平衡位置向下运动7.图(a)为金属四极杆带电粒子质量分析器的局部结构示意图,图(b)为四极杆内垂直于x 轴的任意截面内的等势面分布图,相邻两等势面间电势差相等,下列说法错误的是A.P点电势比M点的高B.P点电场强度大小比M点的小C. M点电场强度方向沿z轴正方向D.带正电的粒子沿x轴正方向运动时,电势能减少8.如图所示,在足够长的光滑斜面上,有一端封闭的导热玻璃管.玻璃管内部液柱封闭了一定量的理想气体,外界温度保持不变.在斜面上静止释放玻璃管,当液柱在玻璃管中相对稳定后,以下说法正确的是A.封闭气体的长度将变长B.封闭气体的分子平均动能减小C.封闭气体压强小于外界大气压D.单位时间内,玻璃管内壁单位面积上所受气体分子撞击次数增加9.已知行星A的同步卫星离A表面高度为其半径的7倍,行星B的同步卫星离B表面高度为其半径的3倍,行星A的平均密度为行星B的平均密度的2倍,行星A与行星B的自转周期之比为A.2B.4C. 12D.1410.如图所示,两小球a,b(可视为质点)通过铰链用刚性轻杆连接,a套在竖直杆M上,b套在水平杆N上. 两根足够长的细杆M、N不接触(a、b球均可越过O点),且两杆间的距离忽略不计,将两小球从图示位置由静止释放,不计一切摩擦.下列说法中正确的是A. a球的机械能守恒B.两球组成的系统水平方向动量守恒C. b球在水平杆上运动过程中存在四个速度可以为零的位置D. a球从初位置下降到最低点的过程中,连接杆对a球的弹力先做负功,后做正功二、非选择题:共5题,共60分,其中第12~15题解答时请写出必要的文字说明、方程式和重要的演算步骤,只写出最后答案的不能得分;有数值计算时,答案中必须明确写出数值和单位.11.(15分)某实验小组测量电源的电动势和内阻时,设计了如图(a)所示的测量电路.使用的器材有量程500mA、内阻为1.00Ω的电流表;量程为3V、内阻约为3kΩ的电压表;阻值未知的定值电阻R1、R2、R3、R4、R5;开关S;-端连有鳄鱼夹P的导线1,其它导线若千.(1)测量时,改变鳄鱼夹P所夹的位置,使R1、R2、R3、R4、R5依次串入电路,记录对应的电压表的示数U和电流表的示数I.在一次测量中电压表的指针位置如图(b)所示,其示数是_______V.(2)其余实验数据如下表所示.根据下表中的数据,在图(c)中的坐标纸上描绘出相应的5个点,并作出U-I图线,(3)根据U-I图线求出电源的内阻r=____Ω(保留三位有效数字).(4)在图(d)中,实线是由实验数据描点得到的U-I图像,虚线表示该电源真实的路端电压和干路电流的关系图像,表示正确的是(5)根据实验测得的数据,判断R3与R4阻值的大小关系并写出依据__________________12.(6分)图a 为“快乐飞机”的游乐项目,模型如图b 所示,已知模型飞机质量为m,固定在长为L 的旋臂上,旋臂与竖直方向夹角为θ,模型飞机绕转轴OO'匀速转动,线速度大小为v ,重力加速度为g.求:(1)模型飞机的向心加速度大小;(2)悬臂对模型飞机的作用力大小.13. (8分)有一种新型光电效应量子材料,当某种光照射该材料时,只产生相同速率的相千电子束.用该电子束照射间距为d 的双缝,在与缝相距为L 的观测屏上形成干涉条纹,测得第1条亮纹与第5条亮纹间距为△x .已知电子质量为m ,普朗克常量为h,该量子材料的逸出功为W 0.求:(1)电子束的德布罗意波长λ和动量p;(2)光子的能量E.14. (15分)如图所示,质量为m ,带电量为+q 的微粒从O 点以初速度v 0沿y 轴负方向射入,从直线MN 上的P 点穿出,MN 左侧存在竖直向上的匀强电场I,电场强度为mg q,以及垂直于纸面向里的匀强磁场,磁感应强度为B.直线MN 的位置为0(1mv qB +(1)求微粒从O 点运动到P 点的时间t;(2)微粒穿过直线MN 后,经过Q 点(图中未画出)速度方向变为水平,求PQ 两点的高度差h;(3)若在直线MN右侧存在匀强电场II(图中未画出),微粒穿过直线MN后,经过Q'点(图中未画出)速度方向水平向右,且速度大小为2v0,求匀强电场II的电场强度E2的最小值及E2的方向.15.(16分)如图所示,足够长的传送带与水平方向的夹角θ=30°,并以v0=2.0m/s的速度逆时针转动.A、B两物体质量均为m=1.0kg,其中A物体和传送带间的摩擦可忽略,B物体与传送带间的摩擦因数为、B之间用长为L=0.4m的不可伸长的轻绳连接.在外力作用下,A、B和传送带相对静止且绳处于伸直状态,t=0时撤去外力作用.A、B之间的碰撞为弹性碰撞,g取10m/s2.求:(1)第一次碰撞前A、B各自的加速度大小;(2)绳子是否会再次伸直?如果会,求出此时的时刻t1;如果不会,求出第一次碰后A、B之间的最大距离;(3)从t=0到t=2s的过程中物体B与传送带间由于摩擦产生的热量Q.。
江苏省海门中学2024-2025学年高三上学期第一次学情检测物理试题

注 意 事 项考生在答题前请认真阅读本注意事项及各题答题要求1.本试卷共6页,满分100分,考试时间为75分钟。
考试结束后,请将答题卷交回。
2.答题前,请您务必将自己的姓名、准考证号、座位号用0.5毫米黑色字迹签字笔填写在答题卷上。
3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、考试证号与你本人的是否相符。
4.作答选择题必须用2B 铅笔把答题卡对应题目的答案标号涂黑。
如需改动,请用橡皮擦干净后,再选涂其它答案。
作答非选择题必须用书写黑色字迹的0.5毫米的签字笔写在答题卷上的指定位置,在其它位置作答一律无效。
2025届高三第一次调研考试物理试卷一、单项选择题:共11题,每题4分,共44分.每题只有一个选项最符合题意.1.现代物理学认为,自然界存在着四种基本相互作用,那么引起原子核β衰变的是以下哪种相互作用A .引力相互作用B .电磁相互作用C .强相互作用D .弱相互作用2.如图所示,半圆形玻璃砖水平放置,一束复色光从其上表面左侧射入玻璃砖,分成a 、b 两束.随着入射角增加,下列说法正确的是A .a 的折射角增大,b 折射角减小B .a 的折射角减小,b 折射角增大C .a 、b 折射角都增大D .a 、b 折射角都减小3.在潜水员看来,岸上的所有景物都出现在一个倒立的圆锥里,若水的折射率n =2,则这个圆锥的顶角是A . 30°B . 60°C . 90°D .120°4.如图,向陶瓷茶杯倒入一定量的热水,迅速盖上杯盖后,发现杯盖被顶起又落下发出“哐哐”的声响,杯盖被顶起前,关于杯内气体说法正确的是A .杯内所有气体分子的速率均增大B .杯内气体的内能不变C .杯内气体的体积变小D .杯内气体压强增大5.如图为两分子系统的势能E p 与两分子间距离r 的关系曲线,甲分子固定于坐标原点O ,乙分子的位置如图中横轴所示,现认为乙分子只受甲分子的作用力,下列说法正确的是A .当r 等于r 1时,分子间的作用力为零B .在r 由r 1变到r 2的过程中,分子间的引力与斥力均减小C .当r 等于r 2时,分子间的作用力最大D .在r 由r 1变到10r 2的过程中,分子间的作用力先增大后减小a b6. “拉曼散射”是光通过介质时,入射光与分子相互作用而引起频率变化的散射.若入射光经过某介质发生散射后,光子波长变长,则A .光子的频率变大B .光子的动量变小C .光传播速度变大D .光子的能量不变7.如图所示为一列沿x 轴传播的简谐波在某时刻的波形图,关于图中 A 、B 、C 、D 三个质点说法正确的是A .A 、B 两点速度方向相同B .A 、C 两点加速度方向相同C .A 、C 同时到达平衡位置D .B 比 D 先到达平衡位置8.如图所示,电动势为E 的电源与定值电阻R 相连,当电源内阻r 取下列哪个值时,电源的输出功率最大A .2R r =B .R r =C .R r 2=D .R r 3=9.如图所示,空间站与微型卫星在机械臂的作用下,同步绕地球做匀速圆周运动.则下列说法正确的是A .空间站的线速度大于微型卫星的线速度B .微型卫星的向心力仅由地球对微型卫星的万有引力提供C .若机械臂断裂,则微型卫星将远离地球D .空间站的向心加速度大于微型卫星的向心加速度10.如图所示,一条轻绳跨过定滑轮,绳的两端各系一个小球A 和B ,已知m B >m A ,A 球静止于地面,用手托住B 球,轻绳刚好被拉紧,然后释放B球.定滑轮的质量及轮与轴间的摩擦均不计,重力加速度为g ,则在B 球落地前A .若增大mB ,绳的拉力减小B .若减小m A ,绳的拉力变大C .A 、B 球的动能变化量相等D .A 、B 球的机械能变化率相等11.如图为一机械手臂,在驾驶员的操作下将质量为m 的工件抓取后,沿与竖直方向夹角为30°由静止开始做匀加速直线运动,经t 时间,上升高度为h ,重力加速度为g .则物体所受的合力为A .2334t mh B .2332t mh C .22t mh mg + D .24t mh mg + R E ry 0-y 0二、非选择题:共5题,共56分.其中第13题~第16题解答时请写出必要的文字说明、方程式和重要的演算步骤,只写出最后答案的不能得分;有数值计算时,答案中必须 明确写出数值和单位.12.(15分)利用如图甲的装置做“探究物体加速度与质量的关系”的实验.气垫导轨上安装了一个光电门,滑块上固定一遮光条.滑块通过绕过滑轮的细绳与槽码相连.请回答下列问题:(1)用螺旋测微器测量遮光条的宽度,如图乙所示,d = ▲ mm ; (2)实验前,需要调整滑轮高度,使细绳与气垫导轨平行,其目的是 ▲ ;(3)多次改变滑块与光电门之间的距离L ,并由静止释放滑块,读出遮光条经过光电门的时间t ,作出L t-21图像,已知其斜率为k ,则滑块加速度的表达式为 ▲ (用题中字母表示); (4)改变槽码质量m ,作出M a 1-图像(M 为滑块的质量),如图丙所示,图像不过原点,原因是 ▲ ,(5)为使图丙中的图像过原点,下列操作中正确的是 ▲A .调节旋钮2 ,降低轨道右侧高度B .调节旋钮1 ,降低轨道左侧高度C .增加滑块的质量,使M 远大于ma 0 调节 旋钮1 调节 旋钮2 光电门图甲 图乙 图丙13.(6分)如图所示,在电场中有A、B、C三个点,若将电子从A点移到B点,静电力做功-6eV,再将电子从B点移到C点,电势能增加6eV.求:(1)AC间的电势差U AC;(2)若A点电势为零,则C点的电势φC.14.(8分)将某个质量为m 的物体以速度v0水平抛出,在运动过程中,除了重力之外,还受到水平方恒力F的作用,已知F=mg,经一段时间垂直落地.(1)物体的运动时间;(2)运动过程中的最小速度.15.(12分)如图所示,两个竖直放置的同轴导体薄圆筒,其电容为C,筒半径为R,两筒间距为d()R d,内外筒分别与电源的正负极连接,在两筒之间靠近内筒有A、B两点,其连线与中央轴平行.一质量为m、电量为-q的粒子从A点以v0垂直纸面方向进入,恰好能经过B点.已知重力加速度为g.求:Array(1)内外筒之间的电场强度大小E;(2)内筒所带的电荷量Q;(3)A、B两点间的高度h.16.(15分)如图所示,在倾角为θ=30°的斜面上运送物体,配重和电动机连接小车的轻绳均与斜面平行,小车质量为m ,配重质量为4m ,小车受到的阻力为车及车上物体总重力的k 倍(k 未知),若电动机输出功率恒为P ,小车装满质量为2m 物体后,在电动机的牵引下运动L 位移,达到最大速度,此后关闭电动机,小车沿斜面上行到最高点,速度恰好为零,卸下物体.轻推小车,小车恰能沿斜面匀速下滑.已知重力加速度为g .求:(1)比例系数k 的值;(2)电动机对小车做的功W ;(3)小车在斜面向上滑行的总时间t .θ。
南京市六校联合体2025届高三上学期学情调研测试数学试题与答案

南京市六校联合体2025届高三上学期学情调研测试数学试题一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}2230,NA x x xB =--≤=∣,则A B = ()A.{}0,1 B.{}1,2,3 C.{}0,1,2,3 D.{}1,0,1,2,3-2.已知复数z 满足)i i z +=,则复数z =()A.13i 22- B.13i 22+ C.31i 22- D.31i 22+3.已知,a b ∈R ,则“22a b --<”是“22a b >”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件4.已知()y f x =,x ∈R 为奇函数,当0x >时,2()log 1f x x =-,则集合{|()()0}x f x f x --<可表示为()A.(2,)+∞ B.(,2)-∞- C.(,2)(2,)-∞-+∞ D.(2,0)(2,)-+∞5.已知向量,a b为单位向量,20a b c ++=且c =,则a与b的夹角为()A.π6B.π4 C.π3D.2π36.已知()()sin cos ,tan tan 3x y x y x y +=-+=,则()tan x y +=()A.-3B.-2C.3D.27.已知圆锥侧面展开图是圆心角为直角,半径为4的扇形,则此圆锥内切球的表面积为()A.12π5B.52π81C.415π25D.52π8.若2e e x y=,则x y -的最小值为()A.4ln25B.4ln23C.3ln24D.5ln24二.多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.抛物线2:2C x py =的焦点为,F P 为抛物线上一动点,当P 运动到(),2t 时,4PF =,直线l 与抛物线相交于A B 、两点,则下列结论正确的是()A.抛物线的方程为:28x y =B.抛物线的准线方程为:4y =-C.当直线l 过焦点F 时,以AF 为直径的圆与x 轴相切D.当直线l 过焦点F 时,以AB 为直径的圆与准线相切10.已知等差数列{}n a 的首项为1a ,公差为d ,其前n 项和为n S ,若867S S S <<,则下列说法正确的是()A.当7n =时,n S 最大B.使得0nS <成立的最小自然数13n =C.6789a a a a +<+ D.数列n n S a ⎧⎫⎨⎬⎩⎭中的最小项为88S a 11.已知定义在实数集R 上的函数()f x ,其导函数为()f x ',且满足()()()()()1,10,12f x y f x f y xy f f +'+=+==,则()A.()()110f x f x -++= B.()21f = C.()202410122023f =⨯ D.20241()20232024k fk '==⨯∑三、填空题:本题共3小题,每小题5分,共15分.12.已知二项式()*3nx n ⎛∈ ⎝N 的展开式中第2项的二项式系数为6,则展开式中常数项为__________.13.若函数()()sin 2(02π)f x x ϕϕ=+<<的图象向右平移ϕ个单位后在区间π0,2⎡⎤⎢⎥⎣⎦上单调递减,则ϕ=______.14.设双曲线2222:1(0,0)x y C a b a b -=>>的左右焦点分别为12,F F ,离心率为2,P 为C 上一点,且12120F PF ∠= ,若12F PF的面积为a =__________.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.已知函数()()1ln 2f x x x ax =+-+.(1)当1a =时,求()f x 的图象在1,1处的切线方程;(2)若函数()f x 在1,+∞上单调递增,求实数a 的取值范围.16.在ABC V 中,角,,A B C 所对的边分别为,,a b c ,设向量()πππ5π4sin ,sin ,cos cos ,2cos2,,,3346m A n A A f A m n A ⎫⎛⎫⎛⎫⎛⎫⎛⎫⎡⎤=-=-=⋅∈⎪ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦⎝⎭⎝⎭⎭.(1)求函数()f A 的最小值;(2)若()0,sin 2f A a B C ==+=,求ABC V 的面积.17.如图,在四棱锥P ABCD -中,四边形ABCD 是边长为2的菱形,60BAD ∠= ,,PB PD PA PC =⊥,点,E F 分别为棱,AD PC 的中点.(1)求证://EF 平面PAB ;(2)若直线PA 与平面ABCD 所成角的大小为60o ,求二面角P BC D --的余弦值.18.某校为了提高教师身心健康号召教师利用空余时间参加阳光体育活动.现有4名男教师,2名女教师报名,本周随机选取2人参加.(1)求在有女教师参加活动的条件下,恰有一名女教师参加活动的概率;(2)记参加活动的女教师人数为X ,求X 的分布列及期望()E X ;(3)若本次活动有慢跑、游泳、瑜伽三个可选项目,每名女教师至多从中选择参加2项活动,且选择参加1项或2项的可能性均为12,每名男教师至少从中选择参加2项活动,且选择参加2项或3项的可能性也均为12,每人每参加1项活动可获得“体育明星”积分3分,选择参加几项活动彼此互不影响,记随机选取的两人得分之和为Y ,求Y 的期望()E Y .19.已知椭圆2222:1(0),x y C a b C a b+=>>的上顶点为A ,左、右焦点为12,F F ,离心率为121,2AF F 的面积l 与椭圆C 交于,D E 两点.(1)求椭圆C 的方程;(2)当直线l 过点1F 且与直线2AF 垂直时,求ADE V 的周长;(3)若OD OE ⊥(O 是坐标原点),求DOE 面积的取值范围.南京市六校联合体2025届高三上学期学情调研测试数学试题答案1.【分析】先求集合A,再求交集运算.【详解】解不等式2230x x --≤得13x -≤≤,所以{|13}A x x =-≤≤,因为N B =,所以{}0,1,2,3A B ⋂=,故选:C.2.【分析】利用复数的运算和共轭复数的定义求解即可.【详解】)i i z ++=,故)22i 21i 3i 422z --====--,故12z =.故选:B3.【分析】分别化简22a b --<和22a b >,再根据充分、必要条件判断即可.【详解】因为2x y =在R 单调递增,且22a b --<,所以a b -<-,即a b>因为22a b >,所以220a b ->,即()()0a b a b +->,所以存在两种情况:0a b +>且a b >,0a b +<且a b <,因此22a b --<推不出22a b >,同样22a b >推不出22a b --<,因此“22a b --<”是“22a b >”的既不充分也不必要条件.故选:D.4.【分析】利用函数奇偶性可得不等式()()0f x f x --<等价于()0f x >,再求出函数解析式,利用对数函数单调性解不等式可得结果.【详解】因为()y f x =为奇函数,所以()()0f x f x --<等价于2()0f x -<,即()0f x >;当0x >时,2()log 1f x x =-,即20()log 1f x x =->,解得2x >;当0x <时,0x ->,可得()()2()log 1f x f x x -=-=--,所以()()21log f x x =--,解不等式()()21log 0f x x =-->,可得20x -<<,综上可得集合{|()()0}x f x f x --<可表示为(2,0)(2,)-+∞ .故选:D5.【分析】由已知可得2a b c +=-,两边平方,结合数量积的定义和运算律及性质可求结论.【详解】设a与b 的夹角为θ,则[]0,πθ∈,因为20a b c ++=,所以2a b c +=-,所以()()222a bc +=-,所以22244a b a b c ++⋅=,即22244cos a b a b cθ++⋅=又1a b == ,c =,所以144cos 7θ++=,所以1cos 2θ=,又[]0,πθ∈,所以π3θ=,即a与b 的夹角为π3.故选:C.6.【分析】根据两角和的正弦公式和两角差的余弦公式对题目所给条件进行化简,再用两角和的正切公式即可.【详解】因为()()sin cos x y x y +=-,所以sin cos cos sin cos cos sin sin x y x y x y x y +=+,所以sin cos cos sin cos cos sin sin cos cos cos cos cos cos cos cos x y x y x y x yx y x y x y x y+=+,即tan tan 1tan tan x y x y +=+,因为tan tan 3x y +=,所以tan tan 2x y =,所以()tan tan 3tan 31tan tan 12x y x y x y ++===---.故选:A.7.【分析】由扇形弧长的计算,可得圆锥底面半径,画组合图形的轴截面,利用三角形内切圆以及勾股定理,最后利用球表面积公式,可得答案.【详解】由题意可知,圆锥的母线4l =,底面周长12π42π4C =⋅⋅=,所以圆锥的底面半径1r =,根据题意可作圆锥与其内切球的轴截面如下:根据圆锥和球的对称性可知,球的截面为圆O ,也即为等腰ABC V 的内切圆,即OE AC ⊥,AD BC ⊥,OD OE =,CD CE =,在Rt ADC 中,222AD CD AC +=,由4AC l ==,1CD r ==,则AD =,在Rt AOE △中,222AE OE AO +=,即()()222AC CE OE AD OD -+=-,可得())22241OE OE -+=,解得155OE =,所以内切球的表面积2124ππ55S ⎛⎫== ⎪ ⎪⎝⎭.故选:A.8.【分析】先对等式进行移项,然后两边同时除以e y ,凑出e x y -,再利用基本不等式即可.【详解】因为2e e ,x y =即122e e 2x y =+,两边同时除以e y ,得到122e e 2e e xyy y+=,即15242ee 2e x yyy -=+≥=,当且仅当2e e y y=,即ln23ln2,42y x ==等号成立,则54e2x y-≥,则545ln2ln24x y -≥=.故x y -的最小值为5ln24.故选:D .9.【分析】对于A,B,根据抛物线的定义即可求解p ,进而知道抛物线方程和准线方程;对于C,D ,由抛物线的性质易知该结论正确.证明过程见详解.【详解】对于A ,如图所示,过点P 作准线2Py =-的垂线,垂足为Q,则由抛物线的定义可知:242pPF PQ ==+=,解得4p =.∴抛物线C 的方程为:28x y =,故A 正确;对于B ,抛物线的准线方程为22py =-=-,故B 错误;对于C ,如图所示,取AF 的中点C ,过点C 作x 轴的垂线,垂足为D,易知抛物线的焦点(0,2)F ,设()11,A x y ,则112,22x y C +⎛⎫⎪⎝⎭,1,02x D ⎛⎫⎪⎝⎭,21121111228·1,224DF DAx y k k x x x ⨯=⨯==--- 所以DF DA ⊥,所以以AF 为直径的圆与x 轴相切,故C 正确;对于D ,当直线l 过抛物线的焦点F 且与抛物线相交于A B 、两点时,直线l 的斜率存在,假设:2l y kx =+,设()()1122,,,A x y B x y ,AB 的中点为M ,则121222x x y y M ++⎛⎫⎪⎝⎭,,如图所示,作MN 垂直于准线于点N ,则12,22x x N +⎛⎫-⎪⎝⎭,联立228y kx x y=+⎧⎨=⎩,消去y 并整理可得28160x kx --=,所以12128,16x x k x x +==-,所以124,2x x k +=所以()4,2N k -,()212121222484y y kx kx k x x k ∴+=+++=++=+,()()22221212121111164886464y y x x x x =⨯==⨯-=,()()()221212122221212124284424221616·1444161648161616NA NBk y y y y y y k k k x k x k x x k x x k k k k k +⨯++++++++=⨯====----++--⨯+-- ,NA NB∴⊥∴以A 为直经的圆与准线相切,故D 正确.故选:ACD.【点睛】结论点睛:如图所示,已知抛物线22x py =,过其焦点0,2p F ⎛⎫ ⎪⎝⎭且与抛物线交于()()1122,,,A x y B x y 两点的直线2py kx =+,则有如下常用结论:(1)1212,,;22p pAF y BF y AB y y p =+=+=++(2)若直线A 的倾斜角为θ,则21122,,,1sin 1sin cos p p pAF BF AB AF BF p θθθ==+==-+;(3)以,AF BF 为直径的圆都与x 轴相切,以AB 为直径的圆与准线相切;(4)221212,4p x x p y y =-=;10.【分析】利用等差数列及867S S S <<,判断出10a d >>,780a a +<,再利用等差数列和等差数列前n 项和的性质逐项判断即可.【详解】若867S S S <<,则77678860,0a S S S a a S =->+=-<,所以8870,0a d a a <=-<,即等差数列为递减数列,对于A ,由870,0a a <>,知等差数列前7项为正数,其余项为负数,故当7n =时,n S 最大,故A 正确;对于B ,114780a a a a +=+< ,故()11313713130,2a a S a ⨯+==>()11414140,2a a S ⨯+=<所以使得0nS <成立的最小自然数不是13,故B 错误;对于C ,()678967897820a a a a a a a a a a +-+=+++=+<,则6789a a a a +<+,故C 正确;对于D ,当7n ≤或14n ≥时,0nn S a >;当714n <<时,0n nS a <;由131********,S 0a a a S S S >>>⋯>>>>⋯>>,所以n n S a ⎧⎫⎨⎬⎩⎭中最小项为88S a ,故D 正确.故选:ACD11.【分析】对于AB ,利用赋值法求得(0)0f =,()21f =,再根据中心对称的定义判断即可;对CD ,利用赋值法后结合数列的性质进行相应的累加及等差数列公式法求和即可得.【详解】对于A ,令0x y ==,则有(0)(0)(0)0f f f =++,即(0)0f =,令1y =,则有()(1)()1()f x f x f x f x x +=++=+,所以()()21f f =110(0)f +=≠=-,所以函数不关于(1,0)中心对称,故A 错误B 正确;对于C ,令1y =,则有()(1)()1()f x f x f x f x x +=++=+,即(1)()f x f x x +-=,则()()(2024)(2024)(2023)(2023)(2022)11f f f f f f f =-+-+⋯-+,(20231)20232023202210101220232+⨯=++++==⨯ ,故C 正确;对于D ,令1y =,则有()(1)()1()f x f x f x f x x +=++=+,即(1)()f x f x x +=+,则()(1)1f x f x ''+=+,即()(1)1f x f x ''+-=,又1(1)2f '=,令()(n a f x n '=,*N )x ∈,则有11n n a a +-=,所以数列{}n a 是等差数列,首项为12,公差为1,所以11(1)122n a n n =+-⨯=-,即11()122f k k k '=+-=-,则2024111(2024)202422()101220242z f k =+-⨯'==⨯∑,故D 错误.故选:BC .12.【分析】根据题意求出n ,再写出二项展开式的通项,令x 的指数部分为0,然后求解即可.【详解】依题意1C 6n =,解得6n =,二项式63x ⎛ ⎝的通项为()36662166C 33C kk k k k k k T x x---+==,令3602k-=,得4k =,所以展开式中常数项为64463C 135-=.故答案为:135.13.【分析】先求出向右平移后的函数图象,再根据正弦函数的单调递减区间列出不等式,进而求解即可.【详解】()f x 向右平移ϕ个单位后得到()()()sin 2sin 2g x x x ϕϕϕ⎡⎤=-+=-⎣⎦因为π0,2x ⎡⎤∈⎢⎥⎣⎦,所以2π,x k ϕϕϕ-≤-≤-∈Z ,因为()g x 在π0,2⎡⎤⎢⎥⎣⎦单调递减,所以π2π,23ππ2π,2k k k k ϕϕ⎧-≥+∈⎪⎪⎨⎪-≤+∈⎪⎩Z Z,即π2π,2π2π,2k k k k ϕϕ⎧-≥+∈⎪⎪⎨⎪-≤+∈⎪⎩Z Z ,所以π2π,2k k ϕ-=+∈Z ,所以π2π,2k k ϕ=--∈Z ,因为02πϕ<<,所以当1k =-时,3π2ϕ=.故答案为:3π2.14.【分析】根据双曲线定义以及余弦定理,由双曲线离心率和12F PF的面积为2a =.【详解】不妨取P点在第一象限,如下图所示:根据双曲线定义可得122PF PF a -=,且122F F c =;由离心率为2可得2ca=,可得2c a =,即124F F a =;设20PF m =>,则12PF a m =+;由12F PF的面积为()1212113sin 2222PF PF F PF m a m ∠=+⨯=,解得()216m a m +=;利用余弦定理可得222121212121cos 22PF PF F F F PF PF PF +-∠==-,即()()()222241222a m m a m a m ++-=-+,整理可得()2224122m am a m a m +-=-+,即()21232a m a m =+,所以21248a =,解得2a =.故答案为:215.【分析】(1)求出()11f '=,切点为()1,1,直接写出切线方程;(2)转化为′≥0对于∈1,+∞恒成立,求实数a 的取值范围.【小问1详解】当1a =时,()()1ln 2f x x x x =+-+,()0x >,()1ln f x x x='+,()11f '=,()11f =,所以()f x 的图象在1x =处的切线方程为:y x =.【小问2详解】()1ln 1f x x a x=++-',若函数()f x 在1,+∞上单调递增,则′≥0对于∈1,+∞恒成立,即1ln 1a x x≤++对于∈1,+∞恒成立,令()()1ln 1,1g x x x x=++>,当1x >时,()210x g x x-'=>,则函数()g x 在1,+∞上单调递增,所以()()12g x g >=,故2a ≤.16.【分析】(1)根据数量积的坐标运算公式,二倍角公式,辅助角公式化简()f A ,结合正弦函数性质求其最小值;(2)解方程()0f A =求A ,由正弦定理可求b c +,再由余弦定理求bc ,根据三角形面积公式求结论.【小问1详解】()ππ4sin cos cos sin 2cos233f A m n A A A⎛⎫⎛⎫=⋅=⋅-+-⋅ ⎪ ⎪⎝⎭⎝⎭ πsin22sin 23A A A ⎛⎫=-=- ⎪⎝⎭因为π5π,46A ⎡⎤∈⎢⎥⎣⎦,所以ππ4π2,363A ⎡⎤-∈⎢⎥⎣⎦,所以当π4π233A -=,即5π6A =时,()f A有最小值【小问2详解】因为()0f A =,所以π2sin 203A ⎛⎫-= ⎪⎝⎭,所以π2π,3A k k -=∈Z ,因为π5π,46A ⎡⎤∈⎢⎥⎣⎦,所以2π3A =由正弦定理,2sin sin sin b c a B C A====,所以sin ,sin 22b c B C ==.又因为sin sin 2B C +=,所以222b c +=,得b c +=,由余弦定理有:2222cos a b c bc A =+-,所以3bc =.所以11333sin 32224ABC S bc A ==⨯⨯=.17.【分析】(1)取PB 中点M ,连接,MF MA ,由已知可证得四边形AMFE 为平行四边形,可得//EF AM ,则得//EF 平面PAB .(2)连接,AC BD ,交于点O ,可得平面ABCD ⊥平面PAC ,则PAO ∠为直线PA 与平面ABCD 所成的角的平面角,以O 为原点,直线OB OC 、所在直线分别为x y 、轴,过点O 垂直于平面ABCD 的直线为z 轴,建立空间直角坐标系,利用向量坐标运算,求得平面PBC的一个法向量()m =,取平面ABCD一个法向量为()0,0,1n =,由cos ,m n m n m n⋅=⋅即可求得二面角P BC D --的余弦值.【小问1详解】如图:取PB 中点M ,连接,MF MA ,因为F 为PC 中点,所以//MF BC 且12MF BC =,又四边形ABCD 为菱形,且E 为AD 中点,所以//AE BC 且12AE BC =,所以//MF AE 且MF AE =,所以四边形AMFE 为平行四边形,所以//EF AM ,又AM ⊂平面,PAB EF ⊄平面PAB ,所以//EF 平面PAB .【小问2详解】如图:连接,AC BD ,交于点O ,因为四边形ABCD 为菱形,所以AC BD ⊥,且O 为,AC BD 的中点,又因为=PB PD ,所以,,PO BD AC PO ⊥⊂平面PAC ,且AC PO O = ,所以BD ⊥平面PAC ,BD ⊂平面ABCD ,所以平面ABCD ⊥平面PAC ,所以AC 是直线PA 在平面ABCD 内的射影,则PAO ∠为直线PA 与平面ABCD 所成的角的平面角,则60PAO ∠= ,又2,,60AB PA PC BAD ∠=⊥= ,所以2,60AC BD PA POA ∠==== ,如图,以O 为原点,直线OB OC 、所在直线分别为x y 、轴,过点O 垂直于平面ABCD 的直线为z 轴,建立空间直角坐标系,则()()()330,0,0,1,0,0,,0,,22O B C P ⎛⎫-⎪ ⎪⎝⎭,所以()331,,,22PB BC ⎛⎫=-=- ⎪ ⎪⎝⎭.取平面ABCD 一个法向量为()0,0,1n =,设平面PBC 的一个法向量为(),,m x y z =,则33002200m PB x y z m BC x ⎧⎧⋅=+-=⎪⎪⇒⎨⎨⋅=⎪⎪-+=⎩⎩,令3x =,得3y z ==,则()m =,则cos ,7m nm n m n ⋅===⋅,所以二面角P BC D --的余弦值为7.18.【分析】(1)由条件概率的计算公式即可求解;(2)参加活动的女教师人数为X ,则X 服从超几何分布,即可写出X 的分布列及期望.(3)根据一名女教师和一名男教师参加活动获得分数的期望,即可得153Y X =-,即可求得()E Y .【小问1详解】设“有女教师参加活动”为事件A ,“恰有一名女教师参加活动”为事件B ,则()114226C C 8C 15P AB ==,()11242226C C C 3C 5P A +==,所以()()()8815|395P AB P B A P A ===.【小问2详解】依题意知X 服从超几何分布,且()()22426C C 0,1,2C k kP X k k -===()2426C 20C 5P X ===,()114226C C 81C 15P X ===,()2226C 12C 15P X ===,所以X 的分布列为:X012P25815115()2812012515153E X =⨯+⨯+⨯=.【小问3详解】设一名女教师参加活动可获得分数为1X ,一名男教师参加活动可获得分数为2X ,则1X 的所有可能取值为3,6,2X 的所有可能取值为6,9,()()111362P X P X ====,()111936222E X =⨯+⨯=,()()221692P X P X ====,()2111569222E X =⨯+⨯=,有X 名女教师参加活动,则男教师有2X -名参加活动,()915215322Y X X X =+-=-,所以()()()2153153153133E Y E X E X =-=-=-⨯=.即两个教师得分之和的期望为13分.19.【分析】(1)由椭圆的离心率为12,可得2a c =,b =,再由12AF F S =△,可求得1c =,进而求得2a =,b =C 的方程;(2)由(1)可得12AF F △为正三角形,得直线DE 为线段2AF 的垂直平分线,则ADE V 的周长为()2211AD AE DE DF EF DF F E ++=+++4a =.(3)当直线,OD OE 的斜率一条为零,另一条不存在时,DOE 的面积为12ab ;当直线,OD OE 的斜率存在且不为零时,设直线:OD y kx =,与椭圆联立消去y 得2234()12x kx +=,则得221243x k =+,2221243k y k =+,则得()22212143k OD k +=+,同理可得,()22212134k OE k +=+,代入12DOE S OD OE =⋅ ,变形后利用基本不等式,即可求得其取值范围.【小问1详解】因为12c e a ==,所以2a c =,又222b a c =-,则b =,即椭圆方程为2222143x y c c+=,因为122AF F S bc === 21c =,即1c =,则2a =,b =,故椭圆方程为22143x y +=.【小问2详解】由(1)知,2a c =,b =,得12AF F △为正三角形,则由2DE AF ⊥,得直线DE 为线段2AF 的垂直平分线,所以2DA DF =且2EA EF =,则ADE V 的周长为()222211AD AE DE DF EF DE DF EF DF F E ++=++=+++()()121248DF DF EF EF a =+++==.【小问3详解】①当直线,OD OE 的斜率一条为零,另一条不存在时,DOE 的面积为12ab =,②当直线,OD OE 的斜率存在且不为零时,设直线:OD y kx =,与椭圆联立消去y ,得2234()12x kx +=,即221243x k =+,则2221243k y k =+,则()2222221211212434343k k OD k k k +=+=+++,同理可得,()22212134k OE k +=+,故DOE 的面积为26112k OD OE +⨯⨯=226161k k ++==127⎡==⎢⎣,当且仅当221k k =,即1k =±时取最小值,综上,DOE 的面积的取值范围为127⎡⎢⎣.【点睛】关键点点睛:第(3)小问,先讨论直线,OD OE 的斜率一条为零,另一条不存在时,DOE 的面积;再讨论直线,OD OE 的斜率存在且不为零时,设直线:OD y kx =,与椭圆联立消去y ,得到2x ,2y ,即可得2OD ,同理得2OE ,则DOE的面积为26112k OD OE +⨯⨯=等式,从而求得DOE 面积的取值范围.。
语文丨江苏省盐城五校联盟2025届高三10月第一次学情调研检测考试语文试卷及答案

2024/2025学年度第一学期联盟校第一次学情调研检测高三年级语文试题(总分150分考试时间150分钟)注意事项:1.本试卷中所有试题必须作答在答题纸上规定的位置,否则不给分.2.答题前,务必将自己的姓名、准考证号用0.5毫米黑色墨水签字笔填写在试卷及答题纸上.3.作答非选择题时必须用黑色字迹0.5毫米签字笔书写在答题纸的指定位置上,作答选择题必须用2B铅笔在答题纸上将对应题目的选项涂黑。
如需改动,请用橡皮擦干净后,再选涂其它答案,请保持答题纸清洁,不折叠、不破损。
一、现代文阅读(35分)(一)现代文阅读1(本题共5小题,19分)阅读下列文字,完成下面小题。
你对于某个问题没有调查,就停止你对于某个问题的发言权。
这不太野蛮了吗?一点也不野蛮,你对那个问题的现实情况和历史情况既然没有调查,不知底里,对于那个问题的发言便一定是瞎说一顿。
瞎说一顿之不能解决问题是大家明了的,那末,停止你的发言权有什么不公道呢?许多的同志都成天地闭着眼睛在那里瞎说,这是共产党员的耻辱,岂有共产党员而可以闭着眼睛瞎说一顿的吗?要不得!要不得!注重调查!反对瞎说!你对于那个问题不能解决吗?那末,你就去调查那个问题的现状和它的历史吧!你完完全全调查明白了,你对那个问题就有解决的办法了。
一切结论产生于调查情况的末尾,而不是在它的先头。
只有蠢人,才是他一个人,或者邀集一堆人,不作调查,而只是冥思苦索地“想办法”,“打主意”。
须知这是一定不能想出什么好办法,打出什么好主意的。
换一句话说,他一定要产生错办法和错主意。
许多巡视员,许多游击队的领导者,许多新接任的工作干部,喜欢一到就宣布政见,看到一点表面,一个枝节,就指手画脚地说这也不对,那也错误。
这种纯主观地“瞎说一顿”,实在是最可恶没有的。
他一定要弄坏事情,一定要失掉群众,一定不能解决问题。
许多做领导工作的人,遇到困难问题,只是叹气,不能解决。
他恼火,请求调动工作,理由是“才力小,干不下”。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高三数学综合四
―、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题纸相应的位
1.已知2T-3<0},若实数XA,则a的取值范围是
2.若复数U + 是纯虚数,则实数a的值是
3.如果数据禺一砲"3 ’…g:的平均数是10,则数据0込1 一2,&規一—Eq…,6巧一£的平均数为
4.盒中装有形状、大小完全相同的3个球,其中红色球2个,黄色球1个.
若从中随机取出2个球,则所取出的2个球颜色不同的概率等于
5.右图是某程序的流程图,则其输出结果为
6.已知伽匕斗® = 亍怕叩=—y,则里竺二
7.已知双曲线/in的焦点到一条渐近线的距离等于
实轴长,那么该双曲线的离心率为
8.巳知二次函数心=心一卄的值域是[0,+心,则++知勺
最小值是
9.用一张长8cm宽6 cm的矩形铁皮围成圆柱形的侧面,则这个圆柱的体积为
cm3.(用含兀的式子表
示)
k
Y
*
W
—阳丽IV , ,
)—!/輸出
I 血一丘+1 II I
(第5
题〕
10.设函数= —+2,若不等式f(3+2血的<>1对任意&WR恒成立,则实数
的取值范围为
11.在AABC中,AB边上的中线CO =2,若动点P满足
AP护和& •如)+ g*补•处(胆R),则(丙+丙)云的最小值是
12.将所有的奇数排列如右表,其中第i行第j个数表示为5,例如畑=9.若
Hi/-445,则i + j =
13.若实数a,b,c成等差数列,点P(-1,0)在动直线耳工+上的射影为M,已知
点N(3,3),则线段MN长度的最大值是
14.下图展示了一个由区间(0,k)k为一正实数)到实数集R上的映射过程:区间(0,k)中的实数m对应线段AB上的点M,如图1;将线段AB围成一个离心率为警的椭圆,使两
端点A 、B 恰好重合于椭圆的一个短轴端点,如图 2;再将这个椭圆放在平面直角坐标系
中,使其中心在坐标原点,长轴在
x 轴上,已知此时点 A 的坐标为(0, 1),如图3,在图
AM 的长度对应于图3中的椭圆弧 ADM 的长度.图3中直线
N(n,_2),则与实数 m 对应的实数就是 n ,记作f (m) = n 。
现给出下列命题:①..f(y)= 6 ;②贰刃是奇函数;③在定义域上单调递增;④ .g 的
图象关于点(J , 0)对称;⑤f(m
)=3j 耳时,AM 过椭圆右焦点.
二、解答题:本 大题共6小题,共计90分,请在答题纸指定区域内作答,解答时应写出文 字说明、证明过程或演算步骤.
15.(本小题满分14分)已知△ ABC 中,角A , B, C 的对边分别为 a , b , c,且
72 acosB = e?cosB+氐osU
(1)求角B 的大小;
⑵ 设向量f»=CcosA,cos2A) ,n=(12, — ^),求当m ? n 取最大值时,tanC 的值.
16.(本小题满分14分)如图,直四棱柱 ABCD-AB 1C D 中,底面ABCD 是直角梯形,
ZEAD=ZADC=9丁,/W=
, CD^AD,
(1)求证:民C 丄AC ;
形变化过程中,图1中线段 AM 与直线y = -2交于点
其中所有的真命题是 __ (
写出所有真命题的序号)
(2)在AiB上是否存在一点P,使得DP既与平面BCB平行,又与平面ACB平行?并证明你
17.(本小题满分14分)某商场对A品牌的商品进行了市场调查,预计2012年从1月起前x 个月顾客对A品牌的商品的需求总量P(x)件与月份x的近似关系是:
= 十1)(41—2工心©2且疋N・)
(1)写出第x月的需求量f (x)的表达式;
<7 且xEN* ,
⑵若第X月的销售量宮⑺=住(扣—to工十96)昇H 且工WN■(单位:件),每件利润q(x)元与月份x的近似关系为:輕丈)二业,问:该商场销售A品牌商品,预计
第几月的月利润达到最大值?月利润最大值是多少?
18.(本小题满分16分)如图,已知中心在原点0、焦点在x轴上的椭圆T过点M(2,1),离I
心率为纟L抛物线C顶点在原点,对称轴为x轴且过点M .
(1)当直线10经过椭圆T的左焦点且平行于0M时,求直线10的方
程;
(2)若斜率为一石的直线丨不过点M,与抛物线C交于
A、B两个不同的点,求证:直线MA,MB与x轴总围成
等腰三角形.
19.(本小题满分16分)已知函数了〔工)=互心一■(加+ 1)工十21njr>,其中常数a A 0 .
(1)求f (x)的单调区间;
⑵ 如果函数在公共定义域D上,满足fQyHQYgS,那么就称
H(丁;为只迂)与g(x)的"和谐函数”.设g〔工)=丄工一4応丹(刃=_fG) + (2 —]n2'u J为常
数,且O<A<1),求证:当2<a<y时,在区间(0,2]上,H (x)是函数f (x)与g(x)的
“和谐函数”.
20.
(本小题满分16分)巳知无穷数列仙」的各项均为正整数,久为数列{偽}的前n项和, 若数列}是等差数列,且对任意正整数n都有成立,求数列{心}的通项公
式;
对任意正整数n ,从集合他厂1也"}中不重复地任取若干个数,这些数之间经过加减运算后所得数的绝对值为互不相同的正整数,且这些正整数与至S n全体正整数组成的集合.
(i)求血心的值;(ii)求数列W H}的通项公式.。
