大一高等数学第五章定积分习题

合集下载

高等数学第五章定积分习题课

x
x
∴ ∵
∴
Q( x ) ≡ c , Q ( 0) = 0 ,
Q( x ) ≡ 0 . 证毕 .
d x f (t)(x −t)dt 0 d x∫ = f (x) (x − x) =0?
13
例 6 . 设 f ( x ) 在 [ a , b ] 上连续且 f ( x ) > 0 ,
F ( x ) = ∫ f ( t ) dt + ∫
(1) . 若在 [ a , b ] 上 , f ( x ) ≥ 0 , 且 ∫ f ( x ) dx = 0 ,
a
b
则在 [ a , b ] 上 f ( x ) ≡ 0 .
( 2) . 若在 [ a , b ] 上 , f ( x ) ≥ 0 , 且 f ( x ) ≡ 0 , /
则 ∫ f ( x ) dx > 0 .
由于 f ( x ) 连续 ,
2h
h
对于 ε = h , ∃δ > 0 , 当 x − c < δ 时 ,
f ( x ) − f (c ) < ε
b
c −δ
a
b
(
c
)
f (c ) − ε < f ( x ) < f (c ) + ε 成立 ,
即 h < f ( x ) < 3h .
∫a f ( x ) dx = ∫a
∫a f = ∫a f + ∫c f ∫a
b b c b b b
b
5 . 在[a , b]上
f ( x) ≥ 0 f ( x) ≤ 0
⇒ ⇒
f ( x ) ≥ g( x ) ⇒
∫a f ≥ 0 b ∫a f ≤ 0 b b ∫a f ≥ ∫a g

高等数学第05章定积分及其应用习题详解

x

0

x 1 sin tdt 0dt 1 ， 2

b a
f ( x)dx 在几何上表示由曲线 y f ( x) ，直线
x a, x b 及 x 轴所围成平面图形的面积. 若 x a, b时，f ( x) 0, 则 b f ( x)dx 在几何 a
上表示由曲线 y f ( x) ，直线 x a, x b 及 x 轴所围平面图形面积的负值. （1）由下图（1）所示， 1 xdx ( A1 ) A1 0 .
n
2
i
i 1
n
2
1 1 1 1 1 n(n 1)(2n 1) = (1 )(2 ) 3 n 6 6 n n 1 1 2 当 0时（即 n 时），由定积分的定义得： x d x = ． 0 3
= 5. 利用定积分的估值公式，估计定积分
4 3

1 1
(4 x 4 2 x 3 5) dx 的值.
上任取一点 i 作乘积 f ( i ) xi 的和式：
n
f ( i ) xi c ( xi xi1 ) c(b a) ,
i 1 i 1
n
n
记 max{xi } , 则
1i n

b a
cdx lim f ( i ) xi lim c(b a) c(b a) .

x
0
(t 1)dt ，求 y 的极小值
解：当 y x 1 0 ，得驻点 x 1 ， y '' 1 0. x 1 为极小值点，极小值 y (1)
( x 1)dx - 2

定积分习题与答案

第五章定积分(A)1．利用定积分定义计算由抛物线12+=x y ，两直线)(,a b b x a x >==与横轴所围成的图形的面积。

2．利用定积分的几何意义，证明下列等式： 3．估计下列各积分的值4．根据定积分的性质比较下列各对积分值的大小 ⎰21ln )1xdx 与dx x ⎰212)(ln dx e x⎰10)2与⎰+10)1(dx x5．计算下列各导数 6．计算下列极限7．当x 为何值时，函数⎰-=xt dt te x I 02)(有极值？8．计算下列各积分⎰2)()8dx x f ，其中⎪⎩⎪⎨⎧+=2211)(x x x f11>≤x x9.设k ，l 为正整数，且l k ≠，试证下列各题： 10.计算下列定积分11.利用函数的奇偶性计算下列积分12．设f （x ）在[]b a ,上连续，证明：⎰⎰-+=ba ba dx xb a f dx x f )()(13．证明：)0(1111212>+=+⎰⎰x x dx x dx x x14．计算下列定积分15.判定下列反常积分的收敛性，如果收敛，计算反常积分的值。

1）⎰∞+14xdx2）⎰+∞-0dx e ax ()0>a3）dx ee x x ⎰∞+-+014）⎰+∞->>0)0,0(sin ωωp tdt e pt5）⎰-121x xdx 6）⎰-211x xdx7）⎰∞+∞-++222x x dx8）()⎰-e x x dx 12ln 1 (B)1．填空： 1）________)12111(lim =++++++∞→nn n n n 。

2）估计定积分的值：_____sin 1____342≤+≤⎰ππx dx。

3）运用积分中值定理可得：⎰-→xa a x x f dt t f a x )(()(1lim 是连续函数）＝________，______)0(sin lim =>⎰+∞→a dx xxa n n n 。

高等数学第五章定积分试题

第五章定积分§5—1 定积分概念一、填空题1． )(x f 在[a,b]上可积的充分条件是。

2． nn knk n ∑=∞→1lim用定积分表示可表示成。

3．由定积分的几何意义知⎰-ππxdx sin = ，⎰-ππxdx sin = 。

4．定积分dx x a aa⎰--22的几何意义是。

二．判断题。

1．若f(x)在[ a,b]上有界，则f(x)在[a,b]上可积。

（） 2．若f(x)在[a,b]上可积，则f(x)在[ a,b]上有界。

（） 3．若f(x)、g(x)在[a,b]上都不可积，则f(x)+g(x)在[a,b]上必不可积。

（） 5．若f(x)在[a,b]上可积，则g(x) )在[a,b]上不可积，则f(x)+g(x)在[a,b]上一定不可积。

（）三．单项选择题。

1．定积分⎰badx x f )(表示和式的极限是。

（A ）、))((1l i ma b nkf n a b n k n --∑=∞→ （B ）、))(1(1l i ma b nk f n a b n k n ---∑=∞→ （C ）∑=∞→∆nk k kn x f 1)(l i m ξ（i ξ为i x ∆中任一点）（D ）、∑=∞→∆nk k kx f 1)(l i m ξλ（}{max 1i ni x ∆=≤≤λ，i ξ为i x ∆中任一点）2．定积分⎰badx x f )(=∑=∞→∆nk kkxf 1)(l i m ξλ表明（A ）、[b a ,]必须n 等分,k ξ是[x k-1,x k ]的端点。

（B ）、[b a ,]可以任意分,ξk必是[x k-1,x k ]的端点。

（C ）、[b a ,]可以任意分, }m ax{1x k nk ∆≤≤=λ，k ξ可在[x k-1,x k ]上任取。

（D ）、[b a ,]必须等分, }m ax{1x k nk ∆≤≤=λ，k ξ可在[x k-1,x k ]上任取四．利用定积分定义计算 ⎰baxdx )(b a <§5—2 定积分的性质中值定理一、判断题1．若函数)(x f 在[b a ,]上连续，且0)(2=⎰dx x f ba则在[b a ,]上f(x)0≡ （）2．若f(x),g(x)在[b a ,]上可积且f(x)<g(x),则dx x g dx x f baba⎰⎰<)()( （）3．若函数)(x f 在[b a ,]上可积且[d c ,]⊂ [b a ,] 则⎰⎰≤badcdx x f dx x f )()( （）4．若函数)(x f 在[b a ,]上可积，则至少有一点∈δ[b a ,],使⎰-baa b f ))((δ （）5．不等式 32a r c t a n 9331ππ≤≤⎰x d x x 成立。

高等数学题库第05章(定积分)

第五章定积分习题一一．选择题 1.⎰b xt dt e dx d 2的结果为( ) A.2x e B. 2x e - C. 22x b e e - D. 22x xe - 2.设()x f 连续,则()⎰=-→xa ax dt t f ax x lim( ) A.0 B.a C.()a af D. ()a f 3.设函数()⎰-=xdt t y 01,则y 有( )A.极小值21 B. 极小值21- C. 极大值21 D. 极大值21- 4.若()()⎰-=xdt x t dxd x f 0cos ,则()=x f ( ) A.x cos B. x cos - C.x sin D.x sin -5.若()⎰=+122dx k x ,则=k ( )A.0B.-1C.1D.21 6.曲线x y -=42与y 轴所围图形的面积为( ) A.()⎰--2224dy y B. ()⎰-224dy y C.dx x ⎰-44 D. dx x ⎰--444二．填空题1.若物体以速度()()()0≥=t v t v v 作直线运动,用定积分表示从时刻1t 到时刻2t 所经过的路程S,则S= .2.设平面图形由直线)1(,>==b b x x y 和曲线1=xy 所围(第一象限部分),该图形的面积I 的定积分表达式为 .3.()()[]=--⎰-dx x f x f a a.4.⎰-=-11221sin dx xx arc x .5.⎰=bdx x 0.6.设()x f '在[]b a ,连续,且()()1,0==b f a f ,则()()[]⎰=+badx x f x f 2'1 .7.设()x f 在()+∞∞-,一阶可导,()()()⎰≠=x x dt t xf x F 1,0则()=x F '' . 8.⎰=++∞→10421limdx x n nxn .9.若广义积分()⎰+∞2ln kx x dx发散,则k 的取值为 .10.由0,1,4>≥≤x y xy 所夹图形绕y 轴旋转所成旋转体体积V = . 三、计算题 1. 计算⎰+1313arctan dx xx x .2. 计算⎰+∞-0sin xdx e x .3. 求⎰-=xt dt e x f 02)(对x 的导数.4. 计算⎰-⎪⎪⎭⎫⎝⎛-++112)2ln(cos 3tan sin dx x x x x . 5. 计算⎰--22232)1(dx x .6. ⎰e dx x 13)(ln 7. ⎰-1)1(arcsin dx x x x习题二一．选择题1.()x f 在[]b a ,上连续是()⎰ba dx x f 存在的( )A.必要条件B.充分条件C. 充分必要条件D.以上A 、B 、C 都不对 2.在积分中值定理()()()a b f dx x f ba -=⎰ξ中,ξ是( )A. []b a ,内任意一点B. []b a ,的中点C. []b a ,内某一点D. []b a ,内至少存在的某一点3.若()x f 可导,()()20,00'==ff ,则()2limxdt t f xx ⎰→的值为( )A.0B.1C.2D.不存在4.设()()⎪⎩⎪⎨⎧=≠-=⎰0,0,122x a x x dte xf x t 若()x f 在0=x 连续则必有( ) A.1=a B.2=a C.0=a D.1-=a 5.⎰=+b a dx xdx d 211( D ) A.211x + B. 211b + C. 211a+- D.0 6.设()()⎰-=x x f dt t f 02121，且()10=f ,则()x f =( )A.2xe B.x e 21 C.x e 2 D.x e 2217.若()()()⎰+==xtxCdt t e x f e x x g 02122213,,且()()23lim '=+∞→x g x f x ,则必有( ) A.C=0 B.C=1 C.C=-1 D.C=2 8.=⎰-112dx x ( )A.0B.21C.1D.2 9.设()x f ''在[]b a ,连续,且()()b a f a b f =='',,则()()⎰∙b adx x f x f '''=( )A.b a -B. )(21b a -C.22b a -D.)(2122b a -10.若10=⎰+∞-dx ae x 收敛,则=a ( )A.1B.2C.21D. 21- 二．填空题1.设()x f 在积分区间上连续,则()()[]=--⎰-dx x f x f x aa2 .2.定积分⎰-=22cos ππxdx x .3.定积分⎰-=22cos ππxdx x .4.定积分()⎰-=+ππdx x xsin 2.5.定积分⎰-=+222cos 1sin ππdx x x.6.设()⎰=x tdt x f 0tan ,则()=x f ' . 7.设()⎰+∙=20321x dt t t x f ,则()=x f ' .8.设()⎰=xtdt x f 1arctan ,则()=x f ' .9.设()⎰=x tdt x f 0sin ,则=⎪⎭⎫⎝⎛2'πf .10.⎰+∞-=02dx e x .三、计算题1. 设⎪⎩⎪⎨⎧≤<+≤≤-=-10 ,1101 ,)(2x x x xe x f x ,求⎰-2 0.)1(dx x f2. 求极限)cos 1()1arctan(lim 0002x x du dt t xu x -⎥⎥⎦⎤⎢⎢⎣⎡+⎰⎰→. 3. ⎰+1)1ln(dx x .4. 将2)(2--=x x xx f 展成x 的幂级数.5. 已知⎪⎩⎪⎨⎧≥+<=+0,)1ln(0,)1(2x x x x xe x f x，求⎰-41)2(dx x f .6.求定积分⎰------6)6)(5)(4)(3)(2)(1(dx x x x x x x x .7．设连续函数)(x f 满足方程x xe dt tf x f +=⎰0)()(，求)(x f .习题三一．选择题1.设()x f 在区间[]b a ,上连续,则()()⎰⎰-babadt t f dx x f 的值( )A.小于0B.大于0C.等于0D.不能确定2.设()x f 在[]b a ,上连续,x 是[]b a ,上的任一点,则下式中是()x f 的一个原函数的是( )A.()⎰dx x fB.()⎰badx x f C.()⎰xadt t f D.()⎰xadt t f '3.设函数()x f 在区间[]b a ,上连续,则下列结论不正确的是( ) A.()⎰badx x f 是()x f 的一个原函数 B.()⎰xadt t f 是()x f 的一个原函数()b x a <<C.()⎰bxdt t f 是-()x f 的一个原函数 D. ()x f 在[]b a ,上是可积的4.设函数()x f 在[]1,0上连续,令x t 4=,则()⎰=14dx x f ( )A.()⎰40dt t f B.()⎰1041dt t f C. ()⎰404dt t f D. ()⎰441dt t f 5.广义积分⎰+∞-+222x x dx( )A.收敛于2ln 32B. 收敛于2ln 23C. 收敛于41ln 31 D.发散6.⎰baxdx dx d arctan 等于( ) A.x arctan B.211x + C.a b arctan arctan - D.07.若函数()x x x f +=3,则()⎰-22dx x f 的值等于( )A.0B.8C. ()⎰20dx x f D. ()⎰22dx x f8.下列定积分等于零的是( )A.⎰-112cos xdx x B. ⎰-11sin xdx x C. ⎰-+11)sin (dx x x D. ⎰-+11)(dx x e x9.变上限积分()⎰xadt t f 是( )A.()x f ' 的一个原函数B.()x f '的全体原函数C.()x f 的一个原函数D.()x f 的全体原函数10.极限⎰⎰→x xx tdttdtsin lim等于( )A.-1B.0C.1D.2二．填空题1.根据定积分的几何意义,有()⎰=-101dx x .2.设(),sin 12dt t x x⎰=ϕ则导数()=x 'ϕ .3.⎰--=121dx x . 4.()⎰=xa dt t f dx d . 5.()⎰=2x a dt t f dx d . 6.()⎰=ua dt t f du d . 7.()⎰=badx x f dx d . 8.=++⎰4122dx x x .9.=⎰210arcsin xdx .10.设()()⎪⎩⎪⎨⎧<+≥+=+,0,1,0,111x e x x x x f x 则定积分()=-⎰201dx x f .三、计算题1. 计算⎰++102132dx x x . 2. 设xxe x f =+)12(, 求⎰53)(dt t f .3. 已知⎰+=+12)1ln()()(2x x f dx x f x , 求⎰1)(dx x f .4. 讨论级数∑∞=-⎪⎭⎫ ⎝⎛--111co s 1)1(n n n 的敛散性, 若收敛,指出其条件收敛或绝对收敛.5. 计算⎰-20)2sin(1πdx x .6. 已知⎪⎩⎪⎨⎧≥<=1,ln 1,)(2x x x x xe x f x ，求.)2(41⎰-dx x f7. 求.)2()1ln(102⎰-+dx x x习题四一．选择题 1.()⎰=+xdt t dx d 021ln （） A ．()1ln 2+x B.()1ln 2+t C.()1ln 22+x x D.()1ln 22+t t 2.=⎰→320sin limx dt t xx ( )A.0B.1C.31D.∞3.下列积分中,使用变换正确的是( )A.⎰+π03,sin 1dx xdx 令t x arctan = B.⎰-3023,1dx x x 令t x sin = C.()⎰-++2122,11ln dx xx x 令21x u += D.⎰--112,1dx x 令31t x = 4.下列积分中,值为零的是( )A.⎰-112dx x B.⎰-213dx x C.⎰-11dx D.⎰-112sin xdx x二．填空题1. 若2x e -为)(x f 的一个原函数，则='⎰1)(dx x f x .2. 函数⎰--=xdt t t y 02)2()1(的极小值点是 .3. 若)(x f 在R 上连续，则=⎰-aadt x f x )(cos 3 .4. 若⎰+=yx t dt e y x f 402),(，则='),(y x f x .5. 若⎰=x t dt xe x f 0)(，则=dxdf. 6. ⎰+∞-=04dx e x x .7. 若平面区域{}0,4),(22≥≤+=y y x y x D ，则=⎰⎰Ddxdy .8. =⎰∞→32sin limt xdx x tt . 9. 设,sin )(C xxdx x f +=⎰则=⎰362)(ππdx x xf .10. 设,)sin 3()( 02⎰+=x dt t t x f 则=→23)(limx x f x . 三、计算题1. 求连续函数),(x f 使其满足20)(2)(x dt t f x f x=+⎰.2. 计算⎰-12112dx ex .3. 计算⎰-0|cos sin |πdx x x .4. 讨论⎰+∞dx e ax 的敛散性.5. 设x e x f -=)(，（1）求dx x f ⎰)(;（2）若)()(x f x F ='，且1)0(=F ，求)(x F 的表达式；（3）计算⎰ba dx x f )(；（4）判别⎰+∞1)(dx x f 的收敛性，若收敛，求其值；（5）求202)(lim2xdt t f x x ⎰→；6. 计算⎰-12112dx ex .7. 可微函数)(x f y =满足⎰-=-xdt t f x f 0]1)(2[1)(，求：（1）)0(f ; （2）)(x f答案习题一一．选择题 1.⎰b xt dt e dx d 2的结果为( B ) A.2x e B. 2x e - C. 22x b e e - D. 22x xe - 2.设()x f 连续,则()⎰=-→xa ax dt t f ax x lim( C ) A.0 B.a C.()a af D. ()a f 3.设函数()⎰-=xdt t y 01,则y 有( B )A.极小值21 B. 极小值21- C. 极大值21 D. 极大值21-4.若()()⎰-=xdt x t dx d x f 0cos ,则()=x f ( A ) A.x cos B. x cos - C.x sin D.x sin -5.若()⎰=+122dx k x ,则=k ( C )A.0B.-1C.1D.21 6.曲线x y -=42与y 轴所围图形的面积为( A ) A.()⎰--2224dy y B. ()⎰-224dy y C.dx x ⎰-44 D. dx x ⎰--444二．填空题1.若物体以速度()()()0≥=t v t v v 作直线运动,用定积分表示从时刻1t 到时刻2t 所经过的路程S,则S= . ()⎰21t t dt t v2.设平面图形由直线)1(,>==b b x x y 和曲线1=xy 所围(第一象限部分),该图形的面积I 的定积分表达式为 . ⎰⎪⎭⎫⎝⎛-b dx x x 113.()()[]=--⎰-dx x f x f aa. 04.⎰-=-11221sin dx xx arc x . 05.⎰=b dx x 0 . 221b ± 6.设()x f '在[]b a ,连续,且()()1,0==b f a f ,则()()[]⎰=+badx x f x f 2'1 .4π 7.设()x f 在()+∞∞-,一阶可导,()()()⎰≠=x x dt t xf x F 1,0则()=x F '' . ⎪⎭⎫⎝⎛x f x 11'3 8.⎰=++∞→10421limdx x n nx n . 4π9.若广义积分()⎰+∞2ln kx x dx发散,则k 的取值为 . 1>k10.由0,1,4>≥≤x y xy 所夹图形绕y 轴旋转所成旋转体体积V = . π 三、计算题 1. 计算⎰+1313arctan dx xx x .2. 计算⎰+∞-0sin xdx e x .3. 求⎰-=xt dt e x f 02)(对x 的导数.4. 计算⎰-⎪⎪⎭⎫⎝⎛-++112)2ln(cos 3tan sin dx x x x x . 5. 计算⎰--22232)1(dx x .6. ⎰e dx x 13)(ln 7. ⎰-1)1(arcsin dx x x x习题二一．选择题1.()x f 在[]b a ,上连续是()⎰ba dx x f 存在的( B )A.必要条件B.充分条件C. 充分必要条件D.以上A 、B 、C 都不对 2.在积分中值定理()()()a b f dx x f ba -=⎰ξ中,ξ是( D )A. []b a ,内任意一点B. []b a ,的中点C. []b a ,内某一点D. []b a ,内至少存在的某一点 3.若()x f 可导,()()20,00'==ff ,则()2limx dt t f xx ⎰→的值为( B ) A.0 B.1 C.2 D.不存在4.设()()⎪⎩⎪⎨⎧=≠-=⎰0,0,122x a x x dte xf x t 若()x f 在0=x 连续则必有( C ) A.1=a B.2=a C.0=a D.1-=a 5.⎰=+b a dx x dx d 211( D ) A.211x + B. 211b + C. 211a+- D.06.设()()⎰-=xx f dt t f 02121，且()10=f ,则()x f =( C ) A.2xe B.x e 21 C.x e 2 D.x e 2217.若()()()⎰+==xtxCdt t e x f e x x g 02122213,,且()()23lim '=+∞→x g x f x ,则必有( B ) A.C=0 B.C=1 C.C=-1 D.C=2 8.=⎰-112dx x ( C )A.0B.21C.1D.2 9.设()x f ''在[]b a ,连续,且()()b a f a b f =='',,则()()⎰∙b adx x f x f '''=( D )A.b a -B. )(21b a -C.22b a -D.)(2122b a -10.若10=⎰+∞-dx ae x 收敛,则=a ( C )A.1B.2C.21D. 21- 二．填空题1.设()x f 在积分区间上连续,则()()[]=--⎰-dx x f x f x aa2 . 02.定积分⎰-=22cos ππxdx x . 03.定积分⎰-=22cos ππxdx x . 04.定积分()⎰-=+ππdx x xsin 2. 332π5.定积分⎰-=+222cos 1sin ππdx x x. 06.设()⎰=x tdt x f 0tan ,则()=x f ' . x tan7.设()⎰+∙=20321x dt t t x f ,则()=x f ' . 34312x x +∙8.设()⎰=xtdt x f 1arctan ,则()=x f ' . x arctan9.设()⎰=x tdt x f 0sin ,则=⎪⎭⎫⎝⎛2'πf . 110.⎰+∞-=02dx e x .21三、计算题1. 设⎪⎩⎪⎨⎧≤<+≤≤-=-10 ,1101 ,)(2x x x xe x f x ,求⎰-2 0.)1(dx x f2. 求极限)cos 1()1arctan(lim0002x x du dt t xu x -⎥⎥⎦⎤⎢⎢⎣⎡+⎰⎰→. 3. ⎰+1)1ln(dx x .4. 将2)(2--=x x xx f 展成x 的幂级数.5. 已知⎪⎩⎪⎨⎧≥+<=+0,)1ln(0,)1(2x x x x xe x f x，求⎰-41)2(dx x f .6.求定积分⎰------6)6)(5)(4)(3)(2)(1(dx x x x x x x x .7．设连续函数)(x f 满足方程x xe dt tf x f +=⎰0)()(，求)(x f .习题三一．选择题1.设()x f 在区间[]b a ,上连续,则()()⎰⎰-babadt t f dx x f 的值( C )A.小于0B.大于0C.等于0D.不能确定2.设()x f 在[]b a ,上连续,x 是[]b a ,上的任一点,则下式中是()x f 的一个原函数的是( C )A.()⎰dx x fB.()⎰badx x f C.()⎰xadt t f D.()⎰xadt t f '3.设函数()x f 在区间[]b a ,上连续,则下列结论不正确的是( A ) A.()⎰b adx x f 是()x f 的一个原函数 B.()⎰xadt t f 是()x f 的一个原函数()b x a <<C.()⎰b xdt t f 是-()x f 的一个原函数 D. ()x f 在[]b a ,上是可积的 4.设函数()x f 在[]1,0上连续,令x t 4=,则()⎰=104dx x f ( D )A.()⎰4dt t f B. ()⎰1041dt t f C. ()⎰404dt t f D. ()⎰441dt t f5.广义积分⎰+∞-+222x x dx( A )A.收敛于2ln 32B. 收敛于2ln 23C. 收敛于41ln 31 D.发散6.⎰baxdx dx d arctan 等于( D ) A.x arctan B.211x + C.a b arctan arctan - D.07.若函数()x x x f +=3,则()⎰-22dx x f 的值等于( A )A.0B.8C. ()⎰20dx x f D. ()⎰22dx x f8.下列定积分等于零的是( C )A.⎰-112cos xdx x B. ⎰-11sin xdx x C. ⎰-+11)sin (dx x x D. ⎰-+11)(dx x e x9.变上限积分()⎰xadt t f 是( C )A.()x f ' 的一个原函数B.()x f '的全体原函数C.()x f 的一个原函数D.()x f 的全体原函数10.极限⎰⎰→x xx tdttdtsin lim等于( C )A.-1B.0C.1D.2二．填空题1.根据定积分的几何意义,有()⎰=-101dx x .21 2.设(),sin 12dt t x x⎰=ϕ则导数()=x 'ϕ . 2sin x3.⎰--=121dx x . 2ln - 4.()⎰=xa dt t f dx d . ()x f 5.()⎰=2x a dt t f dx d . ()22x xf 6.()⎰=ua dt t f du d . ()u f 7.()⎰=badx x f dx d . 0 8.=++⎰4122dx x x .322 9.=⎰210arcsin xdx .12312-+π10.设()()⎪⎩⎪⎨⎧<+≥+=+,0,1,0,111x e x x x x f x 则定积分()=-⎰201dx x f . 2ln 1+三、计算题1. 计算⎰++102132dx x x . 2. 设x xe x f =+)12(, 求⎰53)(dt t f .3. 已知⎰+=+12)1ln()()(2x x f dx x f x , 求⎰1)(dx x f .4. 讨论级数∑∞=-⎪⎭⎫ ⎝⎛--111co s 1)1(n n n 的敛散性, 若收敛,指出其条件收敛或绝对收敛.5. 计算⎰-20)2sin(1πdx x .6. 已知⎪⎩⎪⎨⎧≥<=1,ln 1,)(2x x x x xe x f x ，求.)2(41⎰-dx x f7. 求.)2()1ln(102⎰-+dx x x习题四一．选择题 1.()⎰=+xdt t dx d 021ln （ A ） A ．()1ln 2+x B.()1ln 2+t C.()1ln 22+x x D.()1ln 22+t t2.=⎰→320sin limx dt t xx ( C )A.0B.1C.31D.∞3.下列积分中,使用变换正确的是( C )A.⎰+π03,sin 1dx xdx 令t x arctan = B.⎰-3023,1dx x x 令t x sin =C.()⎰-++2122,11ln dx xx x 令21x u += D.⎰--112,1dx x 令31t x = 4.下列积分中,值为零的是( A )A.⎰-112dx x B.⎰-213dx x C.⎰-11dx D.⎰-112sin xdx x二．填空题1. 若2x e -为)(x f 的一个原函数，则='⎰1)(dx x f x .2. 函数⎰--=xdt t t y 02)2()1(的极小值点是 .3. 若)(x f 在R 上连续，则=⎰-aadt x f x )(cos 3 .4. 若⎰+=yx t dt e y x f 402),(，则='),(y x f x .5. 若⎰=x t dt xe x f 0)(，则=dxdf. 6. ⎰+∞-=04dx e x x .7. 若平面区域{}0,4),(22≥≤+=y y x y x D ，则=⎰⎰Ddxdy .8. =⎰∞→32sin limt xdx x tt . 9. 设,sin )(C xxdx x f +=⎰则=⎰362)(ππdx x xf .10. 设,)sin 3()( 02⎰+=x dt t t x f 则=→23)(limx x f x . 三、计算题1. 求连续函数),(x f 使其满足20)(2)(x dt t f x f x=+⎰.2. 计算⎰-12112dx ex .3. 计算⎰-20|cos sin |πdx x x .4. 讨论⎰+∞dx e ax 的敛散性.5. 设x e x f -=)(，（1）求dx x f ⎰)(;（2）若)()(x f x F ='，且1)0(=F ，求)(x F 的表达式；（3）计算⎰ba dx x f )(；（4）判别⎰+∞1)(dx x f 的收敛性，若收敛，求其值；（5）求202)(lim2xdt t f x x ⎰→；6. 计算⎰-12112dx ex .7. 可微函数)(x f y =满足⎰-=-xdt t f x f 0]1)(2[1)(，求：（1）)0(f ; （2）)(x f。

高等数学第五章定积分习题课

∫
b
a
f ( x )dx ≤ ∫ g ( x )dx
a
b
⑧估值定理：设M 和 m 分别是函数 f ( x )在区间[a, b ]上的估值定理：最大值和最小值，最大值和最小值，则
m (b − a ) ≤ ∫ f ( x )dx ≤ M (b − a )
a b
上连续, ⑨定积分中值定理：如果函数 f ( x ) 在闭区间[a, b ] 上连续定积分中值定理：则至少存在一点ξ ∈(a , b) ,使下式成立：使下式成立：使下式成立
b b b
b
a
b
b
∫
b
a
f ( x )dx = ∫ f ( x )dx + ∫ f ( x )dx
a c
c
b
⑤区间长： ∫ 1dx = b − a 区间长：
a
b
保号性： ⑥保号性：如果在区间[a, b ]上, f ( x ) ≥ 0 ，则∫ a f ( x )dx ≥ 0
b
⑦单调性：如果在区间 [a, b ] 上, f ( x ) ≤ g ( x ) 则单调性：
b
∫
b
a
f ( x )dx = lim ∫ f ( x )dx −
t →b a
t
设 c ( a < c < b ) 为 f ( x ) 的瑕点，则有的瑕点，
∫
b a
f ( x )dx = ∫ f ( x )dx + ∫ f ( x )dx
a c
c
b
= lim ∫ f ( x )dx + lim ∫ f ( x )dx − +
∫
b
a
f ′( x )dx = [ f ( x )] a = f (b) − f (a ) = a − b

大学高等数学第五章定积分及其应用答案

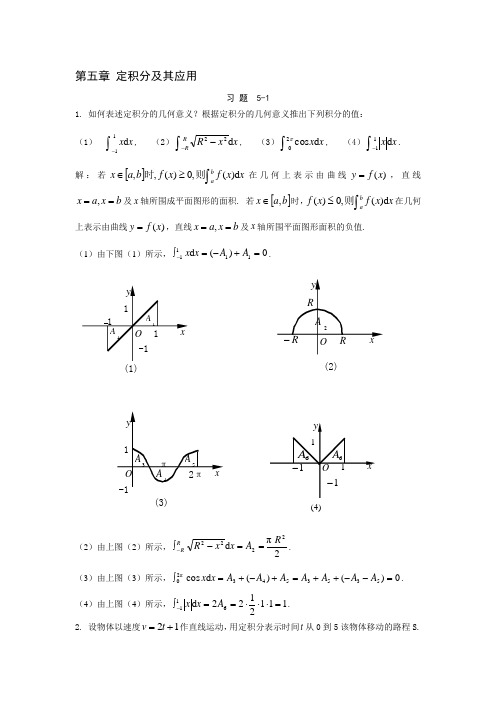
第五章定积分及其应用习题 5-11. 如何表述定积分的几何意义？根据定积分的几何意义推出下列积分的值：（1）⎰-x x d 11, （2）⎰--x x R R R d 22, （3）⎰x x d cos 02π, （4）⎰-x x d 11.解：若[]⎰≥∈x x f x f b a x ab d )(,0)(,,则时在几何上表示由曲线)(x f y =，直线b x a x ==,及x 轴所围成平面图形的面积. 若[]b a x ,∈时，⎰≤x x f x f ab d )(,0)(则在几何上表示由曲线)(x f y =，直线b x a x ==,及x 轴所围平面图形面积的负值. （1）由下图（1）所示，0)(d 1111=+-=⎰-A A x x .（2）由上图（2）所示，2πd 2222R A x x R R R==-⎰-.（3）由上图（3）所示，0)()(d cos 5353543π20=--++=+-+=⎰A A AA A A A x x . （4）由上图（4）所示，1112122d 611=⋅⋅⋅==⎰-A x x . 2. 设物体以速度12+=t v 作直线运动，用定积分表示时间t 从0到5该物体移动的路程S.( 2 )( 1 )( 3 )(4)解：=s ⎰+t t d )12(053. 用定积分的定义计算定积分⎰bax c d ,其中c 为一定常数.解：任取分点b x x x x a n =<<<<= 210,把],[b a 分成n 个小区间],[1i i x x -)2,1(n i =，小区间长度记为x ∆i =i x -1-i x )2,1(n i =,在每个小区间[]i i x x ,1-上任取一点i ξ作乘积i i x f ∆⋅)(ξ的和式：∑∑==--=-⋅=∆⋅n i ni i iiia b c x xc x f 111)()()(ξ,记}{max 1i n i x ∆=≤≤λ, 则)()(lim )(lim d 0a b c a b c x f x c ni i i b a-=-=∆⋅=∑⎰=→→λλξ.4. 利用定积分定义计算120d x x ⎰.解：上在]1,0[)(2x x f =连续函数，故可积，因此为方便计算，我们可以对[]0,1 n 等分，分点i i n i nix ξ;1,,2,1,-==取相应小区间的右端点，故 ∑∑∑===∆=∆=∆ni i i ni i i ni i i x x x x f 12121)(ξξ=∑∑===ni ni in n n i 1232111)(=311(1)(21)6n n n n ⋅++ =)12)(11(61nn ++ 当时0→λ（即时∞→n ），由定积分的定义得： 120d x x ⎰=31．5. 利用定积分的估值公式，估计定积分⎰-+-1134)524(x x x d 的值.解：先求524)(34+-=x x x f 在[]1,1-上的最值，由0616)(23=-='x x x f , 得0=x 或83=x . 比较 35093(1)11,(0)5,(),(1)781024f f f f -====的大小，知min max 5093,111024f f ==，由定积分的估值公式，得[])1(1d )524()]1(1[max 1134min --⋅≤+-≤--⋅⎰-f x x x f ,即14315093(425)d 22512x x x -≤-+≤⎰. 6. 利用定积分的性质说明⎰1d xe x与⎰1d 2x e x ，哪个积分值较大？解：在[]0,1区间内：22xx x x e e ≥⇒≥ 由性质定理知道：⎰1d xe x≥⎰1d 2x e x7. 证明：⎰---<<2121212d 22x e ex 。

(完整版)定积分习题及答案

第五章定积分(A 层次)1．⎰203cos sin πxdx x ； 2．⎰-adx x a x222； 3．⎰+31221xxdx ；4．⎰--1145x xdx ； 5．⎰+411x dx ； 6．⎰--14311x dx ；7．⎰+21ln 1e xx dx； 8．⎰-++02222x x dx； 9．dx x ⎰+π02cos 1； 10．dx x x ⎰-ππsin 4； 11．dx x ⎰-224cos 4ππ； 12．⎰-++55242312sin dx x x xx ；13．⎰342sin ππdx x x； 14．⎰41ln dx x x ； 15．⎰10xarctgxdx ； 16．⎰202cos πxdx e x ； 17．()dx x x ⎰π2sin ； 18．()dx x e⎰1ln sin ；19．⎰--243cos cos ππdx x x ； 20．⎰+4sin 1sin πdx xx ； 21．dx x xx ⎰+π02cos 1sin ；22．⎰-+2111ln dx xxx ； 23．⎰∞+∞-++dx x x 4211； 24．⎰20sin ln πxdx ； 25．()()⎰∞+++0211dx x x dxα()0≥α。

(B 层次)1．求由0cos 0=+⎰⎰xyttdt dt e 所决定的隐函数y 对x 的导数dxdy 。

2．当x 为何值时，函数()⎰-=xt dt te x I 02有极值？3．()⎰x x dt t dxd cos sin 2cos π。

4．设()⎪⎩⎪⎨⎧>≤+=1,211,12x x x x x f ，求()⎰20dx x f 。

5．()1lim22+⎰+∞→x dt arctgt xx 。

6．设()⎪⎩⎪⎨⎧≤≤=其它,00,sin 21πx x x f ，求()()⎰=x dt t f x 0ϕ。

7．设()⎪⎪⎩⎪⎪⎨⎧<+≥+=时当时当0,110,11x e x xx f x，求()⎰-21dx x f 。

大一高等数学第五章定积分习题

记为
a f ( x )dx I lim f ( i )xi . 0 i 1
b
n
3、存在定理
可积的两个充分条件：
定理1 当函数 f ( x ) 在区间[a , b] 上连续时，
称 f ( x ) 在区间[a , b] 上可积.
定理2 设函数 f ( x ) 在区间[a , b] 上有界，
x
a
x
f ( t )dt 就是
f ( x ) 在[a , b]上的一个原函数.
定理 3（微积分基本公式）如果F ( x ) 是连续函数
f ( x ) 在区间[a , b] 上的一个原函数，则
a f ( x )dx F (b) F (a )
也可写成
b

b
a
f ( x )dx [ F ( x )]b . a

0
xf (sin x ) f (sin x ) dx dx. 2 2 2 0 1 cos x 1 cos x
例9 设 f ( x ) 在区间 [a , b] 上连续，且 f ( x ) 0. b b dx 证明 f ( x )dx ( b a )2 . a a f ( x) 证作辅助函数
则 f ( x )dx g( x )dx
a a b b
(a b)
（2）
a f ( x )dx a
b
b
f ( x )dx
(a b)
性质6 设 M 及 m 分别是函数 f ( x ) 在区间[a , b]
上的最大值及最小值，
则
m (b a ) a f ( x )dx M (b a ) .
一、主要内容

(完整版)高等数学第五章定积分综合测试题

二、选择题
1.（B）；2.（B）; 3.（A）; 4（D）; 5.（B）.
三、解答题
1.解：
.
2.解:
3.解:
.
4.解:反常积分，被积函数求出后，方可代入或取极限.
.
5.解:令，则
.
6.解:令，则 .
因为，故，
，
由于在上单调递减，，
因此，即 .
6、（10分）设在可积且单调递减，试证对任一，有
.
综合测试A卷答案
一、填空题
1.解:设函数， ,则 = .应填 .
2.解:在区间内，，由积分的性质可知 .应填<.
3.解: .应填 .
4.解: .
应填 .
5.解: .从而 =3.应填3.
二、选择题
1.（C）；2.（B）; 3.（C）; 4（C）; 5.（D）.
第五章定积分测试题B卷
一、是非题正确者画√，错者画（每小题3分共30分）
1、设在上有界，且存在，则
.[]
2、设在上可积且有连续点，当时， .[]
3、设在上连续，且，则时，
[]
4、设是奇函数，则 .[]
5、因为是奇函数，因此 []
6、设，由积分中值定理，存在，使，
从而证出 []
使，由于，
.
3.【√】，因为，，故 .
4.【√】，是奇函数，则也是奇函数，令， .
5.【】, 是无穷间断点且积分发散.
6.【】，不一定存在.
7.【】，函数在其每个有定义的区间上不一定有界的，区间也不一定是闭区间，故不能保证可积.
8.【√】，令 .
9.【√】，是奇函数.

高等数学第五章课后习题答案

班级姓名学号1 第五章定积分1．证明定积分性质：òò=b abadxx f kdx x kf )()(（k 是常数）. 证：òåòå=D =D ==®=®banii ban ii x kf x kf x f k x f k)()(lim )(lim )(1010x x l l 2．估计下列积分值：（1）dxx )sin 1(4542ò+p p解：令x x f 2sin 1)(+=，则02sin cos sin 2)(===x x x x f ‘得驻点：,,221p p==x x 由23)4(,23)4(,1)(,2)2(====p p p pf f f f ，得2)(max ,1)(min ==x f x f 由性质，得pp p p2)(454££òdx x f （2）ò333arctan xdxx 解：令x x x f arctan )(=，01arctan )(2>++=xxx x f ‘，所以)(x f 在]333[，上单调增加，p p33)(max ,36)(min ==\x f x f ，）（）（33333arctan 33336333-££-\òp pxdx x ，即pp32a r c t a n 9333££òx d x x班级班级姓名姓名学号学号3．比较下列积分值的大小：．比较下列积分值的大小：（1）dx x ò12与dxx ò13解：当10££x 时，有23x x £，且23x x -不恒等于0，0312>-\òdx x x ）（，即，即 dxx dxx òò>1212。

（2）ò6pxdx 与ò6sin pxdx解：当60p££x 时，有x x £sin ，且x x sin -不恒等于0，0sin 10>-\òdx x x ）（，即，即 dx x dx x òò>1010sin 。

高数上学期第五章习题部分解答打印稿

选择题(3)解答
练习一2．填充题
填充题(1)解答
填充题(2)解答
由函数ex的马克劳林公式知
填充题(3)解答
填充题(4)解答
填充题(5)解答
综上讨论有：I3<I1<I2．
练习一3．估计积分值的大小
3(1)解答
定积分估值的基本原理是通过被积函数进行估值，即通过被积函数在积分区间上的最大
值和最小值进行估值。对本题
因为f(x)在[a,b]上连续，由连续函数的介值定理，存在[a,b]，使得
练习二1．计算下列函数的导数
1(1)解答
这是一个变上限函数的求导问题。由于其上限是x的函数，且被积式中还含有自变量x，
因此需注意根据导数规则进行计算。
1(2)解答
1(3)解答
这是一个变上限隐函数的求导问题。由隐函数求导法，方程两边对自变量x求导有
9(2)．解答
练习二10．解答
(1)求(x)的表达式
由于(x)是分段函数，故(x)也是分段函数，因而需逐段确定其表达式。
·当x[0,1)时，
·当x[1,2]时，
(2)考察(x)的连续性
由于(x)在其各子段上都是初等函数，要考察(x)的连续性只需考虑其在分段点
x=1处的连续性，即考察(x)在x=1处是否左连续和右连续。
练习四2．解答
此广义积分含参数k，因此需就k的不同取值进行讨论。
由定义，当k=1时
当k1时
练习四3．解答
以此类推可得In=nIn-1=n(n-1)In-2=…=n!I0．
练习四4．解答
(1)求曲线y=ex过原点的切线方程
设切点为(x0,y0)，则曲线y=ex在点(x0,y0)处的切线斜率为ex0，

高等数学课后习题及参考答案(第五章)

高等数学课后习题及参考答案（第五章）习题5-11. 利用定积分定义计算由抛物线y =x 2+1, 两直线x =a 、x =b (b >a )及横轴所围成的图形的面积.解第一步: 在区间[a , b ]内插入n -1个分点i nab a x i -+=(i =1, 2, ⋅ ⋅ ⋅, n -1), 把区间[a , b ]分成n 个长度相等的小区间, 各个小区间的长度为: nab x i -=∆(i =1, 2, ⋅ ⋅ ⋅, n ). 第二步: 在第i 个小区间[x i -1, x i ] (i =1, 2, ⋅ ⋅ ⋅, n )上取右端点i nab a x i i -+==ξ, 作和 nab i n a b a x f S ni i i ni n -⋅+-+=∆=∑∑==]1)[()(211ξ ∑=+-+-+-=n i i na b i n a b a a n a b 12222]1)()(2[ ]6)12)(1()(2)1()(2[)(222n n n n n a b n n n a b a na n a b +++⋅-++⋅-+-= ]16)12)(1()()1)(()[(222+++-++-+-=n n n a b n n a b a a a b . 第三步: 令λ=max{∆x 1, ∆x 2, ⋅ ⋅ ⋅ , ∆x n }nab -=, 取极限得所求面积 ∑⎰=→∆==ni i i ba x f dx x f S 10)(lim )(ξλ]16)12)(1()()1)(()[(lim 222+++-++-+-=∞→n n n a b n n a b a a a b n a b a b a b a b a a a b -+-=+-+-+-=)(31]1)(31)()[(3322.2. 利用定积分定义计算下列积分:(1)xdx ba ⎰(a <b ); (2)dx e x ⎰10.解 (1)取分点为i n a b a x i -+=(i =1, 2, ⋅ ⋅ ⋅, n -1), 则nab x i -=∆(i =1, 2, ⋅ ⋅ ⋅, n ). 在第i 个小区间上取右端点i nab a x i i -+==ξ (i =1, 2, ⋅ ⋅ ⋅, n ). 于是 ∑∑⎰=∞→=∞→-⋅-+=∆=ni n ni i i n ba nab i n a b a x xdx 11)(lim lim ξ )(21]2)1()()([lim )(22222a b n n n a b a b a a b n -=+-+--=∞→. (2)取分点为n i x i =(i =1, 2, ⋅ ⋅ ⋅, n -1), 则nx i 1=∆(i =1, 2, ⋅ ⋅ ⋅, n ). 在第i 个小区间上取右端点nix i i ==ξ (i =1, 2, ⋅ ⋅ ⋅, n ). 于是) (1lim 1lim 21110n n n n n n i n i n xe e e nn e dx e +⋅⋅⋅++==∞→=∞→∑⎰1)1(]1[lim1])(1[1lim 11111-=--=--⋅=∞→∞→e e n e e e e e nnn n nn n n n .3. 利用定积分的几何意义说明下列等式: (1)1210=⎰xdx ; (2)41102π=-⎰dx x ;(3)⎰-=ππ0sin xdx ;(4)⎰⎰=-2022cos 2cos πππxdx xdx .解 (1)⎰102xdx 表示由直线y =2x 、x 轴及直线x =1所围成的面积, 显然面积为1.(2)⎰-1021dx x 表示由曲线21x y -=、x 轴及y 轴所围成的四分之一圆的面积, 即圆x 2+y 2=1的面积的41:41411212ππ=⋅⋅=-⎰dx x .(3)由于y =sin x 为奇函数, 在关于原点的对称区间[-π, π]上与x 轴所夹的面积的代数和为零, 即⎰-=ππ0sin xdx .(4)⎰-22cos ππxdx 表示由曲线y =cos x 与x 轴上]2,2[ππ-一段所围成的图形的面积. 因为cos x为偶函数, 所以此图形关于y 轴对称. 因此图形面积的一半为⎰20cos πxdx , 即⎰⎰=-2022cos 2cos πππxdx xdx .4. 水利工程中要计算拦水闸门所受的水压力, 已知闸门上水的压强p (单位面积上的压力大小)是水深h 的函数, 且有p =9⋅8h (kN/m 2). 若闸门高H =3m , 宽L =2m , 求水面与闸门顶相齐时闸门所受的水压力P .解建立坐标系如图. 用分点i nHx i =(i =1, 2, ⋅ ⋅ ⋅, n -1)将区间[0, H ]分为n 分个小区间, 各小区间的长为nHx i =∆(i =1, 2, ⋅ ⋅ ⋅, n ). 在第i 个小区间[x i -1, x i ]上, 闸门相应部分所受的水压力近似为 ∆P i =9.8x i l ⋅∆x i . 闸门所受的水压力为22118.42)1(lim 8.9lim 8.98.9lim H L nn n H L n Hi n H L x L x P n ni n ni i i n ⋅=+⋅=⋅=∆⋅⋅=∞→=∞→=∞→∑∑.将L =2, H =3代入上式得P =88.2(千牛).5. 证明定积分性质: (1)⎰⎰=ba b a dx x f k dx x kf )()(; (2)a b dx dx ba b a -==⋅⎰⎰1.证明 (1)⎰∑∑⎰=∆=∆==→=→ba ni i i ni i i ba dx x f k x f k x kf dx x kf )()(lim )(lim )(1010ξξλλ.(2)a b a b x x dx ni i ni i ba -=-=∆=∆⋅=⋅→=→=→∑∑⎰)(lim lim 1lim 101010λλλ.6. 估计下列各积分的值: (1)⎰+412)1(dx x ; (2)⎰+ππ4542)sin 1(dx x ;(3)⎰331arctan xdx x ;(4)⎰-022dx e xx.解 (1)因为当1≤x ≤4时, 2≤x 2+1≤17, 所以 )14(17)1()14(2412-⋅≤+≤-⋅⎰dx x , 即 51)1(6412≤+≤⎰dx x . (2)因为当ππ454≤≤x 时, 1≤1+sin 2x ≤2, 所以 )445(2)sin 1()445(14542ππππππ-⋅≤+≤-⋅⎰dx x ,即 ππππ2)sin 1(4542≤+≤⎰dx x .(3)先求函数f (x )=x arctan x 在区间]3 ,31[上的最大值M 与最小值m .21arctan )(xx x x f ++='. 因为当331≤≤x 时, f '(x )>0, 所以函数f (x )=x arctan x 在区间]3 ,31[上单调增加. 于是3631arctan31)31(π===f m , 33arctan 3)3(π===f M .因此)313(3arctan )313(36331-≤≤-⎰ππxdx x ,即32arctan 9331ππ≤≤⎰xdx x . (4)先求函数xx e x f -=2)(在区间[0, 2]上的最大值M 与最小值m .)12()(2-='-x e x f xx , 驻点为21=x .比较f (0)=1, f (2)=e 2,41)21(-=e f ,得41-=e m , M =e 2. 于是)02()02(220412-⋅≤≤-⎰--e dx e e xx,即 41022222---≤≤-⎰e dx dx e e xx .7. 设f (x )及g (x )在[a , b ]上连续, 证明:(1)若在[a , b ]上 f (x )≥0, 且0)(=⎰ba dx x f , 则在[a ,b ]上f (x )≡0; (2)若在[a , b ]上, f (x )≥0, 且f (x )≢0, 则0)(>⎰ba dx x f ;(3)若在[a , b ]上, f (x )≤g (x ), 且⎰⎰=b a ba dx x g dx x f )()(, 则在[ab ]上f (x )≡g (x ).证明 (1)假如f (x )≢0, 则必有f (x )>0. 根据f (x )在[a , b ]上的连续性, 在[a , b ]上存在一点x 0, 使f (x 0)>0, 且f (x 0)为f (x )在[a , b ]上的最大值.再由连续性, 存在[c , d ]⊂[a , b ], 且x 0∈[c , d ], 使当x ∈[c , d ]时, 2)()(0x f x f >. 于是0)(2)()()()()()(0>-≥≥++=⎰⎰⎰⎰⎰c d x f dx x f dx x f dx x f dx x f dx x f dc bd d c c a b a . 这与条件0)(=⎰ba dx x f 相矛盾. 因此在[a ,b ]上f (x )≡0.(2)证法一因为f (x )在[a , b ]上连续, 所以在[a , b ]上存在一点x 0, 使f (x 0)>0, 且f (x 0)为f (x )在[a , b ]上的最大值.再由连续性, 存在[c , d ]⊂[a , b ], 且x 0∈[c , d ], 使当x ∈[c , d ]时, 2)()(0x f x f >. 于是⎰⎰>-≥≥badcc d x f dx x f dx x f 0)(2)()()(0. 证法二因为f (x )≥0, 所以0)(≥⎰ba dx x f . 假如0)(>⎰ba dx x f 不成立. 则只有0)(=⎰ba dx x f , 根据结论(1), f (x )≡0, 矛盾. 因此0)(>⎰ba dx x f . (3)令F (x )=g (x )-f (x ), 则在[a ,b ]上F (x )≥0且0)()()]()([)(=-=-=⎰⎰⎰⎰ba b a b a b a dx x f dx x g dx x f x g dx x F ,由结论(1), 在[a , b ]上F (x )≡0, 即f (x )≡g (x ).4. 根据定积分的性质及第7题的结论, 说明下列积分哪一个的值较大: (1)⎰102dx x 还是⎰103dx x ？(2)⎰212dx x 还是⎰213dx x ？ (3)⎰21ln xdx 还是⎰212)(ln dx x ？ (4)⎰10xdx 还是⎰+10)1ln(dx x ？ (5)⎰10dx e x 还是⎰+10)1(dx x ？解 (1)因为当0≤x ≤1时, x 2≥x 3, 所以⎰⎰≥103102dx x dx x . 又当0<x <1时, x 2>x 3, 所以⎰⎰>103102dx x dx x . (2)因为当1≤x ≤2时, x 2≤x 3, 所以⎰⎰≤213212dx x dx x . 又因为当1<x ≤2时, x 2<x 3, 所以⎰⎰<213212dx x dx x .(3)因为当1≤x ≤2时, 0≤ln x <1, ln x ≥(ln x )2, 所以⎰⎰≥21221)(ln ln dx x xdx . 又因为当1<x ≤2时, 0<ln x <1, ln x >(ln x )2, 所以⎰⎰>21221)(ln ln dx x xdx . (4)因为当0≤x ≤1时, x ≥ln(1+x ), 所以⎰⎰+≥1010)1ln(dx x xdx . 又因为当0<x ≤1时, x >ln(1+x ), 所以⎰⎰+>1010)1ln(dx x xdx .(5)设f (x )=e x -1-x , 则当0≤x ≤1时f '(x ) =e x -1>0, f (x )=e x -1-x 是单调增加的. 因此当0≤x ≤1时, f (x )≥f (0)=0, 即e x ≥1+x , 所以⎰⎰+≥1010)1(dx x dx e x .又因为当0<x ≤1时, e x >1+x , 所以⎰⎰+>1010)1(dx x dx e x .习题5-21. 试求函数⎰=xtdt y 0sin 当x =0及4π=x 时的导数.解 x tdt dx dy x sin sin 0=='⎰, 当x =0时, y '=sin0=0;当4π=x 时, 224sin =='πy .2. 求由参数表示式⎰=tudu x 0sin , ⎰=tudu y 0cos 所给定的函数y 对x的导数.解 x '(t )=sin t , y '(t )=cos t ,t t x t y dx dy cos )()(=''=. 3. 求由⎰⎰=+xy ttdt dt e 00cos 所决定的隐函数y 对x 的导数dxdy. 解方程两对x 求导得 0cos =+'x y e y , 于是ye x dx dy cos -=. 4. 当x 为何值时, 函数⎰-=xt dt te x I 02)(有极值？解 2)(x xe x I -=', 令I '(x )=0, 得x =0.因为当x <0时, I '(x )<0; 当x >0时, I '(x )>0, 所以x =0是函数I (x )的极小值点. 5. 计算下列各导数:(1)⎰+2021x dt t dx d ; (2)⎰+32411x x dt tdx d ; (3)⎰x x dtt dxd cos sin 2)cos(π.解 (1)dxdu dt t du d u x dt t dx d u x ⋅+=+⎰⎰02202112令 421221x x x u +=⋅+=.(2)⎰⎰⎰+++=+323204044111111x x x x dt t dx d dt t dx d dt t dx d ⎰⎰+++-=3204041111x x dt t dx d dt t dx d )()(11)()(11343242'⋅++'⋅+-=x x x x 12281312xx x x +++-=. (3)⎰⎰⎰+-=x x x x dt t dx d dt t dx d dt t dx d cos 02sin 02cos sin 2)cos()cos()cos(πππ))(cos cos cos())(sin sin cos(22'+'-=x x x x ππ )cos cos(sin )sin cos(cos 22x x x x ππ⋅-⋅-= )sin cos(sin )sin cos(cos 22x x x x πππ-⋅-⋅-= )sin cos(sin )sin cos(cos 22x x x x ππ⋅+⋅-= )sin cos()cos (sin 2x x x π-=.6. 计算下列各定积分: (1)⎰+-adx x x 02)13(;解a a a x x x dx x x a a+-=+-=+-⎰230230221|)21()13(.(2)⎰+2142)1(dx xx ;解852)11(31)22(31|)3131()1(333321332142=---=-=+---⎰x x dx x x . (3)⎰+94)1(dx x x ;解94223942194|)2132()()1(x x dx x x dx x x +=+=+⎰⎰6145)421432()921932(223223=+-+=.(4)⎰+33121x dx ; 解 66331arctan 3arctan arctan 13313312πππ=-=-==+⎰x x dx . (5)⎰--212121x dx ; 解3)6(6)21arcsin(21arcsin arcsin 1212121212πππ=--=--==---⎰x x dx .(6)⎰+ax a dx 3022;解aa a ax a x a dx a a30arctan 13arctan 1arctan 1303022π=-==+⎰.(7)⎰-1024x dx ;解60arcsin 21arcsin 2arcsin 41012π=-==-⎰x x dx .(8)dx x x x ⎰-+++012241133; 解 01301221224|)arctan ()113(1133---+=++=+++⎰⎰x x dx x x dx x x x 41)1arctan()1(3π+=----=.(9)⎰---+211e xdx ; 解1ln 1ln ||1|ln 12121-=-=+=+------⎰e x xdx e e .(10)⎰402tan πθθd ;解4144tan )(tan )1(sec tan 4040242πππθθθθθθπππ-=-=-=-=⎰⎰d d .(11)dx x ⎰π20|sin |;解⎰⎰⎰-=ππππ2020sin sin |sin |xdx xdx dx xπππ20cos cos x x +-==-cos π +cos0+cos2π-cos π=4. (12)⎰2)(dx x f , 其中⎪⎩⎪⎨⎧>≤+=1 2111)(2x x x x x f . 解38|)61(|)21(21)1()(213102212102=++=++=⎰⎰⎰x x x dx x dx x dx x f . 7. 设k 为正整数. 试证下列各题: (1)⎰-=ππ0cos kxdx ;(2)⎰-=ππ0sin kxdx ;(3)⎰-=πππkxdx 2cos ;(4)⎰-=πππkxdx 2sin .证明 (1)⎰--=-=--==ππππππ000)(sin 1sin 1|sin 1cos k kk k kx k kxdx . (2))(cos 1cos 1cos 1sin ππππππ-+-=-=--⎰k kk k x k k kxdxcos 1cos 1=+-=ππk kk k(3)πππππππππ=+=+=+=---⎰⎰22|)2sin 21(21)2cos 1(21cos 2kx k x dx kx kxdx . (4)πππππππππ=+=-=-=---⎰⎰22|)2sin 21(21)2cos 1(21sin 2kx k x dx kx kxdx . 8. 设k 及l 为正整数, 且k ≠l . 试证下列各题: (1)⎰-=ππ0sin cos lxdx kx ;(2)⎰-=ππ0cos cos lxdx kx ;(3)⎰-=ππ0sin sin lxdx kx .证明 (1)⎰⎰----+=ππππdx x l k x l k lxdx kx ])sin()[sin(21sin cos0])cos()(21[])cos()(21[=----++-=--ππππx l k l k x l k l k .(2)⎰⎰---++=ππππdx x l k x l k lxdx kx ])cos()[cos(21cos cos0])sin()(21[])sin()(21[=--+++=--ππππx l k l k x l k l k .(3)⎰⎰----+-=ππππdx x l k x l k lxdx kx ])cos()[cos(21sin sin . 0])sin()(21[])sin()(21[=--+++-=--ππππx l k l k x l k l k .9. 求下列极限: (1)xdt t xx ⎰→020cos lim ; (2)⎰⎰→xt xt x dttedt e 0220022)(lim.解 (1)11cos lim cos lim20020==→→⎰x xdt t x xx . (2)22222200022)(2lim)(limx xt x t x xt xt x xedt e dt e dttedt e '⋅=⎰⎰⎰⎰→→222220202lim2limx xt x x x xt x xedte xeedt e ⎰⎰→→=⋅=2212lim 22lim 2020222=+=+=→→x e x e e x x x x x . 10. 设⎩⎨⎧∈∈=]2 ,1[ ]1 ,0[ )(2x x x x x f . 求⎰=x dt t f x 0)()(ϕ在[0, 2]上的表达式,并讨论ϕ(x )在(0, 2)内的连续性.解当0≤x ≤1时, 302031)()(x dt t dt t f x xx===⎰⎰ϕ;当1<x ≤2时, 6121212131)()(2211020-=-+=+==⎰⎰⎰x x tdt dt t dt t f x xxϕ.因此 ⎪⎩⎪⎨⎧≤<-≤≤=21 612110 31)(23x x x x x ϕ.因为31)1(=ϕ, 3131lim )(lim 30101==-→-→x x x x ϕ,316121)6121(lim )(lim 20101=-=-=+→+→x x x x ϕ,所以ϕ(x )在x =1处连续, 从而在(0, 2)内连续.11. 设⎪⎩⎪⎨⎧><≤≤=ππx x x x x f 或0 00 sin 21)(. 求⎰=x dt t f x 0)()(ϕ在(-∞, +∞)内的表达式.解当x <0时,00)()(0===⎰⎰xxdt dt t f x ϕ;当0≤x ≤π时,21cos 21|cos 21sin 21)()(000+-=-===⎰⎰x t tdt dt t f x xxxϕ;当x >π时,πππϕ000|cos 210sin 21)()(t dt tdt dt t f x x x-=+==⎰⎰⎰10cos 21cos 21=+-=π.因此 ⎪⎩⎪⎨⎧≥≤≤-<=ππϕx x x x x 10 )cos 1(210 0)(.12. 设f (x )在[a , b ]上连续, 在(a , b )内可导且f '(x )≤0,⎰-=x a dt t f ax x F )(1)(. 证明在(a , b )内有F '(x )≤0.证明根据积分中值定理, 存在ξ∈[a , x ], 使))(()(a x f dt t f xa -=⎰ξ.于是有)(1)()(1)(2x f ax dt t f a x x F x a -+--='⎰ ))(()(1)(12a x f a x x f a x ----=ξ )]()([1ξf x f ax --=.由 f '(x )≤0可知f (x )在[a , b ]上是单调减少的, 而a ≤ξ≤x , 所以f (x )-f (ξ)≤0. 又在(a , b )内, x -a >0, 所以在(a , b )内)]()([1)(≤--='ξf x f a x x F .习题5-31. 计算下列定积分:(1)⎰+πππ2)3sin(dx x ;解 0212132cos 34cos)3cos()3sin(22=-=+-=+-=+⎰ππππππππx dx x . (2)⎰-+123)511(x dx;解51251110116101)511(2151)511(22122123=⋅+⋅-=+-⋅=+-----⎰x x dx. (3)⎰203cos sin πϕϕϕd ;解⎰⎰-=20323sin cos cos sin ππϕϕϕϕϕd s d410cos 412cos 41cos 4144204=+-=-=πϕπ.(4)⎰-πθθ03)sin 1(d ; 解⎰⎰⎰⎰-+=+=-πππππθθθθθθθθ02002003cos )cos 1(cos sin )sin 1(d d d d34)cos 31(cos 03-=-+=πθθππ.(5)⎰262cos ππudu ;解2626262622sin 4121)2cos 1(21cos ππππππππu u du u udu +=+=⎰⎰836)3sin (sin 41)62(21-=-+-=πππππ.(6)dx x ⎰-2022;解dt t tdt t t x dx x ⎰⎰⎰+=⋅=-202022)2cos 1(cos 2cos 2sin 22ππ令2)2sin 21(20ππ=+=t t .(7)dy y ⎰--22228;解⎰⎰⎰---⋅=-=-44222222cos 2cos 22sin 24228ππxdx x xy dy y dy y 令)2(2)2sin 21(22)2cos 1(224444+=+=+=--⎰πππππy x dx x .(8)⎰-121221dx xx ;解41)cot ()1sin 1(cos sin cos sin 12424224212122πππππππ-=--=-=⋅=-⎰⎰⎰t t dt t tdt t t t x dx x x 令.(9)⎰-adx x a x 0222; 解⎰⎰⎰=⋅⋅=-2024202202222sin4cos cos sin sin ππtdt a tdt a t a t a t a x dx x a xa令164sin 328)4cos 1(84204204204ππππa t a t a dt t a =-=-=⎰. (10)⎰+31221xxdx ;解⎰⎰⋅⋅=+34223122secsec tan 1tan 1ππtdt t t tx xxdx 令3322sin 1sin cos 34342-=-==⎰ππππt dt tt. (11)⎰--1145xxdx ;解61)315(81)5(81454513133211=--=-=--⎰⎰-u u du u u x x xdx 令. (12)⎰+411xdx ;解)32ln 1(2|)1|ln (2)111(2211121212141+=+-=+-=⋅+=+⎰⎰⎰u u du u udu u u x x dx 令.(13)⎰--14311x dx ;解2ln 21|)1|ln (2)111(2)2(11111210210021143-=-+=-+=-⋅-=---⎰⎰⎰u u du u du u u ux x dx 令.(14)⎰-axa xdx 20223;解)13(3)3(3121320202222222022-=--=---=-⎰⎰a x a x a d x a xa xdx a a a.(15)dt te t ⎰-1022;解2110102221021)2(222-----=-=--=⎰⎰e etd e dt tet t t .(16)⎰+21ln 1e x x dx; 解)13(2ln 12ln ln 11ln 1222111-=+=+=+⎰⎰e e e xx d xxx dx .(17)⎰-++02222x x dx;解 2)1arctan(1arctan )1arctan()1(112202022022π=--=+=++=++---⎰⎰x dx x x x dx .(18)⎰-222cos cos ππxdx x ;解32)sin 32(sin sin )sin 21(2cos cos 22322222=-=-=---⎰⎰ππππππx x x d x xdx x . (19)⎰--223cos cos ππdx x x ;解⎰⎰---=-222223cos 1cos cos cos ππππdx x x dx x x34cos 32cos 32sin cos )sin (cos 20230223202=-=+-=--⎰⎰ππππx xxdx x dx x x (20)⎰+π02cos 1dx x .解22cos 2sin 22cos 1000=-==+⎰⎰πππxxdx dx x .2. 利用函数的奇偶性计算下列积分: (1)⎰-ππxdx x sin 4;解因为x 4sin x 在区间[-π, π]上是奇函数, 所以0sin 4=⎰-ππxdx x . (2)⎰-224cos 4ππθθd ;解⎰⎰⎰+==-202204224)22cos 1(8cos 42cos 4ππππθθθθθd x d d ⎰⎰++=++=20202)4cos 212cos 223(2)2cos 2cos 21(2ππθθd x x d x x23)4sin 412sin 23(20πθπ=++=x x . (3)⎰--2121221)(arcsin dx xx ;解⎰⎰⎰=-=--21221022212122)(arcsin )(arcsin 21)(arcsin 21)(arcsin x d x dx xx dx xx324)(arcsin 3232103π==x .(4)⎰-++55242312sin dx x x xx . 解因为函数12sin 2423++x x x x 是奇函数, 所以012sin 552423=++⎰-dx x x x x .3. 证明:⎰⎰-=aa adx x dx x 022)(2)(ϕϕ, 其中ϕ(u )为连续函数.证明因为被积函数ϕ(x 2)是x 的偶函数, 且积分区间[-a , a ]关于原点对称, 所以有⎰⎰-=aa adx x dx x022)(2)(ϕϕ.4. 设f (x )在[-b , b ]上连续, 证明⎰⎰---=bb bb dx x f dx x f )()(. 证明令x =-t , 则dx =-dt , 当x =-b 时t =b , 当x =b 时t =-b , 于是⎰⎰⎰----=--=b b bb bbdt t f dt t f dx x f )()1)(()(,而 ⎰⎰---=-bb bb dx x f dt t f )()(, 所以⎰⎰---=bb bb dx x f dx x f )()(.5. 设f (x )在[a , b ]上连续., 证明⎰⎰-+=ba ba dx xb a f dx x f )()(. 证明令x =a +b -t , 则dx =d t , 当x =a 时t =b , 当x =b 时t =a , 于是 ⎰⎰⎰-+=--+=b a ba ab dt t b a f dt t b a f dx x f )()1)(()(, 而 ⎰⎰-+=-+ba badx x b a f dt t b a f )()(,所以⎰⎰-+=ba ba dx xb a f dx x f )()(.6. 证明:⎰⎰>+=+11122)0(11x x x x dxx dx. 证明令t x 1=, 则dt tdx 21-=, 当x =x 时x t 1=, 当x =1时t =1, 于是⎰⎰⎰+=-⋅+=+11121122211)1(1111xx xdt t dt t tx dx , 而 ⎰⎰+=+x x dx x dt t 1121121111,所以 ⎰⎰+=+1112211x xxdx x dx.7. 证明:⎰⎰-=-1010)1()1(dx x x dx x xm n n m.证明令1-x =t , 则⎰⎰⎰⎰-=-=--=-10100110)1()1()1()1(dx x x dt t t dt t t dx x x m n n m n m n m , 即⎰⎰-=-1010)1()1(dx x x dx x x m n n m . 8. 证明: ⎰⎰=ππ020sin 2sinxdx xdx n n.证明 ⎰⎰⎰+=ππππ2020sin sin sin xdx xdx xdx nn n,而⎰⎰⎰⎰==---=2020202sin sin ))((sin sinπππππππxdx tdt dt t t x xdx n n nn 令,所以⎰⎰=ππ020sin 2sinxdx xdx n n.9. 设f (x )是以l 为周期的连续函数, 证明⎰+1)(a a dx x f 的值与a 无关.证明已知f (x +l )=f (x ). ⎰⎰⎰⎰⎰⎰⎰-+=++=+++ala ll la ll a a adx x f dx x f dx x f dx x f dx x f dx x f dx x f 00001)()()()()()()(,而 ⎰⎰⎰⎰=+=++=+a a ala ldx x f dx l x f dt l t f l t x dx x f 000)()()()(令,所以 ⎰⎰=+la adx x f dx x f 01)()(.因此⎰+1)(a adx x f 的值与a 无关.10. 若f (t )是连续函数且为奇函数, 证明⎰xdt t f 0)(是偶函数; 若f (t )是连续函数且为偶函数, 证明⎰xdt t f 0)(是奇函数. 证明设⎰=xdt t f x F 0)()(.若f (t )是连续函数且为奇函数, 则f (-t )=-f (t ), 从而)()()()1)(()()(0000x F dx x f dx u f du u f u t dt t f x F x x xx ===---==-⎰⎰⎰⎰-令,即⎰=xdt t f x F 0)()(是偶函数.若f (t )是连续函数且为偶函数, 则f (-t )=f (t ), 从而)()()()1)(()()(0000x F dx x f dx u f du u f u t dt t f x F x x x x -=-=-=---==-⎰⎰⎰⎰-令,即⎰=xdt t f x F 0)()(是奇函数.11. 计算下列定积分: (1)⎰-10dx xe x ; 解11011010101021--------=--=+-=-=⎰⎰⎰e e e dx e xe xde dx xe xx x x x .(2)⎰e xdx x 1ln ; 解)1(414121121ln 21ln 21ln 21220212121+=-=⋅-==⎰⎰⎰e x e dx x x x x xdx xdx x ee e e e.(3)⎰ωπω20sin tdt t (ω为常数); 解⎰⎰⎰+-=-=ωπωπωπωπωωωωωωω20202020cos 1cos 1cos 1sin tdt tt t td tdt t 220222sin 12ωπωωωπωπ-=+-=t.(4)⎰342sin ππdx xx;解34343434342sin ln 4313cot cot cot sin ππππππππππππxxdx xx x xd dx x x++⋅-=+-=-=⎰⎰⎰23ln 21)9341(+-=π.(5)⎰41ln dx x x; 解 ⎰⎰⎰⋅-==4141414112ln 2ln 2ln dx xx x x x xd dx xx )12ln 2(442ln 8122ln 84141-=-=-=⎰x dx x.(6)⎰10arctan xdx x ;解x d x x x x xdx xdx x ⎰⎰⎰+⋅-==1022102102101121arctan 21arctan 21arctan214)41(218)arctan (218)111(21810102-=--=--=+--=⎰πππππx x x d x. (7)⎰202cos πxdx e x ; 解⎰⎰⎰-==202202202202sin 2sin sin cos ππππxdx e xe x d e xdx e x x x x⎰⎰⎰-+=-+=+=202202202202cos 42cos 4cos 2cos 2πππππππxdx e e xdx e xe e x d e e x x xx所以)2(51cos 202-=⎰ππe xdx e x ,于是(8)⎰212log xdx x ; 解⎰⎰⎰⋅-==212212221222122ln 121log 21log 21log dx x x x x xdx xdx x2ln 432212ln 212212-=⋅-=x . (9)⎰π02)sin (dx x x ; 解⎰⎰⎰-=-=ππππ02302022sin 4161)2cos 1(21)sin (x d x x dx x x dx x x πππππππ03000332cos 41622sin 412sin 416⎰⎰-=⋅+-=xxd xdx x xx 462sin 81462cos 412cos 416303003ππππππππ-=+-=+-=⎰x xdx x x .(10)⎰edx x 1)sin(ln ; 解法一 ⎰⎰⋅=101sin ln )sin(ln dt e t tx dxx te令.因为⎰⎰⎰-==⋅10101010cos sin sin sin tdt e te tde dt e t t tt t⎰⎰--⋅=-⋅=101010sin cos 1sin cos 1sin tdt e t e e tde e t t t⎰-+⋅-⋅=10sin 11cos 1sin tdt e e e t , 所以 )11cos 1sin (21sin 10+⋅-⋅=⎰e e tdt e t .因此)11cos 1sin (21)sin(ln 1+⋅-⋅=⎰e e dx x e. 解法二⎰⎰⎰-⋅=⋅⋅-⋅=e e eedx x e dx x x x x x dx x 1111)cos(ln 1sin 1)cos(ln )sin(ln )sin(ln ⎰⋅⋅-⋅-⋅=e edx x x x x x e 111)sin(ln )cos(ln 1sin ⎰-+⋅-⋅=edx x e e 0)sin(ln 11cos 1sin , 故)11cos 1sin (21)sin(ln 1+⋅-⋅=⎰e e dx x e . (11)dx x e e⎰1|ln |; 解⎰⎰⎰⎰⎰-++-=+-=eee eee e e dx dx xx x x dx x dx x dx x 1111111111ln ln ln ln |ln |)11(2)1()11(1ee e e e -=---++-=.(12)⎰-1022)1(dx xm (m 为自然数); 解⎰⎰+=-2011022cos sin )1(πtdt t x dx xm m 令.根据递推公式⎰⎰--=20220cos 1cos ππxdx n n xdx n n ,⎪⎩⎪⎨⎧⋅⋅⋅⋅⋅--⋅--⋅+⋅⋅⋅⋅⋅⋅--⋅--⋅+=-⎰为偶数为奇数m m m m m m m m m m m m m m dx x m325476 34121 2214365 34121)1(1022π. (13)⎰=π0sin xdx x J m m (m 为自然数). 解因为⎰⎰⎰⎰-=----=ππππππππ0000sin sin )1)((sin )(sin tdt t tdt dt t t t x xdx x mm m m 令,所以 ⎰⎰⎰⎰=⋅===20200sin sin 22sin 2sin πππππππxdx xdx xdx xdx x J m m mmm (用第8题结果).根据递推公式⎰⎰--=20220sin 1sin ππxdx n n xdx n n , ⎪⎩⎪⎨⎧⋅⋅⋅⋅⋅--⋅--⋅-⋅⋅⋅⋅⋅⋅--⋅--⋅-=为奇数为偶数m m m m m m m m m m m m m m J m 325476 45231 2214365 452312ππ.习题5-71. 判别下列各反常积分的收敛性, 如果收敛, 计算反常积分的值:(1)⎰+∞14xdx; 解因为3131)31(lim 3131314=+-=-=-+∞→+∞-+∞⎰x x x dx x , 所以反常积分⎰+∞14x dx收敛, 且3114=⎰∞+x dx . (2)⎰+∞1xdx ;解因为+∞=-==+∞→+∞∞+⎰22lim 211x xxdx x , 所以反常积分⎰+∞1xdx 发散.(3)dx e ax ⎰+∞-0(a >0); 解因为aa e a e adx e ax x ax ax 11)1(lim 100=+-=-=-+∞→+∞-+∞-⎰, 所以反常积分dx e ax ⎰+∞-0收敛, 且adx e ax 10=⎰+∞-.(4)⎰+∞-0ch tdt e pt (p >1); 解因为1]1111[21][21ch 2)1()1(0)1()1(0-=+--=+=+∞+--∞++--∞+-⎰⎰p p e pe p dt e e tdt e tp t p t p tp pt ,所以反常积分⎰+∞-0ch tdt e pt 收敛, 且1ch 20-=⎰∞+-p p tdt e pt .(5)⎰+∞-0sin tdt e pt ω(p >0, ω>0); 解⎰⎰+∞-+∞--=0cos 1sin t d e tdt e pt pt ωωω⎰⎰+∞-+∞-+∞--=-⋅+-=020sin 1)(cos 1cos 1t d e pdt pe t te pt pt pt ωωωωωωω⎰+∞-+∞--⋅+-=0202)(sin sin 1dt pe t pte p ptpt ωωωωω⎰+∞--=022sin 1tdt e p pt ωωω,所以 22sin w p tdt e pt +=⎰+∞-ωω.(6)⎰+∞∞-++222x x dx;解 πππ=--=+=++=++⎰⎰+∞∞-+∞∞-+∞∞-)2(2)1arctan()1(12222x x dxx x dx .(7)dx xx ⎰-121;解这是无界函数的反常积分, x =1是被积函数的瑕点.11)1(lim 112110212=+--=--=--→⎰x x dx x x x . (8)⎰-22)1(x dx;解这是无界函数的反常积分, x =1是被积函数的瑕点. 因为⎰⎰⎰-+-=-212102202)1()1()1(x dxx dx x dx , 而 +∞=--=-=--→⎰111lim 11)1(110102xx x dx x ,所以反常积分⎰-202)1(x dx发散. (9)⎰-211x xdx ;解这是无界函数的反常积分, x =1是被积函数的瑕点.21232121]12)1(32[)111(1-+-=-+-=-⎰⎰x x dx x x x xdx322]12)1(32[lim 38231=-+--=+→x x x . (10)⎰-ex x dx 12)(ln 1.解这是无界函数的反常积分, x =e 是被积函数的瑕点.2)arcsin(ln lim )arcsin(ln ln )(ln 11)(ln 111212π===-=--→⎰⎰x x x d x x x dx ex e ee.2. 当k 为何值时, 反常积分⎰+∞)(ln kx x dx收敛? 当k 为何值时, 这反常积分发散? 又当k 为何值时, 这反常积分取得最小值?解当k <1时, +∞=-==+∞+-+∞+∞⎰⎰2122)(ln 11ln )(ln 1)(ln k k k x k x d x x x dx ;当k =1时, +∞===+∞+∞+∞⎰⎰222)ln(ln ln ln 1)(ln x x d x x x dxk ; 当k >1时,k k kkk x kx d x x x dx -+∞+-+∞+∞-=-==⎰⎰12122)2(ln 11)(ln 11ln )(ln 1)(ln . 因此当k >1时, 反常积分⎰+∞0)(ln k x x dx 收敛; 当k ≤1时, 反常积分⎰+∞0)(ln k x x dx发散. 当k >1时, 令k kk x x dx k f -∞+-==⎰10)2(ln 11)(ln )(, 则 )2ln ln 11()1(2ln ln )2(ln 2ln ln )2(ln 11)2(ln )1(1)(21112+---=----='---k k k k k f k kk. 令f '(k )=0得唯一驻点2ln ln 11-=k . 因为当2ln ln 111-<<k 时f '(k )<0, 当2ln ln 11->k 时f '(k )>0, 所以2ln ln 11-=k 为极小值点,同时也是最小值点, 即当2ln ln 11-=k 时, 这反常积分取得最小值 3. 利用递推公式计算反常积分⎰+∞-=0dx e x I x n n . 解因为101000-+∞--+∞-+∞-+∞-=+-=-==⎰⎰⎰n x n x n x n x n n nI dx e x n e x de x dx e x I ,所以 I n = n ⋅(n -1)⋅(n -2)⋅ ⋅ ⋅2⋅I 1. 又因为 1000001=-=+-=-==+∞-+∞-+∞-+∞-+∞-⎰⎰⎰xx xx x e dx e xe xde dx xe I ,所以 I n = n ⋅(n -1)⋅(n -2)⋅ ⋅ ⋅2⋅I 1=n !.总习题五1. 填空:(1)函数f (x )在[a , b ]上(常义)有界是f (x )在[a , b ]上可积的______条件, 而f (x )在[a , b ]上连续是f (x )在[a , b ]上可积______的条件;解函数f (x )在[a , b ]上(常义)有界是f (x )在[a , b ]上可积的___必要___条件, 而f (x )在[a , b ]上连续是f (x )在[a , b ]上可积___充分___的条件;(2)对[a , +∞)上非负、连续的函数f (x ), 它的变上限积分⎰xa dx x f )(在[a , +∞)上有界是反常积分⎰+∞a dx x f )(收敛的______条件;解对[a , +∞)上非负、连续的函数f (x ), 它的变上限积分⎰xa dx x f )(在[a , +∞)上有界是反常积分⎰+∞a dx x f )(收敛的___充分___条件;(3)绝对收敛的反常积分⎰+∞a dx x f )(一定______; 解绝对收敛的反常积分⎰+∞a dx x f )(一定___收敛___;(4)函数f (x )在[a , b ]上有定义且|f (x )|在[a , b ]上可积, 此时积分⎰ba dx x f )(______存在. 解函数f (x )在[a ,b ]上有定义且|f (x )|在[a , b ]上可积, 此时积分⎰b a dx x f )(___不一定___存在.2. 计算下列极限:(1)∑=∞→+n i n nin 111lim ;解 )122(32)1(32111lim 103101-=+=+=+⎰∑=∞→x dx x n i n n i n . (2)121lim+∞→+⋅⋅⋅++p pp p n nn (p >0);解 11111])( )2()1[(lim 21lim 101101+=+==⋅⋅⋅⋅++=+⋅⋅⋅+++∞→+∞→⎰p x p dx x n n n n n n n p p p p p n p p p p n . (3)nn nn !lnlim ∞→; 解 ]ln 1)ln 2ln 1(ln 1[lim !lnlim n n nn n n n n nn ⋅-+⋅⋅⋅++=∞→∞→nn n n n n 1)]ln (ln )ln 2(ln )ln 1[(ln lim ⋅-+⋅⋅⋅+-+-=∞→⎰=⋅+⋅⋅⋅++=∞→10ln 1)ln 2ln 1(ln lim xdx n n n n n n1)ln ()ln (10101010-=-=-=⎰xx x dx x x .(4)⎰-→xaa x dt t f a x x )(lim, 其中f (x )连续; 解法一 )()(lim )(lima af xf dt t f ax x axa ax ==-→→⎰ξξ (用的是积分中值定理). 解法二 )(1)()(lim )(lim )(lim a af x xf dt t f a x dt t f x dt t f a x x xaa x xa a x x a a x =+=-=-⎰⎰⎰→→→ (用的是洛必达法则). (5)1)(arctan lim 22+⎰+∞→x dtt xx .解4)(arctan 1lim 1)(arctan lim 1)(arctan lim 22222202π=+=+=+∞→+∞→+∞→⎰x x x x x x x dtt x x xx . 3. 下列计算是否正确, 试说明理由:(1)⎰⎰----=-=+-=+111111222)1arctan ()1(1)1(1πx xx d x dx ;解计算不正确, 因为x 1在[-1, 1]上不连续. (2)因为⎰⎰--++-=++111122111t t dt tx x x dx , 所以⎰-=++11201x x dx .解计算不正确, 因为t1在[-1, 1]上不连续.(3)01lim 122=+=+⎰⎰-∞→+∞∞-A A A dx x xdx x x . 解不正确, 因为⎰⎰⎰⎰-+∞→+∞→+∞∞--∞→+≠+++=+A A A b b a a dx xxdx x x dx x x dx x x 2020221lim 1lim 1lim 1. 4. 设p >0, 证明⎰<+<+10111p x dx p p. 证明 p pp p p p px x x x x x x ->+-=+-+=+>11111111. 因为⎰⎰⎰<+<-1010101)1(dx x dxdx x pp,而 110=⎰dx , pp p x x dx x p p+=+-=-+⎰1)1()1(10110, 所以⎰<+<+10111pxdx p p. 5. 设f (x )、g (x )在区间[a , b ]上均连续, 证明: (1)⎰⎰⎰⋅≤ba ba ba dx x g dx x f dx x g x f )()(])()([222;证明因为[f (x )-λg (x )]2≥0, 所以λ2g 2(x )-2λ f (x )g (x )+f 2(x )≥0, 从而 0)()()(2)(222≥+-⎰⎰⎰ba ba ba dx x f dx x g x f dx x g λλ.上式的左端可视为关于λ的二次三项式, 因为此二次三项式大于等于0, 所以其判别式小于等于0, 即0)()(4])()([4222≤⋅-⎰⎰⎰ba ba ba dx x g dx x f dx x g x f ,亦即 ⎰⎰⎰⋅≤ba ba ba dx x g dx x f dx x g x f )()(])()([222. (2)()()()212212212)()()]()([⎰⎰⎰+≤+b ab a b a dx x g dx x f dx x g x f , 证明⎰⎰⎰⎰++=+ba ba ba ba dx x g x f dx x g dx x f dx x g x f )()(2)()()]()([222。

定积分专项习题

第五章定积分(A)1．利用定积分定义计算由抛物线12+=x y ，两直线)(,a b b x a x >==及横轴所围成的图形的面积。

2．利用定积分的几何意义，证明下列等式： ⎰=112)1x d x 41)212π=-⎰dx x⎰-=ππ0s i n )3x d x ⎰⎰-=2220cos 2cos )4πππxdx xdx3．估计下列各积分的值 ⎰331a r c t a n )1x d x x dx exx ⎰-022)24．根据定积分的性质比较下列各对积分值的大小 ⎰21ln )1xdx 与dx x ⎰212)(ln dx e x ⎰10)2与⎰+1)1(dx x5．计算下列各导数dt t dx d x ⎰+2021)1 ⎰+3241)2x x t dt dx d⎰xxdt t dx d cos sin 2)cos()3π6．计算下列极限xdt t xx ⎰→020cos lim)1 xdt t xx cos 1)sin 1ln(lim)20-+⎰→2220)1(lim)3x xt x xedt e t ⎰+→7．当x 为何值时，函数⎰-=xt dt tex I 02)(有极值？8．计算下列各积分 dx xx )1()12142⎰+dx x x )1()294+⎰⎰--21212)1()3x dx ⎰+ax a dx3022)4⎰---+211)5e x dx⎰π20sin )6dx xdx x x ⎰-π3sin sin )7⎰2)()8dx x f ，其中⎪⎩⎪⎨⎧+=2211)(x x x f11>≤x x9.设k ，l 为正整数，且l k ≠，试证下列各题：⎰-=ππ0c o s )1k x d x πππ=⎰-kxdx 2cos )2⎰-=⋅ππ0s i n c o s )3l x d x kx ⎰-=ππ0sin sin )4lxdx kx10.计算下列定积分 ⎰-πθθ03)s i n 1()1d ⎰262cos )2ππududx xx ⎰-121221)3 dx x a x a 2202)4-⎰ ⎰+31221)5xxdx dx x ⎰-2132)1(1)6⎰-2221)7x x dx ⎰--1145)8xxdx⎰-axa x d x 20223)9 dt tet ⎰-1022)10⎰-++02222)11x x dx⎰-222cos cos )12ππxdx x⎰--223c o s c o s )13ππdx x x ⎰-++2221)(cos )14xdxx x x ⎰+π2c o s 1)15dx x11.利用函数的奇偶性计算下列积分⎰-224c o s 4)1ππθθd dx xx ⎰--2121221)(arcsin )2dx x x xx ⎰-++55242312sin )312．设f （x ）在[]b a ,上连续，证明：⎰⎰-+=babadx x b a f dx x f )()(13．证明：)0(1111212>+=+⎰⎰x x dx x dx xx14．计算下列定积分⎰-10)1dx xe x⎰342sin )2ππdx x xdx xx⎰41ln )3 ⎰10arctan )4xdx x⎰202c o s )5πx d x e x dx x x ⎰π2)sin ()6⎰edx x 1)sin(ln )7 dx x ee⎰1ln )815.判定下列反常积分的收敛性，如果收敛，计算反常积分的值。

高等数学第五章习题课1定积分

第五章定级分
解
原式 lim
2e
x2
0 e
2 x2
x t2
dt
x
e
0
lim
2 e dt e
x2
x t2
x
lim
2e
x2
2
x 2 xe x
1 lim 0 x x
- 17 -
习题课（一）
3 解
第五章定级分
tf ( x t )dt lim 0 ,
1 i 1 2 lim sin sinxdx n 0 n n i 1
n
-2-

习题课（一）
第五章定级分
i 1 n i 1 lim sin lim sin n n n n 1 n n n i 1 i 1 1 2 sinxdx 0 2 原式 1 n1 n 2 n nn 3 lim n n n n
1 2 F ( x )dx 0
存在一点 , 使得 F ( ) 0, 即 f ( ) f ( )

-9-
习题课（一）
第五章定级分
设在 [0,1] 上 f ( x ) 0, 证明： 1 1 2 0 f ( x )dx f ( 3 ) 证由于 y f ( x ) 在区间 [0,1] 是上凸的，所以曲线 1 1 y f ( x ) 在过 ( , f ( )) 处的切线下方，即 3 3 1 1 1 f ( x ) f ( ) f ( )( x ) 3 3 3 1 1 2 1 2 f ( x ) f ( ) f ( )( x ) 3 3 3

大一高等数学第五章定积分习题

THANKS FOR WATCHING
感谢您的观看
基础题目解析
总结词：计算能力
详细描述：基础题目中还包括一些简单的计算题，主要考察学生的计算能力。这些题目通常涉及定积分的计算、求导和微分等基本运算。
基础题目解析
总结词：应用能力
详细描述：基础题目中还有一些应用题，主要考察学生运用定积分解决实际问题的能力。这些题目通常涉及几何、物理等领域的实际问题，要求学生能够建立数学模型并运用定积分求解。
03 定积分的应用
平面图形的面积
直角三角形面积
定积分可用于计算直角三角形的面积，只需计算三角形的底和对应的高，然后使用公式计算面积。
矩形面积
矩形面积可以通过计算其长度和宽度，然后使用公式计算面积。
梯形面积
梯形面积可以通过计算其两个平行边和斜边，然后使用公式计算面积。
体积
圆柱体体积
大一高等数学第五章定积分习
目录
• 定积分的基本概念 • 定积分的计算方法 • 定积分的应用 • 定积分习题解析 • 总结与思考
01 定积分的基本概念
定积分的定义
积分上限函数
定积分定义为积分上限函数在积分区间上的增量。
微积分基本定理
定积分可以通过微积分基本定理计算，即通过原函数计算。
牛顿-莱布尼茨公式
对定积分习题的反思与建议
反思解题方法
反思解题思路
在解决定积分习题时，我经常采用的方法是利用微积分基本定理将定积分转换为求和的形式，然后利用函数的性质进行计算。这种方法虽然有效，但在处理复杂函数时可能会遇到困难。因此，我需要更加深入地理解定积分的概念和性质，以便更好地应用其他解题方法。
在解决定积分习题时，我有时会陷入思维僵化的状态，导致解题思路不清晰。为了避免这种情况，我需要更加注重培养自己的思维灵活性和创造性，尝试从不同的角度去思考问题。

（完整版）定积分习题及答案

第五章定积分(A 层次)1．203cos sin xdx x ；2．a dx x ax222；3．31221xxdx ；4．1145x xdx ；5．411xdx ；6．14311xdx ；7．21ln 1e xx dx ；8．02222xxdx ；9．dx x 02cos 1；10．dx x x sin 4；11．dx x 224cos 4；12．55242312sin dx xxx x ；13．342sin dx xx ；14．41ln dx xx ；15．1xarctgxdx ；16．202cosxdx e x ；17．dx x x 02sin ；18．dx x e 1ln sin ；19．243cos cos dx x x ；20．40sin 1sin dx x x ；21．dx xxx 02cos 1sin ；22．2111lndx xx x ；23．dx xx 4211；24．20sin ln xdx ；25．211dx xxdx0。

(B 层次)1．求由0cos 0x y ttdtdte 所决定的隐函数y 对x 的导数dxdy 。

2．当x 为何值时，函数x tdt tex I 02有极值？3．x xdt t dxd cos sin 2cos 。

4．设1,211,12xx x x xf ，求20dx x f 。

5．1lim22xdtarctgt xx 。

6．设其它,00,sin 21xx xf ，求x dt t f x。

7．设时当时当0,110,11xex xxf x，求201dx xf 。

8．2221limnn nnn。

9．求nk nknknnen e 12lim 。

10．设x f 是连续函数，且12dt t f x x f ，求x f 。

11．若2ln 261xtedt ，求x 。

12．证明：212121222dxeex。

13．已知axxx dx ex axa x 224lim，求常数a 。

中国人民大学出版社(第四版)高等数学一第5章课后习题详解

高等数学一第5章课后习题详解课后习题全解习题5-1★★1.利用定积分的定义计算由抛物线21y x =+，直线x a =，x b =()b a >及横轴所围成的图形的面积知识点：定积分的定义及几何意义思路：根据求定积分的三步骤做解:将[],a b 分成n 等分,取(1,2,)i i n ξ=为第i 个小区间1[(),()]i ia b a a b a n n-+-+-的右端点,则,i b a x n λ-=∆=,i b aa i nξ-=+ 显然, 0,n λ→⇔→∞于是根据定积分的几何意义,该图形面积lim ()nbi i ai A ydx y x λξ→===∆∑⎰ 21lim [()1]nn i b a b aa in n→∞=--=++∑ 22221()lim [12]n n i b a b a b a a ai i n n n→∞=---=+++∑222211()lim [(1)2]nnn i i b a b a b a n a a i in n n →∞==---=+++∑∑22232()(1)()1lim{()[1(1)(21)]}26n a b a n n b a b a a n n n n n →∞-+-=-+++++221()11()lim[1()(1)(1)(2)]6n b a b a a a b a n n n→∞-=-++-++++ 222()()[1]3b a b a a ab a -=-++-+33().3b a b a -=+- ★★2.利用定积分的定义计算下列积分：知识点：定积分的定义思路：根据求定积分的三步骤做(1)baxdx ⎰()a b <.解:易见函数[](),f x x C a b =∈，从而可积，将[],a b 分成n 等分，则,i b ax nλ-=∆=于是0,n λ→⇔→∞；取(1,2,)i i n ξ=为第i 个小区间的右端点，则,0,1,2,,1,ib aa ii n nξ-=+=-所以110lim ()lim ()n n bi i an i i b a b axdx f x a in nλξ--→→∞==--=∆=+∑∑⎰1()lim{[(0121)]}n b ab a na n n n→∞-=-+++++-2(1)()lim[]2n b a n n b a a n →∞--=-+1()lim[(1)]2n b a b a a n→∞-=-+-221()()().22b a b a a b a -=-+=-(2)1ln exdx ⎰解:用分点(0,1,,)i ni x e i n ==划分区间[]1,e ：11,1,2,,i i nni i i x x x e e i n --∆=-=-=，取i ξ是区间右端点，则 ,()ln()ln ,i i nnii i i i x e f e nξξξ=====作和，并取极限得：111ln lim ()lim ()i i nnenn i i n n i i i xdx f x e e nξ-→∞→∞===∆=-∑∑⎰111111lim{[()]}i i i nn n n nn i i i i e e e n n n --→∞==-=-+∑∑11111(1)lim lim (1)i nn n n i n e e e e n n e -→∞→∞=-=-=--∑111(1)lim ()1n n e e n e →∞=--- 记()1xx g x e =-，则当0x →时，()g x 是0型的，由洛必达法则，有 001lim lim 11x xx x x e e →→==---从而，当n →+∞时，有111lim 11n nne →+∞=--，故1ln (1) 1.exdx e e =+-=⎰★3．利用定积分的几何意义，说明下列等式：(1)121xdx =⎰.知识点：定积分的几何意义思路：定积分的几何意义为被积函数与边界所形成曲边梯形的面积解:等式左边为直线2y x =与x 轴和1x =三条直线所围成的面积，该面积等于11212==等式右边. (2)sin 0xdx ππ-=⎰解: 等式左边为正弦曲线sin y x =与x 轴在x π=及x π=-之间所围成的面积，其左右两边面积互为相反数. 则sin ()0xdx A A ππ-=-+==⎰等式右边★★4.用定积分的几何意义求a⎰(0)b >的值.知识点：定积分的几何意义思路：定积分的几何意义为被积函数与边界所形成曲边梯形的面积解:=是以2a b +为圆心，2b a-为半径的上半圆，其面积为：2221()()2228b a b a S r πππ--===由定积分的几何意义知：2().8ab a π-=⎰★★★5.试将和式的极限112lim p p pp n n n +→∞+++(0)p >表示成定积分.知识点：定积分的定义思路：根据定积分的定义推导过程可知,求和的极限公式可表示为定积分解: 112112limlim [()()()]p p p p pp p n n n n n n n nn +→∞→∞+++=+++11lim ()n pn i i n n→∞==∑设()p f x x =，则用定义求解1()f x dx ⎰为：①、等分[0,1]为n 个小区间：11[,], 1,2,, i i ii n x n nn-=∆=②、求和：取区间1[,]i i n n -上的右端点为i ξ，即i in ξ=，作和：111()n ni i i i i f x nn ξ==∆=⨯∑∑③、求极限：011111lim()lim ()lim ()nnn p pi i n n i i i i i f x nn n n λξ→→∞→∞===∆=⨯=∑∑∑∴1101121lim lim ()p p p n pp p n n i n i x dx n n n+→∞→∞=+++==∑⎰ ★★★6.有一河，宽为200米，从一岸到正对岸每隔20米测量一次水深，测得数据如下：试用梯形公式求此河横截面面积的近似值.知识点：定积分的几何意义思路：由定积分定义知：求定积分（曲边梯形面积）的第二步：用小矩形面积近似代替小曲边梯形面积，即1()()ii x i i x f x f x dx ξ-∆≈⎰，若用小梯形面积近似代替小曲边梯形面积则为：111[()()]()2i i x i i i x f x f x x f x dx --+∆≈⎰。

定积分习题及答案

(A层次）1. 4.7. 兀f 。

2 s in x cos3 xdx ; r xdx -1✓5-4x ，e 2dx f 1 x ✓l +I n x ;10. f 一冗九x 4s in 汕；冗13. f f-�dx; 4 Sill X 冗16. f 。

2产co sx dx ;冗第五章定积分2. f 。

a x 2✓a 2—x 2dx; 5.「I✓x dx +l ；8. f -o 2 x 2 + d 2xx + 2 ; 冗11. f� 冗4c os 4xdx ;14. 17. 2f14 Jn X｀dx ;f 。

兀(xsinx)2dx ;冗19. f� ✓cosx-cos 3 xdx;20. f 。

4 smx dx · 1 + S lll . X ， 22. 4If 0 2 xln l +x dx ; l -x25. f +00dx0 (1 + x 2 XI + xa \ (B层次）23. f +oo l +x 2 dx · -oo 1 +X 4' 心(a�o )。

3. 6.9. 厂dx1 X 飞l +x2 r dx｀3 斤言-1;f。

冗✓1+ c os2xdx;3· 212 fs x sm xdx · ·-5 x 4 + 2x 2 + 1' 15. f 。

1 xa rct gxdx ; 18. {es in(lnx 雇21. 24. f 。

冗xs mx dx .1 +C OS 2X 冗f 。

2 ln sin x dx ;d y 1. 求由f 。

:e r dt+f x costd t=O所确定的隐函数对x 的导数odx 2. 当x 为何值时，函数I(x)= f x t e -t 2dt有极值？。

3.d厂cos矿t。

dx si n x(}Ix+l, x�14. 设八x )�{归，X > 1'求l。

勹(x )dx 。

2f x(a rc tg t) 2d t5. lirn 。

大一高等数学第五章定积分习题

高等数学 第五章 定积分 习题课

高等数学第05章 定积分及其应用习题详解

定积分习题与答案

高等数学第五章定积分试题

高等数学题库第05章(定积分)

高等数学 第五章定积分习题课

大学高等数学第五章 定积分及其应用答案

(完整版)定积分习题及答案

大一高等数学第五章定积分习题

(完整版)高等数学第五章定积分综合测试题

高等数学第五章课后习题答案

高数上学期第五章习题部分解答打印稿

高等数学课后习题及参考答案(第五章)

定积分专项习题

高等数学第五章习题课1定积分

大一高等数学第五章定积分习题

（完整版）定积分习题及答案

中国人民大学出版社(第四版)高等数学一第5章课后习题详解

定积分习题及答案

高等数学第五章定积分习题课

高等数学第05章定积分及其应用习题详解

高等数学第五章定积分习题课

大学高等数学第五章定积分及其应用答案