初中数学动点问题专项练习题
初中数学动点题试卷及答案

一、选择题(每题5分,共50分)1. 下列关于动点的说法正确的是()A. 动点在平面直角坐标系中一定沿着直线运动B. 动点的运动轨迹可以是曲线C. 动点的速度和加速度都是不变的D. 动点的位置随时间变化而变化2. 设动点P的坐标为(x,y),则下列关于P点的运动轨迹方程正确的是()A. x+y=0B. x-y=0C. x^2+y^2=1D. x^2-y^2=13. 一个动点在平面直角坐标系中,从原点出发,先向x轴正方向运动2个单位,然后向y轴负方向运动3个单位,最后向x轴负方向运动4个单位。
则该动点的运动轨迹是()A. 直线B. 抛物线C. 圆D. 双曲线4. 设动点P的坐标为(x,y),则下列关于P点的运动轨迹方程正确的是()A. x^2+y^2=1B. x^2+y^2=4C. x^2-y^2=1D. x^2-y^2=4然后向y轴负方向运动3个单位,最后向x轴负方向运动4个单位。
则该动点的运动轨迹是()A. 直线B. 抛物线C. 圆D. 双曲线6. 设动点P的坐标为(x,y),则下列关于P点的运动轨迹方程正确的是()A. x^2+y^2=1B. x^2+y^2=4C. x^2-y^2=1D. x^2-y^2=47. 一个动点在平面直角坐标系中,从原点出发,先向x轴正方向运动2个单位,然后向y轴负方向运动3个单位,最后向x轴负方向运动4个单位。
则该动点的运动轨迹是()A. 直线B. 抛物线C. 圆D. 双曲线8. 设动点P的坐标为(x,y),则下列关于P点的运动轨迹方程正确的是()A. x^2+y^2=1B. x^2+y^2=4C. x^2-y^2=1D. x^2-y^2=4然后向y轴负方向运动3个单位,最后向x轴负方向运动4个单位。
则该动点的运动轨迹是()A. 直线B. 抛物线C. 圆D. 双曲线10. 设动点P的坐标为(x,y),则下列关于P点的运动轨迹方程正确的是()A. x^2+y^2=1B. x^2+y^2=4C. x^2-y^2=1D. x^2-y^2=4二、填空题(每题5分,共50分)1. 动点的运动轨迹可以是()、()、()等。
中考数学动点问题(含答案)

中考数学之动点问题一、选择题:1. 如图,在矩形ABCD中,动点P从点B出发,沿BC、CD、DA运动至点A停顿,设点P运动的路程为*,△ABP的面积为y,如果y关于*的函数图象如图2所示,则△ABC的面积是〔〕A、10B、16C、18D、20二、填空题:1. 如上右图,C为线段AE上一动点〔不与点A,E重合〕,在AE同侧分别作正三角形ABC和正三角形CDE、AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.恒成立的结论有_______________________〔把你认为正确的序号都填上〕。
三、解答题:1.〔2008年大连〕如图12,直角梯形ABCD中,AB∥CD,∠A = 90°,CD = 3,AD = 4,tan B = 2,过点C作CH⊥AB,垂足为H.点P为线段AD上一动点,直线PM∥AB,交BC、C H于点M、Q.以PM为斜边向右作等腰Rt△PMN,直线MN交直线AB于点E,直线PN交直线A B于点F.设PD的长为*,EF的长为y.⑴求PM的长(用*表示);⑵求y与*的函数关系式及自变量*的取值范围(图13为备用图);⑶当点E在线段AH上时,求*的取值范围(图14为备用图).2.〔2008年福建宁德〕如图1,在Rt△ABC中,∠C=90°,BC=8厘米,点D在AC上,CD=3厘米.点P、Q分别由A、C两点同时出发,点P沿AC方向向点C匀速移动,速度为每秒k厘米,行完AC全程用时0<x<,△DCQ的8秒;点Q沿CB方向向点B匀速移动,速度为每秒1厘米.设运动的时间为*秒()8面积为y1平方厘米,△PCQ的面积为y2平方厘米.⑴求y1与*的函数关系,并在图2中画出y1的图象;⑵如图2,y2的图象是抛物线的一局部,其顶点坐标是〔4,12〕,求点P的速度及AC的长;⑶在图2中,点G是*轴正半轴上一点〔0<OG<6=,过G作EF垂直于*轴,分别交y1、y2于点E、F.①说出线段EF的长在图1中所表示的实际意义;②当0<*<6时,求线段EF长的最大值.3.〔2008年白银〕如图,在平面直角坐标系中,四边形OABC 是矩形,点B 的坐标为〔4,3〕.平行于对角线AC 的直线m 从原点O 出发,沿*轴正方向以每秒1个单位长度的速度运动,设直线m 与矩形OABC 的两边..分别交于点M 、N ,直线m 运动的时间为t 〔秒〕. (1) 点A 的坐标是__________,点C 的坐标是__________; (2) 当t=秒或秒时,MN=21AC ; (3) 设△OMN 的面积为S ,求S 与t 的函数关系式;(4) 探求(3)中得到的函数S 有没有最大值?假设有,求出最大值;假设没有,要说明理由.参考答案一、选择 A二、填空:〔1〕〔2〕〔3〕〔5〕 三、解答: 2、解:⑴∵CD CQ S DCQ ⋅⋅=∆21,CD =3,CQ =*, ∴x y 231=. 图象如下图.⑵方法一:CP CQ S PCQ ⋅⋅=∆21,CP =8k -*k ,CQ =*, ∴()kx kx x kx k y 42182122+-=⋅-⨯=.∵抛物线顶点坐标是〔4,12〕,∴12444212=⋅+⋅-k k . 解得23=k .图1C Q → B图2则点P 的速度每秒23厘米,AC =12厘米. 方法二:观察图象知,当*=4时,△PCQ 面积为12. 此时PC =AC -AP =8k -4k =4k ,CQ =4.∴由CP CQ S PCQ ⋅⋅=∆21,得 12244=⨯k .解得23=k . 则点P 的速度每秒23厘米,AC =12厘米.方法三:设y 2的图象所在抛物线的解析式是c bx ax y ++=2. ∵图象过〔0,0〕,〔4,12〕,〔8,0〕,∴⎪⎩⎪⎨⎧=++=++=.0864124160c b a c b a c ,, 解得 ⎪⎪⎩⎪⎪⎨⎧==-=.0643c b a ,, ∴x x y 64322+-=. ①∵CP CQ S PCQ ⋅⋅=∆21,CP =8k -*k ,CQ =*,∴kx kx y 42122+-=. ②比拟①②得23=k .则点P 的速度每秒23厘米,AC =12厘米.⑶①观察图象,知线段的长EF =y 2-y 1,表示△PCQ 与△DCQ 的面积差〔或△PDQ 面积〕. ②由⑵得 x x y 64322+-=.〔方法二,x x x x y 643232382122+-=⋅⎪⎭⎫ ⎝⎛-⨯⨯=〕∵EF =y 2-y 1, ∴EF =x x x x x 29432364322+-=-+-, ∵二次项系数小于0,∴在60<x<范围,当3=x 时,427=EF 最大. 3、解:(1)〔4,0〕,〔0,3〕; 2分 (2) 2,6; 4分 (3) 当0<t ≤4时,OM =t .由△OMN ∽△OAC ,得OCONOA OM =, ∴ ON =t 43,S=283t . 6分 当4<t <8时,如图,∵ OD =t ,∴ AD = t-4. 方法一:由△DAM ∽△AOC ,可得AM =)4(43-t ,∴ BM =6-t 43. 7分 由△BMN ∽△BAC ,可得BN =BM 34=8-t ,∴ CN =t-4. 8分S=矩形OABC 的面积-Rt △OAM 的面积- Rt △MBN 的面积- Rt △NCO 的面积=12-)4(23-t -21〔8-t 〕〔6-t 43〕-)4(23-t =t t 3832+-. ·························· 10分方法二:易知四边形ADNC 是平行四边形,∴ CN =AD =t-4,BN =8-t .7分 由△BMN ∽△BAC ,可得BM =BN 43=6-t 43,∴ AM =)4(43-t .8分 以下同方法一. (4) 有最大值.方法一: 当0<t ≤4时,∵ 抛物线S=283t 的开口向上,在对称轴t=0的右边, S 随t 的增大而增大, ∴ 当t=4时,S 可取到最大值2483⨯=6; 11分当4<t <8时, ∵ 抛物线S=t t 3832+-的开口向下,它的顶点是〔4,6〕,∴ S <6. 综上,当t=4时,S 有最大值6. 12分 方法二:∵ S=22304833488t t t t t ⎧<⎪⎪⎨⎪-+<<⎪⎩,≤,∴ 当0<t <8时,画出S 与t 的函数关系图像,如下图. 11分显然,当t=4时,S有最大值6. 12分说明:只有当第〔3〕问解答正确时,第〔4〕问只答复"有最大值〞无其它步骤,可给1分;否则,不给分.。
初二数学动点练习题

初二数学动点练习题1. 直线上的动点问题- 题目:在直线AB上,点C是动点,当点C沿着直线AB移动时,求证∠ACB是一个恒定的角度。
2. 圆上的动点问题- 题目:圆O的半径为5,点P是圆上的动点。
求证:无论点P在圆上如何移动,OP的长度始终为5。
3. 动点与线段的关系- 题目:线段AB的长度为10,点C是线段AB上的动点。
当点C从A向B移动时,求线段AC的长度与线段BC的长度之和是否恒定。
4. 动点与三角形的面积- 题目:三角形ABC的面积为30平方单位,点D是边AB上的动点。
求证:无论点D在AB上如何移动,三角形ACD的面积始终是三角形ABC面积的一半。
5. 动点与平行四边形的对角线- 题目:平行四边形ABCD中,点E是边AB上的动点,点F是边CD 上的动点,且EF始终是平行四边形的对角线。
求证:无论点E和点F如何移动,EF的长度始终等于AB和CD的长度之和。
6. 动点与圆的切线- 题目:圆O的半径为6,点P是圆O外的一点,点Q是圆O上的动点。
当点Q沿着圆O移动时,求证:点P到圆O的切线长度始终等于点P到点Q的距离。
7. 动点与相似三角形- 题目:三角形ABC与三角形DEF相似,点G是三角形ABC的动点,点H是三角形DEF的动点,且GH始终是三角形ABC和三角形DEF的对应边的平行线。
求证:无论点G和点H如何移动,三角形AGH与三角形DEF始终相似。
8. 动点与坐标系- 题目:在平面直角坐标系中,点A的坐标为(2,3),点B的坐标为(5,6)。
点C是线段AB上的动点,其坐标为(x,y)。
求证:无论点C如何移动,x和y的和始终等于点A和点B坐标的和。
练习题答案提示:- 对于直线上的动点问题,可以利用角度的恒定性,结合直线的性质来证明。
- 对于圆上的动点问题,可以利用圆的半径性质来证明。
- 对于动点与线段的关系问题,可以利用线段长度的加法性质来证明。
- 对于动点与三角形的面积问题,可以利用三角形面积的计算公式来证明。
(完整word版)初中数学动点问题专题复习及答案

初中数学动点问题练习题1、佇夏回族自治区)已知:等边三角形ABC的边长为4厘米,长为1厘米的线段MN在△ ABC的边AB上沿AB方向以1厘米/秒的速度向B点运动(运动开始时,点M与点A重合,点N到达点B 时运动终止),过点M、N分别作AB边的垂线,与△ ABC的其它边交于P、Q两点,线段MN运动的时间为t秒.1、线段MN在运动的过程中,t为何值时,四边形MNQP恰为矩形?并求出该矩形的面积;(2)线段MN在运动的过程中,四边形MNQP的面积为S,运动的时间为t .求四边形MNQP的面C积S随运动时间t变化的函数关系式,并写岀自变量t的取值范围.QPAM N B2、如图,在梯形ABCD中,AD // BC,AD 3,DC 5,AB 4. 2,Z B 45 .动点M 从B点出发沿线段BC以每秒2个单位长度的速度向终点C运动;动点N同时从C点出发沿线段CD 以每秒1个单位长度的速度向终点D运动•设运动的时间为t秒.(1)求BC的长.(2)当MN // AB时,求t的值.(3)试探究:t为何值时,△ MNC为等腰三角形.3、如图,在平面直角坐标系中,四边形OABC是梯形,OA// BC,点A的坐标为(6,0),点B 的坐标为(4,3),点C在y轴的正半轴上.动点M在OA上运动,从O点出发到A点;动点N在AB上运动,从A点出发到B点.两个动点同时出发,速度都是每秒1个单位长度,当其中一个点到达终点时,另一个点也随即停止,设两个点的运动时间为t(秒).(1)求线段AB的长;当t为何值时,MN // OC?⑵设△ CMN的面积为S,求S与t之间的函数解析式, 并指出自变量t的取值范围;S是否有最小值?若有最小值,最小值是多少?x(3)连接AC,那么是否存在这样的 t ,使MN 与AC 互相垂直? 若存在,求出这时的t 值;若不存在,请说明理由.4、(河北卷)如图,在 Rt A ABC 中,/ C = 90°, AC = 12, BC = 16,动点P 从点A 出发沿 AC 边向点C 以每秒3个单位长的速度运动,动点Q 从点C 出发沿CB 边向点B 以每秒4个单位长的速度运动.P, Q 分别从点A , C 同时出发,当其中一点到达端点时,另一点也随之 停止运动.在运动过程中,△ PCQ 关于直线PQ 对称的图形是△ PDQ.设运动时间为t (秒). (1 )设四边形PCQD 的面积为y ,求y 与t 的函数关系式; (2) t 为何值时,四边形 PQBA 是梯形?(3) 是否存在时刻t ,使得PD // AB ?若存在,求出t 的值;若不存在,请说明理由; (4) 通过观察、画图或折纸等方法,猜想是否存在时刻t ,使得PD 丄AB ?若存在,请估计t 的值在括号中的哪个时间段内( O W t < 1 ; 1 v t w 2 ; 2v t w 3; 3 v t < 4);若不存在,请简要说明理由.5、(山东济宁)如图, A 、B 分别为x 轴和y 轴正半轴上的点。
初一数学动点问题20题及答案

初一数学动点问题20题及答案数轴上动点问题1.已知:如图,数轴上点A表示的数为6,点B表示的数为2,点C表示的数为﹣8,动点P从点A出发,沿数轴向左运动,速度为每秒1个单位长度.点M为线段BC中点,点N为线段BP中点.设运动时间为t秒.(1)线段AC的长为__________个单位长度;点M表示的数为;(2)当t=5时,求线段MN的长度;(3)在整个运动过程中,求线段MN的长度.(用含t的式子表示).2.已知数轴上点A,B,C所表示的数分别是x,﹣6,4.(1)线段BC的长为_________,线段BC的中点D所表示的数是;(2)若AC=8,求x的值;(3)在数轴上有两个动点P,Q,P的速度为1个单位长度/秒,Q的速度为2个单位/秒,点P,Q分别从点B,C同时出发,在数轴上运动,则经过多少时间后P,Q两点相距4个单位?3.动点A、B同时从数轴上的原点出发向相反的方向运动,且A、B的速度之比是1:4(速度单位:长度单位/秒),3秒后,A、B两点相距15个单位长度.(1)求出两个动点运动的速度,并在数轴上标出A、B两点从原点出发运动3秒时的位置.(2)若A、B两点从(1)中的位置同时向数轴负方向运动,几秒后原点恰好处在两个动点正中间?4.如图A、B两点在数轴上分别表示﹣10和20,动点P从点A出发以10个单位每秒的速度向右运动,动点Q从点B出发以每秒5个单位的速度出向右运动.设运动时间为t.(1)当点P运动到B点时,求出t的值;(2)当t为何值时,P、Q两点相遇,并求出此时P点对应的数?(3)在此运动过程中,若P、Q相距10个单位,直接写出运动时间t?5.已知a,b满足(a+2)2+|b﹣1|=0,请回答下列问题:(1)a=_______,b=_______;(2)a,b在数轴上对应的点分别为A,B,在所给的数轴上标出点A,点B;(3)若甲、乙两个动点分别从A,B两点同时出发沿x轴正方向运动,已知甲的速度为每秒2个单位长度,乙的速度为每秒1个单位长度,更多好题请进入:437600809,请问经过多少秒甲追上乙?6.在数轴上有A、B两动点,点A起始位置表示数为﹣3,点B起始位置表示数为12,点A的速度为1单位长度/秒,点B的运动速度是点A速度的二倍.(1)若点A、B同时沿数轴向左运动,多少秒后,点B与点A相距6单位长度?(2)若点A、点B同时沿数轴向左运动,是否有一个时刻,表示数﹣3的点是线段AB 的中点?如果有,求出运动时间;如果没有,说明理由.7.如图,已知数轴上点A表示的为8,B是数轴上一点,且AB=14,动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.(1)写出数轴上点B表示的数,点P表示的数(用含t的代数式表示);(2)动点H从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、H 同时出发,问点P运动多少秒时追上点H?8.如图,数轴上的点A,B对应的数分别为﹣10,5.动点P,Q分别从A,B同时出发,点P以每秒3个单位长度的速度沿数轴向右匀速运动,点Q以每秒2个单位长度的速度沿数轴向左匀速运动,设运动时间为t秒.(1)求线段AB的长;(2)直接用含t的式子分别表示数轴上的点P,Q对应的数;(3)当PQ=AB时,求t的值.9.如图,已知数轴上点A表示的数为6,B是你数轴上一点,且AB=10,动点P从点O 出发,以每秒6个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.(1)写出数轴上点B所表示的数______;当t=3时,OP=_______.(2)动点R从点B出发,以每秒8个单位长度的速度沿数轴向右匀速运动,若点P,R 同时出发,问点R运动多少秒时追上点P?10.如图.点A、点C是数轴上的两点,0是原点,0A=6,5AO=3CO.(1)写出数轴上点A、点C表示的数;(2)点P、Q分别从A、C同时出发,点P以每秒1个单位长度的速度沿数轴向右匀速运动,点Q以每4个单位长度的速度沿数轴向左匀速运动,问运动多少秒后,这两个动点到原点O的距离存在2倍关系?11.已知数轴上两点A,B对应的数分别为﹣1,3,P为数轴上的动点,其对应的数为x.(1)数轴上是否存在点P,使P到点A、点B的之和为5?若存在,请求出x的值;若不存在,说明理由;(2)当点P以每分钟1个单位长度的速度从O点向左运动时,点A以每分钟5个单位长度的速度向左运动,点B以每分钟20个单位长度的速度向左运动.问,它们同时出发几分钟时点P到点A、点B的距离相等?12.A、B两个动点在数轴上做匀速运动,它们的运动时间以及位置记录如下.(1)根据题意,填写下列表格;(2)A、B两点能否相遇?如果相遇,求相遇时的时刻及在数轴上的位置;如果不能相遇,请说明理由;(3)A、B两点能否相距18个单位长度?如果能,求相距18个单位长度的时刻;如不能,请说明理由.13.如图1,点A,B是在数轴上对应的数字分别为﹣12和4,动点P和Q分别从A,B 两点同时出发向右运动,点P的速度是5个单位/秒,点Q的速度是2个单位/秒,设运动时间为t秒.(1)AB=.(2)当点P在线段BQ上时(如图2):①BP=______________(用含t的代数式表示);②当P点为BQ中点时,求t的值.。
(中考数学)动点问题专题训练(含答案)

中考专题训练 动点问题例1. 如图, 在ABC ∆中,AB AC =,AD BC ⊥于点D ,10BC cm =,8AD cm =. 点P 从点B 出发, 在线段BC 上以每秒3cm 的速度向点C 匀速运动, 与此同时, 垂直于AD 的直线m 从底边BC 出发, 以每秒2cm 的速度沿DA 方向匀速平移, 分别交AB 、AC 、AD 于E 、F 、H ,当点P 到达点C 时, 点P 与直线m 同时停止运动, 设运动时间为t 秒(0)t >.(1) 当2t =时, 连接DE 、DF ,求证: 四边形AEDF 为菱形;(2) 在整个运动过程中, 所形成的PEF ∆的面积存在最大值, 当PEF ∆的面积最大时, 求线段BP 的长;(3) 是否存在某一时刻t ,使PEF ∆为直角三角形?若存在, 请求出此时刻t 的值;若不存在, 请说明理由 .【解答】(1) 证明: 当2t =时,4DH AH ==,则H 为AD 的中点, 如答图 1 所示 . 又EF AD ⊥ ,EF ∴为AD 的垂直平分线,AE DE ∴=,AF DF =.AB AC = ,AD BC ⊥于点D ,AD BC ∴⊥,B C ∠=∠.//EF BC ∴,AEF B ∴∠=∠,AFE C ∠=∠,AEF AFE ∴∠=∠,AE AF ∴=,AE AF DE DF ∴===,即四边形AEDF 为菱形 .(2) 解: 如答图 2 所示, 由 (1) 知//EF BC ,AEF ABC ∴∆∆∽, ∴EF AH BC AD =,即82108EF t -=,解得:5102EF t =-. 221155510(10)210(2)10(0)222223PEF S EF DH t t t t t t ∆==-=-+=--+<< , ∴当2t =秒时,PEF S ∆存在最大值, 最大值为210cm ,此时36BP t cm ==.(3) 解: 存在 . 理由如下:①若点E 为直角顶点, 如答图 3①所示,此时//PE AD ,2PE DH t ==,3BP t =.//PE AD ,∴PE BP AD BD =,即2385t t =,此比例式不成立, 故此种情形不存在; ②若点F 为直角顶点如答图 3②所示,此时//PF AD ,2PF DH t ==,3BP t =,103CP t =-.//PF AD ,∴PF CP AD CD =,即210385t t -=,解得4017t =;③若点P 为直角顶点,如答图③所示 .过点E 作EM BC ⊥于点M ,过点F 作FN BC ⊥于点N ,则2EM FN DH t ===,////EM FN AD .//EM AD ,∴EM BM AD BD =,即285t BM =,解得54BM t =, 57344PM BP BM t t t ∴=-=-=. 在Rt EMP ∆中, 由勾股定理得:2222227113(2)()416PE EM PM t t t =+=+=. //FN AD ,∴FN CN AD CD =,即285t CN =,解得54CN t =, 5171031044PN BC BP CN t t t ∴=--=--=-. 在Rt FNP ∆中, 由勾股定理得:22222217353(2)(10)85100416PF FN PN t t t t =+=+-=-+. 在Rt PEF ∆中, 由勾股定理得:222EF PE PF =+, 即:2225113353(10)()(85100)21616t t t t -=+-+ 化简得:21833508t t -=, 解得:280183t =或0t =(舍 去) 280183t ∴=. 综上所述, 当4017t =秒或280183t =秒时,PEF ∆为直角三角形 .例2. 如图, 在同一平面上, 两块斜边相等的直角三角板Rt ABC ∆和Rt ADC ∆拼在一起,使斜边AC 完全重合, 且顶点B ,D 分别在AC 的两旁,90ABC ADC ∠=∠=︒,30CAD ∠=︒,4AB BC cm ==(1) 填空:AD = )cm ,DC = ()cm(2) 点M ,N 分别从A 点,C 点同时以每秒1cm 的速度等速出发, 且分别在AD ,CB 上沿A D →,C B →方向运动, 当N 点运动到B 点时,M 、N 两点同时停止运动, 连接MN ,求当M 、N 点运动了x 秒时, 点N 到AD 的距离 (用 含x 的式子表示)(3) 在 (2) 的条件下, 取DC 中点P ,连接MP ,NP ,设PMN ∆的面积为2()y cm ,在整个运动过程中,PMN ∆的面积y 存在最大值, 请求出y 的最大值 .(参考数据sin 75︒=sin15︒=【解答】解: (1)90ABC ∠=︒ ,4AB BC cm ==,AC ∴===,90ADC ∠=︒ ,30CAD ∠=︒,12DC AC ∴==,AD ∴==;故答案为:,;(2) 过点N 作NE AD ⊥于E ,作NF DC ⊥,交DC 的延长线于F ,如图所示:则NE DF =,90ABC ADC ∠=∠=︒ ,AB BC =,30CAD ∠=︒,45ACB ∴∠=︒,60ACD ∠=︒,180456075NCF ∴∠=︒-︒-︒=︒,15FNC ∠=︒,sinFC FNCNC ∠=,NC x=,FC x∴=,NE DF x∴==+,∴点N到ADx+;(3)sinFN NCFNC ∠=,FN x∴=,P为DC的中点,PD CP∴==PF x∴=PMN∴∆的面积y=梯形MDFN的面积PMD-∆的面积PNF-∆的面积111)) 222x x x x=+-+--+2x x=+,即y是x的二次函数,0<,y∴有最大值,当x==时,y=.例3. 如图,BD 是正方形ABCD 的对角线,2BC =,边BC 在其所在的直线上平移, 将通过平移得到的线段记为PQ ,连接PA 、QD ,并过点Q 作QO BD ⊥,垂足为O ,连接OA 、OP .(1) 请直接写出线段BC 在平移过程中, 四边形APQD 是什么四边形?(2) 请判断OA 、OP 之间的数量关系和位置关系, 并加以证明;(3) 在平移变换过程中, 设OPB y S ∆=,(02)BP x x =……,求y 与x 之间的函数关系式,并求出y 的最大值 .【解答】(1) 四边形APQD 为平行四边形;(2)OA OP =,OA OP ⊥,理由如下:四边形ABCD 是正方形,AB BC PQ ∴==,45ABO OBQ ∠=∠=︒,OQ BD ⊥ ,45PQO ∴∠=︒,45ABO OBQ PQO ∴∠=∠=∠=︒,OB OQ ∴=,在AOB ∆和OPQ ∆中,AB PQABO PQO BO QO=⎧⎪∠=∠⎨⎪=⎩()AOB POQ SAS ∴∆≅∆,OA OP ∴=,AOB POQ ∠=∠,90AOP BOQ ∴∠=∠=︒,OA OP ∴⊥;(3) 如图, 过O 作OE BC ⊥于E .①如图 1 ,当P 点在B 点右侧时,则2BQ x =+,22x OE +=, 1222x y x +∴=⨯,即211(1)44y x =+-, 又02x ……,∴当2x =时,y 有最大值为 2 ;②如图 2 ,当P 点在B 点左侧时,则2BQ x =-,22x OE -=, 1222x y x -∴=⨯ ,即211(1)44y x =--+, 又02x ……,∴当1x =时,y 有最大值为14; 综上所述,∴当2x =时,y 有最大值为 2 .例4. 如图, 在平面直角坐标系中,O 为原点, 四边形ABCO 是矩形, 点A ,C 的坐标分别是(0,2)A 和C ,0),点D 是对角线AC 上一动点 (不 与A ,C 重合) ,连结BD ,作DE DB ⊥,交x 轴于点E ,以线段DE ,DB 为邻边作矩形BDEF .(1) 填空: 点B 的坐标为 ;(2) 是否存在这样的点D ,使得DEC ∆是等腰三角形?若存在, 请求出AD 的长度;若不存在, 请说明理由;(3)①求证:DE DB =; ②设AD x =,矩形BDEF 的面积为y ,求y 关于x 的函数关系式 (可 利用①的结论) ,并求出y 的最小值 .【解答】解: (1) 四边形AOCB 是矩形,2BC OA ∴==,OC AB ==90BCO BAO ∠=∠=︒,B ∴2).故答案为2).(2) 存在 . 理由如下:2OA = ,OC =,tan AO ACO OC ∠== , 30ACO ∴∠=︒,60ACB ∠=︒①如图 1 中, 当E 在线段CO 上时,DEC ∆是等腰三角形, 观察图象可知, 只有ED EC =,30DCE EDC ∴∠=∠=︒,60DBC BCD ∴∠=∠=︒,DBC ∴∆是等边三角形,2DC BC ∴==,在Rt AOC ∆中,30ACO ∠=︒ ,2OA =,24AC AO ∴==,422AD AC CD ∴=-=-=.∴当2AD =时,DEC ∆是等腰三角形 .②如图 2 中, 当E 在OC 的延长线上时,DCE ∆是等腰三角形, 只有CD CE =,15DBC DEC CDE ∠=∠=∠=︒,75ABD ADB ∴∠=∠=︒,AB AD ∴==,综上所述, 满足条件的AD 的值为 2 或(3)①如图 1 ,过点D 作MN AB ⊥交AB 于M ,交OC 于N ,(0,2)A 和C ,0),∴直线AC 的解析式为2y x =+,设(,2)D a +,2DN ∴=+,BM a =90BDE ∠=︒ ,90BDM NDE ∴∠+∠=︒,90BDM DBM ∠+∠=︒,DBM EDN ∴∠=∠,90BMD DNE ∠=∠=︒ ,BMD DNE ∴∆∆∽,∴DE DN BD BM ===②如图 2 中, 作DH AB ⊥于H .在Rt ADH ∆中,AD x = ,30DAH ACO ∠=∠=︒,1122DH AD x ∴==,AH x ==,BH x ∴=, 在Rt BDH ∆中,BD ==,DE ∴==, ∴矩形BDEF的面积为22612)y x x ==-+,即2y x =-+,23)y x ∴=-+,0>,3x ∴=时,y .例5. 已知Rt OAB ∆,90OAB ∠=︒,30ABO ∠=︒,斜边4OB =,将Rt OAB ∆绕点O 顺时针旋转60︒,如图 1 ,连接BC .(1) 填空:OBC ∠= 60 ︒;(2) 如图 1 ,连接AC ,作OP AC ⊥,垂足为P ,求OP 的长度;(3) 如图 2 ,点M ,N 同时从点O 出发, 在OCB ∆边上运动,M 沿O C B →→路径匀速运动,N 沿O B C →→路径匀速运动, 当两点相遇时运动停止, 已知点M 的运动速度为 1.5 单位/秒, 点N 的运动速度为 1 单位/秒, 设运动时间为x 秒,OMN ∆的面积为y ,求当x 为何值时y 取得最大值?最大值为多少?【解答】解: (1) 由旋转性质可知:OB OC =,60BOC ∠=︒,OBC ∴∆是等边三角形,60OBC ∴∠=︒.故答案为 60 .(2) 如图 1 中,4OB = ,30ABO ∠=︒,122OA OB ∴==,AB ==11222AOC S OA AB ∆∴==⨯⨯=BOC ∆ 是等边三角形,60OBC ∴∠=︒,90ABC ABO OBC ∠=∠+∠=︒,AC ∴==2AOC S OP AC ∆∴===.(3)①当803x <…时,M 在OC 上运动,N 在OB 上运动,此时过点N 作NE OC ⊥且交OC 于点E .则sin 60NE ON x =︒= ,11 1.522OMN S OM NE x x ∆∴==⨯ ,2y x ∴=.83x ∴=时,y 有最大值, 最大值=. ②当843x <…时,M 在BC 上运动,N 在OB 上运动 .作MH OB ⊥于H . 则8 1.5BM x =-,sin 60 1.5)MH BM x =︒=- ,212y ON MH x ∴=⨯⨯=+.当83x =时,y 取最大值,y < ③当4 4.8x <…时,M 、N 都在BC 上运动, 作OG BC ⊥于G .12 2.5MN x =-,OG AB ==,12y MN OG ∴== ,当4x =时,y 有最大值, 最大值=,综上所述,y 有最大值, .。
七年级数学动点题50道

七年级数学动点题50道一、数轴上的动点问题(20道)1. 已知数轴上点A表示的数为 3,点B表示的数为1,点P以每秒2个单位长度的速度从点A出发向左运动,同时点Q以每秒3个单位长度的速度从点B出发向右运动,设运动时间为t秒。
(1)当t = 1时,求PQ的长度。
(2)求经过多少秒后,PQ = 5。
解析:(1)当t = 1时,点P表示的数为公式,点Q表示的数为公式。
所以公式。
(2)运动t秒后,点P表示的数为公式,点Q表示的数为公式。
则公式。
当公式时,即公式。
则公式或公式。
当公式时,公式,公式(舍去,因为时间不能为负)。
当公式时,公式,公式。
2. 数轴上点A对应的数为 2,点B对应的数为4,点C对应的数为x,若点C在点A、B之间,且公式,求x的值。
解析:因为点C在点A、B之间,公式,公式。
又因为公式,所以公式。
去括号得公式。
移项得公式。
合并同类项得公式。
解得公式。
3. 数轴上有A、B两点,A表示的数为 1,B表示的数为3,点P以每秒1个单位长度的速度从点A出发向右运动,设运动时间为t秒。
(1)当t为何值时,点P到点B的距离为2?(2)点Q以每秒2个单位长度的速度从点B出发向左运动,当公式时,求t的值。
解析:(1)点P表示的数为公式。
当点P到点B的距离为2时,公式。
则公式或公式。
解得公式或公式。
(2)点Q表示的数为公式,公式。
当公式时,公式。
即公式。
则公式或公式。
当公式时,公式,公式。
当公式时,公式,公式。
4. 数轴上点A表示的数为5,点B表示的数为 3,点M从点A出发,以每秒1个单位长度的速度向左运动,点N从点B出发,以每秒2个单位长度的速度向右运动,设运动时间为t秒。
(1)求t秒后,点M表示的数和点N表示的数。
(2)当t为何值时,点M与点N相距4个单位长度?解析:(1)t秒后,点M表示的数为公式,点N表示的数为公式。
(2)当点M与点N相距4个单位长度时,公式。
则公式或公式。
当公式时,公式,公式。
当公式时,公式,公式。
初中数学几何的动点问题专题练习-附答案版

动点问题专题练习 【1 】1.如图,已知ABC △中,10AB AC ==厘米,8BC =厘米,点D 为AB 的中点.(1)假如点P 在线段BC 上以3厘米/秒的速度由B 点向C 点活动,同时,点Q 在线段CA 上由C 点向A 点活动.①若点Q 的活动速度与点P 的活动速度相等,经由1秒后,BPD △与CQP △是否全等,请解释来由;②若点Q 的活动速度与点P 的活动速度不相等,当点Q 的活动速度为若干时,可以或许使BPD △与CQP △全等?(2)若点Q 以②中的活动速度从点C 动身,点P 以本来的活动速度从点B 同时动身,都逆时针沿ABC △三边活动,求经由多长时光点P 与点Q 第一次在ABC △的哪条边上相遇? 1.解:(1)①∵1t =秒, ∴313BP CQ ==⨯=厘米, ∵10AB =厘米,点D 为AB 的中点, ∴5BD =厘米.又∵8PC BC BP BC =-=,厘米, ∴835PC =-=厘米, ∴PC BD =. 又∵AB AC =, ∴B C ∠=∠,∴BPD CQP △≌△. ············································································· (4分) ②∵P Q v v ≠, ∴BP CQ ≠,又∵BPD CQP △≌△,B C ∠=∠,则45BP PC CQ BD ====,, ∴点P ,点Q 活动的时光433BP t ==秒, ∴515443Q CQ v t===厘米/秒. ·································································· (7分)(2)设经由x 秒后点P 与点Q 第一次相遇,由题意,得1532104x x =+⨯, 解得803x =秒.∴点P 共活动了803803⨯=厘米.∵8022824=⨯+,∴点P .点Q 在AB 边上相遇,∴经由803秒点P 与点Q 第一次在边AB 上相遇. ········································· (12分) 2.直线364y x =-+与坐标轴分离交于A B 、两点,动点P Q 、同时从O 点动身,同时到达A点,活动停滞.点Q 沿线段OA 活动,速度为每秒1个单位长度,点P 沿路线O →B →A 活动.(1)直接写出A B 、两点的坐标;(2)设点Q 的活动时光为t 秒,OPQ △的面积为S ,求出S 与t 之间的函数关系式; (3)当485S =时,求出点P 的坐标,并直接写出以点O P Q 、、为极点的平行四边形的第四个极点M 的坐标. 2.解(1)A (8,0)B (0,6) ················· 1分 (2)86OA OB ==,10AB ∴=点Q 由O 到A 的时光是881=(秒) ∴点P 的速度是61028+=(单位/秒) ·1分 当P 在线段OB 上活动(或03t ≤≤)时,2OQ t OP t ==,2S t = ·········································································································· 1分当P 在线段BA 上活动(或38t <≤)时,6102162OQ t AP t t ==+-=-,, 如图,作PD OA ⊥于点D ,由PD AP BO AB =,得4865tPD -=, ······································· 1分21324255S OQ PD t t ∴=⨯=-+ ······································································· 1分 (自变量取值规模写对给1分,不然不给分.)(3)82455P ⎛⎫ ⎪⎝⎭, ···························································································· 1分12382412241224555555I M M 2⎛⎫⎛⎫⎛⎫-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,,,,, ···················································· 3分5.在Rt △ABC 中,∠C=90°,AC = 3,AB = 5.点P 从点C 动身沿CA 以每秒1个单位长的速度向点A 匀速活动,到达点A 后连忙以本来的速度沿AC 返回;点Q 从点A 动身沿AB 以每秒1个单位长的速度向点B 匀速活动.陪同着P.Q 的活动,DE 保持垂直等分PQ,且交PQ 于点D,交折线QB-BC-CP 于点E .点P.Q 同时动身,当点Q 到达点B 时停滞活动,点P 也随之停滞.设点P.Q 活动的时光是t 秒(t >0).(1)当t = 2时,AP =,点Q 到AC 的距离是;(2)在点P 从C 向A 活动的进程中,求△APQ 的面积S与t 的函数关系式;(不必写出t 的取值规模)(3)在点E 从B 向C 活动的进程中,四边形QBED 可否成为直角梯形?若能,求t 的值.若不克不及,请解释来由; (4)当DE 经由点C 时,请直接写出t 的值. 5.解:(1)1,85;(2)作QF ⊥AC 于点F,如图3, AQ = CP= t,∴3AP t =-. 由△AQF ∽△ABC,4BC =, 得45QF t =.∴45QF t =. ∴14(3)25S t t =-⋅, 即22655S t t =-+.(3)能.①当DE ∥QB 时,如图4.∵DE ⊥PQ,∴PQ ⊥QB,四边形QBED 是直角梯形. 此时∠AQP=90°.P图16P图4由△APQ ∽△ABC,得AQ APAC AB=, 即335t t -=. 解得98t =. ②如图5,当PQ ∥BC 时,DE ⊥BC,四边形QBED 是直角梯形. 此时∠APQ =90°. 由△AQP ∽△ABC,得AQ APAB AC=, 即353t t -=. 解得158t =.(4)52t =或4514t =. ①点P 由C 向A 活动,DE 经由点C . 衔接QC,作QG ⊥BC 于点G,如图6.PC t =,222QC QG CG =+2234[(5)][4(5)]55t t =-+--.由22PC QC =,得22234[(5)][4(5)]55t t t =-+--,解得52t =.②点P 由A 向C 活动,DE 经由点C,如图7. 22234(6)[(5)][4(5)]55t t t -=-+--,4514t =】6如图,在Rt ABC △中,9060ACB B ∠=∠=°,°,2BC =.点O 是AC 的中点,过点O 的直线l 从与AC 重合的地位开端,绕点O 作逆时针扭转,交AB 边于点D .过点C 作CE AB ∥交直线l 于点E ,设直线l 的扭转角为α.(1)①当α=度时,四边形EDBC 是等腰梯形,此时AD 的长为;②当α=度时,四边形EDBC 是直角梯形,此时AD 的长为; (2)当90α=°时,断定四边形EDBC 是否为菱形,并解释来由.6.解(1)①30,1;②60,1.5; ……………………4分 (2)当∠α=900时,四边形EDBC 是菱形. ∵∠α=∠ACB=900,∴BC//ED.∵CE//AB, ∴四边形EDBC 是平行四边形. ……………………6分 在Rt △ABC 中,∠ACB=900,∠B=600,BC=2,∴∠A=300.OE CDAα lOCA (备用图)ACBPQ E D 图5AC (E ) BPQD图6GA C (E )B PQD图7G∴∴AO=12AC. ……………………8分 在Rt △AOD 中,∠A=300,∴AD=2. ∴BD=2. ∴BD=BC.又∵四边形EDBC 是平行四边形,∴四边形EDBC 是菱形 ……………………10分7如图,在梯形ABCD 中,3545AD BC AD DC AB B ====︒∥,,,.动点M 从B 点动身沿线段BC 以每秒2个单位长度的速度向终点C 活动;动点N 同时从C 点动身沿线段CD 以每秒1个单位长度的速度向终点D 活动.设活动的时光为t 秒. (1)求BC 的长.(2)当MN AB ∥时,求t 的值.(3)试探讨:t 为何值时,MNC △为等腰三角形.7.解:(1)如图①,过A .D 分离作AK BC ⊥于K ,DH BC ⊥于H ,则四边形ADHK 是矩形∴3KH AD ==. ················································································ 1分 在Rt ABK △中,sin 4542AK AB =︒==.2cos 454242BK AB =︒== ··························································2分 在Rt CDH △中,由勾股定理得,3HC ==∴43310BC BK KH HC =++=++= ················································· 3分(2)如图②,过D 作DG AB ∥交BC 于G 点,则四边形ADGB 是平行四边形 ∵MN AB ∥ ∴MN DG ∥ CM ADCB KHAD CBG MN∴3BG AD ==∴1037GC =-= ············································································· 4分 由题意知,当M .N 活动到t 秒时,102CN t CM t ==-,. ∵DG MN ∥ ∴NMC DGC =∠∠ 又C C =∠∠ ∴MNC GDC △∽△∴CN CMCD CG =··················································································· 5分 即10257t t -= 解得,5017t = ······················································································ 6分(3)分三种情形评论辩论:①当NC MC =时,如图③,即102t t =- ∴103t =·························································································· 7分②当MN NC =时,如图④,过N 作NE MC ⊥于E解法一:由等腰三角形三线合一性质得()11102522EC MC t t ==-=- 在Rt CEN △中,5cosEC t c NC t-== 又在Rt DHC △中,3cos 5CH c CD ==∴535t t -=解得258t = ······················································································· 8分解法二:∵90C C DHC NEC =∠=∠=︒∠∠, ∴NEC DHC △∽△ ∴NC ECDC HC= ADCB MN(图③) (图④)AD CB M NH E即553t t-=∴258t = ·························································································· 8分③当MN MC =时,如图⑤,过M 作MF CN ⊥于F 点.1122FC NC t ==解法一:(办法同②中解法一)132cos 1025tFC C MC t ===-解得6017t =解法二:∵90C C MFC DHC =∠=∠=︒∠∠, ∴MFC DHC △∽△∴FC MCHC DC =即1102235tt -= ∴6017t =综上所述,当103t =.258t =或6017t =时,MNC △为等腰三角形 ······················ 9分10数学课上,张先生出示了问题:如图1,四边形ABCD 是正方形,点E 是边BC 的中点.90AEF ∠=,且EF 交正方形外角DCG ∠的平行线CF 于点F,求证:AE=EF .经由思虑,小明展现了一种准确的解题思绪:取AB 的中点M,衔接ME,则AM=EC,易证AME ECF △≌△,所以AE EF =.在此基本上,同窗们作了进一步的研讨:(1)小颖提出:如图2,假如把“点E 是边BC 的中点”改为“点E 是边BC 上(除B,C 外)的随意率性一点”,其它前提不变,那么结论“AE=EF”仍然成立,你以为小颖的不雅点准确吗?假如准确,写出证实进程;假如不准确,请解释来由;(2)小华提出:如图3,点E 是BC 的延伸线上(除C 点外)的随意率性一点,其他前提不变,结论“AE=EF”仍然成立.你以为小华的不雅点准确吗?假如准确,写出证实进程;假如不(图⑤)A DCBH N MF10.解:(1)准确. ················································· (1分) 证实:在AB 上取一点M ,使AM EC =,衔接ME . ···· (2分)BM BE ∴=.45BME ∴∠=°,135AME ∴∠=°. CF 是外角等分线, 45DCF ∴∠=°, 135ECF ∴∠=°. AME ECF ∴∠=∠.90AEB BAE ∠+∠=°,90AEB CEF ∠+∠=°,∴BAE CEF ∠=∠.AME BCF ∴△≌△(ASA ). ··································································· (5分) AE EF ∴=. ························································································· (6分) (2)准确. ····················································· (7分) 证实:在BA 的延伸线上取一点N .使AN CE =,衔接NE . ····································· (8分)BN BE ∴=.45N PCE ∴∠=∠=°.四边形ABCD 是正方形,AD BE ∴∥.DAE BEA ∴∠=∠. NAE CEF ∴∠=∠.ANE ECF ∴△≌△(ASA ). ································································· (10分) AE EF ∴=.(11分)11已知一个直角三角形纸片OAB ,个中9024AOB OA OB ∠===°,,.如图,将该纸片放置在平面直角坐标系中,折叠该纸片,折痕与边OB 交于点C ,与边AB 交于点D . A DF C GEBM ADFC GE BN则ACD BCD △≌△.设点C 的坐标为()()00m m >,. 则4BC OB OC m =-=-. 于是4AC BC m ==-.在Rt AOC △中,由勾股定理,得222AC OC OA =+, 即()22242m m -=+,解得32m =. ∴点C 的坐标为302⎛⎫⎪⎝⎭,. ··················································································· 4分(Ⅱ)若折叠后点B 落在边OA 上的点为B ',设OB x '=,OC y =,试写出y 关于x 的函数解析式,并肯定y 的取值规模;(Ⅱ)如图②,折叠后点B 落在OA 边上的点为B ', 则B CD BCD '△≌△. 由题设OB x OC y '==,, 则4B C BC OB OC y '==-=-,在Rt B OC '△中,由勾股定理,得222B C OC OB ''=+.()2224y y x ∴-=+,即2128y x =-+ ···························································································· 6分 由点B '在边OA 上,有02x ≤≤,∴解析式2128y x =-+()02x ≤≤为所求.∴当02x ≤≤时,y 随x 的增大而减小,y ∴的取值规模为322y ≤≤. ····································································· 7分 (Ⅲ)若折叠后点B 落在边OA 上的点为B ',且使B D OB '∥,求此时点C 的坐标.(Ⅲ)如图③,折叠后点B 落在OA 边上的点为B '',且B D OB ''∥. 则OCB CB D ''''∠=∠.又CBD CB D OCB CBD ''''∠=∠∴∠=∠,,有CB BA ''∥.Rt Rt COB BOA ''∴△∽△.有OB OCOA OB''=,得2OC OB ''=. ····································································· 9分 在Rt B OC ''△中,设()00OB x x ''=>,则02OC x =. 由(Ⅱ)的结论,得2001228x x =-+, 解得000808x x x =-±>∴=-+,∴点C 的坐标为()016. ··································································· 10分 12如图(1),将正方形纸片ABCD 折叠,使点B 落在CD 边上一点E (不与点C ,D 重合),压平后得到折痕MN .当CE/CD=1/2时,求AM/BN 的值.类比归纳在图(1)中,若13CE CD =,则AM BN 的值等于;若14CE CD =,则AM BN 的值等于;若1CE CD n =(n 为整数),则AMBN的值等于.(用含n 的式子暗示) 接洽拓广如图(2),将矩形纸片ABCD 折叠,使点B 落在CD 边上一点E (不与点C D ,重合),压平后得到折痕MN ,设()111AB CE m BC m CD n =>=,,则AMBN的值等于.(用含m n ,的式子暗示)12解:办法一:如图(1-1),衔接BM EM BE ,,.由题设,得四边形ABNM 和四边形FENM 关于直线MN 对称.∴MN 垂直等分BE .∴BM EM BN EN ==,. ··············································· 1分 ∵四边形ABCD 是正方形,∴902A D C AB BC CD DA ∠=∠=∠=====°,. ∵112CE CE DE CD =∴==,.设BN x =,则NE x =,2NC x =-. 在Rt CNE △中,222NE CN CE =+.∴()22221x x =-+.解得54x =,即54BN =. ······················································ 3分 在Rt ABM △和在Rt DEM △中, 办法指点: 为了求得AM BN 的值,可先求BN .AM 的长,无妨设:AB =2 图(2) NAB C D EFM图(1)A B CDEFMNN 图(1-1)A B C EFM222AM AB BM +=,222DM DE EM +=,∴2222AM AB DM DE +=+. ····························································· 5分 设AM y =,则2DM y =-,∴()2222221y y +=-+. 解得14y =,即14AM =. ····································································· 6分 ∴15AM BN =. ································································································ 7分 办法二:同办法一,54BN =. ·································································· 3分 如图(1-2),过点N 做NG CD ∥,交AD 于点G ,衔接BE .∵AD BC ∥,∴四边形GDCN是平行四边形. ∴NG CD BC ==. 同理,四边形ABNG 也是平行四边形.∴54AG BN ==. ∵90MN BE EBC BNM ⊥∴∠+∠=,°. 90NG BC MNG BNM EBC MNG ⊥∴∠+∠=∴∠=∠,°,.在BCE △与NGM △中90EBC MNG BC NG C NGM ∠=∠⎧⎪=⎨⎪∠=∠=⎩,,°.∴BCE NGM EC MG =△≌△,. ·································· 5分 ∵114AM AG MG AM =--=5,=.4 ····················································· 6分 ∴15AM BN =. ··················································································· 7分 12..如图所示,在直角梯形ABCD 中,AD//BC,∠A =90°,AB =12,BC =21,AD=16.动点P 从点B 动身,沿射线BC 的偏向以每秒2个单位长的速度活动,动点Q 同时从点A 动身,在线段AD 上以每秒1个单位长的速度向点D 活动,当个中一个动点到达端点时另一个动点也随之停滞活动.设活动的时光为t (秒).(1)设△DPQ 的面积为S,求S 与t 之间的函数关系式;(2)当t 为何值时,四边形PCDQ 是平行四边形?(3)分离求出出当t 为何值时,① PD =PQ,② DQ =PQ ?类比归纳N 图(1-2) A B C D EF M G25(或410);917;()2211n n -+ ······································································ 10分 接洽拓广 2222211n m n n m -++ ······················································································· 12分 解1:依题意,得AQ=t,BP=2t,QD=16-t.过点Q 作QF ⊥BP,又∵AQ‖BF,∴∠ABP=90°∴四边形AQFB 是矩形∴AQ=BF=t ∵BP=2t ∴FP=t,∴在Rt △QFP 中,QP=√(12²+t²)又∵QD=QP=PD ∴√(12²+t²)=16-t ∴12²+t²=16²-2*16*t+t²∴解得:t=7/2解2:如图所示,:这P 作PE 垂直AD 于E,垂足为E 点,则ABPE 为矩形.PE=AB=12;AE=BP(1).s=1/2×AB×DQ=1/2×12×(AD-AQ)=6×(16-t)=96-6t;(2).当 BC-2t=21-2t=PC=DQ=AD-t=16-t,即t=5时,四边形PCDQO 为平形四边形.(3).①QE=AE-AQ=BP-AQ=2t-t=t,而ED=AD-AE=16-BP=16-2t;当QE=ED 时,PE 为QD 的垂直等分线时,PQ=PD,而此时t=16-2t; t=16/3;所以当t=16/3时,PD=PQ;.②在Rt △PEQ 中,PE=AB=12; EQ=AE-AQ=PB-AQ=2t-t=t; PQ²=QE²+PE²=t²+12²; QD²=(AD-AQ)²=(16-t)²; 所以当t²+12²=(16-t)²,即:t=3.5时,DQ=PQ;解:因为∠C=90°,∠CBA=30°,BC=20√3所以可求出AB =40如图,圆心从A 向B 的偏向活动时,共有三个地位能使此圆与直线AC 或直线BC 相切当圆心在O1点时,设切点为P显然PO1=6,∠APO1=90°,∠AO1P=30°所以AO1=4√3因为圆O以2个单位长度/秒的速度向右活动所以当t1=4√3/2=2√3(秒)时,圆O与直线AC相切当圆心在O2点时,设切点为Q显然QO2=6,∠BQO2=90°,∠QBO2=30°所以BO2=12,AO2=40-12=28因为圆O以2个单位长度/秒的速度向右活动所以当t2=28/2=14(秒)时,圆O与直线BC相切当圆心在O3点时,设切点为R显然RO3=6,∠BRO3=90°,∠RBO3=30°所以BO3=12,AO3=40+12=52因为圆O以2个单位长度/秒的速度向右活动所以当t3=52/2=26(秒)时,圆O与直线BC相切综上所述,当圆O活动2√3秒.14秒.26秒时与△ABC的一边地点的直线相切.。
七年级动点问题大全

七年级动点问题大全(一)例1:如图,在数轴上A点表示数a,B点表示数b,AB表示A点和B点之间的距离,且a、b满足|a+2|+(b+3a)2=0(1)求A、B两点之间的距离;(2)若在数轴上存在一点C,且AC=2BC,求C点表示的数;(3)若在原点O处放一挡板,一小球甲从点A处以1个单位/秒的速度向左运动;同时另一小球乙从点B处以2个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为t(秒),①分别表示甲、乙两小球到原点的距离(用t表示);①求甲、乙两小球到原点的距离相等时经历的时间.例2:如图,有一数轴原点为O,点A所对应的数是-12,点A沿数轴匀速平移经过原点到达点B.(1)如果OA=OB,那么点B所对应的数是什么?(2)从点A到达点B所用时间是3秒,求该点的运动速度.(3)在(2)的条件下,从点A沿数轴匀速平移经过点K到达点C,所用时间是9秒,且KC=KA,分别求点K和点C所对应的数。
例3动点A从原点出发向数轴负方向运动,同时,动点B也从原点出发向数轴正方向运动,3秒后,两点相距15个单位长度.已知动点A、B的速度比是1:4.(速度单位:单位长度/秒)(1)求出两个动点运动的速度,并在数轴上标出A、B两点从原点出发运动3秒时的位置;(2)若A、B两点从(1)中的位置同时向数轴负方向运动,几秒后原点恰好处在两个动点正中间;(3)在(2)中A、B两点继续同时向数轴负方向运动时,另一动点C同时从B点位置出发向A运动,当遇到A后,立即返回向B点运动,遇到B点后立即返回向A点运动,如此往返,直到B追上A时,C立即停止运动.若点C一直以20单位长度/秒的速度匀速运动,那么点C从开始到停止运动,运动的路程是多少单位长度.例4:已知数轴上两点A、B对应的数分别为-1、3,点P为数轴上一动点,其对应的数为x.(1)若点P到点A,点B的距离相等,求点P对应的数;(2)数轴上是否存在点P,使点P到点A、点B的距离之和为6?若存在,请求出x的值;若不存在,说明理由;(3)点A、点B分别以2个单位长度/分、1个单位长度/分的速度向右运动,同时点P以6个单位长度/分的速度从O点向左运动.当遇到A时,点P立即以同样的速度向右运动,并不停地往返于点A与点B之间,求当点A与点B重合时,点P所经过的总路程是多少?例5数轴上两个质点A、B所对应的数为-8、4,A、B两点各自以一定的速度在上运动,且A点的运动速度为2个单位/秒.(1)点A、B两点同时出发相向而行,在原点处相遇,求B点的运动速度;(2)A、B两点以(1)中的速度同时出发,向数轴正方向运动,几秒钟时两者相距6个单位长度;(3)A、B两点以(1)中的速度同时出发,向数轴负方向运动,与此同时,C点从原点出发作同方向的运动,且在运动过程中,始终有CB:CA=1:2,若干秒钟后,C停留在-10处,求此时B点的位置?例6:在数轴上,点A表示的数是-30,点B表示的数是170.(1)求A、B中点所表示的数.(2)一只电子青蛙m,从点B出发,以4个单位每秒的速度向左运动,同时另一只电子青蛙n,从A点出发以6个单位每秒的速度向右运动,假设它们在C点处相遇,求C点所表示的数.(3)两只电子青蛙在C点处相遇后,继续向原来运动的方向运动,当电子青蛙m处在A 点处时,问电子青蛙n处在什么位置?(4)如果电子青蛙m从B点处出发向右运动的同时,电子青蛙n也向右运动,假设它们在D点处相遇,求D点所表示的数例7、已知数轴上有A、B、C三点,分别代表- 24,- 10,10,两只电子蚂蚁甲、乙分别从A、C两点同时相向而行,甲的速度为4个单位/秒。
初中数学动点题百题训练专题练习(含答案解析)
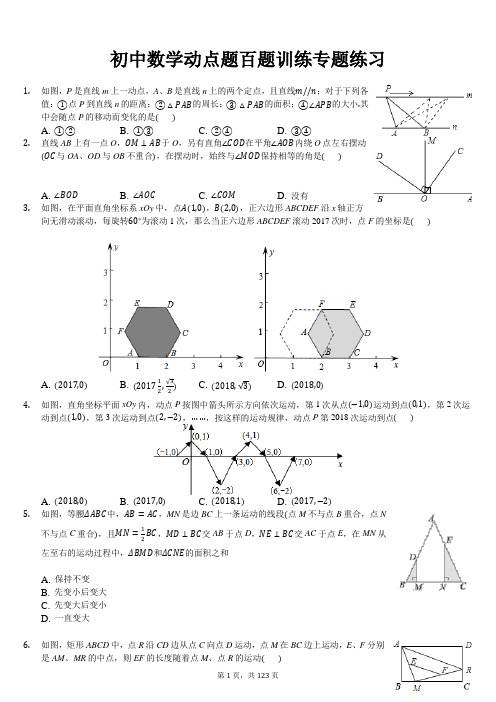
初中数学动点题百题训练专题练习1.如图,P是直线m上一动点,A、B是直线n上的两个定点,且直线m//n;对于下列各值:①点P到直线n的距离;②△PAB的周长;③△PAB的面积;④∠APB的大小.其中会随点P的移动而变化的是()A. ①②B. ①③C. ②④D. ③④2.直线AB上有一点O,OM⊥AB于O,另有直角∠COD在平角∠AOB内绕O点左右摆动(OC与OA、OD与OB不重合),在摆动时,始终与∠MOD保持相等的角是()A. ∠BODB. ∠AOCC. ∠COMD. 没有3.如图,在平面直角坐标系xOy中,点A(1,0),B(2,0),正六边形ABCDEF沿x轴正方向无滑动滚动,每旋转60∘为滚动1次,那么当正六边形ABCDEF滚动2017次时,点F的坐标是()A. (2017,0)B. (201712,√32) C. (2018,√3) D. (2018,0)4.如图,直角坐标平面xOy内,动点P按图中箭头所示方向依次运动,第1次从点(−1,0)运动到点(0,1),第2次运动到点(1,0),第3次运动到点(2,−2),……,按这样的运动规律,动点P第2018次运动到点()A. (2018,0)B. (2017,0)C. (2018,1)D. (2017,−2)5.如图,等腰ΔABC中,AB=AC,MN是边BC上一条运动的线段(点M不与点B重合,点N不与点C重合),且MN=12BC,MD⊥BC交AB于点D,NE⊥BC交AC于点E,在MN从左至右的运动过程中,ΔBMD和ΔCNE的面积之和A. 保持不变B. 先变小后变大C. 先变大后变小D. 一直变大6.如图,矩形ABCD中,点R沿CD边从点C向点D运动,点M在BC边上运动,E、F分别是AM、MR的中点,则EF的长度随着点M、点R的运动()A. 变短B. 变长C. 不变D. 无法确定7.如图,在△ABC中,AB=AC,BC=4,面积是14,AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为()A. 6B. 8C. 9D. 108.如图,已知,,,点是线段上的一个动点,连接,动点始终与点关于直线对称,当点由点位置向右运动至点位置时,相应的点所经过的路程为()A.B.C.D.9.如图,在△ABC中,∠ACB=90∘,AC=2,BC=1,点A、C分别在x轴、y轴上,当点A在x轴运动时,点C随之在y轴上运动,在运动过程中,点B到原点O的最大距离为()A. √5B. √6C. 1+√2D. 310.如图,在▱ABCD中,对角线AC、BD交于点O,并且∠DAC=60∘,∠ADB=15∘.点E是AD边上一动点,延长EO交BC于点F.当点E从D点向A点移动过程中(点E与点D,A不重合),则四边形AFCE的变化是()A. 平行四边形→矩形→平行四边形→菱形→平行四边形B. 平行四边形→菱形→平行四边形→矩形→平行四边形C. 平行四边形→矩形→平行四边形→正方形→平行四边形D. 平行四边形→矩形→菱形→正方形→平行四边形11.如图,点P是边长为1的菱形ABCD对角线AC上一个动点,点M,N分别为AB,BC边上的中点,则MP+NP的最小值是()A. 2B. 1C.D.12.如图,在Rt△ABC中,∠C=90∘,AC=4cm,BC=6cm,动点P从点C沿CA,以1cm/s的速度向点A运动,同时动点O从点C沿CB,以2cm/s的速度向点B运动,其中一个动点到达终点时,另一个动点也停止运动.则运动过程中所构成的△CPO的面积y(cm2)与运动时间x(s)之间的函数图象大致是()A. B. C. D.13.如图,在△ABC中,∠B=90∘,tan∠C=34,AB=6cm.动点P从点A开始沿边AB向点B 以1cm/s的速度移动,动点Q从点B开始沿边BC向点C以2cm/s的速度移动.若P,Q两点分别从A,B两点同时出发,在运动过程中,△PBQ的最大面积是()A. 18cm2B. 12cm2C. 9cm2D. 3cm214.抛物线y=x2−2x−15,y=4x−23,交于A、B点(A在B的左侧),动点P从A点出发,先到达抛物线的对称轴上的某点E再到达x轴上的某点F,最后运动到点B.若使点P动的总路径最短,则点P运动的总路径的长为( )A. 10√5B. 7√10C. 5√21D. 8√1015.如图,抛物线y=x2−12x−32与直线y=x−2交于A、B两点(点A在点B的左侧),动点P从A点出发,先到达抛物线的对称轴上的某点E,再到达x轴上的某点F,最后运动到点B.若使点P运动的总路径最短,则点P运动的总路径的长为()A. √292B. √293C. 52D. 5316.如图,在△ABC中,∠C=90∘,AB=10cm,BC=8cm,点P从点A沿AC向点C以1cm/s的速度运动,同时点Q从点C沿CB向点B以2cm/s的速度运动(点Q运动到点B停止),在运动过程中,四边形PABQ的面积最小值为()A. 19cm2B. 16cm2C. 15cm2D. 12cm217.如图,抛物线y=x2−2x−3与x轴交于A,B两点,过点B的直线与抛物线在第二象限交于点C,且tan∠CBA=43,点D为线段BC上一点(不含端点).现有一动点P从点A出发,沿线段AD以每秒1个单位长度的速度运动到D点,再沿线段DC以每秒54个单位长度的速度运动到C点,则动点P运动到C点的最短时间需()秒.A. 7B. 649C. 10 D. 75818.如图,在△ABC中,∠B=90∘,AB=12mm,BC=24mm,动点P从点A开始沿边AB向B以2mm/s的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以4mm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,那么经过()秒,四边形APQC的面积最小.A. 1B. 2C. 3D. 419.如图,在钝角三角形ABC中,AB=6cm,AC=12cm,动点D从A点出发到B点止,动点E从C点出发到A点止.点D运动的速度为1cm/秒,点E运动的速度为2cm/秒.如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间是()A. 4或4.8B. 3或4.8C. 2或4D. 1或620.如图,矩形ABCD中,AB=4,BC=10,点P为BC边上一动点,AP交BD于点Q.点P从B点出发沿BC边以每秒1个单位长度的速度向C点移动,移动时间为x秒.设S△AQD+S△PQB=y,写出y与x之间的函数关系式,并探究P点运动到第几秒与第几秒之间时,y取得最小值.()A. 3到4B. 4到5C. 5到6D. 6到721.在矩形ABCD中,BC=10cm、DC=6cm,点E、F分别为边AB、BC上的两个动点,E从点A出发以每秒5cm的速度向B运动,F从点B出发以每秒3cm的速度向C运动,设运动时间为t秒.若∠AFD=∠AED,则t的值为()A. √2−1B. 0.5C. 23D. 122.如图,△ABC内接于⊙O,∠A=60∘,BC=4√3,当点P在B^C上由B点运动到C点时,弦AP的中点E运动的路径长为()A. 4√33πB. 43πC. 83πD. 2√323.如图,在平面直角坐标系中,M、N、C三点的坐标分别为(12,1),(3,1),(3,0),点A 为线段MN上的一个动点,连接AC,过点A作AB⊥AC交y轴于点B,当点A从M运动到N时,点B随之运动.设点B的坐标为(0,b),则b的取值范围是()A. −14≤b≤1 B. −54≤b≤1 C. −94≤b≤12D. −94≤b≤124.如图,在△ABC中,∠ACB=90∘,∠A=30∘,BC=1.P是AB边上一动点,PD⊥AC于点D,点E在P的右侧,且PE=1,连结CE.P从点A出发,沿AB方向运动,当E到达点B时,P停止运动.在整个运动过程中,阴影部分面积S1+S2的大小变化情况是()A. 一直不变B. 一直减小C. 一直增大D. 先减小后增大25.如图,在反比例函数y=32x的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第二象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y=kx的图象上运动,若tan∠CAB=2,则k的值为()A. −3B. −6C. −9D. −1226.如图,在点O处测得远处动点P作匀速直线运动,开始位置在A点,一分钟后到达B点,再过一分钟到达C点,测得∠AOB=90∘,∠BOC=30∘,则tan∠OAB=()A. 32B. √32C. 2√33D. 2327.如图,四边形ABCD和四边形BEFG均为正方形,且A、B、E三点共线,正方形ABCD的边长为4,则S△ACF的面积为______ .28.20.如图,矩形ABCD中,点M是CD的中点,点P是AB上的一动点,若AD=1,AB=2,则PA+PB+PM的最小值是.29.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…按这样的运动规律,经过第2017次运动后,动点P的坐标是______,经过第2018次运动后,动点P的坐标是______.30.15.如图1,在直角梯形ABCD中,动点P从B点出发,沿B→C→D→A匀速运动,设点P运动的路程为x,△ABP的面积为y,若y与x的关系图象如图2所示,则AB的长为_______,梯形ABCD的面积为__________.31.18、正方形中,为上一动点,连接交于,过点作交于,。
七年级上册数轴上的动点压轴题专练

七年级上册数轴上的动点压轴题专练一、数轴上动点问题相关知识点回顾1. 数轴的三要素原点、正方向和单位长度。
在数轴上,数与点是一一对应的关系。
2. 两点间的距离公式设数轴上两点公式、公式所表示的数分别为公式、公式,则公式和公式两点间的距离公式。
例如,若公式表示公式,公式表示公式,则公式;若公式表示公式,公式表示公式,则公式。
3. 动点在数轴上的表示设动点公式从数轴上表示数公式的点出发,以速度公式沿数轴正方向运动,经过时间公式后,点公式所表示的数为公式;若沿数轴负方向运动,则点公式所表示的数为公式。
二、典型例题及解析1. 已知数轴上公式、公式两点对应的数分别为公式和公式,点公式为数轴上一动点,其对应的数为公式。
(1)若点公式到点公式、点公式的距离相等,求点公式对应的数。
解析:因为点公式到点公式、点公式的距离相等,根据两点间距离公式公式,公式。
又因为公式,所以公式。
当公式时,方程无解。
当公式时,公式,公式,解得公式。
所以点公式对应的数为公式。
(2)若点公式在点公式、点公式之间,且公式,求点公式对应的数。
解析:因为公式,公式,且公式,所以公式。
因为点公式在公式、公式之间,即公式,所以公式。
去括号得公式。
移项得公式。
合并同类项得公式,解得公式。
所以点公式对应的数为公式。
(3)点公式以每分钟公式个单位长度的速度从原点公式向左运动,同时点公式以每分钟公式个单位长度的速度向左运动,点公式以每分钟公式个单位长度的速度向左运动,设运动时间为公式分钟。
问公式为何值时,点公式到点公式、点公式的距离相等?解析:公式分钟后,点公式表示的数为公式,点公式表示的数为公式,点公式表示的数为公式。
根据公式,公式。
当公式时,即公式。
当公式时,公式,公式,解得公式。
当公式时,公式,公式,公式,解得公式。
2. 数轴上点公式表示的数为公式,点公式表示的数为公式。
(1)求线段公式的长。
解析:根据两点间距离公式公式。
(2)若点公式是线段公式的中点,则点公式表示的数为多少?解析:设点公式表示的数为公式,因为公式是公式中点,所以公式。
初中数学动点题试卷

一、选择题(每题4分,共20分)1. 下列关于动点P在平面直角坐标系中的运动轨迹,正确的是()。
A. 以原点为圆心,半径为2的圆B. 以原点为圆心,半径为3的圆C. 以点(2,0)为圆心,半径为1的圆D. 以点(-2,0)为圆心,半径为1的圆2. 动点A在直线y=2x+1上运动,若点A到点B(2,3)的距离为3,则动点A的轨迹方程为()。
A. (x-2)²+(y-3)²=9B. (x-2)²+(y-3)²=16C. (x-2)²+(y-3)²=25D. (x-2)²+(y-3)²=363. 动点P在抛物线y²=4x上运动,若P到焦点F的距离等于到准线的距离,则P 的轨迹方程为()。
A. y²=2xB. y²=8xC. y²=16xD. y²=32x4. 动点P在直线y=kx+b上运动,若P到点A(2,3)的距离为定值d,则直线y=kx+b的斜率k和截距b的关系为()。
A. k²+d²=1B. k²+d²=4C. k²+d²=9D. k²+d²=165. 动点P在抛物线y²=2px上运动,若P到焦点F的距离等于到准线的距离,则p 的值为()。
A. 1B. 2C. 4D. 8二、填空题(每题5分,共25分)6. 动点P在抛物线y²=4x上运动,若P到焦点F的距离等于到准线的距离,则P 的轨迹方程为______。
7. 动点P在直线y=kx+b上运动,若P到点A(2,3)的距离为定值d,则直线y=kx+b的斜率k和截距b的关系为______。
8. 动点P在抛物线y²=2px上运动,若P到焦点F的距离等于到准线的距离,则p 的值为______。
9. 动点P在椭圆x²/4+y²/9=1上运动,若P到焦点F1的距离等于到焦点F2的距离,则P的轨迹方程为______。
动点综合问题(共32题)(解析版)--2023年中考数学真题分项汇编(全国通用)

专题动点综合问题(32题)1(2023·四川遂宁·统考中考真题)如图,在△ABC 中,AB =10,BC =6,AC =8,点P 为线段AB 上的动点,以每秒1个单位长度的速度从点A 向点B 移动,到达点B 时停止.过点P 作PM ⊥AC 于点M 、作PN ⊥BC 于点N ,连接MN ,线段MN 的长度y 与点P 的运动时间t (秒)的函数关系如图所示,则函数图象最低点E 的坐标为()A.5,5B.6,245C.325,245D.325,5【答案】C【分析】如图所示,过点C 作CD ⊥AB 于D ,连接CP ,先利用勾股定理的逆定理证明△ABC 是直角三角形,即∠C =90°,进而利用等面积法求出CD =245,则可利用勾股定理求出AD =325;再证明四边形CMPN 是矩形,得到MN =CP ,故当点P 与点D 重合时,CP 最小,即MN 最小,此时MN 最小值为245,AP =325,则点E 的坐标为325,245.【详解】解:如图所示,过点C 作CD ⊥AB 于D ,连接CP ,∵在△ABC 中,AB =10,BC =6,AC =8,∴AC 2+BC 2=62+82=100=102=AB 2,∴△ABC 是直角三角形,即∠C =90°,∴S △ABC =12AC ⋅BC =12AB ⋅CD ,∴CD =AC ⋅BC AB=245,∴AD =AC 2-CD 2=325;∵PM ⊥AC ,PN ⊥BC ,∠C =90°,∴四边形CMPN 是矩形,∴MN =CP ,∴当MN 最小时,即CP 最小,∴当点P 与点D 重合时,CP 最小,即MN 最小,此时MN 最小值为245,AP =AD =325,∴点E 的坐标为325,245,故选:C .【点睛】本题主要考查了勾股定理和勾股定理的逆定理,矩形的性质与判断,垂线段最短,坐标与图形等等,正确作出辅助线是解题的关键.2(2023·广东深圳·统考中考真题)如图1,在Rt △ABC 中,动点P 从A 点运动到B 点再到C 点后停止,速度为2单位/s ,其中BP 长与运动时间t (单位:s )的关系如图2,则AC 的长为()B.427C.17D.53A.1552【答案】C【分析】根据图象可知t=0时,点P与点A重合,得到AB=15,进而求出点P从点A运动到点B所需的时间,进而得到点P从点B运动到点C的时间,求出BC的长,再利用勾股定理求出AC即可.【详解】解:由图象可知:t=0时,点P与点A重合,∴AB=15,∴点P从点A运动到点B所需的时间为15÷2=7.5s;∴点P从点B运动到点C的时间为11.5-7.5=4s,∴BC=2×4=8;在Rt△ABC中:AC=AB2+BC2=17;故选:C.【点睛】本题考查动点的函数图象,勾股定理.从函数图象中有效的获取信息,求出AB,BC的长,是解题的关键.3(2023·黑龙江绥化·统考中考真题)如图,在菱形ABCD中,∠A=60°,AB=4,动点M,N同时从A 点出发,点M以每秒2个单位长度沿折线A-B-C向终点C运动;点N以每秒1个单位长度沿线段AD 向终点D运动,当其中一点运动至终点时,另一点随之停止运动.设运动时间为x秒,△AMN的面积为y 个平方单位,则下列正确表示y与x函数关系的图象是()A. B.C. D.【答案】A【分析】连接BD ,过点B 作BE ⊥AD 于点E ,根据已知条件得出△ABD 是等边三角形,进而证明△AMN ∽ABE 得出∠ANM =∠AEB =90°,当0<t <4时,M 在AB 上,当4≤t <8时,M 在BC 上,根据三角形的面积公式得到函数关系式,【详解】解:如图所示,连接BD ,过点B 作BE ⊥AD 于点E ,当0<t <4时,M 在AB 上,菱形ABCD 中,∠A =60°,AB =4,∴AB =AD ,则△ABD 是等边三角形,∴AE =ED =12AD =2,BE =3AE =23∵AM =2x ,AN =x ,∴AM AN =AB AE =2,又∠A =∠A ∴△AMN ∽ABE∴∠ANM =∠AEB =90°∴MN =AM 2-AN 2=3x ,∴y =12x ×3x =32x2当4≤t <8时,M 在BC 上,∴y =12AN ×BE =12x ×23=3x ,综上所述,0<t <4时的函数图象是开口向上的抛物线的一部分,当4≤t <8时,函数图象是直线的一部分,故选:A .【点睛】本题考查了动点问题的函数图象,二次函数图象的性质,一次函数图象的性质,菱形的性质,勾股定理,等边三角形的性质与判定,相似三角形的性质与判定,熟练掌握以上知识是解题的关键.4(2023·黑龙江齐齐哈尔·统考中考真题)如图,在正方形ABCD 中,AB =4,动点M ,N 分别从点A ,B 同时出发,沿射线AB ,射线BC 的方向匀速运动,且速度的大小相等,连接DM ,MN ,ND .设点M 运动的路程为x 0≤x ≤4 ,△DMN 的面积为S ,下列图像中能反映S 与x 之间函数关系的是()A. B.C. D.【答案】A【分析】先根据S =S 正方形ABCD -S △ADM -S △DCN -S △BMN ,求出S 与x 之间函数关系式,再判断即可得出结论.【详解】解:S =S 正方形ABCD -S △ADM -S △DCN -S △BMN ,=4×4-12×4x -12×4(4-x )-12x (4-x ),=12x 2-2x +8,=12(x -2)2+6,故S 与x 之间函数关系为二次函数,图像开口向上,x =2时,函数有最小值6,故选:A .【点睛】本题考查了正方形的性质,二次函数的图像与性质,本题的关键是求出S 与x 之间函数关系式,再判断S 与x 之间函数类型.5(2023·河南·统考中考真题)如图1,点P 从等边三角形ABC 的顶点A 出发,沿直线运动到三角形内部一点,再从该点沿直线运动到顶点B .设点P 运动的路程为x ,PBPC=y ,图2是点P 运动时y 随x 变化的关系图象,则等边三角形ABC 的边长为()A.6B.3C.43D.23【答案】A【分析】如图,令点P 从顶点A 出发,沿直线运动到三角形内部一点O ,再从点O 沿直线运动到顶点B .结合图象可知,当点P 在AO 上运动时,PB =PC ,AO =23,易知∠BAO =∠CAO =30°,当点P 在OB 上运动时,可知点P 到达点B 时的路程为43,可知AO =OB =23,过点O 作OD ⊥AB ,解直角三角形可得AD =AO ⋅cos30°=3,进而可求得等边三角形ABC 的边长.【详解】解:如图,令点P 从顶点A 出发,沿直线运动到三角形内部一点O ,再从点O 沿直线运动到顶点B .结合图象可知,当点P 在AO 上运动时,PBPC=1,∴PB =PC ,AO =23,又∵△ABC 为等边三角形,∴∠BAC =60°,AB =AC ,∴△APB ≌△APC SSS ,∴∠BAO =∠CAO ,∴∠BAO =∠CAO =30°,当点P 在OB 上运动时,可知点P 到达点B 时的路程为43,∴OB =23,即AO =OB =23,∴∠BAO =∠ABO =30°,过点O 作OD ⊥AB ,∴AD =BD ,则AD =AO ⋅cos30°=3,∴AB =AD +BD =6,即:等边三角形ABC 的边长为6,故选:A .【点睛】本题考查了动点问题的函数图象,解决本题的关键是综合利用图象和图形给出的条件.6(2023·四川乐山·统考中考真题)如图,在平面直角坐标系xOy 中,直线y =-x -2与x 轴、y 轴分别交于A 、B 两点,C 、D 是半径为1的⊙O 上两动点,且CD =2,P 为弦CD 的中点.当C 、D 两点在圆上运动时,△PAB 面积的最大值是()A.8B.6C.4D.3【答案】D【分析】根据一次函数与坐标轴的交点得出OA =OB =2,确定AB =22,再由题意得出当PO 的延长线恰好垂直AB 时,垂足为点E ,此时PE 即为三角形的最大高,连接DO ,利用勾股定理求解即可.【详解】解:∵直线y =-x -2与x 轴、y 轴分别交于A 、B 两点,∴当x =0时,y =-2,当y =0时,x =-2,∴A -2,0 ,B 0,-2 ,∴OA =OB =2,∴AB =OA 2+OB 2=22,∵△PAB 的底边AB =22为定值,∴使得△PAB 底边上的高最大时,面积最大,点P 为CD 的中点,当PO 的延长线恰好垂直AB 时,垂足为点E ,此时PE 即为三角形的最大高,连接DO ,∵CD =2,⊙O 的半径为1,∴DP=22∴OP=OD2-DP2=22,∵OE⊥AB,∴OE=12AB=2,∴PE=OE+OP=322,∴S△PAB=12×22×322=3,故选:D.【点睛】题目主要考查一次函数的应用及勾股定理解三角形,垂径定理的应用,理解题意,确定出高的最大值是解题关键.7(2023·河北·统考中考真题)如图是一种轨道示意图,其中ADC和ABC均为半圆,点M,A,C,N依次在同一直线上,且AM=CN.现有两个机器人(看成点)分别从M,N两点同时出发,沿着轨道以大小相同的速度匀速移动,其路线分别为M→A→D→C→N和N→C→B→A→M.若移动时间为x,两个机器人之间距离为y,则y与x关系的图象大致是()A. B.C. D.【答案】D【分析】设圆的半径为R,根据机器人移动时最开始的距离为AM+CN+2R,之后同时到达点A,C,两个机器人之间的距离y越来越小,当两个机器人分别沿A→D→C和C→B→A移动时,此时两个机器人之间的距离是直径2R,当机器人分别沿C→N和A→M移动时,此时两个机器人之间的距离越来越大.【详解】解:由题意可得:机器人(看成点)分别从M,N两点同时出发,设圆的半径为R,∴两个机器人最初的距离是AM+CN+2R,∵两个人机器人速度相同,∴分别同时到达点A,C,∴两个机器人之间的距离y越来越小,故排除A,C;当两个机器人分别沿A→D→C和C→B→A移动时,此时两个机器人之间的距离是直径2R,保持不变,当机器人分别沿C→N和A→M移动时,此时两个机器人之间的距离越来越大,故排除C,故选:D.【点睛】本题考查动点函数图像,找到运动时的特殊点用排除法是关键.8(2023·江苏苏州·统考中考真题)如图,在平面直角坐标系中,点A的坐标为9,0,点C的坐标为0,3,以OA,OC为边作矩形OABC.动点E,F分别从点O,B同时出发,以每秒1个单位长度的速度沿OA,BC向终点A,C移动.当移动时间为4秒时,AC⋅EF的值为()A.10B.910C.15D.30【答案】D【分析】根据题意,得出E4,0,勾股定理求得EF=10,AC=310,即可求解.,F5,3【详解】解:连接AC、EF∵点A的坐标为9,0,以OA,OC为边作矩形OABC.,点C的坐标为0,3∴B9,3,AC=32+92=310则OA=9,BC=OA=9依题意,OE=4×1=4,BF=4×1=4∴AE=9-4=5,则E4,0,∴CF=BC-BF=9-4=5∴F5,3,∴EF=5-42+32=10,∵C0,3,∴AC⋅EF=310×10=30故选:D.【点睛】本题考查了坐标与图形,勾股定理求两点坐标距离,矩形的性质,求得E,F的坐标是解题的关键.9(2023·山东滨州·统考中考真题)已知点P 是等边△ABC 的边BC 上的一点,若∠APC =104°,则在以线段AP ,BP ,CP 为边的三角形中,最小内角的大小为()A.14°B.16°C.24°D.26°【答案】B【分析】将△ABP 绕点A 逆时针旋转60°得到△ACQ ,可得以线段AP ,BP ,CP 为边的三角形,即△PCQ ,最小的锐角为∠PQC ,根据邻补角以及旋转的性质得出∠AQC =∠APB =76°,进而即可求解.【详解】解:如图所示,将△ABP 绕点A 逆时针旋转60°得到△ACQ ,∴AP =AQ ,∠PAQ =60°,BP =CQ ,∠AQC =∠APB ,∴△APQ 是等边三角形,∴PQ =AP ,∴以线段AP ,BP ,CP 为边的三角形,即△PCQ ,最小的锐角为∠PQC ,∵∠APC =104°,∴∠APB =76°∴∠AQC =∠APB =76°∴∠PQC =76°-60°=16°,故选:B .【点睛】本题考查了旋转的性质,等边三角形的性质与判定,熟练掌握旋转的性质是解题的关键.10(2023·甘肃武威·统考中考真题)如图1,正方形ABCD 的边长为4,E 为CD 边的中点.动点P 从点A 出发沿AB →BC 匀速运动,运动到点C 时停止.设点P 的运动路程为x ,线段PE 的长为y ,y 与x 的函数图象如图2所示,则点M 的坐标为()A.4,23B.4,4C.4,25D.4,5【答案】C【分析】证明AB =BC =CD =AD =4,∠C =∠D =90°,CE =DE =2,则当P 与A ,B 重合时,PE 最长,此时PE =22+42=25,而运动路程为0或4,从而可得答案.【详解】解:∵正方形ABCD 的边长为4,E 为CD 边的中点,∴AB =BC =CD =AD =4,∠C =∠D =90°,CE =DE =2,当P 与A ,B 重合时,PE 最长,此时PE =22+42=25,运动路程为0或4,结合函数图象可得M 4,25 ,故选:C .【点睛】本题考查的是从函数图象中获取信息,正方形的性质,勾股定理的应用,理解题意,确定函数图象上横纵坐标的含义是解本题的关键.11(2023·浙江绍兴·统考中考真题)如图,在△ABC 中,D 是边BC 上的点(不与点B ,C 重合).过点D作DE ∥AB 交AC 于点E ;过点D 作DF ∥AC 交AB 于点F .N 是线段BF 上的点,BN =2NF ;M 是线段DE 上的点,DM =2ME .若已知△CMN 的面积,则一定能求出()A.△AFE 的面积B.△BDF 的面积C.△BCN 的面积D.△DCE 的面积【答案】D【分析】如图所示,连接ND ,证明△FBD ∽△EDC ,得出FB ED =FD EC ,由已知得出NF ME =BF DE ,则FDEC=NFME,又∠NFD =∠MEC ,则△NFD ∽△MEC ,进而得出∠MCD =∠NDB ,可得MC ∥ND ,结合题意得出S △EMC =12S △DMC =12S △MNC ,即可求解.【详解】解:如图所示,连接ND ,∵DE ∥AB ,DF ∥AC ,∴∠ECD =∠FDB ,∠FBD =∠EDC ,∠BFD =∠A ,∠A =DEC .∴△FBD ∽△EDC ,∠NFD =∠MEC .∴FB ED =FD EC .∵DM =2ME ,BN =2NF ,∴NF =13BF ,ME =13DE ,∴NF ME =BF DE .∴FD EC=NF ME .又∵∠NFD =∠MEC ,∴△NFD ∽△MEC .∴∠ECM =∠FDN .∵∠FDB =∠ECD ∴∠MCD =∠NDB .∴MC ∥ND .∴S △MNC =S △MDC .∵DM =2ME ,∴S △EMC =12S △DMC =12S △MNC .故选:D .【点睛】本题考查了相似三角形的性质与判定,证明MC ∥ND 是解题的关键.12(2023·安徽·统考中考真题)如图,E 是线段AB 上一点,△ADE 和△BCE 是位于直线AB 同侧的两个等边三角形,点P ,F 分别是CD ,AB 的中点.若AB =4,则下列结论错误的是()A.PA +PB 的最小值为33B.PE +PF 的最小值为23C.△CDE 周长的最小值为6D.四边形ABCD 面积的最小值为33【答案】A【分析】延长AD ,BC ,则△ABQ 是等边三角形,观察选项都是求最小时,进而得出当E 点与F 重合时,则Q ,P ,F 三点共线,各项都取得最小值,得出B ,C ,D 选项正确,即可求解.【详解】解:如图所示,延长AD ,BC ,依题意∠QAD =∠QBA =60°∴△ABQ 是等边三角形,∵P 是CD 的中点,∴PD =PC ,∵∠DEA =∠CBA ,∴ED ∥CQ∴∠PQC =∠PED ,∠PCQ =∠PDE ,∴△PDE ≌△PCQ ∴PQ =PE ,∴四边形DECQ 是平行四边形,则P 为EQ 的中点如图所示,设AQ ,BQ 的中点分别为G ,H ,则GP =12AE ,PH =12EB∴当E 点在AB 上运动时,P 在GH 上运动,当E 点与F 重合时,即AE =EB ,则Q ,P ,F 三点共线,PF 取得最小值,此时AE =EB =12AE +EB =2,则△ADE ≌△ECB ,∴C ,D 到AB 的距离相等,则CD ∥AB ,此时PF =32AD =3此时△ADE 和△BCE 的边长都为2,则AP ,PB 最小,∴PF =32×2=3,∴PA =PB =22+3 2=7∴PA +PB =27,或者如图所示,作点B 关于GH 对称点B ,则PB =PB ,则当A ,P ,B 三点共线时,AP +PB =AB此时AB =AB 2+BB =42+23 2=27故A 选项错误,根据题意可得P ,Q ,F 三点共线时,PF 最小,此时PE =PF =3,则PE +PF =23,故B 选项正确;△CDE 周长等于CD +DE +CE =CD +AE +EB =CD +AB =CD +4,即当CD 最小时,△CDE 周长最小,如图所示,作平行四边形GDMH ,连接CM ,∵∠GHQ =60°,∠GHM =∠GDM =60°,则∠CHM =120°如图,延长DE ,HG ,交于点N ,则∠NGD =∠QGH =60°,∠NDG =∠ADE =60°∴△NGD 是等边三角形,∴ND =GD =HM ,在△NPD 与△HPC 中,∠NPD =∠HPC∠N =∠CHP =60°PD =PC∴△NPD ≌△HPC∴ND =CH∴CH =MH∴∠HCM =∠HMC =30°∴CM ∥QF ,则CM ⊥DM ,∴△DMC 是直角三角形,在△DCM 中,DC >DM∴当DC =DM 时,DC 最短,DC =GH =12AB =2∵CD =PC +2PC∴△CDE 周长的最小值为2+2+2=6,故C 选项正确;∵△NPD ≌△HPC∴四边形ABCD 面积等于S △ADE +S △EBC+S △DEC =S △ADE +S 平行四边NEBH∴当△BGD的面积为0时,取得最小值,此时,D,G重合,C,H重合∴四边形ABCD面积的最小值为3×34×22=33,故D选项正确,故选:A.【点睛】本题考查了解直角三角形,等边三角形的性质,勾股定理,熟练掌握等边三角形的性质,得出当E点与F重合时得出最小值是解题的关键.二、填空题13(2023·四川达州·统考中考真题)在△ABC中,AB=43,∠C=60°,在边BC上有一点P,且BP= 12AC,连接AP,则AP的最小值为.【答案】213-2【分析】如图,作△ABC的外接圆,圆心为M,连接AM、BM、CM,过M作MD⊥AB于D,过B作BN⊥AB,交BP的垂直平分线于N,连接AN、BN、PN,以N为圆心,BN PN为半径作圆;结合圆周角定理及垂径定理易得AM=BM=CM=4,再通过圆周角定理、垂直及垂直平分线的性质、三角形内角和定理易得∠AMC=∠PNB,从而易证△AMC∼△PNB可得CMPN=ACPB=21即PN=12CM=2勾股定理即可求得AN=213在△APN中由三角形三边关系AP≥AN-PN即可求解.【详解】解:如图,作△ABC的外接圆,圆心为M,连接AM、BM、CM,过M作MD⊥AB于D,过B作BN ⊥AB,交BP的垂直平分线于N,连接AN、BN、PN,以N为圆心,BN PN为半径作圆;∵∠C=60°,M为△ABC的外接圆的圆心,∴∠AMB=120°,AM=BM,∴∠MAB=∠MBA=30°,∴MD=12AM,∵MD⊥AB,∴AD=12AB=23,在Rt△ADM中,∵AM2=MD2+AD2,∴AM2=12AM2+232,∴AM=4,即AM=BM=CM=4,由作图可知BN⊥AB,N在BP的垂直平分线上,∴∠PBN=∠BPN=90°-∠ABC,∴∠PNB=180°-∠PBN+∠BPN=2∠ABC,又∵M为△ABC的外接圆的圆心,∴∠AMC=2∠ABC,∴∠AMC=∠PNB,∵CM PN =AMBN,∴△AMC∼△PNB,∴CM PN =ACPB,∵BP=12AC,∴CM PN =ACPB=21,即PN=12CM=2,∴PN=BN=2,在Rt△ABN中,AN=AB2+BN2=432+22=213,在△APN中,AP≥AN-PN=213-2,即AP最小值为213-2,故答案为:213-2.【点睛】本题考查了圆周角定理,垂径定理,勾股定理解直角三角形,相似三角形的判定和性质,垂直平分线的性质,30°角所对的直角边等于斜边的一半,三角形三边之间的关系;解题的关键是结合△ABC的外接圆构造相似三角形.14(2023·浙江宁波·统考中考真题)如图,在Rt△ABC中,∠C=90°,E为AB边上一点,以AE为直径的半圆O与BC相切于点D,连接AD,BE=3,BD=35.P是AB边上的动点,当△ADP为等腰三角形时,AP的长为.【答案】230或6【分析】连接OD,勾股定理求出半径,平行线分线段成比例,求出CD的长,勾股定理求出AC和AD的长,分AP=AD和AP=PD两种情况进行求解即可.【详解】解:连接OD,∵以AE为直径的半圆O与BC相切于点D,∴OD⊥BC,OA=OE=OD,∴∠ODB=90°设OA=OE=OD=r,则OB=OE+BE=3+r,在Rt△ODB中:OD2+BD2=OB2,即:r2+352=3+r2,解得:r=6,∴OA=OE=OD=6,∴OB=9,AB=15,AE=12,∵∠C=∠ODB=90°,∴OD∥AC,∴OB OA =DBDC=96=32,∵DB=35,∴CD=25,∴BC=DB+CD=55,∴AC=AB2-BC2=10,∴AD=AC2+CD2=230;∵△ADP为等腰三角形,当AD=AP时,AP=230,当PA=PD时,∵OA=OD,∴点P与点O重合,∴AP=OA=6,不存在PD=AD的情况;综上:AP的长为230或6.故答案为:230或6.【点睛】本题考查切线的性质,平行线分线段成比例,勾股定理,等腰三角形的定义.熟练掌握切线的性质,等腰三角形的定义,确定点P的位置,是解题的关键.15(2023·四川凉山·统考中考真题)如图,边长为2的等边△ABC的两个顶点A、B分别在两条射线OM、ON上滑动,若OM⊥ON,则OC的最大值是.【答案】1+3【分析】如图所示,取AB的中点D,连接OD,CD,先根据等边三角形的性质和勾股定理求出CD=3,再根据直角三角形的性质得到OD=12AB=1,再由OC≤OD+CD可得当O、C、D三点共线时,OC有最大值,最大值为1+3.【详解】解:如图所示,取AB的中点D,连接OD,CD,∵△ABC是边长为2的等边三角形,∴CD⊥AB,BC=AB=2,∴BD=AD=1,∴CD=BC2-BD2=3,∵OM⊥ON,即∠AOB=90°,∴OD =12AB =1,∵OC ≤OD +CD ,∴当O 、C 、D 三点共线时,OC 有最大值,最大值为1+3,故答案为:1+3.【点睛】本题主要考查了等边三角形的性质,勾股定理,直角三角形斜边上的中线的性质等等,正确作出辅助线确定当O 、C 、D 三点共线时,OC 有最大值是解题的关键.16(2023·四川泸州·统考中考真题)如图,E ,F 是正方形ABCD 的边AB 的三等分点,P 是对角线AC 上的动点,当PE +PF 取得最小值时,AP PC的值是.【答案】27【分析】作点F 关于AC 的对称点F ,连接EF 交AC 于点P ,此时PE +PF 取得最小值,过点F 作AD 的垂线段,交AC 于点K ,根据题意可知点F 落在AD 上,设正方形的边长为a ,求得AK 的边长,证明△AEP∽△KF P ,可得KP AP=2,即可解答.【详解】解:作点F 关于AC 的对称点F ,连接EF 交AC 于点P ,过点F 作AD 的垂线段,交AC 于点K ,由题意得:此时F 落在AD 上,且根据对称的性质,当P 点与P 重合时PE +PF 取得最小值,设正方形ABCD 的边长为a ,则AF =AF =23a ,∵四边形ABCD 是正方形,∴∠F AK =45°,∠P AE =45°,AC =2a∵F K ⊥AF ,∴∠F AK =∠F KA =45°,∴AK =223a ,∵∠F P K =∠EP A ,∴△E KP ∽△EAP ,∴F K AE =KP AP=2,∴AP =13AK =292a ,∴CP =AC -AP =792a , ∴AP CP =27,∴当PE +PF 取得最小值时,AP PC 的值是为27,故答案为:27.【点睛】本题考查了四边形的最值问题,轴对称的性质,相似三角形的证明与性质,正方形的性质,正确画出辅助线是解题的关键.17(2023·河南·统考中考真题)矩形ABCD 中,M 为对角线BD 的中点,点N 在边AD 上,且AN =AB =1.当以点D ,M ,N 为顶点的三角形是直角三角形时,AD 的长为.【答案】2或2+1【分析】分两种情况:当∠MND =90°时和当∠NMD =90°时,分别进行讨论求解即可.【详解】解:当∠MND =90°时,∵四边形ABCD 矩形,∴∠A =90°,则MN ∥AB ,由平行线分线段成比例可得:AN ND =BM MD,又∵M 为对角线BD 的中点,∴BM =MD ,∴AN ND =BM MD=1,即:ND =AN =1,∴AD =AN +ND =2,当∠NMD =90°时,∵M 为对角线BD 的中点,∠NMD =90°∴MN 为BD 的垂直平分线,∴BN =ND ,∵四边形ABCD 矩形,AN =AB =1∴∠A=90°,则BN=AB2+AN2=2,∴BN=ND=2∴AD=AN+ND=2+1,综上,AD的长为2或2+1,故答案为:2或2+1.【点睛】本题考查矩形的性质,平行线分线段成比例,垂直平分线的判定及性质等,画出草图进行分类讨论是解决问题的关键.18(2023·湖南·统考中考真题)如图,在矩形ABCD中,AB=2,AD=7,动点P在矩形的边上沿B→C→D→A运动.当点P不与点A、B重合时,将△ABP沿AP对折,得到△AB P,连接CB ,则在点P的运动过程中,线段CB 的最小值为.【答案】11-2【分析】根据折叠的性质得出B 在A为圆心,2为半径的弧上运动,进而分类讨论当点P在BC上时,当点P在DC上时,当P在AD上时,即可求解.【详解】解:∵在矩形ABCD中,AB=2,AD=7,∴BC=AD=7,AC=BC2+AB2=7+4=11,如图所示,当点P在BC上时,∵AB =AB=2∴B 在A为圆心,2为半径的弧上运动,当A,B ,C三点共线时,CB 最短,此时CB =AC-AB =11-2,当点P在DC上时,如图所示,此时CB >11-2当P 在AD 上时,如图所示,此时CB >11-2综上所述,CB 的最小值为11-2,故答案为:11-2.【点睛】本题考查了矩形与折叠问题,圆外一点到圆上的距离的最值问题,熟练掌握折叠的性质是解题的关键.19(2023·广西·统考中考真题)如图,在边长为2的正方形ABCD 中,E ,F 分别是BC ,CD 上的动点,M ,N 分别是EF ,AF 的中点,则MN 的最大值为.【答案】2【分析】首先证明出MN 是△AEF 的中位线,得到MN =12AE ,然后由正方形的性质和勾股定理得到AE =AB 2+BE 2=4+BE 2,证明出当BE 最大时,AE 最大,此时MN 最大,进而得到当点E 和点C 重合时,BE 最大,即BC 的长度,最后代入求解即可.【详解】如图所示,连接AE ,∵M ,N 分别是EF ,AF 的中点,∴MN 是△AEF 的中位线,∴MN =12AE ,∵四边形ABCD 是正方形,∴∠B =90°,∴AE =AB 2+BE 2=4+BE 2,∴当BE 最大时,AE 最大,此时MN 最大,∵点E 是BC 上的动点,∴当点E 和点C 重合时,BE 最大,即BC 的长度,∴此时AE =4+22=22,∴MN =12AE =2,∴MN 的最大值为2.故答案为:2.【点睛】此题考查了正方形的性质,三角形中位线的性质,勾股定理等知识,解题的关键是熟练掌握以上知识点.20(2023·山东·统考中考真题)如图,在四边形ABCD中,∠ABC=∠BAD=90°,AB=5,AD=4,AD <BC,点E在线段BC上运动,点F在线段AE上,∠ADF=∠BAE,则线段BF的最小值为.【答案】29-2【分析】设AD的中点为O,以AD为直径画圆,连接OB,设OB与⊙O的交点为点F ,证明∠DFA=90°,可知点F在以AD为直径的半圆上运动,当点F运动到OB与⊙O的交点F 时,线段BF有最小值,据此求解即可.【详解】解:设AD的中点为O,以AD为直径画圆,连接OB,设OB与⊙O的交点为点F ,∵∠ABC=∠BAD=90°,∴AD∥BC,∴∠DAE=∠AEB,∵∠ADF=∠BAE,∴∠DFA=∠ABE=90°,∴点F在以AD为直径的半圆上运动,∴当点F运动到OB与⊙O的交点F 时,线段BF有最小值,∵AD=4,AD=2,,∴AO=OF =12∴BO=52+22=29,BF的最小值为29-2,故答案为:29-2.【点睛】本题考查了平行线的性质,圆周角定理的推论,勾股定理等知识,根据题意分析得到点F的运动轨迹是解题的关键.21(2023·四川内江·统考中考真题)出入相补原理是我国古代数学的重要成就之一,最早是由三国时期数学家刘徽创建.“将一个几何图形,任意切成多块小图形,几何图形的总面积保持不变,等于所分割成的小图形的面积之和”是该原理的重要内容之一、如图,在矩形ABCD中,AB=5,AD=12,对角线AC与BD交于点O,点E为BC边上的一个动点,EF⊥AC,EG⊥BD,垂足分别为点F,G,则EF+EG=.【答案】6013【分析】连接OE ,根据矩形的性质得到BC =AD =12,AO =CO =BO =DO ,∠ABC =90°,根据勾股定理得到AC =AB 2+BC 2=13,求得OB =OC =132,根据三角形的面积公式即可得到结论.【详解】解:连接OE ,∵四边形ABCD 是矩形,∴∠ABC =90°,BC =AD =12,AO =CO =BO =DO ,∵AB =5,BC =12,∴AC =AB 2+BC 2=13,∴OB =OC =132,∴S △BOC =S △BOE +S △COE =12×OB ⋅EG +12OC ⋅EF =12S △ABC =12×12×5×12=15,∴12×132EG +12×132EF =12×132(EG +EF )=15,∴EG +EF =6013,故答案为:6013.【点睛】此题考查了矩形的性质、勾股定理.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.22(2023·山东烟台·统考中考真题)如图1,在△ABC 中,动点P 从点A 出发沿折线AB →BC →CA 匀速运动至点A 后停止.设点P 的运动路程为x ,线段AP 的长度为y ,图2是y 与x 的函数关系的大致图象,其中点F 为曲线DE 的最低点,则△ABC 的高CG 的长为.【答案】732【分析】过点A 作AQ ⊥BC 于点Q ,当点P 与Q 重合时,在图2中F 点表示当AB +BQ =12时,点P 到达点Q ,此时当P 在BC 上运动时,AP 最小,勾股定理求得AQ ,然后等面积法即可求解.【详解】如图过点A 作AQ ⊥BC 于点Q ,当点P 与Q 重合时,在图2中F 点表示当AB +BQ =12时,点P 到达点Q ,此时当P 在BC 上运动时,AP 最小,∴BC =7,BQ =4,QC =3在Rt △ABQ 中,AB =8,BQ =4∴AQ =AB 2-BQ 2=82-42=43∵S △ABC =12AB ×CG =12AQ ×BC ,∴CG =BC ×AQ AB=7×438=732,故答案为:732.【点睛】本题考查了动点问题的函数图象,勾股定理,垂线段最短,从函数图象获取信息是解题的关键.23(2023·新疆·统考中考真题)如图,在▱ABCD 中,AB =6,BC =8,∠ABC =120°,点E 是AD 上一动点,将△ABE 沿BE 折叠得到△A BE ,当点A 恰好落在EC 上时,DE 的长为.【答案】37-3【分析】过点C作CH⊥AD交AD的延长线于点H,根据平行四边形的性质以及已知条件得出∠ADC=∠ABC=120°,∠HDC=60°,进而求得DH,HC,根据折叠的性质得出CB=CE,进而在Rt△ECH中,勾股定理即可求解.【详解】解:如图所示,过点C作CH⊥AD交AD的延长线于点H,∵在▱ABCD中,AB=6,BC=8,∠ABC=120°,∴∠ADC=∠ABC=120°,∠HDC=60°,CD=AB=6,AD=CB=8,DC=3,∴DH=DC×cos∠HDC=12在Rt△ECH中,HC=CD2-DH2=62-32=33∵将△ABE沿BE折叠得到△A BE,当点A 恰好落在EC上时,∴∠AEB=∠CEB又AD∥BC∴∠EBC=∠AEB∴∠EBC=∠CEB∴CE=BC=8设ED=x,∴EH=x+3在Rt△ECH中,EC2=EH2+HC2∴82=x+322+33解得:x=37-3(负整数)故答案为:37-3.【点睛】本题考查了折叠的性质,平行四边形的性质,解直角三角形,熟练掌握折叠的性质是解题的关键.24(2023·四川眉山·统考中考真题)如图,在平面直角坐标系xOy中,点B的坐标为-8,6,过点B分别作x轴、y轴的垂线,垂足分别为点C、点A,直线y=-2x-6与AB交于点D.与y轴交于点E.动点M在线段BC上,动点N在直线y=-2x-6上,若△AMN是以点N为直角顶点的等腰直角三角形,则点M的坐标为【答案】M-8,6或M-8,2 3【分析】如图,由△AMN是以点N为直角顶点的等腰直角三角形,可得N在以AM为直径的圆H上,MN= AN,可得N是圆H与直线y=-2x-6的交点,当M,B重合时,符合题意,可得M-8,6,当N在AM的上方时,如图,过N作NJ⊥y轴于J,延长MB交BJ于K,则∠NJA=∠MKN=90°,JK=AB=8,证明△MNK≌△NAJ,设N x,-2x-6,可得MK=NJ=-x,KN=AJ=-2x-6-6=-2x-12,而KJ=AB =8,则-2x-12-x=8,再解方程可得答案.【详解】解:如图,∵△AMN是以点N为直角顶点的等腰直角三角形,∴N在以AM为直径的圆H上,MN=AN,∴N是圆H与直线y=-2x-6的交点,当M,B重合时,∵B-8,6,则H-4,3,∴MH=AH=NH=4,符合题意,∴M-8,6,当N在AM的上方时,如图,过N作NJ⊥y轴于J,延长MB交BJ于K,则∠NJA=∠MKN=90°,JK= AB=8,∴∠NAJ+∠ANJ=90°,∵AN =MN ,∠ANM =90°,∴∠MNK +∠ANJ =90°,∴∠MNK =∠NAJ ,∴△MNK ≌△NAJ ,设N x ,-2x -6 ,∴MK =NJ =-x ,KN =AJ =-2x -6-6=-2x -12,而KJ =AB =8,∴-2x -12-x =8,解得:x =-203,则-2x -6=223,∴CM =CK -MK =223-203=23,∴M -8,23 ;综上:M -8,6 或M -8,23 .故答案为:M -8,6 或M -8,23.【点睛】本题考查的是坐标与图形,一次函数的性质,等腰直角三角形的判定与性质,全等三角形的判定与性质,圆周角定理的应用,本题属于填空题里面的压轴题,难度较大,清晰的分类讨论是解本题的关键.25(2023·四川自贡·统考中考真题)如图,直线y =-13x +2与x 轴,y 轴分别交于A ,B 两点,点D 是线段AB 上一动点,点H 是直线y =-43x +2上的一动点,动点E m ,0 ,F m +3,0 ,连接BE ,DF ,HD .当BE +DF 取最小值时,3BH +5DH 的最小值是.【答案】392【分析】作出点C 3,-2 ,作CD ⊥AB 于点D ,交x 轴于点F ,此时BE +DF 的最小值为CD 的长,利用解直角三角形求得F 113,0 ,利用待定系数法求得直线CD 的解析式,联立即可求得点D 的坐标,过点D 作DG ⊥y 轴于点G ,此时3BH +5DH 的最小值是5DG 的长,据此求解即可.【详解】解:∵直线y =-13x +2与x 轴,y 轴分别交于A ,B 两点,∴B 0,2 ,A 6,0 ,作点B 关于x 轴的对称点B 0,-2 ,把点B 向右平移3个单位得到C 3,-2 ,作CD ⊥AB 于点D ,交x 轴于点F ,过点B 作B E ∥CD 交x 轴于点E ,则四边形EFCB 是平行四边形,此时,BE =B E =CF ,∴BE +DF =CF +DF =CD 有最小值,作CP ⊥x 轴于点P ,则CP =2,OP =3,∵∠CFP =∠AFD ,∴∠FCP =∠FAD ,∴tan ∠FCP =tan ∠FAD ,∴PF PC =OB OA ,即PF 2=26,∴PF =23,则F 113,0 ,设直线CD 的解析式为y =kx +b ,则3k +b =-2113k +b =0,解得k =3b =-11 ,∴直线CD 的解析式为y =3x -11,联立,y =3x -11y =-13x +2 ,解得x =3910y =710,即D3910,710;过点D 作DG ⊥y 轴于点G ,直线y =-43x +2与x 轴的交点为Q 32,0 ,则BQ =OQ 2+OB 2=52,∴sin ∠OBQ =OQ BQ =3252=35,∴HG =BH sin ∠GBH =35BH ,∴3BH +5DH =535BH +DH =5HG +DH =5DG ,即3BH +5DH 的最小值是5DG =5×3910=392,故答案为:392.【点睛】本题考查了一次函数的应用,解直角三角形,利用轴对称求最短距离,解题的关键是灵活运用所学知识解决问题.三、解答题26(2023·重庆·统考中考真题)如图,△ABC 是边长为4的等边三角形,动点E ,F 分别以每秒1个单位长度的速度同时从点A出发,点E沿折线A→B→C方向运动,点F沿折线A→C→B方向运动,当两者相遇时停止运动.设运动时间为t秒,点E,F的距离为y.(1)请直接写出y关于t的函数表达式并注明自变量t的取值范围;(2)在给定的平面直角坐标系中画出这个函数的图象,并写出该函数的一条性质;(3)结合函数图象,写出点E,F相距3个单位长度时t的值.【答案】(1)当0<t≤4时,y=t;当4<t≤6时,y=12-2t(2)图象见解析,当0<t≤4时,y随x的增大而增大(3)t的值为3或4.5【分析】(1)分两种情况:当0<t≤4时,根据等边三角形的性质解答;当4<t≤6时,利用周长减去2AE即可;(2)在直角坐标系中描点连线即可;(3)利用y=3分别求解即可.【详解】(1)解:当0<t≤4时,连接EF,由题意得AE=AF,∠A=60°,∴△AEF是等边三角形,∴y=t;当4<t≤6时,y=12-2t;(2)函数图象如图:。
初中数学动点问题测试卷

一、选择题(每题4分,共20分)1. 下列关于动点问题的说法,正确的是()A. 动点问题只涉及几何知识B. 动点问题需要运用方程思想和数形结合思想C. 动点问题与实际生活无关D. 动点问题只出现在高中数学中2. 在等腰三角形ABC中,AB=AC,点D在边BC上,AD垂直于BC,点E在AD上,若BE=ED,则下列结论正确的是()A. ∠BAC=∠BCAB. ∠B=∠CC. ∠A=∠BD. ∠A=∠C3. 在矩形ABCD中,AB=3cm,BC=4cm,点P从点A开始沿AB边以1cm/s的速度向点B运动,点Q从点C开始沿CD边以2cm/s的速度向点D运动,则下列结论正确的是()A. 当P运动到B点时,Q运动到D点B. 当P运动到B点时,Q运动到C点C. 当Q运动到D点时,P运动到B点D. 当Q运动到D点时,P运动到C点4. 在等腰三角形ABC中,AB=AC,点D在边BC上,AD垂直于BC,若BD=3cm,则AD的长度为()A. 3cmB. 4cmC. 5cmD. 6cm5. 在矩形ABCD中,AB=3cm,BC=4cm,点P从点A开始沿AB边以1cm/s的速度向点B运动,点Q从点C开始沿CD边以2cm/s的速度向点D运动,则下列结论正确的是()A. 当P运动到B点时,Q运动到D点B. 当P运动到B点时,Q运动到C点C. 当Q运动到D点时,P运动到B点D. 当Q运动到D点时,P运动到C点二、填空题(每题4分,共16分)1. 在等腰三角形ABC中,AB=AC,点D在边BC上,AD垂直于BC,若BD=3cm,则AD的长度为______cm。
2. 在矩形ABCD中,AB=3cm,BC=4cm,点P从点A开始沿AB边以1cm/s的速度向点B运动,点Q从点C开始沿CD边以2cm/s的速度向点D运动,则当P运动到B 点时,Q运动到______点。
3. 在等腰三角形ABC中,AB=AC,点D在边BC上,AD垂直于BC,若∠BAC=30°,则BD的长度为______cm。
初二数学动点问题专项试卷

一、选择题(每题3分,共30分)1. 在平面直角坐标系中,点P(a,b)在直线y=2x+1上运动,那么a与b的关系是:A. a+b=1B. a=2bC. a=2b+1D. a=2b-12. 已知点A(2,3),点B在x轴上,且AB=5,那么点B的坐标可能是:A. (7,0)B. (-3,0)C. (-7,0)D. (3,0)3. 在△ABC中,AB=AC,点D在BC上,且BD=CD,那么∠ADB与∠ADC的关系是:A. ∠ADB=∠ADCB. ∠ADB=∠BACC. ∠ADB=∠BAC/2D. ∠ADB=∠BAC/34. 在平面直角坐标系中,点M在直线y=x+1上运动,那么点M的坐标满足:A. x=y-1B. x=y+1C. y=x-1D. y=x+15. 已知直线l的方程为2x-3y+6=0,那么直线l与x轴的交点坐标是:A. (3,0)B. (-3,0)C. (0,2)D. (0,-2)6. 在△ABC中,AB=AC,点D在BC上,且BD=CD,那么∠ADB与∠ADC的关系是:A. ∠ADB=∠ADCB. ∠ADB=∠BACC. ∠ADB=∠BAC/2D. ∠ADB=∠BAC/37. 已知点P(a,b)在直线y=-2x+3上运动,那么a与b的关系是:A. a+b=3B. a=2bC. a=2b+3D. a=2b-38. 在平面直角坐标系中,点Q(m,n)在直线y=3/2x-2上运动,那么m与n的关系是:A. m=n+4B. m=2n-4C. m=n-4D. m=2n+49. 已知直线l的方程为x+4y-12=0,那么直线l与y轴的交点坐标是:A. (0,3)B. (0,-3)C. (4,0)D. (-4,0)10. 在△ABC中,AB=AC,点D在BC上,且BD=CD,那么∠ADB与∠ADC的关系是:A. ∠ADB=∠ADCB. ∠ADB=∠BACC. ∠ADB=∠BAC/2D. ∠ADB=∠BAC/3二、填空题(每题5分,共20分)11. 在平面直角坐标系中,点P(2,3)在直线y=mx+1上运动,那么m的取值范围是______。
7年级动点题10道

7年级动点题10道一、数轴上的动点问题。
1. 已知数轴上点A表示的数为 -2,点B表示的数为4,点P从点A出发,以每秒2个单位长度的速度沿数轴向右运动,同时点Q从点B出发,以每秒1个单位长度的速度沿数轴向左运动,设运动时间为t秒。
- 当t = 1时,求点P和点Q所表示的数。
- 求经过多少秒,点P与点Q相遇?- 求经过多少秒,点P与点Q之间的距离为2个单位长度?解析:- 点P从 - 2出发,速度为每秒2个单位长度,当t = 1时,点P表示的数为-2 + 2×1=0;点Q从4出发,速度为每秒1个单位长度,当t = 1时,点Q表示的数为4-1×1 = 3。
- 设经过t秒点P与点Q相遇。
点P向右运动的路程为2t,点Q向左运动的路程为t,相遇时2t + t=4 - (-2),即3t = 6,解得t = 2秒。
- 分两种情况:- 相遇前相距2个单位长度:2t+t+2 = 4-(-2),3t+2 = 6,3t = 4,解得t=(4)/(3)秒。
- 相遇后相距2个单位长度:2t + t-2=4 - (-2),3t-2 = 6,3t = 8,解得t=(8)/(3)秒。
2. 数轴上点A对应的数为 -1,点B对应的数为3,点P为数轴上一动点,其对应的数为x。
- 若点P到点A、点B的距离相等,求点P对应的数。
- 数轴上是否存在点P,使点P到点A、点B的距离之和为5?若存在,求出x的值;若不存在,请说明理由。
- 当点P以每分钟1个单位长度的速度从原点向左运动时,点A以每分钟5个单位长度的速度向左运动,点B以每分钟20个单位长度的速度向左运动,问几分钟时点P到点A、点B的距离相等?解析:- 因为点P到点A、点B的距离相等,所以x=(-1 + 3)/(2)=1。
- 存在。
当点P在点A左侧时,-1 - x+3 - x = 5,-2x+2 = 5,-2x = 3,解得x =-(3)/(2);当点P在点B右侧时,x - (-1)+x - 3 = 5,2x - 2 = 5,2x = 7,解得x=(7)/(2)。
初中数学动点问题及练习题附参考答案

例1.如图,已知在矩形ABCD 中,AD =8,CD =4,点E 从点D 出发,沿线段DA 以每秒1个单位长的速度向点A 方向移动,同时点F 从点C 出发,沿射线CD 方向以每秒2个单位长的速度移动,当B ,E ,F 三点共线时,两点同时停止运动.设点E 移动的时间为t (秒). (1)求当t 为何值时,两点同时停止运动;(2)设四边形BCFE 的面积为S ,求S 与t 之间的函数关系式,并写出t 的取值范围; (3)求当t 为何值时,以E ,F ,C 三点为顶点的三角形是等腰三角形; (4)求当t 为何值时,∠BEC =∠BFC .例2. 正方形ABCD 边长为4,M 、N 分别是BC 、CD 上的两个动点, 当M 点在BC 上运动时,保持AM 和MN 垂直, (1)证明:Rt Rt ABM MCN △∽△;(2)设BM x ,梯形ABCN 的面积为y ,求y 与x 之间的函数关系式;当M 点运动到什么位置时,四边形ABCN 面积最大,并求出最大面积;(3)当M 点运动到什么位置时Rt Rt ABM AMN △∽△,求此时x 的值. ‘ABD E FODMA B CN例3.如图,在梯形ABCD中,3545 AD BC AD DC AB B====︒∥,,,.动点M从B点出发沿线段BC以每秒2个单位长度的速度向终点C运动;动点N同时从C点出发沿线段CD以每秒1个单位长度的速度向终点D运动.设运动的时间为t秒.(09年济南中考)(1)求BC的长。
(2)当MN AB∥时,求t的值.(3)试探究:t为何值时,MNC△为等腰三角形.例4.如图,在Rt△AOB中,∠AOB=90°,OA=3cm,OB=4cm,以点O为坐标原点建立坐标系,设P、Q分别为AB、OB边上的动点它们同时分别从点A、O向B点匀速运动,速度均为1cm/秒,设P、Q移动时间为t(0≤t≤4)(1)求AB的长,过点P做PM⊥OA于M,求出P点的坐标(用t表示)(2)求△OPQ面积S(cm2),与运动时间t(秒)之间的函数关系式,当t为何值时,S有最大值?最大是多少?(3)当t为何值时,△OPQ为直角三角形?(4)若点P运动速度不变,改变Q 的运动速度,使△OPQ为正三角形,求Q点运动的速度和此时t的值.C。
初中数学动点题型试卷

一、选择题(每题5分,共20分)1. 在平面直角坐标系中,点P在直线y=kx+b上运动,若点P到原点O的距离为定值r,则直线y=kx+b的斜率k为:A. 0B. 1C. rD. r²2. 动点M从点A(2,0)出发,沿x轴正方向运动,速度为每秒2个单位,动点N从点B(0,2)出发,沿y轴正方向运动,速度为每秒2个单位。
则动点M和N相距最远的时刻为:A. 1秒B. 2秒C. 3秒D. 4秒3. 在等腰三角形ABC中,AB=AC,动点D在BC边上运动,若∠BDC=90°,则动点D在BC边上的位置:A. 与B、C重合B. 位于BC中点C. 在BC上任意一点D. 不存在4. 动点P在圆O上运动,圆O的半径为r,若动点P到直线l的距离为d,则动点P到圆心O的距离为:A. r+dB. r-dC. r+d/2D. r-d/25. 动点M从点A(0,0)出发,沿x轴正方向运动,速度为每秒1个单位,动点N从点B(0,b)出发,沿y轴正方向运动,速度为每秒1个单位。
则动点M和N的轨迹方程为:A. x+y=bB. x-y=bC. x²+y²=b²D. x²+y²=2b二、填空题(每题5分,共20分)1. 在平面直角坐标系中,点P在直线y=kx+b上运动,若点P到原点O的距离为定值r,则直线y=kx+b的截距b为______。
2. 动点M从点A(2,0)出发,沿x轴正方向运动,速度为每秒2个单位,动点N从点B(0,2)出发,沿y轴正方向运动,速度为每秒2个单位。
则动点M和N相距最远时,它们之间的距离为______。
3. 在等腰三角形ABC中,AB=AC,动点D在BC边上运动,若∠BDC=90°,则动点D在BC边上的位置是______。
4. 动点P在圆O上运动,圆O的半径为r,若动点P到直线l的距离为d,则动点P到圆心O的距离为______。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C
C1 C2
C1
C2
P
A
D
图1
BA
D1 D2 图2
F
E
B A D2
D1 B
图3
8. 梯形 ABCD 中,AD∥BC,∠B=90°,AD=24cm,AB=8cm,BC=26cm,动点 P 从点 A 开始,沿
P.
(1)当 AC1D1 平移到如图 3 所示的位置时,猜想图中的 D1E 与 D2F 的数量关系,并证明
你的猜想;
3
(2)设平移距离 D2D1为 x ,AC1D1 与 BC2D2 重叠部分面积为 y ,请写出 y 与 x 的函数
关系式,以及自变量的取值范围;
(3)对于(2)中的结论是否存在这样的 x 的值;使得重叠部分的面积等于原 ABC 面积 的 1 ?若不存在,请说明理由.
A
D
N
B
M
C
3(河北卷)如图,在 Rt△ABC 中,∠C=90°,AC=12,BC=16,动点 P 从点 A 出发沿 AC 边向点 C 以每秒 3 个单位长的速度运动,动点 Q 从点 C 出发沿 CB 边向点 B 以每秒 4 个单位长的速度运动.P,Q 分别从点 A,C 同时出发,当其中一点到达端点时,另一点也 随之停止运动.在运动过程中,△PCQ 关于直线 PQ 对称的图形是△PDQ.设运动时间为 t (秒). (1)设四边形 PCQD 的面积为 y,求 y 与 t 的函数关系式; (2)t 为何值时,四边形 PQBA 是梯形?
(2)线段 MN 在运动的过程中,四边形 MNQP 的面积为 S ,运动的时间为 t .求四边形
MNQP 的面积 S 随运动时间 t 变化的函数关系式,并写出自变量 t 的取值范围.
C Q
P
AM N
B
2、如图,在梯形 ABCD 中, AD∥BC,AD 3,DC 5,AB 4 2,∠B 45.动点
经过的时间为 t s 时, BPQ 的面积为 y cm2 (如图 2)。分别以 t, y 为横、纵坐标建立直
角坐标系,已知点 P 在 AD 边上从 A 到 D 运动时, y 与 t 的函数图象是图 3 中的线段 MN 。 (1)分别求出梯形中 BA, AD 的长度; (2)写出图 3 中 M , N 两点的坐标;
M 从 B 点出发沿线段 BC 以每秒 2 个单位长度的速度向终点 C 运动;动点 N 同时从 C 点
出发沿线段 CD 以每秒 1 个单位长度的速度向终点 D 运动.设运动的时间为 t 秒.
(1)求 BC 的长.
(2)当 MN ∥ AB 时,求 t 的值.
(3)试探究: t 为何值时, △MNC 为等腰三角形.
1
(3)是否存在时刻 t,使得 PD∥AB?若存在,求出 t 的值;若不存在,请说明理由; (4)通过观察、画图或折纸等方法,猜想是否存在时刻 t,使得 PD⊥AB?若存在,请估计 t 的值在括号中的哪个时间段内(0≤t≤1;1<t≤2;2<t≤3;3<t≤4);若不存在,请简 要说明理由.
APBiblioteka D初中数学动点问题专项练习题
1、已知:等边三角形 ABC 的边长为 4 厘米,长为 1 厘米的线段 MN 在 △ABC 的边 AB 上 沿 AB 方向以 1 厘米/秒的速度向 B 点运动(运动开始时,点 M 与点 A 重合,点 N 到达点 B 时运动终止),过点 M、N 分别作 AB 边的垂线,与△ABC 的其它边交于 P、Q 两点,线 段 MN 运动的时间为 t 秒. 1、线段 MN 在运动的过程中,t 为何值时,四边形 MNQP 恰为矩形?并求出该矩形的面积;
2
(3)分别写出点 P 在 BA 边上和 DC 边上运动时, y 与 t 的函数关系式(注明自变量的 取值范围),并在图 3 中补全整个运动中 y 关于 t 的函数关系的大致图象。
y
AD
AD
30
P
B
C
(图 1)
BQC
(图 2)
O
t
(图 3)
6、两块完全相同的直角三角板 ABC 和 DEF 如图 1 所示放置,点 C、F 重合,且 BC、DF 在一条直线上,其中 AC=DF=4,BC=EF=3.固定 Rt△ ABC 不动,让 Rt△ DEF 沿 CB 向左平移,直到点 F 和点 B 重合为止.设 FC=x,两个三角形重叠阴影部分的面积为 y.
(1)如图 2,求当 x= 1 时,y 的值是多少? 2
(2)如图 3,当点 E 移动到 AB 上时,求 x、y 的值; (3)求 y 与 x 之间的函数关系式;
7(重庆课改卷)如图 1 所示,一张三角形纸片 ABC,∠ACB=90°,AC=8,BC=6.沿斜边 AB
的中线 CD 把这张纸片剪成 AC1D1 和 BC2D2 两个三角形(如图 2 所示).将纸片 AC1D1 沿直线 D2B (AB)方向平移(点 A, D1, D2, B 始终在同一直线上),当点 D1 于点 B 重合 时,停止平移.在平移过程中, C1D1 与 BC2 交于点 E, AC1 与 C2D2、BC2 分别交于点 F、
CQ
B
4、在 ABC 中, C Rt, AC 4cm, BC 5cm,点D在BC上,且以CD=3cm, 现有
两个动点 P、Q 分别从点 A 和点 B 同时出发,其中点 P 以 1cm/s 的速度,沿 AC 向终点 C 移动;点 Q 以 1.25cm/s 的速度沿 BC 向终点 C 移动。过点 P 作 PE∥BC 交 AD 于点 E,连 结 EQ。设动点运动时间为 x 秒。 (1)用含 x 的代数式表示 AE、DE 的长度;
(2)当点 Q 在 BD(不包括点 B、D)上移动时,设 EDQ 的面积为 y(cm2 ) ,求 y 与月 份 x 的函数关系式,并写出自变量 x 的取值范围; (3)当 x 为何值时, EDQ 为直角三角形。
A
P E
B
QD
C
5、(杭州)在直角梯形 ABCD 中, C 90 ,高 CD 6cm (如图 1)。动点 P,Q 同时 从点 B 出发,点 P 沿 BA, AD, DC 运动到点 C 停止,点 Q 沿 BC 运动到点 C 停止,两点运动 时的速度都是1cm / s 。而当点 P 到达点 A 时,点 Q 正好到达点 C 。设 P,Q 同时从点 B 出发,
