双向板设计与计算
双向板设计与计算
②荷载等效
将板上永久荷载g和活荷载q分成为对称荷载和反对称荷载两 种情况,取
对称荷载
g’=g+q/2
反对称荷载
q’=±q/2
, ③对称型荷载作用下
近似认为板的中间支座处转角为零
中间区格板可按四边固定的板来计算内力 边区格板的三个内支承边、角区格的两个 内支承边都可以看成固定边。
④反对称型荷载作用下
M max
1 8
(g
q
)
l
2 0
式中 g 、q ——作用于梯段板上的沿水平投影方向的
恒载及活载设计值; l0 — — 梯 段 板 的 计 算 跨 度 。
简支斜板(梁)在竖向均布荷载作用下的最大剪力为:
1 V max 2 ( g q ) l n
式 中 ln — — 净 跨 的 水 平 投 影 长 度 。
但 在 配 筋 计 算 时 ,考 虑 到 梯 段 板 与 平 台 梁 整 体 连 接 ,平
台梁对梯段板有一定的弹性约束作用,计算时最大弯矩可
取:
M
1 10
(g
q
)
l
2 0
○6 由于梯段板为斜向搁置的受弯构件,还将产生轴向力, 但其影响很小,设计时可不考虑。
○7 梯段斜板和一般板计算一样,可不必进行斜截面抗剪承 载力验算。
长度为≥ ln / 4 (图 7.3.12)。
(2)斜边梁 1)计算要点
○1 斜边梁两端支承在平台梁上,承受踏步传板传来的荷载
和本身自重,内力计算时与板式楼梯中梯段斜板的计算原理相
同,斜边梁的计算不考虑平台梁的弹性约束作用,按两端简支
计算,即:
M max
1 8
(g
q
)l
双向板设计与计算

双向板设计与计算双向板是指在接触面上都有点对称排列一定间距的钢筋,并成网状结构的预制板。
双向板设计与计算是指根据双向板的使用要求和实际情况,对其进行结构设计和力学计算的过程。
以下将从双向板的设计和计算两个方面进行详细介绍。
1.双向板的设计:(1)确定双向板的使用要求:首先需要确定双向板的设计使用要求,包括承载能力、刚度要求、使用环境要求等。
(2)确定双向板的尺寸和形状:根据双向板的使用要求和实际情况,确定双向板的尺寸和形状,包括长度、宽度、厚度等。
(3)确定双向板的钢筋布置:根据双向板的使用要求和受力情况,确定双向板的钢筋布置方式,包括钢筋的直径、间距、排列形式等。
(4)设计双向板的混凝土强度等级:根据双向板的使用要求和实际情况,确定双向板的混凝土强度等级,从而确定混凝土的配合比。
(5)设计双向板的钢筋:根据双向板的使用要求和受力情况,设计双向板的钢筋数量和直径,并进行受力计算。
2.双向板的计算:(1)受力分析:根据双向板的使用要求和受力情况,对双向板进行受力分析,包括活载荷、自重荷载、温度荷载等。
(2)按规范计算:根据相关的规范要求,对双向板进行弯曲计算、截面变形计算、刚度计算等。
(3)验算:对双向板进行验算,确保其承载能力和稳定性满足使用要求。
(4)结构分析:对双向板进行结构分析,探讨双向板的破坏机理,确定结构的敏感部位和安全系数。
(5)材料选择:根据设计要求和实际情况,选择适当的混凝土材料和钢筋材料,以保证双向板的性能和安全性。
综上所述,双向板的设计与计算是一个复杂而细致的工作。
它涉及到多个方面的知识和技术,需要根据双向板的使用要求和实际情况进行综合考虑和判断。
通过合理的设计和精确的计算,可以确保双向板具有足够的承载能力和稳定性,满足实际工程的要求。
双向板计算步骤

双向板计算步骤双向板是一种常见的建筑材料,由两片薄木板或薄钢板之间夹有一层胶合材料组成的。
双向板具有良好的强度和刚性,常用于建筑结构中的地板、墙壁和屋顶等。
在进行双向板的计算时,需要按照以下步骤进行:1.确定双向板的尺寸和几何形状。
这包括板的长度、宽度和厚度等。
根据具体的应用需求和设计规范,确定双向板的尺寸和几何形状。
2.确定双向板的边界条件。
双向板在使用中会受到一定的边界条件的约束,例如支座、固定点和荷载等。
根据具体的应用情况和设计规范,确定双向板的边界条件。
3.计算双向板的荷载。
根据具体的使用情况和设计规范,确定在双向板上的荷载情况。
这包括静荷载、动荷载和温度荷载等。
对于不同类型的荷载,需要进行相应的计算和分析。
4.进行双向板的弯曲计算。
双向板在受到荷载作用时会发生弯曲变形,需要计算板的弯曲应力和变形情况。
在进行弯曲计算时,考虑到双向板的材料性质、截面形状和边界条件等因素。
5.进行双向板的剪切计算。
双向板在受到荷载作用时还会发生剪切变形,需要计算板的剪切应力和变形情况。
在进行剪切计算时,考虑到双向板的材料性质、截面形状和边界条件等因素。
6.进行双向板的轴向计算。
双向板在受到荷载作用时还会发生轴向拉力或压力,需要计算板的轴向应力和变形情况。
在进行轴向计算时,考虑到双向板的材料性质、截面形状和边界条件等因素。
7.进行双向板的稳定性计算。
双向板在受到较大荷载作用时,可能会发生稳定性失效。
需要根据具体的使用情况和设计规范,进行双向板的稳定性计算,以确定板的稳定性。
8.进行双向板的传力计算。
双向板在使用中的荷载会通过板的结构传递到支座或其他受力构件上,需要进行传力计算,以确定板的传力情况。
9.进行双向板的疲劳计算。
双向板在反复荷载作用下,可能会出现疲劳断裂。
需要进行双向板的疲劳计算,以确定板的安全使用寿命。
10.进行双向板的验算。
根据计算结果,对双向板的尺寸和材料进行验算,以保证板的安全性和可靠性。
在进行双向板计算时,需要参考相关的设计规范和建筑准则,按照合理的假设和计算方法进行。
1-3双向板计算截面与设计共44页文档

♠④两个方向配筋相同的四边简支正方形板,由于跨中正弯 矩Mx,My的作用,板的第一批裂缝出现在底面中间部分; ♠随后由于主弯矩MI的作用,沿着对角线方向向四角发展, 图1.34a所示。 ♠随着荷载不断增加,板底裂缝继续向四角扩展,直至板的 底部钢筋屈服而破坏。 ♠当接近破坏时,由于主弯矩MII的作用,板顶面靠近四角附 近,出现了垂直于对角线方向的、大体上呈圆形的裂缝。这 些裂缝的出现,又促进了板底对角线方向裂缝的进一步扩展。
♠对于满布荷载 g q 2 的情况,板在支座处的转角较小,
可认为各区格板中间支座都是固定支座; ♠对于间隔布置的情况,可认为在支座两侧的转角大小都相 等、方向相同,无弯矩产生,可认为各区格板在支座都是简 支支座; ♠楼盖周边则按实际支承条件采用。 ♠从而可对上述两种荷载情况分别求出其跨中弯矩,而后叠 加,即可求出各区格的跨中最大弯矩。
♠支承梁的内力可按弹性理论或考虑塑性内力重分布的调幅 法计算,分述如下: ♠ (1)按弹性理论计算
♥对于等跨或近似等跨(跨度相差不超过10%)的连续梁, 可先将支承梁的三角形或梯形分布荷载化为等效均布荷 载(根据支座弯矩相等的原则确定 ),再利用均布荷载 下等跨连续梁的计算表格计算梁的内力(弯矩、剪力)。
♠精确地确定双向板传给支承梁的荷载是困难的,也是不必 要的。在确定双向板传给支承梁的荷载时,可根据荷载传递 路线最短的原则按如下方法近似确定。 ♠即从每一区格的四角作45o线与平行于底边的中线相交,把 整块板分为四块,每块小板上的荷载就近传至其支承梁上。 因此,短跨支承梁上的荷载为三角形分布,在长跨支承梁上 的荷载为梯形分布,见图1.36。
1.2.2 双向板肋梁楼盖
♠双向板定义 ♠1.2.2.1 双向板的受力特点 ♠(1)双向板的受力特点 ♠ ①沿两个方向弯曲和传递荷载 ♠ ②同时承受剪力、扭矩和主弯矩
双向板的课程设计计算书

双向板的计算书1.设计资料1)楼面活荷载标准值2.0kN ∕m ²2)楼面面层为地砖地面,梁、板底为20mm 粉刷层。
3)材料选用混凝土:采用C30(1c a f =14.3 N ∕2mm )钢筋:一律采用CRB550冷扎钢筋(y f =360 N ∕2mm )2.结构平面布置采用弹性理论分区计算,根据板的支撑条件和几何尺寸以及结构的对称性,将板分化为A 、B 、C 、D 、E 、F 、G 、H 各区格。
3.荷载计算荷载计算取1m 宽板带作为计算单元 恒荷载:板自重:0.12×25=3kN ∕m 板底粉刷:0.02×17=0.34kN ∕m地砖地面:0.05×1×20=1kN ∕m标准值:k g =4.34kN ∕m设计值:g =4.34×1.2=5.21kN ∕m活荷载:标准值:k q =2kN ∕m设计值:q =2×1.4=2.8kN ∕m4.弯矩计算区格Ax l =3.00m ;y l =3.00m ;x y l l =33=1x M =0.0281×(g +q )/2×2x l +0.0429×2q ×2x l=0.0281×(5.21+2.8)/2×3²+0.0429×2.82×3²=1.55 kN •my M =0.0289×(g +q )/2×2x l +0.0429×2q ×2x l=0.0289×(5.21+2.8)/2×3²+0.0429×2.82×3²=1.58 kN •m'x M =-0.0677×(g +q )×2x l =-0.0677×(5.21+2.8) ×3²=-4.88 kN •m'yM =-0.0677×(g +q )×2x l =-0.0677×(5.21+2.8) ×3² =-4.88 kN •m区格Bx l =3.00m ;y l =3.00m ;x y l l =33=1x M =0.0306×(g +q )/2×2x l +0.0429×2q ×2x l=0.0306×(5.21+2.8)/2×3²+0.0429×2.82×3²=1.64 kN •my M =0.0388×(g +q )/2×2x l +0.0429×2q ×2x l=0.0388×(5.21+2.8)/2×3²+0.0429×2.82×3²=1.94kN •m'x M =-0.0839×(g +q )×2x l =-0.0839×(5.21+2.8) ×3²=-6.05 kN •m'yM =-0.0839×(g +q )×2x l =-0.0839×(5.21+2.8) ×3² =-6.05 kN •m区格C 同区格B区格Dx l =3.00m ;y l =3.30m ;x y l l =33=0.9x M =0.0438×(g +q )/2×2x l +0.0516×2q ×2x l=0.0438×(5.21+2.8)/2×3²+0.0516×2.82×3²=2.23 kN •my M =0.0293×(g +q )/2×2x l +0.0434×2q ×2x l=0.0293×(5.21+2.8)/2×3²+0.0434×2.82×3²=1.60kN •m'x M =-0.0767×(g +q )×2x l =-0.0767×(5.21+2.8) ×3²=-5.53 kN •m'yM =-0.0926×(g +q )×2x l =-0.0926×(5.21+2.8) ×3² =-6.68kN •m区格Ex l =3.00m ;y l =3.00m ;x y l l =33=1 x M =0.0388×(g +q )/2×2x l +0.0429×2q ×2x l=0.0388×(5.21+2.8)/2×3²+0.0429×2.82×3²=1.94 kN •my M =0.0306×(g +q )/2×2x l +0.0429×2q ×2x l=0.0306×(5.21+2.8)/2×3²+0.0429×2.82×3²=1.64kN •m'x M =-0.0839×(g +q )×2x l =-0.0839×(5.21+2.8) ×3²=-6.05 kN •m'yM =-0.0839×(g +q )×2x l =-0.0839×(5.21+2.8) ×3² =-6.05 kN •m区格Fx l =3.00m ;y l =3.00m ;x y l l =33=1x M =0.0205×(g +q )/2×2x l +0.0429×2q ×2x l=0.0205×(5.21+2.8)/2×3²+0.0429×2.82×3²=1.28 kN •my M =0.0205×(g +q )/2×2x l +0.0429×2q ×2x l=0.0205×(5.21+2.8)/2×3²+0.0429×2.82×3²=1.28kN •m'x M =-0.0513×(g +q )×2x l =-0.0513×(5.21+2.8) ×3²=-3.70 kN •m'yM =-0.0513×(g +q )×2x l =-0.0513×(5.21+2.8) ×3² =-3.70 kN •m区格G 同区格F区格Hx l =3.00m ;y l =3.30m ;x y l l =33=0.9x M =0.0249×(g +q )/2×2x l +0.0516×2q ×2x l=0.0249×(5.21+2.8)/2×3²+0.0516×2.82×3²=1.55 kN •my M =0.0202×(g +q )/2×2x l +0.0429×2q ×2x l=0.0202×(5.21+2.8)/2×3²+0.0429×2.82×3²=1.38kN •m'x M =-0.0588×(g +q )×2x l =-0.0588×(5.21+2.8) ×3²=-4.24kN •m'yM =-0.0541×(g +q )×2x l =-0.0541×(5.21+2.8) ×3² =-3.90 kN •m 5.截面设计板跨中截面两个方向有效高度o h 的确定: 暂定钢筋选用A R8则:ox h =h -x a =(120-15-5)mm =100mm ox h =h -x a -d =(120-15-5-8)mm =92mm支座有效高度:ox h =h -x a =(120-15-5)mm =100mm5.配筋计算简化计算受拉钢筋s A ,可近似按以下公式计算:S A =0.95y oM f h配筋计算结果见下表:Hxl 1.55 92 49.26 A R8@200251 yl 1.38 100 40.35 A R8@200251支座A→B4.88 6.052+100 159.42 A R8@200251 B→C6.05 6.052+100 176.90 A R8@200251 C→D6.05 6.342+100 182.46 A R8@200251 E→F4.88 6.052+100 142.69 A R8@200251 F→G3.70 3.702+100 108.19 A R8@200251 G→H3.70 3.902+100 111.11 A R8@200251 A→E4.88 6.052+100 159.42 A R8@200251 B→F6.05 3.702+100 142.69 A R8@200251 C→G6.05 3.702+100 142.69 A R8@200251 D→H5.53 4.242+100 157.60 A R8@2002516.配筋图如下所示。
弹性双向板计算

弹性双向板计算
在进行弹性双向板的计算时,需要使用一些基本的公式和原理。
下面是关于弹性双向板计算的一些基本原理和公式:
1.位移和应变的关系:
ε=(ΔL/L)=(y/r)
其中,ε是单位长度的应变,ΔL是位移,L是板的边长,y是位移距离,r是板的曲率半径。
2.应力和应变的关系:
σ=Eε=Ey/r
其中,σ是单位面积的应力,E是材料的弹性模量。
3.弯曲方程:
弯曲是弹性双向板最主要的变形形式。
根据弯曲理论,弹性双向板的弯曲方程可以表示为:
M=Dη/z
其中,M是弯矩,D是抵抗弯曲的几何刚度系数(弯曲刚度),η是受力方式的常数(取决于荷载类型和边界条件),z是抵抗弯曲的几何形状参数。
4.抵抗弯曲的几何刚度系数:
抵抗弯曲的几何刚度系数D可以通过以下公式计算:
D=(Eh^3/12(1-μ^2))
其中,E是材料的弹性模量,h是板的厚度,μ是材料的泊松比。
5.抵抗弯曲的几何形状参数:
抵抗弯曲的几何形状参数z可以通过以下公式计算:
z=(h^2/6)
其中,h是板的厚度。
以上是弹性双向板计算中的一些基本原理和公式。
需要根据具体的设计条件和要求,结合实际情况选取适合的公式和原理进行计算。
通过应用这些公式和原理,可以对弹性双向板进行合理的设计和计算,以满足结构的强度和稳定性要求。
双向板按弹性理论的计算方法

双向板按弹性理论的计算方法双向板是一种常见的结构元件,其受力特点与单向板有所不同。
在计算双向板的设计参数时,可以采用弹性理论中的一些方法来进行计算。
双向板的受力分析主要涉及以下几个方面:弯矩、剪力和扭矩的计算、板的变形以及板的稳定性计算。
首先,我们来看双向板的弯矩计算。
在双向板上,由于受到两个方向的载荷作用,会同时产生正弯矩和负弯矩。
在计算弯矩时,可以采用叠加法。
假设双向板在x和y方向上的弯矩分别为Mx和My,那么总弯矩M为M=Mx+My。
其次,剪力的计算也是双向板设计时需要考虑的问题。
在计算剪力时,可以将双向板看作一个复杂的梁结构,采用横截面法来计算剪力。
与此同时,双向板还会产生扭矩。
扭矩的计算可以借助于剪力的计算结果,具体方法可以参考弹性理论中的扭矩公式。
双向板的变形分为平面变形和空间变形两种情况。
在计算平面变形时,可以采用等效弹性模量法。
通过考虑不同方向上的刚度系数和位移系数,将双向板的变形进行等效处理,从而简化计算过程。
而空间变形的计算则需要考虑额外的因素,例如板的高度、边界条件等。
最后,双向板的稳定性也是需要进行计算的重要参数。
在计算稳定性时,可以引入边界条件、支撑条件等因素,采用弹性理论中的稳定性计算方法进行分析。
总之,双向板按照弹性理论的计算方法主要包括弯矩、剪力和扭矩的计算、板的变形以及板的稳定性计算。
在实际工程中,双向板的设计与计算还需要综合考虑其他因素,例如材料的强度特性、施工工艺、荷载条件等。
因此,在进行双向板的设计与计算时,需要综合运用弹性理论以及其他相关知识,进行全面而准确的分析。
双向板_计算步骤

LB-1矩形板计算一、构件编号: LB-1二、示意图三、依据规范《建筑结构荷载规范》 GB50009-2001《混凝土结构设计规范》 GB50010-2010四、计算信息1.几何参数计算跨度: Lx = 3000 mm; Ly = 4600 mm板厚: h = 120 mm2.材料信息混凝土等级: C25 fc=11.9N/mm2 ft=1.27N/mm2 ftk=1.78N/mm2Ec=2.80×104N/mm2钢筋种类: HRB400 fy = 360 N/mm2Es = 2.0×105 N/mm2最小配筋率: ρ= 0.200%纵向受拉钢筋合力点至近边距离: as = 40mm保护层厚度: c = 20mm3.荷载信息(均布荷载)永久荷载分项系数: γG = 1.200可变荷载分项系数: γQ = 1.400准永久值系数: ψq = 1.000永久荷载标准值: qgk = 4.100kN/m2可变荷载标准值: qqk = 2.000kN/m24.计算方法:弹性板5.边界条件(上端/下端/左端/右端):固定/简支/简支/简支6.设计参数结构重要性系数: γo = 1.00泊松比:μ = 0.200五、计算参数:1.计算板的跨度: Lo = 3000 mm2.计算板的有效高度: ho = h-as=120-40=80 mm六、配筋计算(lx/ly=3000/4600=0.652<2.000 所以按双向板计算):1.X向底板钢筋1) 确定X向板底弯矩Mx = 表中系数(γG*qgk+γQ*qqk)*Lo2= (0.0634+0.0307*0.200)*(1.200*4.100+1.400*2.000)*32= 4.829 kN*m2) 确定计算系数αs = γo*Mx/(α1*fc*b*ho*ho)= 1.00*4.829×106/(1.00*11.9*1000*80*80)= 0.0633) 计算相对受压区高度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2*0.063) = 0.0664) 计算受拉钢筋面积As = α1*fc*b*ho*ξ/fy = 1.000*11.9*1000*80*0.066/360 = 173mm25) 验算最小配筋率ρ = As/(b*h) = 173/(1000*120) = 0.144%ρ<ρmin = 0.200% 不满足最小配筋要求所以取面积为As = ρmin*b*h = 0.200%*1000*120 = 240 mm2采取方案?8@200, 实配面积251 mm22.Y向底板钢筋1) 确定Y向板底弯矩My = 表中系数(γG*qgk+γQ*qqk)*Lo2= (0.0307+0.0634*0.200)*(1.200*4.100+1.400*2.000)*32 = 3.012 kN*m2) 确定计算系数αs = γo*My/(α1*fc*b*ho*ho)= 1.00*3.012×106/(1.00*11.9*1000*80*80)= 0.0403) 计算相对受压区高度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2*0.040) = 0.0404) 计算受拉钢筋面积As = α1*fc*b*ho*ξ/fy = 1.000*11.9*1000*80*0.040/360 = 107mm25) 验算最小配筋率ρ = As/(b*h) = 107/(1000*120) = 0.089%ρ<ρmin = 0.200% 不满足最小配筋要求所以取面积为As = ρmin*b*h = 0.200%*1000*120 = 240 mm2采取方案?8@200, 实配面积251 mm23.Y向上边支座钢筋1) 确定上边支座弯矩M o y = 表中系数(γG*qgk+γQ*qqk)*Lo2= 0.1131*(1.200*4.100+1.400*2.000)*32= 7.861 kN*m2) 确定计算系数αs = γo*M o y/(α1*fc*b*ho*ho)= 1.00*7.861×106/(1.00*11.9*1000*80*80)= 0.1033) 计算相对受压区高度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2*0.103) = 0.1094) 计算受拉钢筋面积As = α1*fc*b*ho*ξ/fy = 1.000*11.9*1000*80*0.109/360 = 289mm25) 验算最小配筋率ρ = As/(b*h) = 289/(1000*120) = 0.241%ρ≥ρmin = 0.200% 满足最小配筋要求采取方案?8@160, 实配面积314 mm2七、跨中挠度计算:Mk -------- 按荷载效应的标准组合计算的弯矩值Mq -------- 按荷载效应的准永久组合计算的弯矩值1.计算荷载效应Mk = Mgk + Mqk= (0.0634+0.0307*0.200)*(4.100+2.000)*32 = 3.816 kN*mMq = Mgk+ψq*Mqk= (0.0634+0.0307*0.200)*(4.100+1.0*2.000)*32 = 3.816 kN*m2.计算受弯构件的短期刚度 Bs1) 计算按荷载荷载效应的两种组合作用下,构件纵向受拉钢筋应力= 3.816×106/(0.87*80*251) = 218.438 N/mm= 3.816×106/(0.87*80*251) = 218.438 N/mm2) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积: Ate = 0.5*b*h = 0.5*1000*120= 60000mm2= 251/60000 = 0.418%3) 计算裂缝间纵向受拉钢筋应变不均匀系数ψ= 1.1-0.65*1.78/(0.418%*218.438) = -0.166因为ψ不能小于最小值0.2,所以取ψk = 0.2= 1.1-0.65*1.78/(0.418%*218.438) = -0.166因为ψ不能小于最小值0.2,所以取ψq = 0.24) 计算钢筋弹性模量与混凝土模量的比值αEαE = Es/Ec = 2.0×105/2.80×104 = 7.1435) 计算受压翼缘面积与腹板有效面积的比值γf矩形截面,γf=06) 计算纵向受拉钢筋配筋率ρρ = As/(b*ho)= 251/(1000*80) = 0.314%7) 计算受弯构件的短期刚度 BsBsk = Es*As*ho2= 2.0×105*251*802/[1.15*-0.166+0.2+6*7.143*0.314%/(1+3.5*0.0)]= 5.692×102 kN*m2Bsq = Es*As*ho2= 2.0×105*251*802/[1.15*-0.166+0.2+6*7.143*0.314%/(1+3.5*0.0)]= 5.692×102 kN*m23.计算受弯构件的长期刚度B1) 确定考虑荷载长期效应组合对挠度影响增大影响系数θ2) 计算受弯构件的长期刚度 B= 3.816/(3.816*(2.0-1)+3.816)*5.692×102= 2.846×102 kN*m2= 5.692×102/2.0= 2.846×102 kN*m2B = min(Bk,Bq)= min(284.588,284.588)= 284.5884.计算受弯构件挠度f max = f*(q gk+q qk)*Lo4/B= 0.00677*(4.100+2.000)*34/2.846×102= 11.749mm5.验算挠度挠度限值fo=Lo/200=3000/200=15.000mmfmax=11.749mm≤fo=15.000mm,满足规范要求!八、裂缝宽度验算:1.跨中X方向裂缝1) 计算荷载效应Mx = 表中系数(qgk+ψqqk)*Lo2= (0.0634+0.0307*0.200)*(4.100+1.00*2.000)*32= 3.816 kN*m2) 光面钢筋,所以取值v i=0.73) 因为C > 65,所以取C = 654) 计算按荷载效应的准永久组合作用下,构件纵向受拉钢筋应力=3.816×106/(0.87*80*251)=218.438N/mm5) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积,Ate=0.5*b*h=0.5*1000*120=60000 mm2=251/60000 = 0.0042因为ρte=0.0042 < 0.01,所以让ρte=0.016) 计算裂缝间纵向受拉钢筋应变不均匀系数ψ=1.1-0.65*1.780/(0.0100*218.438)=0.5707) 计算单位面积钢筋根数nn=1000/dist = 1000/200=58) 计算受拉区纵向钢筋的等效直径d eqd eq= (∑n i*d i2)/(∑n i*v i*d i)=5*8*8/(5*0.7*8)=119) 计算最大裂缝宽度=1.9*0.570*218.438/2.0×105*(1.9*20+0.08*11/0.0100)=0.1532mm ≤ 0.30, 满足规范要求2.跨中Y方向裂缝1) 计算荷载效应My = 表中系数(qgk+ψqqk)*Lo2= (0.0307+0.0634*0.200)*(4.100+1.00*2.000)*32= 2.380 kN*m2) 光面钢筋,所以取值v i=0.73) 因为C > 65,所以取C = 654) 计算按荷载效应的准永久组合作用下,构件纵向受拉钢筋应力=2.380×106/(0.87*80*251)=136.228N/mm5) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积,Ate=0.5*b*h=0.5*1000*120=60000 mm2=251/60000 = 0.0042因为ρte=0.0042 < 0.01,所以让ρte=0.016) 计算裂缝间纵向受拉钢筋应变不均匀系数ψ=1.1-0.65*1.780/(0.0100*136.228)=0.2517) 计算单位面积钢筋根数nn=1000/dist = 1000/200=58) 计算受拉区纵向钢筋的等效直径d eqd eq= (∑n i*d i2)/(∑n i*v i*d i)=5*8*8/(5*0.7*8)=119) 计算最大裂缝宽度=1.9*0.251*136.228/2.0×105*(1.9*20+0.08*11/0.0100)=0.0420mm ≤ 0.30, 满足规范要求3.支座上方向裂缝1) 计算荷载效应M o y = 表中系数((qgk+ψqqk)*Lo2)= 0.1131*(4.100+1.00*2.000)*32= 6.211 kN*m2) 光面钢筋,所以取值v i=0.73) 因为C > 65,所以取C = 654) 计算按荷载效应的准永久组合作用下,构件纵向受拉钢筋应力=6.211×106/(0.87*80*314)=284.215N/mm5) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积,Ate=0.5*b*h=0.5*1000*120=60000 mm2=314/60000 = 0.0052因为ρte=0.0052 < 0.01,所以让ρte=0.016) 计算裂缝间纵向受拉钢筋应变不均匀系数ψ=1.1-0.65*1.780/(0.0100*284.215)=0.6937) 计算单位面积钢筋根数nn=1000/dist = 1000/160=68) 计算受拉区纵向钢筋的等效直径d eqd eq= (∑n i*d i2)/(∑n i*v i*d i)=6*8*8/(6*0.7*8)=119) 计算最大裂缝宽度=1.9*0.693*284.215/2.0×105*(1.9*20+0.08*11/0.0100)=0.2421mm ≤ 0.30, 满足规范要求。
双向板计算步骤范文

双向板计算步骤范文第一步:几何模型建立根据实际工程情况,确定双向板的几何尺寸和形状,包括板的长度、宽度和厚度等参数。
根据这些参数,建立双向板的有限元模型,通常采用三维有限元模型进行计算。
第二步:荷载分析确定双向板受力的荷载情况,包括静载和动载的荷载大小和作用位置。
例如,静载可以包括自重、活载和风载等;动载可以包括地震和风荷载等。
将荷载应用于有限元模型,得出板的受力情况。
第三步:边界条件设定根据双向板的支座情况,确定边界条件。
双向板一般有四个边界面,边界条件可以是固定端、简支或自由端。
根据实际情况,设定边界条件,以便计算出正确的受力情况。
第四步:弹性材料性质确定双向板的材料性质,包括弹性模量和泊松比等。
这些参数反映了材料的刚度和变形性质。
根据材料的特性,计算板在受力时的应力和变形情况。
第五步:受力计算通过有限元分析,在给定的荷载和边界条件下,计算双向板的受力情况。
这包括剪力、弯矩和轴力等受力情况。
计算的过程可以采用迭代方法,通过不断调整单元尺寸和网格密度,直至达到收敛。
第六步:挠度计算计算双向板的挠度情况。
挠度是指板在受力过程中的弯曲变形,也是判断双向板是否满足强度和刚度要求的重要指标。
通过有限元分析,计算双向板在给定荷载下的挠度情况,并与规范要求进行对比。
第七步:验算与优化根据计算结果,进行双向板的验算与优化。
验证计算结果是否符合规范要求,包括受力和挠度等方面。
如果不满足要求,需要对双向板进行优化设计,调整其几何尺寸和材料性质,满足规范要求。
第八步:结果分析与总结对计算结果进行分析和总结。
对双向板的受力和挠度进行评价,了解其强度和刚度情况。
根据分析结果,可以对双向板的设计和施工提出建议和改进措施,以提高结构的安全性和可靠性。
总而言之,双向板计算是一项复杂的结构力学计算,需要建立几何模型、进行荷载分析、设定边界条件、确定材料性质、进行受力计算和挠度计算,最后对结果进行分析与总结。
通过这些步骤,可以得到双向板结构的受力和变形情况,为工程设计和施工提供参考和指导。
毕业设计--2010新规范--双向板及计算
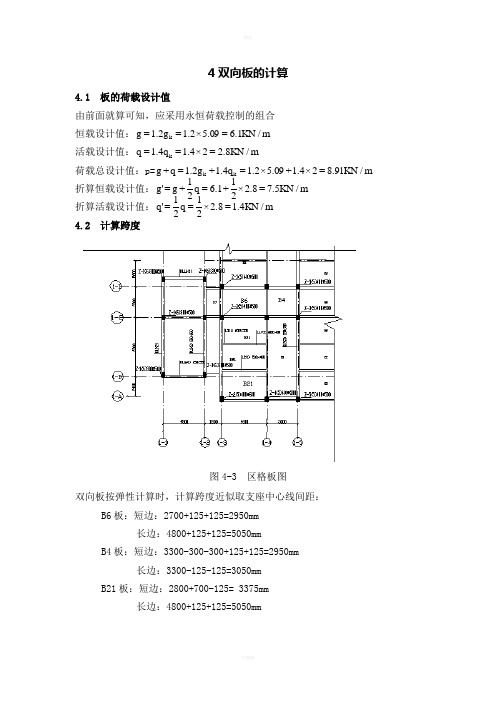
4双向板的计算4.1 板的荷载设计值由前面就算可知,应采用永恒荷载控制的组合 恒载设计值:m /KN 1.609.52.1g 2.1g k =×== 活载设计值:m /KN 8.224.1q 4.1q k =×==荷载总设计值:p=m /KN 91.824.109.52.1q 4.1g 2.1q g k k =×+×=+=+折算恒载设计值:m /KN 5.78.2211.6q 21g 'g =×+=+=折算活载设计值:m /KN 4.18.221q 21'q =×==4.2 计算跨度图4-3 区格板图双向板按弹性计算时,计算跨度近似取支座中心线间距:B6板:短边:2700+125+125=2950mm 长边:4800+125+125=5050mm B4板:短边:3300-300-300+125+125=2950mm 长边:3300-125-125=3050mm B21板:短边:2800+700-125= 3375mm 长边:4800+125+125=5050mm4.3 弯矩计算取每米板宽计算,在'g作用下,各内支座均可视为固定,边支座按固支考虑。
在'q作用下,各区格板四边均可视作简支,边支座按固支考虑,跨内最大正弯矩则在中心点处,计算时,可近似取二者之和作为跨内最大正弯矩值。
在求各中间支座最大负弯矩(绝对值)时,按恒荷载及活荷载均满布各区格板计算。
具体计算结果见表4-1。
表4-1 双向板弯矩计算表区格B6B42950/50500.5842950/30500.97跨内计算简图g’q’μ=01m2(0.03737.50.0843 1.4)2.953.46kN m2(0.01897.50.0393 1.4)2.95 1.71kN m2m2(0.006967.50.0232 1.4)2.950.737kN m2(0.017367.50.0366 1.4)2.95 1.58kN mμ=0.21m 3.460.20.737 3.607kN m 1.710.2 1.58 2.026kN m2m0.7370.2 3.46 1.426kN m 1.580.2 1.71 1.922kN m支座计算简图g+q g+q'1m0.0799×8.9kN/m2×(2.95m)2= 6.188 kN·m0.0535×8.9kN/m2×(2.95m)2= 4.14kN·m 2'm0.0571×8.9kN/m2×(2.95m)2= 4.423kN·m0.0522×8.9kN/m2×(2.95m)2= 4.028 kN·m+区格B213375/50500.67跨内 计算简图μ=01m2(0.03357.50.0447 1.4) 3.375 3.575kN m 2m2(0.0107.50.0159 1.4) 3.375 1.108kN mμ=0.21m3.5750.2 1.108 3.796kN m 2m1.1080.2 3.575 1.823kN m支座计算简图g+q'1m20.075368.9 3.3757.64kN m2'm20.0578.9 3.375 5.78kN m由上表可知:板间支座弯矩是不平衡的,实际应用时可以近似取的绝对值较大者,根据对称性取代表区格AB 相邻两区格板支座弯矩取较大值即m=-4.423KN.m4.4 截面配筋计算 短跨方向:012080h h mm长跨方向:023070h h mmC30混凝土:HPB2100级钢筋:2270/yf N mm中间区格板带,各内驱格板四周与梁整体连接,故各跨跨内和中间支座考虑板的内拱作用,计算配筋量降低20%,但须满足最小配筋率: 板的最小配筋率:0.2%0.450.238%max0.238%tyf f板的最小配筋面积:2,minmin0.238%100080190.4s A bh mm为便于计算,近似取0.95,s配筋计算如图:表4-2 连续板各截面配筋计算截面M0h选配钢筋实配钢筋 跨中 B601l 方向3.6070.8 2.5980109.6Ф8@20025102l 方向1.4260.8 1.1470 57.1 Ф8@200 251B401l 方向2.0260.8 1.6280 71 Ф8@200 25102l 方向1.9220.8 1.5377077.04 Ф8@200 251B2101l 方向3.79680166.49Ф8@20025102l 方向1.8237091.38Ф8@200251 截面 M 0h s A 选配钢筋 实配钢筋 支座B6-B4 -4.423 80 194.1 Ф8@200 251 B21-B21-7.6480334Ф8@150335布置时,短方向钢筋放在长方向钢筋外侧。
双向板梁板结构设计

所有塑性铰线所作的内功:U=10maθ
外功:W=Puθa/2 所以,解得Pu=20m
假定双向板的破坏图示
板的跨内及支座截面钢筋通常均匀布置。
板底钢筋弯起
跨内正弯矩钢筋在 距支座lx/4处弯起 50%
跨内钢筋弯起过早或弯起数量过多,可 能使余下的钢筋不能承受该处的正弯矩 ,致使该处的钢筋比跨内钢筋先达到屈 服而出现塑性铰线,形成“倒锥台形” 破坏机构,并导致双向板极限荷载降低 。
支座钢筋截断
支座负弯矩钢筋在 距支座边lx/4处切 断
* 塑性铰线出现 在弯矩最大处:
塑性铰线位置的确定规则
①塑性铰线发生在弯矩最大处 ②塑性铰线是直线,对称结构 具有对称的塑性铰线分布; ③正弯矩部位出现正塑性铰线 ,负弯矩部位出现负塑性铰线 ④当板块产生竖向位移时,板 块必绕一旋转轴产生转动; ⑤转动轴线必通过支承板的柱 ;板的支承边也是转动轴。 ⑥两块板之间的塑性铰线必通 过两块板转动轴的交点; ⑦塑性铰线的数量应使整块板 成为一个几何可变体系。
板跨中最大正弯矩计算(活荷载棋盘式布置)
在正对称荷载作用下,连 续板的各中间支座两侧的荷 载相同,可认为支承处板的 转角为零,当作固定支座, 则中间区格可视为四边固定 在反对称荷载作用下,连 续板的支承处左右截面旋转 方向一致,即板在支承处的 转动变形基本自由,可将板 的各中间支座当作简支支座 ,中间各区格板均可视为四 边简支。 边区格和角区格按楼盖周 边实际支承情况确定。 棋盘式荷载布置 两种荷载作用下的弯矩叠 加,即得跨中最大弯矩。
整体式双向板课程设计计算书

1设计资料 (1)1.1楼面做法 (1)1.2楼面荷载 (1)1.3材料选用 (1)1.4建筑设计规范要求 (1)1.4结构平面布置 (2)2双向板计算 (2)2.1确定板的厚度H和梁的截面 (2)2.2荷载计算 (3)2.3按塑性理论计算 (3)3支承梁计算(按弹性理论) (5)3.1纵向支承梁 (6)3.2纵向支承梁 (9)4跨中挠度验算 (13)4.1挠度和裂缝验算参数 (13)4.2在荷载效应的标准组合作用下,受弯构件的短期刚度B S (13)4.3考虑荷载长期效应组合对挠度影响增大影响系数 (14)4.4受弯构件的长期刚度B,可按下列公式计算 (14)5裂缝宽度验算 (14)5.1X方向板带跨中裂缝 (14)5.2Y方向板带跨中裂缝 (15)5.3左端支座跨中裂缝 (15)5.4右端支座跨中裂缝 (15)5.5上端支座跨中裂缝 (16)6基础设计 (16)6.1荷载的确定 (16)6.2初定承台尺寸 (16)致谢 (18)参考文献 (17)施工图 (20)1设计资料墙体厚度370mm ,结构横向长1L =30m ,结构纵向长2L =30m 。
楼梯位于该层平面的外部,本设计不予考虑。
楼盖采用整体式双向板肋形结构;1.1 楼面做法水泥砂浆面层(25mm 厚,容重320kN /m ) 钢筋混凝土现浇板(容重325kN /m )板底混合砂浆抹灰(15mm 厚,容重317kN /m )1.2 楼面荷载永久荷载分项系数G 1.2γ=; 可变荷载标准值为2Q 3.5KN /m γ=; 分项系数1.4;1.3 材料选用板混凝土强度等级:C20(22c t f 11.9N /mm ,f 1.27N /mm ==);板中钢筋、梁中箍筋、构造钢筋HPB235级(2y f 210N /mm =),梁中受力筋HRB335级(2y f 300N /mm =);1.4建筑设计规范要求该建筑位于非地震区; 建筑物安全级别为二级; 结构环境类别二类;结构平面布置及初估尺寸:板的支承长度为120mm ,梁的支承长度为240mm 。
双向板计算.doc

(一)双向板按弹性理论的计算方法1.单跨双向板的弯矩计算为便于应用,单跨双向板按弹性理论计算,已编制成弯矩系数表,供设计者查用。
在教材的附表中,列出了均布荷载作用下,六种不同支承情况的双向板弯矩系数表。
板的弯矩可按下列公式计算:M = 弯矩系数×(g+p)l x2式中M 为跨中或支座单位板宽内的弯矩(kN·m/m);g、p为板上恒载及活载设计值(kN/m2);l x为板的跨度(m)。
错误!未找到引用源。
错误!未找到引用源。
2.多跨连续双向板的弯矩计算(1)跨中弯矩双向板跨中弯矩的最不利活载位置图多跨连续双向板也需要考虑活载的最不利位置。
当求某跨跨中最大弯矩时,应在该跨布置活载,并在其前后左右每隔一区格布置活载,形成如上图(a)所示棋盘格式布置。
图(b)为A-A剖面中第2、第4区格板跨中弯矩的最不利活载位置。
为了能利用单跨双向板的弯矩系数表,可将图(b)的活载分解为图(c)的对称荷载情况和图(d)的反对称荷载情况,将图(c)与(d)叠加即为与图(b)等效的活载分布。
在对称荷载作用下,板在中间支座处的转角很小,可近似地认为转角为零,中间支座均可视为固定支座。
因此,所有中间区格均可按四边固定的单跨双向板计算;如边支座为简支,则边区格按三边固定、一边简支的单跨双向板计算;角区格按两邻边固定、两邻边简支的单跨双向板计算。
在反对称荷载作用下,板在中间支座处转角方向一致,大小相等接近于简支板的转角,所有中间支座均可视为简支支座。
因此,每个区格均可按四边简支的单跨双向板计算。
将上述两种荷载作用下求得的弯矩叠加,即为在棋盘式活载不利位置下板的跨中最大弯矩。
错误!未找到引用源。
错误!未找到引用源。
(2)支座弯矩支座弯矩的活载不利位置,应在该支座两侧区格内布置活载,然后再隔跨布置,考虑到隔跨活载的影响很小,可假定板上所有区格均满布荷载(g+p)时得出的支座弯矩,即为支座的最大弯矩。
这样,所有中间支座均可视为固定支座,边支座则按实际情况考虑,因此可直接由单跨双向板的弯矩系数表查得弯矩系数,计算支座弯距。
双向板-计算步骤

双向板-计算步骤⼀、构件编号: LB-1⼆、⽰意图三、依据规范《建筑结构荷载规范》 GB50009-2001《混凝⼟结构设计规范》 GB50010-2010四、计算信息1.⼏何参数计算跨度: Lx = 3000 mm; Ly = 4600 mm板厚: h = 120 mm2.材料信息混凝⼟等级: C25 fc=mm2 ft=mm2 ftk=mm2Ec=×104N/mm2钢筋种类: HRB400 fy = 360 N/mm2Es = ×105 N/mm2最⼩配筋率: ρ= %纵向受拉钢筋合⼒点⾄近边距离: as = 40mm保护层厚度: c = 20mm3.荷载信息(均布荷载)永久荷载分项系数: γG =可变荷载分项系数: γQ =准永久值系数: ψq =永久荷载标准值: qgk = m2可变荷载标准值: qqk = m24.计算⽅法:弹性板5.边界条件(上端/下端/左端/右端):固定/简⽀/简⽀/简⽀6.设计参数结构重要性系数: γo =泊松⽐:µ =五、计算参数:1.计算板的跨度: Lo = 3000 mm2.计算板的有效⾼度: ho = h-as=120-40=80 mm六、配筋计算(lx/ly=3000/4600=< 所以按双向板计算):向底板钢筋1) 确定X向板底弯矩Mx = 表中系数(γG*qgk+γQ*qqk)*Lo2= +***+**32= kN*m2) 确定计算系数αs = γo*Mx/(α1*fc*b*ho*ho)= *×106/**1000*80*80)=3) 计算相对受压区⾼度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2* =4) 计算受拉钢筋⾯积As = α1*fc*b*ho*ξ/fy = **1000*80*360= 173mm25) 验算最⼩配筋率ρ = As/(b*h) = 173/(1000*120) = %ρ<ρmin = % 不满⾜最⼩配筋要求所以取⾯积为As = ρmin*b*h = %*1000*120 = 240 mm2采取⽅案?8@200, 实配⾯积251 mm2向底板钢筋1) 确定Y向板底弯矩My = 表中系数(γG*qgk+γQ*qqk)*Lo2= +***+**32= kN*m2) 确定计算系数αs = γo*My/(α1*fc*b*ho*ho)= *×106/**1000*80*80)=3) 计算相对受压区⾼度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2* =4) 计算受拉钢筋⾯积As = α1*fc*b*ho*ξ/fy = **1000*80*360= 107mm25) 验算最⼩配筋率ρ = As/(b*h) = 107/(1000*120) = %ρ<ρmin = % 不满⾜最⼩配筋要求所以取⾯积为As = ρmin*b*h = %*1000*120 = 240 mm2采取⽅案?8@200, 实配⾯积251 mm2向上边⽀座钢筋1) 确定上边⽀座弯矩M o y = 表中系数(γG*qgk+γQ*qqk)*Lo2= **+**32= kN*m2) 确定计算系数αs = γo*M o y/(α1*fc*b*ho*ho)= *×106/**1000*80*80)=3) 计算相对受压区⾼度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2* =4) 计算受拉钢筋⾯积As = α1*fc*b*ho*ξ/fy = **1000*80*360= 289mm25) 验算最⼩配筋率ρ = A s/(b*h) = 289/(1000*120) = %ρ≥ρmin = % 满⾜最⼩配筋要求采取⽅案?8@160, 实配⾯积314 mm2七、跨中挠度计算:Mk -------- 按荷载效应的标准组合计算的弯矩值Mq -------- 按荷载效应的准永久组合计算的弯矩值1.计算荷载效应Mk = Mgk + Mqk= +**+*32 = kN*mMq = Mgk+ψq*Mqk= +**+**32 = kN*m2.计算受弯构件的短期刚度 Bs1) 计算按荷载荷载效应的两种组合作⽤下,构件纵向受拉钢筋应⼒σsk = Mk/*ho*As) 混规= ×106/*80*251) = N/mmσsq = Mq/*ho*As) 混规= ×106/*80*251) = N/mm 2) 计算按有效受拉混凝⼟截⾯⾯积计算的纵向受拉钢筋配筋率矩形截⾯积: Ate = *b*h = *1000*120= 60000mm2ρte = As/Ate 混规 = 251/60000 = %3) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψk = 混规 = =因为ψ不能⼩于最⼩值,所以取ψk =ψq = 混规 = =因为ψ不能⼩于最⼩值,所以取ψq =4) 计算钢筋弹性模量与混凝⼟模量的⽐值αEαE = Es/Ec = ×105/×104 =5) 计算受压翼缘⾯积与腹板有效⾯积的⽐值γf矩形截⾯,γf=06) 计算纵向受拉钢筋配筋率ρρ = As/(b*ho)= 251/(1000*80) = %7) 计算受弯构件的短期刚度 BsBsk = Es*As*ho2/[ψk++6*αE*ρ/(1+ γf')](混规 = ×105*251*802/[*++6**%/(1+*] = ×102 kN*m2Bsq = Es*As*ho2/[ψq++6*αE*ρ/(1+ γf')](混规 = ×105*251*802/[*++6**%/(1+*] = ×102 kN*m23.计算受弯构件的长期刚度B1) 确定考虑荷载长期效应组合对挠度影响增⼤影响系数θ当ρ'=0时,θ= 混规 2) 计算受弯构件的长期刚度 BBk = Mk/(Mq*(θ-1)+Mk)*Bs (混规= *+*×102= ×102 kN*m2Bq = Bsq/θ (混规= ×102/= ×102 kN*m2B = min(Bk,Bq)= min,=4.计算受弯构件挠度f max = f*(q gk+q qk)*Lo4/B= *+*34/×102=5.验算挠度挠度限值fo=Lo/200=3000/200=fmax=≤fo=,满⾜规范要求!⼋、裂缝宽度验算:1.跨中X⽅向裂缝1) 计算荷载效应Mx = 表中系数(qgk+ψqqk)*Lo2= +**+**32= kN*m2) 光⾯钢筋,所以取值v i=3) 因为C > 65,所以取C = 654) 计算按荷载效应的准永久组合作⽤下,构件纵向受拉钢筋应⼒σsq=Mq/*ho*As) 混规=×106/*80*251)=mm5) 计算按有效受拉混凝⼟截⾯⾯积计算的纵向受拉钢筋配筋率矩形截⾯积,Ate=*b*h=*1000*120=60000 mm2ρte=As/Ate 混规 =251/60000 =因为ρte= < ,所以让ρte=6) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψ= 混规 = =7) 计算单位⾯积钢筋根数nn=1000/dist = 1000/200=58) 计算受拉区纵向钢筋的等效直径d eqd eq= (∑n i*d i2)/(∑n i*v i*d i)=5*8*8/(5**8)=119) 计算最⼤裂缝宽度ωmax=αcr*ψ*σsq/Es**C+*Deq/ρte) (混规=**×105**20+*11/ = ≤ , 满⾜规范要求2.跨中Y⽅向裂缝1) 计算荷载效应My = 表中系数(qgk+ψqqk)*Lo2= +**+**32= kN*m2) 光⾯钢筋,所以取值v i=3) 因为C > 65,所以取C = 654) 计算按荷载效应的准永久组合作⽤下,构件纵向受拉钢筋应⼒σsq=Mq/*ho*As) 混规=×106/*80*251)=mm5) 计算按有效受拉混凝⼟截⾯⾯积计算的纵向受拉钢筋配筋率矩形截⾯积,Ate=*b*h=*1000*120=60000 mm2ρte=As/Ate 混规 =251/60000 =因为ρte= < ,所以让ρte=6) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψ= 混规 = =7) 计算单位⾯积钢筋根数nn=1000/dist = 1000/200=58) 计算受拉区纵向钢筋的等效直径d eqd eq= (∑n i*d i2)/(∑n i*v i*d i)=5*8*8/(5**8)=119) 计算最⼤裂缝宽度ωmax=αcr*ψ*σsq/Es**C+*Deq/ρte) (混规=**×105**20+*11/ = ≤ , 满⾜规范要求3.⽀座上⽅向裂缝1) 计算荷载效应M o y = 表中系数((qgk+ψqqk)*Lo2)= *+**32= kN*m2) 光⾯钢筋,所以取值v i=3) 因为C > 65,所以取C = 654) 计算按荷载效应的准永久组合作⽤下,构件纵向受拉钢筋应⼒σsq=Mq/*ho*As) 混规=×106/*80*314)=mm5) 计算按有效受拉混凝⼟截⾯⾯积计算的纵向受拉钢筋配筋率矩形截⾯积,Ate=*b*h=*1000*120=60000 mm2ρte=As/Ate 混规 =314/60000 =因为ρte= < ,所以让ρte=6) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψ= 混规 = =7) 计算单位⾯积钢筋根数nn=1000/dist = 1000/160=68) 计算受拉区纵向钢筋的等效直径d eqd eq= (∑n i*d i2)/(∑n i*v i*d i)=6*8*8/(6**8)=119) 计算最⼤裂缝宽度ωmax=αcr*ψ*σsq/Es**C+*Deq/ρte) (混规=**×105**20+*11/ = ≤ , 满⾜规范要求。
双向板的计算课程设计

双向板的计算课程设计一、课程目标知识目标:1. 学生能理解双向板的基本概念,掌握其结构特点及工作原理。
2. 学生能运用数学公式进行双向板的计算,解决实际问题。
3. 学生了解双向板在现代工程技术中的应用和价值。
技能目标:1. 学生能运用所学知识,对双向板进行受力分析,并正确绘制力的作用图。
2. 学生能熟练运用计算公式,完成双向板的内力计算,提高解决问题的能力。
3. 学生通过实际操作,培养观察能力、动手能力和团队协作能力。
情感态度价值观目标:1. 学生对双向板的相关知识产生兴趣,激发学习热情,树立求真务实的学习态度。
2. 学生通过学习双向板,认识到科学技术在工程领域的重要性,增强创新意识。
3. 学生在课程学习过程中,培养合作精神,提高沟通能力,形成良好的团队意识。
课程性质:本课程为四年级下学期的工程技术类课程,旨在让学生掌握双向板的计算方法,培养解决实际问题的能力。
学生特点:四年级学生具有一定的数学基础和动手能力,对新鲜事物充满好奇,喜欢探索和实践。
教学要求:结合学生的特点和课程性质,课程目标具体、明确,注重理论与实践相结合,培养学生的动手操作能力和团队协作精神。
通过课程学习,使学生能够独立完成双向板的计算任务,提高综合运用知识的能力。
二、教学内容1. 双向板的基本概念与结构特点- 双向板的定义- 双向板的分类- 双向板的结构特点2. 双向板的受力分析- 受力分析的基本原理- 受力图的绘制方法- 双向板受力分析的步骤3. 双向板的内力计算- 弯矩、剪力的计算公式- 支座反力的计算方法- 内力计算的步骤与实例4. 双向板的应用与实例分析- 双向板在现代工程技术中的应用- 实际工程案例的受力分析与计算- 双向板的优化设计方法5. 实践操作与团队协作- 双向板模型制作- 受力分析与计算的实际操作- 团队协作完成双向板项目教学内容安排与进度:第一周:双向板的基本概念与结构特点第二周:双向板的受力分析第三周:双向板的内力计算第四周:双向板的应用与实例分析第五周:实践操作与团队协作教材章节关联:本教学内容与教材第四章“桥梁结构”相关,涉及第4.2节“双向板的设计与计算”。
双向板楼板设计

双向板设计计算板厚的确定:连续双向板的厚度一般大于或等于(1/40~l/50)l ox =4800/50=96~120mm,且双向板的厚度不宜小于80mm,故取板厚为100mm。
支撑梁截面尺寸:根据经验,支撑梁的截面高度h=l/14~l/8,长跨梁截面高度h=(6000/14~6000/8)=428.57~750mm,故取h=600mm。
长跨梁截面宽b=h/3~h/2=(600/3~600/2)=200~300mm,故取b=200mm。
短跨梁截面高 h=(4800/14~4800/8)mm=342.9~600mm,故取h=500mm。
短跨梁截面宽 b= h/3~h/2=166.7~250mm,故取b=200mm。
由于活荷载标准值等于5kN/m2,则取r Q =1.3。
18mm厚水泥砂浆底面0.018×20kN/m3=0.36kN/m2100mm厚钢筋砼现浇板0.10×25kN/m3=2.5kN/m215mm厚石灰砂浆抹底0.015×17kN/m3=0.26kN/m212mm厚水磨石面层 0.65kN/m2g K=0.36+2.5+0.26+0.65=3.77kN/m2可变荷载:楼面面层活荷载标准值5kN/m2。
(学号1015041224)混凝土:板强度等级C25,梁强度等级C30。
钢筋:板HPB300级:梁:主筋HRB400级,箍筋HPB300级恒荷载设计值:g=r G g K=1.2×g K=1.2×3.77=4.6kN/m2活荷载设计值:q=r Q q K =1.3×5.0=6.5kN/m2g+q/2=4.6+6.5/2=7.85kN/m2 q/2=6.5/2=3.25 kN/m2g+q=4.6+6.5=11.1kN/m2区格板A计算跨度:l ox=l n+a/2+b/2>l n+h/2+b/2=(3000-200)+100/2+200/2=2950mm l ox=2950mml oy=l n+a/2+b/2>l n+h/2+b/2=(4800-200)+100/2+200/2=4750mm l oy=4750mm区格板B计算跨度:L ox=l c=2400mm<1.1l n=1.1*(2400-200)=2420mml ox=2400mml oy=l n+a/2+b/2>l n+h/2+b/2=(4800-200)+100/2+200/2=4750mm l oy=4750mm区格板C计算跨度:l ox=l n+a/2+b/2>l n+h/2+b/2=(3000-200)+100/2+200/2=2950mm l ox=2950mml oy=l c=4800mm<1.1l n=1.1*(4800-200)=5060mml oy=4800mm区格板D计算跨度:l ox=l c=2400mm<1.1l n=1.1*(2400-200)=2420mml ox=2400mmL oy= l c=4800mm<1.1l n=1.1*(4800-200)=5060mml oy =4800mm区格板E 计算跨度:L ox =l c =3000mm<1.1l n =1.1*(3000-200)=3080mm l ox =3000mml oy =l n +a/2+b/2>l n +h/2+b/2=(4800-200)+100/2+200/2=4750mm l oy =4750mm 区格板F 计算跨度:l ox =l c =3000mm<1.1l n =1.1*(3000-200)=3080mm l ox =3000mmL oy = l c =4800mm<1.1l n =1.1*(4800-200)=5060mm l oy =4800mm按弹性理论设计板此法假定支承梁不产生竖向位移且不受扭,并且要求同一方向相邻跨度比值75.0max0min0≥l l ,以防误差过大。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2)平台板 1)计算要点
○1 平台板板厚可取 l0 / 35 (l 0 为平台板计算跨度),常
取 60~80mm,平台板一般均为单向板(有时也可能是双向 板),取 1m 宽板带作为计算单元。
○2 当板的两边均与梁整体连接时,考虑梁对板的弹性约束
(图
7.3.4b),板的跨中弯矩可按
M
1 10
(g
中间区格板可按四边固定的板来计算内力 边区格板的三个内支承边、角区格的两个 内支承边都可以看成固定边。
④反对称型荷载作用下
将板的各中间支座看成铰支承,因此在
q’=±q/2作用下,各板均可按四边简支 的单区格板计算内力,计算简图取附表3-2 中的第1种(图3-51),求得反对称荷载 作用下当μ = 0时各区格板的跨中最大弯矩。
M
1 (g 10
q
Hale Waihona Puke )l2 0○6 由于梯段板为斜向搁置的受弯构件,还将产生轴向力, 但其影响很小,设计时可不考虑。
○7 梯段斜板和一般板计算一样,可不必进行斜截面抗剪承 载力验算。
2)构造要求
梯段斜板配筋可采用弯起式或分离式。采用弯起式配筋时,一半 钢筋伸入支座,一半靠近支座处弯起,支座截面负筋的用量一般可取 与跨中截面相同。受力钢筋的弯起点位置见图7.3.3。在垂直受力钢 筋方向仍应按构造配置分布钢筋φ6@250,并要求每一个踏步下至少 放置一根钢筋。
2. 考虑泊桑比(μ≠ 0) 时的内力计算
M M ( ) M
x
x
y
M M ( ) M
y
y
x
μ——泊桑比,钢筋混凝土的μ通常取1/6;
注意:计算支座截面弯矩时,不考虑泊桑比的影响, 即可直接按式(3-20)计算内力。
(三)多区格等跨连续双向板的实用计算法 1. 求跨中最大弯矩 ①活荷载的最不利布置
3. 内力折减
(1)中间各区格板的跨中截面及支座截面弯矩,折减系数为0.8。
(2)边区格各板的跨中截面及自楼盖边缘算起的第一内支座截面:
当 l / l 1.5 时,折减系数为0.8; b
,
当1.5≤ l / l ≤2时,折减系数为0.9 b
当 l / l >2时,不予折减 b
(3)对角区格板块,不予折减。
④钢筋弯起
在四边固定的单块双向板及连续双向板中,板底钢筋可在距支座边 l /4处 x
弯起钢筋总量的1/2~1/3,作为支座负筋,不足时,另加板顶负钢筋。 在四边简支的双向板中,由于计算中未考虑支座的部分嵌固作用,板底
钢筋可在距支座边 l /4处弯起1/3作为构造负筋。 x
双向板钢筋分板带布置示意图
(2)板中构造钢筋
直径、间距、位置参见单向板。
图3-47两个方向的板带受力变形示意图
(二)双向板肋梁楼盖中支承梁的设计要点与配筋构造 1. 梁的设计要点 (1)支承梁梁的截面形式
对现浇楼盖,梁跨中按T形截面,梁支座处按矩形截面。
(2)支承梁截面有效高度h0
同单向板肋梁楼盖中梁一样取值 (3)支承梁上荷载分布
②板的整体工作
实际上,图3-47中从双向板内截出的两个方向的板带并不是孤立的, 它们都是受到相邻板带的约束,这将使得其实际的竖向位移和弯矩有所减小。
图3-47两个方向的板带受力变形示意图
二、双向板按弹性理论的计算方法
(一)计算简图确定 1. 基本假定 (1)双向板为各向同性板;板厚远小于板平面尺寸;
2)构造要求 踏步板的最小厚度 d 40mm ,踏步板的配筋需按计算确 定,且每一级踏步受力钢筋不得少于 2φ6,沿梯段宽度应布置 间距不大于 250mm 的φ6 分布钢筋(图 7.3.11)。 梁式楼梯的踏步板同时应配置负弯矩钢筋,即每两根受力 钢筋中有一根在伸入支座后,再弯向上部,负筋部分伸出梁边
○5 内力计算:7.3.2b 图所示的简支斜板可简化为 7.3.2c
图所示的水平板计算,计算跨度按斜板的水平投影长度取值, 斜板自重可化作沿斜板的水平投影长度上的均布荷载。
由结构力学可知,简支斜板(梁)在竖向均布荷载下(沿 水平投影长度)的最大弯距与相应的简支水平梁的最大弯矩 是相等的,即:
式中
度),截面宽度可取 b h / 3 ~ h / 2 。平台梁与平台板为整体现浇,配筋 计算时按倒 L 形截面计算。
○3 计算踏步板正载面受弯承载力时,可近似地按宽度为
b,高度为折算高度 h 的矩形截面计算(图 7.3.11),梯形截面 的折算高度(平均高度)可按下式计算:
hc d
2 cos
1. 现浇板式楼梯的计算与构造
(1)梯段板
1)计算要点 ○1 为 保 证 梯 段 板 有 一 定 的 刚 度 , 梯 段 板 厚 度 可 取 l0 / 25 ~ l0 / 35 ( l0 为梯段板水平方向的跨度),常取 80~120mm。 ○2 计算梯段板时,可取 1m 宽板带或以整个梯段板作为计算 单元。 ○3 计算简图:梯段板(图 7.3.2a)内力计算时可简化为两 端简支的斜板(图 7.3.2b)。 ○4 荷载计算:荷载包括活荷载、斜板及抹灰层自重、栏杆 自重等。活荷载及栏杆自重是沿水平方向分布的,斜板及抹灰层 自重是沿板的倾斜方向分布的,为了计算方便,一般将其换算成 沿水平方向分布的荷载后再进行计算。
三、双向板肋梁楼盖的截面设计及构造
(一)双向板的截面设计与构造 1. 双向板设计要点
(1)内力计算:双向板的内力计算可以采用弹性理论与塑性理论的方法
(2)板的计算宽度:通常取 1 000 mm,板的厚度按表3-2取值。 (3)截面有效高度 h0:双向板中短跨方向弯矩较长跨方向弯矩大,
因此短跨方向钢筋应放在长跨方向钢筋之下,
(4)假定梁的抗扭刚度很小,在荷载作用下,支承梁绕自身纵轴 可自由转动。
2. 计算简图
根据基本假定,按支座情况不同,矩形双向板有如图3-48所 示六种计算简图。
(1)四边简支板
(2)一边固定、三边简支板(3)两对边固定、两对边简支板
(4)四边固定板 (5)两邻边固定、两邻边简支板 (6)三边固定、一边简支板
2.平台梁的计算截面按倒L形截面计算。 3.平台梁横截两侧荷载不同,因此平台梁受有一定的扭距作用,一般 不需计算,但应适当增加配箍量。平台梁受有斜边梁的集中荷载,所以在 平台梁中位于斜边梁支座两侧处,应设置附加横向箍筋。
2)构造要求
平台梁一般构造要求与简支受弯构件相同,平台梁的高度应保证斜边 梁的主筋能放在平台梁的主筋上,即平台梁的底面应低于斜边梁的底面, 或与斜边梁底面齐平。
M max
1 (g 8
q)l02
g 、q ——作用于梯段板上的沿水平投影方向的
恒载及活载设计值;
l0 ——梯段板的计算跨度。
简支斜板(梁)在竖向均布荷载作用下的最大剪力为:
Vmax
1 (g 2
q)ln
式中 ln ——净跨的水平投影长度。
但在配筋计算时,考虑到梯段板与平台梁整体连接,平 台梁对梯段板有一定的弹性约束作用,计算时最大弯矩可 取:
,
⑤跨内最大正弯矩
通过上述荷载的等效处理,等区格连续双向板在荷载g’ 、q’作用下,都可转化成 单区格板利用附表3-2计算出跨内弯矩值。最后按式(3-21)计算出两种荷载情 况的实际跨中弯矩,并进行叠加,即可作为所求的跨内最大正弯矩。
2.求支座弯矩
假定全板各区格满布活荷载时支座弯矩最大,内区格可按四边固定的单跨双向板计算 其支座弯矩,边区格,其边支座边界条件按实际情况考虑,内支座按固定边考虑, 计算其支座弯矩。
3 折线形楼梯的计算与构造要点 (1)计算要点 为满足建筑使用要求,在房屋中有时需要采用折线形楼梯。 折线形楼梯梁(板)的计算与普通梁(板)式楼梯一样,一 般将斜梯段上的荷载化为沿水平长度方向分布的荷载,然后再按
简支梁计算 M max及Vmax 值。
(2)构造要求 由于折线形楼梯在梁(板)曲折处形成内折角,在配筋时, 若钢筋沿内折角连续配置,则此处受拉钢筋将产生较大的向外的 合力,可能使该处砼保护层崩落,钢筋被拉出而失去作用(图 7.3.19a)。 因此,在内折角处,配筋时应采取将钢筋断开并分别予以锚 固的措施(见图 7.3.19b)。在梁的内折角处,箍筋应适应加密。
支座边缘 ln / 4 (见图 7.3.5)。 (3)平台梁 1)计算要点
○1 平台梁一般支承在梯间横墙上或柱上,计算简图如 7.3.6 图所示。
○2 内力计算时可不考虑上、下梯段板之间的空隙,荷载按全 跨满布考虑,按简支梁计算。
○3 平台梁截面高度可取 h ≥ l0 / 12 ( l 0 为平台梁计算跨
2)构造要求 斜边梁构造要求与一般简支受弯构件相同,斜边梁的 纵筋在平台梁中应有足够的锚固长度。
(3)平台板 梁式楼梯平台板的计算及构造与板式楼梯相同。
(4)平台梁
1)计算要点
1.平台梁支承在两侧楼梯间的横墙上,按简支梁计算。平台梁承受斜 边梁传来的集中荷载,平台板传来的均布荷载以及平台梁自重,计算简图 见7.3.11图所示。
(g
q)ln
cos
○2 斜边梁的计算截面形式与斜边梁和踏步板的相对位置
有关,当踏步板在斜边梁上部时(图 7.3.12a),若仅有一根斜 梁,可按矩形截面计算;若有两根斜梁,则按倒 L 形截面计算。 当踏步板在斜边梁的中下部时(图 7.3.12b)应按矩形截面计算。
○3 斜边梁截面高度取垂直于斜梁轴线的高度,一般取 h ≥ l0 / 20 ( l0 为斜边梁水平投影的计算跨度)。
(二)单区格矩形双向板的内力计算 按照弹性理论计算钢筋混凝土双向板的内力可利用图表进行。 1. 不考虑泊桑比(μ = 0 )时的内力计算
M = 表中系数×ql 2
(3-20)
l——计算跨度,取板两个方向计算跨度lx、ly的较小者,计算跨度取值同单向板。 , M——跨中或支座截面单位板宽上的弯矩,单位板宽通常取1000 mm;
