新版立体几何题型解题技巧适合总结提高用-新版-精选.pdf
数学立体几何高考题答题技巧全版.doc

数学立体几何高考题答题技巧高中数学的学习对学生来讲非常重要,尤其是几何部分可以提升学生的思维能力。
下面我给高考考生带来数学立体几何答题技巧,希望对你有帮助。
高考数学立体几何答题技巧01、合理安排,保持清醒。
数学考试在下午,建议中午休息半小时左右,睡不着闭闭眼睛也好,尽量放松。
然后带齐用具,提前半小时到考场。
02、通览全卷,摸透题情。
刚拿到试卷,一般较紧张,不宜匆忙作答,应从头到尾通览全卷,尽量从卷面上获取更多的信息,摸透题情。
这样能提醒自己先易后难,也可防止漏做题。
03、解答题规范有序。
一般来说,试题中容易题和中档题占全卷的80%以上,是考生得分的主要来源。
对于解答题中的容易题和中档题,要注意解题的规范化,关键步骤不能丢,如三种语言文字语言、符号语言、图形语言的表达要规范,逻辑推理要严谨,计算过程要完整,注意算理算法,应用题建模与还原过程要清晰,合理安排卷面结构……对于解答题中的难题,得满分很困难,可以采用“分段得分”的策略,因为高考阅卷是“分段评分”。
比如可将难题划分为一个个子问题或一系列的步骤,先解决问题的一部分,能解决到什么程度就解决到什么程度,获取一定的分数。
有些题目有好几问,前面的小问你解答不出,但后面的小问如果根据前面的结论你能够解答出来,这时候不妨引用前面的结论先解答后面的,这样跳步解答也可以得分。
高考数学立体几何知识1、有关平行与垂直线线、线面及面面的问题,是在解决立体几何问题的过程中,大量的、反复遇到的,而且是以各种各样的问题包括论证、计算角、与距离等中不可缺少的内容,因此在主体几何的总复习中,首先应从解决“平行与垂直”的有关问题着手,通过较为基本问题,熟悉公理、定理的内容和功能,通过对问题的分析与概括,掌握立体几何中解决问题的规律--充分利用线线平行垂直、线面平行垂直、面面平行垂直相互转化的思想,以提高逻辑思维能力和空间想象能力。
2、判定两个平面平行的方法:1根据定义--证明两平面没有公共点;2判定定理--证明一个平面内的两条相交直线都平行于另一个平面;3证明两平面同垂直于一条直线。
立体几何大题方法和技巧讲解

立体几何大题方法与技巧讲解空间向量问题基础知识:线面平行:1.线面平行的判定定理:如果平面外一条直线和平面内的一条直线平行,那么这条直线和这个平面平行.2.线面平行的性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个相交那么这条直线和交线平行.3.平行平面的判定定理:如果一个平面内两条相交的直线都平行于另一平面,那么这两个平面互相平行.4.平行平面的性质定理:如果两个平行平面同时与第三个平面相交,那么它们的交线平行.5.性质:如果两个平面平行,那么其中一个平面内的直线平行于另一个平面.线面垂直:1.直线与平面垂直的判定定理:如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面.2.直线与平面垂直的性质定理:垂直于同一个平面的两条直线平行.3.两平面垂直的判定定理:如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直.4.两平面垂直的性质定理:若两个平面互相垂直,那么在一个平面内垂直于它们的交线的直线垂直于另一个平面.证明方法:如何证明线面平行常用方法①构造三角形中位线,线面位置落差大时(平移法)② 构造平行四边形, 线面位置相当时 ③ 通过面面平行,证明线面平行 ● 如何证明线面垂直 1) 题目中给出的垂直条件2) 特殊的图形(菱形,正方形,等腰三角形,等边三角形等等) 3) 勾股定理证明垂直(偶尔利用相似证明垂直) 4) 通过面面垂直证明线面垂直 ● 空间向量建系问题① 找出和底面垂直的直线 ② 找出底面相垂直的直线 ③ 建立直角坐标系 ● 三个角异面直线所成的角的范围]90,0(00 两异面直线的方向向量分别为 ,2121cos l l l l ⋅=θ直线和平面所成的角的范围]90,0[0, 直线的方向向量为,平面的法向量为nl nl ⋅==φθcos sin平面和平面所成的角的范围]180,0[00, 两个平面的法向量分别为,2121cos n n n n⋅=φθ1l 2l θl nθ1n 2n如果面面所成的角为锐角,则2121cos cos n n n n ⋅==φθ,如果面面所成的角为钝角,则2121cos cos n n n n ⋅=-=φθ是否存在一点问题线段BD 上是否存在点M ,使得直线//CE 平面AFM 即证:线CE 和法向量垂直 判断线段BE 上是否存在点Q ,使得平面CDQ ⊥平面BEF 即证:两个面的法向量垂直证明 直线FG (不在平面BCD 里面)与平面BCD 相交. 即证:线和面的法向量不垂直例子1.(本小题满分14分)如图,在多面体ABCDEF 中,平面ADEF ⊥平面ABCD .四边形ADEF 为正方形,四边形ABCD 为梯形,且//AD BC ,90BAD ∠=︒,1AB AD ==,3BC =.(Ⅰ)求证:AF CD ⊥;(Ⅱ)求直线BF 与平面CDE 所成角的正弦值;(Ⅲ)线段BD 上是否存在点M ,使得直线//CE 平面AFM ? 若存在,求BMBD的值;若不存在,请说明理由. 1.(本小题满分14分)解:(Ⅰ)证明:因为ADEF 为正方形,所以AF AD ⊥.又因为平面ADEF ⊥平面ABCD , 且平面ADEF平面ABCD AD =,所以AF ⊥平面ABCD .所以AF CD ⊥.………………4分EDCBA F(Ⅱ)由(Ⅰ)可知,AF ⊥平面ABCD ,所以AF AD ⊥,AF AB ⊥. 因为90BAD ∠=︒,所以,,AB AD AF 两两垂直.分别以,,AB AD AF 为x 轴,y 轴,z 轴建立空间直角坐标系(如图). 因为1AB AD ==,3BC =,所以(0,0,0),(1,0,0),(1,3,0),(0,1,0),(0,1,1),(0,0,1)A B C D E F , 所以(1,0,1),(1,2,0),(0,0,1)BF DC DE =-==. 设平面CDE 的一个法向量为(,,)x y z =n ,则0,0.DC DE ⎧⋅=⎪⎨⋅=⎪⎩n n 即20,0. x y z +=⎧⎨=⎩令2x =,则1y =-, 所以(2,1,0)=-n .设直线BF 与平面CDE 所成角为θ, 则|2(1)|10sin |cos ,|552BF θ⨯-=〈〉==⨯n .……………….9分 (Ⅲ)设( (01])BMBDλλ=∈,, 设()111,,M x y z ,则()1111,,(1,1,0)x y z λ-=-, 所以1111,,0x y z λλ=-==,所以()1,,0M λλ-, 所以()1,,0AM λλ=-.设平面AFM 的一个法向量为000(,,)x y z =m ,则0,0.AM AF ⎧⋅=⎪⎨⋅=⎪⎩m m因为()0,0,1AF =,所以000(1)0,0. x y z λλ-+=⎧⎨=⎩令0x λ=,则01y λ=-,所以(,1,0)λλ=-m .在线段BD 上存在点M ,使得//CE 平面AFM 等价于存在[0,1]λ∈,使得0CE ⋅=m .z D y DxDEDCB A FM因为()1,2,1CE =--,由0CE ⋅=m , 所以2(1)0λλ---=, 解得2[0,1]3λ=∈, 所以线段BD 上存在点M ,使得//CE 平面AFM ,且23BM BD =.……………….14分2 .主要是C 点的坐标怎么表示(一是画出底面的平面图找出相应关系,二是利用向量平行BA CD 21=) (本小题14分)如图,四边形ABCD 和三角形ADE 所在平面互相垂直,AB ∥CD ,AB BC ⊥,60DAB ∠=,4AB AD ==,AE DE ⊥,AE DE =,平面ABE 与平面CDE 交于EF . (Ⅰ)求证:CDEF ;(Ⅱ)若EF CD =,求二面角--A BC F 余弦值;(Ⅲ)在线段BC 上是否存在点M 使得AM EM ⊥?若存在,求BM 的长;若不存在,说明理由. (17)(共14分)解:(Ⅰ)在四边形ABCD 中,AB ∥CD . 因为AB ⊂平面ABE ,CD ⊄平面ABE , 所以CD ∥平面ABE .因为CD ⊂平面CDE ,且平面ABE平面CDE EF =,所以CD ∥EF . ........4分(Ⅱ)如图,取AD 的中点N ,连接BN ,EN .在等腰△ADE 中,.EN AN ⊥因为平面ADE ⊥平面ABCD ,交线为AD ,又EN AD ⊥,所以EN ⊥平面ABCD .所以.EN BN ⊥ 由题意易得.AN BN ⊥如图建立空间直角坐标系N xyz -,则(0,0,0),N (2,0,0)A ,(0,23,0)B ,(3,0)C -, (2,0,0)D -,(0,0,2)E .因为EF CD =,所以(3,2)F -.设平面BCF 的法向量为(,,)x y z =,n (1,3,2),(3,3,0),BF BC =--=-- 则0,0,BF BC ⎧⋅=⎪⎨⋅=⎪⎩n n 即320,330.x y z x y ⎧--+=⎪⎨-=⎪⎩ 令3y =1,1x z =-=.于是(3,1)=-n .又平面ABCD 的法向量为(0,0,2)NE =,所以5cos ,5NE NE NE⋅〈〉==n n n 由题知二面角--A BC F 为锐角, 所以二面角--A BC F 的余弦值为5分 (Ⅲ)不存在满足条件的点M ,使AM EM ⊥,理由如下:若AM EM ⊥,则0EM AM ⋅=.因为点M 为线段BC 上的动点,设(01),CM tCB t =≤≤,(,,0)M u v .则(3,3,0)(3,3,0)u v t +-=, 解得(33,3+3,0)M t t -.所以(33,33,2)EM t t =-+-,(35,33,0)AM t t =-+. 所以(33,33,2)(35,33,0)=0EM AM t t t t ⋅=-+-⋅-+. 整理得22330t t -+=,此方程无实根.所以线段BC 上不存在点M ,使AM EM ⊥. ............................14分3.如图,在多面体ABCDEF 中,梯形ADEF 与平行四边形ABCD 所在平面互相垂直, //AF DE ,DE AD ⊥,AD BE ⊥,112AF AD DE ===,2AB =.(Ⅰ)求证://BF 平面CDE ; (Ⅱ)求二面角B EF D --的余弦值;(Ⅲ)判断线段BE 上是否存在点Q ,使得平面CDQ ⊥平面BEF ?若存在,求出BQBE的值,若不存在,说明理由. 3.(本小题满分14分)解:(Ⅰ)由底面ABCD 为平行四边形,知//AB CD ,又因为AB ⊄平面CDE ,CD ⊂平面CDE ,所以//AB 平面CDE . ……………… 2分DABCEF同理//AF 平面CDE , 又因为ABAF A =,所以平面//ABF 平面CDE . ……………… 3分又因为BF ⊂平面ABF ,所以//BF 平面CDE . ……………… 4分(Ⅱ)连接BD ,因为平面ADEF ⊥平面ABCD ,平面ADEF 平面ABCD AD =,DE AD ⊥,所以DE ⊥平面ABCD . 则DE DB ⊥. 又因为DE AD ⊥,AD BE ⊥,DEBE E =,所以AD ⊥平面BDE ,则AD BD ⊥.故,,DA DB DE 两两垂直,所以以,,DA DB DE 所在的直线分别为x 轴、y 轴和z 轴,如图建立空间直角坐标系, ……………… 6分则(0,0,0)D ,(1,0,0)A ,(0,1,0)B ,(1,1,0)C -,(0,0,2)E ,(1,0,1)F , 所以(0,1,2)BE =-,(1,0,1)EF =-,(0,1,0)=n 为平面DEF 的一个法向量. 设平面BEF 的一个法向量为(,,)x y z =m ,由0BE ⋅=m ,0EF ⋅=m ,得20,0,y z x z -+=⎧⎨-=⎩令1z =,得(1,2,1)=m . ………………8分所以6cos ,||||3⋅<>==m n m n m n .如图可得二面角B EF D --为锐角,D A B CEyxzF所以二面角B EF D --6.………………10分(Ⅲ)结论:线段BE 上存在点Q ,使得平面CDQ ⊥平面BEF . ………………11分证明如下:设(0,,2)([0,1])BQ BE λλλλ==-∈,所以(0,1,2)DQ DB BQ λλ=+=-.设平面CDQ 的法向量为(,,)a b c =u ,又因为(1,1,0)DC =-,所以0DQ ⋅=u ,0DC ⋅=u ,即(1)20,0,b c a b λλ-+=⎧⎨-+=⎩………………12分若平面CDQ ⊥平面BEF ,则0⋅=m u ,即20a b c ++=, (13)分解得1[0,1]7λ=∈.所以线段BE 上存在点Q ,使得平面CDQ ⊥平面BEF ,且此时17BQ BE =. …… 14分4(本小题满分14分)如图,在直三棱柱111ABC A B C -中,1,2AC BC AC BC CC ⊥===,点,,D E F 分别为棱11111,,AC B C BB 的中点. (Ⅱ)求证:1AC ∥平面DEF (Ⅱ)求证:平面1ACB ⊥平面DEF ;(Ⅲ)在线段1AA 上是否存在一点P ,使得直线DP 与平面1ACB 所成的角为300?如果存在,求出线段AP 的长;如果不存在,说明理由. 4.(共14分)解:(Ⅰ)方法一:连结1BC因为,D E 分别为11A C ,11B C 中点, 所以11//DE A B 又因为11//AB A B ,所以//DE AB因为,E F 分别为11B C ,1B B 中点,所以1//EF BC 又因为DEEF E =DE ⊂平面DEF ,EF ⊂平面DEF AB ⊂平面1ABC ,1BC ⊂平面1ABC所以平面1ABC 平面DEF又1AC ⊂平面1ABC ,所以1AC 平面DEF方法二:取1AA 中点为G ,连结FG 由11AA BB 且11AA BB =又点F 为1BB 中点,所以11FG A B又因为,D E 分别为11A C ,11B C 中点,所以11DE A B所以DEFG所以,,,D E F G 共面于平面DEF 因为D ,G 分别为111,AC AA 中点, 所以1AC DG1AC ⊄平面DEFDG ⊂平面DEF所以1AC 平面DEF方法三:在直三棱柱111ABC A B C -中,1CC ⊥平面ABC 又因为AC BC ⊥以C 为原点,分别以1,,CA CB CC 为x 轴,y 轴,z 轴,建立空间直角坐标系C xyz -由题意得1(2,0,0),(0,0,2),(1,0,2)A C D ,(0,1,2),(0,2,1)E F .所以(1,1,0)DE =-,(0,1,1)EF =-设平面DEF 的法向量为111(,,)x y z =n ,则00DE EF ⎧⋅=⎪⎨⋅=⎪⎩n n ,即111100x y y z -+=⎧⎨-=⎩ 令11x =,得111,1y z ==于是(1,1,1)=n 又因为1(2,0,2)AC =-所以12020AC ⋅=-++=n 又因为1AC ⊄平面DEF ,所以1AC 平面DEF(Ⅱ)方法一:在直棱柱111ABC A B C -中,1CC ⊥平面ABC因为AC ⊂ABC ,所以1CC AC ⊥ 又因为AC BC ⊥,且1CC BC C =所以AC ⊥平面11BB C C EF ⊂平面11BB C C ,所以AC EF ⊥又1BC CC =,四边形11BB C C 为正方形所以11BC B C ⊥ 又1BC EF ,所以1B C EF ⊥又AC EF ⊥,且1AC B C C =所以EF ⊥平面1ACB又EF ⊂平面DEF所以平面1ACB ⊥平面DEF方法二:设平面1ACB 的法向量为222(,,)x y z =m ,1(2,0,0),(0,2,2)CA CB == 100CA CB ⎧⋅=⎪⎨⋅=⎪⎩m m ,即22220220x y z =⎧⎨+=⎩ 令21y =,得220,1x z ==-于是(0,1,1)=-m (1,1,1)(0,1,1)0⋅=⋅-=n m即⊥n m ,所以平面1ACB ⊥平面DEF (Ⅲ)设直线DP 与平面1ACB 所成角为θ,则30θ=︒设1(01)AP AA λλ=≤≤,则(0,0,2)AP λ=(1,0,22)DP λ=-所以1cos sin302DP DP θ⋅===︒=m m 解得12λ=或32λ=(舍) 所以点P 存在,即1AA 的中点,1AP =5.(本小题满分14分)在三棱柱111ABC A B C -中,底面ABC 是正三角形,侧棱1AA ⊥底面ABC . D ,E 分别是边BC ,AC的中点,线段1BC 与1B C 交于点G ,且4AB =,1BB =(Ⅰ) 求证://EG 平面1AB D ;(Ⅱ) 求证:1BC ⊥平面1AB D ;(Ⅲ) 求二面角1A B C B --的余弦值.5.(本小题满分14分)(I)因为E 为AC 中点,G 为1B C 中点.所以1//EG AB . 又因为EG ⊄平面1AB D ,1AB ⊂平面1AB D ,所以//EG 平面1AB D . ………….4分(Ⅱ) 取11B C 的中点1D ,连接1DD .显然DA ,DC ,1DD 两两互相垂直,如图,建立空间直角坐标系D xyz -, 则(0,0,0)D,A ,(0,2,0)B -,1(0,B -,1C, E ,(0,2,0)C .所以1(0,DB =-,(2DA =,1BC =.又因为12300400BC DA ⋅=+⨯+⨯=,1100(2)40BC DB ⋅=⨯+-⨯+=,所以111,BC DA BC DB ⊥⊥.又因为1DA DB D =,所以1BC ⊥平面1AB D . ………….9分 (Ⅲ)显然平面1B CB 的一个法向量为1(1,0,0)=n .设平面1AB C 的一个法向量为2(,,)x y z =n ,又(AC =-,1(0,4,B C =-, 由2210,0,AC BC ⎧⋅=⎪⎨⋅=⎪⎩n n 得20,40.y y⎧-+=⎪⎨-=⎪⎩设1x =,则y=,z =,则2=n.1B所以121212cos,⋅<>===n nn nn n设二面角1A B C B--的平面角为θ,由图可知此二面角为锐二面角,所以cos10θ=. ………….14分。
数学解题解决立体几何题目的技巧

数学解题解决立体几何题目的技巧在解决立体几何题目时,很多学生常常遇到困惑,因为立体几何题目相比平面几何更为复杂,需要更加细致的观察和分析。
本文将为大家介绍一些解决立体几何题目的技巧,帮助大家更好地应对这类题目。
一、理解立体图形的基本概念在解决立体几何题目之前,我们首先要熟悉一些基本概念。
比如,什么是正方体、长方体、圆柱体等。
掌握了这些基本概念,我们才能更好地理解题目中所描述的立体图形,从而思考解题的方向。
二、画图解题的技巧立体几何题目通常需要我们进行绘图才能更好地理解和解决。
在绘图时,我们需要注意以下几点。
1. 选择合适的比例为了能够清晰地展示立体图形,我们需要选择合适的比例进行绘图。
通常情况下,我们可以根据题目中给出的尺寸信息来确定比例,保证图形的各个部分都能够清晰显示。
2. 采用多视图绘图法有些立体图形由于其特殊的形状,无法用一张平面图来表示。
这时,我们可以采用多视图绘图法,即将立体图形从不同的角度进行绘制,以便更好地观察和分析。
3. 注意标注图形的关键信息在绘制过程中,我们需要将图形的关键信息标注清楚,如边长、角度、对称轴等。
这有助于我们在解决问题时更加明确和有针对性地进行分析,避免犯错。
三、利用立体几何的性质和定理解决立体几何题目的关键在于运用立体几何的性质和定理。
下面列举一些常见的立体几何性质和定理,供大家参考:1. 对称性:很多立体图形都具有对称性,可以利用对称性简化解题过程。
比如,正方体的各个面都是对称的,我们可以根据对称性来推断各个面的性质。
2. 平行关系:平行关系在立体几何题目中经常出现,我们应该注意观察图形中的平行线、平面等,利用平行关系进行推导和计算。
3. 相似关系:相似关系是解决立体几何题目时常用的思想工具。
当两个立体图形相似时,它们的对应边长、对应角度都成比例关系。
通过寻找相似关系,我们可以得到一些所需的未知量。
4. 体积和表面积公式:熟练掌握立体图形的体积和表面积公式是解决立体几何题目的基础。
初中数学立体几何解题技巧归纳

初中数学立体几何解题技巧归纳立体几何是数学的一个重要分支,主要研究三维物体的形状、结构和性质。
在初中数学中,掌握一些立体几何解题技巧对于解决各类几何问题非常重要。
本文将针对初中数学立体几何解题技巧进行归纳总结。
一、立体几何基本概念的应用1. 图形投影法:当我们需要求取立体图形在平面上的投影时,可以利用正交投影的方法将其进行投影。
这样可以在二维空间中更好地理解和解决问题。
2. 空间向量法:在解决立体几何题目时,可以利用向量的方法来进行推导和计算。
特别是在求取距离、中点坐标等问题时,利用向量的性质可以更加简便地解决问题。
3. 平行关系的应用:当两个平面平行时,它们的任意一对平行直线的夹角等于两个平面的夹角。
当两条直线相交于某一点,并且它们与同一个平面的夹角相等时,可以判断这两条直线平行于平面。
二、常见立体几何的解题方法1. 平面切割法:当遇到一个复杂的立体图形时,我们可以通过将其用平面进行切割,将问题转化为几个简单的平面图形,从而更好地理解和解决问题。
2. 空间旋转法:在解决立体几何问题时,有时我们可以将整个空间进行旋转,利用旋转后的图形特点来简化问题。
这种方法常用于求取旋转体的体积、表面积等问题。
3. 截面法:当需要求取一个立体图形的体积时,我们可以通过截面法来解决。
选择一个与图形相交的平面,求出这个平面上的面积并乘以图形的高,就可以得到图形的体积。
三、立体几何解题技巧的例题分析1. 例题一:一个正方体的一个顶点被一个平面截到,并且截下的部分是一个正三角形。
求这个正方体的体积。
解析:我们将这个正方体绕截面上的边作旋转,可以发现旋转后的图形是一个锥体,三角形为底面。
我们知道,锥体的体积等于底面积乘以高除以3。
所以,这个正方体的体积就等于正三角形的面积乘以高除以3。
2. 例题二:一个长方体的长、宽、高分别为a、b、c,如果长a增加d,宽b减少d,高c不变,那么长方体的体积变成原来的多少倍?解析:长方体的体积等于长乘以宽乘以高。
立体几何高考常见题型解题思路及知识点总结
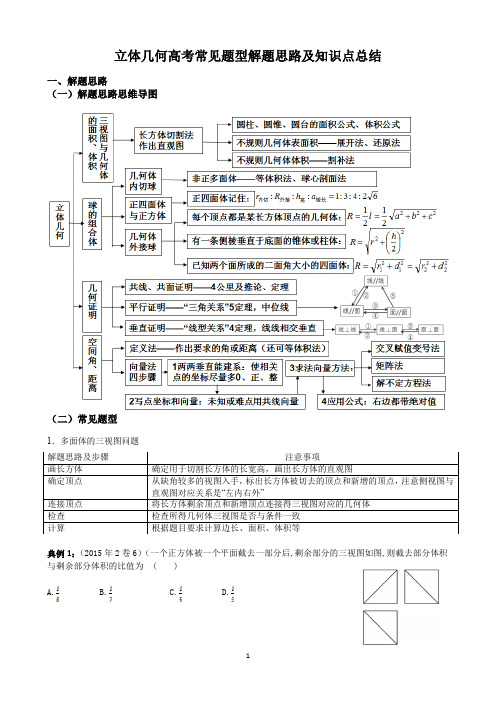
立体几何高考常见题型解题思路及知识点总结一、解题思路(一)解题思路思维导图(二)常见题型1.多面体的三视图问题解题思路及步骤注意事项画长方体确定用于切割长方体的长宽高,画出长方体的直观图确定顶点从缺角较多的视图入手,标出长方体被切去的顶点和新增的顶点,注意侧视图与直观图对应关系是“左内右外”连接顶点将长方体剩余顶点和新增顶点连接得三视图对应的几何体检查检查所得几何体三视图是否与条件一致计算根据题目要求计算边长、面积、体积等典例1:(2015年2卷6)(一个正方体被一个平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为( )A. B. C. D.解:由三视图得,在正方体ABCD-A 1B 1C 1D 1中,截去四面体A-A 1B 1D 1, 如图所示,设正方体棱长为a,则,故剩余几何体体积为a 3-a 3=a 3,所以截去部分体积与剩余部分体积的比值为.选D.典例2:(2017年1卷7)某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形,这些梯形的面积之和为( )A .10B .12C .14D .16解:将三视图还原可得右图图形,故而多面体有两个面是梯形,此时可得,故而选B.2.多面体的外接球问题典例3(类型1):(2019年1卷12)已知三棱锥P −ABC 的四个顶点在球O 的球面上,PA =PB =PC ,△ABC 是边长为2的正三角形,E ,F 分别是PA ,AB 的中点,∠CEF =90°,则球O 的体积为 A .68π B .64π C .62πD .6π解:,PA PB PC ABC ==△为边长为2的等边三角形,P ABC ∴-为正三棱锥,PB AC ∴⊥,又E ,F 分别为PA ,AB 的中点,EF PB ∴∥,11133111326A AB D V a a -=⨯=()12242122S =⨯+⨯=解题思路及步骤 注意事项根据条件确定类型类型1:可补成长方体且所有顶点为所补长方体的顶点的几何体的外接球问题,主要特征是由较多的垂直关系,例如墙角三棱锥;类型2:有侧棱⊥底面条件几何体外接球问题,例如直三棱柱;类型3:顶点到底边各点距离相等的锥体的外接球问题,例如正三棱锥;类型4:已知相邻两个面所成二面角的大小多面体的外接球问题,例如已知两个面垂直画出基本图形 类型2类型3画出解决问题的截面图 求截面半径 若截面为三角形,则)3,60;2,90,sin 2ar A a r A A a r =====特别地代入公式计算类型1公式:2222121c b a l R ++==,类型2公式:222⎪⎭⎫ ⎝⎛+=h r R ,类型3公式:()222R r R h =+-,类型4公式:22222121d r d r R +=+=EF AC ∴⊥,又EF CE ⊥,,CE AC C EF =∴⊥平面PAC ,∴PB ⊥平面PAC ,2APB PA PB PC ∴∠=90︒,∴===,P ABC ∴-为正方体的一部分,22226R =++=,即364466,π62338R V R =∴=π=⨯=π,故选D .典例4(类型2):三棱锥的三视图如图所示,则该三棱锥外接球的 体积为________.解:由三视图可得几何体为三棱锥D -ABC (如图所示),若以△ACD 为底,则侧棱BC ⊥底面ACD.因为底面半径160sin 23==r ,22=BC ,所以外接球半径3222=⎪⎭⎫ ⎝⎛+=h r R ,即外接球的体积为ππ34343=R典例5(类型3):(2018年3卷10) 设是同一个半径为4的球的球面上四点,为等边三角形且其面积为,则三棱锥体积的最大值为A. B. C. D.解:如图所示,点M 为三角形ABC 的重心,E 为AC 中点,当平面时,三棱锥体积最大此时,,,,点M 为三角形ABC 的重心,中,有,故选B.典例6(类型4):已知等边⊥ABC 的边长为4,D 、E 分别为AB 、AC 的中点,将⊥ABC 沿DE 折成120°的二面角,求四棱锥A -BCED 外接球的表面积.解:如图所示,作出截面四边形OO 1MO 2,延长O 1M ,OO 2相交于点F ,由已知得∠O 1MO 2=120°,31=M O ,332=M O , 所以332=FM ,3351=FO ,3511==OO d ,因为21=r ,所以9612121=+=d r R (也可以求出22,r d 求出R ),924442ππ==R S .3.平行关系证明问题典例7:(2014年全国Ⅱ卷)如图,四棱锥P -ABCD 中,底面ABCD 为矩形,PA ⊥平面ABCD ,E 为PD 的中点.(Ⅰ)证明:PB ∥平面AEC ;证明:连接BD 交AC 于点为G ,连接EG ,⊥E ,G 分别为PD ,BD 的中点, ⊥中位线EG⊥PB ,⊥PB ⊄平面AEC ,EG ⊂平面AEC ,⊥PB⊥平面AEC.典例8:(2016年全国Ⅲ卷)如图,四棱锥中,底面面,AD ∥BC ,,,为线段上一点,,为的中点. (I )证明平面;4.垂直关系证明问题典例9:(2016年全国Ⅱ卷)如图,菱形的对角线与交于点,,点P ABC -PA ⊥ABCD 3AB AD AC ===4PA BC ==M AD 2AM MD =N PC MN PAB ABCD AC BD O 5,6AB AC ==,E F解题思路及步骤 注意事项在图形上标注已知条件 作辅助线 线线平行关系在直观图中是不变形的,若需找面外直线与面内直线平行,可将面外直线平移到面内,以确定辅助线位置写出证明思路 按照平行的“三角关系”把证明的思路写出来 完善证明过程 把定理所需要的条件写出,特别是立体几何中的定理 解题思路及步骤 注意事项在图形上标注已知条件 垂直关系在直观图中是变形的,因此,相交直线垂直一定要用直角符号标注出来 作辅助线 等腰三角形由三线合一,菱形对角垂直 写出证明思路 按垂直的“线型关系”写出证明的思路,在证明线线垂直时,若是相交两条直线垂直,还需考虑用平面几何知识证明. 常用的有勾股定理逆定理,等腰三角形三线合一定理,菱形对角线互相垂直平分,直径所对的圆周角是直角等完善证明过程 把定理所需要的条件写出,特别是立体几何中的定理分别在上,,交于点.将沿折到位置,. (Ⅰ)证明:平面;证明:∵54AE CF ==,∴AE CF AD CD=,∴EF AC ∥.∵四边形ABCD 为菱形,∴AC BD ⊥,∴EF BD ⊥,∴EF DH ⊥,∴EF D H '⊥.∵6AC =,∴3AO =;又5AB =,AO OB ⊥,∴4OB =,∴1AEOH OD AO=⋅=,∴3DH D H '==, ∴222'OD OH D H '=+,∴'D H OH ⊥. 又∵OH EF H =,∴'D H ⊥面ABCD .典例10:(2018年全国Ⅲ卷)如图,边长为2的正方形所在的平面与半圆弧所在平面垂直,是上异于,的点.(Ⅰ)证明:平面平面; 证明:由题设知,平面CMD ⊥平面ABCD ,交线为CD .因为BC ⊥CD , BC平面ABCD ,所以BC ⊥平面CMD ,故BC ⊥DM .因为M 为上异于C ⊥D 的点,且DC 为直径,所以 DM ⊥CM .又 BC CM =C ,所以DM ⊥平面BMC . 而DM平面AMD ,故平面AMD ⊥平面BMC .5.求空间角和空间距离问题典例11:如图,在三棱柱111ABC A B C -中,侧面11AA B B ⊥底面ABC ,,AD CD 54AE CF ==EF BD H DEF ∆EF 'D EF ∆10OD '=D H '⊥ABCD ABCD CD M CD C D AMD ⊥BMC 解题思路及步骤 注意事项建系 先找垂直于底面的直线作为z 轴或z 轴平行线,若没有则先证明,再把底面直观图还原,找底面相互垂直两条直线作为x 轴和y 轴,若有多种选择,则尽量使相关点在坐标轴上 写点的坐标点的坐标尽量写在图上,先写坐标轴上的点的坐标,再写坐标标平面上的点的坐标,最后写其余点的坐标,其余点的坐标一般是找出其在底面上的射影来求其坐标;求坐标目的是求向量,若所求向量涉及比较难确定坐标的点时,可观察是否有相等向量来替代;对于棱上动点坐标,一般用共线向量关系来假设,例如P 为棱AB 上的一点,设()10≤≤=λλAB AP ,则P 点坐标可用参数λ表示求向量 求平面法向量有解不定方程法、观察法、矩阵法3种,不管哪种方法,规范书写过程,求出后先检验正确后再往下写,并且通过共线向量把法向量坐标去分母.应用公式根据所求问题正确选用公式:线线角><=b a ,cos cos θ,线面角><=n a ,cos sin θ,面面角><=m n ,cos cos θ,点到面的距离.n MP d n⋅=ABC ∆和1ABB ∆都是边长为2的正三角形.求1AC 与平面11BCC B 所成角的正弦值.解:⊥面11AA B B ⊥底面ABC 且交线为AB ,1,AB OC AB OB ⊥⊥,B B AA O B 111面⊂, ⊥ABC O B 面⊥1以O 为原点,OB 方向为x 轴方向建立如图所示的空间直角坐标系,则()()1,0,0,1,0,0B A -,()()()110,3,0,0,0,3,1,3,3C B C - ()3,3,01111=+==+=BB AC AC CC AC AC设平面11BCC B 的一个法向量为(),,n x y z =,因为()()()111,3,0,1,0,3,0,3,3CB B B AC =-=-=,由130{ {30x y n CB n B Bx z -=⊥⇔⊥-= 得平面11BCC B 的一个法向量为()3,1,1n =1113310cos ,565AC n AC n AC n⋅+===⋅⋅, 所以1AC 与平面11BCC B 所成角的正弦值为105典例12:(2017全国Ⅱ卷改编)如图所示,在四棱锥P ABCD -中,侧面PAD 为等边三角形且垂直于底面ABCD ,12AB BC AD ==,o 90BAD ABC ∠=∠=, E 是PD 的中点,点M 在棱PC 上,且直线BM 与底面ABCD 所成的锐角为45,(Ⅰ)求二面角M AB D --的余弦值; (Ⅱ)求点E 到平面ABM 的距离. 解:(Ⅰ)取AD 的中点O ,连接PO ,CO .则AD PO ⊥,AD CO ⊥,因为面PAD ⊥底面ABCD ,且交线为AD ,PAD PO 面⊂,所以ABCD PO 面⊥以O 为坐标原点,建立如图所示的空间直角坐标系.设1AB BC ==, 则()010A -,,,()110B -,,,()100C ,,,()003P ,,,(100)AB =,,. 设()()()103,0,3,0,1≤≤-=-==λλλλλ,CP CM , ()()()λλλλ3,1,3,0,0,1,0-=-+=+=CM BC BM ,底面ABCD 的法向量()1,0,0=n ,由题意><=n BM ,cos 45sin,即241322λλ+=,解之得,22=λ,所以⎪⎪⎭⎫ ⎝⎛-=26,1,22BM . 设平面ABM 的法向量,()z y x m ,,=,由⎪⎩⎪⎨⎧=⋅=⋅0m AB m BM ,得,()2,6,0-=m ,从而10cos ,5⋅==⋅m n m n m n , 故二面角M AB D --的余弦值为105. EM DCBAP(Ⅱ)因为⎪⎪⎭⎫ ⎝⎛23210,,E ,所以⎪⎪⎭⎫ ⎝⎛=23230,,AE , 所以求点E 到平面ABM 的距离1030153-=⋅=mm AE d .典例13:(2018年全国Ⅱ卷)如图,在三棱锥中,⊥⊥为的中点, ⊥Ⅰ)证明:平面⊥⊥Ⅱ)若点在棱上,且二面角为,求与平面所成角的正弦值. 解:(Ⅰ)因为⊥为的中点,所以,且.连结.因为,所以为等腰直角三角形,且⊥.由知.由知平面.⊥Ⅱ)如图,以为坐标原点,的方向为轴正方向,建立空间直角坐标系. 由已知得取平面的法向量.方法1:设,则.设平面的法向量为.由得,可取⊥所以.由已知得.所以.解得(舍去),.所以.又,所以,所以与平面所成角的正弦值为.方法2:设()10,≤≤=λλBC BM ,则()02222,,λλλ+-=+=+=BC AB BM AB AM , ()3220,,=AP ,设面PAM 的一个法向量为()z y x n ,,=,由⎪⎩⎪⎨⎧=⋅=⋅00n AP n AM ,得()()()λλλ-+=1,1-3,13n ,由()()()23141313,,cos 22=-+++==λλλnOB n OB n OB ,解之得31=λ,3=λ(舍去),所以⎪⎪⎭⎫ ⎝⎛-=32332334,,n ,又,所以,所以与平面所成角的正弦值为.二、知识点总结 (一)知识点思维导图(二)常用定理、公式及其变形1.面积、体积公式2.正四面体的外接球与内切球方法(1):将问题转换为等腰三角形ADF 线段关系问题,易证r :R :h=1:3:4(h 为正四面体的高AE). 方法(2):将正四面体看成正方体切割而来,由正四面体棱长求出正方体棱长,再求出R ,根据比例可求r ,h .(1)外接球:球心是正四面体的中心;半径R=64a(a 为正四面体的棱长); (2)内切球:球心是正四面体的中心;半径r=612a(a 为正四面体的棱长). →方法(1) 方法(2)3.已知两个面所成的二面角大小的四面体外接球问题其本公式:22222121d r d r R +=+=,d 为球心到截面距离,r 为该截面半径.基本图形:有两个直角的四边形21MO OO (或两个相似直角三角形),21MO O ∠为二面角的平面角,多数题目所给条件中易求出O 1M ,O 2M ,r 1,r 2的值,此时,将四边形补成直角三角形,只需求出d 1或d 2的值,代入公式即可求R .4.共线、共面证明思路及定理(1)证明思路:①三点共线:转换为有公共点的向量共线;②点、线共面:转换为直线平行或相交.(2)公里1-4、定理、推论公里2推论:①直线和直线外的一个点确定一个平面;②两条相交直线确定一个平面;③两条平行直线确定一个平面.5.平行关系证明思路及定理(1)证明思路:(3)定理6.垂直关系证明思路及定理 (1)证明思路:(2)定理7.空间向量坐标运算:已知(),,z y x a OA ==,()222,,z y x b OB == (1)则(2d x AB =AB =(2)若a 、b 为非零向量,则12121200a b a b x x y y z z ⊥⇔⋅=⇔++=; (3)若0b ≠,则121212//,,a b a b x x y y z z λλλλ⇔=⇔===;(4)222111a a a x y z =⋅=++.(5)121212222222111222cos ,x x y y z z a b a b a b x y z x y z ++⋅〈〉==++⋅++.8.求平面法向量方法:解不定方程法、观察法、矩阵法 例如:已知⎪⎪⎭⎫ ⎝⎛=21,23,0AE ,()0,3,a AC =,设平面ACE 的一个法向量为()z y x m ,,=(1)解不定方程法:先任意确定其中一个坐标值(不能是0),再代入方程求其余坐标.书写格式:设平面ACE 的法向量为()z y x m ,,=,⊥⎪⎪⎭⎫⎝⎛=21,23,0AE ,()0,3,a AC = 由⎪⎩⎪⎨⎧=+=+⎪⎩⎪⎨⎧=⋅=⋅030212300y ax z y m AC m AE ,即,得()a a m 3,,3--= (2)观察法:情形1:两个0,非0对0,其余两坐标再交换,其中一个变号; 情形2:一个0,非0先交换,其中一个变号,最后一个坐标由另一个向量确定;书写格式:设平面ACE 的法向量为()z y x m ,,=,⊥⎪⎪⎭⎫ ⎝⎛=21,23,0AE , ()0,3,a AC = 由,⎪⎩⎪⎨⎧=⋅=⋅0m AC m AE 可得()a a m 3,,3--=(3)矩阵法:面上两个向量坐标上下对齐,求谁盖谁,交叉相乘再相减. 书写格式:设平面ACE 的法向量为()z y x m ,,=, ⊥⎪⎪⎭⎫ ⎝⎛=21,23,0AE , 由⎪⎪⎭⎫⎝⎛--=⎪⎪⎪⎭⎫⎝⎛-=⨯23,2,233230,0210,032123a a aaAC AE ,可得()a a m 3,,3--= 9.空间向量求空间角公式若直线a 、b 的方向向量分别为a 和b ,则><=b a ,cos cos θ.若直线AP 方向向量为a ,平面α的法向量为n ,则><=n a ,cos sin θ.若平面α、β的法向量分别为n 和m ,则><=m n ,cos cos θ.()0,3,a AC =10.空间向量求空间距离公式斜线l 与平面α交于点M ,P 为斜线l 上任一点,平面α的法向量分别为n , 则P 到平面α的距离为MP 在n 上投影的绝对值,即.n MP d n⋅=。
高中数学中的立体几何问题解析与技巧总结

高中数学中的立体几何问题解析与技巧总结在高中数学学习中,立体几何是一个重要的内容,掌握立体几何的解析方法和技巧对于解题非常有帮助。
本文将针对高中数学中的立体几何问题进行解析,并总结出一些解题技巧,帮助读者更好地理解和应用立体几何知识。
立体几何是研究立体图形的性质和关系的数学分支,它与平面几何相辅相成,共同构成了几何学的基础。
在立体几何中,我们经常遇到的问题主要包括计算体积、表面积、求解空间几何体之间的位置关系等。
一、计算体积和表面积的方法在计算立体几何体的体积和表面积时,我们需要根据给定的条件和几何体的性质来选择合适的计算方法。
1. 计算体积的方法计算立体几何体的体积,需要根据几何体的形状和给定的条件,选择合适的公式进行计算。
下面以常见几何体为例,列举一些计算体积的公式:- 矩形长方体的体积公式:V = lwh,其中l为长,w为宽,h为高。
- 正方体的体积公式:V = a^3,其中a为边长。
- 圆柱体的体积公式:V = πr^2h,其中r为底面半径,h为高。
- 圆锥体的体积公式:V = (1/3)πr^2h,其中r为底面半径,h为高。
- 球体的体积公式:V = (4/3)πr^3,其中r为半径。
2. 计算表面积的方法计算立体几何体的表面积,同样需要根据几何体的形状和给定的条件,选择合适的公式进行计算。
下面以常见几何体为例,列举一些计算表面积的公式:- 矩形长方体的表面积公式:S = 2lw + 2lh + 2wh,其中l为长,w 为宽,h为高。
- 正方体的表面积公式:S = 6a^2,其中a为边长。
- 圆柱体的表面积公式:S = 2πrh + 2πr^2,其中r为底面半径,h为高。
- 圆锥体的表面积公式:S = πrl+ πr^2,其中r为底面半径,l为母线长。
- 球体的表面积公式:S = 4πr^2,其中r为半径。
二、解决立体几何问题的技巧在解决立体几何问题时,除了熟悉计算公式外,还需要灵活运用几何知识和解题技巧。
最新整理高中数学立体几何解题技巧

最新整理高中数学立体几何解题技巧最新整理高中数学立体几何解题技巧导语:许多高中生认为立体几何很难,但只要打好基础,立体几何将会变得很容易。
下面是小编为大家整理的,受助学生感谢信,更多相关信息请关CNFLA学习网!1.平行、垂直位置关系的论证的策略:(1)由已知想性质,由求证想判定,即分析法与综合法相结合寻找证题思路。
(2)利用题设条件的性质适当添加辅助线(或面)是解题的常用方法之一。
(3)三垂线定理及其逆定理在高考题中使用的频率最高,在证明线线垂直时应优先考虑。
2.空间角的计算方法与技巧:主要步骤:一作、二证、三算;若用向量,那就是一证、二算。
(1)两条异面直线所成的角①平移法:②补形法:③向量法:(2)直线和平面所成的角①作出直线和平面所成的角,关键是作垂线,找射影转化到同一三角形中计算,或用向量计算。
②用公式计算.(3)二面角①平面角的作法:(i)定义法;(ii)三垂线定理及其逆定理法;(iii)垂面法。
②平面角的计算法:(i)找到平面角,然后在三角形中计算(解三角形)或用向量计算;(ii)射影面积法;(iii)向量夹角公式.3.空间距离的计算方法与技巧:(1)求点到直线的距离:经常应用三垂线定理作出点到直线的垂线,然后在相关的三角形中求解,也可以借助于面积相等求出点到直线的距离。
(2)求两条异面直线间距离:一般先找出其公垂线,然后求其公垂线段的长。
在不能直接作出公垂线的情况下,可转化为线面距离求解(这种情况高考不做要求)。
(3)求点到平面的'距离:一般找出(或作出)过此点与已知平面垂直的平面,利用面面垂直的性质过该点作出平面的垂线,进而计算;也可以利用“三棱锥体积法”直接求距离;有时直接利用已知点求距离比较困难时,我们可以把点到平面的距离转化为直线到平面的距离,从而“转移”到另一点上去求“点到平面的距离”。
求直线与平面的距离及平面与平面的距离一般均转化为点到平面的距离来求解。
4.熟记一些常用的小结论,诸如:正四面体的体积公式是;面积射影公式;“立平斜关系式”;最小角定理。
高中立体几何最佳解题方法及考题详细解答精选文档

高中立体几何最佳解题方法及考题详细解答精选文档TTMS system office room 【TTMS16H-TTMS2A-TTMS8Q8-高中立体几何最佳解题方法总结一、二、线线平行的证明方法1、2、利用平行四边形;3、4、利用三角形或梯形的中位线;5、6、如果一条直线和一个平面平行,经过这条直线的平面与这个相交,那么这条直线和交线平行。
(线面平行的性质定理)7、8、如果两个平行平面同时和第三个平面相交,那么它们的交线平行。
(面面平行的性质定理)9、10、如果两条直线垂直于同一个平面,那么这两条直线平行。
(线面垂直的性质定理)11、12、平行于同一条直线的两个直线平行。
13、14、夹在两个平行平面之间的平行线段相等。
三、四、线面平行的证明方法1、2、定义法:直线和平面没有公共点。
3、4、如果平面外的一条直线和这个平面内的一条直线平行,那么这条直线就和这个平面平行。
(线面平行的判定定理)5、6、两个平面平行,其中一个平面内的任意一条直线必平行于另一个平面。
7、8、反证法。
五、六、面面平行的证明方法1、2、定义法:两个平面没有公共点。
3、4、如果一个平面内的两条相交直线都平行于另一个平面,那么这两个平面平行。
(面面平行的判定定理)5、6、平行于同一个平面的两个平面平行。
7、8、经过平面外一点,有且只有一个平面与已知平面平行。
9、10、垂直于同一条直线的两个平面平行。
七、八、线线垂直的证明方法1、2、勾股定理; 2、等腰三角形;3、菱形对角线;4、圆所对的圆周角是直角;5、点在线上的射影;6、如果一条直线和这个平面垂直,那么这条直线和这个平面内的任意直线都垂直。
7、在平面内的一条直线,如果和这个平面一条斜线垂直,那么它也和这条斜线的射影垂直。
(三垂线定理)15、16、在平面内的一条直线,如果和这个平面一条斜线的射影垂直,那么它也和这条斜线垂直。
17、18、如果两条平行线中的一条垂直于一条直线,那么另一条也垂直于这条直线。
立体几何题的解题技巧

立体几何题的解题技巧立体几何是数学中的一个重要分支,主要研究与空间有关的图形、物体以及它们之间的关系。
解立体几何题需要掌握一定的几何知识和解题技巧。
在本文中,将介绍一些常用的解题技巧,并通过一些例题来加深理解。
一、了解基本几何概念在解立体几何题前,首先要对一些基本几何概念进行了解。
比如,需要熟悉各种几何体的定义、性质和性质定理。
同时,要掌握几何图形的投影、展开和截面等概念。
只有对这些基本概念有清晰的理解,才能更好地解答问题。
二、画准确的图形画图是解立体几何题的基础,准确的图形可以帮助我们更好地理解题目。
在画图时,要准确地根据题目中给出的要求,按照比例和尺寸画出几何体。
三、根据已知条件引入辅助线常常会遇到一些复杂的立体几何题,此时可以通过引入辅助线来简化问题。
辅助线有时可以分解图形、构造相似三角形或等腰三角形等。
通过引入辅助线,可以将原问题转化为更简单的几何问题。
四、利用相似关系或等价关系求解在解立体几何题时,经常会用到相似关系或等价关系来求解。
例如,利用相似三角形的性质可以求解连线比等问题,利用等腰三角形的性质可以求解边长、高度等问题。
因此,在解题过程中要善于利用相似关系和等价关系。
五、利用平面几何知识辅助解题立体几何和平面几何之间存在一定的联系,有时可以通过运用平面几何知识来辅助解决立体几何问题。
例如,平面几何中的角平分线定理可以在立体几何中用来求解面的分割线等问题。
六、注意投影关系与可视性在有关几何体的投影、展开以及截面的问题中,需要注意投影关系和可视性。
投影关系是指物体在不同位置或角度下的投影特征。
在解题过程中要善于利用投影关系来推导或求解。
另外,要考虑立体几何体的可视性,即在不同视角下,哪些部分能够被看到,哪些部分被遮挡住。
七、灵活运用体积和表面积计算公式在解立体几何题时,经常需要计算体积和表面积。
要熟练掌握各种几何体的体积和表面积计算公式,并在解题过程中灵活运用。
有时可以通过求两个几何体的体积或表面积之差来解题。
高中立体几何最佳解题方法及考题详细解答

高中立体几何最佳解题方法总结一、线线平行的证明方法1、利用平行四边形;2、利用三角形或梯形的中位线;3、如果一条直线和一个平面平行,经过这条直线的平面与这个相交,那么这条直线和交线平行。
(线面平行的性质定理)4、如果两个平行平面同时和第三个平面相交,那么它们的交线平行。
(面面平行的性质定理)5、如果两条直线垂直于同一个平面,那么这两条直线平行。
(线面垂直的性质定理)6、平行于同一条直线的两个直线平行。
7、夹在两个平行平面之间的平行线段相等。
二、线面平行的证明方法1、定义法:直线和平面没有公共点。
2、如果平面外的一条直线和这个平面内的一条直线平行,那么这条直线就和这个平面平行。
(线面平行的判定定理)3、两个平面平行,其中一个平面内的任意一条直线必平行于另一个平面。
4、反证法。
三、面面平行的证明方法1、定义法:两个平面没有公共点。
2、如果一个平面内的两条相交直线都平行于另一个平面,那么这两个平面平行。
(面面平行的判定定理)3、平行于同一个平面的两个平面平行。
4、经过平面外一点,有且只有一个平面与已知平面平行。
5、垂直于同一条直线的两个平面平行。
四、线线垂直的证明方法1、勾股定理;2、等腰三角形;3、菱形对角线;4、圆所对的圆周角是直角;5、点在线上的射影;6、如果一条直线和这个平面垂直,那么这条直线和这个平面内的任意直线都垂直。
7、在平面内的一条直线,如果和这个平面一条斜线垂直,那么它也和这条斜线的射影垂直。
(三垂线定理)8、在平面内的一条直线,如果和这个平面一条斜线的射影垂直,那么它也和这条斜线垂直。
9、如果两条平行线中的一条垂直于一条直线,那么另一条也垂直于这条直线。
五、线面垂直的证明方法:1、定义法:直线与平面内的任意直线都垂直;2、点在面内的射影;3、如果一条直线和一个平面内的两条相交直线垂直,那么这条直线就和这个平面垂直。
(线面垂直的判定定理)4、如果两个平面互相垂直,那么在一个平面内垂直于它们交线的直线必垂直于另一个平面。
立体几何的解题技巧

△ BCD LE H ^S A 州BD_d , . d 二"△BCD 二-23S A A BD 2立体几何新题型的解题技巧【命题趋向】 在高考中立体几何命题有如下特点: 1. 线面位置关系突出平行和垂直,将侧重于垂直关系2. 多面体中线面关系论证,空间“角”与“距离”的计算常在解答题中综合出现.3. 多面体及简单多面体的概念、性质多在选择题,填空题出现4. 有关三棱柱、四棱柱、三棱锥的问题,特别是与球有关的问题将是高考命题的热点 此类题目分值一般在 17---22分之间,题型一般为 1个选择题,1个填空题,1个解答题. 【考点透视】 掌握两条直线所成的角和距离的概念,对于异面直线的距离,只要求会计算已给出公垂线时的距离掌握 斜线在平面上的射影、直线和平面所成的角、直线和平面的距离的概念 •掌握二面角、二面角的平面角、两个平行平面 间的距离的概念. 空间距离和角是高考考查的重点 :特别是以两点间距离,点到平面的距离,两异面直线的距离,直线与平面的距 离以及两异面直线所成的角,直线与平面所成的角,二面角等作为命题的重点内容,高考试题中常将上述内容综合在 一起放在解答题中进行考查,分为多个小问题,也可能作为客观题进行单独考查 .考查空间距离和角的试题一般作为整 套试卷的中档题,但也可能在最后一问中设置有难度的问题 不论是求空间距离还是空间角,都要按照“一作,二证,三算”的步骤来完成,即寓证明于运算之中,正是本专 题的一大特色. 求解空间距离和角的方法有两种:一是利用传统的几何方法,二是利用空间向量。
考点1点到平面的距离 求点到平面的距离就是求点到平面的垂线段的长度,其关键在于确定点在平面内的垂足,当然别忘了转化法与等 体积法的应用. 例1如图,正三棱柱 ABC _AB i C i 的所有棱长都为2 , D 为cC i 中点. (【)求证:AB 1丄平面A 1BD ;(n)求二面角 A-AD-B 的大小;(川)求点C 到平面ABD 的距离. 考查目的:本小题主要考查直线与平面的位置关系,二面角的 大小,点到平面的距离等知识,考查空间想象能力、逻辑思维 能力和运算能力. 解答过程:解法一:(I )取BC 中点0,连结A0. ABC 为正三角形,.AO 丄BC . B iC1DT 正三棱柱ABC _ABG 中,平面 ABC 丄平面BCC 1B 1,二AO 丄平面BCC 1 B . 连结B 10,在正方形BB 1C 1C 中,0, D 分别为BC , CC 1的中点,• BQ 丄BD , . AB 1丄BD . 在正方形 ABB 1A 中,AB 1丄AB , . AB 1丄平面 ABD • (n )设AB 1与A B 交于点G ,在平面A BD 中,作GF 丄A D 于F ,连结AF ,由(I )得AB AB 1C1.AF 丄AD , ■ / AFG 为二面角A-AD-B 的平面角.在 △ AA D 中,由等面积法可求得 'AG *AB 1川,曲AFGdAIA-AD -B 的大小为AF B 45AF = 5arcsin 一4(川)△ ABD 中,BD=AD=、5, AB =2 2, S A A 1BD 「6 ,BCD=1 •在正三棱柱中, A 到平面BCC 1B 1的距离为 3 .设点C 到平面ABD 的距离为d •由V A 』CD =V c 」BD ,得1 Sz △ A 1BD.点C 到平面ABD 的距离为_2 .2•点C 到平面ABD 的距离d = B 0A Bi =丄-2 =・2 . |A B ;| 2^2小结:本例中(川)采用了两种方法求点到平面的距离•解法二采用了平面向量的计算方法,把不易直接求的面AMB 1的距离转化为容易求的点 K 到平面AMB 1的距离的计算方法,这是数学解题中常用的方法;解法一采用了等 体积法,这种方法可以避免复杂的几何作图,显得更简单些,因此可优先考虑使用这一种方法 .考点2异面直线的距离此类题目主要考查异面直线的距离的概念及其求法,考纲只要求掌握已给出公垂线段的异面直线的距离 例2已知三棱锥S-ABC ,底面是边长为4.、2的正三角形,棱SC 的长为2,且垂直于底面.E 、D 分别为BC 、AB 的 中点,求CD 与SE 间的距离. 思路启迪:由于异面直线 CD 与SE 的公垂线不易寻找,所以设法将所求异面直线的 距离,转化成求直线与平面的距离,再进一步转化成求点到平面的距离 解答过程:如图所示,取 BD 的中点F ,连结EF , SF , CF ,-EF 为 BCD 的中位线,.EF // CD,. CD //面 SEF ,解法二:(I )取BC 中点0 ,连结A0 • ':△ ABC 为正三角形,.A0丄BC .V 在正三棱柱 ABC _ABG 中,平面ABC 丄平面 BCC 1B 1 , . AD 丄平面 BCGB . 取BG 中点。
立体几何题型及解题方法总结

立体几何题型及解题方法总结1. 立体几何题型啊,那可是个神奇的领域!有求各种立体图形体积的题型,就像求一个装满水的古怪形状瓶子能装多少水一样。
比如说正方体,正方体的体积公式就是边长的立方。
要是有个正方体边长是3厘米,那它的体积就是3×3×3 = 27立方厘米,简单吧!这类型的题就像是数糖果,一个一个数清楚就行。
2. 还有求立体图形表面积的题型呢。
这就好比给一个形状奇怪的礼物包装纸,得算出需要多少纸才能把它包起来。
像长方体,表面积就是六个面的面积之和。
假如一个长方体长4厘米、宽3厘米、高2厘米,那表面积就是2×(4×3 + 4×2 + 3×2) = 52平方厘米。
哎呀,可别小瞧这表面积,有时候算错一点就像给礼物包了个破纸一样难看。
3. 立体几何里关于线面关系的题型也不少。
这就像在一个迷宫里找路,线和面的关系复杂得很。
比如说直线和平面平行的判定,就像在一个方方正正的房间里,一根直直的杆子和地面平行,只要杆子和地面内的一条直线平行就行。
像有个三棱柱,一条棱和底面的一条棱平行,那这条棱就和底面平行啦,是不是很有趣呢?4. 线面垂直的题型也很重要哦。
这就像是建房子时的柱子和地面的关系,必须垂直才稳当。
判断一条直线和一个平面垂直,就看这条直线是不是和平面内两条相交直线都垂直。
就像搭帐篷,中间那根杆子要和地面上交叉的两根绳子都垂直,帐篷才能稳稳地立起来。
比如一个正四棱锥,它的高就和底面垂直,因为高和底面两条相交的对角线都垂直呢。
5. 面面平行的题型有点像照镜子。
两个平面就像两面镜子,要想平行,得看一个平面内的两条相交直线和另一个平面内的两条相交直线分别平行。
就像有两个一样的盒子,一个盒子里面两条交叉的边和另一个盒子里面对应的两条交叉边平行,那这两个盒子的面就是平行的关系。
想象一下,如果两个平行的黑板,是不是很有画面感?6. 面面垂直的题型就像是打开的书页。
立体几何新题型的解题技巧

立体几何新题型的解题技巧引言立体几何是数学中一个重要的分支,涉及到空间图形的性质和相关计算方法。
随着学习和教学的不断进展,立体几何的题型也在不断演化和创新。
本文将介绍一些新的立体几何题型以及解题的技巧和方法。
球和圆锥的交点在立体几何中,球和圆锥是常见的几何图形。
当球与圆锥相交时,我们可以利用一些几何性质来解题。
首先,当球和圆锥的底面相切时,交点为一个单点,即切点。
此时,可以通过计算切点的坐标和其他相关属性,解决与此题型相关的问题。
其次,当球与圆锥的侧面相交时,交点为一个圆。
我们可以通过确定圆心坐标和圆的半径来解题。
同时,利用圆和圆锥的几何性质,可以推导出一些关键结果,如切线的性质和相切点的计算方法。
空间旋转问题在立体几何中,空间旋转是一个常见的题型。
利用空间旋转的性质,可以推导出一些重要的结论。
首先,考虑一个立方体绕着一个轴线旋转的情况。
我们可以观察到,旋转后的立方体仍然是一个立方体,边长可能发生变化,但是形状保持不变。
利用这个性质,我们可以解决一些与立方体旋转相关的问题。
其次,如果我们考虑一个长方体绕着一个轴线旋转的情况,同样可以得出类似的结论。
我们可以利用旋转后的长方体的性质,确定旋转后的长方体的体积和表面积等。
平行关系的判断在立体几何中,平行是一个重要的关系,涉及到平面与直线、平面与平面之间的关系判断。
对于平行关系的判断,我们可以利用一些特殊的性质和定理。
首先,平行的直线具有相同的斜率。
我们可以利用直线的斜率来判断两条直线是否平行。
如果两条直线的斜率相等,则它们是平行的。
其次,我们可以通过考虑两个平面之间的夹角来判断它们是否平行。
如果两个平面之间的夹角为零或180度,则它们是平行的。
三棱柱的表面积与体积计算三棱柱是一个常见的立体几何图形,具有三个棱面和两个底面。
计算三棱柱的表面积和体积是一个重要的题型。
首先,三棱柱的底面积可以通过底面的形状和尺寸计算得出。
如果底面是一个正三角形,可以使用三角形的面积公式计算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例 17.如图,四棱锥 P— ABCD 中,底面是一个矩形, ∠PAD = 60° ① 求四棱锥的体积; ② 求二面角 P- BC- D 的大小 .
AB= 3,AD = 1,又 PA⊥AB ,PA=4, P
H D
A
E C
B
例 18 . ( 2006 年全国卷Ⅱ)已知圆 O1 是半径为 R 的球 O 的一
D. 90
D1
C1
A1
B1
D
C
2
C.
2
3
D.
4
A
B
5.已知在 ABC 中 ,AB=9,AC=15 , BAC 120 ,它所在平面外一点 P 到 ABC 三顶 点的距离都是 14,那么点 P 到平面 ABC 的距离为( )
A. 13
B. 11
C. 9
D. 7
6.如图,在棱长为 3 的正方体 ABCD -A1B1C1D 1中, M 、 N 分别
考点 2 异面直线的距离
例 3 已知三棱锥 S ABC ,底面是边长为 4 2 的正三角形,棱 SC 的长为 2,且垂直于底面 . E、 D 分别为 BC、 AB 的中点,求
CD 与 SE 间的距离 .
考点 3 直线到平面的距离
例 4. 如图,在棱长为 2 的正方体 AC1 中, G 是 AA1 的中点,求 BD 到平面 GB1D1 的距离 .
4 / 12
例 11.( 2006 年全国Ⅰ卷)
如图 ,l1、l2 是互相垂直的两条异面直线, MN 是它们的公垂线段,点 A、B 在
C
l 1 上, C 在 l2 上, AM =MB =MN (I )证明 AC NB;
A
M
N
(II )若 ACB 60 ,求 NB 与平面 ABC 所成角的余弦值 .
A1 D
B A
3.在一个 45 的二面角的一平面内有一条直线与二面角的棱成
的另一平面所成的角为(
)
A. 30
B. 45
C. 60
4.如图,直平行六面体 ABCD -A1B1C1D1 的棱长均为 2,
BAD 60 ,则对角线 A1C 与侧面 DCC 1D 1 所成
的角的正弦值为(
)
1
A.
2
3
B.
2
45 角,则此直线与二面角
(Ⅱ)设 PA= k·AB,且二面角 E-BD-C 的平面角大于 30 ,求 k 的取
值范围 .
考点 7 利用空间向量求空间距离和角 例 10.( 2007 年江苏卷)
如图,已知 ABCD A1B1C 1D1 是棱长为 3 的正方体,
点 E 在 AA1 上,点 F 在 CC1 上,且 AE FC1 1.
(1)求证: E, B,F,D1四点共面;
(2)若点 G 在 BC 上, BG
2 ,点 M 在 BB1上,
3
GM ⊥ BF ,垂足为 H ,求证: EM ⊥ 平面 BCC1B1 ;
D1 C
A1 B1
F
E
M
D
A
H
C
GB
(3)用 表示截面 EBFD1 和侧面 BCC1B1 所成的锐二面角的大小,求 tan .
3
又 CM ⊥AC 1; (1) 求证: CM ⊥ C1D;
(2) 求 AA 1 的长 .
2 . 如图, 在四棱锥 P-ABCD 中, 底面是矩 形且 AD=2 , AB=PA= 2 , PA⊥底面 ABCD ,E 是 AD 的中点, F 在 PC 上 . (1) 求 F 在何处时, EF ⊥平面 PBC ; (2) 在 (1) 的条件下, EF 是不是 PC 与 AD 的公垂线段 .若是,求 出公垂线段的长度;若不是,说明理由; (3) 在 (1) 的条件下,求直线 BD 与平面 BEF 所成的角 .
B、 60°
C、 45°
D、 0°
5 / 12
例 14.长方体 ABCD - A1B1C1D1 中,
D1 ① 设对角线 D 1B 与自 D 1出发的三条棱分别成 α 、 β 、 角
求证: cos2α + cos2β +cos2 = 1 ② 设 D 1B 与自 D1 出发的三个面成 α 、 β 、
cos2α +cos2β+ cos2 = 2
例 13 .如图左,在正三角形 ABC 中, D、 E、F 分别为各边的中点, G、H、 I、J 分别为 AF、
AD 、BE、 DE 的中点,将△ ABC 沿 DE 、EF、 DF 折成三棱锥后, GH 与 IJ 所成角的度数为
(
)
A
G
F
(A、B、C) C
H D
J E
I
B
H
D J E
G
I F
A、 90°
(II )求异面直线 AO 与 CD 所成角的大小.
E
O
B
C
2 / 12
例 6.( 2006 年广东卷)如图所示, AF 、DE 分别是⊙ O、⊙ O1 的直径 .AD 与两圆所在的平 面均垂直, AD = 8,BC 是⊙ O 的直径, AB= AC= 6,OE//AD . (Ⅰ )求二面角 B— AD— F 的大小; (Ⅱ )求直线 BD 与 EF 所成的角 .
C B
D
C1
B1
P
例 2.( 2006 年湖南卷 )如图 ,已知两个正四棱锥 P-ABCD 与
Q-ABCD 的高分别为 1 和 2,AB=4.
(Ⅰ )证明 PQ⊥平面 ABCD ; (Ⅱ )求异面直线 AQ 与 PB 所成的角; (Ⅲ )求点 P 到平面 QAD 的距离 .
D
C
M A
O B
Q
1 / 12
D1
P A1
C1 B1
你认为正确的一个答案即可)
3.边长为 1 的等边三角形 ABC 中 ,沿 BC 边高线 AD 折起 ,使得折后二面角 B-AD-C 为 60° ,则点 A 到 BC 的距离为 _________,点 D 到平面 ABC 的距离 A 为 __________.
4.在水平横梁上 A、 B 两点处各挂长为 50cm 的细绳, AM、 BN、 AB 的长度为 60cm,在 MN 处挂长为 60cm 的木条, MN 平行于横梁,木条的中点为 O,若木条 绕过 O 的铅垂线旋转 60°,则木条比原来升高了
_________.
5.多面体上,位于同一条棱两端的顶点称为相邻的 方体的一个顶点 A 在 平面内 .其余顶点在
.如图正 的同侧,
正方体上与顶点 A 相邻的三个顶点到 的距离分别是
1、 2 和 4. P 是正方体其余四个顶点中的一个,则
① 3;② 4;③ 5;④ 6;⑤ 7.
以上结论正确的为
.
P 到平面
D1 O1
C1
A1
B1
H
G
D
C
O
A
B
考点 4 异面直线所成的角
A
例 5( 2007 年北京卷文)
如图,在 Rt△AOB中, OAB π,斜边 AB 4 . Rt△ AOC 可以通过 Rt△ AOB
6
D
以直线 AO 为轴旋转得到, 且二面角 B AO C 的直二面角. D 是 AB 的中点.
(I )求证:平面 COD 平面 AOB ;
B
考点 8 简单多面体的有关概念及应用,主要考查多面体的概念、性质,主要以填空、选择
题为主,通常结合多面体的定义、性质进行判断
.
例 12 . 如图( 1),将边长为 1 的正六边形铁皮的六个角各切去一个全等的四边形,再沿虚
线折起, 做成一个无盖的正六棱柱容器, 当这个正六棱柱容器的底面边长为
时
容积最大 .
考点 5 直线和平面所成的角 例 7.( 2007 年全国卷Ⅰ理) 四棱锥 S ABCD 中,底面 ABCD为平行四边形,侧面 SBC 底面 ABCD.已知 ∠ABC 45 ,
S
AB 2 , BC 2 2 , SA SB 3 .
(Ⅰ)证明 SA BC ; (Ⅱ)求直线 SD 与平面 SAB 所成角的大小.A.3B.4C1
10 C. arctan
4
6 D. arcsin
4
2.直线 a 与平面 成 角, a 是平面 的斜线, b 是平面
内与 a 异面的任意直线,则 a 与 b 所成的角( )
C
A. 最小值 ,最大值 C. 最小值 ,无最大值
B. 最小值 ,最大值
2
D. 无最小值,最大值
4
7 / 12
B1
第六讲 立体几何新题型的解题技巧
考点 1 点到平面的距离 例 1( 2007 年福建卷理) 如图,正三棱柱 ABC A1B1C1 的所有棱长都为 2 , D 为 CC1 中点.
(Ⅰ)求证: AB1 ⊥平面 A1 BD ;
A
A1
(Ⅱ)求二面角 A A1D B 的大小; (Ⅲ)求点 C 到平面 A1 BD 的距离.
(写出所有正确结论的编号..)
D
E
C
B
的距离可能是:
9 / 12
O1
6. 如图,棱长为 1m 的正方体密封容器的三个面上有三个锈蚀的小孔 (不计小孔直径) O1、O2、O3 它们分别是所在面的中心 .如果恰当放置容 器,容器存水的最大容积是 _______m3.
O2 O3
三、解答题
1
1. 在正三棱柱 ABC — A 1B1C1中,底面边长为 a,D 为 BC 为中点,M 在 BB 1上,且 BM= B 1M ,
角一定不等于( )
A. 30
B. 45
C. 60
D. 90
D1
C1
二、填空题
B1
1.如图,正方体 ABCD -A1B1C1D1 的棱长为 1,E 是 A1B1 A1
