度上海市九校第一学期联考试卷
上海市闵行区九校九年级(上)期中物理联考试卷

C.可以通过查阅资料、观察实验等方法去验证观点是否正确
D.到目前为止没人反对的观点我们就可以放心接受
为了了解浮力的大小,“验证阿基米德原理”,继续进行了实验。他们用弹簧测力计、量筒、
水、金属块等器材,按图 2 所示的实验方法测量了实验数据,排开液体的重力表示
为:
,(F1﹣F2)表示的是
。
28.(6 分)为了探究影响物体对支持面压力大小的有关因素,小汇同学用形状大小相同、
水的多少有关。他先用弹簧测力计测出木块的重力(如图 1 甲).再将木块放入烧杯内的
水中,木块处于漂浮状态(如图 1 乙).然后他
(填操作),发现木块仍然漂浮。
经分析可知,木块两次受到的浮力都为
牛。从而得出木块漂浮时浮力大小与水的
多少无关。
(2)小常进一步开展了如图 1 丙实验。往两个形状相同的塑料盆 A、B 中各加入 10 牛的水,
再将 B 盆放入 A 盆,B 盆漂浮。这时 B 盆所受浮力:F 浮=GB 盆+10N>10N.继续往 B
盆内加 30 牛水,B 盆仍漂浮。小常此实验的目的是
。
第7页(共10页)
(3)结合小常的探究活动,你认为面对前人的观点,应采取的做法是
。
A.普通人的观点可以质疑,科学家的观点也可以质疑
B.只要多数人认同的观点我们就要全盘接受
同学用两个半球组成的球形容器进行实验,他们将 A、B、C 三个容器中的空气抽出至各容 器中压强相等,然后分别用仪器测出恰好将它们拉开时的力 FA、FB、FC,且 FA=FB< FC,如图(a)、(b)、(c)所示。已知实验时半球的横截面积 SA=SB<SC,表面积 SA′ <SB′<SC′。
①分析比较图(a)和(b)可得:当球形容器内外的压强差相同时,
上海市虹口区九校联考2020-2021学年八年级上学期期中语文试题(原卷版)

2020学年第一学期期中考试八年级语文试卷一、古诗文阅读(30分)(一)默写(11分)1.根据原文默写填空。
(1)巴东三峡巫峡长,________________。
(2)________________,行止依林阻。
(3)夕日欲颓,________________。
(4)经纶世务者,________________。
(5)《野望》一诗中表达了作者归隐之心的诗句是:___________,___________。
(二)课内文言文阅读(9分)阅读下面文字,完成下列小题。
记承天寺夜游元丰六年十月十二日夜,解衣欲睡,月色入户,欣然起行。
念无与为乐者,遂至承天寺寻张怀民。
怀民亦未寝,相与步于中庭。
庭下如积水空明,水中藻荇交横,盖竹柏影也。
何夜无月?何处无竹柏?但少闲人如吾两人者耳。
2.解释加点字。
(1)但.少闲人如吾两人者耳。
(2)念.无与为乐者3.用现代汉语翻译下列句子。
怀民亦未寝,相与步于中庭。
4.下列选项中对文章的理解不正确的一项是()A.运用比喻描写月色,独具匠心,十分精妙,真可谓如诗如画,一个宁静淡雅的境界,真让人心醉神迷。
B.这篇短文,真实地记录了作者当时生活的一个片段,透露出作者在遭贬谪中的那种凄凉、孤寂的特殊心境。
C.这篇随笔性的小品,叙事简洁,写景如绘,而抒情则寓于叙事、写景之中。
叙事、写景、抒情又都集中于写人;写人又突出一点“闲”。
D.本文语言简洁、准确、形象,作者观察事物细致入微,抓住了佳境瞬间最敏感的特征,以极其少的文字,包罗较多的内容,凝练含蓄。
(三)课外文言文阅读(10分)阅读下面文字,完成下列小题。
大抵大峨之上,凡草木禽虫悉非世间所有。
昔固传闻,今亲验之。
余来以季夏,数日前雪大降,木叶犹有雪渍斓斑①之迹。
草木之异,有如八仙②而深紫,有如牵牛而大数倍,有如蓼③而浅青。
闻春时异花尤多,但是时山寒,人鲜能识之。
草叶之异者亦不可胜数。
山高多风,木不能长,枝悉下垂。
古苔如乱发鬖鬖④,挂木上,垂至地,长数丈。
上海市-闵行区-九校联考-初一-上学期语文-期末考试

语文-2016-上海市-闵行区-九校联考-初一-上学期-期末考试120-100-7总分:100分日期:____________ 班级:____________ 姓名:____________一、填空题(每小题12 分,共1题,共12分)1、默写(1)人生自古谁无死,_________。
(《过零丁洋》)(2)山随平野尽,_______。
(《渡荆门送别》)(3)_______ ,天涯共此时。
(《望月怀远》)(4)怪石奔秋涧,_______。
(《草书屏风》)(5)_________,何人不起故园情。
(《春夜洛城闻笛》)(6)凄神寒骨,______。
(《小石潭记》二、篇章阅读(共5题,共46分)2、(4 分)阅读古诗,完成下列各题题破山寺后禅院【唐】常建清晨入古寺,初日照高林。
竹径通幽处,禅房花木深。
山光悦鸟性,潭影空人心。
万籁此俱寂,但余钟磬音。
(1)“万籁”意思是______。
(2)下列对本诗理解错误的一项是___A、首联点明诗人出游的时间和地点以及入寺所见。
B、颔联形象地描绘了山寺的美妙、幽深和清寂。
C、颈联诗人想借鸟儿之乐来排遣自己的苦闷。
D、尾联以有声衬无声,烘托山寺的宁静气氛。
3、(8 分)阅读课内文言文,完成下列各题愚公移山太行、王屋二山,方七百里,高万仞。
本在冀州之南,河阳之北。
北山愚公者,年且九十,面山而居。
惩山北之塞,出入之迂也。
聚室而谋曰:“吾与汝毕力平险,指通豫南,达于汉阴,可乎?”杂然相许。
其妻献疑曰:“以君之力,曾不能损魁父之丘,如太行、王屋何?且焉置土石?”杂曰:“投诸渤海之尾,隐土之北。
”遂率子孙荷担者三夫,叩石垦壤,箕畚运于渤海之尾。
邻人京城氏之孀妻有遗男,始龀,跳往助之。
寒暑易节,始一反焉。
河曲智叟笑而止之曰:“甚矣,汝之不惠。
以残年余力,曾不能毁山之一毛,其如土石何?”北山愚公长息曰:“汝心之固,固不可彻,曾不若孀妻弱子。
虽我之死,有子存焉;子又生孙,孙又生子;子又有子,子又有孙;子子孙孙无穷匮也,而山不加增,何苦而不平?”河曲智叟亡以应。
2021届上海市高三上学期九校联考一模物理试卷(解析版)

上海市2021届九校联考高三一模试卷物理一、单项选择题(每小题只有一个正确答案,第1-8 题,每题 3 分,第9-12 题,每题4 分,共40 分)1.5G 是“ 第五代移动通信网络” 的简称,目前世界各国正大力发展5G 网络。
5G 网络使用的无线电波通信频率在3.0 GHz 以上的超高频段和极高频段(如图所示),比目前4G 及以下网络(通信频率在0.3GHz ~ 3.0GHz 间的特高频段)拥有更大的带宽和更快的传输速率.未来5G 网络的传输速率(指单位时间传送的数据量大小)可达10G bps (bps 为bits per second 的英文缩写,即比特率、比特/ 秒),是4G 网络的50-100 倍.关于5G 网络使用的无线电波,下列说法正确的是A .在真空中的传播速度更快B .在真空中的波长更长C .衍射的本领更强D .频率更高,相同时间传递的信息量更大【答案】D【解析】A 、无线电波(电磁波)在真空的传播速度与光速相同,保持不变,其速度与频率没有关系,故 A 错误;BC 、由公式可知:,频率变大,波长变短,衍射本领变弱,故BC 错误;D 、无线电波(电磁波)频率越高,周期越小,相同时间内可承载的信息量越大,故D 正确.2.如图所示,质量为M 的小车的表面由光滑水平面和光滑斜面连接而成,其上放一质量为m 的球,球与水平面的接触点为 a ,与斜面的接触点为 b ,斜面倾角为θ。
当小车和球一起在水平桌面上做直线运动时,下列说法正确的是()A .若小车匀速运动,则球对斜面上b 点的压力大小为mgcosθB .若小车匀速运动,则球对水平面上a 点的压力大小为mgsinθC .若小车向左以加速度gtanθ 加速运动,则球对水平面上a 点无压力D .若小车向左以加速度gtanθ 加速运动,小车对地面的压力小于(M+m )g 【答案】C【解析】AB .小车和球一起匀速运动时,小球受到竖直向下的重力和水平面对小球竖直向上的支持力,二力平衡,所以小球对 b 点无压力,根据牛顿第三定律可知小球对a 点的压力大小为mg ,AB 错误;C .若小车向左以加速度gtanθ 加速运动,假设小球对a 点无压力,根据牛顿第二定律解得假设成立,所以小球对 a 点无压力, C 正确;D .对小车和球构成的系统整体受力分析可知,系统在竖直方向上加速度为0 ,竖直方向受到重力和支持力,二者等大反向,根据牛顿第三定律可知小车对地面的压力等于(M+m )g , D 错误。
2023-2024学年上海市29校联考九年级上学期月考数学试题及解析

2023学年第一学期九年级数学学科素养测试(满分:150分 完成时间:100分钟)一、选择题:(本大题共6小题,每题4分,满分24分)1. 如果ABC DEF ∽△△(其中顶点A 、B 、C 依次与顶点D 、E 、F 对应)那么下列等式中,不一定成立的是( ) A. A D ∠=∠ B.A DB E∠∠=∠∠ C. AB DE =D.AB DEAC DF=【答案】C 【解析】【分析】本题考查了相似三角形的性质,主要利用了相似三角形对应角相等,对应边成比例.根据相似三角形对应角相等,对应边成比例解答即可. 【详解】解:ABC DEF △∽△,A ∴、A D ∠=∠正确,故本选项错误;B 、A DB E∠∠=∠∠正确,故本选项错误; C 、AB DE =不一定成立,故本选项正确; D 、AB DEAC DF=正确,故本选项错误. 故选:C .2. 已知点D 、E 分别是ABC 的边AB 、AC 上,DE BC ∥,且:1:3ADE DBCE S S =△四边形,那么:AD DB 的值是( ).A.14B.13C.12D. 1【答案】D 【解析】【分析】由:1:3ADE DBCE S S =△四边形可得:1:4ADE ABC S S =△△ 再证ADE ABC △△∽可得12AD AB =,则AD BD =即可解答;掌握相似三角形的面积比等于相似比的平方是解题的关键.【详解】解:如图:∵:1:3ADE DBCE S S =△四边形 ∴()::1:4ADE ABCADE ADE DBCE S SS S S =+=△△△四边形∵DE BC ∥, ∴ADE ABC △△∽,∴12AD AB == 即AD BD =, ∴:1AD DB =.故选D .3. 如果抛物线2y ax bx c =++不经过第二象限,且在y 轴的左侧是上升的,那么下列对其顶点的描述中,正确的是( ).A. 其顶点一定不在第一、二象限B. 其顶点一定不在第二、三象限C. 其顶点一定不在第三、四象限D. 其顶点一定不在第四、一象限【答案】B 【解析】【分析】根据题意可知a<0、对称轴bx 02a=−>,然后根据对称轴确定顶点的可能位置即可;根据题意确定对称轴的位置是解题的关键.【详解】解:∵抛物线2y ax bx c =++不经过第二象限,且在y 轴的左侧是上升的, ∴a<0,对称轴bx 02a=−>, ∴顶点不可能在第二、三象限. 故选B .4. 已知在四边形ABCD 中,记AB a =,BC b =,CD c =,DA d =.如果向量a 、b 、c 、d 都是单位向量,那么下列描述中,正确的是( ) A. 向量a 与b 方向相同,且向量c 与d 方向相同 B. 向量a 与c 方向相同,且向量b 与d 方向相同 C. 向量a 与b 方向相反,且向量c 与d 方向相反D. 向量a 与c 方向相反,且向量b 与d 方向相反 【答案】D 【解析】【分析】本题考查了向量的定义,根据题意作出图形,根据向量的定义及数形结合即可求解,熟练掌握向量的定义,利用数形结合思想解决问题是解题的关键. 【详解】解:如图:∴向量a 与c 方向相反,且向量b 与d 方向相反,故选D .5. 如图,在ABC 中,CD 是边AB 上的高,已知90ACB ∠=︒,1AB =.下列线段中,其长为sin 2A 的是( )A. BCB. ACC. BDD. AD【答案】C 【解析】【分析】本题考查正弦的定义,掌握sin A A ∠=的对边斜边是解题的关键.【详解】解:∵CD 是边AB 上的高,已知90ACB ∠=︒, ∴90A ACD ACD DCB ∠+∠=∠+∠=︒, ∴A DCB ∠=∠, 又∵sin BC A AB =,sin BDDCB BC∠=, ∴2sin sin sin =BC BDA A DCB BD AB BC=⋅∠⋅=, 故选C .6. 已知抛物线M :2y ax bx c =++的顶点为P ,抛物线N :2y ax bx d =−++的顶点为Q .命题1:如果点P 在抛物线N 上,那么点Q 也在抛物线M 上;命题2:如果点P 不在抛物线N 上,那么点Q 也不在抛物线M 上.下列说法中,正确的是( ) A. 命题1是真命题,命题2也是真命题 B. 命题1是真命题,命题2是假命题 C. 命题1是假命题,命题2是真命题 D. 命题1是假命题,命题2也是假命题【答案】A 【解析】【分析】根据题意可知抛物线M 、抛物线N 开口方向相反,对称轴互为相反数,据此判断即可;根据二次函数的性质的抛物线M 、抛物线N 的关系是解题的关键.【详解】解:∵抛物线M :2y ax bx c =++的顶点为P ,抛物线N :2y ax bx d =−++的顶点为Q . ∴抛物线M 、抛物线N 开口方向相反,对称轴互为相反数;∴如果点P 在抛物线N 上,那么点Q 也在抛物线M 上;原说法是真命题; 如果点P 不在抛物线N 上,那么点Q 也不在抛物线M 上;即原说法是真命题. 故选A二、填空题:(本大题共12题,每题4分,满分48分)7. 已知::1:3:6a b c =,30a b c ++=,那么−−=c b a ________. 【答案】6 【解析】【分析】设a n =,则3,6b n c n ==,然后代入30a b c ++=求得n ,进而求得a 、b 、c 的值,最后代入计算即可;掌握一元一次方程的应用是解题的关键.【详解】解:设a n =,则3,6b n c n ==,则3630n n n ++=,解得:3n =; ∴3,9,18a b c ===, ∴18936c b a −−=−−=. 故答案为6.8. 已知抛物线2y ax bx c =++的顶点在直线y x =上,且开口向下,请写出一个满足上述条件的抛物线的表达式:________.【答案】2y x =−(答案不唯一)【解析】【分析】先根据开口向下可知a<0,再根据顶点在y x =上,即2424b ac ba a−−=,整理得2240b b ac −−=,然后确定符合条件的值即可解答.【详解】解:∵抛物线2y ax bx c =++开口向下, ∴a<0,∵抛物线2y ax bx c =++的顶点在直线y x =上,∴2424b ac b a a−−=,即2240b b ac −−=,如:当1a =−,0b c ==符合题意. 故答案为:2y x =−(答案不唯一). 9. 已知点()11,A y 和()22,By 在二次函数()220y axax c a =++<图像上,则12y y −________0.(填“>”、“<”或“=”) 【答案】> 【解析】【分析】本题主要考查对二次函数图象上点的坐标特征,二次函数的性质等知识点的理解和掌握,能熟练地运用二次函数的性质进行推理是解此题的关键.根据二次函数的解析式得出图象的开口向下,对称轴是直线=1x −,根据1x >−时,y 随x 的增大而减小,即可得出答案. 【详解】解:()220y ax ax c a =++<,∴图象的开口向下,对称轴是直线212ax a=−=−, ∴1x >−时,y 随x 的增大而减小, 112−<<,21y y ∴<, 120y y ∴−>,故答案为>.10. 已知平面直角坐标系中点()3,4A 和()0,B b ,满足1tan 2ABO ∠=(O 为原点),那么b 的值为________.【答案】2−或10##10或2− 【解析】【分析】本题考查的是坐标与图形,锐角三角函数的应用,分当点B 在y 轴的正半轴上和负半轴上两种情况,分别画出图形、根据正切的定义列方程求解即可;清晰的分类讨论是解答本题的关键. 【详解】解:①如图:当点B 在y 轴的正半轴上时,则4BC b =−,∵1tan 2ABO ∠=, ∴12AC BC =,即3142b =−,解得:10b =;②如图:当点B 在y 轴的负半轴上时,则4BC b =−,∵1tan 2ABO ∠=,∴12AC BC =,即3142b =−+,解得:=2b −.故答案为2−或10.11. 平面直角坐标系中点()30A ,、()02B ,、()53C −,,设OA a =,OB b =,那么向量CO =________.(用向量a 、b 表示) 【答案】5332a b − 【解析】【分析】本题考查了向量的线性运算:平面向量的加法法则,利用作平面直角坐标系更快速解题,掌握()CO OC =−是解题的关键【详解】解:依题意,如图所示:故()535353323232CO OC OA OB OA OB a b ⎛⎫=−=−−+=−=− ⎪⎝⎭ 故答案为:5332a b − 12. 如果轮船甲位于轮船乙的北偏东35︒方向,那么轮船乙位于轮船甲的________.(注明方向) 【答案】南偏西35︒ 【解析】【分析】根据方位角的相对性进行解答即可;理解相对性是解题的关键. 【详解】解:∵轮船甲位于轮船乙的北偏东35︒方向, ∴轮船乙位于轮船甲的南偏西35︒. 故答案为:南偏西35︒.13. 已知等腰三角形两腰上的中线相互垂直,那么其顶角的正弦值为________. 【答案】35##0.6 【解析】【分析】如图:过B 作BE AC ⊥ 设2BC = 则1BG CG == 再根据直角三角形的性质可得112DG BC ==;根据三角形的重心是中线的三等分点可得3AG =;再运用等腰三角形的性质和勾股定理可得AB AC ==35BE CE ==,最后根据正弦的定义即可解答.【详解】解:如图:过B 作BE AC ⊥ 设2BC = 则1BG CG ==∵D 是重心,BD CD ⊥ ∴112DG BC ==∴BD CD === 22AD DG == 即3AG =∵AD 是中线 AB AC = ∴AG BC ⊥∴AB AC ====∵1tan 3BE AG ACB CE CF ∠=== ∴3BE CE =∵222BC CE BE =+∴()2223BC CE CE =+ 解得:5CE =∴3BE CE ==,∴3sin5BE BAC AB ∠===.故答案为35.【点睛】本题主要考查了等腰三角形的性质、勾股定理、三角形重心的性质、正切、正弦的定义等知识点,掌握三角形的重心是中线的三等分点成为解题的关键.14. 已知菱形的周长为C ,其一个内角(锐角)的正切值为2,设其面积为S ,那么S 关于C 的函数关系式是________.(不必写出定义域)【答案】2S =【解析】【分析】本题考查正切的定义,菱形的性质和面积以及勾股定理.正切等于对边比邻边,菱形的四边长度相等.根据菱形的性质得出菱形的边长,由正切的定义得出2DEAE=,再由勾股定理得出DE 的长,由菱形的面积等于底乘以高即可求解.【详解】解:如图,四边形ABCD 是菱形,DE 是AB 边上的高,∵菱形的周长为C , ∴4C AB AD ==, ∵A ∠的正切值为2, ∴2DEAE=, ∴12AE DE =, 由勾股定理可得222AD AE DE =+,∴222142C DE DE ⎛⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭解得:10DE =,菱形面积为241040C S AB DE C C =⋅=⋅=,2.15. 已知一张等腰直角纸片,其底边长为3cm ,将其沿过其重心且平行于底边的直线折叠,则折叠后重叠部分的面积为________2cm . 【答案】34【解析】【分析】本题考查平行线分线段成比例及三角形中位线的性质、勾股定理,熟知相关性质是正确解决本题的关键.过AC 中点E 作EF AB ∥,交CD 于F ,利用平行线分线段成比例求出重叠部分的上底、下底、高,再利用梯形面积公式即可求出.【详解】解:如图所示,3AB =,CD BE 、是中线,M 是重心,PQ 过点M 且PQ AB ∥,将CPQ 沿直线PQ 折叠,重叠部分是梯形GHPQ ,EF AB ∥,12EF FM BD DM ∴==, 3AB =,32BD AD CD ∴===,2AC BC ==, 34EF CF ∴==, 1142FM ,DM ∴==,1CM QM ∴==,2PQ =,CQ =2AQ ∴=, 1AG ∴=,同理1BH =,1GH ∴=,()11312224GHPQ S ∴=⨯+⨯=梯形.故答案为:34.16. 已知在ABC 中,5AB =,4BC =,3CA =,G 是其重心,那么以GA 、GB 、GC 为三边的三角形的面积是________. 【答案】2 【解析】【分析】如图:延长AG 交BC 于D 再延长GD 使得DE DG = 根据题意可证四边形CGBE 是平行四边形,即CE BG =、BE CG =,最后根据三角形的重心将三角形三等分以及等底等高即可解答;掌握三角形的重心是三角形的中线的三等分点是解答本题的关键.【详解】解:如图:延长AG 交BC 于D 再延长GD 使得DE DG = ∵AD 是中线, ∴21,,33CD BD AG AD GD AD ===, AG GE = ∴四边形CGBE 是平行四边形, ∴CE BG =,BE CG = ∵AG GE =,∴那么以GA 、GB 、GC 为三边的三角形为BEG ∵111342333BCGABCSS ==⨯⨯⨯=, ∴平行四边形CGBE 的面积为24BCGS =,∴122BEGCGBE SS ==. 故答案为2.17. 如图,将矩形ABCD 分别沿AE 、DF 折叠,恰好使点B 、C 重合于形内点G 处,如果EFG 与ADG △的面积比为1:4,那么:AB AD =________.【答案】58【解析】【分析】本题考查了矩形与折叠问题,勾股定理,相似三角形的性质与判定,过点G 作MN AD ⊥交AD 于点N ,交BC 于点M ,证明EGM GAN ∽得出12EG EM MG AG NG AN ===,设,EM x MG y ==,分别表示出,MN AB ,得出43y x =,进而表示出,AB AD ,即可求解. 【详解】如图所示,过点G 作MN AD ⊥交AD 于点N ,交BC 于点M ,依题意,,AG AB DG DC ==, 又AB CD =, ∴AG GD =,∴GAD GDA ∠=∠,则BAG CDG ∠=∠, ∵折叠, ∴AGEB ∠=∠,DGFC ∠=∠,∴360180BAG BEG B AGE ∠+∠=︒−∠−∠=︒,又180BEG MEG ∠+∠=︒, ∴MEG BAG ∠=∠, ∵90EGA ∠=︒∴90EGM AGN ∠+∠=︒∴90GAN AGN EGM ∠=︒−∠=∠ ∴EGM GAN ∽ 同理可得MGF NDG ∽∵EFG 与ADG △的面积比为1:4, ∴12EG EM MG AG NG AN === 设,EM x MG y == ∴2,2NG x AN y ==,∴EG =AB AG ==∴222BC BE EM x =+= ∴2AB MN MG NG y x ==+=+∴2y x =+ 解得:43y x =∴410233AB x x x =+=,1623AD BC x x === ∴58AB AD = 故答案为:58.18. 如图,直线123l l l ∥∥,等边ABC 的三个顶点分别在直线1l 、2l 、3l 上,如果直线1l 、2l 间的距离与直线2l 、3l 的距离之比为1:2,那么AB 与直线1l 夹角的正切值是________.【答案】5【解析】【分析】本题考查旋转性质,等边三角形的性质,解直角三角形,过点C 作2CD l ⊥于点D ,然后把CDB 绕点C 顺时针旋转60︒得到CEA ,过点E 作3FG l ⊥于点F ,交1l 于点G ,过点B 作1BH l ⊥于点H ,设BH a =,得到12EF EC a ==,然后求出正切值即可. 【详解】解:过点C 作2CD l ⊥于点D ,然后把CDB 绕点C 顺时针旋转60︒得到CEA ,过点E 作3FG l ⊥于点F ,交1l 于点G ,过点B 作3BH l ⊥于点H ,设BH a =,则2CD a =,则2CE CD a ==,90FCD CDB FEC ∠=∠=∠=︒,60ECD ∠=︒,3FG a = ∴30ECF ∠=︒, ∴12EF EC a ==, ∴32EG FG EF a a a =−=−=,又∵90ECF FEC GEA FEC ∠+∠=∠+∠=︒, ∴30GEA ∠=︒∴2cos cos303EG a EA a GEA ===∠︒,∴3AC a ===,又∵等边ABC , ∴3AB AC a ==,∴3AH a ===,∴tan 5BH BAH AH∠===,故答案为:5. 的三、解答题:(本大题共7题,满分78分)19. 计算:()043tan 30tan 60cot 60cos701sin 60cos 45︒︒+︒+︒−−︒︒. 【答案】7 【解析】【分析】本题考查了实数的运算,掌握特殊角的三角函数值是解题的关键,将特殊角的三角函数值代入并结合零次幂的性质计算即可. 【详解】解:()043tan 30tan 60cot 60cos701sin 60cos 45︒︒+︒+︒−−︒︒431=+−⎝⎭114=−61=+− 7=.20. 如图,在等腰梯形ABCD 中,AD BC ∥,2AD =,4BC =,3AB =,BE CD ⊥,垂足为E .(1)设AB a =,AD b =,求作向量EC 分别在AB 、AD 方向上的分向量; (2)求sin ABE ∠的值.【答案】(1)见解析 (2)79【解析】【分析】(1)如图:作,AM BC DN BC ⊥⊥ 则四边形AMND 是矩形.可以得到2MN AD ==、1BM CN ==,再根据三角函数可得43CE =,进而可得49EC CD =,再根据向量的和差可得DC a b =+,即4499EC a b =+,据此作图即可; (2)如图:如图:设AM 与BE 交于点H ,由等腰梯形的性质可得1BF =,再根据勾股定理可得AM =BE =4HM =、BH =AH =;再根据三角函数可得HI =73AI =,进而得到23BI =,最后根据正弦的定义即可解答. 【小问1详解】解:如图:作,AM BC DN BC ⊥⊥ 则四边形AMND 是矩形.∴2MN AD == ∴1BM CN ==∴1cos 3CE NC C BC DC ∠=== 即143CE =,即43CE = ∴49CE CD = 即49EC CD = ∵AD BC ∥,2BC AD = ∴22BC AD b ==,∴2DC DA AB BC b a b a b =++=−++=+, ∴4499EC a b =+ ∴向量EC 在AB 、AD 的分向量分别为4499a b 、;作图见图:小问2详解】解:如图:设AM 与BE 交于点H ,∵等腰梯形ABCD 中,AD BC ∥,2AD =,4BC =, ∴1BF = ∴AM ==BE ==∵4tan 43HM CE EBC BM BE ∠====即14HM =,解得:4HM =;∴BH ==∴AH AM MH =−= 如图:作HIAB ⊥∴1sin 3HI BM BAM AH AB ∠=== 即173HI =,解得:HI = 同理可得:73AI =,∴72333BI =−=,∴712sin 39IH ABE BH ∠===.【点睛】本题主要考查了等腰梯形的性质、矩形的判定与性质、解直角三角形、三角函数、向量等知识点,正确作出辅助线、灵活运用三角函数解直角三角形是解题的关键.【21. 已知函数2423y x x =++.(1)试着通过列表、描点、连线的方式,画出其图像的草图; (2)根据所画草图,请写出该函数的三条图像特征.【答案】(1)见解析 (2)①函数图像的对称轴为=1x −;②当1x >−,y 随x 的增大而减小;③函数图像无限靠近x 轴,但不会和x 轴相交(不唯一合理即可). 【解析】【分析】(1)根据列表、描点、连线的步骤画出函数图像即可;掌握作图步骤是解题的关键; (2)根据函数图像,总结归纳性质即可;掌握数形结合思想是解题的关键. 【小问1详解】 解:①列表如下:②描点、连线如下:【小问2详解】解:由(1)所得图像可得如下性质:①函数图像的对称轴为=1x −;②当1x >−,y 随x 的增大而减小;③函数图像无限靠近x 轴,但不会和x 轴相交(不唯一合理即可).22. 小明想利用建筑CD 玻璃幕墙的反射作用来测建筑AB 的高度.如图所示,他先在建筑AB 的底部A 处用测角仪测得其顶部B 在建筑CD 玻璃幕墙上的反射点E 的仰角为α,然后他沿AC 前进了10米到达点F 处,再用测角仪测得建筑AB 的顶部B 在建筑CD 玻璃幕墙上的反射点G 的仰角为β.已知1tan 3α=,sin 13β=,测角仪置于水平高度1.5米的M 、N 处.求建筑AB 的高度.【答案】31.5 【解析】【分析】延长BE BG ,分别交MN 的延长线于M N '',,MM '于CD 相交于H ,设m NH x =,则()()()10m,210m,220m MH x N M x MM x '=+=+'=+,然后在Rt MM B '和Rt MN B '中解直角三角形可得()1·tan 2103BM MM x α==+'、·tan BM MN β'=,由sin 13β=可得tan 4β=,进而得到()2104BM x =+,据此列方程解得35x =,最后代入即可解答.正确的作出辅助线、灵活应用解直角三角形解实际问题是解题的关键.【详解】解:如图:延长BE BG .分别交MN 的延长线于M N '',,MM '于CD 相交于H ,设m NH x = 则()()()10m,210m,220m MH x N M x MM x '=+=+'=+在Rt MM B '中,()1·tan 2103BM MM x α==+'; Rt MN B '中,·tan BM MN β'=, ∵sin 13β=,∴cos 3β=,∴tan 4β=,∴()2104BM x =+,∴())122021034x x +=+,解得:35x =+,∴()()123520 1.531.5m 3AB ⎡⎤=⨯++=+⎣⎦.答:建筑AB 的高度为()31.5m +.23. 如图,正方形纸片ABCD .现对纸片做如下操作:第一步,对折纸片,使边AD 与BC 重合,得到折痕EF ;第二步,将BCF △折叠,得到折痕BF ;第三步,将ABP 折叠,使顶点A 落在折痕BF 上点Q 处.(1)求证:点P 恰为线段AD 的黄金分割点;(2)现有矩形纸片ABCD ,其中AB BC <,如图所示.请你借助这张纸片,设法折出一个30︒的角.要求写出折纸的步骤(可仿照上面的表述),并在图中画出各步骤的折痕位置,注明30︒角的位置,不需要证明.【答案】(1)见解析 (2)见解析 【解析】【分析】本题考查折叠作图,黄金分割点的定义,勾股定理,掌握黄金分割的比值是解题的关键.(1)先运用勾股定理得到2BF =,然后在Rt QPF 和Rt DGF 中,运用2222FQ PQ DF DP +=+解题计算即可证明;(2)先对折矩形,然后再折叠,使得点A 落在第一次的折痕上,即可得到30︒角. 【小问1详解】 证明:如图,连接PF ,设正方形ABCD 的边长为1,则12DF =.在Rt BCF 中,2BF ==,则12QF BF BQ =−=−. 设AP PQ x ==,则1PD x =−, 在Rt QPF 和Rt DGF 中,有2222FQ PQ DF DP +=+, 即()222211122x x ⎛⎫⎛⎫−++− ⎪ ⎪ ⎪⎝⎭⎝⎭=, 解得512x √−=, 即点P 是AD 的黄金分割点(AG GD >); 【小问2详解】方法如图所示:第一步:对折矩形纸片ABCD ,使 AD 与BC 重合,得到折痕EF ,把纸片展平;第二步:再一次折叠纸片,使点A 落在EF 上,落点为点N ,并使折痕经过点B ,得到折痕BM ,同时,得到线段BN .则30ABM MBN NBC ∠∠∠===︒.24. 如图,直线1l :122y x =+与x 、y 轴的交点为A 、B ,点P 是该直线上位于第一象限内的一点,满足12PB BA =.(1)以B 为顶点的抛物线2y ax bx c =++与线段AB (不含点A 、B )有交点,求a 的取值范围; (2)将直线1l 平移得到直线2l ,直线2l 与x 、y 轴的交点为C 、D ,且使BC CD ⊥,问:直线1l 平移到直线2l ,至少需要平移多少距离?(3)如果(1)中抛物线2y ax bx c =++与直线2l 在抛物线对称轴右侧的交点为Q ,当PQA △与PQB △相似时,求此时抛物线的表达式.【答案】(1)108a −<<(2 (3)2129y x =−+ 【解析】【分析】(1)根据题意可得:a<0、0b =、()()4,0,0,2A B −,然后求出抛物线过临界点时的a 的取值,进而完成解答;确定a 、b 的取值范围是解答本题的关键; (2)设平移后的直线2l 的解析式为:212y x t =+;BC 的解析式为3y kx b =+,根据垂直直线的关系可得2k =−,进而确定(),0,0,2b C D t ⎛⎫⎪⎝⎭;再根据点C 在2l 上可得4b t =−,则0,4b D ⎛⎫− ⎪⎝⎭;再运用勾股定理列方程可得2b =,然后确定()11,0,0,2C D ⎛⎫− ⎪⎝⎭,最后根据两点间距离公式即可解答;明确各直线间的关系是解题的关键; (3)设1,22P a a ⎛⎫+ ⎪⎝⎭,根据题意和勾股定理可得()2,3P ;再根据PQA PQB ∽可得3PA PQ AQ PB BQ PQ ===;设Q 的坐标为11,22n n ⎛⎫− ⎪⎝⎭,根据两点间距离公式可得3=,解得:3n =或92n =(舍),即Q 的坐标为()3,1;再结合(1)、(2)即可解答;灵活运用相似三角形的性质和两点间距离公式是解题的关键. 【小问1详解】解:∵以B 为顶点的抛物线2y ax bx c =++与线段AB (不含点A 、B )有交点, ∴抛物线的开口一定向下,即a<0;且对称轴为y 轴,则02ba−=、0b =, 当0x =时,1222y x =+=;当0y =时,4x =−, ()()4,0,0,2A B −;当2y ax bx c =++恰好过()0,2B 点时,则2c =,()220y ax a =+<;当2y ax bx c =++恰好过()()4,0,0,2A B −两点时,有0162a =+,即18a =−; 综上,a 的取值范围为108a −<<. 【小问2详解】解:设平移后的直线2l 的解析式为:212y x t =+;BC 的解析式为3y kx b =+, ∵BC CD ⊥, ∴112k =−,即2k =−, ∴32y x b =−+,∴(),0,0,2b C D t ⎛⎫⎪⎝⎭由点C 在2l 上,则1022b t ⨯+=,解得:4b t =−,即0,4b D ⎛⎫− ⎪⎝⎭,在Rt BCD 中有222BC CD BD +=,即2222422244b b b b ⎛⎫⎛⎫⎛⎫⎛⎫+++=+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,解得:2b =,∴()11,0,0,2C D ⎛⎫− ⎪⎝⎭21122y x =−∴平移距离BC ==【小问3详解】 解:设1,22P a a ⎛⎫+ ⎪⎝⎭, ∵12PB BA =, ∴2BA PB =∴=,解得:2a =,即()2,3P ; ∵PQA PQB ∽∴3PA PQ AQPB BQ PQ=== 设Q 的坐标为11,22n n ⎛⎫− ⎪⎝⎭3=,解得:3n =或92n =(舍), ∴Q 的坐标为()3,1,(1)可得由22y ax =+,则192a =+,解得:19a =−. ∴抛物线表达式为:2129y x =−+;25. 如图,在ABC 中,90ACB ∠=︒,3AC =,4BC =,O 是边AC 的中点,点D 位于边AB 上,连接DO 并延长交BC 的延长线于点E ,过点D 作DF BC ⊥,垂足为F .(1)当DE AB ⊥时,求tan AED ∠的值; (2)当EA AB ⊥时,求证:2DF DA DB =⋅;(3)作射线OP ,使其平行于BC ,且在AC 的右侧.试问:在射线OP 上是否存在点Q ,使得OQD OQE ∠=∠如果存在,请求出OQ 的长;如果不存在,请说明理由.【答案】(1)1241(2)见解析 (3)4 【解析】【分析】(1)由中点的性质可得32OA OC ==,再直角三角形可得65OD =、910AD =、158OE = 进而得到12340ED =;最后根据正切的定义即可解答; (2)如图:延长EA FD 、相交于G ,根据平行线等分线段定理可得,,OA EO CO EODG ED DF ED==再说明GD DF =,可得sin ADG DG ∠=;再说明sin DF B DB ∠= 则B G ∠=∠;然后可得AD DF DG BD =,再结合GD DF =即可证明结论;(3)如图:作AI BC ∥交BD 延长线于I ,过O 作射线OP 交AB 于G ,,连接CG 交DF 于H DF 与OG 交于J ,再证DJG HJG ≌可得,DJ JH DG HG ==,进而说明DQO EQO ∠=∠,即H 在EQ上;再根据平行线等分线段定理可得GQ HG DGCE CH AD==;然后再说明OG CQ =即可解答. 【小问1详解】解:∵O 是边AC 的中点,3AC = ∴32OA OC ==∵DE AB ⊥,∴346sin 255BC OD OA CAB OA AB =⋅∠=⋅=⨯= 339cos 2510AC AD OA CAB OA AB =⋅∠=⋅=⨯=631553cos cos 282OC OC OE COE AOD ===÷=∠∠∴1561238540ED =+= ∴912312tan 104041AD AED DE ∠==÷=. 【小问2详解】解:如图:延长EA FD 、相交于G , ∵AC GF ∥∴,,OA EO CO EODG ED DF ED == ∴OA CODG DF=, ∵OA OC = ∴GD DF = ∵EA AB ⊥, ∴sin ADG DG∠=在Rt DFB △中,sin DFB DB∠= 则B G ∠=∠ ∴AD DFDG BD= ∵GD DF =, ∴AD DFDF BD= 即2DF DA DB =⋅. 【小问3详解】解:如图:假设Q 存,作AI BC ∥交BD 延长线于I ,过O 作射线OP 交AB 于G ,,连接CG 交DF于H DF 与OG 交于J ,∵OG AC ⊥ AG CG = OG BC ∥ ∴G 是AB 的中点,∴,AG CG BG AGO CGO ==∠= ∵DF OP ⊥ JG GJ = ∴DJG HJG ≌ ∴,DJ JH DG HG ==∴DQ HQ = DQO HQO ∠=∠ 又∵DQO EQO ∠=∠ ∴H 在EQ 上, ∵CE QG ∥ ∴GQ HG DGCE CH AD == ∵AI OG ∥ ∴OG DG AI AD= 则OG GQAI CE = ∵,AO CO AI CE =∥ ∴AI CE = ∴OG CQ = ∴12OG AO OB AC == 即12OG OB = ∴24OQ OG BC ===.【点睛】本题主要考查了中点的性质、解直角三角形、三角函数、平行线等分线段定理、全等三角形的判定与性质等知识点,灵活运用相关知识成为解答本题的关键.,。
2019—2020年最新(沪科版)上海市九校联考七年级上学期期末数学模拟试卷及答案解析【精品提分试卷】.doc

第一学期期末模拟教学质量检测七年级数学试卷一、选择题(每题2分,满分12分)1.下列代数式中,单项式的个数是①2x ﹣3y ;②;③;④﹣a ;⑤;⑥;⑦﹣7x 2y ;⑧0( )A .3个B .4个C .5个D .6个2.下列运算正确的是( )A .2a+3b=5abB .(3a 3)2=6a 6C .a 6÷a 2=a 3D .a 2•a 3=a 53.若分式中的x 和y 都扩大5倍,那么分式的值( )A .不变B .扩大5倍C .缩小到原来的D .无法判断4.下列从左到右的变形,其中是因式分解的是()A.2(a﹣b)=2a﹣2b B.x2﹣2x+1=x(x﹣2)+1C.(m+1)(m﹣1)=m2﹣1 D.3a(a﹣1)+(1﹣a)=(3a﹣1)(a﹣1)5.很多图标在设计时都考虑对称美.下列是几所国内知名大学的图标,若不考虑图标上的文字、字母和数字,其中是中心对称图形的是()A.清华大学B.浙江大学C.北京大学D.中南大学6.如图,小明正在玩俄罗斯方块,他想将正在下降的“L”型插入图中①的位置,他需要怎样操作?()A.先绕点O逆时针旋转90°,再向右平移3个单位,向下平移6个单位B.先绕点O顺时针旋转90°,再向右平移3个单位,向下平移6个单位C.先绕点O逆时针旋转90°,再向右平移4个单位,向下平移5个单位D.先绕点O顺时针旋转90°,再向右平移3个单位,向下平移6个单位二、填空题(每题2分,满分24分)7.计算:(﹣a2b)3= .8.计算:(x﹣1)(x+3)= .9.计算:(8a2b﹣4ab2)÷(﹣ab)= .10.PM2.5是指大气中直径小于或等于2.5微米(0.0000000025米)的颗粒物,也称为可入肺颗粒物,2.5微米用科学记数法表示为米.11.分解因式:4x2﹣12xy+9y2= .12.如果关于x的多项式x2﹣kx+9是一个完全平方式,那么k= .13.如果单项式﹣xy b+1与x a﹣2y3是同类项,那么(b﹣a)2016= .14.当x= 时,分式无意义.15.关于x的方程+=2有增根,则m= .16.如图所示,把△ABC沿直线DE翻折后得到△A′DE,如果∠A′EC=32°,那么∠A′ED= .17.已知a,b,c是三角形ABC的三边,且b2+2ab=c2+2ac,则三角形ABC 的形状是三角形.18.若2x+3y﹣2=0,则9x﹣3•27y+1= .三、计算题(每题6分,满分42分)19.计算:(2x﹣1)2﹣2(x+3)(x﹣3).20.计算:+﹣.21.分解因式:9a2(x﹣y)+(y﹣x)22.因式分解:(x2+x)2﹣8(x2+x)+12.23.解方程:.24.计算:•.25.先化简,后求值:(x+1﹣)÷,其中x=.四、解答题(满分22分)26.如图,(1)请画出△ABC关于直线MN的对称图形△A1B1C1.(2)如果点A2是点A关于某点成中心对称,请标出这个对称中心O,并画出△ABC关于点O成中心对称的图形△A2B2C2.27.“新禧”杂货店去批发市场购买某种新型儿童玩具,第一次用1200元购得玩具若干个,并以7元的价格出售,很快就售完.由于该玩具深受儿童喜爱,第二次进货时每个玩具的批发价已比第一次提高了20%,他用1500元所购买的玩具数量比第一次多10个,再按8元售完,问该老板两次一共赚了多少钱?28.如图,四边形ABCD是正方形,BM=DF,AF垂直AM,M、B、C在一条直线上,且△AEM与△AEF恰好关于AE所在直线成轴对称,已知EF=x,正方形边长为y.(1)图中△ADF可以绕点按顺时针方向旋转°后能与△重合;(2)用x、y的代数式表示△AEM与△EFC的面积.参考答案与试题解析一、选择题(每题2分,满分12分)1.下列代数式中,单项式的个数是①2x﹣3y;②;③;④﹣a;⑤;⑥;⑦﹣7x2y;⑧0()A.3个B.4个C.5个D.6个【考点】单项式.【分析】根据单项式的概念即可判断.【解答】解:③;④﹣a;⑥;⑦﹣7x2y;⑧0是单项式,故选(C)2.下列运算正确的是()A.2a+3b=5ab B.(3a3)2=6a6C.a6÷a2=a3D.a2•a3=a5【考点】同底数幂的除法;合并同类项;同底数幂的乘法;幂的乘方与积的乘方.【分析】直接利用积的乘方法则以及合并同类项、同底数幂的乘法运算法则进而得出答案.【解答】解:A、2a+3b无法计算,故此选项错误;B、(3a3)2=9a6,故此选项错误;C、a6÷a2=a4,故此选项错误;D、a2•a3=a5,故此选项正确;故选:D.3.若分式中的x和y都扩大5倍,那么分式的值()A.不变B.扩大5倍C.缩小到原来的 D.无法判断【考点】分式的基本性质.【分析】根据分式的分子分母都乘以(或除以)同一个不为零整式,分式的值不变,可得答案.【解答】解:分式中的x和y都扩大5倍,那么分式的值不变,故选:A.4.下列从左到右的变形,其中是因式分解的是()A.2(a﹣b)=2a﹣2b B.x2﹣2x+1=x(x﹣2)+1C.(m+1)(m﹣1)=m2﹣1 D.3a(a﹣1)+(1﹣a)=(3a﹣1)(a﹣1)【考点】因式分解的意义.【分析】根据因式分解的意义,看每个选项是不是把一个多项式写成整式积的形式,得出结论.【解答】解:选项A、C是多项式的乘法,选项B不是积的形式,不是因式分解.选项D把多项式变形成了整式积的形式,属于因式分解.故选D.5.很多图标在设计时都考虑对称美.下列是几所国内知名大学的图标,若不考虑图标上的文字、字母和数字,其中是中心对称图形的是()A.清华大学B.浙江大学C.北京大学D.中南大学【考点】中心对称图形.【分析】根据中心对称图形的定义旋转180°后能够与原图形完全重合即是中心对称图形,即可判断出答案.【解答】解:A、不中心对称的图形,故此选项错误;B、不是中心对称图形,故此选项错误;C、不是中心对称图形,故此选项错误;D、是中心对称图形,故此选项正确;故选:D.6.如图,小明正在玩俄罗斯方块,他想将正在下降的“L”型插入图中①的位置,他需要怎样操作?()A.先绕点O逆时针旋转90°,再向右平移3个单位,向下平移6个单位B.先绕点O顺时针旋转90°,再向右平移3个单位,向下平移6个单位C.先绕点O逆时针旋转90°,再向右平移4个单位,向下平移5个单位D.先绕点O顺时针旋转90°,再向右平移3个单位,向下平移6个单位【考点】旋转的性质;平移的性质.【分析】由旋转的性质和平移的性质即可得出结论.【解答】解:小明正在玩俄罗斯方块,他想将正在下降的“L”型插入图中①的位置,他需要先绕点O顺时针旋转90°,再向右平移3个单位,向下平移6个单位;故选:D.二、填空题(每题2分,满分24分)7.计算:(﹣a2b)3= ﹣a6b3.【考点】幂的乘方与积的乘方.【分析】利用(a m b n)p=a mp b np计算即可.【解答】解:原式=﹣a6b3.故答案是=﹣a6b3.8.计算:(x﹣1)(x+3)= x2+2x﹣3 .【考点】多项式乘多项式.【分析】多项式与多项式相乘的法则:多项式与多项式相乘,先用一个多项式的每一项乘另外一个多项式的每一项,再把所得的积相加.依此计算即可求解.【解答】解:(x﹣1)(x+3)=x2+3x﹣x﹣3=x2+2x﹣3.故答案为:x2+2x﹣3.9.计算:(8a2b﹣4ab2)÷(﹣ab)= ﹣16a+8b .【考点】整式的除法.【分析】直接利用多项式除法运算法则计算得出答案.【解答】解:(8a2b﹣4ab2)÷(﹣ab)=8a2b÷(﹣ab)﹣4ab2÷(﹣ab)=﹣16a+8b.故答案为:﹣16a+8b.10.PM2.5是指大气中直径小于或等于2.5微米(0.0000000025米)的颗粒物,也称为可入肺颗粒物,2.5微米用科学记数法表示为 2.5×10﹣9米.【考点】科学记数法—表示较小的数.【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.【解答】解:0.00 000 000 25=2.5×10﹣9,故答案为:2.5×10﹣9.11.分解因式:4x2﹣12xy+9y2= (2x﹣3y)2.【考点】提公因式法与公式法的综合运用.【分析】利用完全平方公式即可直接分解.【解答】解:原式=(2x﹣3y)2.故答案是:(2x﹣3y)2.12.如果关于x的多项式x2﹣kx+9是一个完全平方式,那么k= ±6 .【考点】完全平方式.【分析】利用完全平方公式的结构特征判断即可.【解答】解:∵关于x的多项式x2﹣kx+9是一个完全平方式,∴k=±6,故答案为:±613.如果单项式﹣xy b+1与x a﹣2y3是同类项,那么(b﹣a)2016= 1 .【考点】同类项.【分析】根据同类项的定义,所含字母相同且相同字母的指数也相同的项是同类项,可得答案.注意同类项与字母的顺序无关,与系数无关.【解答】解:由题意,得a﹣2=1,b+1=3,解得a=3,b=2.(b﹣a)2016=(﹣1)2016=1,故答案为日:1.14.当x= ﹣3 时,分式无意义.【考点】分式有意义的条件.【分析】根据分式无意义的条件可得x+3=0,再解即可.【解答】解:由题意得:x+3=0,解得:x=﹣3,故答案为:﹣3.15.关于x的方程+=2有增根,则m= .【考点】分式方程的增根.【分析】分式方程去分母转化为整式方程,由分式方程有增根,求出x的值,代入整式方程计算即可求出m的值.【解答】解:去分母得:5x﹣3﹣mx=2x﹣8,由分式方程有增根,得到x﹣4=0,即x=4,把x=4代入整式方程得:20﹣3﹣4m=0,快捷得:m=,故答案为:16.如图所示,把△ABC沿直线DE翻折后得到△A′DE,如果∠A′EC=32°,那么∠A′ED= 74°.【考点】翻折变换(折叠问题).【分析】根据折叠的性质可知,∠A′ED=∠AED,再根据平角的定义和已知条件即可求解.【解答】解:∵把△ABC沿直线DE翻折后得到△A′DE,∴∠A′ED=∠AED,∵∠A′EC=32°,∴∠A′ED=÷2=74°.故答案为:74°.17.已知a,b,c是三角形ABC的三边,且b2+2ab=c2+2ac,则三角形ABC 的形状是等腰三角形.【考点】因式分解的应用.【分析】根据b2+2ab=c2+2ac,可以求得a、b、c之间的关系,从而可以求得三角形的形状.【解答】解:∵b2+2ab=c2+2ac,∴b2+2ab+a2=c2+2ac+a2,∴(a+b)2=(a+c)2,∴a+b=a+c,∴b=c,∴三角形ABC是等腰三角形,故答案为:等腰.18.若2x+3y﹣2=0,则9x﹣3•27y+1= .【考点】同底数幂的除法;同底数幂的乘法.【分析】直接利用幂的乘方运算法则将原式变形,进而求出答案.【解答】解:∵2x+3y﹣2=0,∴2x+3y=2,9x﹣3•27y+1=(32)x﹣3•(33)y+1=32x﹣6•33y+3=32x+3y﹣3,=3﹣1=.故答案为:.三、计算题(每题6分,满分42分)19.计算:(2x﹣1)2﹣2(x+3)(x﹣3).【考点】平方差公式;完全平方公式.【分析】先根据完全平方公式和平方差公式计算,再根据合并同类项法则合并即可.【解答】解:(2x﹣1)2﹣2(x+3)(x﹣3)=4x2﹣4x+1﹣2x2+9=2x2﹣4x+10.20.计算:+﹣.【考点】分式的加减法;负整数指数幂.【分析】根据分式运算的法则以及负整数指数幂的意义即可求出答案.【解答】解:原式=+﹣=+﹣=﹣+﹣=021.分解因式:9a2(x﹣y)+(y﹣x)【考点】提公因式法与公式法的综合运用.【分析】直接提取公因式(x﹣y),进而利用平方差公式分解因式得出答案.【解答】解:9a2(x﹣y)+(y﹣x)=(x﹣y)(9a2﹣1)=(x﹣y)(3a+1)(3a﹣1).22.因式分解:(x2+x)2﹣8(x2+x)+12.【考点】因式分解-十字相乘法等.【分析】先把x2+x看做一个整体,然后根据十字相乘法的分解方法和特点分解因式.【解答】解:(x2+x)2﹣8(x2+x)+12,=(x2+x﹣2)(x2+x﹣6),=(x﹣1)(x+2)(x﹣2)(x+3).23.解方程:.【考点】解分式方程.【分析】观察可得最简公分母是(x+3)(2﹣x),方程两边乘最简公分母,可以把分式方程转化为整式方程求解.【解答】解:方程两边同乘以(x+3)(2﹣x),得x(2﹣x)﹣x(x+3)=2(x+3)(2﹣x)2x﹣x2﹣3x﹣x2=12﹣2x﹣2x2∴x=12检验:当x=12时,(x+3)(2﹣x)≠0∴原方程的解为x=12.24.计算:•.【考点】分式的乘除法.【分析】先将分式的分子与分母进行因式分解【解答】解:原式=•=•=25.先化简,后求值:(x+1﹣)÷,其中x=.【考点】分式的化简求值.【分析】首先把括号内的分式通分相加,再把除法转化为乘法,计算乘法即可化简,最后代入数值计算即可.【解答】解:原式=•==.当x=时,原式==.四、解答题(满分22分)26.如图,(1)请画出△ABC关于直线MN的对称图形△A1B1C1.(2)如果点A2是点A关于某点成中心对称,请标出这个对称中心O,并画出△ABC关于点O成中心对称的图形△A2B2C2.【考点】作图-旋转变换;作图-轴对称变换.【分析】(1)分别作出A、B、C三点关于直线MN的对称点后顺次连接即可.(2)找到AA2的中点即为O点位置,再利用中心对称图形的性质得出对应点坐标连接即可.【解答】解:(1)如图所示:画出△ABC关于直线MN的对称图形△A1B1C1;(2)如图所示:找出对称中心O,画出△ABC关于点O成中心对称的图形△A2B2C2.27.“新禧”杂货店去批发市场购买某种新型儿童玩具,第一次用1200元购得玩具若干个,并以7元的价格出售,很快就售完.由于该玩具深受儿童喜爱,第二次进货时每个玩具的批发价已比第一次提高了20%,他用1500元所购买的玩具数量比第一次多10个,再按8元售完,问该老板两次一共赚了多少钱?【考点】分式方程的应用.【分析】设这种新型儿童玩具第一次进价为x元/个,则第二次进价为1.2x元/个,分别可以表示出第一次购买玩具的数量和第二次购买玩具的数量,根据两次购买玩具的数量之间的关系建立方程求出其解就可以了.【解答】解:设这种新型儿童玩具第一次进价为x元/个,则第二次进价为1.2x 元/个,根据题意,得﹣=10,变形为:1500﹣1440=12x,解得:x=5,经检验,x=5是原方程的解,则该老板这两次购买玩具一共盈利为:(7﹣1.2×5)+×(7﹣5)=730(元).答:该老板两次一共赚了730元.28.如图,四边形ABCD是正方形,BM=DF,AF垂直AM,M、B、C在一条直线上,且△AEM与△AEF恰好关于AE所在直线成轴对称,已知EF=x,正方形边长为y.(1)图中△ADF可以绕点 A 按顺时针方向旋转90 °后能与△ABM 重合;(2)用x、y的代数式表示△AEM与△EFC的面积.【考点】旋转的性质;轴对称的性质.【分析】(1)利用旋转的定义求解;(2)由于△AEM≌△AEF,则EF=EM,即x=BE+BM=DF+BE,则根据三角形面积公式得到S△AME=xy,然后利用S△CEF=S正方形ABCD﹣S△AEF﹣S△ABE﹣S△ADF可表示出△EFC的面积.【解答】解:(1)图中△ADF可以绕点A按顺时针方向旋转90°后能够与△ABM 重合;故答案为:A、90°,ABM.(2)∵△AEM与△AEF恰好关于所在直线成轴对称,∴EF=EM,即x=BE+BM,∵BM=DF,∴x=DF+BE,∴S△AME=•AB•ME=xy,S△CEF=S正方形ABCD﹣S△AEF﹣S△ABE﹣S△ADF=y2﹣xy﹣•y•BE﹣•y•DF=y2﹣xy﹣•y(BE+DF)=y2﹣xy﹣•y•x=y2﹣xy.2017年2月20日。
2024届九校联考语文试卷

九校联考语文试题一、语言文字基础1.对下列句子所用修辞手法的分析,正确的一项是()①汗水在他那络腮胡根上聚成了一粒粒晶亮的露珠。
②军队驻扎一个月,没有动过群众的一针一线。
③他的日历上是工作,工作,工作,从来没有节假日。
2.下列交际用语使用不得体的一项是( )A.我校将于9月1日如期开学,相关事宜欢迎家长来函垂问。
B.拙作已经寄出,心中惶恐不安,望君哂笑之余不吝赐教。
C.感谢您的家父雪中送炭,明日我将从百忙中专程到府上致谢。
D.令郎不愧生在丹青世家,他的奔马图惟妙惟肖,栩栩如生。
3.把下列句子组成语意连贯的语段,排序最恰当的一项是( )①以及乐曲与你之间的故事,如《童年》让你想起无忧无虑的童年生活。
②不管你什么年龄,无论你走到哪里,只要你重新听到那熟悉的旋律,就会触动你那颗敏感的心,引起你久久的怀念。
③这些故事包括乐曲本身的故事,如《月光曲》与贝多芬、《二泉映月》与阿炳。
④感人的乐曲留给人的记忆是长久的。
⑤想一想,哪一首最让你怀念,哪一支曲子最让你浮想联翩,由此你联想起怎样的故事。
A.②④①⑤③ B.②④⑤①③C.④②⑤③① D.④②①③⑤4.依次填入下列各句横线处的词语,最恰当的一组是( )①最新研究指出,南极冰层因气候变化而加速_______,将使南极皇帝企鹅数目锐减。
②她的目光从我身旁扫过,一直移到窗子,________着窗外,好像在想着什么。
③由于全球化的现实,如今新的对华大战略既不能以________为基础,也不能突然丢弃长期以来让中国融入国际体系的做法。
A.融解凝视遏制 B.溶解窥视遏制C.溶解凝视遏止 D.融解窥视遏止二、古代诗文阅读(34分)(一)阅读下面这首宋诗,回答各题。
篇1:鹧鸪天范成大嫩绿重重看得成,曲阑幽槛小红英。
酴醿①架上蜂儿闹,杨柳行间燕子轻。
春婉娩②,客飘零,残花浅酒片时清。
一杯且买明朝事,送了斜阳月又生。
【注】①酴醿:一种植物,古有“酴醿花开春事了”的说法。
②婉娩:亦作“婉晚”。
2020-2021学年上海市闵行区九校联考七年级(上)期中语文试卷含解析

2020-2021学年上海市闵行区九校联考七年级(上)期中语文试卷一、文言文。
(25分)1. 默写。
(1)远芳侵古道,________。
(《赋得古原草送别》)(2)________,但余钟磬音。
(《题破山寺后禅院》)(3)周公恐惧流言日,________。
(《放言五首(其三)》)(4)俶尔远逝,________。
(《小石潭记》)(5)________,日暮客愁新。
(《宿建德江》)(6)夜来城外一尺雪,________。
(《卖炭翁》)三、标题2. 阅读下面的诗,完成第下列各题。
酬乐天扬州初逢席上见赠刘禹锡巴山楚水凄凉地,二十三年弃置身。
怀旧空吟闻笛赋,到乡翻似烂柯人。
沉舟侧畔千帆过,病树前头万木春。
今日听君歌一曲,暂凭杯酒长精神。
(1)诗中的“长精神”的含义是________。
(2)沉舟侧畔千帆过,病树前头万木春”在诗中的含义是________。
现在引申的含义是________。
3. 阅读下文,完成第下列各题。
伤仲永金溪民方仲永,世隶耕。
仲永生五年,未尝识书具,忽啼求之。
父异焉,借旁近与之,即书诗四句,并自为其名。
其诗以养父母、收族为意,传一乡秀才观之。
自是指物作诗立就,其文理皆有可观者。
邑人奇之,稍稍宾客其父,或以钱币乞之。
父利其然也,日扳仲永环谒于邑人,不使学。
余闻之也久。
明道中,从先人还家,于舅家见之,十二三矣。
令作诗,不能称前时之闻。
又七年,还自扬州,复到舅家问焉。
曰:“泯然众人矣”。
(1)本文作者是宋朝的________(人名)。
(2)解释下列加点字。
(3)用现代汉语翻译下面的句子。
邑人奇之,稍稍宾客其父。
(4)这个故事告诫人们________。
4. 阅读下文,完成第下列各题。
北人食菱北人生而不识菱①者,仕于南方,席上食菱,并壳入口。
或曰:“食菱须去壳。
”其人自护所短,曰:“我非不知,并壳者,欲以去热也。
”问者曰:“北土亦有此物否?”答曰:“前山后山,何地不有?”夫菱生于水而曰土产,此坐强不知以为知也。
沪教版六年级数学试卷:上海市闵行区九校联考六年级(上)期中数学试卷(PDF版 含解析)

部分的面积是大长方形面积的 ( )
A .1 2
B .1 3
C .2 5
D .1 5
【解答】解: 设一个小长方形的面积为 1 ,则大长方形的面积为 5 , 4 个小长方形的面
积为 4 ,求得阴影面积为 2 ,
则25 2, 5
所以阴影部分的面积是大长方形面积的 2 , 5
故选: C .
-8-
三、计算题(本大题共 5 题,每题 5 分,满分 25 分)
则 123 至少加上 3 才能同时被 2 和 3 整除.
故答案是:3. 4.(2 分)已知 A 2 2 3 5 , B 2 3 5 7 ,那么 A 和 B 两数的最大公因数是 30 . 【解答】解: A 2 2 3 5 , B 2 3 5 7 , 那么 A 和 B 两数的最大公因数是: 2 3 5 30 ,
.
5.(2 分)分母是 8 的最简真分数有
个.
6.(2 分)比较大小: 5
2.
8
5
7.(2 分)11 ( ) . 3 18
8.(2 分)我们做一次眼保健操大约需要 5 分钟,每天做两次.我们每天做眼保健操的时间
大约占 1 小时的
.
9.(2 分)
和 3 的积是 12. 4
10.(2 分)请写出一个大于 1 而小于 1 的最简分数可以是
故答案为 5 . 3
12.(2 分)如图,把一个正方形各边中点连结起来组成第二个正方形,再把第二个正方形
各边的中点连结起来组成第三个正方形,按照这样的方法连结得到的第五个正方形的面
积占第一个正方形面积的 1 .(填几分之几) 16
-6-
【解答】解:正方形的边长是 1,
2021届上海市高三上学期九校联考一模物理试卷

上海市2021届九校联考高三一模试卷物理一、单项选择题(每小题只有一个正确答案,第1-8 题,每题 3 分,第9-12 题,每题4 分,共40 分)1.5G 是“ 第五代移动通信网络” 的简称,目前世界各国正大力发展5G 网络。
5G 网络使用的无线电波通信频率在3.0 GHz 以上的超高频段和极高频段(如图所示),比目前4G 及以下网络(通信频率在0.3GHz ~ 3.0GHz 间的特高频段)拥有更大的带宽和更快的传输速率.未来5G 网络的传输速率(指单位时间传送的数据量大小)可达10G bps (bps 为bits per second 的英文缩写,即比特率、比特/ 秒),是4G 网络的50-100 倍.关于5G 网络使用的无线电波,下列说法正确的是A .在真空中的传播速度更快B .在真空中的波长更长C .衍射的本领更强D .频率更高,相同时间传递的信息量更大【答案】D2.如图所示,质量为M 的小车的表面由光滑水平面和光滑斜面连接而成,其上放一质量为m 的球,球与水平面的接触点为 a ,与斜面的接触点为 b ,斜面倾角为θ。
当小车和球一起在水平桌面上做直线运动时,下列说法正确的是()A .若小车匀速运动,则球对斜面上b 点的压力大小为mgcosθB .若小车匀速运动,则球对水平面上a 点的压力大小为mgsinθC .若小车向左以加速度gtanθ加速运动,则球对水平面上a 点无压力D .若小车向左以加速度gtanθ加速运动,小车对地面的压力小于(M+m )g【答案】C3.如图所示,小船以大小为v( 船在静水中的速度) 、方向与上游河岸成θ的速度从O 处过河,经过一段时间,正好到达正对岸的O '处。
现要使小船在更短的时间内过河并且也正好到达正对岸O '处,在水流速度不变的情况下,可采取的方法是()A.θ角不变且v 增大B.θ角减小且v 增大C.θ角增大且v 减小D.θ角增大且v 增大【答案】D4.如图所示,一个质量为m 的物体(可视为质点),由斜面底端的A 点以某一初速度冲上倾角为30°的固定斜面做匀减速直线运动,减速的加速度大小为g ,物体沿斜面上升的最大高度为h ,在此过程中()A .重力势能增加了2mghB .机械能损失了mghC .动能损失了 mghD .系统生热【答案】 B5.如图所示,在空间中水平面 MN 的下方存在竖直向下的匀强电场,质量为 m 的带电小球由 MN 上方的 A 点以一定初速度水平抛出,从 B 点进入电场,到达 C 点时速度方向恰好水平, A 、 B 、 C 三点在同一直线上,且电场力为 3mg 。
2021届上海市第九中学高三语文第一次联考试题及答案解析

2021届上海市第九中学高三语文第一次联考试题及答案解析一、现代文阅读(36分)(一)现代文阅读I(9分)阅读下面的文字,完成下列小题。
材料一:我国已步入老龄化社会。
2019年,我国60周岁及以上人口已增至2.54亿,占总人口的18.1%。
有人预计,到2050年前后,我国老年人口将增至4.87亿,人口老龄化水平将升至34.8%左右。
当老龄化社会遭遇“手机扫码时代”,两者如何并行不悖,让老年人也安享便利?2020年重阳节之际,记者对此展开走访调查。
因疫情原因,如今很多公园要求游客出示健康码,因为不会用智能手机,一些老年人连公园的门都进不去;交手机费、打出租车、到商店买东西,被频频拒收现金;因为不会用手机买票、挂号,很多老人只能一趟趟跑火车站、跑医院……记者走访中,不少老年人感叹,智能手机应用为现代生活打开了一扇“快捷之门”,却把不少老年人档在了快捷之外。
(摘编自新华社《“手机扫码”时代,如何让老年人也安享便利?》)材料二:今年年初,央行在我国7省份进行抽样调查,获取有效问卷2万余份。
调查显示,未使用电子支付工具的受访者比例为17.6%,人物特点是老年人、低学历、低收入、退休人员、农村地区。
其中,60岁以上人群当中使用电子支付的仅为51%。
“由于身心特点、思想观念、知识结构等多方面原因,老年人接受新信息、学习新技能的能力较弱,对智能设备与智慧生活的适应比年轻人慢。
”上海社会科学院城市与人口发展研究所副研究员于宁说,尤其是高龄老人,这方面遇到的困难相对更多。
她分析说,当前很多场合需要智能手机扫码或下载安装App才能开展相应服务与操作,但部分手机产品并没考虑到老年人的群体特点,产品让老人学习起来较为复杂。
况且,不少老年人用的还是“老人机”,扫码功能都不具备,更无法进行其他操作。
事实上,适合老年人用的手机不需过多附加功能与高端配置,只要能够具备基本的扫码支付与App安装使用等功能即可。
但记者走访中发现,目前,符合老年人生理心理特点、适合老年人使用的智能手机,市场上还不多见。
2021年上海市第九中学高三英语第一次联考试题及答案

2021年上海市第九中学高三英语第一次联考试题及答案第一部分阅读(共两节,满分40分)第一节(共15小题;每小题2分,满分30分)阅读下列短文,从每题所给的A、B、C、D四个选项中选出最佳选项ATwitter humorist and TV writer Jonny Sun is the author of the 2017 best-sellereveryone'sa aliebn when ur a aliebn too. This time, he recommends some emotionally powerful books.The Book of Delightsby Ross Gay(2019)Gay's collection of 102 short but emotional stories, begun in mid-2016 and written in the order of time over a year in America, focuses on the careful observation of ordinary delights in daily life. The writing is personal and grounded in thoughtful joy.100 Essays I Don't Have Time to Writeby Sarah Ruhl(2014)Seemingly a collection of essays on theater, Ruhl's book feels instead like the playwright's thoughts all of life. Her writing here is deeply personal, sharply argued but also playful. The book is actually a detailed description of the artist herself.They Can't Kill Us Until They Kill Usby Hanif Abdurraqib(2017)I am always so moved by Abdurraqib's writing. He combines cultural criticism and personal memory in such a beautiful way, making the two styles naturally bound.Space Struckby Paige Lewis(2019 )This poetry collection awakened emotions in me that I did not know existed, or that I could feel, or that one could ever put words to. Every line is playful, honest, complex, and gentle.If you want to get more books, you can click here:Try more books1. Which book is a collection of short stories of daily happiness?A. The Book of Delights.B. 100 Essays I Don't Have Time to Write.C. They Can't Kill Us Until They Kill Us.D. Space Struck.2. Who is probably a poet?A. Ross Gay.B. Sarah Ruhl.C. Hanif Abduraqib.D. Paige Lewis.3. Where is the text most likely from?A. A diary.B. A brochure.C. A website.D. A magazine.BWe all know that a healthy lifemeans getting both plenty of exercise and enough good-quality sleep, but reality often gets in the way. The new research indicates that doing enough exercise could make up for some of the unhealthy impacts of bad sleep. While the health benefits of exercise and sleep are nothing new, it's the relationship between them that is interesting in this particular study — it could even give doctors another option to suggest for patients dealing with sleep problems.“We found those who had both the poorest sleep quality and who exercised the least were most at risk of death from heart disease, stroke, and cancer,” says epidemiologist Bo-Huei Huang, from the University of Sydney in Australia.Participants were grouped into three levels of physical activity (high, medium or low) and were also given a sleep quality score from 0-5 based on the amount of shut-eye they got, how late they stayed up, insomnia, snoring and daytime sleepiness.Those with the highest risk of dying from cancer or heart disease during the study period were those with the worst quality sleep and who didn't meet the WHO recommended guidelines for exercise. That risk went down for people with poor quality sleep but who did meet the exercise guidelines.In the case of all forms of cancer, for example, those at the unhealthiest end of the sleep and exercise scale had a 45 percent higher risk of dying from cancer than those with good sleep scores who kept physically active. However, that risk just about disappeared for those who didn't score well on sleep but did score well on physical activity.For now it's not clear why more exercise might make up for poor sleep, as far as our health goes. It could be that the increased activity iscounteractinginflammation (炎症), or reducing irregularities in glucose metabolism, suggest the researchers.“Considering that physical activity is perhaps more modifiable than sleep, our study offers people more health incentives to be physically active.” says population health researcher Emmanuel Stamatakis, from the University of Sydney.4. This research is of particular interest in that ________.A. it’s in this study that exercise is known to be beneficial to sleep.B. this study offers people more health treatments to be physical active.C. it could enable doctors to cure patients of their sleeping condition.D. the relationship between exercise and sleep is updated in this study.5. Which of the following statements istrueaccording to the passage?A. Those who had the poorest sleep quality were most at risk of death from heart disease.B. Those scoring lowest on sleep and exercise scale were more likely to die from cancer.C. There’s no risk of cancer for those who didn't sleep well but did score well on physical activity.D. It's evident that in terms of health more exercise could make up for poor sleep.6. What does the underlined word in Paragraph 6 mean?A. interactingB. increasingC. preventingD. causing7. Where can this passage most probably be taken from?A. A research findings reportB. A medical examination reportC. A poor sleep study reportD. A physical activity study reportCIt’s a little before8 a.m. when Mathias Schergen pushes open the side door at Chicago’s Jenner Elementary Academy for the Arts. He walks down the hall toward the office to sign in. It’s the same routine he’s had as Jenner’s art teacher for nearly a quarter century. “It’s going to be a good day,” a colleague calls out. “It’s a good day.” They hug. It seems like a typical Friday. Except it’s not. After 23 years at Jenner Elementary, Schergen is retiring. Even on his last day, there are still art projects to finish.Schergen leaves behind a richlegacyat this school. He’s won grants (拨款) for art projects. He turned an empty classroom into a museum. He’s pushed his students to make art about their lives. And he was awarded a Golden Apple — the most honorable teaching award in Chicago. But it wasn’t always easy. For years, Schergen taught in one of the city’s toughest neighborhoods. “When I first got my room, I noticed there were bullet holes in the window. That made me nervous,” he says. So he stuffed Beanie Babies in the holes to make it “look kind of funny”. “I didn’t even tell my wife for a whole year,” he says. “I didn’t want her to know.”With one hour to go, Schergen piles the chairs and sweeps the floor. He cleans out the sink for the last time. Fifth-grader Deontae Barnes, one of his best helpers, has watched him say goodbye all day. He wanders in the doorway. “Ah, come here, son,” Schergen says, signaling him over. He bends down for a hug. “Thank you for making these last days special and being a help to me.”When Deontae leaves, a reporter asks Schergen: When your kids ask why you’re retiring, what do you tellthem? “I just tell them that grown people have dreams too,” he says. “I have other things in my life I have to do. It’s time. It’s just time.”8. Why is it a special Friday for Schergen?A. He was retiring on that day.B. He won an honor for his school.C. He was interviewed by a reporter.D. He received a Golden Apple award.9. What does the underlined word “legacy” in Paragraph 2 refer to?A. Art projects.B. Great achievements.C. Respect from students.D. Change in teaching.10. What made Schergen nervous when he first got to the school?A. Safety concerns in the school.B. The poorly-equipped classroom.C. Being misunderstood by his family.D. Students’ poor academic performance.11. What is the best title for the text?A.A Typical Day for an Art TeacherB. Time for Art ProjectsC. A Teacher’s Final Day at SchoolD. The Last Art ClassDTo show empathy is to identify with another’s feelings. It is to emotionally put yourself in the place of another. The ability to empathize is directly dependent on your ability to feel your own feelings and identify them.If you have never felt a certain feeling, it will be hard for you to understand how another person is feeling. If you have never put your hand in a flame, you will not know the pain of fire. If you have not experienced jealousy, you will not understand its power.Readingabout a feeling and intellectually knowing about it is very different than actually experiencing it for yourself.Among those with an equal level of emotional intelligence, the person who has actually experienced the widest range and variety of feelings — the great depths of depression and the heights of fulfillment, for example, — is the one who is most able to empathize. On the other hand, when we say that someone “can’t relate” to other people, it is likely because they haven’t experienced, acknowledged or accepted many feelings of their own.Once you have felt discriminated against, for example, it is much easier to relate with someone else who has been discriminated against. Our innate emotional intelligence gives us the ability to quickly recall those instances and form associations when we encounter discrimination again. We then can use the “reliving” of those emotions to guide our thinking and actions. This is one of the ways nature slowly evolves towards a higher level of survival.For this process to work, the first step is that we must be able to experience our own emotions. This meanswe must be open to them and not distract ourselves from them or try to numb ourselves from our feelings through drugs, alcohol, etc.Next, we need to become aware of what we are actually feeling — to acknowledge, identify, and accept our feelings. Only then can we empathize with others. That is one reason why it is important to work on your own emotional awareness and sensitivity — in other words, to be “in touch with” your feelings.12. How does the author explain the feelings of empathy?A. By giving examples.B. By having classification.C. By making comparison.D. By providing data.13. Which statement may the author agree with?A. Low level of empathy leads to fewer varieties of feelings.B. The deeper one’s feelings are, the more empathetic one is.C. Empathy is a way we recently picked up for better survival.D. Rich experiences may not go with a high level of empathy.14. What’s the purpose of the last two paragraphs of the text?A. To advise a sincere attitude to one’s experiences.B To suggest a right understanding of empathy.C. To require a realbond with one’s emotions.D. To call for true acceptance of one’s feelings.15. What is the best title for the text?A. How Empathy UnfoldsB. Be Open to Your EmotionsC. Why Is Empathy ImportantD. Accept Your True Self第二节(共5小题;每小题2分,满分10分)阅读下面短文,从短文后的选项中选出可以填入空白处的最佳选项。
上海市崇明区九校联考(五四制)2024-2025学年六年级上学期期中考试数学试题

上海市崇明区九校联考(五四制)2024-2025学年六年级上学期期中考试数学试题一、单选题1.下列等式中表示整除的是()A .202412024÷=B .202436742÷= C .20245404.8÷=D .20240.54048÷=2.下列各式中,表示分解素因数的式子是()A .3622331=⨯⨯⨯⨯B .223336⨯⨯⨯=C .36433=⨯⨯D .362233=⨯⨯⨯3.下列各组数中,不是互素的有()A .13和15B .27和28C .1和20D .21和494.下列分数中,可以化为有限小数的是()A .56B .312C .815D .2185.图中网状阴影部分可以用算式()表示.A .3143⨯B .2334⨯C .2133⨯D .3144⨯6.一个分数的分子扩大为原来的3倍,分母缩小到原来的13,则分数值()A .扩大为原来的9倍B .扩大为原来的6倍C .缩小到原来的16D .不变二、填空题7.用分数表示:35÷=.8.18的因数有.9.243的倒数是.10.比较大小:2.4115(填“>”或“<”号).11.一根绳子长4米,把它平均剪成5段,每段是这根绳子的(),每段长()米.12.在括号内填入适当的整数:()()224918+==,括号内应依次填入:()、().13.要使15x是真分数,14x 是假分数,x 应该是.14.请写出一个介于14和13之间的最简分数,这个分数可以是.15.23,35a m b m =⨯⨯=⨯⨯(m 是自然数且0m ≠),如a 和b 的最大公约数是21,则a 和b 的最小公倍数是().16.一堆煤有15吨,先运走它的13,再运走余下的13,还剩下()吨.17.“转化”是一种解决问题的常用策略,有时画图可以帮助我们找到转化的方法,例如借助图(1),可以把算式1357911+++++转化为26=36,请你观察图(2),可以把算式111112481632++++转化为.18.如图,两条线段把长方形分成了大、中、小三个三角形,小三角形的面积是大三角形面积15,中三角形的面积是长方形面积的().三、解答题19.计算:2113122-+.20.计算:14131393÷⨯.21.164133534÷-⨯.22.计算:8710.759164⎡⎤⎛⎫⨯-- ⎪⎢⎥⎝⎭⎣⎦23.解方程:2734x =.24.一个数的23是92的倒数,求这个数.25.请分别写出点A 、点B 和点C 所对应的数,点A 是______,点B 是_______,点C 是_______,并在数轴上,画出点D :103,比较A 、B 、C 、D 四个数的大小,并用“<”连接_________.26.“学生艺术节”快到了,六年级学生排练舞蹈.舞蹈老师要求除了领舞的1人外,其余的人要作队形变换,既要能平均分成4组,又要能平均分成6组.那么至少要选拔多少名学生参加跳舞?27.星期天,小明去新华书店买书,他共带了60元钱.首先他买了一本科普读物,恰好花了他所带钱数的13,接着他又用余下钱数的35买了一本小说,那么,此时他还剩下多少元钱?28.六年级某班一次数学成绩的统计图如图所示,回答下列问题:(1)成绩在80分以上(含80分)的同学人数是全班人数的几分之几?(2)成绩在70~79分的同学人数是成绩在80~89分的的同学人数的几分之几?29.阅读与理解:我们把形如1n(n 是正整数,2n ≥)的分数叫做单位分数,如111234⋅⋅⋅、、(1)任何一个单位分数都可以拆成两个不同的单位分数之和,如11111111123634124520=+=+=+⋅⋅⋅、、,观察上述式子的规律,回答下面的问题:①把18写成两个单位分数之和:18=_______.②把1n (n 是正整数,2n ≥)写成两个单位分数之和:1n=_______.(2)某些单位分数也可以拆成两个分母是相邻自然数的单位分数的差,如11111111162312342045=-=-=-⋅⋅⋅、、,观察上述式子的规律,回答下面的问题:①在单位分数1111234100⋅⋅⋅、、中,能按上述要求拆分的有________个.②若在单位分数1111234n⋅⋅⋅、、中,能按上述要求拆分的有30个,则n 的最大值为________.。
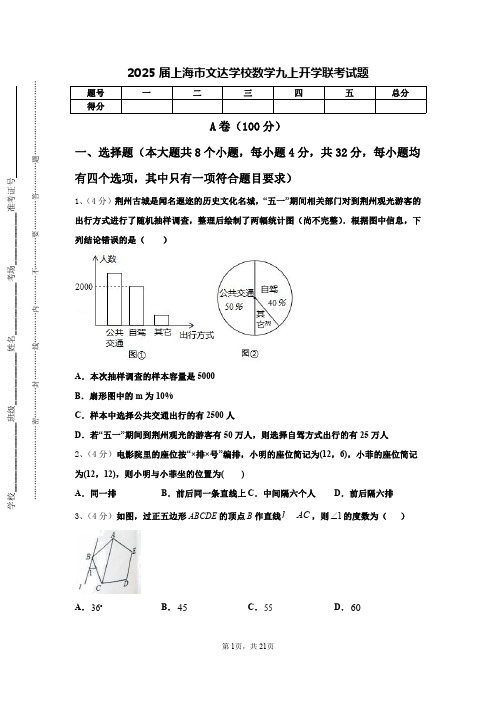
2025届上海市文达学校数学九上开学联考试题【含答案】
2025届上海市文达学校数学九上开学联考试题题号一二三四五总分得分A 卷(100分)一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求)1、(4分)荆州古城是闻名遐迩的历史文化名城,“五一”期间相关部门对到荆州观光游客的出行方式进行了随机抽样调查,整理后绘制了两幅统计图(尚不完整).根据图中信息,下列结论错误的是()A .本次抽样调查的样本容量是5000B .扇形图中的m 为10%C .样本中选择公共交通出行的有2500人D .若“五一”期间到荆州观光的游客有50万人,则选择自驾方式出行的有25万人2、(4分)电影院里的座位按“×排×号”编排,小明的座位简记为(12,6),小菲的座位简记为(12,12),则小明与小菲坐的位置为()A .同一排B .前后同一条直线上C .中间隔六个人D .前后隔六排3、(4分)如图,过正五边形ABCDE 的顶点B 作直线l AC ,则1 的度数为()A .36oB .45C .55D .604、(4分)如果一组数据1、2、x 、5、6的众数是6,则这组数据的中位数是()A .1B .2C .5D .65、(4分)在Rt ABC ∆中,90C ∠=︒,30A ∠=︒,A ∠、B Ð、C ∠的对边分别是a 、b 、c ,则下列结论错误的是()A .2c a =B .222+=a b c C .:1:a b =D .222b a =6、(4分)点()111,P x y ,点()222,P x y 是一次函数43y x =-+图象上的两个点,且12x x <,则1y 与2y 的大小关系是()A .12y y >B .120y y >>C .12y y <D .12y y =7、(4分)某校生物小组11人到校外采集标本,其中2人每人采集到6件,4人每人采集到3件,5人每人采集到4件,则这个小组平均每人采集标本()A .3件B .4件C .5件D .6件8、(4分)如图,在ABC ∆中,4AC =,3BC =,5AB =,D 为AB 上的动点,连接CD ,以AD 、CD 为边作平行四边形ADCE ,则DE 长的最小值为()A .3B .4C .165D .125二、填空题(本大题共5个小题,每小题4分,共20分)9、(4分)数据1、x 、-1、2的平均数是12,则这组数据的方差是_______.10、(4分)若关于x 的一元二次方程2240x mx m ++-=有一个根为0x =,则m =________.11、(4分)若平行四边形中两个内角的度数比为1:2,则其中一个较小的内角的度数是________°.12、(4分)点A (a ,b )是一次函数y =x +2与反比例函数4y x =的图像的交点,则22a b ab -=__________。
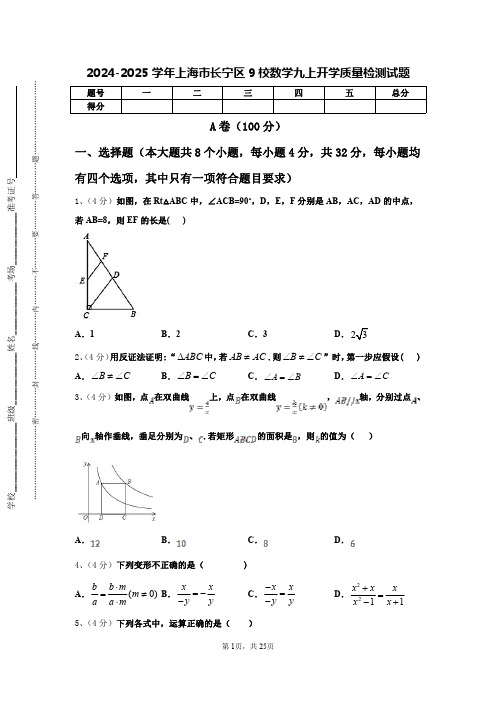
2024-2025学年上海市长宁区9校数学九上开学质量检测试题【含答案】
2024-2025学年上海市长宁区9校数学九上开学质量检测试题题号一二三四五总分得分A 卷(100分)一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求)1、(4分)如图,在Rt △ABC 中,∠ACB=90˚,D ,E ,F 分别是AB ,AC ,AD 的中点,若AB=8,则EF 的长是()A .1B .2C .3D .2、(4分)用反证法证明:“ABC ∆中,若AB AC ≠.则B C ∠≠∠”时,第一步应假设()A .B C ∠≠∠B .B C ∠=∠C .A B ∠=∠D .A C ∠=∠3、(4分)如图,点在双曲线上,点在双曲线,轴,分别过点、向轴作垂线,垂足分别为、.若矩形的面积是,则的值为()A .B .C .D .4、(4分)下列变形不正确的是()A .(0)b b m m a a m ⋅=≠⋅B .x x y y =--C .xxy y -=-D .2211x x xx x +=-+5、(4分)下列各式中,运算正确的是()A .2=-B .3=C 3=D .26、(4分)在一次统考中,从甲、乙两所中学初二学生中各抽取50名学生进行成绩分析,甲校的平均分和方差分别是82分和245分,乙校的平均分和方差分别是82分和190分,根据抽样可以粗略估计成绩较为整齐的学校是()A .甲校B .乙校C .两校一样整齐D .不好确定哪校更整齐7、(4分)因式分解x 2﹣9y 2的正确结果是()A .(x+9y )(x ﹣9y )B .(x+3y )(x ﹣3y )C .(x ﹣3y )2D .(x ﹣9y )28、(4分)若a,b 为等腰△ABC 的周长为()A .9B .12C .15或12D .9或12二、填空题(本大题共5个小题,每小题4分,共20分)9、(4分)如图是小强根据全班同学喜爱四类电视节目的人数而绘制的两幅不完整的统计图,则喜爱“体育”节目的人数是_____人.10、(4分)已知一个直角三角形的斜边长为6cm ,那么这个直角三角形斜边上的中线长为________cm.11、(4分)已知,函数y=(k-1)x+k 2-1,当k ________时,它是一次函数.12、(4分)如图,已知中,边上的高,则的面积是______,边上的高的长是______.13、(4分)某老师为了了解学生周末利用网络进行学习的时间,在所任教班级随机调查了10名学生,其统计数据如下表:时间(单位:小时)43210人数24211则这10名学生周末利用网络进行学均时间是小时.三、解答题(本大题共5个小题,共48分)14、(12分)某中学九年级1班同学积极响应“阳光体育工程”的号召,利用课外活动时间积极参加体育锻炼,每位同学从长跑、篮球、铅球、立定跳远中选一项进行训练,训练前后都进行了测试.现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图表.项目选择统计图训练后篮球定时定点投篮测试进球统计表进球数(个)876543人数214782请你根据图表中的信息回答下列问题:(1)选择长跑训练的人数占全班人数的百分比是___________,该班共有同学___________人;(2)求训练后篮球定时定点投篮人均进球数;(3)根据测试资料,训练后篮球定时定点投篮的人均进球数比训练之前人均进球数增加25%.请求出参加训练之前的人均进球数.15、(8分)实验中学学生在学习等腰三角形性质“三线合一”时(1)(探究发现)如图1,在△ABC中,若AD平分∠BAC,AD⊥BC时,可以得出AB=AC,D 为BC中点,请用所学知识证明此结论.(2)(学以致用)如果Rt△BEF和等腰Rt△ABC有一个公共的顶点B,如图2,若顶点C与顶点F也重合,且∠BFE=12∠ACB,试探究线段BE和FD的数量关系,并证明.(3)(拓展应用)如图3,若顶点C与顶点F不重合,但是∠BFE=12∠ACB仍然成立,(学以致用)中的结论还成立吗?证明你的结论.16、(8分)甲、乙两人参加操作技能培训,他们在培训期间参加的5次测试成绩(满分10分)记录如下:5次测试成绩(分)平均数方差甲8878980.4乙5971098 3.2(1)若从甲、乙两人中选派一人参加操作技能大赛,你认为应选谁?为什么?(2)如果乙再测试一次,成绩为8分,请计算乙6次测试成绩的方差(结果保留小数点后两位).17、(10分)如图,在平行四边形ABCD中,∠ABC=45°,E、F分别在CD和BC的延长线上,AE∥BD,∠EFC=30°,AB=1.求CF的长.18、(10分)学完第五章《平面直角坐标系》和第六章《一次函数》后,老师布置了这样一道思考题:已知:如图,在长方形ABCD 中,BC=4,AB=2,点E 为AD 的中点,BD 和CE 相交于点P.求△BPC 的面积.小明同学应用所学知识,顺利地解决了此题,他的思路是这样的:建立适合的“平面直角坐标系”,写出图中一些点的坐标.根据“一次函数”的知识求出点P 的坐标,从而可求得△BPC 的面积.请你按照小明的思路解决这道思考题.B 卷(50分)一、填空题(本大题共5个小题,每小题4分,共20分)19、(4分)如图,OP=1,过P 作PP 1⊥OP 且PP 1=1,得OP 1;再过P 1作P 1P 2⊥OP 1且P 1P 2=1,得OP 2又过P 2作P 2P 3⊥OP 2且P 2P 3=1,得OP 3=2…依此法继续作下去,得20142015OP P S ∆=____.20、(4分)若分式3||3x x -+的值为零,则x 的值为_____21、(4分)存在两个变量x 与y ,y 是x 的函数,该函数同时满足两个条件:①图象经过(1,1)点;②当x >0时,y 随x 的增大而减小,这个函数的解析式是▲(写出一个即可).22、(4分)直角三角形的三边长分别为a 、b 、c ,若3a =,4b =,则c =__________.23、(4分)如图,矩形ABCD 中,3AB =,4BC =,CE 是ACB ∠的平分线与边AB 的交点,则BE 的长为______.二、解答题(本大题共3个小题,共30分)24、(8分)如图,点C 在线段AB 上,过点C 作CD ⊥AB ,点E ,F 分别是AD ,CD 的中点,连结EF 并延长EF 至点G ,使得FG =CB ,连结CE ,GB ,过点B 作BH ∥CE 交线段EG 于点H .(1)求证:四边形FCBG 是矩形.(1)己知AB =10,.①当四边形ECBH 是菱形时,求EG 的长.②连结CH ,DH ,记△DEH 的面积为S 1,△CBH 的面积为S 1.若EG =1FH ,求S 1+S 1的值.25、(10分)某童装网店批发商批发一种童装,平均每天可售出20件,每件盈利40元.经调查,如果每件童装降价1元,那么平均每天就可多售出2件.(1)设每件童装降价x 元,那么每天可售出多少件童装?每件童装的利润是多少元?(用含x 的代数式表示)(2)为了迎接“六一”儿童节,商家决定降价促销、尽快减少库存,又想保证平均每天盈利1200元,求每件童装应降价多少元?26、(12分)再读教材:宽与长的比是2(约为0.618)的矩形叫做黄金矩形,黄金矩形给我们以协调,匀称的美感.世界各国许多著名的建筑.为取得最佳的视觉效果,都采用了黄金矩形的设计,下面我们用宽为2的矩形纸片折叠黄金矩形.(提示;MN=2)第一步,在矩形纸片一端.利用图①的方法折出一个正方形,然后把纸片展平.第二步,如图②.把这个正方形折成两个相等的矩形,再把纸片展平.第三步,折出内侧矩形的对角线AB,并把AB 折到图③中所示的AD 处,第四步,展平纸片,按照所得的点D 折出DE,使DE ⊥ND,则图④中就会出现黄金矩形,问题解决:(1)图③中AB=________(保留根号);(2)如图③,判断四边形BADQ 的形状,并说明理由;(3)请写出图④中所有的黄金矩形,并选择其中一个说明理由.(4)结合图④.请在矩形BCDE 中添加一条线段,设计一个新的黄金矩形,用字母表示出来,并写出它的长和宽.参考答案与详细解析一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求)1、B【解析】利用直角三角形斜边中线定理以及三角形的中位线定理即可解决问题.【详解】解:在Rt△ABC中,∵AD=BD=4,∴CD=12AB=4,∵AF=DF,AE=EC,∴EF=12CD=1.故选:B.本题考查三角形的中位线定理、直角三角形斜边上的中线的性质等知识,解题的关键是熟练掌握三角形的中位线定理以及直角三角形斜边上的中线的性质解决问题,属于中考常考题型.2、B【解析】熟记反证法的步骤,直接选择即可【详解】解:用反证法证明命题“在△ABC中,AB≠AC,求证:∠B≠∠C”的过程中,第一步应是假设∠B=∠C.故选:B本题结合角的比较考查反证法,解此题关键要懂得反证法的意义及步骤.反证法的步骤是:(1)假设结论不成立;(2)从假设出发推出矛盾;(3)假设不成立,则结论成立.在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定.3、A 【解析】首先得出矩形EODA 的面积为:4,利用矩形ABCD 的面积是8,则矩形EOCB 的面积为:4+8=1,再利用xy=k 求出即可.【详解】过点A 作AE ⊥y 轴于点E ,∵点A 在双曲线上,∴矩形EODA 的面积为:4,∵矩形ABCD 的面积是8,∴矩形EOCB 的面积为:4+8=1,则k 的值为:xy=k=1.故选A .此题主要考查了反比例函数关系k 的几何意义,得出矩形EOCB 的面积是解题关键.4、D【解析】根据分式的基本性质:分式的分子和分母扩大还是缩小相同的倍数,分式的值不变进行解答.【详解】()0bb mm a a m ⋅=≠⋅,A 正确;x x y y =--,B 正确;x x y y -=-,C 正确;2211x x x x x +=--,D 错误,故选D .本题考查的是分式的基本性质,解题的关键是正确运用分式的基本性质和正确把分子、分母进行因式分解.5、C 【解析】根据二次根式的性质对A 进行判断;根据二次根式的除法法则对C 进行判断;根据二次根式的加减运算对B 、D 进行判断.【详解】A.原式=|−2|=2,所以A 选项错误;B.原式=,所以B 选项错误;C.3=,所以C 选项正确;D.2D 选项错误。
上海市崇明区九校联考(五四制)2024-2025学年八年级上学期期中考试物理试题

上海市崇明区九校联考(五四制)2024-2025学年八年级上学期期中考试物理试题一、单选题1.初中阶段的物理课程偏重于对物理现象、物理概念和物理规律的直观把握、()和简单分析。
A.定量描述B.定性描述C.直观描述D.简要描述2.下列物体的质量最接近150克的是()A.一只鸡B.一个苹果C.一头大象D.一枚大头针3.12岁的李明一年内明显长高了,他增长的高度可能是()A.8cm B.8mm C.8dm D.8µm4.“五一”联欢会期间,小王在演出前调节了二胡弦的松紧程度。
他是在调()A.音调B.响度C.音色D.振幅5.声波在下列介质中传播最快是()A.空气B.水C.木材D.铁6.下列关于运动和静止的说法,正确的是()A.校园里的教学楼,若以地面为参照物,教学楼是运动的B.飞机在空中加油时,若以受油机为参照物,加油机是运动的C.运稻谷的车辆和联合收割机以同样快慢、向同一方向前进,以地面为参照物,它们都在运动D.以地面为参照物,站在正在运行的自动扶梯上的乘客是静止的二、填空题7.测量的目的是为了进行可靠的比较。
在利用测量工具测量时,要观察测量工具的和。
8.质量是物体本身的一种。
质量在国际单位制中的单位是。
一块冰融化成水以后,没有发生变化的量是(选填“质量”或“体积”或“形状”)。
9.某次测量活动中,一位粗心同学忘了写单位,请你给他补完整。
(1)人正常行走时,一步长约0.8 ;(2)一节1号电池的高度约0.6 ;(3)一位中学生的质量是55 ;(4)某同学百米赛跑的成绩为14 。
10.水中的游鱼被站在岸上的人讲话声吓跑,鱼听到声音是经历了和两种物质传播.这个现象说明气体能传声以外,同时说明也能传声.11.有时候我们形容一种声音“脆如银铃”指的是声音三个特征中的高,反映发声体振动的频率(选填“高”或“低”);“震耳欲聋”指的是声音的大;在听熟人打来的电话时,容易听出对方是谁,原因是不同的人讲话时声音的不同。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2006-2007学年度上海市九校第一学期联考试卷
一. 填空题(本大题共12小题,每小题4分,共48分) 1. 抛物线y x 42
=的焦点坐标为___________
2. 角α的终边过点)3,4(a a P -)0(>a ,则=+ααCos Sin 2_____________
3. 设集合{}
R x x x A ∈≥-=,914,⎭
⎬⎫⎩⎨⎧∈>+=R x x x x
B ,03,则B A ⋂=_____________ 4. 若z 与()i z 822
-+都是纯虚数,则z =_________
5. 函数)0(12
)(>+=-x x f x
的反函数是_____________
6. 7位同学中需选派4位按一定的顺序参加某演讲比赛,要求甲,乙两人必须参加,且甲
必须在乙之前出场,那么不同的安排方法有____________种。
7. ABC ∆的三内角
,,A B C 所对边的长分别为,,a b c 设向量
),(b c a +=,),(a c a b --= ,若//,则角C 的大小为___________
8. 定义域为R 的函数)(x f y =的值域为[]b a ,,则函数)(a x f y +=的值域为___________ 9. 若数列}{n a 满足: 3
1
1=
a , 且对任意正整数n m ,都有n m n m a a a ⋅=+, 则=++++∞
→)......(lim 21n n a a a ___________
10. 若直线022=+-by ax ),(R b a ∈始终平分圆01422
2
=+-++y x y x 的周长,则
ab 的最大值是___________
11. 已知函数)1(log )(2
1x
a
x x f -
+=在区间[)+∞,1上单调递减,则实数a 的取值范围是___________ 12.
观察下列数表,问此表最后一个数是___________
1 2 3 4......97 98 99 100 3 5 7 ...... 195 197 199 8 12 ...... 392 396 20 (788)
二.选择题(本大题共4小题,每小题4分,共16分)
13.直线0=++b y xCosa ),(R b a ∈的倾斜角的取值范围是( ) A 、[)π,0 B 、⎪⎭⎫⎢⎣⎡⋃⎥⎦⎤⎢⎣⎡πππ,434,
0 C 、⎥⎦⎤⎢⎣⎡43,4ππ D 、⎥⎦
⎤
⎝⎛⋃⎪⎭⎫⎢⎣⎡43,22,4ππππ 14.命题甲:x
)4
1(、x -2、42-x 成等比数列;命题乙:x lg 、)2lg(+x 、)12lg(+x 成等
差数列,则甲是乙的( )
A 、充分不必要条件
B 、必要不充分条件
C 、充要条件
D 、既不充分也不必要条件 15.若函数)(x f y =)(R x ∈满足)()2(x f x f =+,且(]1,1-∈x 时,x x f =)(,则函数
)(x f y = 的图象与函数x y 4log =的图象的交点的个数为( )
A 、3
B 、4
C 、6
D 、8
16.某地一年的气温Q (t )(单位:ºc )与时间t (月份)之间的关系如图(1)所示,已知该年的平均气温为10ºc ,令G (t )表示时间段〔0,t 〕的平均气温,G (t )与t 之间的函数关系用下列图象表示,则正确的应该是( )
三.简答题:(本大题共6题,满分86分,解答下列各题必须写出必要的步骤)
C
17.(本题满分12分)
已知函数2
()22cos f x x x a =-+ (a R ∈,a 为常数),
(Ⅰ)求()f x 的周期和单调递增区间;
(Ⅱ)若[,]46
x ππ
∈-
时,()f x 的最小值为4,求a 的值。
18.(本题满分12分)
记函数()2
7
2++-
=x x x f 的定义域为A ,()()()[]()R a b ax b x x g ∈>+-=,012lg 的定义域为B ,
(1)求A ; (2)若B A ⊆,求a 、b 的取值范围。
19.(本题满分14分)
设1F 为椭圆1C :112
16)1(2
2=+-y x 的左焦点,1C M 是上任意一点,M F P 1是线段的中点, (1)求动点P 的轨迹C 的方程;
(2)若直线2-=kx y 交轨迹C 于A 、B 两点,AB 中垂线交轴y 于点)3
1
,0(Q ,求k 的值。
20.(本题满分14分)
某企业2005年的纯利润为500万元,因设备老化等原因,企业的生产能力将逐年下降。
若不能进行技术改造,预测从今年起每年比上一年纯利润少20万元,今年初该企业一次性投入资金600万元进行技术改造,预测在未扣除技术改造资金的情况下,第n 年(今年为第一年)的利润为1
500(1)2n
+
万元(n 为正整数)。
(Ⅰ)设从今年起的前n 年,若该企业不进行技术改造的累计纯利润为n A 万元,进行技术
改造后的累计纯利润为n B 万元(须扣除技术改造资金),求n A 、n B 的表达式; (Ⅱ)依上述预测一下:从长远效益来看,该企业有没有进行技术改造的必要?如有必要,
则至少要经过多少年后,才能初见进行技术改造的成效?请说明理由。
21.(本题满分16分)
已知2()log ,f x x =当点(,)M x y 在()y f x =的图象上运动时,点(2,)N x ny -在函数
()n y g x =的图象上运动(n N ∈).
1) 求()n y g x =的表达式;
2)
求集合A ={a 关于x 的方程12()(2)g x g x a =-+有实根,a R ∈};
3)
设)
()2
1()(x g n n x H =,函数11()()()(0)F x H x g x a x b =-<≤≤
的值域为
22[log ,log ]22
b a ++,求实数,a b 的值。
22.(本题满分18分)
在杨辉三角形中,除“两腰”上的数字外,其余任意数都等于它上一行“左右两肩”上的
数之和。
将杨辉三角形中的每一个数r
n C 都换成分数
1
(1)r n
n C +,得到莱布尼茨三角形
杨辉三角形 莱布尼茨三角形
(1)
类比杨辉三角形的上述性质,得真命题:莱布尼茨三角形中,每一个数都等于______________(只须填上类比而得的结论,不必证明)
(2)
在莱布尼茨三角形中,称“左腰”上的数字为“第1层”,紧靠“第1层”且与之平行的称为“第2层”,猜测“第2层”中各数按从上到下的顺序构成的数列{}n a 的一个通项公式(不必证明),并据此求该数列的前n 项和n S 。
设n n
n S a n b 2)1(+=)10(<<a ,若存在唯一的自然数k )2(≥k ,使得
1
12+<<-k k
a k k 成立,问数列{}n
b 中是否存在唯一的最大项,试证明你的结论。
2
131613
14
1121301121415
120
15120161
30
160
130
160
16
1 (1)
2
1112
1
1
3
6
3
1
141
4
1
5
10
5
10
1
(11)。
