整理诱导公式计算题100题
正弦、余弦的诱导公式

学科: 数学 年级: 高一 期数: 144正弦、余弦的诱导公式一、知识要点:熟记诱导公式,并能灵活应用进行求值、化简、证明,在应用中要特别注意诱导公式中符号(函数名和正负号)的变化,要了解已知三角函数值求角的方法。
二、典型例题:例1. 已知cos(-100︒)=k, 用k 表示ctg10︒.分析:首先知道cos(-100︒)=cos100︒, 根据题意,进行角的变换100︒=90︒+10︒, 再利用诱导公式及同角基本关系式即可求得。
解: ∵cos(-100︒)=cos100︒=cos(90︒+10︒)=-sin10︒又cos(-100︒)=k,∴ -sin10︒=k 即sin10︒=-k又10︒∈(0︒, 90︒) ∴cos10︒=110122-︒=-sin k∴ctg10︒=cos sin 10101122︒︒=--=--k k k k另解:sin10︒= -k 求法同前∵10︒∈(0︒, 90︒)∴ctg10︒=csc sin ||22221011101111︒-=︒-=-=-k k k 又sin10︒= -k>0 ∴k<0 ∴ctg10︒=--12k k例2. 若sin(α-π)=2cos(α-π)求sin()cos()sin()sin()παπαπαα++-+--5232分析:先利用诱导公式化简已知式可求得sin α, cos α之间的关系,然后再用诱导公式化简所求式,把sin α, cos α之间的其中一个消元即得。
解:由sin(α-π)=2cos(α-2π)得:-sin(π-α)=2cos(2π-α)-sin α=2cos α∴ sin α=-2cos α原式=-+-+=+--=-sin cos cos sin cos cos cos cos αααααααα53253275三.巩固训练(一) 选择题:1. 124364362+-+-tg tg ()()ππ的值是( ) A. 333+ B. 333- C. -3+1 D. 1+32. 已知cos(180︒+α)=-35, 则tg(360︒-α)的值等于( ) A. 43 B. -43C. ±43D. 333. tg(k πθ2+), k ∈Z 的值等于( ) A. ctg θ B. ±ctg θC. tg θ或ctg θD. tg θ或-ctg θ4. 若sin 57π=m, 则cos(4π-57π), ctg(-4π+27π)的值分别是( ) A. 1122--m m m , B. ---1122m m m, C. ----1122m m m , D. 1122---m m m, 5. 下列各式的值与sinA 相同的是( )A. sin(90︒-A)B. cos(90︒+A)C. cos(270︒+A)D. sin(180︒+A)6. sin(α-π4)+cos(α+π4)可化简为( ) A. 2sin(α-π4) B. 2cos(α+π4) C. 0 D. 17. 如果cos(π-x)=32, x ∈(-π, π], 则x 的值为( ) A. 5676ππ, B. ±π6 C. ±56π D. ±23π 8. 若sin(π-α)=log 814, 且α∈(π2, 0), 则tg(32π+α)的值为( ) A. -52 B. 52 C. ±52 D. -259. 已知cos(x+π3)=0, 则x 等于( ) A. π6 B. -56πC. π6或-56πD. kx+π6(k∈Z)10. c tg(323πα+=), 则sin(32πα-)等于( )A. 12B. -12C. 12或-12D.2211. 若12-sin x=-cosx 则x为( )A. 2kπ+π2<α<2kπ+π(k∈Z)B. 2kπ+π≤α≤2kπ+34π(k∈Z)C. 2kπ+π2≤α<2kπ+32π(k∈Z)D. 2kπ+π2≤α≤2kπ+32π(k∈Z)12. 已知tg(π-α)=12, 则ctg(π2+α)的值为( )A. 12B. -12C. 2D. -213. 若集合A={α|sinα=22, α∈[0, 2π]}, B={β|cosβ=-22, β∈[-π, π]}, 则A⋃B为( )A. {π4} B. {34π}C. {π4,5474ππ,} D. {π4,34π, -34π}14. 若log2sin(3π-α)= -2, 且ctgα<0, 则cos(α+5π)等于( )A.54B.13C. 154D. -15415. 若sin(π+α)=110, 则的值为( )A. -13B. ±127C. 13D.33(二) 填空题:16. 化简2901801 1270222cos()[sec()]sin()︒+︒----︒ααα17. 已知sin(3224252παπαπ+=),且〈〈), 则tg α-sec α=__________18. 求值 136822550188263898tg ︒+︒-︒︒+︒sin cos()cos cos =_____________19. 若2sinx =2, 则x=_________ (其中x ∈[0, 2π])(三) 解答题:20. 求值: sin(-1230︒)cos1380︒+cos(-930︒)sin(-30︒)+tg945︒21. 已知sin θ=33, 求cos()(cos )[sin()]cos()cos()sin()sin()πθθπθπθπθπθπθ-⋅--+-++-+3212232的值.22. 已知log sin θcos θ=log cos θsin θ, 且θ∈(0, π2)求21log cot θ+(sin θcos θ)的值.23. 化简: 2223sin ()sin()cos()223csc (2)1()2cot ππααααπαπ+-++---四. 参考答案:(一) 选择题:1. B2. C3. D4. B5.C 6. C 7. C 8. B 9.D 10.C 11.D 12. A 13. D 14. C 15.B (二) 填空题:16. 2tg 2α 17. 3418. 0提示: 原式=182308288tg ︒+︒-︒︒-︒sin (cos)sin sin=ctg8︒-21288⨯︒︒cos sin=ctg8︒-ctg8︒=019. ππ656或(三) 解答题:20. 解: 原式=sin(-1440︒+210︒)cos(1440︒-60︒)+cos(-1080︒+150︒)sin(-30︒)+tg(1080︒-135︒) =sin210︒cos60︒+cos150︒(-sin30︒)-tg135︒ =(-sin30︒)cos60︒+cos30︒sin30︒+tg45︒=-⨯+⨯+121232121 =11434-+ =334- 21. 解: 原式=---+-+cos (cos )[cos ]cos (cos )cos cos θθθθθθθ1 =1111++-cos cos θθ=21222-=cos sin θθ∵sin θ =33∴ 公式=2332()=6 22. 解: ∵θ ∈(0, π2) ∴0<sin θ<1, 0<cos θ<1 ∴lgsin θ<0, lgcos θ<0由log sin θcos θ=log cos θsin θ得:lgcos lgsin lgsin lgcos θθθθ= lg 2cos θ=lg 2sin θ∴ lgcos θ=lgsin θ∴cos θ=sin θ∴log 12+tg θ(sin θcos θ)=log sec 2θ(sin θcos θ)=log (cos )cos 12θθ= -123. 解: 原式=cos csc sin (sin )2221ααααα-+--tg =cos sin 2222ααααctg tg + =sin 2α+cos 2α=1。
02三角函数诱导公式(含经典例题+答案)
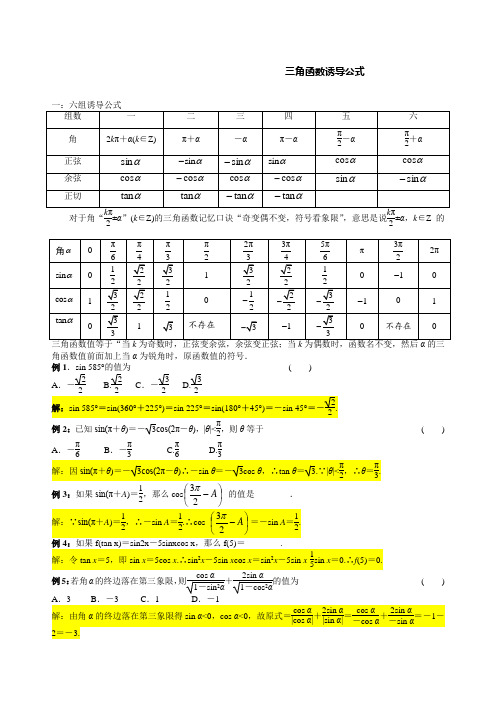
三角函数诱导公式对于角“k π2±α”(k ∈Z)的三角函数记忆口诀“奇变偶不变,符号看象限”,意思是说k π2±α,k ∈Z 的角函数值前面加上当α为锐角时,原函数值的符号.例1.sin 585°的值为 ( )A .-2 B.2 C .-3 D.3例2:已知sin(π+θ)=-3cos(2π-θ),|θ|<π2,则θ等于 ( )A .-πB .-π C.π D.π例3:如果sin(π+A )=12,那么cos ⎪⎫⎛-A 3 的值是________. 例5:若角α的终边落在第三象限,则cos α1-sin 2α+2sin α1-cos 2α的值为 ( )例6:已知α∈(-π,0),tan(3π+α)=31,则cos ⎪⎭⎫⎝⎛+απ23的值为 ( ) A.1010 B .-1010 C.31010 D .-31010解:tan α=13,cos ⎪⎭⎫⎝⎛+απ23=sin α.∵α∈(-π,0),∴sin α=-1010. A .-32 B.32 C.3-12 D.3+12解:sin 600°+tan 240°=sin(720°-120°)+tan(180°+60°)=-sin 120°+tan 60°=-32+3=32. ( ) A .3 B .5 C .1 D .不能确定解:f(2 011)=asin(2 011π+α)+bcos(2 011π+β)+4=asin(π+α)+bcos(π+β)+4=-asin α-bcos β+4 =5.∴asin α+bcos β=-1.∴f(2 012)=asin(2 012π+α)+bcos(2 012π+β)+4=asin α+bcos β+4 =-1+4=3.1.诱导公式在三角形中经常应用,常用的变形结论有:A +B =π-C ; 2A +2B +2C =2π;A 2+B 2+C 2=π2.2.求角时,一般先求出该角的某一三角函数值,再确定该角的范围,最后求角.例9:△ABC 中,cos A =13,则sin(B +C )=________.解:∵△ABC 中,A +B +C =π,∴sin(B +C )=sin(π-A )=sin A =1-cos 2A =223.例10:在△ABC 中,若sin(2π-A )=-2sin(π-B ),3cos A =-2cos(π-B ),求△ABC 的三个内角. 解:由已知得⎩⎨⎧sin A =2sin B ①3cos A =2cos B ②①2+②2得2cos 2A =1,即cos A =22或cos A =-22.(1)当cos A =22时,cos B =32,又A 、B 是三角形的内角,∴A =π4,B =π6,∴C =π-(A +B )=712π. A .B .C .D .2.cos (﹣30°)的值是( ) A .B .C .D .3.下列能与sin20°的值相等的是( ) A .cos20° B .sin (﹣20°) C .sin70° D .sin160°4.已知,则下列各式中值为的是( )A .B .sin (π+α)C .D .sin (2π﹣α)换元法与诱导公式例11:已知41)3sin(=+απ,则=-)6cos(απ 。
三角函数诱导公式练习题集附答案解析

三角函数诱导公式练习题一、选择题(共21小题)1、已知函数f(x)=sin,g(x)=tan(π﹣x),则()A、f(x)与g(x)都是奇函数B、f(x)与g(x)都是偶函数C、f(x)是奇函数,g(x)是偶函数D、f(x)是偶函数,g(x)是奇函数2、点P(cos2009°,sin2009°)落在()A、第一象限B、第二象限C、第三象限D、第四象限3、已知,则=()A、B、C、D、4、若tan160°=a,则sin2000°等于()A、B、C、D、﹣5、已知cos(+α)=﹣,则sin(﹣α)=()A、﹣B、C、﹣D、6、函数的最小值等于()A、﹣3B、﹣2C、D、﹣17、本式的值是()A、1B、﹣1C、D、8、已知且α是第三象限的角,则cos(2π﹣α)的值是()A、B、C、D、9、已知f(cosx)=cos2x,则f(sin30°)的值等于()A、B、﹣C、0 D、110、已知sin(a+)=,则cos(2a﹣)的值是()A、B、C、﹣D、﹣11、若,,则的值为()A、B、C、D、12、已知,则的值是()A、B、C、 D、13、已知cos(x﹣)=m,则cosx+cos(x﹣)=()A、2mB、±2mC、D、14、设a=sin(sin20080),b=sin(cos20080),c=cos(sin20080),d=cos(cos20080),则a,b,c,d的大小关系是()A、a<b<c<dB、b<a<d<cC、c<d<b<aD、d<c<a<b15、在△ABC中,①sin(A+B)+sinC;②cos(B+C)+cosA;③tan tan;④,其中恒为定值的是()A、②③B、①②C、②④D、③④16、已知tan28°=a,则sin2008°=()A、B、C、D、17、设,则值是()A、﹣1B、1C、D、18、已知f(x)=asin(πx+α)+bcos(πx+β)+4(a,b,α,β为非零实数),f(2007)=5,则f(2008)=()A、3B、5C、1D、不能确定19、给定函数①y=xcos(+x),②y=1+sin2(π+x),③y=cos(cos(+x))中,偶函数的个数是()A、3B、2C、1D、020、设角的值等于()A、B、﹣C、D、﹣21、在程序框图中,输入f0(x)=cosx,则输出的是f4(x)=﹣csx()A、﹣sinxB、sinxC、cosxD、﹣cosx二、填空题(共9小题)22、若(﹣4,3)是角终边上一点,则Z的值为.23、△ABC的三个内角为A、B、C,当A为°时,取得最大值,且这个最大值为.24、化简:=25、化简:=.26、已知,则f(1)+f(2)+f(3)+…+f(2009)=.27、已知tanθ=3,则(π﹣θ)=.28、sin(π+)sin(2π+)sin(3π+)…sin(2010π+)的值等于.29、f(x)=,则f(1°)+f(2°)+…+f(58°)+f(59°)=.30、若,且,则cos(2π﹣α)的值是.答案与评分标准一、选择题(共21小题)1、已知函数f(x)=sin,g(x)=tan(π﹣x),则()A、f(x)与g(x)都是奇函数B、f(x)与g(x)都是偶函数C、f(x)是奇函数,g(x)是偶函数D、f(x)是偶函数,g(x)是奇函数考点:函数奇偶性的判断;运用诱导公式化简求值。
诱导公式小测试

高一年级上学期诱导公式小测试(测试时间:45分钟,满分100分)姓名: 班级: 分数:一、选择题:(每小题4分,共40分)1、对于α∈R ,下列等式中恒成立的是 ( ) A .cos (-α)=-cos α B .sin (2π-α)=sin αC .tan (π+α)=tan (2π+α)D .cos (π-α)=cos (π+α) 2、sin (-6π19)的值是 A . 21B .-21C .23 D .-23( ) 3、已知sin(π+α)=45,且α是第四象限角,则cos(α-2π)的值是 ( )(A)-53 (B)53 (C)±53 (D)544、tan300°+0405sin 405cos 的值是 ( )A .1+3B .1-3C .-1-3D .-1+35、若cos (π+α)=-510,且α∈(-2π,0),则tan (2π3+α)的值为 ( ) A .-36 B .36C .-26 D .26 6、下列各式不正确的是 ( )A . sin (α+180°)=-sin αB .cos (-α+β)=-cos (α-β)C . sin (-α-360°)=-sin αD .cos (-α-β)=cos (α+β)7、7、若cos100°= k ,则tan ( -80°)的值为 ( )(A)(D)8、设A ,B ,C 是三角形的三个内角,下列关系恒等成立的是 ( ) (A)cos(A +B )=cos C(B)sin(A +B )=sin C (C)tan(A +B )=tan C(D)sin2A B+=sin 2C 9、)2cos()2sin(21++-ππ等于 ( ) A .sin2-cos2 B .cos2-sin2 C .±(sin2-cos2)D .sin2+cos210、设tan (α+5π)=m ,则s i n (3)c o s ()s i n ()c o s ()αππααπα-+----的值是 ( )A .B .C .D .二、填空题:(每小题4分,共16分)11、=-︒)945cos( . 12、tan(150)cos(570)cos(1140)tan(210)sin(690)-︒⋅-︒⋅-︒-︒⋅-︒= .13、tan5π+tan 52π+tan 53π+tan 54π= . 14、已知cos (π6 +α)= 33,则cos (7π6 +α)的值= .三、解答题:(4个小题,共44分)15(10分)、求值22sin 120cos180tan 45cos (330)sin(210)︒+︒+︒--︒+-︒16(10分)、求证:)π5sin()πcos()π6cos()π2sin()π2tan(θθθθθ+-----=tan θ.17(12分)、化简:(1)︒+︒︒︒+790cos 250sin 430cos 290sin 21 (2).23tan()sin ()cos(2)2cos ()tan(2)ππααπααπαπ-⋅+⋅---⋅-18(12分)、设()f θ=)cos()7(cos 221)cos(2)(sin cos 2223θθππθπθθ-++++---+-,求()3f π的值.。
诱导公式计算题100题

2.求∫x n cosx dx.3.求∫sinxsin(x+a) dx.4.求∫cosxcos(x+a) dx.5.求∫sinxcosx dx.6.求∫sinxcos2x dx.7.求∫cosxsin2x dx.8.求∫sin2x dx.9.求∫cos2x dx.10.求∫tanx dx.11.求∫cotx dx.12.求∫secx dx.13.求∫cscx dx.14.求∫tan2x dx.15.求∫cot2x dx.16.求∫sec2x dx.17.求∫csc2x dx.18.求∫sinxtanx dx.19.求∫cosxcotx dx.20.求∫sinxsecx dx.21.求∫cosxcscx dx. dx.22.求∫sinxcos2x23.求∫cosx dx.sin2x dx.24.求∫tanxcos2xsin x dx.26.求∫secxtan2x dx.27.求∫cscxcot2x28.求∫sin3x dx.29.求∫cos3x dx.30.求∫tan3x dx.31.求∫cot3x dx.32.求∫sec3x dx.33.求∫csc3x dx.34.求∫sin4x dx.35.求∫cos4x dx.36.求∫tan4x dx.37.求∫cot4x dx.38.求∫sec4x dx.39.求∫csc4x dx.40.求∫sin5x dx.41.求∫cos5x dx.42.求∫tan5x dx.43.求∫cot5x dx.44.求∫sec5x dx.45.求∫csc5x dx.46.求∫sin n x dx.47.求∫cos n x dx.48.求∫tan n x dx.49.求∫cot n x dx.51.求∫csc n x dx. dx. 52.求∫sin n xcos m x dx. 53.求∫cos n xsin m x dx. 54.求∫tan n xcos m x55.求∫cot n x dx.sin m x dx. 56.求∫sec n xtan m x57.求∫csc n x dx.cot m x dx. 58.求∫1sin n x dx. 59.求∫1cos n x60.求∫1 dx.tan n x dx. 61.求∫1cot n x dx. 62.求∫1sec n x dx. 63.求∫1csc n x dx.64.求∫1sin n xcos m x dx.65.求∫1sin n xtan m x dx.66.求∫1cos n xtan m x dx.67.求∫1sin n xsec m x dx.68.求∫1cos n xsec m x 69.求∫1 dx.sin n xcsc m x 70.求∫1 dx.cos n xcsc m x71.求∫1 dx.tan n xsec m x dx. 72.求∫1cot n xsec m x dx.73.求∫sinxsin(x+a)74.求∫cosx dx.cos(x+a) dx.75.求∫tanxtan(x+a) dx.76.求∫cotxcot(x+a) dx.77.求∫secxsec(x+a) dx.78.求∫cscxcsc(x+a) dx.79.求∫sinxsin(x+a)cos(x+a) 80.求∫cosx dx.sin(x+a)cos(x+a) dx.81.求∫tanxsin(x+a)cos(x+a) 82.求∫cotx dx.sin(x+a)cos(x+a) dx.83.求∫secxsin(x+a)cos(x+a) 84.求∫cscx dx.sin(x+a)cos(x+a) 85.求∫sinx dx.cos(x+a)sin(x+a) dx.86.求∫cosxcos(x+a)sin(x+a) dx.87.求∫tanxcos(x+a)sin(x+a) dx.88.求∫cotxcos(x+a)sin(x+a) dx.89.求∫secxcos(x+a)sin(x+a) dx.90.求∫cscxcos(x+a)sin(x+a) dx.91.求∫sinxsin(x+a)sin(x+2a)92.求∫cosx dx.sin(x+a)sin(x+2a) dx.93.求∫tanxsin(x+a)sin(x+2a) dx.94.求∫cotxsin(x+a)sin(x+2a)95.求∫secx dx.sin(x+a)sin(x+2a) dx.96.求∫cscxsin(x+a)sin(x+2a)97.求∫sinx dx.sin(x+a)sin(x+2a)sin(x+3a) dx.98.求∫cosxsin(x+a)sin(x+2a)sin(x+3a) 99.求∫tanx dx.sin(x+a)sin(x+2a)sin(x+3a) 100.求∫cotx dx.sin(x+a)sin(x+2a)sin(x+3a)。
高中数学运用诱导公式化简求值精选题

运用诱导公式化简求值精选题42道一.选择题(共16小题)1.记cos(﹣80°)=k,那么tan100°=()A.B.﹣C.D.﹣2.已知cos()=,则sinθ=()A.B.C.﹣D.﹣3.计算:cos210°=()A.B.C.D.4.cos300°=()A.B.﹣C.D.5.已知,则=()A.B.C.D.6.已知sin(α﹣)=,则cos()=()A.﹣B.C.﹣D.7.sin225°=()A.B.C.﹣D.8.cos330°=()A.B.C.D.9.角α的终边在直线y=2x上,则=()A.B.1C.3D.﹣1 10.已知cos(﹣θ)=,则sin()的值是()A.﹣B.﹣C.D.11.已知,则的值等于()A.B.C.D.12.已知,则=()A.B.C.D.13.若,则等于()A.B.C.D.14.sin330°等于()A.B.C.D.15.已知tanθ=3,则等于()A.B.C.0D.16.已知f(α)=,则的值为()A.B.C.D.二.填空题(共18小题)17.已知tan(3π+α)=2,则=.18.已知,则=.19.化简:=.20.设tanα=3,则=.21.已知,且,则=.22.已知,则=.23.化简:的值为.24.化简:=.25.若cos(﹣α)=,则sin(+α)=26.已知,则的值为.27.sin600°=.28.已知,则sinα=.29.已知角α终边上一点P(﹣4,3),则的值.30.化简:=.31.若角θ的终边经过点(﹣3,4),则sin(+θ)+cos(π﹣θ)+tan(2π﹣θ)=.32.已知,则tan(π﹣α)的值是.33.若α∈(0,π),且,则=.34.已知sin(π﹣α)+2cos(π+α)=0,则=.三.解答题(共8小题)35.已知α是第二象限角,且sinα=.(1)求tanα的值;(2)求的值.36.已知α是第三象限角,f(α)=.(1)化简f(α);(2)若cos(α﹣π)=,求f(α)的值;(3)若α=﹣1860°,求f(α)的值.37.若α为第二象限角,sin(+α)=﹣,(1)求sinα的值;(2)若f(α)=,求f(α)的值.38.已知角α为第一象限角,且sinα=.(1)求cosα,tanα的值;(2)求的值.39.已知f(α)=.(1)若α=﹣,求f(α)值;(2)若α为第三象限角,且,求f(α)的值.40.已知角α的终边与单位圆交于点P(,).(1)求sinα、cosα、tanα的值;(2)求的值.41.已知.(1)化简f(α);(2)若,求的值.42.已知,f(α)=.(1)化简f(α);(2)若=﹣,求tanα.运用诱导公式化简求值精选题42道参考答案与试题解析一.选择题(共16小题)1.记cos(﹣80°)=k,那么tan100°=()A.B.﹣C.D.﹣【分析】法一:先求sin80°,然后化切为弦,求解即可.法二:先利用诱导公式化切为弦,求出求出结果.【解答】解:法一:,所以tan100°=﹣tan80°=.法二:cos(﹣80°)=k⇒cos(80°)=k,=.故选:B.【点评】本小题主要考查诱导公式、同角三角函数关系式等三角函数知识,并突出了弦切互化这一转化思想的应用.2.已知cos()=,则sinθ=()A.B.C.﹣D.﹣【分析】利用二倍角的余弦公式、诱导公式,求得sinθ的值.【解答】解:∵cos()=,∴cos(﹣θ)=2﹣1=﹣=sinθ,即sinθ=﹣,故选:C.【点评】本题主要考查二倍角的余弦公式、诱导公式的应用,属于基础题.3.计算:cos210°=()A.B.C.D.【分析】把所求式子中的角210°变为180°+30°,利用诱导公式cos(180+α)=﹣cosα及特殊角的三角函数值化简,即可求出原式的值.【解答】解:cos210°=cos(180°+30°)=﹣cos30°=﹣.故选:B.【点评】此题考查了运用诱导公式化简求值,其中灵活变换角度,熟练掌握诱导公式是解本题的关键.4.cos300°=()A.B.﹣C.D.【分析】利用三角函数的诱导公式,将300°角的三角函数化成锐角三角函数求值.【解答】解:∵.故选:C.【点评】本小题主要考查诱导公式、特殊三角函数值等三角函数知识.5.已知,则=()A.B.C.D.【分析】由诱导公式,化简已知条件以及所求的表达式,然后求解即可.【解答】解:∵,∴sin[]=sin()=,则=sin(π﹣α+)=﹣sin(α+)=﹣,故选:C.【点评】本题主要考查给值求值问题,熟记诱导公式即可,属于基础题型.6.已知sin(α﹣)=,则cos()=()A.﹣B.C.﹣D.【分析】运用﹣α、﹣α的诱导公式,计算即可得到.【解答】解:sin(α﹣)=,即为sin(﹣α)=﹣,即有sin[﹣(+α)]=﹣,即cos()=﹣.故选:A.【点评】本题考查三角函数的求值,考查三角函数的诱导公式的运用,考查运算能力,属于基础题.7.sin225°=()A.B.C.﹣D.【分析】把225°写为180°+45°由诱导公式二得特殊角的正弦角,由特殊角正弦值得结果.【解答】解:sin225°=sin(180°+45°)=﹣sin45°=﹣.故选:A.【点评】本题考查用诱导公式化简求值,诱导公式一到四可以把任意角的三角函数化为锐角的三角函数,是基础题.8.cos330°=()A.B.C.D.【分析】由cos(α+2kπ)=cosα、cos(﹣α)=cosα解之即可.【解答】解:cos330°=cos(360°﹣30°)=cos(﹣30°)=cos30°=,故选:C.【点评】本题考查余弦函数的诱导公式.9.角α的终边在直线y=2x上,则=()A.B.1C.3D.﹣1【分析】由已知求得tanα,再由同角三角函数基本关系式化弦为切求解.【解答】解:∵角α的终边在直线y=2x上,∴tanα=2.∴===.故选:C.【点评】本题考查三角函数的化简求值,考查诱导公式及同角三角函数基本关系式的应用,是基础题.10.已知cos(﹣θ)=,则sin()的值是()A.﹣B.﹣C.D.【分析】由已知及诱导公式即可计算求值.【解答】解:cos(﹣θ)=sin[﹣(﹣θ)]=sin()=,故选:C.【点评】本题主要考查了诱导公式在三角函数求值中的应用,属于基础题.11.已知,则的值等于()A.B.C.D.【分析】观察发现,那么=cos(α+)利用诱导公式求解即可.【解答】解:由,则=cos(α+)=sin(α﹣)=.故选:A.【点评】本题主要考查诱导公式的灵活应用和构造思想,属于基本知识的考查.12.已知,则=()A.B.C.D.【分析】由已知直接利用三角函数的诱导公式化简求值.【解答】解:∵,∴=cos[﹣()]=,故选:C.【点评】本题考查三角函数的化简求值,考查诱导公式的应用,是基础题.13.若,则等于()A.B.C.D.【分析】直接利用诱导公式化简求解即可.【解答】解:,则=sin(﹣)=,故选:A.【点评】本题考查诱导公式的应用,三角函数化简求值.14.sin330°等于()A.B.C.D.【分析】根据330°=360°﹣30°,由诱导公式可得答案.【解答】解:∵故选:B.【点评】本题主要考查根据三角函数的诱导公式进行化简求值的问题.属基础题.对于三角函数的诱导公式一定要强化记忆.15.已知tanθ=3,则等于()A.B.C.0D.【分析】由题意利用诱导公式、同角三角函数的基本关系,化简所给的式子,可得结果.【解答】解:∵tanθ=3,则====,故选:B.【点评】本题主要考查应用诱导公式化简三角函数式,同角三角函数的基本关系,要特别注意符号的选取,这是解题的易错点,属于基础题.16.已知f(α)=,则的值为()A.B.C.D.【分析】已知关系式右边利用诱导公式化简确定出f(α),即可求出所求式子的值.【解答】解:f(α)==cosα,则f(﹣)=cos(﹣)=cos(8π+)=cos=.故选:B.【点评】此题考查了运用诱导公式化简求值,熟练掌握诱导公式是解本题的关键.二.填空题(共18小题)17.已知tan(3π+α)=2,则=2.【分析】利用诱导公式把tan(3π+α)=2化简,得tanα=2,再利用诱导公式化简所求表达式,令分式的分子分母同除cosα,得到只含有tanα的式子,把tanα=2代入即可.【解答】解:由tan(3π+α)=2,可得tanα=2,则=====2,故答案为:2.【点评】本题主要考查诱导公式和同角三角函数关系式在三角函数化简求值中的应用,应用诱导公式时,注意符号的正负.18.已知,则=.【分析】原式利用诱导公式化简,将sinα的值代入计算即可求出值.【解答】解:∵sinα=,∴cos(+α)=﹣sinα=﹣.故答案为:﹣【点评】此题考查了运用诱导公式化简求值,熟练掌握诱导公式是解本题的关键.19.化简:=tanα.【分析】由已知利用诱导公式,同角三角函数基本关系式即可化简求值得解.【解答】解:===tanα.故答案为:tanα.【点评】本题主要考查了诱导公式,同角三角函数基本关系式在三角函数化简求值中的应用,属于基础题.20.设tanα=3,则=2.【分析】利用诱导公式、同角三角函数的基本关系化简所给的式子,可得结果.【解答】解:∵tanα=3,则=====2,故答案为:2.【点评】本题主要考查同角三角函数的基本关系、诱导公式的应用,属于基础题.21.已知,且,则=.【分析】先利用同角三角函数基本关系求得sinα的值,在利用诱导公式对原式化简整理,把cosα和sinα的值代入即可求得答案.【解答】解:∵∴sinα=﹣=﹣∴原式===﹣2故答案为:﹣2【点评】本题主要考查了运用诱导公式化简求值的问题.解题时注意三角函数的正负.22.已知,则=.【分析】利用诱导公式化简求解即可.【解答】解:.故答案为:﹣.【点评】本题主要考查诱导公式.三角函数求值,是基本知识的考查.23.化简:的值为1.【分析】运用诱导公式及特殊角的三角函数值即可求值.【解答】解:=﹣sin(3π+)+cos2640°+tan1665°=sin+cos(360°×7+120°)+tan(360°×4+225°)=+cos(180°﹣60°)+tan(180°+45°)=﹣cos60°+tan45°=﹣+1=1.故答案为:1.【点评】本题主要考查了诱导公式及特殊角的三角函数值的应用,属于基础题.24.化简:=﹣1.【分析】利用诱导公式化简即可求解.【解答】解:===﹣1.故答案为:﹣1.【点评】本题主要考查了诱导公式在三角函数化简求值中的应用,属于基础题.25.若cos(﹣α)=,则sin(+α)=【分析】由题意利用诱导公式,求得所给式子的值.【解答】解:cos(﹣α)=,则sin(+α)=cos[﹣(﹣α)]=cos(﹣α)=,故答案为:.【点评】本题主要考查诱导公式的应用,属于基础题.26.已知,则的值为.【分析】由已知利用诱导公式可求tanα的值,进而利用诱导公式,同角三角函数基本关系式化简所求即可求解.【解答】解:因为,可得tanα=,所以====.故答案为:.【点评】本题主要考查了诱导公式,同角三角函数基本关系式在三角函数化简求值中的应用,考查了转化思想,属于基础题.27.sin600°=.【分析】利用诱导公式直接化简sin600°为﹣sin60°,然后求出它的值即可.【解答】解:sin600°=sin(360°+240°)=sin240°=sin(180°+60°)=﹣sin60°=﹣.故答案为:.【点评】本题考查三角函数求值与化简,正确应用诱导公式是解决三角函数求值的重点,一般思路,负角化简正角,大角化小角(锐角).28.已知,则sinα=﹣.【分析】由已知利用诱导公式即可计算得解.【解答】解:因为,所以﹣sinα=,则sinα=﹣.故答案为:﹣.【点评】本题主要考查了诱导公式在三角函数化简求值中的应用,属于基础题.29.已知角α终边上一点P(﹣4,3),则的值.【分析】由条件利用任意角的三角函数的定义,求得sinα和cosα的值,再利用同角三角函数的基本关系、诱导公式求得所给式子的值.【解答】解:∵角α终边上一点P(﹣4,3),∴x=﹣4,y=3,r=|OP|=5,∴sinα==,cosα==﹣,∴原式==﹣=﹣=.故答案为:.【点评】本题主要考查任意角的三角函数的定义,同角三角函数的基本关系、诱导公式的应用,属于基础题.30.化简:=1.【分析】由条件利用诱导公式进行化简所给的式子,可得结果.【解答】解:=••=1,故答案为:1.【点评】本题主要考查诱导公式的应用,属于基础题.31.若角θ的终边经过点(﹣3,4),则sin(+θ)+cos(π﹣θ)+tan(2π﹣θ)=.【分析】运用诱导公式化简所求,根据任意角的三角函数的定义即可求解.【解答】解:由诱导公式可得,又角θ的终边经过点(﹣3,4),所以,所以.故答案为:.【点评】本题主要考查了诱导公式,任意角的三角函数的定义在三角函数化简求值中的应用,考查了转化思想,属于基础题.32.已知,则tan(π﹣α)的值是﹣2.【分析】由已知利用诱导公式可得﹣2cosα=﹣sinα,根据同角三角函数基本关系式可求tanα的值,利用诱导公式化简所求即可得解.【解答】解:∵,∴﹣2cosα=﹣sinα,可得tanα=2,∴tan(π﹣α)=﹣tanα=﹣2.故答案为:﹣2.【点评】本题主要考查了诱导公式,同角三角函数基本关系式在三角函数化简求值中的应用,考查了转化思想,属于基础题.33.若α∈(0,π),且,则=.【分析】由题意,利用诱导公式可得,从而根据诱导公式及同角三角函数的基本关系求解即可.【解答】解:∵α∈(0,π),且,∴,∴,故答案为.【点评】本题考查了诱导公式及同角三角函数的基本关系,考查了推理能力与计算能力,属于基础题.34.已知sin(π﹣α)+2cos(π+α)=0,则=.【分析】由已知利用诱导公式,同角三角函数基本关系式可求tanα=2,进而利用同角三角函数基本关系式化简所求即可求值得解.【解答】解:∵sin(π﹣α)+2cos(π+α)=0,∴sinα﹣2cosα=0,可得tanα=2,∴====.故答案为:.【点评】本题主要考查了诱导公式,同角三角函数基本关系式在三角函数化简求值中的应用,考查了转化思想,属于基础题.三.解答题(共8小题)35.已知α是第二象限角,且sinα=.(1)求tanα的值;(2)求的值.【分析】(1)由已知利用同角三角函数基本关系式即可求值得解;(2)利用诱导公式,同角三角函数基本关系式化简所求即可求值得解.【解答】(本小题满分14分)解:(1)因为α是第二象限角,且sinα=,所以cosα=﹣=﹣,所以tanα==﹣2.(2)=====.【点评】本题主要考查了同角三角函数基本关系式,诱导公式在三角函数化简求值中的应用,考查了计算能力和转化思想,属于基础题.36.已知α是第三象限角,f(α)=.(1)化简f(α);(2)若cos(α﹣π)=,求f(α)的值;(3)若α=﹣1860°,求f(α)的值.【分析】(1)f(α)利用诱导公式及同角三角函数间的基本关系化简即可得到结果;(2)由已知等式求出sinα的值,代入计算即可求出f(α)的值;(3)把α度数代入计算即可求出f(α)的值.【解答】解:(1)f(α)==cosα;(2)∵cos(α﹣π)=﹣sinα=,即sinα=﹣,且α为第三象限角,∴cosα=﹣=﹣,则f(α)=cosα=﹣;(3)把α=﹣1860°代入得:f(﹣1860°)=cos(﹣1860°)=cosα1860°=cos(5×360°+60°)=cos60°=.【点评】此题考查了同角三角函数基本关系的运用,运用诱导公式化简求值,熟练掌握基本关系是解本题的关键.37.若α为第二象限角,sin(+α)=﹣,(1)求sinα的值;(2)若f(α)=,求f(α)的值.【分析】(1)由已知利用诱导公式可求cosα的值,根据同角三角函数基本关系式可求sinα的值.(2)利用诱导公式即可化简求值得解.【解答】解:(1)∵α为第二象限角,sin(+α)=cosα=﹣,∴sinα==;(2)∵f(α)===sinα,∴f(α)=.【点评】本题主要考查了诱导公式,同角三角函数基本关系式在三角函数化简求值中的应用,考查了计算能力和转化思想,属于基础题.38.已知角α为第一象限角,且sinα=.(1)求cosα,tanα的值;(2)求的值.【分析】(1)由已知利用同角三角函数基本关系式即可求解;(2)利用诱导公式,同角三角函数基本关系式即可化简求解.【解答】解:(1)∵角α为第一象限角,且sinα=,∴cos=,tanα==.(2)==3+=3+=7.【点评】本题主要考查了诱导公式,同角三角函数基本关系式在三角函数化简求值中的应用,考查了转化思想,属于基础题.39.已知f(α)=.(1)若α=﹣,求f(α)值;(2)若α为第三象限角,且,求f(α)的值.【分析】(1)利用诱导公式化简函数解析式,进而根据特殊角的三角函数值即可计算得解.(2)利用诱导公式化简已知等式,结合α为第三象限角,利用同角三角函数基本关系式即可计算得解.【解答】解:(1)由于,又,所以f(α)===﹣.(2)因为,又因为α为第三象限角,所以.【点评】本题主要考查了诱导公式,特殊角的三角函数值,同角三角函数基本关系式在三角函数化简求值中的应用,考查了转化思想,属于基础题.40.已知角α的终边与单位圆交于点P(,).(1)求sinα、cosα、tanα的值;(2)求的值.【分析】(1)根据已知角α的终边与单位圆交于点P(,).结合三角函数的定义即可得到sinα、cosα、tanα的值;(2)依据三角函数的诱导公式化简即可:=,最后利用第(1)小问的结论得出答案.【解答】解:(1)已知角α的终边与单位圆交于点P(,).∴x==,r=1,∴sinα=;cosα=;tanα=;(6分)(2)==.(14分)【点评】本题考查任意角的三角函数的定义,运用诱导公式化简求值.本题是基础题,解答关键是熟悉任意角的三角函数的定义,单位圆的知识.41.已知.(1)化简f(α);(2)若,求的值.【分析】(1)利用诱导公式化简f(α)的解析式,可得结果.(2)由题意利用同角三角函数的基本关系求得sinα+cosα和sinα•cosα的值,从而求得要求式子的值.【解答】解:(1)=+cosα=sinα+cosα.(2)若=sinα+cosα,∴平方可得1+2sinαcosα=,∴sinαcosα=﹣.∴===﹣.【点评】本题主要考查利用诱导公式进行化简求值,同角三角函数的基本关系,属于基础题.42.已知,f(α)=.(1)化简f(α);(2)若=﹣,求tanα.【分析】(1)利用诱导公式,同角三角函数基本关系式即可化简得解.(2)由(1)及已知利用诱导公式可得cosα=﹣,分类讨论,利用同角三角函数基本关系式即可计算得解.【解答】解:(1)f(α)===sinα.(2)∵=﹣,∴sin(﹣α)=﹣,可得cosα=﹣,∴α是第二或第三象限角,当α是第二象限角时,sinα==,tan=﹣,当α是第三象限角时,sinα=﹣=﹣,tan=.【点评】本题主要考查了诱导公式,同角三角函数基本关系式在三角函数化简求值中的应用,考查了计算能力和转化思想,属于基础题.。
高中数学复习:诱导公式练习及答案

高中数学复习:诱导公式练习及答案1.sin210°cos120°的值为( ) A .14 B .-√34C .√32D .122.已知sin(π+α)=35,且α是第四象限角,则cos(α-2π)的值是( ) A .-45 B .45 C .±45 D .353.设cos(-80°)=k ,那么tan100°等于( ) A .√1−k 2kB .-√1−k 2kC .√1−k 2D .-√1−k 24.设sin20°=k ,那么cos160°等于( ) A .√1−k 2 B .-√1−k 2 C .k D .-k5.若sin(π-α)=log 814,且α∈(−π2,0),则cos(π+α)的值为( )A .√53B .-√53C .±√53D .以上都不对6.已知cos(α-75°)=-13,且α为第四象限角,求sin(105°+α)的值.7.计算cos300°-sin(-330°)+tan675°·8.设tan(5π+α)=m,则sin(α-3π)+cos(π-α)sin(−α)−cos(π+α)的值为( )A.m-1m+1B.-1C.m+1m−1D.19.α∈(-π2,0),sinα=-35,则cos(π-α)的值为( )A.-45B.45C.35D.-3510.已知sin(α-180°)-sin(270°-α)=m,则sin(180°+α)·sin(270°+α)用m表示为( )A.m2−12B.m2+12C.1−m22D.-m2+1211.求下列各三角函数式的值: (1)sin1320°;(2)cos (−31π6);(3)tan(-945°).12.已知cos(π6−α)=√33,求cos(56π+α)-sin 2(α−π6)的值.13.若sin(3π+α)=-12,则cos (7π2−α)等于( )A .-12 B .12 C .√32D .-√3214.若sin(π+α)+cos (π2+a)=-m ,则cos (32π−α)+2sin(2π-α)的值为( ) A .-2m 3B .2m 3C .-3m 2D .3m 215.已知角α终边与单位圆x 2+y 2=1的交点为P (12,y ),则sin(π2+2α)等于( ) A .-12B .12C .-√32D .116.已知sin(5π-θ)+sin (52π−θ)=√72,求sin 4(π2−θ)+cos 4(32π+θ)的值.17.已知tan θ=2,则sin(π2+θ)−cos(π−θ)sin(π2−θ)−sin(π−θ)等于( )A .2B .-2C .0D .2318.已知sin(π3-x )=35,则cos(x +π6)等于( ) A .35 B .45 C .-35 D .−45 19.已知cos(52π-θ)=13,求sin?(π+θ)sinθ[sin (π−θ)−1]+sin?(θ−2π)cos?(θ+32π)sin?(θ−π)−cos?(θ−32π)的值.20.已知sin (α−π5)=a (a ≠±1,a ≠0),求cos (α+14π5)·tan (α−11π5)+tan?(α+9π5)cos?(26π5−α)的值.21.设f (θ)=2cos 3θ+sin 2(2π−θ)+sin?(π2+θ)−32+2cos 2(π+θ)+cos?(−θ),求f (π3)的值.22.已知cos (π6−α)=√33,求证:sin (4π3+α)+cos 2(2π3−α)=2−√33.23.若sin(π-α)=log 814,且α∈(−π2,0),则cos(π+α)的值为( )A .√53B .-√53C .±√53D .以上都不对24.设cos(π+α)=√32(π<α<32π),那么sin(2π-α)的值是( )A .-12 B .√32C .-√32D .1225.√1+2sin(π-3)·cos(π+3)的化简结果为( )A .sin3-cos3B .cos3-sin3C .±(sin3-cos3)D .以上都不对26.集合P ={α|α=90°-k ·180°,k ∈Z },Q ={β|β=90°-k ·360°,k ∈Z },则P 与Q 关系是( ) A .PQ 且QP B .PQ C .P =Q D .P Q 27.sin25π6+cos10π3+tan(-25π4)+sin(-7π3)·cos(-13π6)=________.28.化简:sin(θ-5π)cos(−π2−θ)cos(8π−θ)sin(θ−3π2)sin(-θ-4π).29.设tan (α+8π7)=m .求证:sin(α+157π)+3cos(α−13π7)sin(−α+20π7)-cos(α+22π7)=m+3m+1.30.已知sin(α+β)=1,求证:tan(2α+β)+tan β=0. 答案1.sin210°cos120°的值为( ) A .14B .-√34C .√32D .12 【答案】A【解析】sin210°cos120°=-sin30°·(-sin30°)=14.2.已知sin(π+α)=35,且α是第四象限角,则cos(α-2π)的值是( ) A .-45 B .45 C .±45 D .35 【答案】B【解析】∵sin(π+α)=-sin α=35,∴sin α=-35, ∵α是第四象限角,∴cos(α-2π)=cos α=√1−sin 2α=45. 3.设cos(-80°)=k ,那么tan100°等于( ) A .√1−k 2kB .-√1−k 2kC .√1−k 2D .-2 【答案】B【解析】∵cos80°=cos(-80°)=k ,∴sin80°=√1−k 2,tan80°=√1−k 2k,∴tan100°=tan(180°-80°)=-tan80°=-√1−k 2k.4.设sin20°=k ,那么cos160°等于( ) A .√1−k 2 B .-√1−k 2 C .k D .-k 【答案】B【解析】∵sin20°=k ,∴cos20°=√1-sin 220°=√1−k 2, ∴cos160°=-cos20°=-√1−k 2. 5.若sin(π-α)=log 814,且α∈(−π2,0),则cos(π+α)的值为( )A .√53B .-√53C .±√53D .以上都不对 【答案】B【解析】∵sin(π-α)=sin α=log 232−2=-23, ∴cos(π+α)=-cos α=-√1-sin 2a =-√1−49=-√53.6.已知cos(α-75°)=-13,且α为第四象限角,求sin(105°+α)的值. 【答案】∵cos(α-75°)=-13<0,且α为第四象限角,∴α-75°是第三象限角.∴sin(α-75°)=-√1-cos 2(α-75°)=-√1−(−13)2=-2√23, ∴sin(105°+α)=sin[180°+(α-75°)]=-sin(α-75°)=2√23. 7.计算cos300°-sin(-330°)+tan675°·【答案】原式=cos(360°-60°)+sin(360°-30°)+tan(720°-45°)=cos60°-sin30°-tan45°=12-12-1=-1. 8.设tan(5π+α)=m ,则sin(α-3π)+cos(π-α)sin (−α)−cos(π+α)的值为( )A .m -1m +1 B .-1 C .m+1m−1 D .1 【答案】C【解析】∵tan(5π+α)=m , ∴tan α=m , ∴sin(α-3π)+cos(π-α)sin (−α)−cos(π+α)=-sinα-cosα-sinα+cosα=tanα+1tanα-1=m+1m−1. 9.α∈(-π2,0),sin α=-35,则cos(π-α)的值为( ) A .-45 B .45 C .35 D .-35【答案】A【解析】∵α∈(-π2,0),sin α=-35,∴cos(π-α)=-cos α=-√1-sin 2α=-45. 10.已知sin(α-180°)-sin(270°-α)=m ,则sin(180°+α)·sin(270°+α)用m 表示为( ) A .m 2−12B .m 2+12C .1−m 22D .-m 2+12【答案】C【解析】sin(α-180°)-sin(270°-α)=-sin(180°-α)-sin[180°+(90°-α)] =-sin α+sin(90°-α)=cos α-sin α=m , sin(180°+α)sin(270°+α)=-sin α·(-cos α) =sin αcos α=12[1-(cos α-sin α)2]=1−m 22.11.求下列各三角函数式的值: (1)sin1320°;(2)cos (−31π6);(3)tan(-945°).【答案】(1)方法一 sin1320°=sin(3×360°+240°)=sin240°=sin(180°+60°)=-sin60°=-√32.方法二 sin1320°=sin(4×360°-120°)=sin(-120°)=-sin(180°-60°)=-sin60°=-√32.(2)方法一 cos (−31π6)=cos31π6=cos (4π+7π6)=cos(π+π6)=-cos π6=-√32.方法二 cos (−31π6)=cos (−6π+5π6)=cos (π−π6)=-cos π6=-√32.(3)tan(-945°)=-tan945°=-tan(225°+2×360°)=-tan225°=-tan(180°+45°)=-tan45°=-1.12.已知cos(π6−α)=√33,求cos(56π+α)-sin 2(α−π6)的值.【答案】cos (56π+α)-sin 2(α−π6)=cos [π−cos(π6−α)]-sin 2(π6−α)=-cos (π6−α)-[1−cos 2(π6−α)]=cos 2(π6−α)-cos (π6−α)-1=(√33)2-√33-1=-2+√33.13.若sin(3π+α)=-12,则cos (7π2−α)等于( )A .-12 B .12 C .√32D .-√32【答案】A【解析】∵sin(3π+α)=-sin α=-12,∴sin α=12. ∴cos (7π2−α)=cos (3π2−α)=-cos (π2−α)=-sin α=-12.14.若sin(π+α)+cos (π2+a)=-m ,则cos (32π−α)+2sin(2π-α)的值为( ) A .-2m 3B .2m 3C .-3m 2D .3m 2【答案】C【解析】∵sin(π+α)+cos (π2+α) =-sin α-sin α=-m , ∴sin α=m2,故cos (32π−α)+2sin(2π-α)=-sin α-2sin α =-3sin α=-32m.15.已知角α终边与单位圆x 2+y 2=1的交点为P (12,y ),则sin(π2+2α)等于( ) A .-12 B .12 C .-√32D .1 【答案】A【解析】由题意可得,cos α=12,则sin (π2+2α)=cos2α=2cos 2α-1=2×14-1=-12.16.已知sin(5π-θ)+sin (52π−θ)=√72,求sin 4(π2−θ)+cos 4(32π+θ)的值.【答案】∵sin(5π-θ)+sin (52π−θ)=sin(π-θ)+sin (π2−θ)=sin θ+cos θ=√72,∴sin θcos θ=12[(sin θ+cos θ)2-1]=12[(√72)2−1]=38,∴sin 4(π2−θ)+cos 4(32π+θ)=cos 4θ+sin 4θ=(sin 2θ+cos 2θ)2-2sin 2θcos 2θ=1-2×(38)2=2332.17.已知tan θ=2,则sin(π2+θ)−cos(π−θ)sin(π2−θ)−sin(π−θ)等于( )A .2B .-2C .0D .23 【答案】B【解析】由sin(π2+θ)−cos(π−θ)sin(π2−θ)−sin(π−θ)=cosθ+cosθcosθ-sinθ=21−tanθ=21−2=-2.18.已知sin(π3-x )=35,则cos(x +π6)等于( ) A .35 B .45 C .-35 D .−45 【答案】A【解析】cos(x +π6)=sin[π2-(x +π6)]=sin(π3-x ),故cos(x +π6)=35. 19.已知cos(52π-θ)=13,求sin?(π+θ)sinθ[sin (π−θ)−1]+sin?(θ−2π)cos?(θ+32π)sin?(θ−π)−cos?(θ−32π)的值.【答案】∵cos(52π-θ)=cos(2π+π2-θ)=sin θ=13,∴sin θ=13.∴原式=−sinθsin?θ(sin?θ−1)+sin?θcos?(θ+32π)sin?θ−cos?(θ−32π)=11−sin?θ−sin?θcos?(θ+π2+π)sin?θ+cos?(θ−π2−π)=11−sin?θ−sin?θ−sin 2?θ+sinθ=21−sin?θ=3.20.已知sin (α−π5)=a (a ≠±1,a ≠0),求cos (α+14π5)·tan (α−11π5)+tan?(α+9π5)cos?(26π5−α)的值.【答案】cos (α+14π5)·tan (α−11π5)+tan?(α+9π5)cos?(26π5−α)=-cos (α−π5)·tan (α−π5)+tan?(α−π5)−cos?(π5−α)=-sin (α−π5)-sin?(α−π5)cos?2(α−π5)=-a -a1−a 2=a 3−2a 1−a 2.21.设f (θ)=2cos 3θ+sin 2(2π−θ)+sin?(π2+θ)−32+2cos 2(π+θ)+cos?(−θ),求f (π3)的值.【答案】∵f (θ)=2cos 3θ+sin 2θ+cosθ-32+2cos 2θ+cosθ=2cos 3θ+1-cos 2θ+cosθ-32+2cos 2θ+cosθ=2cos 3θ−2−(cos 2θ−cosθ)2+2cos 2θ+cosθ=2(cos 3θ−1)−cosθ(cosθ-1)2+2cos θ+cosθ=2(cosθ-1)(cos 2θ+cosθ+1)−cosθ(cosθ-1)2+2cos 2θ+cosθ=(cosθ-1)(2cos 2θ+cosθ+2)2+2cos 2θ+cosθ=cos θ-1,∴f (π3)=cos π3-1=12-1=-12. 22.已知cos (π6−α)=√33,求证:sin (4π3+α)+cos 2(2π3−α)=2−√33.【答案】因为cos (π6−α)=√33,所以sin (4π3+α)+cos 2(2π3−α)=sin [3π2−(π6−α)]+cos 2[π2+(π6−α)]=-cos (π6−α)+[−sin?(π6−α)]2=-√33+[1−(1−√33)2]=2−√33.23.若sin(π-α)=log 814,且α∈(−π2,0),则cos(π+α)的值为( )A .√53B .-√53C .±√53D .以上都不对 【答案】B【解析】由sin(π-α)=log 814==-23,∴sin α=-23,cos(π+α)=-cos α=-√53.24.设cos(π+α)=√32(π<α<32π),那么sin(2π-α)的值是( )A .-12 B .√32C .-√32D .12 【答案】D【解析】cos(π+α)=√32,cos α=-√32,又π<α<32π,所以sin α=-12,所以sin(2π-α)=-sin α=12. 25.√1+2sin(π-3)·cos(π+3)的化简结果为( ) A .sin3-cos3B .cos3-sin3C .±(sin3-cos3)D .以上都不对 【答案】A【解析】√1+2sin(π-3)·cos(π+3)=√1−2sin3cos3=sin3-cos3.26.集合P ={α|α=90°-k ·180°,k ∈Z },Q ={β|β=90°-k ·360°,k ∈Z },则P 与Q 关系是( ) A .PQ 且QP B .PQ C .P =Q D .P Q 【答案】C【解析】α=90°(-2k +1),β=90°(-4k +1),而-2k +1,-4k +1,k ∈Z ,都表示所有奇数,∴P =Q . 27.sin25π6+cos10π3+tan(-25π4)+sin(-7π3)·cos(-13π6)=________.【答案】-74 【解析】sin25π6+cos10π3+tan(-25π4)+sin(-7π3)·cos(-13π6)=sin π6+cos4π3+tan(-π4)+sin(-π3)cos(-π6)=sin π6-cos π3-tan π4-sin π3cos π6=12-12-1-√32×√32=-74.28.化简:sin(θ-5π)cos(−π2−θ)cos(8π−θ)sin(θ−3π2)sin(-θ-4π).【答案】原式=−sin(-θ+5π)cos(π2+θ)cosθ-sin(θ+3π2)[-sin(θ+4π)]=-sin(-θ+π)(-sinθ)cosθcosθ(-sinθ)=-sin θ.29.设tan (α+8π7)=m .求证:sin(α+157π)+3cos(α−13π7)sin(−α+20π7)-cos(α+22π7)=m+3m+1.【答案】左边=sin[π+(α+8π7)]+3cos[(α+8π7)−3π]sin[4π−(α+8π7)]−cos[2π+(α+8π7)]=−sin(α+8π7)-3cos(α+8π7)−sin(α+8π7)-cos(α+8π7)=tan(α+87π)+3tan(α+87π)+1=m+3m+1=右边.所以原式成立.30.已知sin(α+β)=1,求证:tan(2α+β)+tan β=0. 【答案】∵sin(α+β)=1, ∴α+β=2k π+π2(k ∈Z ), ∴α=2k π+π2-β(k ∈Z ).∴tan(2α+β)+tan β=tan [2(2k π+π2−β)+β]+tan β=tan(4k π+π-2β+β)+tan β =tan(4k π+π-β)+tan β =tan(π-β)+tan β =-tan β+tan β=0.∴tan(2α+β)+tan β=0.所以原式成立.。
高三数学同角三角函数的基本关系式和诱导公式试题答案及解析

高三数学同角三角函数的基本关系式和诱导公式试题答案及解析1.已知,则.【答案】3【解析】===3.【考点】同角三角函数基本关系式2.若tan α=3,则 sin2α-2 sin αcos α+3 cos2α=______.【答案】【解析】sin2α-2 sin αcos α+3 cos2α====.3.已知f(α)=,则f的值为________.【答案】-【解析】∵f(α)==-cos α,∴f=-cos=-cos=-cos=-.4.化简+=________.【解析】原式=+=-sin α+sin α=0.5.已知α∈(,π),tanα=-,则sin(α+π)=()A.B.-C.D.-【答案】B【解析】由题意可知,由此解得sin2α=,又α∈(,π),因此有sinα=,sin(α+π)=-sinα=-,故选B.6.记cos(-80°)=k,那么tan100°=()A.B.-C.D.-【答案】B【解析】解法一:因为cos(-80°)=cos80°=k,sin80°==,所以tan100°=-tan80°=-=-.解法二:因为cos(-80°)=k,所以cos80°=k,所以tan100°=-tan80°==-.7.已知sinαcosα=,且π<α<,则cosα-sinα的值为()A.-B.C.-D.【答案】B【解析】∵π<α<,∴cosα>sinα,∴cosα-sinα>0,又∵(cosα-sinα)2=1-2cosαsinα=,∴cosα-sinα=.8.若3cos(-θ)+cos(π+θ)=0,则cos2θ+sin2θ的值是________.【答案】【解析】∵3cos(-θ)+cos(π+θ)=0,即3sinθ-cosθ=0,即tanθ=.∴cos2θ+sin2θ======.9.(5分)(2011•福建)若α∈(0,),且sin2α+cos2α=,则tanα的值等于()A.B.C.D.【答案】D【解析】把已知的等式中的cos2α,利用同角三角函数间的基本关系化简后,得到关于sinα的方程,根据α的度数,求出方程的解即可得到sinα的值,然后利用特殊角的三角函数值,由α的范围即可得到α的度数,利用α的度数求出tanα即可.解:由cos2α=1﹣2sin2α,得到sin2α+cos2α=1﹣sin2α=,则sin2α=,又α∈(0,),所以sinα=,则α=,所以tanα=tan=.故选D点评:此题考查学生灵活运用二倍角的余弦函数公式及同角三角函数间的基本关系化简求值,是一道基础题.学生做题时应注意角度的范围.10.已知sin α=+cos α,且α∈,则的值为________.【答案】-【解析】将sin α-cos α=两边平方,得2sin α·cos α=,(sin α+cos α)2=,sin α+cos α=,==-(sin α+cos α)=-.11.在△ABC中,若sinA,cosA是关于x的方程3x2-2x+m=0的两个根,则△ABC是 ( )A.钝角三角形B.直角三角形C.锐角三角形D.不能确定【答案】A【解析】∵sinA,cosA是关于x的方程3x2-2x+m=0的两个根∴sinA+cosA=∴(sinA+cosA)2=1+2sinAcosA=即sinAcosA=-∵0o<A<180o,∴sinA>0,所以cosA<0,即90o<A<180o故知△ABC是钝角三角形12.已知,则()A.B.C.D.【答案】A【解析】∵,∴,∴,∴,∴,∴,∴.【考点】三角函数求值.13.在中,角A,B,C的对边a,b,c成等差数列,且,则 .【答案】【解析】∵成等差数列,∴,∴,∵,∴,∴,∴,(1)∵且,∴代入(1)式中,,∴,∴,∴,∴.【考点】1.等差中项;2.倍角公式;3.诱导公式.14.已知,,则.【答案】【解析】由题意,,.【考点】同角间的三角函数关系.15.若则【答案】【解析】,得,∴.【考点】求三角函数值.16.α是第二象限角,tanα=-,则sinα=________.【答案】【解析】由解得sinα=±.∵α为第二象限角,∴sinα>0,∴sinα=.17. cos=________.【答案】-【解析】cos=cos=cos(17π+)=-cos=-.18.已知其中若.(1)求的值;(2)求的值.【答案】(1);(2).【解析】(1)先由已知条件求得的值,再由平方关系可得的值,把拆为,最后利用两角和的余弦公式即可求得的值;(2)考查了三角函数中知一求三的思想,即这几个量“知一求三”.可先利用差角余弦公式将展开,求得的值,两边平方即可求得的值,再由平方关系即可求得的值,最后由商关系即可求得的值.试题解析:(1)由已知得:,(2)由,得,两边平方得:,即,∵,且,从而. 12分【考点】1.平面向量的数量积运算;2.应用三角恒等变换求三角函数的值.19.已知x∈(0,),则函数f(x)=的最大值为()A.0B.C.D.1【答案】C【解析】由已知得,f(x)==tanx-tan2x=-(tanx-)2+,∵x∈(0,),∴tanx∈(0,1),=.故当tanx=时,f(x)max20.已知sinθ,cosθ是关于x的方程x2-ax+a=0(a∈R)的两个根.(1)求cos3(-θ)+sin3(-θ)的值.(2)求tan(π-θ)-的值.【答案】(1) -2 (2) 1+【解析】【思路点拨】先由方程根的判别式Δ≥0,求a的取值范围,而后应用根与系数的关系及诱导公式求解.解:由已知,原方程的判别式Δ≥0,即(-a)2-4a≥0,∴a≥4或a≤0.又(sinθ+cosθ)2=1+2sinθcosθ,则a2-2a-1=0,从而a=1-或a=1+(舍去),因此sinθ+cosθ=sinθcosθ=1-.(1)cos3(-θ)+sin3(-θ)=sin3θ+cos3θ=(sinθ+cosθ)(sin2θ-sinθ·cosθ+cos2θ)=(1-)[1-(1-)]=-2.(2)tan(π-θ)-=-tanθ-=-(+)=-=-=1+.21.若sinθcosθ>0,则θ在()A.第一、二象限B.第一、三象限C.第一、四象限D.第二、四象限【答案】B【解析】∵sinθcosθ>0,∴sinθ,cosθ同号.当sinθ>0,cosθ>0时,θ在第一象限,当sinθ<0,cosθ<0时,θ在第三象限,因此,选B.22.=()A.-B.-C.D.【解析】====sin 30°=.23.设当x=θ时,函数f(x)=sin x-2cos x取得最大值,则cos θ=________.【答案】-【解析】f(x)=sin x-2cos x==sin(x-φ),其中sin φ=,cos φ=,当x-φ=2kπ+ (k∈Z)时,函数f(x)取得最大值,即θ=2kπ++φ时,函数f(x)取到最大值,所以cos θ=-sin φ=-.24. 4cos 50°-tan 40°=________.【答案】【解析】4cos 50°-tan 40°======.25.已知α∈,且cos α=-,则tan α=________.【答案】2【解析】利用同角三角函数的基本关系求解.由条件可得sin α=-,所以tan α===2.26.若α,β∈,cos =,sin =-,则cos (α+β)=________.【答案】【解析】∵α,β∈,∴-<α-<,-<-β<,由cos =和sin =-得α-=±,-β=-,当α-=-,-β=-时,α+β=0,与α,β∈矛盾;当α-=,-β=-时,α=β=,此时cos (α+β)=-.27.若cos =,则cos =().A.-B.-C.D.【答案】D【解析】∵cos =,∴cos =2cos 2-1=-,即sin 2x=,∴cos =sin 2x=.28.已知sin θ+cos θ=,则sin θ-cos θ的值为________.【答案】-【解析】∵sin θ+cos θ=,∴(sin θ+cos θ)2=1+2cos θsin θ=,∴2cos θsin θ=,∴(sin θ-cos θ)2=1-=,又θ∈,∴sin θ<cos θ,∴sin θ-cos θ=-.29.已知,则=____________.【答案】【解析】,根据,可知:,故答案为.【考点】同角三角函数的基本关系式的运算30.已知,且,则.【答案】【解析】因为,所以。
课时作业12:1.2.4 诱导公式(一)

1.2.4 诱导公式(一)一、选择题1.cos 600°的值为( ) A.32 B.12 C .-32 D .-12答案 D解析 cos 600°=cos(360°+240°)=cos 240°=cos(180°+60°)=-cos 60°=-12. 2.tan 690°的值为( )A .-33 B.33C. 3 D .- 3 答案 A解析 tan 690°=tan(360°+330°)=tan 330°=tan(360°-30°)=-tan 30°=-33. 3.若cos(π+α)=-12,32π<α<2π,则sin(2π+α)等于( ) A.12 B .±32 C.32 D .-32答案 D解析 由cos(π+α)=-12,得cos α=12,故sin(2π+α)=sin α=-1-cos 2 α=-32(α为第四象限角).4.化简sin 2(π+α)-cos(π+α)·cos(-α)+1的值为( )A .1B .2sin 2αC .0D .2考点 同名诱导公式的综合应用题点 同名诱导公式的综合应用答案 D解析 原式=(-sin α)2-(-cos α)·cos α+1=sin 2α+cos 2α+1=2.5.记cos(-80°)=k ,那么tan 100°等于( ) A.1-k 2k B .-1-k 2kC.k 1-k 2 D .-k 1-k 2答案 B解析 ∵cos(-80°)=k ,∴cos 80°=k ,∴sin 80°=1-k 2,则tan 80°=1-k 2k . ∴tan 100°=-tan 80°=-1-k 2k. 6.tan(5π+α)=m ,则sin (α-3π)+cos (π-α)sin (-α)-cos (π+α)的值为( ) A.m +1m -1B.m -1m +1 C .-1D .1 答案 A解析 ∵tan(5π+α)=tan α=m ,∴原式=sin α+cos αsin α-cos α=tan α+1tan α-1=m +1m -1. 7.已知n 为整数,化简sin (n π+α)cos (n π+α)所得的结果是( ) A .tan nαB .-tan nαC .tan αD .-tan α 答案 C解析 当n =2k ,k ∈Z 时,sin (n π+α)cos (n π+α)=sin (2k π+α)cos (2k π+α) =sin αcos α=tan α; 当n =2k +1,k ∈Z 时,sin (n π+α)cos (n π+α)=sin (2k π+π+α)cos (2k π+π+α) =sin (π+α)cos (π+α)=-sin α-cos α=tan α.故选C. 二、填空题8.cos (-585°)sin 495°+sin (-570°)的值是________. 答案2-2 解析 原式=cos (360°+225°)sin (360°+135°)-sin (210°+360°)=cos 225°sin 135°-sin 210°=cos (180°+45°)sin (180°-45°)-sin (180°+30°)=-cos 45°sin 45°+sin 30°=-2222+12=2-2. 9.已知a =tan ⎝⎛⎭⎫-7π6,b =cos 23π4,c =sin ⎝⎛⎭⎫-33π4,则a ,b ,c 的大小关系是________. 答案 b >a >c解析 ∵a =-tan 7π6=-tan π6=-33, b =cos ⎝⎛⎭⎫6π-π4=cos π4=22, c =-sin 33π4=-sin π4=-22, ∴b >a >c .10.已知cos(π+α)=-35,π<α<2π,则sin(α-3π)+cos(α-π)=________. 答案 15解析 ∵cos(π+α)=-cos α=-35, ∴cos α=35,又∵π<α<2π,∴3π2<α<2π, ∴sin α=-45. ∴sin(α-3π)+cos(α-π)=-sin(3π-α)+cos(π-α)=-sin(π-α)+(-cos α)=-sin α-cos α=-(sin α+cos α) =-⎝⎛⎭⎫-45+35=15. 11.设f (x )=a sin(πx +α)+b cos(πx +β),其中a ,b ,α,β为非零常数,若f (2 017)=-1,则f (2 018)=________.答案 1解析 ∵f (2 018)=a sin(2 018π+α)+b cos(2 018π+β)=a sin(π+2 017π+α)+b cos(π+2 017π+β)=-a sin(2 017π+α)-b cos(2 017π+β)=-f (2 017),又f (2 017)=-1,∴f (2 018)=1.12.sin ⎝⎛⎭⎫-193πcos 76π=________. 答案 34解析 sin ⎝⎛⎭⎫-193πcos 76π =-sin ⎝⎛⎭⎫6π+π3cos ⎝⎛⎭⎫π+π6=sin π3cos π6=34. 三、解答题13.若cos(α-π)=-23,求 sin (α-2π)+sin (-α-3π)cos (α-3π)cos (π-α)-cos (-π-α)cos (α-4π)的值. 解 原式=-sin (2π-α)-sin (3π+α)cos (3π-α)-cos α-(-cos α)cos α=sin α-sin αcos α-cos α+cos 2α=sin α(1-cos α)-cos α(1-cos α)=-tan α. ∵cos(α-π)=cos(π-α)=-cos α=-23, ∴cos α=23. ∴α为第一象限角或第四象限角.当α为第一象限角时,cos α=23,sin α=1-cos 2α=53, ∴tan α=sin αcos α=52,∴原式=-52. 当α为第四象限角时,cos α=23, sin α=-1-cos 2α=-53, ∴tan α=sin αcos α=-52,∴原式=52. 综上,原式=±52. 四、探究与拓展14.已知f (x )=⎩⎪⎨⎪⎧sin πx ,x <0,f (x -1)-1,x >0,则f ⎝⎛⎭⎫-116+f ⎝⎛⎭⎫116的值为________. 答案 -2解析 因为f ⎝⎛⎭⎫-116=sin ⎝⎛⎭⎫-11π6=sin ⎝⎛⎭⎫-2π+π6=sin π6=12; f ⎝⎛⎭⎫116=f ⎝⎛⎭⎫56-1=f ⎝⎛⎭⎫-16-2 =sin ⎝⎛⎭⎫-π6-2=-12-2=-52, 所以f ⎝⎛⎭⎫-116+f ⎝⎛⎭⎫116=-2. 15.已知f (α)=sin (π+α)cos (2π-α)tan (-α)tan (-π-α)sin (-π-α). (1)化简f (α);(2)若α是第三象限角,且sin(α-π)=15,求f (α)的值; (3)若α=-31π3,求f (α)的值. 解 (1)f (α)=-sin αcos α(-tan α)(-tan α)sin α=-cos α. (2)∵sin(α-π)=-sin α=15, ∴sin α=-15.又α是第三象限角,∴cos α=-265. ∴f (α)=265. (3)∵-31π3=-6×2π+5π3, ∴f ⎝⎛⎭⎫-31π3=-cos ⎝⎛⎭⎫-6×2π+5π3 =-cos 5π3=-cos π3=-12.。
高一数学 三角函数诱导公式练习

同角三角函数的基本关系、三角函数的诱导公式(测试时间:40分钟,总分:100分)班级:____________ 姓名:____________ 座号:____________ 得分:____________一、选择题(本大题共9小题,每小题4分,共36分)1.8tan3π的值为A B . C D .2.4sin 3⎛⎫-π ⎪⎝⎭=A B . C .12D .12-3.已知()sin 30α︒+=,则cos (60°–α)的值为A .12B .12- CD . 4.若α为第二象限的角,且tan α=–512,则cos α=A .513B .–513C .1213D .–12135.已知1sin 3θ=,2θπ⎛⎫∈π ⎪⎝⎭,,则tanθ=A .–2B .C .D . 6.已知α是第一象限角,tan α=34,则sin α等于 A .45B .35C .–45D .–357.若()cos 2απ-=且02απ⎛⎫∈- ⎪⎝⎭,,则sin (π–α)A .B .23-C .13-D .23±8.已知()3cos 5x π+=,x ∈(π,2π),则tan x 等于A.34-B.43-C.34D.439.454sin cos tan363⎛⎫π⋅π⋅-π⎪⎝⎭的值是A.B C.D二、填空题(本大题共5小题,每小题4分,共20分)10.cos660°=___________.11.tan240°=___________.12.已知tanα=2,则3sin cos2sin3cosαααα-=+___________.13.已知sinα+cosα=13,则sinαcosα=___________.14.已知4cos45απ⎛⎫-=⎪⎝⎭,则sin4απ⎛⎫+=⎪⎝⎭___________.三、解答题(本大题共4小题,每小题11分,共44分)15.计算:sin 2526cos63ππ++tan(254π-).16.若5sin coscos sinαααα-+=1.(1)求tanα的值;(2)求cos sincos sinαααα+-+sinαcosα的值.17.已知α为第三象限角,()()()()3sin cos tan22tan sinfααααααππ⎛⎫⎛⎫-+π-⎪ ⎪⎝⎭⎝⎭=--π--π,(1)化简f(α);(2)若31cos25απ⎛⎫-=⎪⎝⎭,求f(α)的值.18.已知f (α)=()()()()3sin 3cos 2sin 2cos sin αααααπ⎛⎫π-π-- ⎪⎝⎭π--π-, (1)化简f (α);(2)若α是第二象限角,且cos (2π+α)=–13,求f (α)的值.。
专题08 诱导公式的化简求值(解析版)-高考数学计算题型精练(新高考通用版)

诱导公式的化简求值1.已知π0,2α⎛⎫∈ ⎪⎝⎭,3sin 5α=,则9πsin sin(8π)25πsin sin(7π)2αααα⎛⎫+++ ⎪⎝⎭=⎛⎫+++ ⎪⎝⎭______.【答案】7【详解】因为3sin 5α=,且π0,2α⎛⎫∈ ⎪⎝⎭,所以4cos 5α==,所以sin 3tan cos 4ααα==.所以9πsin sin(8π)25πsin sin(7π)2αααα⎛⎫+++ ⎪⎝⎭⎛⎫+++ ⎪⎝⎭31cos sin 1tan 473cos sin 1tan 14αααααα+++====---.故答案为:7.2.若π2cos 123α⎛⎫+= ⎪⎝⎭,则2πsin 23α⎛⎫+= ⎪⎝⎭__________.【答案】19-【详解】2ππππsin 2sin 2cos 2312212ααα⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫+=++=+ ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦22π212cos 1211239α⎛⎫⎛⎫=+-=⨯-=- ⎪ ⎪⎝⎭⎝⎭.故答案为:19-.3.计算7π5πcos sin 644πtan 3的结果为__________.【答案】4【详解】因为7πππcoscos πcos 666⎛⎫=+=-= ⎪⎝⎭5πππsin sin πsin 444⎛⎫=+=-=- ⎪⎝⎭4πππtan tan πtan 333⎛⎫=+= ⎪⎝⎭所以7π5πcos sin 22644πtan 3⎛⎫⎛⎫-⨯ ⎪ ⎪=故答案为:4.4.点()3,4A 在角θ的终边上,则sin(π)2cos πcos()cos 2θθθθ++=--__________.【答案】2【详解】因为点()3,4A 在角θ的终边上,则4tan 3θ=,所以42sin(π)2cos sin 2cos tan 232π4sin cos tan 1cos()cos 123θθθθθθθθθθ-+++-+-+===-----.故答案为:25.若1sin 3α=,则πcos 2α⎛⎫+= ⎪⎝⎭__________.【答案】13-【详解】π1cos sin 23αα⎛⎫+=-=- ⎪⎝⎭.故答案为:13-6.已知角α终边上一点()2,3P -,则()()πcos sin π23πcos πcot 2αααα⎛⎫+- ⎪⎝⎭=⎛⎫++ ⎪⎝⎭________.【答案】【详解】由诱导公式知,()()πcos sin πsin sin 2sin 3πcos (tan )cos πcot 2ααααααααα⎛⎫+- ⎪-⋅⎝⎭===--⋅-⎛⎫++ ⎪⎝⎭,因为角α终边上一点()2,3P -,所以sin α所以原式sin 13α=-=-.故答案为:7.23πtan 3⎛⎫-= ⎪⎝⎭____.【详解】23π23π2π2ππtan(tan tan(7π)tan tan 33333-=-=-+=-=8.cos660︒=________.【答案】12/0.5【详解】()()1cos660cos 236060cos 60cos602︒=⨯︒-︒=-︒=︒=故答案为:129.化简:()()()()sin 2πcos 6πcos πsin 5πθθθθ---=-+_____.【答案】1-【详解】原式=()()()()()()()sin cos sin cos 1cos πsin πcos sin θθθθθθθθ-⋅--⋅==-+⋅+-⋅-.故答案为:1-.10.若()sin π3α-=,则πcos 2α⎛⎫+= ⎪⎝⎭______.【答案】【详解】因为()sin sin παα-=所以πcos sin 2αα⎛⎫+=-=- ⎪⎝⎭.故答案为:11.()()cos πππsin cos sin π22αααα-⎛⎫⎛⎫-+ ⎪ ⎪-⎝⎭⎝⎭=____________【答案】2cos α-【详解】原式()()()2cos cos sin cos sin ααααα-=⋅⋅-=--故答案为:2cos α-.12.已知()1cos π2α+=-,3π2π2α<<,则()sin 3πα+=_________.【答案】2【详解】()1cos π2α+=- ,1cos 2α∴-=-,即1cos 2α=,3π2π2α<<,sin 2α∴==()sin 3πsin αα∴+=-=13.()()()()tan 2πsin 2πcos 6πcos π3ππsin cos 22x x x x x x -----=⎛⎫⎛⎫+- ⎪ ⎪⎝⎭⎝⎭__________【答案】sin x【详解】()()()tan 2πtan ,sin 2πsin sin x x x x x -=---=-=-,()()()cos 6πcos cos ,cos πcos x x x x x -=-=-=-,3ππsin cos ,cos sin 22x x x x ⎛⎫⎛⎫+=-= ⎪ ⎪⎝⎭⎝⎭,原式()()()()tan sin cos cos tan cos sin cos sin x x x x x x x x x-⨯-⨯⨯-==⨯=-⨯,故答案为:sin x .14.若α的终边过点()1,2-,则()()sin ππsin cos π2ααα-=⎛⎫+-+ ⎪⎝⎭______.【答案】1-【详解】因为α的终边过点(1,2)-,由三角函数的定义可得2tan 21α==--,所以()()sin πsin 11tan (2)1πcos cos 22sin cos π2ααααααα-===⨯-=-+⎛⎫+-+ ⎪⎝⎭.故答案为:1-15.已知()1sin π3α+=,则πcos()2α+=_________________.【答案】13【详解】由已知1sin(π)sin 3αα+=-=,1sin 3α=-,所以π1cos()sin 23αα+=-=.故答案为:13.16.若角α的终边过点()1,2-,则πsin 2α⎛⎫-= ⎪⎝⎭__________.【答案】【详解】角α的终边过点(1,2)-,由三角函数的定义得cos α=由诱导公式得ππsin sin cos 225ααα⎛⎫⎛⎫-=--=-=- ⎪ ⎪⎝⎭⎝⎭,故答案为:17.1717cos πsin π44⎛⎫⎛⎫---= ⎪ ⎪⎝⎭⎝⎭______.【详解】17π17π17π17πππcos sin cos sin cos 4πsin 4π444444⎛⎫⎛⎫⎛⎫⎛⎫---=+=+++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭ππcos sin 4422=+=;.18.7πsin 3的值为__________【答案】2【详解】7πππsinsin 2πsin 3332⎛⎫=+== ⎪⎝⎭.19.已知5sin 13α=,则πcos 2α⎛⎫+= ⎪⎝⎭______.【答案】513-【详解】由π5cos sin 213αα⎛⎫+=-=- ⎪⎝⎭.故答案为:513-20.已知tan 3α=,求sin(4)3cos()92sin()sin(7)2παπαπαπα-+--=-+-+_________【答案】-6【详解】原式=sin 3cos tan 33362cos sin 2tan 23αααααα------===--+-+-+.故答案为:-6.21.已知角x 在第二象限,且π4cos ,25x ⎛⎫+=- ⎪⎝⎭则tan 2x =______.【答案】247/337【详解】π4cos 25x ⎛⎫+=- ⎪⎝⎭,即4sin 5x -=-,则4sin 5x =, 角x在第二象限,则3cos 5x ==-,则4tan 3x =-,22tan 24tan 21tan 7x x x ∴==-.故答案为:247.22.若()1sin π2A +=-,则3πcos 2A ⎛⎫-= ⎪⎝⎭____________.【答案】12-/-0.5【详解】因为()2π3π5π2A A ⎛⎫-= ⎪⎝⎭+-,所以3πcos 2A ⎛⎫-= ⎪⎝⎭()()()()5πππ1cos πcos πcos πsin π2222A A A A ⎡⎤⎡⎤⎡⎤+-=+-=-+=+=-⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦.故答案为:12-23.化简:()()tan cos 3ππ2co i πt 2πs n 2αααα⎛⎫- ⎪-⎝⎭⋅=+⎛⎫+ ⎪⎝⎭_________.【答案】1【详解】()()tan cos 3πcos cot 21cot 2πcos cot πi 2πs n αααααααα⎛⎫- ⎪---⎝⎭⋅=⋅=+⎛⎫+ ⎪⎝⎭.故答案为:124.已知α是第二象限角,1sin 3α=,则πsin 2α⎛⎫+= ⎪⎝⎭________.【答案】3-/【详解】因为α是第二象限角,1sin 3α=,所以πsin cos 2αα⎛⎫+==-- ⎪⎝⎭故答案为:25.已知1tan 2α=,则()cos ππcos 2αα-=⎛⎫+ ⎪⎝⎭__________.【答案】2【详解】因为1tan 2α=,所以()cos πcos 12πsin tan cos 2ααααα--===-⎛⎫+ ⎪⎝⎭.故答案为:2.26.已知1cos 2α=,3π2π2α<<,则()sin 2πα-=______.【答案】2【详解】因为13πcos ,2π22αα=<<,所以sin2α==-,所以sin(2)sinπαα-=-=.故答案为:2.27.化简:()()()π11πcosπcos cos229πcosπsinπsin2αααααα⎛⎫⎛⎫++-⎪ ⎪⎝⎭⎝⎭=⎛⎫---+⎪⎝⎭______.【答案】tanα【详解】()()()π11πcosπcos cos229πcosπsinπsin2αααααα⎛⎫⎛⎫++-⎪ ⎪⎝⎭⎝⎭⎛⎫---+⎪⎝⎭()()cos sin sin tancos sin cosααααααα-⋅--==-.故答案为:tanα.28.化简πsin(5π)cos()cos(8π)23πsin()sin(4π)2θθθθθ---=---__.【答案】sinθ【详解】πsin(5π)cos()cos(8π)(sin)sin cos2sin3πcos(sin)sin()sin(4π)2θθθθθθθθθθθ----==----.故答案为:sinθ.29.化简222sin(π)cos(π)cos(2π)3π3π1cos cos sin222παααααα+-+-⎛⎫⎛⎫⎛⎫+-++-+⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭的结果为______.【答案】1tanα【详解】222sin(π)cos(π)cos(2π)3π3π1cos cos sin222παααααα+-+-⎛⎫⎛⎫⎛⎫+-++-+⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭222(sin)(cos)cosππ1cos cos cosπ22παααααα--+=⎛⎫⎛⎫+-++-⎪⎡⎤⎡⎤++⎢⎥⎢⎪⎝⎭⎝⎭⎥⎣⎦⎣⎦22222sin cos cos 2sin cos cos 1sin sin cos ππ1cos cos cos 22αααααααααααα++==++-⎡⎤⎛⎫⎛⎫+---+- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦22sin cos cos (2sin 1)cos cos 12sin sin (2sin 1)sin sin tan αααααααααααα++====++.故答案为:1tan α.30.已知角θ的顶点在坐标原点,始边与x 轴的非负半轴重合,终边经过点()()8,60P m m m -->.(1)求sin θ,cos θ的值;(2)求()()()()()()3πsin sin 3πcos πcos 25πsin 2πcos 3πsin sin π2θθθθθθθθ⎛⎫-⋅-⋅+⋅- ⎪⎝⎭⎛⎫-⋅-⋅-⋅- ⎪⎝⎭的值.【答案】(1)3sin 5θ=-,4cos 5θ=-;(2)34-【详解】(1)由题意知,10r m ==,∴63sin 105y m r m θ-===-,84cos 105x m r m θ-===-;(2)原式()()()()()()()322sin sin cos sin sin cos sin cos cos sin sin cos θθθθθθθθθθθθ-⋅-⋅-⋅-⋅==--⋅-⋅⋅-⋅tan θ=-,由(1)知,sin 3tan cos 4θθθ==,∴()()()()()()3πsin sin 3πcos πcos 325π4sin 2πcos 3πsin sin π2θθθθθθθθ⎛⎫-⋅-⋅+⋅- ⎪⎝⎭=-⎛⎫-⋅-⋅-⋅- ⎪⎝⎭.31.已知角θ的始边为x 轴非负半轴,终边过点(A -.(1)3ππcos sin 22θθ⎛⎫⎛⎫-++ ⎪ ⎪.(2)已知角α的始边为x 轴非负半轴,角θ和α的终边关于y 轴对称,求πsin 6α⎛⎫- ⎪⎝⎭的值.【答案】(1)2-(2)6【详解】(1)由题可知OA =则sin ,cos ,tan 33θθθ===3ππcos 222θθ⎛⎫⎛⎫-+++ ⎪ ⎪=-.(2)因为角θ和α的终边关于y 轴对称,所以sin αcos α所以π1sin sin cos 6226ααα⎛⎫-=-= ⎪⎝⎭.32.已知()()ππsin cos 223πcos πsin 2f ααααα⎛⎫⎛⎫-+ ⎪ ⎪⎝⎭⎝⎭=⎛⎫-+ ⎪⎝⎭.(1)若角α的终边经过点(),2m m ,0m ≠,求()f α的值;(2)若()2f α=,求sin cos sin cos αααα+-的值.【答案】(1)2(2)3【详解】(1)()()()()ππsin cos cos sin 22tan 3πcos cos cos πsin 2f αααααααααα⎛⎫⎛⎫-+ ⎪ ⎪-⋅-⎝⎭⎝⎭===-⋅-⎛⎫-+ ⎪⎝⎭,因为角α的终边经过点(),2m m ,0m ≠,所以()2tan 2m f mαα===.(2)由(1)知()tan 2f αα==,所以sin cos tan 1213sin cos tan 121αααααα+++===---.33.已知()()()()()πsin sin tan π2tan 2πsin π+f αααααα⎛⎫--- ⎪⎝⎭=-(1)化简()f α.(2)若α为第三象限角,且3π1cos 25⎛⎫-= ⎪⎝⎭α,求()f α的值.【答案】(1)()f αcos α=(2)()f α=【详解】(1)()()()()()πsin sin tan π2tan sin πf αααααα⎛⎫--- ⎪⎝⎭=-+()()()cos sin tan tan sin ααααα⋅-⋅-=-⋅-cos α=.(2)∵α为第三象限角,且3π1cos sin 25⎛⎫-=-= ⎪⎝⎭αα,∴1sin 5α=-,()cos f αα===.34.已知()()()3πsin 2πsin 2πsin cos π2f ααααα⎛⎫-⋅- ⎪⎝⎭=⎛⎫+⋅- ⎪⎝⎭.(1)化简()f α;(2)若()2f α=,求2222sin 1sin 2cos ααα-+的值【答案】(1)()tan f αα=-(2)12【详解】(1)()()()()()3πsin 2πsin sin cos 2tan cos cos sin cos π2πf αααααααααα⎛⎫-⋅- ⎪-⋅-⎝⎭===-⋅-⎛⎫+⋅- ⎪⎝⎭;(2)由(1)得tan 2α-=,tan 2α∴=-,()2222222222222sin sin cos 2sin 1sin cos sin 2cos sin 2cos sin 2cos αααααααααααα-+--∴==+++221tan ta 1412422n αα--===++.35.(1)化简:3πtan(π)cos(2π)sin()2cos(π)sin(π)ααααα---+----;(2)已知π3cos 45x ⎛⎫+= ⎪⎝⎭,求2sin 22sin 1tan x xx --的值.【答案】(1)1-;(2)725【详解】(1)3πtan(π)cos(2π)sin()2cos(π)sin(π)ααααα---+----=sin cos (tan )cos (cos )cos 1(cos )sin sin ααααααααα⋅-⋅⋅-=-=--⋅;(2)2sin 22sin 2sin (cos sin )2sin cos sin 1tan 1cos x x x x x x xx x x--==--,()2π331818cos cos sin cos sin 12sin cos 4552525x x x x x x x ⎛⎫+==⇒-=⇒-=⎪⎝⎭72sin cos 25x x ⇒=,因此2sin 22sin 71tan 25x x x -=-.36.已知()()()()π3πcos tan πsin 22cos πtan 3πf αααααα⎛⎫⎛⎫+-+ ⎪ ⎪⎝⎭⎝⎭=++.(1)若()0,2πα∈,且()12f α=-,求α的值;(2)若()3π125f f αα⎛⎫-+= ⎪⎝⎭,且π3π,22⎛⎫∈ ⎪⎝⎭α,求tan α的值.【答案】(1)7π6α=或11π6α=(2)4tan 3α=-【详解】(1)()()()()()()π3πcos tan πsin sin tan cos 22sin cos πtan 3πcos tan f αααααααααααα⎛⎫⎛⎫+-+ ⎪ ⎪---⎝⎭⎝⎭===++-,()0,2πα∈,且()1sin 2f αα==-,则7π6α=或11π6α=.(2)()3π3π1sin sin sin cos 225f f αααααα⎛⎫⎛⎫-+=-+=+=⎪ ⎪⎝⎭⎝⎭,则1sin cos 5αα=-,所以22221cos sin cos cos 15αααα⎛⎫+=+-= ⎪⎝⎭,解得4cos 5α=或3cos 5α=-,由π3π,22⎛⎫∈ ⎪⎝⎭α,则3cos 5α=-,得4sin 5α=,所以4sin 45tan 3cos 35ααα===--37.已知tan 3α=,求()()πsin 3sin π23πcos cos 5π2αααα⎛⎫+++ ⎪⎝⎭⎛⎫--+ ⎪⎝⎭的值.【答案】4【详解】因为()πsin cos ,sin πsin 2αααα⎛⎫+=+=- ⎪⎝⎭,()()3πcos sin ,cos 5πcos πcos 2ααααα⎛⎫-=-+=+=- ⎪⎝⎭,所以()()πsin 3sin πcos 3sin 13tan 23πsin cos tan 1cos cos 5π2αααααααααα⎛⎫+++ ⎪--⎝⎭==-+-+⎛⎫--+ ⎪⎝⎭,又tan 3α=,所以()()πsin 3sin π133243π31cos cos 5π2αααα⎛⎫+++ ⎪-⨯⎝⎭==-+⎛⎫--+ ⎪⎝⎭.故答案为:4.38.已知()()5πsin πsin 23π2sin sin π2αααα⎛⎫-++ ⎪⎝⎭=⎛⎫-++ ⎪⎝⎭.(1)求tan α的值;(2)求24sin cos 2cos ααα+的值.【答案】(1)7tan 4α=-(2)1613-【详解】(1)依题意得,()()5πsin πsin sin cos 2π2cos sin 2sin sin π2αααααααα⎛⎫-++ ⎪+⎝⎭=--⎛⎫-++ ⎪⎝⎭tan 132tan αα+==--,解得7tan 4α=-(2)22224sin cos 2cos 4sin cos 2cos sin cos αααααααα++=+24tan 2tan 1αα+=+1613=-.39.已知角α终边上一点(4,3),P -求()πcos()sin π211π9πcos()sin()22a a a α+----++的值.【答案】67【详解】角α终边上一点(4,3),P -3tan ,4y x α∴==-则原式32()sin sin 2tan 64.3sin cos tan 1714αααααα-⨯----====-+-++故答案为:6740.设()322π2cos sin 2cos π222cos 7πcos f θθθθθθ⎛⎫++--- ⎪⎝⎭=+++-()()(),求2023π3f ⎛⎫⎪⎝⎭的值.【答案】12.【详解】因为()322π2cos sin 2cos π222cos 7πcos f θθθθθθ⎛⎫++--- ⎪⎝⎭=+++-()()()=322222cos cos 2cos cos 2cos cos 2cos 22cos cos 22cos cos θθθθθθθθθθθ++++==++++(),所以2023π2023πππ1cos cos 3372πcos 33332f ⎛⎫⎛⎫==⨯+== ⎪ ⎪⎝⎭⎝⎭41.已知1tan 2θ=-,求下列各式的值:(1)22cos 12sin cos θθθ-;(2)tan(π)sin(π)3πππsin cos cos 222θθθθθ--⎛⎫⎛⎫⎛⎫+-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.【答案】(1)34-(2)54【详解】(1)原式()222222cos sin cos cos sin 2sin cos 2sin cos θθθθθθθθθ-+-==22111tan 3212tan 422θθ⎛⎫-- ⎪-⎝⎭===-⎛⎫⨯- ⎪⎝⎭.(2)原式tan sin (cos )sin (sin )θθθθθ=--22221sin cos cos cos θθθθ+==22151tan 124θ⎛⎫=+=+-= ⎪⎝⎭.42.已知()()()()()3sin 3πcos 2πsin π2cos πsin πf αααααα⎛⎫-⋅-⋅-+ ⎪⎝⎭=--⋅-+.(1)化简()f α;(2)若31π3α=-,()f α.【答案】(1)cos α(2)12【详解】(1)由题意可得:()()()()()()()()()3sin 3πcos 2πsin πsin πcos cos 2cos cos πsin πcos sin πf αααααααααααα⎛⎫-⋅-⋅-+ ⎪-+⋅⋅-⎝⎭===--⋅-+-⋅-+,故()cos f αα=.(2)∵31π3α=-,则()3131πππ1πcos πcos 10πcos cos 333332f f α⎛⎫⎛⎫⎛⎫⎛⎫=-=-=--=-== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,∴()12f α=.43.已知3πsin(3π)cos(2π)sin()2()cos(π)sin(π)f αααααα---+=----.(1)化简()f a ;(2)若α是第三象限角,且3π1co (s 52α-=,求π(6f α+的值;【答案】(1)()f α=cos α-;(2)110【详解】(1)3πsin(3π)cos(2π)sin()2()cos(π)sin(π)f αααααα---+=----(sin )cos (cos )cos (cos )sin αααααα-⋅⋅-==--.(2)因为3π1co (s 52α-=,又3ππcos(cos()sin 22ααα-=+=-,所以1sin 5α=-,又α是第三象限的角,所以cos α=-所以ππππ(cos()cos cos sin sin6666f αααα+=-+=-+111(()5210-=-⨯-⨯=.44.sin(2π)sin(π)cos(π)sin(3π)cos(π)ααααα-+----.【答案】sin α【详解】因为sin(2π)sin()sin ,sin(π)sin ,ααααα-=-=-+=-cos(π)cos(π)cos ααα--=+=-,sin(3π)sin(π)sin ,cos(π)cos ,ααααα-=-=-=-所以原式sin (sin )(cos )sin sin (cos )αααααα-⋅-⋅-==⋅-.45.(1)化简:()()()()()()π11πsin 2πcos πcos cos 229πcos πsin 3πsin πsin 2f ααααααααα⎛⎫⎛⎫-++- ⎪ ⎪⎝⎭⎝⎭=⎛⎫----+ ⎪⎝⎭(2)求值:cos21cos24sin159sin 204︒⋅︒+︒⋅︒.【答案】(1)tan α-;(2)2.【详解】(1)()()()()()()π11πsin 2πcos πcos cos 229πcos πsin 3πsin πsin 2f ααααααααα⎛⎫⎛⎫-++- ⎪ ⎪⎝⎭⎝⎭=⎛⎫----+ ⎪⎝⎭()()()()()()πsin cos sin cos 6π2πcos sin πsin πsin 4π2αααααααα⎡⎤⎛⎫----+ ⎪⎢⎥⎝⎭⎣⎦=⎡⎤⎛⎫---+++⎡⎤ ⎪⎣⎦⎢⎥⎝⎭⎣⎦()()()()πsin cos sin cos 2πcos sin sin sin 2αααααααα⎡⎤⎛⎫----+⎪⎢⎥⎝⎭⎣⎦=⎛⎫-+ ⎪⎝⎭()()()2222sin cos cos sin cos sin sin 2tan cos sin cos cos sin cos cos πααααααααααααααα⎛⎫-+ ⎪--⎝⎭===-=---(2)cos 21cos 24sin159sin 204cos 21cos 24sin 21sin 24︒⋅︒+︒⋅︒=︒⋅︒-︒︒()cos 2124cos 452=︒+︒=︒46..化简下列各式:(1)π2912sin cos 6ππtan 54⎛⎫-+⋅ ⎪⎝⎭;(2)3tan(π)cos(2π)sin(π)2cos(3π)sin(π)ααααα+⋅+⋅---⋅--.【答案】(1)12-(2)1-【详解】(1)原式52sin cos 0π6π5=-+⨯2π1sin6=-=-(2)原式tan cos cos 1cos sin ααααα⋅⋅==--⋅47.已知()()()()()5πsin 2πcos πcos 29πcos πsin πsin 2x x x f x x x x ⎛⎫-+- ⎪⎝⎭=⎛⎫---+ ⎪⎝⎭.(1)化简()f x ;(2)已知()2f α=,求sin2α的值.【答案】(1)tan x -(2)45-【详解】(1)由题意得()()()()()5πsin 2πcos πcos 29πcos πsin πsin 2x x x f x x x x ⎛⎫-+- ⎪⎝⎭=⎛⎫---+ ⎪⎝⎭(sin )(cos )sin sin tan (cos )sin cos cos x x x xx x x x x--==-=--.(2)由()2f α=,可得tan 2,tan 2αα-=∴=-,则2222sin cos 2tan 4sin2sin cos tan 15ααααααα===-++.48.(1)已知()2tan π3α-=-,求cos 3sin cos 9sin α-αα+α的值;(2)化简()()()()3πsin πsin tan 2π2πsin tan πcos 2θθθθθθ⎛⎫--- ⎪⎝⎭⎛⎫-+- ⎪⎝⎭.【答案】(1)17-;(2)tan θ.【详解】(1)因为()2tan πtan 3αα-=-=-,可得2tan 3α=,所以213cos 3sin 13tan 132cos 9sin 19tan 7193αααααα-⨯--===-+++⨯;(2)()()()()()()23πsin πsin tan 2πsin cos tan 2tan πcos tan sin tan πcos 2θθθθθθθθθθθθ⎛⎫--- ⎪--⎝⎭==⎛⎫-+- ⎪⎝⎭.49.已知sin 2cos αα=,求:(1)化简()()πcos 2sin 2πcos 2π5πsin 2αααα⎛⎫- ⎪⎝⎭--⎛⎫+ ⎪⎝⎭;(2)求2sin2sin sin cos cos21ααααα+--的值.【答案】(1)45(2)1【详解】(1)因为sin 2cos αα=,22sin cos 1αα+=,所以22sin sin 12αα⎛⎫+= ⎪⎝⎭,即24sin 5α=,()()2πcos sin 42sin 2πcos 2πsin cos sin 5πcos 5sin 2ααααααααα⎛⎫- ⎪⎝⎭--===⎛⎫+ ⎪⎝⎭.(2)sin tan 2cos ααα== ,2sin2sin sin cos cos21ααααα∴+--()222sin cos sin sin cos 2cos 11αααααα=+---222sin cos sin sin cos 2cos αααααα=+-222tan tan tan 2221222ααα=+-⨯==+-.50.化简以下式子:()()()()()7πsin cos πtan 3π2sin 2πtan πcos 9παααααα⎛⎫++- ⎪⎝⎭--+-【答案】1tan α-【详解】()()()()()7πsin cos πtan 3π2sin 2πtan πcos 9παααααα⎛⎫++- ⎪⎝⎭--+-()()()()3πsin cos tan 2sin tan cos παααααα⎛⎫+-- ⎪⎝⎭=--()()()()()cos cos tan sin tan cos αααααα---=--cos 1sin tan ααα=-=-.。
诱导公式练习题

诱导公式练习题诱导公式练习题数学作为一门普遍存在于我们日常生活中的学科,无论是在学校还是在工作中,都扮演着重要的角色。
在数学的学习中,诱导公式是一项重要的技巧,它能够帮助我们解决一些复杂的问题。
本文将通过一些练习题来帮助读者更好地理解和掌握诱导公式。
练习题一:求解二次方程首先,我们来看一个简单的练习题:求解二次方程x^2 + 5x + 6 = 0。
解法一:传统方法我们可以使用传统的方法来求解这个方程。
首先,我们可以尝试将方程进行因式分解,即找到两个数a和b,使得a * b = 6,并且a + b = 5。
很显然,这两个数是2和3。
因此,方程可以写成(x + 2)(x + 3) = 0。
由此可得,x = -2或x= -3。
解法二:诱导公式除了传统的方法外,我们还可以使用诱导公式来求解这个方程。
诱导公式的原理是将二次方程转化为一元二次方程,从而简化求解过程。
首先,我们将方程写成标准形式:x^2 + 5x + 6 = 0。
然后,我们将方程的左侧进行变形,得到(x + 2)(x + 3) = -6。
接下来,我们将方程的右侧移到左侧,得到(x + 2)(x + 3) + 6 = 0。
然后,我们将方程展开,得到x^2 + 5x + 6 + 6 = 0。
最后,我们将方程进行简化,得到x^2 + 5x + 12 = 0。
现在,我们可以使用求根公式来求解这个方程。
根据求根公式,方程的解为x= (-b ± √(b^2 - 4ac)) / 2a。
将方程的系数代入公式中,即可得到x的解。
练习题二:求解三次方程接下来,我们来看一个稍微复杂一些的练习题:求解三次方程x^3 + 2x^2 - 3x - 6 = 0。
解法一:传统方法我们可以使用传统的方法来求解这个方程。
首先,我们可以尝试使用因式分解的方法,找到方程的一个根。
通过尝试,我们可以发现x = 1是方程的一个根。
因此,我们可以将方程进行因式分解,得到(x - 1)(x^2 + 3x + 6) = 0。
三角函数 诱导公式专项练习(含答案)

三角函数诱导公式专项练习(含答案) 三角函数诱导公式专项练一、单选题1.sin(-600°)的值为()A。
-√3/2B。
-1C。
1D。
√3/22.cos(11π/3)的值为()A。
-√3/2B。
-13/2C。
√2D。
23.已知sin(30°+α)=√3/2,则cos(60°-α)的值为A。
1/2B。
-1/2C。
√3/2D。
-√3/24.已知cos(π/3+α)=-5/2,且α∈(2π/5,π),则XXX(α-π)=()A。
-34/4B。
-3C。
4D。
35.已知sin(π-α)=-2/√3,且α∈(-2,0),则tan(2π-α)的值为A。
2√5/5B。
-2√5/2√5C。
±5D。
√5/26.已知cos(π/4-α)=√2/2,则sin(α+π/4)=()A。
-3B。
1C。
√2D。
√14/47.已知sinα=3/5,2<α<π/2,则sin(2-α)=()A。
3/5B。
-3/5C。
4/5D。
-4/58.已知tanx=-12/5π,x∈(π/2,π),则cos(-x+3π/2)=()A。
5/13B。
-5/12C。
13D。
-12/139.如果cos(π+A)=-1,那么sin(π/2+A)=A。
-1/2B。
2C。
1D。
-110.已知cos(π/2-α)-3cosα/(sinα-cos(π+α))=2,则tanα=()A。
12/5B。
-3C。
1/2D。
-511.化简cos480°的值是()A。
1B。
-1C。
√3/2D。
-√3/212.cos(-585°)的值是()A。
√2/2B。
√3/2C。
-√3/2D。
-√2/213.已知角α的终边经过点P(-5,-12),则sin(3π/2+α)的值等于()A。
-5B。
-12/13C。
13D。
12/1314.已知cos(π+α)=2/3,则tanα=()A。
√55/2B。
2√5/52.已知cosα=2/5,-2/5<α<0,则tan(α+α)cos(-α)tanα的值为()答案:D解析:由cosα=2/5可得sinα=-√(21)/5,代入公式可得tan(α+α)cos(-α)tanα=-1/√3=-√3/3,故选D。
诱导公式练习题

诱导公式练习题一、选择题 1. sin11π6的值是( ) A.21 B.-21 C.23 D.-232.已知的值为( )A.B. C.D.3.已知tan ,是关于x 的方程x 2-kx+k 2-3=0的两个实根,且3π<<,则cos +sin= ( )A.B.C. -D. -4.已知tan =2,,则3sin 2-cos sin +1= ( ) A.3 B.-3 C.4 D.-45.在△ABC 中,若sinA,cosA 是关于x 的方程3x 2-2x+m=0的两个根,则△ABC 是 ( ) A.钝角三角形 B.直角三角形 C.锐角三角形 D.不能确定 6.若1sin()33πα-=,则5cos()6πα-的值为() A .13 B.13- C.223 D.223-7.已知3cos()sin()22()cos()tan()f ππ+α-αα=-π-απ-α,则25()3f -π的值为( ) A .12 B .-12C .32D . -328.定义某种运算a S b =⊗,运算原理如上图所示,则式子131100lg ln )45tan 2(-⎪⎭⎫⎝⎛⊗+⊗e π的值为( )A .4B .8C .11D .139.若76πα=,则计算21sin(2)sin()2cos ()αππαα+-⋅+--所得的结果为( ) A. 34- B. 14- C. 0 D. 5410.已知sin()0,cos()0θπθπ+<->,则θ是第( )象限角. A .一 B .二 C .三 D .四11.已知sinx=2cosx,则sin 2x+1=( ) (A) (B) (C) (D)12.设02x π≤≤,sin cos x x =-,则( ) A.0x π≤≤ B.744x ππ≤≤C.544x ππ≤≤D.322x ππ≤≤ 二、填空题13.已知.角α(0)πα-<<的终边与单位圆交点的横坐标是13,则cos()2πα+的值是___. 14.化简:___________)cos()3sin()sin()23cos()3cos()2sin(=---+--+-πααπαπαπαπαπ15.已知32cos =a ,且02<<-a π,求)tan()cos()2sin()tan(a a a a +-+--πππ的值。
同角三角函数的基本关系与诱导公式练习题(基础、经典、好用)

同角三角函数的基本关系与诱导公式一、选择题1.记cos(-80°)=k ,那么tan 100°=( ) A.1-k 2k B .-1-k2k C.k1-k 2 D .-k 1-k 22.1-2sin (π+2)cos (π+2)等于( )A .sin 2-cos 2B .cos 2-sin 2C .±(sin 2-cos 2)D .sin 2+cos 23.(2013·厦门模拟)已知α∈(-π2,0),sin(-α-3π2)=55则sin(-π-α)=() A.55 B.255 C .-55 D .-2554.(2013·惠州模拟)已知tan θ=2,则sin 2θ+sin θcos θ-2cos 2θ=( )A .-43 B.54 C .-34 D.455.若sin α是5x 2-7x -6=0的根, 则sin (-α-3π2)sin (3π2-α)tan 2(2π-α)cos (π2-α)cos (π2+α)sin (π+α)=()A.35B.53C.45D.54二、填空题6.已知sin(π4+α)=32,则sin(3π4-α)的值为________.7.已知tan α=2,则7sin 2α+3cos 2α=________.8.已知sin(x +π6)=14,则sin(7π6+x )+cos 2(5π6-x )=________.三、解答题9.已知函数f (x )=1-sin (x -3π2)+cos (x +π2)+tan 34πcos x .(1)求函数y =f (x )的定义域;(2)设tan α=-43,求f (α)的值.10.已知sin(π-α)-cos(π+α)=23(π2<α<π).求下列各式的值:(1)sin α-cos α;(2)sin 3(π2-α)+cos 3(π2+α).11.已知向量a =(sin θ,cos θ),b =(2,1)满足a ∥b ,其中θ∈(0,π2).(1)求tan θ的值; (2)求2sin (θ+π4)(sin θ+2cos θ)cos 2θ的值.解析及答案一、选择题1.【解析】 由cos(-80°)=k ,得cos 80°=k ,∴sin 80°=1-k 2,∴tan 100°=tan(180°-80°)=-tan 80°=-1-k 2k .【答案】 B2.【解析】 原式=1-2(-sin 2)(-cos 2)=1-2sin 2cos 2=|sin 2-cos 2|,∵sin 2>0,cos 2<0,∴原式=sin 2-cos 2.【答案】 A3.【解析】 ∵sin(-α-3π2)=-sin(3π2+α)=cos α=55,且α∈(-π2,0),∴sin α=-1-cos 2α=-1-525=-255,∴sin(-π-α)=-sin(π+α)=sin α=-255.【答案】 D4.【解析】 sin 2θ+sin θcos θ-2cos 2θ=sin 2θ+sin θcos θ-2cos 2θsin 2θ+cos 2θ=tan 2θ+tan θ-2tan 2θ+1=4+2-24+1=45. 【答案】 D5.【解析】 方程5x 2-7x -6=0的两根为x 1=-35,x 2=2,则sin α=-35.原式=cos α(-cos α)tan 2αsin α(-sin α)(-sin α)=-1sin α=53. 【答案】 B二、填空题6.【解析】 sin(3π4-α)=sin[π-(π4+α)]=sin(π4+α)=32.【答案】 327.【解析】 7sin 2α+3cos 2α=7sin 2α+3cos 2αsin 2α+cos 2α=7tan 2α+3tan 2α+1=7×22+322+1=315. 【答案】 3158.【解析】 原式=-sin(π6+x )+cos 2(π6+x ) =-14+(1-142)=1116.【答案】 1116三、解答题9.【解】 (1)由cos x ≠0,得x ≠π2+k π,k ∈Z ,所以函数的定义域是{x |x ≠π2+k π,k ∈Z}.(2)∵tan α=-43,∴f (α)=1-sin (α-3π2)+cos (α+π2)+tan 34πcos α=1-cos α-sin α-1cos α=-cos α-sin αcos α=-1-tan α=13. 10.【解】 由sin(π-α)-cos(π+α)=23,得sin α+cos α=23,两边平方,得1+2sin α·cos α=29,故2sin α·cos α=-79.又π2<α<π,∴sin α>0,cos α<0.(1)(sin α-cos α)2=1-2sin α·cos α=1-(-79)=169, ∴sin α-cos α=43.(2)sin 3(π2-α)+cos 3(π2+α)=cos 3α-sin 3α =(cos α-sin α)(cos 2α+cos α·sin α+sin 2α) =-43×(1-718)=-2227.11.【解】 (1)∵a ∥b ,∴sin θ2=cos θ1,所以tan θ=2.(2)2sin (θ+π4)(sin θ+2cos θ)cos 2θ =2(22sin θ+22cos θ)(sin θ+2cos θ)cos 2θ-sin 2θ=(sin θ+cos θ)(sin θ+2cos θ)(cos θ+sin θ)(cos θ-sin θ)=sin θ+2cos θcos θ-sin θ=tan θ+21-tan θ =2+21-2=-4.。
诱导公式训练(精选题)(含答案)

诱导公式练习(精选题)一、选择题.(每题5分)1,则()()sin 15cos 105αα-︒+︒-的值是( )2A .3B .-3 C.0 D 解答过程书写:3)A二、填空题.(每题5分)4解答过程书写:5.设f(sin α+cos α)=sin α•cos α,则的值为______. 解答过程书写:67.已知函数3sin )(-+=x x x f π, 为 .解答过程书写:8.已知tan()2θπ-=,则22sin sin cos 2cos 3θθθθ+-+的值为三、解答题(每题10分)9.10.实数,x y 满足22sin()1,x x xy =-求200820075(sin )x y +⋅的值.参考答案1.D 【解析】()()()()sin 15cos 105sin 7590cos 18075αααα-︒+︒-=︒+-︒+︒-︒+⎡⎤⎡⎤⎣⎦⎣⎦()()()()sin 9075cos 75cos 75cos 75αααα=-︒-︒+-︒+=-︒+-︒+⎡⎤⎣⎦考点:利用诱导公式求值.2.A 【解析】 试题分析:设()=x F ()x b x a x f tan sin 2-=-,为奇函数,()()1211-=--=-f F ,那么()()1211=-=f F ,所以()31=f ,故选A .考点:奇函数 3.【答案】C,可得tan 3θ=, 而考点:利用诱导公式求值.4.1-.【解析】试题分析:根据诱导公式可知,故填:1-.考点:诱导公式.5.-38 【解析】略 6考点:诱导公式 7.8058-【解析】43)]2(sin[23sin )2()(-=--+-+-+=-+x x x x x f xf ππ ,【解析】 ,则考点:1、诱导公式;2、同角三角函数基本关系式. 9,即22tan 5tan 20,αα-+=解得或tan 2α=,当tan 2α=时,原式 考点:利用诱导公式化简、求值.10.6【解析】222222222sin()12sin()(sin cos )2sin()sin cos 0(sin )cos 0sin sin 1cos 06x x xy x xy xy xy x x xy xy xy x xy xy x xy x xy xy =-=-+⇒-++=⇒-+==⎧⇒⇒==±⎨=⎩⇒=原式。
(完整版)三角函数诱导公式专项练习(含答案)

三角函数 诱导公式专项练习学校:___________姓名:___________班级:___________考号:___________一、单选题1.()sin (‒600∘)=A . B . C .D .‒32‒1212322.的值为( )cos 11π3A . B .C .D .‒32‒1232123.已知,则cos (60°–α)的值为sin(30°+α)=3A . B .12‒12C .D . –32324.已知,且 ,则()cos(π2+α)=‒35α∈(π2,π)tan (α‒π)=A .B .C .D .‒34‒4334435.已知sin(π-α)=-,且α∈(-,0),则tan(2π-α)的值为( )23π2A .B . -C . ±D .255255255526.已知,则=( )cos (π4‒α)=24sin(α+π4)A .B .C .D .‒3414241447.已知,,则()sinα=35π2<α<3π2sin (7π2‒α)=A .B .C .D .35‒3545‒458.已知 ,则( )tanx =‒125,x ∈(π2,π)cos(‒x +3π2)=A .B .-C .D .-513513121312139.如果,那么cos(π+A)=‒12sin (π2+A)=A .-B .C . 1D . -1121210.已知,则( )cos(π2‒α)‒3cosαsinα‒cos (π+α)=2tanα=A .B .C .D . 15‒2312‒5∘A .B .C .D .12‒1232‒3212.的值是( )cos (‒585°)A .B .C .D .2232‒32‒2213.已知角的终边经过点,则的值等于 αP(‒5,‒12)sin (3π2+α)()A .B .C .D .‒513‒1213513121314.已知,则( )cos (π+α)=23tanα=A .B .C .D .52255±52±25515.已知的值为( )cosα=15,‒π2<α<0,则cos (π2+α)tan(α+π)cos (‒α)tanαA .B .C .D . 26‒26‒61261216.已知则 ()sinα=13,α∈(π2,π)cos (‒α)=A .B .C .D .13‒13223‒22317.已知,且是第四象限角,则的值是( )sin(π+α)=45αcos(α‒2π)A .B .C .D .‒3535±354518.已知sin =,则cos =( )A .B .C . -D . -19.已知cos α=k ,k∈R,α∈,则sin(π+α)=( )A . -B .C . ±D . -k20.=( )A . sin 2-cos 2B . sin 2+cos 2C . ±(sin 2-cos 2)D . cos 2-sin 221.的值为sin 585∘A .B .C .D .22‒2232‒3222.( )sin (‒1020°)=1‒13‒323.若,,则的值为( )α∈(0,π)sin(π‒α)+cosα=23sinα‒cosαA .B .C .D .23‒2343‒4324.已知且,则( )α∈(π2,π)sin (π+α)=‒35tan α=A .B .C .D .‒344334‒4325.已知,则()sin(π2+θ)+3cos (π‒θ)=sin (‒θ)sinθcosθ+cos 2θ=A . B . C . D .1525355526.若,且,则( )sinθ‒cosθ=43θ∈(34π,π)sin(π‒θ)‒cos(π‒θ)=A .B .C .D .‒2323‒434327.已知,则( )sin(π2+θ)+3cos (π‒θ)=sin (‒θ)sinθcosθ+cos 2θ=A . B . C . D .1525355528.已知,则的值为( )sin (2015π2+α)=13cos (π‒2α)A .B .C .D .13-1379‒7929.若,,则的值为( )α∈(0,π)sin(π‒α)+cosα=23sinα‒cosαA .B .C .D .23‒2343‒4330.已知,则的大小关系是( )a =tan (‒π6),b =cos (‒23π4),c =sin25π3a,b,c A .B .C .D . b >a >c a >b >c c >b >a a >c >b31.cos 7500=A .B .C .D .3212‒32‒1232.的值等于( )sin (‒236π)A .B .C .D .32‒1212‒3233.的值的( )sin 300°+tan 600°+cos (‒210°)A . B .C .D .‒30‒12+3212+3234.已知,,则等于().α∈(π2,3π2)tan(α‒π)=‒34sinα+cosαA .B .C .D .±15‒1515‒75A .B .C .D . a ‒a 1‒a 2‒1‒a236.点在直角坐标平面上位于( )A (cos 2018∘,tan 2018∘)A . 第一象限 B . 第二象限C . 第三象限D . 第四象限37.如果,那么等于( )sin (π‒α)=13sin (π+α)‒cos (π2‒α)A .B .C .D .‒2323223‒22338.已知角的终边过点,若,则实数α(a,‒2)tan (π+α)=3a =A . B .C .D .6‒23‒62339.cos (2π+α)tan (π+α)sin (π‒α)cos (π2‒α)cos (‒α)=A .B .C .D . 1‒1tan α‒tan α40.已知,则的值为( )sin (‒α)=-53cos (π2+α)A .B .C .D .53‒5323‒23参考答案1.D 【解析】【分析】直接运用诱导公式,转化为特殊角的三角函数值求解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
诱
导
公
式
计
算
题
100
题
20 年月日A4打印/ 可编辑
三角函数诱导公式检测题
1.全国Ⅱ)若sinα<0且tanα>0,则α是()
A.第一象限角B.第二象限角
C.第三象限角D.第四象限角
2.(07·湖北)tan690°的值为()
A.- B. C. D.-
3.f(sin x)=cos19x,则f(cos x)=()
A.sin19x B.cos19x C.-sin19x D.-cos19x
4.设f(x)=a sin(πx+α)+b cos(πx+β),其中a,b,α,βⅡR,且ab≠0,α≠kπ(kⅡZ).若f(2009)=5,则f(2010)等于()
A.4B.3C.-5D.5
5.(09·全国Ⅱ文)sin585°的值为()
A.- B. C.- D.
6.函数y=5sin的最小正周期是()
A.π
B.π
C.D.5π
7.(2010·重庆文,6)下列函数中,周期为π,且在[,]上为减函数的是()
A.y=sin(2x+) B.y=cos (2x+)
C.y=sin(x+) D.y=cos(x+)
8.函数y=-2tan的单调递减区间是________.
三角函数诱导公式(答案)
1.[答案] C
2.[答案]A
[ 解析]tan690°=tan(-30°+2×360°)=tan(-30°)=-tan30°=-,选A.
3.[答案]C
[解析]f(cos x)=f(sin(90°-x))=cos19(90°-x)=cos(270°-19x)=-sin19x.
4.[答案]C
[解析]Ⅱf(2009)=a sin(2009π+α)+b cos(2009π+β)=-a sinα-b cosβ=5,
Ⅱa sinα+b cosβ=-5.
Ⅱf(2010)=a sinα+b cosβ=-5.
5.[答案]A
[解析]sin585°=sin(360°+225°)=sin225°
=sin(180°+45°)=-sin45°=-.
6.[答案]D[解析]T==5π.
7.[答案]A
[解析]选项A:y=sin(2x+)=cos2x,周期为π,在[,]上为减函数;
选项B:y=cos(2x+)=-sin2x,周期为π,在[,]上为增函数;
选项C:y=sin(x+)=cos x,周期为2π;
选项D:y=cos(x+)=-sin x,周期为2π.故选A.
8. [答案](kⅡZ)
[解析]求此函数的递减区间,也就是求y=2tan的递增区间,由kπ-<3x+<kπ+,kⅡZ 得:-<x<+,
Ⅱ减区间是,kⅡZ.
整理丨尼克
本文档信息来自于网络,如您发现内容不准确或不完善,欢迎您联系我修正;如您发现内容涉嫌侵权,请与我们联系,我们将按照相关法律规定及时处理。
