K-L展开式系数的计算步骤
冲压件展开计算方法

冲压件展开计算方法 The manuscript was revised on the evening of 2021冲压件展开计算方法冲压件是常件的金属件,在冲压前,要对冲压件下料,这时,往往要对冲压件展开计算:1 90?无内R轧形展开K值取值标准:a. t≦,K=b.c.d. t>材料展开长度不易准确计算,应先试轧,得出展开系数后再调整展开尺寸.e. 软料t≦,K=(主要有铝料,铜料).注意:无内R是指客户对内R无要求,或要求不高时,为便于材料的折弯成形,我们的下模做成尖角的形式.有时客户的部品图中有内R,一般客户没有特别指出的条件下我们均以尖角起模.2 非90?无内R轧形展开L=A+B+Kt(C/90)K值取值标准:a. t≦,K=b.c.d. t>材料展开长度不易准确计算,应先试轧,得出展开系数后再调整展开尺寸.e.软料t≦,K=(主要有铝料,铜料).注意:无内R是指客户对内R无要求,或要求不高时,为便于材料的折弯成形,我们的下模做成尖角的形式.有时客户的部品图中有内R,一般客户没有特别指出的条件下我们均以尖角起模.3 有内R轧形展开备注:当客户部品图中没有特别要求做轧形内R时,我们尽量按尖角设计.有要求时按以上方式进行展开.中性层系数确定:弯曲处的中性层是假设的一个层面.首先将材料延厚度方向划分出无穷多个厚度趋于0的层面,那么在材料弯曲的过程中长度方向尺寸不变的层面即为材料弯曲处的中性层.由上述可知中性层的尺寸等于部品的展开尺寸.3) 中性层经验值根据我们的实际设计经验,当产品的材料厚度t≦时,产品弯曲处中性层系数K为;当产品的材料厚度t>时,产品弯曲处中性层系数为1/3.此时只需从弯曲的内侧向材料方向偏移kt即为弯曲处的中性层.4 Z轧展开两次Z轧成形图中t为材料厚度,H为Z轧折弯高度,在设计时材料厚度≦,≦轧形高度H≦的时,我们通常采用两次Z轧的方式完成材料的Z轧成形.这时轧形展开公式为:备注:采用此类Z轧成形法,要求轧形高度为2mm以上以下,材料厚度在以下. 一次成形"Z"轧1) 轧形高度在一倍料厚之内时,一般采用一次成形.轧形展开尺寸为:2) 轧形高度在1倍料厚以上2mm以下时,采用一次成形,展开尺寸为:5 压平展开L=A+B+@=A''+B''+@''@=@''=C=(有压线)C=(无压线)t=材料厚度在模具设计时推平展开按以下公式进行L=A+B+ (t为材料厚度)6 CNC轧形展开展开公式:L=A+B+@上表补偿值适用于折弯内R为0(包括图纸没有要求一般都当0做)的情况,如果客户图纸有内R要求,则展开方法另计.当材料规格不在此表时可以用@=(t为材料的厚度)做补偿进行初步展开,再根据实际情况进行调整.7 U形弯曲的展开L=A+B+(R+ t:为材料厚度8 弯曲拉伸复合结构展开展开原则:先将直边部分按弯曲展开,圆角部分按拉伸展开,然后用三点切圆(PA-PC-PB)的方式作一段与两直边和直径为D圆心与圆角圆心重合的圆(圆形拉伸的展开形状)相切的圆弧.当r≦时,求D值计算公式如下:当r>时,求D值计算公式如下:备注:拉伸处应按等体积法进行计算.9 展开尺寸调整标注公差不对称尺寸调整标注公差不对称尺寸展开时取尺寸公差的中间值.见下例:孔位加工尺寸的调整为防止因冲头的磨损而造成孔尺寸因小而超差.我们在设计一般将孔尺寸(所有类型的孔)做到上公差的60%~80%.例:图纸标注Φ5±,起模时将此孔做到Φ; 图纸标注Φ5±,起模时将此孔做到Φ.但对装钉底孔为保证装配质量,设计时只做大(与装钉类型,材料厚度无关,但对需要进行特质特性要求的产品应根据实际情况而定,如装钉前需进行表面阳极氧化处处理的装钉底孔可以再做大~,但一般也为不表面处理进行再做大处理).有特质特性要求产品展开尺寸调整1)需要进行电镀类产品:原料为单光料(光泊)的产品一般需要电镀处理在设计时应根据客户对镀层厚度的要求适当的做小外形尺寸,做大孔尺寸(此时应根据公差的大小与镀层的厚度对尺寸进行相应调整,且仅进行一次调整),使产品电镀之后,能满足图纸的公差要求.关于需电镀产品镀前尺寸处理(对客户来图公差处理): 图纸圆孔(及方孔)Φ±的,做大;图纸圆孔(及方孔)Φ±的,做大;图纸圆孔(及方孔)Φ±以上的,做大;特别是脚仔,图纸标注公差为±的,做小,角仔公差±以上的,做小.2)需要进行表面阳极氧化类产品,将产品上的孔做大(在孔一般放大之后再做大),其余尺寸(如外形尺寸)不需要进行特别的调整.3)需要进行喷油喷粉的产品,在对产品展开图不进行一般调整,只需将孔做大2倍的最大喷层厚度,将其它有影响的外形尺寸用2倍的最大喷层厚度进行调整(喷后尺寸变大的做小,喷后尺寸变小的做大.。
KL变换和主成分分析

根据经济学知识,斯通给这三个新 变量分别命名为总收入F1、总收入变化 率F2和经济发展或衰退的趋势F3。更有 意思的是,这三个变量其实都是可以直 接测量的。
主成分分析就是试图在力保数据信息丢 失最少的原则下,对这种多变量的数据表进 行最佳综合简化,也就是说,对高维变量空 间进行降维处理。
jd 1
λ j :拉格朗日乘数
g(uj )
uTj Ru j
j
(u
T j
u
j
1)
jd 1
jd 1
用函数 g(u j ) 对 u j 求导,并令导数为零,得
(R j I )u j 0 j d 1, ,
——正是矩阵 R 与其特征值和对应特征向量的关系式。
• 如果这些数据形成一个椭圆形状的 点阵(这在变量的二维正态的假定下 是可能的).
3.2 PCA: 进一步解释
• 椭圆有一个长轴和一 个短轴。在短轴方向上, 数据变化很少;在极端的 情况,短轴如果退化成一 点,那只有在长轴的方向 才能够解释这些点的变化 了;这样,由二维到一维 的降维就自然完成了。
分为: 连续K-L变换 离散K-L变换
1.K-L展开式 设{X}是 n 维随机模式向量 X 的集合,对每一个 X 可以
用确定的完备归一化正交向量系{u j } 中的正交向量展开:
X a juj j 1
d
用有限项估计X时 :Xˆ a juj j 1
aj:随机系数;
引起的均方误差: E[( X Xˆ )T ( X Xˆ )]
总样本数目为 N。将 X 变换为 d 维 (d n) 向量的方法:
K-L变换

K-L 变换(Karhunen-Lo éve )离散K-L 展开式的矩阵表示设非周期随机过程)(t x ,在采样区间[a, b]作均匀采样,采样样本表示为向量⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=)()()(21D t x t x t x x (理解为每个样本向量有D 个特征)其相关函数][T xx E 为D 维方阵,有D 个线性无关的特征向量。
【假如有N 个采样样本,⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⨯DN D D N N ND x x x x x x x x x212222111211x , 相关函数][Txx E =TN D N D N⨯⨯x x 1】 则采样序列x 的展开式仅含有D 项∑-=Dj j c 1jx ϕ,式中,j ϕ为第j 个正交基函数(也叫基向量),j c 为对应的展开式系数。
【对于“K-L 展开式满足正交变换,且是最小均方误差的”证明如下:】假设向量集合),2,1}({ =i i x 中的x 可以用完备正交归一向量系或者称为变换基向量),,2,1(∞= j i u 来展开,则有∑∞==1j j j c u x基向量满足正交性⎩⎨⎧≠==i j ij j T i ,0,1u u在离散情况下使用有限基向量集合来表示,即∑==dj jj c 1ˆux其均方误差为][)]()[()]ˆ()ˆ[(1211∑∑∑∞+=∞+=∞+===--=d j jd j jjT d j jjTcE c c E E u u x x xx ξ将展开式系数x u Tj j c =(理解为x 在基坐标上的投影,而展开式系数就是坐标值)代入均方误差表达式,有∑∑∑∞+=∞+=∞+====111)(][d j jT jd j j TT jd j j TT jE E ψuu u xx uu xx u ξ(理解上式中j TT j j c u x x u ==,因为是行向量和列向量))(T E xx ψ=为自相关矩阵(这是一个对称矩阵,因为T T T xx xx =)()由拉格朗日条件极值法求均方误差的极限,相应的拉格朗日函数为]1[)(11--=∑∑∞+=∞+=jT jd j jd j j Tjj L u u ψu uu λ令0)(=j jL d du u (理解j 从的d +1取到无穷,总共就有这么多方程) 则022=-j j j u ψu λ得0)(=-j j u E ψλ,∞+=,,1 d j 【 这是矩阵的导数问题!相关概念知识如下: 令A 是一个与列向量x 无关的矩阵,则T ∂=∂x A A x , ()T T T ∂=+=+∂x AxAx A x A A x x 特别地,若A 为对称矩阵,则有2T ∂=∂x AxAx x证明:前半部分:假设111221112222111112212211122111222222()()()()Tx a x a x a x a x x a a aa x a x a x a x a x x ∂∂⎡⎤++⎢⎥∂∂⎡⎤∂⎢⎥===⎢⎥∂∂∂⎢⎥⎣⎦++⎢⎥∂∂⎣⎦x A A x 后半部分:11nnTij i j i j A x x ===∑∑x Ax — 一个多项式梯度T ∂∂x Axx(是一个列向量)的第k 个分量为1111[]T n n n nk ij ijik ikjji j i j kA x x A x A xx ====∂∂==+∂∂∑∑∑∑x Ax x()T T T ∂=+=+∂x AxA x Ax A A x x】 其解就是使均方误差为极小的基向量j u ,同时求得的j u 为矩阵ψ的特征向量,其对应的特征值为j λ,则截断均方误差为∑∞+==1d j jλξ(此处用矩阵对角化的概念理解j j T j λ=ψu u ),式中j λ为矩阵ψ的特征值。
(完整版)钣金展开计算方法
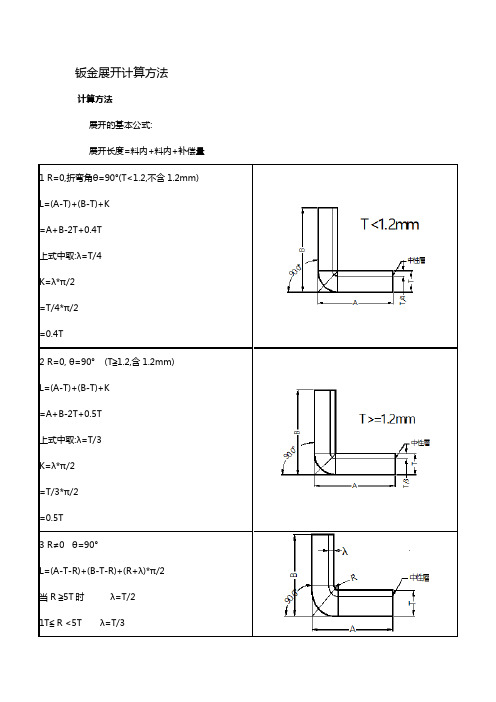
上式中取:λ=T/3
K=λ*π/2
=T/3*π/2
=0.5T
3 R≠0 θ=90°
L=(A-T-R)+(B-T-R)+(R+λ)*π/2
当R ≧5T时 λ=T/2
1T≦ R <5T λ=T/3
0 < R <t λ=t 4<="" p=""></t λ=t>
(实际展开时除使用尺寸计算方法外,也可在确定中性层位置后,通过偏移再实际测量长度的方法.以下相同)
D/2={(r+T/3)2
+2(r+T/3)*(h+T/3)
-0.86*(Rd-2T/3)*[(r+T/3)
+0.16*(Rd-2T/3)]}1/2
12卷圆压平
图(a): 展开长度
L=A+B-0.4T
图(b): 压线位置尺寸 A-0.2T
图(c): 90°折弯处尺寸为A+0.2T
图(d): 卷圆压平后的产品形状
4 R=0 θ≠90°
λ=T/3
L=[A-T*tan(a/2)]+[B
-T*tan(a/2)]+T/3*a
(a单位为rad,以下相同)
5 R≠0 θ≠90°
L=[A-(T+R)* tan(a/2)]+[B
-(T+R)*tan(a/2)]+(R+λ)*a
当R ≧5T时 λ=T/2
1T≦ R <5T λ=T/3
以下Hmax取值原则供参考.
当R≧4MM时:
材料厚度T=1.2~1.4取Hmax =4T
钣金展开计算原理及计算方法!

一、展开计算原理板料在弯曲过程中外层受到拉应力,内层受到压应力,理论上内外层之间有一既不受拉也不受压的过渡层------中性层,中性层为一假想层,在弯曲过程中中性层被假想为与弯曲前状态保持一致,即长度始终不变,所以中性层是计算弯曲件长度的基准。
中性层位置与变形程度有关,当弯曲半径较大,折弯角度较小时,变形程度较小,中性层位置靠近板料厚度的中心处;当弯曲半径变小,折弯角度增大时,变形程度随之增大。
中性层位置逐渐向弯曲中心的内侧移动。
中性层到板料内侧的距离用A表示(图1)。
二、折弯方法的确定折弯方法有单发冲床模具折弯和折弯机模具折弯两种方法。
单发冲床模具折弯的方式及精度是由模具来实现的。
因此只要做出合格的模具,就能够生产出合格的折弯产品。
而采用折弯机折弯不仅需要选用合适的折弯模,还必须调试折弯参数。
因此,如采用折弯机折弯,计算展开尺寸时就必须考虑折弯机的折弯方法。
1.一次一道弯。
此种折弯由普通通用折弯模来完成。
包括折直角,钝角和锐角(图2)。
2. 一次折两道弯——压锻差。
此种折弯由专用特殊模来完成,但折弯难度比普通折弯大(图3)。
3. 压死边。
此种折弯也须用特殊模来完成(图4)。
4.大R圆弧折弯。
些种折弯如R在一定范围内,可用专用R模压成形,如R值过大,则须用小R模多次压制成形(图5)。
这四种折弯的展开计算是不同的。
因此在看图时,要根据零件的折弯尺寸来确定使用何种折弯方法。
其折弯机所配套的普通通用折弯模具V形槽宽度通常为适用该折弯模的板厚的5-6倍。
如采用一次折一道弯的方法,必须考虑到折弯模的V形槽的宽度W1及V形槽一边到模具外侧的宽度L1,如图6所示。
折弯高度H的经验值根据产品形状有如下三种(以90度为例,钝角和锐角与直角相近相似)。
1.简单的90度单边折弯(图7)。
如图7所示,此种折弯只需考虑下模V形槽中心到折弯机定位挡块的距离即可确定。
通常H值为H≥3.5 T + R (R 在1mm 以下)。
四川大学模式识别期末考试内容

四川⼤学模式识别期末考试内容⼀.计算题1、在图像识别中,假定有灌⽊和坦克2种类型,它们的先验概率分别是0.7和0.3,损失函数如下表所⽰。
其中,类型w 1和w 2分别表⽰灌⽊和坦克,判决a 1=w 1,a 2=w 2。
现在做了2次实验,获得2个样本的类概率密度如下:5.02.0)|(1=ωx P 3.06.0)|(2=ωx P(1)试⽤最⼩错误率贝叶斯准则判决2个样本各属于哪⼀类?坦克、灌⽊。
(2)试⽤最⼩风险决策规则判决2个样本各属于哪⼀类?灌⽊、灌⽊。
答:(1)最⼩错误率贝叶斯准则,决策为坦克第⼀个样本:2121221111)|()|(5625.04375.01)|(1)|(4375.032143.0*6.07.0*2.07.0*2.0)()|()()|()|(ωωωωωωωωωω∈?>=-=-===+==∑=x x P x P x P x P P x p P x p x P j j j ,决策为灌⽊第⼆个样本:1121221111)|()|(449205.0795.01)|(1)|(795.044353.0*3.07.0*5.07.0*5.0)()|()()|()|(ωωωωωωωωωω∈?<==-≈-=≈=+==∑=x x P x P x P x P P x p P x p x P j j j(2)最⼩风险决策规则,决策为灌⽊第⼀个样本1212221212122212111211122211211)|()|(3175.25625.0*0.14375.0*4)|()|()|()|(35375.15625.0*24375.0*5.0)|()|()|()|(0.1425.0ωωλωλωλωλωλωλλλλλ∈?<=+=+===+=+======∑∑==x x a R x a R x P x P x P x a R x P x P x P x a R j j j j j j ,决策为灌⽊第⼆个样本12122212121222121112111)|()|(385.3205.0*0.1795.0*4)|()|()|()|(8075.0205.0*2795.0*5.0)|()|()|()|(ωωλωλωλωλωλωλ∈?<=+=+===+=+==∑∑==x x a R x a R x P x P x P x a R x P x P x P x a R j j j j j j2、给出⼆维样本数据(-1,1),(2,2),(1,-1),(-2,-2),试⽤K-L 变换作⼀维数据压缩。
(建筑工程管理)工程展开计算方法

(建筑工程管理)工程展开计算方法壹.目的:统壹展开计算方法,做到展开的快速准确.二.适用范围:晟铭钣金部三.展开计算原理:1.板料在弯曲过程中外层受到拉应力,内层受到压应力,从拉到压之间有壹既不受拉力又不受压力的层称为中性层;中性层在弯曲过程中的长度和弯曲前壹样,保持不变,所以中性层是计算弯曲件展开长的基准.2.中性层位置和变形程度有关,当弯曲半径较大,折弯角度较小时,变形程度较小,中性层位置靠近板料的中心处;当弯曲半径变小,折弯角度增大时,变形程度随之增大,中性层位置逐渐向弯曲中心的内侧移中性层到板料内侧的距离用λ表示.四.展开计算方法:展开计算的基本公式:展开长度=料内+料内+补偿量壹般折弯1(R=0,θ=90°):L=A+B+K1.当0<T≦0.3时,K=02.对于铁材(如﹑SGCC﹑SECC﹑CRS﹑SPTE等):(1)当0.3<T<1.5时,K=0.4T(2)当1.5≦T<2.5时,K=0.35T(3)当T≧2.5时,K=0.3T3.对于其它有色金属材料(如Al﹑Cu等):当T>0.3时,K=0.5T4.对于SUS材料,当T>0.3时,K=0.25T5.当CRS料T≧2.5时,K=0.5T壹般折弯2(R≠0,θ=90°):L=A+B+K(K值取中性层弧长)1.当T<1.5时,λ=0.5T2.当T≧1.5时,λ=0.4T注:当用折刀加工时:1.当R≦2.0时,按R=0处理.2.当2.0<R<3.0时,按R=3.0处理.3.当R≧3.0时,按原值处理.壹般折弯3(R=0,θ≠90°):L=A+B+K’1.当T0.3时,K’=02.当T0.3时,K’=(/90)*K注:K为90∘时的补偿量.壹般折弯4(R≠0,θ≠90°):L=A+B+K(K值取中性层弧长)1.当T 1..5时,λ=0.5T2.当T 1..5时,λ=0.4T注:当用折刀加工时:1.当R2.0时,按R=0处理.2.当2.0<R<3.0时,按R=3.0处理.3.当R≧3.0时,按原值处理.Z折1(直边段差):1.当H5T时,分俩次成型时,按俩个90°折弯计算.2.当H5T时,壹次成型,L=A+B+K注:K值依附件壹中参数取值.Z折2(非平行直边段差):展开方法和平行直边Z折方法相同(如上栏),高度H取值见图示.Z折3(斜边段差样品方桉):1.当H2T时:(1)当θ≦70∘时,L=A+B+C+K(此时K=0.2).(2)当θ>70∘时,按Z折1(直边段差)的方式展开.2.当H2T时,按俩段折弯展开(R=0,θ≠90°).Z折3(斜边段差量产方桉):1.当H2T时:(2)当θ≦70∘时,T≦1.5时,将俩侧倒R=T圆弧偏移0.5T,得到中性层,按中性层展开T>1.5时,连接俩清角处,加上俩θ角处的K值得到变形区(2)当θ>70∘时,按Z折1(直边段差)的方式展开.2.当H2T时,按俩段折弯展开(R=0,θ≠90°).Z折4(过渡段为俩圆弧相切):1.H≦2T段差过渡处为非直线段俩圆弧相切展开时,取基体外侧俩圆弧相切点处作垂线,向内侧偏移料厚按图示处理,然后按Z折1(直边段差)方式展开.2.H>2T,请示后再按指示处理.抽孔和抽牙孔:抽孔尺寸计算原理为体积不变原理,即抽孔前后材料体积不变;壹般抽孔,按下列公式计算,式中参数见图(设预冲孔径为X,且加上修正系数–0.1):1.若抽孔为抽牙孔(抽孔后攻牙),则S取值原则如下:(1)T≦0.5时,取S=100%T(2)0.5<T<0.8时,取S=70%T(3)T≧0.8时取S=65%T注:壹般常见抽牙预冲孔按附件壹取值.2.抽孔展开处理:。
工程展开计算方法

1.当T1..5时,λ=0.5T
2.当T1..5时,λ=0.4T
注:当用折刀加工时:
1.当R2.0时,按R=0处理.
2.当2.0<R<3.0时,按R=3.0处理.
3.当R≧3.0时,按原值处理.
Z折1 (直边段差):
1.当H5T时,分两次成型时,按两个90°折弯计算.
2.0
T=0.8
5.8
2.2
T=1.0
6.0
2.4
T=1.2
6.2
2.6
T=1.5
6.5
3.0
4#40
T=0.6
1.9
2.4
3.4
1.2
T=0.8
3.4
1.4
T=1.0
3.6
1.5
T=1.2
3.8
1.6
T=1.5
4.2
1.8
6#32
T=0.6
T=0.8
注:当用折刀加工时:
1.当R≦2.0时,按R=0处理.
2.当2.0<R<3.0时,按R=3.0处理.
3.当R≧3.0时,按原值处理.
一般折弯3 (R=0,θ≠90°):
L=A+B+K’
1.当T0.3时, K’=0
2.当T0.3时, K’= (/ 90) * K
注: K为90∘时的补偿量.
一般折弯4 (R≠0 ,θ≠90°):
2.2若客户图纸上抽孔没标抽孔孔径尺寸,展开时以下列情形处理:
(1)当T'≧0.7T时,取T'=0.7T,并保证抽孔内径.
(2)当0.5T<T'<0.7T时,按原图抽孔内﹑外径取值.
第三节(泰勒级数展开)

< 1)
1 n −1 = 1 − 2 z + 3z 2 − L + (− 1) nz n−1 + L , 上式逐 项求导: (1 + z )2
(z
< 1)
11
例 求 数 数 主 ln(1+ z)在 = 0处 泰 展 式 对 函 的 值 z 的 勒 开 .
解
奇点z = −1, ∴ 它在 z < 1内可展开成 z的幂级数 . y
∞
ak ( z − z 0 ) k ∑
k =0
f (ζ ) 1 f ( k ) ( z0 ) 其中 ak = ∫CR1 (ζ − z0 ) k +1 dζ = k ! 2πi
包含z且与 R同心的圆。 包含 且与C 同心的圆。 且与
C R1 为圆 R内 为圆C
1
证明: 如图,为避免涉及在圆周C 证明: 如图,为避免涉及在圆周 R上级数的
f ( z ) = ln z , f f ′( z ) = 1 , z (1) = ln 1 = n 2π i ( n ∈ Z ) f ′(1) = + 1
1! , f ′′(1) = − 1 2 z 2! (3) f ( z ) = 3 , f ( 3 ) (1) = + 2! z 3! f ( 4 ) ( z ) = − 4 , f ( 4 ) (1) = − 3! z L L f ′′( z ) = −
可知泰勒级数的收敛半径为无限大,只要 可知泰勒级数的收敛半径为无限大,只要z
是有限的,则泰勒级数就是收敛的! 是有限的,则泰勒级数就是收敛的!
例2
在z0=0的邻域上把 f1 ( z ) = sin z , f 的邻域上把
2
KL变换

顺序后退法Sequential backw. selection
特征 选择
该方法根据特征子集的分类表现来选择特征
搜索特征子集:从全体特征开始,每次剔除
一个特征,使得所保留的特征集合有最大的 分类识别率 依次迭代,直至识别率开始下降为止 用“leave-one-out”方法估计平均识别率:用 N-1个样本判断余下一个的类别,N次取平均。
[W,R] = FEATSELI(A,CRIT,K,T)
特征 选择
顺序前进法Sequential forward selection
自下而上搜索方法。
特征 选择
每次从未入选的特征中选择一个特征,使得
它与已入选的特征组合在一起时所得的J值 为最大,直至特征数增加到d为止。 该方法考虑了所选特征与已入选特征之间的 相关性。
i , j 1 n
u1 x1
x ' Rx y '(U ' RU) y y ' Λy y 2 y2 n yn
2 1 1 2
标准二次 曲线方程
x U y
2
K-L变换的数据压缩图解
取2x1变换矩阵U=[u1],则x的K-L变换y为:
特征 提取
y = UTx = u1T x = y1
分为: 连续K-L变换 离散K-L变换
特征提取与K-L变换
9模式识别第-第九章 K-L变换特征提取

(4)协方差矩阵已知
2、每次使用一个类别样本集合来建立K-L坐 标系,
该K-L变换常用于信息压缩,很少用于分类。
一组具有零均值的样本: 例:
x 1 (1,1) T , x 2 ( 2 , 2 ) T , x 3 ( 1, 1) T , x 4 ( 2 , 2 ) T
n 1
为x(t)的 K-L 展开,其逆过程为K-L变换。 其中n是为使得自相关系数单位化引入的实或 复的系数
计算相关函数
* * * R (, ts ) Ext [ () x( s ) ] E x () t s ) n n n kx k k( k n
9.4 K-L坐标系的生成
数据集合{x}的K-L坐标系是由二阶统计量来 确定的。可以使用以下几种方法来生成 K-L 坐标系: 样本所属类别未知时: 1、可以使用样本的自相关矩阵 Ψ E[xxT ] 2、对于无类别标签的样本集,均值向量无意 义,也常使用协方差矩阵 T Σ E [ ( x μ ) ( x μ )]
反 之 , 为 了 使 xn和 xm互 不 相 关 , 随 机 过 程 必 须 是 周 期 性 的 。
9.2 K-L展开
非周期随机过程: 正弦函数族不能使其傅立叶系数不相关,但是 可以寻找一个新的正交函数族ϕn(t),使得其变 换系数互不相关 。 K-L变换定义
假设一个非周期随机过程,在区间[a, b]展开式为
第9章 基于K-L变换特征提取
线性变换法特征提取
9.1 傅立叶级数展开式
周期随机过程的傅立叶级数(三角级数)
x (t )
n
x n exp( jn 0 t )
KL变换

单独最优特征组合
计算各特征单独使用时的可分性判据J并加 以排队,取前d个作为选择结果 不一定是最优结果 当可分性判据对各特征具有(广义)可加性, 该方法可以选出一组最优的特征来,例:
各类具有正态分布 各特征统计独立 可分性判据基于Mahalanobis距离
特征 选择
j
E y y = E U x x U T = U RU = Λ
T T T
K-L变换的性质 变换的性质
特征 提取
K-L坐标系把矩阵R对角化,即通过K-L R 变换消除原有向量x的各分量间的相关 性,从而有可能去掉那些带有较少信息 的分量以达到降低特征维数的目的
λ1 Λ = 0
ε =
j = d +1
∑
∞
u Tj E x x T u
j
=
j= d +1
∑
∞
u Tj R u
j
求解最小均方误差正交基
用Lagrange乘子法:
if R u
j ∞
特征 提取
= λ ju
j
th e n ε =
j= d +1
∑
u Tj R u j 取 得 极 值
结论:以相关矩阵R的d个本征向量为 R 基向量来展开x时,其均方误差为: x
顺序后退法Sequential backw. 顺序后退法 selection
特征 选择
该方法根据特征子集的分类表现来选择特征 搜索特征子集:从全体特征开始,每次剔除 一个特征,使得所保留的特征集合有最大的 分类识别率 依次迭代,直至识别率开始下降为止 用“leave-one-out”方法估计平均识别率:用 N-1个样本判断余下一个的类别,N次取平均。
模式识别(第九章2010)

方法:
可分性不仅和类内距离有关,还和类间距离有关。 可靠的方法是:希望类间散射大,各维的方差小,∴ 设计判别准则
J (x j ) u T Sb u j j u S wu j
T j
u T Sb u j j
j
由Sw、Sb共同来刻化变换后的分量的可分性
j是Sw的第j个本征值,实际就是第j维方差。
注意:采用K-L作为样本分类的特征提取时,要特别
注意尽可能保留不同类别的样本分类鉴别信息。若
仅考虑准确地提取原来样本的主成分,有时不一定
有利于分类的鉴别。
9.5
利用类平均向量提取判别信息
吸收类均值向量带来的信息进行特征提取 为了使变换后的低维空间尽可能多的保持原有 的分类信息,需进一步研究如何利用类均值向量包 含的大量分类信息,以便更有效提取特征,即需寻 找“最好”的K-L坐标系。
实质上保留了原样本中方差最大的特征成份,突出
了差异性。
j E[C ]
2 j
2 j
除了使用x的自相关阵Rx的本征矢量构成正交变 换矩阵来实现均方误差最小的K-L变换外,还可用x 的协方差阵x的本征矢量构成正交变换矩阵,使均
方误差最小, 即:
E[( x m)( x m)T ]
C T x
j 1, 2,..., D
即C的各量为: c j T x j
其中: T [ j (t1 ), j (t2 ),, j (tD )]T j
∴ C就是随机向量x的一个正交归一化变换的 结果,C的每个值都是选出来的特征。
∵K-L变换的一个非常重要的性质是展开系数ci 互 不相关,即要求:
a [c1 , c2 ,..., cm ]T
钣金展开计算方法简介

2、折弯补偿法
折弯补偿算法是将零件的展开长度描述为零件每段直线长度和折弯 区域展平的长度之和,展平的折弯区域的长度则被称为折弯补偿值 (δ),因此整个零件的长度计算公式为 其中,D1,D2分别为圆弧以外的2段直线长度/mm;δ为圆弧段展 平后的长度/mm。
折弯补偿示意图如图3所示,即把折弯零件的直线段切下来平铺, 然后再将折弯区域展平接在平铺的直线段中,得到的长度就是展开 长度。
本文拟通过K因子参数的设定,及经验计算法,将不同情况下 钣金的折弯展开计算进行简化,提高展开效率和准确度,达到 在设计阶段就可以对钣金工艺性能进行全面考虑和处理的目的。
二、钣金折弯展开长度的改进算法
目前较常规的计算方法是以截面中心层计算展开长度,认为中 心层就是钣金长度始终不变的一个层,其长度就是钣金折弯展 开的长度,它的位置刚好在板厚的一半处,对于一些要求精度 不是太高的薄板大折弯角的零件,这种计算方法相对还是比较 准确的,但对于厚板小折弯角钣金零件的折弯,由于其中心层 长度并非钣金折弯展开的长度,以它的长度下料后再折弯时经 常出现零件尺寸偏大的情况,笔者结合工作实践,采用K因子、 折弯补偿和折弯扣除、经验算法4种方法对该算法加以改进。
一、概述
钣金的展开计算有很多方法,传统的钣金折弯件加工工艺比较 粗放,没有精确的折弯展开算法,多是先近似展开并放样落料, 预留大量加工余量后折弯,然后再进行切割或剪切类加工去除 余料,这种加工方式工艺流程复杂、效率低、浪费材料且加工 质量不易保证。 现代的钣金折弯件加工工艺要求钣金折弯展开精确,折弯加工 后无需后续切割或剪切类加工就可以成为理想的钣金折弯件, 这就要求精确计算钣金折弯展开尺寸,并画出折弯展开图。 1、 K因子法
快速确定 K-L 展开的泽尼克多项式系数的协方差矩阵对经过大气湍流的波前进行模拟

快速确定 K-L 展开的泽尼克多项式系数的协方差矩阵对经过大气湍流的波前进行模拟纪庆楠;付芸;张伶伶【摘要】使用基于zernike多项式的K-L展开法对经过大气湍流的波前进行模拟时,需要根据泽尼克多项式的协方差矩阵对泽尼克多项式的系数进行求解,从而实现对大气湍流的模拟。
本文使用一种快速确定协方差矩阵的方法求得泽尼克多项式系数,进而实现对波前的模拟,并以前15阶泽尼克多项式为例,模拟出经过大气湍流的波前。
【期刊名称】《数字技术与应用》【年(卷),期】2012(000)011【总页数】3页(P107-108,111)【关键词】空地激光通信;自适应光学;波前模拟;大气湍流;泽尼克多项式;协方差矩阵【作者】纪庆楠;付芸;张伶伶【作者单位】长春理工大学吉林长春 130022;长春理工大学吉林长春 130022;长春理工大学吉林长春 130022【正文语种】中文【中图分类】TP212光波在大气中进行传播时,大气湍流会造成空气折射率的随机变化,进而引起光波的振幅和相位的随机变化,导致光强闪烁、波面的畸变、到达角的起伏和光束漂移等现象,大大影响了空地激光通信的质量。
在空地激光通信系统中应用自适应光学系统可以对大气湍流产生的影响进行实时检测和校正,对波面畸变进行改善,提高通信质量。
对受大气湍流引起的波前畸变进行仿真模拟对自适应光学系统的设计、研究和使用有很大的作用,可以大大减少实验成本,提高实验效率,并且能够模拟某些实际条件无法实现的试验场景。
自适应光学系统中受大气湍流影响的光学波前的模拟方法主要有四种:基于zernike多项式的K-L函数展开法、小波法、Fourier法以及ARMA法。
其中无论是精度还是速度上基于zernike多项式的K-L函数展开法都更适合于对经过大气的波前进行模拟[1]。
但是,在使用该方法对波前进行模拟时,需要计算泽尼克多项式系数的协方差矩阵,此过程比较繁琐。
本文介绍了一种快速确定泽尼克多项式系数的协方差矩阵的方法,并应用该方法确定泽尼克多项式系数,进而实现对经过大气湍流的波前进行模拟。
现代数字信号处理及其应用论文――KL变换的应用.

Karhunen-Loeve变换的应用摘要:本文对Karhunen-Loeve变换的原理进行了说明,重点分析了K-L变换的性质,结合K-L变换的性质,对K-L变换的具体应用进行了展示。
利用K-L变换在人脸识别、遥感图像特征提取、地震波噪声抑制、数字图像压缩、语音信号增强中的具体利用,深入总结了K-L变换在模式识别、噪声抑制和数据压缩领域的重要性。
关键字: Karhunen-Loeve变换 K-L变换 K-L展开1、Karhunen-Loeve变换定义1.1Karhunen-Loeve变换的提出在模式识别和图像处理等现实问题中,需要解决的一个主要的问题就是降维,通常我们选择的特征彼此相关,而在识别这些特征时,数据量大且效率低下。
如果我们能减少特征的数量,即减少特征空间的维数,那么我们将以更少的存储和计算复杂度获得更好的准确性。
于是我们需要一种合理的综合性方法,使得原本相关的特征转化为彼此不相关,并在特征量的个数减少的同时,尽量不损失或者稍损失原特征中所包含的信息。
Karhunen-Loeve变换也常称为主成分变换(PCA或霍特林变换,就可以简化大维数的数据集合,而且它的协方差矩阵除对角线以外的元素都是零,消除了数据之间的相关性。
所以可以用于信息压缩、图像处理、模式识别等应用中。
Karhunen-Loeve变换,是以矢量信号X的协方差矩阵Ф的归一化正交特征矢量q 所构成的正交矩阵Q,来对该矢量信号X做正交变换Y=QX,则称此变换为K-L 变换(K-LT或KLT),K-LT是Karhuner-Loeve Transform的简称,有的文献资料也写作KLT。
可见,要实现KLT,首先要从信号求出其协方差矩阵Ф,再由Ф求出正交矩阵Q。
Ф的求法与自相关矩阵求法类似。
1.2Karhunen-Loeve展开及其性质设零均值平稳随机过程u(n构成的M维随机向量为u(n,相应的相关矩阵为R,则向量u(n可以表示为R的归一化特征向量的线性组合,即,此式称为u(n的Karhunen-Loeve展开式,展开式的系数是由内积定义的随机变量,且有,。
模式识别第5章特征选择和提取

第五章 特征选择和提取特征选择和提取是模式识别中的一个关键问题前面讨论分类器设计的时候,一直假定已给出了特征向量维数确定的样本集,其中各样本的每一维都是该样本的一个特征;这些特征的选择是很重要的,它强烈地影响到分类器的设计及其性能;假若对不同的类别,这些特征的差别很大,则比较容易设计出具有较好性能的分类器。
特征选择和提取是构造模式识别系统时的一个重要课题在很多实际问题中,往往不容易找到那些最重要的特征,或受客观条件的限制,不能对它们进行有效的测量;因此在测量时,由于人们心理上的作用,只要条件许可总希望把特征取得多一些;另外,由于客观上的需要,为了突出某些有用信息,抑制无用信息,有意加上一些比值、指数或对数等组合计算特征;如果将数目很多的测量值不做分析,全部直接用作分类特征,不但耗时,而且会影响到分类的效果,产生“特征维数灾难”问题。
为了设计出效果好的分类器,通常需要对原始的测量值集合进行分析,经过选择或变换处理,组成有效的识别特征;在保证一定分类精度的前提下,减少特征维数,即进行“降维”处理,使分类器实现快速、准确和高效的分类。
为达到上述目的,关键是所提供的识别特征应具有很好的可分性,使分类器容易判别。
为此,需对特征进行选择。
应去掉模棱两可、不易判别的特征;所提供的特征不要重复,即去掉那些相关性强且没有增加更多分类信息的特征。
说明:实际上,特征选择和提取这一任务应在设计分类器之前进行;从通常的模式识别教学经验看,在讨论分类器设计之后讲述特征选择和提取,更有利于加深对该问题的理解。
所谓特征选择,就是从n 个度量值集合{x1, x2,…, xn}中,按某一准则选取出供分类用的子集,作为降维(m 维,m<n )的分类特征;所谓特征提取,就是使(x1, x2,…, xn)通过某种变换,产生m 个特征(y1, y2,…, ym) (m<n) ,作为新的分类特征(或称为二次特征);其目的都是为了在尽可能保留识别信息的前提下,降低特征空间的维数,已达到有效的分类。
傅里叶变换 kl展开 渗透系数

傅里叶变换、K-L展开和渗透系数是数学和物理领域中的重要概念,它们在信号处理、光学、量子力学等领域都有着广泛的应用。
在这篇文章中,我将以简到繁的方式,深入探讨这些概念,帮助你更好地理解它们的原理和应用。
一、傅里叶变换1. 傅里叶变换是一种将时域信号转换为频域信号的数学工具,其核心思想是将一个复杂的周期信号分解为若干个简单的正弦波信号的叠加。
通过傅里叶变换,我们可以分析信号的频谱特性,从而更好地理解信号的性质和行为。
2. 以数学公式和图表的形式,展示傅里叶变换的计算方法和结果,以及其在信号处理、通信系统等方面的应用。
重点介绍傅里叶变换在频率分析、滤波器设计等方面的重要性和实际意义。
3. 总结傅里叶变换的基本原理,强调其在不同领域的应用,并共享我对傅里叶变换的理解和看法。
二、K-L展开1. K-L展开是一种基于统计学原理的数据分解方法,通过最小化信息损失,将高维度的数据表示为低维度的子空间。
它在图像压缩、模式识别等领域有着重要的应用,能够提取数据的主要特征并降低维度,从而简化数据分析和处理的复杂度。
2. 通过数学模型和实际案例,详细介绍K-L展开的计算过程和应用场景,重点阐述其在图像处理、语音识别等领域的重要性和实际效果。
3. 总结K-L展开的核心思想和优势,指出其在大数据时代的应用前景和发展趋势,并共享我对K-L展开的个人理解和看法。
三、渗透系数1. 渗透系数是描述物质对流体渗透性的物理指标,它在岩石物理学、地质勘探等领域具有重要的意义。
渗透系数的大小和分布情况对于油气勘探和开发具有重要的指导意义,是地下资源评价和开采的重要参数。
2. 通过理论公式和实验数据,介绍渗透系数的计算方法和影响因素,重点关注其在地质勘探、水文地质等领域的应用和实际意义。
3. 总结渗透系数对地下资源勘探和利用的重要性,展望其在环境保护和地质灾害防治中的潜在价值,并共享我对渗透系数的个人见解和理解。
在对以上三个主题进行深度和广度的探讨之后,我们可以发现傅里叶变换、K-L展开和渗透系数在数学、物理、地质等不同领域都有着重要的应用和意义。
