(完整)2004-2017年体育单招数学分类汇编-圆锥曲线,推荐文档
体育单招数学试题与答案2(K12教育文档)

(直打版)体育单招数学试题与答案2(word版可编辑修改)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((直打版)体育单招数学试题与答案2(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(直打版)体育单招数学试题与答案2(word版可编辑修改)的全部内容。
一.选择题:本大题共10小题,每小题6分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的,请将正确的选项的字母填写在题后的括号内.(1)设集合M = {x|0<x 〈1},集合N={x| -1<x 〈1},则【 】(A )M ∩N=M (B )M ∪N=N(C )M ∩N=N (D )M ∩N= M ∩N(2)已知函数()f x 的图象与函数sin y x =的图象关于y 轴对称,则()f x =【 】(A )cos x - (B )cos x (C )sin x - (D)sin x(3)已知平面向量(1,2),(1,3)a b ==-,则a 与b 的夹角是【 】(A )2π (B )3π (C )4π (D )6π (4)函数1(5)5y x x =≠-+的反函数是【 】 (A )5()y x x R =-∈ (B )15(0)y x x =+≠ (C )5()y x x R =+∈ (D )15(0)y x x=-≠ (5)不等式10x x -<的解集是 【 】 (A ){x |0<x<1} (B){x|1〈x 〈∞}(C ){x|-∞<x 〈0} (D ){x |—∞<x 〈0}(6)已知函数1()cos 222x x f x =+,则()f x 是区间 【 】 (A )28(,)33ππ上的增函数 (B)24(,)33ππ-上的增函数(C )82(,)33ππ--上的增函数 (D )42(,)33ππ-上的增函数 (7)已知直线l 过点(1,1)-,且与直线230x y --= 垂直,则直线l 的方程是【 】(A )210x y +-= (B)230x y +-= (C )230x y --= (D )210x y --=(8) 已知圆锥曲线母线长为5,底面周长为6π,则圆锥的体积是【 】(A )6π (B )12π (C )18π (D )36π(9) n S 是等差数列{}n a 的前n 项合和,已知312S =-,66S =-,则公差d =【 】(A)—1 (B)—2 (C )1 (D )2(10)将3名教练员与6名运动员分为3组,每组一名教练员与2名运动员,不同的分法有【 】(A )90中 (B )180种 (C )270种 (D )360种二.填空题:本大题共6 小题,每小题6 分,共36 分.把答案填在题中横线上。
第19练 圆锥曲线

第19练 圆锥曲线1. 椭圆5522=+y x 的焦点坐标是( ) )0,2(),0,2(.-A )0,4(),0,4(.-B )2,0(),2,0(.-C )4,0(),4,0(.-D2. 双曲线19422=-y x 的实轴长是( ) 4.A 32.B 21.C 1.D 3. 过抛物线x y 62-=焦点F 的弦AB 垂直于轴x ,则弦AB (也称为抛物线的通径)的长的是( )6.A 5.B 4.C 3.D4.双曲线1222=-y x 与1222=-x y 的关系( )A. 有相同的顶点B. 有相同的实轴长、虚轴长C. 有相同的焦距D. 有相同的渐近线5. 椭圆)0(12222>>=+b a by a x 的半焦距为c ,两焦点与椭圆上一点组成的三角形周长为a 3,则椭圆的离心率是( )32.A 35.B 21.C25.D 6. 过抛物线焦点且垂直于y 轴的弦长为8,则该抛物线的标准方程为( )x y A 8.2= x y B 8.2-= x y x y C 8-,8.22==或y x y x D 8-,8.22==或 7. 抛物线以x 轴为对称轴,过焦点F 的弦为AB ,点A 的横坐标为1-,且3=AF ,则抛物线的标准方程为( )x y A 8.2= x y B 8.2-= x y x y C 8-,8.22==或y x y x D 8-,8.22==或8. 过双曲线左焦点的垂线交双曲线于B A ,,分别连接右焦点F 得到的ABF ∆是正三角形,则双曲线的离心率是( )3.A 2.B3.C 5.D9. AB 是过抛物线x y 232=焦点F 的弦,且),(11y x A ,),(22y x B ,则=2121x x y y ( ) 4.-A 4.B 2.C 2.-D10. AB 是过抛物线x y 62=焦点F 的弦,若9=AB ,则线段AB 的中点M 到抛物线准线的距离是( )9.A 29.B 6.C 25.D11. 椭圆)0(122>=+k y k x 的离心率为31,则=k ,焦距是 .12. AB 是过抛物线y x =22焦点F 的弦,若4=AB ,则线段AB 的中点M 到y 轴的距离是 . 13. 点P 是双曲线14522=-y x 与椭圆1162522=+y x 的一个交,双曲线的左右焦点为21,F F ,则=∆21F PF S .14. 已知AB 是过抛物线)0(22>=p px y 焦点F 的弦. )22,2(A ,M 为线段AF 的中点,则点M 到抛物线准线的距离为 .15. 椭圆)0(12222>>=+b a by a x 的半焦距为c ,过一个焦点的直线与椭圆交于B A ,,另一焦点为F ,且ABF ∆的周长为b 62,则椭圆的离心率是 .16. AB 是过抛物线x y 42=焦点F 的弦,且),(11y x A ,),(22y x B ,若直线AB 与y 轴的交点坐标为)2,0(,则=+2111x x ,=+2111y y .。
(完整word版)2004--2017年体育单招数学分类汇编-圆锥曲线

2004--2017年体育单招数学分类汇编--圆锥曲线1、(2017年第6题)已知抛物线y x C 4:2=的焦点为F ,过F 作C 的对称轴的垂线,与C 交于A 、B ,则=||AB( )8 B. 4 C.2 D. 12、(2017年第15题)直线m x y +=与椭圆1222=+y x 有两个不同的交点,则m 的取值范围为 。
3、(2016年第2题)抛物线y 2=2px 过点(1,2),则该抛物线的准线方程为( )A 、x=-1B 、x=1C 、y=-1D 、y=14、(2016年第3题)在一个给定平面内,A ,C 为定点,B 为动点,且|BC|,|AC|,|AB|成等差数列,则点B 的轨迹是( ) A 、圆 B 、椭圆 C 、双曲线D 、抛物线5、(2016年第16题)设双曲线1222=-y a x 与椭圆1162522=+y x 有相同的焦点,则该双曲线的渐近线的方程是_______________.6、(2015年第9题)双曲线12222=-by a x 的一条渐近线的斜率为3,则此双曲线的离心率为 ( ) A. 332 B. 3 C . 2 D. 47、(2015年第12题)若椭圆的焦点为)0,3(-,)0,3(,离心率为53,则该椭圆的标准方程为 。
8、(2015年第18题)已知抛物线C :y x 42=,直线l :0=-+m y x 。
(1)证明:C 与l 有两个交点的充分必要条件是1->m ;(2)设1<m ,C 与l 有两个交点A ,B ,线段AB 的垂直平分线交y 轴于点G ,求GAB ∆面积的取值范围。
9、(2014年第8题)若双曲线22221(0,0)x y a b a b-=>>的两条渐近线相互垂直,则双曲线的离心率为( )A B .2 C 10、(2014年第15题)抛物线24y x =的准线方程是 .11、(2014年第18题)已知椭圆C 中心在原点,焦点在x 轴上,离心率为12,且C 过点3(1,)2- (1) 求C 的方程;(2)如果直线:2l y kx =-与C 有两个交点,求k 的取值范围。
2017年高考数学理试题分类汇编圆锥曲线(供参考)

2017 年高考试题分类汇编之圆锥曲线(理数) 解析一、选择题 .................................................................................................................................... 1 二、填空题 .................................................................................................................................... 3 三、大题 .. (5)一、选择题【浙江卷】2.椭圆22194x y +=的离心率是 ABC .23D .59【解析】e == B.【全国1卷(理)】10.已知F 为抛物线C :y 2=4x 的核心,过F 作两条相互垂直的直线l 1,l 2,直线l 1与C 交于A 、B 两点,直线l 2与C 交于D 、E 两点,那么|AB |+|DE |的最小值为( )A .16B .14C .12D .10【解析】设AB 倾斜角为θ.作1AK 垂直准线,2AK 垂直x 轴 易知11cos 22AF GF AK AK AF P P GP Pθ⎧⎪⋅+=⎪⎪=⎨⎪⎛⎫⎪=--= ⎪⎪⎝⎭⎩(几何关系)(抛物线特性)cos AF P AFθ⋅+=∴同理1cos P AF θ=-,1cos PBF θ=+∴22221cos sin P PAB θθ==- 又DE 与AB 垂直,即DE 的倾斜角为π2θ+2222πcos sin 2P PDE θθ==⎛⎫+ ⎪⎝⎭而24y x =,即2P =.∴22112sin cos AB DE P θθ⎛+=+ ⎝最小值为16,应选A【全国Ⅱ卷(理)】9.假设双曲线C:22221x y a b-=(0a >,0b>)的一条渐近线被圆()2224x y -+=所截得的弦长为2,那么C 的离心率为( )A .2 BCD .3【解析】取渐近线by x a=,化成一样式0bx ay -=,圆心()20,得224c a =,24e =,2e =.【全国III 卷(理)】5.已知双曲线C:22221x y a b -= (a >0,b >0)的一条渐近线方程为y x =,且与椭圆221123x y += 有公共核心,那么C 的方程为( ) A. 221810x y -= B. 22145x y -= C. 22154x y -= D. 22143x y -=【解析】∵双曲线的一条渐近线方程为y =,那么b a =① 又∵椭圆221123x y +=与双曲线有公共核心,易知3c =,那么2229a b c +==②由①②解得2,a b ==,那么双曲线C 的方程为22145x y -=,应选B.【全国III 卷(理)】10.已知椭圆C :22221x y a b+=,(a >b >0)的左、右极点别离为A 1,A 2,且以线段A 1A 2为直径的圆与直线20bx ay ab -+=相切,那么C 的离心率为( )A.6B.3C.23D.13【解析】∵以12A A为直径为圆与直线20bx ay ab-+=相切,∴圆心到直线距离d等于半径,∴222abd aa b==+又∵0,0a b>>,那么上式可化简为223a b=∵222b a c=-,可得()2223a a c=-,即2223ca=∴6cea==,应选A【天津卷】(5)已知双曲线22221(0,0)x ya ba b-=>>的左核心为F,离心率为2.假设通过F和(0,4)P两点的直线平行于双曲线的一条渐近线,那么双曲线的方程为()A.22144x y-= B.22188x y-= C.22148x y-= D.22184x y-=【解析】由题意得224,14,22188x ya b c a bc==-⇒===⇒-=-,故选B.二、填空题【全国1卷(理)】15.已知双曲线C:22221x ya b-=(a>0,b>0)的右极点为A,以A为圆心,b为半径做圆A,圆A与双曲线C的一条渐近线交于M、N两点.假设∠MAN=60°,那么C的离心率为________.【解析】如图,OA a=,AN AM b==∵60MAN∠=︒,∴3AP,222234OP OA PA a b=--∴2232tan34APOPa bθ==-又∵tan b a θ=b a =,解得223a b =∴e ===【全国2卷(理)】16.已知F 是抛物线C:28y x =的核心,M 是C 上一点,FM 的延长线交y 轴于点N .假设M 为FN 的中点,那么FN = .【解析】28y x =则4p =,核心为()20F ,,准线:2l x =-, 如图,M 为F 、N 中点,故易知线段BM 为梯形AFMC 中位线, ∵2CN =,4AF =, ∴3ME =又由概念ME MF =, 且MN NF =, ∴6NF NM MF =+=【北京卷】(9)假设双曲线221y x m-=m =_______________. 【解析】2m =⇒= 【江苏卷】8.在平面直角坐标系xOy 中,双曲线2213x y -= 的右准线与它的两条渐近线别离交于点P ,Q ,其核心是F 1 , F 2 ,那么四边形F 1 P F 2 Q 的面积是 .1(10,0)F -,2(10,0)F ,那么302102310S =⨯=. 【山东卷】14.在平面直角坐标系xOy 中,双曲线()222210,0x y a b a b -=>>的右支与核心为F 的抛物线()220x px p =>交于,A B 两点,假设4AF BF OF +=,那么该双曲线的渐近线方程为 .三、大题【全国I 卷(理)】20.(12分)已知椭圆C :2222=1x y a b+(a >b >0),四点P 1(1,1),P 2(0,1),P 3(–13),P 4(13C 上. (1)求C 的方程;(2)设直线l 不通过P 2点且与C 相交于A ,B 两点.假设直线P 2A 与直线P 2B 的斜率的和为–1,证明:l 过定点. 20.解:(1)依照椭圆对称性,必过3P 、4P又4P 横坐标为1,椭圆必只是1P ,因此过234P P P ,,三点 将()233011P P ⎛- ⎝⎭,,,代入椭圆方程得222113141b ab ⎧=⎪⎪⎨⎪+=⎪⎩,解得24a =,21b = ∴椭圆C 的方程为:2214x y +=.(2)①当斜率不存在时,设()():A A l x m A m y B m y =-,,,,221121A A P A P B y y k k m m m ----+=+==-得2m =,现在l 过椭圆右极点,不存在两个交点,故不知足. ②当斜率存在时,设()1l y kx b b =+≠∶()()1122A x y B x y ,,,联立22440y kx b x y =+⎧⎨+-=⎩,整理得()222148440k x kbx b +++-= 122814kbx x k -+=+,21224414b x x k -⋅=+ 则22121211P A P B y y k k x x --+=+()()21212112x kx b x x kx b x x x +-++-=222228888144414kb k kb kbk b k--++=-+()()()811411k b b b -==-+-,又1b ≠21b k ⇒=--,现在64k ∆=-,存在k 使得0∆>成立. ∴直线l 的方程为21y kx k =-- 当2x =时,1y =- 所以l 过定点()21-,. 【全国II 卷(理)】20. (12分)设O 为坐标原点,动点M 在椭圆C :2212x y +=上,过M 做x 轴的垂线,垂足为N ,点P 知足2NP NM =.(1)求点P 的轨迹方程;(2)设点Q 在直线x =-3上,且1OP PQ ⋅=.证明:过点P 且垂直于OQ 的直线l 过C 的左焦 点F ..解:⑴设()P x y ,,易知(0)N x , (0)NP y =,又0NM ⎛== ⎝∴M x y ⎛⎫⎪⎝⎭,又M 在椭圆上.∴2212x +=,即222x y +=. ⑵设点(3)Q Q y -,,()P P P x y ,,(0)Q y ≠, 由已知:()(3)1P P P Q P OP PQ x y y y y ⋅=⋅---=,,, ()21OP OQ OP OP OQ OP ⋅-=⋅-=,∴213OP OQ OP ⋅=+=,∴33P Q P Q P P Q x x y y x y y ⋅+=-+=. 设直线OQ :3Q y y x =⋅-,因为直线l 与OQ l 垂直. ∴3l Qk y =故直线l 方程为3()P P Qy x x y y =-+, 令0y =,得3()P Q P y y x x -=-, 13P Q P y y x x -⋅=-, ∴13P Q P x y y x =-⋅+,∵33P Q P y y x =+,∴1(33)13P P x x x =-++=-,若0Q y =,那么33P x -=,1P x =-,1P y =±,直线OQ 方程为0y =,直线l 方程为1x =-,直线l 过点(10)-,,为椭圆C 的左核心.【全国III 卷(理)】20.(12分)已知抛物线C :y 2=2x ,过点(2,0)的直线l 交C 与A ,B 两点,圆M 是以线段AB 为直径的圆.(1)证明:坐标原点O 在圆M 上; (2)设圆M 过点P (4,-2),求直线l 与圆M 的方程.解:(1)显然,当直线斜率为0时,直线与抛物线交于一点,不符合题意.设:2l x my =+,11(,)A x y ,22(,)B x y ,联立:222y xx my ⎧=⎨=+⎩得2240y my --=,2416m ∆=+恒大于0,122y y m +=,124y y =-.1212OA OBx x y y ⋅=+ 12(2)(2)my my =++21212(1)2()4m y y m y y =++++ 24(1)2(2)4m m m =-+++0=∴OA OB ⊥,即O 在圆M 上.(2)假设圆M 过点P ,那么0AP BP ⋅= 1212(4)(4)(2)(2)0x x y y --+++= 1212(2)(2)(2)(2)0my my y y --+++=21212(1)(22)()80m y y m y y +--++=化简得2210m m --=解得12m =-或1①当12m =-时,:240l x y +-=圆心为00(,)Q x y ,120122y y y +==-,0019224x y =-+=,半径||r OQ =那么圆229185:()()4216M x y -++=②当1m =时,:20l x y --=圆心为00(,)Q x y ,12012y y y +==,0023x y =+=,半径||r OQ ==那么圆22:(3)(1)10M x y -+-=【北京卷】(18)(14分)已知抛物线C :y 2=2px 过点P (1,1).过点(0,12)作直线l 与抛物线C 交于不同的两点M ,N ,过点M 作x 轴的垂线别离与直线OP 、ON 交于点A ,B ,其中O 为原点. (Ⅰ)求抛物线C 的方程,并求其核心坐标和准线方程; (Ⅱ)求证:A 为线段BM 的中点.(18)解:(Ⅰ)把P (1,1)代入y 2=2Px 得P =12∴C :y 2=x , ∴核心坐标(14,0),准线:x =-14. (Ⅱ)设l :y =kx +12,A (x 1,y 1),B (x 2,y 2),OP :y =x ,ON :y =22yx x ,由题知A (x 1,x 1),B (x 1,122x y x ) 212y kx y x⎧>+⎪⎨⎪=⎩⇒k 2x 2+(k -1)x +14=0,x 1+x 2=21k k -,x 1·x 2=214k . 1112121112221122,22x kx x y x x y kx kx x x x ⎛⎫+ ⎪+⎝⎭+=++=+由x 1+x 2=21k k -,x 1x 2=214k , 上式()2111121122122124kk kx kx k x x x k x -=+=+-⋅=∴A 为线段BM 中点.【江苏卷】17.(14分)如图,在平面直角坐标系xOy 中,椭圆1(0)2222x y E :+a b a b=>>的左、右核心别离为F 1,F 2,离心率为12,两准线之间的距离为8.点P 在椭圆E 上,且位于第一象限,过点F 1作直线PF 1的垂线l 1,过点F 2作直线PF 2的垂线l 2. (1)求椭圆E 的标准方程;(2)假设直线l 1,l 2的交点Q 在椭圆E 上,求点P 的坐标.17.解:(1)∵椭圆E 的离心率为12,∴12c a =①.∵两准线之间的距离为8,∴228a c =②.联立①②得2,1a c ==,∴3b =,故椭圆E 的标准方程为22143x y +=. (2)设00(,)P x y ,那么000,0x y >>,由题意得00001(1)1(1)x y x y x y x y +⎧=-+⎪⎪⎨-⎪=--⎪⎩,整理得0201x x x y y =-⎧⎪-⎨=⎪⎩,∵点00(,)P x y 在椭圆E 上,∴2200143x y +=,∴222002(1)33y x y -=,∴2200169,77x y ==,故点P 的坐标是4737(,)77.【江苏卷】B .[选修4-2:矩阵与变换](本小题总分值10分)已知矩阵A = ,B =. (1) 求AB ;(2)假设曲线C 1;22y =182x + 在矩阵AB 对应的变换作用下取得另一曲线C 2 ,求C 2的方程.B.解:(1)AB ==.(2)设11(,)P x y 是曲线1C 上任意一点,变换后对应的点为1`0210x x y y ⎡⎤⎢⎥⎣⎡⎤⎡⎦⎤=⎢⎥⎢⎥⎣⎦⎣⎦, 因此112x y y x =⎧⎨=⎩,即1112x yy x =⎧⎪⎨=⎪⎩,因为11(,)P x y 在曲线1C 上,因此228x y +=即曲线C 2的方程.【山东卷】(21)(本小题总分值13分)在平面直角坐标系xOy 中,椭圆E :22221x y a b+=()0a b >>的离心率为2,焦距为2.(Ⅰ)求椭圆E 的方程;(Ⅱ)如图,动直线l :13y k x =-交椭圆E 于,A B 两点,C 是椭圆E 上一点,直线OC 的斜率为2k ,且1224k k =,M 是线段OC 延长线上一点,且:2:3MC AB =,M 的半径为MC ,,OS OT 是M 的两条切线,切点别离为,S T .求SOT ∠的最大值,并求取得最大值时直线l 的斜率.(21)解:(I )由题意知 22c e a ==,22c =, 因此 2,1a b ==,因此 椭圆E 的方程为2212x y +=.(Ⅱ)设()()1122,,,A x y B x y ,由题意知0∆>,令2112t k =+,【天津卷】(19)(本小题总分值14分)设椭圆22221(0)x y a b a b +=>>的左核心为F ,右极点为A ,离心率为12.已知A 是抛物线22(0)y px p =>的核心,F 到抛物线的准线l 的距离为12. (I )求椭圆的方程和抛物线的方程;(II )设l 上两点P ,Q 关于x 轴对称,直线AP 与椭圆相交于点B (B 异于点A ),直线BQ 与x 轴相交于点D .假设APD △的面积为2,求直线AP 的方程.(19)(Ⅰ)解:设F的坐标为(,0)c-.依题意,12ca=,2pa=,12a c-=,解得1a=,12c=,2p=,于是22234b a c=-=.因此,椭圆的方程为22413yx+=,抛物线的方程为24y x=.因此,直线AP的方程为3630x y+-=,或3630x y--=.【浙江卷】21.(此题总分值15分)如图,已知抛物线2x y=,点A11()24-,,39()24B,,抛物线上的点11()()24P x y x-<<,.过点B作直线AP的垂线,垂足为Q.(Ⅰ)求直线AP斜率的取值范围;(Ⅱ)求AP PQ⋅的最大值.21.解:(Ⅰ)由题易患P(x,x2),-12<x<32,故k AP=21412xx-+=x-12∈(-1,1),故直线AP 斜率的取值范围为(-1,1).故PA =(-1设直线AP 的斜率为k ,故1(PQ +=又2(1,)PA k k k =---- ,32(1)k PA PQ PA PQ k +==(1)(1)PA PQ k k =+-,令PA PQ 的最大值为。
2005-2024年体育单招历年数学试卷分类汇编 第2章 函数

体育单招历年数学试卷分类汇编目录体育单招历年数学试卷分类汇编第2章函数 (1)2.1 指数运算和指数不等式 (1)2.2 分段函数求值 (1)2.2 对数运算和对数不等式 (1)2.3 二次函数 (1)2.4 函数的定义域 (3)2.5 函数的单调性 (3)2.6 函数的奇偶性 (4)2.7 反函数 (4)2.8 导数 (5)1 第2章 函数2.1 指数运算和指数不等式【例2.1.1】 (2016改编)函数820x−≥的解集为____________.【例2.1.2】 (2019.5)若2x +5>14,则x 的取值范围是( ) A .(-7,+∞) B .(7,+∞) C .(-3,+∞) D .(3,+∞)【例2.1.3】 (2020.10)已知a =0.20.3, b =0.30.3, c =0.2-0.2,则( )A .a <b <cB .b <a <cC .b <c <aD .a <c <b2.2 分段函数求值【例2.1.4】 (2023.2)已知函数23,0()log ,0x x f x x x ⎧≤=⎨>⎩,则1(())3f f =() A.-1 B.1D.32.2 对数运算和对数不等式【例2.1.5】 (2004.03)14lg 23lg5lg 5+−=( ) A .1 B .4 C .18 D .28【例2.1.6】 (2017)=⨯4log 3log 32 .【例2.1.7】 (2005)若63()log f x x =,则(27)f = .【例2.1.8】 (2004)已知函数3log (0)()2(0)x x x f x x >⎧=⎨≤⎩,则1()9f f ⎡⎤⎢⎥⎣⎦的值是 . 【例2.1.9】 (2009)不等式2lg(54)1x x −+<的解集是( )A.(1,6)−B. (1,4)C. (,1)(6,)−∞−+∞ D. (1,1)(4,6)−【例2.1.10】 (2015)若10<<a ,且0)3(log )12(log 2<<+a a a a ,则a 的取值范围是 。
2017年高考数学理试题分类汇编:圆锥曲线

2017 年高考试题分类汇编之圆锥曲线(理数) 解析一、选择题1 二、填空题3 三、大题5一、选择题【XX 卷】2.椭圆22194x y +=的离心率是 AB.23D .59【解析】33e ==,选B.【全国1卷(理)】10.已知F 为抛物线C :y 2=4x 的焦点,过F 作两条互相垂直的直线l 1,l 2,直线l 1与C 交于A 、B 两点,直线l 2与C 交于D 、E 两点,则|AB |+|DE |的最小值为( ) A .16 B .14 C .12 D .10【解析】设AB 倾斜角为θ.作1AK 垂直准线,2AK 垂直x 轴易知11cos 22AF GF AK AK AF P P GP Pθ⎧⎪⋅+=⎪⎪=⎨⎪⎛⎫⎪=--= ⎪⎪⎝⎭⎩(几何关系)(抛物线特性)cos AF P AF θ⋅+=∴同理1cos P AF θ=-,1cos P BF θ=+∴22221cos sin P P AB θθ==-又DE 与AB 垂直,即DE 的倾斜角为π2θ+2222πcos sin 2P PDE θθ==⎛⎫+ ⎪⎝⎭而24y x =,即2P =.∴22112sin cos AB DE P θθ⎛⎫+=+ ⎪⎝⎭2222sin cos 4sin cos θθθθ+=224sin cos θθ=241sin 24θ=21616sin 2θ=≥,当π4θ=取等号 即AB DE +最小值为16,故选A【全国Ⅱ卷(理)】9.若双曲线C:22221x y a b-=(0a >,0b >)的一条渐近线被圆()2224x y -+=所截得的弦长为2,则C 的离心率为()A .2 BCD.3【解析】取渐近线by x a=,化成一般式0bx ay -=,圆心()20,=得224c a =,24e =,2e =.【全国III 卷(理)】5.已知双曲线C:22221x y a b -= (a >0,b >0)的一条渐近线方程为y x =,且与椭圆221123x y +=有公共焦点,则C 的方程为( ) A. 221810x y -= B. 22145x y -= C. 22154x y -= D. 22143x y -=【解析】∵双曲线的一条渐近线方程为y,则b a =又∵椭圆221123x y +=与双曲线有公共焦点,易知3c =,则2229a b c +==②由①②解得2,a b ==C 的方程为22145x y -=,故选B.【全国III 卷(理)】10.已知椭圆C :22221x y a b+=,(a >b >0)的左、右顶点分别为A 1,A 2,且以线段A 1A 2为直径的圆与直线20bx ay ab -+=相切,则C 的离心率为( )A.C.3D.13 【解析】∵以12A A 为直径为圆与直线20bx ay ab -+=相切,∴圆心到直线距离d 等于半径,∴d a == 又∵0,0a b >>,则上式可化简为223a b =∵222b ac =-,可得()2223a a c =-,即2223c a =∴63c e a ==,故选A【XX 卷】(5)已知双曲线22221(0,0)x y a b a b-=>>的左焦点为F ,离心率为2.若经过F和(0,4)P 两点的直线平行于双曲线的一条渐近线,则双曲线的方程为( )A.22144x y -=B.22188x y -=C.22148x y -=D.22184x y -=【解析】由题意得224,14,22188x y a b c a b c ==-⇒===⇒-=- ,故选B.二、填空题【全国1卷(理)】15.已知双曲线C :22221x y a b-=(a >0,b >0)的右顶点为A ,以A 为圆心,b 为半径做圆A ,圆A 与双曲线C 的一条渐近线交于M 、N 两点.若∠MAN =60°,则C 的离心率为________. 【解析】如图,OA a =,AN AM b == ∵60MAN ∠=︒,∴3AP =,222234OP OA PA a b =-=-∴2232tan 34AP OP a b θ=-又∵tan b a θ=b a =,解得223a b =∴e =【全国2卷(理)】16.已知F 是抛物线C:28y x =的焦点,M 是C 上一点,FM 的延长线交y 轴于点N .若M 为FN 的中点,则FN =. 【解析】28y x =则4p =,焦点为()20F ,,准线:2l x =-, 如图,M 为F 、N 中点,故易知线段BM 为梯形AFMC 中位线, ∵2CN =,4AF =, ∴3ME =又由定义ME MF =, 且MN NF =, ∴6NF NM MF =+=【卷】(9)若双曲线221y x m-=m =_______________. 【解析】.21m =⇒= 【XX 卷】8.在平面直角坐标系xOy 中,双曲线2213x y -= 的右准线与它的两条渐近线分别交于点P ,Q ,其焦点是F 1 , F 2 ,则四边形F 1PF 2Q 的面积是.【解析】右准线方程为33101010x ==,渐近线为33y x =±,则31030(,)1010P ,31030(,)1010Q -,1(10,0)F -,2(10,0)F ,则302102310S =⨯=. 【XX 卷】14.在平面直角坐标系xOy 中,双曲线()222210,0x y a b a b -=>>的右支与焦点为F 的抛物线()220x px p =>交于,A B 两点,若4AF BF OF +=,则该双曲线的渐近线方程为.三、大题【全国I 卷(理)】20.(12分)已知椭圆C :2222=1x y a b+(a >b >0),四点P 1(1,1),P 2(0,1),P 3(–1,32 ),P 4(1,32)中恰有三点在椭圆C 上. (1)求C 的方程;(2)设直线l 不经过P 2点且与C 相交于A ,B 两点.若直线P 2A 与直线P 2B 的斜率的和为–1,证明:l 过定点.20.解:(1)根据椭圆对称性,必过3P 、4P 又4P 横坐标为1,椭圆必不过1P ,所以过234P P P ,,三点将()233011P P ⎛- ⎝⎭,,,代入椭圆方程得222113141b ab ⎧=⎪⎪⎨⎪+=⎪⎩,解得24a =,21b =∴椭圆C 的方程为:2214x y +=.(2)①当斜率不存在时,设()():A A l x m A m y B m y =-,,,,221121A A P A P B y y k k m m m ----+=+==-得2m =,此时l 过椭圆右顶点,不存在两个交点,故不满足. ②当斜率存在时,设()1l y kx b b =+≠∶()()1122A x y B x y ,,,联立22440y kx bx y =+⎧⎨+-=⎩,整理得()222148440k x kbx b +++-=122814kbx x k -+=+,21224414b x x k -⋅=+则22121211P A P B y y k k x x --+=+()()21212112x kx b x x kx b x x x +-++-=222228888144414kb k kb kbk b k --++=-+()()()811411k b b b -==-+-,又1b ≠21b k ⇒=--,此时64k ∆=-,存在k 使得0∆>成立.∴直线l 的方程为21y kx k =--当2x =时,1y =-所以l 过定点()21-,.【全国II 卷(理)】20. (12分)设O 为坐标原点,动点M 在椭圆C :2212x y +=上,过M 做x 轴的垂线,垂足为N ,点P 满足2NP NM =.(1)求点P 的轨迹方程;(2)设点Q 在直线x =-3上,且1OP PQ ⋅=.证明:过点P 且垂直于OQ 的直线l 过C 的左焦 点F ..解:⑴设()P x y ,,易知(0)N x , (0)NP y =,又0NM ⎛== ⎝∴M x ⎛⎫⎪⎝⎭,又M 在椭圆上.∴2212x +=,即222x y +=. ⑵设点(3)Q Q y -,,()P P P x y ,,(0)Q y ≠, 由已知:()(3)1P P P Q P OP PQ x y y y y ⋅=⋅---=,,, ()21OP OQ OP OP OQ OP ⋅-=⋅-=,∴213OP OQ OP ⋅=+=, ∴33P Q P Q P P Q x x y y x y y ⋅+=-+=. 设直线OQ :3Q y y x =⋅-,因为直线l 与OQ l 垂直. ∴3l Qk y =故直线l 方程为3()P P Qy x x y y =-+, 令0y =,得3()P Q P y y x x -=-, 13P Q P y y x x -⋅=-, ∴13P Q P x y y x =-⋅+,∵33P Q P y y x =+,∴1(33)13P P x x x =-++=-,若0Q y =,则33P x -=,1P x =-,1P y =±,直线OQ 方程为0y =,直线l 方程为1x =-,直线l 过点(10)-,,为椭圆C 的左焦点.【全国III 卷(理)】20.(12分)已知抛物线C :y 2=2x ,过点(2,0)的直线l 交C 与A ,B 两点,圆M 是以线段AB 为直径的圆. (1)证明:坐标原点O 在圆M 上; (2)设圆M 过点P (4,-2),求直线l 与圆M 的方程.解:(1)显然,当直线斜率为0时,直线与抛物线交于一点,不符合题意.设:2l x my =+,11(,)A x y ,22(,)B x y ,联立:222y x x my ⎧=⎨=+⎩得2240y my --=,2416m ∆=+恒大于0,122y y m +=,124y y =-.1212OA OBx x y y ⋅=+ 12(2)(2)my my =++21212(1)2()4m y y m y y =++++ 24(1)2(2)4m m m =-+++0=∴OA OB ⊥,即O 在圆M 上. (2)若圆M 过点P ,则0AP BP ⋅=1212(4)(4)(2)(2)0x x y y --+++=1212(2)(2)(2)(2)0my my y y --+++=21212(1)(22)()80m y y m y y +--++=化简得2210m m --=解得12m =-或1①当12m =-时,:240l x y +-=圆心为00(,)Q x y ,12012y y y +==-,001924x y =-+=,半径||r OQ ==则圆229185:()()4216M x y -++=②当1m =时,:20l x y --=圆心为00(,)Q x y ,12012y y y +==,0023x y =+=,半径||r OQ ==则圆22:(3)(1)10M x y -+-=【卷】(18)(14分)已知抛物线C :y 2=2px 过点P (1,1).过点(0,12)作直线l 与抛物线C 交于不同的两点M ,N ,过点M 作x 轴的垂线分别与直线OP 、ON 交于点A ,B ,其中O 为原点. (Ⅰ)求抛物线C 的方程,并求其焦点坐标和准线方程; (Ⅱ)求证:A 为线段BM 的中点.(18)解:(Ⅰ)把P (1,1)代入y 2=2Px 得P =12∴C :y 2=x , ∴焦点坐标(14,0),准线:x =-14. (Ⅱ)设l :y =kx +12,A (x 1,y 1),B (x 2,y 2),OP :y =x ,ON :y =22yx x ,由题知A (x 1,x 1),B (x 1,122x y x ) 212y kx y x⎧>+⎪⎨⎪=⎩⇒k 2x 2+(k -1)x +14=0,x 1+x 2=21k k -,x 1·x 2=214k .1112121112221122,22x kx x y x x y kx kx x x x ⎛⎫+ ⎪+⎝⎭+=++=+由x 1+x 2=21k k -,x 1x 2=214k, 上式()2111121122122124kk kx kx k x x x k x -=+=+-⋅=∴A 为线段BM 中点. 【XX 卷】17.(14分)如图,在平面直角坐标系xOy 中,椭圆1(0)2222x y E :+a b a b=>>的左、右焦点分别为F 1,F 2,离心率为12,两准线之间的距离为8.点P 在椭圆E 上,且位于第一象限,过点F 1作直线PF 1的垂线l 1,过点F 2作直线PF 2的垂线l 2. (1)求椭圆E 的标准方程;(2)若直线l 1,l 2的交点Q 在椭圆E 上,求点P 的坐标.17.解:(1)∵椭圆E 的离心率为12,∴12c a =①.∵两准线之间的距离为8,∴228a c =②.联立①②得2,1a c ==,∴3b =,故椭圆E 的标准方程为22143x y +=.【XX 卷】B .[选修4-2:矩阵与变换](本小题满分10分)已知矩阵A = ,B =. (1) 求AB ;(2)若曲线C 1;22y =182x +在矩阵AB 对应的变换作用下得到另一曲线C 2 ,求C 2的方程.B.解:(1)AB ==.(2)设11(,)P x y 是曲线1C 上任意一点,变换后对应的点为1`0210x x y y ⎡⎤⎢⎥⎣⎡⎤⎡⎦⎤=⎢⎥⎢⎥⎣⎦⎣⎦,方程.【XX 卷】(21)(本小题满分13分)在平面直角坐标系xOy 中,椭圆E :22221x y a b+=()0a b >>2.(Ⅰ)求椭圆E 的方程;(Ⅱ)如图,动直线l :1y k x =交椭圆E 于,A B 两点,C 是椭圆E 上一点,直线OC 的斜率为2k ,且12k k =,M 是线段OC 延长线上一点,且:2:3MC AB =,M 的半径为MC ,,OS OT 是M 的两条切线,切点分别为,S T .求SOT ∠的最大值,并求取得最大值时直线l 的斜率.(21)解:(I )由题意知 22c e a ==,22c =, 所以 2,1a b ==,因此 椭圆E 的方程为2212x y +=. (Ⅱ)设()()1122,,,A x y B x y ,联立方程2211,23,2x y y k x ⎧+=⎪⎪⎨⎪=-⎪⎩得()2211424310k x k x +--=, 由题意知0∆>,且()112122211231,21221k x x x x k k +==-++,令2112t k =+,【XX 卷】(19)(本小题满分14分)设椭圆22221(0)x y a b a b +=>>的左焦点为F ,右顶点为A ,离心率为12.已知A 是抛物线22(0)y px p =>的焦点,F 到抛物线的准线l 的距离为12. (I )求椭圆的方程和抛物线的方程;(II )设l 上两点P,Q 关于x 轴对称,直线AP 与椭圆相交于点B (B 异于点A ),直线BQ 与x 轴相交于点D .若APD △AP 的方程.所以,直线AP 的方程为3630x y +-=,或3630x y --=.【XX 卷】21.(本题满分15分)如图,已知抛物线2x y =,点A 11()24-,,39()24B ,,抛物线上的点11()()24P x y x -<<,.过点B 作直线AP 的垂线,垂足为Q .(Ⅰ)求直线AP 斜率的取值范围;(Ⅱ)求AP PQ ⋅的最大值.21.解:(Ⅰ)由题易得P (x ,x 2),-12<x <32, 故k AP=21412x x -+=x -12∈(-1,1), 故直线AP 斜率的取值范围为(-1,1).(Ⅱ)由(Ⅰ)知P (x ,x 2),-12<x <32,故PA =(-1设直线AP 的斜率为k ,故1(PQ +=又2(1,)PA k k k =---- ,32(1)k PA PQ PA PQ k +==3(1)(1)PA PQ k k =+-,令2(1)(24)2(x x x =+-=-时,()0f x '<,PA PQ 的最大值为。
2017年高等职业院校单独招生考试数学考试大纲(可编辑修改word版)

2017 年高等职业院校单独招生考试数学考试大纲数学学科(高中类)一、考试目标与要求1.知识要求知识是指《普通高中数学课程标准(实验)》(以下简称《课程标准》)中所规定的必修课程、选修课程系列 2 中的数学概念、性质、法则、公式、公理、定理以及由其反映的数学思想,还包括按照一定程序与步骤进行运算,处理数据、绘制图表等基本技能。
对知识的要求依次是了解、理解、掌握三个层次。
(1)了解:要求对所列知识的含义有初步的、感性的认识,知道这一知识内容是什么,按照一定的程序和步骤照样模仿,并能(或会)在有关的问题中识别和认识它。
(2)理解:要求对所列知识内容有较深刻的理性认识,知道知识间的逻辑关系,能够对所列知识作正确的描述说明,用数学语言表达,利用所学的知识内容对有关问题作比较、判别、讨论,具备利用所学知识解决简单问题的能力。
(3)掌握:要求对所列的知识内容能够推导证明,利用所学知识对问题能够进行分析、研究、讨论,并且加以解决。
2.能力要求能力是指空间想象能力、抽象概括能力、推理论证能力、运算求解能力以及应用意识。
(1)空间想象能力是对空间形式的观察、分析、抽象的能力。
主要表现为识图、画图和对图形的想象能力。
(2)抽象概括能力是从具体的、生动的实例,在抽象概括的过程中,发现研究对象的本质;从给定的大量信息材料中,概括出一些结论,并能应用于解决问题或作出新的判断。
(3)推理论证能力是根据已知的事实和已获得的正确数学命题来论证某一数学命题真实性初步的推理能力。
(4)运算求解能力:会根据法则、公式进行正确运算、变形和数据处理,能根据问题的条件,寻找与设计合理、简捷的运算途径;能根据要求对数据进行估计和近似计算。
(5)应用意识:能综合应用所学数学知识、思想和方法解决在相关学科、生产、生活中简单的数学问题,能依据现实的生活背景,提炼相关的数量关系,将现实问题转化为数学问题,构造数学模型,并加以解决。
二、考试内容与要求包括《课程标准》的必修内容和选修系列 2 的基本内容。
体育单招数学圆锥曲线专题复习(含答案)
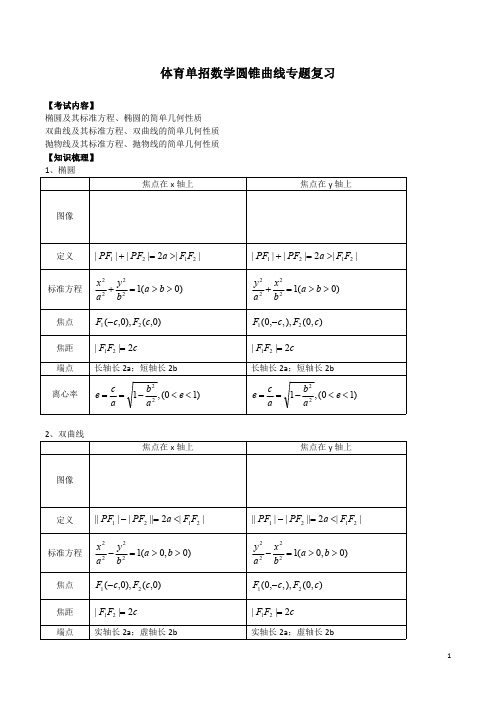
体育单招数学圆锥曲线专题复习【考试内容】椭圆及其标准方程、椭圆的简单几何性质双曲线及其标准方程、双曲线的简单几何性质抛物线及其标准方程、抛物线的简单几何性质【知识梳理】1、椭圆焦点在x 轴上焦点在y 轴上图像定义||2||||2121F F a PF PF >=+||2||||2121F F a PF PF >=+标准方程)0(12222>>=+b a b y a x )0(12222>>=+b a b x a y 焦点)0,(),0,(21c F c F -),0(),,,0(21c F c F -焦距cF F 2||21=cF F 2||21=端点长轴长2a ;短轴长2b长轴长2a ;短轴长2b离心率)10(,122<<-==e a b a c e )10(,122<<-==e ab ac e 2、双曲线焦点在x 轴上焦点在y 轴上图像定义||2||||||2121F F a PF PF <=-||2||||||2121F F a PF PF <=-标准方程)0,0(12222>>=-b a b y a x )0,0(12222>>=-b a b x a y 焦点)0,(),0,(21c F c F -),0(),,,0(21c F c F -焦距cF F 2||21=cF F 2||21=端点实轴长2a ;虚轴长2b实轴长2a ;虚轴长2b离心率)1(,122>+==e a b a c e )1(,122>+==e a b a c e 渐近线x aby ±=x bay ±=3、抛物线焦点在x 轴正半轴焦点在x 轴负半轴焦点在y 轴正半轴焦点在y 轴负半轴图像定义动点到定点的距离等于动点到定直线的距离的点的轨迹标准方程px y 22=px y 22-=py x 22=py x 22-=焦点)0,2(p F )0,2(p F -)2,0(p F )2,0(p F -准线2p x -=2p x =2p y -=2p y =离心率1=e 【题型讲解】题型一、椭圆的定义1.P 是椭圆x 2+4y 2=16上一点,且|PF 1|=7,则|PF 2|=()A .1B .3C .5D .92.已知M 是椭圆C :=1上的一点,则点M 到两焦点的距离之和是()A .6B .9C .14D .103.椭圆+=1上一点P 到它的一个焦点的距离等于3,那么点P 到另一个焦点的距离等于.题型二、椭圆的标准方程4.以(﹣3,0)和(3,0)为焦点,长轴长为8的椭圆方程为()A .B .C .D .5.已知以原点为中心的椭圆C 的左焦点为F (﹣1,0),离心率等于,则C 的方程是()A .B .C .D .6.焦点坐标为(0,﹣4),(0,4),且长半轴长为6的椭圆方程为()A.=1B.=1C.=1D.=1 7.焦点为(﹣2,0),(2,0),离心率为的椭圆的标准方程为()A.=1B.=1C.=1D.=1题型三、椭圆的焦点8.若椭圆+=1的一个焦点为(0,﹣1),则m的值为()A.4B.3C.2D.19.椭圆=1的焦点坐标为()A.(0,﹣4),(0,4)B.(0,),(0,﹣)C.(4,0),(﹣4,0)D.(,0),(﹣,0)10.已知椭圆C:4x2+3y2=12,其焦点坐标为()A.(±1,0)B.(0,±1)C.D.题型四、椭圆的端点11.椭圆的长轴长为()A.16B.8C.D.12.已知椭圆C:=1(a>2)的焦距为2,则C的长轴长为()A.3B.6C.2D.413.已知椭圆的一个焦点为(1,0),则C的短轴的长为()A.B.2C.D.4题型五、椭圆的离心率14.椭圆的离心率为()A.B.C.D.15.直线x﹣2y+2=0经过椭圆的一个焦点和一个顶点,则该椭圆的离心率为()A.B.C.D.16.若椭圆C:(a>b>0)满足2b=a+c,则该椭圆的离心率e=()A.B.C.D.17.已知椭圆的离心率为,则()A.a=2b2B.a=2b C.3a2=4b2D.3a=4b18.已知椭圆C:的一个焦点为(0,2),则C的离心率为()A.B.C.D.题型六、双曲线的定义19.已知点F1(﹣3,0)和F2(3,0),动点P到F1、F2的距离之差为4,则点P的轨迹方程为()A.B.C.D.20.如果方程表示双曲线,则m的取值范围是()A.(2,+∞)B.(﹣2,﹣1)C.(﹣∞,﹣1)D.(1,2)题型七、双曲线的标准方程21.焦距是10,虚轴长是8,经过点(,4)的双曲线的标准方程是()A.B.C.D.22.已知双曲线的中心在原点,焦点在x轴上,焦距为8,离心率为2,则该双曲线的方程为()A.B.C.D.23.已知双曲线的实轴长为2,焦点为(﹣4,0),(4,0),则该双曲线的标准方程为()A.B.C.D.题型八、双曲线的焦点24.双曲线8x2﹣y2=8的焦点坐标是()A.(±3,0)B.(0,±3)C.D.25.双曲线的焦点坐标为()A.B.(±5,0)C.D.(0,±5)题型九、双曲线的离心率26.已知双曲线C:,则C的离心率为()A.B.C.2D.327.已知双曲线的离心率为,则m=()A.2B.4C.8D.12题型十、双曲线的渐近线28.在平面直角坐标系xOy中,双曲线=1的渐近线方程为()A.y=±x B.y=±x C.y=±x D.y=±x29.双曲线﹣y2=﹣4的渐近线方程为()A.y=±2x B.C.y=±4x D.30.双曲线的焦点到C的渐近线的距离为()A.B.C.5D.题型十一、抛物线的标准方程31.已知抛物线的焦点坐标为(﹣,0),则抛物线的方程为()A.x=﹣8y2B.y=﹣8x2C.x=﹣16y2D.y=﹣16x2 32.若抛物线的准线方程为y=2,则该抛物线的标准方程是.题型十二、抛物线的焦点33.抛物线y=ax2(其中a>0)的焦点坐标是()A.B.C.D.34.抛物线x=﹣y2的焦点坐标是()A.(2,0)B.(﹣2,0)C.(0,2)D.(0,﹣2)题型十三、抛物线的准线35.抛物线y2=2x的准线方程是()A.B.C.D.36.抛物线x2=12y的准线方程为()A.y=﹣3B.x=﹣3C.y=﹣6D.x=﹣6 37.抛物线x=4y2的准线方程是()A.B.y=﹣1C.x=﹣D.x=题型十四、解答题38.若椭圆=1(a>b>0)的焦距为2,离心率为.斜率为1的直线经过椭圆的左焦点,交椭圆于A,B两点.(1)求椭圆的标准方程;(2)求|AB|的值.39.已知双曲线的焦点为F1(﹣4,0),F2(4,0),且该双曲线过点P(6,2).(1)求双曲线的标准方程;(2)若双曲线上的点M满足MF1⊥F1F2,求△MF1F2的面积.40.已知抛物线C:y2=2px(p>0)的焦点为F,点A(4,m)在抛物线C.上,且△OAF的面积为(O为坐标原点).(1)求抛物线C的方程;(2)直线l:y=kx+1与抛物线C交于M,N两点,若OM⊥ON,求直线l的方程.【真题再现】1、(2015年)双曲线116922=-y x 的一条渐近线的斜率为3,则它的离心率是()A 、332B 、3C 、2D 、42、(2016年)抛物线px y 22=过点(1,2),则该抛物线的准线方程为()A 、1-=x B 、1=x C 、1-=y D 、1=y 3、(2016年)在一个给定平面内,A ,C 为定点,B 为动点,且|BC |,|AC |,|AB |成等差数列,则点B 的轨迹是()A 、圆B 、椭圆C 、双曲线D 、抛物线4、(2017年)已知抛物线C :y x 42=的焦点为F ,过F 作C 的对称轴的垂线,交C 于A ,B 两点,则|AB |=()A 、8B 、4C 、2D 、15、(2018年)以双曲线C :x 29-y 216=1的中心为顶点,C 的左焦点为焦点的抛物线的方程为()A 、y 2=20xB 、y 2=10xC 、y 2=-10xD 、y 2=-20x6、(2020年)若一个椭圆的两个焦点三等分它的长轴,则该椭圆的离心率为()A 、61B 、31C 、21D 、327、(2020年)双曲线)0,0(12222>>=-b a by a x 的两条渐近线的倾斜角分别为βα,,则=+2cos βα()A 、1B 、23C 、21D 、08、(2017年)直线m x y +=与椭圆1222=+y x 有两个不同的交点,则m 的取值范围是___________9、(2018年)若抛物线px y 22=的准线方程为3-=x ,则P =__________10、(2021年)若椭圆C 的焦点为F 1(-1,0)和F 2(1,0),过F 1的直线交C 于A ,B 两点,且∆ABF 2的周长为12,则C 的方程为______________11、(2021年)双曲线1422=-y x 的离心率是____________12、(2016年)设双曲线1222=-y a x 与椭圆1162522=+y x 有相同的焦点,则该双曲线的渐近线方程是________13、(2015年)若椭圆的焦点为(-3,0),(3,0),离心率为53,则该椭圆的标准方程为___________14、(2015年)已知抛物线C :y x 42=,直线0:=-+m y x l ,(1)证明:C 与l 有两个交点的充分必要条件是1->m ,(2)设1<m ,C 与l 有两个交点A ,B ,线段AB 的垂直平分线交y 轴于点G ,求∆GAB 的面积的取值范围。
2017年高考数学理试题分类汇编:圆锥曲线

2017年高考数学理试题分类汇编:圆锥曲线2017 年高考试题分类汇编之圆锥曲线(理数) 解析一、选择题 .................................................... 2 二、填空题 .................................................... 5 三、大题 .. (8)一、选择题【浙江卷】2.椭圆22194x y +=的离心率是A .133B .53 C .23 D .59【解析】94533e -== B.【全国1卷(理)】10.已知F 为抛物线C :y 2=4x 的焦点,过F 作两条互相垂直的直线l 1,l 2,直线l 1与C 交于A 、B 两点,直线l 2与C 交于D 、E 两点,则|AB |+|DE |的最小值为( ) A .16 B .14 C .12 D .10 【解析】设AB 倾斜角为θ.作1AK 垂直准线,2AK 垂直x 轴 易知11cos 22AF GF AK AK AF P P GP Pθ⎧⎪⋅+=⎪⎪=⎨⎪⎛⎫⎪=--= ⎪⎪⎝⎭⎩(几何关系)(抛物线特性)【全国III 卷(理)】5.已知双曲线C:22221x y a b -= (a>0,b >0)的一条渐近线方程为5y x =,且与椭圆221123x y += 有公共焦点,则C 的方程为( ) A.221810x y -= B.22145x y -= C.22154x y -= D.22143x y -=【解析】∵双曲线的一条渐近线方程为5y =,则5b a =①又∵椭圆221123x y +=与双曲线有公共焦点,易知3c =,则2229a b c +==②由①②解得2,5a b ==,则双曲线C 的方程为22145x y -=,故选B.【全国III 卷(理)】10.已知椭圆C :22221x y a b+=,(a >b >0)的左、右顶点分别为A 1,A 2,且以线段A 1A 2为直径的圆与直线20bx ay ab -+=相切,则C 的离心率为( )A.63B.33C.23 D.13【解析】∵以12A A 为直径为圆与直线20bx ay ab -+=相切,∴圆心到直线距离d 等于半径,∴222ab d a a b ==+又∵0,0a b >>,则上式可化简为223a b =∵222b ac =-,可得()2223a a c =-,即2223c a =∴6c e a == A【天津卷】(5)已知双曲线22221(0,0)x y a b a b-=>>的左焦点为F ,离心率为2.若经过F 和(0,4)P 两点的直线平行于双曲线的一条渐近线,则双曲线的方程为( ) A.22144x y -= B.22188x y -=C.22148x y -=D.22184x y -=【解析】由题意得224,14,22188x y a b c a b c ==-⇒===⇒-=- ,故选B.二、填空题【全国1卷(理)】15.已知双曲线C :22221xy ab-=(a >0,b >0)的右顶点为A ,以A 为圆心,b 为半径做圆A ,圆A 与双曲线C 的一条渐近线交于M 、N 两点.若∠MAN =60°,则C 的离心率为________. 【解析】如图,OA a=,AN AM b == ∵60MAN ∠=︒,∴3AP =,222234OP OA PA a b --∴2232tan 34AP OP a b θ==-又∵tan ba θ=223234b a a b =-,解得223ab =∴22123113b e a ++【全国2卷(理)】16.已知F 是抛物线C:28yx=的焦点,M 是C 上一点,FM 的延长线交y 轴于点N .若M为FN 的中点,则FN = .【解析】28y x =则4p =,焦点为()20F ,,准线:2l x =-, 如图,M 为F 、N 中点,故易知线段BM 为梯形AFMC 中位线, ∵2CN =,4AF =, ∴3ME =又由定义ME MF =, 且MN NF =,∴6NF NM MF =+=lFN M C B AOyx【北京卷】(9)若双曲线221y x m-=3则实数m =_______________. 【解析】.1321mm +=⇒=【江苏卷】8.在平面直角坐标系xOy 中,双曲线2213x y -= 的右准线与它的两条渐近线分别交于点P ,Q ,其焦点是F 1 , F 2 ,则四边形F 1 P F 2 Q 的面积是 .【解析】右准线方程为33101010x ==,渐近线为33y x =±,则31030(,)1010P ,31030(,)1010Q -,1(10,0)F -,2(10,0)F ,则302102310S =⨯=.【山东卷】14.在平面直角坐标系xOy 中,双曲线()222210,0x y a b a b-=>>的右支与焦点为F 的抛物线()220x px p =>交于,A B 两点,若4AF BF OF +=,则该双曲线的渐近线方程为 .三、大题【全国I 卷(理)】20.(12分)已知椭圆C :2222=1x y a b +(a >b >0),四点P 1(1,1),P 2(0,1),P 3(–1,3),P 4(13C 上. (1)求C 的方程;(2)设直线l 不经过P 2点且与C 相交于A ,B 两点.若直线P 2A 与直线P 2B 的斜率的和为–1,证明:l 过定点.20.解:(1)根据椭圆对称性,必过3P 、4P又4P 横坐标为1,椭圆必不过1P ,所以过234P P P ,,三点将()233011P P ⎛- ⎝⎭,,,代入椭圆方程得222113141b ab ⎧=⎪⎪⎨⎪+=⎪⎩,解得24a=,21b =∴椭圆C 的方程为:2214x y+=.(2)①当斜率不存在时,设()():AAl x m A m y B m y =-,,,, 221121A A P A P B y y k k m m m----+=+==-得2m =,此时l 过椭圆右顶点,不存在两个交点,故不满足.②当斜率存在时,设()1l y kx b b =+≠∶()()1122A x y B x y ,,,联立22440y kx bx y =+⎧⎨+-=⎩,整理得()222148440k x kbx b +++-=122814kbx x k -+=+,21224414b x x k -⋅=+则22121211P A P B y y kk x x --+=+()()21212112x kx b x x kx b x x x +-++-=222228888144414kb k kb kbk b k --++=-+()()()811411k b b b -==-+-,又1b ≠21b k ⇒=--,此时64k∆=-,存在k 使得0∆>成立.∴直线l 的方程为21y kx k =-- 当2x =时,1y =- 所以l 过定点()21-,.【全国II 卷(理)】20. (12分)设O 为坐标原点,动点M 在椭圆C :2212x y +=上,过M 做x 轴的垂线,垂足为N ,点P 满足2NP NM=.(1)求点P 的轨迹方程;(2)设点Q 在直线x =-3上,且1OP PQ ⋅=.证明:过点P 且垂直于OQ 的直线l 过C 的左焦 点F ..解:⑴设()P x y ,,易知(0)N x ,(0)NP y =,又1022NM ⎛== ⎝, ∴2M x y ⎛⎫ ⎪⎝⎭,,又M 在椭圆上.∴22122x +=,即222xy +=.⑵设点(3)QQ y -,,()PPP x y ,,(0)Qy ≠,由已知:()(3)1PPPQPOP PQ x y y y y ⋅=⋅---=,,,()21OP OQ OP OP OQ OP ⋅-=⋅-=,∴213OP OQ OP ⋅=+=,∴33PQ P Q P P Q xx y y x y y ⋅+=-+=.设直线OQ :3Qyy x =⋅-, 因为直线l 与OQl 垂直.∴3lQk y =故直线l 方程为3()PPQy x x y y =-+,令0y =,得3()PQP y yx x -=-,13P Q P y y x x -⋅=-, ∴13PQ Px yy x =-⋅+,∵33PQPy yx =+,∴1(33)13PPx x x=-++=-,若0Qy=,则33Px-=,1Px=-,1Py=±,直线OQ 方程为0y =,直线l 方程为1x =-,直线l 过点(10)-,,为椭圆C 的左焦点.【全国III 卷(理)】20.(12分)已知抛物线C :y 2=2x ,过点(2,0)的直线l 交C 与A ,B 两点,圆M 是以线段AB 为直径的圆. (1)证明:坐标原点O 在圆M 上;(2)设圆M 过点P (4,-2),求直线l 与圆M 的方程.解:(1)显然,当直线斜率为0时,直线与抛物线交于一点,不符合题意.设:2l x my =+,11(,)A x y ,22(,)B x y ,联立:222y xx my ⎧=⎨=+⎩得2240y my --=, 2416m ∆=+恒大于0,122y y m +=,124y y =-. 1212OA OB x x y y ⋅=+12(2)(2)my my =++21212(1)2()4m y y m y y =++++ 24(1)2(2)4m m m =-+++0= ∴OA OB ⊥,即O 在圆M 上. (2)若圆M 过点P ,则0AP BP ⋅= 1212(4)(4)(2)(2)0x x y y --+++= 1212(2)(2)(2)(2)0my my y y --+++= 21212(1)(22)()80m y y m y y +--++=化简得2210m m --=解得12m =-或1①当12m =-时,:240l x y +-=圆心为00(,)Q x y , 120122y y y +==-,001924x y =-+=, 半径2291||42r OQ ⎛⎫⎛⎫==+- ⎪ ⎪⎝⎭⎝⎭则圆229185:()()4216M x y -++=②当1m =时,:20l x y --=圆心为0(,)Q x y , 12012y y y +==,0023x y =+=, 半径22||31r OQ ==+则圆22:(3)(1)10M x y -+-= 【北京卷】(18)(14分)已知抛物线C :y 2=2px过点P (1,1).过点(0,12)作直线l 与抛物线C 交于不同的两点M ,N ,过点M 作x 轴的垂线分别与直线OP 、ON 交于点A ,B ,其中O 为原点.(Ⅰ)求抛物线C 的方程,并求其焦点坐标和准线方程;(Ⅱ)求证:A 为线段BM 的中点.(18)解:(Ⅰ)把P (1,1)代入y 2=2Px 得P =12∴C :y 2=x ,∴焦点坐标(14,0),准线:x =-14. (Ⅱ)设l :y =kx +12,A (x 1,y 1),B (x 2,y 2),OP :y =x ,ON :y =22yx x, 由题知A (x 1,x 1),B (x 1,122x y x )212y kx y x⎧>+⎪⎨⎪=⎩⇒k 2x 2+(k -1)x +14=0,x 1+x 2=21kk-,x 1·x 2=214k. 1112121112221122,22x kx x y x x y kx kx x x x ⎛⎫+ ⎪+⎝⎭+=++=+由x 1+x 2=21k k -,x 1x 2=214k, 上式()2111121122122124kk kx kx k x x x k x -=+=+-⋅=∴A 为线段BM 中点.【江苏卷】17.(14分)如图,在平面直角坐标系xOy 中,椭圆1(0)2222x y E :+a b a b=>>的左、右焦点分别为F 1,F 2,离心率为12,两准线之间的距离为8.点P 在椭圆E 上,且位于第一象限,过点F 1作直线PF 1的垂线l 1,过点F 2作直线PF 2的垂线l 2.(1)求椭圆E 的标准方程;(2)若直线l 1,l 2的交点Q 在椭圆E 上,求点P 的坐标.17.解:(1)∵椭圆E 的离心率为12,∴12c a =①.∵两准线之间的距离为8,∴228a c=②.联立①②得2,1a c ==,∴3b =,故椭圆E 的标准方程为22143x y +=.(2)设0(,)P x y ,则000,0xy >>,由题意得00001(1)1(1)x y x y x y x y +⎧=-+⎪⎪⎨-⎪=--⎪⎩,整理得02001x x x y y=-⎧⎪-⎨=⎪⎩,∵点00(,)P x y 在椭圆E 上,∴2200143x y +=,∴2220020(1)33y x y -=,∴2200169,77xy ==,故点P 的坐标是4737(,)77.【江苏卷】B.[选修4-2:矩阵与变换](本小题满分10分)已知矩阵A = ,B =.(1) 求AB ;(2)若曲线C1;22y =182x + 在矩阵AB 对应的变换作用下得到另一曲线C 2 ,求C 2的方程. B.解:(1)AB ==.(2)设11(,)P x y 是曲线1C 上任意一点,变换后对应的点为1`0210x x y y ⎡⎤⎢⎥⎣⎡⎤⎡⎦⎤=⎢⎥⎢⎥⎣⎦⎣⎦,所以112x y y x =⎧⎨=⎩,即1112x y y x =⎧⎪⎨=⎪⎩,因为11(,)P x y 在曲线1C 上,所以228xy +=即曲线C 2的方程.【山东卷】(21)(本小题满分13分)在平面直角坐标系xOy 中,椭圆E :22221x y a b +=()0a b >>的离心率为2,焦距为2. (Ⅰ)求椭圆E 的方程;(Ⅱ)如图,动直线l :13y k x =-交椭圆E 于,A B 两点,C是椭圆E 上一点,直线OC 的斜率为2k ,且122k k=,M是线段OC 延长线上一点,且:2:3MC AB =,M的半径为MC ,,OS OT 是M的两条切线,切点分别为,S T .求SOT ∠的最大值,并求取得最大值时直线l 的斜率.(21)解:(I )由题意知 22c e a ==,22c =,所以2,1a b ==,因此 椭圆E 的方程为2212x y +=.(Ⅱ)设()()1122,,,A x y B x y , 联立方程2211,23,2x y y k x ⎧+=⎪⎪⎨⎪=-⎪⎩得()2211424310kx k x +--=,由题意知0∆>, 且()112122211231,21221k x xx x k k +==-++,所以22112112211181221k k AB kx x k ++=+-=+.由题意知1224k k =,所以2124kk =由此直线OC 的方程为124y x k =.联立方程2211,22,4x y y x k ⎧+=⎪⎪⎨⎪=⎪⎩得2221221181,1414k x y k k ==++,因此2221211814k OC x y k +=+=+.由题意可知1sin21SOT rOC r OCr∠==++,而2121221121181411822321k OC k rk k k ++=+++21221112324141k k k +=++,令2112t k =+,则()11,0,1t t >∈, 因此2223313112221121119224OC t r t t t t t ===≥+-⎛⎫+---+ ⎪⎝⎭,当且仅当112t =,即2t =时等号成立,此时122k =±, 所以1sin22SOT ∠≤,因此26SOT ∠π≤, 所以SOT ∠最大值为3π. 综上所述:SOT ∠的最大值为3π,取得最大值时直线l的斜率为122k =±.【天津卷】(19)(本小题满分14分)设椭圆22221(0)x y a b a b +=>>的左焦点为F ,右顶点为A ,离心率为12.已知A 是抛物线22(0)ypx p =>的焦点,F 到抛物线的准线l 的距离为12. (I )求椭圆的方程和抛物线的方程;(II )设l 上两点P ,Q 关于x 轴对称,直线AP 与椭圆相交于点B (B 异于点A ),直线BQ 与x 轴相交于点D .若APD △6AP 的方程.(19)(Ⅰ)解:设F 的坐标为(,0)c -.依题意,12c a =,2p a =,12a c -=, 解得1a =,12c =,2p =, 于是22234ba c =-=.所以,椭圆的方程为22413y x +=,抛物线的方程为24y x=.所以,直线AP 的方程为3630x y +-=,或3630x y --=.【浙江卷】21.(本题满分15分)如图,已知抛物线2xy=,点A 11()24-,,39()24B ,,抛物线上的点11()()24P x y x -<<,.过点B 作直线AP 的垂线,垂足为Q .(Ⅰ)求直线AP 斜率的取值范围; (Ⅱ)求AP PQ ⋅的最大值.21.解:(Ⅰ)由题易得P (x ,x 2),-12<x <32,故k AP=21412x x -+=x -12∈(-1,1), 故直线AP 斜率的取值范围为(-1,1).(Ⅱ)由(Ⅰ)知P (x ,x 2),-12<x <32, 故PA =(-12-x ,14-x 2), 设直线AP 的斜率为k , 则AP :y =kx +12k +14,BP :y =13924x k k -++, 由112413924y kx k y x k k ⎧=++⎪⎪⎨⎪=-++⎪⎩222234981(,)2244k k k k Q k k +-++⇒++ 故23432221(,)11k k k k k k k PQ k k +----++=++ , 又2(1,)PA k kk =---- , 故323322(1)(1)(1)(1)(1)(1)11k k k k k PA PQ PA PQ k k k k +-+--==+=+-++, 即3(1)(1)PA PQ k k =+-,令3()(1)(1),11f x x x x =+--<<, 则22()(1)(24)2(1)(21)f x x x x x '=+-=-+-,当112x -<<时,()0f x '>,当112x <<时,()0f x '<, 故max 127()()216f x f ==,即PA PQ 的最大值为2716.。
-2017年体育单招历年数学试卷分类汇编-向量123,推荐文档

2005--2017 年体育单招数学分类汇编 --- 向量→→→ →1、(2017 年第 2 题)已知平面向量 a = (1,-1), b = (-1,2) ,则 2 a + b =。
2、(2016 年第 11 题)已知平面向量a = (5,-4), b = (-3, x ), c = (2,1) ,若2a + 3b 与c 垂直,则 x= .→→→→→ →2 → →3、(2015 年第 14 题)若向量 a , b 满足, | a |= 1, | b |= 2 ,a ⋅b = -。
4、(2013 年第 2 题)若平面上单位向量 a , b 的夹角为90︒ ,则 3a - 4b = .5、(2012 年第 2 题),则cos < a , b >=3若平面上向量 a = (1,2), b = (2,1) ,若(a + kb ) ⊥ b ,则 k = .6、(2011 年第 3 题)已知平面向量 a = (1,2), b = (-1, 3) ,则a 与b 的夹角为.7、(2010 年第 12 题) a , b 为平面向量,已知 a = 1, b = 2, a , b 夹角为120︒ ,则 2a + b = . 8、(2009 年第 5 题) 已知非零向量a ,b 满足 b = 4 a ,且2a + b 与a 垂直,则a 与b 的夹角为 .9、(2008 年第 4 题)已知平面向量 a = (1,1),b = (-1, 2) ,则(a + b )(a - b ) =.10、(2007 年第 11 题)已知向量 a = (5,-4), b = (-3,2) 则与2a + 3b 垂直的单位向量是。
(只需写出一个符合题意的答案)11、(2006 年第 7 题)设a 与 b 是平面向量,已知a =(6,-8), b =5 且a ⋅ b =50,则向量a - b =( ) (A )(-3,4)(B )(-4,3) (C )(3,-4) (D )(4,-3)12、(2005 年第 16 题)已知向量 a 与b 的夹角为30︒ , a = 3, b = 2 ,则 a + b =.“”“”At the end, Xiao Bian gives you a passage. Minand once said, "people who learn to learn are very happy people.". In every wonderful life, learning is an eternal theme. As a professional clerical and teaching position, I understand the importance of continuous learning, "life is diligent, nothing can be gained", only continuous learning can achieve better self. Only by constantly learning and mastering the latest relevant knowledge, can employees from all walks of life keep up with the pace of enterprise development and innovate to meet the needs of the market. This document is also edited by my studio professionals, there may be errors in the document, if there are errors, please correct, thank you!。
体育单招数学圆锥曲线答案

一、选择题(本大题共12小题,每小题5分,共60分)1.椭圆x 29+y 2k 2=1与双曲线x 2k -y 23=1有相同的焦点,则k 应满足的条件是( ) A .k >3B .2<k <3C .k =2D .0<k <2考点 双曲线性质的应用题点 双曲线与椭圆结合的有关问题答案 C解析 由9-k 2=k +3,即k 2+k -6=0,解得k =2或-3.又由题意知k 2<9且k >0,所以0<k <3,所以k =2.2.已知双曲线的离心率为2,焦点是(-4,0),(4,0),则双曲线的方程为( )A.x 24-y 212=1 B.x 212-y 24=1 C.x 210-y 26=1 D.x 26-y 210=1 考点 双曲线性质的应用题点 求双曲线的标准方程答案 A解析 依题意得c =4,e =c a =4a=2,a =2,b 2=c 2-a 2=12, 因此所求的双曲线的标准方程为x 24-y 212=1,故选A. 3.若双曲线的顶点为椭圆x 2+y 22=1长轴的端点,且双曲线的离心率与该椭圆的离心率的积为1,则双曲线的方程为( )A .x 2-y 2=1B .y 2-x 2=1C .x 2-y 2=2D .y 2-x 2=2考点 双曲线性质的应用题点 双曲线与椭圆结合的有关问题答案 D解析 椭圆x 2+y 22=1的离心率为22,则双曲线的离心率为2,且双曲线的顶点为(0,±2),故选D.4.设圆锥曲线C 的两个焦点分别为F 1,F 2,若曲线C 上存在点P 满足|PF 1|∶|F 1F 2|∶|PF 2|=4∶3∶2,则曲线C 的离心率等于( )A.12或32B.23或2C.12或2 D.23或32考点 圆锥曲线的综合问题题点 圆锥曲线的综合问题答案 A解析 设|PF 1|=4k ,|F 1F 2|=3k ,|PF 2|=2k .若曲线C 为椭圆,则2a =6k,2c =3k ,∴e =c a =2c 2a =12; 若曲线C 为双曲线,则2a =2k,2c =3k ,∴e =c a =2c 2a =32. 5.设双曲线x 2a 2-y 2b 2=1(a >0,b >0)的虚轴长为2,焦距为23,则双曲线的渐近线方程为( ) A .y =±22x B .y =±2x C .y =±12x D .y =±2x 考点 双曲线性质的应用题点 由双曲线的几何性质求方程答案 A解析 ∵2b =2,2c =23,∴b =1,c =3,则a =c 2-b 2=2,∴b a =22. 故双曲线的渐近线方程为y =±b a x =±22x . 6.M 是抛物线y 2=2px (p >0)上一点,F 为抛物线的焦点,以Fx 为始边,FM 为终边的角为α,且α=60°,若|FM |=4,则p 等于( )A .1B .2C .3D .4考点 抛物线的焦点弦问题题点 与焦点弦有关的其他问题答案 B解析 不妨设M 在第一象限,过点M 作MN ⊥x 轴,垂足为N ,计算可得|MN |=23,|FN |=2,所以M 的坐标为⎝⎛⎭⎫p 2+2,23,代入y 2=2px (p >0),得p =2或p =-6(舍).7.等轴双曲线C 的中心在原点,焦点在x 轴上,C 与抛物线y 2=16x 的准线交于A ,B 两点,|AB |=43,则C 的实轴长为( )A. 2 B .2 2 C .4 D .8考点 抛物线的几何性质题点 抛物线与其他曲线结合有关问题 答案 C解析 设双曲线的方程为x 2a 2-y 2a2=1(a >0), 抛物线的准线为x =-4,且|AB |=43,故可得A (-4,23),B (-4,-23),将点A 坐标代入双曲线方程,得a 2=4,故a =2,故实轴长为4.8.已知点A (0,2),B (2,0).若点C 在抛物线x 2=y 的图象上,则使得△ABC 的面积为2的点C 的个数为( )A .4B .3C .2D .1考点 直线与抛物线的位置关系题点 判断交点个数问题答案 A解析 由已知可得|AB |=22,要使S △ABC =2,则点C 到直线AB 的距离必须为2,设C (x ,x 2),而l AB :x +y -2=0, 所以有|x +x 2-2|2=2, 所以x 2+x -2=±2,当x 2+x -2=2时,有两个不同的C 点;当x 2+x -2=-2时,亦有两个不同的C 点.因此满足条件的C 点有4个,故选A.9.已知双曲线y 22-x 23=1的两个焦点分别为F 1,F 2,则满足△PF 1F 2的周长为6+25的动点P 的轨迹方程为( )A.x 24+y 29=1 B.x 24+y 29=1(x ≠0) C.x 29+y 24=1 D.x 29+y 24=1(x ≠0) 考点 双曲线性质的应用题点 双曲线与椭圆结合的有关问题答案 B解析 ∵双曲线的方程为y 22-x 23=1, ∴a 2=2,b 2=3,可得c 2=a 2+b 2=5,因此双曲线y 22-x 23=1的两个焦点分别为F 1(0,-5),F 2(0,5). ∵△PF 1F 2的周长为6+25,|F 1F 2|=25,∴|PF 1|+|PF 2|=6>25,∴点P 的轨迹是以F 1,F 2为焦点的椭圆(上、下顶点除外).由椭圆的定义,得椭圆长轴长为6,长半轴长为3,∴该椭圆的短半轴长为2,∴点P 的轨迹方程为x 24+y 29=1(x ≠0). 10.我们把焦点相同,且离心率互为倒数的椭圆和双曲线称为一对“相关曲线”.已知F 1,F 2是一对相关曲线的焦点,P 是它们在第一象限的交点,当∠F 1PF 2=60°时,这一对相关曲线中双曲线的离心率是( )A .2 B. 2 C.233D. 3 考点 双曲线性质的应用题点 双曲线与椭圆结合的有关问题答案 D解析 设|F 1P |=m ,|F 2P |=n ,|F 1F 2|=2c ,由余弦定理,得(2c )2=m 2+n 2-2mn cos 60°,即4c 2=m 2+n 2-mn ,设a 1是椭圆的长半轴,a 2是双曲线的实半轴,由椭圆、双曲线定义,得m +n =2a 1,m -n =2a 2,∴m =a 1+a 2,n =a 1-a 2,将它们及离心率互为倒数关系代入前式得3a 22-4c 2+a 21=0,a 1=3a 2,e 1e 2=c a 1·c a 2=⎝⎛⎭⎫c a 223=1, 解得,e 2=3,故选D.11.探照灯反射镜的轴截面是抛物线的一部分,光源位于抛物线的焦点处,已知灯口的直径为60 cm ,灯深40 cm ,则抛物线的标准方程可能是( )A .y 2=254x B .y 2=454x C .x 2=-452y D .x 2=-454y 考点 抛物线的标准方程题点 求抛物线方程答案 C解析 如果设抛物线的方程为y 2=2px (p >0),则抛物线过点(40,30),从而有302=2p ×40,即2p =452, 所以所求抛物线方程为y 2=452x . 虽然选项中没有y 2=452x ,但C 中的2p =452符合题意. 12.已知抛物线y 2=x ,点A ,B 在该抛物线上且位于x 轴的两侧,OA →·OB →=2(其中O 为坐标原点),则△ABO 与△AFO 的面积之和的最小值是( )A .2B .3 C.1728D.10 考点 直线与抛物线的位置关系题点 直线与抛物线相交时的其他问题答案 B解析 如图,可设A (m 2,m ),B (n 2,n ),其中m >0,n <0,则OA →=(m 2,m ),OB →=(n 2,n ),OA →·OB →=m 2n 2+mn =2,解得mn =1(舍)或mn =-2.∴l AB :(m 2-n 2)(y -n )=(m -n )·(x -n 2),即(m +n )(y -n )=x -n 2,令y =0,解得x =-mn =2,∴C (2,0),点C 为直线AB 与x 轴的交点.S △AOB =S △AOC +S △BOC =12×2×m +12×2×(-n )=m -n ,S △AOF =12×14×m =18m ,则S △AOB +S △AOF =m -n +18m =98m -n =98m +2m ≥298m ·2m =3,当且仅当98m =2m ,即m =43时等号成立.故△ABO 与△AFO 的面积之和的最小值为3.二、填空题(本大题共4小题,每小题5分,共20分)13.已知双曲线中心在原点,一个顶点的坐标是(3,0),且焦距与虚轴长之比为5∶4,则双曲线的标准方程为________________.考点 双曲线的标准方程的求法题点 待定系数法求双曲线的标准方程答案 x 29-y 216=1 解析 由题意得双曲线的焦点在x 轴上,且a =3,焦距与虚轴长之比为5∶4,即c ∶b =5∶4, 又c 2=a 2+b 2,所以c =5,b =4,所以双曲线的标准方程为x 29-y 216=1. 14.若椭圆x 2a 2+y 2b2=1过抛物线y 2=8x 的焦点,且与双曲线x 2-y 2=1有相同的焦点,则该椭圆的方程为________________.考点 双曲线性质的应用题点 双曲线与椭圆结合的有关问题答案 x 24+y 22=1 解析 抛物线y 2=8x 的焦点坐标为(2,0),双曲线x 2-y 2=1的焦点坐标为(±2,0)由题意得⎩⎪⎨⎪⎧a 2-b 2=2,4a 2=1,∴a 2=4,b 2=2,∴椭圆的方程为x 24+y 22=1. 15.直线x -2y +3=0与椭圆x 2a 2+y 2b 2=1(a >b >0)相交于A ,B 两点,且P (-1,1)恰好为AB 中点,则椭圆的离心率为________.考点 直线与椭圆的位置关系题点 直线与椭圆相交时弦中点问题答案 22 解析 由⎩⎪⎨⎪⎧x -2y +3=0,b 2x 2+a 2y 2=a 2b 2,消去x , 得(4b 2+a 2)y 2-12b 2y +9b 2-a 2b 2=0,Δ=144b 4-4(a 2+4b 2)(9b 2-a 2b 2)>0,即a 2+4b 2>9.设A (x 1,y 1),B (x 2,y 2),则y 1+y 2=12b 2a 2+4b 2, ∵线段AB 的中点为(-1,1),∴12b 2a 2+4b2=2,得a 2=2b 2. 又a 2=b 2+c 2,∴a 2=2c 2,∴e =c a =22. 16.过抛物线C :y 2=4x 的焦点F 作直线l 交抛物线C 于点A ,B ,若|AF |=3|BF |,则l 的斜率是________.考点 直线与抛物线的位置关系题点 直线与抛物线的综合问题答案 ±3解析 ∵抛物线C 的方程为y 2=4x ,∴它的焦点为F (1,0),由题意知,直线l 的斜率存在,∴设直线l 的方程为y =k (x -1),由⎩⎪⎨⎪⎧y =k (x -1),y 2=4x ,消去x 得k 4y 2-y -k =0. 设A (x 1,y 1),B (x 2,y 2),可得y 1+y 2=4k,① y 1y 2=-4,②∵|AF |=3|BF |,∴y 1+3y 2=0,可得y 1=-3y 2,代入①,②得-2y 2=4k,且-3y 22=-4, 消去y 2,得k 2=3,解得k =±3.三、解答题(本大题共6小题,共70分)17.(10分)已知一个椭圆中心在原点,焦点在同一坐标轴上,焦距为213.一双曲线和这个椭圆有公共焦点,且双曲线的实半轴长比椭圆的长半轴长小4,双曲线离心率与椭圆离心率之比为7∶3,求椭圆和双曲线的标准方程.考点 双曲线性质的应用题点 双曲线与椭圆结合的有关问题解 ①若焦点在x 轴上,设椭圆方程为x 2a 2+y 2b 2=1(a >b >0),c =13. 设双曲线方程为x 2m 2-y 2n 2=1,m =a -4. ∵e 双e 椭=73,易得a =7,m =3. ∴b 2=36,n 2=4.∴椭圆的标准方程为x 249+y 236=1,双曲线的标准方程为x 29-y 24=1. ②若焦点在y 轴上,同理可得椭圆的标准方程为x 236+y 249=1,双曲线的标准方程为y 29-x 24=1. 18.(12分)已知双曲线C 1:x 2-y 24=1. (1)求与双曲线C 1有相同焦点,且过点P (4,3)的双曲线C 2的标准方程;(2)直线l :y =x +m 分别与双曲线C 1的两条渐近线相交于A ,B 两点.当OA →·OB →=3时,求实数m 的值.考点 直线与双曲线的位置关系题点 直线与双曲线的位置关系解 (1)∵双曲线C 1:x 2-y 24=1, ∴焦点坐标为(5,0),(-5,0).设双曲线C 2的标准方程为x 2a 2-y 2b 2=1(a >0,b >0), ∵双曲线C 2与双曲线C 1有相同焦点,且过点P (4,3),∴⎩⎪⎨⎪⎧ a 2+b 2=5,16a 2-3b 2=1,解得⎩⎪⎨⎪⎧a =2,b =1, ∴双曲线C 2的标准方程为x 24-y 2=1. (2)双曲线C 1的两条渐近线分别为y =2x ,y =-2x .由⎩⎪⎨⎪⎧ y =2x ,y =x +m ,可得x =m ,y =2m ,∴A (m,2m ). 由⎩⎪⎨⎪⎧y =-2x ,y =x +m ,可得x =-13m ,y =23m , ∴B ⎝⎛⎭⎫-13m ,23m . ∴OA →·OB →=-13m 2+43m 2=m 2. ∵OA →·OB →=3,∴m 2=3,∴m =±3.19.(12分)已知点P (3,4)是椭圆x 2a 2+y 2b 2=1(a >b >0)上的一点,F 1,F 2为椭圆的两焦点,若PF 1⊥PF 2,试求:(1)椭圆的方程;(2)△PF 1F 2的面积.考点 椭圆的几何性质题点 求椭圆的标准方程解 (1)令F 1(-c,0),F 2(c,0),则b 2=a 2-c 2.因为PF 1⊥PF 2,所以kPF 1·kPF 2=-1,即43+c ·43-c=-1, 解得c =5,所以设椭圆方程为x 2a 2+y 2a 2-25=1. 因为点P (3,4)在椭圆上,所以9a 2+16a 2-25=1. 解得a 2=45或a 2=5.又因为a >c ,所以a 2=5舍去.故所求椭圆的方程为x 245+y 220=1. (2)由椭圆定义知|PF 1|+|PF 2|=65,①又|PF 1|2+|PF 2|2=|F 1F 2|2=100,②①2-②,得2|PF 1|·|PF 2|=80,所以12PF F S =12|PF 1|·|PF 2|=20. 20.(12分)已知抛物线y 2=4x 的焦点为F ,直线l 过点M (4,0).(1)若点F 到直线l 的距离为3,求直线l 的斜率;(2)设A ,B 为抛物线上两点,且AB 不与x 轴垂直,若线段AB 的垂直平分线恰过点M ,求证:线段AB 中点的横坐标为定值.考点 直线与抛物线的位置关系题点 直线与抛物线相交时的其他问题(1)解 由已知,x =4不合题意.设直线l 的方程为y =k (x -4),由已知,抛物线C 的焦点坐标为(1,0),因为点F 到直线l 的距离为3, 所以|3k |1+k 2=3,解得k =±22,所以直线l 的斜率为±22. (2)证明 设线段AB 中点的坐标为N (x 0,y 0),A (x 1,y 1),B (x 2,y 2), 因为AB 不垂直于x 轴,则直线MN 的斜率为y 0x 0-4,直线AB 的斜率为4-x 0y 0, 直线AB 的方程为y -y 0=4-x 0y 0(x -x 0), 联立方程⎩⎨⎧ y -y 0=4-x 0y 0(x -x 0),y 2=4x ,消去x ,得⎝⎛⎭⎫1-x 04y 2-y 0y +y 20+x 0(x 0-4)=0, 所以y 1+y 2=4y 04-x 0, 因为N 为AB 的中点,所以y 1+y 22=y 0,即2y 04-x 0=y 0, 所以x 0=2,即线段AB 中点的横坐标为定值2.21.(12分)已知椭圆M :x 2a 2+y 23=1(a >0)的一个焦点为F (-1,0),左、右顶点分别为A ,B ,经过点F 的直线l 与椭圆M 交于C ,D 两点.(1)求椭圆的方程;(2)记△ABD 与△ABC 的面积分别为S 1和S 2,求|S 1-S 2|的最大值. 考点 圆锥曲线的综合问题题点 圆锥曲线的综合问题解 (1)因为F (-1,0)为椭圆的焦点,所以c =1,又b =3,所以a =2,所以椭圆的方程为x 24+y 23=1. (2)当直线l 的斜率不存在时,直线方程为x =-1, 此时可令D ⎝⎛⎭⎫-1,32,C ⎝⎛⎭⎫-1,-32,所以△ABD ,△ABC 的面积相等,|S 1-S 2|=0.当直线l 的斜率存在时,设直线方程为y =k (x +1)(k ≠0),设C (x 1,y 1),D (x 2,y 2),和椭圆方程联立,消去y 得(3+4k 2)x 2+8k 2x +4k 2-12=0,因为焦点在椭圆内部,所以直线l 与椭圆恒有两个交点, 所以x 1+x 2=-8k 23+4k 2,x 1x 2=4k 2-123+4k 2,此时|S 1-S 2|=2||y 1|-|y 2||=2|y 1+y 2|=2|k (x 2+1)+k (x 1+1)|=2|k (x 2+x 1)+2k |=12|k |3+4k 2=123|k |+4|k |≤12212=3⎝⎛⎭⎫k =±32时等号成立,所以|S 1-S 2|的最大值为 3.22.(12分)如图,抛物线C 1:y 2=4x 的准线与x 轴交于点F 1,焦点为F 2.以F 1,F 2为焦点,离心率为12的椭圆记作C 2.(1)求椭圆的标准方程;(2)直线l 经过椭圆C 2的右焦点F 2,与抛物线C 1交于A 1,A 2两点,与椭圆C 2交于B 1,B 2两点,当以B 1B 2为直径的圆经过F 1时,求|A 1A 2|的长.考点 圆锥曲线的综合问题题点 圆锥曲线的综合问题解 (1)设椭圆的标准方程为x 2a 2+y 2b 2=1(a >b >0),依据题意得c =1,c a =12, 则a =2,b 2=a 2-c 2=3,故椭圆的标准方程为x 24+y 23=1. (2)当直线l 与x 轴垂直时,B 1⎝⎛⎭⎫1,-32,B 2⎝⎛⎭⎫1,32, 又F 1(-1,0),此时B 1F 1→·B 2F 1→≠0,所以以B 1B 2为直径的圆不经过F 1,不满足条件. 当直线l 不与x 轴垂直时,设l :y =k (x -1),由⎩⎪⎨⎪⎧ y =k (x -1),x 24+y 23=1,消去y ,得(3+4k 2)x 2-8k 2x +4k 2-12=0. 因为焦点在椭圆内部,所以直线l 与椭圆恒有两个交点. 设B 1(x 1,y 1),B 2(x 2,y 2),则x 1+x 2=8k 23+4k 2,x 1x 2=4k 2-123+4k 2. 因为以B 1B 2为直径的圆经过F 1,所以B 1F 1→·B 2F 1→=0,又F 1(-1,0),所以(-1-x 1)(-1-x 2)+y 1y 2=0,即(1+k 2)x 1x 2+(1-k 2)(x 1+x 2)+1+k 2=0,解得k 2=97. 由⎩⎪⎨⎪⎧y 2=4x ,y =k (x -1),得k 2x 2-(2k 2+4)x +k 2=0. 设A 1(x 3,y 3),A 2(x 4,y 4),则x 3+x 4=2k 2+4k 2=2+4k 2,所以|A1A2|=x3+x4+2=2+4k2+2=649.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2004--2017年体育单招数学分类汇编--圆锥曲线
1、(2017年第6题)已知抛物线的焦点为F ,过F 作C 的对称轴的垂线,与C 交于A 、B ,则y x C 4:2= (
)8 B. 4 C.2 D. 1=||AB 2、(2017
年第15题)直线与椭圆有两个不同的交点,则的取值范围为
m x y +=1222=+y x m 。
3、(2016年第2题)抛物线y 2=2px 过点(1,2),则该抛物线的准线方程为( )
A 、x=-1
B 、x=1
C 、y=-1
D 、y=1
4、(2016年第3题)在一个给定平面内,A ,C 为定点,B 为动点,且|BC|,|AC|,|AB|成等差数列,则点B 的轨迹是( ) A 、圆 B 、椭圆 C 、双曲线D 、抛物线
5、(2016年第16题)设双曲线与椭圆有相同的焦点,则该双曲线的1222=-y a x 116
2522=+y x 渐近线的方程是_______________.
6、(2015年第9题)双曲线的一条渐近线的斜率为,则此双曲线的离心率为 ( 12222=-b y a x 3)
A. B. C . 2 D. 4
33237、(2015年第12题)若椭圆的焦点为,,离心率为
,则该椭圆的标准方程为 )0,3(-)0,3(53。
8、(2015年第18题)已知抛物线C :,直线:。
y x 42=l 0=-+m y x (1)证明:C 与有两个交点的充分必要条件是;
l 1->m (2)设,C 与有两个交点A ,B ,线段AB 的垂直平分线交轴于点G ,求面积的取值范围。
1<m l y GAB ∆9、(2014年第8题)若双曲线的两条渐近线相互垂直,则双曲线的离心率为22221(0,0)x y a b a b -=>>
( )A B .2 C 10、(2014年第15题)抛物线的准线方程是 .24y x =11、(2014年第18题)
已知椭圆C 中心在原点,焦点在轴上,离心率为,且C 过点x 123(1,2
-
(1)求C 的方程;(2)如果直线与C 有两个交点,求的取值范围。
:2l y kx =-k 12、(2013年第15题)已知椭圆的焦点为、,过斜率为1的直线交椭圆于点、,则的面积为 22
132
x y +=1F 2F 1F A B 2F AB ∆13、(2013年第16题)
已知过点的直线与圆相交于、两点,则 .
(1,2)A -22(3)(2)1x y -++=M N AM AN =14、(2013年第18题)
设、分别为双曲线的左、右焦点,为双曲线右支上一点,且,1F 2F 22
1916
x y -=M 1260F MF ∠=︒(Ⅰ)求的面积;(Ⅱ)求点的坐标。
12MF F ∆M 15、(2012年第7题)
直线交圆于、两点,为圆心,若的面积是,则20(0)x y m m -+=>2220x x y -+=A B P PAB ∆25
( )A B . C D .m =1216、(2012年第16题)已知曲线的一个焦点与一条渐近线,过焦点作渐近线的垂线,垂足的坐标为22
221x y a b
-=F l F l P
,则焦点的坐标是 .4(,3F 17、(2012年第16题)
设是椭圆的右焦点,半圆在点的切线与椭圆交于、两点,F 2
212x y +=221(0)x y x +=≥Q A B (Ⅰ)证明:为常数;(Ⅱ)设切线的斜率为1,求的面积(是坐标原点)。
AF AQ +AB OAB ∆O 18、(2011年第12题)
已知椭圆的两个焦点为与,离心率,则椭圆的标准方程是 .1(1,0)F -2(1,0)F 13
e =19、(2011年第19题)
设是双曲线的右焦点,过点的直线交双曲线于、两点,是(,0)(0)F c c >2
2
12y x -=(,0)F c l P Q O 坐标原点,(Ⅰ)证明:为常数;1OP OQ =- A
(Ⅱ)若原点到直线的距离是,求的面积(是坐标原点)。
O l 32
OPQ ∆O 20、(2010年第8题)是椭圆上的一点,点和为椭圆的两个焦点,已知,P 2212516
x y +=1F 2F 17PF = 以为中心,为半径的圆交线段于,则( )
P 2PF 1PF Q A . B . C . D .1430F Q QP -= 1430F Q QP += 1440F Q QP -= 1340
F Q QP += 21、(2010年第14题)
若双曲线的两条渐近线分别为,,它的一个焦点为,则双曲线的方程是 20x y +=20x y -=(-22、(2010年第18题18分)
已知抛物线,为过的焦点且倾斜角为的直线,设与交于、两点,2:2(0)C y px p =>l C F αl C A B 与坐标原点连线交的准线于点。
(Ⅰ)证明:垂直轴;
A C D BD y (Ⅱ)分析分别取什么范围的值时,与的夹角为锐角、直角或钝角。
αOA OB 23、(2009年第13题)
已知双曲线上的一点到双曲线一个焦点的距离为3,则到另一个焦点的距离为 .22
1916
x y -=P P 24、(2009年第18题)
中心在原点,焦点在轴的椭圆的左、右焦点分别是和,斜率为1的直线过,且x C 1F 2F l 2F
到的距离等于。
(Ⅰ)求的方程;
1F l l (Ⅱ) 与交点、的中点为,已知到轴的距离等于,求的方程和离心率。
l C A B M M x 34
C 25、(2008年第15题)
双曲线的两个焦点是与,离心率,则双曲线的标准方程是 .
1(4,0)F -2(4,0)F 2e =26、(2008年第20题)
过点的直线与圆不相交,则直线的斜率的取值范围是 .(0,2)l 22230x y x +--=l k 27、(2008年第24题)
如图,与是过原点的面积的任意两条互相垂直的直线,分别交的面积于点与点。
1l 2l O 2y x =A B (Ⅰ)证明交轴于固定点;(Ⅱ) 求的面积的最小值。
AB x P OAB ∆28、(2007年第4题) 已知点A (—2.0),C(2.0)。
△ABC 的三个内角∠A , ∠B ,∠C 的对边分别为a,b,c,且a,b,c 成等差数列,则点B 一定在一条曲线上,此曲线是( )
(A )圆 (B) 椭圆 (C) 双曲线 (D) 抛物线
29、(2007年第24题)双曲线 的中心为O ,右焦点为F,右准线和两条渐近线分别交)〉,〉00(122
22b a b
y a x =-
于点。
(Ⅰ)证明四个点同在一个圆上。
21M M 和F M M O 和21,,(Ⅱ)如果,求双曲线的离心率。
||||11F M OM =(Ⅲ)如果,求双曲线的方程。
4||,321==∠OF FM M π
30、(2006年第18题)若圆锥的高H 于底面半径R 都是1,则该圆锥的内切球的表面积S=_____________。
31、(2006年第19题)若抛物线的顶点坐标为(0,2),准线方程为= -1,则这条抛物线的焦点坐y 标为__________________。
32、(2006年第19题)
已知抛物线的顶点在第一象限,且与坐标原点的距离等于5,则( )
2213y x px =++Q Q p =A .3 B .-3 C .4 D .-4
33、(2006年第24题)
设椭圆的中心在直角坐标系的原点,离心率为,右焦点是F(2,0)y x O 3
2(Ⅰ)求椭圆的方程;(Ⅱ)设P 是椭圆上的一点,过点F 与点P 的直线与轴交于点M ,若l y ,求直线的方程式。
PF MP 4=l 34、(2005年第8题)椭圆 的( )
A .离心率是,焦距是8
B .离心率是,焦距是8 2349
C .离心率是,焦距是4
D .离心率是,焦距是42349
35、(2005年第23题)
已知双曲线的两个焦点分别是与,离心率C (e =
(Ⅰ)求双曲线的标准方程;(Ⅱ) 证明:若直线与双曲线有两个不同交点和,则与C l C M N OM 不能相互垂直,其中是坐标原点。
ON O 36、(2004年第15题)
将抛物线绕焦点按逆时针方向旋转后,所得抛物线的方程是 .
24y x =90︒37、(2004年第21题)
若椭圆与双曲线有相同的焦点,又椭圆与双曲线交于点,求椭圆及双22110x y m +=221y x b
-=)P y 曲线的方程。
