及圆有关的动点压轴题.docx

合集下载

2019-2020学年中考数学压轴题分类练习圆与动点专题.doc

2019-2020学年中考数学压轴题分类练习圆与动点专题1.在平面直角坐标系xOy 中的点P 和图形M ，给出如下的定义：若在图形M 上存在一点Q ，使得P Q 、两点间的距离小于或等于1，则称P 为图形M 的关联点．（1）当O 的半径为2时，①在点123115,0,,,0222P P P ⎛⎛⎫⎛⎫⎪ ⎪ ⎝⎭⎝⎭⎝中，O 的关联点是_______________． ②点P 在直线y x =-上，若P 为O 的关联点，求点P 的横坐标的取值范围．（2）C 的圆心在x 轴上，半径为2，直线1y x =-+与x 轴、y 轴交于点A B 、．若线段AB 上的所有点都是C 的关联点，直接写出圆心C 的横坐标的取值范围．2.如图，AB 是O 的直径，,2AC BC AB ==，连接AC ．（1）求证：045CAB ∠=；（2）若直线l 为O 的切线，C 是切点，在直线l 上取一点D ，使,BD AB BD =所在的直线与AC 所在的直线相交于点E ，连接AD ．①试探究AE 与AD 之间的数量关系，并证明你的结论； ②EBCD是否为定值？若是，请求出这个定值；若不是，请说明理由．3. 如图，动点M 在以O 为圆心，AB 为直径的半圆弧上运动（点M 不与点A B 、及AB 的中点F 重合），连接OM .过点M 作ME AB ⊥于点E ，以BE 为边在半圆同侧作正方形BCDE ，过M 点作O 的切线交射线DC 于点N ，连接BM 、BN .（1）探究：如左图，当M 动点在AF 上运动时； ①判断OEMMDN ∆∆是否成立？请说明理由；②设ME NCkMN+=，k是否为定值？若是，求出该定值，若不是，请说明理由；③设MBNα∠=，α是否为定值？若是，求出该定值，若不是，请说明理由；（2）拓展：如右图，当动点M在FB上运动时；分别判断（1）中的三个结论是否保持不变？如有变化，请直接写出正确的结论.（均不必说明理由）4.已知二次函数y=﹣x2+bx+c+1，①当b=1时，求这个二次函数的对称轴的方程；②若c=14b2﹣2b，问：b为何值时，二次函数的图象与x轴相切？③若二次函数的图象与x轴交于点A（x1，0），B（x2，0），且x1＜x2，与y轴的正半轴交于点M，以AB为直径的半圆恰好过点M，二次函数的对称轴l与x轴、直线BM、直线AM分别交于点D、E、F，且满足13DEEF=，求二次函数的表达式．5．已知：AB 是O ⊙的弦，点C 是AB 的中点，连接OB 、OC ，OC 交AB 于点D . (1)如图1，求证：AD BD =；(2)如图2，过点B 作O ⊙的切线交OC 的延长线于点M ，点P 是AC 上一点，连接AP 、BP ，求证：90APB OMB -=∠∠°.(3)如图3，在(2)的条件下，连接DP 、MP ，延长MP 交O ⊙于点Q ，若6MQ DP =，3sin 5ABO =∠，求MP MQ 的值.6.如图，⊙M 的圆心M （﹣1，2），⊙M 经过坐标原点O ，与y 轴交于点A ，经过点A 的一条直线l 解析式为：y=﹣x+4与x 轴交于点B ，以M 为顶点的抛物线经过x 轴上点D （2，0）和点C （﹣4，0）．（1）求抛物线的解析式；（2）求证：直线l 是⊙M 的切线；（3）点P 为抛物线上一动点，且PE 与直线l 垂直，垂足为E ，PF ∥y 轴，交直线l 于点F ，是否存在这样的点P ，使△PEF 的面积最小？若存在，请求出此时点P 的坐标及△PEF 面积的最小值；若不存在，请说明理由．7.如图，在⊙O中，直径CD垂直于不过圆心O的弦AB，垂足为点N，连接AC，点E在AB上，且AE=CE．（1）求证：AC2=AE•AB；（2）过点B作⊙O的切线交EC的延长线于点P，试判断PB与PE是否相等，并说明理由；（3）设⊙O半径为4，点N为OC中点，点Q在⊙O上，求线段PQ的最小值．8.如图，已知△ABC内接于⊙O，点C在劣弧AB上（不与点A，B重合），点D为弦BC的中点，DE⊥BC，DE与AC 的延长线交于点E，射线AO与射线EB交于点F，与⊙O交于点G，设∠GAB=ɑ，∠ACB=β，∠EAG+∠EBA=γ，（1）点点同学通过画图和测量得到以下近似数据：猜想：β关于ɑ的函数表达式，γ关于ɑ的函数表达式，并给出证明：（2）若γ=135°，CD=3，△ABE的面积为△ABC的面积的4倍，求⊙O半径的长．9. 如图，已知线段AB=2，MN⊥AB于点M，且AM=BM，P是射线MN上一动点，E，D分别是PA，PB的中点，过点A，M，D的圆与BP的另一交点C（点C在线段BD上），连结AC，DE．（1）当∠APB=28°时，求∠B和CM的度数；（2）求证：AC=AB。

与圆有关压轴题

与圆有关压轴题一、圆与线（直线、线段）相切问题1、已知二次函数c bx x y ++=221的图象经过点A （-3，6），并与x 轴交于点B（-1，0）和点C ，顶点为P ．（1）求这个二次函数的解析式（2）设D 为线段OC 上的一点，满足∠DPC=∠BAC ，求点D 的坐标；（3）在x 轴上是否存在一点M ，使以M 为圆心的圆与AC 、PC 所在的直线及y 轴都相切？如果存在，请求出点M 的坐标；若不存在，请说明理由．2、在△ABC 中,AB=AC=6,∠B=30°,点O1、O2在BC 上,⊙O1与⊙O2外切于P ；⊙O1与AB 相切于点D,与AC 相离；⊙O2与AC 相切于E,与AB 相离．（1）求证：DP//AC（2）设⊙O1的半径为x,⊙O2的半径为y,求y 与x 的函数解析式,并写定义域；（3） △ADP 能否为直角三角形?如果能够,请求出⊙O2的半径；如果不能,请说明理由．3、三角形ABC中,AB=AC=5,BC=6,P是边AB上的一个动点,过点P作PD⊥AB交BC于点D,以点D为正方形的一个顶点，在三角形ABC内作正方形DEFG，其中D、E在边BC上，F在边AC上，G在三角形内，设BD的长为x,正方形DEFG的边长为y（1）求y与x的函数关系式，并确定函数的定义域（2）记以PD为直径的圆为圆O，当圆O与边AC相切时，求x的值。

4、在矩形ABCD中，BC=4，BG与对角线AC垂直且分别交AC，AD及射线CD于点E，F，G，AB=x．（1）当点G与点D重合时，求x的值；（2）当点F为AD中点时，求x的值及∠ECF的正弦值．（3）是否存在x值，使得以点D为圆心的圆与BC、BG都相切？若存在，求x；若不存在，请说明理由。

5、如图，已知在△ABC中，AB=15，AC=20，cotA=2，P是边AB上的一个动点，⊙P的半径为定长．当点P与点B重合时，⊙P恰好与边AC相切；当点P与点B不重合，且⊙P 与边AC相交于点M和点N时，设AP=x，MN=y．（1）求⊙P的半径；（2）求y关于x的函数解析式，并写出它的定义域；6时，试比较∠CPN与∠A的大小，并说明理由.（3）当AP=5二、圆与圆相切问题1、如图,在直角梯形ABCD中,AD//BC,∠C=90°,BC=12,AD=18,AB=10.动点P、Q 分别从点D、B同时出发,动点P沿射线DA的方向以每秒2个单位长的速度运动,动点Q在线段BC上以每秒1个单位长的速度向点C运动,当点Q运动到点C时,点P随之停止运动.设运动时间为t（秒）.（1）当点P在线段DA上运动时,联结BD若∠ABP=∠ADB,求t的值；（2）当点P在线段DA上运动时,若以BQ为直径的圆与以AP为直径的圆外切,求t的值（3）设射线PQ与射线AB相交于点E,△AEP能否为等腰三角形?如果能,请直接写出t的值；如果不能,请说明理由.2、如图，已知在矩形ABCD 中，AB=3，BC=4，P 是边BC 延长线上的一点，联接AP 交边CD 于点E ，把射线AP 沿直线AD 翻折，交射线CD 于点Q ，设CP=x ，DQ=y ．（1）求y 关于x 的函数解析式，并写出定义域．（2）当点P 运动时，△APQ 的面积是否会发生变化？如果发生变化，请求出△APQ 的面积S 关于x 的函数解析式，并写出定义域；如果不发生变化，请说明理由．（3）当以4为半径的⊙Q 与直线AP 相切，且⊙A 与⊙Q 也相切时，求⊙A 的半径．3、如图，已知△ABC 中，AB=AC=5，BC=4，点O 在BC 边上运动，以O 为圆心，OA 为半径的圆与边AB 交于点D （点A 除外），设OB x =，AD y = ．（1）求ABC ∠sin 的值；（2）求y 关于x 的函数解析式，并写出函数的定义域；（3）当点O 在BC 边上运动时，⊙O 是否可能与以C 为圆心，41BC 长为半径的⊙C 相切？如果可能，请求出两圆相切时x 的值；如果不可能，请说明理由．ABC QD （第25题图） PE C O D BA4、如图，已知Sin ∠ABC=13，⊙O 的半径为2，圆心O 在射线BC 上，⊙O 与射线BA 相交于 E 、F 两点，EF=23，求BO 的长；点P 在射线BC 上，以点P 为圆心作圆，使得⊙P 同时与⊙O 和射线BA 相切，求所有满足条件的⊙P 的半径.5、如图，抛物线()098949422>+--=m m mx x y 与x 轴相交于A ，B 两点，点H 是抛物线的顶点，以AB 为直径作圆G 交y 轴于E ，F 两点，EF=24（1）用含m 的代数式表示圆G 的半径rG 的长；（2）连接AH ，求线段AH 的长；（3）点P 是抛物线对称轴正半轴上的一点，且满足以P 点为圆心的圆P 与直线AH 和圆G 都相切，求点P 的坐标．DC FABO第25题E G6、如图，在△ABC 中∠BAC=90°,AB=AC=2,圆A 的半径1，点O 在BC 边上运动（与点B/C 不重合），设BO=X,△AOC 的面积是y.⑴求y 关于x 的函数关系式及自变量的取值范围；⑵以点O 位圆心，BO 为半径作圆O ，求当○O 与○A 相切时，△AOC 的面积.三、1、将含30度角的直角三角板ABC （∠A=30），绕其直角顶点C 逆时针旋转α角（oo900<<α）,得到AB ,'''与C A C B A Rt ∆交于点D ，过点D 作DE//A ’B ’，交CB ’于点E ，连结BE ，易知在旋转的过程中，三角形BDE 为直角三角形，设BC=1，AD=x ，三角形BDE 的面积为S.(1)当o30=α时，求x 的值(2)求S 与x 的函数关系式，并写出x 的取值范围 (3)以点E 为圆心，BE 为半径作圆E ，当ABC S S ∆=41时，判断圆E 与A ’C 的位置关系，并求相应的tan α的值。

备战中考数学与圆的综合有关的压轴题含答案解析

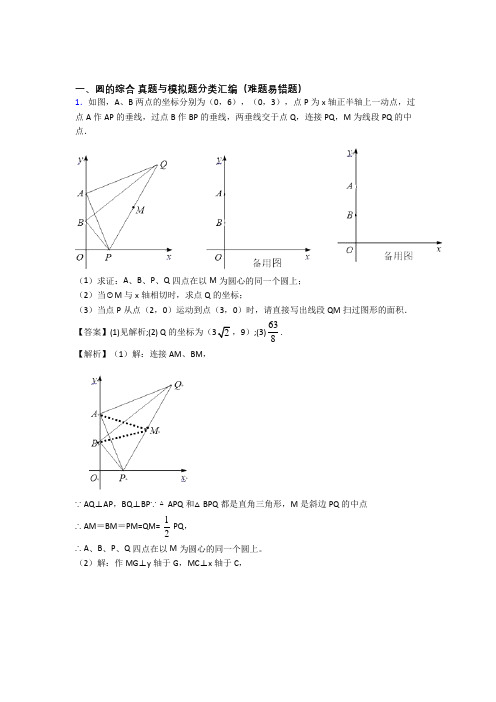
一、圆的综合真题与模拟题分类汇编（难题易错题）1．如图，A、B两点的坐标分别为（0，6），（0，3），点P为x轴正半轴上一动点，过点A作AP的垂线，过点B作BP的垂线，两垂线交于点Q，连接PQ，M为线段PQ的中点．（1）求证：A、B、P、Q四点在以M为圆心的同一个圆上；（2）当⊙M与x轴相切时，求点Q的坐标；（3）当点P从点（2，0）运动到点（3，0）时，请直接写出线段QM扫过图形的面积．【答案】(1)见解析;(2) Q的坐标为（32，9）;(3)63 8.【解析】（1）解：连接AM、BM，∵AQ⊥AP，BQ⊥BP∵△APQ和△BPQ都是直角三角形，M是斜边PQ的中点∴AM＝BM＝PM=QM= 12 PQ，∴A、B、P、Q四点在以M为圆心的同一个圆上。

（2）解：作MG⊥y轴于G，MC⊥x轴于C，∵AM＝BM∴G是AB的中点，由A（0，6），B（0，3）可得MC＝OG＝4.5∴在点P运动的过程中，点M到x轴的距离始终为4.5则点Q到x轴的距离始终为9，即点Q的纵坐标始终为9，当⊙M与x轴相切时则PQ⊥x轴，作QH⊥y轴于H，HB＝9－3＝6，设OP＝HQ＝x由△BOP∽△QHB，得x2＝3×6＝8，x＝2∴点Q的坐标为（2，9）（3）解：由相似可得：当点P在P1（2，0）时，Q1（4，9）则M1（3，4.5）当点P在P2（3，0）时，Q2（6，9），则M2（4.5，4.5）∴M1M2＝92－3＝32， Q1Q2＝6－4＝2线段QM扫过的图形为梯形M1M2Q2Q1其面积为：12×(32＋2)×4.5＝638.【解析】【分析】根据已知可得出三角形APQ和三角形BPQ都是直角三角形，再根据这个条件结合题意直接解答此题.【详解】（1）解：连接AM、BM，∵AQ⊥AP，BQ⊥BP∵△APQ和△BPQ都是直角三角形，M是斜边PQ的中点∴AM＝BM＝PM=QM= PQ，∴A、B、P、Q四点在以M为圆心的同一个圆上。

专题06 圆的有关动点综合问题-突破中考数学压轴题讲义(解析版)

【类型综述】综合题是指学生在不同的学习阶段所学的知识，不同章节所学的知识，特别是代数、几何不同学科中所学的知识，综合运用进行解题的数学题目，它既能考察同学们对数学基础知识基本方法掌握的熟练程度，又能考察综合运用数学知识分析问题、解决问题的能力。

几何中关于圆的综合题大致可分为：（1）以几何知识为主体的综合题；（2）代数、几何知识相结合的综合题；（3）圆中的探索型问题；【方法揭秘】直线与圆的位置关系问题，一般也无法先画出比较准确的图形．解这类问题，一般也分三步走，第一步先罗列两要素：R和d，第二步列方程，第三步解方程并验根．第一步在罗列两要素R和d的过程中，确定的要素罗列出来以后，不确定的要素要用含有x的式子表示．第二步列方程，就是根据直线与圆相切时d＝R列方程．如图1，直线443y x=+与x轴、y轴分别交于A、B两点，圆O的半径为1，点C在y轴的正半轴上，如果圆C既与直线AB相切，又与圆O相切，求点C的坐标．“既……，又……”的双重条件问题，一般先确定一个，再计算另一个．假设圆C与直线AB相切于点D，设CD＝3m，BD＝4m，BC＝5m，那么点C的坐标为(0,4－5m)．罗列三要素：对于圆O，r＝1；对于圆C，R＝3m；圆心距OC＝4－5m．分类列方程：两圆外切时，4－5m＝3m＋1；两圆内切时，4－5m＝3m－1．把这个问题再拓展一下，如果点C在y轴上，那么还要考虑点C在y轴负半轴．相同的是，对于圆O，r＝1；对于圆C，R＝3m；不同的是，圆心距OC＝5m－4．图1【典例分析】例1如图1，直线AB与x轴交于点A(－4,0)，与y轴交于点B(0,3)．点P从点A出发，以每秒1个单位长度的速度沿直线AB向点B移动．同时将直线34y x以每秒0.6个单位长度的速度向上平移，交OA于点C，交OB于点D，设运动时间为t（0＜t＜5）秒．（1）证明：在运动过程中，四边形ACDP总是平行四边形；（2）当t取何值时，四边形ACDP为菱形？请指出此时以点D为圆心、OD长为半径的圆与直线AB 的位置关系并说明理由．图1思路点拨1．用含t的式子把线段OD、OC、CD、AP、AC的长都可以表示出来．2．两条直线的斜率相等，这两条直线平行．3．判断圆与直线的位置关系，就是比较圆心到直线的距离与半径的大小．满分解答（2）如图3，如果四边形ACDP为菱形，那么AC＝AP．所以4－0.8t ＝t ．解得t ＝209．此时OD ＝0.6t ＝43．所以BD ＝433-＝53．作DE ⊥AB 于E ．在Rt △BDE 中，sin B ＝45，BD ＝53，所以DE ＝BD ·sin B ＝43．因此OD ＝DE ，即圆心D 到直线AB 的距离等于圆D 的半径．所以此时圆D 与直线AB 相切于点E （如图4）．图2图3考点伸展在本题情境下，点P 运动到什么位置时，平行四边形ACDP 的面积最大？S 平行四边形ACDP ＝AC ·DO ＝43(4)55t t -⨯＝21212+255t t -＝2125(3252t --+．当52t =时，平行四边形ACDP 的面积最大，最大值为3．此时点P 是AB 的中点（如图5）．图4图5例2如图1，PQ 为圆O 的直径，点B 在线段PQ 的延长线上，OQ ＝QB ＝1，动点A 在圆O 的上半圆上运动（包含P 、Q 两点），以线段AB 为边向上作等边三角形ABC ．（1）当线段AB 所在的直线与圆O 相切时，求△ABC 的面积（如图1）；（2）设∠AOB ＝α，当线段AB 与圆O 只有一个公共点（即A 点）时，求α的范围（如图2，直接写出答案）；（3）当线段AB 与圆O 有两个公共点A 、M 时，如果AO ⊥PM 于点N ，求CM 的长（如图3）．图1图2图3思路点拨1．过点B 画圆O 的切线，可以帮助理解第（1）、（2）题的题意．2．第（3）题发现AO //MQ 很重要，进一步发现NO 、MQ 是中位线就可以计算了．满分解答此时等边三角形ABC 3602︒=，所以S △ABC ＝4．图4图5图6考点伸展第（2）题的题意可以这样理解：如图7，过点B 画圆O 的切线，切点为G ．如图8，弧GQ 上的每一个点（包括点G 、Q ）都是符合题意的点A ，即线段AB 与圆O 只有一个公共点（即A 点）．如图9，弧GP 上的每一个点A （不包括点Q ）与点B 连成的线段AB ，与圆O 都有两个交点A 、M ．图7图8图9例3在Rt △ABC 中，∠C ＝90°，AC ＝6，53sin B ，⊙B 的半径长为1，⊙B 交边CB 于点P ，点O是边AB 上的动点．（1）如图1，将⊙B 绕点P 旋转180°得到⊙M ，请判断⊙M 与直线AB 的位置关系；（2）如图2，在（1）的条件下，当△OMP 是等腰三角形时，求OA 的长；（3）如图3，点N 是边BC 上的动点，如果以NB 为半径的⊙N 和以OA 为半径的⊙O 外切，设NB ＝y ，OA ＝x ，求y 关于x 的函数关系式及定义域．图1图2图3思路点拨1．∠B 的三角比反复用到，注意对应关系，防止错乱．2．分三种情况探究等腰△OMP ，各种情况都有各自特殊的位置关系，用几何说理的方法比较简单．3．探求y 关于x 的函数关系式，作△OBN 的边OB 上的高，把△OBN 分割为两个具有公共直角边的直角三角形．满分解答（1）在Rt △ABC 中，AC ＝6，53sin =B ，所以AB ＝10，BC ＝8．过点M 作MD ⊥AB ，垂足为D ．在Rt △BMD 中，BM ＝2，3sin 5MD B BM ==，所以65MD =．因此MD ＞MP ，⊙M 与直线AB 相离．图4（2）①如图4，MO ≥MD ＞MP ，因此不存在MO ＝MP 的情况．②如图5，当PM ＝PO 时，又因为PB ＝PO ，因此△BOM 是直角三角形．在Rt △BOM 中，BM ＝2，4cos 5BO B BM ==，所以85BO =．此时425OA =．③如图6，当OM ＝OP 时，设底边MP 对应的高为OE ．在Rt △BOE 中，BE ＝32，4cos 5BE B BO ==，所以158BO =．此时658OA =．图5图6图7图8考点伸展第（2）题也可以这样思考：如图8，在Rt △BMF 中，BM ＝2，65MF =，85BF =．在Rt △OMF 中，OF ＝8421055x x --=-，所以222426()()55OM x =-+．在Rt △BPQ 中，BP ＝1，35PQ =，45BQ =．在Rt △OPQ 中，OF ＝4461055x x --=-，所以222463()()55OP x =-+．①当MO ＝MP ＝1时，方程22426()(155x -+=没有实数根．②当PO ＝PM ＝1时，解方程22463()(155x -+=，可得425x OA ==③当OM ＝OP 时，解方程22426()()55x -+22463()(55x =-+，可得658x OA ==．例4如图1，在Rt △ABC 中，∠ACB ＝90°，AC ＝4，cos A ＝14，点P 是边AB 上的动点，以PA 为半径作⊙P ．（1）若⊙P 与AC 边的另一个交点为D ，设AP ＝x ，△PCD 的面积为y ，求y 关于x 的函数解析式，并直接写出函数的定义域；（2）若⊙P 被直线BC 和直线AC 截得的弦长相等，求AP 的长；（3）若⊙C 的半径等于1，且⊙P 与⊙C ，求AP 的长．图1备用图思路点拨1．△PCD 的底边CD 上的高，就是弦AD 对应的弦心距．2．若⊙P 被直线BC 和直线AC 截得的弦长相等，那么对应的弦心距相等．3．⊙C 的半径等于1，公共弦MN ，那么△CMN 是等腰直角三角形．在四边形CMPN 中，利用勾股定理列关于x （⊙P 的半径）的方程．满分解答（1）如图2，在Rt △ABC 中，AC ＝4，cos A ＝14，所以AB ＝16，BC ＝设弦AD 对应的弦心距为PE ，那么AE ＝14AP ＝14x ，PE ＝4AP ＝4x ．所以y ＝S △PCD ＝12CD PE ⋅＝11(4)22x x -＝2x x ．定义域是0＜x ＜8．（2）若⊙P 被直线BC 和直线AC 截得的弦长相等，那么对应的弦心距PF ＝PE ．因此四边形AEPF 是正方形（如图3），设正方形的边长为m ．由S △ABC ＝S △ACP ＋S △BCP ，得AC ·BC ＝m (AC ＋BC )．所以m＝307-．此时AE ＝4AP ＝4AE图2图3图4图5考点伸展第（2）题也可以这样计算：由于PF ＝14BP ＝1(16)4x -，由PE ＝PF ，得1(16)44x x =-．解得87x =．例5如图1，抛物线y ＝ax 2＋bx ＋c （a 、b 、c 是常数，a ≠0）的对称轴为y 轴，且经过(0,0)和1)16两点，点P 在该抛物线上运动，以点P 为圆心的⊙P 总经过定点A (0,2)．（1）求a、b、c的值；（2）求证：在点P运动的过程中，⊙P始终与x轴相交；（3）设⊙P与x轴相交于M(x1,0)、N(x2,0)两点，当△AMN为等腰三角形时，求圆心P的纵坐标．图1思路点拨1．不算不知道，一算真奇妙，原来⊙P在x轴上截得的弦长MN＝4是定值．2．等腰三角形AMN存在三种情况，其中MA＝MN和NA＝NM两种情况时，点P的纵坐标是相等的．满分解答所以在点P运动的过程中，⊙P始终与x轴相交．图2图3②如图4，当MA ＝MN 时，在Rt △AOM 中，OA ＝2，AM ＝4，所以OM ＝3．此时x ＝OH ＝32+．所以点P 的纵坐标为22211(232)(31)4344x ===+③如图5，当NA ＝NM 时，点P 的纵坐标为也为43+．图4图5考点伸展如果点P 在抛物线214y x =上运动，以点P 为圆心的⊙P 总经过定点B (0,1)，那么在点P 运动的过程中，⊙P 始终与直线y ＝－1相切．这是因为：设点P 的坐标为21(,)4x x ．已知B (0,1)，所以222222111(1)(1)1444PB x x x x =+-=++．而圆心P 到直线y ＝－1的距离也为2114x +，所以半径PB ＝圆心P 到直线y ＝－1的距离．所以在点P 运动的过程中，⊙P 始终与直线y ＝－1相切．【变式训练】1.(2017北京第29题)在平面直角坐标系xOy 中的点P 和图形M ，给出如下的定义：若在图形M 上存在一点Q ，使得P Q 、两点间的距离小于或等于1，则称P 为图形M 的关联点．（1）当O 的半径为2时，①在点1231135,0,,,,02222P P P ⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭中，O 的关联点是_______________．②点P 在直线y x =-上，若P 为O 的关联点，求点P 的横坐标的取值范围．（2）C 的圆心在x 轴上，半径为2，直线1y x =-+与x 轴、y 轴交于点A B 、．若线段AB 上的所有点都是C 的关联点，直接写出圆心C 的横坐标的取值范围．【答案】（1）①23,P P ，②－322≤x ≤－22或22≤x ≤322，（2）－2≤x ≤1或2≤x ≤22本题解析：（1）12315,01,22OP P OP ===,点1P 与⊙的最小距离为32，点2P 与⊙的最小距离为1，点3P 与⊙的最小距离为12，∴⊙的关联点为2P 和3P ．（2）∵y=-x+1与轴、轴的交点分别为A、B两点，∴令y=0得，-x+1=0,解得x=1，令得x=0得，y=0，∴A(1,0),B(0,1),分析得：如图1，当圆过点A时，此时CA=3,∴点C坐标为，C(-2,0)如图2，当圆与小圆相切时，切点为D，∴CD=1,如图4,当圆过点B时，连接BC，此时BC=3,-=,C点坐标为2,0)．在Rt△OCB中，由勾股定理得OC=2312考点：切线，同心圆，一次函数，新定义.2.（2017广东广州第25题）如图14，AB 是O 的直径，,2AC BC AB ==，连接AC ．（1）求证：045CAB ∠=；（2）若直线l 为O 的切线，C 是切点，在直线l 上取一点D ，使,BD AB BD =所在的直线与AC 所在的直线相交于点E ，连接AD ．①试探究AE 与AD 之间的数量关系，并证明你的结论；②EB CD 是否为定值？若是，请求出这个定值；若不是，请说明理由．【答案】（1）详见解析；（2）①AE AD =②2BE CD =（2）①如图所示，作BF l ⊥于F由（1）可得，ACB ∆为等腰直角三角形.O 是AB 的中点.CO AO BO ∴==ACB ∴∆为等腰直角三角形.又l 是O 的切线，OC l BF l∴⊥⊥ ∴四边形OBEC 为矩形22AB BF BD BF ∴=∴=303075BDF DBA BDA BAD ∴∠=︒∴∠=︒∠=∠=︒，15901575CBE CEB DEA∴∠=︒∠=︒-︒=︒=∠，,ADE AED AD AE∴∠=∠∴=②当ABD ∠为钝角时，如图所示，同样，1,302BF BD BDC =∴∠=︒1801501509015152ABD AEB CBE ADB ︒-︒∴∠=︒∠=︒-∠=︒∠=︒，，AE AD∴=考点：圆的相关知识的综合运用3.(2017湖南湘潭第26题)如图，动点在以为圆心，为直径的半圆弧上运动（点不与点及的中点重合），连接.过点作于点，以为边在半圆同侧作正方形，过点作的切线交射线于点，连接、.（1）探究：如左图，当动点在上运动时；①判断是否成立？请说明理由；②设，是否为定值？若是，求出该定值，若不是，请说明理由；③设，是否为定值？若是，求出该定值，若不是，请说明理由；（2）拓展：如右图，当动点在上运动时；分别判断（1）中的三个结论是否保持不变？如有变化，请直接写出正确的结论.（均不必说明理由）【答案】(1)①成立，理由见解析；②为定值1；③ 为定值45°；（2）不发生变化.试题解析：（1）①成立，理由如下：过点M作ME⊥AB于点E，以BE为边在半圆同侧作正方形BCDE，∴∠MEO=∠MDN=90°，∴∠MOE+∠EMO=90°过M点的的切线交射线DC于点N，∴∠OMN=90°，∴∠DMN+∠EMO=90°∴∠MOE=∠DMN∴△OEM∽△MDN②k是定值1，理由如下：过点B作BG⊥MN,∵过M点的的切线交射线DC于点N，∴∠OMN=90°，∵BG⊥MN,∴∠BGM=90°，③α为定值45°，理由如下：由②知：∠OBM=∠MBG,△BNG ≌△BCN,∴∠GBN=∠CBN,∵正方形BCDE，∴∠EBC=90°，∴∴∠MBN=01452EBC ∠=(2)不发生变化.4.（2017湖南株洲第26题）已知二次函数y=﹣x 2+bx +c +1，①当b=1时，求这个二次函数的对称轴的方程；②若c=14b 2﹣2b ，问：b 为何值时，二次函数的图象与x 轴相切？③若二次函数的图象与x 轴交于点A （x 1，0），B （x 2，0），且x 1＜x 2，与y 轴的正半轴交于点M ，以AB 为直径的半圆恰好过点M ，二次函数的对称轴l 与x 轴、直线BM 、直线AM 分别交于点D 、E 、F ，且满足13DE EF =，求二次函数的表达式．【答案】①.二次函数的对称轴的方程为x=12；②.b 为2或2时，二次函数的图象与x 轴相切；③.二次函数的表达式为y=﹣x 2+32x +1．出△OAM ∽△OMB ，得出OM 2=OA•OB ，由二次函数的图象与x 轴的交点和根与系数关系得出OA=﹣x 1，OB=x 2，x 1+x 2，=b ，x 1•x 2=﹣（c +1），得出方程（c +1）2=c +1，得出c=0，OM=1，证明△BDE ∽△BOM ，△AOM ∽△ADF ，得出DE BD OM OD =，OM OADF AD=，得出OB=4OA ，即x 2=﹣4x 1，由x 1•x 2=﹣（c +1）=﹣1，得出方程组122114x x x x ⋅=-⎧⎨=-⎩，解方程组求出b 的值即可．试题解析：①二次函数y=﹣x 2+bx +c +1的对称轴为x=2b ，当b=1时，2b =12，∴当b=1时，求这个二次函数的对称轴的方程为x=12．③∵AB 是半圆的直径，∴∠AMB=90°，∴∠OAM +∠OBM=90°，∵∠AOM=∠MOB=90°，∴∠OAM +∠OMA=90°，∴∠OMA=∠OBM ，∴△OAM ∽△OMB ，∴OM OAOB OM=，∴OM 2=OA•OB ，∵二次函数的图象与x 轴交于点A （x 1，0），B （x 2，0），∴OA=﹣x 1，OB=x 2，x 1+x 2，=b ，x 1•x 2=﹣（c +1），∵OM=c +1，∴（c +1）2=c +1，解得：c=0或c=﹣1（舍去），∴c=0，OM=1，∵二次函数的对称轴l 与x 轴、直线BM 、直线AM 分别交于点D 、E 、F ，且满足13DE EF =，∴AD=BD ，DF=4DE ，DF ∥OM ，∴△BDE ∽△BOM ，△AOM ∽△ADF ，∴,DE BD OM OA OM OB DF AD ==，∴DE=BD OB ，DF=AD OA ，∴AD BDOA OB=×4，∴OB=4OA ，即x 2=﹣4x 1，∵x 1•x 2=﹣（c +1）=﹣1，∴122114x x x x ⋅=-⎧⎨=-⎩，解得：12122x x ⎧=-⎪⎨⎪=⎩，∴b=﹣12+2=32，∴二次函数的表达式为y=﹣x 2+32x +1．考点：二次函数综合题；二次函数的性质．5．（2017哈尔滨第26题）已知：AB 是O ⊙的弦，点C 是AB 的中点，连接OB 、OC ，OC 交AB 于点D .(1)如图1，求证：AD BD =；(2)如图2，过点B 作O ⊙的切线交OC 的延长线于点M ，点P 是AC 上一点，连接AP 、BP ，求证：90APB OMB -=∠∠°.(3)如图3，在(2)的条件下，连接DP 、MP ，延长MP 交O ⊙于点Q ，若6MQ DP =，3sin 5ABO =∠，求MPMQ的值.【答案】（1）证明见解析；（2）证明见解析；（3）518PM MQ =.试题解析：（1）如图1，连接OA，∵C 是AB 的中点，∴AC BC =，∴∠AOC=∠BOC，∵OA=OB，∴OD⊥AB，AD=BD；（2）如图2，延长BO 交⊙O 于点T，连接PT∵BT是⊙O的直径，∴∠BPT=90°，∴∠APT=∠APB﹣∠BPT=∠APB﹣90°，∵BM是⊙O的切线，∴OB⊥BM，又∠OBA+∠MBA=90°，∴∠ABO=∠OMB，又∠ABO=∠APT，∴∠APB﹣90°=∠OMB，∴∠APB﹣∠OMB=90°；考点：圆的综合题．6.（2017年贵州省黔东南州第24题）如图，⊙M的圆心M（﹣1，2），⊙M经过坐标原点O，与y轴交于点A，经过点A的一条直线l解析式为：y=﹣x+4与x轴交于点B，以M为顶点的抛物线经过x轴上点D（2，0）和点C（﹣4，0）．（1）求抛物线的解析式；（2）求证：直线l是⊙M的切线；（3）点P为抛物线上一动点，且PE与直线l垂直，垂足为E，PF∥y轴，交直线l于点F，是否存在这样的点P，使△PEF的面积最小？若存在，请求出此时点P的坐标及△PEF面积的最小值；若不存在，请说明理由．【答案】（1）y=﹣29x2﹣49x+169（2）证明见解析（3）50415120试题解析：（1）设抛物线的解析式为y=a（x﹣2）（x+4），将点M的坐标代入得：﹣9a=2，解得：a=﹣29．∴抛物线的解析式为y=﹣29x2﹣49x+169．（2）连接AM，过点M作MG⊥AD，垂足为G．把x=0代入y=﹣12x+4得：y=4，∴∠MAG=∠ABO．∵∠OAB+∠ABO=90°，∴∠MAG+∠OAB=90°，即∠MAB=90°．∴l是⊙M的切线．（3）∵∠PFE+∠FPE=90°，∠FBD+∠PFE=90°，∴∠FPE=∠FBD．∴tan∠FPE=12．5：2：1．∴△PEF的面积=12PE•EF=12×255PF•55PF=15PF2．考点：二次函数综合题7.（2017年四川省内江市第27题）如图，在⊙O中，直径CD垂直于不过圆心O的弦AB，垂足为点N，连接AC，点E在AB上，且AE=CE．（1）求证：AC2=AE•AB；（2）过点B作⊙O的切线交EC的延长线于点P，试判断PB与PE是否相等，并说明理由；（3）设⊙O半径为4，点N为OC中点，点Q在⊙O上，求线段PQ的最小值．【答案】（1）证明见解析；（2）PB=PE；（3）421123．【解析】试题分析：（1）证明△AEC∽△ACB，列比例式可得结论；（2）如图2，证明∠PEB=∠COB=∠PBN，根据等角对等边可得：PB=PE；（3）如图3，先确定线段PQ的最小值时Q的位置：因为OQ为半径，是定值4，则PQ+OQ的值最小时，PQ最小，当P、Q、O三点共线时，PQ最小，先求AE的长，从而得PB的长，最后利用勾股定理求OP 的长，与半径的差就是PQ的最小值．试题解析：（1）如图1，连接BC ，∵CD 为⊙O 的直径，AB ⊥CD ，∴BC AC =，∴∠A =∠ABC ，∵EC =AE ，∴∠A =∠ACE ，∴∠ABC =∠ACE ，∵∠A =∠A ，∴△AEC ∽△ACB ，∴AC AEAB AC=，∴AC 2=AE •AB ；（3）如图3，∵N 为OC 的中点，∴ON =12OC =12OB ，Rt △OBN 中，∠OBN =30°，∴∠COB =60°，∵OC =OB ，∴△OCB 为等边三角形，∵Q 为⊙O 任意一点，连接PQ 、OQ ，因为OQ 为半径，是定值4，则PQ +OQ 的值最小时，PQ 最小，当P 、Q 、O 三点共线时，PQ 最小，∴Q 为OP 与⊙O 的交点时，PQ 最小，∠A =12∠COB =30°，∴∠PEB =2∠A =60°，∠ABP =90°﹣30°=60°，∴△PBE 是等边三角形，Rt △OBN 中，BN ，∴AB =2BN =设AE =x ，则CE =x ，EN =﹣x ，Rt △CNE 中，2222)x x =+，x =433，∴BE =PB =433-=833，Rt △OPB 中，OP =4213，∴PQ =4213﹣4=421123-．则线段PQ 的最小值是421123-．考点：圆的综合题；最值问题；探究型；压轴题．8.（2017年浙江省杭州市第23题）如图，已知△ABC 内接于⊙O，点C 在劣弧AB 上（不与点A，B 重合），点D 为弦BC 的中点，DE⊥BC，DE 与AC 的延长线交于点E，射线AO 与射线EB 交于点F，与⊙O 交于点G，设∠GAB=ɑ，∠ACB=β，∠EAG+∠EBA=γ，（1）点点同学通过画图和测量得到以下近似数据：ɑ30°40°50°60°β120°130°140°150°γ150°140°130°120°猜想：β关于ɑ的函数表达式，γ关于ɑ的函数表达式，并给出证明：（2）若γ=135°，CD=3，△ABE的面积为△ABC的面积的4倍，求⊙O半径的长．【答案】（1）β=α+90°，γ=﹣α+180°（2）5试题解析：（1）猜想：β=α+90°，γ=﹣α+180°连接OB，∴由圆周角定理可知：2∠BCA=360°﹣∠BOA，∵OB=OA，∴∠OBA=∠OAB=α，∴∠BOA=180°﹣2α，∴2β=360°﹣（180°﹣2α），∴β=α+90°，∵D是BC的中点，DE⊥BC，∴OE是线段BC的垂直平分线，∴BE=CE，∠BED=∠CED，∠EDC=90°∵∠BCA=∠EDC+∠CED，∴β=90°+∠CED，∴∠CED=α，∴∠CED=∠OBA=α，∴O、A、E、B四点共圆，∴∠EBO+∠EAG=180°，∴∠EBA+∠OBA+∠EAG=180°，∴γ+α=180°；设CE=3x，AC=x，由（1）可知：BC=2CD=6，∵∠BCE=45°，∴CE=BE=3x，∴由勾股定理可知：（3x）2+（3x）2=62，，考点：1、圆的综合问题，2、勾股定理，3、解方程，4、垂直平分线的性质9.(2017浙江温州第24题)（本题14分）如图，已知线段AB=2，MN⊥AB于点M，且AM=BM，P是射线MN上一动点，E，D分别是PA，PB的中点，过点A，M，D的圆与BP的另一交点C（点C在线段BD 上），连结AC，DE．（1）当∠APB=28°时，求∠B和CM的度数；（2）求证：AC=AB。

(word完整版).中考数学圆压轴题

CBOA D1推理运算如图，AB 为O 直径，CD 为弦，且CD AB ⊥,垂足为H ．（1）OCD ∠的平分线CE 交O 于E ,连结OE ．求证：E 为ADB 的中点；（2）如果O 的半径为1，3CD =，①求O 到弦AC 的距离; ②填空：此时圆周上存在个点到直线AC 的距离为12． 2 如图6，在Rt △ABC 中，∠ABC =90°，D 是AC 的中点，⊙O 经过A 、B 、D 三点,CB 的延长线交⊙O 于点E 。

(1) 求证AE =CE ;(2) EF 与⊙O 相切于点E ,交AC 的延长线于点F ,若CD =CF =2cm ，求⊙O 的直径；（3）若n CDCF = （n 〉0），求sin ∠CAB 。

3 已知:如图，在半径为4的⊙O 中，AB ，CD 是两条直径，M 为OB 的中点，CM 的延长线交⊙O 于点E ，且EM ＞MC ．连结DE ，DE =15。

（1) 求证:AM MB EM MC ⋅=⋅； (2）求EM 的长； (3）求sin ∠EOB 的值.4 如图，已知⊙O 的直径AB ＝2，直线m 与⊙O 相切于点A,P 为⊙O 上一动点（与点A 、点B 不重合），PO 的延长线与⊙O 相交于点C ，过点C 的切线与直线 m 相交于点D ．(1）求证：△APC∽△COD．（2)设AP ＝x ，OD ＝y ，试用含x 的代数式表示y ．（3）试探索x 为何值时，△ACD 是一个等边三角形．5 如图，在以O 为圆心的两个同心圆中,AB 经过圆心O ,且与小圆相交于点A 、与大圆相交于点B ．小圆的切线AC 与大圆相交于点D ，且CO 平分∠ACB ．（1）试判断BC 所在直线与小圆的位置关系，并说明理由；（2）试判断线段AC 、AD 、BC 之间的数量关系，并说明理由;（3）若8cm 10cm AB BC ==，，求大圆与小圆围成的圆环的面积．（结果保留π）6 在Rt △ABC 中，BC =9， CA =12，∠ABC 的平分线BD 交AC 与点D ， DE ⊥DB 交AB 于点E ．（1）设⊙O 是△BDE 的外接圆,求证:AC 是⊙O 的切线；（2）设⊙O 交BC 于点F,连结EF ，求EFAC的值．ABDE OCHABCEDOM7 如图,点A ，B 在直线MN 上，AB ＝11厘米，⊙A ，⊙B 的半径均为1厘米．⊙A 以每秒2厘米的速度自左向右运动，与此同时,⊙B 的半径也不断增大，其半径r （厘米）与时间t （秒）之间的关系式为r ＝1+t （t ≥0）．（1）试写出点A ，B 之间的距离d （厘米）与时间t （秒）之间的函数表达式；（2)问点A 出发后多少秒两圆相切?8 如图,在△ABC 中，∠BAC ＝90°,BM 平分∠ABC 交AC 于M ，以A 为圆心, AM 为半径作⊙A 交BM 于N ,AN 的延长线交BC 于D ，直线AB 交⊙A 于P 、K 两点，作MT ⊥BC 于T ．(1）求证：AK ＝MT ；（2)求证：AD ⊥BC ；（3）当AK ＝BD 时,求证：BMACBP BN =．9 如图,AB 为O 的直径，CD AB ⊥于点E ，交O 于点D ，OF AC ⊥于点F ． (1）请写出三条与BC 有关的正确结论;（2）当30D ∠=，1BC =时，求圆中阴影部分的面积．10 如图，已知O 的直径AB 垂直于弦CD 于点E ,过C 点作CG AD ∥交AB 的延长线于点G ，连接CO 并延长交AD 于点F ，且CF AD ⊥．（1）试问:CG 是O 的切线吗？说明理由；（2）请证明:E 是OB 的中点； (3)若8AB =，求CD 的长．11 如图11，⊙P 与⊙O 相交于A 、B 两点,⊙P 经过圆心O,点C 是⊙P 的优弧上任意一点(不与点A 、B 重合)，连结AB 、AC 、BC 、OC 。

与圆有关的动点问题.doc题

动点问题（4）------与圆有关的动点直线与圆相切1.如图,⊙O 的半径为1,圆心O 在正三角形的边AB 上沿图示方向移动,当⊙O 移动到与AC 边相切时,OA 的长是 .2.如图，已知⊙O 的半径为6cm ，射线PM 经过点O ，10cm OP ，射线PN 与⊙O 相切于点Q ．A B ，两点同时从点P 出发，点A 以5cm/s 的速度沿射线PM 方向运动，点B 以4cm/s 的速度沿射线PN 方向运动．设运动时间为t s ．（1）求PQ 的长；（2）当t 为何值时，直线AB 与⊙O 相切？3如图，ABC ∆中，090C ∠=，4AC =，3BC =.半径为1的圆的圆心P 以1个单位/s 的速度由点A 沿AC 方向在AC 上移动，设移动时间为t （单位：s ）. （1）当t 为何值时，⊙P 与AB 相切；（2）作PD AC ⊥交AB 于点D ，如果⊙P 和线段BC 交于点E ，证明：当165t s=时，四边形PDBE 为平行四边形.4.（2012河北中考25）如图14，(50)(30).A B --，，，点C 在y 轴的正半轴上，CBO∠=45，CD AB ∥，90CDA = ∠.点P 从点(40)Q ，出发，沿x 轴向左以每秒1个单位长的速度运动，运动时间为t 秒.（1）求点C 的坐标；（2）当15BCP =∠时，求t 的值；（3）以点P 为圆心，PC 为半径的P ⊙随点P 的运动而变化，当P ⊙与四边形ABCD 的边（或边所在的直线）相切时，求t 的值．5.如图，形如量角器的半圆O的直径DE=12cm，形如三角板的⊿ABC中，∠ACB=90°，∠ABC= 30°，BC=12cm。

半圆O以2cm/s的速度从左向右运动，在运动过程中，点D、E始终在直线BC 上。

设运动时间为t (s)，当t=0s时，半圆O在⊿ABC的左侧，OC=8cm。

（1）当t为何值时，⊿ABC的一边所在直线与半圆O所在的圆相切？(2)当⊿ABC的一边所在直线与半圆O所在的圆相切时，如果半圆O与直线DE围成的区域与⊿ABC 三边围成的区域有重叠部分，求重叠部分的面积。

关于圆的压轴题

关于圆的压轴题1. 设边长为2a 的正方形的中心A 在直线l 上，它的一组对边垂直于直线l ，半径为r 的⊙O 的圆心O 在直线l 上运动．．，点A 、O 间距离为d ．（1）如图①，当r ＜a 时，根据d 与a 、r 之间关系，将⊙O 与正方形的公共点个数填入下表：与正方形的公共点的个数可能有个；（2）如图②，当r ＝a 时，根据d 与a 、r 之间关系，将⊙O 与正方形的公共点个数填入下表：与正方形的公共点个数可能有个；（3）如图③，当⊙O 与正方形有5个公共点时，试说明r ＝54a ；（4）就r ＞a 的情形，请你仿照“当……时，⊙O 与正方形的公共点个数可能有个”的形式，至少给出一个关于“⊙O 与正方形的公共点个数”的正确结论．[解] （1）所以，当r ＜a 时，⊙O 与正方形的公共点的个数可能有0、1、2个；l图①l图②图③l图①（2）所以，当r ＝a 时，⊙O 与正方形的公共点个数可能有0、1、2、4个；（3）方法一：如图所示，连结OC 则OE ＝OC ＝r ，OF ＝EF －OE ＝2a －r ．在Rt △OCF OF 2＋FC 2＝OC 2即（2a －r ）2＋a 2＝r 24a 2－4ar ＋r 2＋a 2＝ 5a 2＝4ar5a ＝4r ∴r ＝54a ．（4）①当a ＜r ＜54a 时，⊙O 与正方形的公共点个数可能有0、1、2、4、6、7、8个；②当r ＝54a 时，⊙O 与正方形的公共点个数可能有0、1、2、5、8个；③当54a r <<时，⊙O 与正方形的公共点个数可能有0、1、2、3、4、6、8个；④当r =时，⊙O 与正方形的公共点个数可能有0、1、2、3、4个； ⑤当r 时，⊙O 与正方形的公共点个数可能有0、1、2、3、4个．2. 如图，在平面直角坐标系中，以坐标原点O 为圆心，2为半径画⊙O ，P 是⊙O 上一动点，且P 在第一象限内，过点P 作⊙O 的切线与x 轴相交于点A ，与y 轴相交于点B 。

动点问题(与圆相关)

动点问题（与圆相关）1．如图，在平面直角坐标系中，四边形OABC是梯形，BC∥AO，顶点O在坐标原点，顶点A（4，0），顶点B（1，4）．动点P从O出发，以每秒1个单位长度的速度沿OA的方向向A运动；同时，动点Q从A 出发，以每秒2个单位长度的速度沿A→B→C的方向向C运动．当其中一个点到达终点时，另一个也随之停止．设运动时间为t秒．（1）当t为何值时，PB与AQ互相平分？（2）设△PAQ的面积为S，求S与t的函数关系式．当t为何值时，S有最大值？最大值是多少？（3）在整个运动过程中，是否存在某一时刻t，使得以PQ为直径的圆与y轴相切？若存在，求出相应的t值；若不存在，请说明理由．2．如图，矩形ABCD中，AB＝4，BC＝2，动点M、N分别从点A、B同时出发，动点M沿AB边以每秒1个单位的速度向点B运动，动点N沿BC→CD边以每秒32个单位的速度向点D运动，连结MN，设运动时间为t（s）．（1）当t为何值时，MN∥BC？（2）当点N在CD边上运动时，设MN与BD相交于点P，求证：点P的位置固定不变；（3）以AD为直径作半圆O，问：是否存在某一时刻t，使得MN与半圆O相切？若存在，求t的值，并判断此时△MON的形状；若不存在，请说明理由． A C BDMN3（乌鲁木齐）如图，在△ABC中，∠B＝90°，AB＝6米，BC＝8米，动点P以2米/秒的速度从A点出发，沿AC向点C移动，同时，动点Q以1米/秒的速度从C点出发，沿CB向点B移动．当其中有一点到达终点时，它们都停止移动，设移动的时间为t秒．②求△CPQ的面积S（平方米）关于时间t（秒）的函数解析式；（2）在P、Q移动的过程中，当△CPQ为等腰三角形时，直接写出t的值；（3）以P为圆心，PA为半径的圆与以Q为圆心，QC为半径的圆相切时，求出t的值．C4（常州）在平面直角坐标系xOy中，一次函数y＝34x＋3的图象是直线l1，l1与x轴、y轴分别相交于A、B两点，直线l2过点C（a，0）（a＞0）且与l1垂直．点P、Q同时从A点出发，其中点P沿射线AB 运动，速度为每秒4个单位；点Q沿射线AO运动，速度为每秒5个单位．（1）写出A点的坐标和AB的长；（2）当点P、Q运动了t秒时，以点Q为圆心， PQ为半径的⊙Q与直线l2、y轴都相切，求此时a的值．5（无锡）如图，已知O（0，0）、A（4，0）、B（4，3）．动点P从O点出发，以每秒3个单位的速度，沿△OAB的边OA、AB、BO作匀速运动；动直线l从AB位置出发，以每秒1个单位的速度向x轴负方向作匀速平移运动．若它们同时出发，运动的时间为t秒，当点P运动到O时，它们都停止运动．（1）当P在线段OA上运动时，求直线l与以P为圆心、Array 1为半径的圆相交时t的取值范围；（2）当P在线段AB上运动时，设直线l分别与OA、OB交于C、D．试问：四边形CPBD是否可能为菱形？若能，求出此时t的值；若不能，请说明理由，并说明如何改变直线l的出发时间，使得四边形CPBD会是菱形．6（哈尔滨）如图1，在平面直角坐标系中，直线y＝12x＋5与x轴、y轴分别交于A、B两点，将△AOB绕原点O顺时针旋转得到△A′OB′，并使OA′⊥AB，垂足为D，直线AB与线段A′B′相交于点G．动点E从原点O出发，以1个单位/秒的速度沿x轴正方向运动，设动点E运动的时间为t秒．（1）求点D的坐标；（2）连接DE，当DE与线段OB′相交，交点为F，且四边形DFB′G是平行四边形时（如图2），求此时线段DE所在直线的解析式；（3）若以动点为E圆心，以25为半径作⊙E，连接A′E，当t为何值时，tan∠EA′B′＝18？并判断此时直线A′O与⊙E的位置关系，请说明理由．图1 图2 备用图7．如图，等边三角形ABC 的边长为4cm ，AD ⊥BC 于D ．点E 、F 分别从B 、C 两点同时出发，其中点E 以1cm/s 的速度沿BC 向终点C 运动；点F 以2cm/s 的速度沿CA 、AB 向终点B 运动，设运动时间为t （s ）．（1）当t 为何值时，EF ⊥AC ？当t 为何值时，EF ⊥AB ？（2）设△DEF 的面积为S （cm 2），求S 与t 之间的函数关系式；（3）探索以EF 为直径的圆与AC 的位置关系，并写出相应位置关系的t 的取值范围．E DA B C F8（石狮）如图，在平面直角坐标系中，直线l：y＝2x＋b与x轴交于点A（－4，0），与y轴交于点B．点P是y轴上的一个动点，以P为圆心，3为半径作⊙P．（1）若PA＝PB，试判断⊙P与直线l的位置关系，并说明理由；（2）当⊙P与直线l相切时，求点P与原点O间的距离；（3）如果以⊙P与直线l的两个交点和圆心P为顶点的三角形是等边三角形，求点P的坐标．（备用图）9(08无锡模考)已知直线y＝3x－63与x轴、y轴分别相交于A、B两点，点C在射线BA上以每秒3个单位的速度运动，以C点为圆心，半径为1作⊙C．点P以每秒2个单位的速度在线段OA上来回运动，过点P作直线l⊥x轴．（1）填空：A点坐标为（____，____），B点坐标为（____，____）；求直线l与⊙C第二次相切时点P的坐标；（3）在整个运动过程中，直线l与⊙C有交点的时间共有多少秒？10．如图，在平面直角坐标系中，动点P从点A（0，10）出发，以3个单位/秒的速度沿y轴向点O匀速运动，动点Q从点B（5，0）同时出发，以1个单位/秒的速度沿x轴向点O匀速运动，当其中一个点到达终点时，另一点也随即停止运动．设运动的时间为t（秒）．以P、Q为圆心作⊙P和⊙Q，且⊙P和⊙Q的半径分别为4和1．Array（1）若⊙P与Rt△AOB的一边相切，求此时动点P的坐标；（2）若⊙P与线段AB有两个公共点，求t的取值范围；（3）是否存在某一时刻t，使⊙P和⊙Q相切？若存在，求出t的值；若不存在，请说明理由．11．如图，直线l与x轴、y轴分别交于点A（8，0）、点B（0，6），点P以每秒3个单位长度的速度沿BO由B向O运动，点Q以每秒5个单位长度的速度沿AB由A向B运动．已知P、Q两点同时出发，且当一点到达终点时，另一点也随之停止运动，设运动时间为t秒．（1）当四边形PQAO为梯形时，求t的值；（3）在运动过程中，以PQ为直径的圆能否与x轴相切？若能，请求出运动时间t；若不能，请说明理由；（4）在运动过程中，若以点P为圆心、PB为直径的圆与以点Q为圆心、QA为直径的圆相切，请直接写出t的值．12．如图，直线y＝34x－3与x轴、y轴分别交于点A、B，圆心在坐标原点、半径为1的动圆以每秒0.4个单位的速度向x轴正方向运动，动点P从B点同时出发，以每秒0.5个单位的速度沿BA方向运动．设运动时间为t（秒）．（1）直接写出A、B两点的坐标；（2）当t为何值时，动圆与直线AB相切？（3）问在整个运动过程中，点P在动圆的圆面（圆上和圆的内部）上一共运动了多长时间？13．已知直线l：y＝34x＋8与x轴、y轴分别交于点A、B，P是x轴上一点，以P为圆心的⊙P与直线l相切于B点．（1）求点P的坐标和⊙P的半径；（2）若⊙P以每秒103个单位向x轴负方向运动，同时⊙P的半径以每秒32个单位变小，设⊙P的运动时间为t秒，且⊙P始终与直线l有公共点，试求t的取值范围；（3）在（2）中，设⊙P被直线l截得的弦长为a，问是否存在t的值，使a最大？若存在，求出t请说明理由；（4）在（2）中，设⊙P与直线l的一个公共点为Q，若以A、P、Q为顶点的三角形与△ABO相似，请直接写出此时t的值．14．在平行四边形ABCD中，AB在x轴上，D点y轴上，∠C＝60°，BC＝6，B点坐标为（4，0）．点M是边AD上一点，且DM:AD＝1:3．点E、F分别从A、C同时出发，以1个单位/秒的速度分别沿AB、CB向点B运动，当点F运动到点B时，点E随之停止运动，EM、CD的延长线交于点P，FP交AD于点Q．⊙E的半径为52，设运动时间为t秒．（1）求直线BC的解析式；（2）当t为何值时，PF⊥AD？（3）在（2）的条件下，⊙E与直线PF4．15．点M在第一象限，半径为6的⊙M交x轴于点A、B，交y轴于点C、D，且∠AMB＝60°,CD＝5（1）求直线AM的解析式；①当⊙M开始运动时，动点N同时从点A出发，沿x轴正方向以每秒3个单位长的速度匀速运动．在整个运动过程中，点N在动圆的圆面（圆上和圆的内部）上一共运动了多长时间？②在①中，若动点N的运动速度为每秒a个单位，当动点N离开⊙M时，⊙M恰好与x轴相切，求a的值；（3）设P为直线AM上一点，在坐标平面内是否存在点Q，使得以A、B、P、Q为顶点的四边形是一个有三边相等且有一个内角为60°的等腰梯形？若存在，请直接写出点Q16．如图，直线y＝－34x＋9与x轴、y轴分别交于点B、C，抛物线y＝－14x2＋b x＋c经过B，C两点，与x轴的另一个交点为点A，动点P从点A出发沿AB以每秒3个单位长度的速度向点B运动，运动时间为t（0＜t＜5）秒．（1）求抛物线的解析式及点A的坐标；（2）以OC为直径的⊙O′与BC交于点M，当t为何值时，PM与⊙O′相切？请说明理由；（3）在点P从点A出发的同时，动点Q从点B出发沿BC以每秒3个单位长度的速度向点C运动，动点N从点C出发沿CA以每秒3105个单位长度的速度向点A运动，运动时间与点P相同．①记△BPQ的面积为S，当t为何值时，S最大，最大值是多少？②是否存在△NCQ为直角三角形的情形，若存在，求出相应的t值；若不存在，请说明理由．17（苏州）：已知四边形ABCD是边长为4的正方形，以AB为直径在正方形内作半圆，P是半圆上的动点（不与点A、B重合），连接PA、PB、PC、PD．(1)如图①，当PA的长度等于▲时，∠PAB＝60°；当PA的长度等于▲时，△PAD是等腰三角形；(2)如图②，以AB边所在直线为x轴、AD边所在直线为y轴，建立如图所示的直角坐标系（点A即为原点O），把△PAD、△PAB、△PBC的面积分别记为S1、S2、S3．坐标为（a，b），试求2 S1 S3－S22的最大值，并求出此时a，b的值．18（北京）如图，在平面直角坐标系x O y中，我们把由两条射线AE，BF和以AB为直径的半圆所组成的图形叫作图形C（注：不含AB线段）．已知A（﹣1，0），B（1，0），AE∥BF，且半圆与y轴的交点D在射线AE的反向延长线上．（1）求两条射线AE，BF所在直线的距离；（2）当一次函数y=x+b的图象与图形C恰好只有一个公共点时，写出b的取值范围；当一次函数y=x+b的图象与图形C恰好只有两个公共点时，写出b的取值范围；（3）已知平行四边形AMPQ（四个顶点A，M，P，Q按顺时针方向排列）的各顶点都在图形C上，且不都在两条射线上，求点M的横坐标x的取值范围．。

中考圆有关的动点几何压轴题

北辰教育学科老师辅导讲义（2）联结AP 并延长，交边CB 延长线于点D ，设x P A =，y D B =，求y 关于x 的函数解析式，并写出定义域；（3）联结P B ，当点P 是AB 的中点时，求△ABP 的面积与△ABD 的面积比ABDABP S S ∆∆的值．定圆结合直角三角形，考察三角形相似，线段与三角形周长的函数关系2（2010•上海）如图，在Rt △ABC 中，∠ACB=90°．半径为1的圆A 与边AB 相交于点D ，与边AC 相交于点E ，连接DE 并延长，与线段BC 的延长线交于点P ．（1）当∠B=30°时，连接AP ，若△AEP 与△BDP 相似，求CE 的长；（2）若CE=2，BD=BC ，求∠BPD 的正切值；（3）若tan ∠BPD=，设CE=x ，△ABC 的周长为y ，求y 关于x 的函数关系式．定圆结合直角三角形，考察两线段函数关系，圆心距，存在性问题3．如图，在半径为5的⊙O 中，点A 、B 在⊙O 上，∠AOB=90°，点C 是弧AB 上的一个动点，AC 与OB 的延长线相交于点D ，设AC=x ，BD=y ．（1）求y 关于x 的函数解析式，并写出它的定义域；（2）如果⊙O 1与⊙O 相交于点A 、C ，且⊙O 1与⊙O 的圆心距为2，当BD=OB 时，求⊙O 1的半径；（3）是否存在点C ，使得△DCB ∽△DOC ？如果存在，请证明；如果不存在，请简要说明理由．定圆中结合平行线，弧中点，考察两线段函数关系，圆相切4（本题满分14分，第（1）小题6分，第（2）小题2分，第（3）小题6分）在半径为4的⊙O 中，点C 是以AB 为直径的半圆的中点，OD ⊥AC ，垂足为D ，点E 是射线AB 上的任意一点，DF //AB ，DF 与CE 相交于点F ，设EF =x ，DF =y ．（1）如图1，当点E 在射线OB 上时，求y 关于x 的函数解析式，并写出函数定义域；（2）如图2，当点F 在⊙O 上时，求线段DF 的长；（3）如果以点E 为圆心、EF 为半径的圆与⊙O 相切，求线段DF 的长．动圆结合直角梯形，考察圆相切和相似5（14分）（2014•金山区二模）如图，已知在梯形ABCD 中，AD ∥BC ，AB ⊥BC ，AB=4，AD=3，sin ∠DCB=，P 是边CD 上一点（点P与点C 、D 不重合），以PC 为半径的⊙P 与边BC 相交于点C 和点Q ．（1）如果BP ⊥CD ，求CP 的长； O PD C BA 第25题图备用图 O CB A A B E FCD O （第25题图1） A B EF CD O。

人教版九年级数学上册期末圆动点最值问题压轴题

人教版九年级数学上册期末圆动点最值问题压轴题一、单选题1．如图，O的直径12AB=，弦CD垂直平分半径OA，动点M从点C出发在优弧CBD 上运动到点D停止，在点M整个运动过程中，线段AM的中点P的运动路径长为（）A．3πB．4πC．5πD．6π2．如图，在Rt△ABC中，∠C＝90°，AC＝12，BC＝9，点O是AB的三等分点，半圆O与AC相切，M，N分别是BC与半圆弧上的动点，则MN的最大值与最小值之差是（）A．5 B．6 C．7 D．83．如图，线段AB＝6，点C为线段AB外一动点，45∠=︒，连接BC，M，N分别ACB为AB，BC的中点，则线段MN的最大值为（）A．3 B．4 C．2D．24．如图，已知⊙O半径OA＝4，点B为圆上的一点，点C为劣弧AB上的一动点，CD⊥OA，CE⊥OB，连接DE，要使DE取得最大值，则∠AOB等于（）A ．60°B ．90°C ．120°D ．135°5．如图，O 的半径为13，弦AB 的长为24，M 是弦AB 上的动点，则线段OM 长的最小值为（）A ．8B ．7C ．6D ．56．如图，在Rt AOB 中，OA ＝OB ＝42，⊙O 的半径为2，点P 是AB 边上的动点，过点P 作⊙O 的一条切线PQ （点Q 为切点），则线段PQ 长的最小值为（）A ．23B ．3C ．1D ．27．如图，AC 为半圆的直径，弦3AB =，30BAC ∠=︒，点E 、F 分别为AB 和AC 上的动点，则BF EF +的最小值为（）A 3B 33C ．3D ．3328．如图，AB 是⊙O 的弦，AB 长为8，P 是⊙O 上一个动点（不与A ，B 重合），过点O 作OC ⊥AP 于点C ，OD ⊥PB 于点D ，则CD 的长为（）．A ．3B ．23C ．43D ．4二、填空题 9．如图所示，AB 是O 的直径，20AB =，30CAB ∠=︒，点D 为弧BC 的中点，点P 是直径AB 上的一个动点，PC PD +的最小值为__________．10．如图，⊙O 的半径是2，AB 是⊙O 的弦，P 是弦AB 上的动点，且1≤OP ≤2，则弦AB 所对的圆心角的度数是__________．11．如图，AB 是O 的弦，5AB =，点C 是O 上的一个动点，且45ACB ∠=︒，若点M ，N 分别是AB ，AC 的中点，则MN 长的最大值是______．12．如图，在扇形ABD 中，60BAD ∠=︒，AC 平分BAD ∠交弧BD 于点C ，点P 为半径AB 上一动点，若4AB =，则阴影部分周长的最小值为___________．13．在ABC 中，90,2,3ABC AB BC ∠=︒==．点D 为平面上一个动点，45ADB ∠=︒，则线段CD 长度的最小值为_____．14．如图，在扇形AOB 中，45AOB ∠=︒，点C 是AB 的中点，点D ，E 分别为半径OA ，OB 上的动点．若2OB =，则CDE △周长的最小值为______．15．如图，矩形ABCD 中，AB ＝6，BC ＝9，M 是AB 的中点，P 是BC 边上的动点，连结PM ，以点P 为圆心，PM 长为半径作⊙P ．当⊙P 与矩形ABCD 的边CD 相切时，则BP 的长为________．三、解答题16．如图，在正方形ABCD 中，动点E ，F 分别在边DC ，CB 上移动（不与顶点重合），且满足DE CF =．连接AE 和DF ，交于点P ．（1）请你写出AE 与DF 的数量关系和位置关系，并说明理由；（2）由于点E ，F 的移动，使得点P 也随之运动．①请用文字描述并且在图中画出点P 的运动路径；②若10AD =，请求出线段CP 的最小值．17．如图，O为Rt ABC的外接圆，90,43,4∠=︒==，点D是O上的ACB BC AC、分别位于AB的两侧．动点，且点C D（1）求O的半径；∠的度数；（2）当42CD=时，求ACD（3）设AD的中点为M，在点D的运动过程中，线段CM是否存在最大值？若存在，求出CM的最大值；若不存在，请说明理由．18．如图，在△ABC中，AB＝AC，AO⊥BC于点O，OE⊥AB于点E，以点O为圆心，OE的长为半径作半圆，交AO于点F．（1）求证：AC是⊙O的切线；（2）若点F是AO的中点，OE＝3，求图中阴影部分的面积；（3）在（2）的条件下，点P是BC边上的动点，当PE＋PF取最小值时，求出BP的长．19．如图，在平行四边行ABCD 中，AB ＝5，BC ＝8，BC 边上的高AH ＝3，点P 是边BC 上的动点，以CP 为半径的⊙C 与边AD 交于点E ，F （点E 在点F 的左侧）．（1）当⊙C 经过点A 时，求CP 的长；（2）连接AP ，当AP ∥CE 时，求⊙C 的半径及弦EF 的长．20．如图，在Rt ABC 中，90ACB ∠=︒，10AB =，6AC =，点D 为BC 边上的一个动点，以CD 为直径的O 交AD 于点E ，过点C 作//CF AB ，交O 于点F ，连接CE 、EF ．（1）当45CFE ∠=︒时，求CD 的长；（2）求证：BAC CEF ∠=∠；（3）是否存在点D ，使得CFE 是以CF 为底的等腰三角形，若存在，求出此时CD 的长；若不存在，试说明理由．参考答案1．B解：如图，连接OC，设CD交AB于点E．∵CD垂直平分线段OA，∴CA=CO，∵OC=OA，∴AC=OC=OA，∴△AOC是等边三角形，∴∠CAE=60°，当点M与C重合时，连接PE，OP，∵P A=PM，∴OP⊥AM，∴∠APO=90°，∵AE=EO，OA=3，∴EP=12∵PE=AE=3，∠P AE=60°，∴△P AE是等边三角形，∴∠AEP=60°；在点M整个运动过程中，如下图，∵点P 是AM 的中点，点E 是AO 的中点， ∴1122PE OM OA AE EO ====， ∴线段AM 的中点P 的运动轨迹是图中IOJ ，∵260120IEJ ∠=⨯︒=︒，∴IOJ 的圆心角360120240=︒-︒=︒，∴运动路径的长=24034180ππ•=．故选：B ．2．D解：如图，设⊙O 与AC 相切于点D ，连接OD ，过点O 作OP ⊥BC 垂足为P 交⊙O 于F ，此时垂线段OP 最短，PF 最小值为OP ﹣OF ，∵AC ＝12，BC ＝9，∴AB 22AC BC +22129+15，∵∠OPB ＝90°，∴OP ∥AC ，,OPB ACB ∴∽2,3OP OB AC AB ∴== ∵点O 是AB 的三等分点，∴21510,3OB =⨯=， ∴OP ＝8，∵⊙O 与AC 相切于点D ，∴OD ⊥AC ，∴OD ∥BC ，,AOD ABC ∴∽ ∴13OD OA BC AB ==， ∴OD ＝3，∴MN 最小值为OP ﹣OF ＝8﹣3＝5，如图，当N 在AB 边上时，M 与B 重合时，MN 经过圆心，经过圆心的弦最长， MN 最大值＝OB +OE ＝10+3＝13，∴MN 长的最大值与最小值的差是13﹣5＝8．故选：D ．3．C解：由题知A 、B 、C 三点共圆，M ，N 分别为AB ，BC 的中点，12MN AC ∴=， ∴当AC 过圆心即AC 是直径时（如图所示），AC 取得最大值，此时MN 取的最大值， 45ACB =︒∠，90ABC ∠=︒∴此时ABC 是等腰直角三角形，BMN △是等腰直角三角形，132BM BN AB ∴===，MN ∴=故选C ．4．B解：如图，延长CD交⊙O于P，延长CE交⊙O于T，连接PT．∵OA⊥PC，OB⊥CT，∴CD＝DP，CE＝TE，∴DE＝12 PT，∴当PT是直径时，DE的长最大，连接OC，∵OP＝OC＝OT，OD⊥PC，OE⊥CT，∴∠COA＝∠POA，∠COB＝∠BOT，∴∠AOB＝∠COA+∠COB＝12∠POT＝90°，故选：B．5．D解：过O作OM AB'⊥于M'，此时线段OM'的长最短，连接OA，OM '过点O ，OM AB '⊥， 11241222AM AB '∴==⨯=，在Rt AMO △中，由勾股定理得：221691445OM OA AM ''=-=-=．故选：D ．6．A解：连接OQ ．∵PQ 是⊙O 的切线，∴OQ ⊥PQ ；根据勾股定理知PQ 2=OP 2-OQ 2，∴当PO ⊥AB 时，线段PQ 最短，∵在Rt △AOB 中，2∴2OA=8，∴OP=4OA OB AB•=， ∴2223OP OQ =-故选：A ．7．B解：作B 点关于直径AC 的对称点B′，过B′点作B′E ⊥AB 于E ，交AC 于F ，如图，则FB＝FB′，∴FB＋FE＝FB′＋FE＝B′E，此时FB＋FE的值最小，∵∠BAC＝30°，∴∠B′AC＝30°，∴∠BAB′＝60°，∵AB＝AB′，∴△ABB′为等边三角形，∵B′E⊥AB，∴AE＝BE＝32，∴B′E333即BF＋EF33故选：B．8．D∵过点O作OC⊥AP于点C，OD⊥PB于点D，∴AC=PC，BD=PD，∴CD∥AB，且CD=12AB，∵AB=8，∴CD=12AB=4．故选择：D．9．102解：作出D 关于AB 的对称点D ′，连接OC ，OD ′，CD ′．又∵点C 在⊙O 上，∠CAB =30°，D 为弧BC 的中点，即BD BD '=，∴∠BAD ′=12∠CAB =15°．∴∠CAD ′=45°．∴∠COD ′=90°．则△COD ′是等腰直角三角形．∵OC =OD ′=12AB =10，∴CD ′=2故答案为：10210．120︒解：作OD ⊥AB ，∵P 是弦AB 上的动点，且1≤OP ≤2，∴OD=1，∵⊙O 的半径是2，∴12OD OA ， ∵OA=OB ，∴30OAB OBA ==︒∠∠，∴弦AB 所对的圆心角120AOB ∠=︒，故答案为：120︒ ．11．522 解：∵点M ，N 分别是AB ，AC 的中点，∴MN =12BC ， ∵当BC 最大时，线段MN 长的最大，当BC 为⊙O 的直径时，BC 的长度最大，此时，∠A =90°，∠ACB =45°，∴直径BC =2AB =52，则线段MN 长的最大值为522，故答案为：522． 12．2423π+ 解：如图，作点C 关于AB 的对称点C '，连接C D '交OB 于点P '，连接P C '、OC '，此时P C P D ''+最小，即=P C P D C D '''+，由题意得，30DAC CAB BAC '∠=∠=∠=︒，∴90DAC '∠=︒， ∴22224442C D OC OD ''=+=+=，CD 的长3042==1803l ππ⨯， ∴阴影部分周长的最小值为242+3π，故答案为：242+3π． 13．52-如图：以12AB 为半径作圆，过圆心O 作,ON AB OM BC ⊥⊥，以O 为圆心OB 为半径作圆，则点D 在圆O 上，45ADB ∠=︒90AOB ∠=︒∴2AB =1AN BN ==22112AO ∴=+=112ON OM AB ===,3BC = 221(31)5OC ∴=+-=52CO OD ∴-=线段CD 长度的最小值为52-． 52-14．2解：如图，作点C 关于,OA OB 的对称点,M N ，连接,,,,DM EN OM OC ON ，则,,,,,DM CD OM OC AOM AOC EN CE ON OC BON BOC ==∠=∠==∠=∠， CDE ∴的周长为CD DE CE DM DE EN ++=++，由两点之间线段最短得：当点,,,M D E N 共线时，CDE △周长最小，最小值为MN ， ,AOM AOC BON BOC ∠=∠∠=∠，45AOC BOC AOB ∠+∠=∠=︒，2()90MON AOM AOC BON BOC AOC BOC ∴∠=∠+∠+∠+∠=∠+∠=︒，由同圆半径相等得：2OC OB ==，2OM ON ∴==，在Rt MON 中，2222MN OM ON +=即CDE △周长的最小值为22 故答案为：2215．4当⊙P 与直线CD 相切时，设PC ＝PM ＝x ．则PB =9-x ，132BM AB == 在Rt △PBM 中，∵222PM BM PB =+，∴2223(9)x x =+-，∴x ＝5，∴PC ＝5，∴BP ＝BC ﹣PC ＝9﹣5＝4．故答案为：4．16．解：（1）AE DF =，AE DF ⊥，理由是：∵四边形ABCD 是正方形，∴AD DC =，90ADE DCF ∠=∠=︒，∵DE CF =，在ADE 和DCF 中AD DC ADE DCF DE CF =⎧⎪∠=∠⎨⎪=⎩，∴ADE DCF ≅△△，∴AE DF =，DAE FDC ∠=∠∵90ADE ∠=︒，∴90ADP FDC ∠+∠=︒，∴90ADP DAE ∠+∠=︒，∴1809090APD ∠=︒-︒=︒，∴AE DF ⊥；（2）如图，①∵点P 在运动中保持90APD ∠=︒，设正方形ABCD 的中心为O ， ∴得出点P 的运动路径是以AD 为直径的圆的圆弧DPO （去除端点D ，O ），②设AD 的中点（圆心）为G ，连接CG 交圆弧于点P ，此时线段CP 的长度最小．在Rt CDG 中，222210555CG CD DG ++∴555=-=-CP CG GP即线段CP的最小值是555-．17．（1）4；（2）15°；（3）存在，232+解：（1）如图1中，∵AB是直径，∴∠ACB＝90°，∵AC＝4，BC＝3∴AB2222++=8，4(43)AC BC∴⊙O的半径为4．（2）如图1中，连接OC，OD．∵CD＝2，OC＝OD＝4，∴CD2＝OC2+OD2，∴∠COD＝90°，∴∠OCD＝45°，∵AC＝OC＝OA，∴△AOC是等边三角形，∴∠ACO＝60°，∴∠ACD＝∠ACO﹣∠DCO＝60°﹣45°＝15°．（3）如图2中，连接OM，OC．∵AM＝MD，∴OM⊥AD，∴点M的运动轨迹以AO为直径的⊙J，连接CJ，JM．∵△AOC是等边三角形，AJ＝OJ，∴CJ⊥OA，∴CJ22=-=23，AC AJ∵CM≤CJ+JM＝23+2，∴CM的最大值为23+2．18．【详解】（1）证明：如图，过O作AC的垂线OM，垂足为M．∵AB＝AC，AO⊥BC，∴AO平分∠BAC，∵OE⊥AB，OM⊥AC，∴ OE ＝OM ，∵ OE 为⊙O 的半径，∴ OM 为⊙O 的半径，∴ AC 是⊙O 的切线．（2）解：∵OM ＝OE ＝OF ＝3．且F 是OA 的中点，∴ AO ＝6，在Rt ΔAEO 中，AE ＝33， ∴ AEO S ＝12OE AE ＝932． ∵ OE ⊥AB ，在Rt ΔAEO 中，∠OEA ＝90°，AO ＝6，AE ＝33，OE ＝3，∴ ∠EOF ＝60°，∴ OEF S 扇形＝260333602ππ⋅=， ∴ S 阴影AEO OEF S S =-扇形△93322π=-．（3）解：如图，作点F 关于BC 的对称点G ，连接EG 交BC 于P ，∵ =PF PG ，∴ PE PF PE PG EG +=+=，此时EP +FP 最小，∵ OG =OF =OE ，∴ =G OEG ∠∠，而 =+=60AOE G OEG ︒∠∠∠，∴=30G︒∠，∴=G EAG∠∠，∴33EG EA==，即PE PF+最小值为33，在Rt OPG中，333OP OG==，在Rt ABO中，3362333OB OA==⨯=，∴=23-3=3BP，即当PE＋PF取最小值时，BP的长为3．19．（1）CP＝5；（2）⊙C的半径为258，EF＝74．解：（1）连接AC，如图1所示：∵AH⊥BC，∴∠AHB＝∠AHC＝90°，∴BH＝2222534AB AH-=-=，∴CH＝BC﹣BH＝4，∴CA＝225AH CH+=，当⊙C经过点A时，CP＝CA＝5；（2）∵四边形ABCD是平行四边形，∴AD∥BC，当AP∥CE时，四边形APCE是平行四边形，∵CP＝CE，∴四边形APCE是菱形，∴P A＝CP，设P A＝CP＝x，则PH＝4﹣x，在Rt△APH中，由勾股定理得：AH2+PH2＝P A2，即32+（4﹣x ）2＝x 2，解得：x ＝258，即⊙C 的半径为258，作CM ⊥EF 于M ，如图2所示：则CM ＝AH ＝3，ME ＝MF ＝12EF ，在Rt △CEM 中，由勾股定理得：ME ＝2222257()388CE CM -=-=， ∴EF ＝2ME ＝74．20．解：（1）∵45CDE CFE ∠=∠=︒，90ACB ∠=︒∴45DAC CDA ∠=∠=︒∴6CD AC ==（2）∵//CF AB ，∴B FCB ∠=∠，∵FCB DEF ∠=∠，∴B DEF ∠=∠，①又90BAC B ∠+∠=︒②∵CD 是圆O 的直径，90CED ∠=︒，∴90DEF CEF ∠+∠=︒③由①②③可得BAC CEF ∠=∠（3）CFE 是CF 为底的等腰三角形，则EF CE =，则∠EFC =∠ECF ．连接FD ，并延长和AB 相交于G ，∵四边形CEDF为圆内接四边形，∴∠ADG=∠ECF，又∵∠CDE=∠CFE，∴∠ADG=∠CDE，∵CD为⊙O的直径，∴∠DFC=90°，∵FC∥AB，∴∠FGA=90°，∴∠FGA=∠ACD，∵AD=AD，∴△AGD≌△ACD（AAS），∴DG=CD，在Rt△BDG中，设CD=x，BG2+DG2=BD2，∴42+x2=（8-x）2，解得x=3，即CD=3。

中考数学---与圆有关的动点几何压轴题1

中考数学---与圆有关的动点几何压轴题1定圆结合直角三角形：1、已知：如图，在Rt △ABC 中， 90=∠C ，4=BC ，21tan =∠CAB ，点O 在边AC 上，以点O 为圆心的圆过A 、B 两点，点P 为AB 上一动点.（1）求⊙O 的半径；（2）联结AP 并延长，交边CB 延长线于点D ，设x P A =，y D B =，求y 关于x 的函数解析式，并写出x 的取值范围；（3）联结P B ，当点P 是AB 的中点时，求△ABP 的面积与△ABD 的面积比ABDABPS S ∆∆的值．2、如图，在Rt △ABC 中，∠ACB=90°．半径为1的圆A 与边AB 相交于点D ，与边AC 相交于点E ，连接DE 并延长，与线段BC 的延长线交于点P ．（1）当∠B=30°时，连接AP ，若△AEP 与△BDP 相似，求CE 的长；（2）若CE=2，BD=BC ，求∠BPD 的正切值；（3）若tan ∠BPD=，设CE=x ，△ABC 的周长为y ，求y 关于x 的函数关系式．PD第1题图备用图B3、如图，在半径为5的⊙O 中，点A 、B 在⊙O 上，∠AOB=90°，点C 是弧AB 上的一个动点，AC 与OB 的延长线相交于点D ，设AC=x ，BD=y ．（1）求y 关于x 的函数解析式，并写出它的定义域；（2）如果⊙O 1与⊙O 相交于点A 、C ，且⊙O 1与⊙O 的圆心距为2，当BD=OB 时，求⊙O 1的半径；（3）是否存在点C ，使得△DCB ∽△DOC ？如果存在，请证明；如果不存在，请简要说明理由．定圆中结合平行线：2、在半径为4的⊙O 中，点C 是以AB 为直径的半圆的中点，OD ⊥AC ，垂足为D ，点E 是射线AB 上的任意一点，DF //AB ，DF 与CE 相交于点F ，设EF =x ，DF =y ．（1）如图1，当点E 在射线OB 上时，求y 关于x 的函数解析式，并写出函数定义域；（2）如图2，当点F 在⊙O 上时，求线段DF 的长；（3）如果以点E 为圆心、EF 为半径的圆与⊙O 相切，求线段DF 的长．ABEFCDOABF C D O动圆结合直角梯形：5、如图，已知在梯形ABCD 中，AD ∥BC ，AB ⊥BC ，AB=4，AD=3，sin ∠DCB=，P 是边CD 上一点（点P 与点C 、D 不重合），以PC 为半径的⊙P 与边BC 相交于点C 和点Q ．（1）如果BP ⊥CD ，求CP 的长；（2）如果PA=PB ，试判断以AB 为直径的⊙O 与⊙P 的位置关系；（3）联结PQ ，如果△ADP 和△BQP 相似，求CP 的长．动圆结合内切直角三角形：6、在△ABC 中，∠ABC ＝90°，AB ＝4，BC ＝3，O 是边AC 上的一个动点，以点O 为圆心作半圆，与边AB 相切于点D ，交线段OC 于点E ，作EP ⊥ED ，交射线AB 于点P ，交射线CB 于点F 。

2020-2021中考数学与圆的综合有关的压轴题附详细答案.doc

2020-2021 中考数学与圆的综合有关的压轴题附详细答案一、圆的综合1．如图，已知△ ABC中， AC=BC，以 BC 为直径的⊙ O 交 AB 于 E，过点 E 作 EG⊥AC 于G，交 BC的延长线于F．（1）求证： AE=BE；（2）求证： FE是⊙ O 的切线；（3）若 FE=4，FC=2，求⊙ O 的半径及 CG的长．【答案】（ 1）详见解析；（2）详见解析；（3） .【解析】（ 1）证明：连接CE，如图 1 所示：∵BC 是直径，∴ ∠ BEC=90 ，°∴ CE⊥AB；又∵ AC=BC，∴ AE=BE．（2）证明：连接OE，如图 2 所示：∵B E=AE， OB=OC，∴ OE 是△ ABC的中位线，∴ OE∥ AC， AC=2OE=6．又∵ EG⊥ AC，∴ FE⊥OE，∴ FE 是⊙O 的切线．（3）解：∵ EF是⊙ O 的切线，∴ FE2=FC?FB．设FC=x，则有 2FB=16，∴ FB=8，∴ BC=FB﹣ FC=8﹣ 2=6，∴ OB=OC=3，即⊙O 的半径为3；∴OE=3．∵OE∥ AC，∴ △ FCG∽ △ FOE，∴，即，解得：CG=．点睛：本题利用了等腰三角形三线合一定理，三角形中位线的判定，切割线定理，以及勾股定理，还有平行线分线段成比例定理，切线的判定等知识．2．如图，在△ ABC中， AB＝ AC，以 AB 为直径作⊙ O，⊙ O 交 BC 于点 D，交 CA 的延长线于点 E．过点 D 作 DF⊥ AC，垂足为 F．（1）求证： DF 为⊙ O 的切线；（2）若 AB＝ 4，∠ C＝ 30°，求劣弧?的长．BE【答案】（ 1）证明见解析（2）43【解析】分析：（ 1）连接 AD、 OD，根据直径所对的圆周角为直角，可得∠ADB=90°，然后根据等腰三角形的性质求出 BD=CD，再根据中位线的性质求出 OD⊥DF，进而根据切线的判定证明即可；（2）连接 OE，根据三角形的外角求出∠ BAE的度数，然后根据圆周角定理求出∠ BOE 的度数，根据弧长公式求解即可 .详解：（ 1）连接 AD、 OD．∵ AB 是直径，∴ ∠ADB＝ 90°．∵AB＝ AC，∴ BD＝ CD，又∵ OA＝ OB，∴ OD 是△ ABC的中位线，∴ OD∥ AC，∵D F⊥ AC，∴ OD⊥ DF即∠ ODF＝90°．∴ DF 为⊙ O 的切线；（2）连接 OE．∵ AB＝ AC，∴ ∠B＝∠C＝30°，∴∠ BAE＝60°，∵∠ BOE＝ 2∠BAE，∴ ∠ BOE＝ 120 ，°∴＝· 4＝π π．点睛：本题是圆的综合题，考查了等腰三角形的性质和判定、切线的性质和判定、三角形的中位线、圆周角定理，灵活添加辅助线是解题关键．3．如图，在VABC中，ACB 90o，BAC的平分线AD交BC于点D，过点D作DE AD 交AB于点E，以AE为直径作e O．1 求证：BC是 e O 的切线；2 若 AC3 ， BC4 ，求 tan EDB 的值．【答案】（ 1）见解析；（2）tan EDB1 ．2【解析】【分析】1 连接OD，如图，先证明OD/ /AC ，再利用 AC BC 得到 OD BC ，然后根据切线的判定定理得到结论；2 先利用勾股定理计算出AB 5，设 e O 的半径为r，则 OA OD r ， OB 5 r ，再证明 VBDO ∽ VBCA ，利用相似比得到r： 3 5 r ： 5，解得r 15，接着利用勾8股定理计算 BD 5CD3tan1，然后证明，则，利用正切定理得 12 2 21EDB ，从而得到 tan EDB 的值．【详解】1证明：连接 OD，如图，Q AD 平分BAC ，1 2 ，Q OA OD ，2 3 ，1 3 ，OD / / AC ，Q AC BC ，OD BC ，BC 是 e O 的切线；2解：在 RtVACB 中，AB 设e O 的半径为r，则 OA ODQ OD / / AC ，VBDO ∽ VBCA ，OD ： AC BO ：BA，32425，r ， OB 5 r ，即 r：3 5 r ：5 ，解得 r 15，8OD 15 25 ， OB ，8 8在 RtVODB 中， BDOB 2 OD 25 ，2CD BCBD3，2在 RtVACD 中， tanCD31 ，1 2AC3 2Q AE 为直径，ADE 90o ，EDB ADC90o，Q 1ADC90o ，1EDB ，1tan EDB ．2【点睛】本题考查了切线的判定与性质：经过半径的外端且垂直于这条半径的直线是圆的切线；圆的切线垂直于经过切点的半径 .判定切线时 “连圆心和直线与圆的公共点 ”或 “过圆心作这条直线的垂线 ”；也考查了圆周角定理和解直角三角形．4．如图， △ ABC 的内接三角形， P 为 BC 延长线上一点， ∠ PAC=∠ B ， AD 为 ⊙O 的直径，过 C 作 CG ⊥ AD 于 E ，交 AB 于 F ，交 ⊙O 于 G ．（1）判断直线 PA 与 ⊙ O 的位置关系，并说明理由；（2）求证： AG 2=AF ·AB ；（3）若 ⊙ O 的直径为 10， AC=2 5 ， AB=4 5 ，求 △ AFG 的面积 .【答案】（ 1） PA 与 ⊙ O 相切，理由见解析；（ 2）证明见解析；（ 3） 3.【解析】试题分析：（ 1）连接 CD ，由 AD 为⊙ O 的直径，可得 ∠ ACD=90°，由圆周角定理，证得∠B=∠ D ，由已知 ∠ PAC=∠ B ，可证得 DA ⊥ PA ，继而可证得 PA 与⊙ O 相切．（2）连接 BG ，易证得 △ AFG ∽ △ AGB ，由相似三角形的对应边成比例，证得结论.（3）连接 BD ，由 AG 2=AF?AB ，可求得 AF 的长，易证得 △ AEF ∽ △ ABD ，即可求得 AE 的长，继而可求得 EF 与 EG 的长，则可求得答案．试题解析：解：（ 1） PA 与 ⊙ O 相切．理由如下：如答图 1，连接 CD ，∵AD 为 ⊙ O 的直径， ∴ ∠ ACD=90 .°∴∠ D+∠CAD=90 .°∵∠ B=∠D ， ∠PAC=∠ B ， ∴ ∠PAC=∠D.∴∠ PAC+∠ CAD=90 ，°即 DA ⊥PA.∵点 A 在圆上，∴PA 与⊙ O 相切．（2）证明：如答图 2，连接 BG ，∵AD 为 ⊙ O 的直径， CG ⊥ AD ， ∴??.∴ ∠AGF=∠ ABG.AC AD∵∠ GAF=∠ BAG ， ∴ △ AGF ∽ △ABG. ∴AG ： AB=AF ： AG. ∴ AG 2=AF?AB.（3）如答图 3，连接 BD ，∵AD 是直径， ∴ ∠ ABD=90 .°∵AG 2=AF?AB ， AG=AC=2 5 ， AB=4 5 ， ∴ AF= 5 .∵CG ⊥AD ， ∴ ∠AEF=∠ ABD=90 .°AE AF AE 5 ∵∠ EAF=∠ BAD ， ∴△ AEF ∽ △ ABD. ∴，即4 5，解得： AE=2.ABAD10∴ EFAF2AE21.∵EGAG 2 AE 24 ， ∴ FGEG EF 41 3 .∴SAFG1FG AE 13 23 ．22考点： 1. 圆周角定理； 2.直角三角形两锐角的关系； 3. 相切的判定； 4.垂径定理； 5.相似三角形的判定和性质； 6.勾股定理； 7.三角形的面积 .5．四边形 ABCD 的对角线交于点 E ，且 AE ＝ EC ， BE ＝ ED ，以 AD 为直径的半圆过点 E ，圆心为 O ．（1）如图 ① ，求证：四边形ABCD 为菱形；（2）如图 ② ，若 BC 的延长线与半圆相切于点F ，且直径 AD ＝6，求弧 AE 的长．【答案】（ 1）见解析；（ 2）π2【解析】试题分析：（ 1）先判断出四边形ABCD 是平行四边形，再判断出AC ⊥ BD 即可得出结论；（ 2）先判断出 AD=DC 且 DE ⊥ AC ，∠ ADE=∠ CDE ，进而得出 ∠CDA=30°，最后用弧长公式即可得出结论．试题解析：证明：（ 1） ∵ 四边形 ABCD 的对角线交于点 E ，且 AE=EC ，BE=ED ， ∴ 四边形 ABCD 是平行四边形． ∵以 AD 为直径的半圆过点 E ，∴ ∠ AED=90 °，即有 AC ⊥BD ， ∴ 四边形 ABCD 是菱形；（2）由（ 1）知，四边形 ABCD 是菱形， ∴ △ ADC 为等腰三角形， ∴ AD=DC 且 DE ⊥ AC ，∠ADE=∠ CDE．如图 2，过点 C 作 CG⊥AD，垂足为G，连接 FO．∵ BF 切圆 O 于点 F，∴OF⊥ AD，且OF1 AD 3 ，易知，四边形CGOF为矩形，∴CG=OF=3．2在Rt△ CDG中， CD=AD=6， sin∠ADC= CG=1，∴∠ CDA=30°，∴ ∠ ADE=15°．CD 2? 30 3 连接 OE，则∠ AOE=2×∠ADE=30°，∴AE180．2点睛：本题主要考查菱形的判定即矩形的判定与性质、切线的性质，熟练掌握其判定与性质并结合题意加以灵活运用是解题的关键．6．如图， AB 是⊙ O 的直径，点 C，D 是半圆 O 的三等分点，过点 C 作⊙ O 的切线交 AD 的延长线于点 E，过点 D 作 DF⊥AB 于点 F，交⊙ O 于点 H，连接 DC， AC．（1）求证：∠ AEC=90°；（2）试判断以点 A， O， C， D 为顶点的四边形的形状，并说明理由；（3）若 DC=2，求 DH 的长．【答案】（ 1）证明见解析；（2）四边形 AOCD 为菱形；（3） DH=2 ．【解析】试题分析：（ 1）连接 OC，根据 EC与⊙ O 切点 C，则∠ OCE=90°，由题意得，∠DAC=∠ CAB，即可证明AE∥OC，则∠ AEC+∠ OCE=180°，从而得出∠A EC=90 ；°（2）四边形AOCD 为菱形．由（ 1）得平行四边形，再由OA=OC，即可证明平行四边形，则∠DCA=∠ CAB 可证明四边形AOCD是AOCD是菱形（一组邻边相等的平行四边形是菱形）；（3）连接 OD．根据四边形AOCD为菱形，得△ OAD 是等边三角形，则∠ AOD=60°，再由DH⊥ AB 于点 F， AB 为直径，在Rt△OFD 中，根据sin∠AOD=，求得DH的长．试题解析：（ 1）连接 OC，∵EC与⊙ O 切点 C，∴OC⊥ EC，∴∠ OCE=90，°∵点 CD是半圆 O 的三等分点，∴，∴∠ DAC=∠ CAB，∵OA=OC，∴∠ CAB=∠ OCA，∴∠ DAC=∠ OCA，∴AE∥ OC（内错角相等，两直线平行）∴∠ AEC+∠ OCE=180 ，°∴∠ AEC=90 ；°（2）四边形AOCD 为菱形．理由是：∵，∴∠ DCA=∠ CAB，∴CD∥OA，又∵ AE∥ OC，∴四边形 AOCD是平行四边形，∵OA=OC，∴平行四边形AOCD是菱形（一组邻边相等的平行四边形是菱形）；（3）连接 OD．∵四边形 AOCD为菱形，∴OA=AD=DC=2，∵OA=OD，∴O A=OD=AD=2，∴△ OAD 是等边三角形，∴∠ AOD=60 ，°∵DH⊥ AB 于点 F， AB 为直径，∴D H=2DF，在 Rt△ OFD中， sin∠ AOD=，∴D F=ODsin∠ AOD=2sin60 = °，∴D H=2DF=2 ．考点： 1.切线的性质 2.等边三角形的判定与性质 3.菱形的判定与性质 4.解直角三角形．7．如图，△ ABC 内接于⊙ O，且 AB 作⊙ O 的切线 PD 交 CA 的延长线于点F．为⊙ O 的直径．∠ ACB 的平分线交⊙ O 于点 D，过点 D P，过点 A 作 AE⊥ CD 于点 E，过点 B 作 BF⊥ CD 于点（1）求证： DP∥ AB；（2）若 AC=6， BC=8，求线段 PD 的长．【答案】详见解析【解析】【分析】（1）连接 OD，由 AB 为⊙O 的直径，根据圆周角定理得∠ ACB=90°，再由∠ACD=∠ BCD=45 ，°则∠ DAB=∠ ABD=45 ，°所以△DAB 为等腰直角三角形，所以 DO⊥AB，根据切线的性质得 OD⊥PD，于是可得到 DP∥ AB．（2）先根据勾股定理计算出AB=10，由于△ DAB 为等腰直角三角形，可得到AD AB 105 2 ；由△ACE为等腰直角三角形，得到2 2AE CE AC 6DE=4 2，则23 2 ，在Rt△AED中利用勾股定理计算出2CD=7 2，易证得∴△ PDA∽ △PCD，得到PDPA AD 5 2 ，所以 PA= 5 P D，PC PD CD 7 2 77 PC= PD ，然后利用 PC=PA+AC 可计算出 PD ．5【详解】解：（ 1）证明：如图，连接OD ，∵AB 为 ⊙ O 的直径， ∴ ∠ ACB=90 ．°∵∠ ACB 的平分线交 ⊙ O 于点 D ， ∴ ∠ACD=∠BCD=45 ．° ∴∠ DAB=∠ ABD=45 ．°∴ △ DAB 为等腰直角三角形．∴DO ⊥AB ．∵PD 为 ⊙ O 的切线， ∴ OD ⊥ PD ．∴DP ∥ AB ．（2）在 Rt △ACB 中，，∵△ DAB 为等腰直角三角形， ∴．∵AE ⊥ CD ， ∴△ ACE 为等腰直角三角形． ∴在 Rt △ AED 中，∴．∵AB ∥ PD ，∴ ∠ PDA=∠ DAB=45 ．°∴ ∠ PAD=∠ PCD ．又∵ ∠ DPA=∠CPD ， ∴ △ PDA ∽ △ PCD ． ∴7 5∴ P A= PD ， PC= PD ．57又∵ PC=PA+AC ， ∴ 7PD+6= 5 PD ，解得 PD= ．578．如图，已知在 △ ABC 中， ∠ A=90°，．，．（1）请用圆规和直尺作出⊙ P，使圆心 P 在 AC 边上，且与 AB， BC 两边都相切（保留作图痕迹，不写作法和证明）．（2）若∠ B=60°， AB=3，求⊙ P 的面积．【答案】（ 1）作图见解析；（2） 3π【解析】【分析】（1）与 AB、 BC 两边都相切．根据角平分线的性质可知要作∠ ABC的角平分线，角平分线与AC 的交点就是点 P 的位置．（2）根据角平分线的性质和 30°角的直角三角形的性质可求半径，然后求圆的面积．【详解】解：（ 1）如图所示，则⊙ P 为所求作的圆．（2）∵ ∠ ABC=60°， BP平分∠ABC，∴∠ ABP=30 ，°∵ ∠A=90 ，°∴BP=2APRt△ ABP 中 ,AB=3，由勾股定理可得： AP= 3，∴ S⊙P=3 π9．如图，在 Rt△ ABC中，C 90， AD 平分∠ BAC，交 BC于点 D，点 O 在 AB 上，⊙ O 经过A、 D 两点，交 AC于点 E，交 AB 于点 F．（1）求证： BC是⊙ O 的切线；（2）若⊙O 的半径是 2cm， E 是弧 AD 的中点，求阴影部分的面积（结果保留π和根号）【答案】（ 1）证明见解析（ 2）23 3【解析】【分析】（1）连接 OD，只要证明 OD∥ AC即可解决问题；（2）连接 OE，OE 交 AD 于 K．只要证明△AOE是等边三角形即可解决问题．【详解】（1）连接 OD．∵OA=OD，∴∠ OAD=∠ ODA．∵∠ OAD=∠ DAC，∴ ∠ODA=∠ DAC，∴ OD∥ AC，∴ ∠ ODB=∠ C=90 °，∴OD⊥BC，∴ BC 是⊙O 的切线．（2）连接 OE，OE 交 AD 于 K．∵ ??，∴OE⊥AD．AE DE∵∠ OAK=∠ EAK， AK=AK，∠ AKO=∠ AKE=90 ，°∴ △ AKO≌ △ AKE，∴AO=AE=OE，∴△ AOE602 23 222是等边三角形，∴ ∠AOE=60°，∴ S 阴=S 扇形OAE﹣ S△AOE 3 ．360 4 3【点睛】本题考查了切线的判定、扇形的面积、等边三角形的判定和性质、平行线的判定和性质、全等三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，灵活运用所学知识解决问题，属于中考常考题型．10．如图 1，已知⊙ O 是ADB的外接圆，∠ ADB 的平分线D C交 AB 于点 M，交⊙ O 于点C，连接 AC，BC．（1）求证： AC=BC；（2）如图 2，在图 1 的基础上做⊙ O 的直径 CF交 AB 于点 E，连接 AF，过点线AH，若 AH//BC，求∠ ACF的度数；（3）在（ 2）的条件下，若ABD的面积为6 3 ，ABD与ABC的面积比为的长 . A作⊙O 的切2： 9，求 CD【答案】（ 1）证明见解析；（2） 30°；（ 3）233【解析】分析：（ 1）运用“在同圆或等圆中，弧相等，所对的弦相等”可求解；（2）连接 AO 并延长交BC 于 I 交⊙O 于 J,由 AH 是⊙O 的切线且AH∥ BC 得 AI⊥ BC，易证∠I AC=30 ，°故可得∠ ABC=60 =°∠ F=∠ACB，由 CF是直径可得∠ ACF的度数；（3）过点 D 作 DG⊥AB ，连接 AO，知 ABC为等边三角形，求出AB、 AE 的长，在Rt AEO 中，求出AO 的长，得CF的长，再求DG 的长，运用勾股定理易求CD的长 .详解：（ 1）∵ DC平分∠ ADB，∴ ∠ADC=∠ BDC，∴ AC=BC．（2）如图，连接AO 并延长交BC于 I 交⊙ O 于 J∵AH 是⊙ O 的切线且AH∥ BC，∴A I⊥ BC，∴BI=IC，∵AC=BC，1∴I C= AC，2∴∠ IAC=30 ，°∴∠ ABC=60 =°∠ F=∠ ACB．∵FC 是直径，∴∠ FAC=90，°∴∠ ACF=180 -90° -°60 =30° ．°（3）过点 D 作DG AB ，连接AO由（ 1）（ 2）知 ABC为等边三角形∵∠ ACF=30 ，°∴AB CF ，∴A E=BE，∴ S ABC 3 AB2 27 3 ，4∴A B=6 3，∴AE 3 3 ．在Rt AEO中，设 EO=x，则 AO=2x，∴ AO2 AE 2 OE 2，23 3 2∴ 2x x2，∴x=6，⊙ O 的半径为 6，∴C F=12．∵SABD AB DG 1 16 3 DG 6 3 ，2 2∴DG=2．如图，过点 D 作DG CF ,连接OD．∵ AB CF , DG AB ，∴CF//DG，∴四边形 G′DGE为矩形，∴G E 2 ，CG G E CE 6 3 2 11，在 Rt OG D 中，OG 5, OD 6 ，∴DG11，∴ CD DG 2 CG 2 11 112 2 33点睛：本题是一道圆的综合题.考查了圆的基本概念，垂径定理，勾股定理，圆周角定理等相关知识 .比较复杂，熟记相关概念是解题关键.11．如图，点 B 在数轴上对应的数是﹣2，以原点 O 为原心、 OB 的长为半径作优弧AB，使点 A 在原点的左上方，且tan ∠ AOB＝ 3 ，点C为OB的中点，点 D 在数轴上对应的数为 4．（1） S 扇形AOB＝（大于半圆的扇形）；（2）点 P 是优弧 AB 上任意一点，则∠ PDB的最大值为°（3）在（ 2）的条件下，当∠ PDB最大，且∠ AOP＜ 180°时，固定△ OPD 的形状和大小，以原点 O 为旋转中心，将△ OPD 顺时针旋转α（ 0°≤α≤）360°①连接 CP， AD．在旋转过程中，CP与 AD 有何数量关系，并说明理由；②当 PD∥ AO 时，求 AD2的值；③直接写出在旋转过程中，点 C 到 PD 所在直线的距离 d 的取值范围．【答案】（ 1）10（2）30（3）①AD＝2PC②20+8 3 或20+83③1≤d≤3 3【解析】【分析】（1）利用扇形的面积公式计算即可．（2）如图 1 中，当 PD 与⊙ O 相切时，∠ PDB的值最大．解直角三角形即可解决问题．（3）①结论： AD＝ 2PC．如图 2 中，连接 AB， AC．证明△ COP∽ △ AOD，即可解决问题．②分两种情形：如图 3 中，当 PD∥OA 时，设 OD 交⊙ O 于 K，连接 PK 交 OC于 H．求出PC 即可．如图④中，当 PA∥ OA 时，作 PK⊥ OB 于 K，同法可得．③判断出 PC的取值范围即可解决问题．【详解】（1）∵ tan ∠ AOB＝3，∴∠ AOB＝60 °，∴S 扇形AOB＝30022 10 （大于半圆的扇形），360 3（2）如图 1 中，当 PD 与⊙ O 相切时，∠ PDB的值最大．∵PD 是⊙ O 的切线，∴OP⊥ PD，∴∠ OPD＝ 90 °，∵ sin PDOOP 2 1OD 4 2∴∠ PDB＝ 30 °，同法当 DP′与⊙ O 相切时，∠ BDP′＝30°，∴∠ PDB 的最大值为30 °．故答案为 30．（3）①结论： AD＝ 2PC．理由：如图 2 中，连接 AB， AC．∵OA＝OB，∠ AOB＝ 60 °，∴△ AOB 是等边三角形，∵BC＝ OC，∴AC⊥ OB，∵∠ AOC＝∠ DOP＝60 °，∴∠ COP＝∠ AOD，∵AO OD2 ，OC OP∴△ COP∽△ AOD，∴AD AO 2，PC OC∴AD＝ 2PC．②如图 3 中，当 PD∥ OA 时，设 OD 交⊙ O 于 K，连接 PK交 OC于 H．∵OP＝ OK，∠ POK＝ 60 °，∴△ OPK是等边三角形，∵PD∥ OA，∴∠ AOP＝∠ OPD＝ 90 °，∴∠ POH+∠ AOC＝ 90 °，∵∠ AOC＝ 60 °，∴∠ POH＝ 30 °，1∴PH＝ OP＝1， OH＝ 3 PH＝ 3 ，2∴PC＝PH2 CH 2 12 (1 3) 2 5 2 3，∵AD＝ 2PC，∴AD2＝ 4（ 5+2 3 ）＝20+8 3 ．如图④中，当PA∥ OA 时，作 PK⊥ OB 于 K，同法可得：2 2 2＝5﹣PC＝ 1 +（ 3 ﹣1）2 3， AD2＝ 4PC2＝ 20﹣83 ．③由题意 1≤PC≤3，∴在旋转过程中，点 C 到 PD 所在直线的距离 d 的取值范围为 1 ≤d≤3．【点睛】本题属于圆综合题，考查了切线的性质，相似三角形的判定和性质，旋转变换，勾股定理，等边三角形的判定和性质等知识，解题的关键是学会用分类讨论的思想思考问题．12．如图，四边形为菱形，且，以为直径作，与交于点．请仅用无刻度的直尺按下列要求画图．(保留作图痕迹 )(1)在如图中，过点作边上的高．(2)在如图中，过点作的切线，与交于点．【答案】 (1)如图 1 所示． (答案不唯一 ),见解析； (2) 如图 2 所示． (答案不唯一 )，见解析 . 【解析】【分析】（1）连接 AC交圆于一点 F，连接 PF 交 AB 于点 E,连接 CE即为所求．（2）连接 OF交 BC于 Q，连接 PQ 即为所求．【详解】(1)如图 1 所示． (答案不唯一 )(2)如图 2 所示． (答案不唯一 )【点睛】本题考查作图 -复杂作图，菱形和圆的性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．13．如图，已知 AB 是⊙O 的直径， BC 是弦，弦 BD 平分∠ABC交 AC 于 F，弦 DE⊥ AB 于H，交 AC于 G．①求证： AG＝ GD；②当∠ ABC满足什么条件时，△ DFG是等边三角形？③若 AB＝ 10， sin∠ ABD＝3，求 BC 的长．5【答案】（ 1）证明见解析；（2）当∠ ABC＝60°时，△ DFG是等边三角形．理由见解析；（3） BC 的长为14．5【解析】【分析】（1）首先连接 AD，由 DE⊥AB， AB 是e O AD AE的直径，根据垂径定理，即可得到? ? ，然后根据在同圆或等圆中，同弧或等弧所对的圆周角相等，证得∠ ADE＝∠ ABD，又由弦BD 平分∠ABC，可得∠DBC＝∠ABD，根据等角对等边的性质，即可证得AG=GD；（2）当∠ ABC=60°时，△ DFG是等边三角形，根据半圆（或直径）所对的圆周角是直角与三角形的外角的性质，易求得∠DGF=∠ DFG=60°，即可证得结论；（3）利用三角函数先求出tan∠ ABD 3，cos∠ABD＝4，再求出DF、BF，然后即可求出4 5BC.【详解】（1）证明：连接AD，∵DE⊥AB， AB 是⊙ O 的直径，∴?? ，AD AE∴∠ ADE＝∠ ABD，∵弦 BD 平分 ∠ ABC ，∴∠ DBC ＝ ∠ABD ，∵∠ DBC ＝ ∠DAC ，∴∠ ADE ＝∠ DAC ，∴AG ＝ GD ；（ 2）解：当 ∠ ABC ＝ 60°时， △ DFG 是等边三角形．理由： ∵ 弦 BD 平分 ∠ ABC ，∴∠ DBC ＝ ∠ABD ＝30 °， ∵AB 是 ⊙ O 的直径， ∴∠ ACB ＝ 90 °，∴∠ CAB ＝ 90 °﹣ ∠ ABC ＝ 30 °，∴∠ DFG ＝ ∠ FAB+∠ DBA ＝ 60 °，∵DE ⊥AB ，∴∠ DGF ＝ ∠ AGH ＝ 90 °﹣ ∠ CAB ＝ 60 °，∴△ DGF 是等边三角形；（ 3）解： ∵ AB 是 ⊙ O 的直径， ∴∠ ADB ＝∠ ACB ＝ 90 °， ∵∠ DAC ＝ ∠ DBC ＝ ∠ABD ，∵AB ＝ 10， sin ∠ABD ＝ 3，5∴在 Rt △ ABD 中， AD ＝ AB?sin ∠ ABD ＝ 6， ∴BD ＝AB 2 BD 2 ＝ 8，∴tan ∠ ABD ＝AD3 ， cos ∠ ABD ＝ BD =4 ，BD4 AB 5在 Rt △ ADF 中， DF ＝AD?tan ∠ DAF ＝ AD?tan ∠ ABD ＝ 6×3 ＝ 9，42∴ B F ＝ BD ﹣ DF ＝ 8﹣ 9 ＝ 7，2 27 4 ＝ 14 ∴在 Rt △ BCF 中， BC ＝ BF?cos ∠ DBC ＝ BF?cos ∠ ABD ＝×．2 55∴BC 的长为： 14 ．5【点睛】此题考查了圆周角定理、垂径定理、直角三角形的性质、三角函数的性质以及勾股定理等知识．此题综合性较强，难度较大，解题的关键是掌握数形结合思想与转化思想的应用，注意辅助线的作法．14．如图，已知AB 是⊙O 的直径，直线CD 与⊙ O 相切于 C 点， AC平分∠DAB．（1）求证： AD⊥ CD；（2）若 AD＝2， AC= 6，求⊙ O 的半径 R 的长．【答案】（ 1）证明见解析（2）32【解析】试题分析：（ 1）连接 OC，由题意得OC⊥CD．又因为 AC 平分∠ DAB，则1∠1=∠ 2= ∠ DAB．即可得出 AD∥ OC，则 AD⊥ CD；2（2）连接 BC，则∠ ACB=90°，可证明△ ADC∽ △ACB．则试题解析：（ 1）证明：连接 OC，AD AC，从而求得R．AC2R∵直线 CD 与⊙O 相切于 C 点， AB 是⊙ O 的直径，∴OC⊥CD．又∵ AC平分∠ DAB，1∴∠ 1=∠ 2=∠ DAB．2又∠ COB=2∠ 1=∠DAB，∴AD∥ OC，∴AD⊥ CD．（2）连接 BC，则∠ ACB=90°，在△ ADC和△ ACB中∵∠ 1=∠ 2，∠ 3=∠ ACB=90 ，°∴△ ADC∽ △ ACB．∴AC2RAC 2 3 ∴R=22 AD15．如图过点 P 作1，⊙ O 的直径 AB=12， P 是弦PD⊥ OP交⊙ O 于点 D．BC 上一动点（与点B，C 不重合），∠ ABC=30 °，（1）如图 2，当 PD∥ AB 时，求 PD 的长；（2）如图 3，当弧 DC=弧 AC 时，延长 AB 至点 E，使 BE= 1AB，连接 DE．2①求证： DE 是⊙ O 的切线；②求 PC 的长．【答案】（ 1） 2 6 ；（2）① 证明见解析；②3 3 ﹣3．【解析】试题分析：（ 1）根据题意首先得出半径长，再利用锐角三角三角函数关系得出OP， PD 的长；（2）①首先得出△ OBD 是等边三角形，进而得出∠ ODE=∠ OFB=90°，求出答案即可；②首先求出 CF的长，进而利用直角三角形的性质得出PF 的长，进而得出答案．试题解析：（ 1）如图 2，连接 OD，∵OP⊥ PD，PD∥ AB，∴∠ POB=90 ，°∵⊙ O 的直径 AB=12，∴OB=OD=6，在 Rt△ POB中，∠ ABC=30°，∴OP=OB?tan30 ° =6 ×=2 ，在 Rt△ POD中，PD= = =；（2）①如图 3，连接 OD，交 CB于点 F，连接 BD，∵，∴∠ DBC=∠ABC=30 ，°∴∠ ABD=60 ，°∴△ OBD 是等边三角形，∴OD⊥FB，∵B E= AB，∴OB=BE，∴B F∥ ED，∴∠ ODE=∠ OFB=90 ，°∴DE 是⊙O 的切线；②由① 知， OD⊥ BC，∴CF=FB=OB?cos30° =6 =3×，在Rt△ POD中， OF=DF，∴P F= DO=3（直角三角形斜边上的中线，等于斜边的一半），∴C P=CF﹣ PF=3﹣3．考点：圆的综合题。

2024年中考数学高频压轴题训练——圆-动点问题及参考答案

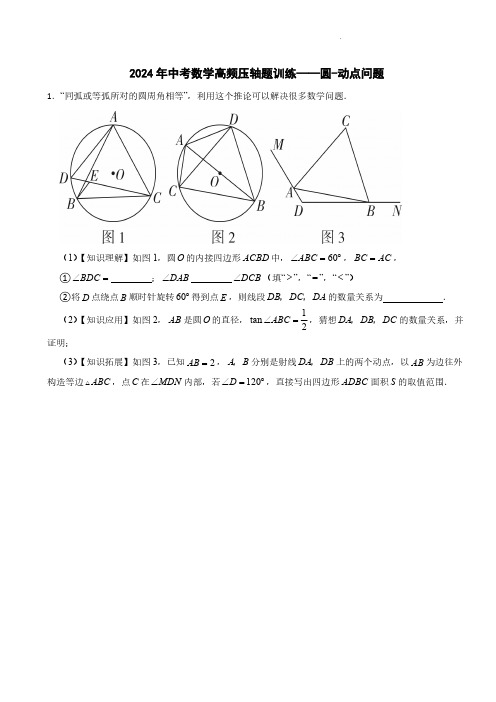
2024年中考数学高频压轴题训练——圆-动点问题1．“同弧或等弧所对的圆周角相等”，利用这个推论可以解决很多数学问题．（1）【知识理解】如图1，圆O 的内接四边形ACBD 中，60ABC ∠=︒，BC AC =，①BDC ∠=；DAB ∠DCB ∠（填“>”，“=”，“<”）②将D 点绕点B 顺时针旋转60︒得到点E ，则线段DB DC DA ，，的数量关系为．（2）【知识应用】如图2，AB 是圆O 的直径，1tan 2ABC ∠=，猜想DA DB DC ，，的数量关系，并证明；（3）【知识拓展】如图3，已知2AB =，A B ，分别是射线DA DB ，上的两个动点，以AB 为边往外构造等边ABC ，点C 在MDN ∠内部，若120D ∠=︒，直接写出四边形ADBC 面积S 的取值范围．2．如图1，对于PMN 的顶点P 及其对边MN 上的一点Q ，给出如下定义：以P 为圆心，PQ 为半径的圆与直线MN 的公共点都在线段MN 上，则称点Q 为PMN 关于点P 的内联点．在平面直角坐标系xOy 中：（1）如图2，已知点(70)A ，，点B 在直线1y x =+上．①若点(34)B ，，点(30)C ，，则在点O ，C ，A 中，点是AOB 关于点B 的内联点；②若AOB 关于点B 的内联点存在，求点B 纵坐标n 的取值范围；（2）已知点(20)D ，，点(42)E ，，将点D 绕原点O 旋转得到点F ．若EOF 关于点E 的内联点存在，直接写出点F 横坐标m 的取值范围．3．在平面直角坐标系xOy 中，O 的半径为1，对于点A 和线段BC ，给出如下定义：若将线段BC 绕点A 旋转可以得到O 的弦B C ''（B C ''，分别是B C ，的对应点），则称线段BC 是O 的以点A 为中心的“关联线段”．（1）如图，点112233A B C B C B C ，，，，，，的横､纵坐标都是整数．在线段112233B C B C B C ，，中，O 的以点A 为中心的“关联线段”是；（2）ABC 是边长为1的等边三角形，点()0A t ，，其中0t ≠．若BC 是O 的以点A 为中心的“关联线段”，求t 的值；（3）在ABC 中，12AB AC ==，．若BC 是O 的以点A 为中心的“关联线段”，直接写出OA 的最小值和最大值，以及相应的BC 长．4．已知：点C 为⊙O 的直径AB 上一动点，过点C 作CD ⊥AB ，交⊙O 于点D 和点E ，连接AD 、BD ，∠DBA 的角平分线交⊙O 于点F ．（1）若DF ＝BD ，求证：GD ＝GB ；（2）若AB ＝2cm ，在（1）的条件下，求DG 的值；（3）若∠ADB 的角平分线DM 交⊙O 于点M ，交AB 于点N ．当点C 与点O 重合时，AD BD DM+＝；据此猜想，当点C 在AB （不含端点）运动过程中，AD BD DM +的值是否发生改变？若不变，请求其值；若改变，请说明理由．5．在平面直角坐标系xOy 中，O 的半径为1，对于ABC 和直线l 给出如下定义：若ABC 的一条边关于直线l 的对称线段PQ 是O 的弦，则称ABC 是O 的关于直线l 的“关联三角形”，直线l 是“关联轴”．（1）如图1，若ABC 是O 的关于直线l 的“关联三角形”，请画出ABC 与O 的“关联轴”（至少画两条）；（2）若ABC 中，点A 坐标为(23)，，点B 坐标为(41)，，点C 在直线3y x =-+的图像上，存在“关联轴l ”使ABC 是O 的关联三角形，求点C 横坐标的取值范围；（3）已知A ，将点A 向上平移2个单位得到点M ，以M 为圆心MA 为半径画圆，B ，C 为M 上的两点，且2AB =（点B 在点A 右侧），若ABC 与O 的关联轴至少有两条，直接写出OC 的最小值和最大值，以及OC 最大时AC 的长．6．如图，在⊙O 中，AB 为弦，CD 为直径，且AB ⊥CD ，垂足为E ，P 为 AC 上的动点（不与端点重合），连接PD ．（1）求证：∠APD ＝∠BPD ；（2）利用尺规在PD 上找到点I ，使得I 到AB 、AP 的距离相等，连接AD （保留作图痕迹，不写作法）．求证：∠AIP+∠DAI ＝180°；（3）在（2）的条件下，连接IC 、IE ，若∠APB ＝60°，试问：在P 点的移动过程中，IC IE 是否为定值？若是，请求出这个值；若不是，请说明理由．7．在平面直角坐标系xOy 中，已知线段AB 和点P ，给出如下定义：若PA PB =且点P 不在线段AB 上，则称点P 是线段AB 的等腰顶点．特别地，当90APB ∠≥︒时，则称点P 是线段AB 的非锐角等腰顶点．（1）已知点(20)A ，，(42)B ，．①在点(40)C ，，(31)D ，，(15)E -，，(05)F ，中，是线段AB 的等腰顶点的是▲；②若点P 在直线3(0)y kx k =+≠上，且点P 是线段AB 的非锐角等腰顶点，求k 的取值范围；（2）直线33y x =-+与x 轴交于点M ，与y 轴交于点N ．⊙P 的圆心为(0)P t ，，半径为，若⊙P 上存在线段MN 的等腰顶点，请直接写出t 的取值范围．8．在平面直角坐标系xOy中，⊙O的半径为1，T（0，t）为y轴上一点，P为平面上一点．给出如下定义：若在⊙O上存在一点Q，使得△TQP是等腰直角三角形，且∠TQP＝90°，则称点P为⊙O的“等直点”，△TQP为⊙O的“等直三角形”．如图，点A，B，C，D的横、纵坐标都是整数．（1）当t＝2时，在点A，B，C，D中，⊙O的“等直点”是；（2）当t＝3时，若△TQP是⊙O“等直三角形”，且点P，Q都在第一象限，求CPOQ的值．9．综合与实践动手操作利用正方形纸片的折叠开展数学活动．探究体会在正方形折叠过程中，图形与线段的变化及其蕴含的数学思想方法．如图1，点E 为正方形ABCD 的AB 边上的一个动点，3AB =，将正方形ABCD 对折，使点A 与点B 重合，点C 与点D 重合，折痕为MN ．思考探索（1）将正方形ABCD 展平后沿过点C 的直线CE 折叠，使点B 的对应点B '落在MN 上，折痕为EC ，连接DB '，如图2．①点B '在以点E 为圆心，的长为半径的圆上；②B M '=；③DB C ' 为三角形，请证明你的结论．（2）拓展延伸当3AB AE =时，正方形ABCD 沿过点E 的直线l （不过点B ）折叠后，点B 的对应点B '落在正方形ABCD 内部或边上．①ABB ' 面积的最大值为；②连接AB '，点P 为AE 的中点，点Q 在AB '上，连接PQ AQP AB E ∠=∠'，，则2B C PQ '+的最小值为．10．在平面直角坐标系xOy 中，过⊙T （半径为r ）外一点P 引它的一条切线，切点为Q ，若0＜PQ≤2r ，则称点P 为⊙T 的伴随点．（1）当⊙O 的半径为1时，①在点A(4，0)，B(0，)，C(1，)中，⊙O 的伴随点是▲；②点D 在直线y ＝x+3上，且点D 是⊙O 的伴随点，求点D 的横坐标d 的取值范围；（2）⊙M 的圆心为M(m ，0)，半径为2，直线y ＝2x ﹣2与x 轴，y 轴分别交于点E ，F ．若线段EF 上的所有点都是⊙M 的伴随点，直接写出m 的取值范围．11．定义：在平面直角坐标系xOy 中，点P 为图形M 上一点，点Q 为图形N 上一点．若存在OP OQ =，则称图形M 与图形N 关于原点O “平衡”．（1）如图，已知⊙A 是以()1,0为圆心，2为半径的圆，点()1,0C -，()2,1D -，()3,2E ．①在点C ，D ，E 中，与⊙A 关于原点O “平衡”的点是；②点H 为直线y x =-上一点，若点H 与⊙A 关于原点O “平衡”，点H 的横坐标的取值范围为：；（2）如图，已知图形G 是以原点O 为中心，边长为2的正方形．⊙K 的圆心在x 轴上，半径为2．若⊙K 与图形G 关于原点O “平衡”，请直接写出圆心K 的横坐标的取值范围．12．阅读下列材料，并按要求解答相关问题：【思考发现】根据直径所对的圆周角是直角，我们可以推出“如果一条定边所对的角始终为直角，那么所有满足条件的直角顶点组成的图形是以定边为直径的圆或圆弧（直径的两个端点除外）”这一正确的结论．如图1，若AB 是一条定线段，且90APB ∠=︒，则所有满足条件的直角顶点P 组成的图形是定边AB 为直径的O （直径两端点A 、B 除外）（1）已知：如图2，四边形ABCD 是边长为8的正方形，点E 从点B 出发向点C 运动，同时点F 从点C 出发以相同的速度向点D 运动，连接AE ，BF 相交于点P ．①当点E 从点B 运动到点C 的过程中，APB ∠的大小是否发生变化？若发生变化，请说明理由；若不发生变化，请直接写出APB ∠的度数．②当点E 从点B 运动到点C 的过程中，点P 运动的路径是（）A ．线段；B ．弧；C ．半圆；D ．圆③点P 运动的路经长是▲．（2）已知：如图3，在图2的条件下，连接CP ，请直接写出E 、F 运动过程中，CP 的最小值．13．对于平面内的图形1G 和图形2G ，记平面内一点P 到图形1G 上各点的最短距离为1d ，点P 到图形2G 上各点的最短距离为2d ，若12d d =，就称点P 是图形1G 和图形2G 的一个“等距点”．在平面直角坐标系xOy 中，已知点()60A ，，(0B ．（1）在()30R ，，()20S ，，(1T 三点中，点A 和点B 的等距点是；（2）已知直线2y =-．①若点A 和直线2y =-的等距点在x 轴上，则该等距点的坐标为▲；②若直线y a =上存在点A 直线2y =-的等距点，求实数a 的取值范围；（3）记直线AB 为直线1l ，直线2l ：33y x =-，以原点O 为圆心作半径为r 的O ．若O 上有m 个直线1l 和直线2l 的等距点，以及n 个直线1l 和y 轴的等距点（0m ≠，0n ≠），求m n ≠时，求r 的取值范围．14．如图，平面上存在点P 、点M 与线段AB ．若线段AB 上存在一点Q ，使得点M 在以PQ 为直径的圆上，则称点M 为点P 与线段AB 的共圆点．已知点P （0，1），点A （﹣2，﹣1），点B （2，﹣1）．（1）在点O （0，0），C （﹣2，1），D （3，0）中，可以成为点P 与线段AB 的共圆点的是；（2）点K 为x 轴上一点，若点K 为点P 与线段AB 的共圆点，请求出点K 横坐标x K 的取值范围；（3）已知点M （m ，﹣1），若直线y ＝12x +3上存在点P 与线段AM 的共圆点，请直接写出m 的取值范围．15．如图，在ABC 中，AB BC =，30CAB ∠=︒，8AC =，半径为2的O 从点A 开始（如图1）沿直线AB 向右滚动，滚动时始终与直线AB 相切（切点为D ），当O 与ABC 只有一个公共点时滚动停止，作OG AC ⊥于点G ．（1）图1中，O 在AC 边上截得的弦长AE =；（2）当圆心落在AC 上时，如图2，判断BC 与O 的位置关系，并说明理由．（3）在O 滚动过程中，线段OG 的长度随之变化，设AD x =，OG y =，求出y 与x 的函数关系式，并直接写出x 的取值范围．16．在平面直角坐标系xOy 中，给出如下定义：若点P 在图形M 上，点Q 在图形N 上，称线段PQ 长度的最小值为图形M ，N 的“近距离”，记为d(M ，N)，特别地，若图形M ，N 有公共点，规定d(M ，N)＝0．已知：如图，点A(2-，0)，B(0，．（1）如果⊙O 的半径为2，那么d(A ，⊙O)＝，d(B ，⊙O)＝．（2）如果⊙O 的半径为r ，且d （⊙O ，线段AB ）=0，求r 的取值范围；（3）如果C(m ，0)是x 轴上的动点，⊙C 的半径为1，使d （⊙C ，线段AB ）<1，直接写出m 的取值范围．17．在平面直角坐标系xOy 中，对于点()P m n ，，我们称直线y mx n =+为点P 的关联直线.例如，点()24P ，的关联直线为24y x =+．（1）已知点()12A ，．①点A 的关联直线为；②若O 与点A 的关联直线相切，则O 的半径为；（2）已知点()02C ，，点()0.D d ，点M 为直线CD 上的动点．①当2d =时，求点O 到点M 的关联直线的距离的最大值；②以()11T -，为圆心，3为半径作.T 在点M 运动过程中，当点M 的关联直线与T 交于E ，F 两点时，EF 的最小值为4，请直接写出d 的值．18．在平面直角坐标系xOy 中，给定圆C 和点P ，若过点P 最多可以作出k 条不同的直线，且这些直线被圆C 所截得的线段长度为正整数，则称点P 关于圆C 的特征值为.k 已知圆O 的半径为2，（1）若点M 的坐标为()11，，则经过点M 的直线被圆O 截得的弦长的最小值为，点M 关于圆O 的特征值为；（2）直线y x b =+分别与x ，y 轴交于点A ，B ，若线段AB 上总存在关于圆O 的特征值为4的点，求b 的取值范围；（3）点T 是x 轴正半轴上一点，圆T 的半径为1，点R ，S 分别在圆O 与圆T 上，点R 关于圆T 的特征值记为r ，点S 关于圆O 的特征值记为.s 当点T 在x 轴正轴上运动时，若存在点R ，S ，使得3r s +=，直接写出点T 的横坐标t 的取值范围．答案解析部分1．【答案】（1）60︒；=；DC DB DA=+（2）解：在AB 上取一点E ，使ADE BDC ∠=∠，如图所示：∵AB 是圆O 的直径，1tan 2ABC ∠=，∴1tan 2AC ABC BC BC =∠⋅=，∴在Rt ACB 中，52AB BC ==，∵ BD BD =，∴DAB DCB ∠=∠，∵ADE BDC ∠=∠，∴ADE CDB ∽，∴ADAECD CB =，∴AD CB CD AE ⋅=⋅，∵ AD AD =，∴DBA DCA ∠=∠，∵ADE CDE CDB CDE ∠-∠=∠-∠，即ADC BDE ∠=∠，∴BDE CDA ∽，∴BDBECD AC =，∴BD AC CD BE ⋅=⋅，∴()AD CB AC BD CD AE CD BE CD AE BE CD AB⋅+⋅=⋅+⋅=⋅+=⋅，∴AB CD AC DB AD BC ⋅=⋅+⋅，∴122BC CD BC DB AD BC ⋅=⋅+⋅，∴5122CD DB AD ⋅=⋅+，∴5122CD DB AD =+，即2DB AD =+，故答案为：2DB AD =+．（3）解：∵A B ，分别是射线DA DB ，上的两个动点，120D ∠=︒，ABC 是等边三角形，∴四边形ADBC 的两个对角180ADB ACB ∠+∠=︒，∴构造四边形ADBC 的外接圆，∴根据四边形外接圆的性质可得：当点A 和点D 重合时，四边形ADBC 面积S 最小；当CD AB ⊥时，四边形ADBC 面积S 最大，①当点A 和点D 重合时，四边形ADBC 面积S 最小，∵CBD 时等边三角形，且2AB =，∴60CBD ∠=︒，2AB BD BC ===∴1sin 602CBD S BC BD =⋅⋅⋅= ，②当CD AB ⊥时，四边形ADBC 面积S 最大，∵CBD 时等边三角形，且2AB =，∴30ACD ∠=︒，2AC =，∴tan 233AD ACD AC =∠⋅==，∴11232322233ADC S AD DC =⋅⋅=⨯= ，∴23ADC ADBC S S == 四边形；433S <≤．2．【答案】（1）解：①O ，C ②当点B 的坐标为（0，1）时，如图，此时以BO 为半径的B 与线段OA 相切于点O ，∴点O 是OAB 关于点B 的内联点；当点B 移动到在y 轴左侧时，作图发现B 与x 轴有相交，且有一个交点不在线段OA 上，∴不再有OAB 关于点B 的内联点；当点B 的坐标为（7，8）时，以BA 为半径的B 与x 轴相切于点A ，∴点A 是OAB 关于点B 的内联点；当点B 直线x=7的右侧时，以BA 为半径的B 与x 轴相交，且有一个交点不在线段OA 上∴不再有OAB 关于点B 的内联点；综上所述，若AOB 关于点B 的内联点存在，求点B 纵坐标n 的取值范围为18n ≤≤；（2）80m 555m -≤≤≤≤或3．【答案】（1）22B C （2）解：由题意可得：当BC 是O 的以点A 为中心的“关联线段”时，则有AB C '' 是等边三角形，且边长也为1，当点A 在y 轴的正半轴上时，如图所示：设B C ''与y 轴的交点为D ，连接OB '，易得B C y ''⊥轴，∴12B D DC ''==，∴32OD ==，32==，∴OA =，∴t =；当点A 在y 轴的正半轴上时，如图所示：同理可得此时的OA =，∴t =；（3）当1min OA =时，此时BC =；当2max OA =时，此时2BC =．4．【答案】（1）证明：∵CD ⊥直径AB ，∴ BDBE =，∵DF ＝BD ，∴ DFBD =，∴ BEDF =，∴∠1＝∠2，∴DG ＝BG（2）解：∠DBA 的角平分线交⊙O 于点F ，∴∠2＝∠3，由（1）知，∠1＝∠2，∴∠1＝∠2＝∠3，∵∠BCD ＝90°，∴∠1+∠2+∠3＝90°，∴∠1＝∠2＝∠3＝30°，∵AB 是⊙O 的直径，∴∠ADB ＝90°，∴∠4＝90°﹣∠2﹣∠3＝30°，∵AB ＝2，∴BD ＝1，在Rt △BCD 中，∠1＝30°，∴BC ＝12BD ＝12，在Rt △BCG 中，∠3＝30°，∴CG ＝＝6，∴BG ＝2CG ＝33，由（1）知，DG ＝BG ＝33（3）5．【答案】（1）解：如图1，作BM ⊥x 轴，垂足为M ，根据题意AB=AE=EF=BF=，且∠EFO=∠BFM=45°，∴∠EFB=90°，∴四边形ABFE 是正方形，∴边AE ，BF 的中点所在直线就是ABC 与O 的一条“关联轴”；∵O 的半径为1，∴，且∠EFG=90°，∴四边形EFGH 是正方形，∵∠EFG+∠EFB=180°，∴B 、F 、G 三点共线，∴直线EF 是ABC 与O 的一条“关联轴”．（2）解：如图2，根据A （2，3），B （4，1），C （4，1），计算2=，故AB 不能落在圆的内部；过点A 作AN ⊥y 轴，垂足为N ，则AN=2，等于圆的直径，存在“关联轴l ”使ABC 是O 的关联三角形，此时0C x =；作点B 关于x 轴的对称点P ，此时BP=2，等于圆的直径，存在“关联轴l ”使ABC 是O 的关联三角形，此时4C x =，综上所述，点C 横坐标的范围是04C x ≤≤．（3）解：OC 的最小值为2-；OC 最大，根据勾股定理，AC=4.6．【答案】（1）证明：∵直径CD ⊥弦AB ，∴ AD BD=，∴∠APD=∠BPD ；（2）解：如图，作∠BAP 的平分线，交PD 于I ，证：∵AI 平分∠BAP ，∴∠PAI=∠BAI ，∴∠AID=∠APD+∠PAI=∠APD+BAI ，∵ AD BD=，∴∠DAB=∠APD ，∴∠DAI=∠DAB+∠BAI=∠APD+∠BAI ，∴∠AID=∠DAI ，∵∠AIP+∠DAI=180°，∴∠AIP+∠DAI=180°；（3）解：如图2，连接BI ，AC ，OA ，OB ，∵AI 平分∠BAP ，PD 平分∠APB ，∴BI 平分∠ABP ，∠BAI=12∠BAP ，∴∠ABI=12∠ABP ，∵∠APB=60°，∴∠PAB+∠PBA=120°，∴∠BAI+∠ABI=12（∠BAP+∠ABP ）=60°，∴∠AIB=120°，∴点I 的运动轨迹是 AB ，∴DI=DA ，∵∠AOB=2∠APB=120°，∵AD ⊥AB ，∴ AD BD=，∴∠AOB=∠BOD=60°，∵OA=OD ，∴△AOD 是等边三角形，∴AD=AO ，∵CD 是⊙O 的直径，∴∠DAC=90°，∵CD ⊥AB ，∴∠AED=90°，∴∠AED=∠CAD ，∵∠ADC=∠ADE ，∴△ADE ∽△CDA ，∴AD DE CD AD=，∴AD 2=DE•CD ，∵DI′=DI=AD ，∴DI 2=DE•CD ，∵∠I′DE 是公共角，∴△DIE ∽△DCI ，∴2IC CD IE DI==．7．【答案】（1）解：①C(4，0)，E(-1，5)；②（Ⅰ）当点(40)，在直线3y kx =+上时，430k +=，34k =-；（Ⅱ）当点(31)，在直线3y kx =+上时，331k +=，23k =-；（Ⅲ）当点(22)，在直线3y kx =+上时，232k +=，12k =-；结合图象可得3142k -≤≤-且23k ≠-；（2）解：直线333y x =-+与x 轴的交点M 坐标为()30，，与y 轴交点N 的坐标为(03，，∴tan 3NMO ∠=，∴30NMO ∠=︒，如图，作出线段MN 的垂直平分线，如图为两个临界情况：，利用待定系数法求得MN 垂直平分线解析式为y =，∴(0R -，，12230ORQ P RQ ∠=∠=︒，∴1112PR PQ ==，2222P R P Q ==，∴(10P ，(20P -，，∴t -≤<．8．【答案】（1）A 、B 、D（2）解：如图，依题意作⊙O 的“等直三角形”△TQP∴TQ=PQ ，∠TQP=90°过Q 点作MH //x 轴，交y 轴于M 点，过点P 作PH ⊥MH 于H 点∴∠TMQ=∠QHP=90°∴∠TQM+∠MTQ=∠TQM+∠HQP=90°∴∠MTQ=∠HQP∴△TMQ ≌△QHP （AAS ）∴TM=QH ，MQ=HP设Q （x ，y ）∴HM=MQ+QH=MQ+TM=x+3-y ，PH=MQ=x∴P （x-y+3，x+y ）∵C （3，0）∴∵∴CP OQ ．9．【答案】（1）BE ；3332-；等边；证明：B′D=BC CD ==，∴△DB'C 为等边三角形（2）310．【答案】（1）B ，C ；解：②如图2中，设点D 的坐标为(3)d d +，当过点D 的切线长为22r =时，OD ==由两点之间的距离公式得：OD =解得1221d d =-=-，结合图象可知，点D 的横坐标d 的取值范围是21d -≤≤-；（2）解：对于22y x =-当0y =时，220x -=，解得1x =，则点E 的坐标为(10)E ，当0x =时，2y =-，则点F 的坐标为(02)F -，⊙M 的半径为2，⊙M 的圆心为(0)M m ，24r ∴=，OM m=由题意，由以下两种情况：如图3-1中，点M 在点E 的右侧设FT 是⊙M 的切线则有两个临界位置：4FT =和点E 对应的切线长为0当4FT =时，则4OM m FT ===当点E 对应的切线长为0，即2EM =12EM m ∴=-=解得3m =结合图象得，当34m <≤时，线段EF 上的所有点都是⊙M 的伴随点②如图3-2和3-3中，点M 在点E 的左侧则有如下两个临界位置：如图3-2，设ET 是⊙M 的切线，连接MT ，则90MTE ∠=︒当4ET =时，2222245EM MT ET =+=+此时15m -=解得15m =-如图3-3，当⊙M 在直线EF 的左侧与EF 相切时，设切点为T ，连接MT∵(10)(02)E F -，，，∴12OE OF ==，∴22125EF =+=∵EF 是切线∴EF MT⊥∴90MTE FOE ∠=∠=︒∵MET FEO∠=∠∴MTE FOE~ ∴EM MTEF OF =，即22=解得EM =，即1m -=解得1m =-结合图象得，当11m -≤<-时，线段EF 上的所有点都是⊙M 的伴随点综上，m 的取值范围是11m -≤<-或34m <≤．11．【答案】（1）点C 、D ；22H x -≤≤-或22H x ≤≤（2）解：图形G 是以原点O 为中心，边长为2的正方形，∴原点O 到正方形的最短距离是1d =，最长距离是d =，⊙K 与图形G 关于原点O “平衡”，∴原点O 到⊙K 上一点的距离1d ≤≤，⊙K 的圆心在x 轴上，半径为2，∴当⊙K 在x 轴正半轴时，圆心K 的横坐标的取值范围为：22x -≤≤+，当⊙K 在x 轴负半轴时，圆心K 的横坐标的取值范围为：22x --≤≤，综上所述，圆心K 的横坐标的取值范围22x -≤≤+或22x --≤≤．12．【答案】（1）解：①90°；②B ；③2π（2）解：413．【答案】（1）S(2，0)（2）解：①（4，0）或（8，0）；②如图，设直线y a =上的点Q 为点A 和直线2y =-的等距点，连接QA ，过点Q 作直线2y =-的垂线，垂足为点C ．点Q 为点A 和直线2y =-的等距点，QA QC ∴=．22QA QC ∴=．点Q 在直线y a =上，∴可设点Q 的坐标为()Q x a ，．()()22262x a a ∴-+=--⎡⎤⎣⎦．整理得2123240x x a -+-=．由题意得关于x 的方程2123240x x a -+-=有实数根．()()()212413241610a a ∴∆=--⨯⨯-=+≥．解得1a ≥-．（3）解：如图．直线l 1和直线l 2的等距点在直线l 3：33y x =-+上，直线l 1和y 轴的等距点在直线4l y =+：或33y x =+上，点O 与l 4的距离为32，点O 与l 3的距离为，点O 与l 5的距离为3，当r ＜时，n=0不符合题意，当r=时，m=2，n=0，符合题意，当＜r ＜3时，m=n=2，不符合题意，当r≥3时，m=2，n=3或4，符合题意，综上所述，r=或r≥3.14．【答案】（1）C（2）解：∵P （0，1），点A （﹣2，﹣1），点B （2，﹣1）．∴AP ＝BP ＝＝2，如图2，分别以PA 、PB 为直径作圆，交x 轴于点K 1、K 2、K 3、K 4，∵OP＝OG＝1，OE∥AB，∴PE＝AE＝，∴OE＝12AG＝1，∴K1（﹣1﹣，0），k2（1﹣，0），k3（﹣1，0），k4（1+，0），∵点K为点P与线段AB的共圆点，∴﹣1﹣≤x k≤1﹣或﹣1≤x k≤1+（3）解：分两种情况：①如图3，当M在点A的左侧时，Q为线段AM上一动点，以PQ为直径的圆E与直线y＝12x+3相切于点F，连接EF，则EF⊥FH，当x＝0时，y＝3，当y＝0时，y＝12x+3＝0，x＝﹣6，∴ON＝3，OH＝6，∵tan∠EHF＝ON EFOH FH＝36＝12，设EF＝a，则FH＝2a，EH＝a，∴OE＝6﹣a，Rt △OEP 中，OP ＝1，EP ＝a ，由勾股定理得：EP 2＝OP 2+OE 2，∴2221(6)a =+-，解得：a ＝2+（舍去）或2，∴QG ＝2OE ＝2（6﹣a ）＝﹣3+2，∴m≤3﹣2；②如图4，当M 在点A 的右侧时，Q 为线段AM 上一动点，以PQ 为直径的圆E 与直线y ＝12x+3相切于点F ，连接EF ，则EF ⊥FH ，同理得QG ＝3+2，∴m≥3+2，综上，m 的取值范围是m≤3﹣2或m≥3+215．【答案】（1）2（2）解：BC 与O 相切；理由：如图2，过点O 作OH BC ⊥于H ，连接OD ，∵O 与AB 相切于D ，∴OD AB ⊥，在Rt AOD 中，30BAC ∠=︒，∴24OA OD ==，∵8AC =，∴4OC =，在ABC 中，AB BC =，∴30C BAC ∠=∠=︒，在Rt OHC 中，30C ∠=︒，∴122OH OC OD ===，∴BC 与O 相切，（3）解：①当点O 在AC 的左侧时，连接OD 交AC 于F ，如备用图1，∵O 与AB 相切于D ，∴OD AB ⊥，∵OG AC ⊥，∴30FOG BAC ∠=∠=︒，在Rt FDA 中，tan FD BAC AD ∠=，∴tan 3FD AD BAC x =⋅∠=，∴23OF x =-，在Rt FOG 中，331cos 2322y OG OF FOG ⎛⎫==⋅∠=-⨯-+ ⎪ ⎪⎝⎭，即12y x =-+，此时x 的取值范围为0x ≤≤；②当点O 在AC 的右侧时，连接DO 并延长交AC 于F ，如备用图2，同①的方法得，33FD x =，∴23OF x =-，∵FD AB ⊥，∴90BAC AFD ∠+∠=︒，∴30FOG BAC ∠=∠=︒，在Rt FOG 中，331cos 2322y OG OF FOG x x ⎛⎫==⋅∠=-⨯- ⎪⎪⎝⎭，即12y x =-，此时x 的取值范围为1433x ≤≤．16．【答案】（1）0；2-（2）解：过点O 作OD ⊥AB 于点D ，∵点A(2-，0)，B(0，．∴2OA OB ==，，∴4AB ==，∵1122OA OB AB OD ⋅=⋅，∴112422OD ⨯⨯=⨯⨯∴DO =，∵d （⊙O ，线段AB ）=0，∴当⊙O 的半径等于OD 时最小，当⊙O 的半径等于OB 时最大，∴r r ≤≤（3）43423m -<<-17．【答案】（1）2y x =+（2）解：①当2d =时，()20D ，，设直线CD 的解析式为：y kx b =+，()02C ，，202k b b +=⎧∴⎨=⎩，解得：12k b =-⎧⎨=⎩，∴直线CD 的解析式为：y x =-+，设点M 的坐标为()2m m -+，，∴点M 的关联直线为：()212y mx m m x =-+=-+，∴点M 的关联直线经过定点()12N ，，如图2，过点O 作直线2y mx m =--+的垂线，垂足为H ，连接ON ，ON OH ∴≥，∴当点H与点N重合时，OH最大，即点O到点M的关联直线的距离最大，∴点O到点M=；2 d=②或2 3-18．【答案】（1）；3（2）解：设点G是O的特征值为4的点，∴经过一点G且弦长为4(最长弦)的直线有1条，弦长为3的直线有2条，弦长为2的直线有且只有1条，经过点G的直线被O截得的弦长的最小值为2，=，∴关于O的特征值为4的所有点都在以O为半径的圆周上，直线y x b=+分别与x，y轴交于点A、B，()0A b∴-，，()B b，，OA OB b∴==，45OBH∴∠=︒，当0b>时，线段AB与以O为半径的圆相切时，点G特征值为4，设切点为为H，连接OH，则OH=，OB∴==，b∴=，设以O 为半径的圆与y 轴正半轴的交点记为1B ，则1OB =，当线段AB 与以O 1B 时，可得b =，b ≤≤同理可求当0b <时，b ≤≤，综上，b b b ≤≤-≤（3）当372122t -≤≤+时，存在点R ，S ，使得3r s +=。

挑战中考压轴题_圆压轴100题

第100题(2010.广东省深圳市中考模拟)如图是一圆形纸片，AB 是直径，BC 是弦，将纸片沿弦BC 折叠后，劣弧BC 与AB 交于点D ，得到BDC ．（1）若BD ︵＝CD ︵，求证：BDC 必经过圆心O ；（2）若AB ＝8，BD ︵＝2CD ︵，求BC 的长．如图甲，分别以两个彼此相邻的正方形OABC与CDEF的边OC、OA 所在直线为x轴、y轴建立平面直角坐标系（O、C、F三点在x轴正半轴上）．若⊙P过A、B、E三点（圆心在x轴上），抛物线y=14x2+bx+c经过A、C两点，与x轴的另一交点为G，M是FG的中点，正方形CDEF的面积为1．（1）求B点坐标；（2）求证：ME是⊙P的切线；如图，△ABC内接于⊙O，AD⊥BC，OE⊥BC，OE=12 BC．（1）求∠BAC的度数；（2）将△ACD沿AC折叠为△ACF，将△ABD沿AB折叠为△ABG，延长FC和GB相交于点H；求证：四边形AFHG是正方形；（3）若BD=6，CD=4，求AD的长．已知：如图，抛物线y=13x2-233x+m与x轴交于A、B两点，与y轴交于C点，∠ACB=90°，（1）求m的值及抛物线顶点坐标；（2）过A、B、C的三点的⊙M交y轴于另一点D，连接DM并延长交⊙M于点E，过E点的⊙M的切线分别交x轴、y轴于点F、G，求直线FG的解析式；（3）在条件（2）下，设P为CBD上的动点（P不与C、D重合），连接PA交y轴于点H，问是否存在一个常数k，始终满足: AH•AP=k？如果存在，请写出求解过程；如果不存在，请说明理由．如图1所示，以点M（-1，O）为圆心的圆与y轴、x轴分别交于点A，B，C，D，直线y=3-3x-533与⊙M相切于点H，交x轴于点E，交y轴于点F．（1）请直接写出OE、⊙M的半径r、CH的长；（2）如图2所示，弦HQ交x轴于点P，且DP：PH=3：2，求cos∠QHC的值；（3）如图3所示，点K为线段EC上一动点（不与E，C重合），连接BK交⊙M于点T，弦AT交x轴于点N．是否存在一个常数a，始终满足MN•MK=a，如果存在，请求出a的值；如果不存在，请说明理由．第095题(自选)如图，E点为x轴正半轴上一点，⊙E交x轴于A、B两点，交y轴于C、D两点，P点为劣弧BC上一个动点，且A（-1，0），E（1，0）．（1）求点C的坐标；（2）连接PA，PC．若CQ平分∠PCD交PA于Q点，当P点在运动时，线段AQ的长度是否发生变化；若不变求出其值，若发生变化，求出变化的范围；（3）连接PD，当P点在运动时（不与B、C两点重合），求证：PC PDPA的值不变如图，等腰梯形ABCD中，AD∥BC，AB=DC，以HF为直径的圆与AB、BC、CD、DA相切，切点分别是E、F、G、H．其中H 为AD的中点，F为BC的中点．连接HG、GF．（1）若HG和GF的长是关于x的方程x2-6x+k=0的两个实数根，求⊙O的直径HF（用含k的代数式表示），并求出k的取值范围．（2）如图，连接EG、DF. EG与HF交于点M，与DF交于点N，求GNNE的值．直线y=-x+m与直线y=3-3x+2相交于y轴上的点C，与x轴分别交于点A、B．（1）求A、B、C三点的坐标；（2）经过上述A、B、C三点作⊙E，求∠ABC的度数，点E的坐标和⊙E的半径；（3）若点P是第一象限内的一动点，且点P与圆心E在直线AC的同一侧，直线PA、PC分别交⊙E于点M、N，设∠APC=θ，试求点M、N的距离．（可用含θ的三角函数式表示）AB是⊙O的直径，点E是半圆上一动点（点E与点A、B都不重合），点C是BE延长线上的一点，且CD⊥AB，垂足为D，CD与AE交于点H，点H与点A不重合．（1）求证：△AHD∽△CBD；（2）连HO，若CD=AB=2，求HD+HO的值．如图，在平面直角坐标系中，直线l：y=-2x-8分别与x轴，y轴相交于A，B两点，点P（0，k）是y轴的负半轴上的一个动点，以P为圆心，3为半径作⊙P．（1）连接PA，若PA=PB，试判断⊙P与x轴的位置关系，并说明理由；（2）当k为何值时，以⊙P与直线l的两个交点和圆心P为顶点的三角形是正三角形．在平面直角坐标系xoy中，点M在x轴的正半轴上，⊙M交x轴于A、B两点，交y轴于C、D两点，且C为AE的中点，AE交y轴于G点，若点A的坐标为（-2，0），AE=8．（1）求点C的坐标；（2）连接MG、BC，求证：MG∥BC；（3）过点D作⊙M的切线，交x轴于点P．动点F在⊙M的圆周上运动时，OFPF的比值是否发生变化？若不变，求出比值；若变化，说明变化规律．如图1，⊙O中AB是直径，C是⊙O上一点，∠ABC=45°，等腰直角三角形DCE中∠DCE是直角，点D在线段AC上．（1）若M是线段BE的中点，N是线段AD的中点，证明：MN= 2OM；（2）将△DCE绕点C逆时针旋转α（0°＜α＜90°）后，记为△D1CE1（图2），若M1是线段BE1的中点，N1是线段AD1的中点，M1N1= 2OM1是否成立？若是，请证明；若不是，说明理由．如图，AB、BC、CD分别与⊙O切于E、F、G，且AB∥CD．连接OB、OC，延长CO交⊙O于点M，过点M作MN∥OB交CD于N．（1）求证：MN是⊙O的切线；（2）当0B=6cm，OC=8cm时，求⊙O的半径及MN的长．如图，直线AB经过⊙O上的点C，并且OA=OB，CA=CB，⊙O交直线OB于E，D，连接EC，CD．（1）求证：直线AB是⊙O的切线；（2）试猜想BC，BD，BE三者之间的等量关系，并加以证明；（3）若tan∠CED=12，⊙O的半径为3，求OA的长．如图，⊙O是△ABC的外接圆，且AB=AC，点D在弧BC上运动，过点D作DE∥BC，DE交AB的延长线于点E，连接AD、BD．（1）求证：∠ADB=∠E；（2）当点D运动到什么位置时，DE是⊙O的切线？请说明理由．（3）当AB=5，BC=6时，求⊙O的半径．第085题(2009.北京市房山区九上期末)如图，在直角坐标系xoy中，点A（2，0），点B在第一象限且△OAB为等边三角形，△OAB的外接圆交y轴的正半轴于点C，过点C的圆的切线交x轴于点D．（1）判断点C是否为弧OB的中点？并说明理由；（2）求B、C两点的坐标及直线CD的函数解析式；（3）点P在线段OB上，且满足四边形OPCD是等腰梯形，求点P坐标．第084题(自选)如图，直角坐标系中，已知两点O（0，0），A（2，0），点B在第一象限且△OAB为正三角形，△OAB的外接圆交y轴的正半轴于点C，过点C的圆的切线交x轴于点D．（1）求B，C两点的坐标；（2）求直线CD的函数解析式；（3）设E，F分别是线段AB，AD上的两个动点，且EF平分四边形ABCD的周长．试探究：△AEF的最大面积．在Rt△ABC中，BC=9，CA=12，∠ABC的平分线BD交AC与点D，DE⊥DB交AB于点E．（1）设⊙O是△BDE的外接圆，求证：AC是⊙O的切线；（2）求⊙O的半径；（3）设⊙O交BC于点F，连接EF，求EFAC的值．如图，△ABC内接于⊙O，过点B作⊙O的切线，交于CA的延长线于点E，∠EBC=2∠C．（1）求证：AB=AC；（2）当ABBC=54时，①求tan∠ABE的值；②如果AE=2011，求AC的值．如图，Rt△ABC内接于⊙O，AC=BC，∠BAC的平分线AD与⊙O交于点D，与BC交于点E，延长BD，与AC的延长线交于点F，连接CD，G是CD的中点，连接OG．（1）判断OG与CD的位置关系，写出你的结论并证明；（2）求证：AE=BF；（3）若OG⋅DE=3（2-2），求⊙O的面积．如图，AB、AC分别是⊙O的直径和弦，点D为劣弧AC上一点，弦ED分别交⊙O于点E，交AB于点H，交AC于点F，过点C的切线交ED的延长线于点P．（1）若PC=PF，求证：AB⊥ED；（2）点D在劣弧AC的什么位置时，才能使AD2=DE•DF，为什么？如图，AB、AC分别是⊙O的直径和弦，点D为劣弧AC上一点，弦DE⊥AB分别交⊙O于E，交AB于H，交AC于F．P是ED延长线上一点且PC=PF．（1）求证：PC是⊙O的切线；（2）点D在劣弧AC什么位置时，才能使AD2=DE•DF，为什么？（3）在（2）的条件下，若OH=1，AH=2，求弦AC的长．如图，以BC为直径的⊙O交△CFB的边CF于点A，BM平分∠ABC交AC于点M，AD⊥BC于点D，AD交BM于点N，ME⊥BC于点E，AB2=AF•AC，cos∠ABD=35，AD=12．（1）求证：△ANM≌△ENM；（2）求证：FB是⊙O的切线；（3）证明四边形AMEN是菱形，并求该菱形的面积S．（1）如图1，圆内接△ABC中，AB=BC=CA，OD、OE为⊙O的半径，OD⊥BC于点F，OE⊥AC于点G，求证：阴影部分四边形OFCG的面积是△ABC的面积的1 3（2）如图2，若∠DOE保持120°角度不变，求证：当∠DOE绕着O点旋转时，由两条半径和△ABC的两条边围成的图形（图中阴影部分）面积始终是△ABC的面积的1 3第076题(2010.辽宁省铁岭市)如图，已知矩形ABCD内接于⊙O，BD为⊙O直径，将△BCD沿BD所在的直线翻折后，得到点C的对应点N仍在⊙O上，BN交AD与点M．若∠AMB=60°，⊙O的半径是3cm．（1）求点O到线段ND的距离；（2）过点A作BN的平行线EF，判断直线EF与⊙O的位置关系并说明理由．如图，已知△ABC中，AB=BC，以AB为直径的⊙O交AC于点D，过D作DE⊥BC，垂足为E，连接OE，CD=3，∠ACB=30°．（1）求证：DE是⊙O的切线；（2）分别求AB，OE的长；（3）如果以点E为圆心，r为半径的圆上总存在不同的两点到点O的距离为1，则求r的取值范围.如图，⊙O是△ABC的外接圆，FH是⊙O的切线，切点为F，FH∥BC，连接AF交BC于E，∠ABC的平分线BD交AF于D，连接BF．（1）证明：AF平分∠BAC；（2）证明：BF=FD；（3）若EF=4，DE=3，求AD的长．如图，在⊙O上位于直径AB的异侧有定点C和动点P，AC=12AB，点P在半圆弧AB上运动（不与A、B两点重合），过点C作直线PB的垂线CD交PB于D点．（1）如图1，求证：△PCD∽△ABC；（2）当点P运动到什么位置时，△PCD≌△ABC？请在图2中画出△PCD并说明理由；（3）如图3，当点P运动到CP⊥AB时，求∠BCD的度数．第072题(2006.山东省莱芜市)半径为2.5的⊙O中，直径AB的不同侧有定点C和动点P．已知43BCCA，点P在AB上运动，过点C作CP的垂线，与PB的延长线交于点Q．（1）当点P与点C关于AB对称时，求CQ的长；（2）当点P运动到AB的中点时，求CQ的长；（3）当点P运动到什么位置时，CQ取到最大值？求此时CQ的长．第071题(2010.湖北省荆门市中考)如图，圆O的直径为5，在圆O上位于直径AB的异侧有定点C和动点P，已知43BCCA，点P在半圆弧AB上运动（不与A、B重合），过C作CP的垂线CD交PB的延长线于D点．（1）求证：AC•CD=PC•BC；（2）当点P运动到AB弧中点时，求CD的长；（3）当点P运动到什么位置时，△PCD的面积最大？并求这个最大面积S．第070题(2006.山东省烟台市中考)如图，已知点C在⊙O上，延长直径AB到点P，连接PC，∠COB=2∠PCB．（1）求证：PC是⊙O的切线；（2）若AC=PC，且PB=3，M是⊙O下半圆弧上一动点，当M点运动到使△ABM的面积最大时，CM交AB于点N，求MN•MC的值．第069题(2011.江苏省镇江市实验学校中考数学二模)如图，已知AB是⊙O的直径，点C在⊙O上，过点C的直线与AB的延长线交于点P，AC=PC，∠COB=2∠PCB．（1）求证：PC是⊙O的切线；（2）求∠P的度数；（3）点M是弧AB的中点，CM交AB于点N，AB=4，求线段BM、CM及弧BC所围成的图形面积．第068题(2011.北京市昌平区中考数学二模试卷)如图，已知点C在⊙O上，延长直径AB到点P，连接PC，∠COB=2∠PCB．（1）求证：PC是⊙O的切线；（2）若AC=PC，且PB=3，M是⊙O下半圆弧的中点，求MA的长．第067题(自选)如图，已知AB是⊙O的直径，点C在⊙O上，过点C的直线与AB的延长线交于点P，AC=PC，∠COB=2∠PCB．（1）求证：PC是⊙O的切线；（2）点M是弧AB的中点，CM交AB于点N，求∠CNA的度数．第066题(2010.内蒙古包头市中考)如图，已知AB是⊙O的直径，点C在⊙O上，过点C的直线与AB的延长线交于点P，AC=PC，∠COB=2∠PCB．（1）求证：PC是⊙O的切线；（2）求证：BC=12 AB；（3）点M是AB的中点，CM交AB于点N，若AB=4，求MN•MC的值．第065题(2012.江苏省南京市江宁区中考数学一模)如图，在Rt△ABC中，∠ABC=90°，∠ACB=30°，斜边AC的垂直平分线交BC于D点，交AC于E点，连接BE．（1）直线BE是否与△DEC的外接圆⊙O相切？为什么？（2）当AB=3时，求图中阴影部分的面积．第064题(2010.陕西省中考)如图，在Rt△ABC中∠ABC=90°，斜边AC的垂直平分线交BC与D点，交AC与E点，连接BE．（1）若BE是△DEC的外接圆的切线，求∠C的大小；（2）当AB=1，BC=2时，求△DEC外接圆的半径．第063题(2011.江苏省无锡市锡中实验学校九上期中考试)四边形ABCD是平行四边形，以AB为直径的⊙O经过点D，E是⊙O上任意一点，且CD切⊙O于点D．（1）试求∠AED的度数．（2）若⊙O的半径为32cm，试求：△ADE面积的最大值．如图，在△ABC中，AB=AC，D是BC中点，AE平分∠BAD交BC于点E，点O是AB上一点，⊙O过A、E两点，交AD于点G，交AB于点F．（1）求证：BC与⊙O相切；（2）若AB=5，BC=8，求⊙O的半径．（3）若∠BAC=120°时，求∠EFG的度数．如图，△ABC内接于⊙O，且∠B=60°．过点C作圆的切线l与直径AD的延长线交于点E，AF⊥l，垂足为F，CG⊥AD，垂足为G．（1）求证：△ACF≌△ACG；（2）若AF=43，求图中阴影部分的面积．如图，已知AD是△ABC的外角∠EAC的平分线，交BC的延长线于点D，延长DA交△ABC的外接圆于点F，连接FB、FC．（1）求证：FB=FC；（2）求证：FB2=FA•FD；（3）若AB是△ABC外接圆的直径，∠EAC=120°，BC=6cm，求AD的长．如图，AD为△ABC外接圆的直径，AD⊥BC，垂足为点F，∠ABC的平分线交AD于点E，连接BD，CD．（1）求证：BD=CD；（2）请判断B，E，C三点是否在以D为圆心，以DB为半径的圆上？并说明理由．如图，BD是⊙O的直径，OA⊥OB，M是劣弧AB上一点，过点M点作⊙O的切线MP交OA的延长线于P点，MD与OA交于N点．（1）求证：PM=PN；（2）若BD=4，PA=32AO，过点B作BC∥MP交⊙O于C点，求BC的长．如图，在以O为圆心的两个同心圆中，AB经过圆心O，且与小圆相交于点A、与大圆相交于点B．小圆的切线AC与大圆相交于点D，且CO平分∠ACB．（1）试判断BC所在直线与小圆的位置关系，并说明理由；（2）试判断线段AC、AD、BC之间的数量关系，并说明理由；（3）若AB=8cm，BC=10cm，求大圆与小圆围成的圆环的面积．（结果保留π）如图，△ABC内接于⊙O，∠BAC=60°，点D是BC的中点．BC，AB边上的高AE，CF相交于点H．试证明：（1）∠FAH=∠CAO；（2）四边形AHDO是菱形．第055题(2008.陕西省中考)如图，在Rt△ABC中，∠ACB=90°，AC=5，CB=12，AD是△ABC的∠ACB的角平分线，过A、C、D三点的圆O与斜边AB 交于点E，连接DE．（1）求证：AC=AE；（2）求AD的长．第054题(2008.山东省枣庄市中考)已知：如图，在半径为4的⊙O中，AB、CD是两条直径，M为OB的中点，CM的延长线交⊙O于点E，且EM＞MC．连接DE，DE=15．（1）求证：AM•MB=EM•MC；（2）求EM的长；（3）求sin∠EOB的值．第053题(2012.四川省成都市金牛区重点学校中考二模)已知：如图，在半径为4的⊙O中，AB，CD是两条直径，M为OB的中点，CM的延长线交⊙O于点E，且EM＞MC．连接DE，DE=15．（1）求证：AM•MB=EM•MC；（2）求sin∠EOB的值；（3）若P是直径AB延长线上的点，且BP=12，求证：直线PE是⊙O的切线．如图，AB为⊙O的直径，OE交弦AC于点P，交AM于点M，且AM=CM．（1）求证：OP=12 BC；（2）如果AE2=EP•EO，且AE=65，BC=6，求⊙O的半径．如图，已知点C是以AB为直径的⊙O上一点，CH⊥AB于点H，过点B作⊙O的切线交直线AC于点D，点E为CH的中点，连接AE并延长交BD于点F，直线CF交AB的延长线于G．（1）求证：AE•FD=AF•EC；（2）求证：FC=FB；（3）若FB=FE=2，求⊙O的半径R的长．。

专题09 与圆有关的综合压轴题(解析版)

专题9 与圆有关的综合压轴题题型一：圆与三角函数相似的结合【例1】如图，AB为⊙O的直径，C为⊙O上一点，D是弧BC的中点，BC与AD、OD分别交于点E、F．（1）求证：DO∥AC；（2）求证：DE•DA＝DC2；（3）若tan∠CAD=12，求sin∠CDA的值．【答案】见解析【解析】（1）因为点D是弧BC的中点，所以∠CAD＝∠BAD，即∠CAB＝2∠BAD，而∠BOD＝2∠BAD，所以∠CAB＝∠BOD，所以DO∥AC；（2）∵CD=BD，∴∠CAD＝∠DCB，∴△DCE∽△DAC，∴CD2＝DE•DA；（3）∵tan∠CAD=12，连接BD，则BD＝CD，∠DBC＝∠CAD，在Rt△BDE中，tan∠DBE=DEBD =DECD=12，设：DE＝a，则CD＝2a，而CD2＝DE•DA，则AD＝4a，∴AE＝3a，∴AEDE=3，而△AEC∽△DEF，即△AEC和△DEF的相似比为3，设：EF＝k，则CE＝3k，BC＝8k，tan∠CAD=12，∴AC＝6k，AB＝10k，∴sin∠CDA=35．【例2】已知，在Rt ABC △中，90C Ð=°，AD 平分BAC Ð交BC 于点D ，点O 为AB 上一点，经过点A ，D 的O e 分别交AB ，AC 于点E ，F ，连接DF ，连接OF 交AD 于点G ．（1）求证：BC 为O e 的切线．（2）（2）求证：ABD ADF V V ∽（3）若5BE =，3sin 8B =，求DG 的长度．【答案】见解析【解析】（1）证明：如图，连接OD ，AD Q 平分BAC Ð，BAD CAD \Ð=Ð，OA OD =Q ，ODA OAD \Ð=Ð，ODA CAD \Ð=Ð，//OD AC \，∴ODB C Ð=Ð，90C Ð=°Q ，∴90ODB C Ð=Ð=°，OD BC \^，又∵OD 为O e 的半径，∴BC 为O e 的切线；（2）证明：如图，连接EF ，AE ∵为O e 的直径，90AFE C \Ð=Ð=°，//EF BC \，B AEF \Ð=Ð，∵AEF ADF Ð=Ð，B ADF \Ð=Ð，又BAD DAF Ð=ÐQ ，ABD ADF \△△∽；（3）解：设圆的半径为r ，则OD r =，5=+OB r ，在Rt BOD V 中，3sin 8==OD B OB ，即358=+r r ，解得：3r =，26AE r \==，2511AB r =+=，在Rt V AEF 中，39sin sin 684AF AE AEF AE B =Ð==´=g g ，∵ABD ADF V V ∽，∴AB AD AD AF=，AD \=//AF OD Q ，\34934===DG DO AG AF ，∴47=DG AD，47DG AD \==．【例3】如图，AB 是⊙O 的直径，AC 是弦，点E 在圆外，OE ⊥AC 于D ，BE 交⊙O 于点F ，连接BD ，BC ，CF ，∠BFC ＝∠AED ．（1）求证：AE 是⊙O 的切线；（2）求证：△BOD ∽△EOB ；（3）设△BOD 的面积为S 1，△BCF 的面积为S 2，若tan ∠ODB =，求S 1S 2的值．【答案】见解析【解析】（1）∵∠BFC ＝∠AED ，∵AB 是⊙O 的直径，∴∠BFC ＝∠BAC ，∴∠AED ＝∠BAC ，∵OE ⊥AC 于D ，∴∠ADE＝90°，∴∠AED+∠DAE ＝90°，∴∠BAC+∠DAE ＝90°，∵AB 是⊙O 的直径，∴AE 是⊙O 的切线；（2）∵AD ⊥OE ，∴∠OAE ＝∠ODA ＝90°，∵∠AED ＝∠OAD ，∴△AOD ∽△EOA ，∴OAOE =ODOA ，∴OA 2＝OD×OE ，∵OB ＝OA ，∴OB 2＝OD×OE ，∴OBOD =OEOB ，又∵∠BOD ＝∠EOB ，∴△BOD ∽△EOB ；（3）∵AB 是⊙O 的直径，∴∠ACB ＝90°，∵OE ⊥AC 于D ，∴OE ∥BC ，∴∠ODB ＝∠DBC ，∴在直角三角形BCD 中，tan ∠ODB ＝tan ∠DBC =DCBC =3，∴设CD =，BC ＝3k ，∴BD =，∵△BOD ∽△EOB ，∴∠OBD ＝∠OEB ，∵OE ∥BC ，∴∠OEB ＝∠FBC ，∴∠OBD ＝∠FBC ，∵∠BAC ＝∠BFC ，∴△ABD ∽△FBC ，∴S △ABD S 2=（BDBC ）22=149，∵O 是AB 的中点，∴S △ABD ＝2S 1，∴S 1S 2=79．题型二：圆与三角形、四边形的综合【例1】如图，ABD △内接于O e 中，弦BC 交AD 于点E ，连接CD ，BG CD ^交CD 的延长线于点G ，BG 交O e 于点H ，2ABC GBD Ð=Ð．(1)如图1，求证：DB 平分GDE Ð；(2)如图2，CN AB ^于点N ，CN ＝CG ，求证：AN ＝HG ；(3)如图3．在（2）的条件下，点F 在AE 上，连接BF 、CF ，且BF CF ^，2BCN CBF Ð=Ð，BC ＝5．求A E 的长．【答案】见解析【解析】（1）解：∵∠ABC=∠ADC ，∠ABC=2∠GBD ，∴∠ADC=2∠GBD ，∵BG ⊥CG ，∴∠G=90°，∴∠GBD+∠GDB=90°，∵∠GDB+∠BDE+∠ADC=180°，∴∠GDB+∠BDE+2∠GBD=180°，∴∠BDE+∠GBD=90°，∴∠BDE=∠GDB ，∴BD 是∠GDE 是平分线；（2）解：如图所示，连接CH ，CA ，∵四边形ABHC 是圆内接四边形，∴∠BAC+∠BHC=180°，又∵∠BHC+∠CHG=180°，∴∠CHG=∠CAN ，∵CG ⊥BG ，CN ⊥AB ，∴∠CGH=∠CNA=90°，又∵CG=CN ，∴△CGH ≌△CNA （AAS ），∴GH=AN ；（3）解：如图所示，过点D 作DK ⊥BF 分别交BC 于R ，BF 于K ，过点C 作CM ⊥DK 于M ，连接CH ，AC ，∵DK ⊥BF ，CM ⊥DK ，CF ⊥BF ，∴四边形CFKM 是矩形，∴CM=FK ，CF=KM ；∵∠ABC=2∠GBD=∠GBD+∠CBD ，∴∠ABC=2∠GBD=2∠CBD=∠CBG ，设∠GBD=∠CBD=x ，则∠ABC=∠CBG=2x ，∴∠BCG=90°-∠CBG=90°-2x=∠BAD ，∠BCN=90°-∠CBN=90°-2x ，∴∠BAD+∠ABC=90°，∴∠AEB=90°，∴∠EBF+∠EFB=90°，∵∠BCN=2∠CBF ，∴∠CBF=45°-x ，∴∠DBK=∠CBD+∠CBF=45°，又∵∠DKB=∠DKF=90°，∴∠KBD=∠KDB=45°，∠DFK+∠FDK=90°，∴BK=DK ，∠KDF=∠EBF ，∴△KDF ≌△EBF （ASA ）∴RK=KF=CM ；∵∠CRM=∠BRK=90°-∠RBK=45°+x ，∴∠RCM=90°-∠CRM=45°-x ，∴∠DCM=∠BCD-∠RCM=45°-x ，∴∠RCM=∠DCM ，又∵CM ⊥DR ，∴∠CMD=∠CMR ，∵CM=CM ，∴△CMD ≌△CMR （ASA ），∴DM=MR ，设DM=MR=a ，RK=MC=KF=b ，∴MK=CF=MK+RK=a+b ，BK=DK=DM+MR+RK=2a+b ，∴BF=BK+KF=2a+2b ，∴BF=2CF ，∵222+=BF CF BC ，∴22245CF CF +=，∴CF∴BF 11=22BCF S CF BF BC EF ×=×△，∴2CF BFEF BC ×==，∴BE =，由（2）可知△CGH ≌△CAN ，∴∠ACN=∠GCH=∠GBD=x ，∴∠BCA=∠BCN+∠∠CAN=90°-x ，∴∠BAC=180°-∠ABC-∠BCA=90°-x ，∴∠BAC=∠BCA ，∴AB=BC=5，∴3AE ==．【例2】如图，在△ABC 中，90C =o∠，D 为边BC 上一点，DE AB ^于点E ，以DE 为直径的⊙O 分别交线段BD ，AD 于点F ，G ，连结EF ，EG ．(1)求证：DEF ABC D D :．(2)若6,8AC BC ==，当DG 与四边形DGEF 其它三边中的一边相等时，求所有满足条件的BD 的长．(3)当AC BC =时，连结OC 交AD 于点H ，记△DOH 的面积为1S ，△ACH 的面积为2S ，若OC EG ∥，则12S S 的值为．（在横线上直接写出答案）【答案】(1)证明过程见解析；(2)BD=254或507或8；(3)227．【解析】（1）证明：∵DE ⊥AB ，∴∠BED=90°，∴∠EDF+∠B=90°，∵∠=90°，∴∠B+∠BAC=90°，∴∠EDF=∠BAC ，∵DE 是⊙O 的直径，∴∠DFE=90°，∴∠EFD=∠C ，∴△DEF ∽△ABC ；（2）当DG=DF 时，DF DG =，∴∠FED=∠DEG ，∵DE 是⊙O 的直径，∴∠EFD=∠EGD=90°，∴∠EDF=∠EDA，∵DE⊥AB，∴∠AED=∠BED=90°，∴∠B=∠BAD，∴AD=BD，在Rt△ACD中，∵CD2+AC2=AD2，∴（8-BD）2+62=BD2，∴BD=25 4，当DG=EG时，∵∠EGD=90°，∴∠EDG=∠DEG=45°，∵∠AED=90°，∴∠BAD=90°-∠EDG=45°，∴DE=AE，∵∠B=∠B，∠BED=∠ACB=90°，∴△BED∽△BCA，∴BD DE BEAB AC BC==，∴1068BD DE BE==，∴BE=43DE∵BE+AE=10，∴43DE+DE＝10，∴DE=307，∴307106BD=，∴BD=507，当DG=EF时，∴EF DG=，，∴∠EDF=∠DEG，∵∠EFD=∠EGD=90°，∴∠FED=∠EDG，∴EF∥DG，∴四边形EFDG是平行四边形，∴▱EFDG是矩形，∴∠FDG=90°，∵∠C=90°，∴此时点D和C重合，∴BD=8，综上所述：BD=254或507或8；（3）如图，作OV⊥BC于V，∴∠OVC=90°，∠EGD=90°，∴∠AHC=90°，∴∠DAC+∠ACH=90°，∵∠ACB=90°，∴∠OCV+∠ACH=90°，∴∠OCV=∠DAC，∵∠ONC=∠ACD=90°，∴△OCV∽△DAC，∴CD OV AC VC=，设CD=a，AC=BC=b，在等腰直角三角形BDE中，BD(b−a)，∴OD=12(b−a)，在等腰直角三角形DOV中，OD=14(b−a)，∴VC=VD+CD=14 (b−a)+a=14b+34a，∴1()41344b a a b b a -=+，∴b=3a ，∴AC=3a ，OV=14 (3a −a)=12a ，∴tan ∠OCV=tan ∠DAC=13CD AC =，∴sin ∠OVC=sin ∠cos ∠OVC=cos ∠S △COD=12CD•OV=12a•12a=14a2，∴DH=a•sin ∠，，，∴22113,2220CDH S DH CH a =×==V，2211272220ACH S CH AH a=×==V ，∴22213142010DOH S a a a =-=V ，∴21221210272720aS S a ==，故答案是：227．【例3】．在△ABC 中，点D 在边BC 上，连接AD ．(1)如图1，已知AB ⊥AC ，点D 为BC 中点，CE ⊥AD 于点E ．若AD ＝7，CE ＝AE 的长度：(2)如图2，当∠B ＝45°，AC ＝AD 时，过点C 作CE ⊥AD 交AD 于点E ，交AB 于点F ，连接DF ，求证：DC＝．(3)如图3，当∠B ＝45°，AC ＝12，点D 是边BC 中点时，过点D 作DN ⊥AC 交AC 于点N ，当线段DN 取最大值时，请直接写出2AD 的值．【答案】(1)6(2)证明见解析(3)108+【解析】(1)解：∵AB ⊥AC ，点D 为BC 中点∴AD 是Rt ABC V 斜边BC 的中线∴7AD BD CD ===∵CE ⊥AD ∴90CED Ð=°在Rt CDE △中，由勾股定理得1DE ==∴6AE AD DE =-=∴AE 的长为6．(2)证明：如图2，作AM BC ^于M ，FN BC ^于N∵AD AC =∴ADC ACD Ð=Ð，12DM CM DC ==设1BAD Ð=Ð则451ACD ADC Ð=Ð=°+Ð，901BAC Ð=°-Ð∴90451CAM ACD Ð=°-Ð=°-Ð∵CE AD^∴90901AFC BAD Ð=°-Ð=°-Ð，90451DCE ADC Ð=°-Ð=°-Ð∴AFC BAC Ð=Ð，CAM DCE Ð=Ð∴AC CF=在ACM △和CFN V 中∵90CAM FCNAMC CNF AC CF Ð=ÐìïÐ=Ð=°íï=î∴()ACM CFN AAS V V ≌∴FN MC =∴2DC FN =∵45B Ð=°，90BNF Ð=°∴BF =∴DC =．(3)解：如图3，以AC 为斜边作等腰直角三角形AOC ，∴=90AOC Ð°∵1452B AOCÐ=°=Ð∴B 在以O 为圆心，OC 为半径的圆上运动连接OD ∵D 为BC 中点∴90ODC Ð=°∴D 在以OC 为直径的圆上运动，圆心为I ∵DN AC ^∴当DN 过圆心I 时，线段DN 取最大值∵12AC =，45OCA OAC Ð=Ð=°∴OC =12CI DI OC ===3IN CN ==∴DN DI IN =+3=+在Rt AD N △中，由勾股定理得222AD DN AN=+()()223123108=+-=+∴2AD 的值为108+【例4】(1)发现：如图1，在平面内，已知⊙A 的半径为r ，B 为⊙A 外一点，且AB ＝a ，P 为⊙A 上一动点，连接PA ，PB ，易得PB 的最大值为，最小值为；（用含a ，r 的代数式表示）(2)应用：①如图2，在矩形ABCD 中，AB ＝6，BC ＝4，E 为AD 边中点，F 为AB 边上一动点，在平面内沿EF 将△AEF 翻折得到△PEF ，连接PB ，则PB 的最小值为；②如图3，点P 为线段AB 外一动点，分别以PA 、PB 为直角边，P 为直角顶点，作等腰Rt △APC 和等腰Rt △BPD ，连接BC 、AD ．若AP ＝AB ＝7，求AD 的最大值；(3)拓展：如图4，已知以AB 为直径的半圆O ，C 为弧AB 上一点，∠ABC ＝60°，P 为弧BC 上任意一点，CD ⊥CP 交AP 于D ，连接BD ，若AB ＝6，则BD 的最小值为．【答案】(1)a+r，a﹣r(2)①﹣2②13﹣【解析】（1）解：（1）当P在BA延长线上时，PB最大，如图：∴PB最大为：AB+PA＝a+r，当P在线段BA上时，PB最小，如图：∴PB最小为：AB﹣PA＝a﹣r，（2）①如图：∵沿EF将△AEF翻折得到△PEF，∴EA＝EP＝12AD＝12BC＝2，即P的轨迹是以E为圆心，以2为半径的半圆，∴当E、P、B共线时，PB最小，此时BE，∴PB最小值为：BE﹣EP＝﹣2；②连接BC，如图：∵△APC和△BPD是等腰直角三角形，∴PD＝PB，PA＝PC，∠DPB＝∠APC，∴∠DPB+∠APB＝∠APC+∠APB，即∠DPA＝∠BPC，∴△DPA≌△BPC（SAS），∴AD＝BC，∴当BC最大时，AD就最大，∵AP＝APC是等腰直角三角形，∴AC＝AP＝6，∵AB＝7，∴当C、A、B共线时，BC最大，如图：∴此时BC＝AC+AB＝13，∴AD最大为13；（3）以AC为边，在△ABC异侧作等边△GAC，连接GD、GB，如图：∵AB 为半圆O 的直径，∠ABC ＝60°，∴∠ACB ＝90°，∠APC ＝∠ABC ＝60°，∴∠CAB ＝30°，∴AC ＝AB•cos30°＝CD ⊥CP ，∴∠ADC ＝∠DCP+∠APC ＝150°，∵△GAC 是等边三角形，∴∠AGC ＝∠GAC ＝60°，GA ＝AC ＝∴∠ADC+12∠AGC ＝180°，即D 的轨迹是以G 为圆心， AC ，而∠GAB ＝∠GAC+∠CAB ＝90°，∴BG ，△BGD 中，BD ＞BG ﹣GD ，∴BD ＞﹣∴当G 、D 、B 共线时，BD 最小，如图∴BD 最小值为﹣﹣题型三：瓜豆原理【例1】如图，在平面直角坐标系中，C （0，4），A （3，0），⊙A 半径为2，P 为⊙A 上任意一点，E 是PC 的中点，则OE 的最小值是（）C．2DA．1B．32【答案】B【解析】如图，连接AC，取AC的中点H，连接EH，OH．∵CE＝EP，CH＝AH，PA＝1，∴EH=12∴点E的运动轨迹是以H为圆心半径为1的圆，∵C（0，4），A（3，0），∴H（1.5，2），∴OH= 2.5，∴OE的最小值＝OH﹣EH＝2.5﹣1＝1.5，所以选：B．【例2】如图，等边△ABC中，AB＝2，点D是以A为圆心，半径为1的圆上一动点，连接CD，取CD的中点E，连接BE，则线段BE的最大值与最小值之和为．【答案】【解析】延长CB到T，使得BT＝BC，连接AT，DT，AD．∵△ABC是等边三角形，∴BA＝BC＝AC＝BT＝2，∠ACB＝60°，∴∠CAT＝90°，∴AT＝CT•sin60°＝∵AD＝1，∴1≤DT≤1，∵CB＝BT，CE＝DE，DT，∴BE=12≤BE≤∴线段BE的最大值与最小值之和为x+3与坐标轴交于A、B两点，⊙O的半径为2，点P是⊙O上动点，△ABP面积【例3】如图，直线y=34的最大值为 cm2．【答案】11【解析】如图，∵直线y =34x +3与坐标轴交于A 、B 两点，∴A （﹣4，0），B （0，3），∴OA ＝4，OB ＝3，在Rt △AOB 中，根据勾股定理得，AB ＝5，∵△PAB 中，AB ＝5是定值，∴要使△PAB 的面积最大，即⊙O 上的点到AB 的距离最大，∴过点O 作OC ⊥AB 于C ，CO 的延长线交⊙O 于P ，此时S △PAB 的面积最大，∴S △AOB =12OA •OB =12AB •OC ，∴OC =OA⋅OB AB =4×35=125，∵⊙O 的半径为2，∴CP ＝OC +OP =225，∴S △PAB =12AB •CP =12×5×225=11．所以答案为11．【例4】如图，在直角坐标系中，⊙A 的半径为2，圆心坐标为（4，0），y 轴上有点B （0，3），点C 是⊙A 上的动点，点P 是BC 的中点，则OP 的范围是．【答案】32≤OP ≤72　【解析】如图，在y 轴上取点B '（0，﹣3），连接B 'C ，B 'A ，∵点B （0，3），B '（0，﹣3），点A （4，0），∴OB ＝OB '＝3，OA ＝4，∴B 'A =5，∵点P 是BC 的中点，∴BP ＝PC ，∵OB ＝OB '，BP ＝PC ，∴B 'C ＝2OP ，当点C 在线段B 'A 上时，B 'C 的长度最小值＝5﹣2＝3，当点C 在线段B 'A 的延长线上时，B 'C 的长度最大值＝5+2＝7，∴32≤OP ≤72，所以答案为32≤OP ≤72．【例5】如图，∠BAD ＝90°，AB ＝AD ＝4，点C 为平面内一动点，且BC ＝2，点M 为线段CD 中点，则线段AM 的取值范围为．【答案】1≤AM ≤+1【解析】如图1，连接BD ，取BD 的中点N ，连接AN ．MN ，∵点M 为线段CD 中点，∴MN 是△BCD 的中位线，∴MN =12BC =12×2＝1，∵∠BAD ＝90°，AB ＝AD ＝4．∴BD =又∵点N 为BD 的中点，∴AN =12BD ＝（1）如图1，当点A ，N ，M 不共线时，由三角形的三边关系得：AN ﹣MN ＜AM ＜AN +MN 即1＜AM ＜1；（2）如图2，当点A，N，M共线，且点N位于点A，M中间时，则AM＝AN+MN＝+1；（3）如图3，当点A，N，M共线，且点M位于点A，N中间时，则AM＝AN﹣MN＝1；综上，线段AM的取值范围为1≤AM≤+1，解法二：倍长DA到F，得到AM等于二分之一CF，点C的运动轨迹是以点B为圆心，BC＝2为半径的圆，同时当FC经过圆心B的时候，FC1是最大，也就是AM最大，FC2最小也就是AM最小，∵点M为线段CD中点，AF＝AD，FC，AF＝AD＝AB＝4，∴AM=12∵∠BAD＝90°，∴BF＝当FC经过圆心B的时候，FC1是最大为2，也就是AM最大，AM＝1，FC2最小也就是AM最小为2，也就是AM最小，AM＝1，∴线段AM的取值范围为1≤AM≤1，所以答案为：1≤AM≤+1．课后作业:1、如图，矩形ABCD中，E是BC的中点，连接DE，P是DE上一点，∠BPC＝90°，延长CP交AD于点F．⊙O经过P、D、F，交CD于点G．（1）求证DF＝DP；（2）若AB＝12，BC＝10，求DG的长；的值．（3）连接BF，若BF是⊙O的切线，直接写出ABBC【答案】见解析【解析】证明：（1）∵∠BPC＝90°，点E是BC中点，∴BE＝EC＝PE，∴∠EPC＝∠ECP，∵四边形ABCD是矩形，∴AD∥BC，∠ABC＝∠ADC＝90°，∴∠DFP＝∠ECP，∴∠DFP＝∠EPC＝∠DPF，∴DF＝DP；（2）连接FG，∵∠ADC＝90°，∴FG是直径，∵BE＝EC＝PE=12BC＝5，∴DE=13，∴DP＝DE﹣EP＝13﹣5＝8＝DF，∵∠DGF＝∠DPF＝∠DFP，∠FDG＝∠FDC＝90°，∴△FDG∽△CDF，∴DFDG =DCDF，∴8DG=128，∴DG=163；（3）如图2，连接BF，FG，PG，∵FG是直径，∴∠FPG＝90°，∴∠FPG+∠BPF＝180°，∴点B，点P，点G三点共线，∵BF是⊙O切线，∴∠BFG＝90°，∴∠AFB+∠DFG＝90°，∵∠DFG+∠DGF＝90°，∴∠DGF＝∠AFB，又∵∠A＝∠FDG，∴△AFB∽△DGF，∴AFDG =ABDF，∠DFG＝∠ABF，∴AF•DF＝AB•DG，由（2）可得△FDG∽△CDF，∴DFDG =DCDF，∠DFG＝∠DCF，∴DF2＝DC•DG，∠ABF＝∠DCF，又∵AB＝CD，∠A＝∠FDC，∴△ABF≌△DCF（ASA）∴AF＝DF=12AD，BF＝CF，∵∠CBG+∠PCB＝90°，∠PCB+∠PCG＝90°，∴∠GBC＝∠PCG＝∠DFG，又∵∠FDC＝∠GCB＝90°，∴△CBG∽△DFG，∴DFBC =DGCG=12，∴CG＝2DG，∴（12BC）2=13AB•AB，∴ABBC=2、（2021•泰安中考）如图1，O为半圆的圆心，C、D为半圆上的两点，且＝．连接AC并延长，与BD 的延长线相交于点E．（1）求证：CD＝ED；（2）AD与OC，BC分别交于点F，H．①若CF＝CH，如图2，求证：CF•AF＝FO•AH；②若圆的半径为2，BD＝1，如图3，求AC的值．【答案】见解析【解析】（1）证明：如图1中，连接BC．∵＝，∴∠DCB＝∠DBC，∵AB是直径，∴∠ACB＝∠BCE＝90°，∴∠E+∠DBC＝90°，∠ECD+∠DCB＝90°，∴∠E＝∠DCE，∴CD＝ED．（2）①证明：如图2中，∵CF＝CH，∴∠CFH＝∠CHF，∵∠AFO＝∠CFH，∴∠AFO＝∠CHF，∵＝，∴∠CAD＝∠BAD，∴△AFO∽△AHC，∴＝，∴＝，∴CF•AF＝OF•AH．②解：如图3中，连接OD交BC于G．设OG＝x，则DG＝2﹣x．∵＝，∴∠COD＝∠BOD，∵OC＝OB，∴OD⊥BC，CG＝BG，在Rt△OCG和Rt△BGD中，则有22﹣x2＝12﹣（2﹣x）2，∴x＝，即OG＝，∵OA＝OB，∴OG是△ABC的中位线，∴OG＝AC，∴AC＝．3、（2021•宁波中考）如图1，四边形ABCD内接于⊙O，BD为直径，上存在点E，满足＝，连结BE 并延长交CD的延长线于点F，BE与AD交于点G．（1）若∠DBC＝α，请用含α的代数式表示∠AGB．（2）如图2，连结CE，CE＝BG．求证：EF＝DG．（3）如图3，在（2）的条件下，连结CG，AD＝2．①若tan∠ADB＝，求△FGD的周长．②求CG的最小值．【答案】见解析【解析】解：（1）∵BD为⊙O的直径，∴∠BAD＝90°，∵＝，∴∠ABG＝∠DBC＝α，∴∠AGB＝90°﹣α；（2）∵BD为⊙O的直径，∴∠BCD＝90°，∴∠BEC＝∠BDC＝90°﹣α，∴∠BEC＝∠AGB，∵∠CEF＝180°﹣∠BEC，∠BGD＝180°﹣∠AGB，∴∠CEF＝∠BGD，又∵CE＝BG，∠ECF＝∠GBD，∴△CFE≌△BDG（ASA），∴EF＝DG；（3）①如图，连接DE，∵BD为⊙O的直径，∴∠A＝∠BED＝90°，在Rt△ABD中，tan∠ADB＝，AD＝2，∴AB＝×AD＝，∵＝，∴+＝+，即＝，∴AD＝CE，∵CE＝BG，∴BG＝AD＝2，∵在Rt△ABG中，sin∠AGB＝＝，∴∠AGB＝60°，AG＝BG＝1，∴EF＝DG＝AD﹣AG＝1，∵在Rt△DEG中，∠EGD＝60°，∴EG＝DG＝，DE＝DG＝，在Rt△FED中，DF＝＝，∴FG+DG+DF＝，∴△FGD的周长为；②如图，过点C作CH⊥BF于H，∵△BDG≌△CFE，∴BD＝CF，∠CFH＝∠BDA，∵∠BAD＝∠CHF＝90°，∴△BAD≌△CHF（AAS），∴FH＝AD，∵AD＝BG，∴FH＝BG，∵∠BCF＝90°，∴∠BCH+∠HCF＝90°，∵∠BCH+∠HBC＝90°，∴∠HCF＝∠HBC，∵∠BHC＝∠CHF＝90°，∴△BHC∽△CHF，∴＝，设GH＝x，∴BH＝2﹣x，∴CH2＝2（2﹣x），在Rt△GHC中，CG2＝GH2+CH2，∴CG2＝x2+2（2﹣x）＝（x﹣1）2+3，当x＝1时，CG2的最小值为3，∴CG的最小值为．4．如图1，菱形ABCD的边长为12cm，∠B＝60°，M，N分别在边AB，CD．上，AM＝3cm，DN＝4cm，点P 从点M出发，沿折线MB﹣BC以1cm/s的速度向点C匀速运动（不与点C重合）；△APC的外接圆⊙O与CD 相交于点E，连接PE交AC于点F．设点P的运动时间为ts．(1)∠APE＝ °；(2)若⊙O与AD相切，①判断⊙O 与CD 的位置关系；②求 APC 的长；(3)如图3，当点P 在BC 上运动时，求CF 的最大值，并判断此时PE 与AC 的位置关系；(4)若点N 在⊙O 的内部，直接写出t 的取值范围．【答案】(1)60°(2)①⊙O 与CD 相切；② APC =(3)CF 的最大值为3cm ，此时AC ⊥PE(4)当0<t<1时或17<t<21时，点N 在圆内部；【解析】（1）解：∵四边形ABCD 为菱形，∠B ＝60°，∴∠D=∠B ＝60°，AD=CD ，∴△ACD 为等边三角形，∴∠ACE=60°，∴∠APE=∠ACE=60°，故答案为：60°．（2）如图，当点P 运动到点B 时，⊙O 与AD 相切，①∵四边形ABCD 为菱形，∴AD=CD ，∵⊙O 与AD 相切，∴⊙O 与CD 相切；②连接OD ，由（1）可知，∠ADC=60°，∵AD 、CD 分别与⊙O 相切，∴∠ADO=12∠ADC=30°，∴AO=tan 30AD ´°=12= 2(23APC p =´´=；（3）由图可知：CF=AC-AF ，∵AB=BC ，∠B=60°，∴△ABC 为等边三角形，则AC=12cm ，∠ACB=60°，∴要使CF 取得最大值，则AF 应该取最小值，当AC ⊥PE 时，AF 最小，此时CF 取得最大值，∵点O 为△APC 外接圆圆心，∴OA=OC=OP=12AC =6cm ，∵∠ACB=60°，∴CF=cos 60CP °g =3cm ，综上：CF 的最大值为3cm ，此时AC ⊥PE ．（4）①当点P 在AB 上时，∵四边形APCE 为圆的内接四边形，∴∠APC+∠AEC=180°，∵∠AED++∠AEC=180°，∴∠APC=∠AED ，在△APC 和△DEA 中，AC=AD ，∠PAC=∠D ，∠APC=∠AED ，∴△APC ≌△DEA ，∴AP=DE ，当点E 与点N 重合时，DE=DN=AP=4，∴MP=4-3=1cm ，∴t=1s ，当0<t<1时，点N 在圆内部；②当点P 在BC 上运动时，∵∠AEP=∠ACP=60°，∴△APE 为等边三角形，∴AP=AE ，∠PAE=60°，∵∠BAC=60°，∴∠BAP=∠CAE ，在△BAP 和△CAE 中，AB=AC ， ∠BAP=∠CAE ， AP=AE ，∴△BAP ≌△CAE ，∴BP=CE ，当点E 与带你N 重合时，CE=CN=BP=12-4=8cm ，此时t=1MP BP+=9+8=17s ，当点P 到达点C 时，t=21s ，当17<t<21时，点N 在圆内部；综上：当0<t<1时或17<t<21时，点N 在圆内部．5．为了解决一些较为复杂的数学问题，我们常常采用从特殊到一般的思想，先从特殊的情形入手，从中找到解决问题的方法．已知四边形ABCD 是⊙O 的内接四边形，对角线AC 与BD 相交于点E ．【特殊情形】(1)如图①，AC BD ^，过圆心O 作OF AD ^，垂足为F ．当BD 是圆O 的直径时，求证：12OF BC =．【一般情形】(2)如图②，AC BD ^，过圆心O 作OF AD ^，垂足为F ．当BD 不是圆O 的直径时，求证：12OF BC =．【经验迁移】(3)如图③，60AED Ð=° ，12AD = ， F 为 AB 上的一点，AF BC =，若M 为DF 的中点，连接AM ，则AM 长的最小值为___________．【答案】(1)见解析(2)见解析(3)【解析】（1）Q 在⊙O 中，OF AD ^，DF AF \=OD OB =Q \OF 是△ADB 的中位线，12OF AB \=∵BD 为⊙O 的直径，BD AC ^， AB BC \=AB BC \=12OF BC \=（2）作直径DG ，连接AG ．Q 在⊙O 中，OF AD ^DF AF \=DO OG =Q \OF 是△ADG 的中位线，12OF AG \= AD AD =Q G ACD\Ð=ÐQ DG 是⊙O 的直径，90DAG \Ð=°Q AC BD ^，180DAG ADG AGD DEC EDC ACD ÐÐÐ=ÐÐÐ=°＋＋＋＋ADG EDC \Ð=Ð AG BC \=AG BC \= 12OF BC \=．（3）Q AF BC = AF BC \= ADF BDC \Ð=ÐF ACDÐ=ÐQ 60ADF F BDC ACD AED \Ð+Ð=Ð+Ð=Ð=°()180120DAF ADF F \Ð=°-Ð+Ð=°\在ADF △中，120DAF Ð=°，12AD =，M 是DF 的中点，如图⑤所示，当AF 的长度发生变化时：Q 点M 是DF 中点\点M 始终保持在平行于AF 的直线上\当AM 的长度取最小值时，AM AF^如图④，此时AM AF ^，取AD 中点H ，连接MH ，则162AH AD ==Q H 、M 分别是AD 、DF 中点\MH 是DAF △的中位线，MH AF ∥AM AF ^Q 90HMA MAF \Ð=Ð=°1209030HAM DAF MAF Ð=Ð-Ð=°-°=°Q \在Rt AMH V 中，132MH AH ==，AM \===故答案为：6．如图，在四边形ABCD中，连接BD，AD＝BD＝CD＝4，∠BDC＝120°，E为AB的中点，则线段CE 的最大值为　．【答案】【解析】如图，点F为BD中点，连接EF，FC．∵AD＝BD＝CD＝4，AD＝2，∴EF=12在Rt△HDC中，DC＝4，∠CDH＝180﹣∠HDC＝60°，∴DH＝2，HC＝FH＝4，在Rt△HFC中，FC==∴CE≤EF+FC＝∴CE的最大值为。

中考数学压轴题突破-圆的双动点最值问题

中考数学压轴题突破圆的双动点最值问题1．如图，在Rt△ABC中，∠C=90°，AC=6，BC=8，点F在边AC上，并且CF=2，点E为边BC上的动点，将△CEF沿直线EF翻折，点C落在点P处，则点P到边AB距离的最小值是_____．分析：本题中，要求点P到边AB距离的最小值，先要确定点P的运动轨迹．因为FP=FC=2，所以点P的运动轨迹是以点F为圆心，2为半径的圆弧（如图），过点F作FQ⊥AB，以F为圆心的弧与FQ的交点为满足条件的点P．答案： 6/5这是动点轨迹为圆弧的一种类型，动点满足到定点的距离等于定长，确定动点的运动轨迹为以定点为圆心，定长为半径的圆（或一段弧）．2. 如图，点P是正方形ABCD的对角线BD上的一个动点(不与B、D重合)，连结AP，过点B作直线AP 的垂线，垂足为H，连结DH，若正方形的边长为4，则线段DH长度的最小值是_______．分析：要求线段DH长度的最小值，先要确定动点H的运动轨迹。

在点P的运动过程中，∠AHB=90°，点H 的运动轨迹是以AB为直径的半圆，题目转化为圆外一点到圆上一点之间的最小距离的问题（如图），连结点D和AB中点O，与半圆O交于点H，此时DH长度最小．答案：这一类动点满足与定线段构成一个直角三角形，且为直角顶点，则这个动点的轨迹是以定线段为直径的圆（或圆弧）。

由特殊到一般，如果动点与定线段构成的三角形中，以动点为顶点的角度确定，这个动点的运动轨迹是以定线段为弦的圆（或圆弧）.3. 如图，正方形OABC的边长为4，以O为圆心，EF为直径的半圆经过点A，连接AE，CF相交于点P，将正方形OABC从OA与OF重合的位置开始，绕着点O逆时针旋转90°，交点P运动的路径长是（）分析：这题看似动点很多，其实点A、B、C可看成是同一个动点，点P是第二动点，要求点P运动的路径长，先要确定点P的运动轨迹。

因为四边形OABC是正方形，所以∠AOC=90°，所以∠AFC=45°，因为EF是直径，所以∠EAF=90°，∠APF=45°，∠EPF=135°，点P的运动轨迹是以EF为弦且该弦所对的一个圆周角为135°的一段圆弧（如图）。