种群的相互竞争模型中数值计算与结果分析
种群竞争模型研究

物种混居,必然会出现以食物、空间等资源为核心的种间关系。从理论上讲, 任何物种对其他物种的影响只可能有三种形式,即有利、有害、或无利无害的中 间态。因此,全部的种间关系只是这三种作用形式的可能组合。最常见的关系为 种间竞争、捕食和寄生。当环境中同时存在着两个种群,且两个种群存在着竞争
时可建立方程进行讨论,得到两种不同种群之间竞争的结果。研究种群竞争的关 系有很多应用,现举例如下:
假如人口数真能保持每 34.6 年增加一倍,那么人口数将以几何级数的方式 增长(如图 1)
例如,到 2515 年,人口约达 2×1014 人,即使海洋全部变成陆地,每人也 只有 9.3 平方英尺的活动范围,而到 2665 年,人口约达 4×1015 人,只好一个 人站在另一人的肩上排成二层了。故马尔萨斯模型是不完善的。
r
人口统计数据与 Malthus 模型计算数据对比:
年
1625
人口(亿) 5
表 2.2.1 世界人 口数量统计数据
1830 1930 1960 1974
10
20
30
40
1987 50
1999 60
年
1908
人口(亿) 3.0
表 2.2.2 中国人口数量统计数据
1933
1953 1964 1982
4.7
关键词:种群 竞争 数学模型 环境条件
1.2 英文摘要 Biological populations have different biomass at different growth
stages, and the changes of biomass over time are restricted by various complex factors. The competition between the biological populations is often reflected in the competition between the limited space resources and other living conditions, and the change of environmental conditions has an effect on the real growth rate of the biological population. In this paper, we give the mathematical model of the competition of biological populations, and then apply it in ecology, and then predict the competition outcome of the biological species. The relationship between the species is important for food and living space. Darwin wrote in the book "natural selection and the origin of the species": "because of the similarities in the habits and qualities especially in terms of structure, so if they are in a state of mutual competition, they are more intense than those of different biological species." In this paper, we give a mathematical model of population competition, and apply it to some aspects of ecology, and then predict the results of biological competition.
实例 动物种群的相互竞争与相互依存的模型

实例动物种群的相互竞争与相互依存的模型实例2 动物种群的相互竞争与相互依存的模型在生物的种群关系中,一种生物以另一种生物为食的现象,称为捕食.一般说来,由于捕食关系,当捕食动物数量增长时,被捕食动物数量就逐渐下降,捕食动物由于食物来源短缺,数量也随之下降,而被捕食动物数量却随之上升.这样周而复始,捕食动物与被捕食动物的数量随时间变化形成周期性的震荡.田鼠及其天敌的田间种群消长动态规律也是如此.实验调查数据表明:无论是田鼠还是其天敌的数量都呈周期性的变化,天鼠与天敌的作用系统随时间序列推移,田鼠密度逐渐增加,其天敌随之增加,但时间上落后一步.由于天敌密度增加,则田鼠密度降低,而田鼠密度的降低,则其天敌密度亦减少,如此往复循环,从而形成一定的周期.试用数学模型来概括这一现象,并总结出其数量变化的近似公式.一问题分析及模型的建立设x(t)和y(t)分别表示t时刻田鼠与其天敌的数量,如果单独生活,田鼠的增长速度正比于当时的数量,即dx=λx dtdy=-μy dt而田鼠的天敌由于没有被捕食对象,其数量减少的速率正比于当时的数量,即现在田鼠与其天敌生活一起,田鼠一部分遭到其天敌的消灭,于是以一定的速率α减少,减少的数量正比于天敌的数量,因此有dx=(λ-αy)x dt类似地,田鼠的天敌有了食物,数量减少的速率μ减少β,减少的量正比于田鼠的数量,因此有dy=-(μ-βx)y dt上述公式,最后两个方程联合起来称为Volterra-Lot方程,这里α,β,λ,μ均为正数,初始条件为x(0)=x0,y(0)=y0现在通过实验调查所得到的数据如表,此数据为每隔两个月田间调查一次,得到的田鼠及其天敌种群数量的记录,数量的单位经过处理.试建立合理的数学模型.表田鼠种群数量记录29.7 33.1 32.5 69.1 134.2 236.0 269.6 162.2 69.6 39.8 34.0 20.7 22.0 37.6 57.6 124.6 225.0 272.7 195.7 94.5 41.9 25.7 10.9 22.5 33.5 48.2 92.5 183.3 268.5 230.6 115.5表田鼠天敌种群数量记录1.6 1.3 1.1 1.2 1.1 1.3 1.82.2 2.4 2.2 1.9 1.5 1.5 1.2 0.91.1 1.3 1.62.3 2.4 2.2 1.7 1.8 1.5 1.2 1.0 0.9 1.1 1.3 1.9 2.3二模型的求解Volterra-Lotok方程的解析解即x,y的显示解难求出,因此公式的参数方程不宜直接用Matlab函数来拟合解,可用如下的方法来求其近似解.Volterra-Lotok可转化为⎧dlnx=(λ-αy)dt ⎧dlny=(-μ+βx)dt⎧在区间[ti-1,ti]上积分,得lnxi-lnxi-1=λ(ti-ti-1)-αS1ilnyi-lnyi-1=-μ(ti-ti-1)+βS2i这里,S1i=⎧titi-1ydt,S2i=⎧xdt, i=1, ,m ti-2ti于是得到方程组⎧A1P1=B1 ⎧ AP=B2⎧22这里⎧t1-t0 t-tA1= 21t-t⎧mm-1-S11⎧⎧t1-t0⎧ -S12⎧ t2-t1A= 2 ⎧ ⎧ t-t-Sim⎧m-1⎧⎧m-S⎧⎧-S22⎧ ⎧⎧-S2m⎧⎧⎧-μ⎧⎧λ⎧ ⎧ P=P1= 2 β⎧⎧ α⎧⎧⎧⎧⎧B1=(lnxyx1y, ,lnm)T B=(ln1, ,lnm)T x0xm-1y0ym-1T-1TA2B2 因此方程组参数的最小二乘解为 T-1T P=(AA)A1B1 P=(A2A2)111由于x(t)和y(t)均为未知,因此S1i,S2用数值积分方法的梯形公式解S1i=⎧⎧titi-1ydt≈ti-ti-1(yi+yi-1) 2 S2=titi-1xdt=ti-ti-1(xi+xi-1) 2这样就可求得参数的近似值.模型参数求解的程序为clear all,clcX=[29.7 33.1 32.5 69.1 134.2 236.0 269.6 162.2 69.6 39.8 ...34.0 20.7 22.0 37.6 57.6 124.6 225.0 272.7 195.7 94.5 41.9 25.7 ... 10.9 22.5 33.5 48.2 92.5 183.3 268.5 230.6 115.5];Y=[1.6 1.3 1.1 1.2 1.1 1.3 1.8 2.2 2.4 2.2 1.9 1.5 1.5 1.2 0.9 ...1.1 1.3 1.62.3 2.4 2.2 1.7 1.8 1.5 1.2 1.0 0.9 1.1 1.3 1.9 2.3];N=[X;Y];T=[0:2:60];for i=1:30A(i,1)=T(i+1)-T(i);A(i,[2 3])=((T(i+1)-T(i))/2)*[-(N(1,i+1)+N(1,i)),-(N(2,i+1)+N(2,i))];B(i,[1 2])=[log(N(1,i+1)/N(1,i)),log(N(2,i+1)/N(2,i))];end;A1=A(:,[1 3]);P1=inv((A1'*A1))*A1'*B(:,1)A2=A(:,[1 2]);P2=inv((A2'*A2))*A2'*B(:,2)上述结果代入Volterra-Lotok方程,用MATLAB函数ode45求方程在时间[0,60]的数值解.作图可看到田鼠及其天敌数量的周期震荡.求方程Volterra-Lotok的数值解的程序为定义函数vlok为[vlok.m]function dydt=vlok(T,Y)dydt=[(0.8765-0.5468*Y(2))*Y(1);(-0.1037+0.0010*Y(1))*Y(2)];clear all, clcX=[29.7 33.1 32.5 69.1 134.2 236.0 269.6 162.2 69.6 39.8 ...34.0 20.7 22.0 37.6 57.6 124.6 225.0 272.7 195.7 94.5 41.9 25.7 ... 10.9 22.5 33.5 48.2 92.5 183.3 268.5 230.6 115.5];Y=[1.6 1.3 1.1 1.2 1.1 1.3 1.8 2.2 2.4 2.2 1.9 1.5 1.5 1.2 0.9 ...1.1 1.3 1.62.3 2.4 2.2 1.7 1.8 1.5 1.2 1.0 0.9 1.1 1.3 1.9 2.3]; N=[X,Y];T=[0:2:60];[t,Y]=ode45(@vlok,[0:0.5:60],[29.7 1.6]);plot(t,Y(:,1)/100,'k');hold on;plot(t,Y(:,2),'-.k');title('田鼠及其天敌的Volterra-Lotok模型拟合曲线');xlabel('时间');ylabel('数量(只/每百)');gtext('田鼠');gtext('天敌');legend('田鼠','天敌');legend('田鼠','天敌');图田鼠及其天敌的模拟曲线实线和虚线分别为田鼠和天敌的实际值,田鼠的数量为y坐标乘以100.。
种群相互竞争模型

数学实验设计课题:两种群相互竞争模型如下:()1(11)12()2(12)12x y x t r x s n n x y y t r y s n n ⎧=--⎪⎪⎨⎪=--⎪⎩其中x (t ),y(t)分别是甲乙两种群`的数量,r1,r2为它们的固有增长率,n1,n2为它们的最大容量。
s1的含义是,对于供养甲的资源而言,单位数量乙(相对n2)的消耗量为单位数量甲(相对n1)消耗的s1倍,对于s2也可做相应的解释。
分析:这里用x (t)表示甲种群在时刻t 的数量,即一定区域内的数量。
y(t)表示乙种群在时刻t 的数量。
假设甲种群独立生活时的增长率(固有增长率)为r1,则x (t)/ x=r1,而种群乙的存在会使甲的增长率减小,且甲种群数量的增长也会抑制本身数量的增长,即存在种间竞争。
这里,我们设增长率的一部分减少量和种群乙的数量与最大容纳量的比值成正比,与s1(s1表示最大容纳量乙消耗的供养甲的资源是最大容纳量甲消耗该资源的s1倍)成正比。
另一部分的减少量和种群甲的数量与甲的最大容纳量的比值成正比。
则我们可以得到如下模型:x(t)=r1*x*(1-x/n1-s1*y/n2)同样,我们可以得到乙种群在t时刻的数量表达式:y(t)=r2*y*(1-s2*x/n1-y/n2)如果给定甲、乙种群的初始值,我们就可以知道甲、乙种群数量随时间的演变过程。
对于上述的模型,我们先设定好参数以后,就可以用所学的龙格库塔方法及MATLAB 软件求其数值解;问题一:设r1=r2=1,n1=n1=100,s1=0.5,s2=2, 初值x0=y0=10,计算x(t),y(t),画出它们的图形及相图(x,y),说明时间t充分大以后x(t),y(t)的变化趋势(人民今天看到的已经是自然界长期演变的结局)。
编写如下M文件:function xdot=jingzhong(t,x)r1=1;r2=1;n1=100;n2=100;s1=0.5;s2=2; xdot=diag([r1*(1-x(1)/n1-s1*x(2)/n2),r 2*(1-s2*x(1)/n1-x(2)/n2)])*x;然后运行以下程序:ts=0:0.1:10;x0=[10,10];[t,x]=ode45(@jingzhong,ts,x0);[t,x]plot(t,x),grid,gtext('\fontsize{12}x(t)'),gtext('\fontsize {12}y(t)'),pause,plot(x(:,1),x(:,2)),grid, xlabel('x'),ylabel('y')得到10年间甲、乙两种群数量变化的图象为:123456789100102030405060708090100相图为:1020304050607080901000510152025xy结论:当t 充分大时,x 和y 的数量悬殊变大,最终是一方灭绝,一方繁荣。
7种群的相互竞争模型中数值计算与结果分析

7种群的相互竞争模型中数值计算与结果分析在生态系统中,物种之间存在着各种类型的相互关系,其中最为常见的是竞争关系。
而在生态学中,研究相互竞争的模型可以帮助我们理解不同物种之间的相互作用以及生态系统的稳定性。
本文将介绍基于7种群的相互竞争模型,并进行数值计算与结果分析。
1.模型的建立考虑一个由7种群(A、B、C、D、E、F、G)组成的竞争关系网络。
我们可以用以下方程来描述每个种群的变化率:dA/dt = rA(1-(A+αB+βC+γD+εE+ζF+ηG)/K1)(1)dB/dt = rB(1-(B+αA+βC+γD+εE+ζF+ηG)/K2)(2)dC/dt = rC(1-(C+αA+βB+γD+εE+ζF+ηG)/K3)(3)dD/dt = rD(1-(D+αA+βB+γC+εE+ζF+ηG)/K4)(4)dE/dt = rE(1-(E+αA+βB+γC+δD+ζF+ηG)/K5)(5)dF/dt = rF(1-(F+αA+βB+γC+δD+εE+ηG)/K6)(6)dG/dt = rG(1-(G+αA+βB+γC+δD+εE+ζF)/K7)(7)其中,r为生殖率,K为环境容纳量,α、β、γ、δ、ε、ζ和η为不同群体之间的竞争系数。
为了进行模拟计算,我们需要选择合适的参数值和初始条件。
首先,我们将初始种群密度设定为随机数,并将参数值设定为0.1接下来,我们使用数值计算方法(如欧拉法或四阶龙格-库塔法)来求解上述方程。
通过迭代计算,可以得到在不同时间点上每个种群的密度变化。
在得到结果之后,我们可以对数据进行统计和分析,以了解不同种群之间的竞争关系。
常用的分析方法包括计算平均密度、最大和最小密度、竞争强度等。
此外,我们还可以通过绘制种群密度随时间的变化曲线来直观地观察群体之间的竞争过程。
通过曲线的变化趋势,可以分析群体的生长速率、竞争关系的稳定性以及群体的周期性波动等。
最后,我们可以对不同的参数进行敏感性分析,以探讨不同竞争系数和环境容纳量对种群竞争模型的影响。
种群实验

实验四 种间竞争
三、实验准备 2.将土壤和腐熟厩肥充分拌匀,取等量分装在
花盆里,使土面稍低于盆口(2cm); 3.按上述比例,每盆均匀播种100粒种子,并将
每个花盆贴上标签,注明处理、重复编号和播种日 期;把花盆放在温室内(冬季);
4.种子萌发后,统计其发芽率、幼苗成活情况 等;
5.在植物生长季节内,定期浇水,以利生长。
实验三 种内竞争
五、实验步骤 5.根据花盆的口径和花盆中油菜的株数计算植
株密度; 6.以单株平均干重的对数值对植株密度的对数
值作图; 7.计算平均干重对数值对密度对数值的回归系
数。在5%的置信度内,-1.5斜率的5%边线值是-1.25 和-1.83,若斜率在这一限度之内,则在5%水平,与 指数法则显著吻合。
种群数量 (P) 最初标记数 (a)
取样样本数 (n) 样本中标记个体数
(r)
实验二 标记重捕法估计动物种群密度
在Lincoln法中重捕取样的停止点很重要,不同 的取样方法进行估计的方法不同。
实验二 标记重捕法估计动物种群密度
二、目的要求 1.掌握标记重捕法的原理; 2.学会标记重捕技术; 3.掌握单次、多次重捕法估计动物种群大
实验四 种间竞争
四、实验步骤 1.植物成熟后,分盆分种收获、脱粒,记录种
子数目,将种子放入纸袋内。计算种子输出比率; 2.把每次重复的实验处理及结果分别登记在不
同的表格内; 3.用大麦与燕麦种子的输出比率(三次重复的
平均值)对输入比率作图,利用图解法进行分析。 不管大麦对燕麦的种子输入比率如何,如果
实验三 种内竞争
实验四 种间竞争
一、实验原理 种间竞争是种间关系研究的一个重要方面,
两种群间的相互竞争

两种群间的相互竞争摘要本文针对两种群间的竞争问题作了详细的论述,主体分为两部分,第一部分主要通过理论分析的方法来阐述模型,第二部分主要利用MATLAB通过数值分析的方法从另一个角度来阐述模型,两个部分相辅相成,从不同的角度对同一个模型进行分析,并在最后得到一致的结果。
另外本文在第一部分主要以理论的方式对模型进行数学上的描述,在第二部分主要以生物间的角度对模型进行描述,与此同时对第一部分作一个总结。
关键词:稳定性平面动力系统增广相空间轨线一、问题提出两种群竞争模型很好的描述了种群间的各种关系,而如果从发展的眼光来看待问题,我们不禁对两种群在未来很长一段时间内的状态产生兴趣,换句话说,我们要研究的是在无穷远的将来,两个种群的数量变化关系,这对我们进一步研究生物学的各种问题是有意义的。
二、基本假设假设1: 有甲乙两个种群,它们独自生存时的数量变化服从Logistic 规律。
假设2: 两种群一起生存时,乙种群对甲种群增长的阻滞作用与乙种群的数量成正比,甲种群对乙种群增长的阻滞作用与甲种群的数量也成正比。
三、问题分析根据“假设1”,我们容易得到方程组如下1122()(1)()(1)dx t x r x dt n dy t y r y dtn ⎧=-⎪⎪⎨⎪=-⎪⎩ (1) 其中()x t ,()y t 分别为甲乙两种群随时间变化的数量;1r ,2r 为它们的固有增长率;1n 和2n 为环境允许条件下,甲乙两种群的最大数量。
再由“假设2”,对方程组(1)变形,我们得到方程组如下11122212()(1)()(1)dx t x y r x s dt n n dy t x y r y s dt n n ⎧=--⎪⎪⎨⎪=--⎪⎩(2) 其中1s 的含义是,对于供养甲种群的资源而言,单位数量乙(相对于2n )的消耗为单位数量甲(相对于1n )消耗的1s 倍;2s 的含义是,对于供养乙种群的资源而言,单位数量甲(相对于1n )的消耗为单位数量乙(相对于2n )消耗的2s 倍。
数学模型_种群的相互竞争

的根
0
若从P0某邻域的任一初值出发,都有 lim x 1 ( t ) x 1 , t
lim x 2 ( t ) x 2 , 称P0是微分方程的稳定平衡点 t
0
模型
x1 x2 x 1 ( t ) r1 x 1 1 1 N1 N2
x1 x 2 x 2 ( t ) r2 x 2 1 2 N1 N 2
种群的相互竞争
• 一个自然环境中有两个种群生存,它们之间的 关系:相互竞争;相互依存;弱肉强食。 • 当两个种群为争夺同一食物来源和生存空间相 互竞争时,常见的结局是,竞争力弱的灭绝, 竞争力强的达到环境容许的最大容量。 • 建立数学模型描述两个种群相互竞争的过程, 分析产生这种结局的条件。
模型假设 • 有甲乙两个种群,它们独自生存
t 时 x 1 ( t ), x 2 ( t )的趋向
(平衡点及其稳定性)
(二阶)非线性 x 1 ( t ) f ( x 1 , x 2 ) 的平衡点及其稳定性 (自治)方程 x ( t ) g ( x , x ) 2 1 2
平衡点P0(x10, x20) ~ 代数方程
f ( x1 , x 2 ) 0 g ( x1 , x 2 ) 0
时数量变化均服从Logistic规律;
x 1 ( t ) r1 x 1 (1 x1 N1 )
x 2 ( t ) r2 x 2 (1
x2 N2
)
• 两种群在一起生存时,乙对甲增长的阻滞作 用与乙的数量成正比; 甲对乙有同样的作用。
模型
x1 x2 x2 x1 x 2 ( t ) r2 x 2 1 2 x 1 ( t ) r1 x 1 1 1 N1 N1 N 2 N2
种群竞争模型

泰山教育版权所有 淘宝ID:liuxingma123
结果分析
最后数值稳定在x=100,y=0上,即物种甲达 到最大值,物种乙灭绝。
泰山教育版权所有 淘宝ID:liuxingma123
结果分析
改变r1,r2: r1=r2=0.3
我们可以看到甲乙两物种最终结果仍然是甲达到数量 极限而乙灭绝,但与原先不同的是变化速度减缓了,这 是由于自然增长率r1,r2变小的缘故(相当于变化率减 小)。
泰山教育版权所有 淘宝ID:liuxingma123
结果分析
改变n1,n2: n1=10000, n2=100
由于一开始甲物种的数量相对较少,所以乙物种 得以快速增长,数量一度达到90以上,但最终 仍然灭绝。物种容量的改变并不能影响最终谁会 灭绝。
泰山教育版权所有 淘宝ID:liuxingma123
s1>1,s2<1 s1=1.5,s2=0.7
最后甲物种灭绝,乙物种存活并达到数量极 限。
泰山教育版权所有 淘宝ID:liuxingma123
结果分析
s1<1,s2<1 s1=0.8,s2=0.7
最后稳定在x= 45.4546 y=68.1818上。两物种共存。
泰山教育版权所有 淘宝ID:liuxingma123
结果分析
改变x10,x20: x10=10,x20=100:
乙物种的初始数量大使其灭绝时间稍稍延后,但它灭绝的 趋势不变。综上,无论怎样改变r1,r2,n1,n2,x0,y0,都改变 不了最后甲物种存活并达到数量最大且乙物种灭绝的结果。
泰山教育版权所有 淘宝ID:liuxingma123
结果分析
其中x(t),y(t)分别为甲乙两种群的数量,r1 r2为它们的固有增长率, n1 n2为它们的最 大容量。s1的含义是对于供养甲的资源来说, 单位数量的乙(相对n2)的消耗为单位数量甲 (相对n1)消耗的s1倍,s2同理。
种内竞争与种间竞争数学模型实例分析

种内竞争与种间竞争数学模型实例分析1.1问题提出问题一:甲和乙两类群均能独立生存,比方将鲤鱼群放生,其在水中和卿鱼间的相互作用。
问题二:甲可以独自存活,但乙却只能依存甲而生活,这两者在一起能相互促进,令甲乙都得到存活,比方,植物能独自存活,但以花粉为食的昆虫却放须依靠其生存,而昆虫同时会帮助植物授粉推动其繁殖。
问题三:甲乙双方都无法独立生存,只能依靠彼此获得共生。
1.2问题分析(1)在某自然环境下只存在单类生物群体(即生态学中的种群)生存的情况下,人们往往通过Logistic 模型描述该种群数量产生的演变,公式为:)1()(N x rx t x -=')(t x 为种群为时刻t 的数量,r 代表固有增长率,N 代表环境资源下所能接受的最大种群量。
其中)1(N x -反应了一些种群对有限资源的消耗造成的影响其自身增长的作用,N x 代表着相对于N 来讲,单位数量中某个种群所消耗的食量(假设总量=1)(2)若同一自然环境内存在2个或多个种群,即其会产生竞争或依存关系,又或是供应链的关系,以下我们会由稳定转态角度展开对其依存关系的探讨。
1.3模型假设甲乙两种群各种独立于某个环境生存时,其数量产生的演变将遵守Logisti 规律。
设)(),(21t x t x 为两个种群数量,21,r r 为其固有增长率,21,N N 是它们的最大容量。
于是对于甲种群有:)1()(11111N x x r t x -=' 同理对于乙种群有 )1()(22221N x x r t x -=' 1.4模型建立与稳定性分析对于问题一:1、建立模型:)1()(22111111N x N x x r t x σ+-=' ④ )1()(11222222N x N x x r t x σ+-=' ⑤ 1σ的含义:单位数量乙(相对于2N )提供给甲的食量为单位数量(相对于1N )消耗食量的1σ2σ的含义:单位数量甲(相对于1N )提供给乙的食量为单位数量乙(相对于2N )消耗食量的1σ2、稳定性分析:3、数学建模过程与结果:根据数学实验以及数学建模的相关知识,利用数学软件Matlab 分别求解微分方程的图形和相轨线图形:Matlab 模型:function xdot=sheir(t ,x)n1=16;n2=1;r1=25;r2=18;q1=05;q2=16;xdot=[r1*x(1)*(1-(x(1)/n1)+q1*(x(2)/n2));r2*x(2)*(1-(x(2)/n2)+q2*(x(1)/n1))];>> ts=0:01:15;>> x0=[01,01];>> [t,x]=ode45('sheir',ts,x0);[t,x],>> plot(t,x),grid,gtext('x(t)'),gtext('y(t)'),>> plot(t,x),grid,gtext('x1(t)'),gtext('x2(t)'),>> ts=0:01:15;>> x0=[01,01];>> [t,x]=ode23('sheir',ts,x0);[t,x],>> plot(t,x),grid,gtext('x1(t)'),gtext('x2(t)'),相轨线:4、由上图可知:甲乙可以彼此立生存。
种群的相互竞争模型中数值计算与结果分析报告

河北大学《数学模型》实验实验报告一、实验目的1.学会编写程序段。
2.能根据m文件的结果进行分析。
3.根据图像进行比较和分析。
二、实验要求8-1捕鱼业的持续收获运行下面的m文件,并把相应结果填空,即填入“_________”。
clear;clc;%无捕捞条件下单位时间的增长量:f(x)=rx(1-x/N)%捕捞条件下单位时间的捕捞量:h(x)=Ex%F(x)=f(x)-h(x)=rx(1-x/N)-Ex%捕捞情况下渔场鱼量满足的方程:x'(t)=F(x)%满足F(x)=0的点x为方程的平衡点%求方程的平衡点syms r x N E; %定义符号变量Fx=r*x*(1-x/N)-E*x; %创建符号表达式x=solve(Fx,x) %求解F(x)=0(求根)%得到两个平衡点,记为:% x0=______________ , x1=___________x0=x(2);x1=x(1);%符号变量x的结构类型成为<2×1sym>%求F(x)的微分F'(x)syms x; %定义符号变量x的结构类型为<1×1sym>dF=diff(Fx,'x');dF=simple(dF) %简化符号表达式%得 F'(x)=________________%求F'(x0)并简化dFx0=subs(dF,x,x0); %将x=x0代入符号表达式dFdFx0=simple(dFx0)%得 F’(x0)=_______%求F’(x1)dFx1=subs(dF,x,x1)%得 F’(x1)=________%若 E<r,有F'(x0)<0,F'(x1)>0,故x0点稳定,x1点不稳定(根据平衡点稳定性的准则);%若 E>r,则结果正好相反。
%在渔场鱼量稳定在x0的前提下(E<r),求E使持续产量h(x0)达到最大hm。
种群的相互竞争模型.

2 x1 x2 x1 r1 (1 1 ) r1 1 f x1 f x2 N1 N2 N2 A x2 x1 2 x2 g x1 g x2 r2 2 r2 (1 2 ) N1 N1 N 2 因此, p ( f x1 g x2 ) |Pi , q de t A |Pi , i 1,2,3,4.
对P1 ( N1 ,0), p r1 r2 (1 2 ), q r1r2 (1 2 )
稳定条件 2
1.
其它平衡点类似处理.
N 1 (1 1 ) N 2 (1 2 ) P1 ( N 1 ,0), P2 (0, N 2 ), P3 ( , ), P4 (0,0). 1 1 2 1 1 2 2 x1 x2 x1 r1 1 r1 (1 N 1 N ) N 1 2 2 A x2 x1 2 x2 r2 2 r2 (1 2 ) N1 N1 N 2
模型假设
的对其本身增长的阻滞 作用, x1 / N 1可理解为相对于N 1 而言, 数量为x1时供养甲的食物量 ( 设食物总量为 1).
于是对种群甲我们有
x1 1 ( t ) r1 x1 (1 x ) N1
这里因子1 x1 / N 1反映由于甲对有限资源 的消耗导致 的对其本身增长的阻滞 作用, x1 / N 1可理解为相对于N 1 而言, 数量为x1时供养甲的食物量 ( 设食物总量为 1).
1 ( t ) r1 x1 (1 x
N1
1
N2
)
假设种群乙离开了甲便不能独立存在,设其死亡 率为r2,于是其独立存在时的数量x2(t)满足
种群增长和竞争的数学模型

2013年06月05日 15:31:35在地中海中每平方米就有30至40只水母,种群增长和竞争的数学模型摘 要:本文首先简要介绍Malthus 和Logistic 两种单种群增长模型,然后详细介绍双种群竞争的Volterra 模型,最后介绍了多种群的Gause-Lotka-Volterra 和三种群的RPS 博弈模型,对其做了比较和分析,得出了一些有益的启示。
为了保持自然资料的合理开发与利用,人类必须保持并控制生态平衡,甚至必须控制人类自身的增长。
本文首先简要介绍Malthus 和Logistic 两种单种群增长模型,然后详细介绍双种群竞争的V olterra 模型,最后介绍了三种群的Gause-Lotka-V olterra 和RPS 博弈模型。
一般生态系统的分析可以通过一些简单模型的复合来研究,根据生态系统的特征建立相应的模型。
种群的数量本应取离散值,但由于种群数量一般较大,为建立微分方程模型,可将种群数量看作连续变量,甚至允许它为可微变量,由此引起的误差将是十分微小的。
1.1 马尔萨斯(Malthus )模型马尔萨斯在分析人口出生与死亡情况的资料后发现,人口净增长率r 基本上是一常数,(r =b -d , b 为出生率,d 为死亡率),既: 1dN r N dt = 或 dNrN dt= (1)其解为0()0()r t t N t N e -=(2)其中N 0=N (t 0)为初始时刻t 0时的种群数。
马尔萨斯模型的一个显著特点:种群数量翻一番所需的时间是固定的。
令种群数量翻一番所需的时间为T ,则有: 002rT N N e =(3)ln 2T r=(4)人口统计数据与Malthus 模型计算数据对比:表1 世界人口数量统计数据表2 中国人口数量统计数据比较历年的人口统计资料,可发现人口增长的实际情况与马尔萨斯模型的预报结果基本相符,例如,1961年世界人口数为30.6亿(即3.06×1010),人口增长率约为2%,人口数大约每35年增加一倍。
两个生物种群竞争的模型分析

c2N2m c1c2
,N21m
-
c1N1m c1c2
当直线 L1 和 L2 在第一象限内相交时 , 会出现如
图 3 的情形 3 或者如图 4 的情形 4 。
图3
图4 (3) 在图 3 中 , 直线 L1 和 L2 把第一象限分成 Ⅰ、 Ⅱ、 Ⅲ、 Ⅳ共四个部分 。在各部分区域内 , dN1和dN2的符号分别为负负 、负正 、正正 、正负 。 dt dt 如果点 (N1 ,N2) 在区域 Ⅱ或 Ⅳ, 点 (N1 ,N2) 的变化 趋势会指向稳定点 (0 , N2m) 和 (N1m , 0) ; 如果 点 (N1 ,N2) 在区域 Ⅰ或 Ⅲ内 , 其变化趋势指向直线 L1 和 L2 , 最终达到稳定平衡点 (N1m , 0) 或 (0 , N2m) 。可见 , 点 (N1 ,N2) 一旦偏离了 A 点 , 将会逐 渐趋向 稳 定 平 衡 点 ( N1m , 0) 或 ( 0 , N2m) 。因 此 , 点 A 是不稳定平衡点 。 (4) 在图 4 中 , 直线 L1 和 L2 也把第一象限分 成 Ⅰ、 Ⅱ、 Ⅲ、 Ⅳ共四个部分 。在各部分区域内 , dN1和dN2的符号分别为负负 、正负 、正正 、负正 。 dt dt 如果点 (N1 ,N2) 在区域 Ⅱ或 Ⅳ, 其变化趋势指向稳 定点 A ; 如果点 (N1 ,N2) 在区域 Ⅰ或 Ⅲ内 , 其变化 趋势指向直线 L1 和 L2 , 最终仍然达到稳定点 A 。 可见 , 点 (N1 ,N2) 即便是偏离了 A 点 , 也会逐渐 趋向平衡点 A 。因此 , 点 A 是稳定平衡点 。 综合以上四种情况 , 只有情形 (4) 才会维持 两个种群的稳定并存 。其它情形一旦发生 , 就会 导致两个种群之一发生灭顶之灾 。
第 26 卷 第 6 期 2006 年 12 月
种内竞争与种间竞争相互作用的Lotka-Volterra模型

种内竞争与种间竞争相互作用的Lotka-Volterra 模型Lotka-Volterra 模型(Lotka-Volterra 种间竞争模型)是logistic 模型(阻滞增长模型)的延伸。
现设定如下参数:N 1、N 2:分别为两个物种的种群数量 K 1、K 2:分别为两个物种的环境容纳量 r 1、r 2:分别为两个物种的种群增长率 从逻辑斯蒂模型可以得知: dN 1/dt=r 1N 1(1-N 1/K 1)上式中:N/K 表示在某区域内的种群生活空间(即已利用空间项),那么(1-N/K )就表示在该区域内种群生活没有涉及到的空间(即未利用空间项)。
如果不同物种的已利用空间项出现了重叠,那么“已利用空间项”还要将N2种群占用的空间计算在内,那么可以得到:dN 1/dt=r 1N 1(1-N 1/K 1-αN 2/K 1) (7)上式中,α代表物种2对物种1的竞争系数,也就是α个N 1个体所需要的生存空间和一个N2个体所需要的生存空间是相等的。
那么,β代表物种1对物种2的竞争系数,也就是β个N 2个体所需要的生存空间和一个N1个体所需要的生存空间是相等的。
则另有:dN 2/dt=r 2N 2(1-N 2/K 2-βN 1/K 2) (8) 如我们所知:如果在某一区域能够容纳K 1个N 1种群数量时,那么该种群每个个体给种群数量上升产生的负面作用即为1/K 1;同样的道理,N2种群内各个体对自身种群的增长抑制作用是21/K 。
同时,由(1)、(2)方程和α、β的定义中可知: N2种群内各个体对N1种群的影响:1α/K N1种群内各个体对N2种群的影响:2β/K由此可见,当物种2可用于抑制物种1时,可得出,物种2对物种1的影响超过了物种2对本身的影响,也就是211/K >α/K 。
整理后得:K 2>K 1/α,同理有: 物种2不能抑制物种1:K 2<K 1/α 物种1可以抑制物种2:K 1>K 2/β 物种1不能抑制物种2:K 1<K 2/β如此一来,竞争时,K1、K2、α以及β存在不同数值,便会造成下列四在N2种群达到怎样的密度之下,令N1种群能维持超过0水平,也就是说,各种群需要达到何种密度才将阻上止其他种群的增长?结论是,N2种群达到K1/α,N1就再也不能增长换言之,N1种群达到/βK2,N2便不再增长可以得到两个物种的各自的平衡线如下:叠合两平衡线,会得到四类结局:平衡指的是N1与N2的种群数量不会产生改变,也就是:N 1/dt=r1N1(1-N1/K1-αN2/K1)=0 (9)N 2/dt=r2N2(1-N2/K2-βN1/K2)=0 (10)合乎上述两个方程时,则种群之间达到平衡,焦点也就是平衡点。
种群的相互竞争

§ 7 种 群 的 相 互 竞 争*[问题的提出] 当某个自然环境中只有一种生物的群体(生态学上称为种群)生存时,人们常用Logisdc 模型来描述这个种群数量的演变过程,即)(t x 是种群在时刻t 的数量,r 是固有增长率,N 是环境资源容许的种群最大数量,在1.5节和6.1节我们曾应用过这种模型.由方程(1)可以直接得到,0x =N 是稳定平衡点,即r ∞→时)(t x →N .从模型本身的意义看这是明显的结果.如果一个自然环境中有两个或两个以上种群生存,那么它们之间就要存在着或是相互竞争,或是相互依存,或是弱肉强食(食饵与捕食者)的关系.本节和下面两节将从稳定状态的角度分别讨论这些关系. 当两个种群为了争夺有限的同一种食物来源和生活空间而进行生存竞争时,最常见的结局是竞争力较弱的种群灭绝,竞争力较强的种群达到环境容许的最大数量.人们今天可以看到自然界长期演变成的这样的结局.例如一个小岛上虽然有四种燕子栖息,但是它们的食物来源各不相同,一种只在陆地上觅食,另两种分别在浅水的海滩上和离岸稍远的海中捕鱼,第四种则飞越宽阔的海面到远方攫取海味,每一种燕子在它各自生存环境中的竞争力明显的强于其他几种.本节要建立一个模型解释类似的现象,并分析产生这种结局的条件.[模型建立] 有甲乙两个种群,当它们独自在一个自然环境中生存时,数量的演变均遵从logistic 规律.记)(1t x ,)(2t x 是两个种群的数量,1r ,2r 是它们的固有增长率,1N ,2N 是它们的最大容量.于是对于种群甲有 其中因子⎪⎪⎭⎫ ⎝⎛-111N x 反映由于甲对有限资源的消耗导致的对它本身增长的阻滞作用,11N x 可解释为相对于1N 而言单位数量的甲消耗的供养甲的食物量(设食物总量为1).当两个种群在同一自然环境中生存时,考察由于乙消耗同一种有限资源对甲的增长产生的影响,可以合理地在因子⎪⎪⎭⎫ ⎝⎛-111N x 中再减去一项,该项与种群乙的数量2x (相对于2N 而言)成正比,于是得到种群甲增长的方程为这里1σ的意义是:单位数量乙(相对2N 而言)消耗的供养甲的食物量为单位数量甲(相对1N )消耗的供养甲的食物量的1σ倍.类似地,甲的存在也影响了乙的增长,种群乙的方程应该是对2σ可作相应的解释.在两个种群的相互竞争中1σ,2σ是两个关键指标.从上面对它们的解释可知,1σ >l 表示在消耗供养甲的资源中,乙的消耗多于甲,因而对甲增长的阻滞作用乙大于甲,即乙的竞争力强于甲.对2σ>l 可作相应的理解.一般地说,1σ与2σ之间没有确定的关系,但是可以把这样一种特殊情况作为较常见的一类实际情况的典型代表,即两个种群在消耗资源中对甲增长的阻滞作用与对乙增长的阻滞作用相同.具体地说就是:因为单位数量的甲和乙消耗的供养甲的食物量之比是l :1σ,消耗的供养乙的食物量之比是2σ:l ,所谓阻滞作用相同即1:1σ =2σ:1,所以这种特殊情形可以定量地表示为即1σ,2σ互为倒数.可以简单地理解为,如果一个乙消耗的食物是一个甲的1σ=k 倍,则一个甲消耗的食物是一个乙的2σ=l /k .下面我们仍然讨论1σ,2σ相互独立的一般情况,而将条件(4)下对问题的分析留给读者(习题3).[稳定性分析] 为了研究两个种群相互竞争的结局,即r+oo 时11(f), J2(r)的趋向,不必要解方程(2),(3)*,只需对它的平衡点进行稳定性分析.首先根据微分方程(2),(3)解代数方程组得到4个平衡点:因为仅当平衡点位于平面坐标系的第一象限时(1x ,2x ≥0)才有实际意义,所以对3P 而言要求1σ,2σ同时小于1,或同时大于1.按照判断平衡点稳定性的方法(见6,6节(18),(19)式)计算将4个平衡点p ,q 的结果及稳定条件列入表2.注意:按照6.6节(15)式给出的p>0,q>0得到的1P 的稳定条件只有2σ>l ,表2中的1σ<1是根据以下用相轨线分析的结果添加的.2P 的稳定条件2σ<l 有类似的情况.对于由非线性方程(2),(3)描述的种群竞争,人们关心的是平衡点的全局稳定(即不论初始值如何,平衡点是稳定的),这需要在上面得到的局部稳定性的基础上辅之以相轨线分析.在代数方程组(5)中记对于1σ,2σ的不同取值范围,直线0=ϕ和0=φ在相平面上的相对位置不同,图4给出了它们的4种情况.下面分别对这4种情况进行分析.1.1σ<l ,2σ>1.图4(1)中0=ϕ和0=φ两条直线将相平面(1x ,2x ≥0)划分为3个区域: 可以证明,不论轨线从哪个区域的任一点出发,∞→t 时都将趋向)0,(11N P .若轨线从1S 的某点出发,由(6)可知随着t 的增加轨线向右上方运动,必然进入2S ;若轨线从2S 的某点出发,由(7)可知轨线向右下方运动,那么它或者趋向1P 点,或者进入但是进入3S 是不可能的,因为,如果设轨线在某时刻1t 经直线0=ϕ进入3S ,则)(11t x=0,由方程(2)不难算出 由(7),(8)知)(12t x<0,故)(11t x >0,表明)(1t x 在1t 达到极小值,而这是不可能的,因为在2S 中1x >0,即)(1t x 一直是增加的;若轨线从3S 的某点出发,由(8)可知轨线向左下方运动,那么它或者趋向1P 点,或者进入2S 。
种群的相互竞争模型-精选文档

因此 ,p (fx g )|P ,q det A |P ,i 1 , 2 , 3 , 4 . x 1 2 i i
对 P ( N , 0 ), p r r ( 1 ), q r r ( 1 ) 1 1 1 2 2 1 2 2
稳定条件 2
( 1 ) r N ( 1 ) r 1 1 1 1 1 1 1 N ( 1 ) 1 2 2 1 2 对 P ,A 3 r N ( 1 ) r ( 1 ) 2 2 2 2 2 2 ( 1 ) 1 1 1 2 1 2 N
N ( 1 ) N ( 1 1 1 2 2) P ( , ), P ( 0 ,0 ). 3 4 1 1 1 2 1 2
(5)
其中的第三个平衡点是在σ1,σ2 <1或σ1,σ2 >1的情形 下才会得到.
N ( 1 ) N ( 1 ) 1 1 2 2 P ( N , 0 ), P ( 0 , N ), P ( , ), P ( 0 , 0 ). 1 1 2 2 3 4 1 1 2 1 1 2
模型假设
的对其本身增长的阻滞 作用 ,x 可理解为相 N 1/ N 1 1 而言 ,数量为 x 时供养甲的食物量 ( 设食物总量 1 ). 1
于是对种群甲我们有
x 1 1(t)r x x ( 1 ) 1 1 N 1
这里因子 1 x 反映由于甲对有限资 的消耗导 1/ N 1
的对其本身增长的阻滞 作用 ,x 可理解为相 N 1/ N 1 1
种群的相互竞争模型
1.模型建立
当某个自然的环境中只有一种生物的群体(种群)生 存时,我们常用Logistic模型来描述它的数量的演变 过程,即 x
种群的相互竞争模型

的
对
其
本
身
增
长
的
阻
滞作 用,
x1
/
N
可
1
理 解 为 相 对 于N1
而 言, 数 量 为x1时 供 养 甲 的 食 物 量(设 食 物 总 量 为1).
于是对种群甲我们有
x1(t )
r1 x1 (1
x1 N1
)
这
里
因
子1
x1
/
N
反
1
映
由
于
甲
对
有
限
资
源的
消
耗
导
致
的
对
其
本
身
增
长
的
阻
滞作 用,
x1
/
N
可
)
,
N 2 (1 2 1 1 2
)
)
r1(1 1 ) r2 (1 2 ) 1 1 2
r1r2 (1 1 )(1 2 ) 1 1 2
P4 (0,0)
(r1 r2 )
r1r2
1 1, 2 1
不稳定
注意到平衡点的定义我们可以看出,它是一个局部的
性质.对于非线性方程(4)所描述的种群竞争,我们更
x1 N1
1
x2 N2
( x1 , x2 )
12
x1 N1
x2 N2
x2 N 2 • P2
N2 /1
(2)1 1, 2 1
P2(0, N2 )全局稳定
0
0
O
N1
N1 / 2 x1
x2
N2 /1
N2
P3
•
0
(3)1 1, 2 1
微分方程数值解(生物种群的相互竞争模型)
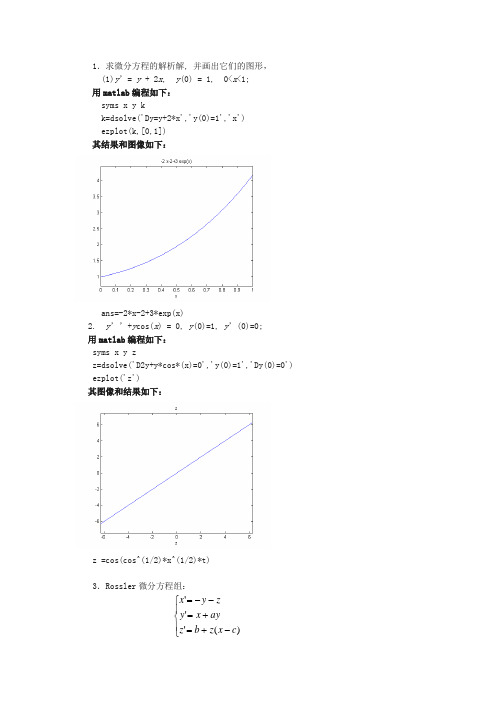
1.求微分方程的解析解, 并画出它们的图形, (1)y ’= y + 2x , y (0) = 1, 0<x <1;用matlab 编程如下: syms x y kk=dsolve('Dy=y+2*x','y(0)=1','x') ezplot(k,[0,1]) 其结果和图像如下:ans=-2*x-2+3*exp(x)2. y ’’+y cos(x ) = 0, y (0)=1, y ’(0)=0; 用matlab 编程如下: syms x y zz=dsolve('D2y+y*cos*(x)=0','y(0)=1','Dy(0)=0') ezplot('z')其图像和结果如下:z =cos(cos^(1/2)*x^(1/2)*t)3.Rossler 微分方程组:⎪⎩⎪⎨⎧-+=+=--=)('''c x z b z ay x y z y x当固定参数b=2, c=4时,试讨论随参数a 由小到大变化(如a ∈(0,0.65))而方程解的变化情况,并且画出空间曲线图形,观察空间曲线是否形成混沌状? 用matlab 编程建立rossler.m 文件: function r=rossler(t,x) global a; global b; global c;r=[-x(2)-x(3);x(1)+a*x(2);b+x(3)*(x(1)-c)]; 建立exp4-3.m 如下: global a; global b; global c; b=2; c=4;t0=[0,200];for a=0:0.03:0.65[t,x]=ode45('rossler',t0,[0,0,0]); subplot(1,2,1);plot(t,x(:,1),'r',t,x(:,2),'g',t,x(:,3),'b');title('x(红色),y(绿色),z(蓝色)随t 变化情况');xlabel('t'); subplot(1,2,2);plot3(x(:,1),x(:,2),x(:,3))title('相图');xlabel('x');ylabel('y');zlabel('z'); end(1)当a=0时,图像如下:所以当a=0时,(x,y,z)收敛于(0,0.5,0.5) (2)当a=0.12时,图像如下:x(红色),y(绿色),z(篮色)随t 变化情况t相图z当a=0.27时,(x,y,z)仍然收敛,但是收敛速度大大降低。
第七 种群竞争模型

种群竞争模型一.问题的提出Causs 根据实验分析,得出结论“吃同种食物的两种不同生物是不能长期共存的。
”你如何理解这句话这里不妨将我们讨论的对象想象为生活在同一草原上的羚羊和老鼠。
二.模型假设1.假设种群密度相当。
2.假设种群个体都是健康的。
3.假设没有受自然灾害的影响,只是靠搞自身的竞争力三.符号说明以)(1t x 、)(2t x 表示处于相互竞争关系中甲、乙二种群在时刻t 的数量,1. 资源有限,设其总量为1,)2,1(=i N i 分别表示甲、乙二种群在单种群情况下自然资源所能承受的最大种群数量;2. 种群数量的增长率)2,1)((=i t xi 与该种群数量)2,1)((=i t x i 成正比,同时也与有闲资源)2,1)((=i t s i 成正比;3. 各种群在对所占据资源的利用上是不充分的,)2,1(=i i σ分别表示甲、乙二种群对对方已占用资源的相对挑剔程度,通俗的讲,是在对方用过的盘子里捡“剩骨头”。
比方,若)1,0(1∈σ时,表示在乙种群看来,甲种群是“奢侈的”,它可以在甲种群用过的盘子里捡到“剩骨头”,若11>σ时,说明乙种群在食物选择上是“过分”挑剔的,或者可理解为,对于乙种群,甲种群在资源利用上对资源有破坏性;换一个说法,)2,1(=i i σ反映了甲、乙二种群适应能力,1σ越小、2σ越大,则甲种群的相对适应能力越强;4. )2,1(=i r i 分别表示甲、乙二种群的固有增长率。
四.模型建立根据模型假设,可得如下数学模型:⎪⎪⎩⎪⎪⎨⎧-⋅-=⋅--=⋅⋅=⋅⋅=22112222111122221111//1//1N x N x s N x N x s s x r x s x r x σσ经化简,得:⎩⎨⎧-⋅-⋅⋅=⋅--⋅⋅=)//1()//1(2211222222111111N x N x x r x N x N x x r x σσ五.模型求解与分析模型方程的解没有解析表达式,我们的兴趣和目的是:当t 充分大时,)(1t x 、)(2t x 的变化趋势怎样?利用平衡点的稳定性,对两种群的变化趋势可作出判断。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
河北大学《数学模型》实验实验报告一、实验目的1.学会编写程序段。
2.能根据m文件的结果进行分析。
3.根据图像进行比较和分析。
二、实验要求8-1捕鱼业的持续收获运行下面的m文件,并把相应结果填空,即填入“_________”。
clear;clc;%无捕捞条件下单位时间的增长量:f(x)=rx(1-x/N)%捕捞条件下单位时间的捕捞量:h(x)=Ex%F(x)=f(x)-h(x)=rx(1-x/N)-Ex%捕捞情况下渔场鱼量满足的方程:x'(t)=F(x)%满足F(x)=0的点x为方程的平衡点%求方程的平衡点syms r x N E; %定义符号变量Fx=r*x*(1-x/N)-E*x; %创建符号表达式x=solve(Fx,x) %求解F(x)=0(求根)%得到两个平衡点,记为:% x0=______________ , x1=___________x0=x(2);x1=x(1);%符号变量x的结构类型成为<2×1sym>%求F(x)的微分F'(x)syms x; %定义符号变量x的结构类型为<1×1sym>dF=diff(Fx,'x');dF=simple(dF) %简化符号表达式%得 F'(x)=________________%求F'(x0)并简化dFx0=subs(dF,x,x0); %将x=x0代入符号表达式dFdFx0=simple(dFx0)%得 F’(x0)=_______%求F’(x1)dFx1=subs(dF,x,x1)%得 F’(x1)=________%若 E<r,有F'(x0)<0,F'(x1)>0,故x0点稳定,x1点不稳定(根据平衡点稳定性的准则);%若 E>r,则结果正好相反。
%在渔场鱼量稳定在x0的前提下(E<r),求E使持续产量h(x0)达到最大hm。
%通过分析(见教材p216图1),只需求x0*使f(x)达到最大,且hm=f(x0*)。
syms r x Nfx=r*x*(1-x/N);df=diff(fx,'x');x0=solve(df,x)%得 x0*=______hm=subs(fx,x,x0)%得 hm=_______%又由 x0*=N(1-E/r),可得 E*=______%产量模型的结论是:%将捕捞率控制在固有增长率的一半(E=r/2)时,能够获得最大的持续产量。
8-2种群的相互竞争(1)补充如下指出的程序段,然后运行该m文件,对照教材上的相应结果。
clear;clc;%甲乙两个种群满足的增长方程:% x1'(t)=f(x1,x2)=r1*x1*(1-x1/N1-k1*x2/N2)% x2'(t)=g(x1,x2)=r2*x2*(1-k2*x1/N1-x2/N2)%求方程的平衡点,即解代数方程组% f(x1,x2)=0 g(x1,x2)=08-3种群的相互竞争(2)补充如下指出的程序段,然后运行该m文件,对照教材上的相应结果。
clear;clc;%甲乙两个种群满足的增长方程:% x1'(t)=f(x1,x2)=r1*x1*(1-x1/N1-k1*x2/N2)% x2'(t)=g(x1,x2)=r2*x2*(1-k2*x1/N1-x2/N2)%求方程的平衡点,即解代数方程组% f(x1,x2)=0 g(x1,x2)=0编写出该程序段。
三、实验内容8-1捕鱼业的持续收获——产量模型%文件名:p178.mclear;clc;%无捕捞条件下单位时间的增长量:f(x)=rx(1-x/N)%捕捞条件下单位时间的捕捞量:h(x)=Ex%F(x)=f(x)-h(x)=rx(1-x/N)-Ex%捕捞情况下渔场鱼量满足的方程:x'(t)=F(x)%满足F(x)=0的点x为方程的平衡点%求方程的平衡点syms r x N E; %定义符号变量Fx=r*x*(1-x/N)-E*x; %创建符号表达式x=solve(Fx,x) %求解F(x)=0(求根)%得到两个平衡点,记为:% x0=N(1-x/N) , x1=0x0=x(2);x1=x(1);%符号变量x的结构类型成为<2×1sym>%求F(x)的微分F'(x)syms x; %定义符号变量x的结构类型为<1×1sym>dF=diff(Fx,'x');dF=simple(dF) %简化符号表达式%得 F'(x)=___________%求F'(x0)并简化dFx0=subs(dF,x,x0); %将x=x0代入符号表达式dFdFx0=simple(dFx0)%得F’(x0)=E-r%求F’(x1)=r-EdFx1=subs(dF,x,x1)%得F’(x1)=r-E%若 E<r,有F'(x0)<0,F'(x1)>0,故x0点稳定,x1点不稳定(根据平衡点稳定性的准则);%若 E>r,则结果正好相反。
%在渔场鱼量稳定在x0的前提下(E<r),求E使持续产量h(x0)达到最大hm。
%通过分析(见教材p178图1),只需求x0*使f(x)达到最大,且hm=f(x0*)。
syms r x Nfx=r*x*(1-x/N);a)df=diff(fx,'x');x0=solve(df,x)%得 x0*=N/2hm=subs(fx,x,x0)%得 hm=(r*N)/4%又由 x0*=N(1-E/r),可得 E*=r/2%产量模型的结论是:%将捕捞率控制在固有增长率的一半(E=r/2)时,能够获得最大的持续产量。
[提示]符号简化函数simple的格式:simple(S)对符号表达式S尝试多种不同的算法简化,以显示S表达式的长度最短的简化形式。
变量替换函数sub的格式:Subs(S,OLD,NEW)将符号表达式S中的OLD变量替换为NEW变量。
8-2种群的相互竞争%文件名:p186.mclear;clc;%甲乙两个种群满足的增长方程:% x1'(t)=f(x1,x2)=r1*x1*(1-x1/N1-k1*x2/N2)% x2'(t)=g(x1,x2)=r2*x2*(1-k2*x1/N1-x2/N2)%求方程的平衡点,即解代数方程组% f(x1,x2)=0% g(x1,x2)=0%得4个平衡点:% P(1)=P1(N1,0)% P(2)=P2(0,N2)% P(3)=P3(N1*(-1+k1)/(-1+k2*k1),N2*(-1+k2)/(-1+k2*k1))% P(4)=P4(0,0)%平衡点位于第一象限才有意义,故要求P3:k1,k2同时小于1,或同时大于1。
%判断平衡点的稳定性(参考教材p200)fx1=diff(f,'x1');fx2=diff(f,'x2');gx1=diff(g,'x1');gx2=diff(g,'x2');A=[fx1,fx2;gx1,gx2]syms x1 x2;p=subs(-(fx1+gx2),{x1,x2},{P(:,1),P(:,2)});p=simple(p);%简化符号表达式pq=subs(det(A),{x1,x2},{P(:,1),P(:,2)});q=simple(q);[P p q]%得到教材p186表2的前3列,经测算可得该表的第4列,即稳定条件。
8-3种群的相互竞争(2)求微分方程组⎪⎪⎩⎪⎪⎨⎧--=--=••)1()()1()(2211222222111111N x N x x r t x N x N x x r t x σσ 的数值解,分别画出教材p189中的图5-1,图5-2,图5-3。
有关数据参见教材p188中“计算与验证”。
[提示](1)求微分方程组的数值解可参考教材p139的程序。
(2)在figure(1)中画图5-1,在figure(2)中画图5-2,在figure(3)中画图5-3。
在程序中,figure(图形编号)用于定位对应图形。
(3)使用text(x,y,’标识文本’),坐标点(x,y)在“标识文本”的左边,调整(x,y)值,使“标识文本”放在图中的适当位置。
(4)用axis([xmin xmax ymin ymax])控制坐标的刻度范围。
(5)用grid on 打开网格,grid off 关闭网格。
(6)用hold on 把要画的图形保持在之前在同一figure 上所画的图形中(同一坐标系)。
(7)图5-3中的两“点线”直线,一条的两个端点为(0,1)和(1,0),另一条的两个端点为(0,2)和(1.6,0)。
四、实验结果及其分析8-1捕鱼业的持续收获 ——产量模型8-2种群的相互竞争(1)1.实验代码:syms r1 r2 N1 N2 k1 k2 x1 x2;f=r1*x1*(1-x1/N1-k1*x2/N2);g=r2*x2*(1-k2*x1/N1-x2/N2);[x1,x2]=solve(f,g,x1,x2)P=[x1,x2];fx1=diff(f,'x1');fx2=diff(f,'x2');gx1=diff(g,'x1');gx2=diff(g,'x2');A=[fx1,fx2;gx1,gx2]syms x1 x2;p=subs(-(fx1+gx2),{x1,x2},{P(:,1),P(:,2)}); p=simple(p);q=subs(det(A),{x1,x2},{P(:,1),P(:,2)});q=simple(q);[P p q]2.实验结果8-3种群的相互竞争(2)1.实验代码%脚本文件function f=fun(t,x)r1=2.5;r2=1.8;N1=1.6;N2=1;k1=0.5;k2=1.6;f=[r1*x(1).*(1-x(1)./N1-k1.*(x(2)./N2));r2*x(2).*(1-k2*x(1)./N1-x(2)./N2)]; %[t,x]=ode45('fun',[0 8],[0.1;0.1]);plot(t,x(:,1),t,x(:,2));axis([0 8 0 2]);grid on;[t,x]=ode45('fun',[0 8],[1;2]);plot(t,x(:,1),t,x(:,2));axis([0 8 0 2]);grid on;[t,x]=ode45('fun',[0 8],[0.1;0.1]);plot(x(:,1),x(:,2));hold on;[t,x]=ode45('fun',[0 8],[1;2]); plot(x(:,1),x(:,2));x1=0:0.1:1;y1=-x1+1;x2=0:0.1:2;y2=-1.25*x2+2;2.实验结果。
