2020七年级数学下册试题解题技巧专题：平面直角坐标系中的图形面积

平面直角坐标系中的面积计算专题

平面直角坐标系中的面积计算知识点一：已知点的坐标求图形面积类型一：平面直角坐标系中三角形的面积①三角形有一边在坐标轴上例1：平面直角坐标系中，A(4，-4)， B(1，0)，C(6，0). 求△ABC 的面积. x yO A (4,-4)B (1,0)C (6,0)例2：平面直角坐标系中，A(0，3)， B(0，-3)，C(2，1). 求△ABC 的面积. x y123–1–2123–1–2–3OCB A②三角形有一边平行于坐标轴例3：平面直角坐标系中，A(-2，3)， B(-2，-3)，C(2，1). 求△ABC 的面积.xy –1–2–3123–1–2–3123OA （-2,3）B (-2,-3)C (2,1)③三角形没有一边平行于坐标轴变式1.保持A 、C 不动，改变点B 的位置：B (0，-3), 求△ABC 的面积. x y –1–2–3–4123–1–2–31234OA (-2,3）C (2,1）B x y –1–2–3–4123–1–2–31234O A (-2,3）C (2,1）B x y –1–2–3–4123–1–2–31234O A (-2,3）C (2,1）B练习：如图中，A 、B 两点的坐标分别为（2，3）、（4，1），求△ABO 的面积．类型二：平面直角坐标系中不规则多边形的面积例4：平面直角坐标系中，A(-3，-2)，B(3，-2)，C(1，3)，D(-2，1)，求四边形ABCD 的面积. xyO A (-3,-2)B (3,-2)C (1,3)D (-2,1)练习：如图，已知四边形ABCD 四个顶点的坐标分别是A （-5，2），B （1，5），C （5，-2），D （-4，-5）.求四边形ABCD 的面积.知识点二：已知图形面积求点的坐标例5：（1）▲ABC 的两个顶点分别为A （2，3），B （-2，0），且▲ABC 的面积为9，若点C 在x 轴上，求点C 的坐标.（2）已知A （1，0），B （0，3），点P 在x 轴上，且▲PAB 的面积为6，求点P 的坐标.（3）已知O （0，0），B （3，2），点A 在坐标轴上，且6=∆OAB S ，求A 点的坐标.练习1.如图A （﹣4，0），B （6，0），C （2，4），D （﹣3，2）．（1）求四边形ABCD 的面积；（2）在y 轴上找一点P ，使△APB 的面积等于四边形的一半．求P 点坐标．练习2.如图，已知A （﹣2，0），B （4，0），C （2，4），D （0，2）（1）求三角形ABC 的面积；（2）设P 为坐标轴上一点，若S △APC ＝S △ABC ，求P 点的坐标．练习3.如图，已知三点A （0，1），B （2，0），C （4，3）（1）求三角形ABC 的面积；（2）设点P 在坐标轴上，且三角形ABP 与三角形ABC 的面积相等，求点P 的坐标．。

七下数学《平面直角坐标系》——【面积问题】

七下数学《平面直角坐标系》——【面积问题】学校:___________姓名：___________班级：___________考号：___________1．如图，在平面直角坐标系中，,A B 坐标分别是(0,),(,)A a B b a ，且,a b 满足()23|5|0a b -+-=，现同时将点,A B 分别向下平移3个单位，再向左平移1个单位，分别得到点,A B 的对应点,C D ，连接,,AC BD AB ．（1）求点,C D 的坐标及四边形ACDB 的面积ACDB S ；（2）在y 轴上是否存在一点M ，连接,MC MD ，使13MCD ACDB S S ∆=？若存在这样的点，求出点M 的坐标，若不存在，试说明理由．2．如图10，在平面直角坐标系中，点A B ，的坐标分别为(),0A a ，(),0Bb ，且a b 、满足2(1)0a ++=.现同时将点A B ，分别向上平移2个单位，再向右平移1个单位，分别得到点A B ，的对应点C D ，，连接AC BD ，得ACBD ．（1）直接写出点C D ，的坐标和四边形ABDC 的面积；（2）若在坐标轴上存在点M ，使MAC S S =△四边形ABDC ，求出点M 的坐标；（3）若点P 在直线BD 上运动，连接PC PO ，.请画出图形，写出CPO DCP BOP ∠∠∠、、的数量关系并证明．3．如图，在长方形ABCD 中，AB =8cm ，BC =6cm ，点E 是CD 边上的一点，且DE =2cm ，动点P 从A 点出发，以2c m/s 的速度沿A →B →C →E 运动，最终到达点E ．设点P 运动的时间为t 秒．（1）请以A 点为原点，AB 所在直线为x 轴，1cm 为单位长度，建立一个平面直角坐标系，并用t 表示出点P 在不同线段上的坐标．（2）在（1）相同条件得到的结论下，是否存在P 点使△APE 的面积等于20cm 2时，若存在，请求出P 点坐标；若不存在，请说明理由．4．在平面直角坐标系中，A （a ，0），B （b ，0），C （−1，2），且|32a b +=0，（1）求a 、b 的值；（2）在y 轴上是否存在一点M ，使△COM 的面积为△ABC 面积的13，若存在，求出点M 的坐标；若不存在，请说明理由．5．如图1，长方形OABC 的边OA 在数轴上，O 为原点，长方形OABC 的面积为12，OC 边长为3（1）数轴上点A 表示的数为______．（2）将长方形OABC 沿数轴水平移动，移动后的长方形记为O A B C ''''，移动后的长方形O A B C ''''与原长方形OABC 重叠部分（如图2中阴影部分）的面积记为S△设点A 的移动距离AA x '=．当4S =时，x =______．△当S 恰好等于原长方形OABC 面积的一半时，求数轴上点A '表示的数为多少．6．如图，在平面直角坐标系中，已知A （0，a ），B （b ，0），其中a ，b 满足|a ﹣2|+（b ﹣3）2＝0．（1）a ＝，b ＝；（2）如果在第二象限内有一点M （m ，1），请用含m 的式子表示四边形ABOM 的面积；（3）在（2）条件下，当m ＝﹣32时，在坐标轴的负半轴上求点N （的坐标），使得△ABN 的面积与四边形ABOM 的面积相等．（直接写出答案）7．如图，在平面直角坐标系中，四边形OABC 各顶点的坐标分别是()0,0O ，()0,12A ，()10,8B -，()14,0C -，求四边形OABC 的面积．8．如图，平面直角坐标系中，点A在第一象限，AB△x轴于B，AC△y轴于C，A（4m，3m），且四边形ABOC的面积为48．（1）如图△，求A点的坐标；（2）如图△，点D从O出发以每秒1个单位的速度沿y轴正半轴运动，同时点E从A出发，以每秒2个单位的速度沿射线BA运动，DE交线段AC于F，设运动的时间为t，当S△AEF＜S△CDF时，求t的取值范围．9．如图1，在平面直角坐标系中，点A坐标为(2,0),点B在x轴负半轴上，C在y轴正半轴上，△ACB=90°，△ABC=30°.(1)求点B坐标；(2)如图2，点P从B出发，沿线段BC运动,点P运动速度为每秒2个单位长度,设运动时间为t秒，用含t的式子表示三角形△OBP的面积S.10．在平面直角坐标系内，点()0,5A ，点()29,32M x x --在第三象限，（1）求x 的取值范围；（2）点M 到y 轴的距离是到x 轴的2倍，请求出M 点坐标；（3）在（2）的基础上，若y 轴上存在一点P 使得AMP 的面积为10，请求出P 点坐标．11．已知坐标平面内的三个点A(1，3)，B(3，1)，O(0，0)．（1）求三角形AOB 的面积；（2）点P 是x 轴上的一个动点，当三角形AOP 的面积与三角形AOB 的面积相等时，求点P 的坐标．12．如图，在平面直角坐标系中，已知(,0)A a ，(,0)B b ，其中a ，b 满足|1|0a +=．（1）填空：a =______，b =______．（2）如果在第三象限内有一点(2,)M m -，请用含m 的式子表示ABM 的面积．的坐标．13．如图所示，在平面直角坐标系中点()30A -,，()5,0B ，()3,4C ，()2,3D -．（1）求四边形ABCD 的面积（2）点P 为y 轴上一点，且ABP △的面积等于四边形ABCD 的面积的一半，求点P 的坐标．14．如图1，在平面直角坐标系中，A （a ，0），C （b ，4），且满足(a+5)2，过C 作CB△x 轴于B ．（1）a = ，b = ，三角形ABC 的面积= ；（2）若过B 作BD //AC 交y 轴于D ，且AE ，DE 分别平分△CAB ，△ODB ，如图2，求△AED 的度数；（3）在y 轴上是否存在点P ，使得三角形ABC 和三角形ACP 的面积相等？若存在，求出P 点坐标；若不存在，请说明理由．15．如图1，在平面直角坐标系中，A （a ，0）是x 轴正半轴上一点，C 是第四象限一点，CB △y 轴，交y 轴负半轴于B （0，b ），且（a ﹣3）2+|b +4|＝0，S 四边形AOBC ＝16．（1）求C 点坐标；（2）如图2，设D 为线段OB 上一动点，当AD △AC 时，△ODA 的角平分线与△CAE 的角平分线的反向延长线交于点P ，求△APD 的度数．（3）如图3，当D 点在线段OB 上运动时，作DM △AD 交BC 于M 点，△BMD 、△DAO 的平分线交于N 点，则D 点在运动过程中，△N 的大小是否变化？若不变，求出其值，若变化，说明理由．16．如图，在平面直角坐标系中，已知A （a ，0），B （b ，0），C （﹣1，2），且221(24)0a b a b ++++-=．（1）求a ，b 的值；（2）y 轴上是否存在一点M ，使△COM 的面积是△ABC 的面积的一半，求点M 的坐标．17．如图，在平面直角坐标系xOy 中，点(,0)A a ，(,)B b b ，(0,)C b ，且满足2(8)0a +=，P 点从A 点出发沿x 轴正方向以每秒2个单位长度的速度匀速移动，Q 点从O 点出发沿y 轴负方向以每秒1个单位长度的速度匀速移动．（1）直接写出点A 的坐标，点B 的坐标，AO 和BC 位置关系是；（2）在P 、Q 的运动过程中，连接PB ，QB ，使S △PAB ＝4S △QBC ，求出点P 的坐标；（3）在P 、Q 的运动过程中，当△CBQ ＝30°时，请探究△OPQ 和△PQB 的数量关系，并说明理由．18．如图，在平面直角坐标系中，已知A(0，a)，B(b ，0)，C(b ，c)三点，其中a ，b ，c 满足关系式|a －2|＋(b －3)2＝0，(c －4)2≤0．（1）求a ，b ，c 的值；（2）如果在第二象限内有一点P(m ，12)，请用含m 的式子表示四边形ABOP 的面积；（3）在（2）的条件下，是否存在点P ，使四边形ABOP 的面积与三角形ABC 的面积相等？若存在，求出点P 的坐标，若不存在，请说明理由．19．已知点()30A -,，点()0,3C ，且点B 的坐标为()1,4-，计算ABC 的面积．20．如图，在平面直角坐标系中，A 、B 、C 三点的坐标分别为(0，1)(2，0)(2，1.5)， (1)求三角形ABC 的面积．(2)如果在第二象限内有一点P (a )，试用含a 的式子表示四边形ABOP 的面积．(3)在(2)的条件下，是否存在点P ，使得四边形ABOP 的面积与三角形ABC 的面积相等？若存在，请求出点P 的坐标？若不存在，请说明理由．。

部编7年级下册数学求平面直角坐标系中图形的面积

求平面直角坐标系中图形的面积山东于化平一、一边平行于坐标轴或与坐标轴重合的三角形此类问题的求解，只需确定此边上的高即可.例1 如图1，在平面直角坐标系中，三角形ABC的顶点坐标分别为（-4，0），（0，4），（0，-1），求三角形ABC的面积.分析：根据三个顶点的坐标可以看出三角形ABC的边BC在y轴上，且BC边上的高就是点A 的横坐标的绝对值，由此利用三角形的面积公式可直接求解.解：由图形可得BC=5，点A到BC边的距离就是点A到y轴的距离，所以S三角形ABC=12BC×AO=12×5×4=10.二、一边平行于坐标轴或与坐标轴重合的四边形此类问题的求解一般是通过对图形的适当分割，使之转化为特殊四边形或三角形，利用相关的面积公式求解.例2 如图2，四边形ABCD的四个顶点分别为A（-2，1），B（-3，-2），C（3，-2），D（1，4），求四边形ABCD的面积.分析：这个四边形要从整体上去求面积有一定的困难，但由B，C两点的坐标特征，结合图形可知BC平行于x轴，此时想到通过作辅助线，将四边形转化为直角梯形和直角三角形，于是问题得解.解：过点D作DF⊥BC，垂足为F，并过点A作AE⊥DF，垂足为E，易求得F（1，-2），E（1，1），所以AE=3，DE=3，EF=3，BF=4，DF=6，FC=2.所以S四边形ABCD=S三角形AED+S梯形ABFE+S三角形DFC=12AE×DE+12（AE+BF）×EF+12FC×DF=12×3×3+12×（3+4）×3+12×2×6=21.三、没有边与坐标轴平行或重合的图形此类问题的求解一般是要通过转化，使之成为比较规则的图形.例3 已知三角形ABC的三个顶点坐标分别为A（-2，1），B（1，-3），C（4，4），求三角形ABC的面积.分析：通过画图可以发现三角形ABC的每一条边都不与坐标轴重合，也不与坐标轴平行，因此，以三角形ABC的任意一边为底边都不容易求三角形ABC的面积.为了方便求解，可通过补形的方法，使之成为比较规则又易于求解的图形，从而利用相应的图形面积公式求解.解：如图，通过辅助线构造长方形DEFC，其中C为长方形的顶点，A，B分别在长方形的两边上，显然，长方形DEFC的各边与坐标轴平行，易得点D，E，F的坐标分别为D（-2，4），E（-2，-3），F（4，-3），于是DE=7，EF=6，AD=3，DC=6，AE=4，EB=3，BF=3，CF=7.所以S三角形ABC=S长方形DEFC-S三角形ADC-S三角形AEB-S三角形CFB=DE×EF-12DC×AD-12AE×EB-12BF×CF=7×6-12×6×3-12×4×3-12×3×7=16.5.。

人教版数学七年级下册微探究小专题3 平面直角坐标系中的面积问题 PPT课件

微探究小专题3 平面直角坐标系中的面积问题
∵A(3,3),B(5,1),C(-2,-3),
∴D(-2,3),E(5,3),F(5,-3).
∴DC=6,CF=7,DA=5,AE=2,BE=2,BF=4.
∴三角形
=长方形
–三角形
-三角形
-三角形
=

6×7-6×5× -2×2× -7×4× =11.
求三角形ABC的面积.
解:∵C(0,4),D(0,1),∴CD=4-1=3.
∵由题图可知,三角形ACD中,CD边上的高为点A横坐
标的绝对值3;三角形BCD中,CD边上的高为点B横坐
标的绝对值2,

∴三角形
=3×3× =4.5,三角形
=3×2× =3.

∴三角形
=三角形
+三角形

微探究小专题3 平面直角坐标系中的面积问题
4.[2023·沧州盐山县期末改编]如图,已知A(0,2),B(4,0),C(-1,-1),求三角形
ABC的面积.
微探究小专题3 平面直角坐标系中的面积问题
.解:过点A,B,C作长方形DEFC,如图所示.

∴S三角形ABC=S长方形DEFC-S三角形ADC-S三角形AEB-S三角形BCF=5×3-1×3×
微探究小专题3 平面直角坐标系中的面积问题
1.如图,已知A(-2,0),B(4,0),C(-4,4),求三角形ABC的面积.
解:∵A(-2,0),B(4,0),∴AB=4-(-2)=6.
∵C(-4,4),
∴三角形ABC的边AB上的高为4.

数学人教版七年级下册平面直角坐标系中几何图形的面积

• B(5,0)
x
S=S1+S2
6.如图所示，则四边形AOBC的面积是
y
。
方法三：
5 4 3
N
•
s1
C(3,4)
• A(0,2)
2 1 -2 o• -1 -1 -2 1 2 3 4 5
• B(5,0)
x
S=S梯形NOBC – S1
6.如图所示，则四边形AOBC的面积是
y
。
方法四：
5 4 3
N
s1
-4
-3
-2
3
-1
o 1 -1 H
-2 • C(0,-2) -3 -4
选取在坐标轴上的边作为三角形的底。
3.已知：A（-3,-2），B（-1,3），C（3,3）， 10 。则△ ABC的面积是
y 5 4 H B(-1,3)
•
3
4
• C(3,3)
2
5
-4 -3 -2 -1 A(-3,-2) •
1 o -1 -2 -3 -4
坐标易求出这条边的长，再根据这条边所对的顶点的坐标可求出该边上的高，从而求出三角形的面积。
一、坐标系中三角形面积的求法
2、三角形无边在坐标轴上或平行于坐标轴
5.如图所示，求△ OAB的面积。
y 5 4 3 2 1 -2 o• -1 -1 -2 1 2 3 4 5P x
B(3,4)
•
• A(5,2)
4 5
• B(5,0)
x
S=S1+S2 +S3
归纳：不规则的四边形的面积不能直接求出，可以利用“分割” 或“补形”，将图形转化为有边在坐标轴上或与坐标轴平行的图形来求。
巩固练习

(完整版)平面直角坐标系中的面积问题

平面直角坐标系中的面积问题
陈玲萍
问题1 已知平面直角坐标系中，点A（1，-2）， B（-4，-2），C（1,3）.
则①线段AB与x轴的位置关系平行，线段 AB的长度为 5 ； ②线段AC与y轴的位置关系平行，线段 AC的长度为 5 。
平行x轴的直线上的AB两点间的距离为：AB= xA xB 平行y轴的直线上的AC两点间的距离为：AC= yA yC
AD
44 2
8
（2）A（0,5），B（0,3），C（3,1）；
如图，过点C做CD⊥AB
∵A（0,5），B（0,3），C（3,1）
∴CD=3，AB=2
∴
SABC
1 ABCD 1 23 3
2
2
小结
平面直角坐标系中，求三角形的面积，关键在于找到平行x轴或平行y轴的线段作为规则图形的底和高。
F
∴BE=3,CF=3
∴ SABC SABD SACD
1 AD• BE 1 AD• CF
E
2
2
1 33 1 33
2
2
9
F
E
补
补
割
问题4
在平面直角坐标系中，四边形OABC的顶点坐标分别为O(0，0)，A(5，0)，B(3，4)， C(0，3),计算这个四边形的面积。
方法总结
割
割
割
补
补
问题2
• 求下列三角形的面积： • （1）A（1,4），B（0,0），C（4,0）； • （2）A（0,5），B（0,3），C（3,1）；
（1）A（1,4），B（0,0），C（4,0）；由图，过点A作AD⊥BC
∵A（1,4），B（0,0），C（4,0）
∴AD=4，BC=4

人教版七年级数学下册5解题技巧专题平面直角坐标系中的图形面积

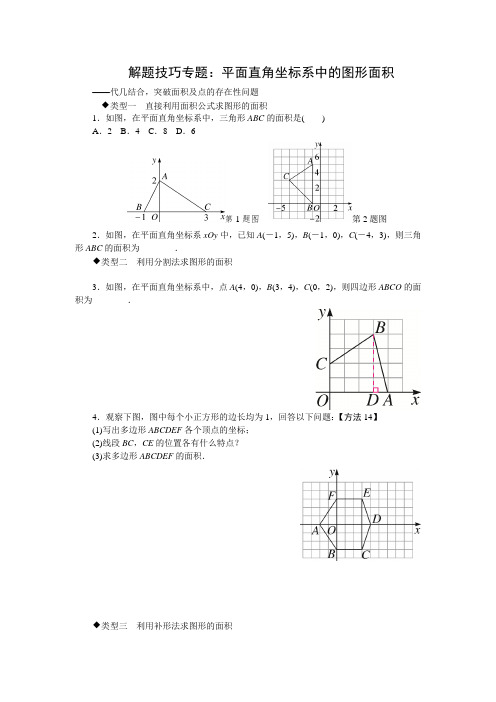
解题技巧专题：平面直角坐标系中的图形面积——代几结合，突破面积及点的存在性问题◆类型一直接利用面积公式求图形的面积1．如图，在平面直角坐标系中，三角形ABC的面积是()A．2 B．4 C．8 D．6第1题图第2题图2．如图，在平面直角坐标系xOy中，已知A(－1，5)，B(－1，0)，C(－4，3)，则三角形ABC的面积为________．◆类型二利用分割法求图形的面积3．如图，在平面直角坐标系中，点A(4，0)，B(3，4)，C(0，2)，则四边形ABCO的面积为________．4．观察下图，图中每个小正方形的边长均为1，回答以下问题：【方法14】(1)写出多边形ABCDEF各个顶点的坐标；(2)线段BC，CE的位置各有什么特点？(3)求多边形ABCDEF的面积．◆类型三利用补形法求图形的面积5．在如图所示的正方形网格中，每个小正方形的边长均为1，三角形ABC的三个顶点恰好是正方形网格的格点．【方法14】(1)写出三角形ABC各顶点的坐标；(2)求出此三角形的面积．◆类型四与图形面积相关的点的存在性问题6．(2017·定州市期中)如图，A(－1，0)，C(1，4)，点B在x轴上，且AB＝3.(1)求点B的坐标；(2)求三角形ABC的面积；(3)在y轴上是否存在点P，使以A，B，P三点为顶点的三角形的面积为10？若存在，请直接写出点P的坐标；若不存在，请说明理由．参考答案与解析1．B 2.1523．11 解析：过点B 作BD ⊥x 轴于D .∵A (4，0)，B (3，4)，C (0，2)，∴OC ＝2，BD ＝4，OD ＝3，OA ＝4，∴AD ＝OA －OD ＝1，则S 四边形ABCO＝S梯形OCBD＋S三角形ABD＝12×(4＋2)×3＋12×1×4＝9＋2＝11.4．解：(1)A (－2，0)，B (0，－3)，C (3，－3)，D (4，0)，E (3，3)，F (0，3)． (2)线段BC 平行于x 轴(或线段BC 垂直于y 轴)，线段CE 垂直于x 轴(或线段CE 平行于y 轴)．(3)S 多边形ABCDEF ＝S 三角形ABF ＋S 长方形BCEF ＋S 三角形CDE ＝12×(3＋3)×2＋3×(3＋3)＋12×(3＋3)×1＝6＋18＋3＝27.5．解：(1)A (3，3)，B (－2，－2)，C (4，－3)．(2)如图，分别过点A ，B ，C 作坐标轴的平行线，交点分别为D ，E ，F .S 三角形ABC ＝S 正方形DECF－S 三角形BEC －S 三角形ADB －S 三角形AFC ＝6×6－12×6×1－12×5×5－12×6×1＝352.6．解：(1)点B 在点A 的右边时，－1＋3＝2，点B 在点A 的左边时，－1－3＝－4，所以点B 的坐标为(2，0)或(－4，0)．(2)S 三角形ABC ＝12×3×4＝6.(3)存在这样的点P .设点P 到x 轴的距离为h ，则12×3h ＝10，解得h ＝203.点P 在y 轴正半轴时，P ⎝⎛⎭⎫0，203，点P 在y 轴负半轴时，P ⎝⎛⎭⎫0，－203，综上所述，点P 的坐标为⎝⎛⎭⎫0，203或⎝⎛⎭⎫0，－203. 高频考点强化训练：三视图的有关判断及计算时间：30分钟分数：50分得分：________ 一、选择题(每小题4分，共24分)乡镇__________________ 学校_____________________ 班级____________ 姓名____________ 座号__________ ……………………密………………………………….封……………………….线…………………………………………………………………………..1．(2016·杭州中考)下列选项中，如图所示的圆柱的三视图画法正确的是( )2．(2016·贵阳中考)如图是一个水平放置的圆柱形物体，中间有一细棒，则此几何体的俯视图是【易错6】( )3．如图所示的主视图、左视图、俯视图是下列哪个物体的三视图( )4．如图所示的几何体的主视图、左视图、俯视图中有两个视图是相同的，则不同的视图是( )5．一个长方体的主视图、俯视图如图所示(单位：cm)，则其左视图的面积为( )A ．36cm 2B ．40cm 2乡镇__________________ 学校_____________________ 班级____________ 姓名____________ 座号__________ ……………………密………………………………….封……………………….线…………………………………………………………………………..C．90cm2 D．36cm2或40cm2第5题图第6题图6．(2016·承德模拟)由一些大小相同的小正方体组成的几何体的俯视图和左视图如图所示，那么组成这个几何体的小正方体个数可能有( )A．8个 B．6个 C．4个 D．12个二、填空题(每小题4分，共16分)7．下列几何体中：①正方体；②长方体；③圆柱；④球．其中，三个视图形状相同的几何体有________个，分别是________(填几何体的序号)．8．如图，水平放置的长方体的底面是边长为3和5的长方形，它的左视图的面积为12，则长方体的体积等于________．9．如图，由五个小正方体组成的几何体中，若每个小正方体的棱长都是1，则该几何体的主视图和左视图的面积之和是________．第8题图第9题图第10题图10．(2016·秦皇岛卢龙县模拟)由若干个相同的小立方体搭成的一个几何体的主视图和俯视图如图所示，俯视图的方格中的字母和数字表示该位置上小立方体的个数，则x 的值为________，y 的值为________．三、解答题(10分)11．如图所示的是某个几何体的三视图． (1)说出这个几何体的名称；(2)根据图中的有关数据，求这个几何体的表面积．中考必考点强化训练专题：简单三视图的识别◆类型一简单几何体的三视图1．(2016·杭州中考)下列选项中，如图所示的圆柱的三视图画法正确的是( )乡镇__________________ 学校_____________________ 班级____________ 姓名____________ 座号__________ ………………………密………………………………….封……………………….线…………………………………………………………………………..第1 题图第2题图第3题图 2．(2016·抚顺中考)如图所示几何体的主视图是( )3．(2016·南陵县模拟)如图，图中的几何体是圆柱沿竖直方向切掉一半后得到的，则该几何体的俯视图是( )4．(2016·肥城市一模)如图所示的四个几何体中，它们各自的主视图与俯视图不相同的几何体的个数是( )A ．1个B ．2个C ．3个D ．4个5．(2016·宁波中考)如图所示的几何体的主视图为( )乡镇__________________ 学校_____________________ 班级____________ 姓名____________ 座号__________ ……………………密………………………………….封……………………….线…………………………………………………………………………..6．(2016·鄂州中考)一个几何体及它的主视图和俯视图如图所示，那么它的左视图正确的是( )7．(2016·菏泽中考)如图所示，该几何体的俯视图是( )◆类型二简单组合体的三视图8．(2016·黔西南州中考)如图，是由几个完全相同的小正方体搭建的几何体，它的左视图是( )9．(2016·营口中考)如图所示的物体是由两个紧靠在一起的圆柱体组成，小明准备画出它的三视图，那么他所画的三视图中的主视图应该是( )10．(2016·日照中考)如图，小明同学将一个圆锥和一个三棱柱组成组合图形，观察其三视图，其俯视图是( )11．(2016·烟台中考)如图，圆柱体中挖去一个小圆柱，那么乡镇__________________ 学校_____________________ 班级____________ 姓名____________ 座号__________……………………密………………………………….封……………………….线…………………………………………………………………………..这个几何体的主视图和俯视图分别为( )。

七年级下平面直角坐标系-面积问题专题

七年级下第七章平面直角坐标系---面积问题
分类
一、直接求面积。二、割补法求面积。三、已知面积求坐标。四、用含未知数的式子表达面积。
一、直接求面积。
例题一，求下列图中三角形的面积
割补法求面积----万能的“补” 例题二：
二、割补法求面积
二、割补法求面积
割补法求面积----万能的“补”
例题三：
已知平面直角坐标系中 A(1，1), B（-3，-1）,
C(2,4),求三角形ABC的
面积。
二、割补法求面积
割补法求面积-----割例题四：
二、割补法求面积
割补法求面积-----割标
例题五：
三、已知面积求坐标
练习：
三、已知面积求坐标
练习：
四、用未知数来表达面积。
例题五：
四、用未知数来表达面积。
例题五：
课堂小结一，今天这堂课学了什么？二，为什么有的三角形面积可以直
接求，而有的需要用割补法？
课堂小结一，今天这堂课学了什么？二，为什么有的三角形面积可以直
接求，而有的需要用割补法？三，哪些问题你觉得比较难？
提高拓展：
已知平面直角坐标系中已知A(1，1),
B（3，3）,
C在Y轴上，三角形ABC的面积为2，求点C的坐标。

人教版七年级下册数学：《平面直角坐标系中面积的计算问题》

进一步认识平面直角坐标系,了解点、图形与坐标的对应关系，能求出给定坐标的点构成的图形的面积；
课后作业
1.已知A(-3,3),B(2,-2),C(6,2)，求△ABC面积？
2.在平面直角坐标系中，已知点A(3,1),B(-2,4)， C（5,6），求三角形CAB的面积。
C
3 1 7 1 1 3 1 1 6
22
2
14 1.5 3
9.5
小结
1.求平面直角坐标系内的三角形面积的方法有几种？ ① 直接法； ② 间接法(构造四边形)；
2.如何判断使用哪种方法？若三角形有一边平行于X轴或者Y轴（与X轴或者Y 轴重合），用直接法；此外，用间接法。
课堂总结
谈谈本节课你的收获：
A B
线段AD长度无法计算
CD
能力提升
例：在平面直角坐标系中，已知点A(-2,1),B(4,0)，
C(-3,-2),求三角形CAB的面积；
解：
∵A(-2,1),B(0,4),C(-3,-2)
∴D(-3,1),E(4,1)
∴AD=1,CD=3,AE=6 BE=1,DE=7
DA
E
B
∴ SABC S梯CDEB SACD S AED
线AC的距离
C
AD
BD=4
∴
SABC
1 2
AC
BD
B
1 54 2
10
能力提升
例4：已知A(-3,3),B(2,-2),C(6,1)，求△ABC面积？
思考1：此时△ABC的
面积可以采用“底×高
÷2”吗？为什么？
A
AB,AC,BC长度无法计算
C
思考2：那如何计算
B
△ABC的面积？

人教版数学七年级下册第七章平面直角坐标系中的面积的求法

5
C
4
3
2
1
-4
-3 A-2
-1
0 -1
-2 -3
-4
1 2 3 B4 5
分析(1)由点C在第二象限，可知x和y的符号，这样可化简绝对值，从而求点C的坐标，求三角形的面积，关键求点C到AB所在的直线即x轴的距离 |y|
问题3
在图(3)中，以OA为边的△OAB的面积为2，试找出符合条件的且顶点是格点的点C，你能找到几
x
-2 -1 O
-1
-2
A(-1,-2)
1234 5 678
y
C`
5
4
C(1,3)
3
2
1
方法4
B`
B(6,2)
x
-2 -1 O A1` 2 3 4 5 6 7 8
-1
-2
A(-1,-2)
已知四边形ABCD中，A(1,-2), B(4,0), C(6,8), D(1,4),求四边形ABCD的面积.
y
8 7 6 5 4 3 2 1
-2 -1O -1 -2 -3
C(6,8)
B(4,0)
1 2 3 4 56 7 8x
A(1,-2)
E(6,3)
B(6,2)
x
-2 -1 O
-1
-2
A(-1,-2)
1234 5 678 D(6,-2)
y
5
4
C(1,3)
3
2
1
方法2
E(6,3)
B(6,2)
x
-2 -1 O
-1
-2
A(-1,-2)
1234 5 678 D(6,-2)
y
5

平面直角坐标系中的面积问题

突破数学压轴题解题策略平面直角坐标系中的面积问题解题策略1【专题攻略】面积问题是初中常考内容，一般应用以下几种方法解决：一是“直接法”，即套用求面积的公式.二是常用“割补法”.割：分割，把图形分割成几部分容易求解的图形，分别求解，然后相加即可.补：补齐，把图形补成一个容易求解的图形，然后再减去补上的那些部分.三是“平行线转化法”，即利用平行线之间的距离处处相等，同底等高模型转化面积来解决.在平面直角坐标系中求面积时，必然会用到线段长度，这里会涉及到利用两点之间的距离公式来求距离.在平面直角坐标系中有两点A（x1,y1）、B（x2,y2），则AB2=（x 1- x2）2 + （y1– y2）2 .若两点平行于坐标轴，则两点之间的距离可以直接用横或纵坐标的差来求.【复习回顾】：例1如图Δ ABC的三个顶点的坐标分别是A（4，0），B（-2，0），C（2，4），求ΔABC的面积.例2如图2，点C为平面直角坐标系中的任意一点，已知点A （-5，0），点B （3, 0）Δ ABC的面积为12，试说明点C的坐标特点.例3如图Δ ABC三个顶点的坐标分别为A （4，1），B （4，5），C （-1，2），求Δ ABC的面积.y >6 -5 - D4 - 3 - 2 - 1 -x-1 01 2 3 4 5 6 7 -1- -2 - 图4图5例4如图4，在四边形ABCD 中，A 、B 、C 、D 的四个点的坐标分别为（0，2），（1，0），（6，2）（2, 4）求四边形 ABCD 的面积.类型3 三边均不与坐标轴平行例5在图5的直角坐标系中，Δ ABC 的顶点都在网格点上，其中，A 点坐标为（2，一 1），则Δ ABC 的面积为 ________________________ .y,:4(?1)〆o123 4 1例6如图，已知Δ ABC中，A（4，1），B （4，5），C （-1，2），求Δ ABC的面积.例7如图，以O A为边的ΔOAB的面积为2，试找出符合条件得且顶点是第一象限格点的点C，你能找出几个这样的例8已知：A（0,1）,B（2,0）,C（4，3）.（1）在坐标系中描出各点，画出ΔABC（2）求ΔABC的面积；（3）设点P在坐标轴上，且ΔABP与ΔABC的面积相等，求点P的坐标.。

解题技巧专题：平面直角坐标系中的图形面积

解题技巧专题：平面直角坐标系中的图形面积解题技巧专题：平面直角坐标系中的图形面积——代数结合，突破面积及点的存在性问题类型一：直接利用面积公式求图形的面积1.在平面直角坐标系中，给定三个点A、B、C，求△ABC的面积。

2.在平面直角坐标系xOy中，已知A(-1.5)，B(-1.0)，C(-4.3)，求△ABC的面积。

类型二：利用分割法求图形的面积3.在平面直角坐标系中，给定四个点A(4.0)，B(3.2)，C(-2.3)，D(-3.0)，求四边形ABCD的面积。

类型三：利用补形法求图形的面积4.已知三个点A(-2.1)，B(1.-3)，C(3.4)，求△ABC的面积。

类型四：探究平面直角坐标系中与面积相关的点的存在性5.在平面直角坐标系中，给定三个点A(4.0)，B(3.4)，C(0.2)。

1) 求四边形ABCO的面积S。

2) 连接AC，求△ABC的面积S。

3) 在x轴上是否存在一点P，使得△PAB的面积S等于10？若存在，求点P的坐标。

6.在平面直角坐标系中，给定三个点A(0.a)，B(b。

0)，C(b。

c)，其中a、b、c满足关系式|a-2|+(b-3)^2≤(c-4)^2.1) 求a、b、c的值。

2) 请用含m的式子表示四边形ABOP的面积，其中m=2.3) 在(2)的条件下，是否存在点P，使得四边形ABOP的面积与△ABC的面积相等？若存在，求出点P的坐标；若不存在，请说明理由。

BF·CF=5×7-3×5-4×3-2×7=22.方法二：将△ABC分成梯形BCDE、△ACD和△ABE三个部分。

则S△ABC=S梯形BCDE-S△ACD-S△ABE=(BE+CD)·DE-AD·CD-AE·BE=（3+5）×7-3×5-4×3=29.方法三：将△ABC分成梯形CAEF、△ABE和△BCF三个部分。

平面直角坐标系中的图形面积问题

例3 如图3，平面直角坐标系中，已知 △ABC三个顶点的坐标分别是A(-3，-1)， B(1，3)，C(2，-3)．
求△ABC的面积．
第6页/共9页
例4 如图，四边形ABCD的四个顶点的坐标分别是A(4， 2)，B(4，-2)，C(0，-4)， D(0，1)．求四边形ABCD的面积．
第7页/共9页
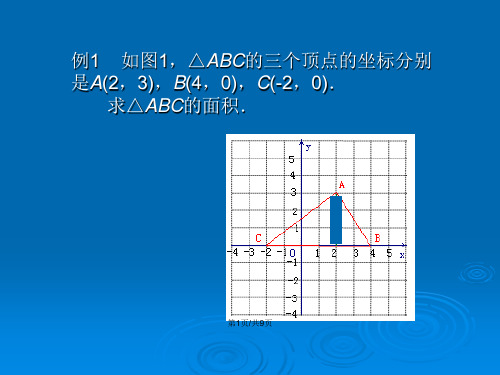
例1 如图1，△ABC的三个顶点的坐标分别是A(2，3)，B(4，0)，C(-2，0)．
求△ABC的面积．
第1页/共9页
例1 如图1，△ABC的三个顶点的坐标分别是A(2，3)，B(4，0)，C(-2，0)．
求△ABC的面积．Zxxk
第2页/共9页
例2 如图，平面直角坐标系中，已知点A(-3，-2)，B(0，3)，C(-3，2)．
求△ABC的面积．
第3页/共9页
例2 如图，平面直角坐标系中，已知点A(-3，-2)，B(0，3)，C(-3，2)．
求△ABC的面积．
第4页/共9页
例3 如图3，平面直角坐标系中，已知 △ABC三个顶点的坐标分别是A(-3，-1)， B(1，3)，C(2，-3)．
求△ABC的面积．
第5页/共9页
例4 如图，四边形ABCD的四个顶点的坐标分别是A(4，2)，B(4，-2)，C(0，4)，D(0，1)．
Zx。xk
求四边形ABCD的面积．
第8页/共9页

专题05平面直角坐标系中求图形面积(解析版)

专题05平面直角坐标系中求图形面积类型一、直接用公式求面积例1.如图，在平面直角坐标系中，点()0,4A b 为y 轴正半轴上一点，点()3,0B b 是x 轴正半轴上一点，其中b 满足()316b +=．（1）求点A ，B 的坐标．（2）点C 为x 轴上一点，且ABC 的面积为12，求C 点的坐标．【答案】（1）()0,4A ，()3,0B ；（2）点C 的坐标为()3,0-或()9,0【解析】（1）由()316b +=得1b =，∴()04A ，，()30B ，．（2）设点C 的坐标为()0x ，，则3BC x =-，由1（）可知4OA =，∴1432ABC S x =⨯⨯-= 12，解得：9x =或3-．∴点C 的坐标为()30-，或()90，．【变式训练1】在平面直角坐标系中，已知点(),0A a ，(),0B b ，a 、b 满足方程组24a b a b +=-⎧⎨-=-⎩，（1）求A 、B 两点的坐标；（2）C 为y 轴正半轴上一点，且6ABC S = ，请求出C 的坐标．【答案】（1）A （-3，0），B （1，0）；（2）C （0，3）【解析】（1）解方程组24a b a b +=-⎧⎨-=-⎩，解得：31a b =-⎧⎨=⎩，∴A （-3，0），B （1，0）；（2）由（1）可知：AB =4，∵S △ABC =12AB •OC =6，∴12×4×OC =6，解得OC =3，∴C （0，3）．故答案为：（1）A （-3，0），B （1，0）；（2）C （0，3）类型二、割补法求面积例1.如图，三角形ABC 的面积等于（）A ．12B ．1122C ．13D ．1132【答案】D【解析】过点A 作AD x ⊥轴于D ，如图所示：由题意可得，3BO =，3OC =，6AD =，3CD =，∴6OD =，∴ABC BOC ACDBODA S S S S ∆∆∆=--梯形111()222BO AD OD BO OC CD AD=+⋅-⋅⋅-⋅⋅111(36)63336222=+⨯-⨯⨯-⨯⨯54918222=--272=，即272ABC S ∆=，故选：D ．【变式训练1】如图，连接AB 、BC 、AC ，则△ABC 的面积是（）A ．312B ．3C ．212D ．2【答案】C【解析】长方形AGDE 的面积为：3×2=6，AGC 的面积：3×1÷2=1.5，CDB △的面积：2×1÷2=1，ABE △的面积：2×1÷2=1，故ABC 的面积为：6-1.5-1-1=2.5，故答案为：C ；【变式训练2】如图，三角形ABO 中，()2,3A --，()2,1B -，A B O ''' 是ABO 平移之后得到的图形，并且O 的对应点O '的坐标为()5,4．（1）作出ABO 平移之后的图形A B O ''' ，并写出A '、B '两点的坐标分别为A '______，B '_____；（2）()00,P x y 为ABO 中任意一点，则平移后对应点P 的坐标为______．（3）求ABO 的面积；【解析】（1）如图，△A 'B 'O '即为所求，A '、B '两点的坐标分别（3，1），（7，3）．故答案为：（3，1），（7，3）．（2）点P '的坐标为（x 0+5，y 0+4）．故答案为：（x 0+5，y 0+4）．（3）S △ABO =3×4-12×2×3-12×1×2-12×4×2=4．【变式训练3】在平面直角坐标系xoy 中，△ABC 的位置如图所示，点A ，B ，C 都在格点上．（1）分别写出下列顶点的坐标：A ________；B ________；（2）请在图中画出△ABC 关于y 轴对称的图形△A ′B ′C ′；（3）计算出△ABC 的面积．【答案】（1）(-1,6)，(-2,0)；（2）见解析；（3）152【解析】（1）由图知，点A 的坐标为(-1,6)，点B 的坐标为(-2,0)，故答案为：(-1,6)，(-2,0)（2）由图得，点C 的坐标为(-4,3)，则点A 、B 、C 关于y 轴的对称点A ′，B ′，C ′坐标分别为(1,6)，(2,0)，(4,3)，依次连接A ′，B ′，C ′，即得△A ′B ′C ′，所得图形如图所示（3）过A 、C 作x 轴的垂线，垂足分别为D 、E则ABC AOD CED ADEC S S S S =-- 梯形111(36)31623222=⨯+⨯-⨯⨯-⨯⨯152=类型三、点的存在性问题例1.如图，在平面直角坐标系中，点B ，C 的坐标分别为(),2a a -、()3,2a a ，其中0a >，点A 为BC 的中点，若4BC =，解决下列问题：（1）BC 所在直线与x 轴的位置关系是；（2）求出a 的值，并写出点A ，C 的坐标；（3）在y 轴上是否存在一点P ，使得三角形PAC 的面积等于5？若存在，求出点P 的坐标；若不存在，请说明理由．【答案】（1）平行；（2）()1,2A ，()3,2C ；（3）存在，P 点坐标为()0,3-或()0,7【解析】（1）∵点B ，C 的坐标分别为(),2a a -、()3,2a a ，∴BC 所在直线与x 轴的位置关系是平行．故答案为：平行．（2）∵4BC =，∴()34a a --=，∴1a =，∴B （-1，2），C （3，2），∵A 为BC 的中点，∴()1,2A ．（3）存在点P ．设()0,P m ，∵2AC =，∴12252m ⨯⨯-=，∴3m =-或7.∴P 为()0,3-或()0,7．【变式训练1】如图，在直角坐标系中，已知()0,2A ，()3,0B ，()3,4C 三点．（1）求四边形AOBC 的面积；（2）是否存在点()0.5P x x ,，使2ABC AOBC S S = 四边形？若存在，求出点P 的坐标．若不存在，请说明理由．【答案】（1）9；（2）存在，()189P --,或(18,9)【解析】如图，∵34C （，），∴33CD ==．∵()34C ，，30B （，），∴404CB =-=，∴4312DCBO S =⨯=四边形．∵()04D ，，()02A ，，∴422DA =-=，∴11236322DCA S =⨯⨯=⨯= ．∵DCA AOBC DCBO S S S =- 四边形四边形，∴1239AOBC S =-=四边形．（2）由（1）得1239AOBC S =-=四边形设存在点()0.5P x x ，，使△AOP 的面积为四边形AOBC 的面积的两倍．∵△AOP 的面积=122x x ⨯⨯=，∴29x =⨯，∴18x =±∴存在点P （18，9）或（-18，-9），使△AOP 的面积为四边形AOBC 的面积的两倍．【变式训练2】如图，A （0，3）是直角坐标系y 轴上一点，动点P 从原点O 出发，沿x 轴正半轴运动，速度为每秒2个单位长度，以P 为直角顶点在第一象限内作等腰Rt △APB ．设P 点的运动时间为t 秒．（1）若AB ∥x 轴，求t 的值；（2）如图2，当t ＝2时，坐标平面内有一点M （不与A 重合）使得以M 、P 、B 为顶点的三角形和△ABP 全等，请直接写出点M 的坐标．【答案】（1）t 的值为1.5；（2）点M 的坐标为（3，7），（8，﹣3），（11，1）．【解析】（1）过点B 作BC ⊥x 轴于点C ，如图所示．∵AO⊥x轴，BC⊥x轴，且AB∥x轴，∴四边形ABCO为矩形，∴AO=BC=3，∵△APB为等腰直角三角形，∴AP=BP，∠PAB=∠PBA=45°，∴∠OAP=90°-∠PAB=45°，∴△AOP为等腰直角三角形，∴OA=OP=3，∴t=3÷2=1.5（秒），故t的值为1.5；（2）当t=2时，OP=4，①如图3，若△ABP≌△MBP，则AP=PM，过点M作MD⊥OP于点D，∵∠AOP=∠PDM，∠APO=∠DPM，∴△AOP≌△MDP（AAS），∴OA=DM=3，OP=PD=4，∴M（8，-3）；②如图，若△ABP≌△MPB，连接AM，则AP=PB=BM，∠APB=∠MBP=90︒，∴AP∥MB，且AP=MB，∴四边形APBM是平行四边形，y轴于点E，又∠APB=∠MBP=90︒，∴四边形APBM是正方形，∴AP=AM，过点M作ME⊥同理可证△AOP≌△MEA（AAS），∴OA=EM=3，OP=AE=4，∴M（3，7）；③如图，若△ABP≌△MPB，则AP=BP=BM，过点M 、B 分别作x 轴的垂线，垂足分别为点F 、G ，过点M 作MH ⊥BF 于点H ，∴四边形FGMH 是矩形，∴MH =FG ，MG =HF ，同理可证△AOP ≌△PFB ≌△BHM （AAS ），∴OA =PF =BH =3，OP =BF =MH =4，∴MG =HF =BF -BH =1，OG =OP +PF +FG =11，∴M （11，1）；综合以上可得点M 的坐标为（3，7），（8，-3），（11，1）．【变式训练3】在平面直角坐标系中，正方形ABCD 的位置如图所示，点A 的坐标为()1,0，点D 的坐标为()0,2．延长CB 交x 轴于点1A ，作第1个正方形111A B C C ；延长11C B 交x 轴于点2A ，作第2个正方形2221A B C C ，…，按这样的规律进行下去，第2021个正方形的面积是______．【答案】404235(2⨯【解析】()()1,0,0,2,A D 正方形ABCD ，1,2OA OD ∴==,,AD AB ===190,DAO ADO DAO BAA ∠+∠=︒=∠+∠1,ADO BAA ∴∠=∠190,DOA ABA ∠=∠=︒ 1,AOD A BA ∴ ∽1,AO OD A B AB ∴=15,2AO AB A B OD ∴== 正方形111A B C C，1113222A B A C ∴====⨯同理可得：22232442A B ⎛⎫=+==⨯ ⎪⎝⎭33332A B ⎛⎫= ⎪⎝⎭······20212021202132A B ⎛⎫= ⎪⎝⎭所以第2021个正方形的面积是22021404233=5.22⎡⎛⎫⎛⎫⨯⎢ ⎪ ⎪⎝⎭⎝⎭⎢⎣⎦故答案为：404235.2⎛⎫⨯ ⎪⎝⎭。

平面直角坐标系下图形面积的计算

19
谈谈我们的收获
1、在平面直角坐标系下，计算图形的面积可以运用什么方法？
割补法求面积
平移
2、今天我们学习了什么数学思想？
转化思想
化复杂为简单
20
C （-14 ， 0 ）
E
D
0 D
X
如图，四边形ABCD各个顶点的坐标分别为（– 2，8），（– 11，6），（– 14，0），（0，0）。（1）确定这个四边形的面积，你是怎么做的? （2）如果把原来ABCD各个顶点纵坐标保持不变，横坐标增加2，所得的四边形面积又是多少？ 5
（2）已知A（－1，0），B（3，0），C（2，－3），
3
例1 平面直角坐标系内,A(2,3),B(4,3),C(3,-5),试求△ABC的面积.
y
4 3 2 1 -5 -4 -3 -2 -1 0 -1 -2 -3 -4 -5
1
2 3
x
平面直角坐标系中求三角形的面积时以与坐标轴重合或平行于坐标轴的边为底.
4
y
A （-2 ， 8 ）（-11 ， 6 ） B
2
复习：
1. 已知P(a,b)，则点P到X轴的距离是 |b| ，到y轴的距离是 |a| 。 2. 若A(a,0)，B(b,0) ，则AB= |a-b| ；
若A(0,a)，B(0,b) ，则AB=|a-b| 。
3. 若A(a,c)，B(b,c) ，则AB= |a-b| ；若A(c,a)，B(c,b) ，则AB= |a-b| 。
C(1,3)
E(6,3)
4 F(-1,3) 3 2 1
B(6,2)
A(-1,-2)
-2
x
17
-2
-1 O -1

人教版初一数学下册在平面直角坐标系内求图形的面积

在平面直角直角坐标系内求图形的面积
教学目标：能用割补法求图形的面积
教学重点：体会转化的数学思想
教学难点：对图形进行合理的分割补形
温故习新，导引自学
题组一
o
y x
A(-3,4)
C(0,2)
B(0,-1)
1、已知(0,4),(3,0),(0,0)A B O ,则△AOB 的面积为。

2、已知(2,4),(2,0),(3,0)A B C -，则△ABC 的面积为。

3、已知(3,4),(0,1),(0,2)A B C --，则△ABC 的面积为。

题组二
4、已知(3,5),(1,2),(5,2)A B C ，则△ABC 的面积为。

5、已知(3,2),(1,3),(5,3)A B C ---，则△ABC 的面积为。

6、已知(2,3),(2,4),(3,1)A B C ----，则△ABC 的面积为。

交流质疑，精讲点拨
例题1、已知(1,2),(3,2),(0,0)A B O --求△AOB 的面积
例题2、已知(0,2),(3,4),(5,0),(0,0)A B C O 求四边形OABC 的面积
变题：在坐标轴上求点P ，使△PBC 的面积是四边形OABC 面积的两倍
当堂反馈，拓展迁移
1、已知(5,2),(3,4),(0,0)A B O 求△AOB 的面积
2、已知(1,2),(4,0),(6,8),(1,4)A B C D 求四边形ABCD 的面积
课堂小结
课后作业。

人教版七下数学第10讲平面直角坐标系中图形面积的求解思路(学生版)

平面直角坐标系中图形面积的求解思路（原卷版）第一部分专题典例剖析+针对训练专题1 规则图形面积求解思路1．求“规则三角形”的面积典例1 （2021春•肥城市期末）△ABC的各顶点坐标为A（﹣5，2），B（1，2），C（3，﹣1），则△ABC 的面积为．针对训练11．如图，已知在平面直角坐标系中，A（0，﹣1）、B（﹣2，0）、C（4，0），求△ABC的面积．2．求规则四边形的面积典例2 如图所示，在平面直角坐标系中，AD∥BC∥x轴，AD＝BC＝7，且A（0，3），C（5，﹣1）．（1）求B，D两点的坐标；（2）求四边形ABCD的面积．典例3（2021春•丰台区校级期末）将长方形OABC先向上平移1个单位长度，再向左平移2个单位长度得新长方形D′A′B′C′，设A′B′与BC交于点M，求四边形A′MCO的面积．针对训练23．长方形ABCD在平面直角坐标系中的位置如图所示，AD∥x轴，AB∥y轴，已知长方形ABCD的长为3，宽为2，且点A的坐标为（﹣1.5，2），求长方形的顶点B、C、D的坐标及矩形AEOM的面积．专题2 不规则图形面积求解思路1．求不规则三角形的面积典例4 （2021秋•靖西市期中）如图，在平面直角坐标系xOy中，A、B、C三点的坐标分别为（﹣5，4）、（﹣3，0）、（0，2）．（1）画出三角形ABC，并求其面积；（2）如图，△A′B′C′是由△ABC经过平移得到的．（3）已知点P（a，b）为△ABC内的一点，则点P在△A′B′C′内的对应点P′的坐标是（，）．针对训练44．如图，已知：A（0，1），B（2，0），C（4，3）（1）在坐标系中描出各点，画出△ABC；（2）求△ABC的面积．2．求不规则多边形的面积典例5 （2021春•凤山县期末）如图，已知四边形ABCD．（1）写出点A，B，C，D的坐标；（2）试求四边形ABCD的面积．（网格中每个小正方形的边长均为1）典例6 （2020秋•罗湖区校级期末）如图，网格中每个小正方形的边长都是1，依次完成下列各问：（1）任选一点作为原点，建立平面直角坐标系；（2）写出A、B、C、D、E各点的坐标；（3）求五边形ABCDE的面积．针对训练55．已知点A（3，0）、B（0，2）、C（﹣2，0）、D（0，﹣1）在同一坐标系中描出A、B、C、D各点，并求出四边形ABCD的面积．6．如图，已知在平面直角坐标系中，四边形各顶点的坐标分别为A（0，0），B（9，0），C（7，4），D（2，8），求四边形ABCD的面积．。