单口网络
合集下载
§4-2单口网络的电压电流关系
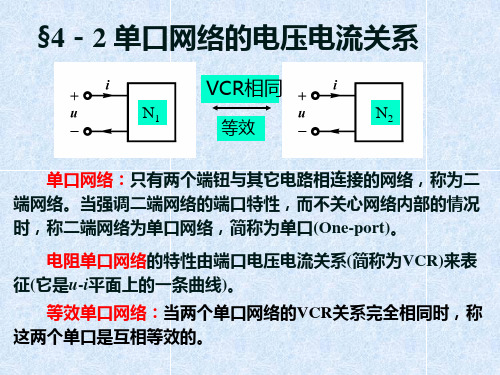
其中:
根据上式所得到的单口等效电路是电导Go和电流源iSC的并联, 如图(b)所示。
例2-6 求图2-10(a)和(c)所示单口的VCR方程,并画出单 口的等效电路。
图2-10
图2-10
解:图(a)所示单口的VCR方程为
u uS
i
根据电压源的定义,该单口网络的等效电路是一个电 压为uS的电压源,如图(b)所示。
而言,等效于一个线性二端电阻,其电导值由上式确定。
两个线性电阻并联单口的等效电阻值,也可用以下公
式计算
R1 R2 R R1 R2
3.线性电阻的串并联 由若干个线性电阻的串联和并联所形成的单口网络, 就端口特性而言,等效于一个线性二端电阻,其等效电阻
值可以根据具体电路,多次利用电阻串联和并联单口的等
假如图 2-13(a) 所示电路 N 能分解为图 2-13(b) 所示的两
个单口网络的连接,就可以用单口的等效电路来代替单口
Nl(或 N2),使电路的支路数和结点数减少,从而简化电路 分析。
图2-13
图2-13
由于单口与其等效电路的VCR方程完全相同,这种代
替不会改变电路其余部分N2(或 Nl)的电压和电流。
14A
5S
图 2- 9 解:在端口外加电压源u,用2b 方程写出端口电流的表达式为 i iS G2u G1 (u uS )
(G1 G2 )u (iS G1uS ) Gou isc
G o G1 G 2 2S 3S 5S isc iS G1u S 4A 2S 5V 14A
图2-10
图(c)所示单口VCR方程为
i iS
u
根据电流源的定义,该单口网络的等效电路是一个电 流为iS的电流源,如图(d)所示。
单口网络_第3讲

R(0, ) R(0, )
2、电阻+独立源:可等效为电阻+独立源
3、电阻+受控源:可等效为电阻
R(, )
4、电阻+独立源+受控源:可等效为电阻+独立源
u Ri U R(, )
五、放大器的作用和意义
作用:小信号放大
u
放大器
y kxቤተ መጻሕፍቲ ባይዱ
ku
x
u1
k
y
u1
第3讲 单口网络
u
u
u
u
一、无源单口网络等效
i
N1
u
i
N2
u
等效:单口网络端口的特性u~i,N1与N2wan完全 相等。
i
6 5
i
7
3
u
u
例:求端口电流i。
8V
i
6 3
4
3
3 3
练习:
例:求端口电流i。
3
8V
i
3
3
各元件电压和电流?
例:
i
1V
2
1.5A
0.5A
7V
1A
4 6V
2i
各元件功率?
例:
(0.5W)
i
2
0.5A
(-3.5W) 7V
1A 1.5A
4
(9W)
2i (-6W)
受控源是有源器件吗?
例:
i
2
u
2i 3
无源单口网络的综合课件

终端开路法
总结词
适用于具有线性电阻和线性电感的无源单口网络
详细描述
终端开路法是一种综合无源单口网络的方法,它适用于具有线性电阻和线性电感 的无源单口网络。通过将单口网络的两个端口开路,并联上适当的电阻和电感, 可以得到一个具有相同端口特性的等效电路。
戴维南等效法
总结词
适用于任何无源单口网络
详细描述
戴维南等效法是一种综合无源单口网络的方法,它适用于任何无源单口网络。通过将单口网络进行戴维南分解, 将其分解为两个或多个二端网络,并分别计算每个二端网络的等效电路,最终得到一个具有相同端口特性的等效 电路。
04
无源单口网络的应用
在通信系统中的应用
频率选择表面(FSS)天线
01
利用无源单口网络设计出具有高性能的FSS天线,可实现高精度
无线传感器网络(WSN)
无源单口网络可以用于WSN中的传感器节点设 计,实现低功耗、长寿命的传感器节点。
3
电磁场探测
无源单口网络可用于电磁场探测系统的设计和优 化,提高探测精度和灵敏度。
在控制系统中的应用
自动控制系统
无源单口网络可以作为自动控制系统的元件,实现精确的信号控 制和传输。
机器人控制系统
、宽频带通信。
微波毫米波滤波器
02
无源单口网络在微波毫米波滤波器设计中应用广泛,可实现高
性能、小型化的滤波器。
电磁波极化技术
03
利用无源单口网络对电磁波进行极化处理,可提高通信系统的
抗干扰能力和数据传输效率。
在测量系统中的应用
1 2
射频识别(RFID)标签
无源单口网络可应用于RFID标签的设计中,实现 低成本、小型化和高效能的RFID标签。
第4章 分解方法及单口网络

i1=i2+0.5i
19/120
u = 2(1 + 0.5i ) + 1 + i + 5 + 3i = 8 + 5i
第四章 分解方法及单口网络
§ 4-1 § 4-2 § 4-3 § 4-4 § 4-5 § 4-6 § 4-7 § 4-8 § 4-9 分解的基本步骤 单口网络的电压电流关系 单口网络的置换- 单口网络的置换-置换定理 单口网络的等效电路 一些简单的等效规律和公式 戴维南定理 诺顿定理 最大功率传递定理 T(Υ 形网络和∏ T(Υ)形网络和∏(Δ)形网络的等效变换
P138 某支路 可推广为一个单口网络 某支路k可推广为一个单口网络
置换定理示意图: 置换定理示意图: + uk – +
ik
支 路 uk k –
ik
ik + uk – R=uk/ik
原因: 替代前后KCL、KVL关系相同 , 其余支路的 关系相同, 原因 : 替代前后 关系相同 其余支路的u、i关 关 系不变。 替代后,其余支路电压不变(KVL),其余支路 系不变。用uk替代后,其余支路电压不变 , 电流也不变,故第k条支路 也不变(KCL)。用ik替代后,其 条支路i 替代后, 电流也不变,故第 条支路 k也不变 。 余支路电流不变(KCL),其余支路电压不变, 故第 条支路 余支路电流不变 , 其余支路电压不变,故第k条支路 uk也不变 也不变(KVL)。 。
+ _
u
i
N
16/120
注意: 注意: 1、单口网络含有受控源时,控制支路和被控 、单口网络含有受控源时, 制支路必须在同一个单口网络中, 制支路必须在同一个单口网络中 , 或者控制量可 以是端口上的电压或电流, 以是端口上的电压或电流 , 但控制量不能在另外 一个网络中。 一个网络中。 2、单口网络的 、 单口网络的VAR只取决于网络内部的参数 只取决于网络内部的参数 和结构, 与外电路无关, 和结构 , 与外电路无关 , 是网络本身固有特性的 反映。 当外电路变化时, 该单口网络的VAR不变 反映 。 当外电路变化时 , 该单口网络的 不变 ,只有当网络内部的连接关系或参数变化时, VAR才变。 才变。 才变
分解方法及单口网络
i
i
例题
试求RL=0.4Ω、0.6Ω和1Ω时的电流 i。(续)
(2)求Ro
1
Ro
电压源置零,即用 短路线代替电压源,可得
例题
计算上题RL的功率, 并问RL取何值时获得的功率最大?
解
1Ω
1Ω
1Ω
1Ω
1 V
R
i
(1)
此为使p为最大的条件——最大功率传递定理
上题 Ro=06Ω, 故 RL=Ro=0.6Ω时 RL所得功率为最大。
(2)基于VCR相同的等效 ——一般所称的等效(equivalence)
N1
N2
N1′
N2
2.5
10
N1
N1′
4Ω
(1)基于工作点相同的等效——置换(substitution)
N1′
N1
u = 6V i =1A
u = 6V i =1A
习题3 答案
最简便方法是把电流源8A与电阻1Ω的并联电路 等效为电压源8V与电阻1Ω的串联电路。由分压关系 得
解
习题课
习题4 已知N的VCR为u=1+0.8i,试求各支路电流。 答案
习题4 答案
解
提问:N用0.5A电流源置换,是否可行?
由N的VCR可得串联等效电路的元件为: 1V电压源与0.8Ω电阻。
N
i
-
u
+
R
习题1 答案
解
结合两个已知条件解得 uoc=40V Ro=8Ω
故得R=24Ω时,i=1.25A
由
习题课
习题2
答案
所示单口网络受控源参数r=1Ω, ab端的戴维南等效 两个参数为 A . 40V, 5Ω B. 30V, 14/6Ω C. 40V, 4Ω D. 4(10-i)V, 8/6Ω ( )
单口网络多口网络

(4.1b)
vN = ZN1i1 + ZN2i2 + ...+ ZNN iN (4.1c) 由此可见,每个端口n不但受到本端口阻抗
Znm的影响而且也受到其他所有端口阻抗线性叠加效果的综合影响,
如果采用更简单的符号,
v1 v2
Z11 Z21
vN ZN1
ห้องสมุดไป่ตู้
Z12 Z22
ZN2
Z1N Z2N
i1 i2
ZNN iN
公式(4.2)
或矩阵符号表达式
V Z I
公式(4.2)中的每个阻抗元素可以通过以下规则求得:
Znm
vn im
ik 0(
for
k m)
这表明,当第 m 端口的输入电流为 im 而且其他端口均
为开路状态(即k m 时,ik 0 )时,第 n 端口测得的电压是vn 。
单端口网络、多端口网络
图4.1
在确定各种网络参数的规则时,我们先根据双脚标阻抗参量Znm建立 电压-电流关系,其中n 和m 的取值从1到N。
各网络端口(n=1...N)的电压为, 1端口:
v1 = Z11i1 + Z12i2 + ...+ Z1NiN 2端口:
(4.1a)
v2 = Z21i1 + Z22i2 + ...+ Z2NiN 和N端口:
例题:
已知导纳矩阵 Y
2 0
0 4
, 求阻抗矩阵
Z
.
Z
1/2 0
0 1/ 4
ABCD参量矩阵(级联矩阵)可定义为:
v1 i1
A C
B v2
D
i2
对于相互级联旳两个多端口网络,则应转化为 ABCD 参量矩阵后相乘。 对于相互并联旳两个多端口网络,则应转化为 Y 参量矩阵后相加。
1-10单口网络

尽 电 模 详 的 路 型 单口网络的描述: 单口网络的描述:端 电 电 关 口 压 流 系 等 电 效 路
单口网络VCR的确定 的确定——外接电路法:通常外接 外接电路法: 单口网络 的确定 外接电路法 返回 一个电压源或一个电流源. 一个电压源或一个电流源.
X
�
u =Us u =Us u = Ri i =Us R
N1
N2
结论:由两元件的 可得到两元件相连的端口的u, 结论:由两元件的VCR可得到两元件相连的端口的 , 可得到两元件相连的端口的 i值. 值 思考:如果在端口11'处相连接的是两个内部结构复杂 思考:如果在端口 处相连接的是两个内部结构复杂 或内部情况不明的单口网络, 或内部情况不明的单口网络,则能否根据这两个单口 网络的VCR求得端口的 ,i值呢? 求得端口的u, 值呢 值呢? 网络的 求得端口的
§1-10 单口网络
北京邮电大学电子工程学院 2007.8
退出
开始
内容提要
网络的分解 单口网络的电压电流关系
X
1.网络的分解 1.网络的分解
求右图所示网络中端口11'处的 求右图所示网络中端口 处的 电压和电流. 电压和电流. 由元件的VCR可得: 可得: 由元件的 可得
i 1
U s
ቤተ መጻሕፍቲ ባይዱ
+ -
+ u 1' R
X
1.网络的分解 1.网络的分解
回答是肯定的.因为同电路元件一样,单口网络 回答是肯定的.因为同电路元件一样, 是由此网络本身所确定的, 的VCR是由此网络本身所确定的,与外接电路无 是由此网络本身所确定的 关. 结论: 结论:一个复杂的网络可以通过将其分解为两个简单 的单口网络的方法进行求解. 的单口网络的方法进行求解. 网络分解法的基本步骤: 网络分解法的基本步骤: 1)将给定的网络划分为两个单口网络 1和N2; )将给定的网络划分为两个单口网络N 2)分别求出 1和N2的VCR; )分别求出N 3)联立两者的 求得N 的端口u, 值 )联立两者的VCR求得 1和N2的端口 ,i值; 求得 4)分别求解 1和N2内部各支路的电压和电流. )分别求解N 返回
单口网络的等效电路

mA 1.5
kΩ
+ u
––
–
–
(a)
(b) 图4-18 例4-7
(c)
解:化简问题也就是要寻求一个最简形式的等效电路问题,也
可以从求单口网络的VAR下手。
电路分析基础——第一部分:4-4
设想在单口网络两端外接电 流为 i 的电流源,则可求得其端 口电压为
u = 1000( i – 0.5i ) + 1000i + 10 = 1500i + 10
电路分析基础——第一部分:第四章 目录
第四章 分解方法及单口电路
1 分解的基本步骤
6 戴维南定理
2 单口网络的伏安关系
7 诺顿定理
3 单口网络的置换 ——置换定理
8 最大功率传递定理
4 单口网络的等效电路
9 T型网络和型网络 的等效变换
5 一些简单的等效规律和公式
电路分析基础——第一部分:4-4 内容回顾 4-4 单口网络的等效电路
– i 1’
解:由例4-1已知该单口网络的VAR为
u = 8 – 4i
图4-17(a)所示的电路也具有同样的 VAR,其电路由两个元件组成,是可能具 有的最简形式,这就是所求的等效电路。
+ 8V 4
+
u
–
–
(a)u = 8 – 4i
电路分析基础——第一部分:4-4
7/16
若把该单口网络的VAR改写为
电路分析基础——第一部分:4-4 内容回顾
其中, 步骤(1)在4-1节中已经完成; 步骤(2)和(3)求VAR在4-2节中通过节点法、
网孔法等方法列解联立方程得到解决;
步骤(4)的工作已在上一次课4-3节中得到解决。
电路分析基础_第9讲(ch4单口网络的等效和化简)

将电压源与电阻的串联等效变换为电流源与电阻的并联。 将电压源与电阻的串联等效变换为电流源与电阻的并联。
将电流源与电阻的并联变换为电压源与电阻的串联等效。 将电流源与电阻的并联变换为电压源与电阻的串联等效。
例2:求 I :
6Ω 9V
_
3Ω
I 8Ω
+
+ _
+ 6V _
2Ω 1V I 8Ω
(三)含受控源电路的等效电路 1. 只含受控源和电阻单口网络 端钮的等效电阻(也叫ab端输入电阻) ab端输入电阻 例1、求 ab 端钮的等效电阻(也叫ab端输入电阻)。 I 100Ω
(一)求二端网络的最简等效电路 最简:一个单回路或单节点的电路。 最简:一个单回路或单节点的电路。 1. 只含电阻的电路 例 1:
3 3 6 12Ω
7
10
5
例2: a 44Ω b
20Ω 60Ω 60Ω
20Ω
20Ω
22Ω
60Ω 结论: 只含电阻单口网络 等效为一个电阻 只含 电阻
R
2.含独立源电路 2.含独立源电路 例3:
N
+ Us
9、电流源与电压源或电阻串联: 、电流源与电压源或电阻串联: N Is Is
结论: 是多余元件, 结论:N——是多余元件,可以去掉。 是多余元件 可以去掉。
10. 受控电压源与受控电流源相互等效
例:
(1)
2Ω
(2)
+
8V
_
10Ω 3A
(4)
(3)
+
5V 5Ω
5Ω 5A
_
二、用等效化简的方法分析电路 用等效化简的方法分析电路 用等效化简的方法
+
电路分析基础第4章分解方法及单口网络

is
is is1 is2 isK
5.电流源的串联 电流值相等的电流源可作方向相同的串联,电 流值不相等的电流源不允许串联。
a is1 is2 b
a
is b
is is1 is2
17
6.电流源与二端网络的串联 N1的等效网络不是理想电流源支路。
a
is N1 b
a is b
3
4-2 单口网络的电压电流关系
单口网络的描述方式:
• 详尽的电路图; • VCR(表现为特性曲线或数学公式); • 等效电路。
VCR只取决于单口本身的性质,与外接电路无关。
因而:
• 可以孤立出单口,而用外施电源法求它的VCR; • 求解单口(例如N2)内各电压、电流时,其外部 (例如N1)可 用适当的电路代替。
a
10
10
-
4
2 24V
I +-
+
b 12V
Isc
-
2 24V
+-
+
12V 图(a)
解:把原电路除4电阻以外的部分化简为诺顿等效电 路。为此先把拟化简的单口网络短路,如图(a)所示:
根据叠加原理求短路电流Isc,可得:
Isc
24 10
12 10 // 2
2.4
7.2
9.6 A
35
N a iK
N' uK NK
b
已知:
uk ,或 ik
a
a
N' isk
N'
usk
b
b
isk
usk
11
例:已知电路中U=1.5V,试用置换定理求U1
戴维宁定理

【例3-4】如图3-10所示电路,已 知E1 = 7 V,E2 = 6.2 V,R1 = R2 = 0.2 ,R = 3.2 ,试应用戴ห้องสมุดไป่ตู้宁定理求 电阻R中的电流I 。
图3-10 例题3-4
解:(1)将R所在支路开路去掉,如图3-11所示,求开路
电压UOC:
E1 E 2 0.8 I1 2A R1 R2 0.4
图3-16 求等效电阻Rab
图3-17 求电阻R中的电流I
(3) 根据戴维宁定理画出等效电路,如图3-17所示,求电 阻R5中的电流
E0 1 I5 0.25 A r0 R5 4
图3-14 例题3-5
解:(1) 将R5所在支路开路去掉,如图3-15所示,求 开路电压Uab:
I1 I 2 E 1A, R1 R2 I3 I4 E 1A R3 R4
Uab = R2I2 R4I4 = 5 4 = 1 V = E0
图3-15 求开路电压Uab
(2) 将电压源短路去掉,如图3-16所示,求等效电阻Rab: Rab = (R1∥R2) + (R3∥R4) = 1.875 + 2 = 3.875 = r0
图3-9
二端网络
(2)戴维宁定理
对外电路而言,线性含源单口网络可以用一个电压源 模型来代替。电压源的电压等于该网络的开路电压UOC; 串联电阻R0等于该网络中所有独立源为零时(即令电压源 短路、电流源开路)所得网络N0的等效电阻(叫做该二端 网络的等效内阻)。
(3)应用戴维宁定理解题步骤
• ①把电路分为待求支路和含源网络两部 分; • ②把待求支路移开,求出含源两端网络 的开路电压UOC; • ③将网络内电源除去,仅保留其内阻, 求出网络的等效电阻R0; • ④画出含源两端网络的等效电路。
《电路原理》第4章 分解方法及单口网络

N
i =0 a + uoc b
i
a b
N0
+ u -
R0
u = i
方法2: uoc 的求法同前;令网络 N 端口短路,求出其短 路电流 isc ,则有 R 0 = u oc i sc 。 证明: a a
N
isc b
uoc
R0
isc b
R0
u oc = i sc
方法3:求出网络 N 的端口VCR,画出由电压源与电 阻串联而成的等效电路。
例1: 求图示二端电 路的VCR及其 解: 等效电路。 设端口电压 u 已知,有 或者
a i 5Ω 10V 20Ω b u u
i = u 20 + ( u − 10 ) 5 = 0 .25 u − 2
u = 8 + 4i
a 2A 4Ω b i u
根据VCR,可得等效电路:
a 4Ω i u b
或者
8V
解法2: 前已求得: U OC = 2 V 将原网络端口短接,得:
1
2Ω 2V
2Ω 2I
- 4V +
a I b
2Ω 2V
0
2Ω 2I
- 4V +
a I b
用节点法,有
(0.5 + 0.5) Un1 = 2 I −1− 2 Un1 = −2 I − 4
a 2V 8Ω b
ISC
解得: I = − 0 .25 A , I = − I = 0 .25 A SC U OC R0 = = 8Ω 戴维南等 I SC 效电路:
电流源与单口电阻网络 N1的串联
N1
a
is
b
a
is
N1的等效网 络不是理想 b 电流源。
6.2 单口网络
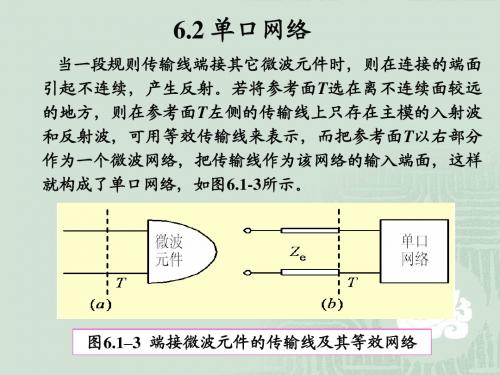
V z 2 1 1 V z 1 P V z I z V z 2 2Z e 2 2 Ze
2 2
双线上传输的有功功率PL等于
1 1 Re V z I z 1 1 PL Re V z I z 2 2 1 2 2 P 1 P P V z I z 1 2
Z in 1 Γ ( z ) 任意点的归一化输入阻抗为 Z in Z e 1 Γ ( z )
这样单口网络就可用传输线理论来分析。
6.2 单口网络
当一段规则传输线端接其它微波元件时, 则在连接的端面 引起不连续Байду номын сангаас 产生反射。若将参考面T选在离不连续面较远 的地方, 则在参考面T左侧的传输线上只存在主模的入射波 和反射波, 可用等效传输线来表示, 而把参考面T以右部分 作为一个微波网络, 把传输线作为该网络的输入端面, 这样 就构成了单口网络, 如图6.1-3所示。
即
V z V z V z I z V z V z
归一化入射波电压模的平方正比于入射波功率,即
V z 1 P V z I z 2 2Z 0 2 1 V z 2
2
1 V z 2 Z0
2
归一化反射波电压模的平方正比于反射波功率,即
I ( z ) A1 1 ( z ) / Z e
式中Ze为等效传输线的等效特性阻抗。 任意点的传输功率为:
A1 1 2 P ( z ) Re[V ( z ) I ( z )] [1 Γ ( z ) ] 2 2 Ze
2
二、 归一化参量
单口网络的等效电路
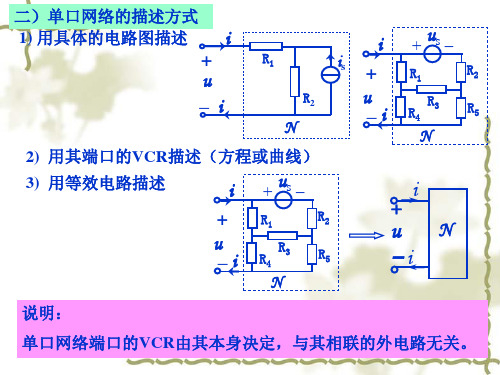
对任意电流 i)可等效成一个电压值为us的电压
源。
i R1
Rm i
n个电压源和m个电阻串联的单口网络,
对任意外电路(即对任意电流 i )可等效 成一个电压源串电阻支路。
例14:求图所示单口网络的等效电路,并写出其VCR。
–+
i
15v 3 +
7
u
–
10v
+
–
5V
–
10
+
思考: 理想电压源的并联?
二)电流源的并联
M
+ u
G
– i N2
i= u G
当G= G1+G2+G3时N1和 N2互为等效电路
说明:1)等效是指对任意的外电路等效。
i
i
+ Mu
G1
– i
G2 G3 N1
i= u (G1+G2+G3)
M
+ u
G
– i N2
i= u G
当G= G1+G2+G3时N1和 N2互为等效电路 2)求单口网络的等效电路,实际上是求该单口网络的VCR。
i
i
is
+
M
RS
uM
i
i–
N1
N2
例17:求图所示单口网络的等效电路,并写出其VCR。
2
++
2A
9v 3v
–
– 3A
+ 2v –
3
5
ia
3A
+ 2v – +
3A
u
3
5 –b
ia
+
u
–
源。
i R1
Rm i
n个电压源和m个电阻串联的单口网络,
对任意外电路(即对任意电流 i )可等效 成一个电压源串电阻支路。
例14:求图所示单口网络的等效电路,并写出其VCR。
–+
i
15v 3 +
7
u
–
10v
+
–
5V
–
10
+
思考: 理想电压源的并联?
二)电流源的并联
M
+ u
G
– i N2
i= u G
当G= G1+G2+G3时N1和 N2互为等效电路
说明:1)等效是指对任意的外电路等效。
i
i
+ Mu
G1
– i
G2 G3 N1
i= u (G1+G2+G3)
M
+ u
G
– i N2
i= u G
当G= G1+G2+G3时N1和 N2互为等效电路 2)求单口网络的等效电路,实际上是求该单口网络的VCR。
i
i
is
+
M
RS
uM
i
i–
N1
N2
例17:求图所示单口网络的等效电路,并写出其VCR。
2
++
2A
9v 3v
–
– 3A
+ 2v –
3
5
ia
3A
+ 2v – +
3A
u
3
5 –b
ia
+
u
–
4-4单口网络的等效

Ri
8 6r
0
意味着该单口网络向外电路发出电功率。
(2)当 r
=
0
时,Ri
8 6r
4 3
当单口网络内仅含电阻时,应用电 阻的串、并联方法,可求得该单口网络 的输入电阻。
4Ω i1 i +
+
r i1
2Ω u
-
-
解法二:用外施电流源法求输入电阻Ri
由电路得方程 u 2i1 u 4(is i1) ri1 0
而N2是理想电流源,N2端口的VCR为:
i2 = 1 A ,是一确定值,与外接电路无关
u2 可为任意值,其电压值取决于外接电路
可见, N1和N2的VCR不同,所以N1和N2不等效!
为进一步说明等效的概念,我们将例题2中的N1和N2外 接同一电路M,再作分析。
N1 i1
+
+
2v u1
-
-
M
2Ω 0.5A
i
+
N1
u
-
任意 外接 电路 ( M)
i
+
N2
u
-
任意 外接 电路 ( M)
对M的作用
对M的作用
等效
(2)若N1和N2两个单口网络端口的VCR完全相同,则N1 和N2等效;反之,若N1和N2 等效,则N1和N2的端口的伏安关 系(VCR)必完全相同。
以下,举例进一步说明等效的含义
例1
i
N1
R+-u0s
N2 i2
1A +
u2
-
M
2Ω 0.5A
图(c)
图(d)
由图(c)得:
由图(d)得:
u1 2V i1 0.5 2 2 1.5 A
电工基础戴维南定理4.5 戴维南 定理

(2)短路电流法:在计算出a、b端口开
路处电的压短u路oc电后流,I将sc,a从b端而口得短R接0 , 求uIosc短c 接
(3)外加电压法:去掉N网络内部的独
立电源,在ab端口处家电压源u,求端
口处的电流I,则
R0
பைடு நூலகம்
u I
(4)外加电流法:去掉N网络内部的独
立电源,在ab端口出加电流源I,求出
端口电压u,则
u R0 I
I
a
+
N
u
-
b
I=0 a +
N
b u
-
aIsc
N b
三.诺顿定理 1.诺顿定理的内容
任一线性含源单口网络,对外而言,总 可以等效为一电流源与一电导并联的实 际电源的电流源模型。
(1)电流源的电流Isc等于该网络的端口端 路电流
(2)等效并联电导G0为该网络去掉内部 独立电源后,从端口处得到的等效电导。
第六章 戴维宁定理与诺顿定 理
一.单口网络 1.单口网络:是指一个网络对外引出两个端钮,构成一个
端口,此网络及其引出的一个端口共同称为单口网络 2.单口网络的等级
(1)不含独立电R源0的单口u2网络电阻R0
(2)含有独立电源的单口网络 这就是戴维宁定理和诺顿定理要解决的问题。
返回本章开头
二.戴维宁定理
3.等效电压源电压Uoc求解方法(1)将外电 路去掉,端口ab处开路,由N网络计算 开路电压Uoc (2)试验测得,将ab端口开路,用电压表 测得开路处的电压Uoc 4.等效电阻R0的求解方法 (1)等效法:去掉N网络的独立电源, 用串、并联简化和Y→△变换等方法计 算出a、b端口看去的等效电阻R0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
125I1-100I2=U 100I1+ (100 + 10000 + 100000) I2 100000 I3= 0 代入 I3 = 0.99I1,得 -99100I1 + 110100I2 = 0
(25 + 100) I1100I2 = U
U
100
110100 0 110100 I1 U 125 100 3852500 99100 110100
I
I1
+
10V
R1 6
解: (1) 用叠加原理求 I
US = —— 10 =1A I' = ——— US 作用 R1 + R2 6+4
−
US
IS
5A
R2
4
R2 IS 4×5 = – 2A IS 作用 I"= – ——— = – —— R1 + R2 6+4 叠加 I = I' +I" = 1– 2 = –1A
I
+ 10V
R1 6 US
图a
用电源等效变换求 I
在图a中 US – US1 10 – 20 I = ———— = ——— = – 1A R1 + R2 6+4
R2 4
+ −
−
20V
US1
第4章 分解方法及单口网络
4- 4
解: (2) 用电源等效变换求 I1
不能在图a中求I1 , ∵电源内部
I
如果US1≠US2, 违背KVL无解
(2)
US + RS
多余元件 可以开路
US
+
与电压源并联 的元件称为多 余元件,多余 元件可开路。
第4章 分解方法及单口网络
4- 4
2. 含源支路的串、并、混联
请注意以下四种情况
(3)
IS1 IS2 IS=IS1=IS2 IS
如果 IS1≠ IS2, 违背KCL无解
等效的概念:如果两个单口网络 N1 和N2 端口上电压、 电流关系完全相同,则 N1 和 N2 等效。
i1 i2 + u1 + u2
N1
N2
若 N1 和 N2 端口上满足 u1 = u2 、i1 = i2 , 则两个单口网络 N1 和 N2 等效。
第4章 分解方法及单口网络
4- 4
二、无独立源单口网络的等效电路
结论:置换后对其他支路没有任何影响。
第4章 分解方法及单口网络
4- 3
例2:已知 N 的VCR为 u = i + 2,用置换定理求 i1。
解: 求左边部分的VCR
u = 7.5 (i1i ) + 15
7.5
i + 5 u i1
N u i1 5 u u 7.5 7.5 i 15 5 将N用3V电压源置换,直接求得: 2.5 u 7.5 i 15 7.5 i u= 3i+6
I1
I1
IS1
R1 6
IS
5A
R2 4
+ 10V US –
R1 6
IS
5A
R2 4
I1 IS1+IS
R1 6
图b
R2 4
+ 20 6 10V = ——— US × — = 4A 3 20V U 6+4 S1
– 注意:欲求支路不能 变换到电源内部。 图a
I1 R1 I1 = ——— ( IS1+IS ) +1 R6 2 + R1R R
IS
R2 I R1 US U
第4章 分解方法及单口网络
4- 3
§4-3 单口网络的置换—置换定理
1. 定理内容
如果一个网络N由两个子网络N1和N2组成,且已求得: u =α,i =β,可用一个电压值为α的电压源或用一个电流 值为β的电流源置换 N2 或 N1,置换后对 N1 或 N2 没有影响。
1. 电阻串联 2. 电阻并联
R =∑Rk
k=1 n n
G =∑Gk
k=1
R1 R2 R R1 R2
公式只适用于 两个电阻并联
3. 电阻的串、并、混联
利用串、并联公式化简
N0
R
第4章 分解方法及单口网络
4- 4
三、含独立源单口网络的等效电路
对外电路等效,对 1. 两种电源模型的等效变换 电源内部不等效。 通常电源可以用电压源或电流源表示, 这两种电源模型之间可进行等效变换。
I
2
4
第4章 分解方法及单口网络
4- 4
四、含受控源单口网络的等效电路
1. 不含独立源的单口网络
I1
25 R1
0.99I1
例1 求图示电路输入电阻Ri。 解:含受控源电路不能用电
阻串、并联公式化简
I3
R3=100k
R4 10k
+ U
Ri
I1 100 I2
R2
(1) 外加电压源 U 求端钮电流 I1
i
1
+
N
3. 采用分解方法的目的
将多个激励或复杂激励电路 化为简单激励电路进行求解。
N1
u
N2 1
N1:u = k1 i + A1 N2:u = k2 i + A2
第4章 分解方法及单口网络
4- 2
§4-2 单口网络的伏安关系
列写单口网络伏安关系的方法:
1. 列电路的方程,求 u、i 关系; 2. 端钮上加电流源,求(输)入端电压,得到 u、i 关系; 3. 端钮上加电压源,求(输)入端电流,得到 u、i 关系。
I1
I3 2 3 2 2 I4 2 I5
+
9V
I2
0.9A 2 2 I2
9 1 I1 0.9 2.7 A 4 2 9 1 I 2 0.9 1.8 A 4 2 1 I 4 I 5 I 3 0.45 A 2
I1
I3
+
9V
2 I4
2 I5
例:求图示电路的 VCR。 解: (1)列电路KVL方程
U = −R2 I + (− I − IS ) R1 − US 利用叠加原理 U = − (R1+R2) I − R1IS − US
IS
R2 I R1 − US U −
第4章 分解方法及单口网络
4- 2
(2) 外加电流源(I),求入端电压
对于含源支路的串、并、混联电路的两端来说, 总可以化简为一个电压源与电阻串联的组合,或者 是一个电流源与电阻并联的组合。 R
US + 戴维南 等效电路
N
IS R 诺顿 等效电路
第4章 分解方法及单口网络
4- 4
2. 含源支路的串、并、混联
请注意以下四种情况
(1)
US1 + + US2 US=US1=US2 US +
代入 u = i + 2 得 i= 1A u=3V i1 = 0.6 A
+ 15V + 5 u i1 + 3V
+ 15V
i1
u 3 0.6 A 5 5
计算结果不变!
第4章 分解方法及单口网络
4- 4
§4-4 单口网络的等效电路 §4-5 简单的等效规律和公式
一、等效单口网络
5 2 I 2 A 5 10 3 4 I 2 I A 3 2 40 P 10 I 2 10 2 W 3 3 4 40 P 5I 2 5 2 W 3 3
结论:等效电路对外电路等效,对电源内部不等效。
第4章 分解方法及单口网络
4- 4
例2 用电源等效变换的方法求图示电路中电流 I。 + 25V _ 5 解: I 5A 5 6A
5 I 11 5 3 55 A 6.875A 8
1
+ 25V_ 6A
I
3 I 5 11A 3
3
第4章 分解方法加原理和电源
的等效变换求 I; (2)用电源的等效变换求 I1 。
I3 = 2.7 1.8 = 0.9A
I1
+
2 2 I2 I1 4 I3
9V
1 I 4 I 5 I 3 0.45 A 2
+
9V
2
4 Ω 3
I1
第4章 分解方法及单口网络
4- 3
2. 应用举例 例1:求图示电路中各支路电流。 解: 将3Ω电阻用电流源置换
I3 = 2.7 1.8 = 0.9A
i=β i=β + u=α N1 +
α
N1
N2
N1
+ u=α
β
第4章 分解方法及单口网络
4- 3
2. 应用举例 例1:求图示电路中各支路电流。 解:方法:从右至左合并电阻,
从左至右分流。
I1
I3 2 3
+
9V
2
I2
2
I4
2
I5
9 I1 2.7 A 2 4/ 3 4 I2 I1 1.8 A 24
解:
6V + 1
a
b
第4章 分解方法及单口网络
4- 4
(1)等效变换的条件:
一般电压源和一般电流源之间可以进行变换; 理想电压源和理想电流源之间不能进行变换。
(2)等效变换的意义:
(1)对电源外部等效: 若接上同一负载,伏安关系相同; (2)对电源内部不等效:
输出端开路时:电流源消耗功率,电压源不消耗功率; 输出端短路时:电流源不消耗功率,电压源消耗功率。 (3)等效变换的目的:简化分析:复杂电路简单电路
(25 + 100) I1100I2 = U
U
100
110100 0 110100 I1 U 125 100 3852500 99100 110100
I
I1
+
10V
R1 6
解: (1) 用叠加原理求 I
US = —— 10 =1A I' = ——— US 作用 R1 + R2 6+4
−
US
IS
5A
R2
4
R2 IS 4×5 = – 2A IS 作用 I"= – ——— = – —— R1 + R2 6+4 叠加 I = I' +I" = 1– 2 = –1A
I
+ 10V
R1 6 US
图a
用电源等效变换求 I
在图a中 US – US1 10 – 20 I = ———— = ——— = – 1A R1 + R2 6+4
R2 4
+ −
−
20V
US1
第4章 分解方法及单口网络
4- 4
解: (2) 用电源等效变换求 I1
不能在图a中求I1 , ∵电源内部
I
如果US1≠US2, 违背KVL无解
(2)
US + RS
多余元件 可以开路
US
+
与电压源并联 的元件称为多 余元件,多余 元件可开路。
第4章 分解方法及单口网络
4- 4
2. 含源支路的串、并、混联
请注意以下四种情况
(3)
IS1 IS2 IS=IS1=IS2 IS
如果 IS1≠ IS2, 违背KCL无解
等效的概念:如果两个单口网络 N1 和N2 端口上电压、 电流关系完全相同,则 N1 和 N2 等效。
i1 i2 + u1 + u2
N1
N2
若 N1 和 N2 端口上满足 u1 = u2 、i1 = i2 , 则两个单口网络 N1 和 N2 等效。
第4章 分解方法及单口网络
4- 4
二、无独立源单口网络的等效电路
结论:置换后对其他支路没有任何影响。
第4章 分解方法及单口网络
4- 3
例2:已知 N 的VCR为 u = i + 2,用置换定理求 i1。
解: 求左边部分的VCR
u = 7.5 (i1i ) + 15
7.5
i + 5 u i1
N u i1 5 u u 7.5 7.5 i 15 5 将N用3V电压源置换,直接求得: 2.5 u 7.5 i 15 7.5 i u= 3i+6
I1
I1
IS1
R1 6
IS
5A
R2 4
+ 10V US –
R1 6
IS
5A
R2 4
I1 IS1+IS
R1 6
图b
R2 4
+ 20 6 10V = ——— US × — = 4A 3 20V U 6+4 S1
– 注意:欲求支路不能 变换到电源内部。 图a
I1 R1 I1 = ——— ( IS1+IS ) +1 R6 2 + R1R R
IS
R2 I R1 US U
第4章 分解方法及单口网络
4- 3
§4-3 单口网络的置换—置换定理
1. 定理内容
如果一个网络N由两个子网络N1和N2组成,且已求得: u =α,i =β,可用一个电压值为α的电压源或用一个电流 值为β的电流源置换 N2 或 N1,置换后对 N1 或 N2 没有影响。
1. 电阻串联 2. 电阻并联
R =∑Rk
k=1 n n
G =∑Gk
k=1
R1 R2 R R1 R2
公式只适用于 两个电阻并联
3. 电阻的串、并、混联
利用串、并联公式化简
N0
R
第4章 分解方法及单口网络
4- 4
三、含独立源单口网络的等效电路
对外电路等效,对 1. 两种电源模型的等效变换 电源内部不等效。 通常电源可以用电压源或电流源表示, 这两种电源模型之间可进行等效变换。
I
2
4
第4章 分解方法及单口网络
4- 4
四、含受控源单口网络的等效电路
1. 不含独立源的单口网络
I1
25 R1
0.99I1
例1 求图示电路输入电阻Ri。 解:含受控源电路不能用电
阻串、并联公式化简
I3
R3=100k
R4 10k
+ U
Ri
I1 100 I2
R2
(1) 外加电压源 U 求端钮电流 I1
i
1
+
N
3. 采用分解方法的目的
将多个激励或复杂激励电路 化为简单激励电路进行求解。
N1
u
N2 1
N1:u = k1 i + A1 N2:u = k2 i + A2
第4章 分解方法及单口网络
4- 2
§4-2 单口网络的伏安关系
列写单口网络伏安关系的方法:
1. 列电路的方程,求 u、i 关系; 2. 端钮上加电流源,求(输)入端电压,得到 u、i 关系; 3. 端钮上加电压源,求(输)入端电流,得到 u、i 关系。
I1
I3 2 3 2 2 I4 2 I5
+
9V
I2
0.9A 2 2 I2
9 1 I1 0.9 2.7 A 4 2 9 1 I 2 0.9 1.8 A 4 2 1 I 4 I 5 I 3 0.45 A 2
I1
I3
+
9V
2 I4
2 I5
例:求图示电路的 VCR。 解: (1)列电路KVL方程
U = −R2 I + (− I − IS ) R1 − US 利用叠加原理 U = − (R1+R2) I − R1IS − US
IS
R2 I R1 − US U −
第4章 分解方法及单口网络
4- 2
(2) 外加电流源(I),求入端电压
对于含源支路的串、并、混联电路的两端来说, 总可以化简为一个电压源与电阻串联的组合,或者 是一个电流源与电阻并联的组合。 R
US + 戴维南 等效电路
N
IS R 诺顿 等效电路
第4章 分解方法及单口网络
4- 4
2. 含源支路的串、并、混联
请注意以下四种情况
(1)
US1 + + US2 US=US1=US2 US +
代入 u = i + 2 得 i= 1A u=3V i1 = 0.6 A
+ 15V + 5 u i1 + 3V
+ 15V
i1
u 3 0.6 A 5 5
计算结果不变!
第4章 分解方法及单口网络
4- 4
§4-4 单口网络的等效电路 §4-5 简单的等效规律和公式
一、等效单口网络
5 2 I 2 A 5 10 3 4 I 2 I A 3 2 40 P 10 I 2 10 2 W 3 3 4 40 P 5I 2 5 2 W 3 3
结论:等效电路对外电路等效,对电源内部不等效。
第4章 分解方法及单口网络
4- 4
例2 用电源等效变换的方法求图示电路中电流 I。 + 25V _ 5 解: I 5A 5 6A
5 I 11 5 3 55 A 6.875A 8
1
+ 25V_ 6A
I
3 I 5 11A 3
3
第4章 分解方法加原理和电源
的等效变换求 I; (2)用电源的等效变换求 I1 。
I3 = 2.7 1.8 = 0.9A
I1
+
2 2 I2 I1 4 I3
9V
1 I 4 I 5 I 3 0.45 A 2
+
9V
2
4 Ω 3
I1
第4章 分解方法及单口网络
4- 3
2. 应用举例 例1:求图示电路中各支路电流。 解: 将3Ω电阻用电流源置换
I3 = 2.7 1.8 = 0.9A
i=β i=β + u=α N1 +
α
N1
N2
N1
+ u=α
β
第4章 分解方法及单口网络
4- 3
2. 应用举例 例1:求图示电路中各支路电流。 解:方法:从右至左合并电阻,
从左至右分流。
I1
I3 2 3
+
9V
2
I2
2
I4
2
I5
9 I1 2.7 A 2 4/ 3 4 I2 I1 1.8 A 24
解:
6V + 1
a
b
第4章 分解方法及单口网络
4- 4
(1)等效变换的条件:
一般电压源和一般电流源之间可以进行变换; 理想电压源和理想电流源之间不能进行变换。
(2)等效变换的意义:
(1)对电源外部等效: 若接上同一负载,伏安关系相同; (2)对电源内部不等效:
输出端开路时:电流源消耗功率,电压源不消耗功率; 输出端短路时:电流源不消耗功率,电压源消耗功率。 (3)等效变换的目的:简化分析:复杂电路简单电路
