6静电场中的导体和电介质PPT课件
合集下载
第六章 静电场中的导体和电介质PPT课件

面
++ + +
+ +
S+
+
++
结论:导体内部无净电荷,电荷只分布在导体表面.
2)空 腔导体,空腔内无电荷
SEdS0 qi0 i
导体内部无净电荷
内表面? 电荷分布在表面 外表面?
高斯 面
S
9
若内表面带电,必等量异号
EdS
qi 0
S
ε0
若有正电荷和负电荷
UAB AB Edl0
与导体是等势体矛盾
结论:空腔内无电荷时,电荷分布在外表面, 内表面无电
荷. 3)空腔导体(q2),空腔内有电荷(q1)
高斯
1+ 2
面
结论: 空腔内有电荷q1时,空 腔内表面有感应电荷- q1 , 外表面有感应电荷q1 + q2 .
+ q1 -q1
S
10
3导体表面的电荷密度分布
1) 孤立导体各处的面电荷密度与其表面的曲率
有关. 1 表面曲率越大,电荷密度约高 r
解(1) q1 q4
1 4
q2 q3 q1q2 qA
q2
qA
qB 2
q3q4 qB
(2) E 2 q2 0 0S
UABEdqA 20SqBd
1 2
A
2 3
dr
qq 40R1 40R2
R2 R2
U
R1 R1 R2 R 1
q
-q
R1q
R2
22
解: q外 0
q U
4 0R2
q外 q U0
U内4q0'R140 q R2 0
第十章 静电场中的导体及电介质PPT课件

+
+
+
+
+
E 感
E +
+
外
+
+
+
E内 =
E 外
+
E 感
=
0
静电平衡——导体中电荷的宏观定向运动 终止,电荷分布不随时间改变。
静电平衡结果:
用场强来描写: 1. 导体内部场强处处为零; 2. 表面场强垂直于导体表面。
用电势来描写: 1. 导体为一等势体; 2. 导体表面是一个等势面。
金属球放入前电场为一均匀场
三、导体的表面场强
s E .dS = 内E .dS +表 E .dS +侧 E .dS
=0
= σεS0
E表
=
σ
ε0
σ
ε E表 = o
+ E表S +
⊥表面 σ
0 E
S
四、静电屏蔽 不接地的导体腔
接地的导体腔
金属罩
仪器
带电体
++++
+ +
静电屏蔽:一个接地的空腔导体可以隔 离内外电场的影响。
[例1]已知两金属板带电分别为 q1 , q2
E 3 E2 E4
E1 E 4 E 1 E 2 E3
ε ε ε ε b点:
σ
2
1+
o
σ
2
2
o
σ
+2
3
o
σ
2
4
o
=0
ε ε ε ε σ σ σ σ a点:
2
1
o
2
2o
第章静电场中的导体和电介质PPT课件

q2
EA
1 2 o
2 2 o
3 2 o
4 2 o
0
EB
1 2 O
2 2 O
3 2 o
4 2 o
0
1
23
4
由电荷守恒:
1S 2 S q1
A
B
3S 4S q2
1
4
q1 q2 2S
2
3
q1 q2 2S
20
1
4
q1 q2 2S
q1
2
3
q1 q2 2S
1
2
上述结果表明:平板相背的两面带电等
R3 R2
R3
RR11
qq1 1
RR33
问题:电势表
达式能直接写
R2 R1
q1
4 or
2
dr
R3
(q q1 )
4 or 2
dr
出来吗?
q1
4 o
1 R1
1 R2
q q1
4 o R3
V1 V2
同理,球壳的电势为:
V2
E dl
R3
R3
(q
4
q1 ) or 2
dr
q q1
2.内屏蔽
+
+
壳外表面上的电荷分布与腔内带电体的位置无关,只 取于导体外表面的形状。
若将空腔接地,则空腔外表面上的感应电荷被大地电荷 中和,腔外电场消失,腔内电荷不会对空腔外产生影响。即 接地空腔对内部电场起到了屏蔽作用,这是静电屏蔽的另外 一种——内屏蔽。
高压设备用金属导体壳接地做保护。 14
五、利用静电平衡条件和性质作定量计算
例1:半径为R和r的球形导体(R>r),用很长的细导线连 接起来,使两球带电Q、q,求两球表面的电荷面密度。
第18章静电场中的导体和电介质PPT课件
2 3 0 ……(3)
在板内任选一点P,其场强是四个面的场强的叠加,有
EP210220230240
又 EP 0 12340 Q
联立四式得:
……(4) 1 2 3 4
12432Q S
I
II III
10
P
由于静电平衡时表面面电荷密度与表面附近场强大小成
正比,即 0 E
所以三区域的场强分别为:
解(1)由于金属球原来不带电,所以产生的感应电荷之
和(即净电荷)为零 q 0
(2)O点的场强EOE点 E球 感 应
又由于金属球处于静电平衡:EO 0
而点电荷在O点的场强:
E点
q
40r2
i
Rl
r
OP
+q 7x
所以E球感应E点4q0r2 i
(3)同上,在P点感应电荷产生的场强:
E 球 感 应 E 点 ( 40 ( q r l)2i) 40 ( q r l)2i
q1 q2 0
联立方程,得:
q1
40(UA
R2
UB)R1R2 R1
q2
40(UB
R2
UA)R1R2 R1
q3 40UBR3
14
电场分布:
E1 0 (r R1)
E2
q1
4 0r 2
(UA UB )R1R2 (R2 R1)r2
(R1 r R2 )
E3 0 (R2 r R3)
E4
q3
4 0r 2
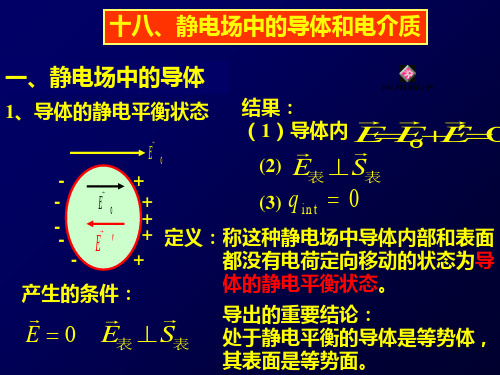
十八、静电场中的导体和电介质
一、静电场中的导体
1、导体的静电平衡状态 结果:
E0
-
+
(1)导体内 EE0E0
(2) E表 S表
--
第10章静电场中导体和电介质 共68页PPT资料

电荷分布
2 3
b E1 E2 E3
1 0
2
3
Q S
A
B
31
电荷分布 1 0
2
3
Q S
1 A 2 3 B
场 两板之间 E Q
强
0S
E
分
布 两板之外 E0
32
例2.已知R1 R2 R3 q Q
Qq
q q
求 ①电荷及场强分布;球心的电势 B A R 1 R2
E dS E S cos00
S 0
E
0
E S
20
2. 电荷面密度与曲率的关系
1 R
R1
l R 1 导线
R2
Q1
证明: 用导线连接两导体球
R2
Q2
则
uR1 uR2
即
Q1 Q2
4 0R1 4 0R2
14R12 24R22 40R1 40R2
R1rR2 B
AR1 R2 O R3
Qq
4 0 r 2
r R3
球心的电势
R 1
R 2
R 3
uoEdrEd rEd rEd rEdr
0
0
R 1
R 2
R 3
4q0(R 11R 12)410qR 3 Q
34
②用导线连接A、B,再作计算 Q q
1) Cn
1U11 1
C q C1 C2
Cn
1 1 1 1
C C1 C2
Cn
44
2.电容器的并联
a U
C1 C2 C3 C4
b q1 C1U, q2 C2U,,qnCnU
2 3
b E1 E2 E3
1 0
2
3
Q S
A
B
31
电荷分布 1 0
2
3
Q S
1 A 2 3 B
场 两板之间 E Q
强
0S
E
分
布 两板之外 E0
32
例2.已知R1 R2 R3 q Q
q q
求 ①电荷及场强分布;球心的电势 B A R 1 R2
E dS E S cos00
S 0
E
0
E S
20
2. 电荷面密度与曲率的关系
1 R
R1
l R 1 导线
R2
Q1
证明: 用导线连接两导体球
R2
Q2
则
uR1 uR2
即
Q1 Q2
4 0R1 4 0R2
14R12 24R22 40R1 40R2
R1rR2 B
AR1 R2 O R3
4 0 r 2
r R3
球心的电势
R 1
R 2
R 3
uoEdrEd rEd rEd rEdr
0
0
R 1
R 2
R 3
4q0(R 11R 12)410qR 3 Q
34
②用导线连接A、B,再作计算 Q q
1) Cn
1U11 1
C q C1 C2
Cn
1 1 1 1
C C1 C2
Cn
44
2.电容器的并联
a U
C1 C2 C3 C4
b q1 C1U, q2 C2U,,qnCnU
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
+
使外部空间不受空
q +
腔内的电场影响. 问:电荷偏离中心,
+ + q+
场强又如何分布 ?
电荷偏心,空腔内的电场、电荷分布改变,空腔外 的电场、电荷分布不变.
例 导体 A含有两个空腔,在腔中心分别有qb、qc导体
本身不带电。在距 A中心 r 较远处有另一电荷qd .
问: qb、qc、 qd 各受多大力?
+ +带+电云+ +
- -- - - -
+ +
静电感应 可靠接地 电晕放电
➢ 避雷针
金属尖端的强电场的应用一例
金属
尖端
场离子显微镜(FIM)
原理:样品制成针尖形 状,针尖与荧光膜之间 加高压,样品附近极强 的电场使吸附在表面的 原 子 电离,氦离子沿 电力线运动, 撞击荧 光膜引起发光,从而获 得样品表面的图象.
间距离大得多,若两板分别带正 Q a , Q b 的电量,
(1)求每块板表面的电荷面密度
解 (1)根据电荷守恒定律,有
Qa
Qb
13
S S
2 4
S S
Qa Qb
S
1 2 3 4
高斯定理
Eds 0
S
2 3
P
Ep2 102 202 302 400 1 4
14
QaQb 2S
2
Qa Qb 2S
3
Qb Qa 2S
3 导体表面电场强度与电荷面密度的关系
E dS S
S
0
E S S 0
E 0
,E; ,E
为表面电荷面密度
E
+ + + + + + + +
+ +
E0
+
作钱币形高斯面 S
表面电场强度的大小与该表面电荷面密度成正比
4 导体表面电荷分布
孤立导体处于静电平衡时, 它的表面各处的面电荷
密度 与各处表面的曲率有关, 曲率半径r越小的地方,
14
QaQb 2S
2
Qa Qb 2S
3
Qb Qa 2S
(2)若 Qa Qb Q,每块板表面的电荷面密度
是多少? 若 Qa Q,Qb 0 呢?
(a)将 QaQ,QbQ代入上
面一组解,有
Qa
Qb
S
140;2Q S;3Q S 1 2 3 4
(b)将 Qa Q,Qb 0 代入
P
上面一组解,有
1 42 Q S;22 Q S;32 Q S
第六章 静电场中的导体和电介质
P229习题6-8, 6-10 6-12,6-13
P229习题6-8, 6-10 6-12,6-13
第六章 静电场中的#43;
++++ + + + +
感应电荷
一 静电平衡条件
感应电荷 电场与外电场 叠加使导体内 电场为零,电 子不再定向运 动.
问 若腔内放置电荷, 导体上电荷如何分布?
空腔内有电荷
问 导体内有电荷吗?
E dS 0 qi 0
S
电荷分布在表面上
问 内表面上有电荷吗?
S2
q
q
S1
EdS0,qi 0
S2
q内 q
结论 当空腔内有电荷 q 时, 内表面因静电感应
出现等值异号的电荷 q,外表面增加感应电荷 q .
(电荷守恒)
解: 两空腔内的电场都不 受外界影响,内表面感应电
qb qc
qd
荷均匀分布,因此,腔内
场强为零,qb、qc 受力为零 A
r
.
根据电荷守恒,导体外表面感应电量 qb qc ,且电荷
均匀分布. 因此,导体外场强分布类似于点电荷的场 ,
电荷qd, 受力为
(qb qc )qd
4 0r2
应用 有导体存在时,可利用导体的静电平衡条
面电荷密度越大.
q1
q2
证:两相互远离的导体球用细导
线连接,静电平衡时电势分别为 r1
r2
V1
q1 4 0 r1
V2
q2 4 0 r2
又 q 114r 1 2,q 224r2 2
V1 V2
q1 q2 r1 r2
1r1 2r2
或
1 2
r2 r1
结论: 孤立导体表面电荷分布, 曲率越大(r越小)地方,
导体球外电场为外电场和感应电荷电场的叠加.
➢ 外电场中的导体平板
+
+
+
+
+
+
E0
+
+
+
+
+
+
E0
+ +
E'
+ + + +
E0
E0+
+
EE 0E 0
导体内电场强度 外电场强度 感应电荷电场强度
➢ 静电平衡条件 (1)导体内部任何一点处的电场强度为零;
(2)导体表面处的电场强度的方向,都与导体表面垂直
He
接真空泵或 充氦气设备
荧光质 导电膜
接地
+ 高压
三 静电屏蔽
1 屏蔽外电场
E
E
外电场
空腔导体屏蔽外电场
空腔导体可以屏蔽外电场, 使空腔内物体不受外电 场影响. 而且整个空腔导体和腔内的电势也处处相等.
2 屏蔽腔内电场
问:空间各处的电场 强度如何分布 ?
接地导体电势为零.
+
+
+
q
接地空腔导体将
电荷密度也越大,附近的电场越强.
, E
++
+ ++
++++
< 电风实验 >
+ +
+++
尖端放电现象 带电导体尖端附近电
场最强,尖端处的强电场 可使尖端附近的空气发生 电离而使导体产生放电现 象,即尖端放电 .
+ +
++ +
尖端放电现象的利与弊:尖端放电也有很广泛的应用, 如避雷针的应用、静电除尘等. 然而, 尖端放电会损耗 电能, 还会对精密测量和通讯产生干扰和危害 .
件 和电荷守恒定律,结合第五章的方法求解相关问题.
例 无限大的带电平面的场中平行放
置一无限大金属平板, 求:金属板
12
两面电荷面密度. 解:设金属板面电荷密度 由对称性和电量守恒
1,2
P2 0
2
1
2 0
2 0
12
导体体内任一点P场强为零
Ep
20
1 20
2 20
0
1
1 2
x
2
1 2
例 两块平行的导体板,面积为S,其线度比两板
例 带电金属球半径R1,带电量q1 ,放在另一个带电
导体球壳内,其内外半径分别为R2、R3,球壳带电量为
q .试求: (1) 此系统的电荷、电场分布以及球与球壳间的
电势差. (2)如果用导线将球壳和球接一下,又将如何?
+
++
S
导体内部无电荷, 电荷分布在导体表面上.
2 有空腔导体 空腔内无电荷
E dS 0 qi 0
S
S
电荷分布在表面上
问 内表面上有电荷吗?
若内表面带电
+
+A
矛 盾
U AB AB Edl0
+S
+
++
+
B+
--
+ +
+ +
导体是等势体
U AB AB Edl0
所以内表面不带电
结论 电荷分布在外表面上(内表面无电荷)
(导体表面也无电荷移动).
导 体 是 等 势 体
➢ 导体表面是等势面
E dl
en
E
U E d l 0
+
➢ 导体内部电势相等 +
U AB AE Bdl0
+
A
+
dl +
eτ
+
B
二 静电平衡时导体上电荷的分布
1 实心导体 根据高斯定理: E 0
qi 0EdS 0
++ + +
+ +
S+
