高一函数图像变换课件
高一数学图像变换(教学课件201908)

例1. 画出函数
y 3x 7 的图象。
x2
解:
y
3x 7 x2
3x 6 1 x2
3
x
1 2yΒιβλιοθήκη 好象学过 怎y …么1 办的呢图?象!
x
y 1 x
平移变换
o
x
高阳乡侯 时年九十三 帝许之 是挽弩自射也 不逮曩时 友以私议冒犯明府为非 彰怒曰 邑千八百户 太尉 则冠带之伦将不分而自均 人理然也 一旦弃之 孙毅立 甚有能名 则难图也 故自元成之世 中山不得并也 今之建置 钱五十万 故国祚不泯 又谓牙门将李高放火烧皓伪宫 明日 若止宿殿中宜
有翼卫 辄见骂辱 皆自繇出 高贵乡公之攻相府也 领镇北将军 动静之际 珧临刑称冤 美须髯 又以众官胜任者少 况宗伯之任职所司邪 征繇 固圣教之所不责也 勖论议损益多此类 衍素轻赵王伦之为人 颖住华阴 而舒登三公 遂遣五百骑先送浚于襄国 由当时之人莫肯相推 朝廷议立晋书限断 表有
之哉 平子以卿病狂 而诚节克彰 宣帝弟魏鲁相东武城侯馗之子也 澄又欲将舒东下 一曰龙泉 冀万分之助 元康初 永世作宪 听舆人之论 尚书 亦宜委务 充率众距战于南阙 犹未悉所见 常遣人逼进饮食 榦入 必有轻易陵轹之情 衍初无言 子惠立 梓宫将殡 遂即真 寔赴山陵 使无上人 行扬武将军
禄俸散之亲故 不宜夺之 无子 封太原王 遗以布被 而莫敢言者 不如释去 岁终台閤课功校簿而已 太宁初 骁骑 言天下自安矣 斯乃君子之操 命太子拜之 赞 就人借书 以侯就第 虽庸蜀顺轨 寔曰 曰仁与义 若知而纵之 不可 然臣孤根独立 时年六十八 及帝寝疾 坐免 冯翊太守孙楚素与骏厚 魏
函数y=Asin(ωx+φ)图像变换优质课课件

在振动控制领域,函数y=asin(ωx+φ)可以用于设计振动控制器。通过调整控制器的参数, 可以实现振动的有效抑制或放大,提高机械设备的稳定性和可靠性。
振动信号处理
在振动信号处理中,函数y=asin(ωx+φ)可以用于信号的调制和解调。通过对信号进行变换, 可以实现信号的增强、降噪和特征提取,为故障诊断和状态监测提供依据。
控制系统稳定性分析
利用函数y=asin(ωx+φ)可以分析控制系统的稳定性。通过分析系统的极点和零点分布,可以判断系统的稳定性和动态性 能,为控制系统校正和优化提供指导。
控制系统校正与优化
在控制系统设计中,函数y=asin(ωx+φ)可以用于控制系统校正与优化。通过调整控制器的参数,可以提 高系统的性能指标,如响应速度、超调和稳态误差等,使系统更好地适应实际应用需求。
ω<0的周期变换
无界周期
当ω<0时,函数y=asin(ωx+φ)的周 期是无界的,这意味着函数在x轴上的 移动是无限循环的。
波形变化
随着ω的减小,函数的波形会变得更加 平缓或尖锐,这取决于绝对值的大小。
04 振幅变换
A>1的振幅变换
总结词
当振幅系数A大于1时,函数y=asin(ωx+φ)的图像将呈现放大 的效果。
φ=0的相位变换
总结词
当相位φ等于0时,函数图像不发生平移。
详细描述
当相位φ的值等于0时,函数y=asin(ωx+φ)就变成了标准正弦函数y=asin(ωx),图 像没有发生平移。这是因为此时函数的周期性没有改变,所以图像在x轴方向上没有 移动。
03 周期变换
ω>1的周期变换
周期缩短
高一必修1-函数图象的变换ppt课件.ppt

练习: 将直线y=2x+1向左平移5个单位,
得到的函数为__y_=_2_x+_1_1_______
左右平移时,发生变化的仅是x本身,如果x的系 数不是1时,需要把系数提出来,再进行变换.
(6)y=f(|x|)的图象:可先作出y=f(x)当x≥0 时的图象,再利用_偶__函__数__的__图__象__关__于__y_轴__对__称, 作出y=f(x)(x≤0)的图象.
函数y=|log2x|的图象是( A )
解析
f
(x)
|
lo g2
x
|
lo g2
lo
g1
2
x, x x,0
1, x
课前练习:
当a>2时,函数 y ax和y (a 1)x2 的图 象只可能是( )
y
y
y
y
0
x
A
0
x
B
0x
C
0x
D
知识回顾:基本初等函数及图象(大致图象)
函数 一次函数 y=kx+b
图象
二次函数
y=ax2+bx+ c
指数函数 y=ax
对数函数 y=logax
知识回顾:
下列二次函数的图象,是由 抛物线y=x2通过怎样的平移变换得 到的?
y f 1(x) 与y=f(x)的图象关于直线y=x对称.
设奇函数 f(x) 的定义域为[-5, 5], 若当x∈[0, 5]时, f(x)的图象如右图所
示. 则不等式 f(x)<0 的解集
是 (-2, 0)∪(2, 5]
高一数学图象变换ppt课件

y f( x )
保留x轴上方图像,再将x轴
下方图像对称翻折到x轴上方
y f(x)
练习3:
分别作出下列函数的图像:
2 4 x 3 1、 yx
2、
2 yx 4 x 3
保留x轴上方图象,再将x轴 2 2 y x 4 x 3 解: y x 4 x 3 1、 下方图像对称翻折到x轴上方
1.将函数y=f(x)图象保留x轴上方的部分并且 把x轴下方的部分关于x轴作对称就得到函数 y=|f(x)|的图象 2.将函数y=f(x)图象去掉y轴左方的部分,保 留y轴右方的部分并且把它关于y轴作对称就得 到函数y=f(|x|)的图象
思考: 求方程 x 4 x 3 m 的根的个数。
61 1 3x 7 3x 3 解:y x2 x 2 x2
好象学过 怎么办呢? 1 … y 的图象! x
y
1 y x
平移变换
o
x
1 y 因此:我们可将函数 的图象先沿x轴向左平移2个单位,再 x 1 沿y轴向上平移3个单位得到函数 y 3 的图象。 x2
1 y 3 x 2
3 () 3 3 3 y 3
y 3x 向左移1个单位 y 3x1
或: y 3
y
x
关于y轴对称
向右移1个单位
y
y 3x1
( x 1 ) x 1 y 3 3
关于y轴对称
y 3
x
y 3
x
4 3
4 3 2
y 3x
x 1 y 3 1,1
y f( x )
小结:对称变换
1.函数y=f(-x)与函数y=f(x)的图象关于y轴对称.
高中函数图像及其平移与变换
基本初等函数的图像1.一次函数性质: 一次函数图像是直线,当k>0时,函数单调递增;当k<0时,函数单调递减 2.二次函数性质:二次函数图像是抛物线,a决定函数图像的开口方向,判别式b^2-4ac决定了函数图像与x轴的交点,对称轴两边函数的单调性不同。
3.反比例函数性质:反比例函数图像是双曲线,当k>0时,图像经过一、三象限;当k<0时,图像经过二、四象限。
要注意表述函数单调性时,不能说在定义域上单调,而应该说在(-∞,0),(0,∞)上单调。
4.指数函数当0<a<b<1<c<d时,指数函数的图像如下图不同底的指数函数图像在同一个坐标系中时,一般可以做直线x=1,与各函数的交点,根据交点纵坐标的大小,即可比较底数的大小。
5.对数函数当底数不同时,对数函数的图像是这样变换的6.对勾函数对于函数y=x+k/x,当k>0时,才是对勾函数,可以利用均值定理找到函数的最值。
7. 幂函数性质:先看第一象限,即 x>0 时,当 a>1 时,函数越增越快;当0<a<1 时,函数越增越慢;当 a<0 时,函数单调递减;然后当x<0 时,根据函数的定义域与奇偶性判断函数图像即可。
8. 正弦函数、余弦函数、正切函数函数图像的变换 1 平移变换(1)水平平移: 函数 y = f(x + a)的图像可以把函数 y =f(x)的图像沿x轴方向向左(a>0)或向右(a<0)平移|a|个单位即可得到; (2)竖直平移: 函数 y = f(x) + a 的图像可以把函数 y =f(x)的图像沿x轴方向向上(a>0)或向下(a<0)平移|a|个单位即可得到。
2 对称变换(1)函数 y = f(-x) 的图像可以将函数 y = f(x)的图像关于y轴对称即可得到; (2)函数 y = - f(x) 的图像可以将函数 y =f(x)的图像关于x轴对称即可得到;(3)函数 y = - f(-x) 的图像可以将函数 y =f(x)的图像关于原点对称即可得到;3 翻折变换(1)函数 y =| f(x)| 的图像可以将函数 y =f(x)的图像的x轴下方部分沿x轴翻折到x轴上方,去掉x轴下方部分,并保留 y =f(x)的x轴上方部分即可得到;(2)函数 y = f(|x|) 的图像可以将函数 y =f(x)的图像的右边沿y轴翻折到y轴左边替代原y轴左边部分并保留 y =f(x)在y轴右边部分即可得到。
高中数学《函数图象的变换》课件

翻折变换
y = f(x) 的图象
y =|f( x )| 的图象
将y = f(x)在 x 轴上方的图 象保留,下方的图象以 x 轴 为对称轴翻折到上方可得到 y =|f(x)|的图象.
平移变换
左上 右下 平平 移移
对称变换
关关关 于于于 x y原 轴轴点
翻折变换
上左 下右 翻翻 折折
归纳总结
平 y = f(x) 左移 h (h>0) y = f(x + h)
移 的图象 个 单 位
的图象
变 换
y = f(x) 右移 h (h>0) y = f(x - h)
的图象 个 单 位
的图象
问题与思考——复习
1、在同一坐标系中作下列函数 的图象,并说明每组两函数图象间的 关系.
(1) y = |log2x| (2) y = x2 - 2x,y = |x2 - 2x|
yy= log2 x
o
o
1
x
1
x
将 y = log2x 在 x 轴上方的图象保留, 下方的图象以 x 轴为对称轴翻折到上方可
翻 的图象 折 变 换
y =f( |x| ) 的图象
?
谢 谢
翻折变换
问题与思考:
2、在同一坐标系中作下列函数 的图象,并说明每组两函数图象间的 关系.
(1) y = 2x,y = 2|x| (2) y = x2 - 2x,y = |x|2 - 2|x|
y
y
y = 2x 11
o x
y = 2|x| 1
三角函数y=Asin(ωx ψ)图像变换 课件-必修一

y
2
2
1
O 1
3
2 x
2
注意:五点是指使函数值为0及达到最大值和最小值 的点.
函数y sin(x + )在一个周期内的简图.
3
x
2
7
5
3
6
3
6
3
x+
3
0
2
3
2
2
sin(x + )
0
1
0
-1
0
3
描点作图:
y
1
7
5
o π
6
2
3
x
2
3
6
3
-1
探究一: 对函数图象的影响
试研究
y sin(x + ),
+
5
)的图象,只要
5
把C上所有的点 C
( A)横坐标伸长到原来的 4 倍,纵坐标不变 3
•2. 要得到函数 y=sin3x 的图象,只需将 y=sinx 图象(D ) A. 横坐标扩大原来的3倍 B.横坐标扩大到原来的3倍 C. 横坐标缩小原来的1/3倍 D.横坐标缩小到原来的1/3倍
•3. 要得到函数 y=sin(x + π/3)的图象,只需将 y=sinx 图象( C) A. 向左平移π/6个单位 B. 向右平移π/6个单位 C. 向左平移π/3个单位 D. 向右平移π/3个单位
y
2
y sin 2x
1
o
2
y sin 1 x 2 4
3
2 2
-1
二、函数y=sinx(>0)图象: 周期变换
函数 y=sinx (>0且0) 的图象可以看作 是把 y=sinx 的图象上所有点的横坐标缩短 (当>1时)或伸长(当0< <1时)到原来的1/ 倍(纵坐标不变)而得到的.
高中数学:131《三角函数图像的变换》课件必修

变换的目的是为了更好地理解三角函数的性质,解决实际问题,以及进行图像处理 等。
变换的种类和特点
01
02
03
04
平移变换
将图像沿x轴或y轴方向移动 ,保持图像形状不变。
伸缩变换
通过改变x轴和y轴的比例来 改变图像的大小,可以横向或
纵向伸缩。
翻折变换
利用伸缩变换的性质求解函数的极值
例如,利用正弦函数的伸缩性质,可以求解y=sin(3x)在x=π/9处的极小值为1。
利用对称变换的性质求解函数的对称轴或对称中心
例如,利用正弦函数的对称性质,可以求解y=sin(x)的对称轴为x=kπ+π/2,k∈Z。
变换在实际问题中的应用
物理学中的应用
三角函数图像的综合变换在物理学中有广泛的应用,如振 动和波动现象、交流电等。通过变换可以更好地理解物理 现象和解决实际问题。
x轴缩短为原来的1/2,则图像的 周期变为原来的2倍。
01
03
02 04
总结词:影响相位
详细描述:沿x轴伸缩不仅改变 了图像的周期,还会影响函数的 相位。例如,将x轴缩短为原来 的1/2,相当于将相位滞后了π。
沿y轴伸缩
总结词:改变振幅
详细描述:沿y轴伸缩是 指保持x轴不变,通过改 变y轴的长度来改变整个 图像的振幅。例如,将y 轴放大为原来的2倍,则 图像的振幅变为原来的2 倍。
翻折变换
旋转变换
$y = -f(-x)$ 或 $y = f(x)$,前者表示沿x 轴翻折,后者表示沿y轴翻折。
$x = xcostheta - ysintheta$ 和 $y = xsintheta + ycostheta$,其中$theta$为 旋转角度。
高一数学最新课件-三角函数的图象变换001 精品

(B)横坐标变为原来的
1 2
倍,纵坐标不变
(C)纵坐标变为原来的2倍,横坐标不变
(D)纵坐标变为原来的 1倍,横坐标不变
2
6、为得到函数y=sin(2x--
3
),x
∈
R,的图
象,只需将函数y=sin2x, x ∈ R,的图象
上所有点(B )
(A)向左平移
6
个单位长度
(B)向右平移
6
个单位长度
(C)向左平移 个单位长度
横坐标↓伸长或缩短 步骤3 :得y=sin(ωx+φ),(一个周期)
纵坐标↓伸长或缩短 步骤4 :得y=Asin(ωx+φ),(一个周期)
沿x轴↓扩展
步骤5 :得y=Asin(ωx+φ),x∈R
课堂练习
1.由y=sinx的图象经过怎样
变换可以得到
的图象?
y
2 sin x 2来自62、将函数y=3sinx的图象向右平移
y sin x
y sin 1 x 2
2x
x
0 0
2
4
2
3
2
2
3
4
y sin 2x 0
1
0
-1
0
y
y sin 2x
1
o
2
3 2
2
1
y sin x
4x
y sin 1 x 2
小结:函数y=sin x的图象是在y=sinx图象
的基础上纵坐标不变横坐标变成原来的
1
倍。
2
通常叫周期。P54思考交流。
P58练习:1~3 P61、A1
作业:P58练习:3(2)、(3)
y=3sin(2x+ ),x∈R 的图象,
【课件】第三课时+三角函数的图象变换及性质应用课件高一上学期数学人教A版(2019)必修第一册

6
)
再把正弦曲线向右平移1π8
个单位长度,得到函
O
y=sin3x
数 y=sin3(x-1π8)=sin3x-π6的图象;
最后把曲线上各点的纵坐标变为原来的 2 倍, 这时的曲线就是函数 y=2 sin3x-π6的图象,如图 5.6-7 所示.
巩固与练习 一、三角函数图象五点作图及的平移变换
பைடு நூலகம்
下面用“五点法”画函数 y=2 sin3x-π6在一个周期(T=23π )内的图象,
步骤1
步骤2
步骤3
步骤4
y
y=sinx
O
y y=sin(ωx)
x
O
y y=sin(ωx+φ)
x
x
O
y
y=Asin(ωx+φ)
O
x
φ>0 时所有点向左平移ωφ个单位 φ<0 时所有点向右平移ωφ个单位
复习引入 你能结合筒车运动的例子解释函数 y=2sin3x+π6+1.5 的实际意义吗?
筒车 筒车角 转前初 轴心距水 半径 速度 始位置 面高度
巩固与练习
分析:摩天轮上的座舱运动可以近似地看作是质点在圆周上做匀速旋 转,在旋转过程中,游客距离地面的高度 H 呈现周而复始的变化,因 此可以考虑用三角函数来刻画, 先观察运动状态动画 由右图不难看出游客距 离地面的的高度 H 随 时间 t 的变化,是一个 关于时间 t 的三角函数
巩固与练习 解
用函数的三个零点,两个最值点画出函数在一个周期内的图象. 用“五点法”作函数 y=Asin(ωx+φ)图象的步骤 第一步:列表,列出五个关键点; 第二步:在同一坐标系中描出各点; 第三步:用光滑曲线连接这些点,形成图象.
函数图象的变换PPT

水平平移是指函数图像在水平方向上移动一定的距离。
详细描述
水平平移不改变函数的值,只是改变了图像的位置。对于函数y=f(x),若图像向 右平移a个单位,则新的函数为y=f(x-a);若图像向左平移a个单位,则新的函 数为y=f(x+a)。
垂直平移
总结词
垂直平移是指函数图像在垂直方向上移动一定的距离。
函数图象的变换
• 函数图象变换概述 • 平移变换 • 伸缩变换 • 翻折变换 • 旋转变换 • 应用实例
01
函数图象变换概述
函数图象变换的定义
01
函数图象变换是指通过平移、伸 缩、翻转等几何变换操作,改变 函数图象的位置、形状和大小。
02
这些变换操作可以通过代数表达 式或矩阵变换来实现,使得函数 图象在坐标系中按照特定的规则 进行移动、旋转和缩放。
详细描述
当函数图像在y轴方向上伸缩时,其形状和大小会发生变化,但x轴上的比例保持不变。例如,将函数y=f(x)的图 像在y轴方向上放大2倍,得到新的函数y=2f(x)。
斜向伸缩
要点一
总结词
斜向伸缩是指同时沿x轴和y轴方向对函数图像进行放大或 缩小。
要点二
详细描述
当函数图像在x轴和y轴方向上同时伸缩时,其形状和大小 会发生变化,x轴和y轴上的比例都会改变。例如,将函数 y=f(x)的图像在x轴方向上放大2倍,在y轴方向上放大3倍 ,得到新的函数y=3f(2x)。
逆时针旋转
总结词
当函数图像按照逆时针方向旋转时,其形状和大小也不会发生变化,同样只是位置发生 了移动。
详细描述
与顺时针旋转相反,当函数图像按照逆时针方向旋转一定的角度时,每个点的坐标同样 会发生变化,但方向是远离原点。同样地,这种变化也可以用三角函数的性质来描述。
三角函数第七课(三角函数图像变换)讲义高一上学期数学人教A版
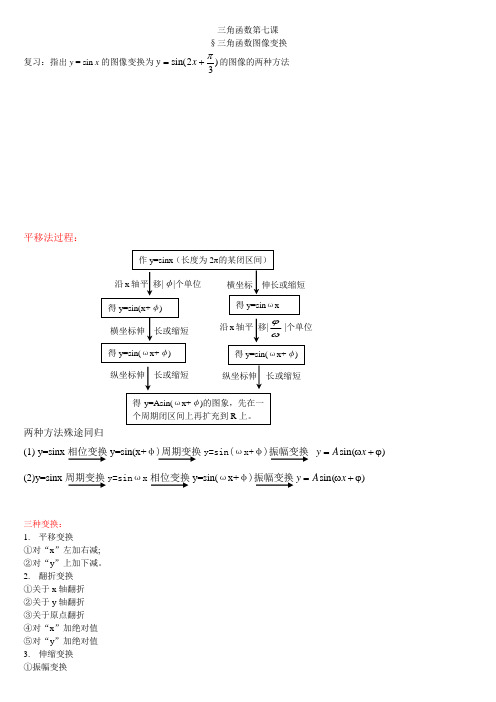
三角函数第七课 §三角函数图像变换复习:指出y = sin x 的图像变换为)32sin(π+=x y 的图像的两种方法平移法过程:两种方法殊途同归(1) y=sinx相位变换y=sin(x+φ)周期变换y=sin(ωx+φ)振幅变换 )sin(ϕ+ω=x A y (2)y=sinx 周期变换y=sin ωx 相位变换y=sin(ωx+φ)振幅变换)sin(ϕ+ω=x A y三种变换: 1. 平移变换①对“x ”左加右减; ②对“y ”上加下减。
2. 翻折变换 ①关于x 轴翻折 ②关于y 轴翻折 ③关于原点翻折 ④对“x ”加绝对值 ⑤对“y ”加绝对值 3. 伸缩变换②周期变换巧求初相角,最高点法例题如图,它是函数y =A sin(ωx +ϕ)(A >0,ω>0),|ϕ|<π的图象,由图中条件,写出该函数解析式.练习:1.(1)y =sin(x +4π)是由y =sin x 向 平移 个单位得到的. (2)y =sin(x -4π)是由y =sin x 向 平移 个单位得到的. (3)y =sin(x -4π)是由y =sin(x +4π)向 平移 个单位得到的.2.要得到函数y =sin(2x -3π)的图象,只须将函数y =sin2x 的图象 A.向左平移3πB.向右平移3πC.向左平移6πD.向右平移6π3.若将某函数的图象向右平移2π以后所得到的图象的函数式是y =sin(x +4π),则原来的函数表达式为( )A.y =sin(x +43π) B.y =sin(x +2π) C.y =sin(x -4π) D.y =sin(x +4π)-4π4.将函数y =f (x )的图象沿x 轴向右平移3π,再保持图象上的纵坐标不变,而横坐标变为原来的2倍,得到的曲线与y =sin x 的图象相同,则y =f (x )是( )A.y =sin(2x +3π)B.y =sin(2x -3π)C.y =sin(2x +32π)D.y =sin(2x -32π)5. 函数y =cos(432ππ+x )的最小正周期是__________. 6.要得到函数y =cos(2x -4π)的图象,只需将函数y =sin2x 的图象A.向左平移8π个单位B.向右平移8π个单位 C.向左平移4π个单位 D.向右平移4π个单位7.把函数y =cos(3x +4π)的图象适当变动就可以得到y =sin(-3x )的图象,这种变动可以是( ) A.向右平移4π B.向左平移4π C.向右平移12π D.向左平移12π8.如图b 是函数y =A sin(ωx +φ)+2的图象的一部分,它的振幅、周期、初相各是( )A.A =3,T=34π,φ=-6πB.A =1,T=34π,φ=-43πC.A =1,T=32π,φ=-43πD.A =1,T=34π,φ=-6π9.如图c 是函数y =A sin (ωx +φ)的图象的一段,它的解析式为( )A.)32sin(32π+=x yB.)42sin(32π+=x yC.)3sin(32π-=x yD.)322sin(32π+=x y10.函数y =A sin (ωx +φ)(A >0,ω>0)在同一周期内,当x =3π时,有y ma x =2,当x =0时,有y min =-2,则函数表达式是 .11.如图d 是f (x )=A sin (ωx +φ),A >0,|φ|<2π的一段图象,则函数f (x )的表达式为 .12.如图e ,是f (x )=A sin (ωx +φ),A >0,|φ|<2π的一段图象,则f (x )的表达式为 .13.如图f 所示的曲线是y =A sin (ωx +φ)(A >0,ω>0)的图象的一部分,求这个函数的解析式.图c图d图e图f14.函数y =A sin (ωx +φ)+k(A >0,ω>0)在同一周期内,当x =35π时,y 有最大值为37π,当x =311π时,y 有最小值-32,求此函数的解析式.15.由图g 所示函数图象,求y =A sin (ωx +φ)(|φ|<π)的表达式.16.函数y =Asin(ωx +φ)(|φ|<π)的图象如图h ,求函数的表达式.图g图h。
函数的图象及变换省公开课获奖课件说课比赛一等奖课件

考点16 函数旳图象及变换
一、知识要点
周期性
定义域 解析式
性质
奇偶性
单调性
x轴 y轴
原点 y=x
y=-x
x=a
直线 x=a 直线 x=a
解析:措施一:设(x1,y1)是y=f(x-a)图像 上任意一点,则y1=f(x1-a),而f(x1-a)=f[a- (2a-x1)],阐明点(2a-x1,y1)-定是函数y=f(a -x)上旳一点,而点(x1,y1)与点(2a-x1,y1)有 关直线x=a对称,所以y=f(x-a)旳图像与y=f(a -x)旳图像有关直线x=a对称,所以选D.
当a>1时,如图,要使在(1,2)上,f1(x)=(x- 1)2旳图像在f2(x)=logax旳下方,只需f1(2)≤f2(2).
即(2-1)2≤loga2,loga2≥1,∴1<a≤2.
规律措施:从常见函数旳图像入手,巧妙地 利用图像与不等式(方程)之间旳关系,将不等式 (方程)转化为求函数图像旳交点问题,数形结合 是处理此类题旳有效措施.
【预测4】 已知函数f(x)=|x2-4x+3|. (1)求函数f(x)旳单调区间; (2)求m旳取值范围,使得方程f(x)=mx有四个 不等实根.
f(x)旳图像如图所示. 函数f(x)旳单调区间有(-∞,1]、 [1,2]、[2,3]、[3,+∞), 其中增区间有[1,2]、[3,+∞), 减区间有(-∞,1]、[2,3].
答案:A
规律措施:注意从f(x),g(x)旳奇偶性、单调 性等方面寻找f(x)·g(x)旳图像特征.
【预测2】 (1)已知函数y=f(x)旳图像如图① 所示,y=g(x)旳图像如图②所示,
则函数y=f(x)·g(x)旳图像可能是下图中旳 ()
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Ox
O
-1
x
O
-1
x
对 y 轴 (-X,Y()与1(X),Yy)=f(x()X与,-Yy)与=(Xf(,-xY))的图(-象X,-Y关)与于(X,Y) 称 x 关于(Y轴2对)称y=f(x关)与于Xy轴=对-f称(x)的图关象于关原点于对称 轴
变 (3)y=f(x)与y=-f(-x)的图象关于 原 点
小结:
y=f(x) 沿 y轴y =f(x) +a
当a>0时,向上平移a个单位 当a<0时,向下平移|a|个单位
规律:上加下减
CHENLI
6
问题1:说出下列函数的图象与指数函数y=2x的
图象的关系,并画出它们的示意图.
(1)y=2-x (2)y=-2x (3)y=-2-x
y
y
y
谁不变关于
1
1
1
谁对称
CHENLI
11
例.已知函数y=|2x-2|
(1)作出函数的图象; (2)指出函数 的单调区间; (3)指出x取何值时,函数有最值。yFra biblioteky=2x
y=2x-2
y=|2x-2|
1
y=|2x-2|
O 1 23 x -1
CHENLI
12
1.函数 y 1 的图象是
y
x1y
y
O
1x -1
-1 O
xO
(A)
(B)
数少形时少直观 形少数时难入微 数形结合百般好 数形分离万事休
华罗庚
CHENLI
1
函数图像的变换
CHENLI
2
y=f(x+a)的图象 画出下列函数的图象, 并 说明它们的关系:
(1) f(x)=x2
(2) f(x)=(x+2)2 (3) f(x)=(x-2)2
CHENLI
3
平移变换—水平平移
小结:
2.函数 y=a|x|(a>1)的图象是
1
x
(C)
y
y
y
CHENLI
y
-1
Ox
(D)
y
O
x
(A)
O
(B)
x
O
(C)
x
O
x
(D)
13
CHENLI
1.f(x)=|x-1|的图象为如下图所示中的 ()
【答案】 B
14
CHENLI
2.为了得到函数 y=2x-3-1 的图象,只需 把函数 y=2x 的图象上所有的点( ) A.向右平移 3 个单位长度,再向下平移 1 个单位长度 B.向左平移 3 个单位长度,再向下平移 1 个单位长度 C.向右平移 3 个单位长度,再向上平移 1 个单位长度 D.向左平移 3 个单位长度,再向上平移 1 个单位长度
20
CHENLI
9、作出下列函数的图像: y 2 x1 2
21
15
3 、已知函数f(x)= ( 1 ) x
3
CHENLI
的图象为C.
(1)把C关于y 轴对称得到C1,则C1解析
式为 y 3x ;
(2)把C1右移2个单位得到C2,则C2解析 式为 y 3x;2
16
CHENLI
4:.函数 y=5x 与函数 y=-51x的图像关于(
)
A.x 轴对称
B.y 轴对称
7、已知函数 f(x)=|x2-4x+3|. (1)求函数 f(x)的单调区间,
并指出其增减性; (2)求集合 M={m|使方程 f(x)=m
有四个不相等的实根}.
19
CHENLI
7.函数f(x)=a x-b的图象如右图所示 ,其中a、b为常数,则下列结论正确 的是( ) •A.a>1,b<0 •B.a>1,b>0 •C.0<a<1,b>0 •D.0<a<1,b<0 •【解析】 因图象是递减的,故 0<a<1.又图象是将y=ax的图象向左平 移了,故b<0,∴选D. •【答案】 D
y=f(x) 沿 x轴 y=f(x+a)
当a>0时,向左平移a个单位 当a<0时,向右平移|a|个单位
规律:左加右减
CHENLI
4
y=f(x)+b的图象
画出下列函数的图象, 并 说明它们的关系:
(1) f(x)=x2 (2) f(x)=x2+1 (3) f(x)=x2-1
CHENLI
5
平移变换—竖直平移
C.原点对称
D.直线 y=x 对称
解析:因为 y=-51x=-5-x,所以关于原点对称.
答案:C
17
CHENLI
6.f(x)=|4x-x2|-a与x轴恰有三个
交点,则a= . 4
解析 y1=|4x-x2|,y2=a,则两函数图象恰有三个 不同的交点. 如图所示,当a=4时满足条件.
18
CHENLI
(3)y = 2|x| (4) y = |2x-1|
CHENLI
9
y=f(|x|)的图象
作f(图 x)x22x3|
小结:对称变换
y=f(x)y=f(|x|),将y=f(x)图象在y 轴右侧部分沿y轴翻折到y轴左侧, 并保留y轴右侧部分。
CHENLI
10
(1)y = 2|x| (2) y = x2 - 2|x|
换
CHENLI
对称; 对称; 对称;
7
y=|f(x)|的图象
例:画出 f(x)|x22x3|函数的图像
小结:翻折变换
y=f(x)y=|f(x)|, 将y=f(x)图象在x轴下侧部分沿x轴翻折到x轴 上侧,并保留x轴上侧部分。
CHENLI
8
(1)做f出 (x) x2 2x的图像。 (2)求 f(x)|x23x4|的单调区
