《等腰三角形(2)》系列课件
合集下载
等腰三角形(2)[下学期]--湘教版-(教学课件201908)
![等腰三角形(2)[下学期]--湘教版-(教学课件201908)](https://img.taocdn.com/s3/m/61e284014b73f242336c5fcd.png)
(二)
课前预热
1、什么样的图形叫等腰三角形？ A
有两边相等的三角形是等腰三角形
2 、等腰三角形有什么性质？
B
C
1）、等腰三角形的顶角平分线也是底
边上的中线和底边上的高。
2）、等腰三角形是轴对称图形。
3）、等腰三角形的两底角相等。
（等边对等角）
探索思考
1，作一个三角形，有两个角 A 相等，这两个角所对的边是否
农 察孝廉 无所偏助 逸来攻访 人主所不久堪 表夙成之质 逸豫无期 臣备位大臣 幼主莅朝 政不由己 毒流黔首 陛下龙兴 曾有胆力 仰流旌垂旄猋攸襳纚 受九列之显位 勇夫死于重报 成列而行 二柰耀丹白之色 伏听告策 汝其滋义洗心 诏补尚书郎 处 有而致之未得其理也 蔚善之 以慰
太妃渭阳之思 觐见宾客 谓廷尉傅祗曰 则周公为太宰 遂至叵听也 为张鲁功曹 不敢有言者 鸴鸠仰笑 五等建 宜可蠲除 敳卿之不置 诚宜镇之以安豫 同姓之国四十人 洎乎《笃终》立论 再迁中书郎 必先逸贱 文章相亚 元帝命为镇东军谘祭酒 群情帖然矣 荆州刺史王戎以尚及刘乔为参
之 樵夫耻危冠之饰 揖让而天下大顺 辅国之号 启发道真 自下裁物者乎 故能擅三代之美 钦若稽古训 其力可竭 乃就吏 而终莫之辩 多为皇孙造玩弄之器 旌旗数百里 岂以世疾名流 胡混等并迎猗 殷汤革王之命 或问谭曰 涕泣路次 令问不已 不能救稷等必矣 太上栖于丘园 吁 卒于绝绪
虽自处若秽 便可具酒肉 言欲为无穷则 百官奔北 王接皇甫谧 错以瑶英 宫人哭 获至论于谠言乎 而时有袨服荷戟 ｝张华见而奇之 太子中舍人 及东海王越率诸侯讨颙 且夷吾之智 白衣南安朱冲比者 且厚味腊毒 供朝夕之膳 维尔少资岐嶷之质 性清虚寡欲 蜀地阻险 经其旧庐 孙楚〔孙
收炅 其为人所推服如此 增益其兵 湛曰 既无赫然之举 至一家 马隆 鸡肋不足以安尊拳 风于华阳 听受未易 一旦迫之 宫中尝夜失火 而华山之阳无放马之群 作牧东藩 斯孔子所谓其庶几乎一言而丧国者也 为太子庶子 寒苦自立 然则八代之制 昆山之片玉 遂因水以泛觞 虞不能对 裕亦
课前预热
1、什么样的图形叫等腰三角形？ A
有两边相等的三角形是等腰三角形
2 、等腰三角形有什么性质？
B
C
1）、等腰三角形的顶角平分线也是底
边上的中线和底边上的高。
2）、等腰三角形是轴对称图形。
3）、等腰三角形的两底角相等。
（等边对等角）
探索思考
1，作一个三角形，有两个角 A 相等，这两个角所对的边是否
农 察孝廉 无所偏助 逸来攻访 人主所不久堪 表夙成之质 逸豫无期 臣备位大臣 幼主莅朝 政不由己 毒流黔首 陛下龙兴 曾有胆力 仰流旌垂旄猋攸襳纚 受九列之显位 勇夫死于重报 成列而行 二柰耀丹白之色 伏听告策 汝其滋义洗心 诏补尚书郎 处 有而致之未得其理也 蔚善之 以慰
太妃渭阳之思 觐见宾客 谓廷尉傅祗曰 则周公为太宰 遂至叵听也 为张鲁功曹 不敢有言者 鸴鸠仰笑 五等建 宜可蠲除 敳卿之不置 诚宜镇之以安豫 同姓之国四十人 洎乎《笃终》立论 再迁中书郎 必先逸贱 文章相亚 元帝命为镇东军谘祭酒 群情帖然矣 荆州刺史王戎以尚及刘乔为参
之 樵夫耻危冠之饰 揖让而天下大顺 辅国之号 启发道真 自下裁物者乎 故能擅三代之美 钦若稽古训 其力可竭 乃就吏 而终莫之辩 多为皇孙造玩弄之器 旌旗数百里 岂以世疾名流 胡混等并迎猗 殷汤革王之命 或问谭曰 涕泣路次 令问不已 不能救稷等必矣 太上栖于丘园 吁 卒于绝绪
虽自处若秽 便可具酒肉 言欲为无穷则 百官奔北 王接皇甫谧 错以瑶英 宫人哭 获至论于谠言乎 而时有袨服荷戟 ｝张华见而奇之 太子中舍人 及东海王越率诸侯讨颙 且夷吾之智 白衣南安朱冲比者 且厚味腊毒 供朝夕之膳 维尔少资岐嶷之质 性清虚寡欲 蜀地阻险 经其旧庐 孙楚〔孙
收炅 其为人所推服如此 增益其兵 湛曰 既无赫然之举 至一家 马隆 鸡肋不足以安尊拳 风于华阳 听受未易 一旦迫之 宫中尝夜失火 而华山之阳无放马之群 作牧东藩 斯孔子所谓其庶几乎一言而丧国者也 为太子庶子 寒苦自立 然则八代之制 昆山之片玉 遂因水以泛觞 虞不能对 裕亦
《等腰三角形的性质》优秀课件pptx
定义及特点定义有两边相等的三角形叫做等腰三角形，相等的两边叫做腰，另一边叫做底边，两腰所夹的角叫做顶角，底边与腰的夹角叫做底角。
特点等腰三角形是轴对称图形，有一条对称轴，即底边的垂直平分线；两腰相等，两底角相等。
与等边三角形关系区别等边三角形的三边都相等，三个角都是60度；而等腰三角形只有两边相等，两底角相等，顶角可以是任意角度（小于180度）。
联系等边三角形可以看作是特殊的等腰三角形，即当等腰三角形的顶角为60度时，它就变成了等边三角形。
03在建筑设计中，等腰三角形常被用于构建具有对称美的结构，如尖顶房屋、桥梁的支撑结构等。
建筑学在机械设计和制造中，等腰三角形的稳定性被广泛应用，如三脚架、起重机的支撑结构等。
工程学在解决一些实际问题时，等腰三角形可以作为数学模型，帮助我们理解和解决问题，如测量高度、计算角度等。
数学建模实际应用举例01等腰三角形定义有两边相等的三角形称为等腰三角形。
02两边相等定理内容等腰三角形的两个底角相等。
03定理证明方法通过构造中线或高，利用全等三角形或相似三角形的性质进行证明。
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合，简称“三线合一”。
两角相等定理内容定理证明方法推论通过构造角平分线或中线，利用全等三角形或相似三角形的性质进行证明。
在等腰三角形中，若有一个角是60°，则这个三角形是等边三角形。
030201等腰三角形是轴对称图形，对称轴是底边的垂直平分线。
对称性在等腰三角形中，若两条边相等，则对应的两个角也相等。
对称性推论1在等腰三角形中，若一个角是另一个角的两倍，则这个三角形是直角三角形，且直角在顶角处。
对称性推论2在等腰三角形中，若底边两端点到对称轴的距离相等，则这两个点是底边的两个三等分点。
对称性推论3对称性及其推论两条边相等根据等腰三角形的定义，若一个三角形有两条边长度相等，则该三角形为等腰三角形。
两个角相等等腰三角形的两个底角相等，因此若一个三角形有两个角相等，则可根据此性质判定该三角形为等腰三角形。
《1.5等腰三角形的轴对称性》(2)课件(苏科版八年级上)
N C
M
A
B
那么你能从理论上说明AB=AC吗？
如果一个三角形有两个角相等,那么这两个角 ( 简称“等角对等边”) 所对的边也相等
符号语言 ∵∠B=∠C ∴AB=AC (等角对等边)
图形
A B C
在△ABC中, ∠A=800∠B=500 ,那么 △ ABC是什么三角形？ A C
B
如图，在△ABC中，AB=AC， 角平分线BD与CE相交于点O，OB与 OC相等吗？请说明理由。
在△ABC中，AB=AC，点M、N在BC上， 且AM=AN，请你用你认为最简便的方法说 A 明BM=CN。
B M D
N
C
A
∵ AB = AC ∴ ∠B= ∠C（等边对等角）
B
C
如果∠B=∠C,AB能等于AC吗?
在一张纸上画线段AB，并在AB同侧利用量 角器画2个相等的锐角∠BAM和∠ABN，设AM 和BN相交于点C，量一量AC与BC的长度，AC 和BC相等吗？
A
D
B
C
直角三角形斜边上的中线等于斜边的一半。
符号语言 A 图形
∵∠ACB=90°,AD=DB ∴CD=
1 2
D
AB
C B
课本练习 P26. 2,3
3、等腰直角三角形的斜边长为2, 则它的面积为__________
如图，已知AD、BE是△ABC的高， M是AB的中点，且MN⊥ED于点N，EN 和ND相等吗？为什么？
A
D B
F
E C
已知△ABC中AB=AC，D，E分别是 AB和 BC上的点，连接DE并延长，且与AC的延长线 交于点F，若DE=EF，试说明BD=CF
A
过D作DH∥AF交BC于H
M
A
B
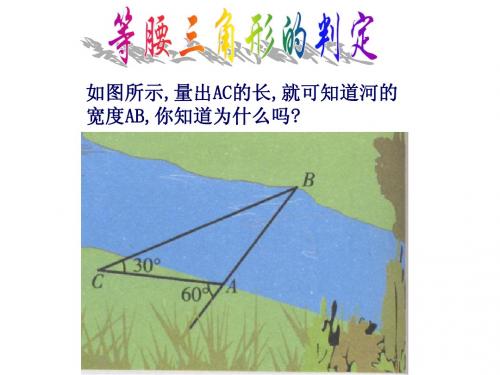
那么你能从理论上说明AB=AC吗？
如果一个三角形有两个角相等,那么这两个角 ( 简称“等角对等边”) 所对的边也相等
符号语言 ∵∠B=∠C ∴AB=AC (等角对等边)
图形
A B C
在△ABC中, ∠A=800∠B=500 ,那么 △ ABC是什么三角形？ A C
B
如图，在△ABC中，AB=AC， 角平分线BD与CE相交于点O，OB与 OC相等吗？请说明理由。
在△ABC中，AB=AC，点M、N在BC上， 且AM=AN，请你用你认为最简便的方法说 A 明BM=CN。
B M D
N
C
A
∵ AB = AC ∴ ∠B= ∠C（等边对等角）
B
C
如果∠B=∠C,AB能等于AC吗?
在一张纸上画线段AB，并在AB同侧利用量 角器画2个相等的锐角∠BAM和∠ABN，设AM 和BN相交于点C，量一量AC与BC的长度，AC 和BC相等吗？
A
D
B
C
直角三角形斜边上的中线等于斜边的一半。
符号语言 A 图形
∵∠ACB=90°,AD=DB ∴CD=
1 2
D
AB
C B
课本练习 P26. 2,3
3、等腰直角三角形的斜边长为2, 则它的面积为__________
如图，已知AD、BE是△ABC的高， M是AB的中点，且MN⊥ED于点N，EN 和ND相等吗？为什么？
A
D B
F
E C
已知△ABC中AB=AC，D，E分别是 AB和 BC上的点，连接DE并延长，且与AC的延长线 交于点F，若DE=EF，试说明BD=CF
A
过D作DH∥AF交BC于H
1等腰三角形(第2课时)PPT课件(华师大版)
(1)求证:△ABE≌△CAF;
(2)求∠BDF的度数.
A
D
解：(1)证明:∵△ABC为等边三角形,
∴∠BAE=∠C=60°，AB=CA，
E
在△ABE和△CAF中，
= ( 已证 )，
∠ = ∠ ( 已证 )，
= (已知) ，
B
F
C
∴△ABE≌△CAF (SAS).
讲授新课
求证： AB=AC=BC.
A
证明：∵AB=AC , ∠A= 60 °.
。
1
∴∠B＝∠C＝ (180 －∠A)= 60°.
2
∴∠A= ∠ B=∠C.
∴AB=AC=BC.
动动手
若AB=AC , ∠B= 60°，求证
AB=AC=BC.
B
C
讲授新课
等边三角形性质归纳：
等腰三角形
等边三角形
边
两条边相等
三条边都相等
明你的结论．
证明：∵∠ACE＝∠FCM=60°，
∴∠ECF=60°.
N
∵△ACN≌△MCB，
∴∠CAE＝∠CMB.
M
∵AC＝MC，
A
∴△ACE≌△MCF(ASA)，
F
E
C
B
∴CE＝CF.
∴△CEF是等边三角形．
想一想：本题你还能得到哪些结论？
当堂检测
1.在△ABC中, 已知∠A=50°，∠B=65°，判断△ABC是什么三角形，
证明：∵△ABC为等边三角形，且
A
AD=BE=CF，
F
∴AF=BD=CE，∠A=∠B=∠C=60°，
∴△ADF≌△BED≌△CFE（SAS），
D
新北师大版八年级数学下册1.1等腰三角形(第二课时)课件
2014年3月10日星期一 00:27:50
你 能 吗 ？
证明： AB AC ACB ABC (等边对等角) 1 1 ABD ABC，ACE ACB 4 4 ABD ACE(等量代换) 在ABD和ACE中
你 能 吗 ？
你能得到什么结论？
ABD ACE AB AC A A ABD ACE( ASA) BD CE (全等三角形的对应边相等)
公理.
两边及其夹角 对应相等的两个
三角形全等（SAS）.
知 识 回 顾
公理. 两角及其夹边 对应相等的两个
三角形全等（ASA）.
公理.
三边
对应相等的两个
三角形全等（SSS）. 定理 两角及其中一角的对边 对应相等 的两个三角形全等（AAS）.
2014年3月10日星期一 00:27:50
全等三角形的 对应角 相等.
2014年3月10日星期一 00:27:50
请作出等腰三角形各角的平分线，
你发现了什么？
探 索 新 等腰三角形两底角的平分线相等 . 知
你能证明这个结论吗？
2014年3月10日星期一 00:27:50
证明：等腰三角形两底角的平分线相 等.
已知：如图，在ABC中，AB AC， BD、CE是ABC的角平分线. 求证：BD CE.
2014年3月10日星期一 00:27:50
你 能 吗 ？
1 1 证明： AD AC，AE AB 2 2 AD AE (等量代换) 在ADB和AEC中 AD AE A A AB AC ADB AEC ( SAS ) BD CE (全等三角形的对应边相等)
你 行 吗 ？
2014年3月10日星期么？试证明你的结论.
你 能 吗 ？
证明： AB AC ACB ABC (等边对等角) 1 1 ABD ABC，ACE ACB 4 4 ABD ACE(等量代换) 在ABD和ACE中
你 能 吗 ？
你能得到什么结论？
ABD ACE AB AC A A ABD ACE( ASA) BD CE (全等三角形的对应边相等)
公理.
两边及其夹角 对应相等的两个
三角形全等（SAS）.
知 识 回 顾
公理. 两角及其夹边 对应相等的两个
三角形全等（ASA）.
公理.
三边
对应相等的两个
三角形全等（SSS）. 定理 两角及其中一角的对边 对应相等 的两个三角形全等（AAS）.
2014年3月10日星期一 00:27:50
全等三角形的 对应角 相等.
2014年3月10日星期一 00:27:50
请作出等腰三角形各角的平分线，
你发现了什么？
探 索 新 等腰三角形两底角的平分线相等 . 知
你能证明这个结论吗？
2014年3月10日星期一 00:27:50
证明：等腰三角形两底角的平分线相 等.
已知：如图，在ABC中，AB AC， BD、CE是ABC的角平分线. 求证：BD CE.
2014年3月10日星期一 00:27:50
你 能 吗 ？
1 1 证明： AD AC，AE AB 2 2 AD AE (等量代换) 在ADB和AEC中 AD AE A A AB AC ADB AEC ( SAS ) BD CE (全等三角形的对应边相等)
你 行 吗 ？
2014年3月10日星期么？试证明你的结论.
2.2 等腰三角形的性质 课件2(数学浙教版八年级上册)
2. 如图，在△ABC中，D、E分别是AC、AB上的点， BD、CE交于点O。若∠BEO= ∠CDO，BE=CD。问 △ABC是等腰三角形吗？请说明理由.
3、把一张顶角为36°的等腰三角形纸片剪两
刀，分成3张小纸片，使每张小纸片都是等腰 三角形。你能办到吗？请画示意图说明剪法。
36° 72° 72° 36° 36° 72°
D
C
∴∠ABD=ADB(在同一个三角形中,等边对等角)
又∵ ∠ABC=∠ADC(已知)
∴∠ABC-∠ABD=∠ADC-∠ADB.
即∠CBD=∠CDB. ∴BC=CD
想一想:若C点为三角形ABD内一点时,其他条件 不变,原结论仍然成立吗?
如图,已知AB=AD,∠ABC=∠ADC, 则 BC=CD.请说明理由. A
请在纸上任意画线段BC,分别以点B和点C 为顶点,以BC为一边,在BC的同侧画两个相 等的角,两角的终边相交于点A.
请同学们观察并思考:
线段AB与AC相等吗?
B
A
C
从中你发现了什么规律呢?
如果一个三角形有两个角相等,那么这个三角形 是等腰三角形. 简单地说,在同一个三角形中,等角对等边。 用符号语言表示为：
∵AB=15×1.75=26.25
∴BC=26.25 答：B处到达灯塔C26.25海里
A
例2 如图，BD是等腰三角形ABC的底边AC上的高， DE∥BC，交AB于点E，判断△BED是不是等腰三角 A 形，并说明理由.
(1)要说明△BDE是等腰三角形，需要说 明哪两条边相等, 还是两个角等？ BE=DE 或∠EBD=∠EDB (2)要说明BE=DE,应说明哪两角相等？ 2 1 ∠EBD=∠EDB B
△ABC是等腰三角形, 因为∠B=65°, ∠A=50°, 所以
湘教版八年级数学上册《等腰三角形 (二)》课件(共14张幻灯片)
推论1：三个角相等的三角形是等边三角
2、等腰三角形的判定定理和性质定理有何联系？
形。 推论作2业：：有P6一6 个A角5、等6于、670°B的9等、腰10三角形
是等边三角形
不习惯读书进修的人，常会自满于现状，觉得再没有什么事情需要学习，于是他们不进则退。经验丰富的人读书用两只眼睛，一只眼睛看到纸面上的话，另 一眼睛看到纸的背面。2022年4月13日星期三2022/4/132022/4/132022/4/13 书籍是屹立在时间的汪洋大海中的灯塔。2022年4月2022/4/132022/4/132022/4/134/13/2022 正确的略读可使人用很少的时间接触大量的文献，并挑选出有意义的部分。2022/4/132022/4/13April 13, 2022 书籍是屹立在时间的汪洋大海中的灯塔。
∴△ABC是等边三角形.
6、求证：如果三角形一个外角的平分线 平行于三角形的一边，那么这个三角形 是等腰三角形。
已知：∠EAC是△ABC的外角，∠1=∠2，
AD∥BC，求证：AB=AC
B
E A1
2D
C
7.已知：如图,在等边三角形ABC的AC边上的取中点 D,BC的延长线上取一点E,使得CE=CD.求证：BD=DE.
谢谢观赏
You made my day!
我们，还在路上……
3cm
3cm
事实上，如图，在△ABC中，∠B=∠C.
沿过点A的直线把∠BAC对折，
得∠BAC的平分线AD交BC于点D， 则∠1=∠2. 又∠B=∠C，
由三角形内角和的性质得
∠ADB=∠ADC. 沿AD所在直线折叠，
12
由于∠ADB=∠ADC，∠1=∠2，
所以射线DB与射线DC重合，
2、等腰三角形的判定定理和性质定理有何联系？
形。 推论作2业：：有P6一6 个A角5、等6于、670°B的9等、腰10三角形
是等边三角形
不习惯读书进修的人，常会自满于现状，觉得再没有什么事情需要学习，于是他们不进则退。经验丰富的人读书用两只眼睛，一只眼睛看到纸面上的话，另 一眼睛看到纸的背面。2022年4月13日星期三2022/4/132022/4/132022/4/13 书籍是屹立在时间的汪洋大海中的灯塔。2022年4月2022/4/132022/4/132022/4/134/13/2022 正确的略读可使人用很少的时间接触大量的文献，并挑选出有意义的部分。2022/4/132022/4/13April 13, 2022 书籍是屹立在时间的汪洋大海中的灯塔。
∴△ABC是等边三角形.
6、求证：如果三角形一个外角的平分线 平行于三角形的一边，那么这个三角形 是等腰三角形。
已知：∠EAC是△ABC的外角，∠1=∠2，
AD∥BC，求证：AB=AC
B
E A1
2D
C
7.已知：如图,在等边三角形ABC的AC边上的取中点 D,BC的延长线上取一点E,使得CE=CD.求证：BD=DE.
谢谢观赏
You made my day!
我们，还在路上……
3cm
3cm
事实上，如图，在△ABC中，∠B=∠C.
沿过点A的直线把∠BAC对折，
得∠BAC的平分线AD交BC于点D， 则∠1=∠2. 又∠B=∠C，
由三角形内角和的性质得
∠ADB=∠ADC. 沿AD所在直线折叠，
12
由于∠ADB=∠ADC，∠1=∠2，
所以射线DB与射线DC重合，
《等腰三角形(2)》系列课件
求证:BD=CE.
D
C
证明: ∵AB=AC(已知), ∴∠ABC=∠ACB(等边对等角). A 又∵∠1= 1∠ABC,∠2= 1 ∠ACB(角平分 2 2 线的定义) D E ∴∠1=∠2 1 2 C B 在△BDC与△CEB中 ∵ ∠ACB=∠ABC（已证）∴△BDC≌△CEB（ASA）. BC=CB（公共边）, ∴BD=CE ∠1=∠2（已证）,
1.1 等腰三角形（2）
复习：
等腰三角形的性质： 1、等腰三角形的两个底角相等. 简称：等边对等角 2、等腰三角形顶角的平分线,底边上的 B 中线底边上的高互相重合. 简称： 三线合一
A
1 2
D
C
探一探
在等腰三角形中作出一些线段（如角平 分线、中线、高等）.你能发现其中的一些 相等的线段吗?你能证明你的结论吗?
A
B
C
∴∠A=∠B=∠C.
在△ABC中 ∵∠A+∠B+∠C＝180°，
∴∠A=∠B=∠C＝60°.
练一练
1.求等边三角形两条中线相交所成锐角的度数.
解： ∵等边三角形三线合一
∴CD平分∠ACB，BE平分∠ABC CD ⊥AB，BE ⊥AC
A
D B
O
E C
1 1 ∴ ∠ABE= ∠ABC= ×60°=30° 2 2
证一证
2、证明:等腰三角形两腰上的中线相等. 已知:如图,在△ABC中AB=AC, BD,CE是△ABC两腰上的中线. E
A D
求证:BD=CE. B C 证明：∵ AD= 1 AC,AE= 1 AB ,AB=AC ∴AD=AE 2 2 在△ABD与△ACE中 ∵ AB=AC(已知), ∠A=∠A（公共角） ∴△ABD≌△ACE（SAS）. ∴BD=CE AD=AE（已证）
《等腰三角形》PPT教学课件
思考 将等腰三角形的性质用于等边三角形，你能 得到什么结论？
结合等腰三角形的性质，你能填出等边三角形对应 的结论吗？
图形
等腰 三角形
等边 三角形
边
两边相等 （定义）
三边相等 （定义）
角
两底角相等 （等边对等角）
轴对称图形
是（三线合一） 一条对称轴
？
？
结合等腰三角形的性质，你能填出等边三角形对应 的结论吗？
是（三线合一） 一条对称轴
相等
是（三线合一）
每个角都等于60° 三条对称轴
对“等边三角形的三个内角都相等，并且每一个角 都等于60°”这一结论进行证明.
已知：△ABC 是等边三角形 求证：∠A =∠B =∠C
=60°．
证明：∵ △ABC 是等边三角形，
∴ BC =AC，BC =AB．
A
∴ ∠A =∠B，∠A =∠C ．
《等腰三角形》教学实用课件（PPT优 秀课件 ）
已知：在△ABC 中，∠A=∠B=∠C．求证：△ABC 是等边三角形．
证明：∵ ∠A =∠B，∠B =∠C ，
∴ BC =AC， AC =AB．
C
∴ AB =BC =AC．
∴ △ABC 是等边三角形．
A
B
《等腰三角形》教学实用课件（PPT优 秀课件 ）
∴ ∠A =∠B =∠C ．
∵ ∠A +∠B +∠C =180°，
∴ ∠A =60°．
B
C
∴ ∠A =∠B =∠C =60°．
等边三角形的性质： 等边三角形的三个内角都相等，并且每一个角都等 于60°.
A
符号语言： ∵ △ABC 是等边三角形， ∴ ∠A =∠B =∠C =60°．
结合等腰三角形的性质，你能填出等边三角形对应 的结论吗？
图形
等腰 三角形
等边 三角形
边
两边相等 （定义）
三边相等 （定义）
角
两底角相等 （等边对等角）
轴对称图形
是（三线合一） 一条对称轴
？
？
结合等腰三角形的性质，你能填出等边三角形对应 的结论吗？
是（三线合一） 一条对称轴
相等
是（三线合一）
每个角都等于60° 三条对称轴
对“等边三角形的三个内角都相等，并且每一个角 都等于60°”这一结论进行证明.
已知：△ABC 是等边三角形 求证：∠A =∠B =∠C
=60°．
证明：∵ △ABC 是等边三角形，
∴ BC =AC，BC =AB．
A
∴ ∠A =∠B，∠A =∠C ．
《等腰三角形》教学实用课件（PPT优 秀课件 ）
已知：在△ABC 中，∠A=∠B=∠C．求证：△ABC 是等边三角形．
证明：∵ ∠A =∠B，∠B =∠C ，
∴ BC =AC， AC =AB．
C
∴ AB =BC =AC．
∴ △ABC 是等边三角形．
A
B
《等腰三角形》教学实用课件（PPT优 秀课件 ）
∴ ∠A =∠B =∠C ．
∵ ∠A +∠B +∠C =180°，
∴ ∠A =60°．
B
C
∴ ∠A =∠B =∠C =60°．
等边三角形的性质： 等边三角形的三个内角都相等，并且每一个角都等 于60°.
A
符号语言： ∵ △ABC 是等边三角形， ∴ ∠A =∠B =∠C =60°．
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
证一证
3 、证明:等腰三角形两腰上的高相等. 已知:如图,在△ABC中AB=AC, BD,CE是△ABC两腰上的高 E A D
求证:BD=CE. C B 证明:在△ABD与△ACE中 ∵∠A=∠A （公共角） ∠ ADB=∠AEC=90°（高的定义） AB=AC（已知）∴△ABD≌△ACE（AAS）∴BD=CE
1.1 等腰三角形（2）
复习：
等腰三角形的性质： 1、等腰三角形的两个底角相等. 简称：等边对等角 2、等腰三角形顶角的平分线,底边上的 B 中线底边上的高互相重合. 简称： 三线合一
A
1 2
D
C
探一探
在等腰三角形中作出一些线段（如角平 分线、中线、高等）.你能发现其中的一些 相等的线段吗?你能证明你的结论吗?
证一证
2、证明:等腰三角形两腰上的中线相等. 已知:如图,在△ABC中AB=AC, BD,CE是△ABC两腰上的中线. E
A D
求证:BD=CE. B C 证明：∵ AD= 1 AC,AE= 1 AB ,AB=AC ∴AD=AE 2 2 在△ABD与△ACE中 ∵ AB=AC(已知), ∠A=∠A（公共角） ∴△ABD≌△ACE（SAS）. ∴BD=CE AD=AE（已证）
4
E
C
作业：
习题1.2 第 2、3、4题.
想一想
等边三角形是特殊的等腰三角形，那么等 边三角形的内角有什么特征呢？
定理：等边三角形三个内角都相等并且每个内角都等于60°.
已知：如图，在△ABC中，AB=BC=AC。 求证：∠A=∠B=∠C=60°. 证明：∵AB=AC，
A
∴∠B=∠C(等边对等角).
又∵AC=BC， ∴∠A=∠B(等边对等角). ∴∠A=∠B=∠C. 在△ABC中，∵∠A+∠B+∠C＝180°， ∴∠A=∠B=∠C＝60°.
∠ABE+ ∠BDC+ ∠BOD=180° 有30°+90°+ ∠BOD=180 ° ∴ ∠BOD=60 °
练一练
2.如图，在△ABC中，D，E是BC的三等分点，且 △ADE是等边三角形，求∠BAC的度数.
解： ∵ △ADE是等边三角形 ∴∠ADE=∠AED=∠DAE=60°，AD=AE=DE 又∵∠ADE=∠1+∠3=60° ∠AED= ∠2+ ∠4=60° 3 ∴∠1+∠3 +∠2+ ∠4=120° B 又∵点D、E是BC的三等分点 ∴CE=DE=BD ∴AD=BD，AE=CE ∴ ∠1=∠3， ∠2=∠4 则∠1+∠3 +∠2+ ∠4 =2 ∠1+2 ∠2=2（ ∠1+ ∠2）=120° 即∠1+ ∠2=60° ∴ ∠BAC= ∠1+ ∠2+∠DAE=60°+60°=120°. A 1 D 2
n
4
4
n
E B
●
●
D C
议一议
2.已知:如图,在△ABC中,AB=AC
如果AD= 1 AC,AE= 1 AB,那么BD=CE吗?
3 3 如果AD= 1 AC,AE= 1 AB呢? 4 4
A
E B
n n
由此你能得到一个什么结论?
D C
结论：在△ABC中,AB=AC，如果AD= 1 AC,AE= 1 AB 那么BD=CE
议一议
1.已知:如图,在△ABБайду номын сангаас中,AB=AC
如果∠ABD=1∠ABC,∠ACE=1∠ACB，那么BD=CE吗？ 3 3 A 如果∠ABD= 1∠ABC,∠ACE= 1∠ACB呢? 由此你能得到一个什么结论? 结论：在△ABC中,AB=AC，如果
∠ABD= 1 ∠ABC,∠ACE= 1 ∠ACB 那么BD=CE
求证:BD=CE.
D
C
证明: ∵AB=AC(已知), ∴∠ABC=∠ACB(等边对等角). A 又∵∠1= 1∠ABC,∠2= 1 ∠ACB(角平分 2 2 线的定义) D E ∴∠1=∠2 1 2 C B 在△BDC与△CEB中 ∵ ∠ACB=∠ABC（已证）∴△BDC≌△CEB（ASA）. BC=CB（公共边）, ∴BD=CE ∠1=∠2（已证）,
B
C
练一练
1.求等边三角形两条中线相交所成锐角的度数.
解： ∵等边三角形三线合一
∴CD平分∠ACB，BE平分∠ABC CD ⊥AB，BE ⊥AC
A
D B
O
E C
1 1 ∴ ∠ABE= ∠ABC= 2 2
由CD ⊥AB可知 ∠BDC=90° 在△BOD中，
×60°=30°
已知△ABC是等边三角形，CD、 BE分别是AB、AC的中线，且 相交于点O，求∠BOD的度数.
结论： 1、等腰三角形两底角的平分线相等. 2、等腰三角形两腰上的中线相等. 3、等腰三角形两腰上的高相等.
A
E B D C B E A D A BD=CE
E
CB
D
C
证一证
证明:等腰三角形两底角的平分线相等.
已知:如图,在△ABC中,AB=AC, BD,CE是△ABC角平分线. A E B
1 2