各种排序方法复杂度总结归纳
各种排序的时间复杂度

排序算法所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
分类在计算机科学所使用的排序算法通常被分类为:计算的复杂度(最差、平均、和最好表现),依据串列(list)的大小(n)。
一般而言,好的表现是O。
(n log n),且坏的行为是Ω(n2)。
对於一个排序理想的表现是O(n)。
仅使用一个抽象关键比较运算的排序算法总平均上总是至少需要Ω(n log n)。
记忆体使用量(以及其他电脑资源的使用)稳定度:稳定排序算法会依照相等的关键(换言之就是值)维持纪录的相对次序。
也就是一个排序算法是稳定的,就是当有两个有相等关键的纪录R和S,且在原本的串列中R出现在S之前,在排序过的串列中R也将会是在S之前。
一般的方法:插入、交换、选择、合并等等。
交换排序包含冒泡排序(bubble sort)和快速排序(quicksort)。
选择排序包含shaker排序和堆排序(heapsort)。
当相等的元素是无法分辨的,比如像是整数,稳定度并不是一个问题。
然而,假设以下的数对将要以他们的第一个数字来排序。
(4, 1) (3, 1) (3, 7) (5, 6)在这个状况下,有可能产生两种不同的结果,一个是依照相等的键值维持相对的次序,而另外一个则没有:(3, 1) (3, 7) (4, 1) (5, 6) (维持次序)(3, 7) (3, 1) (4, 1) (5, 6) (次序被改变)不稳定排序算法可能会在相等的键值中改变纪录的相对次序,但是稳定排序算法从来不会如此。
不稳定排序算法可以被特别地时作为稳定。
作这件事情的一个方式是人工扩充键值的比较,如此在其他方面相同键值的两个物件间之比较,就会被决定使用在原先资料次序中的条目,当作一个同分决赛。
然而,要记住这种次序通常牵涉到额外的空间负担。
排列算法列表在这个表格中,n是要被排序的纪录数量以及k是不同键值的数量。
稳定的冒泡排序(bubble sort)— O(n2)鸡尾酒排序 (Cocktail sort, 双向的冒泡排序) — O(n2)插入排序(insertion sort)— O(n2)桶排序(bucket sort)— O(n); 需要 O(k) 额外记忆体计数排序 (counting sort) — O(n+k); 需要 O(n+k) 额外记忆体归并排序(merge sort)— O(n log n); 需要 O(n) 额外记忆体原地归并排序— O(n2)二叉树排序(Binary tree sort)— O(n log n); 需要 O(n) 额外记忆体鸽巢排序 (Pigeonhole sort) — O(n+k); 需要 O(k) 额外记忆体基数排序(radix sort)—O(n·k); 需要 O(n) 额外记忆体Gnome sort — O(n2)Library sort — O(n log n) with high probability, 需要(1+ε)n 额外记忆体不稳定选择排序(selection sort)— O(n2)希尔排序(shell sort)— O(n log n) 如果使用最佳的现在版本Comb sort — O(n log n)堆排序(heapsort)— O(n log n)Smoothsort — O(n log n)快速排序(quicksort)—O(n log n) 期望时间, O(n2) 最坏情况; 对於大的、乱数串列一般相信是最快的已知排序Introsort — O(n log n)Patience sorting —O(n log n + k) 最外情况时间, 需要额外的 O(n + k) 空间, 也需要找到最长的递增子序列(longest increasing subsequence)不实用的排序算法Bogo排序—O(n × n!) 期望时间, 无穷的最坏情况。
各种排序方法总结

选择排序、快速排序、希尔排序、堆排序不是稳定的排序算法,冒泡排序、插入排序、归并排序和基数排序是稳定的排序算法。
冒泡法:这是最原始,也是众所周知的最慢的算法了。
他的名字的由来因为它的工作看来象是冒泡:复杂度为O(n*n)。
当数据为正序,将不会有交换。
复杂度为O(0)。
直接插入排序:O(n*n)选择排序:O(n*n)快速排序:平均时间复杂度log2(n)*n,所有内部排序方法中最高好的,大多数情况下总是最好的。
归并排序:l og2(n)*n堆排序:l og2(n)*n希尔排序:算法的复杂度为n的1.2次幂这里我没有给出行为的分析,因为这个很简单,我们直接来分析算法:首先我们考虑最理想的情况1.数组的大小是2的幂,这样分下去始终可以被2整除。
假设为2的k次方,即k=log2(n)。
2.每次我们选择的值刚好是中间值,这样,数组才可以被等分。
第一层递归,循环n次,第二层循环2*(n/2)......所以共有n+2(n/2)+4(n/4)+...+n*(n/n) = n+n+n+...+n=k*n=log2(n)*n所以算法复杂度为O(lo g2(n)*n) 其他的情况只会比这种情况差,最差的情况是每次选择到的midd le都是最小值或最大值,那么他将变成交换法(由于使用了递归,情况更糟)。
但是你认为这种情况发生的几率有多大??呵呵,你完全不必担心这个问题。
实践证明,大多数的情况,快速排序总是最好的。
如果你担心这个问题,你可以使用堆排序,这是一种稳定的O(log2(n)*n)算法,但是通常情况下速度要慢于快速排序(因为要重组堆)。
各种排序算法的时间复杂度和空间复杂度(阿里)
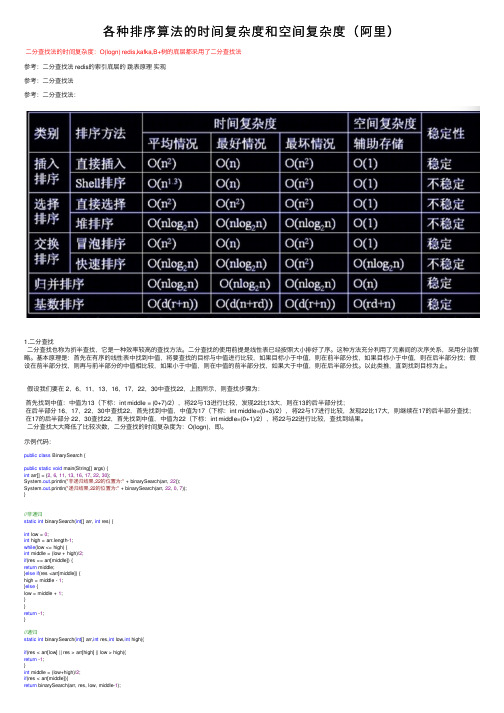
各种排序算法的时间复杂度和空间复杂度(阿⾥)⼆分查找法的时间复杂度:O(logn) redis,kafka,B+树的底层都采⽤了⼆分查找法参考:⼆分查找法 redis的索引底层的跳表原理实现参考:⼆分查找法参考:⼆分查找法:1.⼆分查找⼆分查找也称为折半查找,它是⼀种效率较⾼的查找⽅法。
⼆分查找的使⽤前提是线性表已经按照⼤⼩排好了序。
这种⽅法充分利⽤了元素间的次序关系,采⽤分治策略。
基本原理是:⾸先在有序的线性表中找到中值,将要查找的⽬标与中值进⾏⽐较,如果⽬标⼩于中值,则在前半部分找,如果⽬标⼩于中值,则在后半部分找;假设在前半部分找,则再与前半部分的中值相⽐较,如果⼩于中值,则在中值的前半部分找,如果⼤于中值,则在后半部分找。
以此类推,直到找到⽬标为⽌。
假设我们要在 2,6,11,13,16,17,22,30中查找22,上图所⽰,则查找步骤为:⾸先找到中值:中值为13(下标:int middle = (0+7)/2),将22与13进⾏⽐较,发现22⽐13⼤,则在13的后半部分找;在后半部分 16,17,22,30中查找22,⾸先找到中值,中值为17(下标:int middle=(0+3)/2),将22与17进⾏⽐较,发现22⽐17⼤,则继续在17的后半部分查找;在17的后半部分 22,30查找22,⾸先找到中值,中值为22(下标:int middle=(0+1)/2),将22与22进⾏⽐较,查找到结果。
⼆分查找⼤⼤降低了⽐较次数,⼆分查找的时间复杂度为:O(logn),即。
⽰例代码:public class BinarySearch {public static void main(String[] args) {int arr[] = {2, 6, 11, 13, 16, 17, 22, 30};System.out.println("⾮递归结果,22的位置为:" + binarySearch(arr, 22));System.out.println("递归结果,22的位置为:" + binarySearch(arr, 22, 0, 7));}//⾮递归static int binarySearch(int[] arr, int res) {int low = 0;int high = arr.length-1;while(low <= high) {int middle = (low + high)/2;if(res == arr[middle]) {return middle;}else if(res <arr[middle]) {high = middle - 1;}else {low = middle + 1;}}return -1;}//递归static int binarySearch(int[] arr,int res,int low,int high){if(res < arr[low] || res > arr[high] || low > high){return -1;}int middle = (low+high)/2;if(res < arr[middle]){return binarySearch(arr, res, low, middle-1);}else if(res > arr[middle]){return binarySearch(arr, res, middle+1, high);}else {return middle;}}}其中冒泡排序加个标志,所以最好情况下是o(n)直接选择排序:排序过程:1 、⾸先在所有数据中经过 n-1次⽐较选出最⼩的数,把它与第 1个数据交换,2、然后在其余的数据内选出排序码最⼩的数,与第 2个数据交换...... 依次类推,直到所有数据排完为⽌。
快排复杂度及其证明

快排复杂度及其证明快速排序(Quicksort)是一种经典的排序算法,其平均时间复杂度为O(nlogn)。
该算法的核心思想是通过递归地将数组分割成较小的子数组,然后分别对子数组进行排序。
快速排序的步骤如下:首先选择一个基准元素,然后将数组中比基准元素小的元素放在基准元素的左边,将比基准元素大的元素放在基准元素的右边。
接着递归地对左右两个子数组进行排序,直到整个数组有序。
快速排序的时间复杂度分析如下:在最好情况下,每次划分都能平分数组,时间复杂度为O(nlogn);在最坏情况下,每次划分只能将数组分成一个元素和其余元素两部分,时间复杂度为O(n^2)。
然而,通过随机选择基准元素或者使用三数取中法可以避免最坏情况的发生,从而保证快速排序的平均时间复杂度为O(nlogn)。
快速排序的时间复杂度证明可以通过数学归纳法进行推导。
假设对n个元素的数组进行快速排序的时间复杂度为T(n),则有:T(n) = 2T(n/2) + O(n)。
其中2T(n/2)表示对左右两个子数组进行排序的时间复杂度,O(n)表示划分数组的时间复杂度。
根据主定理(Master Theorem)可知,对于递推式T(n) = aT(n/b) + f(n),其中a>=1,b>1,f(n)是多项式,有以下三种情况:1. 若f(n) = O(n^d),其中d<logba,则T(n) = O(n^logba);2. 若f(n) = Θ(n^d * log^k n),其中d=logba,则T(n) = O(n^d * log^(k+1) n);3. 若f(n) = Ω(n^d),其中d>logba,则T(n) = O(f(n))。
根据快速排序的递推式T(n) = 2T(n/2) + O(n),可以得到a=2,b=2,f(n)=O(n)。
因此,根据主定理可知,快速排序的时间复杂度为O(nlogn)。
快速排序是一种时间复杂度为O(nlogn)的高效排序算法,通过合理选择基准元素和递归地划分子数组,可以在平均情况下实现较快的排序速度。
【十大经典排序算法(动图演示)】 必学十大经典排序算法

【十大经典排序算法(动图演示)】必学十大经典排序算法0.1 算法分类十种常见排序算法可以分为两大类:比较类排序:通过比较来决定元素间的相对次序,由于其时间复杂度不能突破O(nlogn),因此也称为非线性时间比较类排序。
非比较类排序:不通过比较来决定元素间的相对次序,它可以突破基于比较排序的时间下界,以线性时间运行,因此也称为线性时间非比较类排序。
0.2 算法复杂度0.3 相关概念稳定:如果a原本在b前面,而a=b,排序之后a仍然在b的前面。
不稳定:如果a原本在b的前面,而a=b,排序之后a 可能会出现在b 的后面。
时间复杂度:对排序数据的总的操作次数。
反映当n变化时,操作次数呈现什么规律。
空间复杂度:是指算法在计算机内执行时所需存储空间的度量,它也是数据规模n的函数。
1、冒泡排序(Bubble Sort)冒泡排序是一种简单的排序算法。
它重复地走访过要排序的数列,一次比较两个元素,如果它们的顺序错误就把它们交换过来。
走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。
这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
1.1 算法描述比较相邻的元素。
如果第一个比第二个大,就交换它们两个;对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对,这样在最后的元素应该会是最大的数;针对所有的元素重复以上的步骤,除了最后一个;重复步骤1~3,直到排序完成。
1.2 动图演示1.3 代码实现1.unction bubbleSort(arr) {2. varlen = arr.length;3. for(vari = 0; i arr[j+1]) {// 相邻元素两两对比6. vartemp = arr[j+1];// 元素交换7. arr[j+1] = arr[j];8. arr[j] = temp;9. }10. }11. }12. returnarr;13.}2、选择排序(Selection Sort)选择排序(Selection-sort)是一种简单直观的排序算法。
时间复杂度排序大小口诀

时间复杂度排序大小口诀嘿,朋友们,今天咱们聊聊时间复杂度这个话题。
哎呀,这个听上去可能有点高深,但别担心,我来给你捋一捋,保证你听得懂,笑得出来!想象一下,时间复杂度就像咱们生活中的时间管理。
有时候你想做一件事,结果发现一拖再拖,真是急得像热锅上的蚂蚁。
先说说最简单的,那就是常数时间复杂度,记得用O(1)来表示哦。
这就像你去买咖啡,喝一口就能决定味道如何,不管你等了多久,结果都一样。
这种情况下,无论你前面等了多长时间,最后的结果都没变,简单又直接。
是不是觉得很爽快?接下来是对数时间复杂度,O(log n)。
你可以把它想象成是你在翻书,一开始你可能会从头到尾翻一遍,但其实你只需要翻一翻就能找到想要的内容。
就像你在找一本书,找得特别麻烦,结果发现书架上有个小标签,哎呀,直接跳到目标,真是太方便了。
这种方法让你省时省力,简直是居家必备的小技巧。
然后是线性时间复杂度,O(n)。
这就好比你在超市购物,要拿一袋袋的东西,一样样放进购物车,哎,没办法,这就是你不得不面对的事情。
假如你有十件东西,你就得走十趟,这种情况下,你的时间成本是直线增加的,跟着你买的东西多少成正比,实在没办法,只能一步一步走。
咱们聊聊线性对数时间复杂度,O(n log n)。
你可以把它想象成是在举办一个派对,得提前发邀请。
你先要决定谁来,再去一一联系,搞定之后再准备吃的。
虽然每个人的邀请都需要时间,但人数越多,分配的工作量就越复杂,所以最后还是得付出一些时间来准备。
这种复杂度在排序算法中常常出现,比如说归并排序和快速排序,让人不得不佩服程序员的智慧。
然后就是平方时间复杂度,O(n²)。
想象一下你在一个班级里,每个人都要跟其他同学打招呼,结果你就得去和每一个人握手。
假设班里有十个人,你就得握手九次,然后第二个人又得握手八次……这下就得算上所有的握手次数,结果是一堆人都快握不动了。
这样的复杂度简直让人心累,不过在一些简单的算法里,这也算是正常操作了。
排序的五种方法

排序的五种方法一、冒泡排序。
冒泡排序就像水里的泡泡一样,大的泡泡慢慢往上冒。
它的原理是比较相邻的元素,如果顺序不对就交换位置。
比如说有一堆数字,就从第一个数字开始,和它后面的数字比,如果前面的比后面的大,就把它们换过来。
这样一轮一轮地比较,每一轮都会把最大的数字像泡泡一样“冒”到最后面。
这个方法很简单,但是如果数据很多的话,就会比较慢啦。
就像一个小蜗牛,虽然能到达终点,但是速度有点慢哟。
二、选择排序。
选择排序呢,就像是在一群小伙伴里选最高的那个。
它先在未排序的序列里找到最小(或者最大)的元素,然后把这个元素放到已排序序列的末尾。
就好比在一群小朋友里,先找出最矮的那个小朋友,让他站在最前面,然后再在剩下的小朋友里找最矮的,依次类推。
这个方法比冒泡排序在某些情况下会快一点,不过它也有自己的小脾气,不是在所有数据情况下都超级高效的呢。
三、插入排序。
插入排序就像是我们平时整理扑克牌一样。
假设我们手里已经有一部分排好序的牌,然后拿到一张新牌,就把这张新牌插入到合适的位置。
对于一组数字也是这样,从第二个数字开始,把它插入到前面已经排好序的数字里合适的地方。
如果这个数字比前面的大,就往后放,如果比前面的小,就往前找合适的位置插进去。
这个方法在数据比较有序的情况下,速度还是挺快的,就像一个聪明的小助手,能很快地把东西整理好。
四、快速排序。
快速排序就像是一个很厉害的魔法师。
它先选一个基准值,然后把数组里的数字分成两部分,一部分比基准值小,一部分比基准值大。
然后再对这两部分分别进行同样的操作,就像把一个大问题分成很多小问题,然后各个击破。
这个方法在大多数情况下速度都非常快,就像一阵旋风,能迅速把数据排好序。
不过它也有点小复杂,就像魔法师的魔法一样,不是那么容易一下子就完全理解的呢。
五、归并排序。
归并排序就像是两个队伍在合并。
它把数组分成两部分,然后分别对这两部分进行排序,排好序之后再把这两部分合并起来。
这个过程就像是两个已经排好队的小队伍,要合并成一个大队伍,在合并的时候还要保证顺序正确。
堆排序算法复杂度分析及优化思路

堆排序算法复杂度分析及优化思路堆排序是一种高效的排序算法,它的核心思想是通过构建堆来实现排序过程。
在本文中,我们将对堆排序算法的时间复杂度进行分析,并提出一些优化思路。
一、堆排序算法简介堆排序是一种基于二叉堆的排序算法,它包括两个基本步骤:建堆和排序。
建堆的过程是将一个无序序列构建成一个堆,排序的过程是将堆顶元素和堆底元素交换,并将剩余元素重新构建成堆。
二、堆排序算法的时间复杂度分析1. 建堆的时间复杂度:建堆的过程包括从最后一个非叶子节点开始进行下沉操作,因此建堆的时间复杂度为O(n),其中n为待排序序列的长度。
2. 排序的时间复杂度:排序的过程包括将堆顶元素和堆底元素交换,并对剩余元素进行下沉操作。
每次交换后,堆的大小减少1,因此需要进行n-1次交换。
而每次交换和下沉的操作的时间复杂度都是O(logn),因此排序的时间复杂度为O(nlogn)。
综上所述,堆排序算法的时间复杂度为O(nlogn)。
三、堆排序算法的空间复杂度分析堆排序算法的空间复杂度主要取决于堆的建立过程中所使用的辅助空间。
在建堆的过程中,需要使用一个大小为n的辅助数组来存储待排序序列。
因此,堆排序算法的空间复杂度为O(n)。
四、堆排序的优化思路虽然堆排序算法的时间复杂度较好,但在实际应用中,我们可以通过以下几种方式来进一步提高算法的性能。
1. 优化建堆过程:建堆的过程中,我们可以对所有非叶子节点进行下沉操作,但实际上,只有前一半的非叶子节点需要下沉操作。
因此,在建堆过程中,我们可以只对前一半的非叶子节点进行下沉操作,减少了一些不必要的操作,提高了建堆的效率。
2. 优化排序过程:在排序的过程中,每一次交换堆顶元素和堆底元素后,需要重新进行下沉操作。
然而,每次下沉操作都需要遍历堆的高度,时间复杂度为O(logn)。
可以考虑采用堆化的方式,即将堆底元素移至堆顶后,直接对堆顶元素进行下沉操作,减少了遍历的次数,进而提高了排序的效率。
3. 优化空间复杂度:在实际应用中,我们可以使用原地排序的方式来优化空间复杂度。
排序方法的空间复杂度

排序方法的空间复杂度
排序方法的空间复杂度是指算法所需的额外空间与输入数据规模之间的关系。
常用的排序算法的空间复杂度如下:
1. 冒泡排序、插入排序、选择排序的空间复杂度为O(1),即常数级别。
2. 快速排序、归并排序、希尔排序的空间复杂度为O(nlogn),需要递归调用和使用额外的存储空间。
3. 堆排序的空间复杂度为O(1),仅仅需要一个辅助变量来交换元素。
4. 基数排序、计数排序、桶排序的空间复杂度为O(n+k),其中n是元素个数,k是元素的取值范围。
需要注意的是,空间复杂度并不是算法的时间复杂度,它仅仅描述了算法所需的额外空间,与算法的运行时间无关。
排序复杂度总结

排序复杂度总结
嘿,朋友们!今天咱就来唠唠排序复杂度总结。
先说说冒泡排序吧,就好比一群人站成一排,个矮的慢慢往前面挪,一次比较两个,把小的往前放。
比如说咱班同学排队,张三比李四矮,就把张三换到前面去,这一趟趟的重复,最后就排得整整齐齐啦。
这冒泡排序简单易懂,但效率不算高哦!
再看插入排序,这就跟打扑克时整理手牌差不多。
拿到一张牌,就找个合适的位置插进去,慢慢就把牌整理好了。
要是整理一堆乱七八槽的数字,就一个个往里插呗。
那快速排序可厉害啦!它像是一个聪明的指挥家,迅速地把一群人分成两拨,高个子一边,矮个子一边,然后再在这两拨里继续分。
就像分小组比赛,迅速地就把队伍分得明明白白。
归并排序呢,就好像搭积木,先把小部分搭好,再一块一块地拼成完整的形状。
它虽然慢点,但效果还不错哦!
堆排序吧,就像个神奇的小山,把东西堆起来,再按顺序取出来。
哎呀呀,这些排序复杂度可真是各有千秋呀!那咱说到底哪个最好用呢?其实啊,这得看具体情况啊!有时候简单的就是最好的,有时候就得用厉害的快速排序。
没有绝对的好坏,只有适不适合。
所以啊,咱得根据实际需求来选择排序方法,不然就像穿错鞋子,那多别扭呀!你们说是不是这个理儿呢?。
各种排序方式和复杂度分析

#include <stdio.h>#define N 10/*************直接插入排序法******************/ void insertSort(int *a) { //时间复杂度:O(n^2) int i, j, t;for(i=1; i<N; i++) {if(a[i] < a[i-1]) {t = a[i];for(j=i-1; j>=0; j--) {if(a[j] > t) a[j+1] = a[j];else break;}a[j+1] = t;}}}/****************希尔排序*********************/ void shellInsert(int *a, int dk) {int i, j, t;for(i=dk; i< N; i++) {if(a[i] < a[i - dk]) {t = a[i];for(j=i-dk; j>=0; j-=dk) {if(a[j] > t) a[j+dk] = a[j];else break;}a[j+dk] = t;}}}void shellSort(int *a) { //时间复杂度:O(n^1.3) int i;int dlka[3] = {5, 3, 1};for(i=0; i<3; i++) shellInsert(a, dlka[i]);}/****************冒泡排序*********************/void bubbleSort(int *a) { //时间复杂度:O(n^2)int i, j, t;for(i=0; i<N;i++) {for(j=0; j<N-i-1; j++) {if(a[j] > a[j+1]) {t = a[j]; a[j] = a[j+1]; a[j+1] = t;}}}}/****************快速排序*********************/int partition(int *a, int low, int high) {int pivotkey = a[low];while(low < high) {while(low < high && a[high] >= pivotkey) high--;a[low] = a[high];while(low < high && a[low] <= pivotkey) low++;a[high] = a[low];}a[low] = pivotkey;return low;}void qSort(int *a, int low, int high) {int pivotloc;if(low < high) {pivotloc = partition(a, low, high);qSort(a, low, pivotloc - 1); qSort(a, pivotloc + 1, high);}}void quickSort(int *a) {qSort(a, 0, N-1);}/****************选择排序*********************/void selectSort(int *a) { //时间复杂度:O(n^2)int i, j, t, k;for(i=0; i<N; i++) {k = i;for(j=i; j<N; j++) if(a[j] < a[k]) k = j;if(i != k) {t = a[i]; a[i] = a[k]; a[k] = t;}}}/****************堆排序***********************/void heapAdjust(int *a, int s, int n) {int j, rc = a[s];for(j=2*s+1; j<n; j*=2) {if(j < n - 1 && a[j] < a[j+1]) j++;if(rc > a[j]) break;a[s] = a[j]; s = j;}a[s] = rc;}void heapSort(int *a) {int t, i;for(i=N/2-1; i>=0; i--) heapAdjust(a, i, N);//创建大顶堆for(i=N-1; i>0; i--) {t = a[0]; a[0] = a[i]; a[i] = t;heapAdjust(a, 0, i-1);}}/****************归并排序*********************/void merge(int *a, int *b, int i, int m, int n) {int t, k, j;for(j=m+1, k=i; i<=m && j<=n; k++) {if(a[i] < a[j]) b[k] = a[i++];else b[k] = a[j++];}if(i <= m) for(t=i; t<=m; t++)b[k++] = a[t];if(j <= n) for(t=j; t<=n; t++) b[k++] = a[t];}void mSort(int *a, int *b, int s, int t) {int m; static int b1[N]; //只初始化一次if(s == t) b[s] = a[s];else {m = (s + t) / 2; //将a[s..t]平分为a[s..m]和a[m+1..t]mSort(a, b1, s, m); //递归地将a[s..m]归并为有序的b1[s..m]mSort(a, b1, m+1, t); //递归地将a[m+1..t]归并为有序的b1[m+1..t]merge(b1, b, s, m, t); //将b1[s..m]和b1[m+1..t]归并到b[s..m] }}void mergeSort(int *a) {mSort(a, a, 0, N-1);}/*****************main函数*******************/ int main() {int i;int a[N] = {12, 23, 32, 12, 29, 62, 19, 90, 27, 56};printf("原数列为:");for(i=0; i<N; i++) printf("%d ", a[i]);shellSort(a);printf("\n现数列为:");for(i=0; i<N; i++) printf("%d ", a[i]);printf("\n");return 0;}。
计数排序时间复杂度计算方法

计数排序时间复杂度计算方法计数排序是一种非比较排序算法,适用于一定范围内的整数排序。
它的时间复杂度可以通过以下步骤进行计算。
1. 算法步骤回顾首先,我们先回顾一下计数排序的算法步骤:1.找出待排序数组中的最大值,记为max。
2.创建一个计数数组count,长度为max+1,并将所有元素初始化为0。
3.遍历待排序数组,统计每个元素出现的次数,并将其存入计数数组相应的位置。
4.对计数数组进行部分求和操作,使得每个位置存储的值为其对应元素在排序结果中的最终位置。
5.创建一个与待排序数组相同长度的结果数组result。
6.遍历待排序数组,将每个元素根据计数数组中的值,放入结果数组相应的位置。
7.将结果数组的内容复制回待排序数组,完成排序。
2. 时间复杂度分析计数排序的时间复杂度取决于两个因素:待排序数组的长度n和待排序数组中的最大值max。
(1) 初始化计数数组在计数排序的第二步中,需要创建一个计数数组count,并将所有元素初始化为0。
这个操作的时间复杂度为O(k),其中k为max+1,即计数数组的长度。
因为计数数组的长度与待排序数组的最大值有关,所以这个操作的时间复杂度可以看作是O(max)。
(2) 统计元素出现次数在计数排序的第三步中,需要遍历待排序数组,统计每个元素出现的次数,并将其存入计数数组相应的位置。
这个操作的时间复杂度为O(n),其中n为待排序数组的长度。
(3) 求和操作在计数排序的第四步中,需要对计数数组进行部分求和操作,使得每个位置存储的值为其对应元素在排序结果中的最终位置。
这个操作的时间复杂度为O(k),其中k为计数数组的长度,即O(max+1)。
(4) 生成排序结果在计数排序的第六步中,需要遍历待排序数组,将每个元素根据计数数组中的值,放入结果数组相应的位置。
这个操作的时间复杂度为O(n),其中n为待排序数组的长度。
(5) 复制结果数组在计数排序的第七步中,需要将结果数组的内容复制回待排序数组,完成排序。
时间复杂度大小排序口诀

时间复杂度大小排序口诀在这个信息爆炸的时代,时间就像一条飞速奔流的河流,我们常常在思考如何让它流淌得更快些。
说到效率,时间复杂度就是我们不能忽视的话题。
你知道吗?它就像一道神秘的公式,帮我们分析算法的好坏。
咱们今天就来聊聊这个“复杂度”的故事,顺便给你一套排序口诀,保证让你轻松记住。
想象一下,假如你在一个热闹的集市上,摆摊卖东西。
你的摊位前排起了长龙,顾客们急得像热锅上的蚂蚁。
这个时候,时间复杂度就像一块天平,帮助你衡量每个顾客在你摊位前所花的时间。
最简单的情况是O(1),也就是常数时间,顾客们像闪电一样走过来,买完东西就走,爽快得很。
想想看,那样多好,买卖皆欢喜。
再往上走一步,O(log n)就来了。
这就像是你有一把神奇的钥匙,每次进店都能直接跳过一半的顾客。
越来愉快,这种效率简直就是上天的恩赐!可你知道,这样的情况可不常见,更多时候我们需要面对O(n)的线性时间复杂度。
想象一下,你在拥挤的地铁上,得一个个地挤过人群,虽然有点磨蹭,但总能到达目的地,哈哈,真是有点心累。
然后,O(n log n)就像是个狡猾的家伙,它把线性和对数结合在一起,做得特别好。
比如,你的快递要排序,这种情况下就像是你先把快递按区域分好,再慢慢给每个区域里的快递排序,效率就高了不少,心里那个踏实,简直太赞了。
然而,有些时候,我们就要面对O(n²)的二次时间复杂度。
想象一下,参加一个舞会,你得和每一个人跳舞,结果你会发现,你的时间全被消耗在了不停的跳舞中。
即便你舞技了得,这种时间消耗也让人心累,尤其是人越多,问题越大。
最麻烦的情况是O(2^n),这是个指数级的复杂度,感觉就像在参加一场马拉松,谁能熬到最后谁就是赢家。
这种情况下,选手们都快累趴下了,时间就像没完没了的折磨,令人痛苦不已。
想想看,没几个人能熬得过去,简直是“苦不堪言”。
复杂度还可以更高,但我们今天就聊到这里。
简单来说,时间复杂度就像一张地图,指引我们如何更聪明地解决问题。
排序算法总结

排序算法总结【篇一:排序算法总结】1、稳定排序和非稳定排序简单地说就是所有相等的数经过某种排序方法后,仍能保持它们在排序之前的相对次序,我们就说这种排序方法是稳定的。
反之,就是非稳定的。
比如:一组数排序前是a1,a2,a3,a4,a5,其中a2=a4,经过某种排序后为a1,a2,a4,a3,a5,则我们说这种排序是稳定的,因为a2排序前在a4的前面,排序后它还是在a4的前面。
假如变成a1,a4,a2,a3,a5就不是稳定的了。
2、内排序和外排序在排序过程中,所有需要排序的数都在内存,并在内存中调整它们的存储顺序,称为内排序;在排序过程中,只有部分数被调入内存,并借助内存调整数在外存中的存放顺序排序方法称为外排序。
3、算法的时间复杂度和空间复杂度所谓算法的时间复杂度,是指执行算法所需要的计算工作量。
一个算法的空间复杂度,一般是指执行这个算法所需要的内存空间。
功能:选择排序输入:数组名称(也就是数组首地址)、数组中元素个数算法思想简单描述:在要排序的一组数中,选出最小的一个数与第一个位置的数交换;然后在剩下的数当中再找最小的与第二个位置的数交换,如此循环到倒数第二个数和最后一个数比较为止。
选择排序是不稳定的。
【篇二:排序算法总结】在计算机科学所使用的排序算法通常被分类为:计算的复杂度(最差、平均、和最好性能),依据列表(list)的大小(n)。
一般而言,好的性能是O(nlogn),且坏的性能是O(n2)。
对于一个排序理想的性能是O(n)。
仅使用一个抽象关键比较运算的排序算法总平均上总是至少需要O(nlogn)。
内存使用量(以及其他电脑资源的使用)稳定度:稳定排序算法会依照相等的关键(换言之就是值)维持纪录的相对次序。
也就是一个排序算法是稳定的,就是当有两个有相等关键的纪录R和S,且在原本的列表中R出现在S之前,在排序过的列表中R也将会是在S之前。
一般的方法:插入、交换、选择、合并等等。
交换排序包含冒泡排序和快速排序。
关于各种排序方法的比较

各种排序方法的总结一.直接插入排序1.时间复杂度移动次数和比较次数受初始排列的影响。
最好情况o(n) 最坏情况o(n2) 平均情况o(n2)2.空间复杂度:o(1)3.算法特点稳定排序;算法简便,且容易实现适用于顺序和链式两种存储结构,链式存储时不需要移动记录,只修改指针;适合于初始记录基本有序的情况;当记录无序,且n较大时,不宜采用。
二.折半插入排序1.时间复杂度移动次数受初始排列的影响。
最好情况o(nlog2n) 最坏情况o(n2) 平均情况o(n2)2.空间复杂度o(1)3.算法特点稳定排序;算法简便,且容易实现只适用于顺序存储结构,不能用于链式存储结构;适合记录无序、n较大的情况;三.希尔排序1.时间复杂度2.空间复杂度o(1)3.算法特点不稳定排序,记录跳跃式的移动;只适用于顺序存储结构,不能用于链式存储结构;增量序列可以有多种取法,最后一个增量值必须是1;适合记录无序、n较大的情况;四.冒泡排序1.时间复杂度移动次数和比较次数受初始排列的影响。
最好情况o(n) 最坏情况o(n2) 平均情况o(n2)2.空间复杂度o(1)3.算法特点稳定排序;适用于顺序存储结构和链式存储结构;适合记录无序、n较大时不宜采用;五.快速排序1.时间复杂度移动次数和比较次数受初始排列的影响。
最好情况o(nlog2n) 最坏情况o(n2) 平均情况o(nlog2n)2.空间复杂度:o(log2n) 递归算法3.算法特点不稳定排序;算法简便,且容易实现适用于顺序存储结构;适合记录无序,且n较大情况。
六.直接选择排序1.时间复杂度比较次数不受初始排列的影响,移动次数受影响。
最好情况o(n2) 最坏情况o(n2) 平均情况o(n2)2.空间复杂度o(1)3.算法特点不稳定排序;适用于顺序存储结构和链式存储结构;移动记录的次数较多,适合记录占用空间较多时,采用此方法;七.堆排序1.时间复杂度移动次数和比较次数受初始排列的影响。
数组各种排序算法和复杂度分析

数组各种排序算法和复杂度分析Java排序算法1)分类:插⼊排序(直接插⼊排序、希尔排序)交换排序(冒泡排序、快速排序)选择排序(直接选择排序、堆排序)归并排序分配排序(箱排序、基数排序)所需辅助空间最多:归并排序所需辅助空间最少:堆排序平均速度最快:快速排序不稳定:快速排序,希尔排序,堆排序。
2)选择排序算法的时候要考虑数据的规模、数据的类型、数据已有的顺序。
⼀般来说,当数据规模较⼩时,应选择直接插⼊排序或冒泡排序。
任何排序算法在数据量⼩时基本体现不出来差距。
考虑数据的类型,⽐如如果全部是正整数,那么考虑使⽤桶排序为最优。
考虑数据已有顺序,快排是⼀种不稳定的排序(当然可以改进),对于⼤部分排好的数据,快排会浪费⼤量不必要的步骤。
数据量极⼩,⽽起已经基本排好序,冒泡是最佳选择。
我们说快排好,是指⼤量随机数据下,快排效果最理想。
⽽不是所有情况。
3)总结:——按平均的时间性能来分:时间复杂度为O(nlogn)的⽅法有:快速排序、堆排序和归并排序,其中以快速排序为最好;时间复杂度为O(n2)的有:直接插⼊排序、起泡排序和简单选择排序,其中以直接插⼊为最好,特别是对那些对关键字近似有序的记录序列尤为如此;时间复杂度为O(n)的排序⽅法只有,基数排序。
当待排记录序列按关键字顺序有序时,直接插⼊排序和起泡排序能达到O(n)的时间复杂度;⽽对于快速排序⽽⾔,这是最不好的情况,此时的时间性能蜕化为O(n2),因此是应该尽量避免的情况。
简单选择排序、堆排序和归并排序的时间性能不随记录序列中关键字的分布⽽改变。
——按平均的空间性能来分(指的是排序过程中所需的辅助空间⼤⼩):所有的简单排序⽅法(包括:直接插⼊、起泡和简单选择)和堆排序的空间复杂度为O(1);快速排序为O(logn ),为栈所需的辅助空间;归并排序所需辅助空间最多,其空间复杂度为O(n );链式基数排序需附设队列⾸尾指针,则空间复杂度为O(rd )。
——排序⽅法的稳定性能:稳定的排序⽅法指的是,对于两个关键字相等的记录,它们在序列中的相对位置,在排序之前和经过排序之后,没有改变。
算法排序---复杂度o(nlogn)的排序方式

算法排序---复杂度o(nlogn)的排序⽅式上次写的算法排序的⽂章都是O(logn^2)的,这次写两个⽐较常⽤的经典的排序算法:归并排序和快速排序。
1.归并排序也就是合并排序,将两个或两个以上的有序数据序列合并成⼀个新的有序数据序列,它的基本思想是假设数组A有N个元素,那么可以看成数组A有N个有序的⼦序列组成,每个⼦序列的长度为1,然后在将两两合并,得到⼀个N/2个长度为2或1的有序⼦序列,再两两合并,如此重复,直到得到⼀个长度为N的有序序列为⽌。
例如:数组A有7个数据,分别是 23,5,69,85,26,32,15 采⽤归并排序算法的操作过程如下:初始值【23】【5】【69】【85】【26】【32】【15】第⼀次会被分成两组【23】【5】【69】,【85】【26】【32】【15】第⼆次将第⼀组分成【23】,【5】【69】两组第三次将第⼆次分的第⼆组进⾏拆分【5】,【69】两组第四次对第三次拆分数组进⾏合并排序【5 69】第五次第四次排序好的数组和第⼆次拆分的数组合并为【5 23 69】接下来对第⼀次拆分的第⼆数组做同样的过程操作,合并为【15 26 32 85】最后将两个有序的数组做最后的合并【5 15 23 26 32 69 85】该算法的核⼼思想是采⽤了分治思想,即将⼀个数组分成若⼲个⼩数组排序,排序后再两两合并的过程。
⾸先看合并的过程实现,上代码:1//将两个排序好的序列合并2void Merge(int[] left, int[] right, int[] mergeArr)3 {4int i = 0, j = 0, k = 0;56while (i < left.Length && j < right.Length)7 {8if (left[i] < right[j]) //将元素⼩的放在合并的序列内9 {10 mergeArr[k] = left[i];11 i++;12 }13else14 {15 mergeArr[k] = right[j];16 j++;17 }18 k++;19 }2021//有左元素没有右元素的情况22while (i < left.Length)23 {24 mergeArr[k] = left[i];25 i++;26 k++;27 }2829//有右元素没有左元素的情况30while (j < right.Length)31 {32 mergeArr[k] = right[j];33 j++;34 k++;35 }36 }下⾯看看如何将⼀个数组分成若⼲个⼩组的过程:1public int[] MergeSort(int[] arr)2 {3if (arr == null || arr.Length == 0)4return arr;56int middle = arr.Length >> 1;78//左数组9int[] left = new int[middle];1011//右数组12int[] right = new int[arr.Length - middle];1314for (int i = 0; i < arr.Length; i++)15 {16if (i < middle)17 left[i] = arr[i];18else19 right[i - middle] = arr[i];20 }2122if (arr.Length > 1)23 {24//递归左序列25 left = MergeSort(left);2627//递归右序列28 right = MergeSort(right);2930 Merge(left, right, arr);31 }3233 Console.WriteLine("归并排序过程:{0}", String.Join(",", arr.ToArray()));3435return arr;36 }看效果:2.快速排序在平均状况下,排序n个项⽬要Ο(n log n)次⽐较。
各种排序算法的稳定性和时间复杂度小结

各种排序算法的稳定性和时间复杂度小结选择排序、快速排序、希尔排序、堆排序不是稳定的排序算法,冒泡排序、插入排序、归并排序和基数排序是稳定的排序算法。
冒泡法:这是最原始,也是众所周知的最慢的算法了。
他的名字的由来因为它的工作看来象是冒泡:复杂度为O(n*n)。
当数据为正序,将不会有交换。
复杂度为O(0)。
直接插入排序:O(n*n)选择排序:O(n*n)快速排序:平均时间复杂度log2(n)*n,所有内部排序方法中最高好的,大多数情况下总是最好的。
归并排序:log2(n)*n堆排序:log2(n)*n希尔排序:算法的复杂度为n的1.2次幂关于快速排序分析这里我没有给出行为的分析,因为这个很简单,我们直接来分析算法:首先我们考虑最理想的情况1.数组的大小是2的幂,这样分下去始终可以被2整除。
假设为2的k次方,即k=log2(n)。
2.每次我们选择的值刚好是中间值,这样,数组才可以被等分。
第一层递归,循环n次,第二层循环2*(n/2)......所以共有n+2(n/2)+4(n/4)+...+n*(n/n) = n+n+n+...+n=k*n=log2(n)*n所以算法复杂度为O(log2(n)*n)其他的情况只会比这种情况差,最差的情况是每次选择到的middle都是最小值或最大值,那么他将变成交换法(由于使用了递归,情况更糟)。
但是你认为这种情况发生的几率有多大??呵呵,你完全不必担心这个问题。
实践证明,大多数的情况,快速排序总是最好的。
如果你担心这个问题,你可以使用堆排序,这是一种稳定的O(log2(n)*n)算法,但是通常情况下速度要慢于快速排序(因为要重组堆)。
本文是针对老是记不住这个或者想真正明白到底为什么是稳定或者不稳定的人准备的。
首先,排序算法的稳定性大家应该都知道,通俗地讲就是能保证排序前2个相等的数其在序列的前后位置顺序和排序后它们两个的前后位置顺序相同。
在简单形式化一下,如果Ai = Aj, Ai原来在位置前,排序后Ai还是要在Aj位置前。
冒泡排序平均复杂度计算

冒泡排序平均复杂度计算冒泡排序是一种简单而常用的排序算法,其平均复杂度为O(n^2)。
本文将详细介绍冒泡排序算法的原理、步骤及其平均复杂度的计算方法。
一、冒泡排序算法原理冒泡排序算法是一种基于比较的排序算法,其原理是通过相邻元素之间的比较和交换来达到排序的目的。
具体步骤如下:1. 从待排序的序列中,依次比较相邻的两个元素,如果前一个元素大于后一个元素,则交换它们的位置。
2. 对每一对相邻元素进行比较和交换,直到最后一对元素。
3. 针对所有的元素重复以上步骤,除了已经排序好的元素。
4. 重复步骤1~3,直到整个序列排序完成。
二、冒泡排序算法步骤冒泡排序算法的步骤可以简要总结为以下几个阶段:1. 遍历待排序序列,从第一个元素开始,依次比较相邻的两个元素。
2. 如果前一个元素大于后一个元素,则交换它们的位置。
3. 继续遍历序列,重复步骤2,直到最后一个元素。
4. 重复以上步骤,直到所有元素都排好序。
三、冒泡排序算法的平均复杂度计算冒泡排序算法的平均复杂度可以通过以下方式计算:1. 假设待排序序列的长度为n。
2. 在最坏情况下,冒泡排序需要进行n-1次遍历,每次遍历都要比较n-1-i次(i为已排序的元素个数)。
3. 每次比较操作的时间复杂度为O(1)。
4. 因此,冒泡排序的平均时间复杂度可以计算为:平均复杂度= Σ(1 * (n-1-i)) / (n-1)= (n-1) / 2= O(n^2)四、冒泡排序算法的优化尽管冒泡排序算法的平均复杂度较高,但在某些特定情况下,它可能会有一些优化方法:1. 若在某一次遍历中,没有发生元素交换,则说明序列已经有序,可以提前结束排序过程。
2. 在每次遍历时,记录最后一次发生元素交换的位置,下一次遍历只需要比较到该位置即可。
五、总结冒泡排序是一种简单但效率较低的排序算法,其平均复杂度为O(n^2)。
通过比较相邻元素并交换位置,冒泡排序可以将序列逐步排序。
然而,冒泡排序也有一些优化方法可以提高效率。
常见排序算法及对应的时间复杂度和空间复杂度

常见排序算法及对应的时间复杂度和空间复杂度转载请注明出处:(浏览效果更好)排序算法经过了很长时间的演变,产⽣了很多种不同的⽅法。
对于初学者来说,对它们进⾏整理便于理解记忆显得很重要。
每种算法都有它特定的使⽤场合,很难通⽤。
因此,我们很有必要对所有常见的排序算法进⾏归纳。
排序⼤的分类可以分为两种:内排序和外排序。
在排序过程中,全部记录存放在内存,则称为内排序,如果排序过程中需要使⽤外存,则称为外排序。
下⾯讲的排序都是属于内排序。
内排序有可以分为以下⼏类: (1)、插⼊排序:直接插⼊排序、⼆分法插⼊排序、希尔排序。
(2)、选择排序:直接选择排序、堆排序。
(3)、交换排序:冒泡排序、快速排序。
(4)、归并排序 (5)、基数排序表格版排序⽅法时间复杂度(平均)时间复杂度(最坏)时间复杂度(最好)空间复杂度稳定性复杂性直接插⼊排序O(n2)O(n2)O(n2)O(n2)O(n)O(n)O(1)O(1)稳定简单希尔排序O(nlog2n)O(nlog2n)O(n2)O(n2)O(n)O(n)O(1)O(1)不稳定较复杂直接选择排序O(n2)O(n2)O(n2)O(n2)O(n2)O(n2)O(1)O(1)不稳定简单堆排序O(nlog2n)O(nlog2n)O(nlog2n)O(nlog2n)O(nlog2n)O(nlog2n)O(1)O(1)不稳定较复杂冒泡排序O(n2)O(n2)O(n2)O(n2)O(n)O(n)O(1)O(1)稳定简单快速排序O(nlog2n)O(nlog2n)O(n2)O(n2)O(nlog2n)O(nlog2n)O(nlog2n)O(nlog2n)不稳定较复杂归并排序O(nlog2n)O(nlog2n)O(nlog2n)O(nlog2n)O(nlog2n)O(nlog2n)O(n)O(n)稳定较复杂基数排序O(d(n+r))O(d(n+r))O(d(n+r))O(d(n+r))O(d(n+r))O(d(n+r))O(n+r)O(n+r)稳定较复杂图⽚版①插⼊排序•思想:每步将⼀个待排序的记录,按其顺序码⼤⼩插⼊到前⾯已经排序的字序列的合适位置,直到全部插⼊排序完为⽌。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
各种排序方法复杂度总结归纳
一、冒泡排序
主要思路是:
通过交换相邻的两个数变成小数在前大数在后,这样每次遍历后,最大的数就“沉”到最后面了。
重复N次即可以使数组有序。
代码实现
void buadfdsle_sort(int arr[],int len)
{
for (int i = 0; i {
for (int j = len —1; j >= i; j——)
{
if (arr[j] {
int temp = arr[j];
arr[j] = arr[j —1];
arr[j —1] = temp;
}
}
}
}
冒泡排序改进1:
在某次遍历中,如果没有数据交换,说明整个数组已经有序,因
此通过设置标志位来记录此次遍历有无数据交换就可以判断是否要继续循环。
冒泡排序改进2:
记录某次遍历时最后发生数据交换的位置,这个位置之后的数据显然已经有序。
因此设置标志位记录每次遍历中最后发生数据交换的位置可以确定下次循环的范围。
二、直接插入排序
主要思路是:
每次将一个待排序的数组元素,插入到前面已排序的序列中这个元素应该在的位置,直到全部数据插入完成。
类似扑克牌洗牌过程。
代码实现
void _sort(int arr[],int len)
{
for (int i = 1; i {
int j = i —1;
int k = arr[i];
while (j > —1 && k {
arr[j + 1] = arr[j];
j ——;
}
arr[j + 1] = k;
}
}
三、直接选择排序
主要思路是:
数组分成有序区和无序区,初始时整个数组都是无序区,每次遍历都从无序区选择一个最小的元素直接放在有序区最后,直到排序完成。
代码实现
void select_sort(int arr[],int len)
{
for (int i = 0; i {
int index = i;
for (int j = i + 1; j {
if (arr[j] index = j;
}
if (index != i)
{
int temp = arr[i];
arr[i] = arr[index];
arr[index] = temp;
}
}
}
四、快速排序
主要思路是:
“挖坑填数+ 分治法”,首先令i = L;j = R;将a[i]挖出形成打一个坑,称a[i]为基准数。
然后j——从后向前找到一个比基准数小的数,挖出来填到a[i]的坑中,这样a[j]就形成了一个新的坑,再i++从前向后找到一个比基准数大的数填到a[j]坑中。
重复进行这种挖坑填数,直到i = j。
这时a[i]形成了一个新的坑,将基数填到a[i]坑中,这样i 之前的数都比基准数小,i之后的数都比基准数大。
因此将数组分成两部分再分别重复上述步骤就完成了排序。
代码实现
void quick_sort(int arr[],int left,int right)
{
if (left {
int i = left,j = right,target = arr[left];
while (i {
while (i target)
j——;
if (i arr[i++] = arr[j];
while (i i++;
if (i arr[j] = arr[i];
}
arr[i] = target;
quick_sort(arr,left,i —1);
quick_sort(arr,i + 1,right);
}
}
五、希尔排序
主要思路是:
先将整个待排元素序列分割成若干个子序列(由相隔某个“增量”的元素组成的)分别进行直接插入排序,然后依次缩减增量再进行排序,待整个序列中的元素基本有序(增量足够小)时,再对全体元素进行一次直接插入排序。
由于希尔排序是对相隔若干距离的数据进行直接插入排序,因此可以形象的称希尔排序为“跳着插”。
六、归并排序
主要思路是:
当一个数组左边有序,右边也有序,那合并这两个有序数组就完成了排序。
如何让左右两边有序了?用递归!这样递归下去,合并上来就是归并排序。
代码实现
void merge(int arr[],int temp_arr[],int start_index,int mid_index,int end_index)
{
int i = start_index,j = mid_index + 1;
int k = 0;
while (i {
if (arr[i] > arr[j])
temp_arr[k++] = arr[j++];
else
temp_arr[k++] = arr[i++];
}
while (i {
temp_arr[k++] = arr[i++];
}
while (j temp_arr[k++] = arr[j++];
for (i = 0,j = start_index; j arr[j] = temp_arr[i];
}
void merge_sort(int arr[],int temp_arr[],int start_index,int end_index)
{
if (start_index {
int mid_index = (start_index + end_index)/ 2;
merge_sort(arr,temp_arr,start_index,mid_index);
merge_sort(arr,temp_arr,mid_index + 1,end_index);
merge(arr,temp_arr,start_index,mid_index,end_index);
}
}
七、堆排序
堆排序的难点就在于堆的的插入和删除。
堆的插入就是——每次插入都是将新数据放在数组最后,而从这个新数据的父结点到根结点必定是一个有序的数列,因此只要将这个新数据插入到这个有序数列中即可。
堆的删除就是——堆的删除就是将最后一个数据的值赋给根结点,然后再从根结点开始进行一次从上向下的调整。
调整时先在左右儿子结点中找最小的,如果父结点比这个最小的子结点还小说明不需要调整了,反之将父结点和它交换后再考虑后面的结点。
相当于从根结点开始将一个数据在有序数列中进行“下沉”。
因此,堆的插入和删除非常类似直接插入排序,只不是在二叉树上进行插入过程。
所以可以将堆排序形容为“树上插”。
搜集整理,仅供参考学习,请按需要编辑修改。
