11-2动生电动势和感生电动势 涡旋电场
11-2、动生电动势、感生电动势
CA
I
0 I iAB vc iCA 0 B v B 2a v iBC (v B) dl
c dl A x a b
o
iBC
( X d iBC v B)dl C vB cos( )dl dx vB cosdl vB cos dl
注意:
r B L E感 2 t B 0 E感为负值 t
r
S
E感 dS Er dS 0
S
E0 0
3)求切向分量 ( E感 E )
显然违反了感生电场的基本方程,最后只留下 切向分量。
3)求切向分量 ( E感 E )
R
0r R B 与S 一致 作闭合环路L (L+,S+右旋) + t
i
1 BL (负号说明 i实与 i 相反) 2
L
d i (v B) dl L vBdl L d i vBdl lBdl
0 2 0
B
i
解:动生电动势只与运动的导 体部分有关。故可构建一 i实 L 回路0abo。 1)约定 i 右旋
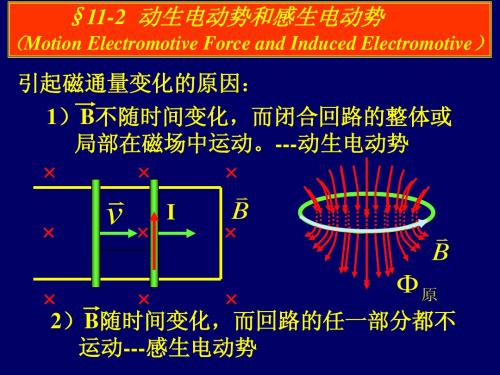
§11-2 动生电动势和感生电动势
(Motion Electromotive Force and Induced Electromotive)
引起磁通量变化的原因: 1)B不随时间变化,而闭合回路的整体或 局部在磁场中运动。---动生电动势
v
11-2动生电动势

v v
方法二
作辅助线,形成闭合回路 作辅助线,形成闭合回路CDEF
r r Φ = ∫ B• dS =
S
∫
a+b
a
εi = −
µ0 Ix a + b ln = 2π a dΦ
dt
µ0 I xdr 2πr
I
方向
D→C →
v v
X
µ0 I a + b dx ln ) = −( 2π a dt µ0 Iv a + b ln =− 2π a
均匀磁场
转动
r 如图,长为L的铜棒在磁感应强度为 例 如图,长为 的铜棒在磁感应强度为 B
求:棒中感应电动势的大小 和方向。 和方向。
的均匀磁场中, 轴转动。 的均匀磁场中,以角速度 ω 绕O轴转动。 轴转动
ω ××××
×××× ××××
O
r A B××× ×
解:方法一
v v v 取微元 dε = ( v × B )⋅ dl
a
+++ + +
r v v f = −e(v × B)
非静电力 它驱使电子沿导线由a向 移动 移动。 它驱使电子沿导线由 向b移动。
v B v v
r f
b
端出现过剩负电荷, 由于洛仑兹力的作用使 b 端出现过剩负电荷, a 端出现过剩正电荷 。
v 在导线内部产生静电场 E
方向a→ 方向 →b 电子受的静电力
S
v S 的法线方向应选得与曲线 L
的积分方向成右手螺旋关系
S
L
v ∂B 是曲面上的任一面元上磁感应强度的变化率 ∂t
不是积分回路线元上的磁感应强度的变化率
动生电动势与感生电动势

【解】由于金属棒处在通电导线的非均匀磁场中,因此必
须将金属棒分成很多长度元dx,规定其方向由A指向B。这样 在每一dx处的磁场可以看作是均匀的,其磁感应强度的大小为
B 0I
2x
根据动生电动势的公式可知,dx小段上的动生电动势为
d动
(v
B)
dl
Bv
cos
dx
0I
2x
vdx
由于所有长度元上产生的动生电动势的方向都相同,所以金
d
dt
d dt
S
B
dS
又根据电动势的定义可得
L EK dl
式中,EK为感生电场的电场强度。感生电场的电场强度是 非静电性场强。
则有
L EK
dl
d dt
B dS B dS
s
s t
dB
s
S t
若闭合回路是静止的,即所包围面积S不随时间变化,即
S 0 ,则上式可写成
t
B L EK dl s t dS
性场强为
Ek
fL (e)
vB
根据电动势的定义可得,动生电动势为
a
动
L Ek
dl
(v B) dl
b
上式是动生电动势的一般表达式。由上式可知,动生电动势
的方向是非静电性场强 Ek v B 在运动导线上投影的指向。
【例9-2】如下图所示,长直导线 中通有电流I=10A,有一长l=0.1m的 金属棒AB,以v=4m·s-2的速度平行于 长直导线作匀速运动,棒离导线较近的 一端到导线的距离a=0.1m,求金属棒 中的动生电动势。
1861年,英国物理学家麦克斯韦提出感生电场的假设,认为 由于磁场变化而产生一种电场,是这个电场使导体中自由电子作 定向运动而形成电流。麦克斯韦还认为,即使没有导体,这种电 场同样存在。这种由变化磁场激发的电场称为感生电场。
感生电动势 涡旋电场
(2). 同一条 E线v 上,E大v 小处处相同,方向沿切线方向(左旋)
(3).
Ev存在于整个空间(管内、外)
6
2.
Ev的分布:
L
Ev
dl
d m dt
(1). r < R 取电力线为回路,
I
R
L Ev
正 方向如图 dl Ev 2 r
d dt
(B
r2)
Ev
L
L
Ev
r 2
dB dt
与L反向
2. 涡旋电场的电力线成闭合线, B和
左旋关系
t
成Ev
B t
Ev
左旋关系
电场有2种: 电荷激发的电场静电场
E
F
E线有源,保守场
q
变化磁场激发的电场涡旋电场
Ev
Fv q
Ev线无源,非保守场
3
三. Ev的性质
客观存在的物质,具有能量、动量,满足叠加原理,对
场中的带电粒子有力的作用。
高斯定理:
b
3. 感应电动势分成动生、感生两种,这种分法 在特殊情况下只有相对意义,如:
但在普遍情况下,不可能通过参照系变换使之互换 N 1v2
P459 变压器铁芯(涡流) 由于变化磁场激起感生电场,则在导体内产生感应电流。 这些感应电流的流线呈闭合的涡旋状,故称涡电流(涡流)
交变电流
交变电流
整块铁芯
彼此绝缘的薄片
由于大块金属电阻很小,形成涡流很大,金属易 被加热到很高温度。涡流的热效应常被用于真空提纯 金属和半导体材料,以及冶炼难溶金属等;而在电机 和变压器等通有交流电的电器设备中,为减少热能损 耗,通常采用叠片式铁芯来减少涡流。
P459 阻尼摆,P461 电子感应加速器——自己选看
感生电动势与涡旋电场
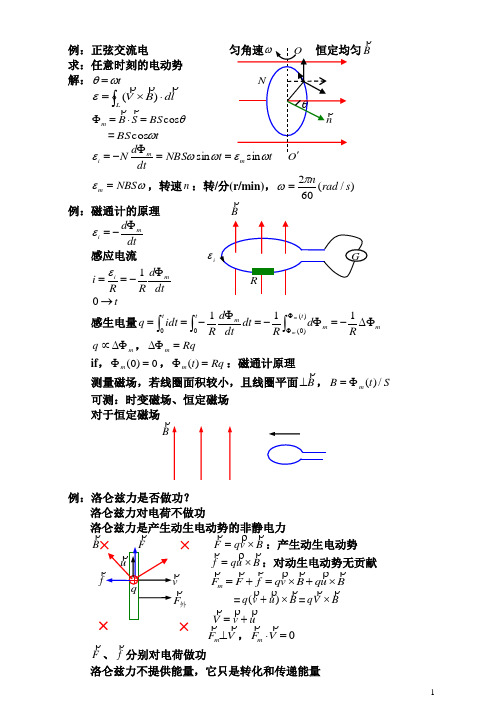
例:正弦交流电B求:任意时刻的电动势解:t ωθ= ⎰⋅⨯=L l d B V)(ε θcos BS S B m =⋅=Φ =t BS ωcost NBS dtd N m mi ωωεsin ==Φ-=ωεNBS m =,转速n :转/分(r/min),)/(602s rad nπω=例:磁通计的原理 Bdtd m i Φ-=ε感应电流 i εdt d R R i mi Φ-==1ε t →0感生电量m t m m t t Rd R dt dt d R idt q m m ∆Φ-=Φ-=Φ-==⎰⎰⎰ΦΦ111)()0(00m q ∆Φ∝,Rq m =∆Φif ,0)0(=Φm ,Rq t m =Φ)(:磁通计原理测量磁场,若线圈面积较小,且线圈平面B⊥,S t B m /)(Φ=可测:时变磁场、恒定磁场 对于恒定磁场B例:洛仑兹力是否做功?洛仑兹力对电荷不做功洛仑兹力是产生动生电动势的非静电力B v q F⨯=:产生动生电动势B u q f ⨯=:对动生电动势无贡献 B u q B v q f F F m ⨯+⨯=+=外 =B u v q⨯+)(=B V q ⨯u v V+=V F m ⊥,0=⋅V F mF、f 分别对电荷做功洛仑兹力不提供能量,它只是转化和传递能量第3节感生电动势与涡旋电场一、涡旋电场假说例:求矩形回路中的感生电动势解:⎰⎰=⋅=ΦSSmdSBS dBtθcos)(=dxlxt Ilrr122)(⎰+πμ,I t Iωs i n)(==rlrtl I210lnsin2+ωπμ,rlrtl Idtdmi210lncos2+-=Φ-=ωωπμε产生电动势的非静电力是什么力?从哪里来的?涡旋电场假说:变化的磁场⇒具有闭合力线的电场:涡旋电场(感应电场),场强VE,非静电场一段导线:⎰⋅=L Vil dEε,闭合回路:⎰Φ-=⋅=LmVi dtdl dEε静电场涡旋电场产生原因静电荷变化的磁场电力线不闭合闭合环路定理0=⋅⎰L l dE⎰Φ-=⋅=LmVi dtdl dEε保守场、电势非保守场,电势高斯定理∑⎰=⋅内iSqS dE1ε=⋅⎰S V S dE对q的作用力EqF=VEqF=⎰Φ-=⋅LmV dtdl dE=0S Sd BB dS dSdt t∂-⋅-⋅<∂⎰⎰固定回路,LVEV tB∂∂t∂二、 涡旋电场的计算⎰Φ-=⋅L mV dt d l d E L H d l I ⋅=∑⎰ 传内 例:半径为R 的无限长 直螺线管内有均匀磁场B设磁场以恒定速率增加,0>∂∂t B求:V E解:tB ∂∂ (1)R r <,沿电力线积分,n向外2)(2cos r tB BS dt d dt d r E dl E l d E L m V LV V ππθ∂∂=--=Φ-===⋅⎰⎰ r tB E V ∂∂=21(2)R r > ⎰Φ-==⋅L m V Vdt d r E l d E π2 22)(R t B R B dt d ππ∂∂=--=rR t B E V 1212∂∂=例:无限长直螺线管(R 、B 0>∂∂tB)求:直导线ab 解:⎰⎰⎰∂∂==⋅=b a L b L a V b L a V ab dl rhr t B dl E l d E 21cos )()()(θε =0)2/(212122>-∂∂=∂∂l R l t B hl t B ,方向b a →,b 端电势高讨论:(1)对于涡旋电场不能引入电势概念,为什么说b 端 电势高?答:b 端积累正电荷,a 端积累负电荷电势概念是针对积累电荷的静电场引入的(2)直导线ab 向上平移ab ε如何变化?答:hl tBab ∂∂=21ε,ab 向上平移,↓h ,↓ab ε直导线通过O 点,0=h ,ab ε=0⎰⋅=baV L ab l d E )(ε,V E l d ⊥,ab ε=0(3)BO a b l ab bO ab Oa OabO εεεεε=++=hl t B hl B dtd dtd m OabO ab 21)21(∂∂=--=Φ-==εε(4)I 、 MN 中有无电动势?II 、 G 中有无电流? B0/≠∂∂t B III 、N M ''中有无电动势? M NIV 、G '中有无电流?M ' N 'G '计算电动势的小结:(1)磁场恒定,回路或其一部分运动:动生电动势一段导线:l d B V bL a ab ⋅⨯=⎰)()(ε闭合回路:⎰⋅⨯=L l d B V )(ε,dtd mi Φ-=ε(2)磁场变化,回路不动:感生电动势一段导线:⎰⋅=LV i l d Eε闭合回路:⎰⋅=L V i l d E ε,dtd mi Φ-=ε(3)磁场变化,且回路或其一部分又运动:既有感生电动势,又有动生电动势,最好使用:dtd mi Φ-=εGh第4节 自感一、 自感现象及其规律I B ∝,I m ∝Φ,LI m =Φ(无铁磁) L :L :自感(系数),SI :亨利(H ) dt d m L Φ-=ε=dtdI L I dt dL LI dt d --=-)(如果L 恒定,=L εdtdIL - L ε L εL ε:自感电动势 自感电动势总是阻碍电流变化 I I。
动生电动势与感生电动势

2r
(r R) (r R)
b
b
Uab a E库 dl a E旋 dl
=
-
b
a E旋cos dl
=-
b k rcos dl a2
=
1 kRcos 2
b a
dl =
k 2
Rcos lab
2
E旋
dl
Ucd
d
d
c E库 dl c E旋 dl
电荷-e所受的洛仑兹力为:
F eV B e(v u) B ev B (e)u B f f
f ev B, f (e)u B
F 中第一项 f 即我们在讨论动生电动势时的非 静电力。 f 与 f 垂直,与导体棒的运动速度 v 反向,即 f 阻碍导体棒的向右运动。要使导体 棒保持以 v 匀速运动,外力必须克服 f 而对棒 作功。
L
E旋
dl
d dt
B dS
S
S
B t
dS
涡旋场呈柱对称,方向沿同心圆切向,逆时针
方向。
2 rE旋
( S
dB dt
)dS=
S
dB dt
dS
(1)r<R时
E旋
2
r
dB dt
r2
E旋
r 2
dB dt
(2)r>R时
E旋
2
ห้องสมุดไป่ตู้
r
dB dt
R2
E旋
麦克斯韦对感生电动势成因的解释,揭示 了电磁感应定律更深层次的物理本质。
动生电动势和感生电动势

Ek
1 2
B t
r
1 2
kr
2. r > R 区域
作半径为 r 的环形路径,并以逆
时针为回路绕向,则同理有
2rEk
S
B t
ds
R2k
R
o
r
r
B
1 B R2 1 R2
Ek 2 t
r
k 2r
Foundation - SJYGGF
§ 13.2 动生电动势和感生电动势
Nov 5, 2002 9/33
随时间均匀增加, dB k dt
若铝圆盘的电导率为γ,求盘内 的感应电流。
见书P212页,例4
R
解: 取半径为r、宽为dr的圆环微 元,并以逆时针方向为正方向,则 微元环中元电动势为
d L Ek dl L Ek dl
1 kr 2r dl kr2
20
o
r
dr
B
微元环中的电阻为 dR 1 2r hdr
Foundation - SJYGGF
§ 13.2 动生电动势和感生电动势
Nov 5, 2002 21/33
4) 电度表记录电量
电度表记录用电量,就是
利用通有交流电的铁心产生交
变的磁场,在缝隙处铝盘上产
o
生涡电流,涡电流的磁场与电
磁铁的磁场作用,表盘受到一
转动力矩,使表盘转动。
o’
Foundation - SJYGGF
感生电动势
1. 感生电动势——回路不动或不变,因磁场随时间变 化产生的电动势。相应的电流称为感生电流。
2. 感生电动势的起源——感生电场Ek 1) Maxwell感生电场(涡旋电场)假设
Maxwell 1861年首先从理论上预言感生电场的存在,后 被Hertz的电磁波实验所证实。Maxwell假设: 变化的磁场要在其周围空间激发一种电场——感生电场
大学物理动生电动势和感生电动势(教学讲课)

非静电力 Fk qEk
Ek 为非静电场的场强
电源的电动势:
+
在电源内将单位正电荷从
+
负极移动到正极的过程中
非静电力所作的功
+
+ -
+
+ +
Fk +
-
+
_ Ek dl
A+
-B
+
-
方向: B A
UA UB
电源的电动势是描述电源非静电力做功本领的物理量
技术教育
3
10 - 2 动生电动势和感生电动势
第十三章电磁感应
冶金炉:把难溶金属放在陶瓷坩锅中,套在
坩锅外的线圈中通交流电 电磁炉:交变磁场作用于金属锅底,产生
大量涡流
2. 电磁阻尼摆
涡电流的弊
热效应过强、温度过高,
易破坏绝缘,损耗电能,还可能造成事故
技术教育
33
10 - 2 动生电动势和感生电动势
第十三章电磁感应
减少涡流 1、选择高阻值材料(硅钢、矽钢等) 2、多片铁芯组合
第十三章电磁感应
dB dt
导体
31
10 - 2 动生电动势和感生电动势
第十三章电磁感应
涡电流或涡流这种交变电流集中于导体表面的效应
涡电流的应用
——趋肤效应
1. 高频感应电炉与电磁灶的原理
利用涡电流进行加热
高频电流 交变磁场 涡旋电场
炼金属 热效应
涡电流
技术教育
32
10 - 2 动生电动势和感生电动势
v。求BP)O两dl端的电B势 差Z ?
P
vB cos dl
rBsin d l
大学物理第二部分电磁场与电磁学之第11章 电磁感应

vB
v
11-2 动生电动势和感生电动势
方法二 作辅助线,形成闭合回路CDEF
m B dS
S
ab
a
i
0 Ix a b ln 2 a d m
dt
0 I xdr 2r
I
方向
DC
v
X
C
D
0 I a b dx ( ln ) 2 a dt 0 Iv a b ln 2 a
11-2 动生电动势和感生电动势
动生电动势的公式 非静电力 Fm e( v B ) Fm vB 定义 E k 为非静电场强 E k e 由电动势定义 i Ek dl
运动导线ab产生的动生电动势为
i
a Ek dl ( v B ) dl
L
11-2 动生电动势和感生电动势
平动
计 算 动 生 电 动 势 分 类 均匀磁场 转动 非均匀磁场
方 法
i
i
b
d m dt
a
(v B) dl
11-2 动生电动势和感生电动势
均匀磁场
例 已知: v , B , , L 求: 解: d ( v B ) dl
a
f
感应电流
产生
阻碍
导线运动
v
感应电流
b
产生 阻碍
磁通量变化
11-1 电磁感应的基本定律
判断感应电流的方向:
1、判明穿过闭合回路内原磁场 的方向; 2、根据原磁通量的变化 , 按照楞次定律的要求确定感 应电流的磁场的方向; 3、按右手法则由感应电流磁场的 方向来确定感应电流的方向。
动生电动势和感生电动势

a
注意Biblioteka r r r ε = ∫ (v × B)⋅ dl
b a
ε 是标量, (1)ε 是标量,ε > 0 时, 的方向由 a ε 到 b ,ε < 0 时, 的方向由 b 到 a ; r r r r B 的速度, (2)v 是导体线元 dl 的速度, 是 dl 所在处的磁感应强度; 所在处的磁感应强度; r r r (3)( v × B ) ⋅ dl 中有两个夹角 α 和 β , r r r r α v 其中 v × B = vB sin α , = 0时, × B = 0 ; r r r (v × B ) ⋅ dl = vB sin α cos βdl .
vµ0 I 0.3 ln = = −4.4 × 10− 6 ( V ) 2π 0.1
指向. 电动势的方向 B 由 A 指向.
一.感生电动势:一个静止的导体回 B 感生电动势: 当它包围的磁场发生变化时, 路,当它包围的磁场发生变化时,
L
穿过它的磁通量也会发生变化, 穿过它的磁通量也会发生变化, 这时回路也会产生感应电动势。 这时回路也会产生感应电动势。 二、感生电动势产生的原因
感生电动势 r r r r dφ m d ε = ∫ E 感 ⋅ dl = − = − ∫∫ B ⋅ dS dt dt S L r r r Q E = E 静 + E感
r r ∫ E 静 ⋅ dl = 0
L
r r r ∂B r ∫ E感 ⋅ dl = − ∫∫ ∂t ⋅ dS L S
r r r ∂B r ∫ E ⋅ dl = − ∫∫ ∂t ⋅ dS L S
r u
实例: 实例:法拉第利用一半径为 R 的铜盘在均 r 中转动, 匀磁场 B 中转动,角速度为ω .求盘上沿半径 方向产生的感应电动势.解法见例1 方向产生的感应电动势.解法见例1.
动生电动势和感生电动势

m1
三、电子感应加速器
原理:在电磁铁的两磁极间放一个真空室,电磁铁是由
交流电来激磁的。
当磁场发生变化时,两极间任意闭合回路的磁通发生变化, 激起感生电场,电子在感生电场的作用下被加速,电子在 Lorentz力作用下将在环形室内沿圆周轨道运动。
轨道环内的磁场 等于它围绕面积 内磁场平均值的 一半。
解:法拉第电机可视为无数铜棒一 端在圆心,另一端在圆周上,即为 并联,因此其电动势类似于一根铜 棒绕其一端旋转产生的电动势。
w
B
o a
R
U0 Ua o Bwl dl
U0
Ua
1 2
BR2w
二、感生电动势
1、感生电动势
由于磁场的变化而在回路中产生的感应电 动势称为感生电动势.
2、感生电场
变化的磁场在其周围空间激发的一种能够产生感生电动势 的电场,这种电场叫做感生电场,或涡旋电场。
是以轴为圆心的一系列同心圆,同一同心圆
上任一点的感生电场的Ek大小相等,并且方
向必然与回路相切。于是沿L取Ek的线积分,
有:
L Ek dl Ek 2 r
EkΒιβλιοθήκη 2rr 2dB dt
若r<R,则 Br 2
L
Ek
dl
- d dt
r 2
dB dt
r dB Ek 2 dt
若r≥R,则
BR2
2、涡流的热效应
电阻小,电流大,能 够产生大量的热量。
3、应用
高频感应炉 真空无按触加热
加热
4、涡流的阻尼作用
当铝片摆动时,穿过运动铝片的磁通量 是变化的,铝片内将产生涡流。根据楞 次定律感应电流的效果总是反抗引起感 应电流的原因。因此铝片的摆动会受到 阻滞而停止,这就是电磁阻尼。
大学物理学-电磁感应教案

dtd R I Φ-=1,在从0=t 到t 时间内,通过电路的电量)(1110000Φ-Φ=Φ⋅=⋅Φ=⋅=⎰⎰⎰ΦΦR d R dt dt d R dt I q t t 可见,q 与)(0Φ-Φ成正比,而与磁通量改变快慢无关。
设0=t 时00=Φ,只要测出R 和q 、即可得到Φ;如果已知回路面积、就可以算出磁感应强度B 。
这就是磁通计原理。
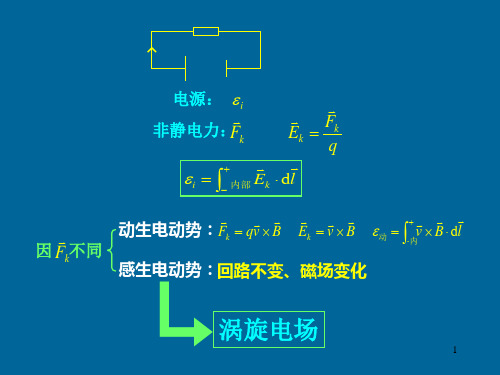
§11. 2 动生电动势与感生电动势一、动生电动势 1.在磁场中运动的导线内的感应电动势 电动势的定义:电源的电动势定义为单位正电荷绕闭合回路运动一周时、电源中非静电力作的功。
即 ⎰⋅=l E k d εk E 为单位正电荷受的非静电力。
如果导线不闭合、则单位正电荷从导线一端a 运动到另一端b 时,非静电力k E 作的功就是导线a 、b 两端的电动势。
即⎰⋅=baab d l E k ε2、动生电动势: 当导线ab 在磁场B 中以速度v 运动时,导线ab 中的电子也以速度v 运动,磁场B 作用在上的电子洛伦兹力 B v f ⨯-=e而单位正电荷受的洛伦兹力B fE k ⨯=-=υe就是动生电动势中的非静电力。
所以,动生电动势⎰⋅⨯=baab )(l Bd υε。
当导线回路闭合时、回路中的动生电动势 ⎰⋅⨯=l B d )(υε。
这是动生电动势的一般表示式。
对此式要注意两个角度的关系: (1) υ与B 的夹角θ1; (2)(υ×B )与dl 的夹角θ2。
如θ1=0(或π),或22πθ=,都会使得0=ε。
例11.1 在长直导线电流I 的附近有一长度为L 的共面导线ab 与长直导线垂直,a 端距长直导线为d 、ab 以平行于长直导线的速度v 向上运动。
求:ab 上的感应电动势。
解:在ab 上取d l 、与长直导线的距离为r ,该点的磁场 r2ΙμB π0= 所以d l 上的感应电动势 dr r2Iv πdr r 2I d d πμπυμυε00cos )(-==⋅⨯=l Bab 上的感应电动势 ⎰++==dL dab d dL πv I μ-dr r πIv μ-εln 2200 感应电动势ab ε为负值表示其方向从b 到a ,即a 点电势高。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
L
ω+ a
+ + b + + dl + +
v
l+ + +
+ + + +
+ + + +
ε ab < 0 ,说明动生电动势的方向由 指 说明动生电动势的方向由b指
第十一章 电磁场的统一理论
1111-2 动生电动势和感生电动势 涡旋电场
a、b之间的电压就等于εab。 、 之间的电压就等于 例11-4 法拉第曾利用圆盘发 电机来演示感应电动势的产 生,金属圆盘在磁场中转动 时能在连接电流计的回路中 产生感应电流。如图所示, 产生感应电流。如图所示, 设圆盘半径R=0.20m,转速为 设圆盘半径 , 50转/秒,匀强磁场的磁感应 转秒 强度B=0.70T,求盘心与盘边 强度 , 缘之间的电势差U。 缘之间的电势差 。
设杆长为 l
∫
l
0
v B d l = v Bl
dε i = (v × B) ⋅ dl
第十一章 电磁场的统一理论
1111-2 动生电动势和感生电动势 涡旋电场
二
动生电动势的计算 动生电动势的产生不要求导体必须是回路, 动生电动势的产生不要求导体必须是回路,一段 电源。 在磁场中运动的导体就像一个电动势为εi的电源。如 果是闭合回路,则会在回路中产生感应电流。 果是闭合回路,则会在回路中产生感应电流。 1) 利用电磁感应定律计算 dΦ dΨ εi = − 或 εi = − dt dt 如果运动导体不是闭合的, 如果运动导体不是闭合的,可以设想一个包含运动 导体的闭合回路,添加的回路的部分最好是静止的。 导体的闭合回路,添加的回路的部分最好是静止的。 2) 利用动生电动势计算公式 电动势的方向是 v× B 的 方向
dΦ ε i = ∫ E涡 ⋅ dl = − L dt
Φ = ∫ B ⋅ ds
S
d ∫L E涡 ⋅ dl = − dt ∫SB ⋅ ds
第十一章 电磁场的统一理论
1111-2 动生电动势和感生电动势 涡旋电场
εi =
∫
L
E涡 ⋅ dl = − ∫
S
dB ⋅ ds dt
涡旋电场沿任意闭合回路的线积分等于该回 路所围面积上的磁感应强度的时间变化率的面积 分的负值。 分的负值。
×
×
r
∂B 2 ε i = E涡 ⋅ 2πr = πR ∂t R 2 ∂B E涡 = , (r > R) 2r ∂t r ∂B E涡 = , (r < R) 2 ∂t
× O R × × ×
× × ×
E涡 O R r
的方向和感生电动势的方向都沿逆时针方向。 E涡的方向和感生电动势的方向都沿逆时针方向。 (2) 求棒中的感应电动势。 棒中的感应电动势。 的感应电动势
第十一章 电磁场的统一理论
1111-2 动生电动势和感生电动势 涡旋电场 × × × × ×
磁场分布具有轴对称性,当磁 解: 磁场分布具有轴对称性,
∂B 变化时, 场按 变化时,产生的涡流电场 ∂t
r O× R ×
× ×
的场线是在垂直轴线平面内、 的场线是在垂直轴线平面内、以轴与 (a) 平面交点为圆心的一系列同心圆。 平面交点为圆心的一系列同心圆。 (1) 在管内,沿某一涡旋电场线作闭合回路,半径 在管内,沿某一涡旋电场线作闭合回路, 为r,逆时针绕行。 ,逆时针绕行。
∫∫ E
S
涡
⋅ dS = 0
感生电场和静电场的对比 感生电场和静电场的对比
E静 和 E涡均对电荷有力的作用. 均对电荷有力的作用
第十一章 电磁场的统一理论
1111-2 动生电动势和感生电动势 涡旋电场
静电场是保守场
∫E
L
静
⋅ dl = 0
dΦ ≠0 感生电场是 电场是非 感生电场是非保守场 ∫ E涡 ⋅ dl = − L dt
× × ×
×
O× R ×
× ×
(a)
× × × (1) 求管内外的涡旋电场 E ,并计 E涡 涡 算图(a)中同心圆形回路中的感生电动势。 × × × × × 算图 中同心圆形回路中的感生电动势。 中同心圆形回路中的感生电动势 × ×O × × × (2) 将长为 的金属棒 垂直于磁场放 将长为l的金属棒 的金属棒ab垂直于磁场放 R × × × × × 置在螺线管内,如图(b)所示 求棒中 所示, 置在螺线管内,如图 所示,求棒中的 a l × b × × 感生电动势的大小和方向。 感生电动势的大小和方向。 (b)
1111-2 动生电动势和感生电动势 涡旋电场
解法二: 解法二: 线圈的磁通量 L1 c O′
bω L2
O n
Φ = SB cos θ = SB cos ωt
θa
B d
dΦ εi = − = SBω sin ωt dt N匝线圈:εi = NSB sinω 匝线圈: 匝线圈 ω t 令 ε max = NSBω ε i = ε max sin ωt
第十一章 电磁场的统一理论
−
+
Ek : 非静电的电场强度 非静电的电场强度.
闭合电路的总电动势
ε =
∫E
l
k
⋅dl
第十一章 电磁场的统一理论
1111-2 动生电动势和感生电动势 涡旋电场
一 动生电动势与洛伦兹力 动生电动势的非 动生电动势的非静电力场来源 洛伦兹力
+ + + + + + + + + +
f m = ( − e) v × B
第十一章 电磁场的统一理论
1111-2 动生电动势和感生电动势 涡旋电场
设回路中的电阻为R, 设回路中的电阻为 ,则回路中的感应电流为
Ii =
说明: 说明:
εi
R
=
ε max
R
sin ωt = I max sin ωt
1)当考虑到线圈存在自感时,感应电流和感应电动 当考虑到线圈存在自感时, 当考虑到线圈存在自感时 势的相位会有差别。 势的相位会有差别。 2) 本例的内容就是交流发电机的基本工作原理。 本例的内容就是交流发电机的基本工作原理。 三 感生电动势与涡旋电场 磁场变化引起的感应电动势称为感生电动势。 磁场变化引起的感应电动势称为感生电动势。 产生感生电动势的根源或者说非静电力是什么?? 产生感生电动势的根源或者说非静电力是什么??
+ + + + + +
B
+ + +
ω+ + +
+ + + + + + + +
+ + + a+ + + + + R+ + + + + + + b
解: 圆盘可以看成由许多小扇形面组成,转动的圆盘 圆盘可以看成由许多小扇形面组成, 产生的电动势可以看成是这些小扇形转动产生的 电动势的并联, 电动势的并联,所以
第十一章 电磁场的统一理论
1111-2 动生电动势和感生电动势 涡旋电场
(一) 麦克斯韦的涡旋电场假说 一 麦克斯韦假设: 不论有无导体或导体回路, 麦克斯韦假设: 不论有无导体或导体回路,变化的 磁场都将在其周围空间激发一种具有闭合电场线的 电场,这个电场叫感生电场或涡旋电场 这个电场叫感生电场或涡旋电场。 电场 这个电场叫感生电场或涡旋电场。 产生感生电动势的非静电场 (二) 涡旋电场的性质 二 闭合回路中的感生电动势 感生电场 E涡
第十一章 电磁场的统一理论
1111-2 动生电动势和感生电动势 涡旋电场
引起磁通量变化的原因: 引起磁通量变化的原因 1)稳恒磁场中的导体运动 , ) 变化、取向变化等 变化、取向变化等. 2)导体不动,磁场变化. )导体不动,磁场变化 电动势
I
或者回路面积 动生电动势 感生电动势
Ek
+
ε = ∫ Ek ⋅ d l
静电场由电荷产生;静电场的电场线起自正电 电场由电荷产生; 终止于负电荷。 荷、终止于负电荷。
∫∫ E
S
静
∑q ⋅ dS =
ε0
内
感生电场是由变化的磁场产生 感生电场是由变化的磁场产生 ;感生电场的电 电场是由变化的磁场 场线是闭合的。 场线是闭合的。
∫∫
S
E涡 ⋅ dS = 0
第十一章 电磁场的统一理论
闭合 计算
闭合的回路 的感生电动势
第十一章 电磁场的统一理论
1111-2 ቤተ መጻሕፍቲ ባይዱ生电动势和感生电动势 涡旋电场 ×
半径为R的无限长直螺线管的电 例11-6 半径为 的无限长直螺线管的电 流随时间线性增加(dI/dt=常数 时,其内 常数)时 流随时间线性增加 常数 ∂B 增加, 部的磁感应强度也以恒定变化率 增加, ∂t 如图(a)所示为在管内产生的均匀磁场的 如图 所示为在管内产生的均匀磁场的 一个横截面。 一个横截面。
第十一章 电磁场的统一理论
1111-2 动生电动势和感生电动势 涡旋电场
1 2 ε i = Bω R 2
U ba
1 = U b − U a = ε i = BωR 2 2 1 2 = × 0.70 × 2π × 50 × 0.20 = 4.4(V ) 2
bω L2 O a B n
例11-5 求在均匀磁场里绕定 L1 轴转动的长方形线圈中的感应 电动势。设长方形的边长为L 电动势。设长方形的边长为 1 c 和L2,旋转的角速度为ω,磁 感应强度大小为B, 感应强度大小为 ,方向垂直 O′ 于线圈轴线,如图。 于线圈轴线,如图。 d
