简单效应SPSS编程
简单效应SPSS编程

被试内、被试间、混合实验设计简单效应分析简单效应(simple effect)分析简单效应(simpleeffect)分析通常是在作方差分析时存在交互效应的情况下的进一步分析。
你需要在SPSS中编写syntax实现。
一、完全随机因素实验中简单效应得分析程序假如一个两因素随机实验中,A因素有两个水平、B因素有三个水平,因变量是Y,检验B因素在A因素的两个水平上的简单效应分析。
TWO-FACTOR RANDOMIZED EXPERIMENTSIMPLE EFFECTS.DATA LIST FREE /A B Y.BEGIN DATA1 3 41 1 21 1 32 2 52 1 61 2 82 1 91 2 82 3 102 3 112 3 92 3 8END DATA.MANOVA y BY A(1,2) B(1,3)/DESIGN/DESIGN=A WITHIN B(1)A WITHIN B(2)A WITHIN B(3).若A与B存在交互作用而进行的进一步分析(即简单效应分析)。
同时你可以再加一个design: /DESIGN=B WITHIN A(1)B WITHIN A(2).自编数据试试y A B4.00 1.00 3.002.00 1.00 1.003.00 1.00 1.005.00 2.00 2.006.00 2.00 1.008.00 1.00 2.009.00 2.00 1.008.00 1.00 2.0010.00 2.00 3.0011.00 2.00 3.009.00 2.00 3.008.00 1.00 2.00当然,你可也直接贴下述语句至syntax编辑框:应会输出下述结果:The default error term in MANOVA has been changed from WITHIN CELLS to WITHIN+RESIDUAL. Note that these are the same for all full factorial designs.* * * * * * A n a l y s i s o f V a r i a n c e * * * * * *12 cases accepted.0 cases rejected because of out-of-range factor values.0 cases rejected because of missing data.6 non-empty cells.3 designs will be processed.- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -* * * * * * A n a l y s i s o f V a r i a n c e -- design 1 * * * * * *Tests of Significance for Y using UNIQUE sums of squaresSource of Variation SS DF MS F Sig of FWITHIN CELLS 10.00 6 1.67X1 15.00 1 15.00 9.00 .024X2 6.46 2 3.23 1.94 .224X1 BY X2 33.00 2 16.50 9.90 .013(Model) 80.92 5 16.18 9.71 .008(Total) 90.92 11 8.27R-Squared = .890Adjusted R-Squared = .798- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -* * * * * * A n a l y s i s o f V a r i a n c e -- design 2 * * * * * *Tests of Significance for Y using UNIQUE sums of squaresSource of Variation SS DF MS F Sig of FWITHIN+RESIDUAL 16.46 8 2.06X1 WITHIN X2(1) 25.00 1 25.00 12.15 .008X1 WITHIN X2(2) 8.15 1 8.15 3.96 .082X1 WITHIN X2(3) 43.74 1 43.74 21.26 .002(Model) 74.46 3 24.82 12.06 .002(Total) 90.92 11 8.27R-Squared = .819Adjusted R-Squared = .751- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -* * * * * * A n a l y s i s o f V a r i a n c e -- design 3 * * * * * *Tests of Significance for Y using UNIQUE sums of squaresSource of Variation SS DF MS F Sig of FWITHIN+RESIDUAL 25.00 7 3.57X2 WITHIN X1(1) 30.30 2 15.15 4.24 .062X2 WITHIN X1(2) 35.58 2 17.79 4.98 .045(Model) 65.92 4 16.48 4.61 .039(Total) 90.92 11 8.27R-Squared = .725Adjusted R-Squared = .568另外,三因素完全随机实验中的简单效应和简单简单效应的分析。
用spss20进行二因素设计的简单效应分析

用SPSS20进行二因素设计的简单效应分析两因素试验要检验互作效应,如果互作显著则应进一步做简单效应分析。
SPSS20图形界面无法简单效应分析,其实SPSS大多数功能均无法利用图形界面实现。
所以SPSS的优点并不是其易用性,而重点在于输出结果丰富、编排合理。
比较SAS、和R软件均能利用图形界面进行简单的统计分析,但其输出结果简单,无法直接发布。
我们用一个两因素裂区试验的产量数据进行简单的说明。
这个试验是一个品种密度试验,品种为主区,种植密度为副区,三次重复,籽粒产量为每公顷公斤产量。
其分析语法为:UNIANOVA 单产BY a b r/RANDOM=r/METHOD=SSTYPE(3)/INTERCEPT=INCLUDE/CRITERIA=ALPHA(0.05)/POSTHOC=a b(DUNCAN LSD)/DESIGN=a b r r(a) a*b/EMMEANS = TABLES(a*b) COMPARE (b) ADJ(LSD)/EMMEANS = TABLES(a*b) COMPARE (a) ADJ(LSD).注意最后两句,采用EMMEANS进行简单效应分析,其选项ADJ表示均值检验方法,有3种方法可供选择,常用的是LSD。
运行该语句(Ctrl+r)的下列结果。
注意,该语句前面还有数据集设置(DATASET ACTIVATE 数据集1.),不能写错数据集的名称。
表1 主体间效应的检验因变量: 单产源III 型平方和df 均方 F Sig.截距假设1524883353.546 1 1524883353.546 41177.914 .000误差74063.167 2 37031.584aa假设5090978.401 2 2545489.201 257.340 .000误差39566.096 4 9891.524bb假设2253126.736 2 1126563.368 79.838 .000误差169326.808 12 14110.567cr假设74063.167 2 37031.584 3.744 .121误差39566.096 4 9891.524br(a)假设39566.096 4 9891.524 .701 .606误差169326.808 12 14110.567ca * b假设836244.524 4 209061.131 14.816 .000误差169326.808 12 14110.567ca. MS(r)b. MS(r(a))c. MS(错误) 主区a 副区b 重复r 籽粒产量xm26 10万 1 6942 xm26 10万 2 6725.3 xm26 10万 3 6692 xm26 15万 1 7658.7 xm26 15万 2 7467 xm26 15万 3 7375.4xm26 20万1 7642 xm26 20万 2 7683.7 xm26 20万3 7467 9398 10万 1 6775.3 9398 10万 2 6900.3 9398 10万 3 6748.7 9398 15万 1 6950.3 9398 15万 2 6825.3 9398 15万 3 6775.3 9398 20万 1 7725.4 9398 20万 2 7575.4 9398 20万 3 7883.7 ts28 10万 1 8167.1 ts28 10万 2 8033.7 ts28 10万 3 7858.7 ts28 15万 1 7975.4 ts28 15万 2 8025.4 ts28 15万 3 7908.7 ts28 20万 1 8450.4 ts28 20万 2 8200.4 ts28 20万 3 8475.4表1显示互作显著,因此有必要进行简单效应分析。
两因素实验设计spss操作技巧
两因素重复测量实验设计SPSS操作
简单效应检验
GLM 无标记短句 无标记中句 无标记长句 有标记短句 有标记中句 有标记长句 /WSFACTOR=标记类型 2 Polynomial 句长类型 3 Polynomial /METHOD=SSTYPE(3) /PLOT=PROFILE(标记类型*句长类型) /EMMEANS=TABLES(标记类型*句长类型) COMPARE(标记类型) ADJ(LSD) /EMMEANS=TABLES(标记类型*句长类型) COMPARE(句长类型) ADJ(LSD) /PRINT=DESCRIPTIVE /CRITERIA=ALPHA(.05) /WSDESIGN=标记类型 句长类型 标记类型*句长类型.
一元方差分析结果表明: ① 标记类型主效应显著, F=37.022,P=.009 ② 句长类型主效应检验。因 其满足球形假设,故参见每项检 验的第一行Sphericity Assumed的结果,即, F=47.79,P=.000,表明b变量 主效应极其显著。 ③ a与b的交互效应检验。因 其满足球形假设,故参见标准一 元方差分析的结果,即, F=34.02,P=.001,表明a与b 的交互效应极显著。
对标记类型,赋值时,分别设定: 1=“无标记” 2=“有标记”
对句子类型赋值时,分别设定: 1=“短句子” 2=“中句子” 3=“长句子”
两因素完全随机实验设计SPSS操作
Data View,进入数据输入窗口, 将原始数据输入SPSS表格区域
两因素完全随机实验设计SPSS操作
第二步:Analyze→General Linear Model → Unvariate
❖ 因变量:句子阅读理解成绩 ❖ 随机抽取24名被试,分配到各实验组。
SPSS统计简单效应分析语法语句

在SPSS里实现被试间设计简单效应分析的方法作者: Highway 发布时间: 2008-7-7简单效应(simple effect)分析通常是在作方差分析时存在交互效应的情况下的进一步分析。
需要在SPSS中编写syntax实现。
比如:MANO y BY x1(1 2) x2(1 3)/DESI/DESI=x1 WITHIN x2(1)x1 WITHIN x2(2)x1 WITHIN x2(3)上述只是一个简单的完全随机设计,若x1与x2存在交互作用而进行的进一步分析(即简单效应分析)。
同时你可以再加一个design:/DESI=x2 WITHIN x1(1)x2 WITHIN x1(2).===========说明=============因变量为Y,自变量1为X1,(两水平),自变量2为X2(三水平),DESI即是DESIGN,表示实验设计效应类型计算,/DESI=X1 WITHIN X2(1)表示在自变量X2水平1层面上考察X1的两个水平之间是否存在显著性差异.余类推.下面那句/DESI=X2 WITHIN X1(1)表示在自变量X1水平1的层面上考察自变量X2的三个水平之间是否存在显著性差异.被试内、被试间、混合实验设计简单效应分析作者: Highway 发布时间: 2008-7-7简单效应(simple effect)分析简单效应(simple effect)分析通常是在作方差分析时存在交互效应的情况下的进一步分析。
你需要在SPSS中编写syntax实现。
一、完全随机因素实验中简单效应得分析程序假如一个两因素随机实验中,A因素有两个水平、B因素有三个水平,因变量是Y,检验B因素在A因素的两个水平上的简单效应分析。
TWO-FACTOR RANDOMIZED EXPERIMENTSIMPLE EFFECTS.DA TA LIST FREE /A B Y.BEGIN DATA1 3 41 1 21 1 32 2 52 1 61 2 82 1 91 2 82 3 102 3 112 3 92 3 8END DATA.MANOV A y BY A(1,2) B(1,3)/DESIGN/DESIGN=A WITHIN B(1)A WITHIN B(2)A WITHIN B(3).若A与B存在交互作用而进行的进一步分析(即简单效应分析)。
SPSS做方差分析交互作用的简单效应分析
SPSS做方差分析交互作用的简单效应分析两个试验因素如果他们的交互作用有统计学意义,此时还需继续考察一个因素在另一个因素各水平上的差异,或者说,要考察两个因素不同水平组合之间到底是哪些组合有统计学差异。
这项工作就是交互作用的两两比较,为了区别于主效应的两两比较,特将交互作用的两两比较叫做简单效应分析。
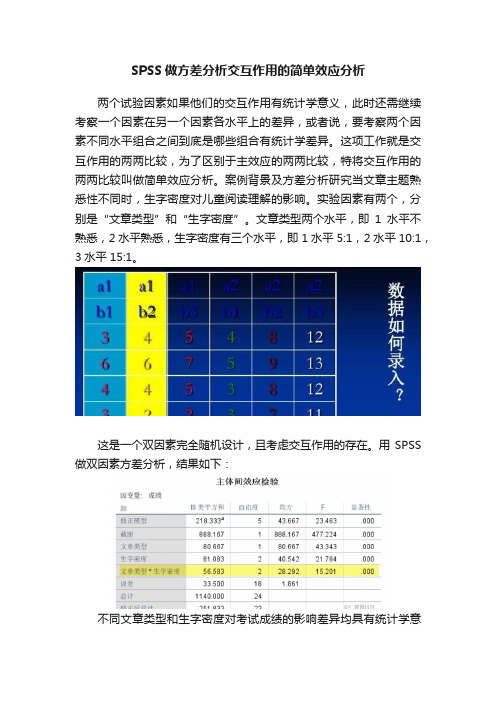
案例背景及方差分析研究当文章主题熟悉性不同时,生字密度对儿童阅读理解的影响。
实验因素有两个,分别是“文章类型”和“生字密度”。
文章类型两个水平,即1水平不熟悉,2水平熟悉,生字密度有三个水平,即1水平5:1,2水平10:1,3水平15:1。
这是一个双因素完全随机设计,且考虑交互作用的存在。
用SPSS 做双因素方差分析,结果如下:不同文章类型和生字密度对考试成绩的影响差异均具有统计学意义(P<0.05),各因素两两比较略,大家可以自己尝试。
文章类型和生字密度对成绩的影响存在交互作用,F(2,18)=15.2,P<0.05。
即当文章主题熟悉性不同时,生字密度对儿童阅读理解的影响有统计学差异。
正如交互效应图所示,当阅读的文章类型不熟悉时,不同生字密度下测试的成绩差距不大(见蓝色线条),而当熟悉文章的类型时,不同生字密度下测试的成绩相差很大(见红色线条)。
6个水平组合中,两两之间的差异到底如何呢?需要进行简单效应分析。
开始分析打开SPSS一般线性模型(单变量)菜单。
因变量“成绩”,固定因子“文章类型”、“生字密度”,打开模型对话框,创建两个因素的主效应加二者的交互作用模型项。
其他参数按软件默认即可,返回主对话框。
SPSS方差分析对话框中并没有内置简单效应参数选项,我们需要使用SPSS的语法代码。
此时在主对话框点击【粘贴】按钮,打开该过程的语法窗口。
如下所示。
请将以下这两行代码粘贴至已有代码中,建议放在最后一行之前。
/EMMEANS=TABLES(文章类型*生字密度)COMPARE(文章类型)ADJ(LSD)/EMMEANS=TABLES(文章类型*生字密度)COMPARE(生字密度)ADJ(LSD)其中:EMMEANSE是estimated marginal means subcommand的缩写,意思是估计边际平均数,TABLES函数以透视表格形式输出边际平均值;COMPARE指定要比较的分组变量;SPSS默认提供lsd ,bonferroni和sidak这三种两两比较方法,本例选择lsd法。
被试内设计及数据处理

Sd ig f . 15
(2-tail .000
Descriptive Statistics
Mean Std. Dev iation
生 字 密 度 1 4.38
1.685
生 字 密 度 2 3.88
1.246
生 字 密 度 3 7.00
1.309
生 字 密 度 410.00
2.268
N 8 8 8 8
描述统计量:平均数和标准差;用于“结果”部分的三线表
单因素重复测量设计方差分析结果的解读
Multiv aria te Tebsts
Ef f ect
Va lue
F Hy pothesis dEfrror df
生 字 密 度 Pillai's Trace
. 954 34.257a
3. 000 5. 000
Wilks' Lambda . 046 34.257a
Test Sphericity Mauchly’s test for sphericity (2 distribution).
Example: ANOVA-2
Mauchly’s test H0: Sphericity 2=11.628 (p=0.043) Reject H0 No sphericity.
2、单因素被试内设计的数据处理方法(SPSS统计软件):
包含的统计变量:实验自变量A的各个处理水平:A1,A2,A3…AP
单因素、交互作用、简单效应分析

8
解 测 验
区组4 区组5
3 5
2 4
7
7
5
12
分 区组6 7
5
6
13
数 区组7 5
3
7
12
区组8 2
3
6
11
数据录入
Tests of Between-Subjects Effects
Dependent Variable: SCORE
S ou rc e Corrected Model
Type III Sum of Squares 216.000a
(I-J)
Std. Error
-2.1250* .68211
3.00
-4.5000* .68211
2.00
1.00
2.1250* .68211
3.00
-2.3750* .68211
3.00
1.00
4.5000* .68211
2.00
2.3750* .68211
Based on observ ed means.
结果2:事后检验即 Post hoc
选中主效应显著,且 水平≥3的自变量
通常用LSD
结果2:事后检验即 Post hoc
Dependent Variable: 成 绩 LSD
Multiple Comparisons
(I) 生 字 密 度 (J) 生 字 密 度
1.00
2.00
Mean
Difference
F值
p值
自由度 组内均方
研究报告中的方差分析结果
One-Way ANOVA通常用文字陈述结果
自由度、均方、F、P 因素较多时则用三线表呈现
三个变量的交互作用简单效应简单效应分析

三个变量的交互作用简单效应简单效应分析Main effect 一个因素的独立效应,即其不同水平引起的方差变异。
三因素的实验有三个主效应。
把某一因素的一个水平同该因素的其他水平比较,不考虑其他因素。
Interaction 多个因素的联合效应,A因素的作用受到B因素的影响,即有交互——two-way interaction. 当一因素作用受到另外两个因素影响,即三因素交互three-way interaction.重复测量一个因素的三因素混合设计3*2*2的混合设计A3*B2*R2 【A, B为被试间因素】需要分析的有——A, B, R 各自主效应二重交互作用,A*B, A*R, B*R三重交互作用,A*B*C结果发现,A, B为被试间因素,交互作用SIG当二重交互作用SIG,需要进行simple effect检验。
A因素水平在B因素某一水平上的变异。
A在B1水平上的简单效应A在B2水平上的简单效应B在A1水平上的简单效应B在A2水平上的简单效应B在A3水平上的简单效应如果三重交互作用SIG,需要进行三因素的简单简单效应分析simple simple effect. 某一因素的水平在另外两个因素的水平结合上的效应在A1B1水平结合上,R1 与 R2 差异在A1B2水平结合上,R1 与 R2 差异在A2B1水平结合上,R1 与 R2 差异在A2B2水平结合上,R1 与 R2 差异在A3B1水平结合上,R1 与 R2 差异在A3B2水平结合上,R1 与 R2 差异重复测量方差分析之后,如果三重交互作用显著,需要编辑语法,得出三个因素各自的简单效应某一因素在其他两个因素的某一实验条件内的简单效应检验三因素重复测量方差分析对应的会有3种简单效应检验结果SPSS在输出简单效应检验结果的同时,也会报告多重比较结果,会有更直观的对比结果。
如果三重交互作用SIG,需要进行简单简单效应检验。
固定某两个因素水平组合,考察研究者最感兴趣的那个变量的效应。
SPSS编程操作入门知识讲解

SPSS编程操作入门知识讲解S P S S编程操作入门第四章 SPSS编程操作入门4.1程序编辑窗口操作入门一、进入程序编辑窗口界面①创建一个新程序File——new——syntax②打开一个旧程序File——open——syntax程序文件的扩展名为*.sps注:syntax窗口的菜单和SPSS窗口的菜单功能基本一致,区别在于RUN菜单。
RUN ALL——运行全部程序RUN SELECTION——运行所选择的部分程序二、熟用Paste 按钮在SPSS所有菜单对话框中均有Paste功能,在所有对话框选择完毕后,不选择 OK,而使用Paste,则程序编辑窗口会自动生成程序。
此功能使得SPSS编程操作变得简单易行,只需要对生成的程序适当加以修改即可。
示例:运用Paste创建一个程序文件。
以xuelin.sav.为例,产生P50页的程序语句,并保存在桌面上备用。
该程序文件可以保存,当下次做相同的分析时,无需重新进行复杂的菜单选择,直接在原有程序文件上进行适当的修改,运行即可。
三、编程进行对话框无法完成的工作示例1:见书示例2:怎么产生连续自然数1~200Input program.Loop #i=1 to 200.Compute x=#i.end case.End loop.End file.End input program.Execute.4.2结构化语句简介一、分支语句(条件语句)①IF语句SPSS程序格式:IF逻辑表达式目标表达式逻辑表达式用于给出判断条件。
目标比达式表示如果满足逻辑表达式后该如何操作。
注:编程基本小知识:①每句命令完成后,以点号结束,否则程序不被执行。
②全部命令编辑完成后,以Execute.结束,否则程序不被执行.③学会使用help——command syntax reference自学编程。
示例1:打开案例数据brain1.sav,要求将年龄小于20,性别为1(男)的病人归为第一组(group=1).GETFILE='F:\chenghongli\spss\数据集\brain1.sav'.if age<20 & sex=1( 逻辑表达式) group=1.(目标表达式)Execute.示例2:打开案例数据brain1.sav,要求将年龄小于等于40岁的女性病人归为组2.GETFILE='F:\chenghongli\spss\数据集\brain1.sav'.if age le 40 group=2.execute.练习1:将血小板大于等于100的列为组1练习2:打开brain1.sav,创造一个新的字符型变量sex1,当sex取值为1时,sex1取值为f, 当sex取值为2时,sex1取值为m. GET FILE='F:\chenghongli\spss\数据集\brain1.sav'.string sex1 (a1).compute sex1='f'.if sex=2 sex1='m'.execute.②DOIF语句如果需要多重分支,有多个条件限制时,需要用到DO IF语句SPSS程序格式:DoIF逻辑表达式目标表达式Else目标表达式EndIF示例1:见书(P52)示例2:编程完成书P31例题练习3:自己完成P33例题二、循环语句在介绍循环语句时,着重介绍Loop/End Loop语句.该语句主要用于建立数据集和数据变换操作。
在SPSS里实现被试间设计简单效应分析的方法

被试内、被试间、混合实验设计简单效应分析作者: Highway 发布时间: 2008-7-7简单效应(simple effect)分析简单效应(simple effect)分析通常是在作方差分析时存在交互效应的情况下的进一步分析。
你需要在SPSS中编写syntax实现。
一、完全随机因素实验中简单效应得分析程序假如一个两因素随机实验中,A因素有两个水平、B因素有三个水平,因变量是Y,检验B因素在A因素的两个水平上的简单效应分析。
TWO-FACTOR RANDOMIZED EXPERIMENTaaaSIMPLE EFFECTS.DATA LIST FREE /A B Y.BEGIN DATA1 3 41 1 21 1 32 2 52 1 61 2 82 1 91 2 82 3 102 3 112 3 92 3 8END DATA.MANOVA y BY A(1,2) B(1,3)/DESIGN/DESIGN=A WITHIN B(1)A WITHIN B(2)A WITHIN B(3).若A与B存在交互作用而进行的进一步分析(即简单效应分析)。
同时你可以再加一个design: /DESIGN=B WITHIN A(1)B WITHIN A(2).自编数据试试y A B4.00 1.00 3.002.00 1.00 1.003.00 1.00 1.005.00 2.00 2.006.00 2.00 1.008.00 1.00 2.009.00 2.00 1.008.00 1.00 2.0010.00 2.00 3.0011.00 2.00 3.009.00 2.00 3.008.00 1.00 2.00当然,你可也直接贴下述语句至syntax编辑框:应会输出下述结果:The default error term in MANOVA has been changed from WITHIN CELLS toWITHIN+RESIDUAL. Note that these are the same for all full factorialdesigns.* * * * * * A n a l y s i s o f V a r i a n c e * * * * * *12 cases accepted.0 cases rejected because of out-of-range factor values.0 cases rejected because of missing data.6 non-empty cells.3 designs will be processed.- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -* * * * * * A n a l y s i s o f V a r i a n c e -- design 1 * * * * * *Tests of Significance for Y using UNIQUE sums of squaresSource of Variation SS DF MS F Sig of FWITHIN CELLS 10.00 6 1.67X1 15.00 1 15.00 9.00 .024X2 6.46 2 3.23 1.94 .224X1 BY X2 33.00 2 16.50 9.90 .013(Model) 80.92 5 16.18 9.71 .008 (Total) 90.92 11 8.27R-Squared = .890Adjusted R-Squared = .798- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -* * * * * * A n a l y s i s o f V a r i a n c e -- design 2 * * * * * *Tests of Significance for Y using UNIQUE sums of squaresSource of Variation SS DF MS F Sig of FWITHIN+RESIDUAL 16.46 8 2.06X1 WITHIN X2(1) 25.00 1 25.00 12.15 .008X1 WITHIN X2(2) 8.15 1 8.15 3.96 .082 X1 WITHIN X2(3) 43.74 1 43.74 21.26 .002(Model) 74.46 3 24.82 12.06 .002 (Total) 90.92 11 8.27R-Squared = .819Adjusted R-Squared = .751- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -* * * * * * A n a l y s i s o f V a r i a n c e -- design 3 * * * * * * Tests of Significance for Y using UNIQUE sums of squaresSource of Variation SS DF MS F Sig of F WITHIN+RESIDUAL 25.00 7 3.57X2 WITHIN X1(1) 30.30 2 15.15 4.24 .062 X2 WITHIN X1(2) 35.58 2 17.79 4.98 .045 (Model) 65.92 4 16.48 4.61 .039 (Total) 90.92 11 8.27R-Squared = .725Adjusted R-Squared = .568另外,三因素完全随机实验中的简单效应和简单简单效应的分析。
简单效应.

简单效应(simple effect分析通常是在作方差分析时存在交互效应的情况下的进一步分析。
你需要在SPSS 中编写syntax实现一、完全随机因素实验中简单效应得分析程序假如一个两因素随机实验中,A因素有两个水平、B因素有三个水平,因变量是Y,检验B因素在A因素的两个水平上的简单效应分析。
TWO-FACTOR RANDOMIZED EXPERIMENTSIMPLE EFFECTSDATA LIST FREE /A B Y.BEGIN DATA1 3 41 1 21 1 32 2 52 1 61 2 82 1 91 2 82 3 102 3 112 3 92 3 8END DATA.MANOVA y BY A(1,2 B(1,3/DESIGN/DESIGN=A WITHIN B(1A WITHIN B(2A WITHIN B(3.若A与B存在交互作用而进行的进一步分析(即简单效应分析。
同时你可以再加一个design:/DESIGN=B WITHIN A(1B WITHIN A(2.另外,三因素完全随机实验中的简单效应和简单简单效应的分析。
当实验设计中的因素多于两个时,做简单效应检验的前提仍然是,方差分析中发现了显著的两次交互作用。
而当三因素完全随机实验中发现了显著的三次交互作用时,可以进一步作简单简单效应检验。
也是DESIGN。
/DESIGN=A WITHIN B(1WITHIN C(1A WITHIN B(2WITHIN C(2.例如:THREE-FACTOR RANDOMIZED EXPERIMENTSIMPLE EFFECTS.SIMPLE SIMPLE EFFECTS. DATA LIST FREE /A B C Y. BEGIN DATA1 3 1 41 1 1 21 1 1 32 2 1 52 1 1 61 2 2 82 1 2 91 2 2 82 3 2 102 3 2 11……2 3 2 92 3 2 8END DATA.MANOVA y BY A(1,2 B(1,3 C(1,2./DESIGN/DESIGN=A WITHIN B(1A WITHIN B(2A WITHIN B(3A WITHIN C(1A WITHIN C(2/DESIGN=A WITHIN B(1 WITHIN C(1A WITHIN B(2 WITHIN C(2.二、被试内因素实验的简单效应分析程序与完全随机实验的不同之处:需要加一个WITHIN关键词说明的WSDESIGN 分命令。
两因素实验设计SPSS操作技巧

两因素完全随机实验设计SPSS操作
第六步:绘制均值图。 在主对话框中点击Plots 横坐标Horizontal Axis 纵坐标Separate Lines 单击Add完成操作。
两因素完全随机实验设计SPSS操作
第七步:点击OK,执行程序。
两因素完全随机实验设计SPSS操作
输出结果
(1)描述统计结果
标记类型主效应显著,F=27.871,P<0.01 句长类型主效应显著,F=8.177,P<0.01 两因素交互效应显著,F(a*b)=5.661,P<0.05。
两因素完全随机实验设计SPSS操作
输出结果
(4)多重比较结果
本例方差齐性检验结果表明,三组方差是齐的。因此,进行多重比较时,应该看用Tukey法进行多重比较的结果。 比较结果为:短句与中句的差异不显著(P=.171)
短句与长句的差异不显著(P=.107) 中句与长句的差异是显著的(P=.002)
两因素完全随机实验设计SPSS操作
输出结果
(5)均值显示图
代表中句和长句的两 条直线大体平行,而代表 短句的直线与两条直线交 叉。因此,大致可以判断 两个因素之间存在交互效 应。
两因素完全随机实验设计SPSS操作
两因素完全随机实验设计SPSS操作
第四步:打开Options 选择Descriptive statistics,对数据进行描述性统计; 选择Homogeneity tests,进行方差齐性检验
两因素完全随机实验设计SPSS操作
第五步:点击Post Hoc按钮,对句长类型(被试间变量)的三个水平进行多重比 较。在方差齐性假设前提条件下可选用Tukey法;在方差非齐性假设前提条件下可 选用Dunnett’s C法。
(整理)三因素溷合方差分析简单效应简单简单效应多重比较语法.

(整理)三因素溷合方差分析简单效应简单简单效应多重比较语法.概念笔记Main effect 一个因素的独立效应,即其不同水平引起的方差变异。
三因素的实验有三个主效应。
把某一因素的一个水平同该因素的其他水平比较,不考虑其他因素。
Interaction 多个因素的联合效应,A因素的作用受到B因素的影响,即有交互——two-way interaction. 当一因素作用受到另外两个因素影响,即三因素交互three-way interaction.重复测量一个因素的三因素混合设计3*2*2的混合设计A3*B2*R2 【A, B为被试间因素】需要分析的有——A, B, R 各自主效应二重交互作用,A*B, A*R, B*R三重交互作用,A*B*C结果发现,A, B为被试间因素,交互作用SIG当二重交互作用SIG,需要进行simple effect检验。
A因素水平在B因素某一水平上的变异。
A在B1水平上的简单效应A在B2水平上的简单效应B在A1水平上的简单效应B在A2水平上的简单效应B在A3水平上的简单效应如果三重交互作用SIG,需要进行三因素的简单简单效应分析simple simple effect. 某一因素的水平在另外两个因素的水平结合上的效应在A1B1水平结合上,R1 与R2 差异在A1B2水平结合上,R1 与R2 差异在A2B1水平结合上,R1 与R2 差异在A2B2水平结合上,R1 与R2 差异在A3B1水平结合上,R1 与R2 差异在A3B2水平结合上,R1 与R2 差异重复测量方差分析之后,如果三重交互作用显著,需要编辑语法,得出三个因素各自的简单效应某一因素在其他两个因素的某一实验条件内的简单效应检验三因素重复测量方差分析对应的会有3种简单效应检验结果SPSS在输出简单效应检验结果的同时,也会报告多重比较结果,会有更直观的对比结果。
如果三重交互作用SIG,需要进行简单简单效应检验。
固定某两个因素水平组合,考察研究者最感兴趣的那个变量的效应。
三因素实验设计

三因素实验设计对三因素重复测量实验设计进行数据处理一、三因素完全随机实验设计数据处理过程:1、打开SPSS软件,点击Data View ,进入数据输入窗口,将原始数据输入SPSS 表格区域;2、在菜单栏中选择分析→一般线性模型→单变量;3、因变量Dependent Variable方框中放入记忆成绩(JY),固定变量(Fixed Factor(s))方框中,放入自变量记忆策略、有无干扰和材料类型;4、点击选项(Options)按钮,选择Descriptive statistics,对数据进行描述性统计;选择Homogeneity tests,进行方差齐性检验;s i o n 2总计 4.2000 1.54238 20 总计实物图片7.3000 3.79889 20 图形图片 5.6500 2.39022 20总计 6.4750 3.2422540被试间变量效应检验结果:A、B、C的主效应均极显著(P<0.01);AB 交互效应显著;AC 交互效应极显著;BC 交互效应不显著;ABC 交互效应极显著。
对于二阶与三阶交互效应显著的,还需进行简单效应与简单简单效应检验。
主体间效应的检验因变量:记忆成绩源III 型平方和df 均方 F Sig.校正模型349.175a7 49.882 26.254 .000 截距1677.025 1 1677.025 882.645 .000A 65.025 1 65.025 34.224 .000B 207.025 1 207.025 108.961 .000C 27.225 1 27.225 14.329 .001 A * B 9.025 1 9.025 4.750 .037A * C 15.625 1 15.625 8.224 .007B *C 4.225 1 4.225 2.224 .146 A * B * C 21.025 1 21.025 11.066 .002 误差60.800 32 1.900总计2087.000 40校正的总计409.975 39主体间效应的检验因变量:记忆成绩源III 型平方和df 均方 F Sig.校正模型349.175a7 49.882 26.254 .000 截距1677.025 1 1677.025 882.645 .000A 65.025 1 65.025 34.224 .000B 207.025 1 207.025 108.961 .000C 27.225 1 27.225 14.329 .001 A * B 9.025 1 9.025 4.750 .037A * C 15.625 1 15.625 8.224 .007B *C 4.225 1 4.225 2.224 .146 A * B * C 21.025 1 21.025 11.066 .002 误差60.800 32 1.900总计2087.000 40校正的总计409.975 39a. R 方= .852(调整R 方= .819)简单效应检验:在主对话框中,单击Paste按钮,SPSS会把原先的全部操作转换成语句并粘贴到新打开的程序语句窗口中,在命令语句中加入EMMEANS引导的语句;结果:当被试使用联想策略进行记忆时,无干扰条件的记忆成绩极显著优于有干扰条件的记忆成绩;当被试使用复述策略进行记忆时,无干扰条件的记忆成绩也极显著优于有干扰条件的记忆成绩。
简单交互效应和简单简单效应分析

between-subject designif three-way interaction is signifcant , compute the simple interaction effect.**********simple interaction effect******************** manovatotal by gender (1,2) depart (1,2) grade(1,3)/design = gender*grade within depart(1)gender*grade within depart(2).if the simple interaction effect is not signifcant , compute the simple effect.如果简单交互效应不显著,那么就计算***************simple effect*********************** manovatotal by gender (1,2) depart (1,2) grade(1,3)/design = grade within depart(1)gender within depart(1).**************multiple comparison s***************** manovatotal by gender (1,2) depart (1,2) grade(1,3)/contrast (grade) = special (1 1 1 1 -1 0 1 0 -1)/design = grade within depart(1).manovatotal by gender (1,2) depart (1,2) grade(1,3)/contrast (grade) = special (1 1 1 1 -1 0 0 1 -1)/design = grade within depart(1).if the simple interaction is significant ,compute the simple simple effect.简单交互效应显著,计算简单简单效应。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
被试内、被试间、混合实验设计简单效应分析简单效应(simple effect)分析简单效应(simple effect)分析通常是在作方差分析时存在交互效应的情况下的进一步分析。
你需要在SPSS中编写syntax实现。
一、完全随机因素实验中简单效应得分析程序假如一个两因素随机实验中,A因素有两个水平、B因素有三个水平,因变量是Y,检验B因素在A因素的两个水平上的简单效应分析。
TWO-FACTOR RANDOMIZED EXPERIMENTSIMPLE EFFECTS.DATA LIST FREE /A B Y.BEGIN DATA1 3 41 1 21 1 32 2 52 1 61 2 82 1 91 2 82 3 102 3 112 3 92 3 8END DATA.MANOVA y BY A(1,2) B(1,3)/DESIGN/DESIGN=A WITHIN B(1)A WITHIN B(2)A WITHIN B(3).若A与B存在交互作用而进行的进一步分析(即简单效应分析)。
同时你可以再加一个design: /DESIGN=B WITHIN A(1)B WITHIN A(2).自编数据试试y A B4.00 1.00 3.002.00 1.00 1.003.00 1.00 1.005.00 2.00 2.006.00 2.00 1.008.00 1.00 2.009.00 2.00 1.008.00 1.00 2.0010.00 2.00 3.0011.00 2.00 3.009.00 2.00 3.008.00 1.00 2.00当然,你可也直接贴下述语句至syntax编辑框:应会输出下述结果:The default error term in MANOVA has been changed from WITHIN CELLS to WITHIN+RESIDUAL. Note that these are the same for all full factorial designs.* * * * * * A n a l y s i s o f V a r i a n c e * * * * * *12 cases accepted.0 cases rejected because of out-of-range factor values.0 cases rejected because of missing data.6 non-empty cells.3 designs will be processed.- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -* * * * * * A n a l y s i s o f V a r i a n c e -- design 1 * * * * * *Tests of Significance for Y using UNIQUE sums of squaresSource of Variation SS DF MS F Sig of FX1 15.00 1 15.00 9.00 .024X2 6.46 2 3.23 1.94 .224X1 BY X2 33.00 2 16.50 9.90 .013(Model) 80.92 5 16.18 9.71 .008(Total) 90.92 11 8.27R-Squared = .890Adjusted R-Squared = .798- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -* * * * * * A n a l y s i s o f V a r i a n c e -- design 2 * * * * * *Tests of Significance for Y using UNIQUE sums of squaresSource of Variation SS DF MS F Sig of FWITHIN+RESIDUAL 16.46 8 2.06X1 WITHIN X2(1) 25.00 1 25.00 12.15 .008X1 WITHIN X2(2) 8.15 1 8.15 3.96 .082X1 WITHIN X2(3) 43.74 1 43.74 21.26 .002(Model) 74.46 3 24.82 12.06 .002R-Squared = .819Adjusted R-Squared = .751- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -* * * * * * A n a l y s i s o f V a r i a n c e -- design 3 * * * * * *Tests of Significance for Y using UNIQUE sums of squaresSource of Variation SS DF MS F Sig of FWITHIN+RESIDUAL 25.00 7 3.57X2 WITHIN X1(1) 30.30 2 15.15 4.24 .062X2 WITHIN X1(2) 35.58 2 17.79 4.98 .045(Model) 65.92 4 16.48 4.61 .039(Total) 90.92 11 8.27R-Squared = .725Adjusted R-Squared = .568另外,三因素完全随机实验中的简单效应和简单简单效应的分析。
当实验设计中的因素多于两个时,做简单效应检验的前提仍然是,方差分析中发现了显著的两次交互作用。
而当三因素完全随机实验中发现了显著的三次交互作用时,可以进一步作简单简单效应检验。
也是DESIGN。
/DESIGN=A WITHIN B(1) WITHIN C(1)A WITHIN B(2) WITHIN C(2).例如:THREE-FACTOR RANDOMIZED EXPERIMENTSIMPLE EFFECTS.SIMPLE SIMPLE EFFECTS.DATA LIST FREE /A B C Y. BEGIN DATA1 3 1 41 1 1 21 1 1 32 2 1 52 1 1 61 2 2 82 1 2 91 2 2 82 3 2 102 3 2 11……2 3 2 92 3 2 8END DATA.MANOVA y BY A(1,2) B(1,3) C(1,2). /DESIGN/DESIGN=A WITHIN B(1)A WITHIN B(2)A WITHIN B(3)A WITHIN C(1)A WITHIN C(2)/DESIGN=A WITHIN B(1) WITHIN C(1)A WITHIN B(2) WITHIN C(2).二、被试内因素实验的简单效应分析程序与完全随机实验的不同之处:需要加一个WITHIN关键词说明的WSDESIGN分命令。
假如一个两因素被试内实验中,A因素有两个水平、B因素有三个水平,因变量是Y,检验B因素在A因素的两个水平上的简单效应分析。
TWO-FACTOR REPEATED MEASURED EXPERIMENT ANOVASIMPLE EFFECTS.DATA LIST FREE /A1B1 A1B2 A1B3 A2B1 A2B2 A2B3.BEGIN DATA3 4 5 4 8 126 67 5 9 134 45 3 8 123 2 2 3 7 11END DATA.MANOVA A1B1 A1B2 A1B3 A2B1 A2B2 A2B3/WSFACTORS=A(2)B(3)/WSDESIGN=A WITHIN B(1)A WITHIN B(2)A WITHIN B(3).三、混合因素实验的简单效应分析一个两因素混合实验中,简单效应检验中既包括被试内因素,有包括被试间因素,这是需要用关键词MWITHIN代替WITHIN去做简单效应检验。
例如,一个两因素混合实验中,A因素是被试间因素,B因素是被试内因素,当要求A因素在B1水平上的简单效应检验时,程序有两处说明:1.被试间因素A应写在DESIGN分命令中。
/DESIGN=A2.B1水平应写在WSDESIGN分命令中,跟在MWITHIN之后。
/WSDESIGN=MWIRHIN B(1)两个命令和起来:/DESIGN=A/WSDESIGN=MWITHIN B(1)这样可以检验到“混合”简单效应。
当要求B因素在A1水平上的简单效应检验时,/WSDESIGN=B/DESIGN=MWITHIN A(1)一个两因素混合实验中,A因素是被试间因素,有两个水平,B因素是被试内因素,有三个水平,要求做B因素在A的两个水平上的简单效应检验,程序如下:TWO-FACTOR MIXED EXPERIMENT ANOVASIMPLE EFFECTS.SIMPLE SIMPLE EFFECTS.DATA LIST FREE /A B1 B2 B3.BEGIN DATA1 3 3 41 1 3 21 6 1 32 5 1 52 4 4 61 2 9 82 1 7 91 4 6 82 3 2 102 3 3 11……2 9 5 92 3 2 8END DATA.MANOVA B1 B2 B3 BY A(1,2)./WSFACTORS=B(3)/WSDESIGN/DESIGN/WSDESIGN=B/DESIGN=MWITHIN A(1) MWITHIN A(2).要求做另一个方向的简单效应检验,做A因素在B的三个水平的简单效应检验时,MWITHIN关键词应被移动到WSDESIGN分命令。
程序如下:TWO-FACTOR MIXED EXPERIMENT ANOVASIMPLE EFFECTS.SIMPLE SIMPLE EFFECTS.DATA LIST FREE /A B1 B2 B3.BEGIN DATA1 3 3 41 1 3 21 6 1 32 5 1 52 4 4 61 2 9 82 1 7 91 4 6 82 3 2 102 3 3 11……2 9 5 92 3 2 8END DATA.MANOVA B1 B2 B3 BY A(1,2)./WSFACTORS=B(3)/WSDESIGN/DESIGN/WSDESIGN=MWITHINB(1) MWITHINB(2) MWITHIN B(3) /DESIGN= A.总结:被试内:WSDESIGN WITHIN被试间:DESIGN WITHIN混合:MWITHIN研究变量的主效应与交互效应在多因素实验研究中,主效应就是在考察一个变量是否会对因变量的变化发生影响的时候,不考虑其他研究变量的变化,或者说将其他变量的变化效应平均掉。
