过不共线三点作圆
《过不在同一直线上的三点作圆》教案-02
《过不在同一直线上的三点作圆》教案【知识与技能】1.理解确定圆的条件及外接圆外心的定义。
2.掌握三角形外接圆的画法。
【过程与方法】经历过不在一直线上的三点确定一个圆的探索过程,让学生会用尺规作过不在同一直线上的三点的圆。
【情感态度与价值观】在探究过不在同一直线上的三点确定一个圆的过程中,进一步培养探究能力和动手能力。
教学重点和难点【重点】(1)确定圆的条件和外心的定义。
(2)三角形外接圆的画法。
【难点】过不共线的三点的圆的圆心的确定。
教学过程一 创设情境,导入新课1.几点确定一条直线?既然一条直线可以由两点确定,那么一个圆需要几点才能确定呢?2.如图一考古学家在马王堆汉墓挖掘时,发现一圆形瓷器碎片,为了便于进行研究,这位考古学家想画出这个碎片所在的圆,你能帮助他解决这个问题吗?为了解决上面问题我来学习:3.1.3过不在同一直线上的三点作圆二合作交流,探究新知 1探究确定圆的条件(1)如何过点A 作圆,可以作多少个圆?(学生独立完成) 教师归纳:任意取点O 作圆心,OA 为半径作圆。
(2)如何过两点作圆?过两点可以作多少个圆?已知点,圆心确定以后,半径也随之确定,因此,关键是确定圆心. ①过A 、B 两点的圆的圆心在哪儿?由于A 、B 两点在圆上,所以OA=OB,因此点O 在AB 的垂直平分线上。
② 如何过A 、B 两点作圆?以线段AB 垂直平分线上任意一点O 为圆心,OA 长为半径作圆。
③ 过A 、B 两点可以作多少个圆?由于AB 垂直平分线上任意一点都可以作为圆心,因此可以作无数个圆。
学生完成作图(3)如何过不在同一直线上的三点作圆? 已知:不在同一直线上的三点A、B、C(如图) 求作:⊙O,使它经过点A、B、C.分析:由于圆O 经过点A 、B 、C ,因此点OA=OB=OC,于是点O 在线段AB 的垂直平分线上,也在BC 的垂直平分线上。
作法:① 连接AB ,作AB 的垂直平分线EF , ② 连接BC ,作BC 的垂直平分线MN 交EF 于O.③ 以O 为圆心,OA 为半径作圆,则圆O 就是要作的圆。
过不共线三点作圆
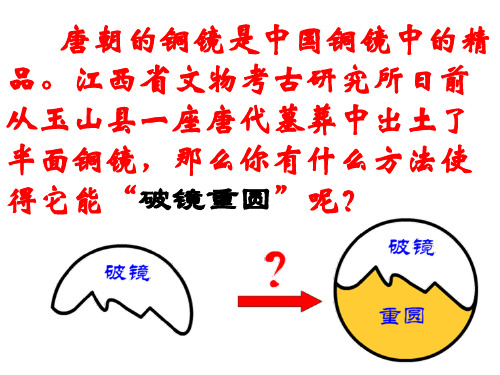
∵直线DE和FG只有一个交点O,并且点O到 A,B,C三个点的距离相等,
∴经过点A,B,C三点可以作一个圆,并且只能作 一个圆.
经过不在同一直线上的三点可以
作一个圆,并且只能作一个圆。
A
定理:
O C
B
不在同一直线上的三
点确定一个圆。
1。由定理可知:经过三角 形三个顶点可以作一个圆. 并且只能作一个圆.
即没有过这三点的圆心
2、三点不共线
已知:不在同一直线上的三点
F
A、B、C
求作:⊙O,使它经过A、B、C
A
B
作法:
O
1、连结AB,作线段AB的
C
垂直平分线DE,
2、连结BC,作线段BC的垂直平 G
分线FG,交DE于点O,
3、以O为圆心,OB为半径作圆,
⊙O就是所求作的圆
请你证明你作得圆符合要求
证明:∵点O在AB的垂直平分线上, ∴OA=OB. 同理,OB=OC. ∴OA=OB=OC. ∴点A,B,C在以O为圆心,OA长为半径的圆上. ∴⊙O就是所求作的圆,
三、为美化校园,学校要把一块三角
形空地扩建成一个圆形喷水池,在三
角形三个顶点处各有一棵名贵花树(A、
B、C),若不动花树,还要建一个
最大的圆形喷水池,请设计你的实施
方案。
A
C B
的中点
钝角三角形外心在 △ABC的外面
如何解决“破镜重圆” 的问题:
B
A
C
O
圆心一定在弦的 垂直平分线上
如图所示,△ABC中,AB=AC=10,BC=12, 求△ABC外接圆的半径.
如图,圆O是△ABC的外接圆,AD是圆O的直径 ,若圆O的半径为3/2,AC=2,则sinB的值是多少?
《过不共线三点作圆》导学案

学习目标
1.了解不共线三点确定一个圆的方法,三角形的外接圆及外心等概念;
2.经历不共线三个点确定一个圆的探索过程,培养学生的探索能力.
重点难点
重点:掌握过不共线三点作圆的方法,了解三角形的外接圆及外心等概念.
难点:怎么样去确定过不在同一条直线上的三点的圆的圆心.
学习过程:
一、课前抽测: A B
A·
B· ·C
2.求边长为a的等边三角形的外接圆的半径.(用含有a的式子表示)
五、达标)⊙O是△ABC的圆.
2. 判断:
(1)经过三个点一定可以作圆;( )
(2)任意一个三角形一定有一个外接圆,并且只有一个外接圆;( )
(3)任意一个圆一定有一个内接三角形,并且只有一个内接三角形;( )
1.(1)经过一个已知点A画圆; ·A
想一想:经过已知点A可以画多少个圆?
(2)经过两个已知点C、B画圆.
想一想:①经过两个已知点可以画多少个圆?
C· · B
②圆心在哪儿?半径怎么确定?
2.设三点A,B,C不在同一直线上.
⑴过三点A,B,C的圆的圆心在哪儿?怎么确定?
A· ·B
C·
⑵过不在同一直线上的三点A,B,C如何作圆?
强调:(1)过同一直线上三点不行; (2)“确定”一词应理解成“有且只有”.
3.三角形的外接圆:.
圆的内接三角形:.
外心:.
三、合作探究:
例1:作出下列三角形的外接圆(只要作图痕迹,不要求作法)
归纳:锐角三角形的外心在三角形的
直角三角形的外心是三角形
钝角三角形的外心在三角形的
四、展示质疑:
1.如图,A、B、C表示三个工厂,要建一个供水站,使它到这三个工厂的距离相等,求供水站的位置(用点P表示,保留作图痕迹)。
点和圆的位置关系-课件

例题
已知⊙O 的半径为10cm,A,B,C 三点到圆心O 的距离分 别为8cm,10cm,12cm,则点A,B,C 与⊙O 的位置关 系点A是在: __圆__内_____. 点B在__圆___上____. 点C在__圆___外____.
点P在圆外
d>r
点P在圆上
d=r
点P在圆内
d<r
这个符号读作“等价于”,它表示从该符号的左端 可以推出右端,右端也能推出左端.
点和圆的位置关系
你知道击中靶上不同位置的成绩是如何计算的吗 ?
射击靶图上,有一组以靶心为圆心的大小不同 的圆,他们把靶图由内到外分成几个区域.
这些区域用由高到底的环数来表示,射击成绩 用弹着点位置对应的环数来表示.
练习
已知⊙O 的半径为5,M 为ON的中点,当OM=3时 ,N点与⊙O 的位置关系是N 在⊙O 外的部_____________.
练习 ⊙O 直径为d,点A到圆心的距离为m,若点 A不在圆
外,则d与m的关系是_____________.
练习
有一张矩形纸片,AB =3cm,AD =4cm,若以A为圆 心作圆,并且要使点D 在⊙A内,而点C 在⊙A外, ⊙A的半径 r 的取值范围是__________________.
例题
如图所示,已知⊙O 和直线l,过圆心O 作OP⊥l,P 为 垂足,A,B,C为直线l上三个点,且PA=2cm,PB =3cm,PC =4cm,若⊙O的半径为5cm,OP=4cm, 判断A,B,C三点与⊙O的位置关系. 点A在__圆___内____.
点B在__圆___上____. 点C在__圆___外____.
九年级数学平面几何过三点的圆和垂径定理人教四年制知识精讲

九年级数学平面几何过三点的圆和垂径定理人教四年制【同步教育信息】一. 本周教学内容:平面几何过三点的圆和垂径定理二. 学习要求:(过三点的圆)1. 定理:不在同一直线上的三个点确定一个圆:它的意思是如果有三个点,它们三点不共线,那么经过这三个点可以作一个圆并且只可以做一个圆。
2. 三角形的外接圆,外心以及圆的内接三角形:经过三角形三个顶点的圆叫做三角形的外接圆,外接圆的圆心叫三角形的外心,这个三角形叫做这个圆的内接三角形,如图:A、(二)学习要点:1. 圆的轴对称性:圆是轴对称图形,经过圆心的每一条直线都是它的对称轴。
2. 垂径定理:垂直于弦的直径平分这条弦且平分这条弦所对的两条弧。
如图:CD 是直径,AB 是弦,AB CD ⊥于E ,则有:AE=EB ,⋂⋂=DB AD ,⋂⋂=CB AC 。
理由是:因为圆是轴对称图形,CD 是直径是圆的对称轴,若延CD 将圆对折,则CD⋂⋂⋂⋂【典型例题】[例1] 如图,已知直径AB 和CD 相交于点E ,︒=∠==60,5,1BED cm BE cm AE ,求:OA B CD证:依题意:OC=OD ,OA=OB∴OD OBOC OA =且夹角O ∠∴OAB ∆∽OCD ∆ ∴ABCD OA OC =∴CD OA AB OC ⋅=⋅ [例3] ABC ∆中,︒=∠90C 直角边a 、b 分别是方程0132=+-x x 的两个根,求ABC Rt ∆外接圆面积。
解:∵a 、b 是0132=+-x x 两个根∴1,3==+ab b a72132)(22222=⨯-=-+==+ab b a c b a∴7=c ,而ABC Rt ∆外接圆半径=27 ∴ππ47)27(2=⋅=圆S [例4] 已知四边形ABCD 中,︒=∠=∠90D B ,求证ABCD 有外接圆。
ADBCO证:连AC ,取AC 中点O在ABC Rt ∆和ADC Rt ∆中,连OB 、OD 则OC AO AC OD OB ====21∴A 、B 、C 、D 在以O 为圆心,以OA 为半径的圆上[例5] 如图,AB 是⊙O 的直径,CD 是⊙O 的一条弦,延长DC 与BA 的延长线交于P ,且PC=OB ,︒=∠99BOD ,求P ∠的度数。
过不共线三点做圆

如图:⊙O是△ABC的
外接圆, △ABC是⊙O
的内接三角形,点O是
O C △ABC的外心
B
外心是△ABC三条边的垂
直平分线的交点,它到三角
形的三个顶点的距离相等。
A
A
A
●O
●O
B
┐
CB
C
●O
B
C
锐角三角形的外心位于三角形内. 直角三角形的外心位于直角三角形斜边中点. 钝角三角形的外心位于三角形外.
运用新知
某一个城市在一块空地新建了三个居 民小区,它们分别为A、B、C,且三个小区 不在同一直线上,要想规划一所中学,使 这所中学到三个小区的距离相等。请问同 学们这所中学建在哪个位置?你怎么确定 这个位置呢?
●A
B●
●C
课堂小结
1、通过本课的学习,你有什么收获?还有什么问题?
2、确定圆的条件——
长沙马王堆一号汉墓的 发掘,在我国的考古界算得 上惊人的发现,在世界考古 学史上,也产生了深远的影 响。一位考古学家在马王堆 汉墓挖掘时,发现一圆形瓷 器碎片,你能帮助这位考古 学家将这个破损的圆形瓷器 复原,以便于进行深入的研 究吗?
知识回顾
1、确定一个圆的基本条件是 什么?
2、如何作线段的垂直平分线, 它有什么性质?
A N
F
作法: 1、连结AB,作线段AB的垂
直平分线MN;
B
EO
M
C 2、连接AC,作线段AC的垂 直平分线EF,交MN于点O;
3、以O为圆心,OA为半径作
圆。
所以⊙O就是所求作的圆。
课题:不在同一条直线 上的三个点确定一个圆
如果三个点在同一直线时可以作圆吗? 为什么?
2024年人教版九年级数学上册教案及教学反思全册第24章 圆(教案) 点和圆的位置关系教案

24.2 点和圆、直线和圆的位置关系24.2.1 点和圆的位置关系一、教学目标【知识与技能】1.掌握点与圆的三种位置关系及数量间的关系.2.探求过点画圆的过程,掌握过不在同一直线上三点画圆的方法.3.了解运用“反证法”证明命题的思想方法.【过程与方法】通过生活中的实例探求点和圆的三种位置关系,并提炼出数量关系,从而渗透数形结合,分类讨论等数学思想.【情感态度与价值观】形成解决问题的一些基本策略,体验解决问题策略的多样性,发展实践能力与创新精神.二、课型新授课三、课时1课时。
四、教学重难点【教学重点】(1)点与圆的三种位置关系.(2)过三点作圆.【教学难点】点与圆的三种位置关系及其数量关系反证法五、课前准备课件、图片、圆规、直尺等.六、教学过程(一)导入新课我国射击运动员在奥运会上获金牌,为我国赢得荣誉.如图是射击靶的示意图,它是由许多同心圆(圆心相同,半径不相同)构成的,你知道击中靶上不同位置的成绩是如何计算的吗?(出示课件2)解决这个问题要研究点和圆的位置关系.(板书课题)(二)探索新知探究一点和圆的位置关系教师问:观察下图中点和圆的位置关系有哪几种?(出示课件4)学生交流,回答问题.教师点评:点与圆的位置关系有三种:点在圆内,点在圆上,点在圆外.教师问:设点到圆心的距离为d,圆的半径为r,量一量在点和圆三种不同位置关系时,d与r有怎样的数量关系?(出示课件5)学生答:教师问:反过来,由d与r的数量关系,怎样判定点与圆的位置关系呢?学生观察思考交流后,师生共同得到结论:(出示课件6)点与圆的三种位置关系及其数量间的关系:边结论.读作“等价于”.⑵要明确“d”表示的意义,是点P到圆心O的距离.出示课件7,8:例如图,已知矩形ABCD的边AB=3,AD=4.(1)以A为圆心,4为半径作⊙A,则点B、C、D与⊙A的位置关系如何?(2)若以A点为圆心作⊙A,使B、C、D三点中至少有一点在圆内,且至少有一点在圆外,求⊙A的半径r的取值范围?(直接写出答案)学生独立思考后,师生共同解答.解:⑴AD=4=r,故D点在⊙A上;AB=3<r,故B点在⊙A内;AC=5>r,故C点在⊙A外.⑵3≤r≤5.巩固练习:(出示课件9)1.⊙O的半径为10cm,A、B、C三点到圆心的距离分别为8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:点A在_______;点B在_______;点C在_______.2.圆心为O的两个同心圆,半径分别为1和2,若,则点P在()A.大圆内B.小圆内C.小圆外D.大圆内,小圆外学生独立思考后口答:1.圆内;圆上;圆外 2.D探究二过不共线三点作圆教师问:如何过一个点A作一个圆?过点A可以作多少个圆?(出示课件10)学生动手探究,作图,交流,得出结论,教师点评并总结.以不与A点重合的任意一点为圆心,以这个点到A点的距离为半径画圆即可;可作无数个圆.教师问:如何过两点A、B作一个圆?过两点可以作多少个圆?(出示课件11)学生动手探究,作图,交流,得出结论,教师点评并总结.作线段AB的垂直平分线,以其上任意一点为圆心,以这点和点A或B的距离为半径画圆即可;可作无数个圆.教师问:过不在同一直线上的三点能不能确定一个圆?(出示课件12)学生思考后师生共同解答:经过A,B两点的圆的圆心在线段AB的垂直平分线上.经过B,C两点的圆的圆心在线段BC的垂直平分线上.经过A,B,C三点的圆的圆心应该在这两条垂直平分线的交点O的位置.教师归纳:不在同一直线上的三点确定一个圆.(出示课件13)出示课件14:例已知:不在同一直线上的三点A、B、C.求作:⊙O,使它经过点A、B、C.学生动手探究,作图,交流后,师生共同解答.作法:1.连接AB,作线段AB的垂直平分线MN;2.连接AC,作线段AC的垂直平分线EF,交MN于点O;3.以O为圆心,OB为半径作圆.所以⊙O就是所求作的圆.教师问:现在你知道怎样将一个如图所示的破损的圆盘复原了吗?(出示课件15)学生动手探究,交流,在教师指导下作图.作法:1.在圆弧上任取三点A、B、C;2.作线段AB、BC的垂直平分线,其交点O即为圆心;3.以点O为圆心,OC长为半径作圆.⊙O即为所求.巩固练习:(出示课件16)如图,CD所在的直线垂直平分线段AB,怎样用这样的工具找到圆形工件的圆心.学生独立思考后口答:∵A、B两点在圆上,所以圆心必与A、B两点的距离相等,又∵和一条线段的两个端点距离相等的点在这条线段的垂直平分线上,∴圆心在CD所在的直线上,因此可以做任意两条直径,它们的交点为圆心.探究三三角形的外接圆及外心已知△ABC,用直尺与圆规作出过A、B、C三点的圆.(出示课件17)学生复述作法.教师对照图形进行归纳:(出示课件18)1.外接圆:经过三角形三个顶点可以作一个圆,这个圆叫做三角形的外接圆.⊙O叫做△ABC的外接圆,△ABC叫做⊙O的内接三角形.2.三角形的外心定义:外接圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的外心.作图:三角形三边中垂线的交点.性质:到三角形三个顶点的距离相等.练一练:判断下列说法是否正确.(出示课件19)(1)任意的一个三角形一定有一个外接圆.( )(2)任意一个圆有且只有一个内接三角形.( )(3)经过三点一定可以确定一个圆. ( )(4)三角形的外心到三角形各顶点的距离相等.( )学生口答:⑴√⑵×⑶×⑷√画一画:分别画一个锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,观察并叙述各三角形与它的外心的位置关系.(出示课件20)学生动手探究,作图,交流后,教师总结.锐角三角形的外心位于三角形内,直角三角形的外心位于直角三角形斜边的中点,钝角三角形的外心位于三角形外.出示课件21,22:例1 如图,将△AOB置于平面直角坐标系中,O为原点,∠ABO=60°,若△AOB的外接圆与y轴交于点D(0,3).(1)求∠DAO的度数;(2)求点A的坐标和△AOB外接圆的面积.学生独立思考后师生共同解答.解:(1)∵∠ADO=∠ABO=60°,∠DOA=90°,∴∠DAO=30°;⑵∵点D的坐标是(0,3),∴OD=3.在Rt△AOD中,∵∠DOA=90°,∴AD为直径.又∵∠DAO=30°,∴AD=2OD=6,OA=因此圆的半径为3.点A的坐标(0),∴△AOB外接圆的面积是9π.教师强调:解题妙招:图形中求三角形外接圆的面积时,关键是确定外接圆的直径(或半径)长度.巩固练习:(出示课件23)如图,已知直角坐标系中,A(0,4),B(4,4),C(6,2).(1)写出经过A,B,C三点的圆弧所在圆的圆心M的坐标.(2)判断点D(5,-2)和圆M的位置关系.学生独立解答.解:(1)在方格纸中,线段AB和BC的垂直平分线相交于点(2,0),所以圆心M的坐标为(2,0).(2)圆的半径AM==线段DM所以点D在圆M内.出示课件24:例2 如图,在△ABC中,O是它的外心,BC=24cm,O到BC的距离是5cm,求△ABC的外接圆的半径.学生独立思考后师生共同解答.解:连接OB ,过点O 作OD ⊥BC.则OD =5cm ,112cm 2BD BC ==在Rt △OBD 中,13cm OB ==,即△ABC 的外接圆的半径为13cm.巩固练习:(出示课件25)在Rt △ABC 中,∠C=90°,AC=6 cm,BC=8cm,则它的外心与顶点C 的距离为( )A.5cmB.6cmC.7cmD.8cm学生思考后口答:A探究四 反证法教师问:经过同一条直线上的三个点能作出一个圆吗?(出示课件26)学生动手探究,作图,交流后,师生共同解答.如图,假设过同一条直线l 上三点A 、B 、C 可以作一个圆,设这个圆的圆心为P.那么点P 既在线段AB 的垂直平分线l 1上,又在线段BC 的垂直平分线l 2上,即点P 为l 1与l 2的交点.而l 1⊥l ,l 2⊥l 这与我们以前学过的“过一点有且只有一条直线与已知直线垂直”相矛盾.所以过同一条直线上的三点不能作圆.教师归纳:(出示课件27)1.反证法的定义先假设命题的结论不成立,然后由此经过推理得出矛盾(常与公理、定理、定义或已知条件相矛盾),由矛盾判定假设不正确,从而得到原命题成立,这种方法叫做反证法.2.反证法的一般步骤⑴假设命题的结论不成立(提出与结论相反的假设);⑵从这个假设出发,经过推理,得出矛盾;⑶由矛盾判定假设不正确,从而肯定命题的结论正确.出示课件28:例求证:在一个三角形中,至少有一个内角小于或等于60°.师生共同解答.已知:△ABC.求证:△ABC中至少有一个内角小于或等于60°.证明:假设△ABC中没有一个内角小于或等于60°,则∠A>60°,∠B>60°,∠C>60°.因此∠A+∠B+∠C>180°.这与三角形的内角和为180度矛盾.假设不成立.因此△ABC中至少有一个内角小于或等于60°.巩固练习:(出示课件29)利用反证法证明“在直角三角形中,至少有一个锐角不大于45°”时,应先假设()A.有一个锐角小于45°B.每一个锐角都小于45°C.有一个锐角大于45°D.每一锐角都大于45°学生口答:D(三)课堂练习(出示课件30-36)1.已知△ABC的三边a,b,c,满足a+b2+|c﹣,则△ABC的外接圆半径=______.2.如图,⊙O是△ABC的外接圆,∠A=45°,BC=4,则⊙O的直径为______.3.如图,请找出图中圆的圆心,并写出你找圆心的方法?4.正方形ABCD的边长为2cm,以A为圆心2cm为半径作⊙A,则点B在⊙A______;点C在⊙A______;点D在⊙A______.5.⊙O的半径r为5cm,O为原点,点P的坐标为(3,4),则点P与⊙O的位置关系为()A.在⊙O内B.在⊙O上C.在⊙O外D.在⊙O上或⊙O外6.已知:在Rt△ABC中,∠C=90°,AC=6,BC=8,则它的外接圆半径=______.7.如图,△ABC内接于⊙O,若∠OAB=20°,则∠C的度数是________.8.如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是()A.点P B.点Q C.点R D.点M9.画出由所有到已知点的距离大于或等于2cm并且小于或等于3cm的点组成的图形.10.某地出土一明代残破圆形瓷盘,如图所示.为复制该瓷盘要确定其圆心和半径,请在图中用直尺和圆规画出瓷盘的圆心.参考答案:1.2582.3.解:如图所示.4.上;外;上5.B6.57.70°8.B9.解:如图所示.10.解:(1)在圆形瓷盘的边缘选A、B、C三点;(2)连接AB、BC;(3)分别作出AB、BC的垂直平分线;(4)两垂直平分线的交点就是瓷盘的圆心.(四)课堂小结本节课你学到了哪些数学知识和数学方法?请与同伴交流.(五)课前预习预习下节课(24.2.2第1课时)的相关内容.七、课后作业1.教材95页练习2.2.配套练习册内容八、板书设计:九、教学反思:本节课通过学生操作,总结出了点与圆的三种位置关系,其中渗透着分类讨论的思想,经过探讨过一点、两点、三点作圆,得出了不在同一直线上三点确定一个圆,从而自然引出三角形外接圆、外心及圆内接三角形的定义,此外还学习了用反证法证明命题的方法和步骤.这些定理都是从学生实践中得出的,培养了学生动手的能力.。
九年级数学下册《过不共线三点作圆》优秀教学案例

在本章节的教学过程中,教师应关注学生的全面发展,将知识与技能、过程与方法、情感态度与价值观有机地结合起来,使学生在掌握基本几何知识的同时,提高自身的综合素质,为未来的学习和发展奠定坚实的基础。
三、教学策略
(一)情景创设
1.创设生活化的教学情境,以学生熟悉的事物或场景作为引入,如校园里的圆形花坛、篮球场的圆形边界等,让学生感受到圆就在我们的身边,激发他们的学习兴趣。
4.通过对几何性质的学习和证明,使学生掌握几何学的基本研究方法和思维方式,提高学生的几何素养。
(三)情感态度与价值观
1.激发学生对数学几何学科的兴趣,培养他们主动探究、勇于创新的科学精神。
2.培养学生严谨、细心的学习态度,使他们认识到几何学习的严密性和逻辑性,从而提高学习的自觉性和自律性。
3.引导学生关注数学与生活的联系,体会数学在现实生活中的广泛应用,增强数学学习的实用性和价值感。
3.教师巡回指导,关注每个小组的讨论情况,给予适当的提示和引导,确保讨论的有效性。
(四)总结归纳
1.邀请各小组代表汇报讨论成果,让学生在倾听他人观点的过程中,加深对知识点的理解。
2.教师针对学生的讨论成果进行点评,总结“过不共线三点作圆”的基本原理、尺规作图方法以及几何证明过程。
3.强调本节课的重点和难点,指导学生掌握几何学习的思维方法和技巧。
4.能够运用所学的知识,解决一些与圆相关的实际问题,如测量圆形场地、设计圆形图案等。
(二)过程与方法
1.通过小组合作和自主探究,培养学生的团队合作意识和解决问题的能力,让学生在实践中学会如何观察、分析和解决问题。
2.引导学生运用尺规作图、直观演示等方法,提高学生的动手操作能力和空间想象能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基础过关:
• • • • 三点确定圆的前提条件是 1.判断正误 “三点不在同一直线上” (1)经过三点可以作一个圆。(×) (2)三角形的外心就是这个三角形两边垂 直平分线的交点。 ( √ ) (3)三角形的外心到三角形三边的距离相 等。(× )
2.如图:已知A、B、C三点都在⊙O上, 内接三角形 ,⊙O是 那么△ABC是⊙O的_________ 外接圆 , △ABC的________ 外心 点O是△ABC的________ 。
1 个外接圆,一个圆 3.一个三角形有_____ 无数 个内接三角形。 有______ 4.三角形的三边分别为3、4、5,则此三 10 角形外接圆的直径是_______ 。 小结:锐角三角形的外心在三角形内 部;直角三角形的外心是斜边中点; 钝角三角形的外心在三角形外部
能力提升:
5.如图:等腰三角形ABC内接于半径为 5的⊙O,AB=AC,且tanB=1/3 。
知识梳理: 1.经过一点可以画 无数个圆;经过两个点可以画无数 个圆;经过不在同一直线上的三点可以画 1 个圆; 圆心和半径分别怎样确定? 2.定理3:不在同一直线上的三点 确定 一个圆。
经过三角形各顶点的圆。 3. 1)三角形的外接圆:
(三边垂直平分线的交点) 2)外心: 外接圆的圆心 。
3)圆的内接三角形:三个顶点在圆上的三角形 。
过不共线三点作圆
【温故知新】 1、圆周角定理:圆周角的度数等于它所 对弧上的圆心角度数的 一半 . 2、在同圆或等圆中,同弧或等弧 ___________所对的 圆周角相等,反之相等的圆周角所对的 直径 所对的圆周角是 弧 相等 ;__________ 直角,反之。90°的圆周角所对的弦是 直径 。 _________ 3、垂径定理:垂直于弦的直径 平分 这 条弦,并且平分弦所对的 两条弧 .
(1)求BC的
