工程数学考试试卷A

合集下载

《工程数学-线性代数》试卷(A)

安徽矿业职业技术学院 2011-2012学年第二学期期末考试《工程数学-线性代数》试卷(A)（时间：120分钟）课程所在系部：公共课教学部适用专业：矿井建设与相关专业考试形式: 闭卷(闭卷/开卷) 命题人：马万早说明：在本卷中，T A 表示矩阵A 的转置矩阵，A*表示矩阵A 的伴随矩阵，E 是单位矩阵，|A|表示方阵A 的行列式. 1A -表示方阵A 的逆矩阵，R （A ）表示矩阵A 的秩。

一、填空题（每小题2分，共20分）1. 行列式任意两行互换行列式。

2. 设D 为一个三阶行列式，第三列元素分别为-2，3，1，其余子式分别为9，6，24，则D= 。

3. 关于线性方程组的克莱姆法则结论是。

4. n 阶矩阵A 可逆的充要条件是。

5. 若n 阶矩阵满足2240A A E --=,则A -1= 。

6. ()⎪⎪⎪⎪⎪⎭⎫ ⎝⎛43214321= ， ()43214321⎪⎪⎪⎪⎪⎭⎫⎝⎛= 。

7. 设向量组321,,ααα线性相关，则向量组332211,,,,,βαβαβα一定线性。

8. 设A 为三阶矩阵，若A=3，则1-A = ,*A = 。

9. n 阶可逆矩阵A 的列向量组为n αααΛ,,21，则r(n αααΛ,,21)= 。

10. 非齐次线性方程组A n m ⨯X=b 有解的充要条件是。

二、选择题（10分，每题2分）1．1221--k k 0≠的充要条件是（）。

（a ） k ≠1（b ） k ≠3（c ） k ≠1且k ≠3（d ）k ≠1或k ≠3 2. A,B,C 为n 阶方阵，则下列各式正确的是（）(a) AB=BA (b) AB=0,则A=0或B=0 (c) （A+B ）（A-B ）=A 2-B2(d) AC=BC 且C 可逆,则A=B3. 设A 为n 阶可逆矩阵，则下述说法不正确的是（）(a) A ,0≠ (b) 1-A 0≠ (c) r(A)=n (d) A 的行向量组线性相关4. 设矩阵A =(a ij )n m ⨯，AX=0仅有零解的充要条件是（） (a) A 的行向量组线性无关 (b) A 的行向量组线性相关 (c) A 的列向量组线性无关 (d) A 的列向量组线性相关5. 向量组s αααΛ,,21的秩为r,则下述说法不正确的是（）(a) s αααΛ,,21中至少有一个r 个向量的部分组线性无关(b) s αααΛ,,21中任何r 个向量的线性无关部分组与s αααΛ,,21可互相线性表示 (c) s αααΛ,,21中r 个向量的部分组皆线性无关 (d)s αααΛ,,21中r+1个向量的部分组皆线性相关三、判断题（正确的划√，错误的划х，共10分，每题2分）1．1112111221222122ka ka a ak ka ka a a =。

工程数学试卷及标准答案

1．某人打靶3发，事件Ai 表示“击中i 发”，i=0,1,2,3. 那么事件A=A1∪A2∪A3表示( )。

A. 全部击中.B. 至少有一发击中.C. 必然击中D. 击中3发 2．对于任意两个随机变量X 和Y ，若E(XY)=E(X)E(Y)，则有( )。

A. X 和Y 独立。

B. X 和Y 不独立。

C. D(X+Y)=D(X)+D(Y)D. D(XY)=D(X)D(Y)3．下列各函数中可以作为某个随机变量的概率密度函数的是（）。

A ．其它1||0|)|1(2)(≤⎩⎨⎧-=x x x f 。

B. 其它2||05.0)(≤⎩⎨⎧=x x fC. 0021)(222)(<≥⎪⎪⎩⎪⎪⎨⎧=--x x e x f x σμπσ D. 其它00)(>⎩⎨⎧=-x e x f x ，4．设随机变量X ～)4,(2μN , Y ～)5,(2μN , }4{1-≤=μX P P ,}5{2+≥=μY P P , 则有（）A. 对于任意的μ, P 1=P 2B. 对于任意的μ, P 1 < P 2C. 只对个别的μ，才有P 1=P 2D. 对于任意的μ, P 1 > P 25．设X 为随机变量，其方差存在，c 为任意非零常数，则下列等式中正确的是（）A ．D(X+c)=D(X). B. D(X+c)=D(X)+c. C. D(X-c)=D(X)-c D. D(cX)=cD(X)6．设3阶矩阵A 的特征值为-1，1，2，它的伴随矩阵记为A*，则|A*+3A –2E|= 。

7．设A= ⎪⎪⎪⎭⎫ ⎝⎛-⎪⎪⎪⎭⎫ ⎝⎛--10000002~011101110x ，则x = 。

8．设有3个元件并联，已知每个元件正常工作的概率为P ，则该系统正常工作的概率为。

9．设随机变量X 的概率密度函数为其它Ax x x f <<⎩⎨⎧=002)(，则概率=≥)21(X P 。

南京理工大学(工程数学(4.0学分)(A)(18.1.5))

6．；
7．；
8．；
9．数量场在点处方向导数最大的方向为；
10．矢量场是场。
二、（10分）已知调和函数，求一个解析函数使得？
第页共页
南京理工大学课程考试试卷(学生考试用)
课程名称：工程数学学分：4教学大纲编号：11024001
试卷编号：A考试方式：闭卷满分分值：100考试时间：120分钟
组卷日期：2018年1月5日组卷教师(签字)：审定人(签字)：
三、（8分）将函数在下列指定的圆环域内展开成洛朗(Laurent)级数
(1) ；(2) 。
八、（4分）若函数在圆周内解析，在圆周上连续，且
，证明：对任意的，都有成立。
所有试题的答案全部写在答题纸上，否则无效！
一、填空题（每题3分，共30分）
1．复数的三分，其中C是从点沿虚轴到点的路径；
4．映射将z平面上区域映射成w平面上区域；
5．幂级数的收敛半径R=；
四、（8分）求一个将z平面上区域映射成w平面上区域的映射？（请画出映射前后的示意图）
五、（20分）计算下列积分
1）；（4分）2）；（6分）
3）；（4分）4）。（6分）
六、（10分）1)设，计算Fourier变换。
2)求。
七、（10分）用Laplace变换求解常微分方程的初值问题？

工程数学试题A及答案

工程数学试题A及答案一、选择题（每题3分，共30分）1. 函数\( f(x) = x^3 - 3x^2 + 2 \)的导数是：A. \( 3x^2 - 6x \)B. \( 3x^2 - 6x + 2 \)C. \( x^3 - 3x^2 + 2 \)D. \( 3x^2 - 6x + 3 \)答案：A2. 极限\( \lim_{x \to 0} \frac{\sin x}{x} \)的值是：A. 0B. 1C. \( \pi \)D. \( \infty \)答案：B3. 函数\( y = e^x \)的不定积分是：A. \( e^x + C \)B. \( \ln x + C \)C. \( x e^x + C \)D. \( \frac{1}{x} + C \)答案：A4. 微分方程\( y' + 2y = 0 \)的通解是：A. \( y = Ce^{-2x} \)B. \( y = Ce^{2x} \)C. \( y = C\sin(2x) \)D. \( y = C\cos(2x) \)答案：A5. 矩阵\( A = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \)的行列式是：A. 5B. -2C. 2D. -5答案：B6. 函数\( f(x) = x^2 \)在区间\( [1, 2] \)上的定积分是：A. 1B. 2C. 3D. 4答案：C7. 函数\( y = \ln x \)的二阶导数是：A. \( \frac{1}{x^2} \)B. \( \frac{1}{x} \)C. \( x \)D. \( x^2 \)答案：A8. 矩阵\( A = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \)的逆矩阵是：A. \( \begin{bmatrix} -1 & 0 \\ 0 & -1 \end{bmatrix} \)B. \( \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} \)C. \( \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \)D. \( \begin{bmatrix} 0 & -1 \\ -1 & 0 \end{bmatrix} \)答案：C9. 函数\( y = x^3 \)的不定积分是：A. \( \frac{x^4}{4} + C \)B. \( \frac{x^3}{3} + C \)C. \( \frac{x^2}{2} + C \)D. \( \frac{x}{3} + C \)答案：B10. 函数\( y = \sin x \)的不定积分是：A. \( \cos x + C \)B. \( \sin x + C \)C. \( -\cos x + C \)D. \( -\sin x + C \)答案：A二、填空题（每题4分，共20分）1. 函数\( f(x) = x^2 - 4x + 4 \)的极小值点是 \( x =\_\_\_\_\_ \)。

工程数学试题(A卷)参考答案(2015.6.29)

工程数学试题(A 卷)参考答案一． (1) 3 ; (2) 5,6; (3) 0,9; (4) 2321+x ; (5)3,121. 二．解. (1) 因为2)(-+=x e x f x 在)1,0(上连续，并且(),]1,0[01)(,01)1(,01)0(∈∀>+='>-=<-=x e x f e f f x所以由零点定理和单调性知原方程在)1,0(内存在唯一实根.*x (4分) (2) 牛顿迭代格式为.,2,1,0,121 =+-+-=+k e x e x x kkx k x k k (8分) ⑶ 因为,])1,0[(0)(∈∀>=''x e x f x ,0)1()1(>''f f 所以牛顿迭代法收敛，且收敛阶为2. (12分)三. 解. 用杜里特尔分解法求解。

按紧凑格式计算得562852137133321----- 于是得.56133,2800710321,152013001⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=y U L ( 9分) 回代求解上三角形线性方程组,Ux y = 得原方程组的解为 .1,1,2123===x x x即 .)2,1,1(),,(321=x x x ( 12分)四．解. 雅可比迭代矩阵,050100100100)(1⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡----=+=-αββαU L D B J 其特征方程为,01003||2=⎪⎭⎫ ⎝⎛-=-αβλλλJ B E ( 4分)J B 的谱半径,10||3)(αβρ=J B 所以J 法收敛的充要条件是3100||<αβ. (8分)赛德尔迭代矩阵,50500010100001000000000500100010)(211⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡---=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=-=--αββαβαβαβααβU L D B G 其特征方程为,01003||2=⎪⎭⎫⎝⎛-=-αβλλλG B E (12分) G B 的谱半径,100||3)(αβρ=G B 所以G-S 法收敛的充要条件是3100||<αβ.(16分)五．解. 由条件得.0c o s 2,0)c o s ()0(,1c o s)0(220202==⎪⎭⎫⎝⎛='='=====ππx x x x P x P x P (3分) .2,0,0]0,0[)0()(22x f x f f x P ⎥⎦⎤⎢⎣⎡++=π ( 6分)作差商表.41)(222x x P π-= ( 9分).2,0,2612!3|s i n ||c o s)(|222⎥⎦⎤⎢⎣⎡∈⎪⎭⎫ ⎝⎛-≤⎪⎭⎫ ⎝⎛-=-πππξx x x x x x x P ( 12分) 记,2)(2⎪⎭⎫⎝⎛-=x x x g π 令,0)3()(=-='x x x g π 得.3,021π==x x 所以,54323)(max 3220πππππ=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=≤≤x g x 故.324|cos )(|max 3220ππ≤-≤≤x x P x ( 16分)六．解. (1) 取,)(,1)(10x x x ==ϕϕ 并设一次最佳平方逼近多项式为,bx a y += 则,1),(,21),(,11),(1001101000======⎰⎰⎰dx xe f xdx dx x ϕϕϕϕϕ,2),(,31),(,21),(10211021101-=====⎰⎰e dx e x f dx x x ϕϕϕϕϕ (6分)正规方程组为 ⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡213121211e b a ( 8分) 解得⎩⎨⎧-=+-=.3012,166e b e a 故所求的最佳平方逼近多项式为.616)3012(e x e y -+-= ( 12分)七．解.9767267.09896158.09973978.0(21[161)(18++⨯+=≈⎰T dx x f ]8414709.0)8771925.09088516.09361556.09588510.0+++++ .9456908.0=. ( 6分))8771925.09361556.09767267.09973978.0(41[241)(14+++⨯+=≈⎰S dx x f ]8414709.0)9088516.09588510.09896158.0(2+++⨯+ =.9460833.0 ( 12分)。

工程数学本科试题及答案

工程数学本科试题及答案一、选择题（每题2分，共20分）1. 下列哪个选项是微分方程 \( y'' - y' - 2y = e^{2x} \) 的一个解？A. \( y = e^{-x} \)B. \( y = e^{2x} \)C. \( y = e^{x} \)D. \( y = e^{3x} \)2. 在复数域中，下列哪个表达式是正确的？A. \( |z|^2 = z \cdot \bar{z} \)B. \( |z|^2 = z + \bar{z} \)C. \( |z|^2 = z - \bar{z} \)D. \( |z|^2 = z / \bar{z} \)3. 对于向量 \( \mathbf{A} = (2, -3, 4) \) 和 \( \mathbf{B} = (1, 2, -1) \)，它们的点积 \( \mathbf{A} \cdot \mathbf{B} \) 等于：A. 1B. 2C. 3D. 54. 在 \( z = x^2 + y^2 \) 中，如果 \( \frac{\partialz}{\partial x} = 2x \)，那么 \( \frac{\partial z}{\partial y} \) 等于：A. \( 2y \)B. \( -2y \)C. \( 2x \)D. \( -2x \)5. 一个函数 \( f(x) \) 在点 \( x = a \) 处连续的充分必要条件是：A. \( \lim_{x \to a^-} f(x) = \lim_{x \to a^+} f(x) \)B. \( \lim_{x \to a} f(x) = f(a) \)C. \( f(a) \) 存在D. \( f(x) \) 在 \( x = a \) 处可导6. 微分方程 \( y' = y^2 \) 的解的形式是：A. \( y = Ce^x \)B. \( y = \frac{1}{Ce^x + 1} \)C. \( y = Ce^{-x} \)D. \( y = \frac{1}{Cx + 1} \)7. 傅里叶级数中的 \( a_n \) 系数是由以下哪个积分计算得出的？A. \( a_n = \frac{2}{L} \int_{-L}^{L} f(x) \cos(\frac{n\pi x}{L}) dx \)B. \( a_n = \frac{1}{L} \int_{-L}^{L} f(x) \cos(\frac{n\pi x}{L}) dx \)C. \( a_n = \frac{2}{L} \int_{0}^{L} f(x) \cos(\frac{n\pi x}{L}) dx \)D. \( a_n = \frac{1}{L} \int_{0}^{L} f(x) \cos(\frac{n\pi x}{L}) dx \)8. 矩阵 \( A = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \) 的行列式 \( |A| \) 等于：A. 7B. 2C. 1D. -29. 函数 \( f(x) = x^3 - 6x^2 + 11x - 6 \) 的零点个数是：A. 1B. 2C. 3D. 410. 拉普拉斯变换 \( \mathcal{L} \{ f(t) \} \) 的定义是：A. \( \mathcal{L} \{ f(t) \} = \int_{0}^{\infty} e^{-st} f(t) dt \)B. \( \mathcal{L} \{ f(t) \} = \int_{-\infty}^{\infty} e^{-st} f(t) dt \)C. \( \mathcal。

浙江大学大一桥梁工程专业《工程数学》考试A卷及答案

第 1 页共2页第 1 页共2页工程数学试卷 A适用专业：考试日期：试卷类型：闭卷考试时间：120分钟试卷总分：100分一．填空题（每题3分，共计3⨯8＝24分）1、设行列式123020001D =, 则D =2、设,9,3,A B A B ==三阶方阵有则 1AB -=3、设向量,101,121⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=βα 则αβ+=4、设向量111,0,11αβ⎛⎫⎛⎫ ⎪ ⎪== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭则内积[],αβ=5、已知2BA B E =+,2112A ⎛⎫= ⎪-⎝⎭, 则 B =6、设矩阵A =220210⎛⎫ ⎪⎝⎭,则矩阵的秩()TR A =7. 设A 的列向量为123,,ααα，且1A =，则132,,ααα=8、设123012111D =，则111213A A A ++=二.选择题（3分⨯4＝12分）1、设α是矩阵A 对应于λ的特征向量，则1P AP -对应的特征向量为（）（A ）1P α- （B ）P α （C ） T P α （D ） α2、设n 阶矩阵A 的行列式1A =，下列说法错误的是（）（A ）存在B 使AB E = （B ）1T A = （C ）A 能相似于对角阵 (D) ()r A n = 3、设四阶方阵A ，B 有秩()4,()3R A R B ==，则()R AB =（）。

（A ） 1 （B ） 2 （C ） 3 （D ） 44、设A 为m n ⨯的矩阵，()R A n =，则非齐次线性方程组Ax b =的解为（）（A ）一定有唯一解（B ）一定无解（C ）一定有无穷多解（D ）可能有解三. 设矩阵方程254621321X -⎡⎤⎡⎤+=⎢⎥⎢⎥⎣⎦⎣⎦，求矩阵X （8分）四、设矩阵31111311,11311113A ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦求（1）行列式A ；（2）秩()R A （12分）第 2 页共2页第 2 页共2页五、已知向量组123423240,1,1,22100αααα⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪==== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭，（1）求向量组的秩；（2）向量组的一个最大无关组；（3）将其余向量用最大无关组线性表示。

15~16_1_工程数学(1)试卷A

.
⎡5⎤
⎡−1⎤
7、设向量
u
=
⎢ ⎢
2
⎥ ⎥
与
v
=
⎢ ⎢
4
⎥ ⎥
正交，则
λ
=
.
⎢⎣−1⎥⎦
⎢⎣ λ ⎥⎦
8、矩阵
A
=
⎡4 ⎢⎣2
−3⎤ −1⎥⎦ 的特征值为
，对应的特征向量为
.
9、二次型 f (x1, x2 , x3 ) = 3x12 + x22 + 5x32 + 8x2 x3 对应的矩阵 A =
，
八、(10 分) 设 u1, u2 , u3 是两两正交的 3 维单位向量，令 A = E − 2u1u1T , 其中 E 是单位阵. （1）验证 u1, u2 , u3 是 A 的特征向量，并指出对应的特征值 λ1, λ2 , λ3 ；（2）给出正交变换 x = P y ，将二次型 f ( x) = xT Ax 化为标准形，并写出新的二次型；（3）证明 A = λ1u1u1T + λ 2u2u2T + λ3u3u3T .
的是
.
⎡ 1 −1 5 ⎤
5、设矩阵
A
=
⎢ ⎢
2
0
7
⎥ ⎥
,
则方程 Ax
= 0 的通解为
.
⎢⎣−3 −5 −3⎥⎦
6、设向量 u，v 是方程 ( A − λ E) x = b 的两个不同的解， E 是单位阵，则 u 、 v 、 u + v 、
u − v 中一定是矩阵 A 对应特征值 λ 的特征向量为
东华大学 2015--2016 学年第一学期期末试题 A 卷
踏实学习，弘扬正气；诚信做人，诚实考试；作弊可耻，后果自负。

14~15_2_工程数学(1)试卷A

东华大学 2014--2015 学年第二学期期末试题A 卷踏实学习，弘扬正气；诚信做人，诚实考试；作弊可耻，后果自负。

考试科目工程数学（1）使用专业卓越工程教师班号____ 学号姓名考试教室一二三四五六七八九总分试题得分一、填空题（每小题4分，共40分）.1、设ABC Δ的三个顶点分别是(1,0),(2,5),(1,3),A B C − 则ABC Δ的面积为 .2、已知2424,1236A B −⎛⎞⎛⎞==⎜⎟⎜⎟−−−⎝⎠⎝⎠,则AB = .3、若向量组123(,1,1),(1,,1),(1,1,)TTTαλαλαλ===的秩为2，则=λ . 4、设三阶矩阵A 的特征值为1,1,4,−则2A E −特征值为，2A E −= .5、设矩阵322232223A ⎛⎞⎜⎟=⎜⎟⎜⎟⎝⎠, 则行列式A = ，伴随矩阵*A 的逆阵*1()A −= .6、设=Ax b ，其中1213A −⎛⎞=⎜⎟−⎝⎠, 12b ⎛⎞=⎜⎟⎝⎠，则=x . 7、行列式1201035001561234= . 8、设A 为43×矩阵，0≠b ，且()3R A =，则线性方程组b Ax = . （有唯一解; 有无穷多解；无解; 可能无解）9、设111232121A ⎛⎞⎜⎟=⎜⎟⎜⎟⎝⎠，则解空间{}x Ax O =的基为，维数为 . 10、矩阵21102043A t −⎛⎞⎜⎟=⎜⎟⎜⎟−⎝⎠的特征值为，又当t = 时，矩阵A 可对角化.二、（7分）已知行列式213142751D−=−，求D的第三行余子式313233,,M M M的和.三、（7分）设301111114A⎛⎞⎜⎟=⎜⎟⎜⎟⎝⎠，且2,AB A B=+用初等行变换法求矩阵.B四、（7分）确定向量312b⎛⎞⎜⎟=−⎜⎟⎜⎟⎝⎠是否为1231020,1,2110a a a⎛⎞⎛⎞⎛⎞⎜⎟⎜⎟⎜⎟===−⎜⎟⎜⎟⎜⎟⎜⎟⎜⎟⎜⎟⎝⎠⎝⎠⎝⎠的线性组合？若是，求出其表示式.五、（8分）设向量12,1⎛⎞⎜⎟=⎜⎟⎜⎟−⎝⎠α求与α正交的所有向量x y z ⎛⎞⎜⎟⎜⎟⎜⎟⎝⎠。

工程数学试卷及答案

一、选择填空题1. 某数x 的有四位有效数字且绝对误差限是4105.0-⨯的近似值是（A ）（A ）0.693 (B)0.6930 （C ）0.06930 (D)0.006930 2. n 次拉格朗日插值多项式的余项是( A)(A))()!1()()(1)1(x n f x R n n n +++=ωξ (B)()()()()!n n n f R x x n ξω= (C))!1()()()1(+=+n f x R n n ξ (D)()()()!n n f R x n ξ=3. 求积公式)1()1()(11f f dx x f +-≈⎰-具有（A ）次代数精度（A ）1 （B ）2 （C ）4 （D ）34. 用牛顿法计算)0(>a a n ，构造迭代公式时，下列方程不可用的是（A ）（A ）0)(=-≡n a x x f （B ）0)(=-≡n a x x f （C ）0)(=-≡nx a x f （D ）01)(=-≡nx ax f 5. 由数据0051152252171 022 42......x y --- 所确定的插值多项式是次数不大于（ D ）的多项式．（A ）二次（B ）三次（C ）四次（D ）五次 6. 在牛顿—柯特斯公式()()()()nbn i i ai f x dx b a C f x =≈-∑⎰中，当系数()n i C 有负值时，公式的稳定性不能保证，所以实际应用中，当n （ B ）时的牛顿—柯特斯公式不使用。

（A ）10≥ （B ）8≥ （C ）6≥ （D ）4≥ 7. 经过点)3,2(),2,1(),1,0(C B A 的插值多项式=)(x P （ B ） 8. （A ）x （B ） 1+x （C ）12+x （D ）12+x 9. 给定向量Tx )4,3,2(-=，则∞xx x,,21分别为（ A ）（A ）4,29,9 （B ）5,29,9 （C ）4,29,5.8 （D ）5,29,5.8 10. 精确值x =36.85用四舍五入保留三位有效数字的近似数为 36.9 。

工程数学考试试卷A

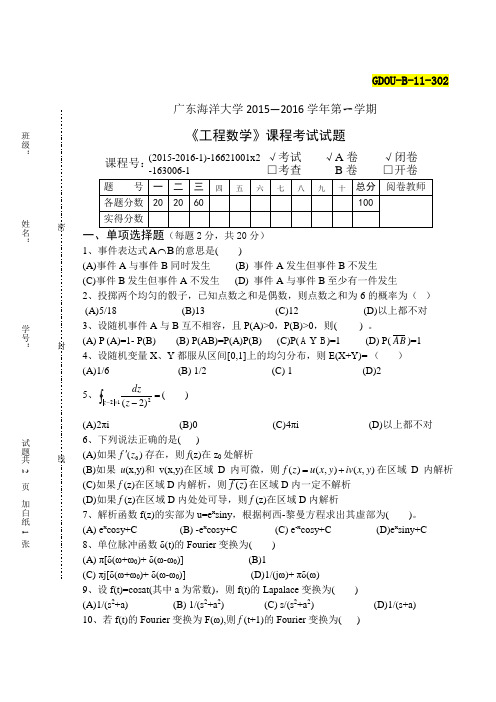
广东海洋大学2015—2016学年第一学期《工程数学》课程考试试题课程号： (2015-2016-1)-16621001x2 -163006-1√ 考试 √ A 卷 √ 闭卷 □ 考查 B 卷 □ 开卷（每题2分，共20分）1、事件表达式B A ⋂的意思是( ) (A)事件A 与事件B 同时发生 (B) 事件A 发生但事件B 不发生 (C)事件B 发生但事件A 不发生 (D) 事件A 与事件B 至少有一件发生 2、投掷两个均匀的骰子，已知点数之和是偶数，则点数之和为6的概率为（） (A)5/18 (B)13 (C)12 (D)以上都不对 3、设随机事件A 与B 互不相容，且P(A)>0，P(B)>0，则( ) 。

(A) P (A)=1- P(B) (B) P(AB)=P(A)P(B) (C)P(B A )=1 (D) P(AB )=1 4、设随机变量X 、Y 都服从区间[0,1]上的均匀分布，则E(X+Y)= （） (A)1/6 (B) 1/2 (C) 1 (D)2 5、=⎰=-12z ( ) (A)2πi (B)0 (C)4πi (D)以上都不对 6、下列说法正确的是( ) (A)如果)(0z f '存在，则f (z)在z 0处解析 (B)如果u (x,y)和v(x,y)在区域D 内可微，则),(),()(y x iv y x u z f +=在区域D 内解析 (C)如果f (z)在区域D 内解析，则)(z f 在区域D 内一定不解析 (D)如果f (z)在区域D 内处处可导，则f (z)在区域D 内解析 7、解析函数f(z)的实部为u=e x siny ，根据柯西-黎曼方程求出其虚部为( )。

(A) e x cosy+C (B) -e x cosy+C (C) e -x cosy+C (D)e x siny+C 8、单位脉冲函数δ(t)的Fourier 变换为( ) (A) π[δ(ω+ω0)+ δ(ω-ω0)] (B)1(C) πj[δ(ω+ω0)+ δ(ω-ω0)] (D)1/(j ω)+ πδ(ω)9、设f(t)=cosat(其中a 为常数)，则f(t)的Lapalace 变换为( )(A)1/(s 2+a) (B) 1/(s 2+a 2) (C) s/(s 2+a 2) (D)1/(s+a)10、若f(t)的Fourier 变换为F(ω),则f (t+1)的Fourier 变换为( ) 班级：姓名：学号：试题共 2页加白纸1张密封线GDOU-B-11-302(A)e j ωF(ω) (B)e -j ωF(ω) (C)F(ω+1) (D)F(ω-1)3、已知随机变量X 的概率密度函数为⎩⎨⎧≤≤+=其它,020,1)(x kx x f ，则k= 。

工程数学A卷答案及评分标准

临沂大学2011—2012学年度第二学期《工程数学》A 卷答案及评分标准（适用于2009级机械设计制造及其自动化专业2+2、2011 级3+2专升本学生，开卷考试，时间120分钟）一、选择题：（共10小题，每小题2分，共20分）请将下列各题正确的答案填入下表中。

二、填空题：（共10空，每空2分，共20分）1、-125 2、-2 3、2 4、4 5、13a =，0b =6、0.187、0.18、67\49、 8 三、计算题：（共5小题，第1题8分，第2、3、4题各10分，第5题12分，共50分）1、解：对系数矩阵作初等行变换，有：110011*********~001010011100010⎛⎫⎛⎫⎪ ⎪- ⎪ ⎪⎪ ⎪⎝⎭⎝⎭得：1253540x x x x x x =--⎧⎪=-⎨⎪=⎩ 4分令251,0x x == 得：()11,1,0,0,0Tη=- 1分令250,1x x == 得：()11,0,1,0,1Tη=-- 1分基础解系为12,ηη 1分通解为1122k k ηη+ k 1，k 2为任意常数 1分2、解：（1）()1f x dx +∞-∞=⎰所以2221cx dx +-=⎰则316c =2分（2）()()22323016E X x f x dx x dx +∞+-∞-===⎰⎰2分()()22242312165E X x f x dx x dx +∞+-∞-===⎰⎰()()()22125D XE X E X =-=⎡⎤⎣⎦ （3）()(){}12||||15P X E X D X P X ⎧⎫-<=<=⎨⎬⎩⎭ 2分3、解：()12341122112202150215~203100111104000r A αααα⎛⎫⎛⎫⎪ ⎪⎪ ⎪== ⎪ ⎪-- ⎪ ⎪⎝⎭⎝⎭4分一个最大无关组为：123,,ααα 2分41233αααα=+- 2分4、(1) 由()F x 右连续性得()()00F F +=，即0A B +=, 又由()1F +∞=得，1A =，解得1,1A B ==- 5分(2) ()22,0()0,xxe x f x F x -⎧⎪>'==⎨⎪⎩其它, 3分 (3) )2PX <<()2F F=-12ee --=- 2分5、解：（1）因为A~B ，故其特征多项式相同。

工程数学(本)

一、单项选择题1. 设2321321321=c c c b b b a a a ，则=---321332211321333c c c b a b a b a a a a （A ）． A . 2- 2. 设A 是n s ⨯矩阵，B 是m s ⨯矩阵，则下列运算中有意义的是（ D ）．D . AB '3. 已知⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡-=21101210,20101B a A ，若⎥⎦⎤⎢⎣⎡=1311AB ，则=a （ B ）． B . 1- 4.B A ,都是n 阶矩阵（)1>n ，则下列命题正确的是 ( D ) ．D ．B A AB = 5. 若A 是对称矩阵，则等式（C ）成立． C . A A =' 6. 若⎥⎦⎤⎢⎣⎡=5321A ，则=*A （D ）． D . ⎥⎦⎤⎢⎣⎡--1325 7. 若⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=4321432143214321A ，则秩=)(A （B ）． B . 1 8. 向量组10001200123012341111⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥,,,,的秩是（A ）． A . 49. 向量组]532[,]211[,]422[,]321[4321'='='='=αααα的一个极大无关组可取为（B ）．B .21,αα10. 向量组[][][]1,2,1,5,3,2,2,0,1321==-=ααα，则=-+32132ααα（B ）．[]2,3,1-- 11. 线性方程组⎩⎨⎧=+=+013221x x x x 解的情况是（D ）D . 有无穷多解12. 若线性方程组AX =0只有零解，则线性方程组AX b =（C ）．C . 可能无解13. 若n 元线性方程组AX =0有非零解，则（ A ）成立．A . r A n ()< 14. 下列事件运算关系正确的是（ A ）．A . BA A B B +=15. 对于随机事件A B ,，下列运算公式（ A ）成立．A . )()()()(AB P B P A P B A P -+=+16. 袋中有3个红球，2个白球，第一次取出一球后放回，第二次再取一球，则两球都是红球的概率是（D ）．25917. 若随机事件A ,B 满足AB =∅，则结论（B ）成立．A 与B 互不相容18. 若A B ,满足（C ），则A 与B 是相互独立．C . )()()(B P A P AB P = 19. 下列数组中，（C ）中的数组可以作为离散型随机变量的概率分布．163161412120. 设⎥⎦⎤⎢⎣⎡2.04.03.01.03210~X ，则=<)2(X P （B ）． B ．0.4 21. 随机变量)21,3(~B X ，则=≤)2(X P （D ）． D . 87 22. 已知)2,2(~2N X ，若)1,0(~N b aX +，那么（C ）．1,21-==b a23. 若)4,2(~N X ，Y =（C ），则Y N ~(,)01． C . 22-X24. 设n x x x ,,,21 是来自正态总体22,)(,(σμσμN 均未知）的样本，则（ A ）是统计量．A . 1x 25. 设x x x n 12,,, 是来自正态总体N (,)μσ2的样本，则（D ）是μ无偏估计．D .321535151x x x ++ ⒈设a a a b b b c c c 1231231232=，则a a a a b a b a b c c c 123112233123232323---=（D ）．D. －6 ⒉若000100002001001a a=，则a =（A ）⒊乘积矩阵1124103521-⎡⎣⎢⎤⎦⎥-⎡⎣⎢⎤⎦⎥中元素c 23=（C ）．C. 10 ⒋设A B ,均为n 阶可逆矩阵，则下列运算关系正确的是（ B ）⒌设A B ,均为n 阶方阵，k >0且k ≠1，则下列等式正确的是（D ）⒍下列结论正确的是（ A ）．若A 是正交矩阵，则A -1也是正交矩阵⒎矩阵1325⎡⎣⎢⎤⎦⎥的伴随矩阵为（ C ）．5321--⎡⎣⎢⎤⎦⎥⒏方阵A 可逆的充分必要条件是（B） ⒐设A B C ,,均为n 阶可逆矩阵，则()ACB '=-1（D ）．()B C A ---'111⒑设A B C ,,均为n 阶可逆矩阵，则下列等式成立的是（A ）．()A B A AB B +=++2222⒈用消元法得x x x x x x 12323324102+-=+=-=⎧⎨⎪⎩⎪的解x x x 123⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥为（C ）．[,,]--'1122 ⒉线性方程组x x x x x x x 12313232326334++=-=-+=⎧⎨⎪⎩⎪（B ）．有唯一解⒊向量组100010001121304⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥,,,,的秩为（ A ）．A. 3⒋设向量组为αααα12341100001110101111=⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥=⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥=⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥=⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥,,,，则（B ）⒌A 与A 分别代表一个线性方程组的系数矩阵和增广矩阵，若这个方程组无解，则（D ⒍若某个线性方程组相应的齐次线性方程组只有零解，则该线性方程组（A ）．可能无解⒎以下结论正确的是（D ）．齐次线性方程组一定有解⒏若向量组ααα12,,, s 线性相关，则向量组内（A ）可被该向量组内其余向量线性表出．至少有一个向量 10．设Ａ，Ｂ，Ｐ为n 阶矩阵，若等式（Ｃ）成立，则称Ａ和Ｂ相似．B PAP =-1 ⒈A B ,为两个事件，则（B ）成立．()A B B A +-⊂⒉如果（C ）成立，则事件A 与B 互为对立事件．AB =∅且AB U =⒊10张奖券中含有3张中奖的奖券，每人购买1张，则前3个购买者中恰有1人中奖的概率为（D ）．307032⨯⨯.. 4. 对于事件A B ,，命题（C ）⒌某随机试验的成功率为)10(<<p p ,则在3次重复试验中至少失败1次的概率为（D ）．)1()1()1(223p p p p p -+-+-6.设随机变量X B n p ~(,)，且E X D X ().,().==48096，则参数n 与p 分别是（A ）． A. 6, 0.87.设f x ()为连续型随机变量X 的密度函数，则对任意的a b a b ,()<，E X ()=（A ）．xf x x ()d -∞+∞⎰8.在下列函数中可以作为分布密度函数的是（B ）9.设连续型随机变量X 的密度函数为f x ()，分布函数为F x ()，则对任意的区间(,)a b ，则=<<)(b X a P （ D ）．f x x ab()d ⎰10.设X 为随机变量，E X D X (),()==μσ2，当（C ）时，有E Y D Y (),()==01．⒈设x x x n 12,,, 是来自正态总体N (,)μσ2（μσ,2均未知）的样本，则（A ）是统计量．x 1⒉设x x x 123,,是来自正态总体N (,)μσ2（μσ,2均未知）的样本，则统计量（D ）不是μ的无偏估计．x x x 123--1. 若0351021011=---x ，则=x （A ）．A . 3 2. 已知2维向量组4321,,,αααα，则),,,(4321ααααr 至多是（B ）． A 1 B 2 C 3 D 43. 设B A ,为n 阶矩阵，则下列等式成立的是（C ）．B A B A '+'='+)(4. 若A B ,满足（B ），则A 与B 是相互独立．)()()(B P A P AB P =5. 若随机变量X 的期望和方差分别为)(X E 和)(X D ，则等式（D ）成立．22)]([)()(X E X E X D -=1. 设A 为43⨯矩阵，B 为25⨯矩阵，当C 为（B ）矩阵时，乘积B C A ''有意义．42⨯2. 向量组[][][][]αααα1234000*********====,,,,,,,,,,,的极大线性无关组是（A ）．ααα234,, 3. 若线性方程组的增广矩阵为⎥⎦⎤⎢⎣⎡=41221λA ，则当λ＝（D ）时线性方程组有无穷多解．124. 掷两颗均匀的骰子，事件“点数之和为4”的概率是（C ）. 1215. 在对单正态总体N (,)μσ2的假设检验问题中，T检验法解决的问题是（B ）．未知方差，检验均值二、填空题1. 1111111---x x 是关于x 的一个多项式，该式中一次项x 系数是 2 ．2. 设B A ,是3阶矩阵，其中2,3==B A ，则='-12B A 12 ．3. 设D C B A ,,,均为n 阶矩阵，其中C B ,可逆，则矩阵方程D BXC A =+的解=X 11)(---C A D B ．4. 若方阵A 满足A A '=，则A 是对称矩阵．5．设矩阵⎥⎦⎤⎢⎣⎡=1111A ，则r A ()= 1 ． 6. =⎥⎦⎤⎢⎣⎡-12514⎥⎦⎤⎢⎣⎡--451231． 7. 向量组)01(),110(),011(321k ===ααα线性相关，则_____=k .1-8．含有零向量的向量组一定是线性相关的．9. 若n 元线性方程组0=AX 满足r A n ()<，则该线性方程组有非零解．10. 线性方程组b AX =中的一般解的自由元的个数是2，其中A 是54⨯矩阵，则方程组增广矩阵)(b A r = 3 ． 11. 齐次线性方程组0=AX 的系数矩阵经初等行变换化为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--→→000020103211 A则方程组的一般解为 4342431,(22x x x x x x x ⎩⎨⎧=--= ．是自由未知量）12. 当λ= 1 时，方程组⎩⎨⎧-=--=+112121x x x x λ有无穷多解．13. 若5.0)(,1.0)(,9.0)(===+B A P B A P B A P ，则)(AB P 3.0 ． 14. 设A ，B 为两个事件，若)()()(B P A P AB P =，则称A 与B 相互独立．15. 设随机变量⎥⎦⎤⎢⎣⎡-25.03.0101~a X ，则a =45.0．16. 设随机变量的概率密度函数为⎪⎩⎪⎨⎧≤≤+=其它,010,1)(2x x kx f ，则常数k =π4．17. 设随机变量⎥⎦⎤⎢⎣⎡5.02.03.0210~X ，则=≠)1(X P 8.0．18. 设随机变量X 的概率密度函数为⎩⎨⎧≤≤=其它103)(2x x x f ，则=<)21(X P 81．19. 已知随机变量⎥⎦⎤⎢⎣⎡-5.05.05.05.05201~X ，那么=)(X E 3 ．20. 设随机变量)15.0,100(~B X ，则=)(X E 15 ． 21. 设随机变量X 的期望存在，则E X E X (())-= 0 ．22. 设随机变量X ，若5)(,2)(2==X E X D ，则=)(X E 3．23. 不含未知参数的样本函数称为统计量．24. 设1021,,,x x x 是来自正态总体)4,(μN 的一个样本，则~101101∑=i i x )104,(μN ．25. 若参数θ的两个无偏估计量1ˆθ和2ˆθ满足)ˆ()ˆ(21θθD D >，则称2ˆθ比1ˆθ更有效．⒈210140001---= 7 ．⒉---11111111x 是关于x 的一个一次多项式，则该多项式一次项的系数是 2 ． ⒊若A 为34⨯矩阵，B 为25⨯矩阵，切乘积AC B ''有意义，则C 为 5×4 矩阵．⒋二阶矩阵A =⎡⎣⎢⎤⎦⎥=11015⎥⎦⎤⎢⎣⎡1051．⒌设A B =-⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥=--⎡⎣⎢⎤⎦⎥124034120314,，则()A B +''=⎥⎦⎤⎢⎣⎡--815360 ⒍设A B ,均为3阶矩阵，且A B ==-3，则-=2AB 72 ．⒎设A B ,均为3阶矩阵，且A B =-=-13,，则-'=-312()A B －3 ．⒏若A a =⎡⎣⎢⎤⎦⎥101为正交矩阵，则a = 0 ．⒐矩阵212402033--⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥的秩为 2 ．⒑设⒈当λ= １时，齐次线性方程组x x x x 12120+=+=⎧⎨⎩λ有非零解．⒉向量组[][]αα12000111==,,,,,线性相关．⒊向量组[][][][]123120100000,,,,,,,,,,,的秩是３． ⒋设齐次线性方程组ααα1122330x x x ++=的系数行列式ααα1230=，则这个方程组有无穷多解，且系数列向量ααα123,,是线性相关的．⒌向量组[][][]ααα123100100===,,,,,的极大线性无关组是21,αα． ⒍向量组ααα12,,, s 的秩与矩阵[]ααα12,,, s 的秩相同．⒎设线性方程组AX =0中有5个未知量，且秩()A =3，则其基础解系中线性无关的解向量有２个． ⒏设线性方程组AX b =有解，X 0是它的一个特解，且AX =0的基础解系为X X 12,，则AX b =的通解为22110X k X k X ++．9．若λ是Ａ的特征值，则λ是方程0=-A I λ 的根．10．若矩阵Ａ满足A A '=-1 ，则称Ａ为正交矩阵．是两个可逆矩阵，则A O O A 121⎡⎣⎢⎤⎦⎥=-⎥⎦⎤⎢⎣⎡--1211A O O A ． ⒈从数字1,2,3,4,5中任取3个，组成没有重复数字的三位数，则这个三位数是偶数的概率为52． 2.已知P A P B ().,().==0305，则当事件A B ,互不相容时，P A B ()+= 0.8 ，P AB ()= 0.3 ． 3.A B ,为两个事件，且B A ⊂，则P A B ()+=()A P ． 4. 已知P AB P AB P A p ()(),()==，则P B ()=P -1．5. 若事件A B ,相互独立，且P A p P B q (),()==，则P A B ()+=pq q p -+．6. 已知P A P B ().,().==0305，则当事件A B ,相互独立时，P A B ()+= 0.65 ，P A B ()= 0.3 ． 7.设随机变量X U ~(,)01，则X 的分布函数F x ()=⎪⎩⎪⎨⎧≥<<≤111000x x x x ．8.若X B ~(,.)2003，则E X ()= 6 ．9.若X N ~(,)μσ2，则P X ()-≤=μσ3)3(2Φ．10.E X E X Y E Y [(())(())]--称为二维随机变量(,)X Y 的协方差．1．统计量就是不含未知参数的样本函数．2．参数估计的两种方法是点估计和区间估计．常用的参数点估计有矩估计法和最大似然估计两种方法．3．比较估计量好坏的两个重要标准是无偏性，有效性．4．设x x x n 12,,, 是来自正态总体N (,)μσ2（σ2已知）的样本值，按给定的显著性水平α检验H H 0010:;:μμμμ=≠，需选取统计量nx U /0σμ-=．5．假设检验中的显著性水平α为事件u x >-||0μ（u 为临界值）发生的概率．1. 设B A ,均为n 阶可逆矩阵，逆矩阵分别为11,--B A ，则='--11)(A BB A )(1'-2. 向量组),0,1(),1,1,0(),0,1,1(321k ===ααα线性相关，则_____=k .1-3. 已知2.0)(,8.0)(==AB P A P ，则=-)(B A P 6.0．4. 已知随机变量⎥⎦⎤⎢⎣⎡-5.01.01.03.05201~X ，那么=)(X E 4.2．5. 设1021,,,x x x 是来自正态总体)4,(μN 的一个样本，则~101101∑=i ix )104,(μN ． 1. 设B A ,均为3阶矩阵，且3==B A ，则=--12AB 8-．2.设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=070040111A ，则_________________)(=A r ．2 3. 设A B C ,,是三个事件，那么A 发生，但C B ,至少有一个不发生的事件表示为)(C B A +.4. 设随机变量)15.0,100(~B X ，则=)(X E 15．5. 设n x x x ,,,21 是来自正态总体N (,)μσ2的一个样本，∑==ni ix n x 11，则=)(x D n2σ．三、计算题1. 已知⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=244213001,543322011B A ，证明B A -可逆，并求1)(--B A ．解： ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=-301111010B A ，因为023111301111010≠=---=--=-B A ，所以B A - 可逆且⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡--=--212121001212323)(1B A 2. 设矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=423532211A ，求（1）A ，（2）1-A ．解：（1）1100110211210110211423532211=---=---=---=A （2）利用初等行变换得⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-----→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---103210012110001211100423010532001211 →-----⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥→-----⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥112100011210001511112100011210001511→------⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥→-----⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥110922010721001511100201010721001511即 A -=-----⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥121721511 3. 设矩阵A B =--⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥=⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥101011111122212221,，求A -1及A BA -1．解：利用初等行变换得101100011010111001101100011010012101--⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥→-⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥ →⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥→⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥10110001101000311110110011010001131313 →--⎡⎣⎢⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥⎥→----⎡⎣⎢⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥⎥101100010132313001131313100231313010132313001131313 即 A -=----⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥1132******** 由矩阵乘法得A BA -=----⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥--⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥1132111211111222122211010111114. 已知B AX X +=，其中02323347,5858901A B --⎡⎤⎡⎤⎢⎥⎢⎥=---=⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦，求X ．解：由方程B AX X +=，得()I A X B -=，且1233575810I A ⎡⎤⎢⎥-=⎢⎥⎢⎥⎣⎦利用初等行变换得⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡1055200132100013211001085010753001321 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---→121100255010364021121100013210001321 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-----→121100255010146001 即 1()I A --=641552121--⎡⎤⎢⎥-⎢⎥⎢⎥--⎣⎦ 由矩阵乘法得164123813()55258152312101812X I A B ---⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=-=-=--⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦5. 设矩阵11512112353181913978A --⎡⎤⎢⎥-⎢⎥=⎢⎥-⎢⎥-⎣⎦，求矩阵A 的秩．解：用初等行变换将矩阵化为阶梯形⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-----→⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-----68144034720347202151187931918135321121511 11512027430000000000--⎡⎤⎢⎥-⎢⎥→⎢⎥⎢⎥⎣⎦ 由此可知矩阵的秩为2．6. 求向量组[]11,3,2,1,1α=---，[]23,8,4,1,0α=---，[]32,1,4,2,1α=--，[]41,2,6,1,2α=---的秩，并求该向量组的一个极大无关组．解：将向量组组成的矩阵化为阶梯形1321138410214211261213211012230580305803-----------⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥→--------⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥1321101223002101200000---⎡⎤⎢⎥-⎢⎥→⎢⎥-⎢⎥⎣⎦ 由此可知该向量组的秩为3，且321,,ααα是一个极大无关组．7. 分别说明当a b ,取何值时，线性方程组x x x x x x x x x x x x x x x ax b12341234123412343127224321248-+-=-+-+=--++=-++=⎧⎨⎪⎪⎩⎪⎪无解、有唯一解、有无穷多解．在有无穷多解的情况下求出一般解．解：将方程组的增广矩阵化为阶梯形13111272121432124813111010100123002622-------⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥→----+-⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥a b a b →---+-⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥→-----⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥1311101010*******64213111010100022000022a b a b …当a b =≠22,时，方程组无解。

工程数学期末考试试题与标准答案及评分标准模板

《工程数学》试题（A 卷）（考试时间： 90 分钟）一、选择题（共30分，共10小题，每小题3分）1.函数293x x xy -++=的定义域是（）． A.{}3|-≥x x ； B.{}3|≤x x ；C.{}33|≤≤-x x ； D .{}33|≤<-x x . 2.函数x y =在0=x 处( ) ．A.连续且可导；B.不连续且不可导； C 不可导但连续；D.不连续但可导. 3.x x arctan lim +∞→=﹙ ）.A.0；B.不存在；C. 2π-； D.2π. 4.若11,1,22()3,1,1,1x x f x x x ⎧+<⎪⎪==⎨⎪>⎪⎩，则1lim ()x f x →=（）. A.2； B. 1； C.1-； D.不存在. 5.函数11)(-=x x f 的水平渐近线是（）. A. 1=x ； B. 1-=y ； C. 0=x ； D. 0=y . 6.函数()y f x =在x 处可导是该点可微的（）条件.A.必要；B.充分；C.充要；D.无关.7.若),)(b a x f 在（内二阶可导，且0)(,0)(<''<'x f x f ，则在),(b a 内函数（）． A.单调减，凸函数； B. 单调增，凸函数； C. 单调减，凹函数； D. 单调增，凹函数.8.函数22,1(),1x x f x x x >⎧=⎨≤⎩，在点1x =处（）.A.不连续；B.连续；C. ()2f x '=可导且；D.无法判断. 9.设函数()f x ，()g x 在[,]a b 上连续，且()()f x g x ≥，则（）.A.()d ()d bbaaf x xg x x ≥⎰⎰ ； B.()d ()d bbaaf x xg x x ≤⎰⎰；C.()d ()d f x x g x x ≥⎰⎰ ； D.()d ()d f x x g x x ≤⎰⎰.10. 曲线x y x y ==与2所围成的平面图形绕x 轴旋转而成的旋转体的体积为（）.A. ⎰-124d )(x x x π； B. ⎰-142d )(x x x π；C.⎰-12d )(y y y π； D. ⎰-12d )(y y y π.二、填空题（共20分，共5小题，每小题4分）1．函数654)(22+--=x x x x f ，则2=x 是_______间断点，3=x 是 _______间断点.2. 复合而成和是由函数函数 e arcsin x y =． 3．点()1,0是曲线b ax x y +-=233 的拐点，则=a ______,=b ______. 4. 设 ()f x 的一个原函数为1x，则=)(x f . 5. ⎪⎩⎪⎨⎧==tty x 2ee,=x y d d __________.2.已知y x x y '+=求,cos sin 22.三、计算题（共42分，共6小题，每小题7分）1.求x x x2)51(lim +∞→ 2.已知y x x y '+=求,cos sin 22. 3. 已知.d ,2cos e 2y x y x 求= 4.求x x x d e 2⎰. 5.求⎰exdx x 1ln .6.求由曲线2,,1===x x y xy 围成的平面图形的面积. 四、证明题（共8分，共1小题，每小题8分）1．证明不等式()()0,1ln 1><+<+x x x xx.《工程数学》试题（B 卷）（考试时间： 90 分钟）一、选择题（共30分，共10小题，每小题3分）1．函数242y x x x-++=的定义域是（）．.A {}2|-≥x x ； B.{}2|≤x x ；C.{}22|≤≤-x x ； D . {}22|≤<-x x2．当0→x 时，下列变量为无穷小的是（）A.;cos x x B. ;sin xxC.;12-xD..sin 1x - 3．x x arctan lim ∞→=﹙ ﹚．A.0 ；B.不存在；C. —2π ； D.2π. 4．若⎩⎨⎧>-≤=1,21,)(2x x x x x f ，则1lim ()x f x →=（）.2;A .1;B .1;C - .;D 不存在5．函数xx f 1)(=的水平渐近线是（）. A. 1=x B. 1-=y C. 0=x D. 0=y6．函数()y f x =在x 处可导是该点连续的（）条件.;A 必要 .;B 充分 .;C 充要 .;D 无关7.若),)(b a x f 在（内二阶可导，且0)(,0)(///>>x f x f ，则在),(b a 内函数（）．A.单调减，凸函数B. 单调增，凸函数C. 单调减，凹函数D. 单调增，凹函数8．函数⎪⎩⎪⎨⎧>+≤=1,21211,)(2x x x x x f ，在点1x =处（）A.连续且可导；B.不连续且不可导； C 不可导但连续；D.不连续但可导.9．设函数()f x 在[,]a b 上连续，则（）dx x f dx x f A b ab a⎰⎰≤)()(. dx x f dx x f B bab a⎰⎰≥)()(.dx x f dx x f C b ab a⎰⎰=)()(. dx x f dx x f D bab a⎰⎰>)()(.10. 曲线12==x x y 与及x 轴所围成的平面图形绕x 轴旋转而成的旋转体的体积为（） A. ⎰14dx x πB. ⎰102dx x π C. ⎰10ydy π D. ⎰12dy y π二、填空题（共20分，共5小题，每小题4分）1．函数231)(22+--=x x x x f ,则2=x 是_______间断点，1=x 是 _______间断点. 2. 复合而成和是由函数函数 sin x e y =． 3．点（1，3）是曲线y=23bx ax + 的拐点，则a=______,b=______. 4. 设 ()f x 的一个原函数为x sin ，则=)(x f .5. ⎩⎨⎧==3x bt y at ,=dxdy__________. 三、计算题（共42分，共6小题，每小题7分）1.x x x2)31(lim +∞→2.已知')),ln(ln(ln y x y 求=.3. 已知.dy ,2sin 求x x y =4.求dx xe x ⎰.5.求⎰-224dx x .6.求由曲线0,1,2===y x x y 围成的平面图形的面积.四、证明题（共8分，共1小题，每小题8分）1．证明：当x x x 211,0+>+>时一、单项选择题（共30分，共10小题，每小题3分）1、D2、C3、D4、B5、D6、C7、A8、A9、A 10、B 二、填空题（共20分，共5小题，每小题4分）1、可去（或者第一类）；无穷（或者第二类）2、x u e y u arcsin ,==；3、a=0,b=1；4、21x-；5、t2e . 三、计算题（共42分，共6小题，每小题7分）1..7(5())5111(lim (3()5111(lim )51(lim 101051)51(102分）分）分）e x x xx x x x x x =+=+=+∞→∞→∞→ 2..7(sin 2cos sin 24()(sin )(sin sin 22'22''分）分）x x x x x x x x y -=-= 3..7()2sin 2(cos 23(2cos 2cos 222分）分）dx x x e x d e xde dy x x x -=+= 4. C e x d e dx e x dx xe x x x x +===⎰⎰⎰2222215)((213()(212'2分）分）.（7分） 5.1ln ex xdx ⎰=211ln 2exdx ⎰（3分）=2221111111ln 2244ee x x x dx e x -⋅=+⎰(7分).6..72ln 235(|)ln 21(3()1(21221分）（分）分）-=-=-=⎰x x dx x x S 四、证明题（共8分，共1小题，每小题8分）1、证：令f(x)=ln(1+x), 在[]x 0，上连续,在（0，x ）内可导， )(x f '=x11+,（2分）由拉格朗日中值定理，在（0，x ）内至少存在一点ξ，使得ξ+=-+-+110)01ln()x 1ln x （（4分）有 ln(1+x)=ξ+1x ,又 0<x <ξ, 1<1+x +<1ξ, x xx x <+<+ξ11,（7分）所以，x x xx<+<+)1ln(1 （8分）一、单项选择题（共30分，共10小题，每小题3分）1、D2、C3、B4、B5、D6、B7、D8、C9、A 10、A . 二、填空题（共20分，共5小题，每小题4分）1、无穷（或者第二类）；可去（或者第一类）2、x u e y u sin ,==；3、29,23=-=b a ；4、x cos ；5、abt 23.三、计算题（共42分，共6小题，每小题7分）1..7(5())3111(lim (3()3111(lim )31(lim 6631)31(62分）分）分）e x x xx x x x x x =+=+=+∞→∞→∞→ 2..7(1ln 1)ln(ln 16()(ln ln 1)ln(ln 13())(ln(ln )ln(ln 1'''分）分）分）xx x x x x x x y ===3..7()2cos 22(sin 3(2sin 2sin 分）分）dx x x x x xd xdx dy +=+=4. .7(4()(''分）分）C e xe dx e x xe dx ex dx xe x x x x x x +-=-==⎰⎰⎰5.令2,2;0,0,cos 2sin 2π======t x t x tdt dx t x 当当则.（1分）⎰-224dx x =tdt ⎰202cos 4π（3分）=⎰+20)2cos 1(2πdt t （4分）=20|)2sin 21(2πt t +(6分)=π.（7分））6..7315(|313(10312分）（分）分）===⎰x dx x S 四、证明题（共8分，共1小题，每小题8分）1、证：令x x x f 211)(+-+=, )(x f '=02x1121>+-+x ,0>x （3分）0)0()(,0],0[)(=>>f x f x x x f 单调递增，在，（6分） ,0211)(>+-+=x x x f 即x x 211+>+.（8分）。

高等工程数学I 试题(A)与答案(2019.11.23)

2019年高等工程数学试题答案一、（15分）设210120003⎛⎫⎪= ⎪ ⎪⎝⎭A ，计算()ρA 、225max =x Ax 及()2cond A 。

解：12321012001;3003λλλλλλλ---=--=⇒===-I A ()3ρ=A 2||||()3是正规矩阵ρ∴== A A A 2222515max 5max 5155==∞===x x xAx AA ()2331是正规矩阵∴== A cond A 二、（10分）讲述一下求解矩阵A 的最靠近*λ的特征值的思路、步骤。

答：**对使用逆幂法，求出其按模最小的特征值再加上。

λλ-A I 000u v =≠任取*11()max()k k k k k u A I v u v u λ--⎧=-⎪⎨=⎪⎩*1()max()k k kk k A I u v u v u λ-⎧-=⎪⎨=⎪⎩即**()A I P A I LUλλ--=对进行选列主元的三角分解有1max()k k k kk k k Ly PvUu y u v u -⎧⎪=⎪⎪∴=⎨⎪⎪=⎪⎩1max()max()k ik i u x v x λλ*⎧→⎪⎪⎨⎪→⎪⎩－有三、（18分）已知矩阵200226044-⎛⎫⎪= ⎪ ⎪⎝⎭A ，求P 使得1-P AP 为A 的Jordan 标准型，同时需要求出A 的Jordan 标准型。

解：200226044λλλλ+-=-----I A ()()23+28λλ=-D 211D D ==()()23+28λλ=-d 211d d ==初等因子：()()2+2 8，λλ-Jordan 标准形：2128-⎛⎫ ⎪=- ⎪ ⎪⎝⎭J 1123212,[]8令--⎛⎫⎪==-= ⎪ ⎪⎝⎭P AP J P p p p 11121223332[032]512[0]228[011]∴=-∴=-=-=-==TT TAp p p Ap p p p Ap p p 15002131,2201使得-⎛⎫⎪ ⎪⎪∴=-= ⎪ ⎪- ⎪⎝⎭P P AP J四、(20分)已知241111212,212211⎛⎫⎛⎫⎪ ⎪=-= ⎪ ⎪ ⎪ ⎪---⎝⎭⎝⎭A b ，（1）求A 的满秩分解；（2）求A +；（3）判断Ax b =是否有解，有解时求极小范数解，无解时求极小范数最小二乘解。

工程数学试题及答案

工程数学参考答案及评分标准
一、选择题（每小题3分，共15分）
1、B2、C3、D4、A5、A
二、填空题（每小题3分，共15分）
6、97、18、1–(1–P)39、3/410、12
三、计算题（每题10分，共50分）
1、解答：函数f(t)的付氏变换为：
F(w)= （3分）
= (2分)
由付氏积分公式有
f(t)= F(w)]= (2分)
7、设A= ，则 =。
8、设有3个元件并联，已知每个元件正常工作的概率为P，则该系统正常工作的概率为。
9、设随机变量的概率密度函数为，则概率。
10、设二维连续型随机变量的联合概率密度函数为，则系数。
三、计算题（每小题10分，共50分）
1、求函数的傅氏变换(这里 )，并由此证明：
2、发报台分别以概率0、6和0、4发出信号“1”和“0”。由于通讯系统受到干扰，当发出信号“1”
(3)A对称，故A必相似于对角阵Λ，
Λ=diag(║a║2, 0,…,0) (2分)
五、应用题（共10分）
解答:
设y为预备出口的该商品的数量，这个数量可只介于2000与4000之间，用Z表示国家的收益（万元）,（1分）
则有（4分）
因 X服从R(2000,4000), 故有
(1分)
所以
=–( y2–7000y + 4•106) /1000(3分)
时，收报台未必收到信号“1”，而是分别以概率0、8和0、2收到信号“1”和“0”；同时，当发出信号“0”时，收报台分别以概率0、9和0、1收到信号“0”和“1”。求
（1）收报台收到信号“1”的概率；
（2）当收报台收到信号“1”时，发报台确是发出信号“1”的概率。

中国矿业大学11-12(上)《工程数学A》试题(A)卷

11-12学年第一学期《工程数学A 》试题（A ）卷一、填空题（每空4分，共40分）1) ()()f t u t =的傅氏变换为 .2) 函数3232()(3)f z my nx y i x xy =++−为解析函数，则m = .3) 201lim(sin d )t t t t i t t j e k →++=∫ . 4) 矢量场k z j y i x A ++=从下向上通过有向曲面22z x y =+(02)z <<的通量为 .5) 函数()sin t f t e t =的拉氏变换为 .6) 矢量场222A xi x y j yzk =−+ 在点)1,2,1(−M 处散度为 . 7) 设()tan f z z =则Res[(),]2f z π= . 8) 函数20()sin 2d t t f t te t t −=∫的拉氏变换为 . 9) C 是直线OA ，O 为原点，A 为i +2, 则d C z z =∫ .10) 复数ln i i = .二、（10分）求矢量场22()A x i y j x y zk =+++ 通过点)1,1,2(−M 的矢量线方程. 三、（10分）求常系数二阶线性微分方程t e t y t y t y −=+′−′′2)()(2)(满足条件0)0(,0)0(=′=y y 的解.四、（10分）求函数222()(413)s F s s s +=++的拉氏逆变换.五、（10分）证明矢量场k yz x j y z x i xyz A 22222)cos (2+++=为保守场，并求积分∫⋅B Al A d ，其中(1,0,1),(2,1,3)A B . 六、（10分）将函数21()(1)f z z z =−在圆环域1|1|z <−<+∞展开成洛朗级数. 七、（10分）用留数计算积分201d 5cos t tπ+∫.。

南京理工大学(工程数学(4.0学分)(A)(16.1.12))

南京理工大学课程考试试卷(学生考试用)
课程名称：工程数学学分：4.0教学大纲编号：11024001
试卷编号：A考试方式：闭卷满分分值：80考试时间：120分钟
组卷日期：2016年1月12日组卷教师(签字)：命题组审定人(签字)：
三．（每小题5分，共15分）：
1．计算积分，其中是0到的直线段；
2．求积分，从而证明；
3．计算积分。
四．（7分）将函数在下列圆环域内展开成洛朗级数：
1．；2．。
五．计算下列各题（每小题5分，共10分）：
1．设，求的Fourier变换；
2．设，求的Laplace变换。
六．（7分）用积分变换法求解微分积分方程。
七．（7分）求一映射，将z平面的区域：映射成w平面
上的区域：。
八．（6分）设与是区域内的调和函数，，，证明是内的解析函数。
所有解答必须写在答题纸上，写在试卷上无效!
一．填空题（每小题2分，共20分），则；
4．；
5．映射将映射成，并满足，则映射
；
6．；
7．设，则Laplace逆变换；
8．曲线在处的切向量为；
9．矢量场在点处沿方向
的环量面密度为；
10．设，为矢径的模，为拉普拉斯算子，则在点(1,1,1)处。
二．（8分）证明矢量场是有势场，并求其势函数。
第1页共1页