图论中的几个实际例子
将士渡河——最短路径问题的实际应用

将士渡河——最短路径问题的实际应用引言最短路径问题是图论中的经典问题之一,它在现实生活中有着广泛的应用。
本文将讨论一个实际应用场景——将士渡河问题,并探讨如何使用最短路径算法来解决该问题。
问题描述将士渡河是一个经典的智力游戏,游戏规则如下:有一条河,河岸上有若干士兵和一艘船。
游戏目标是将所有士兵从一岸安全地运送到另一岸,而且船每次只能运送一定数量的士兵。
同时,游戏规定在任何一侧的岸边,士兵的数量不能超过敌军的数量,否则士兵将会被敌军消灭。
现在的问题是,如何通过最短路径算法确定士兵的最佳运输方案,以确保所有士兵都能安全渡河。
解决方案为了解决将士渡河问题,我们可以使用最短路径算法来确定士兵的最佳运输方案。
以下是解决该问题的步骤:1. 建立图模型:将河岸、士兵和船分别表示为图的节点,将船的运输能力表示为图的边。
根据游戏规则,我们可以将每一种状态(即河岸上士兵的分布情况)作为图的一个节点,并根据船的运输能力建立相应的边。
2. 权重设定:根据题目要求,我们需要找到最短路径来确保士兵的安全渡河。
因此,我们需要为图的每条边设定一个权重,使得最短路径算法能够在搜索过程中优先选择权重较小的路径。
可以根据士兵的数量、敌军的数量等因素来设定权重。
3. 应用最短路径算法:使用最短路径算法(如Dijkstra算法或A*算法)来确定从起点到终点的最短路径。
算法将根据权重和图的拓扑结构来搜索最短路径,直到找到目标节点或者搜索完整个图。
4. 输出结果:根据最短路径算法的结果,我们可以得到士兵的最佳运输方案。
可以将路径中的边转化为实际操作,即哪些士兵应该上船、哪些士兵应该下船,以及船的运输方向等。
实际应用将士渡河问题在实际生活中有着广泛的应用。
以下是一些例子:1. 军事行动:在实际的军事行动中,士兵的运输和部署是非常重要的。
通过使用最短路径算法,可以确定最佳的运输方案,以确保士兵能够安全快速地到达目的地。
2. 物流管理:在物流管理中,货物的运输是一个重要的环节。
图论模型实例优秀课件

存在,考虑增环,增环后权值应减小 ▪ 换枝原则 环路上某顶点长出一条枝,该枝末梢和环路另
一顶点接近,可考虑换枝
问题1的分析与求解--最小生成树法
问题1的分析与求解 --TSP方法
公路边的数字为该路段的公里数.
问题分析:
本题给出了某县的公路网络图,要求的是在不 同的条件下,灾情巡视的最佳分组方案和路线.
将每个乡(镇)或村看作一个图的顶点,各乡 镇、村之间的公路看作此图对应顶点间的边,各条 公路的长度(或行驶时间)看作对应边上的权,所 给公路网就转化为加权网络图,问题就转化图论中 一类称之为旅行售货员问题,即在给定的加权网络 图中寻找从给定点O出发,行遍所有顶点至少一次 再回到点O,使得总权(路程或时间)最小.
图论模型实例
专题
❖ 图的表示与锁具问题 ❖ 最小生成树、TSP和灾区巡视问题 ❖ 最短路、网络流和运输问题 ❖ 作业
图的表示与锁具问题
不积硅步,无以至千里 --荀子·劝学
图的矩阵表示
邻接矩阵: (以下均假设图为简单图).
1) 对无向图 G,其邻接矩阵 A(aij),其中:
1, aij 0,
若vi与vj相邻 , 若vi与vj不相.邻
i1
定义 称
为最大容许均衡度.
为该分组的实际均衡度.
显然0 0 1,0越小,说明分组的均衡性越 好. 取定一个 后,0与 满足条件 3)的分组是
一个均衡分组. 条件 4)表示总巡视路线最短.
此问题包含两方面:a)对顶点分组, b)在每组中求 (单个售货员)最佳旅行售货员回路.
因单个售货员的最佳旅行售货员回路问题不存在多 项式时间内的精确算法.因此多个售货员的最佳旅行售 货员回路问题也不存在多项式时间内的精确算法.
图论思想在生活中的运用

图论思想在生活中的运用
图论思想在生活中的应用很多,例如:
1、交通出行:在城市的出行,经常会用到从一个地点到另一地点的最短路径,而解决此问题最好的方法就是使用图论,用最短路径算法来找到最优路线,比如驾车、打车、乘地铁等都会使用图论来算出最短路径。
2、网络传输:现在的互联网系统都是使用图论的方法来进行网络传输。
当多台计算机连接到网络时,都会形成一个图,通过图论,可以找到最佳的传输路径,以优化路径走向,从而提高网络的传输速度。
3、调度系统:调度系统中的人员调度及运输路线调度,也是依靠图论思想。
人员调度时,可以建立一个移动关系图,找到每一步最短路径,从而得到最佳的调动方案;而运输路线则可通过最短路线算法,计算出从一个点到另一点最短的路径,从而达到节约时间,提高工作效率的效果。
4、信息检索:在海量数据的环境下检索合适的信息,也是利用图论来解决的。
例如搜索引擎,会建立一个链接关系图,根据各页面间的链接关系来确定最优的信息检索结果。
图论知识及运用举例

图论知识及运用举例1 概论图论中的“图”是指某类具体事物和这些事物之间的联系。
如果我们用点表示这些具体事物,用连接两点的线段(直的或曲的)表示两个事物的特定的联系,就得到了描述这个“图”的几何形象。
图论为任何一个包含了一种二元关系的离散系统提供了一个数学模型,借助于图论的概念、理论和方法,可以对该模型求解。
图是运筹学(Operations Research )中的一个经典和重要的分支,所研究的问题涉及经济管理、工业工程、交通运输、计算机科学与信息技术、通讯与网络技术等诸多领域。
下面将要讨论最短路问题、最大流问题、最小费用流问题和匹配问题等。
2 图的基本概念2.1 无向图一个无向图(undirected graph)G 是由一个非空有限集合)(G V 和)(G V 中某些元素的无序对集合)(G E 构成的二元组,记为))(),((G E G V G =。
其中},,,{)(21n v v v G V =称为图G 的顶点集(vertex set )或节点集(node set ), )(G V 中的每一个元素),,2,1(n i v i =称为该图的一个顶点(vertex )或节点(node );},,,{)(21m e e e G E =称为图G 的边集(edge set ),)(G E 中的每一个元素k e (即)(G V 中某两个元素j i v v ,的无序对) 记为),(j i k v v e =或i j j i k v v v v e == ),,2,1(m k =,被称为该图的一条从i v 到j v 的边(edge )。
当边j i k v v e =时,称j i v v ,为边k e 的端点,并称j v 与i v 相邻(adjacent );边k e 称为与顶点j i v v ,关联(incident )。
如果某两条边至少有一个公共端点,则称这两条边在图G 中相邻。
边上赋权的无向图称为赋权无向图或无向网络(undirected network )。
图论及其应用
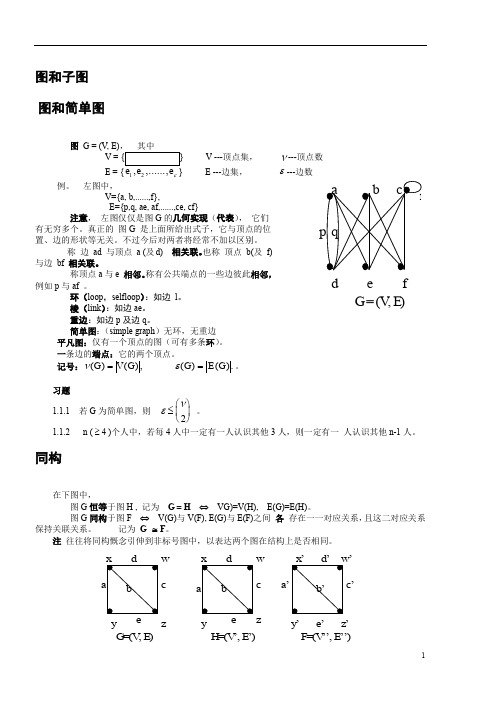
图和子图 图和简单图图 G = (V, E)V ---顶点集,ν---顶点数12ε E ---边集, ε---边数例。
左图中, V={a, b,......,f}, E={p,q, ae, af,......,ce, cf} 注意, 左图仅仅是图G 的几何实现(代表), 它们有无穷多个。
真正的 图G 是上面所给出式子,它与顶点的位置、边的形状等无关。
不过今后对两者将经常不加以区别。
称 边 ad 与顶点 a (及d) 相关联。
也称 顶点 b(及 f) 与边 bf 相关联。
称顶点a 与e 相邻。
称有公共端点的一些边彼此相邻,例如p 与af 。
环(loop ,selfloop ):如边 l 。
棱(link ):如边ae 。
重边:如边p 及边q 。
简单图:(simple graph )无环,无重边 平凡图:仅有一个顶点的图(可有多条环)。
一条边的端点:它的两个顶点。
记号:νε()(),()().G V G G E G ==。
习题1.1.1 若G 为简单图,则εν≤⎛⎝ ⎫⎭⎪2 。
1.1.2 n ( ≥ 4 )个人中,若每4人中一定有一人认识其他3人,则一定有一 人认识其他n-1人。
同构在下图中, 图G 恒等于图H , 记为 G = H ⇔ VG)=V(H), E(G)=E(H)。
图G 同构于图F ⇔ V(G)与V(F), E(G)与E(F)之间 各 存在一一对应关系,且这二对应关系保持关联关系。
记为 G ≅F。
注 往往将同构慨念引伸到非标号图中,以表达两个图在结构上是否相同。
de f G = (V , E )yz w cG =(V , E )w cyz H =(V ’, E ’)’a ’c ’y ’e ’z ’F =(V ’’, E ’’)注 判定两个图是否同构是NP-hard 问题。
完全图(complete graph) Kn空图(empty g.) ⇔ E = ∅ 。
V’ ( ⊆ V) 为独立集 ⇔ V’中任二顶点都互不相邻。
数学建模——图论篇

软件学院
图论原理 一. 图的概念 一个图 G=<V(G),E(G)>, 其中结点集V(G):是G的结 点的非空集合.(V(G)≠Φ),简记成V;边集E(G):是 G的边的集合. 有时简记成E. 结点: 用 表示, 旁边标上该结点的名称. 边:有向边:带箭头的弧线.从u到v的边表示成(u,v) 无向边:不带箭头的弧线.u和v间的边表示成(u,v)
v3
软件学院
图论原理
回路:如果一条路的起点和终点是一个结点,则称此路 是一个回路. 如果一条路中所有边都不同,则称此路为迹或简单通路. 如果一条回路中所有边都不同,则称此回路为闭迹或简 单回路. 如果一条路中所有结点都不同,则称此路为基本通路. 如果一条回路中所有结点都不同,则称此路为基本回路. 一条基本通路一定是简单通路,但是一条简单通路不 一定是基本通路
图论原理
图的同构 设G=<V,E>和G’=<V’,E’>是图,如果存在双射f:VV’ 且任何 vi,vj∈V,若边(vi,vj)∈E,当且仅当 边(f(vi),f(vj))∈E’, (则称G与G’同构,记作G≌G’. (同构图要保持边的“关联”关系) 例如:右边所示的两个图: a b 1 4 G=<V,E> G’=<V’,E’> c d 3 2 构造映射f:VV’ a 1 b 2 c 3 d 4 a 1 b 2 c 3 d 4
软件学院
图论原理
2.汉密尔顿图的判定: 到目前为止并没有判定H图的充分必要条件. 定理1 (充分条件):G是完全图,则G是H图.
K2
K3
K4
K5
定理2(充分条件)设G是有n(n>2)个结点的简单图,若对G中每 对结点度数之和大于等于n,则G有一条H路(H回路)。
图论的基本概念和应用

图论的基本概念和应用图论是数学中的一个重要分支,研究的是图的性质和图之间的关系。
图论在计算机科学、网络科学、运筹学等领域有着广泛的应用。
本文将介绍图论的基本概念和一些常见的应用。
图的定义图是由节点(顶点)和边组成的一种数据结构。
节点表示对象,边表示对象之间的关系。
图可以分为有向图和无向图两种类型。
有向图有向图中,边是有方向的,表示从一个节点到另一个节点的关系。
如果从节点A到节点B存在一条边,那么我们称节点A指向节点B。
无向图无向图中,边是没有方向的,表示两个节点之间的关系。
如果两个节点之间存在一条边,那么我们称这两个节点是相邻的。
图的表示方法图可以用多种方式进行表示,常见的有邻接矩阵和邻接表两种方法。
邻接矩阵邻接矩阵是一个二维数组,其中行和列分别表示图中的节点,数组元素表示节点之间是否存在边。
如果节点i和节点j之间存在边,则邻接矩阵中第i行第j列的元素为1,否则为0。
邻接表邻接表是一种链表的形式,其中每个节点都有一个链表,链表中存储了与该节点相邻的节点。
邻接表更加节省空间,适用于稀疏图。
图的遍历图的遍历是指从图中的某个节点出发,按照一定规则依次访问图中的所有节点。
常见的图遍历算法有深度优先搜索(DFS)和广度优先搜索(BFS)。
深度优先搜索(DFS)深度优先搜索是一种递归的遍历算法,从起始节点开始,沿着一条路径尽可能深入地访问图中的节点,直到无法继续深入为止,然后回溯到上一个节点,继续访问其他未被访问过的节点。
广度优先搜索(BFS)广度优先搜索是一种非递归的遍历算法,从起始节点开始,按照距离起始节点的距离逐层访问图中的节点。
首先访问起始节点,然后访问与起始节点相邻的所有节点,再访问与这些相邻节点相邻的所有未被访问过的节点,以此类推。
图的应用图论在许多领域都有着广泛的应用,下面介绍几个常见的应用场景。
社交网络分析社交网络是一个典型的图结构,其中节点表示用户,边表示用户之间的关系。
通过对社交网络进行图论分析,可以研究用户之间的关系、社区发现、信息传播等问题。
面试中图论基本知识

面试中图论基本知识1. 引言在计算机科学中,图论是一门研究图的性质和图的应用的学科。
图由节点(顶点)和边组成,这些节点和边可以表示各种复杂的现实世界问题。
图论在计算机科学中有着广泛的应用,如网络路由算法、社交网络分析等。
本文将介绍面试中常见的图论基本知识。
2. 图的定义和术语图由节点和边组成,节点表示对象,边表示对象之间的关系。
以下是图的一些基本术语:•节点(或顶点):表示图中的对象,可以是任何东西,如人、地点、事件等。
•边:表示节点之间的关系,可以是有向的(箭头指向某个方向)或无向的。
•有向图:图中的边有方向,表示关系具有方向性。
•无向图:图中的边没有方向,表示关系是双向的。
•权重:边可以带有权重,表示关系的强度或代价。
•路径:节点之间的序列,沿着边从一个节点到达另一个节点。
•循环:路径的起点和终点相同,形成一个环。
•连通图:图中任意两个节点之间都存在路径。
•子图:图的一部分,由图的节点和边的子集组成。
3. 常见的图算法在图论中,有许多用于解决不同问题的算法。
以下是一些常见的图算法:3.1 广度优先搜索(BFS)广度优先搜索是一种用于图的遍历和搜索的算法。
它从一个节点开始,依次访问它的邻居节点,然后再访问邻居节点的邻居节点,以此类推。
广度优先搜索通常用于寻找最短路径或找到两个节点之间的最短距离。
3.2 深度优先搜索(DFS)深度优先搜索也是一种用于图的遍历和搜索的算法。
它从一个节点开始,访问它的邻居节点,然后再访问邻居节点的邻居节点,一直深入到没有未访问节点为止。
深度优先搜索通常用于查找连通分量或判断图是否有环。
3.3 最小生成树(MST)最小生成树是一个连通图的子图,它包含了图中所有的节点,并且边的权重之和最小。
最小生成树通常用于在一个有权图中找到一个最小的连接子图,即把所有节点连接起来的代价最小的方式。
3.4 最短路径算法最短路径算法用于寻找两个节点之间的最短路径。
其中最著名的算法是迪杰斯特拉算法(Dijkstra)和贝尔曼-福特算法(Bellman-Ford)。
图论(基础篇)

根据此图便可找到渡河方法.
(1,1,1,1) (1,1,1,0) (1,1,0,1) (1,0,1,1) (1,0,1,0) (0,0,0,0) (0,0,0,1) (0,0,1,0) (0,1,0,0) (0,1,0,1)
-1,所以该图有一哈密尔顿路,故本题有解。
问题:
7位客人入席,A只会讲英语,B会讲英,汉语,C会 讲英,意大利,俄语,D会讲日,汉语,E会讲德,意 大利语,F会讲法,日,俄语,G会讲法,德语.能否 安排圆桌席位使每位客人与其左右邻不用翻译 便可交谈?
解:首先建立无向图模型:
结点为客人;会共同语言的2结点相邻接.则问 题归结为求此图的一条Hamilton回路.
• 对它们进行数学抽象————图。
C
A
B
D 哥尼斯堡七桥示意图
问题1(哥尼斯堡七桥问题): 能否从任一陆地出发通过每座桥恰好一次而回到出发
点?
C
A
B
D
七桥问题模拟图
欧拉指出: 如果每块陆地所连接的桥都是偶数座,则从任一陆
地出发,必能通过每座桥恰好一次而回到出发地.
例1: 一摆渡人欲将一只狼,一头羊,一篮菜从河西渡过河 到河东.由于船小,一次只能带一物过河,并且狼与羊,羊 与菜不能独处.给出渡河方法.
解 把33盏灯看成树叶,将5插头的接线板看成分 枝点,这样本问题可理解为求一个完全5叉树的分 枝点的个数的问题。 由m叉树定理1知, 有 由此得 =8 所以至少需要8个5插头的接线板。
例5:一笔画问题
Euler路径与Euler图
• 经过于(有向或无向)图 G 的每条边一次且仅一次的路径(回 路)称为 Euler 路径(回路). 具有 Euler 回路的连通图称为Euler图.
图论及其应用—典型图

4.3Hamilton图
定理4.3.2:设G是p(G)≥3的图,如果G中任意 两个不相邻的顶点u和v,均有 dG(u)+dG(v)≥p(G), 则G是若G是Hamilton图。
推论4.3.3:若G是具有p(≥3)个顶点的简单图, 且每个顶点的度至少是p/2,则G是Hamilton图 。
定理5.2.5:对k≥1,2k-正则图G有2-因子。 注:若H是G的k-正则生成子图,则称H是G的 k-因子。
5.3二分图最大对集算法
匈牙利算法。
k
w(C)定 义 为 w(ei)。 i 1
w(C)包 含 两 部 分 权 和 ,
一 部 分 是 w(C),即 每 条 边 的 和 ; eE (G)
另 外 一 部 分 是 重 复 走 的街 道E E(G),即 w(e)。 eE
因 此 , 对 于G的 人 一 个 环 游C, w(C) w(C), eE (G )
图论及其应用—典型图
4.1Euler环游 4.2中国邮路问题 4.3Hamilton图 4.4旅行售货员问题 5.1对集 5.2二分图的对集 5.3二分图最大对集算法
4.1Euler环游
定义4.1.1:经过G的每条边的迹称为G的Euler迹,如
果这条迹是闭的,则称这条迹为G的Euler环游。 一般情况下,我们把不是Euler环游的迹称为G的Euler 通路,而把含有Euler环游的图称为Euler图。
推论4.3.9:设图G的度序列为(d1,d2,…,dp) ,d1≤d2≤…≤dp,p≥3。若对任何k,1≤k<(p-1)/2 ,均有dk>k,若p为奇数,更有d(p+1)/2>(p-1)/2, 则G是Hamilton图。
最短路径实际生活中的应用

最短路径实际生活中的应用
最短路径算法是一种常用的图论算法,可以在图中寻找两个节点之间最短的路径。
在实际生活中,最短路径算法可以被应用于多种场景,下面将列举几个例子:
1.导航系统
众所周知,导航系统是基于地图数据实现的,而地图就是一个图。
最短路径算法可以帮助导航系统找到两个地点之间最短的路径,并在地图上标出路线,为司机提供导航服务。
2.物流配送
在物流配送过程中,物流企业需要将货物从仓库运送到客户处。
最短路径算法可以帮助物流企业确定货车的行驶路线,节约时间和成本。
此外,最短路径算法还可以帮助物流企业规划仓库的位置,让仓库与客户的距离更近,提高效率。
3.电力网络
电力网络中的电线杆和变电站可以看作是节点,它们之间的电线可以看作是边。
最短路径算法可以帮助电力公司确定电线的布局,让电线的长度更短,降低电力损耗和成本。
4.社交网络
社交网络中的用户可以看作是节点,他们之间的关注和好友关系可以看作是边。
最短路径算法可以帮助社交网络推荐好友或者关注对象,让用户之间的连接更加紧密。
总之,最短路径算法在实际生活中有着广泛的应用,它可以帮助
我们优化决策,提高效率和降低成本。
数学建模-图论篇

data
firstarc
nextvex
边结点表中的结点的表示:
data:结点的数据场,保存结点的 数据值。
firstarc:结点的指针场,给出自该 结点出发的的第一条边的 边结点的地址。
nextvex:结点的指针场,给出该结 点的下一结点的地址。
info:边结点的数据场,保存边的 权值等。
adjvex:边结点的指针场,给出本
2C 3D
20 30 ∧
data firstin firstout
tailvex headvex hlink tlink
0
1
02
∧
31∧
2
3
∧∧
3 2 ∧∧
图的存储结构
4、邻接多重表
•结点表中的结点的表示
:
data
firstedge
data:结点的数据域,保存结点的 数据值。
firstedge: 结点的指针域,给出自该
A
B
E
表示成右图矩阵
C
D
011 00 100 11 1000 1 0100 1 0111 0
图的存储结构
1、邻接矩阵和加权邻接矩阵(labeled adjacency matrix)(续)
•有向图的加权邻接矩阵
设有向图具有 n 个结点,则用 n 行 n 列的矩阵 A 表示该有向图;
并且 A[i,j] = a , 如果i 至 j 有一条有向边且它的权值为a。A[i,j] =无穷,如果 i 至 j 没有一条有向边。
邻接表
十字链表
邻接多重表
1、邻接矩阵和加权邻接矩阵(labeled adjacency matrix) •无权值的有向图的邻接矩阵
设有向图具有 n 个结点,则用 n 行 n 列的布尔矩阵 A 表示该有向图;
图论在实际生活中的应用

一、图论的基本知识
图论起源于举世闻名的柯尼斯堡七桥问题。在柯尼斯堡的普莱格尔河上面有七座桥将河中的岛及岛与河岸是连接起来的,有一个问题是要从这四块陆地中任何一块开始,通过每一座桥而且正好只能一次,再回到起点。然而许多人经过无数次的尝试都没有成功。在1736年欧拉神奇般的解决了这个问题,他用抽像分析法将这个问题化为第一个图论问题:即用点来代替每一块陆地,将每一座桥用联接相应的两个点的一条线来代替,所以相当于得到一个“图”(如下图)。
{
int i=0;
while(i<G.vexnum && v!=G.vexs[i])
i++;
if(i<G.vexnum)
return i;
else
return -1;
}
int CreateUDG(MGraph &G) //数组邻接矩阵表示法构造无向图
{
char v1,v2;
int weight;
cout<<"请输入图的顶点数和边的条数"<<endl;
cin>>G.vexnum>>G.arcnum;
cout<<"请输入顶点的名称(0--9)"<<endl;
for(int i=0;i<G.vexnum;i++)
cin>>G.vexs[i];
for(int q=0;q<G.vexnum;q++)
for(int p=0;p<G.vexnum;p++)
G.arcs[q][p]=0;
数学中的图论问题研究

数学中的图论问题研究图论是数学中一个重要的分支,研究的是描述多个对象之间关系的图模型的性质和结构。
图论问题广泛应用于计算机科学、运筹学、电路设计等领域,并在实际生活中有很多应用。
本文将从几个重要的图论问题入手,探讨它们的理论背景和实际应用。
一、最短路径问题在图论中,最短路径问题是指连接图中两个顶点的路径中,边权之和最小的那条路径。
解决最短路径问题的方法有很多,常用的有迪杰斯特拉算法和弗洛伊德算法。
迪杰斯特拉算法适用于求解单源最短路径问题,而弗洛伊德算法则能够求解全局最短路径问题。
最短路径问题在实际生活中有广泛应用,比如地图导航、物流路径规划等。
地图导航中,我们需要找到起点和终点之间的最短路径,而物流路径规划中,我们需要找到运输货物所需的最短路径。
通过最短路径算法,我们可以高效地解决这些实际问题。
二、最小生成树问题最小生成树问题是指在带权无向图中找到一个边的子集,使得这个子集包含图中的所有顶点,并且边的权值之和最小。
在解决最小生成树问题时,常用的算法有普利姆算法和克鲁斯卡尔算法。
最小生成树问题在实际应用中也有很多。
比如,我们在设计电力输电网络时,需要将各个电力站点用最小的输电线路连接起来,以降低成本和能量损耗。
此外,最小生成树问题还可以应用于通信网络、铁路规划等领域。
三、旅行商问题旅行商问题是指在带权完全图中找到一条经过所有顶点的哈密顿回路,并且使得回路总权值最小。
旅行商问题是一个典型的NP完全问题,没有多项式时间的解法。
即使旅行商问题没有高效解法,但是它在实际生活中有很多应用。
比如,物流公司需要规划送货员的路线,使得送货员能够高效地访问每个客户。
其他应用还包括航空航天领域中的轨道规划、城市旅游规划等。
四、最大流问题最大流问题是指在有向图中找到从一个源点到一个汇点的最大流量。
最大流问题与最小割问题密切相关,可以通过最大流最小割定理相互转化。
最大流问题在网络流中有重要应用。
比如,在通信网络中,我们需要确定数据流从源点到目的地的最大传输量。
图论知识及运用举例

图论知识及运用举例1 概论图论中的“图”是指某类具体事物和这些事物之间的联系。
如果我们用点表示这些具体事物,用连接两点的线段(直的或曲的)表示两个事物的特定的联系,就得到了描述这个“图”的几何形象。
图论为任何一个包含了一种二元关系的离散系统提供了一个数学模型,借助于图论的概念、理论和方法,可以对该模型求解。
图是运筹学(Operations Research )中的一个经典和重要的分支,所研究的问题涉及经济管理、工业工程、交通运输、计算机科学与信息技术、通讯与网络技术等诸多领域。
下面将要讨论最短路问题、最大流问题、最小费用流问题和匹配问题等。
2 图的基本概念2.1 无向图一个无向图(undirected graph)G 是由一个非空有限集合)(G V 和)(G V 中某些元素的无序对集合)(G E 构成的二元组,记为))(),((G E G V G =。
其中},,,{)(21n v v v G V =称为图G 的顶点集(vertex set )或节点集(node set ), )(G V 中的每一个元素),,2,1(n i v i =称为该图的一个顶点(vertex )或节点(node );},,,{)(21m e e e G E =称为图G 的边集(edge set ),)(G E 中的每一个元素k e (即)(G V 中某两个元素j i v v ,的无序对) 记为),(j i k v v e =或i j j i k v v v v e == ),,2,1(m k =,被称为该图的一条从i v 到j v 的边(edge )。
当边j i k v v e =时,称j i v v ,为边k e 的端点,并称j v 与i v 相邻(adjacent );边k e 称为与顶点j i v v ,关联(incident )。
如果某两条边至少有一个公共端点,则称这两条边在图G 中相邻。
边上赋权的无向图称为赋权无向图或无向网络(undirected network )。
图论中的树与森林

图论中的树与森林图论是一门研究图的结构和性质的数学分支,而树和森林则是图论中重要的概念。
本文将对图论中的树与森林进行介绍与分析。
一、树的定义及性质树是一种特殊的图,它是连通且无环的无向图。
树可以看作具有分支结构的图,其中每个节点只有一个入度(除了根节点)和零到多个出度。
树的定义具有以下性质:1. 树中任意两个节点之间都存在唯一的路径,这个路径是唯一的。
2. 树中的边数比节点数少1,记作|E| = |V| - 1,其中|E|表示边数,|V|表示节点数。
3. 删除树中任意一条边后,将得到两个单独的树。
二、树的特殊类型在图论中,树有一些特殊的类型,包括二叉树、平衡树、最小生成树等。
1. 二叉树:二叉树是每个节点最多只有两个子节点的树。
它可以是空树,或者由一个根节点及左子树、右子树组成。
2. 平衡树:平衡树是一种特殊的二叉树,它的左子树和右子树的高度差不大于1。
3. 最小生成树:最小生成树是指在一个连通带权无向图中,选择一个权值最小的子图,使得这个子图是一个树,并且覆盖了图中的所有节点。
三、森林的定义及性质森林是由零个或多个不相交的树组成的图。
和树类似,森林也是一个连通且无环的无向图。
森林的定义具有以下性质:1. 森林中每个树的边数比节点数少1。
2. 森林的节点数等于所有树的节点数之和。
3. 森林中的任意两个节点之间可能存在多个路径。
四、树与森林在实际应用中的意义树和森林在实际应用中有着广泛的意义和应用,以下是一些例子:1. 计算机科学中,树和森林常用于构建数据结构,例如二叉搜索树、哈夫曼树等。
2. 在网络领域,树和森林可以用于路由算法、拓扑结构等。
3. 在人工智能中,决策树常用于分类和回归问题。
4. 遗传学中,基因进化树可以用于研究不同物种的进化关系。
五、总结图论中的树和森林是重要的概念,在数学和计算机科学中都有着广泛的应用。
树具有连通且无环的特点,可以看作是一种具有分支结构的图。
而森林由零个或多个不相交的树组成,是一种更加复杂的结构。
2.4图论的一些简单的应用引言生活中许多实际的问题往往都要用到图

2.4 图论的一些简单的应用引言生活中许多实际的问题往往都要用到图论和算法理论的思想去解决.所以一些图论的简单的知识已经陆续地进入到不同层次的中学教材中,例如俄罗斯的高中选修课教材中就介绍了一些图论的知识,在我国最近制定的新大纲(高中)中把组合数学(图论)初步知识放在任意选择的选修课中.在高中、初中的数学竞赛和数学知识应用竞赛中需要运用图论知识解决的问题也日渐增多,无论是中学教师还是中学生都应该注意到这种趋势.另外掌握基本的图论知识也不是一件难事,何况掌握它们对思考生活中的数学问题的确是很有用的.这一节我们将用很少的篇幅结合一些实际问题介绍图论的初步知识和思想.1.从哥尼斯堡七桥问题到一笔画在18世纪哥尼斯堡是位于东普鲁士的一座城市,现在属于立陶宛共和国,并更名为加里宁格勒.在通过哥尼斯堡的皮格尔河(pregel)上架有七座桥,如图4-1所示把城市分为四个部分A、B、C、D.很久以前当地居民热衷于一个难题:是否能一次走遍七座桥,每座桥只允许走一次,最后回到原出发点.这样的问题通常称做一笔画问题.例如以下图形是否可以用笔把所有边画出来而不允许笔离开纸呢?看起来哥尼斯堡七桥问题与后面图形一笔画的问题有些不同,但是如果我们对哥尼斯堡七桥问题稍加改进,就会发现它们是完全相同的,七座桥连接着四块土地,A、B、C和D,我们不妨把它们看做平面上的四个点,把连接这些不同土地的桥看做连接不同点的边,这样哥尼斯堡的七座桥就变成了如图4—3的图形(N).显然,图形Ⅳ与图形Ⅰ、Ⅱ和Ⅲ就很相像了.我们通常可以用一个抽象的模型把这些图形的共性刻画出来.它们都是由一些顶点和一些连接某些顶点的边组成,例如Ⅰ中,顶点集V={A,B,C,D,E},边集E={a,b,c,d,e,f,g,h},图Ⅳ中,顶点集V={A,B,C,D},边集E={a,b,c,d,e,f,g}.从图中可以看出每一条边是连接哪两个顶点的,一般每条边可以附加上被它连接的顶点,例如图Ⅳ中,a(C,D),b(C,B),等等.并且边连接的顶点是没有顺序的,即无起点和终点之分.如果我们用G表示上述的图,顶点集V和边集E是其两个组成部分,可以表示为G=(V,E),而E中的每个元素对应着两个顶点,不妨表示为e∈E,e =(A,B)或e(A,B),其中A、B是V中的元素.给定一个图,每一边与顶的关系也就被确定了.与一个顶点连接的边数通常称做这个顶点的度.而我们把由顶点、边、顶点、边…、边、顶点组成的序列,称做道路,当然,道路序列的起点和终点都是顶点,道路序列的每一顶点都是与其相邻的边的顶点,并且顶点与边是交替出现在道路序列中.如果道路序列的起点与终点是同一个顶点,则称这条道路为回路.如果一条道路通过一个图的每一条边,且仅通过一次,则称这种道路为欧拉道路,如果一条欧拉道路又是一个回路,则称这样的回路为欧拉回路.这样哥尼斯堡七桥问题实际上变成问图Ⅳ是否存在欧拉回路.而一笔画问题则变成是否存在欧拉道路的问题.我们所以起名欧拉道路和欧拉回路就是为纪念这位伟大的数学家在18世纪时已经圆满地解决了这个问题.在我们叙述欧拉对这些问题的解答之前,再引入一个连通图的概念,如果一个图的任意两个顶点都可以用一条道路把这两个点连接,并做为道路的起点和终点,则这样的图称为连通图.欧拉对这两个问题的回答是:结论(1) 一个图有欧拉回路的充分必要条件是这个图是连通的且每一个顶点的度是偶数.结论(2) 一个图有欧拉道路的充分必要条件是这个图是连通的且仅有两个顶点的度是奇数.在中学我们所见到的数学命题的证明大体上可以分为两类.一类是逻辑演绎和归纳类的证明,即或从已知条件出发,利用所学过的其他事实,推导结论的正确性,或从所需证明的问题出发,逐步分析,看是否可以归纳为已知条件和学过的事实;等等.这类证明都可作为逻辑推理能力的一种训练.另外一类是构造性的,即可从已知条件和事实把结论或结论的要求通过确定的做法“将其构造出来”.例如:一元二次方程ax2+bx+c=0,当b2-4ac≥0时方程一定有实根.就是用构造的方法(配方法)把该方程的实根具体地构造出来.后一类“构造式”证明方式在中学生的学习中是强调不够的,或者说没有给予足够的注意.而在现实生活中的很多情况下,仅仅知道事实的存在是远远不够的,更为关心的是“实现”出来.这里简单介绍的算法思想可以看做“构造式证明”的一种.先从一个实例出发.在欧拉的结论(1)中,我们要证明这样的事实,如果一个连通图每一个顶点的度是偶数,则一定存在欧拉回路.事实上,这个结论蕴含着这样的结果:从每一顶点出发都可以产生一个欧拉回路.当然,如果我们可以确定出一系列做法,确保从每一顶点出发都可以构造出一个欧拉回路,证明自然就完成了.我们可以按以下步骤完成欧拉回路的构造.第一步:任意选定一个顶点A,做为回路的起点.第二步:由于G是一个连通图,故顶点A的度不为0,至少存在一条边以A点为端点,我们可任取一条这样的边e,另一个端点为A′.由于A′的度数为偶数,则必然至少还有另一条不同于e的边e′,若e′的另一端点是A,则我们得到了一以A为起点,同时A又是终点的回路C.否则,我们又可从A′沿不同于e的边走下去.直到得到一个以A为起点和终点的回路C,每条边在C中仅可出现一次.第三步:如果C包含了图G的全部边则我们完成了工作.否则,至少存在回路C的一个顶点B,还有过B的边不在C上,图G的连通性保证了这一点.由B出发重复第一步、第二步,我们又可以得到一个以B为起点和终点的另一回路C′,而C′中没有C中的边.把C和C′合并成一个新的回路.第四步:反复第三步直到作出欧拉圈.从这样一个实例,我们可以看出这是一个可操作的步骤序列,无论遇到怎样的图,只要这个图每一顶点的度是偶数,我们都可以按照上面给定的步骤序列构造出或者说找出一个欧拉圈.我们可以把给定图看做一个输入,把要求的欧拉圈看做输出,上面给出的步骤就是从输入得到输出的操作步骤序列.很多的数学问题都可以概括成这样的形式,这里再举几个平面几何的例子.例1 我们可以把给定“线段AB和自然数n”看做输入,而把求“AB何的同学都知道可采用以下步骤序列完成“从输入得到输出的任务”.第一步过A点作一条射线AN;第二步在AN中任取一点A1;第三步在射线A1N中取一点A2,使|AA1|=|A1A2|,…第n+1步在射线An-1N中取一点A n,使|AA1|=|A n-1A n|,第n+2步连结BAn,第n+3步过A1做BAn的平行线,交AB于M.则M是要求的点,称之为n分点.读者可以想出很多这样的数学问题.我们把这一类问题称作“计算问题”.计算问题是具有一般性的问题,输入和输出是确定的,我们把“从输入求出输出的操作步骤序列”称作解决这一计算问题的一种算法.我们希望读者了解到当我们谋求计算机帮助时,首先要设计出算法.我们请读者为前面给出的第二个问题设计出算法,并且运用这些算法,去寻求图Ⅰ,Ⅱ,Ⅲ,Ⅳ的欧拉圈或欧拉道路,或者指出某图没有欧拉圈或欧拉道路.2.最小生成树有一个石油公司计划为它拥有的许多存储站设计一个管道连接系统,它共有九个存储站,如果两个存储站之间可以修管道,我们就用一条边连接起来,用一个数表示修这两站之间的管道所需的费用,这样这个公司所有的存储站和可能修管道的情况完全可以通过下面这个图表示.公司设计计划要求:管道网可以把任何两个存储站都连接起来,且装修费用最小.从图论的角度来说,图4—4是一个连通图,每一个边都被赋予了一个数,通常我们称之为赋权图.我们的目的是确定出另一个连通图,其顶点集与原图的顶点集一样,仅保留原图中的一部分边,通常我们把这样确定的新图称作原图的生成子图,并且使子图的所有边的权之和最小.我们来简单分析一下子图的属性.首先,我们要找的子图必须是连通的,直观地说子图具有的边应尽量地少,即这个子图不能含有任何回路,因为去掉回路中的任何边都不会影响它的连通性质,我们把不包含回路的生成子图称为原图的生成树.下面的图都是不含回路的连通图,又称为树.很容易看出树中的顶点有两类,一类是度数为1的顶点,称为悬挂点,另一类是度数大于1的顶点,称为割点.一旦去掉割点及与之相联的边,图就不连通了.我们很容易得出这样一些结论:一个具有n个顶点的连通图,(1)连通子图是生成树的充要条件为它具有n-1条边.(2)子图是生成树的充要条件为它有n-1条边且无回路.简述一下(1)和(2)的证明,实际上只需做这样一循环的推理:从一个树即无回路的连通图推出它具有n-1条边,可以用数学归纳法来证明.n=2时结论是显然的.假设对有n个顶点的树结论正确.我们可任取一条边,由于过这条边的两个端点只能有一条边(否则会出现回路),我们可去掉这条边,而把那两个端点看做一个点,这样就得到一个具有k个顶点的树,而它具有k-1条边,所以具有k+1个顶点的树有k条边.若一个仅有n-1条边的连通图有回路,我们可从回路中去掉一条边,并不妨碍其连通性,这样就得到了一个边数少于n-1的具有n个顶点的树,这与上一个结果是矛盾的.若图不连通,至少它可以分解为两个连通分支,由于它们都无回路,故每一个分支都是树,而它们的边数一定少于n-2条,这与具有n-1条边矛盾.我们开始的问题变成了求权重最小的生成树了,我们简称为最小生成树.下面我们来介绍一个求最小生成树的算法:第一步:我们把所有的边按其权重从小到大排列起来.第二步:先选定第一条边.第三步:边序列中选择下一条边的原则是此边与前面的边全在一起不构成回路.第四步:直至选出n-1条边.这样就得到了一个生成树,关于它一定是最小生成树的证明这里省略.这个算法是1956年由Kruskal提出的又称做Kruskal算法.由于在不出现回路的前提下取权小的边,故又称做“贪婪算法”.下面我们用Kruskal算法讨论本节的例子.第一步:我们按权重从小到大把边排列为:h(90)→g(90)→f(90)→e(100)→a(100)→b(100)→d(100)→i(150)→c(200)→j(200)→l(200)→p(300)→n(300)→m(400)→o(400)→k(500).第二步:确定h为第一条边.第三步:h(90)→g(90)→t(90)→e(100)→a(100)→b(100)→d(100)→i(150).第四步:上面八条边组成了最小生成树.3.最短行程问题例1 下面给出的是一个城市(用大写字母表示)和道路(用小写字母表示)的分布图(如图4—6),道路的长度附在道路字母的括弧里.问题是如何确定任意两个城市之间的最短道路?例2 购车策略(美国例子)有一个小公司计划买一辆同一型号的小卡车,他们可以用上一段时间(一年、二年或三年)再把车卖掉,例如:他们今年买了一辆车,用了两年,再卖掉,他们需要用的花费是18000美元,我们可以把从现在起三年购车所需费用用图4—7表示出来.为了理解这个图的含义,再花费14000美元.问题是这个小公司采取怎样的策略,可以使得三年内他们始终有一辆卡车使用而且总的花费最少.(边上加一个箭头是表明一个方向,标志采取的策略是只能从箭头的起始顶点指向终止顶点.在图论中我们称之为定向图.)1959年E.W.Dijkatra提示了解决这一类问题的一种算法.这种算法可以解决从确定的起始点到任何其他点的最短行程.下面我们来介绍这种算法,设G=(V,E)是一个加权连通图.第一步:首先确定起始点,将其放入确定集D.给每一个顶点设定一个权数,若有边连接起点与该点,则把这边权数设定为这点的权数,若没有边连接起点与该点,则设定该点的权重为∞(无穷),而且确定集中起点的权为0,表示与起点的最短行程.每做一步都将把某个顶点加入确定集,并修正所有点的权重.第二步:把权重最小的顶点放入确定集D,其权数仍做为它在确定集中点的权——即是从起点到这一点的最短行程.对每一个没有被列入确定集的点A,我们考虑每一个确定集中的点B,如果有边连接A与B,这样可以得到B的权与这点连接边的权的和,所有这样的和一定有最小的值,令其为A的新的权数,当然,如果确定集中没有点能有与之连接成边,则A的权仍是无穷.用式子写出应是:A的新权数w(A)为:w(A)=min{w(B)+w(e(B-A)):e(B-A)∈E}其中e(B-A)表示有边e连接B与A点,w(e)表示e的权.w(B)表示起点到确定集点B的最短行程.第三步:反复进行第二步骤就可以不断地扩大确定集,直到所有顶点进入确定集.下面我们分别用Dijkatra算法分析例1和例2.例1解:第一步:令D={A},w(A)=0,又w(B)=2,w(C)=8,w(D)=1,其余点的权均为无穷.这样的点排成如下序列:D,B,C,E,F,G,I,J,K,F.第二步(1)把D放入确定集D={A,D}(w(D)=1,)w(B)=2,w(C)=8,w(G)=10,其余的点权均为无穷.(2)把B放入确定集D={A,D,B}(w(B)=2),w(E)=3,w(C)=8,w(G)=10,其余的点权均为无穷.(3)把E放入确定集D={A,D,B,E}(w(E)=3),w(I)=5,w(F)=6,w(C)=8,w(G)=10,w(J)=12,其余点的权为无穷.(4)把I放入确定集D={A,D,B,E,I}(w(I)=5),调整后各点的权如下:w(F)=6,w(C)=7,w(G)=10,w(J)=12,w(L)=14,其余点的权均为无穷.(5)把F放入确定集D={A,D,B,E,I,F}(w(F)=6),调整后各点的权重为w(C)=7,w(G)=10,w(J)=12,w(L)=14,其余点的权为无穷.(6)把C放入确定集D={A,D,B,E,I,F,C}(w(C)=7),调整后各点的权重为w(G)=10,w(J)=12,w(L)=14,w(K)=10;(7)把G放入确定集D={A,D,B,E,I,F,C,G}(w(G)=10),调整后各点的权重为w(K)=11,w(J)=12,w(L)=14;(8)把K放入确定集D={A,D,B,E,I,F,C,G,K}(w(k)=11),调整后各点权重为w(J)=12,w(L)=14;(9)把J放入确定集D={A,D,B,E,I,F,C,G,K,J}(w(J)=12),调整后w(L)=14.(10)D={A,D,B,E,I,F,C,G,K,J,L}.第三步:这样就完成了确定从起点到任何点最短行程的工作.例2解:第一步:把0放入确定集D={0},(w(0)=0).w(1)=10,000,w(2)=18,000,w(3)=34,000.第二步:(1)把1放入确定集D={0,1}(w(1)=10,000),修正后各点的权数为w(2)=18,000,w(3)=34,000;(2)把2放入确定集D={0,1,2}(w(2)=18,000),修正后:w(3)=32,000.(3)把3放入确定集.第三步:三年最少的花费是32,000,所采取的策略是先买一辆卡车,用两年后卖掉,再买一辆新车,用一年再卖掉,这样的决策是花费最少的.在我国这样事情也很多,重要的是要有准确的市场预测.图论的应用是非常广泛的,我们仅仅列举了几个例子.我们希望读者从中受到启发,学会用图这样的模型(模式)刻画出我们周围生活中的一些实际问题,这是一种重要的本领.4.2 几何概率在高中数学中的应用本节主要内容编译自Richard Dahlke,Robert Fakler编写的大学数学及其应用教学单元第660号(Modules in Under-graduate Mathematics and its Applications Module 660(UMAP Module 660))“Applications of High School Mathematics in Geometrical Probability”一文.这是由美国一个名为“数学及其应用联合会”的非赢利公司(Consortium for Mathematics and its Application(COMAP),Inc.)与美国工业与应用数学学会(Society for Industrial and Applied Mathematics(SIAM)),美国数学协会(Mathematical Association of America(MAA))美国全国数学教师联合会(National Council of Teachers of Mathematics(NCTM)),以及美国两年制学院数学协会(American Mathematical Association of Two Year Colleges(AMSTYC))合作开发由专家编写的供大、中学进行数学建模和数学应用教学和课外活动用的教学单元.教学单元(Module)的含义是指这是一种能在一定时间内进行教学的单一主题或更广泛的主题的一节,并能在教学中具有较高师生比的教学材料,这是一种值得我们借鉴的形式.4.2.1 引论1.什么是几何概率?几何概率讨论的是无限样本空间上的概率,在此空间上实验的每一结果都是等可能发生的.几何概率中一个随机事件的概率通过将一次随机实验中所有可能结果的样本空间等同于一个几何区域R,而将实验中可能发生的事件等同于R中的子区域r后进行计算的.下面我们利用几何知识来求得所要的概率.2.为什么几何概率使人感兴趣并值得研究?几何概率充满了适合于高中不同数学水平的有趣问题:从初等代数到三角(涉及事件的运算,尽管我们这里将不考虑这类问题),几何概率问题的求解只需要求四边形的面积、图解不等式或用勾股定理等方面的知识,而几何概率的一个特别好的优点在于它的定义非常直观,可用很短的时间描述出来.因此使得学生几乎马上就可以处理重要问题了.几何概率可以有助于培养学生的解题技巧,而这是数学研究中的一个重要论题.应用问题都需要将实际情况转化为数学模型,做这种转化依赖于解决问题的基本功,而任何对这种思维的训练无疑都是有益的.最后,几何概率是研究连续型(而不是离散型的)样本空间及其事件的,正是这种概率可作为学生将在大学中学习的重要的以微积分为工具的概率知识和统计研究的基础,因此现在对这个方面的训练将有助于将来对所学知识的更好理解.4.2.2几何概率模型1.定义一些基本术语我们需要对将要用到的一些基本概念术语加以定义:一个实验的所有可能结果的全体构成的集合叫做样本空间,样本空间的子集叫做事件.对给定的一个事件而言,我们称这个事件发生,当且仅当试验的结果属于这事件的集合.2.为某类具体实验建立模型从一个具体的具有随机结果的实验开始,我们希望求得在一次试验中发生某事件的概率,建模的第一步是将实验的每一结果与几何区域中某点建立对应关系.这个几何区域可以是一段曲线(一维区域),或是一个平面区域(二维区域),一旦我们做了这种对应,则具体实验中的一个随机发生的结果就对应于在称为样本空间的几何区域中随机地取了一点,而这样由几何区域中随机选点的数学试验即是具体实验的数学模型.我们将利用这一数学模型来求我们所关心的概率.我们将用R表示数学试验中的几何区域,其代表实验的样本空间,而实验中的一个事件则被表示为R中的子区域r,这种记号见图4—8.例1 一个实验是这样做的,将一条5米长的绳子随机地切断成两条.考虑这两段绳子都不短于1米的事件,把样本空间可以等同于长度为5的线段R,而实验的结果对应于在R中随机地选一点.区域R和对应两段都不短于1米的事件r如图4—9所示.(注意到事件r发生对应于绳子被切断的点到绳两端的距离一定都要大于1米).这就是说随机选的点必须属于r区域.例2 投镖游戏中的靶子由边长为1米的四方板构成,并将此板分功.这个实验对应的数学试验是从边长为1个单位的正方形中随机地选一点,而事件对应于选到的点恰为阴影部分的点,区域R的子域r对应实验的成功.如图4—10.3.几何概率模型的定义当具体的实验被转化为相应的数学试验后,实验中一个事件发生的概率就转化为数学试验中相应事件r发生的概率,即随机地从R中选一点恰好属于r的概率.回过头来看例1和例2,它们相应事件的概率是什么呢?在例1中看来将随机地从R中选的点恰好属于r的概率p如下计算是合理的:(由于r的长度为3,R的长度为5,我们可以期待,在重复多次试验时,在五次中平均有三次事件r发生,或100次试验中平均有60次事件r发生.本例还表明概率可用分数、小数或百分数表示).同理,在例2中,从一个大正方形中随机地选一点,而这一点恰好属于小正方形的概率为因此,我们归结为对一般的数学试验,从R中随机地选一点,而这一点恰好属于某子集r的概率为这里测度对一维的R来说是长度,对二维的R来说是面积(若R是三维区域,测度将是什么?)4.概率上下界的确定由于事件r是样本空间R的子集,于是我们有0≤r的测度≤R的测度.在不等式两侧同时除以R的测度(一般假定其为正数)则有即0≤p≤1,这个不等式表明几何概率被0和1在下方和上方界住.注意到当p =0时,r的测度一定为0(一个点的长度是0,一条曲线的面积是0).且当p=1时,r的测度必须等于R的测度.我们经常用p(r)来表示事件r发生的概率,记号p(r)读作“r的概率”,并且表明我们定义的概率是r的函数(请考虑概率函数p(r)定义域和值域是什么?).例3 样本空间R和事件r如图4—11表示,试求从R中随机地选一点,而这点恰好属于r的概率.例4 样本空间R和事件r如图4—12所示.试求从R中随机选一点恰好落入r中的概率.5.练习Ⅰ在每个习题中区域R和r都已表示出来(r为阴影部分).试计算随机地从R 中选一点恰好落入r中的概率.4.2.3应用1.从应用问题开始例5 (电话线问题)一条长50米的电话线架于两电线杆之间,其中一个杆上装有变压器.在暴风雨天气中,电话线遭到雷击的点是随机的.试求雷击点距离变压器小于20米情况发生的概率.解:将电话线表为长度为50的线段,此线段即代表试验的样本空间,事件为区域r(属于它的点距离装有变压器的端点不超过20).如图4—14所示.因此,例6 (意大利馅饼问题)山姆的意大利馅饼屋中设有一个投镖靶.该靶为正方形板,边长为18厘米,挂于前门附近的墙上,顾客花两角伍分的硬币便可投一镖并可有机会赢得三种意大利馅饼中的一个,投镖靶中画有三个同心圆,圆心在靶的中心,当投镖击中半径为1厘米的最内层圆域时,可得到一个大馅饼;当击中半径为1厘米到2厘米之间的环城时,可得到一个中馅饼;如果击中半径为2厘米到3厘米之间的环域时,可得到一个小馅饼,如果击中靶上的其他部分,则得不到馅饼,我们假设每一个顾客都能投镖中靶,并假设每个圆的周边线没有宽度,即每个投镖不会击中线上,试求一顾客将赢得:(a)一张大馅饼,(b)一张中馅饼,(c)一张小馅饼,(d)没得到馅饼的概率.解:我们实验的样本空间可由一个边长为18的正方形表示.图4—15表明R 和子区域门r 1,r 2,r 3和r 4,它们分别表示得大馅饼、中馅饼、小馅饼或没得到馅饼的事件.例7 (磁带问题)乔和摩进行了一次关于他们前一天夜里进行的活动的谈话,然而谈话却被监听录音机记录了下来,联邦调查局拿到磁带并发现其中有10秒钟长的一段内容包含有他们俩犯罪的信息.然而后来发现,这段谈话的一部分被联邦调查局的一名工作人员擦掉了,该工作人员声称她完全是无意中按错了键,并从即刻起往后的所有内容都被擦掉了.试问如果这10秒钟长的谈话记录开始于磁带记录后的半分钟处,那么含有犯罪内容的谈话被部分或全部偶然擦掉的概率将是多大?。
图论中的排列与组合问题

图论中的排列与组合问题图论作为数学的一个分支,在各个领域都有着广泛的应用。
其中,排列与组合问题是图论中的重要内容之一。
通过对图的排列与组合进行研究,可以揭示图的性质和特征,解决现实中的实际问题。
本文将以图论中的排列与组合问题为主题,探讨其应用和解决方法。
一、图论中的排列问题在图论中,排列是指将图中的节点按照一定的顺序进行排列。
对于给定的图,其所有的节点排列方式就构成了图的排列集合。
排列的具体算法有很多,常见的有深度优先搜索算法和回溯算法。
排列问题的一个经典例子是旅行商问题(Traveling Salesman Problem,TSP)。
TSP是指一个旅行商从某个节点出发,经过图中的每个节点且只经过一次,最终回到出发节点的最短路径问题。
通过对图的排列进行穷举和计算,可以找到解决TSP的最优路径,并且可以扩展到更复杂的情况。
二、图论中的组合问题与排列不同,组合是指从图中选取一部分节点进行组合,忽略节点的排列顺序。
组合问题在图论中也有着重要的应用。
典型的组合问题包括子图问题、最小支配集问题等。
子图问题是指从给定图中选取一部分节点和边,构成一个新的子图。
选取子图的方式有很多种,可以是包含某些特定节点的子图或者是满足某种性质的子图。
通过研究不同的子图组合方式,可以揭示图的局部特征和结构。
最小支配集问题是指在一个图中选择最小数目的节点,使得每个节点要么在选中的节点集合中,要么与选中的节点直接相连。
这个问题与组合密切相关,通过对不同的节点组合方式进行计算,可以找到最小支配集。
最小支配集问题在无线传感器网络、社交网络等领域有着广泛的应用。
三、排列与组合的应用案例排列与组合在图论中的应用非常广泛。
下面列举几个常见的案例:1. 电路布线问题:在电路设计中,需要将不同的元件进行布线,以满足电路的要求。
通过对元件的排列与组合,可以找到最优的布线方式。
2. 交通网络优化:在城市交通网络规划中,需要考虑路线的选择和交通流量的分配。
图论中的几个实际例子

1
电信总局要如何配接电缆才能使各电信局能互通 讯息, 但同时令配线经费最低? 讯息 但同时令配线经费最低?
最 短 路 的 应 用 第 八 讲 最
大公司部门之间的沟通管道: 大公司部门之间的沟通管道:
2
最 短 路 的 应 用
第 八 讲 最
汽车导航问题 汽车导航问题
3
最 短 路 的 应 用
第 八辅助设备, 汽车导航是近年兴起的一种汽车驾驶辅助设备, 驾车者只要将目的地输入汽车导航系统, 驾车者只要将目的地输入汽车导航系统,系统就 根据电子地图自动计算出最合适的路线, 会根据电子地图自动计算出最合适的路线,并在 车辆行驶过程中(例如转弯前 例如转弯前)提醒驾驶员按照计算 车辆行驶过程中 例如转弯前 提醒驾驶员按照计算 的路线行驶。在整个行驶过程中, 的路线行驶。在整个行驶过程中,驾车者根本不 用考虑该走哪条路线就能快捷地到达目的地。 用考虑该走哪条路线就能快捷地到达目的地。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
电信局配接电缆问题: 电信局配接电缆问题:
1
电信总局要如何配接电缆才能使各电信局能互通 讯息, 但同时令配线经费最低? 讯息 但同时令配线经费最低?
最 短 路 的 应 用 第 司部门之间的沟通管道:
2
最 短 路 的 应 用
第 八 讲 最
汽车导航问题 汽车导航问题
3
最 短 路 的 应 用
第 八 讲 最
汽车导航是近年兴起的一种汽车驾驶辅助设备, 汽车导航是近年兴起的一种汽车驾驶辅助设备, 驾车者只要将目的地输入汽车导航系统, 驾车者只要将目的地输入汽车导航系统,系统就 根据电子地图自动计算出最合适的路线, 会根据电子地图自动计算出最合适的路线,并在 车辆行驶过程中(例如转弯前 例如转弯前)提醒驾驶员按照计算 车辆行驶过程中 例如转弯前 提醒驾驶员按照计算 的路线行驶。在整个行驶过程中, 的路线行驶。在整个行驶过程中,驾车者根本不 用考虑该走哪条路线就能快捷地到达目的地。 用考虑该走哪条路线就能快捷地到达目的地。
