图论第01讲
1网络图论

§1-2 树和树余·树支和连支
树(tree):
树是一个连通图的子图,该子图中包含了连通图G
的全部节点,但不包含任何回路。
树余(cotree) :
连通图中与树互补的子图叫做树余。
树支(tree branch): 树中的支路叫做树支。
连支(link) : 树余中的支路叫做连支。
基本回路(fundamental loop): 只包含一条连支的回路叫做基本回路。 基本回路是唯一的。
对于具有s个分离部分的非连通图,符合下列条件的 支路集叫做割集 。
(1) 该支路集中的所有支路被移去(但所有节点予以 保留)后,原非连通图留下的图形将具有s+1个分离部 分;
(2) 该支路集中,当保留任一支路,而将其余的所有 支路移去后,原非连通图留下的图形仍然只具有s个 分离部分。
基本割集(fundamental cut set) : 只包含一条树支的割集叫做基本割集 。 由每一树支决定的基本割集是唯一的。
B
2
0
1 1 0 1 0
3 1 1 1 0 0 1
B [E Il ]
§1-8 矩阵Q与矩阵B之间的关系
12 3
b1 b2
C1 1 0 QBT C2 0 1
C3 0 0
b3 0 0 1
b4 b5 10 1 1 01
b6 1
1 1
1
1
0 1
0
0 1 1 0 1
1 b1 1 b2
路径(path): 由m条不同的支路和m+1个不同的节点依次联接成的一 条通路称为路径。
回路 (loop):
如果路径的始端节点和终端节点重合,这样的路径称 为回路。
连通图(connected graph)和非连通图(disconnected graph) :
图论(王树禾编著)PPT模板

2
0
2
0
感谢聆听
长算法
03
3.3极大平 面图
06
习题
04
第四章匹配理论及其应用
第四章匹配理论及 其应用
4.1匹配与许配 4.2匹配定理 4.3匹配的应用 4.4图的因子分解 习题
05
第五章着色理论
第五章着色理 论
5.1图的边 着色
5.6Rams
01
5.2图的顶
e y 数 06
着色
02
05
5.5独立
集
04
5.4颜色多 项式
10.1图的线性空间 10.2图矩阵 习题
11
第十一章图论中的NPC问题
第十一章图论中的 NPC问题
11.1问题、实例和算法的时间复杂 度 11.2Turing机和NPC 11.3满足问题和Cook定理 11.4图论中的一些NPC问题 习题
12习题解答与ຫໍສະໝຸດ 示习题解答与提示13
参考文献
参考文献
04
2.4求最优 树的算法
02
2.2生成树 的个数
05
2.5有序二 元树
03
2.3求生成 树的算法
06
2.6n顶有序 编码二元树
的数目
第二章树
*2.7最佳追捕问题 习题
03
第三章平面图
第三章平面图
01
3.1平面图 及其平面嵌
入
04
3.4平面图 的充要条件
02
3.2平面图 Euler公式
05
*3.5平面嵌 入的灌木生
08
第八章最大流的算法
第八章最大流的算 法
8.12F算法 *8.2Dinic分层算法 8.3有上下界网络最大流的算法 8.4有供需要求的网络流算法 习题
图论第01讲

•
两个问题:
(1)经过每个顶点一次且仅一次; (2)代价最小的Hamilton回路。
(目前无有效的方法求解)
•
货郎问题(Traveling Salesman Problem)
一个货郎到各村去卖货,要求每个村子 至少去一次,最后返回出发点,为其设计一 种销售路线,使总耗时最短。
求解方法:把路线全排列,求其中最小的。
1930年,波兰数学家库拉托父斯基 (Kuratowski)证明了平面图可以画在平面上;
•
里程碑:1936年,匈牙利数学家寇尼希 (D.Konig)发表名著《有限图和无限图理论》 ,使得图论成为一门独立的数学学科;
蓬勃发展:1946年,随着世界上第一台计算机 的问世,使图论的发展突飞猛进。 其后,图论在现代数学、计算机科学、工程技 术、优化管理等领域有大用而得以大力发展。
图论第01讲
•
课程简介
▪ 《图论》是计算机科学与技术专业、信息 安全专业的选修课程。 通过本课程的学习,使学生对图论的 历史背景、研究内容、相关技术及其发展 有一个较为全面地了解,从而将所学知识 和技术运用于实际应用领域奠定基础。
•
▪ 本课程所介绍的内容包括:
图论的发展历程和经典问题; 图的基本概念; 有关树和图的算法; 网络流问题; 匹配问题、色数问题;
•如何才能在所有桥都恰巧只走一遍的前提下,回到原出发点?
•
不少数学家都尝试去解析这个事例。而 这些解析,最后发展成为了数学中的图论。
莱昂哈德·欧拉(Leonhard Euler)在1736 年圆满地解决了这一问题,证明这种方法并 不存在。他在圣彼得堡科学院发表了图论史 上第一篇重要文献。欧拉把实际的问题抽象 简化为平面上的点与线组合,每一座桥视为 一条线,桥所连接的地区视为点。这样若从 某点出发后最后再回到这点,则这一点的线 数必须是偶数。
组合数学与图论

● 02
第2章 图论基础
什么是图论
图论是研究图结构的 数学分支,用于描述 对象之间的关系。图 由节点和边组成,节 点表示对象,边表示 对象之间的关系。
基本概念
无向图
边没有方向的图
权重图
边带有权重的图
度
节点相连的边数 称为节点的度
91%
有向图
边有方向的图
图的表示方法
01 邻接矩阵
02 邻接表
判断图中的节点是否都是连通的
02 组合数学方法
连通性定理和算法可以用于判断和求解
03
总结
组合数学和图论相互结合,能够解决图的同构、 着色、匹配和连通性等各种问题,通过组合数学 方法的运用,可以更好地探索图论中的难题。
● 04
第四章 组合数学与图论在计 算机科学中的应用
图数据库与图搜索
图数据库是一种专门用于存储和查询图结构数据 的数据库系统。在计算机科学中,图搜索算法如 Dijkstra算法、A*算法等被广泛应用于图数据库 的查询和分析,帮助用户快速准确地获取所需信 息。
03
● 05
第五章 组合数学与图论在统 计学中的应用
基于图的统计分 析
利用组合数学和图论 的方法进行统计学分 析,如图的频繁模式 挖掘、图数据的聚类 分析等。这些方法能 够帮助研究人员从大 量数据中提取出有用 的信息并进行深入分 析。
网络数据采样与推断
节点采样
通过在网络中随 机选择节点来获
取样本数据
使得相邻节点颜 色不同
图的匹配问题
图的匹配问题是指在 图中找到一些相互不 相邻的边,使得边的 数量最大化。组合数 学的匹配定理和匹配 算法可以用于解决图 的匹配问题。
图的连通性问题
图论及其应用

顶点染色
定理:对于任何一个图χ(G)≤ω(G)。 ω(G)为图G的团数,用来描述χ(G)的下 界,其中ω(G)=max{k|Kk属于G}。
顶点染色
给定图G=(V,E)的一个k-点染色。用Vi表示G中染以 第i色的顶点集合(i=1,2,…,k),则每个Vi都是G 的独立集。因而G的每一个K-点染色对应V(G)的一个划 分[V1,V2,…,Vk],其中每一个Vi是一个独立集。反之 ,给出V(G)的这样一个划分(V1,V2,…,Vk),其中每 一个Vi均是独立集(1≤i≤k),则相应得到G的一个k点染色,称V(G)的这样一个划分为G的一个色划分,每 一个Vi称为色类。因此,G的色数χ(G)就是使这种划 分成为可能最小自然数k。
推论:若G是p(G) 3且g(G) 3的平图,则 q(G) g(G) ( p(G) 2)。 g(G) 2
平面图的性质
推论:任何一个简单平面图G,有 q(G)≤3p(G)-6
推论:设G是简单平面图,则δ(G)≥6.
定理:仅存在5种正多面体,即正四面体、正 方体、正八面体、正十二面体和正二十面体。
定理:每一个平面的色数不超过5
边染色
定义:无环图G的一个正常染色k-边染色(简 称k-边染色)是指一个映射φ:E(G)→{1,2, …,k},使对G中任意两条相邻的边e1和e2,有 φ(e1)≠φ(e2)。若G有一个正常k-边染色,则 称G是k-边染色的。G的边色数是指G为k-边染 色的最小整数k的值,记为
χ'(G)。若χ'(G)=k,则称G是k-边可色的。
边染色
设G有一个正常k-边染色,置Ei为G中所有染 以第i种颜色的边的全体,则E1,E2,…,Ek 是G的k个边不相交的对集,并且
图论及其应用
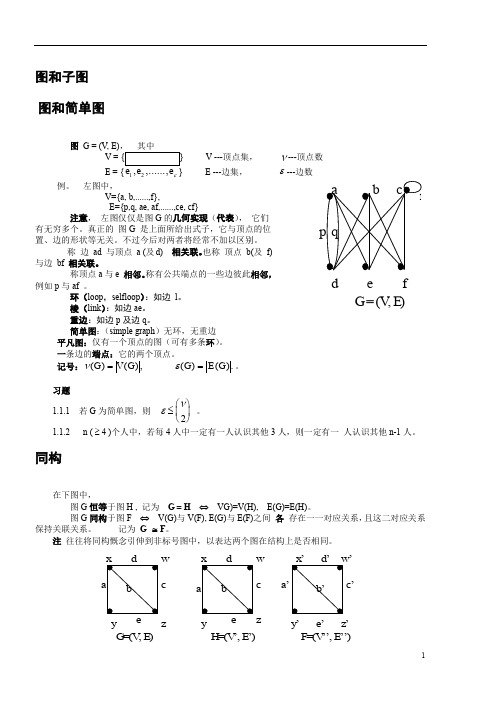
图和子图 图和简单图图 G = (V, E)V ---顶点集,ν---顶点数12ε E ---边集, ε---边数例。
左图中, V={a, b,......,f}, E={p,q, ae, af,......,ce, cf} 注意, 左图仅仅是图G 的几何实现(代表), 它们有无穷多个。
真正的 图G 是上面所给出式子,它与顶点的位置、边的形状等无关。
不过今后对两者将经常不加以区别。
称 边 ad 与顶点 a (及d) 相关联。
也称 顶点 b(及 f) 与边 bf 相关联。
称顶点a 与e 相邻。
称有公共端点的一些边彼此相邻,例如p 与af 。
环(loop ,selfloop ):如边 l 。
棱(link ):如边ae 。
重边:如边p 及边q 。
简单图:(simple graph )无环,无重边 平凡图:仅有一个顶点的图(可有多条环)。
一条边的端点:它的两个顶点。
记号:νε()(),()().G V G G E G ==。
习题1.1.1 若G 为简单图,则εν≤⎛⎝ ⎫⎭⎪2 。
1.1.2 n ( ≥ 4 )个人中,若每4人中一定有一人认识其他3人,则一定有一 人认识其他n-1人。
同构在下图中, 图G 恒等于图H , 记为 G = H ⇔ VG)=V(H), E(G)=E(H)。
图G 同构于图F ⇔ V(G)与V(F), E(G)与E(F)之间 各 存在一一对应关系,且这二对应关系保持关联关系。
记为 G ≅F。
注 往往将同构慨念引伸到非标号图中,以表达两个图在结构上是否相同。
de f G = (V , E )yz w cG =(V , E )w cyz H =(V ’, E ’)’a ’c ’y ’e ’z ’F =(V ’’, E ’’)注 判定两个图是否同构是NP-hard 问题。
完全图(complete graph) Kn空图(empty g.) ⇔ E = ∅ 。
V’ ( ⊆ V) 为独立集 ⇔ V’中任二顶点都互不相邻。
图论及应用课件-欧拉图与中国邮路问题

解:
d
f
h
a
b
c
e
g
i
j
图G
例4 某博物馆的一层布置如下图,其中边代表走廊, 结点e是入口,结点g是礼品店,通过g我们可以离开博物 馆。请找出从博物馆e进入,经过每个走廊恰好一次,最 后从g处离开的路线。
d
j
b a
h
i
e
g
c
f
10
1
0.5 n 0
0.5
1 2 1.5 t1
0.5
00
1 0.8
0.6 0.4 x 0.2
0.5
00
1 0.8
0.6 0.4 x 0.2
(二)、Fleury算法
该算法解决了在欧拉图中求出一条具体欧拉环游的方 法。方法是尽可能避割边行走。
1、 算法 (1)、 任意选择一个顶点v0,置w0=v0;
8
1
0.5 n 0
0.5
1 2 1.5 t1
0.5
00
1 0.8
0.6 0.4 x 0.2
(2)、 假设迹wi=v0e1v1…eivi已经选定,那么按下述方 法从E-{e1,e2,…,ei}中选取边ei+1:
问题 某地区的双车道公路如图1的图G(单 位是千米),路上积满了雪 。一辆扫雪车从
v1点出发,扫除公路上的所有积雪,最后回 到v1 。
要求1) 请你为扫雪车选择一条路径,使它 经过的总路程最短。
要求2) 现在先进的喷气扫雪车只需沿公 路一侧行驶,就能清除两个车道的积雪。如
v1
4 v2 2
v3
1
v7
2 9
v8
5 3
1
v4
1
图论_李煜东

• 拓扑排序
– 判定有向无环图(DAG)
3
Graph Theory
图论 目录页
最短路
任意两点间的最短路问题
• 使用动态规划求解?需要定义状态、阶段、决策。 • 以长度为阶段?
– 经过k条边从x到y的最短路F[k,x,y] = Min{F[i,x,z]+F[k-i,z,y]},O(N^4)
• 倍增优化?
15
Graph Theory
图论 目录页
最短路
欧拉回路(POJ2230)
• 欧拉回路:经过每条边恰好一次的回路(一笔画问题) • 欧拉回路存在 连通图中每个点的度数都是偶数。
• 初始时,1号点入栈。 • 依次把与栈顶节点有未标记的边相连的节点入栈并递归,递归前标记该边。 • 如果当前栈顶结点出发已经没有未标记边,把该节点出栈,并记录到答案序 列中。 • 重复上述步骤直到栈为空。 • 倒序输出答案序列,就是一条欧拉回路。
最短路
Floyd求最小环(POJ1734)
• 最小环:从一个点出发经过至少一条边回到该点,不能重复经过 某条边,距离最短的回路。 • 有向图最小环: • 令dist[i,i]=+∞,然后floyd求最短路。 • 无向图最小环: • 在最外层循环开始进行k时,用“i到k、再到j、再经过编号<k的 节点从j到i”的最短路w(i,k)+w(k,j)+dist[i,j]来更新最小环。
24
Graph Theory
图论 目录页
生成树
生成树
POJ1639
• 题意:求n<=30个点的图的MST,满足根节点的度数<=S。 • 1. 去掉根节点,对得到的每个连通分量求MST,并对每个连通分 量选择一个到根节点距离最近的点连到根节点上,此时得到的生 成树T已经满足度数<=S。 • 2. 枚举每个点,若该点与根节点有边相连,设长度为D1,设该 点在T中到根节点的路径上的最长边长度为D2。找出D2-D1最大 的点,若D2-D1>0,删除边D2,加入边D1,形成一棵更小的生 成树;若D2-D1<=0,说明当前方案已经最优。 • 3. 重复第二步K次,K为第一步后根节点还能连边的条数。
《离散数学》图论 (上)

无向图与有向图
v2
e1
e2
e3
v3
e4
v1
e5 (e1)={( v42, v24 )}
v4
(e2)={( v32, v23 )} (e3)={( v3, v4 )}
(e4)=({ v43, v34 )}
(e5)=({ v4,}v4 )
13
无向图与有向图
A B C
D E F
14
无向图与有向图
第八章 图论
第八章 图论
§8.1 基本概念
§8.1.1 无向图、有向图和握手定理 §8.1.2 图的同构与子图 §8.1.3 道路、回路与连通性 §8.1.4 图的矩阵表示
§8.2 欧拉图 §8.3 哈密尔顿图 §8.4 平面图 §8.5 顶点支配、独立与覆盖
2
无向图与有向图
3
无向图与有向图
一个无向图(undirected graph, 或graph) G 指一个三元组 (V, E, ),其中
vV
vV
24
特殊的图
假设 G=(V, E, ) 为无向图,若 G 中所有 顶点都是孤立顶点,则称 G 为零图(null graph)或离散图(discrete graph);若 |V|=n,|E|=0,则称 G 为 n 阶零图 所有顶点的度数均相等的无向图称为正 则图(regular graph),所有顶点的度数 均为 k 的正则图称为k度正则图,也记作 k-正则图 注:零图是零度正则图
19
握手定理
定理(图论基本定理/握手定理)
假设 G=(V, E, ) 为无向图,则deg(v) 2 E , vV
即所有顶点度数之和等于边数的两倍。
推论
在任何无向图中,奇数度的顶点数必是偶 数。
程序员的数学4:图论入门

内容摘要
这一章通过分析图的连通性,让读者理解图中的信息流动和路径问题。 第四章介绍了图的遍历算法,包括深度优先遍历和广度优先遍历。这两种算法是常用的图遍历算 法,通过这一章的学习,读者可以掌握如何遍历一个图并获取所需信息。 第五章介绍了最小生成树算法,包括Prim算法和Kruskal算法。这两种算法是最常用的最小生成 树算法,通过这一章的学习,读者可以掌握如何找到一个图中连接所有节点的最小代价的树。 第六章介绍了拓扑排序算法,包括Kahn算法和DFS算法。拓扑排序是解决有向无环图(DAG)上 的一种排序算法,通过这一章的学习,读者可以掌握如何对一个有向无环图进行拓扑排序。 《程序员的数学4:图论入门》这本书是一本非常适合程序员阅读的数学书籍,它介绍了图论的 基本概念和应用,并提供了很多实例和练习题帮助读者理解和应用所学知识。这本书不仅可以提 高程序员的数学素养,还可以帮助程序员更好地理解和应用图论来解决实际问题。
精彩摘录
精彩摘录
《程序员的数学4:图论入门》是一本面向程序员群体的数学入门指南,其作 者罗博·福布斯将带大家探索图论的基础概念和算法,从而更好地理解和应用编 程技术。本书将选取一些精彩的摘录,供大家欣赏。
精彩摘录
“图论是一个研究图形和结构的学科,其中节点和边分别表示对象和它们之 间的关系。”
精彩摘录
这是本书最基本的概念之一,通过节点和边这两个概念,我们可以描述各种 复杂的结构。在编程中,我们通常会使用节点和边来表示数据结构,例如树、图 等。
精彩摘录
“一个图G=(V,E)由一组节点V和一组边E组成。”
精彩摘录
这个定义简洁明了,很好地概括了图论的基本构成要素。在许多应用场景中, 节点可以表示人、物体或其他实体,而边则表示这些实体之间的关系。
01-中国邮递员问题

欧拉图及判定定理
顶点可能重复
一进一出
经过一次 且不重复
偶点
如果一个连通图有欧拉环游,即从某个顶点出发,经过该图所有边一次,且不 重复,最后回到出发点,则对中间经过的任一顶点都是一进一出,而出发点开始出 去最后又进来,也是一进一出。注意有的顶点可能有若干次一进一出。不论如何, 都意味着该图的每个顶点都应该是偶点(即进出总共偶数条边)。
中国邮递员问题
厦门大学数学科学学院 金贤安
引言
中 国 邮 递 员 问 题 是 由 山 东 师 范 大 学 管 梅 谷 同 志 1960年首先提出的。
这是数学中为数不多的几个以“中国”命名的问题 或定理之一。
该问题涉及著名的的哥尼斯堡(Königsberg) 七桥问题。
七桥问题是图论和拓扑学的起源。
以交叉路口为顶点,街道为边,街道的长度为边的权得 到 一赋权图,我们称之为街道图。 不妨设邮局在一条街道上。 若街道图是欧拉图,有欧拉环游,无需重复走街道,沿 着 一个欧拉环游作为投递路线即可。
中国邮递员问题
若街道图不是欧拉图,则有些街道需要重复 走,那么中国邮递员问题就变为:重复走哪 些街道,使总路程最短?
给定一个连通图,我们称经过图的所有边一次且只有一次 的走法为一个欧拉通路。
如果进一步该走法还回到出发点,则称之为欧拉环游(回 路)。
具有欧拉环游的图称之为欧拉图。
C
哥尼斯堡问题即图3是否是欧拉图的问题。
A
B
D
图3 七桥问题对应图
欧拉图及判定定理
一笔画问题:什么样的图形可以一笔画成,笔不离纸,而 且每条线都只画一次不准重复?
(1) 在最优方案中,对街道图的任意一边,所添加的平行边的次数不会超过1。 事实上,若在某可行方案中,对街道图的某边,所添加的平行边的次数 大于等于2,那么在该方案中去掉该边2次,将得到一个新的更优的可行 方案,矛盾。
图的基本概念与握手定理

9
二、 图旳类型
注意:完全图是 n-1 正则图
完全图旳每个结点都与其他 n-1 个结点相邻接,即与 n-1条边有关联,所以是n-1正则图,反之正则图不一定 是完全图。
1.完全图:
2.正则图:
是3正则图
完全图,
不是完全图
10
二、 图旳类型
子图:
设G=<V,E>, G`=<V`,E`>为两个图,满足V` V 且E` E,则称G`为G旳子图, G为G`旳母图,记 作G`G。 (1)G`为G旳真子图:若G` G且V` V或E` E。 (2)G`为G旳生成子图:若G` G且V` = V。 (3)V1导出旳导出子图:顶点集≠V1 V,边集为 两端点均在V1中旳全体边构成旳子图。 (4) E1导出旳导出子图:≠E1E,以E1中边关联旳 顶点旳全体为顶点集旳G旳子图。
定理2 设D=<V,E>为任意有向图,V={v1,v2,…,vn}, |E|=m, 则
n
n
n
d(vi ) 2m, 且
d (vi ) d (vi ) m
i 1
i 1
i 1
16
握手定理推论及应用
推论 任何图 (无向或有向) 中,奇度顶点旳个数是 偶数.
例1 无向图G有16条边,3个4度顶点,4个3度顶 点,其他顶点度数均不大于3,问G旳阶数n为几?
分别为D旳最大出度、最小出度、最大入度、最小 入度。简记作△、、 △+、+ 、 △- 、- 。
15
四、握手定理
定理1 设G=<V,E>为任意无向图,V={v1,v2,…,vn},
|E|=m, 则
n
边 (涉及环) 都有两个端点,所以在计算G中各顶点 度数之和时,每条边均提供2度,m 条边共提供 2m 度.
运筹学基础-图论方法
间V的弧即为最小V截集,最小截集容量即为该网络最大流量;
最大流最小截 的标号法步骤
第二步:增广过程
1、对增广链中的前向弧,令 f=f +q (t),q(t) 为节点 t 的标记 值
2、对增广链中的后向弧,令 f=fq (t) 3、非增广链上的所有支路流量保持不变
第三步:抹除图上所有标号,回到第一步
1
2
3
5
6 Θ=2
1
2
4
3 截止
截止,最大流量=9+5=14(或者最大流量=7+5+2=14
(六)利用 EXCEL求网 络最大流量
建立各结点间的流量矩阵
各结点间的流量矩阵
v1
v2
v3
v1
30
80
v2
v3
10
v4
v5
20 60
v6
2
20 30
1 80
10
100 3
v4
v5
60 100
10
4 70
10
5(34)
2(0)
6(01)
t
最大流量为5+9=14
7(65)
2
4
(s+, 1) 9(9)
10(98)
第二条链:(s+,)→(s+,1) → (2-,1) → (1+,1)截止
又例:利用标 号法(确定最 小截集)求最
大流量
(3-,1)
(1+,1)
1
3(2)
4
5(5)
(s+,) s
3(3)
3(3(5) -,41()4)
1(0)
(s+,)
图论课件-图的因子分解

因子分解的应用场景
虽然图的因子分解在理论计算机科学中有广泛的应用,但在实际应 用中,如何将理论应用于实际问题仍需进一步探索。
未来可能的研究方向和挑战
寻找高效算法
01
未来研究的一个重要方向是寻找更高效的算法来解决图的因子
分解问题。
04
图的因子分解的应用
在计算机科学中的应用
计算机网络
图的因子分解可以用于优化路由算法,通过将网络分解为 若干个连通子图,可以更有效地进行路由选择和流量控制 。
并行计算
在并行计算中,图的因子分解可以用于任务分配,将一个 大任务分解为若干个小任务,并分配给不同的处理器执行 ,从而提高计算效率。
数据挖掘和机器学习
一个图,其中任意两个不 同的顶点之间都恰有一条 边相连。
空图
一个图,其中任意两个不 同的顶点之间都无边相连 。
图的因子分解的重要性
理论意义
图的因子分解是图论中的重要概 念,它有助于深入理解图的性质 和结构。
应用价值
图的因子分解在计算机科学、运 筹学、电子工程等领域有广泛的 应用,如网络设计、电路优化等 。
资源配置和调度。
金融风险管理
在金融风险管理中,图的因子分 解可以用于识别和评估风险因素 之间的关联关系,从而更好地进
行风险管理和控制。
在网络设计中的应用
01
社交网络分析
在构和群体关系,
从而更好地理解社交行为的模式和规律。
02 03
推荐系统
在推荐系统中,图的因子分解可以用于用户兴趣分析和物品关联推荐, 通过将用户和物品之间的关系进行分解和分析,可以更有效地进行个性 化推荐。
图论与代数结构第一二三章习题解答

习题一1. 一个工厂为一结点;若两个工厂之间有业务联系,则此两点之间用边相联;这样就得到一个无向图。
若每点的度数为3,则总度数为27,与图的总度数总是偶数的性质矛盾。
若仅有四个点的度数为偶数,则其余五个点度数均为奇数,从而总度数为奇数,仍与图的总度数总是偶数的性质矛盾。
(或者利用度数为奇数的点的个数必须为偶数个)2.若存在孤立点,则m 不超过K n —1的边数, 故m 〈= (n-1)(n-2)/2, 与题设矛盾。
3.4。
用向量(a 1,a 2,a 3)表示三个量杯中水的量, 其中a i 为第i 杯中水的量, i = 1,2,3。
以满足a 1+a 2+a 3 = 8 (a 1,a 2,a 3为非负整数)的所有向量作为各结点, 如果(a 1,a 2,a 3)中某杯的水倒满另一杯得到 ( a ’1, a'2, a ’3 ) , 则由结点到结点画一条有向边。
这样可得一个有向图。
本题即为在此图中找一条由( 8, 0, 0 )到( 4, 4, 0 )的一条有向路,以下即是这样的一条:5. 可以。
6 若9个人中没有4个人相互认识,构造图G ,每个点代表一个点,两个人相互认识则对应的两个点之间有边。
1) 若可以找到点v,d (v)>5,则与v 相连的6个点中,要么有3个相互认识,要么有3个相互不认识(作K 6并给边涂色:红=认识,蓝=不认识,只要证图中必有同色三角形。
v 1有5条边,由抽屉原则必有三边同色(设为红),这三边的另一顶点设为v 2, v 3, v 4。
若 △v 2v 3v 4有一边为红,则与v 1构成红色△,若△v 2v 3v 4的三边无红色,则构成蓝色△)。
若有3个人相互认识,则这3个人与v 相互认识,这与假设没有4个人相互认识矛盾,所以这6个人中一定有3个人相互不认识∑∑∑∑∑∑∑==+====-=++=-==---=--=ni i n i i n i n i n i ni i i n i i n i i i i a a n n a a a n n n a n a v v 12 12 12112212 12 i i 2/)1(C )1(2)1(])1[(a a 。
图论简介

关于有 n 结点 m 边的(n,m)图度的定理
• 定理1-1 令 v1,…,vn为图的所有结点,则 i=1n deg(vi)=2m. (1) 定理1-2 任何图中度为奇数的结点必பைடு நூலகம்偶数个.
图的同构
定义:对给定两个图 G=V,E,G=V,E,若存在 双射 f:VV 使对任意a,bV, (a,b)E (f(a),f(b))E,并且(a,b)与 (f(a),f(b))有相同重数,则称 G 与 G同构,记 为 GG. 注:① 两图同构是相互的: GG GG. ② 两图同构时不仅结点之间要有一一对应关系, 而且要求这种对应关系保持结点间的邻接关系. 对有向图同构还要求保持边的方向. ③ 寻求判断图同构的简单有效方法仍是图论待 解决的重要问题.
无向图 G 能否一笔画的问题等价于 G 是 否有一条Euler路径(回路)的问题
a
1 b 2 3 9 6 4 5 8 7
若图只有两个奇结点,则任何Euler路径必 从其中一点开始到另一点结束.利用这条规律, 先在此2奇点之间加条边使之变成Euler图并画 出一条Euler回路,然后再去掉所加的边即得一 条Euler路径.
同构图举例
4 2 1 a c 3 1 2 3
G
4 a 5 d 6
H H’
b
G’
d b
f c e
G G’ 1a,2b,3c, 4d
H H’ 1a,2b,3c, 4d,5e,6f
非同构图举例
存在结点数及每个结点对应度都相等的两个图 仍然不同构的情况.; 如下:(注意:两个4度点 或邻接或不相邻接)
图的定义与记号
• 图G是一个二重组:G=V,E,其中V是非空有限集 合,它的元素称为结点或顶点, E 也是(可空)有 限集合,它的元素称为边. • 图G的边e是一个结点二重组:a,b,a,bV,e可 以是有序的,称为有向边,简称为弧,a称为弧e 的始点,b称为e的终点; e也可以是无序的,称 为无向边.e=a,b时,称e与a,b关联,或a,b与e 关联,或a与b相邻接;关联于同一顶点的一条边 称为自回路或环. • 每条边都是无向边的图称为无向图;每条边都 是有向边的图称为有向图;我们仅讨论无向图 和有向图.
运筹学图论

其中:
bi j
wi j 0
(vi , v j ) E (vi , v j ) E
24 2019/11/19
图的基本概念与模型
例6.3 下图所表示的图可以构造邻接矩阵M如下:
v1
v4
e9
v6
e1 v2
e2
e3
e5 e6
v3
e12
e10
v5
e11 v7
e4
e7
v8 v1
e8
v2
v3
2019/11/19
无向图
有向图 8
图与网络的基本知识
环, 多重边, 简单图
多重边
如果边e的两个端点相重,称该边为 环。如右图中边e1为环。如果两个点 之间多于一条,称为多重边,如右图 中的e4和e5,对无环、无多重边的图 称作简单图。含多重边的图称为多重 图。
e2 v2
e6
v4
e1 e4 v1 e3 e5 e7
定义6 在有向图中,以顶点v为始点的边数称为顶点v的 出次,记为d+(v);以v为终点的边数称为v的入次,记为 d-(v)。顶点v的出次与入次的和称为点v的次。
定义7 图G=(V, E), 若E'是E的子集,若V'是V的子集,且 E'中的边仅与V'中的顶点相关联,则称G' = (V', E')为图 G的一个子图,特别地,若V' =V, 则称G'为G的一个生 成子图(支撑子图)。
1. 邻接矩阵 对于图G=(V,E),| V |=n, | E |=m,有nn阶方矩阵
A=(aij) nn,其中
aij
1, 0,
(vi , v j ) E 其他
《图论》第2章 基本概念(1)

[有向图] 设V是一个非空有限集,A是V上的二元关
系。二元组 G=(V,A) 称为(有向)图,V 中元素
称为顶点,A 中元素称为弧(有向边)。
关系A的关系图就是图G的图解。
[自环] A中的自反性图解为环形,称为自环。
[多重边] 在表达实际问题的图解中可能出现重复的
关系定义,称为多重边。
平凡图是任何图的子图。(零图无类似结论)
3
2.1 图的概念
[生成子图] G=(V, A)是 G=(V, A) 的一个子图且 V = V ,则称 G 是 G 的一个生成子图或支撑子图。
[极大子图] G=(V, A)是 G=(V, A) 的一个子图,若对
u,vV, <u,v>A 必有 <u,v>A,则称G 是G的一
S=(a1,a2,…,an,…),即存在一个正整数,使对任何
正整数 n,都有an+= an。S 的一个 k 阶子式 Si 定义 为k 元组 Si = (ai, ai+1,…, ai+k1)。具有最大的周期 使得 S1, S2, … , S 各不相同的 S 序列称为 k 阶 De Bruijn 序列。
记为 (a1, a2, a3, …, ak1) 的点v,引入两条外向弧分
别与点 (a2, a3, …, ak1, 0) 和点 (a2, a3, …, ak1, 1) 邻 接,并将上述的弧分别标记为 k 位的 (a1, a2, a3, …, ak1 , 0) 和 (a1, a2, a3, …, ak1 , 1) 。显然点 v 同时也 被点 (1, a1, a2, …, ak2) 和点 (0, a1, a2,…, ak2) 分别
(即以4除n余0或余1)
matlab图论方法

哈密顿圈(环球旅行游戏)
问题3(四色问题): 对任何一张地图进行着色,两个共同边界的
国家染不同的颜色,则只需要四种颜色就够了.
问题4(关键路径问题): 一项工程任务,大到建造一座大坝,一座体育
中心,小至组装一台机床,一架电视机, 都要包括 许多工序.这些工序相互约束,只有在某些工序完 成之后, 一个工序才能开始. 即它们之间存在完 成的先后次序关系,一般认为这些关系是预知的, 而且也能够预计完成每个工序所需要的时间.
V = {v1 , v2 , v3 , v4}, E = { v1v2 , v1v3 , v1v4 , v2v3 , v2v4 , v3v4}.
今后将不计较这种外形上的差别,而用一个容 易理解的、确定的图解去表示一个图.
有边联结的两个点称为相邻的点, 有一个公共 端点的边称为相邻边. 边和它的端点称为互相关联. 常用d(v)表示图G中与顶点v关联的边的数目, d(v) 称为顶点v的度数. 用N(v)表示图G中所有与顶点v相 邻的顶点的集合.
这时工程领导人员迫切希望了解最少需要多 少时间才能够完成整个工程项目, 影响工程进度 的要害工序是哪几个?
6.1 图论的基本概念
图论中的“图”并不是通常意义下的几何图 形或物体的形状图, 而是以一种抽象的形式来表 达一些确定的事物之间的联系的一个数学系统.
定义1 一个有序二元组(V, E ) 称为一个图, 记 为G = (V, E ), 其中
(0,1,0,1) (0,1,0,0) (0,0,1,0) (0,0,0,1) (0,0,0,0) (1,0,1,0) (1,0,1,1) (1,1,0,1) (1,1,1,0) (1,1,1,1)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
如何才能在所有桥都恰巧只走一遍的前提下,回到原出发点?
A
C D
桥所连接的地区 视为点
A
C
D
B B 每一座桥视为一 条线
求从图中任一点出发,通过每条边一次,最后回到起点。
如果通奇数座桥的地方不止两个,那麽 满足要求的路线便不存在了。
如果只有两个地Biblioteka 通奇数座桥,则可从 其中一地出发可找到经过所有桥的路线。
r(3,5)=14, r(3,8)=28, r(4,5)=25.
计算Ramsey数是一个NPC问题,匈牙利 数学家厄尔多斯(Erdos)曾用下面的话比喻 计算Ramsey数的艰巨性:
某年某月某日,一伙外星强盗入侵地球, 并威胁到,若不能在一年内计算出r(5,5),他 们便灭绝人类!面对危机,人类最好的选择 是调动地球上所有的计算机、数学家、计算 机专家,日以继夜的计算r(5,5),以求人类免 于灭顶之灾;如果外星人威胁说要求得r(6,6), 那我们别无选择,只能和外星人战斗到底了!
蓬勃发展:1946年,随着世界上第一台计算机 的问世,使图论的发展突飞猛进。 其后,图论在现代数学、计算机科学、工程技 术、优化管理等领域有大用而得以大力发展。
一、Konisberg七桥问题(Euler问题)
柯尼斯堡七桥问题是图论中 的著名问题。
这个问题是基于一个现实 生活中的事例:位于当时东 普鲁士柯尼斯堡(今日俄罗斯 加里宁格勒)有一条河,河中 心有两个小岛。小岛与河的 两岸有七条桥连接。如何才 能在所有桥都恰巧只走一遍 的前提下,回到原出发点?
1857年,Cayley在有机化学领域发现了 一种重要的图,称为“树”,解决了计算饱和 氢化物同分异构体的数目;
1930年,波兰数学家库拉托父斯基 (Kuratowski)证明了平面图可以画在平面上;
里程碑:1936年,匈牙利数学家寇尼希 (D.Konig)发表名著《有限图和无限图理论》, 使得图论成为一门独立的数学学科;
1878~1880年两年间,著名的律师兼数学家肯 普和泰勒两人分别提交了证明四色猜想的论文,宣布 证明了四色定理,大家都认为四色猜想从此也就解决 了。
1890年,在牛津大学就读的年仅29岁的赫伍德 以自己的精确计算指出了肯普在证明上的漏洞。不久, 泰勒的证明也被人们否定了。后来,人们开始认识到, 这个貌似容易的题目,其实是一个可与费马猜想相媲 美的难题。
如何才能在所有桥都恰巧只走一遍的前提下,回到原出发点?
不少数学家都尝试去解析这个事例。而 这些解析,最后发展成为了数学中的图论。
莱昂哈德·欧拉(Leonhard Euler)在1736 年圆满地解决了这一问题,证明这种方法并 不存在。他在圣彼得堡科学院发表了图论史 上第一篇重要文献。欧拉把实际的问题抽象 简化为平面上的点与线组合,每一座桥视为 一条线,桥所连接的地区视为点。这样若从 某点出发后最后再回到这点,则这一点的线 数必须是偶数。
1930年, Ramsey因腹部手术并发症不幸逝世, 年仅26岁。但他关于Ramsey数的遗产却永泽数学 界。
▪ 有n+1只鸽子进入n个笼子,那么必然有至少 两只鸽子在同一个笼子中。
Ramsey问题的证明
证:设6个人分别用v1,v2,v3,v4,v5,v6表示。 任取一点vi,它与其他5点联线中,至少有
3条同为实线或3条同为虚线:
vi
vi
或
vj
vj
vp
vp
vq
实线表示相互认识
vq
虚线表示相互不认识
证毕。
而5个人的人群,可能出现既没有3个人彼此不 认识,也没有3个人相互认识,如下图:
1928年, 英国数学家Ramsey提出了 Ramsey数与相关理论,直观的讲,就是:
任意6个人在一起,6人中要不是有3个人 彼此相互认识,就必然有3个人相互不认识; 即两种情况至少存在一种。
记作:r(3,3)=6 推广:r(p,q)是任给出的人群中必有p人 彼此认识或有q人彼此不相识的最小值。
鸽巢原理
>>
六、妖怪(snark graph)
妖怪图每个点都关联着3条边,用4种颜 色可以把每条边涂上颜色,使得有公共端点 的边异色,而用3种颜色办不到,切断任意3 条边不会使它断裂成2个有边的图。
单星妖怪
双星妖怪
七、过河问题
参看课本p7~p11。
由此可见
图论中蕴含着强有力的思想、漂亮的图 形和巧妙的理论,即使是非常困难尚未解决 的问题,它的表述也可以是非常平易的。图 论是最接近百姓生活、最容易阐述的一门数 学分支,具有实质性的难度又有简朴的外表 是很多图论问题的特点之一。
这类问题称为NPC问题。
哈密顿回路和七桥问题的区别
▪ Hamilton回路: 侧重顶点(一次行遍顶) ;
▪ 七桥问题: 侧重边(一次行遍桥/边) 。
▪ 两者相似,但在难度上不是同一级别的问题。
三、四色问题
四色问题是世界近代三大数学 难题之一。
四色问题的内容是:任何一张 地图只用四种颜色就能使具有共 同边界的国家着上不同的颜色。
小行星欧拉2002是为了纪念欧拉而命名的。
莱昂哈德·欧拉
弗兰克·拉姆赛(Frank Ramsey 1904~1930), 英国剑桥的数学家、哲学家、经济学家。
是20世纪最显赫的两大经济学家之一约翰·梅纳 德·凯恩斯的得意弟子。
1928年,拉姆赛在伦敦数学会宣读了一篇数学 奇文,提出了Ramsey数的计算和相关理论。科学 界一致认为, Ramsey理论是离散数学中最漂亮的 成就。
1976年6月,美国伊利诺大学哈肯与阿佩尔在 两台不同的电子计算机上,用了1200个小时,作了 100亿判断,终于完成了四色定理的证明,轰动了 世界。
然而,真正数学上的严格证明仍然没有得到! 数学家仍为此努力,并由此产生了多个不同的图论 分支。
四、计算机程序的流程图
具体可参看课本P13~P14
五、Ramsey问题
为什么要学习图论? ▪ 可以采用图论的成果和方法; ▪ 最重要的是:
可以培养我们思考问题和解决问题的能力。
▪ 图论诞生和孕育于民间游戏。
创生:1736年 瑞士数学家欧拉——图论之父; 进展:1847年,基尔霍夫(Kirchhoff)运用图论解
决了电路理论中求解联立方程的问题,引进了 “树”概念;
欧拉的一生很虔诚。然而,那个广泛流传的传说却不 是真的。传说中说到,欧拉在叶卡捷琳娜二世的宫廷里,
挑战德尼·狄德罗:“先生,(a+b)n/n = x;所以上帝存在, 这是回答!”
欧拉的离世也很特别:据说当时正是下午茶时间, 正在逗孙儿玩的时候,被一块蛋糕卡在喉头窒息而死。
欧拉是第一个使用“函数”一词来描述包含各种参数 的表达式的人,例如:y = F(x) (函数的定义由莱布尼兹在 1694年给出)。他是把微积分应用于物理学的先驱者之一。 欧拉是有史以来最多产的数学家,他的全集共计75卷。欧 拉实际上支配了18世纪的数学,对于当时新发明的微积分, 他推导出了很多结果。在他生命的最后7年中,欧拉的双 目完全失明,尽管如此,他还是以惊人的速度产出了生平 一半的著作。
自我介绍
阙(quē)夏 自2001年开始讲授《算法与数据结构》课程
2005年开始讲授《图论》课程
quexia@
课程简介
➢《图论》是计算机科学与技术专业、信息 安全专业的选修课程。 通过本课程的学习,使学生对图论的 历史背景、研究内容、相关技术及其发展 有一个较为全面地了解,从而将所学知识 和技术运用于实际应用领域奠定基础。
求解算法(算法)
用大量数据验证
测试
编程实现
什么是图论?
▪ 图论是离散数学的分支: 图(graph): 是一个离散集和某些两元素子集的集合。 数学形象是:纸上画几个顶点,把其中一些点
用曲线段或直线连起来。图显示的是点与点 之间的二元关系。
图论的分支很多,例如: ▪ 图论 ▪ 算法图论 ▪ 极值图论 ▪ 网络图论 ▪ 模糊图论 ▪ 代数图论 ▪ 随机图论 ▪ 超图论
若没有一个地方通奇数座桥,则从任何 一地出发,所求的路线都能实现。
>>
二、哈密顿回路问题到货郎问题
1856年,哈密顿(Hamilton)提出了所谓环 球旅行问题:
在正12面体上的注2意0个!顶!点分别表示20个城市, 两点间的连线表不示是城所市有间图的道都路能。要求旅行者从 某个城市出发找,到到达这各样个的城路市线一!次且仅一次,最
v1
v2
v3 实线表示相互认识
虚线表示相互不认识
v4
v5
所以r(3,3)≥6
>>
自Ramsey在1928年提出了Ramsey数与 相关理论70多年以来,至今求得的Ramsey 数仅仅9个,它们是:
r(3,3)=6, r(3,6)=18, r(3,9)=36,
r(3,4)=9, r(3,7)=23, r(4,4)=18,
进入20世纪以来,科学家们对四色猜想的证明 基本上是按照肯普的想法在进行。后来美国数学家 富兰克林于1939年证明了22国以下的地图都可以用 四 色 着 色 。 1950 年 , 有 人 从 22 国 推 进 到 35 国 。 1960年,有人又证明了39国以下的地图可以只用四 种颜色着色;随后又推进到了50国。
➢本课程所介绍的内容包括:
图论的发展历程和经典问题; 图的基本概念; 有关树和图的算法; 网络流问题; 匹配问题、色数问题;
图论及其应用
第一章 图的基本概念 第二章 树 第三章 图的算法
第六章 网络流图问题 第七章 匹配理论、色数问题及其他
参考书籍
▪ 《图论》 王树禾著 科学出版社 2004
后返回出发城市。
两个问题:
(1)经过每个顶点一次且仅一次; (2)代价最小的Hamilton回路。
(目前无有效的方法求解)
