32第三十二讲 运算电路的分析网络函数极点和零点
零点与极点的关系PPT课件

零点与极点的相互影响
零点对极点的影响
在函数图像上,零点是函数值为0的 点,而极点是函数值无穷大的点,因 此零点的位置会影响极点的位置。
极点对零点的影响
极点的位置也会影响零点的位置,因 为函数值在极点附近会变得非常大或 非常小,从而影响函数的零点。
零点与极点的性质比较
01
零点的性质
零点是函数值为0的点,是函数图像与x轴的交点。
2023
PART 05
总结与展望
REPORTING
零点与极点的重要性和意义
零点与极点在数学、物理和工程领域中具有广泛的应用,是解决复杂问题的关键。 零点与极点的概念和性质在数学分析、复变函数、信号处理等领域中占有重要地位。
零点和极点的分析有助于深入理解函数的性质、系统的稳定性和信号的传播等。
未来研究方向和展望
02
极点的性质
极点是函数值无穷大的点,是函数图像上凹凸性改变的点。
03
零点和极点的关系
在函数图像上,零点和极点可以重合,也可以不重合。如果重合,则该
点既是函数的零点也是函数的极点;如果不重合,则该点只可能是零点
或只可能是极点。
2023
PART 03
零点与极点的应用
REPORTING
在信号处理中的应用
2023
PART 04
零点与极点的实际案例
REPORTING
信号处理中的零点与极点案例
总结词
信号处理中的零点与极点案例展示了零点与极点在信号处理中的实际应用和影响。
详细描述
在信号处理中,零点和极点是影响信号频域特性的重要因素。零点可以改变信号的相位,而极点则影响信号的幅 度。通过在信号处理过程中合理地设计零点和极点,可以实现信号的滤波、均衡、调制和解调等操作,从而提高 信号的质量和性能。
极点和零点电路中的意义

极点和零点电路中的意义摘要:一、极点和零点电路的基本概念二、极点和零点电路的意义1.极点:电压、电流的转折点2.零点:电压、电流的平衡点三、极点和零点在电路分析中的应用1.电压、电流的计算2.电路元件的特性分析四、实际电路案例分析正文:极点和零点电路中的意义在电路领域,极点和零点是两个非常重要的概念。
它们在电路分析、计算和实际应用中具有显著的意义。
本文将从基本概念、意义以及在电路分析中的应用等方面进行详细阐述。
一、极点和零点电路的基本概念1.极点:在电路中,极点通常指的是电压或电流发生转折的点。
例如,在交流电压或电流的正负半周期之间,电压或电流的值会发生剧变,这个转折点就称为极点。
在电路分析中,极点常常用于描述电容、电感等元件的电压或电流变化。
2.零点:零点是指电压或电流的平衡点,即电压或电流的值为零的点。
在直流电路中,电源的正负极之间的电压为零点;在交流电路中,电压或电流的瞬时值为零的点即为零点。
零点在电路分析中也具有重要作用,如用于电路元件的特性的描述和计算。
二、极点和零点电路的意义1.极点:在电路分析中,极点有助于我们理解电压、电流的变化规律。
通过分析极点,可以研究电容、电感等元件的充放电过程,以及电路中的共振现象等。
此外,在信号处理领域,极点还与信号的频率响应密切相关。
2.零点:零点在电路分析中具有实用性意义。
首先,在计算电路中的电压、电流时,零点可以作为参考点,便于进行数值计算。
其次,通过分析零点,可以研究电路元件的特性,如电阻、电容、电感等。
此外,零点还在交流电路的相位分析中起到关键作用。
三、极点和零点在电路分析中的应用1.电压、电流的计算:在电路分析中,我们需要对电压、电流进行计算。
通过分析极点和零点,可以得到电压、电流的波形和幅值,从而为电路的性能评估提供依据。
2.电路元件的特性分析:极点和零点有助于我们了解电路元件的特性,如电容、电感的充放电过程,以及电阻、电容、电感等元件对交流信号的阻抗特性。
网络函数的零极点图

网络函数的零极点图
式中,K是比例因子K的绝对值;φ0是K的幅角, 当K为正时,φ0=0°,当K为负时,φ0=180°。 上式告诉我们,H(s)在s=s0处的模
l1l2 L lm H ( s0 ) = K d1d 2 L d n
幅角 H ( s0 ) = φ0 + (φ1 + φ2 + L + φm ) − (ϕ1 + ϕ2 + L + ϕn ) 显而易见,在图上量得长度li(i=1,2,…,m)和 dj(j=1,2,…,n)后,便能定出 H(s0);量得 φi(i=1,2,…,m)和ϕj(j=1,2,…,n)后,便能 定出H(s0)。
利用这几个关系式算出li、dj、φi和ϕj后,也能求 出 H(s0)和H(s0)。
网络函数的零极点图
网络函数的零极点图
网络函数的零点和极点都是实数和复数,因此 现讨论如何利用作图的方法来求出网络函数H(s)在 不同s下的模值与幅角值。现设s=s0,得
H ( s ) s = s = H ( s0 ) = K
网络函数的零极点图
因为(s0-zi)和(s0-pj)还可表示成代数形式,即 (s0-zi) = γi+ηi (s0-pj) = ζj+ξj 所以又有关系式 2 2 −1 η i li = γ i + ηi , φi = tg γi
2 j 2 j −1
ξj d j = ζ + ξ , ϕ j = tg ζj
0
∏ (s − z ) ∏ (s − p )
j =1 j i =1 n i
m
网络函数的零极点图
在上式中,无论是分子还是分母的因式都可在s平 面上用一矢量来表示,现以(s0-zi)为例,因为s0和 zi都是复数,故可在s平面上找到它们的位置,并 用矢量表示(见下图)。 jω
电子电路中网络函数的分析与应用

0 t
e( t ) * h( t )
例:已知 R 500k, C 1F , is (t ) 2e t A
uc (0 ) 0, 求uc (t )。
+ is
R C
Is( s)
R 1/sC
+
Uc(s)
uc
解: 电路的单位冲激响应为
(t)
1 零 状 态
h( t ) = r( t )
R(s)
R( s ) H ( s) 1 L1[ H ( s)] h(t )
网络函数和冲激响应构成一对拉氏变换对
R( s ) H ( s) E( s)
1Hale Waihona Puke t 0R( s ) E ( s ) H ( s )
r (t ) L [ E( s) H ( s)] e( )h( t )d
+
_
1 设H 0 RC
U c ( s) + H ( s) 1 U s ( s) R uc 1 sC C us _ RC 1 s 1 RC 有一个极点 p1 RC
H0 H ( j ) H ( j ) ( j ) j 1 / RC
R
1 sC
H0 H0 H ( j ) j 1 / RC j p1
0
f1 ( x ) ( x ) f 2 ( )e s e sx ddx
sx
f1 ( x ) ( x )e
0
dx f 2 ( )e s d
0
F1 ( s)F2 ( s)
同理可证
L[ f 2 (t ) * f1 (t )] F2 ( s)F1 ( s) f1 (t ) * f 2 (t ) f 2 (t ) * f1 (t ) L1[F1 ( s)F2 ( s)]
极点和零点——精选推荐

极点和零点在信号处理系统中,当输⼊幅度不为零且输⼊频率使系统输出为零时,此输⼊频率值即为零点。
当系统输⼊幅度不为零且输⼊频率使系统输出为⽆穷⼤(系统稳定破坏,发⽣振荡)时,此频率值即为极点。
对于⼀个信号处理系统,其输⼊输出之间存在⼀定的关系,这种关系⽆论在时域还是频域都可以⽤数学表达式来表⽰。
⽽这数学表达式⼜是分⼦分母都是多项式的表达式(称为传递函数),这样满⾜使传递函数的分⼦为零的是零点,满⾜使传递函数分母为零的就是其极点。
(什么是相位裕度?相位裕度就是系统进⼊不稳定状态之前可以增加的相位变化,相位裕度越⼤,系统越稳定,但同时时间响应速度减慢了,因此必须要有⼀个⽐较合适的相位裕度)零点与极点怎么产⽣的:将电阻电容电感器件简单串并联就产⽣了。
其实我很简单的了。
电容接地单极点、电阻接地单零点。
电感电容双极点。
先记住这三⼝诀吧。
然后你再看看低通滤波器,⾼通滤波器吧。
你就了解我了。
在这⾥我先想说⼀下我的另⼀个兄弟转折频率:从转折频率理解零点与极点作⽤吧。
转折频率:例如单极和单零点电路中,此电路都有电容和电阻构成,当输⼊信号频率发⽣变化时,电容阻抗会随着的频率发⽣变化。
当电容阻抗等于电阻阻抗时候。
此是的频率点就是转折频率。
在单极点(低通滤波器中)从0HZ(直流)~转折频率的范围内,增益是⼀条⽔平直,经过转折频率后,增益以-20dB/dec下降。
输出的信号的幅度降为输⼊的⼀半,并输出信号相位相对与输⼊信号是落后了45度,输⼊信号被延迟了。
当电容阻抗远⼤与电阻时,输出信号相位最⼤会被延迟90度,从经验上说这个相位在转折频率正负10倍受到了影响。
在单零点(⾼通滤波器中)它与极点作⽤正好相反,它从0HZ(直流)~转折频率范围内增益响应是⼀条⽔平的直线,过转折频率后+20dB/dec上升,相位在转折频率点超前了45度,当信号频率继续上升⼤于10倍转折频率时候,相位超前了90度。
总结,何为转折,⽆论在单极电,还是单零点,或双极双零点中。
电路分析基础-第12章网络函数课件

2et teξdξ 0
2(et e2t )V (t 0)
解法二:H (s) L[h(t )] 106 s2
H (s) R(s)
iS(t) 2etμA时
E(s)
IS(s)
ℒ[iS (t )]
2 106 s1
由网络函数定义得:
UC (s) IS (s)H(s)
106 2 106
5(s 1)2 5(s 1)
(1)
uS(t) δ(t)V。
i2 (t ) h(t ) ℒ-1[H (s)]
(1 et 5
1 5
tet )ε(t )A
(2) uS(t) 2e3tε(t)V。
I2(s)
H (s)US (s)
5(s
2s 3)(s
1)2
3 3 1 10(s 3) 10(s 1) 5(s 1)2
0称Z1
Z
为
m
零
点
j 1
当s Pj时H (s) 称P1 Pn为 极 点
jω
复频率平面 s σ jω
p1
z1
在复平面上极点用“”表示 ,
p0
零点用“。”表示。
零、极点分布图 p2
z0
z2
应用举例
例: 12-3已知网络函数
H(s)
=
s2
+
s 2s
+
4
,试求:
(1)网络的零、极点; (2)绘出零、极点分布图;
r(t ) ℒ-1 [R(s)]
=ℒ-1[ E ( s) H ( s)] = e(t) * h(t)
t
= 0e(ξ)h(t ξ)dξ
t
= 0e(t - ξ )h(ξ )dξ
学习要点MainContents1网络函数的概念驱动点阻抗

• 学习要点(Main Contents): • 1网络函数的概念 • 2、驱动点阻抗、驱动点导纳、转移阻抗、转移导纳、
转移电压比、转移电流比
3、极点和零点的概念
4、极点、零点与冲激响应的关系
§11.5.1 网络函数的定义 (Definition of Network Function)
与激励无关
网络函数是实系数的有理函数
网络函数的具体形式(Concrete Form of Network Function)
1.驱动点(Driving Point )函数
Z(s) U(s) I(s)
驱动点阻抗
I(s) U(s)
Y(s) I(s) U(s)
H(s) U2(s) I1(s)
若E(S)=1,则H(S)=R(S) , 即 h(t)=r(t)
网络函数的原函数h(t)是电路的冲激响应。
补例:
R
+
_ uS
C
H(s) UC (s) U s (s)
+
_
uC
R +
_ Us(s)
1/sC
1
sC R 1
sC
1 RsC 1
+ _ UC(s)
网络函数是由网络的结构和参数决定,
极点用“”表示 ,零点用“。”表示。
补例:
H(s)
2( s 2) s( s 3)( s 2 2s 2)
绘出其极零点图
j
-3
j。
0 -j
2
H (s)的零点为Z1 2
H (s)的极点为P1 0 P2 3 , P3,4 1 j1
网络函数的零点和极点分析

电感电压作为输出
设 R 1, C 1F , L 1H
电容电压作为输出 :
低通滤波器
1 H1 ( s ) 2 s s 1 1 H1 ( j ) j 1 2
Frequency3.m
电阻电压作为输出
s H 2 (s) 2 s s 1 j H 2 ( j ) j 1 2
s (t )的导数(零状态)
d h(t ) s (t ) dt 证明: 冲击响应 R冲 (S ) H (S ) E(S ) H (S )
(冲击激励时 E ( S ) 1 ) 阶跃激励时
r冲 (t ) h(t )
1 S阶 ( S ) H ( S ) E ( S ) H ( S ) S
R( S ) H ( s) E (S )
[e(t ) (t )] 时,
n Kn 1 (设无重极点) S Sn i 1 S Si
K1 K2 R( S ) H ( S ) S S1 S S2
则
r (t ) h(t ) K1e
Байду номын сангаас
s1t
Kne
snt
0 0
t
特别注意,当激励为分段连续函数 时(见图),有
e1 (t ) e2 (t )
t t0
(t0 t )
R1
r (t ) t e ( )h(t )d (0 t t0 ) 0 1 t0 t r (t ) e1 ( )h(t )d e2 ( )h(t )d 0 t0
Ki e
i 1
n
sit
每一个极点代表着一个响应分量的形式,极点在复平面 上的分布决定其响应形态。(如图)
网络函数的零点和极点分析

目录
• 引言 • 网络函数的零点分析 • 网络函数的极点分析 • 网络函数的零极点与系统稳定性 • 实际应用案例
01 引言
零点和极点的定义
零点
函数值为零的点,即 $f(z) = 0$ 的 解。
极点
函数在某点的值趋于无穷的点,即函 数在该点附近的导数趋于无穷。
零点和极点在网络分析中的重要性
极点分析在网络路由优化中的应用
极点分析在网络路由优化中具有重要价值,通过分析网络函数的极点,可以确定最 佳的网络路由路径。
极点分析可以用于优化路由算法,提高网络路由的效率和稳定性,降低网络传输延 迟。
极点分析还可以用于故障排查和网络性能评估,通过分析极点的变化,可以快速定 位网络故障和评估网络性能。
05 实际应用案例
零点分析在网络拥塞控制中的应用
零点分析在网络拥塞控制中起到 关键作用,通过分析网络函数的 零点,可以确定网络中数据传输
的稳定性。
零点分析可以预测网络拥塞的情 况,提前采取措施进行预防,提
高网络传输的效率和稳定性。
零点分析还可以用于优化网络拥 塞控制算法,通过调整算法参数,
降低网络拥塞发生的概率。
极点对网络性能的影响
稳定性
极点的位置决定了系统的稳定性。如果极点位于复平面的左半部分, 系统是稳定的;如果极点位于右半置和数量会影响系统的动态响应特性,如系统的超调和调 节时间等。
噪声抑制
极点的位置和数量也会影响系统对外部噪声的抑制能力。
极点分析在网络设计中的应用
数值法
通过迭代或搜索算法在复平面上找到零点,适用于复杂或难以解析 求解的网络。
图形法
通过绘制网络函数的极坐标图或奈奎斯特图来直观地找到零点,适 用于具有直观几何意义的网络。
极点和零点重合-概述说明以及解释

极点和零点重合-概述说明以及解释1.引言1.1 概述极点和零点是在数学分析中常见的概念,它们分别代表了函数在特定点处的奇点和使函数为零的点。
通常情况下,极点和零点是不会重合的,因为它们代表了函数在不同情况下的性质。
然而,有时候极点和零点会重合在同一个点上,这种情况在数学分析中被称为极点和零点重合。
本文将对极点和零点的定义、特征以及它们之间的关系进行详细的探讨,同时还将分析极点和零点重合的意义和影响。
通过深入研究极点和零点的重合现象,我们可以更好地理解函数的性质和行为,为进一步的数学研究提供有益的参考。
1.2文章结构1.2 文章结构本文将首先介绍极点和零点的定义和特征,包括它们在数学和物理领域的重要性以及相互之间的区别。
然后,我们将讨论极点和零点之间的关系,探讨它们在数学和物理问题中的应用。
最后,我们将深入探讨极点和零点重合的意义,探讨这种现象在实践中的重要性和可能的应用领域。
通过对极点和零点的研究和分析,我们希望读者能够更深入地理解这两个概念,并从中获得一些启发和新的见解。
1.3 目的本文的目的在于探讨极点和零点在数学和物理学中的重要性和作用,并深入研究极点和零点在数学领域的定义、特征以及它们之间的关系。
通过对极点和零点的探讨,我们希望能够更深入地理解它们在数学和物理学中的应用,以及它们在解决问题和预测某些现象中起到的重要作用。
同时,本文还将探讨极点和零点重合的意义,从而帮助读者更好地理解这一现象对于数学和物理学的意义和影响。
最终,通过本文的研究,我们将能够更全面地认识极点和零点的重要性,以及它们在数学和物理学领域的作用。
2.正文2.1 极点的定义和特征在复数域上,一个函数在某点处的极点是指在该点处函数取无穷大值或无穷小值的点。
具体来说,如果一个函数在某点处取无穷大值,我们称这个点为函数的极点。
极点是一种特殊的奇点,它在函数的定义域内是孤立的点。
极点具有以下特征:1. 极点是函数在某点处的奇点,也就是说这个点不能满足函数的定义。
电网络分析-网络函数课件

H jk s k 1,2,q 是表征零状态响应象函数和激励象
函数之间关系的复频变量s 的函数
H
jk (s)
Rj (s) Ek (s)
除Ek (s)外其余激励置0
2021/3/11
电网络分析第三章
3-1. 网络函数及其极点和零点
3、网络函数
➢ 线性时不变网络在单一激励源作用下,某一零 状态响应的象函数与激励象函数之比称为网络函 数。
《电网络分析-网络函数》
2021/3/11
电网络分析第三章
第三章 网络函数
网络函数是描述线性时不变网络 (零初始条件)输入-输出关系的复频 域函数
2021/3/11
电网络分析第三章
3-1. 网络函数及其极点和零点
一、网络函数
由若干独立电(压、流)源激励的线性时 不变网络,设其中电容电压、电感电流的初始值 为0,以节点电压方程
i j i 1,2,nt ; j 1,2,nt
2021/3/11
电网络分析第三章
3-3. 不定导纳矩阵
(2)写出各类二端元件(VCCS,回转器,耦合 电感元件,理想变压器等)对原始不定导纳矩 阵的贡献。
(3)将由以上步骤所得的各类元件对原始不定 导纳矩阵的贡献相加,即得原始不定导纳矩阵 。
i 1
k 1
m
n
H ( j) K ( j Zi ) / ( j pk )
i 1
k 1
m
n
K lie ji / dke j
i 1
k 1
m
n
H j k li dk
i1
k 1
m
n
i k
i1
k 1
0 , H j和的变化规律
网络函数

求H(s)的步骤: 1)先作出S域模型 2)按元件VAR关系以及KCL、KVL列出响应R(s)与激励 E(s)之比即H(s)。具体的可利用电路元件的串并联化 简或分压、分流等关系,必要时可借助戴维宁定理, 叠加定理等间接方法。 另外一般方法:列写回路方程或节点方程来求 H(s) 。
§14-7 网络函数的极点和零点
pi为H(s)的极点
n k h(t ) L1[ i ] k i e pit i 1 s pi i 1 n
pi t e 衰减指数函数 h(t )单调下降(指数形式) ① pi为负实数
i
② pi为正实数 e p t 增长指数函数 h(t )单调上升(指数形式) ③ pi为共轭复数时(实部 0) 振荡且幅值衰减 ④ pi 为共轭复数时(实部 0) 振荡且幅值增加 ⑤ pi 为纯虚数( 0) 等幅振荡
-2
2
4
§14-8极点、零点与冲激响应 极点与冲激响应:冲激响应h(t)
n ki h(t ) L [ ] k i e pit i 1 s pi i 1 1 n
若H(s)为真分式且分母具有单根 则 h(t ) L1[ H (s)] L1[ N (s) ]
D( s )
I 2 (S ) 1 S 2S 2S 1
3 2
U1 (S )
H1 (S )
U 2 (S ) 1 3 U 1 ( S ) S 2S 2 2S 1
I1 (S ) 2S 2 4S 3 H 2 (S ) U1 (S ) 3(S 3 2S 2 2S 1)
H ( s)
U C (s) U s ( s)
1 R sL 1 sC
1 sC
零点和极点详解

零点和极点详解一、引言零点和极点是复变函数中非常重要的概念,它们在数学中的应用非常广泛,包括电路分析、信号处理、控制系统等领域。
本文将详细介绍零点和极点的定义、性质以及在实际应用中的意义。
二、零点的定义与性质1. 零点的定义设f(z)是一个复变函数,z0是复平面上的一个复数,如果f(z0)=0,则称z0为f(z)的一个零点。
2. 零点的性质(1)零点是函数图像与x轴交点处。
(2)如果f(z)在z0处有一个k阶零点,则f(z)在z0处可以表示为:f(z)=(z-z0)^k g(z)其中g(z)是在z=z0处不为0且解析的函数。
(3)如果f(z)有无穷多个不同的零点,那么f(z)必须恒等于0。
三、极点的定义与性质1. 极点的定义设f(z)是一个复变函数,z0是复平面上的一个复数,如果满足以下条件:(1)存在某个正整数k使得g(z)=(z-z0)^kf(z)在z=z0处解析;(2)当z趋近于z0时,|f(z)|趋近于无穷大;则称z0为f(z)的一个k阶极点。
2. 极点的性质(1)极点是函数图像在z0处的奇异点,也就是说,函数在z0处没有定义。
(2)如果f(z)在z0处有一个k阶极点,则可以表示为:f(z)=h(z)/(z-z0)^k其中h(z)是在z=z0处不为0且解析的函数。
(3)如果f(z)有无穷多个不同的极点,那么f(z)必须恒等于无穷大或者恒等于零。
四、零点与极点之间的关系1. 零点与极点之间的关系如果f(z)在z0处既有零点又有极点,那么它们之间存在以下关系:(1)当k>0时,称z0为可去奇异点。
此时,当我们把这个可去奇异点消去后,就得到了一个新的解析函数g(z),它在原来的可去奇异点处具有一个正常的值g(z0)=lim_(z→z_0)f(z),并且g(z)和f(z)在其他地方完全相同。
(2)当k<0时,称z0为本性奇异点。
此时,它是一个真正意义上的奇异点。
如果f(z)在z0的某个邻域内解析,那么称z0为孤立奇异点。
电路分析基础12-网络函数

12.1 网络函数的定义 12.2 网络函数的极点和零点 12.3 极点、零点与冲激响应 (,★) 12.4 极点、零点与频率响应 () 12.5 卷积 () 12.6 应用实例 ——交叉网络
12.1 网络函数的定义
一、网络函数的定义及类型 1.网络函数的定义 线性电路在单一电源激励下,其零状态响应r(t)的像 函数R(s)与激励e(t)的像函数E(s)之比定义为该电路的网 络函数H(s)。
-
)
-
I1 ( s ) U 2 ( s) 电压转移函数 H ( s) U 1 ( s) I 2 ( s ) 电流转移函数 H ( s) I1 ( s )
二、网络函数的性质
1.网络函数是单位冲击响应的象函数。
R( s ) R( s ) , R( s ) 当 e(t ) (t ) 时,E ( s) 1 H ( s) E ( s) 1
U(s)
-
(2)转移函数(传递函数):输入和输出是双口的电压(电流) I 2 ( s) 转移导纳 H ( s) U1 ( s) I2 ( s + + I1 ( s U 2 ( s ) 转移阻抗 U1(s) ) ) U2(s H ( s)
I ( s) H ( s) 驱动点导纳 U ( s)
+ u1 +
uS(t) R1
+ + R2 α u1 (a) L C
U 1 ( s) R1
+
R2
+
US(s i2 ) -
sL
-
-
αU 1 ( s )
I2 ( s)
1 sC
(b)
解: U1 ( s) US ( s) αU1 ( s)
电路中极点与零点的产生与影响

请问电路中极点与零点的产生与影响一、电路中经常要对零极点进行补偿,想问,零点是由于前馈产生的吗?它产生后会对电路造成什么样的影响?是说如果在该频率下,信号通过这两条之路后可以互相抵消还是什么??极点又是怎么产生的呢?是由于反馈吗?那极点对电路的影响又是什么?产生振荡还是什么??请大家指教一下。
1.(不能这么简单的理解其实电路的每个node都有一个极点只是大部分的极点相对与所关心的频率范围太大而忽略了运放中我们一般关心开环的0dB带宽那么>10*带宽频率的极点我们就不管了因为它们对相位裕度贡献太小而被忽略;只要输入和输出之间有两条通路就会产生一个零点:同样的高于所关心频率范围的零点也不用管一个在所关心频率范围内的零点需要看是左半平面还是右半平面的左半平面的零点有利于环路稳定右半平面的则不利具体的看拉扎维的书吧写的还是蛮详细的看不懂就多看几遍自己做个电路仿下)2.好问题,希望彻底了解的人仔细解答。
我也同样疑惑。
但是我总觉得极点,零点并不能单单的说是由于前馈,反馈,或者串联并联一个电容产生的。
产生的原因还是和具体的电路结构相关联的。
比如一个H(s)的系统和一个电容并联或串联在输入输出之间,谁能说他一定产生一个极点或零点呢?这因该和H(s)的具体形式有关。
大多书上说的应该大多针对的是运放结构,它的结构具有特殊性。
具有以点盖全的嫌疑。
还请达人细说。
3.一般的说,零点用于增强增益(幅度及相位),极点用于减少增益(幅度及相位),电路中一般零点极点是电容倒数的函数(如1/C)。
当C变大时,比如对极点来说,会向原点方向变化,造成增益减少加快(幅度及相位)~一般运放电路的米勒效应电容就是这个原理,当增益迅速下降倒-3dB时,其他的零点极点都还没对系统增益起到啥作用(或作用很小,忽略了),电路就算七窍通了六窍半了~你就可以根据自己的需要补上带宽,多少多大的裕度就KO了极点是由于结点和地之间有寄生电容造成的,零点是由于输入和输出之间有寄生电容造成的,一般输入和输出之间的零极点考虑多一点,主要是因为输入输出有较大的电阻,造成了极点偏向原点.4.个人的一点理解极点决定的是系统的自然响应频率,通常在电路中就是对地电容所看进去的R 和对地电容C 共同决定的。
网络函数的零极点图

式中,分子和分母的各项系数都为实数。 如果将上式的分子、分母写成因式连乘形式又有
( s z1 )( s z2 ) ( s zm ) H (s) K K ( s p1 )( s p2 ) ( s pn )
(s z ) (s p )
j 1 j i 1 n i
此式证明了引理中的第一条。
由于
P( z) 0 P( z ) 0 0
网络函数的零极点图
以及根据 P(s) P(s ) ,所以必有
P( z ) 0 P( z ) 0
这又证明了引理中的第二条。至此,引理全部得 证。 由此引理之(2)可立即推得N(s)和D(s)的零点 不是实数,就是复共轭对,于是有如下的结论: 网络函数H(s)的零点和极点或者是实数,或者是 共轭复数对。当然应该注意到这个结论并不排 斥在零点和极点中可能有重零点和重极点。
m
网络函数的零极点图
b0 K 式中, a0 是一个实因子,可正可负;zi(i=1,
2,…,m)是分子多项式的零点,当s=zi时,网络 函数为零,所以称它们为网络函数的零点;pj(j=1, 2,…,n)是分母多项式的零点,当s= pj时,网络 函数为无穷大,所以称它们为网络函数的极点。
对于实系数的s多项式,有下面的引理成立。
证明 设
P(s) a0 sn a1sn1
an1s an
式中的系数ai(i=0,1,2,…,n)都是实数,于 是,对任一复数s有
P(s) a0 s n a1s n1 a0 s n a1 s n1 an1s an a0an1s an
至此引理全部得由此引理之2可立即推得ns和ds的零点不是实数就是复共轭对于是有如下的结论
网络函数的零极点图

网络函数的零极点图
网络函数一般可以表示成如下的形式,即
N (s) b0 s m b1s m1 H ( s) D(s) a0 s n a1s n1 bm1s bm an1s an
式中,分子和分母的各项系数都为实数。 如果将上式的分子、分母写成因式连乘形式又有
P(s) a0 s n a1s n1 a0 s n a1 s n1 an1s an a0 s n a1s n1 an1 s an P(s ) an1s an
此式证明了引理中的第一条。
由于
P( z) 0 P( z ) 0 0
( s z1 )( s z2 ) ( s zm ) H (s) K K ( s p1 )( s p2 ) ( s pn )
(s z ) (s p )
j 1 j i 1 n i
m
网络函数的零极点图
b0 K 式中, a0 是一个实因子,可正可负;zi(i=1,
P(s) P(s ),
s
(2) P(s)的零点或者是实数,或者是复共轭对,即
P( z ) 0 P( z ) 0
式中z代表多项式P(s)的零点。
网络函数的零极点图
证明 设
P(s) a0 sn a系数ai(i=0,1,2,…,n)都是实数,于 是,对任一复数s有
网络函数的零极点图
以及根据 P(s) P(s ) ,所以必有
P( z ) 0 P( z ) 0
这又证明了引理中的第二条。至此,引理全部得 证。 由此引理之(2)可立即推得N(s)和D(s)的零点 不是实数,就是复共轭对,于是有如下的结论: 网络函数H(s)的零点和极点或者是实数,或者是 共轭复数对。当然应该注意到这个结论并不排 斥在零点和极点中可能有重零点和重极点。
零点与极点计算和分析
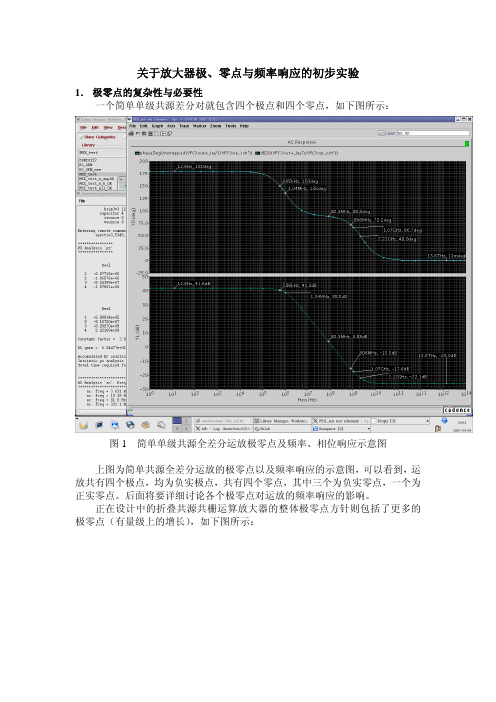
关于放大器极、零点与频率响应的初步实验1.极零点的复杂性与必要性一个简单单级共源差分对就包含四个极点和四个零点,如下图所示:图1 简单单级共源全差分运放极零点及频率、相位响应示意图上图为简单共源全差分运放的极零点以及频率响应的示意图,可以看到,运放共有四个极点,均为负实极点,共有四个零点,其中三个为负实零点,一个为正实零点。
后面将要详细讨论各个极零点对运放的频率响应的影响。
正在设计中的折叠共源共栅运算放大器的整体极零点方针则包括了更多的极零点(有量级上的增长),如下图所示:图2 folded-cascode with gain-boosting and bandgap all-poles details图3 folded-cascode with gain-boosting and bandgap all-zeros details从上述两张图可以看到,面对这样数量的极零点数量(各有46个),精确的计算是不可能的,只能依靠计算机仿真。
但是手算可以估计几个主要极零点的大致位置,从而预期放大器的频率特性。
同时从以上图中也可以看到,详细分析极零点情况也是很有必要的。
可以看到46个极点中基本都为左半平面极点(负极点)而仿真器特别标出有一个正极点(RHP )。
由于一般放大器的极点均应为LHP ,于是可以预期这个右半平面极点可能是一个设计上的缺陷所在。
(具体原因现在还不明,可能存在问题的方面:1。
推测是主放大器的CMFB 的补偿或者频率响应不合适。
2。
推测是两个辅助放大器的带宽或频率响应或补偿电容值不合适)其次可以从极零点的对应中看到存在众多的极零点对(一般是由电流镜产生),这些极零点对产生极零相消效应,减少了所需要考虑的极零点的个数。
另外可以看到46个零点中45个为负零点,一个为正零点,这个正零点即是需要考虑的对放大器稳定性产生直接影响的零点。
以上只是根据仿真结果进行的一些粗略的分析,进一步的学习和研究还需要进行一系列实验。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(3)、反变换得出时间函数 )、反变换得出时间函数
−4 5 U L ( s) = + S + 2 S + 2.5
u L (t ) = L [U L ( s )] = − 4e
−1
(
−2 t
+ 5e
−2.5t
)V (t ≥ 0)
§14-6 网络函数的定义 14-
运算形式KCL、KVL 、 运算形式
∑ I (S) = ∑ U (S )
KCL KVL
=0 ∑u = 0
∑i
0 =0
U ( s ) = Z ( s ) I ( s ) 元件 → 运算阻抗、运算导纳 运算阻抗、
I(S) R
U ( S ) = RI ( S )
I ( S ) = GU ( S )
+ U(S) -
K3 K1 K2 I L (s) = + + S S + 50 S + 150
+ 50/S 1.33S _
IL
10000/S
50 ×104 K1 = 199.5s 2 + 2.66 ×104 s + 50 ×104
=1
s =0
50 ×10 4 K2 = 199.5s 2 + 2.66 ×104 s + 50 ×104
I L ( s) =
50 s
S
50 iL
100µF
50 + 1.33s // 10 s
4
1.33s // • 1.33s
10 4 s
50 ×10 4 = s (66.5s 2 + 1.33 × 10 4 s + 50 ×10 4 )
+ 50V 1.33H _
50
(t=0)
S 1 = 0 , S 2 ≈ − 50 , S 3 ≈ − 150
1 K1 = I (s)s s=0 = 2
1 2 1 2(1+ j) 1 2(1− j) I (s) = − − s s +1− j (s +1+ j)
14- 2、举例: 例14-10 举例:
解: 1)、画出运算电路 ( )、画出运算电路
is = ε (t ), u c ( 0 − ) = 0, I ( s ) =
§14-5 应用拉普拉斯变换法分 14- 析线性电路 §14-6 网络函数的定义 14- §14-7 网络函数的极点和零点 14-
重点: 重点: 1、运算法; 运算法; 网络函数; 2、网络函数; 3、网络函数的极点和零点的分布。 网络函数的极点和零点的分布。
一、知识回顾
1、拉普拉斯反变换 2、拉普拉斯反变换的部分分式展开 3、运算电路 4、作业讲解:P377 14-2(1) 作业讲解: 14-
sL
i (0 − ) / s
I(s )
+
U(s)
-
1 u c (0 − ) U c (S ) = I c (S ) + SC S I C ( S ) = SCU C ( S ) − Cuc (0 − )
1/sC Uc(s)
1/sC
Cuc(0-) Ic(s) Uc(s)
Z ( s ) = 1 sC Y ( s ) = sC
1 I L (s) = I a (s) = s ( s 2 + 2 s + 2)
(3)、反变换得出时间函数 )、反变换得出时间函数
待定系数法
1 1 s +1 1 I L ( s) = − − 2 2 2 S (S + 1) + 1 (S + 1) + 1
1 −t −t iL (t ) = L [ I L ( s )] = 1 − e cos t − e sin t A (t ≥ 0) 2
1、运算法 2、举例: 例14-9 14- 举例: 例14-10 14- 例14-11 14-
1、运算法
运算法是把时间函数变换为对应的 象函数, 象函数,从而把问题归结为求解以象函 数为变量的线性代数方程。 数为变量的线性代数方程。 (1)、画出运算电路 )、画出运算电路 (2)、象函数的运算 )、象函数的运算 (3)、反变换得出时间函数 )、反变换得出时间函数
3s + 5 K1 K2 解:F ( s ) = 2 + = 2+ + 2 s + 3s + 2 s +1 s + 2
3s + 5 K1 = =2 s + 2 s =−1
3s + 5 K2 = =1 s + 1 s =−2
f (t ) = 2δ (t ) + 2e + e
−t
−2 t
14- 4、作业讲解:P377 14-5 作业讲解: 解:
−1
(
)
•
(4)反变换求原函数 反变换求原函数
1 I1(s) = I (s) = 2 s(s + 2s + 2)
D(s) = 0有 个根: p1 = 0 p2 = −1+ j,p3 = −1− j 3 ,
K1 K2 K3 I (s) = + + s s +1− j (s +1+ j)
1 K2 = I (s)(s +1− j) s=−1+ j = − 2(1+ j) 1 K3 = I (s)(s +1+ j) s=−1−j = − 2(1− j)
3 1 − 2t 3 − 4t f (t ) = + e + e 8 4 8
( s + 1)(s + 3) 1 = = s( s + 4) s = −2 4 ( s + 1)( s + 3) 3 = = s ( s + 2) s = −4 8
14- 4、作业讲解:P377 14-2(3) 作业讲解:
50 ×104 K3 = 199.5s 2 + 2.66 ×104 s + 50 ×104
≈ −1.5
s = −50
≈ 0.5
s = −150
1 − 1.5 0.5 I L ( s) = + + S S + 50 S + 150
iL (t ) = 1 − 1.5e
−50 t
+ 0.5e
−150 t
§14-5 应用拉普拉斯变换法分析线性电路 14-
(3)、分母多项式具有共轭复根 )、分母多项式具有共轭复根 一对共轭复根为
k1,k2也是一对共轭复数
k1 k2 F ( s) = + S − α − j ω S − α + jω
αt
p1 = α + jω
p 2 = α − jω
f (t ) = 2 K1 e cos(ωt + θ1 )
(4)、分母多项式具有重根 1 )、分母多项式具有重根p 分母多项式具有重根 k2 k13 k12 k11 F (S ) = + + + 2 3 (S − p ) + ⋅ ⋅ ⋅ S − p1 ( S − p1 ) ( S − p1 ) 2 k11 = [( S − p1 ) 3 F ( S )] S = p1
H ( s) = U 2 ( s) I1 ( s)
转移阻抗
I1(s) U1(s)
I2(s)
U 2 ( s) H (S) = 转移电压比 U1 ( s) U2(s)
1、网络函数的定义 2、网络函数的具体形式 3、举例:例14-15 举例: 14- 例14-16 14-
1、网络函数的定义
e(t) E(s)
零 状 态
r(t) R(s)
单个独立源作用的线性网络
L[r(t )] H(s) = L[e(t )]
R(s) 零状态 = E(s)
零状态
当e( t ) = δ ( t )时,E ( s ) = 1,则有 H ( s ) = R( s )
U(S) −
u (t ) = R − Re
1 − RC t
V (t ≥ 0)
14- 2、举例: 例14-11 举例:
解: 1)、画出运算电路 ( )、画出运算电路 R1 + 2 _ s+2
5 ①
R2
5
u S 1 = 2e
−2 t
,U S1 ( s) =
2 s+2
u S 2 = 5, U S 2 ( s ) = 5 s us 2 5 iL (0 − ) = = = 1A R2 5
UL(s)
sL _ +
Li (0 − )
+ _
5 s
0
(2)、象函数的运算,采用结点分析法 )、象函数的运算, 象函数的运算
5 2 1 1 1 Li (0 − ) s+2 s + R R + sL U L ( s ) = R + R − sL 2 1 2 1
2 1 1 2 1 + − + U L ( s ) = 5( s + 2) s s 5 s
Z ( s) = R Y ( s) = G
I(s)
sL U(s)
Li (0 − )
U ( S ) = SLI ( S ) − Li (0 − )
U ( S ) i (0 − ) I (S ) = + SL S
Z ( s ) = sL Y ( s ) = 1 sL uc(0-)/S I (S)
C
+
