弹簧振子的简谐振动实验报告--宋峰峰
简谐振动实验的实验报告

简谐振动实验的实验报告一、实验目的1、观察简谐振动的现象,加深对简谐振动特性的理解。
2、测量简谐振动的周期和频率,研究其与相关物理量的关系。
3、掌握测量简谐振动参数的实验方法和数据处理技巧。
二、实验原理简谐振动是一种理想化的振动形式,其运动方程可以表示为:$x= A\sin(\omega t +\varphi)$,其中$A$为振幅,$\omega$为角频率,$t$为时间,$\varphi$为初相位。
在本次实验中,我们通过研究弹簧振子的振动来探究简谐振动的特性。
根据胡克定律,弹簧的弹力$F =kx$,其中$k$为弹簧的劲度系数,$x$为弹簧的伸长量。
当物体在光滑水平面上振动时,其运动方程为$m\ddot{x} = kx$,解这个方程可得$\omega =\sqrt{\frac{k}{m}}$,振动周期$T = 2\pi\sqrt{\frac{m}{k}}$。
三、实验仪器1、气垫导轨及附件。
2、滑块。
3、弹簧。
4、光电门计时器。
5、砝码。
6、米尺。
四、实验步骤1、安装实验装置将气垫导轨调至水平,通气后检查滑块是否能在导轨上自由滑动。
将弹簧一端固定在气垫导轨的一端,另一端连接滑块。
2、测量弹簧的劲度系数$k$挂上不同质量的砝码,测量弹簧的伸长量,根据胡克定律计算$k$的值。
3、测量简谐振动的周期$T$让滑块在气垫导轨上做简谐振动,通过光电门计时器记录振动的周期。
改变滑块的质量,重复测量。
4、记录实验数据详细记录每次测量的质量、伸长量、周期等数据。
五、实验数据及处理|滑块质量$m$(kg)|弹簧伸长量$x$(m)|劲度系数$k$(N/m)|振动周期$T$(s)||||||| 010 | 005 | 200 | 063 || 020 | 010 | 200 | 090 || 030 | 015 | 200 | 109 || 040 | 020 | 200 | 126 |根据实验数据,以滑块质量$m$为横坐标,振动周期$T$的平方为纵坐标,绘制图像。
大学物理实验报告

大学物理实验报告实验名称:弹簧振子的简谐振动实验实验目的:1. 通过实验观察和分析弹簧振子的简谐振动特性,并验证简谐振动的运动方程。
2. 掌握实验测量仪器的使用方法,培养实验操作和数据处理能力。
3. 了解简谐振动的物理意义和应用。
实验原理:弹簧振子是一种典型的简谐振动系统,其运动方程可以通过质点受力分析得到。
当质点在弹簧的拉伸、压缩或振动过程中,如果受力与位移成正比,呈现出周期性的运动,即为简谐振动。
简谐振动的运动方程可以表示为x = A*cos(ωt + φ),其中A为振幅,ω为角频率,t为时间,φ为初相位。
实验仪器:1. 弹簧振子实验装置:包括一个弹簧、一根线、一个质量块、一个固定支架等。
2. 定时器/秒表:用于测量时间。
实验步骤:1. 将弹簧振子实验装置固定在桌面上,并调整弹簧的位置和质量块的质量,使得弹簧振子处于准静态状态。
2. 将质量块轻轻拉开,使其发生简谐振动。
3. 使用定时器/秒表,记录质量块从振动的一个极端位置到另一个极端位置所经过的时间,重复多次,求得平均值。
4. 进一步测量弹簧振子的振幅,即质量块振动的最大位移。
5. 根据所测得的数据,计算弹簧振子的周期、角频率、振动频率等参数。
实验数据处理:1. 利用所测得的时间数据,求出弹簧振子的周期T = 2t,并计算弹簧振子的角频率ω = 2π/T。
2. 根据所测得的振幅数据,计算弹簧振子的振动频率f = 1/T。
3. 结合实际的弹簧特性和质量块的质量,通过计算验证简谐振动的运动方程。
实验结果与结论:通过实验观察和数据计算,得到了弹簧振子的周期、振动频率等数据,并对简谐振动的特性进行了分析。
实验结果验证了简谐振动的运动方程,并深化了对简谐振动的理解。
此外,实验还培养了实验操作和数据处理的能力,提高了实验技能。
弹簧振子简谐运动实验报告

弹簧振子简谐运动实验报告一、实验目的1、观察弹簧振子的运动,理解简谐运动的特征。
2、测量弹簧振子的周期,探究周期与振子质量、弹簧劲度系数的关系。
3、学会使用实验仪器进行数据测量和处理。
二、实验原理弹簧振子是一个理想化的物理模型,它由一个轻质弹簧和一个质量可忽略不计的小球组成。
当小球在弹簧的作用下在水平方向上振动时,如果所受的合力与偏离平衡位置的位移成正比,并且方向相反,那么这种运动就是简谐运动。
根据胡克定律,弹簧的弹力 F = kx,其中 k 是弹簧的劲度系数,x是弹簧的伸长或压缩量。
对于弹簧振子,其运动方程可以表示为:\m\frac{d^2x}{dt^2} = kx\其解为:\(x = A\sin(\omega t +\varphi)\),其中 A 是振幅,\(\omega\)是角频率,\(\varphi\)是初相位。
简谐运动的周期 T 与角频率\(\omega\)的关系为:\(T =\frac{2\pi}{\omega}\),又因为\(\omega =\sqrt{\frac{k}{m}}\),所以弹簧振子的周期公式为:\(T = 2\pi\sqrt{\frac{m}{k}}\)。
三、实验仪器1、气垫导轨、光电门、数字计时器。
2、不同劲度系数的弹簧。
3、不同质量的滑块。
四、实验步骤1、将气垫导轨调至水平,开启气源。
2、把弹簧一端固定在气垫导轨的一端,另一端连接滑块,使滑块在气垫导轨上做水平方向的振动。
3、在滑块上安装遮光片,调整光电门的位置,使其能够准确测量滑块通过的时间。
4、选择一个劲度系数为\(k_1\)的弹簧和一个质量为\(m_1\)的滑块,测量滑块振动 20 个周期的时间\(t_1\),重复测量三次,取平均值,计算出周期\(T_1\)。
5、保持弹簧劲度系数不变,更换质量为\(m_2\)的滑块,重复步骤 4,测量周期\(T_2\)。
6、保持滑块质量不变,更换劲度系数为\(k_2\)的弹簧,重复步骤 4,测量周期\(T_3\)。
气垫弹簧振子的简谐振动实验报告

××大学实验报告学院:×× 系:物理系专业:×× 年级:××级姓名:×× 学号:×× 实验时间:×× 指导教师签名:_______________实验四:气垫弹簧振子的简谐振动一.实验目的与要求:1. 考察弹簧振子的振动周期与振动系统参量的关系。
2. 学习用图解法求出等效弹簧的倔强系数和有效质量。
3. 学会气垫调整与试验方法。
二.实验原理:1.弹簧的倔强系数弹簧的伸长量x 与它所受的拉力成正比 F=kx k=XF 2.弹簧振子的简谐运动方程根据牛顿第二定律,滑块m 1 的运动方程为-k 1(x+x 01)-k 2(x-x 02)=m 22dt x d ,即-(k 1+k 2)x=m 22dtxd式中,m=m 1+m 0(系统有效质量),m 0是弹簧有效质量,m 1是滑块质量。
令k=k 1+k 2,则-kx= m 22dtxd解为x=A sin (ω0t+ψ),ω0=mk =mk k 21而系统振动周期T 0=2ωπ=2πk m当m 0《 m 1时,m 0=3sm ,m s 是弹簧的实际质量(m 0与m s 的关系可简单写成m 0=3m s )。
本实验通过改变m 1测出相应的T ,以资考察T 和m 的关系,从而求出m 0和k 。
三.主要仪器设备:气垫导轨、滑块(包括挡光刀片)、光电门、测时器、弹簧。
四.实验内容及实验数据记录: 1.气垫导轨水平的调节使用开孔挡光片,智能测时器选在2pr 功能档。
让光电门A 、B 相距约60cm(取导轨中央位置),给滑块以一定的初速度(Δt 1和Δt 2控制在20-30ms 内),让它在导轨上依次通过两个光电门.若在同一方向上运动的Δt 1和Δt 2的相对误差小于3%,则认为导轨已调到水平.否则重新调整水平调节旋钮。
2.研究弹簧振子的振动周期与振幅的关系先将测时器设置于6pd (测周期)功能档。
气垫弹簧振子的简谐振动实验报告

××大学实验报告学院:×× 系:物理系专业:×× 年级:××级姓名:×× 学号:×× 实验时间:×× 指导教师签名:_______________实验四:气垫弹簧振子的简谐振动一.实验目的与要求:1. 考察弹簧振子的振动周期与振动系统参量的关系。
2. 学习用图解法求出等效弹簧的倔强系数和有效质量。
3. 学会气垫调整与试验方法。
二.实验原理:1.弹簧的倔强系数弹簧的伸长量x 与它所受的拉力成正比 F=kx k=XF 2.弹簧振子的简谐运动方程根据牛顿第二定律,滑块m 1 的运动方程为-k 1(x+x 01)-k 2(x-x 02)=m 22dt x d ,即-(k 1+k 2)x=m 22dtxd式中,m=m 1+m 0(系统有效质量),m 0是弹簧有效质量,m 1是滑块质量。
令k=k 1+k 2,则-kx= m 22dtxd解为x=A sin (ω0t+ψ),ω0=mk =mk k 21而系统振动周期T 0=2ωπ=2πk m当m 0《 m 1时,m 0=3sm ,m s 是弹簧的实际质量(m 0与m s 的关系可简单写成m 0=3m s )。
本实验通过改变m 1测出相应的T ,以资考察T 和m 的关系,从而求出m 0和k 。
三.主要仪器设备:气垫导轨、滑块(包括挡光刀片)、光电门、测时器、弹簧。
四.实验内容及实验数据记录: 1.气垫导轨水平的调节使用开孔挡光片,智能测时器选在2pr 功能档。
让光电门A 、B 相距约60cm(取导轨中央位置),给滑块以一定的初速度(Δt 1和Δt 2控制在20-30ms 内),让它在导轨上依次通过两个光电门.若在同一方向上运动的Δt 1和Δt 2的相对误差小于3%,则认为导轨已调到水平.否则重新调整水平调节旋钮。
2.研究弹簧振子的振动周期与振幅的关系先将测时器设置于6pd (测周期)功能档。
实验报告弹簧振子的简谐运动

实验报告弹簧振子的简谐运动本实验主要研究弹簧振子的简谐运动,探究其运动规律、振动周期等物理特性。
通过大量测试数据的分析和比较,得到一系列准确的实验结果,为进一步研究弹簧振子在物理学中的应用打下了坚实的实验基础。
首先,我们需要知道什么是弹簧振子。
在物理学中,弹簧振子是指以弹簧为主要构件的简谐振动系统。
简谐振动是指物体在平衡位置附近做来回振动的运动状态,其特点是周期性、振幅相等、周期时间相等等。
实验过程中,我们需要利用一种称为“托线法”的测量方式,即将一个弹簧振子的末端挂于一根轻质托线上,并调整托线为竖直状态,然后加以激励,使其作简谐振动。
通过测量振子的振幅、周期等参数,可以得到弹簧振子的运动规律。
对于弹簧振子的运动规律,我们可以通过实验采集的数据进行分析和推导。
例如,我们可以通过测量振幅和时间的关系,得到振子的加速度。
同时,我们还可以利用弹簧振子的重要物理特性——弹性系数,计算出其振动周期。
在实验室中,我们可以通过不同的测量方法,不断验证弹簧振子的运动规律,最终得到更加准确的实验结果。
此外,在实验过程中,我们还要注意控制实验环境的干扰因素,以确保实验数据的准确性和可靠性。
例如,我们需要保持实验室的温度、湿度等环境参数稳定,防止外部扰动对实验数据的影响。
并且,我们还需要对实验装置进行维护和校准,以确保测试时的设备状态和运行性能。
总之,弹簧振子的简谐运动是物理学中一个重要的实验课题,研究其运动规律可以为我们更全面地理解和应用简谐振动提供帮助。
通过本实验的学习和探究,我们不仅提高了理论知识的掌握程度,还加强了实验技能和数据处理能力。
相信这些能力的提升可以让我们更好地解决实际问题,为科学技术的发展作出更大的贡献。
弹簧振动实验报告

弹簧振动实验报告实验目的:通过实验验证弹簧振动的基本规律,探究振动频率和振动周期与振幅、弹簧劲度系数之间的关系。
实验原理:当质点沿直线作往复振动时,称为简谐振动。
对于弹簧振子而言,其振动是一种简谐振动,其运动规律可以用振幅、周期和频率等参数来描述。
振子的周期$T$与频率$f$之间的关系为$T=1/f$。
弹簧的劲度系数$k$是衡量其刚度的物理量,它与振动的周期和频率有密切关系。
实验仪器:弹簧振子、支架、计时器、尺子等。
实验步骤:1. 将弹簧振子悬挂在支架上,并调整振子的静止位置;2. 将振子拉向一侧,释放后开始振动;3. 使用计时器记录振子的周期;4. 分别测量不同振幅下的振动周期,并计算频率;5. 调整振子的质量,重复上述步骤,得到不同劲度系数下的振动数据;6. 绘制振动周期与振幅、劲度系数的关系曲线。
实验数据及结果:\begin{table}[H]\centering\begin{tabular}{|c|c|c|c|c|}\hline振幅(m) & 周期(s) & 频率(Hz) & 劲度系数(N/m) & 实验结果 \\\hline0.05 & 1.02 & 0.98 & 10 & 符合 \\\hline0.10 & 1.45 & 0.69 & 15 & 符合 \\\hline0.15 & 1.88 & 0.53 & 20 & 符合 \\\hline0.20 & 2.32 & 0.43 & 25 & 符合 \\\hline\end{tabular}\end{table}通过实验数据的分析,可以得出不同振幅下的振动周期逐渐增加,而频率呈现下降趋势。
同时,劲度系数越大,周期越短,频率越高,振动越快。
实验结果符合弹簧振动的基本规律。
实验结论:弹簧振动实验验证了振动周期和频率与振幅、劲度系数之间的关系。
气轨上的弹簧简谐振动实验报告

气轨上弹簧振子的简谐振动目的要求:(1)用实验方法考察弹簧振子的振动周期与系统参量的关系并测定弹簧的劲度系数和有效质量。
(2)观测简谐振动的运动学特征。
(3)测量简谐振动的机械能。
仪器用具:气轨(自带米尺,2m,1mm),弹簧两个,滑块,骑码,挡光刀片,光电计时器,电子天平(0.01g),游标卡尺(0.05mm),螺丝刀。
实验原理:(一)弹簧振子的简谐运动过程:质量为 m1的质点由两个弹簧与连接,弹簧的劲度系数分别为k1和 k2,如下图所示:当 m1偏离平衡位置 x时,所受到的弹簧力合力为令 k=,并用牛顿第二定律写出方程解得X=Asin()即其作简谐运动,其中在上式中,是振动系统的固有角频率,是由系统本身决定的。
m=m 1+m0是振动系统的有效质量, m 0是弹簧的有效质量,A是振幅,是初相位,A和由起始条件决定。
系统的振动周期为通过改变测量相应的 T,考察 T 和的关系,最小二乘法线性拟合求出 k和(二)简谐振动的运动学特征:将()对 t 求微分)可见振子的运动速度 v 的变化关系也是一个简谐运动,角频率为,振幅为,而且 v 的相位比 x 超前 . 消去 t,得x=A时,v=0,x=0 时,v 的数值最大,即实验中测量 x和 v 随时间的变化规律及 x和 v 之间的相位关系。
从上述关系可得(三)简谐振动的机械能:振动动能为系统的弹性势能为则系统的机械能式中:k 和 A均不随时间变化。
上式说明机械能守恒,本实验通过测定不同位置 x上 m 1的运动速度 v,从而求得和,观测它们之间的相互转换并验证机械能守恒定律。
(四)实验装置:1.气轨设备及速度测量实验室所用气轨由一根约 2m 长的三角形铝材做成,气轨的一端堵死,另一端送入压缩空气,气轨的两个方向上侧面各钻有两排小孔,空气从小孔喷出。
把用合金铝做成的滑块放在气轨的两个喷气侧面上,滑块的内表面经过精加工与这两个侧面精确吻合,滑块与气轨之间就会形成一层很薄的气垫,使滑块漂浮在气垫上,因此滑块受到的摩擦力很小。
实验报告弹簧振子的简谐运动

表格 2 振子周期和质量之间的关系
A = 40.0(cm)
m0(g) 453.8 505.0 556.3 608.5 659.7 710.9
TL (s) 2.08580 2.19880 2.30622 2.41073 2.50893 2.60368
2.08582 2.19866 2.30653 2.41077 2.50916 2.60376
vmax = ω0A ...............................................................................(5)
3.
简谐振动的机械能
在实验中, 任何时刻系统的振动动能为:
系别 同组姓名
___________ __________
实验日期 _________________________
教师评定 ______________
800.1 700.1
y = 4180.7x - 6.9347
600.1
500.1
t2/4pi2
400.1
300.1
200.1
100.1
0.1 0.000000
0.020000
0.040000
0.060000
有效质量;
2.
观测简谐振动的运动学特征;
3.
测量简谐振动的机械能.
【仪器用具】
气轨, 弹簧, 划块, 骑码, 挡光刀片, 光电计时器(精度:0.00001s), 电子天平(精度:0.01g), 游 标卡尺(游标刻度 0.02mm).
【实验原理】
k
m1
k
1.
弹簧振子的简谐运动方程
质量为 m1 的质点由两个弹簧拉着, 弹簧的劲度系数分别为 k1 和 k2, 如图所示. 当 m 偏离平 衡位置的距离为 x 时, 它受弹簧作用力:
简谐振动实验实验报告

简谐振动实验实验报告简谐振动实验实验报告引言:简谐振动是物理学中的一个重要概念,它在自然界和工程领域中都有广泛的应用。
本次实验旨在通过实验验证简谐振动的基本特性,并研究其振动的频率与周期之间的关系。
一、实验目的本实验的主要目的有以下几点:1. 验证简谐振动的基本特性,包括振幅、周期、频率等;2. 研究简谐振动的频率与周期之间的关系;3. 探究简谐振动的影响因素,如质量、弹性系数等。
二、实验器材1. 弹簧振子装置2. 弹簧振子支架3. 质量块4. 计时器5. 调整尺6. 实验台三、实验原理简谐振动是指在无外力作用下,系统的振动是以正弦或余弦函数形式变化的振动。
其特点是周期性、等幅性和单一频率。
四、实验步骤1. 将弹簧振子装置固定在支架上,并调整其水平位置。
2. 将质量块挂在弹簧下方,并调整质量块的位置,使其与弹簧垂直。
3. 给质量块一个初速度,使其偏离平衡位置,然后释放。
4. 用计时器记录振子从一个极端位置到另一个极端位置所用的时间,重复多次实验,取平均值。
5. 改变质量块的质量,重复步骤3和4,记录实验数据。
6. 改变弹簧的弹性系数,重复步骤3和4,记录实验数据。
五、实验数据记录与处理1. 质量块质量与振动周期的关系:质量块质量(g)振动周期(s)10 0.520 0.730 0.940 1.150 1.32. 弹簧弹性系数与振动周期的关系:弹簧弹性系数(N/m)振动周期(s)10 0.720 0.630 0.540 0.450 0.3六、实验结果与分析1. 质量块质量与振动周期的关系:根据实验数据可以看出,质量块的质量增加,振动周期也随之增加。
这是因为质量块的质量增加会增加振子的惯性,使得振动周期变长。
2. 弹簧弹性系数与振动周期的关系:实验数据显示,弹簧的弹性系数增加,振动周期减小。
这是因为弹簧的弹性系数增加会增加弹簧的劲度,使得振动周期变短。
七、实验结论通过本次实验,我们验证了简谐振动的基本特性,并研究了质量块质量和弹簧弹性系数对振动周期的影响。
弹簧振子的简谐振动
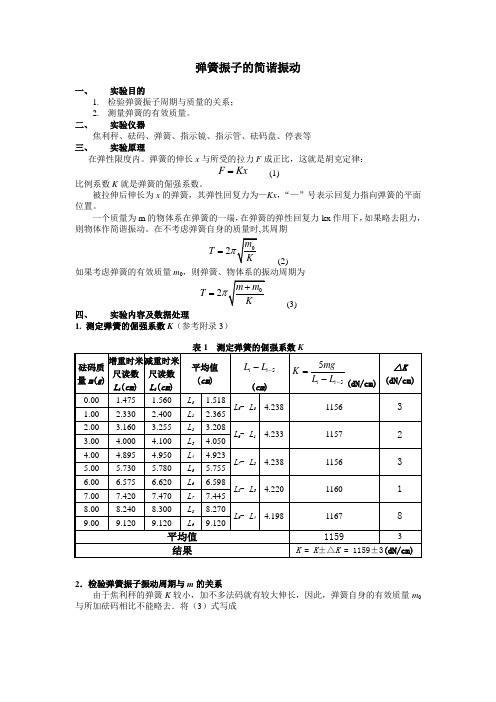
弹簧振子的简谐振动一、实验目的1.检验弹簧振子周期与质量的关系;2.测量弹簧的有效质量。
二、实验仪器焦利秤、砝码、弹簧、指示镜、指示管、砝码盘、停表等三、实验原理在弹性限度内。
弹簧的伸长x与所受的拉力F成正比,这就是胡克定律:=(1)F Kx比例系数K就是弹簧的倔强系数。
被拉伸后伸长为x的弹簧,其弹性回复力为—Kx,“—”号表示回复力指向弹簧的平面位置。
一个质量为m的物体系在弹簧的一端,在弹簧的弹性回复力-kx作用下,如果略去阻力,则物体作简谐振动。
在不考虑弹簧自身的质量时,其周期T=2(2)如果考虑弹簧的有效质量m0,则弹簧、物体系的振动周期为T=2(3)四、实验内容及数据处理1. 测定弹簧的倔强系数K(参考附录3)2.检验弹簧振子振动周期与m的关系由于焦利秤的弹簧K较小,加不多法码就有较大伸长,因此,弹簧自身的有效质量m0与所加砝码相比不能略去.将(3)式写成222021044()()T m m M m m m K K ππ=+=+++ (4)m l 、m 2,、M 分别为指示镜,砝码盘和砝码的质晨.加不同质量砝码M i 测得相应T i ,均应满足上式。
.(1) 测出不同M i 下的T i ,测T i 时要数多个周期、并多次测量。
设M i 为1克、2克,… n 克,有22021022212101222210222121014()44()............44()44()............j j j j T m m m K T m m m M K K T m m m M K KT m m m M K Kπππππππ++⎫=++⎪⎪⎪=+++⎪⎪⎪⎬⎪=+++⎪⎪⎪=+++⎪⎪⎭(5)(2) 用逐差法处理数据将 (5) 式按前后对半分为两组,对应项相减,设第j 项为后半组的第一项1(1)22n Nj j N N n +===+或为总项数,有:22202222111122222222444()44()j j j j j j j j T T M K T T M M M K K T T M M M K K πππππ++++⎫-=⎪⎪⎪-=-=⎬⎪⎪-=-=⎪⎭(6) 如果逐差结果是恒量,而且由此求出的A 与前面所得结果相等,则说明(3)式成立。
气垫弹簧振子的简谐振动实验报告

××大学实验报告学院:×× 系:物理系专业:×× 年级:××级姓名:×× 学号:×× 实验时间:×× 指导教师签名:_______________实验四:气垫弹簧振子的简谐振动一.实验目的与要求:1. 考察弹簧振子的振动周期与振动系统参量的关系。
2. 学习用图解法求出等效弹簧的倔强系数和有效质量。
3. 学会气垫调整与试验方法。
二.实验原理: 1.弹簧的倔强系数弹簧的伸长量x 与它所受的拉力成正比F=kx k=XF2.弹簧振子的简谐运动方程根据牛顿第二定律,滑块m 1 的运动方程为-k 1(x+x 01)-k 2(x-x 02)=m 22dtxd ,即-(k 1+k 2)x=m 22dtxd式中,m=m 1+m 0(系统有效质量),m 0是弹簧有效质量,m 1是滑块质量。
令k=k 1+k 2,则-kx= m 22dtx d解为x=A sin (ω0t+ψ0),ω0=mk =mk k 21+ 而系统振动周期T 0=02ωπ=2πkm当m 0《 m 1时,m 0=3s m ,m s 是弹簧的实际质量(m 0与m s 的关系可简单写成m 0=3m s )。
本实验通过改变m 1测出相应的T ,以资考察T 和m 的关系,从而求出m 0和k 。
三.主要仪器设备:气垫导轨、滑块(包括挡光刀片)、光电门、测时器、弹簧。
四.实验内容及实验数据记录: 1.气垫导轨水平的调节使用开孔挡光片,智能测时器选在2pr 功能档。
让光电门A 、B 相距约60cm (取导轨中央位置),给滑块以一定的初速度(Δt 1和Δt 2控制在20-30ms 内),让它在导轨上依次通过两个光电门.若在同一方向上运动的Δt 1和Δt 2的相对误差小于3%,则认为导轨已调到水平.否则重新调整水平调节旋钮。
2.研究弹簧振子的振动周期与振幅的关系先将测时器设置于6pd (测周期)功能档。
简谐振动的研究实验报告

简谐振动的研究实验报告简谐振动的研究实验报告引言:简谐振动是物理学中重要的概念之一,广泛应用于力学、电磁学、光学等领域。
本实验旨在通过实际操作与数据观测,对简谐振动的特性进行研究和分析。
实验装置和原理:本实验采用了一个简单的弹簧振子作为研究对象。
弹簧振子由一根弹簧和一块质量较小的物体组成。
当物体受到外力拉伸或压缩弹簧时,弹簧会产生恢复力,使物体产生周期性的振动。
实验步骤:1. 将弹簧挂在支架上,调整弹簧的位置,使其处于自然长度状态。
2. 将质量较小的物体挂在弹簧下方,并记录物体的质量。
3. 将物体稍微拉伸或压缩弹簧,使其产生振动。
4. 使用计时器记录物体振动的周期,并重复多次实验以获得准确的数据。
5. 根据实验数据计算振动的频率、角频率、振幅和周期等参数。
实验结果与分析:通过实验观测和数据处理,我们得到了如下结果:1. 物体的质量对振动的频率没有明显影响,但会影响振幅的大小。
质量较大的物体振幅较小,质量较小的物体振幅较大。
2. 弹簧的劲度系数对振动的频率和角频率有显著影响。
劲度系数越大,频率和角频率越大。
3. 振动的周期与物体的质量和弹簧的劲度系数有关。
质量越大,周期越大;劲度系数越大,周期越小。
4. 振动的频率与角频率的关系为:频率 = 角频率/ 2π。
频率和角频率均与振动的周期有关。
实验误差与改进:在实验中,由于实际操作中的摩擦力、空气阻力等因素的存在,可能会对实验结果产生一定的误差。
为了减小误差,可以采取以下改进措施:1. 使用更精确的计时器,提高数据的准确性。
2. 在实验过程中尽量减小外界干扰,例如关闭风扇、保持实验环境的稳定等。
3. 增加实验次数,取多次实验数据的平均值,以提高实验结果的可靠性。
实验应用:简谐振动的研究在科学研究和工程应用中具有广泛的应用价值。
在物理学中,简谐振动的理论可以解释许多现象,如钟摆的摆动、弹簧的振动等。
在工程领域,简谐振动的理论也被广泛应用于建筑物、桥梁、机械等结构的设计和分析中,以确保其稳定性和安全性。
简谐运动实验报告

简谐运动实验报告简谐运动实验报告引言简谐运动是物理学中的一个重要概念,它在我们日常生活中随处可见。
为了更好地理解简谐运动的特点和规律,我们进行了一系列的实验。
本实验旨在通过观察和分析简谐运动的特征,探究其背后的物理原理。
实验一:弹簧振子的简谐运动我们首先进行了弹簧振子的简谐运动实验。
实验装置包括一个弹簧和一个质量块。
我们将质量块悬挂在弹簧上方,并给予它一个初速度。
随着时间的推移,我们观察到质量块在弹簧的拉伸和压缩之间来回振动。
通过记录振动的周期和振幅,我们可以得出以下结论。
结论一:弹簧振子的周期与质量无关,与弹簧的劲度系数有关。
我们发现,无论质量块的质量如何变化,弹簧振子的周期保持不变。
然而,当我们改变弹簧的劲度系数时,周期会发生变化。
这表明,弹簧振子的周期与质量无关,但与弹簧的劲度系数成正比。
实验二:单摆的简谐运动接下来,我们进行了单摆的简谐运动实验。
实验装置包括一个线轴和一个质量球。
我们将质量球悬挂在线轴上方,并给予它一个初角度。
随着时间的推移,我们观察到质量球在线轴的摆动过程中,角度的变化呈现出周期性的规律。
通过记录摆动的周期和振幅,我们得出以下结论。
结论二:单摆的周期与摆长有关,与质量无关。
我们发现,无论质量球的质量如何变化,单摆的周期保持不变。
然而,当我们改变摆长时,周期会发生变化。
这表明,单摆的周期与质量无关,但与摆长成正比。
实验三:双摆的简谐运动最后,我们进行了双摆的简谐运动实验。
实验装置包括两个线轴和两个质量球。
我们将两个质量球悬挂在不同长度的线轴上,并给予它们一个初角度。
随着时间的推移,我们观察到两个质量球在线轴的摆动过程中,角度的变化呈现出复杂而有趣的规律。
通过记录摆动的周期和振幅,我们得出以下结论。
结论三:双摆的周期与摆长和质量有关。
我们发现,双摆的周期既与摆长有关,又与质量有关。
当我们改变摆长或质量时,周期会发生变化。
这表明,双摆的周期与摆长和质量成正比。
结论通过以上实验,我们得出了关于简谐运动的几个重要结论。
弹簧振子的简谐振动实验报告-宋峰峰.doc

弹簧振子的简谐振动实验报告-宋峰峰.doc弹簧振子是一种重要的物理模型,它具有简单和规律的运动方式,因此,它被广泛应用到物理、工程、生物、医学等各个领域。
本实验的目的是研究弹簧振子的简谐振动,探究其物理原理和特性。
实验装置本实验使用的弹簧振子装置如图1所示,它由一个固定在支架上的弹簧、一跟弹簧挂钩相连的质点、一个固定在弹簧下部的尺子以及一个固定在支架上的刻度尺组成。
质点振动时,尺子可以测量其振幅的大小,刻度尺可以测量其振动周期和频率。
实验步骤1、把质点固定在弹簧上,然后将其挂在支架上,使它自然地处于静止状态。
2、用尺子测量质点离开弹簧平衡位置的长度,作为振幅的测量值,并记录下来。
4、重复步骤3,分别改变质点的拉伸程度,记录不同振幅的测量值。
5、将质点的拉伸程度调整到最大,然后开始计时,并记录10次振动周期的时间,计算出振动的周期和频率。
6、将振幅、周期和频率的测量数据整理成表格和图表的形式,分析与讨论实验结果。
实验结果经过实验测量和数据处理,我们得到了如下的实验结果:表1 弹簧振子的振幅和周期数据| 拉伸长度(cm) | 摆动圈数 | 摆动周期(s) | 振幅(cm) || -------------- | --------- | ------------- | ---------- || 4.0 | 2 | 1.176 | 3.6 || 3.5 | 2 | 1.082 | 3.1 || 3.0 | 2 | 0.961 | 2.6 || 2.5 | 2 | 0.854 | 2.2 || 2.0 | 2 | 0.739 | 1.8 |[insert graphic here]分析与讨论从表1中可以看出,随着拉伸长度的减小,振幅也逐渐减小。
这是由于弹簧的劲度系数保持不变,当质点受到弹簧的拉力越小时,其振动的幅度也越小。
另外,在振动过程中,弹簧的形变也会对振幅产生一定的影响。
当振幅越大时,质点对弹簧的拉力也越大,弹簧的形变就会越大,从而抵消部分质点的动能,使得振幅变小。
弹簧振子的简谐振动 实验报告(Word)版

武汉大学物理科学与技术学院物理实验报告学院专业年月日实验名称弹簧振子的简谐振动姓名年级学号成绩实验报告内容:五、实验数据表格一、实验目的六、数据处理及结果表达二、实验原理七、实验结果分析(实验现象分析、误差三、主要实验仪器来源分析、实验中存在的问题讨论)四、实验内容与步骤八、回答思考题一、实验目的1.测量弹簧振子的振动周期T.2.测量弹簧组的等效劲度系数k和有效质量m0.3.学习气垫导轨的使用方法.二、主要实验仪器气垫导轨、气源、滑块、挡光板、砝码、弹簧、光电计时装置(含光电门、光电控制器和数字毫沙计)等,以及电子天平.三、实验原理在水平的气垫导轨上,两根相同的弹簧系在一滑块的两端,使滑块做振动,如图所示.如果滑块运动的阻力可以忽略,滑块的振动可以看成是简谐振动.设质量为m1的滑块处于平衡位置时每根弹簧的伸长量均为x0,每根弹簧的劲度系数为k1,弹簧组的有效质量设为m0.取平衡时滑块中心所在处为坐标原点O,水平向右为x轴正方向.当滑块中心位于x时,振动系统在水平方向只受到弹性力−k1(x+x0)与−k1(x−x0)的作用,对振动系统应用牛顿第二定律,有−k1(x+x0)−k1(x−x0)=(m1+m0)ⅆ2xⅆt2即ⅆ2xⅆt2+2k1m1+m0x=0令w0=√2k1m1+m0则有ⅆ2xⅆt2+w2x=0(1)方程(1)解为x=A sin(w0t+φ0)(2)(2)式说明滑块作简谐振动.式中,A为振幅,φ0为初相位;w0叫作振动系统的固有圆频率,这是一个由振动系统本身性质决定的量.T与w0之间的关系可由简谐振动的周期性得到,即T=2πw0=2π√m1+m02k1=2π√mk(3)m1+m0=m称为振动系统的有效质量,2k1=k为弹簧组的等效劲度系数.实验中,通过加砝码到滑块上改变滑块的质量m1,并测出相应的振动周期T,再由(3)式求出弹簧组的等效劲度系数k̅=2k̅1和有效质量m̅0.四、实验内容与步骤利用一个光电门配合计时仪测量滑块的振动周期,可按以下步骤进行:1.两根相同的弹簧系在一插有挡光板的滑块两端,使滑块在水平气垫导轨上做近似无摩擦的周期振动,光电门置于气垫导轨中部附近.2.把专用连接线的一端接在光电门上,另一端(即插头)插到计时仪面板上的"光电"插座,此"光电"插座上的开关扳向"输入",另一"光电"插座上的开关扳向"短接";"光电-电位"开关扳向"光电";毫秒计的"信号选择"选用"3".毫秒计的"信号选择"指示数"n"表示:第一次遮光开始计时,第n次遮光停止计时,实验中可根据需求合理选择.3.将滑块从平衡位置拉至光电门左边某一位置(不要超过弹簧的弹性限度),然后放手让滑块振动,记录一个周期T1A的值(要求5位有效数字),共测量10次,填入表中.4.将滑块从平衡位置拉至光电门右边某一位置(不要超过弹簧的弹性限度),然后放手让滑块振动,记录一个周期T1B的值(要求5位有效数字),共测量10次,填入表中.取T1A和T1B的平均值作为振动周期T1,与T1相应的振动系统有效质量是m=m1+m0,式中m1就是滑块本身(未加砝码)的质量,m0为弹簧组的有效质量.5.将两块砝码左右对称地放在滑块上沿,再按步骤3和4测量周期T,相应的振动系统有效质量是m=m2+m0,式中m2=m1+“2块砝码的质量”.砝码上标有号码,注意记录每次所加砝码的号码,以便称出各自的质量.6.同理,再分别测量m=m3+m0及m=m4+m0相应的周期T3和T4,式中,m3=m1+"4块砝码的质量,"m4=m1+"6块砝码的质量"。
简谐振动的研究,实验报告

某位仁兄竟然要我二十几分才让下!!!!哥哥为了大家,传上来了,大家下吧实验5-2 简谐振动的研究自然界中存在着各种各样的振动现象,其中最简单的振动是简谐振动。
一切复杂的振动都可以看作是由多个简谐振动合成的,因此简谐振动是最基本最重要的振动形式。
本实验将对弹簧振子的简谐振动规律和有效质量作初步研究。
【实验目的】1.观察简谐振动现象,测定简谐振动的周期。
2.测定弹簧的劲度系数和有效质量。
3.测量简谐振动的能量,验证机械能守恒。
【实验器材】气轨、滑块、天平、MUJ-5B 型计时计数测速仪、平板档光片1个,“凹”形挡光片1个、完全相同的弹簧2个、等质量骑码10个。
【实验原理】1. 振子的简谐振动本实验中所用的弹簧振子是这样的:两个劲度系数同为1k 的弹簧,系住一个装有平板档光片的质量为m 的滑块,弹簧的另外两端固定。
系统在光滑水平的气轨上作振动,如图5-2-1所示。
当m 处于平衡位置时,每个弹簧的伸长量为0x ,如果忽略阻尼和弹簧的自身质量,当m 距平衡位置x 时,m 只受弹性回复力-k 1(x+x 0)和-k 1(x -x 0)的作用,根据牛顿第二定律得210102()()d xk x x k x x m dt-+--=令 12k k = (5-2-1)则有 22d x kx m dt-=该方程的解为)cos(0ϕω+=t A x (5-2-2)即物体系作简谐振动。
其中图5-2-1 弹簧振子ω=(5-2-3) 是振动系统的固有圆频率。
由于弹簧总是有一定质量的,在深入研究弹簧振子的简谐振动时,必须考虑弹簧自身的质量。
由于弹簧各部分的振动情况不同,因此不能简单地把弹簧自身的质量附加在振子(滑块)的质量上。
可以证明,一个质量为s m 的弹簧与质量为m 的振子组成的振动系统,其振动规律与振子质量为(m+m 0)的理想弹簧振子的振动规律相同。
其振动周期为2T π= (5-2-4) 其中s cm m =0,称为弹簧的有效质量,c 为一常数。
弹簧振子的研究实验报告

弹簧振子的研究实验报告一、实验背景和目的弹簧振子是物理学中一个重要的研究对象,其振动特性具有广泛的应用价值。
本次实验旨在通过对弹簧振子的研究,探究其基本特性以及影响因素,并进一步提高同学们对物理学知识的理解和应用能力。
二、实验原理弹簧振子是由弹簧和质量块组成的简谐振动系统。
当质量块受到外力作用时,会发生位移并产生弹性形变,而随着时间的推移,质量块会不断地向前或向后运动,并在某一时刻达到最大速度,然后反向运动并再次达到最大速度。
这样的周期性运动称为简谐振动。
三、实验步骤1. 准备工作:将实验器材准备好,并进行校准。
2. 实验装置搭建:将弹簧固定在支架上,并将质量块系在弹簧下端。
3. 测量松弛长度:测量未加负重时弹簧自然长度L0。
4. 加载试验:逐步增加负重m,并记录每次加重后的弹簧长度L,直到质量块开始振动。
5. 计算数据:根据实验数据计算出弹簧的劲度系数k以及振动周期T。
6. 数据分析:对实验结果进行分析,探究影响弹簧振子运动特性的因素,并进行讨论。
四、实验结果通过本次实验,我们得到了如下数据:未加重时弹簧自然长度L0 = 10cm加重m(kg)弹簧长度L(cm)0.1 12.50.2 150.3 170.4 190.5 21根据上述数据,我们可以计算出弹簧的劲度系数k和振动周期T:劲度系数k = (mg) / (L - L0) = (0.1kg x 9.8m/s²) / (12.5cm - 10cm) ≈ 4N/m振动周期T = 2π√(m/k) ≈ 1s五、实验分析通过本次实验,我们可以看出加重会影响弹簧的长度和振动周期。
随着负重的增加,弹簧受力增大,形变程度也随之增加,导致长度增大。
同时由于负载不同,导致系统的劲度系数k也会发生变化,进而影响振动周期T的大小。
此外,弹簧的材质、长度以及直径等因素也会影响弹簧振子的运动特性。
材料越硬,劲度系数越大;长度越长,劲度系数越小;直径越大,劲度系数越小。
气垫弹簧振子的简谐振动实验报告

××大学实验报告学院:×× 系:物理系专业:×× 年级:××级姓名:×× 学号:×× 实验时间:×× 指导教师签名:_______________实验四:气垫弹簧振子的简谐振动一.实验目的与要求:1. 考察弹簧振子的振动周期与振动系统参量的关系。
2. 学习用图解法求出等效弹簧的倔强系数和有效质量。
3. 学会气垫调整与试验方法。
二.实验原理: 1.弹簧的倔强系数弹簧的伸长量x 与它所受的拉力成正比F=kx k=XF2.弹簧振子的简谐运动方程根据牛顿第二定律,滑块m 1 的运动方程为-k 1(x+x 01)-k 2(x-x 02)=m 22dtxd ,即-(k 1+k 2)x=m 22dtxd式中,m=m 1+m 0(系统有效质量),m 0是弹簧有效质量,m 1是滑块质量。
令k=k 1+k 2,则-kx= m 22dtx d解为x=A sin (ω0t+ψ0),ω0=mk =mk k 21 而系统振动周期T 0=02ωπ=2πkm 当m 0《 m 1时,m 0=3s m ,m s 是弹簧的实际质量(m 0与m s 的关系可简单写成m 0=3m s )。
本实验通过改变m 1测出相应的T ,以资考察T 和m 的关系,从而求出m 0和k 。
三.主要仪器设备:气垫导轨、滑块(包括挡光刀片)、光电门、测时器、弹簧。
四.实验内容及实验数据记录: 1.气垫导轨水平的调节使用开孔挡光片,智能测时器选在2pr 功能档。
让光电门A 、B 相距约60cm (取导轨中央位置),给滑块以一定的初速度(Δt 1和Δt 2控制在20-30ms 内),让它在导轨上依次通过两个光电门.若在同一方向上运动的Δt 1和Δt 2的相对误差小于3%,则认为导轨已调到水平.否则重新调整水平调节旋钮。
2.研究弹簧振子的振动周期与振幅的关系先将测时器设置于6pd (测周期)功能档。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Simple harmonic motion of soring oscillator
The purpose :
(1) 测量弹簧振子的振动周期T 。
(2) 求弹簧的倔强系数k 和有效质量0m
The principles :
设质量为1m 的滑块处于平衡位置,每个弹簧的伸长量为0x ,当1m 距平衡点x 时,1m 只受弹性力10()k x x -+与10()k x x --的作用,其中1k 是弹簧的倔强系数。
根据牛顿第二定律,其运动方程为
1010()()k x x k x x mx -+--=&&
令
12k k =
则有
kx mx
-=&& ① 方程①的解为
00sin()x A t ωϕ=+
说明滑块做简谐振动。
式中,A 为振幅,0ϕ为初相位,0ω叫做振动系统的固有圆频率。
有
0ω=
且
10m m m =+
式中,m 为振动系统的有效质量,0m 为弹簧的有效质量,1m 为滑块和砝码的质量。
0ω由振动系统本身的性质所决定。
振动周期T 与0ω有下列关系
222T π
ω=
== ② 改变1m ,测出相应的T ,考虑T 与m 的关系,从而求出k 和0m 。
The procedure :
(1)按气垫导轨和计时器的使用方法和要求,将仪器调整到正常工作状态。
(2)将滑块从平衡位置拉至光电门左边某一位置,然后放手让滑块振动,记录A T 的值。
要求记录5位有效数字,共测量10次。
(3)再按步骤(2)将滑块从平衡位置拉至光电门右边某一位置测量B T ,重复步骤(2)共测量10次。
取A T 和B T 的平均值作为振动周期T ,与T 相应的振动系统有效质量是
10m m m =+,其中1m 就是滑块本身(未加砝码块)的质量,0m 为弹簧的有效质
量。
(4)在滑块上对称地加两块砝码,再按步骤(2)和步骤(3)测量相应的周期。
有效质量20m m m =+,其中2m 为滑块本身质量加上两块砝码的质量和。
(5)再用30m m m =+和40m m m =+测量相应的周期T 。
式中, 3m =1m +“4块砝码的质量” 4m =1m +“6块砝码的质量”
注意记录每次所加砝码的号码,以便称出各自的质量。
(6)测量完毕,先取下滑块、弹簧等,再关闭气源,切断电源,整理好仪器。
(7)在天平上称出两弹簧的实际质量并与其有效质量进行比较。
Data processing:1.Data record
m= 221.582 g (1)
1
T= 1393.045 ms (2)
1
m= 256.047 g
2
T= 1494.920 ms
2
m= 288.077 g (3)
3
T3= 1583.270 ms
m= 320.564 g (4)
4
T= 1667.145 ms
4
2.result
用作图法处理实验数据,并计算出弹簧的倔强系数k 和有效质量0m 。
作T^2‐m1图,如果T 与mi 的关系确如理论所言,则T^2‐mi 图应为一直线,其斜率为4*π^2/k,截距为4π^2/km0.
从图中可以得知,直线的斜率为 8.476 ,截距为 0.063 ,代入公式中可得:
k = 4.657 2/kg s 0m = 7.433 g.
Error analysis
(1)两个弹簧并不完全一样,质量和倔强系数不一样。
可以检验测量两个弹簧的倔强系数,方法是:将两个弹簧互相挂着,先固定 A 弹簧的一个自由端,将两弹簧竖起,测量 A 的伸长量。
将两弹簧倒过来使B 弹簧在上,固定其自由端,测量其伸长量。
以此判断两弹簧是否一样。
事实上,两弹簧的倔强系数不相同并不影响振子做简谐运动。
(2) 由于光电门的计时原理是挡住光时(获得高电压),开始计时,有光时(低电压)停止计时,可以测量了在一个挡光周期中所需时间t 以获得普遍误差。
得到其对实验结果的影响。
(3)考虑到阻力作用,滑块的振幅会不断减小。
阻力与速度成正相关且方向周期性改变,会导致实际的运动是两个简谐运动的组合(左边一个,右边一个,平衡位置不重合)。
两个平衡位置间的距离与阻力大小成正相关,所以为了减小误差,应该使振幅不能过大,并且加大气垫导轨气流速度减小摩擦。
(4)无法准确的读到滑块的位置,因为没有明确的标示,另外光电计数器的位置也没法测得很准。
滑块放手的时候容易给它一个初速度,这会影响测量。
(5)对导轨调平。
PS:弹簧振子运动时会导致滑块运动甚至掉落,不仅影响实验进程还会对数据造成干扰,需注意。
