luttinger kohn 哈密顿矩阵
哈密尔顿图的充分必要条件(精品)

哈密尔顿图的充分必要条件摘要图论在现实生活中有着较为广泛的应用, 到目前为止,哈密尔顿图的非平凡充分必要条件尚不清楚,事实上,这是图论中还没解决的主要问题之一,但哈密尔顿图在实际问题中,应用又非常广泛,因此哈密尔顿图一直受到图论界以及运筹学学科研究人员的大力关注.关键词:哈密尔顿图;必要条件;充分条件;1 引言 (3)2 哈密尔顿图的背景 (3)3 哈密尔顿图的概念 (4)4 哈密顿图的定义 (5)4.1定义 (5)4.2定义 (5)4.3哈密顿路是遍历图的所有点。
(6)4 哈密尔顿图的充分条件和必要条件的讨论 (7)5 结论 (8)参考文献 (8)指导老师 (9)1 引言图论是一门既古老又年轻的学科,随着科学技术的蓬勃发展,它的应用已经渗透到自然科学以及社会科学的各个领域之中,利用它我们可以解决很多实际生活中的问题,给你一个图,你怎么知道它是否是哈密尔顿图呢?当然如果图的顶点不多,你可以用最古老的”尝试和错误”的方法试试找哈密尔顿回路就可以解决和判断.但是,数学家们并不满足这样的碰得焦头烂额后才找到的真理方法.是否存在一组必要和充分的条件,使得我们能够简单轻易地判断一个图是否是哈密尔顿图?有许多智者通过各种方式去尝试过了,遗憾的是至今尚未找到一个判别哈密尔顿回路和通路的充分必要条件.虽然有些充分非必要或必要非充分条件,但大部分还是采用尝试的办法,不过这些条件也是非常有用的.2 哈密尔顿图的背景美国图论数学家奥在1960年给出了一个图是哈密尔顿图的充分条件:对于顶点个数大于2的图,如果图中任意两点度的和大于或等于顶点总数,那这个图一定是哈密尔顿图。
闭合的哈密顿路径称作哈密顿圈,含有图中所有顶的路径称作哈密顿路径.1857年,哈密尔顿发明了一个游戏(Icosian Game).它是由一个木制的正十二面体构成,在它的每个棱角处标有当时很有名的城市。
游戏目的是“环球旅行”。
为了容易记住被旅游过的城市,在每个棱角上放上一个钉子,再用一根线绕在那些旅游过的城市上(钉子),由此可以获得旅程的直观表示(如图1)。
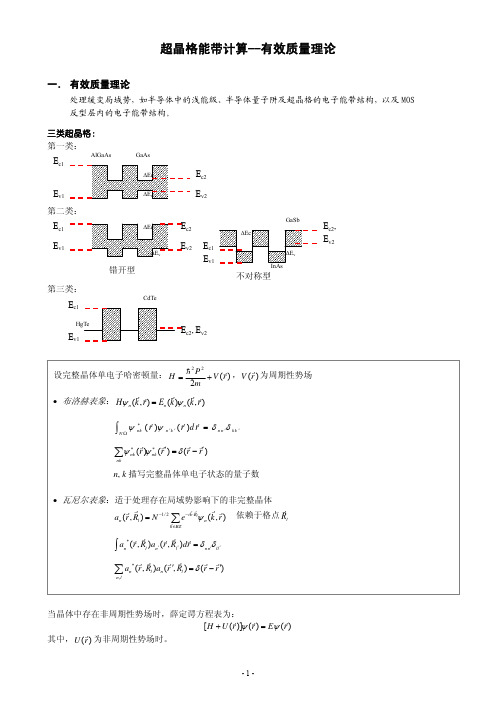
超晶格能带计算 有效质量理论
+
∂2 ∂y 2
+
∂2 ∂z 2
)
其中,m*是电子有效质量(导带底附近是各项同性的),假设了能量极值点在Γ点(
r k0
=
0 )。
有效质量方程为:
⎢⎡− ⎣
h2 2m∗
∂2 ( ∂x2
+
∂2 ∂y 2
+
∂2 ∂z 2
)
+
U
(rr)⎥⎤ ⎦
F
(rr
)
= [E
−
En (0)]F (rr)
波函数:
ψ (rr) = F (rr)unk0 (rr) = F (rr)usk0 (rr)
= 0 , ki2
=
2mi h2
(E −Vi )
其解的形式是沿 z 轴正负两个方向平面波的叠加:
-∞ ≤
z
<
z1: G0
=
A eik0 ( z−z1) 0
+
B e −ik0 ( z−z1) 0
z1 ≤ z < z2: ……
G = A e + B e ik1(z−z1)
−ik1( z−z1)
1
1
1
(注意取 z0 = z1)
注意此式中
Fj
(rr)
与
a
j
r (k
)
的关系[?]。
-4-
二. 导带的计算
1.导带不参与其他带的耦合
----单带模型的有效质量方程(抛物带模型)
导带底等能面是球面,抛物型能量色散关系为:
En
r (k )
=
En
(0)
+
h2k 2 2m∗
图论-哈密尔顿图-课内专题报告

{n-3,n-1},{n-1,1}组成。这条哈密顿圈与第一条圈没有公共边。当n ≥7时,按照这种
k 2 方法把图?中的圈旋转角度 n 1 ,其中2 ≤k ≤(n-3)/2,就得到总数为(n-1)/2条哈密顿
圈,它们满足任意两个圈没有公共边。所以这17名学生在此科学营地中一直可以共进 (17-1)/2=8天午餐,直到某些同学不得再次坐在其它人旁边。 5 5 7 n-2 3 3 2 4 1 n 2 1 n n-1 (b)
2014-4-14 图论之哈密尔顿图 16
Xi’an Jiaotong University
定理 3 设G =(V,E)是一个无环图并且|V| 2。如果对于所有的x,y V并且x y 都有deg(x)+deg(y) n-1,则G中有哈密顿路径。 使得x是C1中的一个顶点,y是C2中的一个顶点。设Ci具有n i 个顶点,其中i=1,2。 则deg(x) n1 1, deg( y ) n2 1, 从而有 deg( x) deg( y) ( n1 n2 ) 2, 这就与定理中 给出的条件矛盾。因此,G是连通的。 现在构造G中的一条哈密顿路径。对于m 2,pm是长度为m 1的路径
2
Xi’an Jiaotong University
哈密尔顿周游世界问题
1857年,著名的爱尔兰数学家Sir William Hamilton设计了一个游 戏:它是由一个木制的正十二面体构成,在它的每个棱角处标有当 时很有名的城市。游戏目的是“环球旅行”。为了容易记住被旅游 过的城市 ,在每个棱角上放上一个钉子,再用一根线绕在那些旅游 过的城市上(钉子),由此可以获得旅程的直观表示。给定世界上20个 城市,用一个代表地球的十二面体的20个顶点分别代表这20个城市。 从某一个顶点出发,沿着十二面体的棱,经过每个顶点恰好一次, 最后回到出发点。
kohn-sham方程

kohn-sham方程Kohn-Sham方程式是密度泛函理论(DFT)的核心数学表达式,用于描述多电子体系的基态性质。
密度泛函理论是一种计算量子力学体系的方法,它基于电子密度而不是波函数。
Kohn-Sham方程的推导始于一组基本假设,其中最重要的假设是将多电子体系的总能量表达为从单电子波函数派生的泛函。
这样的波函数被称为Kohn-Sham波函数,它们是通过求解一组单电子方程获得的。
每个单电子方程描述了一个虚拟的非相互作用粒子在一个有效外势场中运动。
Kohn-Sham方程的形式如下:[-(h^2/2m)∇^2+ V(r) + V_H(r) + V_{xc}(r)] ψ_i(r) = ε_iψ_i(r)其中,h是普朗克常数除以2π,m是电子的质量,V(r)是电子在外势场下的有效势能,V_H(r)是Hartree势,它描述了电子之间的经典库伦相互作用,V_{xc}(r)是交换-相关势,它描述了电子之间的量子力学交换和相关效应。
ψ_i(r)是Kohn-Sham波函数,ε_i是对应的能量。
这个方程是一个自洽方程,因为V_H(r)和V_{xc}(r)依赖于电荷密度ρ(r),而电荷密度本身又依赖于Kohn-Sham波函数。
因此,需要通过迭代求解来确定一个自洽的解。
Kohn-Sham方程的求解可以通过各种数值方法来实现。
其中最常用的方法是使用基组(expansion basis)来表示波函数,并将方程离散化为一个矩阵特征值问题。
这个矩阵特征值问题可以通过对角化得到波函数的能量和形式。
Kohn-Sham方程被广泛应用于材料科学、凝聚态物理、化学和生物物理等领域的计算研究中。
它可以用于计算分子的电子结构、材料的能带结构和光谱性质等。
密度泛函理论和Kohn-Sham方程的发展使得计算材料性质和分子模拟等变得更加可行和准确。
尽管Kohn-Sham方程是密度泛函理论一个重要的数学表达式,但它也存在一些局限性。
其中一个主要的问题是交换-相关泛函的近似。
24-哈密尔顿图

F
C
C
E
D
E
D
旅行推销员(TSP)问题 问题 旅行推销员
问题:n个城市间均有道路,但距离不等,旅行推销员从某地出发, 走过其它n-1个城市,且只经过一次,如何选择最短路线? 数学模型: 构造无向带权图G, VG中的元素对应于每个城市, EG中每个元素 对应于城市之间的道路,道路长度用相应边的权表示。 则问题的解对应于G中包含所有边的权最小的哈密尔顿回路。 G是带权完全图, 总共有n!/2条哈密尔顿回路。因此,问题是如何 从这n!/2条中找出最短的一条。 (给你一点感觉 给你一点感觉:含20个顶点的完全图中不同的哈密尔顿回路有约 给你一点感觉 6000万亿条-(1.21645×1017)/2,若机械地检查,每秒处理10万条, 需2万年。)
若v1,vk相邻,结论成立。 若v1,vk不相邻,令T={vj|vj与vk相邻} ,S={vi|v1与vi+1相邻} ; 注意:|S|+|T|= d(v1)+d(vk)≥n-1, |S|+|T|= Qvk∉S⋃T, ∴|S⋃T|≤k-1<n-1, ∴|S⋂T|=|S|+|T|-|S⋃T|>0, 即 ⋃ ⋃ ⋂ ⋃ S⋂T非空,令vi∈S⋂T, 则vi+1与v1相邻,vi与vk相邻。于是 C=v1…vivkvk-1…vi+1v1是包含Γ中所有顶点的初级回路。
闭合图与哈密尔顿图的判定
图G是哈密尔顿图当且仅当C(G)是哈密尔顿图。 只须证明在构造闭合图(加边)过程中的每一步,图的哈密 过程中的每一步,
尔顿性质均双向保持
若u,v∈VG, u,v不相邻,且d(u)+d(v)≥|VG|,则G是哈密尔顿 图当且仅当G+e(u,v)是哈密尔顿图。 必要性显然。 反之,若G+{uv}是哈密尔顿图,但G不是,则G是半哈 密尔顿图,且uv-路径是哈密尔顿通路,由 d(u)+d(v)≥|VG|,可以将uv-路径改造成哈密尔顿回路, 矛盾。
哈密顿表象中的投影算子及性质分析

佳木斯大学学报(自然科学版)Vol. 38 No. 6Nov. 2020第38卷第6期2020 年11月Journal of Jiamusi University ( Natural Science Edition )文章编号:1008 -1402(2020)06 -0168 -03哈密顿表象中的投影算子及性质分析①徐丽雯a ,张海丰a ,刘明达b,;,韩海生a ,李慕勤c(佳木斯大学a.理学院,b.附属第二医院,c.材料科学院,黑龙江佳木斯154007)摘要:利用哈密顿算符表象中的封闭关系定义了哈密顿算符表象中的投影算子,并给出了两 个衍生算符,最后讨论了投影算子性质及应用。
研究结果表明投影算子p n 作用在I 〃〉后,只保 留了 In 〉的分量,并且投影系数显示I n >分量的几率不变;投影算子q n 对I 忙作用的是在I 帕 中去掉了 I n 〉的分量,只保留了其他分量,且几率大小不变;投影算子p mn 对任意态矢I 〃〉作用后,只留下了 I 〃〉中的I m 〉分量,且其几率I n 〉分量的几率,投影算子的作用效果在很多量子 体系的研究中具有重要的意义。
关键词:哈密顿表象;投影算子;衍生算子中图分类号:O431文献标识码:A0引言在量子力学中,哈密顿算符表象是很重要的基本表象之一,很多体系的哈密顿算符本征值问题的求解都是在哈密顿算符表象下进行的,因而在大量的研究中被使用,例如:张鹏程等在哈密顿算符表象中对一维谐振子做了计算[1];李重石给出了三维谐振子哈密顿算符表象下径向矩阵元的简要形式[2];韩菊等在坐标表象和哈密顿算符表象中对 电场中带电谐振子进行了求解[3];马春生等在哈 密顿算符表象中使用应变补偿对多量子阱价带结构哈密顿方程进行了求解。
此外,投影算子也在国内外的量子体系研究中被大量的应用[5-8]。
1哈密顿算符表象以氢原子体系为例,由于其能级构成分离谱,该表象的基本矢量是由相互对易的三个算符(H 、L 2和L 2 )的共同本征态构成正交归一完备函数系I I nlm) < nlm I = I(1)nlm任意波函数向该本征函数系基矢投影后就得到了哈密顿算符表象下的波函数。
Kohn-Sham方程及其解法

Kohn-Sham方程及其解法Kohn-Sham 方程及其解法1. Kohn-Sham 方程如果原子核不动,材料可以看成是“外场下的非均匀电子气”,体系的基态性质是其电子密度的唯一泛函,而该电子密度)(r n 满足Kohn-Sham 方程:写在一起就是:∑=ψ=Ni i r r n 12)()(对所研究的体系解出该Kohn-Sham 方程,就可得到其电子密度,而体系的性质由该电子密度决定:物理量 F = F [n]2. Kohn-Sham 方程中的各项:第1项:动能项(电子的动能,原子核不动)第3项:称为 Hartree 势(哈特利势),可以类比为库仑势。
(')'21122()()()()()'([()]())()(()()())n r H r eff i i i Ni i eff xc xc xc r r v r dr v r v E n V n r V r r V r r r r V r n r r ψεψδδφφψ=-=??=+-?+=?==++=?∑)()()]}('')()([21{2n V r d r r r n V i i i xc ext ψ=ψ+-++?-?ε第2和第4项需要很多的说明。
第2项:外势项。
由原子核(或原子芯)的空间排列(即材料的结构)构成。
原子由: {原子核+全部的电子} 构成→ all-electrons cal. 或 {原子芯+价电子} 构成→ pseudo-potential cal.由于全电子的计算工作量大(波函数在靠近原子核的地方振荡很厉害),非全电子的计算通常有优势。
我们这里就将使用非全电子的计算(V ASP 程序包)。
所以,需要有“赝势”的概念:赝势方程:如果不考虑原子的芯电子,则原子就成为“赝原子”(原子芯+价电子)。
这时,价电子运动受处的势场就相当于来自原子芯的“赝势”(原来是原子芯内所有电子提供的势场)。
n模二次型哈密顿量对角化的一种简单方法_逯怀新[1]
![n模二次型哈密顿量对角化的一种简单方法_逯怀新[1]](https://img.taocdn.com/s3/m/a24cf92bdd36a32d737581f8.png)
1 2
(
A
2 1
+
A
2 2
)
+
2
(
C
2 1
+
C 22) +
2( B 21+
B22) ∋
[
(
A
2 1
-
A
2 2
)
2
+
4(
C
2 1
+
C22) ( A 1+
A 2) 2+
4
(
B
2 1
+
B 22)(
1
( A 1-
A 2)2+
16( B21+
B
2 2
)
(
C
21+
C
2 2
)
]
1 2
2
参考文献:
[ 1] 玻戈留玻夫 H H, 玻戈留玻夫 H H( 小) . 量子统计力学导 论[ M ] . 刘典宪, 郭新凯, 王锡绂 译. 北京: 高 等教育出 版 社, 1992. 266~ 292.
如下对易关系:
[ i, j ] =
!
B
1
ij , ! B =
0 -I
I 0
( 2)
为使式( 1) 对角化, 作如下量子变换:
∃= U - 1 U = M
( 3)
这里, M 为 2n 2 n 复辛矩 阵, 满足下列辛条 件[6]:
M ! BM = ! B
( 4)
在式( 3) 中, 如果算符 U 是幺正的, 则相应的矩
[ 4] Zhang Y D , Tang Z. Q uant um transf ormation theory in f ermion Fock space[ J] . J M at h Phys, 1993, 34: 5 639.
哈密顿正则方程课件

解析解的意义
解析解能够精确地描述系统的运 动状态,对于理解和分析物理现 象具有重要意义。
哈密顿正则方程的物理意义
系统能量守恒
哈密顿正则方程描述了系统的能量守恒关系,即系统的总能量保持 不变。
运动状态演化
哈密顿正则方程描述了系统运动状态的演化过程,即随着时间的推 移,系统的运动状态会发生怎样的变化。
广义哈密顿正则方程
广义哈密顿正则方程是经典哈密顿正则方程的扩展,它允许系统具有非保守力和非完整约束。
广义哈密顿正则方程的形式为:$frac{d}{dt}frac{partial L}{partial q'} - frac{partial L}{partial q} = Q$, 其中$L$是系统的拉格朗日函数,$q'$和$q$是系统的广义坐标,$Q$是非保守力。
在统计物理中的应用
描述系统微观状态
哈密顿正则方程在统计物理学中用于描述系统的微观 状态和能量。
分析系统宏观性质
通过哈密顿正则方程,可以分析系统的宏观性质,如 温度、压强和熵等。
研究相变和临界现象
哈密顿正则方程可以用来研究相变和临界现象,包括 对称性破缺和标度律等。
05
CATALOGUE
哈密顿正则方程的扩展与深化
广义哈密顿正则方程在分析力学、动力学和控制系统等领域有广泛应用。
非完整约束系统中的哈密顿正则方程
非完整约束系统是指具有非完整约束的力学系 统,这些约束不能由牛顿第三定律完全确定。
在非完整约束系统中,哈密顿正则方程需要考 虑约束对系统运动的影响,其形式与完整约束 系统中的哈密顿正则方程有所不同。
非完整约束系统中的哈密顿正则方程在机器人 学、航天器和车辆动力学等领域有重要应用。
哈密尔顿图的充分必要条件之欧阳语创编

哈密尔顿图的充分必要条件摘要图论在现实生活中有着较为广泛的应用, 到目前为止,哈密尔顿图的非平凡充分必要条件尚不清楚,事实上,这是图论中还没解决的主要问题之一,但哈密尔顿图在实际问题中,应用又非常广泛,因此哈密尔顿图一直受到图论界以及运筹学学科研究人员的大力关注.关键词:哈密尔顿图;必要条件;充分条件;1 引言42 哈密尔顿图的背景43 哈密尔顿图的概念54 哈密顿图的定义64.1定义64.2定义64.3哈密顿路是遍历图的所有点。
74哈密尔顿图的充分条件和必要条件的讨论85 结论9参考文献9指导老师101 引言图论是一门既古老又年轻的学科,随着科学技术的蓬勃发展,它的应用已经渗透到自然科学以及社会科学的各个领域之中,利用它我们可以解决很多实际生活中的问题,给你一个图,你怎么知道它是否是哈密尔顿图呢?当然如果图的顶点不多,你可以用最古老的”尝试和错误”的方法试试找哈密尔顿回路就可以解决和判断.但是,数学家们并不满足这样的碰得焦头烂额后才找到的真理方法.是否存在一组必要和充分的条件,使得我们能够简单轻易地判断一个图是否是哈密尔顿图?有许多智者通过各种方式去尝试过了,遗憾的是至今尚未找到一个判别哈密尔顿回路和通路的充分必要条件.虽然有些充分非必要或必要非充分条件,但大部分还是采用尝试的办法,不过这些条件也是非常有用的.2 哈密尔顿图的背景美国图论数学家奥在1960年给出了一个图是哈密尔顿图的充分条件:对于顶点个数大于2的图,如果图中任意两点度的和大于或等于顶点总数,那这个图一定是哈密尔顿图。
闭合的哈密顿路径称作哈密顿圈,含有图中所有顶的路径称作哈密顿路径.1857年,哈密尔顿发明了一个游戏(Icosian Game).它是由一个木制的正十二面体构成,在它的每个棱角处标有当时很有名的城市。
游戏目的是“环球旅行”。
为了容易记住被旅游过的城市,在每个棱角上放上一个钉子,再用一根线绕在那些旅游过的城市上(钉子),由此可以获得旅程的直观表示(如图1)。
第三章 哈密顿图

(1) G的每条边在G*至多重复一次;
(2) G的每个(初级)圈在G*重复边权的和不超过该圈 权的一半。
算法过程
–
1.用Dijstra算法求所有奇度顶点对之间的最短路径。 (若G是欧拉图,直接用Fleury算法) 2.以G中所有奇度顶点构造带权完全图G2k, 每边的 权是两端点间最短路径长度。
1
2
20
17
19
18Biblioteka 义: 图G中的一圈,若它通过G中每个顶 点恰好一次,则该圈称为哈密尔顿圈,具 有哈密尔顿圈的图称为哈密尔顿无向图。 完全图必是哈密尔顿图。
从定义可知,一个图的Hamilton圈与
Euler环游是很相似的,差别在于Hamilton
圈是环游G的所有顶点圈(点不重,当然
边也不重),而Euler环游是环游G的所
道的交叉点,街道长度用相应边的权表示。 则问题的解对应于G中包含所有边的权最小 的圈,称为最优圈(注意:未必是简单圈)。 当G是欧拉图,则最优圈即欧拉圈。 若G不是欧拉图,则通过加边来消除G中的 奇度顶点,要求使加边得到的欧拉图G'中重复边
的权和最小。
C是带正权无向连通图G中的最优圈当且仅当对 应的欧拉图G*满足:
边外,,每经过G中顶点xi(包括a和b),都为顶点xi
贡献2度,而C的第一边为a贡献1度,C的最后一条
边为b贡献1度.因此,a和b的度数均为奇数,其余
结点度数均为偶数.
充分性:设连通图G恰有两个奇数度结点,
不妨设为a和b,在图G中添加一条边e={a,b} 得G’,则G’的每个结点的度数均为偶数,因 而G’中存在欧拉圈,故G中必存在欧拉路.
J K
例3 一张纸上画有如下图所示的图,你能否用剪刀 一次连续剪下图中的三个正方形和两个三角形?
哈密顿猜想

哈密顿猜想
哈密顿猜想是图论中的一个经典问题,也被称为哈密顿回路问题。
该问题的正式陈述如下:对于给定的无向图,是否存在一条路径,使得这条路径经过图中的每个顶点一次且仅一次,然后回到起点,这条路径被称为哈密顿回路。
更具体地说,给定一个无向图G=(V, E),其中V表示顶点的集合,E表示边的集合。
如果存在一个回路,它包含图中的每个顶点一次且仅一次,我们称其为哈密顿回路。
而哈密顿猜想则是询问对于任意给定的无向图,是否都存在哈密顿回路。
哈密顿猜想的提出者是爱尔兰数学家威廉·哈密顿(William Hamilton),他在19世纪中叶提出了这个问题。
虽然经过多年的努力,数学家们已经找到了许多特殊情况下的哈密顿回路,但至今仍没有一个普遍适用于所有情况的证明或反例。
哈密顿猜想是NP完全问题的一种,意味着在通常情况下,要解决这个问题需要指数级时间复杂度。
虽然现代计算机科学和数学领域已经提出了一些启发式算法和近似解法,但它们并不能给出该问题的确定性解答。
因此,哈密顿猜想仍然是一个未解决的数学问题,吸引了众多数学家和计算机科学家的兴趣。
对于该猜想的证明或反例的发现将对图论和组合优化等领域产生重大影响。
1。
第3章赝势平面波方法(I)

第3章赝势平面波方法(I)-49-基于密度泛函理论的赝势平面波方法可以计算很大范围不同体系的基态属性,它采用了平面波来展开晶体波函数,用赝势方法作有效的近似处理。
由于平面波具有标准正交化和能量单一性的特点,对任何原子都适用且等同对待空间中的任何区域,不需要修正重叠误差。
因此平面波函数基组适合许多体系,其简单性使之成为求解Kohn-Sham方程的高效方案之一另外,赝势的引入可以保证计算中用较少的平面波数就可以获得较为可靠的结果。
该方法具有较高的计算效率,使之日益发展成为有效的计算方法。
本章首先对赝势平面波方法进行重点讨论,其次介绍了基于第一性原理计算软件一般步骤,最后结合MaterialStudio软件包应用,对锐钛矿型TiO2(101)表面及其点缺陷结构进行建模和计算。
3.1基本原理基于密度泛函理论的第一性原理计算实质是求解Kohn-Sham方程。
实际求解Kohn-Sham方程时,由于原子核产生的势场项在原子中心是发散的波函数变化剧烈,需要采用大量的平面波展开,因而计算成本变得非常大,所以在计算中选取尽可能少的基函数。
计算中选择的基函数与最终波函数较接近则收敛较快,当然包含的维度也应该尽量少。
众所周知,根据研究对象不同,选择基函数的方法也不同的,如原子轨道线性组合法(LCA0-TB)、正交平面波法(0PW)、平面波贋势法(PW-PP)、缀加平面波法(APW)、格林函数法(KKR)、线性缀加平面波法(LAPW)、Muffin-tin轨道线性组合法(LMTO)等,选取典型代表方法在随后的章节中重点展开讨论。
与LAPW,LMTO等精度较高的第一性原理计算方法比较,平面波贋势法是计算量较少的方法,适用于计算精度要求不严格,因原胞较复杂而导致计算量陡增加的体系。
为此,本章将重点学习赝势平面波方法,先学习电子能带的平面波基底展开以及赝势等相关基本概念,然后再讨论赝势引入原理。
3.1.1平面波展开与截断能1.平面波展开平面波是自由电子气的本征函数,由于金属中离子芯与类似的电子气有很小的作用,因此很自然的选择是用它描述简单金属的电子波函数。
闪锌矿结构GaN的能带结构和有效质量性质研究

闪锌矿结构GaN的能带结构和有效质量性质研究王焕友;李亚兰;王龙【摘要】从第一性原理赝势平面波( PP-PAW)方法出发,计算了闪锌矿结构半导体材料GaN的能带结构,利用对价态的相对论处理,研究了布里渊区中心点附近价带顶( VBM)的自旋轨道分裂能。
基于有效质量近似理论,计算了导带底(CBM)附近电子的有效质量,以及Γ点附近沿着[100],[110]和[111]方向的轻、重空穴的有效质量。
利用计算的轻、重空穴有效质量,研究了Luttinger 参数γ1、γ2和γ3,这些参数是光电子材料颇有价值的重要参数。
%With the pseudo-potential plane-wave ( PP-PAW) method of the first principle, the energy-band structures ofzinc-blende GaN are calculated. According to relativism for valence states, the spin-orbit splitting energy DSO are calculated. Based on the effective-mass approximation theory, we calculated electron effective-mass around the conduction-band minimum, and heavy-hole (mhh) ,light-hole (mlh) effective-mass in [100], [110] and [111] direction aroundΓ, Using above data, Lut tinger parametersγ1,γ2andγ3 are calculated, because these parameters are important parameters for optoelectronic materials.【期刊名称】《湘南学院学报》【年(卷),期】2016(037)005【总页数】6页(P13-17,65)【关键词】闪锌矿结构;GaN;电子结构;有效质量【作者】王焕友;李亚兰;王龙【作者单位】湘南学院电子信息与电气工程学院,湖南郴州423000;湘南学院电子信息与电气工程学院,湖南郴州423000; 华中师范大学物理科学与技术学院,湖北武汉430079;湘南学院电子信息与电气工程学院,湖南郴州423000【正文语种】中文【中图分类】O472;O482闪锌矿结构半导体材料GaN不仅在发光二极管,激光二极管,光电调制器和光探测器等方面有着广泛的应用,而且是制作异质结,超晶格和量子阱的基本材料.研究该晶体的能带结构和有效质量,可为半导体新材料的开发提供理论依据和实验指导,如定量的解释材料的光电转换效率,载流子的迁移率,以及与价带顶简并态相关的受主杂质,激发能级等物理现象.此外,III-V化合物半导体光电子材料的光传输、量子点和量子阱材料和器件的性能与布里渊区中心的电子结构密切相关,因此获取布里渊区中心附近区域的电子结构信息对光电子器件的设计有着重要意义.近年来,许多的科研小组对闪锌矿结构GaN的能隙和有效质量进行了理论计算和实验研究,如Ramos L E[1]小组和Suzuki M[2]等人采用了全势线性缀加平面波法(FLAPW),Fan W J[3]基于经验赝势进行了计算,Ahn D[4]等人采用k.p理论进行了计算.在实验方面,Perlin[5]小组用反射谱和霍尔效应测出了电子的有效质量,还有Gass M H[6],Shokhovets S[7] 和Shokhovets S [8]等人用不同的实验方法测出了电子的有效质量.但是Perlin的间接实验结果遭到质疑,因为测量电子有效质量的最佳方法是回旋共振技术,而霍尔效应得不到所需要的高迁移率和高磁场;另外样品本身的缺陷和不纯会高度影响带边反射率和吸收率.本文基于第一性原理,采用赝势平面波法(PP-PAW)计算了闪锌矿结构GaN价带顶(VBM)和导带底(CBM)附近的能带结构,并将计算结果与有效质量近似理论相结合,得到了布里渊区中心附近电子和空穴的有效质量,以及相应的Luttinger参数[9],这将有利于提高GaN材料光电性能的研究.本文基于密度泛函理论,从第一性原理赝势平面波方法出发,利用文献[10]中的局域密度近似(LDA)构造单电子势中的交换关联项,并利用了文献[11]中的方法产生模守恒赝势,自洽求解Kohn-Sham方程,得到了闪锌矿结构半导体材料GaN的能带结构.考虑到Ga-3d10电子能量高,相对局域的特点,并与N-2s2电子有比较强的杂化,对能带的描述扮有重要的角色,故把Ga-3d10与Ga-4s24p1和N-2s22p3一样作为价态处理.电荷密度采用四面体积分的方法计算,对应的积分区域为简约布里渊区(IBZ),按8×8×8划分空间网格,同时考虑到Ga原子的质量较大,在计算中对价态作相对论效应处理.通过计算布里渊区几个高对称性方向的色散谱,把电子带结构计算与有效质量联系起来,为价带拟合,一个6×6 Luttinger-Kohn 哈密顿量[12]是被采用的.由于在Γ点CBM属于非简并带,故采用抛物线逼近法求得电子有效质量,此次计算的收敛判据取波函数平方余数1×10-12.2.1 结构和电子性质闪锌矿结构GaN空间群为F-43M(216),由阳离子和阴离子分别以面心立方结构沿空间对角线1/4套构而成,本文采用优化的理论晶格常数,由于只有一个晶格常数,仅需利用能量最低原理对Monkhorst-Pack格子和截断能作收敛测试,计算得到理论晶格常数为4.552?倗,与实验值4.50[13]和4.531[14]相比,误差仅为1%.基于计算的理论格子参数,计算了第一布里渊区几个主要对称性方向的色散关系曲线,在未考虑自旋-轨道相互作用时的的带隙值Eg和价带宽度Ev分别为1.84 eV和17.02 eV,当考虑自旋-轨道相互作用时的带隙值Eg和价带宽度Ev分别为1.83 eV和17.07 eV.此次计算值与文献[1]、[2]采用的FLAPW计算值有比较好的一致,但与带隙值Eg的实验值3.21 eV [15]和3.3 eV [3]比较,有较大的误差,这是由于用LDA方法求解激发态能量时本身存在的不足,忽略了交换关联势的非局域特性所致,但本文关注的体系局部结构的性质并不会受这一误差的影响.由于自旋-轨道相互作用,布里渊区Γ点价带顶Γ15分裂为四重简并的Γ8态和二重简并的Γ7态,它们的分裂能Δso和其它的理论方法值和实验值列于表2中.a 本次计算-PP-PAW,b文献[1]-FLAPW方法,c文献[16]-实验值,d文献[17]-全势线性原子轨道叠加法(FLMTO),e文献[18]-经验赝势法.为了更进一步了解能量区间的电子组合情况,计算了考虑自旋轨道相互作用后总的态密度和分态态密度分布.从图2可以看出,闪锌矿结构的能带结构主要是由四个部分组成,即三个电子填充带(价带)和一个能量最高的非电子填充带(导带).能量最低的填充带对应-9.88 eV至-8.14eV,主要是由N的2s电子态和Ga的4s态组成.能量居中的电子填充带位于-6.45 eV至-4.10eV之间,该能带区域明显的表现出Ga的3d电子态的局域特征,说明Ga原子成为负电中心;能量最高的电子填充带位于-1.08 eV至6.19eV之间,在该能带的低能部分主要由Ga的4s态和N 的2p态组成,在该能带的高能部分由Ga的4p和N的2p态组成.能量最高的能带称为导带,CBM位于Γ点,值为8.03eV,在导带的低能边除Ga的3d少有贡献外,其余的四个分态对导带的低能边的贡献相差不大.2.2 有效质量与Luttinger参数电子和空穴的有效质量不同于真实的电子和空穴的质量,它们的大小有赖于k空间很小区域的电子结构,更确切的说有赖于布里渊区附近区域的电子结构.有效质量决定了它们的惯性和迁移率,对半导体材料的光现象及电子的输运有直接的影响. 有效质量与能带之间关系可有下面的方程求解,把布洛赫波函数代入到能量本征方程得到对非简并带,解方程(1)可得到小波矢k点的波函数和能量本征值这里m*满足以下方程对于简并带,简并带之间的耦合需用扰动的方法加以处理,任意波矢间的能量变化用k.p[19]方法进行对角化矩阵得到总的来说,有效质量是一个张量,与能带结构有关根据有效质量近似理论具有闪锌矿对称结构的半导体材料在CBM附近的能带为抛物线,为非简并带,具有类s特征,成略微的各向异性,故可以取不同的k方向的电子有效质量的平均值作为CBM附近电子的有效质量.VBM由原来的六重简并态在计入自旋-轨道藕合后分裂为四重简并的态和二重简并态,总的哈密顿量分解为k.p部分的HK.P和自旋-轨道相互作用的HSO.如果分别用|jmj〉表示轻重空穴价带态,通过计算,对四重简并的Γ8v态有这里;对双重简并的Γ7v态有这里因为闪锌矿结构为直接带隙半导体,所以我们仅对布里渊区中心Γ点附近电子和空穴的有效质量感兴趣,通过用抛物线逼近法分别计算了沿高对称性方向ΓX,ΓL 和ΓK(见图3)的5%范围内的电子有效质量,在每个方向取40个点,通过拟合得到Γ点附近沿Δ轴,Σ轴和Λ轴的电子有效质量,并取其平均值作为CBM附近电子的有效质量.为了系统研究轻、重空穴和自旋轨道分裂耦合与有效质量的关系,首先对Luttinger-Kohn公式[12]对角化计算六个本征值,然后采用最小二乘法对VBM附近的色散关系进行拟合,并运用Luttinger [9]参数表达式,即可得到沿[100],[110]和[111]方向的轻重空穴的有效质量,计算结果和其它文献的理论和实验值列于表3中.从表3中可以看出无论沿哪一个方向都有这是因为载流子的有效质量仅仅依赖于能谱,从能带图可以看出VBM附近重空穴带的曲率半径明显大于轻空穴带的曲率半径,使得重空穴的有效质量是轻空穴的几倍甚至十几倍.由于VBM沿[100],[110]和[111]方向的曲率半径不同,使得空穴的有效质量呈各向异性,尤其是重空穴的有效质量相差较大,而轻空穴的有效质量相差较小.我们将拟合求得的空穴有效质量代入到Luttinger参数表达式得到Luttinger参数γ1,γ2,γ3.γ1,γ2,γ3以及Δso是其它系统,如量子阱和超晶格等的重要输入参数.本文通过局域密度近似内的第一性原理PP-PAW计算了闪锌矿结构半导体材料GaN的结构和电子性质.计算的格子常数,带隙和自旋-轨道分裂能与其它的理论和实验方法值加以比较,有较好的一致.在有效质量近似理论的基础上,对布里渊区中心点附近CBM和VBM色散关系进行拟合,得到了一些对光电子材料颇有价值的重要参数,如在CBM附近电子的有效质量以及在Γ点附近沿[100],[110]和[111]方向的轻重空穴的有效质量mlh和mhh.从这些有效质量,计算了Luttinger参数γ1,γ2和γ3.从Luttinger参数和轨道分裂能可为其它的体系,如量子阱和超晶格等提供重要的理论帮助.【相关文献】[1] Ramos L E,Teles L K,Scolfaro L M R,et al.Structure,electronic,and effective-mass properties of silicon and zinc-blende group-III nitride semiconductor compounds[J].Phys Rev B,2001,63: 165210-165219.[2]Suzuki M and Uenoyama T.Optical gain and crystal symmetry in III-V nitridelasers[J].Appl Phys Lett,1996,69: 3378-3380.[3] Fan W J,Li M F and Chong T C.Electronic properties of zinc-blende GaN,AlN,and their alloys Ga1-xAlxN[J].J Appl Phys,1996,79: 188-194.[4]Doyeol Ahn.Optical gain of InGaP and cubic GaN quantum-well lasers with very strong spin-orbit coupling[J].J Appl Phys,1996,79: 7731-7737.[5] Perlin P and Litwin-Staszewska E.Determination of the effective mass of GaN from infrared reflectivity and Hall effect[J].Appl Phys Lett,1996,66: 1114-1116.[6] Gass M H,Papworth A J,and Beanland R,et al.Mapping the effective mass of electronsin III-V semiconductor quantum confined structures[J].Phys Rev B,2006,73:35312-35318. [7] Shokhovets S,Ambacher O and Gobsch G.Conduction-band dispersion relation and electron effective mass in III-V and II-VI zinc-blende semiconductors[J].Phys Rev B,2007,76: 125203-125208.[8] Shokhovets S and Gobsch G.Momentum matrix element and conduction band nonparabolicity in wurtzite GaN[J].Appl Phys Lett,2005,86: 161908-161910.[9] Luttinger J M and Kohn W.Motion of Electrons and Holes in Perturbed PeriodicFields[J].Phys Rev,1955,97: 869-873.[10] Perdew J P and Zunger A.Self-interaction correction to density-functional approximations for many-electron systems[J].Phys Rev B,1991,23: 5048-5079.[11] Hartwigsen C,Goedecker S and Hutter J.Relativistic separable dual-space Gaussian pseudopotentials from H to Rn[J].Phys Rev B,1998,58,3641-3647.[12] Luttinger J M,Ward J C.Ground-State Energy of a Many-Fermion System II[J].Physical Review,1960,118 (5): 1417-1427.[13] Lei T and Moustakas T D.Epitaxial growth and characterization of zinc-blende gallium nitride on (001) silicon[J].J Appl Phys,1992,71: 4933-4943.[14] Kim K,Lambrecht W R,and Segall.Elastic constants and related properties of tetrahedrally bonded BN,AlN,GaN,and InN[J].Phys Rev B,1996,53: 16310-16326.[15] Powell R C,Lee N E and Greene.Heteroepitaxial wurtzite and zinc-blende structure GaN grown by reactive-ion molecular-beam epitaxy: Growth kinetics,microstructure,and properties[J].J Appl Phys,1993,73: 189-204.[16] Ramirez-Flores,Navarro-Contreras H,Lastras-Martinez A,et al.Temperature-dependent optical band gap of the metastable zinc-blende structure -GaN[J].Phys Rev B,1994,50: 8433-8438.[17] Kim K,Lambrecht W R L and Segall B.Effective masses and valence-band splittings in GaN and AlN[J].Phys Rev B,1997,56: 7363-7369.[18] Sánchez A M,Gass M,Papworth A J and Goodhew P J.Nanoscale EELS analysis of InGaN/GaN heterostructures[J].Phys Rev B,2004,70: 035325-035332.[19] Fanciulli T,Lei T and Moustakas T D.Conduction-electron spin resonance in zinc-blende GaN thin films[J].Phys Rev B,1993,48: 15144-15149.[20] Gass M H,Papworth A J and Joyce T B,et al.Measurement of the effective electron mass in GaInNAs by energy-loss spectroscopy[J].Appl Phys Lett,2004,84: 1453-1455.。
k.p方法计算应变量子阱空穴能级[整理版]
![k.p方法计算应变量子阱空穴能级[整理版]](https://img.taocdn.com/s3/m/ba1ebcfde109581b6bd97f19227916888486b920.png)
Spin-orbit-coupling effects on the valence-band structure of strained semiconductor quantum wellsCalvin Yi-Ping Chao and Shun Lien ChuangDepartment of Electrical and Computer Engineering, University of Illinois摘要:找到一组将6×6 Luttinger-Kohn 哈密顿量对角化为两个3×3块的酉变换,使得计算量子阱能带时更有效。
使用这些公式,系统的研究了应变量子阱中重空穴、轻空穴和自旋轨道分裂耦合。
给出应变对k空间能量表面的影响,给出包含与不包含自旋轨道分裂能带的结果。
结果显示,自旋轨道分裂耦合对能带特别是高应变量子阱能态影响很明显,不能忽略。
1.简介应变可以是调整半导体能带参数的有力工具,在量子阱激光器,调制器,探测器等中有重要的应用。
例如对于应变量子阱激光器,应变使得量子阱价带带边在k=0处分裂,降低平面有效质量,从而降低态密度,降低阈值电流。
各向同性(静水力学的)应变改变带隙,各向异性(单轴或切应变)使得价带在k=0处简并分离。
应变导致重空穴、轻空穴、自旋轨道分裂带额外的耦合,这些耦合在非应变量子阱计算中通常被忽略,但对于高应变量子阱,忽略这些耦合将导致计算能级误差几十个meV,有效质量误差高于30%。
本文的目的就是证明应变如何影响半导体价带能级,着重于重空穴、轻空穴、自旋轨道分裂带额外的耦合。
使用的公式基于Luttinger-Kohn 哈密顿量和包络函数近似。
以下第二部分研究应变体材料带边能量公式和有效质量。
第三部分结合应变和量子效应,集中讨论应变量子阱的能级计算,在轴近似下,得到一组将6×6 Luttinger-Kohn 哈密顿量对角化为两个3×3块的酉变换,由这简单的哈密顿量,可以计算应变量子阱的能级。
哈密顿原理的推导 ppt课件

0
21
ppt课件
k
j 1
d
dt
T q j
T q j
V q j
q j
0
引入拉格朗日函数L=T-V(质点系动能与势能 之差,称为动势),则上式可表示为:
k
j 1
d dt
L q j
q j
的两个关系式:
q j dt q j
(1)
ri
ri t
k ri j1 q j
q j
(ri ri (q1, q2,,t) (6)
q j 称为广义速度,为广义坐标对时间的变化率,
因 ri 和 ri 仅是广义坐标和时间的函数,与广义 t q j
速度 q j 无关,
L q j
q j
0
(11a)
22
ppt课件
广义力:Q j
V q j
代入(11a)式中,而拉格朗日
函数L=T-V(质点系的动能与势能之差又称为动势)
(11a)式又可以写为:
k
j 1
d dt
L q j
q
j
L q j
q j
量函数:
11
ppt课件
r i
r i
(q1
,
q2
,,
qk
,
t
)
(i 1,2,n) (1)
n为质点的数目,为了将质点系中质点Mi 的 虚位移δri表示为广义坐标的变分 q j ( j 1,2,, k,) 求(1)式的变分:
第七章哈密顿正则方程

H p q j dt 0 j t0 j1 q j
t1 k
对于完整系统,由于δqj 是相互独立的,且可取任何值, 则 H
j p
j
即得关于变量
q , p , t
j
q j
的Hamilton正则方程
t1
k t1 k k j H Qj q j dt L Qj q j dt p j q t0 t0 j j j 1
H H j p j p j q j q qj p j Qj q j dt t0 q j p j j 1
H j p Q j q j
j
1,2, ,k
其中Qj 为系统的非有势力对应于广义坐标 qj 的广义力。
例7-1 试用Hamilton正则方程求出水平弹簧质量振动 系统的运动微分方程 解:单自由度系统, x为广义坐标
L T V
1 2 1 2 1 2 kx L mx V kx 2 2 2 px L x mx 构造H函数 p x m x 1 2 1 2 L px x mx kx H Px x 2 2 px 2 1 2 kx H x, px 2m 2
t1 t1
对上式进行变分运算,得
H H p q q p p q dt 0 j j j j j j t0 p q j 1 j j
t1 k
将上式中的第一项改写成
d j p j q j p j q dt j 1 j 1
j H p j q j H q j p
Kohn-Sham方程

绝热近似:电子和核 的分离 考虑到核质量很大,可以把 核动能项 从 Hamiltonian中分离出来,写成
H (r,R) TN (R) H 0 (r,R) 其中 H 0 (r,R) U N (R) Te (r) U e (r) U eN (r.R )
因为 H0 不含核坐标的微分算苻,所以核坐标可以认为是该 Hamiltonian的一个经典的变量。 对于核位置为已知(作为固定参数),则有:
1 (rN ) 2 (rN ) N (rN )
** 最佳的 i (ri ) 满足 Hartree–Fock 方程:
* * ( r ' ) ( r ' ) ( r ' ) ( r ') 2 j j j i 2 2 [ V (r ) e d ' ] i ( r ) e j ( r ) d ' i i ( r ) 2m r r ' r r ' j j
非均匀电子气
2) 原子,分子…凝聚态体系
基础理论 基本量 从
F
n( r ) F* F
一大进步 (至少从计算科学的角度。
Kohn 获1998年Nobel 化学奖)
这样,
所有量 (对比:
F=F [n]
F F * FFd )
** 已不必求出反对称的波函数 F,它非常难求。
(如果密度可求)
即必须过渡到新的理论21schrdinger方程的困难哈密顿量的复杂性方程本身的复杂性绝熱近似电子和核动力学的分离电子的schrdinger方程2波函数的复杂性反对称性要求hartree方程hartreefock方程薛定谔方程
