最新高三数学第一次联考试题理科数学
2021年高三数学第一次联考试题 理

2021年高三数学第一次联考试题理一、选择题(本大题共10小题,每小题5分,共50分,在每个小题给出的四个选项中,只有一个选项符合题意)1.已知全集,集合,则()A. B.C. D.2.已知,则是的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件3.若某市8所中学参加中学生比赛的得分用茎叶图表示(如图)其中茎为十位数,叶为个位数,则这组数据的平均数和方程分别是()A.91 5.5B.91 5C.92 5.5D.92 54.执行如图所示的程序框图,则输出的值为()A. B. C.0 D.5.在等腰中,→→→→====︒=∠AEACBDBCACABBAC32,2,90,,则的值为()A. B. C. D.6.某几何体的三视图(单位:)如图所示,其中侧视图是一个边长为2的正三角形,则这个几何体的体积是()A. B. C. D.7.已知函数图像经过点,则该函数的一条对称轴方程为()A. B. C. D .8.设不等式组所表示的区域为,函数的图像与轴所围成的区域为,向内随机投一个点,则该点落在内的概率为()A. B. C. D.9.函数的图像大致为()10.已知映射,设点,点是线段上一动点,。
当在线段上从点开始运动到点结束时,点对应点所经过的路线长度为()A. B. C. D.二、填空题(本大题共5小题,每小题5分,共25分)11.在数列中,,则通项。
12.已知是直线的动点,是圆的一条切线,是切点,那么的面积的最小值是。
13.已知表示两数中的最大值。
若,则的最小值为。
14.已知函数()xaxaxf cos123sin321⎪⎪⎭⎫⎝⎛++⎪⎭⎫⎝⎛-=,将图像向右平移个单位长度得到函数的图像,若对任意,都有成立,则的值为。
15.已知{}+++∈∈=<<=NnNmmxxxA nnn,,3,22|1,若表示集合中元素的个数则。
三、解答题(本大题共6小题,共75分,解答要写出必要的文字说明,证明过程或演算步骤)16.(本小题满分12分)已知圆和圆外一点。
江西五校(江西师大附中、临川一中、鹰潭一中、宜春中学、新余四中)高三数学第一次联考试题 理

五校(江西师大附中、临川一中、鹰潭一中、宜春中学、新余四中)联考高三年级数学(理)学科试题一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知z 是z 的共轭复数,若1z i =+(i 是虚数单位),则z z ⋅=( )A .2-B .1-C .0D .22.已知集合2{|20}A x x x =--…,{|ln(1)}B x y x ==-,则A B =( )A .(1,2)B .(1,2]C .[1,1)-D .(1,1)-3.已知命题p :存在x R ∈,使得10lg x x ->;命题q :对任意x R ∈,都有20x >,则( ) A .命题“p 或q ”是假命题 B .命题“p 且q ”是真命题C .命题“非q ”是假命题D .命题“p 且‘非q ’”是真命题4.已知α为第二象限角,sin cos αα+=,则cos 2α=( )A .3B .9C .3-D .9-5.一只蚂蚁从正方体1111ABCD A BC D -的顶点A 处出发,经正方体的表面,按最短路线爬行到达顶点1C 位置,则下列图形中可以表示正方体及蚂蚁最短爬行路线的正视图是( )A .①②B .①③C .③④D .②④6.某教研机构随机抽取某校20个班级,调查各班关注汉字听 写大赛的学生人数,根据所得数据的茎叶图,以组距为5将数据分组成[)5,0,[)10,5,[)15,10,[)20,15,[)25,20,[)30,25,[)35,30,[]40,35时,所作的频率分布直方图如图所示,则原始茎叶图可能是( )7.若如下框图所给的程序运行结果为35S =,那么判断框中应填入的关于k 的条件是( )A. 7=kB. 6k …C. 6<kD. 6>k 8.已知定义在区间[3,3]-上的函数()y f x =满足()()0f x f x -+=,对于函数()y f x =的图像上任意两点1122(,()),(,())x f x x f x 都有1212()[()()]0x x f x f x -⋅-<.若实数,a b 满足22(2)(2)0f a a f b b -+-…,则点(,)a b 所在区域的面积为( ) A .8 B . 4 C . 2 D . 19.已知直线0x y k +-=(0)k >与圆224x y +=交于不同的两点A 、B ,O 是坐标原点,且有3||||3OA OB AB +≥,那么k 的取值范围是( )A. )+∞B.C. )+∞D.10.如图,半径为2的圆内有两条圆弧,一质点M 自点A 开始沿弧A B C O A D C ------做匀速运动,则其在水平方向(向右为正)的速度()v v t =的图象大致为( )二、选做题:请考生在下列两题中任选一题作答.若两题都做,则按做的第一题评阅计分,本题共5分. 11. (1) (不等式选做题)如果存在实数x 使不等式2315x x a a +---…成立,则实数a 的取值范围为____________.(2) (坐标系与参数方程选做题)在极坐标系中,曲线2cos4sin ρθθ=的焦点的极坐标___________.(规定:0,02ρθπ<厔)三.填空题:本大题共4小题,每小题5分,共20分. 12.设矩形区域Ω是由直线2x π=±和1y =±所围成的平面图形,区域D 是由余弦函数cos y x =、2x π=±和1y =-所围成的平面图形.在区域Ω内随机的抛掷一粒豆子,则该豆子落在区域D 内的概率是___________.13.已知曲线1()()n f x x n N +*=∈与直线1x =交于点P ,若设曲线()y f x =在点P 处的切线与x 轴交点的横坐标为n x ,则201412014220142013log log log x x x +++的值为___________. 14.已知平面向量,()αβαβ≠满足2α=,且α与βα-的夹角为120︒,t R ∈,则(1)t t αβ-+的最小值是________________.15.如图,12,F F 是双曲线221:13y C x -=与椭圆2C 的公共焦点,点A 是12,C C 在第一象限的公共点.若121F F F A =,则2C 的离心率是________.四、解答题:本大题共6个题,共75分.解答应写出文字说明、证明过程或演算步骤. 16.(本小题满分12分)已知函数2()2sin ()2,,442f x x x x πππ⎡⎤=+∈⎢⎥⎣⎦.设x α=时()f x 取到最大值. (1)求()f x 的最大值及α的值;(2)在ABC ∆中,角,,A B C 所对的边分别为,,a b c ,12A πα=-,且2sin sin sin B C A =,求b c -的值.17.(本小题满分12分)某学校为了增强学生对消防安全知识的了解,举行了一次消防安全知识竞赛,其中一道题是连线题,要求将4种不同的工具与它们的4种不同的用途一对一连线,规定:每连对一条得5分,连错一条得-2分.某参赛者随机用4条线把消防工具与用途一对一全部连接起来.(1)求该参赛者恰好连对一条的概率;(2)设X 为该参赛者此题的得分,求X 的分布列与数学期望.18.(本小题满分12分)已知三棱柱ABC —A1B 1C 1,A 1在底面ABC 上的射影恰为 AC 的中点O ,∠BCA=90°,AC=BC=2,又知BA 1⊥AC 1。
河南省2023届高三上学期第一次考试数学理科试题(解析版)

“顶尖计划”2023届高中毕业班第一次考试理科数学一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}{}223,N ,18400A x x n nB x x x ==+∈=--<∣∣,则A B 中的元素个数为()A.8B.9C.10D.11【答案】B 【解析】【分析】解一元二次不等式化简集合B ,再根据已知列出不等式,求解判断作答.【详解】解不等式218400x x --<得:220x -<<,即{|220}B x x =-<<,而{}23,N A x x n n ==+∈∣,由22320n -<+<解得:51722n -<<,又N n ∈,显然满足51722n -<<的自然数有9个,所以A B 中的元素个数为9.故选:B 2.已知复数33i2i z =+,则z =()A.1B.35C.355D.3【答案】C 【解析】【分析】利用复数的除法化简复数z ,利用复数的模长公式可求得结果.【详解】因为()()()33i 2i 3i 3i 36i 2i 2i 2i 2i 55z +====-++--+,因此,5z ==.故选:C.3.已知非零向量a 、b满足a b =r r ,且()2a b b +⊥ ,则,a b <>= ()A.π6B.π3C.2π3D.5π6【答案】C 【解析】【分析】由已知可得出()20a b b +⋅= ,利用平面向量数量积的运算性质求出cos ,a b <> 的值,结合平面向量夹角的取值范围可求得结果.【详解】因为()2a b b +⊥ ,则()222cos ,0a b b a b a b b +⋅=⋅<>+= ,a b = ,可得1cos ,2a b <>=- ,因为0,πa b ≤<>≤ ,因此,2π,3a b <>= .故选:C.4.某士兵进行射击训练,每次命中目标的概率均为34,且每次命中与否相互独立,则他连续射击3次,至少命中两次的概率为()A.2732B.916C.2764D.932【答案】A 【解析】【分析】根据相互独立事件的概率乘法公式及互斥事件的概率加法公式即可求解.【详解】解:因为每次命中目标的概率均为34,且每次命中与否相互独立,所以连续射击3次,至少命中两次的概率322333327C 144432P ⎛⎫⎛⎫⎛⎫=+-= ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭,故选:A.5.已知函数()2sin 3cos f x x x =+在x ϕ=处取得最大值,则cos ϕ=()A.13 B.13C.13-D.31313-【答案】A 【解析】【分析】根辅助角公式和正弦函数最值求解即可.【详解】()()2sin 3cos f x x x x θ=+=+,其中θ为锐角,sin 13θ=.因为当x ϕ=处取得最大值,所以22πϕθπ+=+k ,k Z ∈,即22πϕθπ=-+k ,k Z ∈,所以313cos cos 2sin 213πϕθπθ⎛⎫=-+== ⎪⎝⎭k .故选:A6.已知定义域为R 的偶函数()f x 满足()(4)0f x f x +-=,且当[2,2)x ∈-时,2()4f x x =-,则(2021)f =()A.3-B.1- C.1D.3【答案】D 【解析】【分析】根据给定条件,探讨出函数()f x 的周期,再结合已知函数式求解作答.【详解】因R 上的偶函数()f x 满足()(4)0f x f x +-=,即有()()()4f x f x f x -=-=--,则(8)(4)()f x f x f x -=--=-,因此,函数()f x 是周期为8的周期函数,2(2021)(25285)(5)(1)[(1)4]3f f f f =⨯+==--=---=.故选:D7.我国古代经典数学名著《九章算术》中有一段表述:“今有圆堡壔(dăo ),周四丈八尺,高一丈一尺”,意思是有一个圆柱,底面周长为4丈8尺,高为1丈1尺.则该圆柱的外接球的表面积约为()(注:1丈=10尺,π取3)A.1185平方尺B.1131平方尺C.674平方尺D.337平方尺【答案】B 【解析】【分析】根据题意作图,再由底面周长求得底面半径,连接上下底面圆心,取中点为外接圆的圆心,根据勾股定理,可得外接圆半径,可得答案.【详解】由1丈=10尺,则4丈8尺=48尺,1丈1尺=11尺,如下图:则11,2·48BC AB π==,即8AB =,假设点D 为圆柱外接圆的圆心,即AD 为外接圆的半径,且112BD DC ==,在Rt ABD △中,222AB BD AD +=,解得294.25AD =,则外接球的表面积241131S AD π=⋅=,故选:B.8.甲、乙、丙、丁、戊五名志愿者去,,A B C 三个不同的小区参加新冠疫情防控志愿服务,每个小区至少去1人,每人只去1个小区,且甲、乙去同一个小区,则不同的安排方法有()A.28种B.32种C.36种D.42种【答案】C 【解析】【分析】先将甲、乙看成一个元素,然后先分组后排列可得.【详解】将甲、乙看成一个元素A ,然后将A 、丙、丁、戊四个元素分为3组,共有21142122C C C 6A =种,再将3组分到3个不同小区有33A =6种,所以满足条件的安排方法共有66=36⨯种.故选:C9.已知角α的顶点在坐标原点,始边与x 轴的非负半轴重合,终边经过点(,4)m -,其中0m <,若7cos 225α=-,则πtan 2m α⎛⎫+= ⎪⎝⎭()A.2B.12-C.43-D.34-【答案】D 【解析】【分析】利用三角函数定义求出tan α,再利用二倍角的余弦公式结合齐次式法求解作答.【详解】依题意,4tan 0mα=->,又22222222cos sin 1tan 7cos 2cos sin cos sin 1tan 25ααααααααα--=-===-++,解得4tan 3α=,从而得3m =-,所以3πsin()π3πcos 132tan(tan()3π22sin tan 4cos(2m ααααααα-+=-===-=---.故选:D10.过抛物线()2:20C y px p =>的焦点F 且斜率为1-的直线交C 于A 、B (其中A 在x轴上方)两点,交C 的准线于点M ,且16AB =,O 为坐标原点,则OM =()A.2B.C.D.【答案】D 【解析】【分析】将直线AB 的方程与抛物线的方程联立,利用韦达定理结合抛物线的焦点弦长公式求出p 的值,可求得点M 的坐标,再利用平面间两点间的距离公式可求得OM 的值.【详解】抛物线C 的焦点为,02p F ⎛⎫⎪⎝⎭,准线方程为2p x =-,直线AB 的方程为2⎛⎫=--⎪⎝⎭p y x ,设点()11,A x y 、()22,B x y ,联立222p y x y px⎧⎛⎫=--⎪ ⎪⎝⎭⎨⎪=⎩可得22304p x px -+=,2290p p ∆=->,由韦达定理可得123x x p +=,则12416x x p A p B =++==,可得4p =,联立22p x p y x ⎧=-⎪⎪⎨⎛⎫⎪=-- ⎪⎪⎝⎭⎩可得2p x y p ⎧=-⎪⎨⎪=⎩,即点()2,4M -,因此,OM ==.故选:D.11.已知32()2(2)3f x x a x x =+--是奇函数,则过点(1,2)P -向曲线()y f x =可作的切线条数是()A.1B.2C.3D.不确定【答案】C 【解析】【分析】根据给定条件,求出a ,再求出函数()f x 的导数,设出切点坐标,借助导数的几何意义列出方程求解作答.【详解】因函数()f x 是奇函数,则由()()0f x f x -+=得()2220a x -=恒成立,则2a =,即有3()23f x x x =-,2()63'=-f x x ,设过点(1,2)P -向曲线()y f x =所作切线与曲线()y f x =相切的切点为3000(,23)Q x x x -,而点(1,2)P -不在曲线()y f x =上,则320000232631x x x x ---=+,整理得32004610x x +-=,即2000(21)(221)0x x x ++-=,解得012x =-或0132x -±=,即符合条件的切点有3个,所以过点(1,2)P -向曲线()y f x =可作的切线条数是3.故选:C12.设双曲线2222:1(0,0)x y a b a bΓ-=>>的左、右焦点分别为点12(,0),(,0)F c F c -,过点(2,0)P c -且斜率为12的直线与双曲线的左、右两支分别交于,M N 两点,若||3||PN PM =,且直线2F N 的斜率为3,则Γ的离心率为()A.132B.2C.2D.2【答案】B 【解析】【分析】通过题意可以得到直线PN 和直线2NF 的方程,两条方程联立可以得到N 的坐标,代入双曲线即可求出答案【详解】解:由题意可得直线PN 的方程为()122y x c =+,直线2NF 的方程为()3y x c =-,所以()()1223y x c y x c ⎧=+⎪⎨⎪=-⎩,解得8595c x cy ⎧=⎪⎪⎨⎪=⎪⎩,即89,55c c N ⎛⎫ ⎪⎝⎭,将89,55c c N ⎛⎫ ⎪⎝⎭代入双曲线可得2222648112525c c a b-=即()22222648112525c c a c a -=-,所以2264811125251e e -=⎛⎫- ⎪⎝⎭,因为1,e >所以e =故选:B二、填空题:本题共4小题,每小题5分,共20分.13.已知函数2()log (1)f x x a =-+在区间(2,3)上有且仅有一个零点,则实数a 的取值范围为_____.【答案】(1,0)-【解析】【分析】结合函数的单调性和零点的存在定理,即可求解【详解】解:由对数函数的性质,可得()f x 为单调递增函数,且函数()f x 在(2,3)上有且仅有一个零点,所以()()230f f ⋅<,即(1)0a a ⋅+<,解得10a -<<,所以实数a 的取值范围是(1,0)-,故答案为:(1,0)-14.写出一个同时具有下列性质①②③的函数:()f x =_____.①()()()1212f x x f x f x =+;②当,()0x ∈+∞时,()f x 单调递减;③()f x 为偶函数.【答案】12log x (不唯一)【解析】【分析】根据对数函数性质即可做出判断.【详解】性质①显然是和对数有关,性质②只需令对数的底01a <<即可,性质③只需将自变量x 加绝对值即变成偶函数.故答案为:12log x (不唯一)15.已知平面上的动点P 到点(0,0)O 和(2,0)A 的距离之比为32,则点P 到x 轴的距离最大值为_____.【答案】【解析】【分析】设(,)P x y ,然后根据题意列方程化简可得点P 的轨迹是以(6,0)-为圆心,为半径的圆,从而可求得答案.【详解】设(,)P x y ,因为动点P 到点(0,0)O 和(2,0)A 的距离之比为32,2=,22223(2)4x y x y +=-+,2222443(44)3x y x x y +=-++,221212x y x ++=22(6)48x y ++=,所以点P 的轨迹是以(6,0)-为圆心,所以点P 到x 轴的距离最大值为故答案为:16.微型航空遥感技术以无人机为空中遥感平台,为城市经济和文化建设提供了有效的技术服务手段.如图所示,有一架无人机在空中P 处进行航拍,水平地面上甲、乙两人分别在,A B 处观察该无人机(两人的身高忽略不计),C 为无人机在水平地面上的正投影.已知甲乙两人相距100m ,甲观察无人机的仰角为45︒,若再测量两个角的大小就可以确定无人机的飞行高度PC ,则这两个角可以是_____.(写出所有符合要求的编号)①BAC ∠和ABC ∠;②BAC ∠和PAB ∠;③PAB ∠和PBA ∠;④PAB ∠和ABC ∠.【答案】①③④【解析】【分析】①:根据已知先解ABC 得AC ,然后可得;②:根据已知直接判断可知;③:先解PAB △得PA ,然后可得;④:先由最小角定理的BAC ∠,解ABC 可得AC ,然后可得.【详解】①:当已知BAC ∠和ABC ∠时,在ABC 利用内角和定理和正弦定理可得AC ,然后在Rt PAC △中,由三角函数定义可得PC ,故①正确;②:当已知BAC ∠和PAB ∠时,在ABC 已知一角一边,在PAB △中已知一角一边,显然无法求解,故②错误;③:当已知PAB ∠和PBA ∠时,在PAB △中已知两角一边,可解出PA ,然后在Rt PAC △中,由三角函数定义可得PC ,故③正确;④:当已知PAB ∠和ABC ∠时,可先由最小角定理求得BAC ∠,然后解ABC 可得AC ,最后在Rt PAC △中,由三角函数定义可得PC ,故④正确.故答案为:①③④三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17-21题为必考题,每个试题考生都必须作答.第22,23题为选考题,考生根据要求作答.(一)必考题:共60分.17.设等差数列{}n a 的前n 项和为n S ,已知251,15a S ==.(1)求数列{}n a 的通项公式;(2)若23log 2n n n b a a +=,求数列{}n b 的前n 项和n T .【答案】(1)23n a n =-(2)1(25)210n n T n +=-⨯+【解析】【分析】(1)根据等差数列的通项公式和前n 项和公式列方程组直接求解可得;(2)由错位相减法可得.【小问1详解】设数列{}n a 的公差为d ,由题设可得111,51015a d a d +=⎧⎨+=⎩解得112,a d =-⎧⎨=⎩所以1(1)223n a n n =-+-⨯=-.【小问2详解】由(1)知2log 23n b n n =-,所以223nn bn =-可得(23)2nn b n =-⨯,所以231121232(25)2(23)2n n n T n n -=-⨯+⨯+⨯++-⨯+-⨯ ①23412121232(25)2(23)2n n n T n n +=-⨯+⨯+⨯++-⨯+-⨯ ②②减①可得:341112222(23)2n n n T n ++=⨯----+-⨯ 118(12)(23)2212n n n -+⨯-=-⨯+--1(25)210n n +=-⨯+18.某工厂共有甲、乙两个车间,为了比较两个车间的生产水平,分别从两个车间生产的同一种零件中各随机抽取了100件,它们的质量指标值m 统计如下:质量指标值m [)0,20[)20,40[)40,60[)60,80[]80,100甲车间(件)152025319乙车间(件)510153931(1)估计该工厂生产这种零件的质量指标值m 的平均数;(同一组中的数据用该组区间的中点值作代表)(2)根据所给数据,完成下面的22⨯列联表(表中数据单位:件),并判断是否有99%的把握认为甲、乙两个车间的生产水平有差异.60m <60m ≥合计甲车间乙车间合计附:22()()()()()n ad bc K a b c d a c b d -=++++,其中n a b c d =+++.()2P K k≥0.050.010.001k3.8416.63510.828【答案】(1)58;(2)列联表见解析,有99%把握认为甲乙两个车间的生产水平有差异.【解析】【分析】(1)根据给定的数表,求出各组数据的频率,再列式计算作答.(2)完善22⨯列联表,计算2K 的观测值,再与临界值比对作答.【小问1详解】由所给数据,各组的频率分别为0.1,0.15,0.2,0.35,0.2,所以该工厂生产这种零件的质量指标值m 的平均数的估计值为:100.1300.15500.2700.35900.258⨯+⨯+⨯+⨯+⨯=.【小问2详解】22⨯列联表如下:60m <60m ≥合计甲车间6040100乙车间3070100合计90110200所以22200(60704030)18.18210010090110K ⨯⨯-⨯=≈⨯⨯⨯因为18.182大于6.635,所以有99%把握认为甲乙两个车间的生产水平有差异.19.如图,在直三棱柱111ABC A B C -中,190,24,ACB AA AC BC M ︒∠====为棱1AA 上靠近1A 的三等分点,N 为棱AC 的中点,点P 在棱BC 上,且直线PN ∥平面1BMC .(1)求PC 的长;(2)求二面角1P BM C --的余弦值.【答案】(1)23PC =(2)22110【解析】【分析】(1)在1CC 上取一点Q ,使得CP CQ =,根据面面平行判定定理证明平面PQN平面1BMC ,再根据面面平行性质定理确定CQ 的长即可,(2)建立空间直角坐标系,求出平面PBM ,平面1BC M 的法向量,根据二面角向量公式求二面角1P BM C --的余弦值.【小问1详解】在1CC 上取一点Q ,使得CP CQ =,连接,PQ NQ .由已知得11CC AA CB ==,所以1CQ CPCC CB=所以1PQ BC ∥.因为PQ ⊄平面1BMC ,1BC ⊂平面1BMC ,所以PQ ∥平面1BMC .又因为PN ∥平面1,BMC PN PQ P ⋂=,,PN NQ ⊂平面PQN ,所以平面PQN 平面1BMC .平面11ACC A 平面PQN QN =,平面11ACC A 平面11BC M MC =,根据面面平行的性质可知1//MC QN .在矩形11ACC A 中,可得11CQN A MC ∽,所以11123A M CQ CN A C ==,所以2233PC CQ CN ===.【小问2详解】以C 为坐标原点,分别以1,,CA CB CC 所在直线为,,x y z 轴建立空间直角坐标系.则182(0,0,0),(0,0,4),(0,4,0),2,0,,0,,033C C B M P ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭.114(0,4,4),2,0,3C B C M ⎛⎫=-=- ⎪⎝⎭ ,8102,4,,0,,033BM BP ⎛⎫⎛⎫=-=- ⎪ ⎪⎝⎭⎝⎭ ,设平面1C MB 的法向量为()111,,m x y z =r,则110,0,C B m C M m ⎧⋅=⎪⎨⋅=⎪⎩ ,所以1111440,420,3y z x z -=⎧⎪⎨-=⎪⎩,取13z =得()2,3,3.m = 设平面PMB 的法向量为()222,,n x y z =r ,则0,0,BM n BP n ⎧⋅=⎨⋅=⎩ 所以22228240,3100,3x y z y ⎧-+=⎪⎪⎨⎪-=⎪⎩取23z =-,得()4,0,3.n =- 所以22cos ,110m n m n m n ⨯++⨯-⋅===-⋅结合图可知二面角1PBM C --的余弦值为110.20.过椭圆22:143x y C +=上任意一点P 作直线:l y kx p=+(1)证明:2234p k + ;(2)若0,p O ≠为坐标原点,线段OP 的中点为M ,过M 作l 的平行线,l l ''与C 交于,A B 两点,求ABP △面积的最大值.【答案】(1)证明见解析(2)32.【解析】【分析】(1)联立椭圆方程与直线方程,消元整理一元二次方程,由题意,该方程有解,则判别式大于等于零,可得答案.(2)设出题目中的两点,根据平行,设出另一条直线,根据中点,找出两直线的截距之间的关系,联立椭圆方程与直线方程,消元整理一元二次方程,写出韦达定理,根据三角形的等积变换,利用分割法,整理函数,根据(1),可得答案.【小问1详解】联立221,43,x y y kx p ⎧+=⎪⎨⎪=+⎩,消去y 整理得:()2223484120k x kpx p +++-=,因为点P 在C 上,所以()()2222644412340,k p p k ∆=--+ 化简得2234p k + .【小问2详解】设:l y kx m '=+,点()00,P x y ,则00,22x y M ⎛⎫⎪⎝⎭.由已知得00y kx p =+,所以00222y x p k =⋅+,即点00,22x y M ⎛⎫⎪⎝⎭满足方程2p y kx =+,所以2p m =.由221,43,x y y kx m ⎧+=⎪⎨⎪=+⎩得()2223484120k x kmx m +++-=,设()()1122,,,A x y B x y ,则21212228412,3434km m x x x x k k-+=-=++.所以122.34x x k-==+∣所以121||2ABPABOSS m x x ==-==令2234m t k =+,因为2223444p k m += ,所以10,4t ⎛⎤∈ ⎥⎝⎦.所以32ABPS ==所以ABP △面积的最大值为32.21.设函数()()e xf x mx m m =--∈R .(1)讨论()f x 的单调性;(2)若()f x 有两个零点1x 和2x ,设1202x x x +=,证明:()00f x '>(()f x '为()f x 的导函数).【答案】(1)答案见解析(2)证明见解析【解析】【分析】(1)分0m ≤、0m >两种情况讨论,分析导数的符号变化,由此可得出函数()f x 的增区间和减区间;(2)由函数零点的定义可得出1212e 0e 0x x mx m mx m ⎧--=⎨--=⎩,可得出1212e e x x m x x -=-,将所证不等式等价变形为12212212eex x x x x x --->-,令1202x x t -=>,即证e e 2t t t -->,构造函数()e e 2t t g t t -=--,其中0t >,利用导数分析函数()g t 的单调性,即可证得结论成立.【小问1详解】解:因为()e x f x mx m =--,则()e xf x m '=-,若0m ≤,对任意的x ∈R ,则()0f x '<,函数()f x 的单调递减区间为(),-∞+∞;若0m >,令()e 0xf x m '=-=,得ln x m =,当ln x m <时,()0f x '>,当ln x m >时,()0f x '<.所以()f x 的增区间为(),ln m -∞,减区间为()ln ,m +∞.综上所述,当0m ≤时,函数()f x 的单调递减区间为(),-∞+∞;当0m >时,函数()f x 的增区间为(),ln m -∞,减区间为()ln ,m +∞.【小问2详解】证明:不妨令12x x >,由题设可得1212e 0e 0x x mx m mx m ⎧--=⎨--=⎩,两式相减整理可得1212e e x x m x x -=-.所以()1212121222012e e ee 2x x x x x x x xf x f m x x ++''+-⎛⎫==-=- ⎪-⎝⎭,要证()00f x '>,即证1212212e e e 0x x x x x x +-->-,即证12212212eex x x x x x --->-,令1202x x t -=>,即证e e 2t t t -->,其中0t >,构造函数()e e 2ttg t t -=--,其中0t >,则()e e 220t t g t -'=+->=,所以,函数()g t 在()0,∞+上单调递增,所以,当0t >时,()()00g t g >=,即e e 2t t t -->,故原不等式得证.【点睛】方法点睛:利用导数证明不等式问题,方法如下:(1)直接构造函数法:证明不等式()()f x g x >(或()()f x g x <)转化为证明()()0f x g x ->(或()()0f x g x -<),进而构造辅助函数()()()h x f x g x =-;(2)适当放缩构造法:一是根据已知条件适当放缩;二是利用常见放缩结论;(3)构造“形似”函数,稍作变形再构造,对原不等式同解变形,根据相似结构构造辅助函数.(二)选考题:共10分.请考生在22,23题中任选一题作答,如果多做,则按所做的第一题计分.[选修4-4:坐标系与参数方程]22.在直角坐标系xOy 中,曲线C 的参数方程为2(cos sin )(,0),(cos sin )x m m y m ϕϕϕϕϕ=-⎧≠⎨=+⎩为参数以O 为极点,x 轴正半轴为极轴建立极坐标系,直线l 的极坐标方程为sin 504πθ⎛⎫+-= ⎪⎝⎭.(1)写出l 的直角坐标方程;(2)若l 与C 只有一个公共点,求m 的值.【答案】(1)50x y +-=(2)102=±m 【解析】【分析】(1)利用和差化积的正弦公式把直线l 的极坐标方程展开,再利用极坐标与直角坐标的互化公式即可求解.(2)先得出曲线C 的普通方程,再联立方程,利用判别式等于0即可求解.【小问1详解】由l 的极坐标方程可得sin cos 50ρθρθ+-=,由cos sin x y ρθρθ=⎧⎨=⎩可知,直角坐标方程为:50x y +-=.【小问2详解】由C 的参数方程可得2222x y m m ⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭,即C 的普通方程为222480x y m +-=.联立方程22250480x y x y m +-=⎧⎨+-=⎩得:2254010080x x m -+-=,因为直线l 与曲线C 只有一个公共点,所以()222404510081604000m m∆=-⨯⨯-=-=,解得:2=±m .[选修4-5:不等式选讲]23.已知,,a b c 均为正实数,且1abc =.(1)求124a b c++的最小值;(2)证明:222++≥+++++bc ac ab b c a c a b.【答案】(1)6(2)证明见解析【解析】【分析】(1)利用三元基本不等式求解即可.(2)利用基本不等式证明即可得到答案.【小问1详解】由基本不等式可知1246++≥==a b c ,当且仅当124a b c ==,即1,1,22a b c ===时等号成立,所以124a b c++的最小值为6.【小问2详解】因为1abc =,所以111bc ac ab a b c++=++.11242+≥=≥=++a b a b a b .同理可得114b c b c+≥+,114a c a c+≥+所以4111442⎛⎫++≥++⎪+++⎝⎭a b c b c a c a b,当且仅当a b c==时等号成立.所以111222++≥+++++a b c b c a c a b,即222. ++≥+++++ bc ac abb c a c a b。
陕西省联盟学校2023届高三下学期第一次大联考理科数学试题含答案

绝密★启用前“高考研究831重点课题项目”陕西省联盟学校2023年第一次大联考数学(理科)试题(答案在最后)注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上,并将自己的姓名、准考证号、座位号填写在本试卷上.2.回答选择题时,选出每小题答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号.涂写在本试卷上无效. 3.作答非选择题时,将答案书写在答题卡上,书写在本试卷上无效. 4.考试结束后,将本试卷和答题卡一并交回.一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.集合{}2,1,0,1,2A =--,{}1,0,2AB =-,则B =( )A .{}2-B .{}1C .{}2,1-D .{}2,0,2-2.在复平面内,复数z 与21i-对应的点关于实轴对称,则z 等于( ) A .1i +B .1i --C .1i -+D .1i -3.下列说法中正确的是( )A .回归直线方程为 1.230.08y x =+,则样本点的中心可以为()4,5B .采用系统抽样,从800名学生中抽取一个容量为40的样本,则分组的组距为40C .“a b >”是“22a b >”成立的充分不必要条件D .命题p :x ∀∈R ,20x >,则p ⌝:0x ∃∈R ,020x< 4.二项式()()*1nx n +∈N 的展开式中3x 项的系数为10,则n =( )A .8B .6C .5D .105.已知x ,()0,y ∈+∞,6124yx -⎛⎫= ⎪⎝⎭,则xy 的最大值为( )A .92B .98C .32D .946.某学校拟派2名语文老师、3名数学老师和3名体育老师共8人组成两个支教分队,平均分到甲、乙两个村进行义务支教,其中每个分队都必须有语文老师、数学老师和体育老师,则不同的分配方案有( ) A .72种B .36种C .24种D .18种7.已知圆C :22480x y x y +-+=关于直线32220x ay --=对称,则圆C 中以,22a a ⎛⎫-⎪⎝⎭为中点的弦长为( )A .B CD .8.在xOy 平面内,双曲线22221x y a b-=(0a >,0b >)的左、右焦点分别为1F ,2F ,过左顶点AM ,若122MO FF =,则该双曲线的离心率是( ) ABCD .539.在△ABC 中,如果()cos 2cos 0B C C ++<,那么△ABC 的形状为( ) A .钝角三角形B .直角三角形C .锐角三角形D .不能确定10.在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且cos cos sin sin B C Ab c C+=,则b 的值为( ) A .1BC.2D .211.函数()()πsin 03f x x ωω⎛⎫=+> ⎪⎝⎭在[]0,1上有唯一的极大值,则ω∈( ) A .13ππ,6⎡⎤⎢⎥⎣⎦ B .13ππ,6⎡⎫⎪⎢⎣⎭ C .π13π,66⎡⎫⎪⎢⎣⎭D .13π25π,66⎡⎫⎪⎢⎣⎭ 12.已知偶函数()f x 满足()()8f x f x =-,且当(]0,4x ∈时,()()ln 2x f x x=,关于x 的不等式()()20f x af x +>在[]20,20-上有且只有30个整数解,则实数a 的取值范围是( )A .1ln 2,ln 63⎛⎫-- ⎪⎝⎭B .1ln 2,ln 63⎛⎤-- ⎥⎝⎦C .13ln 2ln 6,34⎛⎫--⎪⎝⎭ D .13ln 2ln 6,34⎛⎤--⎥⎝⎦二、填空题:本题共4小题,每小题5分,共20分. 13.曲线5e2xy -=+在()0,3处的切线方程为________.14.设数列{}n a ,{}n b 均为等差数列,它们的前n 项和分别为n S ,n T ,若2334n n S n T n -=+,则77a b =________. 15.点A ,B 是抛物线C :()220y px p =>上的两点,F 是抛物线C 的焦点,若120AFB ∠=︒,AB 中点D 到抛物线C 的准线的距离为d ,则ABd的最小值为________. 16.在四棱锥P ABCD -中,PA ⊥平面ABCD ,2AP =,点M 是矩形ABCD 内(含边界)的动点,且1AB =,3AD =,直线PM 与平面ABCD 所成的角为π4,当三棱锥P ABM -的体积最小时,三棱锥P ABM -的外接球的体积为________.三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答. (一)必考题:60分17.(12分)数列{}n a 为正项数列,14a =,n +∀∈N ,22112n n n n a a a a ++-=(I )求数列{}n a 的通项公式; (II )若数列{}n b 满足2211log log n n n b a a -=⋅,n T 为数列{}n b 的前项和,求证:1n T <.18.(12分)如图,在四棱锥P ABCD -中,底面ABCD 是正方形,2AD PD ==,PA =120PDC ∠=︒,点E 为线段PC 的中点,点F 在线段AB 上.(I )若12AF =,求证:CD EF ⊥; (II )设平面DEF 与平面DP A 所成二面角的平面角为θ,试确定点F的位置,使得cos θ=. 19.(12分)中国职业男篮CBA 总决赛采用七场四胜制,即若有一队先胜四场,则此队为总冠军,比赛就此结束.现甲、乙两支球队进行总决赛,因两队实力相当,每场比赛两队获胜的可能性均为12.据以往资料统计,第一场比赛可获得门票收入400万元,以后每场比赛门票收入比上一场增加100万元.(I )求总决赛中获得门票总收入恰好为3000万元的概率; (II )设总决赛中获得门票总收入为X ,求X 的数学期望()E X .20.(12分)已知1F ,2F 为椭圆E :22184y x +=的上、下焦点,()00,P x y 为平面内一个动点,其中00x >.(I)若12PF PF +=12FPF △面积的最大值; (II )记射线1F P 与椭圆E 交于()11,M x y ,射线2F P 与椭圆E 交于()22,N x y ,若21MF NF ∥,探求0x ,1x ,2x 之间的关系.21.(12分)已知函数()ln 1e axxf x x ax =+--,a ∈R ,e 为自然对数的底数. (I )当1a =时,求()f x 的单调区间;(II )若函数()f x 有两个不同的零点1x ,2x ,证明:1212elnx x a+>. (二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.22.(10分)选修4-4:坐标系与参数方程 已知曲线C 的参数方程为12cos ,12sin x y ϕϕ=-+⎧⎨=+⎩(ϕ为参数),直线l :θα=([)0,πα∈,ρ∈R )与曲线C 相交于M 、N 两点.以极点O 为原点,极轴为x 轴的非负半轴建立平面直角坐标系.(I )求曲线C 的极坐标方程;(II )记线段MN 的中点为P ,若OP λ≤恒成立,求实数λ的取值范围. 23.(10分)选修4-5:不等式选讲 已知函数()121f x x x =++-. (I )若()11f x m n≥+(m ,0n >)对x ∀∈R 恒成立,求m n +的最小值; (II )若()2f x ax a ≥-+恒成立,求实数a 的取值范围.“高考研究831重点课题项目”陕西省联盟学校2023年第一次大联考数学(理科)试题参考答案一、选择题(本题共12小题,每题5分,共60分)一、选择题(本题共12小题,每题5分,共60分) 1.【参考答案】C 2.【参考答案】D【解析】21i 1i=+-,则1i z =-. 3.【参考答案】A 4.【参考答案】C【解析】由310n C =得,5n =. 5.【参考答案】A 【解析】由题可得,6222x y--=,26x y +=,则2129222x y xy +⎛⎫≤= ⎪⎝⎭,当且仅当3x =,32y =时,等号成立. 6.【参考答案】B【解析】()112212333336C C C C C +=.7.【参考答案】D【解析】直线32220x ay --=过圆C :22480x y x y +-+=的圆心()2,4C -,r =,则2a =,圆C 中以()1,1-为中点的弦长为=8.【参考答案】B【解析】由222,b y x ax y c⎧=⎪⎨⎪+=⎩得(),M a b ,则()03b a a -=--,3b a =,于是3e ==. 9.【参考答案】D 【解析】()()()cos 2cos cos πcos π2cos cos 0B C C B A B A B A ⎡⎤⎡⎤++=+-+-+=-<⎣⎦⎣⎦,则cos cos 0B A >,于是B ,A 均为锐角,则△ABC 的形状无法确定. 10.【参考答案】A【解析】易得22222222a c b a b c aabc abc c+-+-+=,化简得1b =. 11.【参考答案】C 【解析】令ππ2π32x k ω+=+,k ∈Z ,则π2π6x k ω=+,k ∈Z ,在y 轴右侧的第一个极大值点为π6x ω=,第二个极大值点为13π6x ω=,于是π1,613π1,6ωω⎧≤⎪⎪⎨⎪>⎪⎩解得π13π,66ω⎡⎫∈⎪⎢⎣⎭.12.【参考答案】D【解析】由题可知,此函数周期为8,此不等式在(]0,4上恰有3个整数解,又可知()f x 在e 0,2⎛⎫ ⎪⎝⎭上递增,在e ,42⎡⎤⎢⎥⎣⎦上递减,且()1ln 20f =>,()()()3234ln 204f f f >>=>,故0a <,且须()()()4,3,1,a f a f a f ⎧-≥⎪-<⎨⎪-<⎩解得13ln 2ln 6,34a ⎛⎤∈-- ⎥⎝⎦. 二、填空题(本题共4小题,每题5分,共20分) 13.【参考答案】530x y +-=【解析】05x y ='=-,切线方程为35y x -=-即530x y +-=.14.【参考答案】2343【解析】7713771313231343a a Sb b T ===.15.【解析】由抛物线几何性质可得()12d AF BF =+,由余弦定理和基本不等式可得, ()22222cos120AB AF BF AF BF AF BF AF BF =+-⋅︒=+-⋅()()222324AF BF AF BFAF BF⎛⎫+≥+-=+ ⎪⎝⎭,易得ABd≥,当且仅当AF BF =时等号成立. 16.【解析】【详解】如图,易知M 位于底面矩形ABCD 内的以点A 为圆心,2为半径的圆上,记点M 的轨迹为圆弧EF .连接AF ,当点M 位于F 时,三棱锥P ABM -的体积最小,又π2PAF PBF ∠=∠=,则三棱锥P ABM -的外接球球心为PF的中点,此外接球的体积34π3V ==. 三、解答题(解答应写出文字说明,证明过程或演算步骤)17.解:(1)由221120n n n n a a a a ++--=得12n n a a +=,∴12n n a +=;(II )()11111n b n n n n ==-++,∴11111nn n i T b n ===-<+∑.18.解:(I )在△PCD 中,2PD CD ==,∵E 为P C 的中点,∴DE 平分∠PDC ,60PDE ∠=︒, ∴在Rt △PDE 中,cos601DE PD =⋅︒=, 过E 作EH CD ⊥于H ,则12DH =,连结FH , ∵12AF =,∴四边形AFHD 是矩形, ∴CD FH ⊥,又CD EH ⊥,FH EH H =,∴CD ⊥平面EFH ,又EF ⊂平面EFH ,∴CD EF ⊥.(II )∵2AD PD ==,PA =AD PD ⊥,又AD DC ⊥, ∴AD ⊥平面PCD ,又AD ⊂平面ABCD , ∴平面PCD ⊥平面ABCD .过D 作DG DC ⊥交PC 于点G ,则由平面PCD ⊥平面ABCD 知,DG ⊥平面ABCD ,故DA ,DC ,DG 两两垂直,以D 为原点,以DA ,DC ,DG 所在直线分别为x ,y ,z 轴,建立如图所示空间直角坐标系O xyz -,则()2,0,0A ,()2,2,0B ,()0,2,0C,(0,P -,又知E 为PC的中点,10,2E ⎛ ⎝⎭,设()2,,0F t ,02t ≤≤,则10,2DE ⎛=⎝⎭,()2,,0DF t =,(0,DP =-,()2,0,0DA =.设平面DEF 的法向量为()111,,n x y z =,则0,0,n DE n DF ⎧⋅=⎪⎨⋅=⎪⎩∴111110,220,y z x ty ⎧+=⎪⎨⎪+=⎩ 取12z =-,可求得平面DEF 的一个法向量()3,22n t =--,设平面ADP 的法向量为()222,,m x y z =,则0,0,m DP m DA ⎧⋅=⎪⎨⋅=⎪⎩所以2220,20,y x ⎧-+=⎪⎨=⎪⎩取()0,3,1m =.∴cos cos ,23m n θ===⋅43t =,∴当43AF =时满足cos 4θ=.19.解:(I )依题意,每场比赛获得的门票收入组成首项为400,公差为100的等差数列.设此数列为{}n a ,则易知1400a =,100300n a n =+,所以()10070030002n n n S +==. 解得5n =或12n =-(舍去),所以此决赛共比赛了5场.则前4场比赛的比分必为1:3,且第5场比赛为领先的球队获胜,其概率为4341124C ⎛⎫= ⎪⎝⎭. 所以总决赛中获得门票总收入恰好为3000万元的概率为14. (II )随机变量X 可取的值为4S ,5S ,6S ,7S ,即2200,3000,3900,4900.()4112200228P X ⎛⎫==⨯= ⎪⎝⎭,()434113000C 24P X ⎛⎫=== ⎪⎝⎭,()535153900C 216P X ⎛⎫=== ⎪⎝⎭,()636154900C 216P X ⎛⎫=== ⎪⎝⎭, 所以X 的分布列为所以()22003000390049003775841616E X =⨯+⨯+⨯+⨯=.20.解:(I )由题可知,点()00,P x y为椭圆2219122y x +=上一点,且00x >, 则1212011422F PF S F F x =⋅⋅≤⨯⨯=△12F PF △. (II )射线2F N 的方程为()22220y y x x x +=-≥,射线1F M 的方程为()11220y y x x x -=+≥,联立221122,22,y y x x y y x x +⎧=-⎪⎪⎨-⎪=+⎪⎩解得()212112012224y x x y x x x x x -++=,① 又21MF NF ∥,则12212112122222y y y x x y x x x x +-=⇔-=+,② 将②代入①,得012111x x x =+. 21.解:(I )当1a =时,()e ln 1x f x x x x -=+--,0x >,()()11e x f x x x -⎛⎫'=-+ ⎪⎝⎭,当()0,1x ∈时,()0f x '>;当()1,x ∈+∞时,()0f x '<, 则()f x 的单调增区间为区间()0,1,减区间为区间()1,+∞.(II )()ln ln 1e ln 1ex axax x f x x ax x ax -=+--=++--,0x >, 令()e 1x g x x =+-,()e 10x g x '=+>,则()g x 在()0,+∞上单调递增,又()00g =,于是当()0f x =即()ln 0g x ax -=时,ln 0x ax -=,则此关于x 的方程有两个不同的解1x ,2x ,即1122ln ln ,,x ax x ax ==⎧⎨⎩①②构造函数()ln x h x x =,0x >,()21ln xh x x -'=,当()0,e x ∈时,()0f x '>;当()e,x ∈+∞时,()0f x '<,可知()10e e a h <<=,又()10h =,不妨设121e x x <<<, 由②-①,得()2211ln x a x x x -=,令()211xt t x =>,则()11ln ax t t -=,1ln 1t ax t =-,同理可得,2ln 1t t ax t =-, 要证1212eln x x a +>,即证()12112e ln ln 2e ln 1t a x x a t a a a t ++>⇔>--,令()()21ln 1t t t t ϕ-=-+,1t >,()()()22101t t t t ϕ-'=≥+,又()10ϕ=,则()0t ϕ>,1ln 21t t t +>-, 又1ln ea a >-,2e ln 2a a -<,故此题得证.22.解:(I )因为曲线C 的参数方程为12cos ,12sin x y ϕϕ=-+⎧⎨=+⎩(ϕ为参数),故所求方程为()()222112x y ++-=. 又cos sin x y ρθρθ=⎧⎨=⎩,则22cos 2sin 2ρρθρθ+-=,故曲线C的极坐标方程为2πsin 24ρθ⎛⎫--= ⎪⎝⎭. (II )联立θα=和22cos 2sin 20ρρθρθ+--=,得()22cos sin 20ρραα+--=, 设()1,M ρα、()2,N ρα,则()12π2sin cos 4ρρααα⎛⎫+=-=- ⎪⎝⎭, 由122OP ρρ+=,得π4OP α⎛⎫=-≤ ⎪⎝⎭当3π4α=时,OP,故实数λ的取值范围为)+∞.23.解:(I )由题可得,()3,1,11212,1, 213,.2x x f x x x x x x x ⎧⎪-<-⎪⎪=++-=--≤<⎨⎪⎪≥⎪⎩如图所示,()min 32f x =,则1132m n +≤, 可得233222m n m n mn +⎛⎫+≤≤⎪⎝⎭,于是83m n +≥,当且仅当43m n ==时,等号成立. 故m n +的最小值为83. (II )令()()212g x ax a a x =-+=+-,则()g x 恒过()1,2--,当()g x 过点13,22⎛⎫ ⎪⎝⎭时,73a =,结合图像分析可得,733a -≤≤. 故73,3a ⎡⎤∈-⎢⎥⎣⎦.。
高三第一次联考数学试题及答案

高三第一次联考数学试题及答案一、选择题(本题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的)1. 已知函数f(x) = 3x^2 - 2x + 1,求f(1)的值。
A. 2B. 3C. 4D. 52. 计算复数z = (1 + i)^2的模。
A. 2B. 1C. √2D. 03. 已知集合A = {1, 2, 3},B = {2, 3, 4},求A∩B。
A. {1, 2, 3}B. {2, 3}C. {1, 3, 4}D. {1, 2}4. 已知等差数列{a_n}的首项a_1 = 2,公差d = 3,求a_5的值。
A. 17B. 14C. 11D. 85. 已知函数y = x^3 - 6x^2 + 9x + 15,求其导数y'。
A. 3x^2 - 12x + 9B. x^2 - 6x + 9C. 3x^2 - 12x + 15D. x^2 - 6x + 156. 计算定积分∫(0, 1) x^2 dx。
A. 1/3B. 1/2C. 1D. 27. 已知直线l:2x + y - 3 = 0,求直线l与x轴的交点。
A. (3/2, 0)B. (3, 0)C. (0, 3)D. (0, -3)8. 已知圆C:x^2 + y^2 - 6x + 8y + 24 = 0,求圆C的半径。
A. 2B. 4C. 6D. 89. 已知向量a = (1, 2),b = (3, 4),求向量a与向量b的点积。
A. 11B. 10C. 8D. 710. 已知函数f(x) = sin(x),求f'(π/2)的值。
B. 0C. -1D. 2二、填空题(本题共5小题,每小题5分,共25分)11. 已知函数f(x) = 2x^3 - 3x^2 + 1,求f'(x) = ________。
12. 已知等比数列{a_n}的首项a_1 = 4,公比q = 1/2,求a_4的值。
长郡十八校联盟2023届高三第一次联考(全国卷)理科数学试题

长郡十八校联盟2023届高三第一次联考(全国卷)理科数学试题一、单选题 1.已知集合{}21,0,430A y y x xB xx x x ⎧⎫==+>=-+<⎨⎬⎩⎭,则AB =( )A .(1,)+∞B .[2,3)C .(1,2]D .[2,)+∞2.如果一个复数的实部和虚部相等,则称这个复数为“等部复数”,若复数(2i)i z a =+(其中a ∈R )为“等部复数”,则复数iz a +在复平面内对应的点在( )A .第一象限B .第二象限C .第三象限D .第四象限3.若x ,y 满足约束条件201030? x y x y x -+≥⎧⎪+-≥⎨⎪-≤⎩,则23zx y=-的最大值为( )A .2B .4C .8D .124.已知1x <-,那么在下列不等式中,不成立的是A .210x -> B .12x x+<- C .sinx x -> D .co s 0x x +>5.希尔伯特在1990年提出了孪生素数猜想,其内容是:在自然数集中,孪生素数对有无穷多个.其中孪生素数就是指相差2的素数对,即若p 和2p+均是素数,素数对(),2p p +称为孪生素数.从16以内的素数中任取两个,其中能构成孪生素数的概率为( ) A .13B .15C .17D .3286.大衍数列来源于《乾坤谱》中对易传“大衍之数五十”的推论,主要用于解释中国传统文化中的太极衍生原理,数列中的每一项,都代表太极衍生过程中,曾经经历过的两仪数量总和,是中华传统文化中隐藏的世界数学史上第一道数列题.已知该数列{}n a 的前10项依次是0,2,4,8,12,18,24,32,40,50,记(1)nn nb a =-⋅,n *∈N ,则数列{}n b 的前20项和是( ) A .110B .100C .90D .807.某几何体的三视图如图所示,则该几何体的体积是( )A .64B .128C .256D .3848.八一广场是南昌市的心脏地带,江西省最大的城市中心广场,八一南昌起义纪念塔为八一广场标志性建筑,塔座正面携刻“八一南昌起义简介”碑文,东、南、西三面各有一幅反映武装起义的人物浮雕.塔身正面为“八一南昌起义纪念塔”铜胎鎏金大字,塔顶由一支直立的巨型“汉阳造”步枪和一面八一军旗组成.八一南昌起义纪念塔的建成,表达了亿万人民永远缅怀老一辈无产阶级革命家创建和培育解放军的丰功伟绩,鼓励国人进行新的长征.现某兴趣小组准备在八一广场上对八一南昌起义纪念塔的高度进行测量,并绘制出测量方案示意图,A 为纪念塔最顶端,B 为纪念塔的基座(即B 在A 的正下方),在广场内(与B 在同一水平面内)选取C 、D 两点,测得C D 的长为m .兴趣小组成员利用测角仪可测得的角有.A C B∠、A C D∠、B C D ∠、A D C∠、B D C ∠,则根据下列各组中的测量数据,不能计算出纪念塔高度A B 的是( )A .m A CB BCD B D C ∠∠∠、、、 B .m A C B B C D A C D ∠∠∠、、、 C .m A C B A C D A D C ∠∠∠、、、 D .m A C B B C D A D C ∠∠∠、、、9.将函数()c o s 2f x x=的图象向右平移π02ϕϕ⎛⎫<< ⎪⎝⎭个单位长度后得到函数()g x 的图象,若对满足()()122fx g x -=的12,xx ,总有12x x -的最小值等于π6,则ϕ=( )A .π12B .π6C .π3D .5π1210.已知R λ∈,函数21,0,()()412lg ,0,x x f x g x x x x x λ⎧+<==-++⎨>⎩,若关于x 的方程(())f g x λ=有6个解,则λ的取值范围为( )A .10,2⎛⎤ ⎥⎝⎦B .20,3⎛⎫ ⎪⎝⎭C .1,12⎛⎫⎪⎝⎭D .12,23⎛⎫⎪⎝⎭11.双曲线22:13xCy-=的左焦点为F ,过点F 的直线l 与双曲线C 交于A ,B 两点,若过A ,B和点0)M 的圆的圆心在y 轴上,则直线l 的斜率为( )A.2±B.C .1± D .32±12.《九章算术》卷五《商功》中描述几何体“阳马”为“底面为矩形,一棱垂直于底面的四棱锥”,现有阳马P A B C D -(如图),P A ⊥平面,1,2,3A B C D P A A B A D ===,点E ,F 分别在,A B B C 上,当空间四边形P E F D 的周长最小时,三棱锥P A D F-外接球的表面积为( )A .9πB .11πC .12πD .16π二、填空题13.已知7280128(1)(21)x x a a x a x a x-+=++++,则2a 等于___________.14.已知向量()2,1a =r ,()1,0b=,()1,2c=,若()ca mb ⊥+,则m=___________.15.已知ππ,s in 2c o s 2s in c o s 122βαβααβ-<-<+=-=,则πc o s 3α⎛⎫+=⎪⎝⎭___________. 16.设函数1()ln ()f x x a x a x=-+∈R 的两个极值点分别为12,xx .若()()2124124e2e 1fx fx a x x -≤---恒成立,则实数a 的取值范围是___________.三、解答题17.在数列{}n a 中,616a =,点()()1,n n a a n *+∈N在直线30x y -+=上.(1)求数列{}n a 的通项公式; (2)若2nnnb a =,求数列{}n b 的前n 项和nT .18.基础学科招生改革试点,也称强基计划,强基计划是教育部开展的招生改革工作,主要是为了选拔培养有志于服务国家重大战略需求且综合素质优秀或基础学科拔尖的学生.聚焦高端芯片与软件、智能科技、新材料、先进制造和国家安全等关键领域以及国家人才紧缺的人文社会科学领域.某校在一次强基计划模拟考试后,从全体考生中随机抽取52名,获取他们本次考试的数学成绩(x )和物理成绩(y ),绘制成如图散点图:根据散点图可以看出y 与x 之间有线性相关关系,但图中有两个异常点A ,B .经调查得知,A 考生由于重感冒导致物理考试发挥失常,B 考生因故未能参加物理考试.为了使分析结果更科学准确,剔除这两组数据后,对剩下的数据作处理,得到一些统计的值:5015800i i x ==∑,5013900i i y ==∑,501462770i i i x y ==∑,()502128540ii x x=-=∑,()502118930ii y y=-=∑,其中,i i x y 分别表示这50名考生的数学成绩、物理成绩,1i =,2,…,50,y 与x 的相关系数0.45r≈.(1)若不剔除A ,B 两名考生的数据,用52组数据作回归分析,设此时y 与x 的相关系数为0r .试判断0r 与r 的大小关系(不必说明理由);(2)求y 关于x 的线性回归方程(系数精确到0.01),并估计如果B 考生加了这次物理考试(已知B 考生的数学成绩为125分),物理成绩是多少?(精确到0.1)附:线性回归方程ˆˆˆyab x =+中:()()()121ˆˆˆ,niii nii xxy yb ay b x xx==--==--∑∑.19.如图,在四棱锥P A B C D-中,E 为棱A D 上一点,,P E A D P A P C⊥⊥,四边形B C D E为矩形,且13,,//4B CP E B E P F P C P A ====平面B E F .(1)求证:P A⊥平面P C D ;(2)求二面角FA B D--的大小.20.如图,在平面直角坐标系x O y 中,已知直线5y =与椭圆2222:1(0)x y Ca b ab+=>>交于,P Q 两点(P 在x 轴上方),且65P Q a=,设点P 在x 轴上的射影为点N ,P Q N V 的5抛物线2:2(0)Eyp x p =>的焦点与椭圆C的焦点重合,斜率为k 的直线l 过抛物线E 的焦点与椭圆C 交于,A B 两,点,与抛物线E 交于,C D 两点.(1)求椭圆C 及抛物线E 的标准方程;(2)是否存在常数λ||||A B C D λ为常数?若存在,求λ的值;若不存在,说明理由.21.设函数311()s in c o s 0,()()s in 222f x x x x x g x f x x a x π⎛⎫=-<<=+- ⎪⎝⎭.(1)证明:当0,2x π⎛⎫∈ ⎪⎝⎭时,()f x 有唯一零点;(2)若任意[0,)x ∈+∞,不等式()0g x ≤恒成立,求实数a 的取值范围.22.在直角坐标系x O y中,直线l 的参数方程为,x y ⎧=⎪⎨=⎪⎩(t 为参数),以坐标原点O为极点,x 轴为正半轴建立极坐标,椭圆C 的极坐标方程为2222c o s 2s in 4ρθρθ+=,其右焦点为F ,直线l 与椭圆C 交于,A B 两点. (1)求||||F A F B +的值; (2)若点P 是椭圆上任意一点,求P A B的面积最大值.23.已知函数()|21||3|f x x x =---.(1)求()f x 的最小值m ;(2)若a ,b 为正实数,且20a b m ++=,证明不等式225abba+≥.参考答案:1.B【分析】根据基本不等式求得集合A ,解一元二次不等式得集合B ,即可得集合的交集.【详解】∵10,2x y x x >=+≥=,当且仅当1x =时,等号成立,∴[2,)A =+∞,又∵{}{}()2430|131,3Bxx x x x =-+<=<<=,∴[2,3)AB =.故选:B. 2.D【分析】根据“等部复数”得a 的值,即可得22iz =+,从而得iza +,从而可确定其复平面内对应的点所对应的象限. 【详解】∵(2i)i 2iz a a =+=-+,又∵“等部复数”的实部和虚部相等,复数z 为“等部复数”,∴2a -=,解得2a =-, ∴22i z=+,∴22iz=-,即24iza i +=-,∴复数iza +在复平面内对应的点是(2,4)-,位于第四象限.故选:D. 3.D【分析】如图所示,画出可行域,233z y x =-,3z-表示直线与y 轴的截距,截距最小时,z最大,根据图像得到答案. 【详解】画出可行域,如图所示:23z x y=-,则233z yx =-,3z-表示直线与y 轴的截距,截距最小时,z 最大,当直线过交点,310x x y =⎧⎨+-=⎩,即()3,2-时,6612z=+=.故选:D4.D【分析】利用作差法可判断A 、B 选项的正误,利用正弦、余弦值的有界性可判断C 、D 选项的正误.综合可得出结论. 【详解】1x <-Q,则()()21110x x x -=-+>,()22112120x x x x xxx+++++==<,又sin x、[]c o s 1,1x ∈-,sinx x ∴->,co s 0x x +<.可得:ABC 成立,D 不成立. 故选:D.【点睛】本题考查不等式正误的判断,一般利用作差法来进行判断,同时也要注意正弦、余弦有界性的应用,考查推理能力,属于中等题. 5.B【分析】先分析20以内的素数,再分析其中孪生素数的对数,再分别求解所以可能的情况种数以及孪生素数的对数求概率即可.【详解】20以内的素数有2,3,5,7,11,13共6个,从中任取两个共有15种可能,其中构成孪生素数的有3和5,5和7,11和13共3对,∴16以内的素数中任取两个,其中能构成孪生素数的概率31155P ==.故选:B【点睛】本题主要考查了古典概型的问题,需要根据题意分析总的情况数以及满足条件的基本事件数.属于基础题. 6.A【分析】根据所给数列的项归纳出通项公式,利用分组求和法求和即可. 【详解】观察此数列可知,当n为偶数时,22nna =,当n为奇数时,212nn a -=,因为221,2(1)2nn n n n b a nn ⎧--⎪⎪=-⋅=⎨⎪⎪⎩为奇数,为偶数,所以数列{}n b 的前20项和为:(02)++2219120(48)(1218)()22--++-+++-+10(220)246201102⨯+=++++==,故选:A 7.B【分析】根据三视图得到该几何体是一个四棱锥求解. 【详解】解:如图所示:由三视图知:该几何体是一个四棱锥, 其底面积为8864S=⨯=,高为6h=,所以其体积为11283V S h ==,故选:B 8.B【分析】依据解三角形的条件,逐项判断可解三角形求出塔高度A B 的选项即可. 【详解】对于A :由m ,B C D ∠、B D C ∠可以解B C D △,又tan A B B C A C B=⋅∠,可求塔高度A B ;对于B :在B C D △中,由,C D m B C D=∠无法解三角形,在A C D中,由,C Dm A C D=∠无法解三角形,在B C A V 中,已知两角A C B A B C ∠∠、无法解三角形,所以无法解出任意三角形,故不能求塔高度A B ; 对于C :由C Dm=,∠∠A C D A D C 、可以解A C D,可求A C ,又sin A BA C A C B=⋅∠,即可求塔高度A B ;对于D :如图,过点B 作B EC D⊥于点E ,连接A E ,由c o s ,c o s B C E C A C B B C D A CB C∠=∠=,c o s E C A C E A C∠=,知co s c o s c o s A C E A C B B C D∠=∠⋅∠,故可知A C D∠的大小,由A C D∠、A D C∠、m 可解A C D,可求A C ,又s i n AB A CA C B=⋅∠,可求塔高度A B . 故选:B. 9.C【分析】根据函数图象平移规律可得函数()g x 的图象,由()()122fx g x -=、12m inπ6x x -=设1x=,则2π6=±x ,分别利用πc o s 2216ϕ⎛⎫⨯-=- ⎪⎝⎭、πc o s 2216ϕ⎡⎤⎛⎫⨯--=- ⎪⎢⎥⎝⎭⎣⎦,求出ϕ可得答案. 【详解】函数()c o s 2f x x=的周期为π,将函数的图象向右平移π02ϕϕ⎛⎫<< ⎪⎝⎭个单位长度后得到函数()g x 的图象,可得()c o s(22)g x x ϕ=-,由()()122fx g x -=可知,两个函数的最大值与最小值的差为2,且12m inπ6x x -=,不妨设1x=,则2π6=±x ,即()g x 在2π6=±x 时取得最小值,由于πc o s 2216ϕ⎛⎫⨯-=- ⎪⎝⎭,此时ππ,3ϕ=--∈k k Z ,不合题意;πc o s 2216ϕ⎡⎤⎛⎫⨯--=- ⎪⎢⎥⎝⎭⎣⎦,此时2ππ,3ϕ=--∈k k Z,当1k=-时,π3ϕ=满足题意.故选:C. 10.B【分析】数形结合法,令()g x t =,可得方程()f t λ=的解有3个,对应的一元二次方程各有2个不相等的实数根,利用判别式求解λ的范围. 【详解】令()g x t =,则方程()f t λ=的解有3个,由图象可得,01λ<<,且三个解分别为1231,1,10t t t λλλ=--=-+=,则24121x x λλ-++=--,24121x x λλ-++=-+,241210x x λλ-++=,均有两个不相等的实根, 则1∆>,且2∆>,且3∆>,即164(23)0λ-+>且164(2)0λ-+>,解得203λ<<,当203λ<<时,()316412104(3210)λλλλ∆=-+-=-+,因为203λ<<,所以4203λ-<-<,所以53233λ<-<,且100λ>,所以32100λλ-+>,即3∆>恒成立,故λ的取值范围为20,3⎛⎫ ⎪⎝⎭.故选:B. 11.A【分析】利用韦达定理结合P GA B⊥可得283m tm=-,再根据弦长公式表示得A B,结合2221||2rdA B ⎛⎫=+ ⎪⎝⎭即可求直线l 的斜率.【详解】由题意可知:(2,0)F -,设()11,A x y ,()22,B x y ,A B 的中点为P , 过点A ,B ,M 的圆的圆心坐标为(0,)G t,则||G Mr==,由题意知:直线A B 的斜率存在且不为0,设直线A B 的方程为:2xm y =-,联立方程组222,1,3x m y x y =-⎧⎪⎨-=⎪⎩化简整理可得,()223410m y m y --+=,则230m -≠,()222164312120mmm∆=--=+>,12122241,33m y y y y mm+==--,故A B 的中点P 的纵坐标122223p y y m y m+==-,横坐标2623pp x m y m=-=-,则2262,33mP mm⎛⎫⎪--⎝⎭,由圆的性质可知:圆心与弦中点连线的斜率垂直于弦所在的直线,所以222363P Gmtm k m m--==---,化简整理可得:283m tm=-①,则圆心(0,)G t 到直线A B的距离d=)221||3m A B m+===-,2221||2rdA B ⎛⎫=+ ⎪⎝⎭,即()()222222231(2)713mm t tmm+-+=++-,将①代入可得:()()()2222222222282313647133m mm mmmm⎛⎫- ⎪+-⎝⎭+=++--,即()()()()2222222222316436367333mmm mmm+++=+---,整理可得:42560m m -+=,则()()22230m m--=,因为230m -≠,所以220m-=,解得m=∴12km ==±.故选:A. 12.B【分析】把,A P P B 剪开,使得P A B与矩形A B C D 在同一个平面内.延长D C 到M ,使得C MD C=,则四点P ,E ,F ,M 在同一条直线上时,P EE F F D++取得最小值,即空间四边形P E F D 的周长取得最小值.可得122C F PD ==,∴1B F =.∴点E 为A B 的中点.设A F D △的外心为1O ,外接圆的半径为r ,则2s in 45︒=A F r,利用勾股定理进而得出结论. 【详解】如图所示,把,A P P B 剪开,使得P A B与矩形A B C D 在同一个平面内.延长D C 到M ,使得C MD C=,则四点P ,E ,F ,M 在同一条直线上时,P EE F F D++取得最小值,即空间四边形P E F D 的周长取得最小值.可得122C F PD ==,∴1B F=.∴点E 为A B的中点.如图所示,设A F D △的外心为1O ,外接圆的半径为r ,易得45F D A ∠=,则2s in 45==︒A F r设三棱锥PA D F-外接球的半径为R ,球心为O ,连接1O O ,则11122O O P A ==,则222111224R⎛⎛⎫=+= ⎪⎝⎭⎝⎭.∴三棱锥PA D F-外接球的表面积24π11π==R.故选:B. 13.70-【分析】要求2a ,即求展开式中2x 项的系数,进而根据二项式定理求解即可; 【详解】解:因为777(1)(21)(21)(21)x x x x x -+=+-+,对于7(21)x +,其展开式通项为()777177C 22C kkkkkk T x x---+==.所以,7(1)(21)x x -+中含2x 的项为6252772C 2C x x x⋅-,所以展开式中含2x 的项系数为625772C 2C 70⨯-=-.故答案为:70-. 14.4-【分析】用向量的坐标运算即可. 【详解】依题意:()()211211200ca mb ca m cb m +=+=⨯+⨯+⨯+⨯= ,解得m =-4, 故答案为:-4.15.3-【分析】根据已知等式平方后相加可得()1sin 2βα-=-,即()1sin 2αβ-=,根据已知角度范围即可得6παβ-=,从而可得s in3β=πs in 63α⎛⎫-= ⎪⎝⎭得所求.【详解】等式sin 2c o s 2sin c o s 1βααβ+=-=,两边同时平方得22s in 4c o s 4s in c o s 2βαβα++=,24s in c o s 4s in c o s 1αβαβ+-=,两式相加,得414sin c o s 4sin c o s 3βααβ++-=,,整理得()1sin 2βα-=-,即1s i n()2αβ-=,因为ππ22βα-<-<,所以6παβ-=,得π6αβ=+,代入2sin c o s 1αβ-=,得2sin c o s 16πββ⎛⎫+-= ⎪⎝⎭,即s in3β=πs in 63α⎛⎫-= ⎪⎝⎭则ππππc o s c o s s in 36263ααα⎛⎫⎛⎫⎛⎫+=-+=--=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭故答案为:3-16.221e,e ⎡⎫++∞⎪⎢⎣⎭【分析】由函数()f x 有两个极值点分别为12,xx ,可知()f x 不单调,利用导数求得a 的范围,运用韦达定理可得122212ax x x x =+=+>,作差()()12f x fx -,再由条件,结合恒成立思想,运用函数的单调性,构造函数421e 1()ln (1)2eF x x x x x-=-+>,通过求导,判断单调性可得22ex ≥,即可得到a 的范围.【详解】∵函数1()ln ()f x x a x a x=-+∈R 有两个极值点分别为12,x x ,()f x 的定义域为221(0,),()x a x f x x-'++∞=-,令2()1g x x a x =-+,其判别式2Δ4a =-,当22a -≤≤时,Δ0,()0,()f x f x '≤≤在(0,)+∞上单调递减,不合题意.当2a <-时,Δ0,()0g x >=的两根都小于零,在(0,)+∞上,()0f x '<,则()f x 在(0,)+∞上单调递减,不合题意. 当2a>时,Δ0>,设()0g x =的两个根12,xx 都大于零,令1212122x x x x =<==,当10x x <<时,()0f x '<,当12xx x <<时,()0f x '>,当2xx >时,()0f x '<,故()f x 分别在区间()10,x ,()2,x +∞上单调递减,在区间()12,x x 上单调递增,则122212a x x x x =+=+>,∴a 的取值范围是(2,)+∞.∵()()1211221211ln ln ⎛⎫-=-+--+=⎪⎝⎭f x fx x a x x a x x x ()()21211212ln ln x x x x a x x x x -+-+-,∴()()121212121212121ln ln ln ln 12fx fx x x x x aax x x x x x x x ---=--+=-+---,若()()2124124e2e 1fx fx a x x -≤---恒成立,则212412ln ln 4e22e 1x x aa x x --+≤---,∴212412ln ln 4ee 1x x x x -≤--,由12x x <,则()412122e 1lnln 4ex x x x --≤-.又121x x =,∴()422221e 12ln4ex x x --≤-,∴()4222221e 1ln 012ex x x x --+≤>①恒成立,记421e 1()ln (1)2eF x x x x x-=-+>,4221e 1()12e F x xx-=--+',记()0F x '=的两根为4121e 122e x ⎡-⎢=-⎢'⎣,4221e 122e x ⎡-⎢=+⎢'⎣,()F x 在区间()21,x '上单调递增,在区间()2,x '+∞上单调递减,且易知2121e x x <<<<''.又()2(1)0,e0F F ==,∴当()2ex ∈1,时,()0F x >;当)2,e x ⎡∈+∞⎣时,()0F x ≤.故由①式可得,22ex ≥,代入方程()222210g x x a x =-+=,得222211e ea x x =+≥+.又2a>, ∴a 的取值范围是221e,e ⎡⎫++∞⎪⎢⎣⎭.故答案为:221e,e ⎡⎫++∞⎪⎢⎣⎭.【点睛】关键点点睛:本题考查利用导数求单调区间、极值,主要考查极值的运用,运用分类讨论的思想方法是解题的关键,同时考查函数的单调性的运用和基本不等式的运用,考查运算能力,属于难题. 17.(1)32n a n =-;(2)1(35)210n n T n +=-⋅+.【分析】(1)根据给定条件,结合等差数列定义判断求解作答. (2)利用(1)的结论,利用错位相减法求和作答. 【详解】(1)依题意,130n n a a +-+=,即13n na a +-=,因此数列{}n a 是公差为3的等差数列,则63(6)32na a n n =+-=-,所以数列{}n a 的通项公式是32n a n =-.(2)由(1)得(32)2nn b n =-⋅,则1321242(342)22nnT n =⨯+⨯⨯+⋅⋅⋅-⨯++,于是23121242(35)2(32)2nn nT n n +=⨯+⨯+⋅⋅⋅+-⨯+-⨯,两式相减得1231122()23(222(32)2(3212)22)123n n n n nT n n +-+-=+++⋅⋅⋅⋅+--⋅--⋅-=+-1(53)210n n +⋅=--,所以1(35)210n nT n +=-⋅+.18.(1)0r r<(2)0.36 6.4ˆ32yx =+,估计B 考生的物理成绩约为81.2分【分析】(1)根据已知条件,结合散点图,即可求解.(2)根据已知条件,结合最小二乘法,以及线性回归方程的公式,求出线性回归方程,再将125x =代入,即可求解.【详解】(1)0r r<理由如下:由图可知,y 与x 成正相关关系, ①异常点A ,B 会降低变量之间的线性相关程度,②52个数据点与其回归直线的总偏差更大,回归效果更差,所以相关系数更小, ③50个数据点与其回归直线的总偏差更小,回归效果更好,所以相关系数更大, ④50个数据点更贴近其回归直线l , ⑤52个数据点与其回归直线更离散. (2)由题中数据可得:50501111116,785050i i i i xx y y ======∑∑,所以()()5050115010370iii i i i x xy yx y x y ==--=-=∑∑,所以()()()501502110370ˆ0.3628540iii ii xxy ybxx==--==≈-∑∑,780.36ˆˆ11636.24a y b x =-=-⨯=,所以0.36 6.4ˆ32y x =+,将125x =代入,得0.3612536.2481.2481.2y =⨯+=≈,所以估计B 考生的物理成绩约为81.2分. 19.(1)证明见解析 (2)π4【分析】(1)连接A C 交B E 于点G ,连接F G ,利用线面平行的性质得//P A F G ,利用平行线分线段成比例可得线段长度,从而由勾股定理得线线垂直,再利用线面垂直的判定定理证明线面垂直;(2)利用线面关系,证明线线垂直,建立空间直角坐标系,根据空间向量的坐标运算分别确定平面A B F 与平面A B D 的法向量,根据坐标运算得二面角的余弦值,即可确定二面角大小.【详解】(1)连接A C 交B E 于点G ,连接F G ,因为//P A 平面B E F ,平面P A C 平面B E FF G=,P A⊂平面P A C ,所以//P A F G ,又//B E C D,所以13A F A F A G P F D EB CG CF C====,又3D E=,所以1,4A EA D ==.因为P E A D⊥,所以2P A==,P D==所以222P A P D A D+=,所以P A P D⊥,又,,,P AP C P D P C P P D P C ⊥⋂=⊂平面P C D ,所以P A ⊥平面P C D . (2)因为P A ⊥平面P C D ,C D⊂平面P C D ,所以P AC D⊥,又,A D C D P A A D A ⊥⋂=,,P A A D⊂平面P A D ,所以C D⊥平面P A D ,又P E⊂平面P A D ,所以P EC D⊥,又P E A D⊥,A DC D D =,A D C D ⊂平面A B C D所以P E ⊥平面A B C D .如图建系,则3(1,0,0),(0,0),(3,0,0),,444A B D F ⎛-- ⎝⎭,7333,,,(1,3,0)444A F A B ⎛⎫=-- ⎝⎭,设平面A B F 的一个法向量为(,,)mx y z=,则720044400z y A F m x y z x A B m x ⎧⎧=⎧⋅=-++=⎪⎪⎪⇒⇒⎨⎨⎨=⎪⋅=⎪⎩⎪⎩-+=⎩,取1y =,得2)m =,又平面A B D的一个法向量为(0,0,1)n=,所以2c o s ,2||||22m n m n m n ⋅〈〉===FA B D--为锐角,故二面角F A B D--的大小为π4.20.(1)2215xy+=,28yx=(2)存在,16λ=-【分析】(1)设()00005P xx ⎛⎫> ⎪⎝⎭,由2P Q N P O NS S =△△解得1,5⎛⎫⎪ ⎪⎝⎭P ,利用13525O P P Q a====可得a=,再求得b 的值,即可得椭圆C 方程,由抛物线2:2(0)E yp x p =>的焦点与椭圆C 的焦点重合,即可得抛物线E 的标准方程;(2)设直线l 的方程为(2)yk x =-,()()()()11223344,,,,,,,A x yB x yC x yD x y ,分别让直线l 与椭圆、抛物线联立,得交点坐标关系,从而得弦长,即可求得λ的值. 【详解】(1)由题意可设()00005P x x⎛⎫> ⎪⎝⎭,可得2P Q N P O N S S =△△,所以001255P O NS x x =⋅⋅=△,所以01x =,1,5⎛ ⎝⎭P ,所以13525O PP Q a====,所以a=,点P 坐标代入椭圆方程得1b =,所以椭圆C 方程为2215xy+=,所以2c=,即4p=,所以抛物线E 方程为28y x=.(2)设()()()()11223344,,,,,,,A x y B x y C x y D x y .直线l 的方程为(2)yk x =-,与椭圆C 的方程联立()22152x y y k x ⎧+=⎪⎨⎪=-⎩得()222215202050k xk x k+-+-=,则()()()4222Δ4002051412010kkkk=-+-=+>恒成立,所以2212122220205,1515kk x x x x kk-+==++则)221||15kA Bk+==+.直线l 的方程为(2)y k x =-,与抛物线E 的方程联立28,(2),y x y k x ⎧=⎨=-⎩得()22224840k x k x k -++=.()223434228148,||4kkx x C D x x kk+++==++=.()()()22222215(20)4||||218181k kk A B C D kkkλλλ+++=+=+++.||||A B C D λ+为常数,则204λ+=,得16λ=-.故存在16λ=-||||A B C D λ为常数.21.(1)证明见解析 (2)13a ≥【分析】(1)求导,根据导函数判断函数()f x 的单调性,再根据零点存在法则求解; (2)求导,根据导函数的结构,对a 分类讨论. 【详解】(1)π110,,()s in c o s ,()s in c o s 222x f x x x x f x x x x ⎛⎫∈=-=-' ⎪⎝⎭ ,令'()()h x f x = ,则'3()sin co s 02h x x x x =+> ,则π0,,()2x f x '⎛⎫∈ ⎪⎝⎭单调递增,且''1ππ(0),222f f ⎛⎫=-= ⎪⎝⎭,∴'π0,,()02t f t ⎛⎫∃∈= ⎪⎝⎭ ,'(0,),()0,()x t f x f x ∈<单调递减,'π,,()0,()2x t f x f x ⎛⎫∈> ⎪⎝⎭单调递增,且π1(0)0,022f f ⎛⎫==> ⎪⎝⎭,则()0<f t ,∴存在唯一零点0π,2x t ⎛⎫∈ ⎪⎝⎭,使得()00f x =,即()f x 有唯一零点;(2)3()s in c o s g x x x x a x=--,则'()(s in 3)g x x x a x =- ,又令'()s in 3,()c o s 3h x x a x h x x a=-=- ,①当31a≤-,即13a ≤-时,()0h x '≥ 恒成立,∴()h x 在区间[0,)+∞上单调递增,∴()(0)0h x h ≥=,∴'()0g x ≥ ,∴()g x 在区间[0,)+∞上单调递增, ∴()(0)0g x g ≥=(不合题意);②当31a≥即13a ≥时,'()0,()h x h x ≤在区间[0,)+∞上单调递减,∴()(0)0h x h ≤=,∴'()0g x ≤ ,∴()g x 在区间[0,)+∞上单调递减, ∴()(0)0g x g ≤=(符合题意);③当131a -<<,即1133a -<<时,由''(0)130,(π)130h a h a =->=--< ,∴0(0,π)x ∃∈ ,使()'00h x = ,且()00,x x ∈时,''()0,()(0)0,()0h x h x h g x >>=> ,∴()g x 在()00,x x ∈上单调递增,∴()(0)0g x g >=(不符合题意);综上,a 的取值范围是13a≥;【点睛】本题的函数类型是三角函数与非三角函数组合成的,对于这一类函数往往是在一个周期()2π 内讨论或半个周期()π内讨论 ;如果一次求导不能判断清楚导函数的符号,则需要多次求导,而且每次求导后都要研究导函数的解析式能否判断清楚导函数的符号,直至能判断清楚导函数的符号为止.22.(1)83(2)41)3【分析】(1)根据极坐标方程可得椭圆C 的标准方程,又直线l 经过点椭圆焦点F ,将直线参数方程代入椭圆方程,得坐标关系,即可得||||F A F B +的值;(2)设点P 坐标为(2c o s in )θθ,直线l 的直角坐标方程为0x y --=,由点到直线的距离,结合三角函数的图象性质求得距离最大值,即可求得P A B的面积最大值.【详解】(1)由2222c o s 2s in 4ρθρθ+=得椭圆C 的方程为22142xy+=,其焦点F坐标为答案第16页,共16页0),由题意得直线l 经过点F,其参数方程为x y ⎧=⎪⎨=⎪⎩(t 为参数),代入椭圆C 的方程整理得23210t t +-=,所以121221,33t t t t +=-=-,所以121282223F A F B t t t t +==+=-===(2)由椭圆方程22142xy+=,可设点P 坐标为(2c o s ,in )θθ,又直线l 的直角坐标方程为0x y --=,∴点P 到直线l的距离d ==ta n 2φ=,所以m a x 1d =+,因为18||,||||||23P A BS A B d A B F A F B =⋅=+=△,所以P A B323.(1)52m=-(2)证明见解析【分析】(1)讨论去绝对值可得()f x 的解析式及最小值;(2)由(1)可得5a b +=,利用基本不等式可得答案.【详解】(1)当12x <时,5()21322=-++-=--≥-f x x x x ,当132x ≤≤时,5()21334,52⎡⎤=-+-=-∈-⎢⎥⎣⎦f x x x x ,当3x >时,()21325=--+=+>f x x x x ,综上,12,21()34,322,3x x f x x x x x ⎧--<⎪⎪⎪=-≤≤⎨⎪+>⎪⎪⎩,可知当12x=时,()f x 有最小值52-,所以52m=-;(2)由(1)可得5a b +=,因为a ,b 为正实数,所以222,2abb a a bba+≥+≥,所以225aba b b a+≥+=.。
2023年河南省五市高考数学第一次联考试卷(理科)+答案解析(附后)

2023年河南省五市高考数学第一次联考试卷(理科)1. 已知集合,则集合A的所有非空真子集的个数是( )A. 6B. 7C. 14D. 152. 欧拉公式把自然对数的底数e、虚数单位i、三角函数联系在一起,充分体现了数学的和谐美.若复数z满足,则z的虚部为( )A. B. C. 1 D.3. 在等比数列中,已知,,则( )A. 128B. 64C. 64或D. 128或4. 若抛物线上的一点M到坐标原点O的距离为,则点M到该抛物线焦点的距离为( )A. 3B.C. 2D. 15. 变量X与Y相对应的一组数据为,,,,,变量U与V相对应的一组数据为,,,,表示变量Y与X之间的线性相关系数,表示变量V与U之间的线性相关系数,则( )A. B. C. D.6. 如图,已知正三棱柱的各条棱长都相等,M是侧棱的中点,N是的中点,则( )A.B. 平面BAMC. 平面ABMD.7. 是单位圆的内接三角形,角A,B,C的对边分别为a,b,c,且,则a等于( )A. 2B.C.D. 18. 讲桌上放有两摞书,一摞3本,另一摞4本,现要把这7本不同的书发给7个学生,每位学生一本书,每次发书只能从其中一摞取最上面的一本书,则不同取法的种数为( ) A. 20 B. 30 C. 35 D. 2109. 某棋手与甲、乙、丙三位棋手各比赛一盘,各盘比赛结果相互独立.已知该棋手与甲、乙、丙比赛获胜的概率分别为,,,且记该棋手连胜两盘的概率为p,则( )A. p与该棋手和甲、乙、丙的比赛次序无关B. 该棋手在第二盘与甲比赛,p最大C. 该棋手在第二盘与乙比赛,p最大D. 该棋手在第二盘与丙比赛,p最大10. 传说古希腊数学家阿基米德的募碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等.“圆柱容球”是阿基米德最为得意的发现;如图是一个圆柱容球,,为圆柱上下底面的圆心,O为球心,EF为底面圆的一条直径,若球的半径,则( )A. 球与圆柱的表面积之比为1:2B. 平面DEF截得球的截面面积取值范围为C. 四面体CDEF的体积的最大值为16D. 若P为球面和圆柱侧面的交线上一点,则的取值范围11. 某中学开展劳动实习,学生加工制作零件,零件的截面如图单位:所示,四边形AFED为矩形,AB,CD,FE均与圆O相切,B、C为切点,零件的截面BC段为圆O的一段弧,已知,则该零件的截面的周长为结果保留( )A. B. C. D.12. 的展开式的第2项为______.13. 已知向量,满足,且,则______.14.双曲线C:的左,右焦点分别为,,过且倾斜角为的直线与双曲线右支交于A,B两点,若为等腰三角形,则该双曲线的离心率为______ .15. 已知正实数x,y满足,则的最小值为______ .16. 已知是数列的前n项和,且求数列的通项公式;若,是的前n项和,证明:17. 如图,在三棱柱中,,,P为AD的中点,为等边三角形,直线AC与平面ABED所成角大小为求证:平面BCP;求平面ECP与平面CDP夹角的余弦值.18. 某超市采购了一批袋装的进口牛肉干进行销售,共1000袋,每袋成本为30元,销售价格为50元,经过科学测定,每袋牛肉干变质的概率为,且各袋牛肉干是否变质相互独立.依据消费者权益保护法的规定:超市出售变质食品的,消费者可以要求超市退一赔三.为了保护消费者权益,针对购买到变质牛肉干的消费者,超市除退货外,并对每袋牛肉干以销售价格的三倍现金赔付,且把变质牛肉干做废物处理,不再进行销售.若销售完这批牛肉干后得到的利润为X,且,求p的取值范围;已知,若超市聘请兼职员工来检查这批牛肉干是否变质,超市需要支付兼职员工工资5000元,这样检查到的变质牛肉干直接当废物处理,就不会流入到消费者手中.请以超市获取的利润为决策依据,判断超市是否需要聘请兼职员工来检验这批牛肉干是否变质?19. 已知椭圆,过直线l:上一点P作椭圆的切线,切点为A,当P点在x轴上时,切线PA的斜率为求椭圆的方程;设O为坐标原点,求面积的最小值.20. 已知函数若在上恒成立,求实数a的取值范围;若,判断关于x的方程在内解的个数,并说明理由.21. 极坐标系中曲线T的极坐标方程为,以极点为原点,极轴为x轴正半轴建立平面直角坐标系,单位长度不变,直线,均过点,且,直线的倾斜角为写出曲线T的直角坐标方程;写出,的参数方程;设直线,分别与曲线T交于点A,B和C,D,线段AB和CD的中点分别为M,N,求的最小值.22. 已知函数求不等式的解集;若函数的最小值为m,正实数a,b满足,证明:答案和解析1.【答案】A【解析】解:,元素个数为3个,则集合A的所有非空真子集的个数是故选:根据已知条件,结合非空真子集的定义,即可求解.本题主要考查非空真子集的定义,属于基础题.2.【答案】B【解析】解:由已知可得,,则,的虚部为故选:由欧拉公式和复数除法运算可求得z,由复数虚部定义求得结果.本题考查复数代数形式的乘除运算,考查复数的基本概念,是基础题.3.【答案】D【解析】【分析】本题考查等比数列的通项公式,属于简单题.设等比数列的公比为q,利用等比数列通项公式列出方程组,求出首项和公比,由此能求出【解答】解:设等比数列的公比为q,在等比数列中,,,,解得,或,,或故选:4.【答案】B【解析】解:设点,,,或舍去,到抛物线的准线的距离点M到该抛物线焦点的距离等于点M到抛物线的准线的距离,点M到该抛物线焦点的距离为:故选:求得点M的坐标,将点M到该抛物线焦点的距离转化为点M到抛物线的准线的距离即可.本题考查抛物线的简单性质,考查转化思想与方程思想,求得点M的坐标是关键,属于中档题.5.【答案】C【解析】解:变量X与Y相对应的一组数据为,,,,,这组数据的相关系数是,变量U与V相对应的一组数据为,,,,,这组数据的相关系数是,第一组数据的相关系数大于零,第二组数据的相关系数小于零,故选:求两组数据的相关系数的大小和正负,可以详细的解出这两组数据的相关系数,现分别求出两组数据的两个变量的平均数,利用相关系数的个数代入求出结果,进行比较.本题考查用相关系数来衡量两个变量之间相关关系,当相关系数为正时,表示两个变量正相关,也利用散点图判断两个变量之间是否有相关关系.6.【答案】D【解析】解:因为与异面,故A错误;因为的延长线必过点B,则直线与平面BAM相交,故B错误;因为与AB不垂直,所以不垂直于平面ABM,故C错误;取BC的中点P,连接,在正方形中,由,,即,可得,所以连接AP,则,又平面底面ABC,平面底面,所以平面因为平面,所以,且,所以平面因为平面,所以故D正确.故选:由两条直线的位置关系可判断A;由线面的位置关系可判断B;由线面垂直的性质可判断C;由线面垂直的判定与性质可判断本题考查空间中线线、线面的位置关系,主要是平行与垂直的判定和性质,考查转化思想和推理能力,属于中档题.7.【答案】C【解析】解:因为,所以,即,由正弦定理得,所以,因为,所以,由A为三角形内角得,由正弦定理得,所以,故选:由已知结合余弦定理及正弦定理及和差角公式进行化解可求,进而可求A,然后结合正弦定理表示出a,b,c,然后求解即可.本题主要考查了正弦定理,余弦定理,和差角公式在三角化简求值中的应用,属于中档题.8.【答案】C【解析】解:根据题意,问题等价于从一行七个空里选三个空把1、2、3按从小到大自左向右顺序填进去,剩下三个空将4、5、6、7从小到大自左向右顺序填进去,共有填法种.故选:问题等价于从一行七个空里选三个空把1、2、3按从小到大自左向右顺序填进去,剩下三个空将4、5、6、7从小到大自左向右顺序填进去,即得解.本题主要考查了排列组合知识,属于基础题.9.【答案】D【解析】解:A选项,已知棋手与甲、乙、丙比赛获胜的概率不相等,所以P受比赛次序影响,故A错误;设棋手在第二盘与甲比赛连赢两盘的概率为,棋手在第二盘与乙比赛连赢两盘的概率为,棋手在第二盘与丙比赛连赢两盘的概率为,,,,,,所以最大,即棋手在第二盘与丙比赛连赢两盘的概率最大.故选:已知棋手与甲、乙、丙比赛获胜的概率不相等,所以P受比赛次序影响,A错误;再计算第二盘分别与甲、乙、丙比赛连赢两盘的概率,比较大小即可.本题考查概率的求法,是基础题,解题时要认真审题,注意相互独立事件概率乘法公式的灵活运用.10.【答案】D【解析】解:选项A,球表面积为,圆柱全面积是,,A错;选项B,平面DEF过球心O时,截得球的截面最大,此时截面面积为,B错;选项C,EF绕旋转时,由于始终有是圆柱的轴,圆柱的底面垂直,因此与底面上的直线EF垂直,从而为定值,,当时,易得平面,而当EF与AB不垂直时,CD与平面不垂直,因此C到平面的距离小于,D到平面的距离小于,因此,即四面体CDEF的体积的最大值为,C错;选项D,如下图,不妨设E与A重合,F与B重合,设Q是圆柱过点P的母线与下底面的交点,则PQ与底面圆垂直,从而PQ与底面上的直线AQ,BQ,,,设,则,,令,则,,时,,单调递增,时,,单调递减,所以,而,所以,的取值范围是,所以,即的取值范围是,D正确.故选:求出球与圆柱的表面积之比判断A,由截面积最大为球的大圆面积判断B,用割补法求四面体体积判断C,不妨设E与A重合,F与B重合,设Q是圆柱过点P的母线与下底面的交点,计算出,利用导数求出其取值范围从而判断本题考查圆柱与球的表面积、体积以及折线段的最值问题,考查逻辑推理能力,是一道难题.11.【答案】A【解析】解:以A为原点,AD为x轴正方向建立平面直角坐标系如图所示:则,,又,所以直线AB的方程为:,即,直线CD的方程为:,即,直线EF的方程为:,设圆心为,则圆心到直线AB、直线CD、直线的距离均相等且等于r,则,解得,,,所以,,,,由题可知,即,所以可得,,对应弧长为圆的周长,故该零件的截面的周长为故选:以A为原点,建立直角坐标系,根据圆心到直线AB、直线CD、直线EF距离均相等,利用点到直线的距离公式列式,计算出、、的长,即得.本题主要考查直线与圆的位置关系,考查转化能力,属于中档题.12.【答案】【解析】解:的展开式的第2项为,故答案为:利用二项展开式的通项公式,求得的展开式的第2项.本题主要考查二项式定理的应用,二项展开式的通项公式,二项式系数的性质,属于基础题.13.【答案】【解析】解:根据题意,向量,满足,若,则,则,两边平方变形可得,则,则有,则,故答案为:根据题意,有,即可得,变形可得,由向量数量积的计算公式计算可得答案.本题考查向量数量积的计算,涉及向量模的计算,属于基础题.14.【答案】【解析】解:如图,为等腰三角形,,,,,直线AB的倾斜角为,,在三角形中,根据余弦定理得:整理得,同除以得,,即,解得,舍故答案为:先根据为等腰三角形,然后利用双曲线的定义分别将边长表示为a的关系,然后利用余弦定理建立a,c的方程,从而求出双曲线的离心率.本题考查双曲线的离心率的求法,是中档题,解题时要认真审题,注意双曲线的性质的合理运用.15.【答案】0【解析】解:,即,设,则,且,所以在上单调递增,正实数x,y,,即,所以,等价于,即,,设,;,设,,所以单调递增,且,所以在上,,,单调递减;在上,,,单调递增;所以即最小值为0,故答案为:根据,构造函数,得到,然后转化为单变量问题,求导判断单调性即可.本题主要考查了导数与单调性关系在最值求解中的应用,属于中档题.16.【答案】解:已知是数列的前n项和,且,时,,时,,经验证时,,;证明:若,是的前n项和,时,,时,,,【解析】根据题意得到时,,验证即可求解;利用裂项相消求和即可得证.本题考查了数列的递推式和裂项相消求和,属于中档题.17.【答案】解:证明:取BP中点M,连接AM,CM,,P为AD的中点,,,为等边三角形,,,AM,面ACM,平面ACM,平面平面,直线AC在平面ABP的射影在直线AM上,直线AC与平面ABED所成角为,则,,,是正三角形,则,,为等边三角形,,则,在中,由,,得,则,,,,AM,平面ABED,平面ABED,平面ABED,,,在中,,,,又,,,,平面由知MP,MC,MA两两垂直,以M为坐标原点,MA所在直线为x轴,MP所在直线为y轴,MC所在直线为z轴,建立空间直角坐标系,则,,,,是AD的中点,,,,,,,设平面ECP的法向量,则,令,得,设平面PCD的法向量,则,取,得,设平面ECP与平面CDP夹角为,则平面ECP与平面CDP夹角的余弦值为:【解析】先利用线面垂直判定定理证明平面ACM,从而得到AC在平面ABP的射影在直线AM上,即,进而证明,利用线面垂直的判定理得平面ABED,则,再利用勾股定理能证明,由此能证明平面BCP;建立空间直角坐标系,利用向量法能求出平面ECP与平面CDP夹角的余弦值.本题考查线面垂直的判定与性质、二面角的定义及其余弦值的求法、向量法等基础知识,考查运算求解能力,是中档题.18.【答案】解:令Y表示1000袋牛肉干中变质牛肉干的数量,由题意有,则,故,由,有,解得:,故当时,p的取值范围为对这批牛肉干来说,变质牛肉干不管数量有多少,未变质牛肉干的销售后产生的利润与变质牛肉干作废物处理后产生的费用是不变的,是否聘请兼职员工来检查这批牛肉干是否,产生的费用是工资和给消费者赔付的费用,当时,由知,,设需要赔付给消费者的费用为Z元,有,由,以超市获取的利润为决策依据,故超市需要聘请兼职员工来检验这批牛肉干是否变质.【解析】令Y表示1000袋牛肉干中变质牛肉干的数量,由题意有,则,,进而求解;当时,由知,,,由,进而求解.考查数学概率,期望在实际问题中的应用,属于中档题.19.【答案】解:当P点在x轴上时,,PA:,,,椭圆方程为;…设切线为,设,,则, (7)且,则,PA直线为,A到直线PO距离,…则, (13),,此时…【解析】由P在x轴设出P点坐标及直线PA方程,将PA方程与椭圆方程联立,整理关于x的一元二次方程,求得,即可求得椭圆方程;设出切线方程和点P及点A的坐标,将切线方程代入椭圆方程,求得关于x的一元二次方程,,求得A和P点的坐标,求得丨PA丨及A到直线OP的距离,根据三角形的面积公式求得丨丨,平方整理关于k的一元二次方程,,即可求得S的最小值.本题考查曲线方程的求法,考查三角形面积的最小值的求法,综合性强,难度大,解题时要注意推理论证能力的培养,属于中档题.20.【答案】解:由题意在上恒成立,得恒成立,令,则,当时,令,解得,令,解得,所以在为减函数,在上为增函数,故,故,即,所以实数a 的取值范围由,得,等价于,令,,因为在上,,单调递减,在上,故,,单调递增,注意到,,在和上各有一个零点,,共有两个零点,故方程有两个实数根.【解析】由题意转化为即恒成立,由此构造函数,转化为求函数的最值问题,即可求得答案;由题意得,等价于,构造,通过判断导数正负,判断函数单调性,结合零点存在定理,继而判断函数的零点个数.本题考查利用导数研究函数的单调性,极值及最值,考查不等式的恒成立问题,考查函数零点个数判断,考查逻辑推理能力及运算求解能力,属于较难题目.21.【答案】解:曲线T 的极坐标方程为,变形为,则曲线T 的直角坐标方程:,为参数,为参数;将为参数,代入,得,则,同理,当时取等号,且此时满足方程的判别式均大于零,故的最小值为【解析】将代入曲线T的极坐标方程得出直角坐标方程,由直线,均过点,直线的倾斜角为且,可得两直线的参数方程;将直线,的参数方程分别代入曲线T的直角坐标方程,利用韦达定理即可得出,再利用基本不等式即可得出结果.本题主要考查了曲线的极坐标方程与直角坐标方程的互化,考查了直线的参数方程的应用,属于中档题.22.【答案】解:即,或,或解得或,所以原不等式的解集为证明:由知当时,有最小值,所以,因为,所以,因为,,当且仅当时取等号,所以,当且仅当时取等号,所以,当且仅当,时取等号.【解析】将函数化为分段函数的形式,再分类讨论解不等式组,最后将各部分的解集取并集即可得到答案;由知,而,又,再利用基本不等式可得本题考查绝对值不等式的解法以及基本不等式的运用,考查不等式的证明,考查分类讨论思想以及推理计算能力,属于中档题.。
高三数学第一次联考试题 理含解析 试题

卜人入州八九几市潮王学校2021届高三·十三校联考第一次考试理科数学试卷第一卷一、选择题:本大题一一共12个小题,每一小题5分,一共60分.在每一小题给出的四个选项里面,只有一项为哪一项哪一项符合题目要求的.1.集合,那么〔〕A. B. C. D.【答案】D【解析】集合,,所以,应选D.2.记复数的一共轭复数为,假设〔为虚数单位〕,那么复数的模〔〕A. B.1C. D.2【答案】A【解析】由,得,,应选A.3.在等差数列中,,那么数列的前11项和〔〕A.24B.48C.66D.132【答案】C【解析】试题分析:设等差数列公差为,那么,所以有,整理得,,,应选C.考点:等差数列的定义与性质.4.表示不超过实数的最大整数,为取整函数,是函数的零点,那么等于〔〕A.1B.2C.3D.4【答案】B【解析】,故,应选B.5.〔〕A.B.C.D.【答案】C【解析】设:“甲射击一次,击中目的〞为事件,“乙射击一次,击中目的〞为事件,那么“甲射击一次,未击中目的〞为事件,“乙射击一次,击中目的〞为事件,那么,依题意得:,解得,应选C.6.如以下图,是一个算法流程图,当输入的时,那么运行算法流程图输出的结果是〔〕A.10B.20C.25D.35【答案】D【解析】当输入的时,;;;;;否,输出,应选D.7.二项式展开式中,项的系数为〔〕A. B.C. D.【答案】C【解析】二项式展开式的通项为,令,系数为,应选C.8.设为抛物线的焦点,过且倾斜角为60°的直线交曲线于两点〔点在第一象限,点在第四象限〕,为坐标原点,过作的准线的垂线,垂足为,那么与的比为〔〕A. B.2C.3D.4【答案】C【解析】抛物线的焦点,准线为,设,那么,由那么,即有.应选C.9.函数的定义域为,且,又函数的导函数的图象如以下图,假设两个正数满足,那么的取值范围是〔〕A. B. C. D.【答案】A【解析】由导函数图象,可知函数在上为单调增函数,正数满足,又因为表示的是可行域中的点与的连线的斜率。
陕西省汉中市2023届高三上学期教学质量第一次检测理科数学试题(含答案解析)
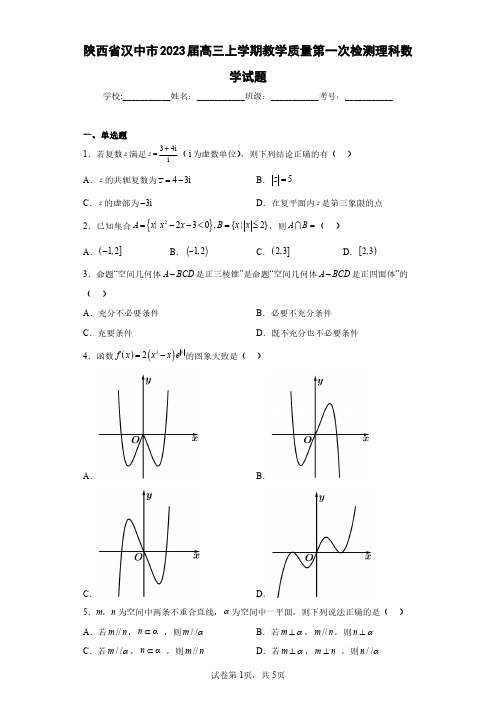
()
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
4.函数 f x 2 x3 x e x 的图象大致是( )
A.
B.
C.
D.
5.m,n 为空间中两条不重合直线, 为空间中一平面,则下列说法正确的是( )
A.若 m // n , n ,则 m / /
B.若 m , m // n ,则 n
7.A 【分析】先将原函数用诱导公式变形为正弦函数表示,再根据“左加右减”的原则判断即可.
【详解】
y
cos
2x
3
cos
2x
5 6
2
sin
2x
5 6
sin
2
x
5 12
故可由
y
sin2x 的图象向左平移
5 12
个单位长度得到.
故选:A.
8.C
【分析】分别安排各场馆的志愿者,利用组合计数和乘法计数原理求解.
三、解答题
17.已知 a,b, c 分别为 ABC 内角 A, B,C 的对边,且 2b a cosC c cosA
(1)求角 C ; (2)若 c2 2ab,ABC 的面积为 3 ,求 a b 的值. 18.如图,多面体 ABCDEF 中,四边形 ABCD 为菱形, ABB FA 2ED 2 .
A.
1 3
B. 2 5
C.
1 2
D. 3 5
11.若双曲线
x2 a2
y2 b2
1(a
0, b
0)
的实轴的两个端点与抛物线
x2
8by
的焦点是一个直
角三角形的顶点,则该双曲线的离心率为( )
江西省重点中学协作体九校2023届高三第一次联考数学(理科)试卷

江西省重点中学协作体2023届高三第一次联考数学(理科)试题2023.2命题人:九江一中李群抚州一中邓述程凌泽广满分:150分考试时间:120分钟一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.设集合{}8|,|14,1A x N N B x N x x ⎧⎫=∈∈=∈-≤≤⎨⎬+⎩⎭则A B = ()A.{0,1,2}B.{0,1,3}C.{1,2,3}D.{1,2,4}2.已知复数z 满足|||4|(),z z i i =-为虚数单位则z 的虚部是()A.2i- B.2iC.2- D.23.已知βα,是两个不同的平面,c b a ,,是三条不同的直线,则下面说法中正确的是()A.若,,αα⊂⊂b a 且,,b c a c ⊥⊥则α⊥cB.若,α⊂a 且,a b ⊥则α⊥b C.若,α⊥b 且,b c ⊥则//c αD.若,,βα⊥⊥b a 且,//,//b c a c 则βα//4.已知单位向量,a b ,满足a a b =+ ,则向量12a b ⎛⎪⎭+⎫ ⎝与b的夹角是()A.120︒B.60︒C.90︒D.30︒5.2021年12月9日15时40分,“天宫课堂”第一课开始,神舟十三号乘组航天员翟志刚、王亚平、叶光富在中国空间站进行太空授课.某中学组织全校学生观看了此次授课,三位太空老师介绍展示了中国空间站的工作生活场景,演示了微重力环境下细胞学实验、物理运动、液体表面张力等现象,并与地面课堂进行了实时交流,极大地激发了学生探索科学的兴趣.为了解同学们对“天宫课堂”这种90人进行调查,已知该校学生共有3600人,30人,则该校高二年级学生共有()A .800人B .1000人C .1200人D .1400人6.在三棱锥P ABC -中,6,8,210,30,PA AB PB BC BPC ====∠=︒则三棱锥P ABC -外接球的表面积为()A .100πB .5003πC .1253πD .25π7.若x ,y 满足约束条件222022x y y x y -≥-⎧⎪+≥⎨⎪+≤⎩,则3z x y =+的最小值为()A .2-B .0C .4D .168.已知抛物线2:2(0)C y px p =>的焦点为,F 点M 是抛物线C 的准线与x 轴的交点,点P 在抛物线上,若5sin ,13PMF ∠=则sin PFM ∠=()A.813B.1213C.512D.349.已知函数(1011)f x +是定义在R 上的奇函数,若()()sin 1g x f x x π=++,则2022()k g k =∑的值是()A .2022-B .2022C .2023-D .202310.已知数列21443n n ⎧⎫⎨⎬+-⎩⎭的前n 项和为n T ,若对任意的*N n ∈,不等式263n T a a <-恒成立,则实数a 的取值范围是()A.[)2,1,3⎛⎤-∞-+∞ ⎥⎝⎦ B.(]2,1,3⎡⎫-∞-+∞⎪⎢⎣⎭C.2,13⎡⎤-⎢⎥⎣⎦D.()2,1,3⎛⎫-∞-+∞ ⎪⎝⎭11.费马点是指三角形内到三角形三个顶点距离之和最小的点.当三角形三个内角均小于120°时,费马点与三个顶点连线正好三等分费马点所在的周角,即该点所对的三角形三边的张角相等且均为120°.根据以上性质,则(,)F x y =()A.4B.2+C.3+D.4+12.已知函数2()|2|x f x a x x e =--在区间[)0,+∞上的最大值为0,则实数a 的取值集合是()1.2A e⋅⎨⎪⎪⎩⎭21.2B e⋅⎨⎪⎪⎩⎭211.22C e e⎫-+⎪⋅⋅⎬⎪⎪⎩⎭21.2D e ⎫+⋅+∞⎪⎪⎣⎭二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)13.已知随机变量),,(~),,6(~2σμN Y p B X 且),()(,21)4(Y E X E Y P ==≥则=p ____.14.已知正项等比数列{}n a 的前n 项积为n T ,若4T 是{}n T 中唯一的最小项,则满足条件的{}n a 的通项公式可以是_____________(写出一个即可).15.已知直线:2l y x t =+与双曲线2222:1x y C a b -=的两条渐近线(0,0)a b >>分别交于点,A B (不重合),与直线:m y x =交于点M ,若AM MB =,则双曲线的离心率为_________.16.已知ABC ∆中,2||29,||3AB AB AC BC +⋅==,则ABC ∆面积的最大值是___________.三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:共60分.17.在ABC ∆中,角,,A B C 所对的边分别是,,a b c ,已知,A C c <=sin (cos sin )C A B -cos (sin cos )C A B =-.(1)若2C π≤,求角C 的值;(2)若23C π=,求ABC ∆的面积.18.卡塔尔世界杯在今年11月21日至12月18日期间举行,赛程如下:第一轮中先将32个国家随机分为ABCDEFGH 8个小组,每个小组中4个国家进行循环积分赛,在积分赛中,每局比赛中胜者积3分,负者积0分,平局各积1分,积分前两名者晋级下一轮淘汰赛;每组的循环积分赛分3轮,其中C 组国家是阿根廷,墨西哥,波兰,沙特,第一轮是阿根廷VS 沙特,墨西哥VS 波兰;第二轮是阿根廷VS 墨西哥,沙特VS 波兰;第三轮是阿根廷VS 波兰,墨西哥VS 沙特。
高三数学第一次联考试题理含解析试题

卜人入州八九几市潮王学校皖江名校联盟2021届高三数学第一次联考试题理〔含解析〕一、选择题:本大题一一共12小题,每一小题5分,一共6分在每一小题给出的四个选项里面,只有一项为哪一项哪一项符合题目要求的{}{}32,ln 0A x x B x x =-≤≤=≥,那么A B =〔〕A.{}3,2,1,0,1---B.{}1,2C.{}31x x -≤≤ D.{}12x x ≤≤【答案】D 【解析】 【分析】根据集合的根本运算进展求解即可. 【详解】由ln 0x ≥得1x ≥,所以{}|1B x x =≥,{|12}A B x x =≤≤,应选D.【点睛】该题考察的是有关集合的运算,属于简单题目.134z i=+,那么以下说法正确的选项是〔〕 A.复数z 的实部为3 B.复数z 的虚部为425i C.复数z 的一共轭复数为342525i + D.复数的模为1【答案】C 【解析】 【分析】直接利用复数的根本概念得选项.【详解】1343434252525i zi i -===-+, 所以z 的实部为325,虚部为425-,z 的一共轭复数为342525i +15=, 应选C.【点睛】该题考察的是有关复数的概念和运算,属于简单题目.221916x y +=的一个焦点坐标为〔〕A.(5,0)B.(0,5)C.)D.(【答案】D 【解析】 【分析】根据题中所给的椭圆的方程,可得,a b 的值,并且可以判断焦点所在轴,从而求得椭圆的焦点的坐标.【详解】因为4,3a b ==,所以c =22+1916x y =的上焦点的坐标是(,应选D.【点睛】该题考察的是有关椭圆的性质,属于简单题目. 4.0.44log m=,0.44n =,0.50.4p =,那么〔〕 A.m n p << B.m p n << C.p n m <<D.n p m <<【答案】B 【解析】 【分析】利用指数函数和对数函数的单调性即可得出结果.【详解】因为0.40.54log 0.40,41,00.41m n p ==<=<,所以m p n <<,应选B .【点睛】该题考察的是有关指数函数和对数函数的单调性,比较大小,属于根底题目.32()x y x x e =+在1x =处的切线方程为〔〕A.75x y e e =-B.79x y e e =+C.35x y e e =+ D.35x y e e =-【答案】A 【解析】 【分析】求出函数的导数,求出切线的斜率,切点坐标,之后应用点斜式写出切线方程,化简得结果. 【详解】()()23232x x y x x e x x e +'=++,所以1|7x y e ==',又1x =时,2y e =,所以所求切线方程为()271y e e x -=-,即75y ex e =-,应选A.【点睛】该题考察的是有关求曲线在某点处的切线方程的问题,涉及到的知识点有导数的几何意义,求导公式,属于简单题目{}n a 的前n 项和为n S ,假设41511,15a S ==,那么2a =〔〕A.18B.16C.14D.12【答案】B 【解析】 【分析】利用等差数列求和公式以及等差数列的性质,可以求得81a =,结合411a =,求得公差111542d -==-,从而求得2a 的值. 【详解】因为()1151581515152a a S a +===,所以81a =,又411a =,所以公差111542d -==-,所以24211516a a d =-=+=. 【点睛】该题考察的是数列的有关问题,涉及到的知识点有等差数列的求和公式,等差数列的性质,通项公式根本量的计算,属于简单题目.3y x =的图象,只需将函数sin 3cos3y x x =+的图象〔〕A.向右平移34π个单位长度 B.向右平移2π个单位长度 C.向左平移个4π单位长度 D.向左平移个2π单位长度 【答案】C 【解析】 【分析】根据三角函数解析式之间的关系即可得到结论.【详解】因为sin3cos334y x x x π⎛⎫=+=+ ⎪⎝⎭,所以将其图象向左平移4π个单位长度,可得()3344y x x x πππ⎡⎤⎛⎫=++=+= ⎪⎢⎥⎝⎭⎣⎦,应选C.【点睛】该题考察的是有关图象的平移变换问题,涉及到的知识点有辅助角公式,诱导公式,图象的平移变换的原那么,属于简单题目.8.假设5个人按原来站的位置重新站成一排,恰有两人站在自己原来的位置上的概率为〔〕A.12B.14C.16D.18【答案】C 【解析】 【分析】根据题意,分2步分析:①先从5个人里选2人,其位置不变,其余3人都不在自己原来的位置,②分析剩余的3人都不在自己原来位置的站法数目,由分步计数原理计算可得答案. 【详解】根据题意,分2步分析: ①先从5个人里选2人,其位置不变,有2510C =种选法,②对于剩余的三人,因为每个人都不能站在原来的位置上, 因此第一个人有两种站法,被站了自己位置的那个人只能站在第三个人的位置上, 因此三个人调换有2种调换方法, 故不同的调换方法有10220⨯=55120A =,所以所求概率为2011206=, 应选C.【点睛】该题考察的是有关古典概型求概率的问题,涉及到的知识点有分步计数原理,排列组合的综合应用,古典概型概率求解公式,属于简单题目.的奇函数()f x 满足,当0x ≤时,()xxf x e e-=-,那么不等式()()2230f x x f --<的解集为〔〕 A.(-1,3) B.(-3,1) C.()(),13,-∞-+∞ D.()(),31,-∞-⋃+∞【答案】A【解析】 【分析】根据题意,可知当x ∈R 时,()1x xf x e e =-,从而利用导数的符号判断得出函数()f x 是R 上的单调递增函数,所以得到()()223f x x f -<,利用函数的单调性得到2230x x --<,解不等式求得结果.【详解】由题意可知,当x ∈R 时,()1x xf x e e =-,所以()10x x f x e e=+>', ()f x 是R 上的单调递增函数,故由()()2230f x x f --<,得()()223f x x f -<, 即2230x x --<,解得13x ,应选A.【点睛】该题考察的是有关函数的问题,涉及到的知识点有奇函数的解析式的求解,函数的单调性的判断与应用,属于简单题目.O 作直线()():2220l m n x m n y m n ++--+=的垂线,垂足为P ,那么P 到直线30x y -+=的间隔的最大值为〔〕12+ C.1 D.2【答案】A 【解析】 【分析】 将直线l :()()2220m n x m n y m n ++--+=化为()()2220x y m x y n +-+--=,可得直线l 经过定点()0,2Q,从而可以判断得出P 的轨迹是以OQ 为直径的圆,圆心为()0,1,半径为1,利用点到直线的间隔公式,可得点P 到直线30x y -+=1.【详解】()()2220m n x m n y m n ++--+=整理得()()2220x y m x y n +-+--=,由题意得22020x y x y +-=⎧⎨--=⎩,解得02x y =⎧⎨=⎩,所以直线l 过定点()0,2Q.因为OP l ⊥,所以点P 的轨迹是以OQ 为直径的圆,圆心为()0,1,半径为1,因为圆心()0,1到直线30x y -+=的间隔为d == 所以P 到直线30x y -+=1.【点睛】该题考察的是有关动点到直线的间隔的最值问题,涉及到的知识点有动直线过定点问题,动点的轨迹,圆上的点到直线的间隔的最值,点到直线的间隔公式,属于简单题目.l 为4,侧面积为S ,体积为V,那么V S获得最大值时圆锥的侧面积为〔〕A.B.C.D.【答案】D 【解析】 【分析】设底面半径为r ,高为h ,利用题的条件,可得22224=16r h l +==,之后应用公式表示出,V S ,利用根本不等式得出V S获得最大值时对应的条件,得出答案.【详解】设圆锥的底面半径为r ,高为h ,那么22224=16r h l +==,所以2221111623121221223r h V rh r h S rl ππ+==≤⨯=⨯=,当且仅当r h ==1242π⨯⨯=.【点睛】该题考察的是有关圆锥的问题,涉及到的知识点有圆锥的性质,母线、高、底面圆的半径之间的关系,圆锥的体积与侧面积公式,根本不等式,属于简单题目.A 是双曲线()222210,0x y a b a b-=>>的右顶点,假设存在过点()3,0N a 的直线与双曲线的渐近线交于一点M ,使得AMN ∆是以点M 为直角顶点的直角三角形,那么双曲线的离心率〔〕A. B.C.存在最小值4D.存在最小值3【答案】B 【解析】 【分析】根据题意,写出其右顶点的坐标(),0A a ,写出双曲线的渐近线方程,取by x a=,设出点M 的坐标,b M m m a ⎛⎫ ⎪⎝⎭,从而得到,b AM m a m a ⎛⎫=- ⎪⎝⎭,3,b NM m a m a ⎛⎫=- ⎪⎝⎭,根据题意可得AM NM ⋅=,从而得到()()230b m a m a m a ⎛⎫--+= ⎪⎝⎭,进一步整理得22221430b m am a a ⎛⎫+-+= ⎪⎝⎭,根据方程有解,利用判别式大于等于零,求得223a b ≥,进一步求得其离心率的范围,得到结果.【详解】双曲线22221(0,0)x y a b a b-=>>的右顶点(),0A a ,双曲线的渐近线方程为by x a=±, 不妨取by x a=, 设,b Mm m a ⎛⎫ ⎪⎝⎭,那么,b AM m a m a ⎛⎫=- ⎪⎝⎭,3,b NM m a m a ⎛⎫=- ⎪⎝⎭. 假设存在过()3,0Na 的直线与双曲线的渐近线交于一点M ,使得AMN ∆是以M 为直角顶点的直角三角形,那么0AM NM ⋅=,即()()230b m a m a m a ⎛⎫--+= ⎪⎝⎭,整理可得22221430b m am a a ⎛⎫+-+= ⎪⎝⎭,由题意可知此方程必有解,那么判别式2222161210b a a a ⎛⎫∆=-+≥ ⎪⎝⎭,得223a b ≥,即22233a c a ≥-,解得1c e a <=≤,所以离心率存在最大值3,应选B.【点睛】该题考察的是有关双曲线的性质的问题,涉及到的知识点有双曲线的渐近线,向量的坐标公式,向量垂直的条件,方程有解的条件,双曲线的离心率,属于简单题目.第二卷二、填空题:本大题一一共4小题,每一小题5分,一共20分,请把正确之答案填在横线上()()2,3,1,a b m ==-,且a 与a b +垂直,那么m =______.【答案】113- 【解析】【分析】根据题意,可求得()1,3a b m +=+,由于a与a b +垂直,结合向量数量积坐标公式可得()2330m ++=,从而求得m 的值,得到结果.【详解】向量()2,3a=,()1,b m =-,()1,3a b m ∴+=+,a 与ab +垂直,()2330m ∴++=,解得113m =-, 故答案是:113-. 【点睛】该题考察的是有关向量的问题,涉及到的知识点有向量加法坐标运算,向量垂直的条件,向量数量积坐标公式,属于简单题目.{}n a 的前项和为n S ,假设11a =,4421S a =+,那么公比q =_________.【答案】4 【解析】 【分析】 根据题意可得321S =,设等比数列的公比为q ,利用等比数列的求和公式表示出3S ,得出关于q 的方程,求解即可得到q 的值. 【详解】由题意得4421S a -=,所以321S =,又11,a =,所以331211q S q-==-,解得4q =或者5q =-〔舍〕, 所以4q=,故答案是:4.【点睛】该题考察的是有关数列的问题,涉及到的知识点有等比数列的求和公式,属于简单题目.7(x 的展开式中,4x 的系数为__________.【答案】283【解析】 【分析】写出二项展开式的通项,由x 的指数等于4,求得r 的值,得到结果.【详解】7x ⎛⎝展开式的通项公式为1377221772233rrr r r rr T C x x C x ---+⎛⎫⎛⎫=⋅⋅-=⋅-⋅ ⎪ ⎪⎝⎭⎝⎭,令3742r -=,解得2r ,故所求系数为22722833C ⎛⎫⋅-=⎪⎝⎭,故答案是:283. 【点睛】该题考察的是有关二项式定理的问题,涉及到的知识点有二项展开式中指定项的系数的问题,二项展开式的通项,属于简单题目.3(,),(0,)22παππβ∈∈,且满足1sin tan cos βαβ+=,那么β=______.(用α表示)【答案】522απ- 【解析】 【分析】化切为弦,整理后得到()sincos αβα-=,利用诱导公式可得()sin sin 2παβα⎛⎫-=-⎪⎝⎭,结合题中所给的角的范围,最后确定出522βαπ=-,从而得到结果.【详解】由1sin tan cos βαβ+=得sin 1sin cos cos αβαβ+=,所以()sin cos cos 1sin αβαβ=+,即()sin cos αβα-=.结合诱导公式得()sinsin 2παβα⎛⎫-=-⎪⎝⎭. 因为3,,0,22ππαπβ⎛⎫⎛⎫∈∈ ⎪ ⎪⎝⎭⎝⎭,所以3,,,222πππαβπαπ⎛⎫⎛⎫-∈-∈-- ⎪ ⎪⎝⎭⎝⎭.由诱导公式可得()sinsin 22παβπα⎡⎤⎛⎫-=+-⎪⎢⎥⎝⎭⎣⎦,易知32,22ππαππ⎛⎫⎛⎫+-∈ ⎪ ⎪⎝⎭⎝⎭,因为sin y x =在3,22ππ⎛⎫ ⎪⎝⎭上单调递减,所以22παβπα⎛⎫-=+- ⎪⎝⎭,即522βαπ=-.法二:由1sin tan cos βαβ+=得sincos tan1222tan tan 24cossin1tan 222ββββπαβββ++⎛⎫===+ ⎪⎝⎭--, 所以tan tan 24βπα⎛⎫=+ ⎪⎝⎭.因为3,,0,22ππαπβ⎛⎫⎛⎫∈∈ ⎪ ⎪⎝⎭⎝⎭,所以,2442βπππ⎛⎫+∈ ⎪⎝⎭. 由诱导公式可得()tantan απα-=,即()tan tan 24βπαπ⎛⎫-=+ ⎪⎝⎭因为tan y x =在0,2π⎛⎫⎪⎝⎭上单调递增,所以24βπαπ-=+,即522βαπ=-.【点睛】该题考察的是有关三角函数恒等变换的问题,涉及到的知识点有同角三角函数关系式,正弦差角公式,诱导公式,属于简单题目.三、解答题:本大题一一共6小题,一共70分解容许写出文字说明、证明过程或者演算步骤解容许写在答题卡上的指定区域内ABC △中,内角,,A B C 所对的边分别为,,a b c ,且222cos cos sin sin sin .C B A A C -=-〔1〕求角B 的大小;〔2〕假设ABC △的面积为b =,求a c +的值.【答案】〔1〕3π;〔2〕7 【解析】 【分析】〔1〕利用同角三角函数关系和正弦定理可将关系式化为222a c b ac +-=;利用余弦定理可求得cos B ,从而得到B ;〔2〕利用三角形面积公式可求得ac ;利用余弦定理可构造关于a c +的方程,解方程求得结果.【详解】〔1〕2222222c cos 1sin 1sin sin si os n sin sin sin C B C B B C A A C -=--+=-=-由正弦定理得:222b c a ac -=-,即222a c b ac +-=〔2〕11sin sin 223S ac B ac π====12ac = 由余弦定理可得:()()222222cos 22cos36133ba c ac B a c ac ac a c π=+-=+--=+-=即()249a c +=7a c ∴+=【点睛】此题考察正弦定理、余弦定理解三角形、三角形面积公式的应用问题,属于常规题型.ABCDEF 中,四边形ABCD 是边长为2的正方形,1//,,,2ED FB DE BF AB FB FB ==⊥平面ABCD .(1)设BD 与AC 的交点为O ,求证:OE ⊥平面ACF ;(2)求二面角E AF C --的正弦值.【答案】〔1〕证明见解析;.【解析】 【分析】〔1〕根据题意,推导出ED ⊥面ABCD ,DE AC ⊥,OE OF ⊥,结合线面垂直的断定定理证得OE ⊥面ACF ;〔2〕以D 为原点,DA ,DC ,DE 方向建立空间直角坐标系,利用面的法向量所成角的余弦值求得二面角的余弦值,之后应用平方关系求得正弦值,得到结果. 【详解】(1)证明:由题意可知:ED ⊥面ABCD ,从而Rt EDA Rt EDC ∆≅∆,EA EC ∴=,又O 为AC 中点,DE AC ∴⊥,在EOF ∆中,3OE OF EF ===,222OE OF EF ∴+=,OE OF ∴⊥又AC OF O ⋂=,OE ∴⊥面ACF .〔2〕ED ⊥面ABCD ,且DA DC ⊥,如图以D 为原点,DA ,DC ,DE 方向建立空间直角坐标系, 从而(0E ,0,1),(2A ,0,0),(0C ,2,0),(2F ,2,2),(1O ,1,0)由〔1〕可知(1EO=,1,1)-是面AFC 的一个法向量,设(n x =,y ,)z 为面AEF 的一个法向量,由·220·20AF n y z AE n x z ⎧=+=⎨=-+=⎩,令1x =得(1n=,2-,2),设θ为二面角E AF C --的平面角,那么·3cos cos ,3·EOn EO n EO nθ===,sin θ∴=.∴二面E AF C --.【点睛】该题考察的是有关立体几何的问题,涉及到的知识点有线面垂直的断定,利用空间向量求二面角的余弦值,同角三角函数关系式,属于简单题目.()2:20C y px p =>的焦点是F ,直线2y =与C 的交点到F 的间隔等于2.(1)求抛物线C 的方程; (2)一直线():1,0l x ky bb k =+≠≠交C 于A ,B 两点,其中点(),b k 在曲线()22348x y --=上,求证:FA 与FB 斜率之积为定值. 【答案】(1)24y x =;(2)证明见解析.【解析】 【分析】〔1〕根据题意,结合抛物线的定义可得点P 的坐标为2,22p P ⎛⎫-⎪⎝⎭,代入抛物线方程可得2p =,从而求得抛物线的方程;〔2〕联立方程组,消元可得2440y ky b --=,设出两点的坐标211,4y A y ,222,4y B y ,由韦达定理可得124y y k +=,124y y b =-,根据点(),b k 在曲线()22349x y --=上,可得22461b k b -=-,整理求得1FA FB k k ⋅=-,得到结果.【详解】〔1〕由2PF =知P 到准线的间隔也是2,P ∴点横坐标是22p -, 将2,22p P ⎛⎫-⎪⎝⎭代入22y px =,得2p =, ∴抛物线C 的方程为24y x =.〔2〕证明:联立24y x x ky b ⎧=⎨=+⎩得2440y ky b --=,设211,4y A y ,222,4y B y ,那么124y y k +=,124y y b =-.因为点(),b k 在曲线()22349x y --=上,所以代入整理可得22461b k b -=-,那么()()12122222221212121241421111441642FA FB y y y y bk k b k b y y y y y y y y -⋅====---+⎛⎫⎛⎫+---++ ⎪⎪⎝⎭⎝⎭.【点睛】该题考察的是有关直线与圆锥曲线的问题,涉及到的知识点有抛物线的定义,直线与抛物线的位置关系,点在曲线上的条件,两点斜率坐标公式,属于简单题目.()sin ,(0,),2f x ax x x a π=-∈为常数(1)假设函数()f x 在0,2π⎛⎫⎪⎝⎭上是单调函数,求a 的取值范围;(2)当1a ≤时,证明31()6f x x ≤. 【答案】(1)][(,01,)-∞⋃+∞;(2)证明见解析.【解析】 【分析】〔1〕对函数求导,单调分单调增和单调减,利用()cos 0f x a x '=-≥或者()cos 0f x a x '=-≤在0,2π⎛⎫⎪⎝⎭上恒成立,求得实数a 的取值范围;〔2〕利用导数研究函数的单调性,求得结果. 【详解】〔1〕由()sin f x ax x =-得导函数()cos f x a x =-',其中0cos 1x <<.当1a ≥时,()0f x '>恒成立,故()sin f x ax x =-在0,2π⎛⎫⎪⎝⎭上是单调递增函数,符合题意;当0a ≤时,()0f x '<恒成立,故()sin f x ax x =-在0,2π⎛⎫⎪⎝⎭上是单调递减函数,符合题意;当01a <<时,由()cos 0f x a x '=-=得cos x a =,那么存在00,2x π⎛⎫∈ ⎪⎝⎭,使得0cos x a =. 当00x x <<时,()00f x '<,当02x x π<<时,()00f x '>,所以()f x 在()00,x 上单调递减,在0,2x π⎛⎫⎪⎝⎭上单调递增,故()f x 在0,2π⎛⎫⎪⎝⎭上是不是单调函数,不符合题意.综上,a 的取值范围是][(),01,-∞⋃+∞.〔2〕由〔1〕知当1a =时,()()sin 00f x x x f =->=,即sin x x <,故22sin 22x x ⎛⎫< ⎪⎝⎭.令()()3311sin ,0,662gx f x x ax x x x π⎛⎫=-=--∈ ⎪⎝⎭, 那么()22222111cos 12sin 12122222x x g x a x x a x a x a ⎛⎫=--=-+-<-+-'=- ⎪⎝⎭,当1a ≤时,()10g x a -'=≤,所以()g x 在0,2π⎛⎫⎪⎝⎭上是单调递减函数,从而()()00gx g <=,即()316f x x ≤. 【点睛】该题考察的是有关导数的应用,涉及到的知识点有根据函数在给定区间上单调求参数的取值范围,利用导数证明不等式,属于中档题目.21.某电子公司新开发一电子产品,该电子产品的一个系统G 有3个电子元件组成,各个电子元件能否正常工作的概率均为12C 中有超过一半的电子元件正常工作,那么G 可以正常工作,否那么就需要维修,且维修所需费用为500元.(1)求系统不需要维修的概率;(2)该电子产品一共由3个系统G 组成,设E 为电子产品需要维修的系统所需的费用,求ξ的分布列与期望; (3)为进步G 系统正常工作概率,在系统内增加两个功能完全一样的其他品牌的电子元件,每个新元件正常工作的概率均为p ,且新增元件后有超过一半的电子元件正常工作,那么C 可以正常工作,问:p 满足什么条件时,可以进步整个G 系统的正常工作概率【答案】(1)12;(2)见解析;(3)当112p <<时,可以进步整个G 系统的正常工作概率.【解析】 【分析】〔1〕由条件,利用HY 重复试验成功的次数对应的概率公式以及概率加法公式求得系统不需要维修的概率;〔2〕设X为维修维修的系统的个数,根据题意可得13,2XB ⎛⎫⎪⎝⎭,从而得到500X ξ=,利用公式写出分布列,并求得期望;〔3〕根据题意,当系统G 有5个电子元件时,分析得出系统正常工作对应的情况,分类得出结果,求得相应的概率,根据题意列出式子,最后求得结果.【详解】〔1〕系统不需要维修的概率为23233311112222C C ⎛⎫⎛⎫⋅⋅+⋅= ⎪ ⎪⎝⎭⎝⎭.〔2〕设X为维修维修的系统的个数,那么13,2XB ⎛⎫⎪⎝⎭,且500X ξ=,所以()()3311500,0,1,2,322kkk P k P X k C k ξ-⎛⎫⎛⎫====⋅⋅= ⎪ ⎪⎝⎭⎝⎭.所以ξ的分布列为所以ξ的期望为()50037502Eξ=⨯⨯=. 〔3〕当系统G 有5个电子元件时,原来3个电子元件中至少有1个元件正常工作,G 系统的才正常工作. 假设前3个电子元件中有1个正常工作,同时新增的两个必须都正常工作,那么概率为21223113228C p p ⎛⎫⋅⋅⋅= ⎪⎝⎭; 假设前3个电子元件中有两个正常工作, 同时新增的两个至少有1个正常工作,那么概率为()()2221222323111131222228C C p p C p p p ⎛⎫⎛⎫⋅⋅⋅⋅⋅-+⋅⋅⋅=- ⎪ ⎪⎝⎭⎝⎭;假设前3个电子元件中3个都正常工作,那么不管新增两个元件能否正常工作,系统G 均能正常工作,那么概率为3331128C ⎛⎫⋅= ⎪⎝⎭.所以新增两个元件后系统G 能正常工作的概率为()2233131288848p p p p +-+=+, 于是由()3113214828p p +-=-知,当210p ->时,即112p <<时,可以进步整个G 系统的正常工作概率.【点睛】该题考察的是有关概率的问题,涉及到的知识点有HY 重复试验,二项分布,分布列与期望,概率加法公式,属于中档题目.请考生从第22、23题中任选一题做答,并用2铅笔将答题卡上所选题目对应的题号右侧方框涂黑,按所涂题号进展评分;多涂、多答,按所涂的首题进展评分;不涂,按本选考题的首题进展评分 选修4-4:坐标系与参数方程22.平面直角坐标系中,曲线1C 的参数方程为2cos 1cos 2x y ϕϕ=⎧⎨=+⎩(ϕ为参数),以原点为极点,x 轴的非负半轴为极轴建立极坐标系,曲线2C 的极坐标方程为()3θρπ=∈R . (1)求曲线2C 的直角坐标方程; (2)求曲线1C 与曲线2C 交点的直角坐标. 【答案】(1)y =;(2)()0,0.【解析】 【分析】〔1〕利用极坐标与平面直角坐标的转换关系求得结果;〔2〕将曲线的参数方程化为普通方程,与直线方程联立,求得方程组的解,结合对应的坐标的范围,求得对应的交点的坐标,得到结果.【详解】〔1〕依题意,曲线2C的直角坐标方程为y =.〔2〕因为曲线1C 的参数方程为2,12,x cos y cos ϕϕ=⎧⎨=+⎩〔ϕ为参数〕,所以曲线1C 的直角坐标方程为[]()212,22y x x =∈-,联立2,1,2y y x ⎧=⎪⎨=⎪⎩解方程组得0,0,x y =⎧⎨=⎩或者6,x y ⎧=⎪⎨=⎪⎩ 根据x的范围应舍去6,x y ⎧=⎪⎨=⎪⎩故交点的直角坐标为()0,0.【点睛】该题考察的是有关坐标系与参数方程的问题,涉及到的知识点有参数方程与普通方程的互化,平面直角坐标方程与极坐标方程的互化,曲线交点的坐标的求解,属于简单题目. 选修4-5:不等式选讲()124f x x x =-++.(1)求不等式()6f x >的解集;(2)假设()10f x m --≥恒成立,务实数m 的取值范围.【答案】(1)()(),31,-∞-⋃+∞;(2)[]2,4-.【解析】 【分析】〔1〕通过讨论x 的范围,求出不等式的解集即可;〔2〕通过求函数()f x 的最小值,将恒成立问题转化为最值问题,得到关于m 的不等关系,从而求得结果. 【详解】〔1〕依题意,1246x x -++>,当2x <-时,原式化为1246x x --->,解得3x <-,故3x <-; 当21x -≤≤时,原式化为1246x x -++>,解得1x >,故无解;当1x >时,原式化为1246x x -++>,解得1x >,故1x >; 综上所述,不等式()6f x >的解集为()(),31,-∞-⋃+∞;〔2〕因为()124122123f x x x x x x x x =-++=-++++≥-++≥,当且仅当2x =-时,等号成立. 故()10f x m --≥恒成立等价于13m -≤;即313m -≤-≤,解得24m -≤≤, 故实数m 的取值范围为[]2,4-.【点睛】该题考察的是有关绝对值不等式的问题,涉及到的知识点有零点分段法解绝对值不等式,恒成立问题向最值靠拢,属于简单题目.。
高三数学第一次统考试题理含解析试题

2021—2021学年高中三年级第一次统一考试制卷人:歐陽文化、歐陽理複;制卷時間:二O二二年二月七日数学试卷(理)第一卷〔一共60分〕一、选择题:本大题一一共12个小题,每一小题5分,一共60分.在每一小题给出的四个选项里面,只有一项是哪一项符合题目要求的.1. 设全集,集合,,那么〔〕A. B. C. D.【答案】C【解析】,,所以,故,应选C................2. 假设〔是虚数单位〕,那么等于〔〕A. 3B. 2C. 0D. -1【答案】A【解析】,因,故,所以,选A.3. 假设函数同时满足以下两个条件,那么称该函数为“优美丽数〞:〔1〕对,都有;〔2〕对,且,都有.①;②;③;④以上四个函数中,“优美函数〞的个数是〔〕A. 0B. 1C. 2D. 3【答案】B【解析】假设,那么为上的奇函数,但在上不单调,故不是优美函数;假设,那么为上的奇函数,且在上为减函数,所以,它是优美函数;假设,因,故它不是上的奇函数,故它不是优美函数;假设,考虑函数在上的单调性,因在为增函数,在为增函数,所以在上为增函数且恒正,故在上为增函数,所以当时,总有,所以也不是优美函数,综上,选B.4. 向量,,假设,那么实数的值是〔〕A. -4B. -1C. 1D. 4【答案】D【解析】因为,故,展开得到,故,,选D.5. 某算法的程序框图如下图,那么该算法的功能是〔〕A. 求首项为1,公差为2 的等差数列前2021项和B. 求首项为1,公差为2 的等差数列前2021项和C. 求首项为1,公差为4 的等差数列前1009项和D. 求首项为1,公差为4 的等差数列前1010项和【答案】C【解析】由题意可知,为求首项为1,公差为4的等差数列的前1009项和.应选C.点睛:算法与流程图的考察,侧重于对流程图循环构造的考察.先明晰算法及流程图的相关概念,包括选择构造、循环构造、伪代码,其次要重视循环起点条件、循环次数、循环终止条件,更要通过循环规律,明确流程图研究的数学问题,是求和还是求项.6. 设满足约束条件,那么的最小值与最大值的和为〔〕A. 7B. 8C. 13D. 14【答案】D【解析】可行域如下图,当动直线过时,;当动直线过时,,故的最大值与最小值的和为14,选D.7. 函数,先将的图象上所有点的横坐标缩短到原来的〔纵坐标不变〕,再将得到的图象上所有点向右平移个单位长度,得到的图象关于轴对称,那么的最小值为〔〕A. B. C. D.【答案】C【解析】因,将其图像上的点的横坐标缩短到原来的后所得函数的解析式为,图像在轴左侧的第一条对称轴,故至少向右平移个单位就可以得到关于轴对称的图像,选C.点睛:假设三角函数的图像平移后得到的图像为奇函数或者偶函数的图像,那么最小的平移往往和轴附近的对称轴或者对称中心有关.8. 一个几何体的三视图如下图,图中的三个正方形的边长均为2,那么该几何体的体积为〔〕A. B. C. D.【答案】A【解析】几何体如下图,它为正方体中挖去两个对顶的圆锥,其体积为.9. 假设,那么二项式的展开式中的常数项为〔〕A. -15B. 15C. -240D. 240【答案】D【解析】,而展开式的通项公式为令,所以,常数项的系数为,选D.10. 在中,角的对边分别为,假设成等比数列,且,那么〔〕A. B. C. D.【答案】B【解析】因为,,故,而,因,故.根据正弦定理有,,故,选B.11. 是抛物线的焦点,曲线是以为圆心,以为半径的圆,直线与曲线从上到下依次相交于点,那么〔〕A. 16B. 4C.D.【答案】A【解析】由可以得到,解得,所以,,故,,选A.点睛:对于抛物线,假设且为焦点弦或者焦半径,那么,,其中为焦点.12. 函数满足,且当时,,那么方程在上的所有根之和为〔〕A. 8B. 9C. 10D. 11【答案】D【解析】由可得总成立,所以是偶函数,由可以得到是周期为的函数.在同一坐标系中,我们画出及的图像,故方程一共有11个根,,其中在内有6个解,其和为零,在内有5个解,得和为11.选D.点睛:对于不可解方程的解的个数,通常转化为两个熟悉函数的图像的交点去考虑.题设中关于的关系式蕴含为偶函数且为周期函数,而且图像的对称轴为,又的对称轴为,故根据两个函数的图像得到11个解,它们的和为8+3=11.第二卷〔一共90分〕二、填空题〔每一小题5分,满分是20分,将答案填在答题纸上〕13. ,那么__________.【答案】【解析】由题设有,所以,所以.14. 某校有4个社团向高一学生招收新成员,现有3名同学,每人只选报1个社团,恰有2个社团没有同学选报的报法数有__________种〔用数字答题〕.【答案】36【解析】先选出学生选报的社团,一共有种选法,再把这3名同学分配到这两个社团,一共有,故恰有2个社团没有同学选报数有.15. 在半径为4的球面上有不同的四点,假设,那么平面被球所截得图形的面积为__________.【答案】【解析】设球心为,那么,所以在平面上射影是的外心,同理在平面上射影也是的外心.因且,故在平面的异侧,如下图,等边三角形中,,故,又为平面截所球得圆的半径,故圆的面积为.点睛:题设中,结合球的半径为,故我们可以确定出在平面的两侧,从而求出的外接圆的半径.16. 为双曲线的左、右焦点,是双曲线右支上的一点,连接并过作垂直于的直线交双曲线左支于,其中,为等腰三角形.那么双曲线的离心率为__________.【答案】【解析】连接并延长交右支于点,设,那么,因为双曲线是中心对称,且,所以四边形是平行四边形.因是等腰三角形,,所以,故,且,根据双曲线的定义,有,所以,解得,所以,所以,.点睛:圆锥曲线的离心率的计算,常常需要寻找一个关于的关系式.假如题设条件与焦点或者准线有关,那么我们需要从几何性质的角度去构建的关系式.三、解答题〔本大题一一共6小题,一共70分.解容许写出文字说明、证明过程或者演算步骤.〕17. 各项均不为零的数列的前项和为,且对任意,满足.〔1〕求数列的通项公式;〔2〕设数列满足,数列的前项和为,求证:.【答案】〔1〕.〔2〕见解析.【解析】试题分析:由,可以得到的大小和的递推关系为,因此为等比数列,从而求得,再根据求出的通项,它是等差数列和等比数列的乘积,利用错位相减法求它的前项和.〔1〕当时,,∵,∴.∵,∴当时,,两式相减得,因,,故,∴数列是首项为4,公比为4的等比数列,∴.〔2〕∵,∴,∴,,两式相减得:.所以.18. 甲、乙两家外卖公司,其送餐员的日工资方案如下:甲公司的底薪80元,每单抽成4元;乙公司无底薪,40单以内〔含40单〕的局部每单抽成6元,超出40单的局部每单抽成7元,假设同一公司送餐员一天的送餐单数一样,现从两家公司各随机抽取一名送餐员,并分别记录其50天的送餐单数,得到如下频数表:甲公司送餐员送餐单数频数表送餐单数38 39 40 41 42天数10 15 10 10 5乙公司送餐员送餐单数频数表送餐单数38 39 40 41 42天数 5 10 10 20 5〔1〕现从甲公司记录的50天中随机抽取3天,求这3天送餐单数都不小于40的概率;〔2〕假设将频率视为概率,答复以下两个问题:①记乙公司送餐员日工资为〔单位:元〕,求的分布列和数学期望;②小王打算到甲、乙两家公司中的一家应聘送餐员,假如仅从日工资的角度考虑,请利用所学的统计学知识为小王作出选择,并说明理由.【答案】〔1〕.〔2〕见解析【解析】试题分析:〔1〕为古典概型,利用组合数公式计算根本领件的总数和随机事件中含有的根本领件的总数即可.〔2〕为计算离散型随机变量的分布列和数学期望,利用公式计算即可.〔1〕记抽取的天送餐单数都不小于40为事件,那么.〔2〕①设乙公司送餐员送餐单数为,那么当时,,当时,,当时,,当时,,当时,.所以的分布列为:228 234 240 247 254所以②依题意,甲公司送餐员日平均送餐单数为所以甲公司送餐员日平均工资为元.,故推荐小王去乙公司应聘.19. 如图,在四棱锥中,分别是的中点,底面是边长为2的正方形,,且平面平面.〔1〕求证:平面平面;〔2〕求平面与平面所成锐二面角的余弦值.【答案】〔1〕见解析〔2〕.【解析】试题分析:〔1〕要证平面因平面,只要证平面,也就是证明和,后者可以由为等边三角形得到,前者由平面得到〔因为平面平面〕.〔2〕要求锐二面角,因几何体比拟规那么,可以建立空间直角坐标系计算两个半平面的法向量的夹角.〔1〕由题,为的中点,可得,∵平面平面,,平面平面,平面,∴平面.又∵平面,∴.,∴平面.∴平面平面.〔2〕取的中点,的中点,连接,∵,∴.∵平面平面平面,∴平面.分别以为轴建立空间直角坐标系,那么,,设平面的法向量为,那么.即.可取.同理,可得平面的法向量..所以平面与平面所成锐二面角余弦值为.20. 短轴长为2的椭圆,直线的横、纵截距分别为,且原点到直线的间隔为.〔1〕求椭圆的方程;〔2〕直线经过椭圆的右焦点且与椭圆交于两点,假设椭圆上存在一点满足,求直线的方程.【答案】〔1〕.〔2〕或者.【解析】试题分析:直线的方程有参数,利用原点到其间隔为可以得到的大小,从而得到椭圆的方程.〔2〕中的三点满足向量关系式,将各点坐标代入,可以得到三个点的坐标之间的关系,而在椭圆上,所以两点的坐标满足关系式,再利用两点在直线上,得到关于的一个关系式,利用韦达定理转化为的方程可以解出的值.〔1〕因为椭圆的短轴长为2,故.依题意设直线的方程为:,由.解得,故椭圆的方程为.〔2〕设当直线的斜率为0时,显示不符合题意.当直线的斜率不为0时,,设其方程为,由,得,所以①.因为,所以.又点在椭圆上,∴.又∵,∴②,将,及①代入②得,即或者.故直线的方程为或者.点睛:一般地,当解析几何中问题出现向量等式时,我们先寻找向量隐含的几何意义,假如没有几何意义,可以转化点的坐标讨论.解决直线与圆锥曲线位置关系式,我们常把给定的关系式转化为含有〔或者〕的关系式,最后利用韦达定理转化为所求参数的方程.21. 函数,〔〕,且曲线在点处的切线方程为.〔1〕务实数的值及函数的最大值;〔2〕当时,记函数的最小值为,求的取值范围.【答案】〔1〕,最大值.〔2〕【解析】试题分析:〔1〕题设给出了在处的切线,也是,从中解出即可.〔2〕中要求的最小值,因此要考虑的单调性,也就是考虑的符号的变化,但的零点不易求得,所以利用〔1〕的结论先确定在给定的范围上有唯一的零点,通过零点满足的关系式化简在零点处的函数值表达式〔也是的最小值〕,最终求出最小值得范围.〔1〕函数的定义域为,,因的图象在点处的切线方程为,所以也即是,解得,所以,故.令,得,当时,,单调递增;当时,,单调递减.所以当时,获得最大值.〔2〕∵,∴,令,由〔1〕知道在是增函数,故在上为增函数,又,,因此存在唯一的,使得,也就是即.当时,,所以,单调递减;当时,,单调递增,所以的最小值为.令,因为,所以在单调递减,从而,即的取值范围是.点睛:在导数问题的讨论中,假如函数的极值点不易求得,那么我们可以利用这个关系式去化简,从而讨论与相关的问题.请考生在22、23两题中任选一题答题,假如多做,那么按所做的第一题记分.22. 选修4-4:坐标系与参数方程在直角坐标系中,曲线的参数方程为〔为参数,〕,以原点为极点,轴的非负半轴为极轴建立极坐标系,曲线的极坐标方程为.〔1〕写出曲线的普通方程和曲线的直角坐标方程;〔2〕点是曲线上一点,假设点到曲线的最小间隔为,求的值.【答案】〔1〕,〔2〕或者.【解析】试题分析:〔1〕消去参数得到的普通方程为.利用可以把的极坐标方程化为直角坐标方程.〔2〕把的直角方程转化为参数方程,利用点到直线的间隔公式算出间隔为,利用得到.因为直线与椭圆是相离的,所以或者,分类讨论就可以得到相应的值.〔1〕由曲线的参数方程,消去参数,可得的普通方程为:.由曲线的极坐标方程得,∴曲线的直角坐标方程为.〔2〕设曲线上任意一点为,,那么点到曲线的间隔为.∵,∴,,当时,,即;当时,,即.∴或者.点睛:一般地,假如圆锥曲线上的动点到直线的间隔有最小值,那么这条直线和圆锥曲线的位置关系式相离的.23. 选修4-5:不等式选讲函数.〔1〕当时,解不等式;〔2〕设不等式的解集为,假设,务实数的取值范围.【答案】〔1〕.〔2〕.【解析】试题分析:〔1〕利用零点分段讨论求解.〔2〕利用化简得到在区间上是恒成立的,也就是是不等式的子集,据此得到关于的不等式组,求出它的解即可.〔1〕当时,原不等式可化为.①当时,原不等式可化为,解得,所以;②当时,原不等式可化为,解得,所以;③当时,原不等式可化为,解得,所以.综上所述,当时,不等式的解集为.〔2〕不等式可化为,依题意不等式在恒成立,所以,即,即,所以.解得,故所务实数的取值范围是.制卷人:歐陽文化、歐陽理複;制卷時間:二O二二年二月七日。
高三数学第一次联考试题 理 试题

阶段性教学质量检测试题高三数学〔理科〕创 作人:历恰面 日 期: 2020年1月1日第一卷〔一共60分〕一、选择题:〔本大题一一共12个小题,每一小题5分,一共60分.在每一小题给出的四个选项中,有且只有一项是哪一项符合题目要求的,请将正确答案填在答题卷的答题卡内〕 1.集合2{|1},{|1}M x N y y x x===-<,那么RN M 等于A.〔1,2〕B. [0,2]C.∅D. [1,2]2.条件:1p x ≤,条件1:1q x<,那么p 是q ⌝成立的C.充要条件D.既非充分也非必要条件3.如图,网格纸的小正方形的边长是1,在其上用粗线画,出了某多面体的三视图,那么这个多面体最长的一条棱的长为 A.3 B. 32C. 4D. 224.如图,矩形OABC 内的阴影局部是由曲线()()()sin 0,f x x x π=∈及直线()()0,x a a π=∈与x 轴围成,向矩形OABC 内随机投掷一点,假设落在阴影局部的概率为14,那么a 的值是 A .712π B.23π C .34π D.56π 5.设)('x f 是函数)(x f 的导函数,将)(x f y =和)('x f y =的图象画在同一个直角坐标系中,不可能正确的选项是6.各项均不为零的数列{}n a ,定义向量1(,)n n n a a +=c ,(,1)n n n =+b ,n ∈*N . 以下命题中真命题是A. 假设n ∀∈*N 总有//n n c b 成立,那么数列{}n a 是等差数列B. 假设n ∀∈*N 总有//n n c b 成立,那么数列{}n a 是等比数列C. 假设n ∀∈*N 总有n n ⊥c b 成立,那么数列{}n a 是等差数列D. 假设n ∀∈*N 总有n n ⊥c b 成立,那么数列{}n a 是等比数列7.,m n ∈R ,a 、b 、c 是一共起点的向量,a 、b 不一共线,b n a m c +=,那么a 、b 、c 的终点一共线的充分必要条件是A .1-=+n mB .0=+n mC .1=-n mD .1=+n m8.101()3x x -的展开式中含x 的正整数指数幂的项数是A .0B .2C .4D .69.简谐振动()sin()f x A x ωφ=+()2πφ<的振幅为32,图象上相邻最高点与最低点之间的间隔 为5,且过点3(0,)4,那么该简谐振动的频率与初相分别为 A .1,66π B .1,86π C .,46ππ D . 1,63π10.设奇函数)(x f 在),0(+∞上是增函数,且0)1(=f ,那么不等式0)]()([<--x f x f x 的解集为A .}1,01|{><<-x x x 或B .}10,1|{<<-<x x x 或C .}1,1|{>-<x x x 或D .}10,01|{<<<<-x x x 或11.设1e ,2e 分别为具有公一共焦点1F 与2F 的椭圆和双曲线的离心率,P 为两曲线的一个公一共点,且满足021=⋅PF PF ,那么2212221)(e e e e +的值是 A .21B .1C .2D .不确定12.函数c bx ax x x f +++=23)(,在定义域∈x [-2,2]上表示的曲线过原点,且在x =±1处的切线斜率均为1-.有以下命题:①()f x 是奇函数;②假设()f x 在[],s t 内递减,那么t s -的最大值为4;③()f x 的最大值为M ,最小值为m ,那么0M m +=; ④假设对[]2,2x ∀∈-,()k f x '≤恒成立,那么k 的最大值为2.其中正确命题的个数为A .1个 B. 2个 C .3个 D. 4个第二卷〔一共90分〕题号 二三总分1718 19 20 21 22 得分二、填空题:〔本大题一一共4小题,每一小题4分,一共16分,把答案填在答题卷中对应题号后的横线上〕13.假设下框图所给的程序运行结果为S=20,那么判断框中应填入的关于k 的条件是 .得 分 评卷人14.3123,cos(),sin(),24135ππβααβαβ<<<-=+=-那么sin cos αα+的值 . 15设,x y 满足约束条件3123x y x y x y +⎧⎪--⎨⎪-⎩≥≥≤,假设目的函数(0,0)x y z a b a b =+>>的最大值为10,那么54a b +的最小值为 .16.如图,在透明塑料制成的长方体1111ABCD A B C D -容器内灌进一些水,将容器底面一边BC 固定于地面上,再将容器倾斜,随着倾斜度的不同,有以下四个说法: ①水的局部始终呈棱柱状; ②水面四边形EFGH 的面积不改变; ③棱11A D 始终与水面EFGH 平行; ④当1E AA ∈时,AE BF +是定值. 其中正确说法是 .三、解答题〔本大题一一共6小题,一共74分。
陕西省2025届高三数学第一次模拟联考试题理含解析

陕西省2025届高三第一次模拟联考理科数学试题一、选择题(本大题共12小题,共60.0分)1.已知集合A={x|-1≤x<2},B={x|0≤x≤3},则A∩B=()A. B. C. D.【答案】B【解析】【分析】利用集合的交集的定义,干脆运算,即可求解.【详解】由题意,集合A={x|-1≤x<2},B={x|0≤x≤3},∴A∩B={x|0≤x<2}.故选:B.【点睛】本题主要考查了集合的交集运算,其中解答中熟记集合的交集定义和精确运算是解答的关键,着重考查了运算与求解实力,属于基础题.2.复数的模是()A. B. C. D.【答案】D【解析】【分析】先将复数化成形式,再求模。
【详解】所以模是故选D.【点睛】本题考查复数的计算,解题的关键是将复数化成形式,属于简洁题。
3.若抛物线y2=2px的焦点坐标为(2,0),则准线方程为()A. B. C. D.【答案】A【解析】【分析】抛物线y2=2px的焦点坐标为(2,0),求得的值,即可求解其准线方程.【详解】由题意,抛物线y2=2px的焦点坐标为(2,0),∴,解得p=4,则准线方程为:x=-2.故选:A.【点睛】本题主要考查了抛物线的标准方程及其性质,其中解答中熟记抛物线的标准方程,及其简洁的几何性质,合理计算是解答的关键,着重考查了运算与求解实力,属于基础题.4.一个空间几何体的三视图如图所示,则该几何体的表面积为()A. 64B.C. 80D.【答案】B【解析】【分析】依据三视图画出几何体的直观图,推断几何体的形态以及对应数据,代入公式计算即可.【详解】几何体的直观图是:是放倒的三棱柱,底面是等腰三角形,底面长为4,高为4的三角形,棱柱的高为4,所求表面积:.故选:B.【点睛】本题主要考查了几何体的三视图,以及几何体的体积计算,其中解答中推断几何体的形态与对应数据是解题的关键,着重考查了推理与计算实力,属于基础题。
5.公元263年左右,我国数学家刘徽发觉当圆内接正多边形的边数无限增加时,多边形面积可无限靠近圆的面积,并创立了“割圆术”,利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是闻名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出n的值为()(参考数据:sin15°=0.2588,sin7.5°=0.1305)A. 12B. 24C. 48D. 96【答案】B【解析】【分析】列出循环过程中S与n的数值,满意推断框的条件,即可结束循环,得到答案.【详解】模拟执行程序,可得:n=6,S=3sin60°=,不满意条件S≥3.10,n=12,S=6×sin30°=3,不满意条件S≥3.10,n=24,S=12×sin15°=12×0.2588=3.1056,满意条件S≥3.10,退出循环,输出n的值为24.故选:B.【点睛】本题主要考查了循环框图的应用,其中解答中依据给定的程序框图,逐次循环,留意推断框的条件的应用是解答的关键,着重考查了运算与求解实力,属于基础题。
高三数学第一次联考试题 理 试题1

卜人入州八九几市潮王学校西路片七校2021届高三第一次联考数学试题〔理科〕 第一卷〔选择题局部,一共60分〕一.选择题:〔一共12小题,每一小题5分,一共60分.在每个小题给出的四个选项里面,只有一项为哪一项哪一项符合题目要求的.〕1.全集U R =,集合{}|lg A x y x ==,集合{}|1B y y x ==+,那么()U AC B =〔〕A.∅B.(0,1)C.(]0,1 D .(1,)+∞ 2.假设复数3i 21z =+,其中i 为虚数单位,那么复数z 的虚部是〔〕 A.1 B.i -C.iD.1-3.假设等差数列{}n a 的公差为2,且5a 是2a 与6a 的等比中项,那么该数列的前n 项和n S 取最小值时,n 的值等于〔〕A .7B .6C .5D .44.R 上的奇函数)(x f 满足:当0x >时,1)(2-+=x x x f ,那么()[]=-1f f 〔〕A.1 B .1- C.2D.2- 〔〕 ①“R x ∈∀都有02≥x 〞的否认是“R x ∈∃0使得020≤x 〞;②“3≠x 〞是“3≠x 〞成立的充分条件;③“假设21≤m ,那么方程0222=++x mxA.0B.1C.2D.3 6.函数()ln x xe ef x x--=的图象大致是〔〕7.某几何体的三视图如下列图(单位:cm ),那么该几何体的体积等于〔〕3cmA .243π+B .342π+ C .362π+D .263π+ 8.元朝著名数学家朱世杰在四元玉鉴中有一首诗:“我有一壶酒,携着游春走,遇店添一倍, 逢友饮一斗,店友经三处,没了壶中酒,借问此壶中, 当原多少酒?〞用程序框图表达如下列图,即最终输出的0x =,那么一开场输入的x 的值是〔〕 A .34B .1516C .4 D .78α假设31)6-sin(=πα,那么=)3- cos(πα() A.6-132 B.82-3C.6612+ D.823+ 10.如下列图,在梯形ABCD 中,∠B =,,BC =2,点E 为AB 的中点,假设向量在向量上的投影为21-, 那么〔〕A .21-B .-2C .0D .2 11.双曲线()222210,0x y a b a b-=>>的两条渐近线与抛物线()220y px p =>的准线分别交于A B、两点,O 为坐标原点.假设双曲线的离心率为2,AOB ∆的面积为3,那么p =〔〕A.2B .1 C .23D .312.函数()223,1,,1,x x x f x lnx x ⎧--+≤=⎨>⎩假设关于x 的方程()12f x kx =-恰有四个不相等的实数根,那么实数k 的取值范围是〔〕 A.1,2e ⎛⎫⎪⎝⎭B.1,2e e ⎛⎫⎪ ⎪⎝⎭C.1,2e ⎡⎫⎪⎢⎣⎭D.1,2e e ⎛⎤⎥ ⎝⎦第二卷〔非选择题局部,一共90分〕二.填空题:〔本大题一一共4小题,每一小题5分,一共20分.〕13.假设某要从5名男生和2名女生中选出3人作为世博会的志愿者,那么选出的志愿者中男女生均不少于1名的概率是_____________.(结果用最简分数表示).14.()20cos a x dx π=-⎰,那么912ax ax ⎛⎫+ ⎪⎝⎭展开式中,3x 项的系数为.15.y x ,满足⎪⎩⎪⎨⎧≤≥-+≤-+,1,033,032y y x y x y x z +=2的最大值为m ,假设正数b a ,满足m b a =+,那么b a 41+的最小值为.16.正三角形ABC 的边长为2,将它沿高AD 翻折,使点B 与点C 2,此时四面体ABCD 的外接球的外表积为.三.解答题:本大题一一共6小题,一共70分.解容许写出文字说明、证明过程或者演算步骤. 17.〔本小题总分值是10分〕等差数列{}n a 的前n 项和为nS ,数列{}n b 是等比数列,满足113,1a b ==,2252310,2.b S a b a +=-=〔Ⅰ〕求数列{}n a 和{}n b 的通项公式; 〔Ⅱ〕令n n nb ac ⋅=,设数列{}n c 的前n 项和为n T ,求n T .18.〔本小题总分值是12分〕向量(3sin cos ,1)mx x ωω=-,1(cos ,)2n x ω=,设函数()f x m n =⋅,假设函数()f x 的图象关于直线3x π=对称且[]0,2ω∈.〔Ⅰ〕求函数()f x 的单调递减区间;〔Ⅱ〕在△ABC 中,角A ,B ,C 的对边分别是a ,b ,c ,假设3a=()1f A =,求b c +的最大值.19.〔本小题总分值是12分〕高考HY 新方案,不分文理科,高考成绩实行“3+3”的构成形式,第一个“3”是语文、数学、外语,每门总分值是150分,第二个“3”由考生在思想政治、历史、地理、物理、化学、生物6个科目中自主选择其中3个科目参加等级性考试,每门总分值是100分,高考录取成绩卷面总分总分值是750分.为了调查学生对物理、化学、生物的选考情况,“将A 某一届学生在物理、化学、生物三个科目中至少选考一科的学生〞记作学生群体B ,从学生群体B 中随机抽取了50名学生进展调查,他们选考物理,化学,生物的科目数及人数统计表如下:选考物理、化学、生物的科目数1 2 3 人数52520〔Ⅰ〕从所调查的50名学生中任选2名,求他们选考物理、化学、生物科目数量不相等的概率;〔Ⅱ〕从所调查的50名学生中任选2名,记X 表示这2名学生选考物理、化学、生物的科目数量之差的绝对值,求随机变量X 的分布列和数学期望;〔Ⅲ〕将频率视为概率,现从学生群体B 中随机抽取4名学生,记其中恰好选考物理、化学、生物中的两科目的学生数记作Y ,求事件“2Y≥〞的概率.20.(本小题总分值是12分)如图,四棱锥P ABCD -中,平面PAD ⊥平面ABCD ,底面ABCD 为等腰梯形,//AB CD ,2AD DC BC ===,4AB =,PAD ∆为正三角形.〔Ⅰ〕求证:BD ⊥平面PAD ;〔Ⅱ〕设AD 的中点为E ,求平面PEB 与平面PDC 所成二面角的平面角的余弦值.21.(本小题总分值是12分)椭圆C :22221(0)x y a b a b+=>>的离心率为32,1F 、2F 分别是椭圆的左、右焦点,M 为椭圆上除长轴端点外的任意一点,且12MF F ∆的周长为423+〔Ⅰ〕求椭圆C 的方程;〔Ⅱ〕过点)2,0(-D 作直线l 与椭圆C 交于A 、B 两点,点N 满足OB OA ON +=〔O 为原点〕,求四边形OANB 面积的最大值,并求此时直线l 的方程. 22.〔本小题总分值是12分〕函数x x a ax x f ln )12()(2---=.〔Ⅰ〕当a >0时,求函数)(x f 的单调递增区间;〔Ⅱ〕当a <0时,求函数)(x f 在]1,21[上的最小值;〔Ⅲ〕记函数)(x f y =的图象为曲线C ,设点A 〔1x ,1y 〕,B 〔1x ,2y 〕是曲线C 上的不同两点,点M为线段AB 的中点,过点M 作x 轴的垂直交曲线C 于点N ,判断曲线C 在点N 处的切线是否平行于直线AB ,并说明理由.西路片七校联考测试卷 理科数学参考答案及评分HY一、选择题:本大题一一共12个小题,每一小题5分,一共60分,在每一小题给出的四个选项里面,只有一项为哪一项哪一项符合题目要求的.13.57;14.212-;15.32;16.5π三、解答题:本大题一一共6小题,一共70分.解容许写出文字说明.证明过程或者演算步骤. 17.解析:(1)设数列{}n a 的公差为d ,数列{}n b 的公比为q ,那么 由2252310,2,b S a b a +=⎧⎨-=⎩得610,34232,q d d q d ++=⎧⎨+-=+⎩解得2,2,d q =⎧⎨=⎩所以32(1)21n a n n =+-=+,12n n b -=.…………………5分(2)由(1)可知1(21)2,n nc n -=+⋅01221325272(21)2(21)2n n n T n n --∴=⋅+⋅+⋅++-⋅++⋅………………①12312325272(21)2(21)2n n n T n n -=⋅+⋅+⋅++-⋅++⋅………………② ①-②得:1213222222(21)2n nnT n --=+⋅+⋅++⋅-+⋅(21)2 1.n n T n ∴=-⋅+…………………10分18.解:〔1〕)1()cos cos 2f x x x x ωωω=-+21cos cos 2x x x ωωω=-+12cos 2sin(2)226x x x πωωω=-=-…………………2分函数()f x 的图象关于直线3x π=对称,那么2,362k k Z ωππππ-=+∈那么312k ω=+,k Z ∈且[0,2]ω∈,那么1ω=…………………4分∴()sin 26f x x π⎛⎫=- ⎪⎝⎭,令3222262k x k πππππ+≤-≤+,解得5,36k x k k Z ππππ+≤≤+∈ ∴函数()f x 的单调递减区间为5,,36k k k Zππππ⎡⎤++∈⎢⎥⎣⎦…………………6分〔2〕()sin 216f A A π⎛⎫=-= ⎪⎝⎭,且A 是△ABC 内角,∴0A π<<,那么112666A πππ-<-<,所以262A ππ-=,那么3A π=,∵a=2222222cos()33a b c bc b c bc b c bc π=+-=+-=+-那么2()33b c bc +-=,而22b c bc +⎛⎫≤ ⎪⎝⎭,所以()22223()3()324b c b c b c bc b c ++⎛⎫=+-≥+-⨯=⎪⎝⎭b c ⇒+≤b c ==所以b c +的最大值为分19.解:〔1〕记“所选取的2名学生选考物理、化学、生物科目数量相等〞为事件A 那么2225252025020()49C C C P A C ++== 所以他们选考物理、化学、生物科目数量不相等的概率为291()49P A -=……………3分〔2〕由题意可知X 的可能取值分别为0,1,22225252025020(0)49C C C P X C ++===,1111525202525025(1)49C C C C P X C +=== 115202504(2)49C C P X C ===…………………6分从而X 的分布列为X 0 1 2P204925494492025433()01249494949E X =⨯+⨯+⨯=…………………8分〔3〕所调查的50名学生中物理、化学、生物选考两科目的学生有25名 相应的概率为251502P ==,所以Y 14,2B ⎛⎫ ⎪⎝⎭…………………10分所以事件“2Y≥〞的概率为22342344441111111(2)112222216P Y C C C ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫≥=-+-+= ⎪⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭…………12分 20.解:〔1〕在等腰梯形ABCD 中,过点D 作DE AB ⊥于点E , 如下列图:有1,3,23AE DE BD ===∴在ABD ∆中,有222AB AD BD =+,即AD BD ⊥又因为平面PAD ⊥平面ABCD 且交线为AD ,∴BD ⊥平面PAD .---5分 〔2〕由平面PAD ⊥平面ABCD ,且PAD ∆为正三角形,E 为AD 的中点, ∴PE AD ⊥,得PE ⊥平面ABCD .如下列图,以D 为坐标原点,DA 所在直线为x 轴,DB 所在直线为y 轴,过点D 平行于PE 所在直线为z 轴,建立空间直角坐标系.由条件2AD DC BC ===,那么1AE DE ==,3PE =23BD = 那么(0,0,0)D ,(1,0,0)E ,(0,23,0)B ,3)P .-------6分 在等腰梯形ABCD 中,过点C 作BD 的平行线交AD 延长线于点F 如下列图:那么在Rt CDF ∆中,有3CF ,1DF =,∴(3,0)C -.-------7分〔另解:可不做辅助线,利用2AB DC =求点C 坐标〕∴(1,3,0)CD =-,(1,0,3)PD =--,设平面PDC 的法向量1111(,,)n x y z =那么1111113030n CD x y n PD x z ⎧⋅==⎪⎨⋅=-=⎪⎩,取13x =,那么11y =,11z =-,∴面PDC 的法向量1(3,1,1)n =-.-------9分同理有(0,0,3)PE =-,(1,23,3)PB =--,设平面PBE 的法向量2222(,,)n x y z =那么222222302330n PE z n PB x y z ⎧⋅=-=⎪⎨⋅=-+=⎪⎩,取21y =,那么223x =20z =,∴面PBE 的法向量2(23,1,0)n =.--10分 设平面PEB 与平面PDC 所成二面角的平面角为θ,∴123231765cos cos ,311121n n θ⨯+=<>==++⨯+. 即平面PEB 与平面PDC 765-------12分 〔2〕∵OB OA ON+=,∴四边形OANB 为平行四边形,显然直线l 的斜率存在,设l 的方程为),(),,(,22211y x B y x A kx y -=,把2-=kx y 代入1422=+y x 得01216)41(22=+-+kx x k , 由0)41(4816222>+-=∆k k 得432>k , ∴2214116k k x x +=+,2214112k x x +=, ∵||||||212121x x x x OD S OAB-=-⋅=∆………………………7分∴21221214)(2||22x x x x x x S S OAB OANB-+=-==∆=222222)41(34841124)4116(2k k k k k +-=+-+,令0342>-=k t,∴243k t =+,∴2161816818)4(82=≤++=+=tt t tS OANB…………………10分 当且仅当4=t ,即27±=k 时取等号,∴2)(max=OANB S ,此时l 的方程为227-±=x y 。
〖人教版〗高三数学复习试卷第一次大联考理科数学

〖人教版〗高三数学复习试卷第一次大联考理科数学第Ⅰ卷一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知21()1i a R ai-∈+是纯虚数,则a =( ) A .12B .12-C .2 D .-22.已知集合U R =,函数y =M ,集合{}2|0N x x x =-≤,则下列结论正确的是( )A .M N N =B .()MC N ⋃=∅C .M N U =D .()M C N ⋃⊆4.已知,a b R ∈>log 1a b <”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件 5.已知tan()24x π+=,则sin 2x =( ) A .110B .15C .35D .9106.如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的体积为( )A .8π+B .82π+C .83π+D .84π+ 7.执行如图所示的程序框图,则该程序运行后输出的i 值为( ) A .8B .9 C .10D .118.已知ABC ∆是边长为1的等边三角形,则(2)(34)AB BC BC CA -+=( )A .132-B .112-C .62--D .62-+ 9.已知1()nx x -的展开式中第3项与第6项的二项式系数相等,则展开式中系数最大的项为第( )项.A .5B .4C .4或5D .5或610.已知抛物线2:8C x y =,过点(0,)(0)M t t <可作抛物线C 的两条切线,切点分别为,A B ,若直线AB 恰好过抛物线C 的焦点,则MAB ∆的面积为( )A .2B .3C .6D .1611.函数()3sin ln(1)f x x x =+的部分图象大致为( )A .B .C .D .12.若函数()f x 在定义域内满足:(1)对于任意不相等的12,x x ,有12211122()()()()x f x x f x x f x x f x +>+;(2)存在正数M ,使得()f x M ≤,则称函数()f x 为“单通道函数”,给出以下4个函数: ①()sin()cos()44f x x x ππ=+++,(0,)x π∈;②()ln x g x x e =+,[]1,2x ∈; ③[]32()3,1,2h x x x x =-∈;④122,10()log (1)1,01x x x x x ϕ⎧--≤<⎪=⎨+-<≤⎪⎩,其中,“单通道函数”有( )A .①③④B .①②④C .①③D .②③第Ⅱ卷二、填空题:本大题共4小题,每小题5分,满分20分.13.已知直线:320l x y b +-=过双曲线2222:1(0,0)x y C a b a b-=>>的右焦点F ,则双曲线的渐近线方程为________.14.已知实数,x y 满足不等式组24024000x y x y x y +-≤⎧⎪--≤⎪⎨≥⎪⎪≥⎩,则92z x y =+的最大值为________. 15.已知,,a b c 是ABC ∆的三边,若满足222a b c +=,即22()()1a b c c+=,ABC ∆为直角三角形,类比此结论:若满足(,3)n n na b c n N n +=∈≥时,ABC ∆的形状为________.(填“锐角三角形”,“直角三角形”或“钝角三角形”).16.关于x 的方程320x x x m --+=,至少有两个不相等的实数根,则m 的最小值为________. 三、解答题:解答应写出文字说明、证明过程或演算步骤.17.(本小题满分12分)已知数列{}n a 满足:1112,92n n n a a a -+=+=⨯.(1)记132n n n b a -=-⨯,求证:数列{}n b 为等比数列;(2)求数列{}n na 的前n 项和n S .18.(本小题满分12分)自1月1日起,我国全面二孩政策正式实施,这次人口与生育政策的历史性调整,使得“要不要再生一个”“生二孩能休多久产假”等成为千千万万个家庭在生育决策上避不开的话题.为了解针对产假的不同安排方案形成的生育意愿,某调查机构随机抽取了200户有生育二胎能力的适龄家庭进行问卷调查,得到如下数据:(1)若用表中数据所得的频率代替概率,面对产假为14周与16周,估计某家庭有生育意愿的概率分别为多少?(2)假设从5种不同安排方案中,随机抽取2种不同安排分别作为备选方案,然后由单位根据单位情况自主选择.①求两种安排方案休假周数和不低于32周的概率;②如果用ξ表示两种方案休假周数和.求随机变量ξ的分布及期望.19.(本小题满分12分)如图,空间几何体ABCDE 中,平面ABC ⊥平面BCD ,AE ⊥平面ABC .(1)证明://AE 平面BCD ;(2)若ABC ∆是边长为2的正三角形,//DE 平面ABC ,且AD 与BD ,CD 所成角的余弦值均为4,试问在CA 上是否存在一点P ,使得二面角P BE A --P 的位置;若不存在,请说明理由.20.(本小题满分12分)已知抛物线2:2(0)E y px p =>,过点(1,1)M -作抛物线E 的两条切线,切点分别为,A B ,直线AB 的斜率为2.(1)求抛物线的标准方程;(2)与圆22(1)1x y -+=相切的直线l ,与抛物线交于,P Q 两点,若在抛物线上存在点C ,使()(0)OC OP OQ λλ=+>,求λ的取值范围.21.(本小题满分12分) 已知函数2()ln (1)2a f x x x a x =+-+. (1)若曲线()y f x =在1x =处的切线方程为2y =-,求()f x 的单调区间;(2)若0x >时,()()2f x f x x '<恒成立,求实数a 的取值范围. 请考生在22、23、24三题中任选一题作答,如果多做,则按所做的第一题计分.22.(本小题满分10分)如图,ABC ∆内接于O ,AB 为其直径,CH AB ⊥于H 延长后交O 于D ,连接DB 并延长交过C 点的直线于P ,且CB 平分DCP ∠.(1)求证:PC 是O 的切线;(2)若4,3AC BC ==,求PC PB 的值. 23.(本小题满分10分)在直角坐标系xOy 中,曲线C 的参数方程为244x t y t⎧=⎨=⎩(其中t 为参数),以O 为极点,x 轴的正半轴为极轴建立极坐标系,直线l 的极坐标方程为(4cos 3sin )0m ρθθ+-=(其中m 为常数).(1)若直线l 与曲线C 恰好有一个公共点,求实数m 的值;(2)若4m =,求直线l 被曲线C 截得的弦长.24.(本小题满分10分)已知定义在R 上的连续函数()f x 满足(0)(1)f f =.(1)若2()f x ax x =+,解不等式3()4f x ax <+; (2)若任意[]12,0,1x x ∈且12x x ≠时,有1212()()f x f x x x -<-,求证:121()()2f x f x -<. 参考答案1.A 2.A 3.C 4.A 5.C 6.B 7.A 8.B 9.A 10.D 11.B 12.A13.0x = 14.6 15.锐角三角形 16.527-所以132(1)n n n na n n -=⨯+⨯-,.....................................................6分设01221122232(1)22n n n T n n --=⨯+⨯+⨯++-⨯+⨯,①12312122232(1)22n n n T n n -=⨯+⨯+⨯++-⨯+⨯,②①–②得012122222212n n n n n T n n --=++++-⨯=--⨯, 所以1(1)2n n T n =+-⨯,...............................................................8分设123(1)n n Q n =-+-++-,即1,2,2n n n Q n n +⎧-⎪⎪=⎨⎪⎪⎩为奇数为偶数,...........................10分 所以53(1)2,2363(1)2,2n n n n n n n n S T Q n n n -⎧-⨯-⎪⎪=+=⎨+⎪-⨯+⎪⎩为奇数为偶数, ..................................12分18.(1)由表中信息可知,当产假为14周时某家庭有生育意愿的概率为14120050P ==; 当产假为16周时某家庭有生育意愿的概率为216220025P == ..........................2分 (2)①设“两种安排方案休假周数和不低于32周”为事件A ,由已知从5种不同安排方案中,随机地抽取2种方案选 法共有2510C =(种),其和不低于32周的选法有14、18、15、17、15、18、16、17、16、18、17、18,共6种,由古典概型概率计算公式得63()105P A ==. ...................................6分 ②由题知随机变量ξ的可能取值为29,30,31,32,33,34,35.1(29)0.110P ξ===,12(30)0.1,(31)0.21010P P ξξ======, 2211(32)0.2,(33)0.2,(34)0.1,(35)0.110101010P P P P ξξξξ============, 因而ξ的公布列为所以()290.1300.1310.2320.2330.2340.1350.132E ξ=⨯+⨯+⨯+⨯+⨯+⨯+⨯=,.........12分19.(1)证明:如图,过点D 作直线DO BC ⊥交BC 于点O ,连接DO .因为平面ABC ⊥平面BCD ,DO ⊂平面BCD ,DO BC ⊥,且平面ABC平面BCD BC =,所以DO ⊥平面ABC . ...............................................1分因为直线AE ⊥平面ABC ,所以//AE DO ,....................................................2分因为DO ⊂平面BCD ,AE ⊄平面BCD ,所以直线//AE 平面BCD . ........................................4分(2)连接AO ,因为//DE 平面ABC ,所以AODE 是矩形,所以DE ⊥平面BCD .因为直线AD 与直线,BD CD 所成角的余弦值均为4,所以BD CD =,所以O 为BC 的中点,所以AO BC ⊥,且cos 4ADC ∠=. 设DO a =,因为2BC =,所以1,OB OC AO ===所以CD AD ==在ACD ∆中,2AC =.所以2222cos AC AD CD AD CD ADC =+-∠,即2243124a a =+++-,223a +=. 解得21,1a a ==. ...................................6分 以O 为坐标原点,,,OA OB OD所在直线分别为x 轴,y 轴,z 轴,建立如图所示的空间直角坐标系. 则(0,1,0),(0,1,0),C B A E -.假设存在点P ,连接,EPBP ,设AP AC λ=,则,,0)P λ-.设平面ABE 的法向量为{},,m x y z =,则030m AE z m BA x y ⎧==⎪⎨=-=⎪⎩,取1x =,则平面ABE 的一个法向量为m =.设平面PBE 的法向量为{},,n x y z =,则(33)(1)030n PB x y n BE x y z λλ⎧=-++=⎪⎨=-+=⎪⎩, 取1x λ=+,则平面PBE 的一个法向量为(133,)n λλ=+--,......................9分设二面角P BE A --的平面角的大小为θ,由图知θ为锐角, 则cos 2m nm nθ===⨯, 化简得2610λλ+-=,解得12λ=-(舍去),.........................11分所以在CA 上存在一点P ,使得二面角P BE A --的余弦值为4.其为线段AC 的三等分点(靠近点A ) ..............................................12分20.(1)设{}1122,,(,)A x y B x y ,则点A 处抛物线的切线为{}11y y p x x =+,过点(1,1)M -,因而11(1)y p x =-;同理,点B 处抛物线的切线为22()y y p x x =+,过点(1,1)M -,因而22(1)y p x =-.两式结合,说明直线(1)y p x =-过,A B 两点,也就是直线AB 的方程为(1)y p x =-.由已知直线AB 的斜率为2,知2p =,故所求抛物线的方程为24y x =................................................5分(2)显然当直线l 的斜率不存在与斜率为0时不合题意.(6分)故可设直线l 的方程为y kx m =+.又直线l 与圆22(1)1x y -+=相切,1=,即221(1)2m km m -=≠...........................................7分与抛物线方程联立,即24y kx m y x =+⎧⎨=⎩, 化简消y 得2222(2)0k x km x m +-+=,设3344(,),(,)P x y Q x y ,则3422(2)km x x k-+=,......................................9分34344()2y y k x x m k+=++=. 由()(0)OC OP OQ λλ=+>,则22(2)4(,)km OC k kλλ-=,.................................10分 又点C 在抛物线上,则222168(2)km k kλλ-=. 即2233244km m λ-+==>,由于0km ≠,因而1λ≠. 所以λ的取值范围为3|14λλλ⎧⎫>≠⎨⎬⎩⎭且,...........................12分 21.(1)由已知得1()(1)f x ax a x'=+-+,则(1)0f '=, 而(1)ln1(1)122a a f a =+-+=--,所以函数()f x 在1x =处的切线方程为12a y =--. 则122a --=-,解得2a =,..............................2分 那么21()ln 3,()23f x x x x f x x x '=+-=+-, 由21231()230x x f x x x x -+'=+-=>,得102x <<或1x >, 因则()f x 的单调递增区间为1(0,)2与(1,)+∞;...................................4分 由1()230f x x x '=+-<,得112x <<, 因而()f x 的单调递减区间为1(,1)2....................................6分 (2)若()()2f x f x x '<,得ln 11(1)2222x a ax a x a x x ++-+<+-, 即ln 1122x a x x +-<在区间(0,)+∞上恒成立. ...................................8分设ln 1()2x h x x x =-,则2221ln 132ln ()22x x h x x x x--'=+=, 由()0h x '>,得120x e <<,因而()h x 在12(0,)e 上单调递增,由()0h x '<,得12x e >,因而()h x 在12(,)e +∞上单调递减 . .................10分 所以()h x 的最大值为1122()h e e -=,因而1212a e -+>, 从而实数a 的取值范围为12|21a a e -⎧⎫>-⎨⎬⎩⎭..........................................12分22.(1)连接OC ,由已知AB 为O 的直径,CH AB ⊥,则CAB DCB ∠=∠,且CAO ACO ∠=∠ ............................................2分 又CB 平分,DCP DCB PCB ∠∠=∠,因而2PCB OCB ACO OCB π∠+∠=∠+∠=,即OC CP ⊥,所以PC 是O 的切线. ............................................5分(2)4,3AC BC ==,则12245,,55AC BC AB CH CD AB ====,3BD BC ==, 因为PC 是O 的切线,所以PCB PDC ∠=∠,所以PCD PBC ∆∆,.................................................8分所以85PC PD CD PB PC BC ===,..............................10分 23.(1)直线l 的极坐标方程可化为直线坐标方程:430x y m +-=,曲线C 的参数方程可化为普通方程:24y x =, 由24304x y m y x +-=⎧⎨=⎩,可得230y y m +-=,...............................2分因为直线l 和曲线C 恰好有一个公共点,所以940m ∆=+=,所以94m =-. ............................................5分(2)当4m =时,直线:4340l x y +-=恰好过抛物线的焦点(1,0)F ,由243404x y y x +-=⎧⎨=⎩,可得241740x x -+=,..................................8分 设直线l 与抛物线C 的两个交点分别为1122(,),(,)A x y B x y , 则12174x x +=, 故直线l 被抛物线C 所截得的弦长为 1217252244AB x x =++=+=,.................................10分24.(1)(0)(1)f f =,即10a +=,得1a =-, 所以不等式化为234x x x -+≤-+. ① 当0x <时,不等式化为234x x x -<-+,所以02x -<<;.......................2分 ② 当01x ≤≤时,不等式化为234x x x --<-+,所以102x ≤<;.....................3分 ③ 当1x >时,不等式化为234x x x -<-+,所以x ∈∅.........................4分 综上所述,不等式的解集为1|22x x ⎧⎫⎪⎪-<<⎨⎬⎪⎪⎩⎭,................................5分(2)由已知任意[]12,0,1x x ∈且12x x ≠,则不妨设21x x >, 则当2112x x -≤时,12121()()2f x f x x x -<-≤,...................................7分 当2112x x ->时,则112x <,且 2112x -<,..........................................8分 那么1212211()(0)(1)()011()2f x f f f x x x x x -+-<-+-=--<. ...............10分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020届高三数学第一次联考试题 理
注意事项:
1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡上,并将考生号条形码粘贴在答题卡上的指定位置。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合2
{30},{17}M x x x N x x =-<=≤≤,则M
N =
A.{13}x x ≤<
B.{13}x x <<
C.{07}x x <<
D.{07}x x <≤ 2.设复数213i
z i
-=
+,则z =
A.
13 C.1
2
3.中国古代用算筹来进行记数,算筹的摆放形式有纵横两种形式(如右图所示),表示一个多位数时,像阿拉伯记数一样,把各个数位的数码从左到右排列,但各位数码的筹式需要纵横相间,其中个位、百位、万位……用纵式表示,十位、千位、十万位……用横式表示,则56846可用算筹表示为46可用算筹表示为
4.为了贯彻落实党中央精准扶贫的决策,某市将其低收入家庭的基本情况经过统计绘制成下图,其中各项统计不重复,若该市老年低收入家庭共有900户,则下列说法错误..
的是
A.该市共有15000户低收入家庭
B.在该市从业人员中,低收入家庭有1800户
C.在该市失无业人员中,低收入家庭有4350户
D.在该市大于18岁在读学生中,低收入家庭有800户
5.运行如图所示的程序框图,若输出的i 的值为99,则判断框中可以填
A.1S ≥
B.S>2
C.S>lg99
D. lg98S ≥
6.已知幕函数()a
f x x =的图象过点(3,5),且11
(),log 4
a
a
a b c e
==
=,则a ,b ,c 的大小关系为
A.c<a<b
B.a<c<b
C.a<b<c
D.c<b<a 7.已知非零向位a ,b 满足a b λ=,若a ,b 夹角的余弦值为19
30
,且(2)(3)a b a b -⊥+,则实数λ的值为
A.49-
B.23
C.32或49-
D.32
8.记单调递增的等比数列{a n }的前n 项和为S n ,若a 2+a 4=10,a 2a 3a 4=64,则 A.S n +1-S n =2
n +1
B.a n =2n
C.S n =2n
-1 D.S n =2
n -1
-1
9.
函数2sin ()6x
f x =的图象大致为
10.设抛物线C :y 2=2px(p>0)的焦点为F ,抛物线C 与圆C':x 2+(y
)2
=3交于M ,N 两
点.
若MN =MNF 的面积为
A.
8 B.3
8
11.关于函数()cos cos 2f x x x =+有下列三个结论:①π是f(x)的一个周期;②f(x)在
35[
,]44
ππ
上单调递增;③f(x)的值域为[-2,2]。
则上述结论中,正确的个数为 A.0 B.1 C.2 D.3
12.已知四棱锥S -ABCD 的底面为矩形,SA ⊥底面ABCD ,点E 在线段BC 上,以AD 为直径的图过点E.若SA
AB =3,则△SED 的面积的最小值为 A.9 B.7 C.
92 D.72
二、填空题:本题共4小题,每小题5分,共20分。
13.若变量x ,y 满足约束条件212420y x x y y ≤+⎧⎪
+≤⎨⎪+≥⎩
,则z =x -2y 的最大值为
14.函数2()x
f x x e
-=⋅的极大值为
15.已知双曲线22
22:1(0,0)x y C a b a b
-=>>,直线l :x =4a 与双曲线C 的两条渐近线分别交
于A ,B 两点,若△OAB(点O 为坐标原点)的面积为32,且双曲线C 的焦距为C 的离心率为
16.记数列{a n }的前n 项和为S n ,已知21(1)n n n S a n a -+=+,且a 2=5。
若2n
n
S m >,则实数m 的取值范围为
三、解答题:共70分。
解答应写出文字说明,证明过程或演算步骤。
第17~21题为必考题,每个试题考生都必须作答,第22、23题为选考题,考生根据要求作答。
(一)必考题:共60分. 17.(12分)
△ABC 的内角A ,B ,C 的对边分别是a ,b ,c ,已知(a -b)2
=c 2
-ab 。
(Ⅰ)求角C ; (Ⅱ)若4cos()sin 02
c A b C π
++=,a =1,求△ABC 的面积。
18.(12分)
如图所示,三棱柱ABC -A 1B 1C 1中,AA 1⊥平面ABC ,点D ,E 分别在线段AA 1,CC 1上,且AD =1
3
AA 1,DE//AC ,F 是线段AB 的中点。
(Ⅰ)求证:EF//平面B 1C 1D ;
(Ⅱ)若AB ⊥AC ,AB =AC ,AA 1=3AB ,求直线BC 与平面B 1DE 所成角的正弦值。
19.(12分)
已知椭圆C :2
214
x y +=,不与坐标轴垂直的直线l 与椭圆C 交于M ,N 两点。
(Ⅰ)若线段MN 的中点坐标为1(1,)2
,求直线l 的方程;
(Ⅱ)若直线l 过点(4,0),点P(x 0,0)满足k PM +k PN =0(k PM ,k PN 分别为直线PM ,PN 的斜率),
求x 0的值。
20.(12分)
已知函数2
1()(ln )2
f x mx x =+。
(Ⅰ)若m =1,求曲线y =f(x)在(1,f(1))处的切线方程; (Ⅱ)当m ≤1时,要使f(x)>xlnx 恒成立,求实数m 的取值范围。
21.(12分)
某机构组织的家庭教育活动上有一个游戏,每次由一个小孩与其一位家长参与,测试家长对小孩饮食习惯的了解程度。
在每一轮游戏中,主持人给出A ,B ,C ,D 四种食物,要求小孩根据喜爱程度对其排序,然后由家长猜测小孩的排序结果,设小孩对四种食物排出的序号依次为x A x B x C x D ,家长猜测的序号依次为y A y B y C y D ,其中x A x B x C x D ,y A y B y C y D 都是1,2,3,4四个数字的一种排列。
定义X =(x A -y A )2
+( x B -y B )2
+(x C -y C )2
+(x D -y D )2
,用X 来衡量家长对小孩饮食习惯的了解程度。
(Ⅰ)若参与游戏的家长对小孩的饮食习惯完全不了解。
(i)求他们在一轮游戏中,对四种食物排出的序号完全不同的概率; (ii)求X 的分布列(简要说明方法,不用写出详细计算过程)。
(Ⅱ)若有一组小孩和家长进行了三轮游戏,三轮的结果都满足X<4,请判断这位家长对小孩的饮食习惯是否了解,说明理由。
(二)选考题:共10分。
请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分。
22.[选修4-4:坐标系与参数方程](10分)
在直角坐标系xOy 中,曲线C 的参数方程为126126x m m
y m m ⎧
=+⎪⎪⎨⎪=-
⎪⎩
(m 为参数),以坐标原点为极点,
x 轴的正半轴为极轴建立极坐标系,直线l 的极坐标方程为cos()13
π
ρθ+=。
(Ⅰ)求曲线C 的普通方程以及直线l 的直角坐标方程; (Ⅱ)已知点M(2,0),若直线l 与曲线C 交于P ,Q 两点,求
11
MP MQ
+的值。
23.[选修4-5:不等式选讲](10分) 已知x ,y ,z 是正数。
(Ⅰ)若xy<1,证明:4x z z y xyz ++>;
(Ⅱ)若1
3
xyz x y z =++,求2xy •2yz •2xz 的最小值。
