新湘教版七年级数学下册《2章 整式的乘法 2.2 乘法公式 2.2.3运用乘法公式进行计算》课件_34
合集下载
新湘教版七年级数学下册《2章 整式的乘法 2.2 乘法公式 2.2.3运用乘法公式进行计算》教案_0
检验学生的掌握程度。
手机授课助手拍照，请学生上台讲解。
四、课堂小结
五、当堂检测
P49练习题第1、2、3题。
班级优化大师随机点名。
板书设计
教学后记
注：由于各学科模式不同，教学内容不同，课堂教学目标及任务不同，可自行对教学模式和教学过程进行调整。
运用平方差、完全平方公式进行运算。
教师进行板书。
请学生先自己解答，利用手机授课助手拍照。
3，
巩固提高
1、运用乘法公式计算：
2.已知(a+b)2=7,(a-b)2=3.求:(1)a2+b2; (2)ab的值.
3.一个正方形的一边增加4cm，另一边减少4cm，所得到的长方形与这个正方形的每一边减少2cm所得到的正方形面积相等，求原来正方形的面积。
教学难点
综合运用乘法公式进行多项式的计算。
教学用具及信息技术手段
Ppt、手机授课助手、班级优化大师
教学
环节
教学过程
Байду номын сангаас设计
意图
备注
一、复习引入
问题：我们学过了哪些乘法公式？
动脑筋：
手机授课助手拍照，请学生上台讲解。
二：知识精讲
例1.运用乘法公式计算：
例2.计算
例3.一个长方形花圃的边长增加到原来的2倍还多1m，它的面积就增加到原来的4倍还多21m2,求这个正方形花圃原来的边长.
教学设计
学科
课题名称
2.2.3运用乘法公式进行计算
课时数
1
授课时间
授课年级
七年级
授课人
授课班级
课的类型
新授课
教学目标
1.通过练习，更进一步理解三个乘法公式；
手机授课助手拍照，请学生上台讲解。
四、课堂小结
五、当堂检测
P49练习题第1、2、3题。
班级优化大师随机点名。
板书设计
教学后记
注：由于各学科模式不同，教学内容不同，课堂教学目标及任务不同，可自行对教学模式和教学过程进行调整。
运用平方差、完全平方公式进行运算。
教师进行板书。
请学生先自己解答，利用手机授课助手拍照。
3，
巩固提高
1、运用乘法公式计算：
2.已知(a+b)2=7,(a-b)2=3.求:(1)a2+b2; (2)ab的值.
3.一个正方形的一边增加4cm，另一边减少4cm，所得到的长方形与这个正方形的每一边减少2cm所得到的正方形面积相等，求原来正方形的面积。
教学难点
综合运用乘法公式进行多项式的计算。
教学用具及信息技术手段
Ppt、手机授课助手、班级优化大师
教学
环节
教学过程
Байду номын сангаас设计
意图
备注
一、复习引入
问题：我们学过了哪些乘法公式？
动脑筋：
手机授课助手拍照，请学生上台讲解。
二：知识精讲
例1.运用乘法公式计算：
例2.计算
例3.一个长方形花圃的边长增加到原来的2倍还多1m，它的面积就增加到原来的4倍还多21m2,求这个正方形花圃原来的边长.
教学设计
学科
课题名称
2.2.3运用乘法公式进行计算
课时数
1
授课时间
授课年级
七年级
授课人
授课班级
课的类型
新授课
教学目标
1.通过练习，更进一步理解三个乘法公式；
新湘教版七年级数学下册《2章 整式的乘法 2.2 乘法公式 2.2.3运用乘法公式进行计算》教案_23
运用乘法公式进行计算教学目标：1、熟练地运用乘法公式进行计算； 2、能正确地根据题目的要求选择不同的乘法公式进行运算。
教学重点：正确选择乘法公式进行运算。
教学难点：综合运用平方差和完全平方公式进行多项式的计算。
教学过程：一、复习乘法公式1、平方差公式：()()22b a b a b a -=-+2、完全平方公式：2222)(b ab a b a ++=+2222)(b ab a b a +-=-3、三个数的和的平方公式：2)(c b a ++＝＝bc ac ab c b a 222222+++++4、运用乘法公式进行计算：（1）()()b a b a --- （2）()()b a b a +--（3）())1)(1(12-++x x x二、范例分析 P106的例1、例2例1运用乘法公式计算：（1）()()22b a b a --+ （2）()()22b a b a -++ 解：（1）()()22b a b a --+ ＝()())]()][([b a b a b a b a --+-++＝()ab b a 2)2(2=•想一想：这道题你还能用什么方法解答？（2）()()22b a b a -++ ＝()()222222b ab a b ab a +-+++＝222222b ab a b ab a +-+++＝2222b a +例2 运用乘法公式计算：（1）)1)(1(-+++y x y x （2）)1)(1(-++-b a b a 解：（1）)1)(1(-+++y x y x＝]1)][(1)[(-+++y x y x＝221)(-+y x=1222-++y xy x(2) )1)(1(-++-b a b a=)]1()][1([-+--b a b a=22)1(--b a=)12(22+--b b a=1222-+-b b a注意灵活运用乘法公式，按要求最好能写出详细的过程。
三、小结与练习。
新湘教版七年级数学下册《2章 整式的乘法 2.2 乘法公式 2.2.3运用乘法公式进行计算》课件_0
知识精讲
例3 一个长方形花圃的边长增加到原来的2倍 还多1 m，它的面积就增加到原来的4倍还多21m2, 求这个正方形花圃原来的边长.
知识精讲
例4.已知a b 3,b c 2, a2 b2 c2 1,求 ab bc ca的值。
巩固提高
1、运用乘法公式计算：
1 a b2 2a ba b a b2; 2 x 2 y 3zx 2 y 3z; 3 2a b2 b 2a2;
a ba b a2 b2
乘法 公式
完全平方和公式 完全平方差公式
a b2 a2 2ab b2 a b2 a2 2ab b2
当堂检测
教材P49练习第1、2、3题。
第2章 整式的乘法
——2公式？ 请利用学过的乘法公式解决以下问题：
(1) x 1x2 1x 1
(2) x y 1x y 1
知识精讲
例1、运用乘法公式计算：
1 a 3a 32; 2 a b ca b c.
知识精讲
例2、计算： a b c2.
4 2 122 124 1 216 1.
巩固提高
2.已知(a+b)2=7,(a-b)2=3.求: (1)a2+b2; (2)ab的值.
巩固提高
3.一个正方形的一边增加4cm，另一边减少4cm， 所得到的长方形与这个正方形的每一边减少2cm 所得到的正方形面积相等，求原来正方形的面积。
课堂小结
平方差公式
七年级数学下册2整式的乘法小结与复习教学课件新版湘教版
解：原式=(x3y2-x2y-x2y+x3y2) ×3x2y =(2x3y2-2x2y) ×3x2y = 6x5y3-6x4y2 .
当x=1,y=3时，原式=6×27-6×9=108.
方法总结 整式的乘法主要包括单项式乘以单项式、单项式乘以多项
式及多项式乘以多项式，其中单项式乘以单项式是整式乘法的 基础，必须熟练掌握它们的运算法则.
转化
有理数的乘法和同底数幂的乘
法.
针对训练
7.计算：（4a-b）•（-2b）2．.
解： 原式=（4a-b）•4b2=16ab2-4b3．
整体思想
例5 若2a+5b-3=0，则4a·32b= 8 . 【解析】已知条件是2a+5b-3=0，无法求出a，b的值因此可以 逆用积的乘方先把4a·32b.化简为含有与已知条件相关的部分， 即4a·32b=22a·25b=22a+5b.把2a+5b看做一个整体，因为2a+5b3=0，所以2a+5b=3，所以4a·32b=23=8.
=-1-（2 ×0.5）300 ×0.5 =-1-0.5 =-1.5. 3. 比较大小：420与1510.
解:∵420=（42）10=1610， 1610>1510, ∴420>1510.
考点二 整式的乘法
例2 计算：[x(x2y2-xy)-y(x2-x3y)]×3x2y,其中x=1,y=3. 【解析】在计算整式的加、减、乘、除、乘方的运算中，一要 注意运算顺序；二要熟练正确地运用运算法则.
针对训练
1.下列计算不正确的是（ D ） A.2a3 ·a=2a4 C. a4 ·a3=a7
B. (-a3)2=a6 D. a2 ·a4=a8
2. 计算：0.252015 ×（-4）2015-8100 ×0.5301. 解:原式=[0.25 ×（-4）]2015-（23）100 ×0.5300 ×0.5
当x=1,y=3时，原式=6×27-6×9=108.
方法总结 整式的乘法主要包括单项式乘以单项式、单项式乘以多项
式及多项式乘以多项式，其中单项式乘以单项式是整式乘法的 基础，必须熟练掌握它们的运算法则.
转化
有理数的乘法和同底数幂的乘
法.
针对训练
7.计算：（4a-b）•（-2b）2．.
解： 原式=（4a-b）•4b2=16ab2-4b3．
整体思想
例5 若2a+5b-3=0，则4a·32b= 8 . 【解析】已知条件是2a+5b-3=0，无法求出a，b的值因此可以 逆用积的乘方先把4a·32b.化简为含有与已知条件相关的部分， 即4a·32b=22a·25b=22a+5b.把2a+5b看做一个整体，因为2a+5b3=0，所以2a+5b=3，所以4a·32b=23=8.
=-1-（2 ×0.5）300 ×0.5 =-1-0.5 =-1.5. 3. 比较大小：420与1510.
解:∵420=（42）10=1610， 1610>1510, ∴420>1510.
考点二 整式的乘法
例2 计算：[x(x2y2-xy)-y(x2-x3y)]×3x2y,其中x=1,y=3. 【解析】在计算整式的加、减、乘、除、乘方的运算中，一要 注意运算顺序；二要熟练正确地运用运算法则.
针对训练
1.下列计算不正确的是（ D ） A.2a3 ·a=2a4 C. a4 ·a3=a7
B. (-a3)2=a6 D. a2 ·a4=a8
2. 计算：0.252015 ×（-4）2015-8100 ×0.5301. 解:原式=[0.25 ×（-4）]2015-（23）100 ×0.5300 ×0.5
七年级数学下册第2章整式的乘法2.2乘法公式教学课件新版湘教版
3.计算： （1）202×198；
（2）49.8×50.2.
答案：（1）39996；（2）2499.96.
我思 我进步
通过本节课，你有什么收获？ 你还存在哪些疑问，和同伴 交流。
2.2.2 完全平方公式
思考
计算下列各式，你能发现什么规律： ( a+1 )2=( a+1 )( a+1 )=a2+a+a+12=a2+2·a·1+12， ( a+2 )2=( a+2 )( a+2 )=a2+2a+2a+22=a2+2·a·2+22， ( a+3 )2=( a+3 )( a+3 )=a2+3a+3a+32=a2+2·a·3+32， ( a+4 )2=( a+4 )( a+4 )=a2+4a+4a+42=a2+2·a·4+42. 我们用多项式乘法来推导一般情况： ( a+b )2=( a+b )=a2+ab+ab+b2=a2+2ab+b2.
（2）1982.
解：（1）1042=( 100+4 )2 （2）1982=( 200-2 )2
= 1002+2×100×4+42
= 2002-2×200×2+22
= 10000+800+16
= 40000-800+16
= 10816.
= 39204.
练习
1.运用完全平方公式计算： （1）( -2a+3 )2； （3）( -x2-4y )2；
湘教版七年级数学下册_2.2 乘法公式
感悟新知
特别解读
知2－讲
1. 弄清公式的特征：公式的左边是一个二项式的平方，公
式的右边是一个三项式，包括左边二项式的各项的平方
和，另一项是这两项的乘积的2倍.
2.理解字母a，b的意义：公式中的字母a，b可以表示具体的
数，也可以表示含字母的单项式或多项式.
3. 口诀记忆：
头平方和尾平方，头(乘)尾两倍在中央，中间符号照原样.
1. 移位置 : 有时交换位置，改变运算顺序，可利用
乘法公式简化计算 .
2. 整体 : 有时将其中几项看成一个整体 ，从而构造
出特殊的结构，利 用 乘法公式简化计算 .
3. 转化 : 将较复杂的未知问题，经过变形，转化为
可轻易解决或已解决的问题 .
感悟新知
解题秘方：紧扣多项式之间的特征，运用移位置、 知3－练 整体或转化的方法寻找乘法公式，进 行计算 .
知1－练
感悟新知
知1－练
方法点拨 运用平方差公式计算两数乘积时， 关键是找到这两个
的平均数，再将原数与这个平均 数进行比较， 变成两 数 的和与差的积的形式 .
感悟新知
知识点 2 测量质量
知2－讲
1. 完全平方公式： 两数和(或差)的平方，等于它们的平方和， 加(或减)它们的积的 2 倍 .
用字母表示为( a+b ) 2=a2+2ab+b2， (a － b) 2=a2 － 2ab+b2.
感悟新知
知3－讲
特别解读 为了体现乘法公式的结构特征，常运用到交换
律和结合律.
感悟新知
例5
计算： (1) ( b － 3 ) ( b2+9 ) ( b+3 ) ；
湘教版七年级下册数学 第2章 整式的乘法 运用乘法公式进行计算(2)
解：设这个正方形的边长是 x 厘米， 由题意，得(x＋4)2－x2＝40，解得 x＝3. 答：这个正方形的边长是 3 厘米．
14．我们知道，(k＋1)2＝k2＋2k＋1，变形得(k＋1)2－k2＝2k＋1， 对上面的等式，依次令 k＝1，2，3，…，得 第 1 个等式：22－12＝2×1＋1； 第 2 个等式：32－22＝2×2＋1； 第 3 个等式：42－32＝2×3＋1； ….
…，
(n＋1)2－n2＝2n＋1，
所以①＋②＋③＋…＋ ，
得(n＋1)2－12＝2(1＋2＋3＋…＋n)＋n，即 n2＋2n＝2S1＋n， n2＋n
所以 S1＝ 2 .Fra bibliotek15．先仔细阅读材料，再尝试解决问题： 完全平方公式(x±y)2＝x2±2xy＋y2 及(x±y)2 的值恒为非负 数的特点在数学中有着广泛的应用，比如探求多项式 2x2＋ 12x－4 的最小值时，我们可以这样处理： 解：原式＝2(x2＋6x－2)＝2(x2＋6x＋9－9－2) ＝2[(x＋3)2－11]＝2(x＋3)2－22. 因为无论 x 取什么数，(x＋3)2 的值都为非负数，
12．解方程： 2x(x－1)－(x－4)(x＋4)＝(x＋2)2.
解：2x(x－1)－(x－4)(x＋4)＝2x2－2x－x2＋16 ＝x2－2x＋16.(x＋2)2＝x2＋4x＋4. 故原方程可化为 6x＝12. 解得 x＝2.
13.如果一个正方形的边长增加 4 厘米，那么它的面积就增加 40 平方厘米，这个正方形的边长是多少？
所以(x＋3)2 的最小值为 0，此时 x＝－3， 进而 2(x＋3)2－22 的最小值是 2×0－22＝－22， 所以原多项式的最小值是－22. 请根据上面的解题思路，探求多项式 3x2－6x＋12 的最小值 是多少，并写出相应的 x 的值．
14．我们知道，(k＋1)2＝k2＋2k＋1，变形得(k＋1)2－k2＝2k＋1， 对上面的等式，依次令 k＝1，2，3，…，得 第 1 个等式：22－12＝2×1＋1； 第 2 个等式：32－22＝2×2＋1； 第 3 个等式：42－32＝2×3＋1； ….
…，
(n＋1)2－n2＝2n＋1，
所以①＋②＋③＋…＋ ，
得(n＋1)2－12＝2(1＋2＋3＋…＋n)＋n，即 n2＋2n＝2S1＋n， n2＋n
所以 S1＝ 2 .Fra bibliotek15．先仔细阅读材料，再尝试解决问题： 完全平方公式(x±y)2＝x2±2xy＋y2 及(x±y)2 的值恒为非负 数的特点在数学中有着广泛的应用，比如探求多项式 2x2＋ 12x－4 的最小值时，我们可以这样处理： 解：原式＝2(x2＋6x－2)＝2(x2＋6x＋9－9－2) ＝2[(x＋3)2－11]＝2(x＋3)2－22. 因为无论 x 取什么数，(x＋3)2 的值都为非负数，
12．解方程： 2x(x－1)－(x－4)(x＋4)＝(x＋2)2.
解：2x(x－1)－(x－4)(x＋4)＝2x2－2x－x2＋16 ＝x2－2x＋16.(x＋2)2＝x2＋4x＋4. 故原方程可化为 6x＝12. 解得 x＝2.
13.如果一个正方形的边长增加 4 厘米，那么它的面积就增加 40 平方厘米，这个正方形的边长是多少？
所以(x＋3)2 的最小值为 0，此时 x＝－3， 进而 2(x＋3)2－22 的最小值是 2×0－22＝－22， 所以原多项式的最小值是－22. 请根据上面的解题思路，探求多项式 3x2－6x＋12 的最小值 是多少，并写出相应的 x 的值．
湘教版七年级数学下册第二章《运用乘法公式进行计算》公开课课件
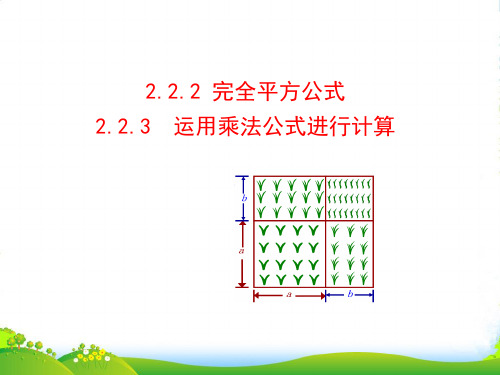
2ab
a2+ ab+
ab+ b2.
a
b
公式: (a+b)2= a2 + 2 ab + b2.
完全平方公式
(a+b)2=a2+2ab+b2 ; (a−b)2= a2 −2ab+b2.
(1) 你能用多项式的乘法法则来说明它们成立吗?
(2) 小颖写出了如下的算式:
(a−b)2= [a+(−b)]2
她是怎么想的?
＝(4a-1)，
所以 (4a-1)(1-4a)＝(4a-1)·[(4a-1)]
＝(4a-1)(4a-1)＝(4a-1)2.
(4) 右边应为:
(4a-1)(4a+1).
一位老人非常喜欢孩子，每当有孩子到他家做客时，老人都要拿出糖果招待 他们.如果来1个孩子，老人就给这个孩子1块糖果，如果来2个孩子，老人就 给每个孩子2块糖果.如果来3个孩子，老人就给每个孩子3块糖果……
•1、使教育过程成为一种艺术的事业。 •2、教师之为教，不在全盘授予，而在相机诱导。2021/10/252021/10/252021/10/2510/25/2021 6:47:28 PM •3、一年之计，莫如树谷；十年之计，莫如树木；终身之计，莫如树人4、智力教育就是要扩大人的求知范围 •5、教育是一个逐步发现自己无知的过程。 •6、要经常培养开阔的胸襟，要经常培养知识上诚实的习惯，而且要经常学习向自己的思想负责任。2021年10月 2021/10/252021/10/252021/10/2510/25/2021
减去 第一个数 与第二个数
乘积 的2倍,
加上 第二个数 的平方.
计算：
(1) ( x1− 2y)2 . 2
七年级数学下册第2章整式的乘法2.2乘法公式2.2.3运用乘法公式进行计算习题课件新版湘教版
6.(5x2-4y2)(-5x2+4y2)运算的结果是( )
(A)-25x4-16y4
(B)-25x4+40x2y2-16y4
(C)25x4-16y4
(D)25x4-40x2y2+16y4
【解析】选B.(5x2-4y2)(-5x2+4y2)
=-(5x2-4y2)(5x2-4y2)=-(5x2-4y2)2
(A)m+3 (B)m+6 (C)2m+3 (D)2m+6
【解析】选C.由题意知，长方形面积为(m+3)2m2=m2+6m+9-m2 =6m+9=3(2m+3)，因为长方形一边长为3，故另一边长为 2m+3.
2.下列选项中，与(x+y)2相等的是( )
(A)(-x+y)2 (B)(-x-y)2
(C)(x-y)2
【预习思考】 添括号后，括号前面是“-”号，括到括号里各项的符号应如何 处理？ 提示：各项都变号.
完全平方公式的应用 【例1】计算:(1)1972.(2)(x-2y+z)2. 【解题探究】(1)完全平方公式适用的前提是两数和(或差)的平 方，应把197看作哪两个数的和(或差)计算比较方便？ 答：200与3的差, 所以1972=(200-3)2
4.计算：(1)592=_____.(2)712=_____. 【解析】(1)592=(60-1)2=3 600-120+1=3 481. (2)712=(70+=5 041. 答案：(1)3 481 (2)5 041
乘法公式的综合运用 【例2】(6分)计算:(m-2n+3t)(m+2n-3t). 【规范解答】原式=［m-(2n-3t)］［m+(2n-3t)］ ……………………………………………………………………1分 =m2-(2n-3t)2 ……………………………………………………4 分 =m2-(4n212nt+9t2) ……………………………………………5分 =m2-4n2+12nt-9t2. ……………………………………………6
2019春七年级数学下册 第2章《整式的乘法》2.2 乘法公式 2.2.3 运用乘法公式进行计算习题
ppt课件
16
根据“杨辉三角”请计算(a＋b)8 的展开式中从左起第
四项的系数为( B )
A．84
B．56
C．35
D．28
【解析】找规律发现(a＋b)4 的第四项系数为 4＝3
＋1；(a＋bቤተ መጻሕፍቲ ባይዱ5 的第四项系数为 10＝6＋4；(a＋b)6 的第四
项系数为 20＝10＋10；(a＋b)7 的第四项系数为 35＝15
ppt课件
14
18. 一个长方形的长增加 4 cm，宽减少 1 cm，面积
保持不变；长减少 2 cm，宽增加 1 cm，面积仍保持不
变．求这个长方形的面积．
解：设这个长方形的长为 a cm，宽为 b cm，由题意
得（（aa＋－42））（（bb－＋11））＝＝aabb，， 即aa－－42bb＋－42＝＝00，. 解得ab＝ ＝83.，
ppt课件
3
知识点 乘法公式的应用
1. 计算(a＋2)(a－2)(a2＋4)的结果是( C )
A．a4＋16
B．－a4－16
C．a4－16
D．16－a4
2. 一个正方形的边长增加了 3 cm，它的面积增加了
51 cm2，这个正方形原来的边长是( C )
A．5 cm
B．6 cm
C．7 cm
D．8 cm
第二章 整式的乘法 2．2 乘法公式
2.2.3 运用乘法公式进行计算
ppt课件
1
1. 灵活运用平方差公式和完全平方公式计算．
ppt课件
2
2. 几种常见的乘法公式的变换技巧： (1)(－a－b)(a－b)＝_b_2_－__a_2 ； (2)(－a－b)(a＋b)＝_－__(_a_2_＋__b_2＋__2_a_b_)____； (3)(a－b)2＝_a_2－__2_a_b_＋__b_2__； (4)(－a－b)2＝_a_2_＋__2_a_b_＋__b_2 _； (5)(a＋b)2－(a－b)2＝__4_a_b__； (6)(a＋b)2＝(a－b)2＋__4_a_b__； (7)(a＋b)(a2－ab＋b2)＝_a_3_＋__b_3 ； (8)(a－b)(a2＋ab＋b2)＝_a3_－__b_3_．
新湘教版七年级数学下册《2章 整式的乘法 2.2 乘法公式 2.2.2完全平方公式》课件_6
a2 2ab b2 2a 2b 1
例7 运用完全平方公式计算：
（1） 1042
解 1042 = (100+4)2 = 1002+2×100×4+42
= 10 000+800+16
= 10பைடு நூலகம்816.
（2） 1982 解 1982
= (200-2)2 = 2002-2×200×2+22 = 40 000-800+4 = 39 204.
然后应用公式计算.
作业：P50 B 5、8
4．若（a＋b）2＝5，（a-b）2＝3，则a2＋b2与ab的 值分别是（ B ）
A. 8与
B. 4与
C. 1与4 D. 4与1
中考 试题
例1 已知 (m-n)2=8，(m+n)2=2，则 m2+n2=（ C）
A．10 B．6
C．5
D． 3
解析
∵（m-n）2=8， ∴m2-2mn+n2=8①，
∵（m+n）2=2， ∴m2+2mn+n2=2②， ①+②得，2m2+2n2=10， ∴m2+n2=5．故选C．
关于完全平方公式的变形：
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
变形一： 由得：(a+b)2-2ab= a2 +b2
由得：(a-b)2+2ab= a2 +b2
变形二： +得：(a+b)2+(a-b)2= 2（a2 +b2 ）
变形三： -得：(a+b)2-(a-b)2= 4ab
例7 运用完全平方公式计算：
（1） 1042
解 1042 = (100+4)2 = 1002+2×100×4+42
= 10 000+800+16
= 10பைடு நூலகம்816.
（2） 1982 解 1982
= (200-2)2 = 2002-2×200×2+22 = 40 000-800+4 = 39 204.
然后应用公式计算.
作业：P50 B 5、8
4．若（a＋b）2＝5，（a-b）2＝3，则a2＋b2与ab的 值分别是（ B ）
A. 8与
B. 4与
C. 1与4 D. 4与1
中考 试题
例1 已知 (m-n)2=8，(m+n)2=2，则 m2+n2=（ C）
A．10 B．6
C．5
D． 3
解析
∵（m-n）2=8， ∴m2-2mn+n2=8①，
∵（m+n）2=2， ∴m2+2mn+n2=2②， ①+②得，2m2+2n2=10， ∴m2+n2=5．故选C．
关于完全平方公式的变形：
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
变形一： 由得：(a+b)2-2ab= a2 +b2
由得：(a-b)2+2ab= a2 +b2
变形二： +得：(a+b)2+(a-b)2= 2（a2 +b2 ）
变形三： -得：(a+b)2-(a-b)2= 4ab
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
注意： 把（x+y）作为一个整体，那么 （x+y）就相当于平方差公式中的a， 1就相当于平方差公式中的b.
(3) (a+b-c)(a-b+c)
解：原式= [a+(b-c)][a- (b-c)]
=a2-(b-c )2
注意符号的变化
=a2-(b2-2bc+c2 )
=a2-b2+2bc-c2
先分析式子的特点，灵活运用乘法公式， 简化运算！
解 设正方形原来的边长为 x cm. 列方程，得 (x +2)2 = x2+16 ， x2+4x+4= x2+16, 4x=12, 解得 x = 3.
答：这个正方形原来的边长为3cm.
拓展延伸：思维训练操：
小刚同学在用公式计算： （2+1）×（22+1）×（24+1)×…×(264+1) 是这样做的：
2. 家庭作业：完成学法大视野中本课时的练习.
下课啦， 再见!
原式=1×（2+1）×（22+1)（24+1)×…×(264+1) =（2-1）×（2+1）×（22+1）×…×(264+1) =（22-1）×（22+1）×（24+1)×…×(264+1) =…… =(264-1)×(264+1) =2128-1
请参考小刚的方法，计算：
(1
1) 2
(1
1 22
)
(1
1 24
)
(1
1 28
)
1 215
课堂小结： 如何运用乘法公式进行计算?
1、先观察式子的特点，选取适当的乘法公式.
2、有时会结合其它运算法则.
3、灵活应用公式进行求值计算.
如果你还有疑问，课后与同学多交流一下学习 心得哦！
作业布置：
1、课堂作业:教材第50页“习题2.2”中第5、6 题.
结果有什么 规律呢？
小试牛刀：
2、计算下列各题 (1) (x+1)2(x-1)2；
(2) (a-b-c)2
答案： (1) x4-2x2+1 (2) a2+b2+c2-2ab-2ac+2bc
用数学，为生活服务：
例2 一个正方形花圃的边长增加到原来2 倍还多1m，它的面积就增加到原来的4倍 还多21m2 ,求这个正方形花圃原来的边长.
★ a2b2=(ab)2
解：(1) 原式=[(a+3)(a-3)]2
= (a2-9)2
= a4-18a2+81.
(2) (a+b+c)2 (2)原式 = [(a+b)+c]2
= (a+b)2+2(a+b)c+c2 = a2+2ab+b2+2ac+2bc+c2 = a2+b2+c2+2ab+2ac+2bc
小试牛刀： 1、计算下列各题:
(1) (x-2)(x2+4)(x+2)
(2) (x+y+4)(x+y-4).
(3) (x+2y-3z)(x-2y+3z)
答案： (1)x4-16 (2) x2+2xy+y2-16 (3) x2-4y2+12yz-9z2
例1 用乘法公式计算下列各题 （1）(a+3)2(a-3)2; (2) (a+b+c)2
解 ：设正方形花圃原来的边长为 x m. 由数量关系 得： （2x +1）2= 4x 2+21,
化简得: 4x 2+4x +1= 4x 2 +21, 即 4x = 20, 解得 x = 5. 答: 这个正方形花圃原来的 边长为 5 m.
小试牛刀： 3. 一个正方形的边长增加2cm，它的面积
就增加16cm2，求这个正方形原来的边长.
湘教版 七年级下册
2.2.3
运用乘法公式进行计算
学习目标
1.能的 乘法公式.
3.提高对乘法公式的综合运用能力， 为以后学习因式分解做好准备.
复习回顾： 我们已经学习了哪些乘法公式？
（1）平方差公式:
(a+b) (a-b)= a²- b².
（2）完全平方公式：
（a+b）2 = a2+2ab+b2. （a-b）²= a2-2ab+b2 .
注意： 公式中的 a 与 b既可以是单项 式 也可以是多项式.
下面我们就一起来运用这 些公式解决几个问题.
请思考： 怎样用乘法公式计算下列各题？
（1）(x+1)(x2+1)(x-1); （2）(x+y+1)(x+y-1).
（3）(a+b-c)(a-b+c)
（1）(x+1)(x2+1)(x-1); 解：原式= (x+1)(x-1)(x2+1) =（x2-1)(x2 +1 ) = x4-1.
（2）(x+y+1)(x+y-1); 解：原式= [(x+y)+1] [(x+y)-1]
= (x+y)2-1 = x2+2xy+y2-1.
(3) (a+b-c)(a-b+c)
解：原式= [a+(b-c)][a- (b-c)]
=a2-(b-c )2
注意符号的变化
=a2-(b2-2bc+c2 )
=a2-b2+2bc-c2
先分析式子的特点，灵活运用乘法公式， 简化运算！
解 设正方形原来的边长为 x cm. 列方程，得 (x +2)2 = x2+16 ， x2+4x+4= x2+16, 4x=12, 解得 x = 3.
答：这个正方形原来的边长为3cm.
拓展延伸：思维训练操：
小刚同学在用公式计算： （2+1）×（22+1）×（24+1)×…×(264+1) 是这样做的：
2. 家庭作业：完成学法大视野中本课时的练习.
下课啦， 再见!
原式=1×（2+1）×（22+1)（24+1)×…×(264+1) =（2-1）×（2+1）×（22+1）×…×(264+1) =（22-1）×（22+1）×（24+1)×…×(264+1) =…… =(264-1)×(264+1) =2128-1
请参考小刚的方法，计算：
(1
1) 2
(1
1 22
)
(1
1 24
)
(1
1 28
)
1 215
课堂小结： 如何运用乘法公式进行计算?
1、先观察式子的特点，选取适当的乘法公式.
2、有时会结合其它运算法则.
3、灵活应用公式进行求值计算.
如果你还有疑问，课后与同学多交流一下学习 心得哦！
作业布置：
1、课堂作业:教材第50页“习题2.2”中第5、6 题.
结果有什么 规律呢？
小试牛刀：
2、计算下列各题 (1) (x+1)2(x-1)2；
(2) (a-b-c)2
答案： (1) x4-2x2+1 (2) a2+b2+c2-2ab-2ac+2bc
用数学，为生活服务：
例2 一个正方形花圃的边长增加到原来2 倍还多1m，它的面积就增加到原来的4倍 还多21m2 ,求这个正方形花圃原来的边长.
★ a2b2=(ab)2
解：(1) 原式=[(a+3)(a-3)]2
= (a2-9)2
= a4-18a2+81.
(2) (a+b+c)2 (2)原式 = [(a+b)+c]2
= (a+b)2+2(a+b)c+c2 = a2+2ab+b2+2ac+2bc+c2 = a2+b2+c2+2ab+2ac+2bc
小试牛刀： 1、计算下列各题:
(1) (x-2)(x2+4)(x+2)
(2) (x+y+4)(x+y-4).
(3) (x+2y-3z)(x-2y+3z)
答案： (1)x4-16 (2) x2+2xy+y2-16 (3) x2-4y2+12yz-9z2
例1 用乘法公式计算下列各题 （1）(a+3)2(a-3)2; (2) (a+b+c)2
解 ：设正方形花圃原来的边长为 x m. 由数量关系 得： （2x +1）2= 4x 2+21,
化简得: 4x 2+4x +1= 4x 2 +21, 即 4x = 20, 解得 x = 5. 答: 这个正方形花圃原来的 边长为 5 m.
小试牛刀： 3. 一个正方形的边长增加2cm，它的面积
就增加16cm2，求这个正方形原来的边长.
湘教版 七年级下册
2.2.3
运用乘法公式进行计算
学习目标
1.能的 乘法公式.
3.提高对乘法公式的综合运用能力， 为以后学习因式分解做好准备.
复习回顾： 我们已经学习了哪些乘法公式？
（1）平方差公式:
(a+b) (a-b)= a²- b².
（2）完全平方公式：
（a+b）2 = a2+2ab+b2. （a-b）²= a2-2ab+b2 .
注意： 公式中的 a 与 b既可以是单项 式 也可以是多项式.
下面我们就一起来运用这 些公式解决几个问题.
请思考： 怎样用乘法公式计算下列各题？
（1）(x+1)(x2+1)(x-1); （2）(x+y+1)(x+y-1).
（3）(a+b-c)(a-b+c)
（1）(x+1)(x2+1)(x-1); 解：原式= (x+1)(x-1)(x2+1) =（x2-1)(x2 +1 ) = x4-1.
（2）(x+y+1)(x+y-1); 解：原式= [(x+y)+1] [(x+y)-1]
= (x+y)2-1 = x2+2xy+y2-1.