《全等三角形》常考题型演练
全等三角形经典题型50题(含答案)

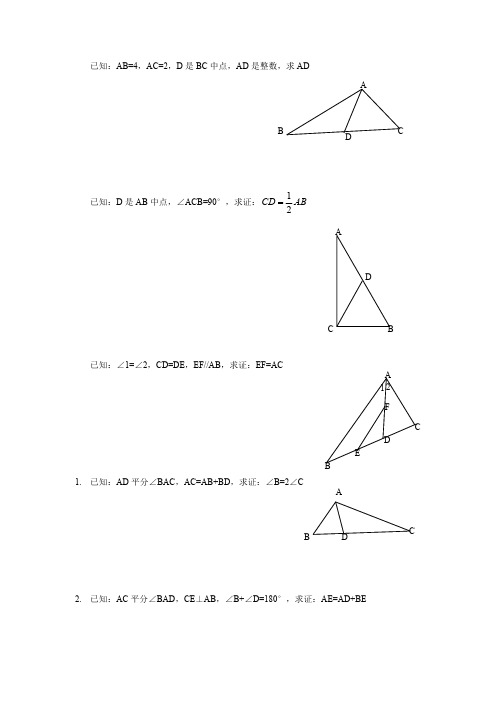
全等三角形证明经典50 题(含答案)1. 已知: AB=4, AC=2, D 是 BC 中点, AD 是整数,求ADAB CD延伸 AD 到 E,使 DE=AD,则三角形ADC全等于三角形EBD即 BE=AC=2 在三角形 ABE 中 ,AB-BE<AE<AB+BE即:10-2<2AD<10+2 4<AD<6又 AD 是整数 ,则 AD=512. 已知: D 是 AB 中点,∠ ACB=90°,求证:CD AB2ADC B3.已知: BC=DE,∠ B=∠ E,∠ C=∠ D, F 是 CD中点,求证:∠ 1=∠ 2A21B EC F D证明:连结 BF 和 EF。
由于 BC=ED,CF=DF,∠ BCF=∠ EDF。
因此三角形 BCF 全等于三角形 EDF(边角边 )。
因此 BF=EF,∠ CBF=∠ DEF。
连结 BE。
在三角形BEF 中 ,BF=EF。
因此∠ EBF=∠ BEF。
又由于∠ ABC=∠AED。
因此∠ABE=∠AEB。
因此 AB=AE。
在三角形 ABF 和三角形 AEF中, AB=AE,BF=EF,∠ABF=∠ ABE+∠ EBF=∠ AEB+∠ BEF=∠ AEF。
因此三角形 ABF 和三角形 AEF全等。
因此∠ BAF=∠ EAF (∠ 1=∠ 2)。
A4. 已知:∠ 1=∠ 2, CD=DE, EF//AB,求证: EF=AC 1 2证明:过 E 点,作 EG//AC,交 AD 延伸线于 G 则∠ DEG=∠ DCA,F ∠DGE=∠ 2又∵CD=DE∴ ⊿ADC≌ ⊿ GDE(AAS)∴EG=AC∵ EF//AB∴∠ DFE=∠ 1∵ ∠ 1=∠ 2∴ ∠ DFE=∠ DGE∴ EF=C EG∴ EF=AC DEB5.已知:AD均分∠ BAC,AC=AB+BD,求证:∠B=2∠C ACB D证明:在 AC上截取AD=AD∴ ⊿ AED≌ ⊿ ABD AE=AB,连结(SASED∵ AD)均分∠ BAC∴ ∠∴ ∠ AED=∠ BEAD=∠ BAD 又∵ AE=AB,,DE=DB∵ AC=AB+BDAC=AE+CE∴ CE=DE∴ ∠ C=∠ EDC∵∠ AED=∠ C+∠ EDC=2∠ C∴∠ B=2∠C6. 已知: AC 均分∠ BAD,CE⊥ AB,∠ B+∠ D=180°,求证:AE=AD+BE证明:在AE上取F,使EF=EB,连结 CF 由于 CE⊥AB 因此∠CEB=∠ CEF= 90 °由于 EB= EF, CE= CE,所以△CEB≌△CEF 所以∠B =∠ CFE 由于∠ B+∠ D= 180 ,°∠CFE+∠ CFA= 180°因此∠ D=∠ CFA 由于AC 均分∠ BAD 因此∠ DAC=∠ FAC 又由于AC= AC因此△ ADC≌ △ AFC( SAS)因此 AD= AF 因此 AE= AF+ FE= AD+ BE12.如图,四边形 ABCD 中, AB∥ DC, BE、 CE 分别均分∠ ABC、∠ BCD,且点 E 在 AD 上。
八年级全等三角形专题练习(解析版)

一、八年级数学全等三角形解做题压轴题〔难〕1. 〔1〕如图〔1〕,:在△ ABC中,N BAC=90.,AB二AC,直线m经过点A, 8口,直线m, CE J_直线m,垂足分别为点D、E.证实:DE=BD+CE.〔2〕如图〔2〕,将〔1〕中的条件改为:在△ ABC中,AB=AC, D、A、E三点都在直线m 上,并且有N BDA=Z AEC=Z BAC=.,其中.为任意锐角或钝角.请问结论DE=BD+CE是否成立? 如成立,请你给出证实;假设不成立,请说明理由.〔3〕拓展与应用:如图〔3〕 , D、E是D、A、E三点所在直线m上的两动点〔D、A、E 三点互不重合〕,点F为N BAC平分线上的一点,且△ ABF和^ ACF均为等边三角形,连接BD、CE,假设N BDA=Z AEC=Z BAC,试判断△ DEF 的形状.【答案】(1)见解析(2)成立(3) 4DEF为等边三角形【解析】解:(1)证实:BDL直线m, CEJ_直线m,,N BDA=N CEA=900.: Z BAC=90°, /. Z BAD+Z CAE=90°.•/ Z BAD+Z ABD=90°, /. Z CAE=Z ABD.又AB二“AC〞,「・△ ADB合△ CEA (AAS) . /. AE=BD, AD=CE./. DE=,,AE+AD=H BD+CE.(2)成立.证实如下:: Z BDA =Z BAC=a , /. Z DBA+Z BAD=Z BAD+Z CAE=180°-O r . /. Z DBA=Z CAE.Z BDA=Z AEC=., AB=AC,「・△ AD於△ CEA (AAS). /. AE=BD, AD=CE.DE二AE+AD=BD+CE.(3)△ DEF为等边三角形.理由如下:由(2)知,△ ADB合△ CEA, BD=AE, Z DBA =Z CAE,: △ ABF 和^ ACF 均为等边三角形,J Z ABF=Z CAF=60°.・•, Z DBA+Z ABF=Z CAE+Z CAF. /. Z DBF=Z FAE.; BF=AF,,•・丛DBF合△ EAF (AAS) . /. DF=EF, Z BFD=Z AFE.・•, Z DFE=Z DFA+z AFE=Z DFA+Z BFD=60°.・•.A DEF为等边三角形.(1)由于DE=DA+AE,故由AAS证△ ADB合4 CEA,得出DA=EC, AE=BD,从而证得DE=BD+CE.(2)成立,仍然通过证实△ ADB2 J CEA,得出BD=AE, AD=CE,所以DE=DA+AE=EC+BD.(3)由△ ADB2△ CEA得BD=AE, NDBA=N CAE,由△ ABF和△ ACF均等边三角形,得Z ABF=Z CAF=60°, FB=FA,所以N DBA+N ABF=N CAE+N CAF,即N DBF二N FAE,所以△ DBF^ △ EAF,所以FD=FE, Z BFD=Z AFE,再根据N DFE=Z DFA+Z AFE=Z DFA+Z BFD=60°得到△ DEF是等边三角形.2.如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE, PE 交CD 于 F〔1〕证实:PC=PE;〔2〕求N CPE的度数:〔3〕如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当N ABC=12〔T时,连接【答案】(1)证实见解析(2) 90° (3) AP=CE【解析】【分析】(1)、根据正方形得出AB=BC, ZABP=ZCBP=45%结合PB=PB得出aABP g^CBP,从而得出结论:⑵、根据全等得出NBAP=NBCP, ZDAP=ZDCP,根据PA=PE得出NDAP=NE,即ZDCP=ZE,易得答案;(3)、首先证实4ABP和^CBP全等,然后得出PA=PC, NBAP=NBCP,然后得出NDCP二NE,从而得出NCPF=NEDF=60°,然后得出AEPC是等边三角形,从而得出AP=CE.【详解】⑴、在正方形ABCD 中,AB=BC, ZABP=ZCBP=45%在ZkABP 和4CBP 中,XV PB=PB AAABP^ACBP (SAS) , ,PA=PC, VPA=PE>:.PC=PE;⑵、由(1)知,A ABP^ACBP,.\ZBAP=ZBCP, JNDAP=NDCP,VPA=PE, .\ZDAP=ZE> /. ZDCP=ZE. VZCFP=ZEFD (对顶角相等), A180° - ZPFC - ZPCF=1800 - ZDFE - NE, BPZCPF=ZEDF=90<>:⑶、AP = CE理由是:在菱形ABCD 中,AB=BC, NABP二NCBP,在2\ABP ^lACBP 中,XV PB=PB /.△ABP^ACBP (SAS),,PA二PC, NBAP=NDCP,VPA=PE,,PC=PE,,NDAP=NDCP, V PA=PC,/DAP=NE, A ZDCP=ZE V ZCFP=ZEFD (对顶角相等),A180°- ZPFC - ZPCF=180° - ZDFE - NE, RPZCPF=ZEDF=180° - ZADC=180° - 120°=60°, AAEPC 是等边三角形,,PC=CE, AAP=CE考点:三角形全等的证实3.如图,在AA8C中,NAC8为锐角,点£>为射线8C上一动点,连接AO.以AO为直角边且在AD的上方作等腰直角三角形ADF.图①图②图③〔1〕假设A3 = AC, ABAC = 90°①当点.在线段BC上时〔与点3不重合〕,试探讨CF与8.的数量关系和位置关系:②当点O在线段C的延长线上时,①中的结论是否仍然成立,请在图2中而出相应的图形并说明理由;〔2〕如图3,假设ABwAC, ABAC90° , ZBC4 = 45°,点.在线段8C上运动,试探究CF与8.的位置关系.【答案】〔1〕①CF_LBD,证实见解析:②成立,理由见解析:〔2〕 CF1BD,证实见解析.【解析】【分析】〔1〕①根据同角的余角相等求出NCAF=NBAD,然后利用"边角边"证实4ACF和4ABD全等,②先求出NCAF=NBAD,然后与①的思路相同求解即可:〔2〕过点A作AE_LAC交BC于E,可得4ACE是等腰直角三角形,根据等腰直角三角形的性质可得AC=AE, NAED=45.,再根据同角的余角相等求出NCAF=NEAD,然后利用“边角边〞证实4ACF 和4AED全等,根据全等三角形对应角相等可得NACF=NAED,然后求出ZBCF=90°,从而得到CFJ_BD.【详解】解:〔1〕①•••NBAC=90°, 4ADF是等腰直角三角形,.\ZCAF+ZCAD=90% ZBAD+ZACD=90°,.\ZCAF=ZBAD,在4ACF和4ABD中,VAB=AC, ZCAF=ZBAD, AD=AF,.,.△ACF^AABD〔SAS〕,.・.CF=BD, ZACF=ZABD=45",ZACB=45",AZFCB=90°,.-.CF±BD:②成立,理由如下:如图2:VZCAB=ZDAF=90%,ZCAB+ ZCAD= ZDAF+ ZCAD, 即NCAF=NBAD,在aACF和AABD中,VAB=AC, ZCAF=ZBAD, AD=AF, AAACF^AABD(SAS), ACF=BD, NACF=NB,VAB=AC, ZBAC=90%AZB=ZACB=45%/. Z BCF= ZACF+ ZACB=45o+45o=90°,ACF1BD:(2)如图3,过点A作AE_LAC交BC于E,•/ ZBCA=45",••.△ACE是等腰直角三角形,,AC=AE, NAED=45°, VZCAF+ZCAD=90°, ZEAD+ZCAD=90%,NCAF=NEAD,在4ACF和4AED中,VAC=AE, NCAF=NEAD, AD=AF,.•.△ACF^AAED(SAS), /. ZACF=ZAED=45\,ZBCF= ZACF+ ZBCA=45o+45°=90°, ACF1BD.【点睛】此题考查全等三角形的动点问题,综合性较强,有一定难度,需要熟练掌握全等三角形的判定和性质进行综合运用.4.如图〔1〕,在△A3C中,ZA = 90°, A3 = AC,点.是斜边8C的中点,点E, 产分别在线段A3, 4c上,且NEDF = 90..〔1〕求证:△.所为等腰直角三角形:〔2〕假设△ABC的面积为7,求四边形AEDF•的面积:〔3〕如图〔2〕,如果点E运动到A8的延长线上时,点尸在射线C4上且保持ZEDF = 90°,△.石尸还是等腰直角三角形吗.请说明理由.【答案】〔1〕证实见解析;〔2〕 3.5:〔3〕是,理由见解析.【解析】【分析】〔1〕由题意连接AD,并利用全等三角形的判定判定△ BD年△ ADF〔ASA〕,进而分析证得△.瓦'为等腰直角三角形;〔2〕由题意分析可得S网边形AEDF=S MDF+S AADE=S ABDE+S ACDF,以此进行分析计算求出四边形AEDF的面积即可;〔3〕根据题意连接AD,运用全等三角形的判定判定△ BDE^ △ ADF〔ASA〕,进而分析证得△.所为等腰直角三角形.【详解】解:〔1〕证实:如图①,连接AD.「N BAC=90°,AB=AC,点D是斜边BC的中点,/. AD±BC , AD=BD,・•, Z 1=Z B=45°,Z EDF=90% Z 2+Z 3=90%又,Z 3+Z 4=90°,/. Z 2=Z 4,在^ BDE 和^ ADF 中,Z 1=Z B, AD=BD,Z 2=Z 4,/. △ BDE合 , ADF(ASA),・•, DE二DF,又;Z EDF=90\・•・ ADEF为等腰直角三角形.(2)由(1)可知DE=DF, NON 6=45., 又「N 2+N 3=90°, Z 2+Z 5=90%J Z 3=Z 5,A ADE级△ CDF,・' S N边H,AEDF=S AADF+S CADE二S ABDE+S^CDF,S MBC=2 S 网边毛AEDF,S wijn;AEDF=3.5.(3)是,如图②,连接AD.•/ Z BAC=90\ AB=AC, D 是斜边BC 的中点,/. AD±BC Z AD=BD ,「・Z 1=45°,Z DAF=180°-Z l=180°-45°=135% Z DBE=180°-Z ABC=180°-45°=135%/. Z DAF=Z DBE,「Z EDF=90\/. Z 3+Z 4=90%又;Z 2+Z 3=90°,「・Z 2=Z 4,在仆BDE 和a ADF 中,Z DAF=Z DBE, AD=BD,N 2=Z 4,△ BDE合△ ADF(ASA),・•.DE=DB又:Z EDF=90\.•.A DEF为等腰直角三角形.【点睛】此题考查等腰直角三角形的性质以及全等三角形的判定与性质,根据题意作辅助线构造出全等三角形是解题的关键.5.如图,在MBC中,ZC = 90°, AC = 3, BC = 7,点.是8c边上的动点,连接AD,以AO为斜边在A.的下方作等腰直角三角形AO石.(1)填空:AABC的面积等于—;(2)连接CE,求证:CE是NAC3的平分线;(3)点.在6C边上,且CO = 1,当.从点.出发运动至点3停止时,求点E相应的运动路程.王O 1 _【答案】〔I〕—:〔2〕证实见解析:〔3〕 3点【解析】【分析】〔1〕根据直角三角形的面积计算公式直接计算可得:〔2〕如下图作出辅助线,证实△AEM名ADEN 〔AAS〕,得至I] ME=NE,即可利用角平分线的判定证实:〔3〕由〔2〕可知点E在NACB的平分线上,当点D向点B运动时,点E的路径为一条直线,再根据全等三角形的性质得出CN=!〔AC + C.〕,根据CD的长度计算出CE的长度即可.【详解】解:〔1〕 ZC = 90°, AC = \ BC = 7= -ACxBC = -x3x7 = — ,故答案为:—2〔2〕连接CE,过点E作EMLAC于点M,作EN_LBC于点N,AZEMA=Z END=90°,XVZACB=90SAZMEN=90%AZMED+Z DEN=90°,•••△ADE是等腰直角三角形AZAED=90\ AE=DEA ZAEM+Z MED=90%, ZAEM=Z DEN,在△AEM 与ZkDEN 中,ZEMA=Z END=90% ZAEM=Z DEN, AE=DEAAAEM^ADEN 〔AAS〕/. ME=NE,点E 在NACB 的平分线上, 即CE 是NAC3的平分线工(3)由(2)可知,点E 在NACB 的平分线上,・•・当点D 向点B 运动时,点E 的路径为一条直线,VAAEM^ADEN,AM=DN,即 AC-CM=CN-CD在 RtZiCME 与 RtZkCNE 中,CE=CE, ME=NE,ARtACME^RtACNE (HL)ACM=CN.,.CN=;(AC + CO),又YNMCE 二NNCE=45°, ZCME=90\・,. CE= y/2CN = —(AC + CD).2当 AC=3, CD=CO=1 时,CE=](3 + 1) = 2&当 AC=3, CD=CB=7 时,5CE=r (3 + 7) = 5 虚,点E 的运动路程为:50-20 = 30,£【点睛】此题考查了全等三角形的综合证实题,涉及角平分线的判定,几何中动点问题,全等三角 形的性质与判定,解题的关键是综合运用上述知识点.6.如图1,在长方形ABCD 中,AB=CD=5 cm, BC=12 cm,点P 从点B 出发,以2cm/s 的 速度沿BC 向点C 运动,设点P 的运动时间为ts.(1) PC=—cm :(用含t 的式子表示)■I) I)(2)当t 为何值时,△ABPg^DCP?.(3)如图2,当点P从点B开始运动,此时点Q从点C出发,以vcm/s的速度沿CD向点D运动,是否存在这样的v值,使得某时刻4ABP与以P, Q, C为顶点的直角三角形全等?假设存在,请求出v的值:假设不存在,请说明理由.【答案】(1) (12-2/); (2)1 = 3;(3)存在,P = 2或忏1【解析】【分析】(1)根据P点的运动速度可得BP的长,再利用BC的长减去BP的长即可得到PC的长:(2)先根据三角形全等的条件得出当BP=CP,列方程求解即得;(3)先分两种情况:当BP=CQ, AB=PC 时,△ABPgZ\PCQ:或当BA=CQ, PB=PC 时,△ABPgaQCP,然后分别列方程计算出t的值,进而计算出v的值.【详解】解:(1)当点P以2cm/s的速度沿BC向点C运动时间为ts时3P = 2/57•・• BC = \2cin:.PC = BC-BP = (n-2i)cm故答案为:(12—27)(2) MBP = ^DCP・•. BP = CP・•・ 2/= 12-2/解得1 = 3.(3)存在,理由如下:①当BP=CQ, AB=PC 时,ZiABP名△PCQ,1. PC=AB=5.•.BP=BC-PC=12-5=7•・• BP = Item:.2t=7解得t=3.5.\CQ=BP=7,那么 3.5v=7解得y = 2.②当B4 = C.,PB = PC 时,MBP = \QCP,: BC = ncm,BP = CP = -BC = 6c7〃 2V BP = Item:.2t = 6解得/ = 3CQ = 3vcm,: AB = CQ = 5cm, 3v = 5解得U3综上所述,当u = 2或i,=,时,A48尸与以P, Q,C为顶点的直角三角形全等.【点睛】此题考查全等三角形的判定及性质和矩形的性质,解题关键是将动态情况化为某一状态情况,并以这一状态为等量关系建立方程求解.7.:在MBC中,AB = AC,ZBAC = 90° ,尸Q为过点4的一条直线,分别过B、C两点作8M_LP0,CN_L尸.,垂足分别为M、N.(1)如图①所示,当P.与BC边有交点时,求证:MN = CN — BM ;(2)如图②所示,当与6C边不相交时,请写出线段8M、CN和MN之间的数量关系,并说明理由. 【答案】(1)见解析:(2) MN = BM + CN (或BM = MN — CN或CN = MN-BM ),理由见解析【解析】【分析】(1)根据条件先证AAA/i运ACN4,得到AM = CN,BM = AN,即可证得MN = CN — BM: (2)由(1)知AAMBYACNA,得到4M =CN,8M = AN,即可确定MN = BM + CN.【详解】证实:・・・BM_LPQ,CN_LP0,・•. ZAMB=ZCAN=90°,V ZBAC=90 ° ,AZCAN+ZACN=90°,ZCAN+ZBAM=90°(或NCW + NAC/V = NC4N+NMM)・•. ZBAM = ZACN,在AAMB和ACN4中,'ZAMB = 4CNA・.• ZBAM = AACN , AB = CA:.AAM“ACN4(A4S),.・.AM =CN,BM =AN,,: MN = AM-AN,:.MN = CN — BM.(2) MN = BM + CN (或BM=MN-CN或CN = MN-BM) .理由:•.・BM_LPQ,CN_LP.,・•・ ZAMB=ZCAN=90°,V ZBAC=90 ° ,.\ZCAN+ZACN=90°,ZCAN+ZBAM=90°(或NCW + NAC/V = NC4N+NBAM ),:.ZBAM = ZACN,在AAMB和ACNA中,'AAMB = ZCNAZ.B\M = ZACN , AB = CA:.AAM*ACNA( AAS),.・.AM =CN,BM =AN,:.MN = AN + AM = BM+CN.【点睛】此题考察三角形全等的应用,正确确定全等三角形是解题关键,由此得到对应相等的线段,确定它们之间的和差关系得到80、CN和MN之间的关系式.8.操作发现:如图,己知"配和"DE均为等腰三角形,AB=AC, AD=AE,将这两个三角形放置在一起,使点8, D, E在同一直线上,连接CE.(1)如图1, ZABC= ZACB= ZADE= ZAED=55Q,求证:△BADgZkCAE;(2)在(1)的条件下,求N8EC的度数:拓广探索:(3)如图2,假设NC48=NEAD=120.,8D=4, CF为aBCE中8E边上的高,请直接写出讦的长度.【答案】(1)见解析:(2) 70°; (3) 2【解析】【分析】(1)根据SAS证实△BADg/kCAE即可.(2)利用全等三角形的性质解决问题即可.(3)同法可证4BAD丝ZkCAE,推出EC=BD=4,由NBEC=NBAC=12O0,推出NFCE=30°即可解决问题.(1)证实:如图1中,图1Z ABC=^ ACB = Z ADE=N AED, /. Z EAD=Z CAB,:.Z EAC=A DAB,AE=AD. AC=AB9:.△ BAD^ & CAE (SAS).(2)解:如图1中,设AC交8E于O. •「N A8C=N4C8 = 55°,/. Z 84c=180° - 110° = 70°,BAD^△ CAE,Z ABO=Z ECO,Z EOC=ZAOB,・•, Z CEO = Z 840=70°,即 N BEC= 70°.(3)解:如图2中,A图2Z C48 = N EAD=120\•. Z BAD=A CAE,:AB=AC, AD=AE.△ BAD^ 4 CAE 〔SAS〕,•. Z BAD=A ACE. 8D=EC=4,同理可证N BEC- 8AC=120°,Z F£C=60%CFLEF,Z F=90",•. Z FCE=30\1•. EF=-EC=2. 2此题属于三角形综合题,考查了全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.9.在等边aABC中,点.是边8C上一点.作射线AO,点3关于射线AO的对称点为点E.连接CE并延长,交射线AO于点〔1〕如图,连接AE,①AE与AC的数量关系是;②设NBA尸=a,用.表示NBCF的大小;〔2〕如图,用等式表示线段A尸,CF.所之间的数量关系,并证实.【答案】⑴①AB二AE;②NBCF=.:(2)AF-EF=CF,理由见详解.【解析】【分析】(1)①根据轴对称性,即可得到答案;②由釉对称性,得:AE二AB, NBAF=NEAF=.,由△A3C是等边三角形,得AB=AC, ZBAC=ZACB=60° ,再根据等腰三角形的性质和三角形内角和等于180°,即可求解:(2)作NFCG=60°交AD于点G,连接BF,易证AFCG是等边三角形,得GF=FC,再证△ACG会ABCF(SAS),从而得AG=BF,进而可得至lj结论.【详解】(1)①•・•点4关于射线的对称点为点E , AAB和AE关于射线AD的对称,AAB=AE.故答案是:AB=AE;②•.•点3关于射线的对称点为点E , ,AE二AB, NBAF=NEAF=.,•二△A3c是等边三角形,AAB=AC, ZBAC=ZACB=60" ,:.ZEAC=60° -2a, AE=AC,ZACE=1[180 - (60 - 2a)] = 60 +6?,A ZBCF=ZACE-ZACB=60 +a-60°=a .(2) AF-EF=CF,理由如下:作NFCG=60.交AD于点G,连接BF,•••NBAF=NBCF=a , NADB=NCDF,A ZABC=ZAFC=60c ,••.△FCG是等边三角形,AGF=FC,•二△A3c是等边三角形,ABC=AC, ZACB=60° , AZACG=ZBCF=« .在AACG和ABCF中,CA = CBZACG = ABCF , CG = CF,AACG 仝ABCF(SAS),.,.AG=BF,•・•点4关于射线AO的对称点为点E , .\AG=BF=EF,VAF-AG=GF,.\AF-EF=CE【点睛】此题主要考查等边三角形的性质和三角形全等的判定和性质定理,添加辅助线,构造全等三角形,是解题的关键.10.如图,AA8C是等边三角形,点.在边4c上〔“点D不与A,C重合〕,点石是射线5c上的一个动点〔点E不与点8,C重合〕,连接OE,以OE为边作作等边三角形hDEF,连接CF.〔1〕如图1,当.石的延长线与A3的延长线相交,且CF在直线OE的同侧时,过点D 作DG//AB, DG 交BC 于点、G ,求证:CF = EG ;〔2〕如图2,当.石反向延长线与A8的反向延长线相交,且.,尸在直线OE的同侧时,求证:CD = CE+CF;〔3〕如图3,当OE反向延长线与线段A8相交,且.,厂在直线O石的异侧时,猜测CD、CE、CP之间的等量关系,并说明理由.【答案】〔1〕证实见详解;〔2〕证实见详解:〔3〕 CF = CO-CE,理由见详解.【解析】【分析】(1)由AABC 是等边三角形,DG//AB,得NCDG=NA=60° , NACB=60.,ACDG 是等边三角形,易证AGDE仝ACDF(SAS),即可得到结论:(2)过点D作DG〃AB交BC于点G,易证A GDE仝△ CDF(SAS),即可得到结论;(3)过点D作DG〃AB交BC于点G,易证A GDE仝A CDF(SAS),即可得到结论.【详解】(1)•・• AA3C是等边三角形,DG//AB, :.ZCDG=ZA=60° , ZACB=60° , ・•. ACQG是等边三角形,.\DG=DC.是等边三角形, .,.DE=DF, ZEDF=60° , A ZCDG-ZGDF=ZEDF-ZGDF,即:ZGDE=ZCDF, 在4 GDE和八CDF中,DE = DFNGDE = NCDF ,DG = DC.,.△GDE^A CDF(SAS),:.CF = EG ;(2)过点D作DG〃AB交BC于点G,如图2,•・• AABC是等边三角形,DG//AB、:.ZCDG=ZA=60° , ZACB=60" ,••・ACDG是等边三角形,:.DG=DC.•••ADE/是等边三角形,,DE=DF, ZEDF=60c ,A ZCDG-ZCDE=ZEDF-ZCDE> 即:ZGDE=ZCDF, 在4 GDE和^ CDF中,DE = DFNGDE = ZCDF ,DG = DC.,.△GDE^ACDF(SAS),:・CF = GE,••. CD = CG = CE+GE = CE+CF(3)CF = CD + CE,理由如下:过点D作DG〃AB交BC于点G,如图3,•・・AA8C是等边三角形,DGUAB, .,.ZCDG=ZA=60° , ZACB=60" ,,ACDG是等边三角形, ADG=DC=GC.•・• ADEF是等边三角形, ,DE=DF, ZEDF=60° ,A ZCDG+ZCDE=ZEDF+ZCDE,即:NGDE=NCDF, 在A GDE和4 CDF中,DE = DFNGDE = ZCDF , DG = DCAAGDE^ACDF(SAS),,CF = G£=GC+CE=CD+CE.【点睛】此题主要考查等边三角形的性质和三角形全等的判定和性质定理,添加辅助线,构造全等三角形,是解题的关键.。
初中数学《全等三角形》基本模型训练含解析

全等三角形基本模型专项训练一、单选题1如图,在Rt△ABC中,AB=AC,∠BAC=90°,点D,E分别在边BC及其延长线上,BD2+CE2=DE2,F为△ABC外一点,且FB⊥BC,FA⊥AE,则结论:①FA=AE;②∠DAE=45°;③S△ADE=14AD⋅EF;④CE2+BE2=2AE2,其中正确的是()A.①②③④B.①②④C.①③④D.①②【答案】A【分析】根据全等三角形的性质,证明△ABF和△ACE全等,即可得到FA=AE;连接DF如图见解析,证明△ADE和△ADF全等,即可得到∠DAE=45°;延长AD交EF于H如图见解析,利用等腰直角△AFE三线合一的性质,∠FAE=90°,∠DAE=45°∠DAE=45°,可知AH⊥EF,S△ADE=12AD⋅EH,HE=HF=12EF,即可判断③;在Rt△EBF和Rt△EAF中,利用勾股定理以及等式的性质,即可判断④.【详解】解:∵AB=AC,∠BAC=90°∴∠ABC=∠ACB=45°∴∠ACE=180°-∠ACB=135°∵FB⊥BC∴∠FBE=90°∴∠ABF=∠ABC+∠FBE=135°∴∠ABF=∠ACE∵FA⊥AE∴∠FAE=90°=∠BAC∴∠FAE-∠FAC=∠BAC-∠FAC即∠CAE=∠BAF在△ABF和△ACE中,∠ACE=∠ABF AC=AB∠CAE=∠BAF∴△ACE≌△ABF ASA∴FA=EA,故①正确;连接DF,如图:∵△ACE≌△ABF∴BF=CE在Rt△BDF中,BD2+BF2=DF2∴BD2+CE2=DF2∵BD2+CE2=DE2∴DE=DF∵AE=AF,AD=AD∴△ADE≌△ADF SSS∴∠DAE=∠DAF∴∠DAE=12∠EAF=45°,故②正确;延长AD交EF于H,如图:∵AE=AF,∠EAD=∠FAD∴AH⊥EF,HE=HF=12EF∴S△ADE=12AD⋅EH=12AD⋅12EF=14AD⋅EF,故③正确;在Rt△EBF中,BE2+BF2=EF2∵CE=BF∴BE2+CE2=EF2∵AE=AF,∠FAE=90°∴EF2=AE2+AF2=2AE2∴BE2+CE2=2AE2,故④正确,综上所述,正确的有①②③④,故选:A.【点睛】本题考查了全等三角形的判定与性质、勾股定理、等腰直角三角形性质等知识,解题的关键是灵活运用所学知识.2如图所示,△ABC中,AC=BC,M、N分别为BC、AC上动点,且BM=CN,连AM、CN,当AM +BN最小时,CMCN=( ).A.2B.32C.54D.1【答案】D 【分析】过B 点在BC 下方作BH ∥AC ,且BH =AC ,链接BH ,AH ,先证明△BCN ≌△HBM ,即有BN =HM ,则AM +BN =AM +MH ,当A 、M 、H 三点共线时,AM +MH 值最小,再证明△ACM ≌△HBM ,问题随之得解.【详解】如图,过B 点在BC 下方作BH ∥AC ,且BH =AC ,链接BH ,AH ,∵BH ∥AC ,∴∠C =∠CBH ,∵BH =AC ,BM =CN ,∴△BCN ≌△HBM ,∴BN =HM ,∴AM +BN =AM +MH ,当A 、M 、H 三点共线时,AM +MH 值最小,如图,此时∵BH ∥AC ,∴∠C =∠CBH ,∠CAM =∠BHM ,∵AC =BC ,∴△ACM ≌△HBM ,∴CM =BM ,∵BM =CN ,∴CM CN=CM BM =1,故选:D .【点睛】本题主要考查了全等三角形的判定与性质,作出辅助线,构造全等三角形是解答本题的关键.3如图,正五边形ABCDE 中,点F 是边CD 的中点,AF ,BC 的延长线交于点N ,点P 是AN 上一个动点,点M 是BN 上一个动点,当PB +PM 的值最小时,∠BPN =()A.72°B.90°C.108°D.120°【答案】C【分析】本题考查了正多边形的定义,全等三角形的判定与性质等知识.连接BF ,EF ,PE ,EM ,根据全等三角形的判定与性质可得EP =BP ,则当E 、P 、M 三点共线,且EM ⊥BC 时,PB +PM 的值最小,过点E 作EH ⊥BC 于H ,交AF 于P ,分别求出∠BAP 和∠ABP 的度数,然后利用三角形外角的性质求解即可.【详解】解:连接BF ,EF ,PE ,EM ,∵正五边形ABCDE ,∴AE =AB =BC =ED ,∠BAE =∠AED =∠BCD =∠EDC =5-2 ×180°5=108°,∵点F 是边CD 的中点,∴CF =DF ,∴△BCF ≌△EDF SAS ,∴BF =EF ,又AE =AB ,AF =AF ,∴△AEF ≌△ABF SSS ,∴∠EAF =∠BAF =12∠BAE =54°,∴△AEP ≌△ABP SAS∴EP =BP ,∴PB +PM =EP +PM ≥EM ,∴当E 、P 、M 三点共线,且EM ⊥BC 时,PB +PM 的值最小,过点E 作EH ⊥BC 于H ,交AF 于P ,同理可求∠ABP =∠AEP =12∠AED =54°,∴∠BP N =∠BAP +∠ABP =108°,即当PB +PM 的值最小时,∠BPN =108°.故选:C .4如图,在Rt △ABC 中,∠ACB =90°,以该三角形的三条边为边向外作正方形ABEF ,正方形BCGH 和正方形ACMN ,给出下列结论:①AB =MG ;②S △ABC =S △AFN ;③过点B 作BI ⊥EH 于点I ,延长B 交AC 于点J ,则AJ =CJ .④若AB =1,则EH 2+FN 2=5.其中正确的结论个数是()A.1个B.2个C.3个D.4个【答案】D 【分析】本题考查勾股定理,全等三角形的性质和判定,解题的关键是正确作出辅助线.首先根据题意证明出△ACB ≌△MCG SAS ,进而得到AB =MG ,即可判断①;过点F 作FO ⊥NA 交NA 延长线于点O ,证明出△AFO ≌△ABC AAS ,得到OF =BC ,然后利用三角形面积公式即可得到S △ABC =S △AFN ,即可判断②;过点A 作AP ⊥BJ 交BJ 的延长线于点P ,过点C 作CQ ⊥BJ ,证明出△ABP ≌△BEI AAS ,得到AP =BI ,同理得到CQ =BI ,得到CQ =AP ,然后证明出△AJP ≌△CJQ AAS ,得到AJ =CJ ,即可判断③;根据全等三角形的性质得到EH =2BJ ,然后利用勾股定理证明出EH 2=AC 2+4BC 2,同理得到NF 2=4AC 2+BC 2,然后得到EH 2+NF 2=5AB 2=5,即可判断④.【详解】∵在Rt △ABC 中,∠ACB =90°,以该三角形的三条边为边向外作正方形ABEF ,正方形BCGH 和正方形ACMN ,∴AC =MC ,BC =GC ,∠MCA =∠GCB =90°∵∠ACB =90°∴∠MCG =∠ACB =90°∴△ACB ≌△MCG SAS∴AB =MG ,故①正确;如图所示,过点F 作FO ⊥NA 交NA 延长线于点O ,∵∠FAO +∠BAO =∠CAB +∠BAO =90°∴∠FAO =∠CAB又∵∠O =∠ACB =90°,AF =AB∴△AFO ≌△ABC AAS∴OF =BC∵AN =AC∵S △ANB =12AN ⋅OF ,S △ACB =12AC ⋅BC ∴S △ABC =S △AFN ,故②正确;如图所示,过点A 作AP ⊥BJ 交BJ 的延长线于点P ,过点C 作CQ ⊥BJ∵∠ABP +∠BEI =90°,∠EBI +∠BEI =90°∴∠ABP =∠BEI又∵∠P =∠BIE =90°,AB =BE∴△ABP ≌△BEI AAS∴AP =BI同理可证,△BCQ ≌△HBI AAS ∴CQ =BI∴CQ =AP∵∠P=∠CQJ=90°,∠AJP=∠CJQ∴△AJP≌△CJQ AAS∴AJ=CJ,故③正确;∵△ABP≌△BEI AAS∴BP=EI∵△BCQ≌△HBI AAS∴BQ=HI∵△AJP≌△CJQ AAS∴PJ=QJ∵EH=EI+HI=PB+BQ=PJ+QJ+BQ+BQ=2BJ ∵AJ=CJ∴BJ2=CJ2+BC2=14AC2+BC2∴EH2=2BJ2=4BJ2=414AC2+BC2=AC2+4BC2同理可证,NF2=4AC2+BC2∴EH2+NF2=AC2+4BC2+4AC2+BC2=5AC2+BC2=5AB2=5×12=5,故④正确.综上所述,正确的结论个数是4.故选:D.5如图,在Rt△AEB和Rt△AFC中,BE与AC相交于点M,与CF相交于点D,AB与CF相交于点N,∠E=∠F=90 °,∠EAC=∠FAB,AE=AF.给出下列结论:①∠B=∠C;②CD=DN;③BE= CF;④△ACN≅△ABM.其中正确的结论是()A.①③④B.①②③④C.①②③D.①②④【答案】A【分析】本题考查了两个全等三角形的判定及性质,根据已知条件判定两个三角形全等,可得到对应边及对应角相等,据此可判断①③,再结合条件证明两个三角形全等,可得到④,即可求得结果,灵活运用两个全等三角形的条件及性质是解题的关键.【详解】解:∵∠EAC=∠FAB,∴∠EAB=∠FAC,在△EAB 和△FAC 中,∠E =∠F =90 °AE =AF ∠EAB =∠FAC,∴△EAB ≌△FAC ASA ,∴∠B =∠C ,BE =CF ,AB =AC ,∴①③都正确,在△ACN 和△ABM 中,∠B =∠CAB =AC ∠CAN =∠BAM,∴△ACN ≌△ABM ASA ,故④正确,根据已知条件无法证明②是否正确,故①③④正确,故选:A .二、填空题6如图,在△ABC 中,AH 是高,AE ⎳BC ,AB =AE ,在AB 边上取点D ,连接DE ,DE =AC ,若S △ABC =5S △ADE ,BH =1,则BC =.【答案】2.5【分析】过点E 作EF ⊥AB ,交BA 的延长线于点F ,先分别证明△ABH ≌△EAF ,Rt △ACH ≌Rt △EDF ,由此可得S △ABH =S △EAF ,S △ACH =S △EDF =S △EAF +S △ADE ,再结合S △ABC =S △ABH +S △ACH =5S △ADE 可得S △ACH S △ABH =32,由此可得CH BH=32,进而即可求得答案.【详解】解:如图,过点E 作EF ⊥AB ,交BA 的延长线于点F ,∵EF ⊥AB ,AH ⊥BC ,∴∠EFA =∠AHB =∠AHC =90°,∵AE⎳BC ,∴∠EAF =∠B ,在△ABH 与△EAF 中,∠AHB =∠EFA∠B =∠EAFAB =EA∴△ABH ≌△EAF (AAS ),∴AH =EF ,S △ABH =S △EAF ,在Rt△ACH与Rt△EDF中,AH=EF AC=DE∴Rt△ACH≌Rt△EDF(HL),∴S△ACH=S△EDF=S△EAF+S△ADE,∵S△ABC=S△ABH+S△ACH=5S△ADE,∴S△ABH+S△EAF+S△ADE=5S△ADE,∴2S△ABH+S△ADE=5S△ADE,解得:S△ABH=2S△ADE,∴S△ACH=5S△ADE-S△ABH=3S△ADE,∴S△ACHS△ABH=3S△ADE2S△ADE=32,∴12CH⋅AH12BH⋅AH=32,即CHBH=32,又∵BH=1,∴CH=1.5,∴BC=BH+CH=2.5,故答案为:2.5.【点睛】本题考查了全等三角形的判定与性质以及三角形的面积公式,作出正确的辅助线并能灵活运用全等三角形的判定与性质是解决本题的关键.7如图,在△ADE和△ABC中,∠E=∠C,DE=BC,EA=CA,过A作AF⊥DE,垂足为F,DE交CB的延长线于点G,连接AG.四边形DGBA的面积为12,AF=4,则FG的长是.【答案】3【分析】过点A作AH⊥BC于H,证△ABC≌△AED,得AF=AH,再证Rt△AFG≌Rt△AHG,同理Rt△ADF≌Rt△ABH,得S四边形DGBA=6,进而得到FG的长.【详解】解:过点A作AH⊥BC于H,如图所示:在△ABC 和△ADE 中,BC =DE∠C =∠E CA =EA,∴△ABC ≌△AED SAS∴AD =AB ,S △ABC =S △AED ,又∵AF ⊥DE ,∴12×DE ×AF =12×BC ×AH ,∴AF =AH ,∵AF ⊥DE ,AH ⊥BC ,∴∠AFG =∠AHG =90°,在Rt △AFG 和Rt △AHG 中,AG =AG AF =AH ,∴Rt △AFG ≌Rt △AHG HL ,同理:Rt △ADF ≌Rt △ABH HL ,∴S 四边形DGBA =S 四边形AFGH =12,∵Rt △AFG ≌Rt △AHG ,∴S Rt △AFG =6,∵AF =4,∴12×FG ×4=6,解得:FG =3;故答案为:3.【点睛】本题考查了全等三角形的判定与性质以及三角形面积等知识,解决问题的关键是作辅助线构造全等三角形,解题时注意:全等三角形的面积相等.8如图,动点C 与线段AB 构成△ABC ,其边长满足AB =9,CA=2a +2,CB =2a -3.点D 在∠ACB 的平分线上,且∠ADC =90°,则a 的取值范围是,△ABD 的面积的最大值为.【答案】a >52454【分析】在△ABC 中,由三角形三边关系“在一个三角形中,任意两边之和大于第三边,任意两边之差小于第三边”可知AC +BC >AB ,代入数值即可确定a 的取值范围;延长AD 、CB交于点E ,首先利用“ASA ”证明△ACD ≌△ECD ,由全等三角形的性质可得AC =EC =2a +2,AD =ED ,进而可求得BE =5,结合三角形中线的性质易知S △ABD :S △ABE =1:2,确定△ABE 面积的最大值,即可获得答案.【详解】解:∵在△ABC 中,AC +BC >AB ,∴2a +2+2a -3>9,解得a >52;如下图,延长AD 、CB 交于点E ,∵CD 为∠ACB 的平分线,∴∠ACD =∠ECD ,在△ACD 和△ECD 中,∠ACD =∠ECDCD =CD ∠ADC =∠EDC =90°,∴△ACD ≌△ECD (ASA ),∴AC =EC =2a +2,AD =ED ,∵CB =2a -3,∴BE =2a +2-(2a -3)=5,∵AD =ED ,∴S △ABD :S △ABE =1:2,当BE ⊥AB 时,△ABE 的面积取最大值,即S △ABE max =12×9×5=452,∴S △ABD max =454.故答案为:a >52,454.【点睛】本题主要考查了三角形三边关系、解一元一次不等式、角平分线、全等三角形的判定与性质、三角形中线的性质等知识,熟练掌握相关知识,正确作出辅助线是解题关键.9如图,AB =AC ,AD=AE ,∠BAC =∠DAE =40°,BD 与CE 交于点F ,连接AF ,则∠AFB 的度数为.【答案】70°/70度【分析】本题考查了全等三角形的判定与性质,三角形内角和定理,构造全等三角形是解答本题的关键.过点A作AM⊥BD于点M,AN⊥CE于点N,根据手拉手模型证明△BAD≌△CAE,得到∠ADM=∠AEN,然后证明△AMD≌△ANE,得到∠DAM=∠EAN,AM=AN,进一步推得∠MAN=∠DAE= 40°,再证明△AMF≌△ANF,可得∠FAM=20°,最后根据三角形内角和定理即得答案.【详解】过点A作AM⊥BD于点M,AN⊥CE于点N,∵∠BAC=∠DAE=40°,∴∠BAD=∠CAE,∵AB=AC,AD=AE,∴△BAD≌△CAE SAS,∴∠ADM=∠AEN,∵∠AMD=∠ANE=90°,AD=AE,∴△AMD≌△ANE AAS,∴∠DAM=∠EAN,AM=AN,∴∠DAM+∠DAN=∠EAN+∠DAN,即∠MAN=∠DAE=40°,∵∠AMF=∠ANF=90°,AM=AN,AF=AF,∴△AMF≌△ANF HL,∴∠FAM=∠FAN=1∠MAN=20°,2∴∠AFB=180°-90°-∠FAM=70°.故答案为:70°.10如图所示,已知△ABC,∠BAC=90°,AB=AC,点D和点E分别是AB和AC边上的动点,满足AD=CE,连接DE,点F是DE的中点,则CDAF的最大值为.【答案】5+1/1+5【分析】作EM⊥ED,且EM=ED,连DM,MC,取ME中点N,连ND、NC、NF,可根据“SAS”证明△ADE≌△CEM,可得∠ECM=90°,再设AF=1,并表示DE,EM,及CN,然后根据勾股定理求出DN,最后根据三角形的三边关系ND+NC≥DC,求出CD最大值,可得答案.【详解】解:过E作EM⊥ED,且EM=ED,连DM,MC.取ME中点N,连ND、NC、NF.∵∠ADE+∠AED=90°,∠AED+∠MEC=90°,∴∠ADE=∠MEC.∵AD=CE,DE=EM,∴△ADE≌△CEM,∴∠ECM=∠DAE=90°.设AF=1,∵F为DE中点,∴DE=2AF=2,∴EM=2.∵N为EM中点,∴CN=EN=1.∴DN=DE2+EN2= 5.∵ND+NC≥DC,∴CD最大值5+1,=5+1.∴CDAF故答案为:5+1.【点睛】本题主要考查了全等三角形的性质和判定,勾股定理,根据三角形的三边关系求最大值,作出辅助线是解题的关键.三、解答题11数学兴趣小组在活动时,老师提出了这样,一个问题:如图1:在△ABC中,AB=3,AC=5,D是BC的中点,求BC边上的中线AD的取值范围.【问题初探】:第一小组经过合作交流,得到如下解决方法:如图2延长AD至E.使得DE=AD,连接BE.利用三角形全等将线段AC转移到线段BE,这样就把线段AB,AC,2AD集中到△ABE中.利用三角形三边的关系即可得到中线AD的取值范围,第二小组经过合作交流,得到另一种解决方法:如图3过点B作AC的平行线交AD的延长线于点F,利用三角形全等将线段AC转移到BF,同样就把线段AB,AC,2AD集中到△ABF中,利用三角形三边的关系即可得到中线AD的取值范围.(1)请你选择一个小组的解题思路.写出证明过程【方法感悟】当条件中出现“中点”“中线”等条件时,可考虑将中线延长一倍或者作一条边的平行线.构造出“平行八字型”全等三角形;这样就把分散的已知条件和所证的结论集中到一个三角形中,顺利解决问题【类比分析】(2)如图4:在△ABC中,∠B=90°,AB=6,AD是△ABC的中线,CE⊥BC,CE=10且∠ADE=90°.求AE的长度.【思维拓展】(3)如图5:在△ABC中,AF⊥BC于点F在AB右侧作AD⊥AB,且AD=AB,在AC的左侧作AE⊥AC,且AE=AC,连接DE,延长AF交DE于点O,证明O为DE中点.【答案】(1)见解析(2)16(3)见解析【分析】(1)选择第一个小组的解题思路:延长AD到点E,使DE=AD,证明△ADC≌△EDB(SAS),得到BE=AC=10,再根据在△ABE中,5-3<AE<5+3,即2<2AD<8,求解即可;选择第二个小组的解题思路:过点B作AC的平行线交AD的延长线于点F,先证明△BDF≌△CDA (AAS),得到DF=AD,BF=AC=5,则2AD=AF,再根据在△ABF中,5-3<AF<5+3,即2<2AD<8,求解即可;(2)延长AD到点F,使DF=AD,连接CF,先证明△ABD≌△FCD SAS,得到∠FCD=∠ABD=90°,CF=AB=6,再证明E、C、F三点共线,得到EF=EC+CF=10+6=16,然后证明△ADE≌△FDE SAS,得到AE=EF=16解决问题;(3)过点E作EM∥AD交AD延长线于M,先证明△AEM≌△CAB AAS,得到EM=AB,再证明△AOD≌△MOE AAS,得到OD=OE,即可得出结论.【详解】解:(1)选择第一个小组的解题思路:如图2,延长AD到点E,使DE=AD,∵D是BC的中点,∴BD=CD,∵∠ADC=∠EDB,∴△ADC≌△EDB(SAS),∴BE=AC=10,△ABE中,5-3<AE<5+3,∴2<2AD<8,∴1<AD<4;选择第二个小组的解题思路:如图3,过点B作AC的平行线交AD的延长线于点F,∵D是BC的中点,∴BD=CD,∵BF∥AC,∴∠FBD=∠C,∠F=∠CAD,∴△BDF≌△CDA(AAS),∴DF=AD,BF=AC=5,∴2AD=AF,在△ABF中,5-3<AF<5+3,∴2<2AD<8,(2)延长AD到点F,使DF=AD,连接CF,如图4,∵D是BC的中点,∴BD=CD,∵∠ADB=∠FDC,DF=AD,∴△ABD≌△FCD SAS,∴∠FCD=∠ABD=90°,CF=AB=6,∵CE⊥BC,∴∠BCD=90°,∴∠FCD+∠ECD=180°,∴E、C、F三点共线,∴EF=EC+CF=10+6=16,∵∠ADE=90°,∴∠FDE=∠ADE=90°,∵DE=DE,AD=DF,∴△ADE≌△FDE SAS,∴AE=EF=16;(3)证明:过点E作EM∥AD交AD延长线于M,如图4,∵AD⊥AB,AE⊥AC,∴∠3+∠2+∠CAD=∠3+∠2+∠BAE=90°,∴∠CAD=∠BAE,又∵AF⊥BC,∴∠3+∠2+∠CAD=∠3+∠BAE+∠B=90°,∴∠2=∠B,∵EM∥AD,∴∠2=∠M,∴∠B=∠M,∵AE⊥AC,AF⊥BC,∴∠3+∠CAM=∠C+∠CAM=90°,∴∠3=∠C,∵AE=AC,∴△AEM≌△CAB AAS,∵AB =AD ,∴EM =AD ,∵∠2=∠M ,∠AOD =∠EOM ,∴△AOD ≌△MOE AAS ,∴OD =OE ,∴O 为DE 中点.【点睛】本题考查三角形三边的关系,全等三角形的判定与性质,余角的性质,平行线的性质,熟练掌握倍长中线,构造出“平行八字型”全等三角形是解题的关键.12已知,在等腰直角三角形ABC 中,AB =AC ,∠BAC =90°,∠ABC =∠ACB =45°,点D 是线段BC 上一点,点D 不与点B ,点C 重合,连接AD ,以AD 为一边作△ADE ,AD =AE ,∠DAE =90°,且点E 与点D 在直线AC 两侧,DE 与AC 交于点H ,连接CE .(1)如图1,求证:△ABD ≌△ACE .(2)如图2,在CE 的延长线上取一点F ,当∠AEF =∠AFE 时,求证:CD =CF .(3)过点A 作直线CE 的垂线,垂足为G ,当CD =6EG 时,直接写出△CDH 与△CEH 的面积比.【答案】(1)见详解(2)见详解(3)32或34【分析】本题主要考查了全等三角形的判定与性质,涉及SAS 、AAS 以及HL 等判定方法,(1)利用“SAS ”证明△ABD ≌△ACE 即可作答;(2)结合(1)的结论,再利用“AAS ”证明△ACD ≌△ACF 即可作答;(3)分类讨论,第一种情况:点G 在点E 的下方,过点A 作AO ⊥BC 于点O ,点H 作HM ⊥BC 于点M ,点H 作HN ⊥CG 于点N ,先证明△AOC ≌△AGC ,即有AO =AG ,CO =CG ,同理可证明:MH =NH ,再证明Rt △AOD ≌Rt △AGE HL ,可得OD =GE ,问题即可作答;第二种情况:点G 在点E 的上方,过点A 作AO ⊥BC 于点O ,点H 作HM ⊥BC 于点M ,点H 作HN ⊥CG 于点N ,按照第一种情况作答即可.【详解】(1)∵∠DAE =90°,∠BAC =90°,∴∠DAE -∠DAH =∠BAC -∠DAH ,∴∠CAE =∠BAD ,又∵AB =AC ,AD =AE ,∴△ABD ≌△ACE SAS ;(2)∵△ABD ≌△ACE SAS ,∴∠ADB =∠AEC ,∠ABD =∠ACE =45°,∴180°-∠ADB =180°-∠AEC ,∠ACB =∠ACE =45°,∴∠ADC =∠AEF ,∵∠AEF =∠AFE ,∴∠ADC =∠AFE ,在△ACD 和△ACF 中,∴∠ACD =∠ACF∠ADC =∠AFC AC =AC,∴△ACD ≌△ACF AAS ,∴CD =CF ;(3)分类讨论:第一种情况:点G 在点E 的下方,过点A 作AO ⊥BC 于点O ,点H 作HM ⊥BC 于点M ,点H 作HN ⊥CG 于点N ,如图,∵AO ⊥BC ,AG ⊥CE∴∠AOC =∠AGC =90°,又∵∠ACB =∠ACE =45°,AC =AC ,∴△AOC ≌△AGC ,∴AO =AG ,CO =CG ,同理可证明:MH =NH ,又∵AD =AE ,∴Rt △AOD ≌Rt △AGE HL ,∴OD =GE ,∵CD =6EG ,∴CO =CD -OD =5EG ,∴CG =CO =5EG ,∴CE =CG -EG =4EG ,∵S △CHD =12×CD ×MH ,S△CHE =12×CE ×NH ,MH =NH ,∴S △CHD S △CHE =12×CD ×MH 12×CE ×NH =CD ×MH CE ×NH ,∵CD =6EG ,CE =4EG ,MH =NH ,∴S △CHD S △CHE =CD ×MH CE ×NH=32;第二种情况:点G 在点E 的上方,过点A 作AO ⊥BC 于点O ,点H 作HM ⊥BC 于点M ,点H 作HN ⊥CG 于点N ,如图,同理可得:OD =GE ,OC =CG ,MH =NH ,∵CD =6EG ,∴CO =CD +OD =7EG ,∴CG =CO =7EG ,∴CE =CG +EG =8EG ,∴S △CHD S △CHE =CD ×MH CE ×NH=34;综上:△CDH 与△CEH 的面积比为32或者34.13如图,在平面直角坐标系中,O 为坐标原点,△ABC 的边BC 在x 轴上,A 、C 两点的坐标分别为A (0,m ),C (n ,0),B (-5,0),且m ,n 满足方程组m +2n =103m -n =9 ,点P 从点B 出发,以每秒2个单位长度的速度沿射线BO 匀速运动,设点P 运动时间为t 秒.(1)求A 、C 两点的坐标;(2)连接P A ,用含t 的代数式表示△AOP 的面积,并直接写出t 的取值范围;(3)当点P 在线段BO 上运动时,在y 轴上是否存在点Q ,使△POQ 与△AOC 全等?若存在,请求出t 的值并直接写出Q 点标;若不存在,请说明理由.【答案】(1)A (0,4),C (3,0);(2)0≤t <52,S △AOP =10-4t ;t >52,S △AOP =4t -10.(3)存在,Q (0,3)或(0,-3)或Q (0,4)或(0,-4).【分析】本题考查了全等三角形的性质和判定,二元一次方程组的解法,坐标与图形性质等知识点的综合运用,关键是利用分类讨论求出符合条件的所有情况.(1)解二元一次方程组求出m ,n 的值即可;(2)分为两种情况:当0≤t <52时,P 在线段OB 上,②当t >52时,P 在射线OC 上,求出OP 和OA ,根据三角形的面积公式求出即可;(3)分为四种情况:①当BP =1,OQ =3时,②当BP =2,OQ =4时,③④利用图形的对称性直接写出其余的点的坐标即可.【详解】(1)解方程组m +2n =103m -n =9 得m =4n =3 ,∴ A 的坐标是0,4 ,C 的坐标是3,0 ;(2)由已知,BP =2t ,OB =5.①0≤t <52,P 在线段OB 上.OP =OB -BP =5-2tS △AOP =12×OP ×OA 2=12×(5-2t )×4=10-4t .②t >52,P 在射线OC 上,OP =BP -OP =2t -5S △AOP =12×OA ×OP =12×4×(2t -5)=4t -10(3)在y 轴上存在点Q ,使△AOC 与△POQ 全等.①△POQ ≌△AOC 时,OQ =OC =3.OP =OA =4.t =5-42=12,Q (0,3)或Q (0,-3)②△POQ ≌△COA 时,OQ =OA =4,OP =OC =3.t =5-32=1 Q (0,4)或(0,-4)t =12,Q (0,3)或(0,-3);t =1,Q (0,4)或(0,-4);综上所述,t =12,Q (0,3)或(0,-3);t =1,Q (0,4)或(0,-4).14某校课后延时兴趣小组尝试用尺规来“作一条线段的三等分点”,请认真阅读下面的操作过程并完成相应的学习任务.如图1,①分别以点A ,B 为圆心,大于12AB 的长为半径在AB 两侧画弧,四段弧分别交于点C ,点D ;②连接AC ,BC ,AD ,作射线BD ;③以D 为圆心,BD 的长为半径画弧,交射线BD 于点E ;④连接CE ,交于AB 点F .点F 即为AB 的一个三等分点(即AF =13AB ).学习任务:(1)填空:四边形ADBC的形状是,你的依据是;(2)证明:AF=13AB;(3)如图2,若CE交AD于点H,∠CAD=60°,AC=6,将CH绕着点C旋转,当点H的对应点H 落在直线FD上时,求DH 的长.【答案】(1)菱形;四条边相等的四边形为菱形(2)见解析(3)DH′的长为33+32或33-32【分析】本题考查了菱形的判定与性质、相似三角形的判定与性质、等边三角形的判定与性质、全等三角形的判定与性质、勾股定理,善于利用特殊叫以及直角三角形中的关系是解题的关键.(1)根据菱形的性质判定即可.(2)证明△AFC∽△BFE,得出AFFB =ACBE,再根据线段关系即可求出.(3)利用菱形及已知条件推出相关信息,证明△ACD为等边三角形,再根据AAS证明△AHC≌△DHE,求得CH ;然后证明△AKF∽△BDF,根据相似三角形的性质得出AK、CK;最后用勾股定理解三角形即可.CH绕着点C旋转,点H的对应点H 需要分情况讨论.【详解】(1)解:由图的作法可知:AC=AD=BC=BD,∴四边形ADBC的形状是菱形,依据是:四条边相等的四边形为菱形.故答案为:菱形;四条边相等的四边形为菱形;(2)证明:∵四边形ADBC的形状是菱形,∴AC∥BE,∴△AFC∽△BFE,∴AF FB =ACBE.∵AC=BD,BD=DE,∴BE=2AC,∴AF FB =12,∴FB=2AF,∴AB=3AF.∴AF=13AB.(3)解:①当点H 在线段FD上时,连接CD,如图,∵AC=AD,∠CAD=60°,∴△ACD为等边三角形,∴CD=AD=6,∠ADC=60°.∵AC∥BE∴∠ACF =∠DEC .在△AHC 和△DHE 中,∠AHC =∠DHE∠ACE =∠DEC AC =DE,∴△AHC ≌△DHE AAS ,∴AH =HD =3,∵△ACD 为等边三角形,∴CH ⊥AD ,∠ACH =∠DCH =30°,∴CH =33.∴CH =CH =33.设FD 与AC 交于点K ,∵AC ∥BE ,∴△AKF ∽△BDF ,∴AK BD =AF FB=12.同理:CK ED =AF FB=12,∴AK BD =CK ED.∵BD =ED ,∴AK =CK =3,∴HK ⊥AC ,∠CDK =12∠ADC =30°.∴H K =CH 2-CK 2=32,DK =33.∴DH =DK -H K =33-32.②当点H 在射线FD 上时,连接CD ,如图,由①知CH =CH =33,HK ⊥AC ,AK =KC =3,∴DK =AD 2-AK 2=33,∴H K =CH 2-CK 2=32.∴DH =H K +DK =33+32.综上,DH 的长为33+32或33-32.15(1)某学习小组在探究三角形全等时,发现了下面这种典型的基本图形.如图1,已知:在△ABC 中,∠BAC =90°,AB =AC ,直线l 经过点A ,BD ⊥直线l ,CE ⊥直线l ,垂足分别为点D 、E .证明:DE =BD +CE .(2)组员小刘想,如果三个角不是直角,那结论是否会成立呢?如图2,将(1)中的条件改为:在△ABC 中,AB =AC ,D 、A 、E 三点都在直线l 上,并且有∠BDA =∠AEC =∠BAC =α,其中α为任意锐角或钝角.请问结论DE =BD +CE 是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:如图3,过△ABC 的边AB 、AC 向外作正方形ABDE 和正方形ACFG ,AH 是BC 边上的高,延长HA 交EG 于点I ,求证:I 是EG 的中点.【答案】(1)见解析;(2)DE =BD +CE ,见解析;(3)见解析【分析】本题主要考查全等三角形的判定和性质,由条件证明三角形全等得到BD =AE 、CE =AD 是解题的关键.(1)由条件可证明△ABD ≌△CAE ,可得DA =CE ,AE =BD ,可得DE =BD +CE ;(2)由条件可知∠BAD +∠CAE =180°-α,且∠DBA +∠BAD =180°-α,可得∠DBA =∠CAE ,结合条件可证明△ABD ≌△CAE ,可得出结论;(3)由条件可知EM =AH =GN ,可得EM =GN ,结合条件可证明△EMI ≌△GNI ,可得出结论I 是EG 的中点.【详解】解:(1)如图1,∵BD ⊥直线l ,CE ⊥直线l ,∴∠BDA =∠CEA =90°,∵∠BAC =90°,∴∠BAD +∠CAE =90°,∵∠BAD +∠ABD =90°,∴∠CAE =∠ABD ,在△ABD 和△CAE 中,∠ABD =∠CAE∠BDA =∠CEA AB =AC,∴△ABD ≌△CAE AAS ,∴AE =BD ,AD =CE ,∴DE =AE +AD =BD +CE ;(2)成立,理由如下:如图,证明如下:∵∠BDA =∠BAC =α,∴∠DBA +∠BAD =∠BAD +∠CAE =180°-α,∴∠DBA =∠CAE ,在△ABD 和△CAE 中.∠BDA =∠AEC∠DBA =∠CAE AB =AC.∴△ABD ≌△CAE AAS∴AE =BD ,AD =CE ,∴DE =AE +AD =BD +CE ;(3)如图3,过E 作EM ⊥HI 于M ,GN ⊥HI 的延长线于N .∴∠EMI =∠EMA =∠GNA =90°,∠BAE =90°,∴∠EAM +BAH =90°,∵AH 是BC 边上的高,∴∠AHB =90°,∴∠BAH +∠ABH =90°,∴∠ABH =EAM ,∵AE =AB ,∴△ABH ≌△EAM ,∴EM =AH ,同理△ACH ≌△GAN ,∴AH =GN ,∴EM =GN ,在△EMI 和△GNI 中,∠EIM =∠GIN∠EMI =∠GNI EM =GN,∴△EMI ≌△GNI AAS ,∴EI =GI ,∴I 是EG 的中点.16如图,在△ABC 中,BC =5,高AD 、BE 相交于点O ,BD =2,且AE =BE.(1)请说明△AOE ≌△BCE 的理由;(2)动点P 从点O 出发,沿线段OA 以每秒1个单位长度的速度向终点A 运动,动点Q 从点B 出发沿射线BC 以每秒4个单位长度的速度运动,P 、Q 两点同时出发,当点P 到达A 点时,P 、Q 两点同时停止运动.设点P 的运动时间为t 秒,求当t 为何值时,△AOQ 的面积为3.(3)在(2)的条件下,点F 是直线AC 上的一点且CF =BO .当t 为何值时,以点B 、O 、P 为顶点的三角形与以点F 、C 、Q 为顶点的三角形全等?(请直接写出符合条件的t 值).【答案】(1)见解析(2)当t 为15或45时,△AOQ 的面积为3(3)t =1或53s 时,△BOP 与△FCQ 全等【分析】本题考查三角形综合题、全等三角形的判定和性质、三角形的面积等知识,(1)首先推导出∠EAO =∠EBC ,通过ASA 即可证明△AOE ≌△BCE ;(2)分两种情形讨论求解即可①当点Q 在线段BD 上时,QD =2-4t ,②当点Q 在射线DC 上时,DQ =4t -2时;依据三角形面积计算公式解答即可;(3)分两种情形求解即可①如图2中,当OP =CQ 时,BOP ≌△FCQ .②如图3中,当OP =CQ 时,△BOP ≌△FCQ .【详解】(1)如图1中,∵AD 是高,∴∠ADC =90°,∵BE 是高,∴∠AEB =∠BEC =90°,∴∠EAO +∠ACD =90°,∠EBC +∠ECB =90°,∴∠EAO =∠EBC ,在△AOE 和△BCE 中,∠EAO =∠EBCAE =BE ∠AEO=∠BEC,∴△AOE ≌△BCE ASA ,(2)解:由(1)知△AOE ≌△BCE ,∴OA =BC =5,∵BD =2,∴CD =3,由题意OP =t ,BQ =4t ,①当点Q 在线段BD 上时,QD =2-4t ,∴S △AOQ =12OA ⋅QD =12×5×2-4t =3,解得:t =15;②当点Q 在BD 延长线上时,DQ =4t -2,∴S △AOQ =12OA ⋅DQ =12×5×4t -2 =3,解得:t =45,综上,当t 为15或45时,△AOQ 的面积为3;(3)存在.①如图2中,当OP =CQ 时,∵OB =CF ,∠POB =∠FCQ ,∴△BOP ≌△FCQ .∴CQ =OP ,∴5-4t =t ,解得t =1,②如图3中,当OP =CQ 时,∵OB =CF ,∠POB =∠FCQ ,∴△BOP ≌△FCQ .∴CQ =OP ,∴4t -5=t ,解得t =53.综上所述,t =1或53s 时,△BOP 与△FCQ 全等.17如图1,在△ABC 中,BD 为AC 边上的高,BF 是∠ABD 的角平分线,点E 为AF 上一点,连接AE ,∠AEF =45°.(1)求证:AE平分∠BAF(2)如图2,连接CE交BD于点G,若△BAE与△CAE的面积相等,求证:BG=CF【答案】(1)见解析;(2)见解析【分析】本题主要考查了全等三角形的证明以及性质运用,角平分线的判定以及基本性质,熟练掌握全等三角形的几种判定方法以及角平分线的判定是解答该题的关键.(1)根据BF是∠ABD的角平分线和,BD为AC边上的高,可得12∠BAD=45°-12∠ABD,由∠AEF=45°得∠BAE=45°-∠ABE=45°-12∠ABD,即可证明∠BAE=12∠BAD;(2)过点E作EM⊥AB于点M,EN⊥AC于点N,由角平分线性质可以得EM=EN,由△BAE与△CAE的面积相等可得AB=AC,证明△ABE≌△ACE(SAS),得出∠AEB=∠CEB=135°,BE=EC,即可得出∠BEG=∠CEF=360°-∠AEB-∠AEC=90°,再根据垂直模型证明△BEG≌△CEF(ASA),即可得出结论.【详解】(1)证明:∵BD为AC边上的高,即∠ADB=90°,∴∠ABD+∠BAD=90°,∴12(∠ABD+∠BAD)=45°,∴1 2∠BAD=45°-12∠ABD∵∠AEF=∠ABF+∠BAE=45°,∴∠BAE=45°-∠ABF,∵∠ABF=12∠ABD,∴∠BAE=45°-12∠ABD,∴∠BAE=12∠BAF,即:AE平分∠BAF.(2)过点E作EM⊥AB于点M,EN⊥AC于点N,∵AE平分∠BAC,且EM⊥AB,EN⊥AC,∴EM=EN.∵S△ABE=S△ACE,∴AB=AC,∵AE平分∠BAC,∴∠BAE=∠CAE,在△ABE和△ACE中,AB=BC∠BAE=∠CAE AE=AE∴△ABE≌△ACE(SAS),∴∠AEB=∠CEB,BE=EC,∵∠AEF=45°,∴∠AEB=∠AEC=135°,∴∠BEG=∠CEF=360°-∠AEB-∠AEC=90°,∵BD为AC边上的高,∴∠ADB=90°,∴∠FBD+∠BFC=∠BFC+∠FCE,∴∠EBG=∠ECF.在△BEG和△CEF中,∠BEG=∠CEF BE=CE∠EBG=∠ECF∴△BEG≌△CEF(ASA).∴BG=CF .18如图,已知A a,0,B0,b,AB=AC且AB⊥AC,AC交y轴于E点.(1)如图1,若a2+b2-4a-8b+20=0,求C点坐标;(2)如图2,A,B两点分别在x轴,y轴正半轴上,E为AC的中点,BC交x轴于G点,连EG,若a=3,求G点的坐标;(3)如图3,A在x轴的负半轴上,以BC为边在BC的右侧作等边△BCD,连OD,当∠BOD=60°时,请探究线段OA、OB、OD之间的数量关系,并证明.【答案】(1)(-2,-2)(2)(-2,0)(3)OD=OB+2OA【分析】(1)利用完全平方公式将等式变形为两个数平方和的形式,即可求出a=2,b=4,如图1中,过点C作CH ⊥x轴于点H,证明△AHC≌△BOA,可得CH=OA=2,AH=OB=4,即可得到点C坐标.(2)根据(1)可得CH=OA=a,AH=OB=b,再由a=3,E为AC的中点,可得点C(-3,-3),AH=OB=6,再利用面积法求出AG =5,即可解题;(3)过点C 作CH ⊥x 轴于点H ,在OD 上取一点M ,使得OM =OB ,证明△OBM 是等边三角形,进而证明△MBD ≌△OBC ,得∠BMD =∠BOC =120°,MD =OC ,再证明∠COH =30°,得OC =2CH =2OA ,即可得出OD =OB +2OA .【详解】(1)解:∵a 2+b 2-4a -8b +20=0,∴(a 2-4a +4)+(b 2-8b +16)=0,即(a -2)2+(b -4)2=0,∴a =2,b =4,∴A 2,0 ,B 0,4如图1中,过点C 作CH ⊥x 轴于点H ,∵∠AHC =∠BOA =∠BAC =90°,∴∠CAH +∠BAO =90°,∠BAO +∠ABO =90°,∴∠CAH =∠ABO ,在△AHC 和△BOA 中,∠AHC =∠BOA∠CAH =∠ABO AC =BA,∴△AHC ≌△BOA (AAS ),∴CH =OA =2,AH =OB =4,∴OH =AH -OA =4-2=2∴点C 坐标为(-2,-2);(2)如图2,同理(1)可证明:CH =OA =a ,AH =OB =b ,∵a =3,E 为AC 的中点,OE 平行于CH ,∴OA =OH =3,CH =3,∴点C (-3,-3),AH =OB =6,AB =AC =OA 2+OB 2=62+32=35,∵S △ABC =S △AGC +S △AGB ,即12×35×35=12×3⋅AG +12×6⋅AG ,∴AG =5,∴GO =AG -OA =5-3=2,∴点G 坐标为(-2,0);(3)结论:OD =OB +2OA ,如图3,过点C 作CH⊥x轴于点H ,同理可得:CH =OA ,AH =OB ,在OD 上取一点M ,使得OM =OB ,∵OM =OB ,∠BOD =60°,∴△OBM 是等边三角形,∴BO =BM ,∠OMB =60°,∴∠BMD =120°,∵△BCD 是等边三角形,∴BC =BD ,∠CBD =∠OBM =60°,∴∠DBM =∠CBO ,在△MBD 和△OBC 中,BM =OB∠DBM =∠CBO BD =BC,∴△MBD ≌△OBC (SAS ),∴∠BMD =∠BOC =120°,MD =OC ,∴∠COH =120°-90°=30°,∵CH ⊥x 轴,∴OC =2CH =2OA ,∵OD =OM +MD ,∴OD =OB +OC =OB +2OA【点睛】本题考查了等腰直角三角形的性质,等边三角形的判定和性质,全等三角形的判定和性质,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.19已知△ABC 为等边三角形,D 是边AC 上的一点,连接BD ,E 为BD 上的一点,连接CE.(1)如图1,延长CE 交AB 于点G .若∠DCG =15°,BG =2,求BC 的长;(2)如图2,将△BEC 绕点B 逆时针旋转60°至△BFA ,延长CB 至点M ,使得BM =DC ,连接AM 交BF 于点N ,探究线段FN ,DE ,BE 之间的数量关系,并说明理由;(3)如图3,在(2)问的条件下,过点A 作AH ⊥BC 于点H ,过点B 作BK ∥AH 且BK =AH ,连接HK ,NK ,NH ,NC .若BC =4,当12BD +NK 的值最小时,请直接写出CD NH的值.【答案】(1)1+3(2)2FN +DE =BE .理由见解析(3)277【分析】(1)作CF⊥BC,解直角三角形BFG求得BF和FG,进而解直角三角形CFG求得CF,从而得出结果;(2)延长BF至G,使FG=DE,连接AG,作BH∥AF,交BF于H,证明△ABG≌△CBD,进而证明△ANG≌ΔMNB,△AFN≌△MHN,△BMH≌△DCE,进一步得出结论;BD+NK最小,此时BG⊥AG,即BD⊥AC,进一步得出(3)可得出当K、N、G共线且与AG垂直时,12结果.【详解】(1)解:如图1,作CF⊥BC于F,∴∠CFG=∠BFG=90°,∵△ABC是等边三角形,∴∠ACB=∠ABC=60°,在Rt△BFG中,BG=2,∠ABC=60°,=1,∴BF=2cos60°=2×12=3,FG=2⋅sin60°=2×32在Rt△CFG中,FG=3,∠FCG=∠ACB-∠ACG=60°-15°=45°,∴CF=FG=3,tan∠FCG∴BC=BF+FC=1+3;(2)证明:如图2,延长BF至G,使FG=DE,连接AG,作BH∥AF,交BF于H,∴∠MHN=∠AFN,∠NMH=∠FAN,∴∠MHB=∠AFG∵△BEC绕点B逆时针旋转60°至△BFA,∴BF=BE,∠ABF=∠CBE,AB=BC,∴BG=BD,∴△ABG≌△CBD,∴AG=CD=BM,∠G=∠BDC=180°-∠CBE-∠ACB=120°-∠CBE,∵∠MBN=180°-∠ABC-∠ABF=120°-∠CBE,∴∠G=∠MBN,∴△ANG≌△MNB,∴AN=MN,∴△AFN≌△MHN,∴FN=NH,∵△ANG ≌△MNB ,∴NG =BN ,∵FN =NH ,∴BH =FG ,∵FG =DE∴BH =DE ,∵旋转,∴CE =AF ,∵△AFN ≌△MHN ,∴AF =MH ,∴MH =CE ,∵CD =BM ,∴△BMH ≌△DCE ,∴BH =DE ,∵FN +NH +BH =BF ,∴2FN +DE =BE ;(3)解:如图3,由(2)知:BD =BG =2BN ,∴12BD +NK =GN +NK ,∴当K 、N 、G 共线且与AG 垂直时,12BD +NK 最小,此时BG ⊥AG ,即BD ⊥AC ,如图4,连接NH ,∵AC =BC =4,∴CD =BH =2,BD =32BC =23,BN =GN =12BG =12BD =3,∵NH =BH 2+BN 2=2+(3)2=7,∴CD NH=277.【点睛】本题考查了等边三角形的性质,全等三角形的判定和性质,解直角三角形等知识,解决问题的关键是作辅助线,构造全等三角形.。
(完整版)全等三角形的判定常考典型例题及练习

(完整版)全等三角形的判定常考典型例题及练习-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN全等三角形的判定一、知识点复习 ①“边角边”定理:两边和它们的夹角对应相等的两个三角形全等。
(SAS )图形分析:书写格式: 在△ABC 和△DEF 中⎪⎩⎪⎨⎧=∠=∠=EFBC E B DEAB∴△ABC ≌△DEF (SAS )②“角边角”定理:两角和它们的夹边对应相等的两个三角形全等。
(ASA)图形分析:书写格式: 在△ABC 和△DEF 中 ⎪⎩⎪⎨⎧∠=∠=∠=∠FC EF BC EB∴△ABC ≌△DEF(ASA)③“角角边”定理:两个角和其中一个角的对边对应相等的两个三角形全等。
(AAS )图形分析:书写格式:在△ABC 和△DEF 中⎪⎩⎪⎨⎧=∠=∠∠=∠EFBC F C EB∴△ABC ≌△DEF(AAS)④“边边边”定理:三边对应相等的两个三角形全等。
(SSS )图形分析:书写格式: 在△ABC 和△DEF 中 ⎪⎩⎪⎨⎧===EF BC DF AC DE AB∴△ABC ≌△DEF(AAS)⑤“斜边、直角边”定理:斜边和一条直角边对应相等的两个直角三角形全等。
(HL )图形分析:书写格式:在△ABC 和△DEF 中 ⎩⎨⎧==DF AC DE AB ∴△ABC ≌△DEF (HL )一个三角形共有三条边与三个角,你是否想到这样一问题了:除了上述四种识别法,还有其他的三角形全等识别法吗比如说“SSA ”、“AAA ”能成为判定两个三角形全等的条件吗两个三角形中对应相等的元素 两个三角形是否全等反例 SSA⨯AAA⨯二、常考典型例题分析第一部分:基础巩固1.下列条件,不能使两个三角形全等的是( )A.两边一角对应相等 B.两角一边对应相等 C.直角边和一个锐角对应相等 D.三边对应相等2.如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD()A.∠B=∠C B.AD=AE C.BD=CE D.BE=CD3.下列各图中a、b、c为三角形的边长,则甲、乙、丙三个三角形和左侧△ABC全等的是()A.甲和乙 B.乙和丙 C.甲和丙 D.只有丙4.如图,E,B,F,C四点在一条直线上,EB=CF,∠A=∠D,再添一个条件仍不能证明△ABC≌△DEF的是()A.AB=DE B.DF∥AC C.∠E=∠ABC D.AB∥DE5.如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是()A.∠A=∠D B.AB=DC C.∠ACB=∠DBC D.AC=BD6.如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合,过角尺顶点C的射线OC便是∠AOB的平分线OC,作法用得的三角形全等的判定方法是()A.SAS B.SSS C.ASA D.HL第二部分:考点讲解考点1:利用“SAS ”判定两个三角形全等1.如图,A 、D 、F 、B 在同一直线上,AD=BF ,AE=BC ,且AE ∥BC .求证:△AEF ≌△BCD .2.如图,AB=AC ,AD=AE ,∠BAC=∠DAE .求证:△ABD ≌△ACE .考点2:利用“SAS ”的判定方法解与全等三角形性质有关的综合问题3.已知:如图,A 、F 、C 、D 四点在一直线上,AF=CD ,AB ∥DE ,且AB=DE ,求证:FEC CBF ∠=∠考点3:利用“SAS ”判定三角形全等解决实际问题 4.有一座小山,现要在小山A 、B 的两端开一条隧道,施工队要知道A 、B 两端的距离,于是先在平地上取一个可以直接到达A 和B 的点C ,连接AC 并延长到D ,使CD=CA ,连接BC 并延长到E ,使CE=CB ,连接DE ,那么量出DE 的长,就是A 、B 的距离,你能说说其中的道理吗?考点4:利用“ASA”判定两个三角形全等5.如图,已知AB=AD,∠B=∠D,∠1=∠2,求证:△AEC≌△ADE.6.如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.求证:△AEC≌△BED;考点6:利用“ASA”与全等三角形的性质解决问题:7.如图,已知EC=AC,∠BCE=∠DCA,∠A=∠E;求证:BC=DC考点7:利用“SSS”证明两个三角形全等8.如图,A、D、B、E四点顺次在同一条直线上,AC=DF,BC=EF,AD=BE,求证:△ABC≌△EDF.考点8:利用全等三角形证明线段(或角)相等9.如图,AE=DF,AC=DB,CE=BF.求证:∠A=∠D.考点9:利用“AAS”证明两个三角形全等10.如图,在△ABC中,AB=AC,BD⊥AC,CE⊥AB,求证:△ABD≌△ACE.考点10:利用“AAS”与全等三角形的性质求证边相等11.(2017秋?娄星区期末)已知:如图所示,△ABC中,∠ABC=45°,高AE与高BD交于点M,BE=4,EM=3.(1)求证:BM=AC;(2)求△ABC的面积.考点11:利用“HL”证明两三角形全等12.如图,在△ABC中,D是BC边的中点,DE⊥AB,DF⊥AC,垂足分别为E、F,且DE=DF。
第12章 全等三角形(基础、常考、易错、压轴)分类专项训练(解析版)

第12章全等三角形(基础、常考、易错、压轴)分类专项训练【基础】一.全等图形(共2小题)1.(2022春•商水县期末)有下列说法,其中正确的有()①两个等边三角形一定能完全重合;②如果两个图形是全等图形,那么它们的形状和大小一定相同;③两个等腰三角形一定是全等图形;④面积相等的两个图形一定是全等图形.A.1个B.2个C.3个D.4个【分析】直接利用全等图形的性质分别分析得出答案.【解答】解:①两个等边三角形不一定能完全重合,故此选项不合题意;②如果两个图形是全等图形,那么它们的形状和大小一定相同,故此选项符合题意;③两个等腰三角形不一定是全等图形,故此选项不合题意;④面积相等的两个图形不一定是全等图形,故此选项不合题意.故选:A.【点评】此题主要考查了全等图形,正确掌握全等图形的性质是解题关键.2.(2022春•永春县期末)如图是由四个相同的小正方形组成的网格图,则∠1+∠2=180°.【分析】根据SAS可证得△ABC≌△EDC,可得出∠BAC=∠DEC,继而可得出答案.【解答】】解:由题意得:AB=ED,BC=DC,∠D=∠B=90°,∴△ABC≌△EDC(SAS),∴∠BAC=∠1,∠1+∠2=180°.故答案为:180°.【点评】本题考查全等图形的知识,比较简单,解答本题的关键是判断出△ABC≌△EDC.二.全等三角形的性质(共3小题)3.(2022春•淄博期末)如图,已知△ABD≌△ACE,AD=3,AB=7,BD=9,则AC的长为()A.3B.7C.9D.无法确定【分析】根据全等三角形的性质即可得到结论.【解答】解:∵△ABD≌△ACE,AB=7,∴AB=AC=7,故选:B.【点评】本题考查了全等三角形的性质,熟练掌握全等三角形的性质是解题的关键.4.(2022春•招远市期末)如图所示,△ABC≌△AEF.在下列结论中,不正确的是()A.∠EAB=∠F AC B.BC=EF C.CA平分∠BCF D.∠BAC=∠CAF 【分析】根据全等三角形的性质即可得到结论.【解答】解:∵△ABC≌△AEF,∴∠BAC=∠EAF,∴∠BAC﹣∠EAE=∠EAF﹣∠EAC,∴∠EAB=∠F AC,故A不符合题意;∵△ABC≌△AEF,∴BC=EF,故B不符合题意;∵△ABC≌△AEF,∴AC=AF,∠ACB=∠F,∴∠ACF=∠F=∠ACB,∴CA平分∠BCF,故C不符合题意;∵△ABC≌△AEF,∴∠BAC=∠EAF,∴∠BAC>∠CAF,故D符合题意,故选:D.【点评】本题考查了全等三角形的性质,熟练掌握全等三角形性质是解题的关键.5.(2022春•元阳县期末)已知△ABC的三边长为x,3,6,△DEF的三边长为5,6,y.若△ABC与△DEF全等,则x+y的值为8.【分析】根据全等三角形对应边相等解答即可.【解答】解:因为△ABC与△DEF全等,所以x=5,y=3,所以x+y=8,故答案为:8.【点评】本题考查了全等三角形的性质,熟练掌握全等三角形的性质并准确识图是解题的关键.三.全等三角形的判定(共4小题)6.(2022春•温江区校级期末)下列说法正确的是()A.两个全等图形面积一定相等B.两个等边三角形一定是全等图形C.形状相同的两个图形一定全等D.两个正方形一定是全等图形【分析】直接利用全等图形的性质以及定义,分别分析得出答案.【解答】解:A.两个全等图形面积一定相等,故此选项合题意;B.两个等边三角形不一定是全等图形,故此选项不合题意;C.形状相同的两个图形不一定全等,故此选项不合题意;D.两个正方形不一定是全等图形,故此选项不符合题意;故选:A.【点评】此题主要考查了正方形的性质以及全等图形,正确掌握全等图形的性质是解题关键.7.(2022春•保定期末)如图三角形纸片被遮住了一部分,小明根据所学知识画出了一个与原三角形完全重合的三角形,他画图的依据是()A.SSS B.AAS C.ASA D.SAS【分析】根据全等三角形的判定定理ASA得出即可.【解答】解:他画图的依据是ASA,即有两角和它们的夹边对应相等的两个三角形全等,故选:C.【点评】本题考查了全等三角形的判定定理,能熟记全等三角形的判定定理是解此题的关键,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,两直角三角形全等还有HL等.8.(2022•连城县校级开学)如图,在△ABC和△DEF中,AB=DE,∠B=∠DEF,请你再补充一个条件,能直接运用“SAS”判定△ABC≌△DEF,则这个条件是()A.∠ACB=∠DEF B.BE=CF C.AC=DF D.∠A=∠F【分析】根据全等三角形的判定方法即可确定.【解答】解:添加条件:BE=CF,理由如下:∵BE=CF,∴BC=EF,在△ABC和△DEF中,,∴△ABC≌△DEF(SAS),故选:B.【点评】本题考查了全等三角形的判定,熟练掌握全等三角形的判定方法是解题的关键.9.(2022春•榕城区期末)如图,已知AB=AD,AE=AC,∠DAB=∠EAC.求证:△ACD ≌△AEB.【分析】先证明∠DAC=∠BAE,然后根据“SAS”可判断△ACD≌△AEB.【解答】证明:∵∠DAB=∠EAC,∴∠DAB+∠BAC=∠EAC+∠BAC,即∠DAC=∠BAE,在△ACD和△AEB中,,∴△ACD≌△AEB(SAS).【点评】本题考查了全等三角形的判定:熟练掌握全等三角形的5种判定方法是解决问题的关键,选用哪一种方法,取决于题目中的已知条件.四.全等三角形的判定与性质(共6小题)10.(2022春•凤翔县期末)如图,锐角△ABC的两条高BD、CE相交于点O,且CE=BD,若∠CBD=20°,则∠A的度数为()A.20°B.40°C.60°D.70°【分析】首先利用直角三角形可得∠BCD得度数,再根据“HL“可得△BEC≌△CDB,进而得到∠BCD=∠CBE,可得∠A.【解答】解:∵BD是高,∠CBD=20°,∴∠BCD=180°﹣90°﹣20°=70°,在Rt△BEC和Rt△CDB中,,∴Rt△BEC≌Rt△CDB(HL),∴∠BCD=∠CBE=70°,∴∠A=180°﹣70°﹣70°=40°.故选:B.【点评】本题考查直角三角形全等的判定和等腰三角形的性质,熟练的掌握全等的判定方法是解题关键.11.(2022春•永州期末)如图,∠AOC=∠BOC,点P在OC上,PD⊥OA与点D,PE⊥OB与点E,若OD=4,OP=5,则PE的长为()A.3B.C.4D.【分析】利用勾股定理列式求出PD,再根据角平分线上的点到角的两边距离相等可得PE=PD.【解答】解:∵OD=4,OP=5,PD⊥OA,由勾股定理得,PD==3,∵∠AOC=∠BOC,PD⊥OA,PE⊥OB,∴PE=PD=3.故选:A.【点评】本题考查了角平分线上的点到角的两边距离相等的性质,勾股定理,是基础题,熟记性质是解题的关键.。
全等三角形的常见题型

全等三角形的常见题型一、全等三角形的性质:1、如图,△ABC ≌△ADE ,则,AB= .若∠BAE=120°,∠BAD=40°,则∠BAC= °.2、如图,△ECD ≌△BCA ,AC ⊥BD 于C ,AB=5 cm ,∠B=60°,则DE= 。
3、已知,如图ΔABE ≌ΔACD ,AB=AC ,BE=CD ,∠B=50°,∠AEC=120°,则∠DAC 的度数为( )A. 120°B. 70°C. 60°D.50°4、如图,ΔABC ≌ΔADE ,AB=AD , AC=AE ,∠B=28º,∠E=95º,∠EAB=20º, 则∠BAD 为( )A.75ºB. 57ºC. 55ºD. 77º5、如图,ΔABC ≌ΔBAD ,A 和B ,C 和D 是对应顶点,如果AB=6cm ,BD=5cm ,AD=4cm ,那么BC 等于( )A .6cm B.5cm C.4cm D.5cm 或4cm6、如图, ΔABC ≌ΔADE,AB 和AD,AC 和AE 是对应边,那么∠DAC 等于 A.∠ACB B.∠CAE C.∠BAE D.∠BAC7、已知图2中的两个三角形全等,则∠ 度数是( )A.72°B.60°C.58°D.50° 8、如图,Rt △ABC 中,∠ACB =90°,∠A =50°,将其折叠,使点A 落在边CB 上A ′处,折痕为CD ,则∠A ′DB =( ) (A)40°. (B)30°. (C)20°. (D)10°.9、如图所示,△ABE 和△ADC 是△ABC 分别沿着AB ,AC 边翻折180°形成的,若∠1∶∠2∶∠3=28∶5∶3,则∠α的度数为A .80°B .100°C .60°D .45°.A 'B DAC ABCDEADEBCABCDCBAED10、如图,在正方形ABCD中,E是AD的中点,F是BA延长线上的一点,AF=AB,已知△ABE≌△ADF.⑴在图中,可以通过平移、翻折、旋转中的哪一种方法,使△ABE变到△ADF的位置;⑵线段BE与DF有什么关系?证明你的结论.二、全等三角形判定SSSC DB CDD如图,已知点E C,在线段BF上,BE=CF,AB=DE,AC=DF.求证:ABC DEF△≌△.如图,A C=B D,CB=A D.求证:∠BAD=∠ABC.已知:如图,AD=BC,AC=BD.求证:OD=OCCEB FDAOD CAADBFECA BCFECA BDE三、全等三角形判定SAS已知AD AE AB AC ==,.试说明:B C =∠∠;(江津区)如图,在△ABE 中,AB =AE,AD =AC,∠BAD =∠EAC, BC 、DE 交于点O. 求证: △ABC ≌△AED ;如图,△ABC 中,∠C=90度,AC=BC ,D 为AB 中点,AE=CF , 求证:DE=DF ,四边形CEDF 面积为定值在ABC △中,AB AC =,点D 是直线BC 上一点(不与B C 、重合),以AD 为一边在AD 的右侧..作ADE △,使AD AE DAE BAC =∠=∠,,连接CE .(1)如图1,当点D 在线段BC 上,如果90BAC ∠=°,则BCE ∠= 度; (2)设BAC α∠=,BCE β∠=.O C EBD A FE D CB AA BC D E①如图2,当点D 在线段BC 上移动,则αβ,之间有怎样的数量关系?请说明理由; ②当点D 在直线BC 上移动,则αβ,之间有怎样的数量关系?请直接写出你的结论.已知Rt ABC △中,90AC BC C D ==︒,∠,为AB 边的中点,90EDF ∠=°,EDF ∠绕D 点旋转,它的两边分别交AC 、CB (或它们的延长线)于E 、F . 当EDF ∠绕D 点旋转到DE AC ⊥于E 时(如图1),易证12DEF CEF ABC S S S +=△△△.当EDF ∠绕D 点旋转到DE AC 和不垂直时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,DEF S △、CEF S △、ABC S △又有怎样的数量关系?请写出你的猜想,不需证明.(2009年重庆)如图,在等腰Rt ABC △中,908C AC ∠==°,,F 是AB 边上的中点,点D 、E 分别在AC 、BC 边上运动,且保持AD CE =.连接DE 、DF 、EF .在此运动变化的过程中,下列结论: ①DFE △是等腰直角三角形; ②四边形CDFE 不可能为正方形, ③DE 长度的最小值为4;④四边形CDFE 的面积保持不变; ⑤△CDE 面积的最大值为8. 其中正确的结论是( ) A .①②③ B .①④⑤ C .①③④ D .③④⑤A EEA C C DB B 图1 图2 A A 备用图 BC B C备用图 AE CF BD图1图3ADFECBADBCE 图2F如图,扇形ODE 的圆心角为120,正三角形ABC 的中心恰好为扇形ODE 的圆心,且点B 在扇形ODE 内.(1)请连接OA OB 、,并证明AOF BOG △≌△;(2)求证:ABC △与扇形ODE 重叠部分的面积等于ABC △面积的13.如图:在△ABC 中,BE 、CF 分别是AC 、AB 两边上的高,在BE 上截取BD=AC ,在CF 的延长线上截取CG=AB ,连结AD 、AG 。
(完整版)全等三角形经典题型50题(含答案),推荐文档
E
∵∠ABD+∠ADB=90°,∠ACF+∠CDE=90°
又∵∠ADB=∠CDE
D
∴∠ABD=∠ACF 在△ABD 和△ACF 中 ∠ABD=∠ACF, AB=AC,
∠BAD=∠CAF=90° ∴△ABD≌△ACF(ASA) ∴BD=CF ∴BD=2CE
B
C
25、(10 分)如图:DF=CE,AD=BC,∠D=∠C。求证:△AED≌△
BFC。
D
EF
C
A
26、(10 分)如图:AE、BC 交于点 M,F 点在 AM 上, BE∥CF,BE=CF。 求证:AM 是△ABC 的中线。 证明: ∵BE‖CF ∴∠E=∠CFM,∠EBM=∠FCM ∵BE=CF
B
ቤተ መጻሕፍቲ ባይዱB A
F
M
C
E
∴△BEM≌△CFM
∴BM=CM ∴AM 是△ABC 的中线.
C
B
D
2. 已知:AC 平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE
6. 如图,四边形 ABCD 中,AB∥DC,BE、CE 分别平分∠ABC、∠BCD,且点 E 在 AD 上。求证:BC=AB+DC。
.
7.已知:AB//ED,∠EAB=∠BDE,AF=CD,EF=BC,求证:∠F=∠C
D
AC 是公共边,所以 AAS==>三角形 ADC 全等于三角形
ABC. 所以 BC 等于 DC,角 3 等于角 4,EC=EC 三角形
A
1 2
5 E6
3 4
C
DEC 全等于三角形 BEC 所以∠5=∠6
13.已知:如图,DC∥AB,且 DC=AE,E 为 AB 的中点,
中考数学复习《全等三角形》专题训练-附带有答案

中考数学复习《全等三角形》专题训练-附带有答案一、选择题1.如图,△ABC≌△EFD,且AB=EF,EC=4,CD=3,则AC等于()A.3 B.4 C.7 D.82.某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事方法是()A.带①去B.带②去C.带③去D.①②③都带去3.如图,为了测量B点到河对面的目标A之间的距离,在B点同侧选择了一点C,测得∠ABC=60°,∠ACB= 40°然后在BC的同侧找到点M使∠MBC=60°,∠MCB=40°,得到△MBC≌△ABC,所以测得MB的长就是A,B两点间的距离,这里判定△MBC≌△ABC的理由是()A.SAS B.AAA C.SSS D.ASA4.如图,在△ABC中,BE是∠ABC的平分线,CE是外角∠ACM的平分线,BE与CE相交于点E,若∠A=60°,则∠BEC是()A.15°B.30°C.45°D.60°5.如图,BP是∠ABC的平分线,AP⊥BP于P,连接PC,若△ABC的面积为1cm2则△PBC的面积为().A.0.4 cm2B.0.5 cm2C.0.6 cm2D.不能确定6.如图,OP平分∠AOB,PA⊥OA,PB⊥OB垂足分别为A,B,下列结论中不一定成立是()A.PA=PB B.PO平分∠APBC.OA=OB D.AB垂直平分OP7.如图,△ABC中∠ACF、∠EAC的角平分线CP、AP交于点P,延长BA、BC,PM⊥BE,PN⊥BF.则下列结论中正确的个数()①BP平分∠ABC ②∠ABC+2∠APC=180°③∠CAB=2∠CPB④S△PAC=S△MAP+S△NCP.A.1个B.2个C.3个D.4个8.如图,已知∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F,AB=6,AC=3,则BE=()A.6 B.3 C.2 D.1.5二、填空题9.如图BA=BE,∠1=∠2要使△ABD≌△EBC还需添加一个条件是.(只需写出一种情况)10.如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等的三角形的对数是.11.如图,在Rt△ABC,∠C=90°,E是AB上一点,且BE=BC,DE⊥AB于点E,若AC=8,则AD+DE的值为.12.如图,在△ABC中AB=AC,BF=CD,BD=CE,∠FDE=70°那么∠A的大小等于度.13.如图,在△ABC中,CD平分∠ACB交AB于点D,DE⊥AC交于点E,DF⊥BC于点F,且BC=4,DE=2,则△BCD的面积是.三、解答题14.如图,AD平分∠BAC,∠B=∠C.(1)求证:BD=CD;(2)若∠B=∠BDC=100°,求∠BAD的度数.15.如图,已知,EC=AC,∠BCE=∠DCA,∠A=∠E.(1)求证:BC=DC;(2)若∠A=25°,∠D=15°,求∠ACB的度数.16.如图,AB=AC,AD=AE,∠BAC=∠DAE.(1)求证:△ABD≌△ACE;(2)若∠1=25°,∠2=30°,求∠3的度数.17.如图,△ABD、△AEC都是等边三角形,直线CD与直线BE交于点F.(1)求证:CD=BE;(2)求∠CFE的度数.18.如图,在△AOB和△COD中OA=OB,OC=OD,OA<OC,∠AOB=∠COD=36°连接AC、BD交于点M,连接OM.求证:(1)∠AMB=36°;(2)MO平分∠AMD.参考答案1.C2.C3.D4.B5.B6.D7.D8.D9.BD =BC 或∠A =∠E 或∠C =∠D (任填一组即可)10.411.812.4013.414.(1)证明:∵AD 平分∠BAC∴∠BAD =∠CAD .在△ABD 和△ACD 中{∠BAD =∠CAD ∠B =∠C AD =AD∴△ABD ≌△ACD(AAS)∴BD =CD .(2)解:由(1)得:△ABD ≌△ACD∴∠C =∠B =100°,∠BAD =∠CAD∵∠BAC +∠B +∠BDC +∠C =360°∴∠BAC =60°∴∠BAD =30°15.(1)证明:∵∠BCE =∠DCA∴∠BCE +∠ACE =∠DCA +∠ECA即∠BCA =∠DCE .在△BCA 和△DCE 中{∠BCA =∠DCE AC =EC ∠A =∠E∴△BCA ≌△DCE (ASA )∴BC =DC ;(2)解:∵△BCA ≌△DCE∴∠B =∠D =15°.∵∠A =25°∴∠ACB =180°−∠A −∠B =140°.16.(1)证明:∵∠BAC =∠DAE∴∠BAC ﹣∠DAC =∠DAE ﹣∠DAC∴∠1=∠EAC在△ABD 和△ACE 中{AB =AC ∠1=∠EAC AD =AE∴△ABD ≌△ACE (SAS )(2)解:∵△ABD ≌△ACE∴∠ABD =∠2=30°∵∠1=25°∴∠3=∠1+∠ABD =25°+30°=55°.17.(1)证明:∵△ABD 、△AEC 都是等边三角形∴AD=AB ,AC=AE ,∠DAB=∠DBA=∠ADB=60°,∠CAE=60°∵∠DAB=∠DAC+∠CAB ,∠CAE=∠BAE+∠CAB∴∠DAC=∠BAE在△DAC 和△BAE 中{AD =AB ∠DAC =∠BAE AC =AE∴△DAC ≌△BAE∴CD=BE(2)解:∵△DAC ≌△BAE∴∠ADC=∠ABE∴∠CFE=∠BDF+∠DBF=∠BDF+∠DBA+∠ABF=∠BDF+∠DBA+∠ADC=∠BDA+∠DBA=60°+60°=120°18.(1)解:证明:∵∠AOB=∠COD=36°∴∠AOB+∠BOC=∠COD+∠BOC,即∠AOC=∠BOD 在△AOC和△BOD中{OA=OB ∠AOC=∠BOD OC=OD∴△AOC≌△BOD(SAS)∴∠OAC=∠OBD∵∠AEB是△AOE和△BME的外角∴∠AEB=∠AMB+∠OBD=∠AOB+∠OAC∴∠AMB=∠AOB=36°;(2)解:如图所示,作OG⊥AC于G,OH⊥BD于H∴OG是△AOC中AC边上的高,OH是△BOD中BD边上的高由(1)知:△AOC≌△BOD∴OG=OH∴点O在∠AMD的平分线上即MO平分∠AMD.。
全等三角形经典题型汇集(培优专练)

;
(2)如图 2,当点 E,F 分别在 CB,DC 的延长线上,CF=2 时,求△CEF 的周长;
拓展提升:
如图 3,在 Rt△ABC 中,∠ACB=90°,CA=CB,过点 B 作 BD⊥BC,连接 AD,在 BC 的延长线上取一 点 E,使∠EDA=30°,连接 AE,当 BD=2,∠EAD=45°时,请直接写出线段 CE 的长度.
7.阅读下面材料:
小炎遇到这样一个问题:如图 1,点 E、F 分别在正方形 ABCD 的边 BC,CD 上,∠EAF=45°,连结 EF,则 EF=BE+DF, 试说明理由.
小炎是这样思考的:要想解决这个问题,首先应想办法将 这些分散的线段相对集中.她先后尝试了翻折、旋转、平 移的方法,最后发现线段 AB,AD 是共点并且相等的,于是找到解决问题的方法.她的方法是将△ABE 绕着 点 A 逆时针旋转 90°得到△ADG,再利用全等的知识解决了这个问题(如图 2).
2.阅读下面材料:
数学课上,老师给出了如下问题:如图,AD 为△ABC 中线,点 E 在 AC 上,BE 交 AD 于点 F,AE=EF.求 证:AC=BF. 经过讨论,同学们得到以下两种思路:
思路一如图①,添加辅助线后依据 SAS 可证得△ADC≌△GDB,再利用 AE =EF 可以进一步证得∠G=∠FAE=∠AFE=∠BFG,从而证明结论.
3.如图,分别以 ABC 的边向外作正方形 ABFG 和 ACDE,连接 EG,若 O 为 EG 的中点,
求证:(1) AO 1 BC ;(2) AO BC . 2
4.如图所示,已知 ⶠࢼ 中, 平分 ⶠ ࢼ, 、 分别在 ⶠ 、 上.
ࢼ,
ࢼ.求证: ∥ ⶠ.
5.如图所示, ⶠ ࢼ
全等三角形的判定常考典型例题及练习

全等三角形的判定常考典型例题及练习三角形是我们初中数学中最基础的概念之一。
在学习三角形的过程中,我们经常会遇到一个重要的概念,即全等三角形。
全等三角形即指两个三角形的对应边长相等,对应角度相等。
在考试中,我们经常会被要求判定两个三角形是否全等。
下面,我将列出一些常见的全等三角形判定例题,并提供一些练习题供大家巩固。
一、例题例题1:已知△ABC和△DEF,已知∠A=∠D,∠B=∠E,AB=DE,判断△ABC≌△DEF。
解析:根据题目给出的信息,∠A=∠D,∠B=∠E,AB=DE,我们可以得出两个对应角相等,一个对应边相等。
根据全等三角形的定义,可以得出△ABC≌△DEF。
例题2:已知△ABC,边AB=5cm,边AC=3cm,边BC=4cm。
△DEF为△ABC的内接三角形,判断△ABC≌△DEF。
解析:由题意可知,△DEF是△ABC的内接三角形,即DEF的三条边分别平行且等于ABC的三条边。
根据题意,我们可以得出DE=5cm,DF=3cm,EF=4cm。
而三个边长相等,因此根据全等三角形的定义,可以得出△ABC≌△DEF。
二、练习题1. 已知△ABC和△DEF,已知∠A=∠D,∠B=∠E,AB=DE+2,判断△ABC≌△DEF。
2. 已知△ABC,边AB=6cm,边AC=8cm,边BC=10cm。
△DEF 为△ABC的外接三角形,判断△ABC≌△DEF。
3. 已知△ABC和△DEF,已知∠A=∠D,∠B=∠E,AB=DE,AC=DF,判断△ABC≌△DEF。
4. 已知△ABC和△DEF,已知∠A=∠D,∠B=∠E,AC=DF,判断△ABC≌△DEF。
5. 已知△ABC,边AB=5cm,边AC=7cm,边BC=9cm。
△DEF为△ABC的内切三角形,判断△ABC≌△DEF。
以上是一些常见的全等三角形判定例题及练习题。
在解答这些题目时,我们需要熟练掌握全等三角形的定义和判定条件,根据题目给出的信息进行推理和判断。
专题 全等三角形的应用---动点运动问题(30题)(解析版)

八年级上册数学《第十二章 全等三角形》专题 全等三角形的应用---动点运动问题(30题)1.(2023春•虹口区校级期末)如图,AB =8,BC =10,CD 为射线,∠B =∠C ,点P 从点B 出发沿BC 向点C 运动,速度为1个单位/秒,点Q 从点C 出发沿射线CD 运动,速度为x 个单位/秒;若在某时刻,△ABP 能与△CPQ 全等,则x = .【分析】设点P 、Q 的速度为ts ,分两种情形构建方程即可解决问题.【解答】解:设点P 、Q 的速度为ts ,分两种情形讨论:①当AB =PC ,BP =CQ 时,△ABP ≌△PCQ ,即8=10﹣t ,解得:t =2,∴2x =2×1,∴x =1;②当BP =PC ,AB =CQ 时,△ABP ≌△QCP ,即t =12×10=5,∴5x =8,x =85,综上所述,x =1或85,故答案为:1或85.【点评】本题考查全等三角形的判定、路程、速度、时间之间的关系等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型.2.(2022秋•攸县期末)如图,在四边形ABCD 中,∠DAB =∠ABC ,AB =5cm ,AD =BC =3cm ,点E 在线段AB上以1cm/s的速度由点A向点B运动,同时,点F在线段BC上由点B向点C运动.设运动时间为t(s),当△ADE与以B,E,F为顶点的三角形全等时,则点F的运动速度为 cm/s.【分析】设点F的运动速度为xcm/s,则AE=tcm,BE=(5﹣t)cm,BF=xtcm,由于∠DAB=∠ABC,则当AD=BE,AE=BF时,根据“SAS”判断△ADE≌△BEF,即5﹣t=3,t=xt;当AD=BF,AE=BE 时,根据“SAS”判断△ADE≌△BFE,即xt=3,t=5﹣t,然后分别解方程求出x即可.【解答】解:设点F的运动速度为xcm/s,则AE=tcm,BE=(5﹣t)cm,BF=xtcm,∵∠DAB=∠ABC,∴当AD=BE,AE=BF时,根据“SAS”判断△ADE≌△BEF,即5﹣t=3,t=xt,解得t=2,x=1;当AD=BF,AE=BE时,根据“SAS”判断△ADE≌△BFE,即xt=3,t=5﹣t,解得t=2.5,x=1.2,综上所述,点F的运动速度为1或1.2cm/s.故答案为:1或1.2.【点评】本题考查了全等三角形的判定:熟练掌握全等三角形的5种判定方法是解决问题的关键.选用哪一种方法,取决于题目中的已知条件.3.(2022春•普宁市期末)如图,∠A=∠B=90°,AB=60,E,F分别为线段AB和射线BD上的一点,若点E从点B出发向点A运动,同时点F从点B出发向点D运动,二者速度之比为3:7,运动到某时刻同时停止,在射线AC上取一点G,使△AEG与△BEF全等,则AG的长为 .【分析】设BE=3t,则BF=7t,使△AEG与△BEF全等,由∠A=∠B=90°可知,分两种情况:情况一:当BE=AG,BF=AE时,列方程解得t,可得AG;情况二:当BE=AE,BF=AG时,列方程解得t,可得AG.【解答】解:设BE=3t,则BF=7t,因为∠A=∠B=90°,使△AEG与△BEF全等,可分两种情况:情况一:当BE=AG,BF=AE时,∵BF=AE,AB=60,∴7t=60﹣3t,解得:t=6,∴AG=BE=3t=3×6=18;情况二:当BE=AE,BF=AG时,∵BE=AE,AB=60,∴3t=60﹣3t,解得:t=10,∴AG=BF=7t=7×10=70,综上所述,AG=18或AG=70.故答案为:18或70.【点评】本题主要考查了全等三角形的性质,利用分类讨论思想是解答此题的关键.4.如图,△ABC中,AB=AC=24cm,BC=16cm,AD=BD.如果点P在线段BC上以2cm/s的速度由B 点向C点运动,同时,点Q在线段CA上以vcm/s的速度由C点向A点运动,那么当△BPD与△CQP 全等时,v=( )A.3B.4C.2或4D.2或3【分析】表示出BD、BP、PC、CQ,再根据全等三角形对应边相等,分①BD、PC是对应边,②BD 与CQ是对应边两种情况讨论即可.【解答】解:∵AB=AC=20cm,BC=16cm,点D为AB的中点,∴BD=12×24=12cm,设点P、Q的运动时间为t,则BP=2t,PC=(16﹣2t)c①当BD=PC时,16﹣2t=12,解得:t=2,则BP=CQ=2t=4,故点Q的运动速度为:4÷2=2(厘米/秒);②当BP=PC时,∵BC=16cm,∴BP=PC=8cm,∴t=8÷2=4(秒),故点Q的运动速度为12÷4=3(厘米/秒);故选:D.【点评】本题考查了全等三角形的对应边相等的性质,等边对等角的性质,根据对应角分情况讨论是本题的难点.5.如图,已知长方形ABCD中,AD=8cm,AB=6cm,点E为AD的中点.若点P在线段AB上以2cm/s 的速度由点A向点B运动.同时,点Q在线段BC上由点C向点B运动,若△AEP与△BPQ全等,则点Q的运动速度是( )A.2或83B.6或83C.2或6D.1或23【分析】设Q运动的速度为xcm/s,则根据△AEP与△BQP得出AP=BP、AE=BQ或AP=BQ,AE=BP,从而可列出方程组,解出即可得出答案.【解答】解:∵长方形ABCD,∴∠A=∠B=90°,∵点E为AD的中点,AD=8cm,∴AE=4cm,设点Q的运动速度为xcm/s,①经过y秒后,△AEP≌△BQP,则AP=BP,AE=BQ,2y=6−2y4=8−xy,解得,x=83 y=32,即点Q的运动速度83cm/s时能使两三角形全等.②经过y秒后,△AEP≌△BPQ,则AP=BQ,AE=BP,2y=8−xy4=6−2y,解得:x=6 y=1,即点Q的运动速度6cm/s时能使两三角形全等.综上所述,点Q的运动速度83或6cm/s时能使两三角形全等.故选:B.【点评】本题考查全等三角形的判定及性质,涉及了动点的问题使本题的难度加大了,解答此类题目时,要注意将动点的运用时间t和速度的乘积当作线段的长度来看待,这样就能利用几何知识解答代数问题了.6.(2022秋•高邑县期中)如图,在Rt△ABC中,AC=6,BC=8,AB=10.点P从点A出发,以每秒2个单位长度的速度沿折线A﹣C﹣B向终点B运动,同时点Q从点B出发,以每秒3个单位长度的速度沿折线B﹣C﹣A向终点A运动,点P,Q都运动到各自的终点时停止.设运动时间为t(秒),直线l经过点C,且l∥AB,过点P,Q分别作直线l的垂线段,垂足为E,F.当△CPE与△CQF全等时,t的值不可能是( )A.2B.2.8C.3D.6【分析】分三种情况讨论得出关于t的方程,解方程求得t的值.【解答】解:当P在AC上,Q在BC上时,如图,过点P,Q,C分别作PE⊥直线l于点E,QF⊥直线l于点F,CD⊥AB于点D,∵∠ACB=90,∴∠PCE+∠QCF=90°,∵PE⊥l于E,QF⊥l于F.∴∠EPC+∠PCE=90°,∠PEC=∠CFQ=90°,∴∠EPC=∠QCF,∵△PCE≌△CQF,∴PC=CQ,∴6﹣2t=8﹣3t,解得t=2;当P在AC上,Q在AC上时,即P、Q重合时,则CQ=PC,由题意得,6﹣2t=3t﹣8,解得t=2.8;当P在BC上,Q在AC上时,即A、Q重合时,则CQ=AC=6,由题意得,2t﹣6=6,解得t=6.综上,当△CPE与△CQF全等时,t的值为2或2.8或6.∴t的值不可能是3.故选:C.【点评】本题考查了三角形全等的判定和性质、作图﹣基本作图、平行线之间的距离、勾股定理,根据题意得出关于t的方程是解题的关键.7.(2022秋•浠水县校级期中)如图,在△ABC中,AB=AC,∠BAC=90°,BC=6cm,直线CM⊥BC,动点D从点C开始沿射线CB方向以每秒2cm的速度运动,动点E也同时从点C开始在直线CM上以每秒1cm的速度运动,连接AD、AE,设运动时间为t秒.当△ABD≌△ACE时,t的值为( )A.2B.4C.6D.2或6【分析】当点E在射线CM上时,D在CB上,BD=CE,当点E在CM的反向延长线上时DB=CE,由全等三角形的性质求出其解即可.【解答】解:∵△ABD≌△ACE,∴AD=AE,AB=AC,BD=CE.如图,当点E在射线CM上时,D在CB上,BD=CE,∵CE=t,BD=6﹣2t,∴6﹣2t=t,∴t=2.如图,当点E在CM的反向延长线上时DB=CE,∵CE=t,BD=2t﹣6,∴t=2t﹣6,∴t=6.综上所述,当t=2或6时,△ABD≌△ACE,故选:D.【点评】本题考查了全等三角形的性质的运用,等腰三角形的性质的运用,三角形的面积公式的运用,解答时分类讨论是重点也是难点.8.(2023春•和平区校级期中)如图,已知Rt△ABC中,∠ACB=90°,满足AC=7,BC=12,点P从A 点出发沿A→C→B路径向终点B运动:点Q从B出发沿B→C→A路径向终点A运动;点P,Q的速度分别以每秒1个单位长度和每秒3个单位长度的速度同时开始运动,两个点都要到达相应的终点时才能停止运动,分别过P,Q作PE⊥l于E,QF⊥l于F.设运动时间为t秒,当以P,E,C为顶点的三角形与以Q,F,C为顶点的三角形全等时,t的值为 (不考虑两三角形重合的情况).【分析】三角形PEC和三角形QFC要全等,P的对应顶点是C,有两种情况:一种是点P在AC上,点P在BC上时;另一种是点Q到达终点,而P在BC上时,先把各线段的长度表示出来,再让对应边相等,即可构造方程解出t.【解答】解:①当点P在线段AC上,点P在线段BC上时;如图:当△PCE≌CQF时,∠QCF=∠EPC,∴PC=CQ.由题意知:AP=t,PC=7﹣t,BQ=3t,CQ=12﹣3t;∴7﹣t=12﹣3t,解得t=2.5.②当P在线段BC上,点Q到达终点时,如图:当△PCE≌CQF时,∠QCF=∠EPC,∴PC=CQ.由题意知:AP=t,PC=t﹣7,CQ=7,∴t﹣7=7,解得t=14.综上所述,t的值为2.5或14.【点评】本题考查全等三角形的性质,找到全等三角形的对应边是解题的关键.9.如图,在△ABC中,BC=8cm,AG∥BC,AG=8cm,点F从点B出发,沿线段BC以4cm/s的速度连续做往返运动,点E从点A出发沿线段AG以2cm/s的速度运动至点G,E、F两点同时出发,当点E到达点G时,E、F两点同时停止运动,EF与直线AC交于点D,设点E的运动时间为t(秒)(1)分别写出当0<t<2和2<t<4时段BF的长度(用含t的代数式表示)(2)当BF=AE时,求t的值;(3)当△ADE≌△CDF时,直接写出所有满足条件的t值.【分析】(1)根据点F从点B出发、点E从点A出发的速度、结合图形解答;(2)根据题意列出方程,解方程即可;(3)分点E从点A运动至点G、从点G返回两种情况,根据全等三角形的性质列式计算即可.【解答】解:(1)当0<t≤2时,BF=4t,当2<t≤4时,BF=16﹣4t;(2)由题意得,16﹣4t=2t,解得t=8 3;(3)当0<t≤2时,△ADE≌△CDF,则AE=CF,即8﹣4t=2t,解得t=4 3,当2<t≤4时,△ADE≌△CDF,则AE=CF,即4t﹣8=2t,解得t=4,则t=43或4时,△ADE≌△CDF.【点评】本题考查的是全等三角形的性质的应用,根据题意求出函数关系式、掌握全等三角形的对应边相等是解题的关键.10.在Rt△ABC中,∠C=90°,AC=10cm,BC=5cm,P,Q两点分别在AC上和过点A且垂直于AC的射线AM上运动,且PQ=AB,问P点运动到AC上什么位置时△ABC才能和△QPA全等.【分析】本题要分情况讨论:①Rt△APQ≌Rt△CBA,此时AP=BC=5cm,可据此求出P点的位置.②Rt△QAP≌Rt△BCA,此时AP=AC,P、C重合.【解答】解:根据三角形全等的判定方法HL可知:①当P运动到AP=BC时,∵∠C=∠QAP=90°,在Rt△ABC与Rt△QPA中,AP=BCPQ=AB∴Rt△ABC≌Rt△QPA(HL),即AP=BC=5cm;②当P运动到与C点重合时,AP=AC,在Rt△ABC与Rt△QPA中,AP=ACPQ=AB,∴Rt△QAP≌Rt△BCA(HL),即AP=AC=10cm,∴当点P与点C重合时,△ABC才能和△APQ全等.综上所述,当P运动到AP=BC、点P与点C重合时,△ABC才能和△APQ全等.【点评】本题考查三角形全等的判定方法和全等三角形的性质,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.由于本题没有说明全等三角形的对应边和对应角,因此要分类讨论,以免漏解.11.(2023春•吉安县期末)如图,△ABC中,D为AB的中点,AD=5厘米,∠B=∠C,BC=8厘米.(1)若点P在线段BC上以3厘米/秒的速度从点B向终点C运动,同时点Q在线段CA上从点C向终点A运动,若点Q的速度与点P的速度相等,经1秒钟后,请说明△BPD≌△CQP;(2)若点P以3厘米/秒的速度从点B向点C运动,同时点Q以5厘米/秒的速度从点C向点A运动,它们都依次沿△ABC三边运动,则经过多长时间,点Q第一次在△ABC的哪条边上追上点P?【分析】(1)根据等腰三角形的性质得到∠B=∠C,再加上BP=CQ=3,PC=BD=5,则可判断△BPD 与△CQP全等;(2)设经过x秒后,点Q第一次追上点P,由题意得5x﹣3x=2×10,解方程得到点P运动的路程为3×10=30,得到此时点P在BC边上,于是得到结果.【解答】解:(1)∵BP=3×1=3,CQ=3×1=3,∴BP=CQ,∵D为AB的中点,∴BD=AD=5,∵CP=BC﹣BP=5,∴BD=CP,在△BPD与△CQP中,BD=CP∠B=∠C,BP=CQ∴△BPD≌△CQP(SAS);(2)设经过x秒后,点Q第一次追上点P,由题意得5x﹣3x=2×10,解得:x=10,∴点P运动的路程为3×10=30,∵30=28+2,∴此时点P在BC边上,∴经过10秒,点Q第一次在BC边上追上点P.【点评】本题考查了全等三角形的判定和性质,找准对应边是解题的关键.12.如图,∠BAC=90°,AB=22,AC=28.点P从B点出发沿B→A→C路径向终点C运动;点Q从C 点出发沿C→A→B路径向终点B运动.点P和Q分别以每秒2和3个单位的速度同时开始运动,只要有一点到达相应的终点时两点同时停止运动;在运动过程中,分别过P和Q作PF⊥l于F,QG⊥l于G.问:点P运动多少秒时,△PFA与△QAG全等?【分析】分类讨论:当点P在BA上,点Q在AC上,如图1,则PB=2t,CQ=3t,AP=22﹣2t,AQ=28﹣3t,利用三角形全等得PA=AQ,即22﹣2t=28﹣3t;当点P、Q都在AB上,即P点和Q点重合时,△PFA与△QAG全等,此时2t+3t﹣28=22,当点P在AC上,点Q在AB上,如图2,则PA=2t﹣22,AQ=3t﹣28,由PA=AQ,即2t﹣22=3t﹣28;当点Q停在点B处,点P在AC上,由PA=QA得2t﹣22=22,然后分别解方程求出t,再根据题意确定t的值.【解答】解:设P、Q点运动的时间为t,(1)当点P在BA上,点Q在AC上,如图1,则PB=2t,CQ=3t,AP=22﹣2t,AQ=28﹣3t,∵△PFA与△QAG全等,∴PA=AQ,即22﹣2t=28﹣3t,解得t=6,即P运动6秒时,△PFA与△QAG全等;(2)当点P、Q都在AB上,即P点和Q点重合时,△PFA与△QAG全等,此时2t+3t﹣28=22,解得t=10,(3)当点P在AC上,点Q在AB上,如图2,则PA=2t﹣22,AQ=3t﹣28,∵△PFA与△QAG全等,∴PA=AQ,即2t﹣22=3t﹣28,解得t=6(舍去);当点Q停在点B处,点P在AC上,由PA=QA得2t﹣22=22,解得t=22,舍去.综上所述:当t等于6秒或10秒时,△PFA与△QAG全等.【点评】本题考查了全等三角形的判定:全等三角形的5种判定方法中,选用哪一种方法,取决于题目中的已知条件,若已知两边对应相等,则找它们的夹角或第三边;若已知两角对应相等,则必须再找一组对边对应相等,且要是两角的夹边,若已知一边一角,则找另一组角,或找这个角的另一组对应邻边.对于动点问题常利用代数的方法解决.13.(2022秋•苍溪县期末)如图,AE与BD相交于点C,AC=EC,BC=DC,AB=8cm,点P从点出发,沿A→B→A方向以2cm/s的速度运动,点Q从点D出发,沿D→E方向以lcm/s的速度运动,P、Q两点同时出发,当点P到达点A时,P、Q两点同时停止运动,设点P的运动时间为t(s).(1)求证:AB∥DE.(2)写出线段AP的长(用含t的式子表示).(3)连接PQ,当线段PQ经过点C时,求t的值.【分析】(1)证明△ABC≌△EDC(SAS),可得∠A=∠E,然后根据内错角相等两直线平行即可得出结论;(2)分两种情况讨论:当0≤t≤4时,AP=2tcm,当4<t≤8时,BP=(2t﹣8)cm,可得AP=8﹣(2t﹣8)=(16﹣2t)cm,进而可以解决问题;(3)先证△ACP≌△ECQ(ASA),得AP=EQ,再分两种情况列方程求解即可.【解答】(1)证明:在△ABC和△EDC中,AC=EC∠ACB=∠ECD,BC=DC∴△ABC≌△EDC(SAS),∴∠A=∠E,∴AB∥DE;(2)解:当0≤t≤4时,AP=2tcm,当4<t≤8时,BP=(2t﹣8)cm,∴AP=8﹣(2t﹣8)=(16﹣2t)cm,∴线段AP的长为2tcm或(16﹣2t)cm;(3)解:根据题意得DQ =tcm ,则EQ =(8﹣t )cm ,由(1)得:∠A =∠E ,ED =AB =8cm ,在△ACP 和△ECQ 中,∠A =∠E AC =EC ∠ACP =∠ECQ,∴△ACP ≌△ECQ (ASA ),∴AP =EQ ,当0≤t ≤4时,2t =8﹣t ,解得:t =83;当4<t ≤8时,16﹣2t =8﹣t ,解得:t =8;综上所述,当线段PQ 经过点C 时,t 的值为83或8.【点评】本题考查了全等三角形的判定与性质,列代数式,一元一次方程的应用,解决本题的关键是得到△ACP ≌△ECQ .14.如图,在等腰△ABC 中,AB =AC =6cm ,BC =10cm ,点P 从点B 出发,以2cm /s 的速度沿BC 向点C 运动,设点P 的运动时间为ts .(1)PC = cm .(用t 的代数式表示)(2)当点P 从点B 开始运动,同时,点Q 从点C 出发,以vcm /s 的速度沿CA 向点A 运动,是否存在这样v 的值,使得△ABP 与△PQC 全等?若存在,请求出v 的值;若不存在,请说明理由.【分析】(1)根据P 点的运动速度可得BP 的长,再利用BC ﹣BP 即可得到CP 的长;(2)此题主要分两种情况①当BP =CQ ,AB =PC 时,△ABP ≌△PCQ ;当BA =CQ ,PB =PC 时,△ABP ≌△QCP ,然后分别计算出t 的值,进而得到v 的值.【解答】解:(1)依题意,得PC=(10﹣2t)(cm).故答案为:10﹣2t;(2)①当BP=CQ,AB=PC时,△ABP≌△PCQ,∵AB=6cm,∴PC=6(cm),∴BP=10﹣6=4(cm),2t=4,解得:t=2,CQ=BP=4(cm),v×2=4,解得:v=2;②当BA=CQ,PB=PC时,△ABP≌△QCP,∵PB=PC,∴BP=PC=12BC=5(cm),2t=5,解得:t=2.5,CQ=BP=6(cm),v×2.5=6,解得:v=2.4.综上所述:当v=2.4或2时△ABP与△PQC全等.【点评】此题主要考查了全等三角形的判定,关键是掌握全等三角形全等的条件,找准对应边.15.如图,已知△ABC中,AB=AC=6cm,∠B=∠C,BC=4cm,点D为AB的中点.(1)如果点P在线段BC上以1cm/s的速度由点B向C运动,同时,点Q在线段CA上由点C向A运动,①若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等?请说明理由;②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?(2)若点Q以(1)②中的运动速度从点C出发,点P以1cm/s的运动速度从B同时出发,都逆时针沿△ABC三边运动,则经过 秒后,点P与点Q第一次在△ABC上相遇.(在横线上直接写出答案,不必书写解题过程)【分析】(1)①根据时间和速度分别求得两个三角形中BP、CQ和BD、PC边的长,根据SAS判定两个三角形全等.②根据全等三角形应满足的条件探求边之间的关系,再根据路程=速度×时间公式,先求得点P运动的时间,再求得点Q的运动速度;(2)根据题意结合图形分析发现:由于点Q的速度快,且在点P的前边,所以要想第一次相遇,则应该比点P多走等腰三角形的两个边长.【解答】解:(1)①△BPD≌△CQP,理由如下:∵t=1秒,∴BP=CQ=1×1=1cm,∵AB=6cm,点D为AB的中点,∴BD=3cm.又∵PC=BC﹣BP,BC=4cm,∴PC=4﹣1=3cm,∴PC=BD.又∵AB=AC,∴∠B=∠C,∴△BPD≌△CQP;②假设△BPD≌△CQP,∵v P≠v Q,∴BP≠CQ,又∵△BPD≌△CQP,∠B=∠C,则BP=CP=2,BD=CQ=3,∴点P,点Q运动的时间t=BP1=2秒,∴v Q=CQt=32=1.5cm/s;(2)设经过x秒后点P与点Q第一次相遇,由题意,得 1.5x=x+2×6,解得x=24,∴点P共运动了24s×1cm/s=24cm.∵24×1.5=36,∴点P、点Q在AC边上相遇,∴经过24秒点P与点Q第一次在边AC上相遇.【点评】此题主要是运用了路程=速度×时间的公式.熟练运用全等三角形的判定和性质,能够分析出追及相遇的问题中的路程关系.16.(2022秋•聊城月考)如图,已知四边形ABCD中,AB=10厘米,BC=8厘米,CD=12厘米,∠B=∠C,点E为AB的中点.如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPE与△CQP是否全等?请说明理由.(2)当点Q的运动速度为多少时,能够使△BPE与△CQP全等.【分析】(1)经过1秒后,可得BP=CQ=3厘米,则PC=8﹣3=5厘米,可证明△BPE≌△CQP;(2)由△BPE与△CQP全等可知有△BEP≌△CQP或△BEP≌△CPQ,全等可得BP=CP或BP=CQ,或可求得BP的长,可求得P点运动的时间,由CQ=BE或CQ=BP可求得Q点运动的路程,可求得其速度.【解答】解:(1)△BPE与△CQP全等,理由如下:当运动1秒后,则BP=CQ=3厘米,∴PC=BC﹣BP=8﹣3=5厘米,∵E为AB中点,且AB=10厘米∴BE=5厘米,∴BE=PC,在△BPE和△CQP中BE=PC∠B=∠CBP=CQ∴△BPE≌△CQP(SAS);(2)∵△BPE与△CQP全等,∴△BEP≌△CQP或△BEP≌△CPQ,当△BEP≌△CQP时,则BP=CP,CQ=BE=5厘米,设P点运动的时间为t秒,则3t=8﹣3t,解得t=4 3,∴Q点的运动的速度=5÷43=154(厘米/秒),当△BEP≌△CPQ时,由(1)可知t=1(秒),∴BP=CQ=3厘米,∴Q点的运动的速度=3÷1=3(厘米/秒),即当Q点每秒运动154厘米或3厘米时△BEP≌△CQP.【点评】本题主要考查全等三角形的判定和性质,掌握全等三角形的判定是解题的关键,即SSS、SAS、ASA、AAS和HL17.如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,P,Q是边AC,BC上的两个动点,PD⊥AB于点D,QE⊥AB于点E,设点P,Q运动的时间是t秒(t>0).(1)若点P,Q分别从A,B两点同时出发,沿AC,BC向点C匀速运动,运动速度都为每秒1个单位,其中一点到达终点C后,另一点也随之停止运动,在运动过程中△APD和△QBE是否保持全等?判断并说明理由;(2)若点P从点C出发沿CA以每秒3个单位的速度向点A匀速运动,到达点A后立刻以原来的速度沿AC返回到点C停止运动;点Q仍从点B出发沿BC以每秒1个单位的速度向点C匀速运动,到达点C后停止运动,当t为何值时,△APD和△QBE全等?【分析】(1)根据∠C=90°,PD⊥AB,QE⊥AB,于是得到∠A+∠APD=∠A+∠B=90°,证得∠APD =∠B,∠ADP=∠QEB=90°,即可得到结论;(2)分两种情况:①0≤t<83时,点P从C到A运动,则AP=AC=CP=8﹣3t,BQ=t,求得t=2,②t≥83时,点P从A到C运动,则AP=3t﹣8,BQ=t,求得t=4.【解答】解:(1)△ADP≌△QBE,理由:∵∠C=90°,PD⊥AB,QE⊥AB,∴∠A+∠APD=∠A+∠B=90°,∴∠APD=∠B,∠ADP=∠QEB=90°,∵AP=BQ=t,在△ADP与△QBE中,∠APD=∠B∠ADP=∠QEB AP=BQ,∴△ADP≌△QBE;(2)①0≤t<83时,点P从C到A运动,则AP=AC=CP=8﹣3t,BQ=t,当△ADP≌△QBE时,则AP=BQ,即8﹣3t=t,解得:t=2,②t≥83时,点P从A到C运动,则AP=3t﹣8,BQ=t,当△ADP≌△QBE时,则AP=BQ,即3t﹣8=t,解得:t=4,综上所述:当t=2s或4s时,△ADP≌△QBE.【点评】本题考查了全等三角形的判定,解方程,垂直的定义,熟练掌握全等三角形的判定定理是解题的关键.18.如图,在长方形ABCD中,AD=6cm,AB=4cm,点E为AD的中点.若点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BC上由点B向点C运动.(注:长方形中,∠A=∠B=∠C=∠D=90°,AB=CD,AD=BC)(1)若点Q的运动速度与点P的运动速度相等:①经过1秒后,△AEP与△BPQ是否全等,请说明理由,并判断此时线段PE和线段PQ的位置关系;②设运动时间为t秒时,△PEQ的面积为Scm2,请用t的代数式表示S.(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为 cm/s时,能够使△AEP与△BPQ全等.【分析】(1)①当t=1时,AP=BQ,∠A=∠B,AE=PB,从而可证明△EAP≌Rt△PBQ;②当t≤4时,AP=BQ=t,S=S梯形AEQB﹣S AEP﹣S PBQ;当4<t≤6时,点P与点B重合,S=2t;(2)如图3所示:因为△AEP≌△BQP,所以AP=PB=2,AE=BQ=3,从而可求得t=2,点Q运动的速度为=3÷2=1.5cm/秒.【解答】解:(1)①当t=1时,AP=1,BQ=1,∴AP=BQ.∵E是AD的中点,∴AE=12AD=3.∵PB=AB=AP=4﹣1=3,∴AE=PB.在Rt△EAP和Rt△PBQ中,AE=PB ∠A=∠B AP=BQ,∴Rt△EAP≌Rt△PBQ.∴∠APE=∠BQP,∵∠BQP+∠BPQ=90°,∴∠APE+∠BPQ=90°,∴∠EPQ=90°,∴PE⊥PQ;②如图1所示连接QE.图1Ⅰ、当t≤4时,AP=BQ=t,S梯形AEQB =12(AE+BQ)•AB=12×4×(3+t)=2t+6.S△AEP =12AE•PA=12×3t=32t,S△PBQ=12PB•BQ=12×(4﹣t)t=2t−12t2.∴S=2t+6−32t﹣(2t−12t2).整理得:S=12t2−32t+6,如图2所示:Ⅱ、当4<t≤6时,点P与点B重合,S=12QB•AB=12×4×t=2t.∴S与t的函数关系式为S=2−32t+6(0<t≤4)<t≤6);(2)如图3所示:∵△AEP≌△BQP,PA≠BQ,∴AP=PB=2,AE=BQ=3.∴t=AP=12AB=12×4=2.∴点Q运动的速度为=3÷2=1.5cm/秒时,△AEP≌△BQP.故答案为:1.5.【点评】此题是四边形综合题,主要考查的是全等三角形的性质和判定、相似三角形的性质和判定、矩形的性质、函数的解析式、一元一次方程的综合应用,根据题意画出符合题意的图形是解题的关键.19.(2023春•碑林区校级期末)如图,△ABC的两条高AD与BE交于点O,AD=BD,AC=6.(1)求BO的长;(2)F是射线BC上一点,且CF=AO,动点P从点O出发,沿线段OB以每秒1个单位长度的速度向终点B运动,同时动点Q从点A出发,沿射线AC以每秒4个单位长度的速度运动,当点P到达点B时,P,Q两点同时停止运动,设运动时间为t秒,当△AOP与△FCQ全等时,求t的值.【分析】(1)由AAS证明Rt△BDO≌Rt△ADC,根据对应边相等求得BO的长;(2)分情况讨论点F分别在BC延长线上或在BC之间时△AOP≌△FCQ,根据对应边相等求得t值.【解答】解:(1)∵∠BOD=∠AOE,∠CAD+∠ACD=∠CAD+∠AOE=90°,∴∠ACD=∠AOE,∴∠BOD=∠ACD.又∵∠BDO=∠ADC=90,AD=BD,∴Rt△BDO≌Rt△ADC(AAS),∴BO=AC=6.(2)①当点F在BC延长线上时:设t时刻,P、Q分别运动到如图位置,△AOP≌△FCQ.∵CF=AO,∠AOP=∠EOD=180°﹣∠DCE=∠FCQ,∴当△AOP≌△FCQ时,OP=CQ.∵OP=t,CQ=6﹣4t,∴t=6﹣4t,解得t=1.2.②当点F在BC之间时:设t时刻,P、Q分别运动到如图位置,△AOP≌△FCQ.∵CF=AO,∠AOP=∠EOD=180°﹣∠DCE=∠FCQ,∴当△AOP≌△FCQ时,OP=CQ.∵OP=t,CQ=4t﹣6,∴t=4t﹣6,解得t=2.综上,t=1.2或2.【点评】本题考查全等三角形的判定.这部分内容是初中几何中非常重要的内容,一定要深刻理解,做到活学活用.20.如图1,长方形ABCD中,AB=CD=7cm,AD=BC=5cm,∠A=∠B=∠C=∠D=90°,点E在线段AB上以1cm/s的速度由点A向点B运动,与此同时点F在线段BC上由点B向点C运动,设运动的时间均为ts.(1)若点F的运动速度与点E的运动速度相等,当t=2时:①判断△BEF与△ADE是否全等?并说明理由;②求∠EDF的度数.(2)如图2,将图1中的“长方形ABCD”改为“梯形ABCD”,且∠A=∠B=70°,AB=7cm,AD=BC=5cm,其他条件不变.设点F的运动速度为xcm/s.是否存在x的值,使得△BEF与△ADE全等?若存在,直接写出相应的x及t的值;若不存在,请说明理由.【分析】(1)①根据SAS证明:△BEF≌△ADE;②由①:△BEF≌△ADE得DE=EF,∠BEF=∠ADE,证明△DEF是等腰直角三角形可得结论;(2)分两种情况:①如图2,当△DAE≌△EBF时,②如图3,当△ADE≌△BFE时,分别根据AD=BE,AE=BF,列方程组可得结论.【解答】解:(1)①△BEF≌△ADE,理由如:当t=2时,AE=BF=2,∴BE=AB﹣AD=7﹣2=5,∵AD=5,∴BE=AD,∵∠A=∠B=90°,∴△BEF≌△ADE;②由①得DE=EF,∠BEF=∠ADE,∵∠A=90°,∴∠ADE+∠AED=90°,∴∠BEF+∠AED=90°,∴∠DEF=180°﹣(∠BEF+∠AED)=90°,∵DE=EF∴∠EDF=∠EFD,∵∠EDF+∠EFD=90°,∴∠EDF=45°;(说明:用其他方法的,请参照此评分标准给分)(2)存在,①如图2,当△DAE≌△EBF时,∴AD=BE,AE=BF,则5=7−t t=xt∴x=1,t=2;②如图3,当△ADE≌△BFE时,AE=BE,AD=BF,则t=7−t 5=xt,∴x=107,t=72.(说明:每正确写出一对x、t的值,给1分.)【点评】本题考查四边形综合题、矩形的判定和性质、等腰直角三角形的判定、三角形全等的性质和判定及动点运动等知识,解题的关键是学会用分类讨论的思想思考问题,学会用方程的思想思考问题,属于中考压轴题.21.在Rt△ABC中,∠C=90°,AC=8cm,BC=6cm,点D在AC上,且AD=6cm,过点A作射线AE⊥AC(AE与BC在AC同侧),若动点P从点A出发,沿射线AE匀速运动,运动速度为1cm/s,设点P运动时间为t秒.连接PD、BD.(1)如图①,当PD⊥BD时,求证:△PDA≌△DBC;(2)如图②,当PD⊥AB于点F时,求此时t的值.【分析】(1)由PD⊥BD、∠C=90°可推出∠PDA=∠CBD,即可根据ASA判定△PDA≌△DBC;(2)由PD⊥AB,AE⊥AC可推出∠APF=∠CAB,即可根据AAS判定△APD≌△CAB,再由全等三角形的性质即可得解.【解答】(1)证明:如图①,∵PD⊥BD,∴∠PDB=90°,∴∠BDC+∠PDA=90°,又∵∠C=90°,∴∠BDC+∠CBD=90°,∴∠PDA=∠CBD,又∵AE⊥AC,∴∠PAD=90°,∴∠PAD=∠C=90°,又∵BC=6cm,AD=6cm,∴AD=BC,在△PAD和△DCB中,∠PAD=∠CAD=CB,∠PDA=∠CBD∴△PDA≌△DBC(ASA);(2)解:如图②,∵PD⊥AB,∴∠AFD=∠AFP=90°,∴∠PAF+∠APF=90°,又∵AE⊥AC,∴∠PAF+∠CAB=90°,∴∠APF=∠CAB,在△APD和△CAB中,∠APD=∠CAB∠PAD=∠C,AD=CB∴△APD≌△CAB(AAS),∴AP=AC,∵AC=8cm,∴AP=8cm,∴t=8.【点评】此题考查了全等三角形的判定与性质,根据ASA判定△PDA≌△DBC、根据AAS判定△APD≌△CAB是解题的关键.22.在平面直角坐标系中,点A(0,6),B(8,0),AB=10,如图作∠DBO=∠ABO,∠CAy=∠BAO,BD交y轴于点E,直线DO交AC于点C.(1)①求证:△ACO≌△EDO;②求出线段AC、BD的位置关系和数量关系;(2)动点P从A出发,沿A﹣O﹣B路线运动,速度为1,到B点处停止运动;动点Q从B出发,沿B﹣O﹣A运动,速度为2,到A点处停止运动.二者同时开始运动,都要到达相应的终点才能停止.在某时刻,作PG⊥CD于点G,QF⊥CD于点F.问两动点运动多长时间时△OPG与△OQF全等?【分析】(1)①根据全等三角形的判定定理ASA证得结论;②利用①中全等三角形的性质得到:AC∥BD,AC=BD﹣10;(2)设运动的时间为t秒,(i)当点P、Q分别在y轴、x轴上时(ii)当点P、Q都在y轴上时,(iii)当点P在x轴上,Q在y轴时若二者都没有提前停止,当点Q提前停止时,列方程即可得到结论.【解答】解:(1)①如图,∵∠DBO=∠ABO,OB⊥AE,∴∠BAO=∠BEO,∴AB=BE,∴AO=OE,∵∠CAy=∠BAO,∴∠CAy=∠BEO,∴∠DEO=∠CAO在△ACO与△EDO中,∠CAO=∠DEO OA=OE∠AOC=∠DOE,∴△ACO≌△EDO(ASA);②由①知,△ACO≌△EDO,∴∠C=∠D,AC=DE,∴AC∥BD,AC=BD﹣10;(2)设运动的时间为t秒,(i)当点P、Q分别在y轴、x轴上时PO=QO得:6﹣t=8﹣2t,解得t=2(秒),(ii)当点P、Q都在y轴上时PO=QO得:6﹣t=2t﹣8,解得t=143(秒),(iii)当点P在x轴上,Q在y轴时若二者都没有提前停止,则PO=QO得:t﹣6=2t﹣8,解得t=2(秒)不合题意;当点Q提前停止时,有t﹣6=6,解得t=12(秒),综上所述:当两动点运动时间为2、143、12秒时,△OPE与△OQF全等【点评】本题考查了全等三角形的判定,坐标与图形的性质,正确的理解题意是解题的关键.23.(2023春•渭滨区期末)如图①,在Rt△ABC中,∠C=90°,BC=9cm,AC=12cm,AB=15cm,现有一动点P,从点A出发,沿着三角形的边AC→CB→BA运动,回到点A停止,速度为3cm/s,设运动时间为ts.(1)如图(1),当t= 时,△APC的面积等于△ABC面积的一半;(2)如图(2),在△DEF中,∠E=90°,DE=4cm,DF=5cm,∠D=∠A.在△ABC的边上,若另外有一个动点Q,与点P同时从点A出发,沿着边AB→BC→CA运动,回到点A停止.在两点运动过程中的某一时刻,恰好△APQ≌△DEF,求点Q的运动速度.【分析】(1)分两种情况进行解答,①当点P在BC上时,②当点P在BA上时,分别画出图形,利用三角形的面积之间的关系,求出点P移动的距离,从而求出时间即可;(2)由△APQ≌△DEF,可得对应顶点为A与D,P与E,Q与F;于是分两种情况进行解答,①当点P 在AC上,AP=4,AQ=5,②当点P在AB上,AP=4,AQ=5,分别求出P移动的距离和时间,进而求出Q的移动速度.【解答】解:(1)①当点P在BC上时,如图①﹣1,若△APC的面积等于△ABC面积的一半;则CP=12BC=92cm,此时,点P移动的距离为AC+CP=12+92=332,移动的时间为:332÷3=112秒,②当点P在BA上时,如图①﹣2若△APC的面积等于△ABC面积的一半;则PD=12AB,即点P为BA中点,此时,点P移动的距离为AC+CB+BP=12+9+152=572cm,移动的时间为:572÷3=192秒,故答案为:112或192;(2)△APQ≌△DEF,即,对应顶点为A与D,P与E,Q与F;①当点P在AC上,如图②﹣1所示:此时,AP=4,AQ=5,∴点Q移动的速度为5÷(4÷3)=154cm/s,②当点P在AB上,如图②﹣2所示:此时,AP=4,AQ=5,即,点P移动的距离为9+12+15﹣4=32cm,点Q移动的距离为9+12+15﹣5=31cm,∴点Q移动的速度为31÷(32÷3)=9332cm/s,综上所述,两点运动过程中的某一时刻,恰好△APQ≌△DEF,点Q的运动速度为154cm/s或9332cm/s.。
中考数学总复习《全等三角形》专项提升练习题(附答案)

中考数学总复习《全等三角形》专项提升练习题(附答案) 学校:___________班级:___________姓名:___________考号:___________一、选择题1.下列各组中的两个图形属于全等图形的是( )A. B. C. D.2.下列叙述中错误的是( )A.能够重合的图形称为全等图形B.全等图形的形状和大小都相同C.所有正方形都是全等图形D.形状和大小都相同的两个图形是全等图形3.下列四个选项图中,与题图中的图案完全一致的是( )A. B. C. D.4.如图,已知△ABE≌△ACD,下列选项中不能被证明的等式是( )A.AD=AEB.DB=AEC.DF=EFD.DB=EC5.如果两个三角形全等,那么下列结论不正确的是( )A.这两个三角形的对应边相等B.这两个三角形都是锐角三角形C.这两个三角形的面积相等D.这两个三角形的周长相等6.已知图中的两个三角形全等,则∠a度数是( )A.72°B.60°C.58°D.50°7.已知下列条件,不能作出唯一三角形的是( )A.两边及其夹角B.两角及其夹边C.三边D.两边及除夹角外的另一个角8.如图,某同学不小心将一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,最省事的办法是( )A.带①去B.带②去C.带③去D.带①和②去9.如图,在四边形ABCD中,AC平分∠BAD,CE⊥AB于点E,∠ADC+∠ABC=180°,有下列结论:①CD=CB;②AD+AB=2AE;③∠ACD=∠BCE;④AB-AD=2BE.其中正确的是( )A.②B.①②③C.①②④D.①②③④10.如图,在△ABC中,高AD和BE交于点H,且∠1=∠2=22.5°.下列结论:①∠1=∠3;②BD+DH=AB;③2AH=BH;④若DF⊥BE于点F,则AE﹣FH=DF.其中正确的结论是( )A.①②③B.③④C.①②④D.①②③④二、填空题11.如图,四边形ABCD≌四边形A/B/C/D/,则∠A的大小是________.12.一个三角形的三边为2、5、x,另一个三角形的三边为y、2、4,若这两个三角形全等,则x+y=.13.工人师傅常用角尺平分一个任意角.作法如下:如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与点M,N重合,过角尺顶点C作射线OC.由此作法得△MOC≌△NOC的依据是.14.如图,AC=BC,DC=EC,∠ACB=∠ECD=90°,且∠EBD=38°,则∠AEB= .15.要测量河两岸相对的两点A,B的距离,先在AB的垂线BF上取两点C,D,使CD =BC,再定出BF的垂线DE,使A,C,E在一条直线上(如图所示),可以说明△EDC ≌△ABC,得ED=AB,因此测得ED的长就是AB的长,判定△EDC≌△ABC最恰当的理由是16.在△ABC中,AB=8,AC=10,则BC边上的中线AD的取值范围是 .三、解答题17.如图,线段AC与线段BD相交于点O,连结AB,BC,CD,∠A=∠D,OA=OD.求证:∠1=∠2.18.如图,在△ABC中,AB=AC.分别以点B,C为圆心,BC长为半径在BC下方画弧,设两弧交于点D,与AB,AC的延长线分别交于点E,F,连结AD,BD,CD.求证:AD平分∠BAC.19.如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.(1)求证:△AEC≌△BED;(2)若∠1=42°,求∠BDE的度数.20.如图,在△ABC中,AB=CB,∠ABC=90°,D为AB的延长线上一点,点E在BC 边上,且BE=BD,连结AE,DE,CD.(1)求证:△ABE≌△CBD.(2)若∠CAE=27°,∠ACB=45°,求∠BDC的度数.21.如图,AD∥BC,∠D=90°.(1)如图1,若∠DAB的平分线与∠CBA的平分线交于点P,试问:点P是线段CD的中点吗?为什么?(2)如图2,如果P是DC的中点,BP平分∠ABC,∠CPB=35°,求∠PAD的度数为多少?22.(1)如图①,在四边形ABCD中,AB∥DC,E是BC的中点,若AE是∠BAD的平分线,试探究AB,AD,DC之间的等量关系,证明你的结论;(2)如图②,在四边形ABCD中,AB∥DC,AF与DC的延长线交于点F,E是BC的中点,若AE是∠BAF的平分线,试探究AB,AF,CF之间的等量关系,证明你的结论.答案1.D.2.C3.A4.B.5.B6.D7.D.8.C9.C10.C.11.答案为:95°.12.答案为:10.13.答案为:SSS.14.答案为:128°.15.答案为:ASA.16.答案为:1<AD <9.17.证明:在△AOB 和△DOC 中∵⎩⎨⎧∠A =∠D ,OA =OD ,∠AOB =∠DOC ,∴△AOB ≌△DOC(ASA)∴AB =DC ,OB =OC.∴OA +OC =OD +OB ,即AC =DB.在△ABC 和△DCB 中∵⎩⎨⎧AC =DB ,AB =DC ,BC =CB ,∴△ABC ≌△DCB(SSS)∴∠1=∠2.18.证明:在△ABD 和△ACD 中∵⎩⎨⎧AB =AC ,BD =CD ,AD =AD ,∴△ABD ≌△ACD(SSS)∴∠BAD =∠CAD即AD 平分∠BAC .19.解:(1)∵AE 和BD 相交于点O∴∠AOD =∠BOE.在△AOD 和△BOE 中∠A =∠B ,∠AOD =∠BOE∴∠BEO =∠2.又∵∠1=∠2∴∠1=∠BEO∴∠AEC =∠BED.在△AEC 和△BED 中⎩⎨⎧∠A =∠B ,AE =BE ,∠AEC =∠BED ,∴△AEC ≌△BED(ASA);(2)∵△AEC ≌△BED∴EC =ED ,∠C =∠BDE.在△EDC 中∵EC =ED ,∠1=42°∴∠C =∠EDC =69°∴∠BDE =∠C =69°.20.证明:(1)∵∠ABC =90°∴∠CBD =90°=∠ABC .在△ABE 和△CBD 中∵⎩⎨⎧AB =CB ,∠ABE =∠CBD ,BE =BD ,∴△ABE ≌△CBD(SAS).(2)∵△ABE ≌△CBD∴∠AEB =∠CDB .∵∠AEB 为△AEC 的一个外角∴∠AEB =∠CAE +∠ACB =27°+45°=72° ∴∠BDC =72°.21.解:点P 是线段CD 的中点. 证明如下:过点P 作PE ⊥AB 于E∵AD ∥BC ,PD ⊥CD 于D∴PC ⊥BC∵∠DAB 的平分线与∠CBA 的平分线交于点P ∴PD =PE ,PC =PE∴PC =PD∴点P 是线段CD 的中点.(2)35°22.解:(1)证明:延长AE 交DC 的延长线于点F∵E 是BC 的中点∴CE =BE∵AB ∥DC∴∠BAE =∠F在△AEB 和△FEC 中∴△AEB≌△FEC∴AB=FC∵AE是∠BAD的平分线∴∠BAE=∠EAD∵AB∥CD∴∠BAE=∠F∴∠EAD=∠F∴AD=DF∴AD=DF=DC+CF=DC+AB(2)如图②,延长AE交DF的延长线于点G∵E是BC的中点∴CE=BE∵AB∥DC∴∠BAE=∠G在△AEB和△GEC中∴△AEB≌△GEC∴AB=GC∵AE是∠BAF的平分线∴∠BAG=∠FAG∵AB∥CD∴∠BAG=∠G∴∠FAG=∠G∴FA=FG∴AB=CG=AF+CF第11 页共11 页。
中考全程演练(第02期)第18课时:全等三角形(含答案)

三角形第18课时全等三角形基础达标训练1. (2021合肥长丰县模拟)如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是()A. 带①去B. 带②去C. 带③去D. 带①和②去第1题图2. 如图,△ABC中,AB=AC,BD=CE,BE=CF,若∠A=50°,则∠DEF的度数是()第2题图A. 75°B. 70°C. 65°D. 60°3. (8分)(2021合肥期末)如图,AC=AE,∠C=∠E,∠1=∠2.求证:△ABC≌△ADE.第3题图4. (8分)(2021泸州) 如图,点A、F、C、D在同一条直线上,已知AF=DC,∠A=∠D,BC∥EF.求证:AB=DE.第4题图5. (8分)(2021广安)如图,四边形ABCD是正方形,E、F分别是AB、AD上的一点,且BF⊥CE,垂足为G.求证:AF=BE.第5题图6. (8分)(2021恩施州)如图,△ABC、△CDE均为等边三角形,连接BD、AE交于点O,BC与AE交于点P.求证:∠AOB=60°.第6题图7. (10分)(2021温州)如图,在五边形ABCDE中,∠BCD=∠EDC =90°,BC=ED,AC=AD.(1)求证:△ABC≌△AED;(2)当∠B=140°时,求∠BAE的度数.第7题图8. (10分)(2021常州)如图,已知在四边形ABCD中,点E在AD 上,∠BCE=∠ACD=90°,∠BAC=∠D,BC=CE.(1)求证:AC=CD;(2)若AC=AE,求∠DEC的度数.第8题图9. (10分)(2021连云港)如图,已知等腰三角形ABC中,AB=AC,点D、E分别在边AB、AC上,且AD=AE,连接BE、CD交于点F.(1)判断∠ABE 与∠ACD 的数量关系,并说明理由; (2)求证:过点A 、F 的直线垂直平分线段BC .第9题图能力提升拓展1. (10分)(2021合肥肥城三模)已知:如图,△ABC 中,∠ABC =45°,CD ⊥AB 于D ,BE 平分∠ABC ,且BE ⊥AC 于E ,与CD 相交于点F .(1)求证:BF =AC ; (2)求证:CE =12BF .第1题图2. (12分)(2021合肥模拟)已知,△ABC 中,AB =AC ,∠BAC =90°,E 为边AC 任意一点,连接BE .(1)如图①,若∠ABE =15°,O 为BE 中点,连接AO ,且AO =1,求BC 的长;(2)如图②,F 也为AC 上一点,且满足AE =CF ,过A 作AD ⊥BE 交BE 于点H ,交BC 于点D ,连接DF 交BE 于点G ,连接AG .若AG 平分∠CAD ,求证:AH=12AC.第2题图教材改编题1. (沪科八上P95习题14.1第2题改编)如图,已知CE⊥AB于E,BD⊥AC于D,AC=AB=6,BE=2,则AD的长为()第1题图A. 2B. 3C. 4D. 52.教材母题(沪科八上P150A组复习题第10题)已知:如图,AD⊥DE,BE⊥DE,AC,BC分别平分∠DAB,∠ABE,点C在线段DE上.求证:AB=AD+BE.第2题图变式1:(8分)如图,已知△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D,E,求证:DE=BD+CE;变式1题图拓展变式:(8分)将直线m绕点A旋转,使其与BC边相交,则结论DE=BD+CE是否还成立?如果成立,请你给出证明;若不成立,请写出所有可能的结论,并在图中画出相应的图形.拓展变式题图变式2:(8分)如图,已知△ABC中,AB=AC,D,A,E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角,请问结论DE=BD+CE是否成立?请说明理由;变式2题图变式3:(8分)如图,D,E是D,A,E三点所在直线m上的两动点(D,A,E三点互不重合),点F为∠BAC平分线上的一点,且△ABF 和△ACF均为等边三角形,连接BD,CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.变式3题图拓展变式:(8分)如图,过△ABC 的边AB 、AC 向外作正方形ABDE 和正方形ACFG ,AH 是BC 边上的高,延长HA 交EG 于点I ,求证:I 是EG 的中点.拓展变式题图答案基础达标训练 1. C2. C 【解析】∵AB =AC ,∴∠B =∠C ,在△DBE 和△ECF 中,⎪⎩⎪⎨⎧=∠=∠=CF EB C B EC BD ∴△DBE ≌△ECF (SAS),∴∠EFC =∠DEB ,∵∠A =50°,∴∠C =(180°-50°)÷2=65°,∴∠CFE +∠FEC =180°-65°=115°,∴∠BED +∠FEC =115°,∴∠DEF =180°-115°=65°.3. 证明:∵∠1=∠2, ∴∠1+∠EAC =∠2+∠EAC , ∴∠BAC =∠DAE , 又∵∠C =∠E ,∴在△ABC 和△ADE 中,⎩⎪⎨⎪⎧∠C =∠E ∠BAC =∠DAE AC =AE, ∴△ABC ≌△ADE (ASA). 4. 证明:∵BC ∥EF , ∴∠ACB =∠DFE , 又∵AF =DC , ∴AF +FC =DC +FC , 即AC =DF .在△ABC 与△DEF 中,⎪⎩⎪⎨⎧∠=∠=∠=∠DFE ACB DFAC D A ∴△A B C ≌△DEF (ASA), ∴AB =DE .5. 证明:∵四边形ABCD 是正方形, ∴AB =BC ,∠A =∠ABC =90°, ∴∠AFB +∠ABF =90°, ∵BF ⊥CE ,垂足为G , ∴∠BEC +∠A B F =90°, ∴∠AFB =∠BEC , 在△AFB 和△BEC 中,⎪⎩⎪⎨⎧=∠=∠∠=∠BC AB BEC AFB ABC A , ∴△AFB ≌△BEC (AAS), ∴AF =BE.6. 证明:∵△ABC 、△CDE 为等边三角形, ∴∠ACB =∠ECD =60°, ∴∠ACE =∠BCD , 在△ACE 与△BCD 中,⎪⎩⎪⎨⎧=∠=∠=CD CE BCD ACE BC AC , ∴△ACE ≌△BCD (SAS), ∴∠CAE =∠CBD ,∵∠AOB +∠CBD +∠BPO =180°, ∠BCA +∠C A E +∠A PC =180°, 且∠BPO =∠APC , ∴∠AOB =∠BCA =60°. 7. (1)证明:∵AC =AD , ∴∠ACD =∠ADC , ∵∠BCD =∠EDC =90°,∴∠BCD -∠ACD =∠EDC -∠ADC , 即∠BCA =∠ADE , 在△ABC 与△AED 中,⎪⎩⎪⎨⎧=∠=∠=AD AC ADE BCA ED BC , ∴△ABC ≌△AED (SAS); (2)解:∵△ABC ≌△AED , ∴∠E =∠B =140°,∵五边形ABCDE 内角和为(5-2)×180°=540°, ∴∠BAE =540°-2×90°-2×140°=80°.8. (1)证明:∵∠BCE =∠ACD =90°,∠BCE =∠ACB +∠ACE , ∠ACD =∠ACE +∠DCE , ∴∠ACB =∠DCE , 在△ABC 和△DEC 中,⎪⎩⎪⎨⎧=∠=∠∠=∠CE BC DCE ACB D BAC , ∴△ABC ≌△DEC (AAS),∴AC =CD ;(2)解:由(1)知AC =CD , ∵∠ACD =90°, ∴∠CAD =45°, ∵AC =AE ,∴∠ACE =∠AEC =12(180°-45°)=67.5°, ∴∠DEC =180°-67.5°=112.5°. 9. (1)解:∠ABE =∠ACD.理由:∵AB =AC ,∠BAE =∠CAD ,AE =AD ,∴△ABE ≌△ACD (SAS),∴∠ABE =∠ACD ;(2)证明:∵AB =AC ,∴∠ABC =∠ACB.由(1)可知∠ABE =∠ACD ,∴∠FBC =∠FCB ,∴FB =FC.又∵AB =AC ,∴点A 、F 均在线段BC 的垂直平分线上,即过点A 、F 的直线垂直平分线段BC.能力提升拓展1. (1)证明:∵CD ⊥AB ,∠ABC =45°,∴△BCD 是等腰直角三角形.∴BD =CD.∵∠DBF =90°-∠BFD ,∠DCA =90°-∠EFC ,且∠BFD =∠EFC ,∴∠DBF =∠DCA .在Rt △DFB 和Rt △DAC 中,⎪⎩⎪⎨⎧=∠=∠∠=∠DC BD DFBA CDA BDF , ∴Rt △DFB ≌Rt △DAC (AAS),∴BF =AC.(2)证明:∵BE 平分∠ABC ,∴∠ABE =∠CBE.在Rt △BEA 和Rt △BEC 中,⎪⎩⎪⎨⎧∠=∠=∠=∠CBE ABE BEBE CEB AEB , ∴Rt △BEA ≌Rt △BEC (ASA).∴CE =AE =12AC ,又∵BF =AC,∴CE =12BF .2. (1)解:如解图①,在AB 上取一点M ,使得BM =ME ,连接ME .第2题解图①在Rt △ABE 中,∵OB =OE ,∴BE =2OA =2,∵MB =ME ,∴∠MBE =∠MEB =15°,∴∠AME =∠MBE +∠MEB =30°,设AE =x ,则ME =BM =2x ,AM =3x , ∵AB 2+AE2=BE 2,∴(2x +3x )2+x 2=22,∴x =2-3(负根已经舍弃),∴AB =AC =(2+3)·2-3=2+3,∴BC =2AB =4+23=(3+1)2=3+1.第2题解图②(2)证明:如解图②中,作CP ⊥AC ,交AD 的延长线于P ,GM ⊥AC 于点M .∵BE ⊥AP , ∴∠AHB =90°,∴∠ABH +∠BAH =90°,∵∠BAH +∠P AC =90°,∴∠ABE =∠P AC ,在△ABE 和△CAP 中,⎪⎩⎪⎨⎧∠=∠=∠=∠ACP BAE ACAB PAC ABE , ∴△ABE ≌△CAP (ASA),∴AE =CP =CF ,∠AEB =∠P ,在△DCF 和△DCP 中,⎪⎩⎪⎨⎧=∠=∠=CP CF DCP DCF CD CD ,∴△DCF ≌△DCP (SAS),∴∠DFC =∠P ,∴∠GFE =∠GEF ,∴GE =GF ,∵GM ⊥EF ,∴FM =ME ,∵AE =CF ,∴AF =CE ,∴AM =CM , 在△GAH 和△GAM 中,⎪⎩⎪⎨⎧=∠=∠∠=∠AG AG AMG AHG GAM GAH ,∴△AGH ≌△AGM (AAS),∴AH =AM =CM =12AC .教材改编题1. C 【解析】∵CE ⊥AB 于E ,BD ⊥AC 于D ,∴∠AEC =∠ADB =90°,∵AC =AB ,∠A =∠A ,∴△ADB ≌△AEC (AAS),∴AD =AE ,∵AB =6,BE =2,∴AE =4,∴AD =4.2.变式1 :证明:∵BD ⊥直线m ,CE ⊥直线m ,∴∠BDA =∠CEA =90°.∵∠BAC =90°,∴∠BAD +∠CAE =90°.∵∠BAD +∠ABD =90°,∴∠CAE =∠ABD.∵∠CAE =∠ABD ,∠ADB =∠CEA =90°,AB =AC ,∴ △ADB ≌△CEA (AAS),∴ AE =BD ,AD =CE ,∴ DE =AE +AD =BD +CE .拓展变式解::当m ⊥BC 时,根据D 和E 重合,则DE =0,BD =CE ;当m 与AC 的夹角小于45°时,如解图,拓展变式题解图∵∠BAD +∠CAE =90°,在Rt △ADB 中,∠ABD +∠BAD =90°, ∴∠CAE =∠ABD ,∴△ABD 和△CAE 中,⎪⎩⎪⎨⎧=∠=∠︒=∠=∠AC AB CAEABD AEC BDA 90, ∴△ABD ≌△CAE (AAS),∴BD =AE ,EC =DA ,又∵DE =AE -AD ,∴DE =BD -CE ;同理,当m与AC的夹角大于45°小于90°时,DE=CE-BD. 变式2:解:成立,理由如下:∵∠BDA=∠BAC=α,∴∠DBA+∠BDA=∠BAC+∠CAE,∴∠DBA=∠CAE.∵∠BDA=∠AEC=α,∠ABD=∠CAE,AB=AC,∴△ADB≌△CEA(AAS),∴AE=BD,AD=CE,∴DE=AE+AD=BD+CE.变式3:解:△DEF为等边三角形,理由如下:由(2)知,△ADB≌△CEA,∴BD=AE,∠BDA=∠CEA.∵△ABF和△ACF均为等边三角形,∴∠ABF=∠CAF=60°,∴∠DBA+∠ABF=∠CAE+∠CAF,∴∠DBF=∠F AE.∵B F=AF,∠DBF=∠F AE,BD=AE,∴△DBF≌△EAF(SAS),∴DF=EF,∠BFD=∠AFE,∴∠DFE=∠DF A+∠AFE=∠DF A+∠BFD=60°,∴△DEF为等边三角形.拓展变式:证明:如解图,过E作EM⊥HI于M,GN⊥HI的延长线于N.拓展变式解题图∴∠EMI =∠GNI =90°,由(1)和(2)的结论可以知道EM =AH =GN , ∴EM =GN ,在△EMI 和△GNI 中,⎪⎩⎪⎨⎧∠=∠=∠=∠GNI EMI GNEM GIN EIM , ∴△EMI ≌△GNI (AAS),∴EI =GI ,∴I 是EG 的中点.。
2022-2023学年八年级数学上册《全等三角形中的辅助线与常考模型问题》精讲与精练高分突破

专题强化训练二:全等三角形中的辅助线与常考模型问题题型一:连接两点做辅助线问题1.已知等腰△ABC中,AB=AC,点D在直线AB上,DE∥BC,交直线AC与点E,且BD=BC,CH⊥AB,垂足为H.(1)当点D在线段AB上时,如图1,求证DH=BH+DE;(2)当点D在线段BA延长线上时,如图2,当点D在线段AB延长线上时,如图3,直接写出DH,BH,DE之间的数量关系,不需要证明.2.已知点P是线段MN上一动点,分别以PM,PN为一边,在MN的同侧作△APM,△BPN,并连接BM,AN.(Ⅰ)如图1,当PM=AP,PN=BP且∠APM=∠BPN=90°时,试猜想BM,AN之间的数量关系与位置关系,并证明你的猜想;(Ⅱ)如图2,当△APM,△BPN都是等边三角形时,(Ⅰ)中BM,AN之间的数量关系是否仍然成立?若成立,请证明你的结论;若不成立,试说明理由.(Ⅲ)在(Ⅱ)的条件下,连接AB得到图3,当PN=2PM时,求∠PAB度数.题型二:倍线中线模型问题V中,AB=6,AC=8,D是BC的中点,3.某数学兴趣小组在活动时,老师提出了这样一个问题:如图,在ABC(1)求证:△ABD≌△ECD(1)延长FD到点G结论.(2)如图(2),四边形与∠BAD满足______(3)如图(3),在某公园的同一水平面上,四条通道围成四边形6.综合与实践(1)如图1,在正方形为 .(2)如图2,在四边形ABCD中,BC∥AD,AB=BC,∠A+∠C=180°,点M1∠ABC,试探索线段MN、AM、CN有怎样的数量关系?请写出猜想,并给予证明.2(3)如图3,在四边形ABCD中,AB=BC,∠ABC+∠ADC=180°,点M、N ∠ABC,试探究线段MN、AM、CN的数量关系为 .=12(2)当直线MN 绕点C 旋转到图(2)的位置时,试问DE 、AD 、BE 具有怎样的等量关系?请直接写出这个等量关系(不写证明过程);(3)当直线MN 绕点C 旋转到图(3)的位置时,试问DE 、AD 、BE 具有怎样的等量关系?请直接写出这个等量关系(不写证明过程).8.如图1,已知ABC V 中,90BAC ∠= ,AB AC =,DE 是过A 的一条直线,且B ,C 在D ,E 的同侧,BD AE ⊥于D ,CE AE ⊥于()E BD CE <.(1)证明:ABD CAE ≅V V ;(2)试说明:BD DE CE =-;(3)若直线DE 绕A 点旋转到图2位置(此时B ,C 在D ,E 的异侧)时,其余条件不变,问BD 与DE ,CE 的关系如何?请证明;(4)若直线DE 绕A 点旋转到图3位置(此时B ,C 在D ,E 的同侧)时()BD CE >其余条件不变,问BD 与DE ,CE 的关系如何?请直接写出结果,不需说明理由.题型五:其它技巧模型9.已知:ACB △和DCE V 都是等腰直角三角形,90ACB DCE ∠=∠=︒,连接AD 、BE 交于点H ,AD 与EC 交于点G ,BE 与AC 交于点F .(1)如图1,求证:AD BE =;A.50A.2<AD<3B.3<ADA .①②③④B .②③C .②③④D .③④二、填空题17.如图,AD 是△ABC 中BC 边上的中线,若AB =6,AC =8,则AD 的取值范围是________________.18.如图,在△ABC 中,∠ACB =90°,将△ABC 绕点A 逆时针旋转到△AEF ,延长BC 交EF 于点D ,若BD =5,BC =4,则DE =___.19.(2016育才周测)如图,正三角形ABC ∆和CDE ∆,A ,C ,E 在同一直线上,AD 与BE 交于点O ,AD 与BC 交于点P ,BE 与CD 交于点Q ,连接PQ .①AD =BE ;②PQ ∥AE ;③AP =BQ ;④DE =DP ;⑤∠AOB =60°.成立的结论有______________.并写出3对全等三角形___________________________.20.如图,在平面直角坐标系中,以A (2,0),B (0,1)为顶点作等腰直角三角形ABC (其中∠ABC =90°,且点C 落在第一象限),则点C 关于y 轴的对称点C'的坐标为______.21.如图,线段AB =8cm ,射线AN ⊥AB ,垂足为点A ,点C 是射线上一动点,分别以AC ,BC 为直角边作等腰直角三角形,得△ACD 与△BCE ,连接DE 交射线AN 于点M ,则CM 的长为__________.22.如图, BD 是ABC ∆的角平分线,延长BD 至点E ,使DE AD =,若60ADB ∠=o ,78BAC ∠= , 则BEC ∠=__________.三、解答题23.在BAC V 中,90BAC ∠=︒,AB AC =,AE 是过A 的一条直线,BD AE ⊥于点D ,CE AE ⊥于E ,(1)如图(1)所示,若B ,C 在AE 的异侧,易得BD 与DE ,CE 的关系是DE =____________;(2)若直线AE 绕点A 旋转到图(2)位置时,(BD CE <),其余条件不变,问BD 与DE ,CE 的关系如何?请予以证明;(3)若直AE 绕点A 旋转到图(3)的位置,(BD CE >),问BD 与DE ,CE 的关系如何?请直接写出结果,不需证明.24.如图1,在△ABC 中,∠BAC =90°,AB =AC ,∠ABC =∠ACB =45°.MN 是经过点A 的直线,BD ⊥MN 于D ,CE ⊥MN 于E .(1)如图1,求证BD=AE ;(2)如图2,点H 为BC 中点,分别连接EH ,DH ,求∠EDH 的度数;(3)如图3,在(2)的条件下,点M 为CH 上的一点,连接EM ,点F 为EM 的中点,连接FH ,过点D 作DG ⊥FH ,交FH 的延长线于点G ,若GH :FH =6:5,△FHM 的面积为30,∠EHB =∠BHG ,求线段EH 的长.28.A 、B 是POQ ∠的边OP 上两定点,E 是边OQ 上一动点,分别以AB 、AE 为边在OP 上方同侧作正方形ABCD 、正方形AEFG .(1)如图①,45POQ ∠=︒,6OB =,2OA =,连接BG 、DE .①求证:BG DE =;②当点E 在边OQ 上运动时,线段BG 的长度是否存在最小值,若存在,请直接写出答案;若不存在,请说明理由;(2)如图②,90POQ ∠>︒,连接CG ,当点E 在边OQ 上运动时,线段CG 的长度是否存在最小值,若存在,请用直尺与圆规作出此时点E 的位置;若不存在,请说明理由.29.如图,CD 是经过∠BCA 顶点C 的一条直线,CA =CB ,E 、F 分别是直线CD 上两点,且(1)若直线CD经过∠BCA的内部,且E、F在射线CD上.α=︒,则BE_________CF.①如图1,若∠BCA=90°,90②如图2,若0°<∠BCA<180°,请添加一个关于α与∠BCA关系的条件__________________,使①中的结论仍然成立,并说明理由;α=∠,请提出关于EF,BE,AF三条线段数量关系的合理猜想,并(2)如图3.若线CD经过∠BCA的外部,BCA简述理由30.我们知道两个全等的直角三角形(△ABD和△ACE)可以拼成一个等腰三角形(如图1),那么对其中一个直角三角形作适当改变又能得到什么结论呢?现在我们一起来探究吧.(1)如图2,将△ACE绕点A逆时针旋转,连接DE,M是DE的中点,连接MB、MC,求证:MB=MC.(2)将CE向上平移,连接DE,M是DE的中点,连接MB、MC.①如图3,当∠CAE=∠BAD时,求证:MB=MC;②当∠CAE>∠BAD时,在图4中补全相应的图形,并直接写出MB、MC的数量关系_______.参考答案:1.(1)见详解;(2)图2:=DH BH DE -,图3:+DE DH BH=【分析】(1)在线段AH 上截取HM BH =,连接CM ,CD ,证明DMC DEC △≌△,可得到DE DM =,即可求解.(2)当点D 在线段BA 延长线上时,在BA 的延长线上截取MH BH =,连接CM ,DC ,由题意可证BHC CHM △≌△,可得B CMB ∠=∠,由题意可得=B AED ∠∠,即可证DMC DEC △≌△,可得DE DM =,则可得DH BH DE =-;当点D 在线段AB 延长线上时,在线段AB 上截取BH HM =,连接CM ,CD ,由题意可证BHC CHM △≌△,可得B CMB ∠=∠,由题意可得B AED ∠=∠,即可证DMC DEC △≌△,可得DE DM =,则可得DE DH BH =+.【详解】解:(1)证明:在线段AH 上截取HM BH =,连接CM ,CD∵CH AB ⊥,HM BH=∴CM BC=∴B CMB∠=∠∵AB AC=∴B ACB∠=∠∵//DE BC∴ADE B AED ACB ∠=∠=∠=∠,CDE BCD∠=∠∴AED BMC∠=∠∴DEC DMC∠=∠∵BD BC=∴BDC BCD EDC∠=∠=∠∵CD CD=∴CDM CDE△≌△∴=DM DE∴+BH DE DM HM DH=+=(2)当点D 在线段BA 延长线上时,DH BH DE=-∵AB AC=∴A ABC CB=∠∠∵BD BC=∴BDC DCB=∠∠∵//DE BC∴E ACB B EDB===∠∠∠∠∵=CH CH ,BH MH =,BHC CHM=∠∠∴BHC CHM△≌△∴=B M∠∠∴E M=∠∠∵+MDC B DCB =∠∠∠,EDC BDC EDB=+∠∠∠∴MDC EDC=∠∠又∵E M =∠∠,DC CD=∴DEC DMC△≌△∴DE DM=∵=DH MH DM-∴DH BH DE=-当点D 在线段AB 延长线上时,DE DH BH=+如图3:当点D 在线段AB 延长线上时,在线段AB 上截取BH HM =,连接CM ,CD∵BH HM =,CH CH =,90CHB MHC ==︒∠∠∵AB AC=∴A ABC CB=∠∠∵BD BC=∴BDC BCD∠=∠∵//BC DE∴BCD CDE ∠=∠,ACB AED∠=∠∴BDC CDE ∠=∠,BMC AED =∠∠,且CD CD=∴CDM CDE△≌△∴DE DM=∵DM DH HM=+∴DE DH BH=+【点睛】本题主要考查了三角形综合题,等腰三角形的性质,全等三角形的性质和判定,合理添加辅助线证全等是解题的关键.2.(1)BM =AN ,BM ⊥AN .(2)结论成立.(3)90°.【分析】(1)根据已知条件可证△MBP ≌△ANP ,得出MB =AN ,∠PAN =∠PMB ,再延长MB 交AN 于点C ,得出MCN 90∠=︒,因此有BM ⊥AN ;(2)根据所给条件可证△MPB ≌△APN ,得出结论BM =AN ;(3) 取PB 的中点C ,连接AC ,AB ,通过已知条件推出△APC 为等边三角形,∠PAC =∠PCA =60°,再由CA =CB ,进一步得出∠PAB 的度数.【详解】解:(Ⅰ)结论:BM =AN ,BM ⊥AN .理由:如图1中,∵MP =AP ,∠APM =∠BPN =90°,PB =PN ,∴△MBP ≌△ANP (SAS ),∴MB =AN .延长MB 交AN 于点C .∵∠PAN+∠PNA=90°,∴∠PMB+∠PNA=90°,∴∠MCN=180°﹣∠PMB﹣∠PNA=90°,∴BM⊥AN.(Ⅱ)结论成立理由:如图2中,∵△APM,△BPN,都是等边三角形∴∠APM=∠BPN=60°∴∠MPB=∠APN=120°,又∵PM=PA,PB=PN,∴△MPB≌△APN(SAS)∴MB=AN.(Ⅲ)如图3中,取PB的中点C,连接AC,AB.∵△APM,△PBN都是等边三角形∴∠APM=∠BPN=60°,PB=PN∵点C是PB的中点,且PN=2PM,∴2PC=2PA=2PM=PB=PN,∵∠APC=60°,∴△APC为等边三角形,∴∠PAC=∠PCA=60°,1AD7∴<<,<<;故答案为1AD7AB BC ⊥ ,EF BC ⊥,ABD FCD ∴∠=∠,在ABD △和FCD V 中,ABD FCD BD CDADB FDC ∠=∠⎧⎪=⎨⎪∠=∠⎩,ABD ∴V ≌FCD V ,2CF AB ∴==,AD DF =,又∵∠FDE =∠ADE =90°ED =ED∴△ADE ≌△FDEAE EF ∴=,426EF CE CF CE AB =+=+=+= ,6AE ∴=.【点睛】本题考查了三角形的三边关系定理和全等三角形的性质和判定,解题关键是熟记全等三角形的判定条件.4.(1)1<AD <7;(2)AC ∥BM ,且AC =BM ,证明见解析;(3)EF =2AD ,证明见解析.【分析】(1)延长AD 到M ,使得DM =AD ,连接BM ,根据题意证明△MDB ≌△ADC ,可知BM =AC ,在△ABM 中,根据AB ﹣BM <AM <AB +BM ,即可;(2)由(1)知,△MDB ≌△ADC ,可知∠M =∠CAD ,AC =BM ,进而可知AC ∥BM ;(3)延长AD 到M ,使得DM =AD ,连接BM ,由(1)(2)的结论以及已知条件证明△ABM ≌△EAF ,进而可得AM =2AD ,由AM =EF ,即可求得AD 与EF 的数量关系.【详解】(1)如图2,延长AD 到M ,使得DM =AD ,连接BM ,∵AD 是△ABC 的中线,∴BD =CD ,在△MDB 和△ADC 中,BD CD =⎧∴△MDB ≌△ADC (SAS ),∴BM =AC =6,在△ABM 中,AB ﹣BM <AM <AB +BM ,∴8﹣6<AM <8+6,2<AM <14,∴1<AD <7,故答案为:1<AD <7;(2)AC ∥BM ,且AC =BM ,理由是:由(1)知,△MDB ≌△ADC ,∴∠M =∠CAD ,AC =BM ,∴AC ∥BM ;(3)EF =2AD ,理由:如图2,延长AD 到M ,使得DM =AD ,连接BM ,由(1)知,△BDM ≌△CDA (SAS ),∴BM =AC ,∵AC =AF ,∴BM =AF ,由(2)知:AC ∥BM ,∴∠BAC +∠ABM =180°,∵∠BAE =∠FAC =90°,∴∠BAC +∠EAF =180°,∴∠ABM =∠EAF ,在△ABM 和△EAF 中,AB EA ABM EAF BM AF =⎧⎪∠=∠⎨⎪=⎩,∴△ABM ≌△EAF (SAS ),∴AM =EF ,∵AD =DM ,∴AM =2AD ,∵AM =EF ,∴EF =2AD ,即:EF =2AD .在△AEF 和△AGF 中,GA EA GAF EAF AF AF =⎧⎪∠=∠⎨⎪=⎩,∴()AEF AGF SAS ≅V V ,∴EF =GF =GD +DF =BE +DF ;(2)解:∠BAD =2∠EAF ,理由如下:如图(2),延长CB 至M ,使BM =DF ,连接AM ,∵∠ABC +∠D =180°,∠ABC +∠ABM =180°,∴∠D =∠ABM ,在△ABM 和△ADF 中,AB AD ABM D BM DF =⎧⎪∠=∠⎨⎪=⎩,∴△ABM ≌△ADF ,∴AF =AM ,∠DAF =∠BAM ,∵∠BAD =2∠EAF ,∴∠DAF +∠BAE =∠BAM +∠BAE =∠EAF ,∴∠EAF =∠EAM ,在△EAF 和△EAM 中,AF AM EAF EAM AE AE =⎧⎪∠=∠⎨⎪=⎩,∴△EAF ≌△EAM ,∴EF =EM =BE +BM =BE +DF ,即EF =BE +DF ;(3)解:如图3,把△ABE 绕点A 逆时针旋转150°至△ADG ,连接AF.∵∠BAD=150°,AE⊥AD,∴∠BAE=150°-90°=60°,又∵∠B=60°,∴△BAE是等边三角形,(3)DE=BE-AD(或AD=BE-DE,BE=AD+DE等).理由见详解.【分析】(1)根据题意由垂直得∠ADC=∠BEC=90°,由同角的余角相等得:∠DAC=∠BCE,因此根据AAS可以证明△ADC≌△CEB,结合全等三角形的对应边相等证得结论;(2)由题意根据全等三角形的判定定理AAS推知△ACD≌△CBE,然后由全等三角形的对应边相等、图形中线段间的和差关系以及等量代换证得DE+BE=AD;(3)由题意可知DE、AD、BE具有的等量关系为:DE=BE-AD(或AD=BE-DE,BE=AD+DE等).证明的方法与(2)相同.(1)证明:如图1,∵AD⊥MN,BE⊥MN,∴∠ADC=∠BEC=90°,∴∠DAC+∠ACD=90°,∵∠ACB=90°,∴∠ACD+∠BCE=90°,∴∠DAC=∠BCE,在△ADC和△CEB中,∵ADC BECDAC BCE AC BC∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ADC≌△CEB;∴DC=BE,AD=EC,∵DE=DC+EC,∴DE=BE+AD.(2)解:DE+BE=AD.理由如下:如图2,∵∠ACB=90°,∴∠ACD+∠BCE=90°.又∵AD⊥MN于点D,∴∠ACD+∠CAD=90°,∴∠CAD=∠BCE.在△ACD和△CBE中,90ADC CEB CAD BCEAC BC ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩,∴△ACD ≌△CBE (AAS ),∴CD =BE ,AD =CE ,∴DE +BE =DE +CD =EC =AD ,即DE +BE =AD .(3)解:DE =BE -AD (或AD =BE -DE ,BE =AD +DE 等).理由如下:如图3,易证得△ADC ≌△CEB ,∴AD =CE ,DC =BE ,∴DE =CD -CE =BE -AD ,即DE =BE -AD .【点睛】本题属于几何变换综合题,考查等腰直角三角形和全等三角形的性质和判定,熟练掌握全等三角形的四种判定方法是关键:SSS 、SAS 、AAS 、ASA ;在证明线段的和与差时,利用全等三角形将线段转化到同一条直线上得出结论.8.(1)见解析;(2)见解析;(3) BD=DE+CE ;证明见解析;(4)BD=DE−CE【分析】(1)根据题意可得ABD EAC ∠=∠,结合BDA AEC ∠=∠,AB AC =直接用AAS 证明三角形全等即可;(2)根据(1)的结论ABD CAE V V ≌,进而可得BD DE CE =-;(3)方法同(1)证明ABD CAE V V ≌,进而可得BD DE CE=+(4)方法同(1)结论同(2)证明ABD CAE V V ≌,进而可得BD DE CE =-.【详解】(1)证明:∵90BAC ∠= ,∴90BAD EAC ∠+∠= .又∵BD AE ⊥ ,CE AE ⊥,∴90BDA AEC ∠=∠=o ,90BAD ABD ∠+∠= ,∴ABD EAC ∠=∠.又∵AB AC =,∴()ABD CAE AAS V V ≌.(2) 解:∵ABD CAE V V ≌,∴BD AE =,AD CE =.又∵ED AD AE =+,∴BD DE CE =-.(3) 解:∵90BAC ∠= ,∴90BAD EAC ∠+∠= .又∵BD AE ⊥ ,CE AE ⊥,∴90BDA AEC ∠=∠=o ,90BAD ABD ∠+∠= ,∴ABD EAC ∠=∠.又∵AB AC =,∴ABD CAE V V ≌.∴BD AE =,AD CE =,AE AD DE =+,∴BD DE CE =+.(4) 解:BD DE CE =-.理由如下:∵90BAC ∠= ,∴90BAD EAC ∠+∠= .又∵BD AE ⊥ ,CE AE ⊥,∴90BDA AEC ∠=∠=o ,90BAD ABD ∠+∠= ,∴ABD CAE ∠=∠.又∵AB AC =,∴ABD CAE V V ≌,∴BD AE =,AD CE =.又∵ED AD AE =+,∴BD DE CE =-.【点睛】本题考查了三角形全等的性质与判定,等腰直角三角形的性质,掌握三角形全等的性质与判定是解题的关键.9.(1)证明见解析;(2)△ACB ≌△DCE ,△BCF ≌△DCG ,△AHF ≌△EHG ,△EHD ≌△AHB【分析】(1)根据SAS 可证明△ACD ≌△BCE ,从而可知AD =BE ;(2)根据条件即可判断图中的全等直角三角形.【详解】解:(1)∵△ACB 和△DCE 都是等腰直角三角形,∠ACB =∠DCE =90°,∴AC =BC ,DC =EC ,∴∠ACB +∠ACE =∠DCE +∠ACE ,∴∠BCE =∠ACD ,在△ACD 与△BCE 中,AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩,∴△ACD ≌△BCE (SAS ),∴AD =BE ;(2)△ACB ≌△DCE ,△BCF ≌△DCG ,△AHF ≌△EHG ,△EHD ≌△AH B .理由:∵AC =DC ,∠ACB =∠DCE ,∴AC =CD =EC =CB ,∴△ACB ≌△DCE (SAS );由(1)可知:∠EBC =∠DAC ,∠ADC =∠BEC ,∴∠AHF =90°,∵∠EBC =∠CEB =∠CDA ,∴△BCF ≌△DCG (ASA ),∴CF =CG ,∴AF =EG ,∵∠AHF =∠EHG ,∠FAH =∠HEG ,∴△AHF ≌△EHG (AAS ),∴AH =EH ,又∵DE =AB ,∴Rt △EHD ≌Rt △AHB (HL ).【点睛】本题考查全等三角形的判定与性质,直角三角形的性质,解题的关键是熟练运用全等三角形的判定条件.10.(Ⅰ)见解析;(Ⅱ)见解析;(Ⅲ)AF =AD +BD【分析】(Ⅰ)先判断出∠ACF =∠AEG ,再用同角的余角相等判断出∠CAF =∠EAG ,即可得出结论;(Ⅱ)先用ASA 判断出△ACM ≌△ABD ,得出AM =AD ,CM =BD ,由(Ⅰ)知,△AGE ≌△AFC ,得出∠AGE =∠AFC ,再判断出CM ∥AB ,得出∠MCF =∠AGC ,进而判断出MF =CM ,即可得出结论;(Ⅲ)同(Ⅱ)的方法,即可得出结论.【详解】解:(Ⅰ)∵AC =AE ,∴∠ACF =∠AEG ,∵AF ⊥AD ,∴∠DAF =90°=∠CAB ,∴∠DAF ﹣∠FAG =∠CAB ﹣∠FAG ,∴∠CAF =∠EAG ,在△AGE 和△AFC 中,AEG ACF AE ACEAG CAF ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△AGE ≌△AFC (ASA );(Ⅱ)如图1,过点C 作CM ⊥AC ,交AF 延长线于点M ,∴∠ACM =90°=∠ABD ,由(Ⅰ)知,∠CAF =∠EAB ,在△ACM 和△ABD 中,90CAF BAE AC AB ACM ABD ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩,∴△ACM ≌△ABD (ASA ),∴AM =AD ,CM =BD ,由(Ⅰ)知,△AGE ≌△AFC ,∴∠AGE =∠AFC ,∴180°﹣∠AGE =180°﹣∠AFC ,∴∠AGC =∠AFG ,∵∠CFM =∠AFG ,∴∠AGC =∠CFM ,∵∠BAC =90°=∠ACM ,∴∠BAC +∠ACM =180°,∴CM ∥AB ,∴∠MCF =∠AGC ,∴∠CFM =∠MCF ,∴MF =CM ,∴AM =AF +CM ,∴AD =AF +BD ;(Ⅲ)AD =AF ﹣BD ;过点C 作CM ⊥AC ,交AF 于点M,在ABD △与ACD △【分析】如图,延长AD 至,E 使,AD ED =再证明,ACD EBD V V ≌可得3,BE AC == 再利用三角形的三边关系可得:53253,AD -<<+从而可得答案.【详解】解:如图,延长AD 至,E 使,AD ED =AD 为ABC V 的中线,,BD CD ∴=,ADC BDE ∠=∠,ACD EBD ∴V V ≌3,AC EB ==5,AB =53253,AD ∴-<<+1 4.AD ∴<<故选:C【点睛】本题考查的是三角形的中线的含义,全等三角形的性质与判定,三角形的三边关系,掌握:“两边及其夹角对应相等的两个三角形全等”是解题的关键.14.C【分析】延长AP 交BC 于点C ,根据题意,通过ASA 判定ABP DBP ≌△△,因为APC △和DPC △同高等底,所以面积相等,根据等量代换便可得出212ABC BPC S S ==△△.【详解】解:延长AP 交BC 于点C ,如图所示,,∵AP BP ⊥,∴90APB DPB ∠=∠=︒,∵BP 是ABC ∠的角平分线,∴ABP DBP ∠=∠,在ABP △和DBP V 中,ABP DBP BP BPAPB DPB ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴ABP DBP ASA ≌()△△,∴AP DP =,∴ABP DBP S S =△△,∵APC △和DPC △同底等高,∴APC DPC S S =△,∴PBC DPB DPC ABP APC S S S S S =+=+△△△△,∴212ABC BPC S S ==△△,故选C .【点睛】本题考查了三角形的角平分线和全等三角形的判定,解题的关键是熟练运用三角形的角平分线和全等三角形的判定.15.D【分析】根据旋转变换的性质判断①;根据全等三角形的判定定理判断②;根据SAS 定理判断③;根据全等三角形的性质、三角形的三边关系判断④.【详解】解:∵△ADC 绕点A 顺时针旋转90°得△AFB ,∴△ADC ≌△AFB ,①正确;∵EA 与DA 不一定相等,∴△ABE 与△ACD 不一定全等,②错误;∵∠FAD =90°,∠DAE =45°,∴∠FAE =∠DAE =45°,在△AED 和△AEF 中AF AD EAF EAD AE AE ⎪∠⎪⎩∠⎧⎨===,∴△AED ≌△AEF ,③正确;∵△ADC ≌△AFB ,∴BF =CD ,∵BE +BF >DE∴BE +DC >DE ,④错误;故选:D .【点睛】本题考查的是全等三角形的判定与性质、旋转变换,掌握全等三角形的判定定理与性质定理、图形旋转的性质等知识是解题的关键.16.C【分析】利用旋转性质可得△ABF ≌△ACD ,根据全等三角形的性质一一判断即可.【详解】解:∵△ADC 绕A 顺时针旋转90°后得到△AFB ,∴△ABF ≌△ACD ,∴∠BAF =∠CAD ,AF =AD ,BF =CD ,故②④正确,∴∠EAF =∠BAF +∠BAE =∠CAD +∠BAE =∠BAC ﹣∠DAE =90°﹣45°=45°=∠DAE 故③正确无法判断BE =CD ,故①错误,故选:C .【点睛】本题考查了旋转的性质:旋转前后两图形全等,解题的关键是熟练掌握基本知识,属于中考常考题型.17.1<AD <7【分析】延长AD 到E ,使DE =AD ,然后利用“边角边”证明△ABD 和△ECD 全等,根据全等三角形对应边相等可得CE =AB ,然后根据三角形任意两边之和大于第三边,两边之差小于第三边求出AE 的取值范围,然后即可得解.【详解】解:如图,延长AD 到E ,使DE =AD ,∵AD 是BC 边上的中线,∴BD =CD ,在△ABD 和△ECD 中,BD CD ADB EDC AD ED =⎧⎪∠=∠⎨⎪=⎩,∴△ABD ≌△ECD (SAS ),∴CE =AB ,∵AB =6,AC =8,∴8-6<AE <8+6,即2<2AD <14,∴1<AD <7,故答案为:1<AD <7.【点睛】本题考查了三角形的三边关系,全等三角形的判定与性质,遇中点加倍延,作辅助线构造出全等三角形是解题的关键.18.3【分析】如图,连接AD .证明Rt △ADF ≌Rt △ADC (HL ),推出DF =DC =1,可得结论.【详解】解:如图,连接AD .在Rt △ADF 和Rt △ADC 中,AD AD AF AC =⎧⎨=⎩,∴Rt △ADF ≌Rt △ADC (HL ),∴DF =DC ,∵BD =5,BC =4,∴CD =DF =5﹣4=1,∵EF =BC =4,∴DE =EF ﹣DF =4﹣1=3.故答案为:3.【点睛】本题考查旋转的性质,全等三角形的性质和判定等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.19. ①②③⑤ △ACD ≌△BCE ,△BCQ ≌△ACP ,△CDP ≌△CEQ【分析】①可证明△ACD ≌△BCE,从而得出AD=BE ;②可通过证明△BCQ ≌△ACP ,从而可证明△PCQ 为等边三角形,再根据内错角相等两直线平行可证明PQ ∥AE .③由②中△BCQ ≌△ACP ,可证AP =BQ ;④通过证明△CDP ≌△CEQ 可得DP=EQ ,又由图可知DE >QE ,从而④错误;⑤通过三角形外角定理和前面△ACD ≌△BCE 可得该结论.由前面的证明过程可得出三个全等三角形.【详解】解:①△ABC 和△DCE 均是等边三角形,点A ,C ,E 在同一条直线上,∴AC=BC ,EC=DC ,∠BCE=∠ACD=120°∴△ACD ≌△BCE∴AD=BE ,故本选项正确;②∵△ACD ≌△BCE ,∴∠CBQ=∠CAP ,又∵∠PCQ=∠ACB=60°,CB=AC ,∴△BCQ ≌△ACP ,∴CQ=CP ,又∠PCQ=60°,∴△PCQ 为等边三角形,∴∠QPC=60°=∠ACB ,∴PQ ∥AE ,故本选项正确;③由②△BCQ ≌△ACP 可得AP =BQ ,故本选项正确;④∵△ACD ≌△BCE ,∴∠ADC=∠BEC ,∵CD=CE ,∠DCP=∠ECQ=60°,∴△CDP ≌△CEQ (ASA ).∴DP=EQ ,∵DE >QE∴DE >DP ,故本选项错误;⑤∠AOB=∠DAE+∠AEO=∠DAE+∠ADC=∠DCE=60°,故本选项正确;∴正确的有:①②③⑤.由上面证明过程可知△ACD ≌△BCE ,△BCQ ≌△ACP ,△CDP ≌△CEQ .故答案为:①②③⑤;△ACD ≌△BCE ,△BCQ ≌△ACP ,△CDP ≌△CEQ .【点睛】本题考查全等三角形的性质和判定,等边三角形的性质.熟练掌握全等三角形的判定定理,并能依据等边三角形三边相等,三角相等都是60°的特征判断三角形全等是解题关键.20.()1,3-【分析】过点C 向y 轴,引垂线CD ,利用△OAB ≌△DBC ,确定DC ,DO 的长度,即可确定点C 的坐标,对称坐标自然确定.【详解】如图,过点C 作CD ⊥y 轴,垂足为D ,∴∠DBC+∠OBA=90°,∵∠OAB+∠OBA=90°,∴∠DBC=∠OAB,∵AB=BC,∠BDC=∠AOB=90°∴△OAB≌△DBC,∴DC=OB,DB=OA,∵A(2,0),B(0,1)∴DC=OB=1,DB=OA=2,∴OD=3,∴点C(1,3),∴点C关于y轴的对称点坐标为(-1,3),故答案为:(-1,3).【点睛】本题考查了点的坐标及其对称点坐标的确定,熟练分解点的坐标,利用三角形全等,把坐标转化为线段的长度计算是解题的关键.21.4cm.【分析】过点E作EF⊥AN于F,先利用AAS证出△ABC≌△FCE,从而得出AB=FC=8cm,AC=FE,然后利用AAS 证出△DCM≌△EFM,从而求出CM的长.【详解】解:过点E作EF⊥AN于F,如图所示∵AN⊥AB,△BCE和△ACD为等腰直角三角形,∴∠BAC=∠BCE=∠ACD=∠CFE =90°,BC=CE,AC=CD∴∠ABC+∠ACB=90°,∠FCE+∠ACB =90°,∵DE =DF ,∠EDC =∠FDC ,DC =DC ,∴△CDE ≌△CDF (SAS ),∴∠E =∠DFC =102°;故答案为:102°.【点睛】本题考查了全等三角形的判定和性质、角平分线的定义以及对顶角相等的性质等知识,正确添加辅助线、构造全等三角形是解题的关键.23.(1)DE BD CE =-;(2)DE BD CE =+,证明过程见解析;(3)DE BD CE=+【分析】(1)根据已知条件证明ABD CAE ≅V V 即可得解;(2)根据已知条件证明ABD CAE ≅V V 即可得解;(3)根据已知条件证明ABD CAE ≅V V 即可得解;【详解】(1)在ABD △和CAE V 中,∵90CAD BAD ∠+∠=︒,90BAD ABD ∠+∠=︒,∴CAD ABD ∠=∠,又∵90ADB AEC ∠=∠=︒,AB AC =,∴ABD CAE ≅V V ,∴BD AE =,AD CE =,又AE AD DE =+,∴AE DE CE =+,即DE BD CE =-;故答案是:BD CE -;(2)答:DE BD CE =+;证明:∵BD AE ⊥于D ,CE AE ⊥于E ,∴90ADB CEA ∠=∠=︒.∴90ABD BAD ∠+∠=︒,∵18090CAE BAD BAC ∠+∠=︒-∠=︒,∴ABD CAE ∠=∠.在ABD △和CAE V 中,ADB CEA ABD CAE AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴ABD CAE V V ≌(AAS ),∴BD AE =,AD CE =,∴DE AE AD BD CE =+=+;(3)∵BD AE ⊥于D ,CE AE ⊥于E ,∴90ADB CEA ∠=∠=︒.∴90ABD BAD ∠+∠=︒,∵18090CAE BAD BAC ∠+∠=︒-∠=︒,∴ABD CAE ∠=∠.在ABD △和CAE V 中,ADB CEA ABD CAE AB CA ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴ABD CAE V V ≌(AAS ),∴BD AE =,AD CE =,∴DE BD CE =+;【点睛】本题主要考查了全等三角形的综合应用,准确分析证明是解题的关键.24.(1)见解析;(2)见解析;(3)见解析【分析】(1)根据同角的余角相等,可得DBA EAC ∠=∠,再由AB AC =,可证得ADB CEA V V ≌,即可求证;(2)根据同角的余角相等,可得DBA EAC ∠=∠,再由AB AC =,可证得ADB CEA V V ≌,即可求证;(3)过B 作BP AC ∥交MN 于P ,可得90PBA BAC ∠=∠=︒,再证明≌ACF BAP △△,可得13∠=∠,AF BP =,再证得≌BFG BPG △△,得到23∠∠=,即可求证.【详解】证明:(1)∵BD MN ⊥,CE MN⊥∴90BDA AEC ∠=∠=︒,∴90DBA DAB ∠+∠=︒,∵90BAC ∠=︒,∴90DAB EAC ∠+∠=︒,∴DBA EAC ∠=∠,∵AB AC =,∴()ADB CEA AAS ≌△△,∴BD AE =;(2)∵BD MN ⊥,CE MN ⊥,∴90BDA AEC ∠=∠=︒,∴90DBA DAB ∠+∠=︒,∵90BAC ∠=︒,∴90DAB EAC ∠+∠=︒,∴DBA EAC ∠=∠,∵AB AC =,∴()ADB CEA AAS ≌△△,∴BD AE =;(3)过B 作BP AC ∥交MN 于P ,∵BP AC ∥,∴180PBA BAC ∠+∠=︒,∵90BAC ∠=︒,∴90PBA BAC ∠=∠=︒,由(2)得:ADB CEA V V ≌,∴BAP ACF∠=∠∵AB AC =,∴()≌ACF BAP ASA △△,∴13∠=∠,AF BP =,∵AB 的中点F ,∵BF AF =,∴BF BP =,∵45ABC ∠=︒,90PBA ∠=︒,∴45PBG PBA ABC ∠=∠-∠=︒,∴ABC PBG ∠=∠,∵BG BG =,∴()BFG BPG SAS △△≌,∴23∠∠=,∵13∠=∠,∴12∠=∠.【点睛】本题主要考查了全等三角形的判定和性质,余角的性质,根据题意得到全等三角形是解题的关键.∴FD=BC;(2)作FD⊥AC于D,由(1)得,FD=AC=BC,AD 在△FDG和△BCG中,90FDG BCG∠∠︒⎧==∵BC=AC=AG+CG=4,∴E点为BC中点;(3)当点E在CB的延长线上时,过BC=AC=4,CE=CB+BE=7由(1)(2)知:△ADF≌△∴CG=GD,AD=CE=7,∴CG=DG=1.5,(3)过点M 作MS ⊥FH 于点S ,过点E 作ER ⊥FH ,交HF 的延长线于点R ,过点E 作ET ∥BC ,根据全等三角形判定和性质解答即可.【详解】证明:(1)∵CE ⊥AE ,BD ⊥AE ,∴∠AEC =∠ADB =90°,∵∠BAC =90°,∴∠ACE +CAE =∠CAE +∠BAD =90°,∴∠ACE =∠BAD ,在△CAE 与△ABD 中ACE BAD AEC ADBAC AB ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△CAE ≌△ABD (AAS ),∴AE =BD ;(2)连接AH∵AB =AC ,BH =CH ,∴∠BAH =11904522BAC ∠=⨯︒=︒,∠AHB =90°,∴∠ABH =∠BAH =45°,∴AH =BH ,∵∠EAH =∠BAH ﹣∠BAD =45°﹣∠BAD ,∠DBH =180°﹣∠ADB ﹣∠BAD ﹣∠ABH =45°﹣∠BAD ,∴∠EAH =∠DBH ,在△AEH 与△BDH 中AE BD EAH DBHAH BH =⎧⎪∠=∠⎨⎪=⎩∴△AEH ≌△BDH (SAS ),∴EH =DH ,∠AHE =∠BHD ,∴∠AHE +∠EHB =∠BHD +∠EHB =90°即∠EHD =90°,∴∠EDH =∠DEH =18090452︒-︒=︒;(3)过点M 作MS ⊥FH 于点S ,过点E 作ER ⊥FH ,交HF 的延长线于点R ,过点E 作ET ∥BC ,交HR 的延长线于点T .∵DG ⊥FH ,ER ⊥FH ,∴∠DGH =∠ERH =90°,∴∠HDG +∠DHG =90°∵∠DHE =90°,∴∠EHR +∠DHG =90°,∴∠HDG =∠HER在△DHG 与△HER 中HDG HER DGH ERH DH EH ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△DHG ≌△HER (AAS ),∴HG =ER ,∵ET ∥BC ,∴∠ETF =∠BHG ,∠EHB =∠HET ,∠ETF =∠FHM ,∵∠EHB =∠BHG ,∴∠HET =∠ETF ,∴HE =HT ,在△EFT 与△MFH 中ETF FHM EFT MFH EF FM ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△EFT ≌△MFH (AAS ),∴HF =FT ,∴22HF MS FT ER =g g ,∴ER =MS ,∴HG =ER =MS ,设GH =6k ,FH =5k ,则HG =ER =MS =6k ,563022HF MS k k ==g g ,k =2,∴FH =52,∴HE =HT =2HF =102.∴()OAE MAG SAS △≌△,∴AOE AMG ∠=∠,∴点G 在射线MG 上运动,作CG MG '⊥于G ',当点G 与G '重合时,CG 的值最小,连接AG ',以A 为圆心,以AG '为半径作弧,交OQ 于点E ',当点E 与E '重合时,CG 的值最小,故点E '即为所求.【点睛】此题主要考查了正方形的性质,全等三角形的判定和性质,垂线段最短等知识,解题关键是正确寻找全等三角形.29.(1)①BE =CF ;②180BCA α+∠=︒,理由见解析(2)EF =BE +AF ,理由见解析【分析】(1)①由∠BCA =90°,∠BEC =∠CFA =α=90°,可得∠CBE =∠ACF ,从而可证△BCE ≌△CAF ,故BE =CF .②若BE =CF ,则可使得△BCE ≌△CAF .根据题目已知条件添加条件,再使得一对角相等,△BCE ≌△CAF 便可得证.(2)题干已知条件可证△BCE ≌△CAF ,故BE =CF ,EC =FA ,从而可证明EF =BE +AF .(1)①∵∠BEC =∠CFA =α=90°,∴∠BCE +∠CBE =180°-∠BEC =90°.又∵∠BCA =∠BCE +∠ACF =90°,∴∠CBE =∠ACF .在△BCE 和△CAF 中,BEC CFA CBE ACF BC AC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△BCE ≌△CAF (AAS ).∴BE =CF .②α+∠BCA =180°,理由如下:∵∠BEC =∠CFA =α,∴∠BEF =180°-∠BEC =180°-α.又∵∠BEF =∠EBC +∠BCE ,∴∠EBC +∠BCE =180°-α.又∵α+∠BCA =180°,∴∠BCA =180°-α.∴∠BCA =∠BCE +∠ACF =180°-α.∴∠EBC =∠FCA .在△BCE 和△CAF 中,CBE ACF BEC CFABC CA ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△BCE ≌△CAF (AAS ).∴BE =CF .故答案为:①BE =CF ;②180BCA α+∠=︒(2)EF =BE +AF ,理由如下:∵∠BCA =α,∴∠BCE +∠ACF =180°-∠BCA =180°-α.又∵∠BEC =α,∴∠EBC +∠BCE =180°-∠BEC =180°-α.∴∠EBC =∠FCA .在△BEC 和△CFA 中,EBC FCA BEC FCABC CA ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△BEC ≌△CFA (AAS ).∴BE =CF ,EC =FA .∴EF =EC +CF =FA +BE ,即EF =BE +AF .【点睛】本题主要考查全等三角形的性质与判定,熟练掌握全等三角形的性质与判定是解题的关键.30.(1)见解析(2)①见解析;②补全图形见解析,MB =MC【分析】(1)根据三角形SAS 判定定理证明三角形△BDM ≌△CEM ,证得MB =MC .(2)先根据三角形ASA 判定定理证明△ECM ≌△DFM ,再证明△BFM 是等边三角形,证得MB =MF =MC ;根据图4直接写出MB =MC .(1)如图2,依题意可知:∠ADB =∠AEC ,BD =CE ,AD =AE ,∴∠ADE =∠AED ,∴∠ADB ﹣∠ADE =∠AEC ﹣∠AED ,即:∠MDB =∠MEC , ∵M 是DE 的中点,∴MD =ME ,在△BDM 和△CEM 中,BD CE BDM CEM DM EM =⎧⎪∠=∠⎨⎪=⎩∴△BDM ≌△CEM (SAS ),∴MB =MC ;。
专题 全等三角形常见的基本模型(6大题型提分练)(原卷版)_1

八年级上册数学《第1章三角形的初步认识》专题全等三角形常见的基本模型平移模型展示沿同一直线 (BC) 平移可得两三角形重合 (BE=CF)1.(2024•荔湾区一模)如图,点E,C在线段BF上,BE=FC,∠A=∠D,∠ACB=∠DEF.求证:△ABC≌△DFE.2.已知:如图,点E是AC的中点,BA⊥AC于A,DE⊥AC于E,⊥B=⊥D,求证:BE=DC.3.(2023秋•枣阳市期末)如图,点B,E,C,F在一条直线上,AB=DE,AB∥DE,BE=CF.求证:AC=DF.4.(2023春•埇桥区期末)如图,点B,E,C,F在一条直线上,AB=DE,AC=DF,BE=CF.试说明:(1)△ABC≌△DEF;(2)∠A=∠EGC.5.已知:如图,点B,E,C,F有同一直线l,AB⊥DE,且AB=DE,BE=CF,试判断线段AC与DF的数量关系以及位置关系.并证明.6.如图,点B,E,C,F在一条直线上,AC与DE相交于点O,AB=DE,AB∥DE,BE=CF.(1)求证:AC∥DF;(2)若∠B=65°,∠F=35°,求∠EOC的度数.7.如图,A、D、B、E四点在同一条直线上,AD=BE,BC∥EF,BC=EF.(1)求证:AC=DF;(2)若CD为∠ACB的平分线,∠A=25°,∠E=71°,求∠CDF的度数.对称模型展示有公共边:有公共顶点:所给图形沿公共边所在直线或者经过公共顶点的某条直线折叠,两个三角形完全重合. 1.(2024春•秦都区校级月考)如图,在△ABC和△AED中,AB=AE,AC=AD,∠BAD=∠EAC,求证:2.(2023•越秀区校级二模)已知:如图,DB⊥AB,DC⊥AC,∠1=∠2.求证:AD平分∠BAC.3.(2023春•桑植县期末)如图,∠A=∠D=90°,点B,E,F,C在同一直线上,AB=CD,BE=CF,求证:∠B=∠C.4.(2024•碑林区校级模拟)如图.已知△ABC中,AB=AC,点D、E分别是边AB、AC上的中点,连接求证:BE=CD.5.(2024春•碑林区校级期末)如图,在△ABC中,AB=AC,过点A作DE∥BC,且AD=AE,连接BD,CE.试说明:BD=CE.6.(2024春•碑林区校级月考)如图,已知∠C=∠E,AC=AE,∠CAD=∠EAB.求证:∠ABD=∠ADB.7.(2024•凉州区校级三模)如图,已知CD⊥AB于点D,BE⊥AC于点E,BE,CD交于点O,且OB=OC.求证:AO平分∠BAC.8.(2023春•明水县期中)如图,在△ABE和△ACF中,∠E=∠F=90°,∠B=∠C,BE=CF.求证:(1)∠1=∠2.(2)CM=BN.旋转模型展示绕公共顶点旋转可得两个三角形重合.1.(2024•海珠区校级二模)如图,AD=AB,∠D=∠B,∠EAC=∠DAB,求证:AE=AC.2.(2023•大连)如图,在△ABC和△ADE中,延长BC交DE于F.BC=DE,AC=AE,∠ACF+∠AED =180°.求证:AB=AD.3.如图,在⊥ABC和⊥ADE中,AB=AC,AD=AE,⊥BAD=⊥CAE.求证:⊥ABD=⊥ACE.4.(2024•阎良区校级二模)如图,点E在△ABC外部,点D在BC边上,若∠1=∠2,∠E=∠C,AE=AC,求证:AB=AD.5.(2024•长沙)如图,点C在线段AD上,AB=AD,∠B=∠D,BC=DE.(1)求证:△ABC≌△ADE;(2)若∠BAC=60°,求∠ACE的度数.6.(2023•宜兴市二模)如图,△ABC和△CDE均为等腰三角形,AC=BC,CD=CE,∠ACB=∠DCE,点D在线段AB上(与A,B不重合),连接BE.(1)证明:△ACD≌△BCE.(2)若BD=3,BE=7,求AB的长.7.(2024•杭州三模)如图,在四边形ABCD中,AD∥BC,点E为对角线BD上一点,∠A=∠BEC,且AD=BE.(1)求证:△ABD≌△ECB;(2)如果∠BDC=75°,求∠ADB的度数.8.(2032秋•大同月考)已知△ABC和△CDE中,CA=CB,CD=CE,∠ACB=∠DCE=α,AE与BD交于点F.(1)如图1.当α=90°时.求证:①△ACE≌△BCD;②AE⊥BD;(2)如图2.当α=60°时,直接写出∠AFB的度数为;(3)如图3,直接写出∠AFD的度数为(用含α的式子表示).题型四旋转不共顶点模型1.(2024•泸州校级二模)如图AE=BD,AC=DF,BC=EF,求证:EF∥BC.2.(2024•江阳区校级三模)如图,点A,B,C,D在同一条直线上,点E,F分别在直线AB的两侧,且AE=BF,∠A=∠B,∠ACE=∠BDF.求证:△ADE≌△BCF.3.(2023秋•翠屏区期末)小明和小亮准备用所学数学知识测一池塘的长度,经过实地测量,绘制如下图,点B、F、C、E在直线l上(点F、C之间的距离为池塘的长度),点A、D在直线l的异侧,且AB∥DE,旋转模型展示∠A=∠D,测得AB=DE.(1)求证:△ABC≌△DEF;(2)若BE=120m,BF=38m,求池塘FC的长度.4.(2023春•连平县期末)已知:如图,A、C、F、D在同一直线上,AF=DC,AB∥DE,AB=DE,求证:(1)△ABC≌△DEF;(2)BC∥EF.5.(2023秋•大化县月考)如图,A、E、F、C四点在同一直线上,AE=CF,过E、F分别作BE⊥AC,DF ⊥AC,且AB=CD.求证:(1)AB∥CD;(2)BD平分EF.6.(2023春•碑林区校级期末)如图,点A,E,F,C在同一条直线上,AF=CE,BE=FD,∠AEB=∠CFD.(1)求证:△AEB≌△CFD;(2)若DF=CF,∠ABE=20°,∠DAC=30°,求∠ADC的度数.7.如图所示,点A、E、F、C在一条直线上,AE=CF,过点E,F分别作DE⊥AC,BF⊥AC,且AB=CD.(1)如图⊥所示,若EF与BD相交于点G,则EG与FG相等吗?试说明理由.(2)如图⊥所示,若将⊥DEC的边EC沿AC方向移动至图中所示位置时,其余条件不变,(1)中结论是否还能成立?请说明理由.题型五三垂直模型已知 A , B , C 三点共线,且∠1=∠2=∠3=90°.1.(2023春•钢城区期末)如图,∠BAC=90°,AD是∠BAC内部一条射线,若AB=AC,BE⊥AD于点E,CF⊥AD于点F.求证:△ABE≌△CAF.2.(2023秋•江州区期末)课间,小明拿着老师的等腰三角板玩,不小心掉在两墙之间,如图所示.(1)求证:△ADC≌△CEB;三垂直模型展示(2)已知DE=49cm,请你帮小明求出砌墙砖块的厚度a的大小和墙AD的高(每块砖的厚度都为a cm).3.(2023春•横山区期末)如图,⊥ABC=90°,F A⊥AB于点A,点D在直线AB上,AD=BC,AF=BD.(1)如图1,若点D在线段AB上,判断DF与DC的数量关系和位置关系,并说明理由;(2)如图2,若点D在线段AB的延长线上,其他条件不变,试判断(1)中结论是否成立,并说明理由.4.如图,AB=BC,AD=DE,且AB⊥BC,AD⊥DE,又CG⊥BD的延长线于点G,EF⊥BD交BD的延长线于点F.求证:CG+EF=BD.5.如图,在⊥ABC中,⊥ACB=90°,AC=BC,直线MN过点C,且AD⊥MN于点D,BE⊥MN于点E,在MN绕点C旋转过程中,以上关系保持不变(1)当直线MN绕点C旋转到图1的位置时,求证:DE=AD+BE;(2)当直线MN绕点C旋转到图2位置时,DE、AD、BE三者之间有怎样的等量关系,证明你的结论;(3)当直线MN绕点C旋转到图3位置时,试问:DE、AD、BE三者之间又有怎样的等量关系?请直接写出结论.6.(2023秋•邓州市期中)已知∠ABC=90°,D是直线AB上的点,AD=BC,作F A⊥AB于点A,且AF =BD,连结DC、DF.(1)自主探究:如图1,当点D在线段AB上,点F在点A右侧时,DF与DC的数量关系为,位置关系为;(2)思考拓展:如图2,当点D在线段AB的延长线上,点F在点A的左侧时,(1)中的结论还成立吗?请说明理由;(3)能力提升:当点D在线段BA的延长线上,点F在点A的侧时,(1)中的两个结论依然成立,若此时BC=2,AB=1,则AF的长度为.7.(203秋•阳信县期中)在△ABO中,∠AOB=90°,AO=BO,直线MN经过点O,且AC⊥MN于C,BD⊥MN于D(1)当直线MN绕点O旋转到图①的位置时,求证:CD=AC+BD;(2)当直线MN绕点O旋转到图②的位置时,求证:CD=AC﹣BD;(3)当直线MN绕点O旋转到图③的位置时,试问:CD、AC、BD有怎样的等量关系?请写出这个等量关系,并加以证明.一线三等角模型展示(1)点P在线段AB上:(2)点P 在线段AB 的延长线上:已知A , P , B 三点共线,且∠1=∠2=∠3 .1.(2023•碑林区一模)如图,在△ABC中,AC=BC,∠A=∠B,D、E分别为AB、BC上一点,∠CDE=∠A.若BC=BD,求证:CD=DE.2.(1)课本习题回放:如图①,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E,AD=2.5cm,DE=1.7cm.求BE的长.(2)探索证明:如图②,点B、C在∠MAN的边AM、AN上,点E,F在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,∠1=∠2=∠BAC.求证:△ABE≌△CAF.3.(2023春•宽甸县期中)已知:CD是经过∠BCA顶点C的一条直线,CA=CB,点E、F分别是直线CD 上两点,且∠BEC=∠CF A=∠α.(1)若直线CD经过∠BCA的内部,且E,F在射线CD上,如图1,若∠BCA=90°,∠a=90°,则BE与CF的数量关系是.(2)如图2,若直线CD经过∠BCA的外部,∠α=∠BCA,请提出关于EF,BE,AF三条线段数量关系的合理猜想:.并说明理由.4.(1)如图1,直线m经过等腰直角△ABC的顶点A,过点B、C分别作BD⊥m,CE⊥m,垂足分别为D、E,求证:BD+CE=DE;(2)如图2,直线m经过△ABC的顶点A,AB=AC,在直线m上取两点D,E,使∠ADB=∠AEC=α,补充∠BAC=(用α表示),线段BD,CE与DE之间满足BD+CE=DE,补充条件后并证明;(3)在(2)的条件中,将直线m绕着点A逆时针方向旋转一个角度到如图3的位置,并改变条件∠ADB =∠AEC=(用α表示).通过观察或测量,猜想线段BD,CE与DE之间满足的数量关系,并予以证明.5.问题情境:如图1,在直角三角形ABC中,∠BAC=90°,AD⊥BC于点D,可知:∠BAD=∠C(不需要证明);(1)特例探究:如图2,∠MAN=90°,射线AE在这个角的内部,点B、C在∠MAN的边AM、AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.证明:△ABD≌△CAF;(2)归纳证明:如图3,点B,C在∠MAN的边AM、AN上,点E,F在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,∠1=∠2=∠BAC.求证:△ABE≌△CAF;(3)拓展应用:如图4,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为3,则△ACF与△BDE的面积之和为.6.(2023春•平阴县期末)已知,在△ABC中,AB=AC,D,A,E三点都在直线m上,∠BDA=∠AEC =∠BAC.(1)如图①,若AB⊥AC,则BD与AE的数量关系为,BD,CE与DE的数量关系为.(2)如图②,当AB不垂直于AC时,(1)中的结论是否成立?请说明理由.(3)如图③,若只保持∠BDA=∠AEC,BD=EF=7cm,DE=10cm,点A在线段DE上以2cm/s的速度由点D向点E运动,同时,点C在线段EF上以xcm/s的速度由点E向点F运动,它们运动的时间为t(s).是否存在x,使得△ABD与△EAC全等?若存在,求出相应的t与x的值;若不存在,请说明理由.7.(2024春•温江区校级期末)【模型熟悉】(1)如图1,已知△ABC和△DCE,点B、C、E在一条直线上,且∠B=∠ACD=∠E,AC=CD,求证:BC=DE;【模型运用】(2)如图2,在等边△ABC中,M、N分别为BC,AB边上的点,且ND=NM,∠DNM=60°,连接AD.若∠DAN=30°,求证:CM=2BN;【能力提升】(3)如图3,等边△ABC的面积是25,AB=6,点D、F分别为AC、BC边上的动点,AD=2CF,连接DF,以DF为边在△ABC内作等边△DEF,连接BE,当点D从点A运动到点C,请在图3中作出点E 的运动轨迹,并求出点E的运动路程.。
8年级数学全等三角形经典例题

8年级数学全等三角形经典例题一、全等三角形经典例题1。
例1:如图,在△ABC中,AB = AC,AD是BC边上的中线,求证:△ABD≌△ACD。
解析:1. 在△ABD和△ACD中:- 已知AB = AC(题目中给出的等腰三角形的两腰相等)。
- 因为AD是BC边上的中线,所以BD = CD(中线的定义)。
- AD = AD(公共边)。
2. 根据SSS(边边边)全等判定定理,可得△ABD≌△ACD。
二、全等三角形经典例题2。
例2:已知:如图,AB = AD,∠B = ∠D,∠1=∠2,求证:△ABC≌△ADE。
解析:1. 因为∠1 = ∠2,所以∠1+∠DAC = ∠2+∠DAC,即∠BAC = ∠DAE。
2. 在△ABC和△ADE中:- 已知AB = AD。
- ∠B = ∠D。
- 且∠BAC = ∠DAE(已证)。
3. 根据ASA(角边角)全等判定定理,可得△ABC≌△ADE。
三、全等三角形经典例题3。
例3:如图,在△ABC中,∠C = 90°,AC = BC,AD平分∠CAB交BC于D,DE⊥AB于E,AB = 6cm,求△DEB的周长。
解析:1. 因为AD平分∠CAB,∠C = 90°,DE⊥AB,根据角平分线的性质,可知CD = DE。
2. 在Rt△ACD和Rt△AED中:- AD = AD(公共边)。
- CD = DE(已证角平分线性质)。
- 根据HL(斜边直角边)定理,可得Rt△ACD≌Rt△AED。
- 所以AC = AE。
3. 因为AC = BC,AB = 6cm,设AC = BC=x,根据勾股定理AC^2+BC^2=AB^2,即x^2+x^2=6^2,2x^2=36,x^2=18,x = 3√(2)。
4. 又因为AE = AC = 3\sqrt{2}\),所以BE=AB - AE = 6 - 3\sqrt{2}\)。
5. 而△DEB的周长为DE+DB+BE,因为CD = DE,BC = BD + CD,所以△DEB的周长为BC+BE = 3\sqrt{2}+6 - 3\sqrt{2}=6cm。
全等三角形的判定(SSS与SAS)(精选精练)(专项练习)(教师版)24-2025学年八年级数学上册

专题12.4全等三角形的判定(SSS 与SAS)(精选精练)(专项练习)一、单选题(本大题共10小题,每小题3分,共30分)1.(23-24八年级上·河南信阳·期末)如图,AB AC =,BD CD =,35BAD ∠=︒,120ADB ∠=︒,则C ∠的度数为()A .25︒B .30︒C .35︒D .55︒2.(23-24八年级上·广西百色·期末)如图,O 为AC 的中点,若要利用“SAS ”来判定△≌△AOB COD ,则应补充的一个条件是()A .A C ∠=∠B .AB CD =C .B C ∠=∠D .OB OD=3.(22-23九年级上·重庆大渡口·期末)如图,在正方形ABCD 中,点E F ,分别在边CD BC ,上,且DE CF =,连接AE DF ,,DG 平分ADF ∠交AB 于点G .若70AED ∠=︒,则AGD ∠的度数为()A .50︒B .55︒C .60︒D .65︒4.(2024·陕西咸阳·三模)如图,在ABC 中,D 为边BC 的中点,1AB =,2AD =,延长AD 至点E ,使得DE AD =,则AC 长度可以是()A .4B .5C .6D .75.(17-18八年级上·辽宁营口·阶段练习)如图,AD 是ABC 的中线,E ,F 分别是AD 和AD 延长线上的点,且DE DF =,连接BF CE ,.则下列说法:①CE BF =;②ABD △和ACD 面积相等;③BF CE ∥;④BDF CDE △△≌.其中正确的有()A .4个B .3个C .2个D .1个6.(23-24八年级上·安徽安庆·期末)如图,已知方格纸中是4个相同的正方形,则1∠与2∠的和为()A .80︒B .90︒C .100︒D .110︒7.(23-24八年级上·湖北孝感·期中)如图,已知48AOB ∠=︒,点C 为射线OB 上一点,用尺规按如下步骤作图:①以点O 为圆心,以任意长为半径作弧,交OA 于点D ,交OB 于点E ;②以点C 为圆心,以OD 长为半径作弧,交OC 于点F ;③以点F 为圆心,以DE 长为半径作弧,交前面的弧于点G ;④连接CG 并延长交OA 于点H .则AHC ∠的度数为()A .24︒B .42︒C .48︒D .96︒8.(23-24八年级上·山东德州·阶段练习)如图,平面上有ACD 与BCE ,其中AD 与BE 相交于P 点,如图,若AC BC AD BECD CE ===,,,55ACE ∠=︒,155BCD ∠=︒,则BPD ∠的度数为()A .110︒B .125︒C .130︒D .155︒9.(23-24七年级下·山西太原·阶段练习)如图1,两个大小不同的三角板叠放在一起,图2是由它得到的抽象几何图形,已知AB AC =,AE AD =,90CAB DAE ∠=∠=︒,且点B ,C ,E 在同一条直线上,10cm BC =,4cm CE =,连接DC .现有一只壁虎以2cm/s 的速度沿B C D --的路线爬行,则壁虎爬到点D 所用的时间为()A .10sB .11sC .12sD .13s10.(21-22八年级上·云南昭通·期末)如图,AD 是ABC 的中线,E ,F 分别是AD 和AD 延长线上的点,且CE BF ,连接BF CE ,,下列说法:①DE DF =;②ABD 和ACD 面积相等;③CE BF =;④BDF CDE ≌;⑤CEF F ∠∠=.其中正确的有()A .1个B .5个C .3个D .4个二、填空题(本大题共8小题,每小题4分,共32分)11.(23-24八年级上·江苏南京·期末)如图,已知12∠=∠,要用“SAS ”判定ABD ACD △≌△,则需要补充的一个条件为.12.(23-24八年级上·河北保定·期末)如图,在ABC 与ADE V 中,E 在BC 边上,AD AB =,AE AC =,DE BC =,若125∠=︒,则DAB ∠=.13.(23-24八年级上·吉林松原·期中)如图,为了测量A 、B 两点之间的距离,在地面上找到一点C ,使90ACB ∠=︒,然后在BC 的延长线上确定点D ,使BC CD =,那么只要测量出AD 的长度就得到A 、B 两点之间的距离,其中ABC ADC △△≌的依据是.14.(23-24八年级上·重庆江津·期中)如图,BE BA =,DE AB ∥,DE BC =,若3825BAC E ∠=︒∠=︒,,则BDE ∠=.15.(23-24八年级上·江苏泰州·期中)如图,在ABC 中,点D 、E 分别在AC 、BC 上,AD DE =,AB BE =,80A ∠=︒,则DEC ∠=︒.16.(23-24八年级上·河南洛阳·期中)如图,在长方形ABCD 中,20cm AB =,点E 在边AD 上,且12cm AE =.动点P 在边AB 上,从点A 出发以4cm/s 的速度向点B 运动,同时,点Q 在边BC 上,以cm/s v 的速度由点B 向点C 运动,若在运动过程中存在EAP 与PBQ 全等的时刻,则v 的值为.17.(23-24八年级上·山东菏泽·阶段练习)已知,如图,在ABC 中,点D 是AB 上一点,CD 平分ACB ∠,2A ADC ∠=∠,6BD =,4AC =,则BC 的长为.18.(23-24九年级下·江苏泰州·阶段练习)如图,AC 平分DCB ∠,CB CD =,DA 的延长线交BC 于点E ,若BAE x ∠=︒,则EAC ∠的度数为.(用含x 的代数式表示).三、解答题(本大题共6小题,共58分)19.(8分)(23-24八年级上·陕西商洛·阶段练习)如图,在ABF △和DCE △中,,,AB DC AF DE BE CF ===,且点,,,B E F C 在同一条直线上.求证:B C ∠=∠.20.(8分)(23-24八年级上·江苏泰州·期中)如图,点B F C E 、、、在一条直线上,AB DE =,,,AC DF BF CE AD ==交BE 于点O .(1)求证:B E ∠=∠;(2)求证:,AD BE 互相平分.21.(10分)(23-24八年级上·天津宁河·期中)如图,已知AD AB AC AE DAB CAE ==∠=∠,,,连接DC BE ,.(1)求证:BAE DAC ≌;(2)若13520CAD D ∠=︒∠=︒,,求E ∠的度数.22.(10分)(23-24七年级下·陕西西安·阶段练习)如图,在ABC 中,D 为AB 上一点,E 为AC 中点,连接DE 并延长至点F 使得EF ED =,连CF .(1)求证:CF AB ∥;(2)若50ABC ∠=︒,连接BE ,CA 平分BCF ∠,求A ∠的度数.23.(10分)(23-24七年级下·陕西西安·阶段练习)已知等腰三角形ABC ,AB AC =,D 为射线BC 上一动点,连接AD ,以AD 为边在直线AD 的右侧作等腰三角形ADE ,DAE BAC ∠=∠,AD AE =,连接CE .(1)如图1,当点D 在边BC 上时,请探究BC ,CD ,CE 之间的数量关系.(2)如图2,当点D 在BC 的延长线上时,(1)中BC ,CD ,CE 之间的数量关系是否仍然成立?若成立,请说明理由;若不成立,请你写出新的结论,并说明理由.24.(12分)(23-24七年级下·陕西咸阳·阶段练习)如图,在ABC 中,AD 是BC 边上的中线,分别以AB ,AC 为直角边作直角ABE 和ACF △,其中AB AE =,90BAE ∠=︒,AC AF =,90CAF =︒∠,连接EF ,延长AD 至点G ,使DG AD =,连接BG .【初步探索】(1)试说明:AC BG ∥;【衍生拓展】(2)探究EF 和AD 之间的数量关系,并说明理由.参考答案:1.A【分析】本题主要考查了全等三角形的性质,正确判断对应角,对应边是解决本题的关键.在ABD △中,根据三角形内角和定理求得B ∠,根据全等三角形的对应角相等即可解决.【详解】解:在ABD △中,18025B BAD ADB ∠=︒-∠-∠=︒,∵AB AC =,BD CD =,AD AD =,∴()SSS ABD ACD ≌,∴25C B ∠=∠=︒.故选:A .2.D【分析】本题主要考查了添加一个条件,使得用“SAS ”来判定△≌△AOB COD ,根据已知条件得出OA OC =,AOB COD ∠=∠,故只需要OB OD =即可使用SAS 证明△≌△AOB COD .【详解】解:∵O 为AC 的中点,∴OA OC =,∵AOB COD ∠=∠,∴当添加OB OD =时,()SAS AOB COD ≌△△.故选:D .3.B【分析】可以先证明ADE DCF ≌,则70ADF ∠=︒,利用角平分线可得35ADG ∠=︒,再利用直角三角形的两锐角互余解题即可.【详解】解:∵正方形ABCD∴90AD DC ADC C DAG AD BC ∠∠∠====︒ ,,,在ADE 和DCF 中,AD DC ADE C DE CF =⎧⎪∠=∠⎨⎪=⎩,∴ADE DCF≌∴70AED DFC ADF ∠∠∠===︒∵DG 平分ADF∠∴1352ADG ADF ∠∠==︒∴9055ADG ADG ∠∠=︒-=︒故选B .【点睛】本题考查正方形的性质,全等三角形的性质和判定,掌握全等三角形的判定方法是解题的关键.4.A【分析】本题考查了全等三角形的判定与性质,三角形三边关系;证明ABD ECD ≌,得1CE AB ==,在AEC △中由三边不等关系确定AC 的取值范围,根据范围即可完成求解.【详解】解:D 为边BC 的中点,BD CD ∴=;在ABD △与BCD △中,BD CD ADB EDC AD DE =⎧⎪∠=∠⎨⎪=⎩,ABD ECD ∴ ≌,1CE AB ∴==;AE CE AC AE CE -<<+ ,4AE AD DE =+=,35AC ∴<<,故AC 可以为4,故选:A .5.D【分析】本题主要考查了全等三角形的判定与性质、等底等高的三角形的面积相等、平行线的判定等知识点,熟练掌握三角形全等的判定方法并准确识图是解题的关键.根据三角形中线的定义可得BD CD =,然后利用“SAS ”证明BDF V 和CDE 全等,根据全等三角形对应边相等可得CE BF =,全等三角形对应角相等可得F CED ∠=∠,再根据内错角相等,两直线平行可得BF CE ∥,最后根据等底等高的三角形的面积相等判断出②正确.【详解】解:∵AD 是ABC 的中线,∴BD CD =,在BDF V 和CDE 中,BD CD BDF CDE DE DF =⎧⎪∠=∠⎨⎪=⎩,∴()SAS BDF CDE ≌ ,故④正确;∴CE BF F CED =∠=∠,,故①正确,∴BF CE ∥,故③正确;∵BD CD =,点A 到BD CD 、的距离相等,∴ABD △和ACD 面积相等,故②正确,综上所述,正确的是①②③④,共4个.故选:D .6.B【分析】本题考查了全等三角形的判定与性质,互余.解题的关键在于对知识的熟练掌握与灵活运用.如图,证明()SAS ABC DFE ≌,则1BAC ∠=∠,由290BAC ∠+∠=︒,可得1290∠+∠=︒,然后作答即可.【详解】解:如图,∵BC ED =,90BCA DEF ∠=∠=︒,AC FE =,∴()SAS ABC DFE ≌,∴1BAC ∠=∠,∵290BAC ∠+∠=︒,∴1290∠+∠=︒,故选:B .7.D【分析】本题考查尺规基本作图-作一角等于已知角,三角形全等的判定和性质,三角形外角的性质,根据作图,由全等三角形的判定定理SSS 可以推知DOE GCF ≌,得到GCF DOE ∠=∠,即48ACO AOB ∠=∠=︒,再利用三角形外角性质求解即可.【详解】解:由作图可知,在DOE 与GCF 中,OD CG DE GF OE CF =⎧⎪=⎨⎪=⎩,则()SSS DOE GCF ≌.∴GCF DOE ∠=∠,即48ACO AOB ∠=∠=︒,∴484896AHC AOB ACO ∠=∠+∠=︒+︒=︒.故选:D .8.C【分析】易证≌ACD BCE V V ,由全等三角形的性质可知:A B ∠=∠,再根据已知条件和四边形的内角和为360︒,即可求出BPD ∠的度数.【详解】解:在ACD 和BCE 中,AC BC CD CE AD BE =⎧⎪=⎨⎪=⎩,∴()SSS ACD BCE ≌,∴BCE ACD ∠=∠,∴BCA ECD ∠=∠,∵55ACE ∠=︒,155BCD ∠=︒,∴100BCA ECD ︒∠+∠=,∴50BCA ECD ︒∠=∠=,∵55ACE ∠=︒,∴105ACD ∠=︒∴75A D ︒∠+∠=,∴75B D ∠+∠=︒,∵155BCD ∠=︒,∴36075155130BPD ︒︒︒︒∠=--=,故选:C .【点睛】本题考查了全等三角形的判定和性质、三角形的内角和定理以及四边形的内角和定理,解题的关键是利用整体的数学思想求出75B D ∠+∠=︒.9.C【分析】先根据等腰直角三角形的性质可以得出ABE ACD ≌,属于手拉手型全等,所以()10414cm CD BE ==+=,最后根据时间=路程÷速度即可解答.本题考查全等三角形的判定和性质、等腰直角三角形的性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.【详解】解:BAC EAD ∠=∠ ,BAC CAE EAD CAE ∴∠+∠=∠+∠,BAE CAD ∴∠=∠,在ABE 与ACD 中,AB AC BAE CAD AD AE =⎧⎪∠=∠⎨⎪=⎩,(SAS)ABE ACD ∴ ≌,10414(cm)CD BE BC CE ∴==+=+=,则()101424cm BC CD +=+= 壁虎以2cm/s 的速度B 处往D 处爬,24212()t s ∴=÷=.故选:C .10.B【分析】根据三角形中线的定义可得BD CD =,然后利用“边角边”证明BDF 和CDE 全等,根据全等三角形对应边相等可得CE BF =,全等三角形对应角相等可得F CED ∠∠=,再根据内错角相等,两直线平行可得BF CE ,最后根据等底等高的三角形的面积相等判断出②正确.【详解】解:∵AD 是ABC 的中线,∴BD CD =,在BDF 和CDE 中,BD CD BDF CDE DF DE =⎧⎪∠=∠⎨⎪=⎩,∴()SAS BDF CDE ≌,故④正确∴CE BF F CED ∠∠==,,故①正确,∵CEF CED ∠∠=,∴CEF F ∠∠=,故⑤正确,∴BF CE ,故③正确,∵BD CD =,点A 到BD CD 、的距离相等,∴ABD 和ACD 面积相等,故②正确,综上所述,正确的有5个,故选:B .【点睛】本题考查全等三角形的判定与性质,熟练掌握全等三角形的判定方法并准确识图是解题的关键.11.BD CD=【分析】本题主要考查对全等三角形的判定的理解和掌握,根据用“SAS ”判定ABD ACD △≌△,已知12∠=∠及公共边AD ,添加的条件是BD CD =.【详解】解:添加的条件是BD CD =,理由是:在ABD △与ACD 中,11AD AD BD CD =⎧⎪∠=∠⎨⎪=⎩,∴()SAS ABD ACD ≌,故答案为:BD CD =.12.25︒/25度【分析】本题主要考查了全等三角形的性质与判定,三角形内角和定理,证明()SSS ABC ADE ≌得到AED C ∠=∠,再根据三角形内角和定理和平角的定义可得2125∠=∠=︒.【详解】解:∵AD AB =,AE AC =,DE BC =,∴()SSS ABC ADE ≌,∴AED C ∠=∠,∵11802C AEC AEC AED ∠++=︒=++∠∠∠∠∠,∴2125∠=∠=︒,故答案为:25︒.13.SAS /边角边【分析】本题考查了全等三角形的判定,根据SAS 即可证明ACB ACD ≌ 是解题的关键.【详解】解:AC BD ^ ,90ACB ACD ∴∠=∠=︒,在ACB △和ACD 中,AC AC ACB ACD BC CD =⎧⎪∠=∠⎨⎪=⎩,()SAS ACB ACD \≌ ,故答案为:SAS .14.117︒/117度【分析】本题考查了全等三角形的判定及其性质等知识,根据平行线的性质得出∠=∠ABC BED ,进而利用SAS 证明ABC 和EBD △全等,利用全等三角形的性质解答即可.【详解】解:∵DE AB ∥,ABC BED ∴∠=∠,在ABC 和EBD △中,BA BE ABC BED BC DE =⎧⎪∠=∠⎨⎪=⎩,()SAS ABC EBD ∴ ≌,38BAC EBD ∴∠=∠=︒,1801803825117BDE EBD E ∴∠=︒-∠-∠=︒-︒-︒=︒,故答案为:117︒.15.100【分析】本题考查了三角形全等的判定与性质,熟练掌握三角形全等的判定方法是解题关键.先证出EBD ABD △≌△,再根据全等三角形的性质可得80BED A ∠=∠=︒,由此即可得.【详解】解:在EBD △和ABD △中,ED AD BE BA BD BD =⎧⎪=⎨⎪=⎩,()SSS EBD ABD ∴ ≌,80BED A ∴∠=∠=︒,180100DEC BED ∴∠=︒-∠=︒,故答案为:100.16.4或245【分析】本题主要考查三角形全等的判定.设运动s t ,则4 cm AP t =,()204cm BP AB AP t =-=-, cm BQ vt =,由于在长方形ABCD 中,90A B ∠=∠=︒,因此①当AE BP =,AP BQ =时,()SAS AEP BPQ ≌,②当AE BQ =,AP BP =时,()SAS AEP BQP ≌,代入即可求解v 的值.【详解】设运动s t ,则4 cm AP t =,()204cm BP AB AP t =-=-, cm BQ vt =,∵在长方形ABCD 中,90A B ∠=∠=︒,∴①当AE BP =,AP BQ =,即12204t =-,4t vt =时,()SAS AEP BPQ ≌,解得:2t =,4v =或当AE BQ =,AP BP =,即12vt =,4204t t =-时,()SAS AEP BQP ≌,解得:52t =,245v =.综上所述,v 的值为4或245.故答案为:4或24517.10【分析】本题考查了全等三角形的判定与性质,解决本题的关键是证明ACD ECD ≌△△,在BC 边上取点E ,使EC AC =,连接DE ,证明ACD ECD ≌△△,再根据已知条件证得6BD BE ==,即可得解.【详解】解:如图,在BC 边上取点E ,使EC AC =,连接DE ,∵CD 平分ACB ∠,∴ACD ECD ∠=∠,∵CD CD =,∴()SAS ACD ECD ≌,∴4AC CE ==,ADC EDC ∠=∠,∵22A ADC ADE ADC EDC ADC ∠=∠∠=∠+∠=∠,,∴A ADE DEC ∠=∠=∠,∴BDE BED ∠=∠,∴6BD BE ==,∴6410BC BE CE =+=+=.故答案为:10.18.1802x-【分析】本题主要考查了全等三角形的判定与性质,角平分线的性质,利用SAS 证明ABC ADC △△≌得D DCA B BCA ∠+∠=∠+∠,根据三角形的外角定理推出B BCA CAE ∠+∠=∠,进而根据三角形内角和定理即可求解,解题的关键是利用SAS 证明ABC ADC △△≌.【详解】解:∵AC 平分DCB ∠,∴BCA DCA ∠=∠,在ABC 和ADC △中,CB CD BCA DCA CA CA =⎧⎪∠=∠⎨⎪=⎩∴ABC ADC △△≌,∴B D ∠=∠,∴B BCA D DCA ∠+∠=∠+∠,∵EAC D DCA ∠=∠+∠,∴B BCA EAC ∠+∠=∠,∵180180B BCA BAC BAE EAC ∠+∠=︒-∠=︒-∠-∠,∴180CAE BAE EAC ∠=︒-∠-∠,∵BAE x ∠=︒,∴1802x EAC -⎛⎫∠=︒ ⎪⎝⎭,故答案为:1802x -.19.见解析【分析】由BE CF =可得BF CE =,然后利用SSS 证明ABF DCE ≌即可证明结论.【详解】解:∵BE CF =,∴BE EF EF FC +=+,即BF CE =,在ABF 和DCE 中AB CD AF DE BF CE =⎧⎪=⎨⎪=⎩,∴ABF DCE ≌,∴B C ∠=∠.【点睛】本题考查全等三角形的判定和性质,掌握全等三角形的判定方法是解题的关键.20.(1)见解析(2)见解析【分析】本题考查了全等三角形的判定与性质,解题的关键是:(1)利用SSS 证明ABC DEF ≌△△,然后根据全等三角形的性质即可得证;(2)利用AAS 证明ABO DEO △△≌,然后根据全等三角形的性质即可得证.【详解】(1)证明:∵BF CE =,∴BC EF =,在ABC 和DEF 中AB DE BC EF AC DF =⎧⎪=⎨⎪=⎩,∴()SSS ABC DEF ≌,∴B E ∠=∠;(2)证明:在ABO 和DEO 中B E AOB DOE AB DE ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴()AAS ABO DEO ≌,∴AO DO =,=BO EO ,即AD ,BE 互相平分.21.(1)见解析(2)25E ∠=︒【分析】本题主要考查了全等三角形的判定与性质;(1)根据题意由DAB BAC CAE BAC ∠+∠=∠+∠,可得DAC BAE ∠=∠,即可求证;(2)由()SAS BAE DAC ≌,可得E C ∠=∠,再由内角和为180︒即可求解.【详解】(1)证明:∵DAB CAE ∠=∠,∴DAB BAC CAE BAC ∠+∠=∠+∠,∴DAC BAE ∠=∠,又∵AD AB AC AE ==,,∴()SAS BAE DAC ≌;(2)∵()SAS BAE DAC ≌,∴E C ∠=∠,∵13520CAD D ∠=︒∠=︒,,∴1801801352025C CAD D ∠=︒-∠-∠=︒-︒-︒=︒,∴25E C ∠=∠=︒.22.(1)见详解(2)65︒【分析】本题考查了全等三角形的性质和判定、平行线的性质和判定、三角形内角和定理等知识点,能综合运用定理进行推理是解此题的关键.(1)求出AED CEF ≌,根据全等三角形的性质得出A ACF ∠=∠,根据平行线的判定得出即可;(2)根据(1)求出A ACB ∠=∠,根据三角形内角和定理求出即可.【详解】(1)证明:∵E 为AC 中点,AE CE ∴=,在AED △和CEF △中AE CE AED CEF DE EF =⎧⎪∠=∠⎨⎪=⎩,()AED CEF SAS ∴ ≌,A ACF ∴∠=∠,∴CF AB ∥;(2)解:∵AC 平分BCF ∠,ACB ACF ∴∠=∠,A ACF ∠=∠ ,A ACB ∴∠=∠,180,50A ABC ACB ABC ∠+∠+∠=︒∠=︒ ,18050652A ︒-︒∴∠==︒,65A ∴∠=︒.23.(1)CE CD BC+=(2)不成立.CE CD BC-=【分析】本题考查的是全等三角形的判定与性质,掌握全等三角形的判定方法是解本题的关键.(1)证明BAD CAE ∠=∠.再证明()SAS BAD CAE ≌△△,可得CE BD =,再进一步可得结论;(2)证明BAD CAE ∠=∠.再证明()SAS BAD CAE ≌△△,可得CE BD =,再进一步可得结论;【详解】(1)解:∵BAC DAE ∠=∠,∴BAC DAC DAE DAC ∠-∠=∠-∠,即BAD CAE ∠=∠.在BAD 与CAE V 中,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩,∴()SAS BAD CAE ≌△△,∴CE BD =,∴CE CD BD CD BC +=+=.(2)不成立.CE CD BC -=.理由:∵BAC DAE ∠=∠,∴BAD CAE ∠=∠.在BAD 与CAE V 中,,,,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩()SAS BAD CAE ∴△≌△,∴CE BD =,∴CE CD BD CD BC -=-=.24.(1)见解析(2)2EF AD =,理由见解析【分析】本题考查了全等三角形的判定和性质、平行线的判定和性质,熟练掌握知识点、推理证明是解题的关键.(1)根据AD 是边BC 的中线,得出BD CD =,利用SAS 证明GDB ADC ≌,得出DBG ACD Ð=Ð,根据“内错角相等,两直线平行”,即可证明AC BG ∥;(2)由(1)得AC BG ∥,GDB ADC ≌,得出180BAC ABG ∠+∠=︒,BG AC =,推出BG AF =,ABG EAF ∠=∠,利用SAS 证明ABG EAF ≌,得出AG EF =,根据DG AD =,AG DG AD =+,得出2AG AD =,即可证明2EF AD =.【详解】解:(1)∵AD 是边BC 的中线,∴BD CD =,在GDB △和ADC △中,DG AD GDB ADC BD CD =⎧⎪∠=∠⎨⎪=⎩,∴()SAS GDB ADC ≌,∴DBG ACD Ð=Ð,∴AC BG ∥;(2)2EF AD =,理由如下,∵由(1)得AC BG ∥,GDB ADC ≌,∴180BAC ABG ∠+∠=︒,BG AC =,∵AC AF =,∴BG AF =,∵3603609090180BAC EAF BAE CAF Ð+Ð=°-Ð-Ð=°-°-°=°,∴ABG EAF ∠=∠,在ABG 和EAF △中,AB AE ABG EAF BG AF =⎧⎪∠=∠⎨⎪=⎩,∴()SAS ABG EAF ≌,∴AG EF =,∵DG AD =,AG DG AD =+,∴2AG AD =,∴2EF AD =.。
全等三角形专题复习(含练习讲评)

一、全等三角形注: ① 判定两个三角形全等必须有一组边对应相等;② 全等三角形面积相等. 2. 证题的思路:⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎨⎧⎩⎨⎧⎪⎪⎩⎪⎪⎨⎧⎪⎩⎪⎨⎧⎪⎩⎪⎨⎧)找任意一边()找两角的夹边(已知两角)找夹已知边的另一角()找已知边的对角()找已知角的另一边(边为角的邻边)任意角(若边为角的对边,则找已知一边一角)找第三边()找直角()找夹角(已知两边AAS ASA ASA AAS SAS AAS SSS HL SAS例1: 如图, 在△ABE 中, AB =AE,AD =AC,∠BAD =∠EAC, BC.DE 交于点O.求证: (1) △ABC ≌△AED ; (2) OB =OE .例2: 如图所示, 已知正方形ABCD 的边BC.CD 上分别有点E 、点F, 且BE +DF =EF, 试求∠EAF 的度数.AD F例3.在△ABC中, ∠ACB=90°,AC=BC, AE是BC的中线, 过点C作CF⊥AE于F,过B作BD⊥CB 交CF的延长线于点D。
(1)求证:AE=CD, (2)若BD=5㎝,求AC的长。
例4:如图, △ABE和△ADC是△ABC分别沿着AB.AC边翻折180°形成的, 若∠1: ∠2: ∠3=28: 5: 3, 则∠a的度数为例5: 如图: 在△ABC中, ∠ACB=90°, AC=BC, D是AB上一点, AE⊥CD于E, BF⊥CD交CD的延长线于F.求证: AE=EF+BF。
练习:1.已知: 如图5—129, △ABC 的∠B.∠C 的平分线相交于点D, 过D 作MN ∥BC 交AB.AC 分别于点M 、N, 求证:BM +CN =MN2.如图(13):已知AB ⊥BD, ED ⊥BD, AB=CD , BC=DE ,请你判断AC 垂直于CE 吗? 并说明理由。
3.如图(14),已知AB=DC , DE=BF, ∠B=∠D , 试说明(1)DE ∥BF (2)AE=CFFDCABE(14)4.如图: 在△ABC中, ∠BAC=90°,∠ABD= ∠ABC, DF⊥BC, 垂足为F, AF交BD于E。
