2011秋高性能计算练习题
全国计算机等级考试三级PC技术机试真题2011年9月_真题-无答案

全国计算机等级考试三级PC技术机试真题2011年9月(总分100,考试时间90分钟)上机题1. 请编制程序ex1.ASM,其功能是:内存中连续存放着20个十进制数字的ASCⅡ字符,把它们转换成10个字节的压缩型(组合型)BCD码。
例如:内存中有:31H('1'),32H('2'),33H('3'),34H('4')…(共20个字节)结果为:21H,43H,…(共10个字节)部分程序已经给出,其中原始数据由过程LOAD从文件INPUT1.DA T中读入SOURCE 开始的内存单元中,运算结果要求从RESULT开始存放,由过程SA VE保存到文件OUTPUT1.DAT中。
填空BEGIN和END之间已给出的源程序使其完整,空白处已用横线标出,每行空白一般只需一条指令,但采用功能相当的多条指令亦可,或删去BEGIN和END 之间原有的代码并自行编程来完成所要求的功能。
对程序必须进行汇编,并与IO.OBJ连接产生ex1.exe可执行文件,最终运行程序产生结果。
调试中若发现整个程序存在错误之处,请加以修改。
[试题程序]EXTRN LOAD:FAR,SA VE:FARN EQU 10STAC SEGMENT STACKDB 128 DUB(?)STAC ENDSDA TA SEGMENTSOURCE DB N*2 Dup(?)RESULT DB N DUP(0)NAME0 DB 'INPUT1.DAT',0NAMEl DB 'OUTPUT1.DA T',0DA TA ENDSCODE SEGMENTASSUMECS:CODE,DS:DA TA,SS:STACSTART PROC FARPUSH DSXORAX,AXPUSH AXMOV AX,DATAMOV DS,AXMOV ES,AXLEA DX,SOURCE ;数据区起始地址LEA SI,NAME0 ;原始数据文件名MOV CX,N*2 ;字节数CALL LOAD ;从'INPUT.DA T'中读取数据 ;****BEGIN****LEA SI,SOURCELEA DI,RESULTMOV CX,NCLDNEXT:LODS ______ANDAL, ______MOVBL,AL ______LODS ______PUSH ______MOV CL, ______SAL AL,CLPOP ______ADDAL, ______STOS ______LOOP NEXT;****END****LEA DX,RESULT ;结果数据区首址LEA SI,NAME1 ;结果文件名MOV CX,N ;结果字节数CALL SAVE ;保存结果到文件RETSTART ENDPCODE ENDSEND START。
2011年9月信息技术高考正式题
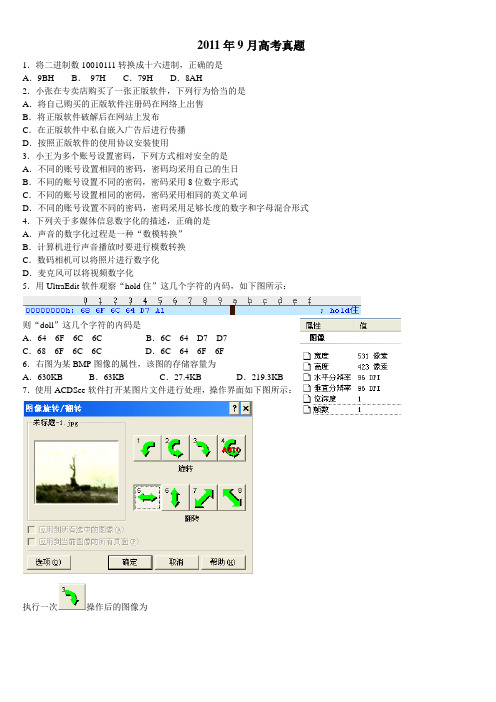
2011年9月高考真题1.将二进制数10010111转换成十六进制,正确的是A.9BH B.97H C.79H D.8AH2.小张在专卖店购买了一张正版软件,下列行为恰当的是A.将自己购买的正版软件注册码在网络上出售B.将正版软件破解后在网站上发布C.在正版软件中私自嵌入广告后进行传播D.按照正版软件的使用协议安装使用3.小王为多个账号设置密码,下列方式相对安全的是A.不同的账号设置相同的密码,密码均采用自己的生日B.不同的账号设置不同的密码,密码采用8位数字形式C.不同的账号设置相同的密码,密码采用相同的英文单词D.不同的账号设置不同的密码,密码采用足够长度的数字和字母混合形式4.下列关于多媒体信息数字化的描述,正确的是A.声音的数字化过程是一种“数模转换”B.计算机进行声音播放时要进行模数转换C.数码相机可以将照片进行数字化D.麦克风可以将视频数字化5.用UltraEdit软件观察“hold住”这几个字符的内码,如下图所示:则“doll”这几个字符的内码是A.64 6F 6C 6C B.6C 64 D7 D7C.68 6F 6C 6C D.6C 64 6F 6F6.右图为某BMP图像的属性,该图的存储容量为A.630KB B.63KB C.27.4KB D.219.3KB 7.使用ACDSee软件打开某图片文件进行处理,操作界面如下图所示:执行一次操作后的图像为A B C D 8该算法输出S 的值A .-2B . 3C .5D .89.小茸想购买一台iPad ,从以下渠道获得的信息,可信度最高的是 A .数码城中经销商的产品介绍 B .网店中的广告C .权威机构的检测报告D .报纸上的用户试用报告10.在Word 文档处理过程中,要接受所选修订,在下图中应单击的按钮是A .B .C .D .11.使用Windows Media Player 软件把CD 中的歌曲转换成MP3时(如下图所示),应该选择的功能按钮是A .媒体库B . 翻录C .刻录D .同步 12.在某论坛注册用户账号时的部分界面如下所示:下列注册信息中符合注册要求的是A.笔名:雪用户名:snow 密码:snowdown 确认:snowdown B.笔名:JBH91 用户名:金不换密码:abcdef 确认:abcdef C.笔名:逐星追月用户名:star 密码:star4 确认:star4 D.笔名:柔情似水用户名:RQSS12 密码:luw4te7 确认:luw4te7 13.下图为某OCR软件识别过程的部分界面:A.单击A区的“体”字,B处的“休”字会变成“体”字B.单击A区的“休”字,C处的“体”字会变成“休”字C.单击B处的“休”字,A区的“体”字会变成“休”字D.单击C处的“体”字,B处的“休”字会变成“体”字14.下列软件中可以用来编辑HTML文件的是A.B.C.D.15.小涛在某网站查询国内航班,查询界面如右图所示,对所要查询的航班信息,以下说法正确的是()A.10月1日从上海到杭州,10月4日从昆明到上海B.10月1日从杭州到上海,10月4日从上海到昆明C.10月1日从上海到昆明,10月4日从昆明到上海D.10月1日从上海到昆明,10月4日从杭州到昆明16.下图为整理收藏夹的部分界面:要将“新华网”移到“新闻网站”文件夹中,有一下操作:1单击“移至文件夹”按钮,弹出“浏览文件夹”对话框2单击“确定”按钮3选择“新华网”4在“浏览文件夹”对话框中,选择“新闻网站”文件夹正确的步骤为A.○1○4○2○3B.○3○1○4○2C.○1○4○3○2D.○1○2○4○3 17.在IE浏览器中,要查看最近访问过的网址,应单击下列按钮中的A.B.C.D.二综合题(18题5分,19题9分,20题7分,共21分)18.小刘要根据第18题-1图所示的表格数据建立一个数据库文件“学生.mdb”。
2011年重庆市普通高等学校招生三校生类统一考试计算机类专业综合试题

2011年重庆市普通高等学校招生三校生类统一考试计算机类专业综合试题计算机类专业综合试题卷共12页。
满分300分。
考试时间150分钟。
注意事项:1.答题前,务必将自己的姓名、准考证号填写在答题卡规定的位置上。
,2.答选择题时,必须使用2B铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦擦干净后,再选涂其他答案标号。
3.答非选择题时,必须使用0.5毫米黑色签字笔,将答案书写在答题卡规定的位置上。
4.所有题目必须在答题卡上作答,在试题卷上答题无效。
5.考试结束后,将试题卷和答题卡一并交回。
本试题卷解密时间:2011年6月8日11:30,说明:试题卷中将Visual FoxPro 6.0简称为VFP。
一、单项选择题(共40小题,每小题3分,共120分)从每个小题的备选答案中,选出一个最符合题目要求的答案。
并将答题卡对应位置上的答案标号涂黑。
1.计算机能够根据“真与假”的结果决定下一步的工作流程,是因为它具有A.运算速度快的能力B.存储容量大的能力C.逻辑判断的能力D.通用性强的能力2.随机存取存储器RAM的特点是A.断电后,存储的数据将会丢失B.存储的数据将永久保存C.只能读出数据,不能写人数据D.只能写人数据,不能读出数据3-下列因素中,对微型计算机工作影响最小的是A.温度B.湿度C.噪声D.磁场4.按打印机输出质量由高到低排列的是A.激光打印机、喷墨打印机、针式打印机B.喷墨打印机、针式打印机、激光打印机C.针式打印机、激光打印机、喷墨打印机D.喷墨打印机、激光打印机、针式打印机5.下列属于系统软件的是A.办公软件B.辅助设计软件C.图形处理软件D.语言处理软件6.关于计算机病毒的叙述错误的是A.能够自我复制B.计算机自己生成的C.具有传染性D.具有破坏性7.关于计算机采用二进制的叙述错误的是A.可以降低硬件成本B.两个状态的系统具有稳定性C.二进制表示的数据简短D.二进制的运算规则简单8.关于BIOS的叙述错误的是A.BIOS固化在主板的ROM芯片中B.BIOS为微机提供最底层的、最直接的硬件设置和控制C.BIOS设置的参数保存在CMOS RAM芯片中D.B10S设置的参数保存在BIOS ROM芯片中9.主板上芯片组的作用不包括A.提对CPU的支持B.提供对内存的支持C.提供对硬盘接口的支持D.提供对应用软件接口的支持10.下列软件不是操作系统的是A.QQ B.Windows XPC.Unix D.Linux1l.在Windows XP的菜单选项中,会看到一些后缀标记,其中表示执行后将弹出一个对话框的标记是A. B.…C D.加下划线的字母12.在windows XP中,剪贴板是应用程序之间用来传递信息的临时存储区,该区域是A.内存的一部分B.硬盘的一部分C.回收站的一部分D.软盘的一部分l 3.点击IE浏览器工具栏中的“主页”按钮,浏览页面将转到A.Microsoft公司的主页B.正在访问的站点的主页C.IE中设定的主页D.用户个人网站的主页14.在Windows XP中,新建文本文件的默认属性是A.只读B.存档C.隐藏D.系统15,关于屏幕分辨率的叙述错误的是A.分辨率的高低由每帧画面的像素数量决定B.分辨率越高,显示的图像就越清晰C.分辨率越高,画面显示越稳定,闪烁感就越小D.分辨率高时,屏幕上显示的项目多,但尺寸比较小16,局域网所覆盖的地理范围比较小,通常不超过A.1km B.10kmC 100kmD 1000km17.下列操作系统中能够升级安装Windows Server 2003的是A.MS-DOS B.Windows 98C.Windows XP D.Windows 2000 Server18.下列网络传输介质中传输速率最高的是A.同轴电缆B.双绞线C.光纤D.电话线19.制定802.11网络标准的组织是A.ARPA B.IEEEC.ITU D.ISO20.在下列网络结构中,可靠性最高的是A.总线型B.星形C.环型D.网状型2l.在网络的通信协议中一般不包括A.信息交换的速率B.传输代码的结构C.信息的正文D.出错控制22.如果组建的局域网规模很大,每台计算机均能独立运行,其局域网类型应选择A.对等式网络B.工作站/服务器网络C.无盘工作站网络D.两两对接网络23.在组建网络时使用配线架能够A.避免使用跳线B.将前端的信息点直接接入到交换机上C.实现不同传输介质的对接D.减少交换机端口的磨损24.关于对等网的叙述错误的是A.需要设置一台计算机做专门的服务器B.网络中的每台计算机既可作为客户机又可作为服务器C.每个用户都可管理本地机上的资源D.网络中的每台计算机可以互相共享资源25.关于Windows Server 2003网络配置的叙述正确的是A.网络客户和协议均自动安装无需再配置B.IP只能是自动获得的C.可为一块网卡绑定多个IPD.只能配置一个默认网关26.在windows XP的对等网内,对计算机之间的相互访问无影响的因素是A.计算机名称是否相同B.工作组名称是否相同C.是否开启GUEST用户D,是否开启防火墙27.在C语言中,可以作为自定义标识符的是A.3x B.x_yC.x-y D.long28.关于C语言函数定义的叙述正确的是A.函数都有返回值B.可以定义空函数C.函数定义允许嵌套D.定义float型的函数时数据类型说明符可以省略29.在C语言中,设int a[6]={l,2,3};则不能表示数组a中元素的是A.a[O] B.a[1]C.a[4] D.a[6]30.在C语言的条件判断中,能正确表示“a不等于0”的表达式是A.a<>O B.aC.a=O D.!a31.在C语言中,设int m,n;在执行语句scanf(”%d%d”,&m,&n);时,如果希望将数据10和20分别赋给变量m和n,则正确的输入格式是A.1020<回车> B.10 20<回车>C.10,20<回车> D.m=10,n=20<回车>32.在C语言中,能正确表示十六进制数79的是A.79 B.079C.X79 D.0X7933.在C语言中,能决定函数返回值类型的是A.函数内变量的类型B.主调函数的类型C.return语句中表达式的类型D.定义该函数时所指定的函数的类型34.用二维表的形式表示实体和实体问联系的数据模型是A.关系模型B.网状模型C.层次模型D.对象模型35.在VFP中,数据表文件和索引文件都已打开,将记录指针定位在第1号记录上的命令是A.G0 TOP B.GO BOTTC.GO 1 D.SKIP 136.SQL SELECT语句中的WHERE子句对应于查询设计器中的A.“筛选”选项卡B.“联接”选项卡C.“字段”选项卡D.“排序依据”选项卡37.在VFP中,SET DEFAULT T0命令的功能是设置A.当前数据库B.主索引C.默认路径D.默认工作区38.在VFP中,关于建立表间永久关系的叙述正确的是A.表间永久关系是设置参照完整性的必要条件B.关闭数据表后表间的永久关系即被取消C.数据库表和自由表之间可以创建永久关系D.表间永久关系只能是一对一的39.在VFP中,使用报表设计器创建报表时,通常将列标题信息放到A.标题区B.页标头区C.细节区D.页注脚40.在VFP中,如果限定性别字段只能输人“男”和“女”。
2011(秋)江苏高校计算机一级摸底测验4

2011〔秋〕江苏高校电脑一级考试<4>必做题单项选择题[1].信息技术是指用来扩展人们信息器官功能、协助人们进行信息处理的一类技术,其中________主要用于扩展手、眼等效应器官的功能。
答案:C[2].以下关于比特的表达中错误的选项是_________。
B.比特可以表示文字、图像、声音等多种不同形式的信息答案:C[3].将十进制数89.625转换成二进制数表示,其结果是_________。
答案:A[4].20世纪四、五十年代的第一代电脑主要应用于________领域。
答案:D[5].以下关于电脑硬件组成的描述中,错误的选项是________。
D.一台电脑中可能有多个处理器,它们都能执行指令答案:B[6].以下关于PC机主板上芯片组的描述中,错误的选项是________。
B.芯片组规定了主板可安装的内存条的类型、内存的最大容量等答案:D[7].PC机加电启动时,电脑首先执行BIOS中的第一部分程序,其目的是_________。
A.读出引导程序,装入操作系统答案:B[8].总线最重要的性能指标是它的带宽。
假设总线的数据线宽度为16位,总线的工作频率为133MHz,每个总线周期传输一次数据,则其带宽为________。
答案:A[9].以下选项中,属于击打式打印机的是________。
答案:A[10].在windows操作系统中,系统约定第一个硬盘的盘符必定是________。
A.A:B.B:C.C:D.D:答案:C[11].PC机上运行的WindowsXP操作系统属于________。
答案:B[12].以下关于操作系统中多任务处理的表达中,错误的选项是:________。
A.将CPU时间划分成许多小片,轮流为多个程序服务,这些小片称为"时间片"B.由于CPU是电脑系统中最珍贵的硬件资源,为了提高CPU的利用率,一般采用多任务处理C.正在CPU中运行的程序称为前台任务,处于等待状态的任务称为后台任务D.在单CPU环境下,多个程序在电脑中宏观上同时运行,微观上由CPU轮流执行答案:C[13].以下关于汇编语言的表达中,错误的选项是____________ 。
2011秋季计算机组成试题(A)答案

哈工大 2011 年 秋 季学期计算机组成技术III(A)试 题1. 计算机内使用的数制是 二进制 。
2. 把一个数连同其符号在计算机中的表示加以数值化,这样的数称为 机器数 。
3. 为了标识数制,规定在十进制数末尾加字母D ,二进制末尾加字母 B ,八进制末尾加字母 O ,十六进制末尾加字母 H 。
4. 宏汇编源程序需要经过汇编程序 MASM 汇编成机器能够识别的机器代码程序,再经过连接程序 LINK 产生一个可执行模块。
5. I/O 与主机数据传送主要有 程序查询 、 程序中断 和DMA 三种控制方式。
6. 所谓指令是指计算机执行某种操作的命令。
指令通常由 操作数 和 操作码 组成。
7. 如果组成一个64K*8的存储体,使用8K*4的芯片需要 16 片,使用16K*8的芯片需要 4 片,使用8K*1的芯片需要 64 片。
8. DB 伪指令以1个字节为单位分配存贮;DW 指令以__2_个字节为单位分配存贮, DD指令以_4_个字节为单位分配存储。
9. 8086CPU 有 16 根数据线, 20 根地址线,寻址空间为 1M 个存储单元。
10. 在8086CPU 中有哪四个段寄存器: CS , ES , SS , DS 。
11. 输入、输出设备的编址方式有 统一编址(存储器映射IO ) 、 独立编址 两种。
12. 一个存储芯片的容量为8k*8,该芯片共有 个存储单元,有 根地址线,有 根数据线。
13. 数的运算可以分为两类,算术运算和逻辑运算,逻辑运算一般包括 与 , 或 , 非 ,异或 。
14. 用ASCII 码表示一个字符需要 1 个字节,用机内码表示一个汉字需要 2个字节。
15. 写出下列英文单词或缩写在计算机中的含义: CPU :__中央处理单元____________; ALU :_算术逻辑处理单元___________; CISC :__复杂指令系统计算机___________; SRAM :__静态RAM__________;ROM :__只读存储器_______; Cache :_____高速缓存_____________;第 1 页 (共 8页)简答题( 每题4分,共16分 )1、简单描述计算机存储系统的层次结构,画出层次结构图并说明各层次的主要特点。
高性能计算习题及答案

高性能计算练习题1、一下哪种编程方式适合在单机并行?哪种适合在多机间并行?单机:Threading线程、OpenMP;多机:MPI。
2、例题:HPC集群的峰值计算能力:一套配置256个双路X5670处理器计算节点的HPC集群。
X5560:2.93GHz Intel XS5670 Westmere六核处理器,目前主流的Intel处理器每时钟周期提供4个双精度浮点计算。
峰值计算性能:2.93GHz*4Flops/Hz*6Core*2CPU*256节点=36003.8GFlops。
Gflops=10亿次,所以36003Gflops=36.003TFlops=36.003万亿次每秒的峰值性能。
3、T op500排名的依据是什么?High Performance Linpack(HPL)测试结果4、目前最流行的GPU开发环境是什么?CUDA5、一套配置200TFlops的HPC集群,如果用双路2.93GHz Intel westmere六核处理器X5670来构建,需要用多少个计算节点?计算节点数=200TFlops/(2*2.93GHz*6*4Flops/Hz)=14226、天河1A参与TOP500排名的实测速度是多少,效率是多少?2.57PFlops 55%7、RDMA如何实现?RDMA(Remote Direct Memory Access),数据发送接收时,不用将数据拷贝到缓冲区中,而直接将数据发送到对方。
绕过了核心,实现了零拷贝。
8、InfiniBand的最低通讯延迟是多少?1-1.3usec MPI end-to-end,0.9-1us InfiniBand latency for RDMA operations9、GPU-Direct如何加速应用程序运行速度?通过除去InfiniBand和GPU之间的存拷贝来加速程序运行。
•GPUs provide cost effective way for building supercomputers【GPUs提供高效方式建立超级计算机】•Dense packaging of compute flops with high memory bandwidth【使用高端存带宽的密级封装浮点计算】10、网络设备的哪个特性决定了MPI_Allreduce性能?集群大小,Time for MPI_Allreduce keeps increasing as cluster size scales,也就是说集群的规模决定了MPI_Allreduce的性能。
并行计算与高性能计算考核试卷

(以下为答题纸区域,请考生在此区域作答,超出此区域作答无效。)
三、填空题(本题共10小题,每小题2分,共20分,请将正确答案填到题目空白处)
1.并行计算中,将一个大的任务分解成多个子任务的过程称为______。
2.在并行计算中,______是指使用多个处理器执行单个任务的不同部分。
3.高性能计算中,______是一种衡量计算机性能的指标,表示每秒能够执行的浮点运算次数。
C. CUDA
D. Java
5.并行计算中,任务分解与任务分配是()
A.相同的过程
B.互相独立的
C.相互依赖的
D.无关的
6.以下哪个部件不是并行计算机的主要组成部分?()
A.处理器
B.存储器
C.网络接口卡
D.显卡
7.高性能计算领域中,计算速度的主要指标是()
A. MIPS
B. MFLOPS
C. GHz
D. OpenCL
11.并行计算中,以下哪种通信方式开销最小?()
A.同步通信
B.异步通信
C.广播通信
D.全局通信
12.以下哪个术语不是高性能计算中的术语?()
A.性能
B.效能
C.并行度
D.带宽
13.并行计算中,以下哪种同步机制可能会导致死锁?()
A.互斥锁
B.条件变量
C.信号量
D.读写锁
14.以下哪个选项不属于并行计算中的数据依赖类型?()
3. MFLOPS
4.点对点
5.数据并行
6.可扩展性
7.图形处理单元
8.互斥锁
9. SRAM
10.并发
四、判断题
1. ×
2. ×
3. √
《2011年9月全国计算机等级考试试题及答案》及相关

《2011年9月全国计算机等级考试模拟试题及答案》1."商品"与"顾客"两个实体集之间的联系一般是(D)A)一对一B)一对多c)多对一D)多对多注意:要能区分一对一,一对多,多对多,题目可扩展为三道。
2.在E-R图中,用来表示实体的图形是(A)A)矩形B)椭圆形C)菱形D)三角形注意:矩形表示实体,椭圆形表示属性,菱形表示联系3.数据库DB、数据库系统DBS、数据库管理系统DBMS之间的关系是(C)A)DB包含DBS和DBMSB)DBMS包含DB和DBSC)DBS包含DB和DBMSD)没有任何关系注意:1)包含关系2)数据库系统的核心软件是DBMS,应用程序通过DBMS来使用数据库中的数据。
4.在Visual FoxPro中以下叙述错误的是(D)A)关系也被称作表B)数据库文件不存储用户数据C)表文件的扩展名是.dbfD)多个表存储在一个物理文件中5.数据库技术的根本目标是要解决数据的(B)。
A)存储问题B)共享问题C)安全问题D)保护问题6.操作对象只能是一个表的关系运算是(C)。
A)联接和选择B)联接和投影C)选择和投影D)自然连接和选择注意:关系运算的定义要熟记。
7.在 Visual FoxPro 中以下叙述正确的是(B)。
A)关系也被称作表单B)数据库文件不存储用户数据C)表文件的扩展名是.DBCD)多个表存储在一个物理文件中8.数据独立性是数据库技术的重要特点之一。
所谓数据独立性是指 (D)A) 数据与程序独立存放B) 不同的数据被存放在不同的文件中C) 不同的数据只能被对应的应用程序所使用D) 以上三种说法都不对9.用树形结构表示实体之间联系的模型是 (C)A) 关系模型B) 网状模型C) 层次模型D) 以上三个都是注意:关系模型的定义要熟记。
10.数据库系统中对数据库进行管理的核心软件是 (A)A) DBMSB) DBC) OSD) DBS11.关系运算中的选择运算是 (A)A)从关系中找出满足给定条件的元组的*作B)从关系中选择若干个属性组成新的关系的*作C)从关系中选择满足给定条件的属性的*作D)A和B都对12.DBMS的含义是(B)A.数据库系统B.数据库管理系统C.数据库管理员D.数据库13.从关系模式中指定若干个属性组成新的关系的运算称为(B)A.联接B.投影C.选择D.排序14.对于“关系”的描述,正确的是(D)A同一个关系中允许有完全相同的元组B同一个关系中元组必须按关键字升序存放C在一个关系中必须将关键字作为该关系的第一个属性D同一个关系中不能出现相同的属性名15.在关系模型中,为了实现“关系中不允许出现相同元组”的约束应使用(B)A) 临时关键字B) 主关键字C) 外部关键字D) 索引关键字注意:熟悉关系的术语16.以下关于关系的说法正确的是(C)A) 列的次序非常重要B) 当需要索引时列的次序非常重要C) 列的次序无关紧要D) 关键字必须指定为第一列17.对于现实世界中事物的特征,在实体-联系模型中使用(A)A)属性描述B)关键字描述C)二维表格描述D)实体描述18.把实体-联系模型转换为关系模型时,实体之间多对多联系在关系模型中是通过(C)A)建立新的属性来实现B)建立新的关键字来实现C)建立新的关系来实现D)建立新的实体来实现19.专门的关系运算不包括下列中的 (D)A)联接运算B)选择运算C)投影运算D)交运算20.对关系S和关系R进行集合运算,结果中既包含S中元组也包含R中元组,这种集合运算称为 (A)A)并运算B)交运算C)差运算D)积运算21如下关系表:RABC112223TABC112223313SABC313则下列操作正确的是(B)A)T=R∩SB)T=R∪SC)T=RхSD)T=R/S注意:要掌握并,交差的概念.P1322.数据库系统与文件系统的最主要区别是(B)A) 数据库系统复杂,而文件系统简单B) 文件系统不能解决数据冗余和数据独立性问题,而数据库系统可以解决C) 文件系统只能管理程序文件,而数据库系统能够管理各种类型的文件D) 文件系统管理的数据量较小,而数据库系统可以管理庞大的数据量23.扩展名为dbf的文件是(A)A.表文件B. 表单文件C.数据库文件D.项目文件24.在Visual FoxPro中“表”是指(B)A) 报表B) 关系C) 表格D) 表单25.VISUAL FOXPRO是一种关系型数据库管理系统,这里关系通常是指(B)A)数据库文件(.DBC文件)B)一个数据库中两个表之间有一顶的关系C)表文件(.DBF文件)D)一个表文件中两条记录之间有一定的关系注意:一个具体的关系模型由若干个关系模式组成.在VISUAL FOXPRO中,一个数据库中包含相互之间存在联系的多个表.这个数据库文件就代表一个实际的关系模型.P11。
2011年九月份计算机等级考试答案

vf:1-20 23112 33432 33432 11232 21-35 43234 32234 11212 1.一对多 2.255 3.白盒测试 4.需求分析 5.DBMS 6.数据库 7.日期型 8.连接 9.having 10.goto 11.primary key 12..F. 13.prg 14.19 15.avg(成绩
2:70,13:for.output.as#1,14:"end" 15
ct,nt
vb前:1-10bbbacdadca11-20abbacbddbb,21-30aabbacabdc,31-35cbaad填空1线性结构2,n-1 3结构化4dbms5属性6on7declare82:259100 101,10doform11autocenter12文本框13mpr14页注脚15readevent
收费明细附表:
工业产品类(机械类)
项目 一级
二级
培训费及资料费
150元
150元
报名及考试费
170元
170元
总计
320元
320元
土木与建筑类
项目 一级
二级
培训费及资料费
150元
150元
ቤተ መጻሕፍቲ ባይዱ
随着物权法立法进程的推进,不少业内人士提出希望此次物权的立法能在该问题的解决上有所突破。因此本报公司法务专刊特别邀请有关专家围绕“在建工程的法律性质”展开讨论,以期能对该问题的解决产生一定积极意义。
问题一:建设工程的施工过程,是将钢筋水泥等建筑材料进行物化的过程,在建工程是否已经构成了一个完整法律意义上的独立的“物”?
问题四:在建工程土地使用权已经抵押给银行的情况下,建设单位将在建工程抵押给承包人,在立法上是否可行?如果允许,那么办理抵押登记的行政机关是“建设行政主管单位”还是“房地产主管单位”?
高性能计算技术练习题

高性能计算与云计算练习题1. 解释以下基本概念●HPC, HPCC, Distributed computing, Cloud computing●MIMD, SIMD, SISDHPC:High Performance Computing 高性能计算,即并行计算。
在并行计算机或分布式计算机等高性能计算系统上所做的超级计算。
HPCC:High Performance Computing and Communication 高性能计算与通信。
指分布式高性能计算、高速网络和Internet的使用。
Distributed computing:分布式计算。
在局域网环境下进行的计算。
比起性能来说,它更注重附加功能。
一个计算任务由多台计算机共同完成,由传统的人和软件之间的交互变成软件和软件之间的数据交互。
Cloud computing:云计算(Cloud Computing)是一种新兴的商业计算模型。
它将计算任务分布在大量计算机构成的资源池上,使各种应用系统能够根据需要获取计算力、存储空间和各种软件服务。
MIMD:多指令多数据流。
每台处理机执行自己的指令,操作数也是各取各的。
SIMD:单指令多数据流。
所有“活动的”处理器在同一时刻执行同一条指令对多个数据流进行操作。
SISD:单指令单数据流。
传统的串行处理机。
CPU执行单一的指令流对单一的数据流进行操作。
2. 试比较PVP、SMP、MPP、DSM和Cluster并行机结构的不同点,以典型系统举例说明。
3. 列出常用静态和动态网络的主要参数(节点度、直径、对剖带宽和链路数)以及复杂度、网络性能、扩展性和容错性等。
常用的标准互联网络有哪些?答:静态网络(Static Networks)是指处理单元间有着固定连接的一类网络,在程序执行期间,这种点到点的链接保持不变;动态网络(Dynamic Networks)是用交换开关构成的,可按应用程序的要求动态地改变连接组态。
2011秋C++试卷(附答案)

2011年秋江苏省计算机等级考试试题C++语言程序设计(第二部分)一、选择题(用答题卡答题,答案依次填在21~30答题号内)21. 以下关于C++变量的存储类型和作用域的叙述中,正确的是(21)。
A.可将变量分为:auto、static、extern、register和array五种存储类型B.自动变量的作用域为整个程序文件C.函数内定义的静态变量的作用域为整个程序文件D.在某花括号“{”开头定义的变量,其作用域为该开花括号至对应的闭花括号内22. 在C++中,没有this指针的函数是(22)。
A.静态成员函数B.构造函数C.析构函数D.非静态的内联成员函数23. 在C++中,设有变量说明“char a[20],*pa=a;”,不存在语法错误的语句是(23)。
A.a[20]="Hello"; B.a="Hello"; C.*pa="Hello"; D.pa="Hello";24. C++的break语句(24)。
A.用在能出现语句的任意位置B.只能用在循环体内C.只能用在循环体内或switch语句中D.能用在任一复合语句中25. 以下有关C++构造函数的叙述中,正确的是(25)。
A.构造函数的名字可与类名不同B.可定义构造函数的返回值类型C.构造函数可由系统自动调用D.可以存在没有构造函数的类26. 在C++中,用非成员函数重载双目运算符时,其参数表中的参数个数为(26)。
A.0个B.1个C.2个D.3个27. 在C++派生类中定义虚函数时,可以与基类中相应的虚函数不同的是(27)。
A. 参数类型B. 函数体C. 参数个数D. 函数返回值的类型28. 以下关于C++标识符的描述中,不正确的是(28)。
A. 标识符必须以字母或下划线开头B. 标识符可以用任何字符开头C. 标识符区分大小写字母D.用户定义的标识符不能与关键字相同29. 以下关于C++函数的叙述中,不正确的是(29)。
2011年秋计算机科学技术A试卷

柳州市鹿寨职业教育中心2011-2012学年度上学期《计算机科学技术》期末试卷A考试时间:90 分钟 满分:150分 考试类型:闭卷一、选择题(每题1.5分 60题共90分)1、计算机中数据的表示形式是 ( )A 八进制B 十进制C 二进制D 十六进制2、下面列出的四种存储器中,易失性(即断电后数据会丢失)存储器是( )A RAMB ROMC PROMD CD-ROM3、计算机硬件能直接识别和执行的只有( )A 高级语言B 符号语言C 汇编语言D 机器语言 4、微机中1K 字节表示的二进制位数是( )A 1000B 8x1000C 1024D 8x1024 5、通常一个完整的计算机系统应包括:( )A 主机、键盘和显示器B 计算机及其外部设备C 系统软件和系统硬件D 硬件系统和软件系统 6、一台计算机的配置为:赛扬466/8.4G/32M:其中466指的是:( )A 内存容量B CPU 型号C 硬盘容量D 主频 7、Windows XP 操作系统是一个( )A 单用户多任务操作系统B 多用户多任务操作系统系统C 多用户单任务操作系统D 单用户单任务操作 8、在Windows XP 中,“任务栏”的作用是( )A 显示系统的所有功能B 只显示当前活动窗口名C 只显示正在后台工作的窗口名D 实现窗口之间的切换9、Word2003的“文件”命令菜单底部显示的文件名所对应的文件是( )A 当前被操作的文件B 当前已经打开的所有文件C 最近被操作过的文件D 扩展名是.doc 的所有文件 10、下面是关于Windows XP 文件名的叙述,错误的是( )A 文件名中允许使用汉字B 文件名中允许使用多个圆点分隔符C 文件名中允许使用空格D 文件名中允许使用竖线("|")11、当选定文件或文件夹后,不将文件或文件夹放到“回收站”中,而直接删除的操作是( )A 按Delete (Del )键B 用鼠标直接将文件或文件夹拖放到“回收站”中C 按Shift +Delete (Del )键D 用“我的电脑”或“资源管理器”窗口中“文件”菜单中的删除命令 12、当个人计算机以拨号方式接入1nternet 网时,必须使用的设备是( )A 网卡B 调制解调器(Modem )C 电话机D 浏览器软件 13、下列有关复制文件和文件夹的错误说法是:( )A 通过资源管理器的编辑菜单命令可以完成复制任务B 使用鼠标拖放将文件或文件夹拖到目标位置可以代替复制操作C 使用鼠标拖放复制文件会丢失文件的格式D 按[ctrl]键的同时使用鼠标拖放文件可以实现文件的复制14、用中、小规模集成电路作为主要元件的计算机,称为( )电子计算机A 、第一代B 、第二代C 、第三代D 、第四代15、计算机系统的开机顺序是( )A 、 先开主机再开外设B 、先开显示器再开打印机C 、 先开外设再开主机 D、先开主机再打开显示器 16、某单位的人事档案程序属于( )A 、工具软件B 、应用软件C 、系统软件D 、字处理软件 17、在计算机中,1GB 表示( )。
08-10江苏计算机三级偏软试卷及答案

2011年秋季江苏省三级偏软考试真题(无答案)2011年(秋)江苏省高等学校非计算机专业学生计算机基础知识和应用能力等级考试试卷三级偏软(本试卷考试时间150分钟)说明:1.本试卷题型分两类:选择题和填空题2.选择题使用答题卡答题。
每一个选择题有A、B、C、D四个可供选择的答案,请将其中一个正确答案按题序涂写在答题卡的相应题号中。
3.填空题使用答题纸答题。
请将答案填入答题纸上的相应题号中,不得转行。
4.请检查答题卡和答题纸上的学校和准考证号等是否已分别按规定填好。
一、选择题(共有70个空格,每格1分,共70分,请务必使用答题卡答题)I.计算机基础知识(14分)1.在2010年11月公布的世界超级计算机TOP 500强名单中,我国研制的天河一号A以峰值性能每秒 4701亿次、实测每秒2566万亿次的运算速度名列榜首,天河一号A配置了14336颗Intel xeon X5670六核处理器和2048颗我国制造的___(1)___飞腾处理器(FT-1000)。
A.双核B.四核C.六核D.八核2. 天河一号A采用的是基于___(2)___内核的麒麟操作系统。
A.UNIXB.LINUXC.WINDOWS 7WARE3.下列4个不同进制的数中,数值最小的是___(3)___。
A.2B.4H B.53.4QC.101110.1BD.454.带符号的16位二进制定点数,用补码表示时,其最大的绝对值是___(4)___A.32767B.32768C.65535D.655365.设有8位字长表示的浮点数,从高位到低位依次为阶符1位、阶码2位(补码),数(尾)符1位,尾数4位(原码),则该浮点数的数值范围为___(5)___。
A.-15/256~+15/2B.-15/2~+15/2C.-15/2~+15/256D.-15/256~+15/2566.根据汉字编码标准(GB2312-80),汉字"微"位于46区的第2位,则它在计算机内部存储时的内码为___(6)___A.CEA2HB.2E02HC.4602HD.4E22H7. 要对二进制数据中的若干位取反,其他位不变,应采用的逻辑操作是___(7)___A.ANDB.ORC.XORD.NOT8. 组成一个微机系统除了需包含CPU、ROM、RAM、总线、外设以外,至少还应包含___(8)___。
全国计算机等级考试三级网络技术真题2011年9月

全国计算机等级考试三级网络技术真题2011年9月(总分:100.00,做题时间:120分钟)一、选择题(每小题1分,共60分)(总题数:60,分数:60.00)1.我国“天河一号”超级计算机的计算速度为2.507PFlops。
这里PFlops的P代表10的15次方,那么该浮点运算速度为每秒钟( )。
(分数:1.00)A.2.507万亿次B.2.507百万亿次C.2.507千万亿次√D.2.507亿亿次解析:[解析] 本题考查计算机速度的概念。
PFlops表示处理速度。
P即10的15次方,计算可知其量级为千万亿次。
所以2.507PFlops即2.507千万亿次。
2.关于计算机应用的描述中,错误的是( )。
(分数:1.00)A.模拟核爆炸需要复杂的科学计算B.中长期气象预报主要是事务处理√C.过程控制大多采用嵌入式计算装置D.CAD、CAM改变了传统制造业的面貌解析:[解析] 模拟核爆炸、模拟经济运行和进行中长期天气预报都属于科学计算的范畴。
3.关于工作站的描述中,正确的是( )。
(分数:1.00)A.RISC加Unix曾是专业工作站主流√B.RISC加Windows曾是PC工作站主流C.图形工作站不支持OpenGL标准D.工作站按体系结构分为CISC和VLIW两种解析:[解析] 工作站根据软、硬件平台的不同,一般分为两类:一类是基于RISC和UNIX操作系统的专业工作站,另一类是基于Intel处理器和Windows操作系统的PC工作站。
4.关于计算机芯片技术的描述中,错误的是( )。
(分数:1.00)A.奔腾芯片是32位的B.安腾芯片是64位的C.哈佛结构把指令缓存与数据缓存分开D.超流水线采用多条流水线执行多处理√解析:[解析] 超流水线技术是通过细化流水、提高主频,使得在一个机器周期内完成一个甚至多个操作。
选项D)中的多条流水线执行多个处理的描述是超标量技术的概念。
5.关于软件概念的描述中,正确的是( )。
2011秋高性能计算练习题

说明:A 组题中任选1题,在B 组任选1题;编写MPI 程序,采用多进程协同完成练习题。
要求: (1) 并行环境正确运行;(2)提交上机实验报告:问题描述、算法设计、重点及难点、并行程序关键代码、计算结果分析等 A01. 从键盘输入一个无符号长整型数n ,计算2~n 之间完数的个数。
所谓完数是指,小于该数的所有因数之和恰好等于该数。
例如6是一个完数,因为小于6的因数有1,2,3且1+2+3=6。
A02. 从键盘输入一个无符号长整型数n ,产生一个长度为n ,取值在[0,1]之间的随机实数数组,计算其去掉一个最大值、去掉一个最小值,剩下n -2个值的平均值。
A03. 从键盘输入一个无符号长整型数n ,产生一个长度为n ,取值在[0,1]之间的随机实数数组,计算其数学期望、方差。
A04. (仿环网络的多圈接力) 设0进程有变量x ,初值为0,要求将x 按进程号的次序,将(圈数*进程号)累加到x 上,完成m 后,输出0进程中x 的值。
A05. (仿完全连接网络的互致问候)所有进程间两两互致问候。
具体要求,例如:进程0传递字符串”greetings from process No.0.”到进程1。
进程1则在收到字符串前添加字符”Process No.1 has received ”并输出。
A06. (仿二维网格Mesh 通信)设创建n m P ⨯=个进程(n m ,为正整数),要求各进程与其相邻的进程(按n m ⨯网格结构)互致问候。
具体要求,例如:若进程0传递字符串”greetings from process No.0.”到进程1。
进程1则在收到字符串前添加字符”Process No.1 has received ”并输出。
A07. (仿二维环形网格2D-Torus Mesh 通信)设创建n m P ⨯=个进程(nm ,为正整数),要求各进程与其相邻的进程(按2维n m ⨯环形网格结构)互致问候。
2011年全国专业技术人员计算机应用能力考试题库每科10套模拟题

中文Windows XP 操作系统模块【第一套】1.请切换鼠标左右键按钮的功能。
2.将当前窗口移动到桌面右上角。
3.将Windows的色彩方案设为橄榄绿。
4.在写字板程序中设置度量单位为“厘米”且文字按窗口自动换行。
5.请通过任务管理器运行“msconfig”程序。
6.通过任务栏添加智能ABC输入法,并设置其词频调整。
7.桌面上有打开的我的电脑窗口,请将窗口的工具栏锁定。
8.隐藏窗口的状态栏。
9.将“回收站”的最大空间设置为每个驱动器的10%。
10.请让鼠标指向文件夹时显示提示信息,并在标题栏中显示完整的路径。
11.在E盘根文件夹下,请利用窗口信息区创建一个新文件夹“联系电话”,并将其属性设置为“隐藏”。
12.从开始菜单设置打印机Epson EPL-3000为默认打印机,并且脱机使用。
13.设置在任务栏上显示时钟。
14.让工具栏的图标显示为小图标。
15.对磁盘E盘进行扫描并恢复坏扇区。
16.利用快捷方式向导,为用户“myFamily”在桌面“游戏”文件夹中,给文件夹“E:\exame”中的应用程序“mshearts.exe”创建名为“红心大战”的快捷方式.17.设置“电源选项属性”,使按下计算机电源按钮时“问我要做什么”。
18.选中“C:\WINDOWS”文件夹下所有文件和文件夹。
19.请注销当前用户。
20.最小化当前桌面上打开的多个窗口,快速显示出桌面。
21.利用控制面板,将日期格式设置为“yyyy-MM-dd”短格式。
22.让任务管理器保持前端显示,大图标显示当前运行的应用程序,然后重新启动计算机。
23.通过对文件夹设置,单击打开setup文件夹。
24.将IE图标移动到我的文档图标下方,并设置桌面图标自动排列。
25.请在当前窗口通过菜单栏创建一个公文包。
26.通过任务栏设置在“开始”菜单中显示“控制面板”项目,并且设置为“显示为菜单”,并查看。
27.请将桌面上的“Word”快捷方式附加到“开始”菜单的“固定项目列表”中,并查看“开始”菜单。
2011秋江苏省计算机等级考试c语言试题答案

A. B. C. D.
BMP JPG GIF PNG
第二部分 C语言程序设计
一.选择题 21. 某程序需要使用一个代表常数3.14的符号常量P,以下定义中正确 的是 (21) A. #define P 3.14 ; B. #define P(3.14) C.#define P=3.14 ; D. #define P 3.14 22. 下列四个选项中,属于C语言关键字的是 (22) A. Float B. single C. double D. real 23. 已知某编译系统中signed int 类型数据的长度是16位,该类型数据的 最大值是 ( 23) A. 32767 B. 32768 C. 127 D. 65535 24. 以下关于if语句和switch语句的叙述中错误的是 (24) A. if语句和switch语句都可以实现算法的选择结构 B. if语句和switch语句都能实现多路(两路以上)选择 C. if语句可以嵌套使用 D. switch语句不可以嵌套使用 25. 已有声明“char *1=”China”,s2[10],*s3=”Nanjing”,*s4;”,以下字符串 赋值语句在执行时可能出现错误的是 (25) A. strcpy(s3,s1); B. strcpy(s4,s1); C. strcpy(s2,s1); D. strcpy(s2,s3); 26. 已有声明“int x=0,*p=&x;”,以下语句中有语法错误的是 (26) A. printf(”%d”,*x); B. printf(”%d”,&x); C. printf(”%d”,*p); D. printf(”%d”,x); 27. 以下叙述中错误的是 (27) A. 在函数外可以声明变量 B. 变量声明的位置决定了该变量名的使用范围 C. 函数调用时在函数内声明的变量所得到的值将无法保存到该函数
2011年9月全国计算机三级数据库技术考试真题及答案

2011年9月全国计算机三级数据库技术考试真题及答案一、选择题(1)计算机软件分为系统软件和应用软件两大类下列哪一个不属于系统软件?( )A) 操作系统 B) 编译程序C) 数据库管理系统 D) 科学和工程计算软件(2)计算机系统的存储介质包括寄存器、Cache、内存和硬盘其中成本最低、访问速度最慢的是( )。
A) 寄存器 B) Cache C) 硬盘 D) 内存(3)下列关于Internet的叙述中哪一个是不正确的?( )A)通信线路的最大传输速率与其带宽成正比B)主机是Internet中信息资源与服务的载体C)搜索引擎的出现使得信息资源得到更合理的组织方式D)路由器的作用是将Internet中的各个局域网、城域网或广域网以及主机互联起来(4)从邮件服务器读取邮件所采用的协议是( )。
A) SMTP B) IMAP C) MIME D) EMAIL(5)通过专门的防范技术可以使系统免受来自恶意软件的威胁。
以下哪种技术不属于恶意软件检测技术?( )A) 签名扫描 B) 行为阻止 C) 启发式扫描 D) 防火墙(6)下列哪一项不是实现访问控制可采用的方法?( )A) 口令 B) 保护键 C) 存取控制表 D) 存取控制矩阵(7)下列哪些是数据结构研究的内容?( )Ⅰ. 数据的存储结构Ⅱ. 数据的逻辑结构Ⅲ. 数据的传输结构Ⅳ. 数据的采集Ⅴ. 数据的运算Ⅵ. 数据的集成A) 仅Ⅰ、Ⅱ和Ⅲ B) 仅Ⅳ、Ⅴ和ⅥC) 仅Ⅰ、Ⅱ和Ⅴ D) 仅Ⅰ、Ⅲ和Ⅵ(8)下列关于链式存储结构的叙述中哪些是正确的?( )Ⅰ. 逻辑上相邻的结点物理上不必邻接Ⅱ. 每个结点都包含恰好一个指针域Ⅲ. 用指针来体现数据元素之间逻辑上的联系Ⅳ. 结点中的指针都不能为空Ⅴ. 可以通过计算直接确定第i个结点的存储地址A) 仅Ⅰ和Ⅱ B) 仅Ⅰ和Ⅲ C) 仅Ⅰ、Ⅲ和Ⅴ D) 仅Ⅱ、Ⅳ和Ⅴ(9)下列关于串的叙述中哪一条是正确的?( )A) 串是由至少1个字符组成的有限序列 B) 串中字符的数目就是串的长度C) 空串就是由空格构成的串 D) 串只能顺序存储(10)栈S最多能容纳4个元素。
哈工大计算机试题2011秋A答案

哈工大 2011 年 秋 季学期大学计算机基础 试题(A)题号 一 二 三 四 五 六 七 八 九 十 总分 分数学号 姓名注:本试卷满分100分,折合为60分记入期末成绩。
如本试卷为补考卷,则按实际分数记录。
一. 单项选择题(每小题2分,共40分)1. 属于电子计算机的是( C )A 、1822年巴贝奇的差分机B 、1944年IBM 的MarkⅠC 、1942年美国宾夕法尼亚大学的ENIACD 、1801年杰卡德的提花编织机2. 因提出通用计算模型而为通用计算机建立理论基础,又因其为机器智能的定义而被称为计算机之父,人工智能之父的是( B )A 、莫希利和埃克特B 、阿兰·图灵C 、冯·诺依曼D 、爱因斯坦3. 按使用的电子元器件将计算机发展分为几个阶段,其中第四代计算机以使用( B )为分界。
A 、集成电路B 、超大规模集成电路C 、晶体管D 、单片机4. 关于逻辑运算以下说法错误的是( D )A 、逻辑运算是一种代数运算。
B 、VB 程序设计语言中的逻辑常量只有两个。
C 、常用的逻辑运算有与、或、非D 、“或”运算的结果只有两种,而"与"运算的结果不只两种。
5. 音频信息在计算机内部表示为( C )A. 连续变化的模拟信号B. 连续变化的数字信号C. 离散变化的数字信号D. 离散变化的模拟信号6.( A )能用来表示文件在磁盘上的位置。
A.路径B.目录C.我的电脑D.扇区7.高级语言程序计算机不能直接理解和执行,需要( C )将其翻译成计算机能直接理解并执行的二进制代码的目标程序。
A、机器语言B、操作系统C、编译程序D、编辑程序8.被称为计算机中央处理机的CPU是由( D )组成的。
A、算术运算器和逻辑运算器B.存储器和运算器C.存储器和控制器D.运算器和控制器9.VB中能向用户单向显示信息,而不能编辑的控件是( A )。
A.标签B.文本框C.命令按钮D.计时器10.在Word编辑状态下,如要调整段落的左右边界,用( C )的方法最为直观、快捷。
2011年特长生测试

一、工具软件问题描述:大家都知道任何数据、符号在计算机中都是以二进制的形式表示的。
小明是某软件公司的工程师,公司应客户的需要,要开发一个小工具程序,用来实现任意进制之间的转换。
可以将给定的m进制数x转化为n进制的P(所有数数据均能在长整型范围内处理)。
现在也将这个任务交给你,请你来完成这个程序。
数据输入:从文件tool.in中读入数据,文件中只有一行,共有三个数x,m,n(2<=m,n<=10)。
数据输出:将结果输出到tool.out中,输出文件中只有一个数,那就是转换后的结果P。
输入输出样例tool.in48 10 8tool.out60解析:把m进制数转化为10进制数之后,再转化为n进制数就可以了。
程序:var x,n,m,a,b,i,j,s,t:longint;d:array[1..20] of integer;beginreadln(x,m,n);s:=x; b:=0; t:=0;while s>0 do begina:=s mod 10; s:=s div 10;t:=t+1; j:=1;for i:=1 to t-1 do j:=j*m;b:=b+a*j;{a:=s mod 10; b:=b*m+a; s:=s div 10;}end;j:=0;while b>0 do begina:=b mod n; b:=b div n;j:=j+1;d[j]:=a;end;for i:=j downto 1 do write(d[i]);writeln;end.二、裁缝师问题描述:老李是某布行资深的裁缝师傅,他经常要将一块布裁剪成若干块小布。
他是这样裁剪布料的:一刀下去,不管布有多长,都是沿直线剪开它为止。
当然,他还可以一次剪多层布料,至于一次能剪多少层,则依赖于该布料的类型。
例如:对于某种布料来说,一次只能剪一层布,那么要把一块2X3的布料剪成6块1X1的小布,总共需要剪5刀,如下图;但是,对于另外一种不同的布料来说,如果这种布料一次可以剪两层布,那么只需要三刀就可以剪开布料了(剪完第一刀后,把剪开的两块布叠在一起,再剪第二、第三刀)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
说明:
A 组题中任选1题,在
B 组任选1题;
编写MPI 程序,采用多进程协同完成练习题。
要求: (1) 并行环境正确运行;
(2)提交上机实验报告:
问题描述、算法设计、重点及难点、并行程序关键代码、计算结果分析等 A01. 从键盘输入一个无符号长整型数n ,计算2~n 之间完数的个数。
所谓完数
是指,小于该数的所有因数之和恰好等于该数。
例如6是一个完数,因为小于6的因数有1,2,3且1+2+3=6。
A02. 从键盘输入一个无符号长整型数n ,产生一个长度为n ,取值在[0,1]之间
的随机实数数组,计算其去掉一个最大值、去掉一个最小值,剩下n -2个值的平均值。
A03. 从键盘输入一个无符号长整型数n ,产生一个长度为n ,取值在[0,1]之间
的随机实数数组,计算其数学期望、方差。
A04. (仿环网络的多圈接力) 设0进程有变量x ,初值为0,要求将x 按进程号
的次序,将(圈数*进程号)累加到x 上,完成m 后,输出0进程中x 的值。
A05. (仿完全连接网络的互致问候)所有进程间两两互致问候。
具体要求,例
如:进程0传递字符串”greetings from process No.0.”到进程1。
进程1则在收到字符串前添加字符”Process No.1 has received ”并输出。
A06. (仿二维网格Mesh 通信)设创建n m P ⨯=个进程(n m ,为正整数),要求各进程与其相邻的进程(按n m ⨯网格结构)互致问候。
具体要求,例如:若进程0传递字符串”greetings from process No.0.”到进程1。
进程1则在收到字符串前添加字符”Process No.1 has received ”并输出。
A07. (仿二维环形网格2D-Torus Mesh 通信)设创建n m P ⨯=个进程(n
m ,为正整数),要求各进程与其相邻的进程(按2维n m ⨯环形网格结构)互致问候。
具体要求,例如:若进程0传递字符串”greetings from process No.0.”到进程m-1。
进程m-1则在收到字符串前添加字符”Process No.m-1 has received ”并输出。
A08. 计算级数()()() +--++-+-=--!
121!7!5!3sin 121753n x x x x x x n n ,要求精度
810-。
B01. 从键盘输入一个正整数n ,由进程0产生一个n 行5列的矩阵A ,该矩阵的
第一行元素依次为-1,0,1,2,3;第
k 行元素依次为(-1)k ,0,1,2-k ,3-k 。
用send 和recv 实现将矩阵A 的各行按“块分布”
分布到各进程。
各进程输出收到的各行数据。
B02. 从键盘输入一个正整数n ,由进程0产生一个n 行5列的矩阵A ,该矩阵的
第一行元素依次为-1,0,1,2,3;第k 行元素依次为(-1)k ,0,1,2-k ,3-k 。
用send 和recv 实现将矩阵A 的各行按“周期分布(亦称为卷帘分布)”分布到各进程。
各进程输出收到的各行数据。
B03. 在各进程上计算:1-5000中,凡是【进程号(myid)+1】的倍数的数的
倒数之和。
并用gather 收集各进程求解的和,并输出。
B04. 从键盘输入一个正整数n ,由进程0产生n 阶方阵A (元素为0~99之间的
随机值),并行计算矩阵A*A*A 。
B05. (超立方体结构从高维到低维的广播算法)设创建p P 2=个进程(p 为正
整数),进程0从键盘接收一个整数n 。
请按照超立方体结构的边,从高维到低维,模仿超立方体结构的广播算法将n 传递到其他所有进程(提示:该算法在P p 2log =步内完成)。
B06. (归并排序)给定无符号长整型数n N 2=(n 为正整数)。
产生长度为N
取值在0~99之间的随机整数数组,用p P 2=(p 为正整数)个进程实现数组的归并排序。
B07. (邻域布雷数)给定两个正整数n m ,,随机产生一个n m ⨯阶矩阵A ,
矩阵A 的元素取0(表示该处未布地雷),或取1(表示该处布有地雷)。
要求计算矩阵A 各点邻域内的地雷数,形成一个n m ⨯阶矩阵B ,并输出矩阵B 。
例如,若⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=00001101110110001001A ,则⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=12243244533555323321B 。
B08. (八皇后问题)在8*8格的棋盘上,放置8个皇后。
要求每行每列放一个
皇后,而且每一条对角线和每一条反对角线上最多只能有一个皇后,即对同时放置在棋盘的任意两个皇后
11(,)i j 和22(,)i j ,不允许1212()()i i j j -=-或者1122()()i j i j +=+的情况出现。
