水位与流量关系曲线作业
白石水库尾水渠水位-流量关系曲线率定与分析

第 3 期2021 年 6 月水利信息化Water Resources InformatizationNO.3Jun .,2021白石水库尾水渠水位-流量关系曲线率定与分析高 峰(辽宁江海水利工程有限公司,辽宁 沈阳 110003)收稿日期:2021-01-26作者简介:高峰(1983-),男,辽宁沈阳人,高级工程师,研究方向为水利信息化与自动化。
E -mail:139****************摘 要:为率定白石水库尾水渠水位-流量关系曲线,以白石水库尾水渠为研究对象,利用实测数据计算出渠道的断面尺寸,根据渠道的实际情况选定理论流量计算公式和比降、糙率等系数,经过计算得出水位-流量关系理论曲线,再通过对水库渠道内低、中、高水位下测流方法的选择,确定在低水位和高水位下采用浮标法,在中水位下采用流速仪法,并将多次实测结果与理论值进行比较,发现两者差值均在误差范围内,吻合度非常高,最终验证所绘制的白石水库尾水渠水位-流量理论关系曲线采用的理论公式和参数准确、合理,曲线精确度符合水库的实际需求,以此为水库流量测验提供可靠的技术支持,同时也为同类型水库的尾水渠计算下泄流量提供宝贵经验,可用于今后的泄洪流量测算。
关键词:白石水库;水位-流量关系曲线;流速仪法;浮标法中图分类号:TV697;P333 文献标志码:A 文章编号:1674-9405(2021)03-0021-04DOI: 10.19364/j.1674-9405.2021.03.005根据实测水位在水位-流量关系曲线上得出相应流量是水库计算下泄流量重要的手段之一。
尤其是在汛期,往往时间紧,流量大,通过常规方法测流具有非常大的难度和危险性,所以水位-流量关系曲线对于水库来说是非常实用和重要的工具,为保证水位-流量关系曲线的准确性,对水位-流量关系曲线的率定是十分紧迫和必要的。
以白石水库尾水渠水位-流量关系曲线率定为研究背景,在下泄渠道内低、中、高水位下采用不同的流量测验方法进行流量率定,通过分析与研究,最终得到适合白石水库尾水渠的水位-流量关系曲线,从而为今后的相关工作提供可靠的技术支持和宝贵经验。
利用Excel规划拟合水位流量关系曲线

“水位-流量”关系近似函数为:H= 0.61Q0.48+96.45
3、Excel 规划求解的H-Q 拟合曲线
根据Excel 规划求解得到 的水位-流量关系近似函 数H=0.61Q0.48+96.45,我 们就可以利用Excel的绘 图功能, 方便地绘制的 出该河流在此测站的水 位-流量关系拟合曲线了, 如图
分析根据散点图人工拟合的“水位-流量”关系曲线,我们可 以看出其线型符合幂函数的曲线类型,因此我们可以利用幂函 数来描述“水位-流量”的关系。用近似的函数表达“水位- 流量”关系,便于利用计算机进行相关的水文分析与计算,具 有统一性和推广性。
(1)加载“规划求解”
规划求解加载宏是一个Excel中的加载项程序,在用Excel作“规划求解”之前,必 须先进行加载。加载“规划求解”的方法如下:
结语
大量的实践已证明,通过Excel 规划求解得到水位 -流量关系拟合曲线相当切合实际河流的水位-流 量关系,拟合结果可以广泛地应用于水文工作的 各个方面,极具推广价值,值得深入研究。Excel 规划求解方法不仅仅能够用于水位-流量关系曲线 (H—Q)的拟合,还可以拟合诸如水位-流速关 系曲线(H-V)、水位-库容关系曲线(H-F)、河 道基面曲线(Z-F)、泄流曲线(H-q)等许多类似曲 线。
11水文 张超嘉
Excel规划求解水位-流量关系曲线
水位-流量关系曲线拟合是河流水文预报中的最重要的工作 之一。研究Excel 规划求解水位-流量关系曲线拟合方法, 可以极大地提高河流水文预报的质量、精度和效率,加快 水文预报科技进步的步伐。 以2009 年某河流水位-流量关系曲线拟合为实例, 详细阐 述水位-流量关系曲线拟合的Excel 规划求解的方法和步骤。
a.在“工具”菜单上,单击“加载宏”; b.在“可用加载宏”框中,选中“规划求解”旁边的复选框,然后单击“确 定”; c.如果出现一条消息,指出您的计算机上当前没有安装规划求解,请单击“是” 进行安装。加载规划求解后,“规划求解”命令就会添加到“工具”菜单中。
石大自然地理实验指导05绘制水位与流量关系曲线图

实验五绘制水位/流量关系曲线图
(一)目的要求
掌握水位/流量关系曲线图的绘制和使用方法。
加深对课堂学习理论知识的理解。
(二)实验准备
坐标纸、铅笔、彩色铅笔、实验教材等。
(三)主要内容
1、绘制水位/流量关系曲线图;
2、分析在一次涨落水过程中,水位/流量关系点的分布及其原因;
3、用水位推求其流量。
(四)实验步骤
1、取用一次涨落水过程的水位和相应的流量资料,以纵坐标为水位(H),横坐标为流量(Q),把水位和对应流量点绘在坐标纸上,再经过点群中心画出一条平滑的曲线,并写上图的名称。
2、分析在涨落水的过程中,水位相同时,水位/流量关系点子分布的情况及其原因。
3、用水位值73m、74m、75m,在已绘制的水位/流量关系曲线图上,推求流量的相应数值。
(五)思考问题
1)用给定的水位、流量资料绘制水位/流量关系曲线图。
2)分析所绘曲线图,说明在涨落水的过程中,关系点子分布的不同及其原因。
3)在所绘曲线图上,用已知水位推求流量。
表1 1960年8月9日—13日广州牛心岭站水位流量资料。
水位流量关系曲线绘制方法实例分析
2019年21期方法创新科技创新与应用Technology Innovation and Application1概述水文资料整编工作中,流量资料整编是重中之重,流量资料整编的前提是水位流量关系曲线的绘制和确定。
曲线质量决定了流量资料的精度,准确定线是用水位资料推算连续流量资料的基础。
随着信息化技术在水文资料整编领域的普及应用,目前水位流量关系曲线绘制可通过多种水位流量关系曲线绘制方法实例分析胡艳娇1,黄琦1,田长涛2(1.黑龙江省大兴安岭水文局,黑龙江大兴安岭165000;2.黑龙江省伊春水文局,黑龙江伊春153000)摘要:针对水位流量关系曲线不同定线方法,以实例测站数据为基础,结合工作实际,分别采用手工方法定线、CAD 软件法和水文资料整编软件三种方式进行了对比分析。
从工作方式繁琐程度、工作效率和成果精度等方面,提出了三种方法的优越性和实用中的注意事项。
关键词:水位流量关系;定线分析;系统拟合;误差评定;对比分析中图分类号:P333文献标志码:A文章编号:2095-2945(2019)21-0132-02Abstract :According to the different alignment methods of the relationship curve of water level and discharge ,based on the da ⁃ta of an example station ,combined with the working practice ,the manual alignment method ,CAD software method and hydrological data compilation software are adopted to make a comparative analysis.From the aspects of tedious working mode ,work efficiencyand result accuracy ,the superiority of the three methods and the matters needing attention in practice are put forward.Keywords :relationship between water level and discharge;alignment analysis;system fitting;error evaluation;comparative analy ⁃sis作者简介:胡艳娇(1980-),女,黑龙江大兴安岭人,工程师,主要从事水文测验分析工作;黄琦(1978-),男,黑龙江大兴安岭人,工程师,主要从事水文预报和水文分析工作。
EXCEL在绘制水闸水位—开度—流量关系曲线中的应用

EXCEL在绘制水闸水位—开度—流量关系曲线中的应用摘要:通过闸门启闭来控制水位和流量,是水库调度运用的一项基本内容。
为了使运行管理人员做好水闸的调度工作,科学调配水量,利用EXCEL软件绘制水位—开度—流量关系曲线,解决了人工绘制复杂工程图表的问题。
关键词:EXCEL;水位—流量关系曲线Abstract: through the gate crane to control water level and flow, is the use of the reservoir regulation a basic content. In order to make the operation management personnel do the damages to the scheduling, scientific allocation of water, use of EXCEL software draw water level-the opening-flow relation curves, solve the artificial drawing complex engineering graphs problems.Keywords: EXCEL; Water level-flow relation curves前言MICROSOFT EXCEL 2007是美国微软公司发布的Office系列办公软件之一,是一个功能强大的电子表格软件,具有数据计算、统计分析、图表制作等多种功能。
EXCEL在表格中输入公式、函数,可自动计算出结果;利用表格中的数据,可生成各种柱状图、拆线图、区域图、饼图、环形图、雷达图、组合图等图形。
用EXCEL软件绘制的图表,图形随着数据的改变而改变,具有成图速度快、容易操作的特点。
工程技术人员掌握EXCEL的基本命令和操作技巧,将EXCEL与水利理论知识相结合,应用于水利工程计算之中,起到事半功倍的效果。
水位流量关系曲线绘制方法实例分析

水位流量关系曲线绘制方法实例分析作者:胡艳娇黄琦田长涛来源:《科技创新与应用》2019年第21期摘要:针对水位流量关系曲线不同定线方法,以实例测站数据为基础,结合工作实际,分别采用手工方法定线、CAD软件法和水文资料整编软件三种方式进行了对比分析。
从工作方式繁琐程度、工作效率和成果精度等方面,提出了三种方法的优越性和实用中的注意事项。
关键词:水位流量关系;定线分析;系统拟合;误差评定;对比分析中图分类号:P333 文献标志码:A 文章编号:2095-2945(2019)21-0132-02Abstract: According to the different alignment methods of the relationship curve of water level and discharge, based on the data of an example station, combined with the working practice, the manual alignment method, CAD software method and hydrological data compilation software are adopted to make a comparative analysis. From the aspects of tedious working mode, work efficiency and result accuracy, the superiority of the three methods and the matters needing attention in practice are put forward.Keywords: relationship between water level and discharge; alignment analysis; system fitting; error evaluation; comparative analysis1 概述水文資料整编工作中,流量资料整编是重中之重,流量资料整编的前提是水位流量关系曲线的绘制和确定。
水位流量关系曲线拟定作业指导书

水位流量关系曲线拟定作业指导书目录1 目的 (2)2 范围 (2)3 职责 (2)4 水位流量关系曲线拟定的主要依据 (2)5 作业实施程序 (2)5.1编写工作大纲和生产计划 (2)5.2基本资料的搜集与复核 (2)5.3关系的拟定 (2)5.4高、低水部分的外延 (2)5.5成果合理性分析 (2)5.6验证与修改 (2)5.7审查 (3)5.8编写设计断面水位流量关系报告 (3)5.9审查上报 (3)1 目的为了统一水位流量关系曲线拟定的作业要求,使成果质量符合GB/T19001-2008和长江委水文局《质量手册》和《程序文件》的要求,特编写本作业指导书。
2 范围本作业指导书适用于水利水电工程各阶段设计断面的水位流量关系分析拟定。
3 职责按“水文水资源处各类人员岗位职责、权限”执行。
4 水位流量关系曲线拟定的主要依据4.1 上级主管部门批复下达的任务书或与业主签定的合同书。
4.2 有关规程规范,如《水利水电工程设计洪水计算规范》SL44-2006、《水利水电工程水文计算规范》SL278-2002、《水文测验规范》等。
5 作业实施程序5.1 编写工作大纲和生产计划设计负责人接受任务后,在长江委内、外搜集设计断面及设计站的基本资料,上阶段分析成果及有关文件等,编写工作大纲和生产计划,并报专业负责人审批后执行。
5.2 基本资料的搜集与复核搜集并按"水文水资源处基本资料作业指导书"对设计依据站、参证站的实测资料进行审查、复核,对设计河段进行洪、枯水进行调查。
5.3 关系的拟定根据资料条件和设计断面河段特点,选择合适的方案拟定天然河道情况下设计断面的水位流量关系。
5.4 高、低水部分的外延水位流量关系高、低水部分的外延。
5.5 成果合理性分析5.6 验证与修改进一步收集实测资料,对提供的水位流量关系进行验证、修改。
5.7 审查设计负责人将水位流量关系成果报专业负责人组织审查,并根据审查意见组织生产设计人员进行修改、补充。
XXX水库坝下水位流量关系曲线

0.163 29.554 3.351
0.286 32.477 4.886
设计流量 Q
1.193 4.026
渠底高程
432.9 432.9
水位H
433.100 433.300
0.394 0.493 0.587 0.678 0.767 0.854 0.941 1.026 1.111 1.195 0.966 0.676
1.50
1.40
1.50
1.40
1.50
1.40
1.50
1.40
1.50
1.40
1.50
1.40
1.50
1.40
1.50
1.40
1.50
1.40
1.50
1.40
1.50
1.40
1.50
1.40
设计流量Q 水位H
1.193
433.10
4.026
433.30
8.482
433.50
14.703
433.70
R
C
0.151 29.179
0.264 32.047
0.368 33.857
0.467 35.227
0.563 36.348
0.658 37.307
0.753 38.149
0.846 38.903
0.940 39.588
设计流速 V
2.058 2.994 3.730 4.371 4.955 5.498 6.012 6.502 6.971
设计流量 Q
0.683 2.539 5.774 10.630 17.342 26.129 37.202 50.764 67.008
渠底高程
427.8 427.8 427.8 427.8 427.8 427.8 427.8 427.8 427.8
水文信息学水位流量关系
当测站控制有变 化时,水位流速 关系在测站控制 的过渡段内有时 也会发生反曲。
因流速与比降和糙 率等因素有关, 当这些因素随水位 有突变时,有时也 会造成水位流速关 系曲线的反曲。
3.水位流量关系曲线
天然河道稳定的水位流量关系的一阶导数和二阶 导数分别为:
dQ dd
K2
1
d
d 2Q
2
K.3 (
2
1)d
dd
dQ
流量是随水深的增大而增加, d d 也随着水深的增 大而增大,水位流量关系的斜率( dZ / dQ)随着水 深的增大而减少,即稳定的水位流量关系曲线是 一条凹向下方的增值曲线。
一般情况下水位流量关系是不会出现反曲的,这是因为一 般天然河道断面开关是开敞的,即随着水位的增大而水面 宽增大。在极少数情况下,由于水位流速、水位面积关系 曲线的反曲也会造成水位流量关系的反曲。
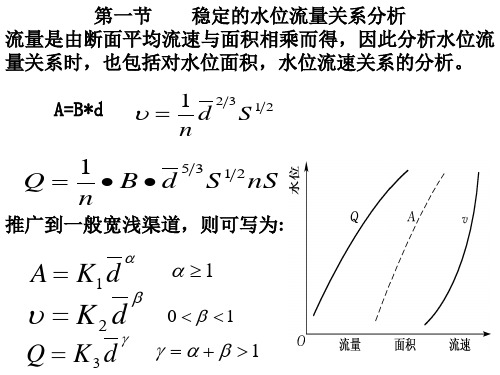
第一节 稳定的水位流量关系分析 流量是由断面平均流速与面积相乘而得,因此分析水位流 量关系时,也包括对水位面积,水位流速关系的分析。
A=B*d 1 d 2 3 S 1 2
n
Q 1 • B • d 5 3S 1 2nS n
推广到一般宽浅渠道,则可写为:
A K1 d
1
K2d 0 1
Q K3d
2. 水位流速关系曲线
水位流量关系稳定时,流速公式的一阶导数和二阶导数分
别为
d
dd
K 2 d 1
d 2
2
K2(
2
1)d
dd
由于 为小于1的正数,所以 d d d 为正数,即流速随水深 的增加而增大;又由于 1 为负数,所以 d 2 / d d 2为负数, 表示水位流量关系曲线为一条凹向上方的曲线。当水深逐 渐增大达一定深度时,流速随水深的增大,增加甚微,所 以高水位时流速近于常数。因此,水位流速关系曲线为一 条以垂直线为渐近线的凹向上方的曲线。当断面有漫滩和 深潭时,水位流速关系曲线发生反曲,这是因为水位流速 关系中的流速是指断面平均流速。漫滩和深潭时,由于过 水断面面积随水深发生变化,合断面平均流速的变化不连 续。
3.2_水位与流量关系

Q KA h
1.4 水位~流量关系曲线
水位~流量关系曲线的延长(低水位时)
纵横断面资料确定法
如测站下游有浅滩、石梁、看直接以滩 顶或者石梁高程作为断流水位;若测站 下游长距离内河底平坦,则基本水尺断 面处河底最低点高程作为断流水位。
1.4 水位~流量关系曲线
• 用途:外延资料,插补资料。
1.4 水位~流量关系曲线
水位~流量关系曲线的绘制
单一关系 “稳定良好”
两者关系
两个以上流量值 “丌稳定”
洪水涨落影响 回水变动影响 河床冲淤影响
1.4 水位~流量关系曲线
水位~流量关系曲线的绘制
一般发生在河床稳定,河道坡度较大,河段顺直的山区河流
1.4 水位~流量关系曲线
• 否则,借用H-A、H-v曲线间接延长H-Q曲线,即:根据 本年实测大断面资料,绘制H-A关系图;考虑高水位时 H-v曲线趋于直线,延长误差小,可延长高水位H-v曲线; 由高水位H查得A和v,求得Q。
1.4 水位~流量关系曲线
水位~流量关系曲线的延长(高水位时)
水力学公式延长法
区别在于延长H-v曲线时,流速v是根据水力学公式计算的。
水位~流量关系曲线的绘制
相同水位条件下,涨潮流速大,则流量大;落潮流速小,则流量小
1.4 水位~流量关系曲线
水位~流量关系曲线的绘制
在同一流量情冴下,受回水影响将会出现丌同水位,普遍偏高
1.4 水位~流量关系曲线
水位~流量关系曲线的延长(高水位时)
水位~面积~流速关系延长法
• 当需延长的水位变幅小于总水位变幅的20%时,可按曲 线相关分析的趋势外延。
v C RI C 1 R1 6
用Excel进行水位~流量关系曲线检验何建华

用Excel进行水位~流量关系曲线检验何建华发布时间:2021-11-04T01:16:47.966Z 来源:基层建设2021年第24期作者:何建华[导读] 水位~流量关系曲线检验是水文资料整编工作的一项主要内容河南省周口水文水资源勘测局摘要:,通过资料整编,可以查找出流量测验中的问题,反映出测验成果及误差,从面进行校正与改进。
关键词:水位;流量;检验正文:一、概述水位~流量关系曲线检验是水文资料整编工作的一项主要内容,在国际标准中,对水位流量关系曲线有四种检验:即符号检验、适线检验、偏离数值检验,和t检验,也叫学生氏检验。
前三种主要用于单一水位流量关系曲线,t检验适用于流量间测站的校测资料检验,以判断原用水位流量关系曲线是否需要重新确定;也适用于相邻年份的水位流量关系曲线或相邻时段的临时曲线是分开或合并定线的判断。
水文资料整编时经常用到的是前三种检验,即:符号检验、适线检验、偏离数值检验,近年来,随着电脑普及应用,利用Excel进行三种检验已成为趋势,通过运用count、countif、if、stdev、average等函数来设置计算公式后,只要将全年实测流量及相应查线流量数据手工输入后,这三种检验结果及关系测点的标准差等便会自动生成,使三种检验的计算准确简便。
针对这几种方法现介绍如下:二、三种检验原理1.符号检验主要检验所定水位流量关系曲线两侧测点数目分配是否均衡合理,借以判断曲线定的是否正确。
应用公式:(1)其中:u——为统计量k——正号或负号个数,n——为测点总数,p、q——正、负号概率,各为0.5,*——连接改正数(离散型换为连续型)具体方法为按给定的显著性水平a=0.25,查得相应临界值U1-a/2=1.15,与计算的U值相比较。
如果U<U1-a/2,则认为合理,即接受原假设;如果U>=U1-a/2,则认为不合理,即拒绝原假设。
2.适线检验按水位递升次序检验实测点偏离曲线正负符号的排列情况,借以检验定线有无明显系统偏离。
水位流量关系

80.00
100.00
0.50
1.00
1.50
2.00
2.50
3.00
断面6-6
水深(z)
高程
断面面积 (m2)
0.00 0.80 1.80 2.80 3.80 4.80
3809.02 3809.82 3810.82 3811.82 3812.82 3813.82
0.00 11.80 28.17 47.54 69.92 95.29
3803.50 3803.00 3802.50 3802.00 3801.50 3801.00 3800.50 3800.00 3799.50 3799.00 3798.50 3798.00
0.00
水位流量关系曲线 水位流量关系曲线
50.00
100.00
150.00
200.00
250.00
300.00
350.00
3803.50 3803.00 3802.50 3802.00 3801.50 3801.00 3800.50 3800.00 3799.50 3799.00 3798.50 3798.00
0.00
0.50
z-R
z-R
1.00
1.50
2.00
2.50
3.00
3803.50 3803.00 3802.50 3802.00 3801.50 3801.00 3800.50 3800.00 3799.50 3799.00 3798.50 3798.00
湿周x (m)
4.00 6.51 14.89 20.34 25.79 29.32
水力半 径R (m) 0.00
1.00
1.21
山区小河流水位流量关系曲线

巴丹土鲁水位站水深~比降关系图
水深(m)
1
0.5 0 0.049
南岔河水文站水位与比降的关系
2.5 2
0.05
0.051
0.052
0.053
0.054
水深()
1.5 1 0.5 0 0 0.0002 0.0004 0.0006 0.0008 0.001 0.0012 0.0014 0.0016 890.2 890
2、恒定均匀流条件下,利用曼宁公式进行 水位流量曲线拟定
2、恒定流均匀流条件下水位流量关系曲线 的计算
断面湿周计算方法示意图
3、明渠恒定非均匀流条件下水位流量关系 曲线采用伯诺力方程进行计算
对于ζ,断面沿程收缩或扩散系数,当断面收缩时, ζ=0;当断面突然扩散时ζ=0.5~1.0,当断面逐 渐扩散时ζ =0.3~0.5。
end
比降
尚义电站水位~比降关系曲线
水位(m)
889.8 889.6 889.4 889.2 889 888.8 0 0.001 0.002 0.003 0.004 0.005 0.006 0.007 0.008
比降
比降
水面比降由于两个水位站观测的资料误差较大,所以点据比较散乱,但定性的分析,对山区河道而 言,水位上升,水面比降总的趋势是增加的。
山区小河流控制断面水位流量 关系曲线拟当明渠中水流的运动要素不随时间而变时,称为明渠 恒定流,否则称为明渠非恒定流。 明渠水流中,如果流线是一族平行线,则水深、断面 平均流速及流速分布均沿程不变,称为明渠恒定均匀 流;如果流线不是平行直线,则称为明渠恒定非均匀 流。 工程设计中提出的水位流量关系曲线一般是在明渠恒 定流及明渠恒定非均流条件下的水位流量关系曲线。
水位~流量关系曲线拟合实例分析

水位~流量关系曲线拟合实例分析文章以永翠河带岭站实测流量资料为例,对该站水位~流量关系曲线进行了函数模型公式拟合分析。
分别采用线性回归和一元图解分析的方法对该站2014年水位~流量关系线进行了公式拟合,得出了拟合关系式并对不同关系类型函数进行了拟合精度对比分析,提出了计算机拟合曲线方程与人工定线推算流量的优缺点及实际工作中对拟合公式的使用建议。
标签:永翠河带岭站;水位~流量关系曲线;曲线拟合方程;人工定线;对比分析1 水位~流量关系曲线介绍流域流量资料在各类水利工程和水资源规划设计工作中发挥着不可替代的重要作用。
水文站测到的流量值是针对某一水位级的瞬时流量,因单次流量测验工作量较大,历时较长,而水位观测简单快捷,为了准确地获得河流任一水位下的实时流量值,往往采用测站水位~流量关系曲线来间接查得瞬时流量。
这种利用测站畅流期各实测流量数据与其同时对应的水位来建立的相关线就称为水位~流量关系曲线。
传统的水位~流量关系曲线定线方法为人工绘图,按相关规范要求首先分别绘制水位~流速、水位~面积曲线,然后据此绘制水位~流量曲线,根据曲线上不同水位级来查读流量。
这种方法虽然得到的流量数值精度较高,但也存在工作量大,效率较低的问题,尤其在一些临时性推算河道流量数据时这种方法非常不便。
文章利用计算机来拟合分析水位~流量函数关系公式,利用关系式可以立即算出某个水位下的河道流量,应用时非常方便快捷。
2 曲线拟合实例应用分析2.1 应用条件分析对水位~流量关系曲线进行公式拟合分析的基本要求是河道横断面必须相对稳定,同一水位级下年内、年际断面面积变化较小,河床冲刷现象不显著,年内水位~流量关系曲线呈单一线型,这样才能使拟合公式具有较长时段的使用性。
实例流域水文站多年断面和水位~流量关系曲线变化情况见表1、图1和图2。
由表1可知,各级水位下断面面积、流量平均偏差分别为4.9%和8.6%,可以说明测站断面年际间变化程度较小,满足水位~流量关系线公式拟合的条件要求。
广义有效水位与流量相关曲线的创建及应用

科学技术创新2020.01广义有效水位与流量相关曲线的创建及应用钱永春乔万亮(黑龙江省绥化水文局,黑龙江绥化152050)1概述此前发表在2014年《东北水利水电》杂志第7期上的《呼兰河法在冰期水文资料整编中的应用》一文,该文只是在大、中河流研究基础上获得的结论,他从一个侧面反映了冰期临时曲线变化的规律和特点,也就是说,该方法仅适用于冰期无底冰、无冰上流水冰情现象时的大、中河流,对于小河常出现冰上流水等现象时就不适用了。
至于冰期出现上述冰情现象的中、小河流是否也能采用这种方法?此文正式针对这一方面问题进行了研究和探索,同时也是对呼兰河法的应用范围进行再扩大。
最终实现冰期有效水位与流量关系曲线在水文资料整编定线中的全面应用。
目前,冰期水流变化稳定封冻一般缓慢,而非稳定封冻期复杂。
冰期资料整编定线都还是使用过程线法,尤其是中、小河流更是使用流量过程线法较多。
在实测流量不能完全控制水流变化过程的前提下,使用过程线法定线整编精度较低。
假如采用相关法定线整编,将会获得更高的精度提升。
2概念的提出与计算2.1广义有效水位定义:某断面或某点的水位与其以下的冰厚之差,就称之为该断面或某点的广义有效水位。
这里的冰厚有两方面涵义,一是指通常的水浸冰厚(包括层冰层水的冰厚)和冰花厚;另一是指河底冰厚。
也就是说,该冰厚是包括水面以下所有的不流动的冰厚和冰花厚等,也可以定义水下冰厚为水浸冰厚,这个水浸冰厚概念不是一般以往所说的概念了,赋予了它新的内涵,或称广义水浸冰厚。
过去讲的有效水位实际上是属于狭义有效水位,因此,广义有效水位就是水位与对应的广义水浸冰厚的差。
相对之下,概念的内涵得到了丰富,这样对于有效水位应用的一些限制条件就完全得到解除。
下文提到的有效水位均指广义有效水位。
2.2有效水位计算公式有效水位计算这里是指实测流量相应有效水位的计算。
有效水位计算大体分为两种情况:一是冰期河流等水体的某一过水断面存在水浸冰或冰花或层冰层水等冰情;另一是具有水底冰或冰上流水等冰情。
综合练习四 单一线法处理流量数据

综合练习四 单一线法处理流量数据一、要求(1)分析稳定的水位一流量关系的特点并用单一线法定线。
(2)推求指定日期的日平均流量。
二、数据(1)衢县水文站1976年实测流量成果表(表2-11)。
(2)衢县水文站1976年6月5~12日部分洪水水文要素摘录表(表2-12)。
(3)衢县水文站的概况:测验河段顺直,河床整齐多卵石,土质坚实,两岸无显著冲淤变化,有电灌机埠5处,水位超过10m ,两岸均发生漫滩。
左岸漫溢约700m ,右岸漫溢约1200m 。
在站上游约2.5km 为江山港、常山港汇流口,lkm 处为常山港叉流汇入口,850m 处左岸有石梁溪汇入,600m 处右岸有德平坝,坝顶高程为10m 。
650m 处有浮桥一座。
在站下游800m 处急滩上筑有捉鱼坝,下游约7.5km 有乌溪江汇入,在1956年9月乌溪江受台风影响水位暴涨时,本站受到严重顶托影响。
三、步骤(1)点绘水位一流量、水位一面积、水位一流速关系点据,并分析其特点。
(2)在水位一流量关系图中,若密集分布成带状,测点无系统偏离,通过点群中心定出单一水位一流量关系曲线。
(3)对突出点进行分析。
(4)对所定的水位一流量关系曲线进行检验,以判断所定曲线是否正确合理(表2-13)。
检验包括: 1)符号检验,公式如下:nn K u 5.05.05.0--=2)适线检验,公式如下:()15.05.015.0----=n n k u3)偏离数值检验,公式如下:/t P S p =其中1i P p n =∑ S p=表2-11 1976年衢县水文站实测流量成果表S =以上检验公式中各符号含义及检验的具体方法详见教科书及水文规范SL 247-1999。
(5)作流率表(表2-14,作表时精确至cm),以供推流时使用,编制流率表时必须注意掌握相邻水位级的流量差是随着水位的增高而递增的。
(6)推流。
推求6月6~11日的逐时流量,再计算出其日平均流量(可在表2-15中进行计算)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
工程水文学第一次作业
题目:原始数据如下表:
水位H/m 流量Q/(m³/s) 断面面积A/㎡水面宽度B/m 256.48 2690 3650 449 258.12 5120 4720 458 259.84 7640 5080 469 260.93 10700 5760 478 262.16 12900 6360 488 262.61 14400 6550 490
263.7 17600 7050 500 264.66 19800 7480 505 266.79 26300 8250 519 267.71 32100 9290 525
270.8 所求?10800 555
解:
一)用MATLAB编程算得下表:
水位H/m
流量
Q/(m³/s)
断面面积
A/㎡
水面宽度
B/m
平均水深
ha(m) ha^(1/2) A*sqrt(ha)
256.48 2690 3650 449 8.13
2.85 10406.77
258.12 5120 4720 458 10.31 3.21 15152.36 259.84 7640 5080 469 10.83 3.29 16718.96 260.93 10700 5760 478 12.05 3.47 19994.92 262.16 12900 6360 488 13.03 3.61 22960.21 262.61 14400 6550 490 13.37 3.66 23947.71 263.7 17600 7050 500 14.1 3.75 26472.73 264.66 19800 7480 505 14.81 3.85 28787.68 266.79 26300 8250 519 15.90 3.97 32892.53 267.71 32100 9290 525 17.70 4.21 39079.04 270.8 ?10800 555 19.46 4.41 47641.91
H=270.8m时,
水力学公式法算得:Q=44112 m³/s
史蒂文森法(Q-A*R2/1延长法)算得:Q=47692m³/s
二)水力学公式延长法:
用MATLAB编程绘图如下:
三)史蒂文森法(Q-A*R2/1延长法):
用MATLAB编程绘图如下:
附(MATLAB编程代码):
H=[256.48 258.12 259.84 260.93 262.16 ...
262.61 263.7 264.66 266.79 267.71 270.8]'; %水位H Q=[2690 5120 7640 10700 12900 ...
14400 17600 19800 26300 32100 0]'; %流量Q A=[3650 4720 5080 5760 6360 ...
6550 7050 7480 8250 9290 10800]'; %断面面积A
B=[449 458 469 478 488 490 500 505 519 525 555]'; %水面宽度B
ha=A./B; %平均水深ha
h1=sqrt(ha); %sqrt(平均水深)---h1
h2=A.*h1; %A*sqrt(平均水深)-----h2
n=length(H); %j计数变量n,存储H、A等的长度
m=[H Q A B ha h1 h2]; %m矩阵用于存储计算过程中所需的数据
v=Q./A; %v是流速
R=A./(2*(B+ha)); %书中道,对于宽浅型天然河道,R=ha(平均水深)
%************************************************************************* %以下为水力学公式延长法
x=v.*R.^(-2/3); %x为1/n*I^(1/2),是水力学中一个公式:1/n*I^(1/2)=v*R^(-2/3)
plot(H(1:n-1),x(1:n-1),'r*');
hold on; %描绘H--1/n*I^(1/2)的离散点分布
P=polyfit(H(1:n-1),x(1:n-1),2);
x1=255:0.5:271;
y1=polyval(P,x1);
plot(x1,y1,'-');
hold on; %拟合并绘出H--1/n*I^(1/2)的关系曲线
%************************************************************************* %以下计算延长水位上的流量-----H=270.80m处
x1=H(11);
y1=polyval(P,x1); %延长线拟合曲线函数
v11=y1.*R(11)^(2/3); %H=270.80m处的流速
Q(11)=v11.*A(11); %H=270.80m处的流量
%************************************************************************* %以下为史蒂文森延长法
E=polyfit(Q(1:n-1),H(1:n-1),3);
x2=0:2000:50000;
y2=polyval(E,x2);
D=polyfit(Q(1:n-1),h2(1:n-1),3);
y3=polyval(D,Q(1:n-1));
C=polyfit(H(1:n-1),h2(1:n-1),3);
y4=polyval(C,H(1:n-1));
plotyy(x2,y2,H(1:n-1)./280*50000,y4',@plot,@plot);
hold on;
E1=polyfit(H(1:n-1),Q(1:n-1),3);
x2=270.80;
y2=polyval(E1,x2);
%y41=polyval(C,270.80/280*50000);
Q(11)=y2;
D1=polyfit(Q(1:n),h2,3);
y3=polyval(D1,Q(1:n));
plotyy(x2,y2,Q(1:n),y3,@plot,@plot);。
