金融数学第-章练习题详解
金融数学课后习题

第一章 利息的度量1.现在投资600元,以单利计息,2年后可以获得150元的利息。
如果以相同的复利利率投资2000元,试确定在3年后的累计值。
2.在第1月末支付314元的现值与第18月末支付的271元的现值之和,等于在第T 月末支付1004元的现值。
年实际利率为5%,求T 。
3.在零时刻,投资者A 在其账户存入X ,按每半年复利一次的年名义利率i 计息。
同时,投资者B 在另一个账户存入2X ,按利率i (单利)来计息。
假设两人在第8年的后6个月中将得到相等的利息,求i 。
3.如果年名义贴现率为6%,每四年贴现一侧,试确定100元在两年末的累计值。
4.一项投资以δ的利息力累积,27.72年后将翻番。
金额为1的投资以每两年复利一次的年名义利率δ累积n 年,累计值将成为7.04.求n 。
5.一直利息力为tt +=21δ,一笔金额为1的投资从0=t 开始的前n 年赚取的总利息是8.求n 。
6.已知利息力为1003t t =δ,求)3(1-a 。
第二章 等额年金1.某人想用分期付款的方式购买一辆现价为10万元的汽车,如果手气支付一笔款项后,在今后5年内每月末付款2000元即可付清车款,假设每月复利一次的年名义利率为8%,试计算他首期付款金额为多少?2.某人将在10年后退休,他打算从现在开始每年初向一种基金存入2000元,如果基金的收益率为6%,试计算他在退休时可以积存多少退休金。
3.某人从2000年3月1日起,每月末可以领取200元,2010年5月末是最后一次领取。
如果每月复利一次的年名义利率是6%,试计算:(1)年金的现值;(2)年金的终值;(3)年金在2005年12月31日的值。
4.某人在今后20年内,每年初向一基金存入10000元。
从第30年开始,每年末可以领取一笔退休金。
该基金的收益率为6%。
(1)如果限期领取20年,每次可以领取多少?(2)如果无限期的领下去(当他死亡后,由其继承人领取),每次可以领取多少?5.借款人原计划在每月末偿付1000元,用5年的时间还清贷款。
(完整版)金融数学课后习题答案

(完整版)金融数学课后习题答案第一章习题答案1. 设总量函数为A(t) = t2 + 2t + 3 。
试计算累积函数a(t) 和第n 个时段的利息In 。
解: 把t = 0 代入得A(0) = 3 于是:a(t) =A(t)A(0)=t2 + 2t + 33In = A(n) ? A(n ?1)= (n2 + 2n + 3) ?((n ?1)2 + 2(n ?1) + 3))= 2n + 12. 对以下两种情况计算从t 时刻到n(t < n) 时刻的利息: (1)Ir(0 < r <n); (2)Ir = 2r(0 < r < n).解:(1)I = A(n) ? A(t)= In + In?1 + + It+1=n(n + 1)2t(t + 1)2(2)I = A(n) ? A(t)=Σnk=t+1Ik =Σnk=t+1Ik= 2n+1 ?2t+13. 已知累积函数的形式为: a(t) = at2 + b 。
若0 时刻投入的100 元累积到3 时刻为172 元,试计算:5 时刻投入的100 元在10 时刻的终值。
第1 页解: 由题意得a(0) = 1, a(3) =A(3)A(0)= 1.72a = 0.08,b = 1∴A(5) = 100A(10) = A(0) ? a(10) = A(5) ? a(10)a(5)= 100 × 3 = 300.4. 分别对以下两种总量函数计算i5 和i10 :(1) A(t) = 100 + 5t; (2) A(t) = 100(1 + 0.1)t. 解:(1)i5 =A(5) ? A(4)A(4)=5120≈4.17%i10 =A(10) ? A(9)A(9)=5145≈3.45%(2)i5 =A(5) ? A(4)A(4)=100(1 + 0.1)5 ?100(1 + 0.1)4100(1 + 0.1)4= 10%i10 =A(10) ? A(9)A(9)=100(1 + 0.1)10 ?100(1 + 0.1)9100(1 + 0.1)9= 10%第2 页5.设A(4) = 1000, in = 0.01n. 试计算A(7) 。
《_金融数学-课后习题答案》

金融数学-课后习题答案本文档为金融数学课后习题的参考答案。
在解答问题时,我会尽量给出详细的步骤和推导过程,帮助读者更好地理解金融数学的概念和方法。
1. 第一章:时间价值1.1 问题一题目:如果我现在存入1000元,年利率是5%,请问5年后我能得到多少钱?解答:首先需要计算每年的复利,即每年利息和本金的总和。
根据复利计算公式:年末总金额 = 本金 * (1 + 年利率)^时间年数代入数据进行计算:年末总金额 = 1000 * (1 + 0.05)^5 = 1000 * 1.2762815625 ≈ 1281.28元因此,5年后你能得到大约1281.28元。
1.2 问题二题目:如果我希望在5年后拥有2000元,年利率是5%,请问我需要存入多少钱?解答:首先需要计算本金与利息的比例,然后根据比例计算需要的本金。
根据复利计算公式:年末总金额 = 本金 * (1 + 年利率)^时间年数可以将该式转化为:本金 = 年末总金额 / (1 + 年利率)^时间年数代入数据进行计算:本金 = 2000 / (1 + 0.05)^5 = 2000 / 1.2762815625 ≈ 1567.45元因此,你需要存入大约1567.45元。
2. 第二章:贴现与现值2.1 问题一题目:如果一笔未来支付3000元的现金流在5年后,年利率是6%,请问它的现值是多少?解答:为了计算现值,我们需要使用贴现率(年利率)和时间年数。
根据贴现计算公式:现值 = 未来支付金额 / (1 + 年利率)^时间年数代入数据进行计算:现值= 3000 / (1 + 0.06)^5 = 3000 / 1.33822557689 ≈ 2241.53元所以,该未来支付的现金流的现值大约为2241.53元。
2.2 问题二题目:如果我希望在5年后得到3000元的现金流,年利率是6%,请问我愿意支付多少现值?解答:为了计算现值,我们使用贴现率(年利率)和时间年数。
金融数学1-期望效用理论

23
序数效用函数定理证明
情况1. 当x~x*时,定义U (x) 1; 情况2. 当x~y*时,定义U (x) 0; 情况3. 当x* x y*时,性质2存在唯一的 (0,1)
使x~x* 1 y*, 此时我们定义U (x) 。
日常生活中,我们时常要比较不同商品或者服 务给我们生理、心理上带来的感受或者说效用 (utility)。
例如,看一场电影还是吃一块鸡腿,是需要经 过激烈思想斗争的,尤其是当荷包里所剩无几 的时候。
这便涉及到效用大小比较的问题。
5
在18世纪的古典经济学家眼中,效用和黄油、 大炮一样是看得见、摸得着的,他们把效用视为快 乐的代名词,看做是一个人的整个福利的指数。
若1 U (x) U ( y) 0,此时令1 U (x),2 U ( y),
由U的定义, x~1x* 11 y*, y~2 x* 12 y*
因为1 U (x) U ( y) 2 , 由性质1
必有x y。
29
(2)证明:x ~ y 当且仅当U (x) U ( y)。
必要性
任取x, y B,设x y, 证U (x) U ( y),
若x y与y x同时成立,则x和y偏好无差异,记作x ~ y。
若x y但y x不成立,则x严格地比y好,记作x y。
自返性保证了消费者对同一商品的偏好具有明显的一 贯性;
可比较性假定保证了消费者具备选别判断的能力; 传递性保证了消费者在不同商品之间选择的首尾一贯性。
12
通常认为这三条并没有给消费者施加过分严格 的限制条件,只要是消费者是理性的都可以做 到这一点。
要解构整个金融体系,要理解金融产品、资本市场、 金融中介在跨期资源配置中的所具有的功能作用及其 实现形式,投资者行为就是一个自然的起点。
孟生旺《金融数学基础》参考答案

孟生旺《金融数学基础》参考答案(中国人民大学出版社,2015年2月第一版)第1章 利息度量1.1360021500.125,2000(1)2848i i i ⨯=⇒=+=1.2 /121/1218/121004314271141.6T v v v T =+⇒= 1.3:(2)2i A X i X =⋅, ()()1615:1/21/2B X i X i +-+ 1615[(1/2)(1/2)]0.09458X i i i X i +-+=⋅⇒=1.427.72e 20.025δδ=⇒=, 当0.5i δ= 时, /2(12)7.0480n n δ+=⇒=1.5 1/42100(146%)114.71-⨯⨯-⨯=1.6 ()()11118//mmm m i i d d m m m -+=+=-=-⇒=⎡⎤⎡⎤⎣⎦⎣⎦1.7 12:()(1.01)tA a t =, 2/12:()e tB a t =, 212/12(1.01)e 1.43t tt =⇒=1.8 2:()exp()/2A a t an bn =+, 2:()exp()/2B a t gn hn =+, 2()/()n a g h b =--1.9 8512()100(1)exp /4(1)d 2600.129a t d t t d --=-⋅⎡⎤+=⇒=⎢⎥⎣⎦⎰ 1.10 11/(1)t δ=+, 222/(1)t t δ=+, 0.41t = 1.11 2()(1)a t t =+1111300(3)600(6)200(2)(5)=315.82a a a X a X ----⨯+⨯=⨯+⨯⇒1.12 ()10.2025330(3)exp e/100d a t t --==-⎰.1.13 20.5()0.040.031,(0.5)/(0.5)0.068a t t t a a δ'=++== 1.14 ()320(3)100exp/100d 109.42A t t X X=⋅+=+⎰()623(6)(109.42)exp /100 1.8776(109.42)A X t dt X =+⋅=+⎰(6)(3)(109.42)(0.87761)784.61A A X X X -=+=⇒=1.15 t = 4时的累积值为:()30.04501000exp0.02d e 1144.54t t ⋅=⎰令名义利率为x , 则 161000(1/4)1144.540.03388x x +=⇒=1.16 ()20.075i=, (4)(2)(2)21/2/2/2ln (1)41(1)0.1466d i i δ⎡⎤⎡⎤-⎢⎥⎢⎥⎣⎦⎣⎦+=++-+= 1.17 ()()510205expd exp/25d 2.71830.414kt t kt t k ⋅=⇒=⎰⎰1.18 0()exp d (2)/2,()(0)/216tt a t t t a n a n n δδ⎡⎤==+=-=⇒=⎢⎥⎣⎦⎰ 1.19 201000exp 1068.94d t t δ⋅=⎡⎤⎢⎥⎣⎦⎰ 1.20 1010267.5, 10(1.0915)30(1.0915), 2.3254nn A B n --==+=第2章等额年金2.1 1363元 2.2 279430元 2.3260052.4 基金在第30年初的现值为658773.91, 如果限期领取20年, 每次可以领取57435, 如果无限期地领下去, 每次可以领取39526 2.5 31941.68元, 21738.97元, 46319.35元 2.6 9年 2.7 29月末2.8 0.1162 2.9 8729.23 2.10 45281.05 2.11 0.2 2.12 302 2.13 4.06%2.14假设最后一次付款的时间为n , 则有:4410000010000(10.05)23.18n a n --=+⇒=假设在23年末的非正规付款额为X , 则有4231910000010000(10.05)(10.05)1762.3a X X --=+++⇒=2.15 601004495.503860000.749329k k a v v k ==⇒=⇒=2.16 20101020153810721072153846600.08688a a v v i =⇒-+=⇒=2.17 设j 为等价利率, 则0.040604j =, 1681000()32430s s =+=&&&&累积值 2.18 以每半年为一个时期, 每个时期的实际利率为/2i , 两年为一个时期的实际利率为()411/2j i =-+, 故 5.891/0.08j i ⇒==2.19 ()20101012126410.7520.09569i s i s i i ⋅⋅+⋅⋅=⇒+=⇒=2.20 {}ln(1)1exp d d 1n nta n r t r==+-+⎰⎰2.21 20()exp d (10.5)tr a t r t δ==+⎡⎤⎣⎦⎰, 5(5)(5)(5)...12.828(1)(2)(5)a a a s a a a =+++=2.22()8888111188100d (1)d tt v a a t v t δδδδ-==-=-=⎛⎫- ⎪⎝⎭⎰⎰()()5/48101810018100v v δδδδ=--⋅⇒=--⎡⎤⎣⎦()[]5/410101181001v a δδδδ----==2.23 1/302.24 1[ln(/)]/i δδ- 2.25 4e 12e 3n n δδ=⇒=, e 112121/6n n s δδδ-=⇒=⇒=第3章变额年金3.1 ()29/229229 /22972.8865.440.1/2j j j s j Is j s j j -⎡⎤=⋅=⋅⇒=⇒=⎢⎥⎢⎥⎣⎦&&&& 3.2 1010900100()a I a += 1088.693.3 2312(1)23......n n n nn i a a v v v nv nv nv id++++++++++==3.4 335792222468...49.89(1)v X v v v v v =++++==-3.5A 的现值为:102010105555()X a a v a ==+B 的现值为:1020101010306090X a v a v a =++ 故 10102055(1)3060900.07177574.74v v vi X +=++⇒=⇒=3.6 1()()n n n n nIa v Da a a -+=⋅&& 3.7 71520()1602146.20Da a +=3.8 11846.663.9每季度复利一次的利率为0.0194, 所有存款在第八年末的终值为40.019480.08()183.01s Is =&&, /0.08183.0114.64X X =⇒= 3.10 3433203.11 166073.12 现值为5197.50, 累积值为9333.98.3.13 111193070()9998.16a Ia +=&&&&, 终值为23312.11. 3.14 现值为111120()2803246.03Da a +=, 在第20年末的终值为10410.46. 3.15 212.343.16 此项投资在第10年末的终值为:106%106%80000(5000)500()X s Ds =-+&&&&80000(5000)(13.97164)500(83.52247)7736.88X X =-+⇒=3.17 ()4106%116%100()200015979.37X v Da a =+=. 3.18 第20年末的终值为:16115%(1)200()19997.38i Ia +=3.19 前5年的现值为77.79, 从第6年开始, 以后各年付款的现值为:()510.092010.09v k k +⎛⎫+ ⎪-⎝⎭, 总现值为335, 故 3.76%k =.3.20 104%104%9010()1735.96s I s +=3.21 第8年的终值为:87%87%605()894.48478s Ds +=第10年末的终值为1024.10. 3.22100(43)exp (0.030.04)d d 89.97t t s s t ⎡⎤+-+=⎢⎥⎣⎦⎰⎰ 3.23 在时刻5的现值为:102255(1.22)exp (0.00060.001)d d 382.88tt t s s s t ⎡⎤+-+=⎢⎥⎣⎦⎰⎰ 时刻零的现值为:50382.88exp (0.0040.01)d 346.44t t⎡⎤-+=⎢⎥⎣⎦⎰ 3.24 ()10100250009exp 1/(9)d d 190131.58t k tk s s t k k ⎡⎤=++=⇒=⎢⎥⎣⎦⎰⎰第4章收益率4.10.1483 4.2 1221.99 4.3 时间加权收益率0.5426, 币值加权收益率0.5226, 两者之差0.0236.4.4 93000 4.5 −10%4.6 120100506565(10050)136,0.1834100120100501009/12503/12D D i D D --+-⋅⋅=⇒===-+-+⨯-⨯ 4.7 0.1327 4.8 7.5% 4.9 236.25 4.100.06194.11 5年末投资者共得到56245.5元. 设购买价格为P , 要得到4%的收益率, 有5(1.04)56245.546229.7P P =⇒=4.12 20.0820/220/25000100000(5000)()34.710.1i i s i Is s i =+⇒=⇒=&&&& 4.13 再投资利率为8.73%. 投资者B 的利息再投资后的积累值为6111.37.4.14 ()10200.75100.7512126410.7520.09569i i i s i s i i ⋅⋅+⋅⋅=⇒+=⇒=4.15 3项投资在2015年初的余额为320.46万元, 在2015年末的余额为344.56万元, 故2015年中所获利息为24.10万元.第5章 贷款偿还方法5.1 X = 704.065.2 设每年的等额分期付款金额为R , 由已知28(1)135R v -=, 147(1)108(1)72R v R v -=⇒-=5.3 301301(1)/32/322.69t t R vR v t -+-+-=⇒=⇒=故在第23年分期付款中利息金额最接近于付款金额的三分之一. 5.4 109832290.35,408.55Rv Rv Rv Rv Rv Rv =++=++0.05,150.03,1158.4i R L ⇒===. 支付的利息总金额为10341.76R L -=5.5 1510.65.6 (1)借款人第2年末向偿债基金的储蓄额应为4438.42(2)第2年末的余额为9231.91 (3)第2年末的贷款净额为10768.095.7 0| 4| 6104.56/20000/8.4911%k i i R L a a i ===⇒= 5.8 第5次偿还中的利息为66.89万元.5.9 22912125,0001 1.02(1.02)(1.02)526i Ra v v v R ⎡⎤=+++⋅⋅⋅⋅+⇒=⎣⎦5.10 各期还款的积累值为 20200.0510*******(1)0.0616s i i =+⇒=5.11 121212155000500.3812 0.09173077.9455000(1)500.38jn njn a i j j s -=⎧⎪⇒==⎨=+-⎪⎩ 5.12 第一笔贷款偿还的本金为490.34, 第二笔贷款偿还的本金为243.93, 两笔贷款的本金之和为 734.27. 5.13 3278.5.14 第3次支付的本金金额为784.7, 第5次支付的利息金额为51.4. 5.15 0.1196. 5.16 64.74.5.17 调整后最后一次的偿还额为1239.1. 5.18 第11年末.5.19 调整后借款人增加的付款为112.5.20 20301019100001900100()5504.7Xa v a v Ia X =++⇒=. 5.21 11190.11.第6章证券定价6.1 价格为957.88元, 账面值为973.27元.6.2价格为974.82元, 账面值为930.26元(理论方法), 929.82(半理论方法), 1015(实践方法.6.37.227% . 6.4 6.986% .6.5 10201010101000.11000.091000.0897.74P a v a v a --=⨯+⨯+⨯=元.6.6债券每年末的息票收入为80元, 故有()()()54321082.27(1)801801801099.84(1)80(1)80 6.5%V V i V i i i i i ==+-=+-+-⎡⎤⎣⎦=+-+-⇒=(3)3 8010001099.8412n n i a v n --⋅+=⇒= 1212 0.065801000(1.065)1122.38P a -=⋅+=元.6.7应用债券定价的溢价公式可以建立下述三个等式:20202040(1) 45(2) 50(3) 2X C i a C Y C i a C X C i a C ⎛⎫-=- ⎪⎝⎭⎛⎫=- ⎪⎝⎭⎛⎫=- ⎪⎝⎭由(3)/(1)得:501302403Ci Ci Ci --=⇒=-由(1)(3)+得:2020(902)902XX Ci a a Ci=-⇒=-所以有 20(45)/25Y Ci a X =-==元. 6.8 t = 7/12, 理论方法的账面值为87.35元, 实践方法的账面值为87.35元.6.9110019019/110910/33n n n v v a =⇒=⇒= 0.0311********.03n n P v a =+=.6.10 40n n P a M v =+⋅, 30n n Q a M v =+⋅, 令债券C 的价格为X , 则有8054n n X a M v X P Q =+⋅⇒=-.6.11 ()()()()1010 0.041010 0.0510*******.040.03581.49100011001.05P r a r P r a --⎧=+⎪⇒=⎨-=+⎪⎩ ()1010 0.0351*******.0351371100 1.0351371070.80X a -=⨯+⨯=6.12 ()()()219202320105050 1.03 1.03 1.03837.78P v v v v v ⎡⎤=+++++=⎣⎦L .6.13 偿还值的现值为55200584.68()v a =元, 未来息票收入的现值为5556012()355.99()a v Da +=元, 故债券的价格为940.67元. 也可以应用Makeham公式计算, 即0.06/0.07(1000584.68)584.68940.67P =⨯-+=元.6.14 2020 10104010001071.06401041.58P a v P P a X v X ⎧=+=⎧⎪⇒⎨⎨=+⋅=⎪⎩⎩6.15 债券每年末的息票收入为60元, 修正息票率为60/1050 = 5.7143%, 小于投资者所要求的收益率8%, 所以赎回越晚(即到期时赎回), 债券的价格越低. 由此可得该债券的价格为1010501050(5.7143%8%)888.94P a =+⨯-⨯=元.6.16 股票在第六年的红利为60.50.2(1.10)⨯⨯, 以后每年增长10%. 应用复递增永续年金的公式, 该股票的价格为6510.50.2(1.10) 1.1110.510.110.1P -=⨯⨯⨯⨯=-元.6.17 投资者每个季度的实际收益率为 2.47%j =, 应用复递增永续年金的公式, 投资者购买该股票的价格为0.3/(2.47%2%)63.83P =-=元. 6.18 1.5/305%10%i =+=. 6.19 30元.6.20 每股利润为109.500.50-=元, 保证金为100.505⨯=元, 保证金所得利息为50.0500.25⨯=元, 每股红利为0.1元, 卖空收益率为(0.50.250.1)/513%+-=.6.21 8.59%第7章利率风险7.115D =马, 基于名义收益率的修正久期为15/(11%)14.85D =+=. 年实际收益率为12.68%i =, 基于实际收益率的修正久期为15/(112.68%)13.31D =+=.7.2 1()/()e 1n nD P P δδδδ'==--7.3 假设债券的面值为100, 则92.648.027.57P D D ===马,, 7.4债券的马考勒久期可以表示为nm j a D m=&&马, 其中()/m j im =. 变形可得:()()()11(1)1(1)(1)n n m m m nm jni v D j a j a m i d--+-=+=+==&&马. 7.5 对年金的现值关于利率i 求导, 应用修正久期的定义公式可得111n nnv D i v +=--.7.6对于期末付永续年金, 现值为()1/P i i =, 2()1/P i i '=-, 所以修正久期为1/D i =, 马考勒久期为=(1)(1)/D D i i i +=+马.7.7对于期初付永续年金, 现值为()(1)/P i i i =+, 2()1/P i i '=-, 所以修正久期为1/[(1]D i i =+), 马考勒久期为=(1)1/D D i i +=马.7.8 24 /2()510096.53()169.29 1.75()i P i P a v P i D P i ''=+=⇒=-⇒=-= 7.97.49D =效7.10 7.8861D D i ==+马, () 1.18%Pi D P∆=-∆⋅= ⇒ 新的债券价格近似为:75.98 1.01876.88⨯= 7.11 8.92D =效, 13.35C =效.2()0.5()8.85%Pi D i C P∆=-∆⋅+⋅∆⋅=-, 债券的新价格近似为95.59元. 7.12 修正久期为8.12, 凸度为101.24. 7.13 马考勒凸度为105.15.7.14 22231d 1d 216.67d d P P P i i i i i==⇒=- = ()116.67()P i D P i i'⇒=-==2()2555.55()P i C P i i''⇒=== 7.152()0.5() 4.28%Pi D i C P∆=-∆⋅+⋅∆⋅=- 7.16 负债的现值为12418.43L P =, 负债的马考勒久期为5LD =马, 负债的马考勒凸度为25L C =马. 不妨假设两种零息债券的面值均为1000元, 则4年期零息债券的价格为441000/(1)683.01P i =+=元, 10年期零息债券的价格为10101000/(1)385.54P i =+=元. 假设有%x 的债券投资4年期的零息债券, (1%)x -的债券投资10年期的零息债券, 由ALD D =马马, 有:(%)(4)(1%)(10)5%83.33%x x x +-=⇒=投资4年期零息债券的金额为10348.28元, 投资10年期零息债券的金额2070.15元. 7.17 债券A 的价格为982.17元, 马考勒久期为1.934, 马考勒凸度为3.8. 债券B 的价格为1039.93元, 马考勒久期为4.256, 马考勒凸度为19.85. 在债券A 上投资11.02%, 在债券B 上投资88.98%, 则债券组合的马考勒久期等于负债的马考勒久期, 均为4年, 债券组合的马考勒凸度为18.08, 大于负债的马考勒凸度16, 满足免疫的条件. 7.18 各种债券的购买数量分别如下:购买5年期债券的数量 80000 购买4年期债券的数量 300000 购买2年期债券的数量 600000 购买1年期零息债券100000购买各种债券以后净负债的现金流如下(单位:万元): 年度 1 2 3 4 5 负债的现金流1794 6744 144 3144 824 5年期债券的现金流 24 24 24 24 824 净负债的现金流 1770 6720 120 3120 0 4年期债券的现金流 120 120 120 3120 0 净负债的现金流 1650 6600 0 0 0 2年期债券的现金流 600 6600 0 0 0 净负债的现金流 1050 0 0 0 0 1年期债券的现金流 1050 0 0 0 0 净负债的现金流第8章利率的期限结构8.1一年期债券的价格为102.78P =;两年期债券的价格为92.96P =;三年期债券的价格为112.43P =.11111102.788%1s s =⇒=+ 2212323123510592.969.03%1(1)1515115112.4310.20%1(1)(1)s s s s s s s =+⇒=++=++⇒=+++8.2现金流分别按对应的即期利率折现得债券的价格为:231010110105.751.05 1.06 1.08P =++= 8.3 各年远期利率分别为8%、10.1%和12.6%. 8.4假设债券的面值为100元, 计算5年期债券的价格:2345234512345234123410101010110101010101101.07 1.07 1.07 1.07 1.071(1)(1)(1)(1)1111 3.741(1)(1)(1)s s s s s s s s s ++++=+++++++++⇒+++=++++每年支付40元的5年期期初付年金按对应的即期利率折现即得其现值为:23412341111401189.751(1)(1)(1)s s s s ⎡⎤++++=⎢⎥++++⎣⎦8.5由远期利率计算的债券价格为:1010110107.251.07(1.07)(1.05)(1.07)(1.05)(1.1)++=(元)8.6假设债券的面值为100元, 则有:001041004%(1)f f =⇒=+1001200101261061008.16%(1)(1)(1)8810810012.69%(1)(1)(1)(1)(1)(1)f f f f f f f f f f f ⇒=+⇒=+++⇒=++⇒=++++++8.7 应用即期利率和远期利率的关系, 有101022012330123116%(1)(1)(1) 5.50%(1)(1)(1)(1) 6.98%s f s f s f f s s f f f s +=+⇒==+=++⇒=+=+++⇒=8.8用t C 表示债券在t 年末的现金流入, 则有:111120%1.21C Cs s =⇒=+ 1212222220%1.2 1.2 1.2(1)C C C C s s +=+⇒=+ 33121232323320%1.2 1.2 1.2 1.2 1.2(1)C C C C C Cs s ++=++⇒=+ 8.91001120%s f f +=+⇒=3211221.21.2(1.2)(1)20%,120%1.2f f f =+⇒==-=8.10 00110106 3.77%1f f =⇒=+ 1001200101251059512.20%1(1)(1)991091029.37%1(1)(1)(1)(1)(1)f f f f f f f f f f f =+⇒=+++=++⇒=++++++用远期利率计算年息票率为15%, 面值为100元的3年期债券的价格:0010121515115117.651(1)(1)(1)(1)(1)P f f f f f f =++=++++++ 8.11 用远期利率分别计算3年期和4年期零息债券的价格可得:01210082(1)(1)(1)f f f =+++,30123100759.33%(1)(1)(1)(1)f f f f f =⇒=++++8.12 21012012115%,(1)(1)(1)6%s f s s f f s +=+⇒=+=++⇒=假设债券的面值为100元, 则有:3233881081008.2%1.05 1.06(1)s s =++⇒=+8.13 通过收益率计算的债券价格为 2610693.061.1(1.1)P =+= 通过即期利率计算的债券价格为2610694.831.07(1.09)P =+= 债券价格被低估了1.77元, 故可以按94.83元的价格购买一个2年期债券, 同时按即期利率出售一个1年期的面值为6元的零息票债券和一个2年期的面值为106元的零息票债券.8.14 与远期利率一致的债券价格为5510597.421.05(1.05)(1.06)(1.05)(1.06)(1.07)P =++=(元) 债券的市场价格为100元, 说明债券被高估了, 因而存在套利机会.套利者可以按100元的价格卖出一个三年期债券, 同时将97.42元按4%的利率投资一年. 在第一年末, 支付已出售债券的5元利息后, 把剩余的资金在第二年按6%的远期利率再投资一年. 在第二年末, 支付已出售债券的5元利息后, 把剩余的资金在第三年按8%的远期利率进行投资. 在第三年末的累积值正好用于支付套利者所售债券在第三年末的偿还值. 完成上述步骤后, 套利者即可在当前时刻获得100 - 97.42 = 2.58元的无风险收益.第9章远期、期货和互换9.1股票多头的回收和盈亏如下表所示: 1年后的股票价格多头的回收多头的盈亏50 50 −16 60 60 −6 70704如果1年后的股票价格为66元时, 则股票多头的回收为66元. 购买股票的初始费用在1年后的累积值为66元, 所以盈亏为0元. 9.2股票空头的回收和盈亏如下表所示, 与多头的回收和盈亏正好相反. 1年后的股票价格空头的回收 空头的盈亏50 −50 16 60 −60 6 70−70−4如果1年后股票的价格是66元时, 则空头的回收为−66元. 初始所得在1年后的累积值为66元, 所以盈亏为 0元. 9.3 40.06/40.061(105 1.7e )e 104.54t t F -==-⨯=∑(元)9.4日股利为0.02/3651050.00575⨯=元. 若在年初持有一单位股票, 年末将持有0.02e 1.0202=单位. 若要在年末持有一单位股股票, 年初应持有0.02e 0.9802-=单位,故投资额为0.02105e 102.92-=元. 9.5(1)0.060.570e 72.13F ⨯=⨯=元. (2)0.0670e 720.032δδ-⨯=⇒=.9.6无套利的远期价格为 0.060.5105108.20F e ⨯==(元)(1)远期价格115 > 108.20, 所以投资者可以先签出一份远期合约, 约定在6个月末以115元的价格卖出股票. 同时借入105元购买股票, 承诺在6个月末还款. 到6个月末, 以115元卖出手中的股票, 同时偿还借款108.20元, 最终无风险获利6.80元. (2)远期价格107 < 108.20, 所以投资者可以先签订一份远期合约, 约定在6个月末以107元购买股票. 同时将手中持有的股票卖出, 获得105元, 将这105元投资于5%的零息债券, 6个月末可以获得108.20元. 6个月末利用远期合约买入股票, 最终获得无风险利润1.20元.9.7 22838483.491.05 1.055 1.05 1.055x xx +=+⇒= 9.8(1)232382838482.981.05 1.055 1.06 1.05 1.055 1.06x x xx ++=++⇒= (2)2323838483.501.055 1.06 1.055 1.06x xx +=+⇒= 9.9四个时期的浮动利率分别为0.06、 0.07、 0.08和 0.09. 互换利率为0.0745.9.10 应用债券组合的定价方法:0.13/120.1059/120.1115/120.13/124e 4e 104e 98.24(5.1100)e 102.5198.24102.51 4.27B B f B B -⨯-⨯-⨯-⨯=++==+==-=-=-固浮浮固第10章 期权10.1 远期多头的回收分别为−10元、−5元、0元、5元和10元, 空头的回收是其相反数. 看涨期权多头的回收分别为0元、0元、0元、5元和10元. 看跌期权的回收分别为10元、5元、0元、0元和0元.10.2 回收分别为0元、0元和5元. 盈亏分别为−6.01元、−6.01元和−1.01元.10.3 看跌期权的回收分别为5元、0元和0元. 盈亏分别为3.96元、−1.04元和−1.04元. 10.4 组合的回收分别为105元、105元、110元和115元. 组合的盈亏分别为−7.56元、−7.56元、−2.56元和2.44元.10.5 组合的回收分别为−105元、−105元、−110元和−115元. 组合的盈亏分别为12.81元、12.81元、7.81元和2.81元.10.6 多头的盈亏为0.95元, 盈亏平衡点为42.05元. 10.7 多头的盈亏为3.47元, 盈亏平衡点为28.53元. 10.8 看跌期权的期权费是3.13元. 10.9 10.2417d =, 20.09167d =.根据Black−Scholes 公式, 欧式看涨期权价格为:12()e () 3.61rTC S d K d -=Φ-Φ=根据平价公式, 欧式看跌期权价格为e 2.38rT P C K S -=+-=10.10 1.0905u =, 1/0.9170d u ==, 0.5266r t e dp u d∆-==- 欧式看跌期权的价值为2.62, 相应的二叉树如下:美式看跌期权的价值为2.71, 相应的二叉树如下:10.11 1.0524u =, 1/0.9502d u ==, ()0.5118r tedp u dτ-∆-==-欧式看涨期权的价值为19.63, 相应的二叉树如下:10.12 回收和盈亏如下表:股票价格 看跌期权回收总回收 成本及其利息 盈亏 90 5 95 −105.98 −10.98 100100−105.98−5.9810.13回收和盈亏如下表:股票价格看涨期权回收股票空头回收总回收净收入及其利息盈亏90 0 −90 −90 94.03 4.03100 5 −100 −95 94.03 −0.97 10.14回收和盈亏如下表:股票价格看涨期权回收空头回收总回收净收入及其利息盈亏100 0 −100 −100 97.44 −2.56 110 5 −110 −105 97.44 −7.5610.15回收和盈亏如下表:股票价格看涨期权回收看跌期权回收贷出资金回收总回收净成本及其利息盈亏90 0 −5 95 90 −105 −15100 5 0 95 100 −105 −5 10.16回收和盈亏如下表:股票价格看涨期权回收看跌期权回收借入资金的回收总回收净收入及其利息盈亏100 0 5 −105 −100 105 5 110 −5 0 −105 −110 105 −510.17105(9.31 1.69) 1.0597--⨯=10.18通过下表可以看到两种交易的盈亏相同:股票价格买进看涨期权的回收卖出看涨期权的回收总回收净成本及其利息盈亏90 0 0 0 −2.46 −2.5100 5 0 5 −2.46 2.54 10.19通过下表可以看到两种交易的盈亏相同:股票价格买进看涨期权的回收卖出看涨期权的回收总回收净成本及其利息盈亏90 0 0 0 3.41 3.41 100 0 −5 −5 3.41 −1.59第11章随机利率11.1 A 10的完整分布如下:概率 A 10 (A 10)2 0.20 1.63 2.65 0.40 2.10 4.41 0.402.918.48(1) 十年末累积值的期望为2330.05元.(2) 十年末累积值的方差为255027.66, 标准差为505.11.2 期望累积值为2593.74元. 累积值的方差为83865.54, 标准差为289.60. 11.3 期望累积值为1560.9元. 11.4 公式(3)和(4)是正确的.11.5 三个投资额的期望累积值分别为6350.4元, 3528元和2240元. 第3年末该账户的期望累积值为12118.4元.11.6 期望累积值为1.1449, 累积值的方差为0.000916.11.7 (1) ln(1)t i +的期望为0.073189, ln(1)t i +的方差为0.000122.(2) ()()25050ln 50, var ln 50E A A μσ==⎡⎤⎡⎤⎣⎦⎣⎦()()()[][]5050Pr 100040000Pr ln ln 40Pr 0.3761Pr 0.376A A Z Z >=> ≈> =-<⎡⎤⎣⎦ []Pr 0.3760.65Z <=, ()50Pr 1000AV 400000.35>= 11.8 累积价值的95%置信区间为(0.81, 1.34). 11.9 (1)t i +的期望和方差分别为222/22E(1)e , var(1)e (e 1)t t i i μσμσσ+++=+=-, 故有E()0.0844, var()0.00235t t i i ==假设年收益率的中位数为k , 则有()ln(1)Pr()0.5Pr ln(1)ln(1)0.5Pr 0.5t t k i k i k Z μσ+-⎛⎫<=⇒+<+=⇒<= ⎪⎝⎭ln(1)08.33%k k μσ+-=⇒=.11.10 利率树:现金流和各节点的价值:可赎回债券的价格为99.19元.11.11 第1年末的即期利率由当前的即期利率发展而来, 在当前利率水平的基础上上调30%的概率为0.75, 下降30%的概率为0.25. 第2年末的即期利率由第1年末的即期利率发展而来, 在第1年末利率水平的基础上上调30%的概率为0.75, 下降30%的概率为0.25. 利率树如下:[]()()()()()()()()()()()()2E 0.750.750.08450.750.250.050.250.750.050.250.250.029596.813%i =+++=。
《数理金融》习题参考答案

《数理金融》习题参考答案第一章〔P52〕题1-1 希德劳斯基模型的金融学含义是什么?解:参考方程〔1.2.13〕式后面的一个自然段。
题1-2 欧拉方程的经济学和金融学的含义是什么?解:参考方程〔1.5.9〕式和方程〔1.5.10〕式后面的一个自然段。
题1-3 假如你借款1000美元,并以年利率8%按每季度计息一次的复利形式支付利息,借期为一年。
那么一年后你欠了多少钱?解: 每季度计息一次的8%的年复合利率,等价于每个季度以2%的单利利率支付一次利息,而每个季度索要的利息,不仅要考虑原有的本金,而且还要加上累计到该时刻的利息。
因此,一个季度后你的欠款为: 1000(1+0.02)两个季度后你的欠款为: 21000(1+0.02)(1+0.02)1000(1+0.02)=三个季度后你的欠款为: 231000(1+0.02)(10.02)1000(1+0.02)+=四个季度后你的欠款为:341000(1+0.02)(10.02)1000(1+0.02)1082.40+==题1-4 许多信用卡公司均是按每月计息一次的18%的年复合利率索要利息的。
假如在一年的年初支付金额为P ,而在这一年中并没有发生支付,那么在这一年的年末欠款将是多少? 解:如此的复合利率相当于每个月以月利率1812%1.5%=支付利息,而累计的利息将加到下一个月所欠的本金中。
因此,一年后你的欠款为:12P(1+0.015)1.1956P =题1-5 假如一家银行所提供的利息是以名义利率5%连续地运算利息,那么每年的有效利率应该是多少?解:有效利率应为:0.050.05eff Pe P r e 10.05127P-==-≈ 即有效利率是每年5.127%。
题1-6 一家公司在以后的5年中需要一种特定型号的机器。
这家公司当前有一台这种机器,价值6000美元,以后3年内每年折旧2000美元,在第三年年末报废。
该机器开始使用后,第一年运转费用在该年年初值为9000美元,之后在此基础上每年增加2000美元。
金融数学引论答案第一章--北京大学出版[1]
![金融数学引论答案第一章--北京大学出版[1]](https://img.taocdn.com/s3/m/0d949b1aa1c7aa00b42acbc4.png)
第一章习题答案1•解:JEt = O 代入得A(O) = 3 于是:a(t) =A(t)/A(O)= (t 2 + 2t + 3) /3 In =A(n) 一 A(n 一 1)= (n 2 + 2n + 3) - ((n - I)2 + 2(n - 1) + 3))= 2n + l 2.解:(1)1 = A(n)-A(t) = I n +I nl + ∙ ∙ ÷I t+1 =n(n+ l)∕2-t(t+ 1)/2 (2)I = A(n)-A(t)= Y J l k = 2π+, -2,+,A-r÷l3•解:由题意得a(0) = I Z a(3) =A(3)/A(O)= => a = , b = 1 ∕∙ A(5) = 100A(IO)=A(O) ∙ a(10) = A(5) ∙ a(10)/ a(5)= 100 X 3 = 300.4.解:(l)i5 =(A(5) - A(4))∕A(4)=5120^ % ilθ =(A(IO) - A ⑼)∕A(9)=5145≈ %(2)i5 =(A(5) 一 A(4))∕A(4)IOO(I + 0.1)5-l∞(l + 0.1)4IOo(I + o.ιy l5•解:A(7) = A(4)(l + i5)(l + i6)(l + i7) =1000 XXX6•解:设年单利率为i500(1 + = 615解得i = %设500元需要累积t 年500(1 + t × %) = 630解得t = 3年4个月 }7•解:设经过t 年后,年利率达到%1 + 4%×t= (1 + 2.5%)1 t Q8. 解ι(l + i)11 = (l + i)5+2*3 = XY 39. 解:设实利辜为i600[(l + i)2 一 1] = 264解彳gi = 20%:• A(3) = 2000(1 + i)3 = 3456 元10•解:设实利站为i10% i K)=(A(10)-A(9))∕A(9) =1∞(1 + 0.1)10-100(1 + 0.1)9 IOO(I + 0.1)910%---------- 1 ------- ~ (l + z)n (l + ∕)2n所以"=导》右11•解:由500×(l+ i)30 = 4∞0 => (l + i)30 = 8IOOOO I(XX)O IOOOo++ i)2°(1 +i)40 (1 +i)60=IOOO ×2 4 (8~+8~+8^2)12 解:(1 + i)a = 2(l + i)b =j (2)(l + i)c = 5 (3)3 + i)n =- (4) 2=> n ∙ In(I. + i) = In 5 -In 3⅝l∕ ⅝l∕11/ /k 牧→ In5 = c × ln(l + i) × (2) => In3 = (a + b) ■ In (1 + i) =C -(a + b)13•解:A ∙ i = 336 A ∙ d = 300 i —d = i ∙ d => A =2800 14•解:(1)10%'1 + 5x10%=%⑵ a-1(t) = 1 一=> a(t) = a(5)III δ A(t)= δ B(t)得t = 5)19・解:依题意,累积函数为a(t) = at2 + bt + 1 a = 0.25a ++ 1 =a(l) = a + b + 1 ==> a =b =于是 δ =≤222= 0.068a(0.5)20∙解:依题意,§ A (t) = J 「J B (t)= ----------------1 + L 1 + tIllJ A (t)> ¾ (t) 1一 1-0.1/=dS = ΦH√1) a(5)=%15∙解:由(l + -r )3=(l-£-)7 3 4i⑶-3二> 〃⑷=4・[1一(1 +寸)-可:⑶ Itl:⑹ z ∕(12)(1 + L_)6=(1_L_)3) 6 12〃(⑵=> 严>=6∙[(1 -------- Γ2-l]1216•解:⑴ 终值为IOO × (1 + i(4)/4 F?=元⑵ 终值为Ioo × [(1 -4d<V4))1/4 ]-2=元17. 解:利用 1/d (FTl)- 1/i (Fn) = I∕m=> m = 818. 解:aA (t) = 1 + => δ A (t)a"1A (t) = l-0.05r=>¾ (a"1B (t))1 aΛ(t) 0.05"l-0.05ra A (I) 1 + 0」/2t 2=> -------- > ---------- 1 +L 1 +t=> t > 121.解:d (4) = 8% ,设复利下月实贴现率为d,单利下实利率为do 。
《金融数学》(第二版)练习题(修订版)

⎧kt,
1.18
假设利息力为 δt
=
⎪
⎨ ⎪⎩
1 25
kt
2
,
0<t ≤5 ,期初存入单位 1 在第 10 年末将会累积到 2.7183。试求 k。
5 < t ≤ 10
1.19
已知利息力为 δt
=
1 2+t
,一笔金额为
1
的投资从 t=0
开始的前
n
年赚取的总利息是
8。试求
n。
1.20 1996 年 1 月 1 日,某投资者向一个基金存入 1000,该基金在 t 时刻的利息力为 0.1(t −1)2 ,求 1998 年 1 月 1 日的累积值。
1.7 基金 A 以每月复利一次的名义利率 12 %累积。基金 B 以 δt = t / 6 的利息力累积。在零时刻,分别存入 1 到两个基金中。请问何时两个基金的金额
1
将相等。
1.8
基金
A
以δ t
=
a
+ bt
的利息力累积。基金
B
以δ t
=
g
+
ht
的利息力累积。基金
A
与基金
B
在零时刻和
n
时刻相等。已知 a
3
2.2 某人将在 10 年后退休。他打算从现在开始每年初向一种基金存入 2000 元,如果基金的收益率为 6%,试计算他在退休时可以积存多少退休金。 2.3 某人从 2000 年 3 月 1 日起,每月末可以领取 200 元,2010 年 5 月末是最后一次领取。如果每月复利一次的年名义利率为 6%,试计算:(1)年金 的现值;(2)年金的终值;(3)年金在 2005 年 12 月 31 日的值。 2.4 某人在今后的 20 年内,每年初向一基金存入 10000 元。从第 30 年开始,每年末可以领取一笔退休金。该基金的收益率为 6%。(1)如果限期领取 20 年,每次可以领取多少?(2)如果无限期地领下去(当他死亡后,由其继承人领取),每次可以领取多少? 2.5 某人留下了 10 万元的遗产,遗嘱规定,该笔遗产前 5 年的利息收入由其长子领取,第二个 5 年的利息由其次子领取,从第 11 年开始,剩余遗产全 部归第三个儿子。如果年实际利率为 8%,试计算三个儿子在该笔遗产中分别占多大份额? 2.6 如果年实际利率为 i,那么一笔在 36 年内每年末支付 4000 元的年金,与另一笔在 18 年内每年末支付 5000 元的年金将有相等的现值。试计算 1000 元的投资在年实际利率为 i 时,经过多长时间可以翻番。 2.7 借款人原计划在每月末偿付 1000 元,用 5 年的时间还清贷款。每月复利一次的年名义利率为 12%。如果他现在希望一次性支付 60000 元还清贷款, 他应该在何时偿还? 2.8 投资者每月初往基金存入一笔款项,5 年后可以积存到 60000 元。如果前 2 年每次存入 1000 元,后 3 年每次存入 500 元。试计算每月复利一次的名 义利率。 2.9 投资者每年末向一基金存入 2000 元,如果在前 2 年的投资按 6%的年实际利率计算,在后两年的投资按 5%的年实际利率计算,投资者在第 4 年末 可以积存多少价值? 2.10 一项 10 年期的年金,在前 5 年的每季度末付款 1000 元,后 5 年的每季度末付款 2000 元。如果年实际利率为 5%,试计算该项年金的现值。 2.11 一项每 3 年末支付 1 元的永续年金,其现值为 125/91,试确定年实际利率是多少? 2.12 某人将一笔遗产(每年末可以领取的永续年金)捐赠给了四家慈善机构 A,B,C 和 D。在前 n 年,每次领取的款项由 A、B、C 三家平均分享,n 年以后,剩余部分均由 D 领取。试确定当(1 + i) n 为多少时,A、B、C、D 四家在该遗产中享有的现值相等。假设年实际利率为 8%。 2.13 一项永续年金在每月初付款 1 元,如果每年结转四次利息的年名义利率为 4%,试计算该项年金的现值。
徐景峰《金融数学》1-4章习题解答

《利息理论》习题详解 第一章 利息的基本概念1.解:(1))()0()(t a A t A =又()25A t t =+(0)5()2()1(0)55A A t a t t A ∴===++ (2)3(3)(2)11(92 2.318I A A =-=== (3)4(4)(3)0.178(3)A A i A -===2.解:15545(4)(3)(1)100(10.04)0.05 5.2nn n I i A I A i A i i -=∴==+=+⨯=3.证明: (1)123(1)()(2)(1)(3)(2)()(1)m m m m k I A m A m I A m A m I A m A m I A m k A m k ++++=+-=+-+=+-+=+-+-123123()()()()()m m m m k m m m n I I I I A m k A m n m k A n A m I I I I m n +++++++∴++++=+-=+-=++++<令有(2)()(1)()1(1)(1)n A n A n A n i A n A n --==---()1(1)()(1)(1)n n A n i A n A n i A n ∴+=-∴=+-4.证明: (1)112123123(1)(0)(0)(2)(0)(0)(0)(3)(0)(0)(0)(0)()(0)(0)(0)(0)(0)k nk i a a a i a a a i a i a a a i a i a i a n a a i a i a i a i ∴=+=++=+++=+++++第期的单利利率是又(0)1a =123123()1()(0)()1nna n i i i i a n a a n i i i i ∴=+++++∴-=-=++++(2)由于第5题结论成立,当取0m =时有12()(0)n A n A I I I -=+++5.解:(1)以单利积累计算1205003i =⨯1200.085003i ∴==⨯800(10.085)1120∴+⨯=(2)以复利积累计算3120500500(1)i +=+0.074337i ∴=5800(10.074337)1144.97∴+=6.解:设原始金额为(0)A 有(0)(10.1)(10.08)(10.06)1000A +++=解得 (0)794.1A =7.证明:设利率是i ,则n 个时期前的1元钱的当前值为(1)ni +,n 个时期后的1元钱的当前值为1(1)ni +又22211[(1)](1)20(1)(1)n n n ni i i i +-=++-≥++,当且仅当221(1)(1)1(1)n n n i i i +=⇒+=+,0i =即或者n=0时等号成立。
孟生旺《金融数学基础》参考答案

孟生旺《金融数学基础》参考答案(中国人民大学出版社,2015年2月第一版)第1章 利息度量1.1360021500.125,2000(1)2848i i i ⨯=⇒=+=1.2 /121/1218/121004314271141.6T v v v T =+⇒= 1.3:(2)2i A X i X =⋅, ()()1615:1/21/2B X i X i +-+ 1615[(1/2)(1/2)]0.09458X i i i X i +-+=⋅⇒=1.427.72e 20.025δδ=⇒=, 当0.5i δ= 时, /2(12)7.0480n n δ+=⇒=1.5 1/42100(146%)114.71-⨯⨯-⨯=1.6 ()()11118//mmm m i i d d m m m -+=+=-=-⇒=⎡⎤⎡⎤⎣⎦⎣⎦1.7 12:()(1.01)tA a t =, 2/12:()e tB a t =, 212/12(1.01)e 1.43t tt =⇒=1.8 2:()exp()/2A a t an bn =+, 2:()exp()/2B a t gn hn =+, 2()/()n a g h b =--1.9 8512()100(1)exp /4(1)d 2600.129a t d t t d --=-⋅⎡⎤+=⇒=⎢⎥⎣⎦⎰ 1.10 11/(1)t δ=+, 222/(1)t t δ=+, 0.41t = 1.11 2()(1)a t t =+1111300(3)600(6)200(2)(5)=315.82a a a X a X ----⨯+⨯=⨯+⨯⇒1.12 ()10.2025330(3)exp e/100d a t t --==-⎰.1.13 20.5()0.040.031,(0.5)/(0.5)0.068a t t t a a δ'=++== 1.14 ()320(3)100exp/100d 109.42A t t X X=⋅+=+⎰()623(6)(109.42)exp /100 1.8776(109.42)A X t dt X =+⋅=+⎰(6)(3)(109.42)(0.87761)784.61A A X X X -=+=⇒=1.15 t = 4时的累积值为:()30.04501000exp0.02d e 1144.54t t ⋅=⎰令名义利率为x , 则 161000(1/4)1144.540.03388x x +=⇒=1.16 ()20.075i=, (4)(2)(2)21/2/2/2ln (1)41(1)0.1466d i i δ⎡⎤⎡⎤-⎢⎥⎢⎥⎣⎦⎣⎦+=++-+= 1.17 ()()510205expd exp/25d 2.71830.414kt t kt t k ⋅=⇒=⎰⎰1.18 0()exp d (2)/2,()(0)/216tt a t t t a n a n n δδ⎡⎤==+=-=⇒=⎢⎥⎣⎦⎰ 1.19 201000exp 1068.94d t t δ⋅=⎡⎤⎢⎥⎣⎦⎰ 1.20 1010267.5, 10(1.0915)30(1.0915), 2.3254nn A B n --==+=第2章等额年金2.1 1363元 2.2 279430元 2.3260052.4 基金在第30年初的现值为658773.91, 如果限期领取20年, 每次可以领取57435, 如果无限期地领下去, 每次可以领取39526 2.5 31941.68元, 21738.97元, 46319.35元 2.6 9年 2.7 29月末2.8 0.1162 2.9 8729.23 2.10 45281.05 2.11 0.2 2.12 302 2.13 4.06%2.14假设最后一次付款的时间为n , 则有:4410000010000(10.05)23.18n a n --=+⇒=假设在23年末的非正规付款额为X , 则有4231910000010000(10.05)(10.05)1762.3a X X --=+++⇒=2.15 601004495.503860000.749329k k a v v k ==⇒=⇒=2.16 20101020153810721072153846600.08688a a v v i =⇒-+=⇒=2.17 设j 为等价利率, 则0.040604j =, 1681000()32430s s =+=&&&&累积值 2.18 以每半年为一个时期, 每个时期的实际利率为/2i , 两年为一个时期的实际利率为()411/2j i =-+, 故 5.891/0.08j i ⇒==2.19 ()20101012126410.7520.09569i s i s i i ⋅⋅+⋅⋅=⇒+=⇒=2.20 {}ln(1)1exp d d 1n nta n r t r==+-+⎰⎰2.21 20()exp d (10.5)tr a t r t δ==+⎡⎤⎣⎦⎰, 5(5)(5)(5)...12.828(1)(2)(5)a a a s a a a =+++=2.22()8888111188100d (1)d tt v a a t v t δδδδ-==-=-=⎛⎫- ⎪⎝⎭⎰⎰()()5/48101810018100v v δδδδ=--⋅⇒=--⎡⎤⎣⎦()[]5/410101181001v a δδδδ----==2.23 1/302.24 1[ln(/)]/i δδ- 2.25 4e 12e 3n n δδ=⇒=, e 112121/6n n s δδδ-=⇒=⇒=第3章变额年金3.1 ()29/229229 /22972.8865.440.1/2j j j s j Is j s j j -⎡⎤=⋅=⋅⇒=⇒=⎢⎥⎢⎥⎣⎦&&&& 3.2 1010900100()a I a += 1088.693.3 2312(1)23......n n n nn i a a v v v nv nv nv id++++++++++==3.4 335792222468...49.89(1)v X v v v v v =++++==-3.5A 的现值为:102010105555()X a a v a ==+B 的现值为:1020101010306090X a v a v a =++ 故 10102055(1)3060900.07177574.74v v vi X +=++⇒=⇒=3.6 1()()n n n n nIa v Da a a -+=⋅&& 3.7 71520()1602146.20Da a +=3.8 11846.663.9每季度复利一次的利率为0.0194, 所有存款在第八年末的终值为40.019480.08()183.01s Is =&&, /0.08183.0114.64X X =⇒= 3.10 3433203.11 166073.12 现值为5197.50, 累积值为9333.98.3.13 111193070()9998.16a Ia +=&&&&, 终值为23312.11. 3.14 现值为111120()2803246.03Da a +=, 在第20年末的终值为10410.46. 3.15 212.343.16 此项投资在第10年末的终值为:106%106%80000(5000)500()X s Ds =-+&&&&80000(5000)(13.97164)500(83.52247)7736.88X X =-+⇒=3.17 ()4106%116%100()200015979.37X v Da a =+=. 3.18 第20年末的终值为:16115%(1)200()19997.38i Ia +=3.19 前5年的现值为77.79, 从第6年开始, 以后各年付款的现值为:()510.092010.09v k k +⎛⎫+ ⎪-⎝⎭, 总现值为335, 故 3.76%k =.3.20 104%104%9010()1735.96s I s +=3.21 第8年的终值为:87%87%605()894.48478s Ds +=第10年末的终值为1024.10. 3.22100(43)exp (0.030.04)d d 89.97t t s s t ⎡⎤+-+=⎢⎥⎣⎦⎰⎰ 3.23 在时刻5的现值为:102255(1.22)exp (0.00060.001)d d 382.88tt t s s s t ⎡⎤+-+=⎢⎥⎣⎦⎰⎰ 时刻零的现值为:50382.88exp (0.0040.01)d 346.44t t⎡⎤-+=⎢⎥⎣⎦⎰ 3.24 ()10100250009exp 1/(9)d d 190131.58t k tk s s t k k ⎡⎤=++=⇒=⎢⎥⎣⎦⎰⎰第4章收益率4.10.1483 4.2 1221.99 4.3 时间加权收益率0.5426, 币值加权收益率0.5226, 两者之差0.0236.4.4 93000 4.5 −10%4.6 120100506565(10050)136,0.1834100120100501009/12503/12D D i D D --+-⋅⋅=⇒===-+-+⨯-⨯ 4.7 0.1327 4.8 7.5% 4.9 236.25 4.100.06194.11 5年末投资者共得到56245.5元. 设购买价格为P , 要得到4%的收益率, 有5(1.04)56245.546229.7P P =⇒=4.12 20.0820/220/25000100000(5000)()34.710.1i i s i Is s i =+⇒=⇒=&&&& 4.13 再投资利率为8.73%. 投资者B 的利息再投资后的积累值为6111.37.4.14 ()10200.75100.7512126410.7520.09569i i i s i s i i ⋅⋅+⋅⋅=⇒+=⇒=4.15 3项投资在2015年初的余额为320.46万元, 在2015年末的余额为344.56万元, 故2015年中所获利息为24.10万元.第5章 贷款偿还方法5.1 X = 704.065.2 设每年的等额分期付款金额为R , 由已知28(1)135R v -=, 147(1)108(1)72R v R v -=⇒-=5.3 301301(1)/32/322.69t t R vR v t -+-+-=⇒=⇒=故在第23年分期付款中利息金额最接近于付款金额的三分之一. 5.4 109832290.35,408.55Rv Rv Rv Rv Rv Rv =++=++0.05,150.03,1158.4i R L ⇒===. 支付的利息总金额为10341.76R L -=5.5 1510.65.6 (1)借款人第2年末向偿债基金的储蓄额应为4438.42(2)第2年末的余额为9231.91 (3)第2年末的贷款净额为10768.095.7 0| 4| 6104.56/20000/8.4911%k i i R L a a i ===⇒= 5.8 第5次偿还中的利息为66.89万元.5.9 22912125,0001 1.02(1.02)(1.02)526i Ra v v v R ⎡⎤=+++⋅⋅⋅⋅+⇒=⎣⎦5.10 各期还款的积累值为 20200.0510*******(1)0.0616s i i =+⇒=5.11 121212155000500.3812 0.09173077.9455000(1)500.38jn njn a i j j s -=⎧⎪⇒==⎨=+-⎪⎩ 5.12 第一笔贷款偿还的本金为490.34, 第二笔贷款偿还的本金为243.93, 两笔贷款的本金之和为 734.27. 5.13 3278.5.14 第3次支付的本金金额为784.7, 第5次支付的利息金额为51.4. 5.15 0.1196. 5.16 64.74.5.17 调整后最后一次的偿还额为1239.1. 5.18 第11年末.5.19 调整后借款人增加的付款为112.5.20 20301019100001900100()5504.7Xa v a v Ia X =++⇒=. 5.21 11190.11.第6章证券定价6.1 价格为957.88元, 账面值为973.27元.6.2价格为974.82元, 账面值为930.26元(理论方法), 929.82(半理论方法), 1015(实践方法.6.37.227% . 6.4 6.986% .6.5 10201010101000.11000.091000.0897.74P a v a v a --=⨯+⨯+⨯=元.6.6债券每年末的息票收入为80元, 故有()()()54321082.27(1)801801801099.84(1)80(1)80 6.5%V V i V i i i i i ==+-=+-+-⎡⎤⎣⎦=+-+-⇒=(3)3 8010001099.8412n n i a v n --⋅+=⇒= 1212 0.065801000(1.065)1122.38P a -=⋅+=元.6.7应用债券定价的溢价公式可以建立下述三个等式:20202040(1) 45(2) 50(3) 2X C i a C Y C i a C X C i a C ⎛⎫-=- ⎪⎝⎭⎛⎫=- ⎪⎝⎭⎛⎫=- ⎪⎝⎭由(3)/(1)得:501302403Ci Ci Ci --=⇒=-由(1)(3)+得:2020(902)902XX Ci a a Ci=-⇒=-所以有 20(45)/25Y Ci a X =-==元. 6.8 t = 7/12, 理论方法的账面值为87.35元, 实践方法的账面值为87.35元.6.9110019019/110910/33n n n v v a =⇒=⇒= 0.0311********.03n n P v a =+=.6.10 40n n P a M v =+⋅, 30n n Q a M v =+⋅, 令债券C 的价格为X , 则有8054n n X a M v X P Q =+⋅⇒=-.6.11 ()()()()1010 0.041010 0.0510*******.040.03581.49100011001.05P r a r P r a --⎧=+⎪⇒=⎨-=+⎪⎩ ()1010 0.0351*******.0351371100 1.0351371070.80X a -=⨯+⨯=6.12 ()()()219202320105050 1.03 1.03 1.03837.78P v v v v v ⎡⎤=+++++=⎣⎦L .6.13 偿还值的现值为55200584.68()v a =元, 未来息票收入的现值为5556012()355.99()a v Da +=元, 故债券的价格为940.67元. 也可以应用Makeham公式计算, 即0.06/0.07(1000584.68)584.68940.67P =⨯-+=元.6.14 2020 10104010001071.06401041.58P a v P P a X v X ⎧=+=⎧⎪⇒⎨⎨=+⋅=⎪⎩⎩6.15 债券每年末的息票收入为60元, 修正息票率为60/1050 = 5.7143%, 小于投资者所要求的收益率8%, 所以赎回越晚(即到期时赎回), 债券的价格越低. 由此可得该债券的价格为1010501050(5.7143%8%)888.94P a =+⨯-⨯=元.6.16 股票在第六年的红利为60.50.2(1.10)⨯⨯, 以后每年增长10%. 应用复递增永续年金的公式, 该股票的价格为6510.50.2(1.10) 1.1110.510.110.1P -=⨯⨯⨯⨯=-元.6.17 投资者每个季度的实际收益率为 2.47%j =, 应用复递增永续年金的公式, 投资者购买该股票的价格为0.3/(2.47%2%)63.83P =-=元. 6.18 1.5/305%10%i =+=. 6.19 30元.6.20 每股利润为109.500.50-=元, 保证金为100.505⨯=元, 保证金所得利息为50.0500.25⨯=元, 每股红利为0.1元, 卖空收益率为(0.50.250.1)/513%+-=.6.21 8.59%第7章利率风险7.115D =马, 基于名义收益率的修正久期为15/(11%)14.85D =+=. 年实际收益率为12.68%i =, 基于实际收益率的修正久期为15/(112.68%)13.31D =+=.7.2 1()/()e 1n nD P P δδδδ'==--7.3 假设债券的面值为100, 则92.648.027.57P D D ===马,, 7.4债券的马考勒久期可以表示为nm j a D m=&&马, 其中()/m j im =. 变形可得:()()()11(1)1(1)(1)n n m m m nm jni v D j a j a m i d--+-=+=+==&&马. 7.5 对年金的现值关于利率i 求导, 应用修正久期的定义公式可得111n nnv D i v +=--.7.6对于期末付永续年金, 现值为()1/P i i =, 2()1/P i i '=-, 所以修正久期为1/D i =, 马考勒久期为=(1)(1)/D D i i i +=+马.7.7对于期初付永续年金, 现值为()(1)/P i i i =+, 2()1/P i i '=-, 所以修正久期为1/[(1]D i i =+), 马考勒久期为=(1)1/D D i i +=马.7.8 24 /2()510096.53()169.29 1.75()i P i P a v P i D P i ''=+=⇒=-⇒=-= 7.97.49D =效7.10 7.8861D D i ==+马, () 1.18%Pi D P∆=-∆⋅= ⇒ 新的债券价格近似为:75.98 1.01876.88⨯= 7.11 8.92D =效, 13.35C =效.2()0.5()8.85%Pi D i C P∆=-∆⋅+⋅∆⋅=-, 债券的新价格近似为95.59元. 7.12 修正久期为8.12, 凸度为101.24. 7.13 马考勒凸度为105.15.7.14 22231d 1d 216.67d d P P P i i i i i==⇒=- = ()116.67()P i D P i i'⇒=-==2()2555.55()P i C P i i''⇒=== 7.152()0.5() 4.28%Pi D i C P∆=-∆⋅+⋅∆⋅=- 7.16 负债的现值为12418.43L P =, 负债的马考勒久期为5LD =马, 负债的马考勒凸度为25L C =马. 不妨假设两种零息债券的面值均为1000元, 则4年期零息债券的价格为441000/(1)683.01P i =+=元, 10年期零息债券的价格为10101000/(1)385.54P i =+=元. 假设有%x 的债券投资4年期的零息债券, (1%)x -的债券投资10年期的零息债券, 由ALD D =马马, 有:(%)(4)(1%)(10)5%83.33%x x x +-=⇒=投资4年期零息债券的金额为10348.28元, 投资10年期零息债券的金额2070.15元. 7.17 债券A 的价格为982.17元, 马考勒久期为1.934, 马考勒凸度为3.8. 债券B 的价格为1039.93元, 马考勒久期为4.256, 马考勒凸度为19.85. 在债券A 上投资11.02%, 在债券B 上投资88.98%, 则债券组合的马考勒久期等于负债的马考勒久期, 均为4年, 债券组合的马考勒凸度为18.08, 大于负债的马考勒凸度16, 满足免疫的条件. 7.18 各种债券的购买数量分别如下:购买5年期债券的数量 80000 购买4年期债券的数量 300000 购买2年期债券的数量 600000 购买1年期零息债券100000购买各种债券以后净负债的现金流如下(单位:万元): 年度 1 2 3 4 5 负债的现金流1794 6744 144 3144 824 5年期债券的现金流 24 24 24 24 824 净负债的现金流 1770 6720 120 3120 0 4年期债券的现金流 120 120 120 3120 0 净负债的现金流 1650 6600 0 0 0 2年期债券的现金流 600 6600 0 0 0 净负债的现金流 1050 0 0 0 0 1年期债券的现金流 1050 0 0 0 0 净负债的现金流第8章利率的期限结构8.1一年期债券的价格为102.78P =;两年期债券的价格为92.96P =;三年期债券的价格为112.43P =.11111102.788%1s s =⇒=+ 2212323123510592.969.03%1(1)1515115112.4310.20%1(1)(1)s s s s s s s =+⇒=++=++⇒=+++8.2现金流分别按对应的即期利率折现得债券的价格为:231010110105.751.05 1.06 1.08P =++= 8.3 各年远期利率分别为8%、10.1%和12.6%. 8.4假设债券的面值为100元, 计算5年期债券的价格:2345234512345234123410101010110101010101101.07 1.07 1.07 1.07 1.071(1)(1)(1)(1)1111 3.741(1)(1)(1)s s s s s s s s s ++++=+++++++++⇒+++=++++每年支付40元的5年期期初付年金按对应的即期利率折现即得其现值为:23412341111401189.751(1)(1)(1)s s s s ⎡⎤++++=⎢⎥++++⎣⎦8.5由远期利率计算的债券价格为:1010110107.251.07(1.07)(1.05)(1.07)(1.05)(1.1)++=(元)8.6假设债券的面值为100元, 则有:001041004%(1)f f =⇒=+1001200101261061008.16%(1)(1)(1)8810810012.69%(1)(1)(1)(1)(1)(1)f f f f f f f f f f f ⇒=+⇒=+++⇒=++⇒=++++++8.7 应用即期利率和远期利率的关系, 有101022012330123116%(1)(1)(1) 5.50%(1)(1)(1)(1) 6.98%s f s f s f f s s f f f s +=+⇒==+=++⇒=+=+++⇒=8.8用t C 表示债券在t 年末的现金流入, 则有:111120%1.21C Cs s =⇒=+ 1212222220%1.2 1.2 1.2(1)C C C C s s +=+⇒=+ 33121232323320%1.2 1.2 1.2 1.2 1.2(1)C C C C C Cs s ++=++⇒=+ 8.91001120%s f f +=+⇒=3211221.21.2(1.2)(1)20%,120%1.2f f f =+⇒==-=8.10 00110106 3.77%1f f =⇒=+ 1001200101251059512.20%1(1)(1)991091029.37%1(1)(1)(1)(1)(1)f f f f f f f f f f f =+⇒=+++=++⇒=++++++用远期利率计算年息票率为15%, 面值为100元的3年期债券的价格:0010121515115117.651(1)(1)(1)(1)(1)P f f f f f f =++=++++++ 8.11 用远期利率分别计算3年期和4年期零息债券的价格可得:01210082(1)(1)(1)f f f =+++,30123100759.33%(1)(1)(1)(1)f f f f f =⇒=++++8.12 21012012115%,(1)(1)(1)6%s f s s f f s +=+⇒=+=++⇒=假设债券的面值为100元, 则有:3233881081008.2%1.05 1.06(1)s s =++⇒=+8.13 通过收益率计算的债券价格为 2610693.061.1(1.1)P =+= 通过即期利率计算的债券价格为2610694.831.07(1.09)P =+= 债券价格被低估了1.77元, 故可以按94.83元的价格购买一个2年期债券, 同时按即期利率出售一个1年期的面值为6元的零息票债券和一个2年期的面值为106元的零息票债券.8.14 与远期利率一致的债券价格为5510597.421.05(1.05)(1.06)(1.05)(1.06)(1.07)P =++=(元) 债券的市场价格为100元, 说明债券被高估了, 因而存在套利机会.套利者可以按100元的价格卖出一个三年期债券, 同时将97.42元按4%的利率投资一年. 在第一年末, 支付已出售债券的5元利息后, 把剩余的资金在第二年按6%的远期利率再投资一年. 在第二年末, 支付已出售债券的5元利息后, 把剩余的资金在第三年按8%的远期利率进行投资. 在第三年末的累积值正好用于支付套利者所售债券在第三年末的偿还值. 完成上述步骤后, 套利者即可在当前时刻获得100 - 97.42 = 2.58元的无风险收益.第9章远期、期货和互换9.1股票多头的回收和盈亏如下表所示: 1年后的股票价格多头的回收多头的盈亏50 50 −16 60 60 −6 70704如果1年后的股票价格为66元时, 则股票多头的回收为66元. 购买股票的初始费用在1年后的累积值为66元, 所以盈亏为0元. 9.2股票空头的回收和盈亏如下表所示, 与多头的回收和盈亏正好相反. 1年后的股票价格空头的回收 空头的盈亏50 −50 16 60 −60 6 70−70−4如果1年后股票的价格是66元时, 则空头的回收为−66元. 初始所得在1年后的累积值为66元, 所以盈亏为 0元. 9.3 40.06/40.061(105 1.7e )e 104.54t t F -==-⨯=∑(元)9.4日股利为0.02/3651050.00575⨯=元. 若在年初持有一单位股票, 年末将持有0.02e 1.0202=单位. 若要在年末持有一单位股股票, 年初应持有0.02e 0.9802-=单位,故投资额为0.02105e 102.92-=元. 9.5(1)0.060.570e 72.13F ⨯=⨯=元. (2)0.0670e 720.032δδ-⨯=⇒=.9.6无套利的远期价格为 0.060.5105108.20F e ⨯==(元)(1)远期价格115 > 108.20, 所以投资者可以先签出一份远期合约, 约定在6个月末以115元的价格卖出股票. 同时借入105元购买股票, 承诺在6个月末还款. 到6个月末, 以115元卖出手中的股票, 同时偿还借款108.20元, 最终无风险获利6.80元. (2)远期价格107 < 108.20, 所以投资者可以先签订一份远期合约, 约定在6个月末以107元购买股票. 同时将手中持有的股票卖出, 获得105元, 将这105元投资于5%的零息债券, 6个月末可以获得108.20元. 6个月末利用远期合约买入股票, 最终获得无风险利润1.20元.9.7 22838483.491.05 1.055 1.05 1.055x xx +=+⇒= 9.8(1)232382838482.981.05 1.055 1.06 1.05 1.055 1.06x x xx ++=++⇒= (2)2323838483.501.055 1.06 1.055 1.06x xx +=+⇒= 9.9四个时期的浮动利率分别为0.06、 0.07、 0.08和 0.09. 互换利率为0.0745.9.10 应用债券组合的定价方法:0.13/120.1059/120.1115/120.13/124e 4e 104e 98.24(5.1100)e 102.5198.24102.51 4.27B B f B B -⨯-⨯-⨯-⨯=++==+==-=-=-固浮浮固第10章 期权10.1 远期多头的回收分别为−10元、−5元、0元、5元和10元, 空头的回收是其相反数. 看涨期权多头的回收分别为0元、0元、0元、5元和10元. 看跌期权的回收分别为10元、5元、0元、0元和0元.10.2 回收分别为0元、0元和5元. 盈亏分别为−6.01元、−6.01元和−1.01元.10.3 看跌期权的回收分别为5元、0元和0元. 盈亏分别为3.96元、−1.04元和−1.04元. 10.4 组合的回收分别为105元、105元、110元和115元. 组合的盈亏分别为−7.56元、−7.56元、−2.56元和2.44元.10.5 组合的回收分别为−105元、−105元、−110元和−115元. 组合的盈亏分别为12.81元、12.81元、7.81元和2.81元.10.6 多头的盈亏为0.95元, 盈亏平衡点为42.05元. 10.7 多头的盈亏为3.47元, 盈亏平衡点为28.53元. 10.8 看跌期权的期权费是3.13元. 10.9 10.2417d =, 20.09167d =.根据Black−Scholes 公式, 欧式看涨期权价格为:12()e () 3.61rTC S d K d -=Φ-Φ=根据平价公式, 欧式看跌期权价格为e 2.38rT P C K S -=+-=10.10 1.0905u =, 1/0.9170d u ==, 0.5266r t e dp u d∆-==- 欧式看跌期权的价值为2.62, 相应的二叉树如下:美式看跌期权的价值为2.71, 相应的二叉树如下:10.11 1.0524u =, 1/0.9502d u ==, ()0.5118r tedp u dτ-∆-==-欧式看涨期权的价值为19.63, 相应的二叉树如下:10.12 回收和盈亏如下表:股票价格 看跌期权回收总回收 成本及其利息 盈亏 90 5 95 −105.98 −10.98 100100−105.98−5.9810.13回收和盈亏如下表:股票价格看涨期权回收股票空头回收总回收净收入及其利息盈亏90 0 −90 −90 94.03 4.03100 5 −100 −95 94.03 −0.97 10.14回收和盈亏如下表:股票价格看涨期权回收空头回收总回收净收入及其利息盈亏100 0 −100 −100 97.44 −2.56 110 5 −110 −105 97.44 −7.5610.15回收和盈亏如下表:股票价格看涨期权回收看跌期权回收贷出资金回收总回收净成本及其利息盈亏90 0 −5 95 90 −105 −15100 5 0 95 100 −105 −5 10.16回收和盈亏如下表:股票价格看涨期权回收看跌期权回收借入资金的回收总回收净收入及其利息盈亏100 0 5 −105 −100 105 5 110 −5 0 −105 −110 105 −510.17105(9.31 1.69) 1.0597--⨯=10.18通过下表可以看到两种交易的盈亏相同:股票价格买进看涨期权的回收卖出看涨期权的回收总回收净成本及其利息盈亏90 0 0 0 −2.46 −2.5100 5 0 5 −2.46 2.54 10.19通过下表可以看到两种交易的盈亏相同:股票价格买进看涨期权的回收卖出看涨期权的回收总回收净成本及其利息盈亏90 0 0 0 3.41 3.41 100 0 −5 −5 3.41 −1.59第11章随机利率11.1 A 10的完整分布如下:概率 A 10 (A 10)2 0.20 1.63 2.65 0.40 2.10 4.41 0.402.918.48(1) 十年末累积值的期望为2330.05元.(2) 十年末累积值的方差为255027.66, 标准差为505.11.2 期望累积值为2593.74元. 累积值的方差为83865.54, 标准差为289.60. 11.3 期望累积值为1560.9元. 11.4 公式(3)和(4)是正确的.11.5 三个投资额的期望累积值分别为6350.4元, 3528元和2240元. 第3年末该账户的期望累积值为12118.4元.11.6 期望累积值为1.1449, 累积值的方差为0.000916.11.7 (1) ln(1)t i +的期望为0.073189, ln(1)t i +的方差为0.000122.(2) ()()25050ln 50, var ln 50E A A μσ==⎡⎤⎡⎤⎣⎦⎣⎦()()()[][]5050Pr 100040000Pr ln ln 40Pr 0.3761Pr 0.376A A Z Z >=> ≈> =-<⎡⎤⎣⎦ []Pr 0.3760.65Z <=, ()50Pr 1000AV 400000.35>= 11.8 累积价值的95%置信区间为(0.81, 1.34). 11.9 (1)t i +的期望和方差分别为222/22E(1)e , var(1)e (e 1)t t i i μσμσσ+++=+=-, 故有E()0.0844, var()0.00235t t i i ==假设年收益率的中位数为k , 则有()ln(1)Pr()0.5Pr ln(1)ln(1)0.5Pr 0.5t t k i k i k Z μσ+-⎛⎫<=⇒+<+=⇒<= ⎪⎝⎭ln(1)08.33%k k μσ+-=⇒=.11.10 利率树:现金流和各节点的价值:可赎回债券的价格为99.19元.11.11 第1年末的即期利率由当前的即期利率发展而来, 在当前利率水平的基础上上调30%的概率为0.75, 下降30%的概率为0.25. 第2年末的即期利率由第1年末的即期利率发展而来, 在第1年末利率水平的基础上上调30%的概率为0.75, 下降30%的概率为0.25. 利率树如下:[]()()()()()()()()()()()()2E 0.750.750.08450.750.250.050.250.750.050.250.250.029596.813%i =+++=。
2020年春季中国精算师《金融数学》过关必做1000题(含历年真题)

目 录第一篇 利息理论第1章 利息的基本概念第2章 年 金第3章 收益率第4章 债务偿还第5章 债券及其定价理论第二篇 利率期限结构与随机利率模型第6章 利率期限结构理论第7章 随机利率模型第三篇 金融衍生工具定价理论第8章 金融衍生工具介绍第9章 金融衍生工具定价理论第四篇 投资组合理论第10章 投资组合理论第11章 CAPM和APT附 录 2011年秋季中国精算师考试《金融数学》真题及详解第一篇 利息理论第1章 利息的基本概念单项选择题(以下各小题所给出的5个选项中,只有一项最符合题目要求,请将正确选项的代码填入括号内)1.已知在未来三年中,银行第一年按计息两次的名义年利率10%计息,第二年按计息四次的名义年利率12%计息,第三年的实际年利率为6.5%。
某人为了在第三年末得到一笔10000元的款项,第一年年初需要存入银行( )元。
[2011年秋季真题]A.7356B.7367C.7567D.7576E.7657【答案】C【解析】由名义年利率和实际年贴现因子的等价关系,可得:每年的贴现因子分别为,,。
因此,第三年末10000元的款项在第一年初的现值为:。
2.已知0时刻在基金A中投资1元到2t时的积累值为(3t+1)元,在基金B中投资1元到3t时的积累值为元。
假设在T时基金B的利息强度为基金A的利息强度的两倍,则0时刻在基金中B投资1000元在5T时的积累值为( )元。
[2011年秋季真题]A.27567B.27657C.27667D.27676E.27687【答案】C【解析】由题得,0时刻在基金A中投资1元到t时的积累值为(1.5t+1)元,即积累因子,利息强度在基金B中投资1元到3t时的积累值为元,因此在基金B中投资1元到t时的积累值为元,因此。
当时,即,解得,因此0时刻在基金中B投资1000元在5T时的积累值为元。
3.已知某基金的积累函数a(t)为三次函数,每三个月计息一次,第一季度每三个月计息一次的年名义利率为10%,第二季度每三个月计息一次的年名义利率为12%,第三季度每三个月计息一次的年名义利率为15.2%,则为( )。
金融数学--第一章

0 x0 x1c x2c xnc
2
n
n
此外,如果 k 0 xk 0 ,那么相应的内部收益率
r=(1/c)-1为正。
证明 构造函数 注意到 f (0) < 0, f(c)为增函数且连续。因此存 在唯一正根。
f (c) x0 x1c x2c xnc
0 x0 x1 / (1 r) x2 / (1 r ) xn / (1 r )
2
n
若令1/(1+r)=c,此时c满足多项式方程:
0 x0 x1c x2c xnc
2
n
这是一个多项式方程,解一般不唯一。
现金流(-2,1,1,1)的内部收益率
0 2 c c c
一、单利与复利的基本计算 二、贴现因子的意义 三、现金流现值与终值的基本计算 四、名利率的基本计算 五、利息力的意义 六、价值方程的应用(现金流分析)
§1.1 利息基本函数
本金:投资的初始资本投入,记为A(0) 。 定义1.1 总量函数:原始投资经过一定时间后投资 价值称之为总量函数。总量函数用 A(t) 表示。 定义1.2 利息:货币的时间变化量。
现金流的等价
现值的重要定理 对于利率为r的永恒的理性银行来说,当且 仅当以该银行利率来评估两个现金流现值 相同时,这两个现金流等价。两个能够相 互转化的现金流称为等价现金流。 例如, (1,0)和(0,1+i) (-2,1,1,1)和(0.487,0,0,0)在利率 为10%的条件下
内部收益率
内部收益率 设 ( x0 , x1 , xn )为一现金流,内部收益率为满足 下列方程的r:
结论1.11 (1)dd
dd 1 e 0 0, di 1 i d
金融数学第一章练习试题详解

1.22已知利息力为 ,2≤t≤10。请计算在此时间区间的任意一年内,与相应利息力等价的每半年贴现一次的年名义贴现率。
1.13资金A以10%的单利累积,资金B以5%的单贴现率累积。请问在何时,两笔资金的利息力相等。
1.14某基金的累积函数为二次多项式,如果向该基金投资1年,在上半年的名义利率为5%(每半年复利一次),全年的实际利率为7%,试确定 。
1.15某投资者在时刻零向某基金存入100,在时刻3又存入X。此基金按利息力 累积利息,其中t > 0。从时刻3到时刻6得到的全部利息为X,求X。
金融数学第一章练习题详解
第1章利息度量
1.1现在投资$600,以单利计息,2年后可以获得$150的利息。如果以相同的复利利率投资$2000,试确定在3年后的累积值。
1.2在第1月末支付314元的现值与第18月末支付271元的现值之和,等于在第T月末支付1004元的现值。年实际利率为5%。求T。
1.3在零时刻,投资者A在其账户存入X,按每半年复利一次的年名义利率i计息。同时,投资者B在另一个账户存入2X,按利率i(单利)来计息。假设两人在第八年的后六个月中将得到相等的利息,求i。
1.4一项投资以δ的利息力累积,27.72年后将翻番。金额为1的投资以每两年复利一次的名义利率δ累积n年,累积值将成为7.04。求n。
1.5如果年名义贴现率为6%,每四年贴现一次,试确定$100在两年末的累积值。
1.6如果 = 0.1844144, = 0.1802608,试确定m。
1.7基金A以每月复利一次的名义利率12 %累积。基金B以 = t / 6的利息力累积。在零时刻,分别存入1到两个基金中。请问何时两个基金的金额将相等。
O《金融数学》练习题参考答案

−1 =
n 2
⇒
n
= 16
∫ 1.29
⎡2 ⎤ AV = 1000 ⋅ exp ⎢⎣ 0 δtdt ⎥⎦ = 1068.94
1.30 500(1 + 2.5i) + 500(1+1.75i) + 500(1+ 0.25i) = 500(3 + 4.5i) = 1635 ⇒ i = 6%
3
1.31
AVJoe = 10[1+10(0.11)]+ 30[1+ 5(0.11)] = 67.5 AVTina = 10(1.0915)10−n + 30(1.0915)10−2n
⇒ 67.5 = 10(1.0915)10−n + 30(1.0915)10−2n ⇒ n = 1.262
∫ ∫ 1.32
a(n)
=
exp
⎡ ⎢⎣
n 2
δ t
dt
⎤ ⎥⎦
=
exp
⎡ ⎢⎣
n 2
t
2 −1
dt
⎤ ⎥⎦
=
(n
− 1) 2
,
d (2)
=
2 ⎡⎣1− (1− d )0.5 ⎤⎦
=
2(1 −
n −1 )
1.12 由已知得 e27.72δ = 2 ⇒ δ = 0.025
n
当 i0.5 = δ 时, (1+ 2δ )2 = 7.04 ⇒ n = 80
1.13 100×(1-4×6%)-1/4×2=114.71
1.14
1+
i
=
⎡⎢⎢⎣1+
im m
⎤⎥⎥⎦ m
=
⎡⎢⎢⎣1−
金融数学智慧树知到课后章节答案2023年下宁波大学

金融数学智慧树知到课后章节答案2023年下宁波大学宁波大学第一章测试1.利息是资金的 ( ) 。
A:指标B:水平C:价格D:价值答案:价格2.现值也叫 ( ) 。
A:贴现值B:贴现C:终值D:贴现系数答案:贴现值3.假定满足下列条件(i) 10 年末支付 X 和20 年末支付 Y 的现值之和等于 15 年末 X + Y 付款的现值。
(ii) X + Y = 100(iii) 年利率i = 5%则X=()A:44B:48C:52D:50答案:444.杰夫将10元存入一个基金,15 年后又存入20元。
利息以名义贴现率d计息,前 10 年每季度复利一次,名义利率为6%,此后每半年一次。
该基金在30年末的累计余额为100。
则名义贴现率()A:4.43%B:4.63%C:4.53%D:4.33%答案:4.53%5.六个月后到期的$1.00 的现值为$0.97。
则按每年贴现4次的名义年贴现率为()A:6.05%B:6.55%C:6.75%D:5.95%答案:6.05%第二章测试1.一项投资需要首付1万元,前10年每年年底支付1000元。
从第11年年底开始,该投资连续5年在每年底回报相等的金额X。
试确定X使得在15年期间产生10%的年回报率()。
A:10,900B:11,050C:11,200D:10,750答案:11,0502.若年利率为6.3%,每年末付款1000元的4N期年金现值为14113,试确定第一个N年付款的现值和第三个N年付款的现值的百分比为()。
A:66%B:57%C:60%D:63%答案:63%3.如果2010年至2021年(含)每年1月1日缴存1500元,实际利率为每年1.75%,试确定这些存款在2030年1月1日的累计价值为()。
A:23,290B:23,390C:23,490D:23,190答案:23,1904.李明将在每季度末存入账户450元,为期10年。
15年后,李明使用账户资金在每年年初支付Y,为期4年,之后账户余额为0,假设年利率为7%。
O《金融数学》练习题参考答案

(1+ i)n +1
(1+ i)n +1
s
(1 + )i 3n −1 (1 + i)2n −1+ (1+ )i 3n −1
1+ 3n = 1+
=
s 2n
(1 + i )2n −1
(1 + )i 2n −1
(1+ i)n +1+ (1+ )i 2n + (1+ i)n +1 (1+ i)2n + 2 (1+ i)n + 2
n
=
2 n
d = a(n + 1) − a(n) = n2 − (n −1)2
a(n +1)
n2
第2章
等额年金
2.1 1363 元
ห้องสมุดไป่ตู้
2.2 27943 元
2.3 月实际利率为 0.5%,年金的领取次数为 123,截至 2005 年 12 月 31 日,领取次数为
70。因此
200a =18341 123 0.5%
2.17 100a = 4495.5038 = 6000vk ⇒ vk = 0.7493 ⇒ k = 29 60
( ) ( ) 2.18 a 1+ v15 + v30 = 1− v15 1+ v15 + v30 = 1+ v15 + v30 − v15 − v30 − v45 = 1− v45 = a
= ⎡⎣(1+ i)n −1⎤⎦2 ⋅ ⎡⎣(1+ i)n + 1⎤⎦2 + ⎡⎣(1+ i)n −1⎤⎦2 ⎡⎣(1+ i)n −1⎤⎦ ⋅ ⎡⎣(1+ i)n −1⎤⎦ ⋅ ⎡⎣(1+ i)n + 1⎤⎦
金融数学习题
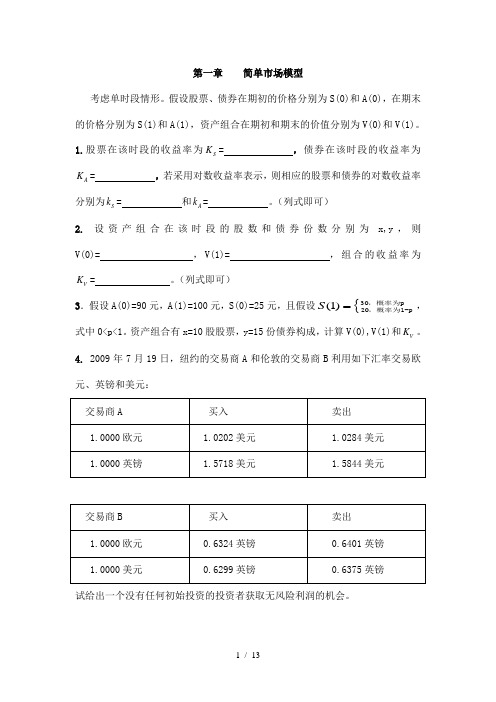
第一章 简单市场模型考虑单时段情形。
假设股票、债券在期初的价格分别为S(0)和A(0),在期末的价格分别为S(1)和A(1),资产组合在期初和期末的价值分别为V(0)和V(1)。
1.股票在该时段的收益率为S K = ,债券在该时段的收益率为A K = ,若采用对数收益率表示,则相应的股票和债券的对数收益率分别为S k = 和A k = 。
(列式即可)2. 设资产组合在该时段的股数和债券份数分别为x,y ,则V(0)= ,V(1)= ,组合的收益率为V K = 。
(列式即可)3.假设A(0)=90元,A(1)=100元,S(0)=25元,且假设{3020(1)S =,概率为p,概率为1-p,式中0<p<1。
资产组合有x=10股股票,y=15份债券构成,计算V(0),V(1)和V K 。
4. 2009年7月19日,纽约的交易商A 和伦敦的交易商B 利用如下汇率交易欧元、英镑和美元:试给出一个没有任何初始投资的投资者获取无风险利润的机会。
第二章无风险资产2.1.某人在未来15 年中每年年初存入银行20 000 元。
前 5 年的年利率为5.2%,中间5 年的年利率下调至3.3%,后 5 年由于通货膨胀率的提高,年利率上调至8.3%。
则第15 年年末时这笔存款的积累值为()元。
(A)496 786 (B) 497 923 (C) 500 010 (D) 501 036 (E) 502 1092.2已知在未来三年中,银行第一年按计息两次的名义年利率10%计息,第二年按计息四次的名义年利率12%计息,第三年的实际年利率为6.5%。
某人为了在第三年末得到一笔10 000元的款项,第一年年初需要存入银行()元。
(A) 7 356 (B) 7 367 (C) 7 567 (D) 7 576 (E) 7 6572.3.将9000元存入银行账户2个月(61天),按单利计算,期末终值9020元。
计算利率r和这个投资的收益率。
金融数学第1、2章作业

第一章 基本概念1.某人存1000元进入银行,第1年末存款余额为1020元,第2年末存款余额为1050元,求1i ,2i ,1d ,2d 分别等于多少?2.确定500元以季度转换8%年利率投资5年的积累值。
3. 确定1000元按如下利息强度投资10年的积累值(1) 0.05δ= (2)20.05(1)t t δ-=+4. 某人为了能在第7年末得到10000元款项,他愿意在第一年末付出1000元,第3年末付出4000元,第8年未付出X 元,如果以6%的年利率复利计息,问X=?5. 某人现在投资4000元,3年后积累到5700元,问季度计息的名义利率等于多少?6.已知(3/2)8%i =,求等价的(12)d ?某人立即付款100元,并在第2年末付132元,以换回第1年末返回230元,求这笔业务的收益率。
7.某人向银行借款1000元,期限1年,并立即收到银行910元,在第8个月末还款300元,假设为单贴现,问在年末该人还应付款多少?8.一家制造商出售产品给零售者,后者可以有两种选择:(1)立即按低于零售价30%的价格付款;(2)6个月后按低于零售价25%的价格付款。
问在什么水平利率情况下,这两种选择无差别?9.10年前,某人存款1000在某账户,以赚取半年度转换4%的利率。
存款后,该人没有再追加新的存款,相反,在每半年他将账户中新产生的利息的一半取出。
求现在该人的账户余额。
10.数学推导证明:()()()()*m m m mi d i dm m m m-=(m>0)第2章年金1.设有年金方式:从1980年6月7日开始,每季度年金金额为100元,直至1991年12月7日。
已知季换算名义利率为6%。
计算:(1)该年金在1979年9月7日的现值;(2)该年金在1992年6月7日的终值。
2.某人将遗产以永久年金的方式留给后代A,B,C和D:前n年,A,B和C三人平分每年的年金,n年后所有年金由D一人继承。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
金融数学第一章练习题详解第 1 章 利息度量1.1 现在投资$600,以单利计息,2 年后可以获得$150 的利息。
如果以相同的复利利率投资$2000,试确定在 3 年后的累积值。
65.2847%)5.121(2000%5.1215026003=+=⇒=∙i i1.2 在第 1 月末支付 314 元的现值与第 18 月末支付 271 元的现值之和,等于在第 T 月末支付 1004 元的现值。
年实际利率为 5% 。
求 T 。
58.1411205.1ln /562352.0ln 562352.0ln 05.1ln 12562352.01004/)05.127105.1314(05.105.1%)51()1(271314100412/1812/112/12/1812/112/=⨯-==-=⨯+⨯==+=+=+=------T T i v v v v T tt t t T 两边取对数,其中1.3 在零时刻,投资者 A 在其账户存入 X ,按每半年复利一次的年名义利率 i 计息。
同时,投资者B在另一个账户存入 2X ,按利率 i (单利)来计息。
假设两人在第八年的后六个月中将得到相等的利息,求 i 。
094588.02)12(2)21(2)21()21()21())21()21((212:))21()21((:215/11515151615161516=⨯-==+∙+=+-+==+-+=⨯⨯+-+i i i i i i i Xi i i X Xi i X B i i X A i A 两边取对数,的半年实际利率为1.4 一项投资以 δ 的利息力累积,27.72 年后将翻番。
金额为 1 的投资以每两年复利一次的名义利率 δ 累积 n 年,累积值将成为 7.04。
求 n 。
()802)05.1ln /04.7(ln 04.7)21025.072.27/2ln 2)1()(1ln 2/5.072.27=⨯==+=====+=+=n i e e i t a i n tt δδδδδδ(1.5 如果年名义贴现率为 6%,每四年贴现一次,试确定$100 在两年末的累积值。
71.114%)641(10024/1=⨯-⨯-1.6 如果 )(m i = 0.1844144 , )(m d= 0.1802608 ,试确定 m 。
81802608.01844144.01802608.01844144.01111111111112=-⨯=-∙=∙=-=∙--+=⎥⎦⎤⎢⎣⎡-∙⎥⎦⎤⎢⎣⎡+=⎥⎦⎤⎢⎣⎡-∙⎥⎦⎤⎢⎣⎡+-=⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡+=+-m m m m mm m m mm m m m m m m m m m m m m d i d i m md i d i m d i m d i m d m i m d m i d m d m i i1.7 基金 A 以每月复利一次的名义利率 12 %累积。
基金 B 以t δ= t / 6 的利息力累积。
在零时刻,分别存入 1 到两个基金中。
请问何时两个基金的金额将相等。
()43.101.1ln 14412/01.1ln 1212/%121212/6/1220=⨯===⎰=+t t t e e t dt t t t 两边取对数,1.8 基金 A 以 t δ= a+bt 的利息力累积。
基金 B 以t δ= g+ht 的利息力累积。
基金 A 与基金 B 在零时刻和 n 时刻相等。
已知 a > g > 0 , h > b > 0 。
求n 。
hb a g n hn gn bn an n b n a b a e e t b e e t a ht gt dt ht g bt at dt bt a t t --=⇒+=+⇒===⎰==⎰=++++)(22121)()(),0()0()()(22)21()()21()(20201.9 在零时刻将100支付利息。
从 t = 2 开始,利息按照 tt +=11δ的利息力支付。
在 t = 5 时,存款的累积值为 260。
求δ。
()()1290.0)2100/(26014260)4/1(100260)4/1(1008/1-)3ln 6(ln 24-1124-52=⨯-⨯==⨯-=⎰⨯--⨯+⨯δδδδe edt t 现率指前两年内的年名义贴1.10 在基金 A 中,资金 1 的累积函数为 t+1,t>0;在基金 B 中,资金 1 的累积函数为1+t 2 。
请问在何时,两笔资金的利息力相等。
41.012012121112,11222=-=⇒=-+⇒+=+⇒=+=+=t t t tt t t t t B A B A δδδδ令 1.11 已知利息力为t t +=12δ。
第三年末支付 300 元的现值与在第六年末支付 600 元的现值之和,等于第二年末支付 200 元的现值与在第五年末支付 X 元的现值。
求 X 。
82.315))51/(())21(200-)61(600)31(300()5()2(200)6(600)3(300)1()()1()(22-221111212)1ln(2120=++⨯+⨯++⨯=⇒⨯+⨯=⨯+⨯+=⇒+==⎰=---------++X a X a a a t t a t e e t a t dt t t1.12 已知利息力为1003t t =δ。
请求)3(1-a 。
8167.0)3(2025.0400/81)03(400/110014303====⎰=---⨯---e e e e a dt t1.13 资金 A 以 10%的单利累积,资金 B 以 5%的单贴现率累积。
请问在何时,两笔资金的利息力相等。
51.011.0-205.0105.01.011.005.0105.0)05.01()(05.01)%51()(:1.011.01.01)%101()(:11=⇒+=⇒-=+⇒=-=⇒-=⇒-=-=+=⇒+=+=--t t t tt t t t a t t t a B tt t t a A B A B A δδδδ令1.14 某基金的累积函数为二次多项式,如果向该基金投资 1 年,在上半年的名义利率为 5%(每半年复利一次),全年的实际利率为 7%,试确定5.0δ。
06829.0103.004.003.008.0103.004.0)(,1,03.0,04.0%71)1(2/%515.025.0)5.0(1)0()(5.025.022=+++=++====⇒+=++=+=++===++==t t t t t t t a c b a c b a a c b a a c a cbt at t a δ设累积函数为1.15 某投资者在时刻零向某基金存入 100,在时刻 3 又存入 X 。
此基金按利息力1002t t =δ累积利息,其中 t > 0。
从时刻 3 到时刻 6 得到的全部利息为 X ,求 X 。
61.784)42.109(8776.0)3()6()42.109(8776.1)42.109()6(42.109100)3(632302100100=⇒=+=-+=⎰+=+=+⎰=X X X A A X e X A XX e A dt t dt t1.16 一位投资者在时刻零投资 1000,按照以下利息力计息:⎩⎨⎧>≤≤=3,045.030,02.0t t t t δ 求前 4 年每季度复利一次的年名义利率。
%39.30339.0)11445.1(41445.11000)4/1(1000,1445.1)4(16/144045.009.0045.002.04330==-⨯=⇒⨯=+==⎰⎰=⨯++x x x e e a dt dt t 设年名义利率为1.17 已知每半年复利一次的年名义利率为 7.5%,求下列两项的和:(1)利息力;(2)每季度贴现一次的年名义贴现率。
14658.007295.0))2/%5.71(-1(4)2/%5.71()4/1(,07363.0)2/%5.71ln()2/%5.71()()4/1(22422=+=+⨯=⇒+=-=+=+=-⨯-x x x x t a t t t t tδδ设名义贴现率为注:个人认为,求这两个数的和并没有实际意义1.18 假设利息力为⎪⎩⎪⎨⎧≤<≤<=105,25150,2t kt t kt t δ,期初存入单位 1 在第 10 年末将会累积到 2.7183。
试求 k 。
0414.07183.2)(1667.24)1251000(751225251105250=⇒===⎰⎰=-++k e e et a k k k dt kt ktdt 1.19 已知利息力为tt +=21δ,一笔金额为 1 的投资从 t=0 开始的前 n 年赚取的总利息是 8。
试求 n 。
1681211)(21)(2ln )2ln(210=⇒=-+=-+==⎰=-++n n n a t e e t a t dt t t1.20 1996 年 1 月 1 日,某投资者向一个基金存入 1000,该基金在 t 时刻的利息力为 0.1(t-1)2 ,求 1998 年 1 月 1 日的累积值。
94.10681000100006667.0)1(1.0202==⎰=-e e A dt t1.21 投资者 A 今天在一项基金中存入 10,5 年后存入 30,已知此项基金按单利 11%计息;投资者 B 将进行同样数额的两笔存款,但是在 n 年后存入 10, 在 2n 年后存入 30,已知此项基金按复利 9.15%计息。
在第 10 年末,两基金的累积值相等。
求 n 。
5244.20915.1ln /8017.0ln 40014.20915.18017.00915.1302)5.67(0915.1304)0915.110(0915.1105.670915.1300915.1100915.1ln /ln ,0915.15.67%)15.91(30%)15.91(10%)15.91(30%)15.91(10:5.67)5%111(30)10%111(10:10101021010210102101021010=-===⨯⨯-⨯⨯⨯-⨯+⨯-==⨯⨯+⨯⨯-===+++⇒+++=⨯++⨯+-----n t t t t n t B A n n n nn 即令注:不知道为什么,笔者算出来的答案恰好是参考答案的两倍,将2.5244带进去右边=66,将1.262代进去,右边=80,由此可得2.5244接近真实结果1.22 已知利息力为12-=t t δ,2 ≤ t ≤10 。
请计算在此时间区间的任意一年内,与相应利息力等价的每半年贴现一次的年名义贴现率。
