A、初中三角函数知识点总结
三角函数的知识点总结

三角函数的知识点总结1. 三角函数的基本概念三角函数源于三角形的角度关系,最开始是根据角度的定义和圆的性质推导得到。
三角函数最常用的有正弦函数(sin)、余弦函数(cos)、正切函数(tan)等。
正弦函数是指直角三角形中对边和斜边的比值,余弦函数是指直角三角形中邻边和斜边的比值,正切函数是指对边和邻边的比值。
这些函数中的输入变量是角度,输出变量是一个无量纲的比值。
2. 三角函数的关系与性质(1)正弦函数与余弦函数的关系:在单位圆上,当一个角为Θ时,其余弦函数值等于该角的补角的正弦函数值,即cos(Θ)=sin(π/2-Θ)。
(2)正切函数与余切函数的关系:在单位圆上,对于角Θ,其正切函数值等于角Θ的补角的余切函数值的倒数,即tan(Θ)=1/cot(Θ)。
(3)函数性质:三角函数具有周期性,正弦函数和余弦函数的周期是2π,而正切函数的周期为π。
3. 三角函数的定义和图像(1)正弦函数的定义和图像:正弦函数sin(x)在整个实数集上都有定义,其图像为一条连续曲线,且在区间[-π, π]上是凹函数,区间[0, π]上是凸函数,在区间[-π/2, π/2]上是单调递增函数,在区间[π/2, 3π/2]上是单调递减函数。
(2)余弦函数的定义和图像:余弦函数cos(x)在整个实数集上都有定义,其图像也是一条连续曲线,且在区间[0, π]上是凹函数,在区间[-π, 0]上是凸函数,在区间[0, π/2]上是单调递减函数,在区间[π/2, 3π/2]上是单调递增函数。
(3)正切函数的定义和图像:正切函数tan(x)在实数集上有定义,其图像是一条有无数间断点的曲线,且在每个周期的中点有一个无穷大的间断点。
4. 三角函数的导数(1)正弦函数和余弦函数的导数:正弦函数sin(x)的导数是cos(x),余弦函数cos(x)的导数是-sin(x)。
(2)正切函数的导数:正切函数tan(x)的导数是sec^2(x)。
5. 三角函数的应用三角函数在物理、工程、计算机科学等领域有着广泛的应用,例如在振动力学中,三角函数用于描述谐波振动的性质;在信号处理中,三角函数用于描述周期信号的特性;在工程中,正切函数用于计算斜面的坡度等。
初中三角函数知识点总结

初中三角函数知识点总结三角函数是数学中重要的概念,对于初中学生来说,掌握三角函数的基本知识是非常重要的。
本文将对初中阶段常见的三角函数知识点进行总结,包括正弦函数、余弦函数和正切函数的定义、性质和应用等方面。
1. 正弦函数(sine function)正弦函数是一个周期函数,用sin表示。
在单位圆中,正弦函数的值等于对应角度的点在单位圆上的纵坐标。
性质:- 正弦函数的值域为[-1, 1],即sin(x) ≤ 1,sin(x) ≥ -1。
- 正弦函数的周期为2π,即sin(x + 2π) = sin(x)。
- 正弦函数在特殊角度上的值为:sin(0) = 0,sin(π/6) = 1/2,sin(π/4) = √2/2,sin(π/3) = √3/2,sin(π/2) = 1。
2. 余弦函数(cosine function)余弦函数是一个周期函数,用cos表示。
在单位圆中,余弦函数的值等于对应角度的点在单位圆上的横坐标。
性质:- 余弦函数的值域为[-1, 1],即cos(x) ≤ 1,cos(x) ≥ -1。
- 余弦函数的周期为2π,即cos(x + 2π) = cos(x)。
- 余弦函数在特殊角度上的值为:cos(0) = 1,cos(π/6) = √3/2,cos(π/4) = √2/2,cos(π/3) = 1/2,cos(π/2) = 0。
3. 正切函数(tangent function)正切函数是一个周期函数,用tan表示。
在单位圆中,正切函数的值等于对应角度的点在单位圆上的纵坐标与横坐标之比。
性质:- 正切函数的定义域为除去所有余弦函数为零的点,即cos(x) ≠ 0的点。
在这些点上,tan(x) = sin(x) / cos(x)。
- 正切函数的值域为全体实数。
- 正切函数的周期为π,即tan(x + π) = tan(x)。
- 正切函数在特殊角度上的值为:tan(0) = 0,tan(π/6) = √3/3,tan(π/4) = 1,tan(π/3) = √3,tan(π/2) 不存在。
九年级三角函数知识点整理

九年级三角函数知识点整理三角函数是数学中一个重要的概念,特别是在处理角度、弧度、三角形和圆等方面。
以下是九年级三角函数知识点整理:1. 锐角三角函数的定义:锐角角A的正弦(sin),余弦(cos)和正切(tan),余切(cot)以及正割(sec),余割(csc)都叫做角A的锐角三角函数。
正弦(sin):等于对边比斜边,即sinA=a/c。
余弦(cos):等于邻边比斜边,即cosA=b/c。
正切(tan):等于对边比邻边,即tanA=a/b。
余切(cot):等于邻边比对边,即cotA=b/a。
正割(sec):等于斜边比邻边,即secA=c/b。
余割(csc):等于斜边比对边,即cscA=c/a。
2. 特殊角的三角函数值:对于一些特定的角度,三角函数有特定的值。
例如,当角度为30°、45°和60°时,正弦、余弦和正切的值分别是1/2、√2/2、√3/3等。
3. 互余角的关系:sin(π-α)=cosα,cos(π-α)=sinα,tan(π-α)=cotα,cot(π-α)=tanα。
4. 平方关系:sin^2(α)+cos^2(α)=1,tan^2(α)+1=sec^2(α),cot^2(α)+1=csc^2(α)。
5. 积的关系:sinα=tanα·cosα,cosα=cotα·sinα。
6. 诱导公式:对于角度的和差、倍角等运算,可以通过诱导公式简化计算。
例如,sin(A+B)和cos(A+B)可以通过诱导公式转化为sinAcosB+cosAsinB 和cosAcosB-sinAsinB。
7. 图像与性质:正弦、余弦和正切的图像是周期函数,具有对称性。
例如,正弦函数在y轴两侧对称,余弦函数在x轴上对称。
此外,三角函数的最大值和最小值以及对应的x值也是重要的知识点。
8. 应用:三角函数在日常生活和科学研究中有着广泛的应用。
例如,在测量、航海、工程、物理和数学等领域中,经常需要用到三角函数的知识。
初中数学三角函数基础知识点总结

初中数学三角函数基础知识点总结初中数学三角函数基础知识点总结总结是对某一特定时间段内的学习和工作生活等表现情况加以回顾和分析的一种书面材料,它可以使我们更有效率,因此,让我们写一份总结吧。
我们该怎么去写总结呢?下面是小编为大家整理的初中数学三角函数基础知识点总结,供大家参考借鉴,希望可以帮助到有需要的朋友。
初中数学三角函数基础知识点总结篇1三角和的公式sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·sinγ-sinα·sinβ·sinγcos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·sinγ-sinα·sinβ·cosγtan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)/(1-tanα·tanβ-tanβ·tanγ-tanγ·tanα)倍角公式tan2A = 2tanA/(1-tan2 A)Sin2A=2SinA?CosACos2A = Cos^2 A--Sin2 A =2Cos2 A-1 =1-2sin^2 A三倍角公式sin3A = 3sinA-4(sinA)3;cos3A = 4(cosA)3 -3cosAtan3a = tan a ? tan(π/3+a)? tan(π/3-a)三角函数特殊值α=0° sinα=0 cosα=1 tαnα=0 cotα→∞ secα=1 cscα→∞α=15°(π/12) sinα=(√6-√2)/4 cosα=(√6+√2)/4 tαnα=2-√3 cotα=2+√3 secα=√6-√2 cscα=√6+√2α=22.5°(π/8) sinα=√(2-√2)/2 cosα=√(2+√2)/2 tαnα=√2-1 cotα=√2+1 secα=√(4-2√2) cscα=√(4+2√2)a=30°(π/6) sinα=1/2 cosα=√3/2 tαnα=√3/3 cotα=√3 secα=2√3/3 cscα=2α=45°(π/4) sinα=√2/2 cosα=√2/2 tαnα=1 cotα=1 secα=√2 cscα=√2α=60°(π/3) sinα=√3/2 cosα=1/2 tαnα=√3 cotα=√3/3 secα=2 cscα=2√3/3α=67.5°(3π/8) sinα=√(2+√2)/2 cosα=√(2-√2)/2 tαnα=√2+1 cotα=√2-1 secα=√(4+2√2) cscα=√(4-2√2)α=75°(5π/12) sinα=(√6+√2)/4 cosα=(√6-√2)/4 tαnα=2+√3 cotα=2-√3 secα=√6+√2 cscα=√6-√2α=90°(π/2) sinα=1 cosα=0 tαnα→∞ cotα=0 secα→∞ cscα=1α=180°(π) sinα=0 cosα=-1 tαnα=0 cotα→∞ secα=-1 cscα→∞α=270°(3π/2) sinα=-1 cosα=0 tαnα→∞ cotα=0 secα→∞ cscα=-1α=360°(2π) sinα=0 cosα=1 tαnα=0 cotα→∞ secα=1 cscα→∞三角函数记忆顺口溜1三角函数记忆口诀“奇、偶”指的是π/2的倍数的`奇偶,“变与不变”指的是三角函数的名称的变化:“变”是指正弦变余弦,正切变余切。
初中三角函数知识点总结
锐角三角函数知识点总结1、勾股定理:直角三角形两直角边a 、b 的平方和等于斜边c 的平方。
2、如下图,在Rt △ABC 中,∠C 为直角,则∠A 的锐角三角函数为(∠A 可换成∠B):3、任意锐角的正弦值等于它的余角的余弦值;任意锐角的余弦值等于它的余角的正弦值。
4、任意锐角的正切值等于它的余角的余切值;任意锐角的余切值等于它的余角的正切值。
5、0°、30°、45°、60°、90°特殊角的三角函数值(重要)6 当0°≤α≤90°时,sin α随α的增大而增大,cos α随α的增大而减小。
7、正切、余切的增减性: 当0°<α<90°时,tan α随α的增大而增大,cot α随α的增大而减小。
1、解直角三角形的定义:已知边和角(两个,其中必有一边)→所有未知的边和角。
依据:①边的关系:222c b a =+;②角的关系:A+B=90°;③边角关系:三角函数A90B 90∠-︒=∠︒=∠+∠得由B A 对边邻边 A90B 90∠-︒=∠︒=∠+∠得由B A的定义。
(注意:尽量避免使用中间数据和除法)2、应用举例:(1)仰角:视线在水平线上方的角;俯角:视线在水平线下方的角。
仰角铅垂线水平线视线视线俯角(2)坡面的铅直高度h 和水平宽度l 的比叫做坡度(坡比)。
用字母i 表示,即h i l=。
坡度一般写成1:m 的形式,如1:5i =等。
把坡面与水平面的夹角记作α(叫做坡角),那么tan hi lα==。
3、从某点的指北方向按顺时针转到目标方向的水平角,叫做方位角。
如图3,OA 、OB 、OC 、OD 的方向角分别是:45°、135°、225°。
4、指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角。
如图4,OA 、OB 、OC 、OD 的方向角分别是:北偏东30°(东北方向) , 南偏东45°(东南方向),南偏西60°(西南方向), 北偏西60°(西北方向)。
三角函数知识点归纳总结

三角函数知识点归纳总结一、三角函数的定义在平面直角坐标系中,设角α的顶点在坐标原点,始边与 x 轴正半轴重合,终边上任意一点 P 的坐标为(x, y),它到原点的距离为 r(r =√(x²+ y²) ,且 r > 0),则角α的正弦、余弦、正切函数分别定义为:正弦函数:sinα = y / r余弦函数:cosα = x / r正切函数:tanα = y / x (x ≠ 0)二、特殊角的三角函数值|角度| 0°| 30°| 45°| 60°| 90°||||||||| sin | 0 | 1/2 |√2/2 |√3/2 | 1 || cos | 1 |√3/2 |√2/2 | 1/2 | 0 || tan | 0 |√3/3 | 1 |√3 |不存在|这些特殊角的三角函数值需要牢记,在解题中经常会用到。
三、同角三角函数的基本关系1、平方关系:sin²α +cos²α = 12、商数关系:tanα =sinα /cosα (cosα ≠ 0)四、诱导公式诱导公式可以将任意角的三角函数转化为锐角三角函数,从而进行计算。
1、终边相同的角的三角函数值相等sin(α +2kπ) =sinα,cos(α +2kπ) =cosα,tan(α +2kπ) =tanα (k ∈ Z)2、关于 x 轴对称sin(α) =sinα,cos(α) =cosα,tan(α) =tanα3、关于 y 轴对称sin(π α) =sinα,cos(π α) =cosα,tan(π α) =tanα4、关于原点对称sin(π +α) =sinα,cos(π +α) =cosα,tan(π +α) =tanα5、函数名改变,符号看象限sin(π/2 α) =cosα,cos(π/2 α) =sinαsin(π/2 +α) =cosα,cos(π/2 +α) =sinα五、两角和与差的三角函数公式1、两角和的正弦公式:sin(α +β) =sinαcosβ +cosαsinβ2、两角差的正弦公式:sin(α β) =sinαcosβ cosαsinβ3、两角和的余弦公式:cos(α +β) =cosαcosβ sinαsinβ4、两角差的余弦公式:cos(α β) =cosαcosβ +sinαsinβ5、两角和的正切公式:tan(α +β) =(tanα +tanβ) /(1tanαtanβ)6、两角差的正切公式:tan(α β) =(tanα tanβ) /(1 +tanαtanβ)六、二倍角公式1、二倍角的正弦公式:sin2α =2sinαcosα2、二倍角的余弦公式:cos2α =cos²α sin²α =2cos²α 1 = 12sin²α3、二倍角的正切公式:tan2α =2tanα /(1 tan²α)七、三角函数的图像和性质1、正弦函数 y = sin x图像:正弦函数的图像是一条波浪线,周期为2π,振幅为 1。
初三三角函数知识点归纳总结

初三三角函数知识点归纳总结
•三角函数基础知识:①三角函数的定义:三角函数是一类特殊的函数,可以通过一个角或一个角的弧度来描述。
②三角函数的公式:sinθ=opp/hyp;cosθ=adj/hyp;tanθ=opp/adj。
③三角函数的图形:三角函数的图形可以分为正弦图形和余弦图形。
•坐标变换:①极坐标系:极坐标系是一种坐标系,它由极点、极轴和极半径构成,用来表示曲线的位置。
②直角坐标系:直角坐标系是一种坐标系,它由原点、横坐标轴和纵坐标轴构成,用来表示点在空间中的位置。
•三角函数的性质:①正弦定理:sinα/a=sinβ/b=sinγ/c;②余弦定理:a^2=b^2+c^2-2bc*cosα;③正弦余弦定理:sinα/a=cosβ/b;④正切定理:tanα/a=tanβ/b;⑤正切余弦定理:tanα/a=cosβ/b;⑥正切正弦定理:tanα/a=sinβ/b。
三角函数中考知识点归纳

三角函数中考知识点归纳三角函数是数学中的一个重要分支,它在中考数学中占有一席之地。
以下是对三角函数中考知识点的归纳:基础概念- 三角函数是直角三角形中,锐角的正弦、余弦和正切函数的简称。
- 正弦(sin):直角三角形中,锐角的对边与斜边的比值。
- 余弦(cos):直角三角形中,锐角的邻边与斜边的比值。
- 正切(tan):直角三角形中,锐角的对边与邻边的比值。
三角函数的图像与性质- 三角函数的周期性:正弦和余弦函数的周期为2π,正切函数的周期为π。
- 三角函数的奇偶性:正弦函数和正切函数是奇函数,余弦函数是偶函数。
- 三角函数的单调性:在每个周期内,正弦函数和余弦函数都有单调递增和递减的区间。
特殊角的三角函数值- 30°、45°、60°角的正弦、余弦和正切值是中考中常见的考点。
- 例如:sin30° = 1/2,cos30° = √3/2,tan30° = √3/3;sin45° = cos45° = √2/2,tan45° = 1;sin60° = √3/2,cos60° = 1/2,tan60° = √3。
三角函数的变换- 函数的平移:将三角函数图像沿x轴或y轴平移。
- 函数的伸缩:改变三角函数图像的振幅或周期。
三角函数的应用- 三角函数在解决实际问题中的应用,如测量、建筑、物理等领域。
- 利用三角函数解决直角三角形问题,如利用三角函数求边长、角度等。
解题技巧- 熟练掌握三角函数的基本公式和性质,能够快速解决相关问题。
- 学会利用图形辅助解题,如通过画图来理解三角函数的性质。
- 掌握特殊角的三角函数值,能够快速计算和应用。
结束语:三角函数在中考数学中是一个重要的知识点,掌握好这些基础知识和解题技巧,可以帮助学生在考试中取得更好的成绩。
希望以上的归纳能够帮助学生更好地理解和运用三角函数。
初中数学中的三角函数知识点归纳

初中数学中的三角函数知识点归纳三角函数是初中数学中的一个重要知识点,它是研究角和角的函数关系的一门数学工具。
三角函数包括正弦函数、余弦函数和正切函数等常见的函数。
在初中数学中,对三角函数的学习主要涉及到下面几个方面的内容:一、角的概念和三角函数的定义1.角的概念:角是由两条半射线构成的一个几何图形,通常用一个大写字母来表示角,如∠A。
2.角的度量:角的度量单位通常有两种,一种是度,另一种是弧度。
在初中数学中,我们主要使用度来度量角。
3.三角函数的定义:在直角三角形中,定义了正弦函数、余弦函数和正切函数。
其中,正弦函数sinA等于角A的对边与斜边的比值,余弦函数cosA等于角A的邻边与斜边的比值,正切函数tanA等于角A的对边与邻边的比值。
二、三角函数的性质和应用1.三角函数的周期性:正弦函数、余弦函数和正切函数都是周期函数,它们的周期都是2π。
2.三角函数的性质:正弦函数、余弦函数和正切函数在定义域内有一些基本的性质,如正弦函数和余弦函数的取值范围是[-1,1],正切函数的定义域是全体实数除去使得tanA不存在的角度。
3.三角函数的运算关系:三角函数之间有一些运算关系,如三角函数的基本关系sin^2A+cos^2A=1,tanA=sinA/cosA等。
4.应用问题:三角函数的知识可用于解决一些实际问题,如物体的运动问题、建筑物高度的测量问题等。
三、三角函数的图像和性质1.正弦函数的图像:正弦函数的图像为一条以原点为中心的周期为2π的正弦曲线,曲线在原点处取得最小值0,在π/2和3π/2处取得最大值1和-12.余弦函数的图像:余弦函数的图像为一条以原点为中心的周期为2π的余弦曲线,曲线在原点处取得最大值1,在π/2和3π/2处取得最小值0和-13.正切函数的图像:正切函数的图像为一组以π为一个周期的势函数曲线,曲线在0和π处有垂直渐近线。
总之,三角函数是初中数学中一个极为重要的知识点,掌握三角函数的基本概念、性质和运算关系对学生发展数学思维和解决实际问题具有重要意义。
初三数学三角函数知识点整理

初三数学三角函数知识点整理
三角函数知识:
(一)基本概念:
1. 三角函数:三角函数是一类变化比较复杂的可以描述出来的函数,它们可以用来描述各种具有特殊的几何关系的函数关系。
2. 周期性特征:三角函数都具有周期性的特征,正弦函数的周期长度为2π,余弦、正切函数的周期有π。
3. 区间形态特征:三角函数的话,一个比较方便的办法是先分析函数图像的区间变化形态,分析一下函数的一般变化规律,进而猜测出变化规律。
(二)三角函数求值
1. 小角度求值法:小角度求值法是把角极限值和角转换为弧度来进行求解,这种方法的优点是可以把角的大小任意进行变量,从而实现任意角度的三角函数求值。
2. 单位圆三角等价:单位圆三角等价是把圆上的位置用三角函数来表示,其中圆心为(0,0),半径为1。
3. 唯一方程法:唯一方程法就是把三角函数问题变成一般代数方程来求解,这样就可以利用代数方法解决三角函数问题了。
(三)三角函数运算
1. 三角函数对数:三角函数对数可以得到两个三角函数的乘积,除法
或求幂的值。
2. 三角形关系:三角形关系是指把一个等腰三角形的一条边的长度按照给定的一定比例缩放得到另外两边的长度。
3. 余弦定理:余弦定理是指任意一个三角形的两边的长度乘积等于它的最短的三条边的三次方再乘以一个特别的常数。
三角函数相关知识点

三角函数相关知识点三角函数知识点学习资料一、基本概念1. 角的概念推广正角、负角和零角:按逆时针方向旋转形成的角为正角,按顺时针方向旋转形成的角为负角,不作任何旋转形成的角为零角。
象限角:使角的顶点与原点重合,角的始边与x轴的非负半轴重合,角的终边落在第几象限,就说这个角是第几象限角。
终边在坐标轴上的角不属于任何象限。
终边相同的角:所有与角α终边相同的角(连同α在内),可构成一个集合S ={β|β=α + k·360^∘,k∈ Z}。
2. 弧度制定义:长度等于半径长的弧所对的圆心角叫做1弧度的角,用符号rad表示。
弧度与角度的换算:180^∘=π rad,所以1^∘=(π)/(180) rad,1 rad = ((180)/(π))^∘。
弧长公式:l =|α|r(其中l为弧长,α为圆心角弧度数,r为半径)。
扇形面积公式:S=(1)/(2)lr=(1)/(2)|α|r^2。
二、三角函数定义设α是一个任意角,它的终边与单位圆交于点P(x,y),那么sinα=y,cosα = x,tanα=(y)/(x)(x≠0)。
对于角α终边上任意一点P(x,y)(r=√(x^2)+y^{2}),则sinα=(y)/(r),cosα=(x)/(r),tanα=(y)/(x)(x≠0)。
2. 三角函数值在各象限的符号正弦函数y = sin x:一、二象限为正,三、四象限为负。
余弦函数y=cos x:一、四象限为正,二、三象限为负。
正切函数y = tan x:一、三象限为正,二、四象限为负。
三、同角三角函数的基本关系1. 平方关系sin^2α+cos^2α = 1。
2. 商数关系tanα=(sinα)/(cosα)(cosα≠0)。
四、诱导公式1. α + 2kπ(k∈ Z)与α的三角函数关系sin(α + 2kπ)=sinα,cos(α+2kπ)=cosα,tan(α + 2kπ)=tanα。
sin(-α)=-sinα,cos(-α)=cosα,tan(-α)=-tanα。
初中数学三角函数知识点梳理

初中数学三角函数知识点梳理三角函数知识点梳理数学是一门抽象而又实用的学科,其中三角函数是一个重要的概念。
它是研究角度的一种数学工具,广泛应用于几何学、物理学、工程学等领域。
在初中数学中,学习三角函数不仅帮助我们理解几何形状和角度的关系,还可以帮助解决各种角度相关的问题。
下面,我们将对初中数学中的三角函数知识点进行梳理。
一、角度的度量在数学中,角度的度量是指用一定的单位来描述角的大小。
常用的单位有度和弧度。
1. 度的概念:度是角度的度量单位,用符号°表示。
一个圆的周长为360°,一个直角为90°,一个平角为180°。
2. 弧度的概念:弧度是角度的另一种度量方式,用符号rad表示。
一个圆的周长为2π(约等于6.28)弧度,一个直角为π/2弧度,一个平角为π弧度。
三角函数的定义中常常用弧度制表示角度。
二、三角比的定义及性质在初中数学中,我们学习了三角函数中的三个基本比较。
1. 正弦函数(sin):在直角三角形中,正弦函数是指某一锐角的对边与斜边之比。
其定义为sinθ = 对边/斜边。
2. 余弦函数(cos):在直角三角形中,余弦函数是指某一锐角的邻边与斜边之比。
其定义为cosθ = 邻边/斜边。
3. 正切函数(tan):在直角三角形中,正切函数是指某一锐角的对边与邻边之比。
其定义为tanθ = 对边/邻边。
三角函数还有诸如余割函数、正割函数和余切函数等,它们都是在三角比的基础上得到的倒数函数。
三、特殊角的数值在初中数学中,掌握一些特殊角的数值是非常重要的。
1. 30°角的三角比:sin30° = 1/2,cos30° = √3/2,tan30° = 1/√3。
2. 45°角的三角比:sin45°= √2/2,cos45° = √2/2,tan45° = 1。
3. 60°角的三角比:sin60° = √3/2,cos60° = 1/2,tan60° = √3。
三角函数知识点归纳

三角函数知识点归纳 一、任意角与弧度制 1.任意角 (I)定义:角可以看成平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形. J 按旋转方向不同分为正角、负角、零角. (2)分类[按终边位置不同分为象限角和轴线角(3)终边相同的角:所有与角a 终边相同的角,连同角a 在内,可构成一个集合S={缈=a+ 2kιt, Λ∈Z!.(3)象限角与轴线角 今1(第一象限角)卜| 第二致限角阳2A"专VaV2痴 2⅛π<α<2⅛π+-g-,⅛∈z} +π,⅛∈ZT 第三敛限角)卜性"τrVaV2"+等"刃 第四象限角]{α∣2⅛π+^<α<2⅛π+2π,⅛∈z}2.弧度制的定义和公式 角a 的弧度数公式 IaI=%/表示弧长)角度与弧度的换算 ①1。
=念 rad ;② 1 rad=, 弧长公式 l=∖a ∖r 扇形面积公式S=»=如/ (1)定义:把长度等于半径长的弧所对的圆心角叫做1弧度的角,弧度记作rad. 3.任意角的三角函数 一、定义:设α是一个任意角,它的终边与单位圆交于点P(x, y),那么Sina=y, cos α=x, tan α=^(x≠()).二、常用结论汇总——规律多一点(1)一个口诀:三角函数值在各象限的符号:一全正、二正弦、三正切、四余弦.(2)三角函数定义的推广:设点P(x, y)是角Q终边上任意一点且不与原点重合,r=∣OP∣,则• V X V,1八、sin a= , COSa=-, tanα=-(Xw0).r rχ∖ ,三、特殊角的三角函数:3.1 象限角及终边相同的角例1、若角。
是第二象限角,则辞()A.第一象限角B.第二象限角C.第一或第三象限角D.第二或第四象限角∩例2、一的终边在第三象限,则。
的终边可能在() 2A.第一、三象限B.第二、四象限C.第一、二象限或y轴非负半轴D.第三、四象限或y轴非正半轴3.2 三角函数的定义例1、已知角α的终边经过点P(一χ, — 6),且COSa=—/,则1;+%½= _________________ .1J SlIl (A IdIl (A例2、已知角α的终边经过点(3, -4),则Sin a+»^=.3.3 、三角函数符号的判定例1、已知Sina < 0旦cosa > 0,则a的终边落在()A.第一象限B.第二象限C.第三象限D.第四象限3.4 扇形面积问题1.已知一个扇形的弧长和半径都等于2,则这个扇形的面积为().A. 2B. 3C. 4D. 6二、同角三角函数的基本关系与诱导公式1 .同角三角函数的基本关系(1)平方关系:siMα+cos2α=l; (2)商数关系:tan α=黑吃.同角三角函数的基本关系式的几种变形(l)sin2α= 1 — cos2α=(l + cos «)(1 —cos a); cos2a= 1 - sin2a=(l ÷sin a)(l — sin a); (sin a±cos a)2 =l±2sin acos a.(2)sin a=tan acos a(a≠5+E, &WZ).2 .诱导公式“奇变偶不变,符号看象限”公式一:sin(a+2⅛π)=sin a, cos(a÷2hc)=cos a»la∏(6Z + <λkτf)= t∏∏OC其中公式二:sin(π+ct)= ~sin a> cos(π+cc)=~cos ct> Ian(Tr+a)=Ian a.公式三:sin(π~a)=sin a,cos(π-a) = — cos ct, ta∏(^-6Z)= —ta∏ OC ∙公式四:sin(-ct)=—sin a, cost—«)=cos a,t<l∏) = -13∏ CX .公式五:Sine-a) =cos a, COSe—a) =Sina 公式六:SinC+a)=cos a,CoSC+«) = -sin a.诱导公式可概括为〃∙]±a的各三角函数值的化简公式.口诀:奇变偶不变,符号看象限.其中的奇、偶是指方的奇数倍和偶数倍,变与不变是指函数名称的变化.若是奇数倍,则函数名称要变(正弦变余弦,余弦变正弦);若是偶数倍,则函数名称不变,符号看象限是指:把a看成锐角时,根据在哪个象限判断厚三曲函数值的符号,最后作为结果符号.8.方法与要点一个口诀I、诱导公式的记忆。
初中三角函数知识点总结

初中三角函数知识点总结一、角和弧度制角是由一条射线绕着一个固定点旋转形成的。
角的单位有度和弧度两种,其中度是最常用的单位。
角的度数决定了它所对应的弧长。
一个角的弧长和它所对应的弧度数之间有一个固定的关系:1弧度等于180°/π。
二、正弦、余弦和正切在直角三角形中,我们可以根据三角形的边长来定义三个比率:正弦、余弦和正切。
1. 正弦(sine)的定义为:sinθ = 对边/斜边。
2. 余弦(cosine)的定义为:cosθ = 邻边/斜边。
3. 正切(tangent)的定义为:tanθ = 对边/邻边。
三、特殊角的三角函数值在一个单位圆上,特殊角的三角函数值有着特定的规律。
1.0°、90°、180°和270°分别对应的三角函数值是:sin0° = 0, sin90° = 1, sin180° = 0, sin270° = -1;cos0° = 1, cos90° = 0, cos180° = -1, cos270° = 0;tan0° = 0, tan90° = 无穷大, tan180° = 0, tan270° = 无穷大。
2.对于30°、45°和60°,它们在单位圆上对应的三角函数值还有特殊的规律:sin30° = 1/2, sin45° = √2/2, sin60° = √3/2;cos30° = √3/2, cos45° = √2/2, cos60° = 1/2;tan30° = 1/√3, tan45° = 1, tan60° = √3四、三角函数的性质三角函数有一些重要的性质:1. sin(-θ) = -sinθ,cos(-θ) = cosθ,tan(-θ) = -tanθ。
初中三角函数的知识要点

初中三角函数的知识要点三角函数是数学中的一个重要分支,它研究了角与其它几何关系之间的函数关系。
初中的三角函数主要包括正弦函数、余弦函数和正切函数,学习三角函数主要掌握以下几个要点。
1.角度的定义和转换在初中数学中,通常采用角度制来表示角的大小。
一个完整的圆周的角度为360°,即360度。
角的大小可以通过直尺量角或者使用传感器测角器来测量。
初中学习时主要以整数度和特殊角度为主,如30°、45°、60°等。
此外,角的转换也很重要,如将弧度制转换为角度制,将角度制转换为弧度制等。
2.正弦函数和余弦函数正弦函数和余弦函数是最基本的三角函数之一、在直角三角形中,对于一个锐角θ,我们可以定义如下:正弦函数sinθ=对边/斜边余弦函数cosθ=邻边/斜边其中,斜边为三角形的斜线,对边为斜边在θ角对应的那条边,邻边为斜边不是θ角的那条边。
初中阶段主要学习如何根据给定的三角函数值求角度大小,或者根据给定的角度大小求三角函数值。
3.正切函数和余切函数正切函数和余切函数也是常见的三角函数。
在直角三角形中,对于一个锐角θ,我们可以定义如下:正切函数tanθ=对边/邻边余切函数cotθ=邻边/对边初中阶段主要学习如何根据给定的三角函数值求角度大小,或者根据给定的角度大小求三角函数值。
4.三角函数的基本性质学习了正弦函数、余弦函数和正切函数后,我们可以了解一些它们的基本性质。
正弦函数和余弦函数是周期函数,其最小正周期T为360°(或者2π弧度)。
正弦函数和余弦函数在定义域内取值范围为[-1,1],即-1≤sinθ≤1,-1≤cosθ≤1正切函数和余切函数没有周期性。
三角函数之间存在一些基本的关系,如sinθ和cosθ之间满足sin^2θ+cos^2θ=1,tanθ和cotθ之间满足tanθ·cotθ=15.三角函数的图像与性质对于三角函数的图像,可以通过绘制函数的曲线来进行观察。
初中三角函数知识点总结

初中三角函数知识点总结初中三角函数主要包括三角比,解三角形,三角方程,向量与三角函数,定理与推论,和三角函数的应用等知识点。
以下是对这些知识点的详细总结:一、三角比1.正弦、余弦、正切-正弦:在直角三角形中,对于一个锐角,其正弦等于对边与斜边的比值。
-余弦:在直角三角形中,对于一个锐角,其余弦等于邻边与斜边的比值。
-正切:在直角三角形中,对于一个锐角,其正切等于对边与邻边的比值。
2.相互之间的关系- 正弦定理:对于任意三角形ABC,有a/sinA=b/sinB=c/sinC。
- 余弦定理:对于任意三角形ABC,有c²=a²+b²-2ab*cosC。
- 正切定理:对于任意三角形ABC,有tanA=(b*sinC)/(a-b*cosC)。
二、解三角形1.根据已知条件求解未知量-已知两边及夹角,可以使用余弦定理求解第三边。
-已知两角及一边,可以使用正弦定理求解其它两边。
-已知两角及两边,可以使用正切定理求解第三边。
三、三角方程1.基本概念-三角方程是含有未知数角的方程,其中角的取值范围在给定区间内。
- 常见的三角方程有sinx=a, cosx=a, tanx=a等形式。
2.解三角方程的一般步骤-利用特殊角的正弦、余弦和正切值,化简方程。
-观察方程的周期性,求解其一个基本解,并利用周期性解得所有解。
4.解三角方程的方法-单调区间法:首先确定方程在一个周期内的单调增区间,然后根据函数图象和方程的特点逐步缩小解的范围。
-观察法:利用特殊角的正弦、余弦和正切值,观察方程在给定区间内的解。
四、向量与三角函数1.向量-平面向量:由大小和方向确定的量,用有向线段表示。
-向量的模长:向量AB的长度。
-向量的方向角:向量与坐标轴正方向的夹角。
2.向量的坐标与分解-向量的坐标:用有序数对表示向量的坐标。
-向量的分解:将一个向量分解为两个方向平行的向量的和。
3.向量的数量积-数量积的定义:向量的数量积等于它们的模长乘积与夹角的余弦值。
初中数学三角函数知识点总结

初中数学三角函数知识点总结三角函数是初中数学中重要的内容之一,它是研究三角形中各个边和角之间关系的一门学科。
通过学习三角函数,我们可以计算未知边长和角度的大小,解决实际生活中的问题。
本文将对初中数学三角函数的知识点进行总结。
一、正弦函数正弦函数是最基本的三角函数之一,用sin记作。
在直角三角形中,正弦函数被定义为对边与斜边的比值。
具体地说,对于一个直角三角形,如果已知一个角的度数为θ,那么三角形中对应的一边长度与斜边的比值就是sinθ。
正弦函数的值域为[-1,1]。
二、余弦函数余弦函数是另一个非常重要的三角函数,用cos记作。
在直角三角形中,余弦函数被定义为邻边与斜边的比值。
具体地说,对于一个直角三角形,如果已知一个角的度数为θ,那么三角形中对应的一边长度与斜边的比值就是cosθ。
余弦函数的值域也是[-1,1]。
三、正切函数正切函数是sin和cos的比值,用tan表示。
在直角三角形中,正切函数被定义为对边与邻边的比值。
具体地说,对于一个直角三角形,如果已知一个角的度数为θ,那么三角形中对应的一边长度与另一边的比值就是tanθ。
正切函数的定义域为除了90度的整数倍的角度之外的所有实数。
四、三角函数的特点与性质1. 周期性:三角函数都具有周期性,即对于任意角θ,sin(θ+2π) = sinθ,cos(θ+2π) = cosθ,tan(θ+π) = tanθ。
这意味着在一定范围内的角度具有相同的三角函数值。
2. 正交性:正弦函数和余弦函数是正交的,即在[0,2π]区间内,它们的乘积的积分为0。
3. 对称性:sin和cos函数具有奇偶性,即sin(-θ) = -sinθ,cos(-θ) = cosθ。
这意味着sin和cos对于角的正负具有对称性。
4. 互逆关系:正弦函数和余弦函数是互逆的,即sin²θ + cos²θ = 1。
五、三角函数的应用三角函数在实际生活中有广泛的应用,特别是在测量、物理学等领域。
九年级数学三角函数全章知识点整理

一、角度与弧度制度量1.角度的定义与表示方法:度、分、秒2.角度的换算:度与弧度的换算3.弧度制度量的定义与表示方法4.弧度与角度之间的换算二、三角函数的定义与基本性质1.正弦函数:定义、图像、性质(周期性、奇偶性、单调性)2.余弦函数:定义、图像、性质(周期性、奇偶性、单调性)3.正切函数:定义、图像、性质(周期性、奇偶性、单调性)4.函数值的范围与周期性5.三角函数的基本关系式和恒等式6.正弦、余弦的诱导公式和和差公式7.三角函数的同角关系式三、常用角的三角函数值1.0度、30度、45度、60度和90度的三角函数值2.零点的三角函数值3.常用角的三角函数值的对称性四、图像与性质1.角度对应的弧度的图像与性质2.角度对应的三角函数图像与性质3.三角函数的周期性、奇偶性和对称性4.幅度与峰值五、三角函数的性质与变换1. 函数y=A*sin(Bx+C)+D和y=A*cos(Bx+C)+D的基本性质和变换2.三角函数的峰值、最小值和最大值3.三角函数图像的平移、伸缩、翻转等变换4.三角函数的同位角恒等式与诱导公式的应用5.反三角函数的性质与定义六、三角函数的应用1.正弦定理与余弦定理:直角三角形、任意三角形的应用2.解三角形的基本步骤和技巧3.短边与短边之间的关系(余弦定理)4.弧度与扇形面积、扇形弧长的关系5.三角函数在测量、工程设计等方面的应用七、用三角函数解直角三角形1.斜边和斜边所对应的角的关系2.已知两边求角度3.已知两边求第三边4.解一般直角三角形问题的基本步骤八、平面向量与复数1.平面向量的定义、表示方法和性质2.平面向量的共线与平行3.向量在平面内的平移九、极坐标与复数1.平面极坐标系的定义与性质2.复数的定义与基本性质3.复数运算:加法、减法、乘法、除法4.复数的共轭、模和辐角5.复数的指数形式与三角形式以上为九年级数学三角函数全章的知识点整理,其中包括角度与弧度制度量、三角函数的定义与基本性质、常用角的三角函数值、图像与性质、三角函数的性质与变换、三角函数的应用、用三角函数解直角三角形、平面向量与复数、极坐标与复数等内容,共计1200字以上。
初中数学三角函数知识点归纳

初中数学三角函数知识点归纳三角函数是初中数学中的重要知识点之一,它涉及到了数学中的几何形状和数值关系。
了解和掌握三角函数的概念、性质和相关计算方法,对于学生理解几何形状和解决实际问题具有重要的作用。
一、三角函数的概念三角函数是以单位圆为基础,通过正弦和余弦的数值关系来描述角度与长度的关系。
常用的三角函数有正弦函数、余弦函数和正切函数。
1. 正弦函数(sin):在单位圆上,对于任意一点P(x, y),以原点O为顶点的弧OP所对应的角的正弦值定义为y坐标。
2. 余弦函数(cos):在单位圆上,对于任意一点P(x, y),以原点O为顶点的弧OP所对应的角的余弦值定义为x坐标。
3. 正切函数(tan):在单位圆上,对于任意一点P(x, y),以原点O为顶点的弧OP所对应的角的正切值定义为y坐标与x坐标的比值。
二、三角函数的性质1. 周期性:正弦函数和余弦函数的周期都是2π,即对于任意实数x,有sin(x+2π) = sinx,cos(x+2π) = cosx。
而正切函数的周期是π,即tan(x+π) = tanx。
2. 奇偶性:正弦函数是奇函数,即sin(-x) = -sinx;余弦函数是偶函数,即cos(-x) = cosx;而正切函数既不是奇函数也不是偶函数,即tan(-x) ≠ -tanx。
3. 函数值的范围:对于正弦函数和余弦函数,函数值的范围是[-1, 1];对于正切函数,函数值的范围是全体实数。
4. 特殊角的函数值:常用的特殊角如0°、30°、45°、60°和90°对应的三角函数值需要熟记,以便在计算中能够快速准确地使用。
三、三角函数的计算方法1. 根据已知角度计算三角函数值:根据已知角度,可以利用计算器或查表法来计算其对应的正弦、余弦和正切值。
需要注意的是,计算器需要设置为弧度制或角度制,以便得到正确的计算结果。
2. 根据已知三角函数值求解角度:根据已知的正弦、余弦或正切值,可以利用逆三角函数来求解对应的角度。
初中数学三角函数知识点汇总

初中数学三角函数知识点汇总三角函数是初中数学中重要且基础的概念之一。
它们在几何形状的测量、图像的描述和数学模型的建立中起着关键作用。
本文将为您汇总初中数学中与三角函数相关的知识点,包括定义、性质、公式等内容,帮助您更好地理解和应用这一概念。
一、三角函数的定义1. 正弦函数(sin)正弦函数是一个周期函数,周期为360°(或2π弧度)。
它的定义域是所有实数,值域是[-1,1]。
在直角三角形中,正弦函数可以表示为对边与斜边之比。
2. 余弦函数(cos)余弦函数同样是一个周期函数,周期也是360°(或2π弧度)。
与正弦函数类似,它的定义域是所有实数,值域也是[-1,1]。
在直角三角形中,余弦函数可以表示为邻边与斜边之比。
3. 正切函数(tan)正切函数是一个周期函数,周期为180°(或π弧度)。
它的定义域包括所有与90°(或π/2弧度)的倍数相差的角度,值域则是所有实数。
在直角三角形中,正切函数可以表示为对边与邻边之比。
二、三角函数的性质1. 奇偶性正弦函数是一个奇函数,即sin(-x)=-sin(x)。
余弦函数是一个偶函数,即cos(-x)=cos(x)。
正切函数则既不是奇函数也不是偶函数。
2. 周期性正弦函数和余弦函数的周期都是360°(或2π弧度)。
正切函数的周期是180°(或π弧度)。
三、三角函数的基本关系1. 三角函数的互相转化利用三角函数的定义和基本关系,我们可以相互转化不同的三角函数,例如sin(x)=cos(90°-x),cos(x)=sin(90°-x),tan(x)=sin(x)/cos(x)等。
2. 三角函数的和差公式三角函数的和差公式是非常重要的公式,它们可以用于化简复杂的三角函数表达式。
例如:- 正弦函数的和差公式:sin(x±y) = sin(x)cos(y) ± cos(x)sin(y)- 余弦函数的和差公式:cos(x±y) = cos(x)cos(y) ∓ sin(x)sin(y)- 正切函数的和差公式:tan(x±y) = (tan(x) ± tan(y))/(1 ∓ tan(x)tan(y))3. 三角函数的倍角公式倍角公式是三角函数中另一个重要的公式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
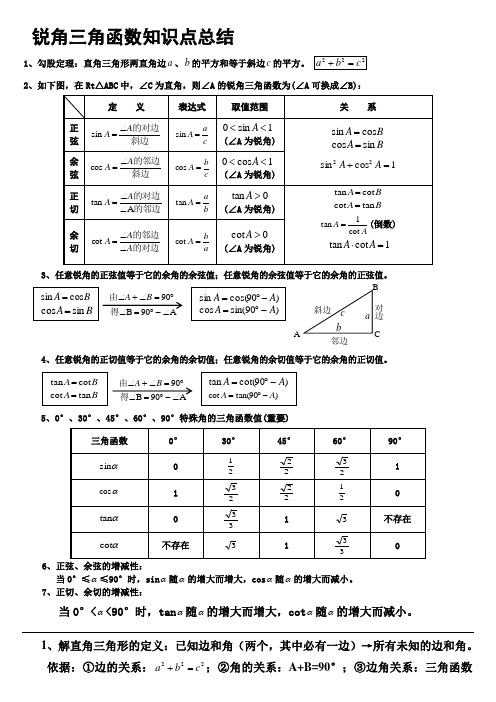
锐角三角函数知识点总结
1、勾股定理:直角三角形两直角边a 、b 的平方和等于斜边c 的平方。
222c b a =+
2、如下图,在Rt △ABC 中,∠C 为直角,则∠A 的锐角三角函数为(∠A 可换成∠B):
定 义
表达式
取值范围
关 系
正弦 斜边的对边A A ∠=
sin c a
A =sin 1sin 0<<A (∠A 为锐角)
B A cos sin =
B A sin cos =
1cos sin 22=+A A
余弦
斜边的邻边A A ∠=
cos c b
A =cos 1cos 0<<A (∠A 为锐角) 正切
的邻边的对边A tan ∠∠=
A A b a
A =tan 0tan >A (∠A 为锐角)
B A cot tan = B A tan cot =
A
A cot 1
tan =
(倒数) 1cot tan =⋅A A
余切
的对边的邻边A A A ∠∠=
cot a b
A =cot 0cot >A (∠A 为锐角) 3、任意锐角的正弦值等于它的余角的余弦值;任意锐角的余弦值等于它的余角的正弦值。
4、任意锐角的正切值等于它的余角的余切值;任意锐角的余切值等于它的余角的正切值。
5、0°、30°、45°、60°、90°特殊角的三角函数值(重要)
三角函数
0° 30°
45°
60°
90° αsin 0
2
1 2
2 2
3
1 αcos
1 2
3 2
2
2
1
αtan 0 3
3
1 3 不存在 αcot
不存在
3
1
3
3
6、正弦、余弦的增减性:
当0°≤α≤90°时,sin α随α的增大而增大,cos α随α的增大而减小。
7、正切、余切的增减性:
当0°<α<90°时,tan α随α的增大而增大,cot α随α的增大而减小。
)
90cot(tan A A -︒=)90tan(cot A A -︒=
B A cot tan = B A tan cot =
)90cos(sin A A -︒=)
90sin(cos A A -︒=
B
A cos sin =
B A sin cos =A
90B 90∠-︒=∠︒=∠+∠得由B A
对边
邻边
斜边 A
C
B
b
a c
A
90B 90∠-︒=∠︒=∠+∠得由B A
1、解直角三角形的定义:已知边和角(两个,其中必有一边)→所有未知的边和角。
依据:①边的关系:222c b a =+;②角的关系:A+B=90°;③边角关系:三角函数的定义。
(注意:尽量避免使用中间数据和除法)
2、应用举例:
(1)仰角:视线在水平线上方的角;俯角:视线在水平线下方的角。
仰角铅垂线
水平线
视线
视线俯角
(2)坡面的铅直高度h 和水平宽度l 的比叫做坡度(坡比)。
用字母i 表示,即h
i l
=。
坡度一般写成1:m 的形式,如1:5i =等。
把坡面与水平面的夹角记作α(叫做坡角),那么tan h
i l
α=
=。
3、从某点的指北方向按顺时针转到目标方向的水平角,叫做方位角。
如图3,OA 、OB 、OC 、OD 的方向角分别是:45°、135°、225°。
4、指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角。
如图4,OA 、OB 、OC 、OD 的方向角分别是:北偏东30°(东北方向) , 南偏东45°(东南方向), 南偏西60°(西南方向), 北偏西60°(西北方向)。
:i h l =h
l
α。
