工程流体力学6明渠水流两种流态及其转换
合集下载
流体力学(第二版)课件：6 明渠流动
f
h
nQ
3
5
i
b 2h 1 m2
b mh
25
迭代计算
h
f
h
nQ i
3
5
b 2h 1 m 2
b mh
25
假定h
h1 f h
h2 f h1
h2 h1
否
是
h1 h2
结束
6.2 明渠恒定均匀流
(3) 求底宽
§6.2.2 明渠均匀流的水力计算
已知渠道设计流量Q、i、n，h、m，求b 方法与求h的相同，采用迭代法、试算图解法
6 明渠流动
§6.1 概述 §6.2 明渠恒定均匀流 §6.3 无压圆管均匀流 §6.4 明渠恒定非均匀流
教学目的和要求
教学目的：使学生理解水力最优断面及允许流速的基本 概念，掌握明渠均匀流各类问题的水力计算方法，并能设计 渠道的断面形式和渠道坡度。
明渠非均匀流中断面单位能量、临界水深等的基本概念， 掌握恒定明渠流其流动状态的判别方法，能进行水面曲线的 分析与绘制。
X /m
8 .0 0 9 .0 0 1 0 .0 0 1 0 .1 0 1 0 .2 0 1 0 .3 0 1 0 .4 0 1 0 .5 0
R
0 .4 4 0 .7 8 1 .0 5 1 .0 7 1 .1 0 1 .1 2 1 .1 4 1 .1 7
n
0 .0 1 3 0 .0 1 3 0 .0 1 3 0 .0 1 3 0 .0 1 3 0 .0 1 3 0 .0 1 3 0 .0 1 3
b /m
b /m
4.0
3.5
3.0
2.5
2.0 24 25 26 27 28 29 30 31 32 33 34 35
工程流体力学课件6明渠水流的两种流态及其转换
工程流体力学课件6：明 渠水流的两种流态及其转 换
本课件将详细讲解明渠水流的均匀流和非均匀流的特点和计算方法，以及两 者之间的转换条件和应用案例。
明渠水流的定义和特点
定义
明渠水流指在开放渠道（或河道）中，水流的 自由表面不受流动约束，而完全暴露在自由空 气中的水流。
特点
明渠水流具有水面自由、水流自然、水深变化 明显、水流路径长等特点，特别适用于小型水 力工程的设计和研究。
均匀流和非均匀流
均匀流
水流速度大小不变，流线平行，一般出现在较宽的 平流区域。
非均匀流
水流速度大小不同，流线不平行，出现在河床陡峭 的变化区域。
转换
均匀流和非均匀流的转换取决于渠道的形状、尺寸 和水流速度等因素。
均匀流的特点和计算方法
1 特点
均匀流速度大小不变，水流线平行，宽度不 变，深度均匀。
均匀流和非均匀流的转换条件和应用
转换条件
均匀流和非均匀流之间的转换一般发生在河道变窄 和陡峭的区域，需要通过计算来判断转换位置。
应用案例
在水坝设计中，需要考虑坝体下游的均匀流和泄洪 段的非均匀流，以做出合理的设计和调整。
转换过程的数学描述和应用
数学描述
均匀流和非均匀流的转换过程一般通过水力学方程 和数学模型来描述和计算。
2 计算方法
通过曼宁公式计算水流的流速和水面坡度等 参数，进而得出均匀流的流量和相关数据。
非均匀流的特点和计算方法
1
特点
非均匀流速度大小不同，水流线不平行，
计算方法
ቤተ መጻሕፍቲ ባይዱ
2
宽度和深度变化大。
通过水力学基本方程、能量方程和持流
方程，计算出非均匀流各点的水位、平
均流速、流量等参数。
本课件将详细讲解明渠水流的均匀流和非均匀流的特点和计算方法，以及两 者之间的转换条件和应用案例。
明渠水流的定义和特点
定义
明渠水流指在开放渠道（或河道）中，水流的 自由表面不受流动约束，而完全暴露在自由空 气中的水流。
特点
明渠水流具有水面自由、水流自然、水深变化 明显、水流路径长等特点，特别适用于小型水 力工程的设计和研究。
均匀流和非均匀流
均匀流
水流速度大小不变，流线平行，一般出现在较宽的 平流区域。
非均匀流
水流速度大小不同，流线不平行，出现在河床陡峭 的变化区域。
转换
均匀流和非均匀流的转换取决于渠道的形状、尺寸 和水流速度等因素。
均匀流的特点和计算方法
1 特点
均匀流速度大小不变，水流线平行，宽度不 变，深度均匀。
均匀流和非均匀流的转换条件和应用
转换条件
均匀流和非均匀流之间的转换一般发生在河道变窄 和陡峭的区域，需要通过计算来判断转换位置。
应用案例
在水坝设计中，需要考虑坝体下游的均匀流和泄洪 段的非均匀流，以做出合理的设计和调整。
转换过程的数学描述和应用
数学描述
均匀流和非均匀流的转换过程一般通过水力学方程 和数学模型来描述和计算。
2 计算方法
通过曼宁公式计算水流的流速和水面坡度等 参数，进而得出均匀流的流量和相关数据。
非均匀流的特点和计算方法
1
特点
非均匀流速度大小不同，水流线不平行，
计算方法
ቤተ መጻሕፍቲ ባይዱ
2
宽度和深度变化大。
通过水力学基本方程、能量方程和持流
方程，计算出非均匀流各点的水位、平
均流速、流量等参数。
第6章 水力学明渠恒定流动
d h
五、棱柱形渠道与非棱柱形渠道
• 棱柱形渠道：A=f ( h) • 非棱柱形渠道：A=f ( h, s).渠流动。 明渠具有自由表面，不存在非恒定明渠均匀流，明 渠均匀流必定为恒定流。 一、明渠均匀流的特性： 过水断面形状、大小、水深沿程不变。
G sin F f
二、 明渠均匀流的产生条件
恒定流 流量沿程不变（无分叉和汇流情况） 渠道为长、直的棱柱体顺坡渠，糙率沿程不变 渠中无闸、坝、跌水等建筑物的局部干扰
均匀流是对明渠流动的一种概化。多数明渠流是非均匀流。 近似符合这些条件的人工渠、河道中一些流段可认为是均匀流。
三、 明渠均匀流的基本计算公式
6 明渠恒定流动
学习重点 §6-1 概述 §6-2 明渠均匀流
• §6-3 明渠恒定非均匀流基本概念 • §6-4 明渠水流的两种急变流现象
学习重点
明渠的几何形态 明渠流动的特点 明渠恒定均匀流的特性、形成条件、基本 计算公式及水力计算。 明渠恒定非均匀流的基本概念、流动状态 及其判别。
§6.1 概述
不冲允许流速 [v ]max v [v ]min 不淤流速
六、 明渠均匀流的水力计算
V C Ri
Q AC Ri
f (m,b, h,i, n)
6个变量：Q，b，h，i，m，n 明渠均匀流的计算类型：校核和设计
（一）校核：校核渠道的过水能力和流速
已知 b、h、m、n、i ，求 Q
Q AC Ri
恒定流连续性方程： Q Av
谢才公式：
v C RJ
明渠均匀流
J=i
Q Av AC Ri K i
K---流量模数， K AC R
C---谢才系数。曼宁公式：C
1 n
工程流体力学第6章明渠均匀流与渠流详解
1、层流的速度分布 定常均匀流速度分布方程
u i y(2h y) 2
y=h，液流表面的速度，
umax
i 2
h2
§6.2 明渠定常均匀流的水力计算
取单位宽度的液体深度为dy，微单元面积为dA=dy×1， 沿液流深度积分得流量
Q udA h i (2h y)dy
A
0 2
Q i h3 3
变的长直明渠称为棱柱形渠道，h=f(i)。
非棱柱形渠道（non-prismatic channel）：断面形状和尺寸
沿程不断变化的明渠称为非棱柱形渠道，h=f(i,s) 2.底坡（ i ）渠道底部沿程单位长度的降低值
i sin z1 z2 z
l
l
§6.1明渠流的概念
平坡（horizontal bed）：i=0，明槽槽底高程沿程不变
1）过水断面的形状和尺寸、断面平均流速、流量和水深 沿程不变。通常将明渠均匀流的水深称为正常水深，
以h0表示。
2）总水头线、测压管水头线（水面坡度）和渠底线互相 平行，即：
§6.1明渠流的概念
列（1）- （2）能量方程得：
§6.1明渠流的概念
物理意义：水流因高程降低而引起的势能减少正好等 于克服阻力所损耗的能量，而水流的动能维持不变
断面平均流速
i h3
v Q 3
A h1
i 3
h2
2 3
umax
§6.2 明渠定常均匀流的水力计算
2、紊流的速度分布
垂线速度分布符合对数分布规律
u u* ln y c 2.3u* lg y c
K
K
式中 u* ghi明渠流动力流速
K紊流系数 c与槽渠粗糙度有一定关系
u 2.3u* K
流体力学 第八章 明渠流动 (2)
利用梯形断面明渠临界水深hc 可以判别明渠水流 的流态： 当明渠内水深h＞hc ，水流为缓流； 当明渠内水深h =hc ，水流为临界流； 当明渠内水深h＜hc ，水流为急流。
例9.1
一矩形断面明渠，流量 Q =30 m3/s，底宽 b = 8 m。要求：
(1) 求渠中临界水深； (2) 计算渠中实际水深 h = 3 m 时，水流的弗劳德数、微波 波速，并据此以不同的角度来判别水流的流态。 解：（1）求临界水深
设水流流速为v，
v gh
v gh
顺水流方向 逆水流方向
则微波传播的绝对速度为
c v c v gh
缓流
急流
缓流时干扰波能向上游传播
临界流
急流时干扰波不能向上游传播
临界流时干扰波恰不能向上游传播
（三）弗劳德数 临界流时，V gh ，所以 定义弗劳德（Froude）数
V gh V
2、当水深很大，即h，则Esh，断面单位能量曲线以45线为渐近线。
3、在Es=f(h)的连续区间内，必有一极小值存在。 4、曲线分上、下两支：上支 dEs 0 ；下支
dh dEs 0 ，且相应于任一Es有两个水深。 dh
h
h h=Es
2 2g
h1
hc
h2
45
q增加
h=2Es/3
q1
根据表中数值，绘制 h ~
关系曲线，如图所示。
（2）计算各级流量下的
并由图中查读临界水深。
Q2 g
值，
1
Fr
gh
当 Fr 1 时,水流为缓流， 当 Fr 1 时,水流为临界流， 当 Fr 1 时,水流为急流，
弗劳德数的物理意义：
V2 V 2g Fr 2 h gh
例9.1
一矩形断面明渠，流量 Q =30 m3/s，底宽 b = 8 m。要求：
(1) 求渠中临界水深； (2) 计算渠中实际水深 h = 3 m 时，水流的弗劳德数、微波 波速，并据此以不同的角度来判别水流的流态。 解：（1）求临界水深
设水流流速为v，
v gh
v gh
顺水流方向 逆水流方向
则微波传播的绝对速度为
c v c v gh
缓流
急流
缓流时干扰波能向上游传播
临界流
急流时干扰波不能向上游传播
临界流时干扰波恰不能向上游传播
（三）弗劳德数 临界流时，V gh ，所以 定义弗劳德（Froude）数
V gh V
2、当水深很大，即h，则Esh，断面单位能量曲线以45线为渐近线。
3、在Es=f(h)的连续区间内，必有一极小值存在。 4、曲线分上、下两支：上支 dEs 0 ；下支
dh dEs 0 ，且相应于任一Es有两个水深。 dh
h
h h=Es
2 2g
h1
hc
h2
45
q增加
h=2Es/3
q1
根据表中数值，绘制 h ~
关系曲线，如图所示。
（2）计算各级流量下的
并由图中查读临界水深。
Q2 g
值，
1
Fr
gh
当 Fr 1 时,水流为缓流， 当 Fr 1 时,水流为临界流， 当 Fr 1 时,水流为急流，
弗劳德数的物理意义：
V2 V 2g Fr 2 h gh
[详细讲解]明渠水流有哪三种流态
![[详细讲解]明渠水流有哪三种流态](https://img.taocdn.com/s3/m/0c23beab970590c69ec3d5bbfd0a79563c1ed475.png)
思考题6.1 明渠水流有哪三种流态，是如何定义的，判别标准是什么？6.2 急流、缓流、临界流各有哪些特点？6.3 弗劳德数的物理意义是什么？为什么可以用它来判别明渠水流的流态？6.4 什么叫断面比能？它与断面单位重量液体的总能量 E 有何区别？6.5 何谓断面比能曲线？比能曲线有哪些特征？6.6 若渠道断面形状，尺寸一定，只使得流量比原来的流量 1Q 增大为2Q (即12Q Q ) ，试在同一图上绘出比能曲线，比较哪一个的临界水深大；如果只增大底坡，K h 又怎样变化？6.7 陡坡、缓坡、临界坡是怎样定义的？如何判别渠道坡度的陡缓？6.8 缓坡渠道只能产生缓流，陡坡渠道只能产生急流，对吗？缓流或急流为均匀流时，只能分别在缓坡或陡坡上发生，对吗？习题6.1 一矩形断面渠道 b 为 3 m , Q 为 4.8 m 3/s ,n 为 0.022 , i 为 0.0005 。
试求：( 1 ) 水流作均匀流时微波波速； ( 2 ) 水流作均匀流时的弗劳德数；( 3 ) 从不同角度判别明渠水流流态。
6.2 一梯形断面渠道,b 为8 m,m 为1,n 为0.014,i 为0.0015 ；当流量分别为 1Q =8 m 3/s,2Q = 16 m 3/s 时。
求：( 1 ) 用试算法计算流量为 1Q 时临界水深；( 2 ) 用图解法计算流量为 2Q 时临界水深；( 3 ) 流量为 1Q 及 2Q 时，判别明渠水流作均匀流的流态。
6.3 有一无压圆管，管径 d 为 4 m ，流量 Q 为15.3 m 3/s 时，均匀流水深 0h 为3 .25 m 。
试求：( 1 ) 临界水深；( 2 ) 临界流速；( 3 ) 微波波速；( 4 ) 判别均匀流时流态。
E以及渠道断面形式、尺寸（b,m）一定时，最大流量相6.4证明：当断面比能S应的水深是临界水深。
6 .5一矩形渠道b为5 m , n为0.015 , i为0.003 ；试计算该明渠在通过流量Q= 10 m3/s 时的临界底坡，并判别渠道是缓坡或陡坡。
水力学第6章明渠恒定流.
设跃前水深为 h’ ,跃后水深为 h’’ 1Q 2 2Q 2 A1 yc1 A2 yc 2 (推导从略) gA gA 1 2 yc1 和 yc2 为水跃前后断面形心淹没深度.(形心到液面距离)
当流量 Q 断面形状一定时
Q2 令 (h) Ayc gA '
A1 , A2 , yc 都是水深 h 的函数.
b 2h 1 m 2 A (b m h)h R b 2h 1 m 2
3.棱柱形渠道和非棱柱形渠道
棱柱形渠道—断面形状,尺寸及底坡沿程不变的长而顺直渠道.
6.2 明渠均匀流
1.明渠均匀流的水力特征
明渠均匀流中流线是与底坡平行的一簇平行直线,所以其水力特征为:
①过流断面形状、大小沿程不变.
可见, ik 与底坡 i 无关.故 ik 是一个计算值,是一个标准.在实际工程中它并 不出现. 综上所述,明渠流态有四个判别标准.(见 P170 表 7-8)
判 别 标 准
流 态
微波波速c
弗劳德数 Fr
临界水深 hk
临界底坡ik
缓流 临界流 急流
v<c v=c v>c
Fr<1 Fr=1 Fr>1
h>hk h=hk h<hk
h’ 和h’ 为共轭水深.(共轭指互相依存.)
为水跃函数
则上式为
(h ） (h" )
四.水跃函数图示
（h) 是水深的连续函数,可绘出水跃函数图形( P157.图7-18)
跃高
a h" h '
六.水跃的能量损失与水跃长度
( h" h ' ) 3 在水跃段内有较大的能量损失.水跃能量损失为 Es 4h ' h"
水力学6.2
解：（1）计算临界水深
q2 Q 2 3 1 30 2 hK 3 3 1.37 m 2 2 g gb 9.8 6
明渠恒定非均匀流
（2）计算共轭水深
3 3 h h 0 . 8 1 . 37 h 1 8 K 1 1 8 1 2.17m 2 h 2 0.8
明渠恒定非均匀流
第一节
明渠水流的三种流态
明渠水流有和大气接触的自由表面，与 有压流不同，具有独特的水流流态，即缓流、 临界流和急流三种 1.缓流 当明渠中水流受到干扰微波后,若干扰微 波即能顺水流方向朝下游传播,又能逆水流方 向朝上游传播,造成在障碍物前长距离的水流 壅起,这时渠中水流就称为缓流。此时水流流 速＜干扰微波流速。
一、明渠水流中干扰波 的传播特点
v~vw
(1) 静水
vw
vw
(2)v<vw
v vw-v vw+v
(3)
v>vw v
v+vw
(4) v=vw
v
2vw
二.明渠水流三种流态
缓流: 急流: 临界流:
v < vw v > vw v = vw
本章着重研究在恒定流情况下，明渠非 均匀渐变流的水流要素沿流程的变化规律， 主要研究明渠水深(或水位)沿流程的变化规 律，也就是要分析研究关于水面曲线的变化 及其计算，以便恰当地确定明渠边墙高度， 以及回水淹没的范围等等。
明渠恒定非均匀流
2.急流 当明渠中水流受到干扰后 ,若干扰微波 只能顺水流方向朝下游传播 ,不能逆水流方 向朝上游传播，这种明渠水流称为急流。 此时水流流速＞干扰微波的流速。 3.临界流 当明渠中水流受到干扰微波后，若干 扰微波向上游传播的速度为零，这正是急 流与缓流这两种流动状态的分界，称为临 界流。此时水流流速=干扰微波的流速。
q2 Q 2 3 1 30 2 hK 3 3 1.37 m 2 2 g gb 9.8 6
明渠恒定非均匀流
（2）计算共轭水深
3 3 h h 0 . 8 1 . 37 h 1 8 K 1 1 8 1 2.17m 2 h 2 0.8
明渠恒定非均匀流
第一节
明渠水流的三种流态
明渠水流有和大气接触的自由表面，与 有压流不同，具有独特的水流流态，即缓流、 临界流和急流三种 1.缓流 当明渠中水流受到干扰微波后,若干扰微 波即能顺水流方向朝下游传播,又能逆水流方 向朝上游传播,造成在障碍物前长距离的水流 壅起,这时渠中水流就称为缓流。此时水流流 速＜干扰微波流速。
一、明渠水流中干扰波 的传播特点
v~vw
(1) 静水
vw
vw
(2)v<vw
v vw-v vw+v
(3)
v>vw v
v+vw
(4) v=vw
v
2vw
二.明渠水流三种流态
缓流: 急流: 临界流:
v < vw v > vw v = vw
本章着重研究在恒定流情况下，明渠非 均匀渐变流的水流要素沿流程的变化规律， 主要研究明渠水深(或水位)沿流程的变化规 律，也就是要分析研究关于水面曲线的变化 及其计算，以便恰当地确定明渠边墙高度， 以及回水淹没的范围等等。
明渠恒定非均匀流
2.急流 当明渠中水流受到干扰后 ,若干扰微波 只能顺水流方向朝下游传播 ,不能逆水流方 向朝上游传播，这种明渠水流称为急流。 此时水流流速＞干扰微波的流速。 3.临界流 当明渠中水流受到干扰微波后，若干 扰微波向上游传播的速度为零，这正是急 流与缓流这两种流动状态的分界，称为临 界流。此时水流流速=干扰微波的流速。
水力学课件 第8章 明渠非均匀流w
Q 2
ds ( 2gA2 ) gA3
dA ds
Q 2
gA3
Bdh ds
Fr2
dh ds
3. dhw ds
J
Q2 K2
i dh Fr2 dh J 0
ds
ds
明渠恒定非均匀渐变流的基本方程
dh
iJ
i
Q2 K2
ds 1 Fr2 1 Fr2
（二） 棱柱体明渠渐变流水面曲线形状分析
单位重量流体所具有的机械能
E z p v2 g 2g
断面单位能量
Es
h v2
2g
h
Q2
2 gA2
(1)断面单位能量（cross-sectional unit energy）
1.
E
z0
Es
z0
h
v2
2g
两者区别
2. dE 0 ds
dEs 0; dEs 0; dEs 0 ds ds ds
1)
水跃分类 波 状 水 跃 1 Fr1 1.7 弱 水 跃 1.7 Fr1 2.5 K j 20% 不 稳 定 水 跃 2.5 Fr1 4.5 K j 20% ~ 45% 稳 定 水 跃 4.5 Fr1 9 K j 45% ~ 70% 强 水 跃 9 Fr1 K j 85%
一.明渠水流的两种流态及其判别
1.明渠水流的两种流态
急流(Supercritical flow ) 当底坡陡峻，水流湍急，遇到障 碍物时，水面在障碍物顶上或稍 向上游隆起。但是障碍物对上游 较远处的水流并不发生影响。这 种水流状态称为急流。
一.明渠水流的两种流态及其判别
1.明渠水流的两种流态
缓流Subcritical Flow 底坡平缓，流速较小，遇到 渠底有阻水的障碍物时，在 障碍物处水面形成跌落，而 在其上游则普遍壅高，一直 影响到上游较远处。这种水
水力学第六章明渠恒定流PPT课件
06 明渠恒定流的研究前沿与 展望
新型流动现象的探索
新型流动现象
随着科学技术的不断进步，越来越多的新 型流动现象在水力学领域被发现。这些现 象不仅拓展了我们对水力学基本规律的理 解，还为解决实际问题提供了新的思路。
探索方法
为了探索这些新型流动现象，研究者们 采用了多种方法，包括理论分析、数值 模拟和实验观测。这些方法相互补充， 有助于更全面地了解流动现象的本质。
明渠恒定流的应用场景
总结词
明渠恒定流的应用场景包括天然河流、 人工渠道、水库等。
VS
详细描述
在自然界中，许多河流的水流状态可以视 为明渠恒定流。通过研究明渠恒定流的流 动规律，可以更好地理解河流的水力学特 性，为河流治理、航道建设等提供理论支 持。此外，在水利工程中，人工渠道和水 库的设计也需要考虑明渠恒定流的流动特 性，以确保水流的稳定和工程的正常运行 。
能量平衡与转化
01能量平衡在恒定流 Nhomakorabea件下，水流系统的总能量保持不变。即水流在运动过程中输
入的能量等于输出的能量加上损失的能量。
02 03
能量转化
水流在运动过程中，由于克服阻力而损失的机械能可以转化为热能或其 他形式的能量。例如，在管路系统中，由于流动摩擦而损失的机械能可 以转化为热能，导致水温升高。
阻力系数与雷诺数
阻力系数是描述流动阻力的一个重要参数，它与流动的几何形状、液体的物理性 质以及流动状态有关。在明渠恒定流中，阻力系数可以通过实验测定或根据经验 公式计算。
雷诺数是描述流动状态的一个无量纲数，它由流速、水力直径和液体动力粘度组 成。在明渠恒定流中，雷诺数的大小决定了流动的形态（如层流或湍流）。不同 的流动形态具有不同的阻力系数和流速分布。
6 明渠流动
6.2 明渠均匀流
6.2.1.2明渠均匀流的产生条件
根据明渠均匀流的上述特征，可以推定它的形成必须具 备下列条件：
(1) 水流必须为恒定流。否则沿流程各断面的水深、流速 随时间变化，任一时刻各断面水深、流速等各不相等，是 非均匀流。 (2) 流量沿程保持不变，没有水流的汇入或分出。否则明 渠上、下游各过水断面的水深和流速将不相同，为非均匀 流。
例1：某梯形断面土渠中发生均匀流动，已知：底宽b=2m，边 坡系数m=1.5，水深h=1.5m，底坡i=0.0004，粗糙系数n=0.0225， 试求渠中流速v，流量Q。
6.3 明渠非均匀流基本概念
6.3.1 明渠非均匀流的定义、形成及特征
明渠水流的流速、水深等水力要素沿程变化的流动，称为 明渠非均匀流。人工渠道和天然河道中的水流多为明渠非 均匀流。 人工渠道或天然河道中的均匀流，由于渠道底坡的变化、 过水断面的几何形状或尺寸的变化、壁面粗糙程度的变化， 或在渠道中修建人工构筑物，都将会形成明渠非均匀流动。
20
6.2 明渠均匀流
6.2.3.2明渠均匀流水力计算
明渠均匀流的基本公式中 Q AC Ri K i f (m, b, h, n, i) ， K 、 i 中，己知任意两 其中K决定于渠道断面特征。在 Q 、 个量，即可求出另一个量，因此渠道水力计算问题可分为 三类。 （1）验算渠道的输水能力 已知渠道断面形状及大小、渠壁的粗糙系数、渠道的底坡， 求渠道的输水能力，即己知 K ， i 求 Q 。求解中需要先计 R、 算出A 、 C 值。
第6章 明渠流动
6 明渠流动
1
6.1 明渠流动概述 6.2 明渠均匀流
6.3 明渠非均匀流基本概念
2 3
第六章 流体力学--明渠恒定流与堰流
三.梯形断面的水力计算：
对于梯形断面的明渠均匀流，有：
Q VA AC Ri f (m,b, h0,i, n) 1. 校核渠道的输水能力：
这类问题，一般已知：m、b、h0、i、n，要求解Q。 可直接代入明渠均匀流的基本公式求解。
2. 决定渠道底坡：
这类问题，一般已知：m、b、h0、n及Q，要求解i。 亦可直接利用明渠均匀流的基本公式求解。
第六章 明渠恒定流与堰流
具有自由表面水流的渠道称为明渠。
§6-1 渠道及明渠流的分类
一.明渠的分类： 1.明渠的横断面：
① 天然河道断面形状：多为“V”形、“U”形或复式断面 ② 人工渠道断面形状：有梯形、矩形、圆形及复式断面 ③ 梯形断面的水力要素：底宽b、水深h、边坡系数m=cot
水面Width：B b 2mh
例：梯形断面水渠。已知: b=5m，m=1，Q=8m3/s。求：hc
解： Fr Q / A 1 gA / B
Q2 gA3
B
1
A (Q2 g
B)1/ 3
0
*§6-5 明渠流的流态——缓流与急流
B b 2mh 5 2h A (b mh)h (5 h)h
§6-3 梯形断面渠道均匀流的水力计算
例1：梯形断面水渠，已知：
m 1.5,i 3104, n 0.025,b 7m,Q 15m3/s
求解：正常水深h0
解： A (b mh)h (7 1.5h)h
b 2h 1 m2 7 3.6056h
Q
i n
J (h) 1 h2b Q2
2
gbh
1 h '2 b Q2 1 h ''2 b Q2
对于梯形断面的明渠均匀流，有：
Q VA AC Ri f (m,b, h0,i, n) 1. 校核渠道的输水能力：
这类问题，一般已知：m、b、h0、i、n，要求解Q。 可直接代入明渠均匀流的基本公式求解。
2. 决定渠道底坡：
这类问题，一般已知：m、b、h0、n及Q，要求解i。 亦可直接利用明渠均匀流的基本公式求解。
第六章 明渠恒定流与堰流
具有自由表面水流的渠道称为明渠。
§6-1 渠道及明渠流的分类
一.明渠的分类： 1.明渠的横断面：
① 天然河道断面形状：多为“V”形、“U”形或复式断面 ② 人工渠道断面形状：有梯形、矩形、圆形及复式断面 ③ 梯形断面的水力要素：底宽b、水深h、边坡系数m=cot
水面Width：B b 2mh
例：梯形断面水渠。已知: b=5m，m=1，Q=8m3/s。求：hc
解： Fr Q / A 1 gA / B
Q2 gA3
B
1
A (Q2 g
B)1/ 3
0
*§6-5 明渠流的流态——缓流与急流
B b 2mh 5 2h A (b mh)h (5 h)h
§6-3 梯形断面渠道均匀流的水力计算
例1：梯形断面水渠，已知：
m 1.5,i 3104, n 0.025,b 7m,Q 15m3/s
求解：正常水深h0
解： A (b mh)h (7 1.5h)h
b 2h 1 m2 7 3.6056h
Q
i n
J (h) 1 h2b Q2
2
gbh
1 h '2 b Q2 1 h ''2 b Q2
《水力学》第六章明渠恒定非均匀流
*
如果我们把参考基准面选在渠底这一特殊位置，把对通过渠底的水平面0′-0′所计算得到的单位能量称为断面比能，并以 来表示，则 在实用上，因一般明渠底坡较小，可认为 故常采用
当流量Q和过水断面的形状及尺寸一定时，断面比能仅仅是水深的函数，即Es＝f(h)，以图表示则称为:比能曲线。
为什么?
*
（6-20） 上式中 ，b为梯形断面的底宽。 上式左端实际上表示一个与梯形断面底宽相等的矩形断面的临界水深。为了与欲求的梯形断面的临界水深 相区别将其以 来表示，即令 （6-21）
*
6-1 明渠水流的三种流态
扰动：在流场的某一点或者某一个区域，由于某种原因，使流动参数发生变化，这种变化叫做扰动。 波：扰动区域与未扰动区域的分界面
*
微弱扰动的一维传播
非定常过程
*
6-1 明渠水流的三种流态
注意：波速与流体质点速度的区别。
*
6-1 明渠水流的三种流态
在t=0、1、2、3、4s，分别有水滴滴入o点，研究t=4s的流动图象 静水中传播的微波速度vw(c)称为相对波速。 当v=0时，水流静止，干扰波能向四周以一定的速度传播。
在t=0、1、2、3、4s，分别有水滴滴入o点，研究t=4s的流动图象
当v＝vw时，水流为临界流，
6-1 明渠水流的三种流态 明渠水流有和大气接触的自由表面，与有压流不同，具有独特的水流流态，即缓流、临界流和急流三种。 静水中传播的微波速度vw称为相对波速。
若将（6-20）式两端同乘以 可得 （6-22） 上式移项后可得 （6-23）
求出与梯形断面底宽相等的矩形断面的临界水深 ；
2然后根据梯形断面已知m , b值算出 ；
3再由 关系曲线上查出相应的 值，从而可算出梯形断面的 值。
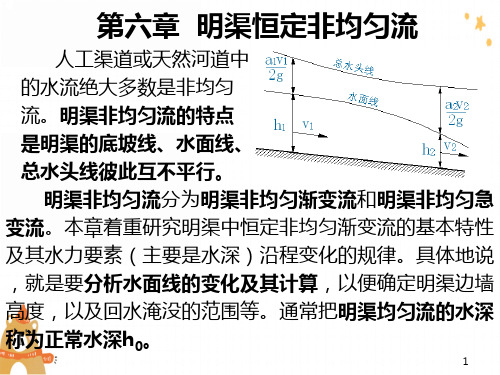
如果我们把参考基准面选在渠底这一特殊位置，把对通过渠底的水平面0′-0′所计算得到的单位能量称为断面比能，并以 来表示，则 在实用上，因一般明渠底坡较小，可认为 故常采用
当流量Q和过水断面的形状及尺寸一定时，断面比能仅仅是水深的函数，即Es＝f(h)，以图表示则称为:比能曲线。
为什么?
*
（6-20） 上式中 ，b为梯形断面的底宽。 上式左端实际上表示一个与梯形断面底宽相等的矩形断面的临界水深。为了与欲求的梯形断面的临界水深 相区别将其以 来表示，即令 （6-21）
*
6-1 明渠水流的三种流态
扰动：在流场的某一点或者某一个区域，由于某种原因，使流动参数发生变化，这种变化叫做扰动。 波：扰动区域与未扰动区域的分界面
*
微弱扰动的一维传播
非定常过程
*
6-1 明渠水流的三种流态
注意：波速与流体质点速度的区别。
*
6-1 明渠水流的三种流态
在t=0、1、2、3、4s，分别有水滴滴入o点，研究t=4s的流动图象 静水中传播的微波速度vw(c)称为相对波速。 当v=0时，水流静止，干扰波能向四周以一定的速度传播。
在t=0、1、2、3、4s，分别有水滴滴入o点，研究t=4s的流动图象
当v＝vw时，水流为临界流，
6-1 明渠水流的三种流态 明渠水流有和大气接触的自由表面，与有压流不同，具有独特的水流流态，即缓流、临界流和急流三种。 静水中传播的微波速度vw称为相对波速。
若将（6-20）式两端同乘以 可得 （6-22） 上式移项后可得 （6-23）
求出与梯形断面底宽相等的矩形断面的临界水深 ；
2然后根据梯形断面已知m , b值算出 ；
3再由 关系曲线上查出相应的 值，从而可算出梯形断面的 值。
工程流体力学课件6明渠水流的两种流态及其转换
流态转换
流态转换定义
当流体在管道或明渠中的流速发生变化时，流体会从一种流态转变 为另一种流态。
流态转换条件
流体的雷诺数（Re）是判断流体是否发生流态转换的重要参数。当 Re值超过某一临界值时，流体将从层流转为紊流。
流态转换的影响因素
除了雷诺数外，管道或明渠的形状、粗糙度、流体性质等因素也会影 响流体的流态。
详细描述
紊流由于其独特的流动特性，在许多工程领域中都有广泛的应用。例如，在水利工程中，可以利用紊 流来提高水流的输水效率；在环境工程中，可以利用紊流来增强废水的处理效果；在石油工业中，可 以利用紊流来提高油气的采收率和输送效率。
04
流态转换
流态转换的定义
流态转换是指水流在流动过程中，由 于受到外部条件或内部因素的影响， 其流动状态发生改变的过程。
在明渠水流中，常见的流态转换包括 从层流到紊流的转换以及从紊流到层 流的转换。
流态转换的条件
流速
01
当流速达到一定阈值时，水流会发生流态转换。具体阈值取决
于渠道的几何形状、水流的物理性质以及外部环境条件。
流量
02
流量的大小也会影响流态转换。当流量增大时，水流更容易发
生紊流化。
渠道粗糙度
03
渠道表面的粗糙度对流态转换有重要影响。粗糙度越大，越容
工程流体力学课件6 明渠水流的两种流态
及其转换
目录
• 明渠水流流态概述 • 层流流动 • 紊流流动 • 流态转换
01
明渠水流流态概述
层流
01
02
03
层流定义
层流是一种相对稳定的流 态，其中流体的流速在垂 直方向上变化较小，呈现 有序的层状流动。
层流特点
(10)第6章(2)明渠流动状态
i <i k
h0 h k = f (i) hk
第 六 章 明 渠 流 动
i >i k
g k Q ik 2 2 2 A Ck Rk Ck Bk
ik i
图6-14 临界水深与流量关系
6.4 明渠流动状态
第 六 章 明 渠 流 动
二、意义： 临界底坡是为便于分析明渠流动而引入的特定坡 度。渠道的实际底坡i与临界底坡ik相比较，有三 种情况： 1.如果实际的渠道底坡小于某一流量的临界坡底,即 i<ik（则h0>hk），此时渠道底坡称为缓坡； 2.如果i>ik（则h0<hk），此时渠道底坡称为急坡或 陡坡； 3.如果渠道底坡i=ik（则h0=hk），此时渠道底坡称 为临界坡。 ——必须指出,因为在断面一定的棱柱形渠道中,临 界水深hk与流量有关(图6-15),因此,底坡i一定的渠 道,坡度的缓、急可能因流量的改变而改变.
★由于水跃的消能效果较好，所以常被采用作为泄
水建筑物下游水流衔接的一种有效的消能方式。
6.5 跌水与水跃
第 六 章 明 渠 流 动
具有上述典型形态的水跃称为完整水跃(图6-20)。 据实验观察，形成完整水跃的条件是跃前断面水 流的佛汝德数Fr>2.9。当1< Fr<2.9时，水跃表面没 有漩滚区，而是形成一系列起伏不平的波浪，称 为波状水跃(图6-21)。
三、用佛汝德数Fr来判别
Fr < 1时，水流状态为缓流； Fr = 1时，水流状态为临界流； Fr> 1时，水流状态为急流。
6.4 明渠流动状态
6.4.5 微幅扰动波与明渠流态的物理意义
第 六 章 明 渠 流 动
明渠流动的三种流态可以解释为明渠中微幅扰动 波(以下简称为微波)相对于水流传播的三种不同 状态.明渠流动的水面线实际上是持续产生的所有 扰动子波相互迭加的结果。
h0 h k = f (i) hk
第 六 章 明 渠 流 动
i >i k
g k Q ik 2 2 2 A Ck Rk Ck Bk
ik i
图6-14 临界水深与流量关系
6.4 明渠流动状态
第 六 章 明 渠 流 动
二、意义： 临界底坡是为便于分析明渠流动而引入的特定坡 度。渠道的实际底坡i与临界底坡ik相比较，有三 种情况： 1.如果实际的渠道底坡小于某一流量的临界坡底,即 i<ik（则h0>hk），此时渠道底坡称为缓坡； 2.如果i>ik（则h0<hk），此时渠道底坡称为急坡或 陡坡； 3.如果渠道底坡i=ik（则h0=hk），此时渠道底坡称 为临界坡。 ——必须指出,因为在断面一定的棱柱形渠道中,临 界水深hk与流量有关(图6-15),因此,底坡i一定的渠 道,坡度的缓、急可能因流量的改变而改变.
★由于水跃的消能效果较好，所以常被采用作为泄
水建筑物下游水流衔接的一种有效的消能方式。
6.5 跌水与水跃
第 六 章 明 渠 流 动
具有上述典型形态的水跃称为完整水跃(图6-20)。 据实验观察，形成完整水跃的条件是跃前断面水 流的佛汝德数Fr>2.9。当1< Fr<2.9时，水跃表面没 有漩滚区，而是形成一系列起伏不平的波浪，称 为波状水跃(图6-21)。
三、用佛汝德数Fr来判别
Fr < 1时，水流状态为缓流； Fr = 1时，水流状态为临界流； Fr> 1时，水流状态为急流。
6.4 明渠流动状态
6.4.5 微幅扰动波与明渠流态的物理意义
第 六 章 明 渠 流 动
明渠流动的三种流态可以解释为明渠中微幅扰动 波(以下简称为微波)相对于水流传播的三种不同 状态.明渠流动的水面线实际上是持续产生的所有 扰动子波相互迭加的结果。
第6章明渠流动
35
b 2h 1 m
均匀流段
非均匀流段
非均匀流段
图 明渠中的流动
•
离开渠进口、或水工建筑物一定距离远的顺直
棱柱体明渠恒定流
6.2.3
明渠均匀流的水力计算
6.2.3.1
基本公式
由谢才公式
v C RJ
基于明渠水流资料获得的经验公式
1769年 谢才（A.Chezy）
在总结了一系列渠道水流实测资料的基础上, 提出明渠均匀流流速与流量的经验公式－谢 才公式，以后又有确定谢才系数的满宁公式 （R.Manning）、 巴普洛甫斯基公式。
Q AC Ri f m, b, h0 , i, n
式中，有6个变量（含Q）
Q AC Ri f m, b, h0 , i, n
式中，共有六个变量（含Q） 边坡系数 m和糙率 n一般根据土质、或衬砌材料用 经验法确定
水力计算任务
给定Q、b、h、i 中三个，求解另一个
计算类型
3
3
人工渠道连接段（扭面）
1
棱 柱 体
非 棱 柱 非棱柱体（纽面） 体 棱 柱 体
1
1
1
2
2
2
2
3
3
3
3
§6.2
6.2.1
明渠均匀流
明渠均匀流的水力特征 过水断面形状、尺寸、水深沿程不变
断面流速分布
断面平均流速
流量 动能修正系数等 沿程不变
6.2.1
明渠均匀流特性
过水断面形状、尺寸、水深沿程不变
【学习重点】
1. 明渠均匀流水力计算； 2. 明渠水流三种流态的判别； 3. 明渠恒定非均匀渐变流水面曲线分析和 计算，这部分也是本章的难点； 4. 水跃的基本特性。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
不淤流速v’’ 渠道中悬沙淤积的临界流速，取决于水流
条件和挟沙的特性以及水中含沙量大小，可根据经 验公式确定。
v'' v v'
【例】一条路基排水沟，底坡i=0.005; n=0.025, m=1.5; 要求通过流量 Q 3.5m3 / s ,试按水力最佳断面
的原理求出此排水沟的底宽和水深。
教学内容、重点及难点
基本内容 1、了解明槽水流的分类和特征，了解棱柱体渠道的概 念，掌握明槽底坡的概念和梯形断面明渠的几何特征和 水力要素。 2、了解明槽均匀流的特点和形成条件，熟练掌握明槽 均匀流公式，并能应用它来进行明渠均匀流水力计算。 3、理解水力最佳断面和允许流速的概念，掌握水力最 佳断面的条件和允许流速的确定方法，学会正确选择明 渠的糙率n值。 4、掌握明槽均匀流水力设计的类型和计算方法，能进 行过流能力和正常水深的计算，能设计渠道的断面尺寸。
【解】 梯形断面最佳宽深比
谢才系数 量纲 流量
C
1
1
R6
n
C
1 L2T
1
[g
1 2
]
Q AC Ri K i
流量模数
K AC R
谢才公式适用条件 : ?
• 恒定均匀流
阻力平方区
i>0
单位 m.s
糙率 n 值的确定
天然河道中影响糙率 n 值的因素 ① 河床表面粗糙 ② 断面的不规则、平弯情况、 滩地交叉、河道阻碍情况 ③ 河堤沙坡影响随水深变化
• 离开渠进口、或水工建筑物一定距离远的顺直 棱柱体明渠恒定流
• 天然河道某些顺直、整齐河段在枯、平水期
三、明渠均匀流基本公式
o 基本公式
1) Q v1A1 v2 A2
2)
vC
Ri
1
21
R3i 2
n
Q AC
Ri
A
21
R 3i 2
K
i
n
(K AC R)
C
1
1
R6
n
谢才公式
dlx
明渠底坡有三种类型
正（顺）坡 i > 0 渠底高程沿流程降低
平
坡 i = 0 渠底高程沿程不变
负（逆）坡 i < 0 渠底高程沿流程增加
i>0
i=0
i<0
三、明渠的分类
按断面形状、尺寸是否沿程变化分 棱柱体明渠、非棱柱体明渠
第二节 明渠均匀流特性 及基本公式
一、明渠均匀流的特性
（1） 过水断面形状、尺寸、水深沿程不变，流速分布、 平均流速均沿程不变
R (b mh)h b 2h 1 m2
B b 2mh
b 2h 1 m2
b
h
m的大小应根据土的种类或护面情况而定，可查表
土壤种类
边坡系数 m
粉砂
3.0~5.3
细沙
2.5~3.5
砂壤土
2.0~2.5
粘砂壤土
1.5~2.0
粘土，密实黄土
1.25~1.5
卵石和砌石
1.25~1.5
第一节 概 述
明渠是人工修建或自然形成的具有自由表面的渠槽。
明渠水流分类：
明渠恒定流 明渠非恒定流
明渠均匀流 明渠非均匀流
无 明渠非均匀流
人工渠道、天然河道以及未被液流所充满的管道都是明渠流.
A Q
A
明渠流与有压流区别
Cross section A-A
有压管流： ① 具有封闭的湿周； ② 压力是流动的主要动力。
例如
一般土渠边坡m > 1，β m < 1，是深
窄形断面，需深挖高填，造成施工不便、维 护管理困难；水深变化大，给通航和灌溉带 来不便，经济上反而不利。因此，限制了水 力最佳断面在实际中应用.
二、允许流速
保证渠道正常运行的允许流速上限和下限值
不冲流速 v’ 渠道冲刷的临界断面平均流速，取决定于
渠壁材料的物理性质和水深，可查阅有关水利设计手册。
半岩性的抗水的土壤
0.5~1.25
风化的岩石
0.25~0.5
未风化的岩石
0.00~0.25
二、明渠底坡
底坡i— 渠底高程沿水流方向单位距离的降落值称为底坡
i sin d z
dl
θ— 渠底线与水平线之间的夹角
如果用水平距离代替实际距离，i dz tg
用垂直水深代替实际水深
（2）总水头线、水面线、渠底线三线平行
J = Jp = i h
（3）摩擦阻力与重力分量相平衡
J Jp v
Gsinθ = FT
i
vh
θ
二、明渠均匀流的形成条件
• 水流恒定，流量沿程不变 • 正坡，底坡沿程不变 • 棱柱体渠道，糙率沿程不变 • 明渠足够长直，不受干扰
均匀流段
非均匀流段
非均匀流段
图 明渠中的流动
注 意: 选择时应谨慎。其选得偏小，渠道断面尺寸偏
小，对实际输水能力影响较大。
第三节 水力最佳断面
及允许流速
一、明渠水力最优断面
51
Q
1 n
21
AR3i 2
1 n
A3i 2
2
3
水力最佳断面：过流断面的面积、糙率、底坡一定,
通过的流量最大的断面形状
当 Q = 一定，要求：A → Amin 当 A = 一定，要求：Q பைடு நூலகம் Qmax
第1章 流体及其主要物理性质
第2章 流体静力学 第3章 流体动力学基础 第4章 流动阻力和水头损失 第5章 孔口、管嘴出流及有压管流 第6章 明渠均匀流 第7章 明渠水流的两种流态及其转换
第六章 明 渠 均 匀 流
第一节 第二节 第三节 第四节
概述 明渠均匀流特性及公式 水力最佳断面及允许流速 无压圆管均匀流
h
断面确定：根据地质条件
岩石中开凿或条石砌筑或混
凝土渠或木渠
— 矩形
排水管道或无压隧道 — 圆形
土质地基
— 梯形
h b
渠道底宽 b 渠中水深 h 水面宽度 B 过水断面面积 A 水力半径 R 断面宽深比
B
h
1
α
m
b
边坡系数m：边坡上高差为1m的两点间的水平距离
m ctg
A (b B )h (b mh)h 2
明渠流： ① 具有自由水面（即水面压强为大气压）； ② 重力是流动的主要动力； ③ 明渠水面线即测压管水头线
一、明渠横断面
1.天然河道的横断面 呈不规则形状，分主槽和滩地 枯水期：水流过主槽 丰水期：水流过主槽和滩地
主槽
滩地
2.人工明渠的横断面
据渠道的断面形状分:
梯形、矩形、圆形、抛物线形等
d
θ
面积、糙率、底坡一定, 流量最大,要求R最大
半圆形断面为水力最佳断面。
R A
梯形断面的最佳宽深比，Rm = hm / 2
“水力最佳”不 是 “技术经济
m
b h
2(
1 m2 m)
最佳”
矩形断面的最佳宽深比，bm = 2 hm
m 2; bm 2hm 4Rm
综合考虑水力最佳断面不太合理
条件和挟沙的特性以及水中含沙量大小，可根据经 验公式确定。
v'' v v'
【例】一条路基排水沟，底坡i=0.005; n=0.025, m=1.5; 要求通过流量 Q 3.5m3 / s ,试按水力最佳断面
的原理求出此排水沟的底宽和水深。
教学内容、重点及难点
基本内容 1、了解明槽水流的分类和特征，了解棱柱体渠道的概 念，掌握明槽底坡的概念和梯形断面明渠的几何特征和 水力要素。 2、了解明槽均匀流的特点和形成条件，熟练掌握明槽 均匀流公式，并能应用它来进行明渠均匀流水力计算。 3、理解水力最佳断面和允许流速的概念，掌握水力最 佳断面的条件和允许流速的确定方法，学会正确选择明 渠的糙率n值。 4、掌握明槽均匀流水力设计的类型和计算方法，能进 行过流能力和正常水深的计算，能设计渠道的断面尺寸。
【解】 梯形断面最佳宽深比
谢才系数 量纲 流量
C
1
1
R6
n
C
1 L2T
1
[g
1 2
]
Q AC Ri K i
流量模数
K AC R
谢才公式适用条件 : ?
• 恒定均匀流
阻力平方区
i>0
单位 m.s
糙率 n 值的确定
天然河道中影响糙率 n 值的因素 ① 河床表面粗糙 ② 断面的不规则、平弯情况、 滩地交叉、河道阻碍情况 ③ 河堤沙坡影响随水深变化
• 离开渠进口、或水工建筑物一定距离远的顺直 棱柱体明渠恒定流
• 天然河道某些顺直、整齐河段在枯、平水期
三、明渠均匀流基本公式
o 基本公式
1) Q v1A1 v2 A2
2)
vC
Ri
1
21
R3i 2
n
Q AC
Ri
A
21
R 3i 2
K
i
n
(K AC R)
C
1
1
R6
n
谢才公式
dlx
明渠底坡有三种类型
正（顺）坡 i > 0 渠底高程沿流程降低
平
坡 i = 0 渠底高程沿程不变
负（逆）坡 i < 0 渠底高程沿流程增加
i>0
i=0
i<0
三、明渠的分类
按断面形状、尺寸是否沿程变化分 棱柱体明渠、非棱柱体明渠
第二节 明渠均匀流特性 及基本公式
一、明渠均匀流的特性
（1） 过水断面形状、尺寸、水深沿程不变，流速分布、 平均流速均沿程不变
R (b mh)h b 2h 1 m2
B b 2mh
b 2h 1 m2
b
h
m的大小应根据土的种类或护面情况而定，可查表
土壤种类
边坡系数 m
粉砂
3.0~5.3
细沙
2.5~3.5
砂壤土
2.0~2.5
粘砂壤土
1.5~2.0
粘土，密实黄土
1.25~1.5
卵石和砌石
1.25~1.5
第一节 概 述
明渠是人工修建或自然形成的具有自由表面的渠槽。
明渠水流分类：
明渠恒定流 明渠非恒定流
明渠均匀流 明渠非均匀流
无 明渠非均匀流
人工渠道、天然河道以及未被液流所充满的管道都是明渠流.
A Q
A
明渠流与有压流区别
Cross section A-A
有压管流： ① 具有封闭的湿周； ② 压力是流动的主要动力。
例如
一般土渠边坡m > 1，β m < 1，是深
窄形断面，需深挖高填，造成施工不便、维 护管理困难；水深变化大，给通航和灌溉带 来不便，经济上反而不利。因此，限制了水 力最佳断面在实际中应用.
二、允许流速
保证渠道正常运行的允许流速上限和下限值
不冲流速 v’ 渠道冲刷的临界断面平均流速，取决定于
渠壁材料的物理性质和水深，可查阅有关水利设计手册。
半岩性的抗水的土壤
0.5~1.25
风化的岩石
0.25~0.5
未风化的岩石
0.00~0.25
二、明渠底坡
底坡i— 渠底高程沿水流方向单位距离的降落值称为底坡
i sin d z
dl
θ— 渠底线与水平线之间的夹角
如果用水平距离代替实际距离，i dz tg
用垂直水深代替实际水深
（2）总水头线、水面线、渠底线三线平行
J = Jp = i h
（3）摩擦阻力与重力分量相平衡
J Jp v
Gsinθ = FT
i
vh
θ
二、明渠均匀流的形成条件
• 水流恒定，流量沿程不变 • 正坡，底坡沿程不变 • 棱柱体渠道，糙率沿程不变 • 明渠足够长直，不受干扰
均匀流段
非均匀流段
非均匀流段
图 明渠中的流动
注 意: 选择时应谨慎。其选得偏小，渠道断面尺寸偏
小，对实际输水能力影响较大。
第三节 水力最佳断面
及允许流速
一、明渠水力最优断面
51
Q
1 n
21
AR3i 2
1 n
A3i 2
2
3
水力最佳断面：过流断面的面积、糙率、底坡一定,
通过的流量最大的断面形状
当 Q = 一定，要求：A → Amin 当 A = 一定，要求：Q பைடு நூலகம் Qmax
第1章 流体及其主要物理性质
第2章 流体静力学 第3章 流体动力学基础 第4章 流动阻力和水头损失 第5章 孔口、管嘴出流及有压管流 第6章 明渠均匀流 第7章 明渠水流的两种流态及其转换
第六章 明 渠 均 匀 流
第一节 第二节 第三节 第四节
概述 明渠均匀流特性及公式 水力最佳断面及允许流速 无压圆管均匀流
h
断面确定：根据地质条件
岩石中开凿或条石砌筑或混
凝土渠或木渠
— 矩形
排水管道或无压隧道 — 圆形
土质地基
— 梯形
h b
渠道底宽 b 渠中水深 h 水面宽度 B 过水断面面积 A 水力半径 R 断面宽深比
B
h
1
α
m
b
边坡系数m：边坡上高差为1m的两点间的水平距离
m ctg
A (b B )h (b mh)h 2
明渠流： ① 具有自由水面（即水面压强为大气压）； ② 重力是流动的主要动力； ③ 明渠水面线即测压管水头线
一、明渠横断面
1.天然河道的横断面 呈不规则形状，分主槽和滩地 枯水期：水流过主槽 丰水期：水流过主槽和滩地
主槽
滩地
2.人工明渠的横断面
据渠道的断面形状分:
梯形、矩形、圆形、抛物线形等
d
θ
面积、糙率、底坡一定, 流量最大,要求R最大
半圆形断面为水力最佳断面。
R A
梯形断面的最佳宽深比，Rm = hm / 2
“水力最佳”不 是 “技术经济
m
b h
2(
1 m2 m)
最佳”
矩形断面的最佳宽深比，bm = 2 hm
m 2; bm 2hm 4Rm
综合考虑水力最佳断面不太合理