GRACE卫星非差简化动力学定轨研究
基于SLR的GRACE卫星定轨中重力场模型对轨道精度的影响

结 果 的精度 高 或相 当 , 能 得 出 比较 符 合 实 际情 况 才
的评 定精度 。
4 1 联合 重力 场 J . GM 模型 序 列和 GGM0 C模 型 2
3 定 轨 软 件
本 文在 进行 定轨 过程使 用 了 C M0 AS RD软件 , 它 是 由 UTO I 软 件演化 而来 的 , 程 序 的文 件结 PA 该
t d i ee c . u edf r n e f
K e r s S ywo d : LR;GRACE;g a iy f l d l r vt i d mo e ;CAS ORD e M
航 天技 术 的迅 速 发 展 , 卫 星 的 应 用 越来 越 广 使 泛 , 二 十年来 , 轨卫 星 由于特 殊 的应用 和科 研 的 近 低
定 轨精 度的影响 ; 以及重力场截断阶引起 的积分轨道差异 ; 同时 , 将定 轨结果与采用 G S确定 的定轨结果进行 比较 , P 分 析与 G S定轨结果 的差异 。实 验证 明 , P 重力场模型选择 G GM0 C的定轨结果 优于选择 J 2 GM- 3的定轨结果 , 于 基 S R的定轨结果与采用 G S确定的定轨结果差异量级为米级 。 L P
l l
I
l
l初 化 始 l
l
况等诸 多 因素 。 定轨结 果 的外符 合精 度是 与使 用其 他方法 获得
的轨 道确定 结果 相 比, 常 要 比被 鉴 定 的轨道 确定 通
l迭 l 代
l
l 结 I 束
图 2 CA MORD程 序 的执 行 流 程 S
d tr n to e u t ee m ie sn e e mi ain r s lsd t r n d u igGPS o b td tr ia in r s lsf rt em ee -c l r e fma n — r i e em n to e u t o h t rsa eo d ro g i
基于星载GPS数据的GRACE卫星动力学法定轨

0 引 言
近几 年 , 低 轨 卫 星 精 密 定 轨 得 到 了 长 足 的 发 展 。国内外 学者 通 过 各 种 定 轨 手 段 ( 包括 S L R定 轨、 D OR I S定轨 和 星 载 G P S定轨 等 ) , 采用 不 同 的 定 轨方 法 , 可 以 获 得厘 米 级 的定 轨 精 度 [ 1 ] 。2 0 0 2
组合 , 观测 方程 为
P3 一p + c・t 一 C・t +e P 3 ,
年, 用 于观 测地球 重 力场 变化 的 GRAC E卫 星成 功
发 射 。通过 GRA C E卫 星数据 , 科 学家 们得 到 了许
理是 : 根 据 牛顿第 二 运 动 定 律 , 建 立 相 应 的卫 星 运
动 方程 , 利用 给定 的初 始 参 考 历元 和速 度 , 就 可 以 通 过对 加速 度 的二 次积 分 得 到 任 意 历元 的低 轨 卫 星 轨道 , 再 由最小 二乘 估计 给 出每个 历元 相对 于初
第 3 8卷 第 5期 2 0 1 3年 1 O月
全 球 定 位 系 统
G N SS W o rl d of Chi na
Vo 1 .3 8, N O. 5 Oc t 0 be r, 2 0 1 3
基 于 星载 GP S数 据 的 GR AC E卫 星 动 力 学 法 定 轨
和 4 . 9 c m; 通过 S LR 观 测 数 据 进 行 校 验 , 残 差 平均值 为 一1 . 6 c m, 均 方根误 差 为 4 . 7 c m.
关 键词 : GR AC E卫 星 ; 星载 G P S观 测 数据 ; 动力学; 低 轨 卫 星定轨
中图分 类号 : P 2 2 8 . 4 文 献标 志码 : A 文 章 编 号 :1 0 0 8 — 9 2 6 8 ( 2 0 1 3 ) 0 5 — 0 0 0 1 - 0 4
几何精度因子对 GRACE 卫星几何轨道精度影响分析

几何精度因子对 GRACE 卫星几何轨道精度影响分析闫志闯;徐君毅;韩少红【摘要】分析了GDOP值与GRACE卫星几何轨道精度之间的关系,发现定轨精度较差的历元其GDOP值普遍较大甚至异常,进一步研究发现GDOP值异常现象是因剔除个别含有粗差的卫星而导致的,进而通过设置GDOP值阈值的方式剔除发生GDOP值异常的历元。
实验结果表明,GDOP值阈值设置为50,将大于该阈值的历元剔除,能够有效抑制个别历元精度较差的情况,最终的RM S在地固系 X ,Y ,Z 3个方向分别为0.029 m ,0.043 m ,0.029 m ,实现了几何法厘米级精密定轨的目标。
%The relationship between GDOP and the accuracy of geometry orbit of GRACE satellite is analyzed .It is found that the GDOP value is lagre or even abnormal when the orbitting accuracy is poor , and most of such phenomenon is caused by the exclusion of outlier w hich leads to bad geometry .T herefore the threshold of GDOP is set as 50 to delete the observations of the whole epoch .The real data is used to verify the method .The result shows the method can avoid the new abnormal values resulting from outlier detection and exclusion .The RMS in X ,Y ,and Z direction are 0.029 m ,0.043 m ,and 0.029 m respectively , and the goal of centimeter level precise orbiting is achieved .【期刊名称】《测绘工程》【年(卷),期】2015(000)011【总页数】5页(P8-12)【关键词】精密定轨;GRACE;GDOP;精密单点定位;SPODAGRS【作者】闫志闯;徐君毅;韩少红【作者单位】信息工程大学,河南郑州 450052; 西安测绘总站,陕西西安710054;西安测绘总站,陕西西安 710054;西安测绘总站,陕西西安 710054【正文语种】中文【中图分类】P228.4低轨卫星精密定轨一般分为几何法定轨、动力法定轨和约化动力法定轨。
利用GRACE重力卫星求解南极洲冰川质量变化的精度研究

利用GRACE重力卫星求解南极洲冰川质量变化的精度研究Lorant FOLDVARY;Annamaria KISS;苏子校;王广才;王林【期刊名称】《地学前缘》【年(卷),期】2015(022)004【摘要】GRACE重力卫星可用于观测南极洲冰川的质量变化.由GRACE重力卫星提供的月解重力场能有效探测质量的年变化及长期变化(周期和非周期性).通过GRACE观测的质量变化时间序列,计算得到南极洲质量的长期变化及周期性年变化.计算结果受多种误差影响,其中GRACE模型误差的影响较小,而研究时段及其跨度的影响较为显著,以不同宽度的时间窗口进行平移,得到无穷时间序列下该误差的参考值为±14.89 mm/a.南极地区的气压修正误差可达±10 mm/a,GIA修正误差与其量级相同.由此我们认为,目前对于南极洲冰川质量变化的一些认识仍需商榷.南极洲西部地区冰川加速消融,Dronning Maud Land和Enderby Land等地区的质量持续累积;其他地区的质量变化情况仍需进一步研究.【总页数】8页(P239-246)【作者】Lorant FOLDVARY;Annamaria KISS;苏子校;王广才;王林【作者单位】Department of Geodesy and Surveying, Budapest University of Technology and Economics, Budapest H-1111, Hungary ;Faculty of Geoinformatics, University of West Hungary, Sopron 9400,Hungary;Department of Geodesy and Surveying, Budapest University of Technology and Economics, Budapest H-1111, Hungary;中国地质大学(北京)水资源与环境学院,北京100083;中国地质大学(北京)水资源与环境学院,北京100083;Faculty of Science, Technology and Communication, University of Luxembourg, Luxembourg L-1359, Luxembourg【正文语种】中文【中图分类】P312.1【相关文献】1.利用GRACE卫星重力数据监测关中地区地下水储量变化 [J], 李婉秋;王伟;章传银;杨强;冯伟;刘阳2.利用GRACE卫星数据研究汶川地震前后重力场的变化 [J], 段虎荣;张永志;刘锋;康荣华3.从GRACE卫星4.6年观测资料分离2004年苏门答腊-安达曼地震的同震和震后重力变化及利用简正振型叠加模拟同震变化 [J], C. de Linage;L. Rivera;J. Hinderer;J.-P. Boy;Y. Rogister;S. Lambotte;R. Biancale;郭树松(译);祝意青(校);陈石(复校)4.GRACE重力卫星研究南极冰盖质量变化的时空特征 [J], 孙成;陈鸿秉5.利用GRACE重力卫星观测研究近7年云南省水储量变化 [J], 王杰;黄英;曹艳萍;王雁因版权原因,仅展示原文概要,查看原文内容请购买。
低轨卫星的非差运动学精密定轨

低轨卫星的非差运动学精密定轨
王伟;汪海洪;罗佳;钟波
【期刊名称】《大地测量与地球动力学》
【年(卷),期】2009(029)002
【摘要】总结了低轨卫星精密定轨的方法,分析了非差运动学定轨的原理、步骤和定轨精度的影响因素.并将非差运动学定轨与双差运动学、非差简化动力学、双差简化动力学定轨进行比较,发现它可以获得与其他定轨方法相近的精度,并且计算简单.
【总页数】3页(P140-142)
【作者】王伟;汪海洪;罗佳;钟波
【作者单位】武汉大学测绘学院,武汉,430079;地球空间环境与大地测量教育部重点实验室,武汉,430079;武汉大学测绘学院,武汉,430079;地球空间环境与大地测量教育部重点实验室,武汉,430079;武汉大学测绘学院,武汉,430079;地球空间环境与大地测量教育部重点实验室,武汉,430079;武汉大学测绘学院,武汉,430079;地球空间环境与大地测量教育部重点实验室,武汉,430079
【正文语种】中文
【中图分类】P227
【相关文献】
1.基于Kalman滤波的低轨卫星运动学精密定轨快速算法 [J], 张守建;赵磊
2.基于历元间差分的低轨卫星运动学精密定轨 [J], 陈俊平;王解先
3.SPODS软件低轨卫星运动学精密定轨精度分析 [J], 阮仁桂;冯来平;吴显兵;
4.Swarm系列卫星非差运动学厘米级精密定轨 [J], 张兵兵;牛继强;王正涛;徐丰;田坤俊
5.非差运动学精密定轨伪距和相位加权分析 [J], 刘荣芳;王文彬
因版权原因,仅展示原文概要,查看原文内容请购买。
应用GRACE卫星星历数据反演地球重力场模型

应用GRACE卫星星历数据反演地球重力场模型张兴福;沈云中【摘要】讨论了基于GRACE卫星星历数据反演地球重力场模型的动力学法,给出了综合考虑估计加速度计尺度、偏差和卫星初始位置的算法.利用26天GRACE卫星精密轨道数据和加速度计数据解算出直到36阶次的地球重力场模型GRACE01S_OR.采用不同模型位系数差的阶方差和不同模型所表示的大地水准面的差值的方法对该模型进行了外部检核.结果表明:该模型的精度优于相同阶次的EGM96模型和EIGEN2模型,而与同阶次的CHAMP03S和CG01C模型的精度非常接近.【期刊名称】《桂林理工大学学报》【年(卷),期】2009(029)001【总页数】4页(P106-109)【关键词】动力学法;GRACE;尺度和偏差参数;初始位置误差;重力场模型【作者】张兴福;沈云中【作者单位】广东工业大学,测绘工程系,广州,510006;同济大学,测量与国土信息工程系,上海,200092【正文语种】中文【中图分类】P2230 引言应用卫星跟踪卫星技术(SST)反演地球重力场模型已经成为当今大地测量学界的研究热点之一,该方法主要是把低轨卫星作为地球重力场的传感器,通过跟踪卫星获得的观测量来反演地球重力场模型。
卫卫跟踪技术可分为高低卫卫跟踪(hl-SST)和低低卫卫跟踪(ll-SST)两种跟踪模式,CHAMP卫星和GRACE卫星是以上两种跟踪方式的代表。
在CHAMP卫星和GRACE卫星发射之前,影响地球重力场模型精度的主要因素为缺乏基准统一并覆盖全球的观测数据。
而卫卫跟踪技术恰恰可以弥补以上缺点,其优越性主要表现在:星载GPS接收机能提供基准统一、高覆盖率、高精度的全球框架下的卫星坐标;星载加速度计能提供高精度的非保守力摄动加速度,除此之外GRACE卫星星间测距系统能提供高精度的星间距离以及相应的衍生观测量——距离变率和距离加速度,这些观测量精度更高,对地球重力场信息的探测更敏感。
GRACE星载GPS非差观测值简化动力学定轨

GPS Onb a d Ze o Dif r n e Ob e v to t o r r - f e e c s r a i n Da a
PA N G Zhe — i , LI N G a— U n x ng A H lO , XI O u , LI io g n ’ A Y n U X a — a g。。
( . ’n Ree rh I siueo u v y n n p n 1 Xia sa c n ttt f S r e i g a d Ma pig,Xia 1 0 4, hia ’n 7 0 5 C n 2.n tt t f S r e i g a d Ma pig, n o ma inEn n e rn ie st , e g h u 4 0 5 ,C ia I siueo u v y n n p n I f r to gier ig Un v riy Zh n z o 5 0 2 h n 3. yLa oa o y o Ke b r tr f GNRS Ree rh sa c ,Mi ity o u a in Wu a ie st , h n 4 0 7 C n n sr f Ed c to , h n Un v riy Wu a 3 0 9, hia)
GRACE卫星星载GPS非差观测值简化动力学定轨方法的研究.

GRACE 卫星星载 GPS 非差观测值简化动力学定轨方法的研究入的是 GRACE 双频载波相位观测量、上步生成的改进轨道、GPS 精密行历、30 秒一点的 GPS 卫星钟差、极移文件,由于处理的是非差观测值,引入了 GPS 星历误差和 GPS 卫星钟的误差,所以在数据处理模块中,当探测到周跳发生时,都不做修复,而是通过设置待解模糊度来消除周跳影响。
5精密星历生成模块此模块利用上步平滑过的载波相位测量数据,30 秒一点的 GRACE 卫星双频伪距观测值、GPS 精密行历、极移文件和 30 秒一点的 GPS 卫星钟差,(2步生成的 GRACE 卫星几何星历,以及(3步生成的标准轨道和光压偏导数文件,估计的参数包括 6 个密切轨道根数、9 光压系数、每 3 分钟一组的 RTN 方向的伪随机脉冲参数和每 30 秒一点的GRACE 卫星精密星历。
步骤(5完成后,利用生成的精密星历重复实施步骤(3~(5,对 GRACE 卫星的标准轨道进行改进,和载波相位数据进行再平滑。
一般重复两遍,即可得到 GRACE 卫星较高精度的轨道。
4.2 算例分析为了验证简化动力学定轨精度,本文采用 GRACE-B(Gravity Recovery and Climate Experiment卫星2004.4.15~17 日三天的星载 GPS 观测数据(ftp://data.gfz-potsdam.de/进行定轨研究,定轨弧长为 3 分钟,每次采用一天的数据进行计算。
为了比较定轨精度,本文将定轨结果与 JPL 精密星历进行了对比分析,并利用当天的激光测距数据进行了检核。
与 JPL 精密星历对比结果如下表 1 和图 1、 2、 3。
从表中可以看出,与JPL 精密星历比较残差在 4.0~6.0cm 之间,平均为 5.1cm。
表 1 与 JPL 精密星历比较结果(cm 最大值 X 方向差值 4.15 Y 方向差值 Z 方向差值 X 方向差值 4.16 Y 方向差值 Z 方向差值 X 方向差值 4.17 Y 方向差值 Z 方向差值 25.4 22.8 13.1 27.6 28.1 22.7 15.6 17.8 18.6 最小值 -13.4 -13.4 -23.1 -17.9 -25.2 -26.5 -17.5 -26.7 -25.1 平均值3.4 3.8 3.1 4.3 4.6 4.1 4.0 4.1 3.8 标准差 4.4 4.7 4.0 5.4 6.0 5.6 5.2 5.5 5.1 6CSNC2010 第一届中国卫星导航学术年会北京图 1 4.15 日定轨结果与 JPL 精密星历比较图图 2 4.16 日定轨结果与 JPL 精密星历比较图图 3 4.17 日定轨结果与JPL 精密星历比较图由于这 3 天 GRACE-B 卫星都有激光测距数据,可以用独立的激光测距数据检核定轨精度,检核结果见下表 2。
【国家自然科学基金】_运动学定轨_基金支持热词逐年推荐_【万方软件创新助手】_20140803
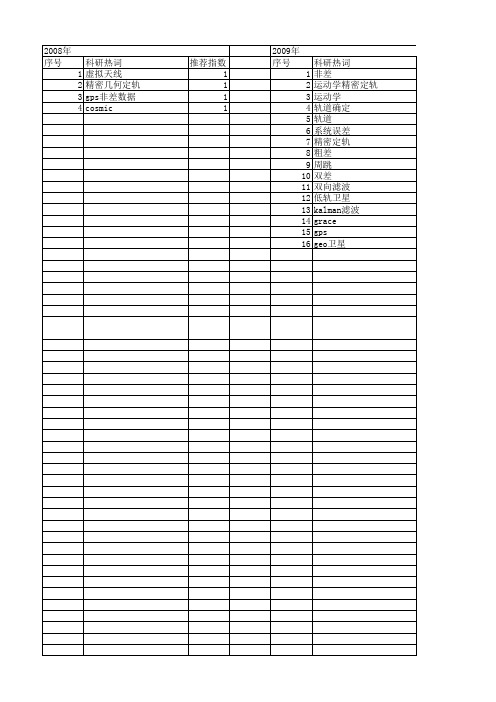
科研热词 虚拟天线 精密几何定轨 gps非差数据 cosmic
推荐指数 1 1 1 1
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
科研热词 非差 运动学精密定轨 运动学 轨道确定 轨道 系统误差 精密定轨 粗差 周跳 双差 双向滤波 低轨卫星 kalman滤波 grace gps geo卫星
推荐指数 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
科研热词 推荐指数 精密定轨 3 运动学 2 grace 2 高度角 1 非差 1 随机模型 1 鉴别 1 运动学方法 1 载噪比 1 轨道确定 1 误差分析 1 落月轨迹 1 统计定轨 1 相位非差 1 有源假目标 1 星载gps 1 探月二期 1 归一化残差 1 弹道目标跟踪 1 嫦娥一号 1 vlbi 1 usb 1 levenberg-marquardt迭代法 1 champ 1
2011年 序号 1 2 3 4 5 6 7 8
2011年 科研热词 航天器 缩减动力学 相位历元差 方法:数据分析 定轨 天体力学 双频gps 卫星 推荐指数 1 1 1 1 1 1 1 1
2012年 序号 1 2 3 4 5 6 7 8 9 10 11 12
科研热词 推荐指数 运动学定轨 1 航天器 1 月面数字高程模型(dem) 1 月球着陆器 1 方法 1 数据分析 1 导航卫星 1 定位 1 天体力学 1 初轨 1 低轨卫星 1 gnss 1
2013年 序号 1 2 3 4 5 6 7 8 9
利用GPS非差观测值的GRACE卫星精密定轨

第2 第3 7卷 期
20 0 6年 5月
宇 航 学 报
Ju l f t n ui o ma r a t s o As o c
Vo . 7 1 2 No. 3 Ma v 20 06
利 用 G S非 差观 测 值 的 G A E卫 星精 密定 轨 P RC
收机 就可 完成 卫星 的高精 度定 轨 。
合作 的空间地 球 重力 测 量 和气 候 实 验计 划 , 由两 颗
完全 相 同 , 间相 距 2 0公 里 的 低 轨 卫 星 组 成 。 空 0 ] 卫 星高 度 5 0公里 , 0 采用 近极轨 道平 面 , 星上 主要 设
备 包括 : P 收机 、 / a 段测 距 系 统 、 星照 相 G S接 KK 波 恒
仪 和 精 密 加 速 度 计 。星 载 加 速 度 计 测 量 精 度 为 lm s, n / 星载恒 星照 相仪 的测 量精度 为 1 度秒 。 0弧
1 卫星 动力法 定轨
最近 国 际 上 研 究 较 多 的 精 密 单 点 定 位 方 法
( P r i o t oioi ) 用 I S提供 的 G S卫 P PPe s P i si n 利 c e n P tn g G P 星精 密星 历和精 密 钟 差 数 据 , 时 采用 多 种 改 正技 同 术对测 量误差 进行 改正 , 然后 进行 非差定 位 , 得 了 取 很好 的定位 结 果 。L cae 在 19 ahpl l 9 5年基 于 G S码 P
度和可 靠性 。本 文采用 星载加 速 度计测量 卫星 非保 守力 , 降低 由于模 型误差 引起 的轨 道误差 , 时提 高 同
卫 星定 轨 的可 靠性 。 本 文 以 G A E 卫 星 为 研 究 对 象。G A E RC R C ( r i eoe n l a x e m n) 划是 美 德 G a t R cvr a dCi t E pr et计 vy y me i
低轨卫星精密定轨算法研究及初步结果分析

低轨卫星精密定轨算法研究及初步结果分析作者:袁凡来源:《硅谷》2014年第19期摘要卫星的精密定轨指的是从观测数据中获取指定预报开始时刻的高精度参数轨道。
由于GPS观测数据中不可避免的带有随机误差和系统误差等非线性影响因素,因而不可能确定一条能够精确地拟合所有观测值的轨道,所以需要利用大量的观测数据使用统计学原理对航天器轨道状态进行估计。
本文以低轨卫星为研究对象,分析了精密定轨的基本理论方法,包括摄动力模型以及最小二乘估计法。
最后分别通过批处理和递推算法对GRACE-A卫星数据进行计算,实现了低轨卫星的定轨,并达到了一定的精度。
关键词精密定轨;非线性影响;最小二乘估计;递推中图分类号:V19 文献标识码:A 文章编号:1671-7597(2014)19-0029-03人造地球卫星的运动,可以当作是一个受摄二体问题,所涉及的数学模型是一个比较复杂的非线性动力学模型。
从数学的角度上看,精密定轨就是将一个常微分方程问题转化为边值问题,再由边值条件反过来确定初值。
同时,在这个过程中,不能简单的将一个初值问题转化为边值问题来求解,还需要用到大量观测数据的统计特性,这将涉及到最优估计问题。
目前,在卫星精密定轨中,最为常用的是最小二乘估计法。
传统的最小二乘估计法是用于卫星的事后轨道确定,也称为批处理算法定轨。
批处理算法的优点是实现简单,稳定性好,对先验知识的要求少。
但是,当观测数据含有非线性误差的时候,批处理算法不具有抗干扰性,得到的估值可能具有较大的偏差。
这种算法在观测数据比较大的情况下,数据存储量太大,不便于计算,因而又有人提出避免量大的递推算法。
递推算法是将观测序列按时间顺序分成若干批,每次处理一批观测量,得到定轨结果后带到下一批数据中,从而递推去处理下一批观测量,与批处理算法中将一批观测量进行处理获得估计值不同。
传统的最小二乘估计是没有初始估计的,但是利用递推算法,也能够导出有初始估计条件下的最小二乘估计公式。
GRACE卫星精密定轨随机模型精化

GRACE卫星精密定轨随机模型精化张守建;李建成;邹贤才;邢乐林【期刊名称】《地球物理学报》【年(卷),期】2010(053)007【摘要】合理的随机模型是确定高精度卫星轨道的前提条件,目前广泛应用于地面观测数据的随机模型主要有高度角模型和载噪比模型,本文通过对GRACE卫星实测数据的分析表明上述随机模型均不能很好地描述GRACE卫星星载GPS观测值的噪声特点,为此,文中提出了扩展的高度角模型和扩展的载噪比随机模型.利用自主研发的精密定轨软件,分别采用高度角模型、扩展的高度角模型、载噪比模型、扩展的载噪比模型对GRACE卫星进行了轨道确定.数值结果表明:(1)高度角模型的运动学轨道径向精度为3.4 cm,扩展的高度角模型的为3.3 cm;(2)载噪比模型的运动学轨道径向精度为4.9 cm,扩展的载噪比模型的则为3.4 cm,精度提高了1.5 cm.经比较分析,文中提出的扩展的高度角模型和载噪比模型能更好地描述GRACE卫星观测值噪声特点,并能取得更高的卫星定轨精度.【总页数】8页(P1554-1561)【作者】张守建;李建成;邹贤才;邢乐林【作者单位】武汉大学测绘学院,武汉,430079;武汉大学测绘学院,武汉,430079;武汉大学地球空间环境与大地测量教育部重点实验室,武汉,430079;武汉大学测绘学院,武汉,430079;中国地震局地震研究所,武汉,430071【正文语种】中文【中图分类】P228【相关文献】1.利用GPS非差观测值的GRACE卫星精密定轨 [J], 杨龙;董绪荣2.北斗GEO/IGSO/MEO卫星观测值精度分析及随机模型精化 [J], 刘永建;江勇3.伪随机脉冲在北斗卫星精密定轨中的应用 [J], 任锴;宋小勇;贾小林;4.GPS天线相位中心校正对GRACE卫星精密定轨的影响 [J], 陈梦;孟瑞祖;袁俊军5.北斗卫星天线相位中心改正模型精化及对精密定轨和定位影响分析 [J], 张勤;燕兴元;黄观文;解世超;曹钰因版权原因,仅展示原文概要,查看原文内容请购买。
重力卫星星载gps简化动力学精密定轨

第34 卷 第4 期
王跃,张德志,张帆.重力卫星星载GPS简化动力学精密定轨
557
SWARM卫星简化动力学轨道与德国地学研究 中心(German Research Centre for Geosciences, GFZ)、ESA提供的精密轨道对比,进行轨道外符 合精度评定。
1简化动力学定轨理论
低轨卫星在复杂的太空环境下绕地球飞行 时会受到多种摄动力的影响,主要包括地球非球 形摄动、多体摄动和地球潮汐摄动等保守摄动力 和太阳辐射压、地球辐射压和大气阻力等非保守 摄动力。在这些摄动力的影响下,低轨卫星运动 方程为"n1# :
向的轨道精度分别达到0 8 cm、1. 3 cm和1. 6 cm$实验表明,基于简化动力学方法,GRACE和SWARM卫
星定轨精度均到达厘米级$
[关键词# 重力卫星;星载全球定位系统(GPS);简化动力学;精密定轨
[中图分类号]P228 4
[文献标识码]A
[文章编号]1007-3000(2020)04-0556-5
的轨道可以表示为:
& rt = r0 () +
r()(p, - p,0) (2)
4p?
式中,p?为轨道参数,星运动方程
中引入伪随机脉冲参数,以充分利用动力学信息
和几何信息,从而提高低轨卫星定轨精度"#。
2定轨策略与数据来源
本文采用 CODE(Center for Orbit Determi
重力卫星星载GPS简化动力学精密定轨
王跃张德志张帆
(山东科技大学测绘科学与工程学院,山东青岛266590)
[摘 要# 利用GRACE和SWARM重力卫星星载GPS观测数据,基于简化动力学方法进行精密定
利用GPS非差观测值的GRACE卫星精密定轨

利用GPS非差观测值的GRACE卫星精密定轨
杨龙;董绪荣
【期刊名称】《宇航学报》
【年(卷),期】2006(027)003
【摘要】参照GPS精密单点定位(PPP,Precise Point Positioning)模型设计了一种新的卫星定轨方法-组合星载加速度计测量数据和IGS提供的GPS精密星历及精密钟差数据进行低轨卫星的精密定轨.利用星载加速度计提高卫星受力模型准确性,使动力法定轨精度和可靠性都得到提升.同时,采用多种改正技术提高GPS非差观测值测量精度,保证最终高精度卫星定轨.本文建立了卫星定轨的轨道滤波模型,得出了有益的结论,即采用星载加速度计测量卫星非保守力可提高卫星定轨精度,在
ITRF2000参考系下三轴精度优于18cm.这种方法不需要在全球建立基准观测站,定轨设备简单,费用低廉.
【总页数】6页(P373-378)
【作者】杨龙;董绪荣
【作者单位】装备指挥技术学院,导航研究中心,北京,101416;装备指挥技术学院,导航研究中心,北京,101416
【正文语种】中文
【中图分类】V19
【相关文献】
1.星载GPS非差精密定轨精度分析 [J], 赵春梅;欧吉坤;孙保琪
2.GRACE星载GPS非差观测值简化动力学定轨 [J], 庞振兴;梁海鸥;肖云;刘晓刚
3.GPS天线相位中心校正对GRACE卫星精密定轨的影响 [J], 陈梦;孟瑞祖;袁俊军
4.基于星载GPS技术GRACE-A卫星非差运动学定轨 [J], 崔腾飞; 王友存; 张涛; 相涛
5.GPS卫星轨道及钟差对GRACE卫星定轨精度影响 [J], 王雅婷;游为;余彪;范东明;熊宇昊
因版权原因,仅展示原文概要,查看原文内容请购买。
用于低轨卫星精密轨道确定的简化动力学法

用于低轨卫星精密轨道确定的简化动力学法
S.C.Wu;C.L.Thornton;柳仲贵;张纪生
【期刊名称】《飞行器测控学报》
【年(卷),期】1996(000)003
【摘要】全球定位系统(GPS)的测量量可促成一种简化动力学法,用于近地卫星的近厘末级定轨。
利用这种方法,不同观测时刻的卫星状态间的转移由正规的动力学模型和由连续GPS载波相位数据以运动学法导出的卫星位置变化来完成。
动力学信息和运动学信息间的相对权重可自由变化。
协方差分析表明:当观测几何差而动力学模型好时,模型支配着状态转移的计算;动力模型差而观测几何好时,载波相位统治着状态转移的计算;而当运动学和动力学信息间没有明显优劣时,简化动力学联合法可显著提高轨道精度。
本文给出简化动力学法中准最佳的择权准则,并研究了求解精度对权的敏感性。
【总页数】1页(P67)
【作者】S.C.Wu;C.L.Thornton;柳仲贵;张纪生
【作者单位】无
【正文语种】中文
【中图分类】V412.41
【相关文献】
1.用单频GPS数据实现低轨卫星动力学法定轨研究 [J], 张德成;郑作亚;王霞迎;李伟
2.基于GPS数据的CHAMP卫星简化动力法轨道确定 [J], 盛传贞;李庆盛;魏忠勇;姬张建;肖长伟
3.风云四号卫星双程测距系统精密轨道确定 [J], 宋叶志; 黄勇; 杨建华; 胡小工; 杨旭海
4.BDS在低轨卫星编队高精度相对轨道确定上的应用分析 [J], 易彬;谷德峰;邵凯;易东云
5.分布式InSAR编队卫星精密绝对和相对轨道确定 [J], 邵凯;张厚喆;秦显平;黄志勇;易彬;谷德峰
因版权原因,仅展示原文概要,查看原文内容请购买。
GRACE卫星非差简化动力学定轨研究

GRACE 卫星非差简化动力学定轨研究益鹏举①②,赵春梅①,郑作亚②(①中国测绘科学研究院 大地测量与地球动力学研究所,北京 100830;②山东科技大学 测绘科学与工程学院,山东 青岛 266510)【摘 要】本文基于卫星精密定轨的基本理论,研究了GRACE 卫星非差简化动力学定轨的方法;并用自行研制的定轨软件CASMORD 对实测的星载GPS 数据进行非差数据的简化动力学定轨,通过比较GRACE 卫星解算的轨道与JPL 事后轨道及SLR 测距信息,结果表明:利用非差观测值进行GRACE 卫星的简化动力学定轨,三维位置精度(3D-RMS )优于7cm ,X 、Y 、Z 方向RMS 约为3~5cm ,从而论证了该方法的可行性、实用性。
【关键词】非差;GRACE 卫星;简化动力学定轨;星载GPS【中图分类号】P228 【文献标识码】A 【文章编号】1009-2307(2011)03- - GRACE reduced-dynamic orbit determination using zero-difference dataAstract: Based on the basic theory of Precise Orbit Determination, the method of the reduced-dynamic orbit determination using zero-difference data onboard GPS observations was researched in this paper. The orbit of GRACE satellite was determined by the autonomic software CASMORD. Compared GRACE orbiting results of reduced-dynam i c m et hod’s solutions with JPL ’s PSO and SLR measurement, the results showed that the 3D-RMS was better than 7 cm and the direction of X ,Y ,Z was about 3~5 cm, to demonstrate the feasibility and practicability of this method.Key words: zero difference ;GRACE satellite ;reduced-dynamic orbit determination ;onboard GPS YI Peng-ju ①②, ZHAO Chun-mei ①, ZHENG Zuo-ya ②(①Institute of Geodesy and Geodynamics, Chinese Academy of Surveying and Mapping, Beijing 100830, China; ②Geomatics College, Shandong University of Science and Technology, Qingdao 266510, China)1 引言随着低轨卫星在国民经济、军事、科研等方面的广泛应用,各国发射的低轨卫星越来越多,这些卫星身负着不同的科学任务,为各国的经济发展及科研事业做出了贡献。
GRACE星载GPS非差观测值简化动力学定轨

GRACE星载GPS非差观测值简化动力学定轨
庞振兴;梁海鸥;肖云;刘晓刚
【期刊名称】《测绘科学技术学报》
【年(卷),期】2010(27)6
【摘要】利用GRACE卫星的实测数据研究了重力卫星精密定轨问题;针对简化动力学精密定轨方法给出了一种有效的星载数据编辑、处理策略.编制了相应的软件,并利用该软件处理了GRACE-B卫星3 d的实测数据;通过与JPL公布的轨道导航解比较,以及激光观测值检验的方式分析了卫星轨道的精度.结果显示,利用简化动力学定轨方法解算的轨道精度在6 cm以内,能够满足重力场反演对轨道精度的要求.【总页数】4页(P412-415)
【作者】庞振兴;梁海鸥;肖云;刘晓刚
【作者单位】西安测绘研究所,陕西西安710054;西安测绘研究所,陕西西安710054;西安测绘研究所,陕西西安710054;信息工程大学测绘学院,河南郑州450052;武汉大学卫星导航与定位教育部重点实验室,湖北武汉430079
【正文语种】中文
【中图分类】P228
【相关文献】
1.基于星载GPS双频观测值的简化动力学定轨方法 [J], 韩保民
2.利用GPS非差观测值的GRACE卫星精密定轨 [J], 杨龙;董绪荣
3.星载GPS相位观测值非差运动学定轨探讨 [J], 郑作亚;蔡五三;黄珹;程宗颐;冯初
刚
4.基于星载GPS技术GRACE-A卫星非差运动学定轨 [J], 崔腾飞; 王友存; 张涛; 相涛
5.基于星载GPS数据的Jason-3卫星简化动力学和运动学法精密定轨 [J], 郭恒洋;郭金运;杨洲铭;齐林虎;赵春梅
因版权原因,仅展示原文概要,查看原文内容请购买。
基于星载 GPS 数据的 GRACE 卫星动力学法定轨

基于星载 GPS 数据的 GRACE 卫星动力学法定轨张德成;郑作亚;刘娴;李兵【期刊名称】《全球定位系统》【年(卷),期】2013(38)5【摘要】利用GRACE A 卫星的星载GPS 观测数据,采用非差动力学低轨卫星定轨方法,解算了2012年1月11日至18日的卫星轨道,将得到的结果与G FZ发布的RS O轨道进行对比分析,并通过SLR观测数据进行轨道的校验。
结果表明:定轨精度满足低轨卫星精密定轨的要求,与RS O轨道比较,在 X、Y 、Z方向的均方根误差的平均值分别为4.7 cm、4.3 cm和4.9cm ;通过SLR观测数据进行校验,残差平均值为-1.6cm,均方根误差为4.7cm.%Using zero-difference satellite-borne GPS data ,the orbit of GRACE A satel-lite by dynamic method with GPS observations is determined during the period from January 11 to 18 ,2012 .The orbit results will be compared with RSO which were released by GFZ , and be verified by SLR observation .The comparison results show that the accuracy of orbit determination canmeet the requirement of LEO satellite .Compared with the RSO orbit inX ,Y ,Z direction ,the average of RMS is 4 .7 cm ,4 .3 cm and 4 .9 cm respectively .Calibra-ted with SLR observation ,the mean of residuals is -1 .6 cm ,and the RMS is 4 .7 cm .【总页数】4页(P1-4)【作者】张德成;郑作亚;刘娴;李兵【作者单位】山东科技大学测绘科学与工程学院,山东青岛266590; 中国测绘科学研究院大地测量与地球动力研究所,北京100830;山东科技大学测绘科学与工程学院,山东青岛266590;北京工业大学计算机学院,北京100124;山东科技大学测绘科学与工程学院,山东青岛266590; 中国测绘科学研究院大地测量与地球动力研究所,北京100830【正文语种】中文【中图分类】P228.4【相关文献】1.用单频GPS数据实现低轨卫星动力学法定轨研究 [J], 张德成;郑作亚;王霞迎;李伟2.GRACE星载GPS非差观测值简化动力学定轨 [J], 庞振兴;梁海鸥;肖云;刘晓刚3.基于星载GPS技术GRACE-A卫星非差运动学定轨 [J], 崔腾飞; 王友存; 张涛; 相涛4.基于星载GPS数据的Jason-3卫星简化动力学和运动学法精密定轨 [J], 郭恒洋;郭金运;杨洲铭;齐林虎;赵春梅5.由星载GPS双差相位数据进行CHAMP卫星动力学定轨 [J], 郭金运;黄金维;胡建国;李建成因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
GRACE 卫星非差简化动力学定轨研究益鹏举①②,赵春梅①,郑作亚②(①中国测绘科学研究院 大地测量与地球动力学研究所,北京 100830;②山东科技大学 测绘科学与工程学院,山东 青岛 266510)【摘 要】本文基于卫星精密定轨的基本理论,研究了GRACE 卫星非差简化动力学定轨的方法;并用自行研制的定轨软件CASMORD 对实测的星载GPS 数据进行非差数据的简化动力学定轨,通过比较GRACE 卫星解算的轨道与JPL 事后轨道及SLR 测距信息,结果表明:利用非差观测值进行GRACE 卫星的简化动力学定轨,三维位置精度(3D-RMS )优于7cm ,X 、Y 、Z 方向RMS 约为3~5cm ,从而论证了该方法的可行性、实用性。
【关键词】非差;GRACE 卫星;简化动力学定轨;星载GPS【中图分类号】P228 【文献标识码】A 【文章编号】1009-2307(2011)03- - GRACE reduced-dynamic orbit determination using zero-difference dataAstract: Based on the basic theory of Precise Orbit Determination, the method of the reduced-dynamic orbit determination using zero-difference data onboard GPS observations was researched in this paper. The orbit of GRACE satellite was determined by the autonomic software CASMORD. Compared GRACE orbiting results of reduced-dynam i c m et hod’s solutions with JPL ’s PSO and SLR measurement, the results showed that the 3D-RMS was better than 7 cm and the direction of X ,Y ,Z was about 3~5 cm, to demonstrate the feasibility and practicability of this method.Key words: zero difference ;GRACE satellite ;reduced-dynamic orbit determination ;onboard GPS YI Peng-ju ①②, ZHAO Chun-mei ①, ZHENG Zuo-ya ②(①Institute of Geodesy and Geodynamics, Chinese Academy of Surveying and Mapping, Beijing 100830, China; ②Geomatics College, Shandong University of Science and Technology, Qingdao 266510, China)1 引言随着低轨卫星在国民经济、军事、科研等方面的广泛应用,各国发射的低轨卫星越来越多,这些卫星身负着不同的科学任务,为各国的经济发展及科研事业做出了贡献。
为了保障不同种类的低轨卫星完成相应的科学任务,卫星的精密定轨便成为卫星顺利完成其任务的重要前提之一。
相对传统的SLR 动力学定轨精度差及纯几何法定轨受观测值品质,卫星观测几何图形等的影响比较大,并且得到的轨道是一组离散的点,轨道外推精度差等原因,1992年,美国和法国联合研制TOPEX/POSEIDON (T/P )卫星,采用星载GPS 定轨的新方法,该方法由Yunck 等科学家于1986年提出,对TOPEX/POSEIDON (T/P )卫星的定轨精度,已达厘米级。
由此,采用星载GPS 定轨便成为众多低轨卫星定轨的新手段。
星载GPS 定轨按观测方程的不同组合分为非差、单差、双差,按是否考虑摄动力及与摄动力模型的关系可分为动力学定轨、几何法定轨、简化动力学定轨。
本文采用非差简化动力学定轨的方法,以GRACE 卫星为例,分析研究了GRACE 卫星的精密定轨。
本文主要探讨利用GRACE 卫星星载GPS 观测值及GPS 精密星历及钟差,采用星载GPS 定轨中的非差简化动力学定轨方法进行GRACE 卫星的定轨。
该方法采用非差定轨,利用星载GPS 观测数据,以无电离层线性组合的相位观测值作为观测量对GRACE 卫星进行简化动力学定轨,并将GRACE 卫星解算的结果与JPL 发布的事后轨道(PSO )及SLR 高精度测距信息进行比较,结果表明:该方法能够充分吸收GPS 几何法定轨和动力学法定轨的优点,同时顾及低轨卫星的动力学状态信息以及几何信息,通过两者权信息的适当调整,以此达到改善定轨精度的目的。
从而论证了该定轨方法及解算方案的可行性、实用性。
2 观测模型2.1 基本观测方程LEO 卫星与GPS 卫星(G )之间的相位观测和伪距观测基本方程分别为[1,2]:,.G G G L i L Lion i i P c t c t e ρδδδρ=+⋅−⋅++ (1) ,,,,,GG G G G L i L L ion i rel pco i pco i i L i i L c t c t N ρδδδρδρδρδρλε=+⋅−⋅−++++⋅+ (2)DOI :CNKI:11-4415/P.20101130.1621.046 网络出版时间:2010-11-30 16:21网络出版地址:/kcms/detail/11.4415.p.20101130.1621.046.html式中,i 表示两个频率1L 和2L ;,G L i L 为相位非差观测值;,G L i P 为伪距观测值(伪距);G L ρ为站星间几何距离;c 为真空中光速;L t δ为低轨卫星钟差改正;G t δ为GPS 卫星钟差改正;i ion ,δρ为电离层延迟;rel δρ为相对论改正;i pco ,δρ为相位中心改正;i λ为GPS 信号波长(1L 或2L );,G L i N 为非差整周模糊度;i ε为相位噪声(1L 或2L );i e 为伪距噪声。
由于GRACE 卫星的轨道高度约485km ,而对流层在40km 以下,所以,星载GPS 接收机不受对流层延迟的影响。
另外,多路径效应也由于经过对天线高度的精心设计而大大削弱,因此,上述方程没有考虑这种影响。
2.2 无电离层LC 组合 为了消除电离层的影响,进行无电离层LC 组合[3]。
码和相位观测的无电离层LC 组合为:2212,3,1,222221212G G G L L L f f P P P f f f f =−−− (3) 2212,3,1,222221212GG G L L L f f L L L f f f f =−−− (4) 由式(3)、(4)得码和相位观测方程为:码观测方程为:,3,33G G G L L L P c t c t e ρδδ=+⋅−⋅+ (5)相位观测方程为:,3,3,3,33GG G G G L L L pco pco L L c t c t B ρδδδρδρε=+⋅−⋅++++ (6)式中: 2212,3,1,222221212pco pco pco f f f f f f δρδρδρ=−−− 2212,3,1,222221212G G G pco pco pco f f f f f f δρδρδρ=−−− (),31,12,22212G G G L L L c B f N f N f f =⋅−⋅− 在非差简化动力学定轨方法中,如果高精度的GPS 卫星轨道和卫星钟是可靠的,则非差简化动力学精密定轨是一个有效的定轨方法,它不涉及繁杂的地面IGS 站并且动力学模型是简化的。
由于精密星历和钟差是事后得到的,IGS 提供的精密星历和钟差约为13天,CODE 提供的约为5-11天。
因此,在无法获得实时GPS 精密星历和钟差的情况下,对LEO 的定轨都为事后处理。
本文即为基于IGS 精密卫星星历及钟差的事后LEO 定轨。
3 简化动力学模型对于遵循牛顿第二定律、在轨运行的低轨卫星来说,除受到地球的中心引力外,还受到各种各样力的作用,在这些力当中,地球的中心引力是主要的,它规定着卫星运行的总体轨迹,而其它力在总体轨道不变的情况下,对卫星起着次要的摄动作用。
中心引力与摄动力共同规定着低轨卫星的运行轨迹。
总体上可将作用于LEO 卫星的力分为:除二体中心引力以外的保守力与非保守力,事实上,中心引力亦为保守力,在这里只不过把作用于LEO 主要的力与次要的力分开,便于问题的分析、说明。
在惯性系中,低轨卫星的运动方程为[4-6]: NG G TB f f f r ΓΓΓ##Γ++= (7) 其中,r ##Γ为卫星的加速度,等式右边为作用于卫星单位质量上的力。
TB f Γ为地球对卫星的二体中心引力;G f Γ,NG f Γ分别为除中心引力外的保守力和非保守力。
并且 RL TD NS NB G f f f f f ΓΓΓΓΓ+++= TH AL DG SR NG f f f f f ΓΓΓΓΓ+++= 式中:NB f Γ为N 体摄动力;NS f Γ为地球非球形部分对卫星的力;TD f Γ为地球潮汐与自转形变对卫星的摄动力;RL f Γ为相对论效应对卫星的压力;SR f Γ为太阳辐射对卫星造成的压力;DG f Γ为大气阻力摄动;AL f Γ为地球红外辐射和地球反射太阳光压摄动;TH f Γ为作用在卫星上的其他力,如姿态控制力等。
对于上述方程,一般来说,很复杂,除二体问题外尚无法得到严格的解析解,只有在某些近似的假设下方可得到近似的解析解,对于轨道精度要求要求不太高的卫星,一阶近似解很有效,对于轨道精度要求较高的卫星,解析解难以获得。
由此,可将运动方程用数值积分的方法表示为:⎪⎩⎪⎨⎧==+=00000)(,)(),,,()(r t r r t r t r r F r F r #Γ#ΓΓΓ#ΓΓΓΓΓ##Γεε (8) 式中,0F Γ是地球中心引力;εF Γ是各种摄动力;0000)(,)(r t r r t r #Γ#ΓΓΓ==为初始条件。
对于低轨卫星来说,上述SLR 动力学定轨随轨道高度降低轨道精度急剧下降的限制。
采用简化的动力学模型,并通过估计载体速度随机噪声,用与时间有关的随机脉冲参数来吸收卫星动力学模型的误差。
