折射和反射定律、菲涅耳公式
Fresnel(菲涅尔)公式

d=z=
2π
λ0
n12 sin2 i1 − n22 ;(3)波矢常数: k2 sin i2 > k2 。
应用:近场光学
15
1.3 反射率和透射率
W1
=
I1σ
cos i1
=
n1 2
ε0 μ0
A1 2 cos i1
W1′ =
I1′σ
cos i1
=
n1 2
ε0 μ0
A1′ 2 cos i1
W2
=
I2σ
cos i2
2.4
2.2
n =1.33 1
n =1
2.0
2
r
r
s
p
1.8
t
t
s
p
1.6
1.4
1.2
i
c
1.0
0.8
0.6
0.4
0.2
i
B
0.0
-0.2 0
10
20
30
40
50
60
i
1
12
全内反射的应用: 1、导波光学 Waveguide / Optical fiber
n 1
n <n , n <n 12 32
n 2
1
Stocks 公式:
A
Ar
Att'
Ar
Arr
Art
At
Atr'
At
Arr + Att′ = A 可知: Art + Atr′ = 0
r2 + tt′ = 1 r + r′ = 0
2
1.2 振幅反射(透射)比 相位跃变(相移) 1、透射比与相位跃变
一、 菲涅耳公式(Fresnel formula)
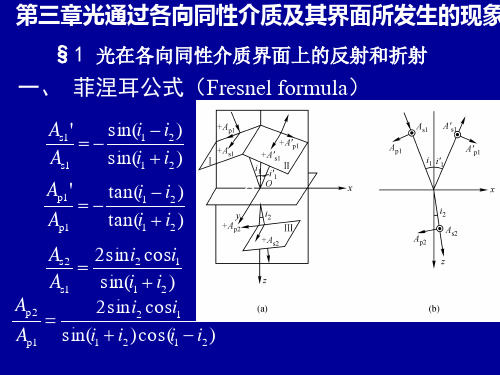
1
4
紫光的散射强度大约是红光的10倍。
4. 偏振性
O z
y p B’
y D A’ B
AP z
x
D’ 实验 自然光入射到散射物质中,观察到:
正侧方(z)线偏振 斜方向(C)部分偏振 对着x方向(x)自然光
解释 用电偶极子次级辐射可解释 实验现象
分解成 +
被微粒散射时,各方向上的振幅可看成以上 两个分振动的合成。 退偏振 线偏振光照射某些气体或液体,从侧向 观察时,散射光变成部分偏振的,称为退偏 振。其机理是介质分子本身是各向异性的。
2.正交棱镜法
研究色散,目的是寻找 n f ( )的函数形式。 正交棱镜装置
三棱镜P1→AH(光谱) P1 P2→A’H’(光谱) n f ( ) ——弯曲光谱的形状。
3.正常色散与反常色散(Normal dispersion and abnormal dispersion)
正常色散曲线的信息
dut余虹一菲涅耳公式fresnelformula第三章光通过各向同性介质及其界面所发生的现象1光在各向同性介质界面上的反射和折射布儒斯特角线偏振光四用反射和折射法获得偏振光布儒斯特定律玻璃片堆要提高反射线偏振光的强度可利用玻璃片堆的多次反射
第三章光通过各向同性介质及其界面所发生的现象 §1 光在各向同性介质界面上的反射和折射 一、 菲涅耳公式(Fresnel formula)
dI Idx dI a Idx I dI d I I 0 a dx a 为吸收系数 I I 0 e a d ,
0
d
a AC ,式中A是一个与浓度无关 稀溶液:
的常量,C为溶液的浓度。
§ 3 光的色散(Dispersion of Light) 1.色散的特点
物理光学折射与反射公式整理

物理光学折射与反射公式整理折射与反射是物理光学中的基本现象,它们描述了光在不同介质间传播时的行为。
在本文中,我们将整理折射与反射公式,以便更好地理解和应用这些概念。
1. 反射公式当光线从一种介质射向另一种介质的界面时,一部分光线会发生反射,即光线回射到原来的介质中。
反射公式用于计算反射角和入射角之间的关系。
根据反射定律,入射角(θ₁)等于反射角(θ₂):θ₁ = θ₂这个公式适用于所有类型的反射,无论是在光滑的表面上还是在粗糙的表面上。
2. 折射公式当光线从一种介质射入另一种介质时,光线会发生偏折,即光线改变传播方向。
折射公式用于计算入射角和折射角之间的关系。
根据斯涅尔定律(也称为折射定律),入射角(θ₁)和折射角(θ₂)满足以下关系:n₁sin(θ₁) = n₂sin(θ₂)其中,n₁和n₂分别代表两个介质的折射率。
折射率是介质中光传播速度与真空中光传播速度的比值。
3. 全反射临界角当光线从光密介质射向光疏介质时,当入射角大于一个特定的角度(临界角),发生全反射。
此时,光线完全反射回原介质,不再折射入另一介质。
临界角可以通过折射公式计算得出。
当折射角(θ₂)等于90度时,入射角(θ₁)即为临界角(θc)。
此时,折射公式可以简化为:n₁sin(θc) = n₂如果入射角小于临界角,则出射角将变大,并根据折射公式计算。
4. 光的菲涅尔公式菲涅尔公式用于计算光线从一个介质射向另一个介质时的反射和透射的强度。
反射分为平行极化光和垂直极化光两种情况。
对于平行极化光,反射系数(r₁)由以下公式给出:r₁ = (n₁cos(θ₁) - n₂cos(θ₂)) / (n₁cos(θ₁) + n₂cos(θ₂))对于垂直极化光,反射系数(r₂)由以下公式给出:r₂ = (n₂cos(θ₁) - n₁cos(θ₂)) / (n₂cos(θ₁) + n₁cos(θ₂))透射系数(t)由以下公式给出:t = 2n₁cos(θ₁) / (n₁cos(θ₁) + n₂cos(θ₂))这些公式描述了反射和透射光的幅度与入射角、折射角以及介质折射率之间的关系。
菲涅尔方程式

菲涅尔方程式
菲涅耳方程式(Fresnel Equations)是用来描述光在两种介质界面上反射和透射的现象和规律的方程式。
它由奥古斯汀·菲涅耳(Augustin-Jean Fresnel)在19世纪提出,并成为光学领域中的重要理论工具。
菲涅耳方程式分为反射方程和透射方程,分别描述了光在界面上的反射和折射(透射)行为。
这些方程式基于电磁波的传播和边界条件,可以通过麦克斯韦方程和边界条件进行推导。
反射方程描述了入射光波在介质界面上的反射行为。
对于垂直入射的光,反射系数(反射光强与入射光强之比)可以通过下述菲涅耳反射方程计算:
r = (n1 - n2) / (n1 + n2)
其中,n1和n2分别是两种介质的折射率,r是反射系数。
透射方程描述了入射光波通过介质界面的折射行为。
同样对于垂直入射的光,透射系数(透射光强与入射光强之比)可以通过下述菲涅耳透射方程计算:
t = 2n1 / (n1 + n2)
其中,n1和n2分别是两种介质的折射率,t是透射系数。
需要注意的是,菲涅耳方程式仅适用于垂直入射的光,并且忽略了光在界面上的散射和吸收行为。
在实际应用中,还需要考虑光的入射角度、极化状态和表面特性等因素,并结合其他衍射、干涉等现象来对界面上的光行为进行更全面的描述。
菲涅耳方程式在材料科学、光学器件设计和表面反射控制等领域中具有广泛的应用,并能解释和预测光在界面上的反射和透射现象。
光线传播的四个基本定律

光线传播的四个基本定律光是一种电磁波,它在空气、水和其他介质中传播时,遵循着一些基本的定律。
这些定律可以帮助我们理解光的传播和反射,也为光学领域的实践应用提供了重要的基础。
本文将介绍光线传播的四个基本定律,分别是折射定律、反射定律、菲涅尔公式和全反射定律。
一、折射定律当光线从一种介质进入另一种介质时,它会发生折射。
折射定律规定了光线在两种介质之间传播时的方向和角度关系。
具体来说,它表明:入射角和折射角的正弦之比在两种介质中是一个常量,这个常量被称为折射率。
这个定律可以用来解释很多现象,比如为什么水中的物体看起来更小,为什么眼镜的镜片可以矫正视力等。
二、反射定律当光线从一种介质射向另一种介质的边界时,一部分光线会被反射回去。
反射定律规定了反射光线的方向和角度关系。
具体来说,它表明:入射角和反射角的大小相等,方向相反,且在同一平面内。
这个定律可以用来解释为什么镜子能够反射图像,为什么光可以在光学器件中进行反射等。
三、菲涅尔公式菲涅尔公式是用来计算反射和折射光线的强度的公式。
它基于电磁波在边界处的边界条件,将电磁波的振幅、相位和入射角考虑在内,可以精确地预测光线的反射和折射情况。
这个公式在光学领域的应用非常广泛,比如用于设计反光镜、光学镜头等。
四、全反射定律当光线从一个介质射向另一个介质时,如果入射角大于某个临界角,就会发生全反射。
全反射定律规定了这个临界角的大小和折射光线的存在性。
具体来说,它表明:入射角大于临界角时,光线将完全反射回去,没有折射光线存在。
临界角的大小取决于两个介质的折射率,可以用折射定律计算得出。
这个定律在光纤通信、光学器件等领域的应用非常广泛。
总结光线传播的四个基本定律是折射定律、反射定律、菲涅尔公式和全反射定律。
它们分别描述了光线在不同介质之间传播时的方向、角度和强度关系,为我们理解光学现象和应用光学技术提供了重要的基础。
在实践中,我们可以根据这些定律来设计光学器件、计算光线的传播和反射等,以实现各种光学应用。
菲涅耳原理

菲涅耳原理
菲涅耳原理指的是一个波从一个介质传播到另一介质时,会发生折射和反射,而这些现象可以通过一组简单的公式进行描述。
这个原理是由法国科学家菲涅耳(Augustin-Jean Fresnel)在19世纪初期提出的,他研究的主要是光的传播和衍射。
后来,这个原理也被推广至其他波动领域。
入射角是波的传播方向与介质界面法线的夹角。
假设波从一般介质A传入到另一介质B,那么入射角就是这个波与介质A表面法线的夹角。
这些参数可以用以下公式计算:
折射角 = 反射角 = i
其中r为反射系数,n1和n2分别是介质A和介质B的折射率,i为入射角。
关于折射率,我们可以根据介质的光密度来计算。
光密度是指在介质中传播的光线数量,它通常与介质的折射率成正比。
菲涅耳原理可以帮助我们理解许多光学现象,例如透明物体、反光镜、玻璃表面的反射、水面反射等等。
总的来说,菲涅耳原理揭示了波在介质间的传播规律和相互作用,使我们能够更加深入地理解和利用波的性质。
玻璃反射率公式

玻璃的反射率可以通过菲涅尔公式来计算。
菲涅尔公式描述了光线从介质1射入介质2时的反射和折射现象。
对于垂直入射的光线,菲涅尔公式可以表示为:
反射率R = ((n1 - n2) / (n1 + n2))^2
其中,n1是入射介质的折射率,n2是出射介质的折射率。
对于平行入射的光线,菲涅尔公式可以表示为:
反射率R = ((n1 * cosθ2 - n2 * cosθ1) / (n1 * cosθ2 + n2 * cosθ1))^2
其中,θ1是入射角,θ2是折射角,n1和n2分别是入射介质和出射介质的折射率。
需要注意的是,菲涅尔公式只适用于光线从一个介质射入另一个介质的情况,且假设介质是均匀的。
在实际应用中,还需要考虑光线的波长、入射角度等因素。
fresnel公式

fresnel公式Fresnel公式是描述光在两种介质之间传播时发生反射和折射的规律。
它由奥古斯汀·让·菲涅耳在19世纪初提出。
Fresnel公式分为反射和折射两个部分,分别描述了光的入射、反射和透射的振幅和相位之间的关系。
根据Fresnel公式,入射光线在介质界面上会发生一部分反射,另一部分则会折射进入下一个介质。
对于垂直入射的光线,反射系数和折射系数可以按以下公式计算:反射系数R = |(n1 - n2) / (n1 + n2)|^2折射系数T = 1 - R其中,n1和n2分别为上一个介质和下一个介质的折射率。
反射系数表示入射光线被反射的比例,折射系数表示入射光线被折射的比例。
对于非垂直入射的光线,Fresnel公式还包括极化方向的影响。
在这种情况下,入射光线可以分为垂直极化(s极化)和平行极化(p极化)两部分。
对于s极化,反射和折射系数分别为:反射系数Rs = |(n1*cos(θ1) - n2*co s(θ2)) / (n1*cos(θ1) + n2*cos(θ2))|^2折射系数Ts = 1 - Rs其中,θ1和θ2分别为入射角和折射角。
对于p极化,反射和折射系数分别为:反射系数Rp = |(n2*cos(θ1) - n1*cos(θ2)) / (n2*cos(θ1) + n1*cos(θ2))|^2折射系数Tp = 1 - RpFresnel公式在光学领域和光学器件设计中具有广泛应用。
例如,它可以被用来优化反射镜、透镜和光学薄膜的性能,以及研究光在介质中的传播和吸收等现象。
总结来说,Fresnel公式描述了光线在介质界面上的反射和折射行为,它提供了计算反射和折射系数的数学表达式,便于研究光的传播和相位的变化。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
21p 1p 2 p
cosi cost
(20) (21) (22) (23)
13
利用折射定律,Fresnel公式还可以写成如下的形式:
rs
sin(i sin(i
t t
) )
(24)
rp
tan(i tan(i
t ) t )
(25)
ts
2cosi sint sin(i t )
Ets
n
H tp
图2
在界面上电场切向分 量连续:
n (E2 E1) 0
Ei0s Er0s Et0s (5)
在界面上磁场的切向分
量连续: n (H2 H1) 0
规定:电场和磁场
的s分量垂直于纸面, 向外为正,向内为负。 Hi0 p cosi H r0 p cosr H t0 p cost (6)
当θi较大时, Eip和Erp中垂直于界面的成分为主要成分,此时尽管rp>0,但因它们 的正向规定基本相反,所以实际上仍有Eip和Erp的主要成分相反向; 因此说,n1<n2时,反射波电场方向总与入射波电场方向相反或接近 相反。
19
4)、θi =0°和90°的情况
θi =0°的情形是一个特殊的情况, 称为正入射。 这时,折射角θt=0°,由Fresnel公 式容易算出在正入射时s和p分量的
例Fr这e如s些n,e数l 公对值式于画计n出2/算了n1=图可1.45得各,到曲r0线:=-的0r.s2=终,-0点.t20。0=401.8,,r在p=-θ0i .1=91509°,时ts=,0.直796接9 tp=0.7973,可见它们分别与r0和t0接近。
由 ,
20
(2)、反射率和透射率的变化
可见,时间频率ω是入射电磁波或光波的固有特性,它不 因媒质而异,也不会因折射或反射而变化;
4
ki r kr r kt r (2)
(kr ki ) r 0 (kt ki ) r 0
写成标量形式,并 约掉共同的位置量
由于
r
n2/n1=2.0
差别消失,用r0和t0分别表示正入射 时的反射和透射系数,则有:
rs
r0
n1 n1
n2 n2
(29)
t0
2n1 n1 n2
图4
(30) 对于n2/n1=2.0,r0=-0.33,t0=0.67
tp ts
rp
(29)、 (30)两式可以看出,两媒质折射率的差别越大,r0的绝对值
位相跃变
n2/n1=2.0
rs
tp ts
rp
图4
ek在xr p界[ir(面kr 上2r任|何tr一|0点)], 反波的这 磁样 波射s位分(,波相光量位)|s差相传分间r别差播量都|。π半与有相2个当入一波于射个长电的π
距离,所以该现象又可称
为半波损失。
17
3)、对于rp,它的代数值随着 入射角θi单调增大,但是经历 了一个由负到正的变化。
越从(2θt二9s大图i=)=媒t、p,94=0质可(0而3°,0里以t)的0还这因值看情可表此越出形以示称小,也用电这。四是来磁种条一估波入曲个计仅射线特小为仅在殊θ掠在iθ(的<i入界1情=5射面0°况°。上),处处‘此的的掠时系斜过,数率’r。都s=,-是1并,零未rp,=真1所。正以进公入式第
n1
cosi
(18)
2p
n2
cost
(19)
12
于是得Fresnel公式的另外一种形式:
rs
Er0s Ei0s
1s 1s
2s 2s
ts
Er0s Ei0s
21s 1s 2s
rp
Er0 p Ei0 p
1p 1 p
2 p 2 p
tp
Et0 p Ei0 p
第七、八次课、折射和反射 定律、菲涅耳公式
内容
一、折射和反射定律 二、菲涅耳公式 三、根据Fresnel公式讨论反射波和 透射波的性质
1
一、折射和反射定律
内容
1、折射和反射定律内容 2、分析
2
1、折射和反射定律的内容是:
时间频率ω是不变的; 反射波和折射波均在入射面内;
反射角等于入射角。
(1)、反射和透射系数的变化:
tp n2/n1=2.0 ts
rp rs
图4
1)、两个透射系 数ts和tp都随着入 射角θi增大而单调 降低,即入射波 越倾斜,透射波 越弱,并且在正 向规定下,ts和tp 都大于零。
16
2)、rs始终小于零,其绝对值 随着入射角单调增大。根据正 方向规定可知,在界面上反射 波电场的s分量振动方向始终
cos(
2
t
)
ki n1 / c kr n1 / c kt n2 / c
θr=θi n2sinθt=n1sinθi
(3)
反射角等于入射角
(4)
折射定律
5
二、菲涅耳公式
内容
1、公式的推导 2、公式的另外两种形式
6
折、反射定律给出了反射波、折射波和入射波传播方向之间的关系。
<2>如果平面波以布儒斯特角入射,反
射角与折射角互为余角,所以kr kt 18
Eip
Erp
H rs
His
ki
界面
θi θr
k r Erp 1
O
2
θt kt
n
Hts
Etp
<3>、当θi较小时,
图3
rp<0, Eip和Erp中平行于界面的成分较多,此时两者的主要成分相 反向;
exp[i(kt
r
tt)]
n
Et
图1
3
界面两侧的总电场为:
E1 Ei Er Ei0 exp[i(ki r it)] Er0 exp[i(kr r rt)]
E2 Et Et0 exp[i(kt r tt)]
n (E2 E1) 0
rp
tan(i tan(i
t ) t )
θi=特定值θB ,rp=0
n2/n1=2.0
rs
tp ts
rp
i B 90 (28) 布儒斯特定律
布儒斯特角
图4
利用折射定律
B
tg 1
n2 n1
<1>如果平面波以布儒斯特角入射,则 不论入射波的电场振动如何,反射波不 再含有p分量,只有s分量;
(26)
tp
2cosi sini sin(t i )sin(t i )
(27)
14
三、根据Fresnel公式讨论反射波和 透射波的性质 内容
1. n1<n2的情况 2. n1>n2的情况
15
1. n1<n2的情况
在光学上,这种情况称为光从光疏媒质向光密媒质入射。 根据折射定律可知:θi>θt 。
与入射波s分量相反。
位相跃变(半波损失)
rs
sin(i sin(i
t t
) )
负号写成 exp(i )
rs | rs | exp(i ) Eis Ei0s exp[i(ki r t 0)] Ers Ei0s rs exp[i(kr r t 0 )] Ei0s | rs | exp[i(kr r t 0 )]
折射定律:折射介质折射率与折射角正弦之积等于入射介质折射率与 入射角正弦之积。
2、分析:
Ei
Ei Ei0 exp[i(ki r it)]
界面
O
z
ki θi
θr kr
Er
Er Er0 exp[i(kr r rt)]
1
O
2
x
θt
kt
Et
Et 0
可以在界面内选取 不同方向 ,
上式实际上意味着 矢量(kr ki )和 (kt ki )
均与界 面的法 线 知,ki 、k r 、kt 与
n n
平行,由此可以推 共面,该平面称为
入射面。
结论:反射波和折射波均在入射面内。
ki
cos(
2
i
)
kr
cos(
2
r
)
kt
tp
Байду номын сангаас
Et0 p Ei0 p
n1
2n1
cost
ctopns2ciEEotis00pp i
2n1
(13co) si
n1 n2
cosi cost
cosi cost
(14) (15)
令: 1s n1 cosi (16) 2s n2 cost (17)
1 p
n2 cosi n2 cosi
(8) (9) (12)
tp
Er0 p Ei0 p
2n1 cosi n1 cost n2 cosi
(13)
11
2、公式的另外两种形式
rs
Er0s Ei0s
n1 cosi n2 cost n1 cosi n2 cost
(8)
公式(8)、(9)、(12)、(13)称为Fresnel公式:
rs
Er0s Ei0s
n1 cosi n2 cost n1 cosi n2 cost
