Eviews异方差性实验报告
异方差性实验报告doc

异方差性实验报告篇一:计量经济学上机实验报告(异方差性)提示:打包保存时自己的文件夹以“学号姓名”为文件夹名,打包时文件夹内容包括:本实验报告、EViews工作文件。
篇二:Eviews异方差性实验报告实验一异方差性【实验目的】掌握异方差性问题出现的来源、后果、检验及修正的原理,以及相关的Eviews操作方法。
【实验内容】以《计量经济学学习指南与练习》补充习题4-16为数据,练习检查和克服模型的异方差的操作方法。
【4-16】表4-1给出了美国18个行业1988年研究开发(R&D)费用支出Y与销售收入X的数据。
请用帕克(Park)检验、戈里瑟(Gleiser)检验、G-Q检验与怀特(White)检验来检验Y关于X的回归模型是否存在异方差性?若存在【实验步骤】一检查模型是否存在异方差性1、图形分析检验(1)散点相关图分析做出销售收入X与研究开发费用Y的散点相关图(SCATX Y)。
观察相关图可以看出,随着销售收入的增加,研究开发费用的平均水平不断提高,但离散程度也逐步扩大。
这说明变量之间可能存在递增的异方差性。
(2)残差图分析首先对数据按照解释变量X由小至大进行排序(SORT X),然后建立一元线性回归方程(LS Y C X)。
因此,模型估计式为: Y?187.507?0.032*X ----------(*) ?(0.17)(2.88) R2=建立残差关于X的散点图,可以发现随着X增加,残差呈现明显的扩大趋势,表明存在递增的异方差。
2、Park检验建立回归模型(LS Y C X),结果如(*)式。
生成新变量序列: GENR LNE2 = LOG(RESID^2)GENR LNX = LOG(X)生成新残差序列对解释变量的回归模型(LS LNE2 C LNX)。
从下图所示的回归结果中可以看出,LNX的系数估计值不为0且能通过显著性检验,即随机误差项的方差与解释变量存在较强的相关关系,即认为存在异方差性。
计量经济学 异方差检验

计量经济学实验报告【实验名称】异方差的检验和修正【实验目的】掌握用Eviews 检验模型中异方差问题的检验和补救方法,能够正确理解和分析Eviews的输出结果【实验内容】(1)试利用OLS法建立人均消费性支出与可支配收入的线性模型;(2)检验模型是否存在异方差性;(3)如果存在异方差性,试采用适当的方法估计模型参数。
【结果分析】1.建立模型打开Eviews软件,选中File\New\Workfile以创建一个工作文件,文件结构类型为undated。
在命令栏中输入“data X Y”,回车后得到一个未命名的组,向组中输入数据。
如下图。
设可支配收入为变量X(横坐标),消费性支出为变量Y(纵坐标),选中Quick\Graph,在出现的对话框中输入“X Y”,点击OK后在新出现的Graph对话框中,在Graph type中选择Categorical Graph下的scatter,点击OK,如下图所示:以X 为解释变量,Y 为被解释变量,建立一元线性回归方程:i 0i i Y =+*X ββ选中Object/New Objects ,在新建对象对话框中选中对象为Equation ,在出现的对话框中输入“y c x ”,进行回归分析,得到如下结果。
可以得出0β=725.3459 1β =0.664746 线性回归方程为:i Y =0β+1β *X=725.3459+0.664746*X(1.589047)(22.49622)2R=0.945802 F=506.0798由散点图可知,原模型很可能存在异方差性,为此,进一步的进行更精确的检验。
G-Q检验:升序排列去掉中间的7个样本,剩余24个样本,再分成两个样本容量为12的子样本,对两个子样本分别用OLS法作回归:键入命令Smpl 1 12Equation eq01.Is Y C XSmpl 20 31Equation eq02.Is Y C X完成对两个子样的回归;0β’=669.5344 1β’=0.677374i Y =0β’+ 1β’*X=669.5344+0.677374*X子样1: (0.281991) (3.490176)RSS1=1971249i Y =1179.053+0.644719*X子样2: (0.954140) (9.951062) RSS2=8403437计算F 统计量:F=197124984034371112/21-1-12/1=--)()(RSS RSS =4.263 在5%的显著性水平下,自由度为(10,10)的F 分布的临界值为4.263,于是拒绝同方差的原假设,表明模型存在异方差。
eviews-异方差性

eviews-异⽅差性3.8(1)根据Y 、X 的相关图分析异⽅差性由上图可知y 与x 的线性相关性差异不是很⼤,基本处在⼀条线性⽅程上(2)利⽤WHITE 检验、帕克检验,和Gleiser 检验进⾏异⽅差检验Ⅰ、White 检验取显著性⽔平05.0=α,由于413667.8n 2=R >841.3)1(205.0=χ,所以理利润函数存在异⽅差性。
Ⅱ、Park 检验根据Park 检验,得到:i i x e ln 8393.16927.7ln 2+-=S 2.2720 0.5713 T -3.3858 3.21953654.02=R 3301.02=R 365.10=F 0047.0=P Ⅲ、Gleiser 检验:利⽤genr 命令⼀次⽣成XX 1,等序列,再建⽴i e 与这些序列的回归⽅程①X e i 0049.05579.1-=White Heteroskedasticity Test: F-statistic 6.1724 Probability 0.0096 Obs*R-squared8.4136Probability0.0148=2R 0.0613 =F 1.1759 =P 0.2924②X e i 0848.08897.1-==2R 0.0639 =F 1.2307 =P 0.2818③Xe i 1970.158811.0+= =2R 0.0683 =F 1.3197 =P 0.2656根据统计检验,得到统计检验最为显著的是:Xe i 1970.158811.0+= =2R 0.0683 =F 1.3197 =P 0.2656;上述四个⽅程表明,利润函数存在着异⽅差(只要取显著性⽔平012.0>α)(3)取权数 e 1w 3= 24e1w =利⽤加权最⼩⼆乘法估计模型:依次键⼊命令:4,3,2,1i )(i ==X C Y W W LS或在⽅程窗⼝中点击Estimate\Options 按钮,并在权数变量栏依次输⼊4321W W W W 、、、,可以得到⼀下估计结果:③ X Y 0387.07076.0?+= e 1w 3=S 0.2082 0.0053 T 3.3978 7.2001=2R 0.7422 =2n R 5.0534 =P 0.000001 ④ X Y0429.05918.0?+= 24e 1w = S 0.1283 0.004 T 4.61144 10.49056=2R 0.8594 =2n R 18.0642 =P 0模型④最优,所以利⽤WLS ⽅法估计的利润函数为 X Y 0429.05918.0?+= 2e 1w = S 0.1283 0.004 T 4.6114 10.49=2R 0.8594 =2n R 18.064 =P 03.9设根据某年全国各地区的统计资料建⽴城乡居民储蓄函数i i i bX a S ε++=时(其中,S 为城乡居民储蓄存款余额、X 为⼈均收⼊),如果经检验得知:228.1i i X e =:(1)说明该检验结果的经济含义;(2)写出利⽤加权最⼩⼆乘法估计储蓄函数的具体步骤;(3)写出使⽤Ewiews 软件估计模型时的有关命令。
EViews计量经济学实验报告-异方差的诊断及修正模板(word文档良心出品)
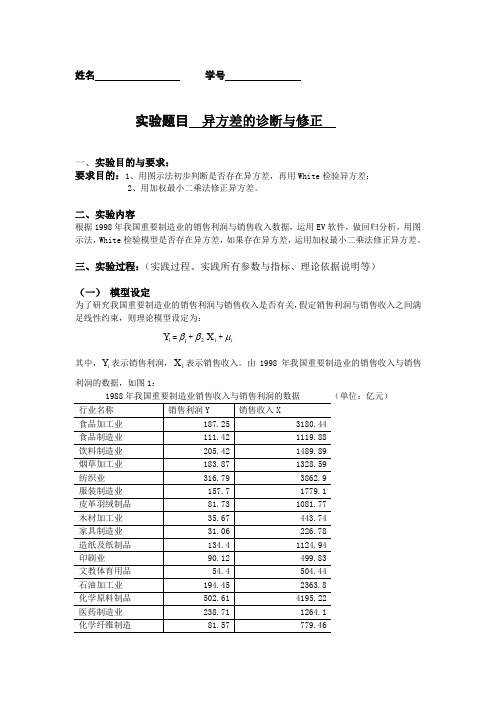
姓名 学号实验题目 异方差的诊断与修正一、实验目的与要求:要求目的:1、用图示法初步判断是否存在异方差,再用White 检验异方差;2、用加权最小二乘法修正异方差。
二、实验内容根据1998年我国重要制造业的销售利润与销售收入数据,运用EV 软件,做回归分析,用图示法,White 检验模型是否存在异方差,如果存在异方差,运用加权最小二乘法修正异方差。
三、实验过程:(实践过程、实践所有参数与指标、理论依据说明等)(一) 模型设定为了研究我国重要制造业的销售利润与销售收入是否有关,假定销售利润与销售收入之间满足线性约束,则理论模型设定为:i Y =1β+2βi X +i μ其中,i Y 表示销售利润,i X 表示销售收入。
由1998年我国重要制造业的销售收入与销售利润的数据,如图1:1988年我国重要制造业销售收入与销售利润的数据 (单位:亿元)(二) 参数估计Dependent Variable: Y Method: Least Squares Date: 10/19/05 Time: 15:27 Sample: 1 28Included observations: 28Variable Coefficient Std. Error t-Statistic Prob. C 12.03564 19.51779 0.616650 0.5428 X0.1043930.008441 12.366700.0000R-squared 0.854696 Mean dependent var 213.4650 Adjusted R-squared 0.849107 S.D. dependent var 146.4895 S.E. of regression 56.90368 Akaike info criterion 10.98935 Sum squared resid 84188.74 Schwarz criterion 11.08450 Log likelihood -151.8508 F-statistic 152.9353 Durbin-Watson stat1.212795 Prob(F-statistic)0.000000估计结果为: iY ˆ = 12.03564 + 0.104393i X (19.51779) (0.008441) t=(0.616650) (12.36670)2R =0.854696 2R =0.849107 S.E.=56.89947 DW=1.212859 F=152.9353这说明在其他因素不变的情况下,销售收入每增长1元,销售利润平均增长0.104393元。
异方差试验报告

《计量经济学》上机实验报告四题目:异方差实验日期和时间:班级:学号:姓名:实验室:实验环境:Windows XP ; EViews 3.1实验目的:掌握异方差检验及修正方法,熟悉EViews软件的相关应用实验内容:利用实例数据和EViews软件,采用有关方法对建立的回归模型进行异方差的检验及处理。
第五章习题5.3实验步骤:一、建立工作文件⒈菜单方式⒉命令方式:CREATE A 起始期终止期二、输入数据三、检验异方差性⒈图示法排序sort X相关图:SCA T 变量名1 变量名2Ls y c x残差图:方程窗口点击RESID按钮⒉戈德菲尔德-匡特检验(C=n/4)①排序:sort X②取样本1 命令:Smpl 1 (n-n/4)/2③估计样本1:Ls y c x得到残差平方和RSS1即∑21i e③取样本1 命令:Smpl (n+n/4)/2 n④估计样本2:Ls y c x得到残差平方和RSS2即∑22i e⑤计算:F = RSS2/ RSS1若给定α,)2/)(,2/)((k c n k c n F F ---->α,表明存在异方差 3.怀特检验步骤:①取样:Smpl 1 n②估计回归模型(或非线性回归模型)计算残差序列:Ls y c x③怀特检验:在方程窗口中依次点击View\Residual Test\White Heteroskedastcity 得到nR 2,给定α,若nR 2>2αχ(q),表明模型存在异方差性 4.帕克(Park )检验 帕克检验的模型形式命令:①估计回归模型得到残差:ls y c x ②生成残差平方序列: genr E2=RESID^2 ③估计帕克检验模型 : ls log(e2) c log(x)给定α,若F>αF (k-1,n-k)或F 统计值的伴随概率p 小于给定α,表明模型存在异方差性 5. 戈里瑟(Gleiser )检验 戈里瑟检验的模型命令:①估计回归模型得到残差:ls y c x 或非线性模型估计 ②生成残差绝对数序列: genr E1=abs(RESID ) ③估计帕克检验模型 :当h=1时 ls e1 c x 当h=2时 ls e1 c x^2当h=1/2时 ls e1 c x^(1/2)或ls e1 c sqr(x ) 等等给定α,若F>αF (k-1,n-k)或F 统计值的伴随概率p 小于给定α,表明模型存在异方差性 四、利用加权最小二乘法估计回归模型命令:①估计回归模型(或非线性回归模型)得到残差 ls y c x ②根据帕克检验结果,生成权数1序列:genr w1=1/x^ 根据戈里瑟检验结果,生成权数2序列:genr w2=1/x^h 生成权数3序列:genr w3=1/abs(RESID) 生成权数4序列:genr w4=1/RESID^2③加权最小二乘法估计回归模型 Ls(w=w1) y c x Ls(w=w2) y c x Ls(w=w3) y c xie x e i i υβα=2ii i x e υβα++=ln ln ln 2ih i i x e υβα++=,21,2,1±±±=h βLs(w=w4) y c x④再运用怀特检验对加权最小二乘法估计回归模型进行异方差检验 试验结果: 写作例题 1、 图示法由相关图和残差图可知模型存在递增型异方差性 2、戈德菲尔德-匡特检验结果给定05.0=α,F=24.7244.3)210,210(05.0=--=>F F α,表明模型存在递增型异方差 3、怀特检验2704.62=nR 99.5)2(2205.0==>χχα,表明模型存在异方差4、帕克(Park )检验ix e i l n 6743.15549.5l n 2+-=2R =0.4655 F=22.64 P=0.0001P 值远小于0.05,上述方程表明利润函数存在异方差 5、戈里瑟(Gleiser )检验(1)ii x e 0153.02394.12+=2R =0.2982 F=11.05 P=0.003(2)ii x e 3862.16768.15+-=2R =0.3279 F=12.68 P=0.001(3)261074.20548.27i i x e -⨯+=2R =0.2177 F=7.24 P=0.012P 值远小于0.05,上述方程表明利润函数存在异方差,且模型(2)最优 6、加权最小二乘估计结果① (W=W1)(3.8823) (0.0099)(注:括号内数据为系数标准差)R 2=0.8483 nr 2=4.92 p=0.085(注:nr 2和p 为加权最小二乘估计模型的怀特检验结果)② (W=W2) (11.1877) (0.0077)x y 1086.09220.5ˆ+=x y1062.06493.8ˆ+=∑∑=24.72=579.5963769.67/2=/2122i i e e fR 2=0.6115 nr 2=3.16 p=0.206③ (W=W3) (3.7798) (0.0035) R 2=0.9754 nr 2=6.64 p=0.036④ (W=W4)(1.6603) (0.0021) t= (3.11) (54.16) R 2=0.9969 nr 2=3.10 p=0.213其中,每个方程下面第一组括号里的数字为系数的标准误差。
计量经济学eviews实习报告.doc
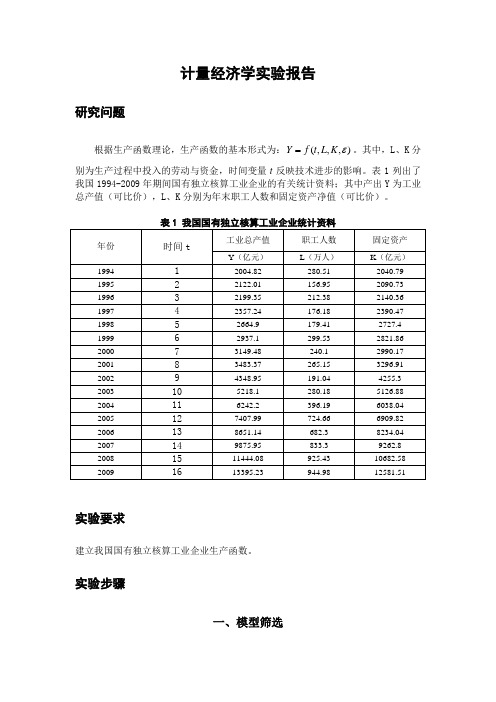
计量经济学实验报告研究问题根据生产函数理论,生产函数的基本形式为:),,,(εK L t f Y =。
其中,L 、K 分别为生产过程中投入的劳动与资金,时间变量t 反映技术进步的影响。
表1列出了我国1994-2009年期间国有独立核算工业企业的有关统计资料;其中产出Y 为工业总产值(可比价),L 、K 分别为年末职工人数和固定资产净值(可比价)。
实验要求建立我国国有独立核算工业企业生产函数。
实验步骤一、模型筛选(一)建立多元线性回归方程回归结果如下:图1因此,我国国有独立工业企业的生产函数为:K L t Y 00998.171897.022674.90897.191+++-=∧(模型1)t =(-5.4) (0.862) (3.57) (40.44)999742.02=R 999677.02=R 57.15483=F模型的计算结果表明,我国国有独立核算工业企业的劳动力边际产出为0.71897,资金的边际产出为1.00998,技术进步的影响使工业总产值平均每年递增9.22674亿元。
回归系数的符号和数值是较为合理的。
999742.02=R ,说明模型有很高的拟合优度,F 检验也是高度显著的,说明职工人数L 、资金K 和时间变量t 对工业总产值的总影响是显著的。
从图1看出,解释变量资金K 的t 统计量值为40.44,表明资金对企业产出的影响是显著的。
但是,模型中时间变量T 的t 统计量值都较小,未通过检验。
因此,需要对以上三元线性回归模型做适当的调整,按照统计检验程序,一般应先剔除t 统计量较小的变量(即时间变量)而重新建立模型。
(二)建立剔除时间变量的二元线性回归模型回归结果如下:图2因此,我国国有独立工业企业的生产函数为:K L Y 026137.1669964.02778.176++-=∧(模型2)t =(-5.76) (3.5) (62.79)999726.02=R 999684.02=R 95.23692=F(三)建立非线性回归模型——C-D 生产函数C-D 生产函数为:εβαe K AL Y =。
计量经济学试验-Eviews

12
0.759316100176
27
13
24.0588008707
0.027744 -0.008265 38.94474 40950.71 -146.3152 1.698005
Mean dependent var S.D. dependent var Akaike info criterion Schwarz criterion F-statistic Prob(F-statistic)
下:
序号
Y
X
序号
Y
X
1
2940
3547
16
1609
1963
2
2322
2769
17
2048
2450
3
1898
2334
18
2087
2688
4
1560
1957
19
3777
4632
5
1585189320源自230328956
1977
2314
21
2404
3072
7
1596
1953
22
2034
2421
8
1660
1960
0.133926 271.8586
7.278296 -1.056384
Mean dependent var S.D. dependent var Akaike info criterion Schwarz criterion F-statistic Prob(F-statistic)
异方差计量实验报告(3篇)

第1篇一、实验目的本实验旨在通过实际操作,验证计量经济学中异方差性的存在,并掌握相应的检验和修正方法。
通过实验,加深对异方差性概念的理解,提高在实际应用中识别和处理异方差问题的能力。
二、实验内容1. 数据来源与处理- 数据来源:本实验使用某地区某年度的居民消费支出数据,包括居民可支配收入和消费性支出两个变量。
- 数据处理:将原始数据进行整理,剔除异常值,并对数据进行对数化处理,以降低异方差性的影响。
2. 模型设定与估计- 模型设定:根据理论分析,设定居民消费支出与可支配收入之间的线性关系模型为:\[ Y = \beta_0 + \beta_1X + \epsilon \]其中,\( Y \) 为居民消费支出,\( X \) 为可支配收入,\( \beta_0 \)和 \( \beta_1 \) 为模型参数,\( \epsilon \) 为随机误差项。
- 模型估计:采用最小二乘法(OLS)对模型进行估计,得到模型参数的估计值。
3. 异方差性检验- 检验方法:采用以下方法检验模型是否存在异方差性:- 观察法:观察残差图,若残差图呈现出明显的曲线关系,则可能存在异方差性。
- Goldfeld-Quandt 检验:通过分组检验残差平方与解释变量之间的关系,判断是否存在异方差性。
- White 检验:采用 White 检验对模型进行异方差性检验,得到统计量值和p 值。
- 检验结果:根据检验结果,判断模型是否存在异方差性。
4. 异方差性修正- 修正方法:若检验结果表明模型存在异方差性,则采用以下方法进行修正:- 加权最小二乘法(WLS):对模型进行加权最小二乘法估计,以降低异方差性的影响。
- 拉格朗日乘数法(LM):采用 LM 检验对模型进行修正,得到修正后的模型参数估计值。
- 修正结果:根据修正结果,比较修正前后模型参数估计值的变化,并分析修正效果。
三、实验结果与分析1. 模型估计结果- 根据最小二乘法估计,得到模型参数的估计值如下:\[ \beta_0 = 1000, \beta_1 = 0.5 \]- 模型拟合优度为 0.8,说明模型对数据的拟合程度较好。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验一异方差性
【实验目的】
掌握异方差性问题出现的来源、后果、检验及修正的原理,以及相关的Eviews操作方法。
【实验内容】
以《计量经济学学习指南与练习》补充习题4-16为数据,练习检查和克服模型的异方差的操作方法。
【4-16】表4-1给出了美国18个行业1988年研究开发(R&D)费用支出Y与销售收入X的数据。
请用帕克(Park)检验、戈里瑟(Gleiser)检验、G-Q检验与怀特(White)检验来检验Y关于X的回归模型是否存在异方差性?若存在
【实验步骤】
一检查模型是否存在异方差性
1、图形分析检验
(1)散点相关图分析
做出销售收入X与研究开发费用Y的散点相关图(SCAT X Y)。
观察相关图可以看出,随着销售收入的增加,研究开发费用的平均水平不断提高,但离散程度也逐步扩大。
这说明变量之间可能存在递增的异方差性。
(2)残差图分析
首先对数据按照解释变量X 由小至大进行排序(SORT X ),然后建立一元线性回归方程(LS Y C X )。
因此,模型估计式为:
X Y *032.0507.187+=∧
----------(*)
(0.17) (2.88) R 2=0.31 s.e.=2850 F=0.011
建立残差关于X 的散点图,可以发现随着X 增加,残差呈现明显的扩大趋势,表明存在递增的异方差。
2、Park检验
建立回归模型(LS Y C X),结果如(*)式。
生成新变量序列:GENR LNE2 = LOG(RESID^2)
GENR LNX = LOG(X)
生成新残差序列对解释变量的回归模型(LS LNE2 C LNX)。
从下图所示的回归结果中可以看出,LNX的系数估计值不为0且能通过显著性检验,即随机误差项的方差与解释变量存在较强的相关关系,即认为存在异方差性。
3、Gleiser 检验
建立回归模型(LS Y C X ),结果如(*)式。
生成新变量序列: GENR E = ABS(RESID)
分别建立新残差序列E 对各解释变量2
12
1
2
12
/////-
--X
X
X
X X X 的回归模
型(LS E C X ),回归结果如各图所示。
由上述各回归结果可知,各回归模型中解释变量的系数估计值显著不为0,且除了2
X的系数,均能通过10%的显著性检验。
所以认为存在异方差性。
4、G-Q检验
将样本按解释变量排序(SORT X)并分成两部分,分别为1到7和11到17,各7个样本。
利用样本1建立回归模型1(SMPL 1 7 LS Y C X),其残差平方和为412586.0。
利用样本2建立回归模型2(SMPL 11 17 LS Y C X ),其残差平方和为94219377。
计算F 统计量:
12/RSS RSS F ==91219377 / 412586 = 221.09,21RSS RSS 和分别是模型1和模型2的残差平方和。
取05.0=α时,查F 分布表得05.5)117,117(05.0=----F ,而
05.509.22105.0=>=F F ,所以存在异方差性。
5、White 检验
建立回归模型(LS Y C X )。
在窗口菜单中选择Heteroskedasticity Test: White ,检验结果如下:
其中F 值为辅助回归模型的F 统计量值。
取显著水平05.0=α,由于
533.1689137.9*1799.5)2(2205.0==<=nR χ,所以存在异方差性。
同时可以直接观察相伴概率P 值的大小,这里P = 0.0022,小于0.05的显著水平,认为存在异方差性。
二 克服异方差 1、确定权数变量
根据Park 检验生成权数变量:GENR W1=1/X^1.5019 根据Gleiser 检验生成权数变量:GENR W2=1/X^2 另外生成:GENR W3=1/ABS(RESID)
GENR W4=1/RESID^2
其中RESID 为最初回归模型LS Y C X 的残差序列。
2、利用加权最小二乘法估计模型
在Eviews 命令窗口中依次键入命令LS(W=i W ) Y C X ,或在回归的权数变量栏里依次输入W1、W2、W3、W4,得到回归结果。
并对所估计的模型再分别进行White 检验,观察异方差的调整情况。
W1:W2:
W3:
Eviews异方差性实验报告
W4:
权数为W1、W2、W4所对应的White检验显示,P值较大,都超过了0.88,所以接受不存在异方差的原假设,即认为已经消除了回归模型的异方差性。
其中以W4=1/RESID^2 作为权数的模型消除了异方差性(P=0.8852),并且拟合程度较好(R2=0.9674)。
