解题技巧专题:平面直角坐标系中的图形面积
2020年中考数学压轴题-专题10 动点产生的面积关系(解析版)
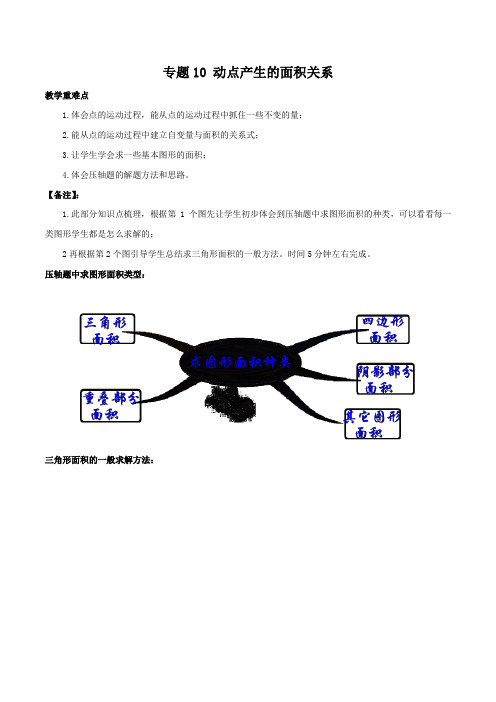
专题10 动点产生的面积关系教学重难点1.体会点的运动过程,能从点的运动过程中抓住一些不变的量;2.能从点的运动过程中建立自变量与面积的关系式;3.让学生学会求一些基本图形的面积;4.体会压轴题的解题方法和思路。
【备注】:1.此部分知识点梳理,根据第1个图先让学生初步体会到压轴题中求图形面积的种类,可以看看每一类图形学生都是怎么求解的;2再根据第2个图引导学生总结求三角形面积的一般方法。
时间5分钟左右完成。
压轴题中求图形面积类型:三角形面积的一般求解方法:【备注】:1.以下每题教法建议,请老师根据学生实际情况参考;2.在讲解时:不宜采用灌输的方法,应采用启发、诱导的策略,并在读题时引导学生发现一些题目中的条件(相等的量、不变的量、隐藏的量等等),使学生在复杂的背景下自己发现、领悟题目的意思;3.可以根据各题的“参考教法”引导学生逐步解题,并采用讲练结合;注意边讲解边让学生计算,加强师生之间的互动性,让学生参与到例题的分析中来;4.例题讲解,可以根据“参考教法”中的问题引导学生分析题目,边讲边让学生书写,每个问题后面有答案提示;5.引导的技巧:直接提醒,问题式引导,类比式引导等等;6.部分例题可以先让学生自己试一试,之后再结合学生做的情况讲评;7.每个题目的讲解时间根据实际情况处理,建议每题7分钟,选讲例题在时间足够的情况下讲解。
例1(2020静安区建承中学一模)在平面直角坐标系xOy 中(如图),已知二次函数2y ax bx c =++(其中a 、b 、c 是常数,且a ≠0)的图像经过点A (0,-3)、B (1,0)、C (3,0),联结AB 、AC .(1)求这个二次函数的解析式;(2)点D 是线段AC 上的一点,联结BD ,如果:3:2ABD BCD S S ∆∆=,求tan∠DBC 的值; (3)如果点E 在该二次函数图像的对称轴上,当AC 平分∠BAE 时,求点E 的坐标.【整体分析】(1)直接利用待定系数法,把A 、B 、C 三点代入解析式,即可得到答案; (2)过点D 作DH ∠BC 于H ,在∠ABC 中,设AC 边上的高为h ,利用面积的比得到32AD DC =,然后求出DH 和BH ,即可得到答案;(3)延长AE 至x 轴,与x 轴交于点F ,先证明△OAB∠∠OFA ,求出点F 的坐标,然后求出直线AF 的方程,即可求出点E 的坐标. 【详解】解:(1)将A (0,-3)、B (1,0)、C (3,0)代入20y ax bx c a =++≠()得,03,0934,300a b a b c =+-⎧⎪=+-⎨⎪-=++⎩解得143a b c =-⎧⎪=⎨⎪=-⎩,∴此抛物线的表达式是:243y x x =-+-.(2)过点D 作DH ⊥BC 于H ,在∠ABC中,设AC边上的高为h,则11:():():3:222ABD BCDS S AD h DC h AD DC∆∆=⋅⋅==,又∠DH//y轴,∴25 CH DC DHOC AC OA===.∵OA=OC=3,则∠ACO=45°,∴△CDH为等腰直角三角形,∴26355 CH DH==⨯=.∴64255 BH BC CH=-=-=.∴tan∠DBC=32 DHBH=.(3)延长AE至x轴,与x轴交于点F,∠OA=OC=3,∴∠OAC=∠OCA=45°,∠∠OAB=∠OAC-∠BAC=45°-∠BAC,∠OFA=∠OCA-∠FAC=45°-∠FAC,∠∠BAC=∠FAC,∴∠OAB=∠OFA . ∴△OAB∠∠OFA , ∴13OB OA OA OF ==. ∴OF=9,即F (9,0);设直线AF 的解析式为y=kx+b (k≠0),可得093k b b =+⎧⎨-=⎩ ,解得133k b ⎧=⎪⎨⎪=-⎩,∴直线AF 的解析式为:133y x =-, 将x=2代入直线AF 的解析式得:73y =-,∴E (2,73-). 【点睛】本题考查了相似三角形的判定和性质,二次函数的性质,求二次函数的解析式,等腰直角三角形的判定和性质,求一次函数的解析式,解题的关键是掌握二次函数的图像和性质,以及正确作出辅助线构造相似三角形.例2..已知9023ABC AB BC AD BC P ∠===°,,,∥,为线段BD 上的动点,点Q 在射线AB 上,且满足PQ AD PC AB =(如图所示)。
平面面积的求法

线等所溯成的区域面积。谯这里不一一介绍。
综上所述,我们看到由特殊曲线湖成的图形面积可由
积分求姆。并且同一图形的瓣积问题逐可以有多攀争不同酶
积分方浚,逶避总络鞍整瑾,我秘迸一步瑾释黎受积分鹃实
质及内涵,为了计算这类区域的面积,我们可归绪为计算特
定结构的和式的极限。同时.我们还可以借助黎曼积分进
一步总络夔线弧妖熬求法、ll|l蘸蠢积憋求法及支体体积的
[收稿日期3zoos-11—16 [作者简介]孛宏(1980--),女。辽宁庄河人,黑龙江幼儿师范i蠹i葶专科学校助理讲师,主要研究穷向为数学与应用数学。 · 132 ·
万方数据
一。疗旧m…m—a曲霄sinz tdt;-2abfT‘c·
一cos2 f)凌;2ab(1一百1 sin2#)|亏=垃兢
1.3 檄坐标系申的面积 若包围平面图形的曲线由极坐标方糨:r;r(口),(a≤口 ≤黟绘窭,篡ee r(鳓褒[a,羽连续,筘一a≤2嚣,麦基线冬巍条 射线疗=a、o=fl所围成的平面翻形s通常称为扇形(如图
1.用定积分求解平面面积 1.1 直角坐标系中的面积
一般情况下,由两条连续的藏线Y一五(z)程Y一 兵(茗)及直线z=a,x—b(a<酗鳜嚣憨乎覆匿影,其嚣积
谛舞公式A=|。阪(工)一苁(烹>鼯。(鞠踅1)
佩一
一l,\LLu x
y。f,∞
j,4
y-)d
‰ 拶j t l
l y_i / l。
O
j
露l
霉2
1帕
4)。则扇形的面积A一÷I‘r2(口)棚.
铡4求双纽线 rz 5 a2 cos2。(Ⅱ>O) 嗣成区域(如图5)的
八胁口。 Y
聋
哆r
\\ 衫 \./f
第七章平面直角坐标系常考题型

平面直角坐标系常考题型一选择题1.若点P(x,y)在第三象限,且点P到x轴的距离为3,到y轴的距离为2,则点P的坐标是( )A.(-2,-3)B.(-2,3)C.(2,-3)D.(2,3)2.若点A(2,m)在x轴上,则点B(m﹣1,m+1)在( )A.第一象限B.第二象限C.第三象限D.第四象限3.一个长方形在平面直角坐标系中,三个顶点的坐标分别是(-1,-1)、(-1,2)、(3,-1),则第四个顶点的坐标是( )A.(2,2)B.(3,2)C.(3,3)D.(2,3)4.若点A(m,n)在第二象限,那么点B(-m,│n│)在( )A.第一象限B.第二象限;C.第三象限D.第四象限5.已知点P(x,y),且,则点P在( )A.第一象限B.第二象限C.第三象限D.第四象限7.如图,在5×4的方格纸中,每个小正方形边长为1,点O,A,B在方格纸的交点(格点)上,在第四象限内的格点上找点C,使三角形ABC的面积为3,则这样的点C共有( )A.2个B.3个C.4个D.5个填空题1.已知点A(0,1),B(0 ,2),点C在x轴上,且S三角形ABC=2,则点C的坐2.在平面直角坐标系中,点C(3,5),先向右平移了5个单位,再向下平移了33.若A(a,b)在第二、四象限的角平分线上,a与b的关系是_________.解题技巧专题:平面直角坐标系中的图形面积——代几结合,突破面积及点的存在性问题◆类型一直接利用面积公式求图形的面积1.如图,在平面直角坐标系中,三角形ABC的面积是( )A.2 B.4 C.8 D.6第1题图第2题图2.如图,在平面直角坐标系xOy中,已知A(-1,5),B(-1,0),C(-4,3),则三角形ABC的面积为________.◆类型二利用分割法求图形的面积3.如图,在平面直角坐标系中,点A(4,0),B(3,4),C(0,2),则四边形ABCO的面积为________.4.观察下图,图中每个小正方形的边长均为1,回答以下问题:【方法14】(1)写出多边形ABCDEF各个顶点的坐标;(2)线段BC,CE的位置各有什么特点?(3)求多边形ABCDEF的面积.◆类型三利用补形法求图形的面积5.在如图所示的正方形网格中,每个小正方形的边长均为1,三角形ABC 的三个顶点恰好是正方形网格的格点.【方法14】(1)写出三角形ABC各顶点的坐标;(2)求出此三角形的面积.◆类型四与图形面积相关的点的存在性问题6.(2017·定州市期中)如图,A(-1,0),C(1,4),点B在x轴上,且AB =3.(1)求点B的坐标;(2)求三角形ABC的面积;(3)在y轴上是否存在点P,使以A,B,P三点为顶点的三角形的面积为10?若存在,请直接写出点P的坐标;若不存在,请说明理由.难点探究专题:平面直角坐标系中动点问题——掌握不同规律,以不变应万变◆类型一沿坐标轴方向运动的点的坐标规律探究1.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2)……按这样的运动规律,经过第2016次运动后,动点P的坐标是________.2.(2017·阿坝州中考)如图,在平面直角坐标系中,一动点从原点O出发,沿着箭头所示方向,每次移动1个单位,依次得到点P1(0,1),P2(1,1),P3(1,0),P4(1,-1),P5(2,-1),P6(2,0),…,则点P2017的坐标是________.3.如图,在直角坐标系中,第一次将三角形OAB变换成三角形OA1B1,第二次将三角形OA1B1变换成三角形OA2B2,第三次将三角形OA2B2变换成三角形OA3B3……已知A(1,3),A1(2,3),A2(3,3),A3(4,3),B(2,0),B1(4,0),B2(8,0),B3(16,0).(1)仔细观察每次变换前后的三角形有何变化,找出规律,按此变换规律将三角形OA3B3变换成三角形OA4B4,则A4的坐标是_________,B4的坐标是_________ ;(2)若按第(1)题的规律将三角形OAB进行了n次变换,得到三角形OAn Bn,比较每次变换中三角形顶点坐标有何变化,找出规律,请推测:An的坐标是_________,Bn的坐标是_________.◆类型二绕原点呈“回”字形运动的点的坐标规律探究1.如图,一个质点在第一象限及x轴、y轴上运动,在第一秒时,它从原点(0,0)运动到(0,1),然后接着按图中箭头所示方向运动,即(0,0)→(0,1)→(1,1)→(1,0)•••,且每秒移动一个单位,那么第80秒时质点所在位置的坐标是( )A.(0,9)B.(9,0)C.(0,8)D.(8,0)2.将自然数按以下规律排列:第一列第二列第三列第四列第五列表中数2在第二行,第一列,与有序数对(2,1)对应;数5与(1,3)对应;数14与(3,4)对应;根据这一规律,数2014对应的有序数对为.。
人教版七年级数学下册解题技巧专题

人教版七年级数学下册解题技巧专题目录:目录:【专题一】平行线中作辅助线的方法【专题一】平行线中作辅助线的方法【专题二】相交线与平行线中的思想方法【专题三】开方运算及无理数判断中的易错题【专题四】平面直角坐标系中的图形面积【专题五】平面直角坐标系中的变化规律【专题六】解二元一次方程组【专题六】解二元一次方程组【专题七】一元一次不等式(组)与学科内知识的综合【专题八】一元一次不等式(组)中含字母系数的问题【专题一】平行线中作辅助线的方法——形成思维定式,快速解题◆类型一类型一 含一个拐点的平行线问题含一个拐点的平行线问题 1.(2017·南充中考)如图,直线a ∥b ,将一个直角三角尺按如图所示的位置摆放.若∠1=58°,则∠2的度数为( ) A .30°B .32°C .42°D .58°第1题图 第2题图题图2.(2017·潍坊中考)如图,∠BCD =90°,AB ∥DE ,则∠α与∠β满足( ) A .∠α+∠β=180°B .∠β-∠α=90°C .∠β=3∠αD .∠α+∠β=90° 3.阅读下列解题过程,然后解答后面的问题.如图①,已知AB ∥CD ,∠B =35°,∠D =32°,求∠BED 的度数.的度数. 解:过E 作EF ∥AB .∵AB ∥CD ,∴CD ∥EF .∵AB ∥EF ,∴∠1=∠B =35°35°..又∵CD ∥EF ,∴∠2=∠D =32°,∴∠BED =∠1+∠2=35°+32°=67°67°. . 如图②、如图②、图③,图③,图③,是明明设计的智力拼图玩具的一部分,是明明设计的智力拼图玩具的一部分,是明明设计的智力拼图玩具的一部分,现在明明遇到两个问现在明明遇到两个问题,请你帮他解决.题,请你帮他解决.(1)如图②,已知∠D =30°,∠ACD =65°,为了保证AB ∥DE ,∠A 应多大?应多大? (2)如图③,要使GP ∥HQ ,则∠G ,∠GFH ,∠H 之间有什么关系?之间有什么关系?◆类型二类型二 含多个拐点的平行线问题含多个拐点的平行线问题4.如图,已知AB ∥DE ,∠ABC =70°,∠CDE =140°,则∠BCD 的大小为( ) A .20°B .30°C .40°D .70°第4题图 第5题图题图5.如图,直线l 1∥l 2,∠α=∠β,∠1=40°,则∠2的度数为________. 6.如图,给出下列三个论断:①∠B +∠D =180°;②AB ∥CD ;③BC ∥DE .请你以其中两个论断作为已知条件,请你以其中两个论断作为已知条件,填入“已知”栏中,填入“已知”栏中,以剩余一个论断作为结论,填入“结论”栏中,使之成为一道由已知可得到结论的题目,并解答该题.已知:______________,结论:______________. 解:解:7.如图①,AB ∥CD ,EOF 是直线AB ,CD 间的一条折线.间的一条折线. (1)试说明:∠EOF =∠BEO +∠DFO ;(2)如果将折一次改为折两次,如图②,则∠BEO ,∠EOP ,∠OPF ,∠PFC 之间会满足怎样的数量关系?并说明理由.【专题二】相交线与平行线中的思想方法——明确解题思想,体会便捷渠道◆类型一方程思想类型一 方程思想1.如图,直线AB,CD相交于点O,∠AOC=60°,OE把∠BOD分成两部分,且∠BOE∶∠EOD=1∶2,则∠AOE的度数为() A.180°B.160°C.140°D.120°题图第1题图第2题图2.(2017·无棣县期末)如图,直线AB,CD相交于点O,OE平分∠BOD,OF平分∠COB,∠AOD∶∠EOD=4∶1,则∠AOF的度数为________.3.如图,已知FC∥AB∥DE,∠α∶∠D∶∠B=2∶3∶4.求∠α,∠D,∠B 的度数.的度数.4.(2017·启东市期末)如图,AD∥BC,BE平分∠ABC交AD于点E,BD平分∠EBC. (1)若∠DBC=30°,求∠A的度数;的度数;(2)若点F在线段AE上,且7∠DBC-2∠ABF=180°,请问图中是否存在与∠DFB相等的角?若存在,请写出这个角,并说明理由;若不存在,请说明理由.由.◆类型二分类讨论思想类型二 分类讨论思想5.若∠α与∠β的两边分别平行,∠α比∠β的3倍少36°,则∠α的度数是() A.18°B.126°C.18°或126°D.以上都不对.以上都不对6.(2017·玄武区期末)在直线MN上取一点P,过点P作射线P A、PB.若P A⊥PB,MPA A=40°,则∠NPB的度数是________________.当∠MP7.(2017·江干区一模)一副直角三角尺按如图①所示方式叠放,现将含45°角的三角尺ADE固定不动,将含30°角的三角尺ABC绕顶点A顺时针转动,使两块三角尺至少有一组边互相平行.如图②,当∠BAD=15°时,BC∥DE,则180°))其他所有可能符合条件的度数为________________.∠BAD(0°<∠BAD<180°8.如图,已知直线l1∥l2,直线l3交l1于C点,交l2于D点,P是线段CD 上的一个动点.当P在直线CD上运动时,请你探究∠1,∠2,∠3之间的关系.之间的关系.第9题图题图第10题图。
专题03 平面直角坐标系(专题详解)(解析版)

专题03 平面直角坐标系专题03 平面直角坐标系 (1)7.1 平面直角坐标系 (2)知识框架 (2)一、基础知识点 (2)知识点1 有序数对 (2)知识点2 平面直角坐标系 (2)知识点3 点的坐标特点 (3)二、典型题型 (6)题型1 有序数对 (6)题型2 平面直角坐标系的概念 (6)题型3 点的坐标的特征 (6)一、点的位置与坐标 (7)二、点的坐标与距离 (8)三、点的坐标与平行于坐标轴的直线(数形结合思想) (8)四、点的坐标与图形的面积 (9)(1)知坐标,求面积 (9)(2)知面积,求坐标(方程思想) (10)(3)分类讨论 (12)三、难点题型 (14)题型1 确定点所在的象限 (14)题型2 点到坐标轴的距离 (14)题型3 探究平面直角坐标系坐标的变化规律 (15)7.2 坐标系的简单运用 (17)知识框架 (17)一、基础知识点 (17)知识点1 用坐标表示地理位置 (17)知识点2 用坐标表示平移 (18)二、典型题型 (20)题型1 用坐标表示地理位置 (20)题型2 用坐标表示平移 (21)一、点的平移 (21)(1)已知点和平移方式,求对应点 (21)(2)已知点和对应点,求平移方式 (21)二、图形的平移 (22)三、难点题型 (23)题型1 动点问题 (23)7.1 平面直角坐标系知识框架{基础知识点{有序数对平面直角坐标系点的坐标的特点典型题型{ 有序数对平面直角坐标系的概念点的坐标的特征{ 点的位置与坐标点的坐标与距离点的坐标与平行于坐标轴的直线(数形结合思想)点的坐标与图形的面积{知坐标,求面积知面积,求坐标(方程思想)分类讨论难点题型{确定点所在的象限点到坐标轴的距离探究平面直角坐标系坐标的变化规律 一、基础知识点知识点1 有序数对1)我们把有顺序的两个数a 与b 组成的数对,用于表示平面中某一确定位置的,叫作有序数对,记作(a ,b )注:①(a ,b )与(b ,a )表达的含义不同,注意有序数对的顺序②在表达有序数对时,一般行在前,列在后。
沪科版八年级上册数学解题技巧精炼专题

沪科版数学解题技巧精炼专题八年级上册目录沪科版八年级上册数学解题技巧精炼专题 (3)解题技巧专题一:平面直角坐标系中的图形面积 (3)◆类型一直接利用面积公式求图形的面积 (3)◆类型二利用分割法求图形的面积 (3)◆类型三利用补形法求图形的面积 (3)◆类型四探究平面直角坐标系中与面积相关的点的存在性 (4)难点探究专题二:平面直角坐标系中点的坐标的变化规律(选做) (5)◆类型一沿坐标轴运动的点的坐标的探究 (5)◆类型二绕原点呈“回”字形运动的点的坐标的探究 (5)◆类型三图形变化的点的坐标的探究 (6)解题技巧专题三:一次函数的图象信息题 (6)◆类型一根据实际问题判断函数图象 (6)◆类型二根据函数图象进行判断 (7)◆类型三一次函数图象与字母系数的关系 (7)难点探究专题四:一次函数与几何的综合问题(选做) (8)◆类型一一次函数与面积问题 (8)◆类型二一次函数与几何图形综合的探究性问题 (9)类比归纳专题五:三角形中内、外角的有关计算 (10)◆类型一直接利用内角和或结合方程思想求角的度数 (10)◆类型二利用外角的性质求角的度数 (11)◆类型三综合内外角求角的度数 (11)◆类型四在三角板或直尺中求角的度数 (11)◆类型五与平行线相结合求角的度数 (12)◆类型六与截取或折叠相关求角的度数 (12)解题技巧专题六:利用全等解决问题的模型与技巧 (13)◆类型一全等三角形的基本模型 (13)◆类型二证明线段间的等量关系 (14)难点探究专题七:动态变化中的三角形全等(选做) (15)◆类型一动点变化与全等三角形 (15)◆类型二图形变换与三角形全等 (15)易错专题八:等腰三角形中易漏解或多解的问题 (16)◆类型一求边长(或周长)时忽略三边关系 (16)◆类型二当腰或底不明时求角度时没有分类讨论 (17)◆类型三三角形的形状不明时与高结合没有分类讨论 (17)难点探究专题九:等腰三角形中辅助线的作法(选做) (17)◆类型一利用“三线合一”作辅助线【方法18】 (17)◆类型二巧用等腰三角形构造全等 (19)◆类型三截长补短构造等腰三角形 (19)模型构建专题十:共顶点的等腰三角形 (20)◆类型一共直角顶点的等腰直角三角形 (20)◆类型二共顶点的等边三角形 (20)类比归纳专题十一:证明线段相等的基本思路 (21)◆类型一已知边的关系或边角关系用全等三角形的性质 (21)◆类型二已知角度、平行关系在同一三角形中用“等角对等边” (21)◆类型三已知线段的垂直平分线或角的平分线+垂直用相应性质 (22)◆类型一求同一顶点的角平分线与高线的夹角的度数 (22)◆类型二求两内角平分线的夹角的度数 (23)◆类型三求一内角平分线与一外角平分线的夹角的度数 (23)◆类型四求两外角平分线的夹角的度数【方法5】 (24)解题技巧专题一:平面直角坐标系中的图形面积参考答案与解析 (25)难点探究专题二:平面直角坐标系中点的坐标的变化规律(选做)参考答案与解析 (26)解题技巧专题三:一次函数的图象信息题参考答案与解析 (27)难点探究专题四:一次函数与几何的综合问题(选做)参考答案与解析 (27)类比归纳专题五:三角形中内、外角的有关计算参考答案与解析 (28)解题技巧专题六:利用全等解决问题的模型与技巧参考答案与解析 (30)难点探究专题七:动态变化中的三角形全等(选做)参考答案与解析 (30)易错专题八:等腰三角形中易漏解或多解的问题参考答案与解析 (32)难点探究专题九:等腰三角形中辅助线的作法(选做)参考答案与解析 (33)模型构建专题十:共顶点的等腰三角形参考答案与解析 (36)类比归纳专题十一:证明线段相等的基本思路参考答案与解析 (37)类比归纳专题十二:与三角形的高、角平分线有关的计算模型参考答案与解析 (38)沪科版八年级上册数学解题技巧精炼专题解题技巧专题1:平面直角坐标系中的图形面积——代几结合,突破面积及点的存在性问题◆类型一直接利用面积公式求图形的面积1.如图,在平面直角坐标系中,△ABC的面积是()A.2 B.4 C.8 D.6第1题图第2题图2.如图,在平面直角坐标系xOy中,已知A(-1,5),B(-1,0),C(-4,3),则△ABC 的面积为________.◆类型二利用分割法求图形的面积3.如图,在平面直角坐标系中,A(4,0),B(3,2),C(-2,3),D(-3,0).求四边形ABCD的面积.◆类型三利用补形法求图形的面积4.如图,已知△ABC,点A(-2,1),B(1,-3),C(3,4),求△ABC的面积.◆类型四 探究平面直角坐标系中与面积相关的点的存在性5.如图,在平面直角坐标系中,点A (4,0),B (3,4),C (0,2).(1)求S 四边形ABCO ;(2)连接AC ,求S △ABC ;(3)在x 轴上是否存在一点P ,使S △P AB =10?若存在,请求点P 的坐标.6.如图,在平面直角坐标系中,已知A (0,a ),B (b ,0),C (b ,c )三点,其中a 、b 、c满足关系式|a -2|+(b -3)2=0和(c -4)2≤0.(1)求a 、b 、c 的值;(2)如果在第二象限内有一点P ⎝⎛⎭⎫m ,12,请用含m 的式子表示四边形ABOP 的面积; (3)在(2)的条件下,是否存在点P ,使得四边形ABOP 的面积与△ABC 的面积相等?若存在,求出点P 的坐标;若不存在,请说明理由.难点探究专题二:平面直角坐标系中点的坐标的变化规律(选做)——掌握不同规律,以不变应万变◆类型一沿坐标轴运动的点的坐标的探究1.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2)……按这样的运动规律,经过第2016次运动后,动点P的坐标是________.2.如图,平面直角坐标系上的点A(1,0)第1次跳至点A1(-1,1),第2次跳至点A2(2,1),第3次跳至点A3(-2,2),第4次跳至点A4(3,2)……依此规律跳下去,点A第100次跳至的点A100的坐标是________.第2题图第3题图3.★如图,一个动点在第一象限内及x轴、y轴上运动,第1分钟从原点运动到(1,0),第2分钟内从(1,0)运动到(1,1),然后它接着按图中箭头所示的方向来回运动(在第一象限内运动时,运动方向与x轴或y轴平行),且每分钟移动1个单位长度.(1)当动点所在位置是(2,2)时,所经过的时间是________;(2)在第2016分钟时,这个动点所在位置的坐标是________.◆类型二绕原点呈“回”字形运动的点的坐标的探究4.(甘孜州中考)如图,正方形A1A2A 3A4,A5A6A7A8,A9A10A11A12,…(每个正方形从第三象限的顶点开始,按顺时针方向顺序,依次记为A1,A2,A3,A4;A5,A6,A7,A8;A9,A10,A11,A12;…)的中心均在坐标原点O,各边均与x轴或y轴平行,若它们的边长依次是2,4,6,…则顶点A20的坐标为________.第4题图第5题图5.★如图,一甲虫从原点出发按图示方向作折线运动,第1次从原点到A1(1,0),第2次运动到A2(1,1),第3次运动到A3(-1,1),第4次运动到A4(-1,-1),第5次运动到A5(2,-1)……则第2015次运动到的点A2015的坐标是________.◆类型三图形变化的点的坐标的探究6.如图,长方形ABCD的两边BC、CD分别在x轴、y轴上,点C与原点重合,点A(-1,2),将长方形ABCD沿x轴向右翻滚,经过1次翻滚点A对应点记为A1,经过2次翻滚点A对应点记为A2……依此类推,经过5次翻滚后点A对应点A5的坐标为() A.(5,2) B.(6,0) C.(8,0) D.(8,1)7.如图,在直角坐标系中,第1次将△OAB变换成△OA1B1,第2次将△OA1B1变换成△OA2B2,第3次将△OA2B2变换成△OA3B3.已知A(1,3),A1(2,3),A2(4,3),A3(8,3),B(2,0),B1(4,0),B2(8,0),B3(16,0).(1)观察每次变换后的三角形有何变化,找出规律,按此变换规律再将△OA3B3变换成△OA4B4,则A4的坐标是________,B4的坐标是________;(2)若按第(1)题找到的规律将△OAB进行了n次变换,得到△OA n B n,比较每次变换中三角形顶点坐标有何变化,找出规律,推测A n的坐标是________,B n的坐标是__________.解题技巧专题三:一次函数的图象信息题——数形结合,快准解题◆类型一根据实际问题判断函数图象1.小明所在学校离家距离为2千米,某天他放学后骑自行车回家,行驶了5分钟后,因故停留10分钟,继续骑了5分钟到家.下面哪一个图象能大致描述他回家过程中离家的距离s(千米)与所用时间t(分钟)之间的关系()◆类型二根据函数图象进行判断2.小亮家与姥姥家相距24km,小亮8:00从家出发,骑自行车去姥姥家.妈妈8:30从家出发,乘车沿相同路线去姥姥家.在同一直角坐标系中,小亮和妈妈的行进路程s(km)与北京时间t(时)的函数图象如图所示.根据图象得到下列结论,其中错误的是() A.小亮骑自行车的平均速度是12km/hB.妈妈比小亮提前0.5小时到达姥姥家C.妈妈在距家12km处追上小亮D.9:30妈妈追上小亮第2题图第3题图3.某复印店复印收费y(元)与复印面数x(面)的函数图象如图所示,从图象中可以看出,复印超过100面的部分,每面收费()A.0.2元B.0.4元C.0.45元D.0.5元◆类型三一次函数图象与字母系数的关系4.如图为一次函数y=kx+b(k≠0)的图象,则下列正确的是()A.k>0,b>0 B.k>0,b<0 C.k<0,b>0 D.k<0,b<05.直线y=ax+b经过第一、二、四象限,则直线y=bx-a的图象只能是图中的()6.下列表示一次函数y=mx+n与正比例函数y=mnx(m,n为常数,且mn≠0)的图象正确的是()7.若函数y=(a-2)x+b-3在直角坐标系中的图象如图所示.化简:|b-a|-|3-b|-|2-a|=________.8.如图,一次函数y=(m-3)x-m+1的图象分别与x轴正半轴、y轴负半轴相交于A、B.(1)求m的取值范围;(2)若该一次函数的图象向上平移4个单位长度后可得某正比例函数的图象.试求这个正比例函数的解析式.难点探究专题四:一次函数与几何的综合问题(选做)◆类型一一次函数与面积问题一、由一次函数图象求面积1.直线y=2x-4与两坐标轴所围成的三角形面积等于()A.8 B.6 C.4 D.162.已知直线l1:y1=2x+3与直线l2:y2=kx-1交于A点,A点横坐标为-1,且直线l1与x轴交于B点,与y轴交于D点,直线l2与y轴交于C点.(1)求出A点的坐标及直线l2的解析式;(2)连接BC,求出S△ABC.二、由面积求一次函数关系式3.若直线y =-2x +b (b >0)与两坐标轴围成的三角形的面积是1,则该直线的解析式为__________.4.在平面直角坐标系中,点O 是坐标原点,过点A (1,2)的直线y =kx +b 与x 轴交于点B ,且S △AOB =4.则该直线的解析式为____________________.三、一次函数上的动点与面积问题5.(盐城中考)如图,在边长为2的正方形ABCD 中剪去一个边长为1的小正方形CEFG ,动点P 从点A 出发,沿A →D →E →F →G →B 的路线绕多边形的边匀速运动到点B 时停止(不含点A 和点B ),则△ABP 的面积S 随着时间t 变化的函数图象大致是( )6.如图所示,直线y =kx -1与x 轴、y 轴分别交于B 、C 两点,OB OC =12. (1)求B 点坐标和k 的值;(2)若点A (x ,y )是直线y =kx -1在第一象限内的部分上的一个动点,试写出在点A 运动过程中,三角形AOB 的面积S 与x 的函数表达式;(3)探索:当动点A (x ,y )可在直线y =kx -1上任意移动时,若S △AOB =14,试确定点A 的位置.【易错4】◆类型二 一次函数与几何图形综合的探究性问题7.如图所示,直线y =x +1与y 轴交于点A 1,以OA 1为边作正方形OA 1B 1C 1,然后延长C 1B 1与直线y =x +1交于点A 2,得到第1个梯形A 1OC 1A 2;再以C 1A 2为边作正方形C 1A 2B 2C 2,同样延长C 2B 2与直线y =x +1交于点A 3得到第2个梯形A 2C 1C 2A 3;再以C 2A 3为边作正方形C 2A 3B 3C 3,延长C 3B 3,得到第3个梯形……则第2个梯形A 2C 1C 2A 3的面积是________;第n (n 是正整数)个梯形的面积是____________(用含n 的式子表示).第7题图 第8题图8.★如图,直角坐标系中,点P (t ,0)是x 轴上的一个动点,过点P 作y 轴的平行线,分别与直线y =12x ,直线y =-x 交于A 、B 两点,以AB 为边向右侧作正方形ABCD .(1)当t =2时,正方形ABCD 的周长是________;(2)当点(2,0)在正方形ABCD 内部时,t 的取值范围是__________________.类比归纳专题五:三角形中内、外角的有关计算◆类型一 直接利用内角和或结合方程思想求角的度数1.△ABC 中,∠A =60°,∠C =70°,则∠B 的度数是( ) A .50° B .60° C .70° D .90°2.(太和县期末)在△ABC 中,已知∠A =2∠B =3∠C ,则△ABC 是( ) A .锐角三角形 B .直角三角形 C .钝角三角形 D .形状无法确定 3.如图,在△ABC 中,∠C =∠ABC =2∠A ,BD 是AC 边上的高,则∠DBC =________度.4.如图,在△ABC 中,AD ⊥BC ,AE 平分∠BAC ,∠B =70°,∠C =30°. (1)∠BAE 的度数为________; (2)∠DAE 的度数为________;(3)探究:小明认为如果只知道∠B -∠C =40°,也能得出∠DAE 的度数?你认为可以吗?若能,请你写出求解过程;若不能,请说明理由.【方法10】◆类型二利用外角的性质求角的度数5.(柳州中考)如图,图中∠1的大小等于()A.40°B.50°C.60°D.70°第5题图第6题图6.如图,BD 、CD分别平分∠ABC和∠ACE,∠A=60°,则∠D的度数是【方法10】()A.20°B.30°C.40°D.60°◆类型三综合内外角求角的度数7.如图,∠B=20°,∠A=∠C=40°,则∠CDE的度数为________.第7题图第8题图8.(和县期末)如图,在△ABC中,D是AB上一点,E是AC上一点,BE,CD相交于F,∠A=70°,∠ACD=20°,∠ABE=28°,则∠CFE的度数为()A.62°B.68°C.78°D.90°9.★如图,△ABC的∠ABC、∠ACB的外角的平分线交于点P.(1)若∠ABC=50°,∠A=70°,求∠P的度数;(2)若∠A=68°,求∠P的度数;(3)根据以上计算,试写出∠P与∠A的数量关系.◆类型四在三角板或直尺中求角的度数10.如图所示,将三角形的直角顶点放在直尺的一边上,∠1=30°,∠3=20°,则∠2=________.第10题图第11题图11.将一副三角板按如图所示摆放,图中∠α的度数是()A.120°B.105°C.90°D.75°12.一副三角板如图所示叠放在一起,则图中∠α的度数是________.◆类型五与平行线相结合求角的度数13.如图,AB∥CD,直线PQ分别交AB、CD于点F、E,EG是∠DEF的平分线,交AB于点G.若∠PF A=40°,那么∠EGB 的度数为()A.80°B.100°C.110°D.120°第13题图第14题图14.如图,BD是△ABC的角平分线,DE∥BC,交AB于点E,∠A=45°,∠BDC=60°,则∠BDE=________度.15.如图,A点在B点的北偏东40°方向,C点在B点的北偏东75°方向,A点在C点的北偏西50°方向.(1)试证明△ABC为直角三角形;(2)求∠ACB的度数.◆类型六与截取或折叠相关求角的度数16.如图,Rt△ABC中,∠ACB=90°,∠A=52°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠A′DB=________.第16题图第17题图17.在△ABC中,∠B=70°,若沿图中虚线剪去∠B,则∠1+∠2等于________.18.如图.(1)将△ABC纸片沿DE折叠成图①,此时点A落在四边形BCDE内部,则∠A与∠1、∠2之间有一种数量关系保持不变,请找出这种数量关系并说明理由;(2)若折成图②或图③,即点A落在BE或CD上时,分别写出图②中∠DAE与∠2、图③中∠DAE与∠1之间的关系式(不必证明);(3)若折成图④,写出∠A与∠1、∠2之间的关系式(不必证明).解题技巧专题六:利用全等解决问题的模型与技巧——明模型,先观察,再猜想,后证明◆类型一全等三角形的基本模型1.如图,AC=AD,BC=BD,∠A=50°,∠B=90°,则∠C=________.【方法12】第1题图第2题图第3题图2.如图,锐角△ABC的高AD、BE相交于F,若BF=AC,BC=7,CD=2,则AF的长为________.3.如图,点A、D、C、E在同一条直线上,AB∥EF,AB=EF,∠B=∠F,AE=10,AC=6,则CD的长为()A.2 B.4 C.4.5 D.34.如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD交AC于点F.(1)求证:△BAD≌△CAE;(2)猜想BD、CE有何特殊位置关系,并说明理由.◆类型二证明线段间的等量关系一、等线段代换5.如图,Rt△ABC中,AB=AC,∠BAC=90°,直线l为经过点A的任一直线,BD⊥l 于D,CE⊥l于E,若BD>CE,试问:(1)AD与CE的大小关系如何?请说明理由;(2)线段BD,DE,CE之间的数量关系如何?并说明理由.【方法13】二、截长补短法6.★如图,在四边形ABDE中,C是BD边的中点,若AC平分∠BAE,∠ACE=90°,猜想线段AE、AB、DE的长度满足的数量关系,并证明.【方法12】三、倍长中线法7.★在△ABC中,AB=8,AC=6,则BC边上的中线AD的取值范围是()A.6<AD<8 B.2<AD<14 C.1<AD<7 D.无法确定难点探究专题七:动态变化中的三角形全等(选做)◆类型一动点变化与全等三角形1.如图,CA⊥AB,垂足为点A,AB=8厘米,AC=4厘米,射线BM⊥AB,垂足为点B,一动点E从A点出发以2厘米/秒的速度沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB,当点E运动______________秒时,△DEB与△BCA 全等.2.★如图,点A的坐标为(-2,0),P为y轴负半轴上一个动点,当点P向y轴负半轴下方运动时,以P为顶点作△APD,并使P A=PD,∠APD=90°,过点D作DE⊥x轴于E点,求OP-DE的值.【方法13】◆类型二图形变换与三角形全等3.如图,在Rt△ABC中,∠ACB=90°,点D、F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CE,连接EF.(1)求证:△BCD≌△FCE;(2)若EF∥CD,求∠BDC的度数.4.如图甲,已知A 、E 、F 、C 在一条直线上,AE =CF ,过E 、F 分别作DE ⊥AC ,BF ⊥AC ,且AB =CD .(1)试问OE =OF 吗?请说明理由;(2)若△DEC 沿AC 方向平移到如图乙的位置,其余条件不变,上述结论是否仍成立?请说明理由.5.★如图,将Rt △ABC 沿斜边翻折得到△ADC ,点E ,F 分别为DC ,BC 边上的点,且∠EAF =12∠DAB .试猜想DE ,BF ,EF 之间有何数量关系,并证明你的猜想.【方法12】易错专题八:等腰三角形中易漏解或多解的问题——易错归纳,各个击破◆类型一 求边长(或周长)时忽略三边关系1.(盐城中考)若一个等腰三角形的两边长分别是2和5,则它的周长为( ) A .12 B .9C .12或9D .9或72.学习了三角形的有关问题后,王老师请同学们交流这样一个问题:“已知一个等腰三角形的周长是12,其中一条边长为3,求另外两条边的长.”同学们经过片刻思考和交流后,小明同学举手讲:“另两条边长为3,6或4.5,4.5”.你认为小明回答是否正确:________,理由是______________________.3.已知一个等腰三角形的两边长a 、b 满足方程组⎩⎪⎨⎪⎧4a -3b =11,2a +b =13.(1)求a 、b 的值;(2)求这个等腰三角形的周长.4.已知等腰三角形ABC中,一腰AC上的中线BD将三角形的周长分成9cm和15cm 两部分,求这个三角形的腰长和底边的长.【易错8】◆类型二当腰或底不明时求角度时没有分类讨论5.已知等腰三角形的一个内角为50°,则这个等腰三角形的顶角为()A.50°B.80°C.50°或80°D.40°或65°6.等腰三角形的一个外角是60°,则它的顶角的度数是________.7.★若一个大的等腰三角形能被分割为两个小等腰三角形,试求该大等腰三角形顶角的度数(要求画出相应图形,写出求解过程).◆类型三三角形的形状不明时与高结合没有分类讨论8.等腰三角形的一内角为80°,则它的一腰上的高与底边的夹角的度数是________.【易错8】9.等腰三角形一腰上的高与另一腰的夹角的度数是20°,试求这个等腰三角形各内角的度数.【易错8】难点探究专题九:等腰三角形中辅助线的作法(选做)——形成精准解题思维◆类型一利用“三线合一”作辅助线【方法18】一、已知等腰作垂线(或中线、角平分线)1.如图,在△ABC 中,AB =AC ,AE ⊥BE 于点E ,且BE =12BC ,若∠EAB =20°,则∠BAC =________.2.(庐江县期末)如图,△ABC 是等边三角形,D 是AC 的中点,E 是BC 延长线上的一点,CE =CD ,DM ⊥BC ,垂足为M .求证:M 是BE 的中点.3.如图,在△ABC 中,AB =AC ,点E 在CA 的延长线上,∠E =∠AFE .求证:EF ⊥BC .二、构造等腰三角形4.如图,△ABC 的面积为1cm 2,AP 垂直∠ABC 的平分线BP 于P ,则△PBC 的面积为( )A .0.4cm 2B .0.5cm 2C .0.6cm 2D .0.7cm 25.★如图,在△ABC 中,AB =AC ,点P 从点B 出发沿线段BA 移动,同时,点Q 从点C 出发沿线段AC 的延长线移动,已知点P 、Q 移动的速度相同,PQ 与直线BC 相交于点D .(1)如图①,当点P 为AB 的中点时,求证:PD =QD ;(2)如图②,过点P 作直线BC 的垂线,垂足为E ,当点P 、Q 在移动的过程中,线段BE 、DE 、CD 中是否存在长度保持不变的线段?请说明理由.◆类型二巧用等腰三角形构造全等6.★如图,△ABC是等边三角形,△BDC是等腰三角形,BD=CD,∠BDC=120°,以点D为顶点作一个60°的角,角的两边分别交AB、AC于M、N两点,连接MN.求证:MN=BM+NC.◆类型三截长补短构造等腰三角形7.★如图,△ABC中,∠C=2∠A,BD平分∠ABC交AC于D.求证:AB=BC+CD.8.★如图,CE、CB分别是△ABC、△ADC的中线,且AB=AC.求证:CD=2CE.模型构建专题十:共顶点的等腰三角形——明模型,记结论◆类型一共直角顶点的等腰直角三角形1.如图,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE =90°,点A、D、E 在同一直线上,CM为△DCE中DE边上的高,连接BE.(1)求∠AEB的度数;(2)探究线段CM、AE、BE之间的数量关系,并说明理由.◆类型二共顶点的等边三角形2.如图,在四边形ABCD中,AB∥CD,AB=CD,AD∥BC,AD=BC,分别延长DC,BC到点E,F,使得△BCE和△CDF都是等边三角形.(1)求证:AE=AF;(2)求∠EAF的度数.类比归纳专题十一:证明线段相等的基本思路——分类型、理条件、定思路◆类型一已知边的关系或边角关系用全等三角形的性质1.如图,在四边形ABCD中,∠B+∠ADC=180°,BC=DC,延长AD到E点,使DE=AB,连接AC,CE.求证:AC=CE.2.★如图,点D在等边三角形ABC的边AB上,点F在边AC上,连接DF并延长交BC的延长线于点E,EF=FD,求证:AD=CE.【方法19】◆类型二已知角度、平行关系在同一三角形中用“等角对等边”3.如图,在△ABC中,CD与CF分别是△ABC的内角、外角平分线,DF∥BC交AC 于点E.求证:DE=EF.4.如图,在△ABC中,∠ACB=2∠B,∠BAC的平分线AD交BC于D,过C作CN⊥AD 交AD于H,交AB于N.(1)求证:AN=AC;(2)试判断BN与CD的数量关系,并说明理由.◆类型三已知线段的垂直平分线或角的平分线+垂直用相应性质5.如图,△ABC中,∠CAB的平分线与BC的垂直平分线DG相交于D,过点D作DE⊥AB,DF⊥AC,求证:BE=CF.6.★如图,∠AOB=90°,OM是∠AOB的平分线,将三角板的直角顶点P在射线OM 上滑动,两直角边分别与OA、OB交于C、D,PC和PD有怎样的数量关系?请说明理由.类比归纳专题十二:与三角形的高、角平分线有关的计算模◆类型一求同一顶点的角平分线与高线的夹角的度数1.如图,AD,AE分别是△ABC的高和角平分线.(1)已知∠B=40°,∠C=60°,求∠DAE的度数;(2)设∠B=α,∠C=β(α<β),请用含α,β的代数式表示∠DAE,并证明.◆类型二 求两内角平分线的夹角的度数2.如图,△ABC 中,∠ABC 和∠ACB 的平分线交于点O .若∠BOC =120°,则∠A =_____.3.如图,△ABC 中,点P 是∠ABC ,∠ACB 的平分线的交点. (1)若∠A =80°,求∠BPC 的度数.(2)有位同学在解答(1)后得出∠BPC =90°+12∠A 的规律,你认为正确吗?请给出理由.◆类型三 求一内角平分线与一外角平分线的夹角的度数4.如图,在△ABC 中,BA 1平分∠ABC ,CA 1平分∠ACD ,BA 1,CA 1相交于点A 1. (1)求证:∠A 1=12∠A ;(2)如图,继续作∠A 1BC 和∠A 1CD 的平分线交于点A 2,得∠A 2;作∠A 2BC 和∠A 2CD 的平分线交于点A 3,得∠A 3……依此得到∠A 2017,若∠A =α,则∠A 2017=_____________.◆类型四求两外角平分线的夹角的度数【方法5】5.(1)如图,BO平分△ABC的外角∠CBD,CO平分△ABC的外角∠BCE,则∠BOC 与∠A的关系为____________;(2)请就(1)中的结论进行证明.解题技巧专题1:平面直角坐标系中的图形面积参考答案与解析1.B 2.7.53.解:分别过C 作CE ⊥x 轴于E ,过B 作BF ⊥x 轴于F .由题意,得DE =1,CE =3,BF =2,AF =1,EF =5.S四边形ABCD =S △CDE +S梯形CEFB +S △ABF =12×1×3+12×(3+2)×5+12×1×2=15.4.解:过点A 作x 轴的垂线,过点B 作y 轴的垂线,过点C 分别作x 轴、y 轴的垂线,交于点D ,E ,F 三点,如图所示.由题意,得CD =EF =5,DE =CF =7,AD =3,CD =5,AE =4,BE =3,BF =2.方法一:S △ABC =S长方形CDEF -S △ACD -S △ABE -S △BCF =CD ·DE -12AD ·CD -12AE ·BE -12BF ·CF =5×7-12×3×5-12×4×3-12×2×7=292.方法二:S △ABC =S梯形BCDE -S △ACD -S △ABE =12(BE +CD )·DE -12AD ·CD -12AE ·BE =12×(3+5)×7-12×3×5-12×4×3=292.方法三:S △ABC =S 梯形CAEF -S △ABE -S △BCF =12(AE +CF )·EF -12AE ·BE -12BF ·CF =12×(4+7)×5-12×4×3-12×2×7=292.方法点拨:本题运用了补形法,对于平面直角坐标系中的三角形,可以通过作垂线,运用补形法将三角形补形,将它转化为便于计算面积的图形,通过这些图形面积的和差关系来求原三角形的面积.5.解:(1)过点B 作BD ⊥OA 于点D .由题意,得OC =2,OD =3,AD =1,BD =4.S 四边形ABCO=S 梯形BCOD +S △ABD =12×(2+4)×3+12×1×4=11;(2)S △ABC =S 四边形ABCO -S △AOC =11-12×2×4=7;(3)存在.设点P 的坐标为(x ,0),则AP =|4-x |,由题意,得12×4×|4-x |=10,∴|4-x |=5,∴x =9或x =-1,∴点P 的坐标为(9,0)或(-1,0).6.解:(1)∵|a -2|+(b -3)2=0,(c -4)2≤0,∴a =2,b =3,c =4;(2)∵P ⎝⎛⎭⎫m ,12在第二象限,∴m <0.S 四边形ABOP =S △ABO +S △AOP =12OA ·OB +12OA ·|m |=12×2×3+12×2×(-m )=3-m ;(3)存在.由B (3,0),C (3,4),A (0,2),得S △ABC =12×3×4=6.由(2)可知S 四边形ABOP =3-m ,∴3-m =6,∴m =-3,∴点P 的坐标为⎝⎛⎭⎫-3,12. 难点探究专题二:平面直角坐标系中点的坐标的变化规律(选做)参考答案与解析1.(2016,0) 解析:结合图象可知,当运动次数为偶数次时,P 点运动到x 轴上,且横坐标与运动次数相等.∵2016为偶数,∴运动2016次后,动点P 的坐标是(2016,0).2.(51,50) 解析:由题意,得A 100在第一象限,纵坐标为1002=50,横坐标比纵坐标大1.∴点A 100的坐标为(51,50).3.(1)6分钟(2)(44,8) 解析:观察图形得第12分钟坐标为(1,0),第22分钟坐标为(0,2),第32分钟坐标为(3,0),第42分钟坐标为(0,4)……∵2016<452=2025,第2025分钟坐标为(45,0),第2024分钟坐标为(44,0),2024-2016=8,∴在第2016分钟时,这个动点所在位置的坐标是(44,8).4.(5,-5) 解析:∵20÷4=5,∴点A 20在第四象限.∵点A 4所在正方形的边长为2,∴点A 4的坐标为(1,-1),同理可得点A 8的坐标为(2,-2),点A 12的坐标为(3,-3),∴点A 20的坐标为(5,-5).5.(-504,504) 解析:观察图形序号(大于4),被4除余数为1的点在第四象限,被4除余数为2的点在第一象限,余数为3的点在第二象限,能被4整除的点在第三象限.2015被4除商为503,余数为3.由A 3(-1,1),A 7(-2,2),可得A 2015(-504,504).6.D 解析:由题意可得下图,经过5次翻滚后点A 对应点A 5的位置如图所示,故A 5的坐标为(8,1).故选D.7.(1)(16,3) (32,0) (2)(2n ,3) (2n +1,0)解析:(1)∵A 1(2,3),A 2(4,3),A 3(8,3),∴A 4的横坐标为24=16,纵坐标为3.故A 4的坐标为(16,3).∵B 1(4,0),B 2(8,0),B 3(16,0),∴B 4的横坐标为25=32,纵坐标为0.故点B 4的坐标为(32,0);(2)由A 1(2,3),A 2(4,3),A 3(8,3),可以发现它们各点坐标的关系为横坐标是2n ,纵坐标都是3.故A n 的坐标为(2n ,3).由B 1(4,0),B 2(8,0),B 3(16,0),可以发现它们各点坐标的关系为横坐标是2n +1,纵坐标都是0.故B n 的坐标为(2n +1,0).解题技巧专题三:一次函数的图象信息题参考答案与解析1.D2.D 解析:根据图象知9:00妈妈追上小亮,故D 选项错误. 3.B 4.C5.B 解析:由直线y =ax +b 经过第一、二、四象限,得a <0,b >0,∴-a >0.∴y =bx -a 的图象经过第一、二、三象限.故选B.6.A 解析:当mn >0时,直线y =mnx 经过第一、三象限,m ,n 同号.m ,n 同正时,直线y =mx +n 经过第一、二、三象限;m ,n 同负时,直线y =mx +n 经过第二、三、四象限,故B 、D 错;当mn <0时,直线y =mnx 经过第二、四象限,mn 异号.m >0,n <0时,直线y =mx +n 经过第一、三、四象限;m <0,n >0时,直线y =mx +n 经过第一、二、四象限,故A 正确,C 错误.故选A.7.1 解析:由图可知y =(a -2)x +b -3的图象经过第一、二、四象限,∴a -2<0,b -3>0,∴a <2,b >3.∴|b -a |-|3-b |-|2-a |=b -a -(b -3)-(2-a )=1.8.解:(1)由图可知y =(m -3)x -m +1经过第一、三、四象限,∴⎩⎪⎨⎪⎧m -3>0,-m +1<0,∴m >3;(2)将y =(m -3)x -m +1的图象向上平移4个单位得y =(m -3)x -m +5,由题意,得-m +5=0,∴m =5,∴这个正比例函数的解析式为y =2x .难点探究专题四:一次函数与几何的综合问题(选做)参考答案与解析1.C2.解:(1)当x =-1时,y 1=-2+3=1,∴A 点的坐标为(-1,1).∵直线l 2:y 2=kx -1经过点A (-1,1),∴1=-k -1,∴k =-2,∴y 2=-2x -1;(2)∵直线y 1=2x +3与y 轴交于D (0,3),直线y 2=-2x -1与y 轴交于C (0,-1),∴CD =4,∴S △ADC =12×4×1=2.∵直线y 1=2x +3与x 轴交于B ⎝⎛⎭⎫-32,0,∴S △BCD =12×4×32=3,∴S △ABC =S △BCD -S △ACD =3-2=1.3.y =-2x +24.y =-23x +83或y =25x +85 解析:设B 点坐标为(m ,0),则S △AOB =12·|m |·2=|m |.又∵S △AOB=4,∴|m |=4,∴m =±4.当m =4时,由直线y =kx +b 过点A (1,2),B (4,0),得⎩⎪⎨⎪⎧2=k +b ,0=4k +b ,。
平面直角坐标系中三角形面积的求法(例题及对应练习)

例析平面直角坐标系中面积的求法我们常常会遇到在平面直角坐标系中求三角形面积的问题.解题时我们要注意其中的解题方法和解题技巧.现举例说明如下.一、有一边在坐标轴上例1 如图1,平面直角坐标系中,△ABC的顶点坐标分别为(-3,0),(0,3),(0,-1),你能求出三角形ABC的面积吗?分析:根据三个顶点的坐标特征可以看出,△ABC的边BC在y轴上,由图形可得BC=4,点A到BC边的距离就是A点到y轴的距离,也就是A点横坐标的绝对值3,然后根据三角形的面积公式求解.解:因为B(0,3),C(0,-1),所以BC=3-(-1)=4.因为A(-3,0),所以A点到y轴的距离,即BC边上的高为3,二、有一边与坐标轴平行例2 如图2,三角形ABC三个顶点的坐标分别为A(4,1),B(4,5),C(-1,2),求三角形ABC的面积.分析:由A(4,1),B(4,5)两点的横坐标相同,可知边AB与y 轴平行,因而AB的长度易求.作AB边上的高CD,则D点的横坐标与A点的横坐标相同,也是4,这样就可求得线段CD的长,进而可求得三角形ABC的面积.解:因为A,B两点的横坐标相同,所以边AB∥y轴,所以AB=5-1=4. 作AB边上的高CD,则D点的横坐标为4,所以CD=4-(-1)=5,所以=.三、三边均不与坐标轴平行例3 如图2,平面直角坐标系中,已知点A(-3,-1),B(1,3),C(2,-3),你能求出三角形ABC的面积吗?分析:由于三边均不平行于坐标轴,所以我们无法直接求边长,也无法求高,因此得另想办法.根据平面直角坐标系的特点,可以将三角形围在一个梯形或长方形中,这个梯形(长方形)的上下底(长)与其中一坐标轴平行,高(宽)与另一坐标轴平行.这样,梯形(长方形)的面积容易求出,再减去围在梯形(长方形)内边缘部分的直角三角形的面积,即可求得原三角形的面积.解:如图,过点A、C分别作平行于y轴的直线,与过点B平行于x 轴的直线交于点D、E,则四边形ADEC为梯形.因为A(-3,-1),B(1,3),C(2,-3),所以AD=4,CE=6,DB=4,BE=1,DE=5.所以=(AD+CE)×DE-AD×DB-CE×BE=×(4+6)×5-×4×4-×6×1=14.平面直角坐标系中的面积问题(提高篇)“割补法”的应用一、已知点的坐标,求图形的面积。
人教版七年级数学下册巧用坐标求涉图形的面积问题的五种方法

5.如图,四边形 OABC 各个顶点的坐标分别是 O(0,0),A(2, 0),B(4,2),C(2,3),过点 C 与 x 轴平行的直线 EF 与 过点 B 与 y 轴平行的直线 EH 交于点 E.
4.如图,已知 A(-2,0),B(4,0),C(2,4), (1)求△ABC 的面积;
解:过 C 作 CD⊥AB 于 D,则 CD=4. 又易知 AB=4-(-2)=6, ∴S(2)设 P 为 x 轴上一点,若 S△APC=12S△PBC,求 P 的坐标.
3.在如图所示的平面直角坐标系中,四边形 OABC 各顶点分别 是 O(0,0),A(-4,10),B(-12,8),C(-14,0).求四边 形 OABC 的面积.
【点拨】本题的解题技巧在于把不规则的四边形 OABC 分割为 几个规则图形,实际上分割的方法是不唯一的,并且不仅可以用 分割法,还可以用补形法.
人教版 七年级下
第七章 平面直角坐标系
阶段核心方法专训 巧用坐标求涉图形的面积问题的五种
方法
1.如图,已知 A(-2,0),B(4,0),C(-4,4),求三角形 ABC 的面积.
解:因为 C 点的坐标为(-4,4), 所以△ABC 的 AB 边上的高为 4. 因为点 A,B 的坐标分别为(-2,0),(4,0),所以 AB=6. 所以 S△ABC=12×6×4=12.
(2)在线段 EH 上是否存在点 P,使得四边形 OAPC 的面积为 7?若不存在,说明理由;若存在,求点 P 的坐标.
专项训练2 巧用坐标求图形的面积的四种方法

专项训练2巧用坐标求图形的面积的四种方法方法总结:1.规则图形的面积可用几何图形的面积公式求解,对于不规则图形的面积,通常可采用补形法或分割法将不规则图形的面积转化为规则图形的面积和或差求解.2.求几何图形的面积时,底和高往往通过计算某些点的横坐标之差的绝对值或纵坐标之差的绝对值去实现.直接求图形的面积1.如图,已知A(-2,0),B(4,0),C(-4,4),求△ABC的面积.(第1题)利用补形法求图形的面积2.已知在四边形ABCD中,A(-3,0),B(3,0),C(3,2),D(1,3),画出图形,求四边形ABCD的面积.3.如图,已知点A(-3,1),B(1,-3),C(3,4),求三角形ABC的面积.(第3题)利用分割法求图形的面积4.在如图所示的平面直角坐标系中,四边形OABC各顶点的坐标分别是O(0,0),A(-4,10),B(-12,8),C(-14,0),求四边形OABC的面积.(第4题)已知三角形的面积求点的坐标5.已知点O(0,0),点A(-3,2),点B在y轴的正半轴上,若△AOB的面积为12,则点B 的坐标为()A.(0,8) B.(0,4) C.(8,0) D.(0,-8)6.已知点A(-4,0),B(6,0),C(3,m),如果三角形ABC的面积是12,求m的值.7.已知A(-3,0),B(5,0),C(x,y).(1)若点C在第二象限内,且|x|=3,|y|=3,求点C的坐标,并求△ABC的面积;(2)若点C在第四象限内,且△ABC的面积为8,|x|=4,求点C的坐标.参考答案1.解:因为C 点的坐标为(-4,4),所以△ABC 的AB 边上的高为4.因为点A ,B 的坐标分别为(-2,0),(4,0),所以AB =6.所以S △ABC =12×6×4=12. 2.解:如图.过D 点作DE 垂直于BC ,交BC 的延长线于点E ,则四边形DABE 为直角梯形. 又由题意知DE =2,AB =6,BE =3,EC =1,所以S 四边形ABCD =S 梯形DABE -S △CDE=12×(2+6)×3-12×1×2 =11.(第2题)3.解:如图,作长方形CDEF ,则S 三角形ABC =S 长方形CDEF -S 三角形ACD -S 三角形ABE -S 三角形BCF =CD·DE -12AD·CD -12AE·BE -12BF·CF =6×7-12×3×6-12×4×4-12×2×7=18. (第3题)(第4题)4.解:如图,过A 点作AD ⊥x 轴,垂足为点D ,过B 点作BE ⊥AD ,垂足为点E.易知OD =4,AD =10,DE =8,BE =-4-(-12)=8,AE =10-8=2,CD =-4-(-14)=10,所以S四边形OABC =S 三角形AOD +S 三角形ABE +S 梯形DEBC =12OD·AD +12AE·BE +12(BE +CD)·DE =12×4×10+12×2×8+12×(8+10)×8=100.方法指导:本题的解题技巧在于把不规则的四边形OABC 分割为几个规则图形,实际上分割的方法不是唯一的,并且不仅可以用分割法,还可以用补形法.5.A6.解:AB =6-(-4)=10.根据三角形的面积公式,得12AB ·|m|=12, 即12×10·|m|=12,解得|m|=2.4. 因为点C(3,m),所以点C 在第一象限或第四象限.当点C 在第一象限时,m >0,则m =2.4;当点C 在第四象限时,m <0,则m =-2.4.综上所述,m 的值为-2.4或2.4.7.解:(1)因为点C 在第二象限内,且|x|=3,|y|=3,所以点C 的坐标为(-3,3),S △ABC =12×[5-(-3)]×3=12. (2)由题意可知AB =8.因为点C 在第四象限内,|x|=4,所以x =4.因为△ABC 的面积为8,所以S △ABC =12×8×|y|=8. 所以|y|=2.又因为点C 在第四象限内,所以y =-2.所以点C 的坐标为(4,-2).。
平面直角坐标系求解题技巧

平面直角坐标系求解题技巧平面直角坐标系是二维坐标系的一种,由两个互相垂直的轴组成,分别为x轴和y轴,通常以原点O为起点,x 轴正方向为右侧,y轴正方向为上方。
这个坐标系在解决各种几何和代数问题时非常有用,以下是一些求解题的技巧:1. 明确问题:在使用直角坐标系求解问题之前,首先需要明确问题中所给出的信息和需要求解的未知量。
通常可以使用字母来代表未知量,并利用已知信息建立方程或关系。
2. 绘制坐标系:在明确问题后,可以根据问题中的条件和已知信息绘制出对应的直角坐标系图。
通过将已知点或线段标记在坐标系中,并与坐标轴进行对应,有助于理清问题的几何关系。
3. 利用距离和斜率:直角坐标系中,两点之间的距离可以根据勾股定理求解。
设点A的坐标为(x1, y1),点B的坐标为(x2, y2),则两点间的距离d为:d = √((x2 - x1)^2 + (y2 - y1)^2) 。
斜率可以用来判断两条直线是否平行、垂直或相交。
设直线L1上两点的坐标分别为(x1, y1)和(x2, y2),直线L2上两点的坐标分别为(x3, y3)和(x4, y4),则两条直线的斜率分别为:m1 = (y2 - y1) / (x2 - x1) 和 m2 = (y4 - y3) / (x4 - x3)。
当两条直线平行时,斜率相等;当两条直线垂直时,斜率乘积为-1。
4. 利用方程和代数关系:通过建立方程或代数关系,可以解决一些几何问题。
例如,已知一条直线上的两点坐标,可以利用点斜式或一般式建立直线的方程。
点斜式方程为:y - y1 = m(x - x1),其中m为斜率,(x1, y1)为已知点的坐标。
一般式方程为:Ax + By + C = 0,其中A、B、C为常数,直线的斜率可表示为m = -A/B。
通过将已知信息转化为方程或代数形式,可以运用代数求解的方法来求解问题。
5. 利用图形的对称性:在直角坐标系中,图形可能具有各种对称性,如关于x轴对称、关于y轴对称、关于原点对称等。
专题11 平面直角坐标系(归纳与讲解)(解析版)

专题11平面直角坐标系【专题目录】技巧1:点的坐标变化规律探究问题技巧2:巧用坐标求图形的面积技巧3:活用有序数对表示点的位置技巧4:巧用直角坐标系中点的坐标特征解相关问题【题型】一、用有序数对表示位置【题型】二、求点的坐标【题型】三、距离与点坐标的关系【题型】四、象限角的平分线上的点的坐标【题型】五、与坐标轴平行的直线上的点的坐标特征【题型】六、点的坐标的规律探索【题型】七、函数图象的应用【考纲要求】1、会画平面直角坐标系,并能根据点的坐标描出点的位置,掌握坐标平面内点的坐标特征.2、了解函数的有关概念和函数的表示方法,并能结合图象对实际问题中的函数关系进行分析.3、能确定函数自变量的取值范围,并会求函数值.【考点总结】一、平面直角坐标系【考点总结】二、函数有关的概念及图象【注意】1、坐标轴上的点不属于任何象限点的坐标:对于坐标轴内任意一点A,过点A分别向x轴、y轴作垂线,垂足在x轴、y轴上的对应的数a、b分别叫做点A的横坐标和纵坐标,有序数对A(a,b)叫做点A的坐标,记作A(a,b)。
2、确定出数自变量力的取值范围的方法 (1)整式:取全体实数 (2)有分母:取值使分母不为零(3)有二次根式:取值使被开方数不小于0 (4)有很多情况:取它们的公共部分 (5)在实际问题中:取值要符合实际意义 【技巧归纳】技巧1:点的坐标变化规律探究问题【类型】一、沿坐标轴运动的点的坐标规律探究1.如图,在平面直角坐标系中,半径均为1个单位长度的半圆O 1,O 2,O 3,…,组成一条平滑的曲线.点P 从原点O 出发,沿这条曲线向右运动,速度为每秒π2个单位长度,则第2 019秒时,点P 的坐标是( )(第1题)A .(2 018,0)B .(2 019,-1)C .(2 019,1)D .(2 020,0)2.如图,动点P 在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2)……按这样的运动规律,经过第2 017次运动后,动点P 的坐标是________,经过第2 018次运动后,动点P 的坐标是________.3.如图,一个粒子在第一象限内及x 轴、y 轴上运动,第一分钟从原点运动到(1,0),第二分钟从(1,0)运动到(1,1),然后它接着按图中箭头所示的方向运动(在第一象限内运动时,运动方向与x 轴或y 轴平行),且每分钟移动1个单位长度.(1)当粒子所在位置是(2,2)时,所经过的时间是________; (2)在第2 017分钟时,这个粒子所在位置的坐标是________.【类型】二、绕原点呈“回”字形运动的点的坐标规律探究4.将正整数按如图所示的规律在平面直角坐标系中进行排列,每个正整数对应一个整点坐标(x ,y),其中x ,y 均为整数,如数5对应的坐标为(-1,1),则数2 018对应的坐标的( )A .(16,22)B .(-15,-22)C .(15,-22)D .(16,-22) 【类型】三、图形变换的点的坐标规律探究5.在平面直角坐标系中有三个点A(1,-1),B(-1,-1),C(0,1),点P(0,2)关于A 的对称点为P 1,P 1关于B 的对称点为P 2,P 2关于C 的对称点为P 3,按此规律继续以A ,B ,C 为对称中心重复前面的操作,依次得到P 4,P 5,P 6,…,则点P 2 018的坐标是( )A .(0,0)B .(0,2)C .(2,-4)D .(-4,2)6.(探究题)如图,在平面直角坐标系中,第一次将三角形OAB 变换成三角形OA 1B 1,第二次将三角形OA 1B 1变换成三角形OA 2B 2,第三次将三角形OA 2B 2变换成三角形OA 3B 3,已知A(1,3),A 1(2,3),A 2(4,3),A 3(8,3),B(2,0),B 1(4,0),B 2(8,0),B 3(16,0).(1)观察每次变换前后的三角形有何变化,找出规律,按此变换规律再将三角形OA 3B 3变换成三角形OA 4B 4,则点A 4的坐标是________,点B 4的坐标是________;(2)若按(1)题中的规律,将三角形OAB 进行n(n 为正整数)次变换,得到三角形OA n B n ,比较每次变换前后三角形顶点坐标有何变化,找出规律,推测点A n 的坐标是__________,点B n 的坐标是__________. 参考答案1.B 点拨:半径为1个单位长度的圆的周长的一半为12×2π×1=π,因为点P 从原点O 出发,沿这条曲线向右运动,速度为每秒π2个单位长度,所以点P 1秒走12个半圆.当点P 从原点O 出发,沿这条曲线向右运动,运动时间为1秒时,点P 的坐标为(1,1); 当点P 从原点O 出发,沿这条曲线向右运动,运动时间为2秒时,点P 的坐标为(2,0); 当点P 从原点O 出发,沿这条曲线向右运动,运动时间为3秒时,点P 的坐标为(3,-1); 当点P 从原点O 出发,沿这条曲线向右运动,运动时间为4秒时,点P 的坐标为(4,0);当点P 从原点O 出发,沿这条曲线向右运动,运动时间为5秒时,点P 的坐标为(5,1); 当点P 从原点O 出发,沿这条曲线向右运动,运动时间为6秒时,点P 的坐标为(6,0); ….因为2 019÷4=504……3,所以第2 019秒时,点P 的坐标是(2 019,-1). 2.(2 017,1);(2 018,0) 3.(1)6分钟 (2)(44,7)4.C 点拨:以原点为中心,数阵图形成多层正方形(不完整),观察图形得出下表:正方形在第四象限的顶点 因为442<2 018<452=(2×22+1)2=2 025, 所以数2 025对应的坐标为(22,-22). 所以数2 018对应的坐标为(15,-22).5.D 点拨:设P 1(x ,y),因为点A(1,-1),点P(0,2)关于A 的对称点为P 1,所以x2=1,y +22=-1,解得x =2,y =-4,所以P 1(2,-4).同理可得P 2(-4,2),P 3(4,0),P 4(-2,-2),P 5(0,0),P 6(0,2),P 7(2,-4),…,所以每6个点循环一次.因为2 018÷6=336……2,所以点P 2 018的坐标是(-4,2).故选D . 6.(1)(16,3);(32,0)(2)(2n ,3);(2n +1,0) 技巧2:巧用坐标求图形的面积 【类型】一、直接求图形的面积1.如图,已知A(-2,0),B(4,0),C(-4,4),求三角形ABC 的面积.【类型】二、利用补形法求图形的面积2.已知在四边形ABCD中,A(-3,0),B(3,0),C(3,2),D(1,3),画出图形,求四边形ABCD 的面积.3.如图,已知点A(-3,1),B(1,-3),C(3,4),求三角形ABC的面积.【类型】三、利用分割法求图形的面积4.在如图所示的平面直角坐标系中,四边形OABC各顶点分别是O(0,0),A(-4,10),B(-12,8),C(-14,0),求四边形OABC的面积.【类型】四、已知三角形的面积求点的坐标5.已知点O(0,0),点A(-3,2),点B在y轴的正半轴上,若三角形AOB的面积为12,则点B 的坐标为()A.(0,8) B.(0,4) C.(8,0) D.(0,-8)6.已知点A(-4,0),B(6,0),C(3,m),如果三角形ABC的面积是12,求m的值.7.已知A(-2,0),B(4,0),C(x,y).(1)若点C在第二象限,且|x|=4,|y|=4,求点C的坐标,并求三角形ABC的面积;(2)若点C在第四象限,且三角形ABC的面积为9,|x|=3,求点C的坐标.参考答案1.解:因为C点坐标为(-4,4),所以三角形ABC 的AB 边上的高为4. 又由题易知AB =6, 所以S 三角形ABC =12×6×4=12.2.解:如图所示.过点D 作DE 垂直于BC ,交BC 的延长线于点E ,则四边形DABE 为直角梯形. S 四边形ABCD =S 梯形DABE -S 三角形C DE =12×(2+6)×3-12×1×2=11.3.解:方法一:如图,作长方形CDEF ,则S 三角形ABC =S 长方形CDEF -S 三角形ACD -S 三角形ABE -S 三角形BCF =CD·DE -12·AD·CD -12AE·BE -12BF·CF =6×7-12×3×6-12×4×4-12×2×7=18.方法二:如图,过点B 作EF ∥x 轴,并分别过点A 和点C 作EF 的垂线,垂足分别为点E ,F.易知AE =4,BE =4,BF =2,CF =7,EF =6,所以S 三角形ABC =S 梯形AEFC -S 三角形ABE -S 三角形BFC =12(AE +CF)·EF -12AE·BE -12BF·CF =12×(4+7)×6-12×4×4-12×2×7=18. 方法三:如图,过点A 作DE ∥y 轴,并分别过点C 和点B 作DE 的垂线,垂足分别为点D ,E. 易知AE =4,BE =4,AD =3,CD =6,DE =7,所以S 三角形ABC =S 梯形BEDC -S 三角形ABE -S 三角形ADC=12(BE +CD)·DE -12AE·BE -12AD·CD =12×(4+6)×7-12×4×4-12×3×6=18.4.解:如图,过点A 作AD ⊥x 轴,垂足为点D ,过点B 作BE ⊥AD ,垂足为点E.易知D(-4,0),E(-4,8),且BE =-4-(-12)=8,AE =10-8=2,CD =-4-(-14)=10,所以S 四边形OABC =S 三角形AOD +S 三角形ABE +S 梯形DEBC =12OD·AD +12AE·BE +12(BE +CD)·DE =12×4×10+12×2×8+12×(8+10)×8=20+8+72=100.点拨:本题的解题技巧在于把不规则的四边形OABC 分割为几个规则图形,实际上分割的方法是不唯一的,并且不仅可以用分割法,还可以用补形法. 5.A6.解:AB =6-(-4)=10.根据三角形的面积公式,得12AB·|m|=12,即12×10·|m|=12,解得|m|=2.4. 因为点C(3,m),所以点C 在第一象限或第四象限. 当点C 在第一象限时,m >0, 则m =2.4;当点C 在第四象限时,m <0,则m =-2.4.综上所述,m 的值为-2.4或2.4.7.解:(1)因为点C 在第二象限,且|x|=4,|y|=4,所以点C 的坐标为(-4,4). 又易知AB =6,所以S 三角形ABC =12×6×4=12.(2)由题意可知AB =6.因为点C 在第四象限,|x|=3,所以x =3.因为S 三角形ABC =12×6×|y|=9,所以|y|=3.所以y =-3.所以点C 的坐标为(3,-3). 技巧3:活用有序数对表示点的位置 【类型】一、利用有序数对表示座位号1.如图,王明同学的座位是1组2排,如果用有序数对(1,2)表示,那么张敏同学和石玲同学的座位怎样用有序数对表示?【类型】二、利用有序数对表示棋子位置2.五子棋深受广大棋友的喜爱,其规则是:在正方形棋盘中,由黑方先行,轮流弈子,在任一方向上连成五子者为胜.如图是两个五子棋爱好者甲和乙对弈时的部分示意图(甲执黑子先行,乙执白子后走),观察棋盘思考:若A点的位置记为(8,4),甲必须在哪个位置上落子,才不会让乙在短时间内获胜?为什么?【类型】三、利用有序数对表示地理位置3.如图是某市市区几个旅游景点示意图(图中每个小正方形的边长为1个单位长度),如果以O为原点建立两条互相垂直的数轴,如果用(2,2.5)表示金凤广场的位置,用(11,7)表示动物园的位置,根据此规定:(1)湖心岛、光岳楼、山陕会馆的位置如何表示?(2)(11,7)和(7,11)是同一个位置吗?为什么?【类型】四、利用有序数对表示运动路径4.如图,小军家的位置点A在经5路和纬4路的十字路口,用有序数对(5,4)表示;点B是学校的位置,点C是小芸家的位置,如果用(5,4)→(5,5)→(5,6)→(6,6)→(7,6)→(8,6)表示小军家到学校的一条路径.(1)请你用有序数对表示出学校和小芸家的位置;(2)请你写出小军家到学校的其他几条路径.(写3条)参考答案1.解:张敏同学的座位可以表示为(3,3),石玲同学的座位可以表示为(4,5).2.解:甲必须在(1,7)或(5,3)处落子,因为若甲不先截断以上两处之一,而让乙在(1,7)或(5,3)处落子,则下一步不论截断何处,乙总有一处落子可连成五子,乙必胜无疑.3.解:(1)湖心岛的位置可表示为(2.5,5);光岳楼的位置可表示为(4,4);山陕会馆的位置可表示为(7,3).(2)不是同一个位置,因为前面一个数字代表横向,后一个数字代表纵向,交换数字的位置后,就会表示不同的位置.4.解:(1)学校和小芸家的位置分别可表示为(8,6),(3,3).(2)答案不唯一,如:①(5,4)→(5,5)→(6,5)→(7,5)→(8,5)→(8,6);②(5,4)→(6,4)→(7,4)→(8,4)→(8,5)→(8,6);③(5,4)→(6,4)→(6,5)→(7,5)→(8,5)→(8,6).技巧4:巧用直角坐标系中点的坐标特征解相关问题【类型】一、象限内的点的坐标1.若点M(x,y)满足(x+y)2=x2+y2-2,则点M所在象限是()A.第一象限或第三象限B.第二象限或第四象限C.第一象限或第二象限D.不能确定2.在平面直角坐标系中,若点P(m,m-2)在第一象限内,则m的取值范围是________.【类型】二、坐标轴上的点的坐标3.若点M的坐标为(-a2,|b|+1),则下列说法中正确的是()A.点M在x轴正半轴上B.点M在x轴负半轴上C.点M在y轴正半轴上D.点M在y轴负半轴上4.已知点P(a-1,a2-9)在y轴上,则点P的坐标为________.【类型】三、平面直角坐标系中一些特殊点的坐标5.已知点P(2m-5,m-1),当m为何值时,(1)点P在第二、四象限的角平分线上?(2)点P在第一、三象限的角平分线上?6.已知A(-3,m),B(n,4),若AB∥x轴,求m的值,并确定n的取值范围.【类型】四、点的坐标与点到x轴、y轴的距离之间的关系7.已知点A(3a,2b)在x轴上方,y轴的左侧,则点A到x轴、y轴的距离分别为() A.3a,-2b B.-3a,2b C.2b,-3a D.-2b,3a8.已知点P到x轴和y轴的距离分别是2和5,求点P的坐标.【类型】五、关于坐标轴对称的点9.点P(-3,4)关于x轴对称的点的坐标是()A.(-4,3)B.(3,-4)C.(-3,-4) D.(3,4)10.已知点P(3,a)关于y轴的对称点为Q(b,2),则ab=________.11.在平面直角坐标系中,点A的坐标是(2,-3),作点A关于x轴的对称点,得到点A′,再作点A′关于y轴的对称点,得到点A″,则点A″的坐标是(______,______).【类型】六、关于特殊直线对称的点12.点P(3,5)关于第一、三象限的角平分线对称的点为点P1,关于第二、四象限的角平分线对称的点为点P2,则点P1,P2的坐标分别为()A.(3,5),(5,3)B.(5,3),(-5,-3)C.(5,3),(3,5) D.(-5,-3),(5,3) 13.点M(1,4-m)关于过点(5,0)且垂直于x轴的直线对称的点的坐标是____________;若点M关于过点(0,-3)且平行于x轴的直线对称的点的坐标为(1,7),则m=________.参考答案1.B2.m>2点拨:第一象限内的点的横、纵坐标必须同时为正,所以m>2.3.C点拨:由-a2可确定a=0,所以-a2=0. 又|b|+1>0,所以点M(-a2,|b|+1)在y轴正半轴上.4.(0,-8)5.解:(1)根据题意,得2m-5+m-1=0,解得m=2.所以当m=2时,点P在第二、四象限的角平分线上.(2)根据题意,得2m-5=m-1,解得m=4.所以当m=4时,点P在第一、三象限的角平分线上.点拨:第一、三象限的角平分线上的点的横、纵坐标相等,第二、四象限的角平分线上的点的横、纵坐标互为相反数.6.解:因为AB∥x轴,所以m=4.因为A,B不重合,所以n≠-3.点拨:与x轴平行的直线上的点的纵坐标相等.7.C点拨:由点A(3a,2b)在x轴上方,y轴的左侧可知点A在第二象限,故3a是负数,2b是正数,所以点A到x轴、y轴的距离分别为2b,-3a.8.解:设点P的坐标为(x, y),依题意,得|x|=5,|y|=2,所以x=±5,y=±2.所以点P的坐标为(5,2)或(5,-2)或(-5,2)或(-5,-2).点拨:(1)点P(x,y)到x轴的距离为|y|,到y轴的距离为|x|.(2)写点P的坐标时,横、纵坐标的前后顺序不能随意改变.(3)找全满足条件的点P的坐标,不要遗漏.9.C10.-611.-2;312.B点拨:任意点A(a,b)关于第一、三象限的角平分线对称的点的坐标为(b,a),关于第二、四象限的角平分线对称的点的坐标为(-b,-a).13.(9,4-m);17点拨:点A(a,b)关于过点(k,0)且垂直于x轴的直线对称的点的坐标为(2k-a,b),关于过点(0,k)且平行于x轴的直线对称的点的坐标为(a,2k-b).【题型讲解】【题型】一、用有序数对表示位置例1、小李、小王、小张、小谢原有位置如图(横为排、竖为列),小李在第2排第4列,小王在第3排第3列,小张在第4排第2列,小谢在第5排第4列.撤走第一排,仍按照原有确定位置的方法确定新的位置,下列说法正确的是().A.小李现在位置为第1排第2列B.小张现在位置为第3排第2列C.小王现在位置为第2排第2列D.小谢现在位置为第4排第2列【答案】B【分析】由于撤走一排,则四人所在的列数不变、排数减一,据此逐项排除即可.【详解】解:A. 小李现在位置为第1排第4列,故A选项错误;B. 小张现在位置为第3排第2列,故B选项正确;C. 小王现在位置为第2排第3列,故C选项错误;D. 小谢现在位置为第4排第4列,故D选项错误.故选:B.【题型】二、求点的坐标例2、如图,四边形OBCD 是正方形,O ,D 两点的坐标分别是()0,0,()0,6,点C 在第一象限,则点C 的坐标是( )A .()6,3B .()3,6C .()0,6D .()6,6【答案】D【分析】利用O ,D 两点的坐标,求出OD 的长度,利用正方形的性质求出OB ,BC 的长度,进而得出C 点的坐标即可.【详解】解:①O ,D 两点的坐标分别是()0,0,()0,6,①OD =6,①四边形OBCD 是正方形,①OB ①BC ,OB =BC =6 ①C 点的坐标为:()6,6, 故选:D .【题型】三、距离与点坐标的关系例3、在平面直角坐标系的第二象限内有一点M ,点M 到x 轴的距离为3,到y 轴的距离为4,则点M 的坐标是( ) A .(3,4)- B .(4,3)-C .(4,3)-D .()3,4-【答案】C 【解析】 由题意,得 x=-4,y=3,即M 点的坐标是(-4,3), 故选C .【题型】四、象限角的平分线上的点的坐标例4、若点N 在第一、三象限的角平分线上,且点N 到y 轴的距离为2,则点N 的坐标是( ) A .(2,2) B .(-2,-2) C .(2,2)或(-2,-2) D .(-2,2)或(2,-2)【答案】C 【解析】已知点M 在第一、三象限的角平分线上,点M 到x 轴的距离为2,所以点M 到y 轴的距离也为2.当点M 在第一象限时,点M 的坐标为(2,2);点M 在第三象限时,点M 的坐标为(-2,-2).所以,点M 的坐标为(2,2)或(-2,-2).故选C . 【题型】五、与坐标轴平行的直线上的点的坐标特征例5、已知点A (a ﹣2,2a +7),点B 的坐标为(1,5),直线AB ①y 轴,则a 的值是( ) A .1 B .3C .﹣1D .5【答案】B 【详解】 解:①AB①y 轴,①点A 横坐标与点A 横坐标相同,为1, 可得:a -2=1,a=3 故选:B .【题型】六、点的坐标的规律探索例6、在平面直角坐标系中,一个智能机器人接到的指令是:从原点O 出发,按“向上→向右→向下→向右”的方向依次不断移动,每次移动1个单位长度,其移动路线如图所示,第一次移动到点1A ,第二次移动到点2A ……第n 次移动到点n A ,则点2019A 的坐标是( )A .()1010,0B .()1010,1C .()1009,0D .()1009,1【答案】C【分析】根据图象可得移动4次图象完成一个循环,从而可得出点2019A 的坐标. 【详解】()10,1A ,()21,1A ,()31,0A ,()42,0A ,()52,1A ,()63,1A ,…,201945043÷=⋅⋅⋅,所以2019A 的坐标为()50421,0⨯+,则2019A 的坐标是()1009,0, 故选C .【题型】七、函数图象的应用例7、如图,一只蚂蚁从O 点出发,沿着扇形OAB 的边缘匀速爬行一周,设蚂蚁的运动时间为t ,蚂蚁到O 点的距离..为s ,则s 关于t 的函数图象大致为( ).【答案】C【分析】利用函数关系和图象分析解决实际问题,要透过问题情境准确地寻找出问题的自变量和函数,探求变量和函数之间的变化趋势,合理地分析变化过程,准确地结合图象解决实际问题. 【详解】本题是典型的数形结合问题,通过对图形的观察,可以看出s 与t 的函数图象应分为三段:(1)当蚂蚁从点O 到点A 时,s 与t 成正比例函数关系;(2)当蚂蚁从点A 到点B 时,s 不变;(3)当蚂蚁从点B 回到点O 时,s 与t 成一次函数关系,且回到点O 时,s 为零.平面直角坐标系(达标训练)一、单选题1.在平面直角坐标系中,点A (a ,2)在第二象限内,则a 的取值可以是( ) A .1 B .-3C .4D .4或-4【答案】B【分析】根据第二象限的坐标特征判断即可; 【详解】解:①点A (a ,2)在第二象限内, ①a <0, A .不符合题意;B .符合题意;C .不符合题意;D .不符合题意; 故选: B .【点睛】本题考查了象限的坐标特征,掌握第二象限内点的横坐标为负数,纵坐标为正数是解题关键. 2.若点(),1A a a -在x 轴上,则点()1,2B a a +-在第( )象限. A .一 B .二 C .三 D .四【答案】D【分析】由点A 在x 轴上求得a 的值,进而求得点B 坐标,进而得到答案. 【详解】解:点(),1A a a -在x 轴上, 10a ∴-=,即1a =,则点B 坐标为()2,1-, ∴点B 在第四象限,故选:D .【点睛】本题主要考查点的坐标,解题的关键是掌握各象限及坐标轴上点的横纵坐标特点. 3.如图,在围棋棋盘上有3枚棋子,如果黑棋①的位置用有序数对(0,−1)表示,黑棋①的位置用有序数对(−3,0)表示,则白棋①的位置可用有序数对表示为( )A .()2,1-B .()1,2-C .()2,1-D .()1,2-【答案】C【分析】根据黑棋①的坐标向上1个单位确定出坐标原点,然后建立平面直角坐标系,再写出白棋①的坐标即可.【详解】解:建立平面直角坐标系如图,白棋①的坐标为(-2,1).故选:C.【点睛】本题考查了坐标确定位置,根据已知点的坐标确定出坐标原点的位置是解题的关键.4.如图,货船A与港口B相距35海里,我们用有序数对(南偏西40°,35海里)来描述货船B相对港口A的位置,那么港口A相对货船B的位置可描述为()A.(南偏西50°,35海里)B.(北偏西40°,35海里)C.(北偏东50°,35海里)D.(北偏东40°,35海里)【答案】D【分析】根据方位角的概念并结合平行线的性质,可得答案.【详解】解:过点B作BD①AC,①①1=①A=40°①港口A相对货船B的位置可描述为(北偏东40°,35海里),故选:D.【点睛】本题考查了方向角的知识点,解答本题的关键是理解确定一个点的位置需要两个量应该是方向角,一个是距离.5.某天早晨,小明从家骑自行车去上学,途中因自行车发生故障而维修,如图所示的图像反映了他骑车上学的整个过程,则下列结论正确的是()A .修车花了25分钟B .小明家距离学校1000米C .修好车后骑行的速度是200米/分钟D .修好车后花了15分钟到达学校【答案】C【分析】根据横坐标,可得时间;根据函数图像的纵坐标,可得路程.【详解】解:A .由横坐标看出,小明修车时间为25-10=15(分钟),故本选项不符合题意; B .由纵坐标看出,小明家离学校的距离2000米,故本选项不合题意;C .小明修好车后骑行到学校的平均速度是:(2000-1000)÷5=200(米/分钟),故本选项符合题意;D .由横坐标看出,小明修好车后花了30-25=5(分钟)到达学校,故本选项不合题意. 故选:D .【点睛】本题考查了函数图像,观察函数图像得出相应的时间,函数图像的纵坐标得出路程是解题关键.二、填空题6.已知点()29,62A m m --在第三象限.则m 的取值范围是______. 【答案】3<m <4.5【分析】在第三象限内的点的横纵坐标均为负数,列式求值即可. 【详解】解:①点A (2m −9,6−2m )在第三象限, ①2m −9<0且6−2m <0, ①3<m <4.5, 故答案为: 3<m <4.5【点睛】本题主要考查了平面直角坐标系中各个象限的点的坐标的符号特点,此特点常与不等式、方程结合起来求一些字母的取值范围.7.如图,两只福娃的发尖所处的位置的坐标分别为M (-2,2)、N (1,-1), 则A 、B 、C 三个点中为坐标系原点的是____.【答案】A【分析】利用平移规律,从M(-2,2)向右平移2个单位长度,向下平移2个单位长度,可得A是坐标原点.【详解】解:①M(-2,2),①A是坐标原点.故答案为A.【点睛】本题考查了平面直角坐标系,利用平移逆向推理是解题关键.三、解答题8.某学校STEAM社团在进行项目化学习时,根据古代的沙漏模型(图1)制作了一套“沙漏计时装置”,该装置由沙漏和精密电子秤组成,电子秤上放置盛沙容器.沙子缓慢匀速地从沙漏孔漏到精密电子称上的容器内,可以通过读取电子秤的读数计算时间(假设沙子足够).该实验小组从函数角度进行了如下实验探究:实验观察:实验小组通过观察,每两小时记录一次电子秤读数,得到表1.表1探索发现:(1)建立平面直角坐标系,如图2,横轴表示漏沙时间x,纵坐标表示精密电子称的读数y,描出以表1中的数据为坐标的各点.(2)观察上述各点的分布规律,判断它们是否在同一条直线上,如果在同一条直线上,请你建立适当的函数模型,并求出函数表达式,如果不在同一条直线上,请说明理由.结论应用:应用上述发现的规律估算:(3)若漏沙时间为9小时,精密电子称的读数为多少?(4)若本次实验开始记录的时间是上午7:30,当精密电子秤的读数为72克时是几点钟? 【答案】(1)作图见解析(2)在同一直线上.函数表达式为:66y x =+ (3)漏沙时间为9小时,精密电子称的读数为60克 (4)下午6:30【分析】(1)根据表中各点对应横、纵坐标,描点即可.(2)通过连线可知这些点大致分布在同一直线上,满足一次函数表达式,所以可假设一次函数表达式,利用待定系数法求解函数表达式.(3)根据(2)中的表达式可求出当9x =时,精密电子秤的读数.(4)根据(2)中的表达式可求出当72y =时,漏沙的时间,然后根据起始时间可求出读数为72克的时间. (1) 解:如图所示(2)解:如图所示,连线可得,这些点在同一线上,并且符合一次函数图像. 设一次函数表达式为:y kx b =+将点(0,6),(2,18)代入解析式中可得6218b k b =⎧⎨+=⎩解得66a b =⎧⎨=⎩∴函数表达式为:66y x =+(3)解:由(2)可知函数表达式为:66y x =+ ∴当9x =时,60y =∴漏沙时间为9小时,精密电子称的读数为60克.(4)解:由(2)可知函数表达式为:66y x =+ ∴当72y =时,11x =起始时间是上午7:30∴经过11小时的漏沙时间为下午6:30.【点睛】本题考查一次函数的实际应用,要求掌握描点法画函数图象,待定系数法求解析式,会求函数自变量或函数值是解决本题的关键.平面直角坐标系(提升测评)一、单选题1.如图,小石同学在正方形网格图中建立平面直角坐标系后,点A 的坐标为(1,1)-,点B 的坐标为(2,0),则点C 的坐标为( )A .(1,2)-B .(2,1)-C .(1,2)--D .(1,1)-【答案】A【分析】利用已知点A 、B 的坐标确定平面直角坐标系,进而可得答案. 【详解】解:根据题意,建立如图所示的直角坐标系, ①点C 的坐标为(1,﹣2). 故选:A .【点睛】此题主要考查了点的坐标的确定,属于基本题型,正确得出原点位置是解题关键. 2.如图所示,从小明家到学校要穿过一个居民小区,小区的道路均是北南或西东方向,小明走下面哪条线路最短( )A .(1,3)→(1,2)→(1,1)→(1,0)→(2,0)→(3,0)→(4,0)B .(1,3)→(0,3)→(2,3)→(0,0)→(1,0)→(2,0)→(4,0)C .(1,3)→(1,4)→(2,4)→(3,4)→(4,4)→(4,3)→(4,2)→(4,0)D .以上都不对 【答案】A【分析】要想线路最短,就应从小明家出发向右及向下走,而不能向左或向上走,所以选A . 【详解】解:要想路线最短,就只应向右及向下走, 故选:A【点睛】本题考查了平面直角坐标系的应用以及数学在实际生活的应用,理解线路最短,应始终向着目标靠近,并明白平面直角坐标系中点的坐标的表示是解题关键.3.道路两旁种植行道树,选择行道树的因素有很多,比如:树形要美、树冠要大、存活率要高、落叶要少…现在只考虑树冠大小、存活率高低两个因素,可以用如下方法将实际问题数学化:设树冠直径为d ,存活率为h .如图,在平面直角坐标系中画出点(d ,h ),其中甲树种、乙树种、丙树种对应的坐标分别为A (d 1,h 1)、B (d 2,h 2)、C (d 3,h 3),根据坐标的信息分析,下列说法正确的是( )A .乙树种优于甲树种,甲树种优于丙树种B .乙树种优于丙树种,丙树种优于甲树种C .甲树种优于乙树种,乙树种优于丙树种D .丙树种优于甲树种,甲树种优于乙树种 【答案】B【分析】根据图象,比较A 、B 、C 三点的存活率和树冠直径即可得出答案. 【详解】根据题意和图象可得,213h h h >>,231d d d >>, ①乙树种是最优的,①甲树种的存活率略高于丙树种,基本相等,但丙树种的树冠直径远远大于甲树种的树冠直径, ①丙树种优于甲树种,①乙树种优于丙树种,丙树种优于甲树种, 故选:B .【点睛】本题考查规律型:点的坐标,准确读出坐标中的信息是解题的关键.4.点A 在第二象限,距离x 轴3个单位长度,距离y 轴5个单位长度,则点A 的坐标为( ) A .()5,3- B .()3,5-C .()5,3-D .()3,5-【答案】A【分析】首先确定点的横纵坐标的正负号,再根据距坐标轴的距离确定点的坐标. 【详解】解:①点A 在第二象限, ①点的横坐标为负数,纵坐标为正数,①点距离x 轴3个单位长度,距离y 轴5个单位长度, ①点的坐标为(-5,3). 故选:A .【点睛】此题主要考查了点的坐标,解决本题的关键是掌握好四个象限的点的坐标的特征:第一象限正正,第二象限负正,第三象限负负,第四象限正负.5.如图,雷达探测器发现了A ,B ,C ,D ,E ,F 六个目标.目标C ,F 的位置分别表示为C (6,120°),F (5,210°),按照此方法表示目标A ,B ,D ,E 的位置时,其中表示正确的是( )A .A (4,30°)B .B (1,90°)C .D ( 4,240°) D .E (3,60°)【答案】C【分析】按已知可得,表示一个点,横坐标是自内向外的环数,纵坐标是所在列的度数,分别写出坐标A (5,30°),B (2,90°),D (4,240°),E (3,300°),即可判断.【详解】解:按已知可得,表示一个点,横坐标是自内向外的环数,纵坐标是所在列的度数, 由题意可知A 、B 、D 、E 的坐标可表示为:A (5,30°),故A 不正确;B (2,90°),故B 不正确;D (4,240°),故C 正确;E (3,300°),故D 不正确.故选择:C .【点睛】本题考查新定义坐标问题,仔细分析题中的C 、F 两例,掌握定义的含义,抓住表示一个点,。
几何图形的面积问题(与函数值域转化)(解析版)

几何图形的面积问题(与函数值域转化)一、考情分析圆锥曲线中几何图形的面积问题,是近几年高考命题的重点和难点。
在2018年的全国卷和2019年的全国卷中,都有圆锥曲线的大题压轴的第二问出现。
题目的难度是可想而知的,这其中涉及到:距离,斜率,切线,直线与圆,三角形的面积,四边形的面积等。
此专题,从这个出发点出发,梳理了最近的高考题和诊断性考试题,得出曲径通幽的解题之法。
归根结底,最终都是转换到函数值域。
二、经验分享圆锥曲线中的几何图形的面积问题,以及围绕与几何图形的面积问题关键是: 其一,选取合适的变量,第二,建立目标函数,转化函数的取值范围与最值问题(也就是转化成函数值域问题), 第三,构造函数,用导数的方法求其最大值与最小值。
其求解策略一般有以下几种:①几何法:根据题目上传达的几何图形以及几何关系,建立目标函数,若目标函数有明显几何特征和意义,则考虑几何图形的性质求解;②代数法: 若目标函数的几何意义不明显,利用基本不等式、导数等方法求函数的值域或最值,注意变量的范围,在对目标函数求最值前,常要对函数进行变换,注意变形技巧,若一个函数式的分母中含有一次式或二次式、分子中含有一次式或二次式的二次根式,则可以通过换元的方法把其转化为分母为二次式、分子为一次式的函数式,这样便于求解此函数式的最值.三、题型分析(一)角的最值问题例1. 已知椭圆22221(0)x y a b a b +=>>上一点A 关于原点O 的对称点为,B F 为其右焦点,若,AF BF ⊥设,ABF α∠=且,,124ππα⎡⎤∈⎢⎥⎣⎦则椭圆离心率的取值范围是 .【答案】26[,]23【点评】本题的关键是利用椭圆的定义建立等量关系式2sin 2cos 2c c a αα+=,然后借助已知条件,,124ππα⎡⎤∈⎢⎥⎣⎦利用三角函数的图象求解离心率的范围. 【变式训练1】【百校联盟2018届TOP202018届高三三月联考】.已知平行四边形ABCD 内接于椭圆()2222:10x y a b a b Ω+=>>,且AB , AD 斜率之积的范围为32,43⎛⎫-- ⎪⎝⎭,则椭圆Ω离心率的取值范围是( ) A. 13,23⎛⎫⎪⎪⎝⎭ B. 32,32⎛⎫⎪ ⎪⎝⎭ C. 13,43⎛⎫⎪ ⎪⎝⎭D. 11,43⎛⎫⎪⎝⎭【答案】A【变式训练2】【2019届河北武邑中学高三周考】已知直线:60l x y +-=和曲线22:2220M x y x y +---=,点A 在直线l 上,若直线AC 与曲线M 至少有一个公共点C ,且030MAC ∠=,则点A 的横坐标的取值范围是( )A .()0,5B .[]1,5C .[]1,3D .(]0,3 【答案】B【解析】设()00,6A x x -,依题意有圆心到直线的距离sin302d AM =≤,即()()22001516x x -+-≤,解得[]01,5x ∈.【变式训练3】【2019届山东省济宁市高三3月模拟】已知双曲线22221(0,0)x y a b a b-=>>的左右焦点分别为12,F F ,焦距为2(0)c c >,抛物线22y cx =的准线交双曲线左支于,A B 两点,且0120(AOB O ∠=为坐标原点),则该双曲线的离心率为 ( ) A.31 B. 2 C. 21 D. 51【答案】A【解析】由题意得,当()22222424c a b cx y a-=-⇒= ,则 ()()2222222244,,2424ca b ca b c cA B aa⎛⎛-- -- ⎝⎝,又因为120AOB ∠=︒, ()22242242244244tan 384084032ca b c c a c a c a a aπ-==-+=⇒-+=4222840423(4231,)331e e e e e ∴-+=⇒=±-<⇒=⇒=舍去.(二)距离的最值问题例2.【2019届山东菏泽一中宏志部高三上学期月考】若过点()2 3 2P --,的直线与圆224x y +=有公共点,则该直线的倾斜角的取值范围是( )A .0 6π⎛⎫ ⎪⎝⎭,B .0 3π⎡⎤⎢⎥⎣⎦, C. 0 6π⎡⎤⎢⎥⎣⎦, D .0 3π⎛⎤ ⎥⎝⎦, 【答案】B【解析】当过点(23,2)P --的直线与圆224x y += 相切时,设斜率为k ,则此直线方程为+2=k(23)y x +,即k 2320x y k -+-=.由圆心到直线的距离等于半径可得2|232|21k k -=+,求得0k =或3k =,故直线的倾斜角的取值范围是[0,]3π,所以B 选项是正确的.【变式训练1】【2020届河北省武邑中学高三上学期测试】在平面直角坐标系x y O 中,圆1C :()()221625x y ++-=,圆2C :()()2221730x y r -+-=.若圆2C 上存在一点P ,使得过点P 可作一条射线与圆1C 依次交于点A ,B ,满足2PA =AB ,则半径r 的取值范围是( ) A .[]5,55 B .[]5,50 C .[]10,50 D .[]10,55 【答案】A【解析】由题,知圆1C 的圆心为(1,6)-,半径为5,圆2C 的圆心为(17,30),半径为r ,两圆圆心距为22(171)(306)30++-=,如图,可知当AB 为圆1C 的直径时取得最大值,所以当点P 位于点1P 所在位置时r 取得最小值,当点P 位于点2P 所在位置时r 取得最大值.因为max ||10AB =,||2||PA AB =,所以min 5r =,max 55r =,故选A .(三)几何图形的面积的范围问题例3.在平面直角坐标系中,,A B 分别是x 轴和y 轴上的动点,若以AB 为直径的圆C 与直线240x y +-=相切,则圆C 面积的最小值为( )A.45πB.34πC.(625)π-D.54π 【答案】A【解析】设直线l :240x y +-=.因为1||||2C l OC AB d -==,所以圆心C 的轨迹为以O 为焦点,l 为准线的抛物线.圆C 半径最小值为11422255O l d -=⨯=,圆C 面积的最小值为1. 【变式训练1】【北京市朝阳区2018届高三第一学期期末】阿波罗尼斯(约公元前262-190年)证明过这样一个命题:平面内到两定点距离之比为常数k (0k >且1k ≠)的点的轨迹是圆.后人将这个圆称为阿氏圆.若平面内两定点,A B 间的距离为2,动点P 与A , B 距离之比为2,当,,P A B 不共线时, PAB ∆面积的最大值是 A. 22 B. 2 C.223 D. 23【答案】A【变式训练2】【吉林省普通中学2020届第二次调研】已知F 为抛物线2y x =的焦点,点,A B 在该抛物线上且位于x 轴的两侧,而且·6OAOB =(O 为坐标原点),若ABO ∆与AFO ∆的面积分别为1S 和2S ,则124S S +最小值是( )A .73 B . 6 C . 132D . 3【答案】B【变式训练3】【2016高考新课标1卷】设圆222150x y x ++-=的圆心为A ,直线l 过点B (1,0)且与x轴不重合,l 交圆A 于C ,D 两点,过B 作AC 的平行线交AD 于点E . (I )证明EA EB +为定值,并写出点E 的轨迹方程;(II )设点E 的轨迹为曲线C 1,直线l 交C 1于M ,N 两点,过B 且与l 垂直的直线与圆A 交于P ,Q 两点,求四边形MPNQ 面积的取值范围.【解析】(Ⅰ)因为||||AC AD =,AC EB //,故ADC ACD EBD ∠=∠=∠, 所以||||ED EB =,故||||||||||AD ED EA EB EA =+=+.又圆A 的标准方程为16)1(22=++y x ,从而4||=AD ,所以4||||=+EB EA . 由题设得)0,1(-A ,)0,1(B ,2||=AB ,由椭圆定义可得点E 的轨迹方程为:13422=+y x (0≠y ). (Ⅱ)当l 与x 轴不垂直时,设l 的方程为)0)(1(≠-=k x k y ,),(11y x M ,),(22y x N .由⎪⎩⎪⎨⎧=+-=134)1(22y x x k y 得01248)34(2222=-+-+k x k x k .可得当l 与x 轴不垂直时,四边形MPNQ 面积的取值范围为)38,12[.当l 与x 轴垂直时,其方程为1=x ,3||=MN ,8||=PQ ,四边形MPNQ 的面积为12.综上,四边形MPNQ 面积的取值范围为)38,12[.(四)函数转化例4.【2019届成都一诊】设椭圆()012222>>=+b a by a x C :的左右顶点为A,B.P 是椭圆上不同于A,B 的一点,设直线AP,BP 的斜率分别为m,n ,则当()||ln ||ln 32323n m mnmn b a +++⎪⎭⎫ ⎝⎛-取得最小值时,椭圆C 的离心率为( )A.51 B.22 C.54D.23【答案】D【解析】设()()(),,,0,,0,00y x P a B a A -,点P 在双曲线上,得()01220220>>=+b a b y a x C :,2202220)(ax a b y -=,所以a x y m +=00,a x y m -=00,化简,22ab mn -=原式⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛+-+⎪⎪⎪⎪⎭⎫⎝⎛--=b a b a b a b a a b a b a b b a ln 63232ln 62323232222所以设1>=b a t ,函数t t t t t f ln 63232)(23++-=,求导可以得到:2t =时,函数取得最小值=)2(f ,2=ba,23=e 。
专题 在平面直角坐标系中求图形的面积(四大题型)(原卷版)

(苏科版)八年级上册数学《第5章 平面直角坐标系》专题训练 在平面直角坐标系中求图形的面积【例题1】(2023春•青龙县期中)如图,已知三角形ABC 如图所示放置在平面直角坐标系中,其中C (﹣4,4).则三角形ABC的面积是( )A.4B.6C.8D.1【变式1-1】如图,已知三角形ABC如图所示放置在平面直角坐标系中,其中C(﹣4,4).则三角形ABC的面积是( )A.4B.6C.12D.24【变式1-2】(2023•岳麓区校级开学)如图,△ABC的三个顶点坐标分别为A(﹣3,2),B(0,3),C(0,﹣1),则△ABC的面积为( )A.4B.6C.4.5D.5【变式1-3】(2023春•思明区校级期中)已知点A(1,2a+1),B(﹣a,a﹣3),若线段AB∥x轴,则三角形AOB的面积为( )A.21B.28C.14D.10.5【变式1-4】(2022春•巴音郭楞州期末)如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中,三角形ABC的三个顶点A(5,2)、B(5,5)、C(1,1)均在格点上.(1)将三角形ABC向左平移5个单位,再向下平移3个单位得到三角形A1B1C1,画出平移后的图形,并写出点A1的坐标;(2)求三角形ABC的面积.【变式1-5】如图所示,将图中的点(﹣5,2),(﹣3,4),(﹣1,2),(﹣4,2),(﹣2,2),(﹣2,3),(﹣4,3)做如下变化:(1)横坐标不变,纵坐标分别减4,再将所得的点用线段依次连接起来,所得的图形与原来的图形相比有什么变化?(2)纵坐标不变,横坐标分别加6,再将所得的点用线段依次连接起来,所得的图形与原来的图形相比有什么变化?(3)求出以点(﹣5,2),(﹣3,4),(﹣1,2)为顶点的三角形的面积?【例题2】如图,A(3,0),B(0,3),C(1,4),求△ABC的面积.【变式2-1】如图,已知:A(3,2),B(5,0),E(4,1),求△AOE的面积.【变式2-2】在如图所示的正方形网格中,每个小正方形的单位长度均为1,△ABC的三个顶点恰好是正方形网格的格点.(1)写出图中所示△ABC各顶点的坐标.(2)求出此三角形的面积.【变式2-3】(2023春•双柏县期中)在直角坐标系中,已知A(﹣3,4),B(﹣1,﹣2),O(0,0),画出三角形并求三角形AOB的面积.【变式2-4】(2022春•雷州市期末)如图,△ABC在直角坐标系中,(1)请写出△ABC各点的坐标;.(2)求出S△ABC【变式2-5】在如图所示的正方形网格中,每个小正方形的边长均为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A、C的坐标分别为(﹣4,5)、(﹣1,3).(1)请在如图所示的网格平面内画出平面直角坐标系;(2)请把三角形ABC先向右平移5个单位长度,再向下平移3个单位长度得到三角形A′B′C′,在图中画出三角形A′B′C′;(3)求三角形ABC的面积.【变式2-6】(2023秋•浏阳市期中)如图,在平面直角坐标系xOy 中,点A 的坐标为(﹣4,4),点B 的坐标为(﹣2,0),点C 的坐标为(﹣1,2).(1)请面出△ABC 关于y 轴的对称图形△A 1B 1C 1;(2)直接写出A 1,B 1,C 1三点的坐标;(3)求△ABC 的面积.【例题3】(2022春•长安区校级月考)如图所示,在平面直角坐标系中,点A (4,0),B (3,4),C (0,2),则四边形ABCO 的面积为( )A .9B .10C .11D .12【变式3-1】(2022春•商南县期末)如图,有一块不规则的四边形图形ABCD,各个顶点的坐标分别为A (﹣2,8),B(﹣11,6),C(﹣14,0),D(0,0)(比例尺为1:100),现在想对这块地皮进行规划,需要确定它的面积.(1)确定这个四边形的面积(2)如果把原来四边形ABCD的各个顶点的纵坐标保持不变,横坐标加2,所得的四边形面积又是多少?【变式3-2】(2022秋•高明区月考)已知:A(﹣5,﹣2),B(﹣1,2),C(5,4),D(6,﹣2).(1)在坐标系中描出各点,画出四边形ABCD;(2)求四边形ABCD的面积.【变式3-3】如图,四边形ABCD四个顶点的坐标分别为A(﹣2,0),B(1,7),C(5,5),D(7,0).试求这个四边形的面积.【变式3-4】如图,面积为12cm 2的△ABC 向x 轴正方向平移至△DEF 的位置,相应的坐标如图所示(a ,b 为常数),(1)求点D 、E 的坐标;(2)求四边形ACED 的面积.【变式3-5】如图,在平面直角坐标系xOy 中,已知A (2,4),B (6,6),C (8,2),求四边形OABC 的面积.【例题4】(2021秋•围场县期末)已知点O (0,0),点A (﹣3,2),点B 在y 轴上,若△AOB 的面积为12,则点B 的坐标为( )A .(0,8)B .(0,4)C .(8,0)D .(0,﹣8)或(0,8)【变式4-1】已知点A(1,0),B(0,2),点P在x轴的负半轴上,且△PAB的面积为5,则点P的坐标为( )A.(0,﹣4)B.(0,﹣8)C.(﹣4,0)D.(6,0)【变式4-2】(2022春•路南区期末)如图,已知A(﹣2,3)、B(4,3)、C(﹣1,﹣3)(1)求点C到x轴的距离;(2)求△ABC的面积;(3)点P在y轴上,当△ABP的面积为6时,请直接写出点P的坐标.【变式4-3】如图,在平面直角坐标系中,点A(4,0),B(3,4),C(0,2).(1)求S;四边形ABCO;(2)连接AC,求S△ABC=8?若存在,请求点P坐标.(3)在x轴上是否存在一点P,使S△PAB【变式4-4】(2022•天津模拟)如图,A(﹣1,0),C(1,4),点B在x轴上,且AB=3.(1)求点B的坐标;(2)求△ABC的面积;(3)在y轴上是否存在点P,使以A、B、P三点为顶点的三角形的面积为10?若存在,请直接写出点P 的坐标;若不存在,请说明理由.【变式4-5】(2022秋•渭滨区期末)如图所示,在平面直角坐标系中,已知A(0,1)、B(2,0)、C (4,3).(1)在平面直角坐标系中画出△ABC,则△ABC的面积是 ;(2)若点D与点C关于y轴对称,则点D的坐标为 ;(3)已知P为x轴上一点,若△ABP的面积为1,求点P的坐标.【变式4-6】(2022•天津模拟)如图,在平面直角坐标系中,已知A(a,0),B(b,0),其中a,b满足|a+1|+(b﹣3)2=0.(1)填空:a= ,b= ;(2)若在第三象限内有一点M(﹣2,m),请用含m的式子表示△ABM的面积;(3)在(2)条件下,当m=−32时,在x轴上是否存在点P(不与点A重合),使得S三角形PBM=S三角形ABM,若存在请求出点P的坐标,不存在说明理由.1.(2022春•湖北期末)已知:如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′.(1)在图中画出△A′B′C′;(2)写出点A′、B′的坐标;(3)连接A′A、C′C,求四边形A′ACC′的面积.2.已知A(0,3),B(﹣4,0),C(﹣2,﹣3),D(4,﹣1),求图中四边形ABCD的面积.专题难点突破练3.(2022春•黄石期末)如图,在平面直角坐标系中,线段AB的坐标分别为A(﹣4,1),B(﹣1,﹣3),把线段AB先向右平移5个单位长度,再向上平移4个单位长度得到线段CD(其中点A与点D、点B与点C是对应点)(1)画出平移后的线段CD,写出点C的坐标为( , ).(2)连接AD、BC,四边形ABCD的面积为 .(3)点E在线段AD上,CE=6,点F是线段CE上一动点,线段BF的最小值为 .4.(2022春•船营区校级期末)如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(3,c)三点,其中a、b、c满足关系式:|a﹣2|+(b﹣3)2+0.(1)求a、b、c的值;(2)如果在第二象限内有一点P(m,12),请用含m的式子表示四边形ABOP的面积;(3)在(2)的条件下,是否存在负整数m,使四边形ABOP的面积等于△AOP面积的两倍?若存在,求出所有满足条件的点P的坐标,若不存在,请说明理由.5.(2022秋•竞秀区期末)已知,如图,方格纸中每个小方格都是边长为1个单位长度的正方形,现有A,B,C三点,其中点A坐标为(﹣4,1),点B坐标为(1,1).(1)请根据点A,B的坐标在方格纸中建立平面直角坐标系,并直接写出点C坐标为 ;(2)依次连接A,B,C,A,得到△ABC,请判断△ABC的形状,并说明理由;(3)若点C关于直线AB的对称点为点D.则点D的坐标为 ;(4)在y轴上找一点F,使△ABF的面积等于△ABD的面积,点F的坐标为 .6.(2022春•青羊区校级月考)在外面直角坐标系中,O为原点,点A(0,2),B(﹣2,0),C(4,0).(1)如图1,△ABC的面积为 ;(2)如图2,将点B向右平移7个单位长度,再向上平移4个单位长度,得到对应点D.①求△ACD的面积;②已知点P(1,m)是一动点,若△PAC的面积等于△ACD的面积,请求出点P的坐标.7.(2022春•梁平区期中)如图1,以长方形ABCD的中心O为原点,平行于BC的直线为x轴建立平面直角坐标系,若点D的坐标为(6,3).(1)直接写出A、B、C的坐标;(2)设AD的中点为E,点M是y轴上的点,且△CME的面积是长方形ABCD面积的16,求点M的坐标;(3)如图2,若点P从C点出发向CB方向匀速移动(不超过点B),点Q从B点出发向BA方向匀速移动(不超过点A),且点Q的速度是P的一半,P、Q两点同时出发,已知当移动时间为t秒时,P点的横坐标为6﹣2t,此时①CP= ,AQ= (用含t的式子表示).②在点P、Q移动过程中,四边形PBQD的面积是否发生变化?若不变,求其值;若变化,求其变化范围.8.(2023春•涵江区期中)如图1,点A(0,a),B(b,0),且a,b满足(a﹣4)2=0.(1)求点A和点B的坐标;(2)如图2,点C(m,n)在线段AB上,且满足n﹣m=5,点D在y轴负半轴上,连接CD交x轴负半轴于点M,且S△MBC =S△MOD,求点D的坐标;(3)平移直线AB,交x轴正半轴于点E,交y轴于点F,P为直线EF上且位于第三象限内的一个点,过点P作PG⊥x轴于点G,若S△PAB=20,且GE=12,求点P的坐标.9.(2023春•武汉期中)在平面直角坐标系中,点A 、B 分别是x 轴和y 轴的正半轴上的点,C 点在第一象限,它们的坐标分别是A (a ,0),B (0,b ),C (a ﹣1,2b ),且满足|a−4|+=0.(1)直接写出四边形AOBC 的面积 ;(2)点P 是x 轴上一个动点,当△APC 的面积等于8时,求点P 的坐标;(3)将线段AC 平移至线段MN (点A 的对应点为M ,点C 的对应点为N ),且点M 在线段OB 上,当△MAC 的面积为152时,求点N 的坐标.。
人教版七年级数学下册专题训练(含答案与解析)

人教版七年级数学下册专题训练(含参考答案与解析)说明:本套训练题包含以下7个专题解题技巧专题:一元一次不等式(组)中含字母系数的问题 考点综合专题:一元一次不等式(组)与学科内知识的综合 难点探究专题:平面直角坐标系中的变化规律 解题技巧专题:平面直角坐标系中的图形面积 解题技巧专题:平行线中作辅助线的方法 思想方法专题:相交线与平行线中的思想方法 解题技巧专题:解二元一次方程组解题技巧专题:一元一次不等式(组)中含字母系数的问题——类比不同条件,体会异同◆类型一 已知解集求字母系数的值或取值范围1.(2017·毕节中考)关于x 的一元一次不等式m -2x3≤-2的解集为x ≥4,则m 的值为( )A.14B.7C.-2D.22.(2017·金华中考)若关于x 的一元一次不等式组⎩⎪⎨⎪⎧2x -1>3(x -2),x <m 的解集是x <5,则m 的取值范围是【易错11】( )A.m ≥5B.m >5C.m ≤5D.m <53.已知关于x 的不等式组⎩⎪⎨⎪⎧x ≥-a -1①,-x ≥-b ②的解集在数轴上表示如图所示,则a b 的值为 .4.若不等式组⎩⎪⎨⎪⎧2x -a <1,x -2b >3的解集为-1<x <1,求代数式(b -1)a +1的值.◆类型二 已知整数解的情况求字母系数的取值范围5.关于x 的不等式x -b >0恰有两个负整数解,则b 的取值范围是( ) A.-3<b <-2 B.-3<b ≤-2 C.-3≤b ≤-2 D.-3≤b <-26.对于任意实数m ,n ,定义一种新运算m ※n =mn -m -n +3,等式的右边是通常的加减和乘法运算,例如:3※5=3×5-3-5+3=10.请根据上述定义解决问题:若a <2※x <7,且解集中有两个整数解,则a 的取值范围是 W.7.(2017·黄石中考)已知关于x 的不等式组⎩⎪⎨⎪⎧5x +1>3(x -1)①,12x ≤8-32x +2a ②恰好有两个整数解,求实数a 的取值范围.◆类型三 已知不等式组有、无解求字母系数的取值范围8.若关于x 的不等式组⎩⎪⎨⎪⎧5-3x ≥0,x -m ≥0有实数解,则实数m 的取值范围是( )A.m ≤53B.m <53C.m >53D.m ≥539.已知关于x 的不等式组⎩⎪⎨⎪⎧x -a ≥0,5-2x >1无解,则实数a 的取值范围是 .10.若关于x 的不等式组⎩⎪⎨⎪⎧x +1<a ①,3x +5>x -7②有解,求实数a 的取值范围.【易错11】参考答案与解析1.D 2.A3.1 解析:由不等式②得x ≤b ,由数轴可得,原不等式组的解集是-2≤x ≤3,∴⎩⎪⎨⎪⎧-a -1=-2,b =3,解得⎩⎪⎨⎪⎧a =1,b =3,∴a b =13=1. 4.解:⎩⎪⎨⎪⎧2x -a <1①,x -2b >3②,解不等式①得x <a +12 .解不等式②得x >2b +3.根据题意得⎩⎪⎨⎪⎧a +12=1,2b +3=-1,解得⎩⎪⎨⎪⎧a =1,b =-2,则(b -1)a +1=(-3)2=9. 5.D6.4≤a <5 解析:根据题意得2※x =2x -2-x +3=x +1.∴a <x +1<7,即a -1<x <6.又∵解集中有两个整数解,∴3≤a -1<4,∴a 的取值范围为4≤a <5.7.解:解不等式①得x >-2,解不等式②得x ≤4+a .∴不等式组的解集是-2<x ≤4+a .∵不等式组恰好有两个整数解,∴0≤4+a <1,解得-4≤a <-3.8.A 9.a ≥210.解:解不等式①得x <a -1.解不等式②得x >-6.∵不等式组有解,∴-6<a -1,∴a >-5.考点综合专题:一元一次不等式(组)与学科内知识的综合——综合运用,全面提升◆类型一 不等式(组)与平面直角坐标系1.(2017·江岸区模拟)已知点P (2a +1,1-a )在第一象限,则a 的取值范围在数轴上表示正确的是( )2.(2017·贵港中考)在平面直角坐标系中,点P (m -3,4-2m )不可能在( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限3.已知点M (3a -9,1-a )在第三象限,且它的横、纵坐标都是整数,则a 的值是 W.4.在平面直角坐标系中,点A (1,2a +3)在第一象限.(1)若点A 到x 轴的距离与到y 轴的距离相等,求a 的值; (2)若点A 到x 轴的距离小于到y 轴的距离,求a 的取值范围.◆类型二 不等式(组)与方程(组)的综合5.(2017·宜宾中考)若关于x ,y 的二元一次方程组⎩⎪⎨⎪⎧x -y =2m -1,x +3y =3的解满足x +y >0,则m 的取值范围是 W.6.(2017·南城县模拟)已知不等式组⎩⎪⎨⎪⎧x +1<2a ,x -b >1的解集是2<x <3,则关于x 的方程ax+b =0的解为 W.7.已知关于x ,y 的方程组⎩⎪⎨⎪⎧x +2y =2m +1①,x -2y =4m -3②的解是一对正数.(1)试确定m 的取值范围;(2)化简|3m -1|+|m -2|.◆类型三 不等式(组)与新定义型问题的综合8.(2017·东胜区二模)我们定义⎪⎪⎪⎪⎪⎪a b c d =ad -bc ,例如⎪⎪⎪⎪⎪⎪2345=2×5-3×4=10-12=-2,则不等式组1<⎪⎪⎪⎪⎪⎪1x 34<3的解集是 W. 9.(2017·龙岩模拟)定义新运算“⊕”如下:当a >b 时,a ⊕b =ab +b ;当a <b 时,a ⊕b =ab -b .若3⊕(x +2)>0,则x 的取值范围是( )A.-1<x <1或x <-2B.x <-2或1<x <2C.-2<x <1或x >1D.x <-2或x >210.(2017·杭州模拟)阅读以下材料:对于三个数a ,b ,c ,用M {a ,b ,c }表示这三个数的平均数,用min{a ,b ,c }表示这三个数中最小的数.例如:M {-1,2,3}=-1+2+33=43;min{-1,2,3}=-1;min{-1,2,a }=⎩⎪⎨⎪⎧a (a ≤-1),-1(a >-1).(1)填空:若min{2,2x +2,4-2x }=2,则x 的取值范围是 ; (2)如果M {2,x +1,2x }=min{2,x +1,2x },求x 的值.参考答案与解析1.C 2.A3.2 解析:由题意得⎩⎪⎨⎪⎧3a -9<0,1-a <0,解得1<a <3.∵横、纵坐标都是整数,∴a 必为整数,∴a =2.4.解:(1)∵点A 到x 轴的距离与到y 轴的距离相等,且点A 在第一象限,∴2a +3=1,解得a =-1.(2)∵点A 到x 轴的距离小于到y 轴的距离,点A 在第一象限,∴⎩⎪⎨⎪⎧2a +3>0,2a +3<1,解得-32<a <-1.5.m >-1 6.x =-127.解:(1)①+②,得2x =6m -2,x =3m -1.①-②得4y =-2m +4,则y =-12m +1.依题意有⎩⎪⎨⎪⎧3m -1>0,-12m +1>0,解得13<m <2.(2)由(1)知13<m <2,∴3m -1>0,m -2<0,∴|3m -1|+|m -2|=3m -1+[-(m -2)]=3m -1-m +2=2m +1.8.13<x <1 9.C 解析:当3>x +2,即x <1时,由题意得3(x +2)+x +2>0,解得x >-2,∴-2<x <1;当3<x +2,即x >1时,由题意得3(x +2)-(x +2)>0,解得x >-2,∴x >1.综上所述,x 的取值范围是-2<x <1或x >1,故选C.10.解:(1)0≤x ≤1 解析:由题意得⎩⎪⎨⎪⎧2x +2≥2,4-2x ≥2,解得0≤x ≤1.(2)方法一:M {2,x +1,2x }=2+x +1+2x3=x +1.当x ≥1时,则min{2,x +1,2x }=2,则x +1=2,∴x =1.当x <1时,则min{2,x +1,2x }=2x ,则x +1=2x ,∴x =1(舍去).∴x =1.方法二:∵M {2,x +1,2x }=2+x +1+2x3=x +1=min{2,x +1,2x },∴⎩⎪⎨⎪⎧2≥x +1,2x ≥x +1,∴⎩⎪⎨⎪⎧x ≤1,x ≥1,∴x =1.难点探究专题:平面直角坐标系中的变化规律——掌握不同规律,以不变应万变◆类型一 沿坐标轴方向运动的点的坐标规律探究1.如图,动点P 在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2)……按这样的运动规律,经过第2016次运动后,动点P 的坐标是________.2.(2017·阿坝州中考)如图,在平面直角坐标系中,一动点从原点O 出发,沿着箭头所示方向,每次移动1个单位,依次得到点P 1(0,1),P 2(1,1),P 3(1,0),P 4(1,-1),P 5(2,-1),P 6(2,0),…,则点P 2017的坐标是________.◆类型二 绕原点呈“回”字形运动的点的坐标规律探究3.在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点.如图,由里向外数第2个正方形开始,分别是由第1个正方形各顶点的横坐标和纵坐标都乘2,3,…得到的,请你观察图形,猜想由里向外第10个正方形四条边上的整点个数共有( )A .10个B .20个C .40个D .80个第3题图 第4题图4.(2017·温州中考)我们把1,1,2,3,5,8,13,21,…这组数称为斐波那契数列,为了进一步研究,依次以这列数为半径作90°圆弧P 1P 2︵,P 2P 3︵,P 3P 4︵,…得到斐波那契螺旋线,然后顺次连接P 1P 2,P 2P 3,P 3P 4,…得到螺旋折线(如图),已知点P 1(0,1),P 2(-1,0),P 3(0,-1),则该折线上的点P 9的坐标为( )A .(-6,24)B .(-6,25)C .(-5,24)D .(-5,25)◆类型三 图形变化中的点的坐标探究5.(2017·河南模拟)如图,点A(2,0),B(0,2),将扇形AOB沿x轴正方向做无滑动的滚动,在滚动过程中点O的对应点依次记为点O1,点O2,点O3…,则O10的坐标是()A.(16+4π,0) B.(14+4π,2)C.(14+3π,2) D.(12+3π,0)6.如图,在直角坐标系中,第一次将三角形OAB变换成三角形OA1B1,第二次将三角形OA1B1变换成三角形OA2B2,第三次将三角形OA2B2变换成三角形OA3B3.已知A(1,3),A1(2,3),A2(4,3),A3(8,3),B(2,0),B1(4,0),B2(8,0),B3(16,0).(1)观察每次变换后的三角形有何变化,找出规律,按此变换规律再将三角形OA3B3变换成三角形OA4B4,则A4的坐标是__________,B4的坐标是__________;(2)若按(1)中找到的规律将三角形OAB进行了n次变换,得到三角形OA n B n,比较每次变换中三角形顶点坐标有何变化,找出规律,推测点A n的坐标是__________,点B n的坐标是__________.参考答案与解析1.(2016,0)解析:结合图象可知,当运动次数为偶数次时,P点运动到x轴上,且横坐标与运动次数相等.∵2016为偶数,∴运动2016次后,动点P的坐标是(2016,0).2.(672,1)解析:由已知得P7(2,1),P13(4,1),所以P6n+1(2n,1).因为2017÷6=336……1,所以P2017(336×2,1),即P2017(672,1).3.C解析:每个正方形四个顶点一定为整点,由里向外第n个正方形每条边上除顶点外的整点个数如下表所示:可见,第n个正方形每条边上除顶点外还有(n-1)个整点,四条边上除顶点外有4(n-1)个整点,加上4个顶点,共有4(n-1)+4=4n(个)整点.当n=10时,4n=4×10=40,即由里向外第10个正方形的四条边上共有40个整点.故选C.4.B解析:由题意,P5在P2的正上方,推出P9在P6的正上方,且到P6的距离为21+5=26,所以P9的坐标为(-6,25),故选B.5.C6.(1)(16,3)(32,0)(2)(2n,3)(2n+1,0)解析:(1)∵A1(2,3),A2(4,3),A3(8,3),∴A4的横坐标为24=16,纵坐标为3.故点A4的坐标为(16,3).又∵B1(4,0),B2(8,0),B3(16,0),∴B4的横坐标为25=32,纵坐标为0.故点B4的坐标为(32,0).(2)由A1(2,3),A2(4,3),A3(8,3),可以发现它们各点坐标的关系为横坐标是2n,纵坐标都是3.故点A n的坐标为(2n,0).由B1(4,0),B2(8,0),B3(16,0),可以发现它们各点坐标的关系为横坐标是2n+1,纵坐标都是0.故点B n的坐标为(2n+1,0).解题技巧专题:平面直角坐标系中的图形面积——代几结合,突破面积及点的存在性问题◆类型一直接利用面积公式求图形的面积1.如图,在平面直角坐标系中,三角形ABC的面积是()A.2 B.4 C.8 D.6第1题图第2题图2.如图,在平面直角坐标系xOy中,已知A(-1,5),B(-1,0),C(-4,3),则三角形ABC的面积为________.◆类型二利用分割法求图形的面积3.如图,在平面直角坐标系中,点A(4,0),B(3,4),C(0,2),则四边形ABCO的面积为________.4.观察下图,图中每个小正方形的边长均为1,回答以下问题:【方法14】(1)写出多边形ABCDEF各个顶点的坐标;(2)线段BC,CE的位置各有什么特点?(3)求多边形ABCDEF的面积.◆类型三利用补形法求图形的面积5.在如图所示的正方形网格中,每个小正方形的边长均为1,三角形ABC的三个顶点恰好是正方形网格的格点.【方法14】(1)写出三角形ABC各顶点的坐标;(2)求出此三角形的面积.◆类型四与图形面积相关的点的存在性问题6.(2017·定州市期中)如图,A(-1,0),C(1,4),点B在x轴上,且AB=3.(1)求点B的坐标;(2)求三角形ABC的面积;(3)在y轴上是否存在点P,使以A,B,P三点为顶点的三角形的面积为10?若存在,请直接写出点P的坐标;若不存在,请说明理由.参考答案与解析1.B 2.1523.11 解析:过点B 作BD ⊥x 轴于D .∵A (4,0),B (3,4),C (0,2),∴OC =2,BD =4,OD =3,OA =4,∴AD =OA -OD =1,则S 四边形ABCO =S 梯形OCBD +S 三角形ABD =12×(4+2)×3+12×1×4=9+2=11. 4.解:(1)A (-2,0),B (0,-3),C (3,-3),D (4,0),E (3,3),F (0,3).(2)线段BC 平行于x 轴(或线段BC 垂直于y 轴),线段CE 垂直于x 轴(或线段CE 平行于y 轴).(3)S多边形ABCDEF =S三角形ABF +S长方形BCEF +S三角形CDE =12×(3+3)×2+3×(3+3)+12×(3+3)×1=6+18+3=27.5.解:(1)A (3,3),B (-2,-2),C (4,-3).(2)如图,分别过点A ,B ,C 作坐标轴的平行线,交点分别为D ,E ,F .S 三角形ABC =S 正方形DECF-S 三角形BEC -S 三角形ADB -S 三角形AFC =6×6-12×6×1-12×5×5-12×6×1=352.6.解:(1)点B 在点A 的右边时,-1+3=2,点B 在点A 的左边时,-1-3=-4,所以点B 的坐标为(2,0)或(-4,0).(2)S 三角形ABC =12×3×4=6.(3)存在这样的点P .设点P 到x 轴的距离为h ,则12×3h =10,解得h =203.点P 在y 轴正半轴时,P ⎝⎛⎭⎫0,203,点P 在y 轴负半轴时,P ⎝⎛⎭⎫0,-203,综上所述,点P 的坐标为⎝⎛⎭⎫0,203或⎝⎛⎭⎫0,-203.解题技巧专题:平行线中作辅助线的方法——形成思维定式,快速解题。
2024年新八年级数学暑假提升精品讲义(北师大版)第14讲 解题技巧专题:平面直角坐标系

第14讲解题技巧专题:平面直角坐标系求面积、规律、新定义问题【题型一利用补形法或分割法求图形的面积】例1.(23-24七年级下·全国·课后作业)如图,在平面直角坐标系中,点,,,,求四边形的面积.【变式1-1】(2023上·安徽滁州·八年级统考期中)如图,在平面直角坐标系中,的顶点坐标分别为,,,过点作轴,过点作轴,轴,过点作轴,分别与和交于点和点,分别与和交于点和点.(1)直接写出下列点的坐标:点____,点____,点____;(2)利用图形求的面积.【变式1-2】如图所示,在平面直角坐标系中,已知,,(1)在平面直角坐标系中画出.(2)求的面积.【变式1-3】已知,在平面直角坐标系中的位置如图所示(1)写出A、B、C三点的坐标;(2)求的面积;(3)中任意一点经平移后对应点为,将作同样的平移得到,画出.【题型二与图形面积相关的点的存在性问题】例2.(23-24七年级上·黑龙江哈尔滨·阶段练习)如图,在平面直角坐标系中,轴,垂足为A,轴,垂足为C,已知,,其中a,c满足关系式,点P从O点出发沿折线的方向运动到点C停止,运动的速度为每秒2个单位长度,设点P的运动时间为t 秒.(1)求点A、C的坐标;(2)在运动过程中,当点P到的距离为2个单位长度时,_________;(3)点,在点P的运动过程中,是否存在这样的t值,使,若存在,请求出t值,若不存在,请说明理由.【变式2-1】(2024上·江西吉安·八年级统考期末)如图,在直角坐标平面内,已做,,(1)求的面积.(2)在y轴上找一点D,使,求点D的坐标.【变式2-2】(2023下·黑龙江牡丹江·七年级统考期末)如图,在平面直角坐标系中,点坐标为,点坐标为,点坐标为,且,,满足关系式(1)请求出、、三点的坐标:(2)如果在第三象限内有一点,请用含的式子表示四边形的面积;(3)在(2)的条件下,当时,在轴上是否存在点,使三角形的面积等于四边形面积的若存在,请直接写出点的坐标,若不存在,请说明理由.【变式2-3】(2023下·七年级课时练习)如图,在平面直角坐标系中,点的坐标分别为,且满足.同时将点分别向上平移2个单位长度,再向右平移1个单位长度,得到点的对应点,连接.(1)求点的坐标及四边形的面积;(2)在坐标轴上是否存在一点,连接,使?若存在,求出点的坐标;若不存在,试说明理由;(3)是线段上的一个动点,连接,当点在上移动时(不与点重合),给出下列结论:①的值不变;②的值不变.其中有且只有一个结论是正确的,请你找出这个结论并求其值.【题型三平面直角坐标系中新定义规律探究问题】例距离的较小值称为点点的若点的若,两点为点的若点是若点的长距为的坐标为,试说明:中的任意一点,给出如下定义:记,那么我们把点与点称为点和谐点”.例如,点的一对“和谐点是点与点点的一对“和谐点”坐标是与;若点的一对重合,则y的值为若点C的一个坐标为,求点“”(1)直接写出点A,B的“-”(2)若点A为B,C的“-3”系和点,求点(3)点D为A,B的“k”系和点.①求点D的坐标(结果用k含的式子表示);②若三角形ABD的面积为6,则符合条件的【题型四平面直角坐标系中点运动规律探究问题】例4. (23-24七年级下·重庆江北·阶段练习)如图,在平面直角坐标中,动点M从点出发,按图中箭头所示方向依次运动,第1次运动到点,第2次运动到点,第3次运动到点,…,按这样的运动规律,动点M第2024次运动到点()A.B.C.D.【变式4-1】(23-24七年级下·黑龙江哈尔滨·阶段练习)如图,动点在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点,第2次接着运动到点,第3次接着运动到点,按这样的运动规律,经过第47次运动后动点的坐标是【变式4-2】如图,在平面直角坐标系中,设一动点自处向下运动1个单位长度至处,然后向左运动2个单位长度至处,再向上运动2个单位长度至处,再向左运动2个单位长度至处,再向下运动2个单位长度至处,,如此继续运动下去,设,,2,3,,则的坐标是.【变式4-3】(23-24七年级上·山东东营·期末)如图,在平面直角坐标系中,一动点从原点O出发,沿着箭头所示方向,每次移动1个单位,依次得到点…,则点的坐标是.【题型五平面直角坐标系中图形变换规律探究问题】例5. (23-24九年级上·山东枣庄·阶段练习)如图,在平面直角坐标系中有一菱形且,点O,B在y轴上,,现在把菱形向右无滑动翻转,每次翻转,点B的落点依次为…,连续翻转2023次,则的坐标为()A.B.C.D.【变式5-1】(2024·云南·模拟预测)如图,将边长为的正方形沿轴正方向连续翻转次,点依次落在点、、、、、的位置上,则点的坐标为( )A.B.C.D.【变式5-2】(23-24七年级上·山东东营·期末)如图,在平面直角坐标系中有一边长为1的正方形,边分别在轴、轴上,如果以对角线为边作第二个正方形,再以对角线为边作第三个正方形……照此规律作下去,则的长为.【变式5-3】(23-24九年级上·四川广安·期末)如图,在平面直角坐标系中,矩形的边在轴上,点,点.将矩形绕点A顺时针旋转,每次旋转,当第2023次旋转结束时,点的对应点的坐标是.一、单选题1.(2024·山东淄博·二模)定义:两点关于某条直线对称,则称这条直线为这两个点的“幸福直线”·若点,幸福直线是,则点A关于这条幸福直线的对称点B的坐标是()A.B.C.D.2.(23-24七年级下·湖北武汉·期中)如图在平面直角坐标系中,点,点,点,则三角形的面积是()A.19B.20C.21D.21.53.(2024七年级下·北京·专题练习)如图,在平面直角坐标系中,已知点,,,,把一条长为2023个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点处,并按的规律紧绕在四边形的边上,则细线另一端所在位置的坐标是( )A.B.C.D.二、填空题4.(23-24七年级下·黑龙江绥化·期中)如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点,,,,…那么点的坐标为5.(23-24七年级下·福建厦门·期中)如图,在平面直角坐标系中,已知点,,,.则四边形的面积(用含有k的式子表示)6.(23-24七年级下·天津·期中)在平面直角坐标系中,给出如下定义:点到轴、轴的距离的较大值称为点的“长距”,点到轴、轴的距离相等时,称点为“完美点”.(1)点的“长距”为;(2)若点是“完美点”,则的值为;三、解答题7.(23-24七年级下·重庆潼南·期中)如图,在平面直角坐标系中,,,,且满足,线段交y轴交于点F.(1)求点A、B的坐标;(2)求点F的坐标;(3)y轴上是否存在一点P,使的面积和的面积相等,若存在求出P点坐标,若不存在说明理由.8.(23-24七年级下·江西赣州·期中)在平面直角坐标系中,给出如下定义:点到轴、轴的距离的较大值称为点的“长距”,点到轴、轴的距离相等时,称点为“完美点”.(1)点的“长距”为______;(2)若点是“完美点”,求的值;(3)若点的长距为4,且点在第二象限内,点的坐标为,试说明:点是“完美点”.9.(2024七年级下·天津·专题练习)如图1,四边形各个顶点的坐标分别为,,,.(1)______,点到轴的距离为______.(2)求四边形的面积.(3)如图2,已知点为轴正半轴上的一个动点,点是否存在一个位置使得的面积是四边形面积的一半?若存在,请求出点的坐标;若不存在,请说明理由.10.(2024七年级下·全国·专题练习)如图,在直角坐标系中,第一次将变换成,第二次将变换成,第三次将变换成,已知,,,;,,,.(1)观察每次变换前后的三角形有何变化,找出规律,按此变化规律再将变换成,则的坐标是,的坐标是.(2)若按(1)找到的规律将进行了次变换,得到,比较每次变换中三角形顶点有何变化,找出规律,推测的坐标是,的坐标是.11.(23-24八年级上·北京丰台·期中)在平面直角坐标系中,对于任意图形G及直线,,给出如下定义:将图形G先沿直线翻折得到图形,再将图形沿直线翻折得到图形,则称图形是图形G的【】伴随图形,例如:点的【x轴,y轴】伴随图形是点.(1)点的【x轴,y轴】伴随图形点的坐标为_________;(2)已知,,,直线经过点.①当,且直线与轴平行时,点的【轴,】伴随图形点的坐标为_________;②当直线经过原点时,若的【轴,】伴随图形上只存在两个与轴的距离为1的点,求的取值范围.12.(23-24七年级下·吉林延边·期中)如图,在平面直角坐标系中,已知,两点,其中、、满足等式.动点从点出发,沿折线以每秒2个单位长度的速度向终点运动.设点运动时间为,当四边形为正方形时,解答下列问题.(1)__________,__________,__________;当点在线段上时,的长度为___________.(用含的代数式表示)(2)当时,求三角形的面积.(3)当时,三角形的面积为__________.(4)当时,直接写出的值.第14讲解题技巧专题:平面直角坐标系求面积、规律、新定义问题【题型一利用补形法或分割法求图形的面积】例1.(23-24七年级下·全国·课后作业)如图,在平面直角坐标系中,点,,,,求四边形的面积.【答案】15【分析】本题主要考查了利用直角坐标系求多边形的面积,过点B,C分别作x轴的垂线,垂足分别为点E,F,即可知,代入求解即可.【详解】解:如下图,过点B,C分别作x轴的垂线,垂足分别为点E,F.∵点,,,∴,,∴,,,,.所以四边形的面积是15.【变式1-1】(2023上·安徽滁州·八年级统考期中)如图,在平面直角坐标系中,的顶点坐标分别为,,,过点作轴,过点作轴,轴,过点作轴,分别与和交于点和点,分别与和交于点和点.(1)直接写出下列点的坐标:点____,点____,点____;(2)利用图形求的面积.【答案】(1),,(2)的面积为9.【分析】本题考查网格中求三角形的面积,坐标与图形.(1)根据点,点,点在坐标系中的位置,直接写出其坐标即可;(2)利用正方形的面积减去周围三个三角形的面积即可求解.【详解】(1)解:点,点,点;故答案为:,,;(2)解:的面积.【变式1-2】如图所示,在平面直角坐标系中,已知,,(1)在平面直角坐标系中画出.(2)求的面积.【答案】(1)见解析(2)15【分析】(1)根据点的坐标画出图形即可;(2)把三角形的面积看成长方形的面积减去周围的三个三角形面积即可.【详解】(1)如图,即为所求;(2)【点睛】本题考查作图-复杂作图,三角形的面积等知识,解题的关键是学会利用面积法解决问题.【变式1-3】已知,在平面直角坐标系中的位置如图所示(1)写出A、B、C三点的坐标;(2)求的面积;(3)中任意一点经平移后对应点为,将作同样的平移得到,画出.【答案】(1),,(2)11.5(3)见解析【分析】(1)根据平面坐标系得出A、B、C三点的坐标即可;(2)根据各点坐标,利用梯形面积与三角形面积公式求出即可;(3)根据点经平移后对应点为判断出平移方式,然后画出三个顶点的对应点即可.【详解】(1)如图所示:A、B、C三点的坐标分别为:,,;(2)的面积;(3)∵点经平移后对应点为,∴把向右平移4个单位,再向下平移3个单位得.如图,【点睛】此题考查了平移的性质,以及平移图形的画法和三角形面积求法,根据平移的性质正确平移对应顶点是解题关键.【题型二与图形面积相关的点的存在性问题】例2.(23-24七年级上·黑龙江哈尔滨·阶段练习)如图,在平面直角坐标系中,轴,垂足为A,轴,垂足为C,已知,,其中a,c满足关系式,点P从O点出发沿折线的方向运动到点C停止,运动的速度为每秒2个单位长度,设点P的运动时间为t 秒.(1)求点A、C的坐标;(2)在运动过程中,当点P到的距离为2个单位长度时,_________;(3)点,在点P的运动过程中,是否存在这样的t值,使,若存在,请求出t值,若不存在,请说明理由.【答案】(1),(2)2秒或8秒(3)当或时【分析】本题主要考查了坐标与图形的性质,平方和二次根式的非负性,一元一次方程的应用,(1)由平方和二次根式的非负性即可求出a,b的值,即可求出点A、C的坐标.(2)由点A,点C的坐标即可求出点B的坐标,然后根据当点P到的距离为2个单位长度时,分两种情况,即可求出t的值.(3)先根据已知条件,求出,然后根据P在上,P在上,P在上,P在上时,根据已知条件,建立关于t的一元一次方程,解方程即可求解.【详解】(1)解∵,∴,,∴,,∴,,∴,(2)由(1)可知,,∴,当点P到的距离为2个单位长度时,运动路程或者,∴秒或秒∴秒或秒,故答案为:2秒或8秒.(3)存在,理由如下:∵,∴,,∵,,轴,轴,∴,∴,,∴,∴,①当P在上时,,即时,,∴∴,解得,舍去②当P在上时,,即时,,∴∴,解得③当P在上时,,即时,∴,∴,解得,舍去④当P在上时,,即时,∴∴,解得综上,当或时【变式2-1】(2024上·江西吉安·八年级统考期末)如图,在直角坐标平面内,已做,,(1)求的面积.(2)在y轴上找一点D,使,求点D的坐标.【答案】(1)16(2)或【分析】本题考查的是坐标与图形面积,理解坐标系的特点是解本题的关键;(1)直接利用三角形的面积公式计算即可;(2)设点D的坐标为,再利用面积公式建立方程求解即可.【详解】(1)解:;(2)设点D的坐标为,.解得.∴满足条件的点D的坐标为或;【变式2-2】(2023下·黑龙江牡丹江·七年级统考期末)如图,在平面直角坐标系中,点坐标为,点坐标为,点坐标为,且,,满足关系式(1)请求出、、三点的坐标:(2)如果在第三象限内有一点,请用含的式子表示四边形的面积;(3)在(2)的条件下,当时,在轴上是否存在点,使三角形的面积等于四边形面积的若存在,请直接写出点的坐标,若不存在,请说明理由.【答案】(1)点坐标为,点坐标为,点坐标为;(2);(3)存在这样的点M,点M的坐标为或.【分析】本题考查非负数的性质,直角坐标系中的面积问题,三角形的面积公式等知识.(1)根据非负数的性质求解即可;(2)求出,,再用计算即可;(3)根据设为,则,,再结合题意列出绝对值方程,求解即可.【详解】(1)解:∵,∴,∴,,;∴点坐标为,点坐标为,点坐标为;(2)解:过点作于,则,∵,,∴,,∴,,∴;(3)解:存在,点M的坐标为或,理由如下:假设存在这样的点M,设为,则,∵,∴∵,由题意得解得:或,∴存在这样的点M,点M的坐标为或.【变式2-3】(2023下·七年级课时练习)如图,在平面直角坐标系中,点的坐标分别为,且满足.同时将点分别向上平移2个单位长度,再向右平移1个单位长度,得到点的对应点,连接.(1)求点的坐标及四边形的面积;(2)在坐标轴上是否存在一点,连接,使?若存在,求出点的坐标;若不存在,试说明理由;(3)是线段上的一个动点,连接,当点在上移动时(不与点重合),给出下列结论:①的值不变;②的值不变.其中有且只有一个结论是正确的,请你找出这个结论并求其值.【答案】(1),(2)存在,或(3)①正确,【详解】(1),.点,点.根据平移规律可得,.(2)坐标轴上存在点满足.当点在轴上时,,..点的坐标为或;当点在轴上时,,..点的坐标为或.综上,点的坐标为或或或.(3)如图,点在线段上(不与点,重合),作交于点,.....①正确.【题型三平面直角坐标系中新定义规律探究问题】例3.(2023上·安徽宿州·八年级统考期中)在平面直角坐标系中,给出如下定义:点A到x轴、y轴距离的较小值称为点A的“短距”,当点P的“短距”等于点Q的“短距”时,称P,Q两点为“等距点”.(1)点的“短距”为______;(2)若点的“短距”为3,求m的值;(3)若,两点为“等距点”,求k的值.【答案】(1)7(2)4或(3)或【分析】本题主要考查新定义下点到坐标轴的距离,(1)根据新定义,求得点B到坐标轴的距离即可;(2)根据新定义得到,求解即可;(3)根据新定义分别找到点C和点D到坐标轴的距离,再分类讨论与2的大小,列出对应的等式即可求得答案;【详解】(1)解:点到x轴、y轴距离分别为和7,根据定义得点的点的“短距,且,∴,解得或.(3)点C到x轴的距离为,到轴的距离为,到当时,,则或,解得或(舍).当时,,则或,解得或(舍).综上,k的值为或.2023上八年级统考期中)轴的距离的较大值称为点点的“长距”若点是若点的长距为的坐标为,试说明:【答案】(1)3(2)或见解析【分析】本题主要考查了平面直角坐标系的知识,属于阅读理解类型题目,关键是要读懂题目里定义的完美点”.)解:根据题意,得点到轴的距离为,到轴的距离为点是∴,∴或,解得或;)解:点的长距为∴,解得,∴,∴点D的坐标为,y轴的距离都是完美点”.中的任意一点,给出如下定义:记,那么我们把点与点称为点和谐点”.例如,点的一对“和谐点是点与点点的一对“和谐点”坐标是与;若点的一对重合,则y的值为若点C的一个坐标为,求点(1)(3)或【分析】(1)根据“2)根据和谐点”的含义及两点重合即可完成;的坐标为,根据)解:由题意得:,,所以点的一对坐标是与;故答案为:;)解:由题意得:,,所以点的一对“和谐点坐标是与;又点的一对重合,,,故答案为:6(3)解:设,的一个“和谐点坐标为,则,,;;若点C的另一个“和谐点”坐标为,则,,;;综上,点C的坐标为或.【点睛】本题是新定义问题,考查了坐标与图形,关键是理解题中“和谐点”的含义.【变式3-3】在平面直角坐标系中,点P(a,b),Q(c,d)给出如下定义:对于实数k(k≠0),我们称点M(ka+kc,kb+kd)为P,Q两点的“k”系和点.例如,点P(3,4),Q(1,-2),则点P.Q的“”系和点的坐标为:(2,1),如图,已知点A(4,-1),B(-2,-1).(1)直接写出点A,B的“-”系和点坐标为_________;(2)若点A为B,C的“-3”系和点,求点C的坐标:(3)点D为A,B的“k”系和点.①求点D的坐标(结果用k含的式子表示);②若三角形ABD的面积为6,则符合条件的k的值为_________(直接写出结果).【答案】(1)(-1,1)(2)(,)(3)①,②或【分析】(1)直接根据系和点的定义分别求出点的横坐标与纵坐标即可;(2)设出点C的坐标,根据系和点的定义列出方程,解方程即可得到答案;(3)①根据系和点的定义将k代入计算即可;②求出AB的长度,同时表示出AB边上的高,列出方程解出k的值即可.【详解】(1)解:∵点A(4,-1),B(-2,-1),∴点A,B的“-”系和点的横坐标为,纵坐标为,∴点A,B的“-”系和点坐标为(-1,1).(2)解:∵点A为B,C的“-3”系和点,设点C坐标为(m,n),∴,,解得,.∴点C的坐标为(,).(3)解:①∵点D为A,B的“k”系和点,设点D坐标为(a,b)则,,∴点D的坐标为;②∵点A(4,-1),B(-2,-1),∴.∵点D到AB的距离为,三角形ABD的面积为6,∴,解得或,∴符合条件的k的值为或.【点睛】本题考查新定义问题,图形与坐标,解题的关键是正确理解新定义的含义列出代数式表示出点的横纵坐标.【题型四平面直角坐标系中点运动规律探究问题】例4. (23-24七年级下·重庆江北·阶段练习)如图,在平面直角坐标中,动点M从点出发,按图中箭头所示方向依次运动,第1次运动到点,第2次运动到点,第3次运动到点,…,按这样的运动规律,动点M第2024次运动到点()A.B.C.D.【答案】D【分析】本题考查点的运动规律,能根据点的运动发现第次为正整数)运动后,动点的坐标是是解题的关键.依次求出前几次运动后点的坐标,再根据坐标的变化规律即可解决问题.【详解】解:由题知,第1次运动后,动点的坐标是;第2次运动后,动点的坐标是;第3次运动后,动点的坐标是;第4次运动后,动点的坐标是;第5次运动后,动点的坐标是;第6次运动后,动点的坐标是;第7次运动后,动点的坐标是;由此可见,第次为正整数)运动后,动点的坐标是.又,即第2024次运动后,动点的坐标是,即.故选:D【变式4-1】(23-24七年级下·黑龙江哈尔滨·阶段练习)如图,动点在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点,第2次接着运动到点,第3次接着运动到点,按这样的运动规律,经过第47次运动后动点的坐标是【答案】【分析】本题主要考查了点的坐标规律,从所给的数据和图形中寻求规律进行解题是解答本题的关键.根据已知提供的数据从横纵坐标分别分析得出横坐标为运动次数,纵坐标为1,0,2,0,每4次一轮这一规律,进而求出即可.【详解】解:根据动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点,第2次接着运动到点,第3次接着运动到点,第4次运动到点,第5次接着运动到点,…,∴点P的横坐标为运动次数,纵坐标为1,0,2,0,每4次一轮,∵,则经过第47次运动后,动点P的横坐标为47,纵坐标为2,即经过第47次运动后,动点P的坐标是∶,故答案为∶.【变式4-2】如图,在平面直角坐标系中,设一动点自处向下运动1个单位长度至处,然后向左运动2个单位长度至处,再向上运动2个单位长度至处,再向左运动2个单位长度至处,再向下运动2个单位长度至处,,如此继续运动下去,设,,2,3,,则的坐标是.【答案】【分析】本题考查点的坐标变化规律,根据点的运动方式,依次求出点的坐标,发现规律即可解决问题,能通过计算发现点坐标变化的规律是解题的关键.【详解】解:根据点的运动方式可知,点的坐标为;点的坐标为;点的坐标为;点的坐标为;点的坐标为;点的坐标为;点的坐标为;点的坐标为;点的坐标为;,由此可见,点的横坐标为,纵坐标为,当时,,,所以点的坐标为,所以点的坐标为,故答案为:.【变式4-3】(23-24七年级上·山东东营·期末)如图,在平面直角坐标系中,一动点从原点O出发,沿着箭头所示方向,每次移动1个单位,依次得到点…,则点的坐标是.【答案】【分析】本题属于平面直角坐标系中找点的规律问题,解答本题的关键是找到循环规律.先根据即可得到,再根据,则,可得.即可作答.【详解】解:由图可得,,,∵∴,即,∴,,故答案为:【题型五平面直角坐标系中图形变换规律探究问题】例5. (23-24九年级上·山东枣庄·阶段练习)如图,在平面直角坐标系中有一菱形且,点O,B在y轴上,,现在把菱形向右无滑动翻转,每次翻转,点B的落点依次为…,连续翻转2023次,则的坐标为()A.B.C.D.【答案】D【分析】连接交y轴于点D,根据条件可以求出,画出第5次、第6次、第7次翻转后的图形,容易发现规律:每翻转6次,图形向右平移4.由于,因此点向右平移1348(即)到点,即可求出点的坐标.【详解】连接交y轴于点D,如图所示,∵四边形是菱形,∴,,∴,,∴是等边三角形,∴,∴,∵,∴,∴,∴,画出第5次、第6次、第7次翻转后的图形,由图可知:每翻转6次,图形向右平移4,∵,∴点向右平移1348(即)到点,,∵的坐标为,∴的坐标为,故选:D.【点睛】本题考查点坐标规律探索,菱形的性质、等边三角形的判定与性质等知识,考查了操作、探究、发现规律的能力.发现“每翻转6次,图形向右平移4”是解决本题的关键.【变式5-1】(2024·云南·模拟预测)如图,将边长为的正方形沿轴正方向连续翻转次,点依次落在点、、、、、的位置上,则点的坐标为( )A.B.C.D.【答案】A【分析】此题主要考查了通过图形观察规律,根据题意分别求出、、、横坐标,再总结出规律即可得出,解题的关键是善于观察,总结规律.【详解】根据规律、、、、、、、、,;每个一个循环,,依次规律在次循环后与纵坐标一致,横坐标分别为:为、为、为、为;为、为、为、为;依次规律与横坐标为减,∴横坐标为,则坐标是,故选:.【变式5-2】(23-24七年级上·山东东营·期末)如图,在平面直角坐标系中有一边长为1的正方形,边分别在轴、轴上,如果以对角线为边作第二个正方形,再以对角线为边作第三个正方形……照此规律作下去,则的长为.【答案】【分析】首先求出的坐标,找出这些坐标之间的规律,然后根据规律计算出点的坐标.【详解】解:正方形边长为,,正方形是正方形的对角线为边,,点坐标为,同理可知,点坐标为,同理可知,点坐标为,点坐标为,点坐标为,,,,,由规律可以发现,每经过次作图后,点的坐标符号与第一次坐标符号相同,每次正方形的边长变为原来的倍,即,,的横纵坐标符号与点相同,横纵坐标相同,且都在第一象限,的坐标为,,故答案为:.【变式5-3】(23-24九年级上·四川广安·期末)如图,在平面直角坐标系中,矩形的边在轴上,点,点.将矩形绕点A顺时针旋转,每次旋转,当第2023次旋转结束时,点的对应点的坐标是.【答案】【分析】本题主要考查旋转的性质、坐标与图形等致死点,熟练根据旋转的知识确定旋转后的位置是解题的关键.先根据矩形的性质作出旋转后的图形,然后找到C点的坐标规律,并按照规律解答即可.【详解】解:如图:将矩形绕点A顺时针旋转,可知:,,则:每旋转4次则回到原位置,∵,∴第2023次旋转结束时,完成了505次循环,又旋转了3次,∴当第2023次旋转结束时,点C对应的坐标是.故答案为:.。
一次函数与面积综合运用(原卷版)

专题07 一次函数与面积综合运用(三大题型)【题型1 常规三角形面积】【题型2 铅垂法求面积】【题型3 等底转化】【题型1 常规三角形面积】【解题技巧】当三角形的底或高在坐标轴上,或者平行于坐标轴上,这样的三角形为常规三角形,可以直接利用三角形的面积公式进行求解。
【典例1】(2023春•永定区期末)综合与探究:如图,平面直角坐标系中,一次函数y=图象分别交x轴、y轴于点A,B,一次函数y=﹣x+b的图象经过点B,并与x轴交于点C,点P是直线AB上的一个动点.(1)求A,B两点的坐标;(2)并直接写出点C的坐标并求直线BC的表达式;(3)试探究直线AB上是否存在点P,使以A,C,P为顶点的三角形的面积为18?若存在,求出点P的坐标;若不存在,说明理由.【变式1-1】(2023春•凤山县期末)如图,在平面直角坐标系中,已知Rt△AOB 的两直角边OA,OB分别在x轴的负半轴和y轴的正半轴上,且OA,OB的长满足|OA﹣8|+(OB﹣6)2=0,∠ABO的平分线交x轴于点C,过点C作AB的垂线,垂足为点D,交y轴于点E.(1)求直线AB的解析式;(2)若△ABC的面积为15,求点C的坐标;【变式1-2】(2023春•涪陵区期末)如图,在平面直角坐标系中,直线l1:y=﹣x﹣3与x轴、y轴分别交于点A,B,直线l2交x轴、y轴分别于点C(﹣6,0),D(0,6),直线l2与直线l1交于点E,连接BC.(1)求直线l2的解析式;(2)求△BCE的面积;(3)连结OE,若点P是x轴上一动点,连结PE,当△POE为等腰三角形时,请直接写出点P的坐标.【变式1-3】(2023春•兰陵县期末)如图,已知函数y=x+1的图象与y轴交于点A,一次函数y=kx+b的图象经过点B(0,﹣1),与x轴以及y=x+1的图象分别交于点C,D,且点D的坐标为(1,n).(1)则k=,b=,n=;(2)求四边形AOCD的面积;(3)在x轴上是否存在点P,使得以点P,C,D为顶点的三角形是直角三角形,请求出点P的坐标.【变式1-4】(2023春•连城县期末)如图,在平面直角坐标系xOy中,直线y =﹣x+4与x轴、y轴分别交于点A、点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.(1)求AB的长;(2)求点C和点D的坐标;(3)y轴上是否存在一点P,使得S△P AB =S△OCD?若存在,直接写出点P的坐标;若不存在,请说明理由.【变式1-5】(2023春•文登区期中)如图,直线l1表达式为y=﹣3x+3,且与x轴交于点D,直线l2经过点A(4,0),B(3,),直线l1,l2交于点C.(1)求直线l2的表达式;(2)在直线l2上存在点P,能使S△ADP=3S△ACD,求点P的坐标.【变式1-6】(2023•花都区一模)在平面直角坐标系中,直线y=kx+4(k≠0)交x轴于点A(8,0),交y轴于点B.(1)k的值是;(2)点C是直线AB上的一个动点,点D和点E分别在x轴和y轴上.①如图,点D的坐标为(6,0),点E的坐标为(0,1),若四边形OECD的面积是9,求点C的坐标;②当CE平行于x轴,CD平行于y轴时,若四边形OECD的周长是10,请直接写出点C的坐标.【题型2 铅垂法求面积】【解题技巧】对于一般三角形,我们可以选择铅垂法求解三角形的面积。
巧用坐标求图形的面积

解:
坐标,并求三角形ABC的面积;
(1)因为点C在第二象限,且|x|=4,|y|=4,
所以点C的坐标为(-4,4).
又易知AB=6,所以S三角0),B(4,0),C(x,y). (2)若点C在第四象限,且三角形ABC的面积为9, |x|=3,求点C的坐标.
2
2×2×7
2.已知在四边形ABCD中,A(-3,0),B(3,0), C(3,2),D(1,3),求四边形ABCD的面积.
解:如图所示.过点D作DE垂直于BC,交BC的延长 线于点E,则四边形DABE为直角梯形.
S四边形ABCD=S梯形DABE-S三角形CDE
=
1 2
×(2+6)×3-
1 ×1×2
训练角度 4 已知三角形的面积求点的坐标
5.已知点O(0,0),点 A(-3,2),点B在y轴 的正半轴上,若三角形AOB的面积为12,则点B 的坐标为( A ) A.(0,8) B.(0,4) C.(8,0) D.(0,-8)
7.已知A(-2,0),B(4,0),C(x,y).
(1)若点C在第二象限,且|x|=4,|y|=4,求点C的
2
=11.
训练角度 3 利用分割法求图形的面积
4.在如图所示的平面直角坐标系中,四边形OABC各 顶点分别是O(0,0),A(-4,10),B(-12, 8),C(-14,0),求四边形OABC的面积.
解: 如图,过点A作AD⊥x轴,垂足为点
D,过点B作BE⊥AD,垂足为点E. 观察图,可知D(-4,0),E(-4,8), 且BE=-4-(-12)=8,AE=10-8= 2,CD=-4-(-14)=10,
根据三角形的面积公式,得
1 2
AB·|m|=12,
专题05平面直角坐标系中求图形面积(解析版)

专题05平面直角坐标系中求图形面积类型一、直接用公式求面积例1.如图,在平面直角坐标系中,点()0,4A b 为y 轴正半轴上一点,点()3,0B b 是x 轴正半轴上一点,其中b 满足()316b +=.(1)求点A ,B 的坐标.(2)点C 为x 轴上一点,且ABC 的面积为12,求C 点的坐标.【答案】(1)()0,4A ,()3,0B ;(2)点C 的坐标为()3,0-或()9,0【解析】(1)由()316b +=得1b =,∴()04A ,,()30B ,.(2)设点C 的坐标为()0x ,,则3BC x =-,由1()可知4OA =,∴1432ABC S x =⨯⨯-= 12,解得:9x =或3-.∴点C 的坐标为()30-,或()90,.【变式训练1】在平面直角坐标系中,已知点(),0A a ,(),0B b ,a 、b 满足方程组24a b a b +=-⎧⎨-=-⎩,(1)求A 、B 两点的坐标;(2)C 为y 轴正半轴上一点,且6ABC S = ,请求出C 的坐标.【答案】(1)A (-3,0),B (1,0);(2)C (0,3)【解析】(1)解方程组24a b a b +=-⎧⎨-=-⎩,解得:31a b =-⎧⎨=⎩,∴A (-3,0),B (1,0);(2)由(1)可知:AB =4,∵S △ABC =12AB •OC =6,∴12×4×OC =6,解得OC =3,∴C (0,3).故答案为:(1)A (-3,0),B (1,0);(2)C (0,3)类型二、割补法求面积例1.如图,三角形ABC 的面积等于()A .12B .1122C .13D .1132【答案】D【解析】过点A 作AD x ⊥轴于D ,如图所示:由题意可得,3BO =,3OC =,6AD =,3CD =,∴6OD =,∴ABC BOC ACDBODA S S S S ∆∆∆=--梯形111()222BO AD OD BO OC CD AD=+⋅-⋅⋅-⋅⋅111(36)63336222=+⨯-⨯⨯-⨯⨯54918222=--272=,即272ABC S ∆=,故选:D .【变式训练1】如图,连接AB 、BC 、AC ,则△ABC 的面积是()A .312B .3C .212D .2【答案】C【解析】长方形AGDE 的面积为:3×2=6,AGC 的面积:3×1÷2=1.5,CDB △的面积:2×1÷2=1,ABE △的面积:2×1÷2=1,故ABC 的面积为:6-1.5-1-1=2.5,故答案为:C ;【变式训练2】如图,三角形ABO 中,()2,3A --,()2,1B -,A B O ''' 是ABO 平移之后得到的图形,并且O 的对应点O '的坐标为()5,4.(1)作出ABO 平移之后的图形A B O ''' ,并写出A '、B '两点的坐标分别为A '______,B '_____;(2)()00,P x y 为ABO 中任意一点,则平移后对应点P 的坐标为______.(3)求ABO 的面积;【解析】(1)如图,△A 'B 'O '即为所求,A '、B '两点的坐标分别(3,1),(7,3).故答案为:(3,1),(7,3).(2)点P '的坐标为(x 0+5,y 0+4).故答案为:(x 0+5,y 0+4).(3)S △ABO =3×4-12×2×3-12×1×2-12×4×2=4.【变式训练3】在平面直角坐标系xoy 中,△ABC 的位置如图所示,点A ,B ,C 都在格点上.(1)分别写出下列顶点的坐标:A ________;B ________;(2)请在图中画出△ABC 关于y 轴对称的图形△A ′B ′C ′;(3)计算出△ABC 的面积.【答案】(1)(-1,6),(-2,0);(2)见解析;(3)152【解析】(1)由图知,点A 的坐标为(-1,6),点B 的坐标为(-2,0),故答案为:(-1,6),(-2,0)(2)由图得,点C 的坐标为(-4,3),则点A 、B 、C 关于y 轴的对称点A ′,B ′,C ′坐标分别为(1,6),(2,0),(4,3),依次连接A ′,B ′,C ′,即得△A ′B ′C ′,所得图形如图所示(3)过A 、C 作x 轴的垂线,垂足分别为D 、E则ABC AOD CED ADEC S S S S =-- 梯形111(36)31623222=⨯+⨯-⨯⨯-⨯⨯152=类型三、点的存在性问题例1.如图,在平面直角坐标系中,点B ,C 的坐标分别为(),2a a -、()3,2a a ,其中0a >,点A 为BC 的中点,若4BC =,解决下列问题:(1)BC 所在直线与x 轴的位置关系是;(2)求出a 的值,并写出点A ,C 的坐标;(3)在y 轴上是否存在一点P ,使得三角形PAC 的面积等于5?若存在,求出点P 的坐标;若不存在,请说明理由.【答案】(1)平行;(2)()1,2A ,()3,2C ;(3)存在,P 点坐标为()0,3-或()0,7【解析】(1)∵点B ,C 的坐标分别为(),2a a -、()3,2a a ,∴BC 所在直线与x 轴的位置关系是平行.故答案为:平行.(2)∵4BC =,∴()34a a --=,∴1a =,∴B (-1,2),C (3,2),∵A 为BC 的中点,∴()1,2A .(3)存在点P .设()0,P m ,∵2AC =,∴12252m ⨯⨯-=,∴3m =-或7.∴P 为()0,3-或()0,7.【变式训练1】如图,在直角坐标系中,已知()0,2A ,()3,0B ,()3,4C 三点.(1)求四边形AOBC 的面积;(2)是否存在点()0.5P x x ,,使2ABC AOBC S S = 四边形?若存在,求出点P 的坐标.若不存在,请说明理由.【答案】(1)9;(2)存在,()189P --,或(18,9)【解析】如图,∵34C (,),∴33CD ==.∵()34C ,,30B (,),∴404CB =-=,∴4312DCBO S =⨯=四边形.∵()04D ,,()02A ,,∴422DA =-=,∴11236322DCA S =⨯⨯=⨯= .∵DCA AOBC DCBO S S S =- 四边形四边形,∴1239AOBC S =-=四边形.(2)由(1)得1239AOBC S =-=四边形设存在点()0.5P x x ,,使△AOP 的面积为四边形AOBC 的面积的两倍.∵△AOP 的面积=122x x ⨯⨯=,∴29x =⨯,∴18x =±∴存在点P (18,9)或(-18,-9),使△AOP 的面积为四边形AOBC 的面积的两倍.【变式训练2】如图,A (0,3)是直角坐标系y 轴上一点,动点P 从原点O 出发,沿x 轴正半轴运动,速度为每秒2个单位长度,以P 为直角顶点在第一象限内作等腰Rt △APB .设P 点的运动时间为t 秒.(1)若AB ∥x 轴,求t 的值;(2)如图2,当t =2时,坐标平面内有一点M (不与A 重合)使得以M 、P 、B 为顶点的三角形和△ABP 全等,请直接写出点M 的坐标.【答案】(1)t 的值为1.5;(2)点M 的坐标为(3,7),(8,﹣3),(11,1).【解析】(1)过点B 作BC ⊥x 轴于点C ,如图所示.∵AO⊥x轴,BC⊥x轴,且AB∥x轴,∴四边形ABCO为矩形,∴AO=BC=3,∵△APB为等腰直角三角形,∴AP=BP,∠PAB=∠PBA=45°,∴∠OAP=90°-∠PAB=45°,∴△AOP为等腰直角三角形,∴OA=OP=3,∴t=3÷2=1.5(秒),故t的值为1.5;(2)当t=2时,OP=4,①如图3,若△ABP≌△MBP,则AP=PM,过点M作MD⊥OP于点D,∵∠AOP=∠PDM,∠APO=∠DPM,∴△AOP≌△MDP(AAS),∴OA=DM=3,OP=PD=4,∴M(8,-3);②如图,若△ABP≌△MPB,连接AM,则AP=PB=BM,∠APB=∠MBP=90︒,∴AP∥MB,且AP=MB,∴四边形APBM是平行四边形,y轴于点E,又∠APB=∠MBP=90︒,∴四边形APBM是正方形,∴AP=AM,过点M作ME⊥同理可证△AOP≌△MEA(AAS),∴OA=EM=3,OP=AE=4,∴M(3,7);③如图,若△ABP≌△MPB,则AP=BP=BM,过点M 、B 分别作x 轴的垂线,垂足分别为点F 、G ,过点M 作MH ⊥BF 于点H ,∴四边形FGMH 是矩形,∴MH =FG ,MG =HF ,同理可证△AOP ≌△PFB ≌△BHM (AAS ),∴OA =PF =BH =3,OP =BF =MH =4,∴MG =HF =BF -BH =1,OG =OP +PF +FG =11,∴M (11,1);综合以上可得点M 的坐标为(3,7),(8,-3),(11,1).【变式训练3】在平面直角坐标系中,正方形ABCD 的位置如图所示,点A 的坐标为()1,0,点D 的坐标为()0,2.延长CB 交x 轴于点1A ,作第1个正方形111A B C C ;延长11C B 交x 轴于点2A ,作第2个正方形2221A B C C ,…,按这样的规律进行下去,第2021个正方形的面积是______.【答案】404235(2⨯【解析】()()1,0,0,2,A D 正方形ABCD ,1,2OA OD ∴==,,AD AB ===190,DAO ADO DAO BAA ∠+∠=︒=∠+∠1,ADO BAA ∴∠=∠190,DOA ABA ∠=∠=︒ 1,AOD A BA ∴ ∽1,AO OD A B AB ∴=15,2AO AB A B OD ∴== 正方形111A B C C,1113222A B A C ∴====⨯同理可得:22232442A B ⎛⎫=+==⨯ ⎪⎝⎭33332A B ⎛⎫= ⎪⎝⎭······20212021202132A B ⎛⎫= ⎪⎝⎭所以第2021个正方形的面积是22021404233=5.22⎡⎛⎫⎛⎫⨯⎢ ⎪ ⎪⎝⎭⎝⎭⎢⎣⎦故答案为:404235.2⎛⎫⨯ ⎪⎝⎭。
专题13几何类比探究题型-2024年中考数学答题技巧与模板构建(解析版)

专题13几何类比探究题型题型解读|模型构建|通关试练几何的类比探究题型是近年中招解答题的必考题型,该题型往往以压轴题的形式出现,有一定的难度。
探究型问题是指命题中缺少一定的条件或无明确的结论,需要经过推断,补充并加以证明的一类问题.根据其特征大致可分为:条件探究型、结论探究型、规律探究型和存在性探究型等四类。
由于探究型试题的知识覆盖面较大,综合性较强,灵活选择方法的要求较高,再加上题意新颖,构思精巧,具有相当的深度和难度,所以要求同学们在复习时,首先对于基础知识一定要复习全面,并力求扎实牢靠;其次是要加强对解答这类试题的练习,注意各知识点之间的因果联系,选择合适的解题途径完成最后的解答.模型01图形旋转模型模型一、A字形(手拉手)及其旋转D模型二、K字型及其旋转CC手拉手模型是有两个等腰的三角形或者两个等边的三角形,他们有一个共同的顶点,且两个等腰三角形的顶角是相等的,那么就可以用角的和差求得共顶点的另外两个角相等等,然后利用等腰的边对应相等,可证明两个三角形全等(边角边)组成这样的图形模样的我们就说他是手拉手模型。
在类比探究题型中,往往会对等腰三角形或者等边三角形进行演变,变成一般三角形进行旋转,通常全等三角形变为相似三角形。
模型特征:双等腰;共顶点;顶点相等;绕着顶点作旋转解题依据:等腰共顶手拉手,旋转全等马上有;左手拉左手,右手拉右手,两根拉线抖一抖,它们相等不用愁;拉线夹角与顶角,相等互补答案有。
模型02图形平移模型探究1.四边形平移变换四边形的平移变换题型中主要考查了全等三角形的判定和性质,相似三角形的判定和性质,平移几何性质、三角形内角和定理的应用,勾股定理,解题的关键是熟练掌握三角形全等或相似的判定方法,画出相应的图形,注意分类讨论.2.三角形平移变换三角形平移变换主要利用三角形全等和三角形相似的判定和性质,勾股定理,矩形的判定和性质,平移性质、平行线的判定和性质,解题的关键是作出辅助线,熟练掌握三角形相似的判定方法.3.其它图形平移类比探究问题综合考查了全等三角形的判定和性质,相似三角形的判定和性质,三角形内角和定理的应用,勾股定理,解题的关键是熟练掌握三角形相似的判定方法,画出相应的图形,注意分类讨论.模型03动点引起的题型探究动点型问题是指题设中的图形中存在一个或多个动点,它们在线段、射线、直线、抛物线、双曲线、弧线等上运动的一类非常具有开放性的题目。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解题技巧专题:平面直角坐标系中的图形面积
——代几结合,突破面积及点的存在性问题
◆类型一直接利用面积公式求图形的面积
1.如图,在平面直角坐标系中,三角形ABC的面积是()
A.2 B.4 C.8 D.6
第1题图
第2题图
2.如图,在平面直角坐标系xOy中,已知A(-1,5),B(-1,0),C(
-4,3),则三角形ABC的面积为________.
◆类型二利用分割法求图形的面积
3.如图,在平面直角坐标系中,点A(4,0),B(3,4),C(0,2),则四边形ABCO的面积为________.
4.观察下图,图中每个小正方形的边长均为1,回答以下问题:【方法14】
(1)写出多边形ABCDEF各个顶点的坐标;
(2)线段BC,CE的位置各有什么特点?
(3)求多边形ABCDEF的面积.
◆类型三利用补形法求图形的面积
5.在如图所示的正方形网格中,每个小正方形的边长均为1,三角形ABC的三个顶点恰好是正方形网格的格点.【方法14】
(1)写出三角形ABC各顶点的坐标;
(2)求出此三角形的面积.
◆
类型四与图形面积相关的点的存在性问题
6.(2017·定州市期中)如图,A(-1,0),C(1,4),点B在x轴上,且AB=3.
(1)求点B的坐标;
(2)求三角形ABC的面积;
(3)在y轴上是否存在点P,使以A,B,P三点为顶点的三角形的面积为10?若存在,请直接写出点P的坐标;若不存在,请说明理由.
参考答案与解析
1.B 2.
15
2
3.11解析:过点B作BD⊥x轴于D.∵A(4,0),B(3,4),C(0,2),∴OC=2,BD =4,OD=3,OA=4,∴AD=OA-OD=1,则S四边形ABCO=S梯形OCBD+S三角形ABD=
1
2×(4+2)×3+
1
2×1×4=9+2=11.
4.解:(1)A(-2,0),B(0,-3),C(3,-3),D(4,0),E(3,3),F(0,3).
(2)线段BC平行于x轴(或线段BC垂直于y轴),线段CE垂直于x轴(或线段CE平行于y轴).
(3)S多边形ABCDEF=S三角形ABF+S长方形BCEF+S三角形CDE=
1
2×(3+3)×2+3×(3+3)+
1
2×(3+3)×1=6+18+3=27.
5.解:(1)A(3,3),B(-2,-2),C(4,-3).
(2)如图,分别过点A,B,C作坐标轴的平行线,交点分别为D,E,F.S三角形ABC=S正方形DECF
-S三角形BEC-S三角形ADB-S三角形AFC=6×6-
1
2×6×1-
1
2×5×5-
1
2×6×1=
35
2.
6.解:(1)点B在点A的右边时,-1+3=2,点B在点A的左边时,-1-3=-4,所以点B的坐标为(2,0)或(-4,0).
(2)S三角形ABC=
1
2×3×4=6.
(3)存在这样的点P.设点P到x轴的距离为h,则
1
2×3h=10,解得h=
20
3.点P在y轴正半轴时,P⎝⎛⎭⎫
0,
20
3,点P在y轴负半轴时,P⎝
⎛
⎭
⎫
0,-
20
3,综上所述,点P的坐标为⎝
⎛
⎭
⎫
0,
20
3或⎝
⎛
⎭
⎫
0,-
20
3.。
