滤波反投影

合集下载

滤波反投影法的实施步骤

滤波反投影法的实施步骤1. 简介滤波反投影法（Filtered Back Projection, FBP）是一种重建计算机体层成像（Computed Tomography, CT）图像的方法。

它通过对一系列飞行时间或射线投影数据进行滤波和反投影操作，来恢复被测物体的内部结构信息。

本文将详细介绍滤波反投影法的实施步骤。

2. 数据获取首先，我们需要获取一系列的投影数据。

投影数据是通过将被测物体从不同角度进行透射扫描而得到的，通常使用X射线或者其他形式的射线。

3. 数据预处理在进行滤波反投影之前，我们需要对投影数据进行一些预处理操作。

这些操作包括：去除背景噪声、校准投影数据以及执行各种纠正操作，以确保数据的准确性和一致性。

4. 滤波操作滤波操作是滤波反投影法中的关键步骤，它通过对投影数据进行频域滤波来增强图像的对比度和细节信息。

常用的滤波方法包括：Ram-Lak、Shepp-Logan、Hann窗等。

5. 反投影操作在经过滤波操作后，我们需要进行反投影操作来恢复原始图像。

反投影是将滤波后的投影数据逆向投影回图像空间的过程。

反投影操作涉及到几何重建算法和数学运算，可以使用快速反投影算法（FFT-based Back Projection）等高效算法来加快图像重建速度。

6. 重建图像优化得到初步的重建图像后，我们可以对其进行一些优化处理，以提高图像质量和视觉效果。

常见的优化方法包括：去除伪影、降噪、增加对比度、增强图像细节等。

7. 结果评估最后，我们需要对重建图像进行结果评估。

这包括比较重建图像和原始物体的差异，评估图像质量和准确性，并根据需要进行后续的调整和改进。

8. 总结滤波反投影法是一种常用的重建CT图像的方法，它通过对投影数据进行滤波和反投影操作，实现了对被测物体的内部结构信息的恢复。

本文介绍了滤波反投影法的实施步骤，包括数据获取、数据预处理、滤波操作、反投影操作、重建图像优化和结果评估等。

通过遵循这些步骤，可以有效地进行CT图像的重建工作，并获得高质量的图像结果。

滤波反投影法

滤波反投影法：
滤波反投影法根据附件三所给接收信息，采用先修正、后投影重建图像的做法，可得到原始图像的吸收率信息。

其原理为：在得到某一角度下的投影函数（一维函数）后，对此函数做滤波处理，得一修正后的滤波函数，再对修正后的滤波函数做反投影运算，得待检测介质吸收率在正方形托盘中的每一点的分布密度函数。

图1给出了滤波反投影法重建原始图像的流程图。

图1滤波反投影法流程图
反投影法重建原始图像的步骤：
（1）在对应于投影函数的角度下对投影函数做一维Fourier变换；
（2）对（1）得到的变换结果乘以权重因子；
（3）对（2）加权后得到的结果做一维傅立叶；
（4）对（3）所得函数做直接反投影；
（5）改变投影角度，得到180个不同的投影角度，对每一角度，重复上述步骤（1）~（4）。

R-L（Ram-Lak）滤波函数：
此函数的基本条件是二维图像函数的频率是有界的，显然，此题所得附件五的所有数据满足此条件。

故频域中的滤波函数可表示为：
其函数图像如图1.
图1R-L滤波函数图像
连续的R-L卷积函数所得结果为：
离散的R-L卷积函数所得结果为：
根据上述滤波原理，在本题中，对附件五中数据的具体滤波过程可用Matlab内置的Ram-Lak命令实现。

基于2017数学建模的滤波反投影算法应用

Image & Multimedia Technology •图像与多媒体技术Electronic Technology & Software Engineering 电子技术与软件工程• 91【关键词】CT 重构 randon 变换滤波反投影1 CT图像重建原理的知识背景CT 系统基本过程是：平行入射的X 射线垂直于探测器平面发射，形成一个发射-接收CT 系统，每个探测器单元都看做是一个接收点，且间隔距离相等。

计算机断层成像图像重建的过程是按照一定的算法将已经检测到的投影数据进行数学运算，最终得到断层图像。

Radon 变换及其逆变换：物体断层被射线扫描后需要用重建算法计算才能得到CT 图像，图像重建的基础是Radon 变换及其逆变换。

假设每条射线相互平行，对于一个二维平面进行射线检测可得到一条投影数据，该投影数据称为二维平面的一个Radon 变换；如果检测中该平面旋转180度，同时将对应的投影数据进行组合，则得到类似正弦分布形式的图像，从正弦图获取二维平面图像的变换称为Radon 反演。

用公式可分别描述为：，由于matlab 中封装有radon 函数，使用时直接调用函数：R=radon （I ，theta ）。

2 滤波反投影算法radon 函数使用的算法是滤波反投影法，反投影算法因为引入“星”状伪影而导致重建的图像失真，为了消除这个伪影，在进行反投影重建之前将数据修正，最后对修正后的投影数据进行反投影，这样就获得没有伪影的重建图像。

该方法是在空间域中把投影的数据直接反向投射到需要重建的图像中，然后将逐个的反投影图像累加起来。

滤波反投影法基本实现步骤：对数据作一维傅里叶变换→滤波函数：R-L 函数→对滤波后的数据作傅里叶逆变换→反投影求图像函数。

本文简要介绍推导傅里叶变换的过程：令为f 的二维傅里叶变换.单变量函G φ(ω)F(ω cosφ,ω sin φ )为通过φ角的F 切片，并记g φ (p)基于2017数学建模的滤波反投影算法应用文/李春梅为由合成方程确定的函数，则 (Ff φV )(ω)=F(ω cos φ,ω sin φ)，其中F 是单变量傅里叶变换算子，它建立了Radon 变换和傅里叶变换的联系.然后采用极坐标u=ω cos φ,v=ω sin φ表示傅里叶合成公式得将这个积分分解成两个积分式，通过变换、合并，最后使用投影切片定律重写这个积分形式为：f(x,y)= d ω d φ由此得到合成方程。

滤波反投影法

滤波反投影法：
滤波反投影法根据附件三所给接收信息，采用先修正、后投影重建图像的做法，可得到原始图像的吸收率信息。

其原理为：在得到某一角度下的投影函数（一维函数）后，对此函数做滤波处理，得一修正后的滤波函数，再对修正后的滤波函数做反投影运算，得待检测介质吸收率在正方形托盘中的每一点的分布密度函数f(x,y)。

图1给出了滤波反投影法重建原始图像的流程图。

图1滤波反投影法流程图
反投影法重建原始图像的步骤：
（1）在对应于投影函数的角度下对投影函数做一维Fourier 变换；
（2）对（1）得到的变换结果乘以权重因子|ρ|；
（3）对（2）加权后得到的结果做一维傅立叶；
（4）对（3）所得函数做直接反投影；
（5）改变投影角度，得到180个不同的投影角度，对每一角度，重复上述步骤（1）
~（4）。

R-L （Ram-Lak ）滤波函数：
此函数的基本条件是二维图像函数的频率是有界的，显然，此题所得附件五的所有数据满足此条件。

故频域中的滤波函数可表示为：
G (ρ)={|ρ|， |ρ|≤ρ0 0，其它
其函数图像如图1.
图1R-L 滤波函数图像
连续的R-L 卷积函数所得结果为：
g (R )=ρ02[2sin c (2ρ0R )−sin c 2(ρ0R )]
离散的R-L 卷积函数所得结果为：
g (nT )={ 14T 2 ， n =0 0 ， n 为偶数−1n 2π2T 2，n 为奇数
根据上述滤波原理，在本题中，对附件五中数据的具体滤波过程可用Matlab 内置的Ram-Lak 命令实现。

ct成像fbp算法公式

ct成像fbp算法公式CT（计算机断层扫描）成像中的FBP（滤波反投影）算法是一种常用的重建方法。

在FBP算法中，首先对投影数据进行滤波，然后对滤波后的数据进行反投影，从而得到重建的图像。

以下是FBP算法的简要步骤：1. 采集投影数据：在CT扫描过程中，X射线源沿某一方向旋转，通过物体照射到探测器上，得到一系列投影数据。

2. 滤波：对投影数据进行滤波，以消除噪声和伪影。

常用的滤波方法有理想低通滤波、高斯滤波等。

3. 反投影：将滤波后的投影数据按照一定的角度间隔进行重新采样，然后对采样数据进行反投影运算，得到重建的图像。

4. 图像重建：对反投影结果进行图像重建，得到最终的CT图像。

关于FBP算法的公式，以中心切片法为例，可以分为以下几个部分：1. 滤波：对投影数据P(x,y)进行滤波，得到滤波后的投影数据P'(x,y)。

滤波公式如下：P'(x,y) = ∫P(x-Δx, y-Δy) * h(Δx, Δy) dx dy其中，h(Δx, Δy)是滤波函数，Δx和Δy分别表示x和y方向上的偏移量。

2. 反投影：将滤波后的投影数据P'(x,y)按照一定的角度间隔进行重新采样，得到采样数据P''(u,v)。

反投影公式如下：u = x -Δx * cos(θ)v = y -Δy * cos(θ)其中，θ是投影方向与水平方向的夹角。

3. 图像重建：对采样数据P''(u,v)进行插值，得到重建的图像I(x,y)。

插值方法有线性插值、双线性插值等。

需要注意的是，FBP算法在实际应用中可能会受到噪声、伪影等因素的影响。

为了提高图像质量，可以采用其他重建方法，如迭代重建算法（如ART、MLEM等）或模型驱动的重建方法（如MBIR等）进行优化。

滤波反投影法迭代方程

滤波反投影法是一种用于图像重建的算法，其迭代方程通常由以下步骤组成：
1. 对当前投影图像进行滤波操作，以去除噪声和伪影。

2. 将滤波后的投影图像进行反投影，得到重建图像的更新值。

3. 将更新值与前一次迭代的重建图像进行叠加，得到新的重建图像。

4. 重复步骤1-3，直到达到预设的迭代次数或满足收敛条件。

具体来说，滤波反投影法的迭代方程可以表示为：
\(I^{k+1} = I^k + \lambda \left( \text{滤波后的投影图像} - \text{反投影图像} \right)\)
其中，\(I^{k+1}\)表示第\(k+1\)次迭代的重建图像，\(I^k\)表示第\(k\)次迭代的重建图像，\(\lambda\)是控制迭代的步长，\(\text{滤波后的投影图像}\)是滤波后的投影图像，\(\text{反投影图像}\)是反投影得到的图像。

需要注意的是，具体的迭代方程可能会因不同的滤波器和反投影方法而有所不同。

基于滤波反投影算法的CT系统成像研究

基于滤波反投影算法的CT系统成像研究摘要：CT系统的安装会使得旋转中心发生偏离，从而影响成像质量，因此需要借助于已知结构的样品来标定CT系统的参数，并且利用标定的参数对未知结构的样品进行图像重建。

首先根据直接反投影算法和滤波反投影算法对收集到的数据中的接收信息分别进行图像重建，通过成像图像可知，滤波反投影算法更优；旋转中心可能发生偏移以及CT系统具有初始角度，依次进行旋转、平移、裁剪和残影去除操作，来校正投影图像，从而得到较高质量的图像。

关键词：CT成像原理（影像医学与核医学）；滤波反投影法；图像重建；吸收率引言CT(Computed Tomography)是用X线束从多个方向对人体检查部位具有一定厚度的层面进行扫描，由探测器而不用胶片接收透过该层面的X线，转变为可见光后，由光电转换器转变为电信号，再经模拟/数字转换器转为数字，输人计算机处理。

数字矩阵中的每个数字经数字/模拟转换器转为由黑到白不等灰度的小方块，称之为像素，并按原有矩阵顺序排列，即构成CT图像。

所以，CT图像是由一定数目像素组成的灰阶图像，是数字图像，是重建的断层图像。

首先根据直接反投影算法和滤波反投影算法对收集到的数据中的接收信息分别进行图像重建，将图像重建[4-6]的两种结果进行对比，得出效果较好的模型；然后，旋转中心可能发生偏移以及CT系统具有初始角度，通过旋转、平移、裁剪和残影去除等操作来校正投影图像，最后对图像进行标准化调整，从而提高了成像质量。

1 模型的准备与建立1.1 CT成像的数学基础Rand变换如图1所示，直线g是xOy平面内任意一条直线，t是原点到直线g的距离，φ为原点到直线g的垂线与x轴的夹角。

对于xOy平面内任意一条直线可以由(t,φ)唯一确定。

二维平面中函数f(x,y)沿着直线的积分等于其Rand变换。

中心切片定理中心切片定理是CT图像重建算法的基础，在非衍射源情况下，含义是图像在某个视角下平行投影的一维Fourier变换等同于该图像二维Fourier变换的一个中心切片。

滤波反投影

滤波反投影法重建CT 图像实验指导书一、实验目的1．了解傅立叶变换法、直接反投影法重建CT 图像的原理；2．掌握滤波反投影法重建CT 图像的原理和基本方法。

二、实验器材装有MATLAB 程序的PC 机，滤波反投影法图像重建演示软件，投影数据。

三、实验原理CT 图像重建问题实际上就是如何从投影数据中解算出成像平面上各像素点的衰减系数。

图像重建的算法有多种，如反投影法、傅立叶变换法、迭代法、滤波反投影法等。

在介绍算法前，有必要先介绍从投影重建图像的重要依据，即中心切片定理。

1．中心切片定理密度函数(,)f x y 在某一方向上的投影函数()g R θ的一维傅立叶变换函数()g θρ是原密度函数(,)f x y 的二维傅立叶变换函数(,)F ρθ在(,)ρθ平面上沿同一方向且过原点的直线上的值。

图1 中心切片定理2．傅立叶变换法如果在不同角度下取得足够多的投影函数数据，并作傅立叶变换，根据中心切片定理，变换后的数据将充满整个(,)u v 平面。

一旦频域函数(,)F u v 或(,)F ρβ的全部值都得到后，将其做傅立叶反变换，就能得到原始的密度函数(,)f x y ，即所要重建的图像。

上述图像重建算法称为傅立叶变换法，图2给出了傅立叶变换重建方法的流程图。

图中指出，对于每次测得的投影数据先作一维傅立叶变换。

根据中心切片定理，可将此变换结果看成二维频率域中同样角度下过原点的直线上的值。

在不同投影角下所得的一维变换函数可在频域中构成完整的二维傅立叶变换函数，将此二维变换函数做一次逆变换，就得到了所要求的空间域中的密度函数。

为了在二维逆变换中采用快速傅立叶变换算法，通常在逆变换前要将极坐标形式的频域函数变换成直角坐标形式的数据。

图2 傅立叶变换重建图像的过程采用傅立叶变换法重建图像时，投影函数的一维傅立叶变换在频域中为极坐标形式，把极坐标形式的数据通过插补运算转换为直角坐标形式的数据时，计算工作量较大。

潘晓川教授的反投影滤波（BPF）新型重建算法介绍

本文详细介绍了潘晓川教授为首的研究小组提出的 BPF 精确重建算法以及 BPF 算法在锥
束扇束 CT 重建中的应用最后介绍了潘晓川等人提出的基于目标的感兴趣区域 ROI 的 BPF
成像策略
2 基于 PI 线的锥束螺旋 BPF 重建算法
2004 年潘晓川等人提出了一种有别于 Katsevich 算法的精确锥束螺旋 CT 重建算法该算法的重建思想是建立在 PI 线的概念基础之上的 PI 线的概念最早是 1997 年由 Danielsson 等提出的在 PI 线的基础上 Danielsson 等提出了用于解决锥束螺旋 CT 近似重建的 PI 算法 PI 线的概
?在锥束螺旋ct精确重建理论中人们已经证明了精确重建螺旋线内的物体三维信息理论上需要的二维探测器上的最少投影数据包含在tamdanielsson窗内9tamdanielsson窗在一系列基于三维radon变换的锥束螺旋ct重建算法中起到了关键的作用katsevich的fbp形式的锥束螺旋ct精确重建算法也用到了tamdanielsson窗的概念但他的重建算法需要比tamdanielsson窗更多的投影数据才能够精确重建出物体的三维图像而潘晓川等人的bpf形式的锥束螺旋ct精确重建算法只需要二维探测器上tamdanielsson窗内的投影数据也就是说bpf重建算法仅仅需要理论上最少的投影数据就可以精确重建出螺旋轨道扫描范围内的物体三维图像这是bpf重建算法相对于其他算法的最重要的不同之处10r20r螺旋线扫描轨道pi线万方数据70ct理论与应用研究15卷根据潘晓川等人的文献bpf算法的重建过程步骤如下1对每个角度下的锥束投影数据进行求导??00rqrpqrqrg??1上式中0qr表示锥束源点轨道上的一个点q都是是该源点的角度坐标r表示从角坐标1到2的pi线上的任意一点?0rqrp表示在锥束源点0qr处的某条方向为?r的x射线穿过物体后的投影2由求导后的投影数据对螺旋轨道内每条pi线上的物体图像点进行加权反投影反投影积分的角度范围是该pi线对应的角度范围12?21?00rrgrrdrg2上式中0r表示锥束源点轨道上的一个点由公式2pi线上r点处的rg是由求导后的投影数据在12的角度范围内进行加权反投影得到的3对加权反投影得到的pi线上的数据沿着该条pi线求hilbert变换得到物体在该线上的重建结果??????????????cxdxgxxxxxxxxxxxfxx21121211212213上式中21x既是公式2中pi线上点r的另外一种表示形式c是沿着pi线方向的投影值1x2x代表pi线的两个端点4对螺旋轨道内所有pi线上的物体重建结果进行重采样得到物体的三维重建图像由公式3得到的是物体沿各条pi线上的采样图像一般情况下我们需要得到的是笛卡儿坐标系下均匀采样的物体三维图像因此需要对3中得到图像进行重采样例如在螺旋锥束ct重建中经过重采样的最终图像可以由下面公式得到21xfzyxf4????????1sinsin1coscos1212121thhtzttryttrx5其中10t2005年潘晓川等人在bpf算法的基础上提

基于FBP算法实现CT图像重建及模板优化

基于FBP算法实现CT图像重建及模板优化一、引言计算机断层扫描（CT）技术是一种医学成像技术，能够通过X射线在人体内部产生的密度差异来获取图像信息。

CT图像重建是CT技术中的重要环节，它可以将X射线的投影数据转换成人体内部结构的精确图像，为医生提供诊断和治疗的依据。

在CT图像重建中，滤波反投影（FBP）算法是一种常用的重建算法，它通过对投影数据进行滤波和反投影操作来实现图像的重建。

本文将介绍基于FBP算法实现CT图像重建及模板优化的方法及应用。

二、FBP算法原理及实现FBP算法是一种基于投影数据的CT图像重建算法，它的基本原理是利用投影数据经过滤波和反投影操作来还原原始图像。

具体来说，FBP算法首先对投影数据进行滤波操作，以修正数据中的衰减和散射效应；然后通过反投影操作将滤波后的数据转换成原始图像。

整个过程可以用数学公式表示为：\[f(x,y) = \int_{0}^{2\pi} g(xcos\theta +ysin\theta,\theta)d\theta\]\(f(x,y)\)表示原始图像，\(g(x,y,\theta)\)表示投影数据，\(\theta\)表示投影角度。

FBP算法通过对投影数据进行滤波和反投影操作来实现\(f(x,y)\)的还原。

FBP算法的实现可以分为三个步骤：投影数据滤波、反投影操作和图像重建。

在投影数据滤波过程中，可以采用不同类型的滤波器来对数据进行滤波操作，例如Ram-Lak滤波器、Shepp-Logan滤波器等。

在反投影过程中，可以采用不同的反投影算法来将滤波后的数据转换成原始图像。

通过图像重建操作来生成CT图像并进行模板优化。

三、模板优化方法及应用1. 模板优化方法在CT图像重建中，模板优化是一种常用的图像后处理技术，它可以通过优化图像的灰度、对比度和边缘信息来改善图像的质量。

在FBP算法中，模板优化可以通过对图像进行局部直方图均衡化、增强边缘信息等方式来实现。

滤波反投影算法原理

《说说滤波反投影算法原理》嘿，朋友们！今天咱来唠唠那个听上去有点高大上的滤波反投影算法原理。

这名字一出来，是不是感觉有点懵？别慌，听我慢慢给你讲讲，其实也没那么难理解。

咱先想象一下哈，你有一张有点模糊的照片，就像那种没对焦好的。

你是不是特想让它变清楚点呢？这滤波反投影算法啊，就有点像给照片变清楚的魔法。

这个算法呢，主要是用在一些图像重建的地方。

比如说医院里的CT 扫描啥的。

医生们想看看咱身体里面到底咋回事，就靠这个算法来帮忙呢。

那它到底咋工作的呢？简单来说，就是先把一个图像分成好多小块。

就好像把一个大蛋糕切成好多小块一样。

然后呢，对每一小块进行处理。

这个处理过程就像是给每一小块图像做个“美容”。

先给它加上一个特殊的“滤镜”。

这个滤镜可不是咱平时拍照用的那种哦，它可厉害啦。

能把图像里不好的东西去掉，留下有用的信息。

接着呢，再把处理过的小块图像给“投影”回去。

就像把一块块小拼图重新拼起来一样。

但是这个投影可不是随便拼的哦，是有讲究的。

得按照一定的规则来，才能把图像变得清楚。

你可能会问啦，为啥要这么麻烦呢？直接看不行吗？哎呀，那可不行。

有些图像直接看根本看不清里面的细节。

就像你在大雾里看东西，模模糊糊的啥也看不清。

但是用了这个滤波反投影算法，就像雾散了一样，一下子就清楚了。

比如说在医院里，医生要是想看你的骨头有没有问题。

用CT 扫描一下，然后这个算法就开始工作啦。

把你的身体图像分成小块，处理完再投影回去。

这样医生就能清楚地看到你的骨头有没有裂缝啊，有没有什么毛病啦。

这个算法虽然很厉害，但是也不是万能的哦。

它也有它的局限性。

有时候可能会出现一些小误差，或者处理得不是那么完美。

但是科学家们一直在努力改进它，让它变得越来越好。

总之啊，滤波反投影算法原理虽然听上去有点复杂，但是其实也挺有趣的。

它就像一个小魔法师，能把模糊的图像变得清楚。

下次你要是听到这个名字，就不会那么害怕啦。

哈哈，现在你是不是对它有点了解了呢？。

滤波反投影重建算法原理

滤波反投影重建算法原理
滤波反投影（Filtered Inverse Projection, FBP）重建算法是一种由计算机系统控制的以迭代方式进行的三维成像算法。

与传统的CT扫描方法相比，FBP具有以下优势：
（1）采用迭代的方式进行重建，避免了多次投影，从而减少了扫描时间。

（2）能够有效地抑制噪声。

（3）重建出的图像质量好，对噪声不敏感。

FBP重建算法是目前应用最广泛的一种三维成像方法，但由于采用迭代的方式进行重建，所需时间长，而且随着扫描次数的增加，其重建图像质量会下降。

为了解决这一问题，人们提出了多种算法来改进FBP算法。

目前最常用的算法是滤波反投影（Filtered Inverse Projection, FBP）算法和最小均方误差（Minimum Mean Square Error, MMSE）算法。

这两种算法均是从FBP算法演变而来。

FBP重建图像时通过多次扫描得到一系列二维数据，这些数据可以看作是原始数据的一部分，称为投影矩阵。

—— 1 —1 —。

滤波反投影程序设计报告

《滤波反投影程序设计报告》课程名称：生物医学图像处理2院系：生物医学工程姓名：学号：完成日期： 2017年4月23日一、设计目的用Matlab实现平行束滤波反投影算法，比较不同滤波函数的效果。

二、实验原理（一）图像重建模型——shepp Logan头模型是图像重建标准体模，由10个位置、大小、方向、密度各异的椭圆组成，代表一个脑部断层。

（二）重建理论推导中心切片定理是从投影图像重建图像的理论基础，表述为：某断层图像f(x,y)在视角为θ时得到的平行投影的一维傅里叶变换等于f(x,y)二维傅里叶变换F（w1,w2）过原点的一个垂直切片，且切片与轴w1相交成θ角。

如下图所示。

公式表述为：F（wcos,wsin）=P(w,) ①将在-坐标系中表达的F（w1,w2）引入新的极坐标系中，新坐标系与原坐标系原点重合，有w1=wcos,w2=wsin.面元换算为dw1dw2=wdwd.有 f(x,y)=== +②注意到在其傅里叶变换存在如下关系：P(w,将上式代入②式，有f(x,y)=③令③式内积分等于g(xcos+ysin),则有g(xcos+ysin)=t=xcosθ+ysinθdw实际上，g(xcos+ysin)就是投射角度为时的滤波投影，在t-s坐标系中表达时，转化为g（t,）=h(t)*p(t,),h(t)是传递函数H（w）=|w|的傅里叶逆变换，p(t,)是P（w,）的傅里叶逆变换。

所以③式可写成f(x,y)=θ④在图中注意到Xr=rcos()=xcos是从原点出发的通过点（r,）的射线方程，④式可写为：f(x,y)=④⑤两式表明：f(x,y)在（x,y）处的重建，等于通过该点的所有角度下滤波投影的累加所得到的像素值，而Xr=rcos()=xcos的变化代表了所有平行投影射线。

（三）Radon变换一个无限薄的切片内相对线性衰减系数的分布是由它的所有线积分的集合唯一决定，揭示了函数和投影之间的关系，若函数为f(x,y),则不同角度下的投影可写为P(t,)=⑥（四）滤波函数由于直接反投影法把取自有限空间的投影均匀回抹到了射线所及的无限空间的各个像素上，使得原来像素值为0的点不为0，从而产生星状伪迹，滤波反投影算法用人为设计的一维滤波函数对所得投影数据进行卷积，而后进行反投影和累加时，由于正负抵消，可一定程度上消除星状伪迹。

滤波反投影图像重建算法分析及MATLAB现实

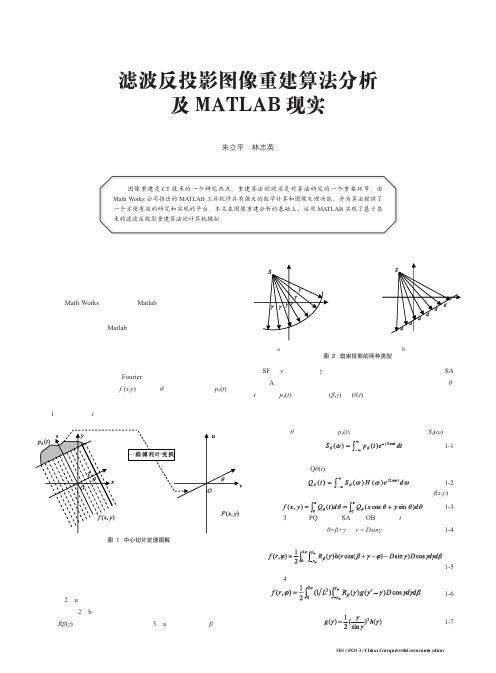
图像重建是CT技术的一个研究热点。

重建算法的现实是对算法研究的一个重要环节。

由Math Works公司推出的MATLAB工具软件具有强大的数学计算和图像处理功能，并为算法提供了
一个方便有效的研究和实现的平台。

本文在图像重建分析的基础上，运用MATLAB实现了基于扇
束的滤波反投影重建算法的计算机模拟。

引言
图像重建技术在诸多领域中发挥着重要作用，在重建算法的研究
和实现过程中，存在着是一系列极其复杂的图像处理问题和数学计算
图５　１２８×１２８的Ｓｈｅｅｐ　
Ｌｏｇａｎ头模型图像
图６　扇束射角增量为０．３°投影值
2. 选取滤波函数，并离散化处理，如：R-L滤波函数，则离散化形式为：
（式1-8）其中：
（式1-9）
图７　重建效果图
总结
本文在分析基于扇束滤波反投影算法的基础上，详细介绍了该算法“模拟产生投影数据——修正投影——加权滤波——反投影重建”整个计算机现实过程，并充分利用Matlab强大的图像处理功能，无需大量的编程，现实了图像重建算法的计算机模拟。

高效的工程计算语言，它从本质上提供了对图像的支持，使用它可以对数字图像形成的离散数据矩阵进行一次性的处理，较其他高级语言。

cbct方法分类

cbct方法分类
CBCT方法可以分为三类：滤波反投影（FBP）、代数重建技术（ART）和统计迭代
法。

1.滤波反投影（FBP）是最常用的CBCT重建方法之一。

该方法首先对每个体
素进行滤波处理，然后通过反投影的方式将滤波后的数据重建为图像。

FBP 方法具有计算效率高、速度快等优点，但可能会产生一些伪影和噪声。

2.代数重建技术（ART）是一种基于数学和代数的重建方法。

它通过迭代的方
式来逐渐逼近真实图像，并利用已知的图像信息来重建未知的图像信息。

ART方法能够处理更复杂的模型和更准确的误差估计，但计算量大，速度
较慢。

3.统计迭代法是一种基于概率统计的重建方法。

它通过迭代的方式来逐渐逼
近真实图像，并利用概率统计的方法来处理图像中的噪声和伪影。

统计迭
代法能够处理更复杂的模型和更准确的误差估计，但计算量大，速度较
慢。

此外，根据应用领域的不同，CBCT方法还可以分为临床CBCT和研究CBCT两大类。

其中，临床CBCT主要用于口腔医学临床实践中的诊断和治疗规划，而研究CBCT则主要用于科学研究和学术交流。

ct滤波反投影算法重建精度研究

CT滤波反投影算法重建精度研究摘要锥形束CT具有射线利用率高、扫描时间短、纵向分辨率高等优点，因此被广泛应用于实际。

锥形束CT重建算法中滤波反投影算法由于数学形式简单，易实现，得到了广泛应用。

但是受实际应用条件的限制，随着扫描半径的减小，锥角增大，重建质量会下降。

基于这个问题，本文主要研究内容如下：（1）首先研究了扫描半径对扇形束FBP算法重建精度的影响，实验结果表明，扫描半径越大，重建图像质量越好；接着研究了加权函数对重建精度的影响，实验结果表明常数0.5加权比一般加权误差更大。

同时将以上结论推广到锥束FDK算法。

（2）平行重排(PFDK)算法是FDK算法的一种推广，针对FDK算法随着锥角增大重建精度下降的问题，给出了一种三维加权PFDK图像重建算法，并研究了重排过程中径向插值间隔对重建图像质量的影响，分别采用三种不同插值总数（插值间隔分别是1单位，0.5单位，0.25单位）重排数据。

实验结果表明给出的三维加权PFDK算法可有效减少锥角对重建结果的影响，且当采用2倍插值总数时重建结果较好。

关键词：短扫描，滤波反投影，平行重排，三维加权算法，插值间隔Research on the Precision of Reconstruction ofCT Filter Back Projection AlgorithmAbstractThe cone beam CT has been widely used in practice because of its advantages such as high radiation efficiency, short scanning time and high resolution. The filtered back projection algorithm of cone beam CT is widely used because of its simple mathematical form and easy implementation. However, due to the limitation of practical application coditions, with the decrease of scanning radius, the cone angle increases, and the quality of reconstruction decreases. Based on this problem, the main contents of this paper are as follows: Firstly, we study the effect to reconstruction accuracy of fan-beam FBP algorithm from the scanning radius of the imaging system, the experimental results show that the reconstruction quality is better with the larger scan radius; and study the effect to reconstruction accuracy from the weighting function, and the experimental results show that the constant weighting causes lager errors than the general weighting. At the same time, the above conclusions are extended to the cone-beam FDK algorithm.The PFDK is the one algorithm of the extending FDK algorithm. Artefacts in images reconstructed by the FDK algorithm deteriorate with increasing cone angle, to solve this problem, a three-dimensional weighted PFDK algorithm for image reconstruction is presented in this paper, Simultaneously studying the effect to quality of reconstruction image from different interpolation interval in the radial direction, we compare the reconstructed results of using the total number of three different interpolation (interpolation interval are 1 unit, 0.5 units, 0.25 units respectively). The experimental results showed that the impact of the cone angle can be effectively reduced by the given algorithm, and we can get satisfactory reconstruction when using two times the total number of interpolation.Key words: short scan, filtered back-projection, parallel rearrangement, a three dimension- al weighted algorithm, interpolation interval目录第一章绪论 (1)1.1课题研究背景及意义 (1)1.2短扫描扇形束FBP重建算法的国内外研究现状 (2)1.3圆轨迹锥形束FDK重建算法的国内外研究现状 (3)1.4论文的主要工作及结构安排 (4)第二章CT成像基础知识 (6)2.1CT成像原理 (6)2.2图像重建的基本理论 (7)2.2.1 Radon变换及其逆变换 (7)2.2.2 傅里叶切片定理 (8)2.3基于滤波反投影的经典CT重建算法 (11)2.3.1 全扫描扇形束FBP重建算法介绍 (11)2.3.1.1 等角采样的重建公式 (11)2.3.1.2 等距采样的重建公式 (13)2.3.2 FDK重建算法介绍 (14)2.4图像重建算法评价 (15)2.5本章小结 (16)第三章短扫描扇形束FBP重建精度研究 (17)3.1短扫描 (17)3.2短扫描FBP重建算法的有误分析 (18)3.3扫描半径对重建精度的影响 (21)3.3.1 短扫描情况 (21)3.3.2 全扫描情况 (26)3.4加权函数对重建精度的影响 (28)3.5锥角对重建精度的影响 (29)3.6本章小结 (32)第四章三维加权PFDK重建算法研究 (33)4.1PFDK重建算法 (33)4.1.1 锥形束平行几何结构 (33)4.1.2 PFDK算法 (34)4.2三维加权PFDK重建算法的提出 (35)4.2.1 二维加权PFDK重建算法 (36)4.2.2 三维加权PFDK重建算法 (36)4.3仿真实验结果及分析 (38)4.4实际实验结果与分析 (41)4.5本章小结 (42)第五章总结与展望 (43)5.1研究主要内容及成果 (43)5.2存在的问题及以后的工作展望 (44)参考文献读硕士学位期间发表的论文致谢第一章绪论1.1 课题研究背景及意义在实际生活中，人们往往需要了解一个物体的内部构造，但由于受到各种条件的限制而无法实现。

实验二扇形束投影数据采集与滤波反投影重建实验

南昌大学实验报告学生姓名：胡文松学号： 6103413007 专业班级：生医131班实验类型：□验证□综合■设计□创新实验日期： 20160516 实验成绩：实验二、扇形束投影数据采集与滤波反投影重建实验一、实验目的及要求：1、用MA TLAB中的fanbeam函数获取Shepp-Logan头模型的扇形束投影数据；2、显示扇形束投影数据并和平行束投影数据进行比较；3、用MA TLAB中的ifanbeam函数实现图像重建；4、改变投影参数，观察对重建图像的影响。

二、实验基本原理：fanbeam 函数，计算扇形束投影。

句法F = fanbeam(I,D)F = fanbeam(...,param1,val1,param1,val2,...)[F,sensor_positions,fan_rotation_angles] = fanbeam(...)F = fanbeam(I,D) 计算图像I的扇形束投影(正弦图) ，D 是扇形束顶点到旋转中心的距离。

F的每一列表示一个角度下的扇形采样数据。

探测器圆弧状排布，探测器间相隔一度，旋转360度[0:359] 。

F = fanbeam(...,param1,val1,param1,val2,...) 指定参数控制扇形投影'FanRotationIncrement' 指定旋转角度增量，单位为度，默认值为1度。

'FanSensorGeometry' 指定探测器的排布方式'arc'—探测器圆弧状排布（默认值）'line' --探测器等距离线性排布'FanSensorSpacing' 指定探测器间的间隔，探测器圆弧状排布的情况，单位为度，默认值为1。

探测器等距离线性排布，单位为像素。

[F,sensor_positions,fan_rotation_angles] = fanbeam(...) 返回探测器位置和旋转角度信息ifanbeam 函数，由扇形束投影数据重建图像句法I = ifanbeam(F,D)I = ifambeam(...,param1,val1,param2,val2,...)[I,H] = ifanbeam(...)I = ifanbeam(F,D) 由投影数据F重建图像I。